大部分觀察性研究的統計結果采用效應量及其 95% 可信區間（95%CI）表示，不符合傳統 Meta 分析使用的數據格式。因此，使用 Review Manager 軟件進行此種類型數據的 Meta 分析時，需要對數據進行特殊轉換，使操作變得復雜、繁瑣。Stata 軟件功能強大，能夠直接應用效應量及其 95%CI 進行 Meta 分析，是進行觀察性研究 Meta 分析必不可少的統計工具。本研究以已發表的 Meta 分析數據為例，主要介紹如何采用 Stata 軟件實現效應量及其 95%CI 的 Meta 分析。
引用本文： 閆小妮, 鄭婕, 厲英超, 黃裕立, 李杰, 曾憲濤, 呂軍. 應用 Stata 軟件實現觀察性研究效應量及可信區間的 Meta 分析. 中國循證醫學雜志, 2018, 18(3): 367-372. doi: 10.7507/1672-2531.201709073 復制
版權信息： ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有，未經授權不得轉載、改編
傳統 Meta 分析常用的數據類型有二分類數據、連續性數據、有序數據、計數數據和時間事件數據。其中，最普遍的數據格式是兩個觀察組的事件發生數和未發生數，或者兩組病例數及結局指標的均數和標準差[1]。但在許多關于病因和預后的研究中，結果數據往往進行了回歸校正，以相對危險度（RR）、比值比（OR）、風險比（HR）及其 95% 可信區間（95%CI）表示，其更能反映研究因素的真實效應[2]，因此此類研究效應量及其 95%CI 進行 Meta 分析更有意義。但這類數據無法轉換成傳統的 Meta 分析數據格式，需要特殊的統計處理。
Stata 軟件是醫學四大統計軟件之一，在 Meta 分析方面功能非常強大[3]，可實現效應量及其 95%CI 的數據合并。本研究以已發表的 Meta 分析數據為例，詳細介紹如何采用 Stata 軟件實現效應量及其 95%CI 的 Meta 分析方法。
1 資料來源
2016 年，Huang 等[4]在 BMJ 雜志上發表了一篇名為《Association between prediabetes and risk of cardiovascular disease and all-cause mortality：systematic review and meta-analysis》的論文，其部分數據見表 1。本研究以該數據為例，介紹采用 Stata 軟件實現 RR 值及其 95%CI 的 Meta 分析的操作過程。其他效應量（OR 或 HR）的 Meta 分析方法與此一致。
表1
RR 值及其 95%CI 的示例數據
2 軟件操作過程
2.1 數據錄入
打開 Stata 軟件（version 14.0，Stata Corp，College Station，Texas），點擊
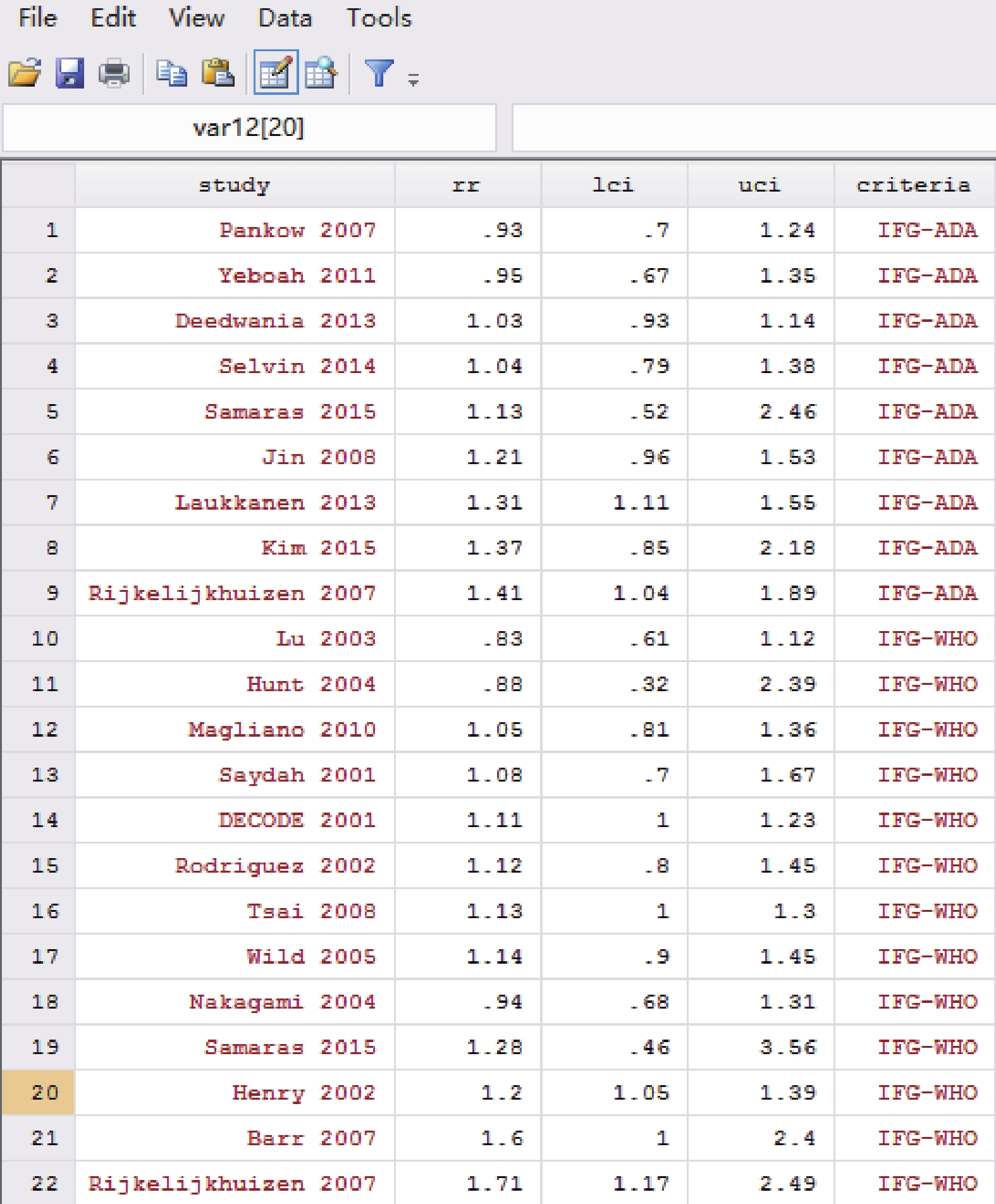
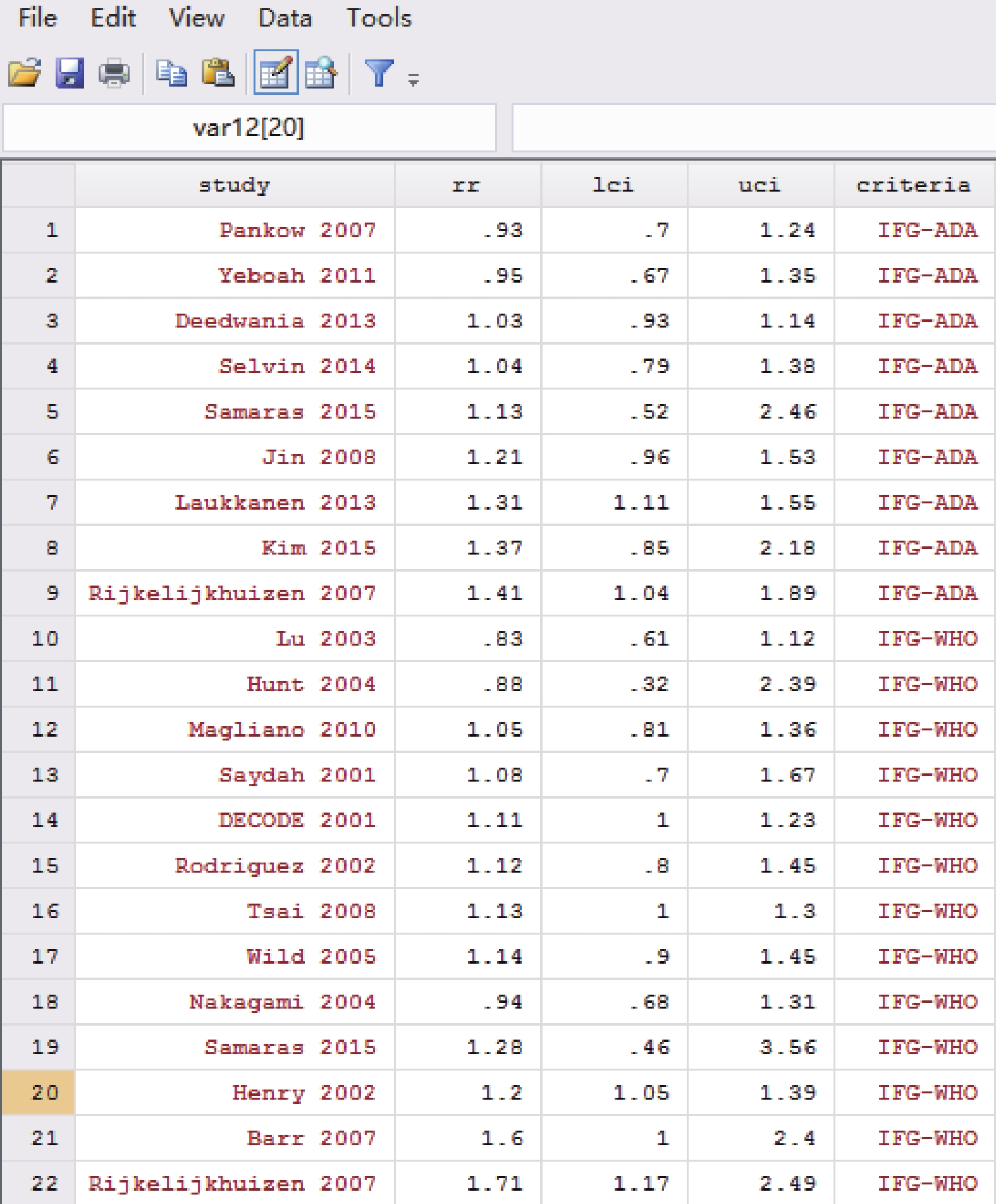圖1
Stata 軟件數據錄入結果圖
2.2 制作森林圖
首先，對 RR 值及其 95%CI 進行對數轉換。在命令框內輸入下述命令：
gen lnrr=ln（rr）
gen lnlci=ln（lci）
gen lnuci=ln（uci）
其次，繪制效應量及可信區間的森林圖，具體操作方法如下：
菜單操作：依次點擊 User→Meta-Analysis→Of Binary and Continuous（metan）。在新出現的面板中，type of Data 選擇 Effect/CI，Vars for Effects 的下拉框里按順序選擇 lnrr、lnlci、lnuci，Label of Data 中 Name 選擇 study（此變量即森林圖左側每個研究的名字），操作見圖 2。隨后在上方 Effect 下選擇 Pooling Model，本次以固定效應模型為例，其次在 Effect Label 中手動輸入 rr，并勾選 Exponentiate（指數轉換），操作見圖 3。需要注意的是，在操作頁面中如果不勾選 Exponentiate，則森林圖中出現的合并效應量是 ln（rr）、ln（lci）和 ln（uci），不易理解。
因該菜單不是 stata 軟件默認，如果使用者不通過一定的編程宏命令不會出現在菜單中，需使用“db metan”命令調用。
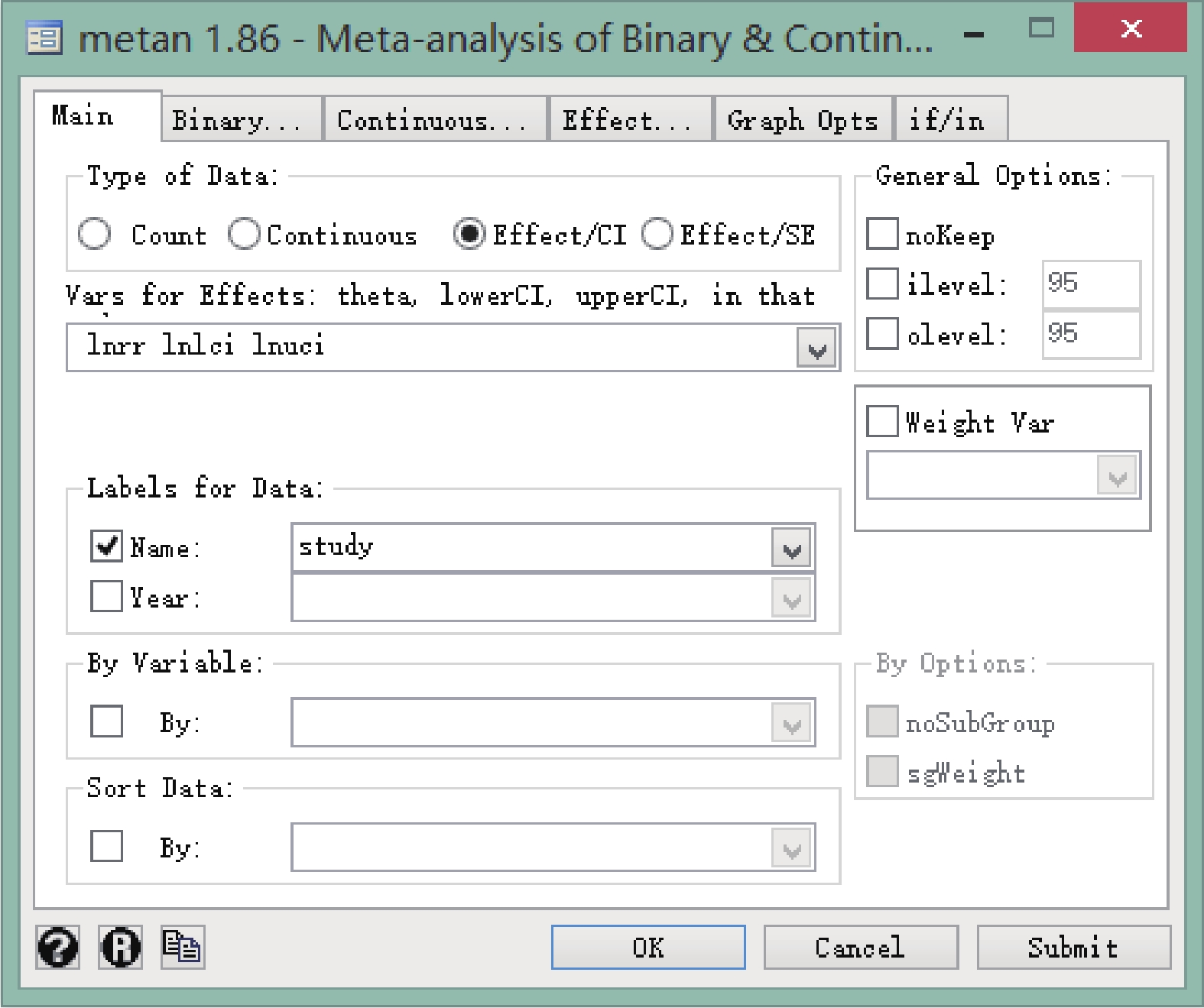圖2
Stata 軟件繪制森林圖時選擇變量對話框
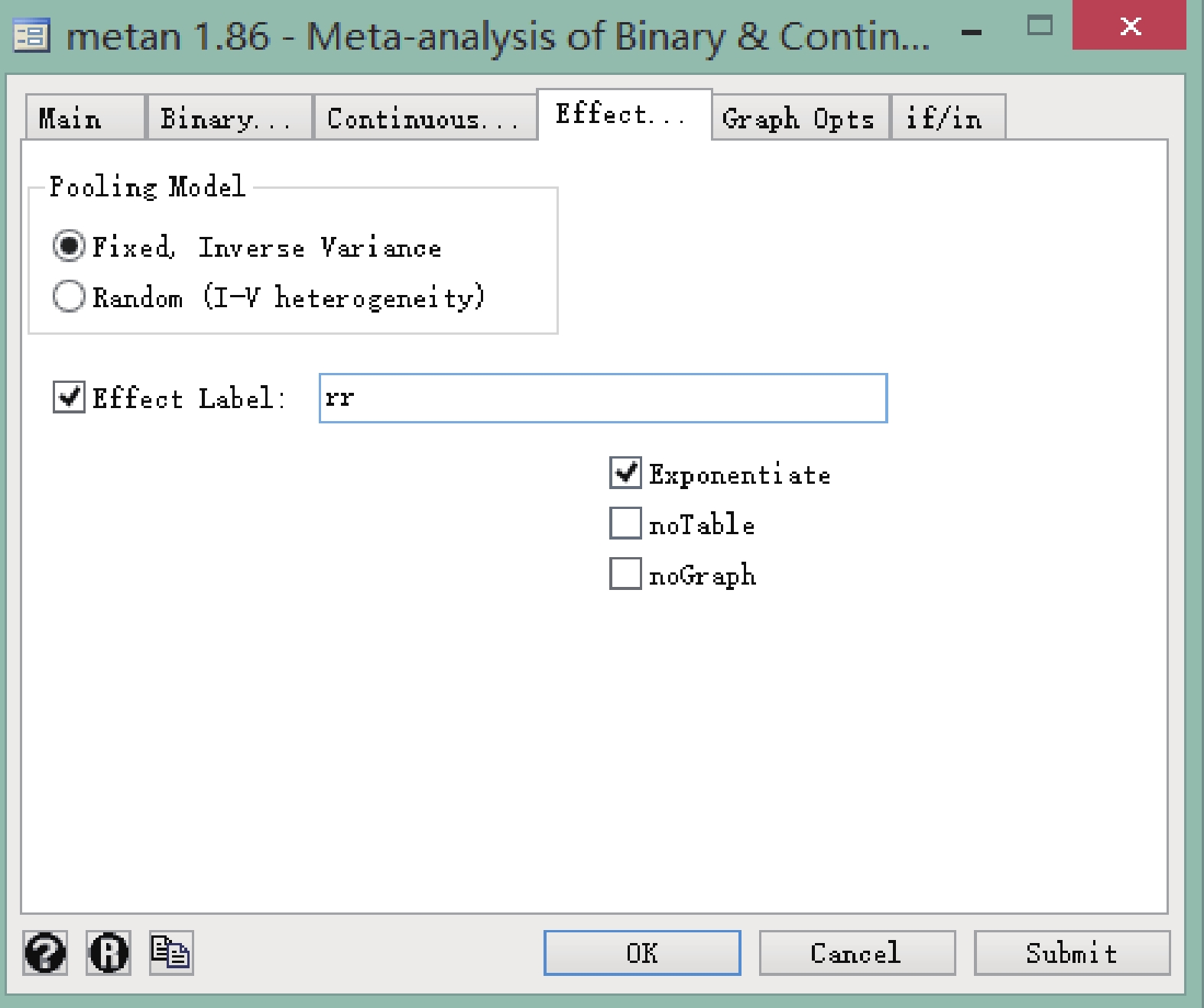圖3
Stata 軟件繪制森林圖時選擇模型對話框
命令操作：在命令框中輸入命令“metan lnrr lnlci lnuci，label（namevar=study） fixed effect（rr） eform”，其中“eform”指對結果進行指數轉換。得到的森林圖結果見圖 4。
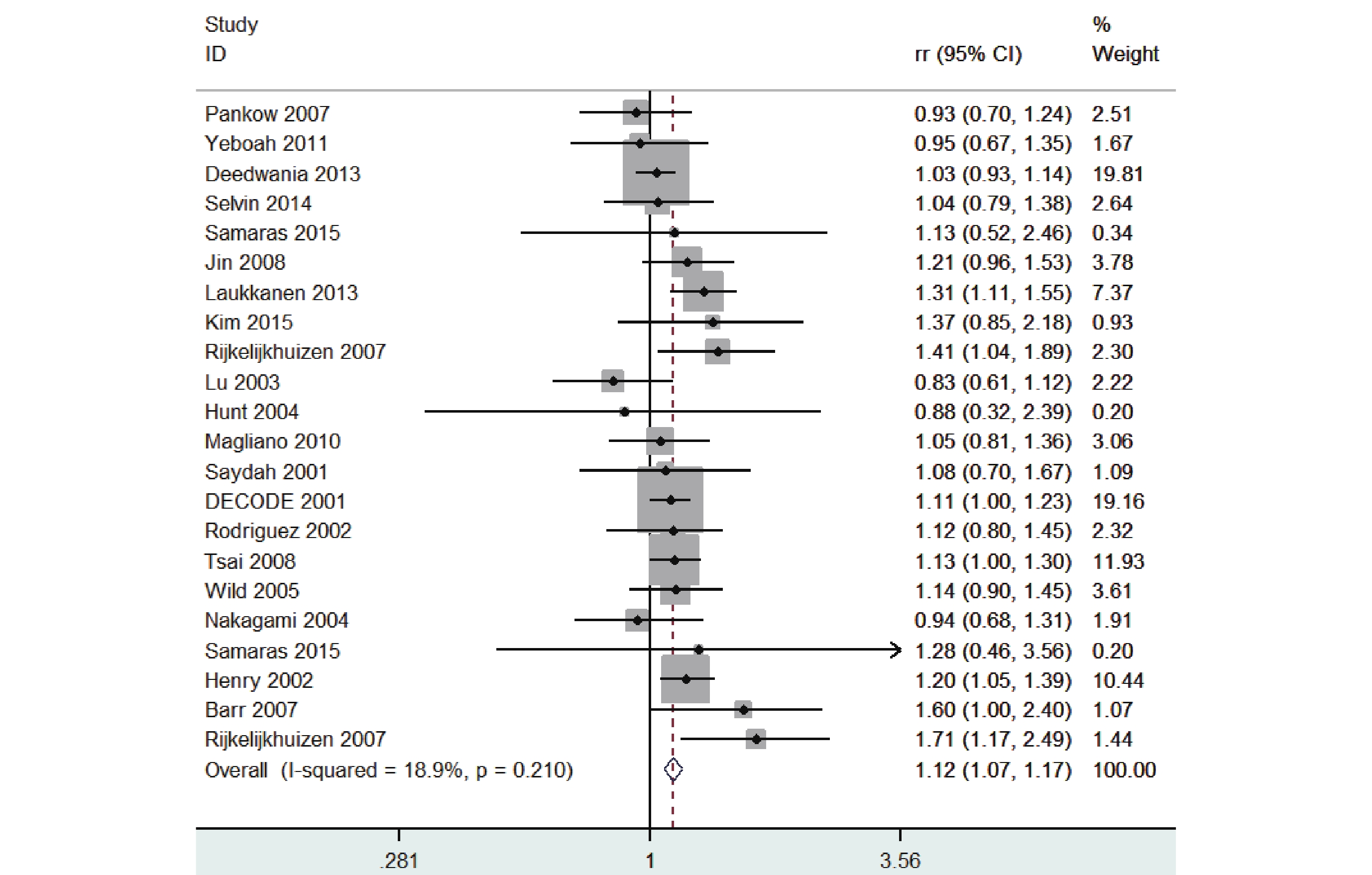圖4
Stata 軟件根據 RR 值及其 95%CI 得出的森林圖
2.3 亞組分析
以不同的診斷標準進行亞組分析為例，具體操作方法如下：
菜單操作：在圖 2 中的 By Variable 下拉框中選擇分組變量 criteria，其他操作同森林圖的菜單操作。
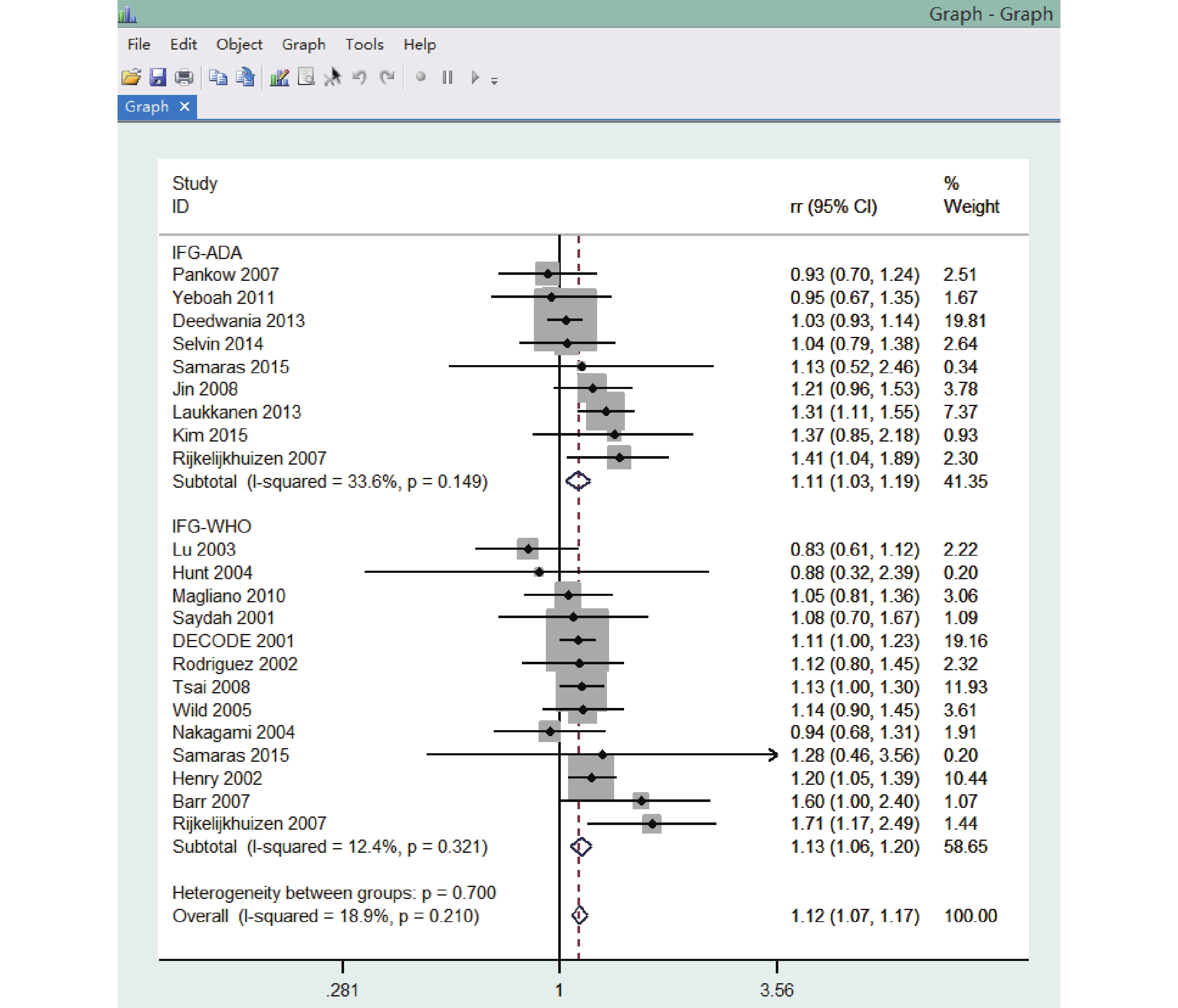
命令操作：在命令框中輸入命令“metan lnrr lnlci lnuci，label（namevar=study） by（criteria） fixed effect（rr） eform”。亞組分析結果見圖 5。
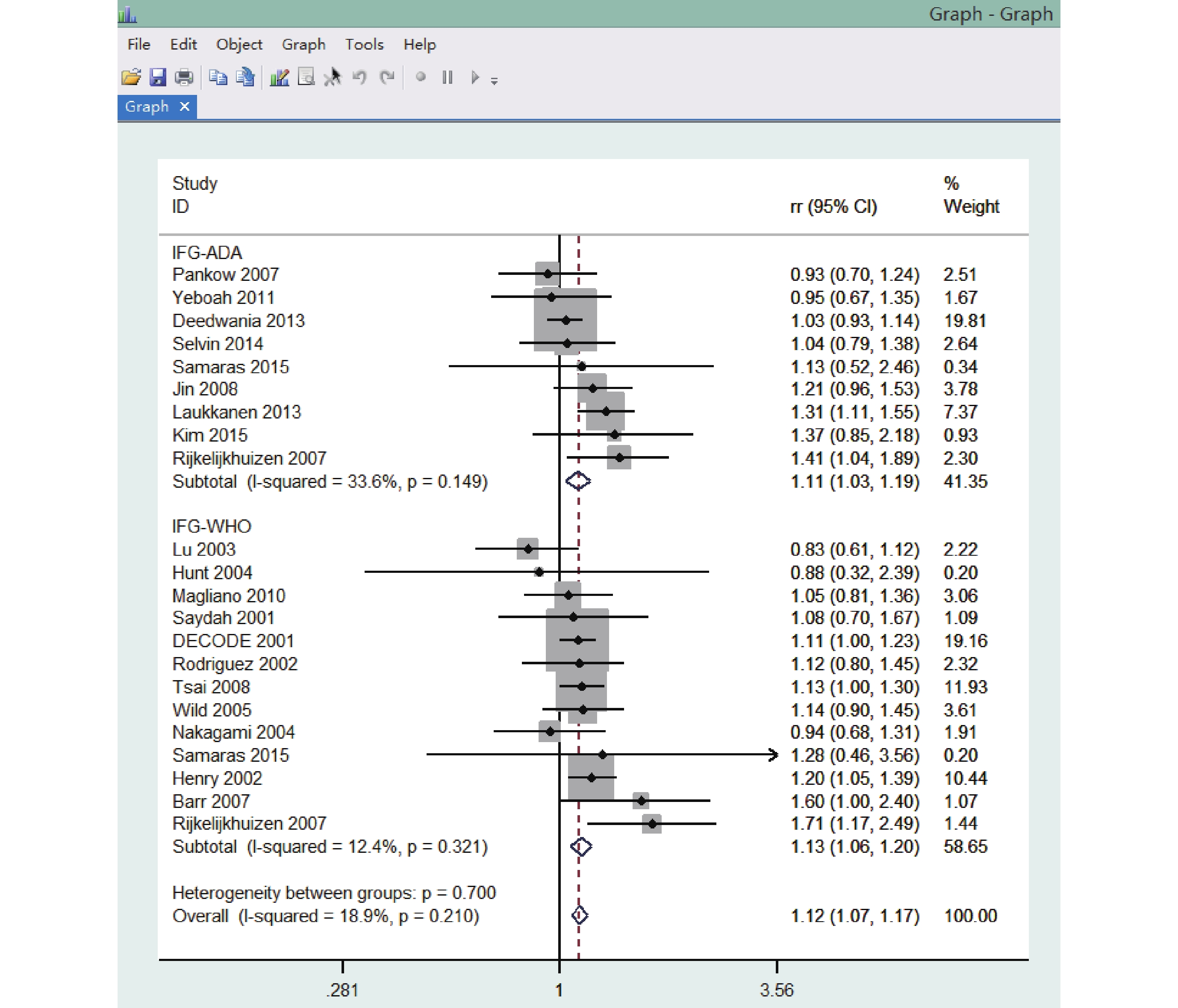圖5
Stata 軟件根據 RR 值及其 95%CI 得出的亞組分析森林圖
2.4 繪制漏斗圖
繪制漏斗圖的方法如下：
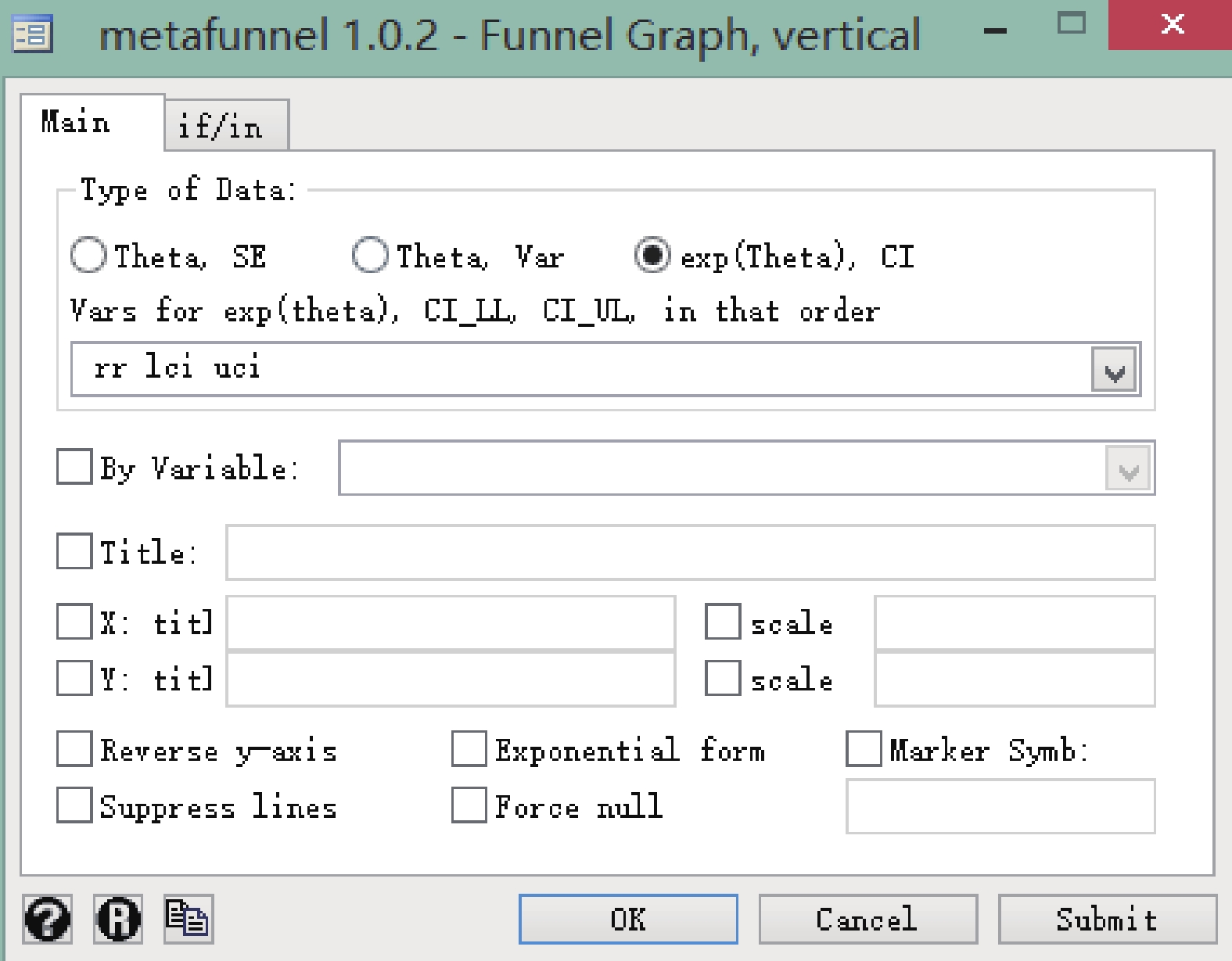
菜單操作：依次點擊 User→Meta-Analysis→Funnel Graph，vertical（metafunnel），Type of Data 選擇 exp（Theta），CI，Vars 中按順序選擇 rr、lci、uci。見圖 6。
因該菜單不是 Stata 軟件默認，需使用“db metafunnel”命令調用。
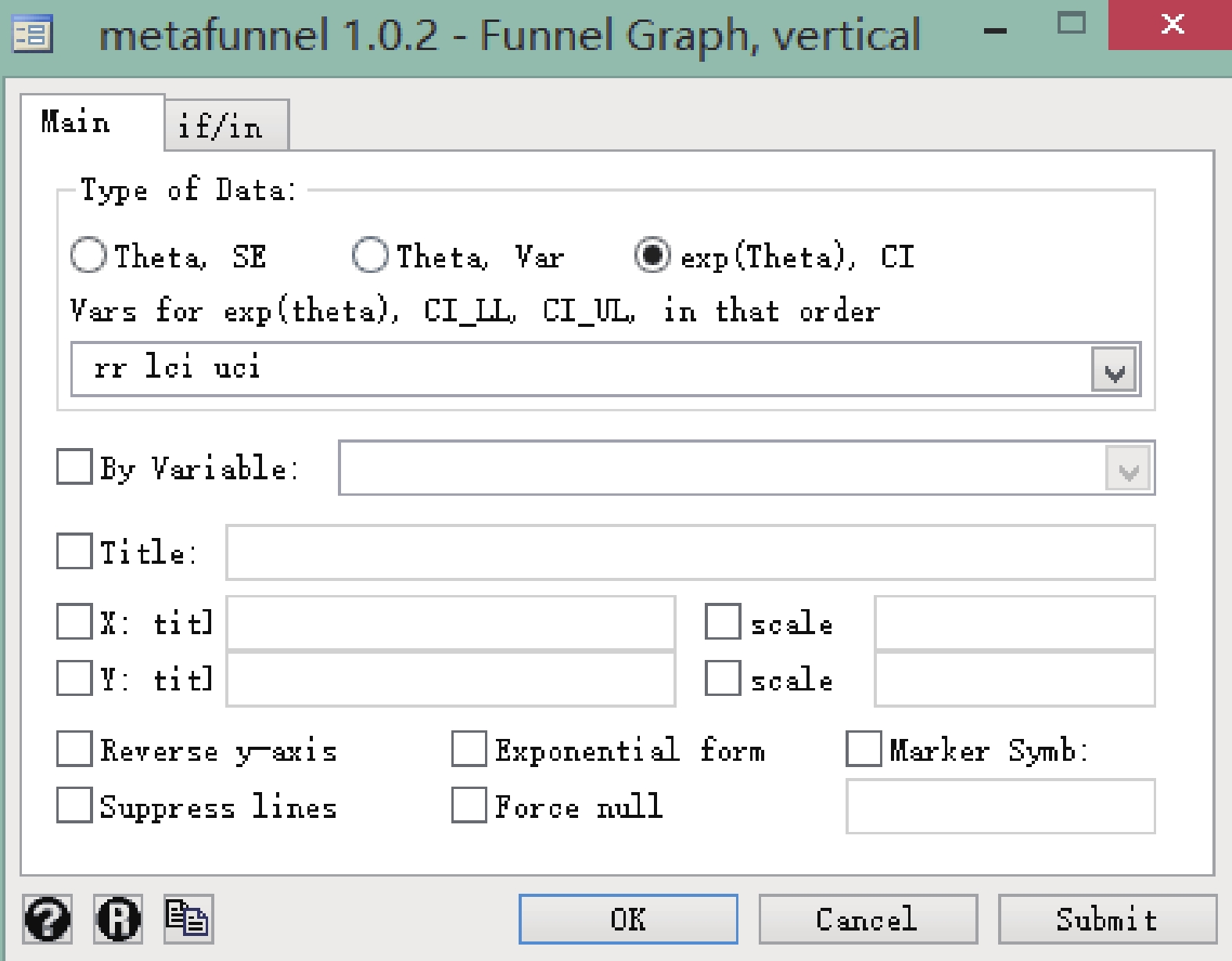圖6
Stata 軟件繪制漏斗圖時選擇模型對話框
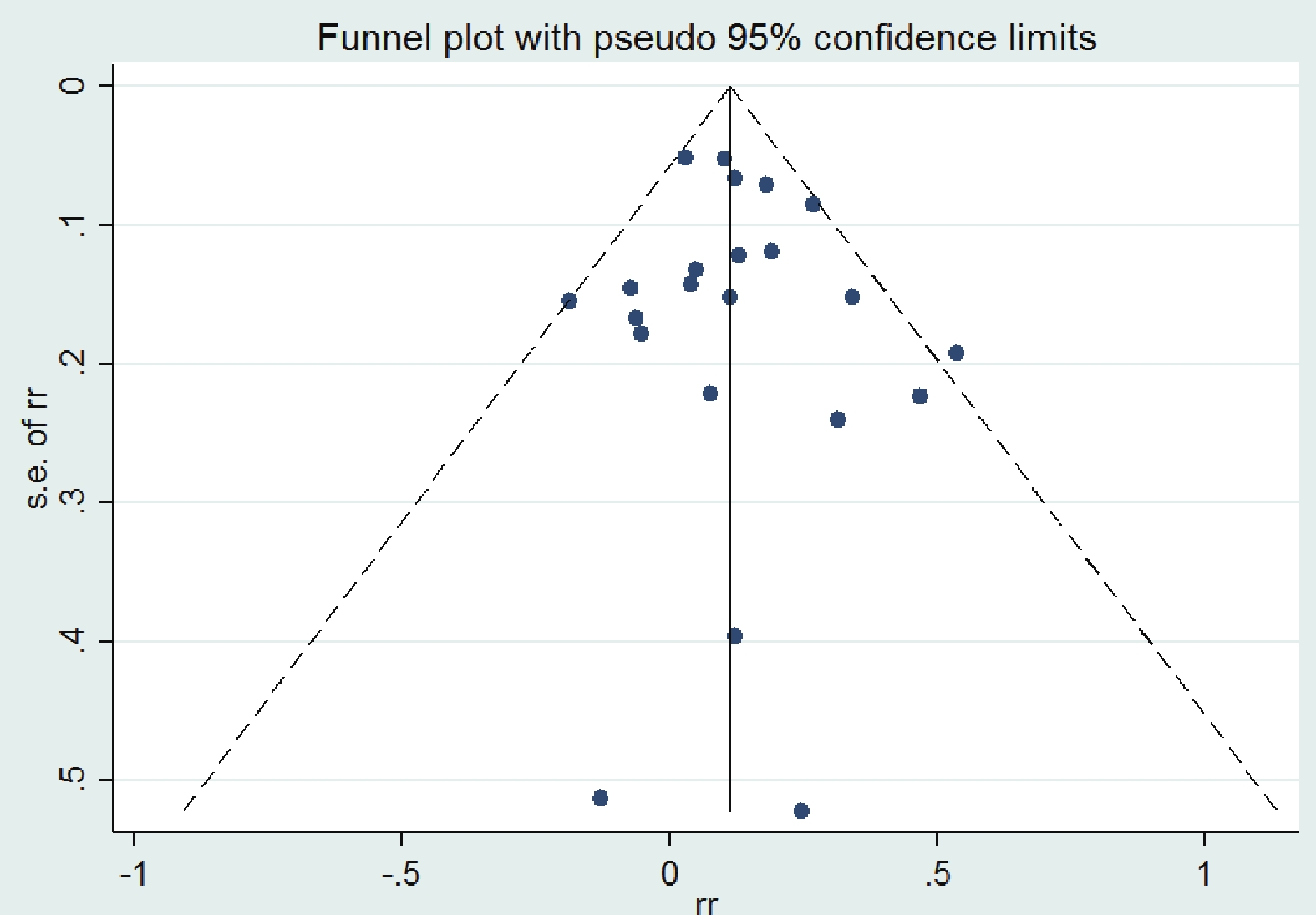
命令操作：在命令框中輸入命令“metafunnel rr lci uci，ci”，漏斗圖結果見圖 7。
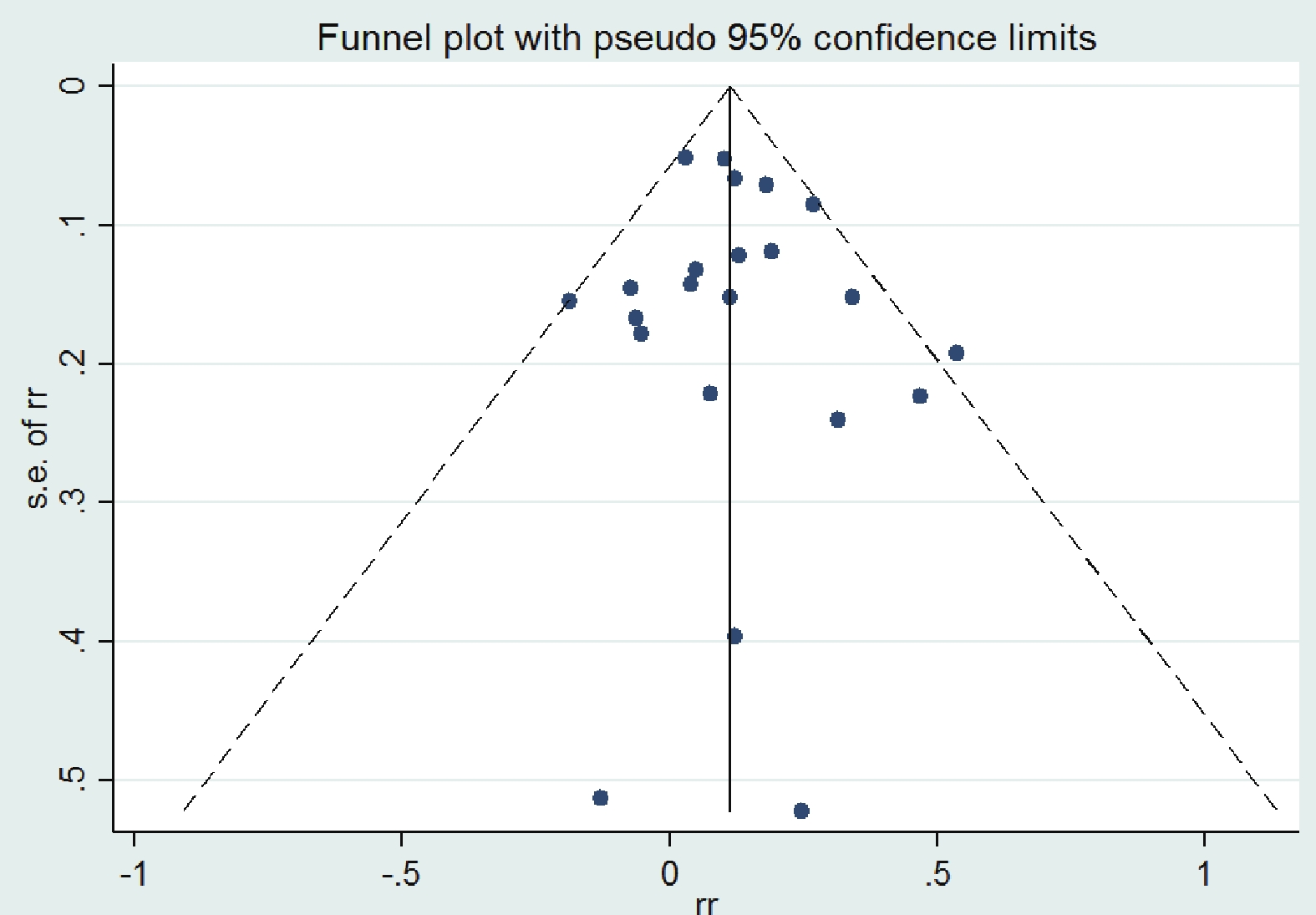圖7
Stata 軟件根據 RR 值及其 95%CI 得出的漏斗圖
2.5 漏斗圖對稱性檢驗
Stata 軟件可對漏斗圖的對稱性行 Egger 或 Begg 檢驗，操作如下：
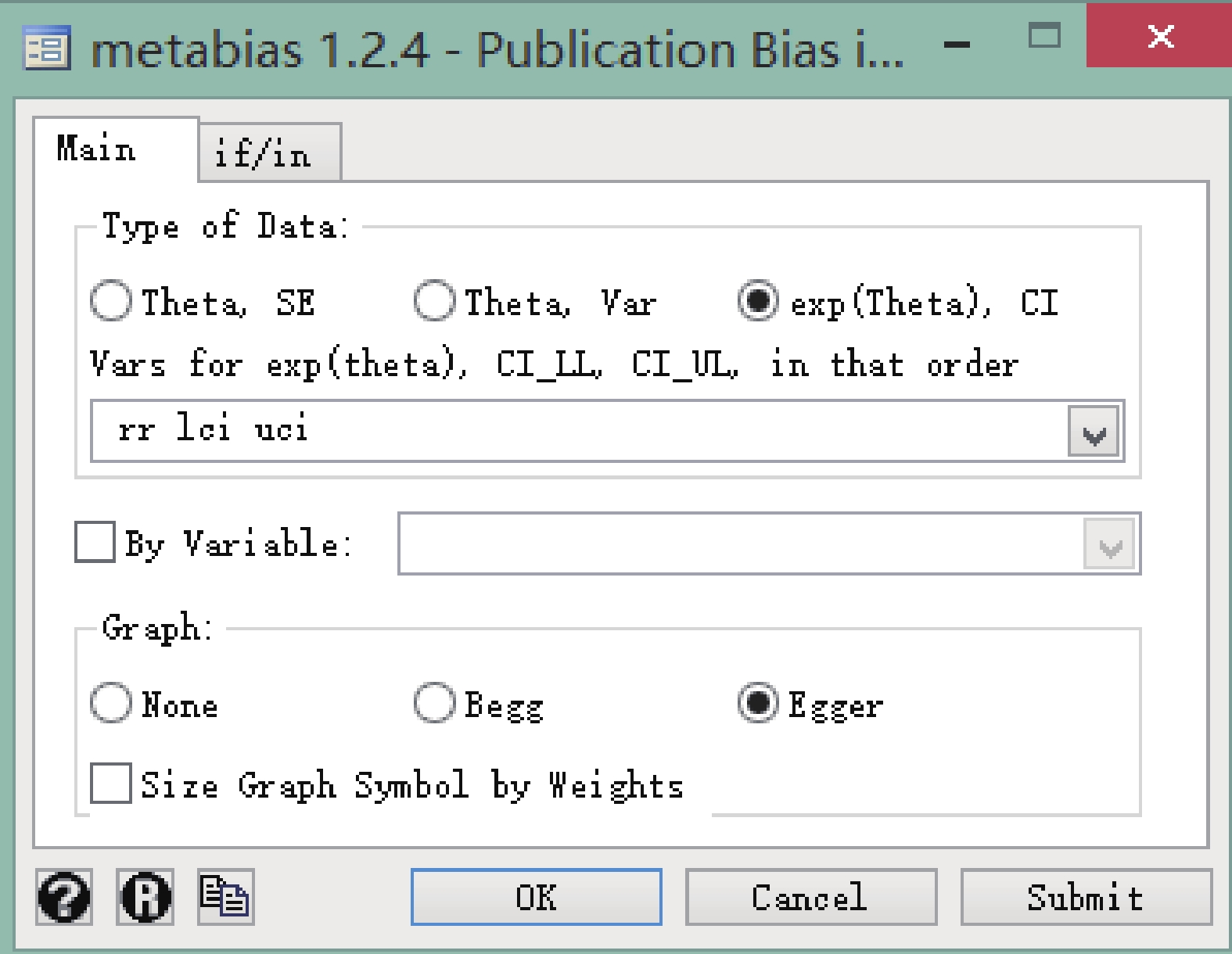
菜單操作：依次點擊 User→Meta-Analysis→Publication Bias（metabias），Type of Data 選擇 exp（Theta），CI，Vars 中按順序選擇 rr、lci、uci，graph 選擇 Egger（也可選 begg），具體操作見圖 8。
因菜單不是 Stata 軟件默認，需使用“db metabias”命令調用。
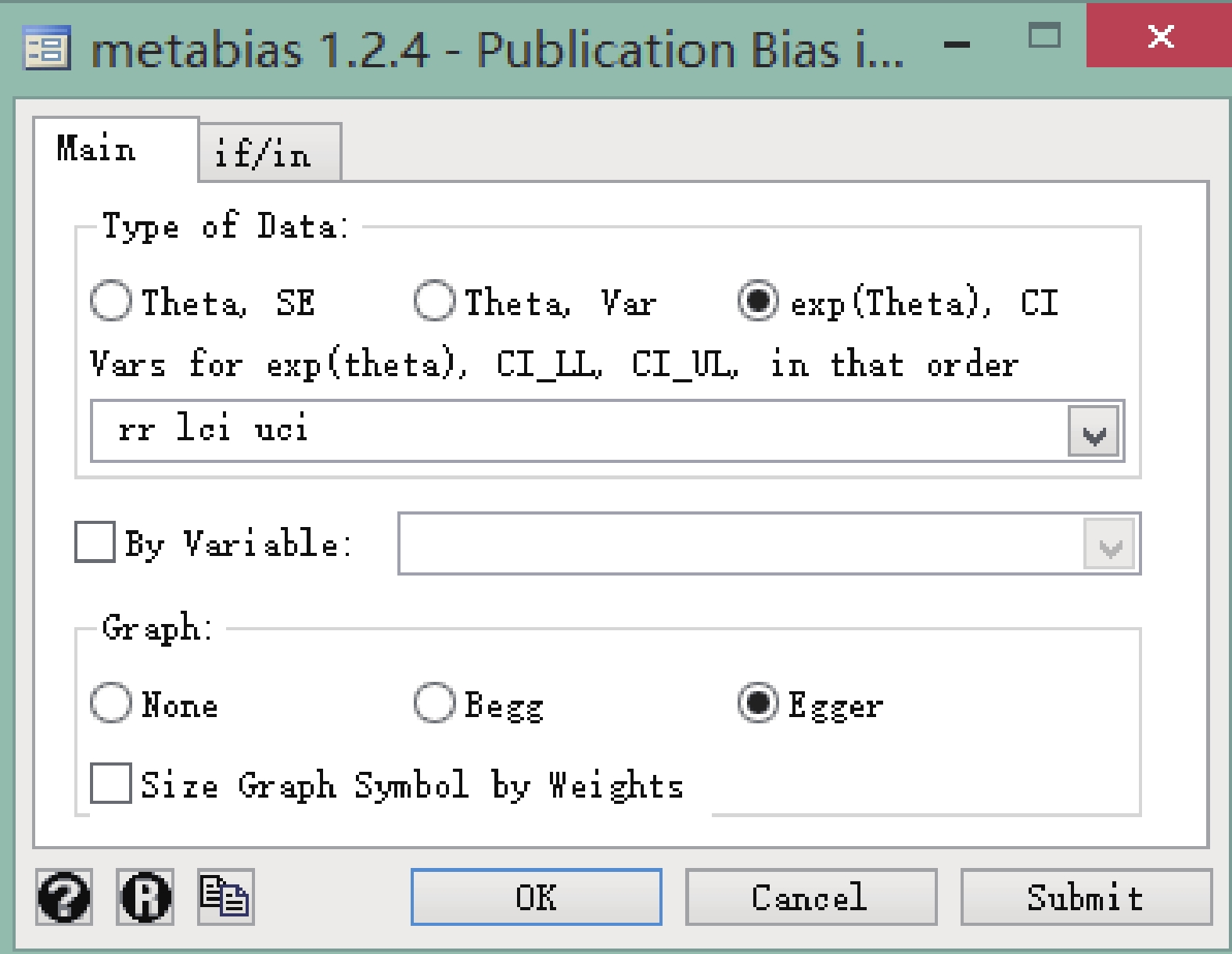圖8
Stata 軟件檢驗漏斗圖對稱性的對話框
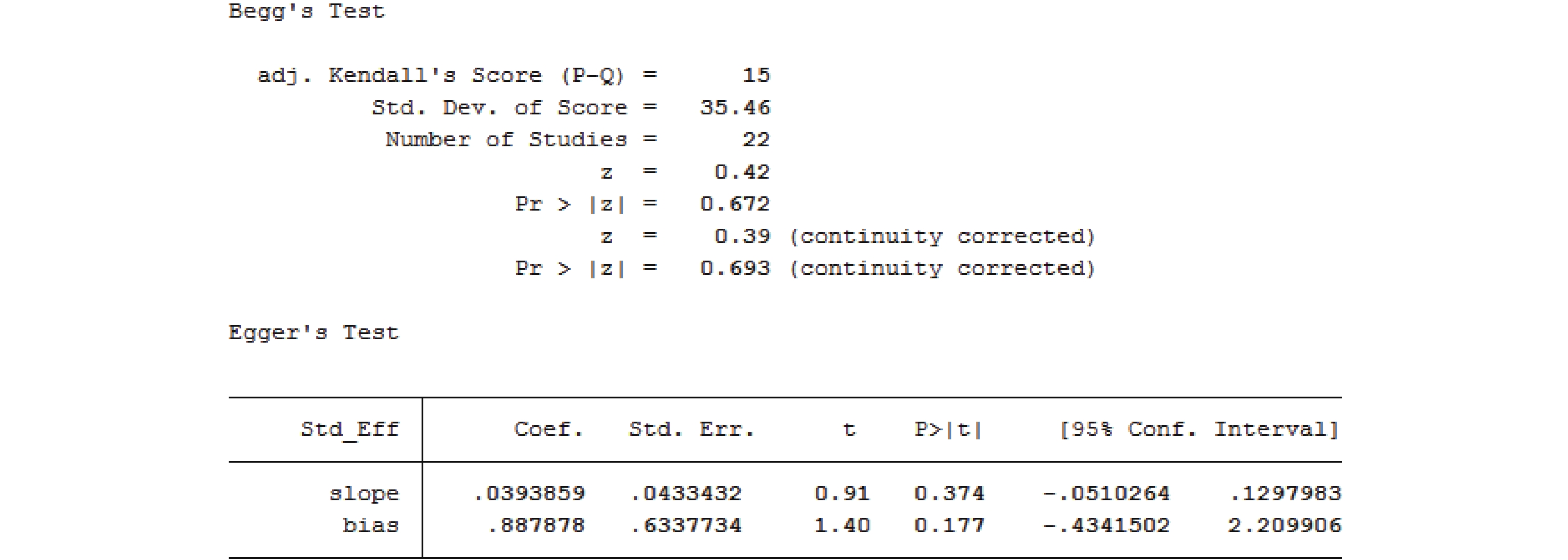
命令操作：在命令框中輸入命令“metabias rr lci uci，ci graph（egger）”，檢驗結果見圖 9。
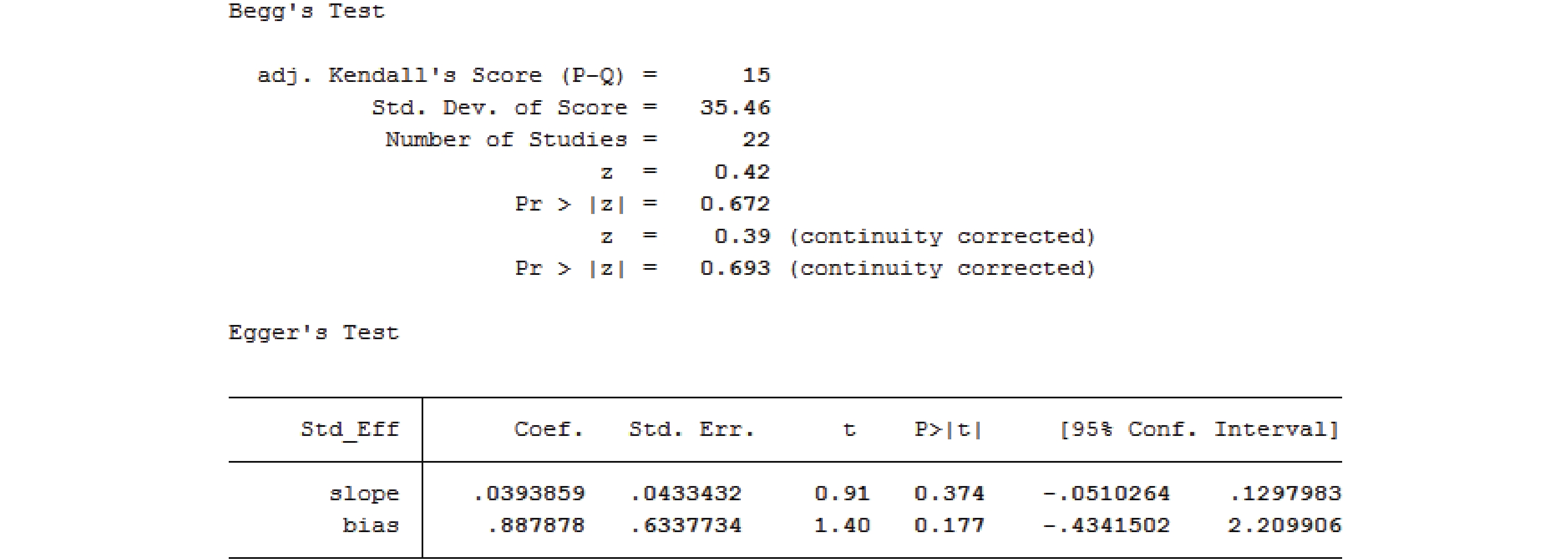圖9
Stata 軟件得出的漏斗圖對稱性的檢驗結果
此外，metabias 命令是 Stata 軟件舊版本的命令，目前已改為 metabias6 命令，新版命令的功能與命令行操作格式均與老版本不同。使用 metabias6 時，命令操作的基本格式為“metabias6 log 效應值 selog 效應值”[5]，其他操作與舊版本相同。
2.6 敏感性分析
Stata 可實現單個研究的影響分析，具體操作如下：
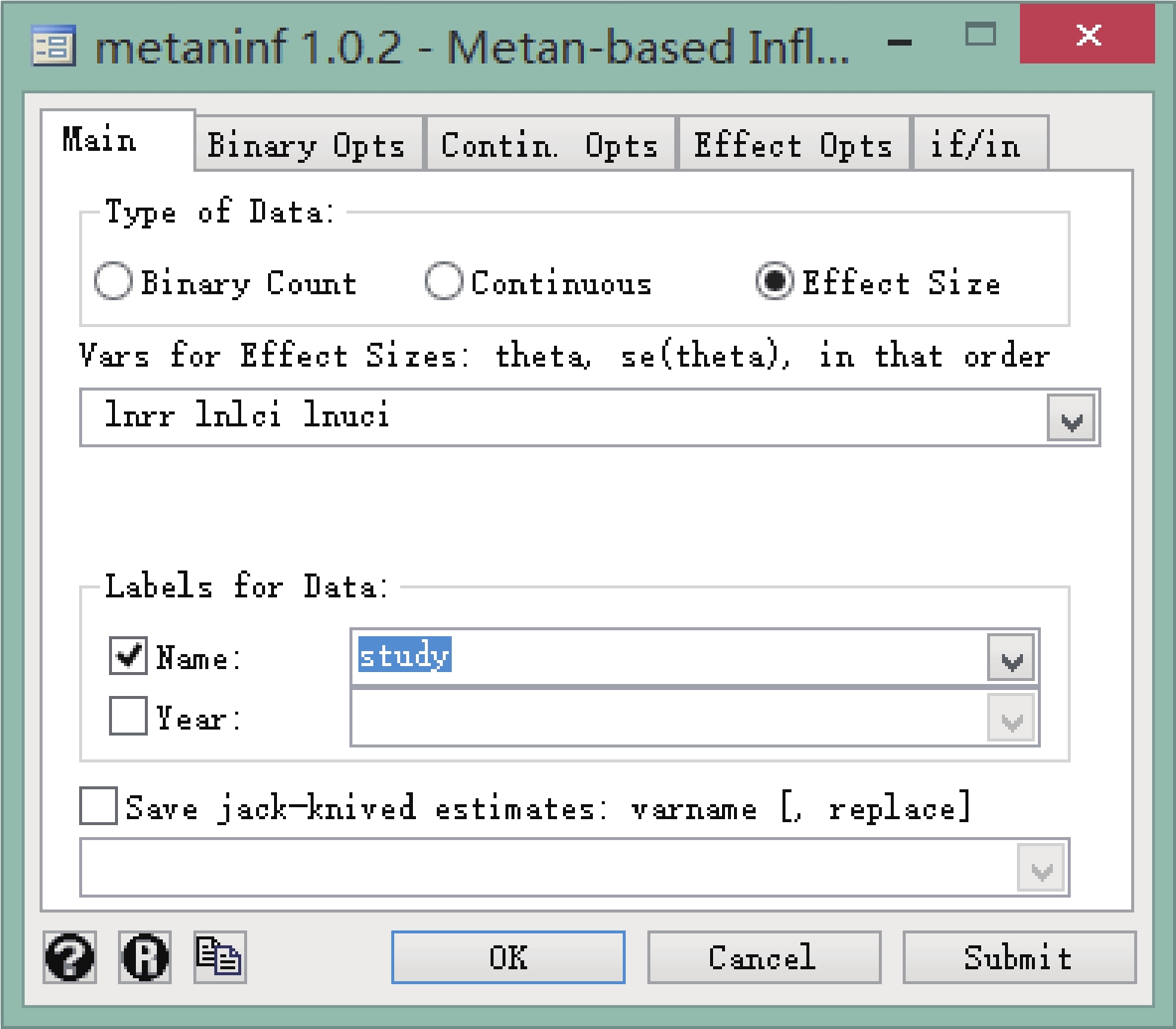
菜單操作：User→Meta-Analysis→Influence Analysis，metan-based（metaninf），Type of Data 選 Effect Size，Vars 依次選擇 lnrr、lnlci、lnuci，具體操作見圖 10。需要特別注意的是，此敏感性分析的結果呈現形式是 ln（rr）、ln（lci）、ln（uci），需對其進行指數轉換得到最終結果。
因該菜單不是 Stata 默認，需使用“db metaninf”命令調用。
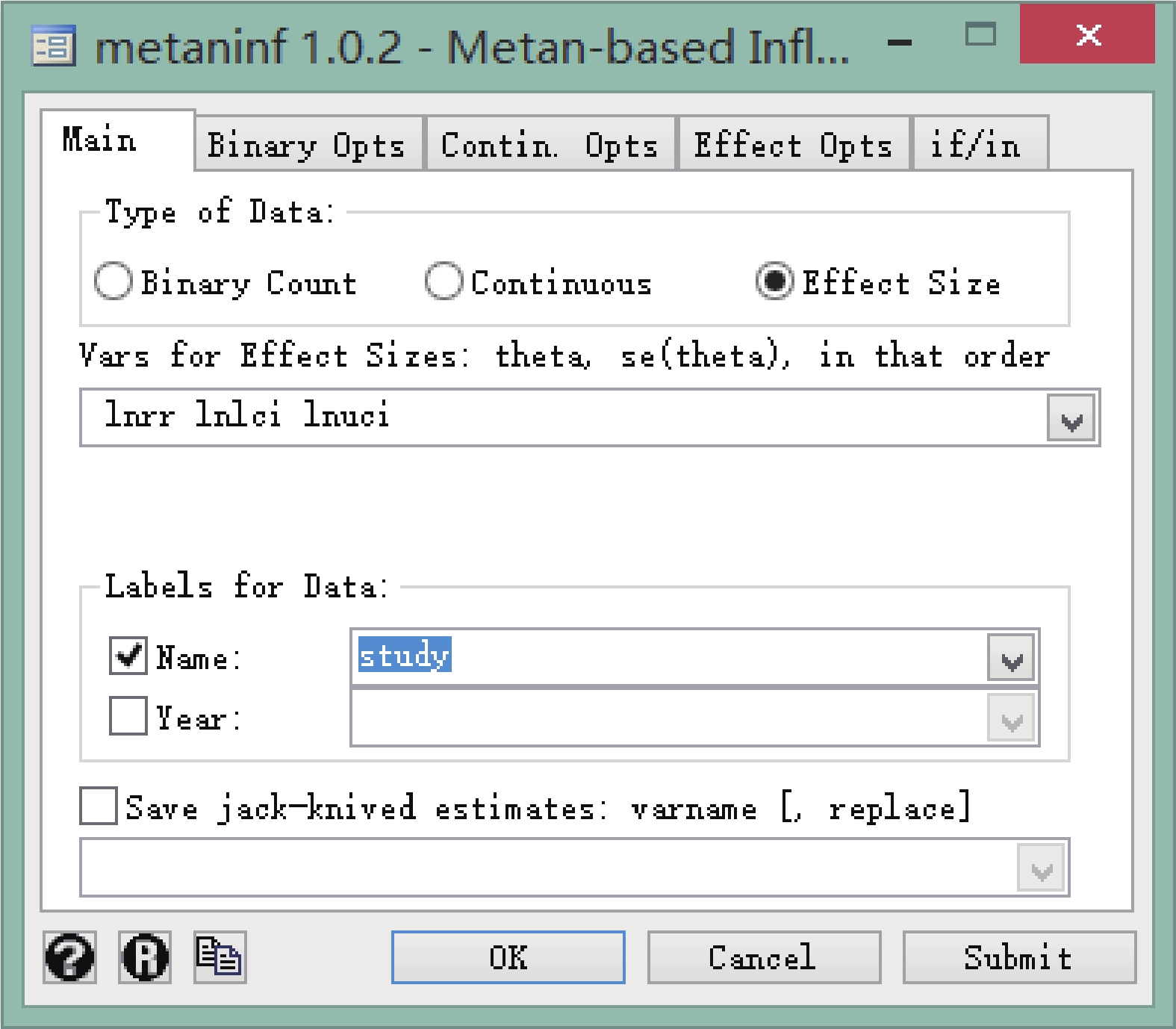圖10
Stata 軟件實現敏感性分析的數據選擇對話框
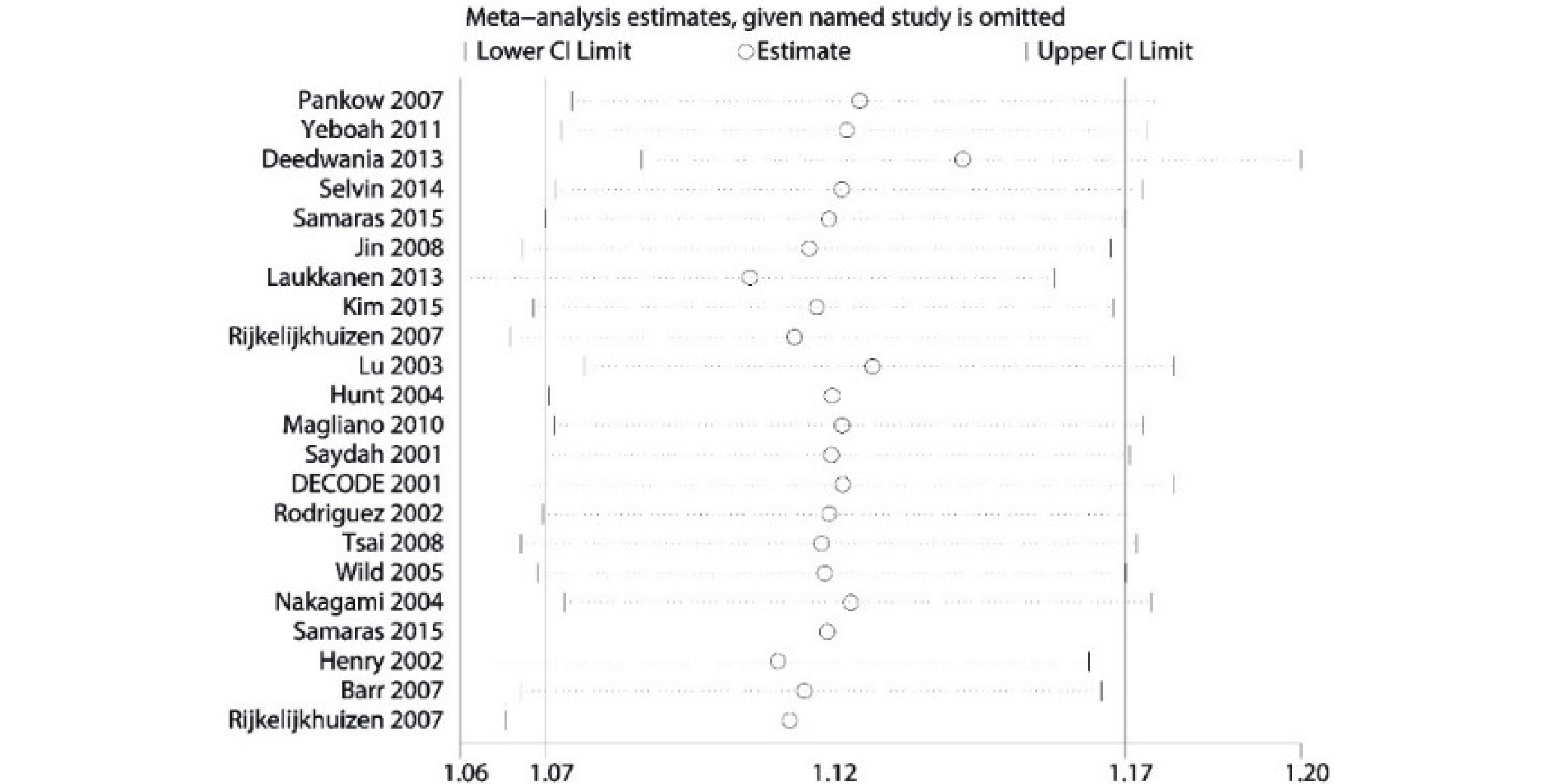
由于菜單中無指數轉換的選項，因此進行敏感性分析最方便的是采用手動輸入命令“metaninf lnrr lnlci lnuci，fixed label（namevar=study）eform”，敏感性分析結果見圖 11，具體的數值結果在結果窗口顯示。
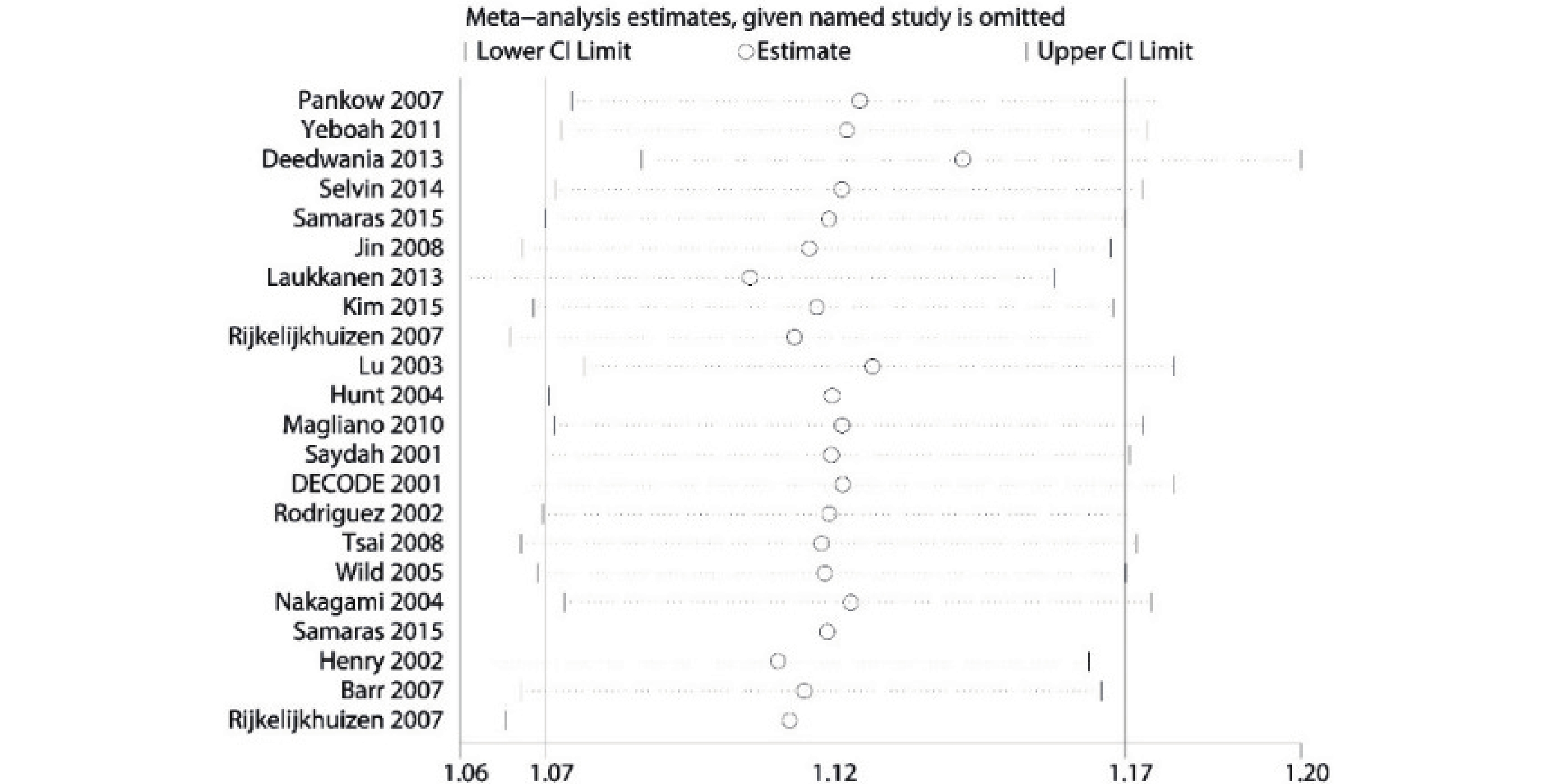圖11
Stata 軟件敏感性分析圖
3 討論
Stata 統計軟件包是目前世界上最著名的統計軟件之一。它同時具有數據管理、統計分析、繪圖、矩陣計算和程序語言的特點，幾乎可完成全部復雜的統計分析工作[6]。Stata 軟件進行統計分析的方法主要有兩種：菜單操作和命令操作。菜單操作簡單易懂，但并不是 Stata 軟件菜單默認，在使用中需要調用“db”命令實現。
使用 Stata 軟件實現效應量及 95%CI 的 Meta 分析時，應注意以下幾個問題：① 命令中注意“eform”的應用。當使用“ln 效應量”和“ln95%CI”進行合并時，應注意對合并結果取冪。當發現森林圖或敏感性分析中單個研究的結果出現負值則很有可能是未進行“eform”的轉換。② 注意數據的錄入格式。Stata 軟件對空格較為敏感，因此字符串前不能有空格，否則會被默認為新的變量或數據。尤其是當進行亞組分析時，空格會影響亞組分組。③ 異質性的分析與干預性研究 Meta 分析的異質性分析方法一樣。但需要注意的是，由于觀察性研究的效應值及其 95%CI 往往是通過回歸分析所得，不同的原始研究進行回歸分析所納入的因素可能不會完全一致，這點可能是統計學異質性的來源。
綜上所述，本文主要介紹了 Stata 實現效應量及其 95%CI 的 Meta 分析的具體操作方法，期望對致力于病因及預后分析的學者提供幫助。
傳統 Meta 分析常用的數據類型有二分類數據、連續性數據、有序數據、計數數據和時間事件數據。其中，最普遍的數據格式是兩個觀察組的事件發生數和未發生數，或者兩組病例數及結局指標的均數和標準差[1]。但在許多關于病因和預后的研究中，結果數據往往進行了回歸校正，以相對危險度（RR）、比值比（OR）、風險比（HR）及其 95% 可信區間（95%CI）表示，其更能反映研究因素的真實效應[2]，因此此類研究效應量及其 95%CI 進行 Meta 分析更有意義。但這類數據無法轉換成傳統的 Meta 分析數據格式，需要特殊的統計處理。
Stata 軟件是醫學四大統計軟件之一，在 Meta 分析方面功能非常強大[3]，可實現效應量及其 95%CI 的數據合并。本研究以已發表的 Meta 分析數據為例，詳細介紹如何采用 Stata 軟件實現效應量及其 95%CI 的 Meta 分析方法。
1 資料來源
2016 年，Huang 等[4]在 BMJ 雜志上發表了一篇名為《Association between prediabetes and risk of cardiovascular disease and all-cause mortality：systematic review and meta-analysis》的論文，其部分數據見表 1。本研究以該數據為例，介紹采用 Stata 軟件實現 RR 值及其 95%CI 的 Meta 分析的操作過程。其他效應量（OR 或 HR）的 Meta 分析方法與此一致。
表1
RR 值及其 95%CI 的示例數據
2 軟件操作過程
2.1 數據錄入
打開 Stata 軟件（version 14.0，Stata Corp，College Station，Texas），點擊
圖1
Stata 軟件數據錄入結果圖
2.2 制作森林圖
首先，對 RR 值及其 95%CI 進行對數轉換。在命令框內輸入下述命令：
gen lnrr=ln（rr）
gen lnlci=ln（lci）
gen lnuci=ln（uci）
其次，繪制效應量及可信區間的森林圖，具體操作方法如下：
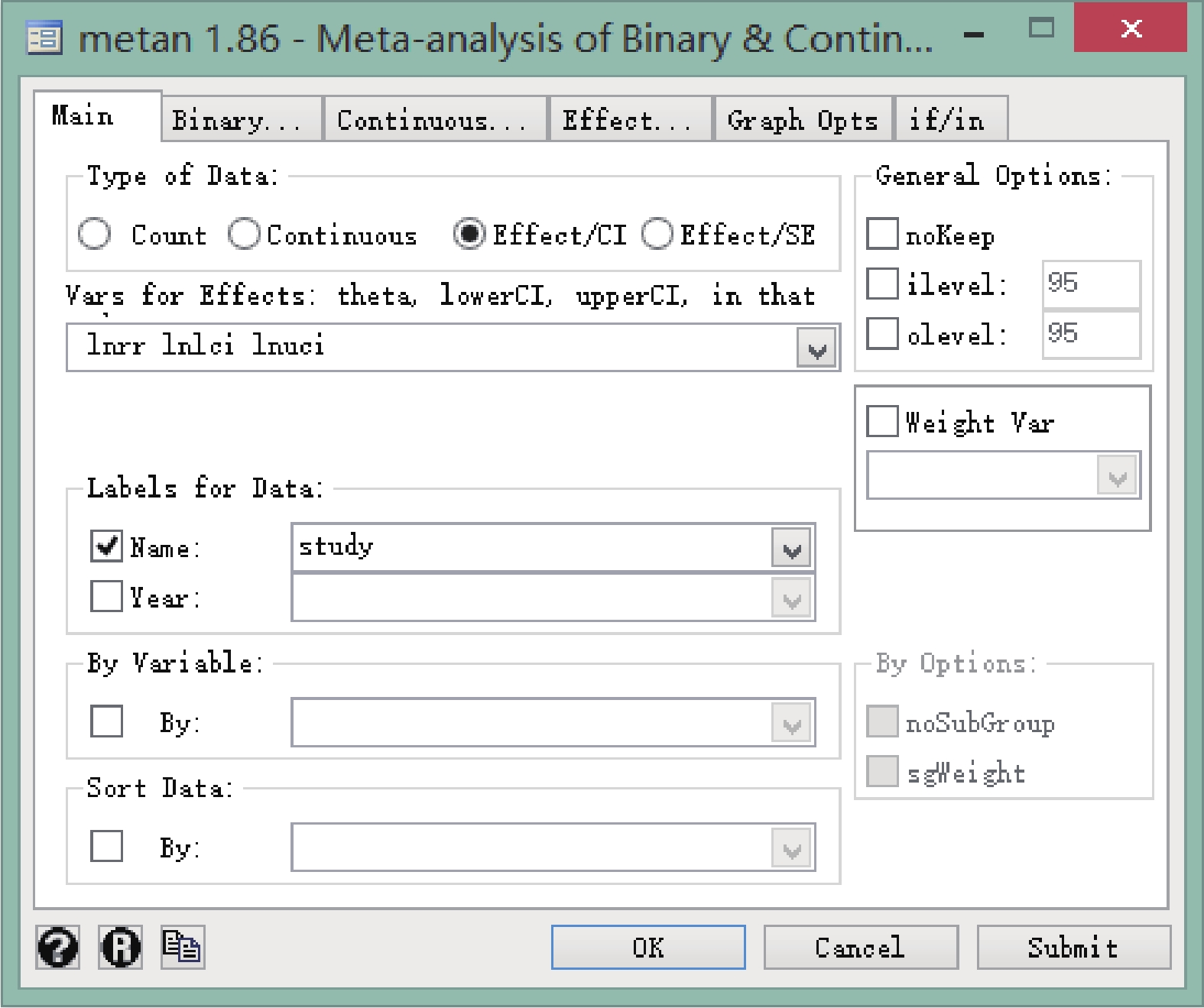
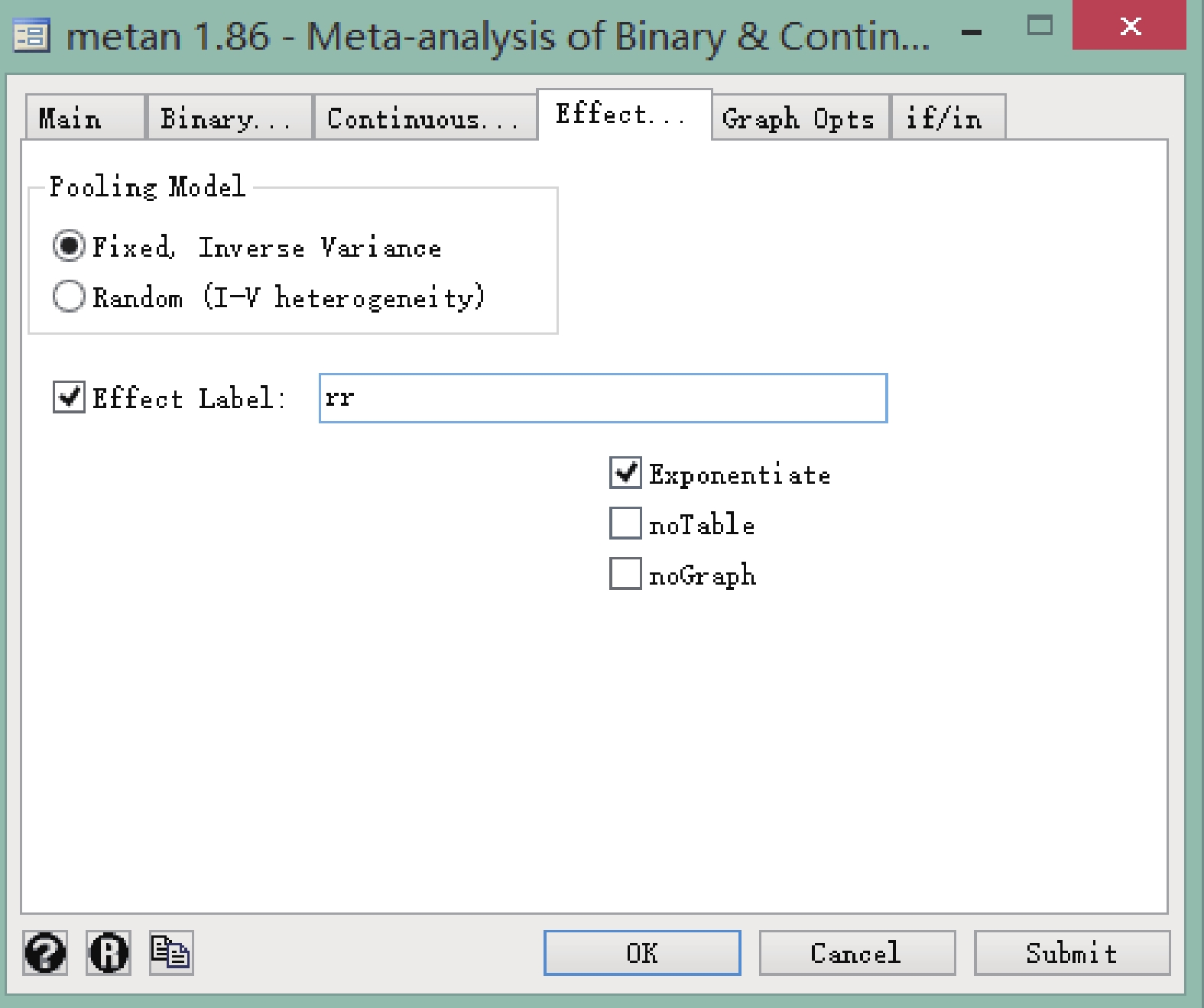
菜單操作：依次點擊 User→Meta-Analysis→Of Binary and Continuous（metan）。在新出現的面板中，type of Data 選擇 Effect/CI，Vars for Effects 的下拉框里按順序選擇 lnrr、lnlci、lnuci，Label of Data 中 Name 選擇 study（此變量即森林圖左側每個研究的名字），操作見圖 2。隨后在上方 Effect 下選擇 Pooling Model，本次以固定效應模型為例，其次在 Effect Label 中手動輸入 rr，并勾選 Exponentiate（指數轉換），操作見圖 3。需要注意的是，在操作頁面中如果不勾選 Exponentiate，則森林圖中出現的合并效應量是 ln（rr）、ln（lci）和 ln（uci），不易理解。
因該菜單不是 stata 軟件默認，如果使用者不通過一定的編程宏命令不會出現在菜單中，需使用“db metan”命令調用。
圖2
Stata 軟件繪制森林圖時選擇變量對話框
圖3
Stata 軟件繪制森林圖時選擇模型對話框
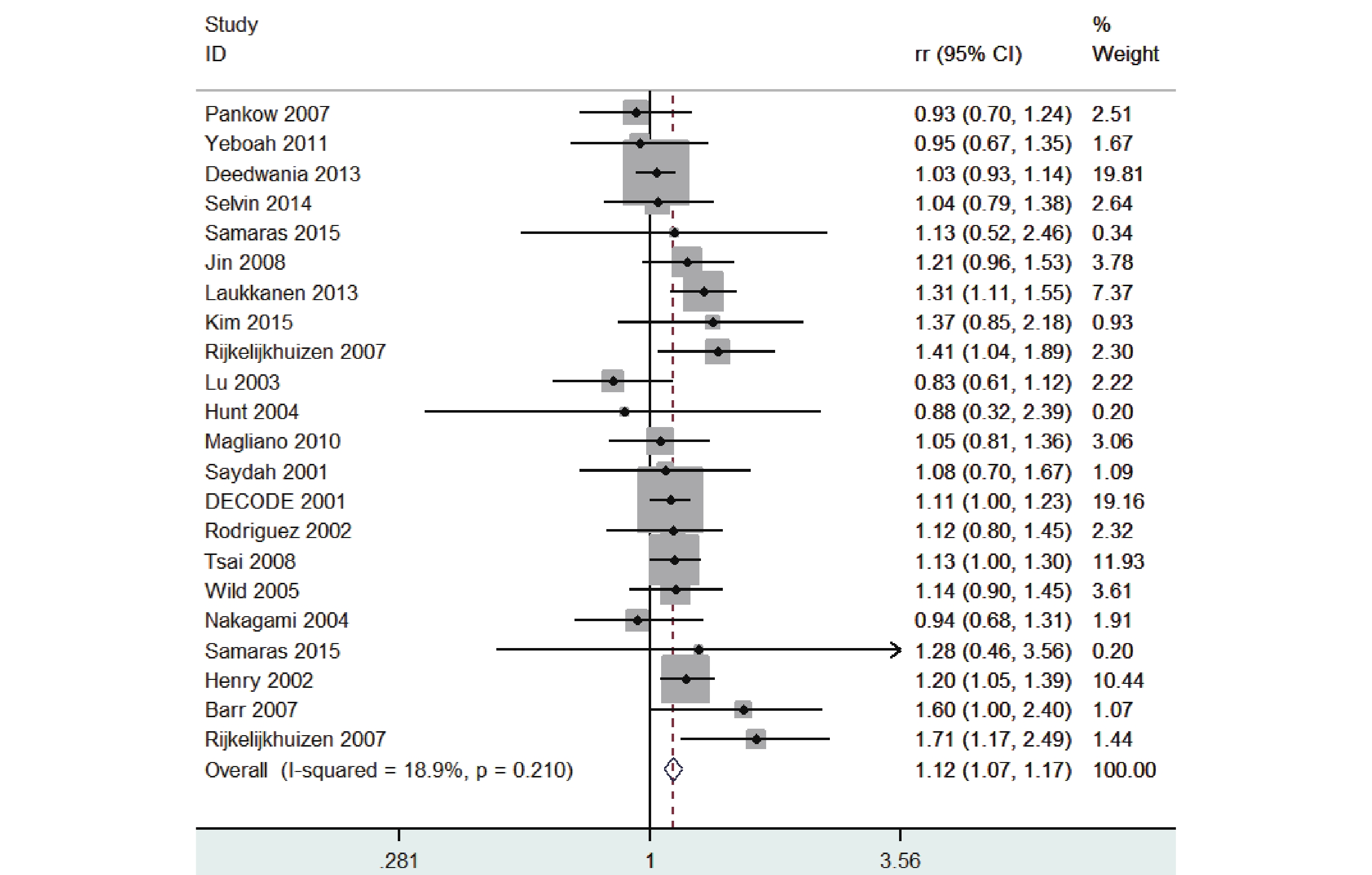
命令操作：在命令框中輸入命令“metan lnrr lnlci lnuci，label（namevar=study） fixed effect（rr） eform”，其中“eform”指對結果進行指數轉換。得到的森林圖結果見圖 4。
圖4
Stata 軟件根據 RR 值及其 95%CI 得出的森林圖
2.3 亞組分析
以不同的診斷標準進行亞組分析為例，具體操作方法如下：
菜單操作：在圖 2 中的 By Variable 下拉框中選擇分組變量 criteria，其他操作同森林圖的菜單操作。
命令操作：在命令框中輸入命令“metan lnrr lnlci lnuci，label（namevar=study） by（criteria） fixed effect（rr） eform”。亞組分析結果見圖 5。
圖5
Stata 軟件根據 RR 值及其 95%CI 得出的亞組分析森林圖
2.4 繪制漏斗圖
繪制漏斗圖的方法如下：
菜單操作：依次點擊 User→Meta-Analysis→Funnel Graph，vertical（metafunnel），Type of Data 選擇 exp（Theta），CI，Vars 中按順序選擇 rr、lci、uci。見圖 6。
因該菜單不是 Stata 軟件默認，需使用“db metafunnel”命令調用。
圖6
Stata 軟件繪制漏斗圖時選擇模型對話框
命令操作：在命令框中輸入命令“metafunnel rr lci uci，ci”，漏斗圖結果見圖 7。
圖7
Stata 軟件根據 RR 值及其 95%CI 得出的漏斗圖
2.5 漏斗圖對稱性檢驗
Stata 軟件可對漏斗圖的對稱性行 Egger 或 Begg 檢驗，操作如下：
菜單操作：依次點擊 User→Meta-Analysis→Publication Bias（metabias），Type of Data 選擇 exp（Theta），CI，Vars 中按順序選擇 rr、lci、uci，graph 選擇 Egger（也可選 begg），具體操作見圖 8。
因菜單不是 Stata 軟件默認，需使用“db metabias”命令調用。
圖8
Stata 軟件檢驗漏斗圖對稱性的對話框
命令操作：在命令框中輸入命令“metabias rr lci uci，ci graph（egger）”，檢驗結果見圖 9。
圖9
Stata 軟件得出的漏斗圖對稱性的檢驗結果
此外，metabias 命令是 Stata 軟件舊版本的命令，目前已改為 metabias6 命令，新版命令的功能與命令行操作格式均與老版本不同。使用 metabias6 時，命令操作的基本格式為“metabias6 log 效應值 selog 效應值”[5]，其他操作與舊版本相同。
2.6 敏感性分析
Stata 可實現單個研究的影響分析，具體操作如下：
菜單操作：User→Meta-Analysis→Influence Analysis，metan-based（metaninf），Type of Data 選 Effect Size，Vars 依次選擇 lnrr、lnlci、lnuci，具體操作見圖 10。需要特別注意的是，此敏感性分析的結果呈現形式是 ln（rr）、ln（lci）、ln（uci），需對其進行指數轉換得到最終結果。
因該菜單不是 Stata 默認，需使用“db metaninf”命令調用。
圖10
Stata 軟件實現敏感性分析的數據選擇對話框
由于菜單中無指數轉換的選項，因此進行敏感性分析最方便的是采用手動輸入命令“metaninf lnrr lnlci lnuci，fixed label（namevar=study）eform”，敏感性分析結果見圖 11，具體的數值結果在結果窗口顯示。
圖11
Stata 軟件敏感性分析圖
3 討論
Stata 統計軟件包是目前世界上最著名的統計軟件之一。它同時具有數據管理、統計分析、繪圖、矩陣計算和程序語言的特點，幾乎可完成全部復雜的統計分析工作[6]。Stata 軟件進行統計分析的方法主要有兩種：菜單操作和命令操作。菜單操作簡單易懂，但并不是 Stata 軟件菜單默認，在使用中需要調用“db”命令實現。
使用 Stata 軟件實現效應量及 95%CI 的 Meta 分析時，應注意以下幾個問題：① 命令中注意“eform”的應用。當使用“ln 效應量”和“ln95%CI”進行合并時，應注意對合并結果取冪。當發現森林圖或敏感性分析中單個研究的結果出現負值則很有可能是未進行“eform”的轉換。② 注意數據的錄入格式。Stata 軟件對空格較為敏感，因此字符串前不能有空格，否則會被默認為新的變量或數據。尤其是當進行亞組分析時，空格會影響亞組分組。③ 異質性的分析與干預性研究 Meta 分析的異質性分析方法一樣。但需要注意的是，由于觀察性研究的效應值及其 95%CI 往往是通過回歸分析所得，不同的原始研究進行回歸分析所納入的因素可能不會完全一致，這點可能是統計學異質性的來源。
綜上所述，本文主要介紹了 Stata 實現效應量及其 95%CI 的 Meta 分析的具體操作方法，期望對致力于病因及預后分析的學者提供幫助。
