利用患者的重復測量數據提升預測模型的分類能力是當前臨床預測模型開發中的關鍵方法問題。本研究擬探索兩階段模型的統計建模策略在基于重復測量數據開展非時變結局預測模型構建中的應用和價值，并以嚴重產后出血風險預測為例，從數據結構、基本原理、軟件操作和模型評價等多個維度，介紹兩階段模型的實現過程，以期為臨床研究者提供方法學指導。
引用本文： 賈玉龍, 任燕, 魏萬強, 徐葉, 劉春容, 趙芃, 劉興會, 孫鑫, 譚婧. 基于重復測量數據預測非時變結局發生風險的兩階段建模方法. 中國循證醫學雜志, 2024, 24(11): 1360-1364. doi: 10.7507/1672-2531.202406045 復制
版權信息： ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有，未經授權不得轉載、改編
1 前言
隨著醫學科學及信息技術的不斷進步，來自醫院電子病歷系統等的多源真實世界診療數據為現階段臨床預測模型的開發提供了大量重復測量的患者信息[1]，既包含了某個單一測量時點上多名患者的診療信息，也包含了同一患者個體多個時點上的重復測量診療信息。但是，在結局變量類型上，多數患者的目標結局往往發生在未來某個特定時期，屬于非時變結局范疇，即相對于重復測量的患者診療信息來說，結局事件并非重復發生，不是隨著患者個體診療信息的重復收集而同時被收集的，如早產、產后出血、低出生體重、兒童期的超重肥胖以及試驗最后一周是否戒煙成功等[2-6]。因此，針對此類基于個體重復測量診療信息預測非時變結局事件發生風險的臨床場景，現有的處理重復測量數據（即預測因子與結局變量均為重復測量）的建模方法，如混合效應模型、廣義估計方程等，均難以通過患者個體重復測量數據來構建非時變結局發生風險的預測模型[7,8]，導致目前研究者常采用單一橫斷面時點上的患者診療信息（如最后一次實驗室檢查指標）來構建預測模型，如logistic回歸模型[9]，但是這一數據處理方式無法充分利用患者多次測量的診療信息，導致預測準確性降低[5]。綜上，本文基于這一臨床預測模型構建中的關鍵方法問題，介紹將混合效應模型與logistic回歸模型相結合的兩階段建模方法，擬合患者個體重復測量信息變化軌跡來預測非時變結局發生風險[6]，并以嚴重產后出血數據為例，介紹兩階段建模方法的R語言軟件操作，為后續研究提供方法學指導。
2 數據結構
重復測量診療信息與患者基本信息及非時變結局信息所組成的數據結構一般為長數據結構（即縱向數據結構），如表1所示，關鍵的變量信息包含：個體編號（id）、重復測量時間（time）、重復測量的實驗室指標（wij）、年齡（age）、體質指數（body mass index，BMI）和非時變結局（Y）。其中，實驗室指標（wij）中i=1，…，n表示患者個體；j=1，…，k表示重復測量時間點，如w12則表示id=1的患者第2次測量的實驗室指標；年齡（age）、BMI和非時變結局（Y）因屬個體水平的變量信息，所以被重復記錄了3次，其中非時變結局（Y）的賦值結果為1=發生，0=未發生。當然，也有的臨床診療數據常被記錄為寬數據結構（即橫向數據結構），其中每次測量的實驗室指標被記錄為獨立變量，需要在分析時轉變為長數據結構，本文不再贅述數據轉置過程。
表1
重復測量診療信息與非時變結局的數據結構
3 兩階段模型基本原理
兩階段模型主要由階段1的“重復測量數據的軌跡建模”和階段2的“非時變結局的風險建模”兩個獨立的建模過程組成，二者通過隨機截距誤差（即每個個體隨機截距與固定截距之差）和隨機斜率誤差（即每個個體隨機斜率與固定斜率之差）進行鏈接，進而達到綜合利用重復測量數據預測非時變結局發生風險的目的[6,7]。其中，隨機截距誤差和隨機斜率誤差共同反映了每個個體對反應變量（本文指重復測量的實驗室指標）的隨機效應，固定截距和固定斜率共同反映了每個個體對反應變量的固定效應。“重復測量數據的軌跡建模”通常采用可以處理具有層次結構數據的混合效應模型來完成，通過最佳線性無偏預測（best linear unbiased prediction，BLUP）法對混合效應模型中的隨機效應進行估計[10]；而“非時變結局的風險建模”通過將階段1所估計的隨機效應作為預測因子[7]，在控制其他個體水平協變量（如年齡、BMI等）的同時，構建結局風險模型。此外，由于階段1和階段2是相對獨立的過程，所以在相應的模型構建階段，需要遵循混合效應模型[11]與logistic回歸模型對應的假設條件[9]。兩階段模型的詳細理論流程描述如下。
3.1 階段1：混合效應模型擬合變化軌跡
基于表1數據擬合混合效應模型，以重復測量次數，即時間標識變量time為1水平；患者個體，即個體編號id為2水平，通過混合效應模型擬合重復測量的實驗室指標隨時間的變化軌跡，通過BLUP法，根據隨機截距和隨機斜率與固定截距和固定斜率的差值，估算每個個體的隨機截距誤差
和隨機斜率誤差
，模型公式列舉如下：
 |
 |
 |
表示隨機截距，即不同個體的起始實驗室指標數值不同，
表示實驗室指標總體均值（即固定截距），
表示圍繞
的隨機個體變異，即隨機截距誤差；
表示隨機斜率，即不同個體的實驗室指標隨時間變化趨勢不同，
表示實驗室指標隨時間變化的總體趨勢（即固定斜率），
表示圍繞
的隨機個體變異，即隨機斜率誤差[11]。
3.2 階段2：logistic回歸模型預測結局發生風險
以階段1估計的個體水平隨機誤差作為自變量，通過logistic回歸模型，構建二元非時變結局的發生風險模型，模型公式列舉如下：
 |
表示隨機截距誤差估計值，
表示隨機斜率誤差估計值，
表示個體水平的混雜變量。此外，需要注意的是：因為
和
是固定不變的，所以將
和
帶入到logistic回歸模型中，與上述結果是一致的。
4 兩階段模型的R語言軟件實現
案例：共納入4 445例孕產婦，于產前分別進行了3次血紅蛋白實驗室檢查；根據產后24 h內的出血量>1 000 mL判斷嚴重產后出血的發生，共90例嚴重產后出血患者，發生率為2.02%。基于實際結局事件數以及目前廣泛應用的EPV>10的經驗原則法，本案例擬將血紅蛋白實驗室檢查作為重復測量預測因子（wij），孕產婦的BMI和年齡（age）作為個體水平的預測因子，將嚴重產后出血作為非時變結局（Y），通過兩階段模型構建嚴重產后出血風險預測模型，并與僅通過產前最后一次的血紅蛋白測量值構建的嚴重產后出血風險預測模型進行比較，以闡明兩階段模型的軟件操作過程和優勢。
4.1 運用lme4軟件包進行階段1的模型構建
參照表1的數據結構（data），擬合重復測量的血紅蛋白值（w）與時間（time）的隨機系數模型（model1），此時患者id作為因子型變量納入模型，time作為數值型變量納入模型。
model1<? lmer(w~time+(time│id),data=data) #模型構建
summary(model1) #展示模型信息
模型固定效應結果展示如下：
4.2 提取隨機截距和隨機斜率
提取每個個體對應的隨機截距和隨機斜率，并依次命名為random_intercept（隨機截距）和random_slope（隨機斜率）。此外，將對應的行名，轉換成列名為id的數據框，便于后期根據id進行數據橫向合并。
coef(model1)$id%>%data.frame()->randomef #提取隨機截距和隨機斜率
names(randomef)[c(1,2)]<?c("random_intercept", "random_slope") #重命名
rownames(randomef)%>%data.frame()->id #行名轉列名
names(id)[1]<-"id"
head(randomef) #展示前6行數據
結果展示如下：
4.3 提取固定效應
提取截距和時間的固定效應，并依次命名為fixed_intercept（固定截距）和fixed_slope（固定斜率）。
fixef(model1)%>%t()%>%data.frame()->fixef #提取固定效應
names(fixef)[c(1,2)]<-c("fixed_intercept", "fixed_slope") #重命名
fixef #展示結果
結果展示如下：
4.4 計算隨機效應
通過隨機截距和隨機斜率（random_intercept和random_slope）與固定截距和固定斜率（fixed_intercept和fixed_slope）對應相減，計算誤差項，并將誤差與原始數據通過id變量橫向合并，同時每例患者根據id變量去重并保留產前最后一次血紅蛋白，生成新的數據集logitdata。此外，研究者也可通過ranef()函數直接估算出隨機截距誤差和隨機斜率誤差，為方便讀者理解具體過程，本文采取逐步計算的方式講解隨機截距誤差和隨機斜率誤差的計算過程。
effect<-cbind(id,fixef,randomef) #數據集橫向合并
effect$error_intercept<-effect$random_intercept-effect$fixed_intercept
effect$error_slope<-effect$random_slope-effect$fixed_slope
data_final<-merge(data,effect,by ="id") #根據id橫向合并數據集
logitdata<-data_final[order(data_final$id,-data_final$week),] #排序
logitdata<-distinct(logitdata,id,.keep_all=TRUE) #保留最后一次血紅蛋白
4.5 根據隨機誤差構建產后出血風險預測模型
通過glm()函數擬合患者年齡，BMI，隨機截距誤差以及隨機斜率誤差與嚴重產后出血之間的風險預測模型（即fit1），同時，擬合患者年齡，BMI以及最后一次血紅蛋白與嚴重產后出血之間的風險預測模型（即fit2），并通過受試者工作特征曲線（receiver operating characteristic curve，ROC）下面積（area under curve，AUC）比較模型鑒別能力。
fit1<-glm(Y~age+BMI+error_intercept+error_slope,data=logitdata,family="binomial")
logitdata$pre1<-predict(fit1,type='response') #計算結局事件預測概率
fit2<-glm(Y~age+BMI+w,data=logitdata,family="binomial")
logitdata$pre2<-predict(fit2,type='response^') #計算結局事件預測概率
library(pROC) #繪制ROC曲線圖，載入pROC包
fit1_roc<-roc(logitdata$Y,logitdata$pre1)
fit2_roc<-roc(logitdata$Y,logitdata$pre2)
plot(fit1_roc,auc.polygon=TRUE,print.thres="best",font=2,font.lab=2,print.auc=TRUE,print.auc.x=-0.01,print.auc.y=0.07)
plot(fit2_roc,add=TRUE,print.thres="best",font=2,print.thres.col="red",col="red",lty=2,print.auc=TRUE,print.auc.x=-0.01,print.auc.y=0.02)
legend(x=0.175,y=0.1,legend=c("fit1","fit2"),col=c("black","red"),text.col=c("black","red"),lty=c(1,2),text.font=2)
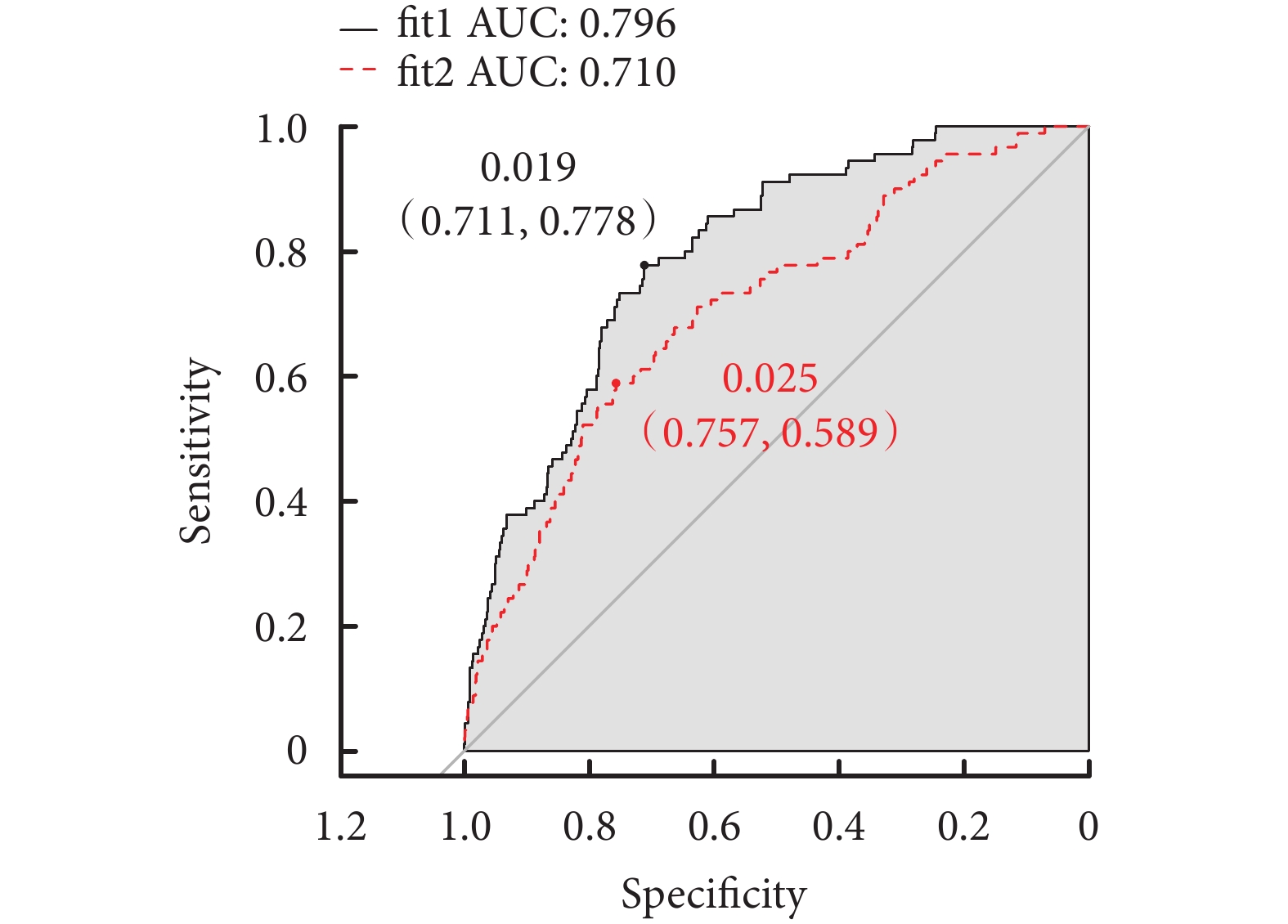
兩種預測模型的ROC曲線如圖1所示，兩階段模型（即fit1）的AUC為0.796，而僅考慮產前最后一次血紅蛋白測量值的預測模型（即fit2）的AUC為0.710。根據ROC曲線選擇最佳截斷值，并計算相應的靈敏度和特異度，結果顯示當兩種預測模型均使用自身最佳截斷值時，fit1相比于fit2，在特異度相近的同時，具有更高的靈敏度（表2）。
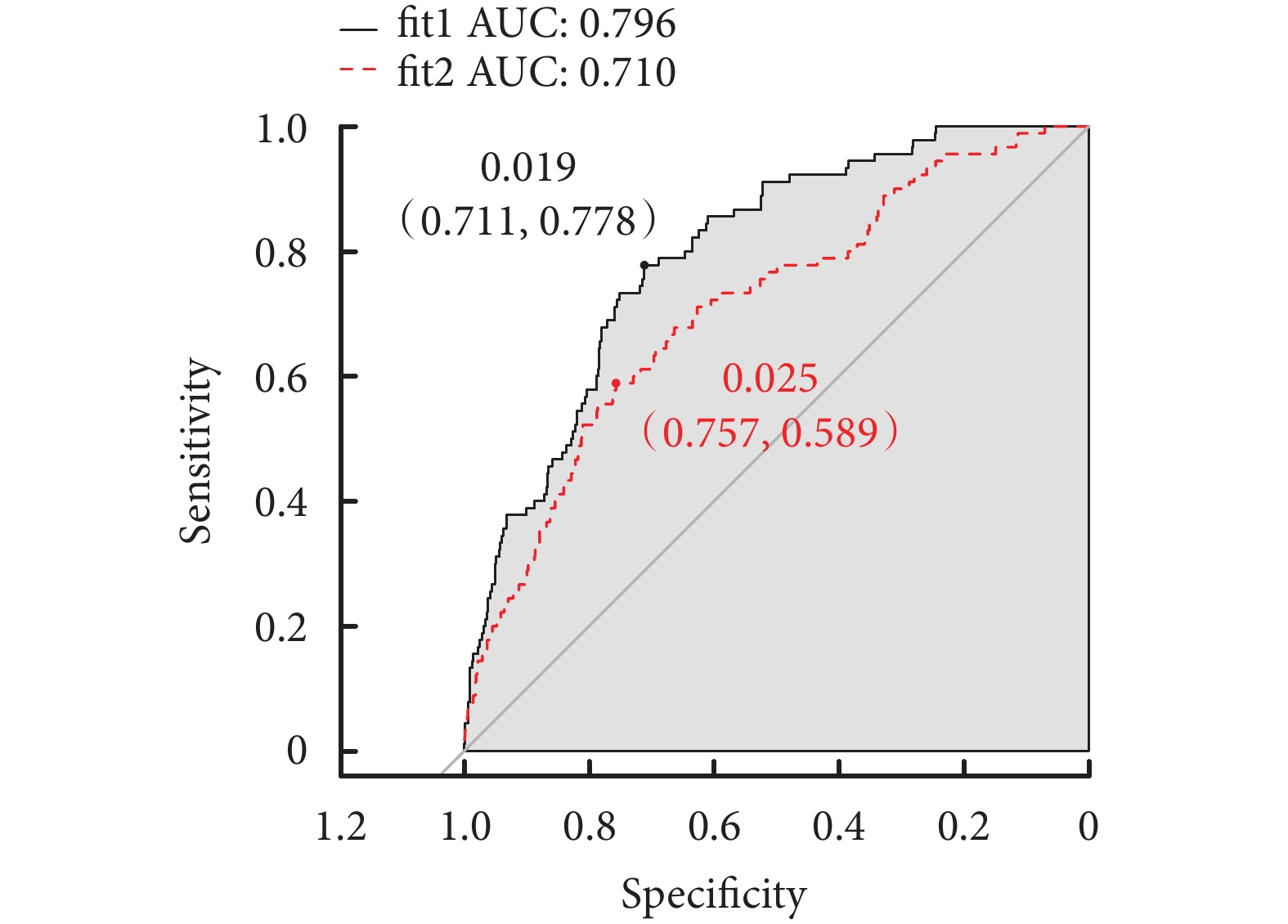圖1
兩種預測模型的受試者工作特征曲線及曲線下面積
表2
基于最佳閾值的模型靈敏度與特異度
5 討論
本研究基于完整的嚴重產后出血示例數據，從臨床預測模型開發實踐的角度，闡述兩階段模型的基本原理和軟件操作過程，比較兩階段模型與僅利用單次實驗室指標的預測模型之間的鑒別能力，并比較兩種預測模型最佳截斷值下的靈敏度和特異度。結果均顯示在嚴重產后出血的臨床場景下，利用重復測量的血紅蛋白實驗室指標作為預測因子的兩階段模型，具備較高的模型分類能力，且在相似特異度的基礎上具備較高的靈敏度，可以較為準確地預測嚴重產后出血的發生風險，為臨床診療和產前預防提供有力的證據支持。
相比于僅利用單次實驗室指標的預測模型，兩階段模型可以充分利用重復測量的指標信息，將個體間變異（即不同的截距）和個體內變異（即不同的隨時間變化趨勢）進行分解，并當作隨機效應通過BLUP法進行準確估計[5]，解決了混合效應模型無法用于個體風險預測的問題[7]，進而提高預測模型的準確性[6]。同時，第一階段中混合效應模型的構建，適當放寬了常規預測模型中對預測因子的獨立性、完整性以及線性變化的強假設要求，有效處理重復測量預測因子之間的相關性，以及可能的缺失值和非線性的變化趨勢[7,12]。此外，兩階段模型以共享隨機效應的形式將混合效應模型與logistic回歸模型兩個獨立的建模方法合理鏈接，解決了非時變結局與重復測量預測因子非一一對應的問題，并且在提高數據利用度的同時未增加軟件實現難度。但是針對特殊的臨床場景，如產前超聲檢查的胎兒腹部直徑預測巨大兒發生風險，因越接近結局事件發生時間窗，預測因子與結局事件的相關性越強，所以利用重復測量預測因子與僅利用最后一次預測因子在總體預測精度上相當，因此需結合具體的臨床場景以及適當的模型評價方法選擇最優預測模型[13]。此外，其他可處理類似重復測量數據預測非時變結局的統計方法以及方法學比較可參考已發表研究[5,7]。
由于本研究的主旨是兩階段建模方法的軟件應用實踐，所以相比于傳統的預測模型研究思路略有不同：① 本研究未根據傳統預測模型構建流程，基于研究目的和研究設計進行樣本量估算，主要考慮本研究的主旨不是為了構建一個完善的嚴重產后出血預測模型并應用于臨床實踐，而是為了介紹兩階段模型構建方法的軟件實現流程，并通過與僅利用單次實驗室指標作為預測因子的logistic回歸，體現利用多次診療信息作為預測因子的模型預測優勢，故臨床研究者可參考本研究的思路，在滿足各水平殘差服從正態分布以及模型的常方差性等混合效應模型的基本假設[11]，以及個體間獨立性和無多重共線性等logistic回歸模型的基本假設前提下，將該兩階段模型應用于適用的臨床場景；② 本研究未充分考慮針對嚴重產后出血這一結局事件本身的預測模型構建過程中所需的關鍵環節，如嚴重產后出血發生率較低，屬于罕見結局事件[14,15]，需要結合不平衡數據處理方法來提高模型預測性能[16-19]；故臨床研究者在應用兩階段模型用于實際臨床預測場景時，需根據具體研究問題和研究設計進行全面考量和相應統計方法的補充；③ 基于軟件操作的考慮，模型中僅納入重復測量的血紅蛋白指標、個體水平的年齡、BMI三個預測因子，未考慮其他臨床上可用于嚴重產后出血風險預測的診療信息，所以AUC僅在0.70～0.80之間，且可能存在高占比的非結局事件過度擬合的問題[19]，但通過最佳截斷值對應的靈敏度比較顯示，兩階段模型在小幅度損失特異度的同時，具備較高的靈敏度，即正確識別結局事件發生的能力，故足以證明利用重復測量的診療信息可以提高模型預測性能；④ 本研究未考慮存在缺失數據的應用場景，一方面階段1的混合效應模型對一定數量的缺失不敏感，另一方面階段2的logistic回歸模型需根據不同缺失模式進行合理的填補和處理。因此，研究者需結合實際臨床場景，綜合利用多源真實世界診療數據，在充分考慮研究設計、數據質量以及模型適用性的同時，選擇科學合理的建模方法。
1 前言
隨著醫學科學及信息技術的不斷進步，來自醫院電子病歷系統等的多源真實世界診療數據為現階段臨床預測模型的開發提供了大量重復測量的患者信息[1]，既包含了某個單一測量時點上多名患者的診療信息，也包含了同一患者個體多個時點上的重復測量診療信息。但是，在結局變量類型上，多數患者的目標結局往往發生在未來某個特定時期，屬于非時變結局范疇，即相對于重復測量的患者診療信息來說，結局事件并非重復發生，不是隨著患者個體診療信息的重復收集而同時被收集的，如早產、產后出血、低出生體重、兒童期的超重肥胖以及試驗最后一周是否戒煙成功等[2-6]。因此，針對此類基于個體重復測量診療信息預測非時變結局事件發生風險的臨床場景，現有的處理重復測量數據（即預測因子與結局變量均為重復測量）的建模方法，如混合效應模型、廣義估計方程等，均難以通過患者個體重復測量數據來構建非時變結局發生風險的預測模型[7,8]，導致目前研究者常采用單一橫斷面時點上的患者診療信息（如最后一次實驗室檢查指標）來構建預測模型，如logistic回歸模型[9]，但是這一數據處理方式無法充分利用患者多次測量的診療信息，導致預測準確性降低[5]。綜上，本文基于這一臨床預測模型構建中的關鍵方法問題，介紹將混合效應模型與logistic回歸模型相結合的兩階段建模方法，擬合患者個體重復測量信息變化軌跡來預測非時變結局發生風險[6]，并以嚴重產后出血數據為例，介紹兩階段建模方法的R語言軟件操作，為后續研究提供方法學指導。
2 數據結構
重復測量診療信息與患者基本信息及非時變結局信息所組成的數據結構一般為長數據結構（即縱向數據結構），如表1所示，關鍵的變量信息包含：個體編號（id）、重復測量時間（time）、重復測量的實驗室指標（wij）、年齡（age）、體質指數（body mass index，BMI）和非時變結局（Y）。其中，實驗室指標（wij）中i=1，…，n表示患者個體；j=1，…，k表示重復測量時間點，如w12則表示id=1的患者第2次測量的實驗室指標；年齡（age）、BMI和非時變結局（Y）因屬個體水平的變量信息，所以被重復記錄了3次，其中非時變結局（Y）的賦值結果為1=發生，0=未發生。當然，也有的臨床診療數據常被記錄為寬數據結構（即橫向數據結構），其中每次測量的實驗室指標被記錄為獨立變量，需要在分析時轉變為長數據結構，本文不再贅述數據轉置過程。
表1
重復測量診療信息與非時變結局的數據結構
3 兩階段模型基本原理
兩階段模型主要由階段1的“重復測量數據的軌跡建模”和階段2的“非時變結局的風險建模”兩個獨立的建模過程組成，二者通過隨機截距誤差（即每個個體隨機截距與固定截距之差）和隨機斜率誤差（即每個個體隨機斜率與固定斜率之差）進行鏈接，進而達到綜合利用重復測量數據預測非時變結局發生風險的目的[6,7]。其中，隨機截距誤差和隨機斜率誤差共同反映了每個個體對反應變量（本文指重復測量的實驗室指標）的隨機效應，固定截距和固定斜率共同反映了每個個體對反應變量的固定效應。“重復測量數據的軌跡建模”通常采用可以處理具有層次結構數據的混合效應模型來完成，通過最佳線性無偏預測（best linear unbiased prediction，BLUP）法對混合效應模型中的隨機效應進行估計[10]；而“非時變結局的風險建模”通過將階段1所估計的隨機效應作為預測因子[7]，在控制其他個體水平協變量（如年齡、BMI等）的同時，構建結局風險模型。此外，由于階段1和階段2是相對獨立的過程，所以在相應的模型構建階段，需要遵循混合效應模型[11]與logistic回歸模型對應的假設條件[9]。兩階段模型的詳細理論流程描述如下。
3.1 階段1：混合效應模型擬合變化軌跡
基于表1數據擬合混合效應模型，以重復測量次數，即時間標識變量time為1水平；患者個體，即個體編號id為2水平，通過混合效應模型擬合重復測量的實驗室指標隨時間的變化軌跡，通過BLUP法，根據隨機截距和隨機斜率與固定截距和固定斜率的差值，估算每個個體的隨機截距誤差和隨機斜率誤差，模型公式列舉如下：
|
|
|
表示隨機截距，即不同個體的起始實驗室指標數值不同，表示實驗室指標總體均值（即固定截距），表示圍繞的隨機個體變異，即隨機截距誤差；表示隨機斜率，即不同個體的實驗室指標隨時間變化趨勢不同，表示實驗室指標隨時間變化的總體趨勢（即固定斜率），表示圍繞的隨機個體變異，即隨機斜率誤差[11]。
3.2 階段2：logistic回歸模型預測結局發生風險
以階段1估計的個體水平隨機誤差作為自變量，通過logistic回歸模型，構建二元非時變結局的發生風險模型，模型公式列舉如下：
|
表示隨機截距誤差估計值，表示隨機斜率誤差估計值，表示個體水平的混雜變量。此外，需要注意的是：因為和是固定不變的，所以將和帶入到logistic回歸模型中，與上述結果是一致的。
4 兩階段模型的R語言軟件實現
案例：共納入4 445例孕產婦，于產前分別進行了3次血紅蛋白實驗室檢查；根據產后24 h內的出血量>1 000 mL判斷嚴重產后出血的發生，共90例嚴重產后出血患者，發生率為2.02%。基于實際結局事件數以及目前廣泛應用的EPV>10的經驗原則法，本案例擬將血紅蛋白實驗室檢查作為重復測量預測因子（wij），孕產婦的BMI和年齡（age）作為個體水平的預測因子，將嚴重產后出血作為非時變結局（Y），通過兩階段模型構建嚴重產后出血風險預測模型，并與僅通過產前最后一次的血紅蛋白測量值構建的嚴重產后出血風險預測模型進行比較，以闡明兩階段模型的軟件操作過程和優勢。
4.1 運用lme4軟件包進行階段1的模型構建
參照表1的數據結構（data），擬合重復測量的血紅蛋白值（w）與時間（time）的隨機系數模型（model1），此時患者id作為因子型變量納入模型，time作為數值型變量納入模型。
model1<? lmer(w~time+(time│id),data=data) #模型構建
summary(model1) #展示模型信息
模型固定效應結果展示如下：
4.2 提取隨機截距和隨機斜率
提取每個個體對應的隨機截距和隨機斜率，并依次命名為random_intercept（隨機截距）和random_slope（隨機斜率）。此外，將對應的行名，轉換成列名為id的數據框，便于后期根據id進行數據橫向合并。
coef(model1)$id%>%data.frame()->randomef #提取隨機截距和隨機斜率
names(randomef)[c(1,2)]<?c("random_intercept", "random_slope") #重命名
rownames(randomef)%>%data.frame()->id #行名轉列名
names(id)[1]<-"id"
head(randomef) #展示前6行數據
結果展示如下：
4.3 提取固定效應
提取截距和時間的固定效應，并依次命名為fixed_intercept（固定截距）和fixed_slope（固定斜率）。
fixef(model1)%>%t()%>%data.frame()->fixef #提取固定效應
names(fixef)[c(1,2)]<-c("fixed_intercept", "fixed_slope") #重命名
fixef #展示結果
結果展示如下：
4.4 計算隨機效應
通過隨機截距和隨機斜率（random_intercept和random_slope）與固定截距和固定斜率（fixed_intercept和fixed_slope）對應相減，計算誤差項，并將誤差與原始數據通過id變量橫向合并，同時每例患者根據id變量去重并保留產前最后一次血紅蛋白，生成新的數據集logitdata。此外，研究者也可通過ranef()函數直接估算出隨機截距誤差和隨機斜率誤差，為方便讀者理解具體過程，本文采取逐步計算的方式講解隨機截距誤差和隨機斜率誤差的計算過程。
effect<-cbind(id,fixef,randomef) #數據集橫向合并
effect$error_intercept<-effect$random_intercept-effect$fixed_intercept
effect$error_slope<-effect$random_slope-effect$fixed_slope
data_final<-merge(data,effect,by ="id") #根據id橫向合并數據集
logitdata<-data_final[order(data_final$id,-data_final$week),] #排序
logitdata<-distinct(logitdata,id,.keep_all=TRUE) #保留最后一次血紅蛋白
4.5 根據隨機誤差構建產后出血風險預測模型
通過glm()函數擬合患者年齡，BMI，隨機截距誤差以及隨機斜率誤差與嚴重產后出血之間的風險預測模型（即fit1），同時，擬合患者年齡，BMI以及最后一次血紅蛋白與嚴重產后出血之間的風險預測模型（即fit2），并通過受試者工作特征曲線（receiver operating characteristic curve，ROC）下面積（area under curve，AUC）比較模型鑒別能力。
fit1<-glm(Y~age+BMI+error_intercept+error_slope,data=logitdata,family="binomial")
logitdata$pre1<-predict(fit1,type='response') #計算結局事件預測概率
fit2<-glm(Y~age+BMI+w,data=logitdata,family="binomial")
logitdata$pre2<-predict(fit2,type='response^') #計算結局事件預測概率
library(pROC) #繪制ROC曲線圖，載入pROC包
fit1_roc<-roc(logitdata$Y,logitdata$pre1)
fit2_roc<-roc(logitdata$Y,logitdata$pre2)
plot(fit1_roc,auc.polygon=TRUE,print.thres="best",font=2,font.lab=2,print.auc=TRUE,print.auc.x=-0.01,print.auc.y=0.07)
plot(fit2_roc,add=TRUE,print.thres="best",font=2,print.thres.col="red",col="red",lty=2,print.auc=TRUE,print.auc.x=-0.01,print.auc.y=0.02)
legend(x=0.175,y=0.1,legend=c("fit1","fit2"),col=c("black","red"),text.col=c("black","red"),lty=c(1,2),text.font=2)
兩種預測模型的ROC曲線如圖1所示，兩階段模型（即fit1）的AUC為0.796，而僅考慮產前最后一次血紅蛋白測量值的預測模型（即fit2）的AUC為0.710。根據ROC曲線選擇最佳截斷值，并計算相應的靈敏度和特異度，結果顯示當兩種預測模型均使用自身最佳截斷值時，fit1相比于fit2，在特異度相近的同時，具有更高的靈敏度（表2）。
圖1
兩種預測模型的受試者工作特征曲線及曲線下面積
表2
基于最佳閾值的模型靈敏度與特異度
5 討論
本研究基于完整的嚴重產后出血示例數據，從臨床預測模型開發實踐的角度，闡述兩階段模型的基本原理和軟件操作過程，比較兩階段模型與僅利用單次實驗室指標的預測模型之間的鑒別能力，并比較兩種預測模型最佳截斷值下的靈敏度和特異度。結果均顯示在嚴重產后出血的臨床場景下，利用重復測量的血紅蛋白實驗室指標作為預測因子的兩階段模型，具備較高的模型分類能力，且在相似特異度的基礎上具備較高的靈敏度，可以較為準確地預測嚴重產后出血的發生風險，為臨床診療和產前預防提供有力的證據支持。
相比于僅利用單次實驗室指標的預測模型，兩階段模型可以充分利用重復測量的指標信息，將個體間變異（即不同的截距）和個體內變異（即不同的隨時間變化趨勢）進行分解，并當作隨機效應通過BLUP法進行準確估計[5]，解決了混合效應模型無法用于個體風險預測的問題[7]，進而提高預測模型的準確性[6]。同時，第一階段中混合效應模型的構建，適當放寬了常規預測模型中對預測因子的獨立性、完整性以及線性變化的強假設要求，有效處理重復測量預測因子之間的相關性，以及可能的缺失值和非線性的變化趨勢[7,12]。此外，兩階段模型以共享隨機效應的形式將混合效應模型與logistic回歸模型兩個獨立的建模方法合理鏈接，解決了非時變結局與重復測量預測因子非一一對應的問題，并且在提高數據利用度的同時未增加軟件實現難度。但是針對特殊的臨床場景，如產前超聲檢查的胎兒腹部直徑預測巨大兒發生風險，因越接近結局事件發生時間窗，預測因子與結局事件的相關性越強，所以利用重復測量預測因子與僅利用最后一次預測因子在總體預測精度上相當，因此需結合具體的臨床場景以及適當的模型評價方法選擇最優預測模型[13]。此外，其他可處理類似重復測量數據預測非時變結局的統計方法以及方法學比較可參考已發表研究[5,7]。
由于本研究的主旨是兩階段建模方法的軟件應用實踐，所以相比于傳統的預測模型研究思路略有不同：① 本研究未根據傳統預測模型構建流程，基于研究目的和研究設計進行樣本量估算，主要考慮本研究的主旨不是為了構建一個完善的嚴重產后出血預測模型并應用于臨床實踐，而是為了介紹兩階段模型構建方法的軟件實現流程，并通過與僅利用單次實驗室指標作為預測因子的logistic回歸，體現利用多次診療信息作為預測因子的模型預測優勢，故臨床研究者可參考本研究的思路，在滿足各水平殘差服從正態分布以及模型的常方差性等混合效應模型的基本假設[11]，以及個體間獨立性和無多重共線性等logistic回歸模型的基本假設前提下，將該兩階段模型應用于適用的臨床場景；② 本研究未充分考慮針對嚴重產后出血這一結局事件本身的預測模型構建過程中所需的關鍵環節，如嚴重產后出血發生率較低，屬于罕見結局事件[14,15]，需要結合不平衡數據處理方法來提高模型預測性能[16-19]；故臨床研究者在應用兩階段模型用于實際臨床預測場景時，需根據具體研究問題和研究設計進行全面考量和相應統計方法的補充；③ 基于軟件操作的考慮，模型中僅納入重復測量的血紅蛋白指標、個體水平的年齡、BMI三個預測因子，未考慮其他臨床上可用于嚴重產后出血風險預測的診療信息，所以AUC僅在0.70～0.80之間，且可能存在高占比的非結局事件過度擬合的問題[19]，但通過最佳截斷值對應的靈敏度比較顯示，兩階段模型在小幅度損失特異度的同時，具備較高的靈敏度，即正確識別結局事件發生的能力，故足以證明利用重復測量的診療信息可以提高模型預測性能；④ 本研究未考慮存在缺失數據的應用場景，一方面階段1的混合效應模型對一定數量的缺失不敏感，另一方面階段2的logistic回歸模型需根據不同缺失模式進行合理的填補和處理。因此，研究者需結合實際臨床場景，綜合利用多源真實世界診療數據，在充分考慮研究設計、數據質量以及模型適用性的同時，選擇科學合理的建模方法。
