針對傳感器非線性校正存在的不足,提出了基于免疫遺傳算法(IGA)的傳感器非線性校正。該算法是在遺傳算法的基礎上引入生物免疫機制,克服了遺傳算法精度差、收斂速度慢和"早熟"等問題。計算機仿真表明,該算法不僅能夠有效保持種群的多樣性,而且收斂速度、精度和穩定性都有了明顯提高。實驗結果表明了該方法的正確性和有效性。
引用本文： 盧莉蓉, 周晉陽, 牛曉東. 基于免疫遺傳算法的傳感器非線性校正. 生物醫學工程學雜志, 2014, 31(4): 751-754. doi: 10.7507/1001-5515.20140140 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
傳感器是能夠感受規定的被測量，并按照一定規律轉化成可用信號輸出的器件或裝置[1]。在科學研究和工業測控中，常用傳感器來檢測研究和控制的對象。人們需要的傳感器能線性地反映被測量的大小，但是大多數實際傳感器的輸入和輸出常常呈現出非線性特點。于是通常采取各種校正措施來解決這一問題。近年來，硬件電路補償和各種軟件補償方法在傳感器非線性校正中得到廣泛的應用。硬件電路校正雖然簡單，但成本高、設計制造繁瑣、效果差；常用的軟件補償法則有最小二乘法、函數校正法、遺傳算法等[2-3]。
遺傳算法[4](genetic algorithm，GA)是模擬生物在自然環境中遺傳和進化過程而形成的一種全局搜索算法。由于遺傳算法較以往傳統的搜索算法具有使用方便、魯棒性強、便于并行處理等特點，因而得到了廣泛的應用。然而，由于交叉和變異兩個遺傳算子都依據一定概率實現，具有較大的隨機性和盲目性；并且沒有先驗知識作為指導，也沒有利用問題自身的特征信息或知識，忽視了問題的特征信息在求解問題時的輔助作用，這很大程度上影響了算法的收斂速度和性能。再者，遺傳算法還容易陷入局部最優解，產生“早熟”問題[5]。
人工免疫系統[6-7](artificial immune systems，AIS)是受生物免疫系統啟發，模仿自然免疫系統功能的一種智能算法，它是基于人類和其他高級動物免疫系統理論而提出的一種新的信息處理系統。
為了克服遺傳算法的不足，在遺傳算法的基礎上引入生物免疫機制，從而形成了免疫遺傳算法(immune genetic algorithm,IGA)[8]。本文研究并應用IGA解決了傳感器系統的非線性校正問題。該算法不僅能夠有效保持種群的多樣性，而且收斂速度和穩定性以及運算效率都有了明顯提高，實驗結果表明了該方法的正確性和有效性。
1 基于IGA的傳感器非線性校正模型
采用IGA的非線性校正模型如圖 1所示。
圖1
IGA算法的非線性校正原理
Figure1.
The theory of the non-linearity rectification with IGA
大多數傳感器滿足關系式：Y=f(X)。若Y為X的單值函數，則上式存在反函數，即X=f-1(Y)。
設校正環節Z=g(Y)，若滿足g(Y)=f-1(Y)，則
| $Z=g\left( Y \right)={{f}^{-1}}\left( Y \right)=X~$ |
從式(1)中可以看出,經過校正環節后的輸出Z與傳感器輸入量X一致。即經過校正后輸出與輸入之間呈線性關系。
Z可以表示為
| $Z={{f}^{-1}}\left( Y \right)={{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+\ldots +{{a}_{n}}{{Y}^{n}},$ |
其中，n的數值由所要求的準確度來確定。在本文中，我們取n=3，即
| $Z={{f}^{-1}}\left( Y \right)={{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}},$ |
式中a0、a1、a2、a3為待定系數。本文就是利用IGA來確定式(3)中的待定系數。
2 利用IGA實現傳感器非線性校正的步驟
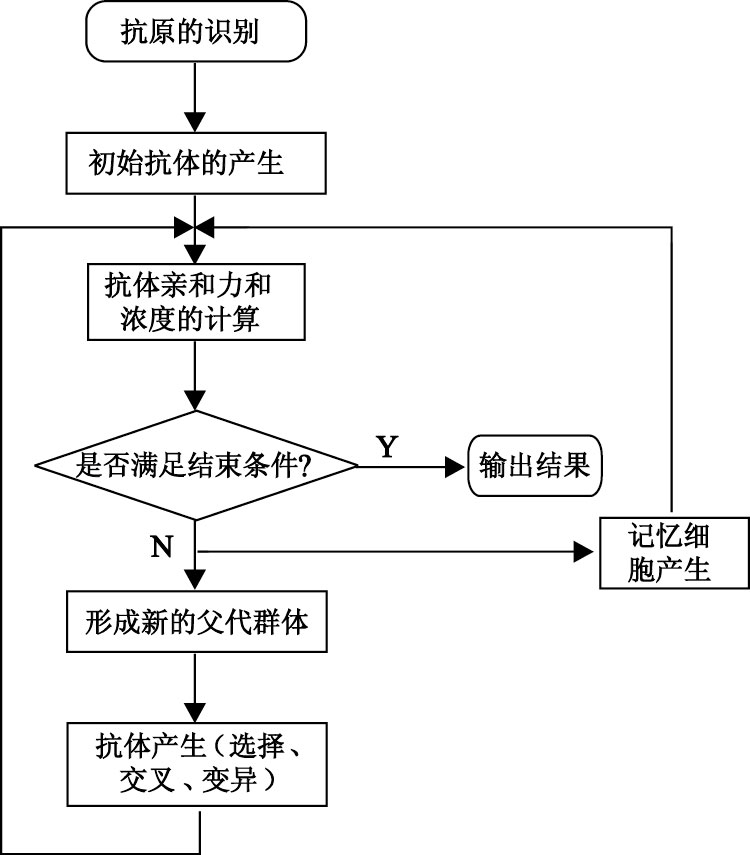
為了克服遺傳算法的不足，在遺傳算法的基礎上引入生物免疫機制，從而形成了IGA。我們研究并應用IGA解決傳感器系統的非線性校正問題。IGA流程圖如圖 2所示。
利用IGA實現傳感器非線性校正的步驟如下：
步驟一： 抗原的識別。根據具體問題，提取抗原，即問題的目標函數形式和約束條件。在本文中我們定義傳感器非線性校正的目標函數為
| $\begin{align} & F\left( x \right)=\sum\limits_{i=1}^{n}{{{\left( Z-X \right)}^{2}}}= \\ & \sum\limits_{i=1}^{n}{{{({{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}}-X)}^{2}}} \\ \end{align}$ |
步驟二： 產生初始抗體群。隨機產生N+m個個體組成初始種群。其中m為記憶庫中個體的數量。
步驟三： 抗體的親和力有兩種，一種是抗體與抗原之間的親和力；另一種是抗體與抗體之間的親和力。
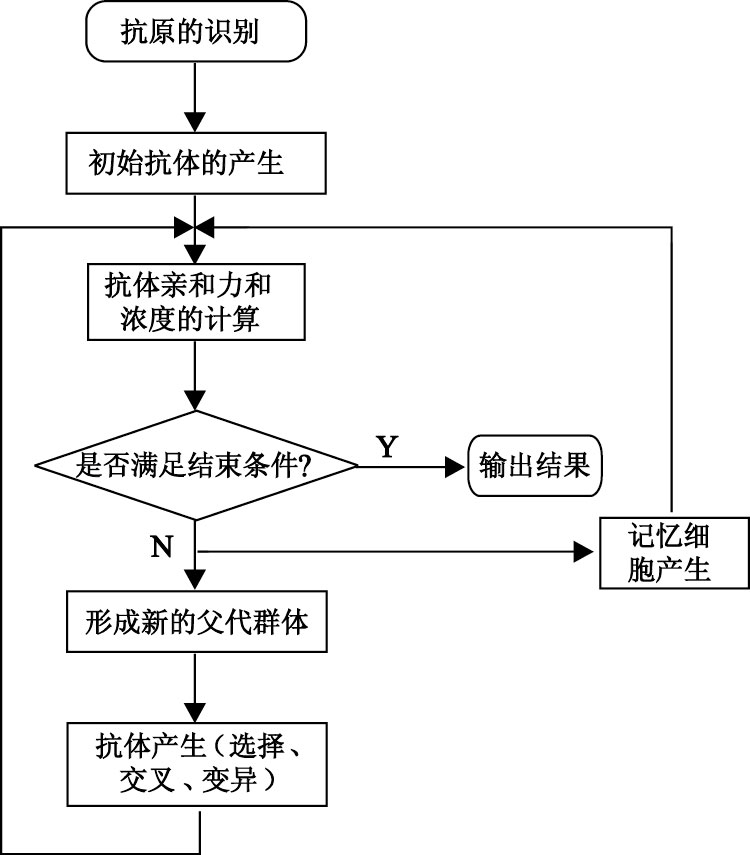圖2
IGA流程圖
Figure2.
IGA flow chart
(1)抗體與抗原之間的親和力。抗體與抗原之間的親和力其實就是適應度，表示的是抗體對抗原的識別程度。本文中親和力函數為
| $\begin{align} & {{A}_{V}}=\frac{1}{F\left( x \right)}=\frac{1}{\sum\limits_{i=1}^{n}{{{\left( Z-X \right)}^{2}}}}= \\ & \frac{1}{\sum\limits_{i=1}^{n}{{{({{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}}-X)}^{2}}}} \\ \end{align}$ |
(2)抗體與抗體間的親和力。抗體與抗體間的親和力反映了抗體之間的相似程度。對于抗體x和y，如果每一個字符都相同，則抗體x和y完全匹配；如果這兩個個體編碼有超過R位的編碼相同，則抗體x和y近似“相同”，否則抗體x和y不同。本文中抗體與抗體間的親和力為
| ${{S}_{x,y}}=\frac{{{k}_{x,y}}}{L~}$ |
其中kx,y是抗體x與抗體y中相同的位數，L為抗體的長度。
(3)抗體的濃度。抗體的濃度就是種群中相似抗體所占的比例，即
| ${{C}_{V}}=\frac{1}{N}\sum\limits_{j\in N}{{{S}_{x,y}}},$ |
其中N為種群中抗體的總數；當Sx,y＞T時，Sx,y=1；當Sx,y≤T時，Sx,y=0。T為設定的閾值。
步驟四： 判斷是否滿足停止條件，即是否達到最大迭代次數。如果是，則結束，輸出最優解；否則，繼續下一步操作。
步驟五： 形成新的父代種群
個體的期望繁殖概率為
| $P=\alpha \frac{{{A}_{V}}}{\Sigma {{A}_{V}}}-(1-\alpha )\frac{{{C}_{V}}}{\Sigma {{C}_{V}}},$ |
其中α為常數。由式(8)可以看出。抗體與抗原之間的親和力越高,則期望繁殖概率越大；抗體的濃度越大，則期望繁殖概率越小。這樣既鼓勵了適應度高的個體，又抑制了濃度高的個體，從而保持了種群的多樣性。
我們將種群按照期望繁殖概率進行降序排列，取前N個個體組成新的父代種群，同時取m個個體存入記憶庫中。
步驟六： 新群體的產生。對新產生的父代種群進行選擇、交叉、變異操作得到新種群，與記憶庫中的m個個體共同組成新一代群體。
步驟七： 轉去執行步驟三。
3 實例分析
這里應用MATLAB工具對紙漿體積分數傳感器[9]予以實例分析，表 1列出了該傳感器的輸出f及對應的實際輸入濃度Cp標定值。
表1
傳感器輸出f及對應的實際輸入濃度值Cp
Table1.
The sensor output f and the corresponding practical input concentration Cp
校正環節
| $\begin{align} & Z={{f}^{-1}}\left( Y \right)={{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}}= \\ & {{a}_{0}}+{{a}_{1}}\frac{f}{fmax}+{{a}_{2}}{{\left( \frac{f}{fmax} \right)}^{2}}+{{a}_{3}}{{\left( \frac{f}{fmax} \right)}^{3}}, \\ \end{align}$ |
其中fmax為2500 Hz，這里我們需要求出待定系數a0、a1、a2、a3。可利用IGA來求得，IGA的參數選取如下：進化代數為100，染色體長度為20，群體規模為50，記憶庫容量為10，交叉概率為0.75，變異概率為0.05，多樣性評價參數為0.95。
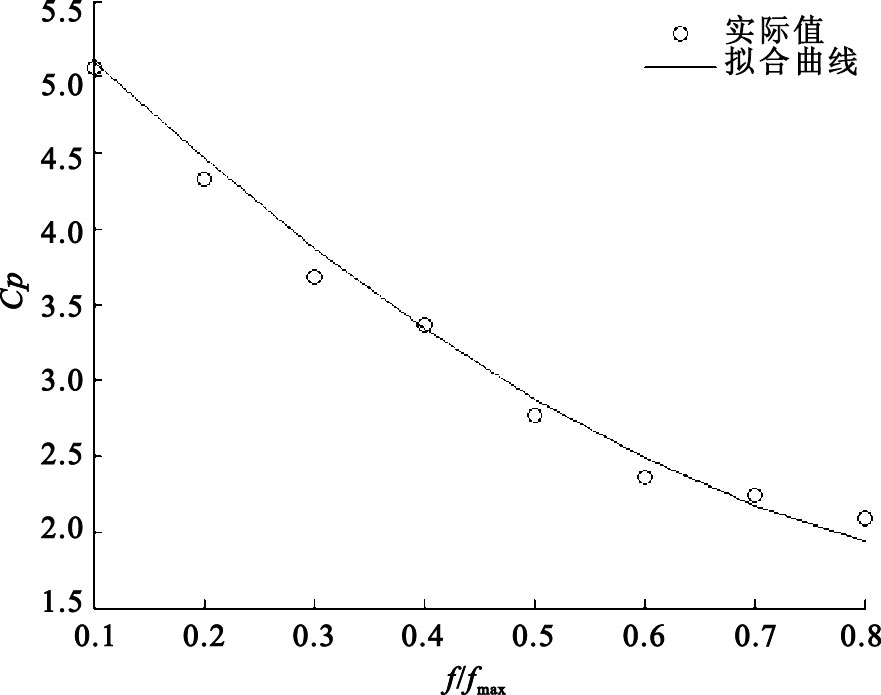圖3
實際值與IGA擬合曲線
Figure3.
The actual value and the fitting curve of IGA
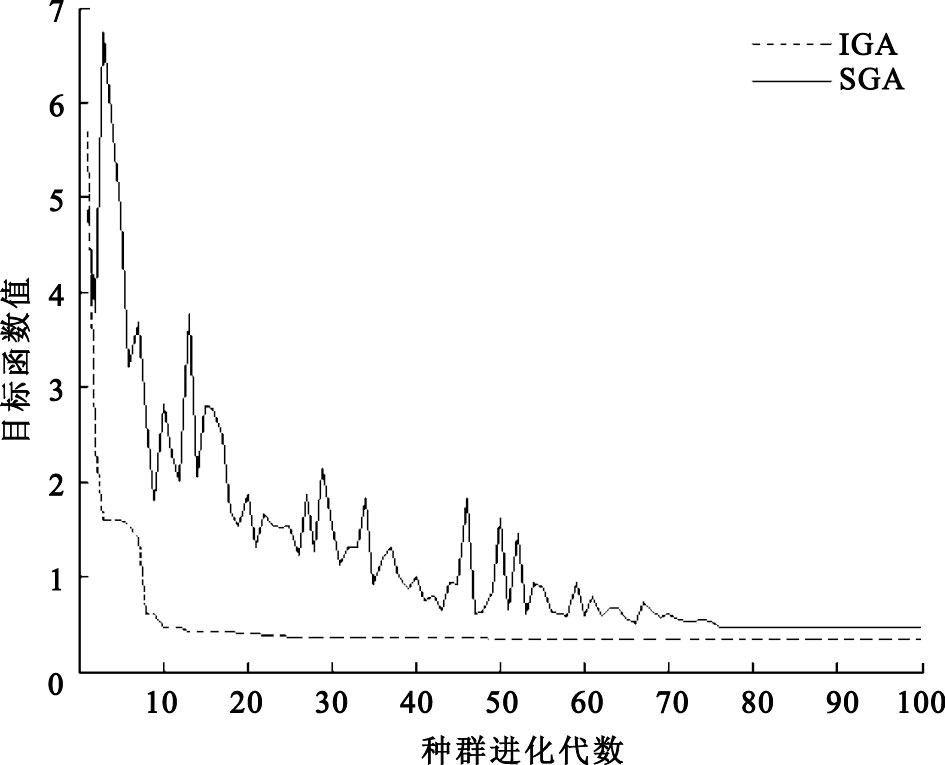圖4
經過100次迭代后最優值的變化
Figure4.
The change of optimum values through 100 times iterations
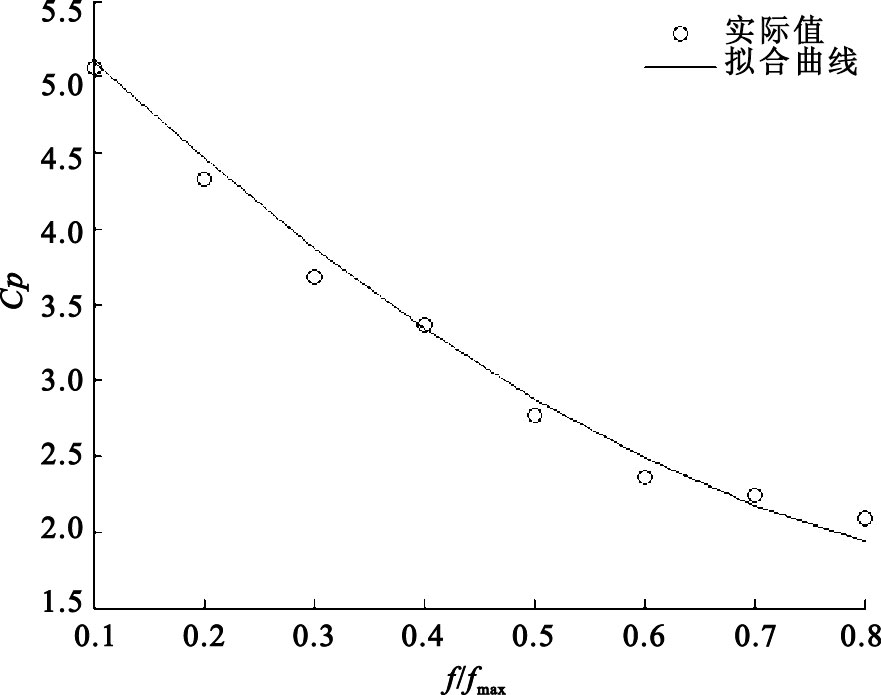
圖 3是實際值與IGA擬合曲線的對比值。從圖 3中可以看出，在傳感器非線性校正問題中，實際值與基于IGA校正傳感器的擬合曲線基本吻合。
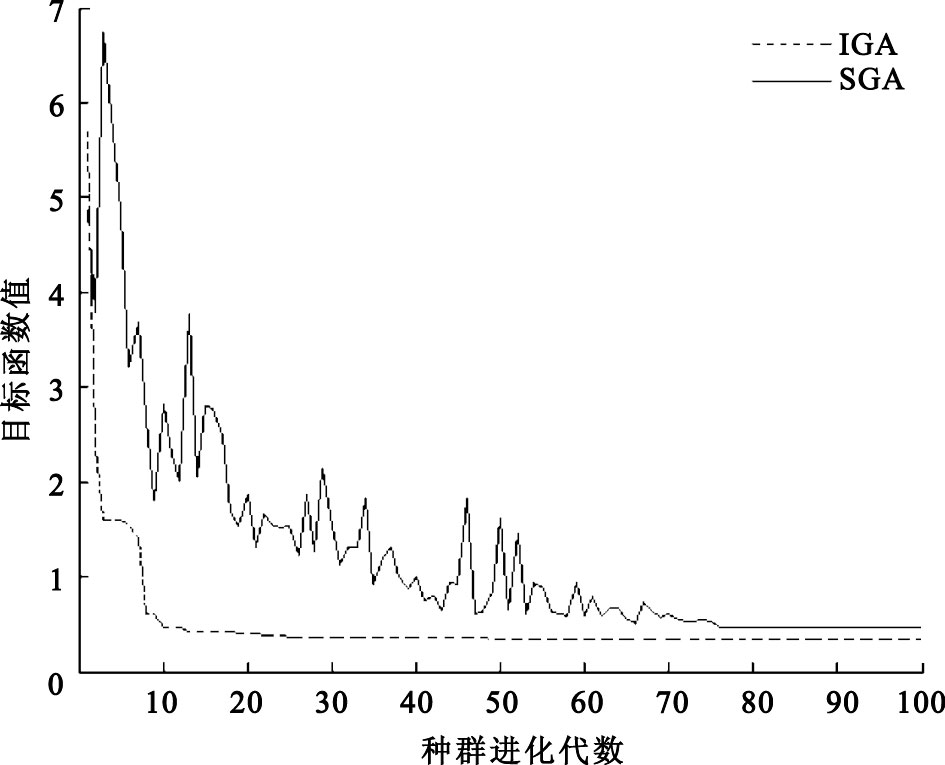
圖 4是利用基本遺傳算法(simple genetic algorithms,SGA)和IGA對紙漿體積分數傳感器進行傳感器的非線性校正經過100次迭代后的最優解變化圖，從圖 4中可以看到利用IGA對傳感器進行校正，群體經過48代進化后最終收斂到全局最優點，也就是式(4)的目標函數值的最小值。得到全局最優點為0.347 7,a0=5.802 2,a1=-7.185 0,a2=2.201 6,a3=0.934 7,也就是校正環節為
| $\begin{align} & Z=5.8022-7.1850\frac{f}{fmax}+ \\ & 2.2016{{\left( \frac{f}{fmax} \right)}^{2}}+0.9347{{\left( \frac{f}{fmax} \right)}^{3}} \\ \end{align}$ |
利用SGA和IGA對紙漿體積分數傳感器進行傳感器的非線性校正，各運行100次，并將二者的測試結果進行比較。測試結果如表 2所示。
表2
SGA與IGA的比較
Table2.
Comparison between SGA and IGA
從表 2可以看出，與SGA相比，IGA的最優值更小，收斂到最優值的比例大大增加，進化代數大大減少。也就是說，利用IGA來進行傳感器的非線性校正具有更高的搜索精度、較強的收斂性以及較快的收斂速度。
4 結論
在許多測控系統中，傳感器作為檢測元件是不可或缺的一部分，其工作上的穩定性和可靠性直接影響整個測控系統的穩定性。針對傳感器的非線性校正問題，本文提出了基于IGA的傳感器非線性校正。IGA是在遺傳算法的基礎上引入生物免疫機制，克服遺傳算法精度差、收斂速度慢和“早熟”等問題。實踐表明,這種算法在搜索精度、收斂性和收斂速度上，比簡單遺傳算法存在明顯優勢。它不但可以用于各種傳感器系統，而且可以用于其它類似系統的非線性校正。
引言
傳感器是能夠感受規定的被測量，并按照一定規律轉化成可用信號輸出的器件或裝置[1]。在科學研究和工業測控中，常用傳感器來檢測研究和控制的對象。人們需要的傳感器能線性地反映被測量的大小，但是大多數實際傳感器的輸入和輸出常常呈現出非線性特點。于是通常采取各種校正措施來解決這一問題。近年來，硬件電路補償和各種軟件補償方法在傳感器非線性校正中得到廣泛的應用。硬件電路校正雖然簡單，但成本高、設計制造繁瑣、效果差；常用的軟件補償法則有最小二乘法、函數校正法、遺傳算法等[2-3]。
遺傳算法[4](genetic algorithm，GA)是模擬生物在自然環境中遺傳和進化過程而形成的一種全局搜索算法。由于遺傳算法較以往傳統的搜索算法具有使用方便、魯棒性強、便于并行處理等特點，因而得到了廣泛的應用。然而，由于交叉和變異兩個遺傳算子都依據一定概率實現，具有較大的隨機性和盲目性；并且沒有先驗知識作為指導，也沒有利用問題自身的特征信息或知識，忽視了問題的特征信息在求解問題時的輔助作用，這很大程度上影響了算法的收斂速度和性能。再者，遺傳算法還容易陷入局部最優解，產生“早熟”問題[5]。
人工免疫系統[6-7](artificial immune systems，AIS)是受生物免疫系統啟發，模仿自然免疫系統功能的一種智能算法，它是基于人類和其他高級動物免疫系統理論而提出的一種新的信息處理系統。
為了克服遺傳算法的不足，在遺傳算法的基礎上引入生物免疫機制，從而形成了免疫遺傳算法(immune genetic algorithm,IGA)[8]。本文研究并應用IGA解決了傳感器系統的非線性校正問題。該算法不僅能夠有效保持種群的多樣性，而且收斂速度和穩定性以及運算效率都有了明顯提高，實驗結果表明了該方法的正確性和有效性。
1 基于IGA的傳感器非線性校正模型
采用IGA的非線性校正模型如圖 1所示。
圖1
IGA算法的非線性校正原理
Figure1.
The theory of the non-linearity rectification with IGA
大多數傳感器滿足關系式：Y=f(X)。若Y為X的單值函數，則上式存在反函數，即X=f-1(Y)。
設校正環節Z=g(Y)，若滿足g(Y)=f-1(Y)，則
| $Z=g\left( Y \right)={{f}^{-1}}\left( Y \right)=X~$ |
從式(1)中可以看出,經過校正環節后的輸出Z與傳感器輸入量X一致。即經過校正后輸出與輸入之間呈線性關系。
Z可以表示為
| $Z={{f}^{-1}}\left( Y \right)={{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+\ldots +{{a}_{n}}{{Y}^{n}},$ |
其中，n的數值由所要求的準確度來確定。在本文中，我們取n=3，即
| $Z={{f}^{-1}}\left( Y \right)={{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}},$ |
式中a0、a1、a2、a3為待定系數。本文就是利用IGA來確定式(3)中的待定系數。
2 利用IGA實現傳感器非線性校正的步驟
為了克服遺傳算法的不足，在遺傳算法的基礎上引入生物免疫機制，從而形成了IGA。我們研究并應用IGA解決傳感器系統的非線性校正問題。IGA流程圖如圖 2所示。
利用IGA實現傳感器非線性校正的步驟如下：
步驟一： 抗原的識別。根據具體問題，提取抗原，即問題的目標函數形式和約束條件。在本文中我們定義傳感器非線性校正的目標函數為
| $\begin{align} & F\left( x \right)=\sum\limits_{i=1}^{n}{{{\left( Z-X \right)}^{2}}}= \\ & \sum\limits_{i=1}^{n}{{{({{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}}-X)}^{2}}} \\ \end{align}$ |
步驟二： 產生初始抗體群。隨機產生N+m個個體組成初始種群。其中m為記憶庫中個體的數量。
步驟三： 抗體的親和力有兩種，一種是抗體與抗原之間的親和力；另一種是抗體與抗體之間的親和力。
圖2
IGA流程圖
Figure2.
IGA flow chart
(1)抗體與抗原之間的親和力。抗體與抗原之間的親和力其實就是適應度，表示的是抗體對抗原的識別程度。本文中親和力函數為
| $\begin{align} & {{A}_{V}}=\frac{1}{F\left( x \right)}=\frac{1}{\sum\limits_{i=1}^{n}{{{\left( Z-X \right)}^{2}}}}= \\ & \frac{1}{\sum\limits_{i=1}^{n}{{{({{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}}-X)}^{2}}}} \\ \end{align}$ |
(2)抗體與抗體間的親和力。抗體與抗體間的親和力反映了抗體之間的相似程度。對于抗體x和y，如果每一個字符都相同，則抗體x和y完全匹配；如果這兩個個體編碼有超過R位的編碼相同，則抗體x和y近似“相同”，否則抗體x和y不同。本文中抗體與抗體間的親和力為
| ${{S}_{x,y}}=\frac{{{k}_{x,y}}}{L~}$ |
其中kx,y是抗體x與抗體y中相同的位數，L為抗體的長度。
(3)抗體的濃度。抗體的濃度就是種群中相似抗體所占的比例，即
| ${{C}_{V}}=\frac{1}{N}\sum\limits_{j\in N}{{{S}_{x,y}}},$ |
其中N為種群中抗體的總數；當Sx,y＞T時，Sx,y=1；當Sx,y≤T時，Sx,y=0。T為設定的閾值。
步驟四： 判斷是否滿足停止條件，即是否達到最大迭代次數。如果是，則結束，輸出最優解；否則，繼續下一步操作。
步驟五： 形成新的父代種群
個體的期望繁殖概率為
| $P=\alpha \frac{{{A}_{V}}}{\Sigma {{A}_{V}}}-(1-\alpha )\frac{{{C}_{V}}}{\Sigma {{C}_{V}}},$ |
其中α為常數。由式(8)可以看出。抗體與抗原之間的親和力越高,則期望繁殖概率越大；抗體的濃度越大，則期望繁殖概率越小。這樣既鼓勵了適應度高的個體，又抑制了濃度高的個體，從而保持了種群的多樣性。
我們將種群按照期望繁殖概率進行降序排列，取前N個個體組成新的父代種群，同時取m個個體存入記憶庫中。
步驟六： 新群體的產生。對新產生的父代種群進行選擇、交叉、變異操作得到新種群，與記憶庫中的m個個體共同組成新一代群體。
步驟七： 轉去執行步驟三。
3 實例分析
這里應用MATLAB工具對紙漿體積分數傳感器[9]予以實例分析，表 1列出了該傳感器的輸出f及對應的實際輸入濃度Cp標定值。
表1
傳感器輸出f及對應的實際輸入濃度值Cp
Table1.
The sensor output f and the corresponding practical input concentration Cp
校正環節
| $\begin{align} & Z={{f}^{-1}}\left( Y \right)={{a}_{0}}+{{a}_{1}}Y+{{a}_{2}}{{Y}^{2}}+{{a}_{3}}{{Y}^{3}}= \\ & {{a}_{0}}+{{a}_{1}}\frac{f}{fmax}+{{a}_{2}}{{\left( \frac{f}{fmax} \right)}^{2}}+{{a}_{3}}{{\left( \frac{f}{fmax} \right)}^{3}}, \\ \end{align}$ |
其中fmax為2500 Hz，這里我們需要求出待定系數a0、a1、a2、a3。可利用IGA來求得，IGA的參數選取如下：進化代數為100，染色體長度為20，群體規模為50，記憶庫容量為10，交叉概率為0.75，變異概率為0.05，多樣性評價參數為0.95。
圖3
實際值與IGA擬合曲線
Figure3.
The actual value and the fitting curve of IGA
圖4
經過100次迭代后最優值的變化
Figure4.
The change of optimum values through 100 times iterations
圖 3是實際值與IGA擬合曲線的對比值。從圖 3中可以看出，在傳感器非線性校正問題中，實際值與基于IGA校正傳感器的擬合曲線基本吻合。
圖 4是利用基本遺傳算法(simple genetic algorithms,SGA)和IGA對紙漿體積分數傳感器進行傳感器的非線性校正經過100次迭代后的最優解變化圖，從圖 4中可以看到利用IGA對傳感器進行校正，群體經過48代進化后最終收斂到全局最優點，也就是式(4)的目標函數值的最小值。得到全局最優點為0.347 7,a0=5.802 2,a1=-7.185 0,a2=2.201 6,a3=0.934 7,也就是校正環節為
| $\begin{align} & Z=5.8022-7.1850\frac{f}{fmax}+ \\ & 2.2016{{\left( \frac{f}{fmax} \right)}^{2}}+0.9347{{\left( \frac{f}{fmax} \right)}^{3}} \\ \end{align}$ |
利用SGA和IGA對紙漿體積分數傳感器進行傳感器的非線性校正，各運行100次，并將二者的測試結果進行比較。測試結果如表 2所示。
表2
SGA與IGA的比較
Table2.
Comparison between SGA and IGA
從表 2可以看出，與SGA相比，IGA的最優值更小，收斂到最優值的比例大大增加，進化代數大大減少。也就是說，利用IGA來進行傳感器的非線性校正具有更高的搜索精度、較強的收斂性以及較快的收斂速度。
4 結論
在許多測控系統中，傳感器作為檢測元件是不可或缺的一部分，其工作上的穩定性和可靠性直接影響整個測控系統的穩定性。針對傳感器的非線性校正問題，本文提出了基于IGA的傳感器非線性校正。IGA是在遺傳算法的基礎上引入生物免疫機制，克服遺傳算法精度差、收斂速度慢和“早熟”等問題。實踐表明,這種算法在搜索精度、收斂性和收斂速度上，比簡單遺傳算法存在明顯優勢。它不但可以用于各種傳感器系統，而且可以用于其它類似系統的非線性校正。
