子波熵是衡量信號復雜程度的指標,本文采用連續子變換的方法對輕、中、重度阿爾茨海默病(AD)患者及正常對照老年人的腦電(EEG)信號進行子波分析,根據子波系數計算EEG信號的子波功率譜分布,提取描述EEG信號復雜程度的定量指標——子波熵。對輕、中、重度AD患者和正常對照的自發狀態下EEG信號的子波熵值進行比較,并將子波熵值與MMSE進行相關性分析。結果顯示,輕、中、重度AD組和正常對照組之間EEG信號的子波熵存在顯著差異(P＜0.01)。組間比較顯示輕、中、重度AD患者EEG信號的子波熵均低于正常對照,差異具有統計學意義(P＜0.05)。這與AD患者EEG信號的功率譜分布單一有關。進一步研究表明EEG信號的子波熵與其MMSE評分均存在顯著相關(r=0.601~0.799,P＜0.01)。子波熵可以作為描述EEG信號復雜程度的定量指標,子波熵值有可能成為AD診斷和病情評估的電生理指標。
引用本文： 張美云, 張本恕, 陳英. 阿爾茨海默病患者自發腦電信號子波熵的研究. 生物醫學工程學雜志, 2014, 31(4): 755-761,770. doi: 10.7507/1001-5515.20140141 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
腦電(electroencephalogram,EEG)是伴隨人生始終的電生理信號，記錄著人腦在生理、病理過程中的神經系統電活動行為，包含了人體神經生理活動的非常豐富的信息。對認知功能及癡呆的研究來說，應該是一種最佳的手段。阿爾茨海默病(Alzheimer’s disease,AD)是最常見的癡呆類型，目前臨床診斷主要依靠神經心理評估量表和神經影像學等檢查。EEG信號對于AD的臨床診斷和預后評估等方面還沒有發揮出應有的作用。
子波熵是衡量非線性信號有序、無序程度的一個量化指標，它可以提供信號非線性動力學過程復雜程度的信息。一個非常有序的信號可以想象為周期性單頻信號，這樣的信號可以用單一的子波尺度來表示，除了信號所在的頻率水平外，其他所有尺度的子波能量幾乎為0，這時單一尺度相對的子波能量為1，而總的子波熵接近0或非常低。隨機信號可以看作極端無序的，這樣的信號子波特征來源于所有頻帶，可以認為所有頻帶對信號的貢獻大致相同，結果不同子波尺度的相對子波能量幾乎相等，子波熵會產生最大值。
傳統的衡量信號有序無序程度的指標是譜熵，它基于傅里葉變換[1]。譜熵也被應用于EEG信號的分析[2]。由于傅里葉變換應用的前提是信號為平穩信號，因此譜熵在EEG信號的分析中受到限制。基于子波變換的子波熵不需要信號是平穩的，適合于EEG信號的分析。AD作為最常見的一種認知功能障礙疾病，其自發EEG信號的子波熵與正常人有何差異，目前還未見相關報道。本研究采用連續子波變換的方法提取AD患者自發EEG信號的頻率分布和子波熵，并與正常同齡進行比較，探討這些新的神經電生理指標在AD的臨床診斷的評估中的價值。
1 研究對象
研究對象來自于2009年1月~2012年5月天津醫科大學神經內科門診治療的認知功能障礙患者，所有患者均行詳細病史采集，神經系統及全身查體，頭核磁共振檢查，部分患者行FDG-PET檢查，行簡易智能精神狀態量表(MMSE)、畫鐘試驗(CDT)和蒙特利爾認知評估量表(MoCA)測試，行血常規、血糖、葉酸、維生素B12、甲狀腺功能、同型半胱氨酸檢查。
納入標準：① 符合美國精神病學會的《精神障礙診斷和統計手冊》(DSM-Ⅳ-TR)中AD的診斷標準。② 符合美國國立神經病學、語言障礙和卒中研究所及AD和相關疾病協會建立AD研究的診斷標準(2007對NINCDS-CADRDA的修訂版)中“很可能AD”的診斷標準；其核心診斷出現早期顯著的情景記憶障礙，并存在陽性的生物學標記物，本研究采用的生物學標記物為頭核磁共振檢查存在內側顳葉萎縮的證據和/或PET檢查顯示雙側顳頂葉葡萄糖代謝減低。③ MMSE評分≤24分。④ HIS評分≤4分。⑤ 具有完整的病歷、化驗和影像學資料。⑥ 患者或家屬知情同意。
排除標準：① 存在2007對NINCDS-CADRDA的修訂版中排除標準的情況或(DSM-Ⅳ-TR)中AD的診斷標準中需除外的引起癡呆的原因。② 頭部MRI檢查發現梗死、出血、占位病變、腦積水或明顯的白質病變，可能影響認知功能者。③ 存在嚴重的心、肺、肝、腎、甲狀腺等臟器疾患，可能影響EEG活動者。④ 有藥物或酒精濫用或依賴史(按照DSM-Ⅳ物質濫用依賴標準)。⑤ 一周內服用鎮靜藥和精神類藥物。
符合上述標準的AD患者共97例，對入組的AD患者按MMSE評分分為三組：輕度AD組(AD Ⅰ)31例，MMSE 19~24分；中度AD組(AD Ⅱ)34例，MMSE 11~18分；重度AD組(AD Ⅲ)32例，MMSE 0~10分。正常對照組34例，來自患者配偶或健康志愿者，無神經精神系統疾病史，無嚴重內科疾病史，MMSE評分≥27分。三個疾病組和一個正常對照組之間年齡和受教育程度差異無統計學意義。
2 方法
2.1 EEG信號采集
對受試者行自發EEG信號描記，描記時間在上午8~11點早餐后進行。采用NIHONKOHDEN公司生產的EEG-2130型數字腦電圖儀，采用Ag/AgCl頭皮電極，按國際標準導聯10/20 系統安裝，以雙耳為參考電極，電阻抗＜5 kΩ，被檢查者在安靜、清醒、閉目狀態下描記EEG信號，描記時間不少于30 min，采樣頻率200 Hz。選擇信號平穩、無偽差的EEG信號片段，每個片段20 s作為分析的EEG信號，每個數據塊包含4 000個數據樣本，用于EEG信號定量分析。
2.2 EEG信號分析
2.2.1 EEG信號的子波分析
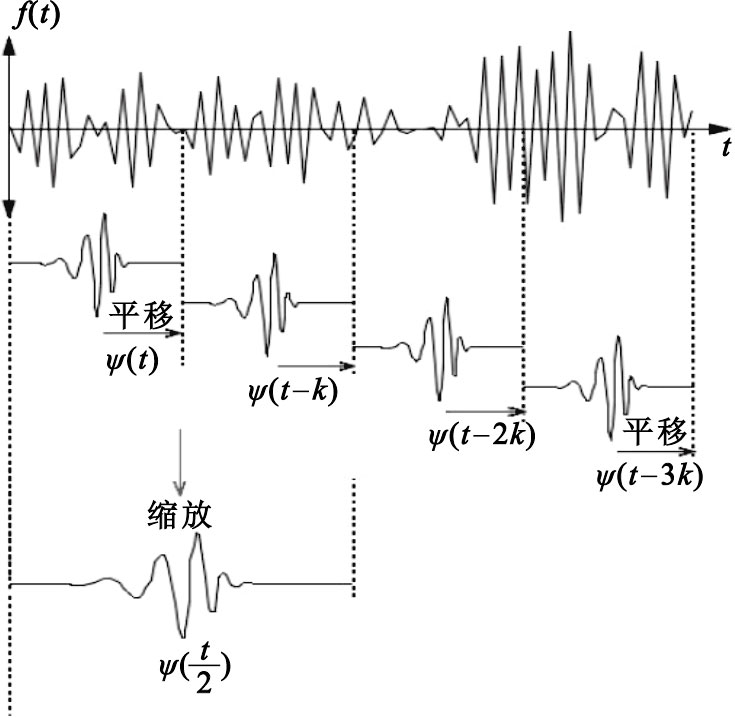
子波分析通過信號與一個被稱為子波的解析函數進行卷積，將含有多尺度成分的復雜信號進行分解。子波變換就是將含有多尺度成分的復雜信號與一定位置、一定尺度下代表特定的物理過程或形狀的子波基函數進行局部互相關分析(見圖 1)，如果其相關性高，表明該信號在該處含有該子波成分，使得信號在該處于該子波具有較好的相似性。利用子波變換可以將含有多尺度成分的復雜信號中的不同成分分解為多種單一尺度的成分。用這一方法可以將貌似隨機、復雜無序的信號分解在不同的頻帶上，實現每一頻帶上的精確表達[3]。
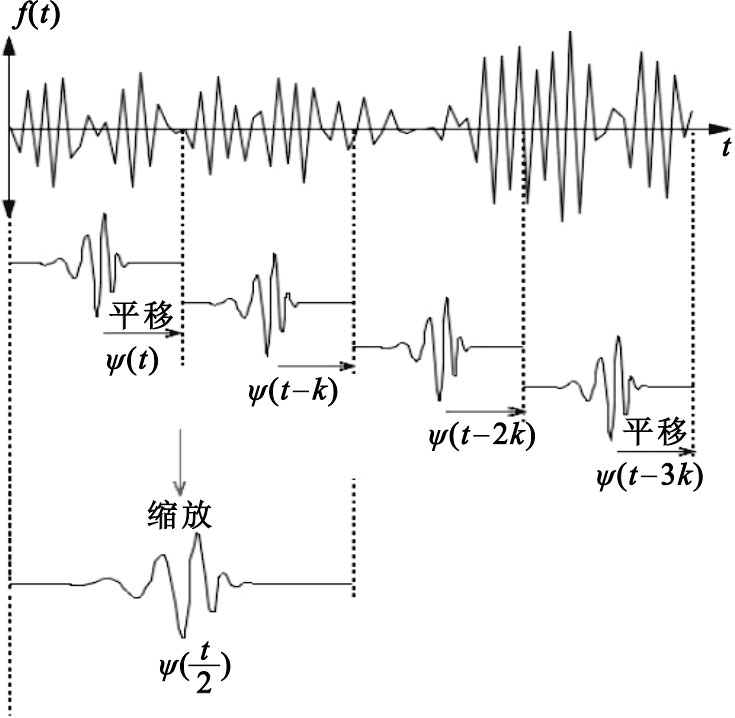圖1
EEG信號與不同尺度的子波函數進行互相關分析
Figure1.
Co-correlation analysis between EEG signal and wavelet function on different scales
一維EEG信號s(t)在子波函數下的子波分析定義為
| ${{W}_{s}}\left( a,b \right)=\int_{-\infty }^{+\infty }{s{{\left( t \right)}_{ab}}\left( t \right)dt}$ |
其中子波函數族Wab(t)是由子波的母波函數W(t)經過平移(參數b)和伸縮變換(參數a)而來：
| ${{W}_{ab}}\left( t \right)=\frac{1}{\sqrt{a}}W\left( \frac{t-b}{a} \right)$ |
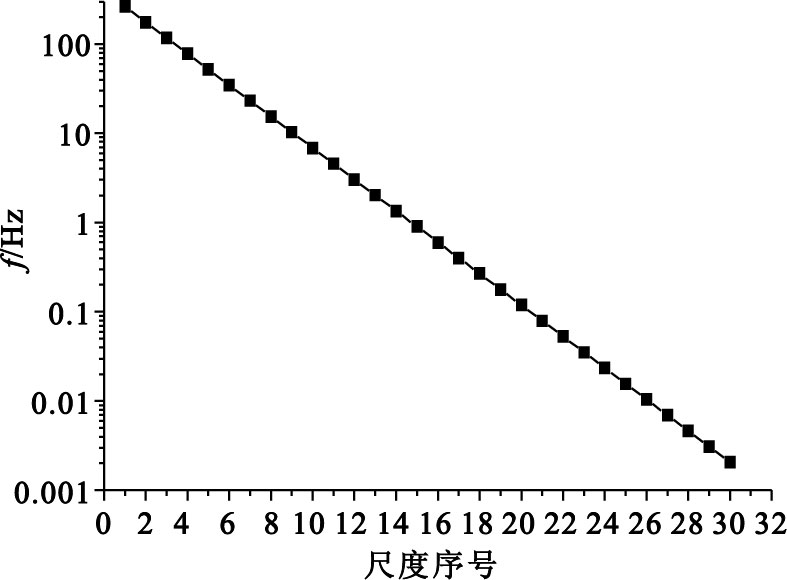
本研究采用Gauss連續子變換的方法對三組受試者不同腦區(21個導聯) EEG信號進行子波分析，共分析30個尺度，尺度所對應的EEG信號的頻率如圖 2所示，由于采樣頻率(200 Hz)和分析片段長度(20 s) 的限制，所觀察的EEG信號的頻率為0.05~100 Hz。
2.2.2 EEG信號的多尺度功率譜分析
根據子波系數Ws(a,b)，EEG信號S(t)的分尺度功率可以用各尺度子波功率譜密度函數表示，描述了分尺度EEG信號的強弱：
| $P\left( a \right)=\frac{2}{{{C}_{W}}}{{\int_{-\infty }^{+\infty }{{{W}_{s}}\left( a,b \right)}}^{2}}db$ |
對于不同類型中樞神經系統疾病的EEG信號，其不同腦區和尺度的子波功率譜密度函數是不同的，反映了不同腦區和頻帶節律性活動的差異。
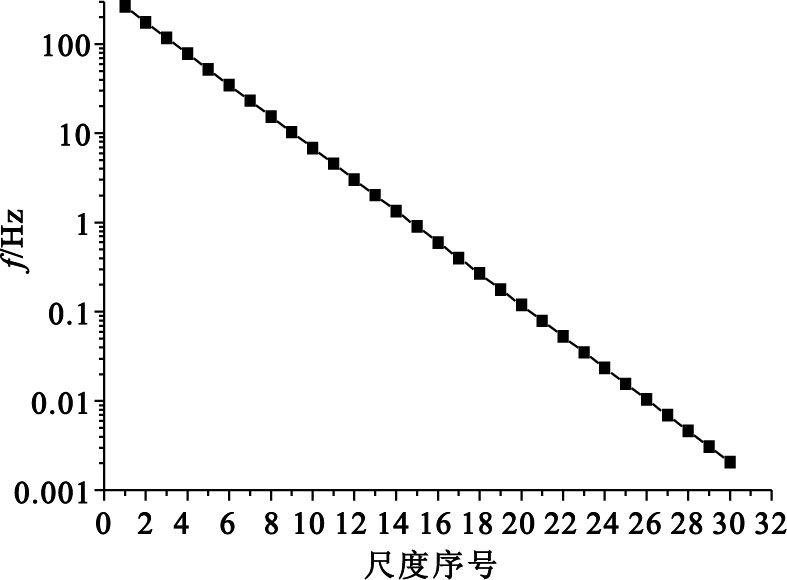圖2
子波尺度序號與所代表的中心頻率的對應關系
Figure2.
Wavelet scale and its corresponding frequency center
2.2.3 EEG信號的子波熵
EEG信號的總功率是各分尺度信號功率的總和：
| $p=\int_{0}^{+\infty }{p\left( a \right)da}$ |
用p對p(a)進行歸一化，得到各分尺度功率在信號總功率中所占的百分比：
| $A\hat{p}G\text{ }\left( a \right)=\frac{p\left( a \right)}{p}$ |
EEG信號的子波熵衡量了EEG信號所含多尺度信息的復雜程度，反映了EEG在人腦神經細胞活動過程中所包含的動力學信息：
| ${{e}_{w}}=-\int_{0}^{+\infty }{A\hat{p}G\text{ }\left( a \right)ln\left[ A\hat{p}G\text{ }\left( a \right) \right]da}\text{ }$ |
子波熵ew表示功率譜寬度所表達的非線性系統復雜性的大小，功率譜越寬，則ew越大；功率譜越窄，則ew越小。極端情況下，若信號只含有一個尺度a的成分，則 A G (a)=1，此時信號尺度單一，復雜性最小，ew=0。
2.3 統計學方法
將輕、中、重度AD組和正常對照組四組之間不同腦區(F3,F4,P3,P4,O1,O2,T3,T4導聯)EEG信號的子波熵進行比較，統計學方法采用單因素方查分析。進一步將組間子波熵兩兩比較，統計學方法采用SNK法。
為進一步觀察子波熵與認知功能障礙的嚴重程度之間的關系，將不同導聯EEG信號子波熵與MMSE評分進行相關性分析，方法采用二元變量相關分析。顯著性檢驗標準為α=0.05。
3 結果
3.1 正常對照和AD患者EEG信號的子波熵比較
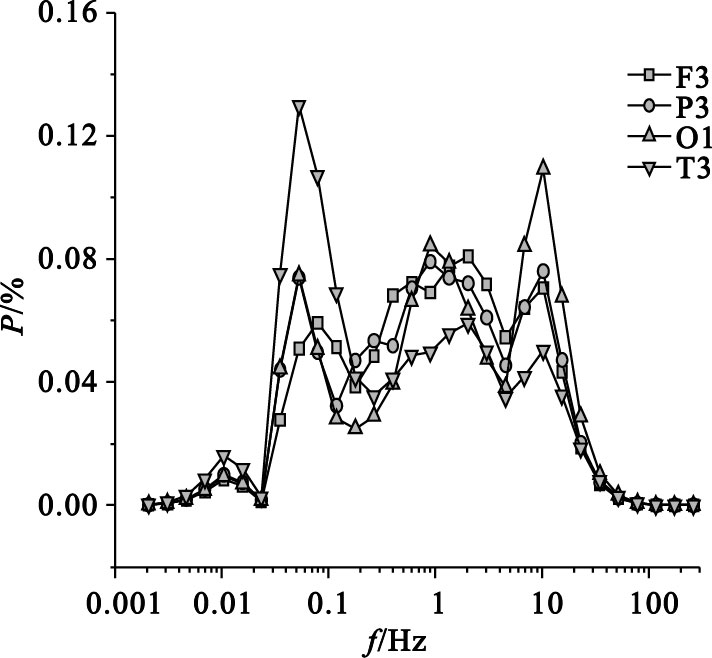
圖 3為正常對照不同導聯EEG信號的子波功率譜分布，正常對照EEG信號在不同導聯上均表現為尺度分布比較廣，從信號的尺度特征看，它的信號是由多尺度成分組成的，EEG信號尺度成分比較復雜。用上述方法計算EEG信號的子波熵，采用子波熵來衡量EEG信號的復雜程度。正常對照左額F3導聯的子波熵為2.73，左頂P3的子波熵為2.75，左枕O1的子波熵為2.77，左顳T3的子波熵為2.69。
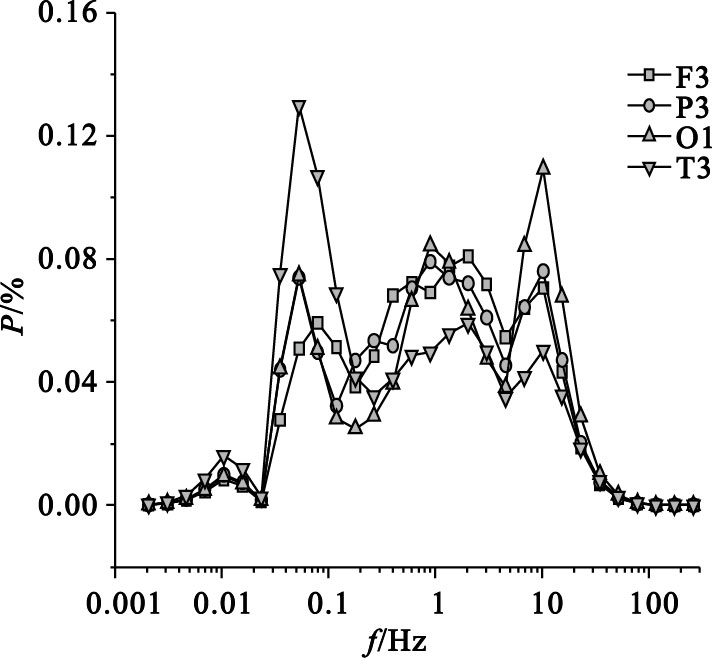圖3
正常對照不同導聯EEG信號的子波功率譜分布
Figure3.
Wavelet power spectrum of different electrode in normal controls
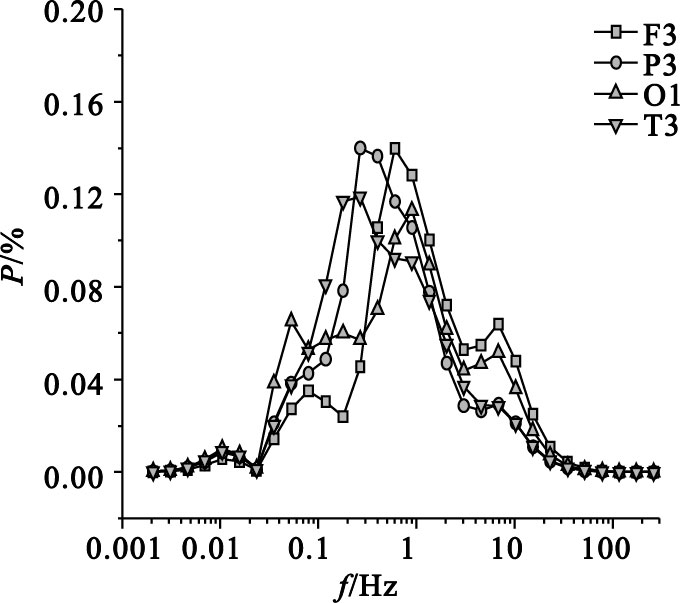
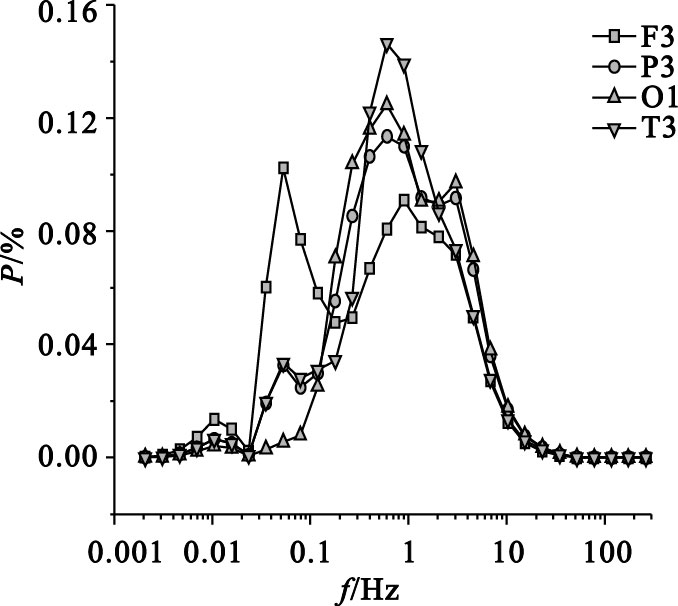
圖 4為EEG信號的子波功率譜分布。從圖中可以看出，輕度 AD患者EEG信號尺度分布較窄，其0.1 Hz和10 Hz附近的功率峰明顯降低，而1 Hz附近的功率峰值明顯增高。輕度AD患者EEG信號尺度成分比較簡單，其左額F3導聯的子波熵為2.57，左頂P3的子波熵為2.50，左枕O1的子波熵為2.67，左顳T3的子波熵為2.61。
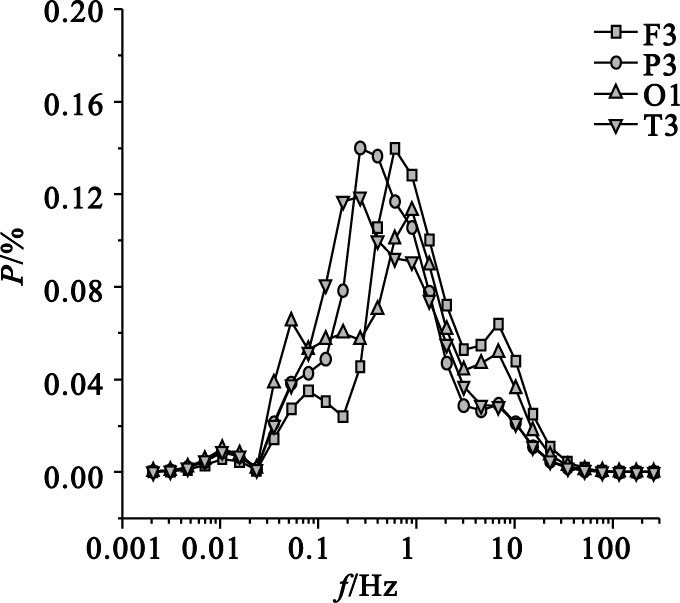圖4
輕度AD患者不同導聯EEG信號的子波功率譜分布
Figure4.
Wavelet power spectrum of different electrode in mild AD patients
圖 5為中度AD患者EEG信號的子波功率譜分布。從圖中可以看出，中度AD患者EEG信號其0.1 Hz和10 Hz附近的功率峰進一步降低乃至消失，逐漸與1 Hz附近的功率峰值融合，形成一個較寬的單峰分布，尺度成分更加簡單。中度AD患者左額F3導聯的子波熵為2.51，左頂P3的子波熵為2.58，左枕O1的子波熵為2.61，左顳T3的子波熵為2.54。
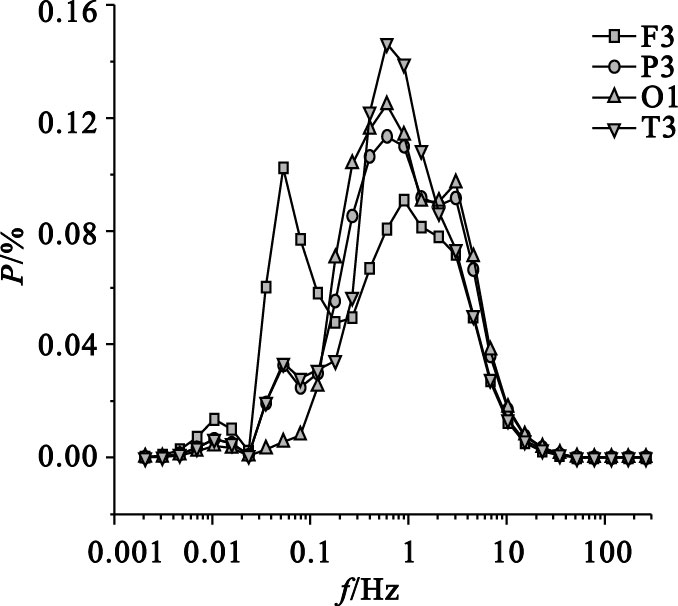圖5
中度AD患者不同導聯EEG信號的子波功率譜分布
Figure5.
Wavelet power spectrum of different electrode in moderate AD patients
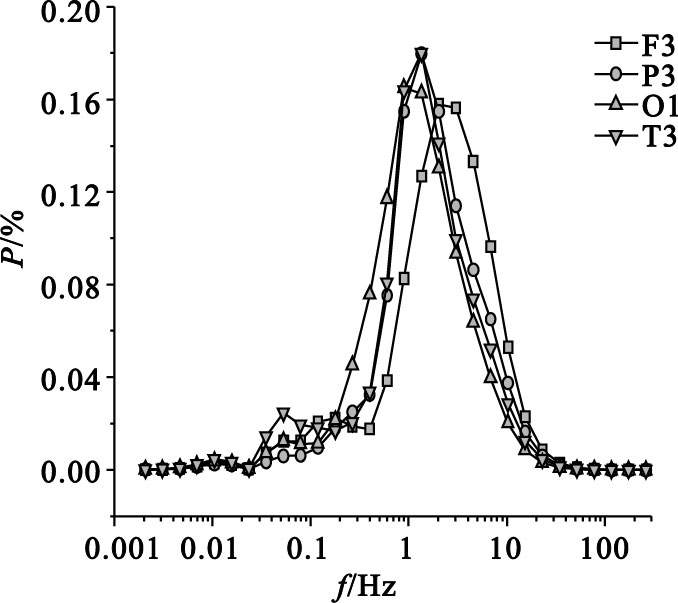
圖 6為重度AD患者EEG信號的子波功率譜分布。從圖中可以看出，重度AD患者EEG信號其0.1 Hz和10 Hz附近的功率峰幾乎完全消失，只在1 Hz附近形成比較高而窄的功率峰，EEG信號尺度成分單一，子波熵值最低，其左額F3導聯的子波熵為2.41，左頂P3的子波熵為2.52，左枕O1的子波熵為2.37，左顳T3的子波熵為2.39。
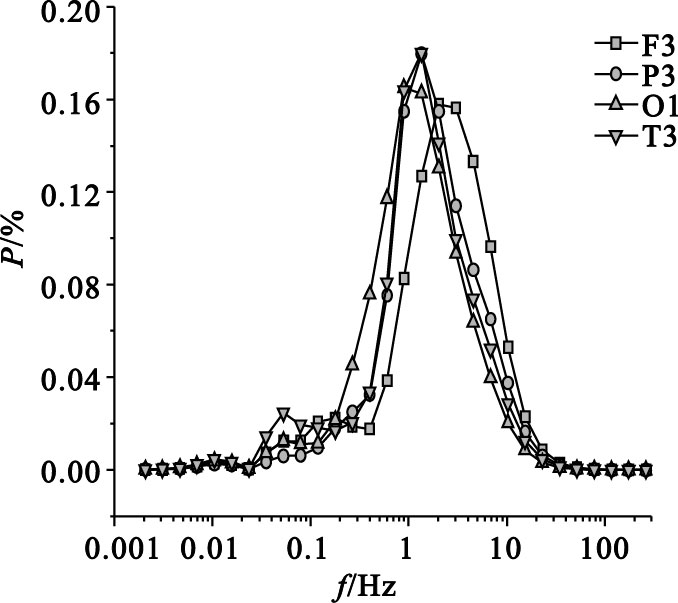圖6
重度AD患者不同導聯EEG信號的子波功率譜分布
Figure6.
Wavelet power spectrum of different electrode in severe AD patients
3.2 子波熵與MMSE評分的關系
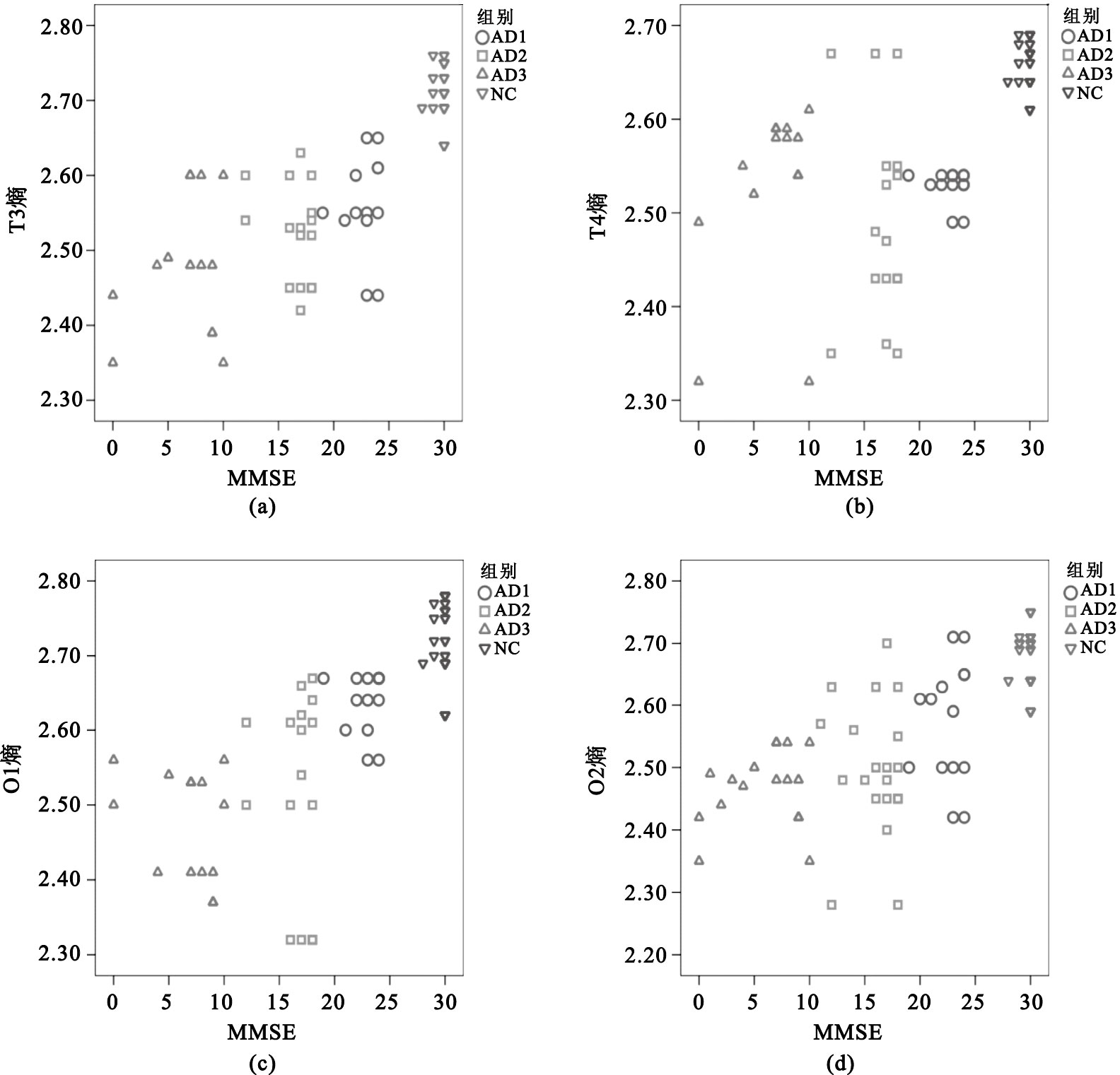
正常對照EEG信號的子波熵高于AD患者，重度AD患者在不同的導聯均明顯降低，這與EEG信號的功率分布單一，信號更加簡單有關，而輕、中度AD患者EEG信號的子波熵介于兩者之間。圖 7為不同導聯EEG信號的子波熵與MMSE評分之間的散點圖。
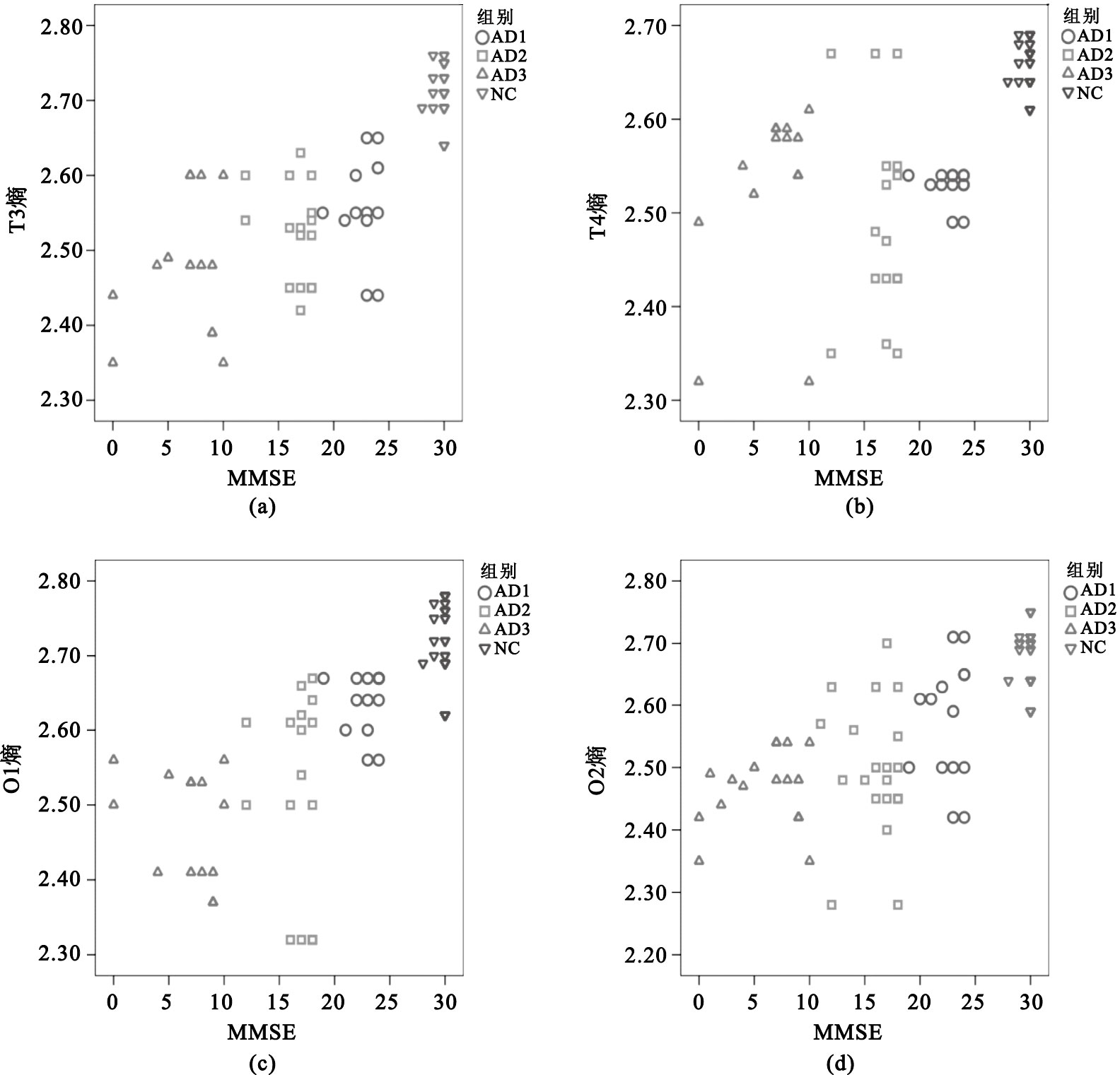圖7
不同導聯EEG信號的子波熵與患者MMSE評分之間關系的散點圖
(a)左顳T3導聯;(b)右顳T4導聯;(c)左枕O1導聯;(d)右枕O2導聯
Figure7. Scatter chart of the relationships between wavelet entropy of EEG signal and MMSE scores of the patients and normal controls at different electrode(a) left temporal T3; (b) right temporal T4; (c) left occipital O1; (d) right occipital O2
3.3 統計學分析
將輕、中、重度AD組和正常對照組之間不同腦區(F3,F4,P3,P4,O1,O2,T3,T4導聯)EEG信號的子波熵進行比較，統計學方法采用單因素方查分析，結果如表 1所示，四組間不同導聯EEG信號的子波熵差異均有統計學意義(P＜0.01)。進一步采用SNK法進行兩兩比較，結果顯示輕、中、重度AD患者不同導聯EEG信號的子波熵與正常對照組比較，差異均有統計學意義(P＜0.05)。
表1
AD患者和正常對照不同導聯EEG信號的子波熵比較
Table1.
Comparison of EEG wavelet entropy between AD patients and normal controls at different electrode
為進一步觀察子波熵與AD患者病情嚴重程度的關系，將不同導聯EEG信號子波熵與AD患者的MMSE評分進行二元變量相關分析。結果如表 2所示，AD患者不同導聯EEG信號子波熵與其MMSE評分均存在相關性(P＜0.01)。
表2
不同導聯EEG信號的子波熵與MMSE評分的相關分析
Table2.
Correlation analysis of EEG wavelet entropy and MMSE score at different electrode
4 討論
EEG信號中蘊藏著非常豐富的信息，對認知功能的研究是一種最佳的工具。如何從EEG信號中提取有價值的定量信息和參數，用于認知功能障礙的診斷，一直是臨床工作和基礎研究領域共同關注的重要課題。
子波熵是衡量非線性信號動力學行為，有序、無序程度的一個量化指標，它可以提供信號非線性動力學過程復雜程度的信息。子波變換可以同時顯示時域頻域兩方面信息，且不需要信號是平穩的，所以非常適合EEG信號的分析。子波熵作為衡量系統的有序程度的指標被應用于EEG信號分析。
Blanco等[4]首先將基于子波變換的子波熵應用于EEG信號的分析。近年來，國內外學者用子波熵研究EEG信號、誘發電位、事件相關電位等的復雜程度，進一步揭示了大腦電活動的動力學機制。其應用主要在大腦感知、認知活動的研究、癲癇EEG信號的動態觀測、睡眠、網絡成癮、頭外傷后腦神經的康復[5-9]等幾個方面。
Rosso等[10]采用正交離散子波變換，對13例健康大學生睜眼、閉眼時自發EEG信號和主動、被動聽覺刺激狀態下的EEG信號進行分析，提出了子波能量(wavelet energy)、子波熵(wavelet entropy)、相對子波熵(relative wavelet entropy)等概念，來研究短片段的自發EEG信號的頻率分布(子波能量)和有序程度(子波熵)，及刺激后EEG信號的子波能量和子波熵的演變過程。結果顯示自發EEG信號的在閉目時α節律占主要優勢，這時的子波熵較睜眼時明顯降低。主動和被動聽覺刺激后自發EEG信號的子波熵均明顯降低。子波熵的降低與EEG信號θ節律性活動的增強有關，表明聽覺刺激后EEG活動向有序狀態轉化。
Quian等[11]對9名健康受試者的視覺誘發電位、目標和非目標視覺刺激三種狀態下EEG信號的子波熵值在刺激前后的動態演變過程進行研究，結果顯示，只有目標刺激后頂枕導聯的子波熵在刺激后約600 ms時出現最低值，這與事件相關的P300相關，而在P100-N200時間窗內未發現子波熵的明顯降低。對事件相關電位的研究不僅要看波幅和潛伏期，子波熵可以提供EEG生理活動中更為豐富的信息，其包含了EEG信號的有序程度、頻率上的同步化及轉化和演變過程。Baser等[12]就EEG和事件相關電位的關系提出EEG是不同頻率電活動的綜合，事件相關電位反映了EEG活動從無序到有序的過程，伴隨著EEG信號在一定頻率上同步化的增強。而子波熵可以顯示受到刺激后EEG信號頻率上同步化的動態演變過程，從而加深了對腦動力學機制的理解，成為認知功能研究的一種新的方法。
Yordanova等[13]對15名健康者主動的視覺刺激、聽覺刺激及視聽覺聯合刺激時事件相關電位的子波熵和頻率分布進行研究，結果表明雙重刺激時子波熵降低更為明顯。子波熵的降低作為衡量EEG活動從有序到無序的轉變的指標，它反映了大腦感知和認識的內源性加工過程，它主要源于前頭部的θ節律同步化增強，與刺激的種類無明顯關聯。Rosso等[14-15]研究了不同狀態下EEG信號子波熵的變化并采用連續子波熵研究聽覺誘發電位，結果顯示較離散子波熵可以發現更多細節特征。
目前的研究表明，子波熵在大腦的認知過程中成動態變化，且與刺激的方式相關，具有一定的規律。它表明子波熵與認知功能明顯相關，那么認知功能障礙患者，它的EEG信號的子波熵與正常對照在一定刺激是其EEG信號的子波熵是否存在差異，認知功能障礙患者的自發EEG信號的子波熵與正常對照是否存在差異，目前尚未見相關報道。AD是認知功能障礙的最主要類型，本研究對AD患者自發EEG信號的子波熵進行研究，并與正常同齡進行比較。結果表明：AD患者自發條件下的EEG信號，其子波熵低于正常對照，而且與AD的嚴重程度明顯相關。
本研究的結果表明，AD患者自發EEG信號的子波熵明顯低于正常對照，而且子波熵與MMSE評分明顯相關。子波熵反映了信號的復雜程度，因此AD 患者EEG信號的子波熵降低，說明AD患者EEG信號的復雜程度降低。從功率譜分布上看說明AD患者EEG信號頻率分布更加單一。因此子波熵這一定量的電生理指標對于AD的臨床診斷和病情的評估具有重要的臨床應用價值。
EEG信號的子波熵降低是如何影響認知功能的，其機制目前還不清楚。Blanco等[4]、Cek等[16]的關于認知功能的子波熵的研究均表明，在受到內、外刺激和工作任務時，EEG信號的子波熵的子波熵降低，這一現象與中樞神經系統在受到刺激后出現神經網絡同步化活動增強，導致EEG信號在某些頻帶上功率值的增高，從而出現頻率分布變窄有關。這種功率分布的在時間和空間上的動態演變過程的模式與刺激的模式和受試者的反映有關。Weiss等[17-18]、Karrasch等[19]對AD患者和正常對照在詞匯記憶任務中EEG信號的和去同步化模式的研究表明，認知功能障礙患者在記憶任務時EEG信號在不同腦區，不同頻率上的同步化模式與正常對照存在差異。AD患者自發EEG信號的子波熵與正常對照的差異的研究，目前尚未見相關報道。自發狀態下EEG信號在一定頻率上的穩定的一種分布模式是良好的認知功能產生的神經電生理基礎，由這種頻率分布模式可以獲得衡量EEG信號的復雜程度的定量電生理指標--子波熵。本研究表明AD患者自發狀態下EEG信號的子波熵低于正常對照，說明AD患者EEG信號復雜程度降低，進一步反映AD患者EEG信號較正常對照功率譜分布單一。推測自發狀態下EEG信號功率譜分布的這種差異可能影響到AD患者在接受外界刺激后神經網絡的反映。一定頻率和空間上刺激相關的同步化和去同步化的精確模式可能是認知功能在EEG信號中的編碼。AD患者子波熵降低，功率譜分布簡單，可能導致刺激后EEG信號的同步化和去同步化過程的混亂，影響信息感知和存儲的準確性，從而造成認知功能的下降。其產生的機制還有待于進一步研究。
5 結論
子波熵作為衡量EEG信號復雜程度的指標，它反映了EEG信號的頻率分布特征。本研究表明：AD患者自發狀態下EEG信號的子波熵明顯低于正常對照，AD患者EEG信號子波熵降低是由其頻率分布單一造成的。通過AD患者和正常對照自發EEG信號的子波熵與MMSE的相關性分析表明，自發狀態下EEG信號的子波熵與MMSE評分呈正相關，提示自發狀態下EEG信號的子波熵有可能成為AD臨床診斷的病情評估的定量電生理參數。
引言
腦電(electroencephalogram,EEG)是伴隨人生始終的電生理信號，記錄著人腦在生理、病理過程中的神經系統電活動行為，包含了人體神經生理活動的非常豐富的信息。對認知功能及癡呆的研究來說，應該是一種最佳的手段。阿爾茨海默病(Alzheimer’s disease,AD)是最常見的癡呆類型，目前臨床診斷主要依靠神經心理評估量表和神經影像學等檢查。EEG信號對于AD的臨床診斷和預后評估等方面還沒有發揮出應有的作用。
子波熵是衡量非線性信號有序、無序程度的一個量化指標，它可以提供信號非線性動力學過程復雜程度的信息。一個非常有序的信號可以想象為周期性單頻信號，這樣的信號可以用單一的子波尺度來表示，除了信號所在的頻率水平外，其他所有尺度的子波能量幾乎為0，這時單一尺度相對的子波能量為1，而總的子波熵接近0或非常低。隨機信號可以看作極端無序的，這樣的信號子波特征來源于所有頻帶，可以認為所有頻帶對信號的貢獻大致相同，結果不同子波尺度的相對子波能量幾乎相等，子波熵會產生最大值。
傳統的衡量信號有序無序程度的指標是譜熵，它基于傅里葉變換[1]。譜熵也被應用于EEG信號的分析[2]。由于傅里葉變換應用的前提是信號為平穩信號，因此譜熵在EEG信號的分析中受到限制。基于子波變換的子波熵不需要信號是平穩的，適合于EEG信號的分析。AD作為最常見的一種認知功能障礙疾病，其自發EEG信號的子波熵與正常人有何差異，目前還未見相關報道。本研究采用連續子波變換的方法提取AD患者自發EEG信號的頻率分布和子波熵，并與正常同齡進行比較，探討這些新的神經電生理指標在AD的臨床診斷的評估中的價值。
1 研究對象
研究對象來自于2009年1月~2012年5月天津醫科大學神經內科門診治療的認知功能障礙患者，所有患者均行詳細病史采集，神經系統及全身查體，頭核磁共振檢查，部分患者行FDG-PET檢查，行簡易智能精神狀態量表(MMSE)、畫鐘試驗(CDT)和蒙特利爾認知評估量表(MoCA)測試，行血常規、血糖、葉酸、維生素B12、甲狀腺功能、同型半胱氨酸檢查。
納入標準：① 符合美國精神病學會的《精神障礙診斷和統計手冊》(DSM-Ⅳ-TR)中AD的診斷標準。② 符合美國國立神經病學、語言障礙和卒中研究所及AD和相關疾病協會建立AD研究的診斷標準(2007對NINCDS-CADRDA的修訂版)中“很可能AD”的診斷標準；其核心診斷出現早期顯著的情景記憶障礙，并存在陽性的生物學標記物，本研究采用的生物學標記物為頭核磁共振檢查存在內側顳葉萎縮的證據和/或PET檢查顯示雙側顳頂葉葡萄糖代謝減低。③ MMSE評分≤24分。④ HIS評分≤4分。⑤ 具有完整的病歷、化驗和影像學資料。⑥ 患者或家屬知情同意。
排除標準：① 存在2007對NINCDS-CADRDA的修訂版中排除標準的情況或(DSM-Ⅳ-TR)中AD的診斷標準中需除外的引起癡呆的原因。② 頭部MRI檢查發現梗死、出血、占位病變、腦積水或明顯的白質病變，可能影響認知功能者。③ 存在嚴重的心、肺、肝、腎、甲狀腺等臟器疾患，可能影響EEG活動者。④ 有藥物或酒精濫用或依賴史(按照DSM-Ⅳ物質濫用依賴標準)。⑤ 一周內服用鎮靜藥和精神類藥物。
符合上述標準的AD患者共97例，對入組的AD患者按MMSE評分分為三組：輕度AD組(AD Ⅰ)31例，MMSE 19~24分；中度AD組(AD Ⅱ)34例，MMSE 11~18分；重度AD組(AD Ⅲ)32例，MMSE 0~10分。正常對照組34例，來自患者配偶或健康志愿者，無神經精神系統疾病史，無嚴重內科疾病史，MMSE評分≥27分。三個疾病組和一個正常對照組之間年齡和受教育程度差異無統計學意義。
2 方法
2.1 EEG信號采集
對受試者行自發EEG信號描記，描記時間在上午8~11點早餐后進行。采用NIHONKOHDEN公司生產的EEG-2130型數字腦電圖儀，采用Ag/AgCl頭皮電極，按國際標準導聯10/20 系統安裝，以雙耳為參考電極，電阻抗＜5 kΩ，被檢查者在安靜、清醒、閉目狀態下描記EEG信號，描記時間不少于30 min，采樣頻率200 Hz。選擇信號平穩、無偽差的EEG信號片段，每個片段20 s作為分析的EEG信號，每個數據塊包含4 000個數據樣本，用于EEG信號定量分析。
2.2 EEG信號分析
2.2.1 EEG信號的子波分析
子波分析通過信號與一個被稱為子波的解析函數進行卷積，將含有多尺度成分的復雜信號進行分解。子波變換就是將含有多尺度成分的復雜信號與一定位置、一定尺度下代表特定的物理過程或形狀的子波基函數進行局部互相關分析(見圖 1)，如果其相關性高，表明該信號在該處含有該子波成分，使得信號在該處于該子波具有較好的相似性。利用子波變換可以將含有多尺度成分的復雜信號中的不同成分分解為多種單一尺度的成分。用這一方法可以將貌似隨機、復雜無序的信號分解在不同的頻帶上，實現每一頻帶上的精確表達[3]。
圖1
EEG信號與不同尺度的子波函數進行互相關分析
Figure1.
Co-correlation analysis between EEG signal and wavelet function on different scales
一維EEG信號s(t)在子波函數下的子波分析定義為
| ${{W}_{s}}\left( a,b \right)=\int_{-\infty }^{+\infty }{s{{\left( t \right)}_{ab}}\left( t \right)dt}$ |
其中子波函數族Wab(t)是由子波的母波函數W(t)經過平移(參數b)和伸縮變換(參數a)而來：
| ${{W}_{ab}}\left( t \right)=\frac{1}{\sqrt{a}}W\left( \frac{t-b}{a} \right)$ |
本研究采用Gauss連續子變換的方法對三組受試者不同腦區(21個導聯) EEG信號進行子波分析，共分析30個尺度，尺度所對應的EEG信號的頻率如圖 2所示，由于采樣頻率(200 Hz)和分析片段長度(20 s) 的限制，所觀察的EEG信號的頻率為0.05~100 Hz。
2.2.2 EEG信號的多尺度功率譜分析
根據子波系數Ws(a,b)，EEG信號S(t)的分尺度功率可以用各尺度子波功率譜密度函數表示，描述了分尺度EEG信號的強弱：
| $P\left( a \right)=\frac{2}{{{C}_{W}}}{{\int_{-\infty }^{+\infty }{{{W}_{s}}\left( a,b \right)}}^{2}}db$ |
對于不同類型中樞神經系統疾病的EEG信號，其不同腦區和尺度的子波功率譜密度函數是不同的，反映了不同腦區和頻帶節律性活動的差異。
圖2
子波尺度序號與所代表的中心頻率的對應關系
Figure2.
Wavelet scale and its corresponding frequency center
2.2.3 EEG信號的子波熵
EEG信號的總功率是各分尺度信號功率的總和：
| $p=\int_{0}^{+\infty }{p\left( a \right)da}$ |
用p對p(a)進行歸一化，得到各分尺度功率在信號總功率中所占的百分比：
| $A\hat{p}G\text{ }\left( a \right)=\frac{p\left( a \right)}{p}$ |
EEG信號的子波熵衡量了EEG信號所含多尺度信息的復雜程度，反映了EEG在人腦神經細胞活動過程中所包含的動力學信息：
| ${{e}_{w}}=-\int_{0}^{+\infty }{A\hat{p}G\text{ }\left( a \right)ln\left[ A\hat{p}G\text{ }\left( a \right) \right]da}\text{ }$ |
子波熵ew表示功率譜寬度所表達的非線性系統復雜性的大小，功率譜越寬，則ew越大；功率譜越窄，則ew越小。極端情況下，若信號只含有一個尺度a的成分，則 A G (a)=1，此時信號尺度單一，復雜性最小，ew=0。
2.3 統計學方法
將輕、中、重度AD組和正常對照組四組之間不同腦區(F3,F4,P3,P4,O1,O2,T3,T4導聯)EEG信號的子波熵進行比較，統計學方法采用單因素方查分析。進一步將組間子波熵兩兩比較，統計學方法采用SNK法。
為進一步觀察子波熵與認知功能障礙的嚴重程度之間的關系，將不同導聯EEG信號子波熵與MMSE評分進行相關性分析，方法采用二元變量相關分析。顯著性檢驗標準為α=0.05。
3 結果
3.1 正常對照和AD患者EEG信號的子波熵比較
圖 3為正常對照不同導聯EEG信號的子波功率譜分布，正常對照EEG信號在不同導聯上均表現為尺度分布比較廣，從信號的尺度特征看，它的信號是由多尺度成分組成的，EEG信號尺度成分比較復雜。用上述方法計算EEG信號的子波熵，采用子波熵來衡量EEG信號的復雜程度。正常對照左額F3導聯的子波熵為2.73，左頂P3的子波熵為2.75，左枕O1的子波熵為2.77，左顳T3的子波熵為2.69。
圖3
正常對照不同導聯EEG信號的子波功率譜分布
Figure3.
Wavelet power spectrum of different electrode in normal controls
圖 4為EEG信號的子波功率譜分布。從圖中可以看出，輕度 AD患者EEG信號尺度分布較窄，其0.1 Hz和10 Hz附近的功率峰明顯降低，而1 Hz附近的功率峰值明顯增高。輕度AD患者EEG信號尺度成分比較簡單，其左額F3導聯的子波熵為2.57，左頂P3的子波熵為2.50，左枕O1的子波熵為2.67，左顳T3的子波熵為2.61。
圖4
輕度AD患者不同導聯EEG信號的子波功率譜分布
Figure4.
Wavelet power spectrum of different electrode in mild AD patients
圖 5為中度AD患者EEG信號的子波功率譜分布。從圖中可以看出，中度AD患者EEG信號其0.1 Hz和10 Hz附近的功率峰進一步降低乃至消失，逐漸與1 Hz附近的功率峰值融合，形成一個較寬的單峰分布，尺度成分更加簡單。中度AD患者左額F3導聯的子波熵為2.51，左頂P3的子波熵為2.58，左枕O1的子波熵為2.61，左顳T3的子波熵為2.54。
圖5
中度AD患者不同導聯EEG信號的子波功率譜分布
Figure5.
Wavelet power spectrum of different electrode in moderate AD patients
圖 6為重度AD患者EEG信號的子波功率譜分布。從圖中可以看出，重度AD患者EEG信號其0.1 Hz和10 Hz附近的功率峰幾乎完全消失，只在1 Hz附近形成比較高而窄的功率峰，EEG信號尺度成分單一，子波熵值最低，其左額F3導聯的子波熵為2.41，左頂P3的子波熵為2.52，左枕O1的子波熵為2.37，左顳T3的子波熵為2.39。
圖6
重度AD患者不同導聯EEG信號的子波功率譜分布
Figure6.
Wavelet power spectrum of different electrode in severe AD patients
3.2 子波熵與MMSE評分的關系
正常對照EEG信號的子波熵高于AD患者，重度AD患者在不同的導聯均明顯降低，這與EEG信號的功率分布單一，信號更加簡單有關，而輕、中度AD患者EEG信號的子波熵介于兩者之間。圖 7為不同導聯EEG信號的子波熵與MMSE評分之間的散點圖。
圖7
不同導聯EEG信號的子波熵與患者MMSE評分之間關系的散點圖
(a)左顳T3導聯;(b)右顳T4導聯;(c)左枕O1導聯;(d)右枕O2導聯
Figure7. Scatter chart of the relationships between wavelet entropy of EEG signal and MMSE scores of the patients and normal controls at different electrode(a) left temporal T3; (b) right temporal T4; (c) left occipital O1; (d) right occipital O2
3.3 統計學分析
將輕、中、重度AD組和正常對照組之間不同腦區(F3,F4,P3,P4,O1,O2,T3,T4導聯)EEG信號的子波熵進行比較，統計學方法采用單因素方查分析，結果如表 1所示，四組間不同導聯EEG信號的子波熵差異均有統計學意義(P＜0.01)。進一步采用SNK法進行兩兩比較，結果顯示輕、中、重度AD患者不同導聯EEG信號的子波熵與正常對照組比較，差異均有統計學意義(P＜0.05)。
表1
AD患者和正常對照不同導聯EEG信號的子波熵比較
Table1.
Comparison of EEG wavelet entropy between AD patients and normal controls at different electrode
為進一步觀察子波熵與AD患者病情嚴重程度的關系，將不同導聯EEG信號子波熵與AD患者的MMSE評分進行二元變量相關分析。結果如表 2所示，AD患者不同導聯EEG信號子波熵與其MMSE評分均存在相關性(P＜0.01)。
表2
不同導聯EEG信號的子波熵與MMSE評分的相關分析
Table2.
Correlation analysis of EEG wavelet entropy and MMSE score at different electrode
4 討論
EEG信號中蘊藏著非常豐富的信息，對認知功能的研究是一種最佳的工具。如何從EEG信號中提取有價值的定量信息和參數，用于認知功能障礙的診斷，一直是臨床工作和基礎研究領域共同關注的重要課題。
子波熵是衡量非線性信號動力學行為，有序、無序程度的一個量化指標，它可以提供信號非線性動力學過程復雜程度的信息。子波變換可以同時顯示時域頻域兩方面信息，且不需要信號是平穩的，所以非常適合EEG信號的分析。子波熵作為衡量系統的有序程度的指標被應用于EEG信號分析。
Blanco等[4]首先將基于子波變換的子波熵應用于EEG信號的分析。近年來，國內外學者用子波熵研究EEG信號、誘發電位、事件相關電位等的復雜程度，進一步揭示了大腦電活動的動力學機制。其應用主要在大腦感知、認知活動的研究、癲癇EEG信號的動態觀測、睡眠、網絡成癮、頭外傷后腦神經的康復[5-9]等幾個方面。
Rosso等[10]采用正交離散子波變換，對13例健康大學生睜眼、閉眼時自發EEG信號和主動、被動聽覺刺激狀態下的EEG信號進行分析，提出了子波能量(wavelet energy)、子波熵(wavelet entropy)、相對子波熵(relative wavelet entropy)等概念，來研究短片段的自發EEG信號的頻率分布(子波能量)和有序程度(子波熵)，及刺激后EEG信號的子波能量和子波熵的演變過程。結果顯示自發EEG信號的在閉目時α節律占主要優勢，這時的子波熵較睜眼時明顯降低。主動和被動聽覺刺激后自發EEG信號的子波熵均明顯降低。子波熵的降低與EEG信號θ節律性活動的增強有關，表明聽覺刺激后EEG活動向有序狀態轉化。
Quian等[11]對9名健康受試者的視覺誘發電位、目標和非目標視覺刺激三種狀態下EEG信號的子波熵值在刺激前后的動態演變過程進行研究，結果顯示，只有目標刺激后頂枕導聯的子波熵在刺激后約600 ms時出現最低值，這與事件相關的P300相關，而在P100-N200時間窗內未發現子波熵的明顯降低。對事件相關電位的研究不僅要看波幅和潛伏期，子波熵可以提供EEG生理活動中更為豐富的信息，其包含了EEG信號的有序程度、頻率上的同步化及轉化和演變過程。Baser等[12]就EEG和事件相關電位的關系提出EEG是不同頻率電活動的綜合，事件相關電位反映了EEG活動從無序到有序的過程，伴隨著EEG信號在一定頻率上同步化的增強。而子波熵可以顯示受到刺激后EEG信號頻率上同步化的動態演變過程，從而加深了對腦動力學機制的理解，成為認知功能研究的一種新的方法。
Yordanova等[13]對15名健康者主動的視覺刺激、聽覺刺激及視聽覺聯合刺激時事件相關電位的子波熵和頻率分布進行研究，結果表明雙重刺激時子波熵降低更為明顯。子波熵的降低作為衡量EEG活動從有序到無序的轉變的指標，它反映了大腦感知和認識的內源性加工過程，它主要源于前頭部的θ節律同步化增強，與刺激的種類無明顯關聯。Rosso等[14-15]研究了不同狀態下EEG信號子波熵的變化并采用連續子波熵研究聽覺誘發電位，結果顯示較離散子波熵可以發現更多細節特征。
目前的研究表明，子波熵在大腦的認知過程中成動態變化，且與刺激的方式相關，具有一定的規律。它表明子波熵與認知功能明顯相關，那么認知功能障礙患者，它的EEG信號的子波熵與正常對照在一定刺激是其EEG信號的子波熵是否存在差異，認知功能障礙患者的自發EEG信號的子波熵與正常對照是否存在差異，目前尚未見相關報道。AD是認知功能障礙的最主要類型，本研究對AD患者自發EEG信號的子波熵進行研究，并與正常同齡進行比較。結果表明：AD患者自發條件下的EEG信號，其子波熵低于正常對照，而且與AD的嚴重程度明顯相關。
本研究的結果表明，AD患者自發EEG信號的子波熵明顯低于正常對照，而且子波熵與MMSE評分明顯相關。子波熵反映了信號的復雜程度，因此AD 患者EEG信號的子波熵降低，說明AD患者EEG信號的復雜程度降低。從功率譜分布上看說明AD患者EEG信號頻率分布更加單一。因此子波熵這一定量的電生理指標對于AD的臨床診斷和病情的評估具有重要的臨床應用價值。
EEG信號的子波熵降低是如何影響認知功能的，其機制目前還不清楚。Blanco等[4]、Cek等[16]的關于認知功能的子波熵的研究均表明，在受到內、外刺激和工作任務時，EEG信號的子波熵的子波熵降低，這一現象與中樞神經系統在受到刺激后出現神經網絡同步化活動增強，導致EEG信號在某些頻帶上功率值的增高，從而出現頻率分布變窄有關。這種功率分布的在時間和空間上的動態演變過程的模式與刺激的模式和受試者的反映有關。Weiss等[17-18]、Karrasch等[19]對AD患者和正常對照在詞匯記憶任務中EEG信號的和去同步化模式的研究表明，認知功能障礙患者在記憶任務時EEG信號在不同腦區，不同頻率上的同步化模式與正常對照存在差異。AD患者自發EEG信號的子波熵與正常對照的差異的研究，目前尚未見相關報道。自發狀態下EEG信號在一定頻率上的穩定的一種分布模式是良好的認知功能產生的神經電生理基礎，由這種頻率分布模式可以獲得衡量EEG信號的復雜程度的定量電生理指標--子波熵。本研究表明AD患者自發狀態下EEG信號的子波熵低于正常對照，說明AD患者EEG信號復雜程度降低，進一步反映AD患者EEG信號較正常對照功率譜分布單一。推測自發狀態下EEG信號功率譜分布的這種差異可能影響到AD患者在接受外界刺激后神經網絡的反映。一定頻率和空間上刺激相關的同步化和去同步化的精確模式可能是認知功能在EEG信號中的編碼。AD患者子波熵降低，功率譜分布簡單，可能導致刺激后EEG信號的同步化和去同步化過程的混亂，影響信息感知和存儲的準確性，從而造成認知功能的下降。其產生的機制還有待于進一步研究。
5 結論
子波熵作為衡量EEG信號復雜程度的指標，它反映了EEG信號的頻率分布特征。本研究表明：AD患者自發狀態下EEG信號的子波熵明顯低于正常對照，AD患者EEG信號子波熵降低是由其頻率分布單一造成的。通過AD患者和正常對照自發EEG信號的子波熵與MMSE的相關性分析表明，自發狀態下EEG信號的子波熵與MMSE評分呈正相關，提示自發狀態下EEG信號的子波熵有可能成為AD臨床診斷的病情評估的定量電生理參數。
