二尖瓣疾病是最多發的心臟瓣膜疾病之一。瓣膜結構的精確定位和顯示是二尖瓣微創手術的前提。本文提出了一種針對三維超聲圖像的多解析度彈性匹配方法來計算運動場函數,運動場函數通過三次B樣條函數構造得到,而待優化的目標函數通過基于超聲斑點噪聲的最大似然方法獲得。該算法被應用于匹配三維超聲圖像中的二尖瓣結構體素點。計算結果充分證明了算法的有效性。
引用本文: 楊近妤, 張婉, 殷然, 鄧宇曉, 魏云峰, 曾俊義, 文通, 丁露, 劉小健, 李軼鵬. 心臟二尖瓣動態追蹤技術. 生物醫學工程學雜志, 2014, 31(5): 1135-1138. doi: 10.7507/1001-5515.20140214 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
心臟二尖瓣結構功能異常是常見的心臟疾病之一[1-4],采用三維超聲圖像對其進行輔助診斷和手術是一項非常重要的技術。為了幫助醫生診斷,需要對三維的二尖瓣結構在不同時刻進行匹配。本文中的“圖像匹配”又稱圖像配準,其含義是對不同時間、不同視場或者不同成像模式的兩幅或者多幅圖像進行空間變換處理,使得各個圖像在幾何上能夠對應起來。圖像配準是圖像處理和分析的關鍵步驟,是圖像對比、數據融合、變化分析、運動檢測和目標識別的重要前提。在本文中,“匹配”指不同時刻對二尖瓣結構進行“跟蹤”,即不同時間、相同視場、相同成像模式的多幅圖像進行配準,在本文中應用于運動檢測。區域匹配算法[5-6]的性能取決于窗口大小,而二尖瓣運動時尺寸大小不一,因此,采用彈性匹配算法[7-9]能夠獲得較好結果。目前二尖瓣追蹤的相關研究[10-12]尚未與圖像配準方法相結合,而圖像配準事實上是一種非常重要的人工智能算法。采用圖像配準方法,不僅能夠追蹤圖像中的二尖瓣結構,而且作為一種普適性匹配方法,還能對圖像中任意感興趣的體素點進行追蹤。本文提出一種針對三維超聲圖像的多解析度彈性匹配算法:通過超聲圖像斑點噪聲的對數函數建立目標函數并采用最大似然方法求解最優值,求解過程分成多個解析度層次由粗至精進行,最后用實例計算來驗證算法的有效性。
1 模型和匹配算法
1.1 二尖瓣結構
二尖瓣結構是位于左心房和左心室之間的單向活門,具體位于左房室口周緣,面積為4~6 cm2。二尖瓣結構和三尖瓣結構統稱為心臟的房室瓣結構,它們位于心房和心室之間并且控制著心臟內血液的流向和流量。在二尖瓣功能正常的情況下,在心臟收縮時,左心室內血液被擠壓而沖擊二尖瓣使其關閉,使得血液不進入左心房。由于二尖瓣不能正常工作引起的疾病包括二尖瓣閉鎖不全、脫垂等,這些疾病的發病率日益增高并且往往需要進行二尖瓣手術。現在的三維醫學超聲成像技術能夠對二尖瓣結構進行三維成像,而根據這些超聲影像進行二尖瓣建模和動態運動追蹤對相關手術有著極其重要的指導意義。
1.2 B樣條函數
樣條函數在數值分析領域的應用十分活躍,屬于函數逼近分支。樣條函數的優點包括充分光滑、插點數目多和插值函數計算穩定等。對于n階樣條函數,其每一段都是一個n階多項式,包括n+1個待定系數,但由于有平滑性的限制(包括函數本身連續性和1至n-1階導數的連續性),所以每個基本的樣條函數只有1個自由度。在本文中,考慮采用均勻插點且插點間間隔為1的樣條函數,這樣的樣條函數可以由一系列B樣條函數用如下方式表達:
| $s\left( x \right)=\sum\limits_{x\in Z}{a}\left( k \right)\beta {{~}^{n}}\left( x-k \right)~,$ |
這是一系列n階B樣條函數β n(x)的平移組合,a(k)為組合權重。而n階B樣條函數β n(x)可以通過0階B樣條函數β 0(x)通過n+1次卷積得到,如下:
| $\eqalign{ & \beta {^0}\left( x \right) = \left\{ \matrix{ 1, - 1/2x1/2 \hfill \cr 1/2,\left| x \right| = 1/2 \hfill \cr 0,otherwise \hfill \cr} \right. \cr & \beta {^n}\left( x \right) = \underbrace {\beta {^0}\left( x \right)*\beta {^0}\left( x \right)* \ldots \beta {^0}\left( x \right)}_{n + 1} \cr} $ |
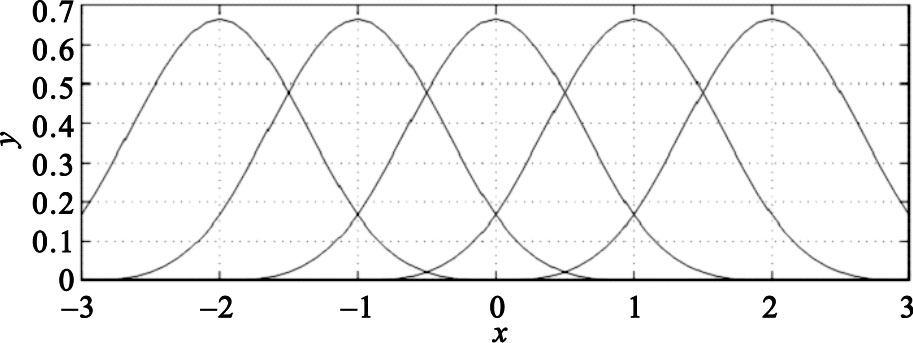
圖 1畫出了一組3次B樣條曲線,為表達簡潔,在本文中使用β(x)表示3次B樣條曲線。
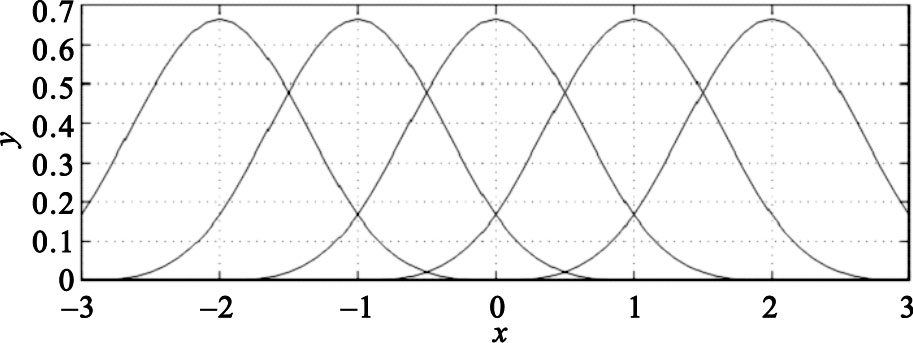 圖1
一組3次B樣條曲線
Figure1.
An example of cubic B-spline
圖1
一組3次B樣條曲線
Figure1.
An example of cubic B-spline
1.3 三維圖像模型
考慮在參考時間r和t的兩幅三維超聲圖像Jr和Jt(分別定義為源和宿圖像),在體素x的灰度值可以表達為Jr(x)=Ir(x)+Sr(x),Jt(x)=It(x)+St(x),其中Ir(x)和It(x)是超聲圖像在x處的真實成像灰度值。而Sr(x),St(x)是對數斑點噪聲,根據超聲圖像的成像原理有S(x)=ln(N(x)),其中N(x)是獨立同分布的噪聲隨機變量,其概率密度服從瑞利分布。
在匹配過程中,需要連續的宿圖像灰度函數,這可以通過對離散圖像灰度函數插值而獲得,在此使用B樣條函數進行如下插值: ,插值系數by可以事先通過求解線性系統得到,而。
1.4 最大似然方法
用f=x+u:G→G表示運動場函數,那么對于源和宿圖像有It(f(x))=Ir(x)。可以定義差異函數:
| $\begin{align} & d\left( x \right)={{J}_{t}}\left( f\left( x \right) \right)-{{J}_{r}}\left( x \right)={{S}_{t}}\left( f\left( x \right) \right)-{{S}_{r}}\left( x \right)= \\ & ln({{N}_{t}}\left( f\left( x \right) \right)/{{N}_{r}}\left( x \right)) \\ \end{align}$ |
經過概率論推導可以得到其概率密度函數pd(z)=2e2z/(e2z+1)2,?z>0。在最大似然方法中,概率密度函數的對數被用來構造似然函數,于是有目標似然函數:
| $K\left( f \right)=\frac{1}{\left| M \right|}\sum\limits_{x\in M}{g\left( d\left( x \right) \right)}$ |
其中g(z)=ln(e2z+1)-z,?z>0,M∈G是圖像中感興趣的體素點集合。根據大數定理以及已知的概率密度函數pd(z),可以得到目標函數最小值滿足。
1.5 彈性匹配
在三維圖像網格G中放置一系列插點L={k=(k1,k2,k3)|1≤ki≤Li}。本文的三維圖像尺寸為N1=224,n2=208,N3=208,定義h=(h1,h2,h3)為插點間隔,于是hi=Ni/Li。用3次B樣條曲線來定義偏移場函數為。
其中ck=(ck1,ck2,ck3)是權重系數,B3(x,h,k)=β(xi/hi-ki+1/2),+1/2是為了把插點中心調整與到圖像中心一致,因此目標似然函數K(f)的優化即是關于權重系數的函數K(c)的優化。
1.6 多解析度優化
使用多解析度層次化的優化方法來求解,多解析度分層既包括圖像模型的分層,也包括運動場函數權重系數的分層。首先建立一個圖像金字塔,即從原始圖像開始,逐級1/2采樣得到下一級的粗略圖像。對于運動場權重系數,從一個粗略插點模型開始,逐級加倍插點數目以得到下一級插點。采用這種多解析度優化的方法實際是一個由粗到精的優化過程,不僅節約計算時間,而且可以有效避免優化過程陷入局部最小值。在每一個解析度層,采用梯度下降算法進行最優化求解。
2 計算結果
三維心臟超聲圖像截面圖如圖 2所示,從中可以由醫生標記出二尖瓣的結構,這通常是一組離散點。為了驗證本文中的算法,根據醫生的標定選取了50對位于二尖瓣結構上的體素點,選取方法為:如圖 3,這是我們建立的三維二尖瓣模型,圖中的點1和點2為源圖像中的兩個標記體素點,為了進行追蹤,我們選擇了這兩個具有明顯特征的點。在第一幅源圖像中,我們選擇這兩個點并記為點R1,1和點R1,2,在第i幅源圖像中(i=2,…,25)類似選取這兩個標記點記為點Ri,1和點Ri,2,然后類似選擇其后某一時刻的宿圖像中的這兩個體素點記為點T1和點T2,就可以得到50對體素點(R1,1,T1),(R2,1,T1),…,(R25,1,T1),(R1,2,T2),(R2,2,T2),…,(R25,2,T2)進行算法的驗證。考慮到每個標記點的人工標記誤差為1個體素點大小,這樣的體素點對距離誤差在2個體素大小可以接受。在匹配之前,這50對體素點之間的距離統計值為:均值10.47,方差3.29。經過匹配算法后,計算運動場函數作用后的源圖像上的標記點與宿圖像對應點之間的距離,50對體素點之間的距離統計值為:均值0.83,方差0.56,這是非常令人滿意的結果。匹配之后,可以得到任意兩幅圖像中體素點的對應關系。即,對于第一幅圖像中的醫生標記體素點,通過匹配計算可以獲得在后來任意時刻圖像中的對應位置。通過這種方法,實現了對二尖瓣的跟蹤。圖 4是一個目標函數最小化的優化過程,可以看出在程序結束時,最小值已經非常接近理論值1。
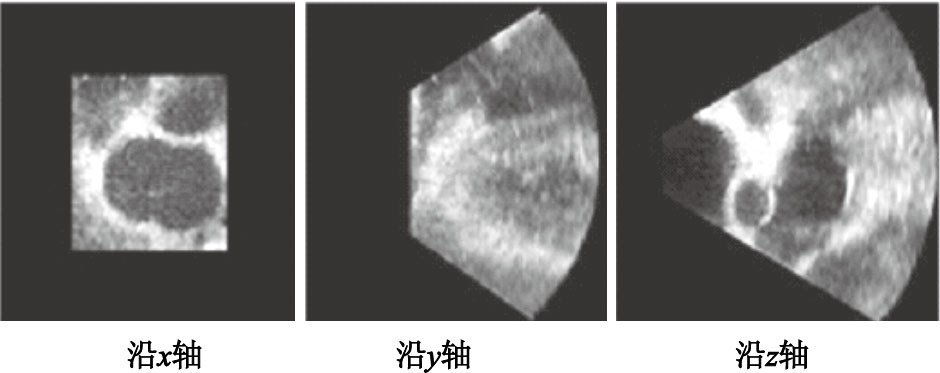 圖2
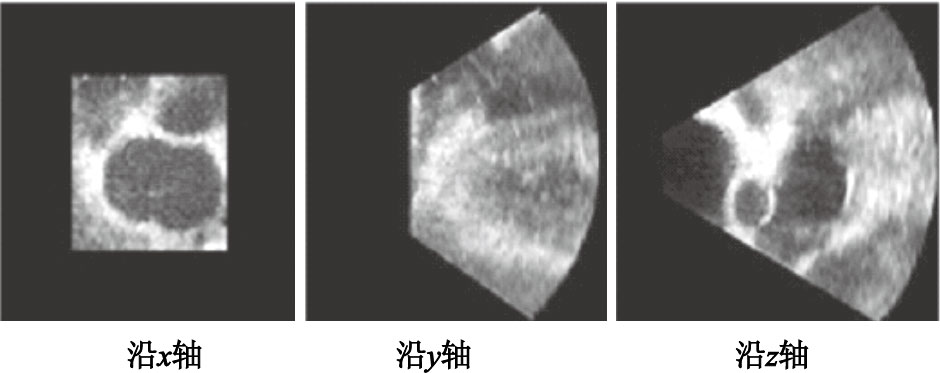
三維心臟超聲圖像截面圖
Figure2.
Sectional views of three dimensional heart ultrasound images
圖2
三維心臟超聲圖像截面圖
Figure2.
Sectional views of three dimensional heart ultrasound images
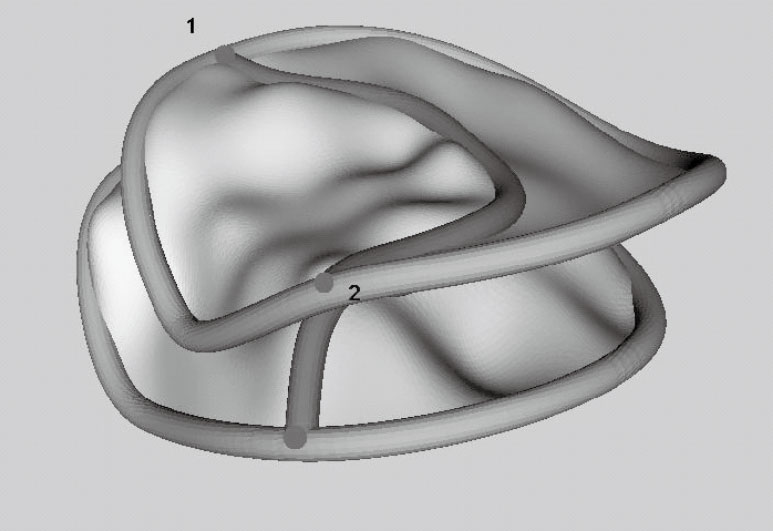 圖3
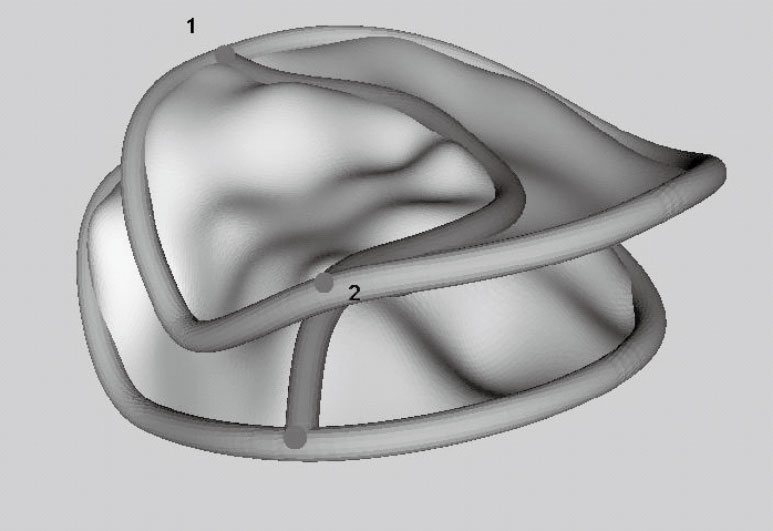
經過匹配計算得到的二尖瓣模型
Figure3.
Mitral valve model after registration computation
圖3
經過匹配計算得到的二尖瓣模型
Figure3.
Mitral valve model after registration computation
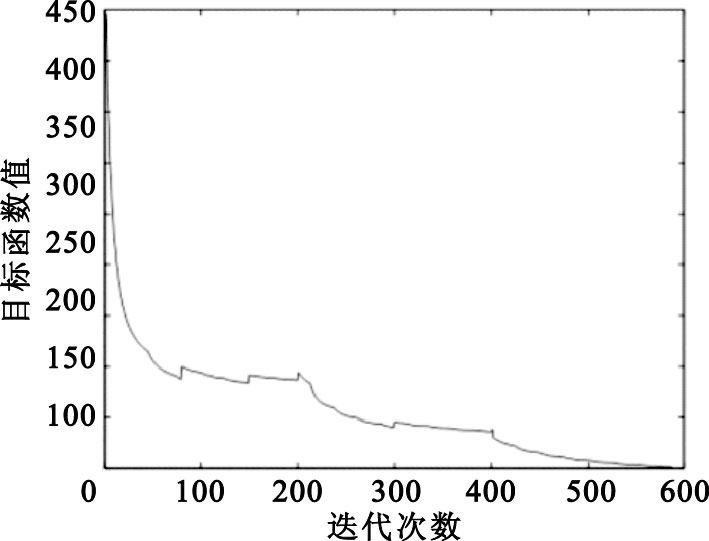 圖4
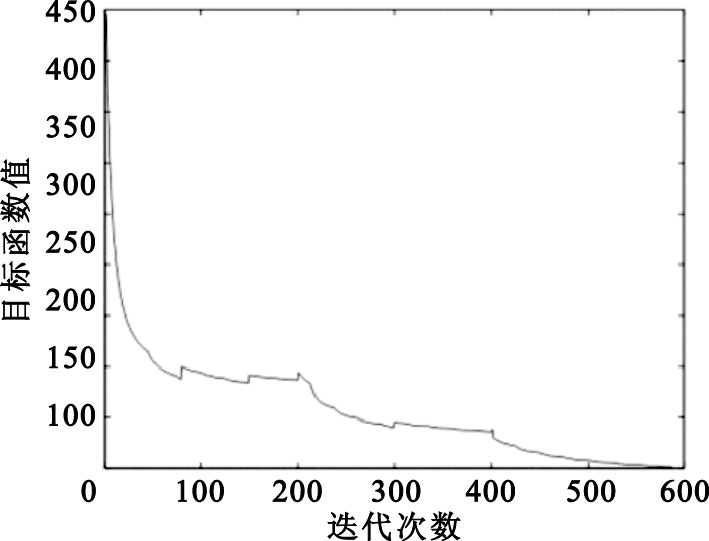
目標函數最小化過程
Figure4.
Minimization process of the cost function
圖4
目標函數最小化過程
Figure4.
Minimization process of the cost function
3 結論
三維醫學影像技術如磁共振波譜(magnetic resonance spectroscopy,MRS)、正電子發射計算機斷層顯像(positron emission computed tomography,PET)、單光子發射計算機斷層成像術(single-photon emission computed tomography,SPECT)、計算機斷層成像(computed tomography,CT)、磁共振成像(magnetic resonance imaging,MRI)、超聲等已經越來越廣泛地應用到醫學診斷之中。采用圖像匹配技術對不同模式、不同時刻或者不同角度的三維醫學圖像進行匹配,可以有效協助診斷的進行。本文提出了一種針對三維超聲圖像同模式不同時刻的多解析度彈性匹配方法,并將其應用至心臟二尖瓣結構的匹配,計算結果充分證明了算法的有效性,該方法的應用將對二尖瓣疾病的診斷和修復手術非常有幫助。
引言
心臟二尖瓣結構功能異常是常見的心臟疾病之一[1-4],采用三維超聲圖像對其進行輔助診斷和手術是一項非常重要的技術。為了幫助醫生診斷,需要對三維的二尖瓣結構在不同時刻進行匹配。本文中的“圖像匹配”又稱圖像配準,其含義是對不同時間、不同視場或者不同成像模式的兩幅或者多幅圖像進行空間變換處理,使得各個圖像在幾何上能夠對應起來。圖像配準是圖像處理和分析的關鍵步驟,是圖像對比、數據融合、變化分析、運動檢測和目標識別的重要前提。在本文中,“匹配”指不同時刻對二尖瓣結構進行“跟蹤”,即不同時間、相同視場、相同成像模式的多幅圖像進行配準,在本文中應用于運動檢測。區域匹配算法[5-6]的性能取決于窗口大小,而二尖瓣運動時尺寸大小不一,因此,采用彈性匹配算法[7-9]能夠獲得較好結果。目前二尖瓣追蹤的相關研究[10-12]尚未與圖像配準方法相結合,而圖像配準事實上是一種非常重要的人工智能算法。采用圖像配準方法,不僅能夠追蹤圖像中的二尖瓣結構,而且作為一種普適性匹配方法,還能對圖像中任意感興趣的體素點進行追蹤。本文提出一種針對三維超聲圖像的多解析度彈性匹配算法:通過超聲圖像斑點噪聲的對數函數建立目標函數并采用最大似然方法求解最優值,求解過程分成多個解析度層次由粗至精進行,最后用實例計算來驗證算法的有效性。
1 模型和匹配算法
1.1 二尖瓣結構
二尖瓣結構是位于左心房和左心室之間的單向活門,具體位于左房室口周緣,面積為4~6 cm2。二尖瓣結構和三尖瓣結構統稱為心臟的房室瓣結構,它們位于心房和心室之間并且控制著心臟內血液的流向和流量。在二尖瓣功能正常的情況下,在心臟收縮時,左心室內血液被擠壓而沖擊二尖瓣使其關閉,使得血液不進入左心房。由于二尖瓣不能正常工作引起的疾病包括二尖瓣閉鎖不全、脫垂等,這些疾病的發病率日益增高并且往往需要進行二尖瓣手術。現在的三維醫學超聲成像技術能夠對二尖瓣結構進行三維成像,而根據這些超聲影像進行二尖瓣建模和動態運動追蹤對相關手術有著極其重要的指導意義。
1.2 B樣條函數
樣條函數在數值分析領域的應用十分活躍,屬于函數逼近分支。樣條函數的優點包括充分光滑、插點數目多和插值函數計算穩定等。對于n階樣條函數,其每一段都是一個n階多項式,包括n+1個待定系數,但由于有平滑性的限制(包括函數本身連續性和1至n-1階導數的連續性),所以每個基本的樣條函數只有1個自由度。在本文中,考慮采用均勻插點且插點間間隔為1的樣條函數,這樣的樣條函數可以由一系列B樣條函數用如下方式表達:
| $s\left( x \right)=\sum\limits_{x\in Z}{a}\left( k \right)\beta {{~}^{n}}\left( x-k \right)~,$ |
這是一系列n階B樣條函數β n(x)的平移組合,a(k)為組合權重。而n階B樣條函數β n(x)可以通過0階B樣條函數β 0(x)通過n+1次卷積得到,如下:
| $\eqalign{ & \beta {^0}\left( x \right) = \left\{ \matrix{ 1, - 1/2x1/2 \hfill \cr 1/2,\left| x \right| = 1/2 \hfill \cr 0,otherwise \hfill \cr} \right. \cr & \beta {^n}\left( x \right) = \underbrace {\beta {^0}\left( x \right)*\beta {^0}\left( x \right)* \ldots \beta {^0}\left( x \right)}_{n + 1} \cr} $ |
圖 1畫出了一組3次B樣條曲線,為表達簡潔,在本文中使用β(x)表示3次B樣條曲線。
 圖1
一組3次B樣條曲線
Figure1.
An example of cubic B-spline
圖1
一組3次B樣條曲線
Figure1.
An example of cubic B-spline
1.3 三維圖像模型
考慮在參考時間r和t的兩幅三維超聲圖像Jr和Jt(分別定義為源和宿圖像),在體素x的灰度值可以表達為Jr(x)=Ir(x)+Sr(x),Jt(x)=It(x)+St(x),其中Ir(x)和It(x)是超聲圖像在x處的真實成像灰度值。而Sr(x),St(x)是對數斑點噪聲,根據超聲圖像的成像原理有S(x)=ln(N(x)),其中N(x)是獨立同分布的噪聲隨機變量,其概率密度服從瑞利分布。
在匹配過程中,需要連續的宿圖像灰度函數,這可以通過對離散圖像灰度函數插值而獲得,在此使用B樣條函數進行如下插值: ,插值系數by可以事先通過求解線性系統得到,而。
1.4 最大似然方法
用f=x+u:G→G表示運動場函數,那么對于源和宿圖像有It(f(x))=Ir(x)。可以定義差異函數:
| $\begin{align} & d\left( x \right)={{J}_{t}}\left( f\left( x \right) \right)-{{J}_{r}}\left( x \right)={{S}_{t}}\left( f\left( x \right) \right)-{{S}_{r}}\left( x \right)= \\ & ln({{N}_{t}}\left( f\left( x \right) \right)/{{N}_{r}}\left( x \right)) \\ \end{align}$ |
經過概率論推導可以得到其概率密度函數pd(z)=2e2z/(e2z+1)2,?z>0。在最大似然方法中,概率密度函數的對數被用來構造似然函數,于是有目標似然函數:
| $K\left( f \right)=\frac{1}{\left| M \right|}\sum\limits_{x\in M}{g\left( d\left( x \right) \right)}$ |
其中g(z)=ln(e2z+1)-z,?z>0,M∈G是圖像中感興趣的體素點集合。根據大數定理以及已知的概率密度函數pd(z),可以得到目標函數最小值滿足。
1.5 彈性匹配
在三維圖像網格G中放置一系列插點L={k=(k1,k2,k3)|1≤ki≤Li}。本文的三維圖像尺寸為N1=224,n2=208,N3=208,定義h=(h1,h2,h3)為插點間隔,于是hi=Ni/Li。用3次B樣條曲線來定義偏移場函數為。
其中ck=(ck1,ck2,ck3)是權重系數,B3(x,h,k)=β(xi/hi-ki+1/2),+1/2是為了把插點中心調整與到圖像中心一致,因此目標似然函數K(f)的優化即是關于權重系數的函數K(c)的優化。
1.6 多解析度優化
使用多解析度層次化的優化方法來求解,多解析度分層既包括圖像模型的分層,也包括運動場函數權重系數的分層。首先建立一個圖像金字塔,即從原始圖像開始,逐級1/2采樣得到下一級的粗略圖像。對于運動場權重系數,從一個粗略插點模型開始,逐級加倍插點數目以得到下一級插點。采用這種多解析度優化的方法實際是一個由粗到精的優化過程,不僅節約計算時間,而且可以有效避免優化過程陷入局部最小值。在每一個解析度層,采用梯度下降算法進行最優化求解。
2 計算結果
三維心臟超聲圖像截面圖如圖 2所示,從中可以由醫生標記出二尖瓣的結構,這通常是一組離散點。為了驗證本文中的算法,根據醫生的標定選取了50對位于二尖瓣結構上的體素點,選取方法為:如圖 3,這是我們建立的三維二尖瓣模型,圖中的點1和點2為源圖像中的兩個標記體素點,為了進行追蹤,我們選擇了這兩個具有明顯特征的點。在第一幅源圖像中,我們選擇這兩個點并記為點R1,1和點R1,2,在第i幅源圖像中(i=2,…,25)類似選取這兩個標記點記為點Ri,1和點Ri,2,然后類似選擇其后某一時刻的宿圖像中的這兩個體素點記為點T1和點T2,就可以得到50對體素點(R1,1,T1),(R2,1,T1),…,(R25,1,T1),(R1,2,T2),(R2,2,T2),…,(R25,2,T2)進行算法的驗證。考慮到每個標記點的人工標記誤差為1個體素點大小,這樣的體素點對距離誤差在2個體素大小可以接受。在匹配之前,這50對體素點之間的距離統計值為:均值10.47,方差3.29。經過匹配算法后,計算運動場函數作用后的源圖像上的標記點與宿圖像對應點之間的距離,50對體素點之間的距離統計值為:均值0.83,方差0.56,這是非常令人滿意的結果。匹配之后,可以得到任意兩幅圖像中體素點的對應關系。即,對于第一幅圖像中的醫生標記體素點,通過匹配計算可以獲得在后來任意時刻圖像中的對應位置。通過這種方法,實現了對二尖瓣的跟蹤。圖 4是一個目標函數最小化的優化過程,可以看出在程序結束時,最小值已經非常接近理論值1。
 圖2
三維心臟超聲圖像截面圖
Figure2.
Sectional views of three dimensional heart ultrasound images
圖2
三維心臟超聲圖像截面圖
Figure2.
Sectional views of three dimensional heart ultrasound images
 圖3
經過匹配計算得到的二尖瓣模型
Figure3.
Mitral valve model after registration computation
圖3
經過匹配計算得到的二尖瓣模型
Figure3.
Mitral valve model after registration computation
 圖4
目標函數最小化過程
Figure4.
Minimization process of the cost function
圖4
目標函數最小化過程
Figure4.
Minimization process of the cost function
3 結論
三維醫學影像技術如磁共振波譜(magnetic resonance spectroscopy,MRS)、正電子發射計算機斷層顯像(positron emission computed tomography,PET)、單光子發射計算機斷層成像術(single-photon emission computed tomography,SPECT)、計算機斷層成像(computed tomography,CT)、磁共振成像(magnetic resonance imaging,MRI)、超聲等已經越來越廣泛地應用到醫學診斷之中。采用圖像匹配技術對不同模式、不同時刻或者不同角度的三維醫學圖像進行匹配,可以有效協助診斷的進行。本文提出了一種針對三維超聲圖像同模式不同時刻的多解析度彈性匹配方法,并將其應用至心臟二尖瓣結構的匹配,計算結果充分證明了算法的有效性,該方法的應用將對二尖瓣疾病的診斷和修復手術非常有幫助。