腦功能網絡探索是揭示大腦處理情緒時潛在神經聯系的重要手段,稀疏貝葉斯網絡(SBN)方法可以分析各區域因果特性及相互影響,逐漸被應用于腦網絡的研究中。本文提取了22名被試情緒腦電(EEG)的theta和alpha頻段,構建了不同情緒喚醒度的有效性腦網絡,并對節點的度、平均聚類系數和特征路徑長度進行分析。結果發現:①相比于低喚醒度的EEG信號,左中顳在高喚醒度狀態的因果影響都很明顯,而右前額的因果影響都不顯著;②高喚醒度的平均聚類系數較高,而低喚醒度的特征路徑長度較短。
引用本文: 高佳, 王蔚. 基于稀疏貝葉斯網絡的情緒腦電的有效性腦網絡研究. 生物醫學工程學雜志, 2015, 32(5): 945-951. doi: 10.7507/1001-5515.20150169 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
目前腦功能研究主要集中在定位不同認知功能活動中的某些功能模塊的激活,其中大腦認知研究則集中在某一特定認知任務中不同區域皮層功能模塊之間的信息流通交互作用,并以此為基礎研究大腦功能整合。隨著功能磁共振成像(functional magnetic resonance imaging,fMRI)、腦電圖(electroencephalogram,EEG)等技術的快速普及發展,腦網絡研究已成為神經信息科學研究中的熱門領域。功能網絡主要是提取感興趣腦區的時間序列,然后通過不同連接方式研究神經耦合關系[1]。由于僅根據腦區功能性信號間統計關系所構建的無向網絡,并不是嚴格意義上的功能網絡,因此必須在無向網絡基礎上繼續考慮信息在節點間的傳播方向,即節點間統計意義上的因果關系,并最終以此獲得有向網絡,才能更加真實地反映大腦的信息傳遞和功能活動[2]。
目前構建兩個腦區之間相互作用大小和方向的常用有效連接模型包括結構方程模型(structural equation modeling,SEM)、動態因果模型(dynamic causal analysis,DCM)和格蘭杰因果分析(Granger causality)等[3]。其中SEM中定義了連接方向,建立反映變量關系的模型,再通過調整連接強度得到最佳擬合模型及數據,估計參數,并檢查其顯著性。但是該模型存在以下缺點:①只用了相關矩陣信息,因此并不能準確建立區域間的交互關系,使得模型與實際神經系統網絡不一致;②忽略了時間序列包含的信息,導致結構方程模型結果不會隨時間序列信息順序的改變而變動。DCM則考察了節點活動的變化,是由外界刺激所引起的節點活動的直接和間接變化的總和,是模型匹配數據,因此如果感興趣區域太多,會極大地增加研究難度。目前DCM最大研究節點個數為8個[3]。根據格蘭杰因果分析,如果第一個節點時間序列當前值和過去值的線性組合能夠更好地預測第二個序列結果,則說明第一節點對第二節點有影響[2],但該分析需假設實際值與預測值間誤差呈正態分布,若實際情況呈其它分布類型將嚴重影響推論的有效性。貝葉斯網絡以概率論和圖論為基礎,將有向無環圖(directed acyclic graph,DAG)和條件概率表有機結合,描述了變量間的相互依賴關系[4]。由于貝葉斯網絡具有獨特的不確定性表達形式、易于綜合先驗知識以及推理結果直觀等特性,因此可以通過神經影像數據研究不同大腦區域的交互。目前該方法已成功應用在任務表現、技能學習和疾病過程診斷等方面。
在情緒認知過程中,大腦中與之相關的信息流向變化速度很快,一般是在毫秒級。因此,EEG的時間分辨率優勢得以凸顯出來[5]。已有研究表明,不同節律EEG可以反映不同認知功能下大腦各個區域的任務分配和功能整合。EEG信號根據不同頻帶可分為delta波(0.5~3 Hz)、theta波(4~7 Hz)、alpha波(8~13 Hz)、beta波(14~30 Hz)和gamma波(30~45 Hz)。其中delta波一般在睡眠時出現;theta波在困倦時可見,它的出現是中樞神經抑制狀態的表現;alpha波在靜息閉目狀態下的幅度比較大,是節律性腦電波中最明顯的波;beta波的出現代表了大腦皮層的興奮,是一種快波;gamma波代表的是大腦皮層的高度興奮。與情緒狀態關聯較大的頻段有theta波和alpha波等[6-7],因此本文將提取這兩個頻段的EEG信號進行研究。情緒的二維空間由愉悅度(valence,效價)和喚醒度(arousal)組成。效價維度的理論基礎是正性情緒和負性情緒的分離激活;喚醒度維度指情緒所激活機體能量的程度,即生理活動和心理警覺的水平差異,低喚醒如睡眠、厭倦、放松等,高喚醒如清醒、緊張等[8]。目前在對情緒認知機制的研究中,多數基于事件相關電位(event-related potentials,ERP)分析愉悅度差異,而基于EEG研究不同喚醒度大腦網絡信息流向、因果關系的報道則較少。因此,本文對不同喚醒度的EEG情緒信號,分別建立theta波和alpha波頻段大腦區域內的因果模型,探索不同喚醒度各頻段的因果調制,從而對比研究不同喚醒度情緒狀態的腦網絡拓撲特性。
1 研究方法
1.1 EEG腦功能網絡構建
對于多通道EEG信號,通常把每個EEG導聯對應的電極覆蓋區域定義為一個節點,然后量化EEG各通道信號之間的關系,以關系強弱作為判定對應腦區之間功能連接強度的指標,從而構建出功能性腦網絡[2]。其步驟可按照以下三步進行:
(1) 量化EEG信號通道關系:對EEG信號進行預處理以及提取特定頻段后,采用一種連接方法確定各節點之間的關系。基于引言中對各種有向連接方法的分析,本研究采用稀疏貝葉斯網絡(sparse Bayesian network,SBN)計算EEG信號各通道之間的兩兩關系。
(2) 確定閾值并構建大腦皮層功能性腦網絡:在量化EEG各通道之間的關系后,需進一步確定合適閾值以構建腦網絡。導聯的EEG信號之間的強度決定了兩個節點之間是否存在連接邊,即若強度大于設定閾值,則兩導聯之間建立連接邊,并設置鄰接矩陣對應元素為1,反之則不建立連接邊,設置鄰接矩陣對應元素為0。通常鄰接矩陣對角線元素為0,該構建網絡稱為0-1 二值網絡。
閾值選取直接影響著腦網絡的統計特性和拓撲結構。SBN構建網絡的過程中,通過一個懲罰變量實現對重要連接的篩選,即控制稀疏性的懲罰變量代替了閾值的作用。
(3) 采用現有復雜網絡測度分析建立的功能性腦網絡:在腦網絡分析中常用復雜網絡測度有節點的度、聚類系數、特征路徑長度等,需計算并分析上述參量可能反映的生理意義。
1.2 稀疏貝葉斯網絡
1986年,美國加州大學Judea Pearl教授首次提出完整的貝葉斯網絡,該網絡通過有向無環圖可以得知n組隨機變量條件概率分配的性質。一般而言,貝葉斯網絡有向無環圖中的節點表示隨機變量,可以是可觀察變量、隱變量、未知參數等。連接兩個節點的箭頭代表此兩個隨機變量具有因果關系或是非條件獨立;而節點中變量間若沒有箭頭相互連接則稱其隨機變量,彼此間為條件獨立。若節點間以一個單箭頭連接在一起,表示其中一個節點是“因(parents)”,另一個是“果(descendants or children)”。
貝葉斯網絡主要由兩部分構成,分別對應問題領域的定性和定量描述,即網絡結構和網絡參數。早期學者依靠專家知識指定的概率分布構建貝葉斯網絡結構,這種方法往往導致與觀測數據產生較大偏差,具有一定的局限性。而SBN采用一種懲罰變量獲得稀疏性,以保證獲得有向無環圖,更加準確高效地實現了貝葉斯網絡的學習[4]。
假設x=[x1,x2,…,xm]T是一個包含m個特征(變量)的樣本,D∈Rn×m是n個樣本數據矩陣,D的第i行為樣本xi,第j列為fj。貝葉斯網絡用有向無環圖表示變量的聯合分布,變量對應圖中相應節點,聯合分布表示為,其中Pa(xi)是xi的所有父節點。每個節點xi可寫成其父節點的回歸表示,即,其中向量θi是回歸系數,εi~N(0,σ2i)。矩陣Θ=[θ1,…,θm]為貝葉斯網絡參數,G(m×m)表示網絡結構,如果從xi到xj存在連接,那么Gij=1;否則Gij=0。矩陣P(p×p)表示路徑,如果從xi到xj存在一條路徑,那么Pij=1;否則Pij=0。
傳統貝葉斯網絡通過兩步學習網絡結構和參數,SBN則通過對貝葉斯網絡執行稀疏約束同時得到網絡結構和參數,具體來說,就是解決一個有約束的最小二乘擬合問題,公式如下:
| $ \begin{array}{l} \mathop {\min }\limits_\theta \sum\limits_{i = 1}^m {\left\| {{f_i} - \theta _i^TPa\left( {{x_i}} \right)} \right\|_2^2} + {\lambda _1}{\left\| {{\theta _i}} \right\|_1}\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\Theta _{ji}} \times {P_{ij}} = 0 \end{array} $ |
其中矩陣Pa(xi)的第i行對應xi的所有父節點,初始化為除xi的所有節點,然后對回歸系數θi的系數約束進行過濾。該約束條件保證了結果為有向無環圖。
1.3 復雜網絡測度
復雜網絡中不依賴于節點具體位置和連線具體形態而表現出來的性質叫做網絡的拓撲性,相應結構稱為網絡的拓撲結構。近年來,基于醫學成像的腦功能網絡研究為刻畫復雜網絡拓撲結構的性質,定義了多個測度用來度量網絡整體或局部特征。其中最主要的概念為:節點的度、聚類系數、特征路徑長度。
節點的度是對節點互相連接統計特性最重要的描述,其度值定義為與節點直接相連的邊數,可由鄰接矩陣第i行或列元素求和得到。如果網絡是有向網絡,節點的度分為兩部分:入度和出度。節點入度是指從其他節點指向該節點的邊數,即該節點作為“果”的連接數目;出度是指從該節點指向其他節點的邊數,即該節點作為“因”的連接數目。總度值為入度與出度值之和。節點入度越大,則影響該節點的連接越多,表明該節點在網絡中是多個節點共同作用的結果。節點出度越大,則該節點在網絡中是多個節點的“因”,表明該節點在網絡中所起作用越大,反之則越小。
聚類系數衡量的是網絡集團程度,表示某一節點的鄰居間互為鄰居的可能。節點i的聚類系數Ci等于該節點鄰居間實際連接邊的數目與可能連接的最大邊數的比值[9],即
| $ {C_i} = \frac{{2{e_i}}}{{{k_i}\left( {k - 1} \right)}} $ |
其中,ei為節點i鄰居間實際連接邊的數目,ki(ki-1)/2為可能連接的最大邊數。對于復雜網絡,由于節點眾多,因此通常不是詳細研究每個節點的聚類系數大小,而是求算整個網絡所有節點總數N聚類系數的平均值,即平均聚類系數,計算如下:
| $ C = \frac{1}{N}\sum\limits_{i = 1}^n {{C_i}} $ |
該系數描述的是網絡中節點形成集團的可能性。C越大,網絡節點越傾向于形成緊密的集團。
網絡特征路徑長度L描述的是網絡全局連接特征,定義為任意兩個節點之間的距離平均值[10],計算公式如下:
| $ L = \frac{1}{{N\left( {N - 1} \right)}}\sum {{d_{ij}}} $ |
其中N代表網絡節點總數,dij表示網絡中節點i、j之間的距離,它被定義為連接這兩個節點最短路徑上的邊數。復雜網絡平均路徑長度大小反映網絡結構的彌散性和連通性,即平均路徑越短,網絡結構越緊湊,網絡連通性也越好,任意兩個節點之間的通信可以較快完成;反之,則網絡結構松散,網絡的連通性差,節點之間的通信較困難。
2 實驗數據
本研究所使用的情緒EEG數據來源于英國帝國理工大學Intelligent Behaviour Understanding小組,在22名被試觀看嚴格篩選的音樂視頻片段時采集,每個視頻結束后被試對喚醒度水平進行自我評價,評價采用9點量表,表示喚醒度水平從平靜(無聊)逐漸過渡到刺激(興奮)[11]。實驗所用腦電采集儀為32導電極帽,電極帽的放置排布按照國際的10/20導聯標準進行。數據經過128 Hz重采樣,去除眼電偽跡,通過4.5~45.0 Hz帶通濾波的預處理數據[11]。每個被試EEG數據以63 s為一段進行分割,按照視頻順序形成40×32×8 064(視頻×導聯×采樣點)的數據文件。依據被試自我評價表中喚醒度的打分,將情緒數據分為高喚醒度和低喚醒度兩類,得到513個高喚醒度的情緒樣本和367個低喚醒度的情緒樣本。
3 數據處理
3.1 EEG頻段信號提取
由于EEG信號具有明顯的非線性和非平穩特性,采用傳統傅里葉變換頻域分析方法不能很好地分析EEG信號。近些年來,隨著小波變換的不斷發展,國內外許多研究者將小波分析用于生物醫學信號的提取及去噪處理。小波變換是一種在時域頻域均能進行分析的信號處理方法,具有良好的時頻局部化特性。本文利用Matlab工具箱中的小波分解方法,選取Daubechies小波函數進行5層小波分解,提取EEG信號中包含的theta波和alpha波,為構建腦功能網絡做好準備。
實驗中,被試進入有效思考要經過數秒時間,而且因為思考時間較長,最后幾秒往往不是很有效,因此EEG數據處理中一般取被試精神狀態比較好、思想集中的時間段內的數據。本研究從第5秒數據點開始,對中間50 s的EEG數據進行小波分解,分別從高喚醒度和低喚醒度的情緒樣本中提取出實驗所需的theta波和alpha波。
3.2 構建不同喚醒度的有效性腦網絡
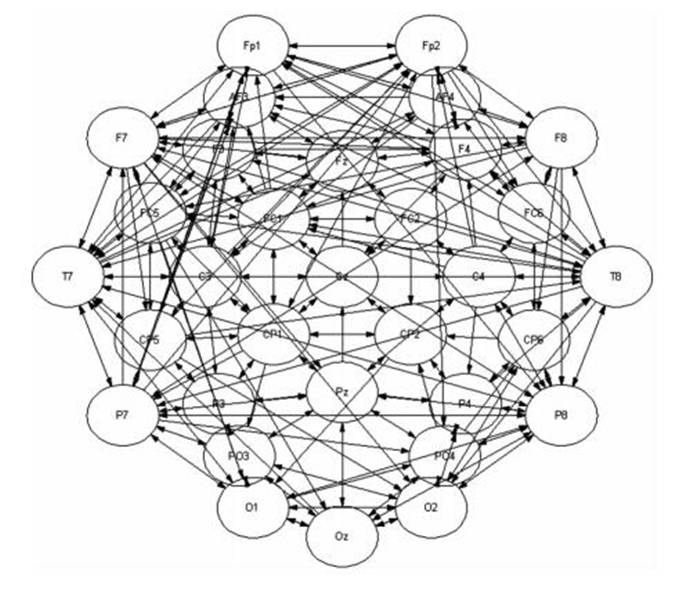
首先利用SBN把每個被試的EEG信號構造為一個二值網絡,在顯著性水平為0.05的條件下對所有節點之間有效連接強度的顯著性進行判定。結果表明在1 024(32×32)個導聯對中,theta頻段有131個連接特征有顯著差異,alpha頻段有171個連接有顯著差異。然后分別把高喚醒度和低喚醒度的矩陣相加,得到theta波和alpha波各兩組不同喚醒度的有效性腦網絡。為了直觀地表示腦網絡連接,更清晰地顯示各個導聯之間的信息流向,以稀疏程度為0.3的腦網絡為例,利用Bsmart工具箱[12]繪制了theta波在低喚醒度下的有效性腦網絡,如圖 1所示。圖中顯示了32個節點在腦電采集設備上的相對位置,節點之間的箭頭表示不同腦區之間的信息流向。在此基礎上,對兩個頻段不同喚醒度的網絡測度進行分析。
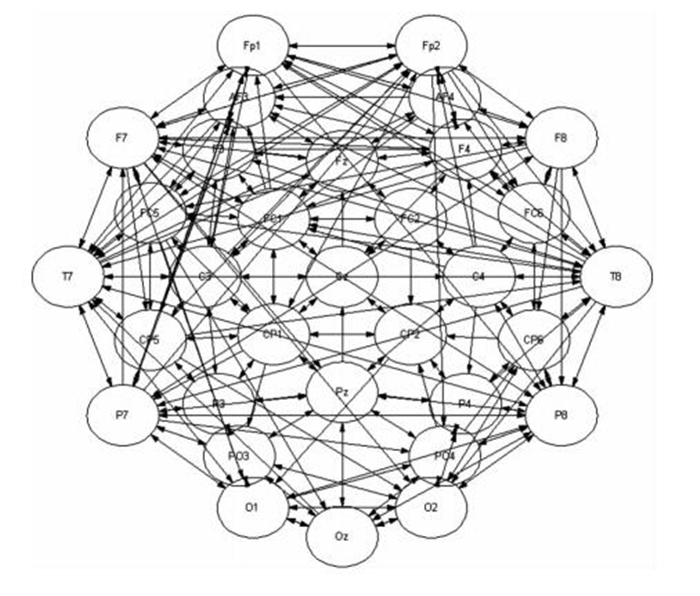 圖1
有效性腦網絡
Figure1.
Effective network
圖1
有效性腦網絡
Figure1.
Effective network
3.3 不同喚醒度的有效性腦網絡測度分析
為得到不同情緒喚醒度的網絡測度的變化規律,本文根據EEG信號所包含的theta波和alpha波繪制了測度隨閾值變化的曲線圖,進一步比較高喚醒度和低喚醒度的EEG信號在不同頻段腦網絡特性的異同,實驗結果借助BCT(Brain Connectivity Toolbox)工具箱[13]用Matlab2010b得到。
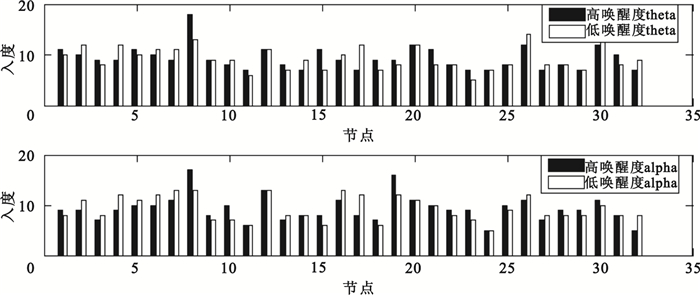
入度和出度是有效網絡特有的屬性,由于這種屬性是針對網絡中的每個節點描述,而閾值為0.3的腦網絡能夠清晰顯示各導聯之間的信息流向,本文將0.3作為閾值得到theta波和alpha波在不同喚醒度下的入度和出度,并進行對比,如圖 2、圖 3所示。從圖 2可知,在theta頻段,高喚醒度下編號為8(T7)、15(Oz)、21(F8)的節點入度均比低喚醒度狀態≥3,17(Fp2)號節點入度比低喚醒度狀態<5;在alpha頻段,高喚醒度下編號為8(T7)、10(CP1)、19(Fz)的節點入度比低喚醒度狀態≥3,編號為4(F7)、17(Fp2)、32(O2)的節點入度比低喚醒度狀態≤3。由此得出,相比于低喚醒度的EEG信號,左中顳在高喚醒度狀態受到更多其他腦區的影響,而右前額所受影響則更少。在對認知障礙患者的情緒發生機制的研究中,顳葉對于情感信號檢測和情感抑制有著重要作用[14]。研究發現前額與情緒有著很大的關聯性,聽積極情緒的樂曲時,左前額會產生較強的腦電活動,而當聽消極情緒的樂曲時,右前額則會產生較強的腦電活動[15]。這些結論在本實驗中也得到了肯定。
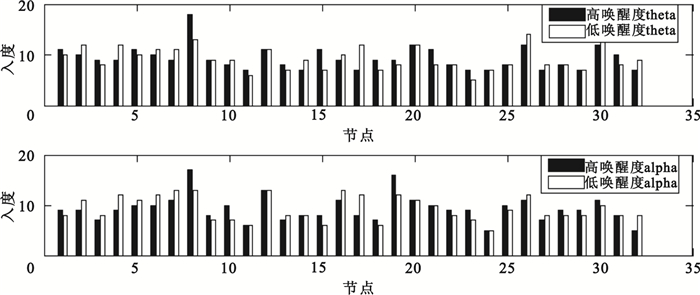 圖2
不同喚醒度的入度
Figure2.
Input degree of different arousal
圖2
不同喚醒度的入度
Figure2.
Input degree of different arousal
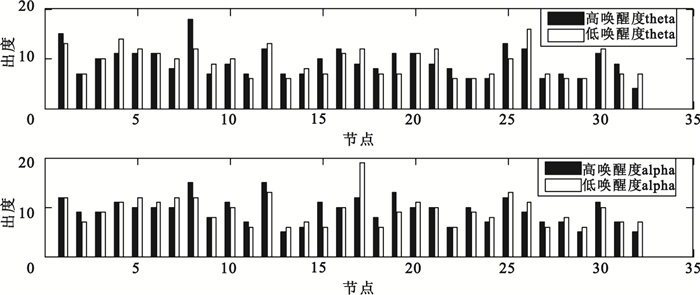 圖3
不同喚醒度的出度
Figure3.
Output degree of different arousal
圖3
不同喚醒度的出度
Figure3.
Output degree of different arousal
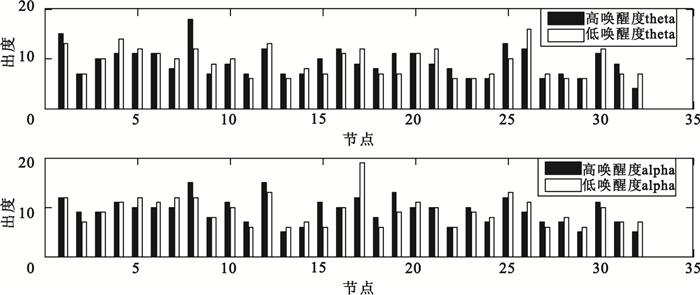
從圖 3可以看出,在theta頻段,高喚醒度下編號為8(T7)、15(Oz)、19(Fz)、25(C4)的節點出度比低喚醒度狀態≥3,編號為4(F7)、17(Fp2)、21(F8)、26(T8)、32(O2)的節點出度比低喚醒度狀態≤3;在alpha頻段,高喚醒度下編號為8(T7)、15(Oz)的節點出度比低喚醒度狀態≥3,編號為17(Fp2)的節點出度比低喚醒度狀態≤3。由此得出,相比于低喚醒度的EEG信號,左中顳和中部枕葉在高喚醒度狀態影響了更多其他腦區,而右前額對其他腦區的影響則更少。左中顳和右前額在入度和出度方面都表現出明顯差異,這與其他研究結論基本一致;而中部枕葉差異性也許是不同喚醒度狀態下所特有的,這為情緒喚醒度的研究提供了借鑒。
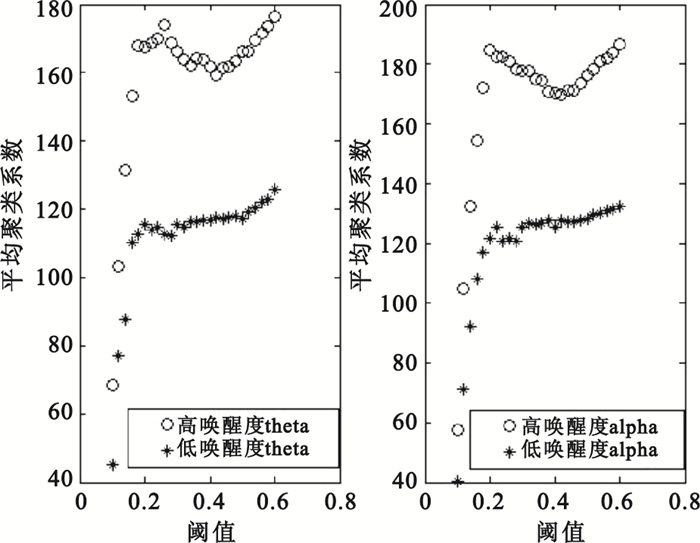
平均聚類系數描述了網絡中節點形成集團的可能性。平均聚類系數越大,網絡中的節點越傾向于形成緊密集團。不同喚醒度平均聚類系數隨閾值變化如圖 4所示。從圖 4可以看出,在theta和alpha頻段不同喚醒度的平均聚類系數隨閾值變化基本一致,在0.1到0.2的閾值范圍內,平均聚類系數迅速增大,隨后趨于平穩,但高喚醒度的平均聚類系數在閾值0.4左右有所降低。整體上,高喚醒度平均聚類系數明顯高于低喚醒度。因此,高喚醒度的腦網絡節點更容易形成集團。
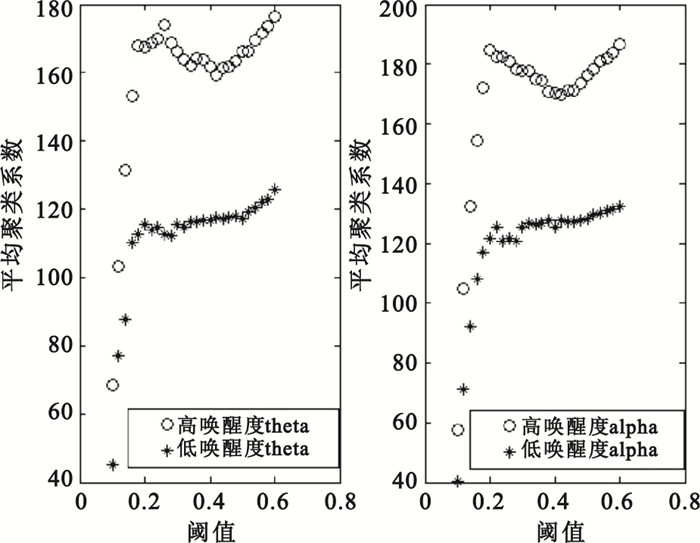 圖4
不同喚醒度的平均聚類系數
Figure4.
Average clustering coefficient of different arousal
圖4
不同喚醒度的平均聚類系數
Figure4.
Average clustering coefficient of different arousal
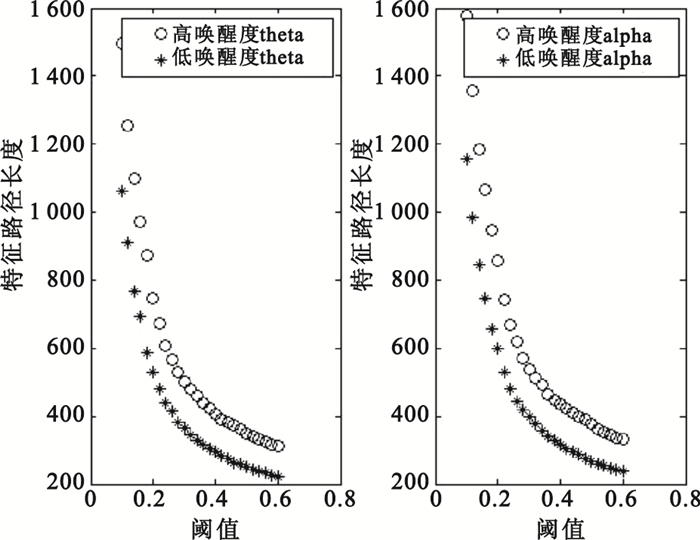
復雜網絡特征路徑長度大小反映了網絡結構的彌散性和連通性,即平均路徑越短,網絡的結構越緊湊,網絡連通性也越好。圖 5是在theta頻段和alpha頻段不同喚醒度的特征路徑長度隨閾值的變化圖。隨著閾值的增大,高喚醒度和低喚醒度的特征路徑長度大體上都呈指數衰減趨勢。由于低喚醒度的平均路徑長度較短,所以低喚醒度的有效性腦網絡結構更緊湊,連通性更好。
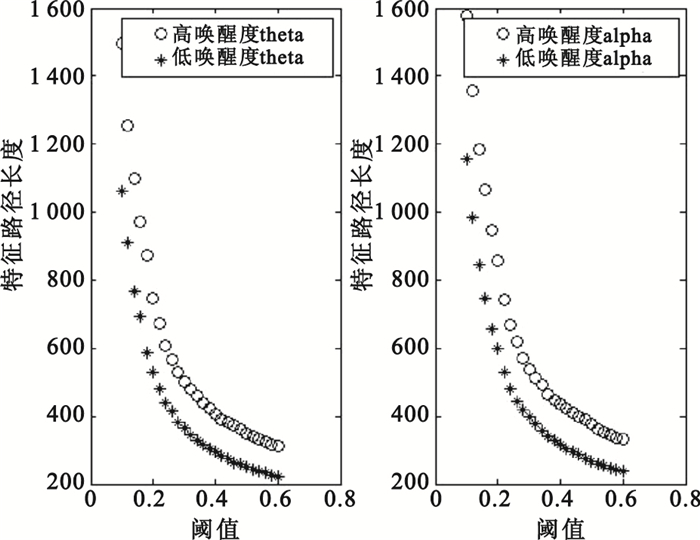 圖5
不同喚醒度的特征路徑長度
Figure5.
Characteristic path length of different arousal
圖5
不同喚醒度的特征路徑長度
Figure5.
Characteristic path length of different arousal
4 結論
本文研究了正常人情緒處于不同喚醒度時theta頻段和alpha頻段各導聯對之間的因果關系,并分析了不同喚醒度的有向性腦網絡的拓撲屬性差異。研究發現相比于低喚醒度的EEG信號,左中顳在高喚醒度狀態的因果影響都很明顯,而右前額因果影響都不顯著。另外,在情緒EEG的有效性腦網絡中,高喚醒度的平均聚類系數較高,而低喚醒度的特征路徑長度較短。
本文僅對不同喚醒度的有效性腦網絡基本測度進行了分析,復雜網絡的測度還包括小世界特性、網絡效率、中心度等,相關分析將在未來進一步展開,以便更加深入地理解不同情緒喚醒度下大腦功能活動規律。
引言
目前腦功能研究主要集中在定位不同認知功能活動中的某些功能模塊的激活,其中大腦認知研究則集中在某一特定認知任務中不同區域皮層功能模塊之間的信息流通交互作用,并以此為基礎研究大腦功能整合。隨著功能磁共振成像(functional magnetic resonance imaging,fMRI)、腦電圖(electroencephalogram,EEG)等技術的快速普及發展,腦網絡研究已成為神經信息科學研究中的熱門領域。功能網絡主要是提取感興趣腦區的時間序列,然后通過不同連接方式研究神經耦合關系[1]。由于僅根據腦區功能性信號間統計關系所構建的無向網絡,并不是嚴格意義上的功能網絡,因此必須在無向網絡基礎上繼續考慮信息在節點間的傳播方向,即節點間統計意義上的因果關系,并最終以此獲得有向網絡,才能更加真實地反映大腦的信息傳遞和功能活動[2]。
目前構建兩個腦區之間相互作用大小和方向的常用有效連接模型包括結構方程模型(structural equation modeling,SEM)、動態因果模型(dynamic causal analysis,DCM)和格蘭杰因果分析(Granger causality)等[3]。其中SEM中定義了連接方向,建立反映變量關系的模型,再通過調整連接強度得到最佳擬合模型及數據,估計參數,并檢查其顯著性。但是該模型存在以下缺點:①只用了相關矩陣信息,因此并不能準確建立區域間的交互關系,使得模型與實際神經系統網絡不一致;②忽略了時間序列包含的信息,導致結構方程模型結果不會隨時間序列信息順序的改變而變動。DCM則考察了節點活動的變化,是由外界刺激所引起的節點活動的直接和間接變化的總和,是模型匹配數據,因此如果感興趣區域太多,會極大地增加研究難度。目前DCM最大研究節點個數為8個[3]。根據格蘭杰因果分析,如果第一個節點時間序列當前值和過去值的線性組合能夠更好地預測第二個序列結果,則說明第一節點對第二節點有影響[2],但該分析需假設實際值與預測值間誤差呈正態分布,若實際情況呈其它分布類型將嚴重影響推論的有效性。貝葉斯網絡以概率論和圖論為基礎,將有向無環圖(directed acyclic graph,DAG)和條件概率表有機結合,描述了變量間的相互依賴關系[4]。由于貝葉斯網絡具有獨特的不確定性表達形式、易于綜合先驗知識以及推理結果直觀等特性,因此可以通過神經影像數據研究不同大腦區域的交互。目前該方法已成功應用在任務表現、技能學習和疾病過程診斷等方面。
在情緒認知過程中,大腦中與之相關的信息流向變化速度很快,一般是在毫秒級。因此,EEG的時間分辨率優勢得以凸顯出來[5]。已有研究表明,不同節律EEG可以反映不同認知功能下大腦各個區域的任務分配和功能整合。EEG信號根據不同頻帶可分為delta波(0.5~3 Hz)、theta波(4~7 Hz)、alpha波(8~13 Hz)、beta波(14~30 Hz)和gamma波(30~45 Hz)。其中delta波一般在睡眠時出現;theta波在困倦時可見,它的出現是中樞神經抑制狀態的表現;alpha波在靜息閉目狀態下的幅度比較大,是節律性腦電波中最明顯的波;beta波的出現代表了大腦皮層的興奮,是一種快波;gamma波代表的是大腦皮層的高度興奮。與情緒狀態關聯較大的頻段有theta波和alpha波等[6-7],因此本文將提取這兩個頻段的EEG信號進行研究。情緒的二維空間由愉悅度(valence,效價)和喚醒度(arousal)組成。效價維度的理論基礎是正性情緒和負性情緒的分離激活;喚醒度維度指情緒所激活機體能量的程度,即生理活動和心理警覺的水平差異,低喚醒如睡眠、厭倦、放松等,高喚醒如清醒、緊張等[8]。目前在對情緒認知機制的研究中,多數基于事件相關電位(event-related potentials,ERP)分析愉悅度差異,而基于EEG研究不同喚醒度大腦網絡信息流向、因果關系的報道則較少。因此,本文對不同喚醒度的EEG情緒信號,分別建立theta波和alpha波頻段大腦區域內的因果模型,探索不同喚醒度各頻段的因果調制,從而對比研究不同喚醒度情緒狀態的腦網絡拓撲特性。
1 研究方法
1.1 EEG腦功能網絡構建
對于多通道EEG信號,通常把每個EEG導聯對應的電極覆蓋區域定義為一個節點,然后量化EEG各通道信號之間的關系,以關系強弱作為判定對應腦區之間功能連接強度的指標,從而構建出功能性腦網絡[2]。其步驟可按照以下三步進行:
(1) 量化EEG信號通道關系:對EEG信號進行預處理以及提取特定頻段后,采用一種連接方法確定各節點之間的關系。基于引言中對各種有向連接方法的分析,本研究采用稀疏貝葉斯網絡(sparse Bayesian network,SBN)計算EEG信號各通道之間的兩兩關系。
(2) 確定閾值并構建大腦皮層功能性腦網絡:在量化EEG各通道之間的關系后,需進一步確定合適閾值以構建腦網絡。導聯的EEG信號之間的強度決定了兩個節點之間是否存在連接邊,即若強度大于設定閾值,則兩導聯之間建立連接邊,并設置鄰接矩陣對應元素為1,反之則不建立連接邊,設置鄰接矩陣對應元素為0。通常鄰接矩陣對角線元素為0,該構建網絡稱為0-1 二值網絡。
閾值選取直接影響著腦網絡的統計特性和拓撲結構。SBN構建網絡的過程中,通過一個懲罰變量實現對重要連接的篩選,即控制稀疏性的懲罰變量代替了閾值的作用。
(3) 采用現有復雜網絡測度分析建立的功能性腦網絡:在腦網絡分析中常用復雜網絡測度有節點的度、聚類系數、特征路徑長度等,需計算并分析上述參量可能反映的生理意義。
1.2 稀疏貝葉斯網絡
1986年,美國加州大學Judea Pearl教授首次提出完整的貝葉斯網絡,該網絡通過有向無環圖可以得知n組隨機變量條件概率分配的性質。一般而言,貝葉斯網絡有向無環圖中的節點表示隨機變量,可以是可觀察變量、隱變量、未知參數等。連接兩個節點的箭頭代表此兩個隨機變量具有因果關系或是非條件獨立;而節點中變量間若沒有箭頭相互連接則稱其隨機變量,彼此間為條件獨立。若節點間以一個單箭頭連接在一起,表示其中一個節點是“因(parents)”,另一個是“果(descendants or children)”。
貝葉斯網絡主要由兩部分構成,分別對應問題領域的定性和定量描述,即網絡結構和網絡參數。早期學者依靠專家知識指定的概率分布構建貝葉斯網絡結構,這種方法往往導致與觀測數據產生較大偏差,具有一定的局限性。而SBN采用一種懲罰變量獲得稀疏性,以保證獲得有向無環圖,更加準確高效地實現了貝葉斯網絡的學習[4]。
假設x=[x1,x2,…,xm]T是一個包含m個特征(變量)的樣本,D∈Rn×m是n個樣本數據矩陣,D的第i行為樣本xi,第j列為fj。貝葉斯網絡用有向無環圖表示變量的聯合分布,變量對應圖中相應節點,聯合分布表示為,其中Pa(xi)是xi的所有父節點。每個節點xi可寫成其父節點的回歸表示,即,其中向量θi是回歸系數,εi~N(0,σ2i)。矩陣Θ=[θ1,…,θm]為貝葉斯網絡參數,G(m×m)表示網絡結構,如果從xi到xj存在連接,那么Gij=1;否則Gij=0。矩陣P(p×p)表示路徑,如果從xi到xj存在一條路徑,那么Pij=1;否則Pij=0。
傳統貝葉斯網絡通過兩步學習網絡結構和參數,SBN則通過對貝葉斯網絡執行稀疏約束同時得到網絡結構和參數,具體來說,就是解決一個有約束的最小二乘擬合問題,公式如下:
| $ \begin{array}{l} \mathop {\min }\limits_\theta \sum\limits_{i = 1}^m {\left\| {{f_i} - \theta _i^TPa\left( {{x_i}} \right)} \right\|_2^2} + {\lambda _1}{\left\| {{\theta _i}} \right\|_1}\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\Theta _{ji}} \times {P_{ij}} = 0 \end{array} $ |
其中矩陣Pa(xi)的第i行對應xi的所有父節點,初始化為除xi的所有節點,然后對回歸系數θi的系數約束進行過濾。該約束條件保證了結果為有向無環圖。
1.3 復雜網絡測度
復雜網絡中不依賴于節點具體位置和連線具體形態而表現出來的性質叫做網絡的拓撲性,相應結構稱為網絡的拓撲結構。近年來,基于醫學成像的腦功能網絡研究為刻畫復雜網絡拓撲結構的性質,定義了多個測度用來度量網絡整體或局部特征。其中最主要的概念為:節點的度、聚類系數、特征路徑長度。
節點的度是對節點互相連接統計特性最重要的描述,其度值定義為與節點直接相連的邊數,可由鄰接矩陣第i行或列元素求和得到。如果網絡是有向網絡,節點的度分為兩部分:入度和出度。節點入度是指從其他節點指向該節點的邊數,即該節點作為“果”的連接數目;出度是指從該節點指向其他節點的邊數,即該節點作為“因”的連接數目。總度值為入度與出度值之和。節點入度越大,則影響該節點的連接越多,表明該節點在網絡中是多個節點共同作用的結果。節點出度越大,則該節點在網絡中是多個節點的“因”,表明該節點在網絡中所起作用越大,反之則越小。
聚類系數衡量的是網絡集團程度,表示某一節點的鄰居間互為鄰居的可能。節點i的聚類系數Ci等于該節點鄰居間實際連接邊的數目與可能連接的最大邊數的比值[9],即
| $ {C_i} = \frac{{2{e_i}}}{{{k_i}\left( {k - 1} \right)}} $ |
其中,ei為節點i鄰居間實際連接邊的數目,ki(ki-1)/2為可能連接的最大邊數。對于復雜網絡,由于節點眾多,因此通常不是詳細研究每個節點的聚類系數大小,而是求算整個網絡所有節點總數N聚類系數的平均值,即平均聚類系數,計算如下:
| $ C = \frac{1}{N}\sum\limits_{i = 1}^n {{C_i}} $ |
該系數描述的是網絡中節點形成集團的可能性。C越大,網絡節點越傾向于形成緊密的集團。
網絡特征路徑長度L描述的是網絡全局連接特征,定義為任意兩個節點之間的距離平均值[10],計算公式如下:
| $ L = \frac{1}{{N\left( {N - 1} \right)}}\sum {{d_{ij}}} $ |
其中N代表網絡節點總數,dij表示網絡中節點i、j之間的距離,它被定義為連接這兩個節點最短路徑上的邊數。復雜網絡平均路徑長度大小反映網絡結構的彌散性和連通性,即平均路徑越短,網絡結構越緊湊,網絡連通性也越好,任意兩個節點之間的通信可以較快完成;反之,則網絡結構松散,網絡的連通性差,節點之間的通信較困難。
2 實驗數據
本研究所使用的情緒EEG數據來源于英國帝國理工大學Intelligent Behaviour Understanding小組,在22名被試觀看嚴格篩選的音樂視頻片段時采集,每個視頻結束后被試對喚醒度水平進行自我評價,評價采用9點量表,表示喚醒度水平從平靜(無聊)逐漸過渡到刺激(興奮)[11]。實驗所用腦電采集儀為32導電極帽,電極帽的放置排布按照國際的10/20導聯標準進行。數據經過128 Hz重采樣,去除眼電偽跡,通過4.5~45.0 Hz帶通濾波的預處理數據[11]。每個被試EEG數據以63 s為一段進行分割,按照視頻順序形成40×32×8 064(視頻×導聯×采樣點)的數據文件。依據被試自我評價表中喚醒度的打分,將情緒數據分為高喚醒度和低喚醒度兩類,得到513個高喚醒度的情緒樣本和367個低喚醒度的情緒樣本。
3 數據處理
3.1 EEG頻段信號提取
由于EEG信號具有明顯的非線性和非平穩特性,采用傳統傅里葉變換頻域分析方法不能很好地分析EEG信號。近些年來,隨著小波變換的不斷發展,國內外許多研究者將小波分析用于生物醫學信號的提取及去噪處理。小波變換是一種在時域頻域均能進行分析的信號處理方法,具有良好的時頻局部化特性。本文利用Matlab工具箱中的小波分解方法,選取Daubechies小波函數進行5層小波分解,提取EEG信號中包含的theta波和alpha波,為構建腦功能網絡做好準備。
實驗中,被試進入有效思考要經過數秒時間,而且因為思考時間較長,最后幾秒往往不是很有效,因此EEG數據處理中一般取被試精神狀態比較好、思想集中的時間段內的數據。本研究從第5秒數據點開始,對中間50 s的EEG數據進行小波分解,分別從高喚醒度和低喚醒度的情緒樣本中提取出實驗所需的theta波和alpha波。
3.2 構建不同喚醒度的有效性腦網絡
首先利用SBN把每個被試的EEG信號構造為一個二值網絡,在顯著性水平為0.05的條件下對所有節點之間有效連接強度的顯著性進行判定。結果表明在1 024(32×32)個導聯對中,theta頻段有131個連接特征有顯著差異,alpha頻段有171個連接有顯著差異。然后分別把高喚醒度和低喚醒度的矩陣相加,得到theta波和alpha波各兩組不同喚醒度的有效性腦網絡。為了直觀地表示腦網絡連接,更清晰地顯示各個導聯之間的信息流向,以稀疏程度為0.3的腦網絡為例,利用Bsmart工具箱[12]繪制了theta波在低喚醒度下的有效性腦網絡,如圖 1所示。圖中顯示了32個節點在腦電采集設備上的相對位置,節點之間的箭頭表示不同腦區之間的信息流向。在此基礎上,對兩個頻段不同喚醒度的網絡測度進行分析。
 圖1
有效性腦網絡
Figure1.
Effective network
圖1
有效性腦網絡
Figure1.
Effective network
3.3 不同喚醒度的有效性腦網絡測度分析
為得到不同情緒喚醒度的網絡測度的變化規律,本文根據EEG信號所包含的theta波和alpha波繪制了測度隨閾值變化的曲線圖,進一步比較高喚醒度和低喚醒度的EEG信號在不同頻段腦網絡特性的異同,實驗結果借助BCT(Brain Connectivity Toolbox)工具箱[13]用Matlab2010b得到。
入度和出度是有效網絡特有的屬性,由于這種屬性是針對網絡中的每個節點描述,而閾值為0.3的腦網絡能夠清晰顯示各導聯之間的信息流向,本文將0.3作為閾值得到theta波和alpha波在不同喚醒度下的入度和出度,并進行對比,如圖 2、圖 3所示。從圖 2可知,在theta頻段,高喚醒度下編號為8(T7)、15(Oz)、21(F8)的節點入度均比低喚醒度狀態≥3,17(Fp2)號節點入度比低喚醒度狀態<5;在alpha頻段,高喚醒度下編號為8(T7)、10(CP1)、19(Fz)的節點入度比低喚醒度狀態≥3,編號為4(F7)、17(Fp2)、32(O2)的節點入度比低喚醒度狀態≤3。由此得出,相比于低喚醒度的EEG信號,左中顳在高喚醒度狀態受到更多其他腦區的影響,而右前額所受影響則更少。在對認知障礙患者的情緒發生機制的研究中,顳葉對于情感信號檢測和情感抑制有著重要作用[14]。研究發現前額與情緒有著很大的關聯性,聽積極情緒的樂曲時,左前額會產生較強的腦電活動,而當聽消極情緒的樂曲時,右前額則會產生較強的腦電活動[15]。這些結論在本實驗中也得到了肯定。
 圖2
不同喚醒度的入度
Figure2.
Input degree of different arousal
圖2
不同喚醒度的入度
Figure2.
Input degree of different arousal
 圖3
不同喚醒度的出度
Figure3.
Output degree of different arousal
圖3
不同喚醒度的出度
Figure3.
Output degree of different arousal
從圖 3可以看出,在theta頻段,高喚醒度下編號為8(T7)、15(Oz)、19(Fz)、25(C4)的節點出度比低喚醒度狀態≥3,編號為4(F7)、17(Fp2)、21(F8)、26(T8)、32(O2)的節點出度比低喚醒度狀態≤3;在alpha頻段,高喚醒度下編號為8(T7)、15(Oz)的節點出度比低喚醒度狀態≥3,編號為17(Fp2)的節點出度比低喚醒度狀態≤3。由此得出,相比于低喚醒度的EEG信號,左中顳和中部枕葉在高喚醒度狀態影響了更多其他腦區,而右前額對其他腦區的影響則更少。左中顳和右前額在入度和出度方面都表現出明顯差異,這與其他研究結論基本一致;而中部枕葉差異性也許是不同喚醒度狀態下所特有的,這為情緒喚醒度的研究提供了借鑒。
平均聚類系數描述了網絡中節點形成集團的可能性。平均聚類系數越大,網絡中的節點越傾向于形成緊密集團。不同喚醒度平均聚類系數隨閾值變化如圖 4所示。從圖 4可以看出,在theta和alpha頻段不同喚醒度的平均聚類系數隨閾值變化基本一致,在0.1到0.2的閾值范圍內,平均聚類系數迅速增大,隨后趨于平穩,但高喚醒度的平均聚類系數在閾值0.4左右有所降低。整體上,高喚醒度平均聚類系數明顯高于低喚醒度。因此,高喚醒度的腦網絡節點更容易形成集團。
 圖4
不同喚醒度的平均聚類系數
Figure4.
Average clustering coefficient of different arousal
圖4
不同喚醒度的平均聚類系數
Figure4.
Average clustering coefficient of different arousal
復雜網絡特征路徑長度大小反映了網絡結構的彌散性和連通性,即平均路徑越短,網絡的結構越緊湊,網絡連通性也越好。圖 5是在theta頻段和alpha頻段不同喚醒度的特征路徑長度隨閾值的變化圖。隨著閾值的增大,高喚醒度和低喚醒度的特征路徑長度大體上都呈指數衰減趨勢。由于低喚醒度的平均路徑長度較短,所以低喚醒度的有效性腦網絡結構更緊湊,連通性更好。
 圖5
不同喚醒度的特征路徑長度
Figure5.
Characteristic path length of different arousal
圖5
不同喚醒度的特征路徑長度
Figure5.
Characteristic path length of different arousal
4 結論
本文研究了正常人情緒處于不同喚醒度時theta頻段和alpha頻段各導聯對之間的因果關系,并分析了不同喚醒度的有向性腦網絡的拓撲屬性差異。研究發現相比于低喚醒度的EEG信號,左中顳在高喚醒度狀態的因果影響都很明顯,而右前額因果影響都不顯著。另外,在情緒EEG的有效性腦網絡中,高喚醒度的平均聚類系數較高,而低喚醒度的特征路徑長度較短。
本文僅對不同喚醒度的有效性腦網絡基本測度進行了分析,復雜網絡的測度還包括小世界特性、網絡效率、中心度等,相關分析將在未來進一步展開,以便更加深入地理解不同情緒喚醒度下大腦功能活動規律。