阿爾茨海默癥(AD)是以進行性認知功能障礙為主要特征的神經系統變性疾病,如何識別其大腦認知障礙的早期改變并干預治療,對延緩癡呆的發生具有重要意義。已有研究表明AD與腦連接的異常變化有關。本文選取AD組和正常對照組各15名志愿者,采集清醒閉目狀態的16導聯腦電圖(EEG)數據,分別對全頻段和alpha頻段(8~13 Hz)EEG進行同步似然分析,選擇合適閾值構建腦網絡并計算網絡的全局效率和聚類系數。結果表明,當閾值0.05≤T≤0.07時,AD組和正常對照組全頻段腦網絡的聚類系數無顯著差異,閾值為0.06和0.07時AD組全頻段網絡全局效率比正常對照組小(P＜0.05);閾值范圍(0.05≤T≤0.07)內,alpha網絡AD組聚類系數和全局效率均低于正常對照組(P＜0.05)。AD患者靜息態腦電alpha網絡可能存在功能連接減弱現象,為從腦網絡角度定量評估AD患者腦功能狀態提供支持。
引用本文： 李莉, 陳靜靜, 鄭旭媛. 基于同步似然分析的阿爾茨海默癥靜息態腦電功能連接特性的研究. 生物醫學工程學雜志, 2015, 32(5): 952-957. doi: 10.7507/1001-5515.20150170 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
阿爾茨海默癥(Alzheimer’s disease,AD)是一種中樞神經系統退行性疾病，表現為進行性記憶力顯著受損引發的腦功能障礙進而導致整體認知功能受損，嚴重威脅老年人身心健康和生活質量。如何定量評價AD患者腦功能狀態并識別其異常表現，對AD早期診斷和延緩癡呆發生具有重要意義。
近年來腦網絡研究快速發展[1]，越來越多的研究者將圖論理論應用于人腦功能網絡研究[2-6]，人腦功能連接網絡在大尺度上通常采用功能磁共振成像(functional magnetic resonance imaging,fMRI)、腦電圖(electroencephalogram,EEG)或腦磁圖(magnetoencephalogram,MEG)數據，以皮爾森相關[7]、相干性[8]、同步似然(synchronization likelihood,SL)分析[9]等方法衡量腦區之間的相關性，從而實現對腦網絡功能連接特性的量化分析。Supekar等[10]利用小波分析的方法研究AD患者基于靜息態fMRI數據的腦功能網絡，發現在低頻區“小世界”屬性表現顯著異常，網絡的拓撲屬性可能有助于區分AD患者和正常老年人。Stam等[11]首次基于靜息態EEG數據，應用圖論分析的方法比較AD組和對照組構建的網絡，發現AD患者腦功能網絡的最短平均路徑長度相對正常人顯著增加，提示AD患者腦功能網絡的小世界屬性可能丟失。Stam等[12]隨后利用靜息態MEG數據研究了AD患者多個頻段的腦功能網絡，發現在低alpha頻段(8~10 Hz)特征路徑長度較大，聚類系數、標準化聚類系數和標準化特征路徑長度較小。de Haan等[13]發現AD患者靜息態EEG信號在多個頻段功能腦網絡存在拓撲結構的改變，和健康對照相比，在低alpha頻段(8~10 Hz)和beta頻段(13~30 Hz)AD患者的標準化聚類系數較低，在低alpha頻段和gamma頻段(30~45 Hz)AD患者的標準化特征路徑長度較短。以上研究表明AD患者存在腦網絡拓撲結構變化，圖論為研究AD患者腦功能連接特性提供了有力工具。
靜息態是人體處于安靜清醒的基準狀態，研究該狀態下的神經活動對了解基本的神經生理機制有著重要的作用[14]。alpha節律是靜息態正常EEG信號的主要節律，研究表明alpha活動在認知、感覺運動、心理情感以及生理過程中扮演著重要角色[15-16]。同步似然算法是Stam等[17]提出的一種基于廣義同步的定義，更適合于非平穩信號分析，用于檢測兩個或更多同時記錄的時間序列信號之間線性和非線性相互依賴關系的標準化估計，在EEG腦網絡研究中應用較多。因此本文以AD患者和正常老年人為研究對象，提取alpha節律，使用同步似然系數衡量靜息態多通道EEG信號之間的同步程度，構建全頻段和alpha頻段腦功能連接網絡，計算網絡的全局效率和聚類系數，從腦網絡層面定量AD患者腦功能狀態。
1 材料和方法
1.1 實驗數據獲取和預處理
本文受試者均來自天津醫科大學總醫院神經內科就診患者，其中AD組15人，男性7名，女性8名，年齡(74.2±9.0)歲；正常對照組15人，男性7名，女性8名，年齡(71.3±6.4)歲。兩組受試者的年齡、性別差異均無統計學意義。采用日本光電Neurofax2130型32導數字化腦電系統，時間常數0.3 s，采樣頻率169 Hz，采樣精度16 bit，電極位置依據國際標準導聯10~20系統放置，記錄AD組和正常對照組受試者在安靜閉目清醒狀態的16導聯(Fp1、Fp2、F3、F4、C3、C4、P3、P4、O1、O2、F7、F8、T3、T4、T5、T6)EEG信號3 min。
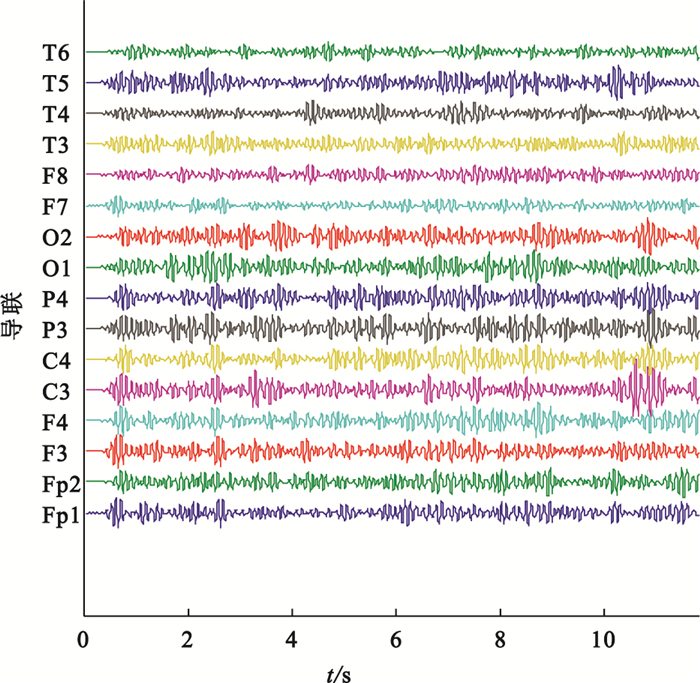
采集到的原始數據選取基線較平穩、無明顯偽差(由于肌肉運動、外界干擾、電極移動等外部因素造成)的EEG信號2 000個采樣點，基于Matlab編程實現基線漂移校正、工頻濾波等預處理，提取EEG信號的alpha節律(8~13 Hz)如圖 1所示，由此得到全頻段和alpha頻段EEG信號用于后續同步似然分析。
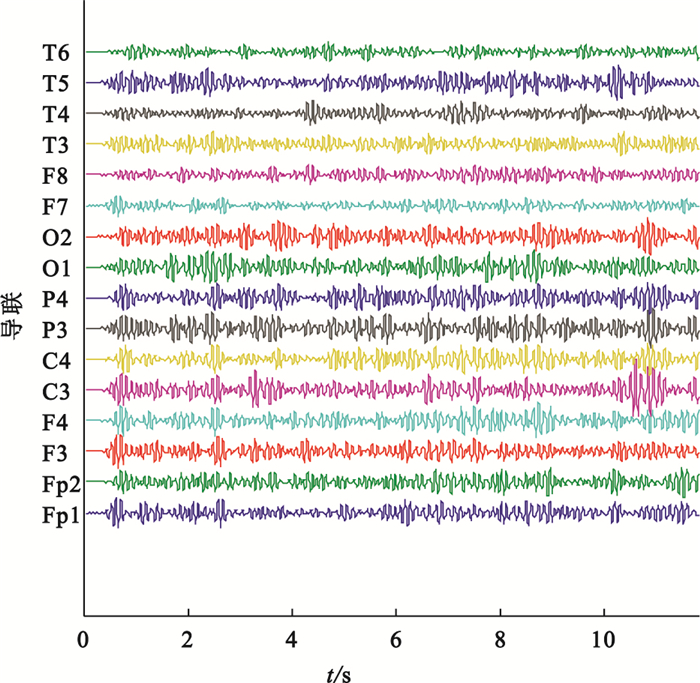圖1
alpha頻段EEG信號
Figure1.
Alpha-band EEGs
1.2 同步似然分析方法
同步似然算法的理論基礎是系統在給定時刻的狀態可以表示為一個插值向量，當再次出現這個系統狀態時，將由一個相似的插值向量表示[17-18]。因此本文計算兩導聯之間同步強度的同步似然分析基本步驟包括：
(1)重建時間序列，將記錄的Channel A時間序列xA,i(i=1,…,N,表示離散時間)，嵌入m維空間中：
| $ {X_{A,i}} = \left( {{x_{A,i}},{x_{A,i + l}},{x_{A,i + 2l}},\cdots ,{x_{A,i + \left( {m - 1} \right)l}}} \right) $ |
其中l是時間延遲，采用同樣的方法對Channel B重構狀態向量空間XB,i。
(2)對Channel A和時間i，假定各向量彼此間的距離小于r的概率為：
| $ P_{A,i}^r = \frac{1}{{2\left( {{w_2} - {w_1}} \right)}}\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {{w_1} < \left| {i - j} \right| < {w_2}} \end{array}}^N {\theta \left( {r - \left| {{X_{A,x}} - {X_{A,j}}} \right|} \right)} $ |
其中：｜·｜表示兩個相空間矢量的歐幾里德距離(Euclidean distance)；θ是Heaviside階梯函數，當x≤0時，θ(x)=0；當x＞0時，θ(x)=1；w1和w2是兩個窗，w1是用于消除自相關的Theiler修正，w2是用來提高時間分辨率的窗，w1和w2需滿足：；
(3)對Channel A和時間i確定其狀態向量的臨界距離：，其中；同樣對Channel B得到其臨界距離為：。
(4)Channel A和B的同步似然值SLAB的確定：SLAB是Channel A和B同時重現其狀態向量的可能性，即當XA,j和給定的XA,i之間的距離小于臨界距離rA,i時，同時XB,j和XB,i之間距離也小于rB,i的可能性。SLAB取值于pref與1之間，SLAB=pref說明兩個導聯完全不同步，SLAB=1說明兩個導聯達到最大程度同步化。依以往文獻經驗，本文選取相關參數為l=10,m=10,pref=0.05,w1=100,w2=200。
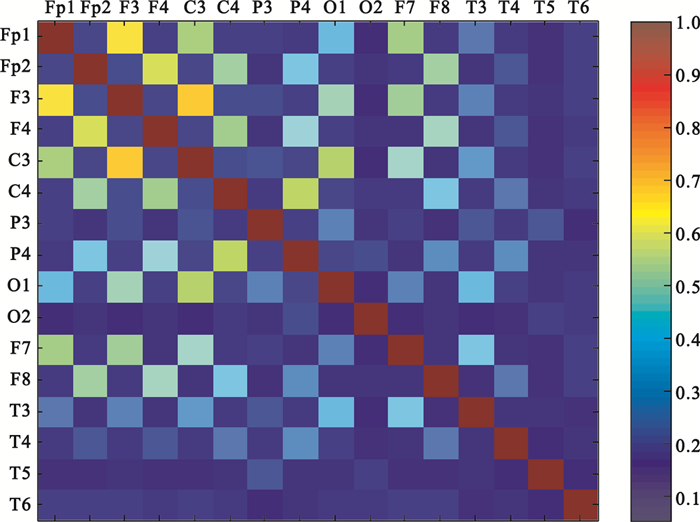
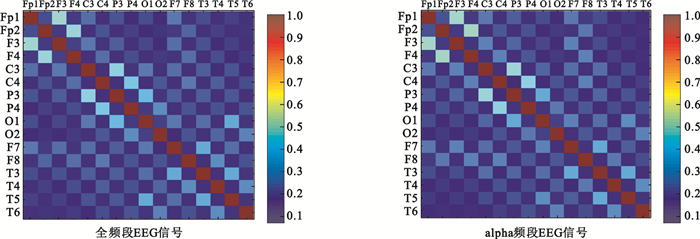
EEG信號進行同步似然分析得到同步似然系數矩陣，如圖 2所示。同步似然系數矩陣是一個16×16的方陣，其大小由導聯數決定，方陣中每一個元素表示橫縱交叉的導聯之間相互作用大小，數值介于pref和1之間(即圖 2右端標尺的范圍)，數值越接近1說明兩個導聯的同步化程度越大。
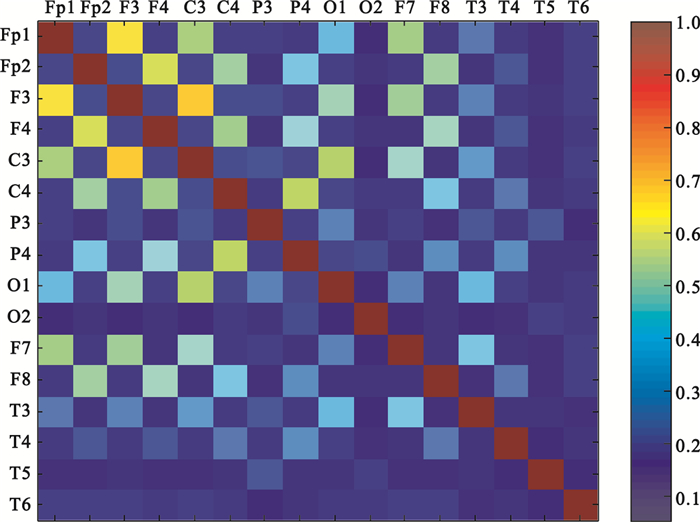圖2
同步似然系數矩陣
Figure2.
Synchronization likelihood coefficient matrix
1.3 構建腦功能網絡及網絡參數計算
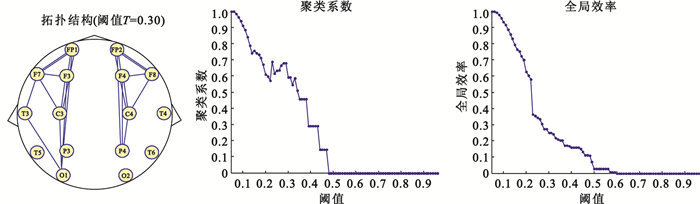
圖論是表征復雜網絡的合適方法[19-20]，由節點和邊構成，文中定義節點為16導聯EEG的電極位置，利用同步似然分析衡量兩兩腦區之間的關聯性大小，得到同步似然系數矩陣，為了消除弱連接的影響，通常設置不同的閾值對關聯矩陣進行二值化，得到圖論中表示邊的二值矩陣(即鄰接矩陣，只包含0或1，1表示節點之間存在連接，0表示節點之間沒有連接)，同步似然系數矩陣即轉換成拓撲結構，計算表征網絡信息整合的全局效率值和表征網絡局部分割特征的聚類系數值。如圖 3所示，分別為設置閾值T=0.30時同步似然系數矩陣進行二值化得到的拓撲結構，以及設置不同閾值(0.05∶0.01∶1)得到的聚類系數和全局效率變化圖。
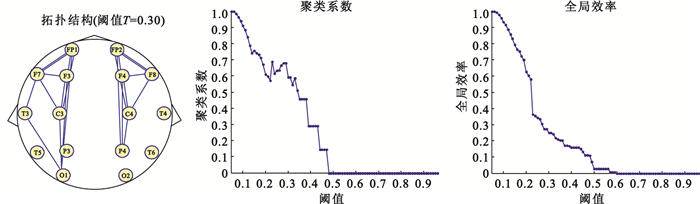圖3
網絡拓撲結構以及聚類系數和全局效率變化圖
Figure3.
Topological structure of network and the clustering coefficient and global efficiency curves
1.4 統計學方法
使用SPSS 20.0統計軟件分析，計量資料用均數±標準差(
2 結果
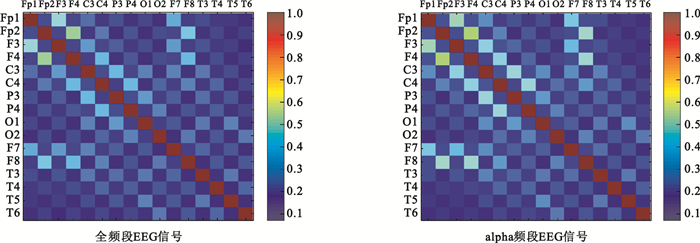
如圖 4所示為正常對照組15名受試者全頻段EEG信號和alpha頻段EEG信號進行同步似然分析得到的平均同步似然系數矩陣，AD組計算結果如圖 5所示。比較圖 4和圖 5，發現與對照組相比，AD組全頻段和alpha頻段EEG信號得到的平均同步似然系數矩陣值均較小，表明EEG信號的同步程度較弱。
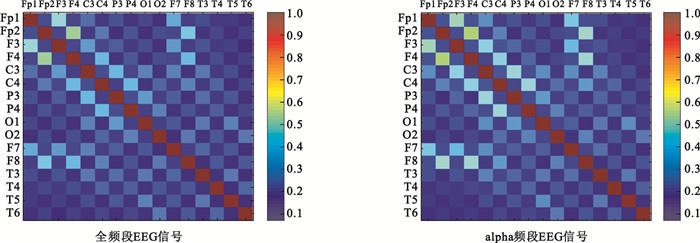圖4
正常對照組平均同步似然系數矩陣(n=15)
Figure4.
Average synchronization likelihood coefficient matrices for the control group (n=15)
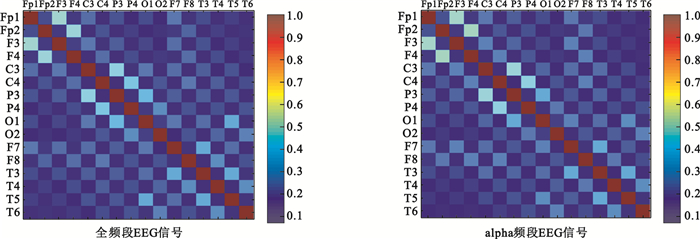圖5
AD組平均同步似然系數矩陣(n=15)
Figure5.
Average synchronization likelihood coefficient matrices for the AD group (n=15)
同步似然系數矩陣是加權矩陣，設置閾值T轉換成拓撲結構，即可計算參數指標進行網絡特性分析。已有研究表明，當網絡平均連接度滿足
表 1和表 2分別為閾值0.05≤T≤0.07范圍內全頻段網絡和alpha網絡聚類系數和全局效率的統計分析結果。隨著閾值的增大，正常對照組和AD組的聚類系數和全局效率均減小。在閾值0.05≤T≤0.07范圍內，AD組和正常對照組全頻段網絡的聚類系數無顯著差異，T=0.06和T=0.07時，AD組全頻段網絡的全局效率比正常對照組小(P＜0.05)；該閾值范圍內AD組alpha網絡的全局效率和聚類系數均比正常對照組小(P＜0.05)。
表1
正常對照組和AD組閾值范圍0.05≤T≤0.07內全頻段網絡連接參數
Table1.
Clustering coefficient and global efficiency for the AD and control groups within values of threshold (0.05≤T≤0.07) in the full band EEGs
表2
正常對照組和AD組閾值范圍0.05≤T≤0.07內alpha網絡連接參數
Table2.
Clustering coefficient and global efficiency for the AD and control groups within values of threshold (0.05≤T≤0.07) in the alpha-band EEGs
3 結論
本文對AD患者和正常老年人靜息態腦電功能連接的研究結果顯示，AD組alpha網絡的全局效率和聚類系數均比正常對照組低(P＜0.05)，表明AD患者靜息態腦電alpha網絡功能連接可能存在減弱，提示alpha網絡的改變可能與AD患者認知能力受損有關。不同研究者采用不同實驗數據和計算方法得到的結果不完全一致，Stam等[12] 使用相位延遲指數(phase lag index，PLI)衡量MEG導聯之間的同步性，de Haan等[13]利用同步似然算法和圖論方法分析靜息態EEG構建大尺度腦功能網絡，均發現AD患者的alpha標準化聚類系數和標準化特征路徑長度減小，而Stam等[11]曾發現AD患者靜息態beta網絡的平均最短路徑長度較長。本文使用同步似然算法衡量不同導聯EEG信號之間同步程度，應用圖論方法定量分析網絡的拓撲特性，發現AD患者的alpha網絡功能連接減弱，該研究思路適用于其他頻段網絡的研究，有助于從網絡層面量化AD患者腦功能狀態，為評估患病程度提供支持。
引言
阿爾茨海默癥(Alzheimer’s disease,AD)是一種中樞神經系統退行性疾病，表現為進行性記憶力顯著受損引發的腦功能障礙進而導致整體認知功能受損，嚴重威脅老年人身心健康和生活質量。如何定量評價AD患者腦功能狀態并識別其異常表現，對AD早期診斷和延緩癡呆發生具有重要意義。
近年來腦網絡研究快速發展[1]，越來越多的研究者將圖論理論應用于人腦功能網絡研究[2-6]，人腦功能連接網絡在大尺度上通常采用功能磁共振成像(functional magnetic resonance imaging,fMRI)、腦電圖(electroencephalogram,EEG)或腦磁圖(magnetoencephalogram,MEG)數據，以皮爾森相關[7]、相干性[8]、同步似然(synchronization likelihood,SL)分析[9]等方法衡量腦區之間的相關性，從而實現對腦網絡功能連接特性的量化分析。Supekar等[10]利用小波分析的方法研究AD患者基于靜息態fMRI數據的腦功能網絡，發現在低頻區“小世界”屬性表現顯著異常，網絡的拓撲屬性可能有助于區分AD患者和正常老年人。Stam等[11]首次基于靜息態EEG數據，應用圖論分析的方法比較AD組和對照組構建的網絡，發現AD患者腦功能網絡的最短平均路徑長度相對正常人顯著增加，提示AD患者腦功能網絡的小世界屬性可能丟失。Stam等[12]隨后利用靜息態MEG數據研究了AD患者多個頻段的腦功能網絡，發現在低alpha頻段(8~10 Hz)特征路徑長度較大，聚類系數、標準化聚類系數和標準化特征路徑長度較小。de Haan等[13]發現AD患者靜息態EEG信號在多個頻段功能腦網絡存在拓撲結構的改變，和健康對照相比，在低alpha頻段(8~10 Hz)和beta頻段(13~30 Hz)AD患者的標準化聚類系數較低，在低alpha頻段和gamma頻段(30~45 Hz)AD患者的標準化特征路徑長度較短。以上研究表明AD患者存在腦網絡拓撲結構變化，圖論為研究AD患者腦功能連接特性提供了有力工具。
靜息態是人體處于安靜清醒的基準狀態，研究該狀態下的神經活動對了解基本的神經生理機制有著重要的作用[14]。alpha節律是靜息態正常EEG信號的主要節律，研究表明alpha活動在認知、感覺運動、心理情感以及生理過程中扮演著重要角色[15-16]。同步似然算法是Stam等[17]提出的一種基于廣義同步的定義，更適合于非平穩信號分析，用于檢測兩個或更多同時記錄的時間序列信號之間線性和非線性相互依賴關系的標準化估計，在EEG腦網絡研究中應用較多。因此本文以AD患者和正常老年人為研究對象，提取alpha節律，使用同步似然系數衡量靜息態多通道EEG信號之間的同步程度，構建全頻段和alpha頻段腦功能連接網絡，計算網絡的全局效率和聚類系數，從腦網絡層面定量AD患者腦功能狀態。
1 材料和方法
1.1 實驗數據獲取和預處理
本文受試者均來自天津醫科大學總醫院神經內科就診患者，其中AD組15人，男性7名，女性8名，年齡(74.2±9.0)歲；正常對照組15人，男性7名，女性8名，年齡(71.3±6.4)歲。兩組受試者的年齡、性別差異均無統計學意義。采用日本光電Neurofax2130型32導數字化腦電系統，時間常數0.3 s，采樣頻率169 Hz，采樣精度16 bit，電極位置依據國際標準導聯10~20系統放置，記錄AD組和正常對照組受試者在安靜閉目清醒狀態的16導聯(Fp1、Fp2、F3、F4、C3、C4、P3、P4、O1、O2、F7、F8、T3、T4、T5、T6)EEG信號3 min。
采集到的原始數據選取基線較平穩、無明顯偽差(由于肌肉運動、外界干擾、電極移動等外部因素造成)的EEG信號2 000個采樣點，基于Matlab編程實現基線漂移校正、工頻濾波等預處理，提取EEG信號的alpha節律(8~13 Hz)如圖 1所示，由此得到全頻段和alpha頻段EEG信號用于后續同步似然分析。
圖1
alpha頻段EEG信號
Figure1.
Alpha-band EEGs
1.2 同步似然分析方法
同步似然算法的理論基礎是系統在給定時刻的狀態可以表示為一個插值向量，當再次出現這個系統狀態時，將由一個相似的插值向量表示[17-18]。因此本文計算兩導聯之間同步強度的同步似然分析基本步驟包括：
(1)重建時間序列，將記錄的Channel A時間序列xA,i(i=1,…,N,表示離散時間)，嵌入m維空間中：
| $ {X_{A,i}} = \left( {{x_{A,i}},{x_{A,i + l}},{x_{A,i + 2l}},\cdots ,{x_{A,i + \left( {m - 1} \right)l}}} \right) $ |
其中l是時間延遲，采用同樣的方法對Channel B重構狀態向量空間XB,i。
(2)對Channel A和時間i，假定各向量彼此間的距離小于r的概率為：
| $ P_{A,i}^r = \frac{1}{{2\left( {{w_2} - {w_1}} \right)}}\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {{w_1} < \left| {i - j} \right| < {w_2}} \end{array}}^N {\theta \left( {r - \left| {{X_{A,x}} - {X_{A,j}}} \right|} \right)} $ |
其中：｜·｜表示兩個相空間矢量的歐幾里德距離(Euclidean distance)；θ是Heaviside階梯函數，當x≤0時，θ(x)=0；當x＞0時，θ(x)=1；w1和w2是兩個窗，w1是用于消除自相關的Theiler修正，w2是用來提高時間分辨率的窗，w1和w2需滿足：；
(3)對Channel A和時間i確定其狀態向量的臨界距離：，其中；同樣對Channel B得到其臨界距離為：。
(4)Channel A和B的同步似然值SLAB的確定：SLAB是Channel A和B同時重現其狀態向量的可能性，即當XA,j和給定的XA,i之間的距離小于臨界距離rA,i時，同時XB,j和XB,i之間距離也小于rB,i的可能性。SLAB取值于pref與1之間，SLAB=pref說明兩個導聯完全不同步，SLAB=1說明兩個導聯達到最大程度同步化。依以往文獻經驗，本文選取相關參數為l=10,m=10,pref=0.05,w1=100,w2=200。
EEG信號進行同步似然分析得到同步似然系數矩陣，如圖 2所示。同步似然系數矩陣是一個16×16的方陣，其大小由導聯數決定，方陣中每一個元素表示橫縱交叉的導聯之間相互作用大小，數值介于pref和1之間(即圖 2右端標尺的范圍)，數值越接近1說明兩個導聯的同步化程度越大。
圖2
同步似然系數矩陣
Figure2.
Synchronization likelihood coefficient matrix
1.3 構建腦功能網絡及網絡參數計算
圖論是表征復雜網絡的合適方法[19-20]，由節點和邊構成，文中定義節點為16導聯EEG的電極位置，利用同步似然分析衡量兩兩腦區之間的關聯性大小，得到同步似然系數矩陣，為了消除弱連接的影響，通常設置不同的閾值對關聯矩陣進行二值化，得到圖論中表示邊的二值矩陣(即鄰接矩陣，只包含0或1，1表示節點之間存在連接，0表示節點之間沒有連接)，同步似然系數矩陣即轉換成拓撲結構，計算表征網絡信息整合的全局效率值和表征網絡局部分割特征的聚類系數值。如圖 3所示，分別為設置閾值T=0.30時同步似然系數矩陣進行二值化得到的拓撲結構，以及設置不同閾值(0.05∶0.01∶1)得到的聚類系數和全局效率變化圖。
圖3
網絡拓撲結構以及聚類系數和全局效率變化圖
Figure3.
Topological structure of network and the clustering coefficient and global efficiency curves
1.4 統計學方法
使用SPSS 20.0統計軟件分析，計量資料用均數±標準差(
2 結果
如圖 4所示為正常對照組15名受試者全頻段EEG信號和alpha頻段EEG信號進行同步似然分析得到的平均同步似然系數矩陣，AD組計算結果如圖 5所示。比較圖 4和圖 5，發現與對照組相比，AD組全頻段和alpha頻段EEG信號得到的平均同步似然系數矩陣值均較小，表明EEG信號的同步程度較弱。
圖4
正常對照組平均同步似然系數矩陣(n=15)
Figure4.
Average synchronization likelihood coefficient matrices for the control group (n=15)
圖5
AD組平均同步似然系數矩陣(n=15)
Figure5.
Average synchronization likelihood coefficient matrices for the AD group (n=15)
同步似然系數矩陣是加權矩陣，設置閾值T轉換成拓撲結構，即可計算參數指標進行網絡特性分析。已有研究表明，當網絡平均連接度滿足
表 1和表 2分別為閾值0.05≤T≤0.07范圍內全頻段網絡和alpha網絡聚類系數和全局效率的統計分析結果。隨著閾值的增大，正常對照組和AD組的聚類系數和全局效率均減小。在閾值0.05≤T≤0.07范圍內，AD組和正常對照組全頻段網絡的聚類系數無顯著差異，T=0.06和T=0.07時，AD組全頻段網絡的全局效率比正常對照組小(P＜0.05)；該閾值范圍內AD組alpha網絡的全局效率和聚類系數均比正常對照組小(P＜0.05)。
表1
正常對照組和AD組閾值范圍0.05≤T≤0.07內全頻段網絡連接參數
Table1.
Clustering coefficient and global efficiency for the AD and control groups within values of threshold (0.05≤T≤0.07) in the full band EEGs
表2
正常對照組和AD組閾值范圍0.05≤T≤0.07內alpha網絡連接參數
Table2.
Clustering coefficient and global efficiency for the AD and control groups within values of threshold (0.05≤T≤0.07) in the alpha-band EEGs
3 結論
本文對AD患者和正常老年人靜息態腦電功能連接的研究結果顯示，AD組alpha網絡的全局效率和聚類系數均比正常對照組低(P＜0.05)，表明AD患者靜息態腦電alpha網絡功能連接可能存在減弱，提示alpha網絡的改變可能與AD患者認知能力受損有關。不同研究者采用不同實驗數據和計算方法得到的結果不完全一致，Stam等[12] 使用相位延遲指數(phase lag index，PLI)衡量MEG導聯之間的同步性，de Haan等[13]利用同步似然算法和圖論方法分析靜息態EEG構建大尺度腦功能網絡，均發現AD患者的alpha標準化聚類系數和標準化特征路徑長度減小，而Stam等[11]曾發現AD患者靜息態beta網絡的平均最短路徑長度較長。本文使用同步似然算法衡量不同導聯EEG信號之間同步程度，應用圖論方法定量分析網絡的拓撲特性，發現AD患者的alpha網絡功能連接減弱，該研究思路適用于其他頻段網絡的研究，有助于從網絡層面量化AD患者腦功能狀態，為評估患病程度提供支持。
