基于自回歸(AR)模型的心率變異性(HRV)分析技術廣泛用于自主神經系統功能狀態評價,其中AR模型階數的選擇對于HRV分析結果的準確性有重要的影響,本文研究了AR模型最佳階數的確定方法。從46名健康成年受試者自然呼吸下的心電信號中提取心跳間期時間序列,用最終預測誤差最小準則來計算AR模型最佳階數,用Burg算法求解AR模型系數,并對殘差序列進行白化檢測來驗證AR模型階數的合理性。將該方法獲得的HRV頻域參數(包括總功率、低頻功率、高頻功率、低高頻功率比以及標準化低頻功率)與Kubios-HRV分析軟件計算得到的結果作對照分析。結果表明通過該方法獲得的HRV的 5個頻域參數均與Kubios -HRV分析軟件的結果高度相關(相關系數r大于0.95),除總功率指標外,均無顯著差異,對應的Bland-Altman圖也有大于95%的點分布在一致性界限內。優化的基于AR模型的HRV分析算法能獲得準確的HRV分析結果,與常用的HRV分析軟件Kubios-HRV的結果有很好的一致性。
引用本文： 柴曉珂, 王步青, 張政波, 王衛東. 心率變異性自回歸模型分析中確定最佳階數的方法研究. 生物醫學工程學雜志, 2015, 32(5): 958-964. doi: 10.7507/1001-5515.20150171 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
心率變異性(heart rate variability,HRV)是指連續竇性心跳間瞬時心率的微小漲落[1]，通過HRV分析技術可獲得反映交感和副交感神經活動性的指標，實現個體自主神經功能狀態無創評估。目前HRV分析技術在臨床的應用研究日益廣泛，既包括急性心肌梗死[2]、心臟性猝死[3]、心力衰竭[4]、冠心病[5]、高血壓[6]等心血管疾病，也用于肝硬化[7]、糖尿病[8]、肥胖[9]、睡眠呼吸暫停綜合征[10]等很多非心血管疾病的相關研究。為規范HRV分析技術及其應用研究，歐洲心臟協會、北美起搏和電生理學會于1996年發表了對各類HRV分析算法及其應用條件的統一技術規范[11]。
HRV分析方法通常可分為線性和非線性兩大類，線性分析方法主要是時域分析法和頻域分析法，在臨床上和科研上應用廣泛,而非線性分析法是近年來研究的熱點，仍處于探索階段[12]。時域分析法有幾何圖形法和統計學方法，比較常用的統計學方法是先繪制心跳間期的直方圖，再計算心跳間期的均值、方差和變異系數等指標。頻域分析方法是將心跳間期時間序列轉換為頻域的功率譜密度函數，然后對代表不同生理意義的各特征譜段進行分析，從而描述自主神經活動性。頻域分析可以在一定程度上分離開各種生理因素對HRV的影響作用(如高頻、低頻、超低頻成分)，可以定量分析正常或疾病狀態的心率變異信號，具有重要的研究意義[13]。HRV頻域分析通過頻譜分析技術實現，根據參數模型的不同可分為基于快速傅里葉變換的經典譜估計技術和基于隨機信號模型的現代譜估計技術。目前在HRV分析中獲得廣泛應用的是基于自回歸(autoregression,AR)模型的現代譜估計技術，比經典譜估計技術頻譜圖曲線更平滑，且譜峰的中心頻率容易識別，對時間序列的長度要求更短。
在HRV分析中最重要的是確定合適階數和系數的AR模型，階數的選擇直接影響了HRV分析結果的準確性[14]。本文在先期基于AR模型的HRV分析算法[15]研究基礎上，進一步研究了影響HRV分析結果準確性的模型階數選擇問題。本研究使用最終預測誤差判據法計算出AR模型最佳階數，對最佳階數的AR模型估計的殘差序列進行白噪聲檢驗，來驗證AR模型參數選擇的合理性。為驗證本文AR模型階數確定方法的有效性，本研究將基于上述方法的HRV分析結果與目前廣泛使用的、免費的HRV分析軟件Kubios -HRV[16]的計算結果做同步對照，以檢驗算法的有效性和準確性。
1 對象與方法
1.1 數據來源
本研究的心電數據來源于課題組之前采集的漸進性引導呼吸實驗數據，參加試驗的46名健康受試者，年齡為(27.6±6.8)歲，均無心血管及循環系統疾病。該試驗采用 Biopac MP150多生理參數采集系統同步采集心電、呼吸、脈搏、血壓、血氧飽和度等生理參數，采樣率設置為1 000 Hz。漸進性引導呼吸試驗開始前，受試者先靜坐休息10 min，試驗開始進行3 min的自主呼吸，之后跟隨引導音樂進行呼吸率依次為14次/分-12.5次/分-11次/分-9.5次/分-8次/分-7次/分的引導呼吸，吸呼比為1∶2，引導音樂停止后保持靜坐自主呼吸5 min后結束試驗。本研究采用引導呼吸開始前3 min的自主呼吸下的心電信號做HRV分析。
1.2 分析方法
1.2.1 基于AR模型的HRV分析
對原始心電信號首先進行帶通濾波后用基于二階差分的R-R間期算法[17]提取R-R間期序列，之后對R-R序列進行通用的4 Hz三次樣條重采樣[18]處理使序列均勻化，并用高通濾波器[19]將超低頻中的趨勢項成分去掉使其變成平穩信號。得到均勻采樣的平穩R-R間期序列之后進行基于AR模型的功率譜分析，AR模型法是HRV測量標準中推薦的頻域參數分析方法，適用于短序列且有良好的譜分辨率[11]。在AR模型的分析方法中，假定所觀測的數據x(n)是用方差為σ2的零均值白噪聲序列w(n)激勵一個全極點的線性系統產生的，模型的階數為p，系數為aj ，用差分方程表示x(n)的AR模型為
| $ x\left( n \right) = - \sum\limits_{j = 1}^p {{a_j}x\left( {n - j} \right) + w\left( n \right),j = 1,2,\cdots p} $ |
1.2.2 AR模型最佳階數計算
(1)判斷準則。基于AR模型的參數模型法需要選擇合適的模型階數，階次選擇得太低，譜分辨率不夠，階次太高，譜估計曲線中又會出現實際不存在的虛假細節(譜分裂現象)[20]。第一種常用的方法是最終預測誤差判據(final prediction error criterion,FPE )[15]，如下式所示：
| $ {\rm{PE}}\left( p \right) = \frac{{N - 1 + p}}{{N - 1 - {p^{{\sigma ^{\left( p \right)}}}}}} $ |
另一種方法是采用信息論判據(Akaika’s information theoretic criterion,AIC)[15]，如下式所示：
| $ ,{\rm{AIC}}\left( p \right) = \frac{{2p}}{N} + \ln {\sigma ^{\left( p \right)}} $ |
其中N為分析數據的長度,σ(p)為p階模型有預測誤差功率的估計。兩種方法均以構造的預測誤差函數的極小值作為判據，實踐證明兩種方法在N趨于無窮大時求得的最佳階數具有等效性[20]。
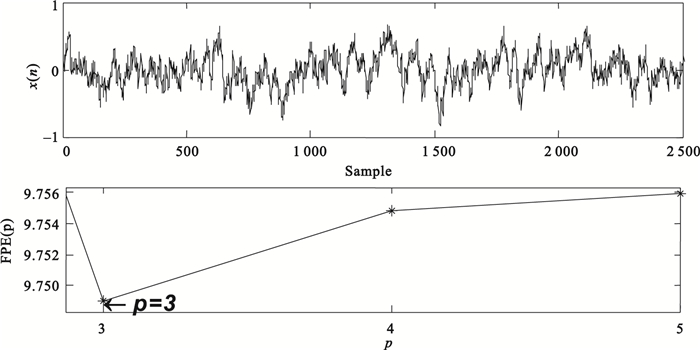
(2) 模擬仿真結果。為驗證FPE準則能否有效確定AR模型階數，我們在Matlab里做了簡單的仿真實驗。由Matlab產生3階AR模型，其中 a1=14/24，a2=9/24，a3=-1/24，v(n)為n=256的隨機白噪聲序列。對x(n)進行最終預測誤差計算得到FPE值與階數的關系如圖 1所示。圖 1中x(n)為仿真AR模型時間序列，下圖所示為FPE值隨階數p的變化關系，可以看到實際計算得到的FPE最小值對應階數為3，與仿真AR模型的實際階數一致，因此使用FPE準則能夠有效確定AR模型最佳階數。
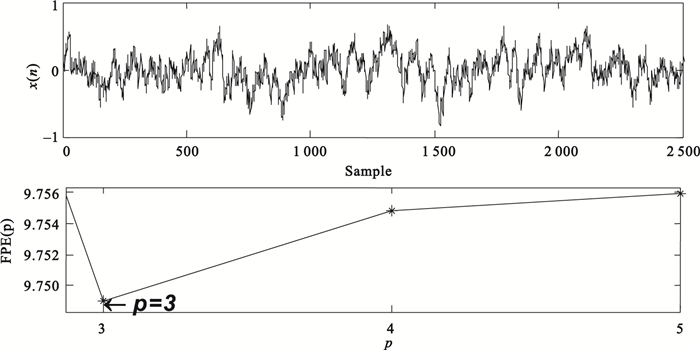圖1
3階AR模型基于FPE準則確定的最佳階數
Figure1.
Optimum order of three order AR model calculated based on FPE criterion
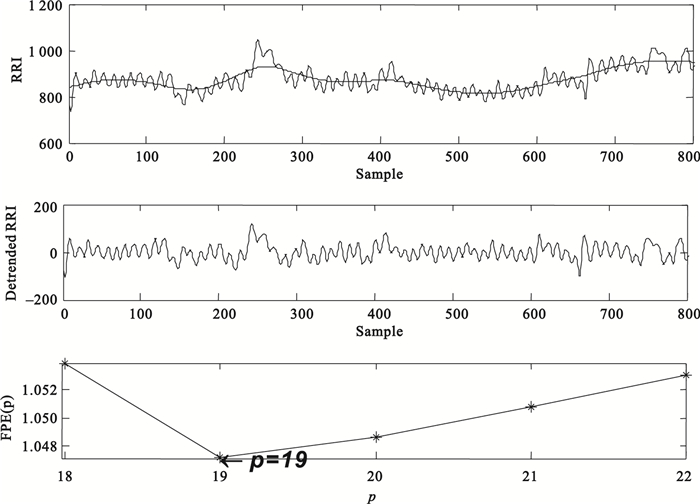
(3) 實測數據結果。圖 2中上圖為一名受試者的原始R-R序列，中圖為去趨勢后的R-R序列，下圖為計算得到的FPE(p)曲線，選擇曲線中的FPE值極小點對應的數值p作為理論最優階次，如圖 2中最佳階次為19。
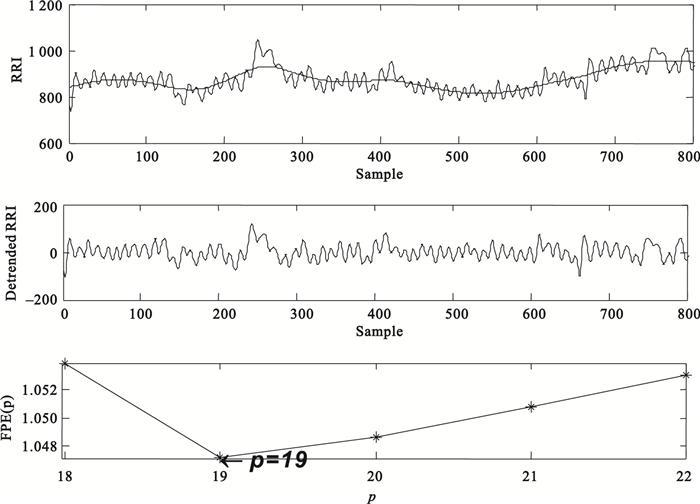圖2
去趨勢的R-R間期序列以及基于FPE準則確定的AR模型最佳階數
Figure2.
Detrended R-R interval series and its optimum order estimated based on FPE criterion method
1.2.3 AR模型殘差白化檢驗
通過FPE準則確定了AR模型的最佳階數后，我們進一步用基于前后相預測誤差功率之和最小的Burg算法求解AR模型的系數，從而建立完整的AR模型。理論上講，若一個信號模型對某個時間序列擬合得好，則通過該信號模型產生的時間序列與原始時間序列的誤差應該滿足隨機分布的白噪聲特性。因此為進一步檢驗AR模型參數的合理性，我們做了AR模型殘差白化檢驗。若通過AR模型估計出的序列與原始序列的殘差能通過白噪聲檢驗，則認為選擇的模型和參數是合適的。歐洲心臟協會、北美起搏和電生理學會發布的HRV分析標準也要求對選擇的模型進行預測誤差白化檢驗[11]，即驗證殘差序列是否為白噪聲。該檢驗是由Box等[21-22]提出并實現的。AR模型預測的時間序列與R-R間期時間序列的殘差計算如式(4)：
| $ e\left( n \right) = x\left( n \right) + \sum\limits_{j = 1}^p {{a_j}x\left( {n - j} \right)} , $ |
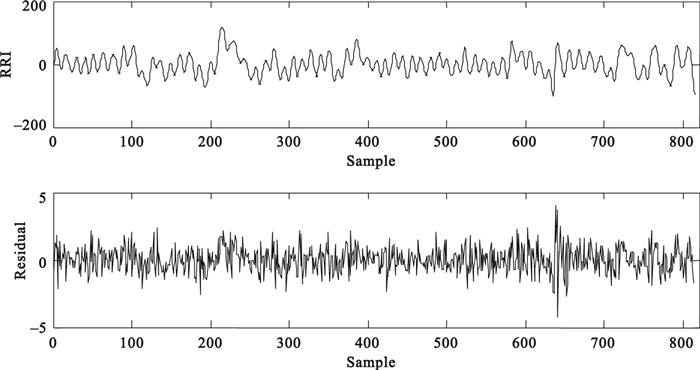
式中aj為AR模型的系數，x(n)為原始R-R序列。用Matlab函數lbqtest對該殘差序列e(n)進行Q檢驗，若檢驗結果h=0，即殘差為白噪聲，則確定p為最佳階數；若Q檢驗結果h=1，即殘差不為白噪聲，則在16~24階范圍內[14]結合FPE值隨階數變化趨勢，選擇其他階數進行Q檢驗，求得滿足殘差白化檢驗的最佳階數。圖 3中上圖RRI為上述受試者的R-R間期序列，下圖為該數據p=19時用式(4)計算得到的殘差序列，該序列經Q檢驗得到h=0，即為白噪聲序列。
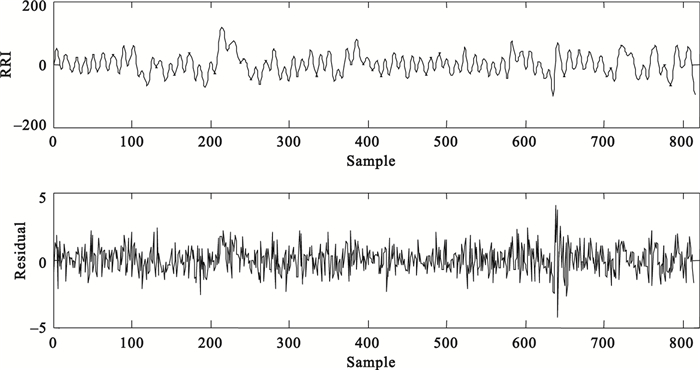圖3
R-R間期序列與AR模型估計得到的殘差序列
Figure3.
R-R interval series and its residual series from AR model estimation
2 數據處理
2.1 AR模型階數的確定
將采集到的受試者自主呼吸3 min的心電信號，去掉前后15 s，取中間平穩的數據段，按照上述方法提取R-R間期序列并將其重采樣后進行功率譜估計。46個數據分別進行理論最佳階數計算和殘差白化驗證，并對未通過驗證的數據結合FPE值隨階數變化趨勢進行微調，找出通過驗證的最佳階數，求得46人的最佳階數的均值為 19.37±2.15，本文選擇p=19作為該批數據的AR模型的功率譜估計的階數。
2.2 HRV功率譜參數的計算
進行基于AR模型的功率譜分析，常用的HRV頻域參數有：總功率(TP)為小于0.4 Hz的所有頻率段的總功率，低頻功率(LF)為0.04~0.15 Hz頻段的功率，高頻功率(HF)為0.15~0.4 Hz頻段的功率，低頻功率標準化值(LFnorm)或高頻功率標準化值(HFnorm)，以及低頻功率與高頻功率比值(LF/HF)。功率譜估計可以通過計算上述各個頻率段的功率，定量評估自主神經系統的狀態[23-25] 。
本文確定了AR模型最佳階數并進一步求得AR模型系數后，通過AR模型實現HRV的頻域分析，計算得到HRV的上述各項參數。為驗證基于AR模型HRV分析的準確性，我們進一步與常用的HRV分析軟件Kubios-HRV的結果作對照分析。將實驗獲得的心電數據轉換為HRV分析軟件Kubios-HRV可讀的txt格式，HRV分析方法選擇基于AR模型的功率譜估計方法，設置階數為p=19，同樣計算得到上述5組頻域參數。
2.3 統計分析
首先檢驗兩組結果是否存在顯著性差異，由于樣本不符合正態分布，用SPSS19.0對本文算法得到的5組頻域參數和Kubios-HRV計算得到的5組參數分別進行Wilcoxon符號秩和檢驗，并對5組參數進行相關系數計算。為進一步比較兩種HRV分析結果的一致性，用Matlab R2012對46人的5組頻域參數(TP、LF、HF、LFnorm、LF/HF)分別與Kubios-HRV的計算結果做Bland-Altman分布圖進行分析。
3 結果
3.1 統計檢驗
對兩種方法得到的5組HRV參數進行秩和檢驗，結果如表 1所示,即本文算法得出的頻域參數除TP外，LF、HF、LFnorm、LF/HF與Kubios-HRV計算得出的結果之間的差異無統計學意義。從表 1中也可以看出，5個參數的兩組結果之間相關系數r均大于0.95，呈顯著相關。由此可以得出，本文基于AR模型的HRV頻域分析結果與常用軟件Kubios-HRV的分析結果有較好的一致性。
表1
本文方法與Kubios-HRV得到的5組頻域參數的統計分析
Table1.
Statistical analysis results of five groups of frequency domain parameters from our method and Kubios-HRV
3.2 Bland-Altman圖分析
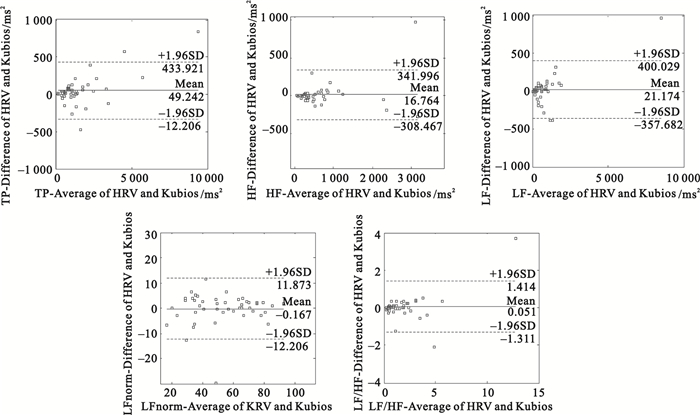
分別對46人的5組頻域參數作Bland-Altman分布圖，如圖 4所示，TP、HF、LF、LFnorm、LF/HF的一致性界限分別為49.5±384.68、16.76±325.23、21.17±378.85、-0.17±12.04、0.05±0.90，功率譜參數的最大差值絕對值為433.92，在實際可接受的范圍內。同時，參數LF、HF、LFnorm、LF/HF小于5%的點在一致性界限外。Bland-Altman分析結果表明本文提出的HRV分析算法與Kubios-HRV分析軟件所得結果具有較好的一致性。
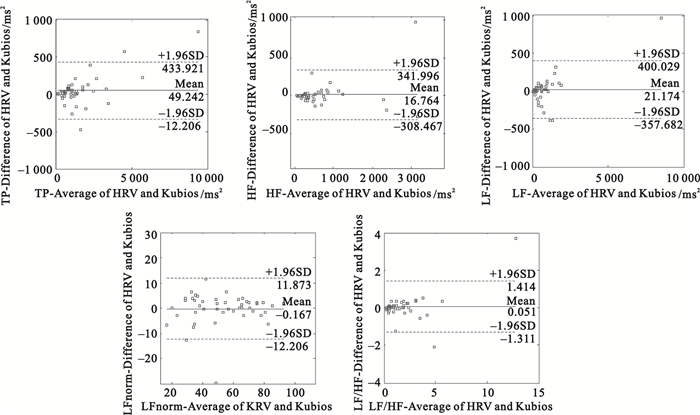圖4
5組參數的 Bland-Altman分布圖
Figure4.
Bland-Altman diagram of five parameters between our methods and Kubios-HRV
4 討論
在基于AR模型進行的HRV頻域分析中，選擇合適的模型和參數直接決定了頻域參數的準確性。本文在課題組先期HRV分析算法研究的基礎上，進一步研究了AR模型最佳階數的確定方法，首先用最終預測誤差判據法計算得到了理論最佳階數，之后對該階的AR模型進行預測誤差白化檢驗，來驗證該模型是否合適。計算最佳階數常用的判據除最終預測誤差判據FPE和信息論判據AIC外，還有自回歸傳遞函數準則和最小描述長度準則。有研究用已知階數的AR模型證實了這4種判據都能準確估計出模型的實際階數[14]，該研究基于這些判據對短時的4 Hz重采樣之后的R-R間期數據進行了分析，得到HRV分析的AR模型最佳階數范圍16~22階。AR模型的階數若小于16階則頻譜分辨率不夠，若大于22階則譜估計曲線中會出現實際不存在的虛假細節[14]。
本文在處理46人的數據時為便于與Kubios-HRV的結果進行統計分析，選擇了統一的19階的AR模型進行計算，但在實際應用中應考慮個體的差異性，分別采用各自驗證得到的最佳階數的AR模型進行功率譜計算。本文在數據處理時發現大多數樣本的FPE趨勢圖中16~22階誤差都較小，并且每個數據滿足殘差白化檢驗的AR模型參數并不是唯一的，這也說明了進行模型合適性驗證的必要性。本文對46人的數據統一使用19階AR模型進行HRV分析，得到與Kubios-HRV分析一致性很好的結果，表明本文針對46名健康成年人的HRV頻域分析，選擇的AR模型階數和系數是合適的。
理論上講，確定AR模型階數的方法有很多，比如可以依據均方誤差最小的原則選定模型階數，也可以觀察殘差序列的自相關函數，檢查其白色性來驗證模型的估計是否合適。本研究中殘差序列白化檢驗使用了Box-Pierce提出的Q統計量來完成，使用Box等提出的修正的Q檢驗方法實現預測誤差的白化檢驗，將殘差為白噪聲的模型作為最合適的模型進行后續的HRV頻域參數計算。
本文的AR模型階數確定方法用于HRV分析時，應該針對每個個體的R-R間期序列進行階數和系數計算，以獲得最優的AR模型參數及準確的HRV分析結果。但是在實際應用中，基于我們的經驗和上述46人的參數模型驗證結果，對于健康成年人AR模型的HRV分析可以統一使用19這個平均階數，再通過殘差序列白化檢驗來進一步確定階數和系數的合理性。但這個平均階數是否適用于個體差異較大的樣本,比如心血管疾病患者或者自主神經病變的群體[26]，或是HRV不同于健康成年人的小兒和老年人群體[27]，還有待于進一步研究。
短時程HRV分析只需采集3~5 min的心電信號，避免了長時間數據記錄過程中各種隨機的偶發因素對數據質量的影響，因此相對長時程HRV分析而言結果更為穩定可靠。但HRV分析存在個體差異性大以及分析結果容易受環境、心理、生理等各種因素影響的問題，HRV分析結果的解讀通常需要綜合考慮多方面的因素，而目前在各個應用領域尚未建立相關標準。本文研究了基于AR模型的HRV分析算法，并與網絡上免費使用的HRV分析軟件Kubios-HRV分析結果作嚴格的對照分析，雖然總功率TP由于數值較大Bland-Altman分析結果顯示有個體存在較大差異，但統計檢驗結果和Bland-Altman分析中一致性界限內點的比例均表明我們的HRV分析算法能夠取得與Kubios-HRV分析相一致的結果。后續研究工作的重點是HRV分析工具的使用，結合醫院臨床應用環境，在精神心理、生物反饋、睡眠醫學、健康狀態辨識等多個領域開展應用研究，更好地解讀HRV分析結果，建立相關臨床應用標準。
5 結論
本文研究了基于AR模型的HRV分析算法中AR模型最佳階數的確定方法，通過最終預測誤差最小準則結合殘差序列白化檢測能夠有效地確定AR模型最佳階數。通過該方法獲得的HRV的5個頻域參數均與Kubios-HRV分析軟件的結果高度相關，除總功率指標外，均無顯著性差異，對應的Bland-Altman圖也有大于95%的點分布在一致性界限內。因此，基于優化的AR模型的HRV分析算法能獲得準確的HRV分析結果，與常用HRV分析軟件Kubios-HRV的結果有很好的一致性。該HRV分析算法在自主神經系統功能狀態評價、心肺交互作用以及精神心理壓力分析等領域將得到更廣泛的應用。
引言
心率變異性(heart rate variability,HRV)是指連續竇性心跳間瞬時心率的微小漲落[1]，通過HRV分析技術可獲得反映交感和副交感神經活動性的指標，實現個體自主神經功能狀態無創評估。目前HRV分析技術在臨床的應用研究日益廣泛，既包括急性心肌梗死[2]、心臟性猝死[3]、心力衰竭[4]、冠心病[5]、高血壓[6]等心血管疾病，也用于肝硬化[7]、糖尿病[8]、肥胖[9]、睡眠呼吸暫停綜合征[10]等很多非心血管疾病的相關研究。為規范HRV分析技術及其應用研究，歐洲心臟協會、北美起搏和電生理學會于1996年發表了對各類HRV分析算法及其應用條件的統一技術規范[11]。
HRV分析方法通常可分為線性和非線性兩大類，線性分析方法主要是時域分析法和頻域分析法，在臨床上和科研上應用廣泛,而非線性分析法是近年來研究的熱點，仍處于探索階段[12]。時域分析法有幾何圖形法和統計學方法，比較常用的統計學方法是先繪制心跳間期的直方圖，再計算心跳間期的均值、方差和變異系數等指標。頻域分析方法是將心跳間期時間序列轉換為頻域的功率譜密度函數，然后對代表不同生理意義的各特征譜段進行分析，從而描述自主神經活動性。頻域分析可以在一定程度上分離開各種生理因素對HRV的影響作用(如高頻、低頻、超低頻成分)，可以定量分析正常或疾病狀態的心率變異信號，具有重要的研究意義[13]。HRV頻域分析通過頻譜分析技術實現，根據參數模型的不同可分為基于快速傅里葉變換的經典譜估計技術和基于隨機信號模型的現代譜估計技術。目前在HRV分析中獲得廣泛應用的是基于自回歸(autoregression,AR)模型的現代譜估計技術，比經典譜估計技術頻譜圖曲線更平滑，且譜峰的中心頻率容易識別，對時間序列的長度要求更短。
在HRV分析中最重要的是確定合適階數和系數的AR模型，階數的選擇直接影響了HRV分析結果的準確性[14]。本文在先期基于AR模型的HRV分析算法[15]研究基礎上，進一步研究了影響HRV分析結果準確性的模型階數選擇問題。本研究使用最終預測誤差判據法計算出AR模型最佳階數，對最佳階數的AR模型估計的殘差序列進行白噪聲檢驗，來驗證AR模型參數選擇的合理性。為驗證本文AR模型階數確定方法的有效性，本研究將基于上述方法的HRV分析結果與目前廣泛使用的、免費的HRV分析軟件Kubios -HRV[16]的計算結果做同步對照，以檢驗算法的有效性和準確性。
1 對象與方法
1.1 數據來源
本研究的心電數據來源于課題組之前采集的漸進性引導呼吸實驗數據，參加試驗的46名健康受試者，年齡為(27.6±6.8)歲，均無心血管及循環系統疾病。該試驗采用 Biopac MP150多生理參數采集系統同步采集心電、呼吸、脈搏、血壓、血氧飽和度等生理參數，采樣率設置為1 000 Hz。漸進性引導呼吸試驗開始前，受試者先靜坐休息10 min，試驗開始進行3 min的自主呼吸，之后跟隨引導音樂進行呼吸率依次為14次/分-12.5次/分-11次/分-9.5次/分-8次/分-7次/分的引導呼吸，吸呼比為1∶2，引導音樂停止后保持靜坐自主呼吸5 min后結束試驗。本研究采用引導呼吸開始前3 min的自主呼吸下的心電信號做HRV分析。
1.2 分析方法
1.2.1 基于AR模型的HRV分析
對原始心電信號首先進行帶通濾波后用基于二階差分的R-R間期算法[17]提取R-R間期序列，之后對R-R序列進行通用的4 Hz三次樣條重采樣[18]處理使序列均勻化，并用高通濾波器[19]將超低頻中的趨勢項成分去掉使其變成平穩信號。得到均勻采樣的平穩R-R間期序列之后進行基于AR模型的功率譜分析，AR模型法是HRV測量標準中推薦的頻域參數分析方法，適用于短序列且有良好的譜分辨率[11]。在AR模型的分析方法中，假定所觀測的數據x(n)是用方差為σ2的零均值白噪聲序列w(n)激勵一個全極點的線性系統產生的，模型的階數為p，系數為aj ，用差分方程表示x(n)的AR模型為
| $ x\left( n \right) = - \sum\limits_{j = 1}^p {{a_j}x\left( {n - j} \right) + w\left( n \right),j = 1,2,\cdots p} $ |
1.2.2 AR模型最佳階數計算
(1)判斷準則。基于AR模型的參數模型法需要選擇合適的模型階數，階次選擇得太低，譜分辨率不夠，階次太高，譜估計曲線中又會出現實際不存在的虛假細節(譜分裂現象)[20]。第一種常用的方法是最終預測誤差判據(final prediction error criterion,FPE )[15]，如下式所示：
| $ {\rm{PE}}\left( p \right) = \frac{{N - 1 + p}}{{N - 1 - {p^{{\sigma ^{\left( p \right)}}}}}} $ |
另一種方法是采用信息論判據(Akaika’s information theoretic criterion,AIC)[15]，如下式所示：
| $ ,{\rm{AIC}}\left( p \right) = \frac{{2p}}{N} + \ln {\sigma ^{\left( p \right)}} $ |
其中N為分析數據的長度,σ(p)為p階模型有預測誤差功率的估計。兩種方法均以構造的預測誤差函數的極小值作為判據，實踐證明兩種方法在N趨于無窮大時求得的最佳階數具有等效性[20]。
(2) 模擬仿真結果。為驗證FPE準則能否有效確定AR模型階數，我們在Matlab里做了簡單的仿真實驗。由Matlab產生3階AR模型，其中 a1=14/24，a2=9/24，a3=-1/24，v(n)為n=256的隨機白噪聲序列。對x(n)進行最終預測誤差計算得到FPE值與階數的關系如圖 1所示。圖 1中x(n)為仿真AR模型時間序列，下圖所示為FPE值隨階數p的變化關系，可以看到實際計算得到的FPE最小值對應階數為3，與仿真AR模型的實際階數一致，因此使用FPE準則能夠有效確定AR模型最佳階數。
圖1
3階AR模型基于FPE準則確定的最佳階數
Figure1.
Optimum order of three order AR model calculated based on FPE criterion
(3) 實測數據結果。圖 2中上圖為一名受試者的原始R-R序列，中圖為去趨勢后的R-R序列，下圖為計算得到的FPE(p)曲線，選擇曲線中的FPE值極小點對應的數值p作為理論最優階次，如圖 2中最佳階次為19。
圖2
去趨勢的R-R間期序列以及基于FPE準則確定的AR模型最佳階數
Figure2.
Detrended R-R interval series and its optimum order estimated based on FPE criterion method
1.2.3 AR模型殘差白化檢驗
通過FPE準則確定了AR模型的最佳階數后，我們進一步用基于前后相預測誤差功率之和最小的Burg算法求解AR模型的系數，從而建立完整的AR模型。理論上講，若一個信號模型對某個時間序列擬合得好，則通過該信號模型產生的時間序列與原始時間序列的誤差應該滿足隨機分布的白噪聲特性。因此為進一步檢驗AR模型參數的合理性，我們做了AR模型殘差白化檢驗。若通過AR模型估計出的序列與原始序列的殘差能通過白噪聲檢驗，則認為選擇的模型和參數是合適的。歐洲心臟協會、北美起搏和電生理學會發布的HRV分析標準也要求對選擇的模型進行預測誤差白化檢驗[11]，即驗證殘差序列是否為白噪聲。該檢驗是由Box等[21-22]提出并實現的。AR模型預測的時間序列與R-R間期時間序列的殘差計算如式(4)：
| $ e\left( n \right) = x\left( n \right) + \sum\limits_{j = 1}^p {{a_j}x\left( {n - j} \right)} , $ |
式中aj為AR模型的系數，x(n)為原始R-R序列。用Matlab函數lbqtest對該殘差序列e(n)進行Q檢驗，若檢驗結果h=0，即殘差為白噪聲，則確定p為最佳階數；若Q檢驗結果h=1，即殘差不為白噪聲，則在16~24階范圍內[14]結合FPE值隨階數變化趨勢，選擇其他階數進行Q檢驗，求得滿足殘差白化檢驗的最佳階數。圖 3中上圖RRI為上述受試者的R-R間期序列，下圖為該數據p=19時用式(4)計算得到的殘差序列，該序列經Q檢驗得到h=0，即為白噪聲序列。
圖3
R-R間期序列與AR模型估計得到的殘差序列
Figure3.
R-R interval series and its residual series from AR model estimation
2 數據處理
2.1 AR模型階數的確定
將采集到的受試者自主呼吸3 min的心電信號，去掉前后15 s，取中間平穩的數據段，按照上述方法提取R-R間期序列并將其重采樣后進行功率譜估計。46個數據分別進行理論最佳階數計算和殘差白化驗證，并對未通過驗證的數據結合FPE值隨階數變化趨勢進行微調，找出通過驗證的最佳階數，求得46人的最佳階數的均值為 19.37±2.15，本文選擇p=19作為該批數據的AR模型的功率譜估計的階數。
2.2 HRV功率譜參數的計算
進行基于AR模型的功率譜分析，常用的HRV頻域參數有：總功率(TP)為小于0.4 Hz的所有頻率段的總功率，低頻功率(LF)為0.04~0.15 Hz頻段的功率，高頻功率(HF)為0.15~0.4 Hz頻段的功率，低頻功率標準化值(LFnorm)或高頻功率標準化值(HFnorm)，以及低頻功率與高頻功率比值(LF/HF)。功率譜估計可以通過計算上述各個頻率段的功率，定量評估自主神經系統的狀態[23-25] 。
本文確定了AR模型最佳階數并進一步求得AR模型系數后，通過AR模型實現HRV的頻域分析，計算得到HRV的上述各項參數。為驗證基于AR模型HRV分析的準確性，我們進一步與常用的HRV分析軟件Kubios-HRV的結果作對照分析。將實驗獲得的心電數據轉換為HRV分析軟件Kubios-HRV可讀的txt格式，HRV分析方法選擇基于AR模型的功率譜估計方法，設置階數為p=19，同樣計算得到上述5組頻域參數。
2.3 統計分析
首先檢驗兩組結果是否存在顯著性差異，由于樣本不符合正態分布，用SPSS19.0對本文算法得到的5組頻域參數和Kubios-HRV計算得到的5組參數分別進行Wilcoxon符號秩和檢驗，并對5組參數進行相關系數計算。為進一步比較兩種HRV分析結果的一致性，用Matlab R2012對46人的5組頻域參數(TP、LF、HF、LFnorm、LF/HF)分別與Kubios-HRV的計算結果做Bland-Altman分布圖進行分析。
3 結果
3.1 統計檢驗
對兩種方法得到的5組HRV參數進行秩和檢驗，結果如表 1所示,即本文算法得出的頻域參數除TP外，LF、HF、LFnorm、LF/HF與Kubios-HRV計算得出的結果之間的差異無統計學意義。從表 1中也可以看出，5個參數的兩組結果之間相關系數r均大于0.95，呈顯著相關。由此可以得出，本文基于AR模型的HRV頻域分析結果與常用軟件Kubios-HRV的分析結果有較好的一致性。
表1
本文方法與Kubios-HRV得到的5組頻域參數的統計分析
Table1.
Statistical analysis results of five groups of frequency domain parameters from our method and Kubios-HRV
3.2 Bland-Altman圖分析
分別對46人的5組頻域參數作Bland-Altman分布圖，如圖 4所示，TP、HF、LF、LFnorm、LF/HF的一致性界限分別為49.5±384.68、16.76±325.23、21.17±378.85、-0.17±12.04、0.05±0.90，功率譜參數的最大差值絕對值為433.92，在實際可接受的范圍內。同時，參數LF、HF、LFnorm、LF/HF小于5%的點在一致性界限外。Bland-Altman分析結果表明本文提出的HRV分析算法與Kubios-HRV分析軟件所得結果具有較好的一致性。
圖4
5組參數的 Bland-Altman分布圖
Figure4.
Bland-Altman diagram of five parameters between our methods and Kubios-HRV
4 討論
在基于AR模型進行的HRV頻域分析中，選擇合適的模型和參數直接決定了頻域參數的準確性。本文在課題組先期HRV分析算法研究的基礎上，進一步研究了AR模型最佳階數的確定方法，首先用最終預測誤差判據法計算得到了理論最佳階數，之后對該階的AR模型進行預測誤差白化檢驗，來驗證該模型是否合適。計算最佳階數常用的判據除最終預測誤差判據FPE和信息論判據AIC外，還有自回歸傳遞函數準則和最小描述長度準則。有研究用已知階數的AR模型證實了這4種判據都能準確估計出模型的實際階數[14]，該研究基于這些判據對短時的4 Hz重采樣之后的R-R間期數據進行了分析，得到HRV分析的AR模型最佳階數范圍16~22階。AR模型的階數若小于16階則頻譜分辨率不夠，若大于22階則譜估計曲線中會出現實際不存在的虛假細節[14]。
本文在處理46人的數據時為便于與Kubios-HRV的結果進行統計分析，選擇了統一的19階的AR模型進行計算，但在實際應用中應考慮個體的差異性，分別采用各自驗證得到的最佳階數的AR模型進行功率譜計算。本文在數據處理時發現大多數樣本的FPE趨勢圖中16~22階誤差都較小，并且每個數據滿足殘差白化檢驗的AR模型參數并不是唯一的，這也說明了進行模型合適性驗證的必要性。本文對46人的數據統一使用19階AR模型進行HRV分析，得到與Kubios-HRV分析一致性很好的結果，表明本文針對46名健康成年人的HRV頻域分析，選擇的AR模型階數和系數是合適的。
理論上講，確定AR模型階數的方法有很多，比如可以依據均方誤差最小的原則選定模型階數，也可以觀察殘差序列的自相關函數，檢查其白色性來驗證模型的估計是否合適。本研究中殘差序列白化檢驗使用了Box-Pierce提出的Q統計量來完成，使用Box等提出的修正的Q檢驗方法實現預測誤差的白化檢驗，將殘差為白噪聲的模型作為最合適的模型進行后續的HRV頻域參數計算。
本文的AR模型階數確定方法用于HRV分析時，應該針對每個個體的R-R間期序列進行階數和系數計算，以獲得最優的AR模型參數及準確的HRV分析結果。但是在實際應用中，基于我們的經驗和上述46人的參數模型驗證結果，對于健康成年人AR模型的HRV分析可以統一使用19這個平均階數，再通過殘差序列白化檢驗來進一步確定階數和系數的合理性。但這個平均階數是否適用于個體差異較大的樣本,比如心血管疾病患者或者自主神經病變的群體[26]，或是HRV不同于健康成年人的小兒和老年人群體[27]，還有待于進一步研究。
短時程HRV分析只需采集3~5 min的心電信號，避免了長時間數據記錄過程中各種隨機的偶發因素對數據質量的影響，因此相對長時程HRV分析而言結果更為穩定可靠。但HRV分析存在個體差異性大以及分析結果容易受環境、心理、生理等各種因素影響的問題，HRV分析結果的解讀通常需要綜合考慮多方面的因素，而目前在各個應用領域尚未建立相關標準。本文研究了基于AR模型的HRV分析算法，并與網絡上免費使用的HRV分析軟件Kubios-HRV分析結果作嚴格的對照分析，雖然總功率TP由于數值較大Bland-Altman分析結果顯示有個體存在較大差異，但統計檢驗結果和Bland-Altman分析中一致性界限內點的比例均表明我們的HRV分析算法能夠取得與Kubios-HRV分析相一致的結果。后續研究工作的重點是HRV分析工具的使用，結合醫院臨床應用環境，在精神心理、生物反饋、睡眠醫學、健康狀態辨識等多個領域開展應用研究，更好地解讀HRV分析結果，建立相關臨床應用標準。
5 結論
本文研究了基于AR模型的HRV分析算法中AR模型最佳階數的確定方法，通過最終預測誤差最小準則結合殘差序列白化檢測能夠有效地確定AR模型最佳階數。通過該方法獲得的HRV的5個頻域參數均與Kubios-HRV分析軟件的結果高度相關，除總功率指標外，均無顯著性差異，對應的Bland-Altman圖也有大于95%的點分布在一致性界限內。因此，基于優化的AR模型的HRV分析算法能獲得準確的HRV分析結果，與常用HRV分析軟件Kubios-HRV的結果有很好的一致性。該HRV分析算法在自主神經系統功能狀態評價、心肺交互作用以及精神心理壓力分析等領域將得到更廣泛的應用。
