心肺復蘇（CPR）過程中實施的胸外按壓引起的偽跡會嚴重降低除顫節律辨識的可靠性。本文提出了一種無需參考信號的CPR偽跡自適應濾除算法。結合經驗模態分解（EMD）和獨立成分分析（ICA），將真正的心電節律信號從受CPR偽跡干擾的心電信號中分離出來。為評估算法的效果，構建了一個用于除顫節律辨識的反向傳播神經網絡。采集了1 484例受CPR偽跡干擾的豬的心電信號用于實驗。實驗結果表明，該算法可以在很大程度上抑制CPR偽跡的影響，從而顯著提高CPR過程中除顫節律辨識的準確性。
引用本文： 余明, 陳鋒, 張廣, 李良喆, 王春晨, 王丹, 詹寧波, 顧彪, 吳太虎. 基于經驗模態分解與獨立成分分析的心肺復蘇偽跡自適應濾除算法. 生物醫學工程學雜志, 2016, 33(5): 834-841. doi: 10.7507/1001-5515.201600135 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
院外心臟驟停是一種嚴重威脅人類健康的致死性疾病[1-3]。高質量的胸外按壓和及時的早期電除顫，是心肺復蘇(cardiopulmonary resuscitation, CPR)的關鍵環節[4-5]。但是，胸外按壓過程中所引起的CPR偽跡會給除顫節律辨識算法帶來嚴重干擾，從而顯著降低辨識結果的可靠性。按照目前的方式，在實施電除顫前，為了準確進行除顫節律辨識，要中斷胸外按壓15 s以上[6]。然而，胸外按壓的長時間中斷，將嚴重阻礙患者建立自主循環，從而導致CPR的失敗[7]。顯然，如果構建一種算法，能在受干擾的心電信號中濾除CPR偽跡，提取出真正的心電節律信號，則可以在不間斷胸外按壓的同時實施可靠的除顫節律辨識，從而有效提高CPR的成功率。
最早關于濾除CPR偽跡的研究是在豬的心臟模型上開展的，研究結果表明一個固定截止頻率的高通濾波器就可以將豬的心電信號和CPR偽跡信號進行頻譜分離[8]。但是，CPR偽跡信號和人類心電信號的頻譜成分有很大一部分重合，使得這種方法無法應用在人類心電的除顫節律辨識上[9]。因此，一些研究者試圖利用一些外部信號作參考，對CPR偽跡建模。其中的一些算法，例如由Eilevstj?nn等[10]提出的多通道遞歸自適應匹配濾波器(multichannel recursive adaptive matching pursuit algorithm, MC-RAMP)、由Irusta等[11]提出的基于按壓頻率的最小均方誤差(least mean-square, LMS)濾波器，以及由Gong等[12]提出的基于胸阻抗信號的自適應濾波算法，都取得了很好的效果。但是，目前通用的大部分除顫儀僅僅記錄心電信號，這些算法所需的每一項外部參考信號，如按壓加速度、按壓深度、呼吸阻抗和胸阻抗等，都意味著另外的硬件支持；連接這些參考通道，既占用了寶貴的急救時間，又對院外急救人員提出了過高的專業要求。
也有研究者提出了一些無需參考信號的CPR偽跡濾除算法。這些算法多建立在傳統濾波器的基礎上，有些試圖用純頻率方法將偽跡濾除，有些試圖僅利用心電信號對偽跡進行建模；然而，由于CPR偽跡是一種頻率成分復雜的非線性信號，這些算法都沒有取得令人滿意的效果[13]。
與諸如傅里葉變換、小波變換等建立在線性分析基礎上的算法相比，經驗模態分解(empirical mode decomposition, EMD)和獨立成分分析(independent component analysis, ICA)作為新興的信號處理方法，更適用于分析短時、非穩態、非線性的復雜信號，已經分別在腦電信號分析、胎兒心電信號提取等生物醫學信號處理領域得到了應用，并取得很好的效果。本文結合EMD和ICA，提出了一種CPR偽跡的自適應濾除算法，試圖在無需任何參考信號的情況下，從受干擾的心電信號中分離出真正的心電節律信號。本文還構建了一個用于區分除顫節律(shockable rhythm)和非除顫節律(nonshockable rhythm)的反向傳播(back propagation，BP)神經網絡，分別對濾波前后的受干擾的心電信號進行除顫節律辨識，并計算其敏感性和特異性，用來評估該算法的性能。
1 算法設計
受干擾的心電信號可以被看作由真正的心電節律信號和疊加其上的CPR偽跡構成，而這兩個成分分別由患者和胸外按壓實施者產生，即信號源完全獨立；經過ICA后，可以有效地將這兩種成分分離開來。由于本文試圖在沒有任何外部參考信號的情況下完成CPR偽跡的濾除，因此進行ICA時所需的參考信號就需要從受干擾的心電信號本身提取。一些研究證明，CPR偽跡可以近似為一個以胸外按壓頻率為基礎頻率的周期信號，且在每一個按壓區間，按壓頻率可以近似為一個常數[11, 14]，如果能直接從受干擾的心電信號中得到胸外按壓頻率，則可以基于該頻率構建參考信號。
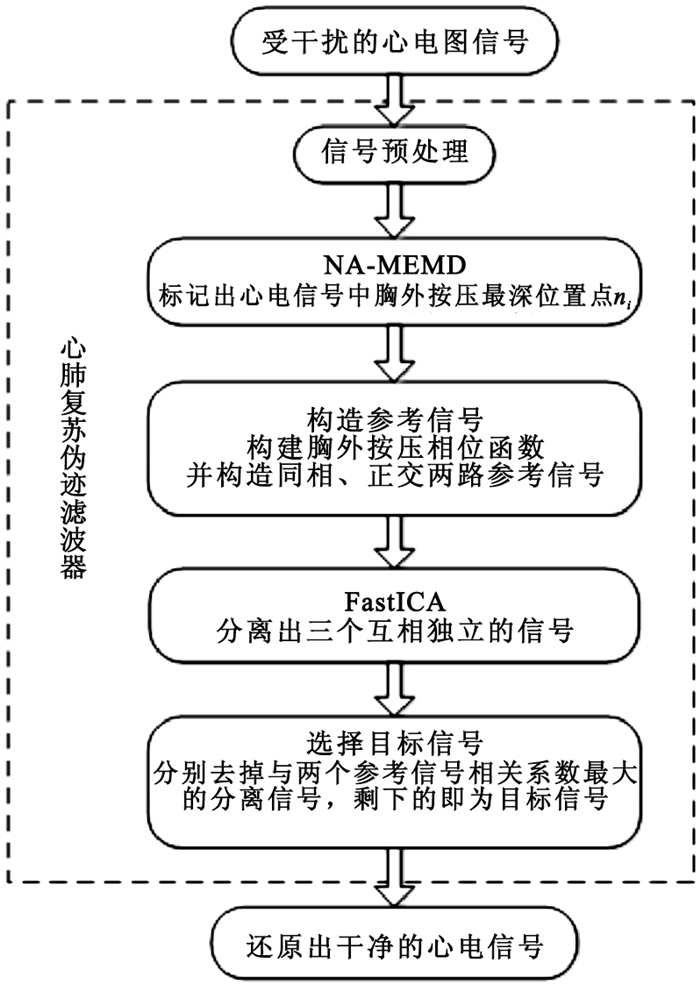
按照上述假設，本文首先利用EMD的方法從受干擾的心電圖信號中近似得到每一次胸外按壓的頻率；基于得到的按壓頻率，構建同相和正交的兩個參考信號；然后將這兩個參考信號和受干擾的心電圖信號一起，進行ICA，得到三個互相獨立的分量；最后從中選擇出所需的分量，即還原出了干凈的心電信號。
整個算法流程如圖 1所示。
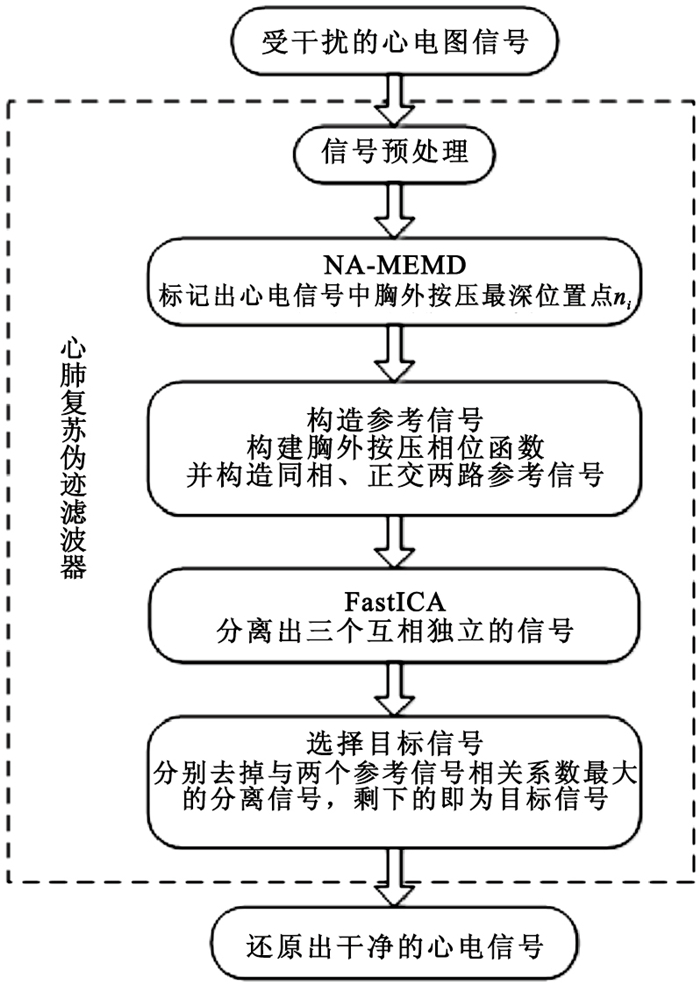圖1
自適應CPR偽跡濾波器算法流程
Figure1.
Flowchart of the CPR artifact cancellation adaptive filter algorithm
1.1 信號預處理
根據Thakor等[15-16]的研究，獲取的心電圖信號需要做三方面的預處理：①截止頻率為1 Hz的高通濾波器，用來去除殘余的基線漂移；②二階30 Hz巴特沃斯低通濾波器，用來抑制主要由肌肉電信號引起的高頻噪聲；③50 Hz陷波濾波器，用來消除工頻噪聲的干擾。
1.2 經驗模態分解
EMD是由Huang等[17]于1998年提出的一種旨在處理非線性、非穩態數據的信號處理方法。基于該方法，任何復雜的信號都能被分解為有限個不同時間尺度上的本征模函數(intrinsic mode function, IMF)，并將它們按照自身攜帶的時間尺度特征依次排列。這種算法根據信號自身的時間尺度進行分解，無需預設任何基函數，特別適合非線性非平穩信號的分析處理。在這一步驟中，需要用EMD提取出的信息代替外部參考信號，得到與CPR偽跡相關的胸外按壓頻率；此時EMD可以起到一個時變濾波器的作用，將與CPR偽跡相關的IMF提取出來[18]；再將這些IMF重新合成一個新的信號，就可以很好地反映CPR偽跡的基礎頻率特征。
為了避免模態混疊，本文采取了在標準EMD上改進的噪聲輔助多通道經驗模態分解(noise-assisted multivariate empirical mode decomposition, NA-MEMD)方法。Rehman等[19]的研究表明，與標準EMD相比，NA-MEMD能有效解決模態混疊問題。實驗發現，當采用三個互相獨立且功率均為1 dB的隨機高斯白噪聲作為MEMD的輔助信號時，效果最好。
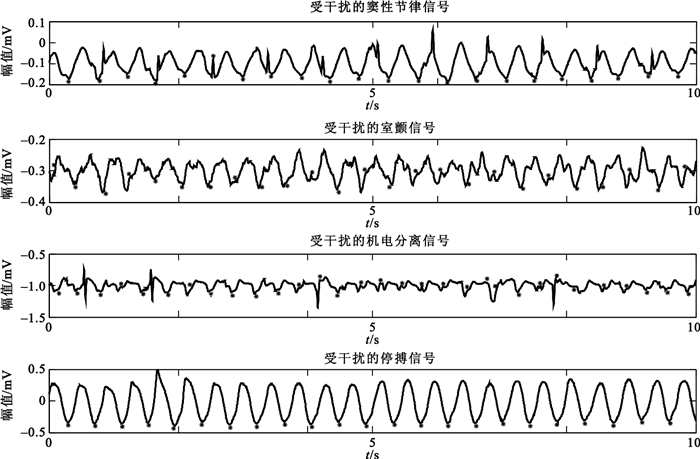
應用上述NA-MEMD方法，將受干擾的心電信號分解為有限個IMF，并選擇相關IMF重新合成一個信號；將該合成信號的每一個極小值點所在的時刻標記在心電圖上，即代表胸外按壓最深位置時刻在心電圖中對應的位置，得到的結果如圖 2所示：從上到下依次是(a)受干擾的竇性節律(sinus rhythm, SR)信號、(b)受干擾的室顫(ventricular fibrillation, VF)信號、(c)受干擾的機電分離(pulseless electrical activity, PEA)信號和(d)受干擾的停搏(asystole, ASYS)信號，圖中的“*”標記胸外按壓最深位置時刻在心電圖上對應的位置，該標記由上述NA-MEMD方法得到。可以看出，這些標記能很好地反映CPR偽跡的基礎頻率特征。
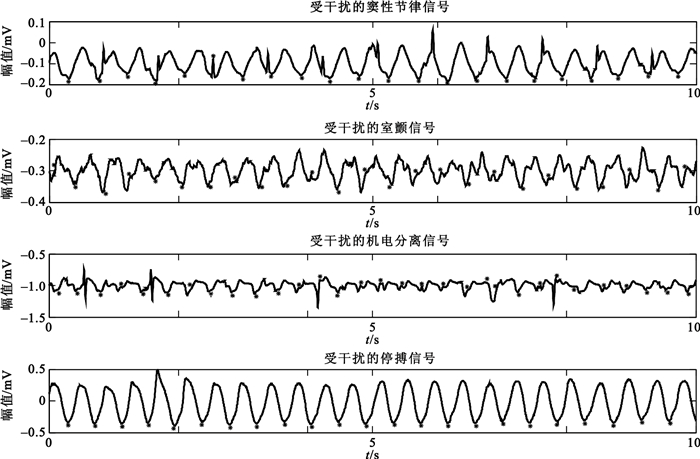圖2
應用NA-MEMD在受干擾的心電信號中標記胸外按壓最深位置時刻
Figure2.
Marks of instant of chest compression obtained from corrupted ECGs by NA-MEMD
將由“*”標記的點依次記為ni，即可得到胸外按壓的相位函數Φ(n)：
| $ \Phi \left( n \right) = \frac{{2{\rm{\pi }}}}{{\nabla {n_i}}}\left( {n - {n_i}} \right) + i \times 2{\rm{\pi }}\;\;{{\rm{n}}_i} \le n < {n_{i + 1}} $ |
得到該相位函數后，構造與CPR同相和正交的兩路參考信號，分別記為r_cos(n)和r_sin(n)：
| $ r\_\cos \left( n \right) = \cos \left( {\Phi \left( n \right)} \right) $ |
| $ r\_\sin \left( n \right) = \sin \left( {\Phi \left( n \right)} \right) $ |
1.3 獨立成分分析
ICA又稱盲信號分離，是一種在源信號及其組合關系均未知的情況下，僅利用觀測信號分離出源信號的方法，在語音處理、圖像處理、生物電信號處理等各個領域均得到廣泛應用。自從ICA的概念提出以來，不同學者基于不同的目標函數和優化算法，提出很多種盲信號分離算法。本文采用Hyv?rinen等[20-22]提出的基于負熵的快速固定點算法(fast fixed-point algorithm for independent component analysis, FastICA)，該算法具有較快的收斂速度，且與基于峭度的算法相比具有更好的魯棒性，更適合于特征多變、噪聲復雜的心電信號處理。
首先結合受干擾的心電信號和上述構造的兩路參考信號，組成矩陣作為觀測信號:
| $ s\left( n \right) = \left[ {{S_{{\rm{ECG\_MIXED}}}}\left( n \right),r\_\cos \left( n \right),r\_\sin \left( n \right)} \right] $ |
將此觀測信號進行去均值和白化處理；處理后的觀測信號按照文獻[20]中描述的方法進行計算，迭代更新分離向量，直至算法收斂；為了避免意外，將最大迭代次數限制為1 000次，如果迭代次數超過上限而算法仍未收斂，則停止迭代，轉而選取白化處理后的觀測信號作為替代結果。
盲信號分離后獲得的結果仍然是一個三維矩陣x(n)，且各個成分出現的順序并不確定，因此需要進行分析選擇：分別計算結果里每個分量與兩路參考信號的相關系數的絕對值：
| $ C\_{\cos _i} = \left| {\frac{{\sum {{x_i}\left( n \right)r\_\cos \left( n \right)} }}{{\sqrt {\sum {x_i^2\left( n \right)} \sum {r\_{{\cos }^2}\left( n \right)} } }}} \right| $ |
| $ C\_{\sin _i} = \left| {\frac{{\sum {{x_i}\left( n \right)r\_\sin \left( n \right)} }}{{\sqrt {\sum {x_i^2\left( n \right)} \sum {r\_{{\sin }^2}\left( n \right)} } }}} \right| $ |
與某一路參考信號相關系數的絕對值最高的分量即為該參考信號在結果中的估計，這種分量不是所需的信號；依次去掉這種分量后剩下的結果，即被認為是還原出的干凈的心電信號。
1.4 BP神經網絡構建
還原出干凈的心電信號后，本文構建了一個BP神經網絡作為二分類器使用，根據心電信號的一些特征值，將其分為除顫節律和非除顫節律兩類。神經網絡已經被廣泛應用于心電節律辨識上，并且取得了良好的效果[23-24]。根據Li等[25]的驗證，結合Jekova等[26]提出的特征值Count2和Kuo等[27]提出的特征值濾波泄露量(Leakage)，進行除顫節律辨識，準確性可高達96.3%；特征值Count2和Leakage分別可用如下方式得到。
(1)Count2：
首先將心電信號S通過如下帶通濾波器：
| $ FS\left( n \right) = \frac{{14 \times FS\left( {n - 1} \right) - 7 \times FS\left( {n - 2} \right) + \frac{{S\left( n \right) - S\left( {n - 1} \right)}}{2}}}{8} $ |
再求得上述濾波器輸出信號的絕對值AbsFS，并計算出每秒鐘該絕對值的最大值max(AbsFS)、平均值mean(AbsFS)和平均絕對偏差MD。
最后，按照以下方法，分別計算出長度為10 s樣本中Count1、Count2、Count3三個值的大小：Count1范圍: 0.5×max(AbsFS)至max(AbsFS); Count2范圍: mean(AbsFS)至max(AbsFS); Count3范圍: mean(AbsFS)-MD至mean(AbsFS)+MD。
(2)Leakage：
將心電信號S通過一個窄帶寬帶阻濾波器，這個濾波器的中心頻率為心電信號的均值頻率，通過濾波器后的殘余信號即為Leakage：
| $ {\rm{Leakage}} = \frac{{\sum\limits_{i = 1}^m {\left| {s\left( i \right) + s\left( {i - \frac{T}{2}} \right)} \right|} }}{{\sum\limits_{i = 1}^m {\left| {s\left( i \right)} \right| + \left| {s\left( {i - \frac{T}{2}} \right)} \right|} }} $ |
其中，T為心電信號的均值頻率：
| $ T = 2{\rm{\pi }}\frac{{\sum\limits_{i = 1}^m {\left| {s\left( i \right)} \right|} }}{{\sum\limits_{i = 1}^m {\left| {s\left( i \right) - s\left( {i - 1} \right)} \right|} }} $ |
這兩個值組成的特征向量metric=[Count2, Leakage]，作為BP神經網絡中的輸入向量。
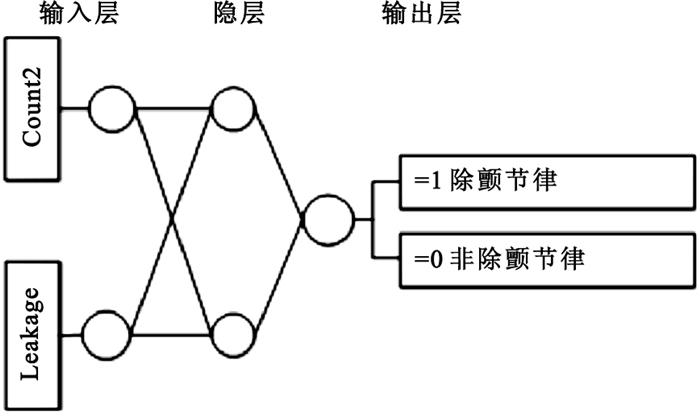
如圖 3所示，本文設計了一個三層BP神經元網絡：輸入層單元數為2，對應二維的輸入向量；輸出層單元數為1，輸出為1表示結果為除顫節律, 輸出為0表示結果為非除顫節律。經試驗，隱層的單元數為2時，神經網絡具有很好的性能。
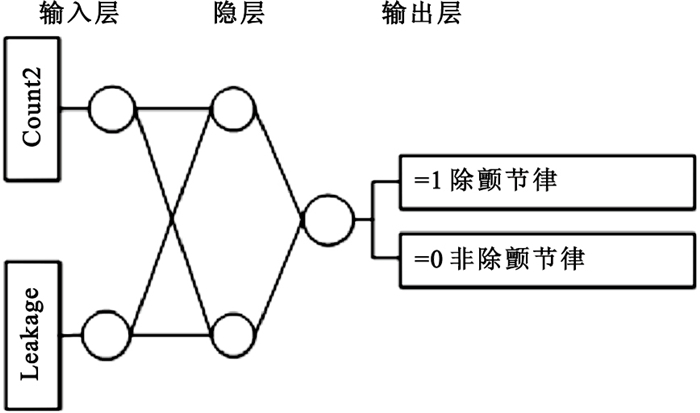圖3
構建的BP神經網絡的結構
Figure3.
Configuration of the constructed BP neural network
2 實驗
2.1 數據庫
實驗所需的心電數據采集自12頭成年豬；在麻醉條件下，將低壓的交流電通入豬的心室壁上，導致其心電變為VF節律，數分鐘后由一名急救科的醫生進行CPR，全程記錄實驗過程中豬的心電、主動脈壓等各項生理信號。
實驗共采集了1 484例受CPR偽跡干擾的心電信號，這些信號由專家綜合當時的心電信號、胸外按壓前后的心電表現和主動脈壓等其他生理參數進行了分類標注：其中810例SR信號，237例VF信號，170例PEA信號和267例ASYS信號。為了對1.4中描述的BP神經網絡進行訓練和驗證，實驗還采集了800例未受CPR偽跡干擾的心電信號，包含SR、VF、PEA、ASYS各200例。將各類信號隨機平均分為兩部分，分別組成神經網絡的訓練集和驗證集。所有的心電信號都以250 Hz的采樣頻率采樣，每個樣本長度均為10 s。
為評估本文提出的濾波算法的性能，實驗選擇了準確性好且應用廣泛的由Ruiz de Gauna等[14]設計的卡爾曼濾波器作為比較：將1 484例受CPR偽跡干擾的心電信號分別在不濾波、通過卡爾曼濾波器和通過本文設計的EMD+ICA自適應濾波器三種情況下，由訓練好的BP神經網絡進行除顫節律辨識，并統計出每一種情況下辨識的敏感性(即正確識別出除顫節律的概率)和特異性(即正確識別出非除顫節律的概率)，以及每一類心電節律辨識的準確性。
2.2 濾波器效果
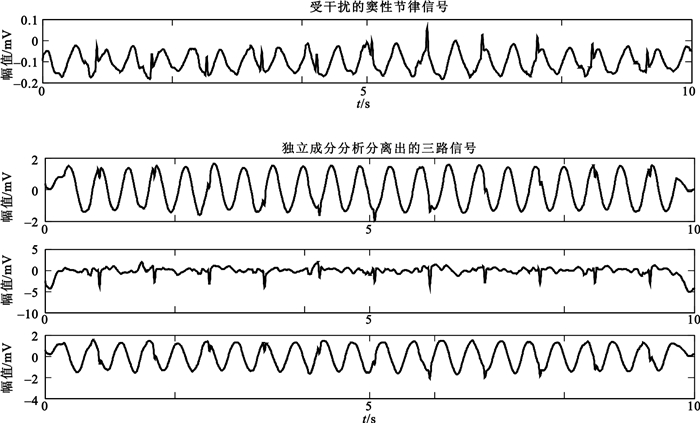
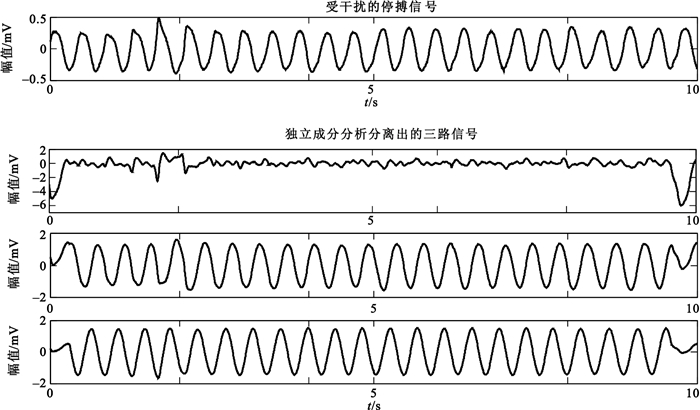
圖 4和圖 5分別是對受干擾的SR信號和ASYS信號進行ICA后的結果。從圖中可以看出，所需的心電信號在分離出的三個獨立分量中出現的位置并不固定，且存在反相現象，這就是本文選擇用相關系數的絕對值作為判斷所需信號依據的原因；與受干擾的心電信號相比，還原出的心電信號中CPR偽跡得到了明顯的抑制，更加接近真實的心電信號。
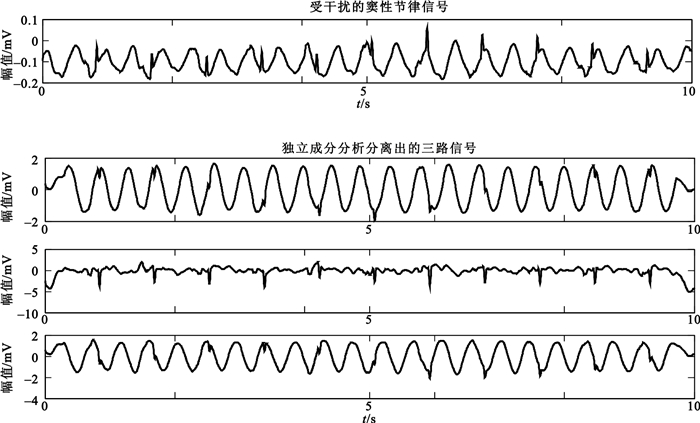圖4
應用FastICA從受干擾的SR信號中分離出的三個獨立分量
Figure4.
Three independent components obtained from corrupted SR signals with FastICA
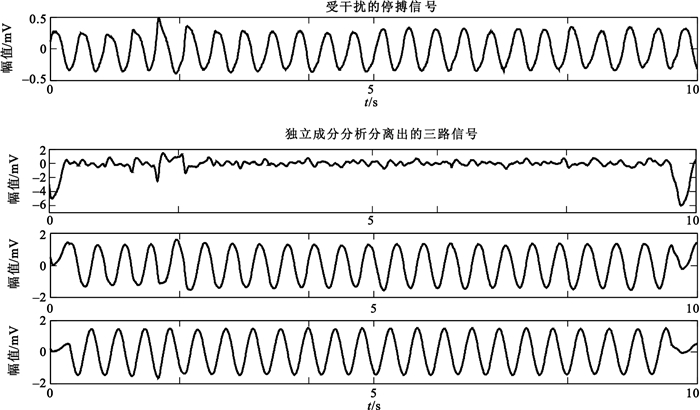圖5
應用FastICA從受干擾的ASYS信號中分離出的三個獨立分量
Figure5.
Three independent components obtained from corrupted ASYS signals with FastICA
2.3 除顫節律辨識結果與分析
表 1展示了不同情況除顫節律辨識的敏感性和特異性。“無CPR偽跡”一欄的結果代表訓練好的BP神經網絡在驗證集中的表現，高達97.00%的敏感性和98.67%的特異性，證明構建的BP神經網絡對于除顫節律辨識具有很好的性能。對比“無CPR偽跡”和“不濾波”兩欄的數據可以看出，CPR偽跡對除顫節律辨識的主要影響是大大降低了辨識算法的特異性，特別是無法正確區分SR節律信號和ASYS信號；這就意味著在CPR偽跡的干擾下，辨識算法更容易將SR信號和ASYS信號判斷為除顫節律。
表1
不同情況下的敏感性(%)和特異性(%)
Table1.
Sensitivities (%) and specificities (%) in different conditions
應用結合NA-MEMD與FastICA設計的自適應濾波器后，除顫節律辨識的特異性有了顯著提升(17.40%)；尤其是極大提高了ASYS信號的辨識準確性(43.82%)，說明自適應濾波器能很好地濾除受干擾的ASYS信號中的CPR偽跡，從而將其正確辨識為非除顫節律。本文設計的EMD+ICA自適應濾波器與性能已得到普遍承認的卡爾曼濾波器的濾波效果相比，在敏感性、特異性和準確性上都有大致相當甚至更好的表現。
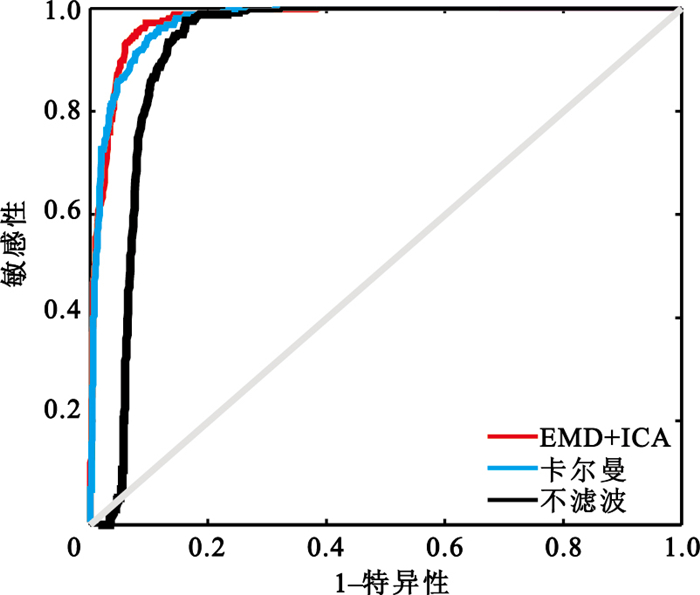
圖 6為不同濾波條件下的除顫節律辨識受試者工作特(receiver operating characteristic, ROC)曲線, 在不濾波、卡爾曼濾波器濾波和EMD+ICA自適應濾波器濾波三種條件下，曲線下面積分別是0.920 5、0.973 8、0.976 2。
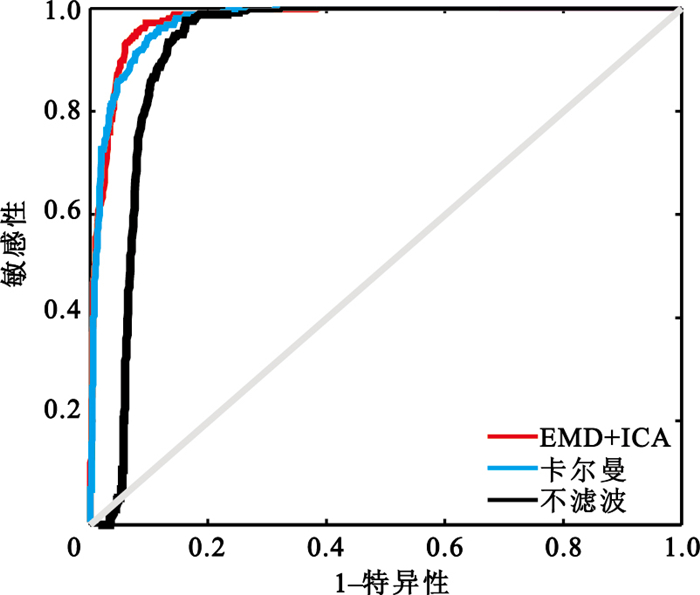圖6
不同濾波條件下的除顫節律辨識ROC曲線
Figure6.
ROC curves of the shockable rhythm detection algorithm derived from ECG signals filtered with different filters
實驗結果表明，應用本文設計的自適應CPR偽跡濾除算法，可以有效抑制CPR偽跡對心電節律辨識的影響，顯著提高除顫節律辨識的分類性能。
3 結論
本文結合EMD和ICA，提出了一種CPR偽跡濾除算法，并且基于一個包含1 484例受CPR偽跡干擾的心電信號的數據庫進行了實驗。實驗證明，對于SR、VF、PEA、ASYS四類心電信號，該算法都可以有效抑制受干擾的心電信號中CPR偽跡的成分，得到干凈的心電信號，從而顯著提高除顫節律辨識的準確性。該算法無需任何外部參考信號，因而可以直接應用在目前的自動體外除顫器(automated external defibrillator, AED)設備中且不必進行任何硬件改動。應用該算法，可以實現在不間斷胸外按壓的情況下，進行除顫節律的可靠分析，最終有效提高CPR的成功率。
引言
院外心臟驟停是一種嚴重威脅人類健康的致死性疾病[1-3]。高質量的胸外按壓和及時的早期電除顫，是心肺復蘇(cardiopulmonary resuscitation, CPR)的關鍵環節[4-5]。但是，胸外按壓過程中所引起的CPR偽跡會給除顫節律辨識算法帶來嚴重干擾，從而顯著降低辨識結果的可靠性。按照目前的方式，在實施電除顫前，為了準確進行除顫節律辨識，要中斷胸外按壓15 s以上[6]。然而，胸外按壓的長時間中斷，將嚴重阻礙患者建立自主循環，從而導致CPR的失敗[7]。顯然，如果構建一種算法，能在受干擾的心電信號中濾除CPR偽跡，提取出真正的心電節律信號，則可以在不間斷胸外按壓的同時實施可靠的除顫節律辨識，從而有效提高CPR的成功率。
最早關于濾除CPR偽跡的研究是在豬的心臟模型上開展的，研究結果表明一個固定截止頻率的高通濾波器就可以將豬的心電信號和CPR偽跡信號進行頻譜分離[8]。但是，CPR偽跡信號和人類心電信號的頻譜成分有很大一部分重合，使得這種方法無法應用在人類心電的除顫節律辨識上[9]。因此，一些研究者試圖利用一些外部信號作參考，對CPR偽跡建模。其中的一些算法，例如由Eilevstj?nn等[10]提出的多通道遞歸自適應匹配濾波器(multichannel recursive adaptive matching pursuit algorithm, MC-RAMP)、由Irusta等[11]提出的基于按壓頻率的最小均方誤差(least mean-square, LMS)濾波器，以及由Gong等[12]提出的基于胸阻抗信號的自適應濾波算法，都取得了很好的效果。但是，目前通用的大部分除顫儀僅僅記錄心電信號，這些算法所需的每一項外部參考信號，如按壓加速度、按壓深度、呼吸阻抗和胸阻抗等，都意味著另外的硬件支持；連接這些參考通道，既占用了寶貴的急救時間，又對院外急救人員提出了過高的專業要求。
也有研究者提出了一些無需參考信號的CPR偽跡濾除算法。這些算法多建立在傳統濾波器的基礎上，有些試圖用純頻率方法將偽跡濾除，有些試圖僅利用心電信號對偽跡進行建模；然而，由于CPR偽跡是一種頻率成分復雜的非線性信號，這些算法都沒有取得令人滿意的效果[13]。
與諸如傅里葉變換、小波變換等建立在線性分析基礎上的算法相比，經驗模態分解(empirical mode decomposition, EMD)和獨立成分分析(independent component analysis, ICA)作為新興的信號處理方法，更適用于分析短時、非穩態、非線性的復雜信號，已經分別在腦電信號分析、胎兒心電信號提取等生物醫學信號處理領域得到了應用，并取得很好的效果。本文結合EMD和ICA，提出了一種CPR偽跡的自適應濾除算法，試圖在無需任何參考信號的情況下，從受干擾的心電信號中分離出真正的心電節律信號。本文還構建了一個用于區分除顫節律(shockable rhythm)和非除顫節律(nonshockable rhythm)的反向傳播(back propagation，BP)神經網絡，分別對濾波前后的受干擾的心電信號進行除顫節律辨識，并計算其敏感性和特異性，用來評估該算法的性能。
1 算法設計
受干擾的心電信號可以被看作由真正的心電節律信號和疊加其上的CPR偽跡構成，而這兩個成分分別由患者和胸外按壓實施者產生，即信號源完全獨立；經過ICA后，可以有效地將這兩種成分分離開來。由于本文試圖在沒有任何外部參考信號的情況下完成CPR偽跡的濾除，因此進行ICA時所需的參考信號就需要從受干擾的心電信號本身提取。一些研究證明，CPR偽跡可以近似為一個以胸外按壓頻率為基礎頻率的周期信號，且在每一個按壓區間，按壓頻率可以近似為一個常數[11, 14]，如果能直接從受干擾的心電信號中得到胸外按壓頻率，則可以基于該頻率構建參考信號。
按照上述假設，本文首先利用EMD的方法從受干擾的心電圖信號中近似得到每一次胸外按壓的頻率；基于得到的按壓頻率，構建同相和正交的兩個參考信號；然后將這兩個參考信號和受干擾的心電圖信號一起，進行ICA，得到三個互相獨立的分量；最后從中選擇出所需的分量，即還原出了干凈的心電信號。
整個算法流程如圖 1所示。
圖1
自適應CPR偽跡濾波器算法流程
Figure1.
Flowchart of the CPR artifact cancellation adaptive filter algorithm
1.1 信號預處理
根據Thakor等[15-16]的研究，獲取的心電圖信號需要做三方面的預處理：①截止頻率為1 Hz的高通濾波器，用來去除殘余的基線漂移；②二階30 Hz巴特沃斯低通濾波器，用來抑制主要由肌肉電信號引起的高頻噪聲；③50 Hz陷波濾波器，用來消除工頻噪聲的干擾。
1.2 經驗模態分解
EMD是由Huang等[17]于1998年提出的一種旨在處理非線性、非穩態數據的信號處理方法。基于該方法，任何復雜的信號都能被分解為有限個不同時間尺度上的本征模函數(intrinsic mode function, IMF)，并將它們按照自身攜帶的時間尺度特征依次排列。這種算法根據信號自身的時間尺度進行分解，無需預設任何基函數，特別適合非線性非平穩信號的分析處理。在這一步驟中，需要用EMD提取出的信息代替外部參考信號，得到與CPR偽跡相關的胸外按壓頻率；此時EMD可以起到一個時變濾波器的作用，將與CPR偽跡相關的IMF提取出來[18]；再將這些IMF重新合成一個新的信號，就可以很好地反映CPR偽跡的基礎頻率特征。
為了避免模態混疊，本文采取了在標準EMD上改進的噪聲輔助多通道經驗模態分解(noise-assisted multivariate empirical mode decomposition, NA-MEMD)方法。Rehman等[19]的研究表明，與標準EMD相比，NA-MEMD能有效解決模態混疊問題。實驗發現，當采用三個互相獨立且功率均為1 dB的隨機高斯白噪聲作為MEMD的輔助信號時，效果最好。
應用上述NA-MEMD方法，將受干擾的心電信號分解為有限個IMF，并選擇相關IMF重新合成一個信號；將該合成信號的每一個極小值點所在的時刻標記在心電圖上，即代表胸外按壓最深位置時刻在心電圖中對應的位置，得到的結果如圖 2所示：從上到下依次是(a)受干擾的竇性節律(sinus rhythm, SR)信號、(b)受干擾的室顫(ventricular fibrillation, VF)信號、(c)受干擾的機電分離(pulseless electrical activity, PEA)信號和(d)受干擾的停搏(asystole, ASYS)信號，圖中的“*”標記胸外按壓最深位置時刻在心電圖上對應的位置，該標記由上述NA-MEMD方法得到。可以看出，這些標記能很好地反映CPR偽跡的基礎頻率特征。
圖2
應用NA-MEMD在受干擾的心電信號中標記胸外按壓最深位置時刻
Figure2.
Marks of instant of chest compression obtained from corrupted ECGs by NA-MEMD
將由“*”標記的點依次記為ni，即可得到胸外按壓的相位函數Φ(n)：
| $ \Phi \left( n \right) = \frac{{2{\rm{\pi }}}}{{\nabla {n_i}}}\left( {n - {n_i}} \right) + i \times 2{\rm{\pi }}\;\;{{\rm{n}}_i} \le n < {n_{i + 1}} $ |
得到該相位函數后，構造與CPR同相和正交的兩路參考信號，分別記為r_cos(n)和r_sin(n)：
| $ r\_\cos \left( n \right) = \cos \left( {\Phi \left( n \right)} \right) $ |
| $ r\_\sin \left( n \right) = \sin \left( {\Phi \left( n \right)} \right) $ |
1.3 獨立成分分析
ICA又稱盲信號分離，是一種在源信號及其組合關系均未知的情況下，僅利用觀測信號分離出源信號的方法，在語音處理、圖像處理、生物電信號處理等各個領域均得到廣泛應用。自從ICA的概念提出以來，不同學者基于不同的目標函數和優化算法，提出很多種盲信號分離算法。本文采用Hyv?rinen等[20-22]提出的基于負熵的快速固定點算法(fast fixed-point algorithm for independent component analysis, FastICA)，該算法具有較快的收斂速度，且與基于峭度的算法相比具有更好的魯棒性，更適合于特征多變、噪聲復雜的心電信號處理。
首先結合受干擾的心電信號和上述構造的兩路參考信號，組成矩陣作為觀測信號:
| $ s\left( n \right) = \left[ {{S_{{\rm{ECG\_MIXED}}}}\left( n \right),r\_\cos \left( n \right),r\_\sin \left( n \right)} \right] $ |
將此觀測信號進行去均值和白化處理；處理后的觀測信號按照文獻[20]中描述的方法進行計算，迭代更新分離向量，直至算法收斂；為了避免意外，將最大迭代次數限制為1 000次，如果迭代次數超過上限而算法仍未收斂，則停止迭代，轉而選取白化處理后的觀測信號作為替代結果。
盲信號分離后獲得的結果仍然是一個三維矩陣x(n)，且各個成分出現的順序并不確定，因此需要進行分析選擇：分別計算結果里每個分量與兩路參考信號的相關系數的絕對值：
| $ C\_{\cos _i} = \left| {\frac{{\sum {{x_i}\left( n \right)r\_\cos \left( n \right)} }}{{\sqrt {\sum {x_i^2\left( n \right)} \sum {r\_{{\cos }^2}\left( n \right)} } }}} \right| $ |
| $ C\_{\sin _i} = \left| {\frac{{\sum {{x_i}\left( n \right)r\_\sin \left( n \right)} }}{{\sqrt {\sum {x_i^2\left( n \right)} \sum {r\_{{\sin }^2}\left( n \right)} } }}} \right| $ |
與某一路參考信號相關系數的絕對值最高的分量即為該參考信號在結果中的估計，這種分量不是所需的信號；依次去掉這種分量后剩下的結果，即被認為是還原出的干凈的心電信號。
1.4 BP神經網絡構建
還原出干凈的心電信號后，本文構建了一個BP神經網絡作為二分類器使用，根據心電信號的一些特征值，將其分為除顫節律和非除顫節律兩類。神經網絡已經被廣泛應用于心電節律辨識上，并且取得了良好的效果[23-24]。根據Li等[25]的驗證，結合Jekova等[26]提出的特征值Count2和Kuo等[27]提出的特征值濾波泄露量(Leakage)，進行除顫節律辨識，準確性可高達96.3%；特征值Count2和Leakage分別可用如下方式得到。
(1)Count2：
首先將心電信號S通過如下帶通濾波器：
| $ FS\left( n \right) = \frac{{14 \times FS\left( {n - 1} \right) - 7 \times FS\left( {n - 2} \right) + \frac{{S\left( n \right) - S\left( {n - 1} \right)}}{2}}}{8} $ |
再求得上述濾波器輸出信號的絕對值AbsFS，并計算出每秒鐘該絕對值的最大值max(AbsFS)、平均值mean(AbsFS)和平均絕對偏差MD。
最后，按照以下方法，分別計算出長度為10 s樣本中Count1、Count2、Count3三個值的大小：Count1范圍: 0.5×max(AbsFS)至max(AbsFS); Count2范圍: mean(AbsFS)至max(AbsFS); Count3范圍: mean(AbsFS)-MD至mean(AbsFS)+MD。
(2)Leakage：
將心電信號S通過一個窄帶寬帶阻濾波器，這個濾波器的中心頻率為心電信號的均值頻率，通過濾波器后的殘余信號即為Leakage：
| $ {\rm{Leakage}} = \frac{{\sum\limits_{i = 1}^m {\left| {s\left( i \right) + s\left( {i - \frac{T}{2}} \right)} \right|} }}{{\sum\limits_{i = 1}^m {\left| {s\left( i \right)} \right| + \left| {s\left( {i - \frac{T}{2}} \right)} \right|} }} $ |
其中，T為心電信號的均值頻率：
| $ T = 2{\rm{\pi }}\frac{{\sum\limits_{i = 1}^m {\left| {s\left( i \right)} \right|} }}{{\sum\limits_{i = 1}^m {\left| {s\left( i \right) - s\left( {i - 1} \right)} \right|} }} $ |
這兩個值組成的特征向量metric=[Count2, Leakage]，作為BP神經網絡中的輸入向量。
如圖 3所示，本文設計了一個三層BP神經元網絡：輸入層單元數為2，對應二維的輸入向量；輸出層單元數為1，輸出為1表示結果為除顫節律, 輸出為0表示結果為非除顫節律。經試驗，隱層的單元數為2時，神經網絡具有很好的性能。
圖3
構建的BP神經網絡的結構
Figure3.
Configuration of the constructed BP neural network
2 實驗
2.1 數據庫
實驗所需的心電數據采集自12頭成年豬；在麻醉條件下，將低壓的交流電通入豬的心室壁上，導致其心電變為VF節律，數分鐘后由一名急救科的醫生進行CPR，全程記錄實驗過程中豬的心電、主動脈壓等各項生理信號。
實驗共采集了1 484例受CPR偽跡干擾的心電信號，這些信號由專家綜合當時的心電信號、胸外按壓前后的心電表現和主動脈壓等其他生理參數進行了分類標注：其中810例SR信號，237例VF信號，170例PEA信號和267例ASYS信號。為了對1.4中描述的BP神經網絡進行訓練和驗證，實驗還采集了800例未受CPR偽跡干擾的心電信號，包含SR、VF、PEA、ASYS各200例。將各類信號隨機平均分為兩部分，分別組成神經網絡的訓練集和驗證集。所有的心電信號都以250 Hz的采樣頻率采樣，每個樣本長度均為10 s。
為評估本文提出的濾波算法的性能，實驗選擇了準確性好且應用廣泛的由Ruiz de Gauna等[14]設計的卡爾曼濾波器作為比較：將1 484例受CPR偽跡干擾的心電信號分別在不濾波、通過卡爾曼濾波器和通過本文設計的EMD+ICA自適應濾波器三種情況下，由訓練好的BP神經網絡進行除顫節律辨識，并統計出每一種情況下辨識的敏感性(即正確識別出除顫節律的概率)和特異性(即正確識別出非除顫節律的概率)，以及每一類心電節律辨識的準確性。
2.2 濾波器效果
圖 4和圖 5分別是對受干擾的SR信號和ASYS信號進行ICA后的結果。從圖中可以看出，所需的心電信號在分離出的三個獨立分量中出現的位置并不固定，且存在反相現象，這就是本文選擇用相關系數的絕對值作為判斷所需信號依據的原因；與受干擾的心電信號相比，還原出的心電信號中CPR偽跡得到了明顯的抑制，更加接近真實的心電信號。
圖4
應用FastICA從受干擾的SR信號中分離出的三個獨立分量
Figure4.
Three independent components obtained from corrupted SR signals with FastICA
圖5
應用FastICA從受干擾的ASYS信號中分離出的三個獨立分量
Figure5.
Three independent components obtained from corrupted ASYS signals with FastICA
2.3 除顫節律辨識結果與分析
表 1展示了不同情況除顫節律辨識的敏感性和特異性。“無CPR偽跡”一欄的結果代表訓練好的BP神經網絡在驗證集中的表現，高達97.00%的敏感性和98.67%的特異性，證明構建的BP神經網絡對于除顫節律辨識具有很好的性能。對比“無CPR偽跡”和“不濾波”兩欄的數據可以看出，CPR偽跡對除顫節律辨識的主要影響是大大降低了辨識算法的特異性，特別是無法正確區分SR節律信號和ASYS信號；這就意味著在CPR偽跡的干擾下，辨識算法更容易將SR信號和ASYS信號判斷為除顫節律。
表1
不同情況下的敏感性(%)和特異性(%)
Table1.
Sensitivities (%) and specificities (%) in different conditions
應用結合NA-MEMD與FastICA設計的自適應濾波器后，除顫節律辨識的特異性有了顯著提升(17.40%)；尤其是極大提高了ASYS信號的辨識準確性(43.82%)，說明自適應濾波器能很好地濾除受干擾的ASYS信號中的CPR偽跡，從而將其正確辨識為非除顫節律。本文設計的EMD+ICA自適應濾波器與性能已得到普遍承認的卡爾曼濾波器的濾波效果相比，在敏感性、特異性和準確性上都有大致相當甚至更好的表現。
圖 6為不同濾波條件下的除顫節律辨識受試者工作特(receiver operating characteristic, ROC)曲線, 在不濾波、卡爾曼濾波器濾波和EMD+ICA自適應濾波器濾波三種條件下，曲線下面積分別是0.920 5、0.973 8、0.976 2。
圖6
不同濾波條件下的除顫節律辨識ROC曲線
Figure6.
ROC curves of the shockable rhythm detection algorithm derived from ECG signals filtered with different filters
實驗結果表明，應用本文設計的自適應CPR偽跡濾除算法，可以有效抑制CPR偽跡對心電節律辨識的影響，顯著提高除顫節律辨識的分類性能。
3 結論
本文結合EMD和ICA，提出了一種CPR偽跡濾除算法，并且基于一個包含1 484例受CPR偽跡干擾的心電信號的數據庫進行了實驗。實驗證明，對于SR、VF、PEA、ASYS四類心電信號，該算法都可以有效抑制受干擾的心電信號中CPR偽跡的成分，得到干凈的心電信號，從而顯著提高除顫節律辨識的準確性。該算法無需任何外部參考信號，因而可以直接應用在目前的自動體外除顫器(automated external defibrillator, AED)設備中且不必進行任何硬件改動。應用該算法，可以實現在不間斷胸外按壓的情況下，進行除顫節律的可靠分析，最終有效提高CPR的成功率。
