充分考慮調強放療計劃系統產生的計劃劑量數據中存在較多梯度邊緣點的特點,提出了一種基于梯度特征的調強放療計劃劑量插值算法(TDAGI)。算法首先改進了傳統Canny邊緣探測方法,并根據計劃劑量數據平面的梯度信息來獲取該平面上各梯度邊緣點和非梯度邊緣點;對梯度邊緣點追蹤梯度剖面并計算其所對應的銳度,對非梯度邊緣點計算自定義的偏離系數。使用銳度和偏離系數,通過TDAGI所構造的分布函數得到以該數據平面上每一點為雙三次插值中心點時對應的雙三次插值核的系數,對每一個待插值點進行特定的雙三次插值,從而得到每一個待插值點的計劃劑量數據。結果表明TDAGI與傳統雙三次插值算法以及目前治療計劃系統中廣為使用的雙線性插值算法相比,在減小誤差的同時,具有梯度保持方面的優勢,因此TDAGI對于調強放療計劃劑量插值有一定的實際應用意義。
引用本文: 翟磊, 黃寧, 王鵬, 范軼翔, 夏翔, 吳慶星. 基于梯度特征的調強放療計劃劑量插值算法. 生物醫學工程學雜志, 2016, 33(6): 1116-1123. doi: 10.7507/1001-5515.20160178 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
調強放射治療(intensity-modulated radiation therapy,IMRT)劑量驗證作為治療計劃可靠性的重要保證,劑量驗證的準確性對放射治療效果以及患者的安全有著重要意義[1-2]。劑量驗證基本思路是用合理的方法比較治療計劃系統(treatment plan system,TPS)產生的計劃劑量數據和測量硬件得到的測量劑量數據[3]。治療計劃劑量數據從產生到進行劑量驗證過程中有時需要經過多次插值計算:一方面,TPS系統對治療計劃使用相關計算模型得到一個較為精確的計劃劑量數據平面,而TPS系統內部有時會改變計劃劑量數據平面上數據點之間的物理間距以滿足不同的輸出要求,因而需要對這個較為精確的數據平面進行插值計算;另一方面,劑量驗證時需要先將計劃劑量數據平面和測量數據平面按等劑量中心進行重合之后再比較相同位置上的點,但兩者數據平面上數據點之間的物理間距可能不相同,因此會導致重合之后兩個平面上的點錯位分布,此時需要進行插值計算從而在計劃劑量數據平面上得到與測量數據平面相同位置的點的劑量值。
目前國內外對于TPS產生的計劃劑量數據插值計算研究較少,實際處理中如DoseLab,MapCkeck等驗證軟件主要采用的方法多為雙線性插值,它利用待求點的四個相鄰點的值在兩個方向上作線性內插[4]。這種插值方法的優點在于時間代價較小,但是由于調強放療的劑量分布中病灶區和正常區域之間存在較大的劑量梯度,大量的研究表明雙線性插值由于算法本身具有平滑以及模糊效應,無法真實地反映梯度邊緣處的梯度分布,從而在梯度邊緣產生較大誤差,并且使結果失去原有的梯度信息,進而對醫生和物理師的判斷產生誤導[5-9]。為了克服上述雙線性插值存在的問題,課題組提出了一種新算法,基于梯度特征的調強放療計劃劑量插值算法(treatment plan dose interpolation algorithm based on gradient feature in intesity-modulated radiation therapy,TDAGI)。算法依據本文對雙三次插值核的系數調節作用的研究,確定以每一個梯度邊緣點或非梯度邊緣點為雙三次插值中心點時所對應的雙三次插值核系數,并對每一個待插值點使用所述雙三次插值核的系數進行特定的雙三次插值得出最終結果,從而充分考慮并有效還原了計劃劑量數據平面上每一點的梯度分布特點。
1 基于梯度特征的調強放療計劃劑量插值算法
1.1 梯度邊緣點和梯度剖面的獲取
假設TPS產生的原始數據平面為IL,首先求得每一點(i,j)的梯度 ?IL(i,j)以及梯度的模‖ ?IL(i,j)‖,然后使用傳統的Canny邊緣探測方法得到原始計劃劑量數據平面上所有梯度邊緣點。
但是,一方面計劃劑量數據由TPS計算而來,是不存在噪聲的,因此不需要傳統Canny算法中的高斯濾波以及上閾值設置;另一方面,傳統Canny算法存在假邊緣效應[10-12]。為了減小傳統Canny算法的假邊緣,在一個3×3鄰域中若存在多個梯度邊緣點,則只取其中梯度模最大點作為所述3×3區域內的唯一梯度邊緣點,用這種方法來代替傳統Canny算法中的下閾值設置。這種評判標準雖然較為嚴格,但是省去了傳統Canny算法中較復雜的上下閾值設置,而且本文算法TDAGI中對于非梯度邊緣點采用了自定義的偏離系數,因此可以從一定程度反映出在減少假梯度邊緣過程中所缺失的梯度邊緣點具有的劑量數據分布特點,從而達到較好的計算結果。因此TDAGI首先對傳統Canny算法作如下改進:
(1) 略去傳統Canny算法中高斯濾波的過程以及上下閾值設置的過程;
(2) 假設點(i′,j′)為所得到的一個梯度邊緣點,且以點(i′,j′)為中心的3×3鄰域中含有其他梯度邊緣點,若點(i′,j′)的梯度模小于所述鄰域中其他梯度邊緣點的梯度模,則需要重新將其標記為非梯度邊緣點。
得到計劃劑量數據平面上所有梯度邊緣點之后,該數據平面上剩下的點則為非梯度邊緣點。對于所獲取的每個梯度邊緣點(i′,j′),如圖 1所示,從該點開始,分別沿著梯度的正方向和負方向追蹤梯度剖面,每次與數據平面的坐標網格交于一個點,根據該交點梯度的方向繼續往下追蹤,直到梯度的模不再減小,最終得到每個點所對應的梯度剖面。在梯度剖面與數據坐標網格形成的各個交點中,若交點不為已存在的數據點(如圖 1所示的方塊),則該點的梯度使用相鄰點的數據線性插值得到[13]。
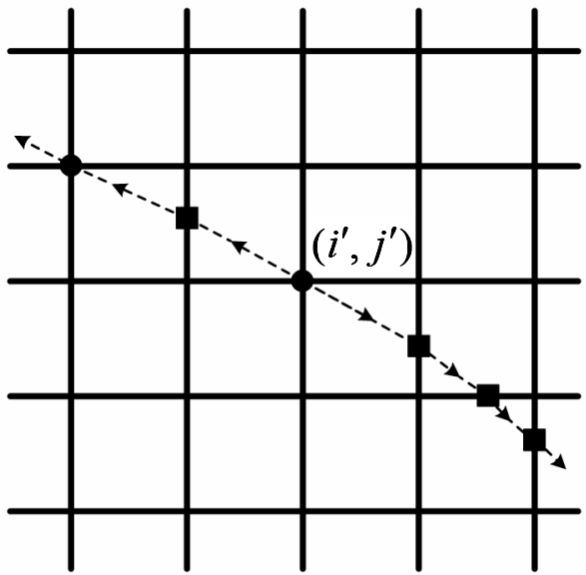 圖1
梯度剖面追蹤示意
Figure1.
Illustration of the gradient profile tracing
圖1
梯度剖面追蹤示意
Figure1.
Illustration of the gradient profile tracing
1.2 雙三次插值核系數調節原理的研究
本文研究了雙三次插值核的系數a對雙三次插值核的影響,并利用系數與雙三次插值核的關系對最終的雙三次插值進行調節。
雙三次插值作為一種傳統的插值方法,其利用待插值點周圍的16個點的值作為基準點,使用如下公式(1)、(2)、(3)、(4)得到待插值點的值[14-15]。
| $f({i_C} + u,{j_C} + v) = ABC$ |
| $A = \left[ {s\left( {1 + u} \right)s\left( u \right)s\left( {1 - u} \right)s\left( {2 - u} \right)} \right]$ |
| $B = \left( {\begin{array}{*{20}{c}} {f({i_C} - 1,{j_C} - 1)} &{f({i_C} - 1,{j_C})} &{f({i_C} - 1,{j_C} + 1)} &{f({i_C} - 1,{j_C} + 2)}\\ {f({i_C},{j_C} - 1)} &{f({i_C},{j_C})} &{f({i_C},{j_C} + 1)} &{f({i_C},{j_C} + 2)}\\ {f({i_C} + 1,{j_C} - 1)} &{f({i_C} + 1,{j_C})} &{f({i_C} + 1,{j_C} + 1)} &{f({i_C} + 1,{j_C} + 2)}\\ {f({i_C} + 2,{j_C} - 1)} &{f({i_C} + 2,{j_C})} &{f({i_C} + 2,{j_C} + 1)} &{f({i_C} + 2,{j_C} + 2)} \end{array}} \right)$ |
| $C = {\left[ {s\left( {1 + v} \right)s\left( v \right)s\left( {1 - v} \right)s\left( {2 - v} \right)} \right]^T}$ |
其中,f(iC+u,jC+v)表示與雙三次插值的中心點(iC,jC)在水平方向和垂直方向距離分別為u和v的待插值點的值(u≥0,v<1),f(iC,jC)表示坐標為(iC,jC)點的值,s(w)表示雙三次插值核。傳統的雙三次插值為了逼近最佳插值函數sin(w)/w,其對應的s(w)如公式(5)所示[15-16]。
| $s\left( w \right) = \left\{ \begin{array}{l} {\left| w \right|^3} - 2{\left| w \right|^2} + 1,{\rm{ }}0 \le \left| w \right| < 1\\ - {\left| w \right|^3} + 5{\left| w \right|^2} - 8\left| w \right| + 4,{\rm{ }}1 \le \left| w \right| < 2\\ 0{\rm{ }},{\rm{ }}\left| w \right| \ge 2 \end{array} \right.$ |
其中w項的實際意義為待插值點到每一個基準點之間的距離,因此s(w)表示16個基準點按照與待插值點之間的距離對應的加權系數。而Keys[17]提出雙三次插值核s(w) 可以有更為普遍的形式,如公式(6)所示(其中a<0):
| $s\left( w \right) = \left\{ \begin{array}{l} \left( {a + 2} \right){\left| w \right|^3} - \left( {a + 3} \right){\left| w \right|^2} + 1 \ge 0,{\rm{ }}0 \le \left| w \right| < 1\\ a{\left| w \right|^3} - 5a{\left| w \right|^2} + 8a\left| w \right| - 4a \le 0,{\rm{ }}1 \le \left| w \right| < 2\\ 0{\rm{ }},{\rm{ }}\left| w \right| \ge 2 \end{array} \right.$ |
可以看出,a=-1時公式(5)與公式(6)等價。假設有兩個雙三次插值核的系數a1和a2且滿足a1<a2<0,則對應的雙三次插值核之差如式(7)所示:
| ${s_{a1}}\left( w \right) - {s_{a2}}\left( w \right) = \left\{ \begin{array}{l} ({a_1} - {a_2}){w^2}\left( {w - 1} \right) \ge 0,{\rm{ }}0 \le \left| w \right| < 1\\ ({a_1} - {a_2})\left( {w - 1} \right){\left( {w - 2} \right)^2} \le 0,{\rm{ }}1 \le \left| w \right| < 2\\ 0{\rm{ }},{\rm{ }}\left| w \right| \ge 2 \end{array} \right.$ |
從式(7)可以看出,0≤|w|<1時,雙三次插值核的系數a絕對值越小,對應雙三次插值核的值越小,此時雙三次插值的中心點(iC,jC)所對應的權重越小,從而待插值點與雙三次插值的中心點(iC,jC)值的差異越大,因而中心點(iC,jC)處容易形成較大梯度;當1≤|w|<2時,雙三次插值核的系數a絕對值越小,對應雙三次插值核的值越大,而且由公式(6)可知此時雙三次插值核的值小于0,故對應雙三次插值核的絕對值也越接近于0,使得雙三插值的中心點(iC,jC)之外的其他基礎點對待插值點的影響越小,從而雙三次插值核的系數a對于待插值點與雙三次插值的中心點(iC,jC)在0≤|w|<1時的調節作用也越明顯,因此可由雙三次插值核的系數a在中心點(iC,jC)處調節出較大的梯度。
從圖 2也可以看出,a的絕對值越小,對應s(w)的絕對值越小,即中心點(iC,jC)的加權系數越小,從而待插值點與中心點(iC,jC)的差異越大,同時中心點之外的其他基礎點對待插值點的影響越小,容易形成較大的梯度。事實上,如圖 3所示,對于每個梯度邊緣點對應的梯度剖面,雙線性插值由于無法真實反映梯度邊緣處的梯度分布,從而在梯度邊緣附近的待插值點處產生較大的計算誤差。我們通過圖 3可以看出,梯度變化越快的剖面(P2)對應的誤差越大。
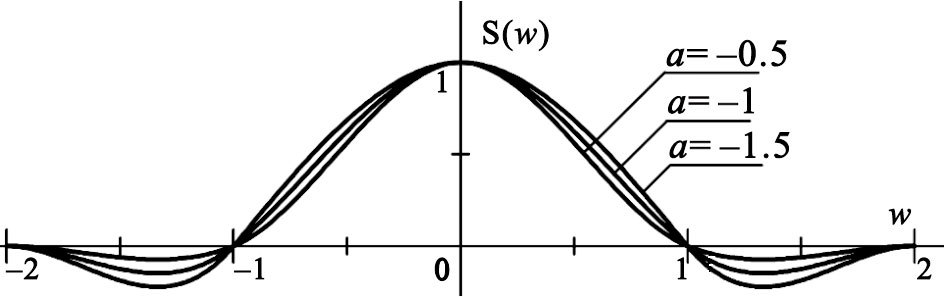 圖2
不同系數下的插值核變化規律
Figure2.
Change pattern of interpolation kernels of different coefficients
圖2
不同系數下的插值核變化規律
Figure2.
Change pattern of interpolation kernels of different coefficients
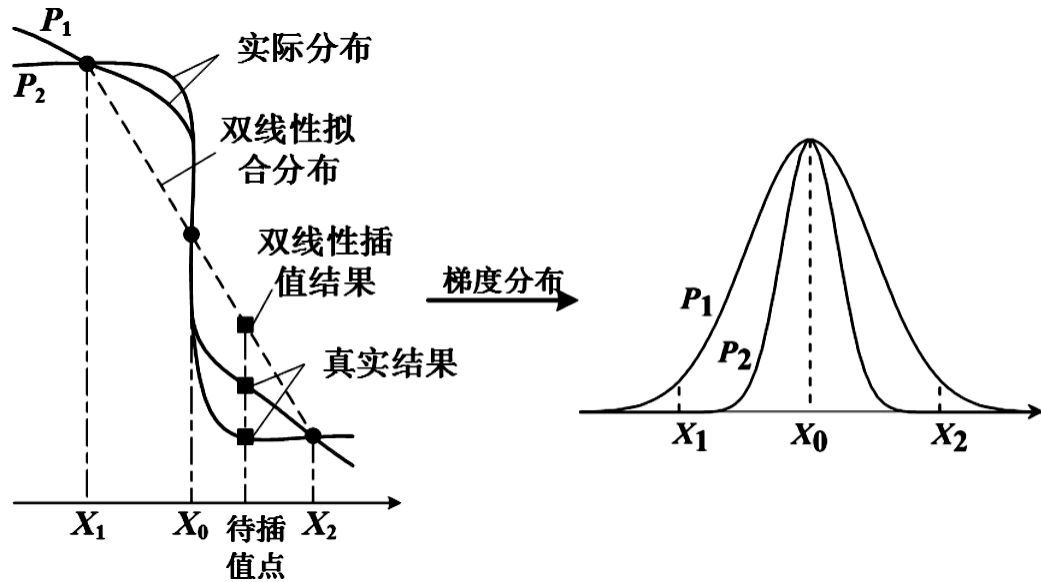 圖3
梯度剖面上的插值以及梯度分布
圖3
梯度剖面上的插值以及梯度分布
對每一個梯度邊緣點(i′,j′),使用公式(8)所定義的銳度σ(i′,j′)來表示該梯度邊緣點對應梯度剖面P(i′,j′)上梯度變化的快慢:
| $\sigma \left( {i\prime ,j\prime } \right) = \sqrt {\sum\nolimits_{x \in P(i\prime ,j\prime )} {} \frac{{m\left( x \right)}}{{M\left( {i\prime ,j\prime } \right)}}d_c^2\left( {x,\left( {i\prime ,j\prime } \right)} \right)} $ |
其中,x是梯度邊緣點(i′,j′)所對應梯度剖面P(i′,j′)上與數據坐標網格相交的每一點,m(x)表示x點處的梯度模,M(i′,j′)表示梯度剖面P(i′,j′)上梯度模的和,dc(x,(i′,j′))表示點x與梯度邊緣點(i′,j′)之間的曲線距離;
對每一個非梯度邊緣點(i″,j″),本文定義偏離系數ρ(i″,j″)為每一點與周圍3×3鄰域整體的平均計劃劑量值偏差,以此來度量該非梯度邊緣點的偏離程度,如式(9)所示:
| $\rho \left( i'',j'' \right)=\frac{\left| \overline{{{I}_{L}}\left( i'',j'' \right)}-{{I}_{L}}\left( i'',j'' \right) \right|}{{{I}_{L}}\left( i'',j'' \right)}$ |
其中IL(i″,j″)為以非梯度邊緣點(i″,j″)為中心的3×3鄰域中除非梯度邊緣點(i″,j″)以外各個點的平均計劃劑量值。IL(i″,j″)為該非梯度邊緣點(i″,j″)的計劃劑量值。
從銳度σ(i′,j′)的定義可以看出,銳度的值越小,對應剖面上的梯度變化越快,從圖 3可以看出,待插值點的值會偏離梯度邊緣點(i′,j′)而接近于兩旁的點,結合對圖 2以及上述公式(6)、(7)的分析可以看出,若以該梯度邊緣點(i′,j′)為雙三次插值中心點(iC,jC) ,此時需要雙三次插值核的系數的絕對值較小,通過這樣的處理,可以使計劃劑量數據平面上梯度邊緣點對應梯度剖面的劑量數據分布更加接近于真實的劑量數據分布;從自定義的非梯度邊緣點(i″,j″)的偏離系數來看,偏離系數ρ(i″,j″)越大則待插值點與非梯度邊緣點(i″,j″)之間的差異越大,結合對圖 2以及式(6)、(7)的分析可以看出,若以該非梯度邊緣點(i″,j″)為雙三次插值中心點(ic,jc),此時需要雙三次插值核的系數的絕對值較小。
通過以上的研究分析結果構造出每一點的銳度或偏離程度與每一點雙三次插值核的系數之間的函數關系。這就是本文算法TDAGI使用雙三次插值核的系數進行調節的思路。
1.3 確定雙三次插值核的系數并得出結果
對于每一個梯度邊緣點(i′,j′),以點(i′,j′)為雙三次插值中心點時,對雙三次插值核的系數a(i′,j′)與該梯度邊緣點對應梯度剖面的銳度σ(i′,j′)之間構造函數關系如式(10)所示:
| $a\left( i',j' \right)=-0.5\frac{1}{1+ln\left( {{\sigma }_{max}}/\sigma \left( i',j' \right) \right)}exp\left\{ {{\left( \frac{1-\sigma \left( i',j' \right)}{{{\sigma }_{max}}} \right)}^{2}} \right\}$ |
其中,σmax表示該計劃劑量數據平面上銳度的最大值;可以看出,式(10)中雙三次插值核的系數a(i′,j′)絕對值隨銳度σ(i′,j′)的減小而減小,滿足前面得出的規律。
對于每一個非梯度邊緣點(i″,j″),以點(i″,j″)為雙三次插值中心點時,對雙三次插值核的系數a(i″,j″)與該非梯度邊緣點的偏離系數ρ(i″,j″)之間構造函數關系如式(11)所示:
| $a\left( i'',j'' \right)=-0.5\left\{ exp-{{\left( \frac{\rho \left( i'',j'' \right)-{{\rho }_{min}}}{{{\rho }_{max}}-{{\rho }_{min}}} \right)}^{2}} \right\}$ |
其中ρmax為計劃劑量數據平面上最大偏離系數,ρmin為計劃劑量數據平面上最小偏離系數。將式(10)和式(11)兩者結果合并,從而得出以計劃劑量數據平面上每一點(i,j)為雙三次插值中心點時所對應的雙三次插值核的系數,記為a(i,j);對于每一個待插值點,設其坐標為(α,β),若α∈[i,i+1) 且β∈[j,j+1) ,則以點(i,j)為雙三次插值中心點,以a(i,j)為雙三次插值核的系數,即可得到該點所對應的雙三次插值核,如式(12)所示:
| $s\left( w \right)=\left\{ \begin{align} & \left( a\left( i,j \right)+2 \right){{\left| w \right|}^{3}}-\left( a\left( i,j \right)+3 \right){{\left| w \right|}^{2}}+1\ge 0,0\le \left| w \right| <1 \\ & a\left( i,j \right){{\left| w \right|}^{3}}-5a\left( i,j \right){{\left| w \right|}^{2}}+8a\left( i,j \right)\left| w \right|-4a\le 0,1\le \left| w \right| <2 \\ & 0,\left| w \right|\ge 2 \\ \end{align} \right.$ |
其中w項的實際意義為待插值點到每一個基準點之間的距離;結合公式(1)、(2)、(3)、(4),以點(i,j)為雙三次插值中心點對該待插值點進行特定的雙三次插值計算,進而得出每一個待插值點的計劃劑量數據。
2 結果與分析
驗證算法最直接的辦法是將各個待插值點處插值所得計劃劑量數據與該點處計劃劑量數據的真實值進行比較。然而一方面對每一個網格,TPS只能輸出該網格中劑量的平均值,無法得到該網格中單個點處的劑量值,因此TPS無法獲取該網格中某一特定待插值點處真實的劑量值;另一方面,TPS內部為了滿足輸出需求會改變數據點之間的距離(網格大小),其往往采用線性插值得到新的計劃劑量數據分布,這種新的劑量數據不是真實值,因此TPS很難得到待插值點的計劃劑量數據的真實值。但是蒙特卡羅程序作為劑量計算的“金標準”,可以用來模擬真實的劑量分布[18]。因此使用蒙特卡羅程序BEAMnrc/Dosxyznrc來替代TPS產生原始計劃劑量數據和待插值點處計劃劑量數據的真實值。分別使用TDAGI、雙線性插值算法以及傳統的雙三次插值算法對原始調強放療計劃劑量數據進行計算,得到各個待插值點處的計劃劑量數據,再與蒙特卡羅程序BEAMnrc/Dosxyznrc輸出的待插值點處計劃劑量數據的真實值進行對比。
對于一個總大小為96 mm×96 mm調強放射治療照射區域,分別以0.40、0.48、0.50、0.60、0.64、0.75、0.80、0.96、1.00、1.20、1.50、1.60、2.00、2.40、3.00、3.20、4.00 mm共17組不同的物理尺寸作為原始調強放療計劃劑量數據平面的網格大小,模擬出該照射區域中17組原始計劃劑量數據平面的劑量數據分布;在相同環境和條件下,從等劑量中心點開始,分別以上述17組物理尺寸為插值間距,模擬出17組待插值點平面上各個待插值點處的計劃劑量數據的真實值。在每一組原始調強放療計劃劑量數據平面上分別運用TDAGI、雙線性插值算法和傳統雙三次插值算法,得出17種插值間距下的插值結果,總共形成17×17組結果,并與模擬得出的各個待插值點處計劃劑量數據的真實值進行比較,得出三種算法各自的誤差。
考慮到實際劑量數據平面的網格大小在0.50 mm左右,因此使用0.40、0.48、0.50、0.60 mm為插值間距來評價算法的精確度。如圖 4所示,展示了用17組原始數據平面分別以0.40、0.48、0.50、0.60 mm為插值間距作插值計算時三種方法的誤差對比(橫坐標為原始計劃劑量數據平面的網格大小)。從結果可以看到,對于所選定的4種插值間距,從誤差的總體變化趨勢來看,TDAGI的誤差小于雙三次插值算法和雙線性插值算法。
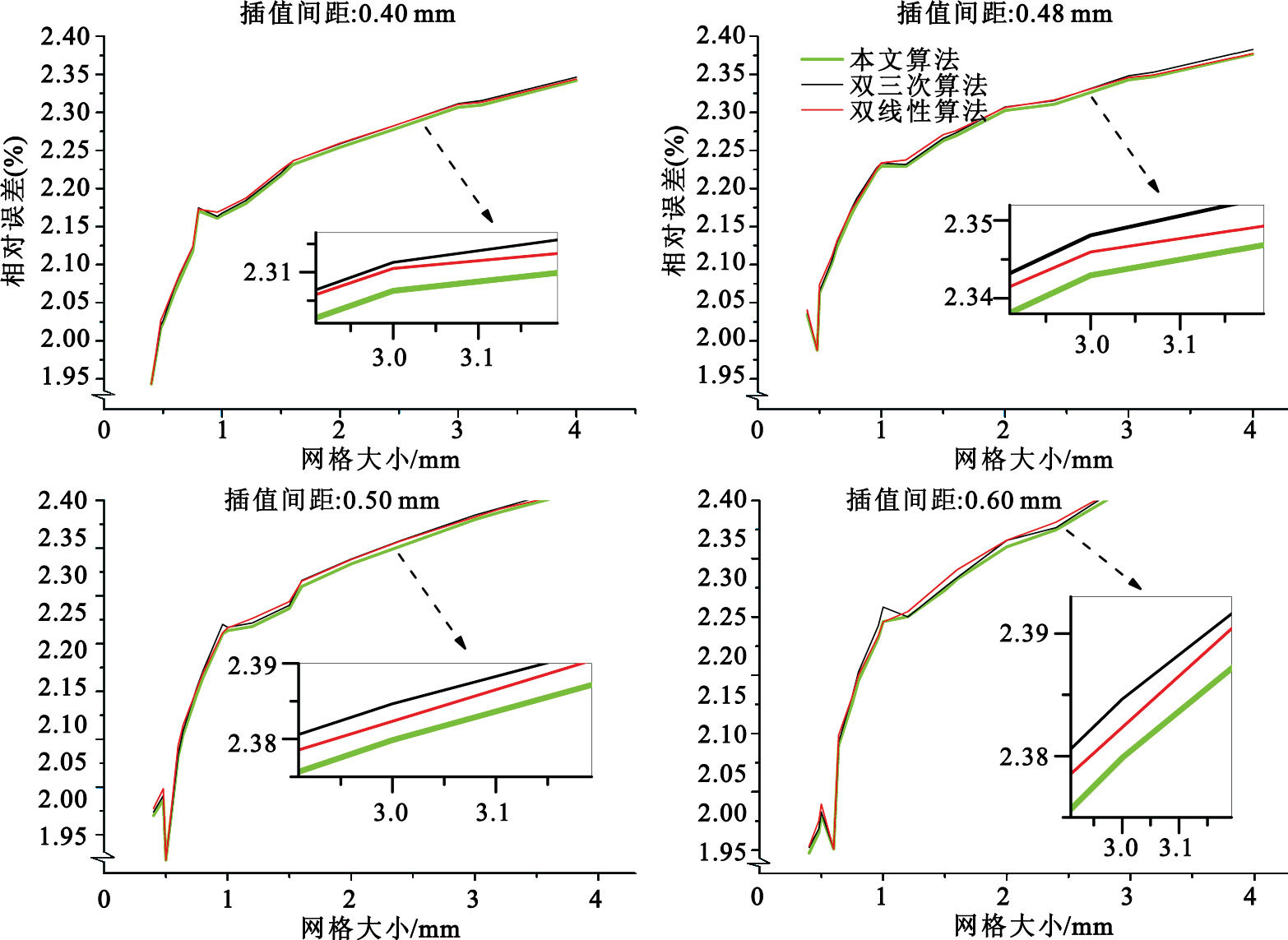 圖4
TDAGI、雙線性插值算法以及雙三次插值算法的誤差對比
Figure4.
Error comparison among TDAGI,Bilinear interpolation and Bi-Cubic interpolation
圖4
TDAGI、雙線性插值算法以及雙三次插值算法的誤差對比
Figure4.
Error comparison among TDAGI,Bilinear interpolation and Bi-Cubic interpolation
對17組原始數據每組都使用上述三種插值方法分別進行上述17種間距的插值計算,求出每組原始數據在不同插值間距下的誤差平均值,將誤差進行對比。結果展示在圖 5中(橫坐標為原始計劃劑量數據平面的網格大小),可以看出,除了原始數據網格大小在1.20~1.50 mm之間時TDAGI誤差大于雙線性插值,其余情況下TDAGI誤差都小于雙線性插值;而且每種情況下TDAGI的誤差都小于傳統雙三次插值結果。
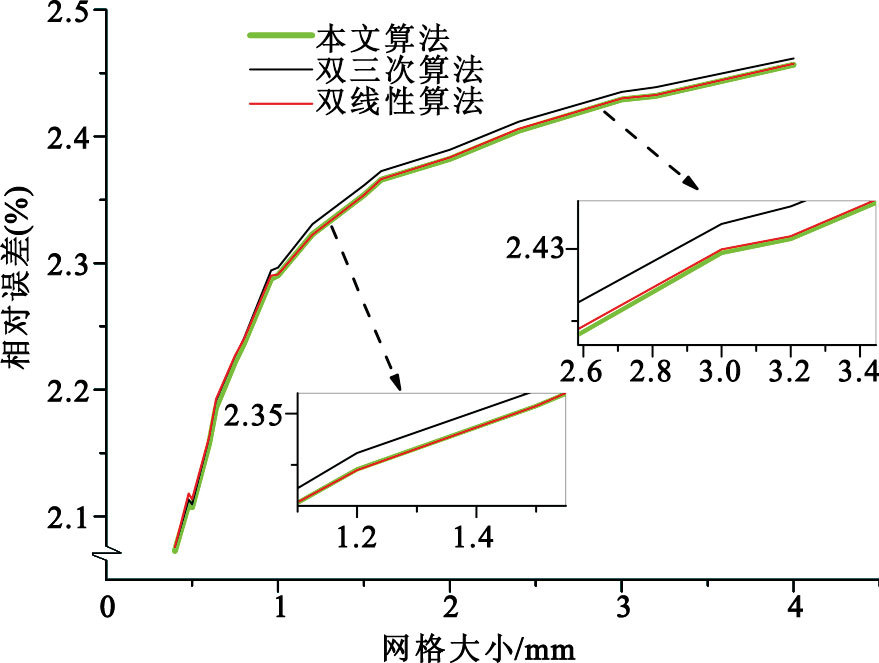 圖5
三種算法在所有插值間距下平均誤差對比
Figure5.
Average error comparison among the three algorithms in all interpolation distances
圖5
三種算法在所有插值間距下平均誤差對比
Figure5.
Average error comparison among the three algorithms in all interpolation distances
圖 6和圖 7分別展示了對于三種算法,每種算法的17×17組結果所對應誤差的累積概率分布和概率密度分布。從圖 6中可以看出,當誤差小于2.358時,TDAGI對應誤差的累積概率大于雙三次插值算法和雙線性插值算法;從圖 7中可以看出,當誤差小于2.163時,TDAGI對應誤差的概率密度大于雙三次插值算法和雙線性插值算法,當誤差大于2.163時,TDAGI對應誤差的概率密度不再是三種算法中的最大。這說明與雙線性插值算法和雙三次插值算法相比,TDAGI產生的誤差多集中在誤差值較小的范圍內,因而可以看到本文算法TDAGI的結果在誤差控制方面較雙線性插值和傳統的雙三次插值有一定優勢。
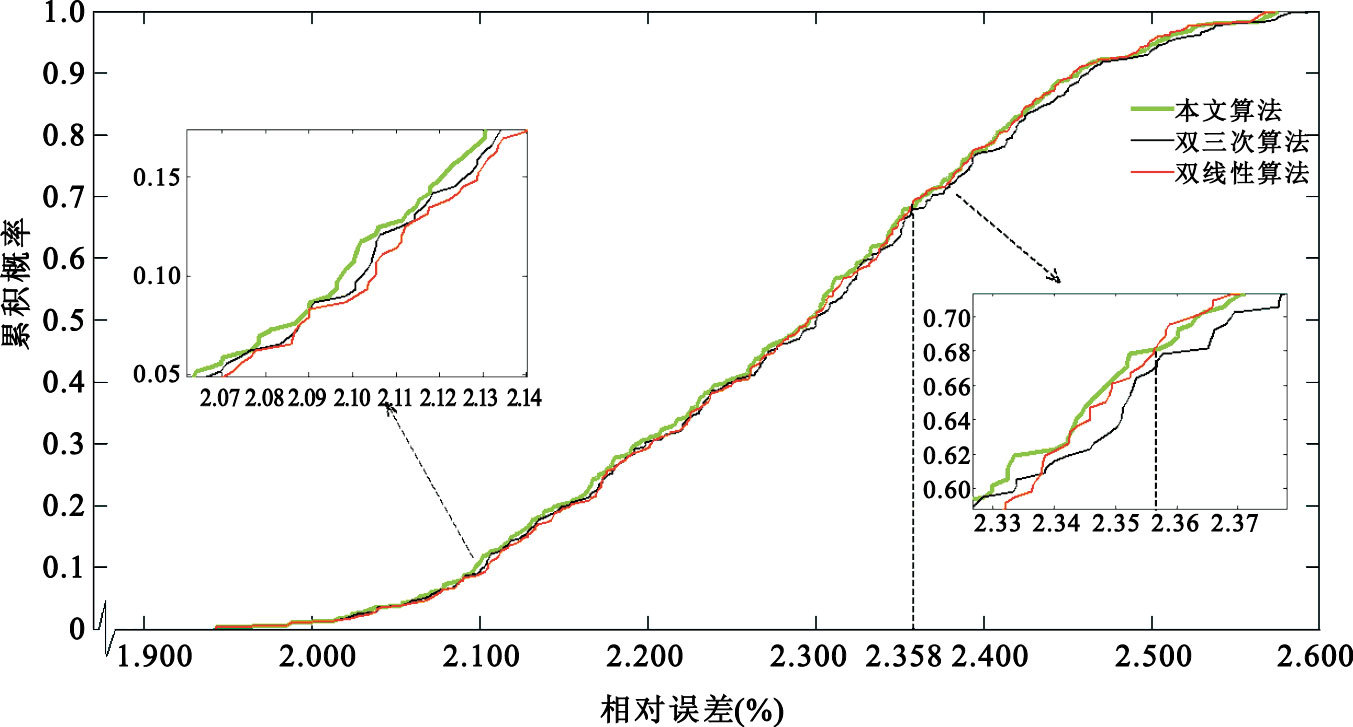 圖6
三種算法誤差的累積概率分布
Figure6.
Cumulative probability distribution for error for the three algorithms
圖6
三種算法誤差的累積概率分布
Figure6.
Cumulative probability distribution for error for the three algorithms
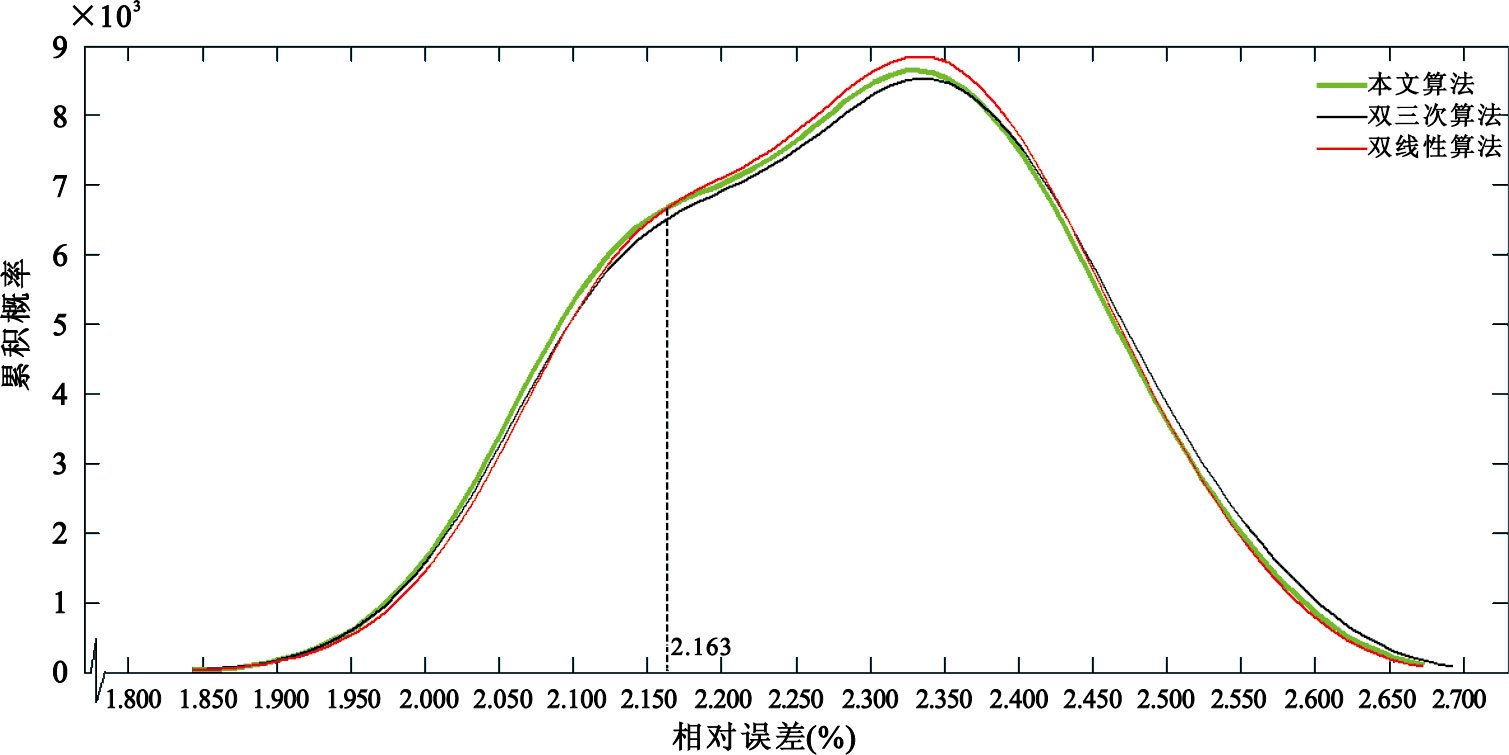 圖7
三種算法誤差的概率密度分布
Figure7.
Probability density distribution for error for the three algorithms
圖7
三種算法誤差的概率密度分布
Figure7.
Probability density distribution for error for the three algorithms
再比較TDAGI和雙線性算法得出平面劑量的平均梯度值。圖 8展示了對17組原始數據每組分別進行17種間距的插值計算后平均梯度的對比(橫坐標為原始計劃劑量數據平面的網格大小),可以看出TDAGI得出結果的平均梯度值均大于雙線性插值算法;同時可以發現,隨著原始數據平面網格大小的增加,雙線性算法對于梯度的平滑效應越發嚴重,而TDAGI卻很好地維持了數據平面的梯度。這種梯度上的改善一方面可以為物理師作判斷時提供良好的梯度信息;另一方面,有些劑量驗證軟件(如MapCheck)在將計劃數據與TPS輸出數據對齊時會采用雙線性插值,TDAGI對劑量梯度的改善可以有效地減小這種多次插值所帶來的多次平滑效應。
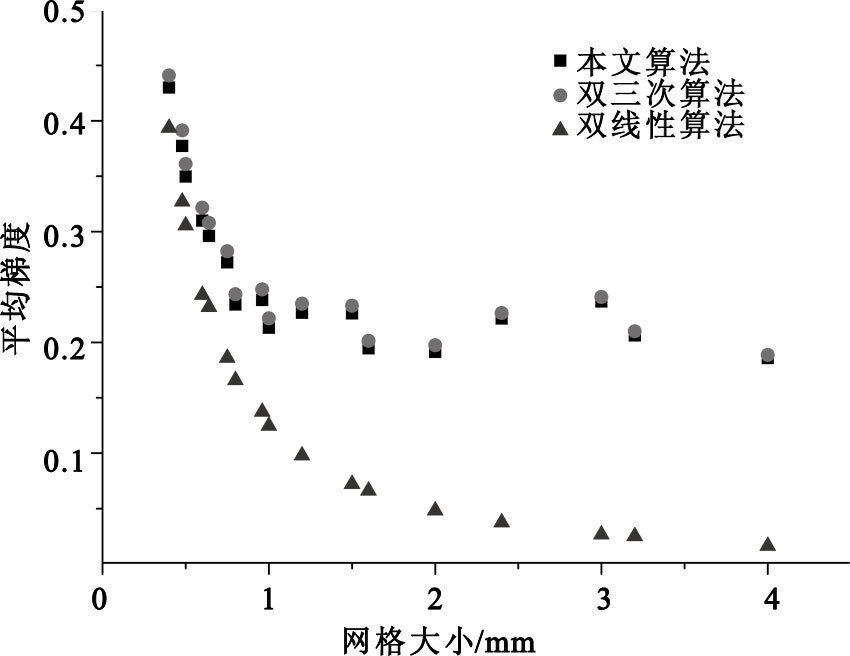 圖8
三種算法結果的平均梯度對比
Figure8.
Average gradient comparison among the three algorithms in all interpolation distances
圖8
三種算法結果的平均梯度對比
Figure8.
Average gradient comparison among the three algorithms in all interpolation distances
表 1展示了三種方法在所有的情況(17×17組)下的平均誤差以及平均梯度。可以看出,TDAGI的整體平均誤差小于雙線性插值和雙三次插值;TDAGI整體平均梯度大于雙線性插值算法,略小于傳統的雙三次插值算法。而事實上改進Canny邊緣探測算法之前TDAGI的平均百分相對誤差為2.283 5,可以看出,改進Canny邊緣探測算法后(平均百分誤差為2.283 4)進一步減小了誤差,這樣可以在提高準確度的同時減小梯度邊緣點的數量從而減小計算復雜度。結果表明,從總體上來看,TDAGI兼具誤差控制方面和梯度保持方面的優勢。
事實上,TPS給出的原始計劃劑量數據平面上每點的劑量是一個個具有一定尺寸的網格內的劑量平均值,而上述三種插值方法都假設網格內的平均劑量等于網格中心點的劑量。而實際上,對于一個有一定大小的網格來說,其中心點的劑量不一定等于網格內的平均劑量,因此這種假設會帶來初始的固有誤差。對17組原始計劃劑量數據平面,通過對比每一個小網格內平均劑量與模擬得出的網格中心點處的劑量,從而得到每組劑量平面的初始固有誤差。圖 9展示了不同原始計劃劑量數據平面插值計算時的初始固有誤差,可以看出,隨著網格尺寸的增大,這種初始固有誤差越來越大。本文算法TDAGI從較大尺度的梯度剖面來估算一個待插值點,可以有效地減小這種初始固有誤差所帶來的影響。
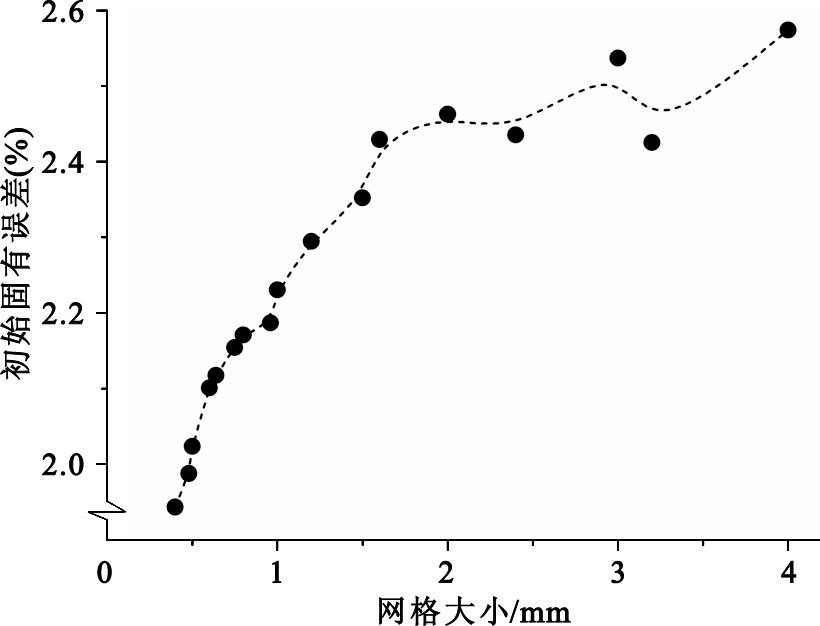 圖9
初始固有誤差與網格大小的關系
Figure9.
Relationship between inherent error and grid size
圖9
初始固有誤差與網格大小的關系
Figure9.
Relationship between inherent error and grid size
3 總結
本文提出了一種基于梯度特征的調強放療計劃劑量插值算法(TDAGI)。該算法根據計劃數據中梯度邊緣點對應的梯度剖面所具有的銳度以及非梯度邊緣點的離散程度,調節雙三次插值核的系數從而使插值結果更接近真實情況。結果顯示TDAGI較雙線性插值算法和傳統的雙三次插值算法在誤差控制和保持梯度特性方面具有一定優勢。課題組下一步工作將進一步提高TDAGI的精確度并將其與具體硬件相結合。
引言
調強放射治療(intensity-modulated radiation therapy,IMRT)劑量驗證作為治療計劃可靠性的重要保證,劑量驗證的準確性對放射治療效果以及患者的安全有著重要意義[1-2]。劑量驗證基本思路是用合理的方法比較治療計劃系統(treatment plan system,TPS)產生的計劃劑量數據和測量硬件得到的測量劑量數據[3]。治療計劃劑量數據從產生到進行劑量驗證過程中有時需要經過多次插值計算:一方面,TPS系統對治療計劃使用相關計算模型得到一個較為精確的計劃劑量數據平面,而TPS系統內部有時會改變計劃劑量數據平面上數據點之間的物理間距以滿足不同的輸出要求,因而需要對這個較為精確的數據平面進行插值計算;另一方面,劑量驗證時需要先將計劃劑量數據平面和測量數據平面按等劑量中心進行重合之后再比較相同位置上的點,但兩者數據平面上數據點之間的物理間距可能不相同,因此會導致重合之后兩個平面上的點錯位分布,此時需要進行插值計算從而在計劃劑量數據平面上得到與測量數據平面相同位置的點的劑量值。
目前國內外對于TPS產生的計劃劑量數據插值計算研究較少,實際處理中如DoseLab,MapCkeck等驗證軟件主要采用的方法多為雙線性插值,它利用待求點的四個相鄰點的值在兩個方向上作線性內插[4]。這種插值方法的優點在于時間代價較小,但是由于調強放療的劑量分布中病灶區和正常區域之間存在較大的劑量梯度,大量的研究表明雙線性插值由于算法本身具有平滑以及模糊效應,無法真實地反映梯度邊緣處的梯度分布,從而在梯度邊緣產生較大誤差,并且使結果失去原有的梯度信息,進而對醫生和物理師的判斷產生誤導[5-9]。為了克服上述雙線性插值存在的問題,課題組提出了一種新算法,基于梯度特征的調強放療計劃劑量插值算法(treatment plan dose interpolation algorithm based on gradient feature in intesity-modulated radiation therapy,TDAGI)。算法依據本文對雙三次插值核的系數調節作用的研究,確定以每一個梯度邊緣點或非梯度邊緣點為雙三次插值中心點時所對應的雙三次插值核系數,并對每一個待插值點使用所述雙三次插值核的系數進行特定的雙三次插值得出最終結果,從而充分考慮并有效還原了計劃劑量數據平面上每一點的梯度分布特點。
1 基于梯度特征的調強放療計劃劑量插值算法
1.1 梯度邊緣點和梯度剖面的獲取
假設TPS產生的原始數據平面為IL,首先求得每一點(i,j)的梯度 ?IL(i,j)以及梯度的模‖ ?IL(i,j)‖,然后使用傳統的Canny邊緣探測方法得到原始計劃劑量數據平面上所有梯度邊緣點。
但是,一方面計劃劑量數據由TPS計算而來,是不存在噪聲的,因此不需要傳統Canny算法中的高斯濾波以及上閾值設置;另一方面,傳統Canny算法存在假邊緣效應[10-12]。為了減小傳統Canny算法的假邊緣,在一個3×3鄰域中若存在多個梯度邊緣點,則只取其中梯度模最大點作為所述3×3區域內的唯一梯度邊緣點,用這種方法來代替傳統Canny算法中的下閾值設置。這種評判標準雖然較為嚴格,但是省去了傳統Canny算法中較復雜的上下閾值設置,而且本文算法TDAGI中對于非梯度邊緣點采用了自定義的偏離系數,因此可以從一定程度反映出在減少假梯度邊緣過程中所缺失的梯度邊緣點具有的劑量數據分布特點,從而達到較好的計算結果。因此TDAGI首先對傳統Canny算法作如下改進:
(1) 略去傳統Canny算法中高斯濾波的過程以及上下閾值設置的過程;
(2) 假設點(i′,j′)為所得到的一個梯度邊緣點,且以點(i′,j′)為中心的3×3鄰域中含有其他梯度邊緣點,若點(i′,j′)的梯度模小于所述鄰域中其他梯度邊緣點的梯度模,則需要重新將其標記為非梯度邊緣點。
得到計劃劑量數據平面上所有梯度邊緣點之后,該數據平面上剩下的點則為非梯度邊緣點。對于所獲取的每個梯度邊緣點(i′,j′),如圖 1所示,從該點開始,分別沿著梯度的正方向和負方向追蹤梯度剖面,每次與數據平面的坐標網格交于一個點,根據該交點梯度的方向繼續往下追蹤,直到梯度的模不再減小,最終得到每個點所對應的梯度剖面。在梯度剖面與數據坐標網格形成的各個交點中,若交點不為已存在的數據點(如圖 1所示的方塊),則該點的梯度使用相鄰點的數據線性插值得到[13]。
 圖1
梯度剖面追蹤示意
Figure1.
Illustration of the gradient profile tracing
圖1
梯度剖面追蹤示意
Figure1.
Illustration of the gradient profile tracing
1.2 雙三次插值核系數調節原理的研究
本文研究了雙三次插值核的系數a對雙三次插值核的影響,并利用系數與雙三次插值核的關系對最終的雙三次插值進行調節。
雙三次插值作為一種傳統的插值方法,其利用待插值點周圍的16個點的值作為基準點,使用如下公式(1)、(2)、(3)、(4)得到待插值點的值[14-15]。
| $f({i_C} + u,{j_C} + v) = ABC$ |
| $A = \left[ {s\left( {1 + u} \right)s\left( u \right)s\left( {1 - u} \right)s\left( {2 - u} \right)} \right]$ |
| $B = \left( {\begin{array}{*{20}{c}} {f({i_C} - 1,{j_C} - 1)} &{f({i_C} - 1,{j_C})} &{f({i_C} - 1,{j_C} + 1)} &{f({i_C} - 1,{j_C} + 2)}\\ {f({i_C},{j_C} - 1)} &{f({i_C},{j_C})} &{f({i_C},{j_C} + 1)} &{f({i_C},{j_C} + 2)}\\ {f({i_C} + 1,{j_C} - 1)} &{f({i_C} + 1,{j_C})} &{f({i_C} + 1,{j_C} + 1)} &{f({i_C} + 1,{j_C} + 2)}\\ {f({i_C} + 2,{j_C} - 1)} &{f({i_C} + 2,{j_C})} &{f({i_C} + 2,{j_C} + 1)} &{f({i_C} + 2,{j_C} + 2)} \end{array}} \right)$ |
| $C = {\left[ {s\left( {1 + v} \right)s\left( v \right)s\left( {1 - v} \right)s\left( {2 - v} \right)} \right]^T}$ |
其中,f(iC+u,jC+v)表示與雙三次插值的中心點(iC,jC)在水平方向和垂直方向距離分別為u和v的待插值點的值(u≥0,v<1),f(iC,jC)表示坐標為(iC,jC)點的值,s(w)表示雙三次插值核。傳統的雙三次插值為了逼近最佳插值函數sin(w)/w,其對應的s(w)如公式(5)所示[15-16]。
| $s\left( w \right) = \left\{ \begin{array}{l} {\left| w \right|^3} - 2{\left| w \right|^2} + 1,{\rm{ }}0 \le \left| w \right| < 1\\ - {\left| w \right|^3} + 5{\left| w \right|^2} - 8\left| w \right| + 4,{\rm{ }}1 \le \left| w \right| < 2\\ 0{\rm{ }},{\rm{ }}\left| w \right| \ge 2 \end{array} \right.$ |
其中w項的實際意義為待插值點到每一個基準點之間的距離,因此s(w)表示16個基準點按照與待插值點之間的距離對應的加權系數。而Keys[17]提出雙三次插值核s(w) 可以有更為普遍的形式,如公式(6)所示(其中a<0):
| $s\left( w \right) = \left\{ \begin{array}{l} \left( {a + 2} \right){\left| w \right|^3} - \left( {a + 3} \right){\left| w \right|^2} + 1 \ge 0,{\rm{ }}0 \le \left| w \right| < 1\\ a{\left| w \right|^3} - 5a{\left| w \right|^2} + 8a\left| w \right| - 4a \le 0,{\rm{ }}1 \le \left| w \right| < 2\\ 0{\rm{ }},{\rm{ }}\left| w \right| \ge 2 \end{array} \right.$ |
可以看出,a=-1時公式(5)與公式(6)等價。假設有兩個雙三次插值核的系數a1和a2且滿足a1<a2<0,則對應的雙三次插值核之差如式(7)所示:
| ${s_{a1}}\left( w \right) - {s_{a2}}\left( w \right) = \left\{ \begin{array}{l} ({a_1} - {a_2}){w^2}\left( {w - 1} \right) \ge 0,{\rm{ }}0 \le \left| w \right| < 1\\ ({a_1} - {a_2})\left( {w - 1} \right){\left( {w - 2} \right)^2} \le 0,{\rm{ }}1 \le \left| w \right| < 2\\ 0{\rm{ }},{\rm{ }}\left| w \right| \ge 2 \end{array} \right.$ |
從式(7)可以看出,0≤|w|<1時,雙三次插值核的系數a絕對值越小,對應雙三次插值核的值越小,此時雙三次插值的中心點(iC,jC)所對應的權重越小,從而待插值點與雙三次插值的中心點(iC,jC)值的差異越大,因而中心點(iC,jC)處容易形成較大梯度;當1≤|w|<2時,雙三次插值核的系數a絕對值越小,對應雙三次插值核的值越大,而且由公式(6)可知此時雙三次插值核的值小于0,故對應雙三次插值核的絕對值也越接近于0,使得雙三插值的中心點(iC,jC)之外的其他基礎點對待插值點的影響越小,從而雙三次插值核的系數a對于待插值點與雙三次插值的中心點(iC,jC)在0≤|w|<1時的調節作用也越明顯,因此可由雙三次插值核的系數a在中心點(iC,jC)處調節出較大的梯度。
從圖 2也可以看出,a的絕對值越小,對應s(w)的絕對值越小,即中心點(iC,jC)的加權系數越小,從而待插值點與中心點(iC,jC)的差異越大,同時中心點之外的其他基礎點對待插值點的影響越小,容易形成較大的梯度。事實上,如圖 3所示,對于每個梯度邊緣點對應的梯度剖面,雙線性插值由于無法真實反映梯度邊緣處的梯度分布,從而在梯度邊緣附近的待插值點處產生較大的計算誤差。我們通過圖 3可以看出,梯度變化越快的剖面(P2)對應的誤差越大。
 圖2
不同系數下的插值核變化規律
Figure2.
Change pattern of interpolation kernels of different coefficients
圖2
不同系數下的插值核變化規律
Figure2.
Change pattern of interpolation kernels of different coefficients
 圖3
梯度剖面上的插值以及梯度分布
圖3
梯度剖面上的插值以及梯度分布
對每一個梯度邊緣點(i′,j′),使用公式(8)所定義的銳度σ(i′,j′)來表示該梯度邊緣點對應梯度剖面P(i′,j′)上梯度變化的快慢:
| $\sigma \left( {i\prime ,j\prime } \right) = \sqrt {\sum\nolimits_{x \in P(i\prime ,j\prime )} {} \frac{{m\left( x \right)}}{{M\left( {i\prime ,j\prime } \right)}}d_c^2\left( {x,\left( {i\prime ,j\prime } \right)} \right)} $ |
其中,x是梯度邊緣點(i′,j′)所對應梯度剖面P(i′,j′)上與數據坐標網格相交的每一點,m(x)表示x點處的梯度模,M(i′,j′)表示梯度剖面P(i′,j′)上梯度模的和,dc(x,(i′,j′))表示點x與梯度邊緣點(i′,j′)之間的曲線距離;
對每一個非梯度邊緣點(i″,j″),本文定義偏離系數ρ(i″,j″)為每一點與周圍3×3鄰域整體的平均計劃劑量值偏差,以此來度量該非梯度邊緣點的偏離程度,如式(9)所示:
| $\rho \left( i'',j'' \right)=\frac{\left| \overline{{{I}_{L}}\left( i'',j'' \right)}-{{I}_{L}}\left( i'',j'' \right) \right|}{{{I}_{L}}\left( i'',j'' \right)}$ |
其中IL(i″,j″)為以非梯度邊緣點(i″,j″)為中心的3×3鄰域中除非梯度邊緣點(i″,j″)以外各個點的平均計劃劑量值。IL(i″,j″)為該非梯度邊緣點(i″,j″)的計劃劑量值。
從銳度σ(i′,j′)的定義可以看出,銳度的值越小,對應剖面上的梯度變化越快,從圖 3可以看出,待插值點的值會偏離梯度邊緣點(i′,j′)而接近于兩旁的點,結合對圖 2以及上述公式(6)、(7)的分析可以看出,若以該梯度邊緣點(i′,j′)為雙三次插值中心點(iC,jC) ,此時需要雙三次插值核的系數的絕對值較小,通過這樣的處理,可以使計劃劑量數據平面上梯度邊緣點對應梯度剖面的劑量數據分布更加接近于真實的劑量數據分布;從自定義的非梯度邊緣點(i″,j″)的偏離系數來看,偏離系數ρ(i″,j″)越大則待插值點與非梯度邊緣點(i″,j″)之間的差異越大,結合對圖 2以及式(6)、(7)的分析可以看出,若以該非梯度邊緣點(i″,j″)為雙三次插值中心點(ic,jc),此時需要雙三次插值核的系數的絕對值較小。
通過以上的研究分析結果構造出每一點的銳度或偏離程度與每一點雙三次插值核的系數之間的函數關系。這就是本文算法TDAGI使用雙三次插值核的系數進行調節的思路。
1.3 確定雙三次插值核的系數并得出結果
對于每一個梯度邊緣點(i′,j′),以點(i′,j′)為雙三次插值中心點時,對雙三次插值核的系數a(i′,j′)與該梯度邊緣點對應梯度剖面的銳度σ(i′,j′)之間構造函數關系如式(10)所示:
| $a\left( i',j' \right)=-0.5\frac{1}{1+ln\left( {{\sigma }_{max}}/\sigma \left( i',j' \right) \right)}exp\left\{ {{\left( \frac{1-\sigma \left( i',j' \right)}{{{\sigma }_{max}}} \right)}^{2}} \right\}$ |
其中,σmax表示該計劃劑量數據平面上銳度的最大值;可以看出,式(10)中雙三次插值核的系數a(i′,j′)絕對值隨銳度σ(i′,j′)的減小而減小,滿足前面得出的規律。
對于每一個非梯度邊緣點(i″,j″),以點(i″,j″)為雙三次插值中心點時,對雙三次插值核的系數a(i″,j″)與該非梯度邊緣點的偏離系數ρ(i″,j″)之間構造函數關系如式(11)所示:
| $a\left( i'',j'' \right)=-0.5\left\{ exp-{{\left( \frac{\rho \left( i'',j'' \right)-{{\rho }_{min}}}{{{\rho }_{max}}-{{\rho }_{min}}} \right)}^{2}} \right\}$ |
其中ρmax為計劃劑量數據平面上最大偏離系數,ρmin為計劃劑量數據平面上最小偏離系數。將式(10)和式(11)兩者結果合并,從而得出以計劃劑量數據平面上每一點(i,j)為雙三次插值中心點時所對應的雙三次插值核的系數,記為a(i,j);對于每一個待插值點,設其坐標為(α,β),若α∈[i,i+1) 且β∈[j,j+1) ,則以點(i,j)為雙三次插值中心點,以a(i,j)為雙三次插值核的系數,即可得到該點所對應的雙三次插值核,如式(12)所示:
| $s\left( w \right)=\left\{ \begin{align} & \left( a\left( i,j \right)+2 \right){{\left| w \right|}^{3}}-\left( a\left( i,j \right)+3 \right){{\left| w \right|}^{2}}+1\ge 0,0\le \left| w \right| <1 \\ & a\left( i,j \right){{\left| w \right|}^{3}}-5a\left( i,j \right){{\left| w \right|}^{2}}+8a\left( i,j \right)\left| w \right|-4a\le 0,1\le \left| w \right| <2 \\ & 0,\left| w \right|\ge 2 \\ \end{align} \right.$ |
其中w項的實際意義為待插值點到每一個基準點之間的距離;結合公式(1)、(2)、(3)、(4),以點(i,j)為雙三次插值中心點對該待插值點進行特定的雙三次插值計算,進而得出每一個待插值點的計劃劑量數據。
2 結果與分析
驗證算法最直接的辦法是將各個待插值點處插值所得計劃劑量數據與該點處計劃劑量數據的真實值進行比較。然而一方面對每一個網格,TPS只能輸出該網格中劑量的平均值,無法得到該網格中單個點處的劑量值,因此TPS無法獲取該網格中某一特定待插值點處真實的劑量值;另一方面,TPS內部為了滿足輸出需求會改變數據點之間的距離(網格大小),其往往采用線性插值得到新的計劃劑量數據分布,這種新的劑量數據不是真實值,因此TPS很難得到待插值點的計劃劑量數據的真實值。但是蒙特卡羅程序作為劑量計算的“金標準”,可以用來模擬真實的劑量分布[18]。因此使用蒙特卡羅程序BEAMnrc/Dosxyznrc來替代TPS產生原始計劃劑量數據和待插值點處計劃劑量數據的真實值。分別使用TDAGI、雙線性插值算法以及傳統的雙三次插值算法對原始調強放療計劃劑量數據進行計算,得到各個待插值點處的計劃劑量數據,再與蒙特卡羅程序BEAMnrc/Dosxyznrc輸出的待插值點處計劃劑量數據的真實值進行對比。
對于一個總大小為96 mm×96 mm調強放射治療照射區域,分別以0.40、0.48、0.50、0.60、0.64、0.75、0.80、0.96、1.00、1.20、1.50、1.60、2.00、2.40、3.00、3.20、4.00 mm共17組不同的物理尺寸作為原始調強放療計劃劑量數據平面的網格大小,模擬出該照射區域中17組原始計劃劑量數據平面的劑量數據分布;在相同環境和條件下,從等劑量中心點開始,分別以上述17組物理尺寸為插值間距,模擬出17組待插值點平面上各個待插值點處的計劃劑量數據的真實值。在每一組原始調強放療計劃劑量數據平面上分別運用TDAGI、雙線性插值算法和傳統雙三次插值算法,得出17種插值間距下的插值結果,總共形成17×17組結果,并與模擬得出的各個待插值點處計劃劑量數據的真實值進行比較,得出三種算法各自的誤差。
考慮到實際劑量數據平面的網格大小在0.50 mm左右,因此使用0.40、0.48、0.50、0.60 mm為插值間距來評價算法的精確度。如圖 4所示,展示了用17組原始數據平面分別以0.40、0.48、0.50、0.60 mm為插值間距作插值計算時三種方法的誤差對比(橫坐標為原始計劃劑量數據平面的網格大小)。從結果可以看到,對于所選定的4種插值間距,從誤差的總體變化趨勢來看,TDAGI的誤差小于雙三次插值算法和雙線性插值算法。
 圖4
TDAGI、雙線性插值算法以及雙三次插值算法的誤差對比
Figure4.
Error comparison among TDAGI,Bilinear interpolation and Bi-Cubic interpolation
圖4
TDAGI、雙線性插值算法以及雙三次插值算法的誤差對比
Figure4.
Error comparison among TDAGI,Bilinear interpolation and Bi-Cubic interpolation
對17組原始數據每組都使用上述三種插值方法分別進行上述17種間距的插值計算,求出每組原始數據在不同插值間距下的誤差平均值,將誤差進行對比。結果展示在圖 5中(橫坐標為原始計劃劑量數據平面的網格大小),可以看出,除了原始數據網格大小在1.20~1.50 mm之間時TDAGI誤差大于雙線性插值,其余情況下TDAGI誤差都小于雙線性插值;而且每種情況下TDAGI的誤差都小于傳統雙三次插值結果。
 圖5
三種算法在所有插值間距下平均誤差對比
Figure5.
Average error comparison among the three algorithms in all interpolation distances
圖5
三種算法在所有插值間距下平均誤差對比
Figure5.
Average error comparison among the three algorithms in all interpolation distances
圖 6和圖 7分別展示了對于三種算法,每種算法的17×17組結果所對應誤差的累積概率分布和概率密度分布。從圖 6中可以看出,當誤差小于2.358時,TDAGI對應誤差的累積概率大于雙三次插值算法和雙線性插值算法;從圖 7中可以看出,當誤差小于2.163時,TDAGI對應誤差的概率密度大于雙三次插值算法和雙線性插值算法,當誤差大于2.163時,TDAGI對應誤差的概率密度不再是三種算法中的最大。這說明與雙線性插值算法和雙三次插值算法相比,TDAGI產生的誤差多集中在誤差值較小的范圍內,因而可以看到本文算法TDAGI的結果在誤差控制方面較雙線性插值和傳統的雙三次插值有一定優勢。
 圖6
三種算法誤差的累積概率分布
Figure6.
Cumulative probability distribution for error for the three algorithms
圖6
三種算法誤差的累積概率分布
Figure6.
Cumulative probability distribution for error for the three algorithms
 圖7
三種算法誤差的概率密度分布
Figure7.
Probability density distribution for error for the three algorithms
圖7
三種算法誤差的概率密度分布
Figure7.
Probability density distribution for error for the three algorithms
再比較TDAGI和雙線性算法得出平面劑量的平均梯度值。圖 8展示了對17組原始數據每組分別進行17種間距的插值計算后平均梯度的對比(橫坐標為原始計劃劑量數據平面的網格大小),可以看出TDAGI得出結果的平均梯度值均大于雙線性插值算法;同時可以發現,隨著原始數據平面網格大小的增加,雙線性算法對于梯度的平滑效應越發嚴重,而TDAGI卻很好地維持了數據平面的梯度。這種梯度上的改善一方面可以為物理師作判斷時提供良好的梯度信息;另一方面,有些劑量驗證軟件(如MapCheck)在將計劃數據與TPS輸出數據對齊時會采用雙線性插值,TDAGI對劑量梯度的改善可以有效地減小這種多次插值所帶來的多次平滑效應。
 圖8
三種算法結果的平均梯度對比
Figure8.
Average gradient comparison among the three algorithms in all interpolation distances
圖8
三種算法結果的平均梯度對比
Figure8.
Average gradient comparison among the three algorithms in all interpolation distances
表 1展示了三種方法在所有的情況(17×17組)下的平均誤差以及平均梯度。可以看出,TDAGI的整體平均誤差小于雙線性插值和雙三次插值;TDAGI整體平均梯度大于雙線性插值算法,略小于傳統的雙三次插值算法。而事實上改進Canny邊緣探測算法之前TDAGI的平均百分相對誤差為2.283 5,可以看出,改進Canny邊緣探測算法后(平均百分誤差為2.283 4)進一步減小了誤差,這樣可以在提高準確度的同時減小梯度邊緣點的數量從而減小計算復雜度。結果表明,從總體上來看,TDAGI兼具誤差控制方面和梯度保持方面的優勢。
事實上,TPS給出的原始計劃劑量數據平面上每點的劑量是一個個具有一定尺寸的網格內的劑量平均值,而上述三種插值方法都假設網格內的平均劑量等于網格中心點的劑量。而實際上,對于一個有一定大小的網格來說,其中心點的劑量不一定等于網格內的平均劑量,因此這種假設會帶來初始的固有誤差。對17組原始計劃劑量數據平面,通過對比每一個小網格內平均劑量與模擬得出的網格中心點處的劑量,從而得到每組劑量平面的初始固有誤差。圖 9展示了不同原始計劃劑量數據平面插值計算時的初始固有誤差,可以看出,隨著網格尺寸的增大,這種初始固有誤差越來越大。本文算法TDAGI從較大尺度的梯度剖面來估算一個待插值點,可以有效地減小這種初始固有誤差所帶來的影響。
 圖9
初始固有誤差與網格大小的關系
Figure9.
Relationship between inherent error and grid size
圖9
初始固有誤差與網格大小的關系
Figure9.
Relationship between inherent error and grid size
3 總結
本文提出了一種基于梯度特征的調強放療計劃劑量插值算法(TDAGI)。該算法根據計劃數據中梯度邊緣點對應的梯度剖面所具有的銳度以及非梯度邊緣點的離散程度,調節雙三次插值核的系數從而使插值結果更接近真實情況。結果顯示TDAGI較雙線性插值算法和傳統的雙三次插值算法在誤差控制和保持梯度特性方面具有一定優勢。課題組下一步工作將進一步提高TDAGI的精確度并將其與具體硬件相結合。




