生物學研究發現，采用簡單線性疊加數學模型不能表達嚙齒類動物大腦皮層海馬區多個激活網格細胞網格野到單一位置細胞位置野輸出特征映射關系。針對這一難題，引入高斯分布激活函數。本文利用其局域化特性，對網格細胞輸入和網格細胞與位置細胞之間連接權值線性疊加輸出進行處理，濾掉激活率比較低的位置野，得到了與生物學研究發現相一致的單一位置細胞位置野。與已有競爭學習算法位置細胞模型、獨立成分分析方法位置細胞模型、貝葉斯位置重建方法位置細胞模型相比，本文實驗結果表明，該模型在神經生理學基礎上不僅能表達嚙齒類動物大腦皮層海馬區多個網格細胞網格野激活得到單一位置細胞位置野輸出特征映射關系，而且算法簡單，所需網格細胞輸入較少，輸出單一位置細胞野準確率高。
引用本文： 于乃功, 方略, 羅子維, 苑云鶴, 蔣曉軍, 蔡建羨. 一種網格細胞到位置細胞的高斯分布激活函數模型. 生物醫學工程學雜志, 2016, 33(6): 1158-1167. doi: 10.7507/1001-5515.20160184 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
海馬結構位于嚙齒類動物大腦皮層中，該結構與動物記憶、認知、學習等高級功能密切相關，是嚙齒類動物進行環境認知的神經生理學基礎。因此，對于該結構深入研究有助于人們深刻理解大腦環境認知機制。從解剖結構上看，海馬結構主要由內嗅皮層(entorhinal cortex,EC)、齒狀回(dentate gyrus,DG)、海馬區(hippocampus)、下托綜合體(subiculum complex,SUB)四部分組成。內嗅皮層共分為6層，Ⅱ、Ⅲ、Ⅴ分別代表的是內嗅皮層第2、3、5層。海馬區由海馬角1區(cornu ammonis1,CA1)和海馬角3區(cornu ammonis3,CA3)構成。下托綜合體進一步分為腦下托(subiculum,S)、前下托(presubiculum,PRS)和傍下托(parasubiculum,PAS)。內嗅皮層與海馬區之間存在有雙向纖維投射，該雙向纖維投射構成了內嗅皮層-海馬區回路。內嗅皮層到海馬區纖維投射表明了內嗅皮層是海馬結構中海馬區的主要輸入來源[1-2]。海馬解剖結構和信息通路如圖 1所示，藍色線條箭頭表示的是內嗅皮層第Ⅱ層到齒狀回和海馬角3區纖維投射，紅色線條箭頭表示的是內嗅皮層第Ⅲ層到海馬角1區和腦下托纖維投射，黃色線條箭頭表示的是海馬角1區和腦下托到內嗅皮層第Ⅴ層纖維投射。
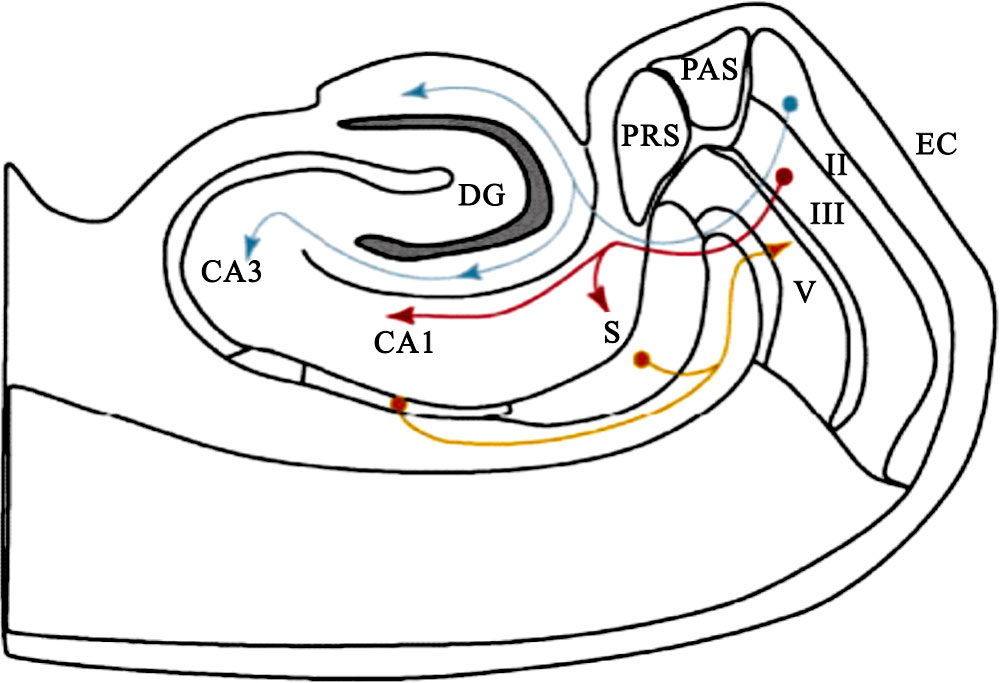圖1
海馬解剖結構和信息通路
Figure1.
Anatomy structure and information pathway of hippocampus
內嗅皮層中主要神經元為網格細胞，多個網格細胞網格野相互交疊成一個個網格節點，以大鼠為例，連接網格節點所形成的正三角形遍及大鼠所處的整個空間環境[3-4]。網格細胞放電空間特征由以下3個參數表征：間距(網格節點之間距離)、定向(相對于外部參考軸傾斜度)、空間位相(相對于外部參考點偏移量)。網格細胞空間特征如圖 2所示，變量λ為網格細胞間距，θ為網格細胞定向，(x0,y0)為網格細胞空間位相。研究發現，沿內側內嗅皮層背腹軸方向，網格細胞網格野間距逐漸增大，相鄰網格細胞具有相似網格野間距和定向，但是它們的空間位相是隨機分散的[3-5]。
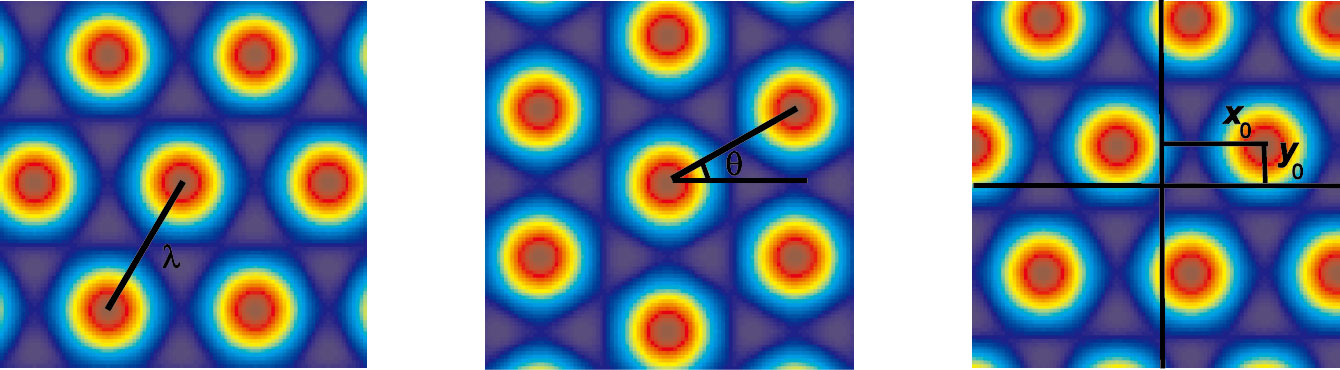圖2
網格細胞空間特征
Figure2.
Spatial characteristics of grid cells
1971年，O’keefe和Dostrovesky在大鼠海馬區首次發現具有空間定位活動的位置細胞神經元[6]。大鼠在二維空間活動時，當其經過環境中某一特定狹小區域時，對應位置細胞就會放電，單個位置細胞對應有單一位置細胞激活域，將此區域稱之為位置細胞位置野[5, 7]。位置細胞位置野與大鼠所處空間位置有著準確的對應關系，位置細胞聯合編碼大鼠所處環境，在大鼠腦內形成“認知地圖”，此后，大鼠能基于該“認知地圖”實現面向空間環境中任一目標的導航任務。2005年，研究人員于大鼠內嗅皮層中發現了另外一種具有強烈空間放電特性的網格細胞神經元，該神經元會呈現出對空間中某一特定區域發生重復性規律放電的特性，此區域被稱之為網格細胞網格野[4]。與位置細胞不同的是，網格細胞能在多個位置放電，多個網格細胞網格野相互交疊成一個個網格節點，連接網格節點所形成的正三角形遍及大鼠所處的整個空間環境。如何構建多個網格細胞網格野到單一位置細胞位置野之間的映射關系呢？自從2005年發現網格細胞以來，一些模型被相繼提出。其中包括基于競爭學習算法的位置細胞模型[8-9]、基于獨立成分分析方法的位置細胞模型[10-12]和基于貝葉斯位置重建方法的位置細胞模型[13-15]。競爭學習算法位置細胞模型算法復雜，而且需要125個網格細胞輸入來實現多個網格細胞野到單一位置細胞野輸出特征映射關系[8]。獨立成分分析方法位置細胞模型約70%輸出為單一位置細胞野[10]。貝葉斯位置重建方法位置細胞模型缺乏神經生理學依據[13]。基于此，本文依據神經生理學上網格細胞到位置細胞神經連接機制，首先將網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加，然后引入高斯分布激活函數，利用其局域化特性，對線性疊加后的輸出進行處理，濾掉激活率比較低的位置野從而得到與生物學研究發現相一致的單一位置細胞位置野，該模型在神經生理學基礎上算法簡單，所需網格細胞輸入較少(本文所需10個網格細胞輸入即可)，選取多組網格細胞輸入得到約90%輸出為單一放電區域位置細胞位置野。位置細胞高斯分布激活函數模型構成與實現流程圖如圖 3所示。位置細胞高斯分布激活函數模型主要由2個模塊構成，如圖 3中藍色框所示，第1個模塊是基于條紋細胞的網格細胞模型，條紋細胞放電活動產生一簇簇條紋波，條紋波疊加形成網格細胞網格野。如圖 3中橙色框所示，第2個模塊是基于網格細胞的位置細胞模型，位置細胞從具有不同空間特征的網格細胞接收信息與相應網格細胞到位置細胞連接權值加權求和后經高斯分布激活函數處理得到位置細胞單一位置野放電特征。此外，本文還對網格細胞數量、網格細胞空間位相、定向、間距等因素對于該模型的影響做了相關研究。
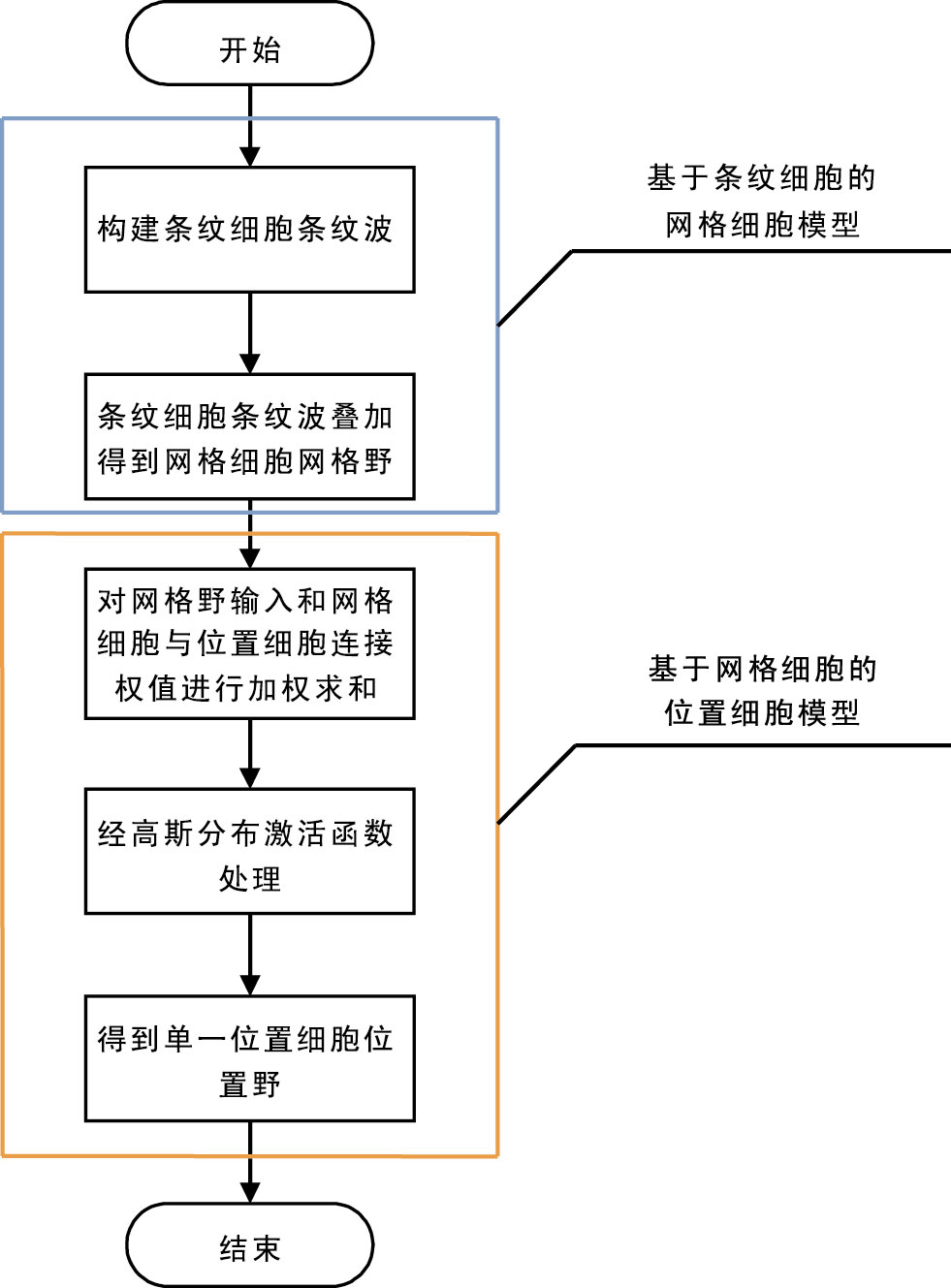圖3
位置細胞高斯分布激活函數模型構成與實現流程圖
Figure3.
Gauss distribution activation function model structure and the flowchart of the realization of place cells
1 方法
1.1 基于條紋細胞的網格細胞模型
條紋細胞被發現存在于內嗅皮層第3層中，該細胞在二維空間環境中的放電活動是一簇簇條紋波，它作為輸入將信息傳遞至內嗅皮層第2層中，其所產生的一簇簇條紋波通過疊加形成具有不同空間位相、定向、間距的網格細胞網格野[16-18]。
對于條紋細胞放電活動，我們用二維cos波來表示，如式(1)所示。
| ${{\varphi }_{1}}=\frac{1}{3}\text{cos}({{k}_{i}}r)$ |
其中，r= (x,y)代表大鼠當前所處環境位置坐標，ki (i=1,2,3) 代表波矢量，其方向表示的是波等相位行進的方向，大小稱之為波數ki。
| ${{k}_{i}}=\frac{2\pi }{{{\lambda }_{\cos }}}$ |
其中，λcos代表cos波波長。
生物學研究證實，網格細胞網格野呈正三角形遍布于大鼠所處的整個環境當中[3-4]。基于此，網格細胞激活率函數可以由三個條紋細胞(三個條紋細胞波矢量朝向相差60°)放電活動疊加來表示，如式(3)所示。
| $\psi \left( r \right)=\frac{\text{cos}({{k}_{1}}r)+\text{cos}({{k}_{2}}r)+\text{cos}({{k}_{3}}r)}{3}$ |
如式(3)所示，r= (0,0)時，ψ(r)有最大值為1。若選擇空間環境中任意一空間位相r0 = (x0,y0)作為網格細胞網格野的某一峰值點，則網格細胞激活率函數轉變為如式(4)所示。
| $\psi \left( r \right)=\psi (r-{{r}_{0}})$ |
ki代表的是波矢量，波矢量是波數ki的函數，網格細胞網格野間距作為表征網格細胞空間放電特征的1個參數。如圖 4所示，紅色實心圓圈表示網格細胞網格野節點，陰影部分表示條紋細胞二維cos波，網格細胞網格野間距λ與二維cos波波長λcos之間的關系如式(5)所示。
| $\lambda =\frac{2}{\sqrt{3}}{{\lambda }_{\cos }}$ |
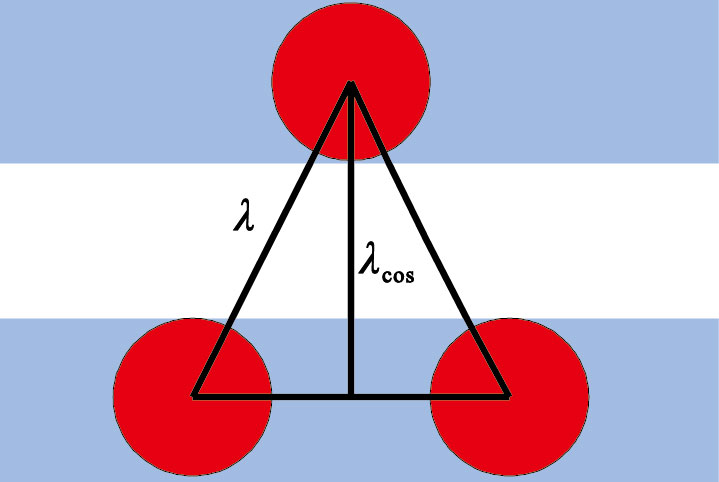圖4
網格細胞網格野間距λ與二維cos波波長λcos之間關系圖
Figure4.
Relationship diagram between grid cells’ grid field spacing λ and two dimensional cos wavelength λcos
又由式(2)可知，波數ki與網格細胞網格野間距λ之間的關系如式(6)所示。
| ${{k}_{i}}=\frac{4\pi }{\sqrt{3}\lambda }$ |
為了得到與生物學上發現相一致的正三角形網格細胞網格野，選取波矢量朝向相差60°的三個條紋細胞疊加后得到所需網格細胞網格野。以0°,60°,120°為例，選取k1,k2,k3，如式(7)所示。
| $\left\{ \begin{array}{*{35}{l}} {{k}_{1}}=\frac{{{k}_{1}}}{\sqrt{2}}[\text{cos}\left( \theta \right)+\sin \left( \theta \right),\text{cos}\left( \theta \right)-\sin \left( \theta \right)] \\ {{k}_{2}}=\frac{{{k}_{2}}}{\sqrt{2}}[\text{cos}\left( \theta +\frac{\pi }{3} \right)+\sin \left( \theta +\frac{\pi }{3} \right), \\ \text{cos}\left( \theta +\frac{\pi }{3} \right)-\sin \left( \theta +\frac{\pi }{3} \right)] \\ {{k}_{3}}=\frac{{{k}_{3}}}{\sqrt{2}}[\text{cos}\left( \theta +\frac{2\pi }{3} \right)+\sin \left( \theta +\frac{2\pi }{3} \right), \\ \text{cos}\left( \theta +\frac{2\pi }{3} \right)-\sin \left( \theta +\frac{2\pi }{3} \right)] \\ \end{array} \right.$ |
其中，θ表示網格細胞網格野定向。
由式(3)可知，ψ(r)取值介于[-1/2,1]之間，為了使網格細胞激活率取值介于0到1之間，網格細胞激活率函數轉變如式(8)所示。
| $g\left( r \right)=\frac{2}{3}\left( \psi \left( r \right)+\frac{1}{2} \right)$ |
將式(3)和式(4)代入式(8)得到網格細胞激活率函數如式(9)所示。
| $g\left( r \right)=\frac{2}{3}\left[ \frac{1}{3}\sum\limits_{i=1}^{3}{\text{cos}{{k}_{i}}(r-{{r}_{0}})+\frac{1}{2}} \right]$ |
1.2 基于網格細胞的位置細胞模型
如圖 3所示為基于網格細胞的位置細胞模型，即位置細胞首先從具有不同空間特征的網格細胞接收信息，然后與其相連接網格細胞之間的權值進行加權求和，最后經高斯分布激活函數處理得到位置細胞放電特征。在1.1小節中得到了作為輸入的網格細胞網格野，接下來就是將網格細胞網格野輸入和網格細胞與位置細胞連接權值進行加權求和，再經高斯分布激活函數處理得到位置細胞的單一激活域放電特征[10]。
網格細胞和位置細胞均為神經細胞，它們是由細胞體和細胞突起構成，而細胞突起是細胞體自身延伸出來的細長部分，細長部分又分為樹突和軸突。每個神經元只有一個軸突，它可以把信號傳遞到其它組織或另一個神經元，每個神經元可以有多個樹突，它可以接收刺激并將興奮傳入細胞體內，網格細胞與位置細胞之間信息傳遞亦是如此。網格細胞與位置細胞之間的連接權值函數如式(10)所示。
| ${{W}_{n}}=\frac{4\pi {{\sigma }^{2}}}{{{\lambda }^{2}}_{n}}3{{e}^{-43{{\sigma }^{2}}{{\pi }^{2}}/{{\lambda }^{2}}_{n}}}$ |
其中，Wn代表第n個網格細胞與位置細胞之間的連接權值，λn代表第n個網格細胞網格野間距，σ(σ=8 cm)代表位置細胞放電激活域標準差。
由式(9)和式(10)可知，位置細胞激活率函數如式(11)所示。
| $P\left( x,y \right)=\sum\limits_{1}^{N}{{{W}_{n}}{{g}_{n}}\left( x,y \right)}$ |
其中，Wn代表第n個網格細胞與位置細胞之間的連接權值，gn(x,y) 代表第n個網格細胞位于空間環境(x,y) 位置點處的激活率，N(N =4,10,20)代表網格細胞數量。
生物學研究發現，單純的對網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加往往得到的輸出是具有多個激活域的位置野，這與已有相關研究所證實單一位置細胞對應有單一位置野的結論不一致[19]。本文在網格細胞網格野輸入和網格細胞與位置細胞之間連接權值加權求和的基礎上，引入高斯分布激活函數，利用其局域化特性，對線性疊加后的輸出進行處理，濾掉激活率比較低的位置野從而得到與生物學研究發現相一致的單一位置細胞位置野，實現網格細胞到單一位置細胞位置野之間的映射關系，如式(12)所示。
| $P\prime \left( x,y \right)={{e}^{-{{\left[ \sum\limits_{1}^{N}{{{W}_{n}}{{g}_{n}}\left( x,y \right)} \right]}^{2}}}}$ |
2 仿真與實驗結果
2.1 基于條紋細胞的網格細胞模型
朝向相差60°的3個條紋細胞放電活動疊加后得到網格細胞網格野如圖 5所示。此處選取的參數為θ=0°，λ=40 cm，r0=(50,50)。
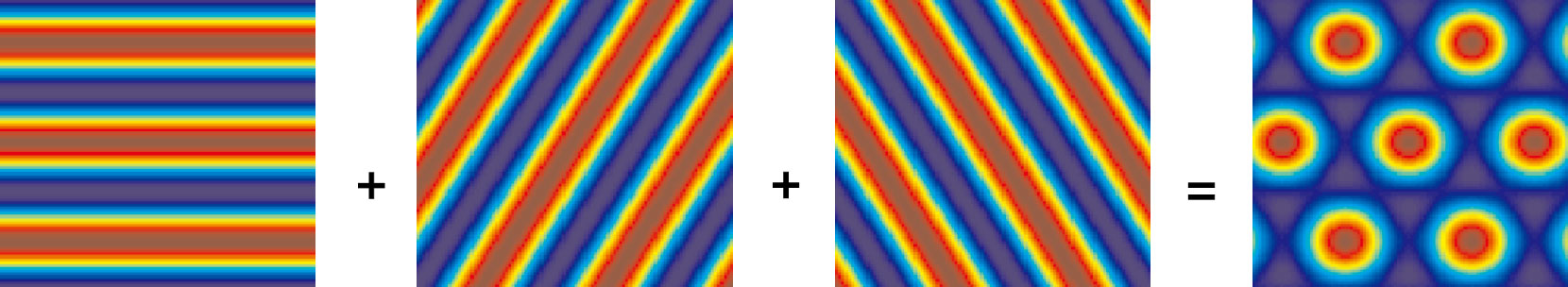圖5
3個條紋細胞條紋波疊加所得網格細胞網格野示意圖
Figure5.
Diagram of grid cells’ grid fields based on superposition of three stripe cells’ stripe wavelength
同樣的，選取不同參數基于條紋細胞得到具有不同空間位相、定向和間距的網格細胞網格野如圖 6所示。
圖6
具有不同空間位相、定向和間距的網格細胞網格野
Figure6.
Grid cells’ grid fields with different spatial phase,orientation and spacing
2.2 基于網格細胞的位置細胞模型
選取10個具有相同空間位相、不同間距、不同定向的網格細胞作為輸入，此處選取的參數定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取，空間位相r0均為(70,40)，實驗結果示意圖如圖 7所示。
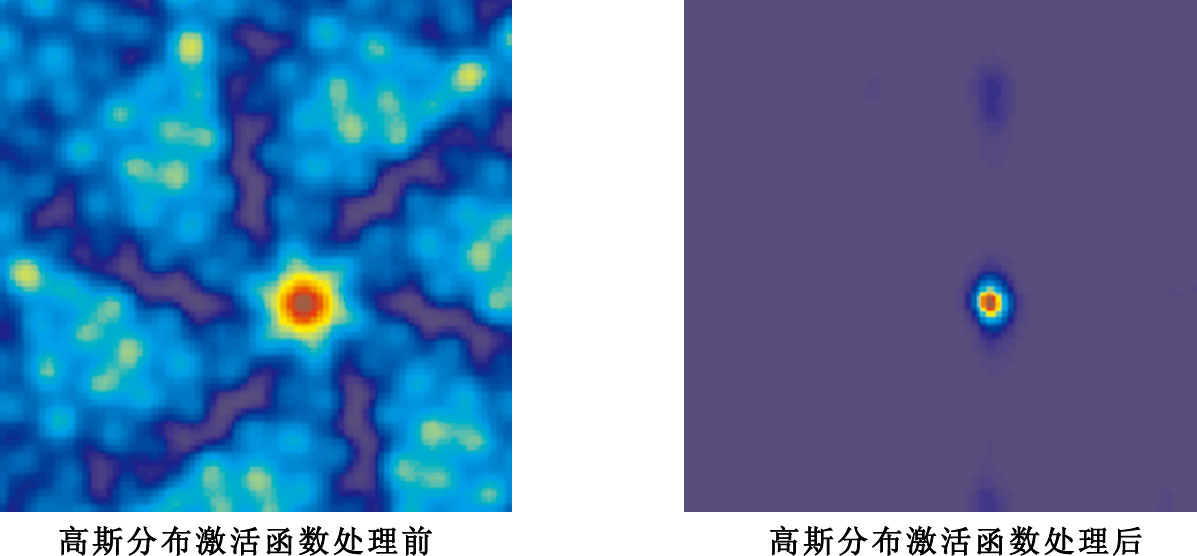圖7
相同空間位相、不同間距、不同定向網格細胞輸入實驗結果示意圖
Figure7.
Experimental results of the same spatial phase,different spacing and different orientation of grid cells input
如圖 7所示，左圖代表的是對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和后未經高斯分布激活函數處理后的輸出結果，可以看出此時位置細胞存在有多個放電區域。右圖則代表的是對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和后經高斯分布激活函數處理后的輸出結果，由圖可以看出此時位置細胞存在有單一位置放電區域。
同樣的，為測試本文所提模型性能，另外選取100組網格細胞輸入進行實驗，每組網格細胞空間位相相同、間距不同、定向不同，而各組網格細胞之間空間位相隨機選取。通過統計100組網格細胞輸入經高斯分布激活函數處理后得到單一放電區域位置細胞位置野比例為基準分析模型的性能。統計仿真實驗結果，隨機選取的100組網格細胞作為輸入經高斯分布激活函數處理后產生單一放電區域位置細胞位置野比例約達到90%，其中10組網格細胞輸入實驗結果示意圖如圖 8所示。
圖8
10組不同空間位相網格細胞輸入實驗結果示意圖
Figure8.
Experimental results of different spatial phases of 10 group grid cells input
10組網格細胞輸入未經高斯分布激活函數處理的輸出結果是具有多個放電區域的位置細胞位置野(如圖 8第1、2行所示)，經高斯分布激活函數處理的輸出結果是具有單一放電區域的位置細胞位置野(如圖 8第3、4行所示)。
2.3 網格細胞輸入數量、網格細胞空間位相、定向、間距變化對于模型影響研究
如圖 1所示，內嗅皮層中主要神經元網格細胞是海馬區主要神經元位置細胞的主要輸入來源，每個網格細胞的放電空間特征由間距、定向和空間位相3個參數來表征，網格細胞到單一位置細胞位置野之間的映射關系可能受這些方面因素影響。本文以下章節會對網格細胞輸入數量、網格細胞網格野空間位相、網格細胞網格野定向、網格細胞網格野間距變化這幾方面對于模型影響進行相關研究。
2.3.1 網格細胞輸入數量
分別選取4個、10個、20個具有相同空間位相、不同間距、不同定向網格細胞網格野作為輸入，此處選取的參數定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取，空間位相r0均為(50,50)，實驗結果如圖 9所示。
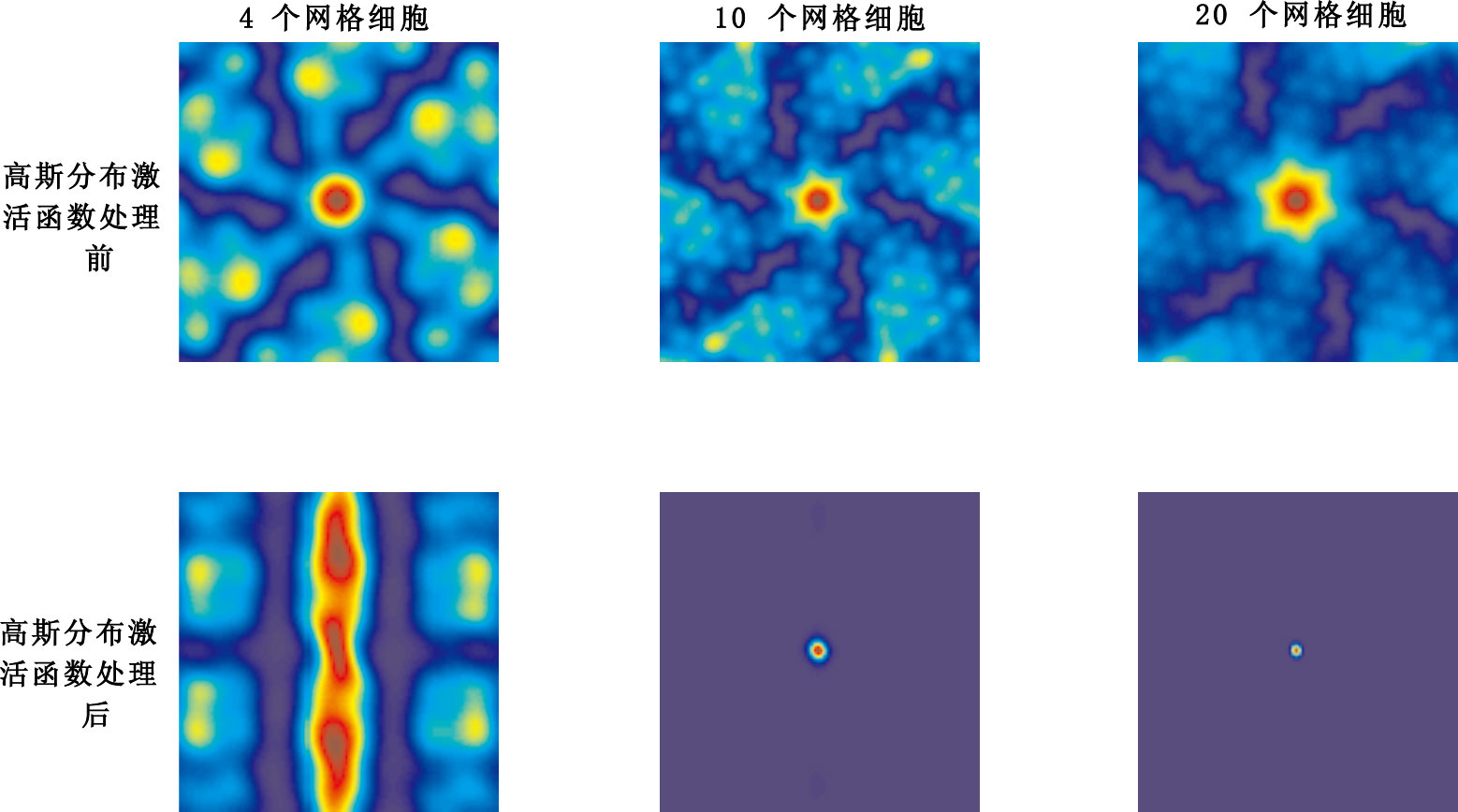圖9
不同數量網格細胞輸入實驗結果示意圖
Figure9.
Experimental results of different quantities of grid cells input
第一行依次從左往右3幅圖分別表示4個、10個、20個網格細胞輸入未經高斯分布激活函數處理后的輸出，第二行依次從左往右3幅圖分別表示4個、10個、20個網格細胞輸入經高斯分布激活函數處理后的輸出。空間位相相同、間距、定向不同的網格細胞作為輸入的情況下，若僅僅對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和，不經高斯分布激活函數處理，得不到單一放電區域位置細胞位置野；若對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和后，再通過高斯分布激活函數處理，當輸入網格細胞數量較少時，同樣不能實現網格細胞到單一位置細胞位置野的映射(如圖 9第二行第1幅子圖所示)；隨著網格細胞輸入數量增加到一定數目(10個網格細胞輸入即可)時，能實現網格細胞到單一位置細胞位置野的映射關系，即網格細胞輸入數量是實現網格細胞到單一位置細胞位置野之間映射的關鍵因素之一。
2.3.2 網格細胞空間位相變化
選取2組網格細胞輸入，其中每組包含有10個網格細胞，第1組網格細胞輸入參數：空間位相r0均為(50,50)，定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取。第2組網格細胞輸入參數：空間位相r0隨機選取，定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取。網格細胞空間位相變化實驗結果示意圖如圖 10所示。
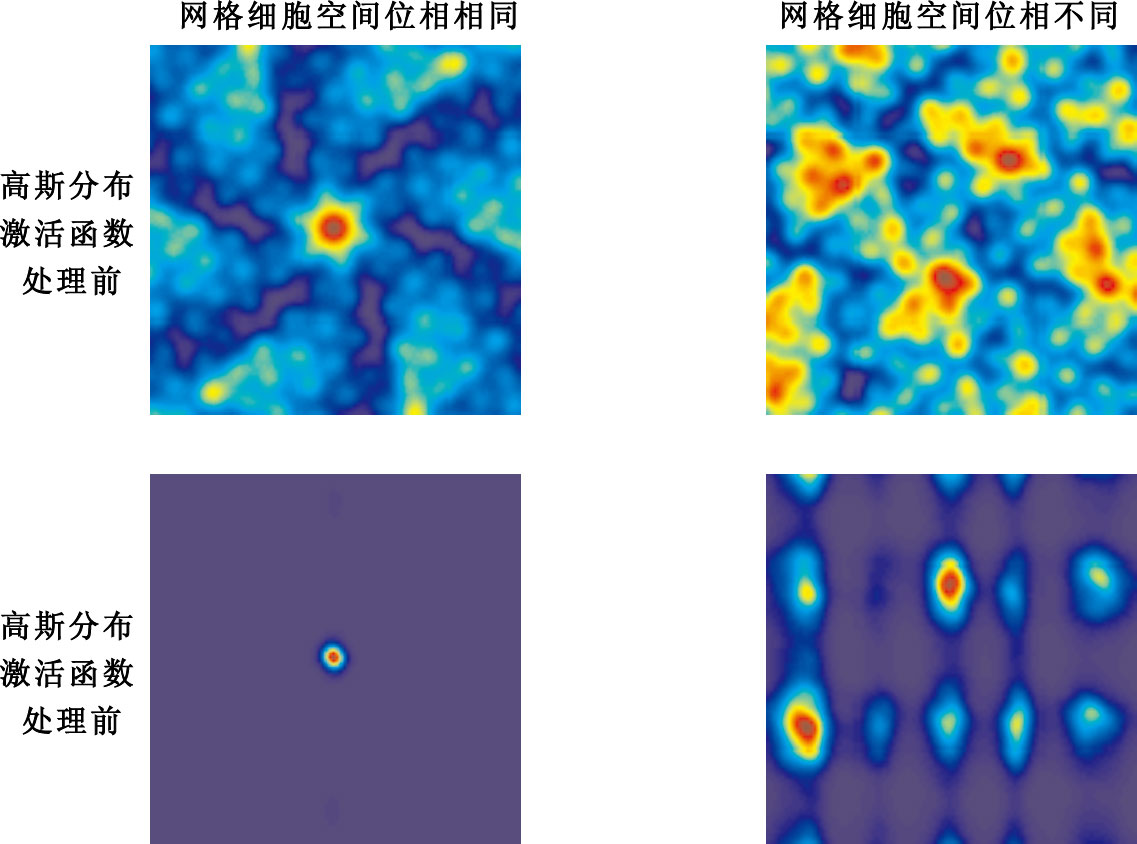圖10
網格細胞空間位相變化實驗結果
Figure10.
Experimental results of grid cells’ spatial phase change
如圖 10所示，第1列分別表示具有相同空間位相的10個網格細胞作為輸入未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出。第2列表示空間位相隨機選取的10個網格細胞作為輸入未經高斯分布激活函數處理、經過高斯分布激活函數處理后的輸出。當網格細胞輸入具有相同的空間位相時，能實現網格細胞到單一位置細胞位置野之間的映射；當網格細胞輸入空間位相發生變化時，不能實現網格細胞到單一位置細胞位置野之間的映射。
2.3.3 網格細胞網格野間距變化
選取2組網格細胞輸入，其中每組包含有10個網格細胞，第1組網格細胞輸入參數：網格野間距λ均為20 cm，定向θ介于[0°,60°]之間任意選取，空間位相r0隨機選取。第2組網格細胞輸入參數：網格野間距λ介于[20,70] cm之間任意選取，定向θ介于[0°,60°]之間任意選取，空間位相r0隨機選取。網格細胞網格野間距變化實驗結果示意圖如圖 11所示。
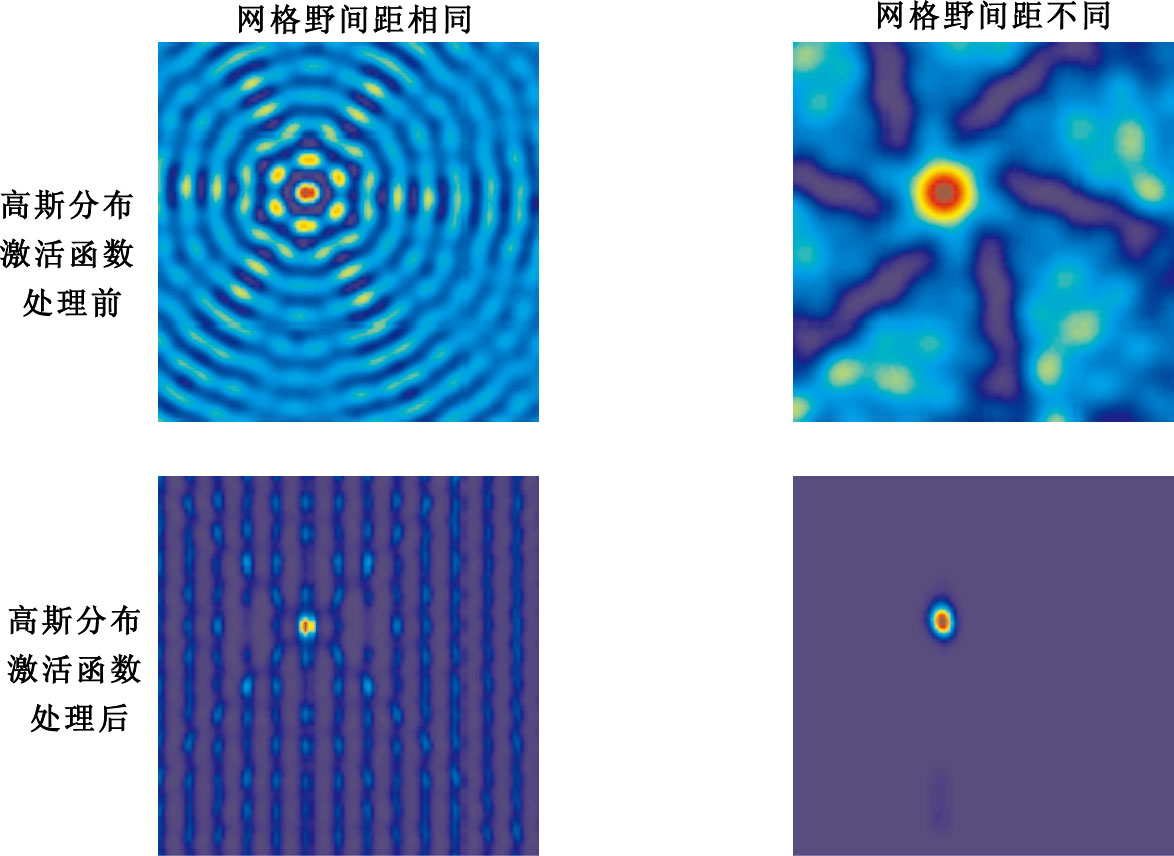圖11
網格細胞網格野間距變化實驗結果
Figure11.
Experimental results of grid fields’ spacing change of grid cells
第1列表示具有相同網格野間距的10個網格細胞作為輸入未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出。第2列表示具有不同網格野間距的10個網格細胞作為輸入未經高斯分布激活函數處理以及經過高斯分布激活函數處理后的輸出。當網格細胞輸入具有相同的網格野間距時，不能實現網格細胞到單一位置細胞位置野之間的映射；當網格細胞輸入具有不同網格野間距時，可實現網格細胞到單一位置細胞位置野之間的映射。
2.3.4 網格細胞網格野定向變化
選取2組網格細胞輸入，其中每組包含有10個網格細胞，第1組網格細胞輸入參數：網格野定向θ均為60°，網格野間距λ介于[20,70] cm之間任意選取，空間位相r0隨機選取。第2組網格細胞輸入參數：定向θ介于[0°,60°]之間任意選取，網格野間距λ介于[20,70] cm之間任意選取，空間位相r0隨機選取。網格細胞網格野定向變化實驗結果示意圖如圖 12所示。
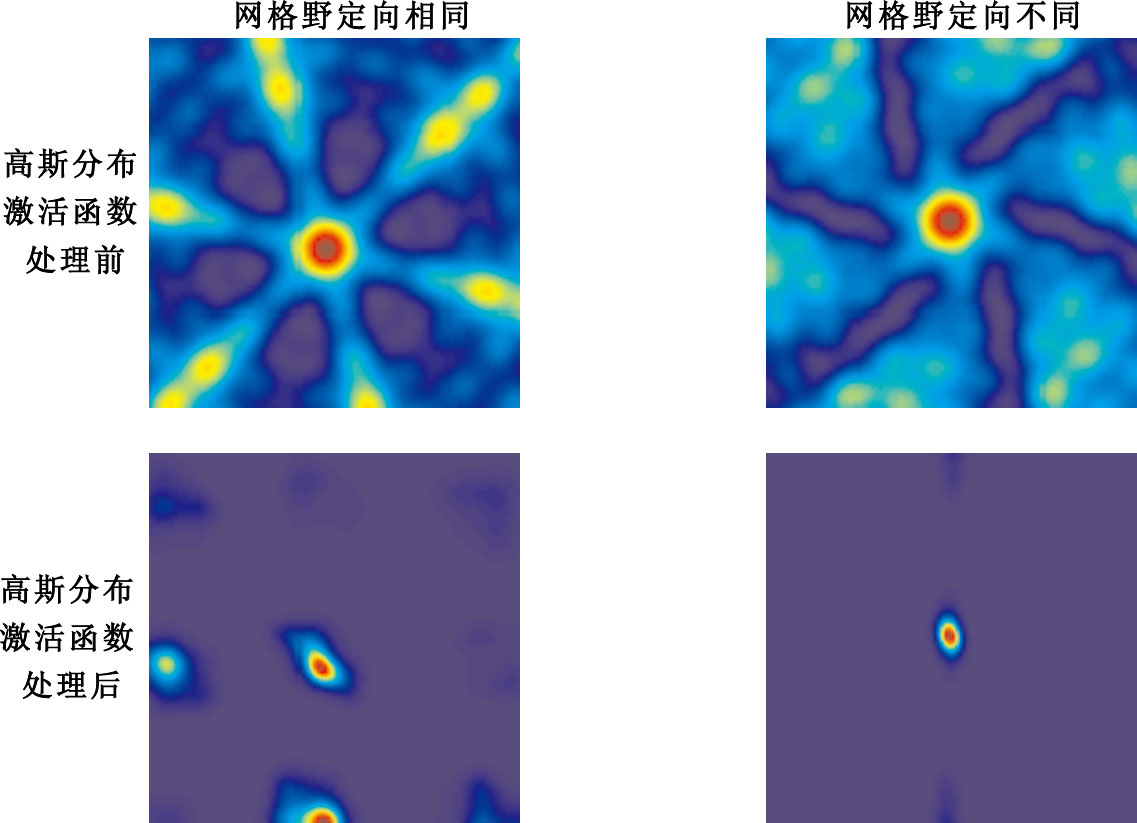圖12
網格細胞網格野定向變化實驗結果
Figure12.
Experimental results of grid fields’ orientation change of grid cells
第1列表示具有相同網格野定向的10個網格細胞作為輸入，然后以未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出結果。第2列表示具有不同網格野定向的10個網格細胞作為輸入，未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出結果。當網格細胞輸入具有相同的網格野定向時，不能實現網格細胞到單一位置細胞位置野之間的映射；而當網格細胞輸入具有不同網格野定向時，能實現網格細胞到單一位置細胞位置野之間的映射。
3 結論
本文提出了一種網格細胞到位置細胞的高斯分布激活函數模型，通過高斯分布激活函數對網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加后的輸出再做處理得到了與生物學研究發現相一致的具有單一激活域的位置細胞位置野[20-21]。在此之前已存在的模型包括基于競爭學習算法的位置細胞模型[8-9]、基于獨立成分分析方法的位置細胞模型[10-12]和基于貝葉斯位置重建方法的位置細胞模型[13-15]，這些模型相比于本文模型都存在有一些缺點，競爭學習算法位置細胞模型算法復雜，而且需要125個網格細胞輸入去表達多個網格細胞野到單一位置細胞野輸出特征映射關系[8]，獨立成分分析方法位置細胞模型約70%輸出為單一放電區域位置細胞位置野[10]，貝葉斯位置重建方法位置細胞模型缺乏神經生理學依據[13]，本文所提模型是依據神經生理學上網格細胞到位置細胞的神經連接機制，首先將網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加，然后引入高斯分布激活函數，利用其局域化特性，對線性疊加后的輸出進行處理，濾掉激活率比較低的位置野從而得到與生物學研究發現相一致的單一位置細胞位置野，實驗結果表明該模型在神經生理學基礎上算法簡單，所需網格細胞輸入較少(10個網格細胞即可)，選取多組網格細胞輸入得到約90%輸出為單一放電區域位置細胞位置野。此外，本文還對網格細胞數量、網格細胞空間位相、定向、間距等因素對于網格細胞到位置細胞映射影響做了相關研究，實驗結果表明在有充足數量網格細胞作為輸入的情況下，選取具有相同空間位相、不同間距、不同定向的網格細胞，該模型能夠很好地實現內嗅皮層中網格細胞到海馬區中單一位置細胞位置野之間的映射。海馬區中單個位置細胞對應單個激活域的位置細胞位置野，大量位置細胞位置野聯合編碼環境，在大鼠腦海馬區內形成“認知地圖”，可以將其應用到機器人等領域，使機器人能夠像人類一樣認知所處空間環境，實現面向所處環境某一目標導航等任務。本文所提出的網格細胞到位置細胞的高斯分布激活函數模型對于認知、記憶、學習、導航等研究具有重要意義。
引言
海馬結構位于嚙齒類動物大腦皮層中，該結構與動物記憶、認知、學習等高級功能密切相關，是嚙齒類動物進行環境認知的神經生理學基礎。因此，對于該結構深入研究有助于人們深刻理解大腦環境認知機制。從解剖結構上看，海馬結構主要由內嗅皮層(entorhinal cortex,EC)、齒狀回(dentate gyrus,DG)、海馬區(hippocampus)、下托綜合體(subiculum complex,SUB)四部分組成。內嗅皮層共分為6層，Ⅱ、Ⅲ、Ⅴ分別代表的是內嗅皮層第2、3、5層。海馬區由海馬角1區(cornu ammonis1,CA1)和海馬角3區(cornu ammonis3,CA3)構成。下托綜合體進一步分為腦下托(subiculum,S)、前下托(presubiculum,PRS)和傍下托(parasubiculum,PAS)。內嗅皮層與海馬區之間存在有雙向纖維投射，該雙向纖維投射構成了內嗅皮層-海馬區回路。內嗅皮層到海馬區纖維投射表明了內嗅皮層是海馬結構中海馬區的主要輸入來源[1-2]。海馬解剖結構和信息通路如圖 1所示，藍色線條箭頭表示的是內嗅皮層第Ⅱ層到齒狀回和海馬角3區纖維投射，紅色線條箭頭表示的是內嗅皮層第Ⅲ層到海馬角1區和腦下托纖維投射，黃色線條箭頭表示的是海馬角1區和腦下托到內嗅皮層第Ⅴ層纖維投射。
圖1
海馬解剖結構和信息通路
Figure1.
Anatomy structure and information pathway of hippocampus
內嗅皮層中主要神經元為網格細胞，多個網格細胞網格野相互交疊成一個個網格節點，以大鼠為例，連接網格節點所形成的正三角形遍及大鼠所處的整個空間環境[3-4]。網格細胞放電空間特征由以下3個參數表征：間距(網格節點之間距離)、定向(相對于外部參考軸傾斜度)、空間位相(相對于外部參考點偏移量)。網格細胞空間特征如圖 2所示，變量λ為網格細胞間距，θ為網格細胞定向，(x0,y0)為網格細胞空間位相。研究發現，沿內側內嗅皮層背腹軸方向，網格細胞網格野間距逐漸增大，相鄰網格細胞具有相似網格野間距和定向，但是它們的空間位相是隨機分散的[3-5]。
圖2
網格細胞空間特征
Figure2.
Spatial characteristics of grid cells
1971年，O’keefe和Dostrovesky在大鼠海馬區首次發現具有空間定位活動的位置細胞神經元[6]。大鼠在二維空間活動時，當其經過環境中某一特定狹小區域時，對應位置細胞就會放電，單個位置細胞對應有單一位置細胞激活域，將此區域稱之為位置細胞位置野[5, 7]。位置細胞位置野與大鼠所處空間位置有著準確的對應關系，位置細胞聯合編碼大鼠所處環境，在大鼠腦內形成“認知地圖”，此后，大鼠能基于該“認知地圖”實現面向空間環境中任一目標的導航任務。2005年，研究人員于大鼠內嗅皮層中發現了另外一種具有強烈空間放電特性的網格細胞神經元，該神經元會呈現出對空間中某一特定區域發生重復性規律放電的特性，此區域被稱之為網格細胞網格野[4]。與位置細胞不同的是，網格細胞能在多個位置放電，多個網格細胞網格野相互交疊成一個個網格節點，連接網格節點所形成的正三角形遍及大鼠所處的整個空間環境。如何構建多個網格細胞網格野到單一位置細胞位置野之間的映射關系呢？自從2005年發現網格細胞以來，一些模型被相繼提出。其中包括基于競爭學習算法的位置細胞模型[8-9]、基于獨立成分分析方法的位置細胞模型[10-12]和基于貝葉斯位置重建方法的位置細胞模型[13-15]。競爭學習算法位置細胞模型算法復雜，而且需要125個網格細胞輸入來實現多個網格細胞野到單一位置細胞野輸出特征映射關系[8]。獨立成分分析方法位置細胞模型約70%輸出為單一位置細胞野[10]。貝葉斯位置重建方法位置細胞模型缺乏神經生理學依據[13]。基于此，本文依據神經生理學上網格細胞到位置細胞神經連接機制，首先將網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加，然后引入高斯分布激活函數，利用其局域化特性，對線性疊加后的輸出進行處理，濾掉激活率比較低的位置野從而得到與生物學研究發現相一致的單一位置細胞位置野，該模型在神經生理學基礎上算法簡單，所需網格細胞輸入較少(本文所需10個網格細胞輸入即可)，選取多組網格細胞輸入得到約90%輸出為單一放電區域位置細胞位置野。位置細胞高斯分布激活函數模型構成與實現流程圖如圖 3所示。位置細胞高斯分布激活函數模型主要由2個模塊構成，如圖 3中藍色框所示，第1個模塊是基于條紋細胞的網格細胞模型，條紋細胞放電活動產生一簇簇條紋波，條紋波疊加形成網格細胞網格野。如圖 3中橙色框所示，第2個模塊是基于網格細胞的位置細胞模型，位置細胞從具有不同空間特征的網格細胞接收信息與相應網格細胞到位置細胞連接權值加權求和后經高斯分布激活函數處理得到位置細胞單一位置野放電特征。此外，本文還對網格細胞數量、網格細胞空間位相、定向、間距等因素對于該模型的影響做了相關研究。
圖3
位置細胞高斯分布激活函數模型構成與實現流程圖
Figure3.
Gauss distribution activation function model structure and the flowchart of the realization of place cells
1 方法
1.1 基于條紋細胞的網格細胞模型
條紋細胞被發現存在于內嗅皮層第3層中，該細胞在二維空間環境中的放電活動是一簇簇條紋波，它作為輸入將信息傳遞至內嗅皮層第2層中，其所產生的一簇簇條紋波通過疊加形成具有不同空間位相、定向、間距的網格細胞網格野[16-18]。
對于條紋細胞放電活動，我們用二維cos波來表示，如式(1)所示。
| ${{\varphi }_{1}}=\frac{1}{3}\text{cos}({{k}_{i}}r)$ |
其中，r= (x,y)代表大鼠當前所處環境位置坐標，ki (i=1,2,3) 代表波矢量，其方向表示的是波等相位行進的方向，大小稱之為波數ki。
| ${{k}_{i}}=\frac{2\pi }{{{\lambda }_{\cos }}}$ |
其中，λcos代表cos波波長。
生物學研究證實，網格細胞網格野呈正三角形遍布于大鼠所處的整個環境當中[3-4]。基于此，網格細胞激活率函數可以由三個條紋細胞(三個條紋細胞波矢量朝向相差60°)放電活動疊加來表示，如式(3)所示。
| $\psi \left( r \right)=\frac{\text{cos}({{k}_{1}}r)+\text{cos}({{k}_{2}}r)+\text{cos}({{k}_{3}}r)}{3}$ |
如式(3)所示，r= (0,0)時，ψ(r)有最大值為1。若選擇空間環境中任意一空間位相r0 = (x0,y0)作為網格細胞網格野的某一峰值點，則網格細胞激活率函數轉變為如式(4)所示。
| $\psi \left( r \right)=\psi (r-{{r}_{0}})$ |
ki代表的是波矢量，波矢量是波數ki的函數，網格細胞網格野間距作為表征網格細胞空間放電特征的1個參數。如圖 4所示，紅色實心圓圈表示網格細胞網格野節點，陰影部分表示條紋細胞二維cos波，網格細胞網格野間距λ與二維cos波波長λcos之間的關系如式(5)所示。
| $\lambda =\frac{2}{\sqrt{3}}{{\lambda }_{\cos }}$ |
圖4
網格細胞網格野間距λ與二維cos波波長λcos之間關系圖
Figure4.
Relationship diagram between grid cells’ grid field spacing λ and two dimensional cos wavelength λcos
又由式(2)可知，波數ki與網格細胞網格野間距λ之間的關系如式(6)所示。
| ${{k}_{i}}=\frac{4\pi }{\sqrt{3}\lambda }$ |
為了得到與生物學上發現相一致的正三角形網格細胞網格野，選取波矢量朝向相差60°的三個條紋細胞疊加后得到所需網格細胞網格野。以0°,60°,120°為例，選取k1,k2,k3，如式(7)所示。
| $\left\{ \begin{array}{*{35}{l}} {{k}_{1}}=\frac{{{k}_{1}}}{\sqrt{2}}[\text{cos}\left( \theta \right)+\sin \left( \theta \right),\text{cos}\left( \theta \right)-\sin \left( \theta \right)] \\ {{k}_{2}}=\frac{{{k}_{2}}}{\sqrt{2}}[\text{cos}\left( \theta +\frac{\pi }{3} \right)+\sin \left( \theta +\frac{\pi }{3} \right), \\ \text{cos}\left( \theta +\frac{\pi }{3} \right)-\sin \left( \theta +\frac{\pi }{3} \right)] \\ {{k}_{3}}=\frac{{{k}_{3}}}{\sqrt{2}}[\text{cos}\left( \theta +\frac{2\pi }{3} \right)+\sin \left( \theta +\frac{2\pi }{3} \right), \\ \text{cos}\left( \theta +\frac{2\pi }{3} \right)-\sin \left( \theta +\frac{2\pi }{3} \right)] \\ \end{array} \right.$ |
其中，θ表示網格細胞網格野定向。
由式(3)可知，ψ(r)取值介于[-1/2,1]之間，為了使網格細胞激活率取值介于0到1之間，網格細胞激活率函數轉變如式(8)所示。
| $g\left( r \right)=\frac{2}{3}\left( \psi \left( r \right)+\frac{1}{2} \right)$ |
將式(3)和式(4)代入式(8)得到網格細胞激活率函數如式(9)所示。
| $g\left( r \right)=\frac{2}{3}\left[ \frac{1}{3}\sum\limits_{i=1}^{3}{\text{cos}{{k}_{i}}(r-{{r}_{0}})+\frac{1}{2}} \right]$ |
1.2 基于網格細胞的位置細胞模型
如圖 3所示為基于網格細胞的位置細胞模型，即位置細胞首先從具有不同空間特征的網格細胞接收信息，然后與其相連接網格細胞之間的權值進行加權求和，最后經高斯分布激活函數處理得到位置細胞放電特征。在1.1小節中得到了作為輸入的網格細胞網格野，接下來就是將網格細胞網格野輸入和網格細胞與位置細胞連接權值進行加權求和，再經高斯分布激活函數處理得到位置細胞的單一激活域放電特征[10]。
網格細胞和位置細胞均為神經細胞，它們是由細胞體和細胞突起構成，而細胞突起是細胞體自身延伸出來的細長部分，細長部分又分為樹突和軸突。每個神經元只有一個軸突，它可以把信號傳遞到其它組織或另一個神經元，每個神經元可以有多個樹突，它可以接收刺激并將興奮傳入細胞體內，網格細胞與位置細胞之間信息傳遞亦是如此。網格細胞與位置細胞之間的連接權值函數如式(10)所示。
| ${{W}_{n}}=\frac{4\pi {{\sigma }^{2}}}{{{\lambda }^{2}}_{n}}3{{e}^{-43{{\sigma }^{2}}{{\pi }^{2}}/{{\lambda }^{2}}_{n}}}$ |
其中，Wn代表第n個網格細胞與位置細胞之間的連接權值，λn代表第n個網格細胞網格野間距，σ(σ=8 cm)代表位置細胞放電激活域標準差。
由式(9)和式(10)可知，位置細胞激活率函數如式(11)所示。
| $P\left( x,y \right)=\sum\limits_{1}^{N}{{{W}_{n}}{{g}_{n}}\left( x,y \right)}$ |
其中，Wn代表第n個網格細胞與位置細胞之間的連接權值，gn(x,y) 代表第n個網格細胞位于空間環境(x,y) 位置點處的激活率，N(N =4,10,20)代表網格細胞數量。
生物學研究發現，單純的對網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加往往得到的輸出是具有多個激活域的位置野，這與已有相關研究所證實單一位置細胞對應有單一位置野的結論不一致[19]。本文在網格細胞網格野輸入和網格細胞與位置細胞之間連接權值加權求和的基礎上，引入高斯分布激活函數，利用其局域化特性，對線性疊加后的輸出進行處理，濾掉激活率比較低的位置野從而得到與生物學研究發現相一致的單一位置細胞位置野，實現網格細胞到單一位置細胞位置野之間的映射關系，如式(12)所示。
| $P\prime \left( x,y \right)={{e}^{-{{\left[ \sum\limits_{1}^{N}{{{W}_{n}}{{g}_{n}}\left( x,y \right)} \right]}^{2}}}}$ |
2 仿真與實驗結果
2.1 基于條紋細胞的網格細胞模型
朝向相差60°的3個條紋細胞放電活動疊加后得到網格細胞網格野如圖 5所示。此處選取的參數為θ=0°，λ=40 cm，r0=(50,50)。
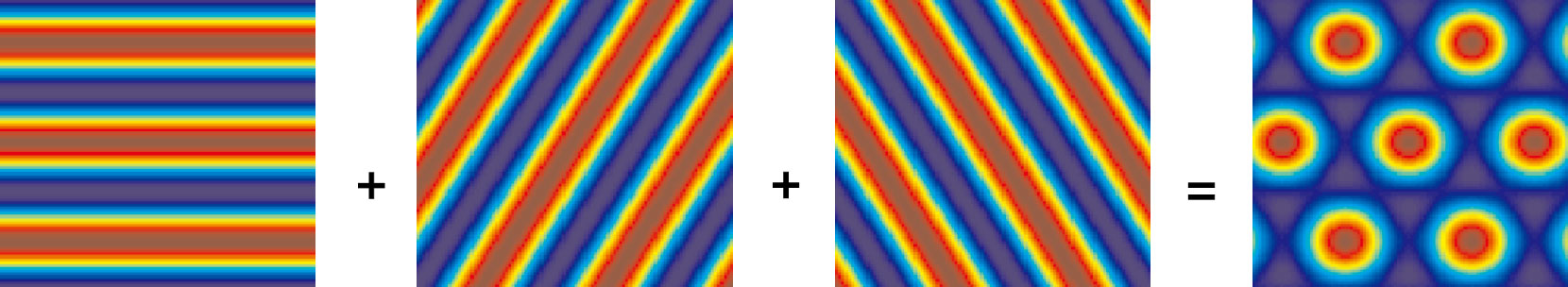圖5
3個條紋細胞條紋波疊加所得網格細胞網格野示意圖
Figure5.
Diagram of grid cells’ grid fields based on superposition of three stripe cells’ stripe wavelength
同樣的，選取不同參數基于條紋細胞得到具有不同空間位相、定向和間距的網格細胞網格野如圖 6所示。
圖6
具有不同空間位相、定向和間距的網格細胞網格野
Figure6.
Grid cells’ grid fields with different spatial phase,orientation and spacing
2.2 基于網格細胞的位置細胞模型
選取10個具有相同空間位相、不同間距、不同定向的網格細胞作為輸入，此處選取的參數定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取，空間位相r0均為(70,40)，實驗結果示意圖如圖 7所示。
圖7
相同空間位相、不同間距、不同定向網格細胞輸入實驗結果示意圖
Figure7.
Experimental results of the same spatial phase,different spacing and different orientation of grid cells input
如圖 7所示，左圖代表的是對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和后未經高斯分布激活函數處理后的輸出結果，可以看出此時位置細胞存在有多個放電區域。右圖則代表的是對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和后經高斯分布激活函數處理后的輸出結果，由圖可以看出此時位置細胞存在有單一位置放電區域。
同樣的，為測試本文所提模型性能，另外選取100組網格細胞輸入進行實驗，每組網格細胞空間位相相同、間距不同、定向不同，而各組網格細胞之間空間位相隨機選取。通過統計100組網格細胞輸入經高斯分布激活函數處理后得到單一放電區域位置細胞位置野比例為基準分析模型的性能。統計仿真實驗結果，隨機選取的100組網格細胞作為輸入經高斯分布激活函數處理后產生單一放電區域位置細胞位置野比例約達到90%，其中10組網格細胞輸入實驗結果示意圖如圖 8所示。
圖8
10組不同空間位相網格細胞輸入實驗結果示意圖
Figure8.
Experimental results of different spatial phases of 10 group grid cells input
10組網格細胞輸入未經高斯分布激活函數處理的輸出結果是具有多個放電區域的位置細胞位置野(如圖 8第1、2行所示)，經高斯分布激活函數處理的輸出結果是具有單一放電區域的位置細胞位置野(如圖 8第3、4行所示)。
2.3 網格細胞輸入數量、網格細胞空間位相、定向、間距變化對于模型影響研究
如圖 1所示，內嗅皮層中主要神經元網格細胞是海馬區主要神經元位置細胞的主要輸入來源，每個網格細胞的放電空間特征由間距、定向和空間位相3個參數來表征，網格細胞到單一位置細胞位置野之間的映射關系可能受這些方面因素影響。本文以下章節會對網格細胞輸入數量、網格細胞網格野空間位相、網格細胞網格野定向、網格細胞網格野間距變化這幾方面對于模型影響進行相關研究。
2.3.1 網格細胞輸入數量
分別選取4個、10個、20個具有相同空間位相、不同間距、不同定向網格細胞網格野作為輸入，此處選取的參數定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取，空間位相r0均為(50,50)，實驗結果如圖 9所示。
圖9
不同數量網格細胞輸入實驗結果示意圖
Figure9.
Experimental results of different quantities of grid cells input
第一行依次從左往右3幅圖分別表示4個、10個、20個網格細胞輸入未經高斯分布激活函數處理后的輸出，第二行依次從左往右3幅圖分別表示4個、10個、20個網格細胞輸入經高斯分布激活函數處理后的輸出。空間位相相同、間距、定向不同的網格細胞作為輸入的情況下，若僅僅對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和，不經高斯分布激活函數處理，得不到單一放電區域位置細胞位置野；若對網格細胞和網格細胞與位置細胞之間連接權值進行加權求和后，再通過高斯分布激活函數處理，當輸入網格細胞數量較少時，同樣不能實現網格細胞到單一位置細胞位置野的映射(如圖 9第二行第1幅子圖所示)；隨著網格細胞輸入數量增加到一定數目(10個網格細胞輸入即可)時，能實現網格細胞到單一位置細胞位置野的映射關系，即網格細胞輸入數量是實現網格細胞到單一位置細胞位置野之間映射的關鍵因素之一。
2.3.2 網格細胞空間位相變化
選取2組網格細胞輸入，其中每組包含有10個網格細胞，第1組網格細胞輸入參數：空間位相r0均為(50,50)，定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取。第2組網格細胞輸入參數：空間位相r0隨機選取，定向θ介于[0°,60°]之間任意選取，間距λ介于[20,70] cm之間任意選取。網格細胞空間位相變化實驗結果示意圖如圖 10所示。
圖10
網格細胞空間位相變化實驗結果
Figure10.
Experimental results of grid cells’ spatial phase change
如圖 10所示，第1列分別表示具有相同空間位相的10個網格細胞作為輸入未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出。第2列表示空間位相隨機選取的10個網格細胞作為輸入未經高斯分布激活函數處理、經過高斯分布激活函數處理后的輸出。當網格細胞輸入具有相同的空間位相時，能實現網格細胞到單一位置細胞位置野之間的映射；當網格細胞輸入空間位相發生變化時，不能實現網格細胞到單一位置細胞位置野之間的映射。
2.3.3 網格細胞網格野間距變化
選取2組網格細胞輸入，其中每組包含有10個網格細胞，第1組網格細胞輸入參數：網格野間距λ均為20 cm，定向θ介于[0°,60°]之間任意選取，空間位相r0隨機選取。第2組網格細胞輸入參數：網格野間距λ介于[20,70] cm之間任意選取，定向θ介于[0°,60°]之間任意選取，空間位相r0隨機選取。網格細胞網格野間距變化實驗結果示意圖如圖 11所示。
圖11
網格細胞網格野間距變化實驗結果
Figure11.
Experimental results of grid fields’ spacing change of grid cells
第1列表示具有相同網格野間距的10個網格細胞作為輸入未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出。第2列表示具有不同網格野間距的10個網格細胞作為輸入未經高斯分布激活函數處理以及經過高斯分布激活函數處理后的輸出。當網格細胞輸入具有相同的網格野間距時，不能實現網格細胞到單一位置細胞位置野之間的映射；當網格細胞輸入具有不同網格野間距時，可實現網格細胞到單一位置細胞位置野之間的映射。
2.3.4 網格細胞網格野定向變化
選取2組網格細胞輸入，其中每組包含有10個網格細胞，第1組網格細胞輸入參數：網格野定向θ均為60°，網格野間距λ介于[20,70] cm之間任意選取，空間位相r0隨機選取。第2組網格細胞輸入參數：定向θ介于[0°,60°]之間任意選取，網格野間距λ介于[20,70] cm之間任意選取，空間位相r0隨機選取。網格細胞網格野定向變化實驗結果示意圖如圖 12所示。
圖12
網格細胞網格野定向變化實驗結果
Figure12.
Experimental results of grid fields’ orientation change of grid cells
第1列表示具有相同網格野定向的10個網格細胞作為輸入，然后以未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出結果。第2列表示具有不同網格野定向的10個網格細胞作為輸入，未經高斯分布激活函數處理和經過高斯分布激活函數處理后的輸出結果。當網格細胞輸入具有相同的網格野定向時，不能實現網格細胞到單一位置細胞位置野之間的映射；而當網格細胞輸入具有不同網格野定向時，能實現網格細胞到單一位置細胞位置野之間的映射。
3 結論
本文提出了一種網格細胞到位置細胞的高斯分布激活函數模型，通過高斯分布激活函數對網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加后的輸出再做處理得到了與生物學研究發現相一致的具有單一激活域的位置細胞位置野[20-21]。在此之前已存在的模型包括基于競爭學習算法的位置細胞模型[8-9]、基于獨立成分分析方法的位置細胞模型[10-12]和基于貝葉斯位置重建方法的位置細胞模型[13-15]，這些模型相比于本文模型都存在有一些缺點，競爭學習算法位置細胞模型算法復雜，而且需要125個網格細胞輸入去表達多個網格細胞野到單一位置細胞野輸出特征映射關系[8]，獨立成分分析方法位置細胞模型約70%輸出為單一放電區域位置細胞位置野[10]，貝葉斯位置重建方法位置細胞模型缺乏神經生理學依據[13]，本文所提模型是依據神經生理學上網格細胞到位置細胞的神經連接機制，首先將網格細胞輸入和網格細胞與位置細胞之間連接權值進行線性疊加，然后引入高斯分布激活函數，利用其局域化特性，對線性疊加后的輸出進行處理，濾掉激活率比較低的位置野從而得到與生物學研究發現相一致的單一位置細胞位置野，實驗結果表明該模型在神經生理學基礎上算法簡單，所需網格細胞輸入較少(10個網格細胞即可)，選取多組網格細胞輸入得到約90%輸出為單一放電區域位置細胞位置野。此外，本文還對網格細胞數量、網格細胞空間位相、定向、間距等因素對于網格細胞到位置細胞映射影響做了相關研究，實驗結果表明在有充足數量網格細胞作為輸入的情況下，選取具有相同空間位相、不同間距、不同定向的網格細胞，該模型能夠很好地實現內嗅皮層中網格細胞到海馬區中單一位置細胞位置野之間的映射。海馬區中單個位置細胞對應單個激活域的位置細胞位置野，大量位置細胞位置野聯合編碼環境，在大鼠腦海馬區內形成“認知地圖”，可以將其應用到機器人等領域，使機器人能夠像人類一樣認知所處空間環境，實現面向所處環境某一目標導航等任務。本文所提出的網格細胞到位置細胞的高斯分布激活函數模型對于認知、記憶、學習、導航等研究具有重要意義。