胰腺癌的診斷非常重要，而細胞抹片顯微圖像的病理分析是其診斷的主要手段。圖像的準確自動分割和分類是病理分析的重要環節，因此本文提出了一種新的胰腺細胞抹片顯微圖像自動分割與分類算法。在分割方面，首先采用多特征 Mean-shift 聚類算法（MFMS）定位細胞核區域；接著采用彈性數學形態學結合角點檢測的去粘連模型（CSM）對粘連重疊細胞核進行去粘連處理，實現了分割的準確性和魯棒性。在分類方面，首先針對分割的細胞核提取了 4 個形狀特征和 138 個不同顏色空間的紋理特征；然后結合支持向量機（SVM）和鏈式遺傳算法（CAGA）實現封裝式特征選擇；最后將優選特征送入 SVM 進行分類，完成了胰腺細胞抹片顯微圖像的分類識別。本文采用了 15 幅圖像一共 461 個細胞核進行測試。實驗結果顯示，本文算法可以實現不同類型的胰腺細胞抹片顯微圖像的自動分割與準確分類。就分割來說，本文算法可獲得較高的正確率（93.46%±7.24%）；就正常和癌變細胞的分類來說，本文算法可獲得較高的分類正確率（96.55%±0.99%）、靈敏度（96.10%±3.08%）和特異度（96.80%±1.48%）。
引用本文： 王品, 劉倩倩, 王力銳, 李勇明, 劉書君, 顏芳. 多特征聚類與粘連分離模型的細胞抹片圖像分割與分類. 生物醫學工程學雜志, 2017, 34(4): 614-621. doi: 10.7507/1001-5515.201605004 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
作為消化道腫瘤發病率排名第二的胰腺癌，具有病情隱匿、發病兇險、難以治愈等特點。胰腺癌在我國的發病趨勢逐漸接近歐美國家[1-2]。據相關報道，世界范圍內的胰腺癌患者在 5 年時間內的存活率最高只有 5%[3]。現階段胰腺癌的診斷方式多種多樣，主要方法有細針穿刺獲取細胞進行病理分析、影像學和超聲內鏡檢查、腫瘤標志物和基因分子診斷等，其中細針穿刺獲取細胞進行病理分析是診斷的重要手段[4-8]。傳統人工病理分析方式主觀性強，診斷正確率不穩定。為了減輕病理醫生的工作量和提高診斷的客觀性，近年來基于計算機技術的自動病理學輔助分析方式已開始用于胰腺細胞抹片顯微圖像，并逐漸成為胰腺癌檢測和診斷的重要方法。
胰腺細胞抹片顯微圖像自動分析包括細胞核分割和分類兩大部分。在分割方面，國內外文獻中提到的大多數分割算法都是圍繞分水嶺、主動輪廓模型、基于像素分類或者是結合預處理和后處理的方法進行研究的。Plissiti 等[9]使用基于標記和彩色梯度圖像的分水嶺分割方法，發現會出現過分割的情況；Kim 等[10]和 George 等[11]利用標記分水嶺對粘連的細胞抹片進行分割；還有研究采用監督機器學習和 k 均值聚類等分類方法來分割細胞抹片顯微圖像[12-13]；其他一些方法如基于動態流的變形模型和輻射梯度向量流蛇模型等也被用于細胞抹片顯微圖像的分割[14-15]。上述研究的分割效果還有待改進，主要原因在于細胞圖像的背景復雜、細胞核染色不均勻，以及對粘連重疊細胞核的準確分割線獲取較難等。
在分類方面，目前公開研究文獻中涉及的特征大多關于形態和紋理，涉及的分類算法主要包括支持向量機（support vector machine，SVM）、k 鄰近算法（k-nearest neighbor，k-NN）、模糊 C 均值（fuzzy C-means，FCM）、人工神經網絡以及它們的組合[11, 16-18]。這些算法大多沒有包含特征選擇，但是研究發現特征選擇能夠提高分類準確率和有效性評價的可靠性[18-19]。
本團隊[20]在前期工作中對乳腺細胞切片圖像進行了分割處理，取得了較好的效果。針對乳腺組織切片圖像存在細胞粘連、細胞邊界不清、細胞內部存在孔洞等問題，提出了一種基于小波多尺度區域生長和雙策略去粘連模型（chain splitting model，CSM）的分割方法。本文胰腺細胞抹片圖像與乳腺組織切片圖像存在較大差別，細胞抹片顯微圖像中存在紅細胞的干擾和細胞核染色不均勻的現象，并且細胞核與細胞質以及背景的密度差別較大。而 Mean-shift 聚類算法具有自適應性強、不需要先驗知識、運行速度快、可有效去除復雜背景干擾等優點，因此本文提出了一種基于多特征的 Mean-shift 聚類算法（multi-feature Mean-shift，MFMS）來取代前期的小波多尺度區域生長以完成胰腺細胞核的定位。前期工作的 CSM 能有效去除粘連細胞，經過調參，可用于本文分割中去除細胞核的粘連。在分類方面，本文提取了 4 個形態特征和 138 個紋理特征作為初始多類型特征集，最后用鏈式遺傳算法（chain-like agent genetic algorithm，CAGA）結合 SVM 來選取最優特征子集并進行分類識別。總的來說，本文算法分為兩部分，第一部分為基于多特征 Mean-shift 聚類和粘連分離模型（MFMS&CSM）的細胞抹片圖像自動分割算法；第二部分為基于 CAGA 和 SVM 的細胞抹片圖像自動分類算法。
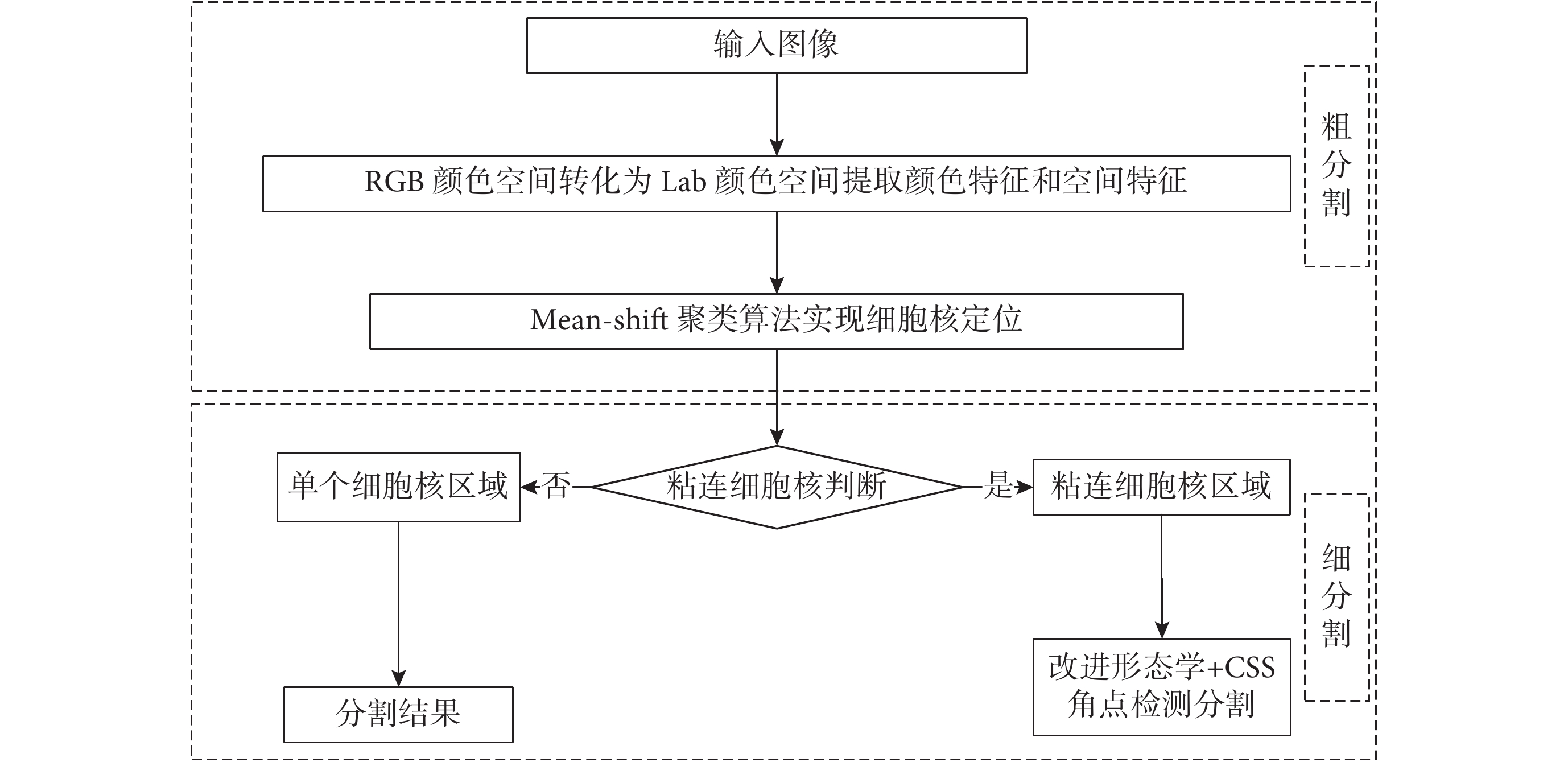
1 基于 MFMS&CSM 的細胞抹片圖像自動分割算法
本分割算法主要由兩部分組成。第一部分為多特征 Mean-shift 聚類的細胞核定位。首先將圖像從 RGB 彩色空間映射到 Lab 彩色空間，并提取 a 和 b 兩個顏色分量作為顏色特征，接著提取細胞圖像的空間特征與顏色特征形成多特征，最后利用 Mean-shift 聚類算法實現多特征聚類提取出細胞核區域，并進行粘連判斷篩選出單個細胞核和粘連細胞核。第二部分采用雙策略去粘連模式對粘連重疊細胞核進行分割，采用彈性數學形態學方法和角點檢測算法對粘連程度不同的細胞核進行分割。該分割算法的主要流程如圖 1 所示。
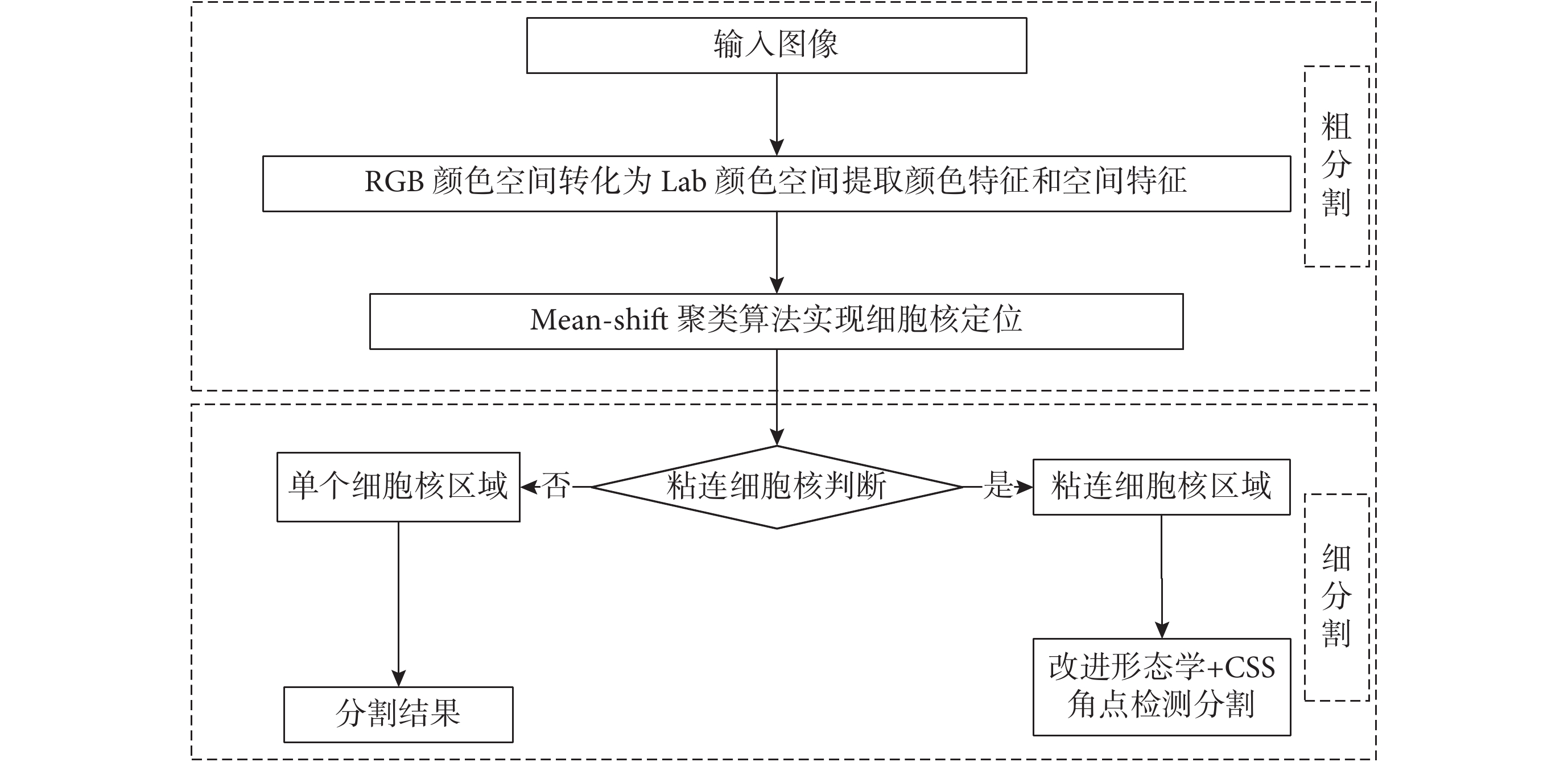圖1
MFMS&CSM 算法總流程圖
Figure1.
Total flow chart of MEMS&CSM
1.1 基于多特征 Mean-shift 聚類的粗分割算法
細胞抹片顯微圖像中細胞核的粗分割是細胞核分割算法中的第一步，主要包括細胞核的定位和單個細胞核與粘連細胞核的區分。粗分割的具體實現過程描述如下：首先把圖像從 RGB 顏色空間映射到 Lab 顏色空間提取每個像素的 a 和 b 分量作為顏色特征，同時提取細胞圖像的空間信息作為空間特征；接著用 Mean-shift 聚類算法對圖像 f 的特征
進行聚類實現細胞核所在區域的提取，并對提取的細胞核區域的邊界進行形態學操作，以將其結果作為掩膜模板；最后用模板把原始彩色胰腺細胞抹片圖像轉化為細胞核為目標前景、其他為背景的二值區域，即為細胞核定位的結果，并對單細胞核與粘連細胞核進行分離。
1.1.1 圖像像素點的多特征提取 在數字圖像處理中，為保留盡量寬闊的色域和豐富的色彩，常選擇將 RGB 顏色空間映射到 Lab 顏色空間[21]。首先將圖像 f 的顏色空間從 RGB 映射成 Lab 得到 f Lab 圖像，然后對 f Lab 提取 a 和 b 分量作為顏色特征，分別用 LabA 和 LabB 表示。圖像 f 的像素為 512×384，像素點（x，y）的位置特征 X、Y 表示如下：
 |
其中
表示取最大值，m 和 n 分別表示圖像行和列的大小，ωxy 表示空間位置特征的權重，一般在 [0 1] 取值，本文取值為 1。將提取的多特征進行高斯平滑處理，則圖像 f 基于像素點的多特征向量可表示為：
。
1.1.2 基于多特征 Mean-shift 聚類的細胞核定位 通過觀察發現，胰腺細胞核、細胞質以及背景三者之間的密度分布是不一樣的，因此考慮用基于密度的聚類算法來分割胰腺細胞核。其中 Mean-shift 算法就是一種有效的密度聚類迭代統計算法，由 Fuku-naga 等[22]于 1975 年在一篇基于非參數概率密度函數的梯度估計的文獻中提出。
通過對圖像像素點提取顏色和空間位置信息，得到 4 個特征向量，并給定 4 維空間 R4 中圖像像素樣本點 xi，
，則在像素點 x 處的 Mean-shift 向量可表示如下：
 |
其中 x 表示被平滑點的像素值；
表示以被平滑點為中心、邊長為 2r 的正方形區域內的像素點的值；r 稱為空域帶寬；K（I）為核函數，實現對區域 Sh 的大小進行控制；Sh 為高維球區域，h 為高維球區域的半徑；k 指在 512×384 個像素樣本點中有 k 個點落入到高維球區域中。從表達式（2）中可知，（xi–x）表示像素點 xi 相對于中心點 x 的偏移量，其中核函數規定了 Mean-shift 向量的貢獻程度，本文選取的核函數如下：
 |
式中 d=4，v 表示 4 維空間單位超球的體積。Mean-shift 向量 Mh（x）是對落入球形區域 Sh 中的 k 個樣本點相對于區域中心點 x 的偏移向量平均數。對圖像 f 的概率密度函數 f（x）進行采樣可以得到樣本點 xi。算法具體實現步驟如下：設像素點窗口（半徑為 r）內外的像素點集合分別用 fsa 和 fsna 表示，聚類的數目用 K 表示，聚類的中心用 Ck 表示。
步驟 1：從圖像 fsna 中隨機選擇一個點 x 作為一次聚類的起始點，該點的特征作為初始聚類中心。
步驟 2：以 x 為中心、r 為半徑建立超球體 Sh 區域，然后計算 Sh 區域內滿足要求的點的個數，同時給這些點投票，并把這些點歸為 fsa。
步驟 3：計算 Mh（x），若
，則聚類平移量已收斂，轉到步驟 4；否則，
，轉到步驟 2，本文
。
步驟 4：當滿足 K=0 或 K>0 且不存在一個 Ck 使得不等式
成立時，則進行如下操作：K=K+1，Ck=x 記錄像素點在窗口平移過程中得到的票數；若 K>0 且存在一個 Ck 滿足 j =
使得不等式
成立，則將 Ck 類合并到第 j 類中，并進行如下操作：
，并將像素點得到的票數相加。
步驟 5：判斷樣本點是否已經處理完
，如果
，則轉到步驟 1，否則轉到步驟 6。
步驟 6：根據聚類過程中得到的票數，將像素點劃歸到得到票數最多的類。
步驟 7：輸出聚類數目 K、聚類中心 Ck 以及每類像素點序號，至此算法結束。
在 Mean-shift 聚類算法中，針對每一幅圖像聚類窗口大小 r 差異，提出了基于類內平均散度（AS）及類間平均分離度（AD）準則來自動尋找最佳聚類數目。AS 和 AD 定義如下：
'/> |
式中 Nk 表示屬于第 k 類的像素點個數。類內平均散度是指同類像素點之間的差異，其值越小，則像素點之間就越相似。類間平均分離度是各個簇中心之間的差異，其值越大，則類與類之間的差異性也就越大。于是用 AR=AS/AD表達式來確定 K 的值，即較小的 AR 值對應的 K 值被選中，實現聚類算法的自適應性分割。
在對細胞核進行正確定位后，需要對定位區域進行單細胞核和粘連細胞核的判斷，以便后面只對粘連細胞核區域進行相應的操作，從而減少算法的時間消耗。單細胞核與粘連細胞核分離的具體步驟如下：
步驟 1：計算每一個區域的圓形度 R=
，A 為區域面積，P 為區域周長。
步驟 2：保存圓形度 R 大于 t 的區域作為分割的區域 f out，其他的作為未分割區域 f usg。
步驟 3：計算 f out 中區域的平均面積作為初始的面積閾值 Ag。
步驟 4：計算 f usg 中每一個區域的面積，然后與之前的面積閾值 Ag 進行比較，大于初始面積的 p 倍作為粘連的細胞核 f ove，需進行進一步的分割，其他的細胞核區域作為 f out 輸出。
經過對樣本圖像和實驗結果的分析，實驗中參數 t 和 p 的取值分別為 0.6 和 1.2。
1.2 基于粘連分離模型的細分割算法
胰腺細胞抹片顯微圖像中非常顯著的特點是粘連現象頻繁和嚴重，不同情況粘連程度不一。為了解決這些問題，本文引入了作者前期提出的粘連分離模型，經過調參處理，來對本文圖像進行分割處理，相關介紹詳見文獻[20]。
2 基于 CAGA 和 SVM 的細胞抹片圖像自動分類算法
有意義的特征能使細胞圖像的分類具有較好的效果。在以往的研究中，形態、比色法、紋理和結構特征已被用于特征提取和特征評價以實現細胞或細胞圖像的分類。本文提取形狀特征和不同顏色空間的紋理特征，并用 CAGA 結合 SVM 來篩選最優特征子集，以便獲得更好的分類效果，同時消耗時間較少。
2.1 特征提取
正常細胞核和癌變細胞核的形態特征存在一定的差異，故提取了 4 個形態特征，分別是面積（area）、周長（perimeter）、離心率（eccentricity）和圓形度（roundness circularity）。紋理特征描述了一個數字化的顯微圖像的像素灰度級的空間布局[23-24]，首先計算圖像中每個像素點的局部特征，然后從局部特征的分布導出一組統計特征，從而得到紋理特征。本研究選取的一階統計特征為灰度直方圖的均值，設
表示一個隨機變量的灰度級，
表示相應的直方圖，L 表示不同的灰度級，統計矩得到的紋理特征是：
（1）平均灰度級方差（mean value）：
 |
（2）標準差（standard deviation）：
 |
（3）平滑度（evenness）：
 |
（4）三階矩（third moment）：
 |
（5）區域灰度一致性（uniformity）：
 |
（6）灰度變化量度熵（entropy）：
 |
顏色空間分別為 RGB、HSV、HSI、YIQ、YCrCb、XYZ、Lab、灰度空間和增強灰度空間。因此，共提取了不同顏色空間的 138 個紋理特征。
2.2 特征選擇
待選特征集包括所有的形態特征和紋理特征。無論這些特征是否有顯著差異，幾乎所有的文獻中都沒有進行特征選擇就直接進行正常和癌變細胞的分類識別，這將導致分類性能較差并耗費更多的時間[21]。文獻中提到 CAGA 結合 SVM 的分類算法獲得了滿意的分類準確率[25]，故本文采用此方法選擇最優特征子集。CAGA 算法描述如下：
輸入：擬提取的多種類型的特征合并在一起得到待選特征集設為
。
初始化：s（t）表示某一代的智能體，個數為 s，每個智能體（即個體）長度為 l，代表 l 個特征序號，M 為設置的最大迭代次數。
過程：（1）對
做樣本處理，得到樣本特征矩陣
，w 代表樣本數，l 代表特征數，即智能體的長度。
（2）將樣本矩陣隨機劃分為訓練樣本矩陣 data_fea_train()、驗證樣本矩陣 data_fea_vali-dation()、測試樣本矩陣 data_fea_test()。
（3）根據初始的第 q 個智能體，對（2）中的驗證樣本矩陣分別進行裁剪，生成該智能體所對應的驗證特征樣本矩陣。
（4）將 data_fea_train() 送入 SVM 進行訓練，然后基于訓練后的 SVM 和 data_fea_validation()ithAgent 輸出測試準確率作為該智能體的適應度值。
（5）最后計算所有代的適應度值，遺傳操作（鄰近競爭選擇、自適應交叉、自適應變異），結果是否滿足確定的狀態，如果是就接著下一步，如果否就返回跳出算法。
（6）輸出最優智能體 p（t）對應的最優特征子集。
（7）基于最優特征子集和測試樣本 data_fea_test() 得到裁剪后的特征樣本矩陣 data_fea_test()p(t)，送入訓練后的 SVM 進行分類，得到分類準確率。
結束
3 實驗結果與分析
本文的胰腺細胞抹片圖像來源于西南醫院，共采集到 10 個患者 15 幅胰腺細胞抹片顯微圖像。為了表明本文算法的有效性，一共組織了 4 組實驗。第一組實驗用于顯示本文分割算法的各個分割中間結果；第二組實驗將本文分割方法與其它有代表性的分割方法進行效果對比；第三組實驗對比統計了本文算法和被比較算法的總的分割準確率；第四組實驗針對正常細胞核和癌變細胞核，統計了分類準確率、敏感度和特異度。
3.1 MFMS&CSM 分割算法中間結果與分析
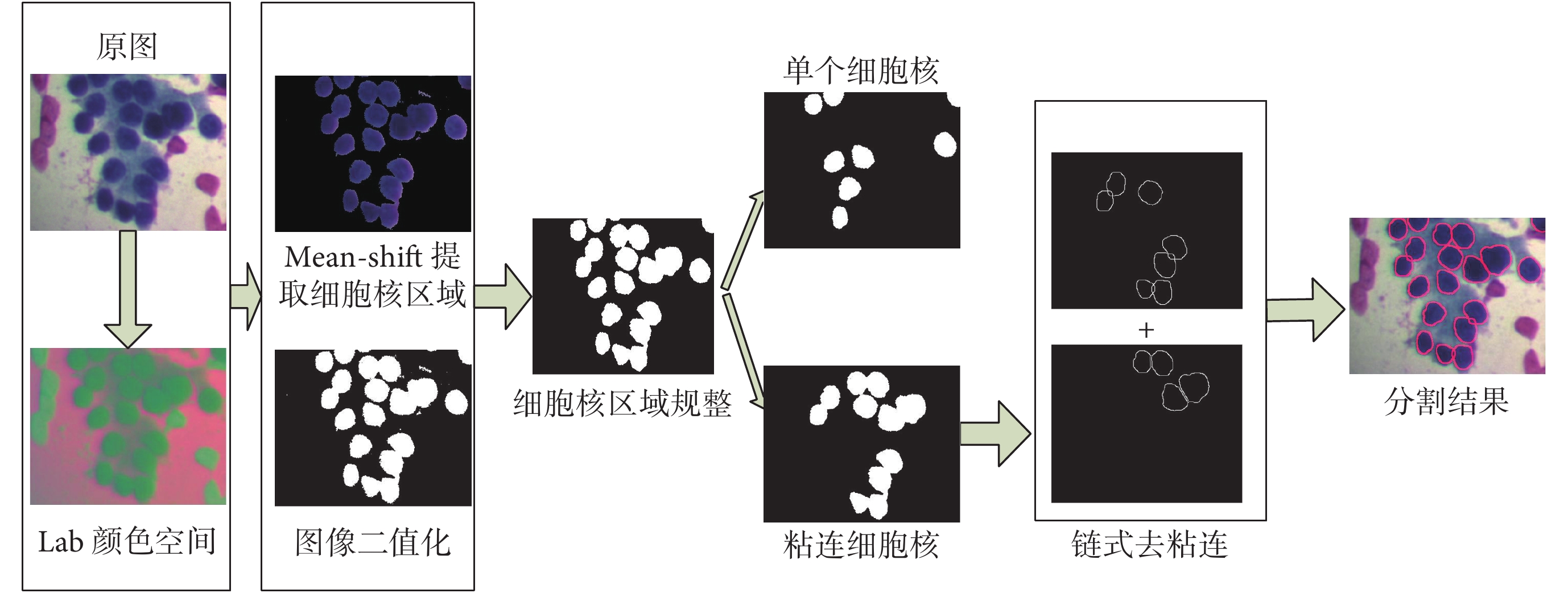
圖 2 顯示了本文分割算法的各個分割中間結果，原圖選自 15 幅圖像中第 7 幅圖像的部分區域。從分割步驟圖可以看出，多特征 Mean-shift 聚類能夠把胰腺細胞核與其它背景很好地分割開來（圖中 Mean-shift 提取細胞核區域和圖像二值化）；聚類后能得到完整、無孔洞和邊緣定位準確的細胞核（圖中細胞核區域規整）；針對粘連重疊細胞核的分割，可以得到準確的分割線（圖中分割結果）。整個分割算法的相關參數均可自適應調整，無需人為干預。
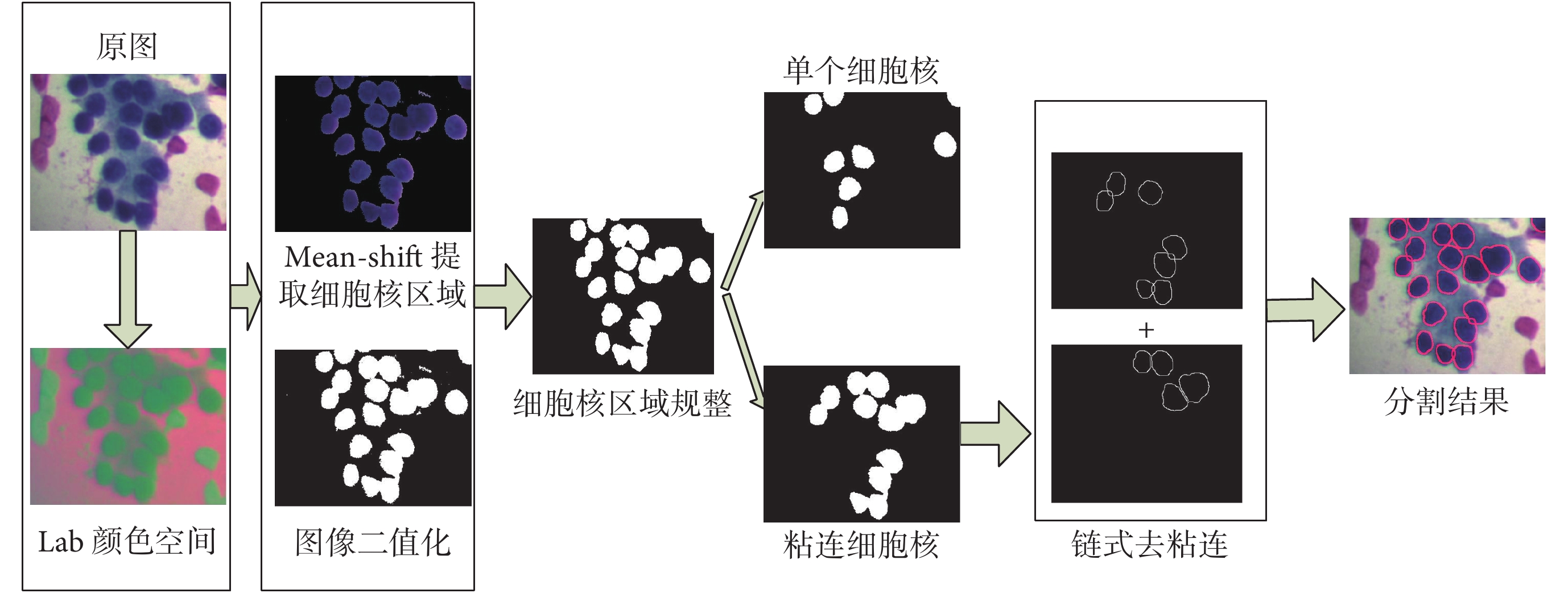圖2
MFMS&CSM 算法分割的中間結果
Figure2.
Intermediate result using method of MFMS&CSM
3.2 不同分割算法的分割結果比較
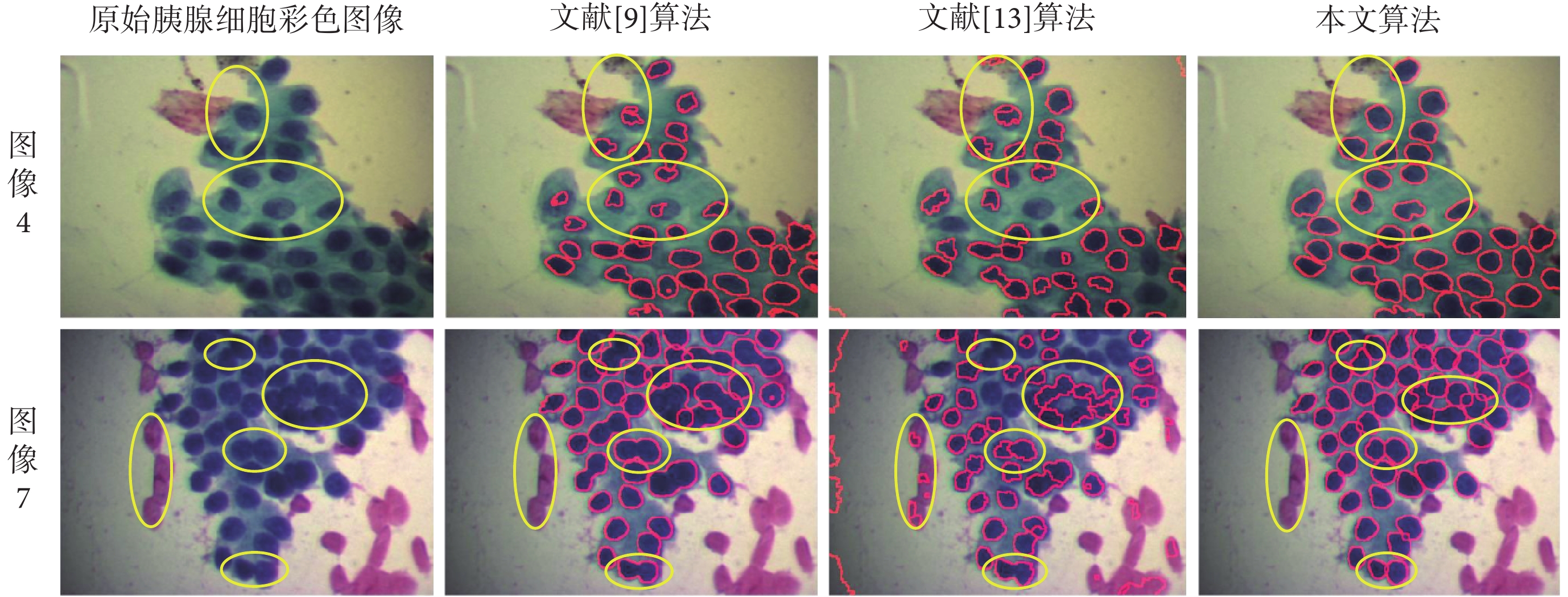
圖 3 為本文算法 MFMS&CSM 與文獻[9]和[13]的最終分割結果對比。這兩篇文獻都是關于細胞抹片顯微圖像分割較新的文獻，并且分割方法可以重現，因此具有較好的比較意義。為了更公平地比較，我們選取了這兩種方法中較好的結果與本文方法的結果進行比較。分割結果如圖 3 所示。
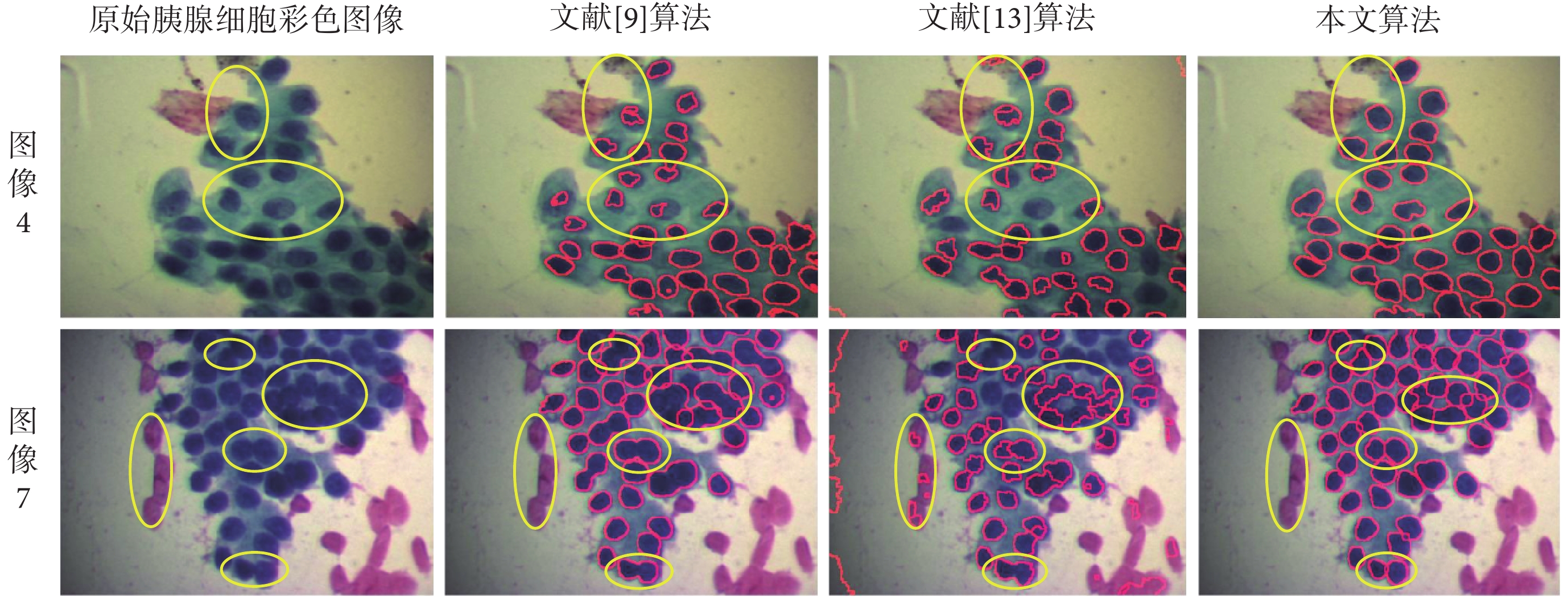圖3
不同分割算法的分割結果對比
Figure3.
Comparison of segmentation results among different segmentation algorithms
從圖 3 可以看出，對于背景簡單、細胞核染色均勻的細胞圖像，被比較算法存在少量錯誤分割，而本文的分割算法基本無錯誤分割，見圖中黃色橢圓區域（如圖像 4）。對于背景復雜、細胞核形態不一、染色不均勻的細胞圖像，被比較算法均存在很多錯誤分割現象，而本文算法仍然有較準確的分割結果（如圖像 7）。
3.3 不同分割算法分割的準確性統計
在細胞圖像分割結果統計中，分割錯誤的類型主要有過分割、錯誤分割、未分割、多分割和欠分割五種。為了更為客觀地定量評估分割結果，將得到的分割結果與人工分割金標準進行比較，并對分割正確的細胞核個數（true number，TN）、分割錯誤的細胞核個數（false number，FN）和實際細胞核個數（real number，RN）進行統計。分割準確性評價指標主要采用正確率（segmentation accuracy，SA）和過分割、錯誤分割、未分割、多分割以及欠分割的個數來表示，正確率定義為：SA=TN/RN。
將本文算法和現有兩種主流算法分別用于所有胰腺細胞抹片圖像的處理，并對各算法的分割結果進行統計。本文算法在 15 幅胰腺細胞圖像上的最高分割正確率為 100%，最低分割準確率為 80.8%。三種分割方法總的分割準確率統計結果如表 1 所示。從分割結果可知，本文分割算法具有精度較高、穩定和普適性好等優點。
表1
不同分割算法的分割正確率
Table1.
Segmentation accuracies of different segmentation algorithms
3.4 分類結果與分析
對于醫學診斷分類器的選擇取決于樣本大小和數據集的相關特征。在本文中細胞核分為兩類：正常細胞核和癌變細胞核。在進行分類性能評估時，采用以下統計量進行分類性能評估，表達式為：
 |
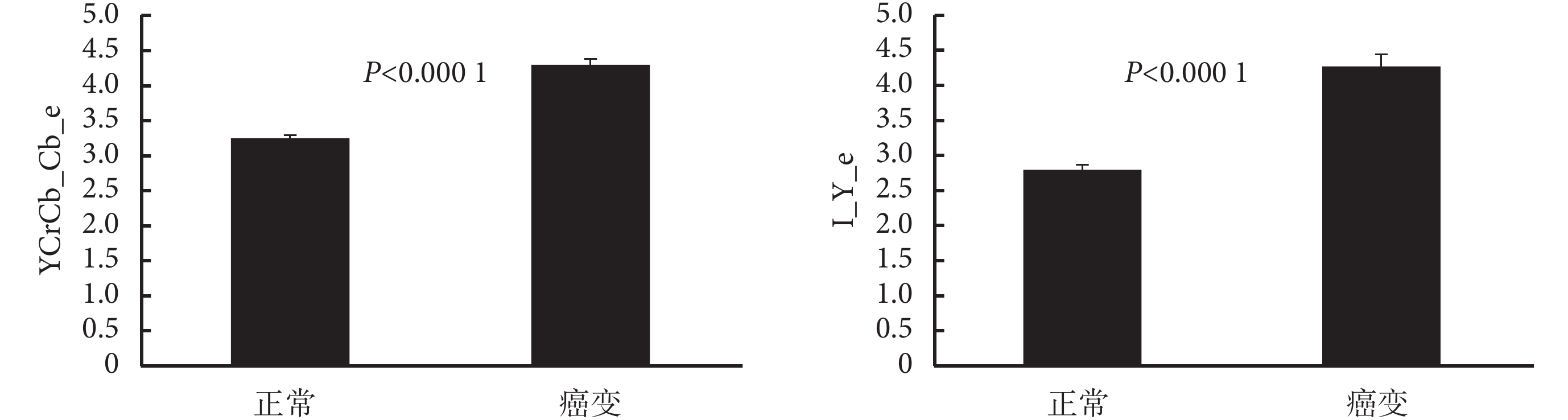
此處 TP、TN、FP 和 FN 分別表示真陽性、真陰性、假陽性和假陰性。本文采用 CAGA結合SVM 方法來選擇特征，獲得了很好的分類效果。按細胞核進行分類，在金標準中正常細胞核有 174 個，癌變細胞核有 287 個。為了使分類結果具有說服力，進行了 10 次實驗，每一次迭代 30 次。記錄 10 次特征選擇結果，其中選擇出特征個數的平均值為 72。本文對 CAGA結合SVM 特征選擇算法選出的特征進行了分析，從選中的特征中挑選了兩個特征，它們分別是 YCrCb_Cb_e 和 I_Y_e，分別代表 YCrCb 顏色空間 B 分量和 XYZ 顏色空間 Y 分量的熵。該特征的柱狀圖如圖 4 所示。從圖中可以看出，兩個特征下，正常細胞核和癌變細胞核之間具有顯著差異，因此本文的 CAGA結合SVM 特征選擇算法能篩選出有效的特征，具有良好的分類性能。
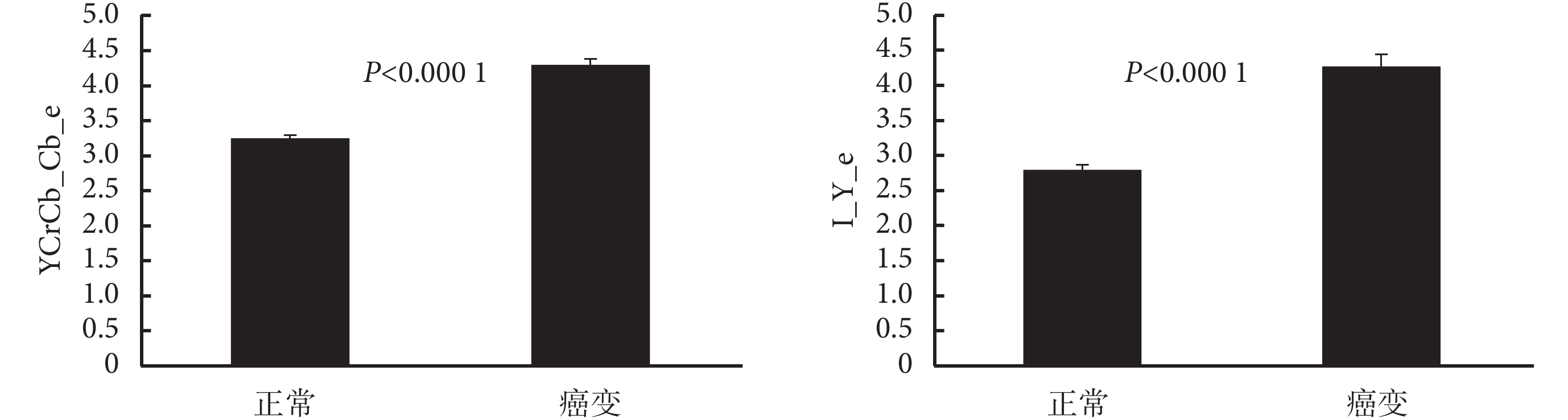圖4
正常細胞核圖像和癌變細胞核圖像特征分類柱狀圖
Figure4.
Scatter diagram of feature classification of normal and malignant cells
根據胰腺細胞核的分類結果，計算正確率為 96.55%±0.99%，靈敏度為 96.10%±3.08%，特異度為 96.80%±1.48%。從這個結果可見，本文提出的算法能夠有效地分類正常和癌變細胞核，且分類準確率達到了 96.55%。此外，三項指標的標準差都較小，表明分類具有很強的穩定性。
4 總結
胰腺細胞抹片顯微圖像的自動分割和分類非常重要，但至今仍未解決。本文針對細胞抹片分割的難點，設計了一種基于多特征 Mean-shift 聚類結合粘連分離模型的胰腺細胞抹片顯微圖像自動分割算法，同時對胰腺細胞抹片顯微圖像的分類識別進行探討，實現了胰腺細胞抹片顯微圖像細胞核的自動分割和分類。該方法首先采用多特征 Mean-shift 算法提取細胞核區域，然后采用彈性數學形態學和角點檢測算法分割粘連區域。通過與其他分割算法進行比較，證實提出的方法有較高的準確率。基于分割出的細胞核的形態和紋理一共 142 個特征作為初始特征集，然后用 CAGA 結合 SVM 選擇最優特征子集用于分類識別。分類結果顯示選擇的特征能夠顯著地區分正常和癌變細胞核，并且有較高的分類準確率。在以后的工作中，將采用更多的圖像進一步測試本文算法性能；同時，算法的自適應和魯棒性也將進一步被測試和改善。
引言
作為消化道腫瘤發病率排名第二的胰腺癌，具有病情隱匿、發病兇險、難以治愈等特點。胰腺癌在我國的發病趨勢逐漸接近歐美國家[1-2]。據相關報道，世界范圍內的胰腺癌患者在 5 年時間內的存活率最高只有 5%[3]。現階段胰腺癌的診斷方式多種多樣，主要方法有細針穿刺獲取細胞進行病理分析、影像學和超聲內鏡檢查、腫瘤標志物和基因分子診斷等，其中細針穿刺獲取細胞進行病理分析是診斷的重要手段[4-8]。傳統人工病理分析方式主觀性強，診斷正確率不穩定。為了減輕病理醫生的工作量和提高診斷的客觀性，近年來基于計算機技術的自動病理學輔助分析方式已開始用于胰腺細胞抹片顯微圖像，并逐漸成為胰腺癌檢測和診斷的重要方法。
胰腺細胞抹片顯微圖像自動分析包括細胞核分割和分類兩大部分。在分割方面，國內外文獻中提到的大多數分割算法都是圍繞分水嶺、主動輪廓模型、基于像素分類或者是結合預處理和后處理的方法進行研究的。Plissiti 等[9]使用基于標記和彩色梯度圖像的分水嶺分割方法，發現會出現過分割的情況；Kim 等[10]和 George 等[11]利用標記分水嶺對粘連的細胞抹片進行分割；還有研究采用監督機器學習和 k 均值聚類等分類方法來分割細胞抹片顯微圖像[12-13]；其他一些方法如基于動態流的變形模型和輻射梯度向量流蛇模型等也被用于細胞抹片顯微圖像的分割[14-15]。上述研究的分割效果還有待改進，主要原因在于細胞圖像的背景復雜、細胞核染色不均勻，以及對粘連重疊細胞核的準確分割線獲取較難等。
在分類方面，目前公開研究文獻中涉及的特征大多關于形態和紋理，涉及的分類算法主要包括支持向量機（support vector machine，SVM）、k 鄰近算法（k-nearest neighbor，k-NN）、模糊 C 均值（fuzzy C-means，FCM）、人工神經網絡以及它們的組合[11, 16-18]。這些算法大多沒有包含特征選擇，但是研究發現特征選擇能夠提高分類準確率和有效性評價的可靠性[18-19]。
本團隊[20]在前期工作中對乳腺細胞切片圖像進行了分割處理，取得了較好的效果。針對乳腺組織切片圖像存在細胞粘連、細胞邊界不清、細胞內部存在孔洞等問題，提出了一種基于小波多尺度區域生長和雙策略去粘連模型（chain splitting model，CSM）的分割方法。本文胰腺細胞抹片圖像與乳腺組織切片圖像存在較大差別，細胞抹片顯微圖像中存在紅細胞的干擾和細胞核染色不均勻的現象，并且細胞核與細胞質以及背景的密度差別較大。而 Mean-shift 聚類算法具有自適應性強、不需要先驗知識、運行速度快、可有效去除復雜背景干擾等優點，因此本文提出了一種基于多特征的 Mean-shift 聚類算法（multi-feature Mean-shift，MFMS）來取代前期的小波多尺度區域生長以完成胰腺細胞核的定位。前期工作的 CSM 能有效去除粘連細胞，經過調參，可用于本文分割中去除細胞核的粘連。在分類方面，本文提取了 4 個形態特征和 138 個紋理特征作為初始多類型特征集，最后用鏈式遺傳算法（chain-like agent genetic algorithm，CAGA）結合 SVM 來選取最優特征子集并進行分類識別。總的來說，本文算法分為兩部分，第一部分為基于多特征 Mean-shift 聚類和粘連分離模型（MFMS&CSM）的細胞抹片圖像自動分割算法；第二部分為基于 CAGA 和 SVM 的細胞抹片圖像自動分類算法。
1 基于 MFMS&CSM 的細胞抹片圖像自動分割算法
本分割算法主要由兩部分組成。第一部分為多特征 Mean-shift 聚類的細胞核定位。首先將圖像從 RGB 彩色空間映射到 Lab 彩色空間，并提取 a 和 b 兩個顏色分量作為顏色特征，接著提取細胞圖像的空間特征與顏色特征形成多特征，最后利用 Mean-shift 聚類算法實現多特征聚類提取出細胞核區域，并進行粘連判斷篩選出單個細胞核和粘連細胞核。第二部分采用雙策略去粘連模式對粘連重疊細胞核進行分割，采用彈性數學形態學方法和角點檢測算法對粘連程度不同的細胞核進行分割。該分割算法的主要流程如圖 1 所示。
圖1
MFMS&CSM 算法總流程圖
Figure1.
Total flow chart of MEMS&CSM
1.1 基于多特征 Mean-shift 聚類的粗分割算法
細胞抹片顯微圖像中細胞核的粗分割是細胞核分割算法中的第一步，主要包括細胞核的定位和單個細胞核與粘連細胞核的區分。粗分割的具體實現過程描述如下：首先把圖像從 RGB 顏色空間映射到 Lab 顏色空間提取每個像素的 a 和 b 分量作為顏色特征，同時提取細胞圖像的空間信息作為空間特征；接著用 Mean-shift 聚類算法對圖像 f 的特征
進行聚類實現細胞核所在區域的提取，并對提取的細胞核區域的邊界進行形態學操作，以將其結果作為掩膜模板；最后用模板把原始彩色胰腺細胞抹片圖像轉化為細胞核為目標前景、其他為背景的二值區域，即為細胞核定位的結果，并對單細胞核與粘連細胞核進行分離。
1.1.1 圖像像素點的多特征提取 在數字圖像處理中，為保留盡量寬闊的色域和豐富的色彩，常選擇將 RGB 顏色空間映射到 Lab 顏色空間[21]。首先將圖像 f 的顏色空間從 RGB 映射成 Lab 得到 f Lab 圖像，然后對 f Lab 提取 a 和 b 分量作為顏色特征，分別用 LabA 和 LabB 表示。圖像 f 的像素為 512×384，像素點（x，y）的位置特征 X、Y 表示如下：
|
其中
表示取最大值，m 和 n 分別表示圖像行和列的大小，ωxy 表示空間位置特征的權重，一般在 [0 1] 取值，本文取值為 1。將提取的多特征進行高斯平滑處理，則圖像 f 基于像素點的多特征向量可表示為：
。
1.1.2 基于多特征 Mean-shift 聚類的細胞核定位 通過觀察發現，胰腺細胞核、細胞質以及背景三者之間的密度分布是不一樣的，因此考慮用基于密度的聚類算法來分割胰腺細胞核。其中 Mean-shift 算法就是一種有效的密度聚類迭代統計算法，由 Fuku-naga 等[22]于 1975 年在一篇基于非參數概率密度函數的梯度估計的文獻中提出。
通過對圖像像素點提取顏色和空間位置信息，得到 4 個特征向量，并給定 4 維空間 R4 中圖像像素樣本點 xi，
，則在像素點 x 處的 Mean-shift 向量可表示如下：
|
其中 x 表示被平滑點的像素值；
表示以被平滑點為中心、邊長為 2r 的正方形區域內的像素點的值；r 稱為空域帶寬；K（I）為核函數，實現對區域 Sh 的大小進行控制；Sh 為高維球區域，h 為高維球區域的半徑；k 指在 512×384 個像素樣本點中有 k 個點落入到高維球區域中。從表達式（2）中可知，（xi–x）表示像素點 xi 相對于中心點 x 的偏移量，其中核函數規定了 Mean-shift 向量的貢獻程度，本文選取的核函數如下：
|
式中 d=4，v 表示 4 維空間單位超球的體積。Mean-shift 向量 Mh（x）是對落入球形區域 Sh 中的 k 個樣本點相對于區域中心點 x 的偏移向量平均數。對圖像 f 的概率密度函數 f（x）進行采樣可以得到樣本點 xi。算法具體實現步驟如下：設像素點窗口（半徑為 r）內外的像素點集合分別用 fsa 和 fsna 表示，聚類的數目用 K 表示，聚類的中心用 Ck 表示。
步驟 1：從圖像 fsna 中隨機選擇一個點 x 作為一次聚類的起始點，該點的特征作為初始聚類中心。
步驟 2：以 x 為中心、r 為半徑建立超球體 Sh 區域，然后計算 Sh 區域內滿足要求的點的個數，同時給這些點投票，并把這些點歸為 fsa。
步驟 3：計算 Mh（x），若
，則聚類平移量已收斂，轉到步驟 4；否則，
，轉到步驟 2，本文
。
步驟 4：當滿足 K=0 或 K>0 且不存在一個 Ck 使得不等式
成立時，則進行如下操作：K=K+1，Ck=x 記錄像素點在窗口平移過程中得到的票數；若 K>0 且存在一個 Ck 滿足 j =
使得不等式
成立，則將 Ck 類合并到第 j 類中，并進行如下操作：
，并將像素點得到的票數相加。
步驟 5：判斷樣本點是否已經處理完
，如果
，則轉到步驟 1，否則轉到步驟 6。
步驟 6：根據聚類過程中得到的票數，將像素點劃歸到得到票數最多的類。
步驟 7：輸出聚類數目 K、聚類中心 Ck 以及每類像素點序號，至此算法結束。
在 Mean-shift 聚類算法中，針對每一幅圖像聚類窗口大小 r 差異，提出了基于類內平均散度（AS）及類間平均分離度（AD）準則來自動尋找最佳聚類數目。AS 和 AD 定義如下：
|
'/> |
式中 Nk 表示屬于第 k 類的像素點個數。類內平均散度是指同類像素點之間的差異，其值越小，則像素點之間就越相似。類間平均分離度是各個簇中心之間的差異，其值越大，則類與類之間的差異性也就越大。于是用 AR=AS/AD表達式來確定 K 的值，即較小的 AR 值對應的 K 值被選中，實現聚類算法的自適應性分割。
在對細胞核進行正確定位后，需要對定位區域進行單細胞核和粘連細胞核的判斷，以便后面只對粘連細胞核區域進行相應的操作，從而減少算法的時間消耗。單細胞核與粘連細胞核分離的具體步驟如下：
步驟 1：計算每一個區域的圓形度 R=
，A 為區域面積，P 為區域周長。
步驟 2：保存圓形度 R 大于 t 的區域作為分割的區域 f out，其他的作為未分割區域 f usg。
步驟 3：計算 f out 中區域的平均面積作為初始的面積閾值 Ag。
步驟 4：計算 f usg 中每一個區域的面積，然后與之前的面積閾值 Ag 進行比較，大于初始面積的 p 倍作為粘連的細胞核 f ove，需進行進一步的分割，其他的細胞核區域作為 f out 輸出。
經過對樣本圖像和實驗結果的分析，實驗中參數 t 和 p 的取值分別為 0.6 和 1.2。
1.2 基于粘連分離模型的細分割算法
胰腺細胞抹片顯微圖像中非常顯著的特點是粘連現象頻繁和嚴重，不同情況粘連程度不一。為了解決這些問題，本文引入了作者前期提出的粘連分離模型，經過調參處理，來對本文圖像進行分割處理，相關介紹詳見文獻[20]。
2 基于 CAGA 和 SVM 的細胞抹片圖像自動分類算法
有意義的特征能使細胞圖像的分類具有較好的效果。在以往的研究中，形態、比色法、紋理和結構特征已被用于特征提取和特征評價以實現細胞或細胞圖像的分類。本文提取形狀特征和不同顏色空間的紋理特征，并用 CAGA 結合 SVM 來篩選最優特征子集，以便獲得更好的分類效果，同時消耗時間較少。
2.1 特征提取
正常細胞核和癌變細胞核的形態特征存在一定的差異，故提取了 4 個形態特征，分別是面積（area）、周長（perimeter）、離心率（eccentricity）和圓形度（roundness circularity）。紋理特征描述了一個數字化的顯微圖像的像素灰度級的空間布局[23-24]，首先計算圖像中每個像素點的局部特征，然后從局部特征的分布導出一組統計特征，從而得到紋理特征。本研究選取的一階統計特征為灰度直方圖的均值，設
表示一個隨機變量的灰度級，
表示相應的直方圖，L 表示不同的灰度級，統計矩得到的紋理特征是：
（1）平均灰度級方差（mean value）：
|
（2）標準差（standard deviation）：
|
（3）平滑度（evenness）：
|
（4）三階矩（third moment）：
|
（5）區域灰度一致性（uniformity）：
|
（6）灰度變化量度熵（entropy）：
|
顏色空間分別為 RGB、HSV、HSI、YIQ、YCrCb、XYZ、Lab、灰度空間和增強灰度空間。因此，共提取了不同顏色空間的 138 個紋理特征。
2.2 特征選擇
待選特征集包括所有的形態特征和紋理特征。無論這些特征是否有顯著差異，幾乎所有的文獻中都沒有進行特征選擇就直接進行正常和癌變細胞的分類識別，這將導致分類性能較差并耗費更多的時間[21]。文獻中提到 CAGA 結合 SVM 的分類算法獲得了滿意的分類準確率[25]，故本文采用此方法選擇最優特征子集。CAGA 算法描述如下：
輸入：擬提取的多種類型的特征合并在一起得到待選特征集設為
。
初始化：s（t）表示某一代的智能體，個數為 s，每個智能體（即個體）長度為 l，代表 l 個特征序號，M 為設置的最大迭代次數。
過程：（1）對
做樣本處理，得到樣本特征矩陣
，w 代表樣本數，l 代表特征數，即智能體的長度。
（2）將樣本矩陣隨機劃分為訓練樣本矩陣 data_fea_train()、驗證樣本矩陣 data_fea_vali-dation()、測試樣本矩陣 data_fea_test()。
（3）根據初始的第 q 個智能體，對（2）中的驗證樣本矩陣分別進行裁剪，生成該智能體所對應的驗證特征樣本矩陣。
（4）將 data_fea_train() 送入 SVM 進行訓練，然后基于訓練后的 SVM 和 data_fea_validation()ithAgent 輸出測試準確率作為該智能體的適應度值。
（5）最后計算所有代的適應度值，遺傳操作（鄰近競爭選擇、自適應交叉、自適應變異），結果是否滿足確定的狀態，如果是就接著下一步，如果否就返回跳出算法。
（6）輸出最優智能體 p（t）對應的最優特征子集。
（7）基于最優特征子集和測試樣本 data_fea_test() 得到裁剪后的特征樣本矩陣 data_fea_test()p(t)，送入訓練后的 SVM 進行分類，得到分類準確率。
結束
3 實驗結果與分析
本文的胰腺細胞抹片圖像來源于西南醫院，共采集到 10 個患者 15 幅胰腺細胞抹片顯微圖像。為了表明本文算法的有效性，一共組織了 4 組實驗。第一組實驗用于顯示本文分割算法的各個分割中間結果；第二組實驗將本文分割方法與其它有代表性的分割方法進行效果對比；第三組實驗對比統計了本文算法和被比較算法的總的分割準確率；第四組實驗針對正常細胞核和癌變細胞核，統計了分類準確率、敏感度和特異度。
3.1 MFMS&CSM 分割算法中間結果與分析
圖 2 顯示了本文分割算法的各個分割中間結果，原圖選自 15 幅圖像中第 7 幅圖像的部分區域。從分割步驟圖可以看出，多特征 Mean-shift 聚類能夠把胰腺細胞核與其它背景很好地分割開來（圖中 Mean-shift 提取細胞核區域和圖像二值化）；聚類后能得到完整、無孔洞和邊緣定位準確的細胞核（圖中細胞核區域規整）；針對粘連重疊細胞核的分割，可以得到準確的分割線（圖中分割結果）。整個分割算法的相關參數均可自適應調整，無需人為干預。
圖2
MFMS&CSM 算法分割的中間結果
Figure2.
Intermediate result using method of MFMS&CSM
3.2 不同分割算法的分割結果比較
圖 3 為本文算法 MFMS&CSM 與文獻[9]和[13]的最終分割結果對比。這兩篇文獻都是關于細胞抹片顯微圖像分割較新的文獻，并且分割方法可以重現，因此具有較好的比較意義。為了更公平地比較，我們選取了這兩種方法中較好的結果與本文方法的結果進行比較。分割結果如圖 3 所示。
圖3
不同分割算法的分割結果對比
Figure3.
Comparison of segmentation results among different segmentation algorithms
從圖 3 可以看出，對于背景簡單、細胞核染色均勻的細胞圖像，被比較算法存在少量錯誤分割，而本文的分割算法基本無錯誤分割，見圖中黃色橢圓區域（如圖像 4）。對于背景復雜、細胞核形態不一、染色不均勻的細胞圖像，被比較算法均存在很多錯誤分割現象，而本文算法仍然有較準確的分割結果（如圖像 7）。
3.3 不同分割算法分割的準確性統計
在細胞圖像分割結果統計中，分割錯誤的類型主要有過分割、錯誤分割、未分割、多分割和欠分割五種。為了更為客觀地定量評估分割結果，將得到的分割結果與人工分割金標準進行比較，并對分割正確的細胞核個數（true number，TN）、分割錯誤的細胞核個數（false number，FN）和實際細胞核個數（real number，RN）進行統計。分割準確性評價指標主要采用正確率（segmentation accuracy，SA）和過分割、錯誤分割、未分割、多分割以及欠分割的個數來表示，正確率定義為：SA=TN/RN。
將本文算法和現有兩種主流算法分別用于所有胰腺細胞抹片圖像的處理，并對各算法的分割結果進行統計。本文算法在 15 幅胰腺細胞圖像上的最高分割正確率為 100%，最低分割準確率為 80.8%。三種分割方法總的分割準確率統計結果如表 1 所示。從分割結果可知，本文分割算法具有精度較高、穩定和普適性好等優點。
表1
不同分割算法的分割正確率
Table1.
Segmentation accuracies of different segmentation algorithms
3.4 分類結果與分析
對于醫學診斷分類器的選擇取決于樣本大小和數據集的相關特征。在本文中細胞核分為兩類：正常細胞核和癌變細胞核。在進行分類性能評估時，采用以下統計量進行分類性能評估，表達式為：
|
此處 TP、TN、FP 和 FN 分別表示真陽性、真陰性、假陽性和假陰性。本文采用 CAGA結合SVM 方法來選擇特征，獲得了很好的分類效果。按細胞核進行分類，在金標準中正常細胞核有 174 個，癌變細胞核有 287 個。為了使分類結果具有說服力，進行了 10 次實驗，每一次迭代 30 次。記錄 10 次特征選擇結果，其中選擇出特征個數的平均值為 72。本文對 CAGA結合SVM 特征選擇算法選出的特征進行了分析，從選中的特征中挑選了兩個特征，它們分別是 YCrCb_Cb_e 和 I_Y_e，分別代表 YCrCb 顏色空間 B 分量和 XYZ 顏色空間 Y 分量的熵。該特征的柱狀圖如圖 4 所示。從圖中可以看出，兩個特征下，正常細胞核和癌變細胞核之間具有顯著差異，因此本文的 CAGA結合SVM 特征選擇算法能篩選出有效的特征，具有良好的分類性能。
圖4
正常細胞核圖像和癌變細胞核圖像特征分類柱狀圖
Figure4.
Scatter diagram of feature classification of normal and malignant cells
根據胰腺細胞核的分類結果，計算正確率為 96.55%±0.99%，靈敏度為 96.10%±3.08%，特異度為 96.80%±1.48%。從這個結果可見，本文提出的算法能夠有效地分類正常和癌變細胞核，且分類準確率達到了 96.55%。此外，三項指標的標準差都較小，表明分類具有很強的穩定性。
4 總結
胰腺細胞抹片顯微圖像的自動分割和分類非常重要，但至今仍未解決。本文針對細胞抹片分割的難點，設計了一種基于多特征 Mean-shift 聚類結合粘連分離模型的胰腺細胞抹片顯微圖像自動分割算法，同時對胰腺細胞抹片顯微圖像的分類識別進行探討，實現了胰腺細胞抹片顯微圖像細胞核的自動分割和分類。該方法首先采用多特征 Mean-shift 算法提取細胞核區域，然后采用彈性數學形態學和角點檢測算法分割粘連區域。通過與其他分割算法進行比較，證實提出的方法有較高的準確率。基于分割出的細胞核的形態和紋理一共 142 個特征作為初始特征集，然后用 CAGA 結合 SVM 選擇最優特征子集用于分類識別。分類結果顯示選擇的特征能夠顯著地區分正常和癌變細胞核，并且有較高的分類準確率。在以后的工作中，將采用更多的圖像進一步測試本文算法性能；同時，算法的自適應和魯棒性也將進一步被測試和改善。
