骨組織內部存在兩大類液體，一類是血液，一類是間隙流。骨細胞新陳代謝主要依賴于間隙流微環境。在骨組織的微觀結構下，骨單元壁中液體的滲流行為是研究的熱點。本文的主要目的是考察中央哈弗管的血管脈動對骨單元壁中的間隙流流動行為的影響。本文利用 COMSOL Multiphysics 軟件分別建立了中空的和考慮哈弗管中血管脈動的骨單元多孔彈性力學有限元模型，并對比了軸向載荷下兩種模型中骨單元壁中的液體滲流行為。結果表明：當考慮哈弗管中的血管脈動時，骨單元壁中液體的壓力會明顯增大，而流速幾乎沒有影響。具體地，骨單元孔隙組織液的壓力幅值隨著血壓脈動幅值的增大而增大，受脈動頻率的變化影響不大，而血壓脈動幅值及頻率對骨單元孔隙組織液的流速基本沒有影響。該有限元模型可用來進一步研究非軸對稱載荷及微裂縫等復雜應力狀態下骨單元的多孔彈性力學行為，并為研究骨的力傳導及力-電傳導機制提供新方法。
引用本文： 武曉剛, 王寧寧, 岑海鵬, 王兆偉, 于緯倫, 陳魁俊, 薛雅楠, 王艷芹, 郭媛, 陳維毅. 血管脈動對骨單元內液體流動行為的影響. 生物醫學工程學雜志, 2017, 34(5): 695-701. doi: 10.7507/1001-5515.201607046 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
骨組織內部存在兩大類液體，一類是血液，一類是間隙組織液。骨細胞新陳代謝主要依賴于間隙流微環境，該間隙組織液也是骨組織力傳導及力電傳導的主要媒介。在密質骨的微觀結構中，骨單元是一個由多級系統組成的結構。其外形是圓柱體結構，半徑大約為 200 μm[1]，中間是哈弗管，包含著血管及神經，外部由一層層的骨板層包裹著。血管脈動的“動力源泉”是心臟，而骨主要承載外力、血管的脈動作用力和附著肌肉的收縮力。看似無關聯的血管脈動與骨之間有著非常緊密的聯系，血管中的血液為骨的生長提供營養，同時也為間隙組織液提供了物質交換的場所。
骨組織受力變形后其內部液體就會流動，同時在骨單元壁中擴散，并進一步產生一系列與骨液流動相關的物理效應，如壓力梯度、流體剪切應力和流動電位等，這些物理效應被細胞（如破骨、成骨細胞）感知并做出反應，以適應外部載荷環境。鑒于骨組織產生的內部液體流動很難通過實驗測定，理論模擬是目前的主要研究手段。描述骨單元的變形并考慮其內部孔隙組織液體的流動，需要用到 Biot 理論[1-2]。Zhang 等[3]較早地提出了一個充液的骨單元多孔介質彈性力學模型，但是是各向同性的；接著 Rémond 等[4]給出了橫觀各向同性的解答；在此基礎上我們[5]發展了不同邊界條件（可能存在的生理邊界條件）的骨單元模型，這樣使得模型更接近于真實情況。但是上述模型都將骨單元視為中空的圓柱體，并沒有考慮哈弗管內的液體壓力，為此我們建立了考慮哈弗管液體壓力的骨單元模型[6]，并與中空骨單元模型做了對比[7]。即使如此，以上模型均為數學模型，且沒有考慮哈弗管內血管血壓的脈動。
因此，本文將建立考慮血管脈動壓力的骨單元多孔彈性力學有限元模型，在骨單元內壁施加脈動壓力考察骨單元孔隙組織液對骨單元壁中的間隙組織液流動行為的影響。
1 控制方程及有限元模型的建立
1.1 幾何模型及控制方程
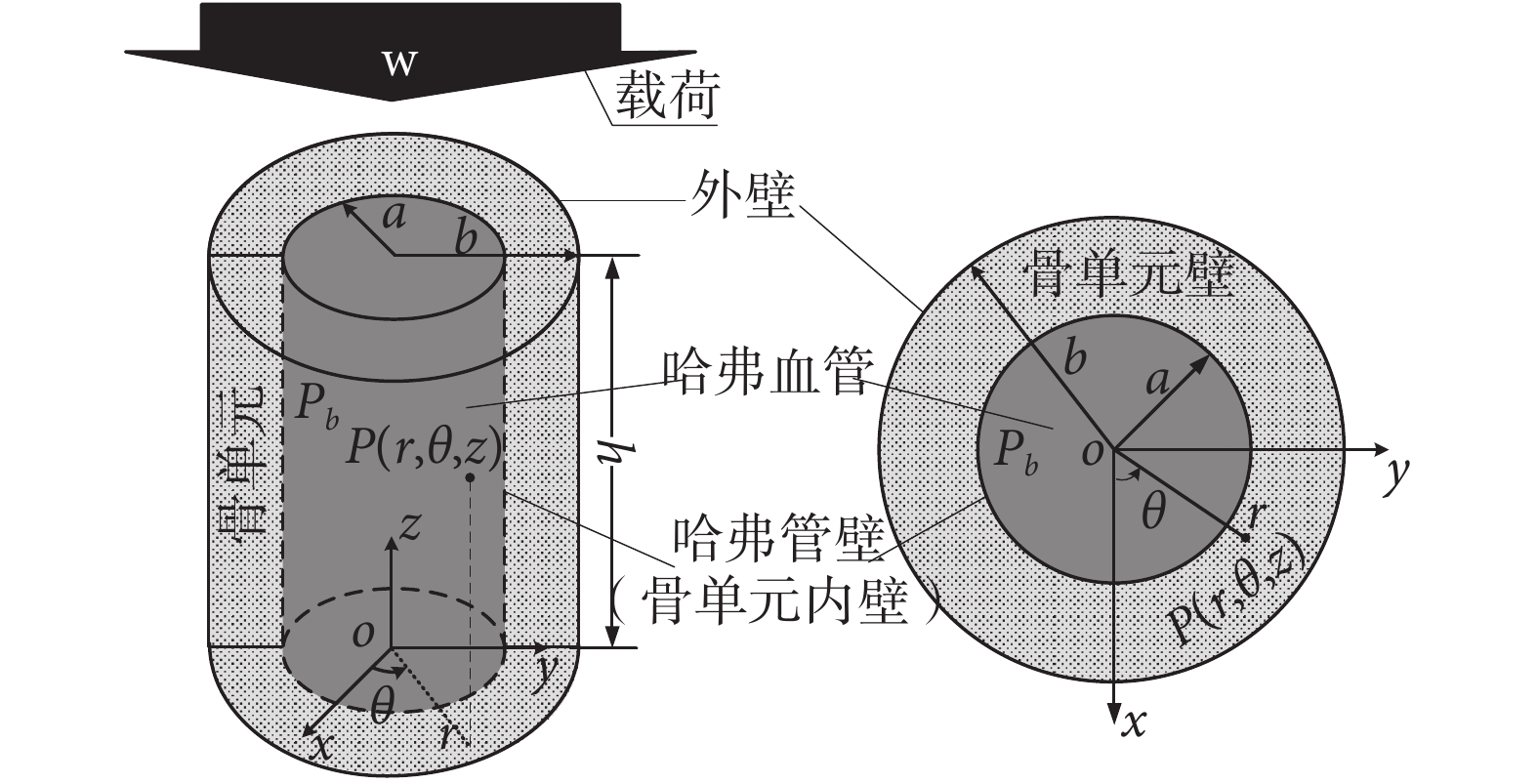
本文將骨單元描述為橫觀各向同性的多孔彈性厚壁圓筒，如圖 1 所示，其中 a = 50 μm 和 b = 150 μm 分別是骨單元的內、外半徑，高為 h = 1 mm。圖 1 為考慮哈弗血管脈動的骨單元模型，其中脈動壓力為 Pb。
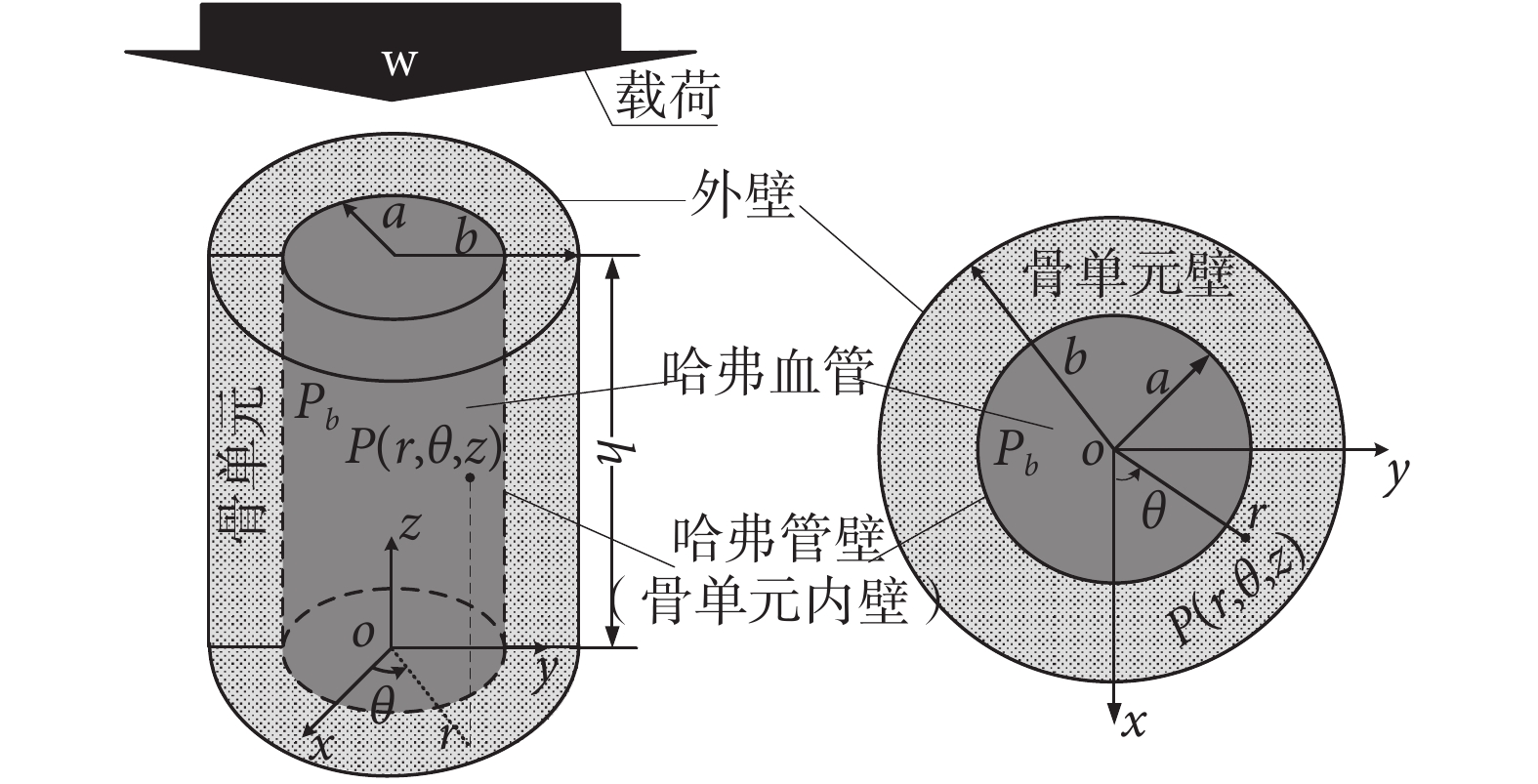圖1
考慮哈弗血管脈動的骨單元模型
Figure1.
Osteon models considering blood pressure oscillation
本構方程可寫為如下：
 |
 |
平衡方程：
 |
幾何方程：
 |
液體的滲流連續性方程:
 |
達西定律:
 |
其中，
和
是總的應力和應變張量；p 是孔隙壓力；ξ 是液體單位體積的改變分數；C 為固體骨架的 4 階張量；α 是 Biot 系數張量；M 稱為 Biot 模量；“:”表示張量間的雙重內積；u 表示位移向量；混合密度
；
為孔隙率，
和
分別表示液體和固體項的密度；V 表示液體速度矢量；
是滲透張量，其中 k 是固有滲透率張量，
是動力粘性系數。
整理上述方程，最終得到系統的控制方程：
 |
在柱坐標系下，考慮橫觀各向同性及低頻（幾個赫茲）下，我們求得了其理論解答，并驗證了相應有限元模型的有效性[8-9]。
1.2 邊界條件
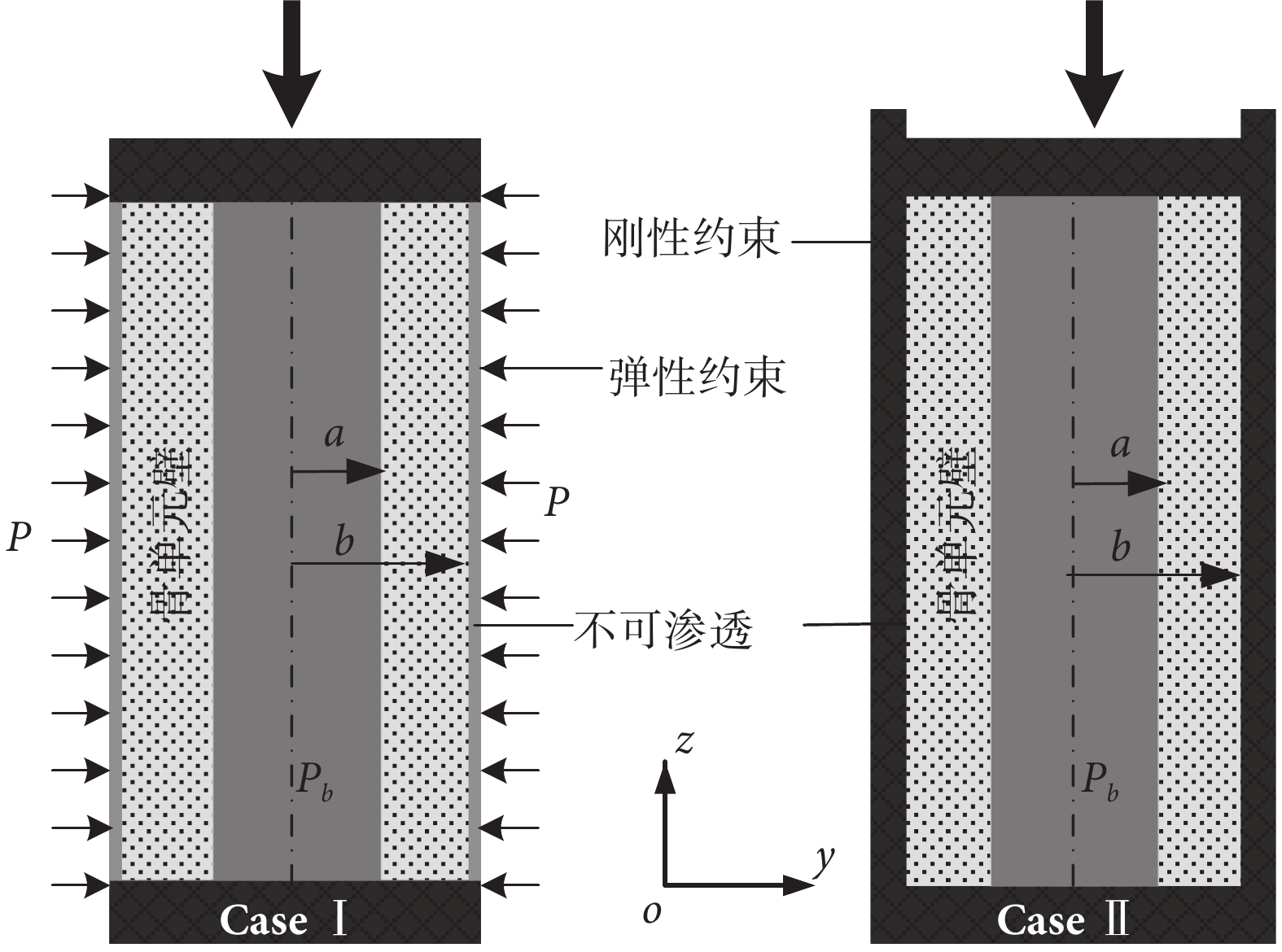
研究中將骨單元外壁分為兩種均不可滲透的邊界條件：一種是彈性約束（Case Ⅰ），一種是剛性位移約束（Case Ⅱ）[5]。骨單元骨架視為橫觀各向同性材料，且施加軸向的位移載荷來研究其孔隙液體壓力及流速分布。軸向位移載荷為 w|z= 1 mm = 0.000 5 [cos（2 × pi × f × t）–1]（以 mm 為單位），應變率幅值最大為 0.001[5]。兩種情況下的邊界條件如圖 2 所示。Case Ⅰ 表示骨單元受到周圍組織的彈性約束，并且不可滲透；Case Ⅱ 表示骨單元外壁受到剛性約束（位移為零），也不能滲透。
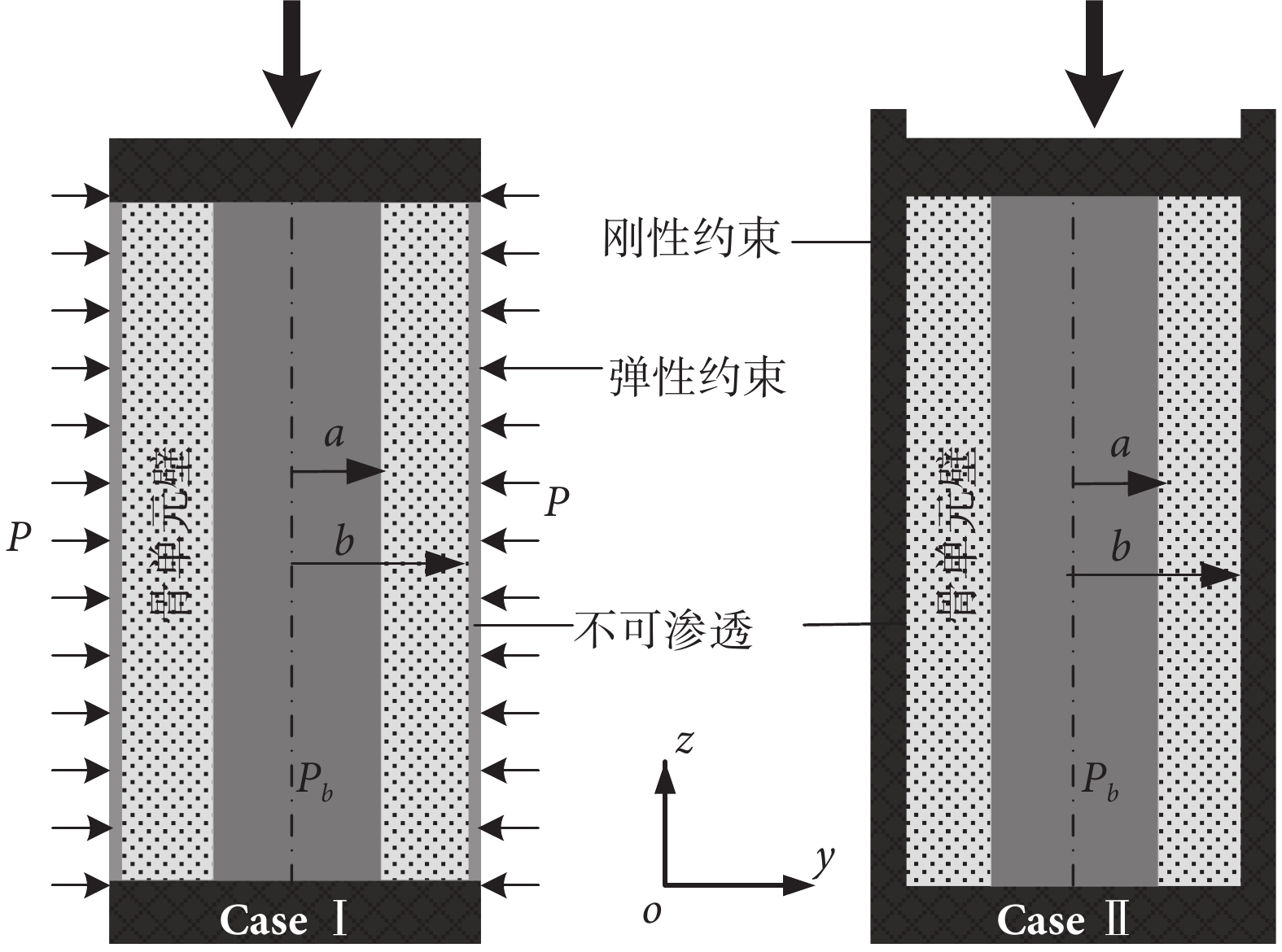圖2
兩種邊界條件
Case Ⅰ：彈性約束邊界；Case Ⅱ：剛性約束邊界
Figure2. Two kinds of boundary conditionsCase Ⅰ: elastic restraints; Case Ⅱ: rigid constraints
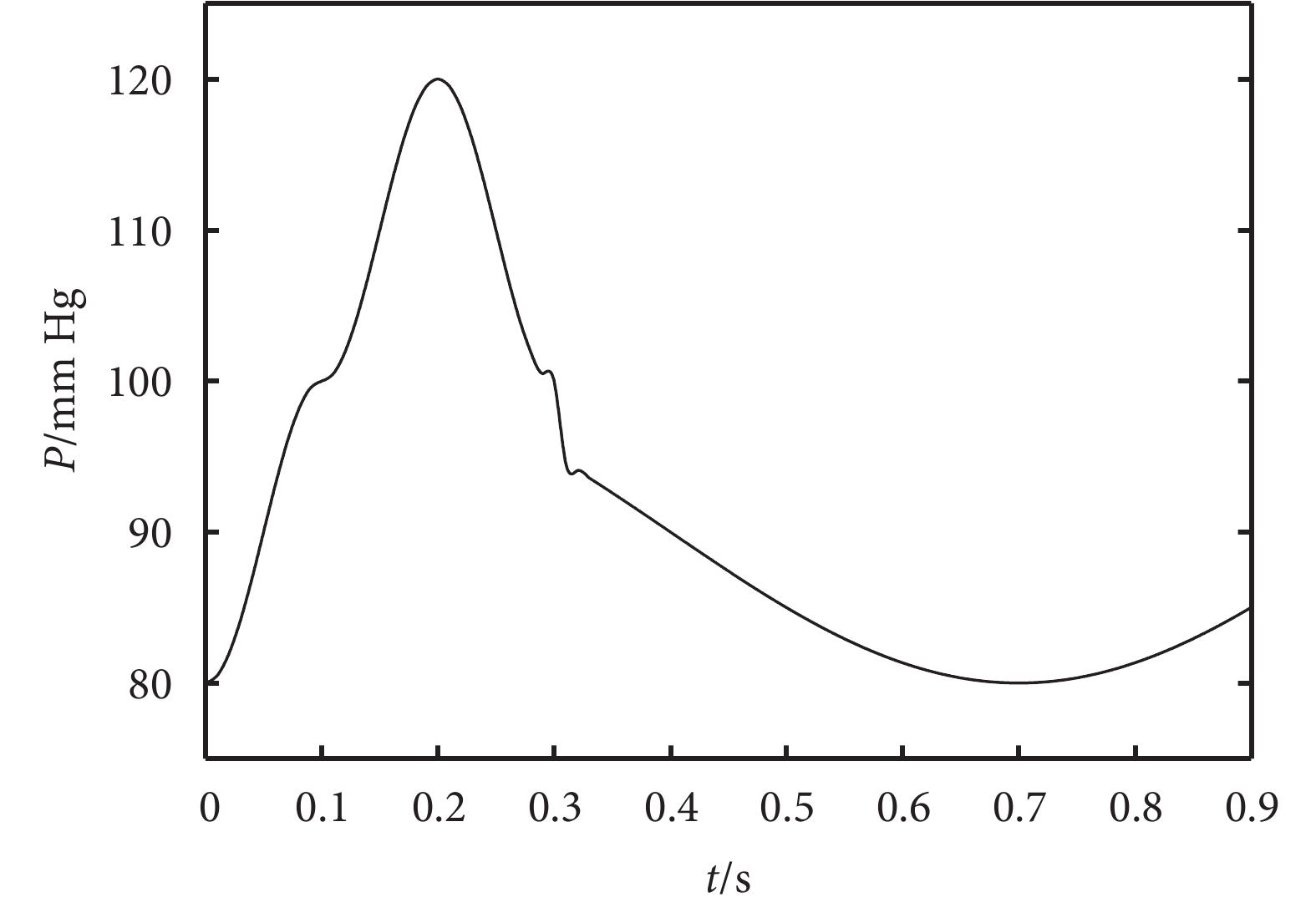
血液脈動壓力設為 Pb = 0.4 × P（以 mm Hg 為單位），其中 P 為主動脈的脈動函數，考慮到哈弗管為微動脈，取其幅值的 40% 作為參考，P 可以由下面的分段函數表示[10-11]：
 |
可知脈動頻率 fb=1/0.9=1.1，并繪制函數圖如圖 3 所示。
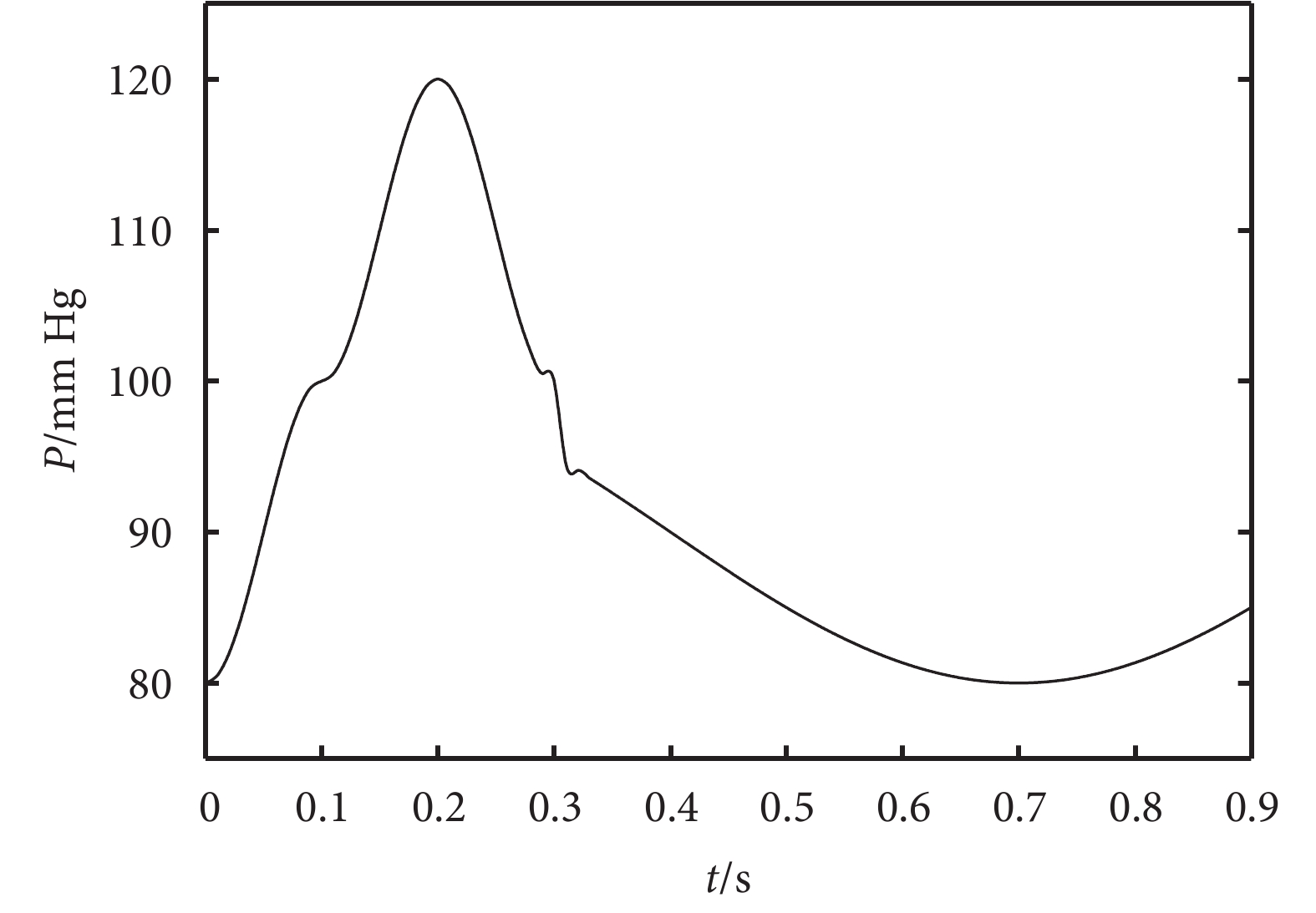圖3
脈動函數 P (t)
Figure3.
Human aortic pulse function P (t)
1.3 材料參數
參數設置如表 1 所示。Cij 表示橫觀各向同性材料脫水的彈性模量矩陣分量，ρS 表示固體的密度，ρf 表示骨單元內流體密度，v 表示泊松比，
表示孔隙率，α 表示 Biot 系數，M 為 Biot 模量，χ f 表示骨內液體的壓縮率，K 表示滲透率，μ 表示液體動力粘度。
2 模擬結果
根據先前的研究發現，當載荷頻率 f=1 Hz、t=0.25 s 時，應變率達到最大值 0.001，這時骨單元孔隙中的液體壓力和流速達到最大[8-9]。本文重點討論在此參數下考慮血管脈動時其孔隙液體壓力和流速的變化規律。
2.1 骨單元內部壓力及流速場分布
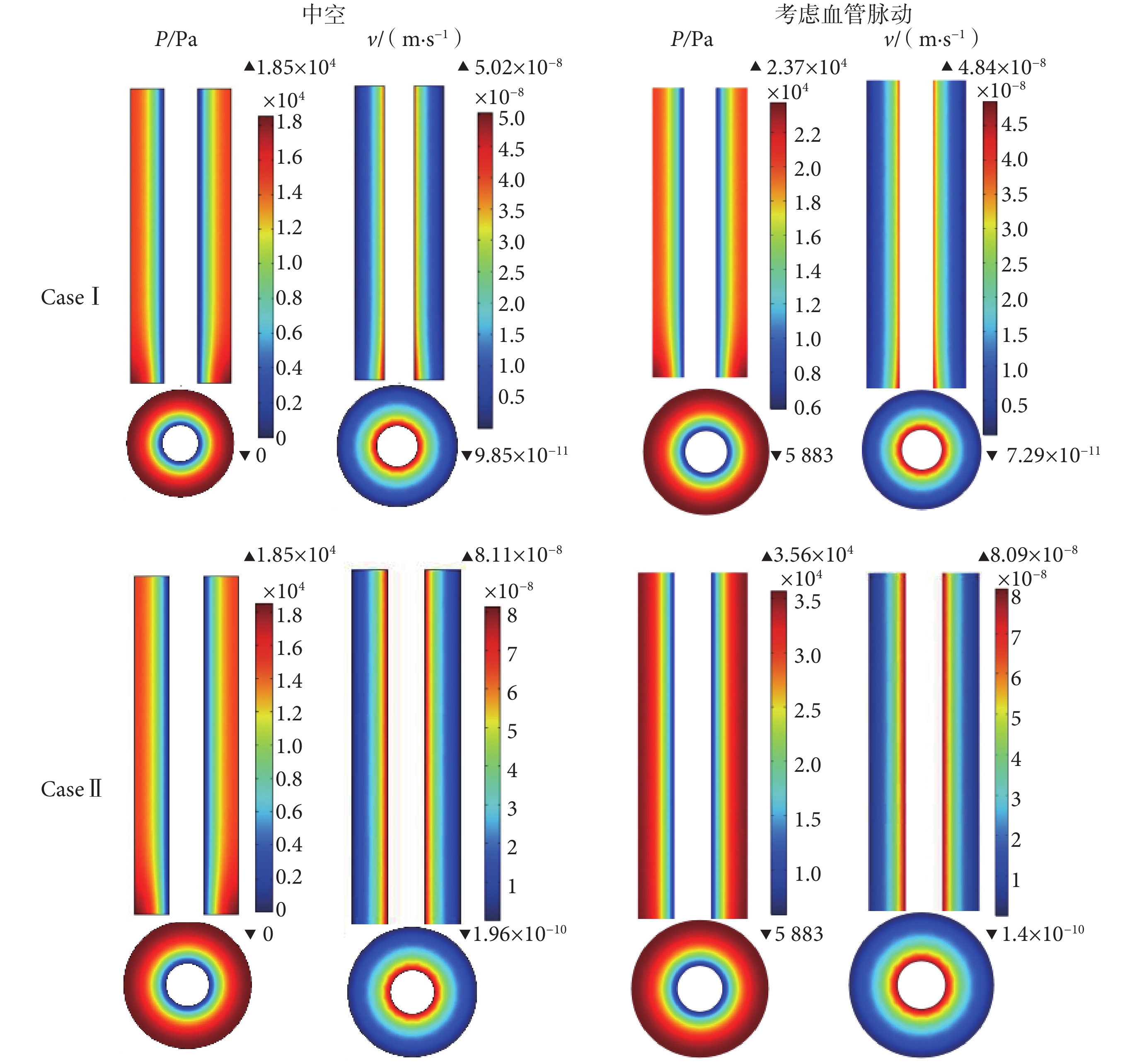
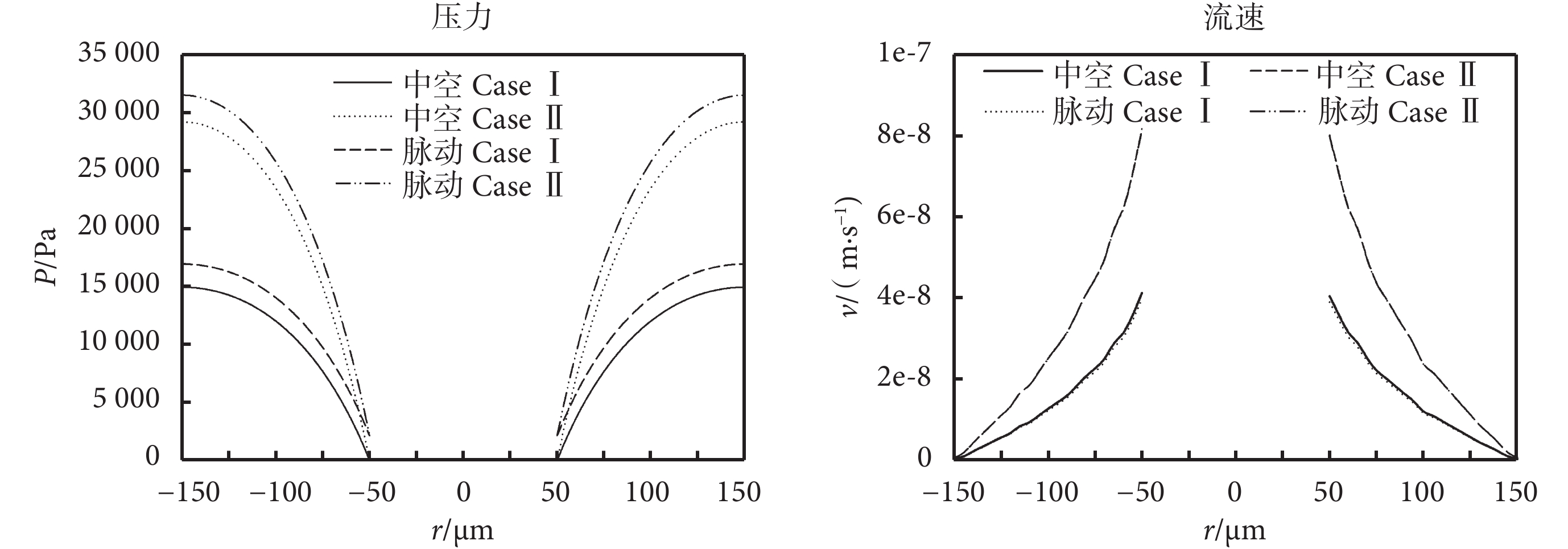
如圖 4 繪制了中空和考慮血管脈動的骨單元孔隙組織液壓力幅值及流速的分布圖。由圖 4 可以看出，在軸向的對稱載荷下，液體的壓力和流速場均為軸對稱分布，并且當考慮血管脈動時骨單元壁中的壓力場分布明顯增大。
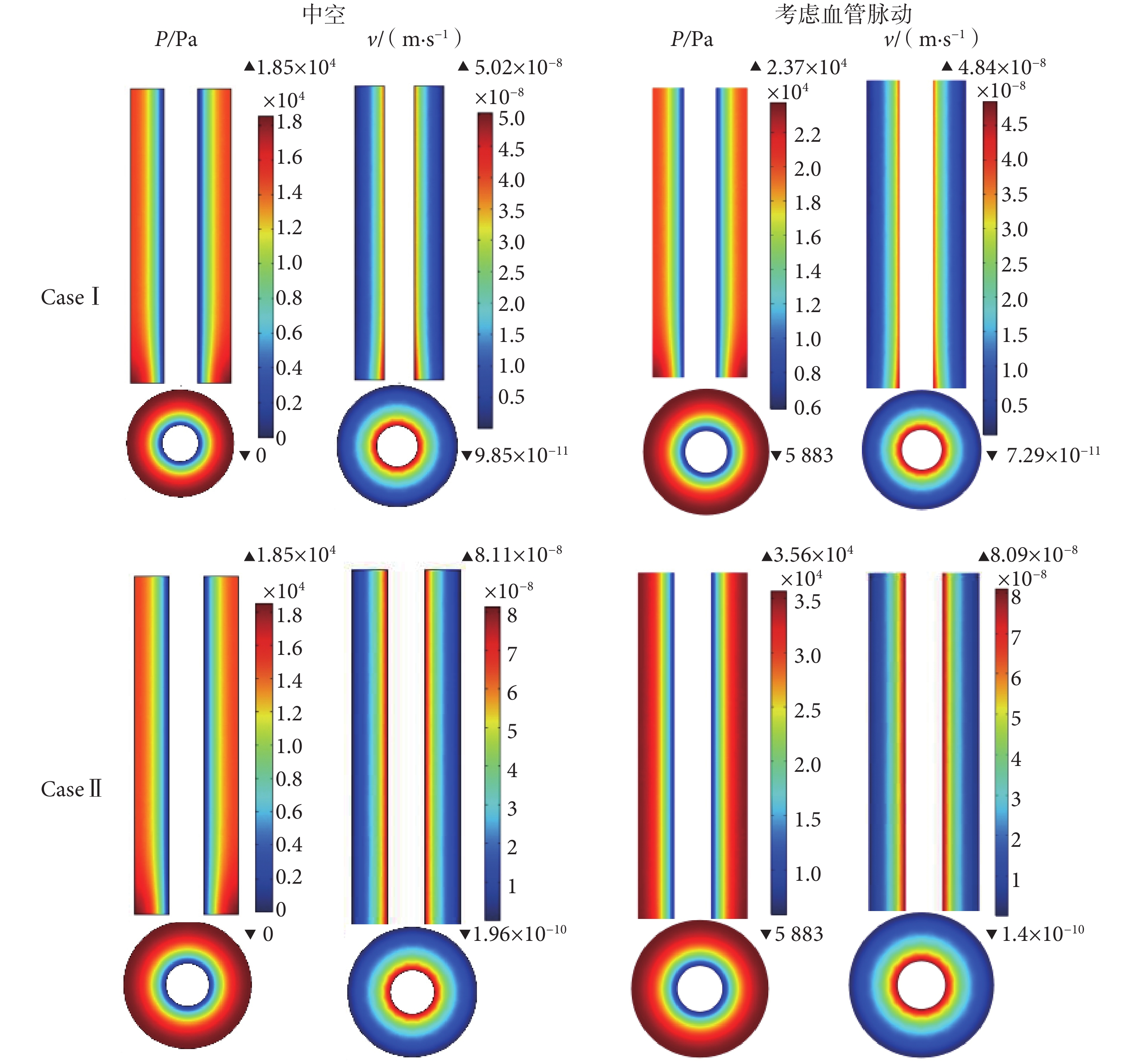圖4
骨單元孔隙組織液壓力幅值及流速的分布圖
Figure4.
Liquid pressure amplitude and the distribution of flow velocity in osteon
2.2 考慮血管脈動時骨單元孔隙組織液壓力和流速的變化
為了考察血管脈動對骨單元孔隙組織液壓力及流速的影響，繪制了圖 5，即血管脈動壓力幅值 A 為 40% 的 P (t)。骨單元孔隙組織液壓力及流速均呈軸對稱分布，這是由其結構及其載荷的軸對稱性所決定的。壓力隨骨單元半徑的增大逐漸增大，流速則反之。在中空不考慮血管脈動的骨單元內壁處（r = 50 μm）壓力最小，在外壁（r = 150 μm）處達到最大，這些結果符合邊界條件和先前的研究結論[5-6, 12]。在考慮血管脈動的骨單元內壁處壓力不為 0，大小為微血管的脈動壓力幅值。對比中空的和考慮微血管脈動的模型發現，當考慮微血管脈動時整個骨單元的壓力場增加，而對流速場基本沒有影響，中空與脈動模型流速值幾乎重合。此外 Case Ⅱ 產生的壓力場和流速場均大于 Case Ⅰ。
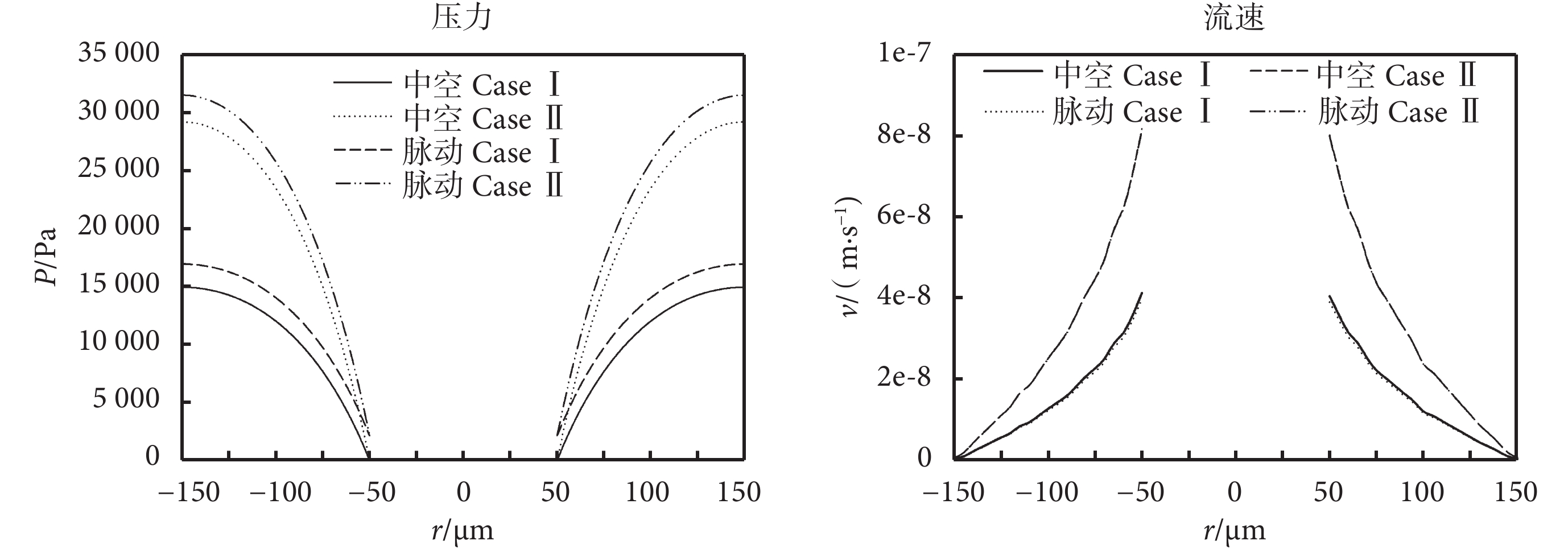圖5
骨單元孔隙組織液壓力幅值及流速沿著半徑方向的分布圖（t=0.25 s，z=0.5 mm）
Figure5.
Liquid pressure amplitude and the distribution of flow velocity varying versus osteon radius of model (t=0.25 s, z=0.5 mm)
2.3 不同脈動幅值的血管壓力對骨單元孔隙組織液壓力及流速的影響
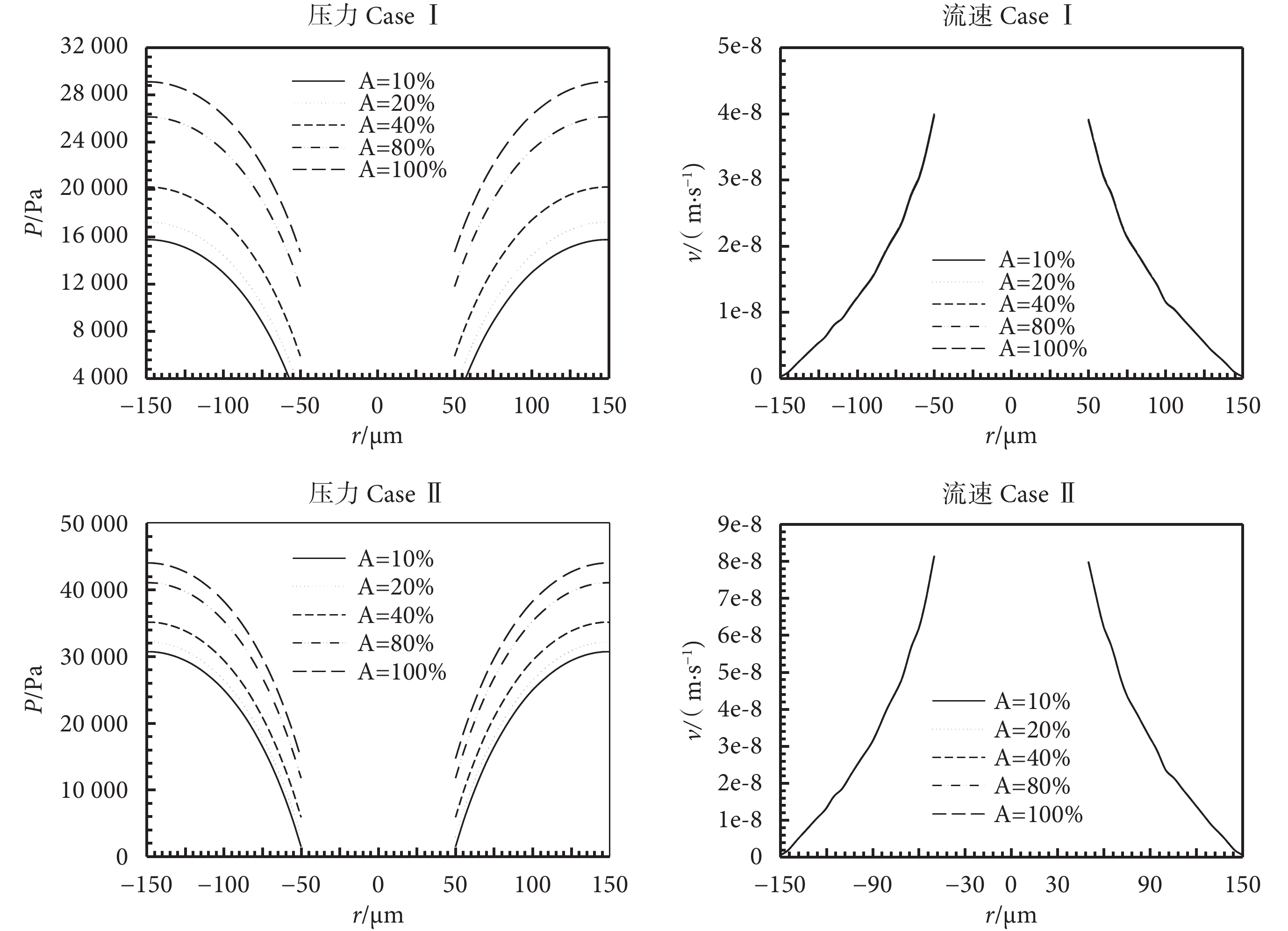
考慮到不同部位骨內微動脈脈動幅值的不同，如圖 6 繪制了當血管脈動頻率 fb = 1.11 Hz、z = 1 mm 情況下，血管壓力幅值 A 分別為 10%、20%、40%、80%、100% 的 P (t) 時骨單元孔隙組織液沿徑向的壓力及流速分布圖。由圖 6 壓力 Case Ⅰ 及壓力 Case Ⅱ 可以看出隨著血管脈動壓力幅值的增大，整個骨單元內部壓力場也增加，而流速場基本不變。對于邊界條件 CaseⅠ 和 Ⅱ 結論基本一致。
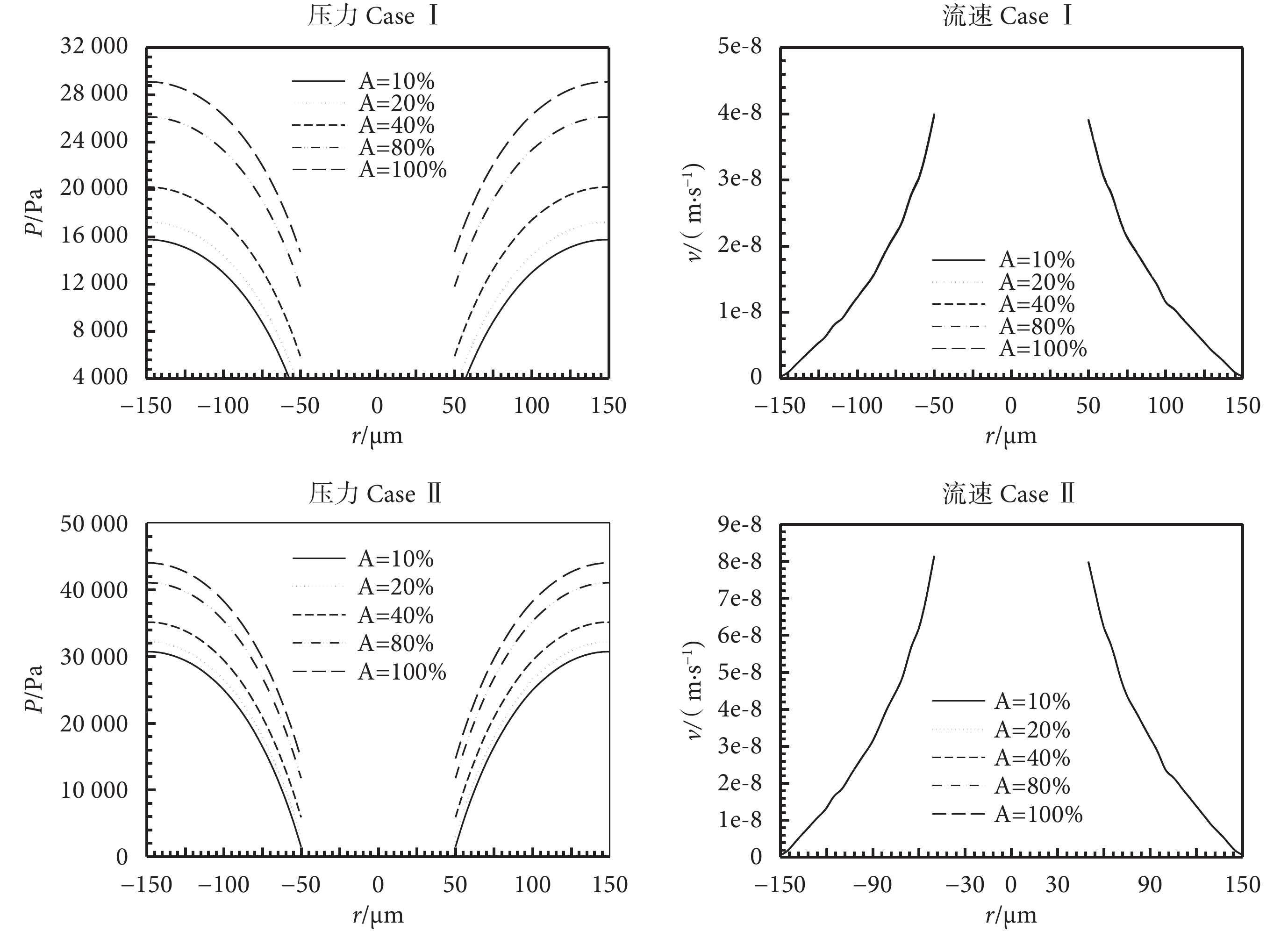圖6
骨單元孔隙組織液壓力幅值及流速隨著脈動壓力幅值 A 的變化（fb=1.11 Hz，z=1 mm）
Figure6.
Liquid pressure amplitude and flow velocity varying versus osteon radius of model with different amplitudes A (fb=1.11 Hz, z=1 mm)
2.4 不同脈動頻率的血管壓力對骨單元孔隙組織液壓力及流速的影響
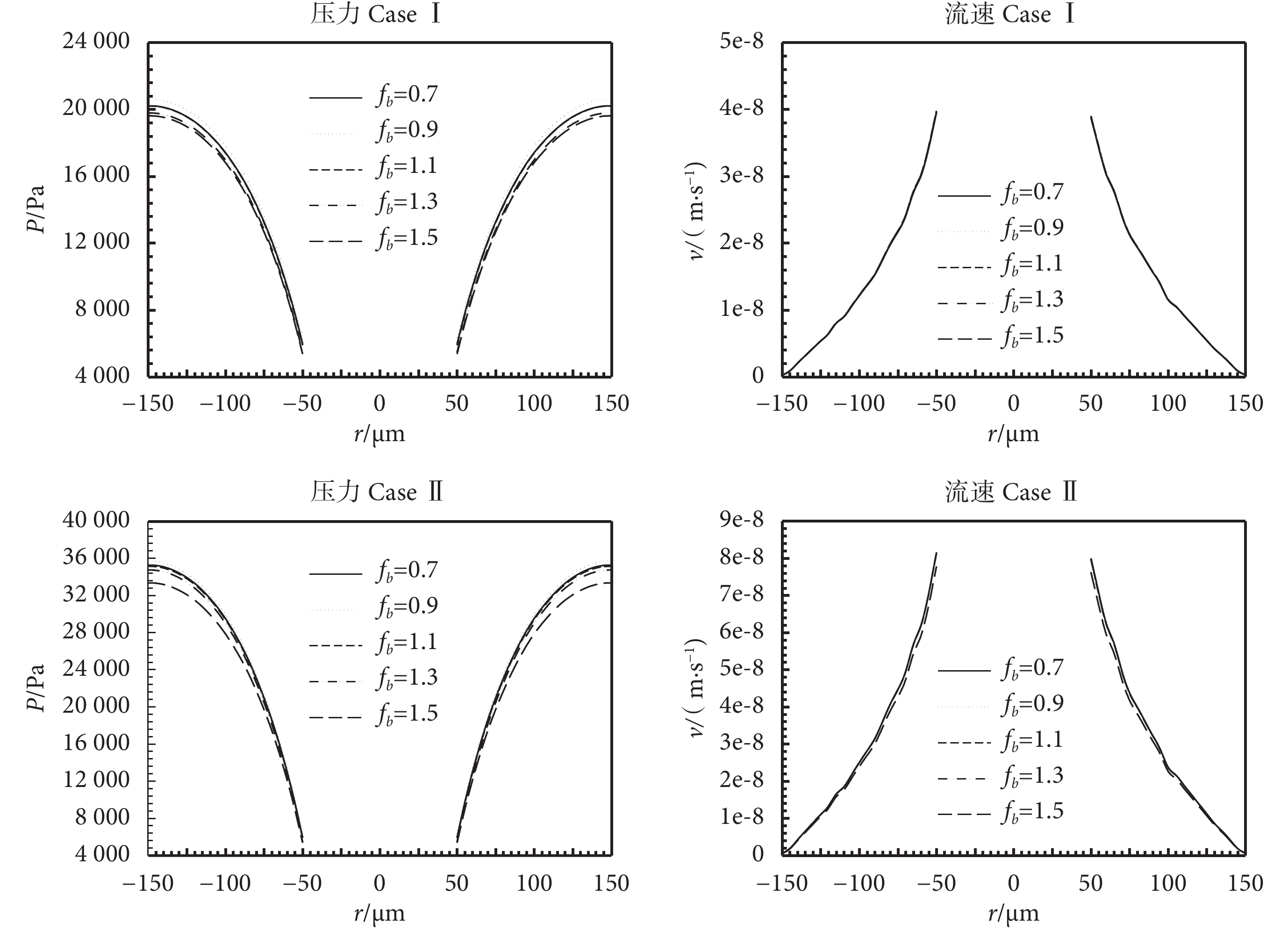
考慮到每個人的心率不同，特別是在心臟搏動紊亂的情況下，圖 7 繪制了當血管脈動幅值 A = 40%P、z = 1 mm 情況下，血管脈動頻率 fb 分別為 0.7、0.9、1.1、1.3、1.5 Hz 時的壓力及流速分布圖。由圖 7 壓力 Case Ⅰ 和壓力 Case Ⅱ 可以看出隨著血管脈動頻率的變化，整個骨單元內部的壓力場也發生變化，并且隨著骨單元半徑的增大，變化愈加明顯，在黏合線 r = 150 μm 處變化最大；而流速場基本沒有受影響。同時可見，整個骨單元孔隙組織液壓力場對于血管脈動頻率的變化不如對幅值變化敏感。
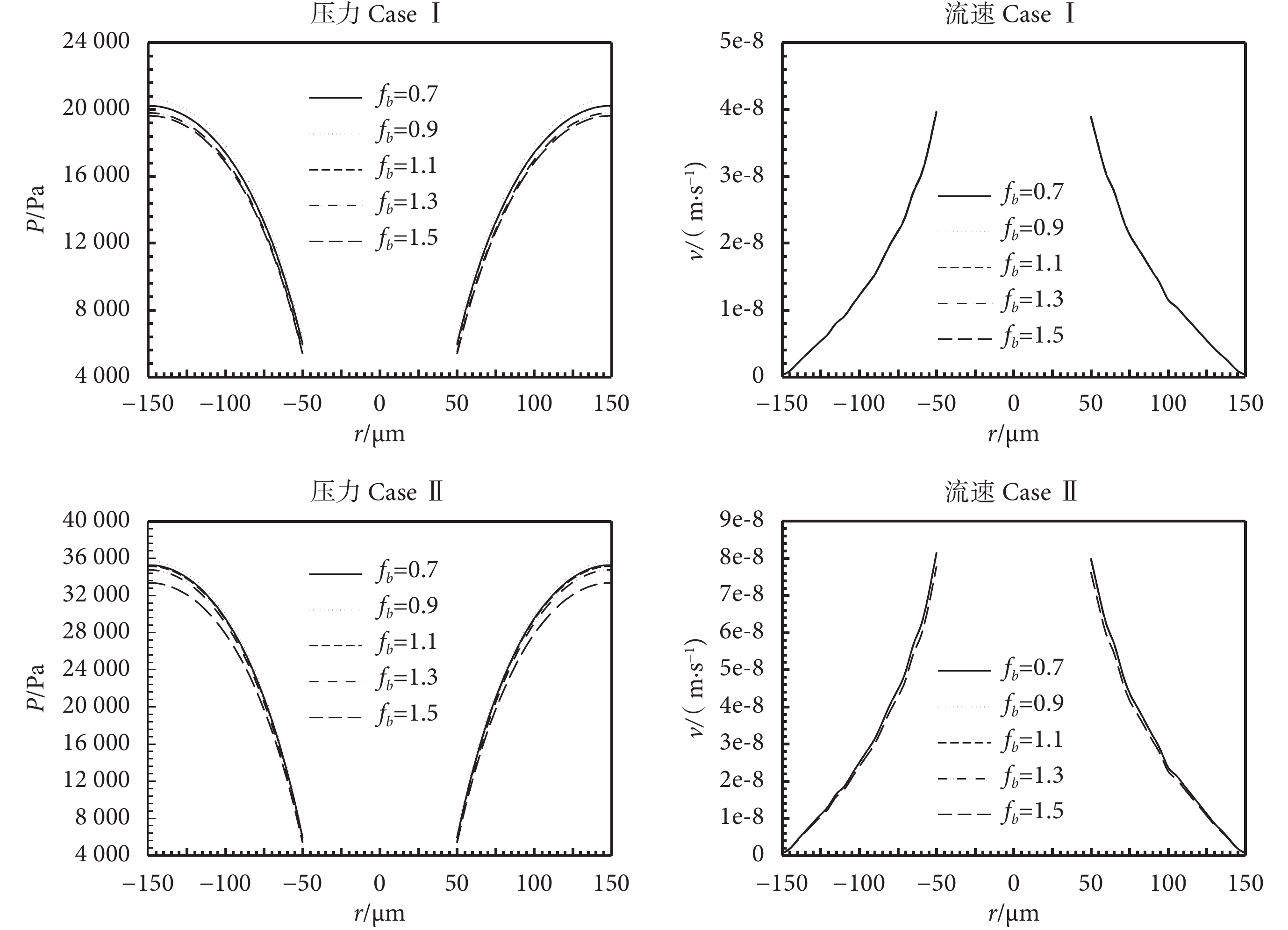圖7
骨單元孔隙組織液壓力幅值及流速隨著脈動頻率 fb 的變化（A=40%P，z=1 mm）
Figure7.
Liquid pressure amplitude and flow velocity varying versus osteon radius of model with different frequencies fb(A=40%P, z=1 mm)
3 討論
本文建立了考慮血管血壓脈動的骨單元有限元模型。根據結果可以看到，當不考慮血管脈動時，骨單元內壁處的壓力為 0，并沿著骨單元半徑逐漸增大，在黏合線（骨單元外壁處 r = 150 μm）處達到最大；流速正好相反：在黏合線處最小，哈弗管處（r = 50 μm）達到最大。這與給定的邊界條件及先前的研究結果[5, 7, 12]一致。邊界條件一（Case Ⅰ）是考慮到骨單元周圍可能受到周圍組織液或部分彈性固體的約束造成該表面不可滲透，在此前工作[5]中詳細討論了其生理意義；而邊界條件二（Case Ⅱ）是大多數學者研究單個骨單元力學行為時采用的邊界條件[13-15]。
對比中空和考慮血管脈動的結果發現，當考慮血管脈動時整個骨單元的孔隙組織液壓力場增大，而流速場基本沒有受影響。此外 Case Ⅱ 產生的壓力場和流速場均大于 Case Ⅰ。血管脈動壓力的高低不僅與心臟功能、血管阻力和血容量密切相關，而且還受到神經、體液等因素的影響。年齡、季節、氣候和職業的不同，血壓脈動幅值及頻率也會有所不同，運動、吃飯、情緒變化等均會導致血壓的升高，而休息、睡眠則會使血壓下降。為此，本文著重考慮哈弗管內血壓脈動的頻率 fb 和幅值 A 對骨單元孔隙組織液的影響。由結果可以看出，血管血壓的脈動幅值對骨單元內部壓力場有明顯的影響。骨單元孔隙組織液壓力隨著脈動幅值的增大而明顯增大，隨脈動頻率的變化則改變不大（小于 5.6%）。另外，血管脈動壓力對骨單元內部流速場基本沒有影響。其潛在的生理意義可能是，血管脈動壓力基本不影響力學信號在骨單元系統的下一個層次——骨小管-骨陷窩-骨細胞系統中的傳導，因為骨小管-骨陷窩-骨細胞系統感受外界載荷，特別是骨細胞感受外界載荷的傳導媒介是間隙組織液的流動，以及液體流動產生的流體剪切力或者粘滯阻力[16-17]。因此大多數情況下，血壓脈動對微管系統中的液體流動基本沒有影響，并不影響骨細胞的力學傳導。但是血管脈動會引起整個骨單元內部壓力場的變化，可能會對結構承載功能或釋放液體壓力的機制造成影響。
在密質骨中大致存在三個尺度[18]的孔隙，第一孔隙是哈弗管及其福爾克曼氏管系統（20 μm 量級）；第二孔隙是骨小管-骨陷窩系統（0.1 μm 量級）；第三孔隙是膠原-羥基磷灰石孔隙（0.01 μm 量級）。血管孔隙相當于一個低壓蓄水庫，可供骨小管-骨陷窩系統中的液體進行液體交換，也是一個高壓緩釋區。本研究中，考慮到骨單元哈弗管中是微動脈，此壓力幅值選為 40% 的主動脈壓力幅值，大約為 6 400 Pa，而骨單元壁中（包含骨小管-骨陷窩系統）孔隙組織液產生的壓力為 15 000～32 000 Pa（見圖 5），因此載荷在骨單元中產生的液體壓力遠大于脈動壓力，而血管是一個低壓緩沖區，同時實現了兩個孔隙系統間的液體交換、營養輸送、廢物排泄等功能。整體密質骨結構的滲透率大約在 10–14 m2 的量級，而骨單元（考慮骨小管-骨陷窩系統）滲透率在 10–17～10–25 m2 量級[18]。本文則選取 1×10–20 m2 進行研究。考慮膠原-羥基磷灰石孔隙的研究較少，也與骨組織內力及力-電信號的傳導關聯不大，因此不是本文研究的熱點。
本文的工作主要考察血管脈動壓力對骨單元孔隙組織液壓力及流動行為的影響，在以前的模型中[5, 13, 15]很多學者忽略了骨單元中央哈弗管的壓力。我們以前的理論工作[6-7]也研究了中央哈弗管的壓力對骨單元多孔彈性力學行為的影響，結果表明哈弗管的壓力會增大液體的壓力場和流速場，而現在的有限元研究結果表明哈弗管內的血管脈動只對壓力場有影響，對流速場基本沒有影響。理論模型[6-7]中的哈弗壓力是一個待求的量，與現在給出已知的脈動力函數不一樣，現在的脈動壓力是作為已知的邊界條件，這可能是得出對流速場是否有影響結論差別的原因所在。盡管這樣，在更多的研究中可以不考慮哈弗管或是血管的脈動[14, 19]，因為通過本文的研究表明血管脈動基本不影響具有力傳導作用的孔隙液體流動行為，該血管區域可以看成很大的低壓蓄水池，因此相對其它由于載荷產生的間隙流孔隙壓力很小，可以略去其效應。當然血管脈動對于局部區域（靠近骨單元內壁附近）的流速場、應力和位移場影響較大，對于遠離此區域的地方則影響甚微。因此在以后的研究中可以酌情考慮血管脈動的影響。
4 結論
本文利用有限元方法，研究了血管脈動壓力對骨單元孔隙組織液壓力及流動行為的影響。本工作為進一步研究其內部骨小管-骨陷窩系統的力傳導及力-電傳導機制提供了基礎，其中包括骨小管內液體流動產生的切應力及流動電位[20-21]等。盡管本文的骨單元模型較為理想化，但初步可以得到以下結論：
（1）當考慮哈弗管中的血管脈動時，骨單元孔隙組織液的壓力會明顯增大，而對流速幾乎沒有影響。
（2）骨單元孔隙組織液的壓力幅值隨著脈動血壓幅值的增大而增大，但受脈動血壓頻率的影響不大；而孔隙液體的流速幅值則不受血壓脈動幅值及頻率的影響。
引言
骨組織內部存在兩大類液體，一類是血液，一類是間隙組織液。骨細胞新陳代謝主要依賴于間隙流微環境，該間隙組織液也是骨組織力傳導及力電傳導的主要媒介。在密質骨的微觀結構中，骨單元是一個由多級系統組成的結構。其外形是圓柱體結構，半徑大約為 200 μm[1]，中間是哈弗管，包含著血管及神經，外部由一層層的骨板層包裹著。血管脈動的“動力源泉”是心臟，而骨主要承載外力、血管的脈動作用力和附著肌肉的收縮力。看似無關聯的血管脈動與骨之間有著非常緊密的聯系，血管中的血液為骨的生長提供營養，同時也為間隙組織液提供了物質交換的場所。
骨組織受力變形后其內部液體就會流動，同時在骨單元壁中擴散，并進一步產生一系列與骨液流動相關的物理效應，如壓力梯度、流體剪切應力和流動電位等，這些物理效應被細胞（如破骨、成骨細胞）感知并做出反應，以適應外部載荷環境。鑒于骨組織產生的內部液體流動很難通過實驗測定，理論模擬是目前的主要研究手段。描述骨單元的變形并考慮其內部孔隙組織液體的流動，需要用到 Biot 理論[1-2]。Zhang 等[3]較早地提出了一個充液的骨單元多孔介質彈性力學模型，但是是各向同性的；接著 Rémond 等[4]給出了橫觀各向同性的解答；在此基礎上我們[5]發展了不同邊界條件（可能存在的生理邊界條件）的骨單元模型，這樣使得模型更接近于真實情況。但是上述模型都將骨單元視為中空的圓柱體，并沒有考慮哈弗管內的液體壓力，為此我們建立了考慮哈弗管液體壓力的骨單元模型[6]，并與中空骨單元模型做了對比[7]。即使如此，以上模型均為數學模型，且沒有考慮哈弗管內血管血壓的脈動。
因此，本文將建立考慮血管脈動壓力的骨單元多孔彈性力學有限元模型，在骨單元內壁施加脈動壓力考察骨單元孔隙組織液對骨單元壁中的間隙組織液流動行為的影響。
1 控制方程及有限元模型的建立
1.1 幾何模型及控制方程
本文將骨單元描述為橫觀各向同性的多孔彈性厚壁圓筒，如圖 1 所示，其中 a = 50 μm 和 b = 150 μm 分別是骨單元的內、外半徑，高為 h = 1 mm。圖 1 為考慮哈弗血管脈動的骨單元模型，其中脈動壓力為 Pb。
圖1
考慮哈弗血管脈動的骨單元模型
Figure1.
Osteon models considering blood pressure oscillation
本構方程可寫為如下：
|
|
平衡方程：
|
幾何方程：
|
液體的滲流連續性方程:
|
達西定律:
|
其中，
和
是總的應力和應變張量；p 是孔隙壓力；ξ 是液體單位體積的改變分數；C 為固體骨架的 4 階張量；α 是 Biot 系數張量；M 稱為 Biot 模量；“:”表示張量間的雙重內積；u 表示位移向量；混合密度
；
為孔隙率，
和
分別表示液體和固體項的密度；V 表示液體速度矢量；
是滲透張量，其中 k 是固有滲透率張量，
是動力粘性系數。
整理上述方程，最終得到系統的控制方程：
|
在柱坐標系下，考慮橫觀各向同性及低頻（幾個赫茲）下，我們求得了其理論解答，并驗證了相應有限元模型的有效性[8-9]。
1.2 邊界條件
研究中將骨單元外壁分為兩種均不可滲透的邊界條件：一種是彈性約束（Case Ⅰ），一種是剛性位移約束（Case Ⅱ）[5]。骨單元骨架視為橫觀各向同性材料，且施加軸向的位移載荷來研究其孔隙液體壓力及流速分布。軸向位移載荷為 w|z= 1 mm = 0.000 5 [cos（2 × pi × f × t）–1]（以 mm 為單位），應變率幅值最大為 0.001[5]。兩種情況下的邊界條件如圖 2 所示。Case Ⅰ 表示骨單元受到周圍組織的彈性約束，并且不可滲透；Case Ⅱ 表示骨單元外壁受到剛性約束（位移為零），也不能滲透。
圖2
兩種邊界條件
Case Ⅰ：彈性約束邊界；Case Ⅱ：剛性約束邊界
Figure2. Two kinds of boundary conditionsCase Ⅰ: elastic restraints; Case Ⅱ: rigid constraints
血液脈動壓力設為 Pb = 0.4 × P（以 mm Hg 為單位），其中 P 為主動脈的脈動函數，考慮到哈弗管為微動脈，取其幅值的 40% 作為參考，P 可以由下面的分段函數表示[10-11]：
|
可知脈動頻率 fb=1/0.9=1.1，并繪制函數圖如圖 3 所示。
圖3
脈動函數 P (t)
Figure3.
Human aortic pulse function P (t)
1.3 材料參數
參數設置如表 1 所示。Cij 表示橫觀各向同性材料脫水的彈性模量矩陣分量，ρS 表示固體的密度，ρf 表示骨單元內流體密度，v 表示泊松比，
表示孔隙率，α 表示 Biot 系數，M 為 Biot 模量，χ f 表示骨內液體的壓縮率，K 表示滲透率，μ 表示液體動力粘度。
2 模擬結果
根據先前的研究發現，當載荷頻率 f=1 Hz、t=0.25 s 時，應變率達到最大值 0.001，這時骨單元孔隙中的液體壓力和流速達到最大[8-9]。本文重點討論在此參數下考慮血管脈動時其孔隙液體壓力和流速的變化規律。
2.1 骨單元內部壓力及流速場分布
如圖 4 繪制了中空和考慮血管脈動的骨單元孔隙組織液壓力幅值及流速的分布圖。由圖 4 可以看出，在軸向的對稱載荷下，液體的壓力和流速場均為軸對稱分布，并且當考慮血管脈動時骨單元壁中的壓力場分布明顯增大。
圖4
骨單元孔隙組織液壓力幅值及流速的分布圖
Figure4.
Liquid pressure amplitude and the distribution of flow velocity in osteon
2.2 考慮血管脈動時骨單元孔隙組織液壓力和流速的變化
為了考察血管脈動對骨單元孔隙組織液壓力及流速的影響，繪制了圖 5，即血管脈動壓力幅值 A 為 40% 的 P (t)。骨單元孔隙組織液壓力及流速均呈軸對稱分布，這是由其結構及其載荷的軸對稱性所決定的。壓力隨骨單元半徑的增大逐漸增大，流速則反之。在中空不考慮血管脈動的骨單元內壁處（r = 50 μm）壓力最小，在外壁（r = 150 μm）處達到最大，這些結果符合邊界條件和先前的研究結論[5-6, 12]。在考慮血管脈動的骨單元內壁處壓力不為 0，大小為微血管的脈動壓力幅值。對比中空的和考慮微血管脈動的模型發現，當考慮微血管脈動時整個骨單元的壓力場增加，而對流速場基本沒有影響，中空與脈動模型流速值幾乎重合。此外 Case Ⅱ 產生的壓力場和流速場均大于 Case Ⅰ。
圖5
骨單元孔隙組織液壓力幅值及流速沿著半徑方向的分布圖（t=0.25 s，z=0.5 mm）
Figure5.
Liquid pressure amplitude and the distribution of flow velocity varying versus osteon radius of model (t=0.25 s, z=0.5 mm)
2.3 不同脈動幅值的血管壓力對骨單元孔隙組織液壓力及流速的影響
考慮到不同部位骨內微動脈脈動幅值的不同，如圖 6 繪制了當血管脈動頻率 fb = 1.11 Hz、z = 1 mm 情況下，血管壓力幅值 A 分別為 10%、20%、40%、80%、100% 的 P (t) 時骨單元孔隙組織液沿徑向的壓力及流速分布圖。由圖 6 壓力 Case Ⅰ 及壓力 Case Ⅱ 可以看出隨著血管脈動壓力幅值的增大，整個骨單元內部壓力場也增加，而流速場基本不變。對于邊界條件 CaseⅠ 和 Ⅱ 結論基本一致。
圖6
骨單元孔隙組織液壓力幅值及流速隨著脈動壓力幅值 A 的變化（fb=1.11 Hz，z=1 mm）
Figure6.
Liquid pressure amplitude and flow velocity varying versus osteon radius of model with different amplitudes A (fb=1.11 Hz, z=1 mm)
2.4 不同脈動頻率的血管壓力對骨單元孔隙組織液壓力及流速的影響
考慮到每個人的心率不同，特別是在心臟搏動紊亂的情況下，圖 7 繪制了當血管脈動幅值 A = 40%P、z = 1 mm 情況下，血管脈動頻率 fb 分別為 0.7、0.9、1.1、1.3、1.5 Hz 時的壓力及流速分布圖。由圖 7 壓力 Case Ⅰ 和壓力 Case Ⅱ 可以看出隨著血管脈動頻率的變化，整個骨單元內部的壓力場也發生變化，并且隨著骨單元半徑的增大，變化愈加明顯，在黏合線 r = 150 μm 處變化最大；而流速場基本沒有受影響。同時可見，整個骨單元孔隙組織液壓力場對于血管脈動頻率的變化不如對幅值變化敏感。
圖7
骨單元孔隙組織液壓力幅值及流速隨著脈動頻率 fb 的變化（A=40%P，z=1 mm）
Figure7.
Liquid pressure amplitude and flow velocity varying versus osteon radius of model with different frequencies fb(A=40%P, z=1 mm)
3 討論
本文建立了考慮血管血壓脈動的骨單元有限元模型。根據結果可以看到，當不考慮血管脈動時，骨單元內壁處的壓力為 0，并沿著骨單元半徑逐漸增大，在黏合線（骨單元外壁處 r = 150 μm）處達到最大；流速正好相反：在黏合線處最小，哈弗管處（r = 50 μm）達到最大。這與給定的邊界條件及先前的研究結果[5, 7, 12]一致。邊界條件一（Case Ⅰ）是考慮到骨單元周圍可能受到周圍組織液或部分彈性固體的約束造成該表面不可滲透，在此前工作[5]中詳細討論了其生理意義；而邊界條件二（Case Ⅱ）是大多數學者研究單個骨單元力學行為時采用的邊界條件[13-15]。
對比中空和考慮血管脈動的結果發現，當考慮血管脈動時整個骨單元的孔隙組織液壓力場增大，而流速場基本沒有受影響。此外 Case Ⅱ 產生的壓力場和流速場均大于 Case Ⅰ。血管脈動壓力的高低不僅與心臟功能、血管阻力和血容量密切相關，而且還受到神經、體液等因素的影響。年齡、季節、氣候和職業的不同，血壓脈動幅值及頻率也會有所不同，運動、吃飯、情緒變化等均會導致血壓的升高，而休息、睡眠則會使血壓下降。為此，本文著重考慮哈弗管內血壓脈動的頻率 fb 和幅值 A 對骨單元孔隙組織液的影響。由結果可以看出，血管血壓的脈動幅值對骨單元內部壓力場有明顯的影響。骨單元孔隙組織液壓力隨著脈動幅值的增大而明顯增大，隨脈動頻率的變化則改變不大（小于 5.6%）。另外，血管脈動壓力對骨單元內部流速場基本沒有影響。其潛在的生理意義可能是，血管脈動壓力基本不影響力學信號在骨單元系統的下一個層次——骨小管-骨陷窩-骨細胞系統中的傳導，因為骨小管-骨陷窩-骨細胞系統感受外界載荷，特別是骨細胞感受外界載荷的傳導媒介是間隙組織液的流動，以及液體流動產生的流體剪切力或者粘滯阻力[16-17]。因此大多數情況下，血壓脈動對微管系統中的液體流動基本沒有影響，并不影響骨細胞的力學傳導。但是血管脈動會引起整個骨單元內部壓力場的變化，可能會對結構承載功能或釋放液體壓力的機制造成影響。
在密質骨中大致存在三個尺度[18]的孔隙，第一孔隙是哈弗管及其福爾克曼氏管系統（20 μm 量級）；第二孔隙是骨小管-骨陷窩系統（0.1 μm 量級）；第三孔隙是膠原-羥基磷灰石孔隙（0.01 μm 量級）。血管孔隙相當于一個低壓蓄水庫，可供骨小管-骨陷窩系統中的液體進行液體交換，也是一個高壓緩釋區。本研究中，考慮到骨單元哈弗管中是微動脈，此壓力幅值選為 40% 的主動脈壓力幅值，大約為 6 400 Pa，而骨單元壁中（包含骨小管-骨陷窩系統）孔隙組織液產生的壓力為 15 000～32 000 Pa（見圖 5），因此載荷在骨單元中產生的液體壓力遠大于脈動壓力，而血管是一個低壓緩沖區，同時實現了兩個孔隙系統間的液體交換、營養輸送、廢物排泄等功能。整體密質骨結構的滲透率大約在 10–14 m2 的量級，而骨單元（考慮骨小管-骨陷窩系統）滲透率在 10–17～10–25 m2 量級[18]。本文則選取 1×10–20 m2 進行研究。考慮膠原-羥基磷灰石孔隙的研究較少，也與骨組織內力及力-電信號的傳導關聯不大，因此不是本文研究的熱點。
本文的工作主要考察血管脈動壓力對骨單元孔隙組織液壓力及流動行為的影響，在以前的模型中[5, 13, 15]很多學者忽略了骨單元中央哈弗管的壓力。我們以前的理論工作[6-7]也研究了中央哈弗管的壓力對骨單元多孔彈性力學行為的影響，結果表明哈弗管的壓力會增大液體的壓力場和流速場，而現在的有限元研究結果表明哈弗管內的血管脈動只對壓力場有影響，對流速場基本沒有影響。理論模型[6-7]中的哈弗壓力是一個待求的量，與現在給出已知的脈動力函數不一樣，現在的脈動壓力是作為已知的邊界條件，這可能是得出對流速場是否有影響結論差別的原因所在。盡管這樣，在更多的研究中可以不考慮哈弗管或是血管的脈動[14, 19]，因為通過本文的研究表明血管脈動基本不影響具有力傳導作用的孔隙液體流動行為，該血管區域可以看成很大的低壓蓄水池，因此相對其它由于載荷產生的間隙流孔隙壓力很小，可以略去其效應。當然血管脈動對于局部區域（靠近骨單元內壁附近）的流速場、應力和位移場影響較大，對于遠離此區域的地方則影響甚微。因此在以后的研究中可以酌情考慮血管脈動的影響。
4 結論
本文利用有限元方法，研究了血管脈動壓力對骨單元孔隙組織液壓力及流動行為的影響。本工作為進一步研究其內部骨小管-骨陷窩系統的力傳導及力-電傳導機制提供了基礎，其中包括骨小管內液體流動產生的切應力及流動電位[20-21]等。盡管本文的骨單元模型較為理想化，但初步可以得到以下結論：
（1）當考慮哈弗管中的血管脈動時，骨單元孔隙組織液的壓力會明顯增大，而對流速幾乎沒有影響。
（2）骨單元孔隙組織液的壓力幅值隨著脈動血壓幅值的增大而增大，但受脈動血壓頻率的影響不大；而孔隙液體的流速幅值則不受血壓脈動幅值及頻率的影響。
