網絡的度量是復雜網絡理論在神經元集群信息處理機制解析中的重要研究內容之一。針對神經元功能網絡的定量度量問題，系統分析了聚類系數、全局效率、特征路徑長度及傳遞性等度量指標與網絡拓撲連接變化的定量描述關系。基于鋒電位發放序列構建了神經元功能網絡，仿真研究表明，構建的網絡可以有效表征神經元之間的連接關系。利用鴿子弓狀皮質尾外側區（NCL）實測數據，研究了神經元功能網絡對鴿子運動行為的編碼特性。研究表明，NCL 區神經元功能網絡可以有效編碼鴿子的運動行為，而且四種度量指標在鴿子左轉、直行和右轉等不同行為時具有顯著差異。研究結果表明本文的神經元功能網絡構建方法可行，對于解析大腦神經信息處理機制具有較高的應用價值。
引用本文： 李珊, 劉新玉, 陳艷, 萬紅. 神經元功能網絡的度量及性能分析. 生物醫學工程學雜志, 2018, 35(2): 258-265. doi: 10.7507/1001-5515.201609010 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
腦是目前自然界中已知的最復雜的系統之一。腦網絡信息處理機制的研究是目前神經信息處理的研究重點，也是腦科學研究的熱點。大腦神經連接網絡可以分為結構性連接網絡、功能性連接網絡和因效性連接網絡三種[1]。結構性連接網絡是由神經元（神經元集群或腦區）之間的解剖連接構成，反映了大腦中真實存在的結構性連接關系；功能性連接網絡是由神經元之間的功能連接構成，反映了神經元之間在特定時間段內形成的功能性連接關系；因效性連接網絡也是由神經元功能連接構成，但反映了神經元之間的相互影響或信息流向。
目前的研究已經表明[2]，復雜網絡理論在腦結構和腦功能分析中是一個十分強大的工具，已經滲透到了腦科學研究的各個方面，可以揭示以往分析手段所不能揭示的腦結構和腦功能的機制和特征。1998 年，Watts 和 Strogatz[3]發現秀麗線蟲（C. elegans）的神經連接網絡具有小世界特性，并推測小世界特性可能是腦神經連接網絡的普遍性質，揭開了復雜網絡在腦科學研究中的序幕。Rubinov 等[4]系統地給出了復雜腦網絡的定量度量指標及其意義，并提供了基于 MATLAB 語言的腦網絡度量工具箱。左西年等[5]闡述了腦結構網絡和腦功能網絡特點，給出了腦網絡的方法學、發展軌跡和行為關聯。Lu 等[6]利用大鼠認知區神經元鋒電位（spike），構建了整體神經元功能網絡和局部神經環路組網絡，成功預測了大鼠在 Y 迷宮和 U 迷宮中的運動行為。Xie 等[7]利用大鼠內側前額葉皮層高發放率的神經元 spike 信號，構建了神經元功能網絡，發現在正確和錯誤試次中網絡的全局效率和聚類系數有顯著差異。Xie 等[8]利用猴子眶額葉皮層 spike 信號構建的神經元功能網絡，揭示了在商品選擇時抉擇行為的神經機制。
現代神經信息采集技術和圖論理論的發展為腦網絡的研究提供了必要的工具和分析方法，但是如何定量度量大腦的神經連接網絡以及這些度量指標隨著網絡節點和連接的變化如何改變依然是目前復雜腦網絡的關鍵問題之一。因此，本文針對神經元功能網絡的定量度量問題，利用仿真數據和鴿子弓狀皮質尾外側區（nidopallium caudolaterale，NCL）實測數據，系統分析了隨機網絡、規則網絡和小世界網絡在不同節點連接概率、節點度和節點數量時聚類系數、全局效率、特征路徑長度和傳遞性等指標的變化特性，并利用 Izhikewich 網絡模型驗證了 spike 序列在構建神經元功能網絡中的有效性；在此基礎上，對鴿子十字迷宮實驗采集的實測數據，利用神經元功能網絡定量度量方法研究了不同度量指標對鴿子轉向行為的編碼特性。
1 原理與方法
根據圖論的概念，神經元功能網絡在數學上可以抽象為一個由節點集
和邊集
組成的圖。節點通常表示為神經元、神經集群、功能腦區等不同尺度上的腦功能單元，邊則代表了節點之間的連接關系。定義兩個節點 ni 和 nj 之間的連接關系為
。
1.1 神經元功能網絡的構建
假設利用微電極陣列胞外采集技術同時可以記錄到 n 個神經元的 spike 發放序列
，其中
為第 i 個神經元在第 t 個 bin 上 spike 發放個數。假設 bin 的寬度足夠小，以至于每一個 bin 中最多只有一個 spike，此處 bin 的寬度設為 1 ms。
對于神經元 i，在給定時間 T 內，假設共記錄到了 n 個 spike，則 spike 發放序列可以表示如下：
 |
其中 ti 為第 i 個 spike 的發放時刻，
，
為 Dirac 函數，
，其他為 0。為了定量度量神經元之間的相關關系，利用滑動時間窗函數對離散的 spike 序列進行了連續化處理，即[9]：
 |
其中，
為窗函數。利用滑動連續的窗函數對 spike 序列連續化處理，避免了窗位置的隨機性，而且估計的 spike 發放率曲線具有更高的時間分辨率。為了得到 spike 發放率的精確估計，這里選用高斯窗函數：
 |
其中，σw 決定發放率的時間分辨率，此處 σw = 400 ms。
在此基礎上，利用 Pearson 相關系數估計神經元之間的相關關系，由于計算簡單、易于實現，Pearson 相關系數在神經元功能網絡的構建中得到了廣泛應用[10]：
 |
其中
表示第 i 個神經元在 t 時刻的發放率，
表示 T 內 spike 的平均發放率。對于 n 個神經元，其相關系數矩陣可以表示如下：
 |
由于神經活動的隨機性和背景噪聲的干擾，并不是所有的連接都是有效的，為了提高網絡構建的準確性，以及網絡拓撲特性定量度量的方便性，對網絡進行了二值化處理。即，對于相關系數矩陣 R，
 |
其中
為閾值，一般根據實際情況設定。定義鄰接矩陣 A 為二值化后的 R 矩陣，鄰接矩陣元素
即為設置閾值后的
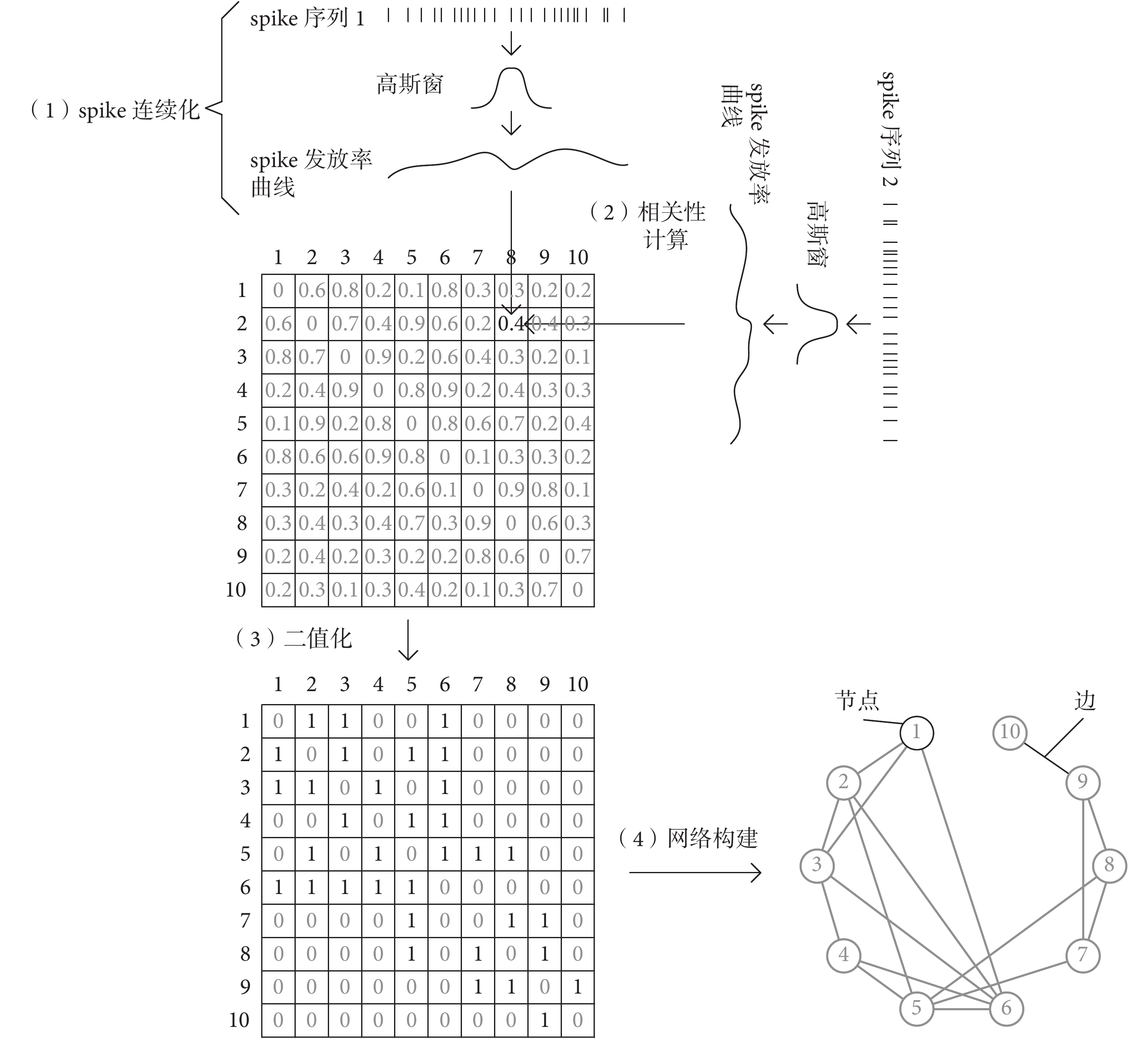
。然后就可以得到二值化后的相關系數矩陣，即鄰接矩陣，由此進行神經元功能網絡的構建。神經元功能網絡的構建過程如圖 1 所示。
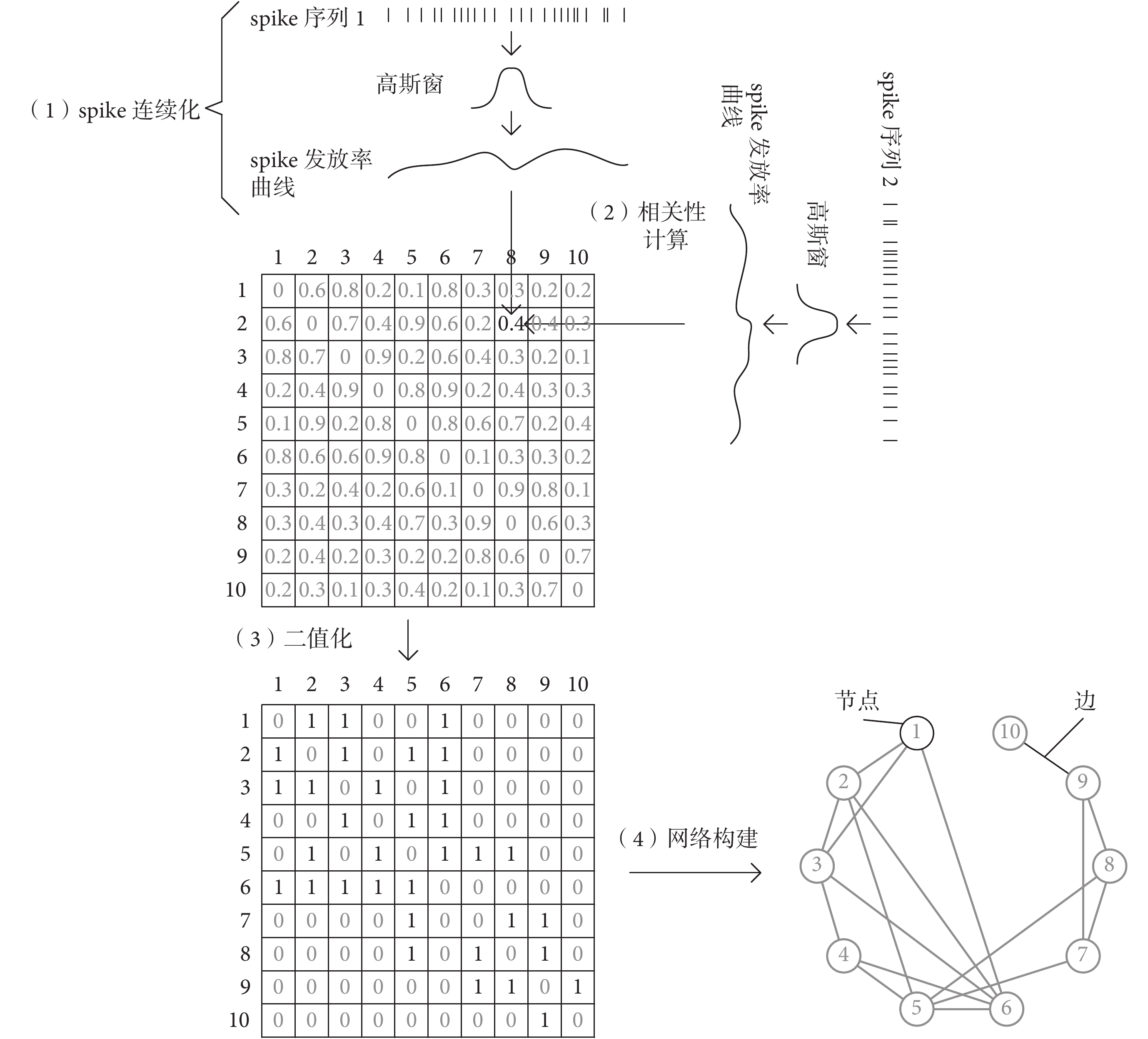圖1
神經元功能網絡的構建示意圖
Figure1.
Establishment of functional neural network
1.2 神經元功能網絡的度量
利用上述構建的神經元功能網絡，基于 spike 相關系數矩陣可以將網絡的度量轉換成對矩陣的計算，特征化神經元之間的連接，量化網絡拓撲特性。在神經元功能網絡的定量度量中，聚類系數、特征路徑長度、全局效率和傳遞性是最常用的四個度量指標，可對網絡的整體特征進行有效度量，其具體計算過程如下。
1.2.1 聚類系數
聚類系數表示某一節點 ni 的鄰居間互為鄰居的可能，反映了節點連接的緊密程度。給定節點 ni，其聚類系數 Ci 定義為節點 ni 鄰居間實際連接邊數與可能的最大連接邊數的比值[4]，
 |
其中
，
，ki 為 ni 的度，
。網絡的聚類系數 C 為所有節點聚類系數的平均值，
 |
其中 n 為網絡中節點的個數，
。聚類系數越大，表明節點之間的連接越緊密。
1.2.2 特征路徑長度
路徑是網絡中特定節點及節點之間連接邊的序列，反映了網絡中信息傳遞的過程。路徑長度是對節點間信息傳遞效率的一個估計。因此，在大腦神經連接網絡的定量度量中，一般用特征路徑長度來刻畫網絡的全局連接特征。特征路徑長度 L 定義為網絡中任意節點對之間最短路徑的平均值[10]，
 |
其中 n 為網絡中節點的個數，
表示節點 ni 和 nj 之間的最短路徑長度，
，
表示節點 ni 和 nj 之間的最短路徑。如果節點 ni 和 nj 之間沒有連接，則
。特征路徑長度越短，表明網絡節點間平均的信息傳遞速率越高。
1.2.3 全局效率
由于當網絡中存在孤立點時，網絡的特征路徑長度將為無窮大，為了解決這一問題，一般用全局效率來代替特征路徑長度。全局效率 E 定義為網絡中所有節點間距離的調和平均的倒數，基于最短路徑的逆進行運算[7]，
 |
其中 n 為網絡中節點的個數，
表示節點 ni 和 nj 之間的最短路徑。全局效率衡量了網絡的全局傳輸能力，網絡的最短路徑長度越短，全局效率就越高，節點間傳遞信息的速率就越快。
1.2.4 傳遞性
傳遞性描述了網絡中節點與鄰居節點間構成三角形的個數與可能構成三角形個數的最大值的比值，反映了網絡中信息的整體傳遞性，即[4]：
 |
其中
，
，
。T 越大，表明網絡的信息傳遞效率越高。
在神經元功能網絡度量中，當網絡為全連通網絡時，聚類系數、全局效率、傳遞性的值可達到 1。
2 實驗及結果分析
大腦神經元功能網絡大多都表現出復雜網絡的特性，復雜網絡是介于隨機網絡和規則網絡之間具有復雜拓撲特性的網絡[11]。小世界網絡是最典型的復雜網絡之一，具有較大的聚類系數和較小的特征路徑長度。為了定量描述各度量指標與神經元功能網絡拓撲結構之間的表征關系，首先對比分析了隨機網絡、規則網絡和小世界網絡的拓撲特性，并利用仿真數據驗證了 spike 序列在神經元功能網絡構建中的可行性，然后將其應用到鴿子十字迷宮實驗中，研究了 NCL 區神經元功能網絡對鴿子運動方向的編碼特性。
2.1 仿真數據及結果分析
2.1.1 典型網絡模型的定量分析
隨機網絡、規則網絡和小世界網絡是三種典型的網絡模型。隨機網絡模型由 n 個節點且節點之間以概率 p 隨機連接而成，網絡的邊數服從期望值為
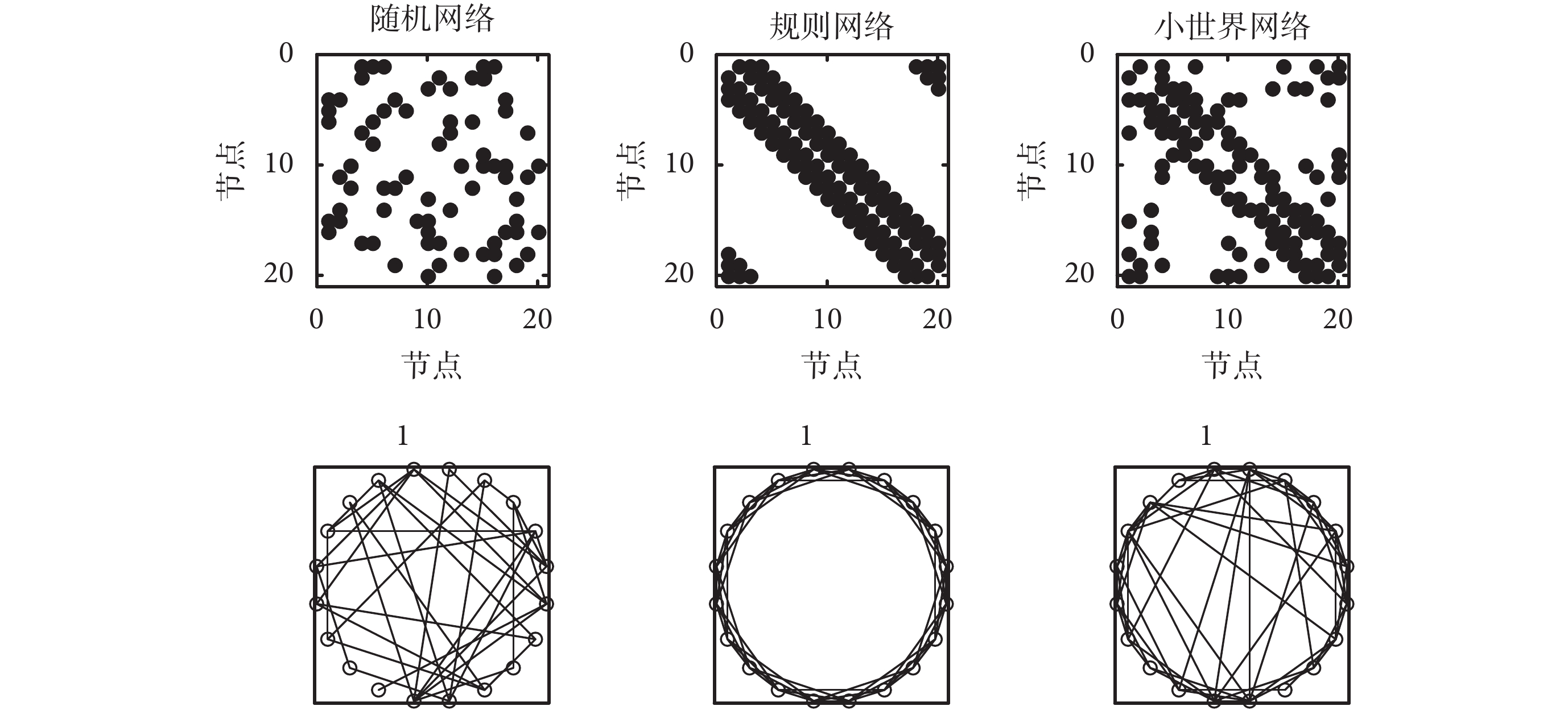
的隨機分布；規則網絡模型由 n 個度為 k 的節點且每個節點與其兩側各 k/2 條邊連接而成，其規則性表現在鄰居節點之間的網狀連接結構，幾乎所有的連接都集中在對角線上；小世界網絡模型的構建分兩步：首先，構建規則網絡，然后，對每條邊以概率 p 隨機進行連接。圖 2 為參數分別為 n = 20、p = 0.2、k = 6 時仿真生成的三種典型網絡節點連接關系和網絡結構圖。
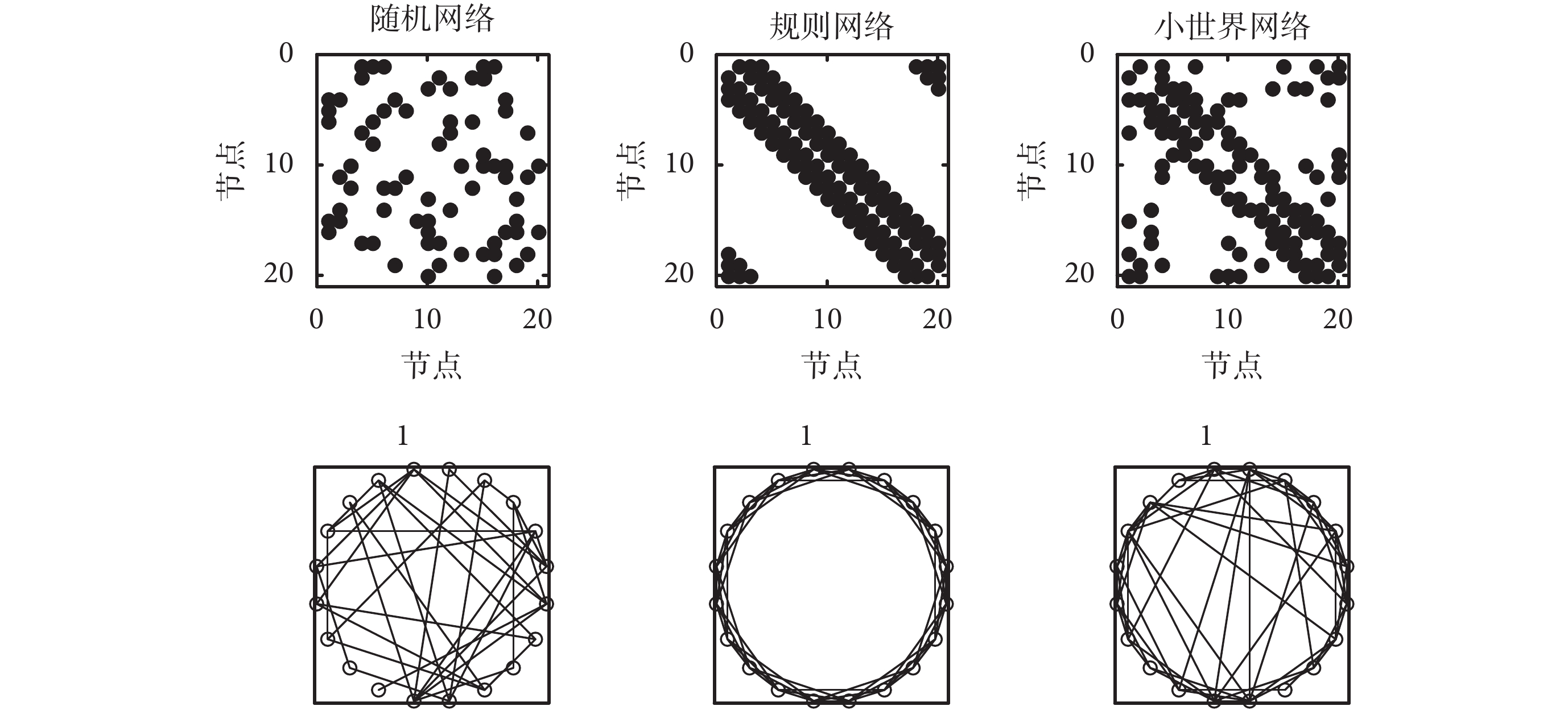圖2
三種典型網絡的節點連接關系和網絡結構圖
Figure2.
Neural connection and network structure of the three typical networks
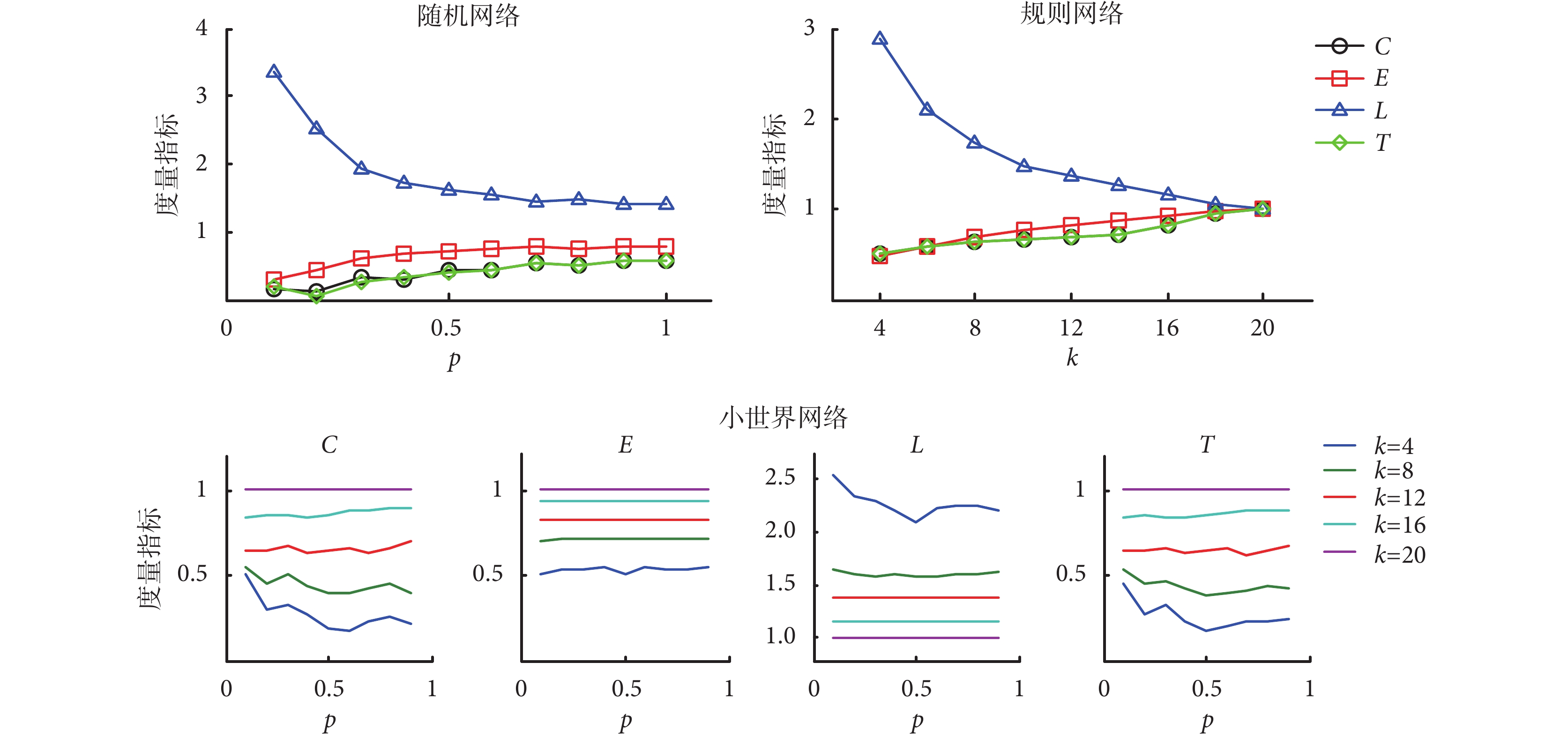
隨機網絡、規則網絡和小世界網絡在不同參數下的四種度量指標變化趨勢如圖 3 所示。由圖可知，連接概率 p 由
的過程中，隨機網絡的聚類系數、全局效率、傳遞性逐漸增大，最后達到穩定狀態，而特征路徑長度逐漸減小，最后也趨于穩定。這表明隨著節點間連接增多，隨機網絡結構更緊密，信息傳遞的路徑減小、傳遞速率升高。隨著節點度 k 的增大，規則網絡的度量指標的變化特性與隨機網絡類似。在連接概率 p 保持不變時，節點度 k 越大，小世界網絡的聚類系數和傳遞性越大；在節點度 k 保持不變時，連接概率增大，聚類系數和傳遞性會出現波動，即當 k ≤ 8 時呈下降趨勢，而當 k > 8 時則保持不變或略有上升。全局效率總體受連接概率 p 的影響不大，但是會隨著節點度 k 的增大逐漸增加。特征路徑長度隨著節點度 k 的增大逐漸減小，且節點度 k 越小，受連接概率 p 的影響越大。
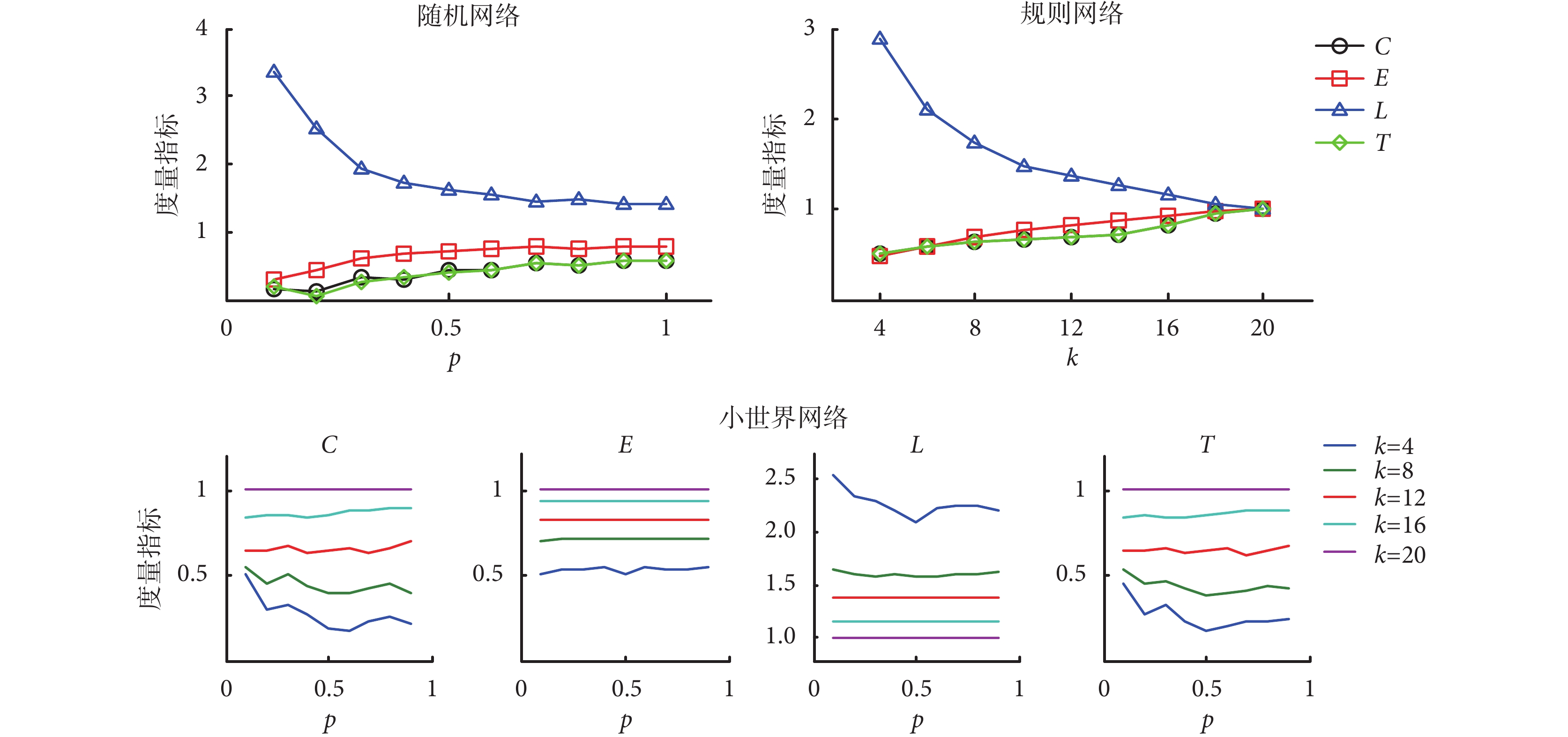圖3
三種典型網絡的聚類系數、全局效率、特征路徑長度、傳遞性等定量度量指標與連接概率 p 和節點度 k 之間的定量變化關系（n = 20）
Figure3.
The quantitative relationship among four measure indexes, clustering coefficient, global efficiency, characteristic path length and transitivity of three typical networks, and the probability as well as the node degree (n = 20)
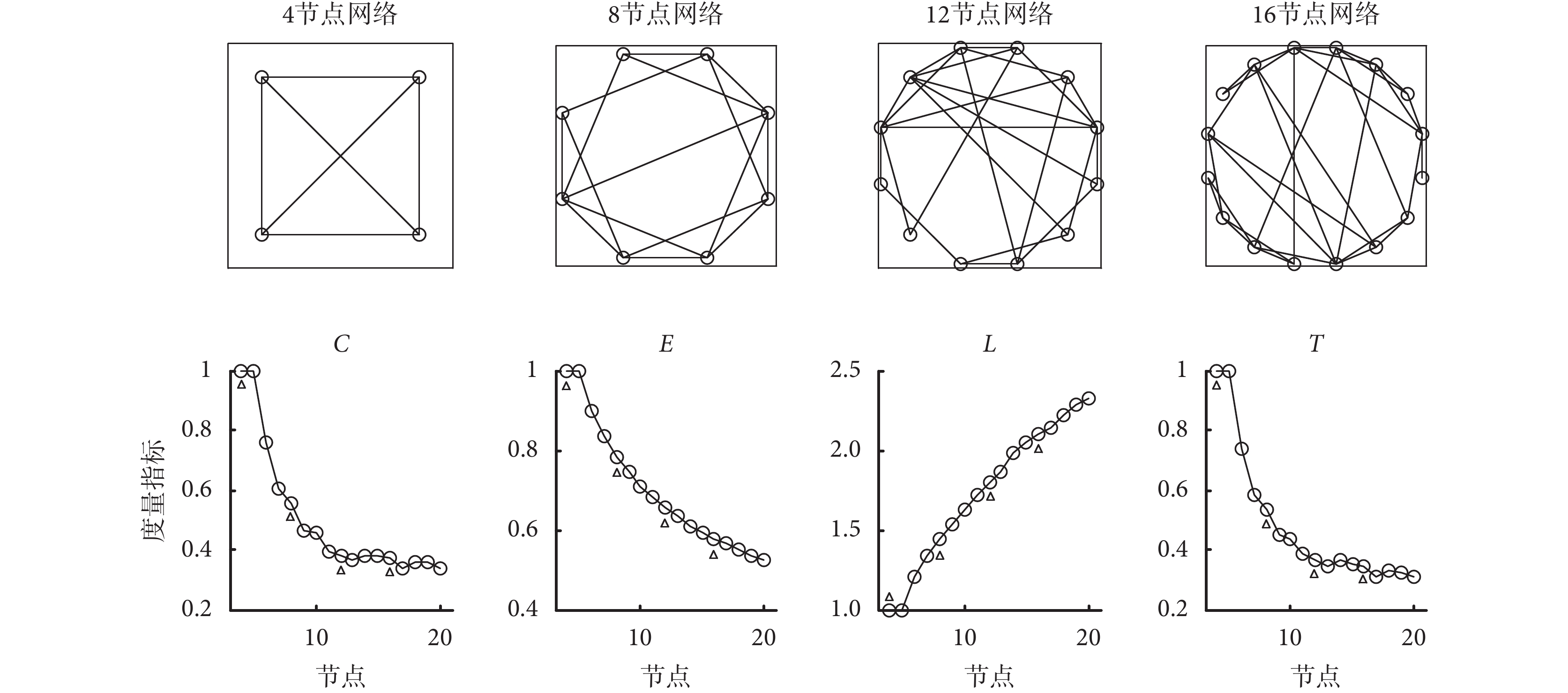
小世界網絡是由規則網絡向隨機網絡過渡的中間狀態得到的網絡模型，對于刻畫復雜網絡拓撲特性具有重要作用。因此，在上述實驗的基礎上，進一步分析在連接概率和節點度保持不變的情況下，節點數的改變對網絡度量指標的影響。對 50 次實驗得到的四種度量指標取平均值，結果如圖 4 所示。
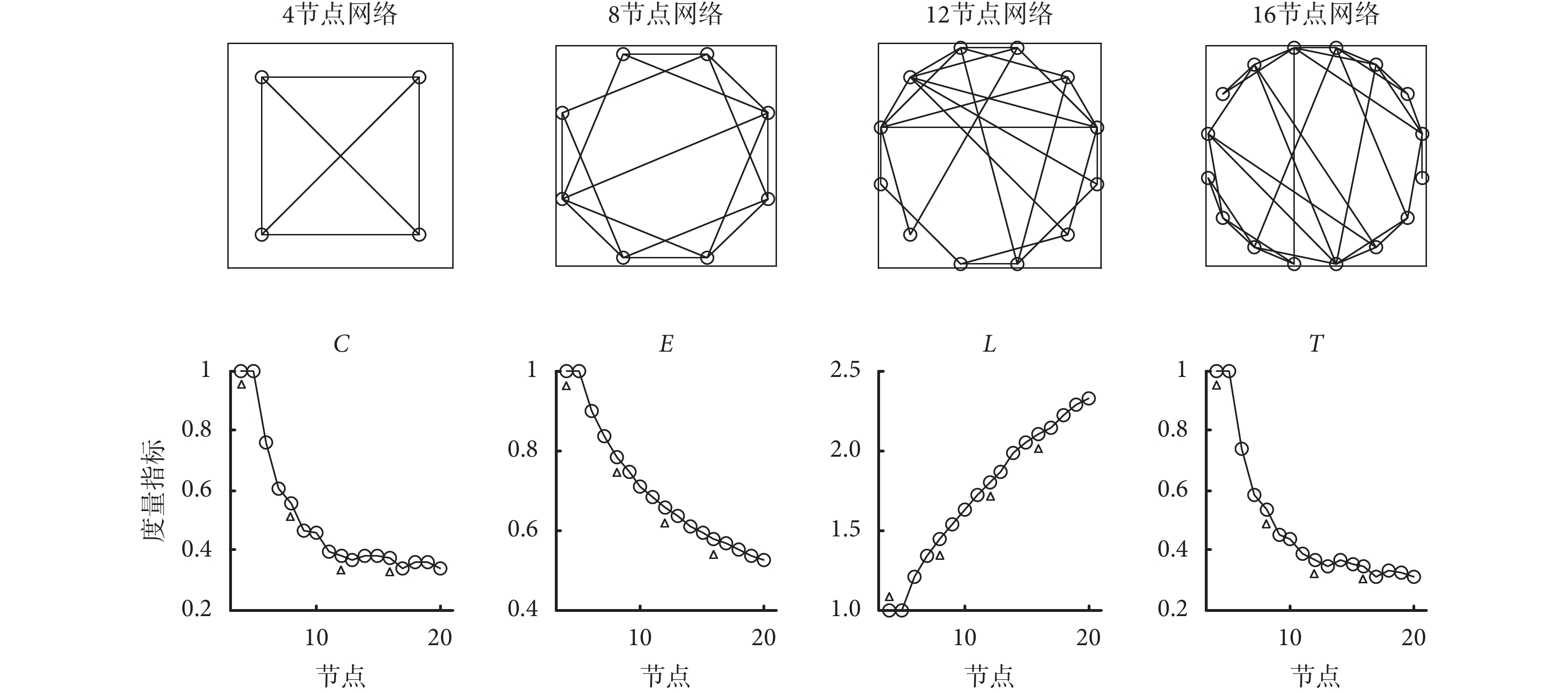圖4
不同節點數量的小世界網絡拓撲結構圖及對應的度量指標變化特性（k = 4，p = 0.2）
Figure4.
The small-world network topology with different number of nodes and its variation characteristics of the measure indexes (k = 4, p = 0.2)
隨著節點數的增加，網絡連接邊的個數也增加，但網絡的連接概率和節點度基本保持不變。在保持網絡的節點度 k 和連接概率 p 不變的情況下，逐漸增加網絡的節點數量，小世界網絡的聚類系數、全局效率和傳遞性都呈下降趨勢，聚類系數和傳遞性減小至 0.3 左右時達到穩定，而全局效率降至 0.5 附近時下降速度逐漸變緩；與上述三種度量指標結果不同，特征路徑長度隨著節點數的增加逐漸增大。總體而言，在節點數為 4 和 5 時，四種度量指標均為 1，網絡為全連通網絡；在節點數為 5 到 7 變化過程中，四種度量指標變化均比較顯著；在節點數大于 7 時，四種度量指標均趨于穩定。
2.1.2 神經元功能網絡模型的性能分析
為了驗證上述神經元功能網絡構建方法的有效性及度量指標的性能，在單個神經元 spike 發放模型的基礎上，構建了以興奮性神經元為主的功能網絡模型。文中使用的神經元發放模型是由 Izhikevich[12]提出的，該模型結合了 Hodgkin-Huxley 模型的生物似真性和積分放電模型計算簡單的優點，模型的微分方程如下：
'/> |
其中，v 表示膜電位，u 表示膜電位的反轉電位，v 和 u 決定了神經元的發放，I 表示膜電流，a、b、c 和 d 是模型參數，可以通過調節這四個參數得到不同的動作電位發放模式。若 v ≥ 30 mV，表示該神經元產生一個動作電位，則
，
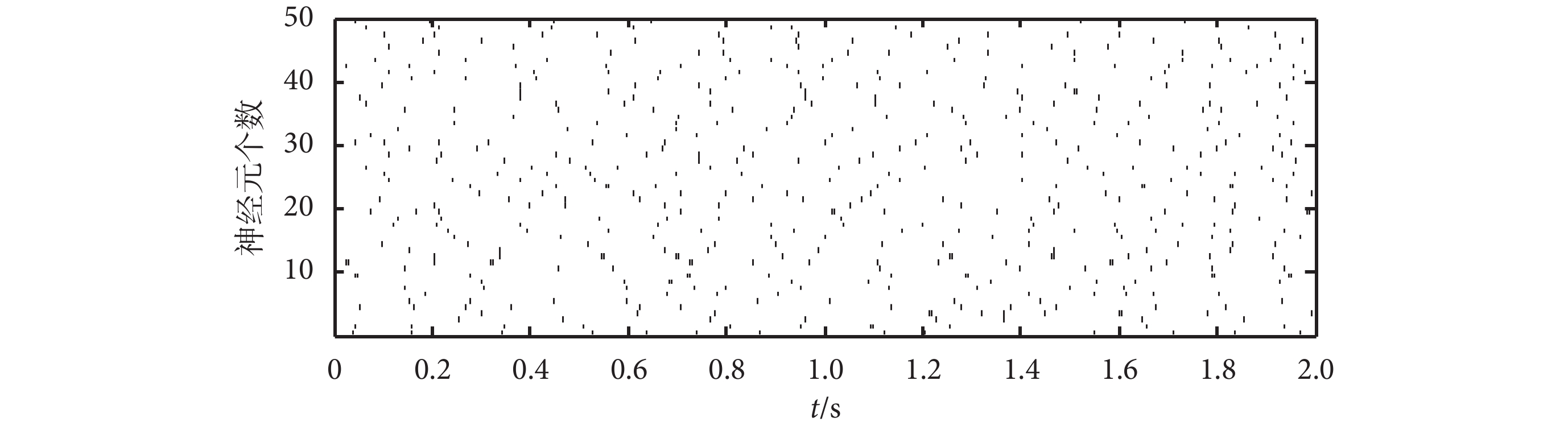
。對于本文使用的興奮性神經元，選取 a = 0.02，b = 0.2，c = –65，d = 8。模擬的 50 個神經元在 2 s 內的 spike 發放序列如圖 5 所示。
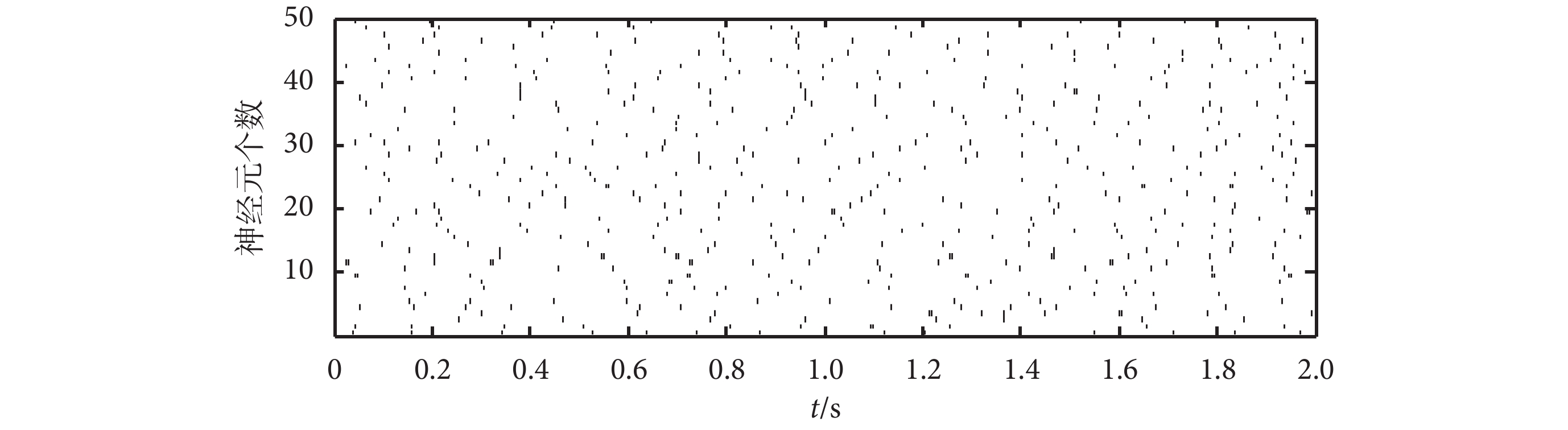圖5
模擬神經元 spike 發放序列
Figure5.
The simulated spike trains
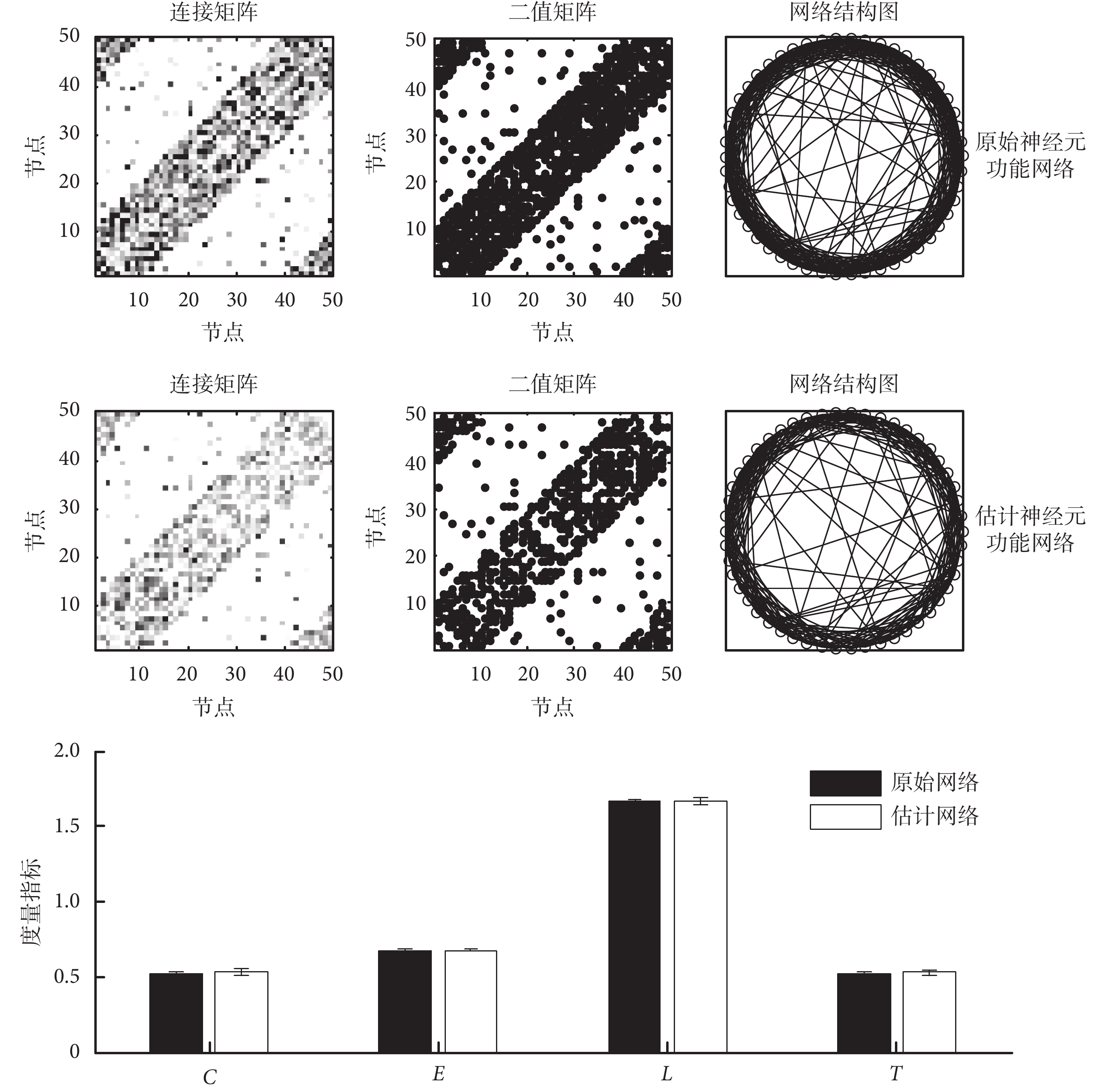
為了驗證 spike 序列在神經元功能網絡構建中的有效性，將原始的神經元功能網絡和利用 spike 序列估計的神經元功能網絡進行了對比，結果如圖 6 所示。由圖可知，估計的和原始的神經元功能連接網絡的拓撲連接特性基本一致，雖然神經元之間的連接強度有所減弱，但是其連接特性并未發生明顯改變。而且這兩個網絡的聚類系數、全局效率、特征路徑長度和傳遞性指標誤差都不超過 2%，其中全局效率和特征路徑長度誤差甚至不超過 0.2%。這表明，基于 spike 發放序列構建的神經元功能網絡與原始網絡特性具有較好的匹配性，可以用于神經元功能網絡的構建。
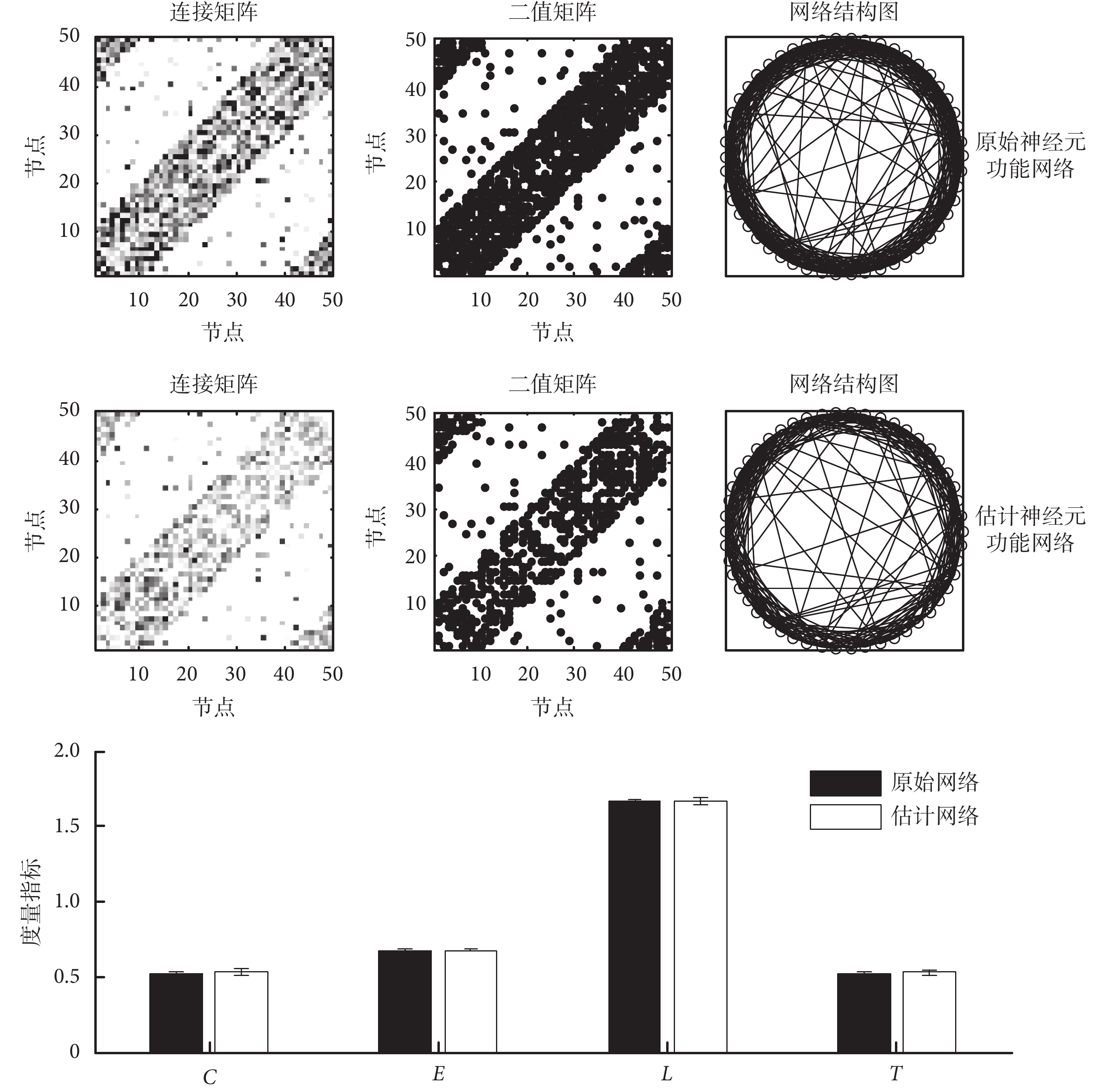圖6
原始的和估計的神經元功能網絡模型對比
Figure6.
Comparison between the original and the estimated functional neural network models
2.2 實測數據及結果分析
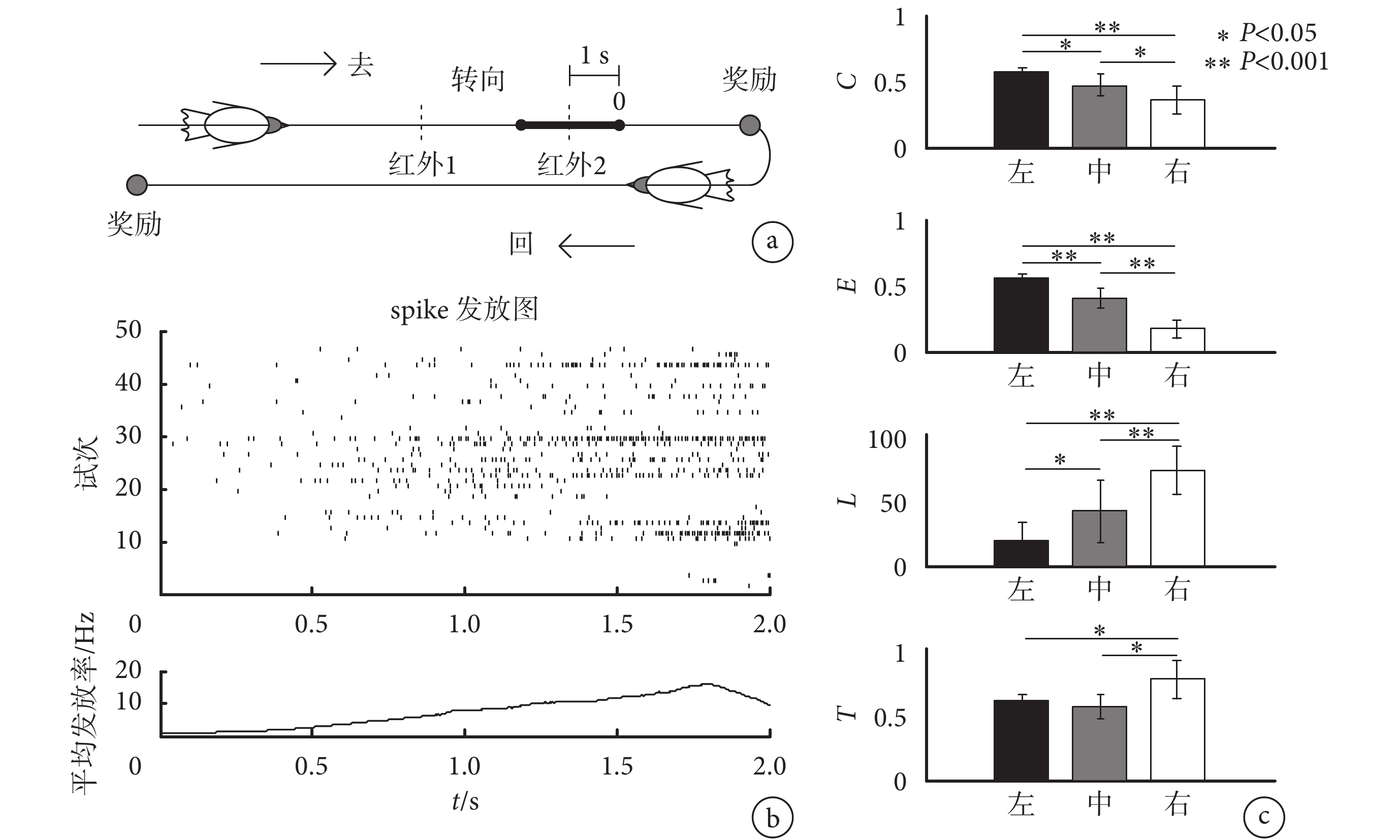
在對實測數據分析中，利用鴿子十字迷宮轉向實驗，采集了鴿子轉向過程中 NCL 區神經元集群 spike 信號，分析了鴿子轉向過程中神經元功能網絡的編碼特性。在鴿子 NCL 區 spike 信號采集中，首先訓練鴿子在十字迷宮中進行食物誘導轉向實驗，實驗范式如圖 7a 所示，在十字路口前后分別設有紅外檢測裝置，以便于分析鴿子轉向過程中的神經活動。待鴿子轉向成功率大于 90% 時，利用慢性植入手術在其 NCL 區植入 2 × 8 微電極陣列，恢復后采用 CerebusTM 信號采集系統（Blackrock Microsystems，美國）采集鴿子轉向時的神經活動。然后，利用二階 Butterworth 帶通濾波器（0.25～5 kHz）對神經信號進行濾波處理，并利用幅度閾值算法進行 spike 檢測，閾值一般設置為 4～5 倍的信號標準差，對于檢測出的 spike 信號，利用基于波形變化率特征和高斯混合模型的聚類算法[13]進行分類，得到每個神經元的 spike 序列。
由于本文使用的是食物誘導鴿子轉向實驗范式，即只有在鴿子看到食物位置時才會進行轉向行為，因此，在研究鴿子神經元功能網絡編碼特性時，僅僅選取了第二個紅外前 1 s 和后 1 s 之間的 spike 信號。圖 7b 給出了單個神經元在 47 個試次中的 spike 發放序列及其平均發放率曲線示例。可以看出，在鴿子轉向過程中，NCL 區神經元 spike 活動有顯著增加。然后利用采集到的 16 個神經元的 spike 發放序列構建了神經元功能網絡。圖 7c 為閾值為 0.2 時的四種網絡度量指標對于鴿子運動行為（左轉、直行、右轉）的編碼特性。由圖可知，在 47 次實驗中（包含 15 次左轉、16 次直行和 16 次右轉），對于三種不同的轉向行為，四種度量指標除了傳遞性指標中左轉和直行外差異均具有統計學意義（P < 0.05，秩和檢驗）。但總的來說，全局效率的編碼特性要優于其他三種度量指標。
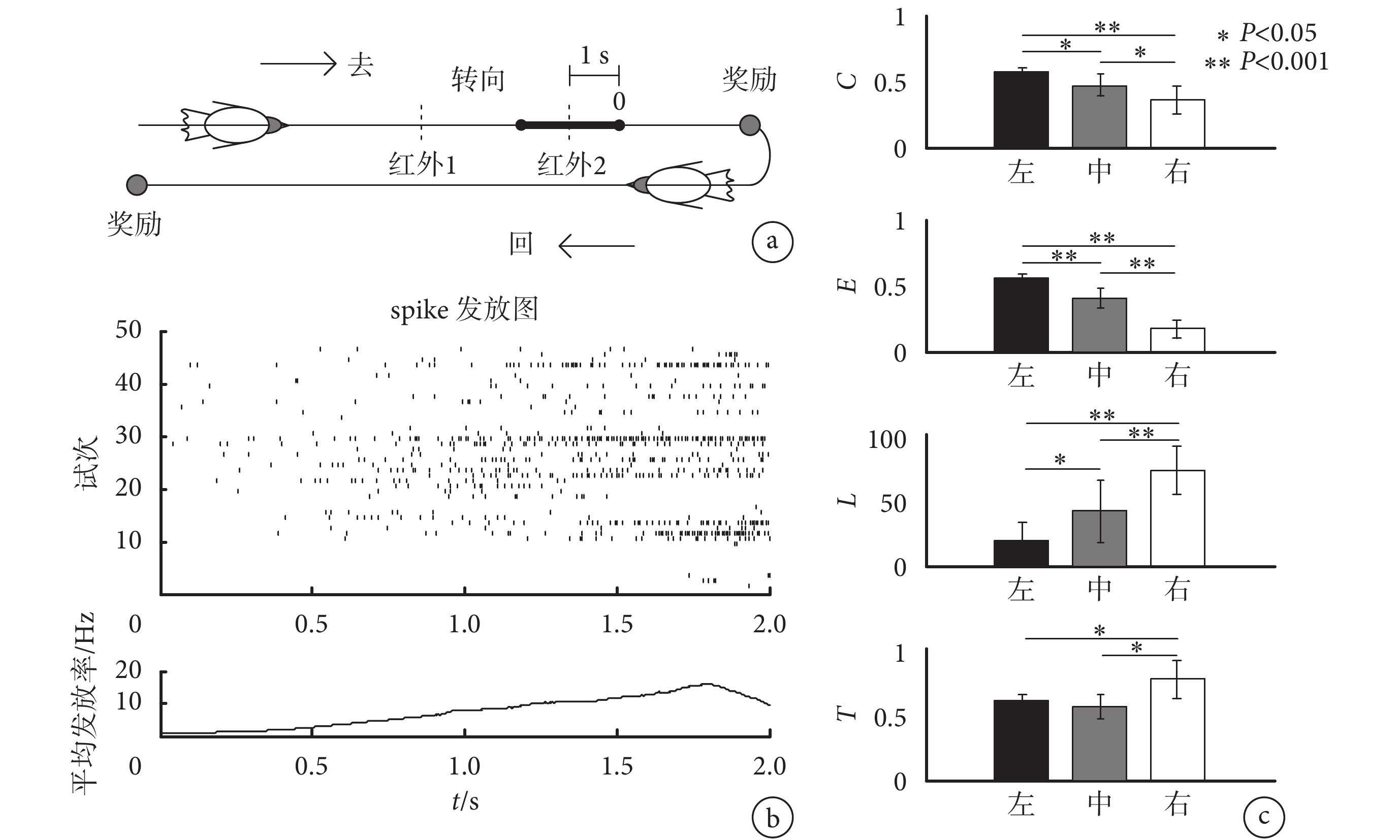圖7
實測數據的神經元功能網絡度量結果
a. 鴿子訓練實驗范式；b. 不同試次神經元 spike 發放圖；c. 不同度量指標對于不同運動方向的編碼特性
Figure7. Measured results of functional neural networks from the real dataa. pigeon's training paradigm; b. the spike trains of different trials; c. the coding property of different indexes for the motion directions
3 討論與結論
大腦中數以億計的神經元構成了龐大而復雜的腦結構網絡，結構網絡上不同神經元、神經元集群或腦區之間動態活動的同步化在時空尺度上的連接形成了腦功能網絡。無論是腦結構網絡還是腦功能網絡，網絡特性的定量度量是其主要的研究內容之一。本文首先描述了一種基于 spike 序列的神經元功能網絡的構建方法，然后介紹了聚類系數、全局效率、特征路徑長度和傳遞性等網絡全局特征的定量度量指標，并在此基礎上利用仿真實驗系統分析了隨機網絡、規則網絡和小世界網絡在不同節點連接概率、節點度和節點數量時的拓撲連接特性，并結合 Izhikewich 模型構建了神經元功能網絡，驗證了 spike 序列在神經元功能網絡構建中的有效性，最后，利用十字迷宮實驗研究了 NCL 區神經元功能網絡對鴿子轉向行為的神經編碼特性。
隨著連接概率的增加，在理論上隨機網絡節點間連接增多，網絡結構更緊密，信息傳遞的路徑減小，傳遞速率升高，這與利用定量度量指標計算的結果一致；與此類似，隨著節點度的增大，規則網絡也表現出了與其一致的變化趨勢；但在網絡結構發生改變時，小世界網絡的網絡特性變化比較復雜，總體上受節點度和網絡節點數量的影響較大，受連接概率的影響較小，而且節點度越大，連接概率對其影響越小。這一結果表明，網絡的節點數量和節點度決定了小世界網絡的結構特性，這也可能是小世界網絡相對于隨機網絡和規則網絡具有更大的全局和局部信息傳輸能力的根本原因。
大腦神經連接網絡大多被認為是小世界網絡，結合小世界網絡模型和 Izhikewich 神經元發放模型模擬了神經元功能網絡響應特性，并將 spike 發放序列估計的神經元功能網絡與原始網絡進行了對比。結果表明估計網絡和原始網絡具有相似的拓撲特性，而且度量指標差異很小，這一結果也驗證了 spike 序列在構建神經元功能網絡時的有效性。在實測實驗中，利用 spike 序列構建的神經元功能網絡，不同的度量指標對鴿子轉向行為都有較好的編碼特性，但相比之下全局效率 > 特征路徑長度 > 聚類系數 > 傳遞性。
對于復雜的神經元功能網絡，分析其拓撲特性可以進一步理解網絡的特性和信息傳遞機制。聚類系數、全局效率、特征路徑長度、傳遞性等是衡量網絡特性的重要指標，聚類系數反映了網絡的集團化程度，全局效率衡量了網絡的全局傳輸能力，特征路徑長度表征了節點間信息傳遞的平均路徑，傳遞性度量了網絡節點間信息傳遞的速率。本文在利用復雜網絡理論對典型網絡系統分析的基礎上，對神經元功能網絡進行了仿真和實測數據分析，研究結果肯定了神經元功能網絡在神經信息處理機制解析中的巨大潛力，相信在未來神經信息處理機制解析中仍將扮演著重要的角色。
引言
腦是目前自然界中已知的最復雜的系統之一。腦網絡信息處理機制的研究是目前神經信息處理的研究重點，也是腦科學研究的熱點。大腦神經連接網絡可以分為結構性連接網絡、功能性連接網絡和因效性連接網絡三種[1]。結構性連接網絡是由神經元（神經元集群或腦區）之間的解剖連接構成，反映了大腦中真實存在的結構性連接關系；功能性連接網絡是由神經元之間的功能連接構成，反映了神經元之間在特定時間段內形成的功能性連接關系；因效性連接網絡也是由神經元功能連接構成，但反映了神經元之間的相互影響或信息流向。
目前的研究已經表明[2]，復雜網絡理論在腦結構和腦功能分析中是一個十分強大的工具，已經滲透到了腦科學研究的各個方面，可以揭示以往分析手段所不能揭示的腦結構和腦功能的機制和特征。1998 年，Watts 和 Strogatz[3]發現秀麗線蟲（C. elegans）的神經連接網絡具有小世界特性，并推測小世界特性可能是腦神經連接網絡的普遍性質，揭開了復雜網絡在腦科學研究中的序幕。Rubinov 等[4]系統地給出了復雜腦網絡的定量度量指標及其意義，并提供了基于 MATLAB 語言的腦網絡度量工具箱。左西年等[5]闡述了腦結構網絡和腦功能網絡特點，給出了腦網絡的方法學、發展軌跡和行為關聯。Lu 等[6]利用大鼠認知區神經元鋒電位（spike），構建了整體神經元功能網絡和局部神經環路組網絡，成功預測了大鼠在 Y 迷宮和 U 迷宮中的運動行為。Xie 等[7]利用大鼠內側前額葉皮層高發放率的神經元 spike 信號，構建了神經元功能網絡，發現在正確和錯誤試次中網絡的全局效率和聚類系數有顯著差異。Xie 等[8]利用猴子眶額葉皮層 spike 信號構建的神經元功能網絡，揭示了在商品選擇時抉擇行為的神經機制。
現代神經信息采集技術和圖論理論的發展為腦網絡的研究提供了必要的工具和分析方法，但是如何定量度量大腦的神經連接網絡以及這些度量指標隨著網絡節點和連接的變化如何改變依然是目前復雜腦網絡的關鍵問題之一。因此，本文針對神經元功能網絡的定量度量問題，利用仿真數據和鴿子弓狀皮質尾外側區（nidopallium caudolaterale，NCL）實測數據，系統分析了隨機網絡、規則網絡和小世界網絡在不同節點連接概率、節點度和節點數量時聚類系數、全局效率、特征路徑長度和傳遞性等指標的變化特性，并利用 Izhikewich 網絡模型驗證了 spike 序列在構建神經元功能網絡中的有效性；在此基礎上，對鴿子十字迷宮實驗采集的實測數據，利用神經元功能網絡定量度量方法研究了不同度量指標對鴿子轉向行為的編碼特性。
1 原理與方法
根據圖論的概念，神經元功能網絡在數學上可以抽象為一個由節點集
和邊集
組成的圖。節點通常表示為神經元、神經集群、功能腦區等不同尺度上的腦功能單元，邊則代表了節點之間的連接關系。定義兩個節點 ni 和 nj 之間的連接關系為
。
1.1 神經元功能網絡的構建
假設利用微電極陣列胞外采集技術同時可以記錄到 n 個神經元的 spike 發放序列
，其中
為第 i 個神經元在第 t 個 bin 上 spike 發放個數。假設 bin 的寬度足夠小，以至于每一個 bin 中最多只有一個 spike，此處 bin 的寬度設為 1 ms。
對于神經元 i，在給定時間 T 內，假設共記錄到了 n 個 spike，則 spike 發放序列可以表示如下：
|
其中 ti 為第 i 個 spike 的發放時刻，
，
為 Dirac 函數，
，其他為 0。為了定量度量神經元之間的相關關系，利用滑動時間窗函數對離散的 spike 序列進行了連續化處理，即[9]：
|
其中，
為窗函數。利用滑動連續的窗函數對 spike 序列連續化處理，避免了窗位置的隨機性，而且估計的 spike 發放率曲線具有更高的時間分辨率。為了得到 spike 發放率的精確估計，這里選用高斯窗函數：
|
其中，σw 決定發放率的時間分辨率，此處 σw = 400 ms。
在此基礎上，利用 Pearson 相關系數估計神經元之間的相關關系，由于計算簡單、易于實現，Pearson 相關系數在神經元功能網絡的構建中得到了廣泛應用[10]：
|
其中
表示第 i 個神經元在 t 時刻的發放率，
表示 T 內 spike 的平均發放率。對于 n 個神經元，其相關系數矩陣可以表示如下：
|
由于神經活動的隨機性和背景噪聲的干擾，并不是所有的連接都是有效的，為了提高網絡構建的準確性，以及網絡拓撲特性定量度量的方便性，對網絡進行了二值化處理。即，對于相關系數矩陣 R，
|
其中
為閾值，一般根據實際情況設定。定義鄰接矩陣 A 為二值化后的 R 矩陣，鄰接矩陣元素
即為設置閾值后的
。然后就可以得到二值化后的相關系數矩陣，即鄰接矩陣，由此進行神經元功能網絡的構建。神經元功能網絡的構建過程如圖 1 所示。
圖1
神經元功能網絡的構建示意圖
Figure1.
Establishment of functional neural network
1.2 神經元功能網絡的度量
利用上述構建的神經元功能網絡，基于 spike 相關系數矩陣可以將網絡的度量轉換成對矩陣的計算，特征化神經元之間的連接，量化網絡拓撲特性。在神經元功能網絡的定量度量中，聚類系數、特征路徑長度、全局效率和傳遞性是最常用的四個度量指標，可對網絡的整體特征進行有效度量，其具體計算過程如下。
1.2.1 聚類系數
聚類系數表示某一節點 ni 的鄰居間互為鄰居的可能，反映了節點連接的緊密程度。給定節點 ni，其聚類系數 Ci 定義為節點 ni 鄰居間實際連接邊數與可能的最大連接邊數的比值[4]，
|
其中
，
，ki 為 ni 的度，
。網絡的聚類系數 C 為所有節點聚類系數的平均值，
|
其中 n 為網絡中節點的個數，
。聚類系數越大，表明節點之間的連接越緊密。
1.2.2 特征路徑長度
路徑是網絡中特定節點及節點之間連接邊的序列，反映了網絡中信息傳遞的過程。路徑長度是對節點間信息傳遞效率的一個估計。因此，在大腦神經連接網絡的定量度量中，一般用特征路徑長度來刻畫網絡的全局連接特征。特征路徑長度 L 定義為網絡中任意節點對之間最短路徑的平均值[10]，
|
其中 n 為網絡中節點的個數，
表示節點 ni 和 nj 之間的最短路徑長度，
，
表示節點 ni 和 nj 之間的最短路徑。如果節點 ni 和 nj 之間沒有連接，則
。特征路徑長度越短，表明網絡節點間平均的信息傳遞速率越高。
1.2.3 全局效率
由于當網絡中存在孤立點時，網絡的特征路徑長度將為無窮大，為了解決這一問題，一般用全局效率來代替特征路徑長度。全局效率 E 定義為網絡中所有節點間距離的調和平均的倒數，基于最短路徑的逆進行運算[7]，
|
其中 n 為網絡中節點的個數，
表示節點 ni 和 nj 之間的最短路徑。全局效率衡量了網絡的全局傳輸能力，網絡的最短路徑長度越短，全局效率就越高，節點間傳遞信息的速率就越快。
1.2.4 傳遞性
傳遞性描述了網絡中節點與鄰居節點間構成三角形的個數與可能構成三角形個數的最大值的比值，反映了網絡中信息的整體傳遞性，即[4]：
|
其中
，
，
。T 越大，表明網絡的信息傳遞效率越高。
在神經元功能網絡度量中，當網絡為全連通網絡時，聚類系數、全局效率、傳遞性的值可達到 1。
2 實驗及結果分析
大腦神經元功能網絡大多都表現出復雜網絡的特性，復雜網絡是介于隨機網絡和規則網絡之間具有復雜拓撲特性的網絡[11]。小世界網絡是最典型的復雜網絡之一，具有較大的聚類系數和較小的特征路徑長度。為了定量描述各度量指標與神經元功能網絡拓撲結構之間的表征關系，首先對比分析了隨機網絡、規則網絡和小世界網絡的拓撲特性，并利用仿真數據驗證了 spike 序列在神經元功能網絡構建中的可行性，然后將其應用到鴿子十字迷宮實驗中，研究了 NCL 區神經元功能網絡對鴿子運動方向的編碼特性。
2.1 仿真數據及結果分析
2.1.1 典型網絡模型的定量分析
隨機網絡、規則網絡和小世界網絡是三種典型的網絡模型。隨機網絡模型由 n 個節點且節點之間以概率 p 隨機連接而成，網絡的邊數服從期望值為
的隨機分布；規則網絡模型由 n 個度為 k 的節點且每個節點與其兩側各 k/2 條邊連接而成，其規則性表現在鄰居節點之間的網狀連接結構，幾乎所有的連接都集中在對角線上；小世界網絡模型的構建分兩步：首先，構建規則網絡，然后，對每條邊以概率 p 隨機進行連接。圖 2 為參數分別為 n = 20、p = 0.2、k = 6 時仿真生成的三種典型網絡節點連接關系和網絡結構圖。
圖2
三種典型網絡的節點連接關系和網絡結構圖
Figure2.
Neural connection and network structure of the three typical networks
隨機網絡、規則網絡和小世界網絡在不同參數下的四種度量指標變化趨勢如圖 3 所示。由圖可知，連接概率 p 由
的過程中，隨機網絡的聚類系數、全局效率、傳遞性逐漸增大，最后達到穩定狀態，而特征路徑長度逐漸減小，最后也趨于穩定。這表明隨著節點間連接增多，隨機網絡結構更緊密，信息傳遞的路徑減小、傳遞速率升高。隨著節點度 k 的增大，規則網絡的度量指標的變化特性與隨機網絡類似。在連接概率 p 保持不變時，節點度 k 越大，小世界網絡的聚類系數和傳遞性越大；在節點度 k 保持不變時，連接概率增大，聚類系數和傳遞性會出現波動，即當 k ≤ 8 時呈下降趨勢，而當 k > 8 時則保持不變或略有上升。全局效率總體受連接概率 p 的影響不大，但是會隨著節點度 k 的增大逐漸增加。特征路徑長度隨著節點度 k 的增大逐漸減小，且節點度 k 越小，受連接概率 p 的影響越大。
圖3
三種典型網絡的聚類系數、全局效率、特征路徑長度、傳遞性等定量度量指標與連接概率 p 和節點度 k 之間的定量變化關系（n = 20）
Figure3.
The quantitative relationship among four measure indexes, clustering coefficient, global efficiency, characteristic path length and transitivity of three typical networks, and the probability as well as the node degree (n = 20)
小世界網絡是由規則網絡向隨機網絡過渡的中間狀態得到的網絡模型，對于刻畫復雜網絡拓撲特性具有重要作用。因此，在上述實驗的基礎上，進一步分析在連接概率和節點度保持不變的情況下，節點數的改變對網絡度量指標的影響。對 50 次實驗得到的四種度量指標取平均值，結果如圖 4 所示。
圖4
不同節點數量的小世界網絡拓撲結構圖及對應的度量指標變化特性（k = 4，p = 0.2）
Figure4.
The small-world network topology with different number of nodes and its variation characteristics of the measure indexes (k = 4, p = 0.2)
隨著節點數的增加，網絡連接邊的個數也增加，但網絡的連接概率和節點度基本保持不變。在保持網絡的節點度 k 和連接概率 p 不變的情況下，逐漸增加網絡的節點數量，小世界網絡的聚類系數、全局效率和傳遞性都呈下降趨勢，聚類系數和傳遞性減小至 0.3 左右時達到穩定，而全局效率降至 0.5 附近時下降速度逐漸變緩；與上述三種度量指標結果不同，特征路徑長度隨著節點數的增加逐漸增大。總體而言，在節點數為 4 和 5 時，四種度量指標均為 1，網絡為全連通網絡；在節點數為 5 到 7 變化過程中，四種度量指標變化均比較顯著；在節點數大于 7 時，四種度量指標均趨于穩定。
2.1.2 神經元功能網絡模型的性能分析
為了驗證上述神經元功能網絡構建方法的有效性及度量指標的性能，在單個神經元 spike 發放模型的基礎上，構建了以興奮性神經元為主的功能網絡模型。文中使用的神經元發放模型是由 Izhikevich[12]提出的，該模型結合了 Hodgkin-Huxley 模型的生物似真性和積分放電模型計算簡單的優點，模型的微分方程如下：
|
'/> |
其中，v 表示膜電位，u 表示膜電位的反轉電位，v 和 u 決定了神經元的發放，I 表示膜電流，a、b、c 和 d 是模型參數，可以通過調節這四個參數得到不同的動作電位發放模式。若 v ≥ 30 mV，表示該神經元產生一個動作電位，則
，
。對于本文使用的興奮性神經元，選取 a = 0.02，b = 0.2，c = –65，d = 8。模擬的 50 個神經元在 2 s 內的 spike 發放序列如圖 5 所示。
圖5
模擬神經元 spike 發放序列
Figure5.
The simulated spike trains
為了驗證 spike 序列在神經元功能網絡構建中的有效性，將原始的神經元功能網絡和利用 spike 序列估計的神經元功能網絡進行了對比，結果如圖 6 所示。由圖可知，估計的和原始的神經元功能連接網絡的拓撲連接特性基本一致，雖然神經元之間的連接強度有所減弱，但是其連接特性并未發生明顯改變。而且這兩個網絡的聚類系數、全局效率、特征路徑長度和傳遞性指標誤差都不超過 2%，其中全局效率和特征路徑長度誤差甚至不超過 0.2%。這表明，基于 spike 發放序列構建的神經元功能網絡與原始網絡特性具有較好的匹配性，可以用于神經元功能網絡的構建。
圖6
原始的和估計的神經元功能網絡模型對比
Figure6.
Comparison between the original and the estimated functional neural network models
2.2 實測數據及結果分析
在對實測數據分析中，利用鴿子十字迷宮轉向實驗，采集了鴿子轉向過程中 NCL 區神經元集群 spike 信號，分析了鴿子轉向過程中神經元功能網絡的編碼特性。在鴿子 NCL 區 spike 信號采集中，首先訓練鴿子在十字迷宮中進行食物誘導轉向實驗，實驗范式如圖 7a 所示，在十字路口前后分別設有紅外檢測裝置，以便于分析鴿子轉向過程中的神經活動。待鴿子轉向成功率大于 90% 時，利用慢性植入手術在其 NCL 區植入 2 × 8 微電極陣列，恢復后采用 CerebusTM 信號采集系統（Blackrock Microsystems，美國）采集鴿子轉向時的神經活動。然后，利用二階 Butterworth 帶通濾波器（0.25～5 kHz）對神經信號進行濾波處理，并利用幅度閾值算法進行 spike 檢測，閾值一般設置為 4～5 倍的信號標準差，對于檢測出的 spike 信號，利用基于波形變化率特征和高斯混合模型的聚類算法[13]進行分類，得到每個神經元的 spike 序列。
由于本文使用的是食物誘導鴿子轉向實驗范式，即只有在鴿子看到食物位置時才會進行轉向行為，因此，在研究鴿子神經元功能網絡編碼特性時，僅僅選取了第二個紅外前 1 s 和后 1 s 之間的 spike 信號。圖 7b 給出了單個神經元在 47 個試次中的 spike 發放序列及其平均發放率曲線示例。可以看出，在鴿子轉向過程中，NCL 區神經元 spike 活動有顯著增加。然后利用采集到的 16 個神經元的 spike 發放序列構建了神經元功能網絡。圖 7c 為閾值為 0.2 時的四種網絡度量指標對于鴿子運動行為（左轉、直行、右轉）的編碼特性。由圖可知，在 47 次實驗中（包含 15 次左轉、16 次直行和 16 次右轉），對于三種不同的轉向行為，四種度量指標除了傳遞性指標中左轉和直行外差異均具有統計學意義（P < 0.05，秩和檢驗）。但總的來說，全局效率的編碼特性要優于其他三種度量指標。
圖7
實測數據的神經元功能網絡度量結果
a. 鴿子訓練實驗范式；b. 不同試次神經元 spike 發放圖；c. 不同度量指標對于不同運動方向的編碼特性
Figure7. Measured results of functional neural networks from the real dataa. pigeon's training paradigm; b. the spike trains of different trials; c. the coding property of different indexes for the motion directions
3 討論與結論
大腦中數以億計的神經元構成了龐大而復雜的腦結構網絡，結構網絡上不同神經元、神經元集群或腦區之間動態活動的同步化在時空尺度上的連接形成了腦功能網絡。無論是腦結構網絡還是腦功能網絡，網絡特性的定量度量是其主要的研究內容之一。本文首先描述了一種基于 spike 序列的神經元功能網絡的構建方法，然后介紹了聚類系數、全局效率、特征路徑長度和傳遞性等網絡全局特征的定量度量指標，并在此基礎上利用仿真實驗系統分析了隨機網絡、規則網絡和小世界網絡在不同節點連接概率、節點度和節點數量時的拓撲連接特性，并結合 Izhikewich 模型構建了神經元功能網絡，驗證了 spike 序列在神經元功能網絡構建中的有效性，最后，利用十字迷宮實驗研究了 NCL 區神經元功能網絡對鴿子轉向行為的神經編碼特性。
隨著連接概率的增加，在理論上隨機網絡節點間連接增多，網絡結構更緊密，信息傳遞的路徑減小，傳遞速率升高，這與利用定量度量指標計算的結果一致；與此類似，隨著節點度的增大，規則網絡也表現出了與其一致的變化趨勢；但在網絡結構發生改變時，小世界網絡的網絡特性變化比較復雜，總體上受節點度和網絡節點數量的影響較大，受連接概率的影響較小，而且節點度越大，連接概率對其影響越小。這一結果表明，網絡的節點數量和節點度決定了小世界網絡的結構特性，這也可能是小世界網絡相對于隨機網絡和規則網絡具有更大的全局和局部信息傳輸能力的根本原因。
大腦神經連接網絡大多被認為是小世界網絡，結合小世界網絡模型和 Izhikewich 神經元發放模型模擬了神經元功能網絡響應特性，并將 spike 發放序列估計的神經元功能網絡與原始網絡進行了對比。結果表明估計網絡和原始網絡具有相似的拓撲特性，而且度量指標差異很小，這一結果也驗證了 spike 序列在構建神經元功能網絡時的有效性。在實測實驗中，利用 spike 序列構建的神經元功能網絡，不同的度量指標對鴿子轉向行為都有較好的編碼特性，但相比之下全局效率 > 特征路徑長度 > 聚類系數 > 傳遞性。
對于復雜的神經元功能網絡，分析其拓撲特性可以進一步理解網絡的特性和信息傳遞機制。聚類系數、全局效率、特征路徑長度、傳遞性等是衡量網絡特性的重要指標，聚類系數反映了網絡的集團化程度，全局效率衡量了網絡的全局傳輸能力，特征路徑長度表征了節點間信息傳遞的平均路徑，傳遞性度量了網絡節點間信息傳遞的速率。本文在利用復雜網絡理論對典型網絡系統分析的基礎上，對神經元功能網絡進行了仿真和實測數據分析，研究結果肯定了神經元功能網絡在神經信息處理機制解析中的巨大潛力，相信在未來神經信息處理機制解析中仍將扮演著重要的角色。
