進行長期空間飛行的航天員處于失重環境，所受力學激勵小于正常值，會面臨骨密度減小和骨丟失的問題。為了探究失重環境下股骨密度和質量的變化趨勢，本文建立了人體股骨的三維模型，進行了臥床條件下基于有限元的人體股骨重建的仿真分析。通過對比臥床實驗數據與仿真數據，驗證了人體股骨有限元模型與重建參數的有效性。繼而進行人體股骨在空間失重條件下的重建仿真，建立關于時間的骨重建速率函數。增大載荷大小和增加載荷循環都能減少骨丟失，仿真結果表明增大載荷大小更能有效減少骨丟失。對股骨骨量恢復的重建速率作出討論，結果表明骨量恢復的重建速率小于骨丟失的重建速率。本文為航天員阻力鍛煉方法及后期恢復訓練提供了理論依據，航天員在空間飛行期間可以通過增大阻力鍛煉強度減少骨量丟失。
引用本文： 楊文婷, 王冬梅, 雷周激欣, 王春慧, 陳善廣. 基于三維有限元仿真的臥床和空間失重下人體股骨重建分析. 生物醫學工程學雜志, 2017, 34(6): 857-862. doi: 10.7507/1001-5515.201609051 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
人體骨骼是一種自適應最優化材料，當所處的力學環境發生變化時，骨骼的結構形態和材料屬性會發生相應的改變，這種調整過程被稱為骨重建。Frost 基于力學穩態理論建立的重建算法最受認可，影響也最廣泛。力學穩態理論認為，骨骼的形態和材料屬性處于動態平衡的狀態，只有當骨骼所處力學環境發生改變，受到的力學激勵超出穩態值時，才會發生骨重建，造成骨吸收或沉淀[1]。
當人體處于空間失重的條件下時，人體所受的力學激勵減小，可能會引發骨吸收。相關研究發現，長時間的空間飛行導致骨丟失，骨丟失量并非隨時間線性增加，上肢沒有觀察到骨量丟失，而下肢的跟骨出現明顯的骨量丟失[2-5]。和平空間站測量了航天員的骨量丟失情況，發現不同骨骼部位骨丟失的情況不一樣[6]，下肢骨量出現了明顯骨丟失。因此本文選擇股骨近端作為空間失重下骨量丟失模擬仿真的研究對象。臥床實驗中骨骼的受力減小，能一定程度上模擬空間失重環境，為空間失重的骨丟失情況提供參考數據[7]，因此本文參考臥床實驗結果對空間失重重建參數作出討論。
為了研究空間失重條件下骨骼密度和質量的變化趨勢，探索減小失重環境下骨量丟失的方法，建立了人體股骨近端的三維模型，通過對比臥床仿真結果與實驗結果，對比空間失重仿真結果與相關文獻結果，驗證重建參數的正確性。對比增大載荷大小和增大載荷循環次數這兩種方法對減小骨量丟失的效果，為航天員空間飛行阻力鍛煉提供理論依據。最后，對失重后的股骨進行骨量恢復仿真。
1 材料與方法
1.1 45 天頭低位臥床實驗
采用 45 天 —6° 頭低位臥床實驗模擬人體處于長期失重環境下的生理效應，共 30 名志愿者參與了此次臥床實驗。30 名志愿者為男性，年齡 25～40 歲，身高 165～175 cm，體重 55～75 kg。使用 DEXA 雙能骨密度測量儀，對臥床期間志愿者的腰椎和髖關節進行骨密度檢測。臥床實驗數據表明，志愿者腰椎骨密度隨臥床時間逐漸降低，并從臥床 30 天后出現顯著降低，臥床 45 天后，腰椎骨密度減少 6.7% ± 1.24%。類似地，志愿者髖關節骨密度隨臥床時間逐漸降低，并在臥床第 30 天達到最低值，臥床 45 天后，髖關節骨密度減少 5.4% ± 1.45%。本臥床試驗得到中國航天員科研訓練中心倫理委員會批準。
1.2 重建控制方程
骨重建計算方法基于 Huikes 的“死區”理論[8]，選擇等效應力作為力學激勵[9]。重建控制方程為：
 |
 |
 |
式中，
是表觀密度（單位為g·cm–3），t 是時間（任意時間單位），φ 是每日等效應力刺激（單位為 MPa），其中 N 為載荷工況的總數，nj 為第 j 種載荷每日循環數，m 為權重系數，
是等效應力，k 是穩態參考值，
是死區寬度，B 是重建速率。骨的單元密度值通過前進歐拉法
得到。
1.3 三維模型的建立
用計算機斷層成像（computed tomography，CT）對一名 28 歲健康男性志愿者的下肢進行掃描，以 DICOM 文件格式輸出到 Mimics 軟件，建立三維模型。將導入 Mimics 的圖片通過閾值分割獲取股骨清晰輪廓，生成股骨三維模型的模板，然后，將股骨三維模型以 STL 格式輸出導入到 Geomagic Studio 軟件進行優化，生成股骨曲面模型。將股骨三維模型以 IGES 格式輸出并導入至 ANSYS。在 ANSYS 中對模型進行網格劃分，采用四面體 Solid92 單元進行自由網格劃分，得到股骨近端三維有限元模型。本文假設骨單元為各向同性材料，骨密度與彈性模量之間的關系由函數式 E = 3 790 ρ3 確定[10]，上式中彈性模量的單位為 MPa，密度單位為 g·cm-3。
在進行臥床和空間失重的重建模擬前，需要獲得正常的股骨密度分布。把 ANSYS 中劃分好網格的模型導回至 Mimics，在 Mimics 的有限元分析（finite element analysis，FEA）模塊中，根據灰度值大小換算得到每個單元的骨密度并賦值給有限元模型。本文采用的灰度值與密度關系式為 ρ = 1.086 × 10–3 × 灰度值 + 0.075，泊松比設為 0.3，分 400 級自動定義密度。將賦值后的模型導出為 ANSYS 的 preprocessor 文件，再在 ANSYS 中讀入即可進行后續的加載求解。
1.4 初始參數設定
在進行臥床實驗的重建模擬前，需要確定股骨模型的網格大小和重建死區寬度。為股骨模型賦初始密度值后，通過控制方程模擬 100 天的骨重建過程，分別用 5、6、7、8 mm 的有限元單元邊長劃分網格。重建 100 次后，每兩次計算結果相差分別為 2.63%、20.26%、13.58%，可以認為當單元邊長不大于 6 mm 時，網格尺寸對于重建計算結果影響不大。為了提高運算速度，在以后的計算中一律選擇 6 mm 的單元劃分網格。
表 1 列出了臥床實驗模擬參數初始值的設置，討論網格大小時，死區寬度固定在 0.1，討論死區寬度時，網格大小固定在 6 mm，其余初始參數相同。
表1
三維股骨重建模擬參數初始值
Table1.
Initial values used in numerical simulation of three-dimensional femur remodeling
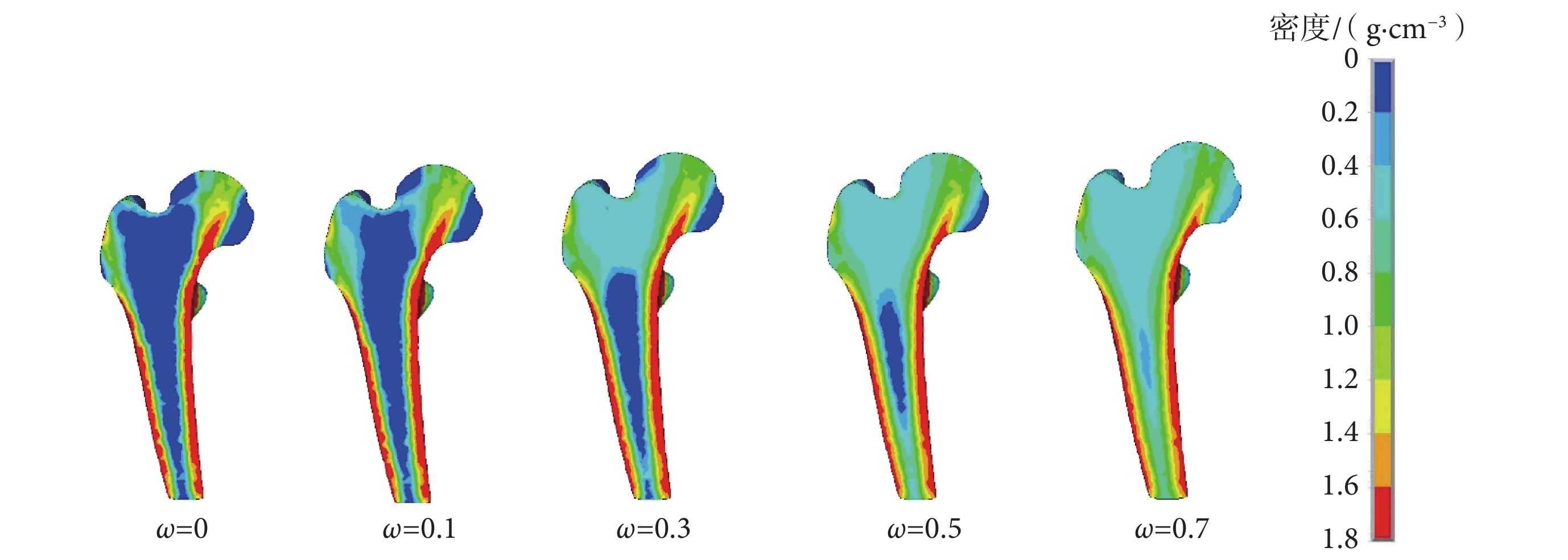
分別改變死區寬度為 0、0.1、0.3、0.5、0.7，其余參數不變，觀察 100 天后的重建情況。發現只有
= 0.1 時的密度分布與實際股骨密度分布相符（見圖 1）。因此在以后的計算中一律選擇死區寬度為 0.1。
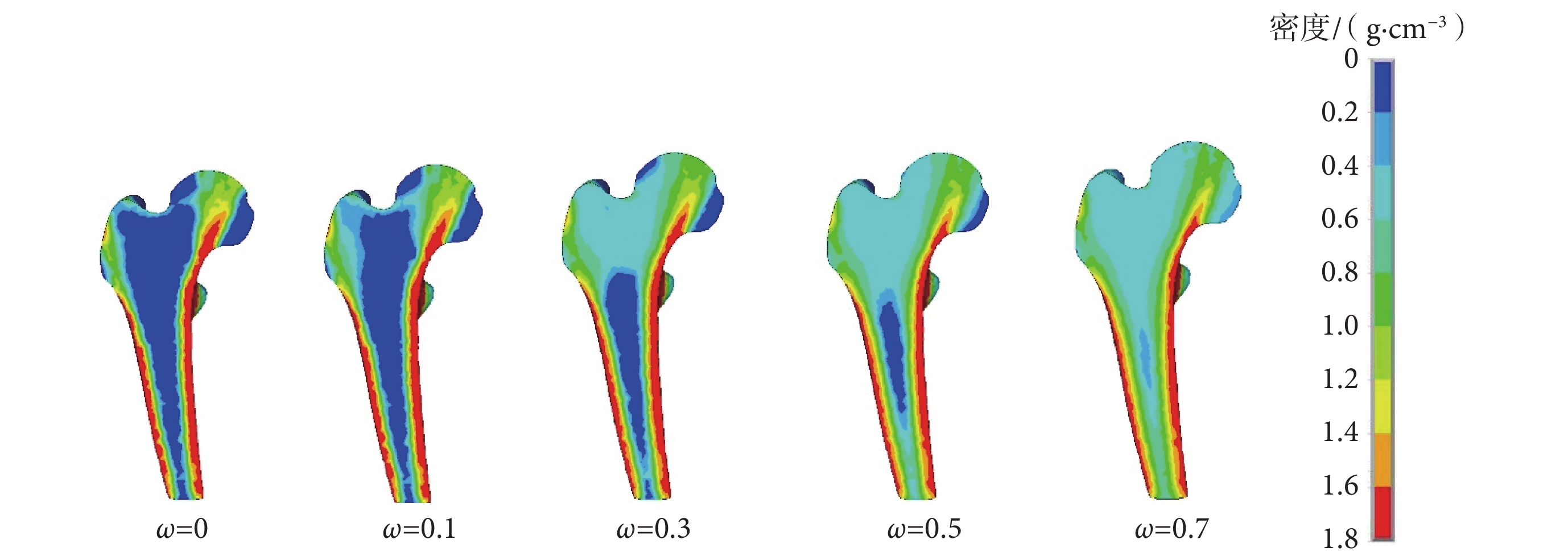圖1
不同死區寬度下股骨近端重建 100 天后密度分布圖
Figure1.
Density distributions under different ω after a 100-day simulation of proximal femur bone remodeling
1.5 臥床實驗模擬加載
基于 1.4 節得到的死區寬度和網格大小，設定重建速率為 B = 0.008，其余初始參數與表 1 相同，模擬臥床 45 天股骨近端的重建過程。選用通過 Mimics 賦值得到的股骨三維模型作為臥床重建的初始模型，對初始模型加載正常步態載荷，計算重建的穩態參考值 k。由于臥床實驗中的志愿者股骨處于無負重狀態，因此對股骨模型不加關節力或肌肉力，只施加穩態慣性力模擬重力。
1.6 空間失重模擬加載
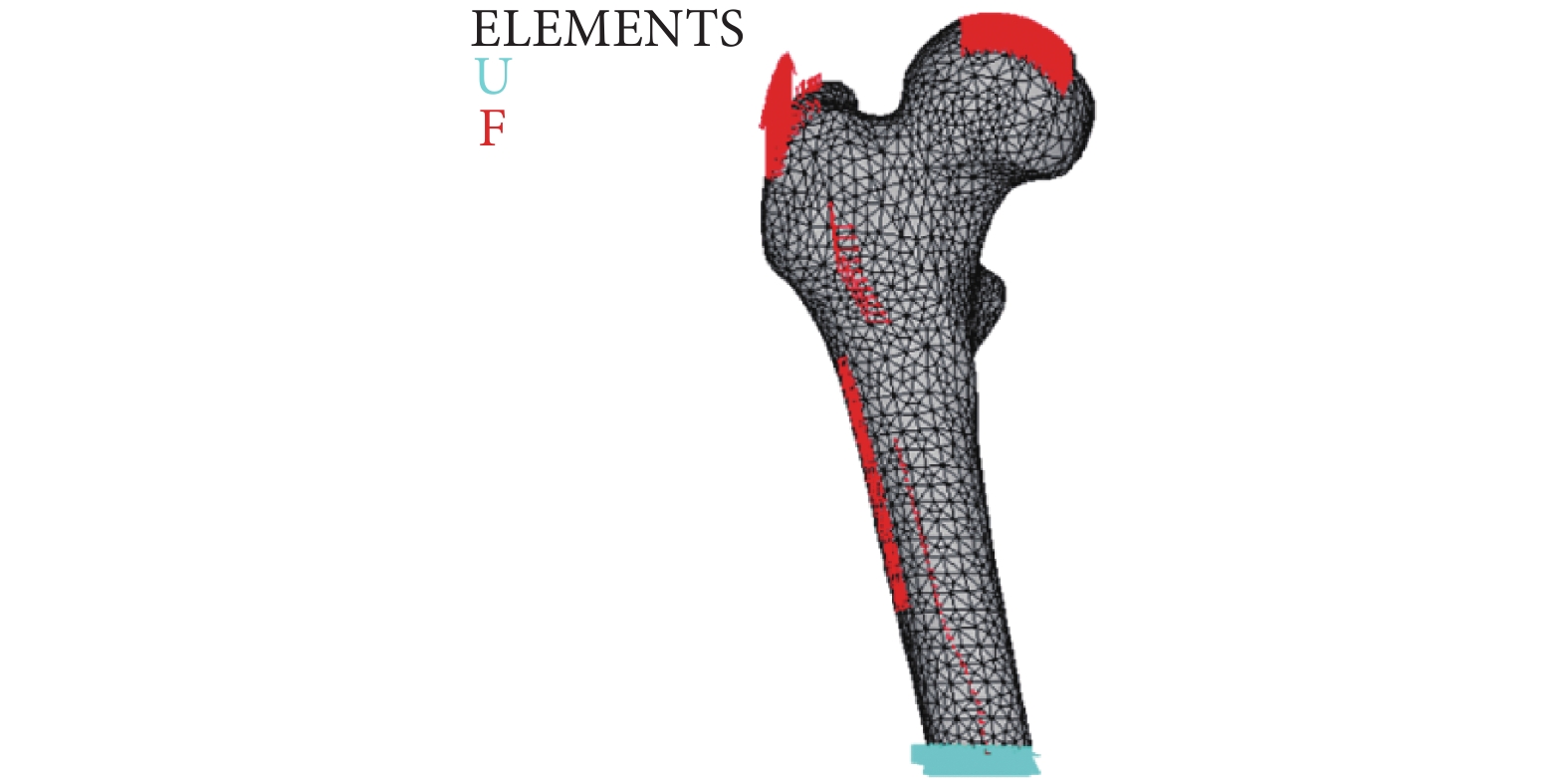
在以往的骨重建研究中，施加在股骨模型上的載荷大多簡化為作用在股骨頭上的關節力和作用在大轉子上的肌肉合力[11-12]。為了更真實地模擬股骨所處的力學環境，本文參考了文獻[13]里各個肌肉力作用在股骨上的面積，考慮了關節力和 7 種肌肉力[14]。圖 2 是空間失重加載示意圖。
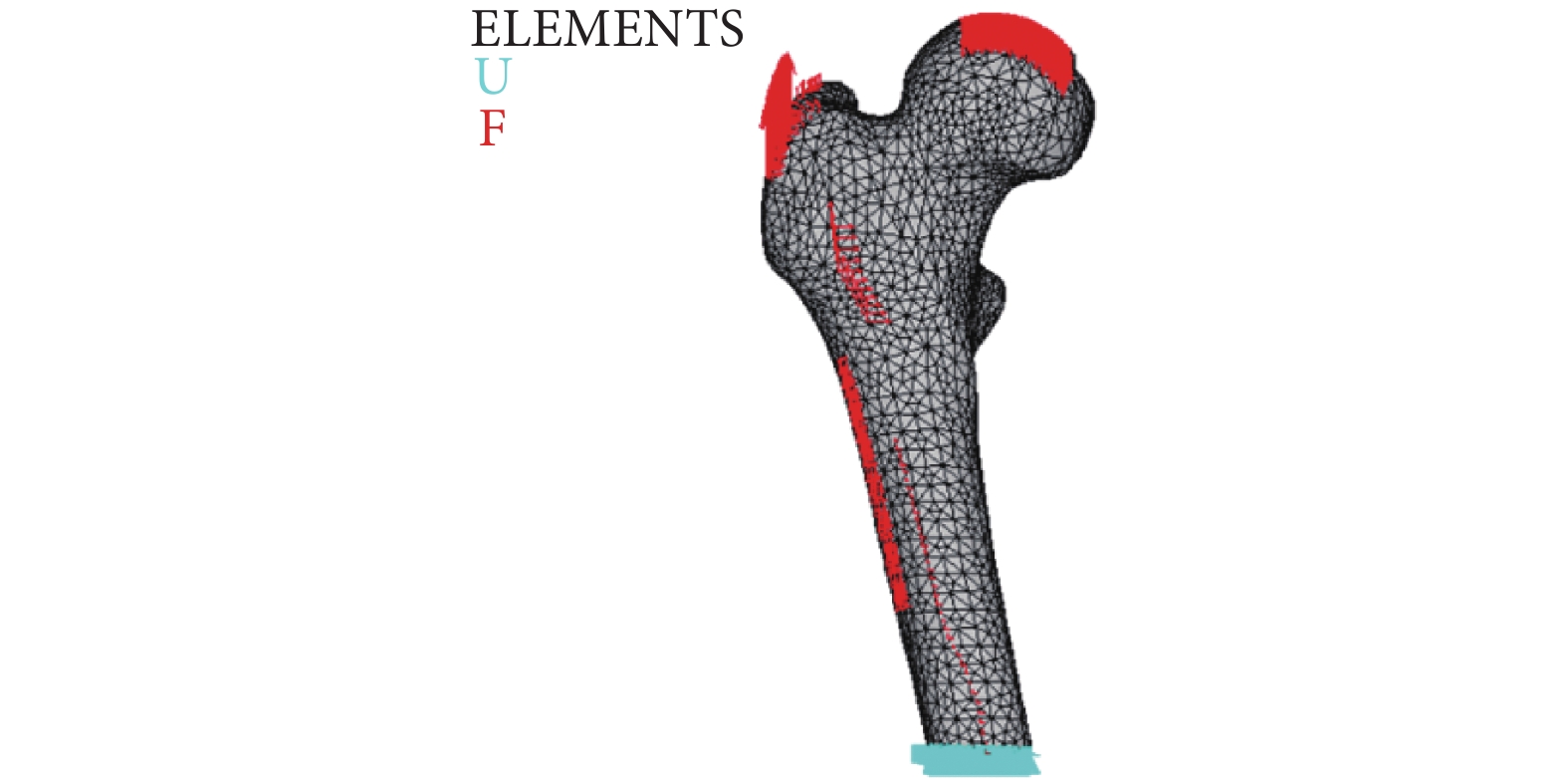圖2
空間失重邊界條件和加載示意圖
Figure2.
Boundary conditions and loading areas for space flight simulation
表 2 列出了關節力與各肌肉力的大小與在全局坐標系下的位置。航天員在空間失重條件下所受關節力大幅減小，肌肉力也相應減弱。由文獻知，–6° 頭低位臥床實驗過程中，下肢肌肉力大小下降 41%～60%[15]，因此在空間失重模擬加載中，只對股骨加載 45% 步態周期時的峰值載荷，其中關節力減小至地面正常值的 20%，肌肉力減小至正常值的 60%。由于航天員在失重環境下活動量顯著減少，因此載荷每日循環數 n 設為 100。
表2
股骨近端模型的正態步態載荷值
Table2.
Loading conditions in three stages during gait cycles of proximal femur
相關研究表明，空間失重前期，重建速率逐漸變快，后期的重建速率基本穩定[5]。事實上，重建率是一個時間相關函數[16]。為了更加準確地模擬空間失重過程，構造式（4）說明骨重建速率與時間的相關性。
 |
式中 B0 = 0.008，與臥床實驗模擬重建率一致，a 的大小能夠控制重建速率的變化速度，分別取為 0.02、0.04、0.06 和 0.08，模擬失重環境下 90 天骨重建的過程，并與 a = 0 即 B = 0.008 時的骨丟失結果對比。
2 結果
2.1 臥床實驗仿真結果
臥床前，股骨近端模型總質量為 154.74 g，模擬臥床實驗 45 天后模型總質量減少至 146.99 g，即臥床結束后骨量丟失了 5%。45 天臥床實驗結束后，志愿者髖關節骨量平均減少 5.4%，模擬結果與實驗數據相近，說明重建參數設定合理。
2.2 空間失重仿真結果
2.2.1 關于時間的骨重建速率函數的確定
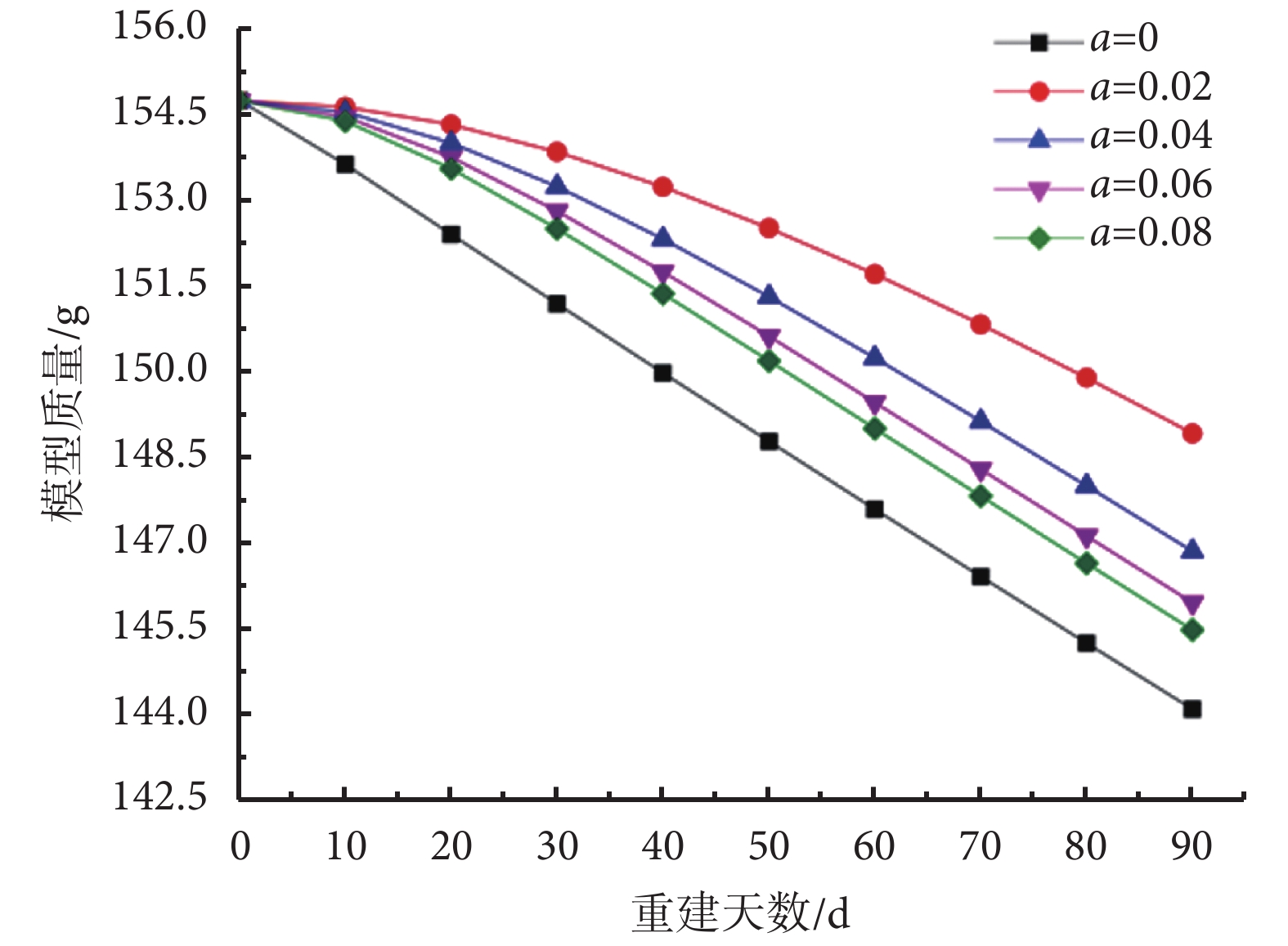
由圖 3 知，當 a 大于 0 時，隨著指數函數中 a 的增大，骨量丟失速度增快。當 a = 0.04 時，失重 20 天至失重 30 天內的骨丟失速率為失重第一個 10 天的 2.52 倍。失重后第 80 天至第 90 天骨量的丟失約為失重第一個 10 天的 5.43 倍。NASA 的研究發現，失重 20 天時的每日鈣丟失量約為失重 10 天時的 2.5 倍，失重 84 天后每日鈣丟失量約為失重 10 天時的 5 倍[15]。因此認為 a = 0.04 時的骨丟失狀況與飛行時的鈣丟失變化基本一致，后續空間失重模擬中重建速率函數取為 B = 0.008（1 — e –0.04t）。
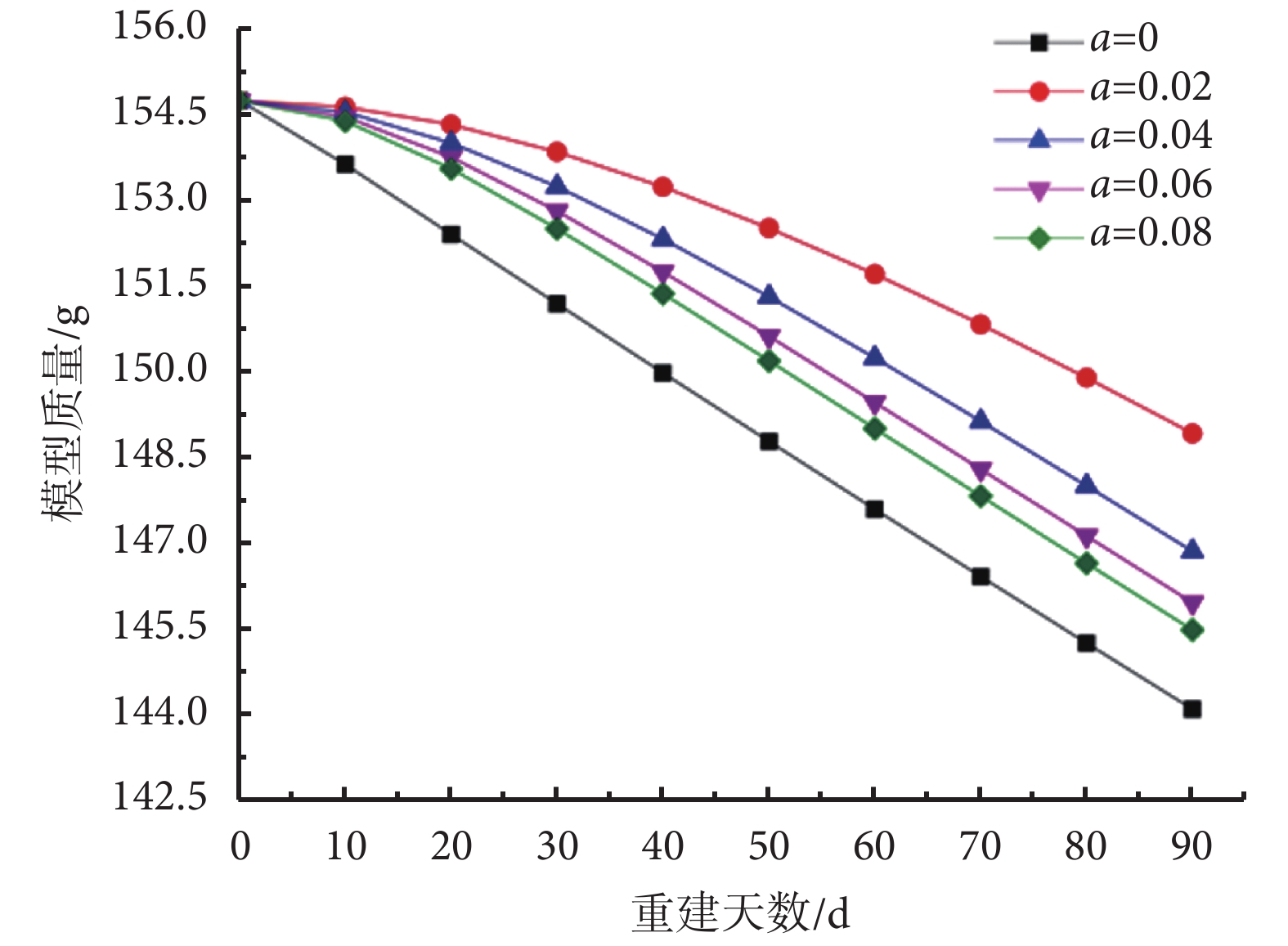圖3
不同重建速率函數下股骨近端模型質量的變化
Figure3.
Variation of proximal femur model mass with different remodeling rate equation
2.2.2 180 天空間失重骨丟失仿真結果
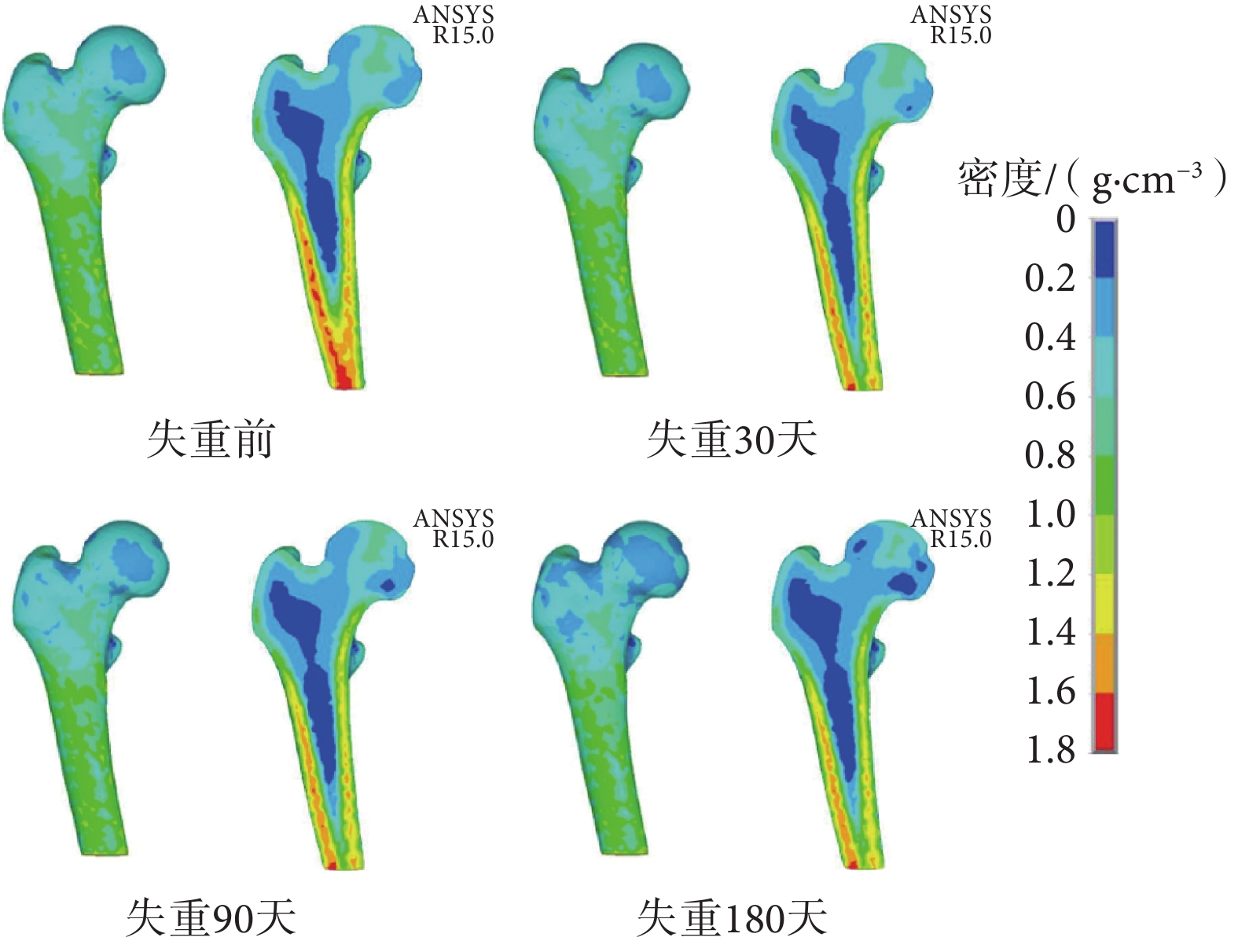
采用重建速率 B = 0.008（1 — e –0.04t），模擬空間失重下股骨近端的重建過程（見圖 4）。模型總質量在失重 30、90、180 天后分別減少至 151.18、144.10、134.37 g，平均每月丟失率為 2.19%。根據文獻[6, 17]中空間飛行時航天員鈣含量變化的測定結果，股骨近端每月骨丟失量為 1%～2%。仿真結果與航天員實際骨丟失情況基本一致。
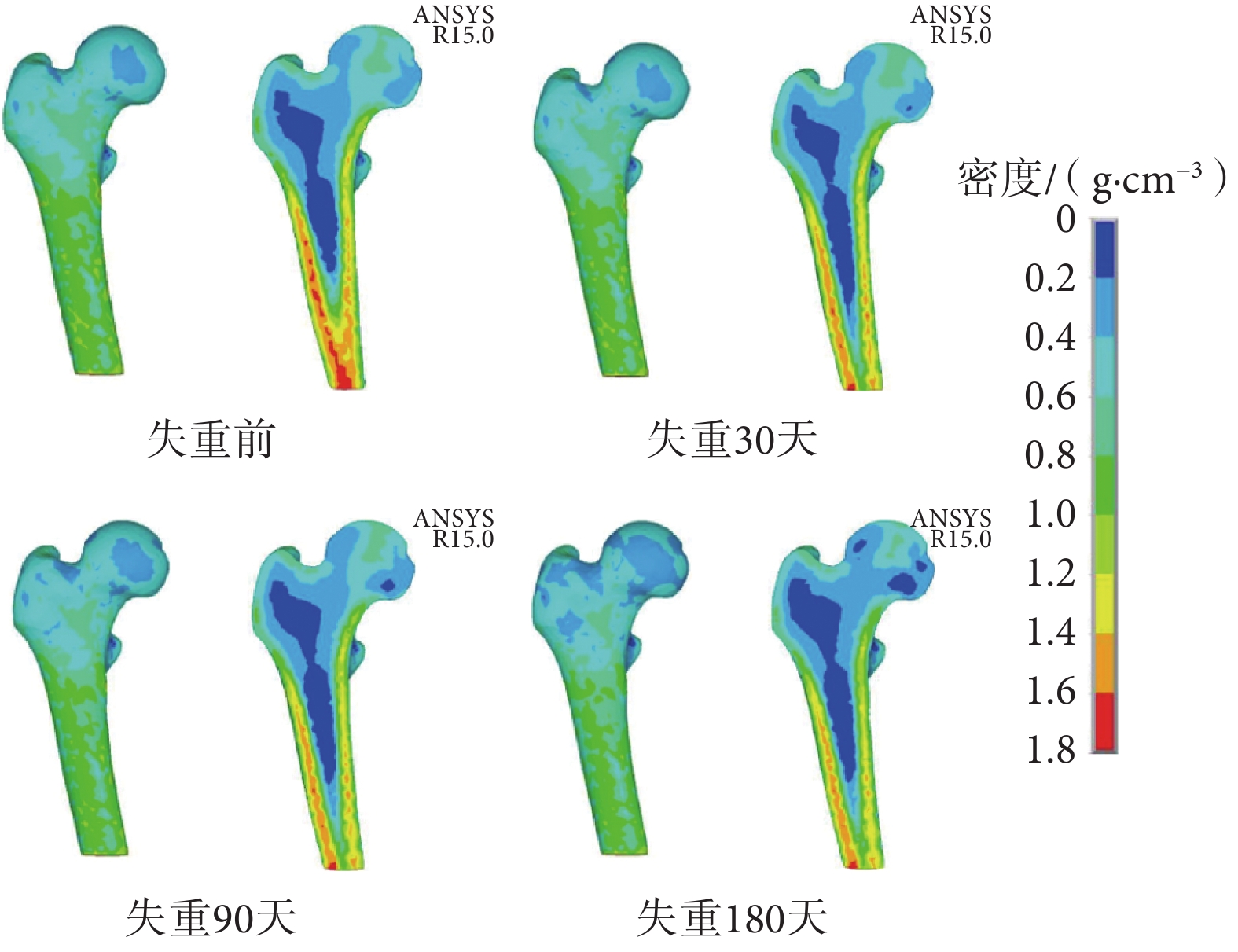圖4
空間失重條件下股骨近端重建密度分布圖
Figure4.
Density distribution of proximal femur remodeling results in space weightless environment
2.2.3 空間失重條件下改變載荷循環次數和載荷大小對重建結果的影響
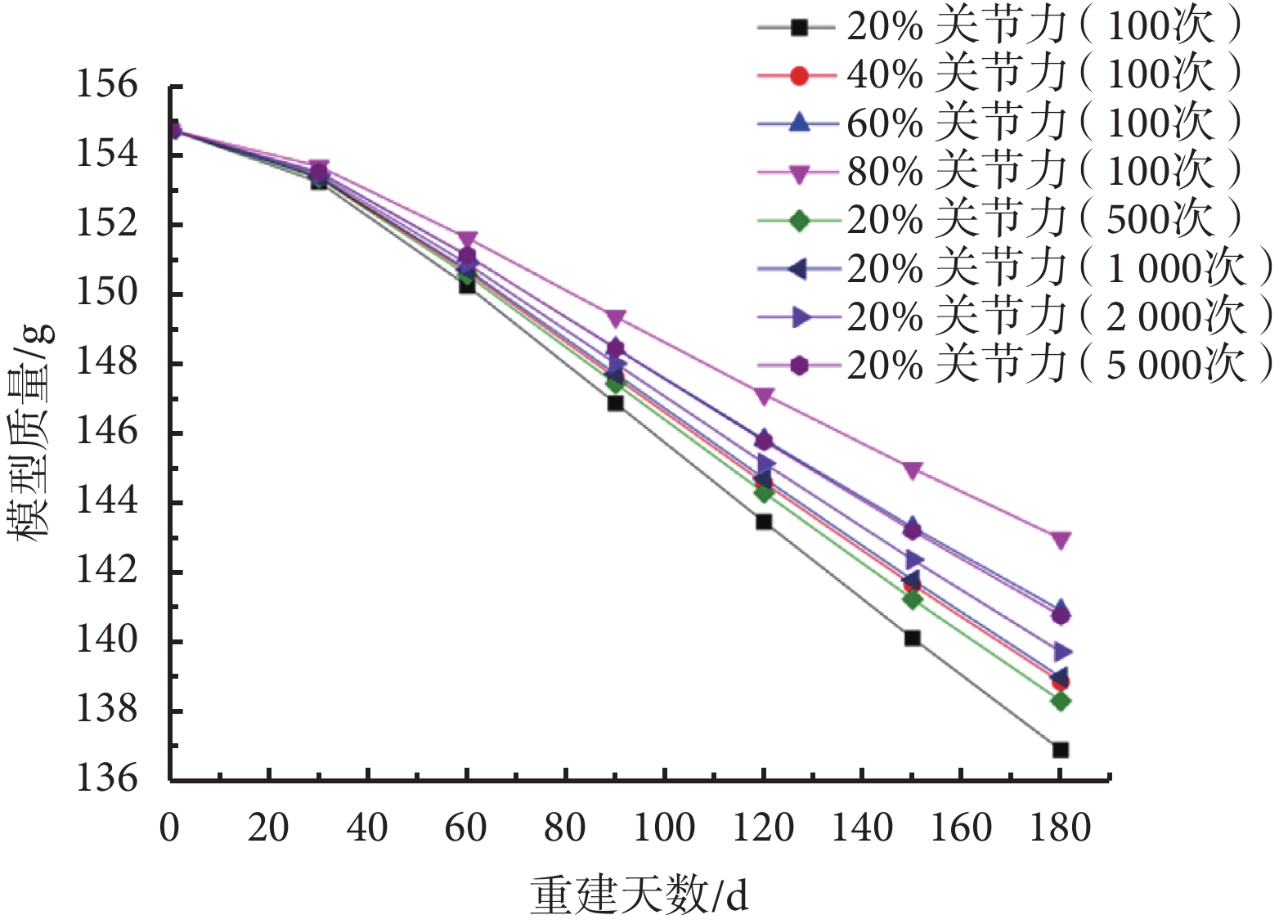
空間飛行期間，航天員會通過跑步等阻力鍛煉模仿重力效應，增加骨骼受載以減少骨丟失。分別調整空間失重時的載荷大小和載荷循環次數，探討兩種方式對于減小骨丟失的影響。由圖 5 可知，當每日載荷循環數分別增加為原循環數（100 次）的 5、10、20、50 倍時，與原循環數（100 次）下的骨丟失量相比，分別減少了 0.92%、1.36%、1.83%、2.5%。當股骨所受關節力分別為地面正常值的 20%、60%、80% 時，與 20% 關節力下相比骨量丟失分別減少了 1.32%、2.66%、4.00%。
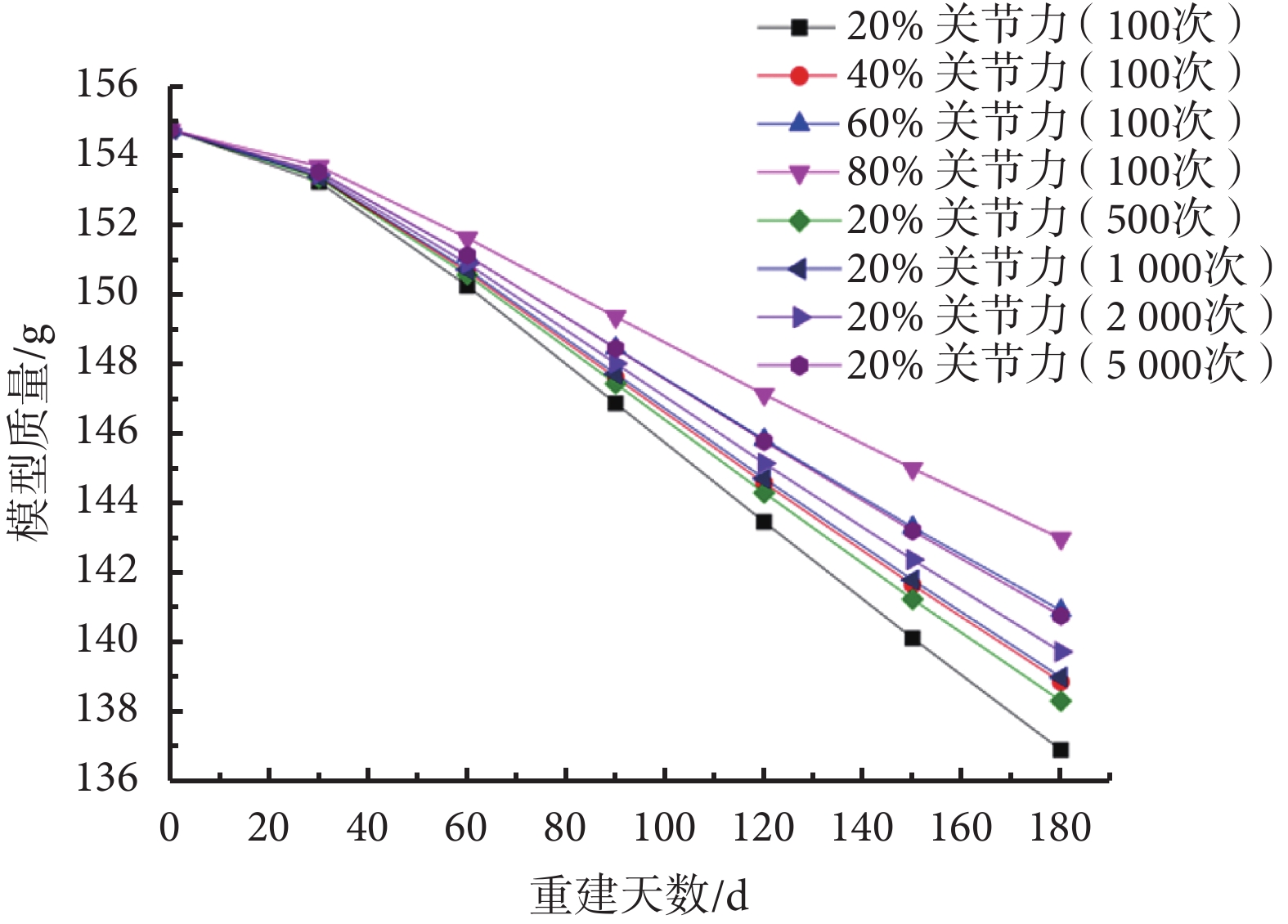圖5
失重條件下增大載荷大小和每日載荷循環數的模型質量
Figure5.
Model mass in weightless condition after increasing loading magnitude and loading cycle
2.2.4 空間失重后的骨量恢復模擬
相關研究顯示，航天員完成 4～6 個月的空間飛行任務回到地球后，需要 1～3 年甚至更長時間骨骼密度才能恢復，并且無法完全恢復至失重前的骨量[17]。若重建速率仍然取 B = 0.008（1 — e –0.04t），恢復載荷 90 天后，模型質量分別恢復到初始質量的 98.13%。這表明恢復載荷為正常值時，三個月內骨量幾乎恢復至原始骨量，與實際情況不符。
因此，減小重建速率至 B = 0.001（1 — e –0.04t），恢復正常載荷后第 360 天時模型質量恢復至初始質量的 95.08%（見圖 6），與文獻[18]相符。這表明骨丟失速率大于骨形成速率，在模擬仿真時，具體部位的骨丟失和骨形成速率需要根據實際情況作出調整，針對空間失重和臥床實驗時骨密度變化的后續研究可以就此問題展開進一步討論。
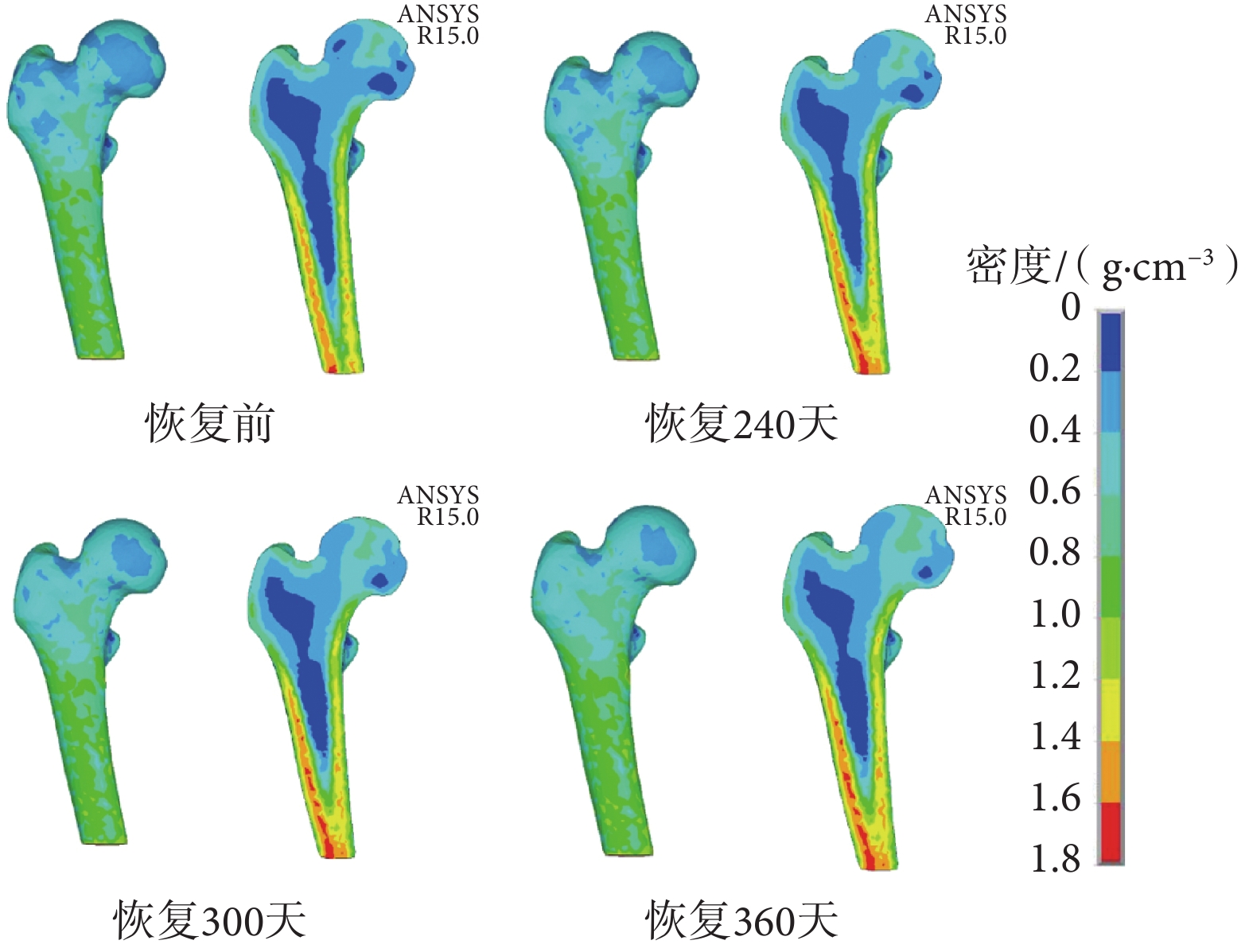圖6
B = 0.001（1 – e–0.04t）恢復正常載荷股骨的密度分布
Figure6.
Density distributions of proximal femur when loading conditions are normal at B = 0.001 (1 – e–0.04t )
3 討論
本文建立了股骨近端三維有限元模型，確定了股骨近端重建死區寬度為 0.1，與 Sarikanat[16]的研究結果一致。圖 1 中死區寬度
= 0.1 時，日常載荷下重建 100 天的密度分布與相關股骨近端重建結果一致[16, 19]，臥床 45 天后密度分布的仿真結果與實驗結果一致，證明了本文重建方法和重建參數設定的正確性。本文確認了空間失重下股骨的重建速率函數為 B = 0.008（1 — e –0.04t）。仿真結果表明，增大關節力大小相比增大每日載荷循環數，更能有效減少骨量丟失。因此，建議航天員在空間飛行時選擇增大每次阻力訓練強度來增大力學刺激，減少骨量丟失。
骨重建過程中，不同區域的密度變化趨勢也不一樣。空間失重過程中，大轉子和股骨頸和股骨頭下側區域密度明顯減小，形成了低密度骨區域，而股骨干皮質骨部分密度減小幅度不大，皮質骨厚度變化也不大（如圖 4 所示）。骨量恢復過程中，大轉子和股骨頸和股骨頭下側區域密度逐漸增大，低密度骨區域面積減小，但與失重前正常密度相比，股骨頭下側區域仍存在低密度區域。可以推測骨重建對于皮質骨和松質骨的影響是不同的，松質骨受骨重建的影響更明顯。Tsouknidas 等[20]發現了股骨密度與材料強度存在明顯的相關性，骨骼密度的大小能夠在一定程度上反映骨折風險。骨量恢復后，股骨頭下側區域仍存在低密度區域，對于經歷過大量骨量丟失的人而言，即使通過鍛煉增加了骨骼密度，也需要評估骨折風險。
本文為航天員阻力鍛煉方法及后期恢復訓練提供了理論依據。由于骨重建速率受到如個體差異、力學環境等因素的影響，因此在為航天員規劃抗骨丟失方案時，需要根據更細致的臨床生理數據和具體的重建參數，定制個性化方案。本文建立的研究方法可以用于評估骨骼在所處應力環境改變時的生長規律，為進行關節置換或植入骨內釘后骨骼的骨折風險評估提供參考。在加載方面，本文未考慮韌帶拉力作用，加載條件基于日常載荷作出了簡化，為了得到更準確的研究結果，可考慮施加更貼近真實情況的邊界條件以及載荷。在材料方面，為了簡化計算，本文認為骨骼材料為各向同性，而真實骨骼由于骨小梁的結構特殊性，實際上是各向異性的，后續研究可以賦予松質骨正交異性的材料屬性，重點探究骨重建對于松質骨的影響。
引言
人體骨骼是一種自適應最優化材料，當所處的力學環境發生變化時，骨骼的結構形態和材料屬性會發生相應的改變，這種調整過程被稱為骨重建。Frost 基于力學穩態理論建立的重建算法最受認可，影響也最廣泛。力學穩態理論認為，骨骼的形態和材料屬性處于動態平衡的狀態，只有當骨骼所處力學環境發生改變，受到的力學激勵超出穩態值時，才會發生骨重建，造成骨吸收或沉淀[1]。
當人體處于空間失重的條件下時，人體所受的力學激勵減小，可能會引發骨吸收。相關研究發現，長時間的空間飛行導致骨丟失，骨丟失量并非隨時間線性增加，上肢沒有觀察到骨量丟失，而下肢的跟骨出現明顯的骨量丟失[2-5]。和平空間站測量了航天員的骨量丟失情況，發現不同骨骼部位骨丟失的情況不一樣[6]，下肢骨量出現了明顯骨丟失。因此本文選擇股骨近端作為空間失重下骨量丟失模擬仿真的研究對象。臥床實驗中骨骼的受力減小，能一定程度上模擬空間失重環境，為空間失重的骨丟失情況提供參考數據[7]，因此本文參考臥床實驗結果對空間失重重建參數作出討論。
為了研究空間失重條件下骨骼密度和質量的變化趨勢，探索減小失重環境下骨量丟失的方法，建立了人體股骨近端的三維模型，通過對比臥床仿真結果與實驗結果，對比空間失重仿真結果與相關文獻結果，驗證重建參數的正確性。對比增大載荷大小和增大載荷循環次數這兩種方法對減小骨量丟失的效果，為航天員空間飛行阻力鍛煉提供理論依據。最后，對失重后的股骨進行骨量恢復仿真。
1 材料與方法
1.1 45 天頭低位臥床實驗
采用 45 天 —6° 頭低位臥床實驗模擬人體處于長期失重環境下的生理效應，共 30 名志愿者參與了此次臥床實驗。30 名志愿者為男性，年齡 25～40 歲，身高 165～175 cm，體重 55～75 kg。使用 DEXA 雙能骨密度測量儀，對臥床期間志愿者的腰椎和髖關節進行骨密度檢測。臥床實驗數據表明，志愿者腰椎骨密度隨臥床時間逐漸降低，并從臥床 30 天后出現顯著降低，臥床 45 天后，腰椎骨密度減少 6.7% ± 1.24%。類似地，志愿者髖關節骨密度隨臥床時間逐漸降低，并在臥床第 30 天達到最低值，臥床 45 天后，髖關節骨密度減少 5.4% ± 1.45%。本臥床試驗得到中國航天員科研訓練中心倫理委員會批準。
1.2 重建控制方程
骨重建計算方法基于 Huikes 的“死區”理論[8]，選擇等效應力作為力學激勵[9]。重建控制方程為：
|
|
|
式中，
是表觀密度（單位為g·cm–3），t 是時間（任意時間單位），φ 是每日等效應力刺激（單位為 MPa），其中 N 為載荷工況的總數，nj 為第 j 種載荷每日循環數，m 為權重系數，
是等效應力，k 是穩態參考值，
是死區寬度，B 是重建速率。骨的單元密度值通過前進歐拉法
得到。
1.3 三維模型的建立
用計算機斷層成像（computed tomography，CT）對一名 28 歲健康男性志愿者的下肢進行掃描，以 DICOM 文件格式輸出到 Mimics 軟件，建立三維模型。將導入 Mimics 的圖片通過閾值分割獲取股骨清晰輪廓，生成股骨三維模型的模板，然后，將股骨三維模型以 STL 格式輸出導入到 Geomagic Studio 軟件進行優化，生成股骨曲面模型。將股骨三維模型以 IGES 格式輸出并導入至 ANSYS。在 ANSYS 中對模型進行網格劃分，采用四面體 Solid92 單元進行自由網格劃分，得到股骨近端三維有限元模型。本文假設骨單元為各向同性材料，骨密度與彈性模量之間的關系由函數式 E = 3 790 ρ3 確定[10]，上式中彈性模量的單位為 MPa，密度單位為 g·cm-3。
在進行臥床和空間失重的重建模擬前，需要獲得正常的股骨密度分布。把 ANSYS 中劃分好網格的模型導回至 Mimics，在 Mimics 的有限元分析（finite element analysis，FEA）模塊中，根據灰度值大小換算得到每個單元的骨密度并賦值給有限元模型。本文采用的灰度值與密度關系式為 ρ = 1.086 × 10–3 × 灰度值 + 0.075，泊松比設為 0.3，分 400 級自動定義密度。將賦值后的模型導出為 ANSYS 的 preprocessor 文件，再在 ANSYS 中讀入即可進行后續的加載求解。
1.4 初始參數設定
在進行臥床實驗的重建模擬前，需要確定股骨模型的網格大小和重建死區寬度。為股骨模型賦初始密度值后，通過控制方程模擬 100 天的骨重建過程，分別用 5、6、7、8 mm 的有限元單元邊長劃分網格。重建 100 次后，每兩次計算結果相差分別為 2.63%、20.26%、13.58%，可以認為當單元邊長不大于 6 mm 時，網格尺寸對于重建計算結果影響不大。為了提高運算速度，在以后的計算中一律選擇 6 mm 的單元劃分網格。
表 1 列出了臥床實驗模擬參數初始值的設置，討論網格大小時，死區寬度固定在 0.1，討論死區寬度時，網格大小固定在 6 mm，其余初始參數相同。
表1
三維股骨重建模擬參數初始值
Table1.
Initial values used in numerical simulation of three-dimensional femur remodeling
分別改變死區寬度為 0、0.1、0.3、0.5、0.7，其余參數不變，觀察 100 天后的重建情況。發現只有
= 0.1 時的密度分布與實際股骨密度分布相符（見圖 1）。因此在以后的計算中一律選擇死區寬度為 0.1。
圖1
不同死區寬度下股骨近端重建 100 天后密度分布圖
Figure1.
Density distributions under different ω after a 100-day simulation of proximal femur bone remodeling
1.5 臥床實驗模擬加載
基于 1.4 節得到的死區寬度和網格大小，設定重建速率為 B = 0.008，其余初始參數與表 1 相同，模擬臥床 45 天股骨近端的重建過程。選用通過 Mimics 賦值得到的股骨三維模型作為臥床重建的初始模型，對初始模型加載正常步態載荷，計算重建的穩態參考值 k。由于臥床實驗中的志愿者股骨處于無負重狀態，因此對股骨模型不加關節力或肌肉力，只施加穩態慣性力模擬重力。
1.6 空間失重模擬加載
在以往的骨重建研究中，施加在股骨模型上的載荷大多簡化為作用在股骨頭上的關節力和作用在大轉子上的肌肉合力[11-12]。為了更真實地模擬股骨所處的力學環境，本文參考了文獻[13]里各個肌肉力作用在股骨上的面積，考慮了關節力和 7 種肌肉力[14]。圖 2 是空間失重加載示意圖。
圖2
空間失重邊界條件和加載示意圖
Figure2.
Boundary conditions and loading areas for space flight simulation
表 2 列出了關節力與各肌肉力的大小與在全局坐標系下的位置。航天員在空間失重條件下所受關節力大幅減小，肌肉力也相應減弱。由文獻知，–6° 頭低位臥床實驗過程中，下肢肌肉力大小下降 41%～60%[15]，因此在空間失重模擬加載中，只對股骨加載 45% 步態周期時的峰值載荷，其中關節力減小至地面正常值的 20%，肌肉力減小至正常值的 60%。由于航天員在失重環境下活動量顯著減少，因此載荷每日循環數 n 設為 100。
表2
股骨近端模型的正態步態載荷值
Table2.
Loading conditions in three stages during gait cycles of proximal femur
相關研究表明，空間失重前期，重建速率逐漸變快，后期的重建速率基本穩定[5]。事實上，重建率是一個時間相關函數[16]。為了更加準確地模擬空間失重過程，構造式（4）說明骨重建速率與時間的相關性。
|
式中 B0 = 0.008，與臥床實驗模擬重建率一致，a 的大小能夠控制重建速率的變化速度，分別取為 0.02、0.04、0.06 和 0.08，模擬失重環境下 90 天骨重建的過程，并與 a = 0 即 B = 0.008 時的骨丟失結果對比。
2 結果
2.1 臥床實驗仿真結果
臥床前，股骨近端模型總質量為 154.74 g，模擬臥床實驗 45 天后模型總質量減少至 146.99 g，即臥床結束后骨量丟失了 5%。45 天臥床實驗結束后，志愿者髖關節骨量平均減少 5.4%，模擬結果與實驗數據相近，說明重建參數設定合理。
2.2 空間失重仿真結果
2.2.1 關于時間的骨重建速率函數的確定
由圖 3 知，當 a 大于 0 時，隨著指數函數中 a 的增大，骨量丟失速度增快。當 a = 0.04 時，失重 20 天至失重 30 天內的骨丟失速率為失重第一個 10 天的 2.52 倍。失重后第 80 天至第 90 天骨量的丟失約為失重第一個 10 天的 5.43 倍。NASA 的研究發現，失重 20 天時的每日鈣丟失量約為失重 10 天時的 2.5 倍，失重 84 天后每日鈣丟失量約為失重 10 天時的 5 倍[15]。因此認為 a = 0.04 時的骨丟失狀況與飛行時的鈣丟失變化基本一致，后續空間失重模擬中重建速率函數取為 B = 0.008（1 — e –0.04t）。
圖3
不同重建速率函數下股骨近端模型質量的變化
Figure3.
Variation of proximal femur model mass with different remodeling rate equation
2.2.2 180 天空間失重骨丟失仿真結果
采用重建速率 B = 0.008（1 — e –0.04t），模擬空間失重下股骨近端的重建過程（見圖 4）。模型總質量在失重 30、90、180 天后分別減少至 151.18、144.10、134.37 g，平均每月丟失率為 2.19%。根據文獻[6, 17]中空間飛行時航天員鈣含量變化的測定結果，股骨近端每月骨丟失量為 1%～2%。仿真結果與航天員實際骨丟失情況基本一致。
圖4
空間失重條件下股骨近端重建密度分布圖
Figure4.
Density distribution of proximal femur remodeling results in space weightless environment
2.2.3 空間失重條件下改變載荷循環次數和載荷大小對重建結果的影響
空間飛行期間，航天員會通過跑步等阻力鍛煉模仿重力效應，增加骨骼受載以減少骨丟失。分別調整空間失重時的載荷大小和載荷循環次數，探討兩種方式對于減小骨丟失的影響。由圖 5 可知，當每日載荷循環數分別增加為原循環數（100 次）的 5、10、20、50 倍時，與原循環數（100 次）下的骨丟失量相比，分別減少了 0.92%、1.36%、1.83%、2.5%。當股骨所受關節力分別為地面正常值的 20%、60%、80% 時，與 20% 關節力下相比骨量丟失分別減少了 1.32%、2.66%、4.00%。
圖5
失重條件下增大載荷大小和每日載荷循環數的模型質量
Figure5.
Model mass in weightless condition after increasing loading magnitude and loading cycle
2.2.4 空間失重后的骨量恢復模擬
相關研究顯示，航天員完成 4～6 個月的空間飛行任務回到地球后，需要 1～3 年甚至更長時間骨骼密度才能恢復，并且無法完全恢復至失重前的骨量[17]。若重建速率仍然取 B = 0.008（1 — e –0.04t），恢復載荷 90 天后，模型質量分別恢復到初始質量的 98.13%。這表明恢復載荷為正常值時，三個月內骨量幾乎恢復至原始骨量，與實際情況不符。
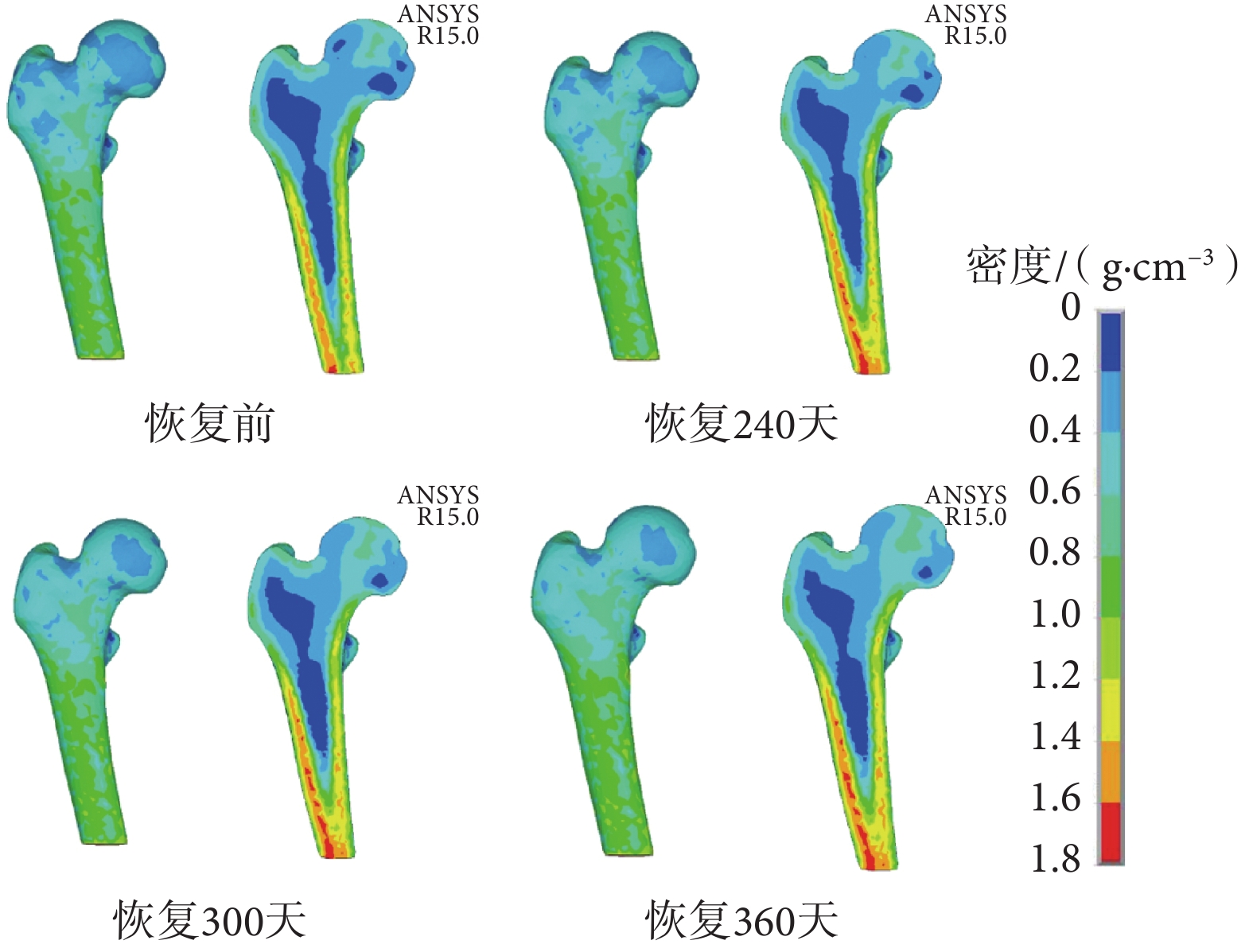
因此，減小重建速率至 B = 0.001（1 — e –0.04t），恢復正常載荷后第 360 天時模型質量恢復至初始質量的 95.08%（見圖 6），與文獻[18]相符。這表明骨丟失速率大于骨形成速率，在模擬仿真時，具體部位的骨丟失和骨形成速率需要根據實際情況作出調整，針對空間失重和臥床實驗時骨密度變化的后續研究可以就此問題展開進一步討論。
圖6
B = 0.001（1 – e–0.04t）恢復正常載荷股骨的密度分布
Figure6.
Density distributions of proximal femur when loading conditions are normal at B = 0.001 (1 – e–0.04t )
3 討論
本文建立了股骨近端三維有限元模型，確定了股骨近端重建死區寬度為 0.1，與 Sarikanat[16]的研究結果一致。圖 1 中死區寬度
= 0.1 時，日常載荷下重建 100 天的密度分布與相關股骨近端重建結果一致[16, 19]，臥床 45 天后密度分布的仿真結果與實驗結果一致，證明了本文重建方法和重建參數設定的正確性。本文確認了空間失重下股骨的重建速率函數為 B = 0.008（1 — e –0.04t）。仿真結果表明，增大關節力大小相比增大每日載荷循環數，更能有效減少骨量丟失。因此，建議航天員在空間飛行時選擇增大每次阻力訓練強度來增大力學刺激，減少骨量丟失。
骨重建過程中，不同區域的密度變化趨勢也不一樣。空間失重過程中，大轉子和股骨頸和股骨頭下側區域密度明顯減小，形成了低密度骨區域，而股骨干皮質骨部分密度減小幅度不大，皮質骨厚度變化也不大（如圖 4 所示）。骨量恢復過程中，大轉子和股骨頸和股骨頭下側區域密度逐漸增大，低密度骨區域面積減小，但與失重前正常密度相比，股骨頭下側區域仍存在低密度區域。可以推測骨重建對于皮質骨和松質骨的影響是不同的，松質骨受骨重建的影響更明顯。Tsouknidas 等[20]發現了股骨密度與材料強度存在明顯的相關性，骨骼密度的大小能夠在一定程度上反映骨折風險。骨量恢復后，股骨頭下側區域仍存在低密度區域，對于經歷過大量骨量丟失的人而言，即使通過鍛煉增加了骨骼密度，也需要評估骨折風險。
本文為航天員阻力鍛煉方法及后期恢復訓練提供了理論依據。由于骨重建速率受到如個體差異、力學環境等因素的影響，因此在為航天員規劃抗骨丟失方案時，需要根據更細致的臨床生理數據和具體的重建參數，定制個性化方案。本文建立的研究方法可以用于評估骨骼在所處應力環境改變時的生長規律，為進行關節置換或植入骨內釘后骨骼的骨折風險評估提供參考。在加載方面，本文未考慮韌帶拉力作用，加載條件基于日常載荷作出了簡化，為了得到更準確的研究結果，可考慮施加更貼近真實情況的邊界條件以及載荷。在材料方面，為了簡化計算，本文認為骨骼材料為各向同性，而真實骨骼由于骨小梁的結構特殊性，實際上是各向異性的，后續研究可以賦予松質骨正交異性的材料屬性，重點探究骨重建對于松質骨的影響。
