通過建立肘關節三維有限元模型,研究內側副韌帶維持肘關節穩定性的作用。本文基于正常人體肘關節計算機斷層掃描(CT)圖像數據,運用逆向工程方法建立肘關節三維幾何模型。在有限元前處理軟件中根據解剖學結構直接構建韌帶和關節面軟骨,并為模型賦予材料及接觸。通過將處于中立 0° 位的肘關節仿真與試驗數據對比,驗證了模型的有效性。繼而計算肘關節中立位分別屈曲 15、30、45、60、75、90、105、120、135° 時內側副韌帶的應力大小及分布。結果表明肘關節在不同屈曲角度受力時,內側副韌帶前束承受的應力最大,后束次之,斜束承受的應力最小,數值趨于 0。由此可以推斷,肘關節內側副韌帶在維持肘關節穩定方面,前束起主導作用,后束起輔助作用,斜束起的作用最小。本研究可為由內側副韌帶損傷所引起的肘關節不穩定的臨床治療提供理論依據。
引用本文: 潘奎, 王芳, 張建國, 李明新, 時培珍, 曹子君, 周勁松. 不同屈曲狀態下肘關節內側副韌帶生物力學的有限元分析. 生物醫學工程學雜志, 2019, 36(3): 401-406. doi: 10.7507/1001-5515.201709018 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
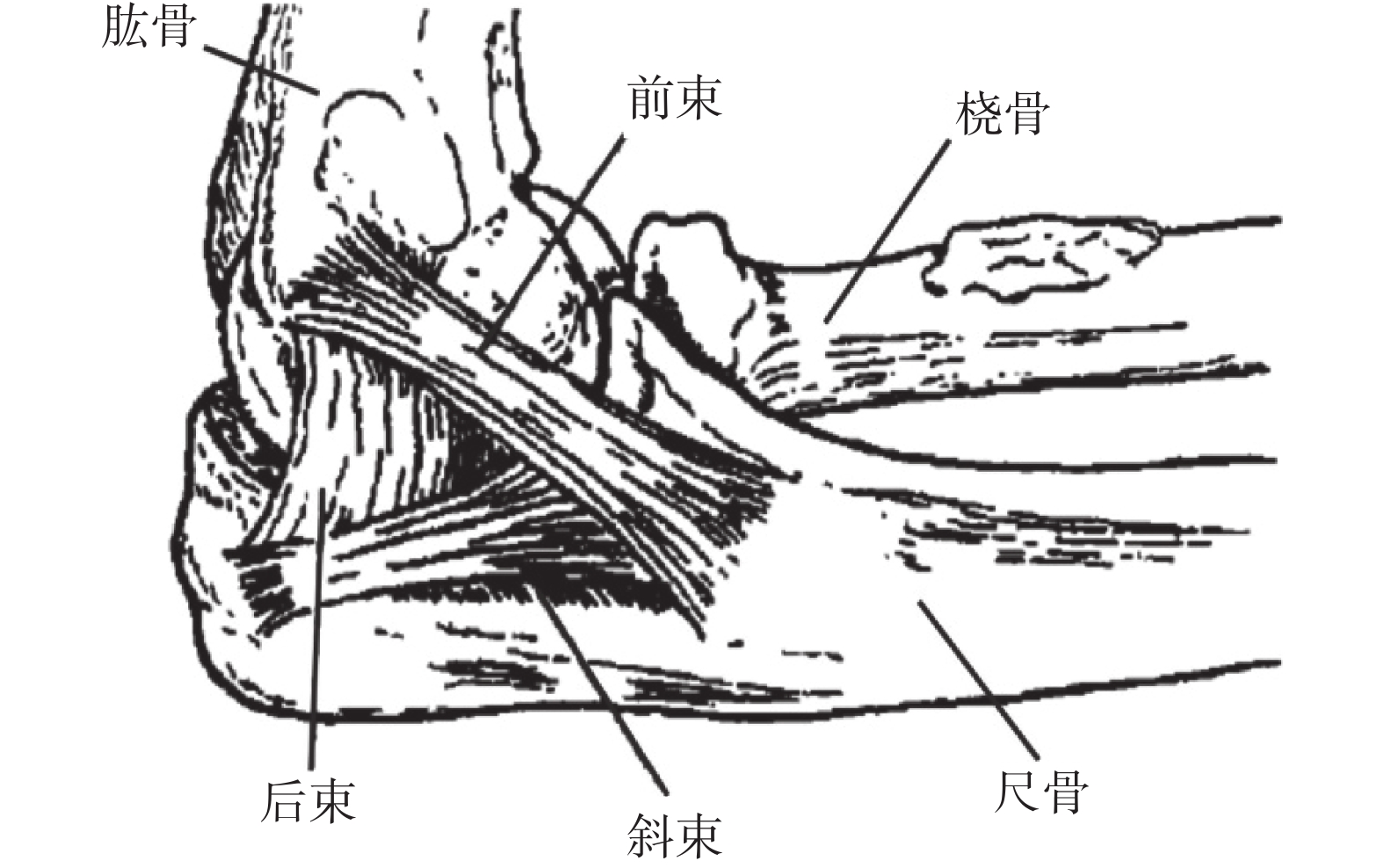
肘關節是人體內對合最好的關節之一,是由肱骨下端和尺骨、橈骨上端構成,包括三個關節,即肱尺關節、肱橈關節和橈尺近側關節(如圖 1 所示),作為肩關節和腕關節的聯結,在上肢功能中起著重要作用,不僅可以擴展手部的活動范圍,而且可以為手部運動提供動力、準確性和穩定性[1]。近年來,因人口老齡化、日常活動及創傷等導致的肘關節功能障礙在臨床上很常見,而我國肘關節領域的整體診斷水平在國際上較為落后,且治療理念不完善,導致其成為臨床治療中的一個難點[2]。肘關節出現功能障礙時常常伴有韌帶損傷,從而導致肘關節不穩定。肘關節內側副韌帶(medial collateral ligament,MCL)是維持肘關節內側穩定的基礎結構[3-4],也是最容易損傷的結構,因此,進一步了解內側副韌帶各部分在肘關節穩定性中的作用顯得尤為重要[5]。目前國內文獻對肘關節內側副韌帶方面的研究相對較少,且大部分集中于關節脫位、外翻、內翻、骨折等對肘關節穩定性的影響,而忽略了內側副韌帶在維持肘關節穩定中所起的作用,導致肘關節內側副韌帶損傷的漏診率較高,以致于相當部分患者得不到有效和及時的治療,進而出現肘關節失穩現象。為從組織層次對肘關節及其周圍韌帶進行生物力學分析,本文基于真實肘關節計算機斷層掃描(computed tomography,CT)圖片,重構了包括完整骨骼、肘關節、關節軟骨以及主要韌帶的人體肘關節三維有限元模型,利用有限元生物力學仿真,觀察肘關節屈曲不同角度時內側副韌帶各部位的應力大小,進而分析內側副韌帶各組成部分在維持肘關節穩定性中所起的作用,為韌帶損傷造成的肘關節屈曲不穩定的臨床診斷和治療提供生物力學理論基礎。
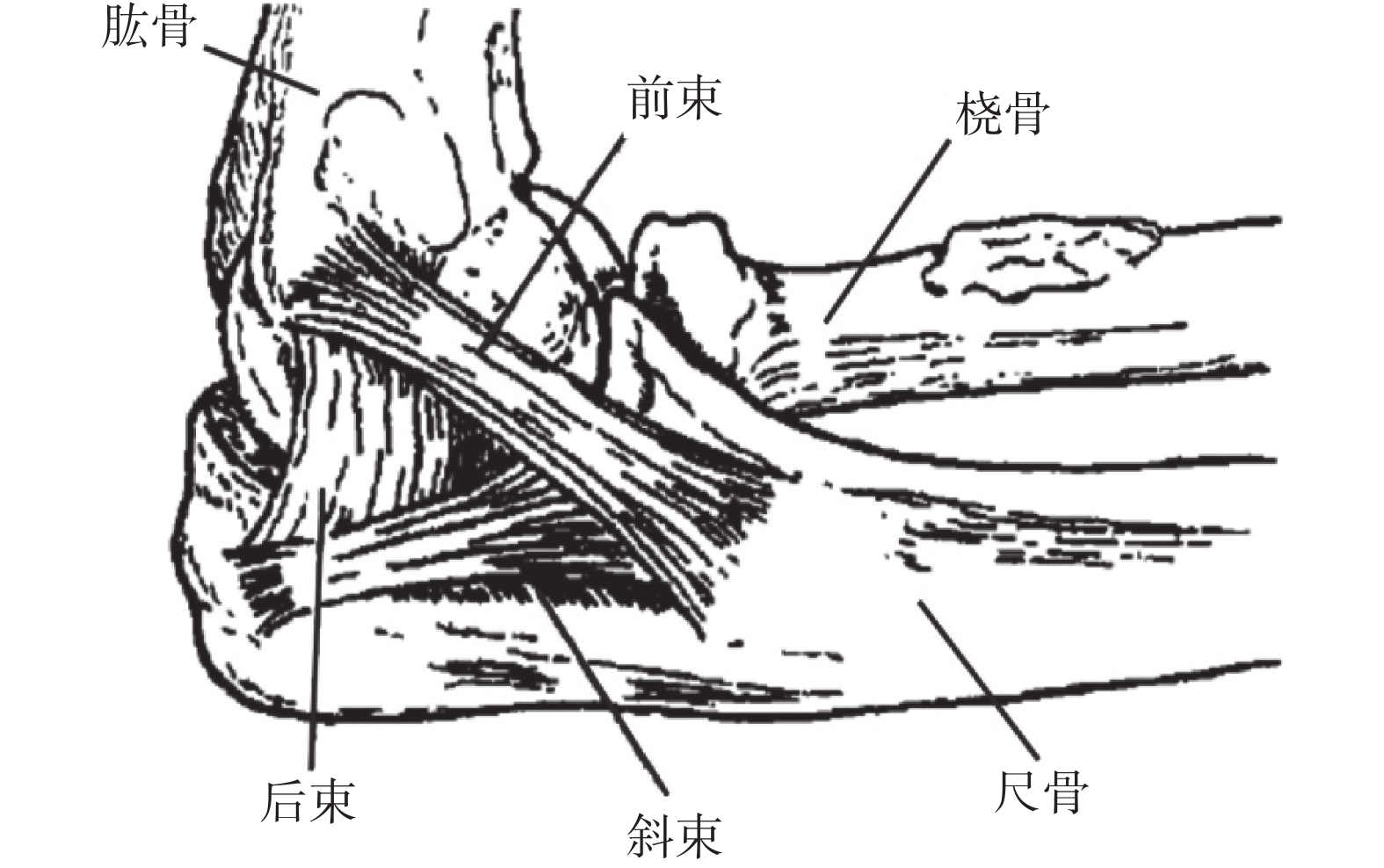 圖1
肘關節解剖示意圖
Figure1.
Anatomical diagram of elbow joint
圖1
肘關節解剖示意圖
Figure1.
Anatomical diagram of elbow joint
1 材料與方法
選擇一位健康中國男性作為測試對象,年齡 43 歲,身高 175 cm,體重 75 kg,無肘關節損傷及相關病史。志愿者自愿參加本次研究,并簽署了知情同意書。采用螺旋 CT 機對其中立 90° 位肘關節進行掃描,層厚為 1 mm,像素為 256 × 256。掃描范圍為左側肱骨遠端至尺、橈骨近端,共獲得 236 張圖像,以醫學數字成像和通信(Digital Imaging and Communications in Medicine,DICOM)格式存儲。
1.1 肘關節有限元模型建立
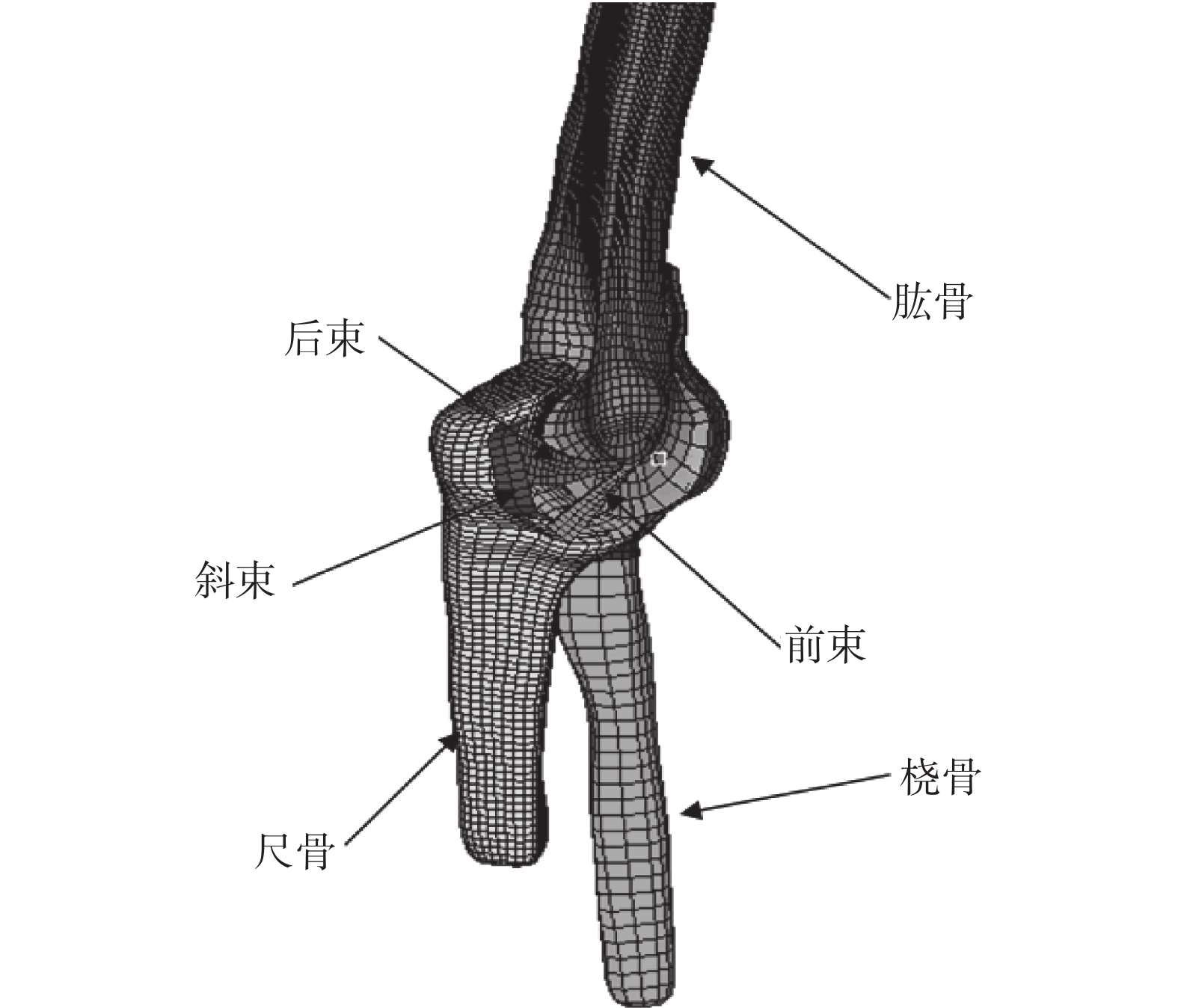
將志愿者 CT 數據以 DICOM 格式導入軟件 Mimics(Materialise Inc.,Leuven,比利時)中進行三維重建,運用區域增長分割等方法,建立包括肱骨遠端及尺、橈骨近端在內的肘關節三維幾何模型。初步提取的肘關節幾何模型表面較粗糙,運用逆向建模軟件 Geomagic(GeomagicInc.,NC,美國)對幾何模型進行光滑和封閉等處理。在有限元前處理軟件 Hypermesh(Altair Engineering Inc,美國)中對骨結構進行有限元網格劃分,并根據解剖學結構,利用直接建模的方法,構建內側副韌帶、關節面軟骨等組織,所有結構均采用八節點六面體單元進行模擬。各模型的相關參數如下:前臂中立位模型節點數 31 009,單元數 24 958,其中骨骼 23 461,關節面軟骨 905,韌帶 205。將模型中骨組織和關節面軟骨簡化為分布均勻且各向同性的均質性彈性體材料,不僅可以大大縮短建模周期,而且大量關于有限元分析的文獻結果證明,采用各向同性特性進行有限元分析也可以得到較準確的分析結果[6]。為更好地反映韌帶的生物力學響應,韌帶定義為超彈性材料,選用 Hypermesh 的 LS-DYNA(Livermore Software Technology Corporation,美國) 模塊下材料庫中的 MATL7。隨后對模型進行有限元網格劃分并建立有限元模型(見圖 2),并在 Hypermesh 中賦予模型材料、屬性、邊界條件、定義接觸等,最后在 LS-DYNA進行仿真計算。材料參數如表 1[7-10]所示。
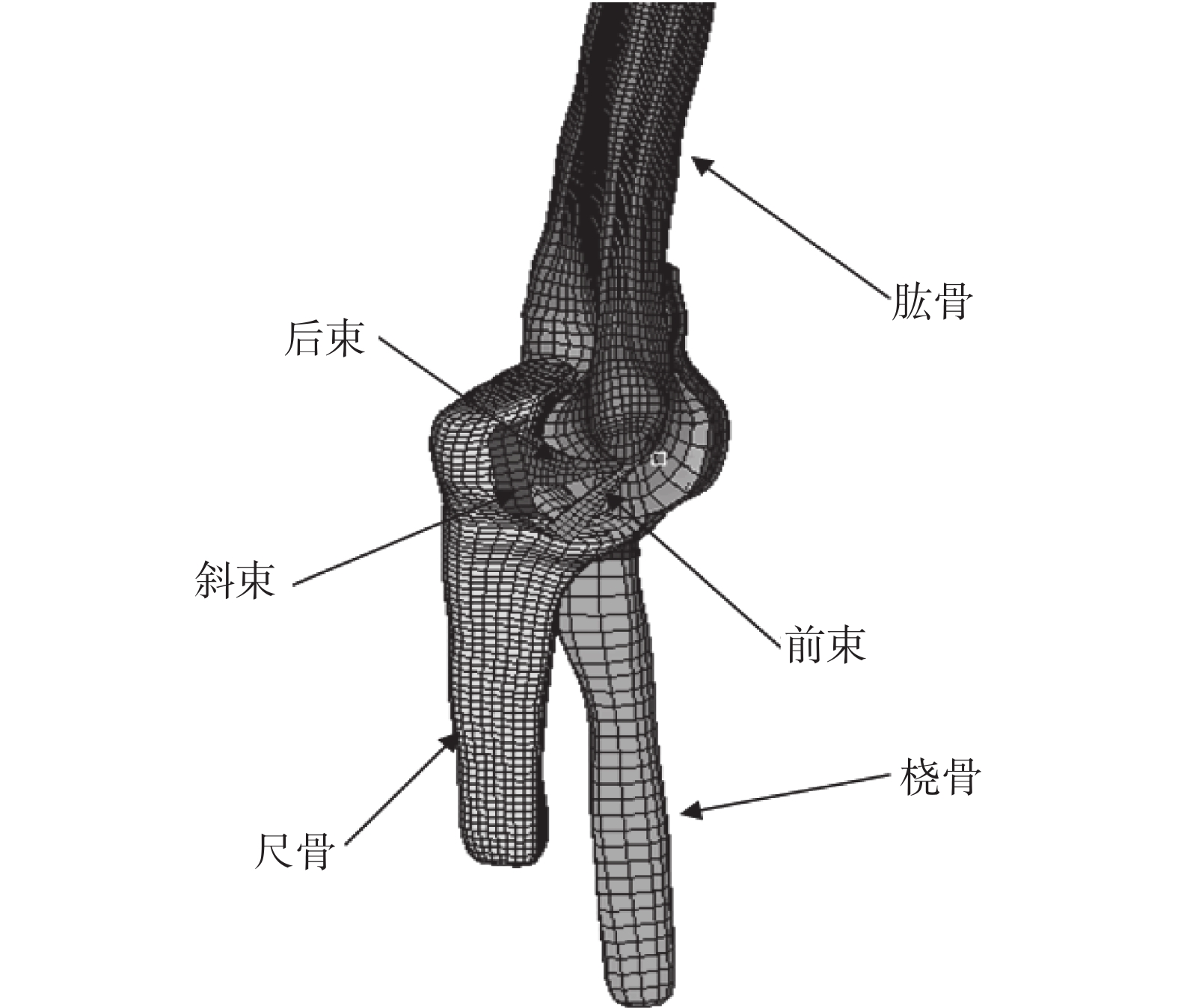 圖2
肘關節三維有限元模型
Figure2.
Three-dimensional finite element model of elbow joint
圖2
肘關節三維有限元模型
Figure2.
Three-dimensional finite element model of elbow joint
1.2 有限元模型有效性驗證
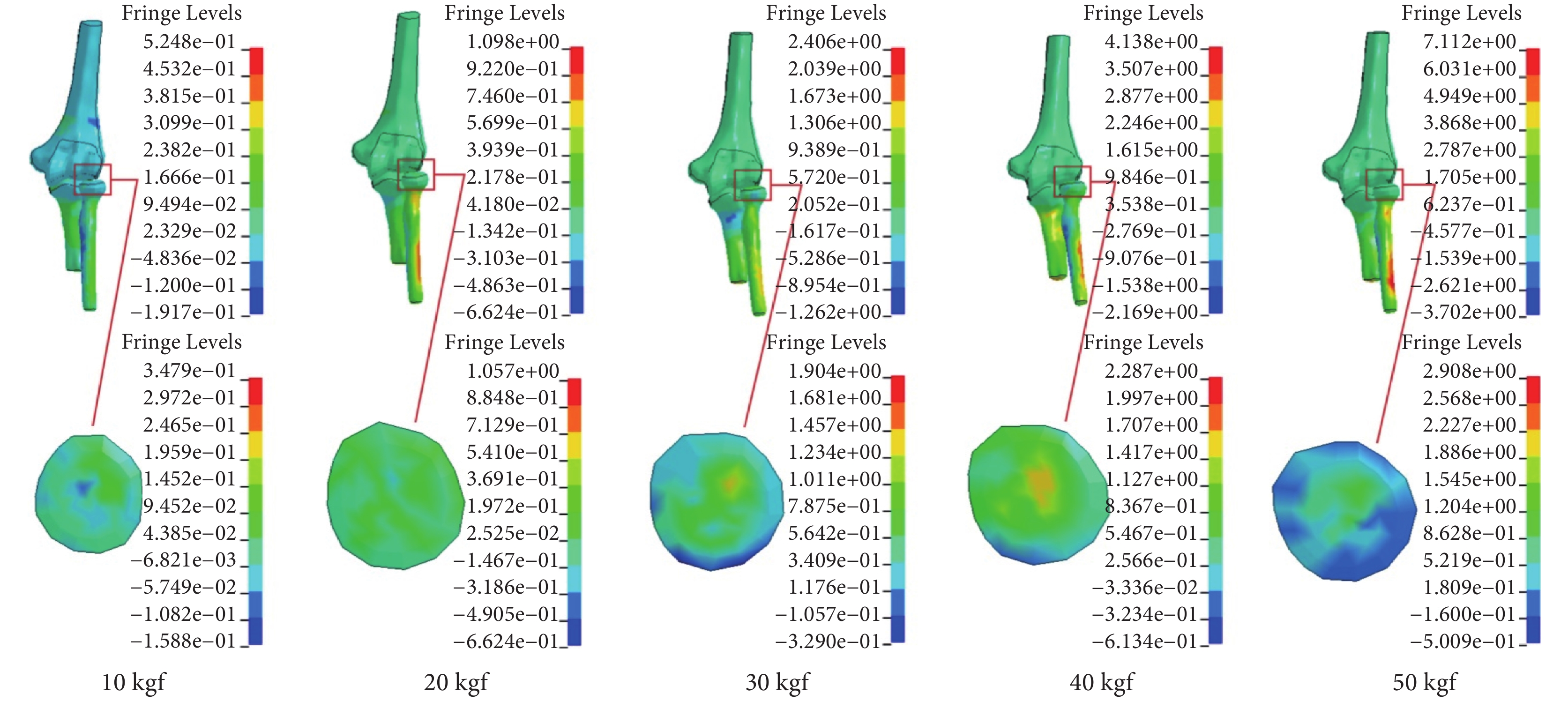
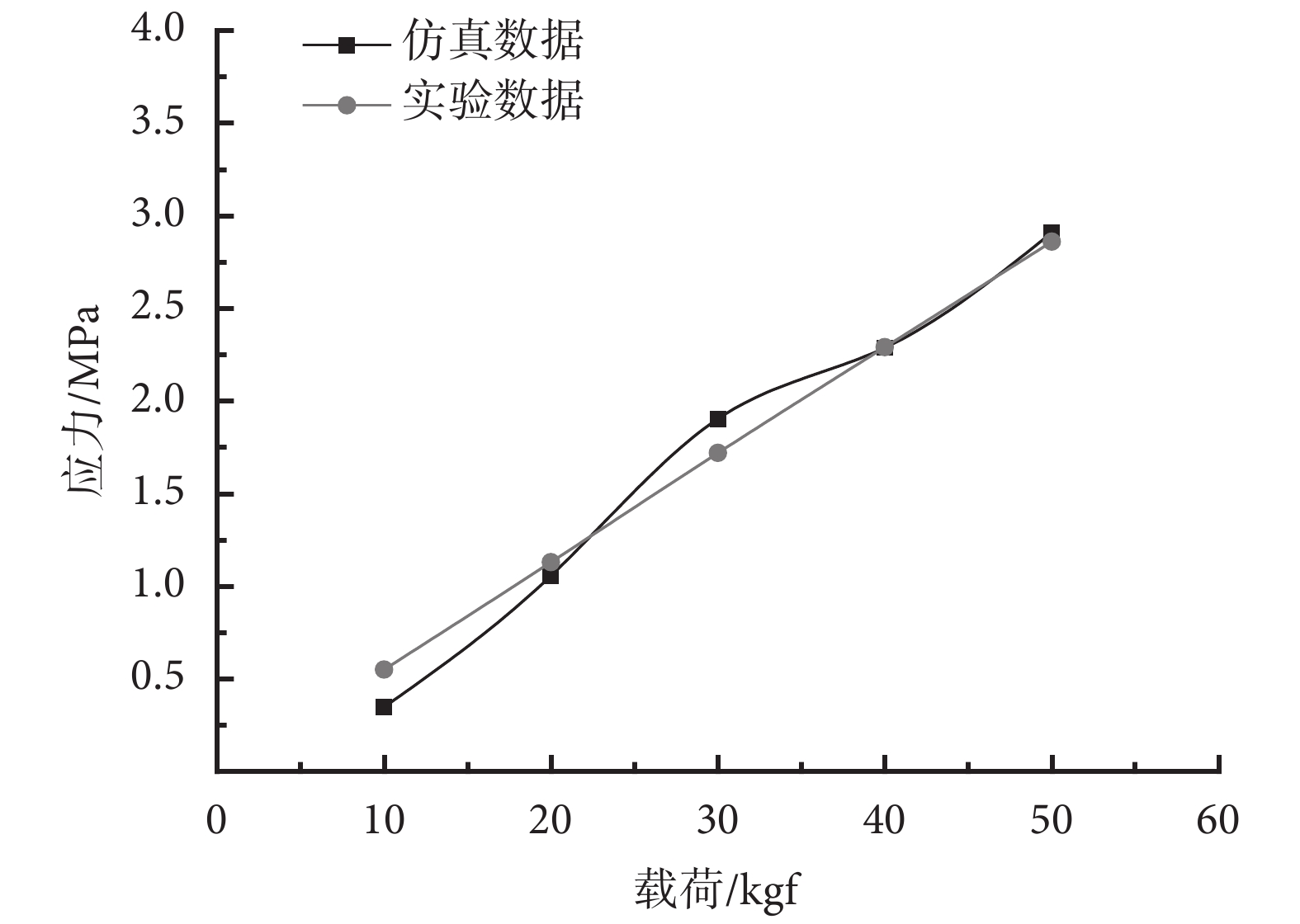
Takatori 等[7]開展了肘關節力學實驗,選取肘關節中立完全伸直位,將肱骨固定,在尺骨和橈骨截面處分別施加 98.06 N(10 kgf)、196.12 N(20 kgf)、294.18 N(30 kgf)、392.24 N(40 kgf)、490.3 N(50 kgf)的壓力,實驗記錄了不同載荷下肱橈關節所受的最大壓力。以此試驗數據定義有限元模型的邊界和載荷,仿真提取了橈骨頭關節面應力峰值數據,如圖 3 所示。由圖 4 可以發現,結果與實驗數據變化趨勢基本吻合,從而驗證了模型的有效性。
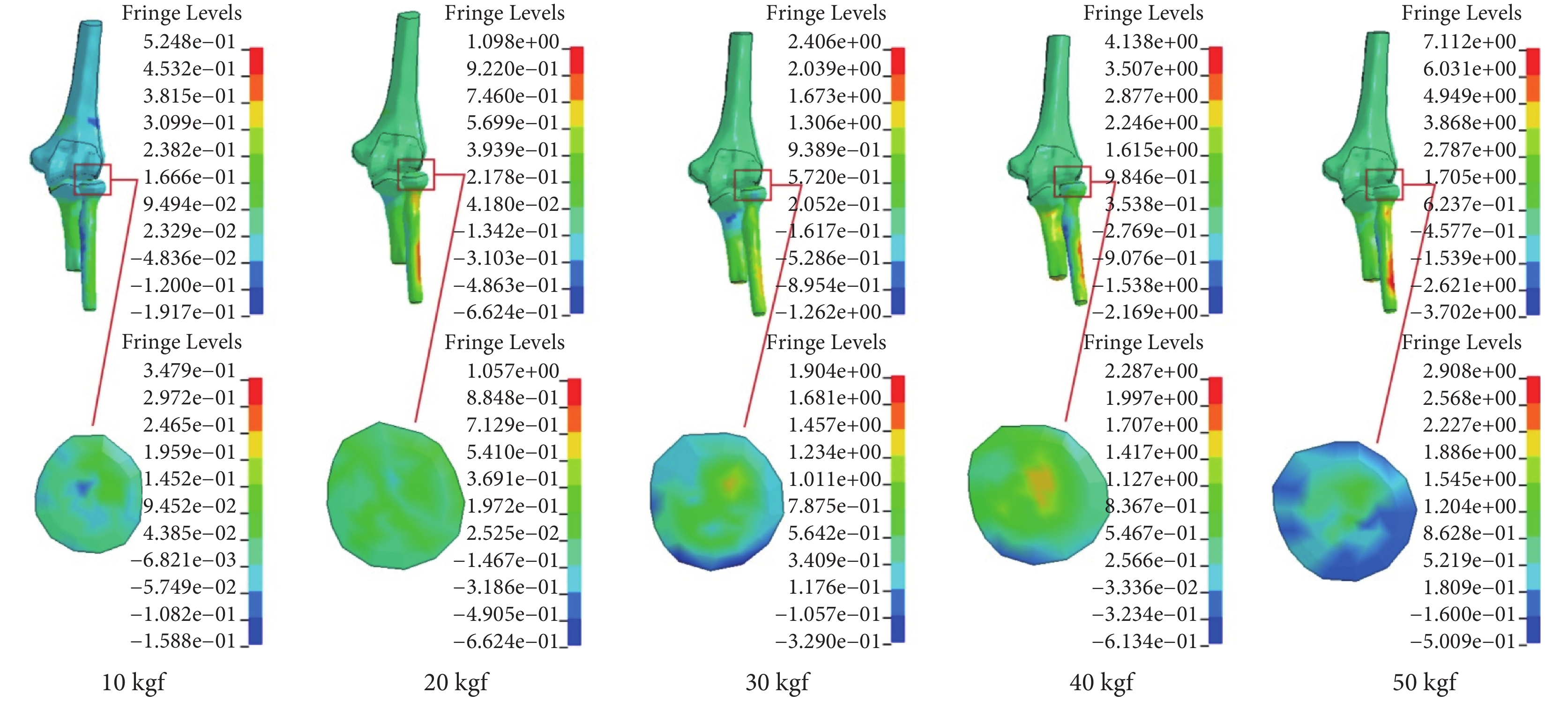 圖3
橈骨頭關節面應力分布
Figure3.
Stress distribution of the radial head articular surface
圖3
橈骨頭關節面應力分布
Figure3.
Stress distribution of the radial head articular surface
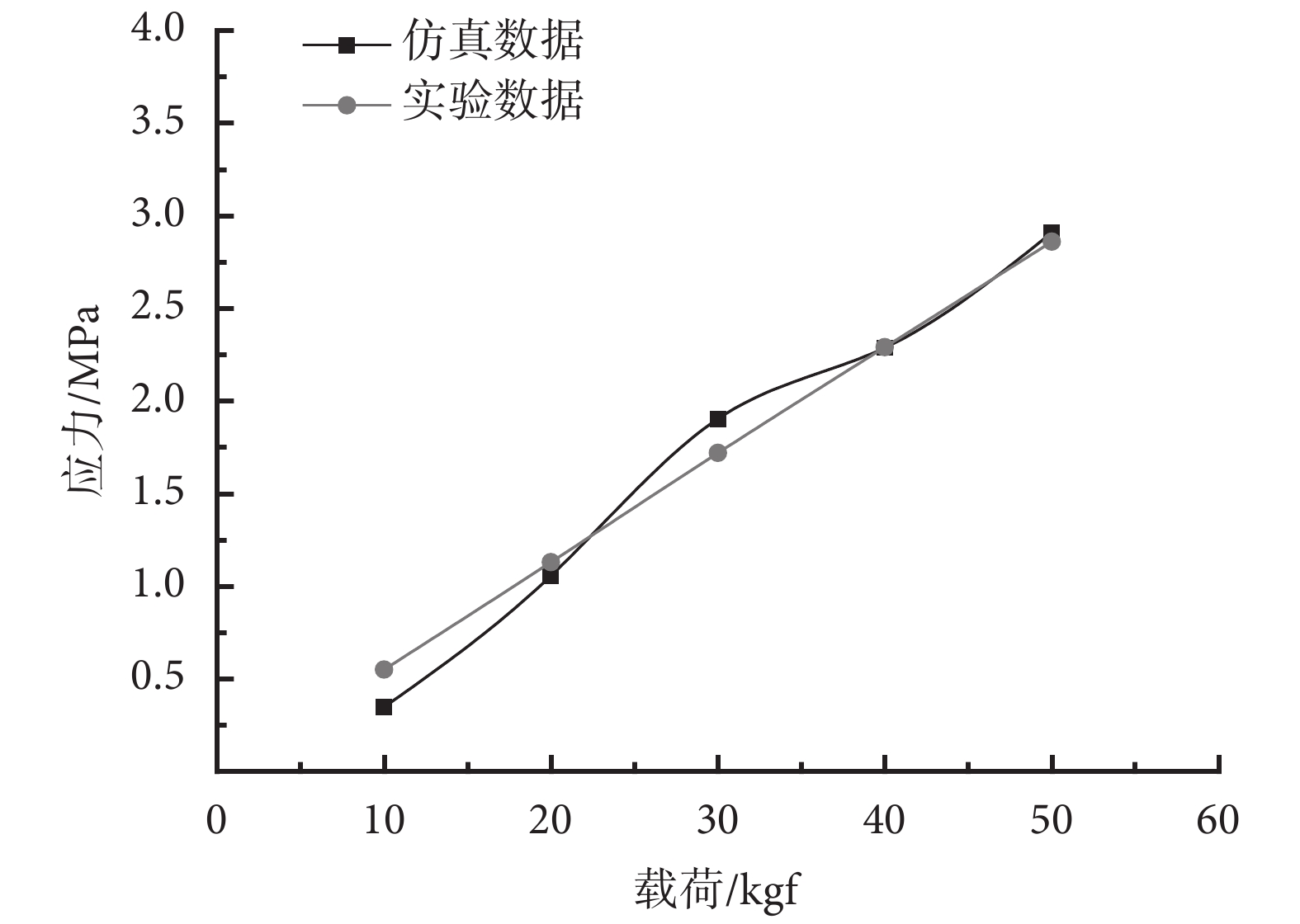 圖4
肱橈關節面峰值應力數據對比圖
Figure4.
The data contrast diagram of the peak stress of the humeroradial joint
圖4
肱橈關節面峰值應力數據對比圖
Figure4.
The data contrast diagram of the peak stress of the humeroradial joint
2 內側副韌帶力學有限元分析
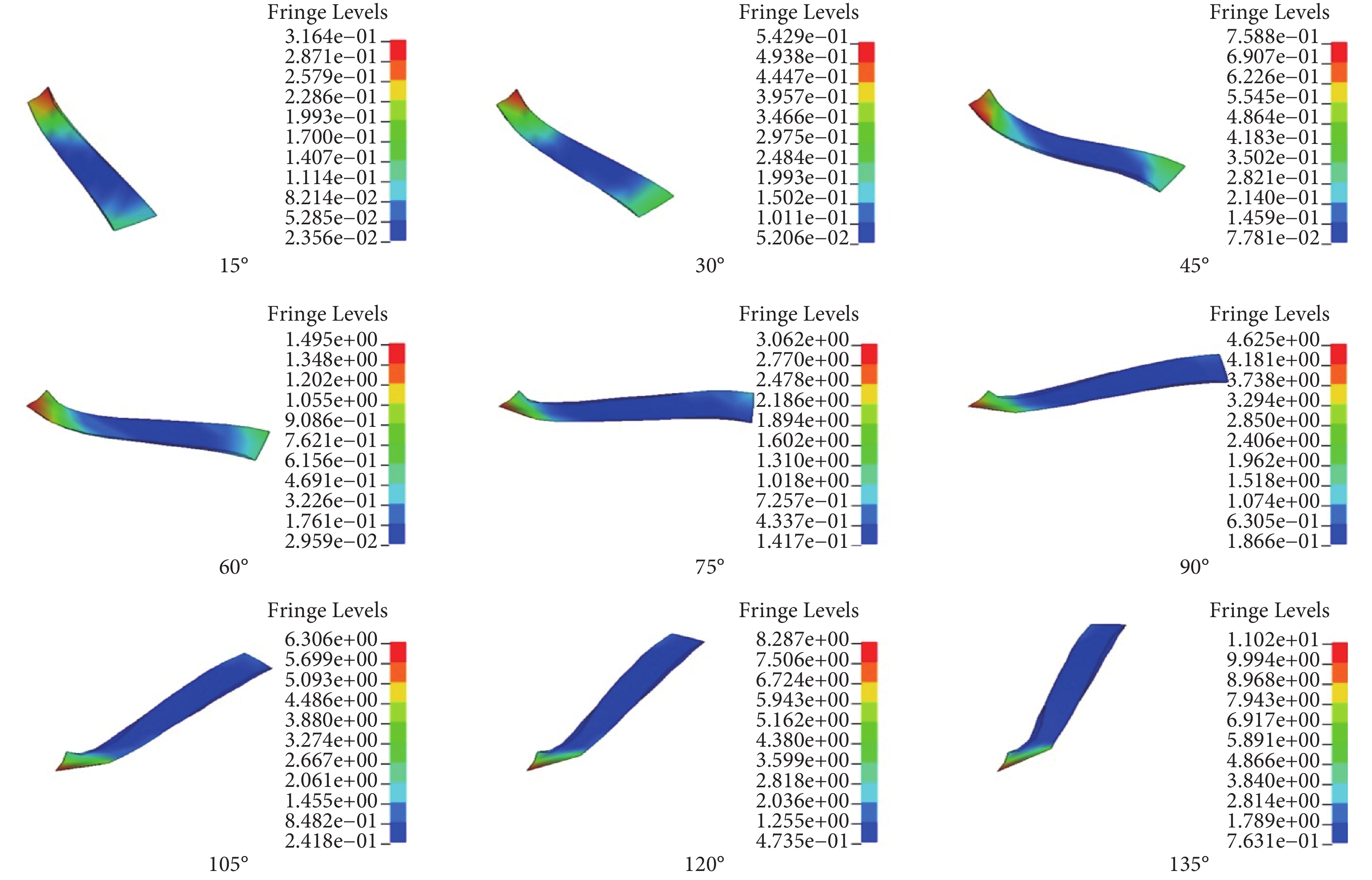
用所建立模型來模擬肘關節屈曲過程的生物力學響應,將模型中肱骨遠端節點自由度進行完全約束,對尺骨和橈骨施加繞額狀軸[8, 11-12]逆時針角速度,大小為 2.46 rad/s,其余方向的自由度進行約束,使肘關節進行 0~135° 的屈曲運動,每隔 15° 提取的內側副韌帶(包括前束、后束和斜束)應力分布如圖 5~7 所示。
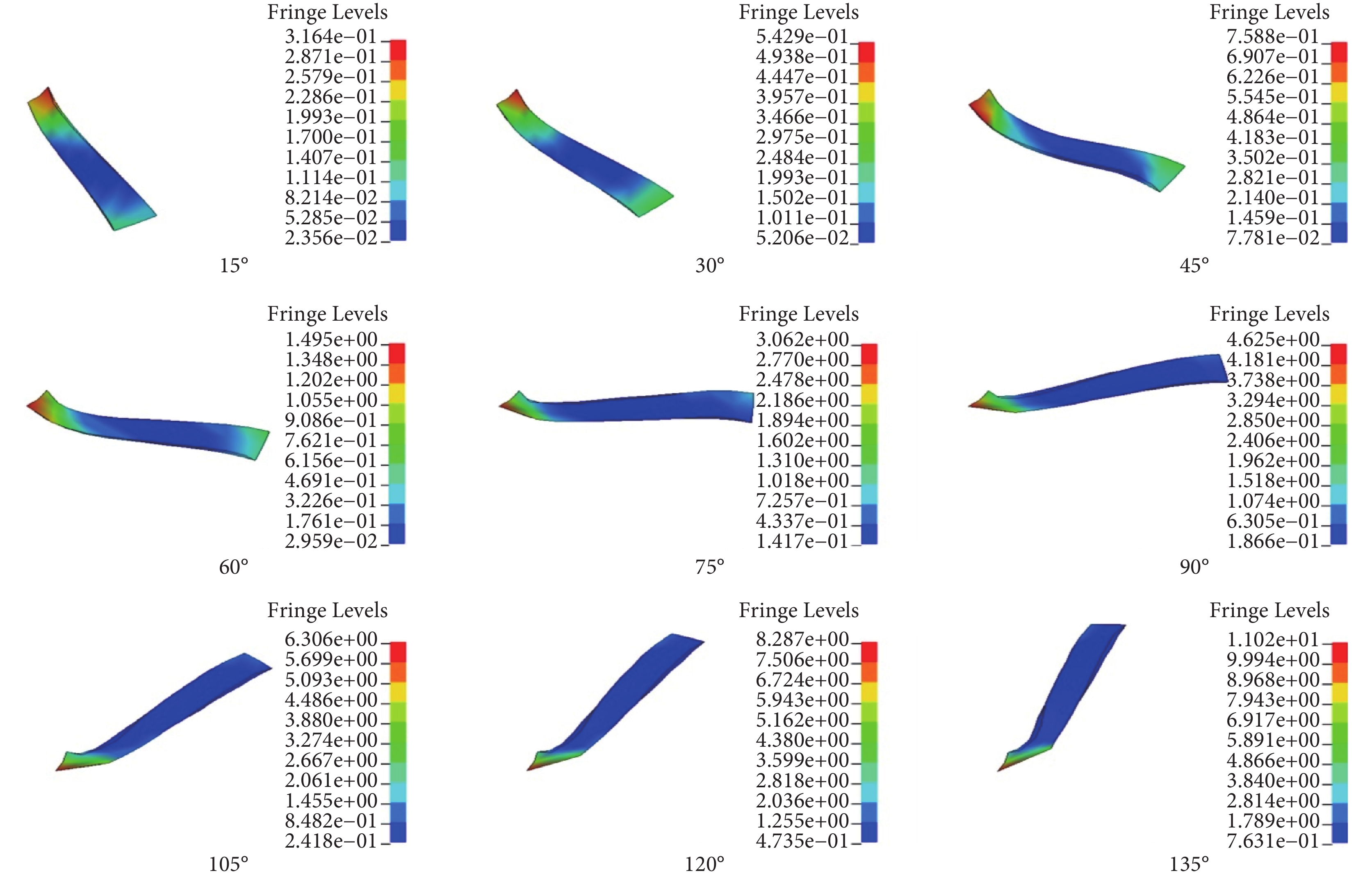 圖5
內側副韌帶前束應力分布
Figure5.
Stress distribution of the anterior bundle of the MCL
圖5
內側副韌帶前束應力分布
Figure5.
Stress distribution of the anterior bundle of the MCL
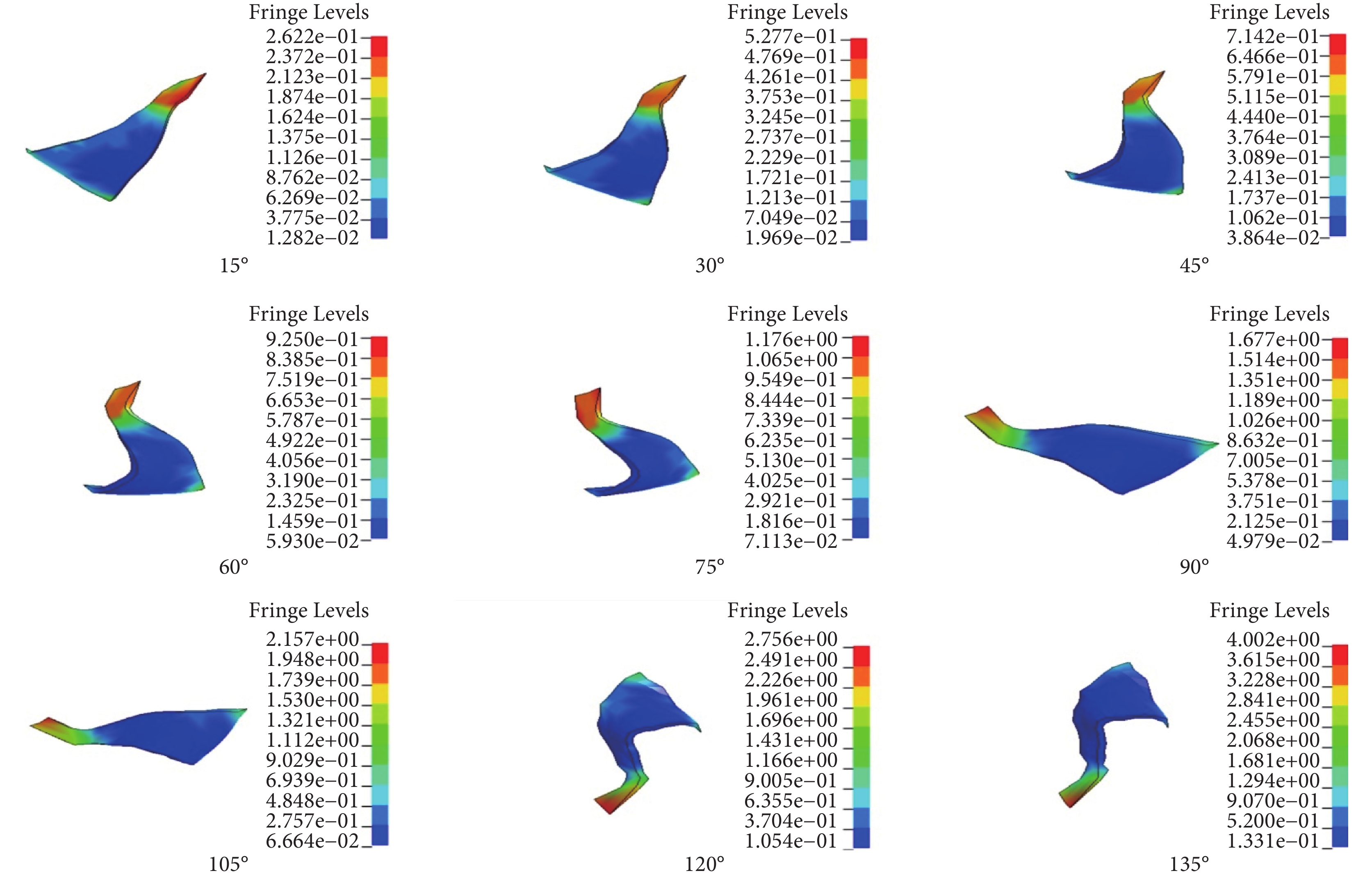
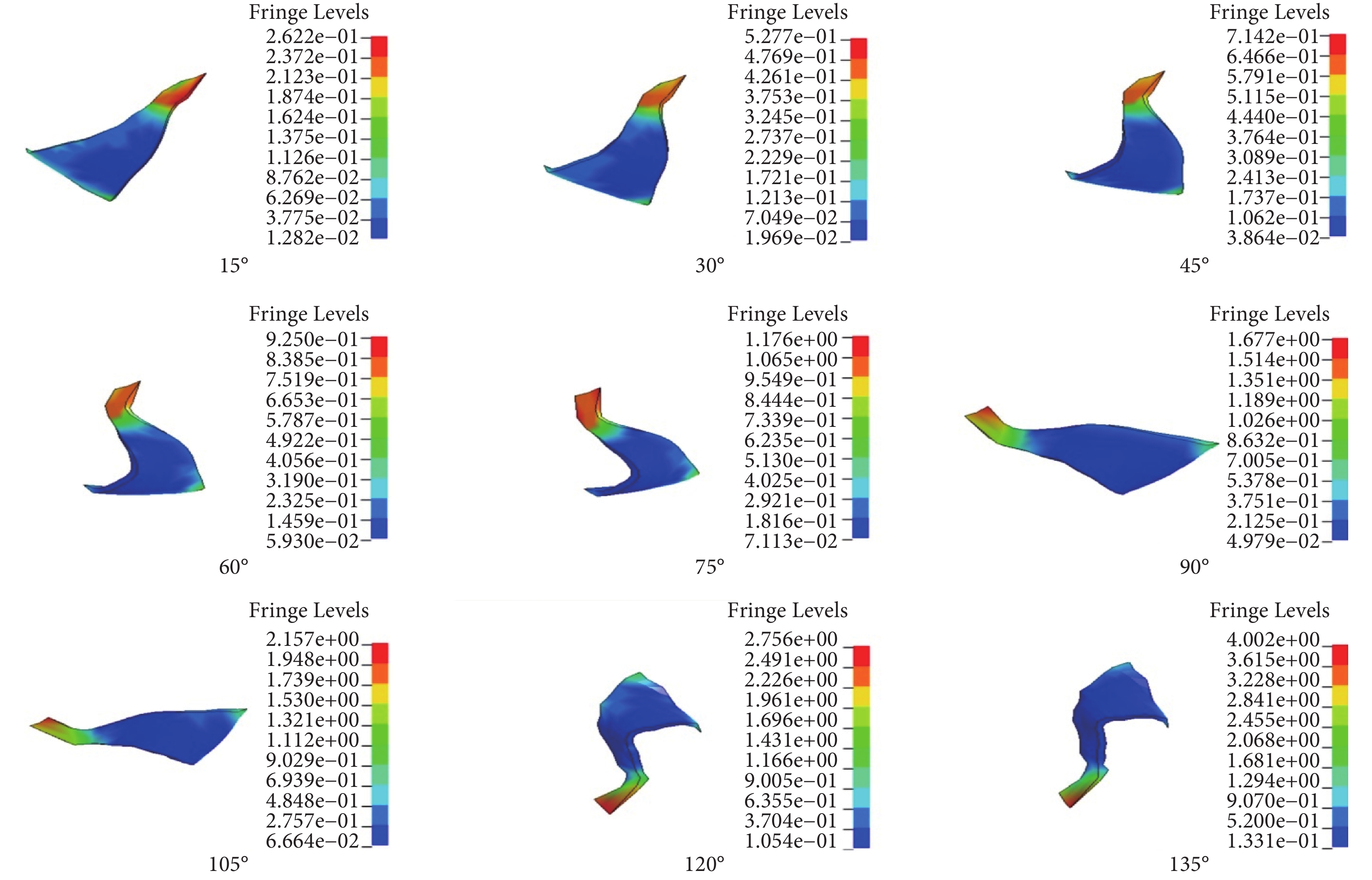 圖6
內側副韌帶后束應力分布
Figure6.
Stress distribution of the posterior bundle of the MCL
圖6
內側副韌帶后束應力分布
Figure6.
Stress distribution of the posterior bundle of the MCL
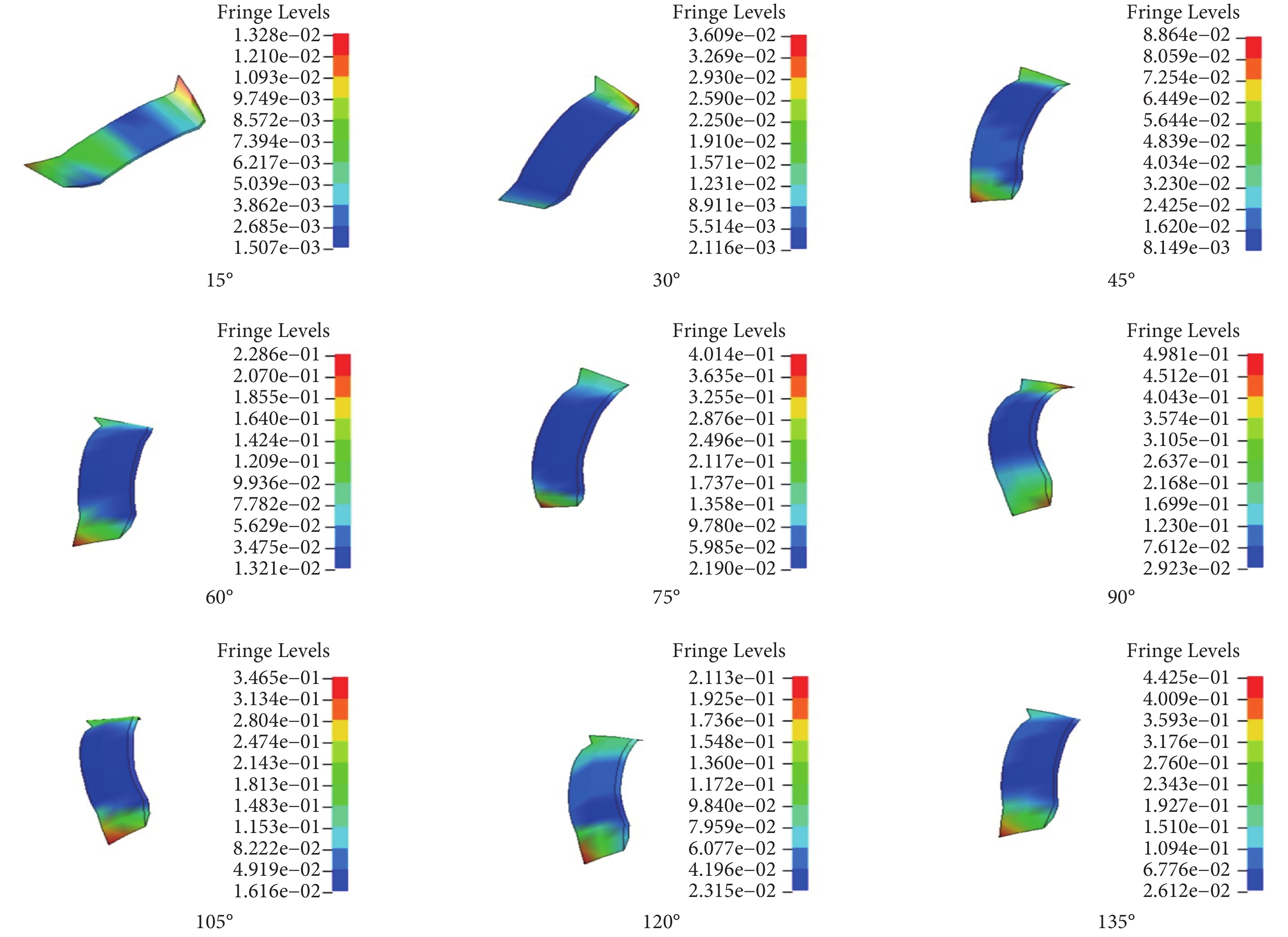
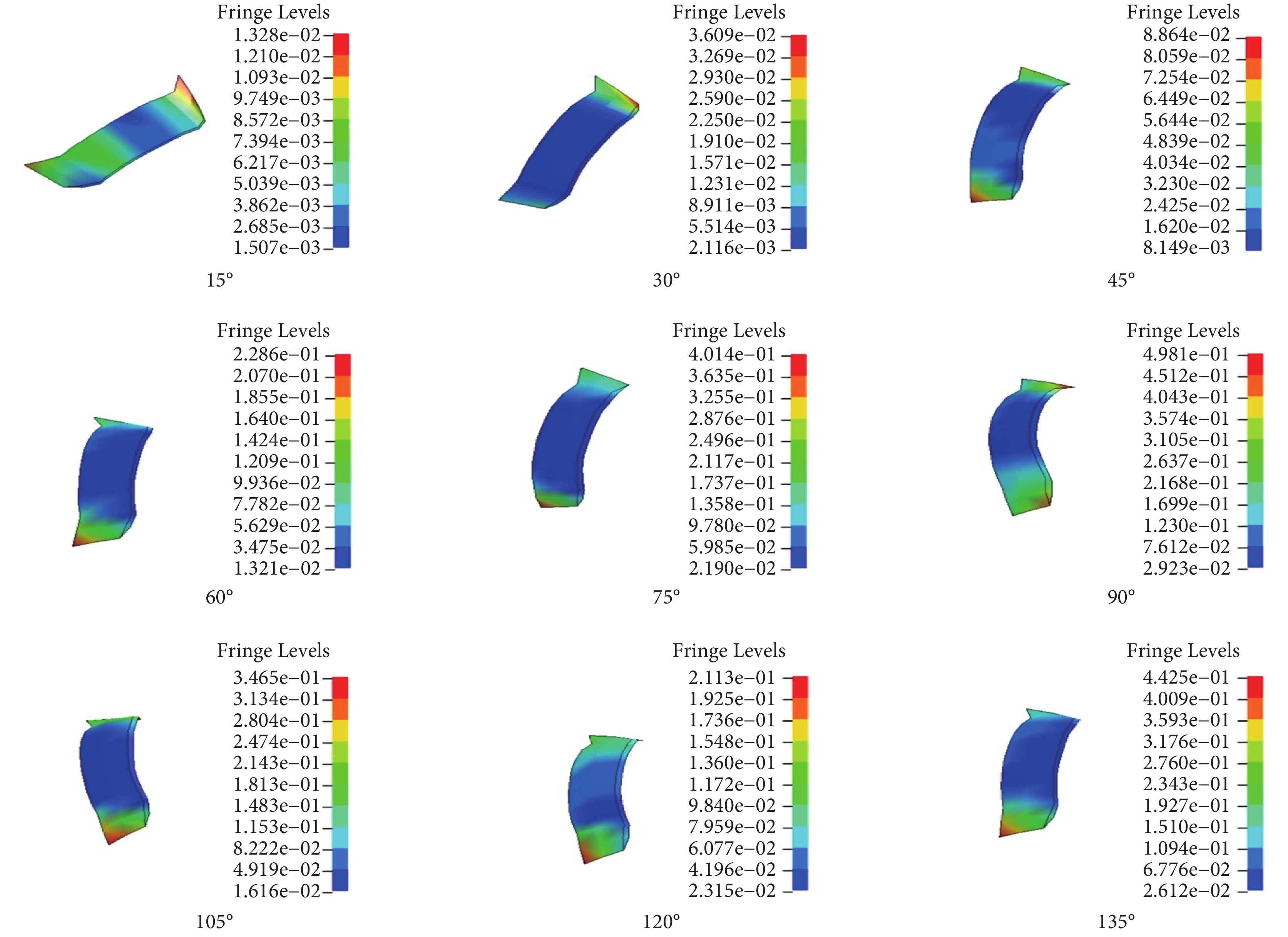 圖7
內側副韌帶斜束應力分布
Figure7.
Stress distribution of the transverse bundle of the MCL
圖7
內側副韌帶斜束應力分布
Figure7.
Stress distribution of the transverse bundle of the MCL
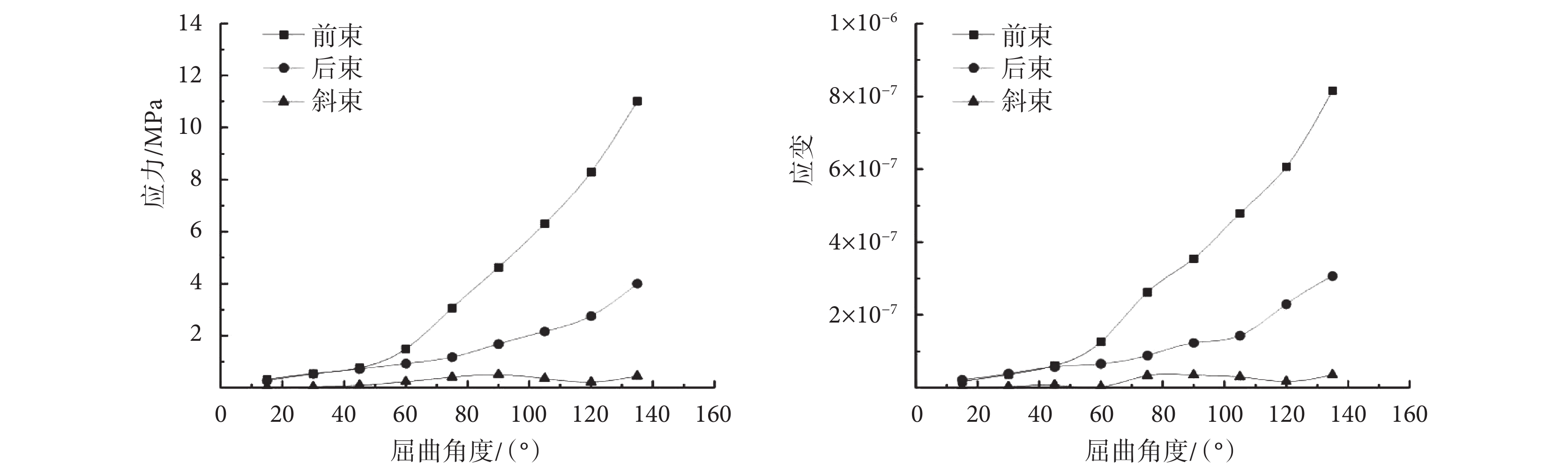
由圖 8 可知,對于前束,肘關節屈曲 0~45° 時應力逐漸增加但應力較小,其最大值為 0.76 MPa;屈曲 45° 以上,其所受應力較大且呈增加趨勢,其最大應力發生于肱骨附著點周圍。后束應力在肘關節屈曲 0~60° 內,隨角度增加而逐漸變大但變化速率較慢,最大值為 0.93 MPa;在屈曲 60° 以上,應力隨角度增大而逐漸增加,最大值為 4 MPa,集中在肱骨附著點周圍。斜束應力最大值為 0.5 MPa,且隨角度增大的變化幅度很小。由圖 8 可知,各韌帶應變隨角度增加的變化趨勢,與應力變化趨勢相似。在相同角度下,三種韌帶中前束所受應變最大而斜束應變最小。可見,肘關節整個屈曲過程中,內側副韌帶所承受的應力和應變在前束最大,后束次之,斜束最小。
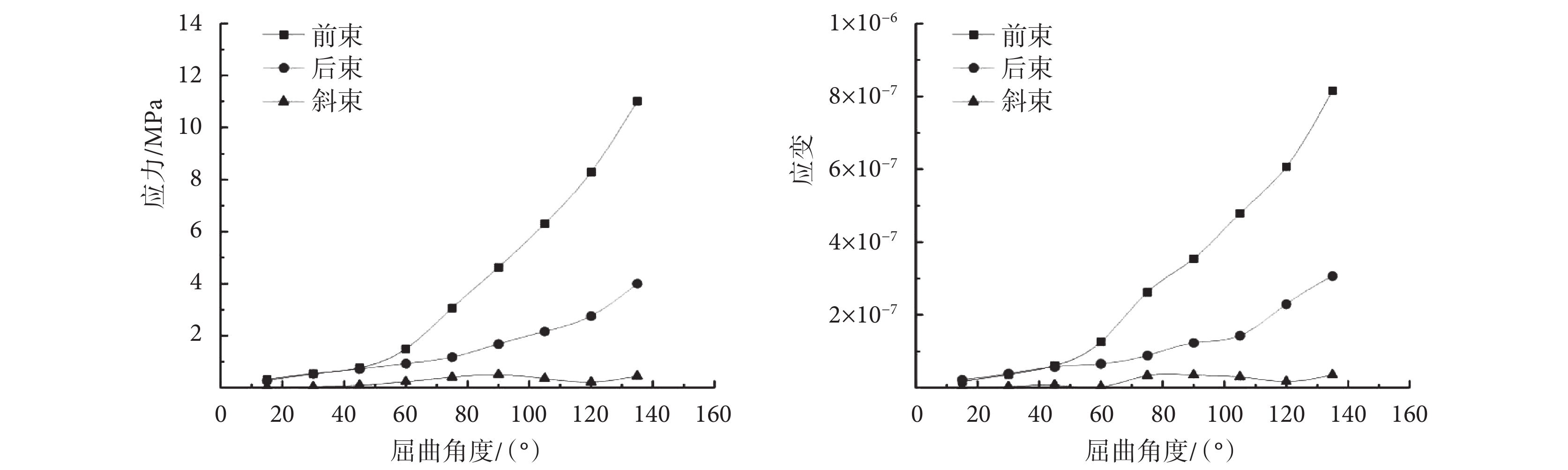 圖8
韌帶峰值應力和峰值應變
Figure8.
Peak stress and strain of ligament
圖8
韌帶峰值應力和峰值應變
Figure8.
Peak stress and strain of ligament
3 討論
本文建立了肘關節三維有限元模型,模型包括肱骨、尺骨、橈骨、各關節軟骨、內側副韌帶等相關組織,其中,特別地將韌帶采用非線性超彈性材料進行模擬,使其更貼近人體組織,并對模型進行了屈曲過程動力學響應分析,分析了隨屈曲角度的變化內側副韌帶的應力及應變的變化趨勢。
紀標等[13]通過解剖正常成年人尸體肘關節標本,并測量內側副韌帶在不同屈曲角度下的長度得出結論:在無外翻力矩的作用下,前束在肘關節屈曲 45° 之前呈松弛狀態,在屈曲超過 45° 之后開始產生張力。本研究中肘關節在 0~135° 屈曲過程中,前束應力值均隨屈曲角度變大而增加,在 0~45° 時其應力值增加速率較小,最大值為 0.76 MPa。當超過 45° 時,前束應力值以較大的速率增加,最小值和最大值分別為 1.5、11.02 MPa。王友華等[14]通過觀察肘關節副韌帶的結構特點及其在不同屈曲角度下的形態變化規律,得出結論:尺側副韌帶的后束在肘關節屈曲超過 60° 后,才隨著屈曲角度的增加而逐漸變得緊張,長度也隨之變長。本研究中后束應力值均隨屈曲角度變大而增加,0~60° 時其應力值增加速率較緩和,最大值為 0.93 MPa。上述研究結論基本吻合。另一方面,當前臂屈曲超過 60° 時,后束承受的應力值較大,最小值和最大值分別為 1.18 MPa 與 4 MPa。肘關節內側副韌帶斜束的峰值應力很小,最大值為 0.50 MPa,且應力值變化不明顯,對肘關節穩定性所起作用較小,正如 Morrey 等[15]認為斜束是內側副韌帶的組成成分,但作用較小。綜上可知,肘關節屈曲 0~90° 位時,前束起到主導作用,當前臂屈曲超過 90° 位時,前束和后束協同起作用;王棕逸等[16]也通過實驗得出結論,肘關節從中立伸直位到屈曲 120° 時,內側副韌帶前束處于緊張狀態并且是抵抗外翻應力最重要的結構,后束在肘關節屈曲 30~120° 時協同抵抗外翻應力。由此可見,臨床上應重視前束損傷的重建和修補,以穩定肘關節。肘關節在屈曲 60° 位以內時,前束、后束和斜束所承受應力均較小,三者中最大值為 1.50 MPa。所以,當肘關節內側副韌帶前束損傷被修復后,應在將肘關節屈曲 60° 以內使用石膏進行外固定。這樣不僅被修復的韌帶承擔的應力較小,并且有助于肘關節的功能恢復。這與王友華等[14]通過實驗得到的,肘關節內側副韌帶修復或重建后肘關節應固定在 45° 或 60° 的結論基本吻合。
另外,通過改變邊界條件和載荷,所建模型可用于進一步聯合模擬內外翻或旋轉等復雜運動,研究肘關節接觸壓力的分布,探討韌帶的生物力學特點;同時可改變材料屬性參數[17],模擬韌帶拉傷、撕裂、斷裂等病理狀態,在今后的分析中,可以通過添加關節囊、肌肉、皮膚等結構使模型更完善,為進一步研究肘關節損傷后的移植物選取、運動安全防護計劃等醫療措施提供理論依據。
引言
肘關節是人體內對合最好的關節之一,是由肱骨下端和尺骨、橈骨上端構成,包括三個關節,即肱尺關節、肱橈關節和橈尺近側關節(如圖 1 所示),作為肩關節和腕關節的聯結,在上肢功能中起著重要作用,不僅可以擴展手部的活動范圍,而且可以為手部運動提供動力、準確性和穩定性[1]。近年來,因人口老齡化、日常活動及創傷等導致的肘關節功能障礙在臨床上很常見,而我國肘關節領域的整體診斷水平在國際上較為落后,且治療理念不完善,導致其成為臨床治療中的一個難點[2]。肘關節出現功能障礙時常常伴有韌帶損傷,從而導致肘關節不穩定。肘關節內側副韌帶(medial collateral ligament,MCL)是維持肘關節內側穩定的基礎結構[3-4],也是最容易損傷的結構,因此,進一步了解內側副韌帶各部分在肘關節穩定性中的作用顯得尤為重要[5]。目前國內文獻對肘關節內側副韌帶方面的研究相對較少,且大部分集中于關節脫位、外翻、內翻、骨折等對肘關節穩定性的影響,而忽略了內側副韌帶在維持肘關節穩定中所起的作用,導致肘關節內側副韌帶損傷的漏診率較高,以致于相當部分患者得不到有效和及時的治療,進而出現肘關節失穩現象。為從組織層次對肘關節及其周圍韌帶進行生物力學分析,本文基于真實肘關節計算機斷層掃描(computed tomography,CT)圖片,重構了包括完整骨骼、肘關節、關節軟骨以及主要韌帶的人體肘關節三維有限元模型,利用有限元生物力學仿真,觀察肘關節屈曲不同角度時內側副韌帶各部位的應力大小,進而分析內側副韌帶各組成部分在維持肘關節穩定性中所起的作用,為韌帶損傷造成的肘關節屈曲不穩定的臨床診斷和治療提供生物力學理論基礎。
 圖1
肘關節解剖示意圖
Figure1.
Anatomical diagram of elbow joint
圖1
肘關節解剖示意圖
Figure1.
Anatomical diagram of elbow joint
1 材料與方法
選擇一位健康中國男性作為測試對象,年齡 43 歲,身高 175 cm,體重 75 kg,無肘關節損傷及相關病史。志愿者自愿參加本次研究,并簽署了知情同意書。采用螺旋 CT 機對其中立 90° 位肘關節進行掃描,層厚為 1 mm,像素為 256 × 256。掃描范圍為左側肱骨遠端至尺、橈骨近端,共獲得 236 張圖像,以醫學數字成像和通信(Digital Imaging and Communications in Medicine,DICOM)格式存儲。
1.1 肘關節有限元模型建立
將志愿者 CT 數據以 DICOM 格式導入軟件 Mimics(Materialise Inc.,Leuven,比利時)中進行三維重建,運用區域增長分割等方法,建立包括肱骨遠端及尺、橈骨近端在內的肘關節三維幾何模型。初步提取的肘關節幾何模型表面較粗糙,運用逆向建模軟件 Geomagic(GeomagicInc.,NC,美國)對幾何模型進行光滑和封閉等處理。在有限元前處理軟件 Hypermesh(Altair Engineering Inc,美國)中對骨結構進行有限元網格劃分,并根據解剖學結構,利用直接建模的方法,構建內側副韌帶、關節面軟骨等組織,所有結構均采用八節點六面體單元進行模擬。各模型的相關參數如下:前臂中立位模型節點數 31 009,單元數 24 958,其中骨骼 23 461,關節面軟骨 905,韌帶 205。將模型中骨組織和關節面軟骨簡化為分布均勻且各向同性的均質性彈性體材料,不僅可以大大縮短建模周期,而且大量關于有限元分析的文獻結果證明,采用各向同性特性進行有限元分析也可以得到較準確的分析結果[6]。為更好地反映韌帶的生物力學響應,韌帶定義為超彈性材料,選用 Hypermesh 的 LS-DYNA(Livermore Software Technology Corporation,美國) 模塊下材料庫中的 MATL7。隨后對模型進行有限元網格劃分并建立有限元模型(見圖 2),并在 Hypermesh 中賦予模型材料、屬性、邊界條件、定義接觸等,最后在 LS-DYNA進行仿真計算。材料參數如表 1[7-10]所示。
 圖2
肘關節三維有限元模型
Figure2.
Three-dimensional finite element model of elbow joint
圖2
肘關節三維有限元模型
Figure2.
Three-dimensional finite element model of elbow joint
1.2 有限元模型有效性驗證
Takatori 等[7]開展了肘關節力學實驗,選取肘關節中立完全伸直位,將肱骨固定,在尺骨和橈骨截面處分別施加 98.06 N(10 kgf)、196.12 N(20 kgf)、294.18 N(30 kgf)、392.24 N(40 kgf)、490.3 N(50 kgf)的壓力,實驗記錄了不同載荷下肱橈關節所受的最大壓力。以此試驗數據定義有限元模型的邊界和載荷,仿真提取了橈骨頭關節面應力峰值數據,如圖 3 所示。由圖 4 可以發現,結果與實驗數據變化趨勢基本吻合,從而驗證了模型的有效性。
 圖3
橈骨頭關節面應力分布
Figure3.
Stress distribution of the radial head articular surface
圖3
橈骨頭關節面應力分布
Figure3.
Stress distribution of the radial head articular surface
 圖4
肱橈關節面峰值應力數據對比圖
Figure4.
The data contrast diagram of the peak stress of the humeroradial joint
圖4
肱橈關節面峰值應力數據對比圖
Figure4.
The data contrast diagram of the peak stress of the humeroradial joint
2 內側副韌帶力學有限元分析
用所建立模型來模擬肘關節屈曲過程的生物力學響應,將模型中肱骨遠端節點自由度進行完全約束,對尺骨和橈骨施加繞額狀軸[8, 11-12]逆時針角速度,大小為 2.46 rad/s,其余方向的自由度進行約束,使肘關節進行 0~135° 的屈曲運動,每隔 15° 提取的內側副韌帶(包括前束、后束和斜束)應力分布如圖 5~7 所示。
 圖5
內側副韌帶前束應力分布
Figure5.
Stress distribution of the anterior bundle of the MCL
圖5
內側副韌帶前束應力分布
Figure5.
Stress distribution of the anterior bundle of the MCL
 圖6
內側副韌帶后束應力分布
Figure6.
Stress distribution of the posterior bundle of the MCL
圖6
內側副韌帶后束應力分布
Figure6.
Stress distribution of the posterior bundle of the MCL
 圖7
內側副韌帶斜束應力分布
Figure7.
Stress distribution of the transverse bundle of the MCL
圖7
內側副韌帶斜束應力分布
Figure7.
Stress distribution of the transverse bundle of the MCL
由圖 8 可知,對于前束,肘關節屈曲 0~45° 時應力逐漸增加但應力較小,其最大值為 0.76 MPa;屈曲 45° 以上,其所受應力較大且呈增加趨勢,其最大應力發生于肱骨附著點周圍。后束應力在肘關節屈曲 0~60° 內,隨角度增加而逐漸變大但變化速率較慢,最大值為 0.93 MPa;在屈曲 60° 以上,應力隨角度增大而逐漸增加,最大值為 4 MPa,集中在肱骨附著點周圍。斜束應力最大值為 0.5 MPa,且隨角度增大的變化幅度很小。由圖 8 可知,各韌帶應變隨角度增加的變化趨勢,與應力變化趨勢相似。在相同角度下,三種韌帶中前束所受應變最大而斜束應變最小。可見,肘關節整個屈曲過程中,內側副韌帶所承受的應力和應變在前束最大,后束次之,斜束最小。
 圖8
韌帶峰值應力和峰值應變
Figure8.
Peak stress and strain of ligament
圖8
韌帶峰值應力和峰值應變
Figure8.
Peak stress and strain of ligament
3 討論
本文建立了肘關節三維有限元模型,模型包括肱骨、尺骨、橈骨、各關節軟骨、內側副韌帶等相關組織,其中,特別地將韌帶采用非線性超彈性材料進行模擬,使其更貼近人體組織,并對模型進行了屈曲過程動力學響應分析,分析了隨屈曲角度的變化內側副韌帶的應力及應變的變化趨勢。
紀標等[13]通過解剖正常成年人尸體肘關節標本,并測量內側副韌帶在不同屈曲角度下的長度得出結論:在無外翻力矩的作用下,前束在肘關節屈曲 45° 之前呈松弛狀態,在屈曲超過 45° 之后開始產生張力。本研究中肘關節在 0~135° 屈曲過程中,前束應力值均隨屈曲角度變大而增加,在 0~45° 時其應力值增加速率較小,最大值為 0.76 MPa。當超過 45° 時,前束應力值以較大的速率增加,最小值和最大值分別為 1.5、11.02 MPa。王友華等[14]通過觀察肘關節副韌帶的結構特點及其在不同屈曲角度下的形態變化規律,得出結論:尺側副韌帶的后束在肘關節屈曲超過 60° 后,才隨著屈曲角度的增加而逐漸變得緊張,長度也隨之變長。本研究中后束應力值均隨屈曲角度變大而增加,0~60° 時其應力值增加速率較緩和,最大值為 0.93 MPa。上述研究結論基本吻合。另一方面,當前臂屈曲超過 60° 時,后束承受的應力值較大,最小值和最大值分別為 1.18 MPa 與 4 MPa。肘關節內側副韌帶斜束的峰值應力很小,最大值為 0.50 MPa,且應力值變化不明顯,對肘關節穩定性所起作用較小,正如 Morrey 等[15]認為斜束是內側副韌帶的組成成分,但作用較小。綜上可知,肘關節屈曲 0~90° 位時,前束起到主導作用,當前臂屈曲超過 90° 位時,前束和后束協同起作用;王棕逸等[16]也通過實驗得出結論,肘關節從中立伸直位到屈曲 120° 時,內側副韌帶前束處于緊張狀態并且是抵抗外翻應力最重要的結構,后束在肘關節屈曲 30~120° 時協同抵抗外翻應力。由此可見,臨床上應重視前束損傷的重建和修補,以穩定肘關節。肘關節在屈曲 60° 位以內時,前束、后束和斜束所承受應力均較小,三者中最大值為 1.50 MPa。所以,當肘關節內側副韌帶前束損傷被修復后,應在將肘關節屈曲 60° 以內使用石膏進行外固定。這樣不僅被修復的韌帶承擔的應力較小,并且有助于肘關節的功能恢復。這與王友華等[14]通過實驗得到的,肘關節內側副韌帶修復或重建后肘關節應固定在 45° 或 60° 的結論基本吻合。
另外,通過改變邊界條件和載荷,所建模型可用于進一步聯合模擬內外翻或旋轉等復雜運動,研究肘關節接觸壓力的分布,探討韌帶的生物力學特點;同時可改變材料屬性參數[17],模擬韌帶拉傷、撕裂、斷裂等病理狀態,在今后的分析中,可以通過添加關節囊、肌肉、皮膚等結構使模型更完善,為進一步研究肘關節損傷后的移植物選取、運動安全防護計劃等醫療措施提供理論依據。