借助信號內在的稀疏性或可壓縮性,壓縮感知利用隨機投影實現以遠低于奈奎斯特頻率的采樣頻率下對壓縮后數據的采集。結合壓縮感知和低秩思想,可以加快心臟磁共振(CMR)圖像的掃描速度,減輕患者不適,提高檢查質量。本文提出 CMR 圖像的多尺度低秩分解模型,并采用交替方向拉格朗日乘子法(ADMM)進行求解。以峰值信噪比(PSNR)和相對誤差(RLNE)作為定量評價指標,結合人眼視覺感受以及局部區域放大,對比分析本文算法與 L + S 分解、kt FOCUSS、k-t SPARSE SENSE 等主流算法的性能優劣。實驗結果表明:本文提出的多尺度低秩分解模型,經過 ADMM 算法重構的效果在性能指標上明顯優于其他對比算法,同時圖像細節和邊緣輪廓成像質量更佳。該方法將推動 CMR 快速成像技術的發展及其在臨床疾病診療中的應用。
引用本文: 衡陽, 陳峰, 徐劍鋒, 湯敏. 基于多尺度低秩的心臟磁共振圖像的高質量重構算法. 生物醫學工程學雜志, 2019, 36(4): 573-580. doi: 10.7507/1001-5515.201803024 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
磁共振成像(magnetic resonance imaging,MRI)是目前主要的無創醫學成像手段之一,心臟磁共振(cardiac magnetic resonance,CMR)則是一種特殊的 MRI 技術,用于無創性評價心臟形態結構和生理功能,已在心臟成像領域成為評價標準[1]。但是,與常規 MRI 技術相比,CMR 成像時間較長,同時具有一定的特殊性,如消除心臟運動偽影、平衡時空分辨率等。
壓縮感知(compressed sensing,CS)理論主要包含稀疏表達、測量矩陣和重構算法三個方面。該理論自 2006 年誕生以來,為加速 MRI 開辟了嶄新的途徑,即利用 MRI 信號的稀疏性,以遠低于奈奎斯特采樣定理的方式來采集數據,設計精確、快速的重構算法,從欠采樣 K 空間數據中恢復出具有診斷價值的圖像,從而大大減少掃描時間[2-4]。此后的研究表明:只要原始矩陣是低秩的,就可以通過求解矩陣核范數最小化問題來恢復原始矩陣[5-6]。壓縮感知是在未知信號向量具有稀疏性的假設條件下進行數據處理;而低秩矩陣恢復則是利用未知矩陣的低秩性來進一步分析,因此低秩矩陣恢復可以看作壓縮感知從一階向量到二階矩陣的拓展和延伸[7-8]。
近兩年來,基于低秩稀疏分解的 CS-MRI 圖像重構始終是研究熱點。文獻[9]首次將低秩稀疏分解模型應用于 MRI 圖像重構,初步應用于心臟灌注、心臟電影、血管成像、胸腹部 MRI 成像等臨床應用。文獻[10]利用魯棒主成分分析提取動態 MRI 中的動態組織部分,提出基于稀疏和低秩先驗分離的重構算法。文獻[11]提出全變差與核范數正則化相結合的動態 MRI 重構算法。文獻[12]采用動態全變差和核范數來增強 MRI 各幀和整個序列的正則化,將重構問題劃分為兩個子問題來求解。文獻[13]利用圖像低秩屬性和全變差,同時考慮圖像本身的局部和非局部信息,提出基于稀疏和低秩先驗的壓縮感知重構算法。文獻[14]提出基于非局部低秩正則化的壓縮感知重構算法,獲得了最好的圖像重構效果;但是僅利用圖像的非局部信息,忽略了局部信息,不能有效重構圖像邊緣。文獻[15]提出基于塊操作的非局部低秩先驗的動態 MRI 重構算法,在此基礎上,文獻[16]提出局部低秩稀疏模型,用于灌注 MRI 圖像的加速成像。此外,文獻[17-18]以張量分解作為稀疏變換,分別提出動態 MRI 重構算法 HOSVD 和 kt-MLSD。文獻[19]提出基于部分可分離模型和壓縮感知相結合的 Stepped-Sparse PS 算法。文獻[20-21]初步提出多尺度和多維低秩矩陣分解,并應用于人臉圖像、監控視頻、動態 MRI 等的多尺度建模和協同濾波。
綜上所述,已有文獻采用低秩稀疏分解來快速重構 MRI 圖像,雖取得一定積極進展,但因稀疏先驗未能充分利用圖像局部空間一致性和圖像塊的平滑性,從而導致重構圖像不夠干凈,重構結果對噪聲敏感。針對這一問題,本文將多分辨率思想引入低秩稀疏分解理論,提出基于多尺度低秩分解模型和交替方向拉格朗日乘子法(alternating direction method of multipliers,ADMM)的 CMR 圖像高質量重構算法,加快成像速度,提高成像質量,改善檢查舒適度,促進循環系統疾病診療新技術的發展。
1 主要關鍵技術
1.1 多尺度低秩模型
CMR 成像所包含的心臟電影和心臟灌注等成像技術均屬于動態 MRI 范疇,時空相關度較高,即序列圖像上保持不變的背景部分較多,變化的動態部分較少,相鄰像素的相似程度較高。因此,把 CMR 圖像的每個時間幀看作時空矩陣的一列,整個圖像序列分離成稀疏先驗和低秩先驗這兩部分,待重構圖像即為兩者疊加,從而建立動態組織和靜態背景的分離模型,即矩陣低秩稀疏分解的基本思想。該方法應用于動態 MRI 圖像重構取得了一定積極進展,但對噪聲敏感,重構圖像不夠干凈,這是因為稀疏先驗沒有充分利用圖像局部空間一致性和圖像塊的平滑性。
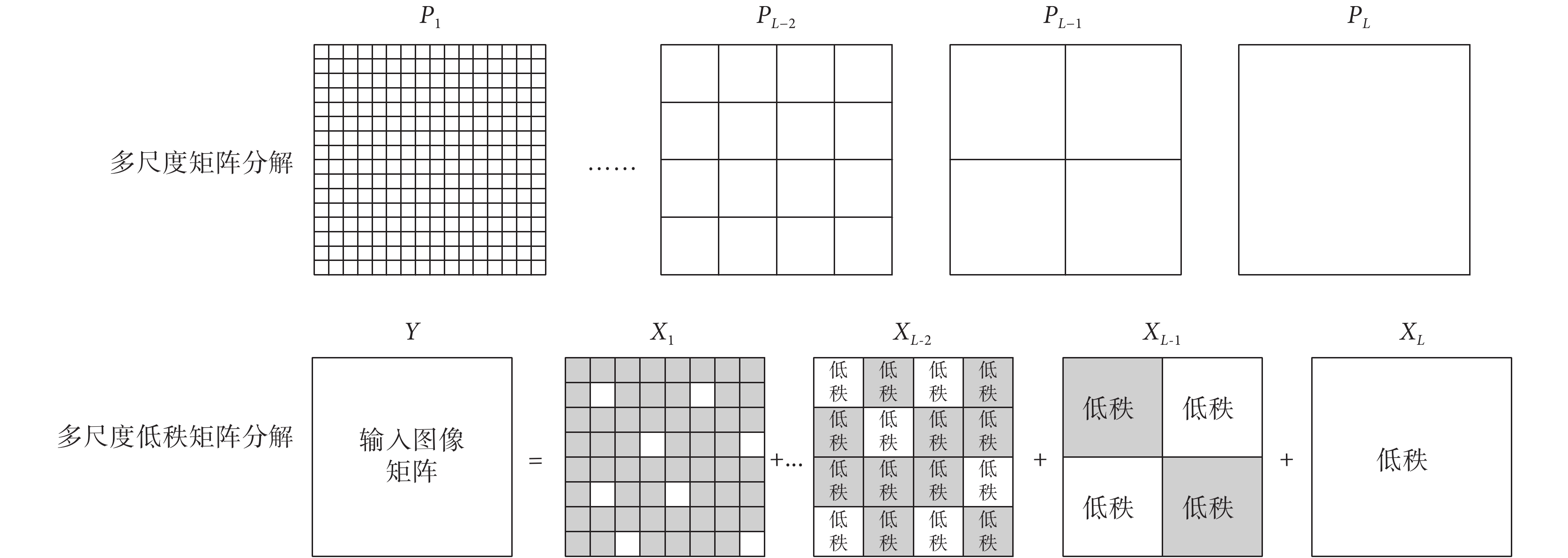
本文將多分辨率思想引入低秩矩陣分解,提出 CMR 圖像的多尺度低秩分解模型,如圖 1 所示。多尺度結構是指信號在不同尺度上展現不同的結構,小波、曲波、多尺度金字塔等均具有多尺度結構。多尺度幾何分析的目的是為了檢測、表示、處理高維空間數據,而這些數據的某些重要特征集中體現在其低維子集中。多尺度低秩矩陣分解可以獲得比傳統低秩模型更精確、更緊湊的信號表達方式,同時具有多尺度模型和低秩矩陣分解的優點。
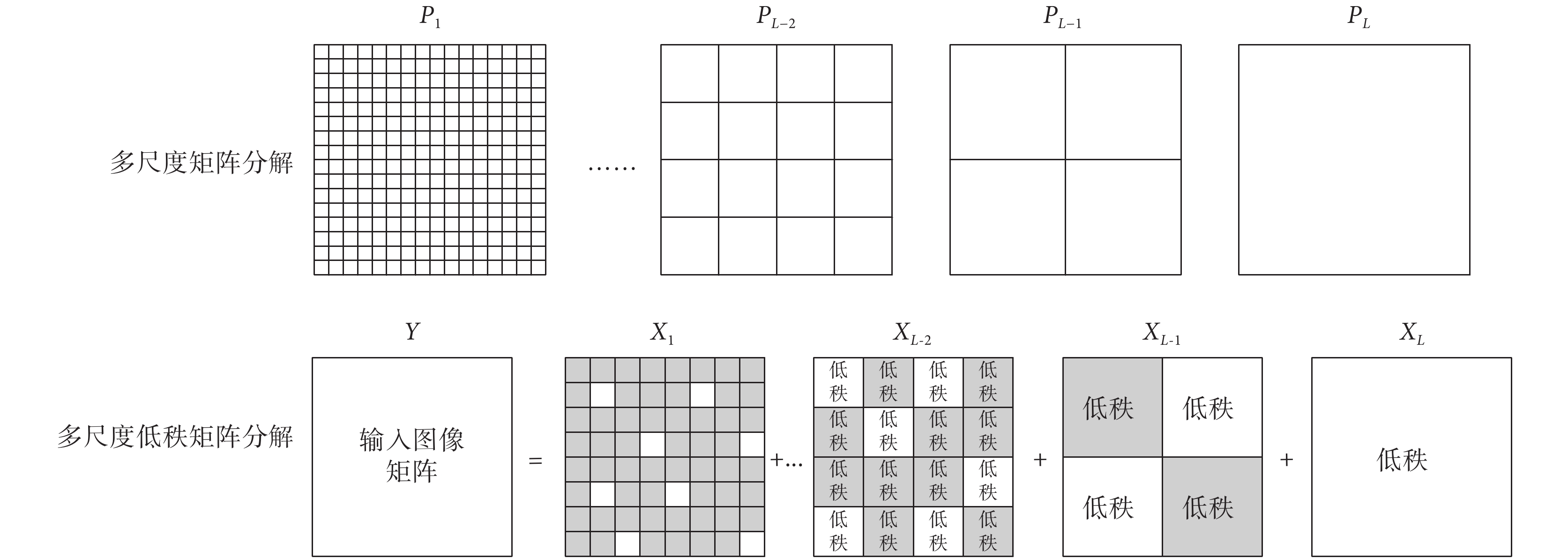 圖1
多尺度低秩分解示意圖
Figure1.
Schematic diagram of multiscale low rank decomposition
圖1
多尺度低秩分解示意圖
Figure1.
Schematic diagram of multiscale low rank decomposition
對于輸入矩陣  (
( ),經過多尺度分解以及塊重構算子
),經過多尺度分解以及塊重構算子  后,其多尺度分解模型可近似寫成如下形式:
后,其多尺度分解模型可近似寫成如下形式:
 |
即輸入矩陣  視為基于圖像分塊
視為基于圖像分塊  的各低秩矩陣
的各低秩矩陣  之和。其中,
之和。其中, 是對應圖像分塊
是對應圖像分塊  部分的低秩矩陣;
部分的低秩矩陣; 表示分解尺度。
表示分解尺度。 是塊重構算子,將塊
是塊重構算子,將塊  從完整矩陣中抽取出來并將其重構成
從完整矩陣中抽取出來并將其重構成  的矩陣,這里
的矩陣,這里  是指第
是指第  個尺度下塊矩陣的大小。
個尺度下塊矩陣的大小。 、
、 和
和  是秩為
是秩為  的塊矩陣
的塊矩陣  的奇異值分解(singular value decomposition,SVD)。
的奇異值分解(singular value decomposition,SVD)。
眾所周知,引入核范數后,矩陣秩最小化問題可以松弛為凸優化問題。遵循這一思路,多尺度低秩分解也可以用凸優化來求解。定義尺度  下的塊核范數為
下的塊核范數為  ,于是多尺度低秩分解模型可寫成如下形式:
,于是多尺度低秩分解模型可寫成如下形式:
 |
其中, 是正則化參數。
是正則化參數。
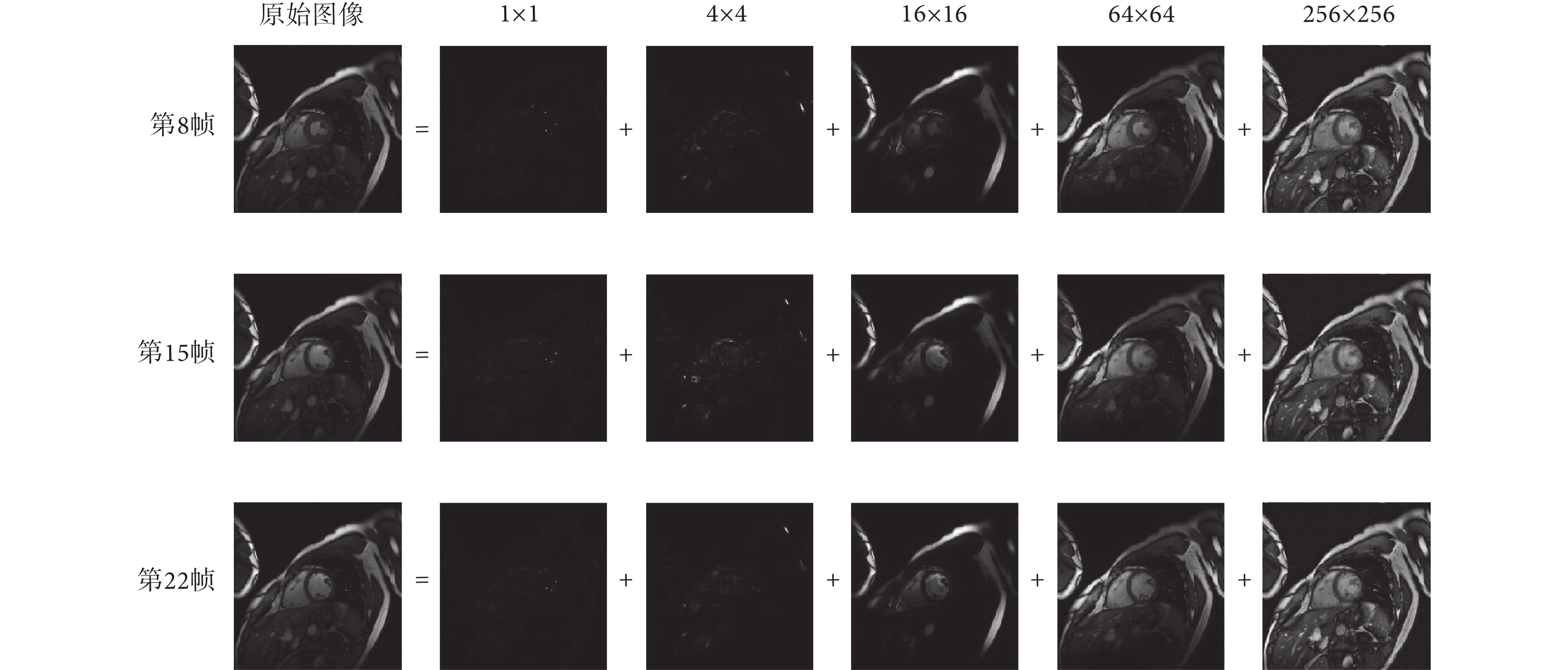
針對  大小的心臟電影成像序列,隨機選取其中第 8、15、22 幀圖像,采用多尺度低秩分解和低秩稀疏分解的結果分別見圖 2、圖 3。圖 2 所示的多尺度低秩分解模型可以清晰顯示靜態和動態組織,對心肌壁等細微結構在
大小的心臟電影成像序列,隨機選取其中第 8、15、22 幀圖像,采用多尺度低秩分解和低秩稀疏分解的結果分別見圖 2、圖 3。圖 2 所示的多尺度低秩分解模型可以清晰顯示靜態和動態組織,對心肌壁等細微結構在  和
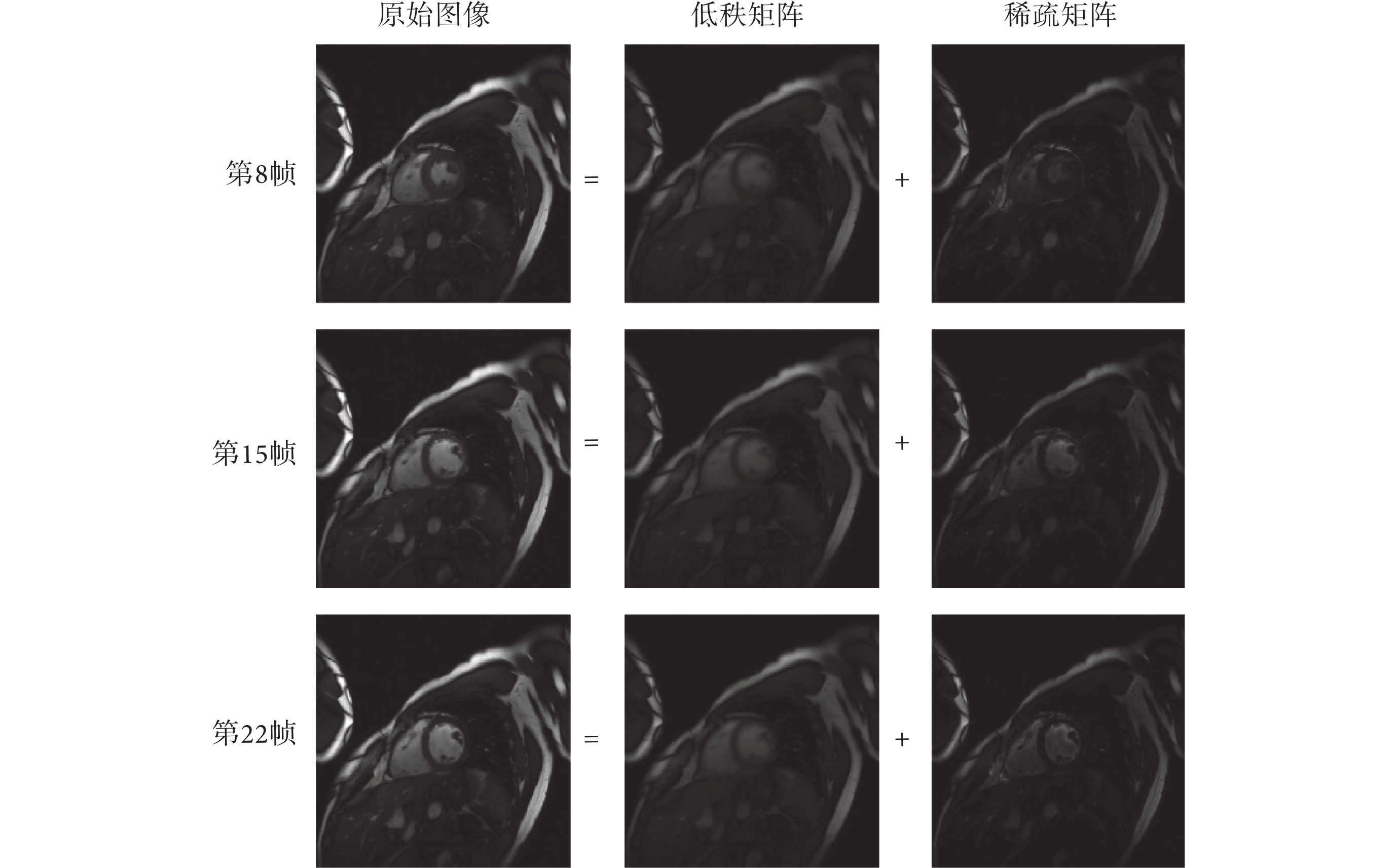
和  尺度上能明確表示,在減少運動偽影的同時更利于提取動態信息。而圖 3 所示的低秩稀疏模型只能大致分離靜態和動態組織,并非嚴格意義上的稀疏或低秩。
尺度上能明確表示,在減少運動偽影的同時更利于提取動態信息。而圖 3 所示的低秩稀疏模型只能大致分離靜態和動態組織,并非嚴格意義上的稀疏或低秩。
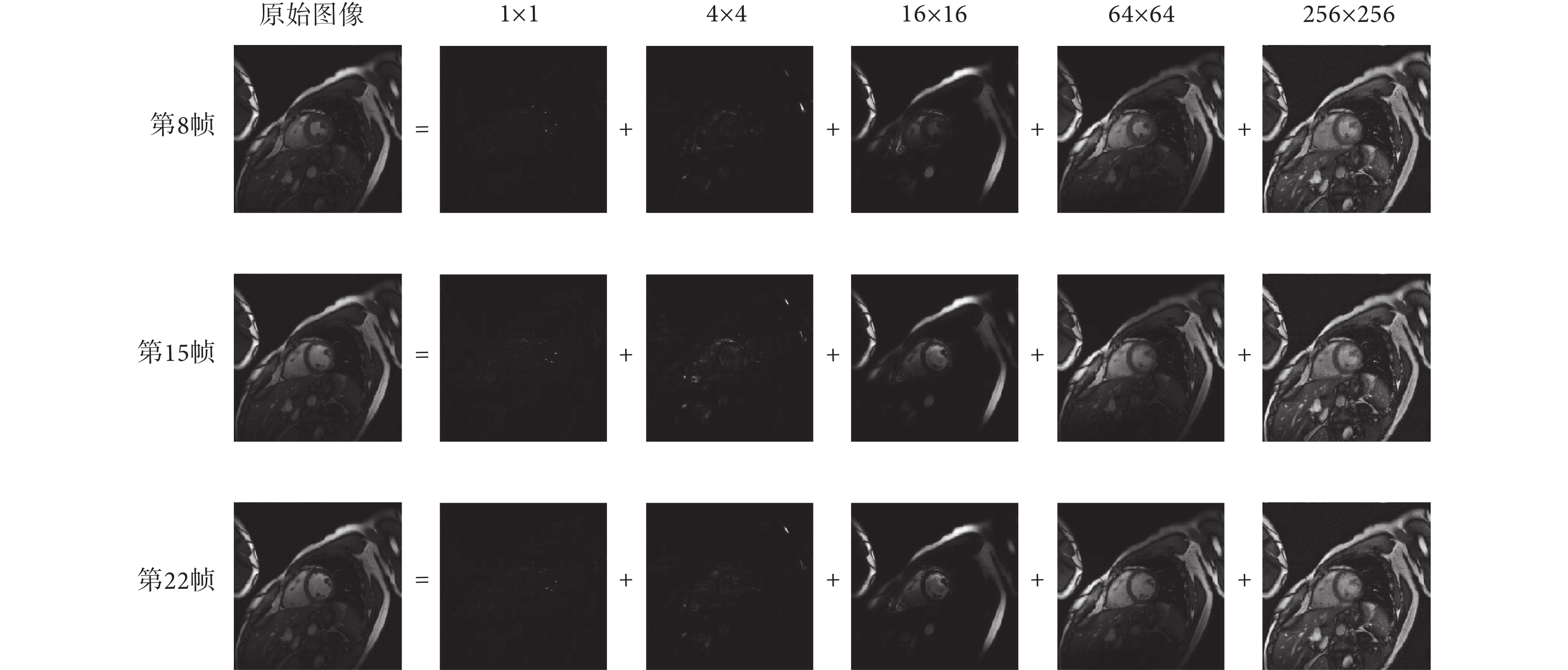 圖2
心臟電影成像序列的多尺度低秩分解
Figure2.
Multiscale low rank decomposition of cardiac cine imaging
圖2
心臟電影成像序列的多尺度低秩分解
Figure2.
Multiscale low rank decomposition of cardiac cine imaging
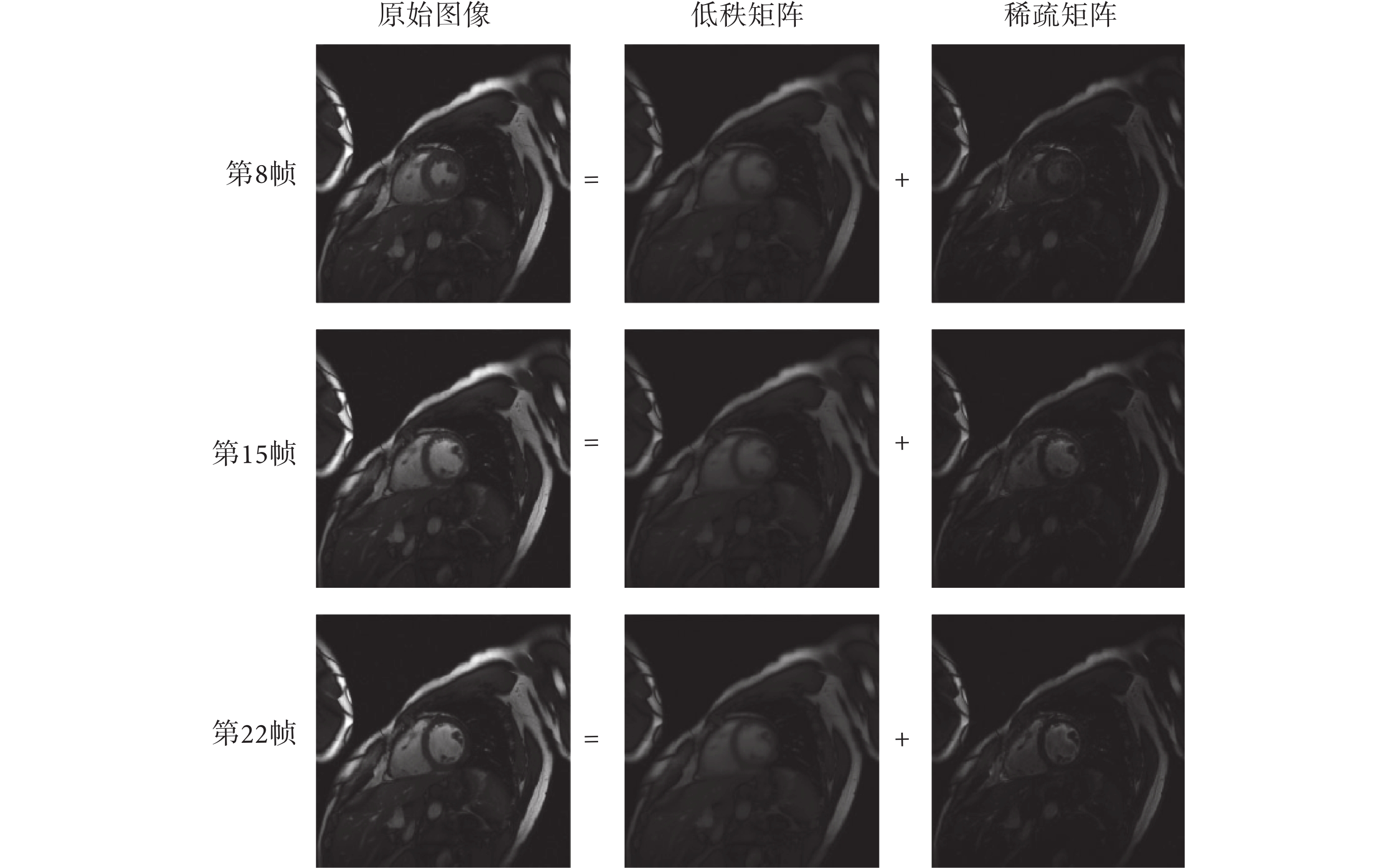 圖3
心臟電影成像序列的低秩稀疏分解
Figure3.
Low rank plus sparse decomposition of cardiac cine imaging
圖3
心臟電影成像序列的低秩稀疏分解
Figure3.
Low rank plus sparse decomposition of cardiac cine imaging
1.2 多尺度低秩模型的 ADMM 重構
壓縮感知重構算法主要分成四類。貪婪算法采用  范數最小化實現,因其非多項式難解問題,一般只能尋找局部最優解,算法簡單快捷,但對于具體應用條件有嚴格規定。約束優化算法采用
范數最小化實現,因其非多項式難解問題,一般只能尋找局部最優解,算法簡單快捷,但對于具體應用條件有嚴格規定。約束優化算法采用  范數最小化來替代原始的無約束問題,雖然重構效果良好,但是計算量劇增。迫近算法將原始問題轉換為相應的迫近算子,計算復雜度低,易于實現,被視為解決非光滑、有約束的大規模數據優化問題的有力工具,但重構精度有待提高。同倫算法通過調整同倫參數,用于
范數最小化來替代原始的無約束問題,雖然重構效果良好,但是計算量劇增。迫近算法將原始問題轉換為相應的迫近算子,計算復雜度低,易于實現,被視為解決非光滑、有約束的大規模數據優化問題的有力工具,但重構精度有待提高。同倫算法通過調整同倫參數,用于  范數最小化不斷迭代尋找最優解。
范數最小化不斷迭代尋找最優解。
ADMM 算法本質上屬于原始-對偶(primal-dual)算法,是用來求解壓縮感知中分解型綜合型模型的流行算法。其基本思想是:利用拉格朗日乘子法將約束問題轉化為無約束問題,結合變量分裂的思想,引入輔助變量替換待求解的變量,通過交替迭代求解一系列低維子問題來求解原來的復雜問題。該算法具有收斂速度快、性能良好以及懲罰參數無需趨向無窮大等優點。
引入變量  將式(2)寫成規范的 ADMM 形式,同時轉化成兩個子問題的求解:
將式(2)寫成規范的 ADMM 形式,同時轉化成兩個子問題的求解:
 |
式(3)中的兩個目標函數分別為  和
和  ,具有可分離性質,可以分為兩組變量,通過固定其中一組變量,然后最小化目標函數求解另外一組變量。對于第一個目標函數,可以采用迫近算子求解。考慮到奇異值分解 X =
,具有可分離性質,可以分為兩組變量,通過固定其中一組變量,然后最小化目標函數求解另外一組變量。對于第一個目標函數,可以采用迫近算子求解。考慮到奇異值分解 X =  ,其中
,其中  和
和  分別為正交矩陣,奇異值
分別為正交矩陣,奇異值  非負。對于第二個目標函數的多尺度核范數,可以通過式(4)的奇異值軟閾值算子求取核范數
非負。對于第二個目標函數的多尺度核范數,可以通過式(4)的奇異值軟閾值算子求取核范數  的參數
的參數  ,即一部分小于
,即一部分小于  的奇異值為 0,而大于
的奇異值為 0,而大于  的奇異值則減去
的奇異值則減去  :
:
 |
由于尺度  下的塊核范數為
下的塊核范數為  ,每個尺度下的塊核范數與尺度都是可分的,其迫近函數可寫作基于塊的奇異值軟閾值算子如式(5),即提取矩陣的每個塊,進行奇異值軟閾值化,然后再重新放回矩陣中:
,每個尺度下的塊核范數與尺度都是可分的,其迫近函數可寫作基于塊的奇異值軟閾值算子如式(5),即提取矩陣的每個塊,進行奇異值軟閾值化,然后再重新放回矩陣中:
 |
將上述式(3)~(5)結合起來,本文提出的多尺度低秩分解模型的 ADMM 求解算法流程為:執行下列迭代過程式(6),直至第  次重構結果與第
次重構結果與第  次重構結果的差值小于等于閾值,或者迭代次數超過設定的最大次數:
次重構結果的差值小于等于閾值,或者迭代次數超過設定的最大次數:
 |
其中, 是 ADMM 算法中影響收斂速度的參數。
是 ADMM 算法中影響收斂速度的參數。
2 實驗結果及分析
本文實驗在 HP 工作站 Z600 上采用 MATLAB 2016 編程實現,系統配置為:Intel Xeon CPU E5606 @2.13 GHz,24 GB 內存,64 位 Windows 7 操作系統。實驗使用的完整采樣數據是心臟電影成像序列  ,多線圈敏感度矩陣為
,多線圈敏感度矩陣為 
 ,使用笛卡爾欠采樣模板,欠采樣率為 25%,沿時間軸進行傅里葉變換作為稀疏表達,來源于文獻[9]。本文以此作為實驗對象,是因為心臟電影成像技術在臨床應用中的廣泛性,以及該成像序列在主流算法文獻[9,22-25]中使用的普遍性。6 種對比算法及本文算法的相關參數設置如表 1 所示。
,使用笛卡爾欠采樣模板,欠采樣率為 25%,沿時間軸進行傅里葉變換作為稀疏表達,來源于文獻[9]。本文以此作為實驗對象,是因為心臟電影成像技術在臨床應用中的廣泛性,以及該成像序列在主流算法文獻[9,22-25]中使用的普遍性。6 種對比算法及本文算法的相關參數設置如表 1 所示。
實驗采用峰值信噪比(peak signal to noise ratio,PSNR)和相對誤差(relative  norm error,RLNE)兩個指標來定量分析和評價算法的性能優劣。PSNR 是一種評價圖像品質的客觀標準,其值越大表示圖像失真越小。RLNE 用于比較完整采樣圖像和重構圖像的相對
norm error,RLNE)兩個指標來定量分析和評價算法的性能優劣。PSNR 是一種評價圖像品質的客觀標準,其值越大表示圖像失真越小。RLNE 用于比較完整采樣圖像和重構圖像的相對  范數誤差,其值越小越好。這兩個指標的計算公式分別如下:
范數誤差,其值越小越好。這兩個指標的計算公式分別如下:
 |
 |
其中, 和
和  分別表示完整采樣圖像和重構圖像,大小均為
分別表示完整采樣圖像和重構圖像,大小均為  (三維)。
(三維)。
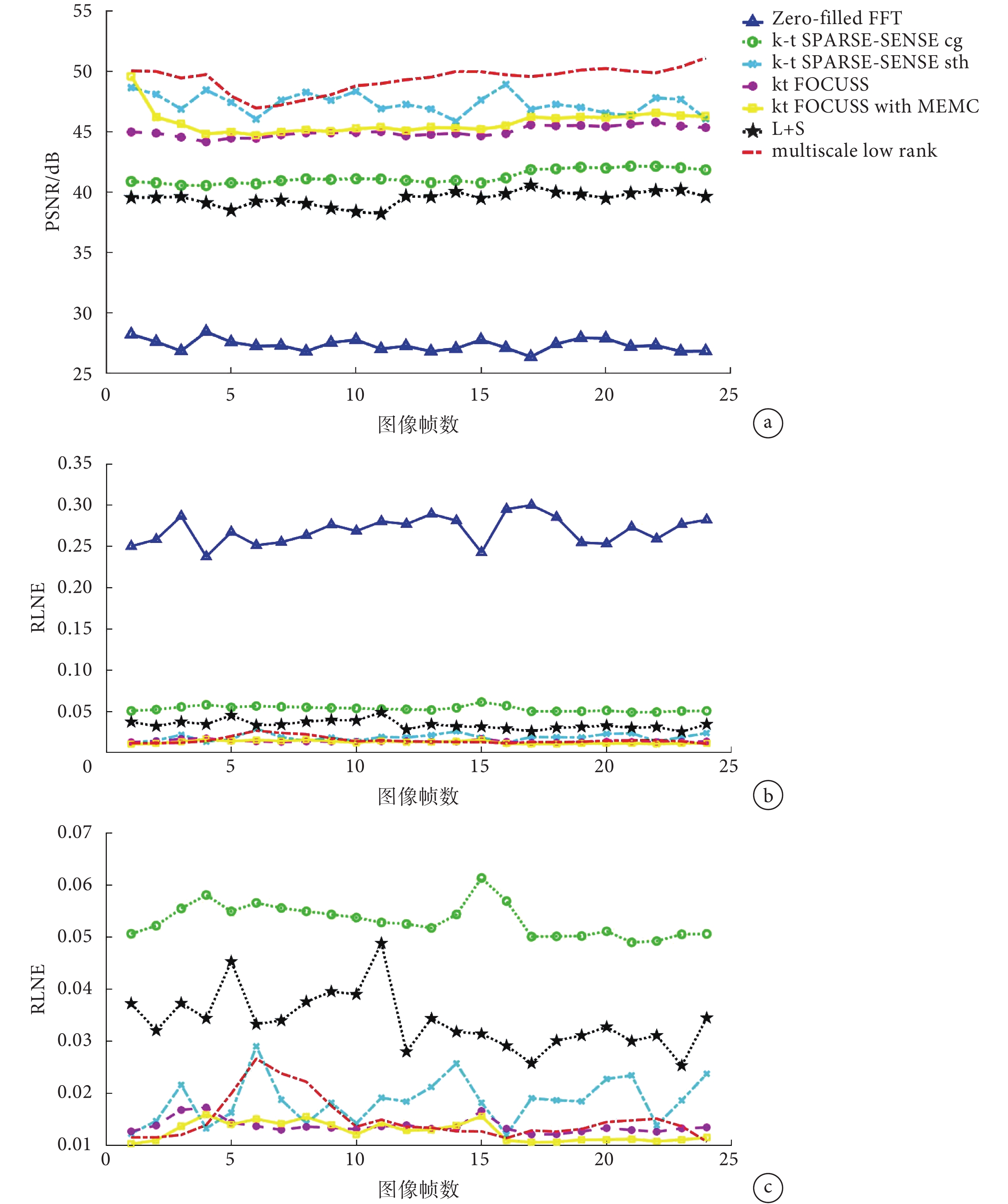
表 1 中列出的 7 種算法重構結果的性能指標如圖 4 所示。由于 Zero-filled FFT 方法性能最差,為進一步觀察其余算法 RLNE 指標的差異,放大顯示于圖 4c。上述 7 種算法的 24 幀圖像的性能指標平均值見表 2。從圖 4a、圖 4c 和表 2 可以看出:本文提出的多尺度低秩模型的 ADMM 求解算法可以獲得 PSNR 均值 49.326 5 dB,RLNE 均值 0.015 0,定量指標表現最優。
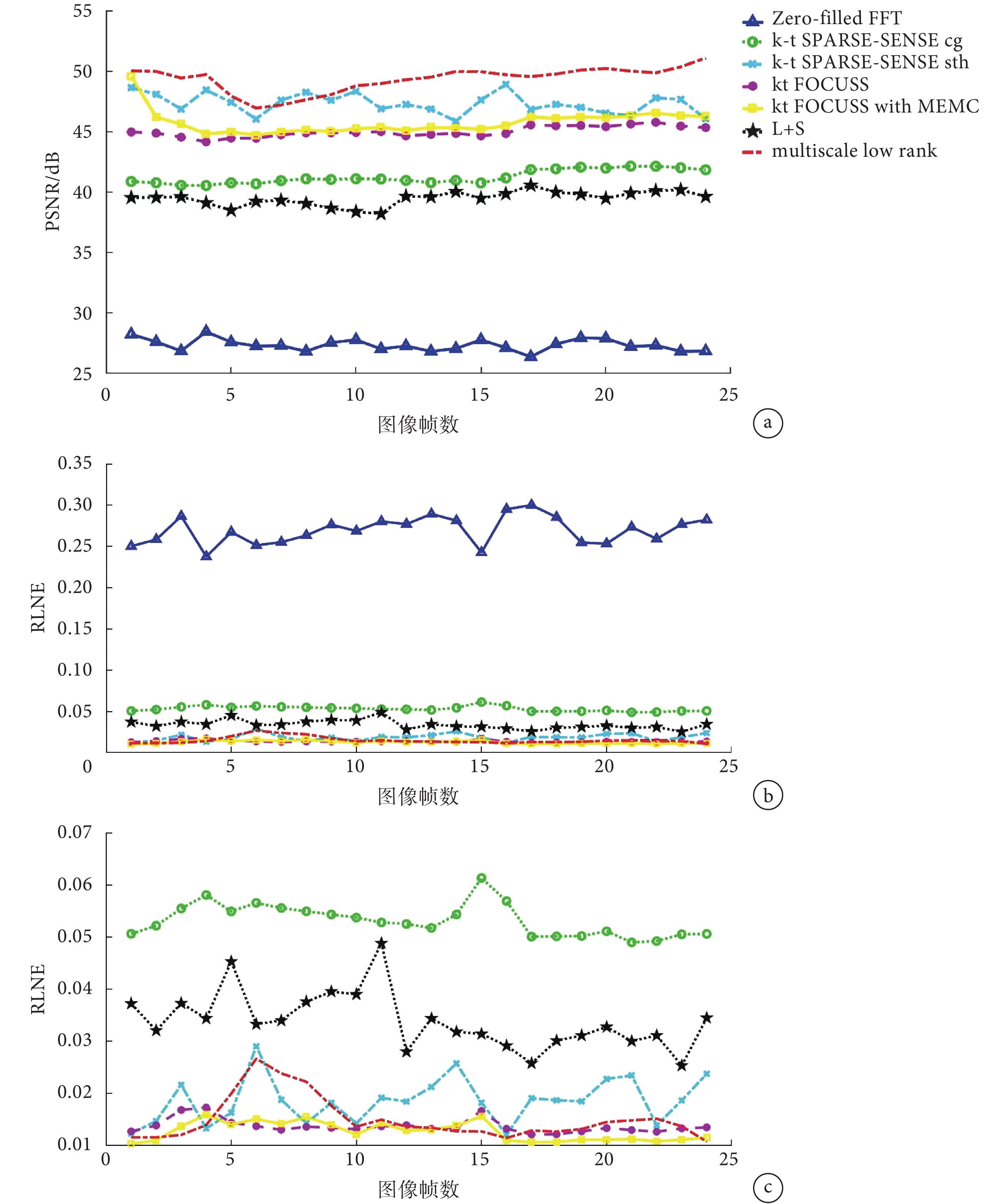 圖4
表 1 所列 7 種算法重構結果的性能指標比較
圖4
表 1 所列 7 種算法重構結果的性能指標比較
a.PSNR;b. RLNE;c. 放大的 RLNE
Figure4. Comparison of the performance indices for 7 algorithmsa.PSNR; b. RLNE; c. magnification of RLNE
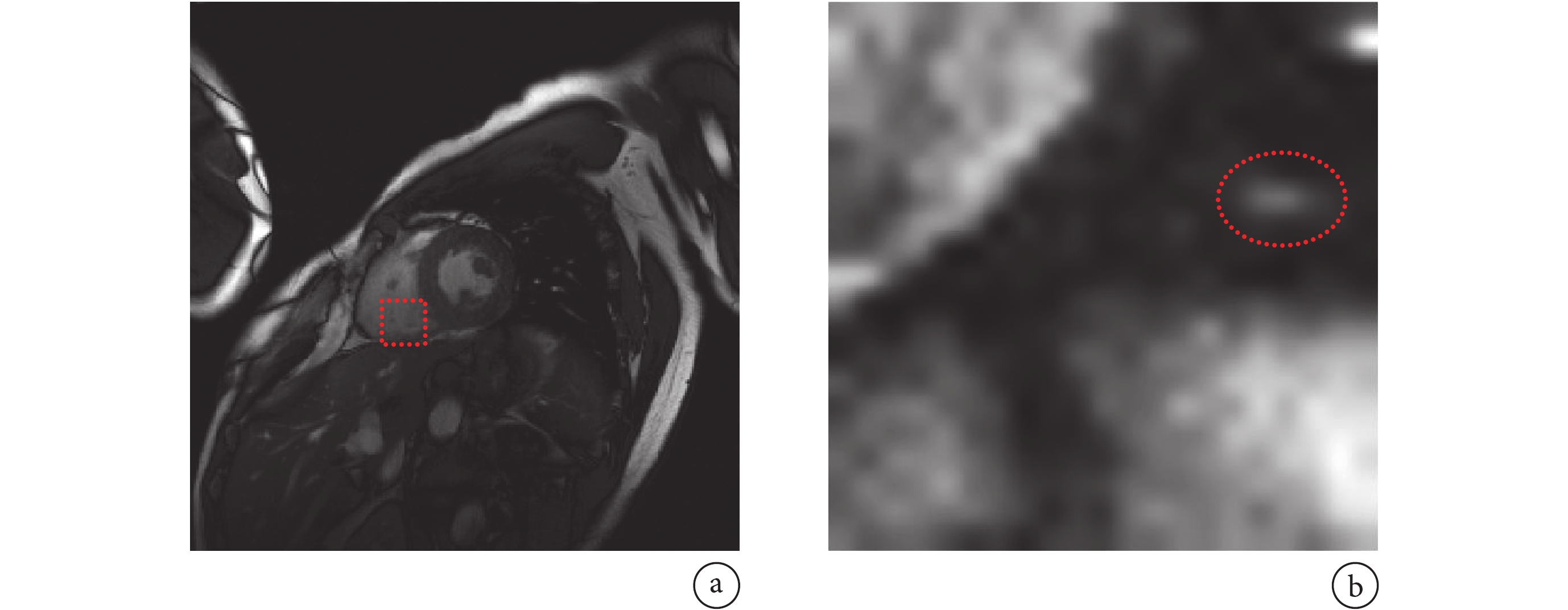
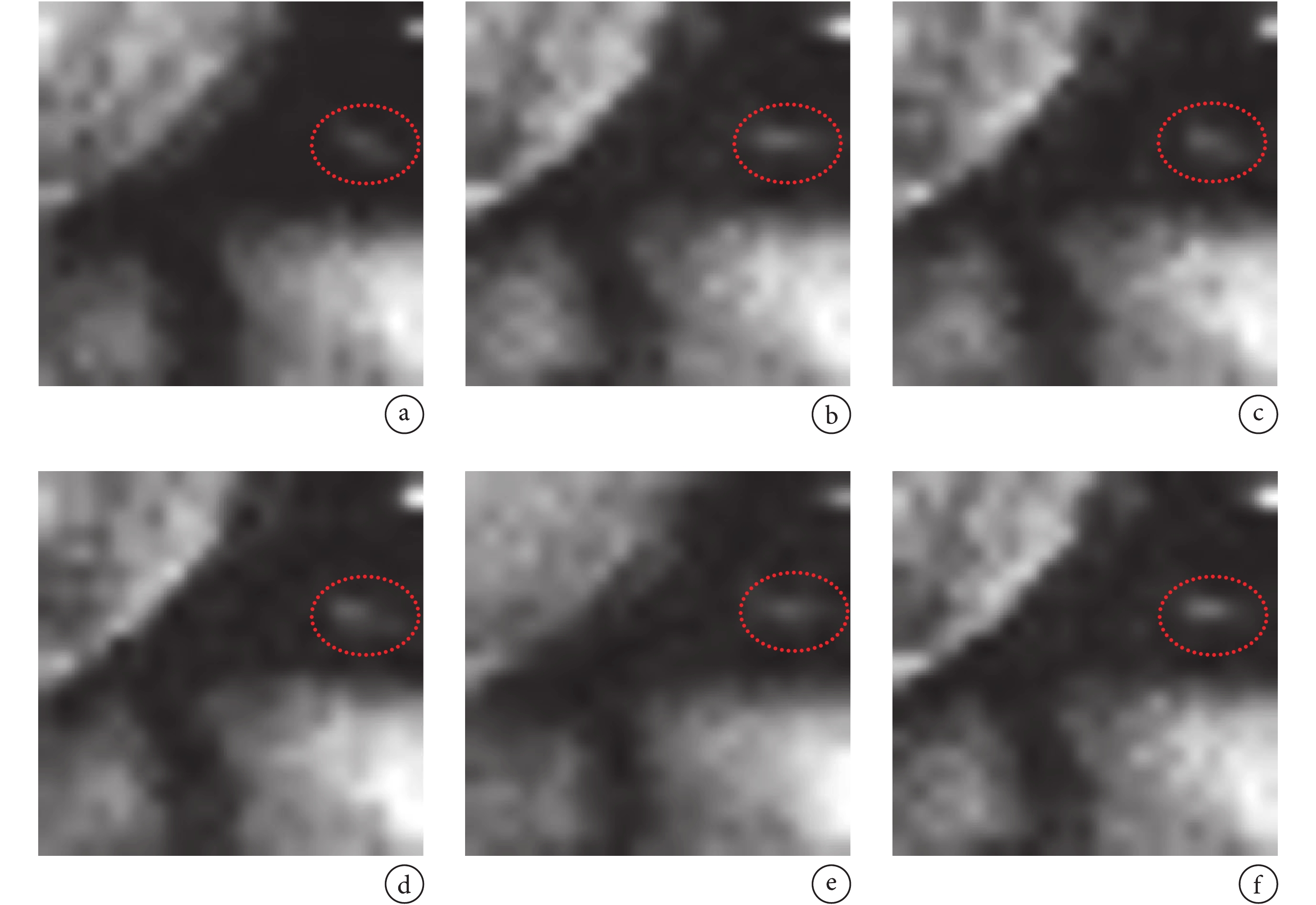
為從人眼視覺系統直觀感受圖像的重構質量,隨機選取完整采樣圖像序列的第 10 幀及其局部放大圖像顯示于圖 5,紅色正方形虛線框表示局部放大區域。將除 Zero-filled FFT 以外的其余 6 種算法的重構結果相同區域局部放大顯示于圖 6。從圖 5b 和圖 6 可以看出:本文算法重構效果最好,圖 6f 紅色橢圓框中的亮點大小和相對位置最接近原始圖像圖 5b,基于軟閾值的 k-t SPARSE-SENSE 算法效果次之,其余算法結果則在亮點的明暗程度和邊緣界限等方面與圖 5b 存在明顯差異。同時,表 2 中的性能指標均值結果也表明:與排名第二的基于軟閾值的 k-t SPARSE-SENSE 算法相比,本文算法的 PSNR 均值高出近 2 dB,RLNE 均值降低了 0.003 6。這充分說明,無論從定量指標入手,還是從定性的人眼視覺感受來說,本文提出的多尺度低秩模型的重構效果均最佳。
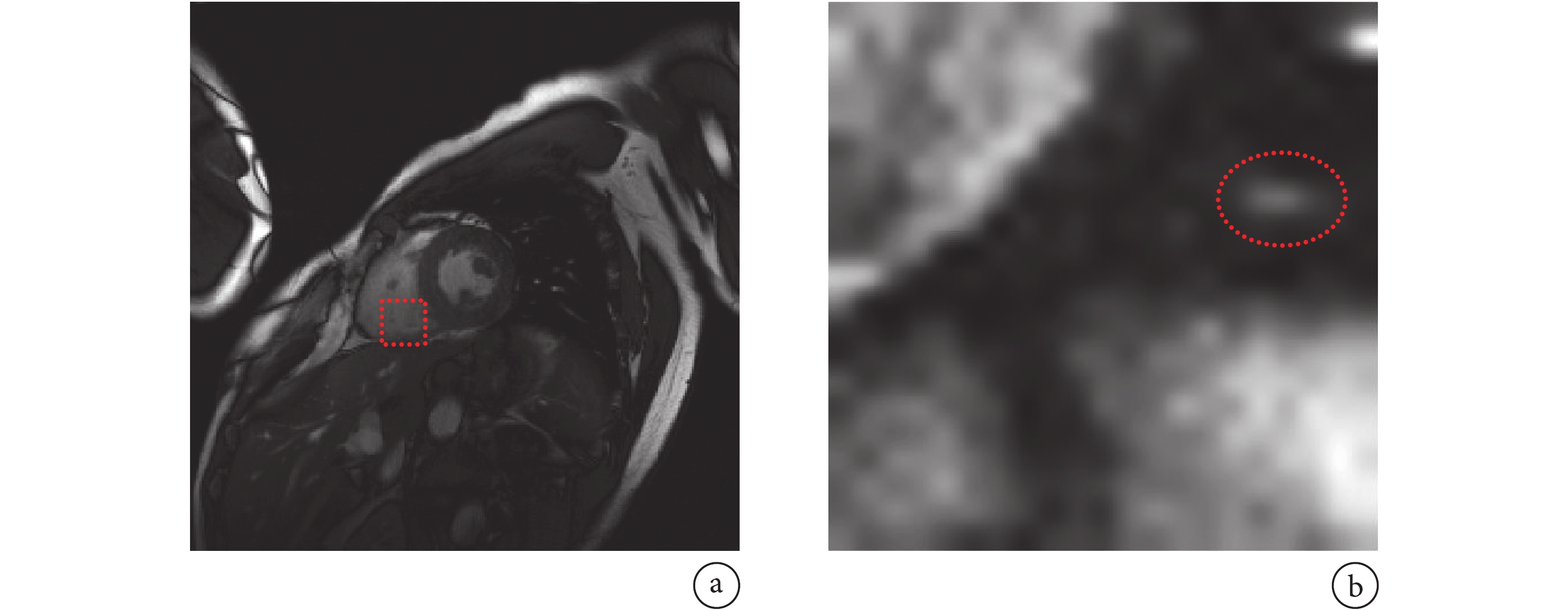 圖5
第 10 幀完整采樣圖像及其局部區域放大顯示
圖5
第 10 幀完整采樣圖像及其局部區域放大顯示
a.完整采樣圖像;b. 局部區域放大
Figure5. The 10th image of full-sampling sequence and its local region magnificationa. full-sampling image; b. local region magnification
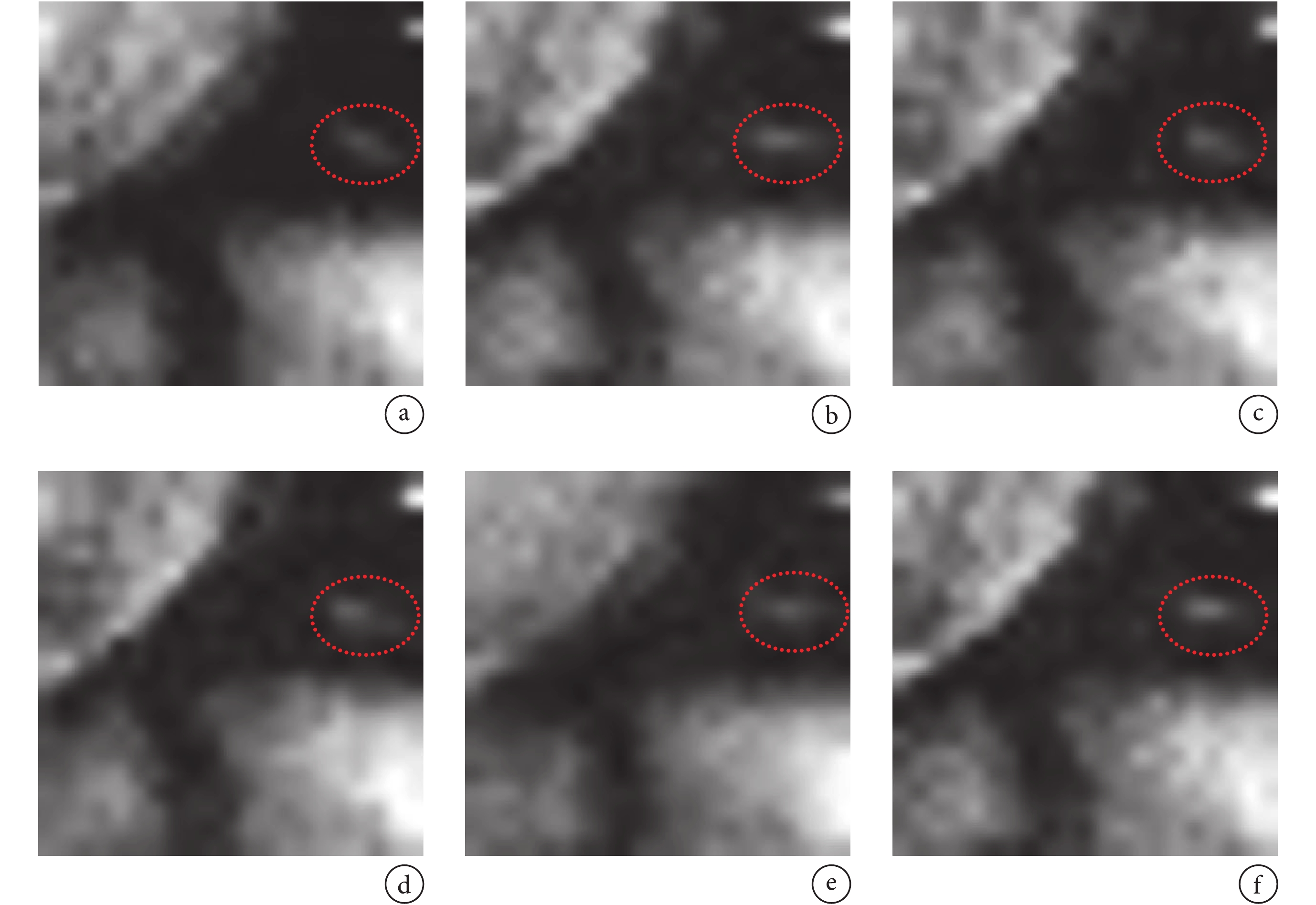 圖6
6 種算法重構結果序列中第 10 幀圖像局部區域放大顯示
圖6
6 種算法重構結果序列中第 10 幀圖像局部區域放大顯示
a. k-t SPARSE-SENSE cg;b. k-t SPARSE-SENSE sth;c. kt FOCUSS;d. kt FOCUSS with MEMC;e. L + S;f. multiscale low rank
Figure6. Comparison of local region magnification of the 10th image from different 6 reconstruction algorithmsa. k-t SPARSE-SENSE cg; b. k-t SPARSE-SENSE sth; c. kt FOCUSS; d. kt FOCUSS with MEMC; e. L + S; f. multiscale low rank
3 討論與結論
心臟磁共振成像 CMR 能夠全面提供心臟及其鄰近結構的信息,在心臟形態結構、心室功能、心肌活性等方面做出準確評價,在心血管成像領域具有廣泛應用。但是,CMR 成像時間較長,檢查過程中需保持制動,小于 8 歲的兒童或者是先天缺陷的大齡兒童、老人以及一些特殊疾病的患者在檢查時難以主動配合,從而制約了其臨床應用。
低秩稀疏分解快速重構 MRI 圖像的方法,因稀疏先驗未能充分利用圖像局部空間一致性和圖像塊的平滑性,從而導致重構圖像不夠干凈以及重構結果對噪聲敏感的缺點。本文將多分辨率思想引入低秩稀疏分解理論,提出基于多尺度低秩分解模型和 ADMM 算法的 CMR 圖像的高質量重構算法。以 PSNR 和 RLNE 為定量評價指標,將本文算法與基于軟閾值的 k-t SPARSE-SENSE 算法、基于非線性共軛梯度的 k-t SPARSE-SENSE 算法、低秩稀疏分解、kt FOCUSS 算法、基于運動補償的 kt FOCUSS 算法等主流算法進行性能比較,并以局部區域放大來進行人眼視覺感受的定性評估。實驗結果表明:本文算法可以取得最優的性能評價指標,同時對圖像細節的處理和邊緣輪廓的顯示更接近完整采樣圖像,對于促進 CMR 快速成像技術的發展及其在臨床疾病診療中的應用具有重要價值。
本文算法在 HP Z600 工作站上運行時間約 1 200 s,考慮到各個欠采樣點間不存在數據相關和控制相關,也無任何數據通信,因此今后將在 GPU 上實現算法加速,在兼顧圖像重構質量的同時進一步提高計算實時性。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
磁共振成像(magnetic resonance imaging,MRI)是目前主要的無創醫學成像手段之一,心臟磁共振(cardiac magnetic resonance,CMR)則是一種特殊的 MRI 技術,用于無創性評價心臟形態結構和生理功能,已在心臟成像領域成為評價標準[1]。但是,與常規 MRI 技術相比,CMR 成像時間較長,同時具有一定的特殊性,如消除心臟運動偽影、平衡時空分辨率等。
壓縮感知(compressed sensing,CS)理論主要包含稀疏表達、測量矩陣和重構算法三個方面。該理論自 2006 年誕生以來,為加速 MRI 開辟了嶄新的途徑,即利用 MRI 信號的稀疏性,以遠低于奈奎斯特采樣定理的方式來采集數據,設計精確、快速的重構算法,從欠采樣 K 空間數據中恢復出具有診斷價值的圖像,從而大大減少掃描時間[2-4]。此后的研究表明:只要原始矩陣是低秩的,就可以通過求解矩陣核范數最小化問題來恢復原始矩陣[5-6]。壓縮感知是在未知信號向量具有稀疏性的假設條件下進行數據處理;而低秩矩陣恢復則是利用未知矩陣的低秩性來進一步分析,因此低秩矩陣恢復可以看作壓縮感知從一階向量到二階矩陣的拓展和延伸[7-8]。
近兩年來,基于低秩稀疏分解的 CS-MRI 圖像重構始終是研究熱點。文獻[9]首次將低秩稀疏分解模型應用于 MRI 圖像重構,初步應用于心臟灌注、心臟電影、血管成像、胸腹部 MRI 成像等臨床應用。文獻[10]利用魯棒主成分分析提取動態 MRI 中的動態組織部分,提出基于稀疏和低秩先驗分離的重構算法。文獻[11]提出全變差與核范數正則化相結合的動態 MRI 重構算法。文獻[12]采用動態全變差和核范數來增強 MRI 各幀和整個序列的正則化,將重構問題劃分為兩個子問題來求解。文獻[13]利用圖像低秩屬性和全變差,同時考慮圖像本身的局部和非局部信息,提出基于稀疏和低秩先驗的壓縮感知重構算法。文獻[14]提出基于非局部低秩正則化的壓縮感知重構算法,獲得了最好的圖像重構效果;但是僅利用圖像的非局部信息,忽略了局部信息,不能有效重構圖像邊緣。文獻[15]提出基于塊操作的非局部低秩先驗的動態 MRI 重構算法,在此基礎上,文獻[16]提出局部低秩稀疏模型,用于灌注 MRI 圖像的加速成像。此外,文獻[17-18]以張量分解作為稀疏變換,分別提出動態 MRI 重構算法 HOSVD 和 kt-MLSD。文獻[19]提出基于部分可分離模型和壓縮感知相結合的 Stepped-Sparse PS 算法。文獻[20-21]初步提出多尺度和多維低秩矩陣分解,并應用于人臉圖像、監控視頻、動態 MRI 等的多尺度建模和協同濾波。
綜上所述,已有文獻采用低秩稀疏分解來快速重構 MRI 圖像,雖取得一定積極進展,但因稀疏先驗未能充分利用圖像局部空間一致性和圖像塊的平滑性,從而導致重構圖像不夠干凈,重構結果對噪聲敏感。針對這一問題,本文將多分辨率思想引入低秩稀疏分解理論,提出基于多尺度低秩分解模型和交替方向拉格朗日乘子法(alternating direction method of multipliers,ADMM)的 CMR 圖像高質量重構算法,加快成像速度,提高成像質量,改善檢查舒適度,促進循環系統疾病診療新技術的發展。
1 主要關鍵技術
1.1 多尺度低秩模型
CMR 成像所包含的心臟電影和心臟灌注等成像技術均屬于動態 MRI 范疇,時空相關度較高,即序列圖像上保持不變的背景部分較多,變化的動態部分較少,相鄰像素的相似程度較高。因此,把 CMR 圖像的每個時間幀看作時空矩陣的一列,整個圖像序列分離成稀疏先驗和低秩先驗這兩部分,待重構圖像即為兩者疊加,從而建立動態組織和靜態背景的分離模型,即矩陣低秩稀疏分解的基本思想。該方法應用于動態 MRI 圖像重構取得了一定積極進展,但對噪聲敏感,重構圖像不夠干凈,這是因為稀疏先驗沒有充分利用圖像局部空間一致性和圖像塊的平滑性。
本文將多分辨率思想引入低秩矩陣分解,提出 CMR 圖像的多尺度低秩分解模型,如圖 1 所示。多尺度結構是指信號在不同尺度上展現不同的結構,小波、曲波、多尺度金字塔等均具有多尺度結構。多尺度幾何分析的目的是為了檢測、表示、處理高維空間數據,而這些數據的某些重要特征集中體現在其低維子集中。多尺度低秩矩陣分解可以獲得比傳統低秩模型更精確、更緊湊的信號表達方式,同時具有多尺度模型和低秩矩陣分解的優點。
 圖1
多尺度低秩分解示意圖
Figure1.
Schematic diagram of multiscale low rank decomposition
圖1
多尺度低秩分解示意圖
Figure1.
Schematic diagram of multiscale low rank decomposition
對于輸入矩陣  (
( ),經過多尺度分解以及塊重構算子
),經過多尺度分解以及塊重構算子  后,其多尺度分解模型可近似寫成如下形式:
后,其多尺度分解模型可近似寫成如下形式:
 |
即輸入矩陣  視為基于圖像分塊
視為基于圖像分塊  的各低秩矩陣
的各低秩矩陣  之和。其中,
之和。其中, 是對應圖像分塊
是對應圖像分塊  部分的低秩矩陣;
部分的低秩矩陣; 表示分解尺度。
表示分解尺度。 是塊重構算子,將塊
是塊重構算子,將塊  從完整矩陣中抽取出來并將其重構成
從完整矩陣中抽取出來并將其重構成  的矩陣,這里
的矩陣,這里  是指第
是指第  個尺度下塊矩陣的大小。
個尺度下塊矩陣的大小。 、
、 和
和  是秩為
是秩為  的塊矩陣
的塊矩陣  的奇異值分解(singular value decomposition,SVD)。
的奇異值分解(singular value decomposition,SVD)。
眾所周知,引入核范數后,矩陣秩最小化問題可以松弛為凸優化問題。遵循這一思路,多尺度低秩分解也可以用凸優化來求解。定義尺度  下的塊核范數為
下的塊核范數為  ,于是多尺度低秩分解模型可寫成如下形式:
,于是多尺度低秩分解模型可寫成如下形式:
 |
其中, 是正則化參數。
是正則化參數。
針對  大小的心臟電影成像序列,隨機選取其中第 8、15、22 幀圖像,采用多尺度低秩分解和低秩稀疏分解的結果分別見圖 2、圖 3。圖 2 所示的多尺度低秩分解模型可以清晰顯示靜態和動態組織,對心肌壁等細微結構在
大小的心臟電影成像序列,隨機選取其中第 8、15、22 幀圖像,采用多尺度低秩分解和低秩稀疏分解的結果分別見圖 2、圖 3。圖 2 所示的多尺度低秩分解模型可以清晰顯示靜態和動態組織,對心肌壁等細微結構在  和
和  尺度上能明確表示,在減少運動偽影的同時更利于提取動態信息。而圖 3 所示的低秩稀疏模型只能大致分離靜態和動態組織,并非嚴格意義上的稀疏或低秩。
尺度上能明確表示,在減少運動偽影的同時更利于提取動態信息。而圖 3 所示的低秩稀疏模型只能大致分離靜態和動態組織,并非嚴格意義上的稀疏或低秩。
 圖2
心臟電影成像序列的多尺度低秩分解
Figure2.
Multiscale low rank decomposition of cardiac cine imaging
圖2
心臟電影成像序列的多尺度低秩分解
Figure2.
Multiscale low rank decomposition of cardiac cine imaging
 圖3
心臟電影成像序列的低秩稀疏分解
Figure3.
Low rank plus sparse decomposition of cardiac cine imaging
圖3
心臟電影成像序列的低秩稀疏分解
Figure3.
Low rank plus sparse decomposition of cardiac cine imaging
1.2 多尺度低秩模型的 ADMM 重構
壓縮感知重構算法主要分成四類。貪婪算法采用  范數最小化實現,因其非多項式難解問題,一般只能尋找局部最優解,算法簡單快捷,但對于具體應用條件有嚴格規定。約束優化算法采用
范數最小化實現,因其非多項式難解問題,一般只能尋找局部最優解,算法簡單快捷,但對于具體應用條件有嚴格規定。約束優化算法采用  范數最小化來替代原始的無約束問題,雖然重構效果良好,但是計算量劇增。迫近算法將原始問題轉換為相應的迫近算子,計算復雜度低,易于實現,被視為解決非光滑、有約束的大規模數據優化問題的有力工具,但重構精度有待提高。同倫算法通過調整同倫參數,用于
范數最小化來替代原始的無約束問題,雖然重構效果良好,但是計算量劇增。迫近算法將原始問題轉換為相應的迫近算子,計算復雜度低,易于實現,被視為解決非光滑、有約束的大規模數據優化問題的有力工具,但重構精度有待提高。同倫算法通過調整同倫參數,用于  范數最小化不斷迭代尋找最優解。
范數最小化不斷迭代尋找最優解。
ADMM 算法本質上屬于原始-對偶(primal-dual)算法,是用來求解壓縮感知中分解型綜合型模型的流行算法。其基本思想是:利用拉格朗日乘子法將約束問題轉化為無約束問題,結合變量分裂的思想,引入輔助變量替換待求解的變量,通過交替迭代求解一系列低維子問題來求解原來的復雜問題。該算法具有收斂速度快、性能良好以及懲罰參數無需趨向無窮大等優點。
引入變量  將式(2)寫成規范的 ADMM 形式,同時轉化成兩個子問題的求解:
將式(2)寫成規范的 ADMM 形式,同時轉化成兩個子問題的求解:
 |
式(3)中的兩個目標函數分別為  和
和  ,具有可分離性質,可以分為兩組變量,通過固定其中一組變量,然后最小化目標函數求解另外一組變量。對于第一個目標函數,可以采用迫近算子求解。考慮到奇異值分解 X =
,具有可分離性質,可以分為兩組變量,通過固定其中一組變量,然后最小化目標函數求解另外一組變量。對于第一個目標函數,可以采用迫近算子求解。考慮到奇異值分解 X =  ,其中
,其中  和
和  分別為正交矩陣,奇異值
分別為正交矩陣,奇異值  非負。對于第二個目標函數的多尺度核范數,可以通過式(4)的奇異值軟閾值算子求取核范數
非負。對于第二個目標函數的多尺度核范數,可以通過式(4)的奇異值軟閾值算子求取核范數  的參數
的參數  ,即一部分小于
,即一部分小于  的奇異值為 0,而大于
的奇異值為 0,而大于  的奇異值則減去
的奇異值則減去  :
:
 |
由于尺度  下的塊核范數為
下的塊核范數為  ,每個尺度下的塊核范數與尺度都是可分的,其迫近函數可寫作基于塊的奇異值軟閾值算子如式(5),即提取矩陣的每個塊,進行奇異值軟閾值化,然后再重新放回矩陣中:
,每個尺度下的塊核范數與尺度都是可分的,其迫近函數可寫作基于塊的奇異值軟閾值算子如式(5),即提取矩陣的每個塊,進行奇異值軟閾值化,然后再重新放回矩陣中:
 |
將上述式(3)~(5)結合起來,本文提出的多尺度低秩分解模型的 ADMM 求解算法流程為:執行下列迭代過程式(6),直至第  次重構結果與第
次重構結果與第  次重構結果的差值小于等于閾值,或者迭代次數超過設定的最大次數:
次重構結果的差值小于等于閾值,或者迭代次數超過設定的最大次數:
 |
其中, 是 ADMM 算法中影響收斂速度的參數。
是 ADMM 算法中影響收斂速度的參數。
2 實驗結果及分析
本文實驗在 HP 工作站 Z600 上采用 MATLAB 2016 編程實現,系統配置為:Intel Xeon CPU E5606 @2.13 GHz,24 GB 內存,64 位 Windows 7 操作系統。實驗使用的完整采樣數據是心臟電影成像序列  ,多線圈敏感度矩陣為
,多線圈敏感度矩陣為 
 ,使用笛卡爾欠采樣模板,欠采樣率為 25%,沿時間軸進行傅里葉變換作為稀疏表達,來源于文獻[9]。本文以此作為實驗對象,是因為心臟電影成像技術在臨床應用中的廣泛性,以及該成像序列在主流算法文獻[9,22-25]中使用的普遍性。6 種對比算法及本文算法的相關參數設置如表 1 所示。
,使用笛卡爾欠采樣模板,欠采樣率為 25%,沿時間軸進行傅里葉變換作為稀疏表達,來源于文獻[9]。本文以此作為實驗對象,是因為心臟電影成像技術在臨床應用中的廣泛性,以及該成像序列在主流算法文獻[9,22-25]中使用的普遍性。6 種對比算法及本文算法的相關參數設置如表 1 所示。
實驗采用峰值信噪比(peak signal to noise ratio,PSNR)和相對誤差(relative  norm error,RLNE)兩個指標來定量分析和評價算法的性能優劣。PSNR 是一種評價圖像品質的客觀標準,其值越大表示圖像失真越小。RLNE 用于比較完整采樣圖像和重構圖像的相對
norm error,RLNE)兩個指標來定量分析和評價算法的性能優劣。PSNR 是一種評價圖像品質的客觀標準,其值越大表示圖像失真越小。RLNE 用于比較完整采樣圖像和重構圖像的相對  范數誤差,其值越小越好。這兩個指標的計算公式分別如下:
范數誤差,其值越小越好。這兩個指標的計算公式分別如下:
 |
 |
其中, 和
和  分別表示完整采樣圖像和重構圖像,大小均為
分別表示完整采樣圖像和重構圖像,大小均為  (三維)。
(三維)。
表 1 中列出的 7 種算法重構結果的性能指標如圖 4 所示。由于 Zero-filled FFT 方法性能最差,為進一步觀察其余算法 RLNE 指標的差異,放大顯示于圖 4c。上述 7 種算法的 24 幀圖像的性能指標平均值見表 2。從圖 4a、圖 4c 和表 2 可以看出:本文提出的多尺度低秩模型的 ADMM 求解算法可以獲得 PSNR 均值 49.326 5 dB,RLNE 均值 0.015 0,定量指標表現最優。
 圖4
表 1 所列 7 種算法重構結果的性能指標比較
圖4
表 1 所列 7 種算法重構結果的性能指標比較
a.PSNR;b. RLNE;c. 放大的 RLNE
Figure4. Comparison of the performance indices for 7 algorithmsa.PSNR; b. RLNE; c. magnification of RLNE
為從人眼視覺系統直觀感受圖像的重構質量,隨機選取完整采樣圖像序列的第 10 幀及其局部放大圖像顯示于圖 5,紅色正方形虛線框表示局部放大區域。將除 Zero-filled FFT 以外的其余 6 種算法的重構結果相同區域局部放大顯示于圖 6。從圖 5b 和圖 6 可以看出:本文算法重構效果最好,圖 6f 紅色橢圓框中的亮點大小和相對位置最接近原始圖像圖 5b,基于軟閾值的 k-t SPARSE-SENSE 算法效果次之,其余算法結果則在亮點的明暗程度和邊緣界限等方面與圖 5b 存在明顯差異。同時,表 2 中的性能指標均值結果也表明:與排名第二的基于軟閾值的 k-t SPARSE-SENSE 算法相比,本文算法的 PSNR 均值高出近 2 dB,RLNE 均值降低了 0.003 6。這充分說明,無論從定量指標入手,還是從定性的人眼視覺感受來說,本文提出的多尺度低秩模型的重構效果均最佳。
 圖5
第 10 幀完整采樣圖像及其局部區域放大顯示
圖5
第 10 幀完整采樣圖像及其局部區域放大顯示
a.完整采樣圖像;b. 局部區域放大
Figure5. The 10th image of full-sampling sequence and its local region magnificationa. full-sampling image; b. local region magnification
 圖6
6 種算法重構結果序列中第 10 幀圖像局部區域放大顯示
圖6
6 種算法重構結果序列中第 10 幀圖像局部區域放大顯示
a. k-t SPARSE-SENSE cg;b. k-t SPARSE-SENSE sth;c. kt FOCUSS;d. kt FOCUSS with MEMC;e. L + S;f. multiscale low rank
Figure6. Comparison of local region magnification of the 10th image from different 6 reconstruction algorithmsa. k-t SPARSE-SENSE cg; b. k-t SPARSE-SENSE sth; c. kt FOCUSS; d. kt FOCUSS with MEMC; e. L + S; f. multiscale low rank
3 討論與結論
心臟磁共振成像 CMR 能夠全面提供心臟及其鄰近結構的信息,在心臟形態結構、心室功能、心肌活性等方面做出準確評價,在心血管成像領域具有廣泛應用。但是,CMR 成像時間較長,檢查過程中需保持制動,小于 8 歲的兒童或者是先天缺陷的大齡兒童、老人以及一些特殊疾病的患者在檢查時難以主動配合,從而制約了其臨床應用。
低秩稀疏分解快速重構 MRI 圖像的方法,因稀疏先驗未能充分利用圖像局部空間一致性和圖像塊的平滑性,從而導致重構圖像不夠干凈以及重構結果對噪聲敏感的缺點。本文將多分辨率思想引入低秩稀疏分解理論,提出基于多尺度低秩分解模型和 ADMM 算法的 CMR 圖像的高質量重構算法。以 PSNR 和 RLNE 為定量評價指標,將本文算法與基于軟閾值的 k-t SPARSE-SENSE 算法、基于非線性共軛梯度的 k-t SPARSE-SENSE 算法、低秩稀疏分解、kt FOCUSS 算法、基于運動補償的 kt FOCUSS 算法等主流算法進行性能比較,并以局部區域放大來進行人眼視覺感受的定性評估。實驗結果表明:本文算法可以取得最優的性能評價指標,同時對圖像細節的處理和邊緣輪廓的顯示更接近完整采樣圖像,對于促進 CMR 快速成像技術的發展及其在臨床疾病診療中的應用具有重要價值。
本文算法在 HP Z600 工作站上運行時間約 1 200 s,考慮到各個欠采樣點間不存在數據相關和控制相關,也無任何數據通信,因此今后將在 GPU 上實現算法加速,在兼顧圖像重構質量的同時進一步提高計算實時性。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。