腎臟腫瘤已經成為威脅人類健康的重要疾病之一。超聲檢查具有普及率高、價格低廉、無輻射等諸多優點,已廣泛應用于腎臟腫瘤的診斷中。超聲圖像中腎臟腫瘤的準確分割是制定治療方案的基礎。腎臟腫瘤往往生長在腎皮質中間,分割容易受到周圍臟器干擾,而且超聲圖像對比度低、斑點噪聲嚴重,使得腫瘤分割困難。本文根據腎臟超聲圖像的特點,提出基于自適應分區演化水平集(ASLSM)的腫瘤分割算法。首先,將感興趣區域圖像分區;然后,融合內外能量項和梯度設計目標函數,并自適應調整二者比例;最后,根據質心原理和零水平集內外相似度自適應卷積半徑及曲率,進行曲線演化。將本算法用于腎臟超聲圖像,實驗結果中豪斯多夫距離(HD)為(8.75 ± 4.21)mm,平均絕對距離(MAD)為(3.26 ± 1.69)mm,戴斯系數(DICE)為 0.93 ± 0.03。與傳統的方法進行比較,實驗結果證明本算法可以獲得更加準確的腫瘤分割結果,今后本算法或可為輔助醫生定位和診斷腎臟腫瘤提供便利。
引用本文: 熊小亮, 郭翌, 汪源源, 張岱, 葉兆祥, 張晟, 忻曉潔. 基于自適應分區演化水平集的腎臟腫瘤超聲圖像分割. 生物醫學工程學雜志, 2019, 36(6): 945-956. doi: 10.7507/1001-5515.201902011 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
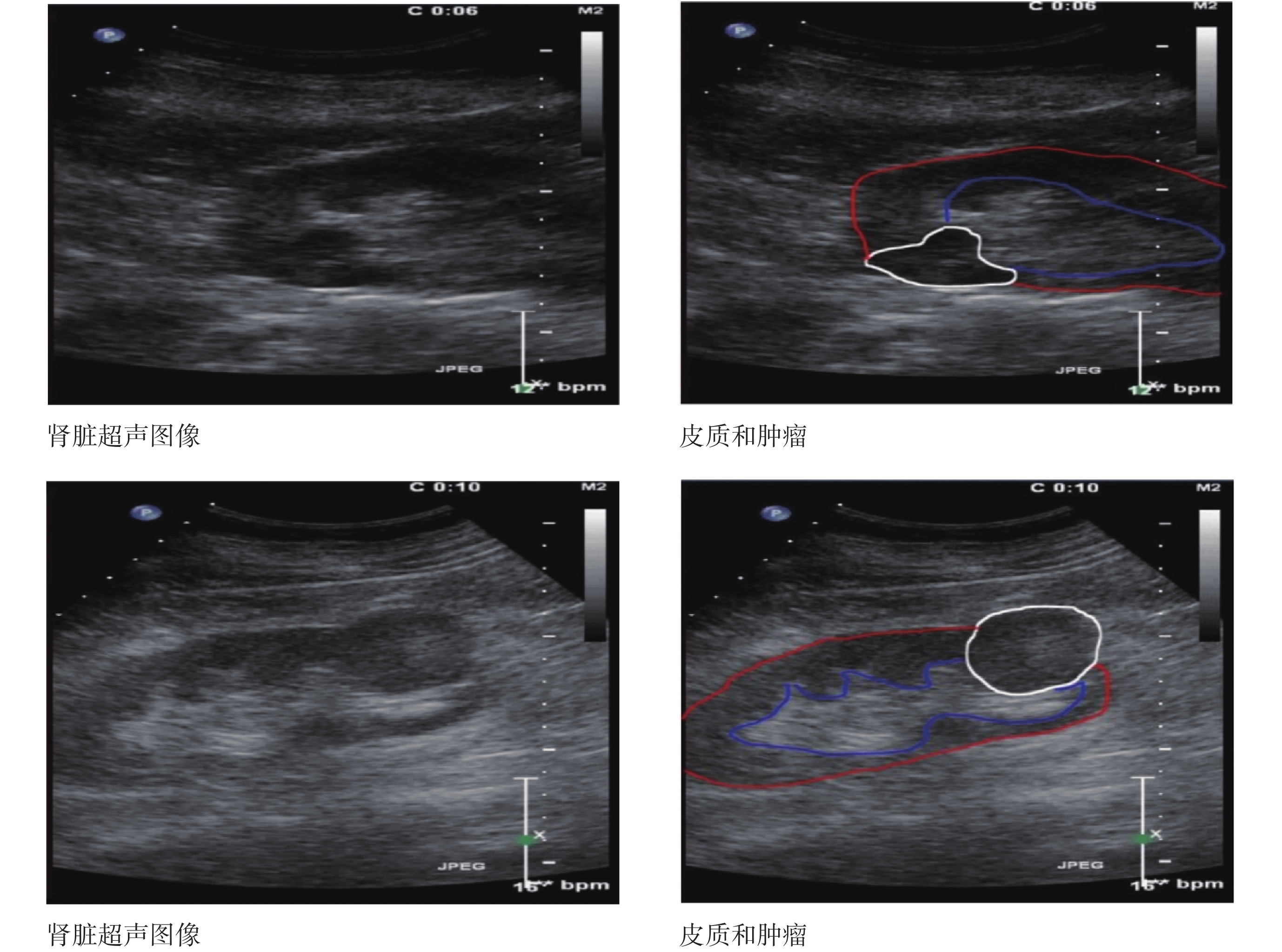
腎臟腫瘤是人體泌尿系統常見腫瘤之一,患病率和死亡率約占腫瘤疾病的 3%[1]。腎臟腫瘤早期臨床癥狀不明顯,晚期可發展到血尿、腹部包塊、疼痛,以致腎功能不全直至患者死亡,所以腎臟腫瘤的早期發現尤為重要[2]。超聲造影以其價格低廉、無輻射、可動態觀察瘤體情況等優勢,已經廣泛應用于腎臟腫瘤檢查[3]。腎臟腫瘤可以根據其造影特征進行分類,以造影劑進入腎皮質和腫瘤的先后順序、造影劑頂峰強度、壞死情況等特征,可區分透明細胞癌、乳頭狀細胞癌和嫌色細胞癌[4]。獲取視頻特征首先要在每幀分割出腫瘤與皮質,因此腫瘤的準確分割尤為關鍵。如圖 1 所示為兩幅典型腎臟超聲圖像,其中左列為兩幅超聲圖像,右列為標注腫瘤和皮質位置的對應圖像,白線內為腫瘤,紅線和藍線之間為皮質。
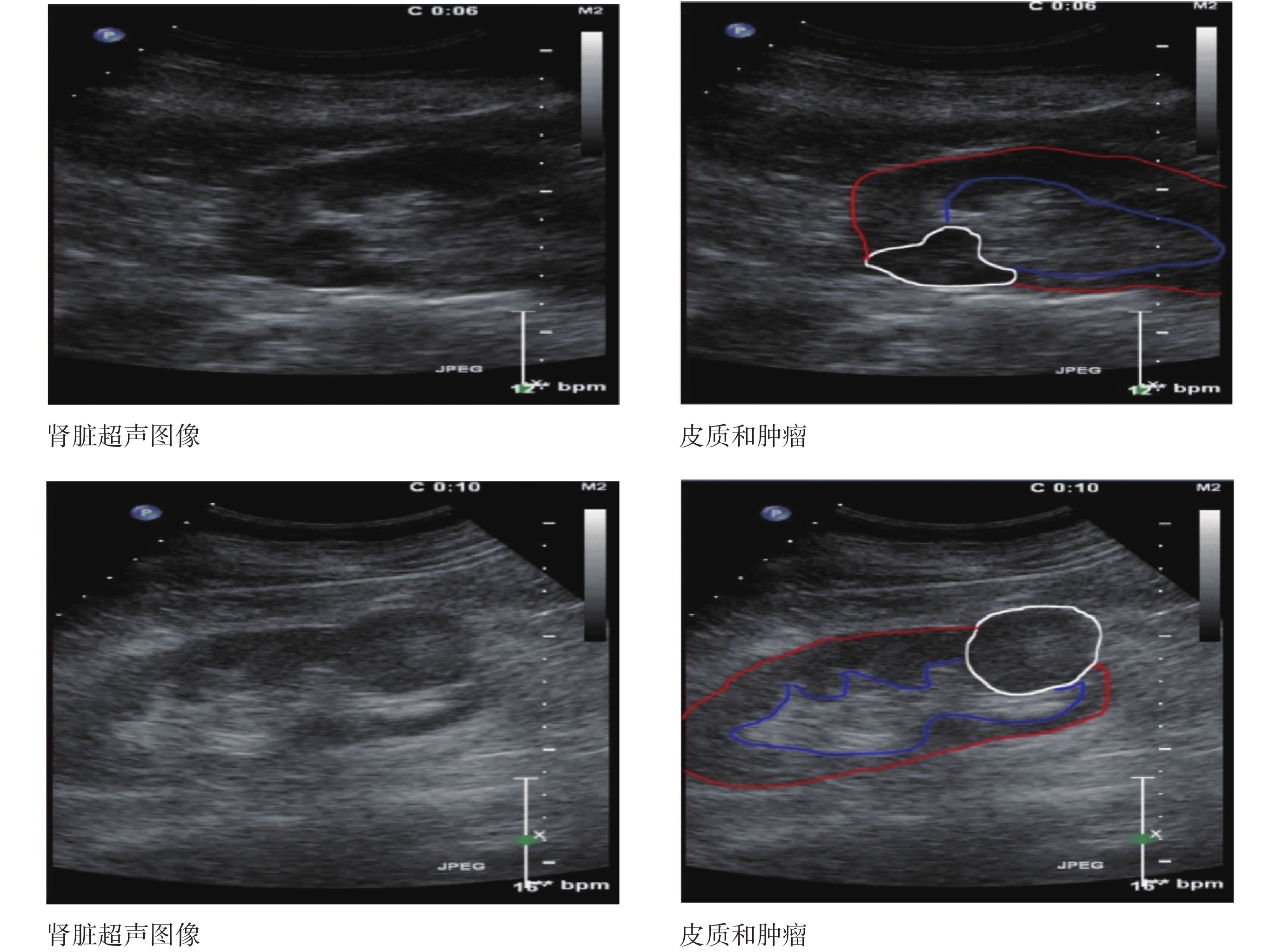 圖1
兩幅腎臟超聲圖像及其對應腫瘤和皮質圖像
Figure1.
Two typical ultrasound kidney images and location of tumor and cortex
圖1
兩幅腎臟超聲圖像及其對應腫瘤和皮質圖像
Figure1.
Two typical ultrasound kidney images and location of tumor and cortex
由于超聲圖像斑點噪聲較大,加之腎臟腫瘤常位于腎臟皮質中間,對腫瘤分割造成很大的干擾。Caselles 等[5]提出了幾何動態模型(geodesic active contours,GAC),使用梯度作為驅動項,僅能夠分割出部分圖像質量好的腫瘤圖像。Li 等[6]提出保持水平集光滑的懲罰項算法,在距離正則化水平集演化模型(distance regularized level set evolution,DRLSE)上改進了懲罰項,取得了更好的效果。然而 DRLSE 僅用梯度驅動演化,當應用于噪聲大的超聲圖像時,如圖 1 所示的第一排圖像,這一演化方式即無法跨越噪聲而到達真正邊界。在 2001 年,Chan 等[7]提出一種以 Chan 和 Vese 兩人名字命名的 Chan-Vese(CV)模型,該方法基于輪廓內外全局能量最小的原則,具有較好的抗噪聲能力,但是容易出現局部演化失敗的問題。在 2008 年,Lankton 等[8]提出區域活動輪廓模型(localizing region-based active contours,LRBAC),其演化只考慮零水平集附近圖像,該取值范圍(下文簡稱:卷積半徑)抗噪聲能力較強。LRBAC 具有 CV 模型同樣的缺陷,即易分裂成小曲線,且會因為卷積半徑過大或者曲率過大所致曲線光滑而出現細節丟失問題,或因卷積半徑過小,演化不到真正邊界。在 2013 年,Zhang 等[9]根據擴散理論簡化了零水平初始問題,避免初始化影響。在 2017 年,Khadidos 等[10]提出根據圖像邊界情況自適應演化速度模型,在邊界模糊處減慢演化速度,而在邊界清晰處加快演化速度。然而在腎臟分割中,文獻[10]的方法沒有比 LRBAC 和 DRLSE 取得更好效果,所以本文主要討論 LRBAC 和 DRLSE。如圖 1 所示的第二排腎臟腫瘤超聲圖像會出現有的區域腫瘤與皮質連在一起,內外相似度大(邊界迷糊);有的區域內外相似度小(邊界清晰);若用同一參數演化不同區域,將導致分割失敗。
針對上述問題,本文提出了基于自適應分區演化水平集(adaptive sub-regional evolution level set models,ASLSM)的腎臟腫瘤分割算法。首先,將感興趣(region of interest,ROI)劃分為多個分區進行演化;然后,將局部內外能量與梯度相融合,以解決 DRLSE 梯度無法跨越大噪聲區域,而 LRBAC 容易出現分裂成小曲線且獲取細節能力差等缺點問題,并根據噪聲自適應二者比值;其次,為解決 LRBAC 的卷積半徑過大易丟失細節、過小則演化不到邊界等問題,本文提出基于質心原理自適應卷積半徑;最后,為解決 LRBAC 曲率過大使得曲線光滑丟失細節、過小則演化曲線跨越真正邊界問題,本文提出基于零水平集內外相似度自適應曲率的解決辦法,期望通過本文研究,能為臨床腎臟腫瘤分割打開新的思路,取得較好的實用效果。
1 方法
1.1 水平集背景
水平集是一種將 n 維曲面投射成 n + 1 維空間曲面的演化算法。
(1)DRLSE 模型,是在 GAC 模型上加入了保持水平集光滑的懲罰項 L(Φ),其能量如式(1)所示:
 |
其中,η1,η2,κ1 為權重參數,εg 為曲線長度項,控制演化精度,如式(2)所示;εa 為輪廓內面積,控制演化速度,如式(3)所示:
 |
 |
其中,H1(Φ)是赫維賽德(Heaviside)函數,如式(4)所示, 是 H1(Φ)求導所得,如式(5)所示;g 為圖像梯度項,如式(6)所示。
是 H1(Φ)求導所得,如式(5)所示;g 為圖像梯度項,如式(6)所示。
 |
其中,? 為常量。
式(4)求導后如式(5)所示:
 |
其中, 為常量。
為常量。
梯度項如式(6)所示:
 |
其中,Gσ 是以 σ 為方差的高斯函數。
懲罰項 L(Φ)如式(7)所示:
 |
(2)LRBAC 模型,引用 CV 模型的內外能量計算方式,并通卷積 B(x,y)區域改進算法。B(x,y)為零水平集附近所取范圍區域,其卷積半徑值定義為 convr(i),能量函數如式(8)所示:
 |
其中,|C|為曲線長度,ψ 為權重參數,εc 為內外能量項,如式(9)所示:
 |
其中,λ1、λ2 是內外能量的權重,H1(Φ)使用式(4)計算,Cin、Cout 為內和外能量項,計算方法如式(10)、式(11)所示:
 |
 |
其中  為所取區域,H1(Φ)如式(4)所示。
為所取區域,H1(Φ)如式(4)所示。
1.2 算法改進
ASLSM 融合內外能量與梯度,并自適應調整其比例,其能量函數如式(12)所示:
 |
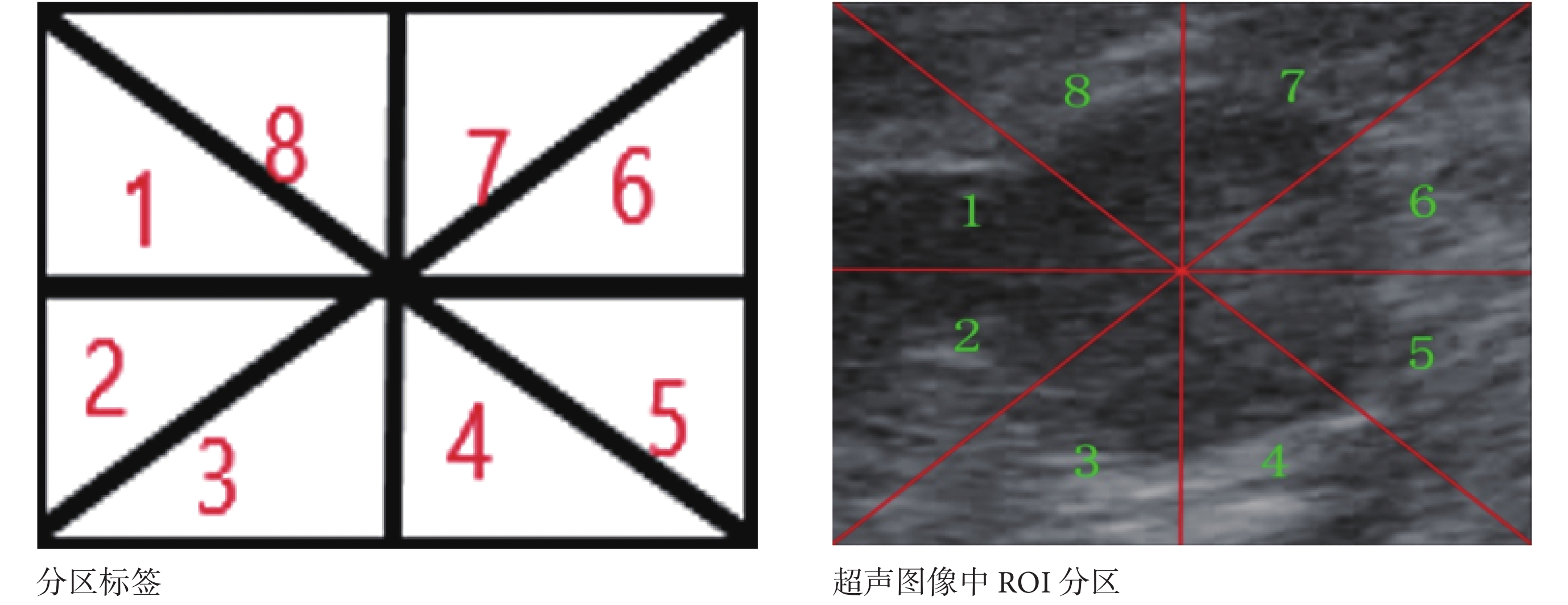
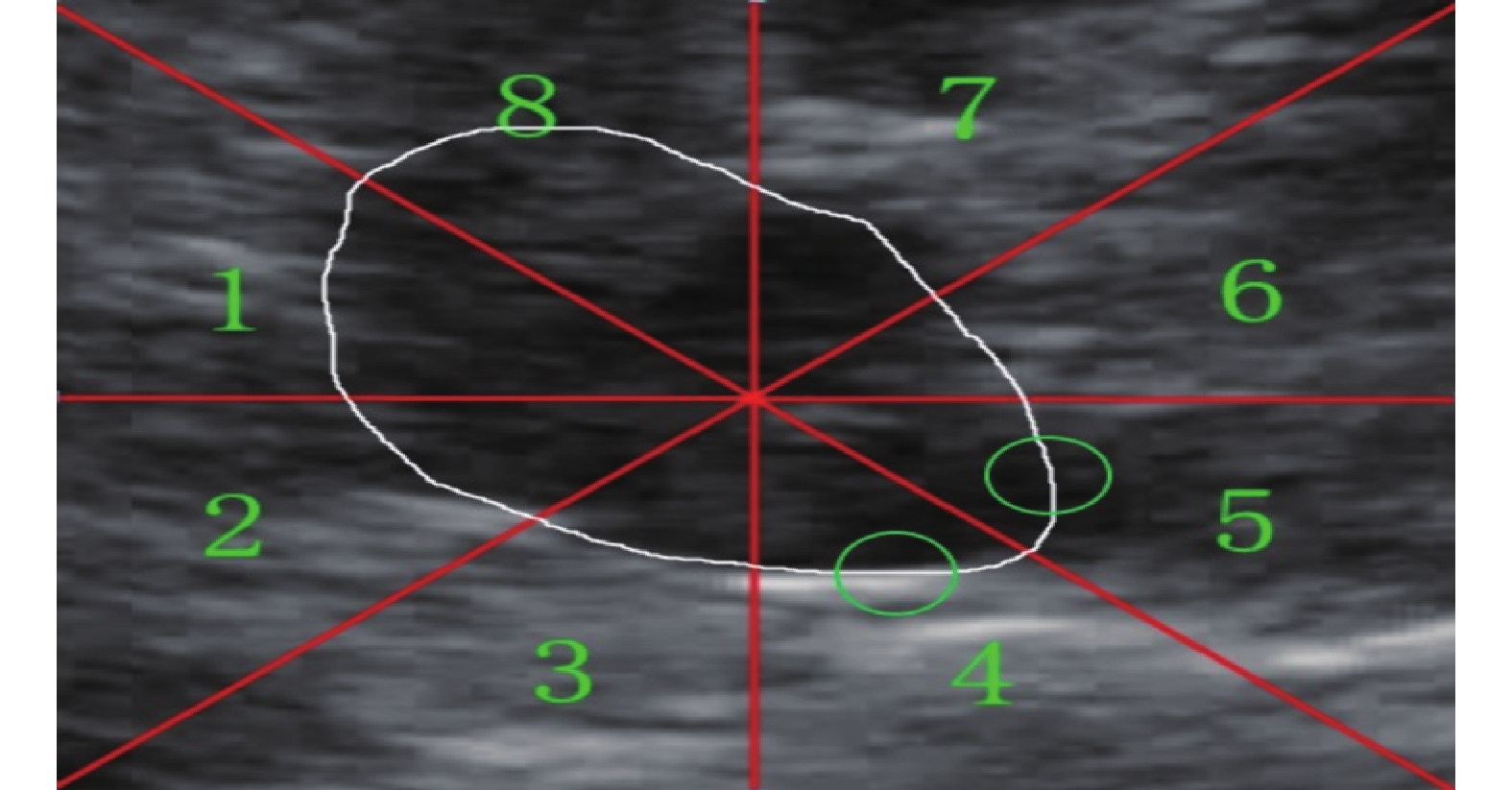
其中,p(i)是第 i 區域 εg 與 εa 權重,分區標簽如圖 2 所示,ROI 被劃分為 8 個區域,分區內圖像噪聲越大,p(i)值越大;εa 是輪廓內面積,增大 β,將會加速演化; 是曲線長度,控制曲線光滑性,q(i)第 i 區域曲率權重。L(Φ)是懲罰項,如式(7)所示,H1(Φ)、δ1(Φ)分別如式(4)、式(5)所示。式(13)中 g 是梯度項,如式(6)所示,B(x,y)的卷積半徑為 convr(i)。梯度下降法求的 EASLSM 導數如式(13)所示:
是曲線長度,控制曲線光滑性,q(i)第 i 區域曲率權重。L(Φ)是懲罰項,如式(7)所示,H1(Φ)、δ1(Φ)分別如式(4)、式(5)所示。式(13)中 g 是梯度項,如式(6)所示,B(x,y)的卷積半徑為 convr(i)。梯度下降法求的 EASLSM 導數如式(13)所示:
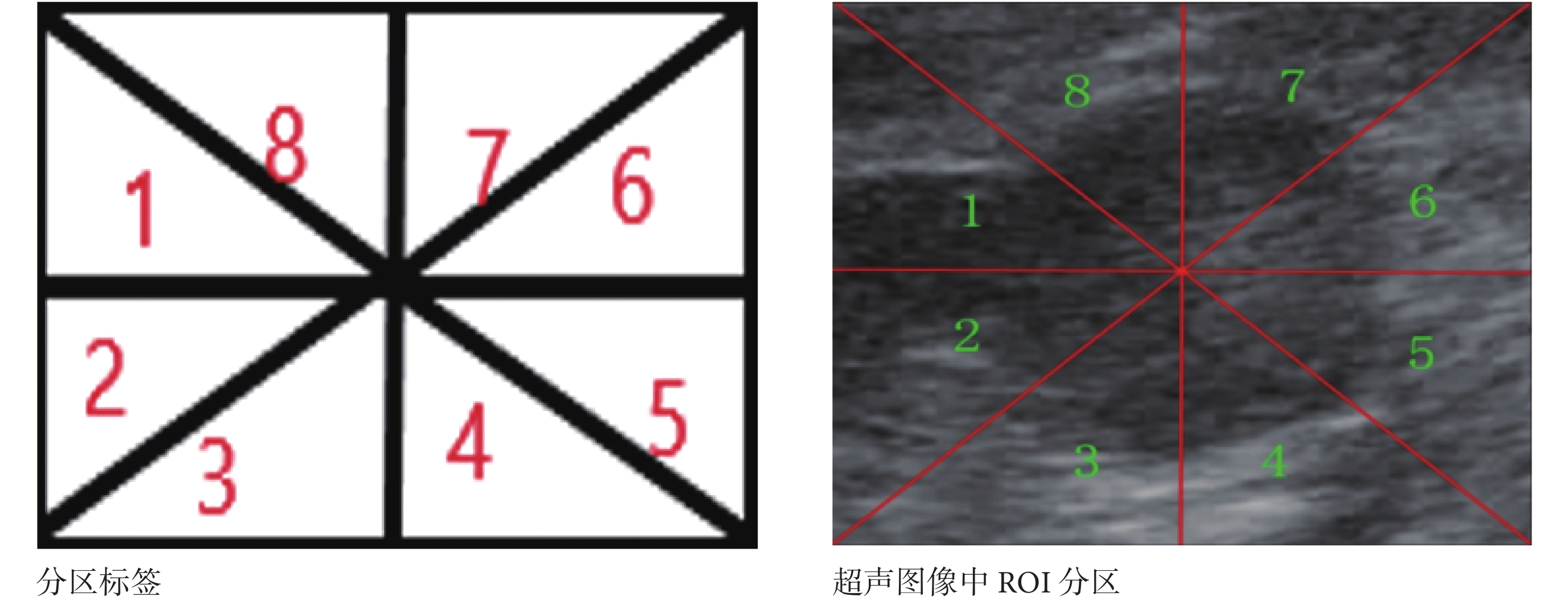 圖2
分區標簽及 ROI 分區示意圖
Figure2.
Sub-regional label and ROI
圖2
分區標簽及 ROI 分區示意圖
Figure2.
Sub-regional label and ROI
 '/> '/> |
演化函數 Phi 如式(14)所示,其中 Δt 為步長。
 |
1.2.1 分區演化
為解決固定參數演化容易造成模糊區域分割失敗等問題,本文提出了分區演化方法。如圖 3 所示,為分區演化總圖。
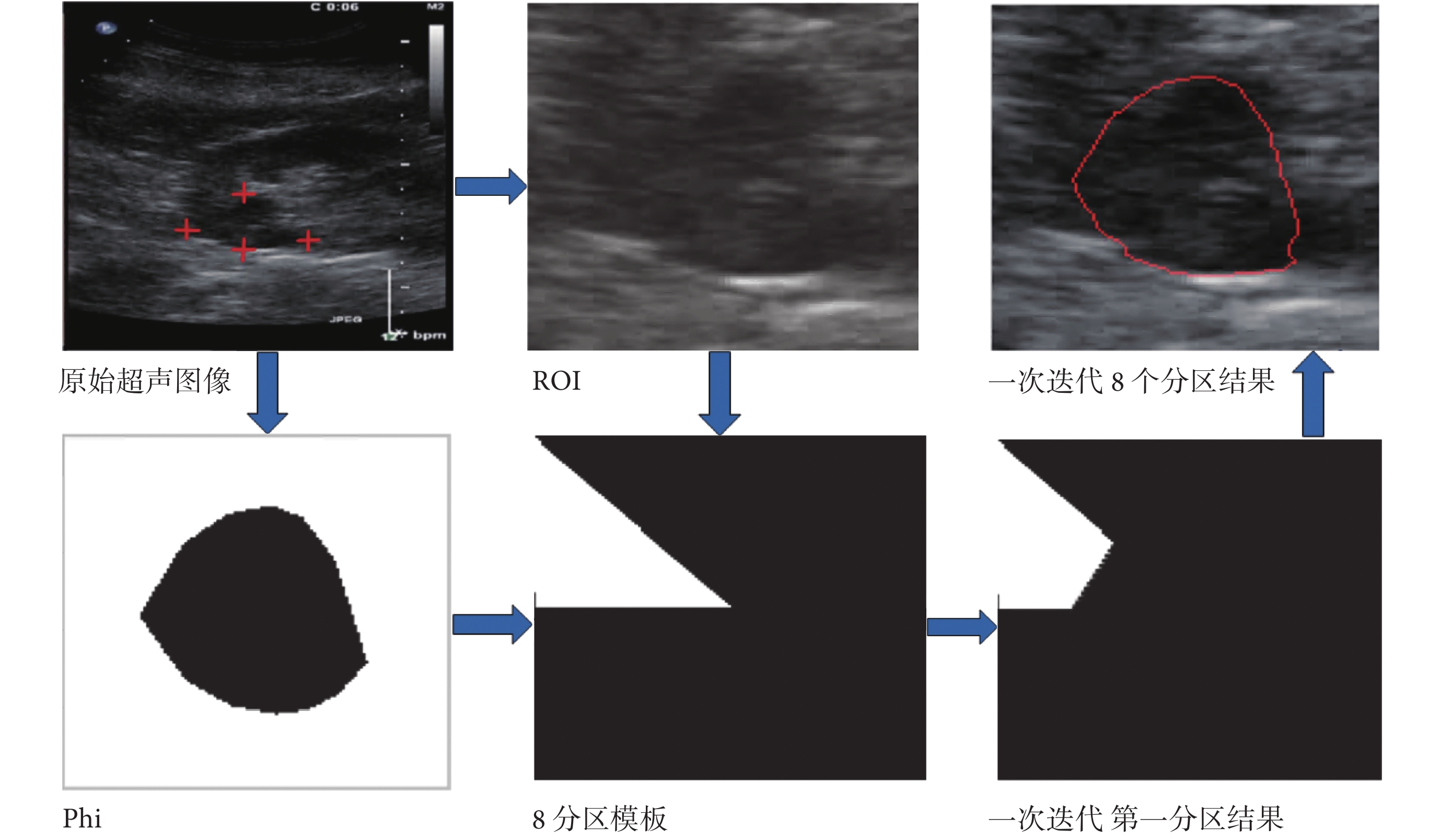 圖3
分區演化整體原理
Figure3.
Principle of sub-regional evolution
圖3
分區演化整體原理
Figure3.
Principle of sub-regional evolution
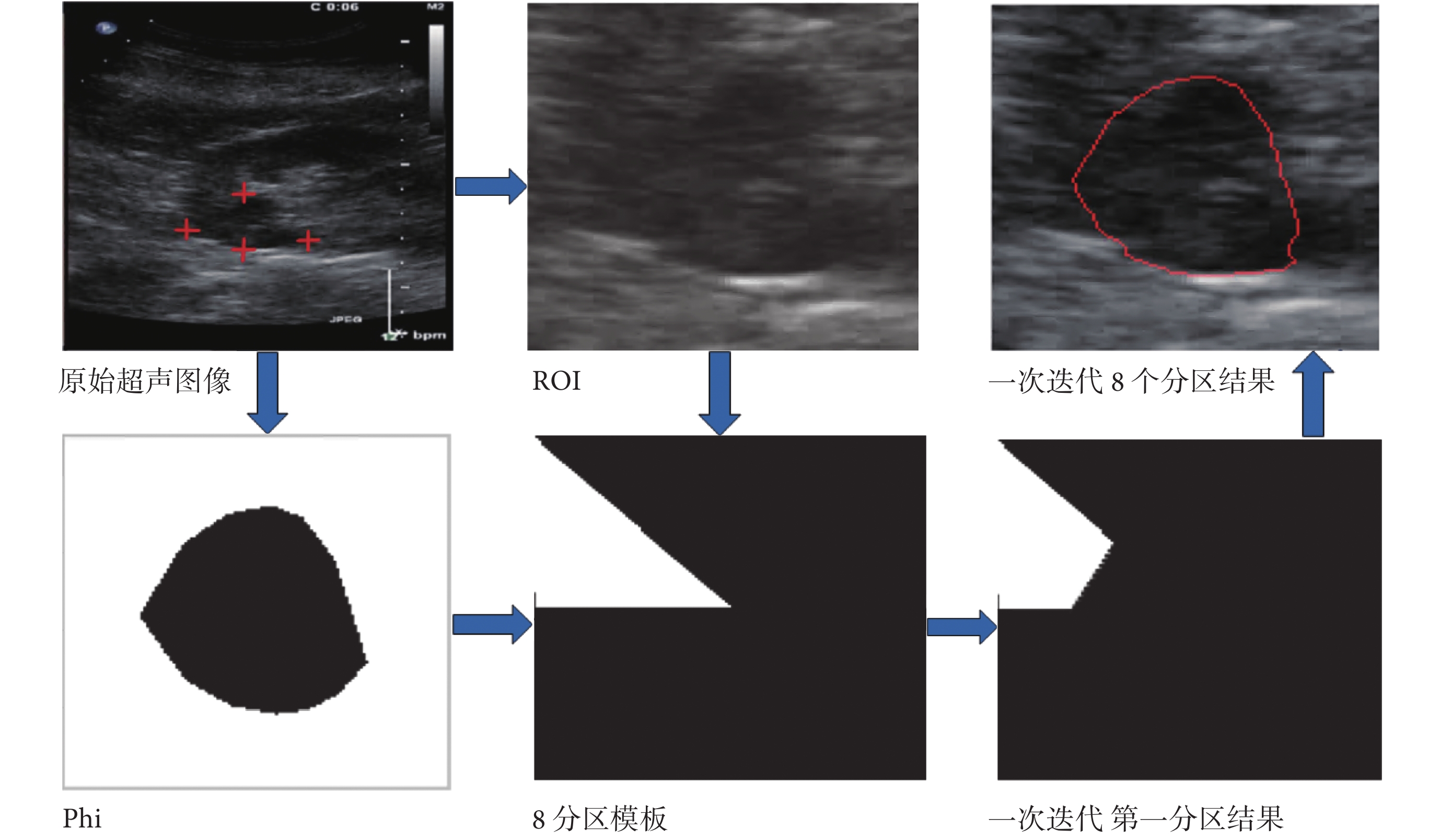
首先本文從原始超聲圖像中的腫瘤邊界選取 4 個點(紅點),根據 4 個點最大長寬,獲取 ROI,制作水平集演化函數 Phi;然后,制作 8 分區模板(每次演化只有一個區域為 1,其他區域為 0),依次與 ROI 和 Phi 相乘,并根據每個分區圖像特征計算 p(i)、q(i)、convr(i),再將上述三個值代入式(14)演化后,得到一次迭代第一分區結果;最后將所有區域的結果合并,獲得所有區域的演化函數 Phi,將其邊界顯示在 ROI 上,即為一次迭代 8 個分區的結果,其中紅線為一次演化結果,完成一次分區演化。
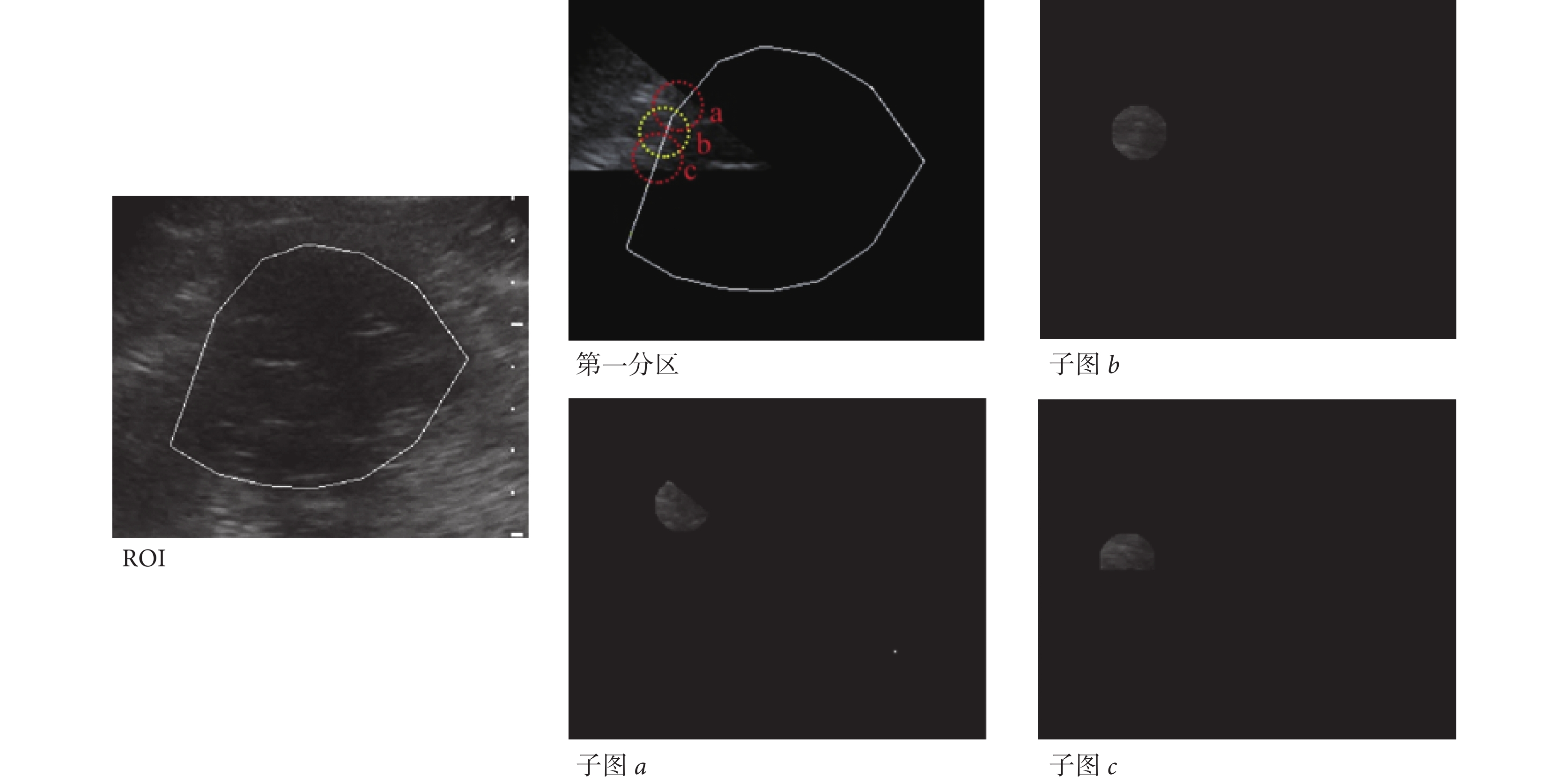
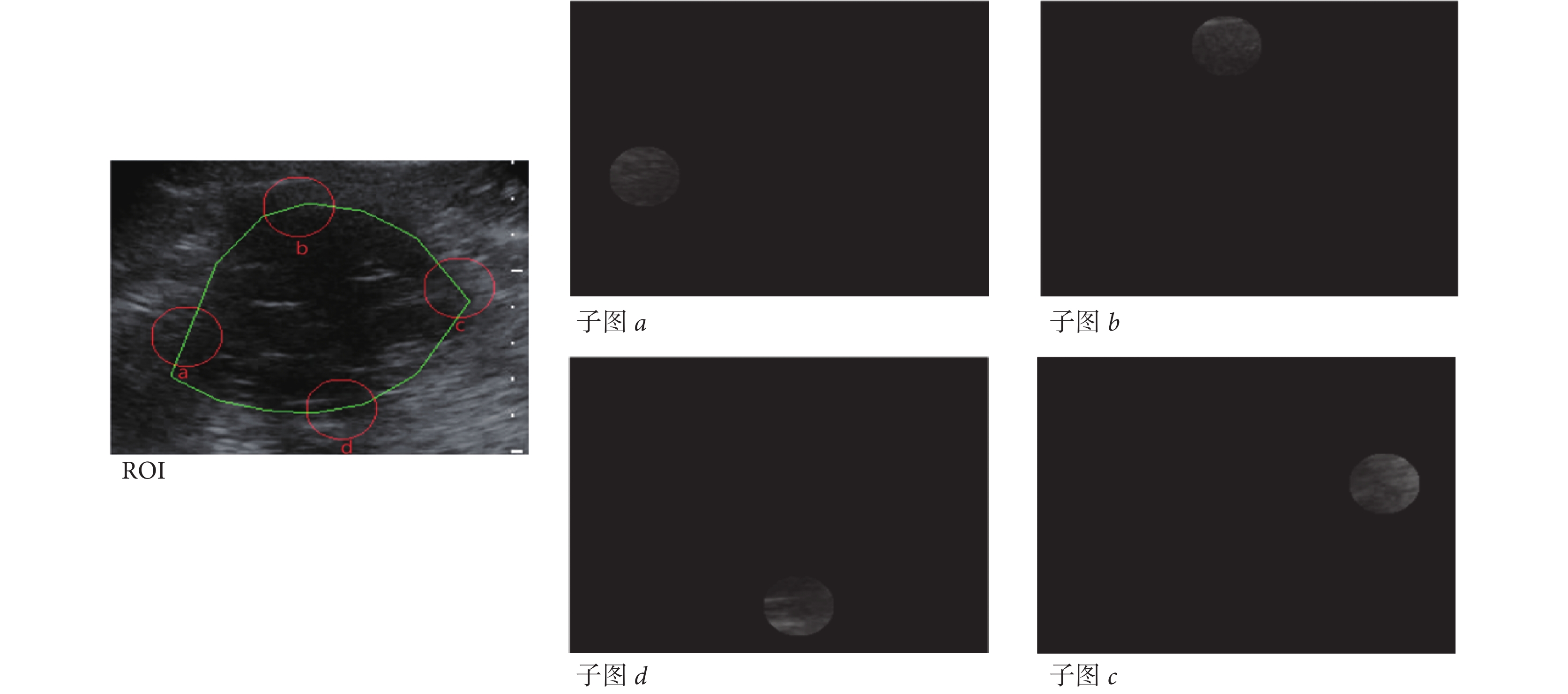
根據每個分區圖像特征計算 p(i)、q(i)和 convr(i),具體算法如圖 4 所示。以計算第一分區參數為例,首先通過將 ROI 點乘 8 分區模板,將第一分區的圖像取出如圖 4 子圖 a 所示;然后在第一分區圖中零水平集(白細線)上等間隔取圓心,半徑采樣 r = 0.1?K,其中 K 為 ROI 長和寬中最小值,取樣圖像如子圖 a、b、c(只顯示 3 個采樣子圖);最后根據采樣子圖 a、b、c 特征取平均值計算第一分區的 p(1)、q(1)、convr(1),具體算法請參照下文。
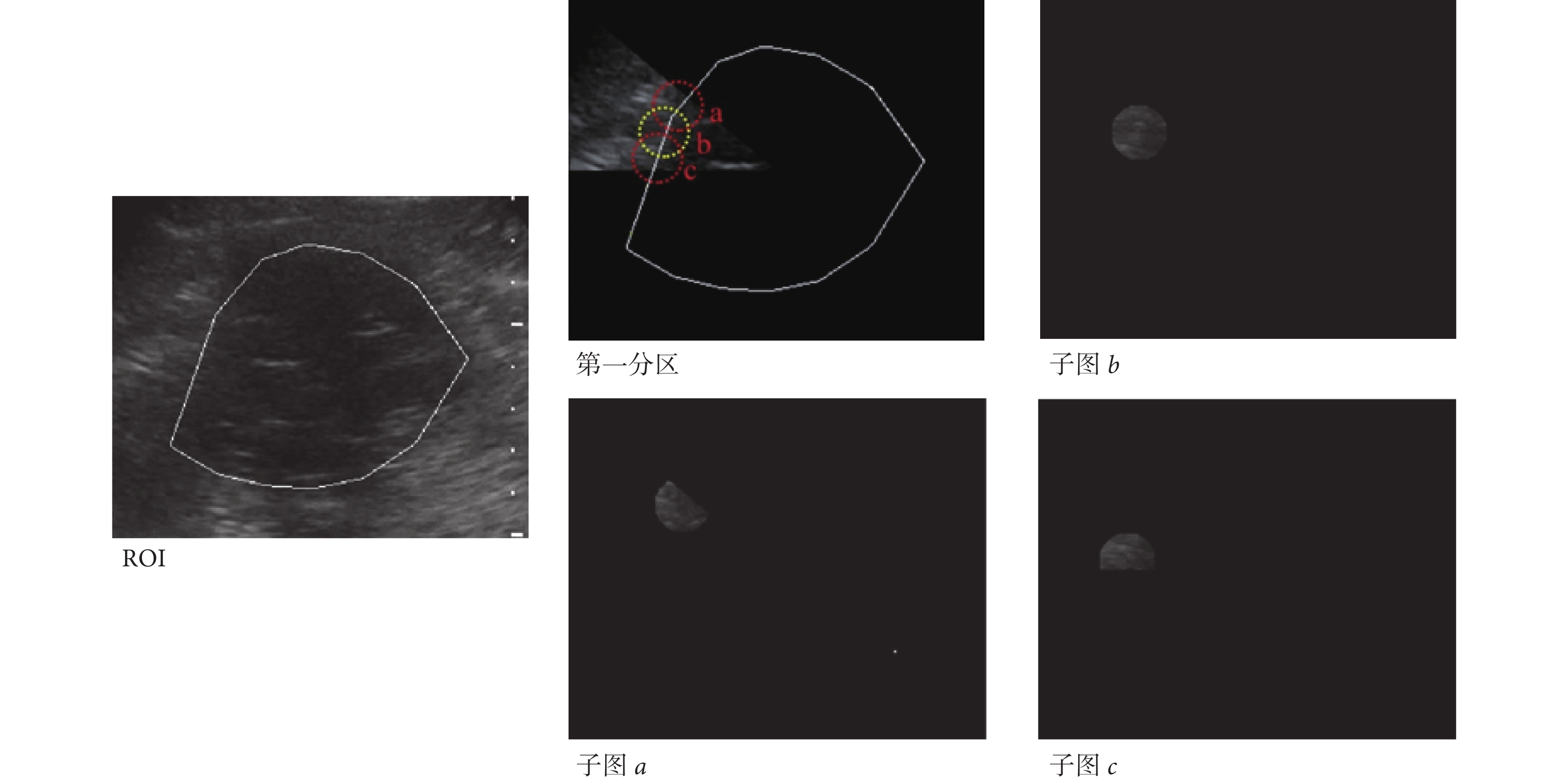 圖4
計算單個分區特征原理
Figure4.
Principle of sub-region feature calculation
圖4
計算單個分區特征原理
Figure4.
Principle of sub-region feature calculation
1.2.2 p(i)值求法
為了解決 DRLSE 梯度無法跨越大噪聲區域和 LRBAC 容易出現分裂小曲線且獲取細節能力差的問題,本文提出將內外能量項與梯度相結合,并根據圖像噪聲自適應二者權重 p(i)的算法。如圖 4 所示原理,本文在零水平集等間隔取圓心,以 r = 0.1?K 為半徑采樣,其中 K 為 ROI 長和寬中最小值。如式(15)所示,本文首先計算分區采樣子圖的方差 var(Img(i,k)),然后計算分區所有采樣子圖方差的平均值,最后除以所有采樣子圖方差的最大值進行歸一化。
 |
其中,var(Img(i,k))是第 i 區域的第 k 采樣子圖方差, 是所有區域采樣子圖方差的最大值。
是所有區域采樣子圖方差的最大值。
作為例子,如圖 5 所示,展示了 ROI 的 4 個區域采樣子圖,為便于展示如圖 2 所示的 1~8 分區的噪聲情況,取樣半徑大于圖 4 設定的半徑。右側 4 幅子圖為左側原始超聲圖像中紅色圓圈的截取圖像,綠圈為零水平集初始輪廓。4 幅采樣子圖中,子圖 d 噪聲最大、方差最大、p(i)值最大;子圖 b 噪聲最小、方差最小、p(i)值最小。1~8 分區的 p(i)取值分別為:0.60、0.53、0.56、0.73、0.67、0.44、0.33、0.29。
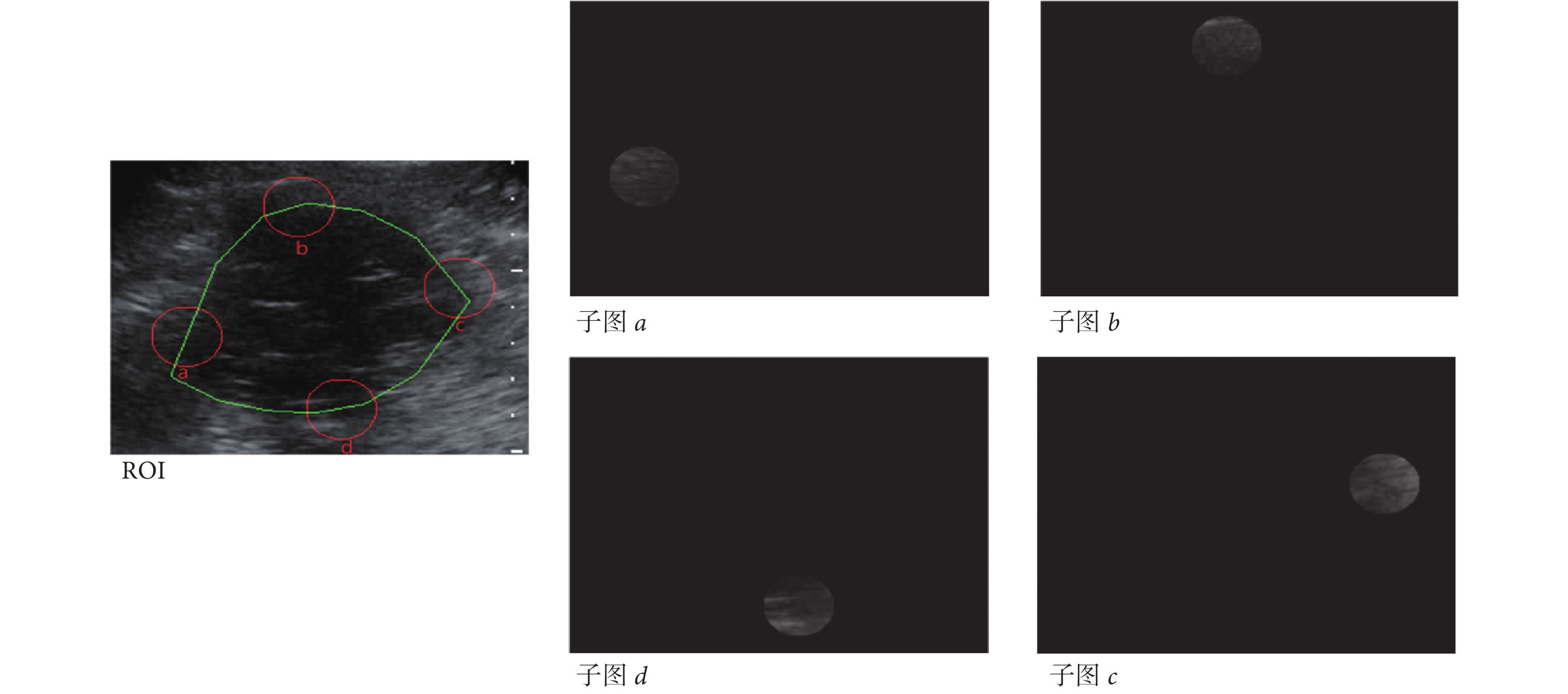 圖5
以方差定量不同區域噪聲原理
Figure5.
Noise calculation method according to variance
圖5
以方差定量不同區域噪聲原理
Figure5.
Noise calculation method according to variance
1.2.3 卷積半徑 convr(i)求法
為解決 LRBAC 卷積半徑過大則易丟失細節而過小則演化不到邊界的問題,本文提出根據質心原理自適應卷積半徑算法。為了便于理解,本文選取一個無噪聲的模擬圖演示卷積半徑計算過程,如圖 6 所示。首先在待分割圖像原始模板圖中任意取點,形成初始輪廓的零水平集曲線;然后求其梯度得到零水平集和真實梯度,其中細線為零水平集,粗線為真實梯度;最后在每個分區零水平集(細線)上等間隔取圓心,半徑采樣 r = 0.1?K,其中 K 為 ROI 長和寬中最小值,計算該點(紅色圓點)到最大梯度值點(紅色叉點)最短距離,該距離即該分區的卷積半徑,半徑依次為 r1、r2、r3 和 r4,以藍色線段顯示。
 圖6
卷積半徑計算原理模型
Figure6.
The model of convolution radius calculation
圖6
卷積半徑計算原理模型
Figure6.
The model of convolution radius calculation
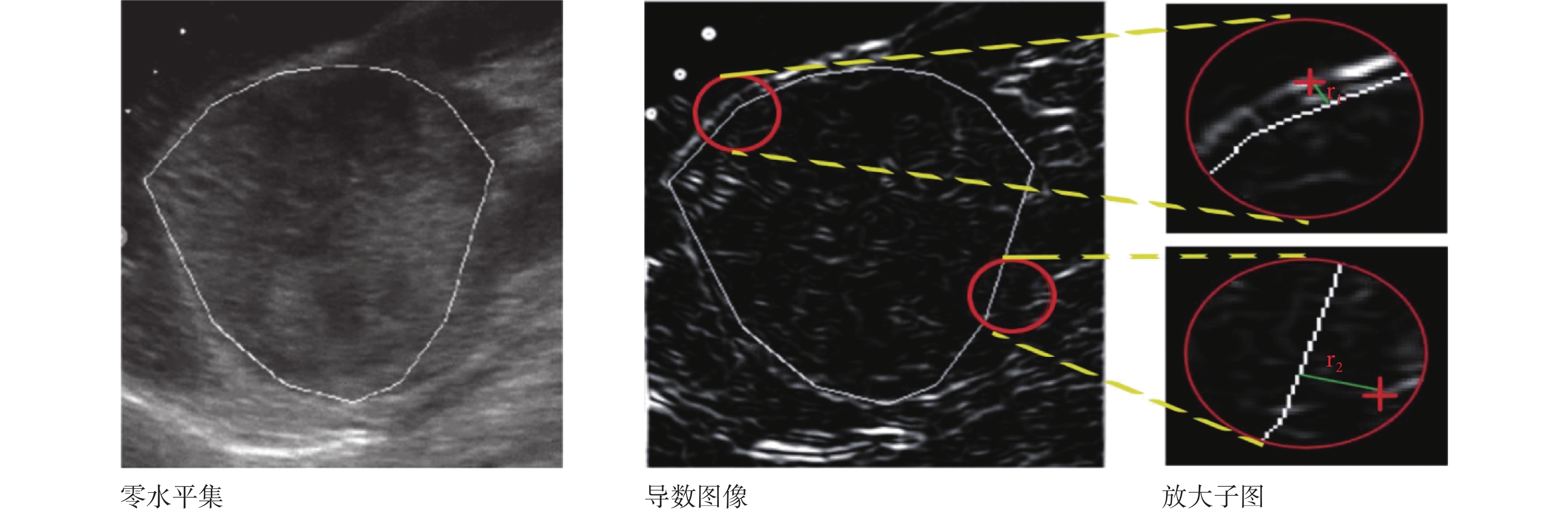
由于超聲圖像對比度低且斑點噪聲大,在同一個區域內很難找到真實的邊界梯度最大值點,故采用質心理論。如圖 4 所示原理,本文在導數圖像零水平集等間隔取圓心,以 r = 0.1?K 為半徑采樣,其中 K 為 ROI 長和寬中最小值。首先計算每個采樣子圖質心如式(16)所示;然后求得質心到最近零水平集的最短距離的平均值,即該子圖的卷積半徑;最后計算分區內所有采樣子圖卷積半徑平均值,即該分區的卷積半徑 convr(i),如式(17)所示。
 |
 |
其中,(x,y)是質心坐標,(xk,yk)是第 i 分區第 k 個采樣子圖零水平集上離質心(x,y)最近的點。
如圖 7 所示,本文將 ROI 求導后得到導數圖像。紅十字即為該采樣子圖質心,計算質心到零水平集(白線)的最短距離,即該采樣子圖的卷積半徑,如放大子圖中 r1、r2;再將分區子圖卷積半徑求平均值,即該分區的卷積半徑 convr(i)。當邊界非常模糊時,若無法獲得質心位置,將所有其他區域卷積半徑的平均值賦予這個區域。1~8 分區的 convr(i)取值分別為 4.21、7.23、6.19、13.90、21.34、9.45、10.43、3.82。
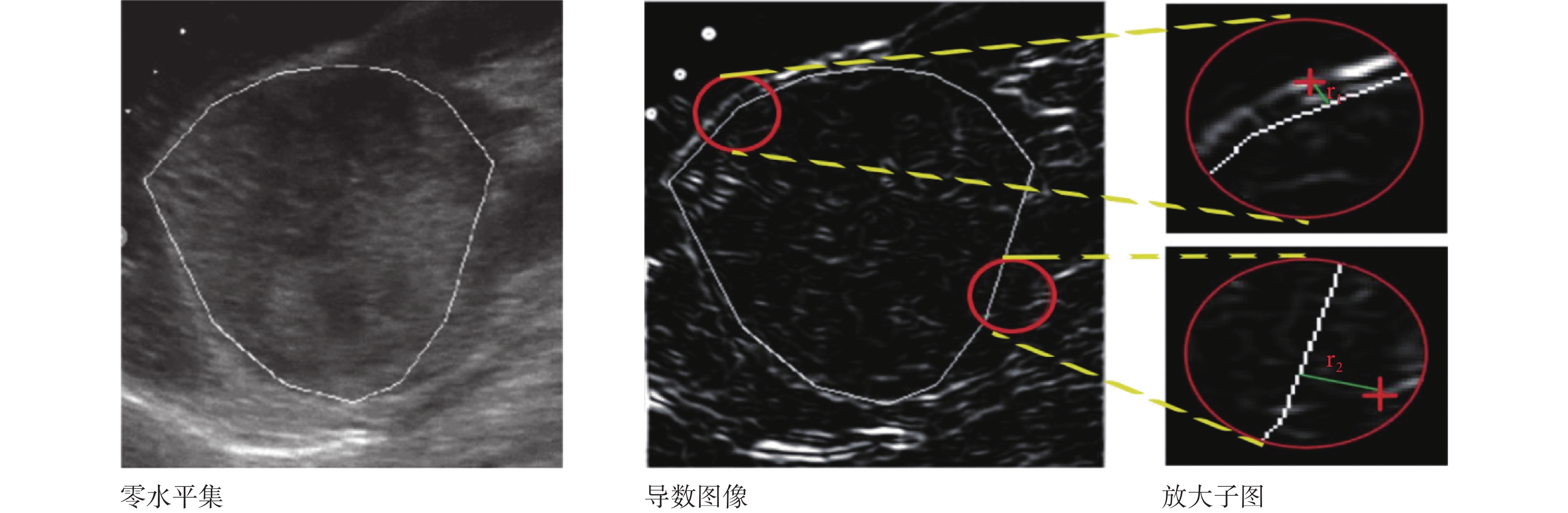 圖7
超聲卷積半徑計算原理
Figure7.
Principle of ultrasound image convolution radius calculation
圖7
超聲卷積半徑計算原理
Figure7.
Principle of ultrasound image convolution radius calculation
1.2.4 曲率權重 q(i)求法
為了解決 LRBAC 曲率過大曲線光滑而失去細節、曲率過小則內外相似度大區域跨越邊界的問題,本文提出根據零水平集內外相似度自適應計算曲率的算法。如圖 4 所示原理,首先在零水平集等間隔取圓心,r = 0.1?K 為半徑采樣,其中 K 為 ROI 長和寬中最小值。采樣子圖內外的相似度 sim 的計算公式,如式(18)所示;分區中采樣子圖 sim 的平均值,即該值乘以相應的參數所得曲率權重 q(i)的計算公式,如式(19)所示:
 |
其中,D_min(i,k)為零水平集內外區域像素平均值較小值,D_max(i,k)則為較大值。
 |
其中,sim(i,k)是第 i 分區域第 k 個采樣子圖內外相似度,δ1、δ2 分別為 ROI 長和寬,這里 γ = 3。
如圖 8 所示,零水平集為白線,4 區和 5 區中的綠圈為采樣子圖區域。4 區內外相似度最小,故 sim(4,k)值最小;5 區內外相似度最大,故 sim(5,k)值最大。本文自適應減小 4 區曲率獲得更多細節,自適應增加 5 區曲率防止內外相似度大區域處跨越邊界。1~8 分區的 sim(i)取值分別為 0.76、0.53、0.46、0.21、0.90、0.40、0.58、0.91。
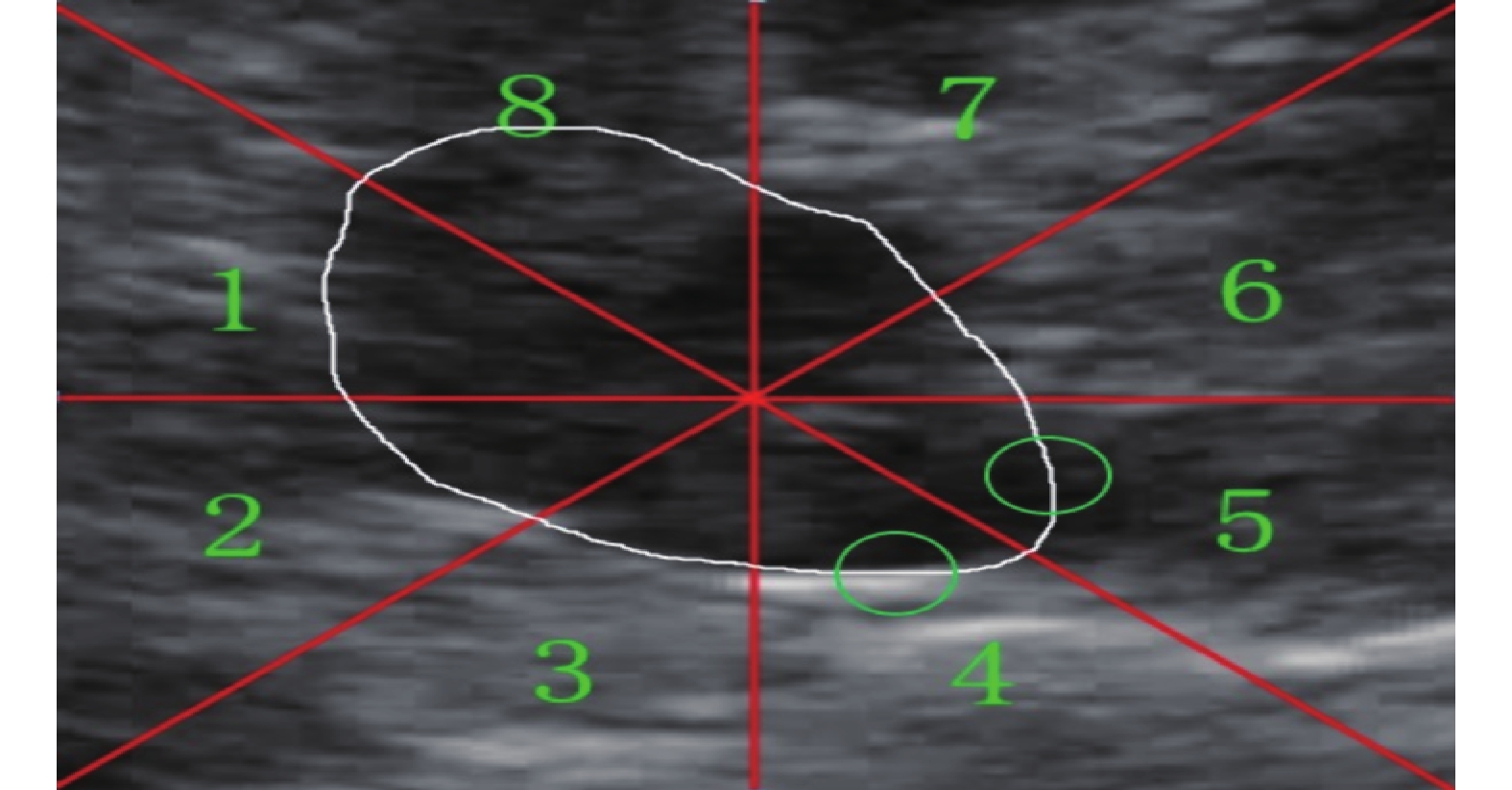 圖8
曲率計算原理
Figure8.
Principle of curvature calculation
圖8
曲率計算原理
Figure8.
Principle of curvature calculation
2 實驗數據、評價指標及計算機配置
2.1 實驗數據
本文數據來自 2012 年 11 月—2016 年 11 月天津醫科大學腫瘤醫院,其中包括:腎臟腫瘤透明細胞癌視頻 67 例、嫌色細胞癌 12 例、乳頭細胞癌 8 例,共 87 例視頻,所有試驗均與患者簽署知情同意書,并經過天津醫科大學腫瘤醫院授權使用該數據。所有患者年齡在 25~75 歲,詳細信息如表 1 所示。每例視頻分別選取造影劑剛進入時、最高峰時和退出時的 3 幀圖像作為本文采樣圖像,共 261 幅超聲圖像,由臨床醫生手工勾勒作為金標準。
為了驗證內外能量項融合梯度的效果,本文選取了一幅無噪聲的模擬圖像,并加入方差 σ = 0.03 的斑點噪聲作為實驗對象。
2.2 量化指標
本文選擇兩輪廓豪斯多夫距離(hausdorff distance,HD)(符號記為:HD),平均絕對距離(mean absolute distance,MAD)(符號記為:MAD)和戴斯系數(dicecoefficient,DICE)(符號記為:DICE)作為評估標準。
假設 A、B 分別對應金標準和算法分割結果,HD 計算的是兩個輪廓間的最大最小距離,如式(20)所示:
 |
其中,a 和 b 分別是兩個輪廓 A 和輪廓 B 上的點,d(a,B)表示 a 到輪廓 B 的最短距離。
MAD 計算的是兩個輪廓所有最小距離的平均值,如式(21)所示:
 |
其中,NA 和 NB 分別為輪廓 A 和輪廓 B 上的點的數量。
DICE 是評價兩輪廓所在區域的重合程度,如式(22)所示:
 |
其中,ΩA 和 ΩB 分別表示以 A 和 B 為輪廓的閉區域,Area(.)為對應的閉區域的面積;DICE = 0 表示沒有完全沒有重合,分割完全錯誤;DICE = 1 表示兩個閉合區域完全重合,分割完全正確。
2.3 計算機硬軟件配置
本文采用的計算機為戴爾工作站(T7920,Dell Inc,美國);使用的軟件為 matlab 2018b(Matlab Inc,美國)。
3 實驗與結果
3.1 融合內外能量項和梯度實驗
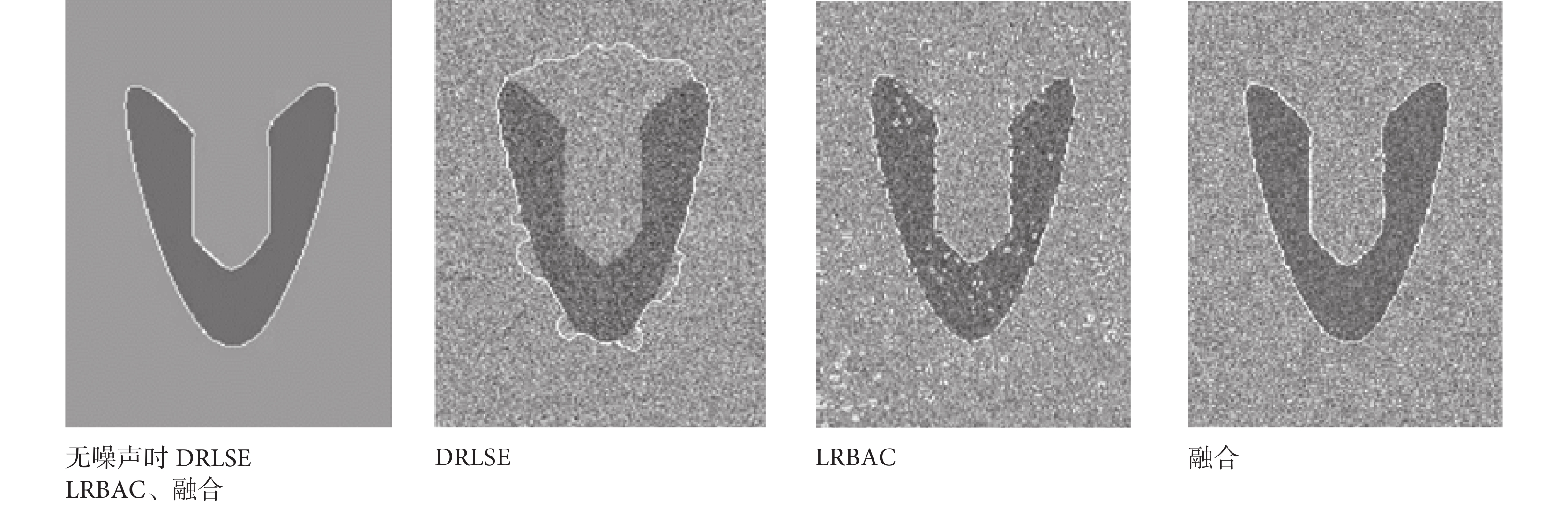
LRBAC 使用的內外能量項,擁有較強抵抗噪聲的能力,但易分裂成小曲線,且當卷積半徑過大的時,演化丟失細節;DRLSE 使用的梯度項能減少分裂小曲線的出現,獲取更多的細節,但跨越大噪聲區域能力較差。融合內外能量項和梯度,既擁有獲取更強細節的能力,又不易分裂成小曲線。如圖 9 所示,白線為演化結果,沒有噪聲時,DRLSE、LRBAC、融合項都能演化到真正邊界;梯度無法跨越大噪聲區域時,DRLSE 無法演化到真正的邊界; LRBAC 模型整幅圖出現很多分裂的小曲線,分割完全失敗;而融合項能夠演化到真正的邊界,且沒有出現分裂的小曲線。
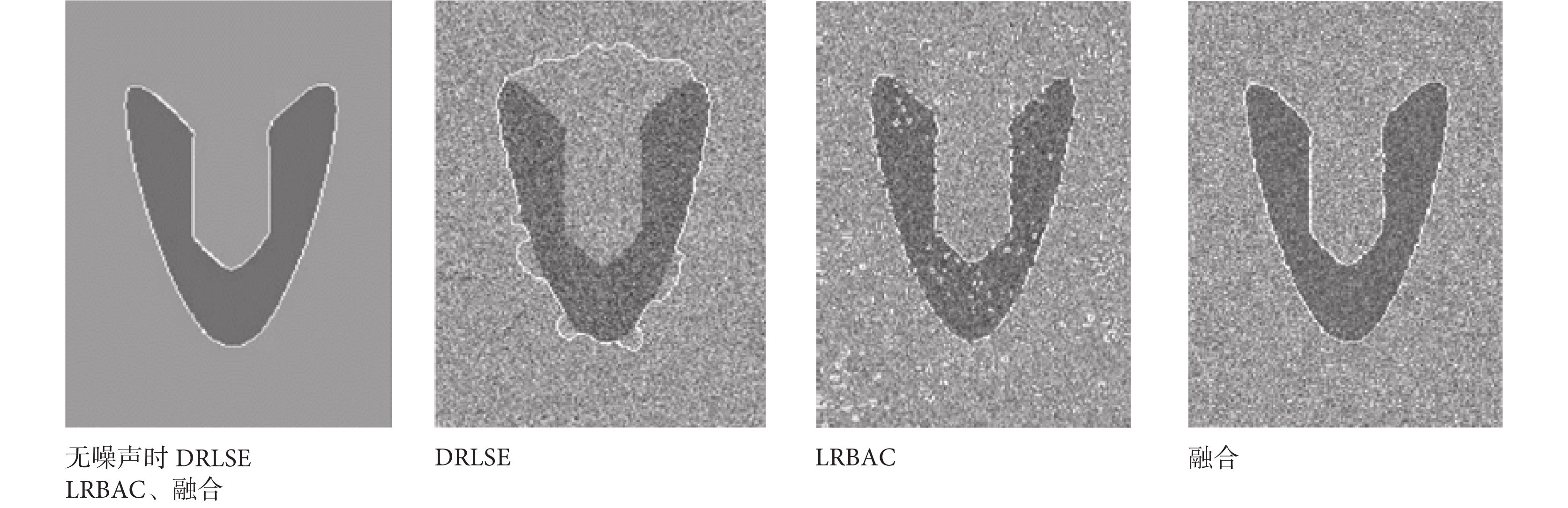 圖9
模擬圖像融合內外能量項和梯度實驗
Figure9.
The experiment of integrating energy and gradient in simulation image
圖9
模擬圖像融合內外能量項和梯度實驗
Figure9.
The experiment of integrating energy and gradient in simulation image
3.2 分區演化實驗
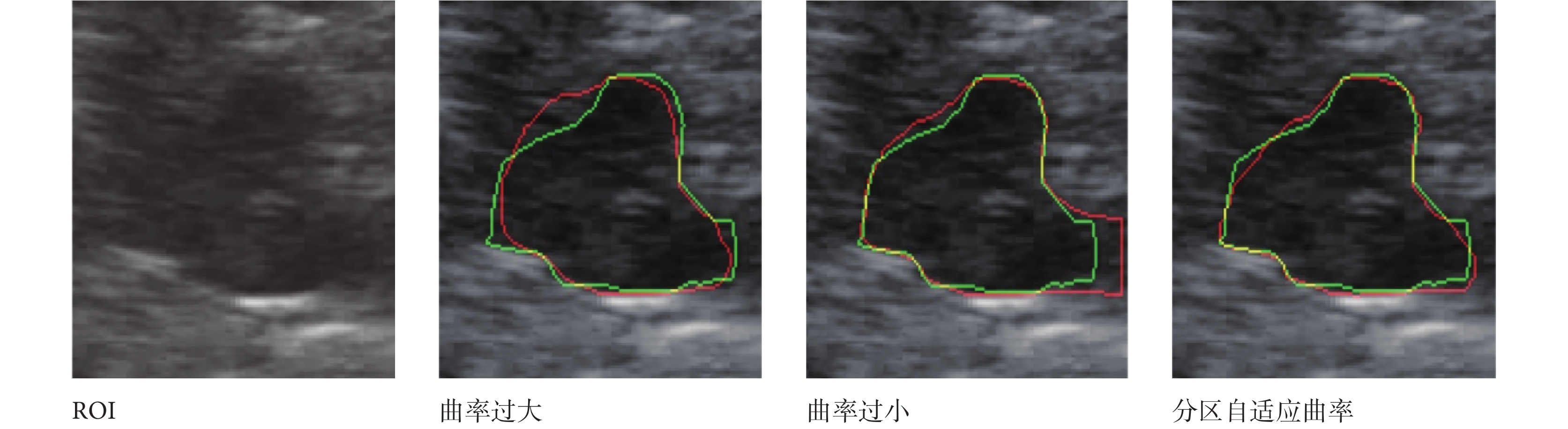
腎臟腫瘤圖像在不同區域內外相似度不同,曲率過大演化曲線變的過于光滑而演化不到邊界,曲率過小內外相似度大的區域演化易跨越邊界。分區演化根據不同區域的噪聲情況,在內外相似度大的區域增大曲率,在內外相似度小的區域減小曲率,可以分割出噪聲較大的腎臟腫瘤圖像。如圖 10 所示,綠線為金標準,紅線為分割結果。左二曲率設定 0.3?δ1?δ2 時,1 區和 2 區曲率過大而演化曲線變得光滑不能到邊界,但 5 區能演化到真正邊界;右二曲率設定為 0.1?δ1?δ2 時,5 區內外相似度大演化跨越邊界;右一分區演化通過自適曲率在 1 區和 2 區減小曲率,5 區增大曲率,各區域均準確演化到邊界。評價參數如表 2 所示,圖 10 證明分區演化效果最好,對所有樣本的分區演化實驗結果如表 2 所示。
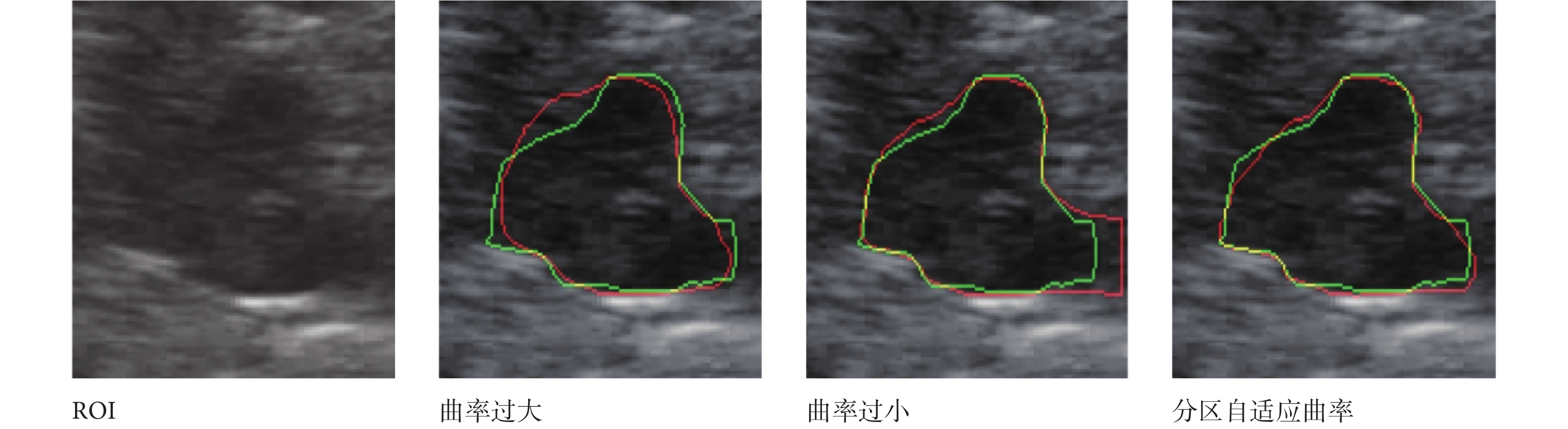 圖10
分區演化實驗
Figure10.
Experiments on sub-region evolution
圖10
分區演化實驗
Figure10.
Experiments on sub-region evolution
3.3 自適應 p(i)值實驗
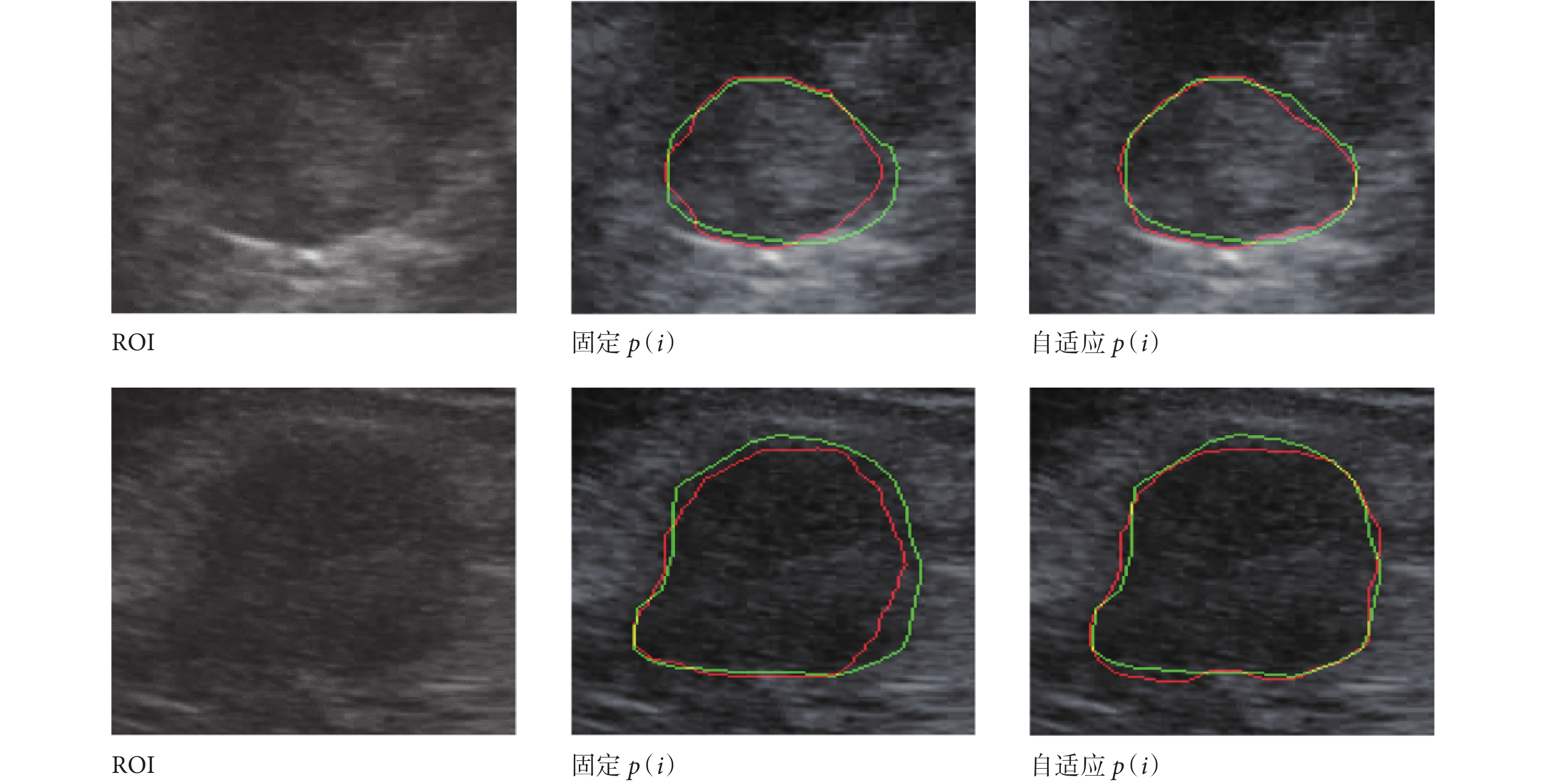
為了解決 DRLSE 梯度無法跨越大噪聲區域和 LRBAC 容易出現分裂小曲線且獲取細節能力差的問題,本文將內外能量項與梯度相融合,并自適應二者比值 p(i)。固定 q(i)值為 0.1?δ1?δ2 和 convr(i)值為 20,其中對照組 p(i)固定為 0.2,對所有的樣本進行自適應 p(i)實驗。實驗結果如表 3 所示,自適應 p(i)值比固定 p(i)值效果有所提升,但梯度在腎臟超聲圖像中獲取細節能力有限。如圖 11 所示,綠線為金標準,紅線為分割結果。其中,如固定 p(i)可見,第一排的 5 區、第二排的 5 區和 6 區域噪聲較大,應增大該區 p(i)值,故固定 p(i)無演化到邊界;而如果是選擇自適應 p(i),則取得更準確的演化效果。
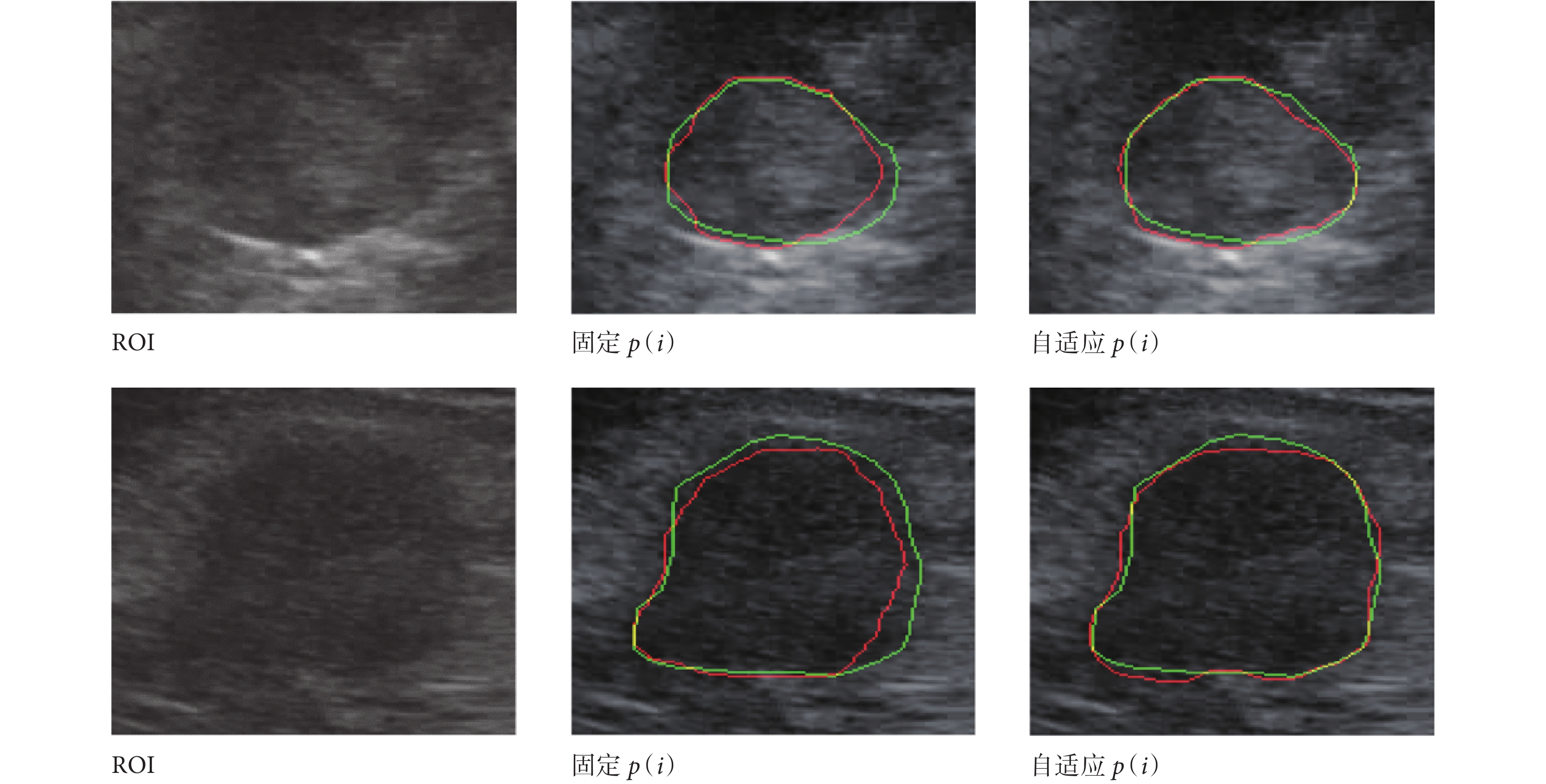 圖11
自適應 p(i)值實驗
Figure11.
Experiments on adaptive p(i)
圖11
自適應 p(i)值實驗
Figure11.
Experiments on adaptive p(i)
3.4 自適應卷積半徑 convr(i)實驗
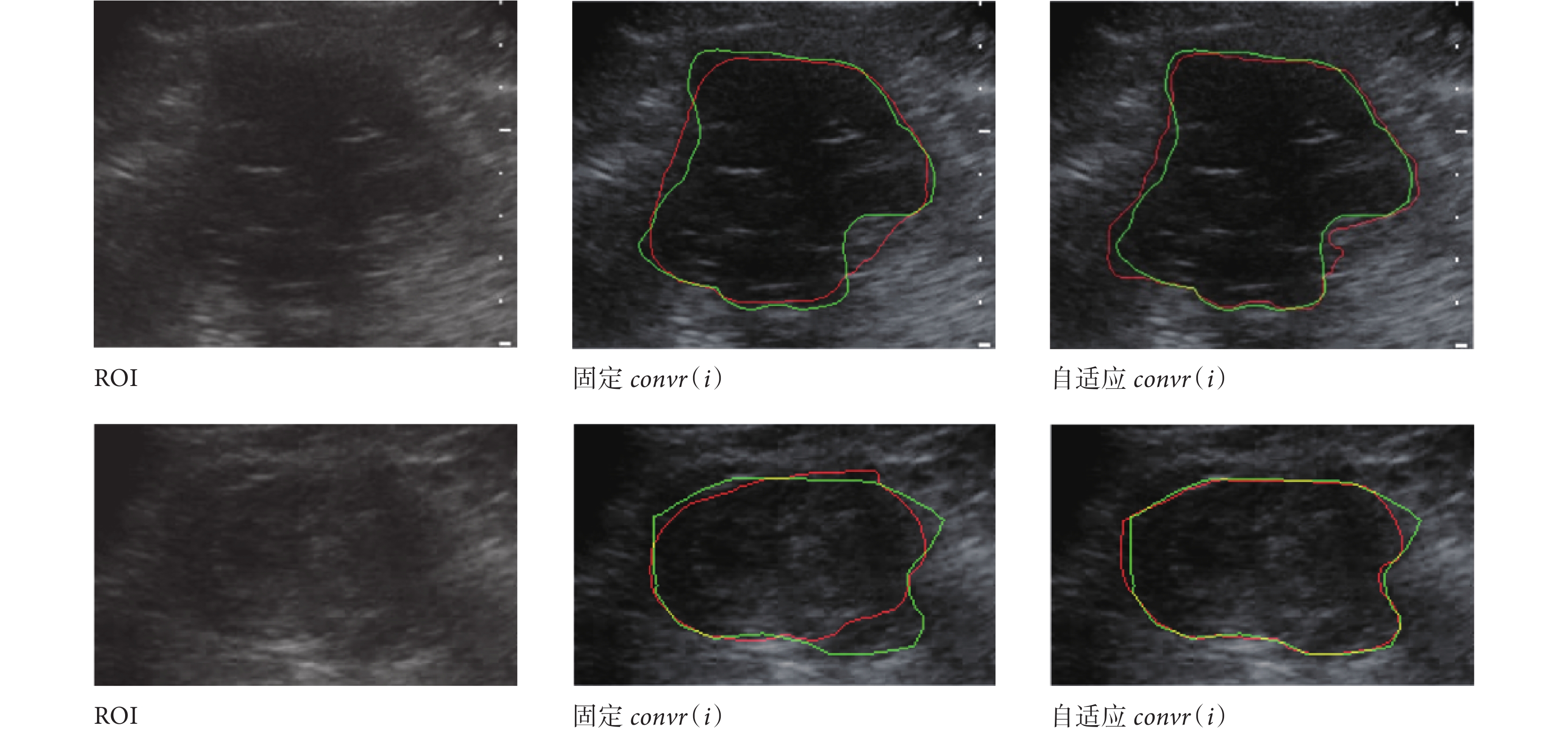
根據質心原理,本文自適應卷積半徑。在初始輪廓離真正邊界較遠的區域增大卷積半徑,在初始輪廓離真正邊界較近的區域減小卷積半徑,增強獲取細節的能力,驅動演化到真正邊界。固定曲率 q(i)值為 0.1?δ1?δ2 和 p(i)值為 0.2,對照組 convr(i)固定為 20,進行自適應卷積半徑實驗。實驗結果如表 4 所示,自適應 convr(i)效果有較大的提升,證明 convr(i)取值對腎臟超聲圖像分割尤其重要。如圖 12 所示,綠線為金標準,紅線為分割結果。左一列是腎臟腫瘤超聲圖像 ROI 區域;左二上在 1 區和 2 區卷積半徑過大,5 區和 6 區卷積半徑過小,演化不到邊界,左二下的 4 區和 5 區卷積半徑過小,演化不到邊界;右一列自適應卷積半徑 convr(i),取得更準確的演化效果。
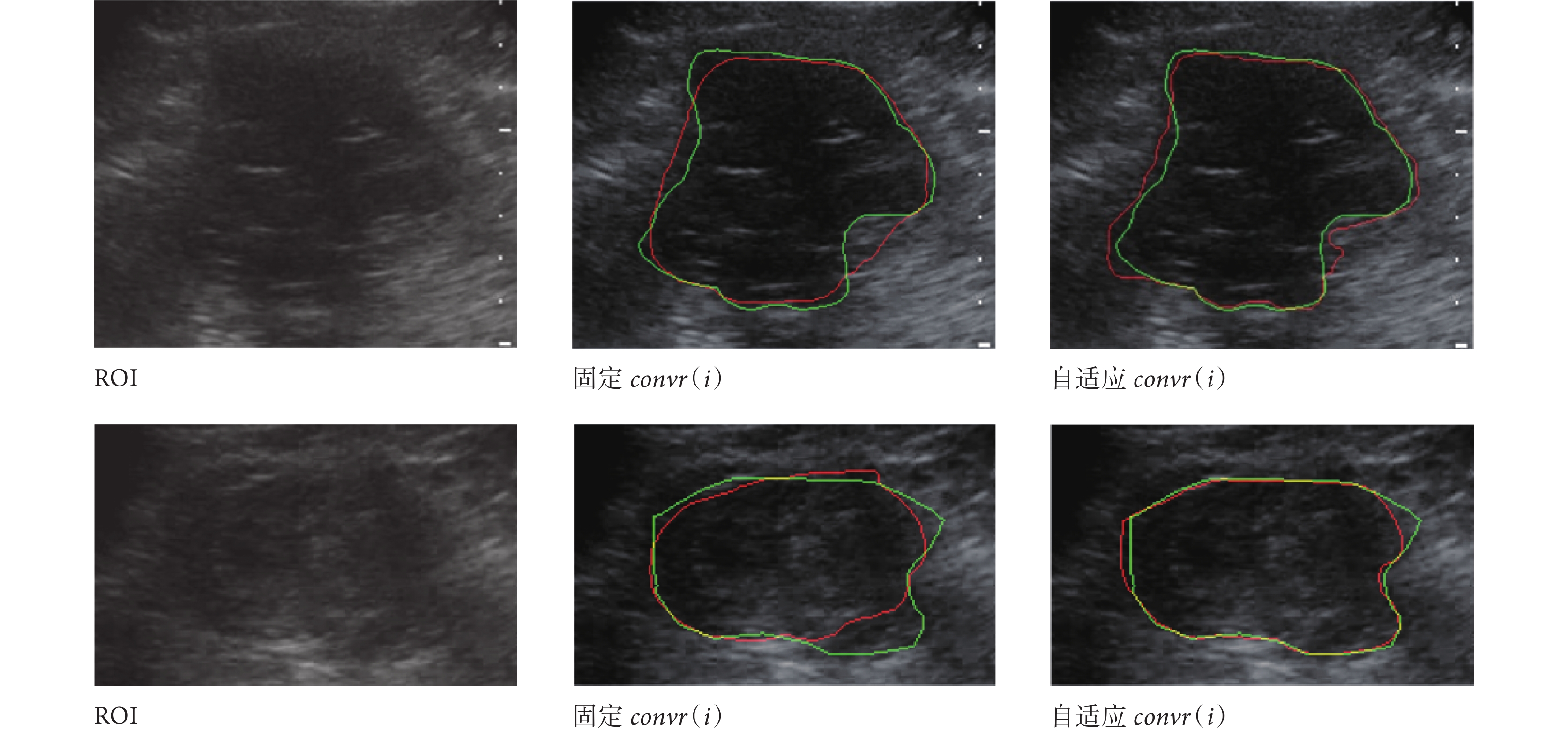 圖12
自適應卷積半徑實驗
Figure12.
Experiments on adaptive convolution radius
圖12
自適應卷積半徑實驗
Figure12.
Experiments on adaptive convolution radius
3.5 自適應曲率 q(i)實驗
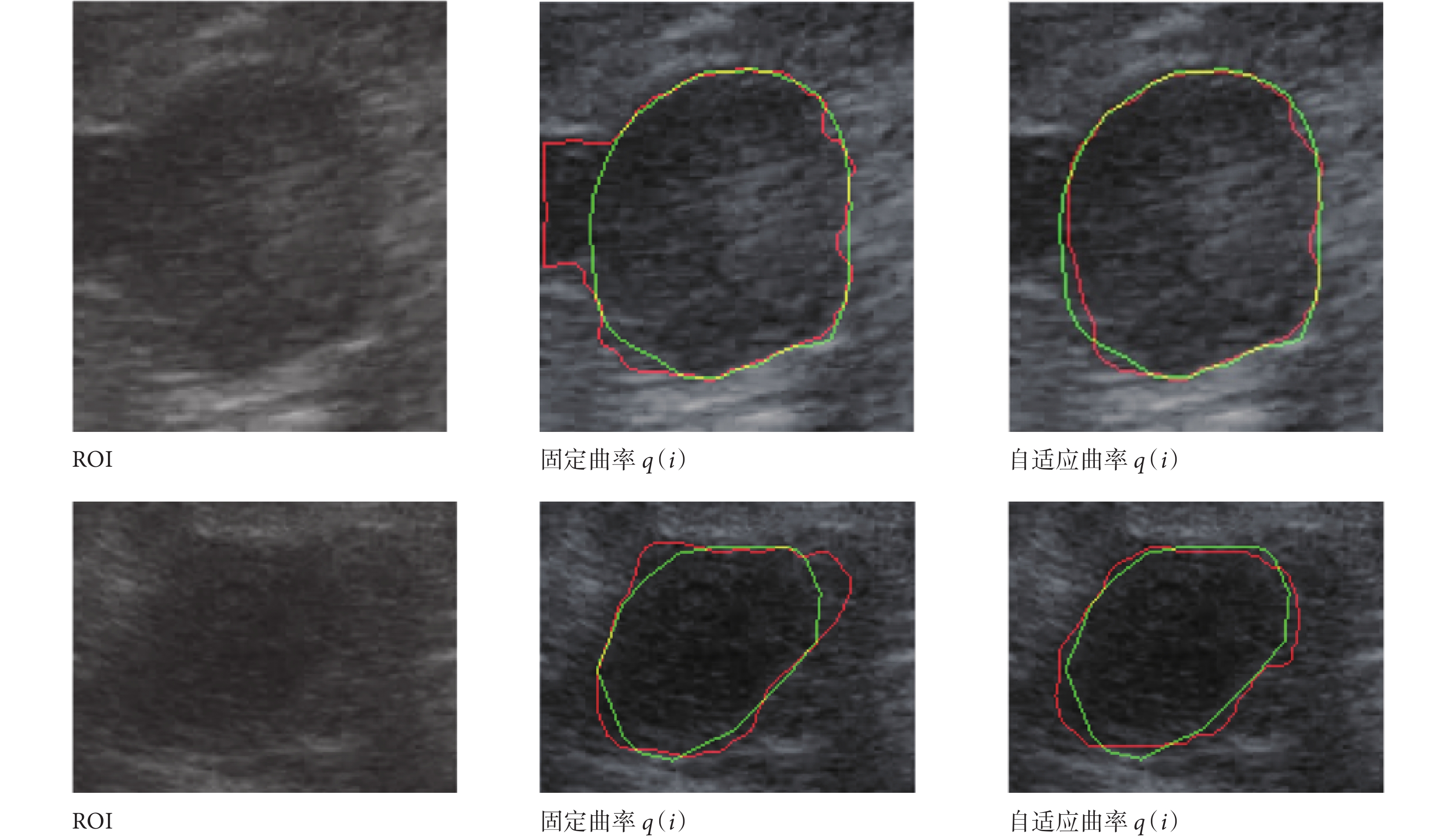
本文根據零水平集內外相似度自適應曲率,在零水平集內外相似度大的區域增大曲率,在相似度小的區域減小曲率,使演化即在邊界模糊處收斂住,又在邊界清晰處獲得更多細節。固定 convr(i)值為 20 和 p(i)值為 0.2,其中對照組 q(i)固定為 0.1?δ1?δ2,對所有的樣本進行自適應曲率實驗。如表 5 所示,自適應 q(i)效果有所提升。如圖 13 所示,綠線為金標準,紅線為分割結果。左二上的 2 區、左二下的 6 區內外相似度大,演化跨越真正邊界;自適應增大了右一上的 2 區、右一下的 6 區曲率,結果顯示二者均取得更準確的演化效果。
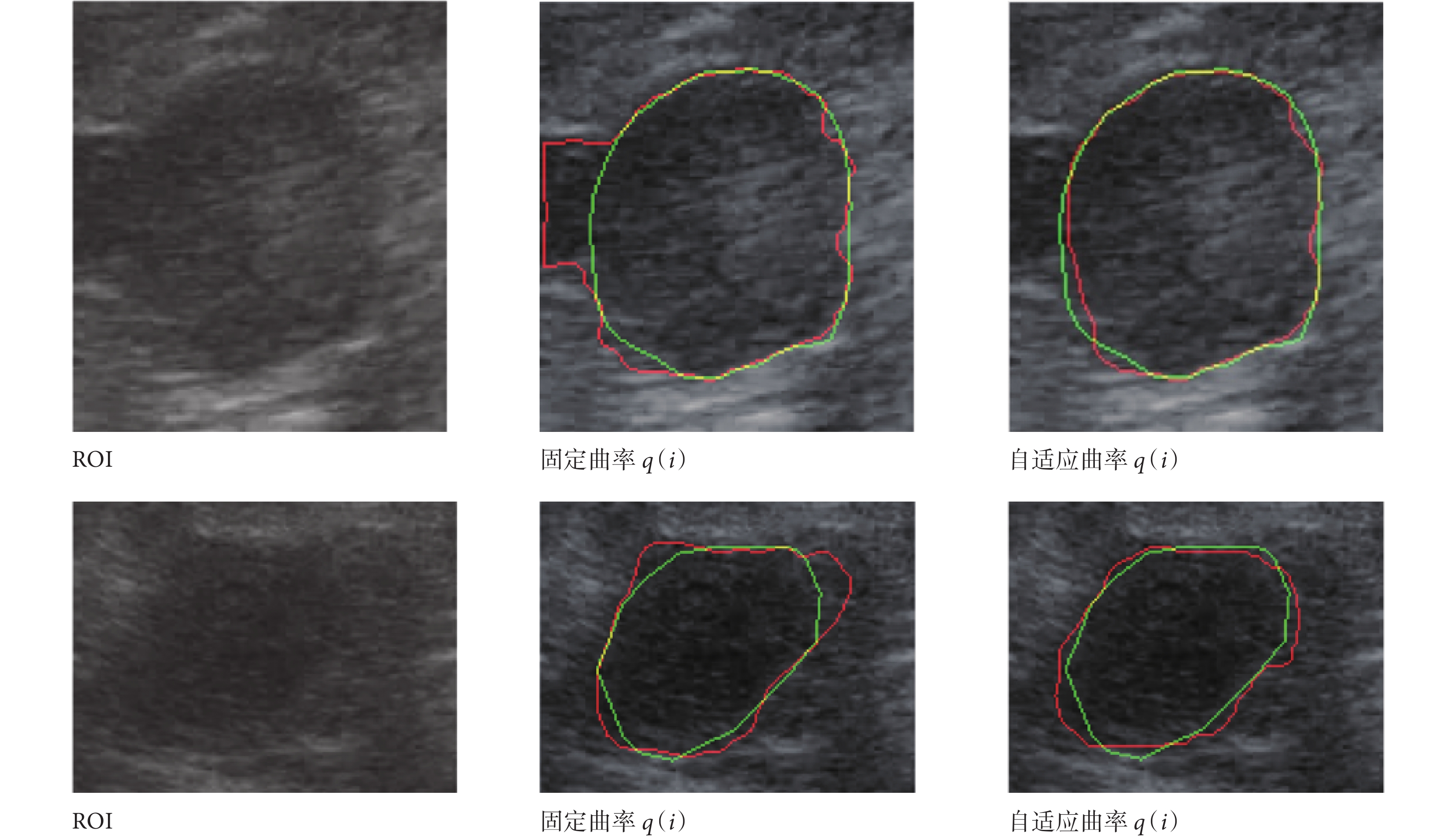 圖13
自適應曲率實驗
Figure13.
Adaptive curvature experiment
圖13
自適應曲率實驗
Figure13.
Adaptive curvature experiment
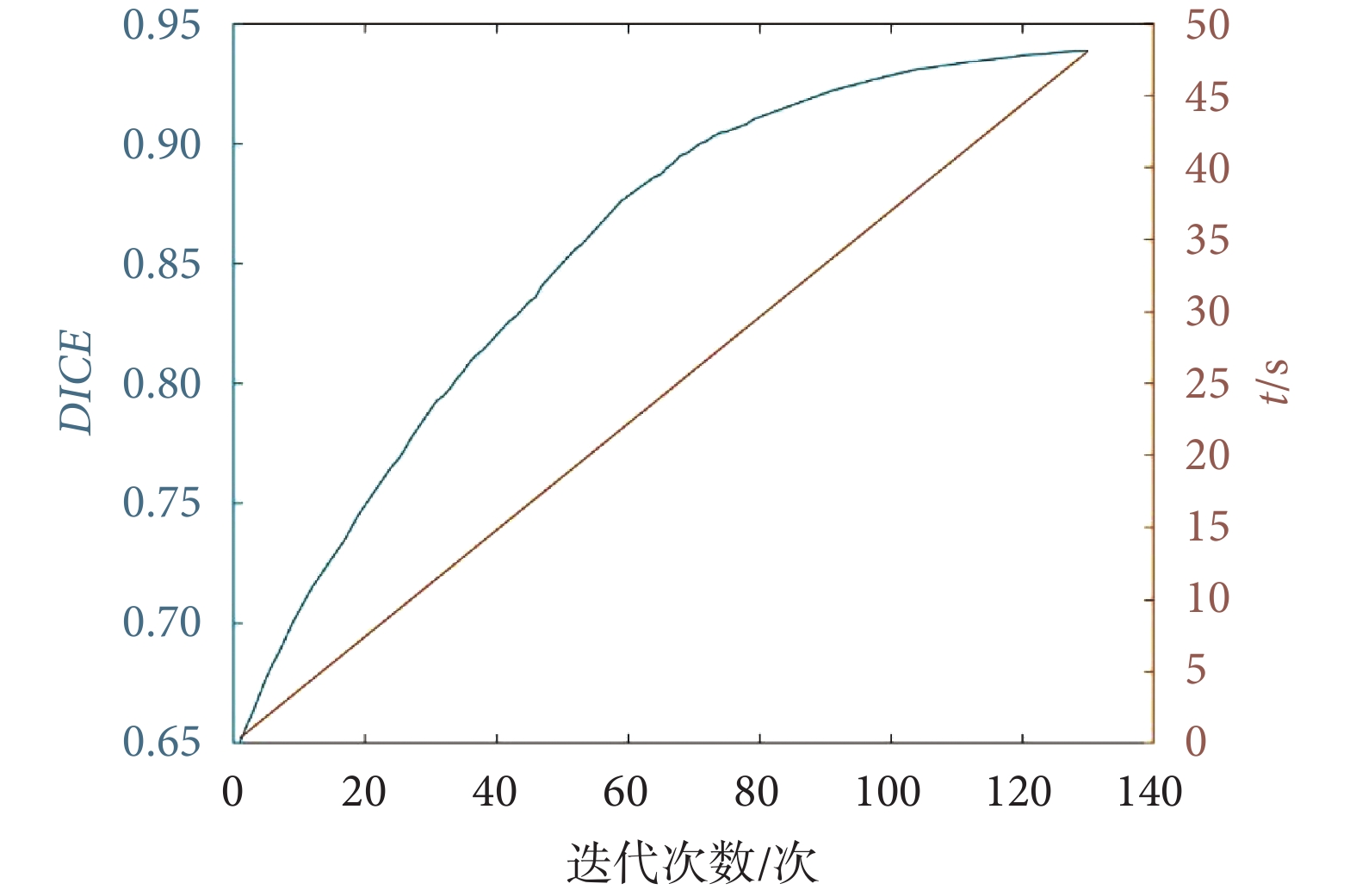
3.6 迭代次數實驗
本文改變 ASLSM 迭代次數,并記錄其 DICE 系數和運行時間,結果如圖 14 所示,藍線為 DICE 系數,棕線為時間。當迭代次數為 0~40 時,DICE 系數值快速提升。40~100 次時提升速度減緩,超過 100 次后,DICE 系數值基本保持不變,運行時間和迭代次數成正比。考慮到有效性和收斂性,故選取 100 次為最優迭代次數。
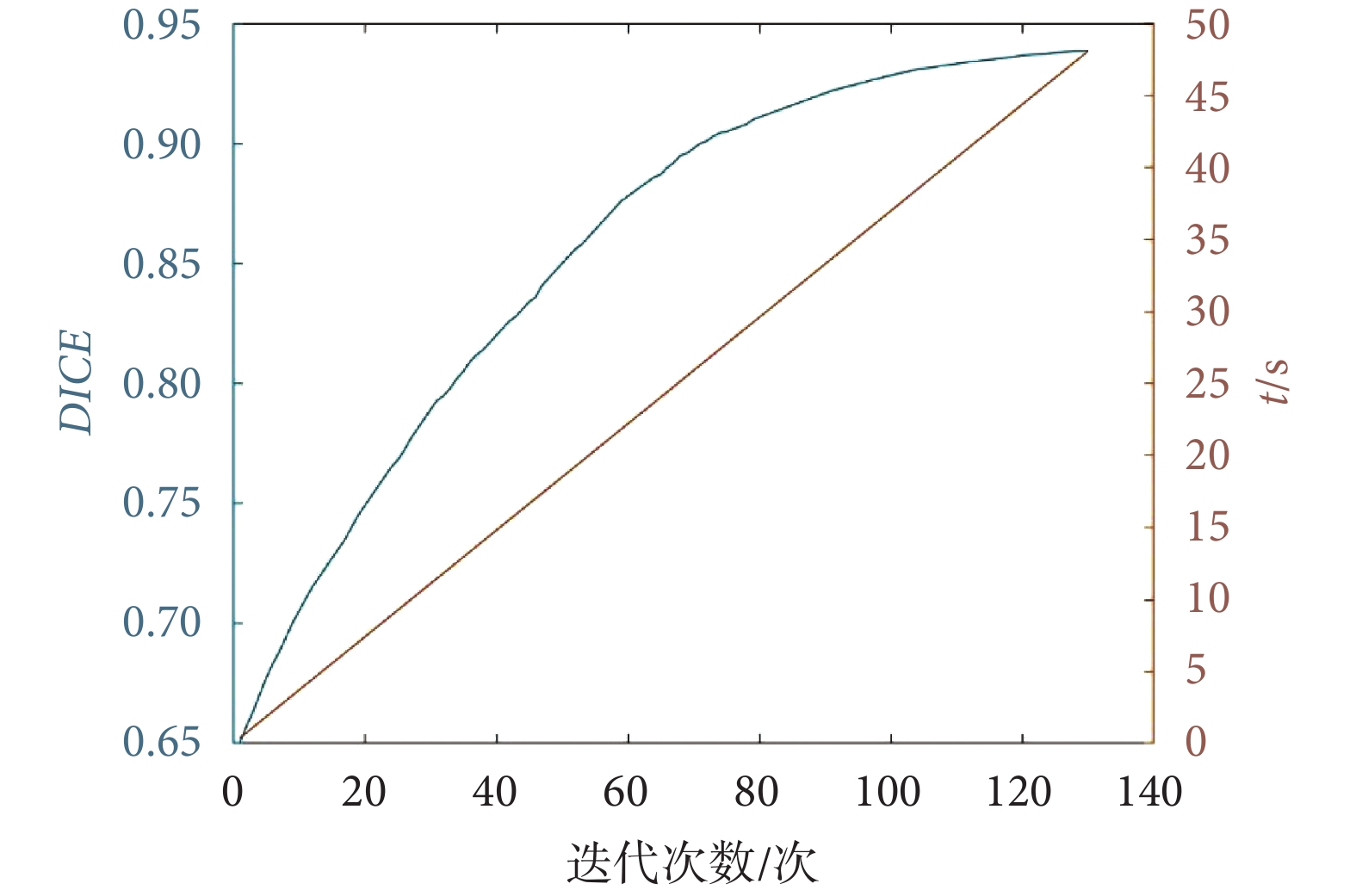 圖14
迭代次數與 DICE 系數和運行時間的關系
Figure14.
Relation between iteration,DICE and running time
圖14
迭代次數與 DICE 系數和運行時間的關系
Figure14.
Relation between iteration,DICE and running time
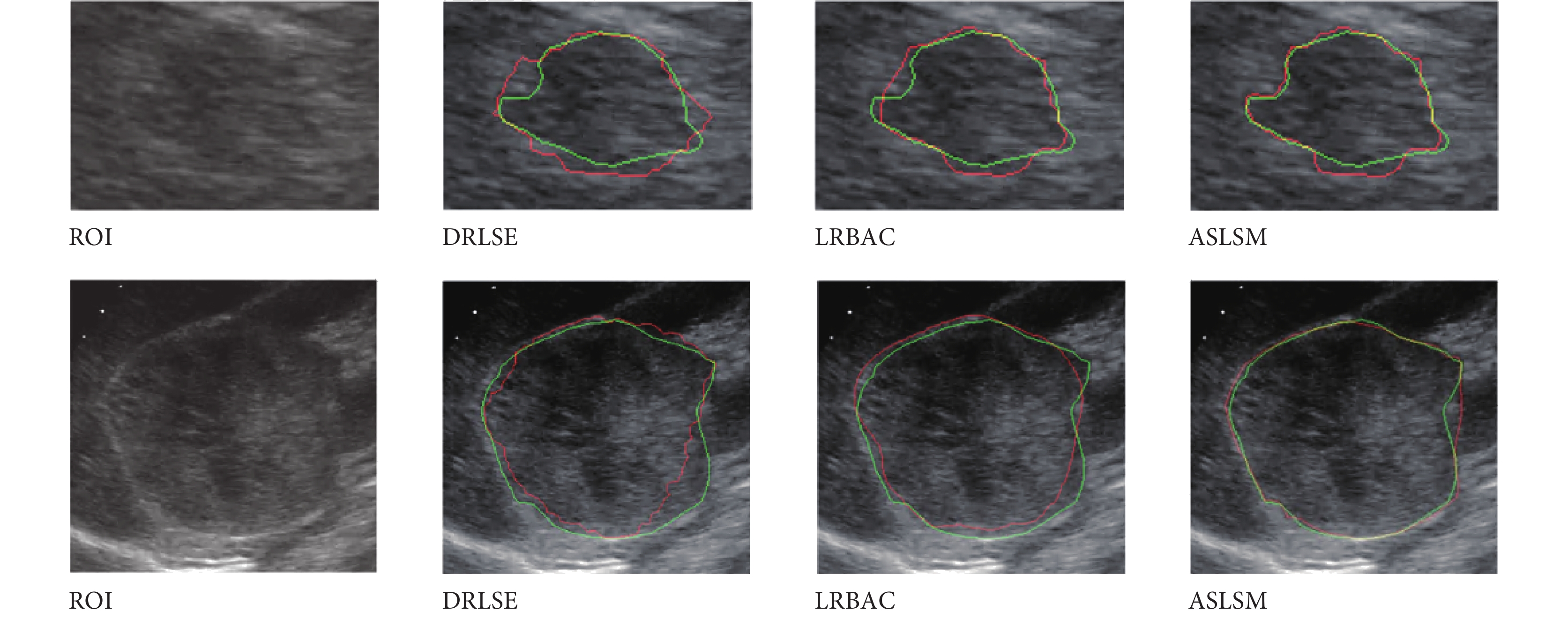
3.7 DRLSE、LRBAC、ASLSM 實驗
DRLSE 僅使用梯度作為驅動項,跨越噪聲能力差,LRBAC 卷積半徑過大丟失細節,過小演化不到真正邊界。ASLSM 通過自適應內外能量和梯度,獲取細節能力明顯增強。本實驗分別使用 DRLSE、LRBAC、ASLSM 分割 261 幅超聲圖像,結果如表 6 所示。ASLSM 犧牲了一定運算時間,效果要明顯好于 DRLSE、LRBAC。如圖 15 所示,綠線為金標準,紅線為分割結果。對應原始的腎臟腫瘤超聲圖像 ROI 區域;DRLSE 結果顯示僅僅使用梯度特征,不能跨越大噪聲區域演化到真正邊界;LRBAC 則過于光滑難以獲取細節,演化不到真正的邊界,而 LRBAC 卷積半徑過小演化不邊界;但采用 ASLSM 自適應 p(i)、convr(i)、q(i),能更加準確演化到真正邊界。
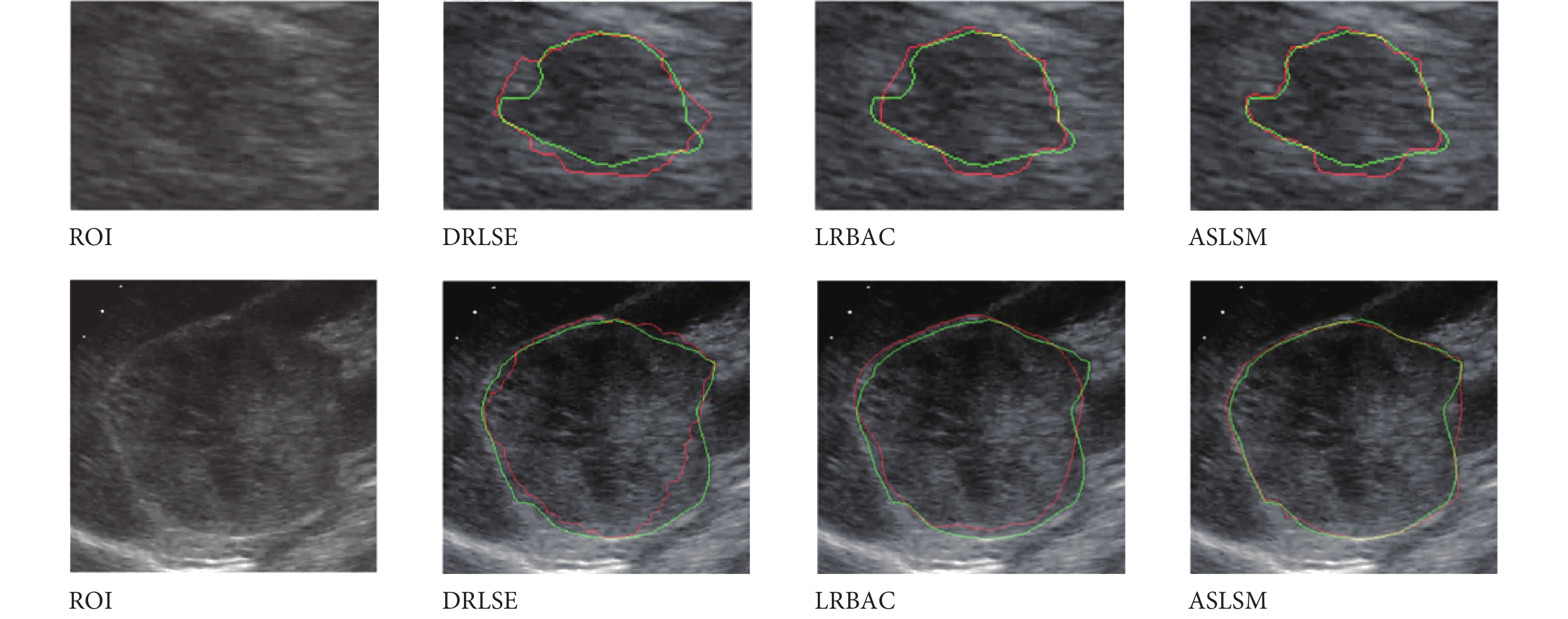 圖15
三種分割算法實驗
Figure15.
Experiment on three segmentation methods
圖15
三種分割算法實驗
Figure15.
Experiment on three segmentation methods
3.8 算法討論
LRBAC 卷積半徑過小演化不到邊界,卷積半徑過大獲取細節能力差,且容易出現分裂成小曲線,造成腎臟超聲圖像分割結果不理想。DRLSE 僅以梯度作為驅動演化項,對于斑點噪聲較大的超聲圖像,同樣分割效果不理想。本文算法融合內外能量項和梯度,彌補了 LRBAC 和 DRLSE 缺點并自適應權重,取得了較好分割效果,但是增加了運行時間。分區演化根據每個區域的圖像特征,計算不同的演化參數,將不同區域的結果合成整個圖像結果,導致運行時間有較大提升,今后本課題組將就此方面進行改進。
4 結論與展望
本文根據腎臟腫瘤超聲圖像特點提出基于分區演化的水平集分割算法。該算法創新性地融合內外能量和梯度,提出了自適應二者能量、卷積半徑和曲率算法,取得了較好的腫瘤分割效果,今后或可為醫生確認腫瘤形態特征提供便利,為超聲視頻跟蹤提取特征提供基礎。基于現有問題,未來還可在如何更精確獲得卷積半徑、減少運行時間和如何根據單幀結果實現腎臟腫瘤視頻跟蹤三方面開展更深入的研究。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
腎臟腫瘤是人體泌尿系統常見腫瘤之一,患病率和死亡率約占腫瘤疾病的 3%[1]。腎臟腫瘤早期臨床癥狀不明顯,晚期可發展到血尿、腹部包塊、疼痛,以致腎功能不全直至患者死亡,所以腎臟腫瘤的早期發現尤為重要[2]。超聲造影以其價格低廉、無輻射、可動態觀察瘤體情況等優勢,已經廣泛應用于腎臟腫瘤檢查[3]。腎臟腫瘤可以根據其造影特征進行分類,以造影劑進入腎皮質和腫瘤的先后順序、造影劑頂峰強度、壞死情況等特征,可區分透明細胞癌、乳頭狀細胞癌和嫌色細胞癌[4]。獲取視頻特征首先要在每幀分割出腫瘤與皮質,因此腫瘤的準確分割尤為關鍵。如圖 1 所示為兩幅典型腎臟超聲圖像,其中左列為兩幅超聲圖像,右列為標注腫瘤和皮質位置的對應圖像,白線內為腫瘤,紅線和藍線之間為皮質。
 圖1
兩幅腎臟超聲圖像及其對應腫瘤和皮質圖像
Figure1.
Two typical ultrasound kidney images and location of tumor and cortex
圖1
兩幅腎臟超聲圖像及其對應腫瘤和皮質圖像
Figure1.
Two typical ultrasound kidney images and location of tumor and cortex
由于超聲圖像斑點噪聲較大,加之腎臟腫瘤常位于腎臟皮質中間,對腫瘤分割造成很大的干擾。Caselles 等[5]提出了幾何動態模型(geodesic active contours,GAC),使用梯度作為驅動項,僅能夠分割出部分圖像質量好的腫瘤圖像。Li 等[6]提出保持水平集光滑的懲罰項算法,在距離正則化水平集演化模型(distance regularized level set evolution,DRLSE)上改進了懲罰項,取得了更好的效果。然而 DRLSE 僅用梯度驅動演化,當應用于噪聲大的超聲圖像時,如圖 1 所示的第一排圖像,這一演化方式即無法跨越噪聲而到達真正邊界。在 2001 年,Chan 等[7]提出一種以 Chan 和 Vese 兩人名字命名的 Chan-Vese(CV)模型,該方法基于輪廓內外全局能量最小的原則,具有較好的抗噪聲能力,但是容易出現局部演化失敗的問題。在 2008 年,Lankton 等[8]提出區域活動輪廓模型(localizing region-based active contours,LRBAC),其演化只考慮零水平集附近圖像,該取值范圍(下文簡稱:卷積半徑)抗噪聲能力較強。LRBAC 具有 CV 模型同樣的缺陷,即易分裂成小曲線,且會因為卷積半徑過大或者曲率過大所致曲線光滑而出現細節丟失問題,或因卷積半徑過小,演化不到真正邊界。在 2013 年,Zhang 等[9]根據擴散理論簡化了零水平初始問題,避免初始化影響。在 2017 年,Khadidos 等[10]提出根據圖像邊界情況自適應演化速度模型,在邊界模糊處減慢演化速度,而在邊界清晰處加快演化速度。然而在腎臟分割中,文獻[10]的方法沒有比 LRBAC 和 DRLSE 取得更好效果,所以本文主要討論 LRBAC 和 DRLSE。如圖 1 所示的第二排腎臟腫瘤超聲圖像會出現有的區域腫瘤與皮質連在一起,內外相似度大(邊界迷糊);有的區域內外相似度小(邊界清晰);若用同一參數演化不同區域,將導致分割失敗。
針對上述問題,本文提出了基于自適應分區演化水平集(adaptive sub-regional evolution level set models,ASLSM)的腎臟腫瘤分割算法。首先,將感興趣(region of interest,ROI)劃分為多個分區進行演化;然后,將局部內外能量與梯度相融合,以解決 DRLSE 梯度無法跨越大噪聲區域,而 LRBAC 容易出現分裂成小曲線且獲取細節能力差等缺點問題,并根據噪聲自適應二者比值;其次,為解決 LRBAC 的卷積半徑過大易丟失細節、過小則演化不到邊界等問題,本文提出基于質心原理自適應卷積半徑;最后,為解決 LRBAC 曲率過大使得曲線光滑丟失細節、過小則演化曲線跨越真正邊界問題,本文提出基于零水平集內外相似度自適應曲率的解決辦法,期望通過本文研究,能為臨床腎臟腫瘤分割打開新的思路,取得較好的實用效果。
1 方法
1.1 水平集背景
水平集是一種將 n 維曲面投射成 n + 1 維空間曲面的演化算法。
(1)DRLSE 模型,是在 GAC 模型上加入了保持水平集光滑的懲罰項 L(Φ),其能量如式(1)所示:
 |
其中,η1,η2,κ1 為權重參數,εg 為曲線長度項,控制演化精度,如式(2)所示;εa 為輪廓內面積,控制演化速度,如式(3)所示:
 |
 |
其中,H1(Φ)是赫維賽德(Heaviside)函數,如式(4)所示, 是 H1(Φ)求導所得,如式(5)所示;g 為圖像梯度項,如式(6)所示。
是 H1(Φ)求導所得,如式(5)所示;g 為圖像梯度項,如式(6)所示。
 |
其中,? 為常量。
式(4)求導后如式(5)所示:
 |
其中, 為常量。
為常量。
梯度項如式(6)所示:
 |
其中,Gσ 是以 σ 為方差的高斯函數。
懲罰項 L(Φ)如式(7)所示:
 |
(2)LRBAC 模型,引用 CV 模型的內外能量計算方式,并通卷積 B(x,y)區域改進算法。B(x,y)為零水平集附近所取范圍區域,其卷積半徑值定義為 convr(i),能量函數如式(8)所示:
 |
其中,|C|為曲線長度,ψ 為權重參數,εc 為內外能量項,如式(9)所示:
 |
其中,λ1、λ2 是內外能量的權重,H1(Φ)使用式(4)計算,Cin、Cout 為內和外能量項,計算方法如式(10)、式(11)所示:
 |
 |
其中  為所取區域,H1(Φ)如式(4)所示。
為所取區域,H1(Φ)如式(4)所示。
1.2 算法改進
ASLSM 融合內外能量與梯度,并自適應調整其比例,其能量函數如式(12)所示:
 |
其中,p(i)是第 i 區域 εg 與 εa 權重,分區標簽如圖 2 所示,ROI 被劃分為 8 個區域,分區內圖像噪聲越大,p(i)值越大;εa 是輪廓內面積,增大 β,將會加速演化; 是曲線長度,控制曲線光滑性,q(i)第 i 區域曲率權重。L(Φ)是懲罰項,如式(7)所示,H1(Φ)、δ1(Φ)分別如式(4)、式(5)所示。式(13)中 g 是梯度項,如式(6)所示,B(x,y)的卷積半徑為 convr(i)。梯度下降法求的 EASLSM 導數如式(13)所示:
是曲線長度,控制曲線光滑性,q(i)第 i 區域曲率權重。L(Φ)是懲罰項,如式(7)所示,H1(Φ)、δ1(Φ)分別如式(4)、式(5)所示。式(13)中 g 是梯度項,如式(6)所示,B(x,y)的卷積半徑為 convr(i)。梯度下降法求的 EASLSM 導數如式(13)所示:
 圖2
分區標簽及 ROI 分區示意圖
Figure2.
Sub-regional label and ROI
圖2
分區標簽及 ROI 分區示意圖
Figure2.
Sub-regional label and ROI
 '/> '/> |
演化函數 Phi 如式(14)所示,其中 Δt 為步長。
 |
1.2.1 分區演化
為解決固定參數演化容易造成模糊區域分割失敗等問題,本文提出了分區演化方法。如圖 3 所示,為分區演化總圖。
 圖3
分區演化整體原理
Figure3.
Principle of sub-regional evolution
圖3
分區演化整體原理
Figure3.
Principle of sub-regional evolution
首先本文從原始超聲圖像中的腫瘤邊界選取 4 個點(紅點),根據 4 個點最大長寬,獲取 ROI,制作水平集演化函數 Phi;然后,制作 8 分區模板(每次演化只有一個區域為 1,其他區域為 0),依次與 ROI 和 Phi 相乘,并根據每個分區圖像特征計算 p(i)、q(i)、convr(i),再將上述三個值代入式(14)演化后,得到一次迭代第一分區結果;最后將所有區域的結果合并,獲得所有區域的演化函數 Phi,將其邊界顯示在 ROI 上,即為一次迭代 8 個分區的結果,其中紅線為一次演化結果,完成一次分區演化。
根據每個分區圖像特征計算 p(i)、q(i)和 convr(i),具體算法如圖 4 所示。以計算第一分區參數為例,首先通過將 ROI 點乘 8 分區模板,將第一分區的圖像取出如圖 4 子圖 a 所示;然后在第一分區圖中零水平集(白細線)上等間隔取圓心,半徑采樣 r = 0.1?K,其中 K 為 ROI 長和寬中最小值,取樣圖像如子圖 a、b、c(只顯示 3 個采樣子圖);最后根據采樣子圖 a、b、c 特征取平均值計算第一分區的 p(1)、q(1)、convr(1),具體算法請參照下文。
 圖4
計算單個分區特征原理
Figure4.
Principle of sub-region feature calculation
圖4
計算單個分區特征原理
Figure4.
Principle of sub-region feature calculation
1.2.2 p(i)值求法
為了解決 DRLSE 梯度無法跨越大噪聲區域和 LRBAC 容易出現分裂小曲線且獲取細節能力差的問題,本文提出將內外能量項與梯度相結合,并根據圖像噪聲自適應二者權重 p(i)的算法。如圖 4 所示原理,本文在零水平集等間隔取圓心,以 r = 0.1?K 為半徑采樣,其中 K 為 ROI 長和寬中最小值。如式(15)所示,本文首先計算分區采樣子圖的方差 var(Img(i,k)),然后計算分區所有采樣子圖方差的平均值,最后除以所有采樣子圖方差的最大值進行歸一化。
 |
其中,var(Img(i,k))是第 i 區域的第 k 采樣子圖方差, 是所有區域采樣子圖方差的最大值。
是所有區域采樣子圖方差的最大值。
作為例子,如圖 5 所示,展示了 ROI 的 4 個區域采樣子圖,為便于展示如圖 2 所示的 1~8 分區的噪聲情況,取樣半徑大于圖 4 設定的半徑。右側 4 幅子圖為左側原始超聲圖像中紅色圓圈的截取圖像,綠圈為零水平集初始輪廓。4 幅采樣子圖中,子圖 d 噪聲最大、方差最大、p(i)值最大;子圖 b 噪聲最小、方差最小、p(i)值最小。1~8 分區的 p(i)取值分別為:0.60、0.53、0.56、0.73、0.67、0.44、0.33、0.29。
 圖5
以方差定量不同區域噪聲原理
Figure5.
Noise calculation method according to variance
圖5
以方差定量不同區域噪聲原理
Figure5.
Noise calculation method according to variance
1.2.3 卷積半徑 convr(i)求法
為解決 LRBAC 卷積半徑過大則易丟失細節而過小則演化不到邊界的問題,本文提出根據質心原理自適應卷積半徑算法。為了便于理解,本文選取一個無噪聲的模擬圖演示卷積半徑計算過程,如圖 6 所示。首先在待分割圖像原始模板圖中任意取點,形成初始輪廓的零水平集曲線;然后求其梯度得到零水平集和真實梯度,其中細線為零水平集,粗線為真實梯度;最后在每個分區零水平集(細線)上等間隔取圓心,半徑采樣 r = 0.1?K,其中 K 為 ROI 長和寬中最小值,計算該點(紅色圓點)到最大梯度值點(紅色叉點)最短距離,該距離即該分區的卷積半徑,半徑依次為 r1、r2、r3 和 r4,以藍色線段顯示。
 圖6
卷積半徑計算原理模型
Figure6.
The model of convolution radius calculation
圖6
卷積半徑計算原理模型
Figure6.
The model of convolution radius calculation
由于超聲圖像對比度低且斑點噪聲大,在同一個區域內很難找到真實的邊界梯度最大值點,故采用質心理論。如圖 4 所示原理,本文在導數圖像零水平集等間隔取圓心,以 r = 0.1?K 為半徑采樣,其中 K 為 ROI 長和寬中最小值。首先計算每個采樣子圖質心如式(16)所示;然后求得質心到最近零水平集的最短距離的平均值,即該子圖的卷積半徑;最后計算分區內所有采樣子圖卷積半徑平均值,即該分區的卷積半徑 convr(i),如式(17)所示。
 |
 |
其中,(x,y)是質心坐標,(xk,yk)是第 i 分區第 k 個采樣子圖零水平集上離質心(x,y)最近的點。
如圖 7 所示,本文將 ROI 求導后得到導數圖像。紅十字即為該采樣子圖質心,計算質心到零水平集(白線)的最短距離,即該采樣子圖的卷積半徑,如放大子圖中 r1、r2;再將分區子圖卷積半徑求平均值,即該分區的卷積半徑 convr(i)。當邊界非常模糊時,若無法獲得質心位置,將所有其他區域卷積半徑的平均值賦予這個區域。1~8 分區的 convr(i)取值分別為 4.21、7.23、6.19、13.90、21.34、9.45、10.43、3.82。
 圖7
超聲卷積半徑計算原理
Figure7.
Principle of ultrasound image convolution radius calculation
圖7
超聲卷積半徑計算原理
Figure7.
Principle of ultrasound image convolution radius calculation
1.2.4 曲率權重 q(i)求法
為了解決 LRBAC 曲率過大曲線光滑而失去細節、曲率過小則內外相似度大區域跨越邊界的問題,本文提出根據零水平集內外相似度自適應計算曲率的算法。如圖 4 所示原理,首先在零水平集等間隔取圓心,r = 0.1?K 為半徑采樣,其中 K 為 ROI 長和寬中最小值。采樣子圖內外的相似度 sim 的計算公式,如式(18)所示;分區中采樣子圖 sim 的平均值,即該值乘以相應的參數所得曲率權重 q(i)的計算公式,如式(19)所示:
 |
其中,D_min(i,k)為零水平集內外區域像素平均值較小值,D_max(i,k)則為較大值。
 |
其中,sim(i,k)是第 i 分區域第 k 個采樣子圖內外相似度,δ1、δ2 分別為 ROI 長和寬,這里 γ = 3。
如圖 8 所示,零水平集為白線,4 區和 5 區中的綠圈為采樣子圖區域。4 區內外相似度最小,故 sim(4,k)值最小;5 區內外相似度最大,故 sim(5,k)值最大。本文自適應減小 4 區曲率獲得更多細節,自適應增加 5 區曲率防止內外相似度大區域處跨越邊界。1~8 分區的 sim(i)取值分別為 0.76、0.53、0.46、0.21、0.90、0.40、0.58、0.91。
 圖8
曲率計算原理
Figure8.
Principle of curvature calculation
圖8
曲率計算原理
Figure8.
Principle of curvature calculation
2 實驗數據、評價指標及計算機配置
2.1 實驗數據
本文數據來自 2012 年 11 月—2016 年 11 月天津醫科大學腫瘤醫院,其中包括:腎臟腫瘤透明細胞癌視頻 67 例、嫌色細胞癌 12 例、乳頭細胞癌 8 例,共 87 例視頻,所有試驗均與患者簽署知情同意書,并經過天津醫科大學腫瘤醫院授權使用該數據。所有患者年齡在 25~75 歲,詳細信息如表 1 所示。每例視頻分別選取造影劑剛進入時、最高峰時和退出時的 3 幀圖像作為本文采樣圖像,共 261 幅超聲圖像,由臨床醫生手工勾勒作為金標準。
為了驗證內外能量項融合梯度的效果,本文選取了一幅無噪聲的模擬圖像,并加入方差 σ = 0.03 的斑點噪聲作為實驗對象。
2.2 量化指標
本文選擇兩輪廓豪斯多夫距離(hausdorff distance,HD)(符號記為:HD),平均絕對距離(mean absolute distance,MAD)(符號記為:MAD)和戴斯系數(dicecoefficient,DICE)(符號記為:DICE)作為評估標準。
假設 A、B 分別對應金標準和算法分割結果,HD 計算的是兩個輪廓間的最大最小距離,如式(20)所示:
 |
其中,a 和 b 分別是兩個輪廓 A 和輪廓 B 上的點,d(a,B)表示 a 到輪廓 B 的最短距離。
MAD 計算的是兩個輪廓所有最小距離的平均值,如式(21)所示:
 |
其中,NA 和 NB 分別為輪廓 A 和輪廓 B 上的點的數量。
DICE 是評價兩輪廓所在區域的重合程度,如式(22)所示:
 |
其中,ΩA 和 ΩB 分別表示以 A 和 B 為輪廓的閉區域,Area(.)為對應的閉區域的面積;DICE = 0 表示沒有完全沒有重合,分割完全錯誤;DICE = 1 表示兩個閉合區域完全重合,分割完全正確。
2.3 計算機硬軟件配置
本文采用的計算機為戴爾工作站(T7920,Dell Inc,美國);使用的軟件為 matlab 2018b(Matlab Inc,美國)。
3 實驗與結果
3.1 融合內外能量項和梯度實驗
LRBAC 使用的內外能量項,擁有較強抵抗噪聲的能力,但易分裂成小曲線,且當卷積半徑過大的時,演化丟失細節;DRLSE 使用的梯度項能減少分裂小曲線的出現,獲取更多的細節,但跨越大噪聲區域能力較差。融合內外能量項和梯度,既擁有獲取更強細節的能力,又不易分裂成小曲線。如圖 9 所示,白線為演化結果,沒有噪聲時,DRLSE、LRBAC、融合項都能演化到真正邊界;梯度無法跨越大噪聲區域時,DRLSE 無法演化到真正的邊界; LRBAC 模型整幅圖出現很多分裂的小曲線,分割完全失敗;而融合項能夠演化到真正的邊界,且沒有出現分裂的小曲線。
 圖9
模擬圖像融合內外能量項和梯度實驗
Figure9.
The experiment of integrating energy and gradient in simulation image
圖9
模擬圖像融合內外能量項和梯度實驗
Figure9.
The experiment of integrating energy and gradient in simulation image
3.2 分區演化實驗
腎臟腫瘤圖像在不同區域內外相似度不同,曲率過大演化曲線變的過于光滑而演化不到邊界,曲率過小內外相似度大的區域演化易跨越邊界。分區演化根據不同區域的噪聲情況,在內外相似度大的區域增大曲率,在內外相似度小的區域減小曲率,可以分割出噪聲較大的腎臟腫瘤圖像。如圖 10 所示,綠線為金標準,紅線為分割結果。左二曲率設定 0.3?δ1?δ2 時,1 區和 2 區曲率過大而演化曲線變得光滑不能到邊界,但 5 區能演化到真正邊界;右二曲率設定為 0.1?δ1?δ2 時,5 區內外相似度大演化跨越邊界;右一分區演化通過自適曲率在 1 區和 2 區減小曲率,5 區增大曲率,各區域均準確演化到邊界。評價參數如表 2 所示,圖 10 證明分區演化效果最好,對所有樣本的分區演化實驗結果如表 2 所示。
 圖10
分區演化實驗
Figure10.
Experiments on sub-region evolution
圖10
分區演化實驗
Figure10.
Experiments on sub-region evolution
3.3 自適應 p(i)值實驗
為了解決 DRLSE 梯度無法跨越大噪聲區域和 LRBAC 容易出現分裂小曲線且獲取細節能力差的問題,本文將內外能量項與梯度相融合,并自適應二者比值 p(i)。固定 q(i)值為 0.1?δ1?δ2 和 convr(i)值為 20,其中對照組 p(i)固定為 0.2,對所有的樣本進行自適應 p(i)實驗。實驗結果如表 3 所示,自適應 p(i)值比固定 p(i)值效果有所提升,但梯度在腎臟超聲圖像中獲取細節能力有限。如圖 11 所示,綠線為金標準,紅線為分割結果。其中,如固定 p(i)可見,第一排的 5 區、第二排的 5 區和 6 區域噪聲較大,應增大該區 p(i)值,故固定 p(i)無演化到邊界;而如果是選擇自適應 p(i),則取得更準確的演化效果。
 圖11
自適應 p(i)值實驗
Figure11.
Experiments on adaptive p(i)
圖11
自適應 p(i)值實驗
Figure11.
Experiments on adaptive p(i)
3.4 自適應卷積半徑 convr(i)實驗
根據質心原理,本文自適應卷積半徑。在初始輪廓離真正邊界較遠的區域增大卷積半徑,在初始輪廓離真正邊界較近的區域減小卷積半徑,增強獲取細節的能力,驅動演化到真正邊界。固定曲率 q(i)值為 0.1?δ1?δ2 和 p(i)值為 0.2,對照組 convr(i)固定為 20,進行自適應卷積半徑實驗。實驗結果如表 4 所示,自適應 convr(i)效果有較大的提升,證明 convr(i)取值對腎臟超聲圖像分割尤其重要。如圖 12 所示,綠線為金標準,紅線為分割結果。左一列是腎臟腫瘤超聲圖像 ROI 區域;左二上在 1 區和 2 區卷積半徑過大,5 區和 6 區卷積半徑過小,演化不到邊界,左二下的 4 區和 5 區卷積半徑過小,演化不到邊界;右一列自適應卷積半徑 convr(i),取得更準確的演化效果。
 圖12
自適應卷積半徑實驗
Figure12.
Experiments on adaptive convolution radius
圖12
自適應卷積半徑實驗
Figure12.
Experiments on adaptive convolution radius
3.5 自適應曲率 q(i)實驗
本文根據零水平集內外相似度自適應曲率,在零水平集內外相似度大的區域增大曲率,在相似度小的區域減小曲率,使演化即在邊界模糊處收斂住,又在邊界清晰處獲得更多細節。固定 convr(i)值為 20 和 p(i)值為 0.2,其中對照組 q(i)固定為 0.1?δ1?δ2,對所有的樣本進行自適應曲率實驗。如表 5 所示,自適應 q(i)效果有所提升。如圖 13 所示,綠線為金標準,紅線為分割結果。左二上的 2 區、左二下的 6 區內外相似度大,演化跨越真正邊界;自適應增大了右一上的 2 區、右一下的 6 區曲率,結果顯示二者均取得更準確的演化效果。
 圖13
自適應曲率實驗
Figure13.
Adaptive curvature experiment
圖13
自適應曲率實驗
Figure13.
Adaptive curvature experiment
3.6 迭代次數實驗
本文改變 ASLSM 迭代次數,并記錄其 DICE 系數和運行時間,結果如圖 14 所示,藍線為 DICE 系數,棕線為時間。當迭代次數為 0~40 時,DICE 系數值快速提升。40~100 次時提升速度減緩,超過 100 次后,DICE 系數值基本保持不變,運行時間和迭代次數成正比。考慮到有效性和收斂性,故選取 100 次為最優迭代次數。
 圖14
迭代次數與 DICE 系數和運行時間的關系
Figure14.
Relation between iteration,DICE and running time
圖14
迭代次數與 DICE 系數和運行時間的關系
Figure14.
Relation between iteration,DICE and running time
3.7 DRLSE、LRBAC、ASLSM 實驗
DRLSE 僅使用梯度作為驅動項,跨越噪聲能力差,LRBAC 卷積半徑過大丟失細節,過小演化不到真正邊界。ASLSM 通過自適應內外能量和梯度,獲取細節能力明顯增強。本實驗分別使用 DRLSE、LRBAC、ASLSM 分割 261 幅超聲圖像,結果如表 6 所示。ASLSM 犧牲了一定運算時間,效果要明顯好于 DRLSE、LRBAC。如圖 15 所示,綠線為金標準,紅線為分割結果。對應原始的腎臟腫瘤超聲圖像 ROI 區域;DRLSE 結果顯示僅僅使用梯度特征,不能跨越大噪聲區域演化到真正邊界;LRBAC 則過于光滑難以獲取細節,演化不到真正的邊界,而 LRBAC 卷積半徑過小演化不邊界;但采用 ASLSM 自適應 p(i)、convr(i)、q(i),能更加準確演化到真正邊界。
 圖15
三種分割算法實驗
Figure15.
Experiment on three segmentation methods
圖15
三種分割算法實驗
Figure15.
Experiment on three segmentation methods
3.8 算法討論
LRBAC 卷積半徑過小演化不到邊界,卷積半徑過大獲取細節能力差,且容易出現分裂成小曲線,造成腎臟超聲圖像分割結果不理想。DRLSE 僅以梯度作為驅動演化項,對于斑點噪聲較大的超聲圖像,同樣分割效果不理想。本文算法融合內外能量項和梯度,彌補了 LRBAC 和 DRLSE 缺點并自適應權重,取得了較好分割效果,但是增加了運行時間。分區演化根據每個區域的圖像特征,計算不同的演化參數,將不同區域的結果合成整個圖像結果,導致運行時間有較大提升,今后本課題組將就此方面進行改進。
4 結論與展望
本文根據腎臟腫瘤超聲圖像特點提出基于分區演化的水平集分割算法。該算法創新性地融合內外能量和梯度,提出了自適應二者能量、卷積半徑和曲率算法,取得了較好的腫瘤分割效果,今后或可為醫生確認腫瘤形態特征提供便利,為超聲視頻跟蹤提取特征提供基礎。基于現有問題,未來還可在如何更精確獲得卷積半徑、減少運行時間和如何根據單幀結果實現腎臟腫瘤視頻跟蹤三方面開展更深入的研究。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。