清晨醒來時刻前后是心血管疾病（CVD）事件發生的高峰期，這一點很可能與夜間睡眠結束時交感神經活動的激增有關。本文以 70 位在兩年隨訪期內發生了 CVD 事件和 70 位未發生 CVD 事件的 140 位受試者為研究對象，提出了一種兩層模型方法以探究覺醒前的心率變異性（HRV）特征是否有利于兩類受試者的區分。在該方法中，第一層采用極端梯度提升算法（XGBoost）構建分類器，通過評估該分類器的特征重要性實現特征篩選；篩選出來的特征作為第二層模型的輸入來構建最終的分類器。在第二層模型中，比較了 XGBoost、隨機森林和支持向量機三種機器學習算法，以確定基于何種算法建立的模型可以得到最優的分類效果。研究結果顯示，基于覺醒前 HRV 特征構建的 XGBoost+XGBoost 模型性能最優，準確率高達 84.3%；在所使用的 HRV 特征中，非線性動力學指標在模型中的重要性優于傳統的時域、頻域分析指標；其中尺度 1 下的排列熵、尺度 3 下的樣本熵較為重要。本研究結果對 CVD 的預防、診斷以及 CVD 風險評估系統的設計有著積極的參考價值。
引用本文： 楊曄, 燕雪雅, 侯鳳貞, 潘蕾. 基于睡眠心率變異性的心血管疾病預測研究. 生物醫學工程學雜志, 2021, 38(2): 249-256. doi: 10.7507/1001-5515.202004039 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
心血管疾病（cardiovascular disease，CVD）是由心臟和血管異常引起的一系列疾病的總稱。目前，我國 CVD 患病率處于持續上升階段，而因 CVD 致死則占城鄉居民總死亡原因的首位[1]，因此 CVD 的早期預測對人類的健康和社會發展有著積極的意義[2]。
睡眠，作為一種復雜的生理過程，與機體的各基本系統密切相關，其中就包括心血管系統[3]。心血管系統的穩定性受到眾多因素的控制，其中自主神經系統對心率的調節起著至關重要的作用。自主神經系統包括交感神經和副交感神經，交感神經興奮時，心率會增加；副交感神經興奮時，心率會降低。自主神經系統活動失衡會增加許多疾病（包括 CVD）的發病率和死亡率[4]。研究表明，在一天的不同時刻，急性 CVD 事件的發生率是不同的，清晨醒來時刻前后是 CVD 事件發生的高峰期[5-9]。雖然導致清晨 CVD 事件增加的原因并未明確，但不少研究認為這一狀況可能與夜間睡眠末期交感神經活動的激增有關[10-14]。
自主神經系統使得心血管系統能夠對機體內外的易變刺激做出迅速反應，導致逐次心跳的心率呈現出細小的波動，通常被稱為心率變異性（heart rate variability，HRV）。HRV 分析方法主要包括時域分析法、頻域分析法和非線性動力學分析法[15]。作為一種非侵入、無創的手段，HRV 分析已經廣泛用于評估自主神經系統功能和心血管系統健康狀況[16-18]。在文獻中，也有利用 HRV 分析進行 CVD 風險評估的報道[19-21]，但這些研究存在著一些不足。首先，使用的 HRV 數據并非針對睡眠狀態。而在本文的前期研究中發現，睡眠 HRV 分析能夠有效預測短時的 CVD 事件[22]。其次，采用的分析方法大都基于時域、頻域分析，鮮有涉及非線性動力學分析。然而大量的研究表明，心臟動力系統富含非線性成分，以熵分析和冪律分析為代表的非線性動力學分析方法現已廣泛用于 HRV 信號的分析中[15]。
因此，鑒于急性 CVD 事件高發于清晨醒來前后的事實、HRV 分析在自主神經功能評估中的重要性以及心臟動力系統的非線性特性，本文綜合使用時域、頻域、非線性動力學分析方法來挖掘夜間睡眠時的 HRV 信號的特征，并利用機器學習算法構建 CVD 自動預測模型，從而探索睡眠末期的 HRV 信號分析是否可以提供更高的 CVD 預測準確率以及哪些 HRV 指標在 CVD 預測中較為重要，這一結果或對 CVD 的早期預測帶來新的突破。
1 研究方法
1.1 研究對象
本文采用的研究數據來源于美國睡眠心臟健康研究項目（sleep heart health study，SHHS）（網址：https://sleepdata.org/datasets/shhs）的開源數據庫[23]，共采納 140 名受試者的相關數據，受試者的篩選過程在本文的前期研究中有詳細的闡述[22]，本文不再贅述。受試者在家中使用便攜式多導睡眠監測儀采集多導睡眠圖（polysomnography，PSG），其中記錄了兩個導聯的心電圖（electrocardiograph，ECG）數據，采樣頻率為 125 Hz。根據 SHHS 的隨訪記錄，其中的 70 人在 PSG 采集后的兩年隨訪期內發生了 CVD 事件，包括心絞痛、急性心肌梗塞等；另外 70 人在隨訪期內未報道任何 CVD 事件。本文將發生 CVD 事件的受試者記為 CVD 組，未發生 CVD 事件的受試者記為 non-CVD 組。兩組人群在年齡、腰臀比、是否有糖尿病病史以及是否有高血壓病史這四個指標上的差異具有統計學意義（P<0.05），而在性別、身高、身體質量指數（body mass index，BMI）、呼吸紊亂指數（apnea hypopnea index，AHI）、呼吸障礙指數（respiratory disturbance index，RDI）、吸煙狀況和吸煙頻率等指標上的差異沒有統計學意義（P>0.05）。
1.2 信號預處理
對于每位受試者，其整夜 ECG 信號經巴特沃斯帶通濾波器（0.5～45 Hz）預處理后，根據潘-湯普金斯（Pan-Tompkins，PT）方法檢測出所有的 R 波頂點[24]，然后計算兩個連續 R 波峰之間的間隔，得到 R-R 間期序列。接著，去除 R-R 間期序列中的異位起搏點或偽跡并進行插值處理[25]，以獲得供后續分析使用的 HRV 信號。
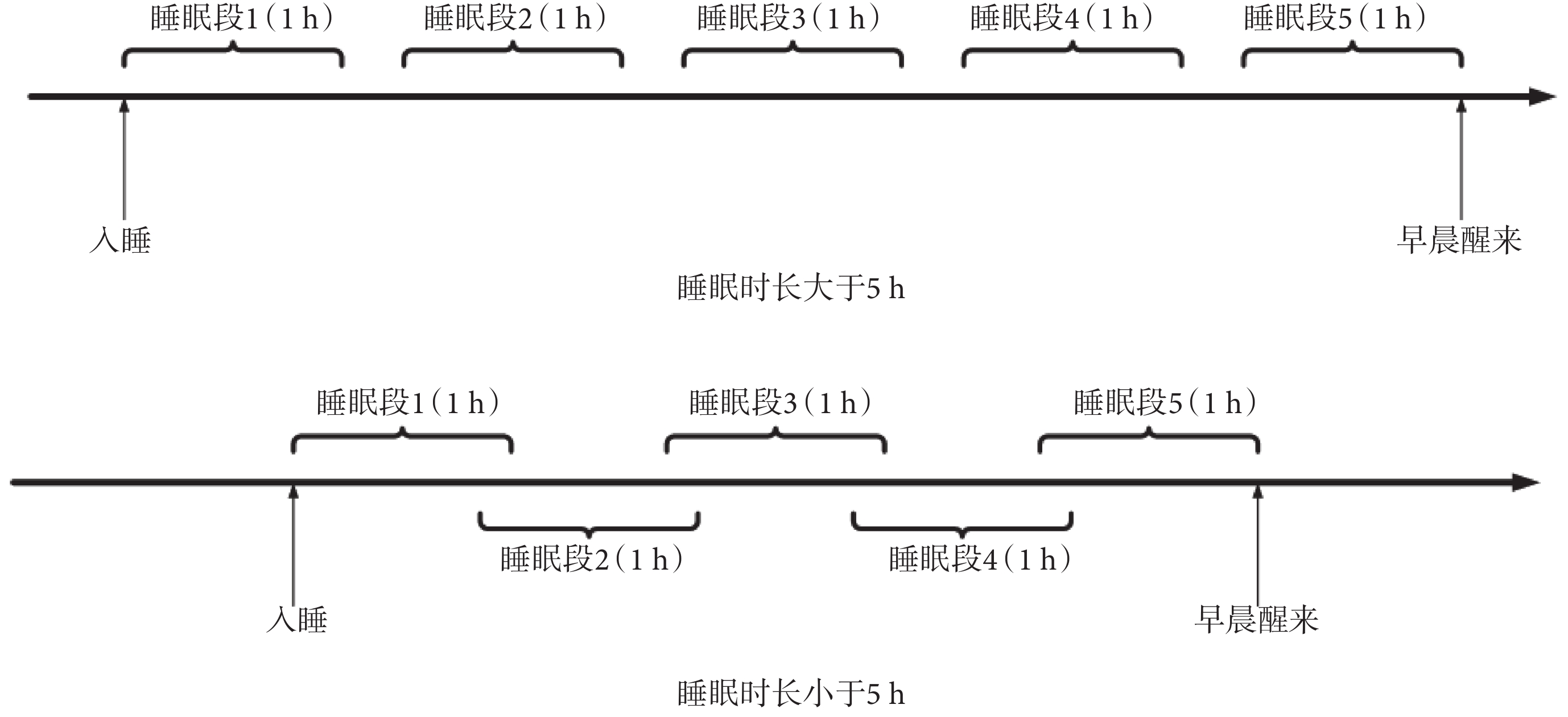
為了對比不同睡眠段 HRV 信號對 CVD 事件的預測能力，如圖 1 所示，本文將每位受試者整夜睡眠 HRV 信號劃分成 5 個 1 h 的片段，分別定義為睡眠段 1～5，其中睡眠段 5 對應為清晨覺醒前 1 h。若整晚睡眠時長大于 5 h，則每個片段互不重疊，片段之間的分離間期相等；若整晚睡眠時長小于 5 h，則每個片段有重疊，片段之間的重疊間期相等。
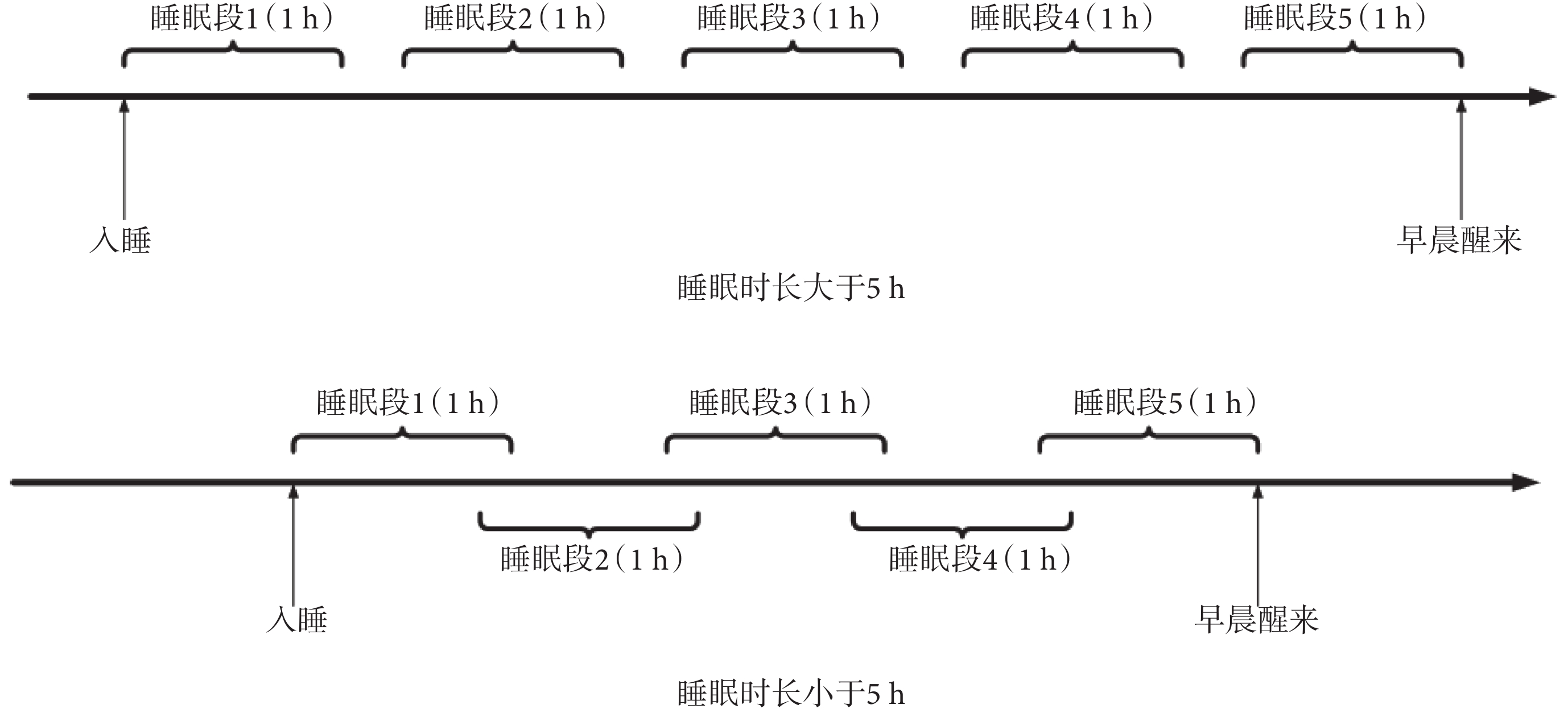圖1
試驗數據抽取示意圖
Figure1.
Schematic diagram of test data extraction
1.3 HRV 分析
本文綜合考慮了 HRV 的時域、頻域和非線性分析方法。時域和非線性分析參數的計算基于每 1 h 的 HRV 數據段進行，而頻域參數的計算則基于每 5 min 的 HRV 片段，然后以 1 h 內的 12 個片段的均值作為對應段的特征值。時域參數包括所有 R-R 間期（NN 間期）的標準差（standard deviation of normal to normal，SDNN）、相鄰 R-R 間期差值的均方根值（root mean square of successive differences，RMSSD），頻域參數包括 0.003～0.4 Hz 頻率范圍內的總功率（total power，TP）、0.04～0.15 Hz 頻率范圍內的低頻功率（power in low frequency，LF）、0.15～0.4 HZ 頻率范圍內的高頻功率（power in high frequency，HF）以及歸一化的高頻段能量（HF power in normalized units，HFnorm）[26]。對于非線性動力學分析，本文采用了去趨勢波動分析（detrend fluctuation analysis，DFA）和多尺度熵分析。
1.3.1 DFA 分析簡介
采用傳統方法研究時間序列的長期冪律關系可能會因為噪聲或者趨勢成分的影響而使得分析結果不可靠[27]。DFA 分析則可以通過去除趨勢項將信號與外部環境的噪聲分離，從而適用于非平穩時間序列的處理。對于長度為 N 的序列
，DFA 算法描述如下：
首先，如式（1）所示，將 
N} 零均值處理后進行一階積分，得到一個新的序列 
：
 |
其次，給定區間長度 n，將 
劃分為不重疊的 m 個區間，m 為 N/n 的整數部分。對于劃分的每一段序列采用最小二乘法線性擬合出局部趨勢 
，最后對 
去除每個區間的局部趨勢并計算出序列的均方根，如式（2）所示：
 |
隨著 n 的變化呈現冪律分布，其中的斜率表示 DFA 指數，本文記為 DFA_alpha，描述了時間序列的粗糙程度，其值越大表明時間序列越光滑。DFA 是一種能夠有效地量化嵌入在非平穩時間序列中的長期相關性的有效方法[28]。
1.3.2 多尺度熵分析
多尺度熵分析引進了時間尺度因子 τ 的概念，通過構造一系列不同粗粒化程度的時間序列，并計算它們的熵值，以獲得原始時間序列在不同尺度下的復雜性測度。其具體計算過程包括粗粒化和熵值計算兩個部分。
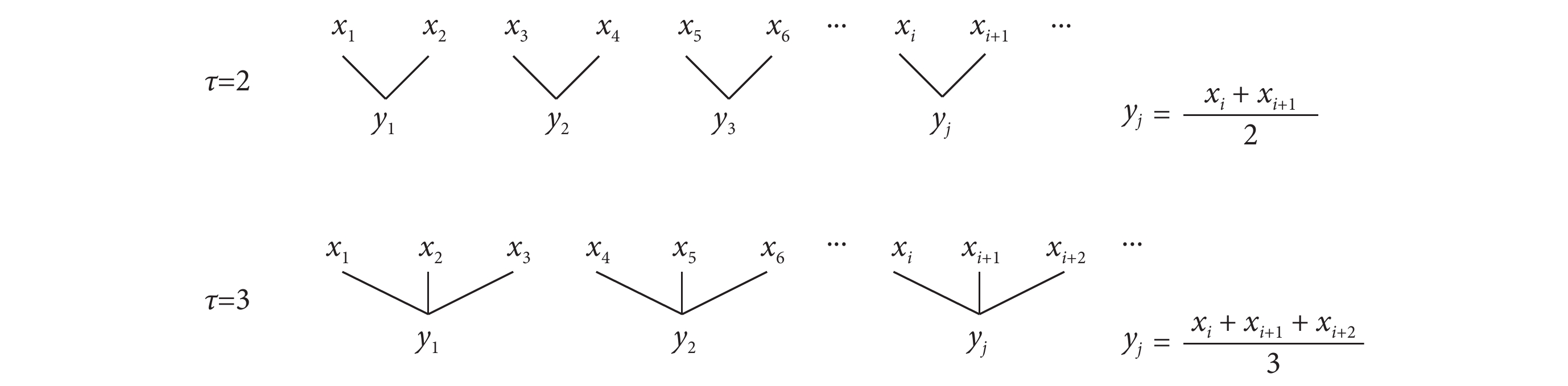
對于 N 點的時間序列 
，粗粒化過程如圖 2 所示[29]。以尺度因子 τ 為長度，依次將原時間序列劃分為 N/τ 段不重疊的子序列，這些子序列的均值就形成了 
在尺度 τ 上的粗粒化序列，記為
。
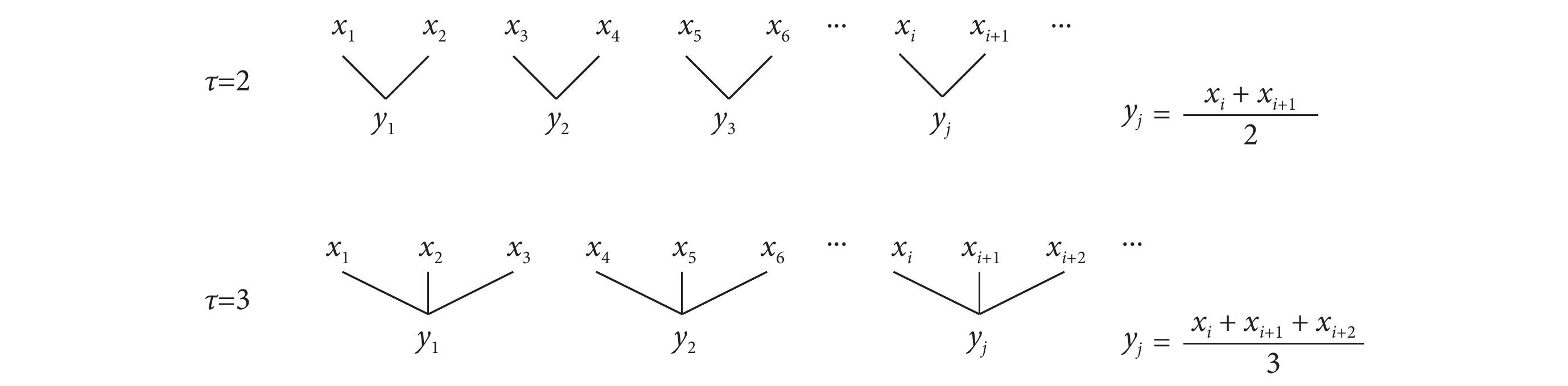圖2
粗粒化示意圖
Figure2.
Schematic diagram of coarse granulation
對于每個粗粒化序列，本文分別采用樣本熵（sample entropy，SE）和改進的排列熵（modified permutation entropy, MPE）算法來進行熵分析。SE 算法如式（3）～（6）所示[30]。
將時間序列
嵌入到 m 維空間中，該空間中向量如式（3）所示：
 |
對于 m 維空間中的向量 Xim，計算它與該空間中其他任一向量 Xim 之間的距離，該距離表示為向量中對應維度上元素距離的最大值，如式（4）所示：
 |
然后，對于每一個向量，計算 m 維空間中與之距離小于給定相似容限 r 的向量占比，記為 
。對于所有向量，計算 
的均值，記為 
，如式（5）所示：
 |
將嵌入空間的維數增加 1 后重復以上步驟得到 
，由此可計算出 SE 值（符號記為 SE），如式（6）所示：
 |
在本文中，嵌入維 m 取值設定為 2，相似容限 r 的取值設定為 0.15×std，std 為原始時間序列的標準差。
具體 PE 算法為[31]：在 m 維的嵌入空間中，對每一個 m 維的向量 Xim 中的元素數值大小按升序重新排列，結果中的每個元素在原始序列中的位序作為一個符號記錄下來，則得到由 m 個符號構成的一個排列。以 Pj 來表示每種可能出現的排列的頻率，并計算它們的香農熵，即可得到序列的 PE 值（符號記為 PE），如式（7）所示：
 |
在 PE 算法中，向量中相等的元素值會被賦予不同的符號。Bian 等[32]提出了 MPE 算法，其中使用相同的符號來表示等值情況。相比 PE 算法，MPE 算法在不同的生理和病理條件下，能夠更有效地表征 HRV 信號的復雜性[32]。因此，本文使用 MPE 算法。
本文對每一段 1 h 的 HRV 信號進行了尺度因子從 1 逐一遞增至 10 的粗粒化；對于每個粗粒化的序列分別計算了 SE、MPE 值，分別記為 SE1～SE10 和 MPE1～MPE10；同時，還計算了 10 個尺度下 SE、MPE 的均值，分別記為 aver_SE 和 aver_MPE。
1.4 CVD 預測模型構建
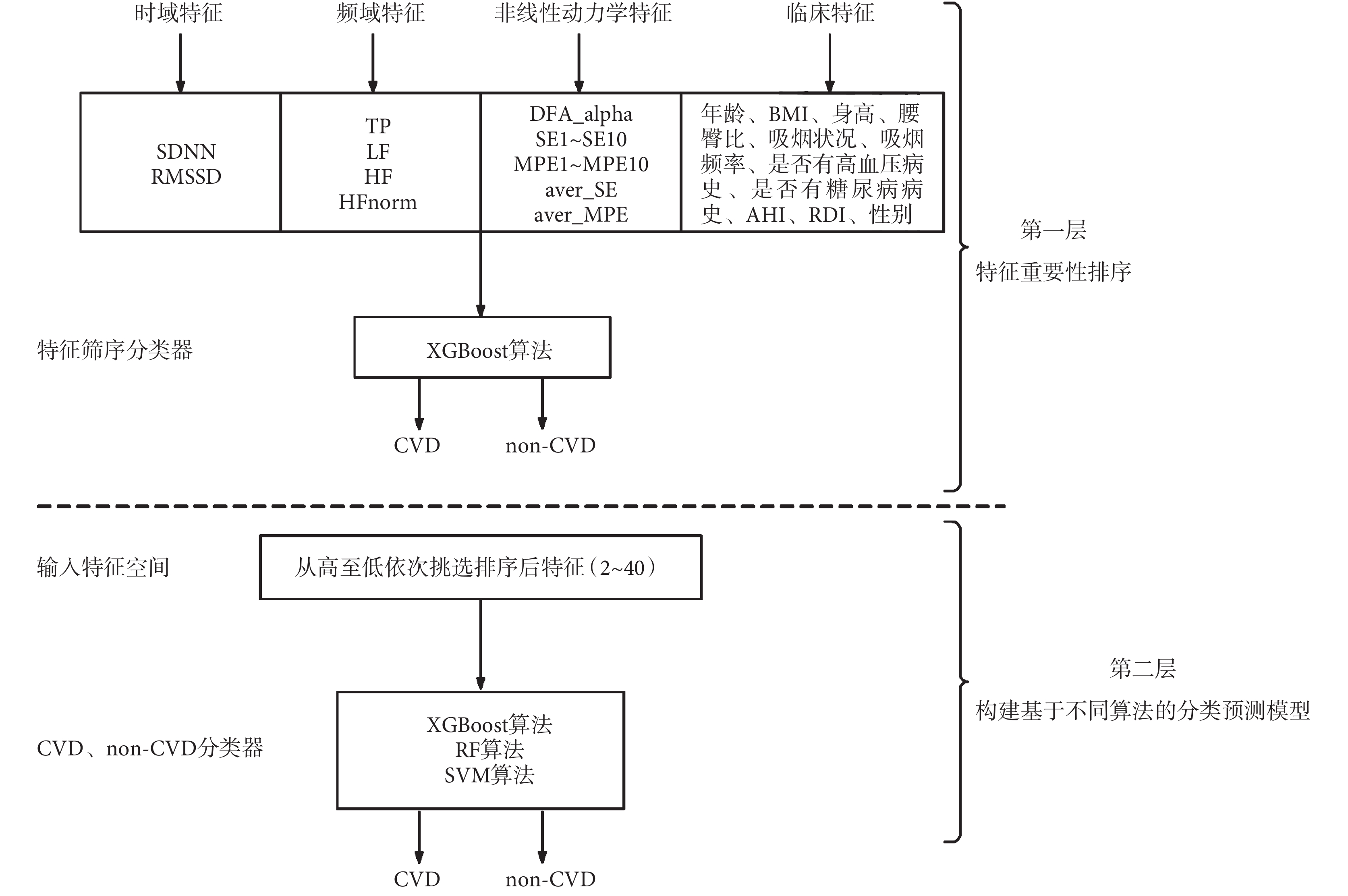
本文提出一種兩層模型方法來實現 CVD 組和 non-CVD 組的二分類，如圖 3 所示。第一層是基于極端梯度提升算法（extreme gradient boosting，XGBoost）的分類器，用于特征篩選。其輸入為某段 HRV 信號的時域特征（SDNN、RMSSD）、頻域特征（TP、LF、HF、HFnorm）、非線性動力學特征（DFA_alpha、SE1～SE10、MPE1～MPE10、aver_SE、aver_MPE）以及 11 個臨床特征（年齡、BMI、身高、腰臀比、吸煙狀況、吸煙頻率、是否有高血壓病史、是否有糖尿病病史、AHI、RDI、性別），共計 40 個特征。使用基于機器學習庫的網格搜索及交叉驗證方法來尋找最優分類器[33]，并對其特征重要性進行排序。在第二層模型中，按照上層模型的特征重要性從高到低依次挑選 2～40 的特征，并構建機器學習模型的輸入特征空間，建立 CVD 和 non-CVD 分類器。對于機器學習算法的選擇，本文考察了 XGBoost、隨機森林（random forest，RF）和支持向量機（support vector machine，SVM）三種算法，來尋找分類性能最優的模型。為了提高機器學習模型的泛化能力，每個模型均采用五折交叉驗證來劃分訓練集和測試集，即將整個數據集隨機劃分為 5 個大小幾乎相同的不相交的子集，使用其中 1 折作為測試數據，其余的 4 折作為訓練數據，直到所有折都被依次用作測試數據集。最終對 5 輪預測結果求平均值，從而能更合理地評估模型的泛化能力[34]。
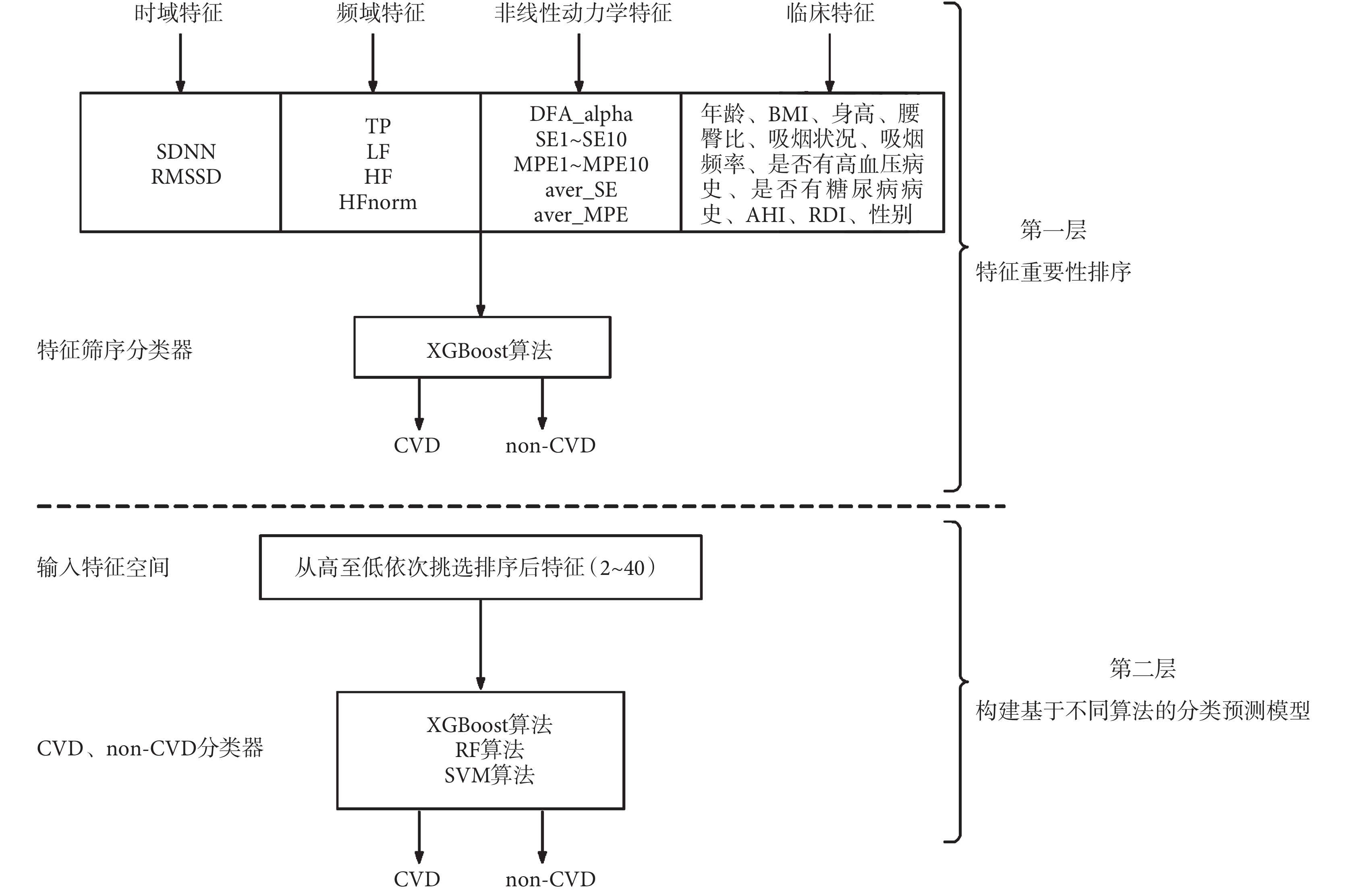圖3
本研究中 CVD 預測模型框架
Figure3.
The proposed framework of CVD prediction
1.5 模型性能評價
典型的二分類問題中存在兩個類，定義為“正類”和“負類”。實際為正類并且被預測為正類的樣本稱為“真正類”（true positive，TP）（符號記為 TP），實際為正類卻被預測為負類的樣本稱為“假負類”（false negative，FN）（符號記為 FN）；類似地，實際為負類并且被預測為負類的樣本稱為“真負類”（true negative，TN）（符號記為 TN），實際為負類卻被預測為正類的樣本稱為“假正類”（false positive，FP）（符號記為 FP）[35-36]。
本文將 CVD 組定義為正類，non-CVD 組定義為負類，并使用六個常用指標評估模型預測性能，即：準確率（accuracy，ACC）（符號記為 ACC），Kappa 系數（符號記為 Kappa），真陰性率（true negative rate，TNR）（符號記為 TNR），真陽性率（true positive rate，TPR）（符號記為 TPR），陽性預測值（positive predictive value，PPV）（符號記為 PPV），F1 值（F1-Score，F1）（符號記為 F1），馬修斯相關系數（matthews correlation coefficient，MCC）（符號記為 MCC）。每個指標具體計算方法如式（8）～（14）所示。ACC、Kappa、MCC 常用于綜合評價正負類的預測表現，而 TPR、PPV 和 F1 偏向于衡量正類預測表現，TNR 偏向于衡量負類預測表現。
 |
 |
 |
 |
 |
 |
 |
2 結果與分析
本文利用提出的兩層模型方法探索了基于哪一個睡眠段的 HRV 信號分析能更好地預測 CVD 的問題。如表 1 所示，以五折交叉驗證的 ACC 值作為比較標準，列出了利用不同睡眠段 HRV 構建的最優模型的分類性能。使用睡眠段 5，第二層模型采用 XGBoost 算法，使用 13 個輸入特征，可以得到正負類綜合預測性能最高的模型，其 ACC 值為 84.3%，Kappa 系數為 0.686，MCC 值為 0.689，表示模型的預測值與真實值之間有高度的一致性。表 1 的結果表明，相比其他睡眠時段，覺醒前 HRV 在預測 CVD 事件上具有更高價值。
表1
不同睡眠段模型預測性能
Table1.
Prediction performance of models in different sleep segments
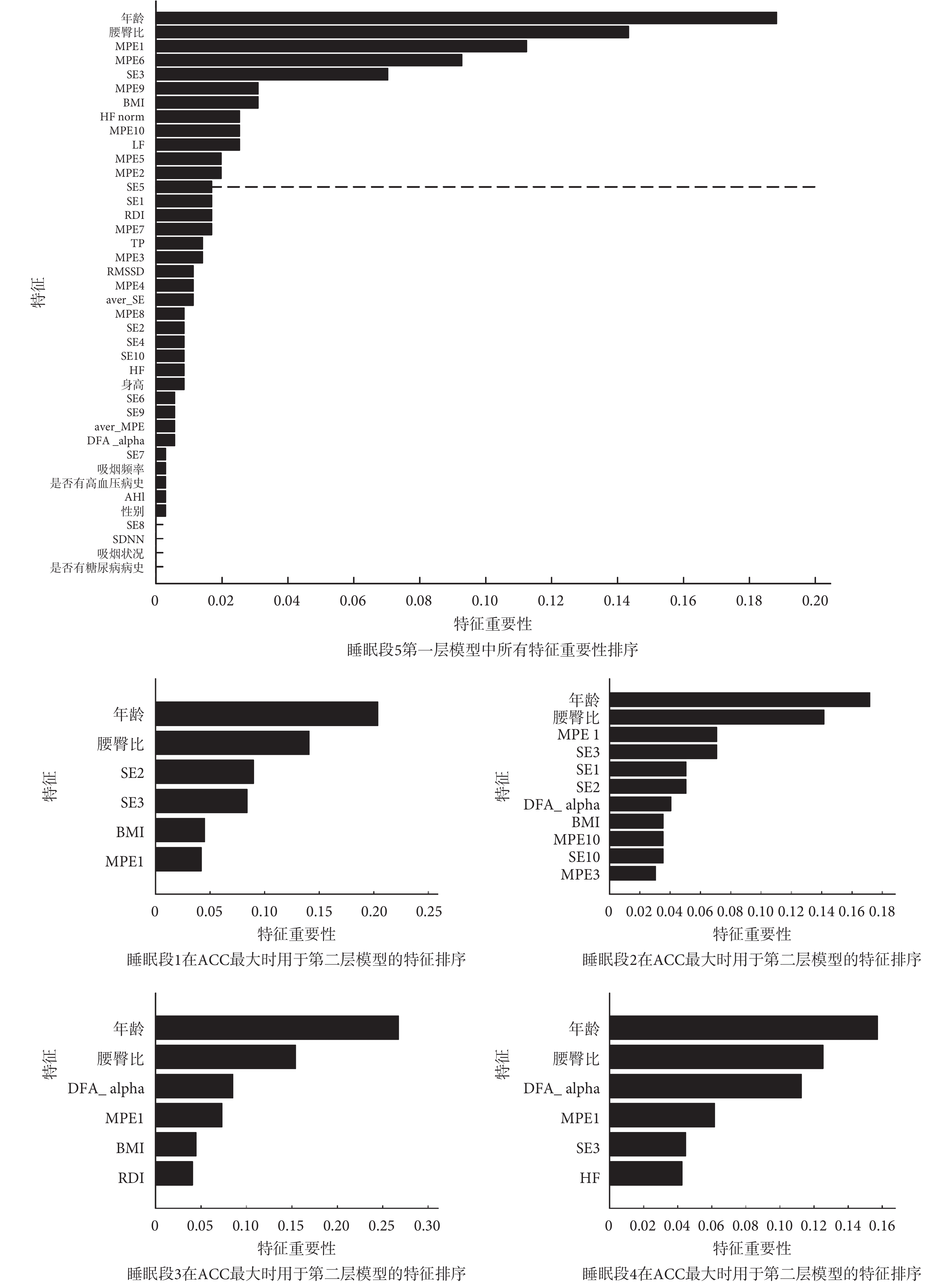
如圖 4 所示，進一步展示了利用不同睡眠段 HRV 構建的最優模型的特征重要性圖。對于睡眠段 5，列出了第一層模型中所有特征的重要性排序；而對于睡眠段 1～睡眠段 4，只列出了 ACC 最大情況下篩選出的用于第二層模型的特征。結果顯示，無論使用哪一段睡眠數據，年齡與腰臀比都是模型中最重要的特征，這與文獻[37]的報道是吻合的；基于非線性動力學分析的 HRV 指標在各個睡眠段，都有入選。對于睡眠段 3，其 ACC 最低（如表 1 所示），入選的特征中 HRV 指標較少。而對于睡眠段 5，在篩選特征個數為 13 時 ACC 數值最大，在這一篩選的特征中 HRV 指標占比較高。這一結果可能意味著模型中 HRV 特征重要性的欠缺會導致較低的 CVD 預測正確率。
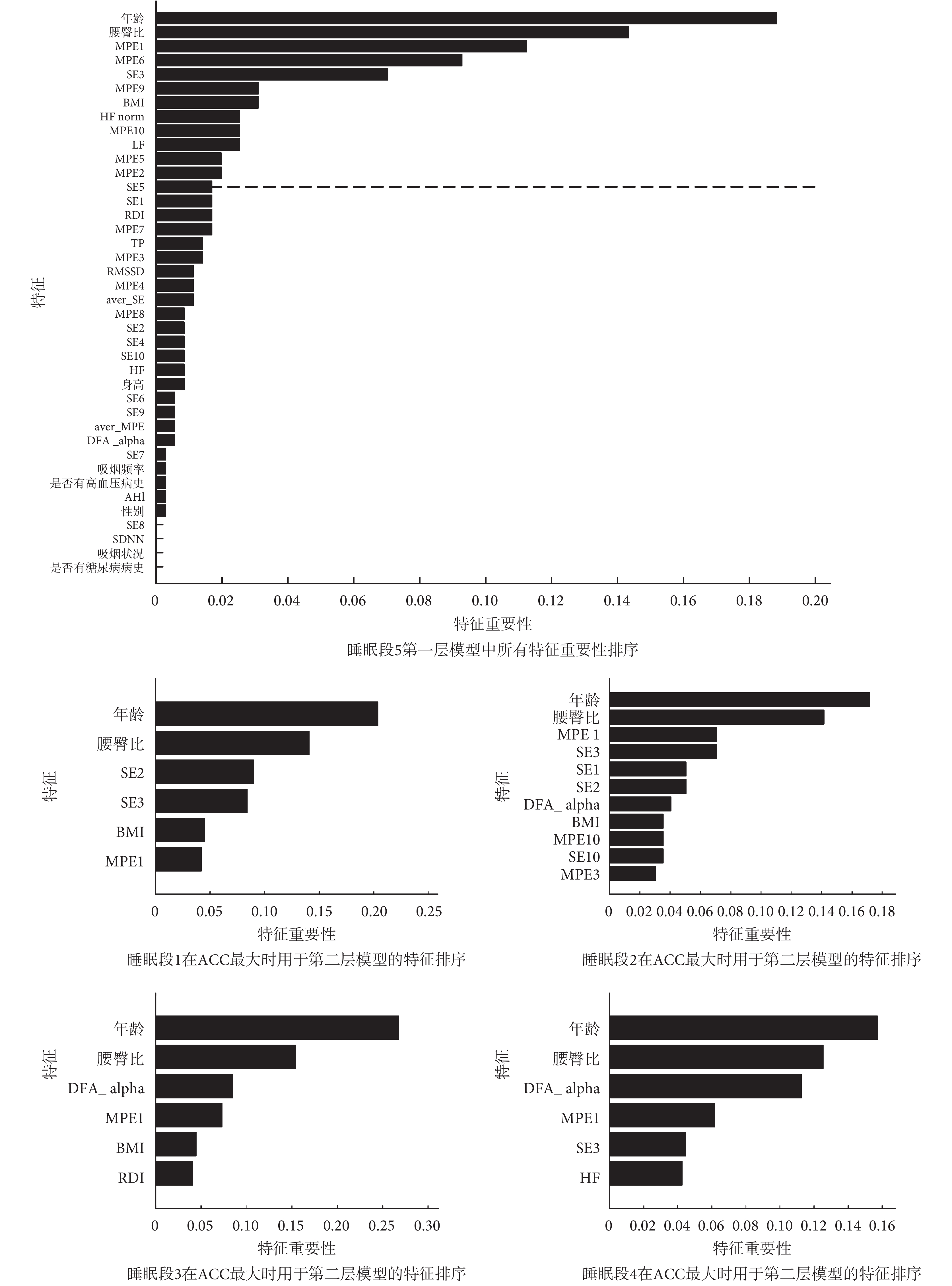圖4
不同睡眠段下第一層模型的特征重要性排序
Figure4.
Feature importance of the 1st layer model during different sleep segments
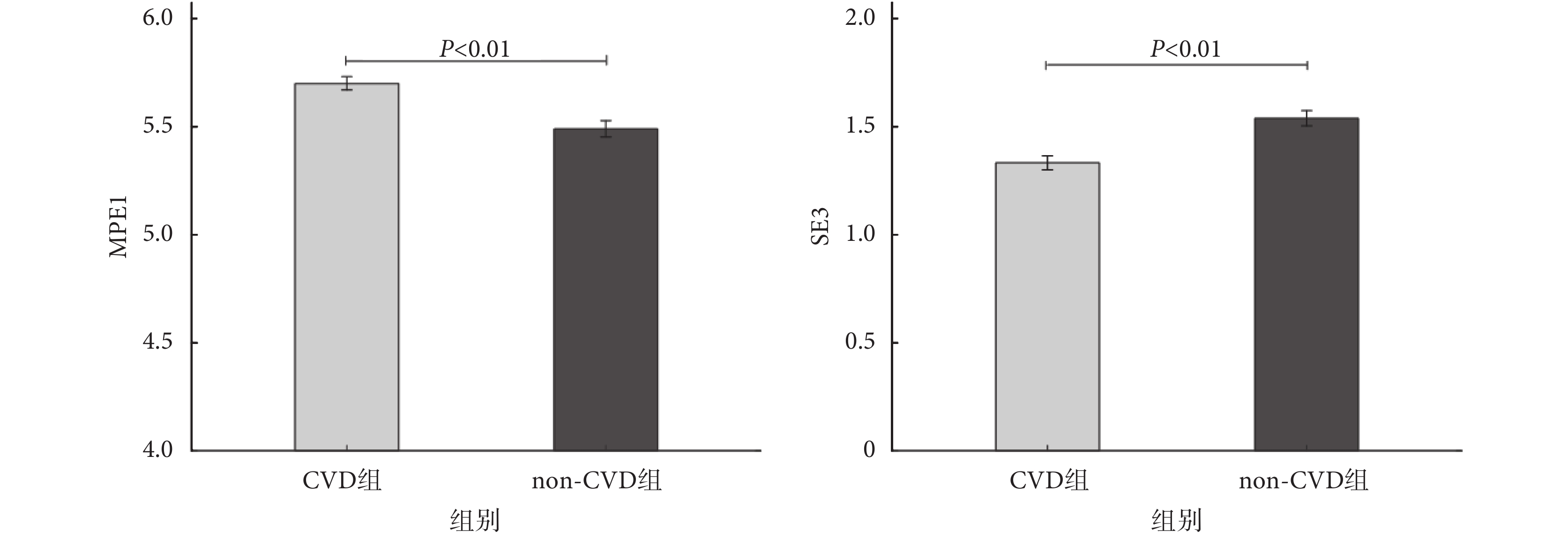
雖然對于各個睡眠段，入選第二層的特征有所不同，如圖 4 所示，但可以發現，基于非線性動力學分析的 MPE1 指標在每一睡眠段中都會出現，SE3 指標也出現在大多數睡眠段中。對于睡眠段 5，如圖 5 所示，組間比較（非配對 t 檢驗）的結果表明，相對于 non-CVD 組而言，CVD 組的 MPE1 上升，SE3 下降，差異具有統計學意義（P<0.01）。
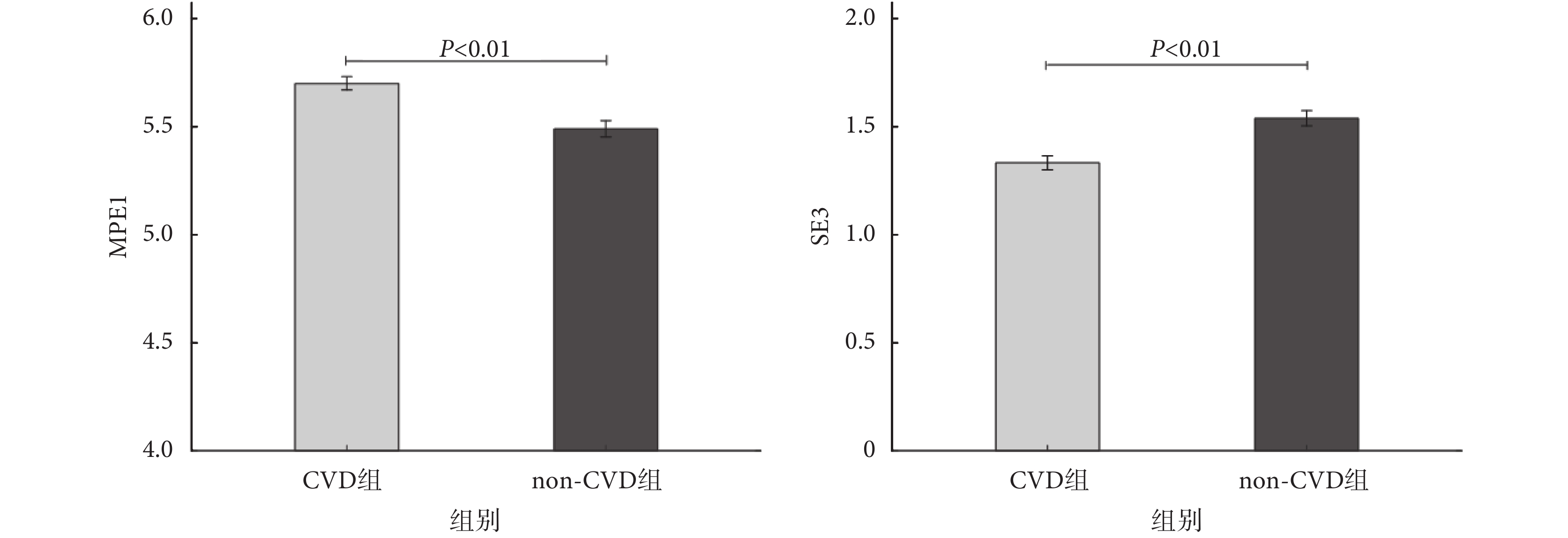圖5
睡眠段 5 的 MPE1 和 SE3 特征值（
）
Figure5.
Values of MPE1 and SE3 indices during sleep segment 5（
）
3 結論
本文提出并采用了一種兩層機器學習模型的方法，通過比較利用不同睡眠時期 HRV 特征構建 CVD 預測模型的性能，來探索是否覺醒前的 HRV 更有利于 CVD 事件預測。在正類和負類均衡的情況下，利用覺醒前 HRV 特征構建的預測模型對于 CVD 組和 non-CVD 組的分類準確率最高，達 84.3%。這一結果表明，與其他睡眠段 HRV 相比，覺醒前 HRV 能更準確地預測 CVD 事件。同時，通過對比不同睡眠段 HRV 構建的最優模型的特征重要性排序圖，發現 CVD 預測正確率的高低與 HRV 特征重要性占比有關，而 HRV 分析的欠缺可能會導致較低的 CVD 預測正確率。
本研究也表明，夜間睡眠時 HRV 信號的非線性動力學分析也許能更好地捕捉心血管系統潛在的危險。相對于 non-CVD 組，CVD 組在覺醒前 HRV 上，MPE1 和 SE3 都出現了顯著的變化。此外，雖然對于各個不同時期的睡眠段，各 HRV 分析指標在模型中的重要性有所不同，但非線性動力學指標 MPE1、SE3 在各睡眠段中均展現出了較高的特征重要性，意味著它們對 CVD 的預測較為重要。本文研究結果進一步證實了心臟動力系統具有非線性特性，在構建 CVD 預測模型時，應綜合 HRV 的線性與非線性動力學指標，才能更好地評估潛在的生理過程。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
心血管疾病（cardiovascular disease，CVD）是由心臟和血管異常引起的一系列疾病的總稱。目前，我國 CVD 患病率處于持續上升階段，而因 CVD 致死則占城鄉居民總死亡原因的首位[1]，因此 CVD 的早期預測對人類的健康和社會發展有著積極的意義[2]。
睡眠，作為一種復雜的生理過程，與機體的各基本系統密切相關，其中就包括心血管系統[3]。心血管系統的穩定性受到眾多因素的控制，其中自主神經系統對心率的調節起著至關重要的作用。自主神經系統包括交感神經和副交感神經，交感神經興奮時，心率會增加；副交感神經興奮時，心率會降低。自主神經系統活動失衡會增加許多疾病（包括 CVD）的發病率和死亡率[4]。研究表明，在一天的不同時刻，急性 CVD 事件的發生率是不同的，清晨醒來時刻前后是 CVD 事件發生的高峰期[5-9]。雖然導致清晨 CVD 事件增加的原因并未明確，但不少研究認為這一狀況可能與夜間睡眠末期交感神經活動的激增有關[10-14]。
自主神經系統使得心血管系統能夠對機體內外的易變刺激做出迅速反應，導致逐次心跳的心率呈現出細小的波動，通常被稱為心率變異性（heart rate variability，HRV）。HRV 分析方法主要包括時域分析法、頻域分析法和非線性動力學分析法[15]。作為一種非侵入、無創的手段，HRV 分析已經廣泛用于評估自主神經系統功能和心血管系統健康狀況[16-18]。在文獻中，也有利用 HRV 分析進行 CVD 風險評估的報道[19-21]，但這些研究存在著一些不足。首先，使用的 HRV 數據并非針對睡眠狀態。而在本文的前期研究中發現，睡眠 HRV 分析能夠有效預測短時的 CVD 事件[22]。其次，采用的分析方法大都基于時域、頻域分析，鮮有涉及非線性動力學分析。然而大量的研究表明，心臟動力系統富含非線性成分，以熵分析和冪律分析為代表的非線性動力學分析方法現已廣泛用于 HRV 信號的分析中[15]。
因此，鑒于急性 CVD 事件高發于清晨醒來前后的事實、HRV 分析在自主神經功能評估中的重要性以及心臟動力系統的非線性特性，本文綜合使用時域、頻域、非線性動力學分析方法來挖掘夜間睡眠時的 HRV 信號的特征，并利用機器學習算法構建 CVD 自動預測模型，從而探索睡眠末期的 HRV 信號分析是否可以提供更高的 CVD 預測準確率以及哪些 HRV 指標在 CVD 預測中較為重要，這一結果或對 CVD 的早期預測帶來新的突破。
1 研究方法
1.1 研究對象
本文采用的研究數據來源于美國睡眠心臟健康研究項目（sleep heart health study，SHHS）（網址：https://sleepdata.org/datasets/shhs）的開源數據庫[23]，共采納 140 名受試者的相關數據，受試者的篩選過程在本文的前期研究中有詳細的闡述[22]，本文不再贅述。受試者在家中使用便攜式多導睡眠監測儀采集多導睡眠圖（polysomnography，PSG），其中記錄了兩個導聯的心電圖（electrocardiograph，ECG）數據，采樣頻率為 125 Hz。根據 SHHS 的隨訪記錄，其中的 70 人在 PSG 采集后的兩年隨訪期內發生了 CVD 事件，包括心絞痛、急性心肌梗塞等；另外 70 人在隨訪期內未報道任何 CVD 事件。本文將發生 CVD 事件的受試者記為 CVD 組，未發生 CVD 事件的受試者記為 non-CVD 組。兩組人群在年齡、腰臀比、是否有糖尿病病史以及是否有高血壓病史這四個指標上的差異具有統計學意義（P<0.05），而在性別、身高、身體質量指數（body mass index，BMI）、呼吸紊亂指數（apnea hypopnea index，AHI）、呼吸障礙指數（respiratory disturbance index，RDI）、吸煙狀況和吸煙頻率等指標上的差異沒有統計學意義（P>0.05）。
1.2 信號預處理
對于每位受試者，其整夜 ECG 信號經巴特沃斯帶通濾波器（0.5～45 Hz）預處理后，根據潘-湯普金斯（Pan-Tompkins，PT）方法檢測出所有的 R 波頂點[24]，然后計算兩個連續 R 波峰之間的間隔，得到 R-R 間期序列。接著，去除 R-R 間期序列中的異位起搏點或偽跡并進行插值處理[25]，以獲得供后續分析使用的 HRV 信號。
為了對比不同睡眠段 HRV 信號對 CVD 事件的預測能力，如圖 1 所示，本文將每位受試者整夜睡眠 HRV 信號劃分成 5 個 1 h 的片段，分別定義為睡眠段 1～5，其中睡眠段 5 對應為清晨覺醒前 1 h。若整晚睡眠時長大于 5 h，則每個片段互不重疊，片段之間的分離間期相等；若整晚睡眠時長小于 5 h，則每個片段有重疊，片段之間的重疊間期相等。
圖1
試驗數據抽取示意圖
Figure1.
Schematic diagram of test data extraction
1.3 HRV 分析
本文綜合考慮了 HRV 的時域、頻域和非線性分析方法。時域和非線性分析參數的計算基于每 1 h 的 HRV 數據段進行，而頻域參數的計算則基于每 5 min 的 HRV 片段，然后以 1 h 內的 12 個片段的均值作為對應段的特征值。時域參數包括所有 R-R 間期（NN 間期）的標準差（standard deviation of normal to normal，SDNN）、相鄰 R-R 間期差值的均方根值（root mean square of successive differences，RMSSD），頻域參數包括 0.003～0.4 Hz 頻率范圍內的總功率（total power，TP）、0.04～0.15 Hz 頻率范圍內的低頻功率（power in low frequency，LF）、0.15～0.4 HZ 頻率范圍內的高頻功率（power in high frequency，HF）以及歸一化的高頻段能量（HF power in normalized units，HFnorm）[26]。對于非線性動力學分析，本文采用了去趨勢波動分析（detrend fluctuation analysis，DFA）和多尺度熵分析。
1.3.1 DFA 分析簡介
采用傳統方法研究時間序列的長期冪律關系可能會因為噪聲或者趨勢成分的影響而使得分析結果不可靠[27]。DFA 分析則可以通過去除趨勢項將信號與外部環境的噪聲分離，從而適用于非平穩時間序列的處理。對于長度為 N 的序列，DFA 算法描述如下：
首先，如式（1）所示，將 N} 零均值處理后進行一階積分，得到一個新的序列 ：
|
其次，給定區間長度 n，將 劃分為不重疊的 m 個區間，m 為 N/n 的整數部分。對于劃分的每一段序列采用最小二乘法線性擬合出局部趨勢 ，最后對 去除每個區間的局部趨勢并計算出序列的均方根，如式（2）所示：
|
隨著 n 的變化呈現冪律分布，其中的斜率表示 DFA 指數，本文記為 DFA_alpha，描述了時間序列的粗糙程度，其值越大表明時間序列越光滑。DFA 是一種能夠有效地量化嵌入在非平穩時間序列中的長期相關性的有效方法[28]。
1.3.2 多尺度熵分析
多尺度熵分析引進了時間尺度因子 τ 的概念，通過構造一系列不同粗粒化程度的時間序列，并計算它們的熵值，以獲得原始時間序列在不同尺度下的復雜性測度。其具體計算過程包括粗粒化和熵值計算兩個部分。
對于 N 點的時間序列 ，粗粒化過程如圖 2 所示[29]。以尺度因子 τ 為長度，依次將原時間序列劃分為 N/τ 段不重疊的子序列，這些子序列的均值就形成了 在尺度 τ 上的粗粒化序列，記為。
圖2
粗粒化示意圖
Figure2.
Schematic diagram of coarse granulation
對于每個粗粒化序列，本文分別采用樣本熵（sample entropy，SE）和改進的排列熵（modified permutation entropy, MPE）算法來進行熵分析。SE 算法如式（3）～（6）所示[30]。
將時間序列嵌入到 m 維空間中，該空間中向量如式（3）所示：
|
對于 m 維空間中的向量 Xim，計算它與該空間中其他任一向量 Xim 之間的距離，該距離表示為向量中對應維度上元素距離的最大值，如式（4）所示：
|
然后，對于每一個向量，計算 m 維空間中與之距離小于給定相似容限 r 的向量占比，記為 。對于所有向量，計算 的均值，記為 ，如式（5）所示：
|
將嵌入空間的維數增加 1 后重復以上步驟得到 ，由此可計算出 SE 值（符號記為 SE），如式（6）所示：
|
在本文中，嵌入維 m 取值設定為 2，相似容限 r 的取值設定為 0.15×std，std 為原始時間序列的標準差。
具體 PE 算法為[31]：在 m 維的嵌入空間中，對每一個 m 維的向量 Xim 中的元素數值大小按升序重新排列，結果中的每個元素在原始序列中的位序作為一個符號記錄下來，則得到由 m 個符號構成的一個排列。以 Pj 來表示每種可能出現的排列的頻率，并計算它們的香農熵，即可得到序列的 PE 值（符號記為 PE），如式（7）所示：
|
在 PE 算法中，向量中相等的元素值會被賦予不同的符號。Bian 等[32]提出了 MPE 算法，其中使用相同的符號來表示等值情況。相比 PE 算法，MPE 算法在不同的生理和病理條件下，能夠更有效地表征 HRV 信號的復雜性[32]。因此，本文使用 MPE 算法。
本文對每一段 1 h 的 HRV 信號進行了尺度因子從 1 逐一遞增至 10 的粗粒化；對于每個粗粒化的序列分別計算了 SE、MPE 值，分別記為 SE1～SE10 和 MPE1～MPE10；同時，還計算了 10 個尺度下 SE、MPE 的均值，分別記為 aver_SE 和 aver_MPE。
1.4 CVD 預測模型構建
本文提出一種兩層模型方法來實現 CVD 組和 non-CVD 組的二分類，如圖 3 所示。第一層是基于極端梯度提升算法（extreme gradient boosting，XGBoost）的分類器，用于特征篩選。其輸入為某段 HRV 信號的時域特征（SDNN、RMSSD）、頻域特征（TP、LF、HF、HFnorm）、非線性動力學特征（DFA_alpha、SE1～SE10、MPE1～MPE10、aver_SE、aver_MPE）以及 11 個臨床特征（年齡、BMI、身高、腰臀比、吸煙狀況、吸煙頻率、是否有高血壓病史、是否有糖尿病病史、AHI、RDI、性別），共計 40 個特征。使用基于機器學習庫的網格搜索及交叉驗證方法來尋找最優分類器[33]，并對其特征重要性進行排序。在第二層模型中，按照上層模型的特征重要性從高到低依次挑選 2～40 的特征，并構建機器學習模型的輸入特征空間，建立 CVD 和 non-CVD 分類器。對于機器學習算法的選擇，本文考察了 XGBoost、隨機森林（random forest，RF）和支持向量機（support vector machine，SVM）三種算法，來尋找分類性能最優的模型。為了提高機器學習模型的泛化能力，每個模型均采用五折交叉驗證來劃分訓練集和測試集，即將整個數據集隨機劃分為 5 個大小幾乎相同的不相交的子集，使用其中 1 折作為測試數據，其余的 4 折作為訓練數據，直到所有折都被依次用作測試數據集。最終對 5 輪預測結果求平均值，從而能更合理地評估模型的泛化能力[34]。
圖3
本研究中 CVD 預測模型框架
Figure3.
The proposed framework of CVD prediction
1.5 模型性能評價
典型的二分類問題中存在兩個類，定義為“正類”和“負類”。實際為正類并且被預測為正類的樣本稱為“真正類”（true positive，TP）（符號記為 TP），實際為正類卻被預測為負類的樣本稱為“假負類”（false negative，FN）（符號記為 FN）；類似地，實際為負類并且被預測為負類的樣本稱為“真負類”（true negative，TN）（符號記為 TN），實際為負類卻被預測為正類的樣本稱為“假正類”（false positive，FP）（符號記為 FP）[35-36]。
本文將 CVD 組定義為正類，non-CVD 組定義為負類，并使用六個常用指標評估模型預測性能，即：準確率（accuracy，ACC）（符號記為 ACC），Kappa 系數（符號記為 Kappa），真陰性率（true negative rate，TNR）（符號記為 TNR），真陽性率（true positive rate，TPR）（符號記為 TPR），陽性預測值（positive predictive value，PPV）（符號記為 PPV），F1 值（F1-Score，F1）（符號記為 F1），馬修斯相關系數（matthews correlation coefficient，MCC）（符號記為 MCC）。每個指標具體計算方法如式（8）～（14）所示。ACC、Kappa、MCC 常用于綜合評價正負類的預測表現，而 TPR、PPV 和 F1 偏向于衡量正類預測表現，TNR 偏向于衡量負類預測表現。
|
|
|
|
|
|
|
2 結果與分析
本文利用提出的兩層模型方法探索了基于哪一個睡眠段的 HRV 信號分析能更好地預測 CVD 的問題。如表 1 所示，以五折交叉驗證的 ACC 值作為比較標準，列出了利用不同睡眠段 HRV 構建的最優模型的分類性能。使用睡眠段 5，第二層模型采用 XGBoost 算法，使用 13 個輸入特征，可以得到正負類綜合預測性能最高的模型，其 ACC 值為 84.3%，Kappa 系數為 0.686，MCC 值為 0.689，表示模型的預測值與真實值之間有高度的一致性。表 1 的結果表明，相比其他睡眠時段，覺醒前 HRV 在預測 CVD 事件上具有更高價值。
表1
不同睡眠段模型預測性能
Table1.
Prediction performance of models in different sleep segments
如圖 4 所示，進一步展示了利用不同睡眠段 HRV 構建的最優模型的特征重要性圖。對于睡眠段 5，列出了第一層模型中所有特征的重要性排序；而對于睡眠段 1～睡眠段 4，只列出了 ACC 最大情況下篩選出的用于第二層模型的特征。結果顯示，無論使用哪一段睡眠數據，年齡與腰臀比都是模型中最重要的特征，這與文獻[37]的報道是吻合的；基于非線性動力學分析的 HRV 指標在各個睡眠段，都有入選。對于睡眠段 3，其 ACC 最低（如表 1 所示），入選的特征中 HRV 指標較少。而對于睡眠段 5，在篩選特征個數為 13 時 ACC 數值最大，在這一篩選的特征中 HRV 指標占比較高。這一結果可能意味著模型中 HRV 特征重要性的欠缺會導致較低的 CVD 預測正確率。
圖4
不同睡眠段下第一層模型的特征重要性排序
Figure4.
Feature importance of the 1st layer model during different sleep segments
雖然對于各個睡眠段，入選第二層的特征有所不同，如圖 4 所示，但可以發現，基于非線性動力學分析的 MPE1 指標在每一睡眠段中都會出現，SE3 指標也出現在大多數睡眠段中。對于睡眠段 5，如圖 5 所示，組間比較（非配對 t 檢驗）的結果表明，相對于 non-CVD 組而言，CVD 組的 MPE1 上升，SE3 下降，差異具有統計學意義（P<0.01）。
圖5
睡眠段 5 的 MPE1 和 SE3 特征值（）
Figure5.
Values of MPE1 and SE3 indices during sleep segment 5（）
3 結論
本文提出并采用了一種兩層機器學習模型的方法，通過比較利用不同睡眠時期 HRV 特征構建 CVD 預測模型的性能，來探索是否覺醒前的 HRV 更有利于 CVD 事件預測。在正類和負類均衡的情況下，利用覺醒前 HRV 特征構建的預測模型對于 CVD 組和 non-CVD 組的分類準確率最高，達 84.3%。這一結果表明，與其他睡眠段 HRV 相比，覺醒前 HRV 能更準確地預測 CVD 事件。同時，通過對比不同睡眠段 HRV 構建的最優模型的特征重要性排序圖，發現 CVD 預測正確率的高低與 HRV 特征重要性占比有關，而 HRV 分析的欠缺可能會導致較低的 CVD 預測正確率。
本研究也表明，夜間睡眠時 HRV 信號的非線性動力學分析也許能更好地捕捉心血管系統潛在的危險。相對于 non-CVD 組，CVD 組在覺醒前 HRV 上，MPE1 和 SE3 都出現了顯著的變化。此外，雖然對于各個不同時期的睡眠段，各 HRV 分析指標在模型中的重要性有所不同，但非線性動力學指標 MPE1、SE3 在各睡眠段中均展現出了較高的特征重要性，意味著它們對 CVD 的預測較為重要。本文研究結果進一步證實了心臟動力系統具有非線性特性，在構建 CVD 預測模型時，應綜合 HRV 的線性與非線性動力學指標，才能更好地評估潛在的生理過程。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
