本文針對以實驗方式研究多室輸液袋構型和工藝存在的低效率、高成本及多參數研究難以開展的問題，提出采用基于流體腔的有限元方法模擬多室輸液袋在外載荷下的受力及變形過程。研究建立了不同尺寸下的輸液袋曲面模型，采用 ABAQUS 中的流體腔方法模擬輸液袋在壓裂實驗條件下的流固耦合變形過程。以弱焊剝離實驗獲取的弱焊剝離應力作為數值模擬的破裂準則，提取破裂時的壓裂力與壓裂實驗結果進行對比，并分析所得應力分布是否滿足壓裂實驗弱焊破裂過程。結果表明：考慮由樣品弱焊差異及偏心壓裂等因素引起的實驗誤差，基于流體腔的有限元方法能夠準確地模擬輸液袋受力及變形過程。本文方法可用于輸液袋構型及工藝改進研究，降低研究成本，提升研究效率。
引用本文： 岳懷俊, 王冠石, 蔣文濤, 譚鴻波, 劉文軍, 朱仲強, 朱麟. 多室軟包裝輸液袋壓裂過程模擬的有限元方法. 生物醫學工程學雜志, 2021, 38(3): 556-562. doi: 10.7507/1001-5515.202005062 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
多室軟包裝輸液袋（多室輸液袋）是一種新的全封閉輸液包裝形式，具有使用方便、無外源性污染等優點，是當前最具發展潛力的輸液包裝容器[1-3]。輸液袋各腔室間通過弱焊方式分隔，弱焊強度需要保證輸液袋使用前不產生脫焊漏液，同時在使用時能順利打開弱焊帶混合液體。然而，由于工藝及運輸過程的影響，弱焊處漏液時常發生，極大地增加了臨床用藥的安全隱患[4-5]。如何防止臨床使用前弱焊處液體滲漏是多室輸液袋生產的關鍵，也是目前亟待解決的問題。
由于國際技術壁壘以及企業間工藝和技術保密，國外針對多室輸液袋的公開研究資料較少。國內研究主要以實驗為主，對生產工藝及輸液袋設計進行改進，如采用剝離實驗、整袋脹破壓力實驗及跌落實驗等評估其焊接強度[6]，再依據技術統計分析調整工藝參數[7-11]，或是通過提升傳熱效率等方式對生產模具進行改進[12-14]。在輸液袋設計上，不同廠家具有不同的設計方案，如 V 型弱焊帶分隔方式[15]、波浪狀弱焊帶[16]等，均能提升弱焊處的防滲漏性能[17-19]。然而，以實驗為主的方式存在成本高、周期長的問題，且針對輸液袋形狀及尺寸對弱焊處液體滲漏影響的多參數研究難以開展。因此，需要發展一種方便快捷、成本低廉的研究方法，提升多室輸液袋優化設計效率。
有限元方法作為一種通用的數值仿真技術，可快速模擬不同參數、不同實驗條件下的結構運動和變形過程，已在其他類型的輸液包裝產品及生產模具設計上得到了廣泛應用[20-22]，有效提升了研究的效率。因此，本文提出采用流體腔方法模擬流體運動，計算多室輸液袋在外載荷下流固耦合變形過程的數值仿真方法，并將仿真結果與壓裂試驗結果進行對比，驗證了該方法的有效性。
1 材料和方法
1.1 研究對象
采用常見包裝氨基酸、葡萄糖、脂肪乳的三室輸液袋為研究對象[23]，選取最易出現弱焊滲漏的最大腔體作為壓裂實驗及計算模型，如圖 1 所示。該模型腔體為三邊實焊一邊“弱焊”的結構，在壓裂實驗時弱焊處率先破裂，便于觀察破裂過程。
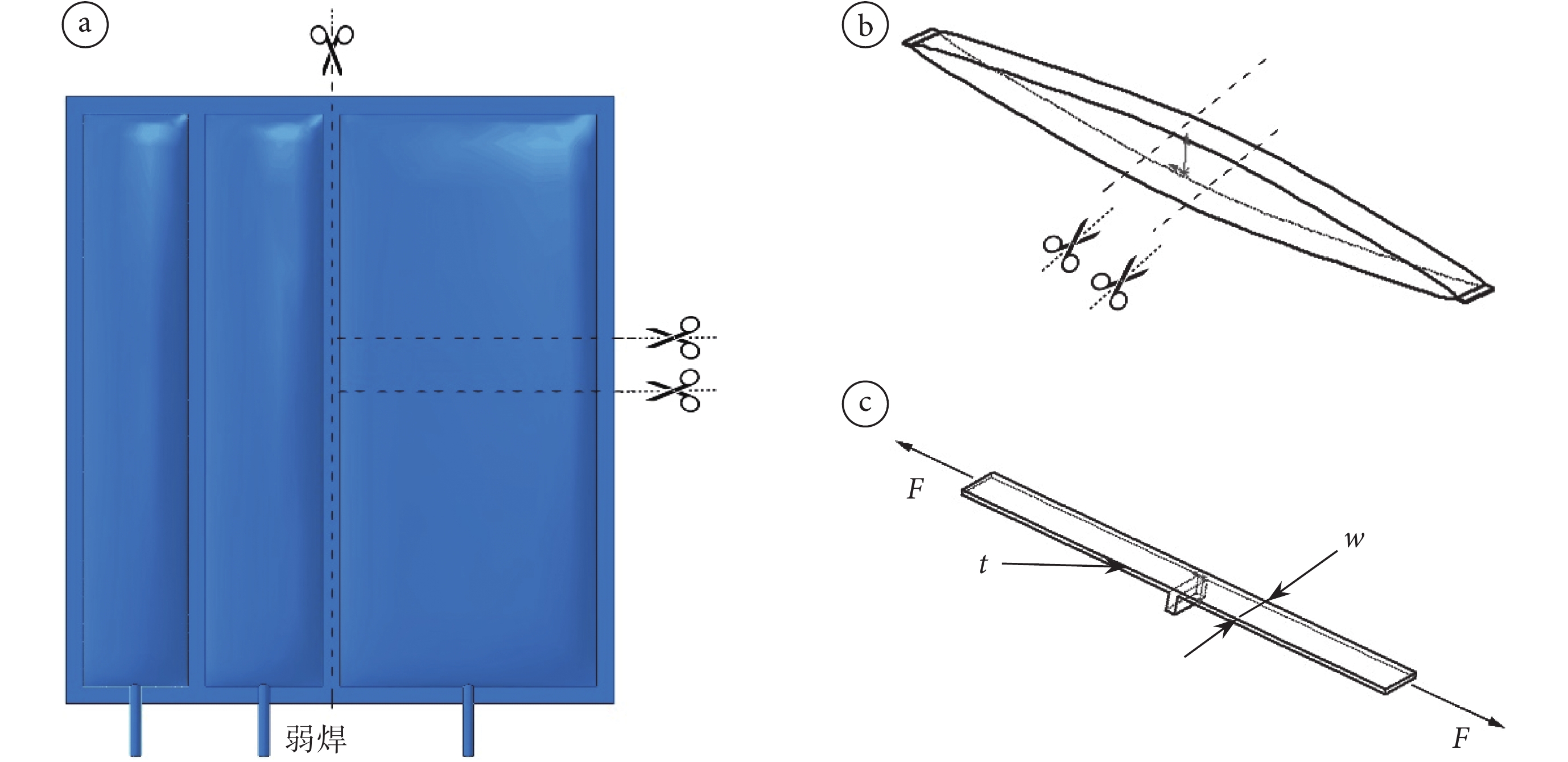圖1
弱焊剝離試驗試樣制備
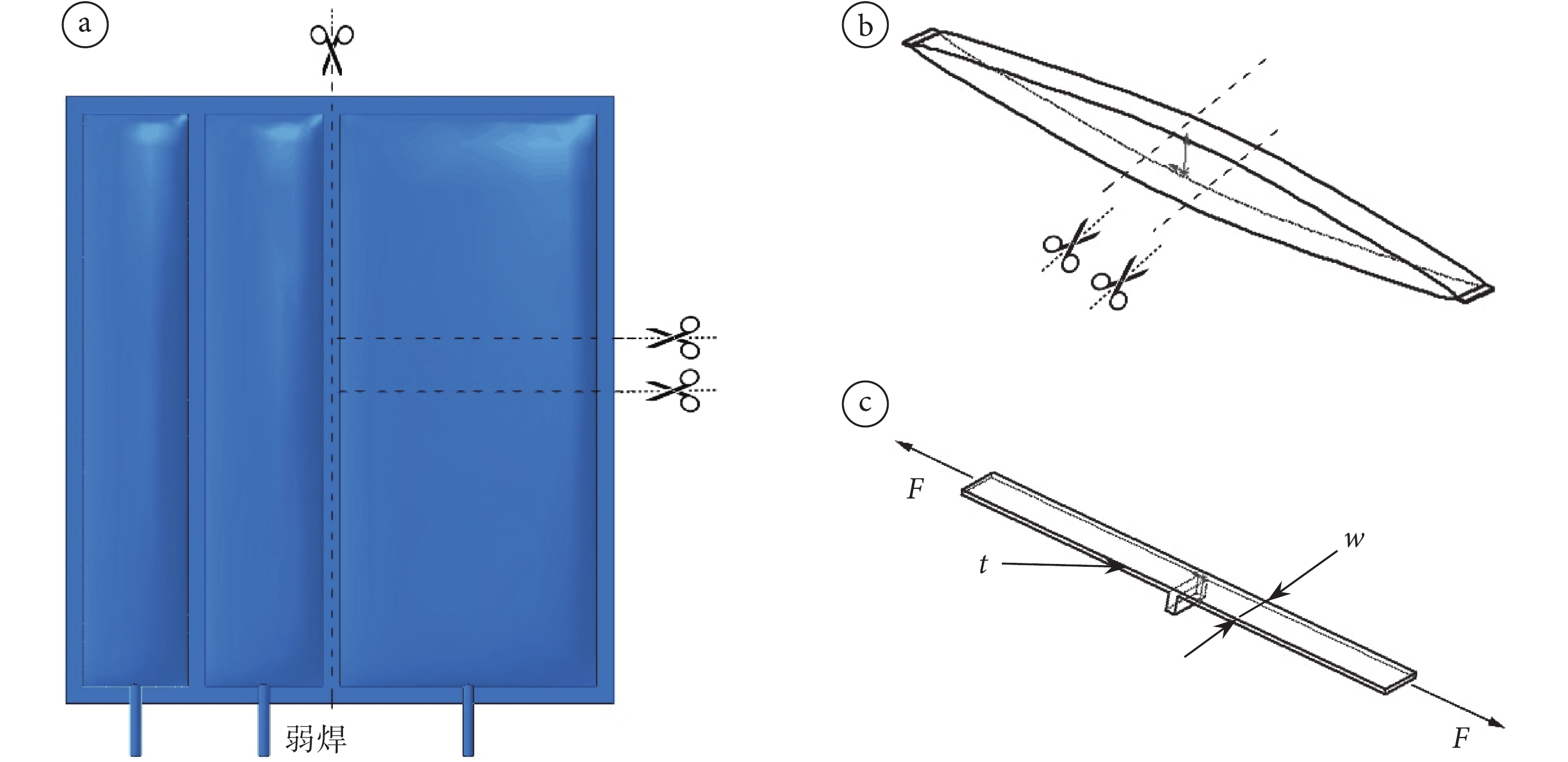
a. 從最大腔室剪裁含弱焊條試樣；b. 對稱剪裁去除實焊側材料；c. 弱焊剝離示意圖
Figure1. Procedure of cutting specimen for peeling testa. the sample containing the weak welding rod was cut from the largest chamber; b. symmetrical clipping to remove solid weld side material; c. schematic diagram of peeling test
1.2 弱焊剝離實驗
采用數值計算分析方法研究弱焊強度需要獲取特定工藝參數下的弱焊脫焊強度，為數值計算提供弱焊破裂準則。為此，本文利用輸液袋薄膜樣品制備了 6 個弱焊位置處的長條拉伸試樣，制備流程如圖 1a-c 所示，每個試樣均寬 15 mm。根據 GBT8808-88 軟質復合塑料材料剝離實驗標準對薄膜試樣進行剝離試驗[24]，試驗采用小量程（5 KN）萬能試驗機（中國，恒準儀器科技有限公司，HZ-1004B），將圖 1c 中制備的試樣兩端分別夾在試驗機豎直方向的上、下夾具上，松緊適中。調整夾持位置使得試樣剝開位置的軸線位于上、下夾具連線的中點并與連線垂直，在拉伸過程中，需保證未剝開部分與試樣所在平面垂直，記錄實驗過程中的力及變形參數，可得輸液袋弱焊處的剝離應力，其大小為：
 |
其中 
為剝離時實驗機拉力，
為剪樣寬度，
為輸液袋厚度。
1.3 數值模擬
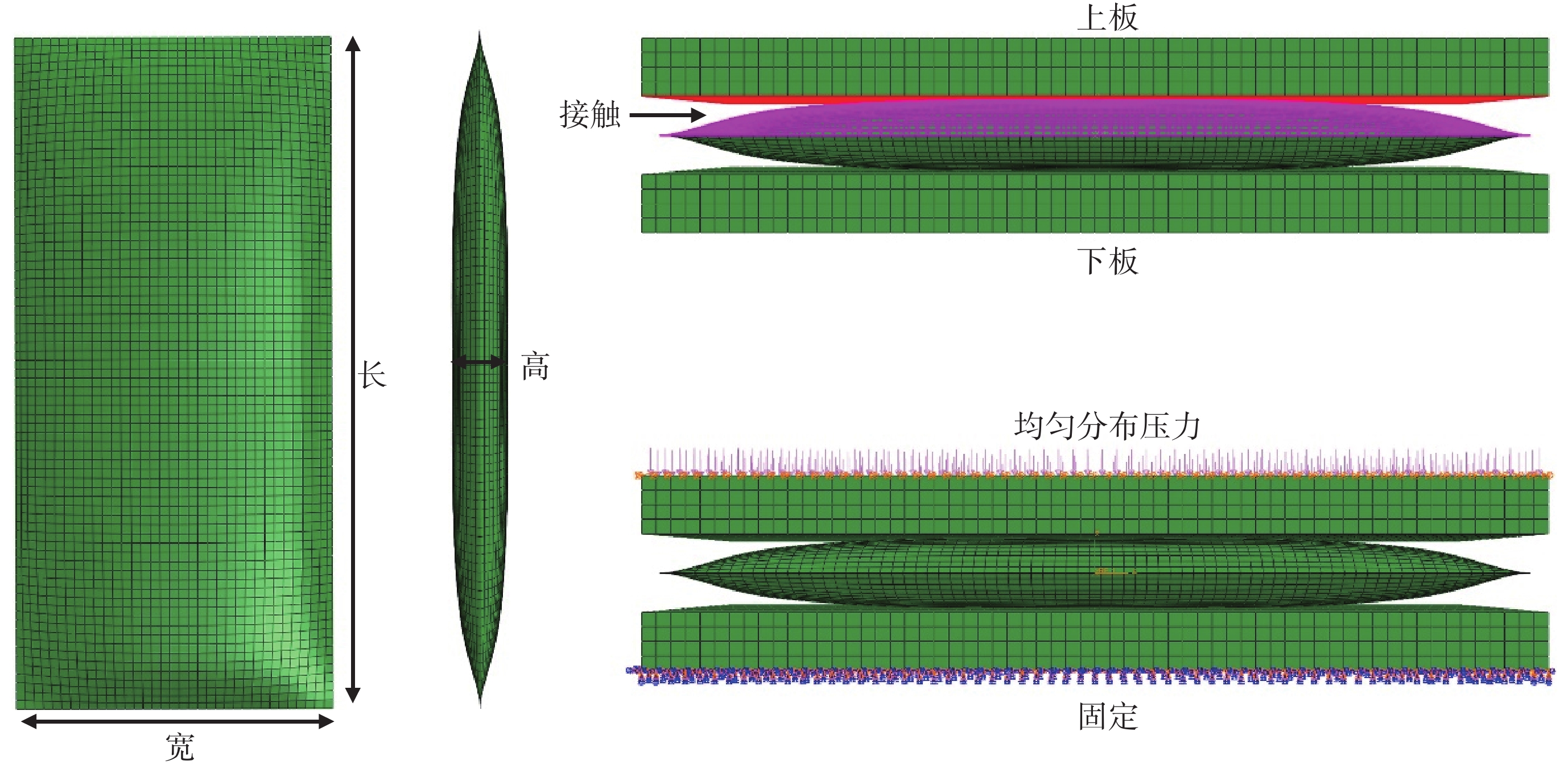
為準確模擬壓裂試驗下輸液袋的變形及應力分布，依照壓裂試驗采用 SolidWorks2017（達索公司，美國）建立數值模型，將所建立的輸液袋三維曲面模型夾在兩塊平板中間，平板尺寸略大于輸液袋尺寸，如圖 2 所示。考慮不同輸液袋尺寸對弱焊破裂的影響及更好地與實驗結果對比，本文建立了不同尺寸的計算模型，具體模型編號及參數如表 1 所示。
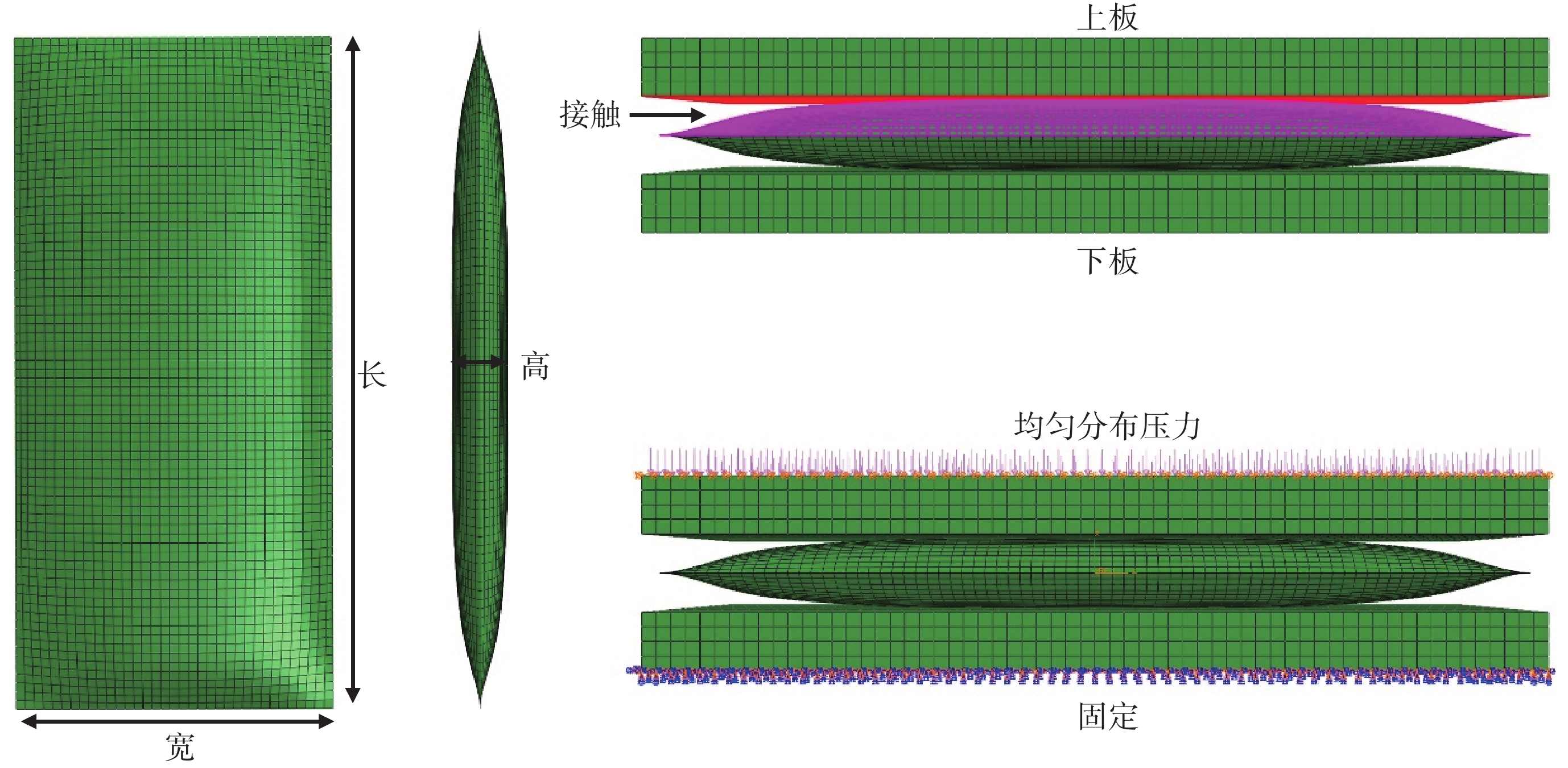圖2
輸液袋計算模型
Figure2.
Computational model of infusion bag
表1
輸液袋腔室壓裂實驗尺寸方案
Table1.
Different size of infusion bag for burst test
將模型導入 ABAQUS2016（達索公司，法國）進行網格劃分，由于輸液袋壁面尺寸較小，本文假設其完全不能承受彎矩[25]，故采用膜單元 M3D4R 生成腔室網格，壓板采用三維實體單元 C3D8R 進行網格劃分。此外，設置上下板與輸液袋對應外表面的摩擦接觸，摩擦系數為 0.2[26]，上板與輸液袋的接觸面如圖 2 中接觸所示，下部分設置與之相同。
模型邊界條件的設置也需要與標準壓裂試驗相對應，因此，約束下板所有自由度，上板施加水平方向的位移約束防止計算過程中由于壓板的水平位移導致的結構失穩，同時在上板施加隨時間增大的均勻分布壓力。
輸液袋中的流體模擬采用 ABAQUS 的流體腔功能，通過定義體積模量模擬近乎不可壓的液體行為[27]。該方法已成功應用在類似輸液袋受力變形的流固耦合分析中[28]。且由前期實驗發現，弱焊帶破裂前袋體材料均處于線彈性區間，因此采用線彈性本構關系進行分析，模型各部分材料參數如表 2 所示。
表2
材料參數
Table2.
Material parameters
1.4 壓裂實驗
為對比數值計算與實驗結果，驗證數值方法的有效性，本文對表 1 中不同尺寸的輸液袋樣品進行了壓裂試驗。壓裂樣品依照數值模型去除了輸液袋管口，相應位置改為實焊。試驗依舊采用小量程萬能試驗機進行加載，上下夾具換作尺寸稍大于輸液袋的水平放置鋼板，充液的輸液袋放置在兩塊鋼板之間，放置位置盡可能保證輸液袋中心與鋼板中心重合。實驗過程中，由上板施加不斷增大的均勻分布壓力直至弱焊處破裂，獲取用于對比的壓裂力及弱焊帶破裂過程，實驗操作如圖 3 所示。
圖3
壓裂試驗
Figure3.
Burst test procedure
2 結果
2.1 剝離試驗結果
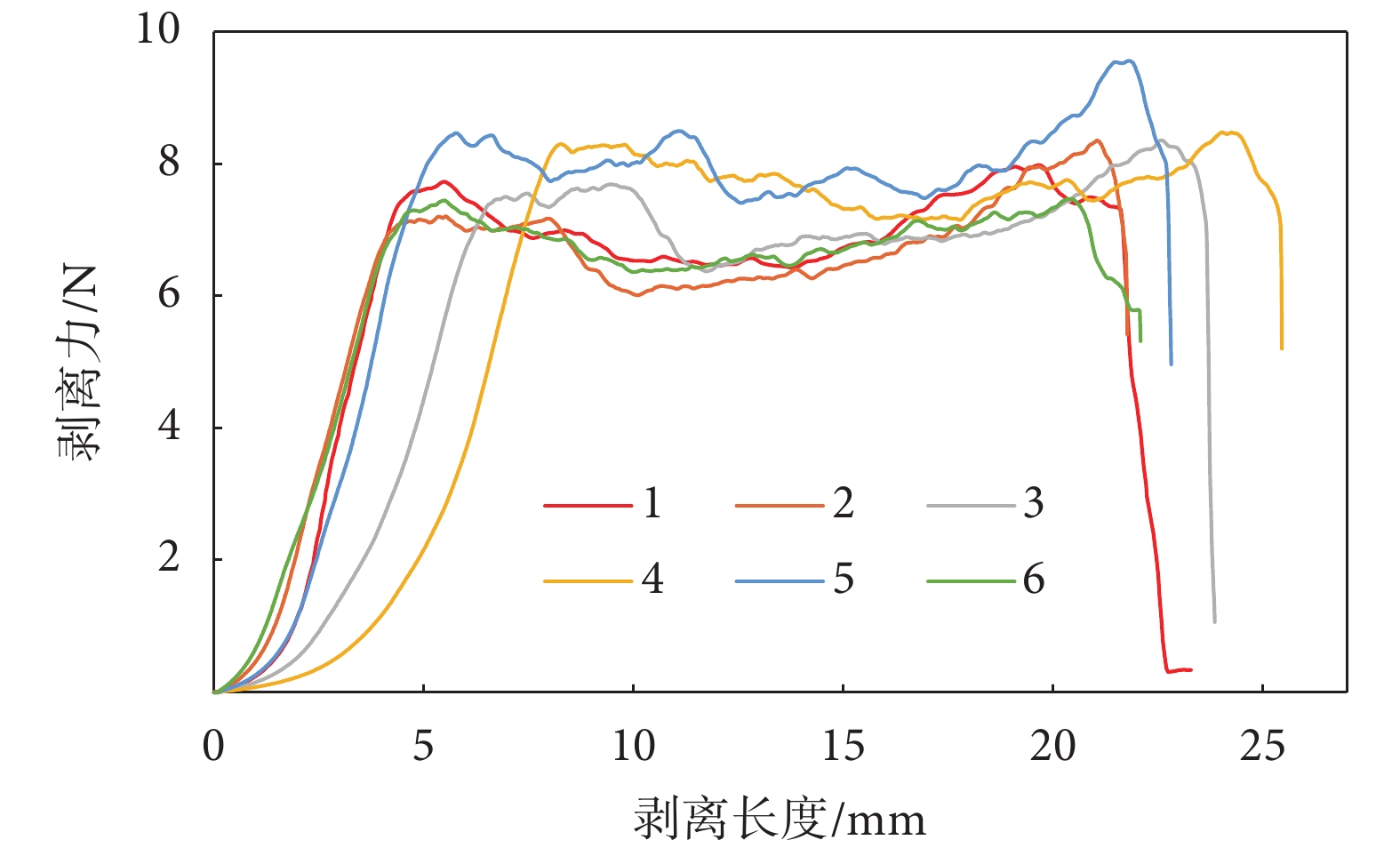
寬度為 15 mm 的輸液袋“弱焊”位置的試樣剝離結果如圖 4 所示，1-6 分別為六個試樣的結果，可以看出剝離過程分為三個階段。在初始階段，剝離力呈線性增大的趨勢，此時試樣尚未達到“弱焊”強度，薄膜在力的作用下被拉長。當達到“弱焊”強度時，試樣開始剝離，剝離力略微呈現先減小后增大的趨勢，但基本穩定在 6～8 N 之間。當剝離結束時，兩段薄膜分開，力隨即陡降至 0。
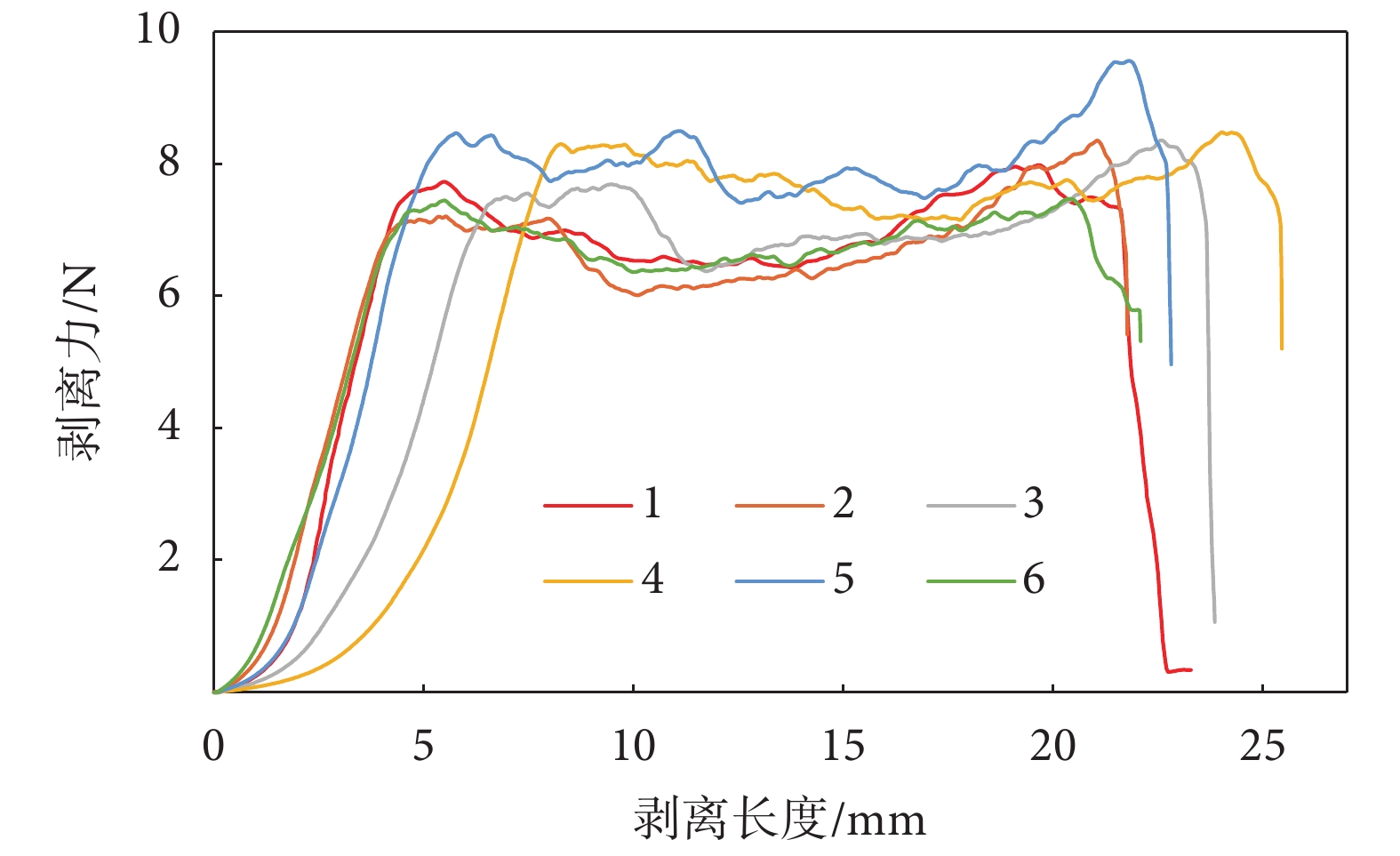圖4
剝離力與剝離長度的關系曲線
Figure4.
The relationship between peeling force and peeling length
從初始階段的曲線可以看出，剛開始拉伸時剝離力隨剝離長度的變化各異，這是由于薄膜初始夾持的松緊不同所造成的，但隨著拉伸的進行逐漸趨于一致。而在剝離剛開始時，試樣形變及剝離伸長兩部分疊加會導致夾具內試樣長度增加速率大于夾具移動速率，因此應力在剝離開始呈現降低的趨勢，與應力降低所對應的是剝離速率的變慢，故隨著剝離的進行，剝離力會逐漸回升直到剝離結束。
從圖 4 可以看出，盡管焊接強度的非均勻性導致了剝離過程中剝離力的浮動，但整體差異較小。依照前文所述公式，所得弱焊剝離應力為 2.63 MPa。
2.2 數值計算結果
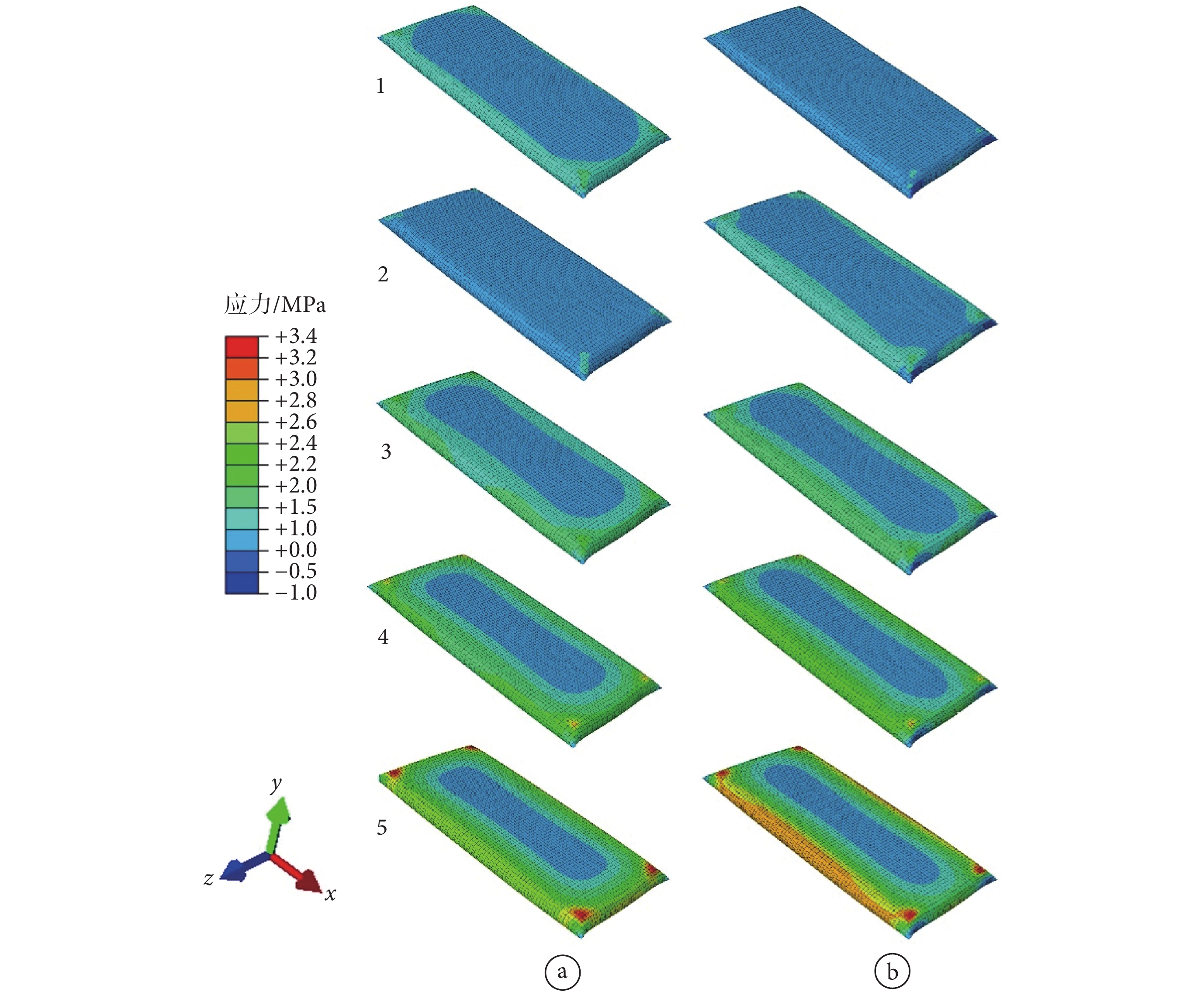
輸液袋在外載荷作用下的應力分布如圖 5 所示，為了便于觀察結果，本文將上壓板剛剛開始接觸輸液袋到壓力達到相應尺寸下的實驗壓裂力這一過程，按時間平均分為 5 個階段。提取各階段輸液袋的 Von Mises 應力和 y 方向（剝離方向）的應力大小，以 250 mm*120 mm*22 mm 腔室的應力結果如圖 5 所示。
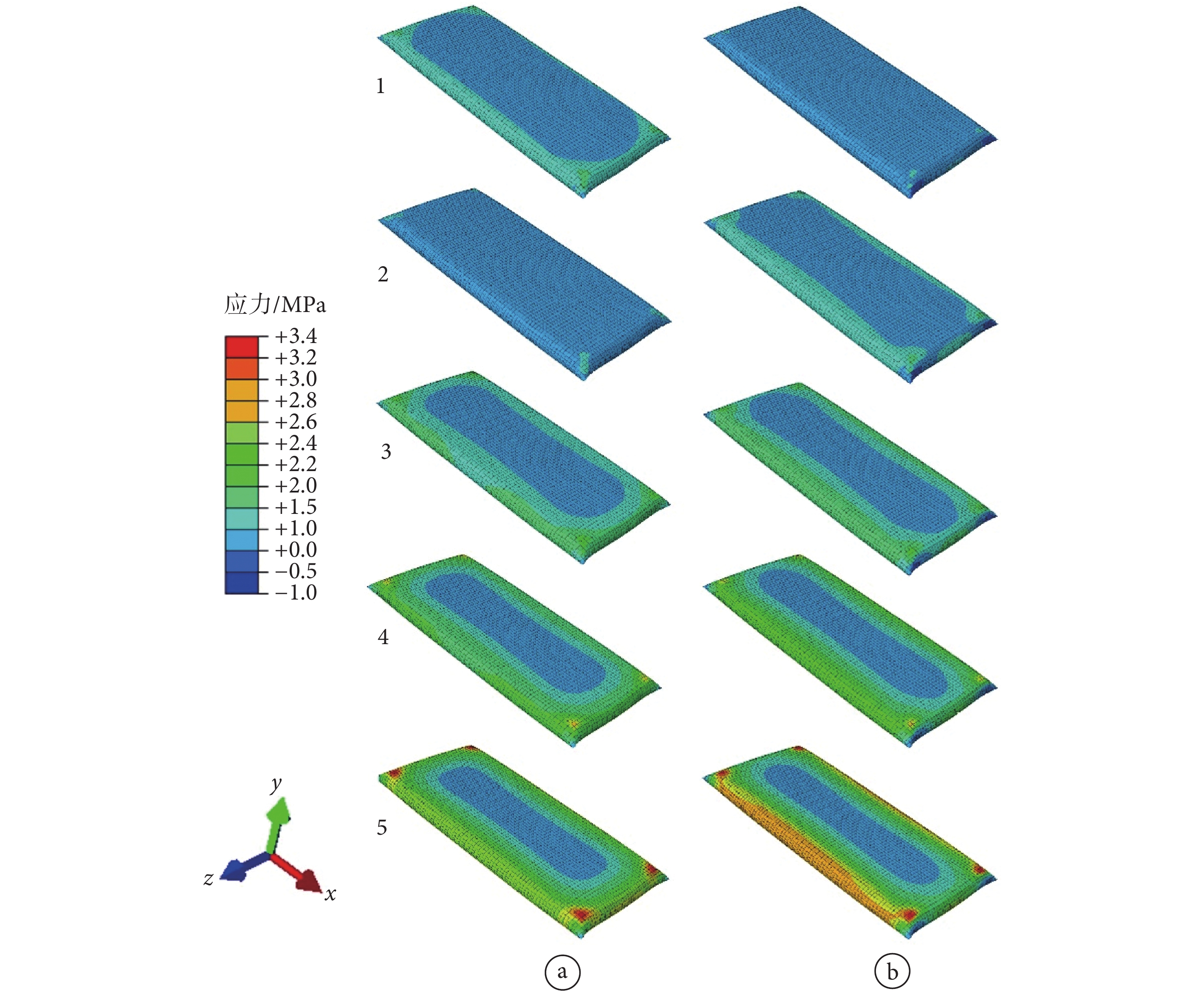圖5
輸液袋受力變化過程
a. Von Mises 應力；b. 剝離方向應力
Figure5. Stress distribution of infusion bag during the pressure break procedurea. Von Mises stress; b. stress along the peeling direction
從計算結果五個階段的 Mises 應力變化可以看出，在加載過程中，輸液袋曲面邊界處的應力變化較為明顯，高應力區域隨著載荷的增加從曲面邊界處向內擴展。由模型的幾何特征可分析產生此結果的原因：在 1、2 階段，壓板接觸輸液袋使得袋中壓強增大，長邊上的曲面結構在內部壓強的作用下產生 y、z 方向的應力分量，短邊上的曲面則在 x、y 方向應力增加較大。輸液袋中部材料由于在變形過程中與壓板貼合較好，部分內壓與壓板抵消，其受力主要來自與曲面邊界的相互作用。故在 3～5 階段，隨著外載荷增加，曲面邊界的應力也不斷升高，與中部材料的相互作用不斷增強，產生了高應力區域向內擴展的現象。
不同階段輸液袋 y 方向的應力分布表明，在載荷增大的過程中，輸液袋中部應力水平變化較小，而曲面邊界處應力變化較為明顯，這也是由邊界的曲面特性所決定的。輸液袋中部位置在 y 方向與內壓的平衡是由壓板與袋體兩部分組成，盡管壓板可平衡大部分內壓，但內壓的增強也會使得袋體的受力發生變化，只是變化較小。
由于輸液袋結構在 xy、yz 截面都是中間平兩頭尖的結構，長邊曲面在 yz 面上沿 z 方向的應力分量會對短邊曲面產生作用，相應的短邊曲面在 xy 平面沿 x 方向的應力分量也會對長邊曲面產生影響。這樣的相互作用會極大地影響輸液袋的變形及應力分布。在長邊與短邊相交的角點處，z 方向作用在長邊上的力對角點的扭矩大于 x 方向作用在短邊上的力對角點的扭矩，因此短邊處靠近角點的位置會產生向內的凹陷。長邊兩端雖也有影響，但因其尺寸較長，影響較小。凹陷后的短邊兩端膨脹小于中間，會導致短邊兩端處的曲面曲率大于中間，減小了短邊兩側在 y 方向的應力分量，因而短邊 y 方向的應力分布呈 u 型分布。長邊由于影響較小，應力分布較為均勻。
2.3 模擬與壓裂實驗結果對比
對比數值模擬與壓裂實驗結果的差異，首先需要比較破裂時壓裂力的大小。為此，本文提取了計算結果中不同尺寸模型 y 方向的應力隨相應的壓力載荷的變化曲線，當與輸液袋試樣對應的弱焊邊界應力達到剝離應力時，記錄外載荷大小，并與實驗所得壓裂力比較，各模型結果如表 3 所示。
表3
輸液袋壓裂實驗值與計算值對比
Table3.
Comparison of break force between the simulation and experiment
可見，除某些特定尺寸下的輸液實驗結果與數值計算存在一定差異外，其余模型的計算值均能與實驗很好地吻合。考慮到實驗過程中由偏心壓裂或輸液袋自身弱焊強度差異造成的實驗誤差，表 3 中的壓裂力差異均在可接受范圍內。因此，數值計算能夠較好地預測壓裂力的大小。
除壓裂力大小外，為更好地驗證計算的有效性，壓裂實驗還記錄了袋體的壓裂過程，圖 6 展示了不同尺寸的輸液袋壓裂后的弱焊條剝離情況，箭頭所指部分為已被剝離的弱焊帶。
圖6
壓裂實驗結果
Figure6.
Results of burst test
從圖 6 可以看出，弱焊帶的剝離并不是只存在于弱焊帶的某一區間，而是在內壓的作用下被全部剝離，這與計算結果中長邊沿 y 方向應力差異較小相符。實際上，依據實驗觀察結果可知，袋體的破裂過程分為弱焊剝離及弱焊剝離擴展兩個階段，當壓力逐漸增大時，弱焊邊上某一位置先被剝離，隨后整個邊上的弱焊條均被剝離并開始向外擴展，直到弱焊條擴展至弱焊邊界產生袋體破裂。
實驗發現，不同輸液袋初始剝離位置不同，對于長寬尺寸均較小的輸液袋，弱焊帶最先從中間開始剝離，而長寬差距較大的輸液袋其起始剝離位置隨機。這在數值模擬結果中得到了極好的驗證。由數值結果分析可知，邊界長度較小的邊由于靠近角點位置，產生的凹陷會使得短邊中間的剝離應力大于兩邊，故弱焊帶最先從中間破裂，而較長邊應力分布差異較小，此時的初始剝離位置由不同區域的弱焊強度差異所決定。
壓裂試驗結果表明，弱焊帶只有部分擴展至邊界，且初始剝離位置的擴展速率高于弱焊帶其余位置。這是由于弱焊帶初始剝離產生后，相應位置的邊界曲率減小，增大了沿剝離方向的應力分量，且液體進入初始剝離位置后，其壓強會對剝離位置兩側的材料產生作用，使得初始剝離位置沿著弱焊帶向兩邊擴展，使得最終的破口大小具有一定的寬度。
因此，從數值分析得到的壓裂力大小關系、應力分布與弱焊破裂的對比分析可知，采用流體腔方式模擬輸液袋是一種行之有效的方式，對不同尺寸的輸液袋均能做到很好的定性及定量分析。
3 討論
實際生產中常用剝離實驗所得拉伸熱封強度及壓裂實驗所得膨脹熱封強度評價輸液袋性能并進行工藝改進，該方式需要大量的實驗數據進行統計分析，且所得結果無法直接用于輸液袋本身的設計改進。將流體腔方法用于多室輸液袋模擬能夠快速地計算出不同條件下的輸液袋的變形過程及應力分布，直觀地指導輸液袋優化設計，同時，可直接研究輸液袋外形、尺寸以及管口大小等參數對輸液袋性能的影響，極大地提升研究效率。
由于弱焊帶破裂過程中，垂直于輸液袋平面的應力起主要作用，因此數值模型采用幾何邊界上 y 方向的應力作為輸液袋是否破裂的判據。然而計算結果中由于輸液袋角點為幾何突變位置，容易造成應力奇異，故在提取 y 方向應力時候需要避免角點處及其附近應力突變的位置。
由剝離實驗可知，即便生產工藝相同，不同輸液袋上的弱焊強度也各不相同，甚至同一弱焊帶上不同位置的弱焊強度也存在一定差異，導致某些樣品的實際剝離強度與所用破裂準則差距較大。此外，若實驗過程中樣品放置失當產生偏心壓裂，則必然與對稱加載的數值模型存在差異，增大實驗誤差。因此，相同工藝下輸液袋的弱焊強度差異及實驗過程中存在的偏心壓裂等因素，均可能導致實驗結果與數值模擬間存在誤差。
盡管本文模擬的是輸液袋在靜載條件下的受力情況，但上述結果顯示流體腔能夠有效地模擬液體與輸液袋的相互作用。這表明采用流體腔方法對輸液袋進行動力學模擬也是可行的，可與傳統的跌落實驗相結合，評估輸液袋的抗沖擊性能并進行優化設計。
4 結論
本文針對以試驗方法對多室輸液袋進行設計改進存在的成本高及多參數研究難以開展的問題，提出了采用基于流體腔的有限元數值計算方法模擬輸液袋在外載荷下的受力及變形情況，為輸液袋的優化設計及性能評估提供新方法。數值模擬采用弱焊剝離實驗提供的剝離應力作為弱焊破裂準則，通過對比不同尺寸輸液袋在破裂時的數值計算與實驗壓裂力大小的差異，并結合對實驗中弱焊破裂過程的分析，驗證了該方法的有效性。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
多室軟包裝輸液袋（多室輸液袋）是一種新的全封閉輸液包裝形式，具有使用方便、無外源性污染等優點，是當前最具發展潛力的輸液包裝容器[1-3]。輸液袋各腔室間通過弱焊方式分隔，弱焊強度需要保證輸液袋使用前不產生脫焊漏液，同時在使用時能順利打開弱焊帶混合液體。然而，由于工藝及運輸過程的影響，弱焊處漏液時常發生，極大地增加了臨床用藥的安全隱患[4-5]。如何防止臨床使用前弱焊處液體滲漏是多室輸液袋生產的關鍵，也是目前亟待解決的問題。
由于國際技術壁壘以及企業間工藝和技術保密，國外針對多室輸液袋的公開研究資料較少。國內研究主要以實驗為主，對生產工藝及輸液袋設計進行改進，如采用剝離實驗、整袋脹破壓力實驗及跌落實驗等評估其焊接強度[6]，再依據技術統計分析調整工藝參數[7-11]，或是通過提升傳熱效率等方式對生產模具進行改進[12-14]。在輸液袋設計上，不同廠家具有不同的設計方案，如 V 型弱焊帶分隔方式[15]、波浪狀弱焊帶[16]等，均能提升弱焊處的防滲漏性能[17-19]。然而，以實驗為主的方式存在成本高、周期長的問題，且針對輸液袋形狀及尺寸對弱焊處液體滲漏影響的多參數研究難以開展。因此，需要發展一種方便快捷、成本低廉的研究方法，提升多室輸液袋優化設計效率。
有限元方法作為一種通用的數值仿真技術，可快速模擬不同參數、不同實驗條件下的結構運動和變形過程，已在其他類型的輸液包裝產品及生產模具設計上得到了廣泛應用[20-22]，有效提升了研究的效率。因此，本文提出采用流體腔方法模擬流體運動，計算多室輸液袋在外載荷下流固耦合變形過程的數值仿真方法，并將仿真結果與壓裂試驗結果進行對比，驗證了該方法的有效性。
1 材料和方法
1.1 研究對象
采用常見包裝氨基酸、葡萄糖、脂肪乳的三室輸液袋為研究對象[23]，選取最易出現弱焊滲漏的最大腔體作為壓裂實驗及計算模型，如圖 1 所示。該模型腔體為三邊實焊一邊“弱焊”的結構，在壓裂實驗時弱焊處率先破裂，便于觀察破裂過程。
圖1
弱焊剝離試驗試樣制備
a. 從最大腔室剪裁含弱焊條試樣；b. 對稱剪裁去除實焊側材料；c. 弱焊剝離示意圖
Figure1. Procedure of cutting specimen for peeling testa. the sample containing the weak welding rod was cut from the largest chamber; b. symmetrical clipping to remove solid weld side material; c. schematic diagram of peeling test
1.2 弱焊剝離實驗
采用數值計算分析方法研究弱焊強度需要獲取特定工藝參數下的弱焊脫焊強度，為數值計算提供弱焊破裂準則。為此，本文利用輸液袋薄膜樣品制備了 6 個弱焊位置處的長條拉伸試樣，制備流程如圖 1a-c 所示，每個試樣均寬 15 mm。根據 GBT8808-88 軟質復合塑料材料剝離實驗標準對薄膜試樣進行剝離試驗[24]，試驗采用小量程（5 KN）萬能試驗機（中國，恒準儀器科技有限公司，HZ-1004B），將圖 1c 中制備的試樣兩端分別夾在試驗機豎直方向的上、下夾具上，松緊適中。調整夾持位置使得試樣剝開位置的軸線位于上、下夾具連線的中點并與連線垂直，在拉伸過程中，需保證未剝開部分與試樣所在平面垂直，記錄實驗過程中的力及變形參數，可得輸液袋弱焊處的剝離應力，其大小為：
|
其中 為剝離時實驗機拉力， 為剪樣寬度， 為輸液袋厚度。
1.3 數值模擬
為準確模擬壓裂試驗下輸液袋的變形及應力分布，依照壓裂試驗采用 SolidWorks2017（達索公司，美國）建立數值模型，將所建立的輸液袋三維曲面模型夾在兩塊平板中間，平板尺寸略大于輸液袋尺寸，如圖 2 所示。考慮不同輸液袋尺寸對弱焊破裂的影響及更好地與實驗結果對比，本文建立了不同尺寸的計算模型，具體模型編號及參數如表 1 所示。
圖2
輸液袋計算模型
Figure2.
Computational model of infusion bag
表1
輸液袋腔室壓裂實驗尺寸方案
Table1.
Different size of infusion bag for burst test
將模型導入 ABAQUS2016（達索公司，法國）進行網格劃分，由于輸液袋壁面尺寸較小，本文假設其完全不能承受彎矩[25]，故采用膜單元 M3D4R 生成腔室網格，壓板采用三維實體單元 C3D8R 進行網格劃分。此外，設置上下板與輸液袋對應外表面的摩擦接觸，摩擦系數為 0.2[26]，上板與輸液袋的接觸面如圖 2 中接觸所示，下部分設置與之相同。
模型邊界條件的設置也需要與標準壓裂試驗相對應，因此，約束下板所有自由度，上板施加水平方向的位移約束防止計算過程中由于壓板的水平位移導致的結構失穩，同時在上板施加隨時間增大的均勻分布壓力。
輸液袋中的流體模擬采用 ABAQUS 的流體腔功能，通過定義體積模量模擬近乎不可壓的液體行為[27]。該方法已成功應用在類似輸液袋受力變形的流固耦合分析中[28]。且由前期實驗發現，弱焊帶破裂前袋體材料均處于線彈性區間，因此采用線彈性本構關系進行分析，模型各部分材料參數如表 2 所示。
表2
材料參數
Table2.
Material parameters
1.4 壓裂實驗
為對比數值計算與實驗結果，驗證數值方法的有效性，本文對表 1 中不同尺寸的輸液袋樣品進行了壓裂試驗。壓裂樣品依照數值模型去除了輸液袋管口，相應位置改為實焊。試驗依舊采用小量程萬能試驗機進行加載，上下夾具換作尺寸稍大于輸液袋的水平放置鋼板，充液的輸液袋放置在兩塊鋼板之間，放置位置盡可能保證輸液袋中心與鋼板中心重合。實驗過程中，由上板施加不斷增大的均勻分布壓力直至弱焊處破裂，獲取用于對比的壓裂力及弱焊帶破裂過程，實驗操作如圖 3 所示。
圖3
壓裂試驗
Figure3.
Burst test procedure
2 結果
2.1 剝離試驗結果
寬度為 15 mm 的輸液袋“弱焊”位置的試樣剝離結果如圖 4 所示，1-6 分別為六個試樣的結果，可以看出剝離過程分為三個階段。在初始階段，剝離力呈線性增大的趨勢，此時試樣尚未達到“弱焊”強度，薄膜在力的作用下被拉長。當達到“弱焊”強度時，試樣開始剝離，剝離力略微呈現先減小后增大的趨勢，但基本穩定在 6～8 N 之間。當剝離結束時，兩段薄膜分開，力隨即陡降至 0。
圖4
剝離力與剝離長度的關系曲線
Figure4.
The relationship between peeling force and peeling length
從初始階段的曲線可以看出，剛開始拉伸時剝離力隨剝離長度的變化各異，這是由于薄膜初始夾持的松緊不同所造成的，但隨著拉伸的進行逐漸趨于一致。而在剝離剛開始時，試樣形變及剝離伸長兩部分疊加會導致夾具內試樣長度增加速率大于夾具移動速率，因此應力在剝離開始呈現降低的趨勢，與應力降低所對應的是剝離速率的變慢，故隨著剝離的進行，剝離力會逐漸回升直到剝離結束。
從圖 4 可以看出，盡管焊接強度的非均勻性導致了剝離過程中剝離力的浮動，但整體差異較小。依照前文所述公式，所得弱焊剝離應力為 2.63 MPa。
2.2 數值計算結果
輸液袋在外載荷作用下的應力分布如圖 5 所示，為了便于觀察結果，本文將上壓板剛剛開始接觸輸液袋到壓力達到相應尺寸下的實驗壓裂力這一過程，按時間平均分為 5 個階段。提取各階段輸液袋的 Von Mises 應力和 y 方向（剝離方向）的應力大小，以 250 mm*120 mm*22 mm 腔室的應力結果如圖 5 所示。
圖5
輸液袋受力變化過程
a. Von Mises 應力；b. 剝離方向應力
Figure5. Stress distribution of infusion bag during the pressure break procedurea. Von Mises stress; b. stress along the peeling direction
從計算結果五個階段的 Mises 應力變化可以看出，在加載過程中，輸液袋曲面邊界處的應力變化較為明顯，高應力區域隨著載荷的增加從曲面邊界處向內擴展。由模型的幾何特征可分析產生此結果的原因：在 1、2 階段，壓板接觸輸液袋使得袋中壓強增大，長邊上的曲面結構在內部壓強的作用下產生 y、z 方向的應力分量，短邊上的曲面則在 x、y 方向應力增加較大。輸液袋中部材料由于在變形過程中與壓板貼合較好，部分內壓與壓板抵消，其受力主要來自與曲面邊界的相互作用。故在 3～5 階段，隨著外載荷增加，曲面邊界的應力也不斷升高，與中部材料的相互作用不斷增強，產生了高應力區域向內擴展的現象。
不同階段輸液袋 y 方向的應力分布表明，在載荷增大的過程中，輸液袋中部應力水平變化較小，而曲面邊界處應力變化較為明顯，這也是由邊界的曲面特性所決定的。輸液袋中部位置在 y 方向與內壓的平衡是由壓板與袋體兩部分組成，盡管壓板可平衡大部分內壓，但內壓的增強也會使得袋體的受力發生變化，只是變化較小。
由于輸液袋結構在 xy、yz 截面都是中間平兩頭尖的結構，長邊曲面在 yz 面上沿 z 方向的應力分量會對短邊曲面產生作用，相應的短邊曲面在 xy 平面沿 x 方向的應力分量也會對長邊曲面產生影響。這樣的相互作用會極大地影響輸液袋的變形及應力分布。在長邊與短邊相交的角點處，z 方向作用在長邊上的力對角點的扭矩大于 x 方向作用在短邊上的力對角點的扭矩，因此短邊處靠近角點的位置會產生向內的凹陷。長邊兩端雖也有影響，但因其尺寸較長，影響較小。凹陷后的短邊兩端膨脹小于中間，會導致短邊兩端處的曲面曲率大于中間，減小了短邊兩側在 y 方向的應力分量，因而短邊 y 方向的應力分布呈 u 型分布。長邊由于影響較小，應力分布較為均勻。
2.3 模擬與壓裂實驗結果對比
對比數值模擬與壓裂實驗結果的差異，首先需要比較破裂時壓裂力的大小。為此，本文提取了計算結果中不同尺寸模型 y 方向的應力隨相應的壓力載荷的變化曲線，當與輸液袋試樣對應的弱焊邊界應力達到剝離應力時，記錄外載荷大小，并與實驗所得壓裂力比較，各模型結果如表 3 所示。
表3
輸液袋壓裂實驗值與計算值對比
Table3.
Comparison of break force between the simulation and experiment
可見，除某些特定尺寸下的輸液實驗結果與數值計算存在一定差異外，其余模型的計算值均能與實驗很好地吻合。考慮到實驗過程中由偏心壓裂或輸液袋自身弱焊強度差異造成的實驗誤差，表 3 中的壓裂力差異均在可接受范圍內。因此，數值計算能夠較好地預測壓裂力的大小。
除壓裂力大小外，為更好地驗證計算的有效性，壓裂實驗還記錄了袋體的壓裂過程，圖 6 展示了不同尺寸的輸液袋壓裂后的弱焊條剝離情況，箭頭所指部分為已被剝離的弱焊帶。
圖6
壓裂實驗結果
Figure6.
Results of burst test
從圖 6 可以看出，弱焊帶的剝離并不是只存在于弱焊帶的某一區間，而是在內壓的作用下被全部剝離，這與計算結果中長邊沿 y 方向應力差異較小相符。實際上，依據實驗觀察結果可知，袋體的破裂過程分為弱焊剝離及弱焊剝離擴展兩個階段，當壓力逐漸增大時，弱焊邊上某一位置先被剝離，隨后整個邊上的弱焊條均被剝離并開始向外擴展，直到弱焊條擴展至弱焊邊界產生袋體破裂。
實驗發現，不同輸液袋初始剝離位置不同，對于長寬尺寸均較小的輸液袋，弱焊帶最先從中間開始剝離，而長寬差距較大的輸液袋其起始剝離位置隨機。這在數值模擬結果中得到了極好的驗證。由數值結果分析可知，邊界長度較小的邊由于靠近角點位置，產生的凹陷會使得短邊中間的剝離應力大于兩邊，故弱焊帶最先從中間破裂，而較長邊應力分布差異較小，此時的初始剝離位置由不同區域的弱焊強度差異所決定。
壓裂試驗結果表明，弱焊帶只有部分擴展至邊界，且初始剝離位置的擴展速率高于弱焊帶其余位置。這是由于弱焊帶初始剝離產生后，相應位置的邊界曲率減小，增大了沿剝離方向的應力分量，且液體進入初始剝離位置后，其壓強會對剝離位置兩側的材料產生作用，使得初始剝離位置沿著弱焊帶向兩邊擴展，使得最終的破口大小具有一定的寬度。
因此，從數值分析得到的壓裂力大小關系、應力分布與弱焊破裂的對比分析可知，采用流體腔方式模擬輸液袋是一種行之有效的方式，對不同尺寸的輸液袋均能做到很好的定性及定量分析。
3 討論
實際生產中常用剝離實驗所得拉伸熱封強度及壓裂實驗所得膨脹熱封強度評價輸液袋性能并進行工藝改進，該方式需要大量的實驗數據進行統計分析，且所得結果無法直接用于輸液袋本身的設計改進。將流體腔方法用于多室輸液袋模擬能夠快速地計算出不同條件下的輸液袋的變形過程及應力分布，直觀地指導輸液袋優化設計，同時，可直接研究輸液袋外形、尺寸以及管口大小等參數對輸液袋性能的影響，極大地提升研究效率。
由于弱焊帶破裂過程中，垂直于輸液袋平面的應力起主要作用，因此數值模型采用幾何邊界上 y 方向的應力作為輸液袋是否破裂的判據。然而計算結果中由于輸液袋角點為幾何突變位置，容易造成應力奇異，故在提取 y 方向應力時候需要避免角點處及其附近應力突變的位置。
由剝離實驗可知，即便生產工藝相同，不同輸液袋上的弱焊強度也各不相同，甚至同一弱焊帶上不同位置的弱焊強度也存在一定差異，導致某些樣品的實際剝離強度與所用破裂準則差距較大。此外，若實驗過程中樣品放置失當產生偏心壓裂，則必然與對稱加載的數值模型存在差異，增大實驗誤差。因此，相同工藝下輸液袋的弱焊強度差異及實驗過程中存在的偏心壓裂等因素，均可能導致實驗結果與數值模擬間存在誤差。
盡管本文模擬的是輸液袋在靜載條件下的受力情況，但上述結果顯示流體腔能夠有效地模擬液體與輸液袋的相互作用。這表明采用流體腔方法對輸液袋進行動力學模擬也是可行的，可與傳統的跌落實驗相結合，評估輸液袋的抗沖擊性能并進行優化設計。
4 結論
本文針對以試驗方法對多室輸液袋進行設計改進存在的成本高及多參數研究難以開展的問題，提出了采用基于流體腔的有限元數值計算方法模擬輸液袋在外載荷下的受力及變形情況，為輸液袋的優化設計及性能評估提供新方法。數值模擬采用弱焊剝離實驗提供的剝離應力作為弱焊破裂準則，通過對比不同尺寸輸液袋在破裂時的數值計算與實驗壓裂力大小的差異，并結合對實驗中弱焊破裂過程的分析，驗證了該方法的有效性。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
