膜片鉗（Patch Clamp）是一種皮安培（pA）級弱電流的測量技術，在基礎醫學研究中廣泛用于細胞電生理記錄，如細胞膜電位和離子通道電流的研究等。為了得到準確的離子通道測量結果，需要同時進行微電極的串聯阻抗和相關電容補償。電容補償包括慢電容補償和快電容補償：慢電容源于細胞脂雙層，其幅度依細胞大小從幾皮法拉（pF）到幾微法拉（μF）不等。快電容由玻璃微電極、導線和溶液及接地線等因素決定，幅值在幾個皮法拉。一般當微電極完成與細胞的吸附，導線和電極位置確定后，只需在實驗前進行一次快、慢電容補償即可記錄到可靠的離子通道電流。但對于伴隨溶液溫度改變的相關研究來說，細胞浴液的變化是如何影響快電容變化的尚沒有報道。本論文在使用膜片鉗研究細胞光熱效應的實驗中，觀察到溶液的溫升可以改變系統快電容的放電特性。基于此提出了一個考慮溫度因素的快電容等效電路，并計算了相關參量變化情況及溫度特性。實驗數據表明快電容以約 0.04 pF/℃ 的速率隨溫度增加而增加，而微電極的串聯阻抗卻隨溫度增加而減小。進一步分析表明：溶液溫度升高對微電極快電容放電時間特性的改變，主要是通過改變微電極內溶液阻抗實現的。這一結果對基于膜片鉗技術開展細胞層面的精細溫度特性研究有參考意義。
引用本文： 孔繁藝, 李新宇, 焦若男, 孫長森. 膜片鉗玻璃微電極快電容溫度特性研究. 生物醫學工程學雜志, 2021, 38(4): 695-702. doi: 10.7507/1001-5515.202007054 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
膜片鉗放大器是實現細胞電生理記錄的主要技術[1]，實驗中通過微米尺度的玻璃微電極負壓吸附細胞膜形成千兆歐級的封接電阻，從而實現對細胞膜選擇性的電學研究，可以對皮安培量級單個離子通道微弱電流進行精密測量。對如此微弱電流的檢測中，需要對細胞膜脂雙層形成的慢電容（slow capacitance，Cslow）[2]以及入液玻璃微電極、導線等引入的分布式快電容（fast capacitance，Cfast）進行補償。其中慢電容大小是細胞尺寸相關的幾皮法拉到幾微法拉量級，快電容的典型值為幾皮法拉量級。
一般來說，電容補償都是首先測量出電容的大小，然后由儀器發生一個大小相同、相位相反的補償電流來抵消電容電流。電容補償的效果取決于儀器發生補償電流與實際電容的差異程度，隨著膜片鉗軟件、硬件技術的高度成熟，電容補償在細胞環境不變的研究中已相當完善[2]。但實際應用膜片鉗實驗系統中有一類伴隨細胞外溶液溫度改變的研究，比如直接改變溫度以研究溫度敏感的離子通道[3-4]、光生物調節[5-8]、磁場調節[9-11]等調制細胞功能的研究。眾多實驗已經證實此類研究主要是以熱效應為基礎[12-15]，因此在這一類實驗中需要對快電容的溫度特性有更深入的認識，但目前的研究中往往缺少此類可靠參數描述。
2009 年 Qin 課題組[16]提出使用膜片鉗空電極測溫方法，由于無需預處理或外置儀器并且有高空間分辨率，其較熱電偶測量、熱敏感攝像機、掃描熱致體積膨脹、染料預處理記錄溫度相關的熒光強度等[17-19]測溫方法更方便且有效，常被應用于伴隨溫度變化的細胞電生理研究中。該方法是通過將玻璃微電極內充滿溶液，并基于恒溫標定得到其電阻與溶液溫度的關系。
本課題組是在使用這種方法的過程中，觀察到溶液溫度的升高可以改變快電容的時間特性。通常情況下，Cfast 被假定為常數僅在實驗前進行一次補償，在實驗過程中不再補償。基于實驗數據我們認為這一假設在熱伴隨實驗中并不成立，因此在溫度實驗中必須進行實時測量電容的自動補償，而一個切合實際的快電容等效電路是這個補償的關鍵，其難點在于快電容是分布式的。
本論文基于不同溫度下記錄到的快電容電流，提出了一個考慮溫度因素的分布式快電容等效電路，并分析了電路參數的溫度特性。使用膜片鉗進行生物信號記錄時，精準補償電容電流對記錄的準確性極為重要[20]，本文的結果將對溫度相關的電生理研究、優化補償電路及改進快電容補償算法的精度和速度具有參考價值。
1 快電容補償原理及實驗方法
1.1 快電容補償原理
分布式快電容是基于動態測量方法測得，即向目標電路輸入一個正弦交流信號，測量其輸入輸出響應后通過計算得到電容值，理論依據是動態電路分析的電容電流 Ic 來描述，即：
 |
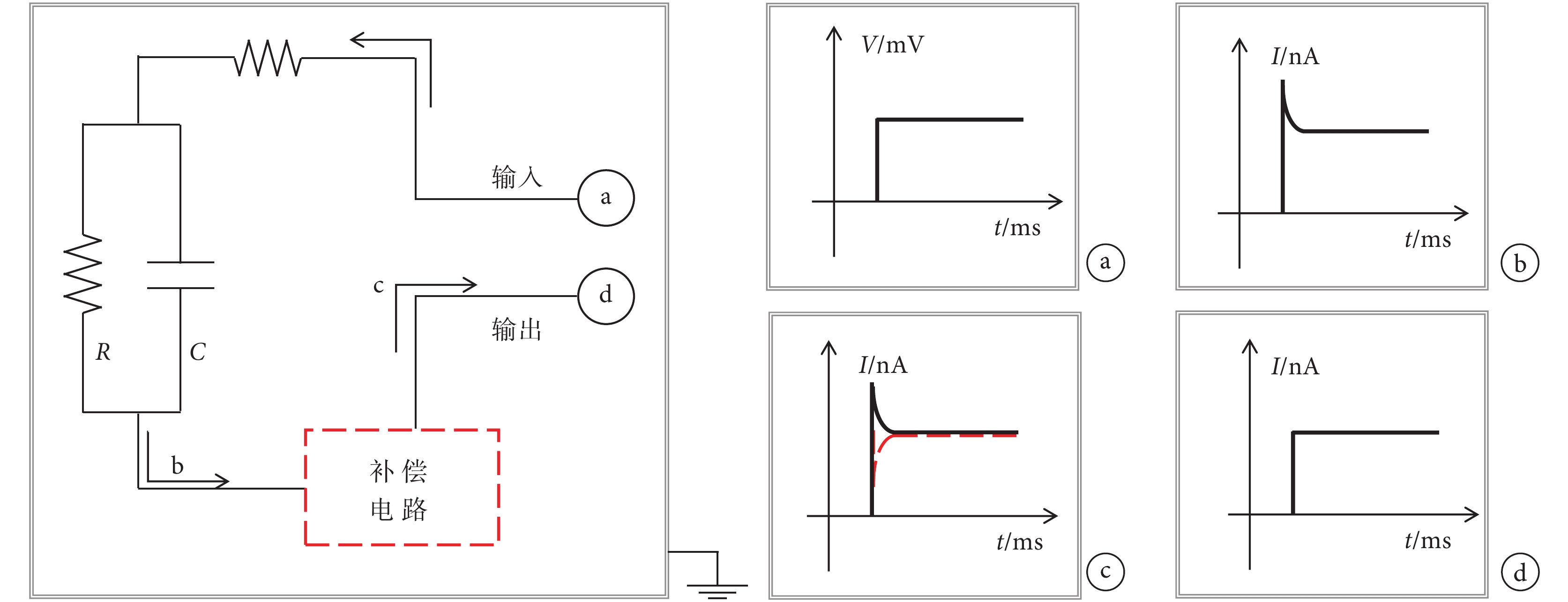
式中 U 為電容兩端電壓，R 為回路電阻，τ 為時間常數。圖 1 左側為德國 Heka 公司生產的 EPC-10 型膜片鉗補償快電容電流的原理圖。圖 1 右側為電路中電壓或電流信號，階躍電壓激勵作為輸入信號（圖 1a）輸入電路后，膜片鉗放大器中的補償電路首先測量出快電容電流的大小（圖 1b），然后輸出一個大小相同、相位相反的補償電流（圖 1c 虛線）來抵消由于快電容的存在而產生的小幅過沖電流，使最終輸出的電流如圖 1d 所示。在多數電生理實驗中，細胞鉗制都已完成的情形下，玻璃微電極、導線等都基本不變，此時快電容基本是一個常數。因此實驗前進行一次補償，系統就可以按照這個電容的幅值進行后續的補償，實現膜片鉗系統的高精度測量。
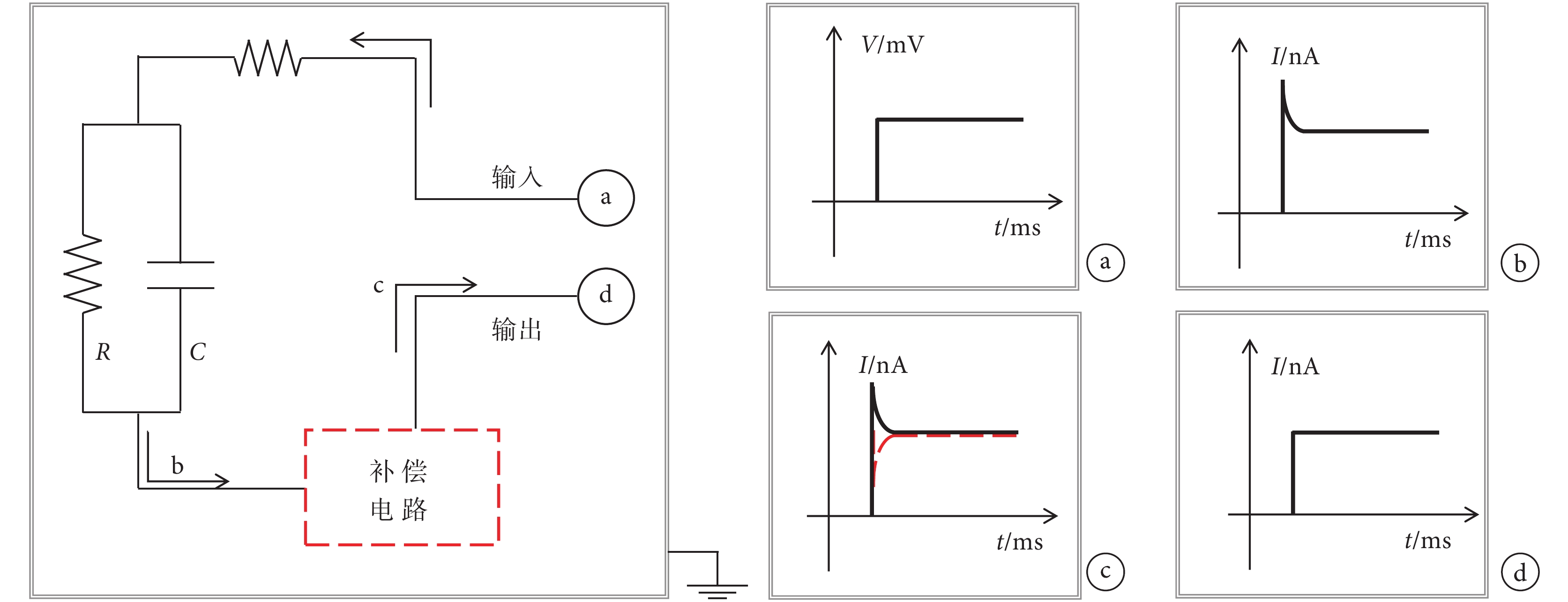圖1
EPC-10 膜片鉗快電容補償原理
左：EPC-10 膜片鉗快電容補償等效電路。右：回路中電壓/電流：a. 輸入激勵電壓；b. 補償前的回路電流；c. 紅色虛線所示為補償電流；d. 補償后的輸出電流
Figure1. The principle of EPC-10 patch clamp fast capacitive compensationLeft: EPC-10 patch clamp fast capacitive compensation equivalent circuit. Right: voltages/currents throughout the circuit: a. input voltage; b. circuit current before compensation; c. compensation current in patch clamp amplifier; d. output current after being compensated
將膜片鉗放大器的補償界面設置為自動補償，其補償信號的發生是基于上一次測量的集總參數來進行。這個集總參數極大地依賴于一個與快電容相關的等效電路。通常電路是不考慮溫度改變情況的，即視由玻璃微電極和導線形成的分布式電容為常數。而當溫度改變時快電容就被分為浴液溫度相關和不相關的兩部分，由于與浴液溫度直接相關的玻璃微電極入液部分的變化，可能出現過補償（補償電容電流大于實際電容電流）或補償不完全（補償電容電流小于實際電容電流）的情況，會極大地干擾正常電生理信號的記錄。因此，下面的實驗將研究溫度相關的快電容特性。
1.2 實驗裝置
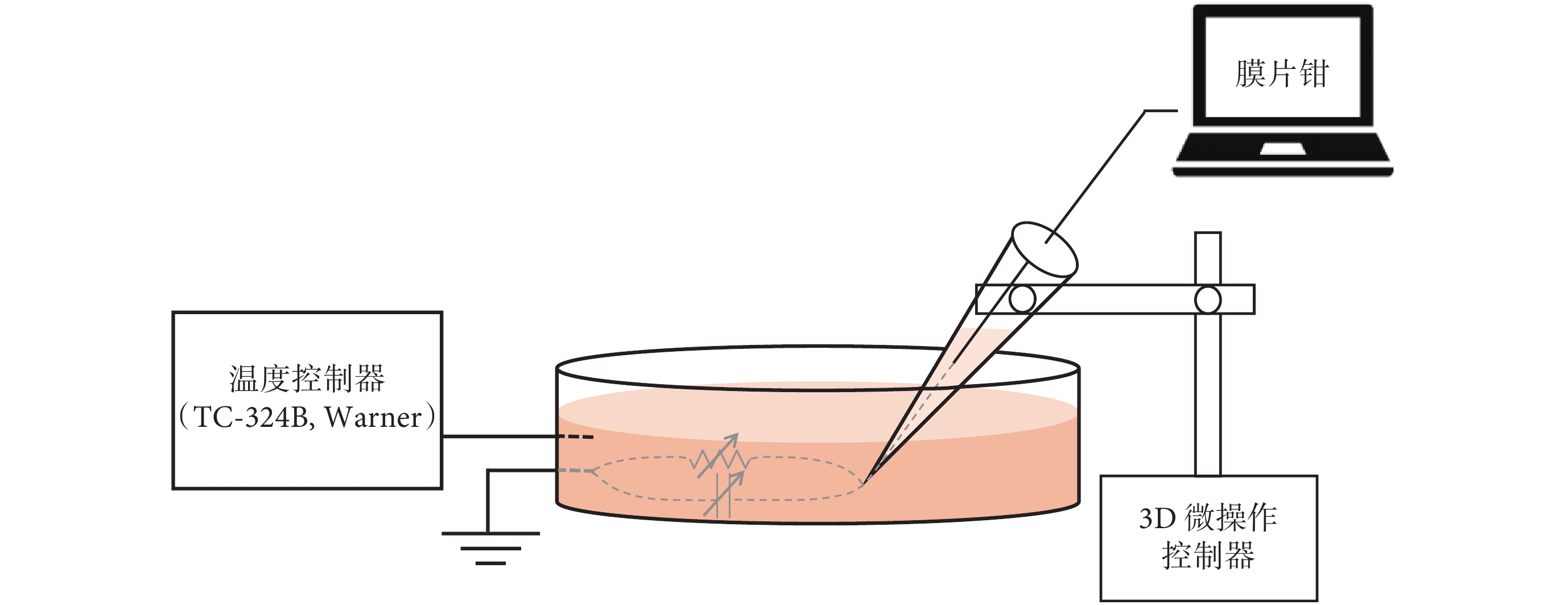
圖 2 為本實驗采用 EPC-10 單通道膜片鉗放大器（HEKA，德國）研究快電容溫度特性的實驗裝置，與用于進行空電極測溫的裝置相同。使用電極拉制儀將玻璃毛細管拉制為電阻為 3～5 MΩ 的玻璃微電極，將尖端為微米量級的空電極充灌標準細胞外液，構成膜片鉗的測量電極，并與細胞外溶液（浴液）中的接地線形成回路。施加的刺激電壓 V 幅值選為 100 mV，電壓時程為 1 s（時間精度為 0.1 ms）。玻璃微電極被固定在微米精度的微操縱器上，在實驗過程中不進行移動。
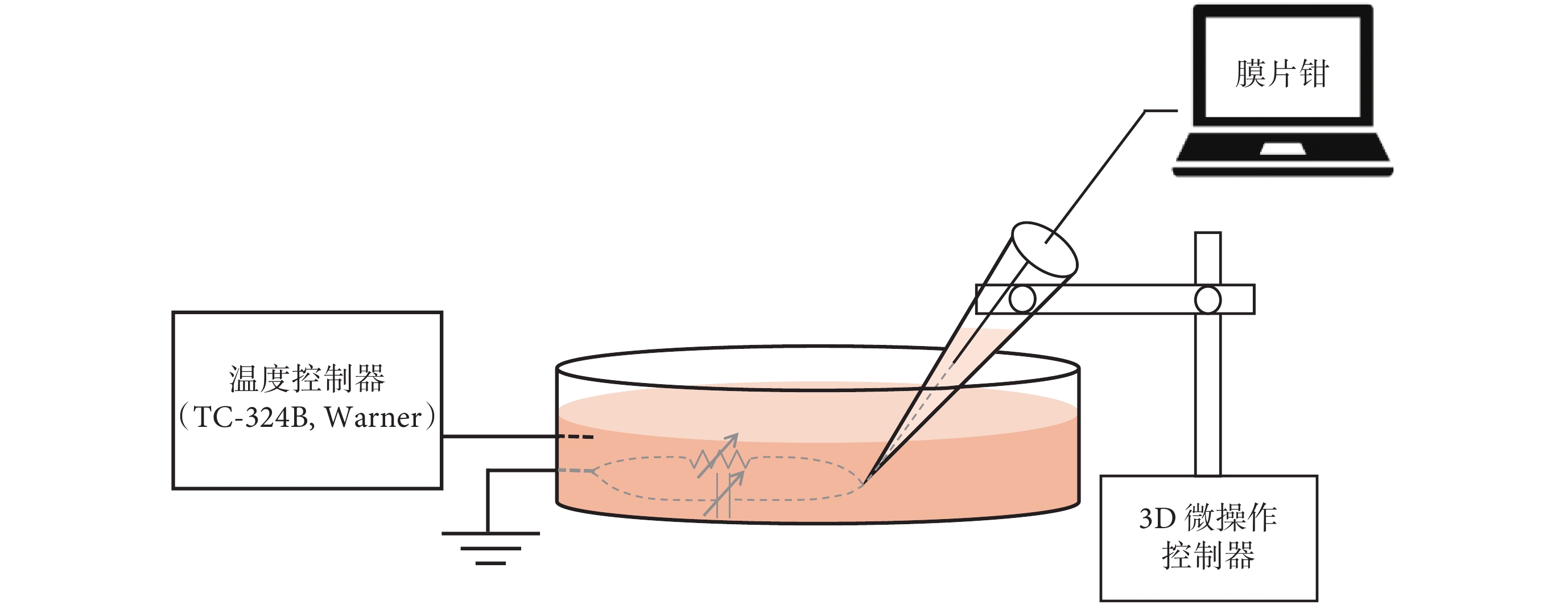圖2
研究快電容溫度特性的實驗裝置
Figure2.
The setup for studying the temperature effect on the fast capacitance
使用恒溫控制器（TC-324B，Warner，美國）控制培養皿中的浴液溫度，參考相關實驗[13,21-22]選擇常見實驗溫度 27.0～55.0 ℃ 并以 1.0 ℃ 遞增，施加 100 mV 激勵電壓。通過膜片鉗測量在相同電壓激勵條件下、不同浴液溫度下的輸出電流，研究快電容的溫度特性。EPC-10 膜片鉗放大器選擇快電容補償方式為手動補償，在開始記錄之前手動補償一次，溫度變化過程中不進行快電容補償操作。
標準細胞外液（mmol/L）：NaCl 150，KCl 5，MgCl2 1.1，CaCl2 2.6，HEPES 10，葡萄糖 10，CdCl2 0.2，使用 Tris-HCl 調節 pH 值至 7.4。
1.3 膜片鉗測溫等效電路
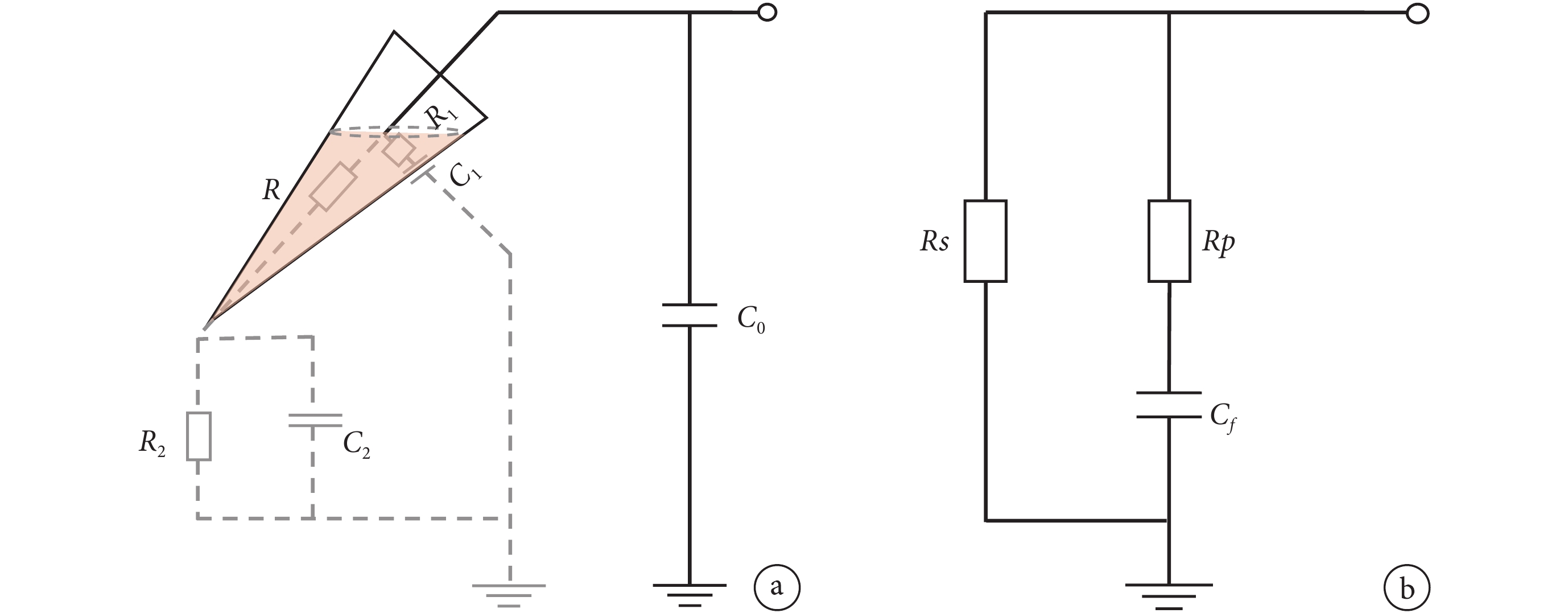
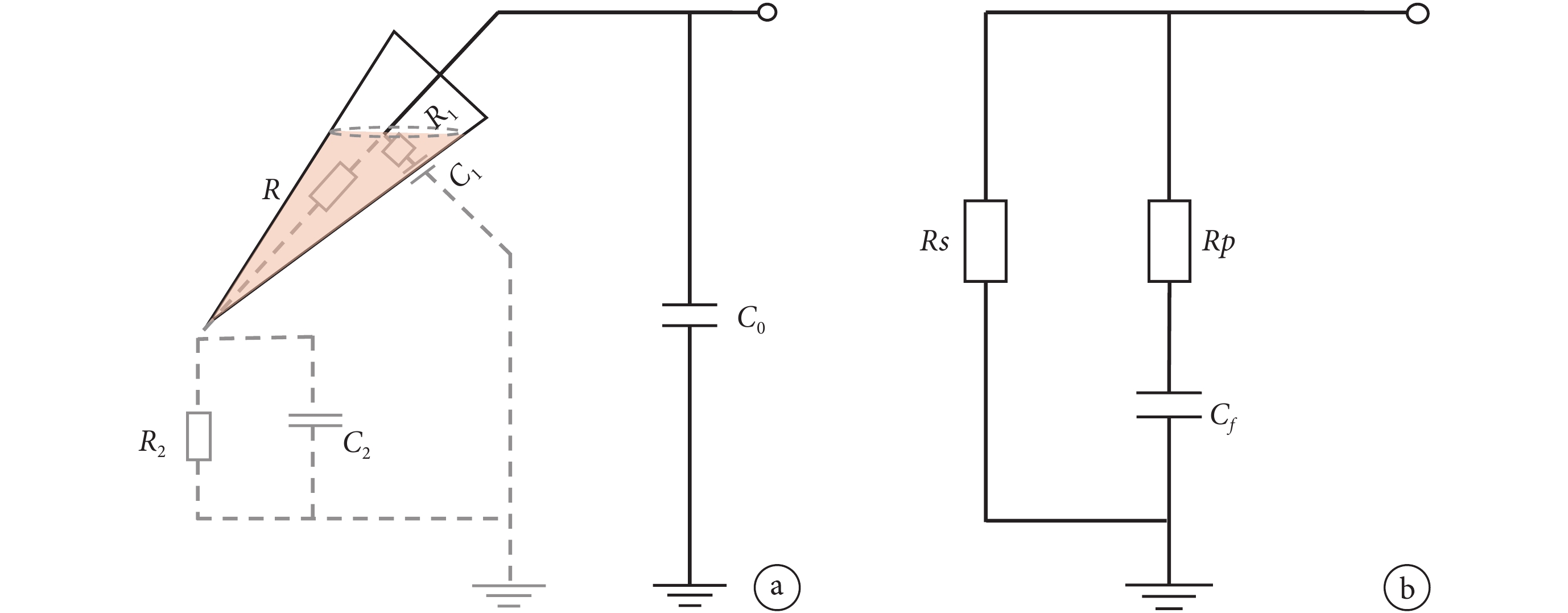
快電容主要來自浴液內的微電極自身、電極與細胞之間和電極與細胞浴液之間的分布電容，以及浴液外導線部分的分布電容。我們的溫度實驗只改變了浴液的溫度，對浴液外的導電回路無影響，因此傳統膜片鉗放大器等效電路[20,23-24]中將快電容僅僅等效為單純的電容來處理是有缺陷的，而瞿安連課題組[25]在設計和改進補償電路時提出的把快電容等效為阻容并聯電路更符合這種情形。文獻[25]中給出如圖 3a 所示不考慮溫度特性的膜片鉗回路，圖中 C0 為浴液之外的電學回路，C1 為電極與細胞浴液之間的跨壁分布電容，C2 為電極與細胞浴液通過尖端的分布電容，R1 為玻璃微電極徑向電阻及溶液電阻，R2 為水槽內細胞浴液等效電阻，而 R 為微電極軸向串聯電阻。
在此基礎上，本論文提出了一個考慮溫度變化的簡化等效回路如圖3 b 所示，以方便描述浴液的溫度特性。圖中略去了圖3 a 中浴液外的分布電容 C0，因為包括探頭中的運算放大器及其電路連線的這一部分分布電容在實驗中是與浴液溫度無關的。將其他參數簡化為由溫度相關的等效電阻，分別為穩態阻抗 Rs、瞬態阻抗 Rp及等效快電容 Cf，并在實驗的基礎上，確定這些參數的典型值及溫度依賴特性。
2 等效電路中參數確定
2.1 穩態阻抗 Rs、瞬態阻抗 Rp 及其溫度特性
細胞浴液是一種電阻隨溫度改變而改變的良導體，已有研究對微電極內溶液對溫度的依賴規律進行了測量[26]，快電容的充放電時間常數也與浴液回路電阻有關系。因此我們首先分析了一定溫度下電路電流的階躍響應，以計算出浴液的穩態阻抗 Rs 和瞬態阻抗 Rp，再結合溫度的變化得到這些阻抗的溫度特性。
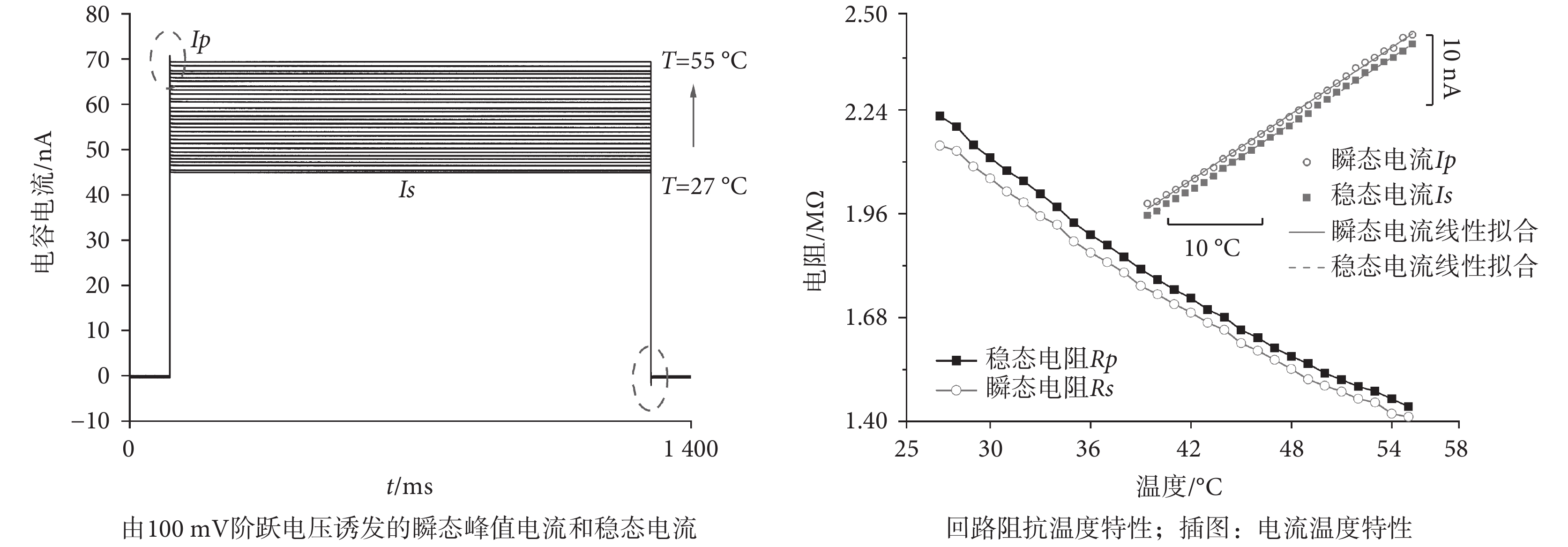
圖 4 是浴液溫度從 27.0 ℃ 增加到 55.0 ℃ 時，在同一膜片鉗階躍電壓下測得的膜片鉗玻璃微電極在接地浴液中構成的回路電流，設置脈寬為 1 s 可以避免因為激勵電壓而引入歐姆熱效應對實驗產生干擾。實驗中測得的電流包括快電容瞬態充電與放電電流 Ip（虛線）以及穩態電流 Is。分別以二者為測試值繪制 Ip、Is 隨溫度的變化關系，通過線性擬合得到溫升和 Ip、Is 改變值的關系如圖 4 內插圖所示（R2 > 0.99）。浴液溫度每增加 1.0 ℃，100 mV 的電壓脈沖引出的峰值快電容電流 Ip 增大 0.890 nA、穩態電流 Is 增大 0.895 nA。同時在相同激勵電壓下，根據測得電流值及圖 3b 等效回路，由歐姆定律可以計算出瞬態阻抗 Rp 和穩態阻抗 Rs。二者在溫度升高的情形下均呈現出隨溫度升高而減小的趨勢，且減小速率隨溫升增大而略有減小。
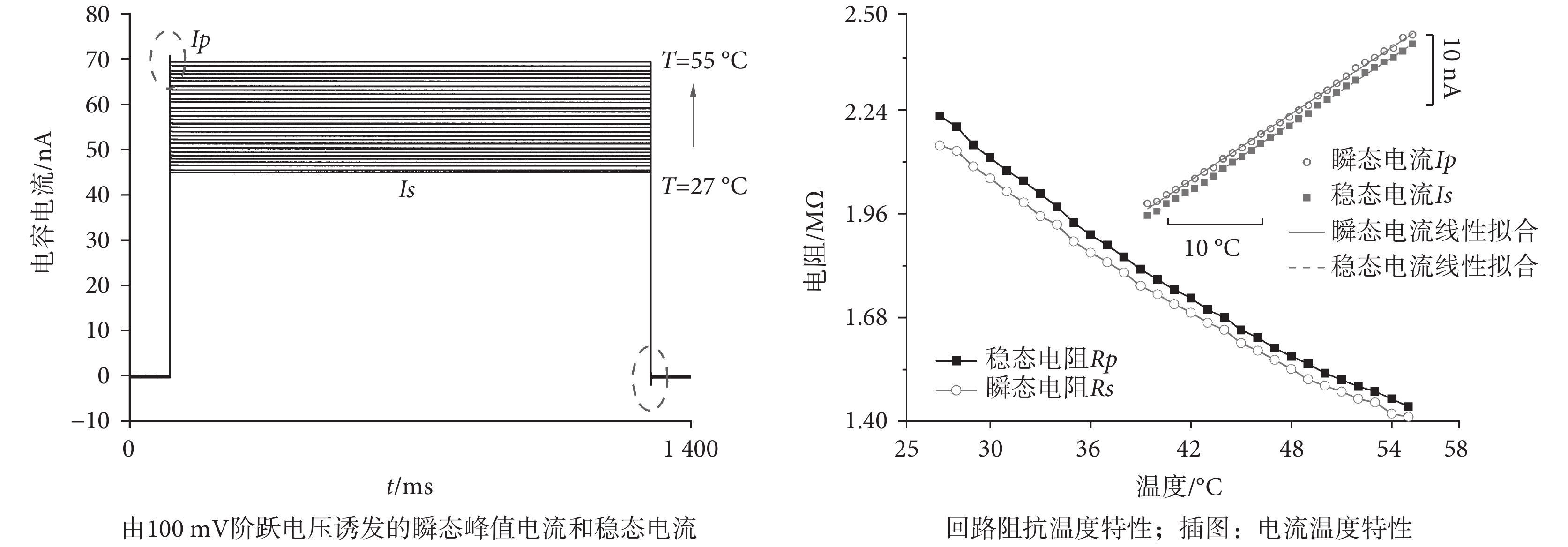圖4
在相同激勵電壓作用下不同溫度條件測得瞬態峰值與穩態電流
Figure4.
Peak transient and steady-state currents under the different temperatures with the same excitation voltages
為進一步驗證等效電路的有效性，對比使用脈沖上、下沿快電容的峰值計算的 Rp 結果。二者計算出的回路電阻 Rp 值一致（見表 1），因此在目前電極拉制儀和導線布置的情形下選擇一個溫度依賴的等效電阻描述快電容回路是合適的。瞬態阻抗 Rp 和穩態阻抗 Rs 隨溫度產生的變化計算結果列于表 1 中。因為玻璃微電極尖端的直徑僅為 1～2 μm，通過標定后電流的變化量也被用來測量浴液的實際溫度，即空電極測溫方法。尤其在對溫度改變響應比較快的情形下，這種方法有很高的空間選擇性與極快的時間分辨率。
表1
穩態阻抗 Rs 和瞬態阻抗 Rp 的溫度特性
Table1.
Temperature characteristics of peak transient and steady-state resistances (Rp, Rs)
影響回路阻值的因素一方面是玻璃具有 10?7/℃ 量級的膨脹系數，溫度升高會產生約 10?6量級的微小膨脹；另一方面是電解質溶液的電離程度隨溫度升高而增大、擔負導電能力的離子數目增加，這一增強效果強于溫升引起的離子間碰撞概率，因此液體的溫度越高則電阻率越小。考慮玻璃微電極為圓錐形，其理論電阻值正比于所處溶液電阻率[27]
 |
其中 ρ 是溶液電阻率，l 為微電極浸入溶液的長度，rs、rt 分別為遠端、尖端開口半徑，c 為溶液比熱容，φ 是尖端夾角。以 170 mmol/L 的 NaCl 溶液為例[28]，溫度由 27.0 ℃ 升至 55.0 ℃ 時電阻率減少了 1.5 Ω·m，因此實驗中使用的包含 150 mmol/L 的 NaCl 及多種其他電解質的標準細胞外液的電阻率也隨溫度升高而降低。理論電阻值在溫度升高情況下隨電阻率降低而發生兆歐姆量級的減小，與我們的記錄到的 0.7～0.8 MΩ 的降低相匹配，也說明阻值減小主要源于玻璃微電極內充灌的浴液。
2.2 等效快電容 Cf 及其溫度特性
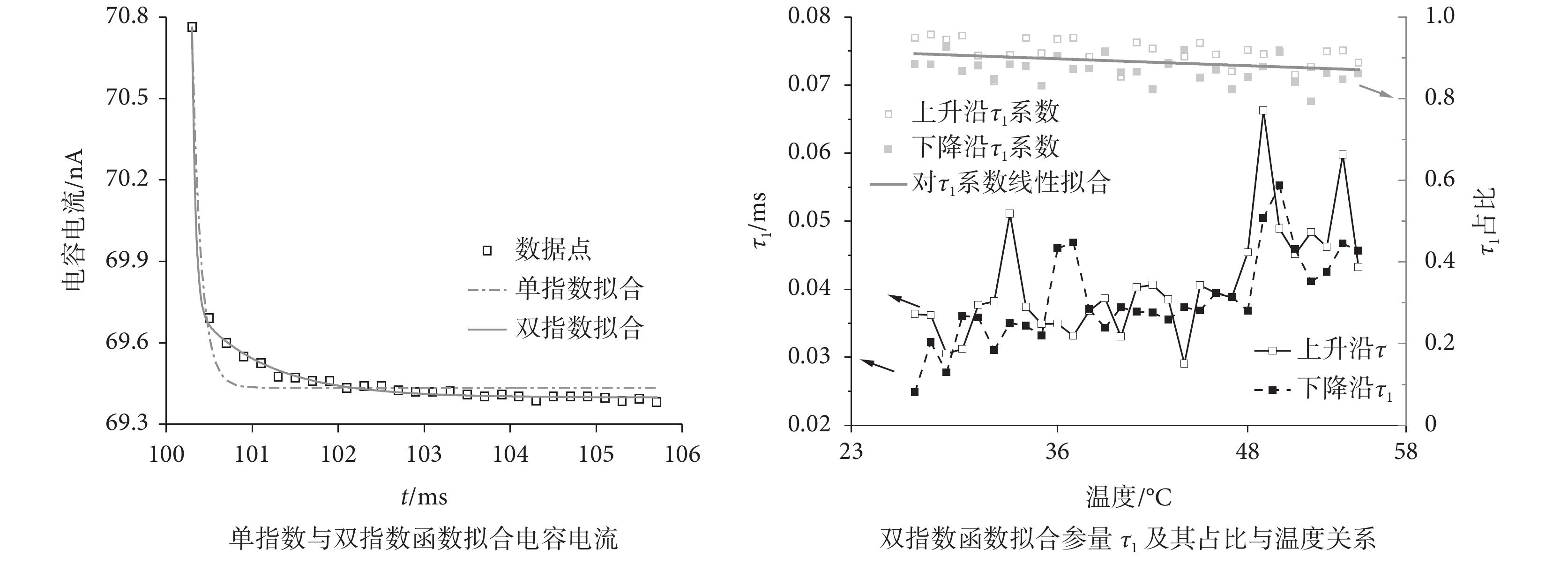
將階躍電壓引起的由快電容充放電決定的電流 Ip 放大于圖 5，以 55.0 ℃ 時電壓上升沿誘發的快電容充放電電流 Ic 為例，分別使用單指數和雙指數函數擬合，式（3）為雙指數擬合函數
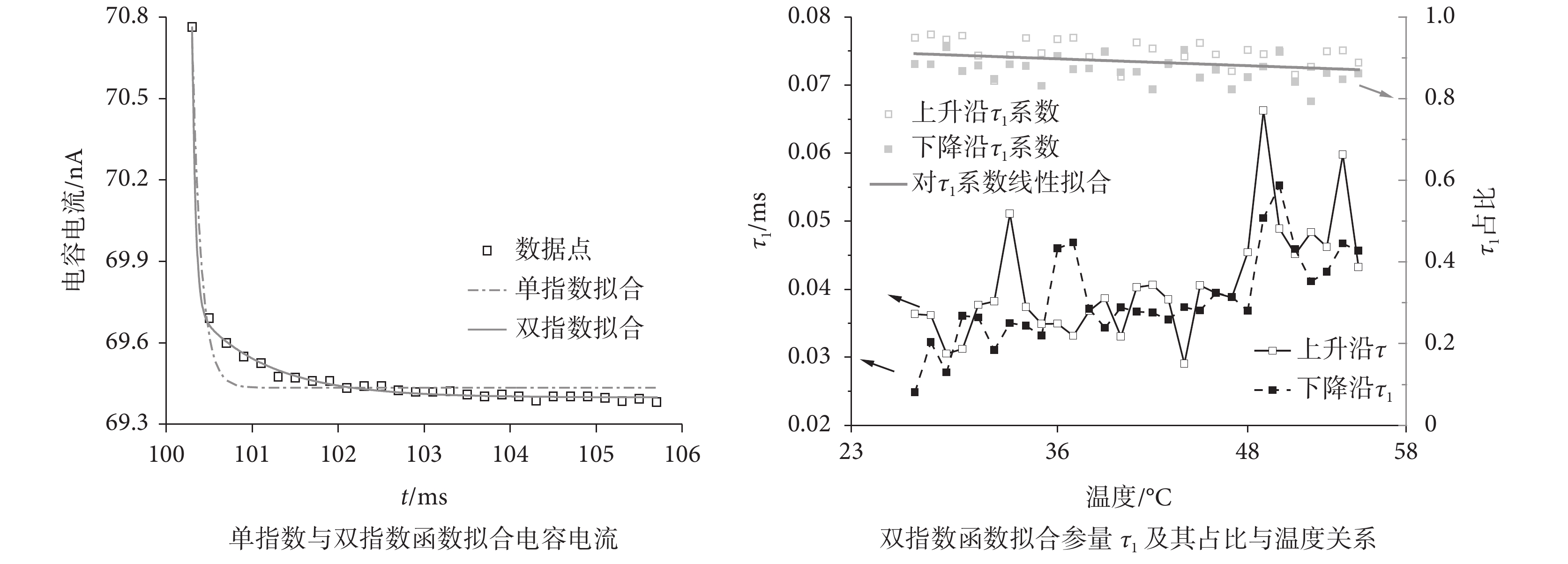圖5
快電容充放電電流擬合及雙指數擬合參數溫度特性
Figure5.
Fast capacitive currents’ fittings and the parameters temperature characteristic of double exponential fitting
 |
其中 A1、A2 為雙指數參數 τ1、τ2 對應的系數，A1/（A1+A2）、A2/（A1+A2）作為兩部分各占的比例。圖 5 為擬合參量與溫度的關系，其中 τ1 所描述組分為平均占比達 0.89 的主要組分，其值及溫度依賴特性與單指數擬合所得到的參數相似，平均每攝氏度增大 0.6 μs。在整個升溫過程中，τ1 隨溫度升高而增大（median（IQR）= 0.039（0.007）ms），該部分占比隨溫度升高而線性減小約 0.14%/℃（見圖 5）；τ2（median（IQR）= 1.304（0.195）ms）在溫升過程中比較穩定，其占比隨溫度略微增大約 0.14%/℃。電壓脈沖的上升、下降沿處兩個擬合方式的時間常數參量有相同的溫度斜率，這表明使用一個等效電容來近似分布電容是合適的。但對快電容放電曲線擬合時間常數參數隨溫度增加增大而回路電阻減小的現象，無法在電容值恒定的假設下進行解釋，因此我們提出快電容與溫度具有相關性。
前述單、雙指數擬合中的時間常數參量比經驗值大 1～2 個量級，這是由于等效快電容放電電流是由多個分布電容逐次、有延遲的放電曲線的疊加而成，而擬合時考慮起始放電時間是相同的，因此直接用于分析等效快電容是非常不準確的。根據分布電容自身特點及圖 3b 等效電路，選取放電特性曲線對應的電荷量作為分析參量來計算快電容的變化量，即：
 |
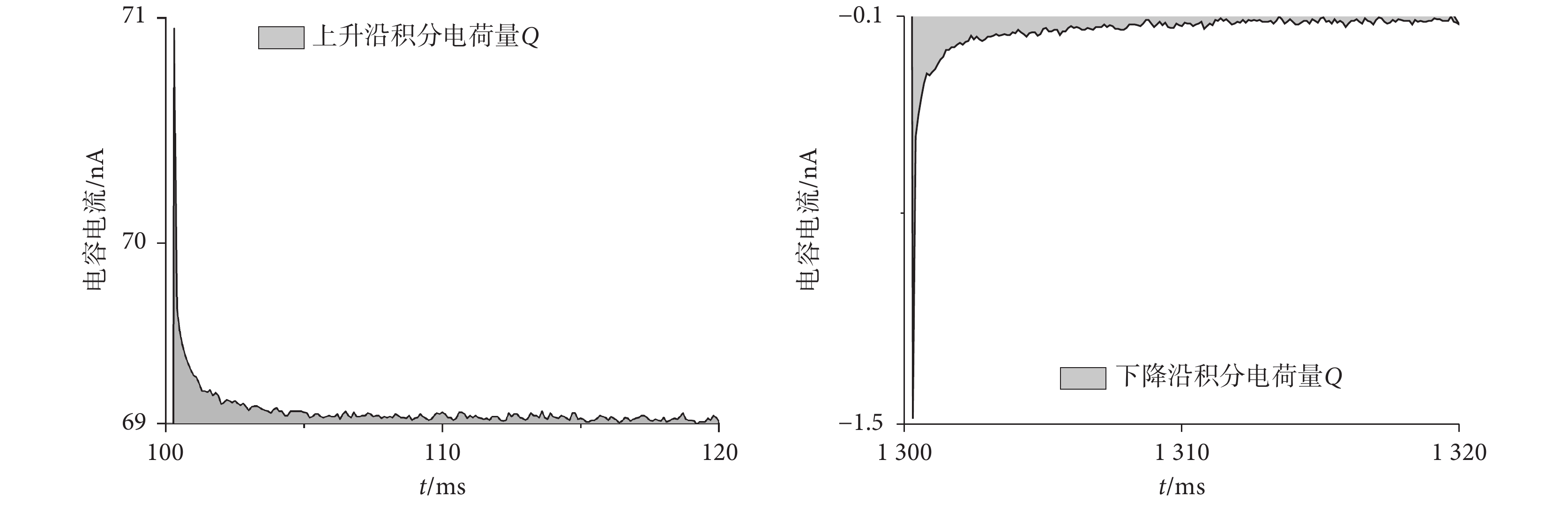
上式中電荷量 Q 包含了 N 個分布電容 Ci 大小及放電延遲情況，Ai、ti、τi 分別為對應的 Ci（i = 1, 2,
, N）系數、起始放電時間以及時間常數參量。選取相關系數更大的雙指數擬合函數（單指數 R2 = 0.915，雙指數 R2 = 0.997）作為近似被積函數，積分區間選取電容放電電流峰值位置至趨于穩態值處。其中上升、下降沿處積分起止位置分別為 100.3～105.7 和 1300.3～1305.7 ms 以排除積分區間的影響進行比較（見圖 6）。
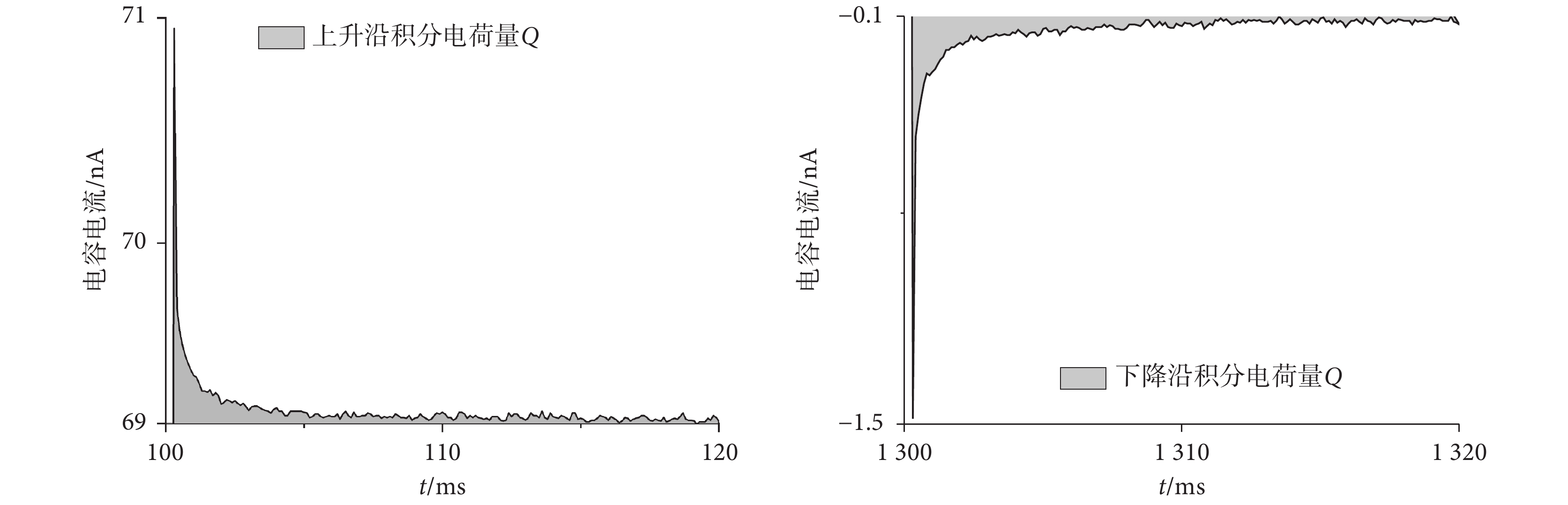圖6
55.0 ℃ 浴液條件下，階躍電壓誘發的電容電流積分電荷 Q
Figure6.
Charge Q integrated by step voltage induced capacitive current at 55.0 ℃
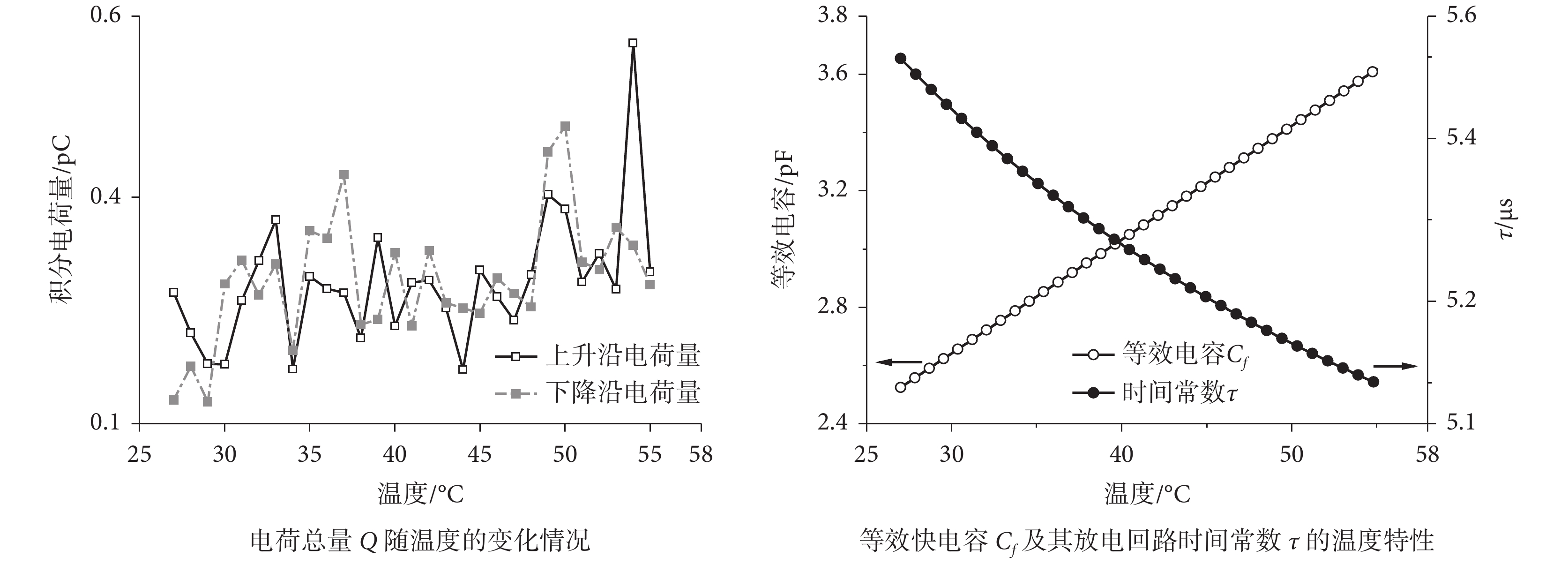
積分結果如圖 7 所示，Q 均隨溫度震蕩、緩慢增大，平均增速為 3.91 × 10?3 pC/℃，據此對電容增量 ΔC（pF/℃）進行估算
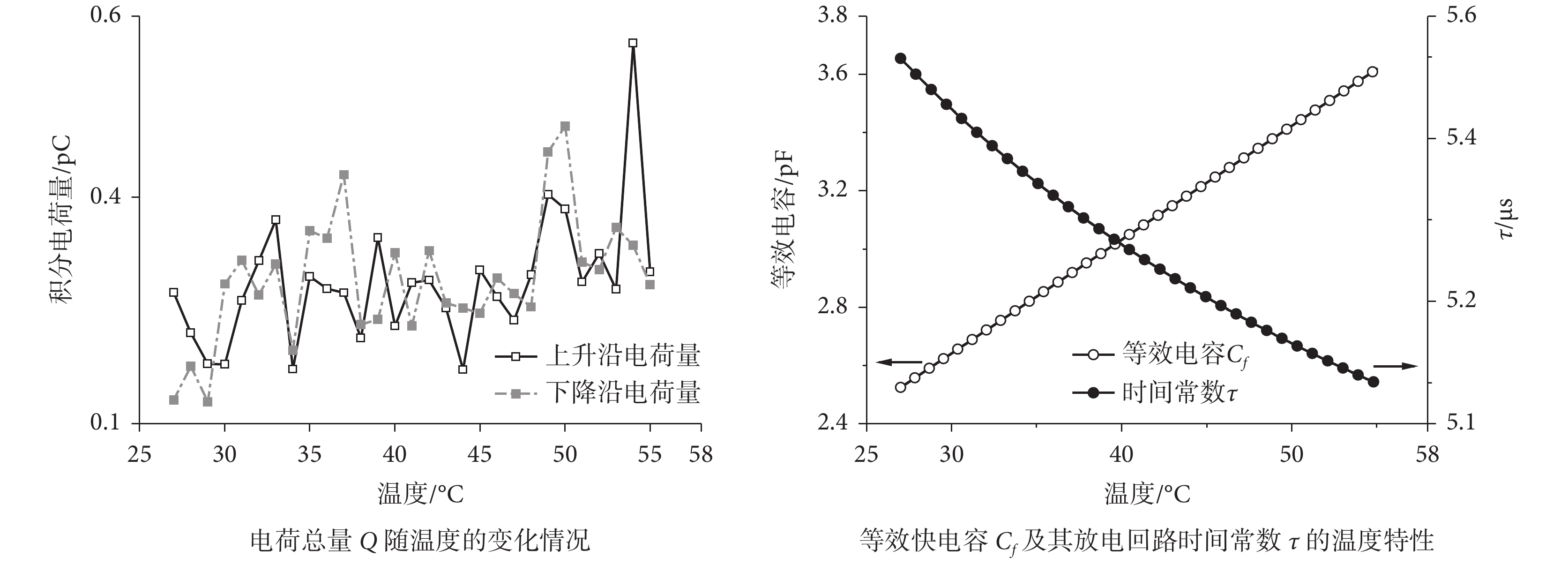圖7
快電容等效回路中參數的溫度特性（電荷總量 Q、等效快電容 Cf 及其時間常數 τ）
Figure7.
Equivalent fast capacitance circuit parameters’ temperature characteristics (Charge Q, equivalent fast capacitance Cf and its time constant τ)
 |
其中 ΔQ = 3.91 × 10?3 pC/℃ 為每攝氏度電荷增量，V 為 100 mV 脈沖電壓。由此我們得到電容每攝氏度增大約 3.91 × 10?2 pF。根據電荷量的線性擬合微電極初始電容為 2.524 2 pF，與經驗快電容值相當[23]，這表明我們計算的等效電容值是合適的。由于影響微電極跨壁電容的參數中除介電常數外均已固定，而介電常數每攝氏度僅增大2.25 × 10?3%左右[20]，因此等效快電容是由微電極跨壁電容和浴液中分布電容共同構成，且溫升通過浴液改變快電容。
為了進一步得出等效快電容的溫度特性，將 Cf 與快電容回路電阻 Rp 乘積得到等效電路的時間常數 τ 并繪于圖 7 中。隨著等效電容由 2.524 2 pF 增大至 3.619 0 pF 過程中（增量 1.094 8 pF），τ 在 28.0 ℃ 溫升中逐漸由 5.498 μs 以減小速度降低的趨勢降至 5.110 μs，整體降幅 0.388 μs。對比快電容放電回路中 Rp 變化，溫升主要通過玻璃微電極內充灌的浴液阻值影響了放電時間常數。
按照這樣的處理，重新計算圖 3b 等效電路中 Cf 的溫度特性，并將 27.0 ℃ 和 55.0 ℃ 時等效電路參數的典型值及其與溫度變化量 ΔT 的關系匯總參數列于表 2中。
3 討論
本文研究了膜片鉗實驗中玻璃微電極形成的分布式快電容的溫度特性，并給出了相應的等效電路和典型參數。由于玻璃微電極及溶液中的分布電容電阻十分復雜，本論文給出了包含溫度依賴的兩個等效電阻和一個等效電容組成的等效電路，如圖 3b 所示。
等效電路各參數計算及擬合如表 2 所示，在 28.0 ℃ 的溫度變化中 Rs 和 Rp 兩個電阻分別減小約 0.73 MΩ 及 0.78 MΩ，同時快電容 Cf 以 3.91 × 10?2 pF/℃ 的速度增大了約 1.1 pF。這樣溫度特性引入了約 0.4 μs 的時間常數 τ 減小量。對比直接擬合放電曲線得到的時間常數 τ1、τ2，不僅數值遠大于 τ 且其值與溫度正相關。結合快電容是由多個分布電容組成的特點，τ1 的誤差來源于忽略了多個分布電容依次、有延遲的放電特性而直接將其視作同時放電而擬合，因此在使用包含各分布電容放電特性的電荷量 Q 計算 τ 時得到的結果與經驗值相符，其值約為 5.5 μs。我們的分析表明在溫升實驗中，溫度改變浴液電阻并通過浴液改變等效快電容，回路 τ 受阻值部分影響較大，主要決定于玻璃微電極內溶液的阻抗。
本論文的結果可以應用到一些物理熱效應相關的細胞研究當中。比如自 2012 年 Shapiro 等[13]提出細胞膜響應熱效應的電容機制后，關于膜電容的實驗和理論研究成為熱點[29]。在使用膜片鉗進行溫度改變的相關細胞實驗[30]研究時，我們估算 28 ℃ 溫升將導致約 1.1 pF 快電容變化。這對巨神經纖維、如平均電容為 200 nF 的卵母細胞[31]等的大細胞來說干擾較小，但對于自身僅為 7～12 pF 的小尺寸細胞[5,32]來說，此量級的快電容補償不徹底會極大地干擾其電生理特性的記錄[20]。
在另外一些體外實驗中，瞬時溫升速率可以達到 500 ℃/s[12]，并最終完成 40～50 ℃ 的溫度變化[5,17]，這時再將快電容視為定值會導致一定的偏差。因此我們的研究結果支持在使用膜片鉗進行熱伴隨研究時需考慮實驗過程中 Cf 的變化，并為伴隨溫度變化的細胞電生理研究提供了良好的參考。同時在進行膜片鉗快電容補償電路的設計與改進時，對時間常數的初值設定及搜索步長將直接決定能否成功、精確地補償，因此本文中給出的時間常數溫度特性對這類實驗中此參數的設定也提供了參考。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
引言
膜片鉗放大器是實現細胞電生理記錄的主要技術[1]，實驗中通過微米尺度的玻璃微電極負壓吸附細胞膜形成千兆歐級的封接電阻，從而實現對細胞膜選擇性的電學研究，可以對皮安培量級單個離子通道微弱電流進行精密測量。對如此微弱電流的檢測中，需要對細胞膜脂雙層形成的慢電容（slow capacitance，Cslow）[2]以及入液玻璃微電極、導線等引入的分布式快電容（fast capacitance，Cfast）進行補償。其中慢電容大小是細胞尺寸相關的幾皮法拉到幾微法拉量級，快電容的典型值為幾皮法拉量級。
一般來說，電容補償都是首先測量出電容的大小，然后由儀器發生一個大小相同、相位相反的補償電流來抵消電容電流。電容補償的效果取決于儀器發生補償電流與實際電容的差異程度，隨著膜片鉗軟件、硬件技術的高度成熟，電容補償在細胞環境不變的研究中已相當完善[2]。但實際應用膜片鉗實驗系統中有一類伴隨細胞外溶液溫度改變的研究，比如直接改變溫度以研究溫度敏感的離子通道[3-4]、光生物調節[5-8]、磁場調節[9-11]等調制細胞功能的研究。眾多實驗已經證實此類研究主要是以熱效應為基礎[12-15]，因此在這一類實驗中需要對快電容的溫度特性有更深入的認識，但目前的研究中往往缺少此類可靠參數描述。
2009 年 Qin 課題組[16]提出使用膜片鉗空電極測溫方法，由于無需預處理或外置儀器并且有高空間分辨率，其較熱電偶測量、熱敏感攝像機、掃描熱致體積膨脹、染料預處理記錄溫度相關的熒光強度等[17-19]測溫方法更方便且有效，常被應用于伴隨溫度變化的細胞電生理研究中。該方法是通過將玻璃微電極內充滿溶液，并基于恒溫標定得到其電阻與溶液溫度的關系。
本課題組是在使用這種方法的過程中，觀察到溶液溫度的升高可以改變快電容的時間特性。通常情況下，Cfast 被假定為常數僅在實驗前進行一次補償，在實驗過程中不再補償。基于實驗數據我們認為這一假設在熱伴隨實驗中并不成立，因此在溫度實驗中必須進行實時測量電容的自動補償，而一個切合實際的快電容等效電路是這個補償的關鍵，其難點在于快電容是分布式的。
本論文基于不同溫度下記錄到的快電容電流，提出了一個考慮溫度因素的分布式快電容等效電路，并分析了電路參數的溫度特性。使用膜片鉗進行生物信號記錄時，精準補償電容電流對記錄的準確性極為重要[20]，本文的結果將對溫度相關的電生理研究、優化補償電路及改進快電容補償算法的精度和速度具有參考價值。
1 快電容補償原理及實驗方法
1.1 快電容補償原理
分布式快電容是基于動態測量方法測得，即向目標電路輸入一個正弦交流信號，測量其輸入輸出響應后通過計算得到電容值，理論依據是動態電路分析的電容電流 Ic 來描述，即：
|
式中 U 為電容兩端電壓，R 為回路電阻，τ 為時間常數。圖 1 左側為德國 Heka 公司生產的 EPC-10 型膜片鉗補償快電容電流的原理圖。圖 1 右側為電路中電壓或電流信號，階躍電壓激勵作為輸入信號（圖 1a）輸入電路后，膜片鉗放大器中的補償電路首先測量出快電容電流的大小（圖 1b），然后輸出一個大小相同、相位相反的補償電流（圖 1c 虛線）來抵消由于快電容的存在而產生的小幅過沖電流，使最終輸出的電流如圖 1d 所示。在多數電生理實驗中，細胞鉗制都已完成的情形下，玻璃微電極、導線等都基本不變，此時快電容基本是一個常數。因此實驗前進行一次補償，系統就可以按照這個電容的幅值進行后續的補償，實現膜片鉗系統的高精度測量。
圖1
EPC-10 膜片鉗快電容補償原理
左：EPC-10 膜片鉗快電容補償等效電路。右：回路中電壓/電流：a. 輸入激勵電壓；b. 補償前的回路電流；c. 紅色虛線所示為補償電流；d. 補償后的輸出電流
Figure1. The principle of EPC-10 patch clamp fast capacitive compensationLeft: EPC-10 patch clamp fast capacitive compensation equivalent circuit. Right: voltages/currents throughout the circuit: a. input voltage; b. circuit current before compensation; c. compensation current in patch clamp amplifier; d. output current after being compensated
將膜片鉗放大器的補償界面設置為自動補償，其補償信號的發生是基于上一次測量的集總參數來進行。這個集總參數極大地依賴于一個與快電容相關的等效電路。通常電路是不考慮溫度改變情況的，即視由玻璃微電極和導線形成的分布式電容為常數。而當溫度改變時快電容就被分為浴液溫度相關和不相關的兩部分，由于與浴液溫度直接相關的玻璃微電極入液部分的變化，可能出現過補償（補償電容電流大于實際電容電流）或補償不完全（補償電容電流小于實際電容電流）的情況，會極大地干擾正常電生理信號的記錄。因此，下面的實驗將研究溫度相關的快電容特性。
1.2 實驗裝置
圖 2 為本實驗采用 EPC-10 單通道膜片鉗放大器（HEKA，德國）研究快電容溫度特性的實驗裝置，與用于進行空電極測溫的裝置相同。使用電極拉制儀將玻璃毛細管拉制為電阻為 3～5 MΩ 的玻璃微電極，將尖端為微米量級的空電極充灌標準細胞外液，構成膜片鉗的測量電極，并與細胞外溶液（浴液）中的接地線形成回路。施加的刺激電壓 V 幅值選為 100 mV，電壓時程為 1 s（時間精度為 0.1 ms）。玻璃微電極被固定在微米精度的微操縱器上，在實驗過程中不進行移動。
圖2
研究快電容溫度特性的實驗裝置
Figure2.
The setup for studying the temperature effect on the fast capacitance
使用恒溫控制器（TC-324B，Warner，美國）控制培養皿中的浴液溫度，參考相關實驗[13,21-22]選擇常見實驗溫度 27.0～55.0 ℃ 并以 1.0 ℃ 遞增，施加 100 mV 激勵電壓。通過膜片鉗測量在相同電壓激勵條件下、不同浴液溫度下的輸出電流，研究快電容的溫度特性。EPC-10 膜片鉗放大器選擇快電容補償方式為手動補償，在開始記錄之前手動補償一次，溫度變化過程中不進行快電容補償操作。
標準細胞外液（mmol/L）：NaCl 150，KCl 5，MgCl2 1.1，CaCl2 2.6，HEPES 10，葡萄糖 10，CdCl2 0.2，使用 Tris-HCl 調節 pH 值至 7.4。
1.3 膜片鉗測溫等效電路
快電容主要來自浴液內的微電極自身、電極與細胞之間和電極與細胞浴液之間的分布電容，以及浴液外導線部分的分布電容。我們的溫度實驗只改變了浴液的溫度，對浴液外的導電回路無影響，因此傳統膜片鉗放大器等效電路[20,23-24]中將快電容僅僅等效為單純的電容來處理是有缺陷的，而瞿安連課題組[25]在設計和改進補償電路時提出的把快電容等效為阻容并聯電路更符合這種情形。文獻[25]中給出如圖 3a 所示不考慮溫度特性的膜片鉗回路，圖中 C0 為浴液之外的電學回路，C1 為電極與細胞浴液之間的跨壁分布電容，C2 為電極與細胞浴液通過尖端的分布電容，R1 為玻璃微電極徑向電阻及溶液電阻，R2 為水槽內細胞浴液等效電阻，而 R 為微電極軸向串聯電阻。
在此基礎上，本論文提出了一個考慮溫度變化的簡化等效回路如圖3 b 所示，以方便描述浴液的溫度特性。圖中略去了圖3 a 中浴液外的分布電容 C0，因為包括探頭中的運算放大器及其電路連線的這一部分分布電容在實驗中是與浴液溫度無關的。將其他參數簡化為由溫度相關的等效電阻，分別為穩態阻抗 Rs、瞬態阻抗 Rp及等效快電容 Cf，并在實驗的基礎上，確定這些參數的典型值及溫度依賴特性。
2 等效電路中參數確定
2.1 穩態阻抗 Rs、瞬態阻抗 Rp 及其溫度特性
細胞浴液是一種電阻隨溫度改變而改變的良導體，已有研究對微電極內溶液對溫度的依賴規律進行了測量[26]，快電容的充放電時間常數也與浴液回路電阻有關系。因此我們首先分析了一定溫度下電路電流的階躍響應，以計算出浴液的穩態阻抗 Rs 和瞬態阻抗 Rp，再結合溫度的變化得到這些阻抗的溫度特性。
圖 4 是浴液溫度從 27.0 ℃ 增加到 55.0 ℃ 時，在同一膜片鉗階躍電壓下測得的膜片鉗玻璃微電極在接地浴液中構成的回路電流，設置脈寬為 1 s 可以避免因為激勵電壓而引入歐姆熱效應對實驗產生干擾。實驗中測得的電流包括快電容瞬態充電與放電電流 Ip（虛線）以及穩態電流 Is。分別以二者為測試值繪制 Ip、Is 隨溫度的變化關系，通過線性擬合得到溫升和 Ip、Is 改變值的關系如圖 4 內插圖所示（R2 > 0.99）。浴液溫度每增加 1.0 ℃，100 mV 的電壓脈沖引出的峰值快電容電流 Ip 增大 0.890 nA、穩態電流 Is 增大 0.895 nA。同時在相同激勵電壓下，根據測得電流值及圖 3b 等效回路，由歐姆定律可以計算出瞬態阻抗 Rp 和穩態阻抗 Rs。二者在溫度升高的情形下均呈現出隨溫度升高而減小的趨勢，且減小速率隨溫升增大而略有減小。
圖4
在相同激勵電壓作用下不同溫度條件測得瞬態峰值與穩態電流
Figure4.
Peak transient and steady-state currents under the different temperatures with the same excitation voltages
為進一步驗證等效電路的有效性，對比使用脈沖上、下沿快電容的峰值計算的 Rp 結果。二者計算出的回路電阻 Rp 值一致（見表 1），因此在目前電極拉制儀和導線布置的情形下選擇一個溫度依賴的等效電阻描述快電容回路是合適的。瞬態阻抗 Rp 和穩態阻抗 Rs 隨溫度產生的變化計算結果列于表 1 中。因為玻璃微電極尖端的直徑僅為 1～2 μm，通過標定后電流的變化量也被用來測量浴液的實際溫度，即空電極測溫方法。尤其在對溫度改變響應比較快的情形下，這種方法有很高的空間選擇性與極快的時間分辨率。
表1
穩態阻抗 Rs 和瞬態阻抗 Rp 的溫度特性
Table1.
Temperature characteristics of peak transient and steady-state resistances (Rp, Rs)
影響回路阻值的因素一方面是玻璃具有 10?7/℃ 量級的膨脹系數，溫度升高會產生約 10?6量級的微小膨脹；另一方面是電解質溶液的電離程度隨溫度升高而增大、擔負導電能力的離子數目增加，這一增強效果強于溫升引起的離子間碰撞概率，因此液體的溫度越高則電阻率越小。考慮玻璃微電極為圓錐形，其理論電阻值正比于所處溶液電阻率[27]
|
其中 ρ 是溶液電阻率，l 為微電極浸入溶液的長度，rs、rt 分別為遠端、尖端開口半徑，c 為溶液比熱容，φ 是尖端夾角。以 170 mmol/L 的 NaCl 溶液為例[28]，溫度由 27.0 ℃ 升至 55.0 ℃ 時電阻率減少了 1.5 Ω·m，因此實驗中使用的包含 150 mmol/L 的 NaCl 及多種其他電解質的標準細胞外液的電阻率也隨溫度升高而降低。理論電阻值在溫度升高情況下隨電阻率降低而發生兆歐姆量級的減小，與我們的記錄到的 0.7～0.8 MΩ 的降低相匹配，也說明阻值減小主要源于玻璃微電極內充灌的浴液。
2.2 等效快電容 Cf 及其溫度特性
將階躍電壓引起的由快電容充放電決定的電流 Ip 放大于圖 5，以 55.0 ℃ 時電壓上升沿誘發的快電容充放電電流 Ic 為例，分別使用單指數和雙指數函數擬合，式（3）為雙指數擬合函數
圖5
快電容充放電電流擬合及雙指數擬合參數溫度特性
Figure5.
Fast capacitive currents’ fittings and the parameters temperature characteristic of double exponential fitting
|
其中 A1、A2 為雙指數參數 τ1、τ2 對應的系數，A1/（A1+A2）、A2/（A1+A2）作為兩部分各占的比例。圖 5 為擬合參量與溫度的關系，其中 τ1 所描述組分為平均占比達 0.89 的主要組分，其值及溫度依賴特性與單指數擬合所得到的參數相似，平均每攝氏度增大 0.6 μs。在整個升溫過程中，τ1 隨溫度升高而增大（median（IQR）= 0.039（0.007）ms），該部分占比隨溫度升高而線性減小約 0.14%/℃（見圖 5）；τ2（median（IQR）= 1.304（0.195）ms）在溫升過程中比較穩定，其占比隨溫度略微增大約 0.14%/℃。電壓脈沖的上升、下降沿處兩個擬合方式的時間常數參量有相同的溫度斜率，這表明使用一個等效電容來近似分布電容是合適的。但對快電容放電曲線擬合時間常數參數隨溫度增加增大而回路電阻減小的現象，無法在電容值恒定的假設下進行解釋，因此我們提出快電容與溫度具有相關性。
前述單、雙指數擬合中的時間常數參量比經驗值大 1～2 個量級，這是由于等效快電容放電電流是由多個分布電容逐次、有延遲的放電曲線的疊加而成，而擬合時考慮起始放電時間是相同的，因此直接用于分析等效快電容是非常不準確的。根據分布電容自身特點及圖 3b 等效電路，選取放電特性曲線對應的電荷量作為分析參量來計算快電容的變化量，即：
|
上式中電荷量 Q 包含了 N 個分布電容 Ci 大小及放電延遲情況，Ai、ti、τi 分別為對應的 Ci（i = 1, 2,, N）系數、起始放電時間以及時間常數參量。選取相關系數更大的雙指數擬合函數（單指數 R2 = 0.915，雙指數 R2 = 0.997）作為近似被積函數，積分區間選取電容放電電流峰值位置至趨于穩態值處。其中上升、下降沿處積分起止位置分別為 100.3～105.7 和 1300.3～1305.7 ms 以排除積分區間的影響進行比較（見圖 6）。
圖6
55.0 ℃ 浴液條件下，階躍電壓誘發的電容電流積分電荷 Q
Figure6.
Charge Q integrated by step voltage induced capacitive current at 55.0 ℃
積分結果如圖 7 所示，Q 均隨溫度震蕩、緩慢增大，平均增速為 3.91 × 10?3 pC/℃，據此對電容增量 ΔC（pF/℃）進行估算
圖7
快電容等效回路中參數的溫度特性（電荷總量 Q、等效快電容 Cf 及其時間常數 τ）
Figure7.
Equivalent fast capacitance circuit parameters’ temperature characteristics (Charge Q, equivalent fast capacitance Cf and its time constant τ)
|
其中 ΔQ = 3.91 × 10?3 pC/℃ 為每攝氏度電荷增量，V 為 100 mV 脈沖電壓。由此我們得到電容每攝氏度增大約 3.91 × 10?2 pF。根據電荷量的線性擬合微電極初始電容為 2.524 2 pF，與經驗快電容值相當[23]，這表明我們計算的等效電容值是合適的。由于影響微電極跨壁電容的參數中除介電常數外均已固定，而介電常數每攝氏度僅增大2.25 × 10?3%左右[20]，因此等效快電容是由微電極跨壁電容和浴液中分布電容共同構成，且溫升通過浴液改變快電容。
為了進一步得出等效快電容的溫度特性，將 Cf 與快電容回路電阻 Rp 乘積得到等效電路的時間常數 τ 并繪于圖 7 中。隨著等效電容由 2.524 2 pF 增大至 3.619 0 pF 過程中（增量 1.094 8 pF），τ 在 28.0 ℃ 溫升中逐漸由 5.498 μs 以減小速度降低的趨勢降至 5.110 μs，整體降幅 0.388 μs。對比快電容放電回路中 Rp 變化，溫升主要通過玻璃微電極內充灌的浴液阻值影響了放電時間常數。
按照這樣的處理，重新計算圖 3b 等效電路中 Cf 的溫度特性，并將 27.0 ℃ 和 55.0 ℃ 時等效電路參數的典型值及其與溫度變化量 ΔT 的關系匯總參數列于表 2中。
3 討論
本文研究了膜片鉗實驗中玻璃微電極形成的分布式快電容的溫度特性，并給出了相應的等效電路和典型參數。由于玻璃微電極及溶液中的分布電容電阻十分復雜，本論文給出了包含溫度依賴的兩個等效電阻和一個等效電容組成的等效電路，如圖 3b 所示。
等效電路各參數計算及擬合如表 2 所示，在 28.0 ℃ 的溫度變化中 Rs 和 Rp 兩個電阻分別減小約 0.73 MΩ 及 0.78 MΩ，同時快電容 Cf 以 3.91 × 10?2 pF/℃ 的速度增大了約 1.1 pF。這樣溫度特性引入了約 0.4 μs 的時間常數 τ 減小量。對比直接擬合放電曲線得到的時間常數 τ1、τ2，不僅數值遠大于 τ 且其值與溫度正相關。結合快電容是由多個分布電容組成的特點，τ1 的誤差來源于忽略了多個分布電容依次、有延遲的放電特性而直接將其視作同時放電而擬合，因此在使用包含各分布電容放電特性的電荷量 Q 計算 τ 時得到的結果與經驗值相符，其值約為 5.5 μs。我們的分析表明在溫升實驗中，溫度改變浴液電阻并通過浴液改變等效快電容，回路 τ 受阻值部分影響較大，主要決定于玻璃微電極內溶液的阻抗。
本論文的結果可以應用到一些物理熱效應相關的細胞研究當中。比如自 2012 年 Shapiro 等[13]提出細胞膜響應熱效應的電容機制后，關于膜電容的實驗和理論研究成為熱點[29]。在使用膜片鉗進行溫度改變的相關細胞實驗[30]研究時，我們估算 28 ℃ 溫升將導致約 1.1 pF 快電容變化。這對巨神經纖維、如平均電容為 200 nF 的卵母細胞[31]等的大細胞來說干擾較小，但對于自身僅為 7～12 pF 的小尺寸細胞[5,32]來說，此量級的快電容補償不徹底會極大地干擾其電生理特性的記錄[20]。
在另外一些體外實驗中，瞬時溫升速率可以達到 500 ℃/s[12]，并最終完成 40～50 ℃ 的溫度變化[5,17]，這時再將快電容視為定值會導致一定的偏差。因此我們的研究結果支持在使用膜片鉗進行熱伴隨研究時需考慮實驗過程中 Cf 的變化，并為伴隨溫度變化的細胞電生理研究提供了良好的參考。同時在進行膜片鉗快電容補償電路的設計與改進時，對時間常數的初值設定及搜索步長將直接決定能否成功、精確地補償，因此本文中給出的時間常數溫度特性對這類實驗中此參數的設定也提供了參考。
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
