心音自動分類技術在先天性心臟病的早期診斷中占有重要地位。本文在不依賴對心音按心動周期進行準確分割的基礎上,提出一種基于子帶包絡特征和卷積神經網絡的心音分類算法。首先對心音信號進行分幀,其次用伽馬通濾波器組對幀級心音信號進行濾波從而得到子帶信號,然后用希爾伯特變換提取子帶包絡并將經過后續處理的子帶包絡堆疊成特征圖,最后使用Ⅰ型與Ⅱ型卷積神經網絡進行分類,經實驗證明該特征在Ⅰ型卷積神經網絡上能達到較優效果。本文用采集的1 000例心音樣本對本文算法進行測試,測試結果表明,本文提出的算法對比其它同類算法的整體性能有明顯提升,期望通過本研究可為先心病的自動分類提供新的方法,并加快心音自動分類技術應用于實際篩查的進程。
引用本文: 王幸之, 楊宏波, 宗容, 潘家華, 王威廉. 基于子帶包絡和卷積神經網絡的心音分類算法. 生物醫學工程學雜志, 2021, 38(5): 969-978. doi: 10.7507/1001-5515.202012024 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
先天性心臟病(congenital heart disease,CHD)占所有先天性出生缺陷的近三分之一[1]。CHD危害極大,及早發現并進行醫療干預是降低患者死亡率的關鍵,因此盡早對兒童和青少年進行CHD篩查尤其重要。心音是由心房與心室的收縮和舒張、瓣膜運動、血流的相互作用引起。此外,還有一些由于心臟結構和功能缺陷所致的雜音[2]。心臟聽診是目前在篩查領域的一種重要手段,它依據心音與雜音的特點輔助臨床醫生進行診斷。但人類聽覺感知在分析心音中的隱藏信息方面存在局限性,有時醫生很難通過聽診來分析心音,從而影響心音診斷的準確性。
由于上述原因,近年來對心音的自動分析研究成為了人工智能在臨床應用的一個重要課題。心音圖(phonocardiogram,PCG)是借助電子聽診器采集得到心音信號的圖形表示,含有能反映心臟功能及心臟生理、病理的重要信息。因此可以通過分析PCG信號來診斷心血管疾病。本文研究目的在于提高心音自動分類技術和CHD篩查效率,降低CHD的死亡風險。
基于計算機的PCG信號分析流程可以總結為以下三個步驟:① 預處理;② 特征提取;③ 分類器的構建。本文研究的重點是PCG信號分析的特征提取部分。典型用于PCG信號分析的特征大致可分為以下幾類:時域特征、頻域特征、時頻域特征[3]。國內外有大量研究者長期將PCG信號的特征提取作為一個重要研究課題。Schmidt等[4]在5個不同頻段中采用了參數譜模型、瞬時頻率、倍頻程功率等方法提取頻譜特征,同時組合多個特征,最后評估得到受試者工作特性(receiver operating characteristic,ROC)曲線與坐標軸圍成的面積(area under curve,AUC)為0.73。Chen等[5]使用短時傅里葉變換(short-time Fourier transform,STFT)提取心音幅度譜,在39個測試樣本中取得了0.954 9的準確率。Zabihi等[6]從時域、頻域、時頻域提取了18個特征,例如梅爾頻率倒譜系數(mel-frequency cepstral coefficients,MFCC)、功率譜密度等,最后在測試集上得到0.859的準確率。Rubin等[7]利用卷積神經網絡(convolutional neural networks,CNN)對時頻域提取的MFCC特征進行訓練,最后測試準確率為0.848。Maknickas等[8]采用梅爾對數頻率系數(log mel-frequency spectral coefficients,MFSC)與CNN,在304例測試樣本上獲得了0.841 5的準確率。Kay等[9]將心動周期的時域特征、時頻域特征和復雜特征(例如頻譜熵、標準偏差等)利用主成分分析(principal component analysis,PCA)進行降維并融合特征,最后該算法在測試集上獲得了0.852的準確率。Hamidi等[10]利用MFCC和分形維數相結合對PCG信號進行分類,并在六個不同的數據集上進行測試,其中三個數據集中達到了0.92、0.81和0.98的準確率。
上述研究中,有些算法研究應用在心音分類上的準確率較高,但是離應用于機器智能輔助聽診階段還有差距。文獻[5]在少量的測試樣本中取得了高準確率,普適性有待驗證。文獻[6]和文獻[9]均提取了多種特征,但提取多種特征耗時高、計算復雜,并且實驗準確率還有待提升。文獻[4]和文獻[9]的算法在進行特征提取前都要對PCG信號進行準確地分割。然而在噪聲環境下很難準確地分割出基本心音,目前也沒有一個較好的方案來解決此問題[11]。文獻[4]利用與時間相關的隱馬爾可夫模型分割心音,但個體心音主成分存在差異,所以很難建立一個統一的模型去進行分析。文獻[9]是基于心電圖(electrocardiogram,ECG)信號對PCG信號進行分割,此方法需要對ECG信號和PCG信號進行同步記錄,但對于新生兒來說ECG信號采集比較困難[12]。對于CHD,能在嬰幼兒時期發現并及時治療,會提高患者存活率。但上述研究使用的數據集來源沒有大量涵蓋嬰幼兒,是否能適用于嬰幼兒的篩查還是個未知數。
針對以上問題,本文使用了一種基于子帶包絡的時頻特征提取方法,并搭建了兩種CNN模型對其驗證。該特征提取方法不需要對PCG信號進行準確分割,減少了計算量。本文在實驗中使用的數據集大部分針對低年齡階段的孩童,以求能在實際篩查中及時發現患者。
1 模型與方法
1.1 數據來源
本文研究所用的心音數據庫由實驗室研究團隊采集構建,其數據來源于云南省阜外心血管病醫院的臨床患者以及在云南省各地州開展CHD免費篩查救治活動時的兒童。作為數據采集來源的志愿者,其年齡限定在6個月至18歲,所有志愿者均簽署了知情同意書。本研究及所有數據均已通過云南大學人體研究材料倫理委員會以及云南省阜外心血管病醫院倫理委員會的審查并批準使用。數據庫中的每一例陽性病例都由心臟病專科醫生根據臨床聽診和超聲心動圖確認和記錄。本實驗室自行研發了一套PCG信號采集設備。采集設備為The ONE心音傳感器(Thinklabs Medical LLC,美國),其輸出為模擬音頻信號,采樣頻率(frequency of sample,Fs)為5 000 Hz,采集時長為20 s。
1.2 心音自動分類流程
在對心音進行分類前,需要對心音組成有個基本的了解。按照心音的產生時間和產生機制可以把一個心動周期分為:第一心音(S1)、第二心音(S2)、第三心音(S3)、第四心音(S4)[13],通常情況只能聽見S1、S2。正確的心臟聽診通常包括分析基本心音(fundamental heart sounds,FHS)和雜音。FHS包括了S1和S2,是心音重要的物理特征。在以往的心音分類研究中,對PCG信號中的FHS進行準確分割是分析PCG信號的前提。但是PCG信號的準確分割是一個有挑戰性的難題,不僅計算復雜,而且分割不準確會導致后續分類精度下降。本文提出一種新穎的框架,無需對FHS進行準確分割來分類PCG信號,降低計算量的同時,也避免了心音分割不準確而導致分類器性能下降。
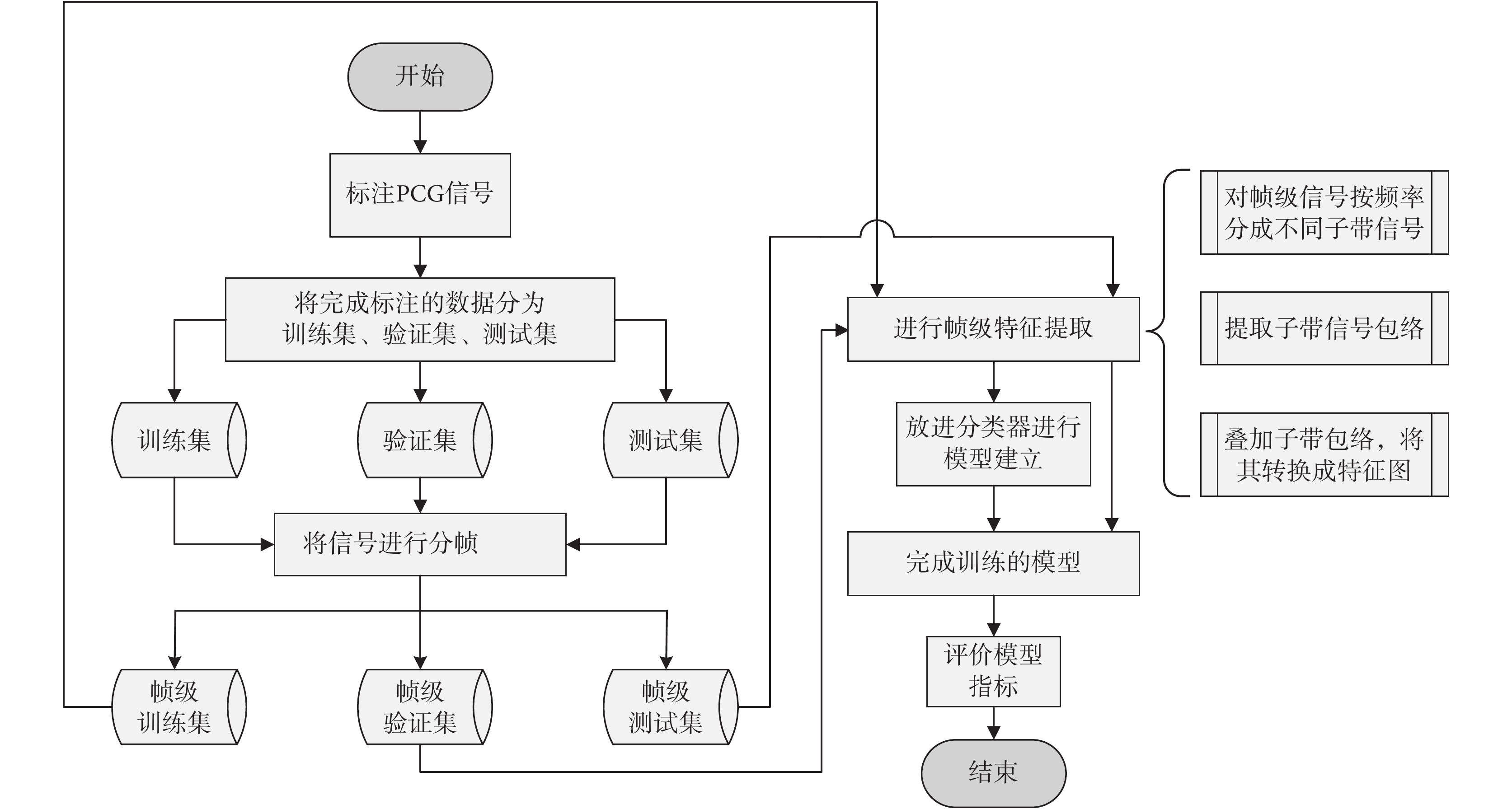
本文研究心音自動分類算法框架如圖1所示,具體步驟如下:
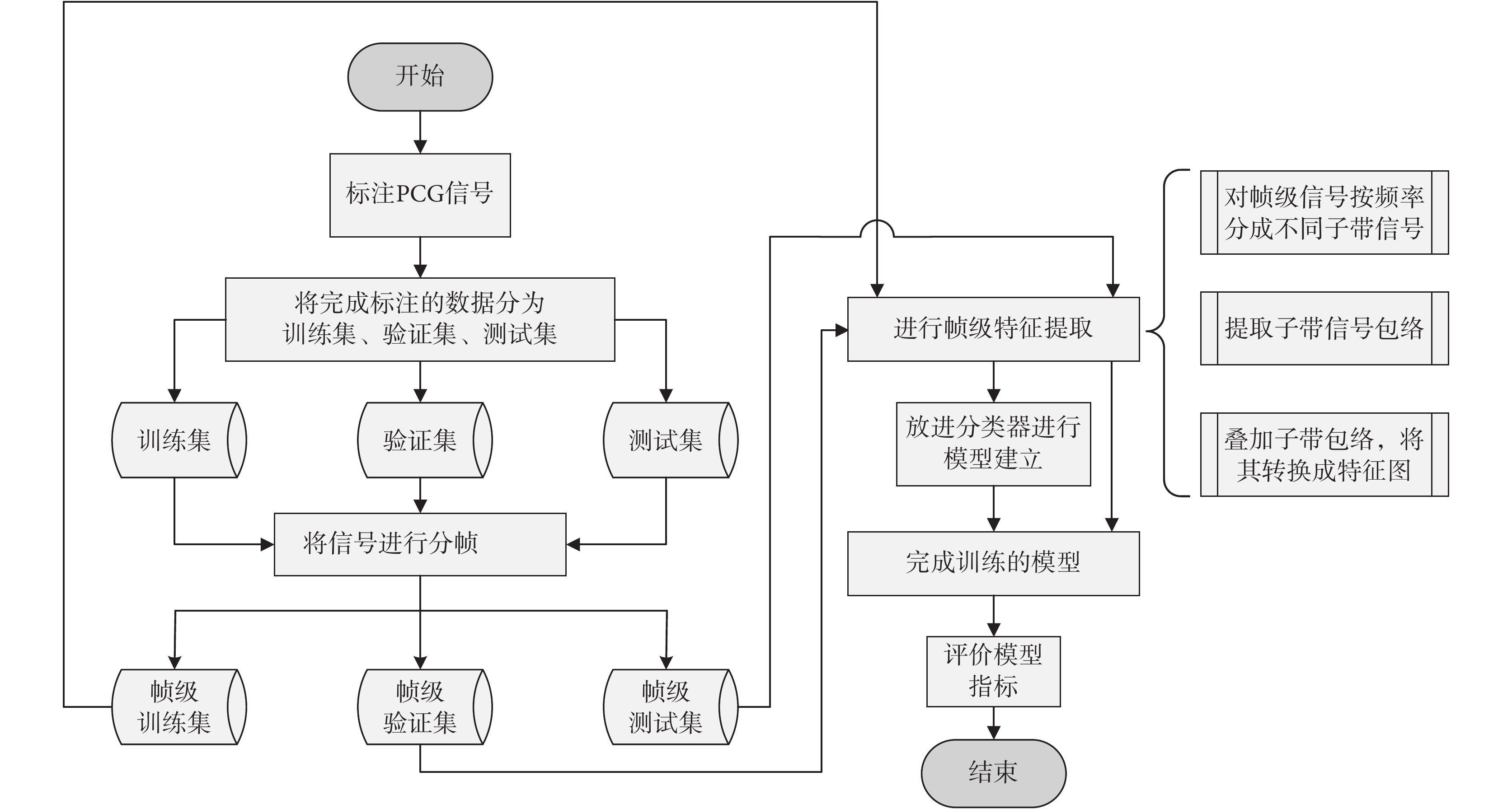 圖1
心音自動分類算法流程圖
Figure1.
Flow chart of automatic classification of heart sounds
圖1
心音自動分類算法流程圖
Figure1.
Flow chart of automatic classification of heart sounds
(1)對PCG信號進行標注,將完成標注的數據分為訓練集、驗證集、測試集。
(2)對標注信號進行預處理,把一段完整的PCG信號分成小段,每一小段為一幀。
(3)將每一幀的PCG信號分為不同的子帶(根據不同頻率范圍劃分),并對每一個子帶信號提取包絡信號。
(4)對所有的子帶包絡下采樣到特定的點數,將其堆疊得到特定尺寸的特征圖(將一維的數據轉換為二維)。
(5)將得到的訓練集與驗證集特征圖放進分類器進行訓練和分類,得到算法模型。
(6)使用測試集評估模型性能。
1.3 預處理
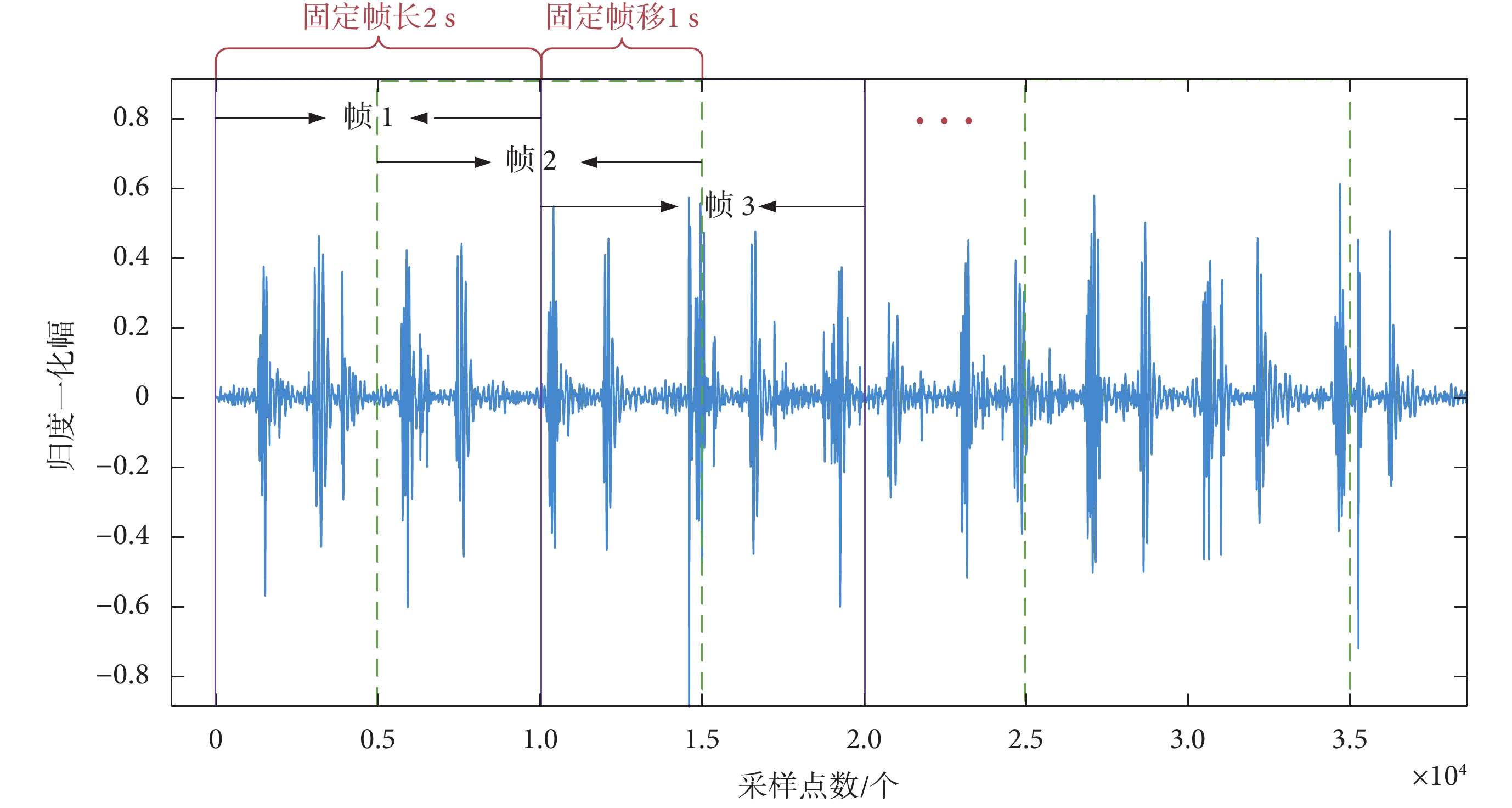
PCG信號的預處理通常指心音分割等步驟。但PCG信號分類的主要目的是檢測信號中是否存在異常而不是進一步去識別它,所以無需對心音進行精確分割[14]。本文采用的預處理方法借鑒了語音信號處理中常用的分幀方式,即使用持續時間的窗口對心音進行逐幀處理[15]。分幀過程是將一個完整的PCG信號樣本分為等長的小段,這在一定程度上起到了擴充數據的作用。在后續的分類過程中每一幀的PCG信號都會有一個分類結果,因此最終結果采用多數投票算法進行綜合判定。本文研究中,選取的固定幀長為2 s,幀移1 s,如圖2所示。正常人平均心率為60~100 次/min。但受生理或者病理的影響,可能導致心率低于或超過此范圍。本文選擇固定幀長為2 s的原因,就是為保證每一幀都能確保至少有一個完整心動周期存在。幀移是為了在幀與幀之間保留重疊部分數據,以滿足連續的要求。通常幀移長度能使幀與幀之間重疊50%。
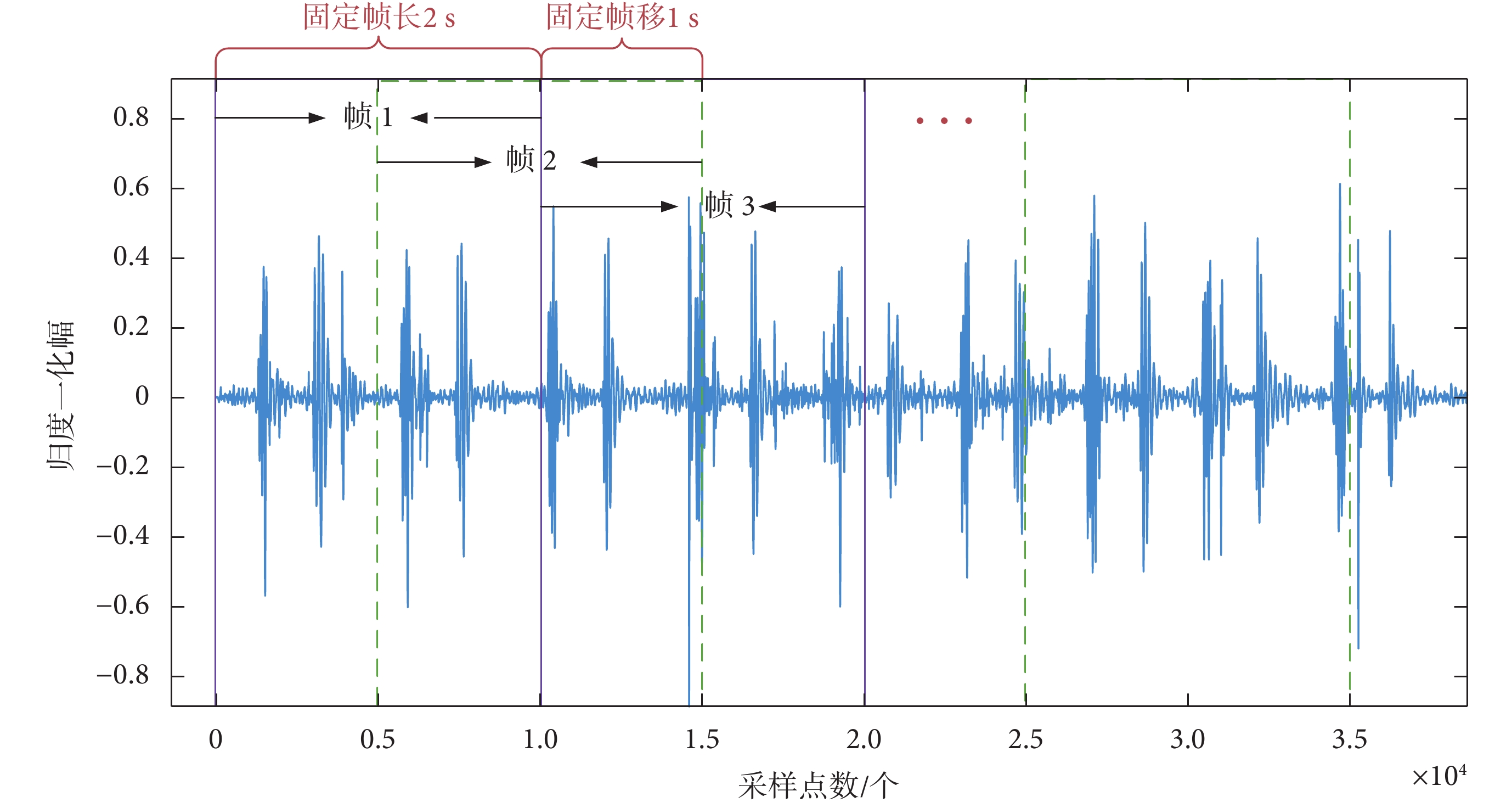 圖2
PCG信號的分幀
Figure2.
Frame division of heart sound signal
圖2
PCG信號的分幀
Figure2.
Frame division of heart sound signal
為使分幀后的PCG信號更平穩,選擇長度為2 s的圖基窗進行加窗操作。圖基窗的特點是旁瓣峰值比低,旁瓣衰減斜率較小,可以有效減少頻譜泄漏。
1.4 特征提取
臨床上可根據雜音產生的時期和心音包絡的形狀,協助醫生診斷某些心臟疾病。在PCG信號分析中,包絡常被提取用于PCG信號的分割[16]。但目前直接用包絡信號當作心音分類主要特征的研究較少。一些基于小波的特征也可以看作是子帶包絡特征,比如Deng等[17]根據離散小波分解系數得到類似于子帶包絡的特征。在本文的自動心音分類系統中,將采取堆疊子帶信號包絡的方法來構建時頻特征。具體步驟如下:
(1)使用伽馬通(Gammatone)濾波器組對分幀后的PCG信號進行濾波并得到子帶信號。Gammatone濾波器組能夠模擬人類聽覺系統特點,可以用于音頻信號的分解[18]。其在時域的脈沖響應h(t)如式(1)所示:
 |
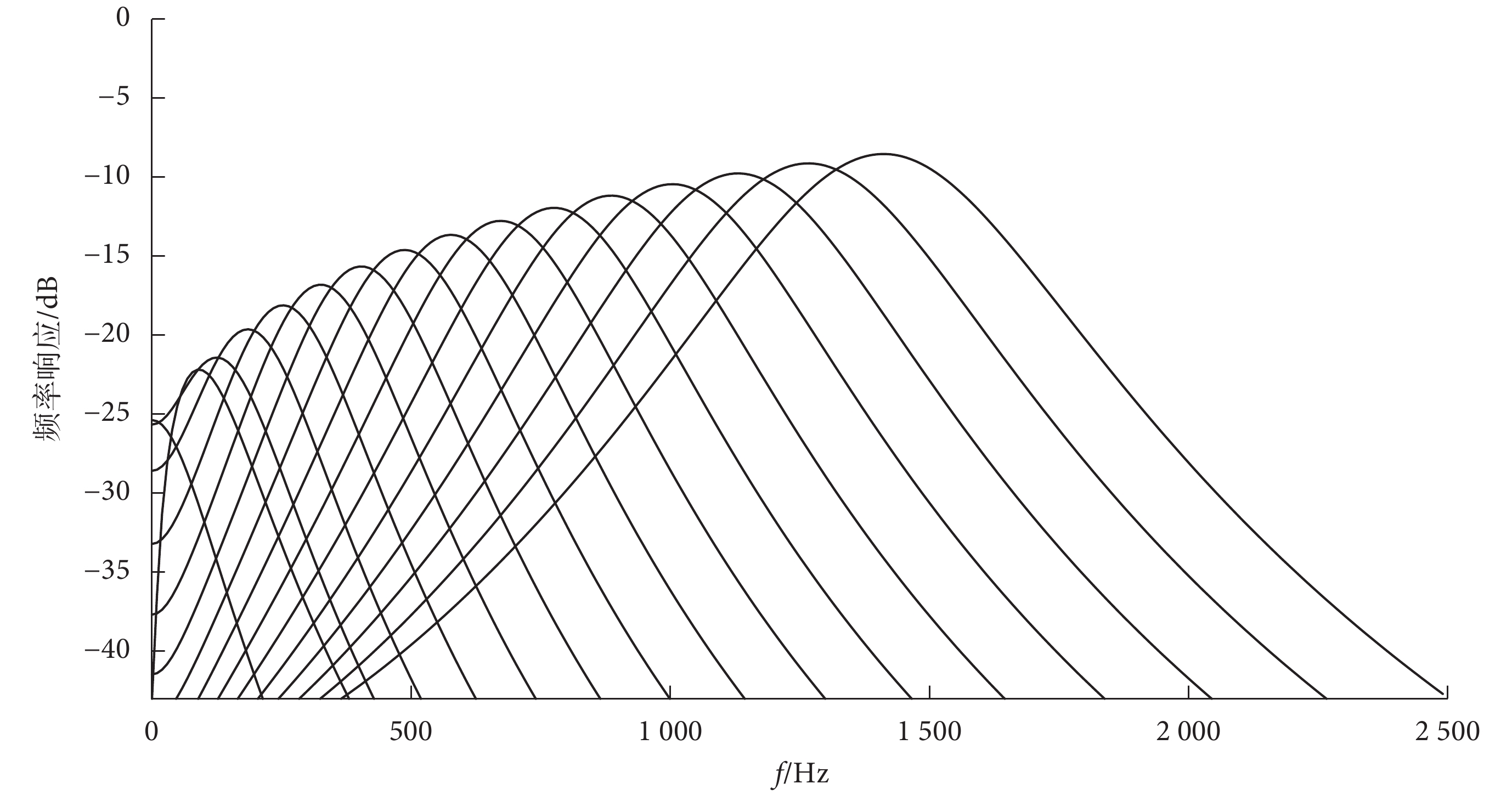
其中,k為輸出增益;t為連續時間;n是濾波器階數,決定了邊緣斜率;B是時間衰減系數,決定了濾波器帶寬;fc是濾波器的中心頻率;φ為相位。本文將多個Gammatone濾波器按中心頻率梯度疊加成一個帶通濾波器組,對PCG信號進行濾波后使每一幀信號轉換為不同的子帶信號。子帶信號數量與濾波器數量相等。在一定程度上濾波器組對信號也進行了降噪處理。其頻率響應如圖3所示(以16個濾波器為例)。
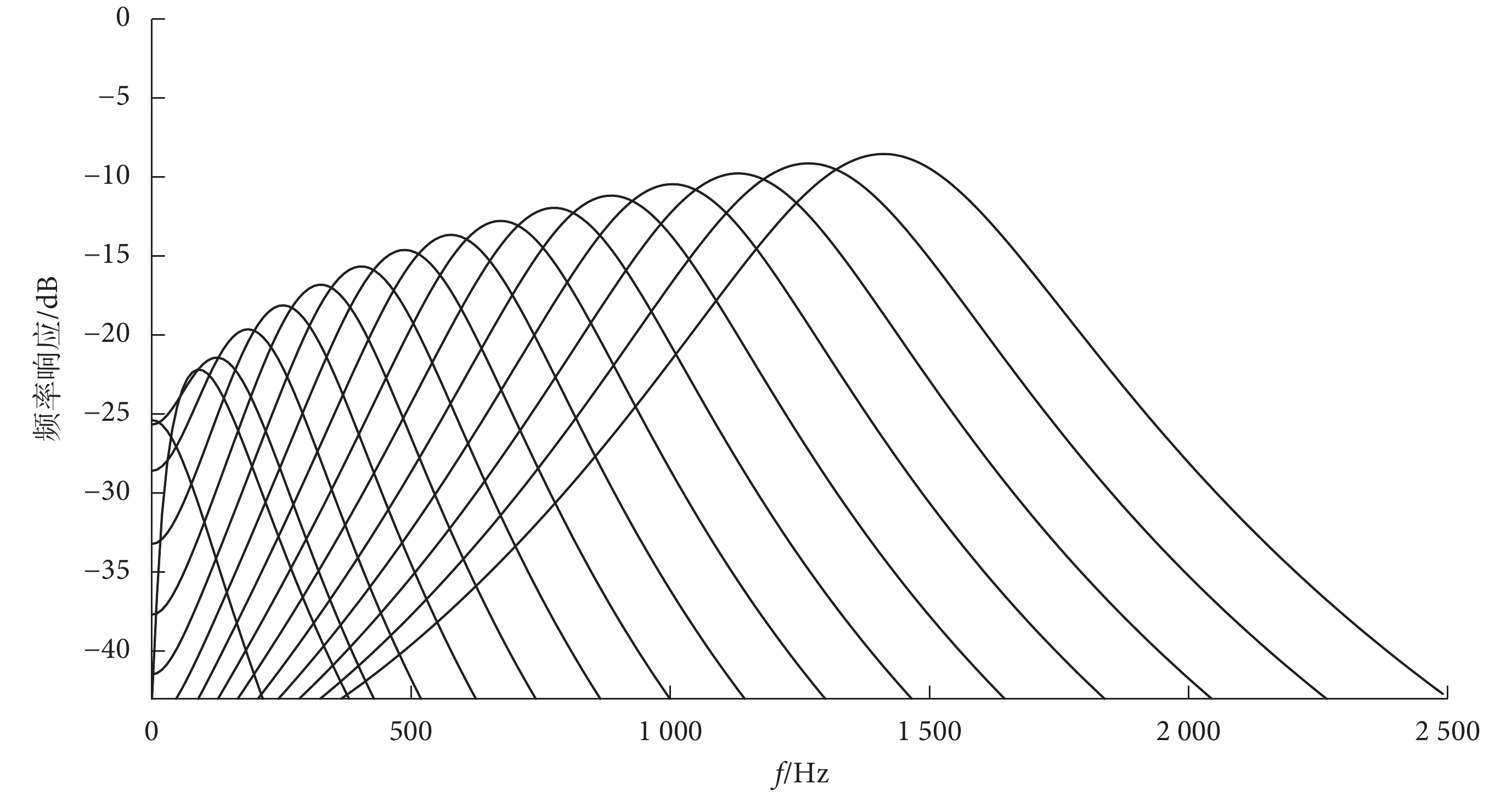 圖3
Gammatone濾波器組的頻率響應
Figure3.
Frequency response of Gammatone filter banks
圖3
Gammatone濾波器組的頻率響應
Figure3.
Frequency response of Gammatone filter banks
(2)將子帶信號通過希爾伯特變換計算得到子帶包絡。希爾伯特變換實際上是連續時間信號x(t)與  之間做卷積[19]。一個實值信號的希爾伯特變換如式(2)所示:
之間做卷積[19]。一個實值信號的希爾伯特變換如式(2)所示:
 |
其中  是x(t)進行希爾伯特變換后的信號。
是x(t)進行希爾伯特變換后的信號。
實信號進行傅里葉變換時,頻譜存在正負頻率,即有一半頻帶攜帶的信息是冗余的。希爾伯特變換在頻域上僅有正頻率部分,能起到消除冗余頻率的作用。如式(2)、式(3)所示,可以構造復信號z(t),z(t)稱為x(t)的解析信號。
 |
其中x(t)為解析信號的實部, 構成虛部,j為虛數單位。最后對式(3)求模即可得到信號的包絡。
構成虛部,j為虛數單位。最后對式(3)求模即可得到信號的包絡。
(3)將子帶包絡下采樣到特定的點數。通常采用抽取的方式進行下采樣,即通過減少數據樣點從而減少運算時間,但可能會造成原始信號特征缺失。本文將子帶包絡分成若干個點數一致的序列片,對每一個序列片求均值并將其設為下采樣后的數值,從而得到新的序列。這種采樣方法被稱為平均下采樣。平均下采樣能較好地保存原始信號特征,還能去除高頻分量,使包絡更平滑。
(4)將平均下采樣后的子帶包絡進行對數運算,如式(4)所示:
 |
其中wi(t)為平均下采樣后的子帶包絡信號,yi(t)為最終得到的子帶包絡信號,m的取值由前面Gammatone濾波器數量即子帶信號個數決定。通過對信號進行對數運算可以將線性轉換為非線性,減少數據間的相關性,有利于后續的分類步驟。對數運算還可以有效對數據進行壓縮,使數據更加平穩,方便計算。
(5)將最終處理得到的子帶包絡yi(t)進行轉置并橫向堆疊成一個二維矩陣Y。對矩陣Y進行中心化得到S,并對S進行幅度歸一化得到Q,如式(5)和(6)所示:
 |
 |
其中  為矩陣Y的均值。
為矩陣Y的均值。
(6)將處理后的矩陣Q的系數利用顏色編碼對應。其中高值對應較亮的顏色,低值對應較暗的顏色,從而得到特征圖。
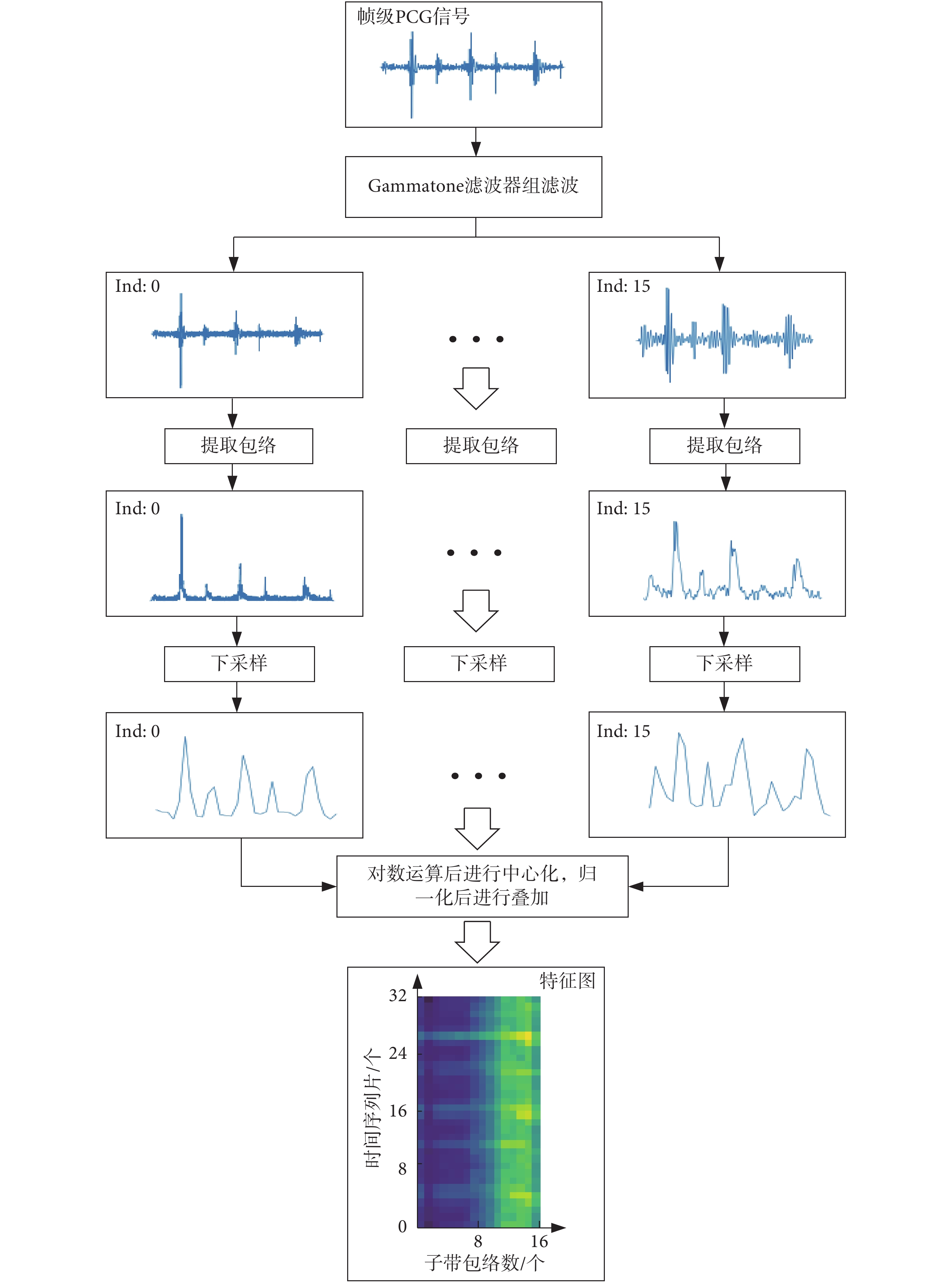
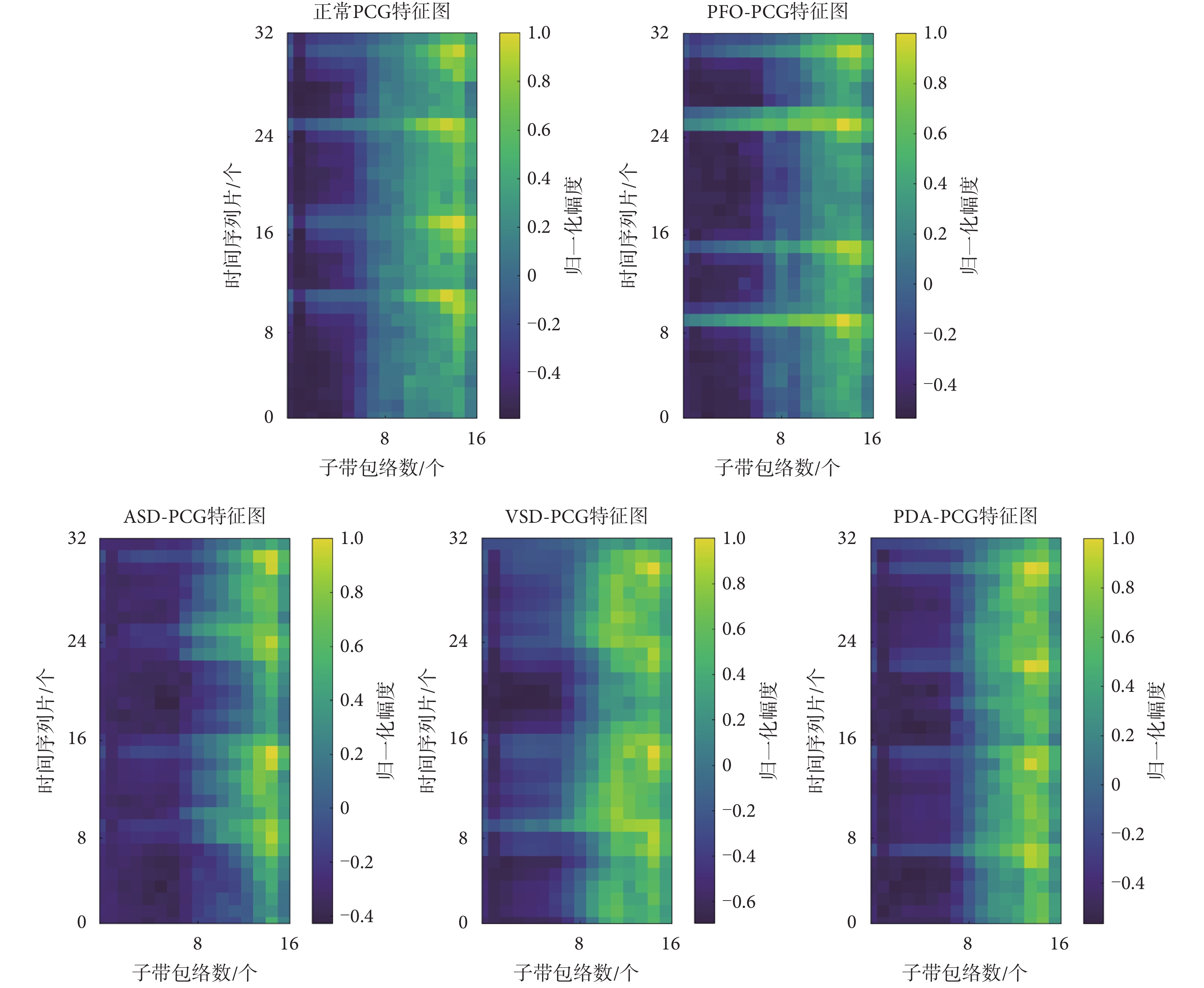
本文是將PCG信號分幀后才進行特征提取,所以一幀PCG信號對應一張特征圖。如圖4所示,給出了特征提取的過程。圖4中“Ind”指的是將一幀完整PCG信號分成不同子帶信息的索引號,由于篇幅限制,中間的省略號指其它的子帶信息。圖4以32×16的特征圖為例,其尺寸分別對應時間序列片數和子帶包絡數。正常PCG信號與異常PCG信號的特征提取結果圖對比如圖5所示。圖5中異常PCG信號為常見CHD病例,包括房間隔缺損(atrial septal defect,ASD)、室間隔缺損(ventricular septal defect,VSD)、動脈導管未閉(patent ductus arteriosus,PDA)、卵圓孔未閉(patent foramen ovale,PFO)。
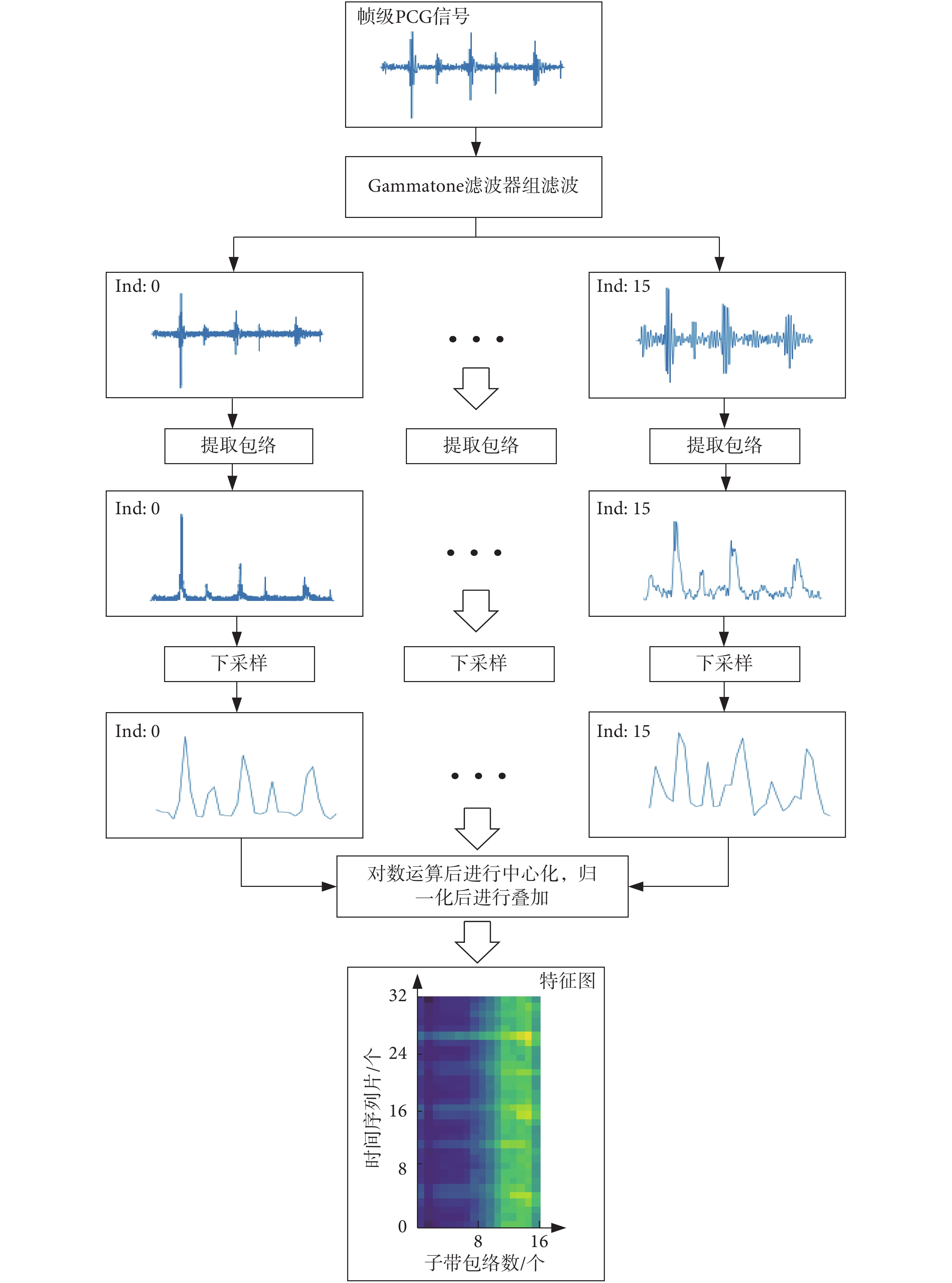 圖4
特征提取整體框架
Figure4.
The overall framework of the feature extraction
圖4
特征提取整體框架
Figure4.
The overall framework of the feature extraction
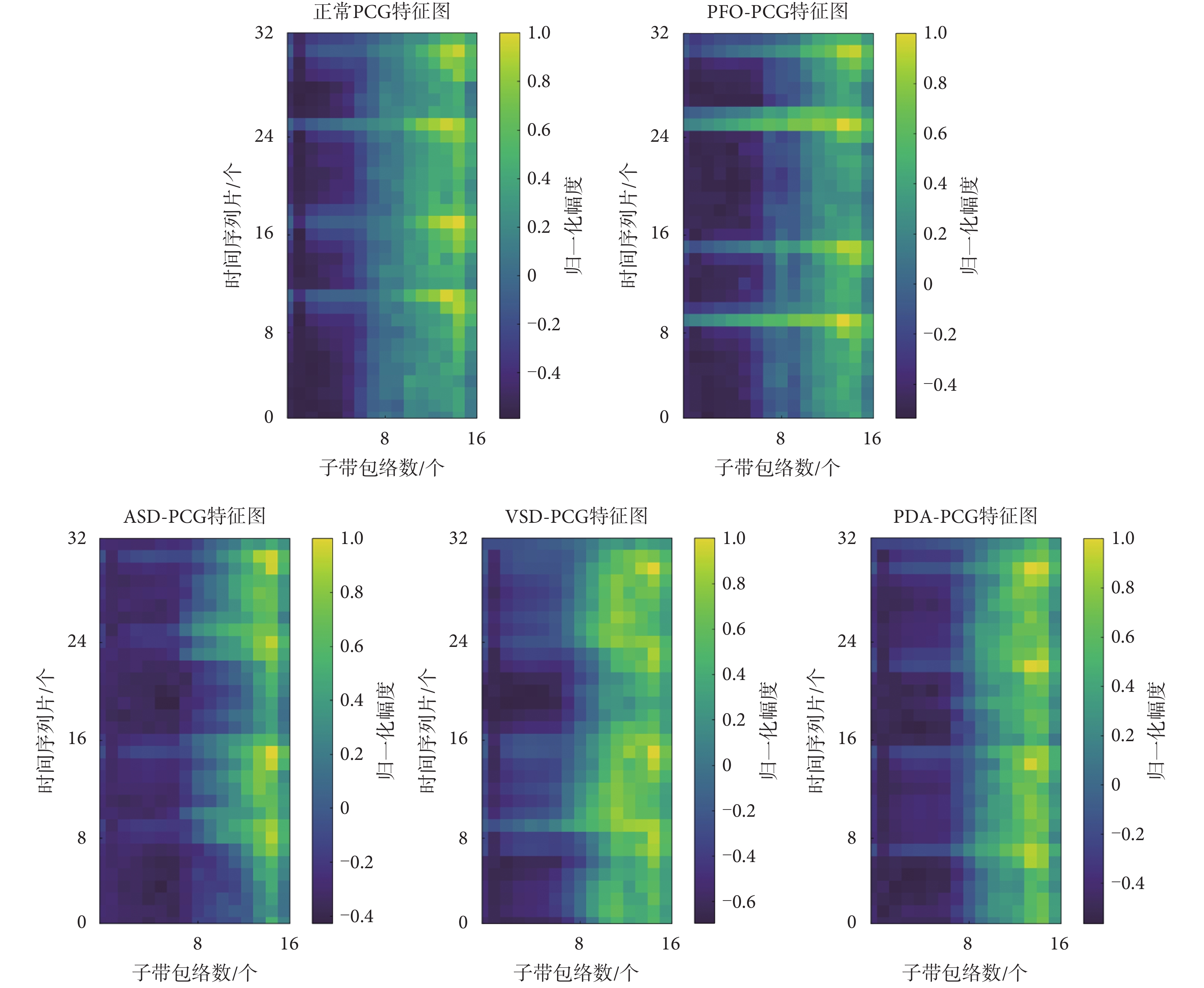 圖5
特征提取結果圖對比
Figure5.
Comparison of feature extraction results
圖5
特征提取結果圖對比
Figure5.
Comparison of feature extraction results
1.5 分類模型
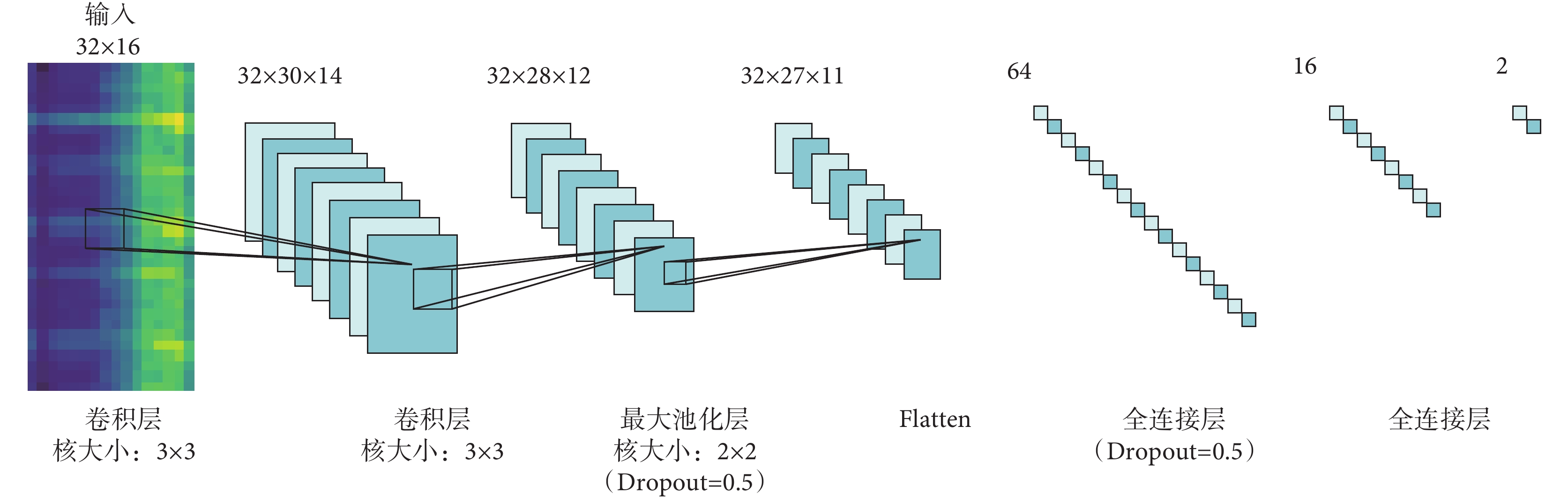
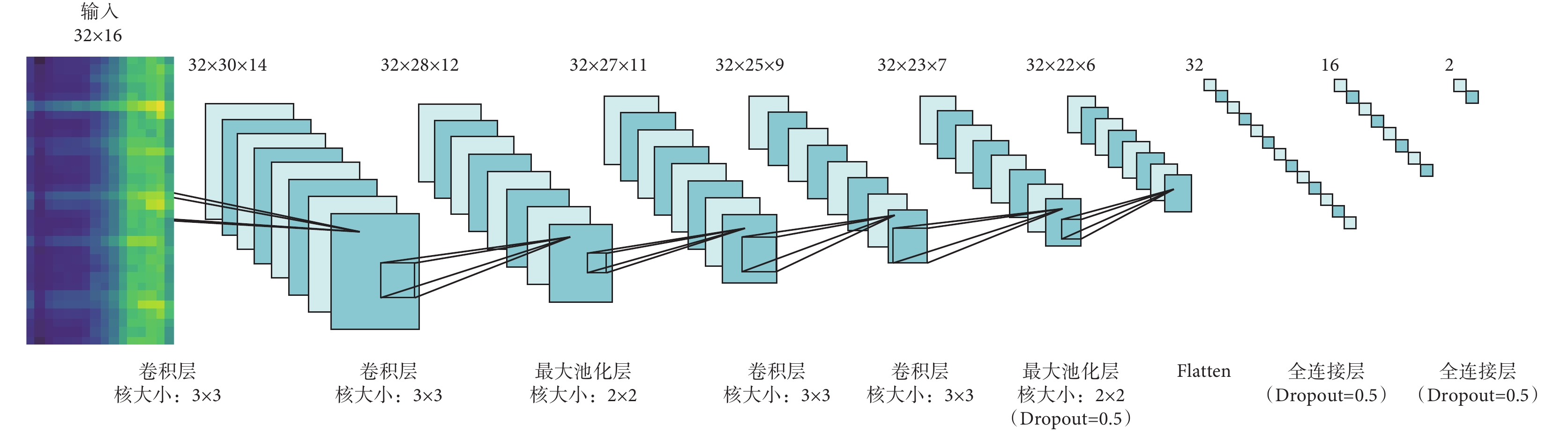
隨著人工智能算法的快速發展,在心音自動分析領域,神經網絡被用于分類的研究日益漸增,并取得不錯的成果。Nilanon等[20]利用CNN對心音進行分類并與傳統分類方式進行了對比。Zhang等[21]利用長短時記憶神經網絡(long short-term memory networks,LSTM)對心音進行分類。因為心音數據庫的規模通常來說相對較小,并且本文提取的特征圖尺寸較小,使用復雜模型容易導致過擬合現象。據此,本文搭建了兩個淺層CNN模型,分別為Ⅰ型與Ⅱ型模型。其中Ⅰ型指具有2層卷積層的CNN,Ⅱ型指具有4層卷積層的CNN。Ⅰ型與Ⅱ型CNN結構示意如圖6和圖7所示。Ⅰ型與Ⅱ型CNN每一個卷積層都是32個核,卷積核大小為3×3,步長為1×1,激活函數選用線性整流函數(rectified linear unit,ReLU)。池化層選用最大池化,池化核大小為2×2。隨機失活(Dropout)層可以有效控制過擬合的現象,Dropout率設置為0.5。展平(Flatten)層用來展平參數,主要用作參數在卷積層與全連接層之間的過渡。本文選用柔性最大(Softmax)回歸方法用于分類,Softmax可以將多個神經元輸出映射到(0,1)區間內,選取概率最大的結點作為最終輸出。本文通過不同特征提取方式和不同卷積層數的CNN模型組合探求適用于臨床環境下的心音自動分類技術。
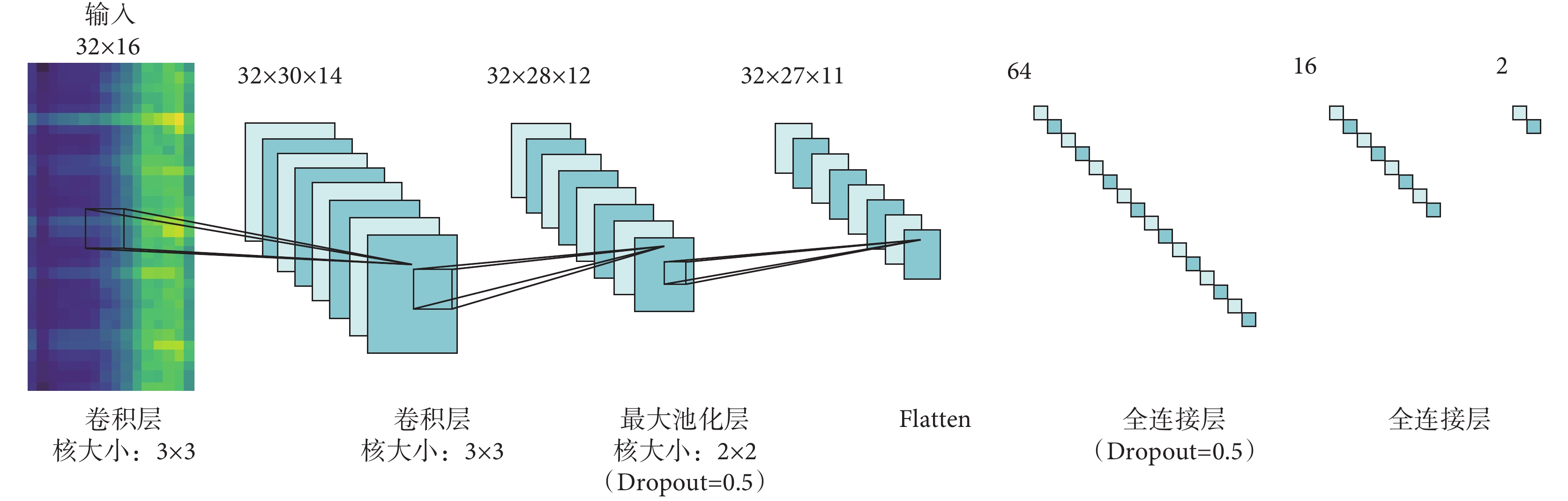 圖6
Ⅰ型CNN結構圖
Figure6.
Structure diagram of type Ⅰ CNN
圖6
Ⅰ型CNN結構圖
Figure6.
Structure diagram of type Ⅰ CNN
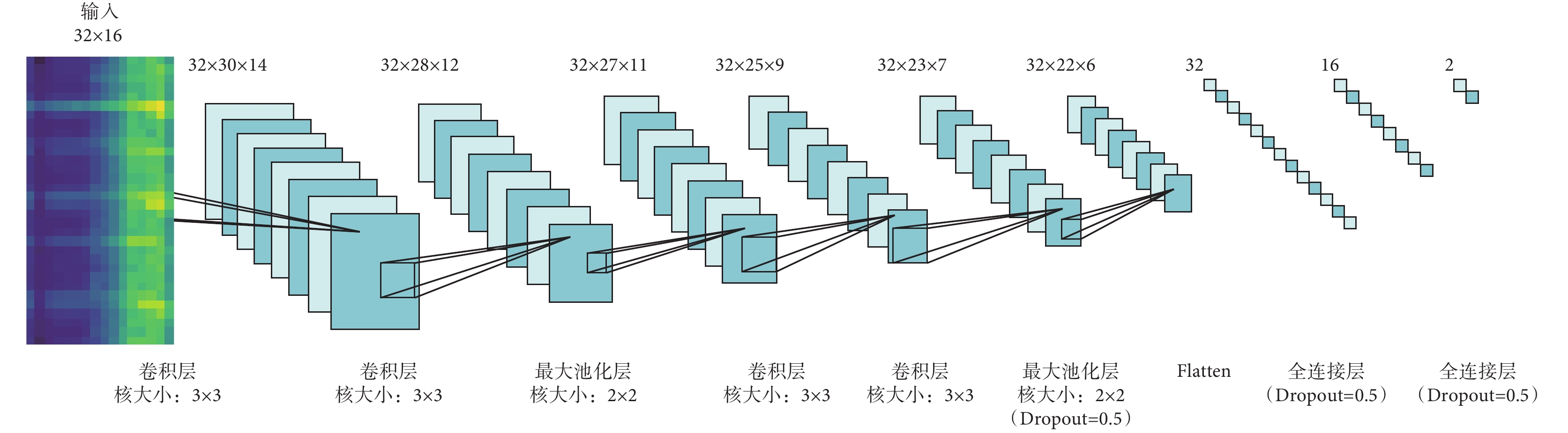 圖7
Ⅱ型CNN結構圖
Figure7.
Structure diagram of type Ⅱ CNN
圖7
Ⅱ型CNN結構圖
Figure7.
Structure diagram of type Ⅱ CNN
2 實驗與分析
2.1 實驗環境與數據說明
本文使用實驗環境的硬件配置如下:中央處理器(Core i7-9750H @2.60GHz,Intel,美國),獨立顯卡(NVIDIA 1660 Ti 6GB, Nvidia,美國)。本文選用的深度學習框架為TensorFlow 2.0(Google,美國),編程語言為Python 3.6(Python Software Foundation,美國)。
為了更有效地進行對比,本文研究實驗與對比實驗均在同一數據集下進行,數據集來自1.1小節所提的心音數據庫。實驗使用的數據來自1 000名志愿者的心音,其中正常和異常心音樣本比例為1∶1,異常心音病例包括了臨床上主要類型的CHD,例如VSD、ASD、PDA、PFO。由于心臟聽診區通常有5個,每個人的心音都按五個聽診點位進行采集,每個點采集時間為20 s,故總的心音數據樣本集為5 000例。將訓練集、驗證集、測試集按照0.65、0.15、 0.2的比例隨機劃分,即訓練集3 250例、驗證集750例、測試集1 000例。1 000例測試集數據中正常和異常心音樣本比例也為1∶1。對比以往的心音分類研究,本文使用的數據量更大,能最大限度地保證本文算法的魯棒性。
2.2 評估指標
為了評估本文所提出的算法,本文的每個實驗均使用以下5種評估標準:準確率(accuracy,acc)、靈敏度(sensitivity,se)、特異度(specificity,sp)、F1、AUC。前三個評估方法的計算公式,如式(7)~式(9)所示:
 |
 |
 |
其中,真陽性(true positive,TP)代表異常心音樣本被正確分類的結果數;真陰性(true negative,TN)代表正常心音樣本被正確分類的結果數;假陽性(false positive,FP)代表正常心音樣本被錯誤分類的結果數;假陰性(false negative,FN)代表異常心音樣本被錯誤分類的結果數。
F1分數是分類問題的一個綜合衡量指標。一些分類問題的機器學習競賽,通常把F1作為最終的測評指標。它結合了精確率(precision,pr)和召回率(recall,re),是這兩者間的調和平均數[22]。其計算公式如式(10)~式(12)所示:
 |
 |
 |
ROC曲線是重要的統計分析方式。ROC關注兩個指標,假陽性率(false positive rate,FPR)和真陽性率(true positive rate,TPR),這兩者分別對應橫坐標和縱坐標。ROC曲線下方與坐標軸形成的面積AUC是度量模型好壞的一個標準[23]。AUC越大,表示性能越好。
2.3 實驗結果與分析
為了對比不同卷積層數對分類效果的影響,本文算法對比實驗均在Ⅰ型和Ⅱ型CNN模型上進行訓練和測試,通過將不同的特征提取方法與不同的CNN模型進行組合來找到最優算法。子帶包絡方法中的參數設置會導致特征圖尺寸不同,從而影響分類效果。為比較特征參數與分類網絡的契合程度,以獲取最佳分類效果。本文通過選取不同的時間序列片數量和Gammatone濾波器數量進行參數對比實驗。時間序列片數量設置為32、64、128。Gammatone濾波器的數量設置為16、32、64。兩組參數一一對應,最后得到三種尺寸的特征圖,分別為32×16、64×32、128×64。根據上述的評估方法,本文算法與其他算法的對比結果如表1和表2所示。
本文對比算法選取文獻[5]、文獻[7]和文獻[8]中的方法。文獻[5]采用STFT與CNN進行心音分類。STFT通過對加窗數據進行傅里葉變換從而得到時頻圖,但會含有過多冗余信息。文獻[7]和文獻[8]均采用梅爾濾波器組相關特征和CNN結合的算法。其中文獻[7]特征提取方法為MFCC,文獻[8]為MFSC。MFCC和MFSC能從音頻數據捕捉到與人類對響度和音調感知相似的特征,所以在語音信號處理領域非常流行。MFSC與MFCC最大的不同是MFCC在MFSC的基礎上又進行離散余弦變換,所以MFSC比起MFCC保留了更多原始特征。從表1與表2的數據來看,四種特征提取方法無論與Ⅰ型還是Ⅱ型CNN模型組合都能較好地對PCG信號進行分類,但是子帶包絡算法整體性能要優于其它算法。從子帶包絡參數對比看,32×16的特征圖效果最佳,更適合應用于心音分類。在表2中,基于Ⅱ型CNN的MFSC算法的sp高于本文基于Ⅱ型CNN的子帶包絡算法,對比其它指標卻略有欠缺。對于CHD的篩查應用,降低漏診率是關鍵,所以提高se比sp更為重要。從兩個表中可看出本文算法的se優于其它算法,降低了臨床誤診的風險。
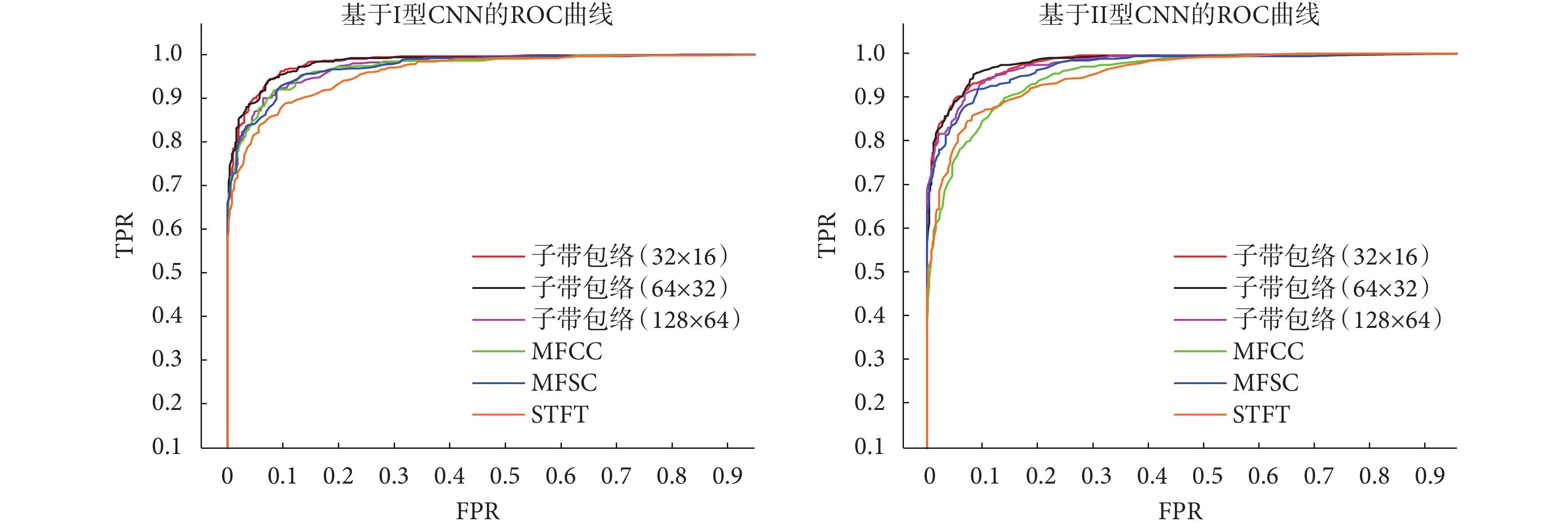
如圖8所示是不同特征提取方法與不同CNN模型組合實驗結果的ROC曲線對比。ROC曲線越靠近左上方表示AUC越大,該系統性能越好。從圖8可以看出不同參數設置的子帶包絡無論搭配2層卷積CNN模型還是4層卷積CNN模型,從整體評估指標上看均優于其它三種算法。PCG信號包絡在信號變化時能呈現出不同的特征信息,例如幅度、峰值間隔等。所以包絡能很好地表示心音的特征。通過不同頻率的子帶包絡疊加,可以將特征信息更加凸顯,作為后續分類會更加有優勢。總的來說,子帶包絡對比STFT、MFCC和MFSC具有更好的性能。
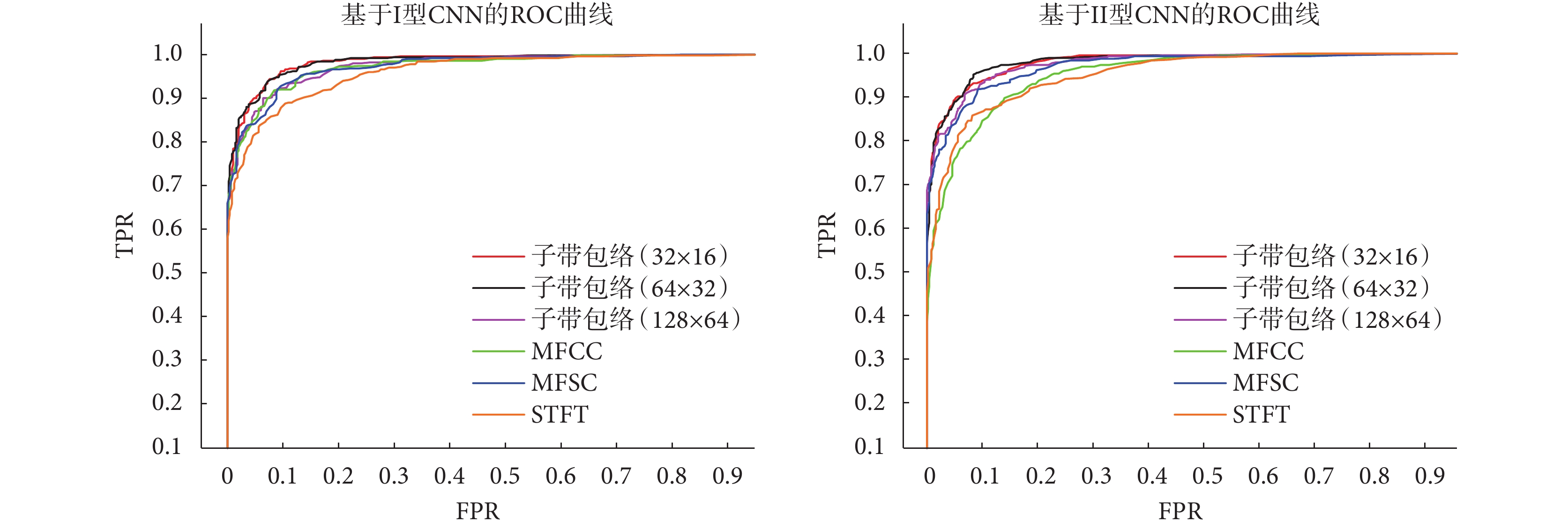 圖8
各算法ROC曲線對比
Figure8.
ROC curve comparison of each algorithm
圖8
各算法ROC曲線對比
Figure8.
ROC curve comparison of each algorithm
通過上述實驗結果分析,基于Ⅰ型CNN的子帶包絡(32×16)優于其它所有對比算法。為了驗證此二分類模型對常見CHD的分類有效性,本文單獨將測試樣本中的500例異常PCG信號進行測試。對常見CHD測試效果如表3所示。可以看出該算法對各類常見CHD能較好地識別,但對于PFO還稍有欠缺。可以從1.4節的圖5中發現 PFO-PCG特征圖較為接近正常PCG特征圖,這是導致準確率稍低的原因。
本文算法實驗以及對比實驗的各項評估指標均在同一測試集上進行測試,并由程序自動計算、統計。對比以往研究,本文使用測試樣本數量更多,進一步表明本文所提算法有較好的魯棒性與泛化能力,可應用于CHD篩查。
3 結論
針對心音自動分類領域多數算法依賴于心音分割的問題,本文提出了一種基于子帶包絡的時頻特征提取方法,不依賴于對心音的準確分割,在降低了運算復雜度的同時也具備較好性能。首先對PCG信號進行預處理,即分幀操作。然后對幀級PCG信號提取子帶包絡,將其疊加成二維特征圖作為CNN分類的主要特征。最后根據所提取的特征,構建合適的CNN分類器模型。本文使用5種不同評價指標對所提算法進行評估。實驗結果表明,本文算法在測試集上的各項指標均取得較好結果,對比其他研究所用的時頻特征提取方法,綜合性能更佳,為心音自動分類技術應用于CHD篩查提供了可行方法。但本文算法對PFO病例分類準確率還有待提高,今后將加深對這方面的研究,進一步提高算法性能。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
先天性心臟病(congenital heart disease,CHD)占所有先天性出生缺陷的近三分之一[1]。CHD危害極大,及早發現并進行醫療干預是降低患者死亡率的關鍵,因此盡早對兒童和青少年進行CHD篩查尤其重要。心音是由心房與心室的收縮和舒張、瓣膜運動、血流的相互作用引起。此外,還有一些由于心臟結構和功能缺陷所致的雜音[2]。心臟聽診是目前在篩查領域的一種重要手段,它依據心音與雜音的特點輔助臨床醫生進行診斷。但人類聽覺感知在分析心音中的隱藏信息方面存在局限性,有時醫生很難通過聽診來分析心音,從而影響心音診斷的準確性。
由于上述原因,近年來對心音的自動分析研究成為了人工智能在臨床應用的一個重要課題。心音圖(phonocardiogram,PCG)是借助電子聽診器采集得到心音信號的圖形表示,含有能反映心臟功能及心臟生理、病理的重要信息。因此可以通過分析PCG信號來診斷心血管疾病。本文研究目的在于提高心音自動分類技術和CHD篩查效率,降低CHD的死亡風險。
基于計算機的PCG信號分析流程可以總結為以下三個步驟:① 預處理;② 特征提取;③ 分類器的構建。本文研究的重點是PCG信號分析的特征提取部分。典型用于PCG信號分析的特征大致可分為以下幾類:時域特征、頻域特征、時頻域特征[3]。國內外有大量研究者長期將PCG信號的特征提取作為一個重要研究課題。Schmidt等[4]在5個不同頻段中采用了參數譜模型、瞬時頻率、倍頻程功率等方法提取頻譜特征,同時組合多個特征,最后評估得到受試者工作特性(receiver operating characteristic,ROC)曲線與坐標軸圍成的面積(area under curve,AUC)為0.73。Chen等[5]使用短時傅里葉變換(short-time Fourier transform,STFT)提取心音幅度譜,在39個測試樣本中取得了0.954 9的準確率。Zabihi等[6]從時域、頻域、時頻域提取了18個特征,例如梅爾頻率倒譜系數(mel-frequency cepstral coefficients,MFCC)、功率譜密度等,最后在測試集上得到0.859的準確率。Rubin等[7]利用卷積神經網絡(convolutional neural networks,CNN)對時頻域提取的MFCC特征進行訓練,最后測試準確率為0.848。Maknickas等[8]采用梅爾對數頻率系數(log mel-frequency spectral coefficients,MFSC)與CNN,在304例測試樣本上獲得了0.841 5的準確率。Kay等[9]將心動周期的時域特征、時頻域特征和復雜特征(例如頻譜熵、標準偏差等)利用主成分分析(principal component analysis,PCA)進行降維并融合特征,最后該算法在測試集上獲得了0.852的準確率。Hamidi等[10]利用MFCC和分形維數相結合對PCG信號進行分類,并在六個不同的數據集上進行測試,其中三個數據集中達到了0.92、0.81和0.98的準確率。
上述研究中,有些算法研究應用在心音分類上的準確率較高,但是離應用于機器智能輔助聽診階段還有差距。文獻[5]在少量的測試樣本中取得了高準確率,普適性有待驗證。文獻[6]和文獻[9]均提取了多種特征,但提取多種特征耗時高、計算復雜,并且實驗準確率還有待提升。文獻[4]和文獻[9]的算法在進行特征提取前都要對PCG信號進行準確地分割。然而在噪聲環境下很難準確地分割出基本心音,目前也沒有一個較好的方案來解決此問題[11]。文獻[4]利用與時間相關的隱馬爾可夫模型分割心音,但個體心音主成分存在差異,所以很難建立一個統一的模型去進行分析。文獻[9]是基于心電圖(electrocardiogram,ECG)信號對PCG信號進行分割,此方法需要對ECG信號和PCG信號進行同步記錄,但對于新生兒來說ECG信號采集比較困難[12]。對于CHD,能在嬰幼兒時期發現并及時治療,會提高患者存活率。但上述研究使用的數據集來源沒有大量涵蓋嬰幼兒,是否能適用于嬰幼兒的篩查還是個未知數。
針對以上問題,本文使用了一種基于子帶包絡的時頻特征提取方法,并搭建了兩種CNN模型對其驗證。該特征提取方法不需要對PCG信號進行準確分割,減少了計算量。本文在實驗中使用的數據集大部分針對低年齡階段的孩童,以求能在實際篩查中及時發現患者。
1 模型與方法
1.1 數據來源
本文研究所用的心音數據庫由實驗室研究團隊采集構建,其數據來源于云南省阜外心血管病醫院的臨床患者以及在云南省各地州開展CHD免費篩查救治活動時的兒童。作為數據采集來源的志愿者,其年齡限定在6個月至18歲,所有志愿者均簽署了知情同意書。本研究及所有數據均已通過云南大學人體研究材料倫理委員會以及云南省阜外心血管病醫院倫理委員會的審查并批準使用。數據庫中的每一例陽性病例都由心臟病專科醫生根據臨床聽診和超聲心動圖確認和記錄。本實驗室自行研發了一套PCG信號采集設備。采集設備為The ONE心音傳感器(Thinklabs Medical LLC,美國),其輸出為模擬音頻信號,采樣頻率(frequency of sample,Fs)為5 000 Hz,采集時長為20 s。
1.2 心音自動分類流程
在對心音進行分類前,需要對心音組成有個基本的了解。按照心音的產生時間和產生機制可以把一個心動周期分為:第一心音(S1)、第二心音(S2)、第三心音(S3)、第四心音(S4)[13],通常情況只能聽見S1、S2。正確的心臟聽診通常包括分析基本心音(fundamental heart sounds,FHS)和雜音。FHS包括了S1和S2,是心音重要的物理特征。在以往的心音分類研究中,對PCG信號中的FHS進行準確分割是分析PCG信號的前提。但是PCG信號的準確分割是一個有挑戰性的難題,不僅計算復雜,而且分割不準確會導致后續分類精度下降。本文提出一種新穎的框架,無需對FHS進行準確分割來分類PCG信號,降低計算量的同時,也避免了心音分割不準確而導致分類器性能下降。
本文研究心音自動分類算法框架如圖1所示,具體步驟如下:
 圖1
心音自動分類算法流程圖
Figure1.
Flow chart of automatic classification of heart sounds
圖1
心音自動分類算法流程圖
Figure1.
Flow chart of automatic classification of heart sounds
(1)對PCG信號進行標注,將完成標注的數據分為訓練集、驗證集、測試集。
(2)對標注信號進行預處理,把一段完整的PCG信號分成小段,每一小段為一幀。
(3)將每一幀的PCG信號分為不同的子帶(根據不同頻率范圍劃分),并對每一個子帶信號提取包絡信號。
(4)對所有的子帶包絡下采樣到特定的點數,將其堆疊得到特定尺寸的特征圖(將一維的數據轉換為二維)。
(5)將得到的訓練集與驗證集特征圖放進分類器進行訓練和分類,得到算法模型。
(6)使用測試集評估模型性能。
1.3 預處理
PCG信號的預處理通常指心音分割等步驟。但PCG信號分類的主要目的是檢測信號中是否存在異常而不是進一步去識別它,所以無需對心音進行精確分割[14]。本文采用的預處理方法借鑒了語音信號處理中常用的分幀方式,即使用持續時間的窗口對心音進行逐幀處理[15]。分幀過程是將一個完整的PCG信號樣本分為等長的小段,這在一定程度上起到了擴充數據的作用。在后續的分類過程中每一幀的PCG信號都會有一個分類結果,因此最終結果采用多數投票算法進行綜合判定。本文研究中,選取的固定幀長為2 s,幀移1 s,如圖2所示。正常人平均心率為60~100 次/min。但受生理或者病理的影響,可能導致心率低于或超過此范圍。本文選擇固定幀長為2 s的原因,就是為保證每一幀都能確保至少有一個完整心動周期存在。幀移是為了在幀與幀之間保留重疊部分數據,以滿足連續的要求。通常幀移長度能使幀與幀之間重疊50%。
 圖2
PCG信號的分幀
Figure2.
Frame division of heart sound signal
圖2
PCG信號的分幀
Figure2.
Frame division of heart sound signal
為使分幀后的PCG信號更平穩,選擇長度為2 s的圖基窗進行加窗操作。圖基窗的特點是旁瓣峰值比低,旁瓣衰減斜率較小,可以有效減少頻譜泄漏。
1.4 特征提取
臨床上可根據雜音產生的時期和心音包絡的形狀,協助醫生診斷某些心臟疾病。在PCG信號分析中,包絡常被提取用于PCG信號的分割[16]。但目前直接用包絡信號當作心音分類主要特征的研究較少。一些基于小波的特征也可以看作是子帶包絡特征,比如Deng等[17]根據離散小波分解系數得到類似于子帶包絡的特征。在本文的自動心音分類系統中,將采取堆疊子帶信號包絡的方法來構建時頻特征。具體步驟如下:
(1)使用伽馬通(Gammatone)濾波器組對分幀后的PCG信號進行濾波并得到子帶信號。Gammatone濾波器組能夠模擬人類聽覺系統特點,可以用于音頻信號的分解[18]。其在時域的脈沖響應h(t)如式(1)所示:
 |
其中,k為輸出增益;t為連續時間;n是濾波器階數,決定了邊緣斜率;B是時間衰減系數,決定了濾波器帶寬;fc是濾波器的中心頻率;φ為相位。本文將多個Gammatone濾波器按中心頻率梯度疊加成一個帶通濾波器組,對PCG信號進行濾波后使每一幀信號轉換為不同的子帶信號。子帶信號數量與濾波器數量相等。在一定程度上濾波器組對信號也進行了降噪處理。其頻率響應如圖3所示(以16個濾波器為例)。
 圖3
Gammatone濾波器組的頻率響應
Figure3.
Frequency response of Gammatone filter banks
圖3
Gammatone濾波器組的頻率響應
Figure3.
Frequency response of Gammatone filter banks
(2)將子帶信號通過希爾伯特變換計算得到子帶包絡。希爾伯特變換實際上是連續時間信號x(t)與  之間做卷積[19]。一個實值信號的希爾伯特變換如式(2)所示:
之間做卷積[19]。一個實值信號的希爾伯特變換如式(2)所示:
 |
其中  是x(t)進行希爾伯特變換后的信號。
是x(t)進行希爾伯特變換后的信號。
實信號進行傅里葉變換時,頻譜存在正負頻率,即有一半頻帶攜帶的信息是冗余的。希爾伯特變換在頻域上僅有正頻率部分,能起到消除冗余頻率的作用。如式(2)、式(3)所示,可以構造復信號z(t),z(t)稱為x(t)的解析信號。
 |
其中x(t)為解析信號的實部, 構成虛部,j為虛數單位。最后對式(3)求模即可得到信號的包絡。
構成虛部,j為虛數單位。最后對式(3)求模即可得到信號的包絡。
(3)將子帶包絡下采樣到特定的點數。通常采用抽取的方式進行下采樣,即通過減少數據樣點從而減少運算時間,但可能會造成原始信號特征缺失。本文將子帶包絡分成若干個點數一致的序列片,對每一個序列片求均值并將其設為下采樣后的數值,從而得到新的序列。這種采樣方法被稱為平均下采樣。平均下采樣能較好地保存原始信號特征,還能去除高頻分量,使包絡更平滑。
(4)將平均下采樣后的子帶包絡進行對數運算,如式(4)所示:
 |
其中wi(t)為平均下采樣后的子帶包絡信號,yi(t)為最終得到的子帶包絡信號,m的取值由前面Gammatone濾波器數量即子帶信號個數決定。通過對信號進行對數運算可以將線性轉換為非線性,減少數據間的相關性,有利于后續的分類步驟。對數運算還可以有效對數據進行壓縮,使數據更加平穩,方便計算。
(5)將最終處理得到的子帶包絡yi(t)進行轉置并橫向堆疊成一個二維矩陣Y。對矩陣Y進行中心化得到S,并對S進行幅度歸一化得到Q,如式(5)和(6)所示:
 |
 |
其中  為矩陣Y的均值。
為矩陣Y的均值。
(6)將處理后的矩陣Q的系數利用顏色編碼對應。其中高值對應較亮的顏色,低值對應較暗的顏色,從而得到特征圖。
本文是將PCG信號分幀后才進行特征提取,所以一幀PCG信號對應一張特征圖。如圖4所示,給出了特征提取的過程。圖4中“Ind”指的是將一幀完整PCG信號分成不同子帶信息的索引號,由于篇幅限制,中間的省略號指其它的子帶信息。圖4以32×16的特征圖為例,其尺寸分別對應時間序列片數和子帶包絡數。正常PCG信號與異常PCG信號的特征提取結果圖對比如圖5所示。圖5中異常PCG信號為常見CHD病例,包括房間隔缺損(atrial septal defect,ASD)、室間隔缺損(ventricular septal defect,VSD)、動脈導管未閉(patent ductus arteriosus,PDA)、卵圓孔未閉(patent foramen ovale,PFO)。
 圖4
特征提取整體框架
Figure4.
The overall framework of the feature extraction
圖4
特征提取整體框架
Figure4.
The overall framework of the feature extraction
 圖5
特征提取結果圖對比
Figure5.
Comparison of feature extraction results
圖5
特征提取結果圖對比
Figure5.
Comparison of feature extraction results
1.5 分類模型
隨著人工智能算法的快速發展,在心音自動分析領域,神經網絡被用于分類的研究日益漸增,并取得不錯的成果。Nilanon等[20]利用CNN對心音進行分類并與傳統分類方式進行了對比。Zhang等[21]利用長短時記憶神經網絡(long short-term memory networks,LSTM)對心音進行分類。因為心音數據庫的規模通常來說相對較小,并且本文提取的特征圖尺寸較小,使用復雜模型容易導致過擬合現象。據此,本文搭建了兩個淺層CNN模型,分別為Ⅰ型與Ⅱ型模型。其中Ⅰ型指具有2層卷積層的CNN,Ⅱ型指具有4層卷積層的CNN。Ⅰ型與Ⅱ型CNN結構示意如圖6和圖7所示。Ⅰ型與Ⅱ型CNN每一個卷積層都是32個核,卷積核大小為3×3,步長為1×1,激活函數選用線性整流函數(rectified linear unit,ReLU)。池化層選用最大池化,池化核大小為2×2。隨機失活(Dropout)層可以有效控制過擬合的現象,Dropout率設置為0.5。展平(Flatten)層用來展平參數,主要用作參數在卷積層與全連接層之間的過渡。本文選用柔性最大(Softmax)回歸方法用于分類,Softmax可以將多個神經元輸出映射到(0,1)區間內,選取概率最大的結點作為最終輸出。本文通過不同特征提取方式和不同卷積層數的CNN模型組合探求適用于臨床環境下的心音自動分類技術。
 圖6
Ⅰ型CNN結構圖
Figure6.
Structure diagram of type Ⅰ CNN
圖6
Ⅰ型CNN結構圖
Figure6.
Structure diagram of type Ⅰ CNN
 圖7
Ⅱ型CNN結構圖
Figure7.
Structure diagram of type Ⅱ CNN
圖7
Ⅱ型CNN結構圖
Figure7.
Structure diagram of type Ⅱ CNN
2 實驗與分析
2.1 實驗環境與數據說明
本文使用實驗環境的硬件配置如下:中央處理器(Core i7-9750H @2.60GHz,Intel,美國),獨立顯卡(NVIDIA 1660 Ti 6GB, Nvidia,美國)。本文選用的深度學習框架為TensorFlow 2.0(Google,美國),編程語言為Python 3.6(Python Software Foundation,美國)。
為了更有效地進行對比,本文研究實驗與對比實驗均在同一數據集下進行,數據集來自1.1小節所提的心音數據庫。實驗使用的數據來自1 000名志愿者的心音,其中正常和異常心音樣本比例為1∶1,異常心音病例包括了臨床上主要類型的CHD,例如VSD、ASD、PDA、PFO。由于心臟聽診區通常有5個,每個人的心音都按五個聽診點位進行采集,每個點采集時間為20 s,故總的心音數據樣本集為5 000例。將訓練集、驗證集、測試集按照0.65、0.15、 0.2的比例隨機劃分,即訓練集3 250例、驗證集750例、測試集1 000例。1 000例測試集數據中正常和異常心音樣本比例也為1∶1。對比以往的心音分類研究,本文使用的數據量更大,能最大限度地保證本文算法的魯棒性。
2.2 評估指標
為了評估本文所提出的算法,本文的每個實驗均使用以下5種評估標準:準確率(accuracy,acc)、靈敏度(sensitivity,se)、特異度(specificity,sp)、F1、AUC。前三個評估方法的計算公式,如式(7)~式(9)所示:
 |
 |
 |
其中,真陽性(true positive,TP)代表異常心音樣本被正確分類的結果數;真陰性(true negative,TN)代表正常心音樣本被正確分類的結果數;假陽性(false positive,FP)代表正常心音樣本被錯誤分類的結果數;假陰性(false negative,FN)代表異常心音樣本被錯誤分類的結果數。
F1分數是分類問題的一個綜合衡量指標。一些分類問題的機器學習競賽,通常把F1作為最終的測評指標。它結合了精確率(precision,pr)和召回率(recall,re),是這兩者間的調和平均數[22]。其計算公式如式(10)~式(12)所示:
 |
 |
 |
ROC曲線是重要的統計分析方式。ROC關注兩個指標,假陽性率(false positive rate,FPR)和真陽性率(true positive rate,TPR),這兩者分別對應橫坐標和縱坐標。ROC曲線下方與坐標軸形成的面積AUC是度量模型好壞的一個標準[23]。AUC越大,表示性能越好。
2.3 實驗結果與分析
為了對比不同卷積層數對分類效果的影響,本文算法對比實驗均在Ⅰ型和Ⅱ型CNN模型上進行訓練和測試,通過將不同的特征提取方法與不同的CNN模型進行組合來找到最優算法。子帶包絡方法中的參數設置會導致特征圖尺寸不同,從而影響分類效果。為比較特征參數與分類網絡的契合程度,以獲取最佳分類效果。本文通過選取不同的時間序列片數量和Gammatone濾波器數量進行參數對比實驗。時間序列片數量設置為32、64、128。Gammatone濾波器的數量設置為16、32、64。兩組參數一一對應,最后得到三種尺寸的特征圖,分別為32×16、64×32、128×64。根據上述的評估方法,本文算法與其他算法的對比結果如表1和表2所示。
本文對比算法選取文獻[5]、文獻[7]和文獻[8]中的方法。文獻[5]采用STFT與CNN進行心音分類。STFT通過對加窗數據進行傅里葉變換從而得到時頻圖,但會含有過多冗余信息。文獻[7]和文獻[8]均采用梅爾濾波器組相關特征和CNN結合的算法。其中文獻[7]特征提取方法為MFCC,文獻[8]為MFSC。MFCC和MFSC能從音頻數據捕捉到與人類對響度和音調感知相似的特征,所以在語音信號處理領域非常流行。MFSC與MFCC最大的不同是MFCC在MFSC的基礎上又進行離散余弦變換,所以MFSC比起MFCC保留了更多原始特征。從表1與表2的數據來看,四種特征提取方法無論與Ⅰ型還是Ⅱ型CNN模型組合都能較好地對PCG信號進行分類,但是子帶包絡算法整體性能要優于其它算法。從子帶包絡參數對比看,32×16的特征圖效果最佳,更適合應用于心音分類。在表2中,基于Ⅱ型CNN的MFSC算法的sp高于本文基于Ⅱ型CNN的子帶包絡算法,對比其它指標卻略有欠缺。對于CHD的篩查應用,降低漏診率是關鍵,所以提高se比sp更為重要。從兩個表中可看出本文算法的se優于其它算法,降低了臨床誤診的風險。
如圖8所示是不同特征提取方法與不同CNN模型組合實驗結果的ROC曲線對比。ROC曲線越靠近左上方表示AUC越大,該系統性能越好。從圖8可以看出不同參數設置的子帶包絡無論搭配2層卷積CNN模型還是4層卷積CNN模型,從整體評估指標上看均優于其它三種算法。PCG信號包絡在信號變化時能呈現出不同的特征信息,例如幅度、峰值間隔等。所以包絡能很好地表示心音的特征。通過不同頻率的子帶包絡疊加,可以將特征信息更加凸顯,作為后續分類會更加有優勢。總的來說,子帶包絡對比STFT、MFCC和MFSC具有更好的性能。
 圖8
各算法ROC曲線對比
Figure8.
ROC curve comparison of each algorithm
圖8
各算法ROC曲線對比
Figure8.
ROC curve comparison of each algorithm
通過上述實驗結果分析,基于Ⅰ型CNN的子帶包絡(32×16)優于其它所有對比算法。為了驗證此二分類模型對常見CHD的分類有效性,本文單獨將測試樣本中的500例異常PCG信號進行測試。對常見CHD測試效果如表3所示。可以看出該算法對各類常見CHD能較好地識別,但對于PFO還稍有欠缺。可以從1.4節的圖5中發現 PFO-PCG特征圖較為接近正常PCG特征圖,這是導致準確率稍低的原因。
本文算法實驗以及對比實驗的各項評估指標均在同一測試集上進行測試,并由程序自動計算、統計。對比以往研究,本文使用測試樣本數量更多,進一步表明本文所提算法有較好的魯棒性與泛化能力,可應用于CHD篩查。
3 結論
針對心音自動分類領域多數算法依賴于心音分割的問題,本文提出了一種基于子帶包絡的時頻特征提取方法,不依賴于對心音的準確分割,在降低了運算復雜度的同時也具備較好性能。首先對PCG信號進行預處理,即分幀操作。然后對幀級PCG信號提取子帶包絡,將其疊加成二維特征圖作為CNN分類的主要特征。最后根據所提取的特征,構建合適的CNN分類器模型。本文使用5種不同評價指標對所提算法進行評估。實驗結果表明,本文算法在測試集上的各項指標均取得較好結果,對比其他研究所用的時頻特征提取方法,綜合性能更佳,為心音自動分類技術應用于CHD篩查提供了可行方法。但本文算法對PFO病例分類準確率還有待提高,今后將加深對這方面的研究,進一步提高算法性能。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。