為建立具有良好生物學性能的骨支架結構,本文基于螺旋(G)型、菱形(D)型三周期極小曲面(TPMS),設計了兩種新型梯度TPMS支架:雙向線性漸變G型(L-G型)支架、D型/G型融合(N-G型)支架,并通過壓縮仿真獲得了兩種支架的結構力學性能參數。然后,本文通過計算流體動力學(CFD)仿真獲得了支架內流體的流動性能參數,并由達西定律計算出兩種支架的滲透率。基于組織分化理論,本研究預測了兩種支架的組織分化面積。研究結果顯示,L-G型支架較N-G型支架的承載能力更強,而N-G型支架在滲透率及軟骨組織分化面積等生物學性能方面更優。L-G型和N-G型支架的建模過程為骨支架的設計提供了一種新思路,文中的仿真分析也可為支架植入人體后的骨整合預測提供參考。
引用本文: 劉志強, 宮赫, 高甲子, 劉哲昊, 鄒姍姍, 田素靜. 基于三周期極小曲面的新型梯度支架設計及其力學、滲透、組織分化特性研究. 生物醫學工程學雜志, 2021, 38(5): 960-968. doi: 10.7507/1001-5515.202102054 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
植入支架作為修復骨缺損的一種有效治療手段,在骨外科領域有著廣泛應用。植入的支架應與宿主骨有良好的整合效果,且具備足夠的力學性能[1]。近年來,越來越多的研究將植入支架設計成多孔結構,原因在于:多孔結構支架與骨結構更接近[2-3];多孔結構能有效降低彈性模量,從而減緩應力遮擋效應[4-6];多孔結構利于營養物質在其內的運輸,促進骨長入[7-8]。
滲透性是評價支架性能的一個重要方面,滲透性好有利于營養物質在支架內運輸及廢物代謝[9-11]。支架的結構、尺寸、孔隙率均能影響其滲透性[12-14]。三周期極小曲面(triply periodic minimal surfaces,TPMS)是一種在三個方向上均呈周期性變化的極小曲面,具有高連通性及幾何參數易控等優點。近年來,越來越多的研究將TPMS引入支架設計[15-16]。TPMS支架的比表面積高,更適宜細胞的黏附、生長[17-19]。菱形(diamond,D)型、螺旋(gyroid,G)型是常用的TPMS支架類型。其中G型支架的結構與人體骨結構最為接近,通過調整其幾何形態可獲得與皮質骨或松質骨相近的力學性能,因此是目前最具應用前景的骨支架結構之一[20-21]。G型支架的滲透性優越,相同孔隙率下,G型支架的滲透率高于截斷八面體及優化晶格結構的支架[22]。而另一種D型支架的特點是比表面積高,相同孔隙率下,相比于G型支架可提供更多的空間供細胞黏附[23]。同時,D型支架在能量吸收性能方面優勢突出,相同孔隙率下,與G型支架相比,D型支架的能量吸收性能更好[16-17]。此外D型與G型支架壁面光滑,承載時可有效減小應力集中[16],在力學性能方面優勢明顯。有研究表明,D型與G型支架的彈性模量與屈服強度均好于傳統的點陣結構支架,如體心立方(body-centered-cubic,BCC)型等[16]。另一方面,多孔支架中的骨細胞生長需要力學載荷刺激,而一定范圍內的壓縮載荷與流體剪應力均能刺激骨細胞生長[24],灌流系統能同時提供壓縮與流體載荷,有研究通過該裝置進行體外細胞培養[25]。
人體骨結構呈各向異性和非均勻性,因此常把多孔支架設計成具有梯度變化的結構[26]。梯度漸變TPMS支架因具備前述優勢而備受青睞。相比于各向同性的TPMS支架,梯度漸變TPMS支架的滲透率更高,且能量吸收性能更好[13, 27]。有研究表明,梯度G型支架具有平臺區長,且平臺區域內應力波動幅度小的特點,能量吸收性能優勢明顯[28]。相同孔隙率下,梯度D型支架的滲透率較均勻結構有明顯提高[13]。不同漸變形式的TPMS支架的力學性能、滲透性及細胞生長情況也不盡相同[29]。目前關于梯度G型、D型支架的研究主要為沿單一方向上的相對密度漸變,而這與變化復雜的人體骨結構差異較大。因此,本文提出兩種新型變化形式的梯度漸變TPMS支架:雙向線性漸變G型(L-G型)支架和D型/G型融合型(N-G型)支架。其中L-G型支架的結構沿X、Y兩個方向均呈線性變化,孔隙尺寸的變化范圍大。N-G型支架由D型、G型兩種胞元結構融合而成,因此具備與D型支架相近的比表面積,同時擁有G型支架的孔隙結構,保證了支架的高滲透率。與現有的梯度漸變TPMS支架不同的是,此兩種支架的結構變化方式更多元,且包含不同形狀與不同尺寸的孔隙,更加符合人體骨結構復雜變化的特點。此外,本文從力學、滲透性及組織分化三個層面對設計的支架展開性能分析,以期實現對兩種新型支架的全面評價,為其植入人體后的承載及骨整合預測提供理論依據。
1 設計
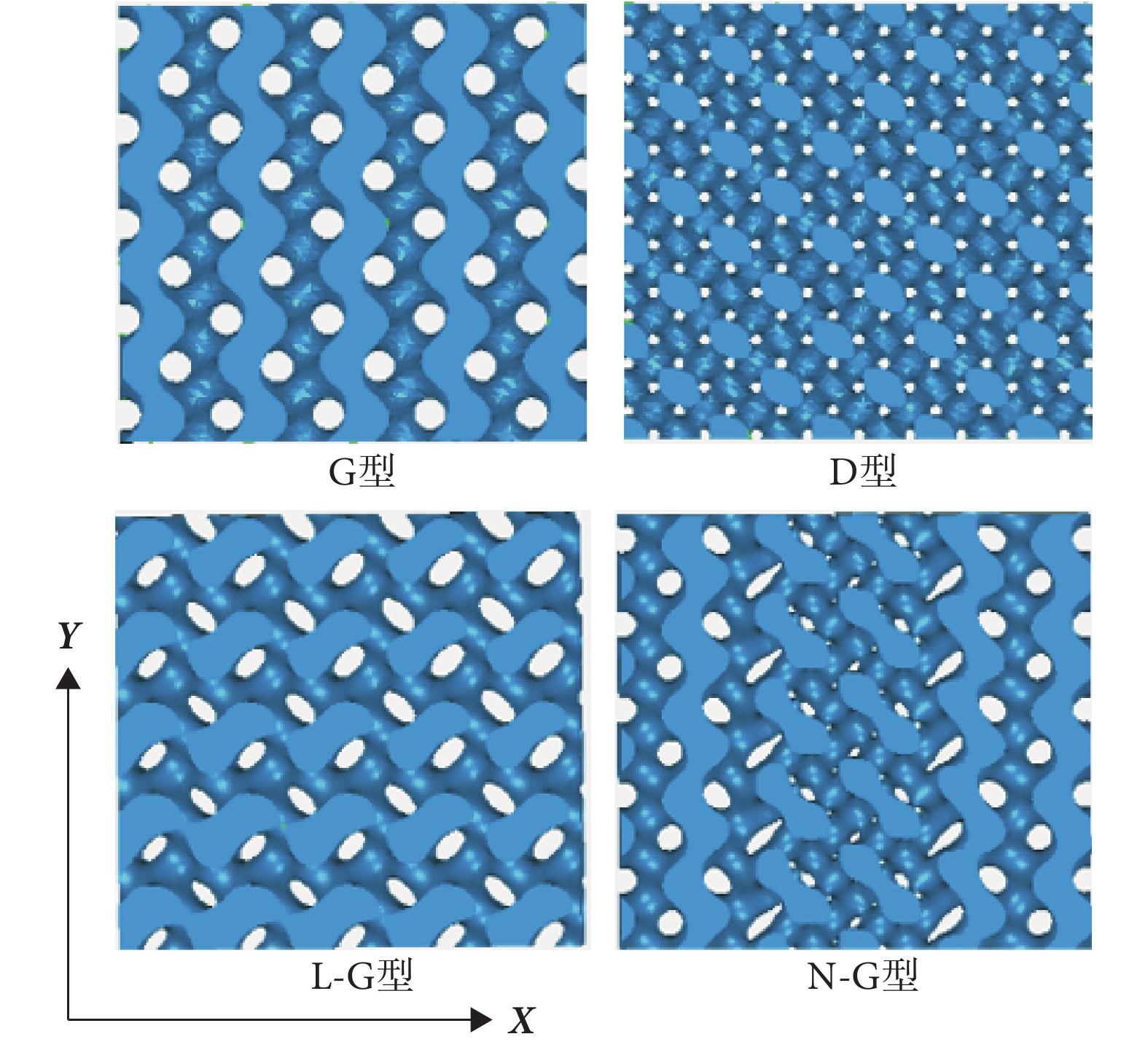
以G型表達式(G(x, y))、D型表達式(D(x, y))為基本公式,在科學計算軟件Mathematica 11.3(Wolfram Inc.,美國)中構建50%、60%、70%三種孔隙率的L-G型支架(L-G-50%、L-G-60%、L-G-70%)及N-G型支架 (N-G-50%、N-G-60%、N-G-70%)。六種支架的胞元尺寸均為3 mm × 3 mm × 3 mm,支架整體尺寸為16 mm × 16 mm × 16 mm。六種支架的結構表達式如表1所示。G型、D型、L-G型及N-G型支架的結構如圖1所示。
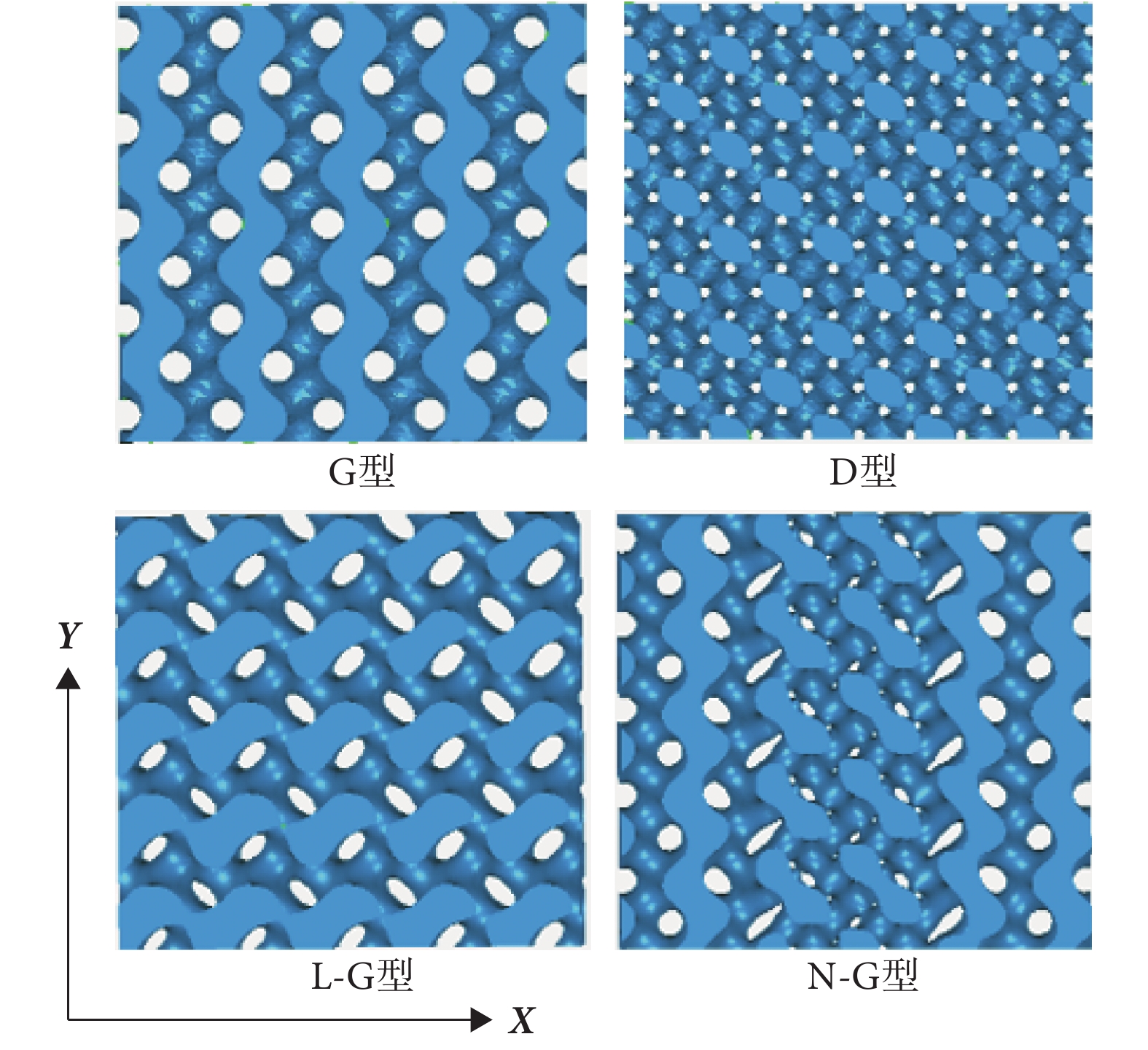 圖1
四種支架結構圖
Figure1.
Four kinds of scaffold structure
圖1
四種支架結構圖
Figure1.
Four kinds of scaffold structure
2 仿真
2.1 壓縮與計算流體動力學仿真
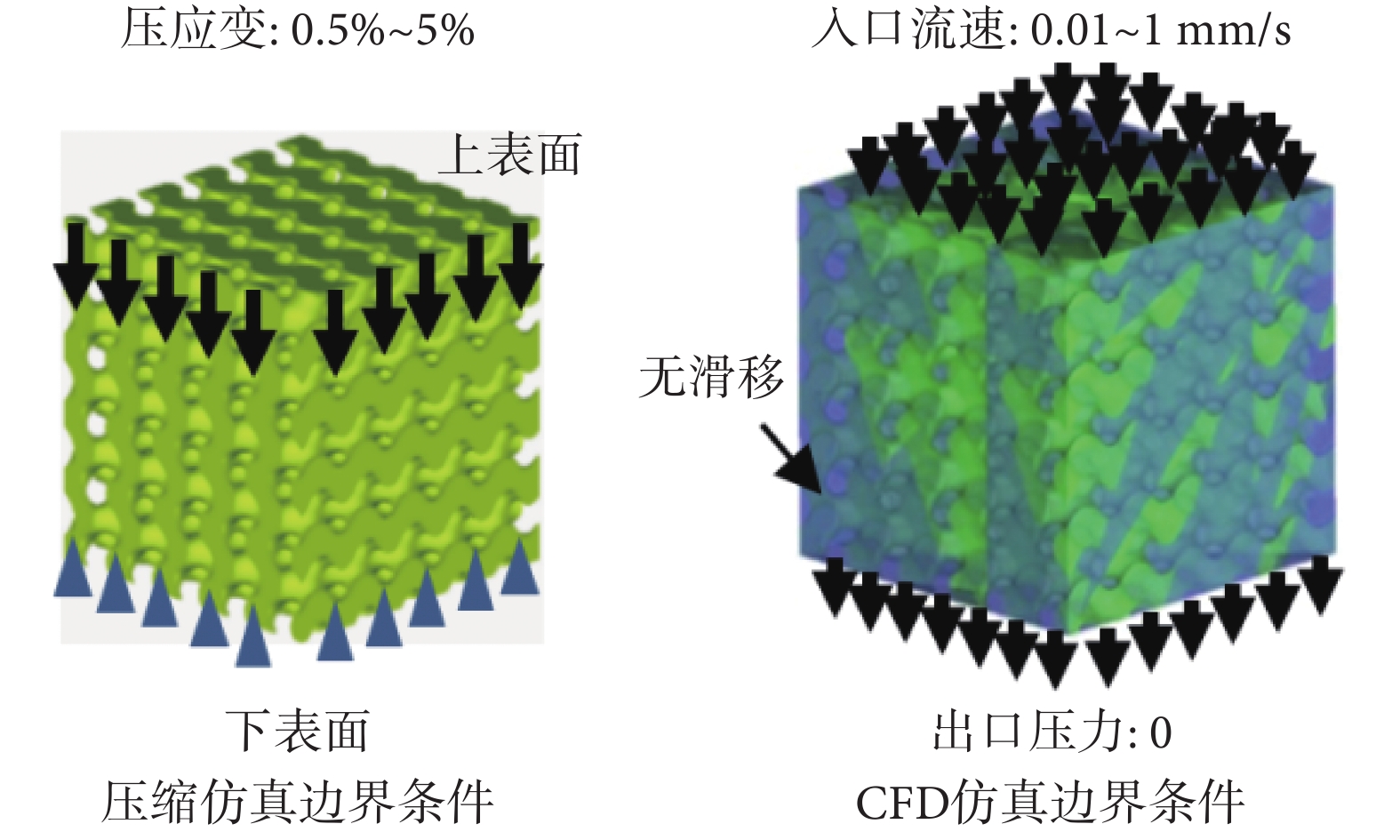
為探究六種支架的力學及滲透性能,分別對其進行壓縮與計算流體動力學(computational fluid dynamics,CFD)仿真。本文模擬在灌注式生物反應器中支架的力學響應。一般而言,支架在該裝置內承受軸向壓縮載荷和培養液灌流作用[25]。
在計算機輔助工程前處理軟件ICEM CFD 15.0 (ANSYS Inc.,美國)中,用16 mm×16 mm×16 mm的立方體與固體域模型進行布爾運算得到流體域模型,對固體及流體域模型進行網格劃分,并保證其流—固交界面上的節點一一對應。將固體域網格用于壓縮仿真,流體域網格用于CFD仿真。壓縮仿真中支架材料選擇外消旋聚乳酸(polyd l-lactide,PDLLA) [24],其彈性模量為3.3 GPa,泊松比為0.3[24]。設置支架下表面為固定約束,上表面為加載面,壓縮應變分別為:0.5%、1%、2.5%、5%[24-25]。CFD仿真中的流體介質為培養液[25],其密度為1 000 kg/m3,黏度為1.45×10-3 Pa﹒s。設置入口流速分別為:0.01 mm/s、0.1 mm/s、0.5 mm/s、1 mm/s[24-25],出口壓力為零,邊界無滑移,根據達西定律計算各支架的滲透率[21]。壓縮與CFD仿真的邊界條件如圖2所示。
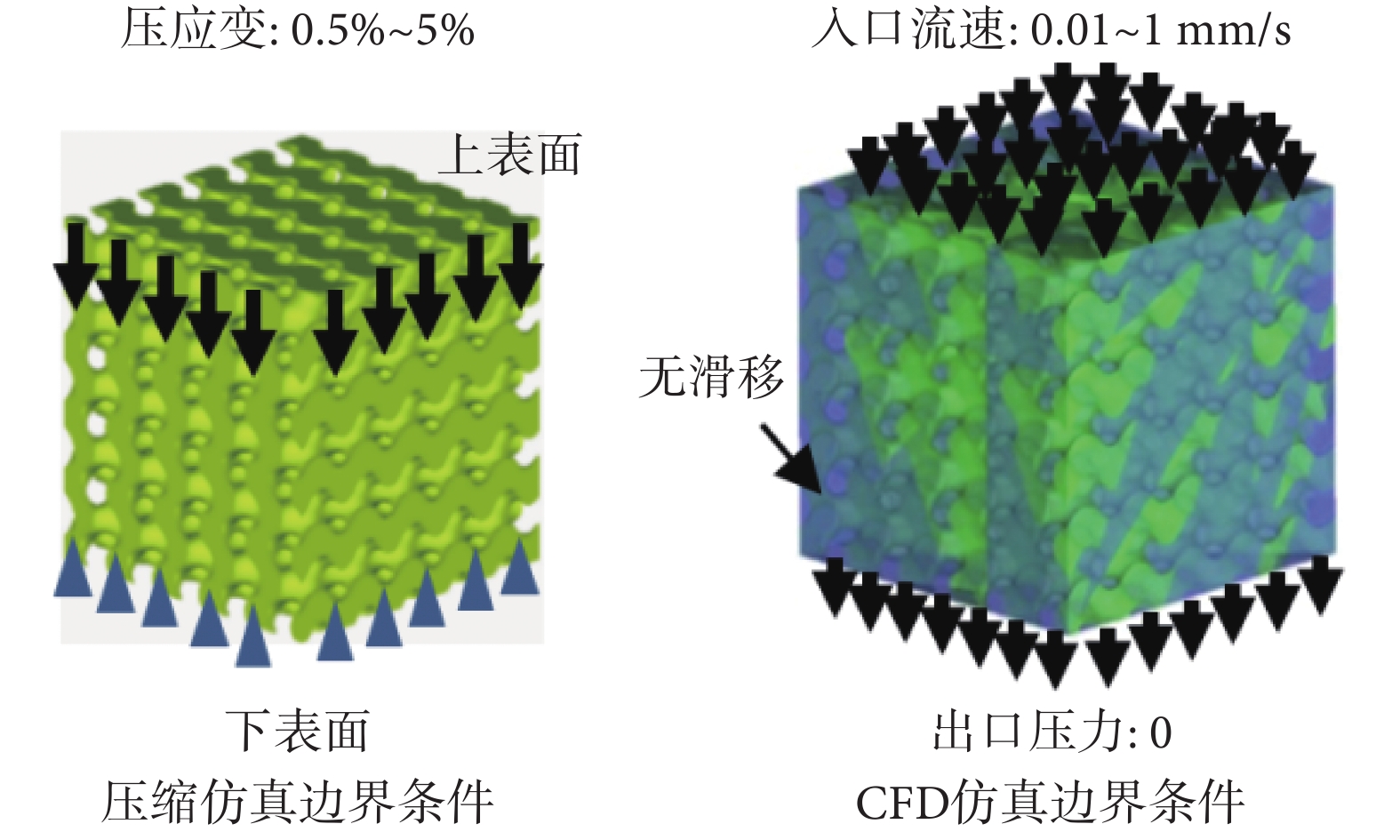 圖2
壓縮與CFD仿真邊界條件示意圖
Figure2.
Boundary condition for compression and CFD simula tion
圖2
壓縮與CFD仿真邊界條件示意圖
Figure2.
Boundary condition for compression and CFD simula tion
2.2 支架壁面上的組織分化計算
為進一步探究六種支架上的組織分化差異,對在體外灌流系統培養條件下支架壁面的組織分化進行計算。體外培養條件下,組織沿多孔支架內壁分化,因此主要受流—固交界面的載荷刺激影響[25],故本文研究的是在流—固交界面上的組織分化情況。Prendergast等[30]提出了組織分化定量理論,建立了組織分化與其黏附面上的力學激勵間的關系。文獻[24-25]運用組織分化定量理論對支架壁面的組織分化情況進行計算,如式(1)~式(2)所示:
 |
 |
其中,r為八面體剪應變;ε1、ε2、ε3分別為第1、2、3主應變;W為流體剪應力;a = 0.037 5%,b = 0.01 Pa。當S<0.01時,激勵值過小不能誘導組織分化;當0.01 ≤ S<1時,分化形成骨組織;當1 ≤ S<3時,分化形成軟骨組織;當3 ≤ S<6時,分化形成纖維組織;而當S ≥ 6時,激勵值過大不能誘導組織分化。
3 結果
3.1 支架的幾何參數
如圖1所示,L-G型支架的結構變化形式主要為孔隙尺寸漸變,而N-G型支架的結構其孔隙尺寸與形狀均發生變化。六種支架的尺寸規格、流—固交界面面積及孔徑尺寸的數值如表2所示。可見,隨著孔隙率的增加,L-G型與N-G型支架的流—固交界面的面積均在減小,而這兩種支架的孔徑尺寸均隨著孔隙率的增加而變大。同時可以看出,在相同孔隙率下,L-G型支架的流—固交界面的面積小于N-G型支架。因此,相同孔隙率下,N-G型支架可提供更大的壁面面積供細胞黏附、生長。此外,相同孔隙率下,L-G型支架孔徑尺寸的數值范圍也小于N-G型支架。換言之,相比于L-G型,N-G型支架的結構漸變程度更高。
3.2 支架的力學性能
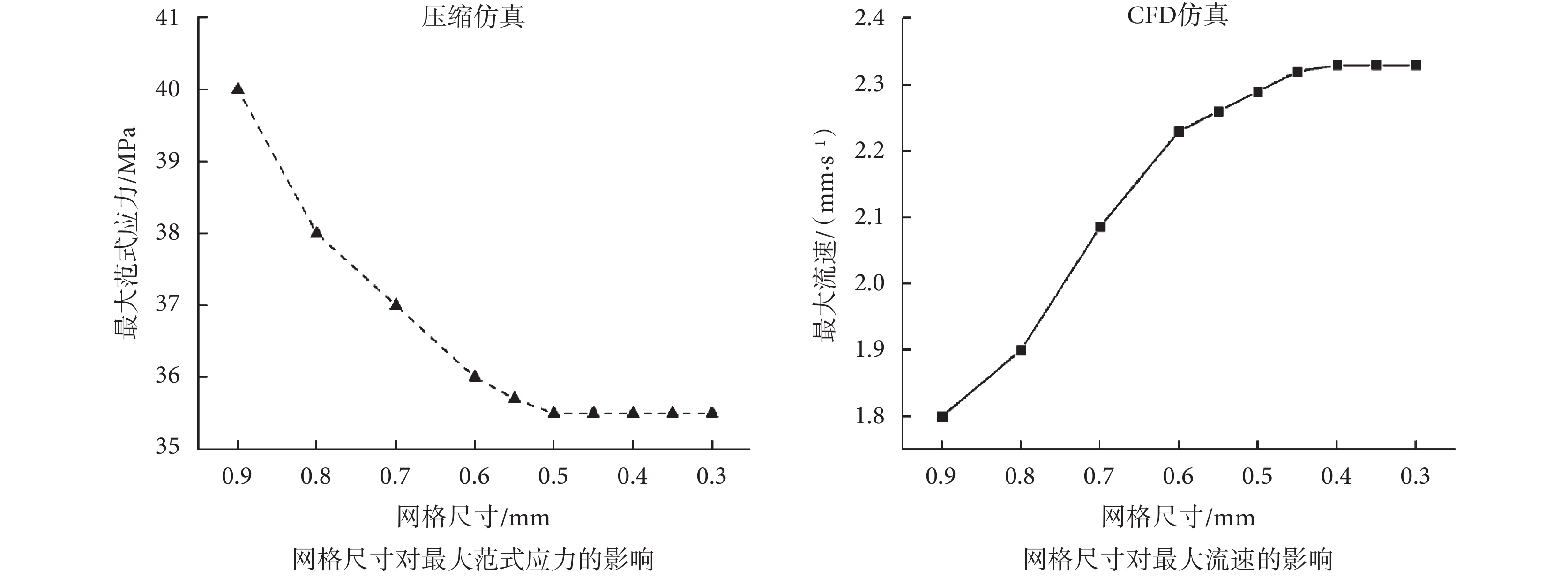
為保證有限元仿真的準確性,以N-G-50%為例進行網格敏感性分析。網格尺寸對仿真結果的影響如圖3所示。當網格尺寸小于0.4 mm時,壓縮仿真與CFD仿真均獲得了穩定的結果,因此為節省計算,設置統一網格尺寸為0.4 mm。
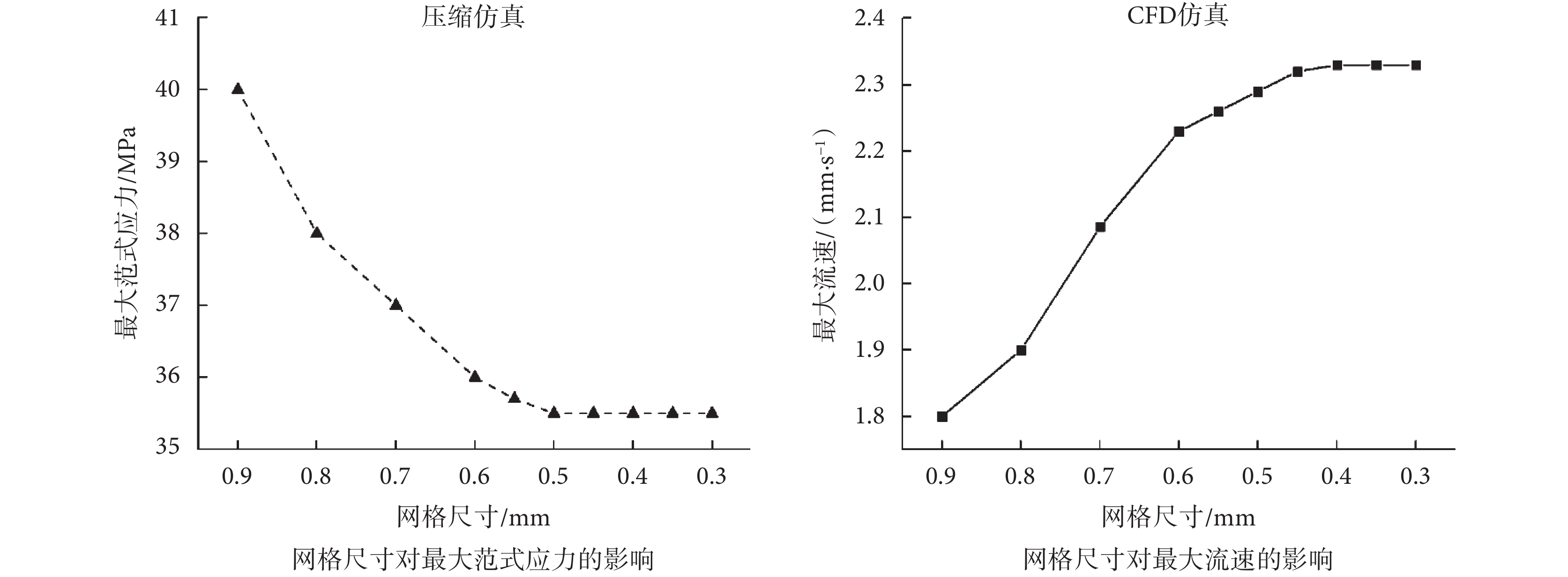 圖3
網格尺寸對最大范式應力及最大流速的影響
Figure3.
The influence of mesh size on maximum von Mises stress and maximum velocity
圖3
網格尺寸對最大范式應力及最大流速的影響
Figure3.
The influence of mesh size on maximum von Mises stress and maximum velocity
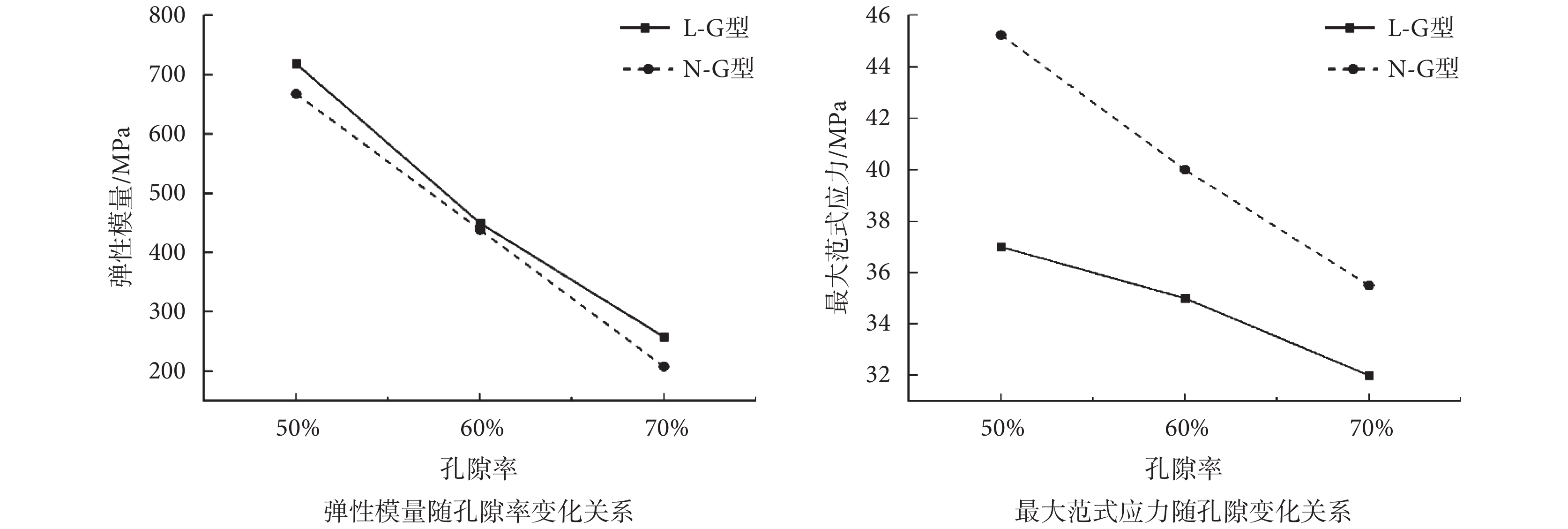
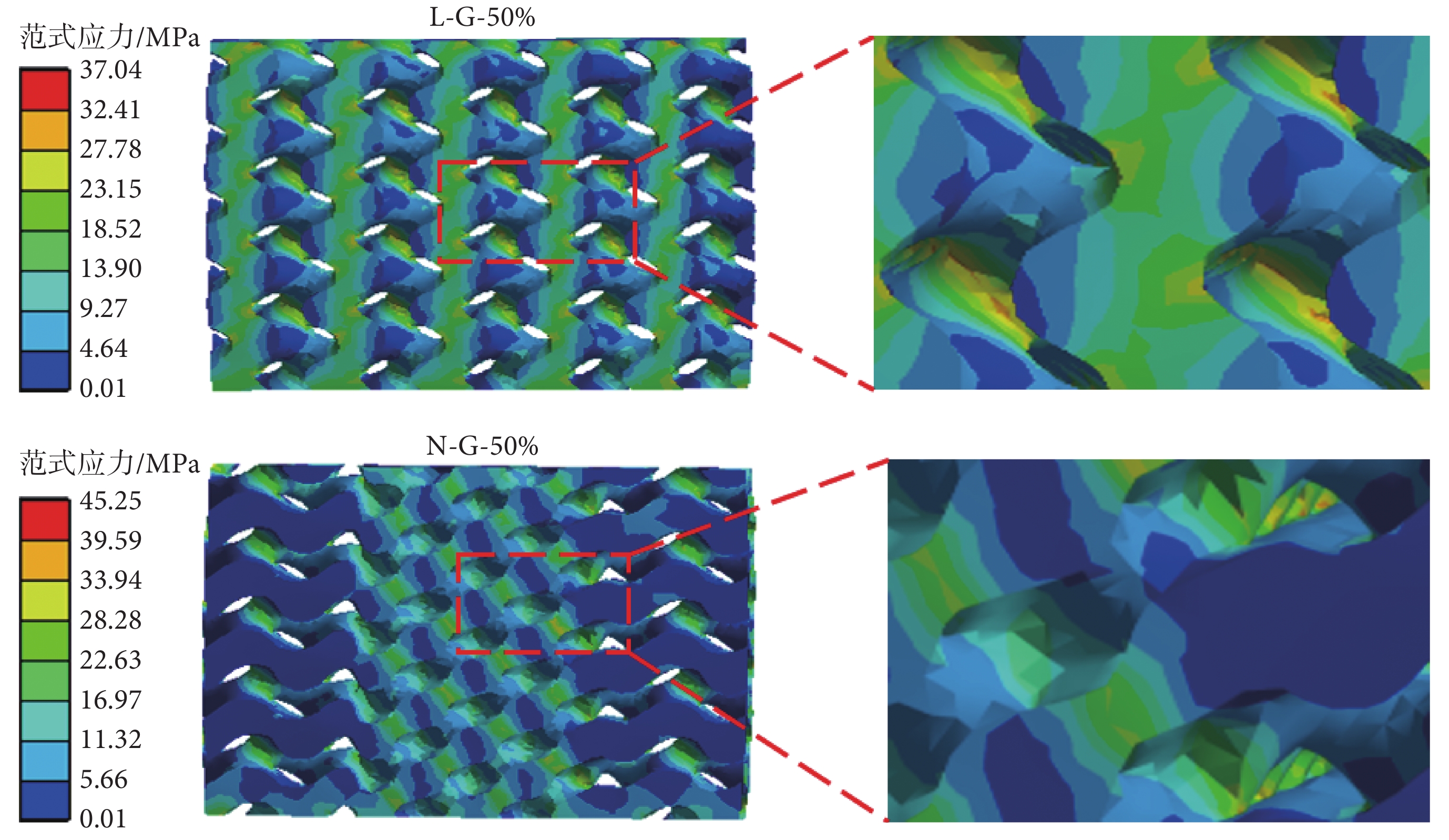
0.5%壓縮應變下,兩種支架上的最大范式應力與彈性模量隨孔隙率的變化關系如圖4所示。可見,L-G型、N-G型支架的最大范式應力與彈性模量均隨孔隙率的增加而減小,其中N-G型支架上的最大范式應力明顯高于L-G型支架。在變化趨勢上,隨孔隙率的提高,N-G型支架的最大范式應力下降得更明顯。彈性模量方面,L-G型支架高于N-G型支架。L-G-50%支架與N-G-50%支架在0.5%的壓縮應變下的范式應力分布情況如圖5所示。其中,N-G型支架的范式應力最大值在不同胞元結構的過渡處,而L-G型支架的范式應力最大值則存在于縱向支桿上,同時可以看出,N-G型支架的應力集中程度高于L-G型支架。
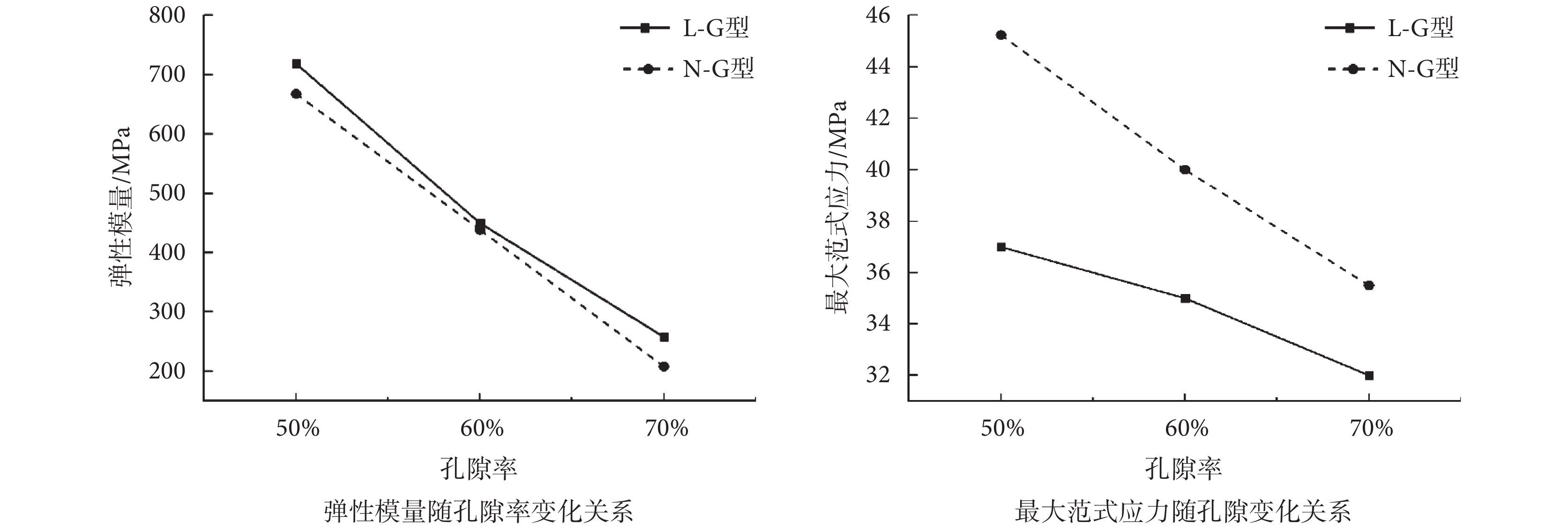 圖4
0.5%壓縮應變下支架最大范式應力與彈性模量隨孔隙率變化關系圖
Figure4.
The relationships of the maximum von Mises stress and elastic modulus with porosity of the scaffolds under the 0.5% compression strain
圖4
0.5%壓縮應變下支架最大范式應力與彈性模量隨孔隙率變化關系圖
Figure4.
The relationships of the maximum von Mises stress and elastic modulus with porosity of the scaffolds under the 0.5% compression strain
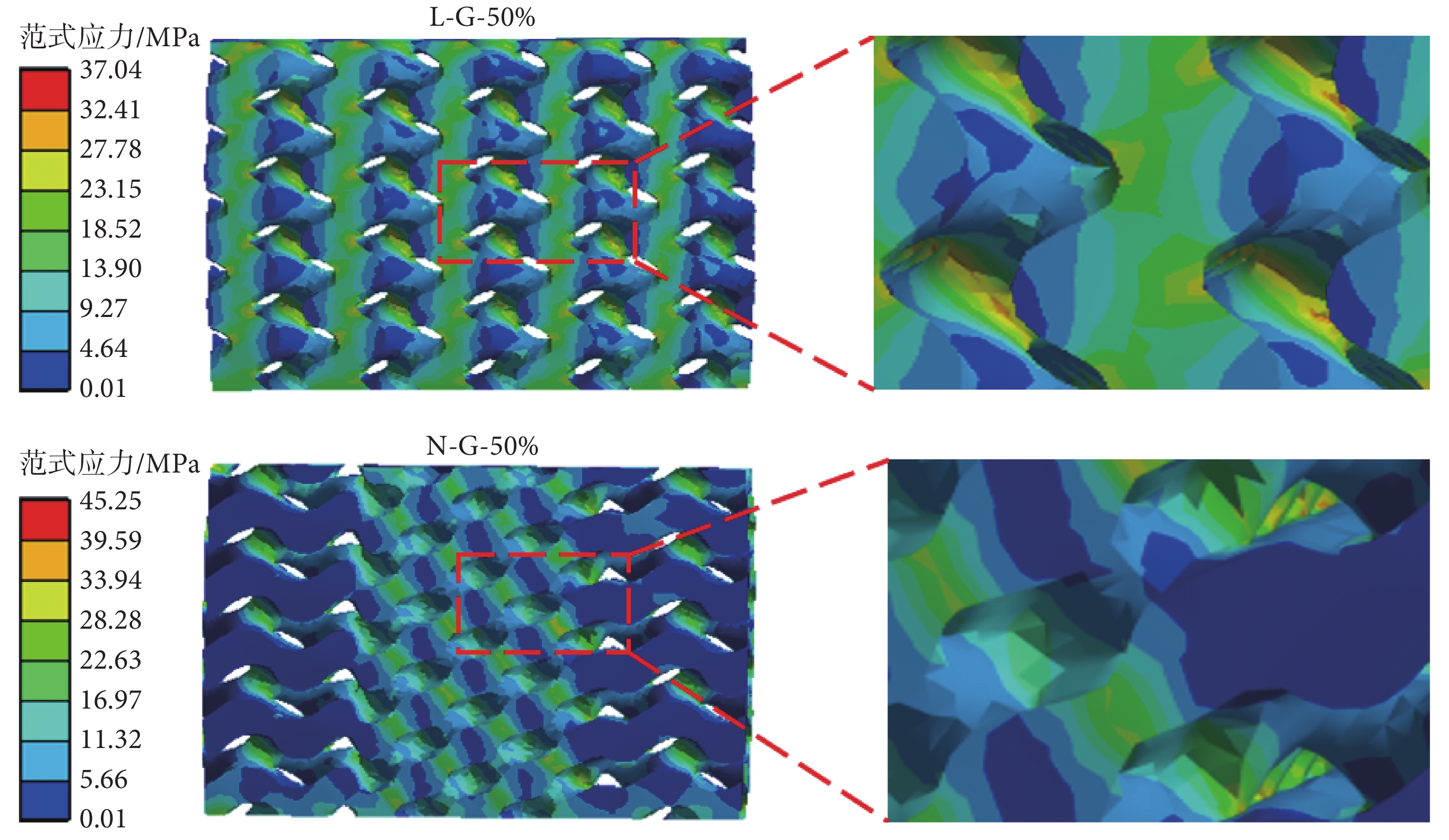 圖5
0.5%壓縮應變下支架上的范式應力分布圖
Figure5.
von Mises stress distribution on the scaffold under 0.5% compression strain
圖5
0.5%壓縮應變下支架上的范式應力分布圖
Figure5.
von Mises stress distribution on the scaffold under 0.5% compression strain
3.3 支架內流體的流動性能
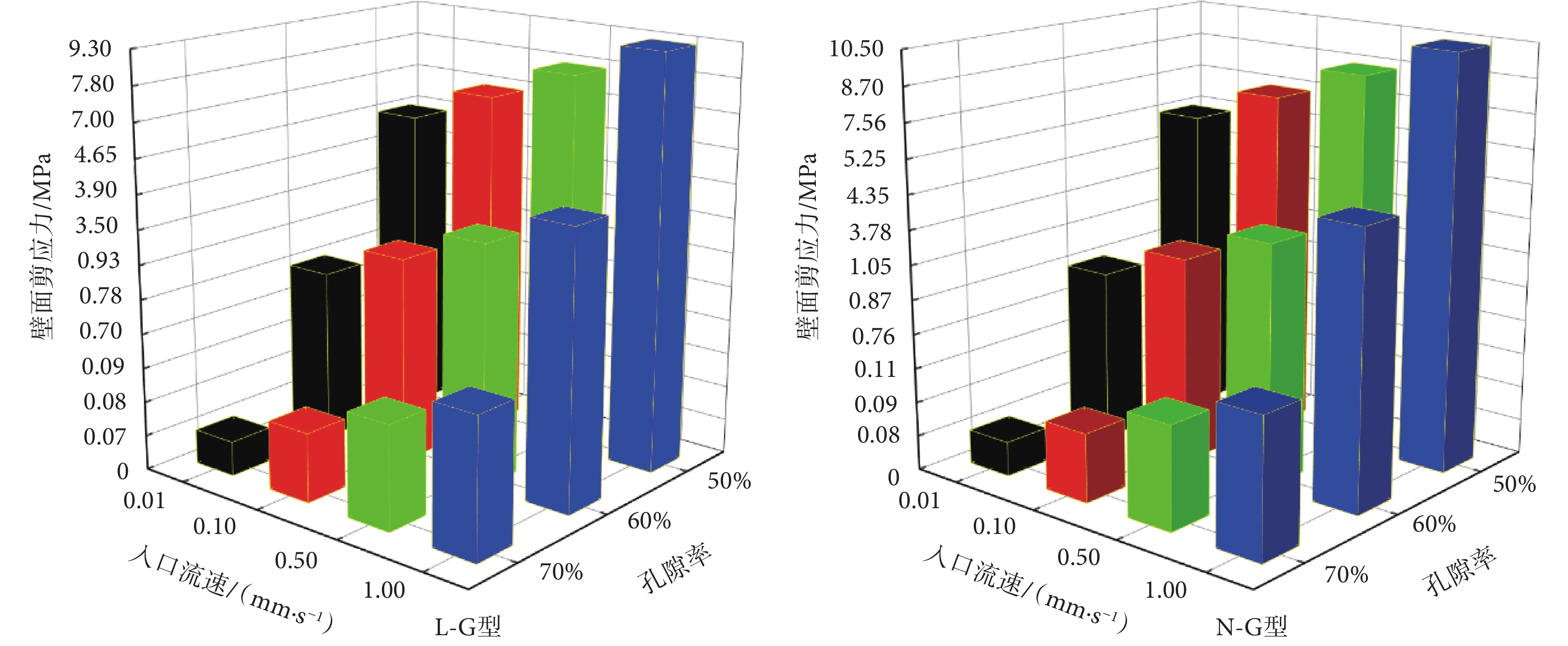
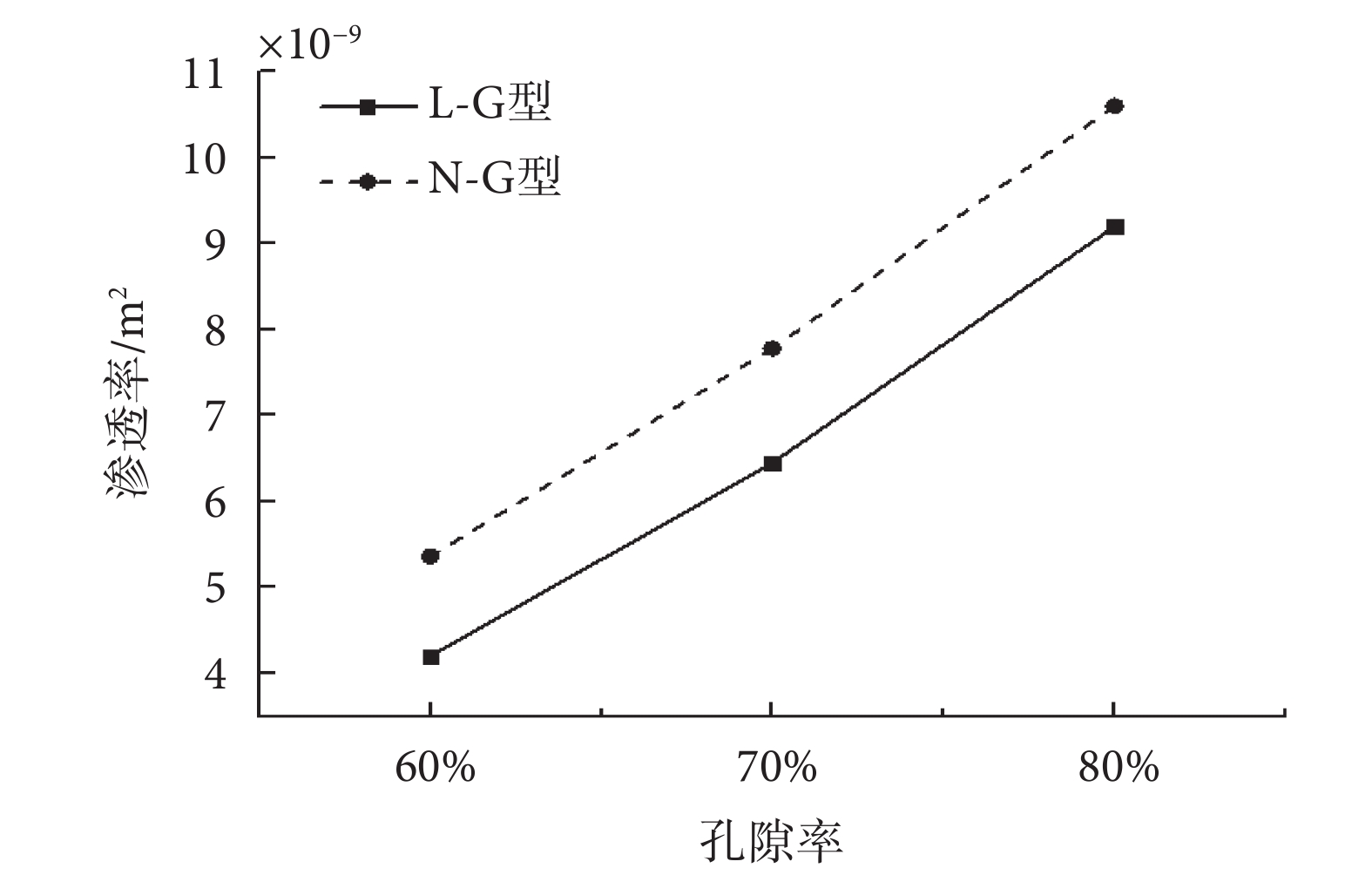
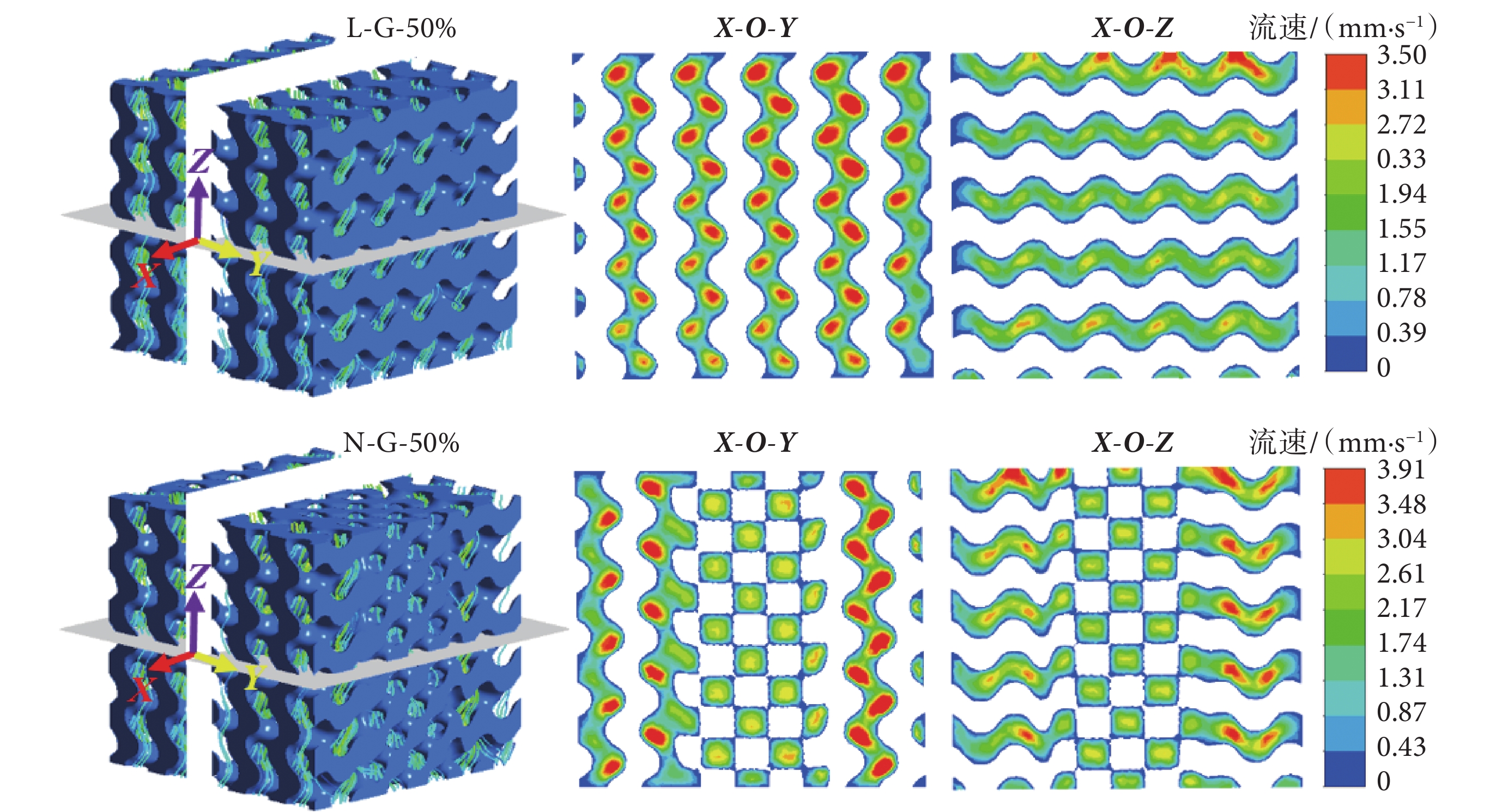
支架的壁面剪應力平均值隨入口流速與孔隙率的變化如圖6所示。其中,支架的壁面剪應力平均值隨入口流速的增加而提高,而當孔隙率增加時,支架的壁面剪應力平均值則明顯降低。兩種支架的滲透率隨孔隙率的變化關系如圖7所示。可見,兩種支架的滲透率均隨孔隙率的增加而提高。相同孔隙率下,N-G型支架的滲透率高于L-G型支架,這是因為孔隙率相同時,N-G型支架孔徑的尺寸范圍大于L-G型支架,因此其滲透性更好。當入口流速為1 mm/s時,L-G-50%及N-G-50%內流體的流線圖,及在X-O-Y、X-O-Z平面上的流速分布如圖8所示。可見,在L-G型支架中,孔隙尺寸大即流道寬處的流速高。N-G型支架中,遠離Z軸的流道結構內的流速高,靠近Z軸的流道結構內的流速低。這是因為N-G型支架靠近Z軸部分為D型結構,孔隙尺寸小,而遠離Z軸的部分為G型結構,孔徑尺寸大,因此產生速度差異。
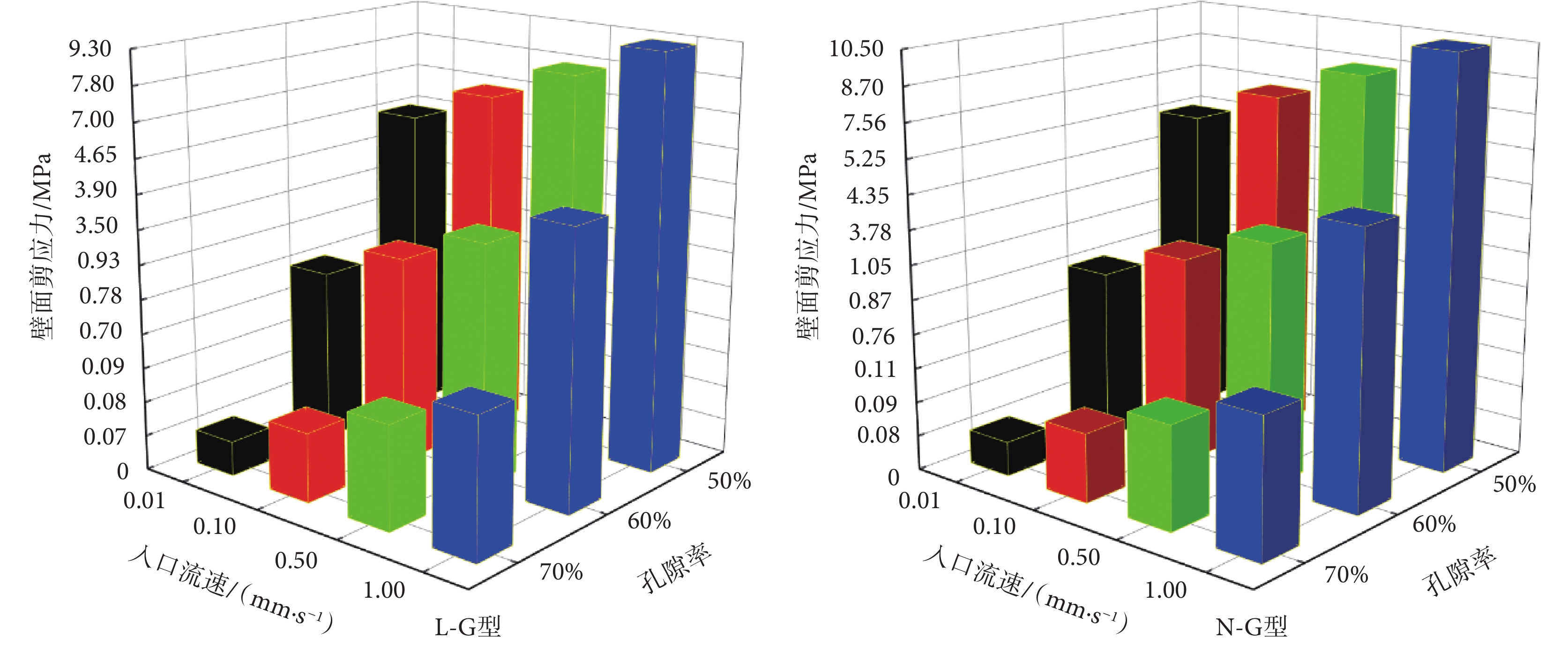 圖6
支架壁面上剪應力平均值隨孔隙率與入口流速變化圖
Figure6.
The change of the average value of the shear stress with porosity and inlet velocity on the scaffold wall
圖6
支架壁面上剪應力平均值隨孔隙率與入口流速變化圖
Figure6.
The change of the average value of the shear stress with porosity and inlet velocity on the scaffold wall
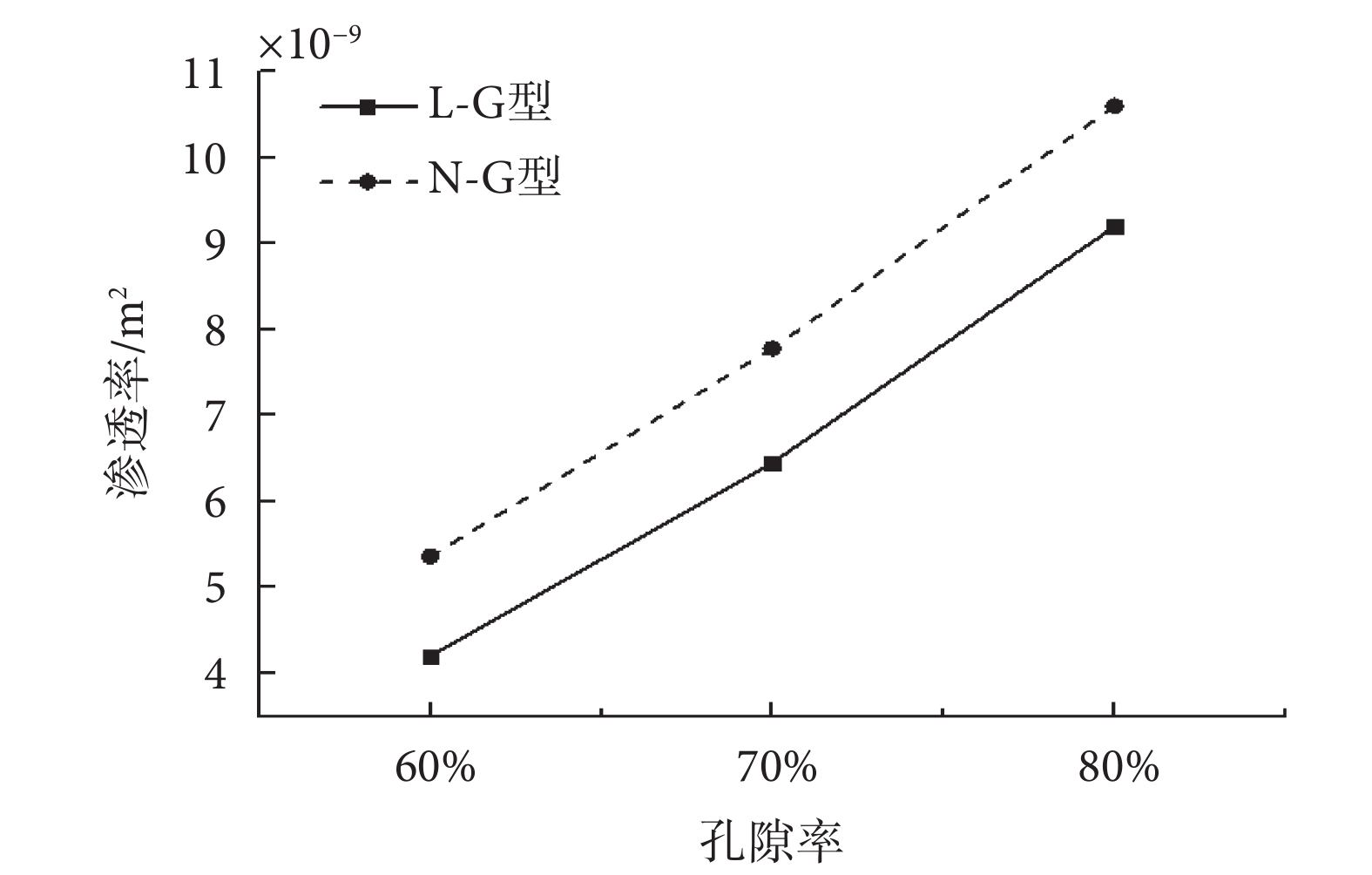 圖7
支架滲透率隨孔隙率變化圖
Figure7.
Permeability of scaffold varies with porosity
圖7
支架滲透率隨孔隙率變化圖
Figure7.
Permeability of scaffold varies with porosity
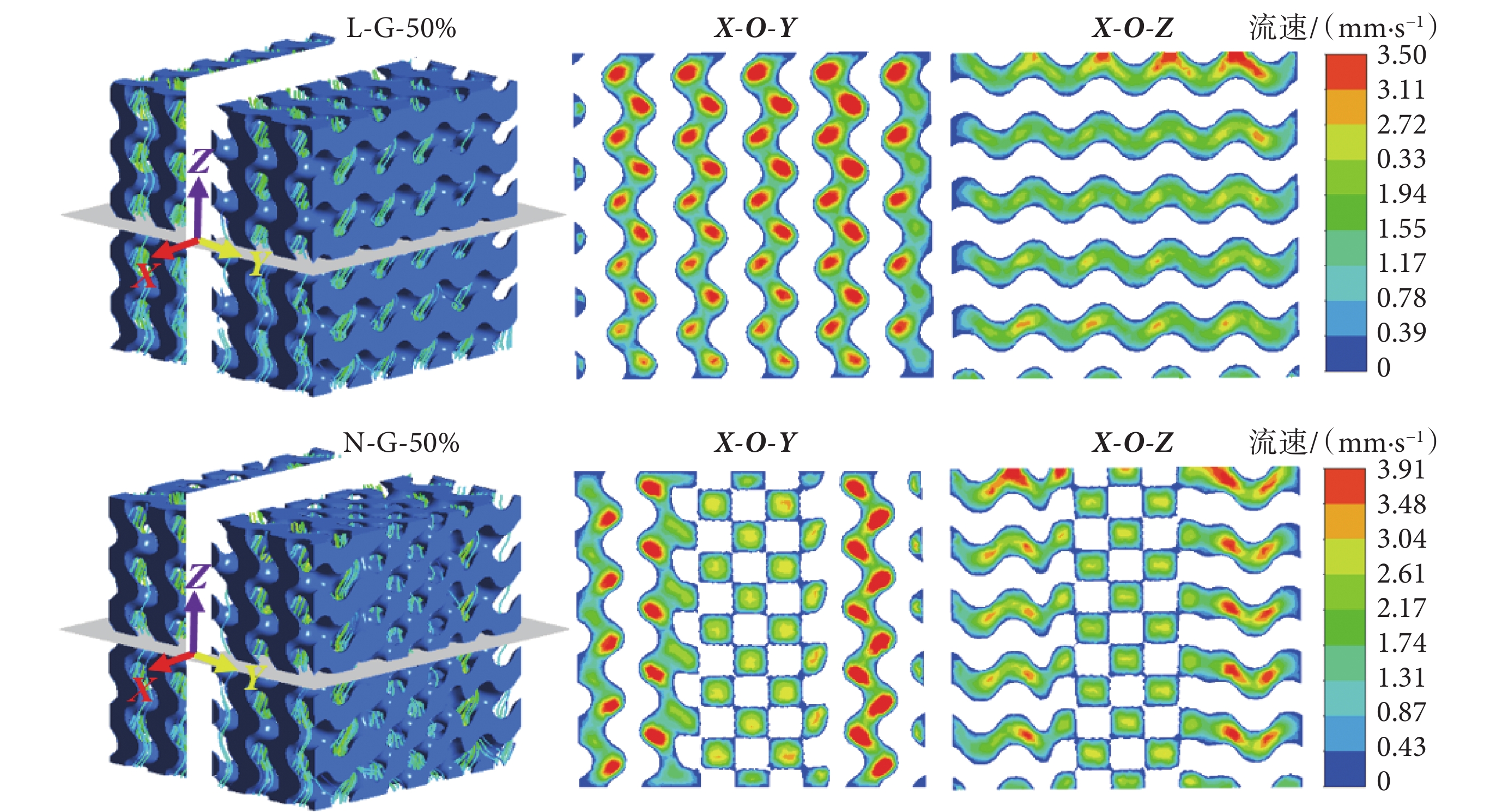 圖8
1 mm/s入口流速下,L-G-50%、N-G-50%支架的流線及流速分布圖
Figure8.
Streamline and velocity distribution of the L-G-50%, N-G50% scaffold at the 1 mm/s inlet velocity
圖8
1 mm/s入口流速下,L-G-50%、N-G-50%支架的流線及流速分布圖
Figure8.
Streamline and velocity distribution of the L-G-50%, N-G50% scaffold at the 1 mm/s inlet velocity
3.4 支架壁面上的組織分化
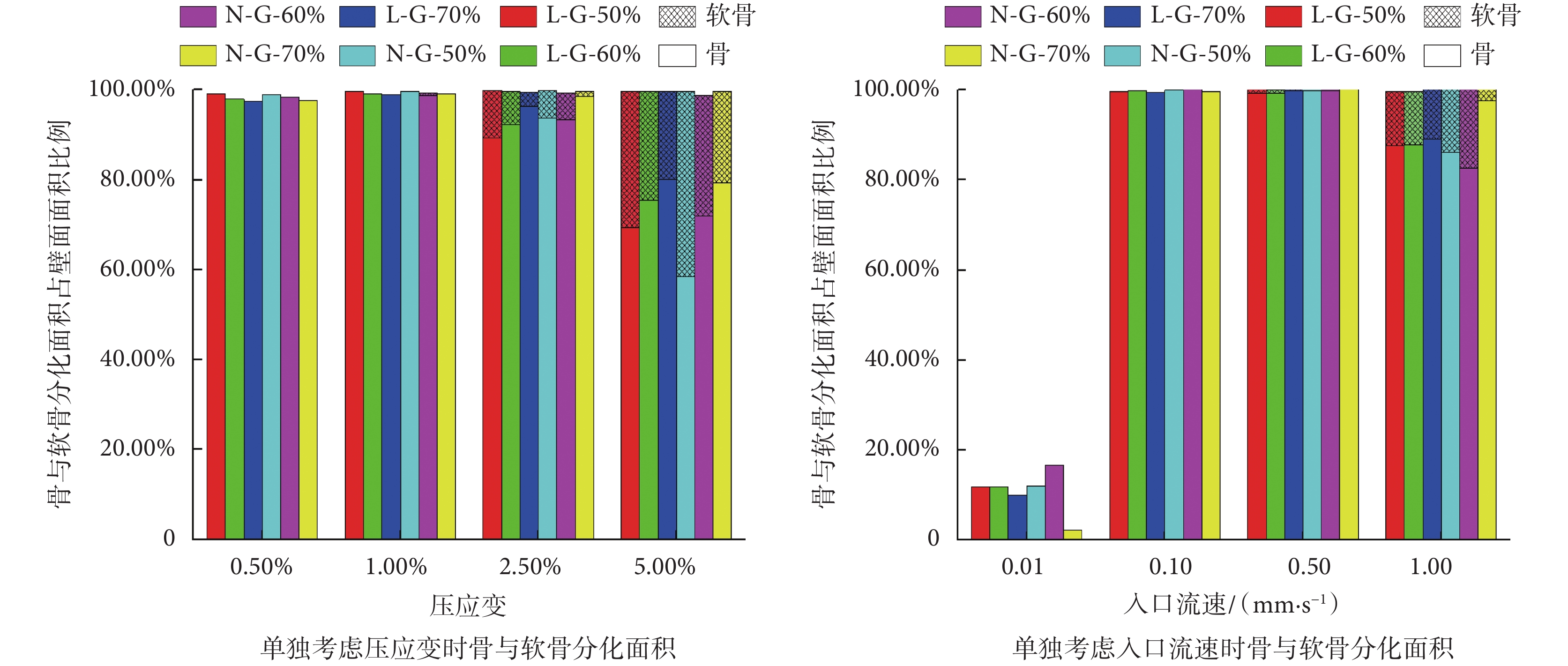
當單獨考慮整體壓應變影響時,支架壁面上骨與軟骨分化面積如圖9所示。可見,當整體壓應變在0.5%~1%時,六種支架壁面均有超過90%的區域分化成骨,但此時因力學刺激過小,無法誘導軟骨分化。而當整體壓應變達到2.5%時,六種支架壁面均出現了軟骨分化;當整體壓應變提高到5%時,軟骨分化面積得到了進一步提高。單獨考慮入口流速影響時,在0.01 mm/s的入口流速作用下,六種支架因力學刺激過小其壁面的骨分化面積均不足50%;而當入口流速在0.1~0.5 mm/s范圍內時,六種支架壁面的骨分化面積均接近100%;當入流速達到1 mm/s時,六種支架壁面有了軟骨分化。由此可得,支架壁面上的骨與軟骨分化程度,相比于整體壓應變,對流體流動產生的剪應力刺激更敏感。這一結論與文獻[24-25]得出的結論一致。
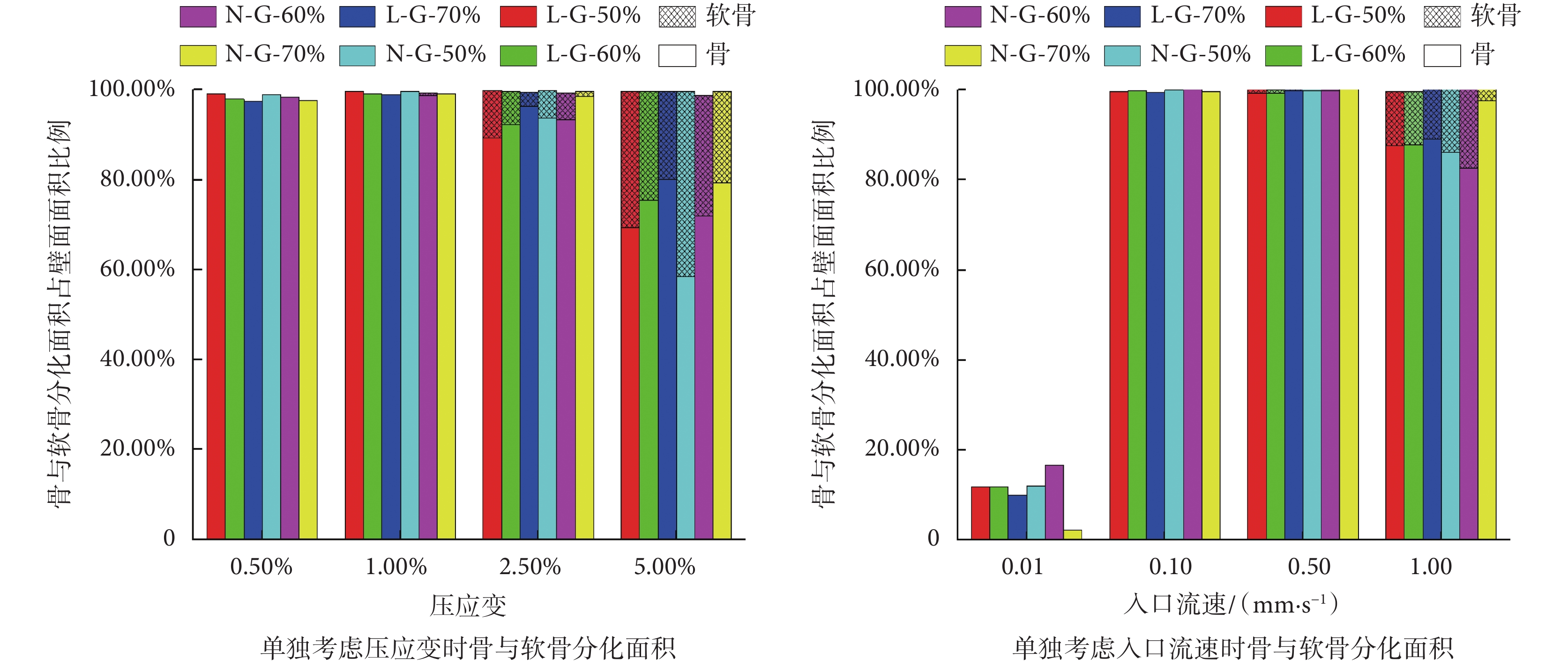 圖9
單獨考慮整體壓應變及流體作用時支架壁面上的骨與軟骨分化面積
Figure9.
The differentiation area of bone and cartilage on the wall of the scaffold when the compressive strain and fluid action are considered separately
圖9
單獨考慮整體壓應變及流體作用時支架壁面上的骨與軟骨分化面積
Figure9.
The differentiation area of bone and cartilage on the wall of the scaffold when the compressive strain and fluid action are considered separately
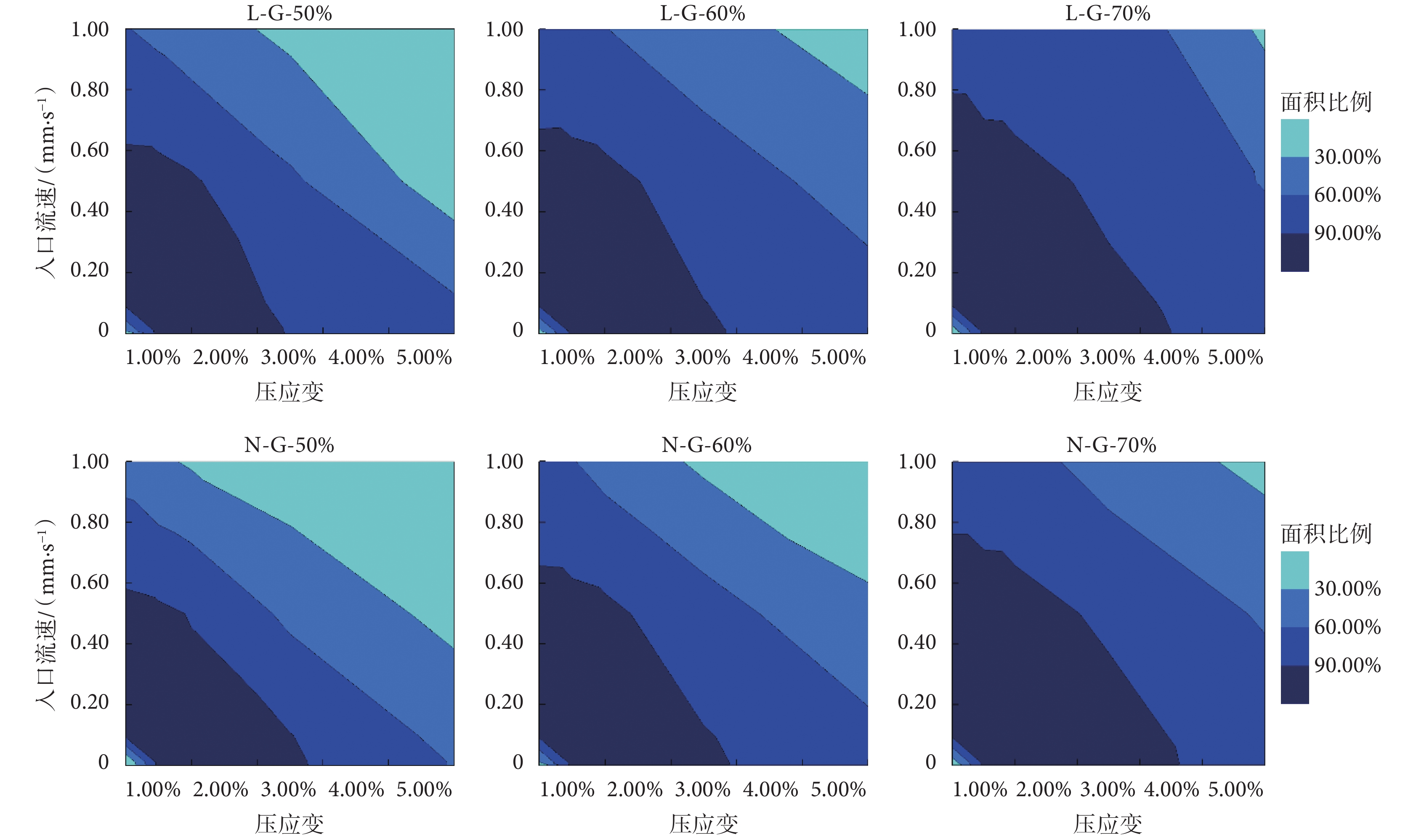
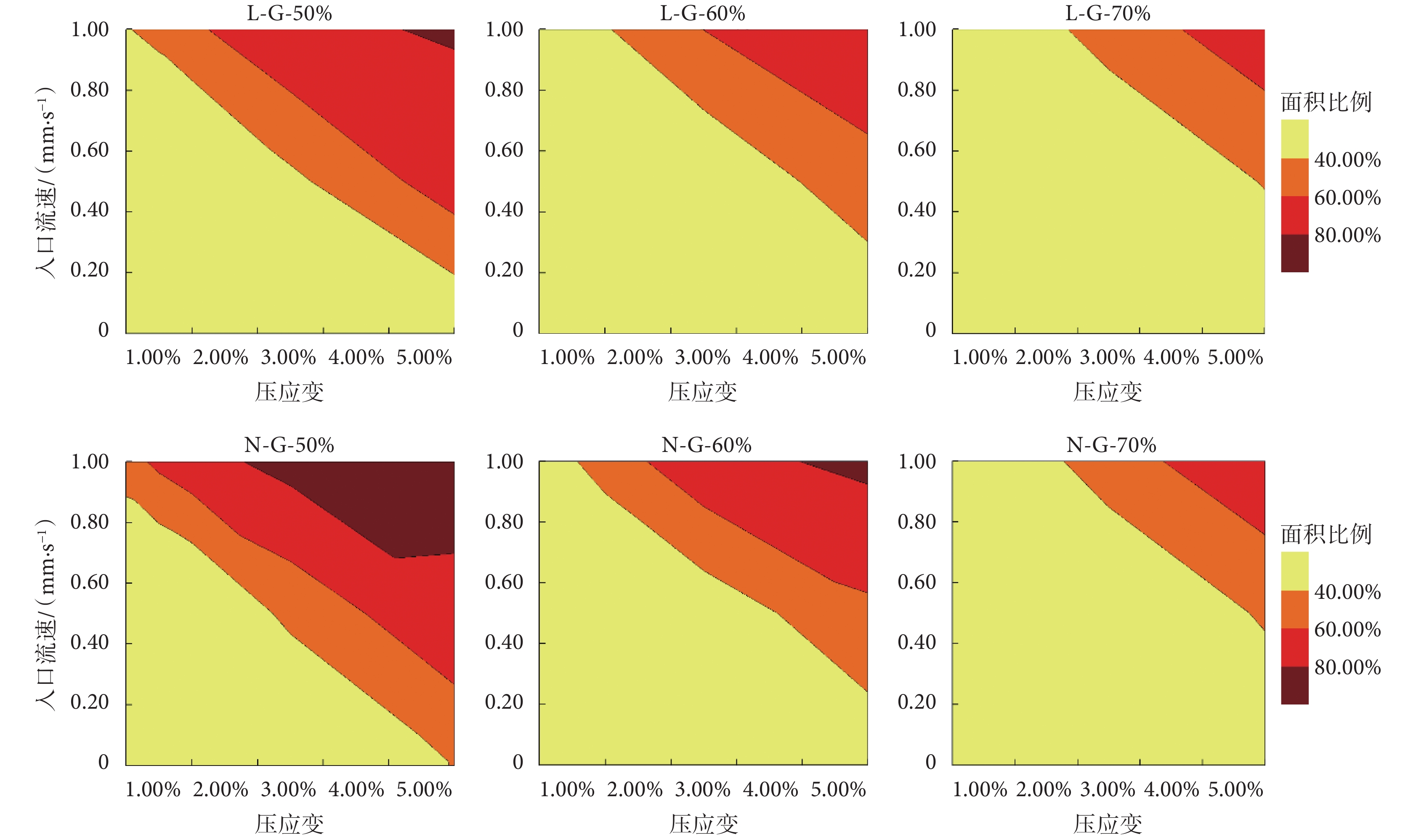
考慮流—固載荷作用時,支架壁面上的骨、軟骨的分化面積如圖10、圖11所示。可見,六種支架均能實現90%壁面面積的骨分化。如圖11所示,在60%孔隙率下,L-G型支架只能實現60%壁面面積的軟骨分化,而N-G型支架則可實現80%壁面面積的軟骨分化。在相同孔隙率及入口流速下,N-G型支架上的壁面剪應力比L-G型支架大,因此N-G型支架較L-G型支架更容易誘導軟骨分化。故為促進軟骨于支架內的分化,在設計支架結構時,應盡量增加支架內部流道的曲折程度以提高支架的壁面剪應力。
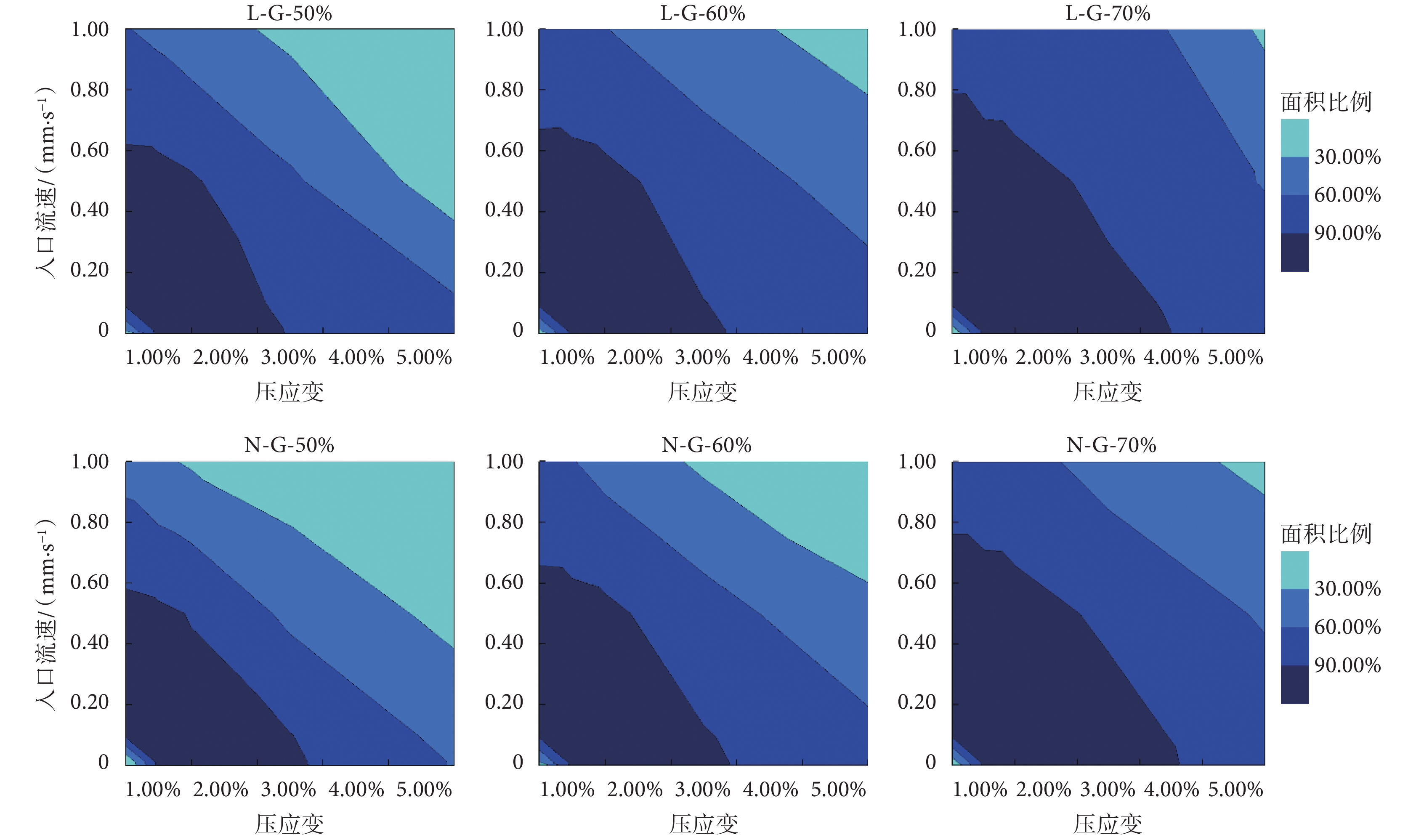 圖10
考慮流-固載荷作用時的骨分化面積
Figure10.
Bone differentiation area considering fluid-solid load
圖10
考慮流-固載荷作用時的骨分化面積
Figure10.
Bone differentiation area considering fluid-solid load
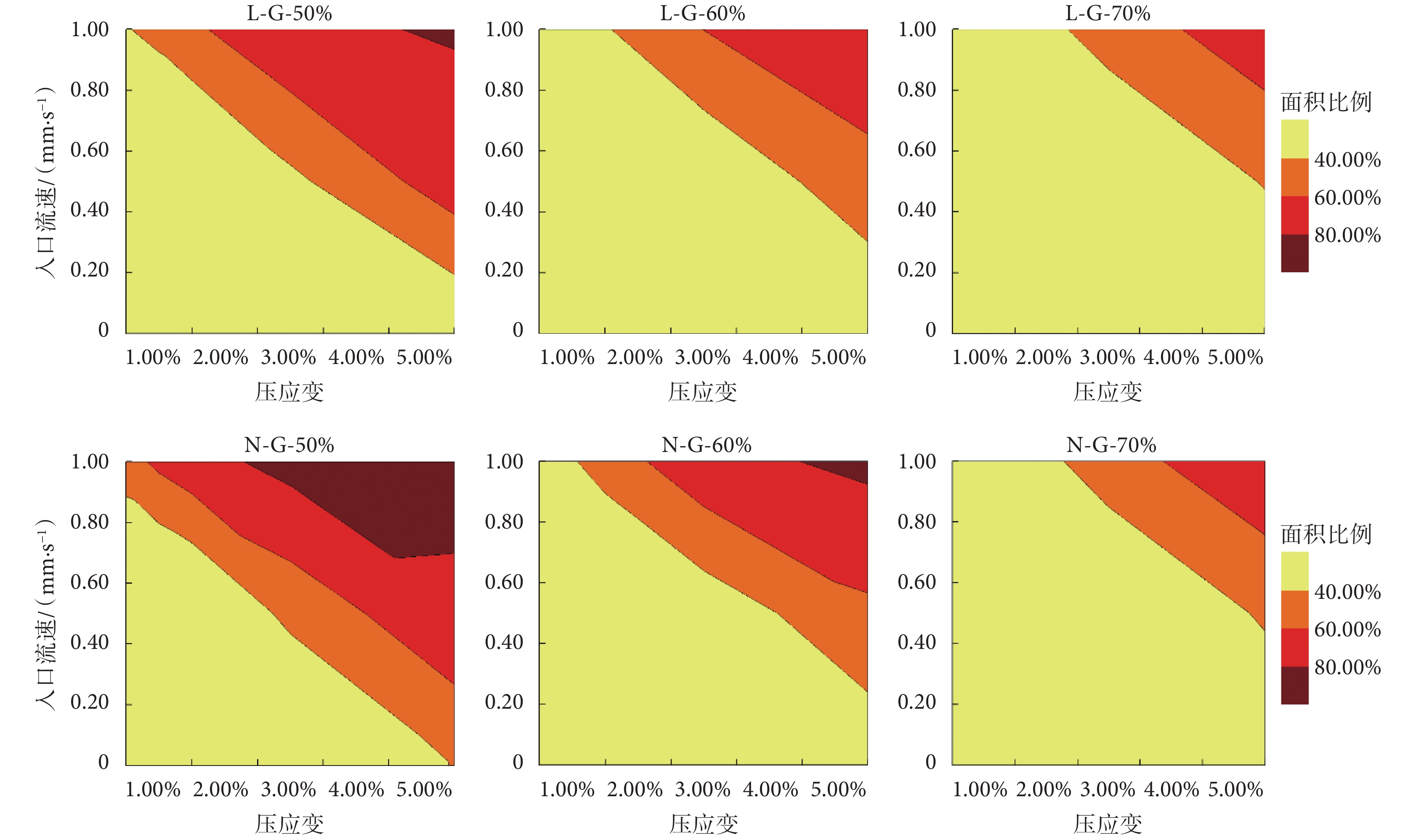 圖11
考慮流-固載荷作用時的軟骨分化面積
Figure11.
Cartilage differentiation area considering fluid-solid load
圖11
考慮流-固載荷作用時的軟骨分化面積
Figure11.
Cartilage differentiation area considering fluid-solid load
4 討論
本文設計了兩種類型的梯度漸變TPMS支架:L-G型和N-G型,通過壓縮仿真與CFD仿真分別獲得了兩種支架的彈性模量、范式應力等結構力學參數及支架內流體的壁面剪應力、滲透率等流體流動性能參數。基于組織分化理論,計算了兩種支架在體外灌流系統培養條件下的骨與軟骨分化面積。
本文中,支架材料選用的是PDLLA,其屈服強度約為0.12 GPa[31],而人體骨的屈服強度范圍為0.002~0.205 GPa[6]。PDLLA是強度與骨接近且可降解的聚合物材料[23],因此廣泛應用于可吸收的骨固定裝置及體外骨細胞培養實驗中[23, 29]。
不同結構形式的G型支架與人體骨的彈性模量對比如表3所示。可見,相同材料及孔隙率下,L-G型與N-G型支架的彈性模量高于文獻[23-24]中的G型與梯度G型支架。人體松質骨的彈性模量范圍為0.067~0.44 GPa[6],可見L-G型與N-G型支架的彈性模量雖高于G型與梯度G型支架,但其數值仍在人體松質骨的彈性模量范圍內,因此可有效避免應力遮擋。相比于N-G型支架,L-G型支架的彈性模量更高且應力分布更均勻,因此其承載能力更強。N-G型支架在兩種胞元的過渡處應力集中現象更明顯,承載時胞元過渡處更容易出現破壞。這是由于N-G型支架由兩種胞元結構融合而成,在過渡處的曲率較大[32],因而承載時出現應力集中。
支架的滲透性主要取決于孔隙率,此外,支架的結構形式是另一個影響因素。支架的滲透率大小應盡量接近宿主骨。本文與一些研究設計的支架及人體骨的滲透率對比如表4所示。可見,一些研究設計的支架雖滲透率較高,但超出人體骨的滲透率數值范圍,而本文設計的六種支架其滲透率均在人體骨的滲透率數值范圍內。相同孔隙率下,相比于L-G型支架,N-G型支架的滲透性能更好,這是由于N-G型支架的最大孔徑尺寸高于L-G型支架,而得益于更大的孔徑尺寸,N-G型支架的滲透性能則明顯好于L-G型支架。細胞在支架內的生長需要載荷刺激,有研究表明,當支架上的壁面剪應力大小在5×10?5~2.5×10?2 Pa時,利于細胞生長;當剪應力大于2.5×10-2 Pa時,將抑制細胞生長[7]。如圖7所示,本文設計的六種支架其壁面剪應力的數值范圍主要集中在2×10-3~1.4×10-2 Pa,因此六種支架均可以提供適宜的細胞生長環境。此外,相同孔隙率下,N-G型支架的壁面剪應力平均值高于L-G型支架。這是由于,N-G型支架內部的流道結構較L-G型支架更復雜,曲折程度更大。這也與表2中兩支架的流—固交界面面積值的差異趨勢相符。
體外灌流系統培養條件下,當灌流速度較低且整體壓應變較小時,L-G型、N-G型支架上均能實現90%壁面面積的骨分化,而隨著力學激勵的增加骨分化面積有所下降,軟骨分化面積上升,這一趨勢與文獻[24-25]中的結論一致。相比于骨,軟骨分化需要更大的載荷刺激,這也導致支架上的骨與軟骨分化程度不同。得益于更大的壁面剪應力,N-G型支架的軟骨分化程度較L-G型支架更高,在孔隙率為60%時仍可實現80%壁面面積的軟骨分化。多孔支架壁面上應能同時保證骨組織與軟骨組織的分化。如文獻[25]中設計的五種支架,在壓縮應變與入口流速較小時,可實現90%壁面面積的骨分化,但該邊界條件下軟骨分化面積小。當壓縮應變與入口流速增加時,軟骨分化面積隨之增加,但最大軟骨分化面積只有30%~60%的壁面面積。由此可知,N-G型支架的結構在保證了骨分化程度的基礎上,提高了軟骨分化的程度。
5 結論
本文設計了兩種新型漸變形式的TPMS支架:L-G型支架、N-G型支架。其中,L-G型支架的固體力學性能更優,承載能力更強,而N-G型支架在壁面面積、滲透性能及組織分化特性方面均優于L-G型支架。考慮到六種支架均滿足松質骨的彈性模量范圍,且N-G型支架的生物學性能更優,因此N-G型支架更適宜植入人體。同時,也可以根據植入部位周圍骨的彈性模量大小,選擇適宜的孔隙率。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
植入支架作為修復骨缺損的一種有效治療手段,在骨外科領域有著廣泛應用。植入的支架應與宿主骨有良好的整合效果,且具備足夠的力學性能[1]。近年來,越來越多的研究將植入支架設計成多孔結構,原因在于:多孔結構支架與骨結構更接近[2-3];多孔結構能有效降低彈性模量,從而減緩應力遮擋效應[4-6];多孔結構利于營養物質在其內的運輸,促進骨長入[7-8]。
滲透性是評價支架性能的一個重要方面,滲透性好有利于營養物質在支架內運輸及廢物代謝[9-11]。支架的結構、尺寸、孔隙率均能影響其滲透性[12-14]。三周期極小曲面(triply periodic minimal surfaces,TPMS)是一種在三個方向上均呈周期性變化的極小曲面,具有高連通性及幾何參數易控等優點。近年來,越來越多的研究將TPMS引入支架設計[15-16]。TPMS支架的比表面積高,更適宜細胞的黏附、生長[17-19]。菱形(diamond,D)型、螺旋(gyroid,G)型是常用的TPMS支架類型。其中G型支架的結構與人體骨結構最為接近,通過調整其幾何形態可獲得與皮質骨或松質骨相近的力學性能,因此是目前最具應用前景的骨支架結構之一[20-21]。G型支架的滲透性優越,相同孔隙率下,G型支架的滲透率高于截斷八面體及優化晶格結構的支架[22]。而另一種D型支架的特點是比表面積高,相同孔隙率下,相比于G型支架可提供更多的空間供細胞黏附[23]。同時,D型支架在能量吸收性能方面優勢突出,相同孔隙率下,與G型支架相比,D型支架的能量吸收性能更好[16-17]。此外D型與G型支架壁面光滑,承載時可有效減小應力集中[16],在力學性能方面優勢明顯。有研究表明,D型與G型支架的彈性模量與屈服強度均好于傳統的點陣結構支架,如體心立方(body-centered-cubic,BCC)型等[16]。另一方面,多孔支架中的骨細胞生長需要力學載荷刺激,而一定范圍內的壓縮載荷與流體剪應力均能刺激骨細胞生長[24],灌流系統能同時提供壓縮與流體載荷,有研究通過該裝置進行體外細胞培養[25]。
人體骨結構呈各向異性和非均勻性,因此常把多孔支架設計成具有梯度變化的結構[26]。梯度漸變TPMS支架因具備前述優勢而備受青睞。相比于各向同性的TPMS支架,梯度漸變TPMS支架的滲透率更高,且能量吸收性能更好[13, 27]。有研究表明,梯度G型支架具有平臺區長,且平臺區域內應力波動幅度小的特點,能量吸收性能優勢明顯[28]。相同孔隙率下,梯度D型支架的滲透率較均勻結構有明顯提高[13]。不同漸變形式的TPMS支架的力學性能、滲透性及細胞生長情況也不盡相同[29]。目前關于梯度G型、D型支架的研究主要為沿單一方向上的相對密度漸變,而這與變化復雜的人體骨結構差異較大。因此,本文提出兩種新型變化形式的梯度漸變TPMS支架:雙向線性漸變G型(L-G型)支架和D型/G型融合型(N-G型)支架。其中L-G型支架的結構沿X、Y兩個方向均呈線性變化,孔隙尺寸的變化范圍大。N-G型支架由D型、G型兩種胞元結構融合而成,因此具備與D型支架相近的比表面積,同時擁有G型支架的孔隙結構,保證了支架的高滲透率。與現有的梯度漸變TPMS支架不同的是,此兩種支架的結構變化方式更多元,且包含不同形狀與不同尺寸的孔隙,更加符合人體骨結構復雜變化的特點。此外,本文從力學、滲透性及組織分化三個層面對設計的支架展開性能分析,以期實現對兩種新型支架的全面評價,為其植入人體后的承載及骨整合預測提供理論依據。
1 設計
以G型表達式(G(x, y))、D型表達式(D(x, y))為基本公式,在科學計算軟件Mathematica 11.3(Wolfram Inc.,美國)中構建50%、60%、70%三種孔隙率的L-G型支架(L-G-50%、L-G-60%、L-G-70%)及N-G型支架 (N-G-50%、N-G-60%、N-G-70%)。六種支架的胞元尺寸均為3 mm × 3 mm × 3 mm,支架整體尺寸為16 mm × 16 mm × 16 mm。六種支架的結構表達式如表1所示。G型、D型、L-G型及N-G型支架的結構如圖1所示。
 圖1
四種支架結構圖
Figure1.
Four kinds of scaffold structure
圖1
四種支架結構圖
Figure1.
Four kinds of scaffold structure
2 仿真
2.1 壓縮與計算流體動力學仿真
為探究六種支架的力學及滲透性能,分別對其進行壓縮與計算流體動力學(computational fluid dynamics,CFD)仿真。本文模擬在灌注式生物反應器中支架的力學響應。一般而言,支架在該裝置內承受軸向壓縮載荷和培養液灌流作用[25]。
在計算機輔助工程前處理軟件ICEM CFD 15.0 (ANSYS Inc.,美國)中,用16 mm×16 mm×16 mm的立方體與固體域模型進行布爾運算得到流體域模型,對固體及流體域模型進行網格劃分,并保證其流—固交界面上的節點一一對應。將固體域網格用于壓縮仿真,流體域網格用于CFD仿真。壓縮仿真中支架材料選擇外消旋聚乳酸(polyd l-lactide,PDLLA) [24],其彈性模量為3.3 GPa,泊松比為0.3[24]。設置支架下表面為固定約束,上表面為加載面,壓縮應變分別為:0.5%、1%、2.5%、5%[24-25]。CFD仿真中的流體介質為培養液[25],其密度為1 000 kg/m3,黏度為1.45×10-3 Pa﹒s。設置入口流速分別為:0.01 mm/s、0.1 mm/s、0.5 mm/s、1 mm/s[24-25],出口壓力為零,邊界無滑移,根據達西定律計算各支架的滲透率[21]。壓縮與CFD仿真的邊界條件如圖2所示。
 圖2
壓縮與CFD仿真邊界條件示意圖
Figure2.
Boundary condition for compression and CFD simula tion
圖2
壓縮與CFD仿真邊界條件示意圖
Figure2.
Boundary condition for compression and CFD simula tion
2.2 支架壁面上的組織分化計算
為進一步探究六種支架上的組織分化差異,對在體外灌流系統培養條件下支架壁面的組織分化進行計算。體外培養條件下,組織沿多孔支架內壁分化,因此主要受流—固交界面的載荷刺激影響[25],故本文研究的是在流—固交界面上的組織分化情況。Prendergast等[30]提出了組織分化定量理論,建立了組織分化與其黏附面上的力學激勵間的關系。文獻[24-25]運用組織分化定量理論對支架壁面的組織分化情況進行計算,如式(1)~式(2)所示:
 |
 |
其中,r為八面體剪應變;ε1、ε2、ε3分別為第1、2、3主應變;W為流體剪應力;a = 0.037 5%,b = 0.01 Pa。當S<0.01時,激勵值過小不能誘導組織分化;當0.01 ≤ S<1時,分化形成骨組織;當1 ≤ S<3時,分化形成軟骨組織;當3 ≤ S<6時,分化形成纖維組織;而當S ≥ 6時,激勵值過大不能誘導組織分化。
3 結果
3.1 支架的幾何參數
如圖1所示,L-G型支架的結構變化形式主要為孔隙尺寸漸變,而N-G型支架的結構其孔隙尺寸與形狀均發生變化。六種支架的尺寸規格、流—固交界面面積及孔徑尺寸的數值如表2所示。可見,隨著孔隙率的增加,L-G型與N-G型支架的流—固交界面的面積均在減小,而這兩種支架的孔徑尺寸均隨著孔隙率的增加而變大。同時可以看出,在相同孔隙率下,L-G型支架的流—固交界面的面積小于N-G型支架。因此,相同孔隙率下,N-G型支架可提供更大的壁面面積供細胞黏附、生長。此外,相同孔隙率下,L-G型支架孔徑尺寸的數值范圍也小于N-G型支架。換言之,相比于L-G型,N-G型支架的結構漸變程度更高。
3.2 支架的力學性能
為保證有限元仿真的準確性,以N-G-50%為例進行網格敏感性分析。網格尺寸對仿真結果的影響如圖3所示。當網格尺寸小于0.4 mm時,壓縮仿真與CFD仿真均獲得了穩定的結果,因此為節省計算,設置統一網格尺寸為0.4 mm。
 圖3
網格尺寸對最大范式應力及最大流速的影響
Figure3.
The influence of mesh size on maximum von Mises stress and maximum velocity
圖3
網格尺寸對最大范式應力及最大流速的影響
Figure3.
The influence of mesh size on maximum von Mises stress and maximum velocity
0.5%壓縮應變下,兩種支架上的最大范式應力與彈性模量隨孔隙率的變化關系如圖4所示。可見,L-G型、N-G型支架的最大范式應力與彈性模量均隨孔隙率的增加而減小,其中N-G型支架上的最大范式應力明顯高于L-G型支架。在變化趨勢上,隨孔隙率的提高,N-G型支架的最大范式應力下降得更明顯。彈性模量方面,L-G型支架高于N-G型支架。L-G-50%支架與N-G-50%支架在0.5%的壓縮應變下的范式應力分布情況如圖5所示。其中,N-G型支架的范式應力最大值在不同胞元結構的過渡處,而L-G型支架的范式應力最大值則存在于縱向支桿上,同時可以看出,N-G型支架的應力集中程度高于L-G型支架。
 圖4
0.5%壓縮應變下支架最大范式應力與彈性模量隨孔隙率變化關系圖
Figure4.
The relationships of the maximum von Mises stress and elastic modulus with porosity of the scaffolds under the 0.5% compression strain
圖4
0.5%壓縮應變下支架最大范式應力與彈性模量隨孔隙率變化關系圖
Figure4.
The relationships of the maximum von Mises stress and elastic modulus with porosity of the scaffolds under the 0.5% compression strain
 圖5
0.5%壓縮應變下支架上的范式應力分布圖
Figure5.
von Mises stress distribution on the scaffold under 0.5% compression strain
圖5
0.5%壓縮應變下支架上的范式應力分布圖
Figure5.
von Mises stress distribution on the scaffold under 0.5% compression strain
3.3 支架內流體的流動性能
支架的壁面剪應力平均值隨入口流速與孔隙率的變化如圖6所示。其中,支架的壁面剪應力平均值隨入口流速的增加而提高,而當孔隙率增加時,支架的壁面剪應力平均值則明顯降低。兩種支架的滲透率隨孔隙率的變化關系如圖7所示。可見,兩種支架的滲透率均隨孔隙率的增加而提高。相同孔隙率下,N-G型支架的滲透率高于L-G型支架,這是因為孔隙率相同時,N-G型支架孔徑的尺寸范圍大于L-G型支架,因此其滲透性更好。當入口流速為1 mm/s時,L-G-50%及N-G-50%內流體的流線圖,及在X-O-Y、X-O-Z平面上的流速分布如圖8所示。可見,在L-G型支架中,孔隙尺寸大即流道寬處的流速高。N-G型支架中,遠離Z軸的流道結構內的流速高,靠近Z軸的流道結構內的流速低。這是因為N-G型支架靠近Z軸部分為D型結構,孔隙尺寸小,而遠離Z軸的部分為G型結構,孔徑尺寸大,因此產生速度差異。
 圖6
支架壁面上剪應力平均值隨孔隙率與入口流速變化圖
Figure6.
The change of the average value of the shear stress with porosity and inlet velocity on the scaffold wall
圖6
支架壁面上剪應力平均值隨孔隙率與入口流速變化圖
Figure6.
The change of the average value of the shear stress with porosity and inlet velocity on the scaffold wall
 圖7
支架滲透率隨孔隙率變化圖
Figure7.
Permeability of scaffold varies with porosity
圖7
支架滲透率隨孔隙率變化圖
Figure7.
Permeability of scaffold varies with porosity
 圖8
1 mm/s入口流速下,L-G-50%、N-G-50%支架的流線及流速分布圖
Figure8.
Streamline and velocity distribution of the L-G-50%, N-G50% scaffold at the 1 mm/s inlet velocity
圖8
1 mm/s入口流速下,L-G-50%、N-G-50%支架的流線及流速分布圖
Figure8.
Streamline and velocity distribution of the L-G-50%, N-G50% scaffold at the 1 mm/s inlet velocity
3.4 支架壁面上的組織分化
當單獨考慮整體壓應變影響時,支架壁面上骨與軟骨分化面積如圖9所示。可見,當整體壓應變在0.5%~1%時,六種支架壁面均有超過90%的區域分化成骨,但此時因力學刺激過小,無法誘導軟骨分化。而當整體壓應變達到2.5%時,六種支架壁面均出現了軟骨分化;當整體壓應變提高到5%時,軟骨分化面積得到了進一步提高。單獨考慮入口流速影響時,在0.01 mm/s的入口流速作用下,六種支架因力學刺激過小其壁面的骨分化面積均不足50%;而當入口流速在0.1~0.5 mm/s范圍內時,六種支架壁面的骨分化面積均接近100%;當入流速達到1 mm/s時,六種支架壁面有了軟骨分化。由此可得,支架壁面上的骨與軟骨分化程度,相比于整體壓應變,對流體流動產生的剪應力刺激更敏感。這一結論與文獻[24-25]得出的結論一致。
 圖9
單獨考慮整體壓應變及流體作用時支架壁面上的骨與軟骨分化面積
Figure9.
The differentiation area of bone and cartilage on the wall of the scaffold when the compressive strain and fluid action are considered separately
圖9
單獨考慮整體壓應變及流體作用時支架壁面上的骨與軟骨分化面積
Figure9.
The differentiation area of bone and cartilage on the wall of the scaffold when the compressive strain and fluid action are considered separately
考慮流—固載荷作用時,支架壁面上的骨、軟骨的分化面積如圖10、圖11所示。可見,六種支架均能實現90%壁面面積的骨分化。如圖11所示,在60%孔隙率下,L-G型支架只能實現60%壁面面積的軟骨分化,而N-G型支架則可實現80%壁面面積的軟骨分化。在相同孔隙率及入口流速下,N-G型支架上的壁面剪應力比L-G型支架大,因此N-G型支架較L-G型支架更容易誘導軟骨分化。故為促進軟骨于支架內的分化,在設計支架結構時,應盡量增加支架內部流道的曲折程度以提高支架的壁面剪應力。
 圖10
考慮流-固載荷作用時的骨分化面積
Figure10.
Bone differentiation area considering fluid-solid load
圖10
考慮流-固載荷作用時的骨分化面積
Figure10.
Bone differentiation area considering fluid-solid load
 圖11
考慮流-固載荷作用時的軟骨分化面積
Figure11.
Cartilage differentiation area considering fluid-solid load
圖11
考慮流-固載荷作用時的軟骨分化面積
Figure11.
Cartilage differentiation area considering fluid-solid load
4 討論
本文設計了兩種類型的梯度漸變TPMS支架:L-G型和N-G型,通過壓縮仿真與CFD仿真分別獲得了兩種支架的彈性模量、范式應力等結構力學參數及支架內流體的壁面剪應力、滲透率等流體流動性能參數。基于組織分化理論,計算了兩種支架在體外灌流系統培養條件下的骨與軟骨分化面積。
本文中,支架材料選用的是PDLLA,其屈服強度約為0.12 GPa[31],而人體骨的屈服強度范圍為0.002~0.205 GPa[6]。PDLLA是強度與骨接近且可降解的聚合物材料[23],因此廣泛應用于可吸收的骨固定裝置及體外骨細胞培養實驗中[23, 29]。
不同結構形式的G型支架與人體骨的彈性模量對比如表3所示。可見,相同材料及孔隙率下,L-G型與N-G型支架的彈性模量高于文獻[23-24]中的G型與梯度G型支架。人體松質骨的彈性模量范圍為0.067~0.44 GPa[6],可見L-G型與N-G型支架的彈性模量雖高于G型與梯度G型支架,但其數值仍在人體松質骨的彈性模量范圍內,因此可有效避免應力遮擋。相比于N-G型支架,L-G型支架的彈性模量更高且應力分布更均勻,因此其承載能力更強。N-G型支架在兩種胞元的過渡處應力集中現象更明顯,承載時胞元過渡處更容易出現破壞。這是由于N-G型支架由兩種胞元結構融合而成,在過渡處的曲率較大[32],因而承載時出現應力集中。
支架的滲透性主要取決于孔隙率,此外,支架的結構形式是另一個影響因素。支架的滲透率大小應盡量接近宿主骨。本文與一些研究設計的支架及人體骨的滲透率對比如表4所示。可見,一些研究設計的支架雖滲透率較高,但超出人體骨的滲透率數值范圍,而本文設計的六種支架其滲透率均在人體骨的滲透率數值范圍內。相同孔隙率下,相比于L-G型支架,N-G型支架的滲透性能更好,這是由于N-G型支架的最大孔徑尺寸高于L-G型支架,而得益于更大的孔徑尺寸,N-G型支架的滲透性能則明顯好于L-G型支架。細胞在支架內的生長需要載荷刺激,有研究表明,當支架上的壁面剪應力大小在5×10?5~2.5×10?2 Pa時,利于細胞生長;當剪應力大于2.5×10-2 Pa時,將抑制細胞生長[7]。如圖7所示,本文設計的六種支架其壁面剪應力的數值范圍主要集中在2×10-3~1.4×10-2 Pa,因此六種支架均可以提供適宜的細胞生長環境。此外,相同孔隙率下,N-G型支架的壁面剪應力平均值高于L-G型支架。這是由于,N-G型支架內部的流道結構較L-G型支架更復雜,曲折程度更大。這也與表2中兩支架的流—固交界面面積值的差異趨勢相符。
體外灌流系統培養條件下,當灌流速度較低且整體壓應變較小時,L-G型、N-G型支架上均能實現90%壁面面積的骨分化,而隨著力學激勵的增加骨分化面積有所下降,軟骨分化面積上升,這一趨勢與文獻[24-25]中的結論一致。相比于骨,軟骨分化需要更大的載荷刺激,這也導致支架上的骨與軟骨分化程度不同。得益于更大的壁面剪應力,N-G型支架的軟骨分化程度較L-G型支架更高,在孔隙率為60%時仍可實現80%壁面面積的軟骨分化。多孔支架壁面上應能同時保證骨組織與軟骨組織的分化。如文獻[25]中設計的五種支架,在壓縮應變與入口流速較小時,可實現90%壁面面積的骨分化,但該邊界條件下軟骨分化面積小。當壓縮應變與入口流速增加時,軟骨分化面積隨之增加,但最大軟骨分化面積只有30%~60%的壁面面積。由此可知,N-G型支架的結構在保證了骨分化程度的基礎上,提高了軟骨分化的程度。
5 結論
本文設計了兩種新型漸變形式的TPMS支架:L-G型支架、N-G型支架。其中,L-G型支架的固體力學性能更優,承載能力更強,而N-G型支架在壁面面積、滲透性能及組織分化特性方面均優于L-G型支架。考慮到六種支架均滿足松質骨的彈性模量范圍,且N-G型支架的生物學性能更優,因此N-G型支架更適宜植入人體。同時,也可以根據植入部位周圍骨的彈性模量大小,選擇適宜的孔隙率。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。