光容積描記圖（PPG）是一種低成本、無創的心率測量技術，目前已經廣泛應用于智能可穿戴設備中。然而PPG信號本身極易受到運動噪聲的干擾，導致在劇烈運動狀態下的心率計算準確率較低。針對這一問題，本文提出一種基于自適應心率搜索模型的心率提取算法。算法首先對加速度信號以及PPG信號進行預處理，之后分別從兩種信號中提取出步頻信息與歷史心率信息，根據兩種信息與當前心率間的關系建立自適應模型，以此動態輸出心率在頻域的可能出現范圍，通過縮小真實心率在頻域的查找范圍來排除劇烈噪聲干擾。在2015年IEEE信號處理杯十二組公開數據中，本文算法結果平均絕對誤差為1.12次/分（皮爾森系數：0.996；一致性誤差：?0.184次/分）；在十組自測運動數據中，本文算法結果平均絕對誤差為3.19次/分（皮爾森系數：0.990；一致性誤差：1.327次/分）。結合實驗結果來看，本文提出的算法能有效提取運動噪聲干擾下的心率信息，在智能臂帶設備中具有投入使用的潛能。
引用本文： 孟戎昊, 李卓識, 于合龍, 鈕旗超. 基于自適應心率搜索模型的心率提取算法. 生物醫學工程學雜志, 2022, 39(3): 516-526. doi: 10.7507/1001-5515.202101091 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
心率作為人體四大生理指標之一，其值的變化可以反映出人體心臟在日常活動以及運動過程中的健康程度。在運動中進行實時心率監測可以幫助運動者了解自身身體機能，制定合理運動計劃，減少患病風險[1]，尤其是針對自身已經患有心血管疾病的患者，在運動中進行實時心率監測就顯得更加重要。目前常見的運動心率監測設備主要基于兩種心率計算方法：① 使用心電信號的心電描記法（electrocardiography，ECG），通過統計ECG信號中“R”波的個數來確定心率。該方法檢測準確率高，但是基于心電信號的運動心率測量設備會受限于使用場景、佩戴方式、價格等因素，因此ECG方法主要應用于心率帶產品，普及率不高。② 基于光電容積脈搏波信號的光電容積描記法（photoplethysmography，PPG）。該方法檢測PPG信號經過人體組織與血液吸收后的強度變化，描記出血管容積在心跳周期內的波動，從脈搏波形中計算心率[2-3]，由于其在心率檢測方面具有極高的連續性、無創性與舒適性且成本較低[4]，與智能可穿戴設備的設計使用理念高度契合，因此是目前最常用的心率檢測方法，也是本文的研究對象。
雖然PPG信號與心跳周期、脈搏變化有很強的關聯性，可以在安靜或輕微運動狀態下獲得準確度較高的心率，但是其信號質量容易受到運動噪聲的干擾，在奔跑時身體的震動會導致PPG信號傳感器與皮膚之間發生相對位移，有時產生的運動噪聲會完全掩蓋PPG信號，導致計算心率與真實心率出現較大誤差[5-6]。如何在噪聲干擾中提取有效的心率信息，盡可能獲取準確度高的心率，一直是通過PPG信號計算心率的難題。對此，Zhang等[7]提出了TROIKA心率計算框架，使用信號分解、稀疏重構、譜峰追蹤等策略來消除運動偽影，提高測試準確度。徐菁等[8]進一步提出將加速度信號估算出的心率與TROIKA框架計算出的心率相結合，使用卡爾曼濾波得到最終心率的方法。Su[9]與Girard[10]兩個團隊則另辟蹊徑，提出了基于跑步機運動的心率計算模型，使用溫度、出汗量、跑步機速度等變化量估算心率值。而近來，Temko[11]提出了WFPV算法，使用相位角修正以及維納濾波濾除噪聲干擾，對周期性運動具有很好的降噪效果，其算法性能和在公開數據集上的計算結果準確度要優于大部分基于PPG信號的心率檢測算法。
上述方法提供了很多解決問題的思路，但是也存在一些不足，其中TROIKA心率計算框架提出時間較早，在12組走路與跑步運動公開數據集的平均絕對誤差（mean absolute error，MAE）為2.34次/分（beat per minute，bpm），算法準確度方面不及后來的WFPV等算法，仍有改進空間。使用卡爾曼濾波的方法在其文章中的測試結果無法滿足本文對準確度的要求。根據速度估計心率變化的方法需要跑步機來確定速度變化，應用場景受到限制，不適用于一般跑步環境。而本文在使用計算準確度最高的WFPV算法從實驗數據中提取心率時發現，其計算結果兩極分化比較嚴重。在慢跑身體震動不劇烈的情況下，WFPV算法擁有較高的準確率，但在跑步運動幅度較大時，心率計算結果與真實值相差甚遠。
針對以上問題，本文提出一種基于自適應心率搜索模型的心率提取算法。該算法對PPG信號與加速度信號進行預處理。提取步頻與歷史心率信息作為關鍵參數，以sigmoid函數作為模型主體，使用改進粒子群算法（improved particle swarm optimization，IPSO）對模型參數進行優化[12-13]，經過30組數據離線訓練后得到了適用性較強的模型參數。隨后使用該模型在經過濾波處理的PPG信號頻域中對真實心率進行動態追蹤，通過縮小真實心率可能出現的范圍來提高心率測量的準確度。
1 方法
基于自適應心率搜索模型的提取算法主要包含以下兩個部分的處理。
（1）數據預處理：PPG信號與加速度信號通過時間窗口位移傳入算法[14]。時間窗口長度為8 s，步長2 s（窗口內包含6 s歷史數據）。數據傳入算法后，首先通過0.4～4 Hz的帶通濾波進行平滑處理；接著對傳入的PPG信號與加速度信號進行快速傅里葉變換，截取1～3 Hz的頻域數據，對應心率變化區間60～180 bpm；最后使用維納濾波進行濾波處理，以加速度信號為噪聲參考得到較為干凈的PPG信號。
（2）自適應心率搜索獲取最終心率：使用自適應心率搜索模型縮小當前時間窗內心率在頻域的可能出現范圍。在該范圍中找到主頻乘以60作為當前心率。
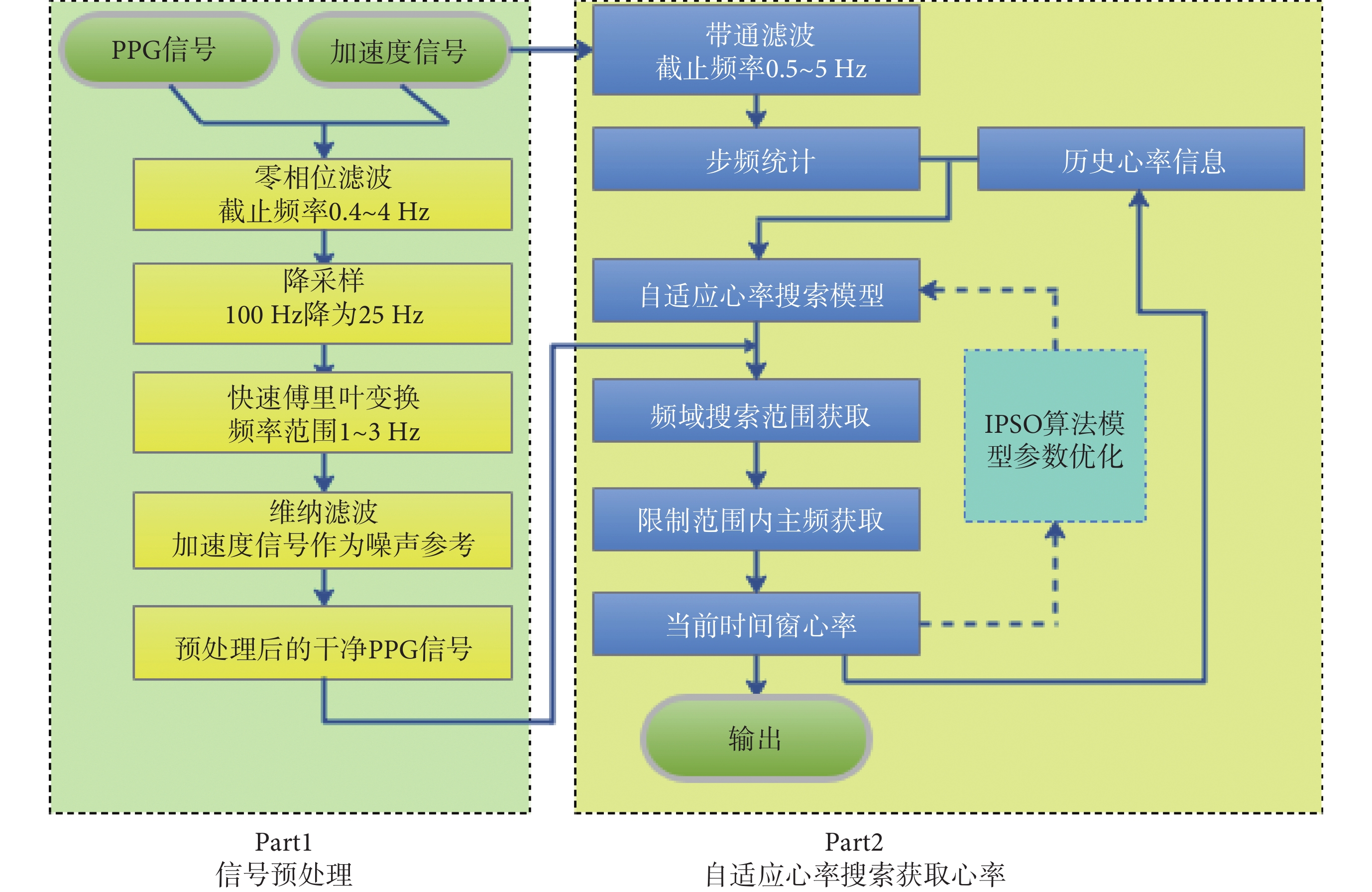
上述步驟（1）數據預處理部分也是標準的PPG信號頻域分析方法，本文論述重點在于步驟（2）中自適應心率搜索模型的搭建與實現以及算法最終的作用效果與測試結果。算法流程如圖1所示。
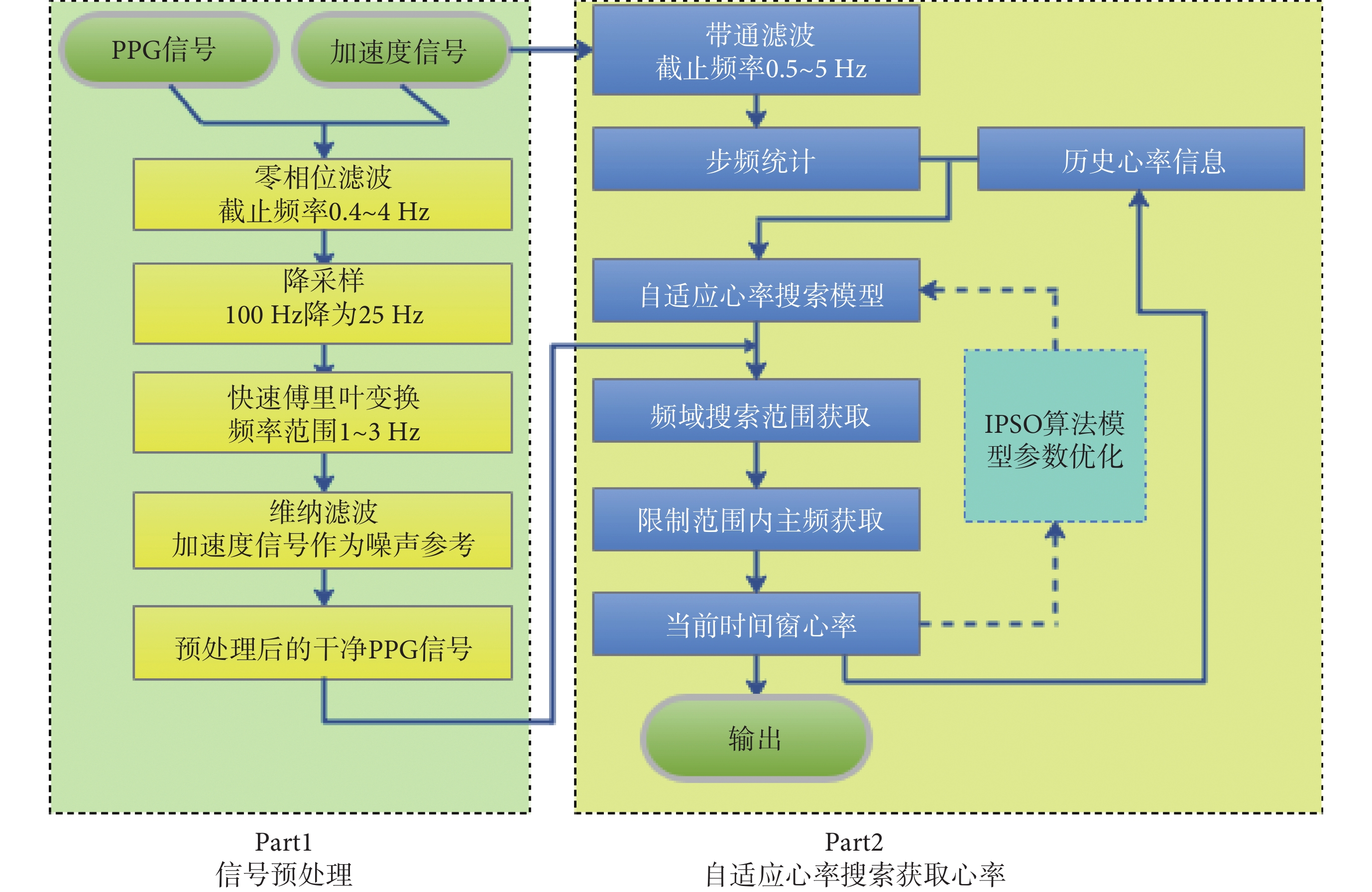圖1
本文方法流程圖
Figure1.
The flow chart of the method in this paper
1.1 自適應心率搜索模型
自適應心率搜索模型的介紹將通過以下三個方面進行：① 步頻計算方法；② 自適應心率搜索模型搭建原理及實現方法；③ IPSO優化模型參數方法。由于在第3部分中，確定非線性模型參數的過程是離線的，IPSO僅作為一種優化方法幫助優化參數，因此該部分內容以及參數優化結果將在1.2節單獨介紹。
1.1.1 步頻計算
步頻計算依賴于加速度信號的處理。三軸加速度傳感器中包含了X軸、Y軸、Z軸的運動數據，為了防止僅使用某一軸數據而丟失部分運動信息的情況，首先根據式(1)對三軸加速度數據求標量和，消除方向影響，最大程度上保留有效的三軸運動信息。其中Acc為處理后的加速度數據，x、y、z代表單個時間窗口內加速度計采集的三個軸數據。本文算法設置時間窗口長度為8 s，采樣頻率100 Hz，因此每800個樣本點處理一次加速度數據。
 |
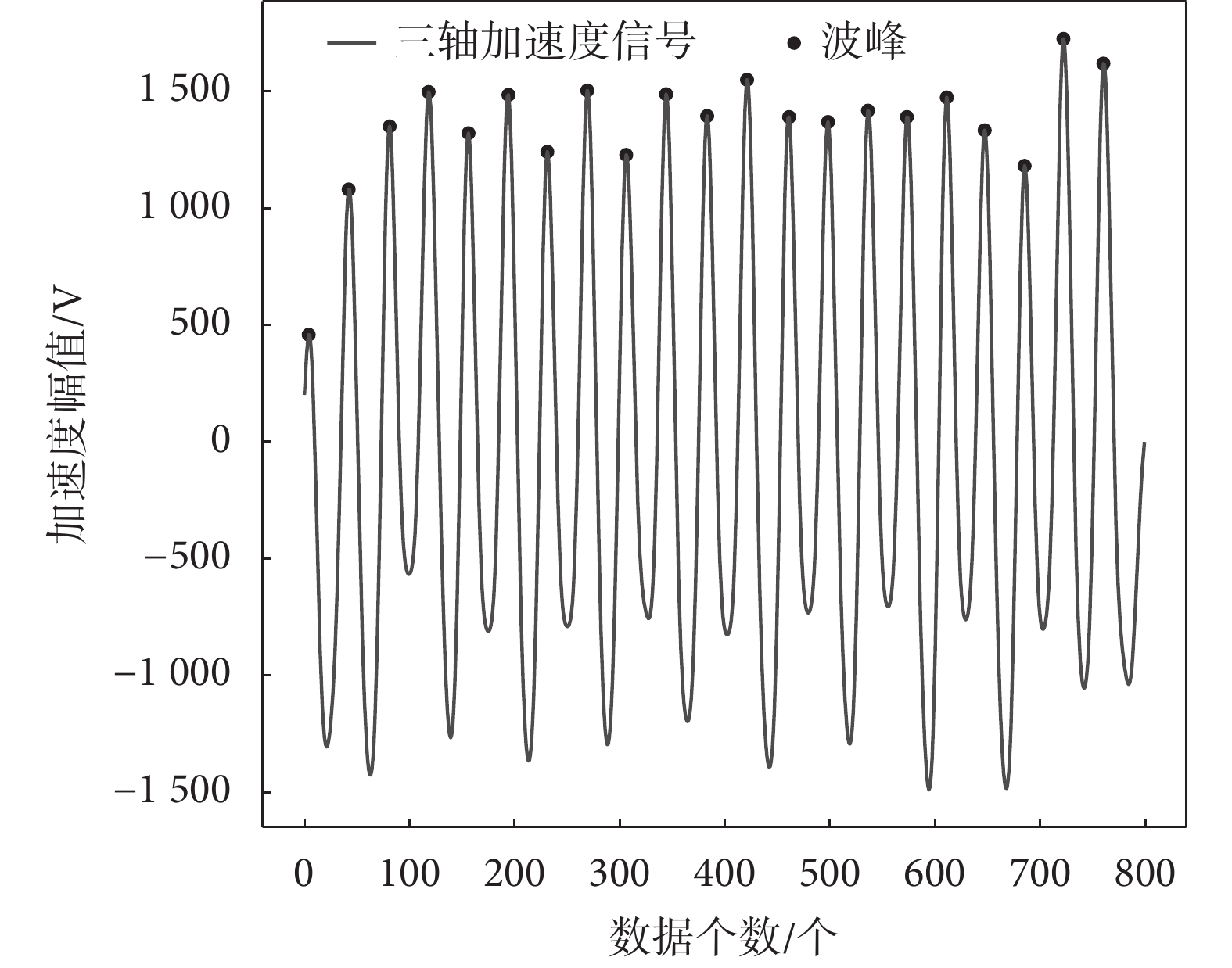
之后使用0.5～5 Hz的帶通濾波過濾加速度信號得到圖2所示的加速度時域波形，選擇Python科學運算庫SciPy中的find_peaks函數統計當前時間窗口內加速度信號的波峰個數。由于加速度傳感器型號以及采樣率設置的不同，導致采集到的信號變化范圍不同，因此需要根據硬件的實際使用情況，靈活設定波峰高度閾值以及連續波峰波谷間的高度差閾值來排除手部運動或局部身體晃動產生的加速度波峰干擾，保留有效的運動波峰[15]。在圖2中，8 s時間窗口內包含21個波峰，意味著此窗口內步數為21，步頻為2.625步/秒。
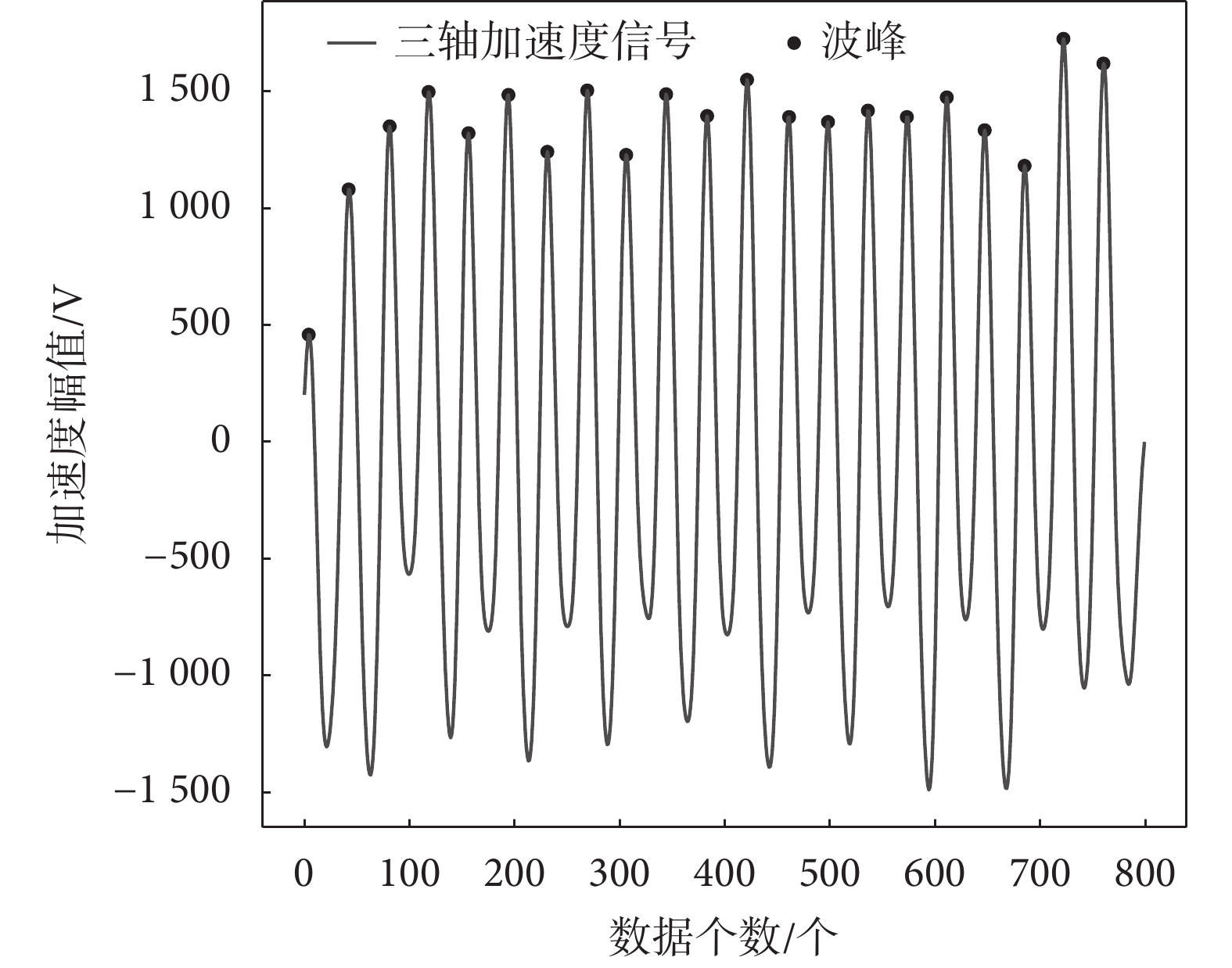圖2
加速度信號
Figure2.
Acceleration signal
1.1.2 自適應心率搜索模型原理及搭建
心率搜索模型的自適應性通過對步頻與歷史心率信息的動態調節實現。其原理包括以下三點：
（1）步頻與心率的聯系：通過步頻反映運動劇烈程度，進而體現心率變化趨勢[16]，是自適應心率搜索模型建立的第一要素。結合實驗發現，步頻變化能在很大程度上體現與影響心率變化。
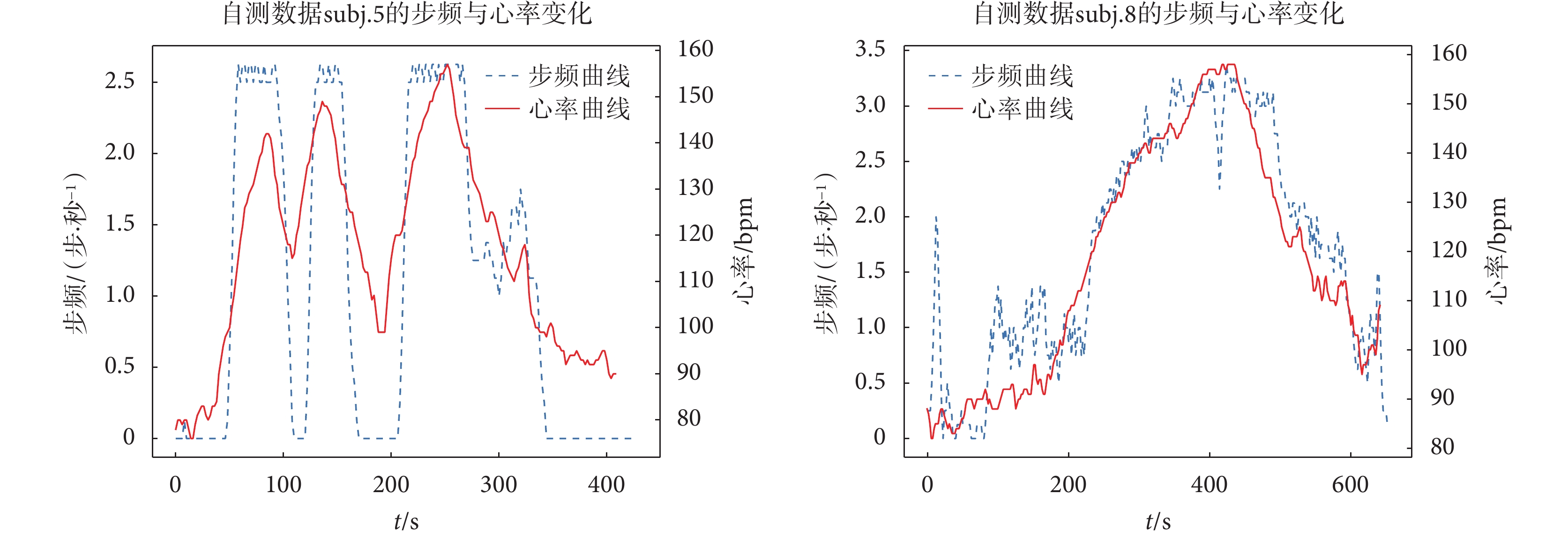
圖3是自測數據subj.5與subj.8兩次計算結果的雙坐標系圖。在subj.5測試中，為了體現步頻對心率的影響，在跑步過程中多次變換步頻，可以看到心率曲線也與步頻曲線一樣呈三個波峰狀，通過步頻的變化可以完整體現心率的變化。而在正常跑步的subj.8測試中，心率曲線與步頻曲線高度吻合，皮爾遜相關系數達到0.933，兩個變量間具有很強的相關性。由于自適應心率搜索模型僅使用步頻信息作為參數，進而得到一個大致的心率變化趨勢和心率追蹤范圍，因此在使用步頻信息調節模型的過程中，步頻與心率相關性不必達到subj.8一樣的高度吻合狀態，能體現心率變化趨勢即可。
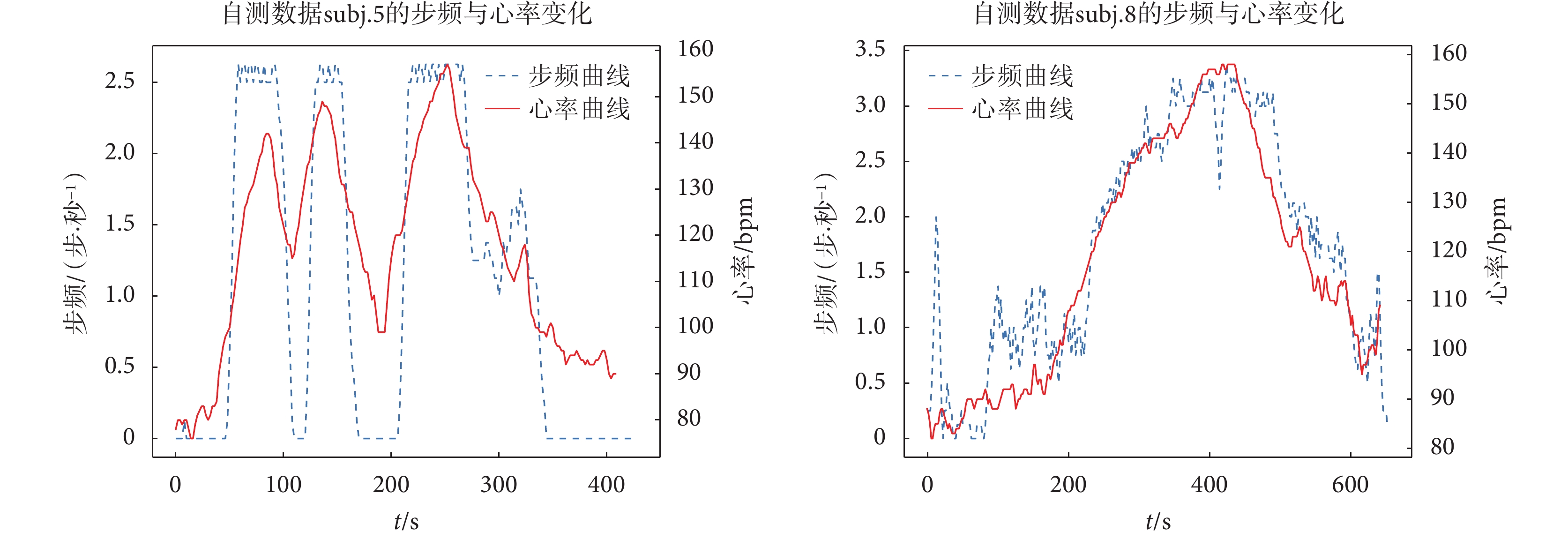圖3
步頻與心率變化曲線
Figure3.
Cadence and heart rate change curve
（2）歷史心率與當前心率的聯系：通過歷史心率確定當前心率的出現范圍是自適應心率搜索模型建立的第二要素。基于一個事實，即人體心率的變化量是有一定范圍的，新計算出的心率與之前一個心率的差值不會太大[14]。該事實在頻域中表現為當前心率所在頻率應當以上一次計算心率對應的頻率為基準點進行變化。
（3）人體運動心率自身變化的特點：通過運動心率的變化特點預測心率變化梯度是自適應心率搜索模型建立的第三要素。在日常活動中，人體心率變化范圍基本維持在60～180 bpm之間。據此，文獻[9]提出，運動心率變化曲線符合“四邊形”變化，即滿足“低心率區間—上升—高心率區間—下降—低心率區間”這一過程。在“上升”與“下降”兩個階段，心率的變化幅度大；在高低心率區間中，心率變化幅度很小。可理解為在歷史心率與當前心率同增同減的情況下，歷史心率越接近人體心率變化的上下限，當前心率可同向變化的空間就越少。因此在模型搭建時，本文選用sigmoid函數［式(2)］作為模型主體。該函數在值域上下限附近梯度最小（對應心率在高低區間中的變化），在中間部分梯度最大（對應心率處于上升和下降階段時的變化），其梯度變化符合運動心率的變化特點。
 |
結合上述觀點，本文通過式(3)～(7)計算時間窗口內心率，可以看出該心率計算是一個循環迭代的過程。
 |
 |
 |
 |
 |
式(3)與式(4)中以歷史譜峰索引Mid(t ? 1)為基準，使用歷史心率搜索范圍Ns(t ? 1)乘以上下界變量φed(t)、φst(t)這一形式，決定當前時間窗口內搜索下界St(t)向PPG信號頻域低頻的變化程度與搜索上界Ed(t)向高頻的變化程度。式(5)則根據下界St(t)與上界Ed(t)得到當前時間窗的心率搜索范圍，為下一次心率計算做準備。式(6)、(7)是最終的心率計算結果，在PPG信號頻域中，以［St(t)，Ed(t)］為界（1 Hz ≤ St(t) < Mid(t ? 1) < Ed(t) ≤ 3 Hz），得到該頻率限制范圍內的譜峰對應頻率Mid(t)并乘以60作為當前時間窗口的計算心率HR(t)。實際上，在式(3)～(7)中，只有下界變量φst(t)與上界變量φed(t)是根據自適應心率搜索模型求出的自變量，其余變量均是因變量。因此，φst(t)與φed(t)實際決定了心率搜索范圍大小與心率搜索區間，進而影響了每一次迭代計算出的心率準確度與最終結果，其中φst(t)作為下界變量關注的是心率在低頻區間（更多發生在心率下降過程中）的界限探索，φed(t)作為上界變量關注的是心率在高頻區間（更多是發生在心率上升過程中）的界限探索
為了得到作用效果好的φst(t)與φed(t)，本文搭建了自適應心率搜索模型。其中加入八個待IPSO擬合的權重參數Parami (i=0, 1, 
, 7)，并使用sigmoid函數作為模型主體。由于心率在上升階段更容易受到噪聲干擾，計算情況更加復雜，因此首先介紹模型中上界變量φed(t)的計算方法，使用負責φed(t)的計算部分［式(8)～(10)］對其進行擬合。
 |
 |
 |
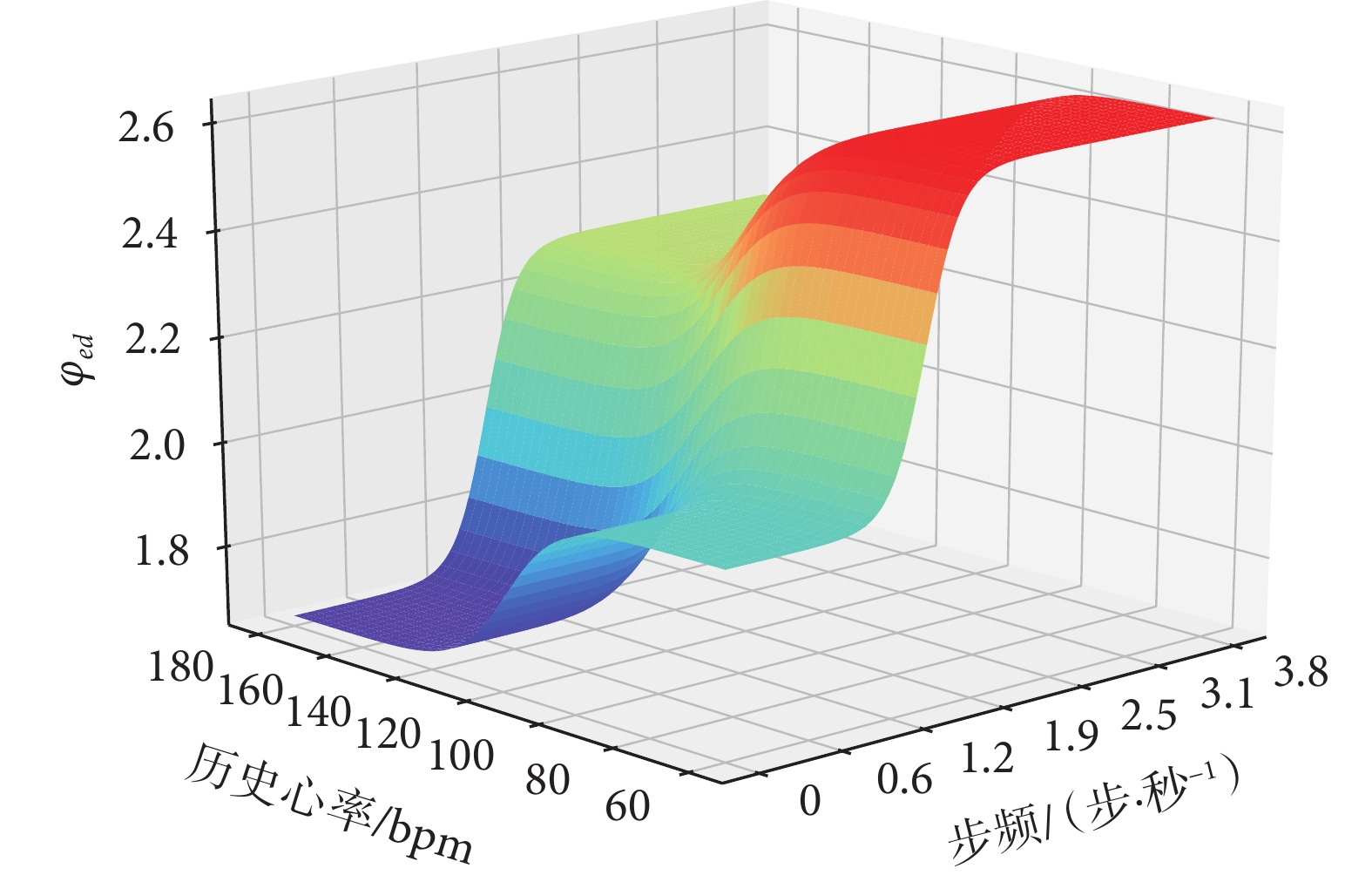
式(8)中，結合待IPSO學習參數Param0、Param1與當前時間窗口內步頻信息Step(t)對參數φ1(t)進行擬合。由于在不考慮歷史心率影響的情況下，步頻變化與心率變化呈正相關（步頻上升導致運動劇烈程度上升進而導致心率上升），因此設定式(8)為常數項與包含步頻參數的未知數項相加的形式，體現φ1(t)與Step(t)同向變化。在式(9)中，使用Param2、Param3與歷史心率參數HR(t?1)相結合對關鍵參數φ2(t)進行擬合。之所以將該公式設置成常數項與未知數項相減的方式，是因為在歷史心率與當前心率同處于上升過程的情況下，歷史心率的值越接近人體心率的上限，當前心率可變化的空間就越小，所以可看作歷史心率與當前心率可變化梯度呈負相關。其中式(8)、(9)的常數項與分子項在文中以經驗常數的方式給出，也可以將其設置為IPSO算法的待學習參數進行擬合。最后根據關鍵參數φ1(t)與φ2(t)，計算出二者均值作為當前時間窗口內自適應心率搜索模型輸出的φed(t)。φed(t)隨Step(t)與HR(t?1)的變化關系如曲面圖4所示。
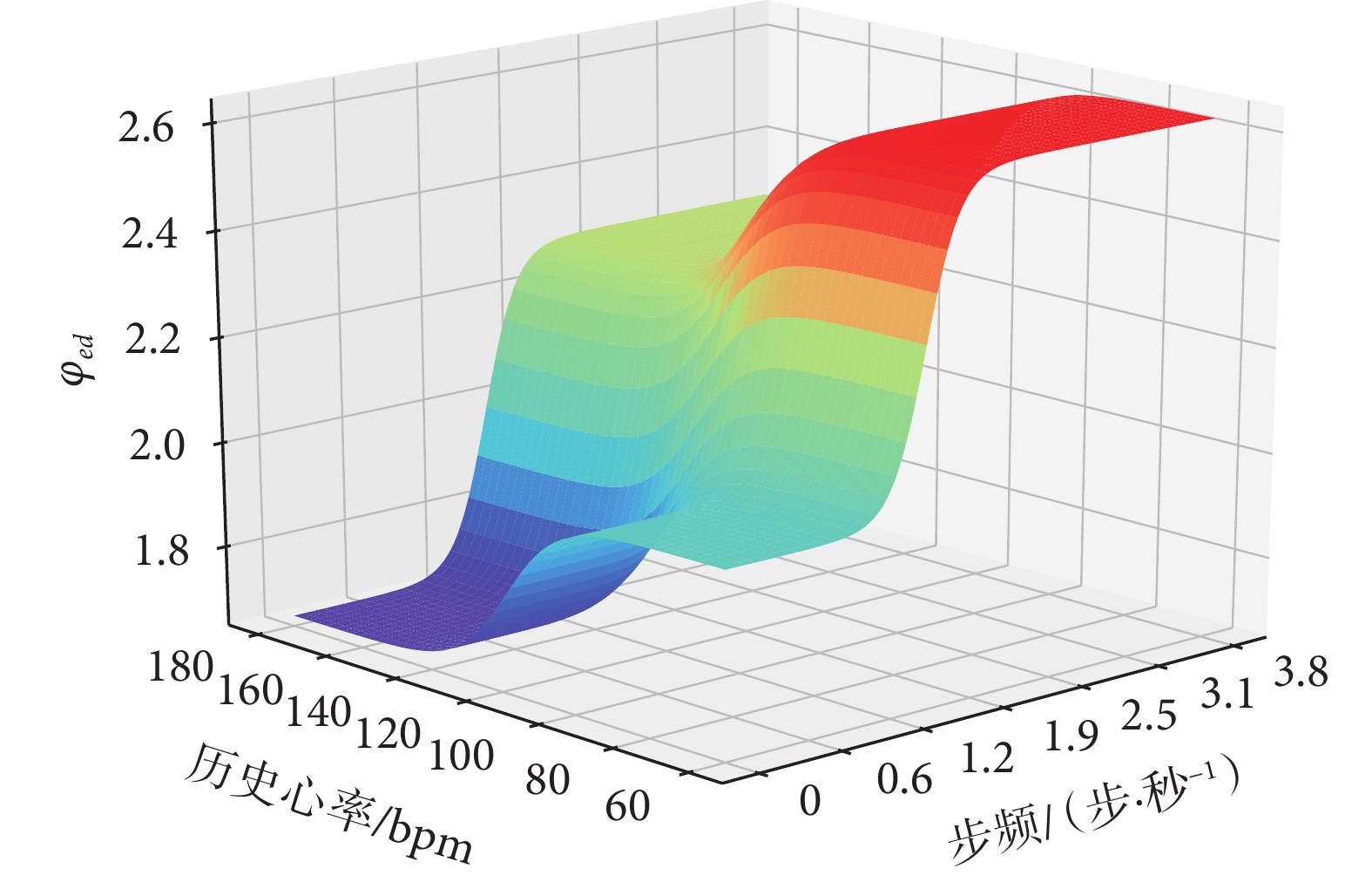圖4
φed隨步頻與歷史心率變化曲線
Figure4.
The curve of φed with step frequency and historical heart rate
圖4中，當歷史心率HR(t?1)較高而步頻Step(t)較低時，上界變量φed(t)偏低，根據式(4)可知此時的上界Ed(t)減小，代表此時心率搜索模型的搜索重心向低心率段偏移，可理解為人體活動趨勢從運動轉變為靜止的過程；當歷史心率處于較低水平而步頻較高時，φed(t)值增加，式(4)中Ed(t)增大，此時心率搜索模型的搜索重心向高心率段偏移，人體活動趨向于從靜止轉變為運動，真實心率更有可能出現在高心率段；當步頻與歷史心率同處于較低水平時，φed(t)維持在一個較小值附近，搜索模型的重心減少偏移，重點在低心率區間尋找真實心率；相反情況下，當步頻與歷史心率值同處于較高水平，φed(t)會維持在一個較大值附近，重點在高心率區間尋找真實心率。
針對下界變量φst(t)，使用模型中式(11)～(13)進行計算。其計算方法與φed(t)相同，只是根據模型使用經驗對公式結構進行了調整，其中4個參數Parami (i=4,5,6,7)同樣作為待學習參數由IPSO算法進行擬合。
 |
 |
 |
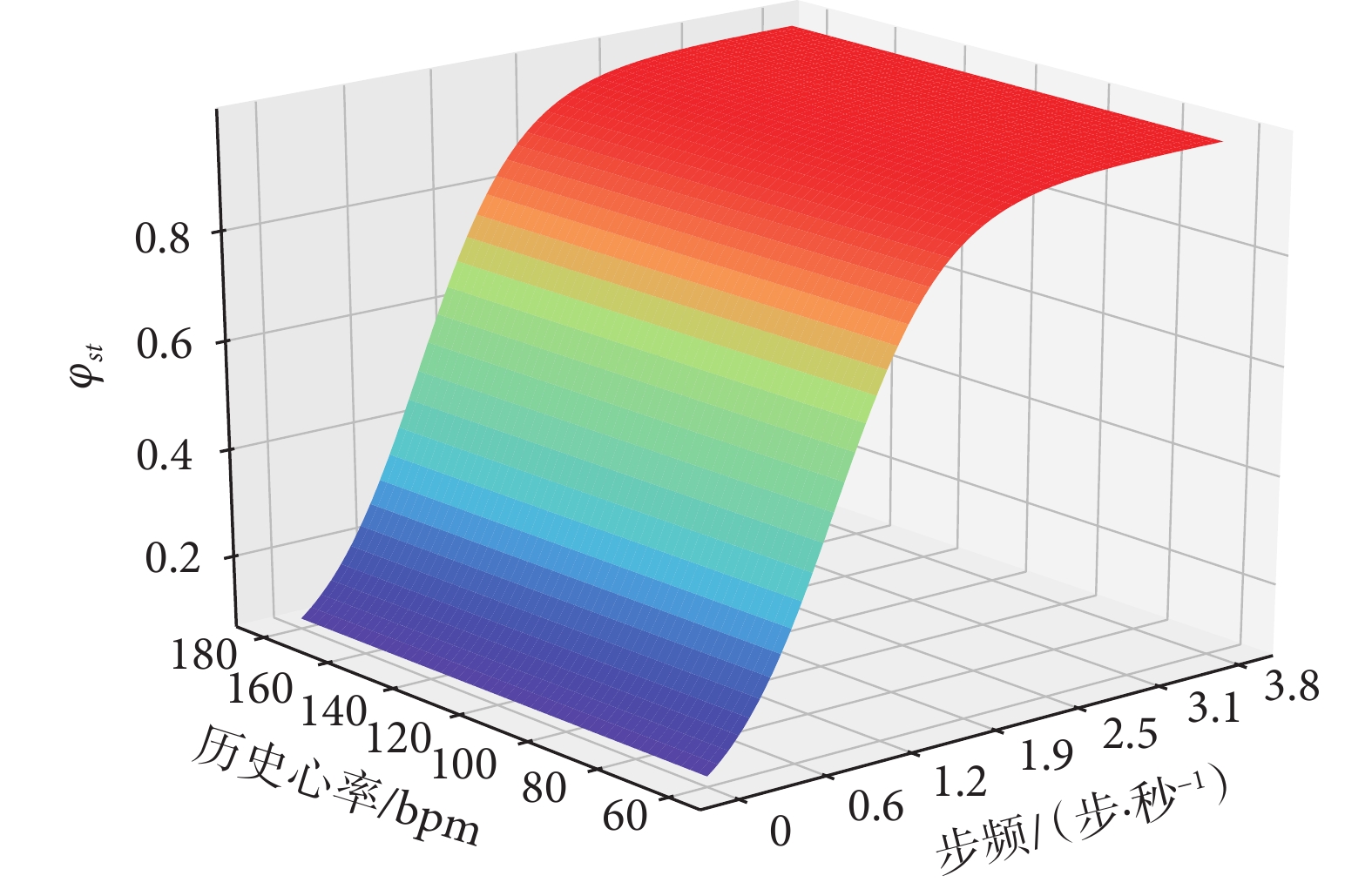
φst(t) 隨Step(t)與HR(t ? 1)的變化關系如曲面圖5所示。在圖5中可以看出，φst(t)在變化上主要受到Step(t)的影響，與步頻變化趨勢相同，這是由于φst(t)主要影響心率在下降階段中的搜索下界變化。而心率下降階段往往出現在運動程度減緩的過程中，在該過程中隨著運動噪聲干擾的減少，PPG信號質量會逐漸上升，因此自適應心率搜索模型只需要根據步頻信息將搜索下界穩步向低頻變化即可。同時根據式(4)可知，Step(t)下降導致φst(t)減小進而使搜索下界St(t)更加靠近歷史譜峰索引Mid(t ? 1)，該表現符合“人體心率越接近心率變化區間的上下限，當前心率與歷史心率可同向變化空間就越小”的理論依據。
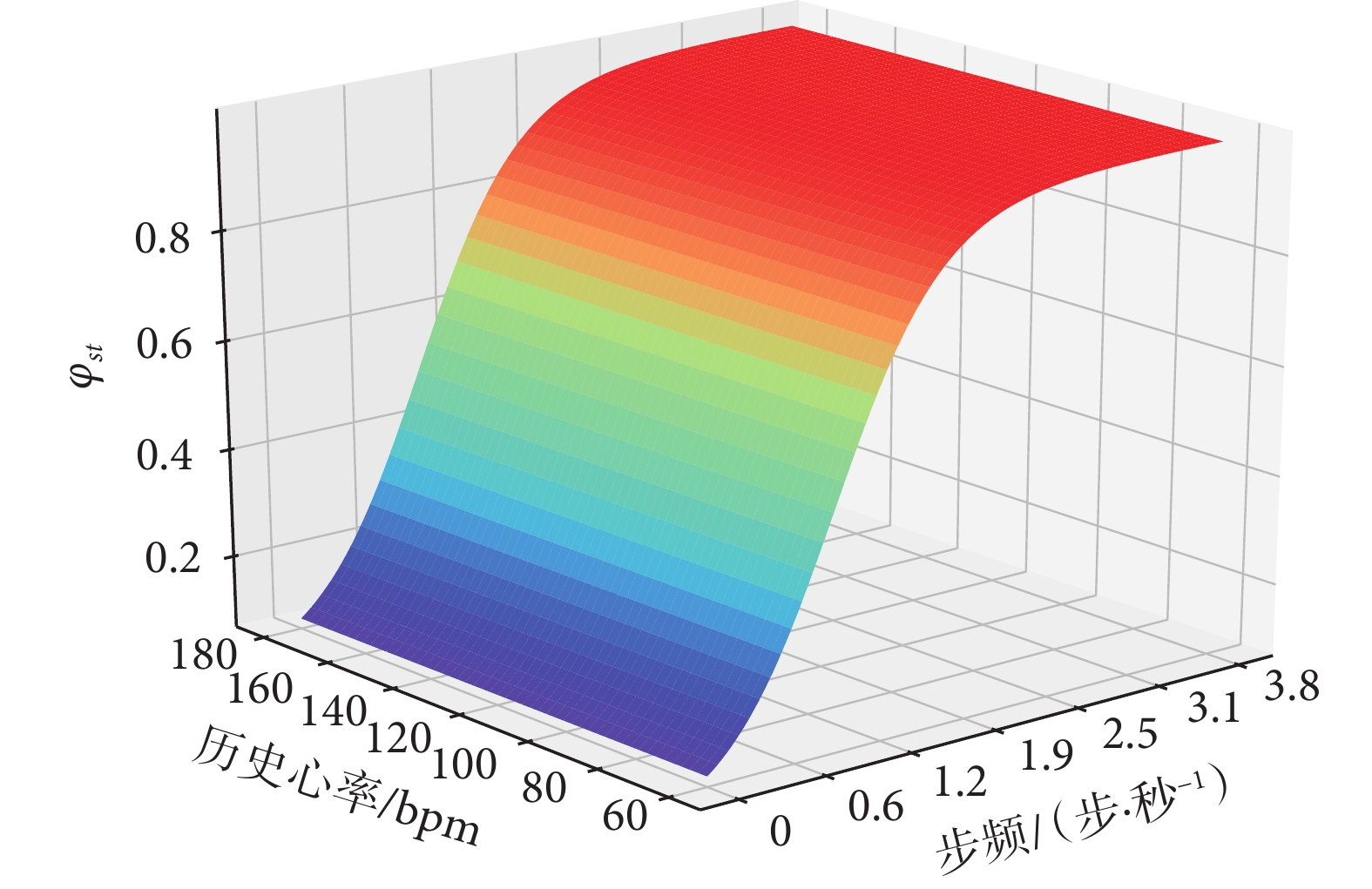圖5
φst隨步頻與歷史心率變化曲線
Figure5.
The curve of φst with step frequency and historical heart rate
優化后的自適應心率搜索模型在頻域的實際作用效果如圖6所示。圖6是實驗自測數據subj.5第47次時間窗口中經過預處理的PPG信號在頻域的表現。為了方便觀察，將橫坐標從頻率轉換為了心率（本文后續頻域圖的橫坐標做了相同處理），其中垂直于X軸的實線代表當前時間窗口內的真實心率，虛線代表計算心率。在圖6a中，經過傳統譜峰追蹤方法得到的PPG信號主頻對應心率為77 bpm，而真實心率為133 bpm，二者相差56 bpm，且真實心率不在任何一個明顯波峰附近，表明當前時間窗內包含心率信息的PPG主頻已經被噪聲掩蓋，只進行譜峰追蹤無法獲取有效心率。而在圖6b中，經過自適應心率搜索模型對心率出現范圍的預測與限制（限制范圍上下限如圖6b中點線所示），得到的計算心率為135 bpm，已經十分貼近真實心率的133 bpm。
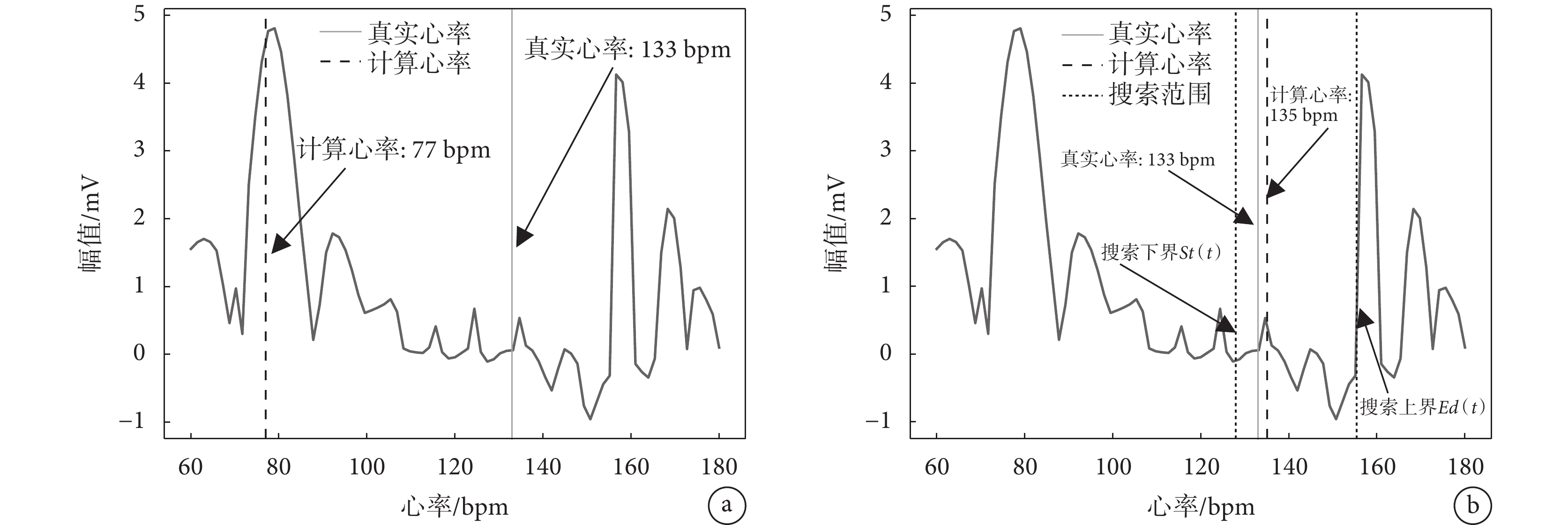圖6
自測數據subj.5的PPG信號頻譜片段
a. 譜峰追蹤；b. 自適應心率搜索+譜峰追蹤
Figure6. PPG signal spectrum fragment of self-test data subj.5a. spectrum peak tracking; b. spectrum peak tracking method based on adaptive heart rate search
1.2 IPSO參數優化
1.2.1 目標函數設計
本文使用IPSO算法的目的是為了減少計算心率與真實心率間的差值，因此在目標函數的設計上，使用平均絕對誤差體現粒子與目標的距離。
 |
 |
式(14)中n代表計算出的心率個數，x(i)表示計算心率值，y(i)表示真實心率值，真實心率值由數據采集時同時佩戴的Polar心率帶測得。Polar心率帶由芬蘭博能公司制造，其心率計算準確度一直處于業界領先水平，本文所用產品型號為H10。式(15)是粒子優化的目標，在每次迭代過程中取平均絕對誤差的最小值。
1.2.2 IPSO作用過程
在IPSO的使用過程中，設定粒子數為20，最大迭代次數1 000次，根據待確定參數的個數，設定每個粒子的維度為8，結合對采集數據的使用經驗設定粒子運動范圍如表1所示。
表1
粒子運動范圍
Table1.
Particle range of motion
在經過預處理的數據中提取步頻信息與歷史心率信息，將二者加入到自適應心率搜索模型中與隨機初始化的粒子
相結合，計算并得到測試心率與真實心率的平均絕對誤差。隨著多次迭代這一過程，以式(15)為目的，評估每個粒子的適應度，儲存每個粒子的個體最優解pbest以及全部pbest中的最佳值gbest，在迭代時，IPSO通過更新速度vt+1來對粒子位置xt+1中的每個維度進行建模，并根據pbest與gbest的線性組合移動粒子。當粒子各維度的移動超出表1對應的范圍時，舍棄該粒子，加入新的隨機粒子以提高IPSO的運行效率。
 |
 |
1.2.3 參數優化結果
IPSO算法參數設置為C1 = C2 = 1.8，R1 = R2
如表2所示。
表2
參數優化結果
Table2.
Parameter optimization results
2 實驗設計與結果
2.1 數據來源
實驗所用的第一部分數據是2015年IEEE信號處理競賽的12組走路與跑步運動公開數據[14]，競賽課題為“Heart Rate Monitoring During Physical Exercise Using Wrist-Type Photoplethymographic Signals”。該部分數據由12位18～35歲間的健康男性受試者采集得到。每組數據中包含2路PPG數據、3路加速度數據和1路ECG數據。在對12組公開數據的PPG信號原始數據進行繪圖觀察后發現，其中大部分數據片段的波形變化都能體現出標準PPG信號的變化特點（如圖7a所示），其所受運動噪聲干擾程度較小。同時對比現有幾種算法在公開數據集的處理結果后發現，不同算法在公開數據集上的計算誤差相差較小，不能很好地體現算法在強運動噪聲干擾下的處理效果，因此在實驗設計中，本文加入10組自測數據作為第二部分數據來源。
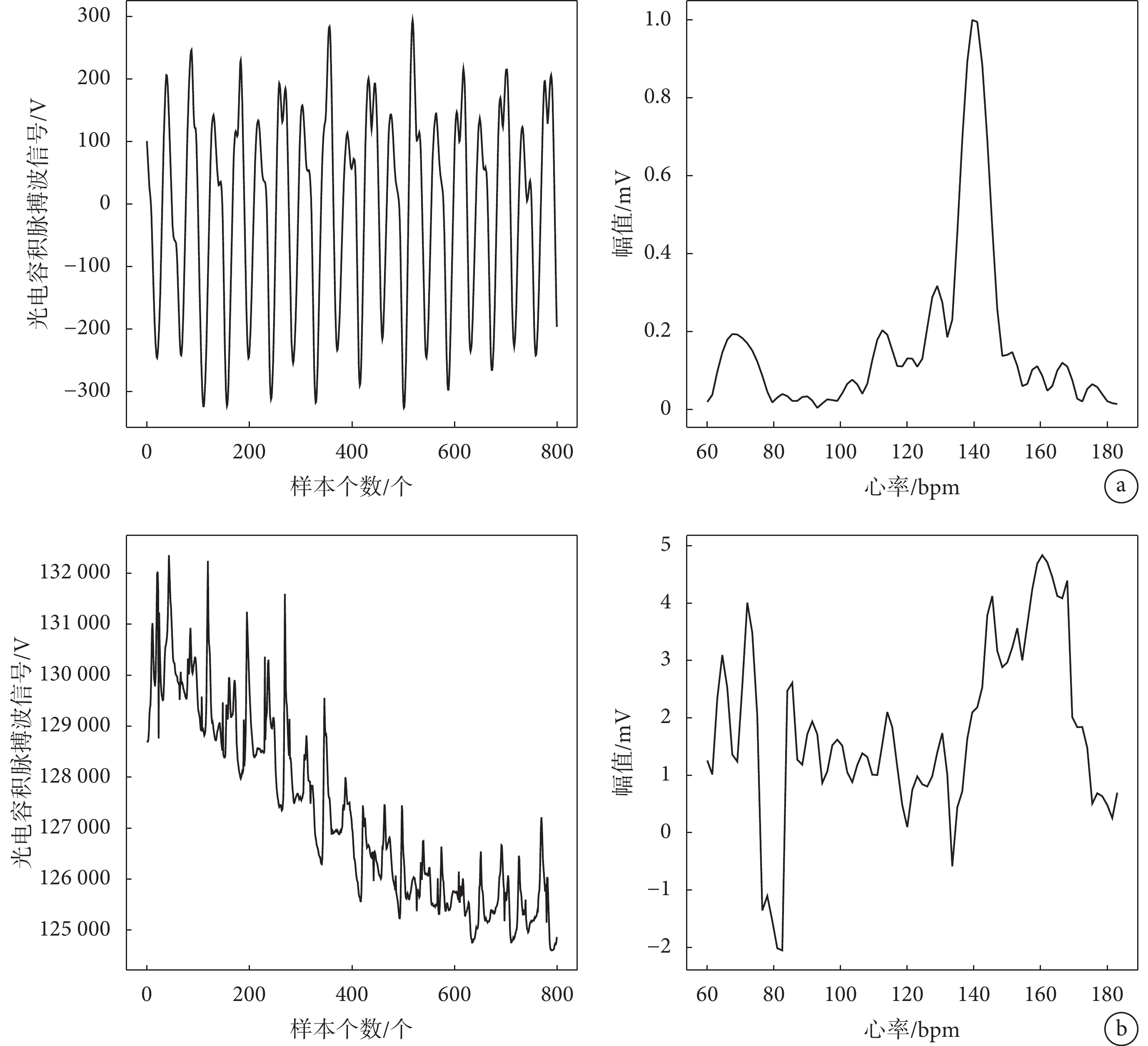圖7
信號質量對比
a. 公開數據庫subj.1數據片段；b. 實驗室自測數據subj.5數據片段
Figure7. Signal quality contrasta. public database subj.1 data fragment; b. laboratory self-test data subj.5 data fragment
實驗室采集的10組自測數據由五位受試者測得，包括四名男性和一名女性，年齡分布在25～33歲之間，身體健康無心臟方面疾病。每位受試者的上臂處無紋身、疤痕，可正常佩戴數據采集裝置（上臂處松緊度滿足測試設備使用要求，受試者對測試設備沒有過敏）。測試前已與受試者簽訂了知情同意書，提倡測試的公正互助性以及保密性。測試過程中尊重受試者的自主自愿原則，在不損害受試者身體健康的前提下完成了數據采集。測試使用的數據采集裝置內主要集成一顆型號為MAX86160EFN+的PPG信號傳感器，一顆型號為LIS2DH12TR的三軸加速度傳感器，通過低功耗藍牙模塊DA14580向移動端傳送傳感器數據，供電由3.7 V鋰電池提供。
在測試時使用綁帶將該裝置固定在上臂處，模擬智能臂帶的工作方式，之所以選擇在上臂處采集PPG信號，是因為在奔跑擺臂時上臂的肌肉會產生收縮與舒張，影響PPG信號的采集質量，在此處采集的PPG信號要比腕部采集的PPG信號更加難以處理。每組測試采集的數據包含1路PPG信號和3路加速度信號，數據采樣率100 Hz。真實心率由測試時同時佩戴的Polar心率帶采集得到。數據采集過程中要求測試人員滿足以下幾點測試要求：
（1）佩戴好設備并開始測試后首先靜待30 s，保證算法初始運行所使用數據的可靠性，之后開始跑步運動。
（2）由于測試環境為真實路跑環境，因此不預先指定跑步速度，但要求受測人員在自身可承受范圍內提高跑步速度，使心率出現較大梯度變化，不可全程慢跑進行測試。
（3）受測人員在一次數據收集過程中至少保證1次急停、1次急跑和4次轉向，不限制受測人員跑步時的擺臂方式，但是不可為了配合測試而故意減少身體震動幅度與擺臂幅度，同時要在測試過程中模擬抬手擦汗與看表。
（4）運動數據采集結束后，受測人員需要在心率持續監測的情況下進行休息，待心率降至90 bpm以內結束測試，保留完整的心率上升、下降過程。
為了體現本文采集數據的強噪聲干擾性，選擇一組自測運動狀態下的PPG信號，截取其中8 s長度的時間片段進行觀察，可以看到圖7b中運動狀態下的PPG信號在時域表現出多個不規則尖峰，尖峰形態以及尖峰間隔不具有規律性，無法從中分辨出有效的PPG信號波形。從頻域來看同樣存在多個偽峰，且偽峰幅值相近，在譜峰檢測方面很難根據每個譜峰的特點篩選出包含有效心率的譜峰。
對比圖7a與圖7b的信號質量表現，發現在時域中：公開數據庫的運動數據片段波形變化比較規律，而自測數據很難從信號波形中找到周期性的規律變化，且波峰多為不規則尖峰，受噪聲污染更加嚴重；在頻域中：公開數據庫運動數據片段譜峰孤立，偽峰數量少且在形態上與主峰存在明顯差別，容易識別出譜峰并得到準確度較高的心率，而自測數據在頻域中包含多個偽峰，偽峰間幅值、形態相近，很難判斷出真實心率所在頻率。因此使用本文采集的運動數據進行心率計算的難度更大，更能體現不同心率算法的性能優劣。
2.2 實驗結果
本文在各類算法的計算結果對比中使用平均絕對誤差與平均絕對誤差百分比（mean absolute percentage error，MAPE）作為評價標準。平均絕對誤差定義如式(14)所示，平均絕對誤差百分比定義如式(18)所示，x(i)表示計算心率值，y(i)表示真實心率值。
 |
在公開數據庫的十二組走路與跑步運動公開數據對比中，本文選擇同樣使用該數據集體現算法準確度的TROIKA[14]、JOSS[17]、自適應濾波器算法（recursive least squares + normalized least mean square，RLS+NLMS）[18]、Random Forest算法[19]、經驗模態分解法（ensemble empirical mode decomposition，EEMD）[20]、WFPV[11]等算法與本文算法相比，統計結果如表3所示。從結果來看，本文算法計算心率的平均絕對誤差為1.12 bpm，平均絕對誤差百分比為0.90%。與其他算法相比：經典算法TROIKA與需要長時間運算的EEMD算法平均絕對誤差分別達到了2.42 bpm與1.83 bpm，計算準確度較低；新近提出的RLS+NLMS算法與Random Forest算法的計算準確度較高，但是仍不及本文算法與WFPV算法；而對周期性運動有很好降噪效果的WFPV算法以平均絕對誤差1.02 bpm優于本文算法。在其中6組數據的計算結果對比上，本文算法計算準確度更高，但是由于在subj.6與subj.10兩組數據的計算結果上與WFPV算法差距較大，導致整體計算結果略差于WFPV算法。
表3
本文算法與各類算法在公開數據的MAE、MAPE對比
Table3.
Comparison of MAE and MAPE between the algorithm proposed in this paper and various algorithm on public data
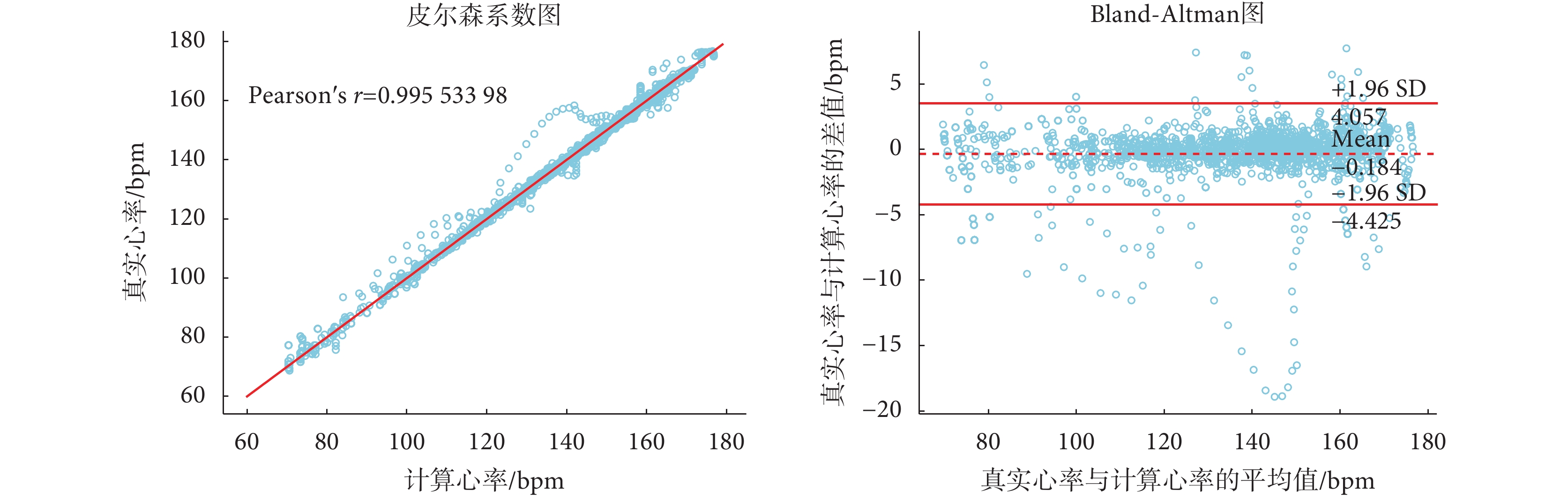
圖8展示了本文算法計算結果的皮爾遜相關系數圖，相關系數為0.995 533 98，已經十分接近于1，表明本文算法計算出的心率與真實心率間存在很強的線性相關關系。圖8還展示了Bland-Altman圖，其一致性界限為[?4.425，4.057]，誤差均值為?0.184 bpm，有95.6%的數據樣本落在置信區間內，表明計算心率與真實心率的一致性極強。
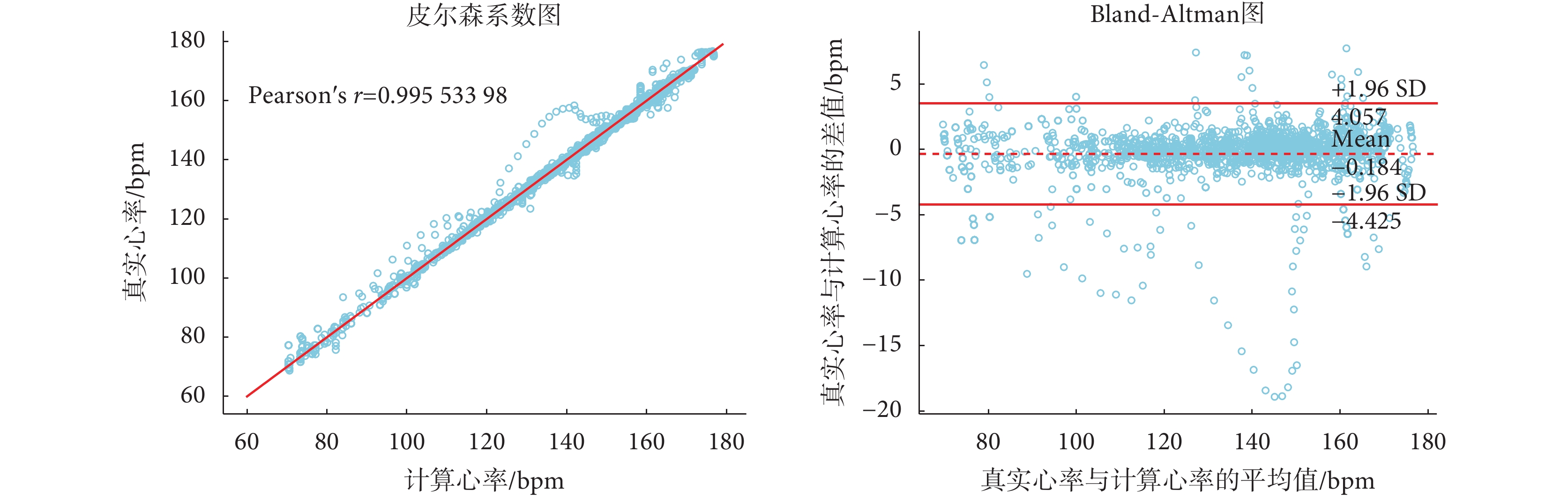圖8
本文算法在IEEE信號處理杯12組訓練數據的統計結果
Figure8.
The statistical results of the proposed algorithm in the 12 sets of training data of IEEE Signal Processing Cup
在實驗室自測數據的結果對比分析中，選擇前述算法中在公開數據集表現最好且具有復現性的WFPV算法與本文算法進行對比，平均絕對誤差與平均絕對誤差百分比如表4所示。
表4
本文算法與WFPV算法在自測數據的MAE、MAPE對比
Table4.
Comparison of MAE and MAPE between the algorithm proposed in this paper and the WFPV algorithm on self-test data
根據表4十組自測數據的處理結果來看，本文算法的平均絕對誤差與平均絕對誤差百分比分別為3.19 bpm與2.57%，明顯優于WFPV算法的5.83 bpm與4.92%。在subj.4～7四組數據中，本文算法的計算精確度雖然有所下降，但總體誤差仍保持在5.5 bpm的可接受范圍內，而WFPV算法則出現了大量計算異常的數據樣本，其中在subj.5測試中的平均絕對誤差更是達到了18.42 bpm。此外，在十組數據共3 174個樣本的t檢驗對比中，本文算法計算得到的心率與真實心率的差異沒有統計學意義（t = 1.931，P = 0.053 5)，而WFPV算法計算得到的心率與真實心率的差異具有統計學意義（t = ?2.670，P = 0.007 6）。統計結果表明在同樣的強噪聲干擾環境下，本文算法的計算結果與真實心率間的差異更小、一致性更高，更加接近真實心率。
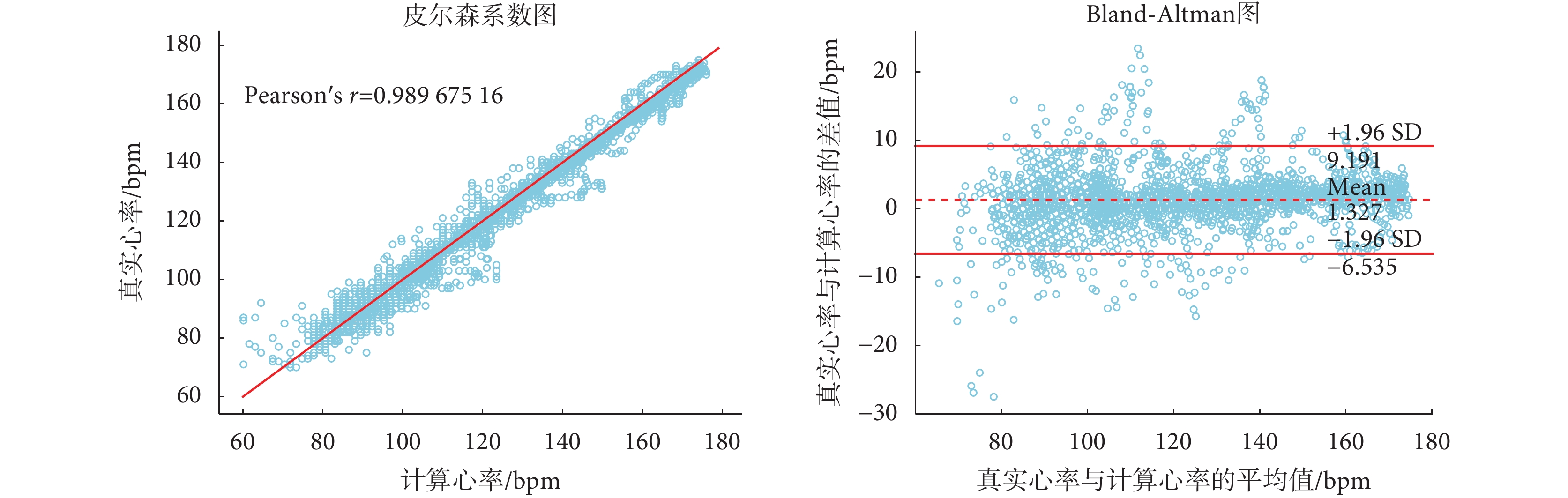
圖9是本文提出算法在自測數據的皮爾森相關系數圖與Bland-Altman圖，其中皮爾森相關系數計算為0.989 675 16、一致性界限為[?6.535，9.191]，誤差均值1.327 bpm，有94.3%的數據點落在了置信區間內。
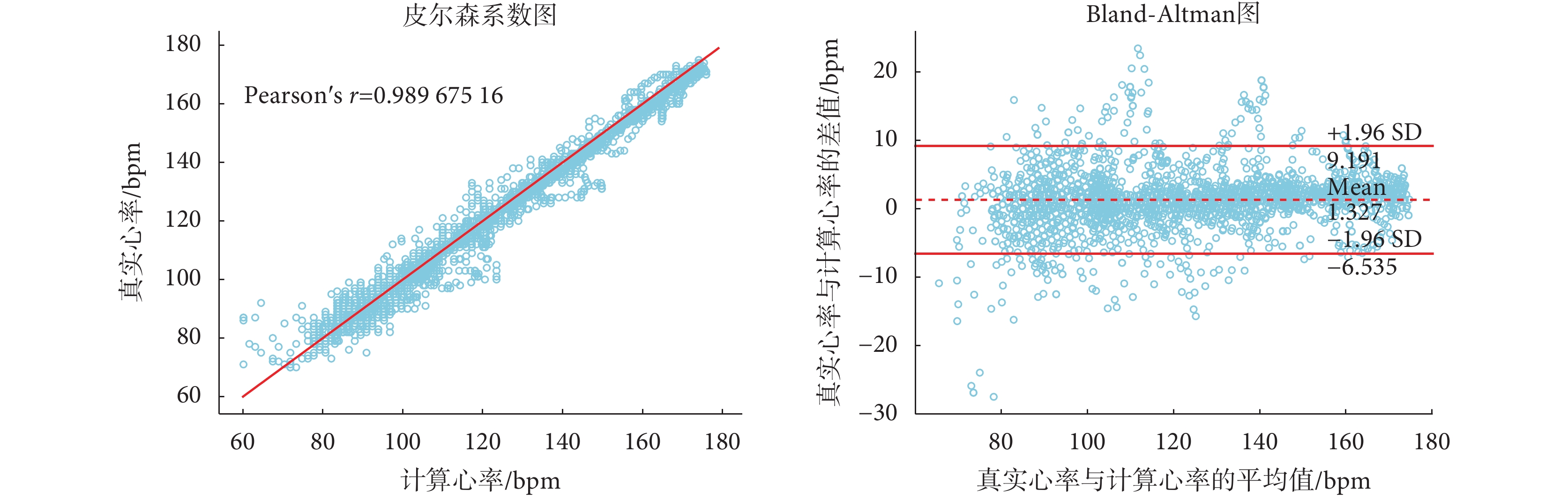圖9
本文算法在10組自測數據的統計結果
Figure9.
The statistical results of the algorithm proposed in this paper on 10 sets of self-test data
3 結論
從實驗結果來看，本文提出的基于自適應心率搜索模型的心率提取算法具有較強的抗運動噪聲干擾性，在PPG信號主頻不突出的情況下，能通過限制其真實心率譜峰的出現范圍來排除噪聲干擾。在十二組公開數據上表現良好，平均絕對誤差均值1.12 bpm，相較于WFPV算法的1.02 bpm仍有改進空間，但是對比TROIKA等心率算法準確率有較大提升。在十組自測運動噪聲較大的數據中，本文提出算法平均絕對誤差均值為3.19 bpm，明顯優于WFPV算法的5.83 bpm。總體來看，本文提出算法能夠在劇烈跑步運動中提取出有效心率信息，具有較高的心率計算準確率與較強的抗噪聲干擾能力，其對于智能臂帶等在上臂處采集PPG信號的心率監測設備具有一定應用前景。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：孟戎昊主要負責算法設計、數據采集與分析、論文編寫工作；李卓識主要提供實驗指導、理論分析指導、論文寫作指導及審閱修訂工作；于合龍為基金項目負責人，主要負責算法分析指導、協調溝通實驗所需資源及落實計劃安排等工作；鈕旗超主要負責數據處理、算法訓練、實驗平臺及設備搭建工作。
引言
心率作為人體四大生理指標之一，其值的變化可以反映出人體心臟在日常活動以及運動過程中的健康程度。在運動中進行實時心率監測可以幫助運動者了解自身身體機能，制定合理運動計劃，減少患病風險[1]，尤其是針對自身已經患有心血管疾病的患者，在運動中進行實時心率監測就顯得更加重要。目前常見的運動心率監測設備主要基于兩種心率計算方法：① 使用心電信號的心電描記法（electrocardiography，ECG），通過統計ECG信號中“R”波的個數來確定心率。該方法檢測準確率高，但是基于心電信號的運動心率測量設備會受限于使用場景、佩戴方式、價格等因素，因此ECG方法主要應用于心率帶產品，普及率不高。② 基于光電容積脈搏波信號的光電容積描記法（photoplethysmography，PPG）。該方法檢測PPG信號經過人體組織與血液吸收后的強度變化，描記出血管容積在心跳周期內的波動，從脈搏波形中計算心率[2-3]，由于其在心率檢測方面具有極高的連續性、無創性與舒適性且成本較低[4]，與智能可穿戴設備的設計使用理念高度契合，因此是目前最常用的心率檢測方法，也是本文的研究對象。
雖然PPG信號與心跳周期、脈搏變化有很強的關聯性，可以在安靜或輕微運動狀態下獲得準確度較高的心率，但是其信號質量容易受到運動噪聲的干擾，在奔跑時身體的震動會導致PPG信號傳感器與皮膚之間發生相對位移，有時產生的運動噪聲會完全掩蓋PPG信號，導致計算心率與真實心率出現較大誤差[5-6]。如何在噪聲干擾中提取有效的心率信息，盡可能獲取準確度高的心率，一直是通過PPG信號計算心率的難題。對此，Zhang等[7]提出了TROIKA心率計算框架，使用信號分解、稀疏重構、譜峰追蹤等策略來消除運動偽影，提高測試準確度。徐菁等[8]進一步提出將加速度信號估算出的心率與TROIKA框架計算出的心率相結合，使用卡爾曼濾波得到最終心率的方法。Su[9]與Girard[10]兩個團隊則另辟蹊徑，提出了基于跑步機運動的心率計算模型，使用溫度、出汗量、跑步機速度等變化量估算心率值。而近來，Temko[11]提出了WFPV算法，使用相位角修正以及維納濾波濾除噪聲干擾，對周期性運動具有很好的降噪效果，其算法性能和在公開數據集上的計算結果準確度要優于大部分基于PPG信號的心率檢測算法。
上述方法提供了很多解決問題的思路，但是也存在一些不足，其中TROIKA心率計算框架提出時間較早，在12組走路與跑步運動公開數據集的平均絕對誤差（mean absolute error，MAE）為2.34次/分（beat per minute，bpm），算法準確度方面不及后來的WFPV等算法，仍有改進空間。使用卡爾曼濾波的方法在其文章中的測試結果無法滿足本文對準確度的要求。根據速度估計心率變化的方法需要跑步機來確定速度變化，應用場景受到限制，不適用于一般跑步環境。而本文在使用計算準確度最高的WFPV算法從實驗數據中提取心率時發現，其計算結果兩極分化比較嚴重。在慢跑身體震動不劇烈的情況下，WFPV算法擁有較高的準確率，但在跑步運動幅度較大時，心率計算結果與真實值相差甚遠。
針對以上問題，本文提出一種基于自適應心率搜索模型的心率提取算法。該算法對PPG信號與加速度信號進行預處理。提取步頻與歷史心率信息作為關鍵參數，以sigmoid函數作為模型主體，使用改進粒子群算法（improved particle swarm optimization，IPSO）對模型參數進行優化[12-13]，經過30組數據離線訓練后得到了適用性較強的模型參數。隨后使用該模型在經過濾波處理的PPG信號頻域中對真實心率進行動態追蹤，通過縮小真實心率可能出現的范圍來提高心率測量的準確度。
1 方法
基于自適應心率搜索模型的提取算法主要包含以下兩個部分的處理。
（1）數據預處理：PPG信號與加速度信號通過時間窗口位移傳入算法[14]。時間窗口長度為8 s，步長2 s（窗口內包含6 s歷史數據）。數據傳入算法后，首先通過0.4～4 Hz的帶通濾波進行平滑處理；接著對傳入的PPG信號與加速度信號進行快速傅里葉變換，截取1～3 Hz的頻域數據，對應心率變化區間60～180 bpm；最后使用維納濾波進行濾波處理，以加速度信號為噪聲參考得到較為干凈的PPG信號。
（2）自適應心率搜索獲取最終心率：使用自適應心率搜索模型縮小當前時間窗內心率在頻域的可能出現范圍。在該范圍中找到主頻乘以60作為當前心率。
上述步驟（1）數據預處理部分也是標準的PPG信號頻域分析方法，本文論述重點在于步驟（2）中自適應心率搜索模型的搭建與實現以及算法最終的作用效果與測試結果。算法流程如圖1所示。
圖1
本文方法流程圖
Figure1.
The flow chart of the method in this paper
1.1 自適應心率搜索模型
自適應心率搜索模型的介紹將通過以下三個方面進行：① 步頻計算方法；② 自適應心率搜索模型搭建原理及實現方法；③ IPSO優化模型參數方法。由于在第3部分中，確定非線性模型參數的過程是離線的，IPSO僅作為一種優化方法幫助優化參數，因此該部分內容以及參數優化結果將在1.2節單獨介紹。
1.1.1 步頻計算
步頻計算依賴于加速度信號的處理。三軸加速度傳感器中包含了X軸、Y軸、Z軸的運動數據，為了防止僅使用某一軸數據而丟失部分運動信息的情況，首先根據式(1)對三軸加速度數據求標量和，消除方向影響，最大程度上保留有效的三軸運動信息。其中Acc為處理后的加速度數據，x、y、z代表單個時間窗口內加速度計采集的三個軸數據。本文算法設置時間窗口長度為8 s，采樣頻率100 Hz，因此每800個樣本點處理一次加速度數據。
|
之后使用0.5～5 Hz的帶通濾波過濾加速度信號得到圖2所示的加速度時域波形，選擇Python科學運算庫SciPy中的find_peaks函數統計當前時間窗口內加速度信號的波峰個數。由于加速度傳感器型號以及采樣率設置的不同，導致采集到的信號變化范圍不同，因此需要根據硬件的實際使用情況，靈活設定波峰高度閾值以及連續波峰波谷間的高度差閾值來排除手部運動或局部身體晃動產生的加速度波峰干擾，保留有效的運動波峰[15]。在圖2中，8 s時間窗口內包含21個波峰，意味著此窗口內步數為21，步頻為2.625步/秒。
圖2
加速度信號
Figure2.
Acceleration signal
1.1.2 自適應心率搜索模型原理及搭建
心率搜索模型的自適應性通過對步頻與歷史心率信息的動態調節實現。其原理包括以下三點：
（1）步頻與心率的聯系：通過步頻反映運動劇烈程度，進而體現心率變化趨勢[16]，是自適應心率搜索模型建立的第一要素。結合實驗發現，步頻變化能在很大程度上體現與影響心率變化。
圖3是自測數據subj.5與subj.8兩次計算結果的雙坐標系圖。在subj.5測試中，為了體現步頻對心率的影響，在跑步過程中多次變換步頻，可以看到心率曲線也與步頻曲線一樣呈三個波峰狀，通過步頻的變化可以完整體現心率的變化。而在正常跑步的subj.8測試中，心率曲線與步頻曲線高度吻合，皮爾遜相關系數達到0.933，兩個變量間具有很強的相關性。由于自適應心率搜索模型僅使用步頻信息作為參數，進而得到一個大致的心率變化趨勢和心率追蹤范圍，因此在使用步頻信息調節模型的過程中，步頻與心率相關性不必達到subj.8一樣的高度吻合狀態，能體現心率變化趨勢即可。
圖3
步頻與心率變化曲線
Figure3.
Cadence and heart rate change curve
（2）歷史心率與當前心率的聯系：通過歷史心率確定當前心率的出現范圍是自適應心率搜索模型建立的第二要素。基于一個事實，即人體心率的變化量是有一定范圍的，新計算出的心率與之前一個心率的差值不會太大[14]。該事實在頻域中表現為當前心率所在頻率應當以上一次計算心率對應的頻率為基準點進行變化。
（3）人體運動心率自身變化的特點：通過運動心率的變化特點預測心率變化梯度是自適應心率搜索模型建立的第三要素。在日常活動中，人體心率變化范圍基本維持在60～180 bpm之間。據此，文獻[9]提出，運動心率變化曲線符合“四邊形”變化，即滿足“低心率區間—上升—高心率區間—下降—低心率區間”這一過程。在“上升”與“下降”兩個階段，心率的變化幅度大；在高低心率區間中，心率變化幅度很小。可理解為在歷史心率與當前心率同增同減的情況下，歷史心率越接近人體心率變化的上下限，當前心率可同向變化的空間就越少。因此在模型搭建時，本文選用sigmoid函數［式(2)］作為模型主體。該函數在值域上下限附近梯度最小（對應心率在高低區間中的變化），在中間部分梯度最大（對應心率處于上升和下降階段時的變化），其梯度變化符合運動心率的變化特點。
|
結合上述觀點，本文通過式(3)～(7)計算時間窗口內心率，可以看出該心率計算是一個循環迭代的過程。
|
|
|
|
|
式(3)與式(4)中以歷史譜峰索引Mid(t ? 1)為基準，使用歷史心率搜索范圍Ns(t ? 1)乘以上下界變量φed(t)、φst(t)這一形式，決定當前時間窗口內搜索下界St(t)向PPG信號頻域低頻的變化程度與搜索上界Ed(t)向高頻的變化程度。式(5)則根據下界St(t)與上界Ed(t)得到當前時間窗的心率搜索范圍，為下一次心率計算做準備。式(6)、(7)是最終的心率計算結果，在PPG信號頻域中，以［St(t)，Ed(t)］為界（1 Hz ≤ St(t) < Mid(t ? 1) < Ed(t) ≤ 3 Hz），得到該頻率限制范圍內的譜峰對應頻率Mid(t)并乘以60作為當前時間窗口的計算心率HR(t)。實際上，在式(3)～(7)中，只有下界變量φst(t)與上界變量φed(t)是根據自適應心率搜索模型求出的自變量，其余變量均是因變量。因此，φst(t)與φed(t)實際決定了心率搜索范圍大小與心率搜索區間，進而影響了每一次迭代計算出的心率準確度與最終結果，其中φst(t)作為下界變量關注的是心率在低頻區間（更多發生在心率下降過程中）的界限探索，φed(t)作為上界變量關注的是心率在高頻區間（更多是發生在心率上升過程中）的界限探索
為了得到作用效果好的φst(t)與φed(t)，本文搭建了自適應心率搜索模型。其中加入八個待IPSO擬合的權重參數Parami (i=0, 1, , 7)，并使用sigmoid函數作為模型主體。由于心率在上升階段更容易受到噪聲干擾，計算情況更加復雜，因此首先介紹模型中上界變量φed(t)的計算方法，使用負責φed(t)的計算部分［式(8)～(10)］對其進行擬合。
|
|
|
式(8)中，結合待IPSO學習參數Param0、Param1與當前時間窗口內步頻信息Step(t)對參數φ1(t)進行擬合。由于在不考慮歷史心率影響的情況下，步頻變化與心率變化呈正相關（步頻上升導致運動劇烈程度上升進而導致心率上升），因此設定式(8)為常數項與包含步頻參數的未知數項相加的形式，體現φ1(t)與Step(t)同向變化。在式(9)中，使用Param2、Param3與歷史心率參數HR(t?1)相結合對關鍵參數φ2(t)進行擬合。之所以將該公式設置成常數項與未知數項相減的方式，是因為在歷史心率與當前心率同處于上升過程的情況下，歷史心率的值越接近人體心率的上限，當前心率可變化的空間就越小，所以可看作歷史心率與當前心率可變化梯度呈負相關。其中式(8)、(9)的常數項與分子項在文中以經驗常數的方式給出，也可以將其設置為IPSO算法的待學習參數進行擬合。最后根據關鍵參數φ1(t)與φ2(t)，計算出二者均值作為當前時間窗口內自適應心率搜索模型輸出的φed(t)。φed(t)隨Step(t)與HR(t?1)的變化關系如曲面圖4所示。
圖4
φed隨步頻與歷史心率變化曲線
Figure4.
The curve of φed with step frequency and historical heart rate
圖4中，當歷史心率HR(t?1)較高而步頻Step(t)較低時，上界變量φed(t)偏低，根據式(4)可知此時的上界Ed(t)減小，代表此時心率搜索模型的搜索重心向低心率段偏移，可理解為人體活動趨勢從運動轉變為靜止的過程；當歷史心率處于較低水平而步頻較高時，φed(t)值增加，式(4)中Ed(t)增大，此時心率搜索模型的搜索重心向高心率段偏移，人體活動趨向于從靜止轉變為運動，真實心率更有可能出現在高心率段；當步頻與歷史心率同處于較低水平時，φed(t)維持在一個較小值附近，搜索模型的重心減少偏移，重點在低心率區間尋找真實心率；相反情況下，當步頻與歷史心率值同處于較高水平，φed(t)會維持在一個較大值附近，重點在高心率區間尋找真實心率。
針對下界變量φst(t)，使用模型中式(11)～(13)進行計算。其計算方法與φed(t)相同，只是根據模型使用經驗對公式結構進行了調整，其中4個參數Parami (i=4,5,6,7)同樣作為待學習參數由IPSO算法進行擬合。
|
|
|
φst(t) 隨Step(t)與HR(t ? 1)的變化關系如曲面圖5所示。在圖5中可以看出，φst(t)在變化上主要受到Step(t)的影響，與步頻變化趨勢相同，這是由于φst(t)主要影響心率在下降階段中的搜索下界變化。而心率下降階段往往出現在運動程度減緩的過程中，在該過程中隨著運動噪聲干擾的減少，PPG信號質量會逐漸上升，因此自適應心率搜索模型只需要根據步頻信息將搜索下界穩步向低頻變化即可。同時根據式(4)可知，Step(t)下降導致φst(t)減小進而使搜索下界St(t)更加靠近歷史譜峰索引Mid(t ? 1)，該表現符合“人體心率越接近心率變化區間的上下限，當前心率與歷史心率可同向變化空間就越小”的理論依據。
圖5
φst隨步頻與歷史心率變化曲線
Figure5.
The curve of φst with step frequency and historical heart rate
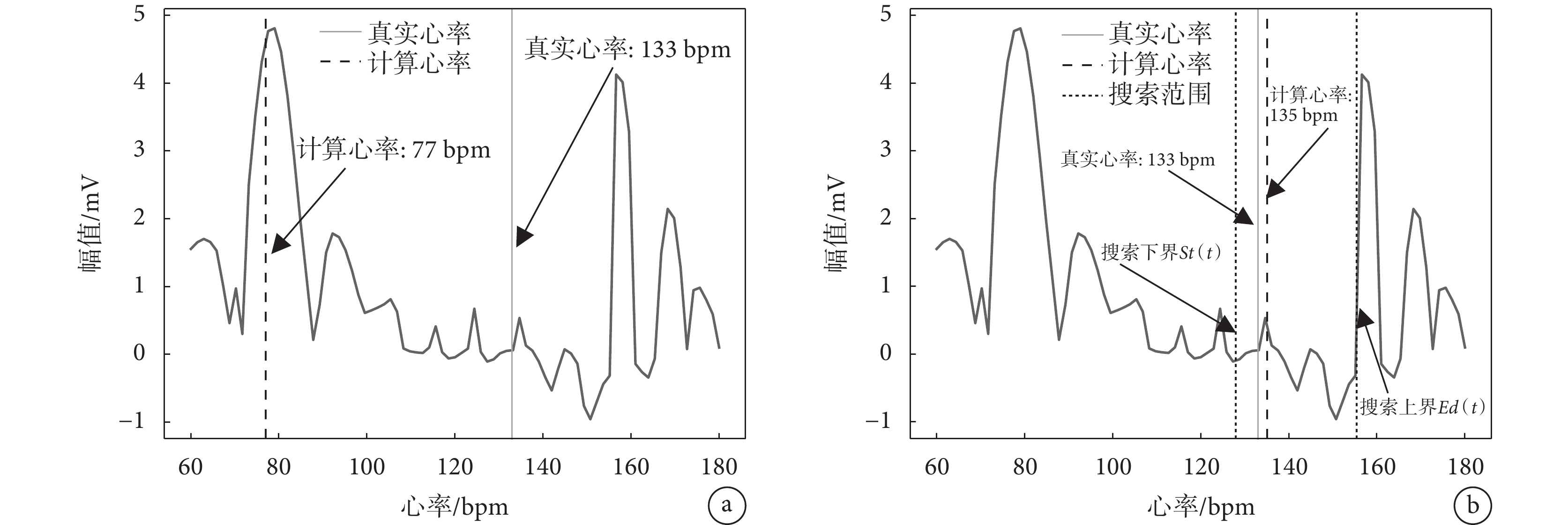
優化后的自適應心率搜索模型在頻域的實際作用效果如圖6所示。圖6是實驗自測數據subj.5第47次時間窗口中經過預處理的PPG信號在頻域的表現。為了方便觀察，將橫坐標從頻率轉換為了心率（本文后續頻域圖的橫坐標做了相同處理），其中垂直于X軸的實線代表當前時間窗口內的真實心率，虛線代表計算心率。在圖6a中，經過傳統譜峰追蹤方法得到的PPG信號主頻對應心率為77 bpm，而真實心率為133 bpm，二者相差56 bpm，且真實心率不在任何一個明顯波峰附近，表明當前時間窗內包含心率信息的PPG主頻已經被噪聲掩蓋，只進行譜峰追蹤無法獲取有效心率。而在圖6b中，經過自適應心率搜索模型對心率出現范圍的預測與限制（限制范圍上下限如圖6b中點線所示），得到的計算心率為135 bpm，已經十分貼近真實心率的133 bpm。
圖6
自測數據subj.5的PPG信號頻譜片段
a. 譜峰追蹤；b. 自適應心率搜索+譜峰追蹤
Figure6. PPG signal spectrum fragment of self-test data subj.5a. spectrum peak tracking; b. spectrum peak tracking method based on adaptive heart rate search
1.2 IPSO參數優化
1.2.1 目標函數設計
本文使用IPSO算法的目的是為了減少計算心率與真實心率間的差值，因此在目標函數的設計上，使用平均絕對誤差體現粒子與目標的距離。
|
|
式(14)中n代表計算出的心率個數，x(i)表示計算心率值，y(i)表示真實心率值，真實心率值由數據采集時同時佩戴的Polar心率帶測得。Polar心率帶由芬蘭博能公司制造，其心率計算準確度一直處于業界領先水平，本文所用產品型號為H10。式(15)是粒子優化的目標，在每次迭代過程中取平均絕對誤差的最小值。
1.2.2 IPSO作用過程
在IPSO的使用過程中，設定粒子數為20，最大迭代次數1 000次，根據待確定參數的個數，設定每個粒子的維度為8，結合對采集數據的使用經驗設定粒子運動范圍如表1所示。
表1
粒子運動范圍
Table1.
Particle range of motion
在經過預處理的數據中提取步頻信息與歷史心率信息，將二者加入到自適應心率搜索模型中與隨機初始化的粒子相結合，計算并得到測試心率與真實心率的平均絕對誤差。隨著多次迭代這一過程，以式(15)為目的，評估每個粒子的適應度，儲存每個粒子的個體最優解pbest以及全部pbest中的最佳值gbest，在迭代時，IPSO通過更新速度vt+1來對粒子位置xt+1中的每個維度進行建模，并根據pbest與gbest的線性組合移動粒子。當粒子各維度的移動超出表1對應的范圍時，舍棄該粒子，加入新的隨機粒子以提高IPSO的運行效率。
|
|
1.2.3 參數優化結果
IPSO算法參數設置為C1 = C2 = 1.8，R1 = R2如表2所示。
表2
參數優化結果
Table2.
Parameter optimization results
2 實驗設計與結果
2.1 數據來源
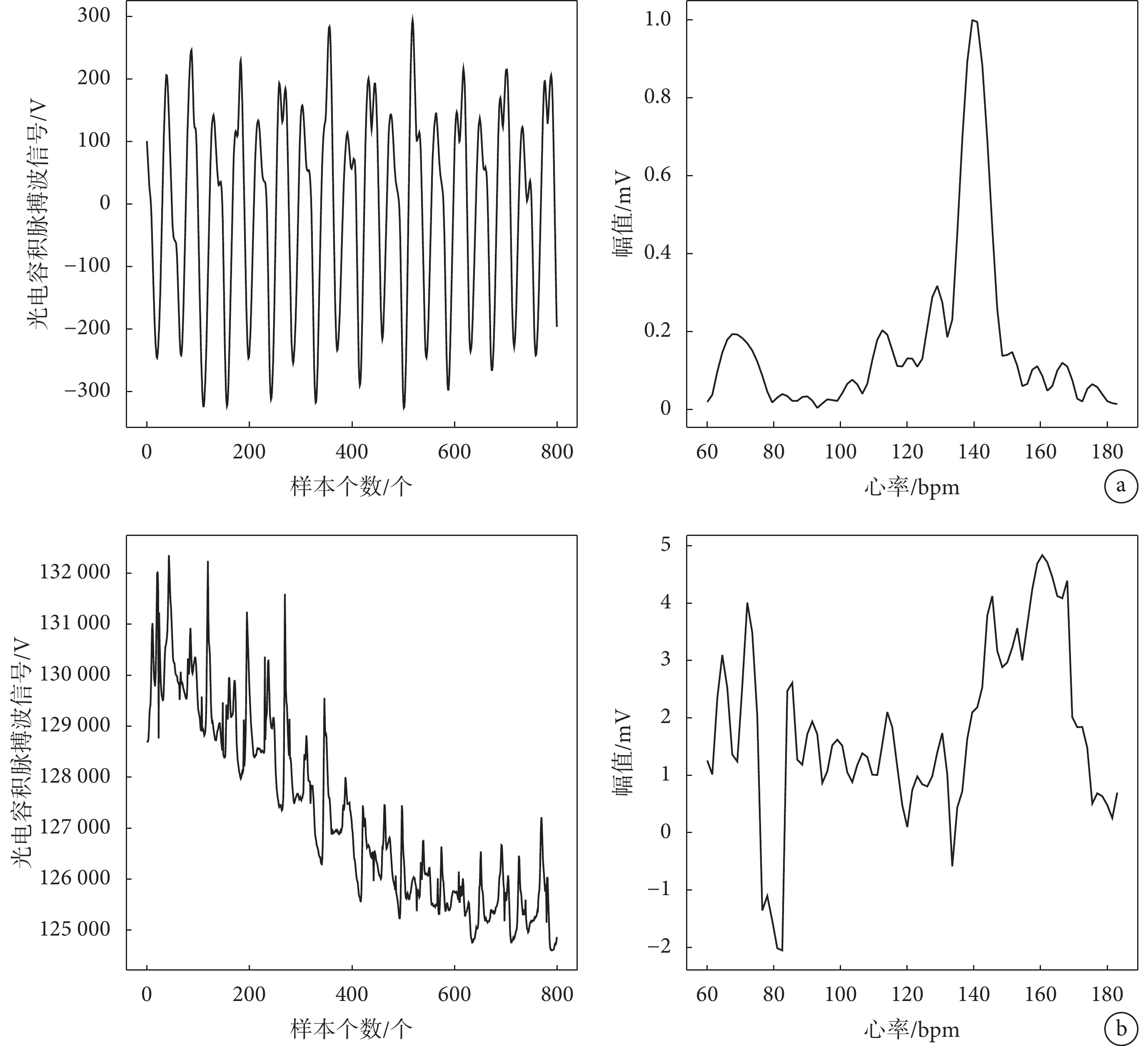
實驗所用的第一部分數據是2015年IEEE信號處理競賽的12組走路與跑步運動公開數據[14]，競賽課題為“Heart Rate Monitoring During Physical Exercise Using Wrist-Type Photoplethymographic Signals”。該部分數據由12位18～35歲間的健康男性受試者采集得到。每組數據中包含2路PPG數據、3路加速度數據和1路ECG數據。在對12組公開數據的PPG信號原始數據進行繪圖觀察后發現，其中大部分數據片段的波形變化都能體現出標準PPG信號的變化特點（如圖7a所示），其所受運動噪聲干擾程度較小。同時對比現有幾種算法在公開數據集的處理結果后發現，不同算法在公開數據集上的計算誤差相差較小，不能很好地體現算法在強運動噪聲干擾下的處理效果，因此在實驗設計中，本文加入10組自測數據作為第二部分數據來源。
圖7
信號質量對比
a. 公開數據庫subj.1數據片段；b. 實驗室自測數據subj.5數據片段
Figure7. Signal quality contrasta. public database subj.1 data fragment; b. laboratory self-test data subj.5 data fragment
實驗室采集的10組自測數據由五位受試者測得，包括四名男性和一名女性，年齡分布在25～33歲之間，身體健康無心臟方面疾病。每位受試者的上臂處無紋身、疤痕，可正常佩戴數據采集裝置（上臂處松緊度滿足測試設備使用要求，受試者對測試設備沒有過敏）。測試前已與受試者簽訂了知情同意書，提倡測試的公正互助性以及保密性。測試過程中尊重受試者的自主自愿原則，在不損害受試者身體健康的前提下完成了數據采集。測試使用的數據采集裝置內主要集成一顆型號為MAX86160EFN+的PPG信號傳感器，一顆型號為LIS2DH12TR的三軸加速度傳感器，通過低功耗藍牙模塊DA14580向移動端傳送傳感器數據，供電由3.7 V鋰電池提供。
在測試時使用綁帶將該裝置固定在上臂處，模擬智能臂帶的工作方式，之所以選擇在上臂處采集PPG信號，是因為在奔跑擺臂時上臂的肌肉會產生收縮與舒張，影響PPG信號的采集質量，在此處采集的PPG信號要比腕部采集的PPG信號更加難以處理。每組測試采集的數據包含1路PPG信號和3路加速度信號，數據采樣率100 Hz。真實心率由測試時同時佩戴的Polar心率帶采集得到。數據采集過程中要求測試人員滿足以下幾點測試要求：
（1）佩戴好設備并開始測試后首先靜待30 s，保證算法初始運行所使用數據的可靠性，之后開始跑步運動。
（2）由于測試環境為真實路跑環境，因此不預先指定跑步速度，但要求受測人員在自身可承受范圍內提高跑步速度，使心率出現較大梯度變化，不可全程慢跑進行測試。
（3）受測人員在一次數據收集過程中至少保證1次急停、1次急跑和4次轉向，不限制受測人員跑步時的擺臂方式，但是不可為了配合測試而故意減少身體震動幅度與擺臂幅度，同時要在測試過程中模擬抬手擦汗與看表。
（4）運動數據采集結束后，受測人員需要在心率持續監測的情況下進行休息，待心率降至90 bpm以內結束測試，保留完整的心率上升、下降過程。
為了體現本文采集數據的強噪聲干擾性，選擇一組自測運動狀態下的PPG信號，截取其中8 s長度的時間片段進行觀察，可以看到圖7b中運動狀態下的PPG信號在時域表現出多個不規則尖峰，尖峰形態以及尖峰間隔不具有規律性，無法從中分辨出有效的PPG信號波形。從頻域來看同樣存在多個偽峰，且偽峰幅值相近，在譜峰檢測方面很難根據每個譜峰的特點篩選出包含有效心率的譜峰。
對比圖7a與圖7b的信號質量表現，發現在時域中：公開數據庫的運動數據片段波形變化比較規律，而自測數據很難從信號波形中找到周期性的規律變化，且波峰多為不規則尖峰，受噪聲污染更加嚴重；在頻域中：公開數據庫運動數據片段譜峰孤立，偽峰數量少且在形態上與主峰存在明顯差別，容易識別出譜峰并得到準確度較高的心率，而自測數據在頻域中包含多個偽峰，偽峰間幅值、形態相近，很難判斷出真實心率所在頻率。因此使用本文采集的運動數據進行心率計算的難度更大，更能體現不同心率算法的性能優劣。
2.2 實驗結果
本文在各類算法的計算結果對比中使用平均絕對誤差與平均絕對誤差百分比（mean absolute percentage error，MAPE）作為評價標準。平均絕對誤差定義如式(14)所示，平均絕對誤差百分比定義如式(18)所示，x(i)表示計算心率值，y(i)表示真實心率值。
|
在公開數據庫的十二組走路與跑步運動公開數據對比中，本文選擇同樣使用該數據集體現算法準確度的TROIKA[14]、JOSS[17]、自適應濾波器算法（recursive least squares + normalized least mean square，RLS+NLMS）[18]、Random Forest算法[19]、經驗模態分解法（ensemble empirical mode decomposition，EEMD）[20]、WFPV[11]等算法與本文算法相比，統計結果如表3所示。從結果來看，本文算法計算心率的平均絕對誤差為1.12 bpm，平均絕對誤差百分比為0.90%。與其他算法相比：經典算法TROIKA與需要長時間運算的EEMD算法平均絕對誤差分別達到了2.42 bpm與1.83 bpm，計算準確度較低；新近提出的RLS+NLMS算法與Random Forest算法的計算準確度較高，但是仍不及本文算法與WFPV算法；而對周期性運動有很好降噪效果的WFPV算法以平均絕對誤差1.02 bpm優于本文算法。在其中6組數據的計算結果對比上，本文算法計算準確度更高，但是由于在subj.6與subj.10兩組數據的計算結果上與WFPV算法差距較大，導致整體計算結果略差于WFPV算法。
表3
本文算法與各類算法在公開數據的MAE、MAPE對比
Table3.
Comparison of MAE and MAPE between the algorithm proposed in this paper and various algorithm on public data
圖8展示了本文算法計算結果的皮爾遜相關系數圖，相關系數為0.995 533 98，已經十分接近于1，表明本文算法計算出的心率與真實心率間存在很強的線性相關關系。圖8還展示了Bland-Altman圖，其一致性界限為[?4.425，4.057]，誤差均值為?0.184 bpm，有95.6%的數據樣本落在置信區間內，表明計算心率與真實心率的一致性極強。
圖8
本文算法在IEEE信號處理杯12組訓練數據的統計結果
Figure8.
The statistical results of the proposed algorithm in the 12 sets of training data of IEEE Signal Processing Cup
在實驗室自測數據的結果對比分析中，選擇前述算法中在公開數據集表現最好且具有復現性的WFPV算法與本文算法進行對比，平均絕對誤差與平均絕對誤差百分比如表4所示。
表4
本文算法與WFPV算法在自測數據的MAE、MAPE對比
Table4.
Comparison of MAE and MAPE between the algorithm proposed in this paper and the WFPV algorithm on self-test data
根據表4十組自測數據的處理結果來看，本文算法的平均絕對誤差與平均絕對誤差百分比分別為3.19 bpm與2.57%，明顯優于WFPV算法的5.83 bpm與4.92%。在subj.4～7四組數據中，本文算法的計算精確度雖然有所下降，但總體誤差仍保持在5.5 bpm的可接受范圍內，而WFPV算法則出現了大量計算異常的數據樣本，其中在subj.5測試中的平均絕對誤差更是達到了18.42 bpm。此外，在十組數據共3 174個樣本的t檢驗對比中，本文算法計算得到的心率與真實心率的差異沒有統計學意義（t = 1.931，P = 0.053 5)，而WFPV算法計算得到的心率與真實心率的差異具有統計學意義（t = ?2.670，P = 0.007 6）。統計結果表明在同樣的強噪聲干擾環境下，本文算法的計算結果與真實心率間的差異更小、一致性更高，更加接近真實心率。
圖9是本文提出算法在自測數據的皮爾森相關系數圖與Bland-Altman圖，其中皮爾森相關系數計算為0.989 675 16、一致性界限為[?6.535，9.191]，誤差均值1.327 bpm，有94.3%的數據點落在了置信區間內。
圖9
本文算法在10組自測數據的統計結果
Figure9.
The statistical results of the algorithm proposed in this paper on 10 sets of self-test data
3 結論
從實驗結果來看，本文提出的基于自適應心率搜索模型的心率提取算法具有較強的抗運動噪聲干擾性，在PPG信號主頻不突出的情況下，能通過限制其真實心率譜峰的出現范圍來排除噪聲干擾。在十二組公開數據上表現良好，平均絕對誤差均值1.12 bpm，相較于WFPV算法的1.02 bpm仍有改進空間，但是對比TROIKA等心率算法準確率有較大提升。在十組自測運動噪聲較大的數據中，本文提出算法平均絕對誤差均值為3.19 bpm，明顯優于WFPV算法的5.83 bpm。總體來看，本文提出算法能夠在劇烈跑步運動中提取出有效心率信息，具有較高的心率計算準確率與較強的抗噪聲干擾能力，其對于智能臂帶等在上臂處采集PPG信號的心率監測設備具有一定應用前景。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：孟戎昊主要負責算法設計、數據采集與分析、論文編寫工作；李卓識主要提供實驗指導、理論分析指導、論文寫作指導及審閱修訂工作；于合龍為基金項目負責人，主要負責算法分析指導、協調溝通實驗所需資源及落實計劃安排等工作；鈕旗超主要負責數據處理、算法訓練、實驗平臺及設備搭建工作。
