針對人體下肢不同步態過程的個體差異和行走過程中步幅隨機變化等問題，本文提出一種利用運動姿態信號進行步態識別與預測的方法。研究采用基于免疫粒子群算法（IPSO）優化門控循環單元（GRU）網絡算法，建立以人體姿態變化數據為輸入，以下一階段姿態變化數據及準確率為輸出的網絡模型，以期實現對人體姿態變化的預測。本文首先明確概述IPSO優化GRU算法的過程，采集多名受試者分別執行平地行走、蹲起、坐姿腿屈伸等動作的人體姿態變化數據，通過對比分析IPSO優化的循環神經網絡(RNN)、長短期記憶網絡(LSTM)、GRU網絡識別與預測情況，以驗證所建模型的有效性。試驗結果顯示，優化后的算法可較好預測人體姿態變化，其中平地行走和蹲起動作的均方根誤差（RMSE）可精確到10?3，坐姿腿屈伸的RMSE可精確到10?2；各種動作的R2值均可達0.966以上。以上研究結果表明，優化后的算法可應用于實現康復治療中人體步態運動評價和步態趨勢預測、假肢和下肢康復設備設計等研究，對今后提高患者肢體功能、活動水平和生活獨立能力的研究提供參考。
引用本文： 高經緯, 馬超, 蘇鴻, 王少紅, 徐小力, 姚杰. 基于改進機器學習算法的步態識別與預測研究. 生物醫學工程學雜志, 2022, 39(1): 103-111. doi: 10.7507/1001-5515.202106072 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
中國乃至全球范圍內，人口老齡化已成為大勢所趨。腦外傷[1]、脊椎損傷[2]、腦卒中[3]、老齡化等引起的神經系統疾病可以導致步行運動失調或步態紊亂等運動障礙問題。輔助康復機器人可最大限度地提高患者肢體功能、活動水平和獨立性，并盡量減少繼發性并發癥[4]，成為患者步行訓練和治療的重要途徑之一，且得到了國內外相關領域的普遍認同[5-6]。
通過獲取人體步態運動姿態信號，并進一步進行穿戴者步態的識別與預測判斷，是實現下肢外骨骼輔助運動功能和康復訓練的重要基礎，也是目前人機交互研究的熱點之一[7]。目前，使用慣性測量單元（inertial measurement unit，IMU）進行步態過程信息獲取技術已成熟，可以采集保存較為豐富的信息數據，同時可以實現無損檢測[8]。基于運動姿態信息的步態識別與預測研究主要包括運動姿態信號的特征提取、識別分類預測等。在運動姿態信號的特征提取方面，主要使用時域、頻域和時頻域。而基于科學研究與工程應用中的實時分析研究需求，時域信號仍然作為主要使用的信號用于識別和預測研究[9-11]。
在運動步態識別預測的研究中，機器學習已逐漸成為一種可行的人體下肢運動變化軌跡識別判斷方法，利用機器學習方法應用大量數據即可實現運動步態的識別和預測判斷[12]。人體姿態變化軌跡可以認為是一種時間序列[13]。而機器學習中長短期記憶網絡（long short term memory，LSTM）算法是處理順序數據最有效的模型之一[14]。Su等[15]使用LSTM算法，實現了預測未來步態軌跡和步態相位的能力。Zebin等[16]提出了一種通過IMU和LSTM算法預測下肢受損角度軌跡的方法，取得了良好的結果。Ma等[17]提出一種基于LSTM神經網絡和時間先進特征的表面肌電圖膝關節角度連續估計方法，其算法均方誤差（mean square error，MSE）、均方根誤差（root mean squared error，RMSE）不高。Su等[18]提出用深度卷積神經網絡區分步態周期中的五個階段，準確率可達90%以上。
綜上可以發現，使用機器學習算法實現人體下肢的步態識別是一種切實可行的研究方法；與其他的生理信息采集的過程和結果相比，使用機器學習算法對運動過程中下肢運動姿態信息進行步態的識別與預測分析，具有過程測試無損、快速實時、采集過程相對便捷等優勢。同時，針對目前國內外研究人體正常狀態下復雜姿態變化預測方法不多、采集設備復雜、對試驗條件要求較高等問題，本文提出一種利用運動姿態信號進行姿態識別與預測的方法，通過采用基于免疫粒子群算法（immune particle swarm algorithm，IPSO）優化門控循環單元（gated recurrent unit，GRU）網絡，建立以人體姿態變化數據為輸入，以下一階段姿態變化數據及準確率為輸出的網絡模型，以期實現預測不同的人體姿態變化，為今后用于下肢外骨骼智能控制研究及相應儀器開發奠定基礎。
1 算法與優化
1.1 GRU算法
循環神經網絡（recurrent neural network，RNN）是將序列按順序分成多個時間步驟來處理定時數據的算法。在每個時間步驟中，RNN輸入取決于之前時間步驟的輸出（存儲單元）和當前輸入信息[19]。RNN在挖掘數據時，其中的時序信息和語義信息在數據分析的過程中會出現梯度消失和梯度爆炸問題，使得長序列數據的RNN在反向傳播時出現漏洞。因此需要通過設定梯度修剪（gradient clipping，GC）閾值來減小梯度爆炸問題；而針對梯度消失問題，則需使用GRU網絡算法[20]進行解決。GRU計算與RNN隱藏狀態相似。GRU前一個隱藏狀態ht ? 1與重置門大小相同，在計算出候選值之后，通過更新門，可以將前一個隱藏狀態的信息傳送到當前隱藏狀態，能夠使GRU存儲長期信息。更新門zt的計算公式如式（1）所示：
 |
式（1）中，
為sigmoid函數，Wz為參數矩陣，xt表示當前的輸入向量，ht ? 1為上一時刻隱藏狀態，當前時刻的隱藏狀態如式（2）所示：
 |
式（2）中，*代表逐元素相乘，
表示當前時刻隱藏狀態候選值。由于每個隱藏單元都擁有獨立的重置門和更新門，因此每個隱藏單元學習捕獲不同時間范圍依賴。
這些學習捕獲短期依賴的單元傾向于使重置門頻繁地激活，導致算法收斂速度降低。針對GRU網絡存在的收斂速度慢、局部極小等問題，本文將引入IPSO算法對其進行優化。
1.2 IPSO算法
標準粒子群算法（particle swarm algorithm，PSO）采用速度-位置搜索模型。將PSO算法初始化為一組隨機粒子后，通過迭代取得最優解。d維空間中t + 1時刻第i個粒子的速度 
—位置 
更新公式如式（3）～式（4）所示：
 |
 |
式（3）和（4）中，
表示d維空間中t時刻個體極值；
為d維空間中t時刻全局極值；
表示d維空間中t時刻第i個粒子的位置；c1、c2表示學習因子，其取值公式如式（5）、（6）所示：
 |
 |
式（5）中，mj表示最大迭代次數；mi表示當前迭代次數；cs表示c1的初始值，取4；ce表示c1的最終值，取1。r1、r2表示0～1 間的隨機數；vi表示粒子當前速度；xi表示粒子當前位置 。分析其速度方程，當t → ∞ 時，
且 
，則如式（7）所示：
 |
式（7）中，Pb表示個體極值；gb為全局極值。由于r1、r2服從均勻分布，求數學期望如式（8）所示：
 |
在PSO算法中，粒子進化收斂過程是持續聚集的過程。收斂極值由pb與gb共同確定，若gb只優化目標局部最優解，則PSO算法會出現早熟收斂的問題。
為解決PSO算法的不足，本文把免疫算法[21]中的“免疫記憶”和“抗體濃度抑制”引入到粒子群算法中。在兩種機制共同作用下，可有效地降低早熟收斂出現的概率，同時保持算法的快速收斂。慣性權重w公式如式（9）所示：
 |
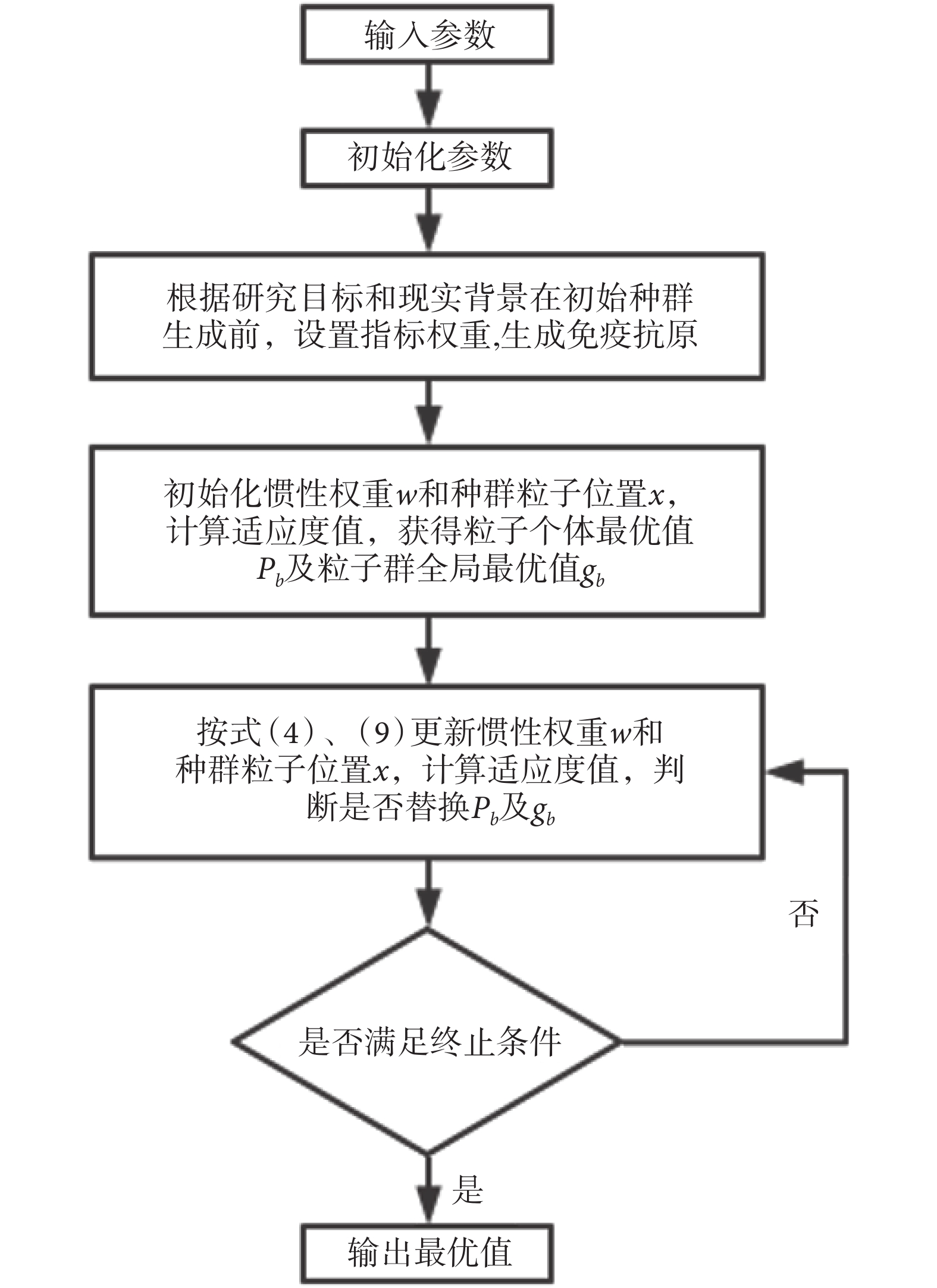
式（9）中，ws表示權重w的初始值，取0.9；we表示權重w的最終值，取0.4。IPSO算法優化步驟如圖1所示。
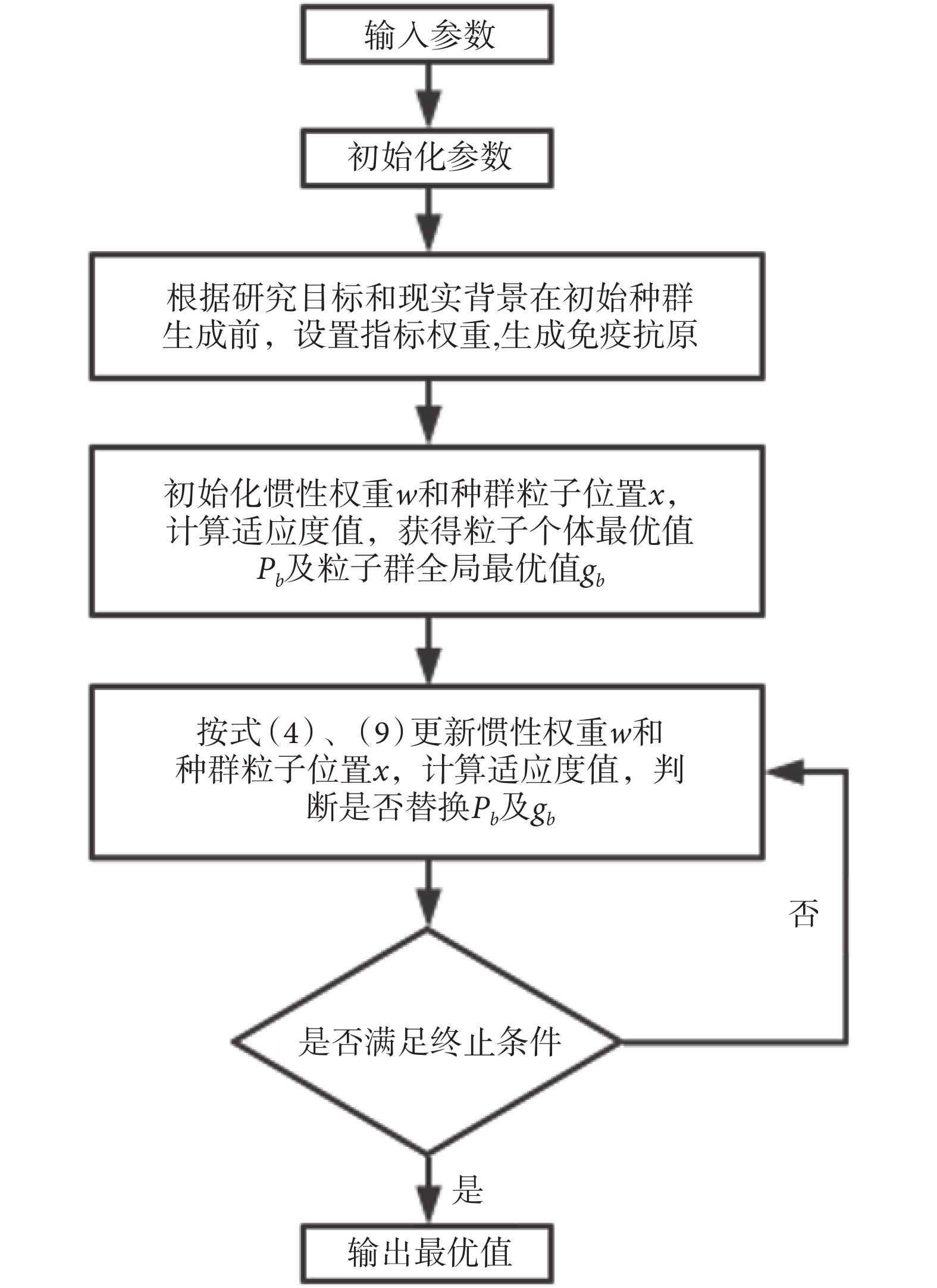圖1
IPSO優化步驟
Figure1.
IPSO optimization algorithm
1.3 基于IPSO優化GRU算法步態預測方法
GRU相較于LSTM算法模型簡單，只有兩個門控[19]。所以從計算角度看，GRU算法有更高效率，因此更適合用于構建復雜下肢姿態變化預測模型。本文采用IPSO優化GRU算法（IPSO-GRU），通過“免疫記憶”和“抗體濃度抑制”兩種機制的共同作用，在保持GRU算法快速收斂的同時有效降低算法早熟收斂概率，減小局部極小等問題，從而提升模型整體運行效率和預測精度。實驗步驟如下：
經實驗設置IPSO算法終止條件迭代次數和種群規模，然后進行種群初始化，給出下肢姿態變化的訓練樣本集、GRU網絡輸出的均方誤差，將其作為網絡訓練問題的適應度函數并迭代尋找最優解，最終根據判斷條件終止。
GRU采用兩個隱藏層，經多次實驗學習率設為0.001；批量大小（batch_size）設為50；期（epochs）為50次時模型效果最優，接下來用IPSO優化兩個隱含層的GRU；對學習率與兩隱含層的節點數進行尋優，超參數優化。經過多次比較分析，粒子數量（N）= 5；d = 3；epochs = 10；mj = 0.8；mi = 0.2；c1 = 1.5；c2 = 1.5；r1 = 0.8；r2 = 0.3時模型效果最優。
初始化粒子和速度后，根據式（3）和（4）對粒子和速度進行更新，之后用式（9）進行迭代循環，加入自適應變異操作，避免陷入局部最優，自適應變異公式如式（10）所示：
 |
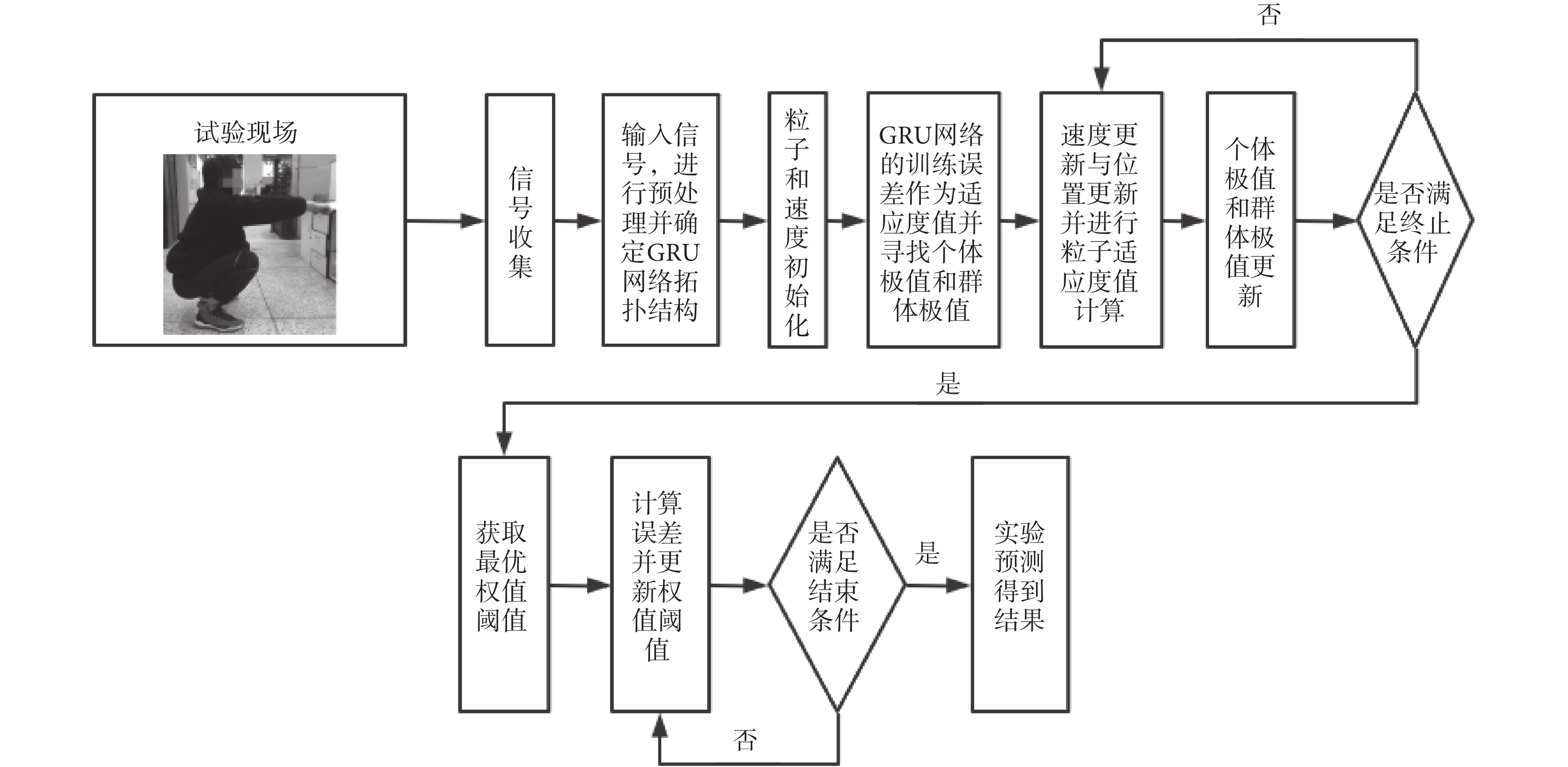
式（10）中，prob表示自適應變異，mj表示最大迭代次數，t為d維空間中t時刻變化情況。IPSO-GRU流程如圖2所示。
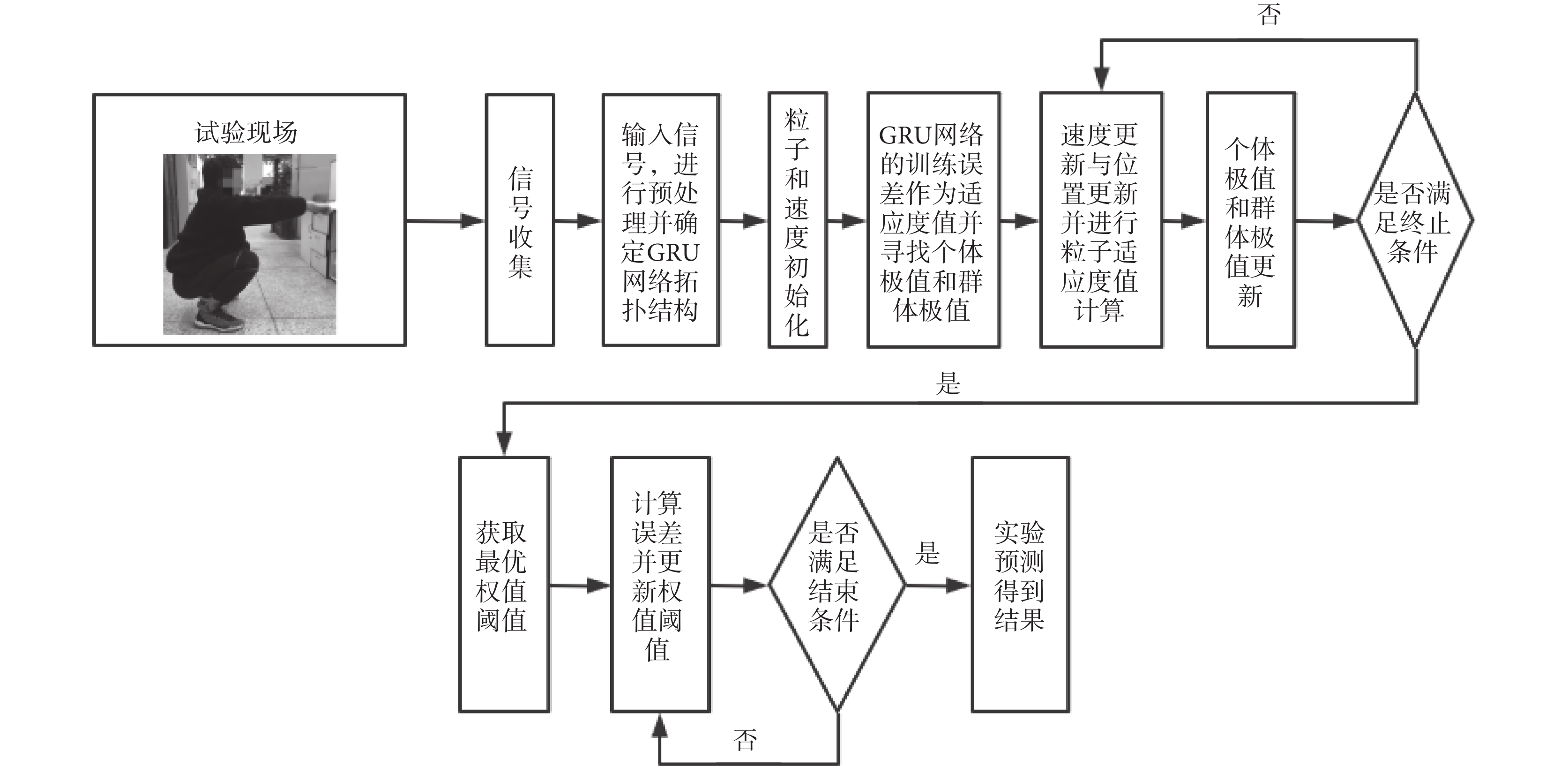圖2
IPSO-GRU流程圖
Figure2.
IPSO-GRU flow chart
2 試驗
2.1 試驗流程
本研究試驗在現代測控技術教育部重點實驗室進行，共采集了10名無任何神經肌肉骨骼異常的受試者［年齡：(24±2)歲，范圍：22～26歲；男/女：6/4；身高：170～185 cm；體重：50～92 kg］的IMU數據。受試者之間年齡、性別比、身高、體重等差異均無統計學意義（P>0.05）。本研究試驗已通過北京航空航天大學生物與醫學倫理委員會批準（BM20200153），所有受試者均由其本人在簽署知情同意書的情況下，自愿參加本試驗。
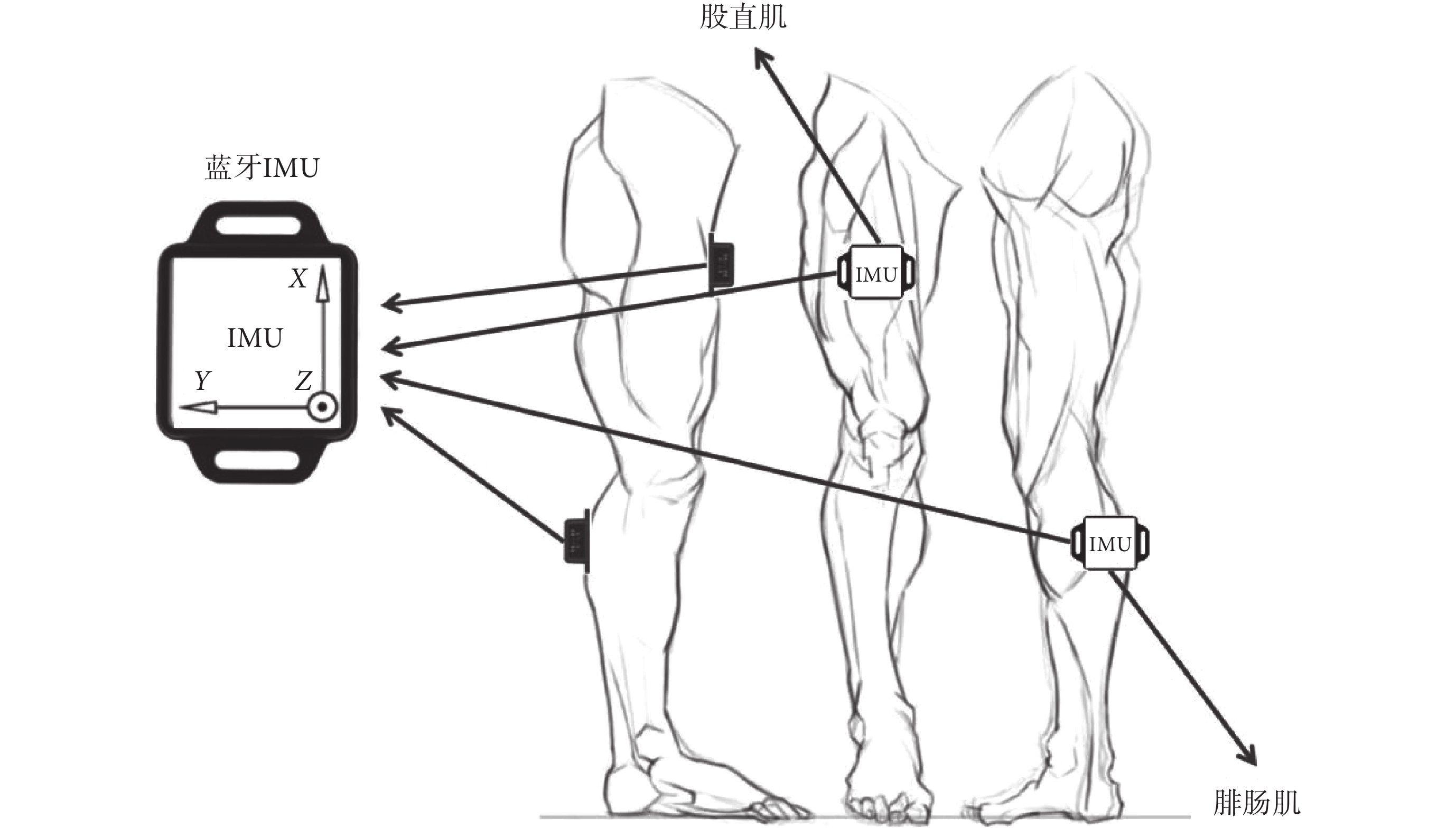
試驗使用IMU以收集人體姿態變化數據，IMU為9軸藍牙帶電池姿態傳感器BWT901CL（Wit-motion，中國）。試驗過程中，IMU分別布置于大腿前側的股直肌和小腿后側腓腸肌上，同時保證IMU的X軸與大腿對齊，試驗時通過測定X軸或Z軸的角度變化量，可以計算人體股關節旋轉的角度，設備分布位置如圖3所示。
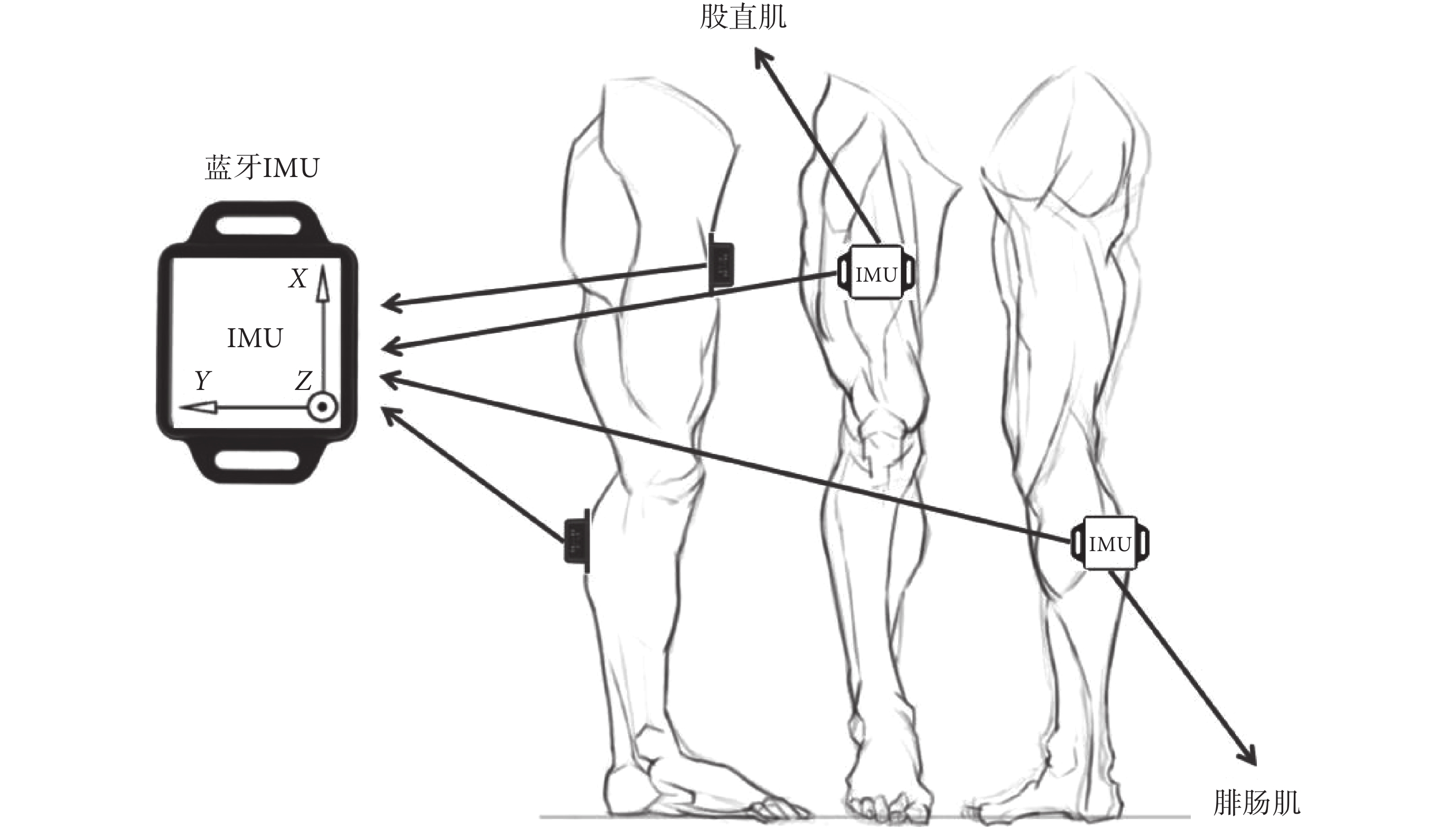圖3
設備在人體分布圖
Figure3.
Distribution of the device on the human body
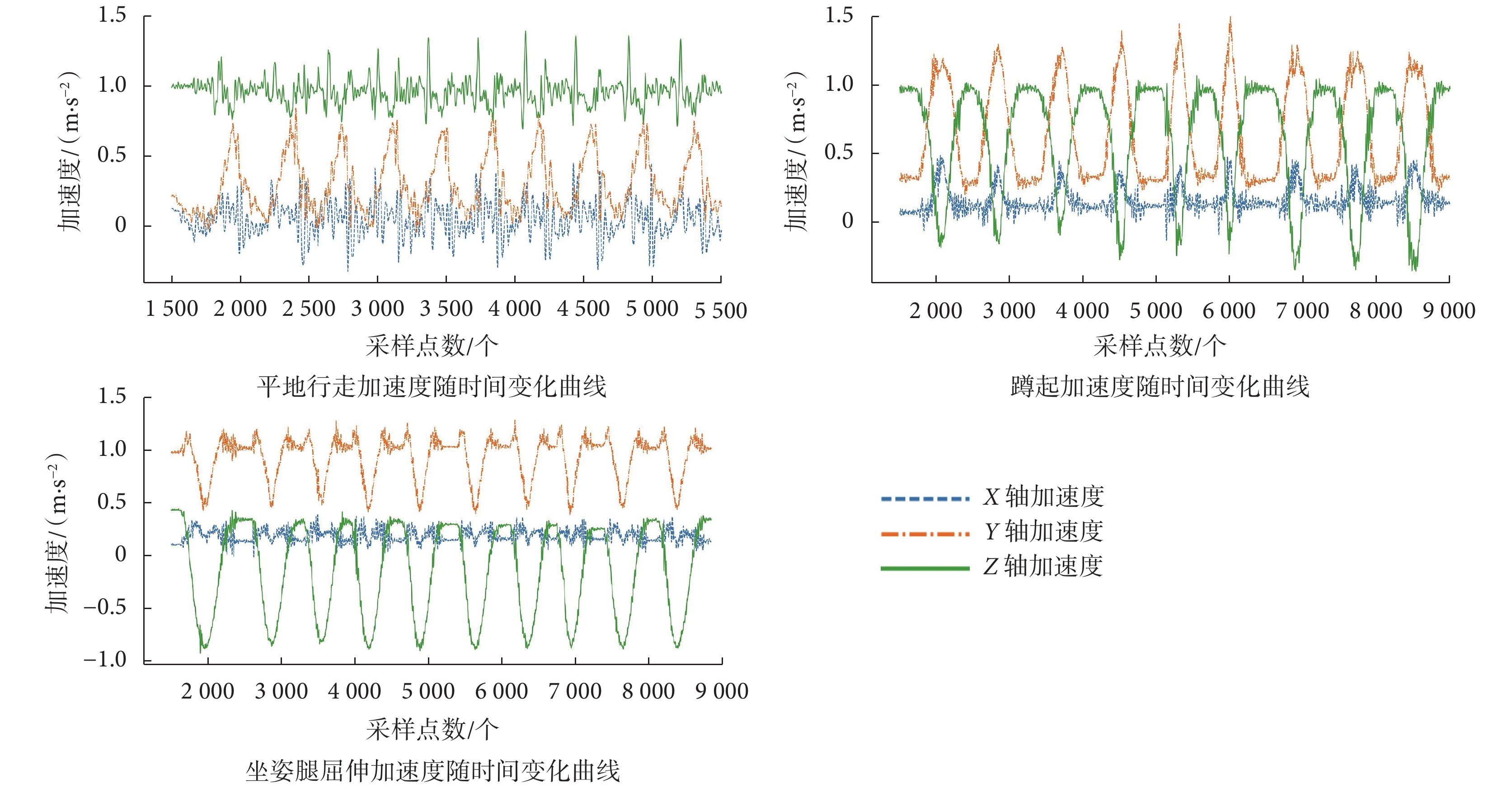
數據采集過程為: ① IMU歸零校準；② 肌肉自然放松；③ 以自選速度行走十步；④ 蹲起十次；⑤ 坐姿腿屈伸十次；⑥ 收集并處理數據。如圖4所示為隨機選取的受試者A大腿前側股直肌的十個步態周期的IMU加速度信號。
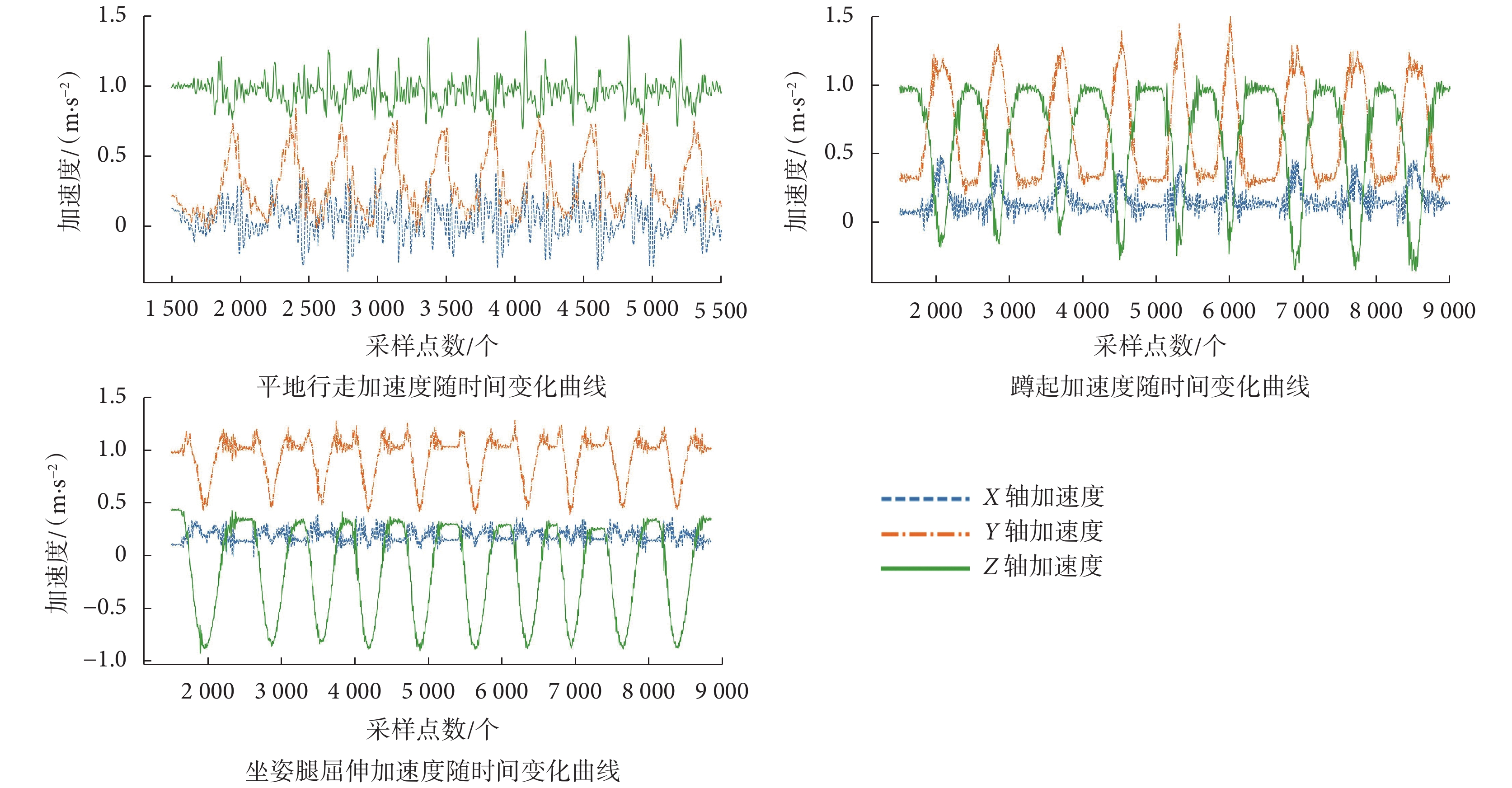圖4
IMU信號加速度運動曲線
Figure4.
Acceleration motion curve of IMU signal
如圖4所示，當人體姿態變化時，IMU獲得的信號可直觀地反應出不同姿態加速度變化。通過對數據質量、可用數據收集時間和潛在參與者疲勞的初步評估，每位受試者平均記錄8、9次試驗（范圍8～10 次）。 最后的數據集包括95項平地行走試驗和85項蹲起試驗，以及95項坐姿腿屈伸試驗。
2.2 模型訓練
本文數據處理的計算機語言為python3.6（Centrum Wiskunde & Informatica，荷蘭），使用軟件機器學習庫sklearn（Institut national de recherche en informatique et en automatique，法國）對數據進行預處理。所有的計算均在臺式機上進行，配備圖形處理器GPU GTX 1650（NVIDIA，美國），8 GB 內存和Windows 10（Microsoft，美國）操作系統。
試驗采用監督學習的方式對IPSO-GRU進行訓練，基于前述試驗提取數據建立樣本庫，對網絡進行訓練，本文訓練集、驗證集和測試集按照8∶1∶1的比例隨機劃分。網絡中加入驗證集，驗證集用來在每個epoch之后計算在驗證集上的分類預測準確度，提升模型泛化能力。為加快模型收斂，在輸入數據之前，需要將原始數據無量綱化。無量綱化公式如式（11）所示：
 |
式（11）中，x為同一時刻粒子位置，max(x)、min(x)分別為同一時刻粒子最大位置和最小位置，
為無量綱化后粒子位置。
3 算法及實驗驗證
為驗證算法的準確率和有效性，將按以下流程對算法進行分析研究：① 對未優化算法預測準確率進行對比分析；② 對IPSO優化后的各算法性能進行對比分析；③ 討論分析受試者個體差異對本應用算法方法的影響。
3.1 未優化算法對比分析
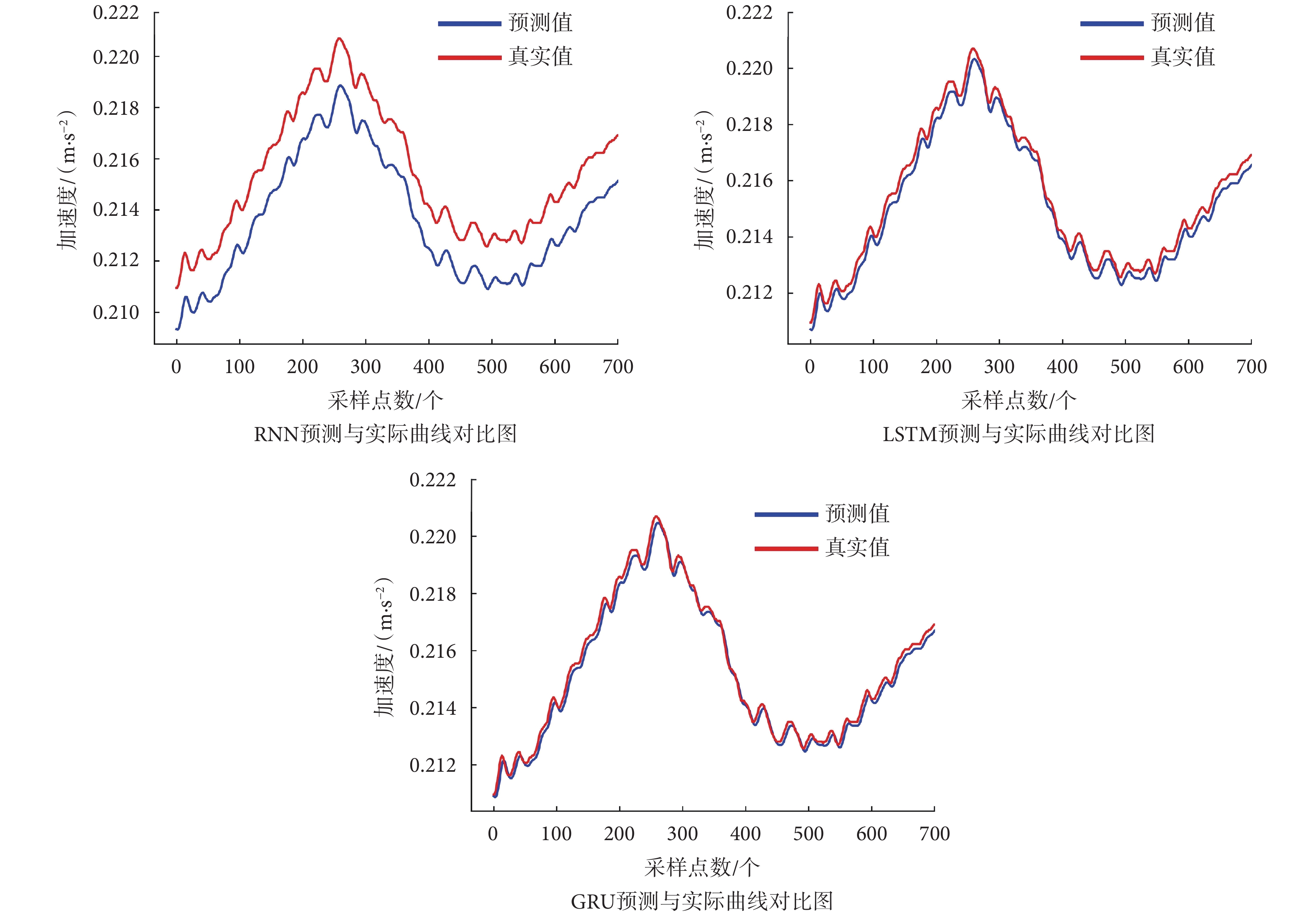
步態過程中IMU震動幅度、人體姿態變化大，預測較難；隨機選取A受試者大腿前側股直肌上IMU采集的Y軸步態加速度信號作為參考。引入RNN、LSTM、GRU算法；并用IPSO分別優化這三種算法進行對比；一組步態周期下各未經IPSO優化算法預測與實測對比如圖5所示。
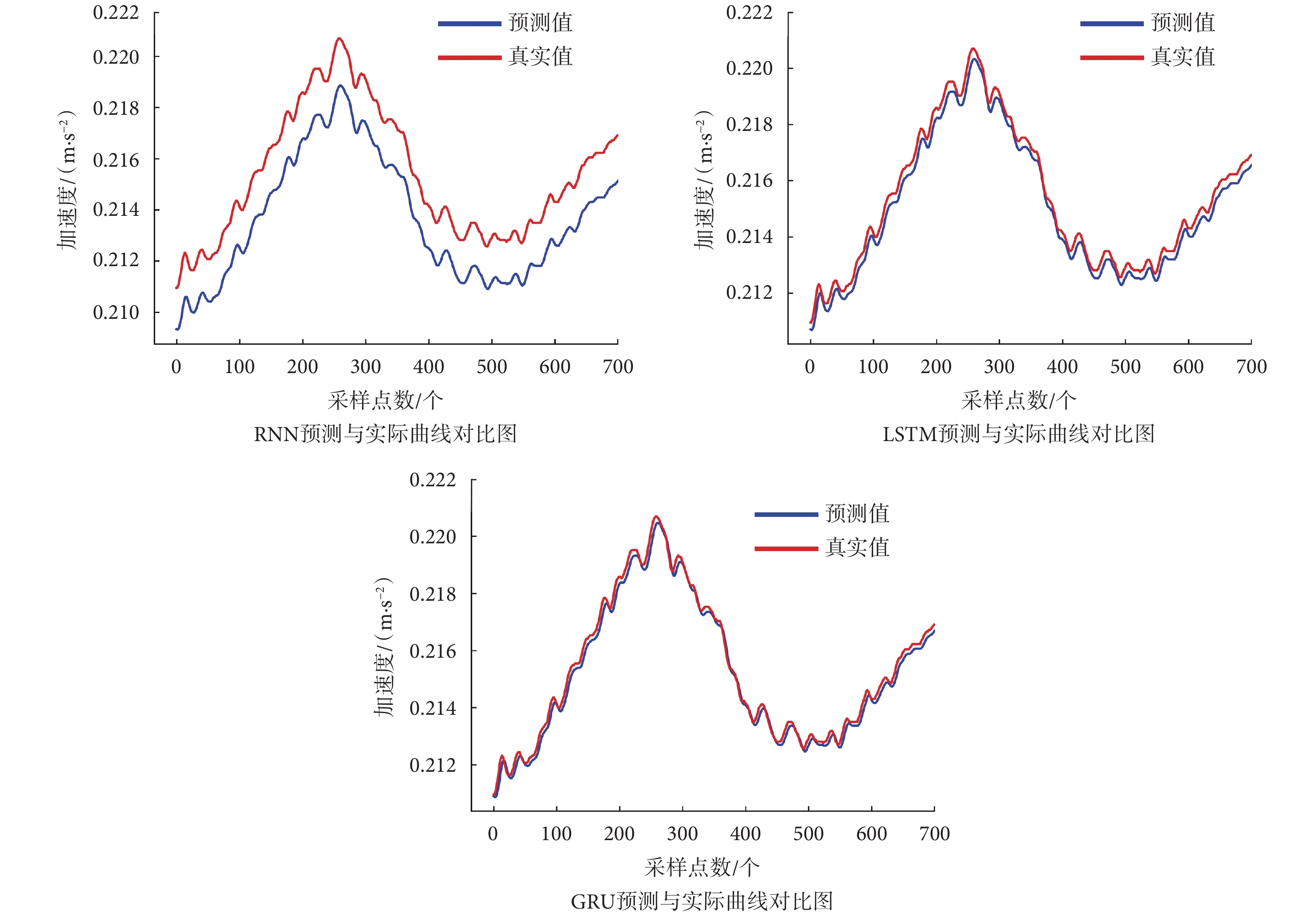圖5
每種未經IPSO優化算法預測和實際對比圖
Figure5.
Comparison of actual and predicted graphs for each algorithm without IPSO optimization
如圖5所示， RNN算法真實值與預測值相差較大，LSTM表現優于RNN，而GRU在三種算法中真實值和預測值最接近。
為深入分析預測模型性能，針對預測回歸類模型本文使用MSE、RMSE、平均絕對誤差（mean absolute error，MAE）、相對誤差（mean absolute percentage error，MAPE）等進行測量，公式如式（12）～（15）所示：
 |
 |
 |
 |
真實值集合Y = {
, yi, 
, yn)，預測值集合 
，MAPE反映模型預測值結果的好壞，MSE和RMSE表示預測值與真值間的偏差程度，可反應模型的泛化能力。做非線性擬合時，MAPE?RMSE越小代表預測結果越精準越穩定。若比較不同量綱下模型好壞，則需要另一個評價指標：R2值。R2值和1越接近，表明模型預測越精確。R2值計算如式（16）所示：
 |
3.2 優化算法對比分析
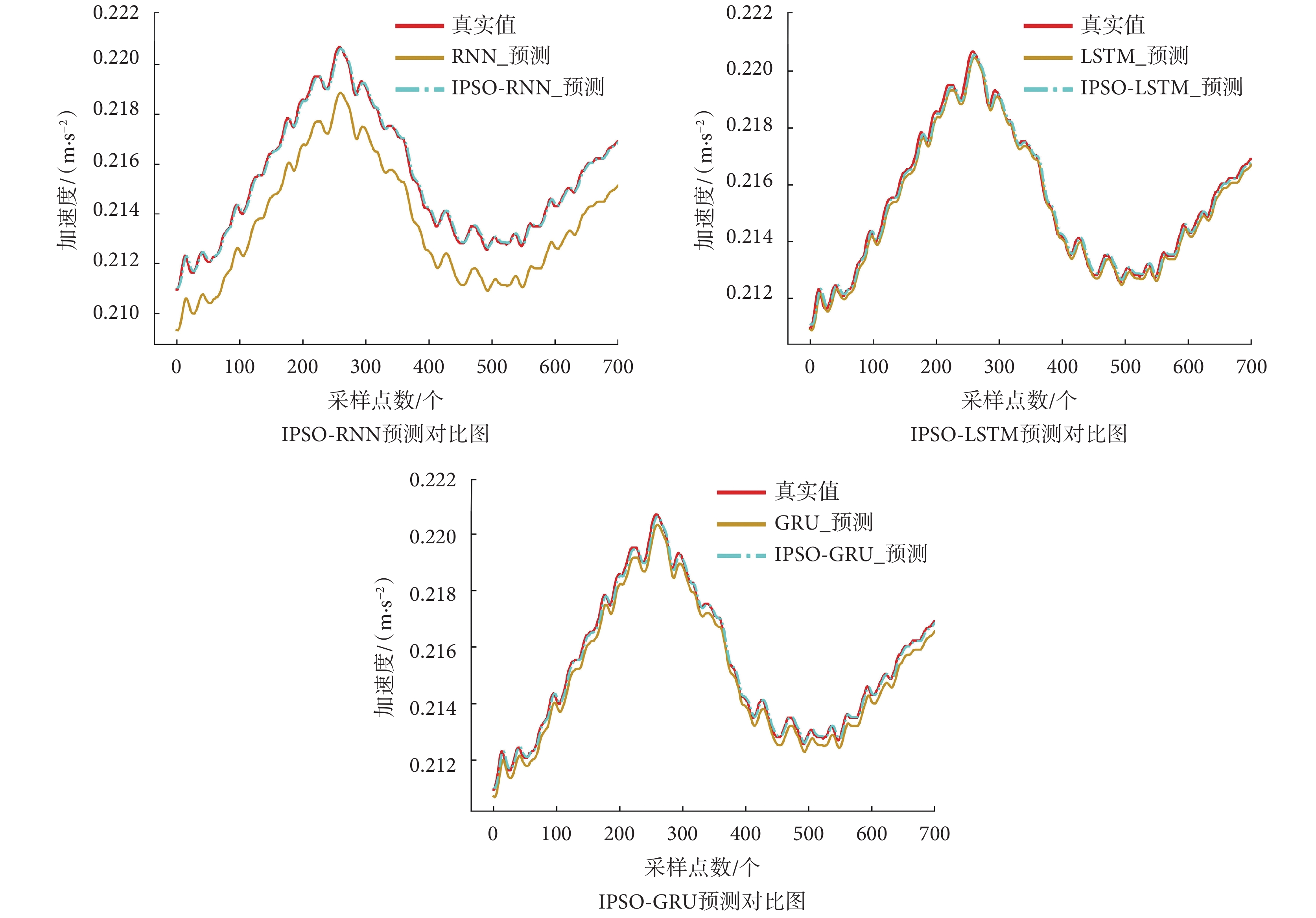
A受試者大腿前側股直肌上IMU采集的Y軸步態加速度信號，在一組步態周期下經過IPSO優化的各算法預測、實際與未經優化的算法對比如圖6所示。
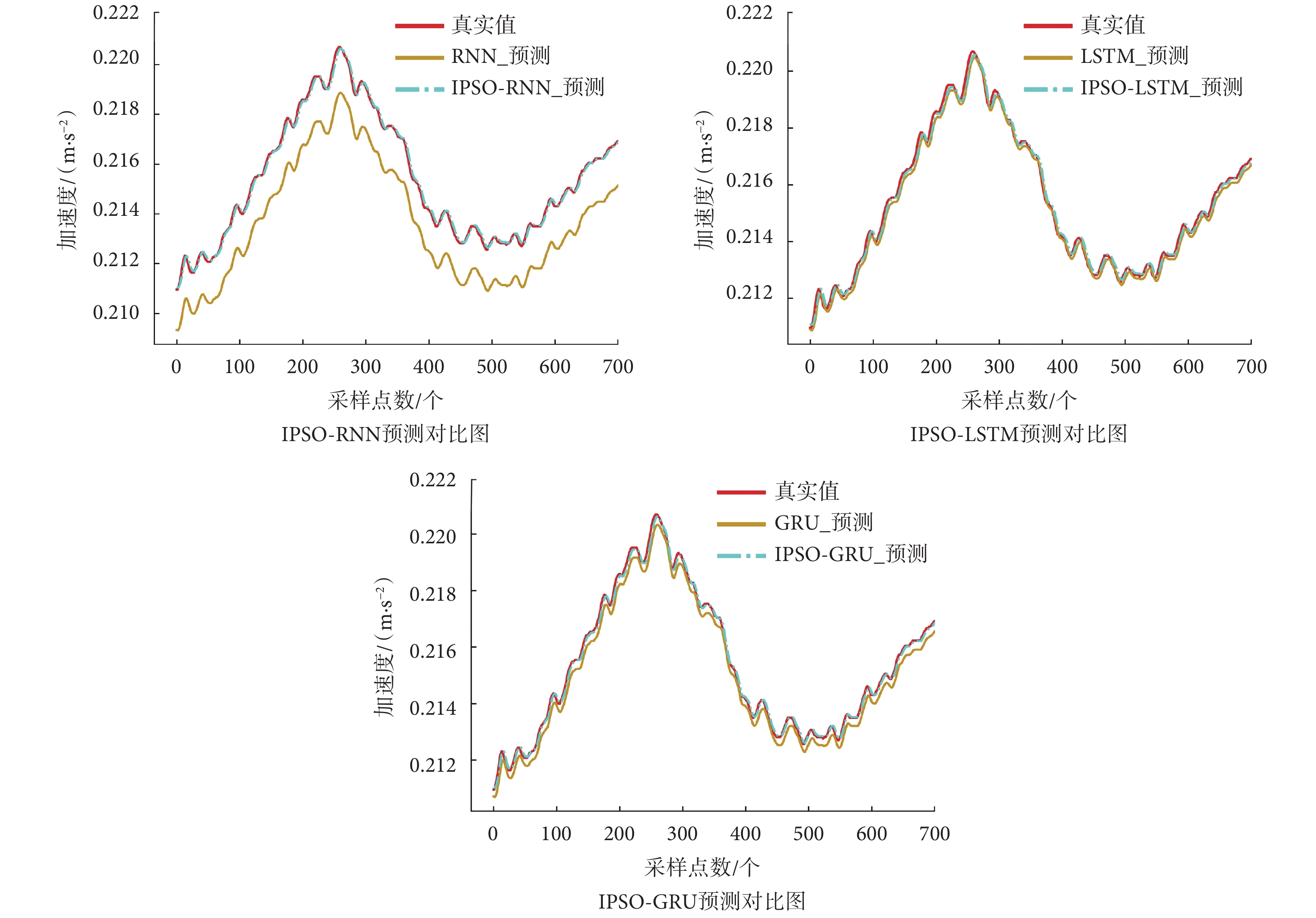圖6
經過IPSO優化算法實際和預測對比圖
Figure6.
Comparison of actual and predicted graphs of each algorithm after IPSO optimization
如圖6所示，三種算法中，IPSO-GRU、IPSO優化LSTM算法（IPSO-LSTM）、IPSO優化RNN算法（IPSO-RNN），比未經過優化的各算法更貼近真實值。而經優化后的各算法由圖中無法直接觀測出哪種算法最優，所以引入MAPE、RMSE、MAE、R2值作為評判依據。A受試者的IMU數據輸入算法得出MAPE、RMSE、MAE、R2值如表1所示。
表1
多種算法評價指標
Table1.
Evaluation index of each algorithm
如表1所示，IPSO優化算法MAPE值比未經優化的算法值低10?2，RMSE、MAE值比未經優化的算法值低約10?1，證明IPSO優化算法預測值與真實值間的偏差程度縮小，而IPSO-GRU算法R2值達到0.997 85，在其中表現最優。
3.3 所有受試者數據試驗分析
為探究個體差異對本試驗方法的影響，將10名合格受試者IMU數據輸入GRU算法，得出其平均MAPE(
)、平均RMSE(
)、平均MAE(
)、平均R2值(
)如表2所示。
表2
GRU算法各項評價指標
Table2.
Evaluation indexes of GRU algorithm
如表2所示，GRU步態預測
值為0.527 32，低于蹲起和屈伸動作的0.707 83和0.970 27，由于平地行走時IMU震動的幅度遠大于另外兩項運動，導致GRU算法的步態預測效果不理想，因此引入IPSO算法對其進行優化。IPSO-GRU算法對全部受試者合格數據各項平均指標如表3所示。
表3
IPSO-GRU算法各項評價指標
Table3.
Evaluation indexes of IPSO-GRU algorithm
由表2與表3對比發現，IPSO-GRU算法的平地行走
值比GRU算法低10?2，蹲起與坐姿腿屈伸的
、
、
值比GRU算法至少低10?1，表明IPSO-GRU算法預測值與真實值間的偏差程度較GRU算法相比更小，且
值都可以達到0.966以上，相較于GRU算法的R2值最多提高0.438 86，證明IPSO-GRU算法可滿足個體差異帶來的影響。
4 結論與討論
針對人體下肢不同步態過程的個體差異和行走中步幅隨機性等問題，本文提出一種基于IPSO和GRU算法利用運動姿態信號進行步態識別與預測的方法。通過采集布置在大腿前側的股直肌和小腿后側腓腸肌上的IMU人體下肢不同運動姿態數據作為輸入，以下一階段姿態變化數據及準確率為輸出的網絡模型，進行步態的識別與預測分析。通過對比分析IPSO優化的RNN、LSTM、GRU網絡識別與預測情況，以驗證所建模型的有效性。結果顯示，經本研究優化后的算法可較好地預測人體的姿態變化，其中平地行走和蹲起動作的均方根誤差（RMSE）可精確到10?3，坐姿腿屈伸的RMSE可精確到10?2，各種動作的R2值均可達0.966以上。上述研究表明：IPSO-GRU算法可準確預測人體下肢的姿態變化，也可適應個體差異，達到了預期效果。
本研究中考慮到下肢外骨骼的穿戴特性，通過將兩個IMU布置于單條腿上的方式減少輸出數據的不確定性，從而提高預測的可靠性[16]。在此基礎上還可進行相應的數據挖掘研究半監督條件下的識別預測，用以降低進行訓練數據的維數，進一步提高識別判斷的實時性能。本研究中主要針對健康的年輕受試者開展研究，本方法同樣可用于如老年人和行走障礙患者等人群的步態識別與預測判斷。因此，本文所提的算法可應用于實現康復治療中人體步態運動評價和步態趨勢預測、假肢和下肢康復設備設計研究等領域，對于提高患者肢體功能、活動水平和生活獨立能力具有工程應用價值。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：高經緯主要負責實驗流程、數據記錄與分析、論文編寫以及算法程序設計；馬超負責項目主持、提供實驗指導，數據分析指導，論文審閱修訂；蘇鴻負責平臺搭建、算法程序設計、協調溝通；王少紅負責實驗設備采集、提供實驗指導，數據分析指導；徐小麗負責數據處理、算法驗證與論文審閱修訂；姚杰負責論文審閱修訂、協調溝通以及計劃安排。
倫理聲明：本研究通過了北京航空航天大學生物與醫學倫理委員會的審批(批文編號：BM20200153)。
引言
中國乃至全球范圍內，人口老齡化已成為大勢所趨。腦外傷[1]、脊椎損傷[2]、腦卒中[3]、老齡化等引起的神經系統疾病可以導致步行運動失調或步態紊亂等運動障礙問題。輔助康復機器人可最大限度地提高患者肢體功能、活動水平和獨立性，并盡量減少繼發性并發癥[4]，成為患者步行訓練和治療的重要途徑之一，且得到了國內外相關領域的普遍認同[5-6]。
通過獲取人體步態運動姿態信號，并進一步進行穿戴者步態的識別與預測判斷，是實現下肢外骨骼輔助運動功能和康復訓練的重要基礎，也是目前人機交互研究的熱點之一[7]。目前，使用慣性測量單元（inertial measurement unit，IMU）進行步態過程信息獲取技術已成熟，可以采集保存較為豐富的信息數據，同時可以實現無損檢測[8]。基于運動姿態信息的步態識別與預測研究主要包括運動姿態信號的特征提取、識別分類預測等。在運動姿態信號的特征提取方面，主要使用時域、頻域和時頻域。而基于科學研究與工程應用中的實時分析研究需求，時域信號仍然作為主要使用的信號用于識別和預測研究[9-11]。
在運動步態識別預測的研究中，機器學習已逐漸成為一種可行的人體下肢運動變化軌跡識別判斷方法，利用機器學習方法應用大量數據即可實現運動步態的識別和預測判斷[12]。人體姿態變化軌跡可以認為是一種時間序列[13]。而機器學習中長短期記憶網絡（long short term memory，LSTM）算法是處理順序數據最有效的模型之一[14]。Su等[15]使用LSTM算法，實現了預測未來步態軌跡和步態相位的能力。Zebin等[16]提出了一種通過IMU和LSTM算法預測下肢受損角度軌跡的方法，取得了良好的結果。Ma等[17]提出一種基于LSTM神經網絡和時間先進特征的表面肌電圖膝關節角度連續估計方法，其算法均方誤差（mean square error，MSE）、均方根誤差（root mean squared error，RMSE）不高。Su等[18]提出用深度卷積神經網絡區分步態周期中的五個階段，準確率可達90%以上。
綜上可以發現，使用機器學習算法實現人體下肢的步態識別是一種切實可行的研究方法；與其他的生理信息采集的過程和結果相比，使用機器學習算法對運動過程中下肢運動姿態信息進行步態的識別與預測分析，具有過程測試無損、快速實時、采集過程相對便捷等優勢。同時，針對目前國內外研究人體正常狀態下復雜姿態變化預測方法不多、采集設備復雜、對試驗條件要求較高等問題，本文提出一種利用運動姿態信號進行姿態識別與預測的方法，通過采用基于免疫粒子群算法（immune particle swarm algorithm，IPSO）優化門控循環單元（gated recurrent unit，GRU）網絡，建立以人體姿態變化數據為輸入，以下一階段姿態變化數據及準確率為輸出的網絡模型，以期實現預測不同的人體姿態變化，為今后用于下肢外骨骼智能控制研究及相應儀器開發奠定基礎。
1 算法與優化
1.1 GRU算法
循環神經網絡（recurrent neural network，RNN）是將序列按順序分成多個時間步驟來處理定時數據的算法。在每個時間步驟中，RNN輸入取決于之前時間步驟的輸出（存儲單元）和當前輸入信息[19]。RNN在挖掘數據時，其中的時序信息和語義信息在數據分析的過程中會出現梯度消失和梯度爆炸問題，使得長序列數據的RNN在反向傳播時出現漏洞。因此需要通過設定梯度修剪（gradient clipping，GC）閾值來減小梯度爆炸問題；而針對梯度消失問題，則需使用GRU網絡算法[20]進行解決。GRU計算與RNN隱藏狀態相似。GRU前一個隱藏狀態ht ? 1與重置門大小相同，在計算出候選值之后，通過更新門，可以將前一個隱藏狀態的信息傳送到當前隱藏狀態，能夠使GRU存儲長期信息。更新門zt的計算公式如式（1）所示：
|
式（1）中，為sigmoid函數，Wz為參數矩陣，xt表示當前的輸入向量，ht ? 1為上一時刻隱藏狀態，當前時刻的隱藏狀態如式（2）所示：
|
式（2）中，*代表逐元素相乘， 表示當前時刻隱藏狀態候選值。由于每個隱藏單元都擁有獨立的重置門和更新門，因此每個隱藏單元學習捕獲不同時間范圍依賴。
這些學習捕獲短期依賴的單元傾向于使重置門頻繁地激活，導致算法收斂速度降低。針對GRU網絡存在的收斂速度慢、局部極小等問題，本文將引入IPSO算法對其進行優化。
1.2 IPSO算法
標準粒子群算法（particle swarm algorithm，PSO）采用速度-位置搜索模型。將PSO算法初始化為一組隨機粒子后，通過迭代取得最優解。d維空間中t + 1時刻第i個粒子的速度 —位置 更新公式如式（3）～式（4）所示：
|
|
式（3）和（4）中， 表示d維空間中t時刻個體極值； 為d維空間中t時刻全局極值； 表示d維空間中t時刻第i個粒子的位置；c1、c2表示學習因子，其取值公式如式（5）、（6）所示：
|
|
式（5）中，mj表示最大迭代次數；mi表示當前迭代次數；cs表示c1的初始值，取4；ce表示c1的最終值，取1。r1、r2表示0～1 間的隨機數；vi表示粒子當前速度；xi表示粒子當前位置 。分析其速度方程，當t → ∞ 時， 且 ，則如式（7）所示：
|
式（7）中，Pb表示個體極值；gb為全局極值。由于r1、r2服從均勻分布，求數學期望如式（8）所示：
|
在PSO算法中，粒子進化收斂過程是持續聚集的過程。收斂極值由pb與gb共同確定，若gb只優化目標局部最優解，則PSO算法會出現早熟收斂的問題。
為解決PSO算法的不足，本文把免疫算法[21]中的“免疫記憶”和“抗體濃度抑制”引入到粒子群算法中。在兩種機制共同作用下，可有效地降低早熟收斂出現的概率，同時保持算法的快速收斂。慣性權重w公式如式（9）所示：
|
式（9）中，ws表示權重w的初始值，取0.9；we表示權重w的最終值，取0.4。IPSO算法優化步驟如圖1所示。
圖1
IPSO優化步驟
Figure1.
IPSO optimization algorithm
1.3 基于IPSO優化GRU算法步態預測方法
GRU相較于LSTM算法模型簡單，只有兩個門控[19]。所以從計算角度看，GRU算法有更高效率，因此更適合用于構建復雜下肢姿態變化預測模型。本文采用IPSO優化GRU算法（IPSO-GRU），通過“免疫記憶”和“抗體濃度抑制”兩種機制的共同作用，在保持GRU算法快速收斂的同時有效降低算法早熟收斂概率，減小局部極小等問題，從而提升模型整體運行效率和預測精度。實驗步驟如下：
經實驗設置IPSO算法終止條件迭代次數和種群規模，然后進行種群初始化，給出下肢姿態變化的訓練樣本集、GRU網絡輸出的均方誤差，將其作為網絡訓練問題的適應度函數并迭代尋找最優解，最終根據判斷條件終止。
GRU采用兩個隱藏層，經多次實驗學習率設為0.001；批量大小（batch_size）設為50；期（epochs）為50次時模型效果最優，接下來用IPSO優化兩個隱含層的GRU；對學習率與兩隱含層的節點數進行尋優，超參數優化。經過多次比較分析，粒子數量（N）= 5；d = 3；epochs = 10；mj = 0.8；mi = 0.2；c1 = 1.5；c2 = 1.5；r1 = 0.8；r2 = 0.3時模型效果最優。
初始化粒子和速度后，根據式（3）和（4）對粒子和速度進行更新，之后用式（9）進行迭代循環，加入自適應變異操作，避免陷入局部最優，自適應變異公式如式（10）所示：
|
式（10）中，prob表示自適應變異，mj表示最大迭代次數，t為d維空間中t時刻變化情況。IPSO-GRU流程如圖2所示。
圖2
IPSO-GRU流程圖
Figure2.
IPSO-GRU flow chart
2 試驗
2.1 試驗流程
本研究試驗在現代測控技術教育部重點實驗室進行，共采集了10名無任何神經肌肉骨骼異常的受試者［年齡：(24±2)歲，范圍：22～26歲；男/女：6/4；身高：170～185 cm；體重：50～92 kg］的IMU數據。受試者之間年齡、性別比、身高、體重等差異均無統計學意義（P>0.05）。本研究試驗已通過北京航空航天大學生物與醫學倫理委員會批準（BM20200153），所有受試者均由其本人在簽署知情同意書的情況下，自愿參加本試驗。
試驗使用IMU以收集人體姿態變化數據，IMU為9軸藍牙帶電池姿態傳感器BWT901CL（Wit-motion，中國）。試驗過程中，IMU分別布置于大腿前側的股直肌和小腿后側腓腸肌上，同時保證IMU的X軸與大腿對齊，試驗時通過測定X軸或Z軸的角度變化量，可以計算人體股關節旋轉的角度，設備分布位置如圖3所示。
圖3
設備在人體分布圖
Figure3.
Distribution of the device on the human body
數據采集過程為: ① IMU歸零校準；② 肌肉自然放松；③ 以自選速度行走十步；④ 蹲起十次；⑤ 坐姿腿屈伸十次；⑥ 收集并處理數據。如圖4所示為隨機選取的受試者A大腿前側股直肌的十個步態周期的IMU加速度信號。
圖4
IMU信號加速度運動曲線
Figure4.
Acceleration motion curve of IMU signal
如圖4所示，當人體姿態變化時，IMU獲得的信號可直觀地反應出不同姿態加速度變化。通過對數據質量、可用數據收集時間和潛在參與者疲勞的初步評估，每位受試者平均記錄8、9次試驗（范圍8～10 次）。 最后的數據集包括95項平地行走試驗和85項蹲起試驗，以及95項坐姿腿屈伸試驗。
2.2 模型訓練
本文數據處理的計算機語言為python3.6（Centrum Wiskunde & Informatica，荷蘭），使用軟件機器學習庫sklearn（Institut national de recherche en informatique et en automatique，法國）對數據進行預處理。所有的計算均在臺式機上進行，配備圖形處理器GPU GTX 1650（NVIDIA，美國），8 GB 內存和Windows 10（Microsoft，美國）操作系統。
試驗采用監督學習的方式對IPSO-GRU進行訓練，基于前述試驗提取數據建立樣本庫，對網絡進行訓練，本文訓練集、驗證集和測試集按照8∶1∶1的比例隨機劃分。網絡中加入驗證集，驗證集用來在每個epoch之后計算在驗證集上的分類預測準確度，提升模型泛化能力。為加快模型收斂，在輸入數據之前，需要將原始數據無量綱化。無量綱化公式如式（11）所示：
|
式（11）中，x為同一時刻粒子位置，max(x)、min(x)分別為同一時刻粒子最大位置和最小位置，為無量綱化后粒子位置。
3 算法及實驗驗證
為驗證算法的準確率和有效性，將按以下流程對算法進行分析研究：① 對未優化算法預測準確率進行對比分析；② 對IPSO優化后的各算法性能進行對比分析；③ 討論分析受試者個體差異對本應用算法方法的影響。
3.1 未優化算法對比分析
步態過程中IMU震動幅度、人體姿態變化大，預測較難；隨機選取A受試者大腿前側股直肌上IMU采集的Y軸步態加速度信號作為參考。引入RNN、LSTM、GRU算法；并用IPSO分別優化這三種算法進行對比；一組步態周期下各未經IPSO優化算法預測與實測對比如圖5所示。
圖5
每種未經IPSO優化算法預測和實際對比圖
Figure5.
Comparison of actual and predicted graphs for each algorithm without IPSO optimization
如圖5所示， RNN算法真實值與預測值相差較大，LSTM表現優于RNN，而GRU在三種算法中真實值和預測值最接近。
為深入分析預測模型性能，針對預測回歸類模型本文使用MSE、RMSE、平均絕對誤差（mean absolute error，MAE）、相對誤差（mean absolute percentage error，MAPE）等進行測量，公式如式（12）～（15）所示：
|
|
|
|
真實值集合Y = {, yi, , yn)，預測值集合 ，MAPE反映模型預測值結果的好壞，MSE和RMSE表示預測值與真值間的偏差程度，可反應模型的泛化能力。做非線性擬合時，MAPE?RMSE越小代表預測結果越精準越穩定。若比較不同量綱下模型好壞，則需要另一個評價指標：R2值。R2值和1越接近，表明模型預測越精確。R2值計算如式（16）所示：
|
3.2 優化算法對比分析
A受試者大腿前側股直肌上IMU采集的Y軸步態加速度信號，在一組步態周期下經過IPSO優化的各算法預測、實際與未經優化的算法對比如圖6所示。
圖6
經過IPSO優化算法實際和預測對比圖
Figure6.
Comparison of actual and predicted graphs of each algorithm after IPSO optimization
如圖6所示，三種算法中，IPSO-GRU、IPSO優化LSTM算法（IPSO-LSTM）、IPSO優化RNN算法（IPSO-RNN），比未經過優化的各算法更貼近真實值。而經優化后的各算法由圖中無法直接觀測出哪種算法最優，所以引入MAPE、RMSE、MAE、R2值作為評判依據。A受試者的IMU數據輸入算法得出MAPE、RMSE、MAE、R2值如表1所示。
表1
多種算法評價指標
Table1.
Evaluation index of each algorithm
如表1所示，IPSO優化算法MAPE值比未經優化的算法值低10?2，RMSE、MAE值比未經優化的算法值低約10?1，證明IPSO優化算法預測值與真實值間的偏差程度縮小，而IPSO-GRU算法R2值達到0.997 85，在其中表現最優。
3.3 所有受試者數據試驗分析
為探究個體差異對本試驗方法的影響，將10名合格受試者IMU數據輸入GRU算法，得出其平均MAPE()、平均RMSE()、平均MAE()、平均R2值()如表2所示。
表2
GRU算法各項評價指標
Table2.
Evaluation indexes of GRU algorithm
如表2所示，GRU步態預測值為0.527 32，低于蹲起和屈伸動作的0.707 83和0.970 27，由于平地行走時IMU震動的幅度遠大于另外兩項運動，導致GRU算法的步態預測效果不理想，因此引入IPSO算法對其進行優化。IPSO-GRU算法對全部受試者合格數據各項平均指標如表3所示。
表3
IPSO-GRU算法各項評價指標
Table3.
Evaluation indexes of IPSO-GRU algorithm
由表2與表3對比發現，IPSO-GRU算法的平地行走值比GRU算法低10?2，蹲起與坐姿腿屈伸的、、值比GRU算法至少低10?1，表明IPSO-GRU算法預測值與真實值間的偏差程度較GRU算法相比更小，且值都可以達到0.966以上，相較于GRU算法的R2值最多提高0.438 86，證明IPSO-GRU算法可滿足個體差異帶來的影響。
4 結論與討論
針對人體下肢不同步態過程的個體差異和行走中步幅隨機性等問題，本文提出一種基于IPSO和GRU算法利用運動姿態信號進行步態識別與預測的方法。通過采集布置在大腿前側的股直肌和小腿后側腓腸肌上的IMU人體下肢不同運動姿態數據作為輸入，以下一階段姿態變化數據及準確率為輸出的網絡模型，進行步態的識別與預測分析。通過對比分析IPSO優化的RNN、LSTM、GRU網絡識別與預測情況，以驗證所建模型的有效性。結果顯示，經本研究優化后的算法可較好地預測人體的姿態變化，其中平地行走和蹲起動作的均方根誤差（RMSE）可精確到10?3，坐姿腿屈伸的RMSE可精確到10?2，各種動作的R2值均可達0.966以上。上述研究表明：IPSO-GRU算法可準確預測人體下肢的姿態變化，也可適應個體差異，達到了預期效果。
本研究中考慮到下肢外骨骼的穿戴特性，通過將兩個IMU布置于單條腿上的方式減少輸出數據的不確定性，從而提高預測的可靠性[16]。在此基礎上還可進行相應的數據挖掘研究半監督條件下的識別預測，用以降低進行訓練數據的維數，進一步提高識別判斷的實時性能。本研究中主要針對健康的年輕受試者開展研究，本方法同樣可用于如老年人和行走障礙患者等人群的步態識別與預測判斷。因此，本文所提的算法可應用于實現康復治療中人體步態運動評價和步態趨勢預測、假肢和下肢康復設備設計研究等領域，對于提高患者肢體功能、活動水平和生活獨立能力具有工程應用價值。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：高經緯主要負責實驗流程、數據記錄與分析、論文編寫以及算法程序設計；馬超負責項目主持、提供實驗指導，數據分析指導，論文審閱修訂；蘇鴻負責平臺搭建、算法程序設計、協調溝通；王少紅負責實驗設備采集、提供實驗指導，數據分析指導；徐小麗負責數據處理、算法驗證與論文審閱修訂；姚杰負責論文審閱修訂、協調溝通以及計劃安排。
倫理聲明：本研究通過了北京航空航天大學生物與醫學倫理委員會的審批(批文編號：BM20200153)。
