特征提取方法和分類器的選擇是心音分類中的兩個重要環節。為了充分捕捉心音信號中的病理性特征，研究中引入了一種結合梅爾頻率倒譜系數（MFCC）和功率譜密度（PSD）的特征提取方法。與目前常規分類器不同，研究中選擇了自適應模糊神經網絡（ANFIS）為分類器。在實驗設計方面，選取了不同時期、不同頻率范圍的PSD進行對比，選出分類效果最佳的特征，并采用均值PSD、標準差PSD、方差PSD和中位PSD四種不同的功率譜統計特性進行對比。通過實驗比較，心音收縮期100～300 Hz的中位PSD和MFCC組合特征有最好的效果，在準確率、精確率、靈敏度、特異度和F1得分上分別達到96.50%、99.27%、93.35%、99.60%和96.35%。結果顯示本研究所提算法對先心病輔助診斷具有較大幫助。
引用本文： 汪琴, 楊宏波, 潘家華, 田英杰, 郭濤, 王威廉. 基于時頻組合特征與自適應模糊神經網絡的心音分類算法. 生物醫學工程學雜志, 2023, 40(6): 1152-1159. doi: 10.7507/1001-5515.202301015 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
先天性心臟病（congenital heart disease，CHD）是威脅嬰幼兒生命的主要疾病之一[1]。到目前為止心臟聽診依然是CHD初診或篩查的主要方式[2]。
心音分析流程[3]一般分為三個步驟：預處理、特征提取、分類。預處理通常是對心音進行去噪以及分割。目前，已經提出了許多不同的心音分割方法，例如基于多尺度的希爾伯特包絡分割、特征幅度閾值分割和隱馬爾可夫模型（hidden Markov model，HMM）分割。Springer等[4]使用隱藏半馬爾可夫模型（hidden semi-Markov mode，HSMM）分割S1和S2聲音，取得了（95.63 ± 0.85）%的平均F1得分；Sedighian等[5]也使用相同的分割模型，分別在分割S1和S2聲音時實現了（92.4 ± 1.1）%和（93.5 ± 1.1）%的精度。特征提取是心音分析中的重要一步，特征提取的好壞決定了分類結果的準確率。Milani等[6]使用線性判別分析（linear discriminant analysis，LDA）分別對時域特征、頻域特征、時頻域組合特征進行降維，再將特征放入人工神經網絡（artificial neural network，ANN）中，分類準確率分別為90%、83.33%和93.33%。Xiang等[7]分別使用對數梅爾譜圖、對數功率譜圖、心音波形圖和希爾伯特包絡圖四種不同特征進行對比，分別得到95.0%、94.7%、88.3%、89.4%的精確度。Roy等[8]提取熵、能量方差和標準差等特征，使用自適應模糊神經網絡（adaptive neuro-fuzzy inference system，ANFIS）檢測心臟的病理狀態，獲得98.33%的準確度。Asmare等[9]使用梅爾頻譜系數（mel-frequency spectral coefficients，MFSC）分量作為特征，使用卷積神經網絡（convolutional neural network，CNN）分類，準確率達到96.10%。Al-Naami等[10]使用了離散傅里葉變換（discrete Fourier transform，DFT）第三個累積量的實分量的平均值、標準差、方差、熵和對數熵作為特征，輸入ANFIS，使用1 837個數據樣本，最高得到了89%的準確率。
文獻[4-5]顯示了HSMM模型在分割上有著良好的表現。文獻[7]驗證了信號時頻域包含更多的信號特征并能獲得更好的分類效果，但是將心音分類轉換為圖像分類增加了計算復雜度，網絡運行較慢。文獻[8]信號共94例，測試集只有23例，樣本量過少，算法的魯棒性和穩定性有待商榷。文獻[9]中分類準確率較高，但是只有170例受試者，樣本數量不足。文獻[10]使用了五個特征輸入ANFIS，最終準確率為89％，準確率較低。
基于以上情況，本研究提出一種基于時頻組合特征和ANFIS的心音分類方法，并在大規模且正負樣本均衡的的數據集上進行驗證，以期為心臟疾病的早期診斷提供更為準確和可靠的工具。
1 算法模型與方法
1.1 數據來源與說明
本文使用心音信號來自昆明醫科大學附屬心血管病醫院與云南大學實驗室聯合采集的心音數據庫。每位被采集志愿者/監護人均簽署知情同意書。庫中數據都已通過云南大學人體研究材料倫理委員會和昆明醫科大學附屬心血管病醫院倫理委員會的審查與批準使用。庫中數據標簽均來自超聲心動圖確診結果。
本文共使用了1 000位志愿者的心音數據，每個人包含五條心音數據，分別來自五個采集點位，共5 000例數據，每條數據采集時間為20 s，采樣頻率為5 000 Hz。其中正常心音2 500例，異常心音2 500例。本研究為二分類，正常與異常的心音信號數量相等。異常心音主要包含了房間隔缺損（atrial septal defect，ASD）、室間隔缺損（ventricular septal defect，VSD）和動脈導管未閉（patent ductus arteriosus，PDA）等常見的異常心音類型。相對于其他的實驗，本實驗正負樣本數量均衡，且大部分信號采集自嬰幼兒和未成年志愿者，本數據集對先心病早期篩查的針對性強，樣本分布合理，保證了算法具有較強的魯棒性。
1.2 算法模型與流程
一個心動周期分為S1、收縮期、S2、舒張期，常見的CHD在收縮期有不同的病理性雜音。臨床上，ASD在收縮期有一種類似吹風的雜音；PDA在收縮期有持續存在的機械性雜音，聲音高亢；VSD有4～5級的收縮期雜音，向心前區傳導，伴收縮期細震顫[11]。因此，本實驗對收縮期心音信號做特征提取。完整算法模型框圖見附件1，具體步驟如下：① 標注心音數據集，將數據集分為訓練集、驗證集和測試集。② 利用小波變換對信號進行去噪，隨后對信號下采樣至1 000 Hz，以降低計算復雜度。③ 使用HSMM模型對心音圖（phonocardiogram，PCG）信號進行分割，提取S1、收縮期、S2、舒張期。④ 對收縮期信號提取頻率在100～300 Hz之間的中位PSD和MFCC。⑤ 將兩種特征輸入模糊神經網絡進行訓練和分類，得到算法模型。⑥ 對訓練出的模型進行性能評估。
1.3 信號預處理
為了降低噪聲對心音分割的影響，本文使用小波去噪去除高頻噪音。正常心音（S1和S2）主要集中在50～100 Hz頻段，而異常心音頻率往往具有較高的頻率特性[12]。經過實驗對比，選用db10小波函數進行5層分解，選擇軟閾值作為降噪閾值，最終有效去除了雜音并保留了病理性噪聲。
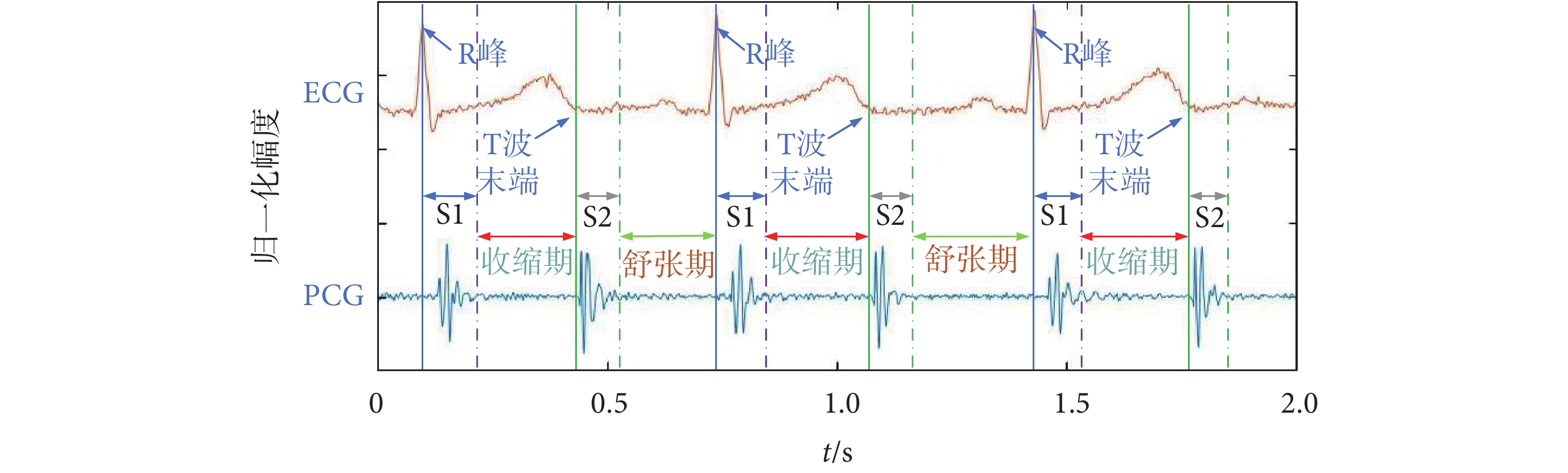
使用HSMM模型對PCG信號進行分割[13]。首先選用心音心電同步采集的信號，對R峰和T波進行位置標注，如圖1所示。
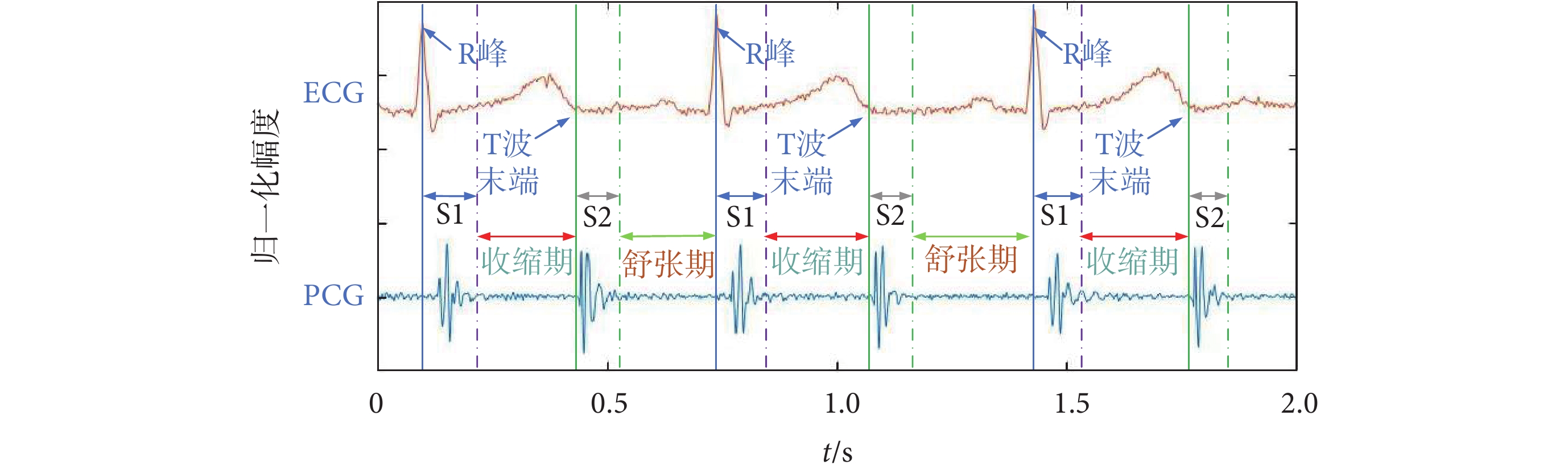圖1
標記R峰與T波末端作為S1和S2起始點參考
Figure1.
Identification of R peak and end of T wave for S1 and S2 initiation
為了評估模型分割信號的能力，使用同步采集的PCG和心電圖（electrocardiograph，ECG）的標簽，評估模型在數據集上準確定位S1、收縮期、S2、舒張期的能力。以ECG的R峰和T波為參考位置，公差為50 ms，經過驗證分割準確率可達91.5%。心音-心電圖評估模型分割圖見附件2。
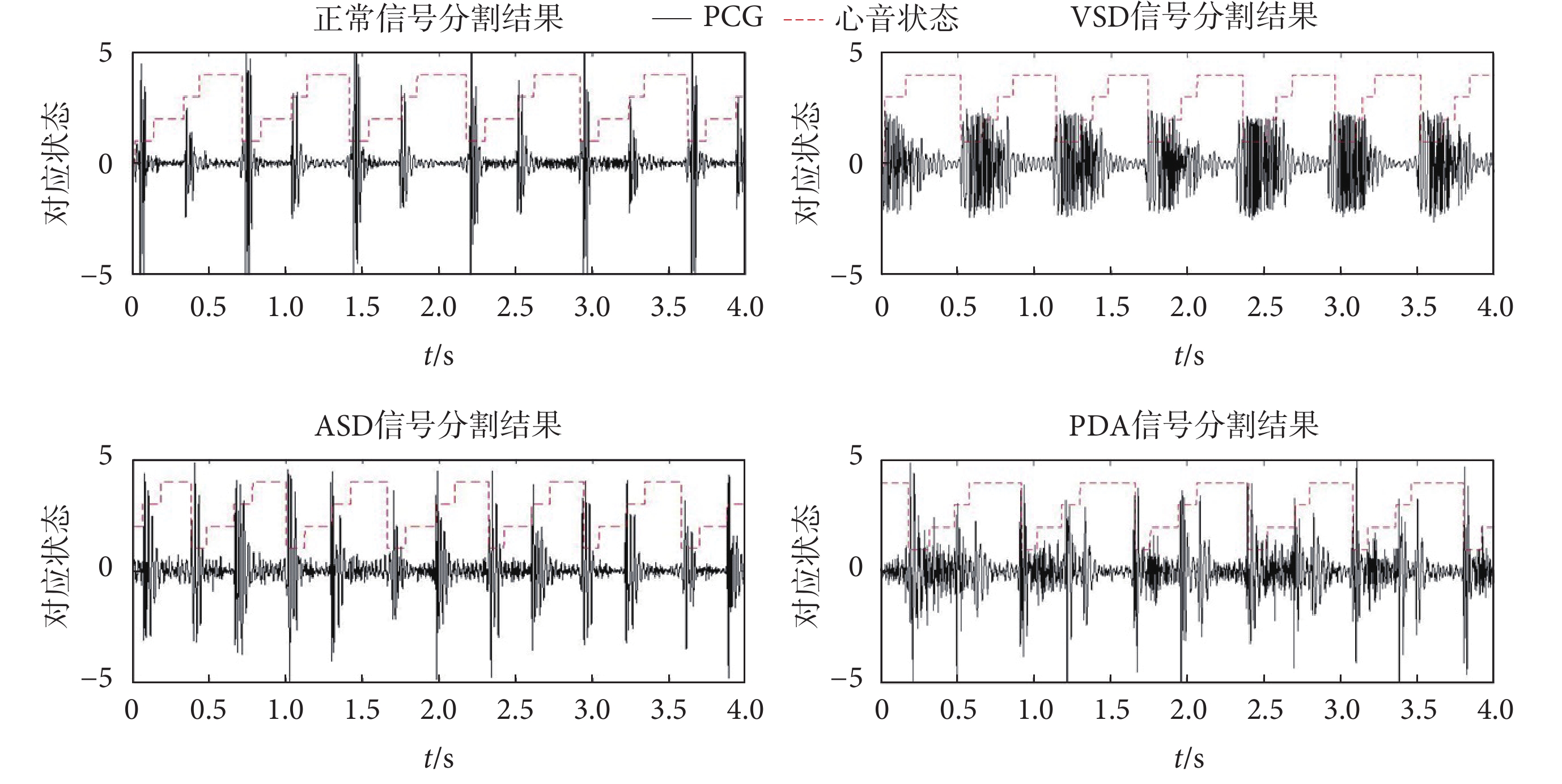
本文參考基于持續時間HMM的分割方法[13]，將每個心動周期四個組成部分的每一個持續時間作為特征，建立每個狀態持續時間的高斯混合模型，提供HSMM所需要的參數。建立HSMM模型，對模型進行訓練，通過估計每種狀態時間的概率密度來估計每個心音狀態的持續時間。使用擴展的維特比算法來解碼最優狀態序列，提高了收縮期雜音掩蓋S2時的分割效果，再提取收縮期信號。對于不同類型信號的分割結果如圖2所示。
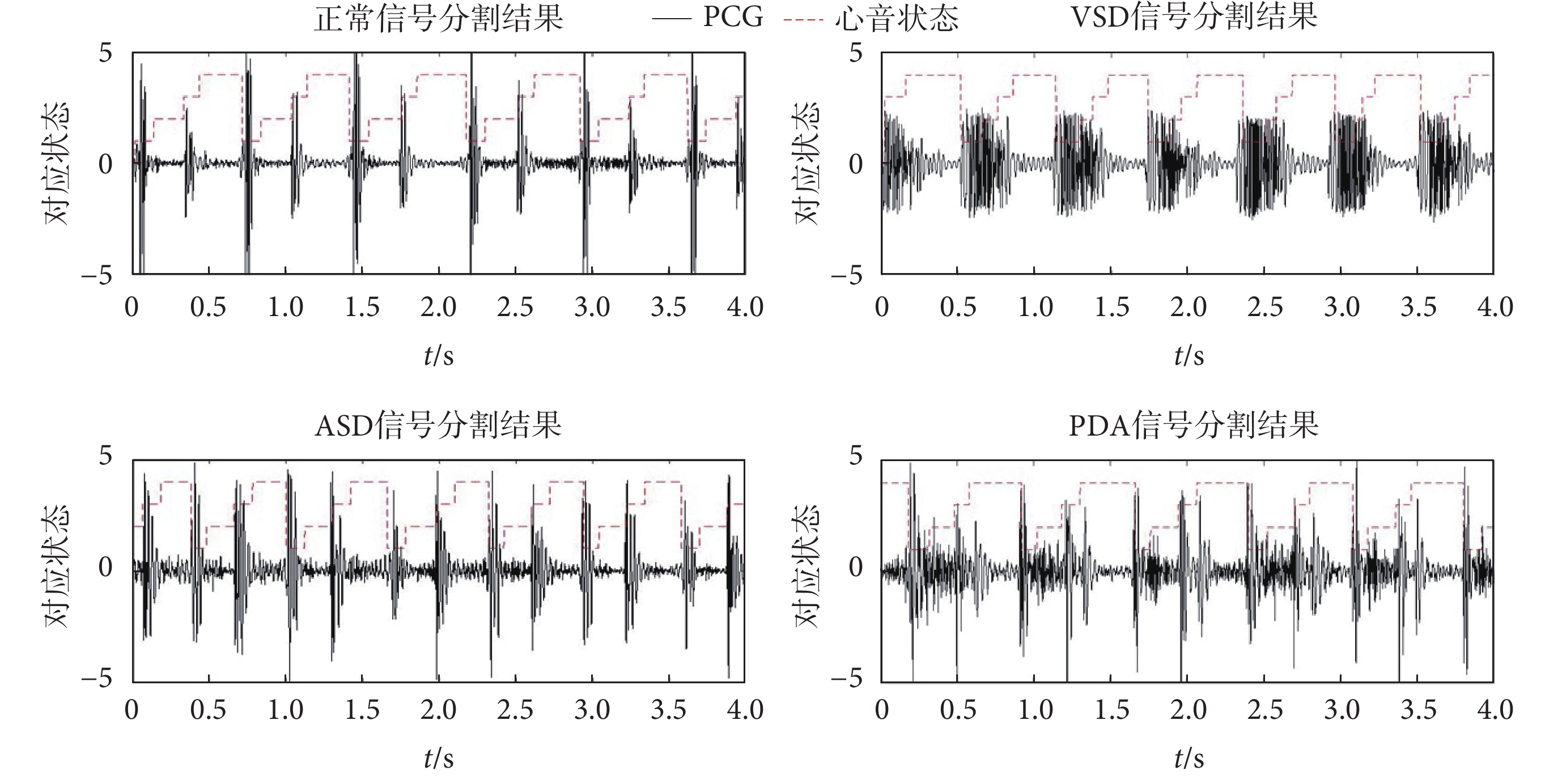圖2
各類信號分割結果
Figure2.
Segmentation results of various signals
1.4 特征提取
僅依靠時域信號可能較難洞察到信號的全部特性[14]，相比之下，時頻分析能夠在時間和頻率兩個維度上展現信號，因此能揭示更多的信號信息。MFCC是語音信號處理中一種常見的特征提取方式，是從低頻到高頻范圍內，設置一組從密集到稀疏的帶通濾波器對信號進行濾波，通過模仿人耳聽覺生理特征提取聲音特征[15]。PSD能準確反映信號功率分布和頻譜分布的相互關系,可以反映心音信號的輸出信號功率在頻域各個點上的功率分布情況[16-17]。基于以上原因，本文選擇MFCC和PSD作為特征。其特征提取流程圖見附件3。
1.4.1 提取MFCC特征
MFCC提取過程包含對心音信號的預處理和特征提取，首先對信號進行預加重，使信號頻譜變得平坦。由于漢明窗能夠減少旁瓣泄露，相比矩形窗等更適合心音信號的分幀，所以本次實驗中使用漢明窗作為窗函數。在每一幀信號乘上旁瓣衰減較大的漢明窗后，通過快速傅里葉變換（fast Fourier transform，FFT）得到心音信號的頻譜能量分布，通過能量分布來觀察信號特性。隨后將能量譜通過一組三角帶通濾波器，得到Mel頻率。最后經過離散余弦變換（discrete cosine transform，DCT）分離基音信號與聲道信號，提取基音信息，得到MFCC特征[18]。
1.4.2 提取中位PSD特征
心臟信號的頻域分析能夠顯示在一個頻率范圍內信號的能量是如何變化的，不同的能量分布代表了不同的心音特性。FFT [19]是一種分析音頻信號頻譜的常用方法，表達式如式(1)所示。
 |
式(1)中的頻譜信息不能識別不同頻率隨時間的變化情況，因此，通過應用50%重疊的漢明窗，使用短時傅里葉變換進行時頻分析，如式(2)所示。
 |
PSD是信號在頻域內的功率分布，顯示了在不同頻率范圍內的能量分布，對進一步的心音分析有一定價值。將信號分成重疊的窗口，并計算每個窗口的PSD，這些PSD提供了各個窗口的頻域信息。
設x為輸入信號，r(x)為輸入信號的自相關：
 |
信號的PSD被視為信號自相關函數的傅里葉變換，并記為:
 |
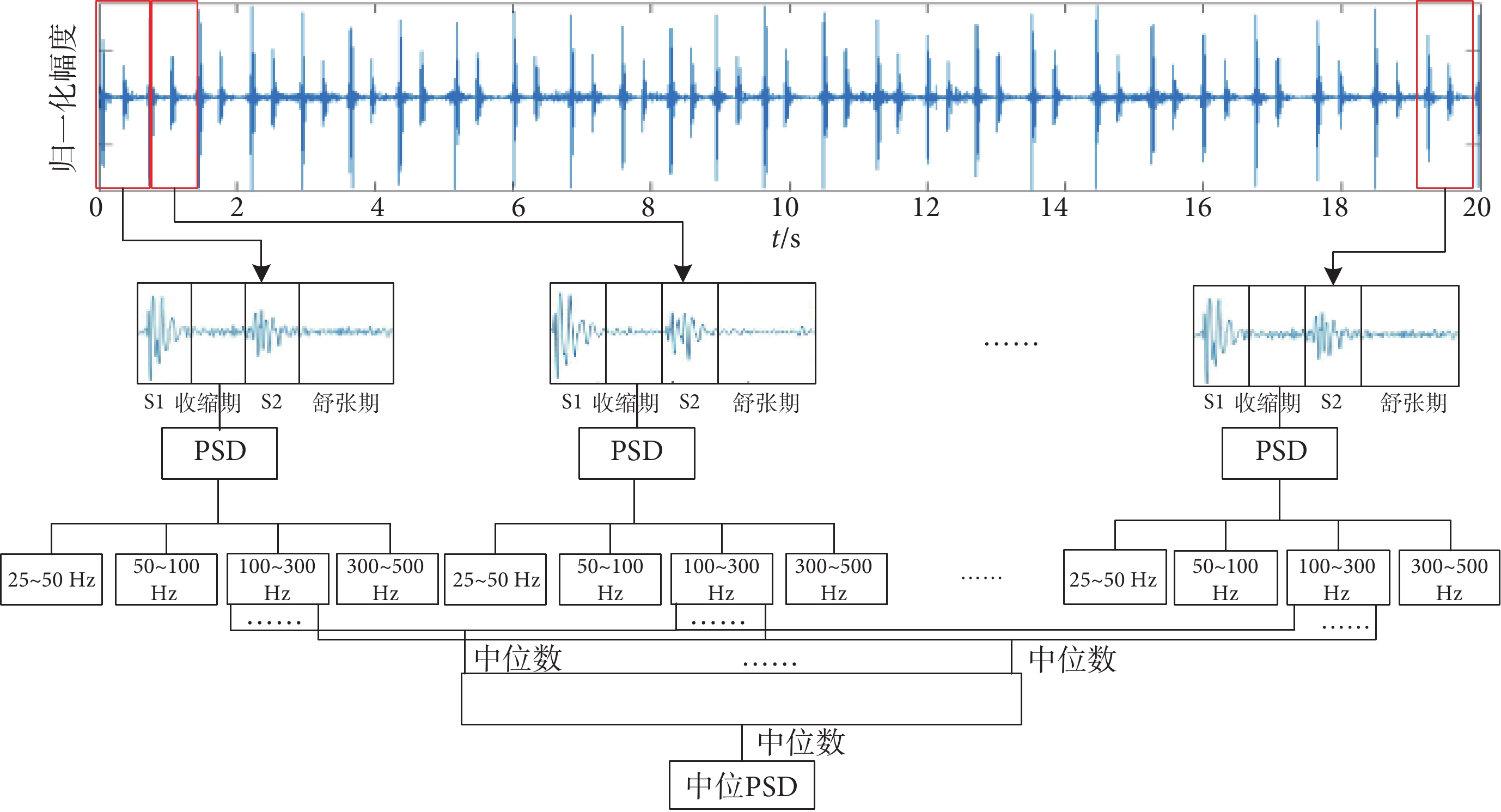
在提取心音特征時，對心音信號中每個心動周期的每個間期都提取了不同頻段的功率譜特征。本文將每個心動周期分割為S1、收縮期、S2、舒張期四個階段，隨后計算心音不同間期的PSD，再將所求的PSD分成25～50、50～100、100～300、300～500 Hz四個頻率段，計算不同頻段的均值PSD、方差PSD、標準差PSD和中位PSD。其中100～300 Hz中位PSD特征提取流程圖如圖3所示。一條心音信號時長為20 s，可分為22～35個心動周期，則一條心音信號可算出22～35個收縮期PSD，將每個收縮期相同位置的PSD進行排序，選擇中位數，將得出的中位數再進行排序提取最后的PSD中位數。
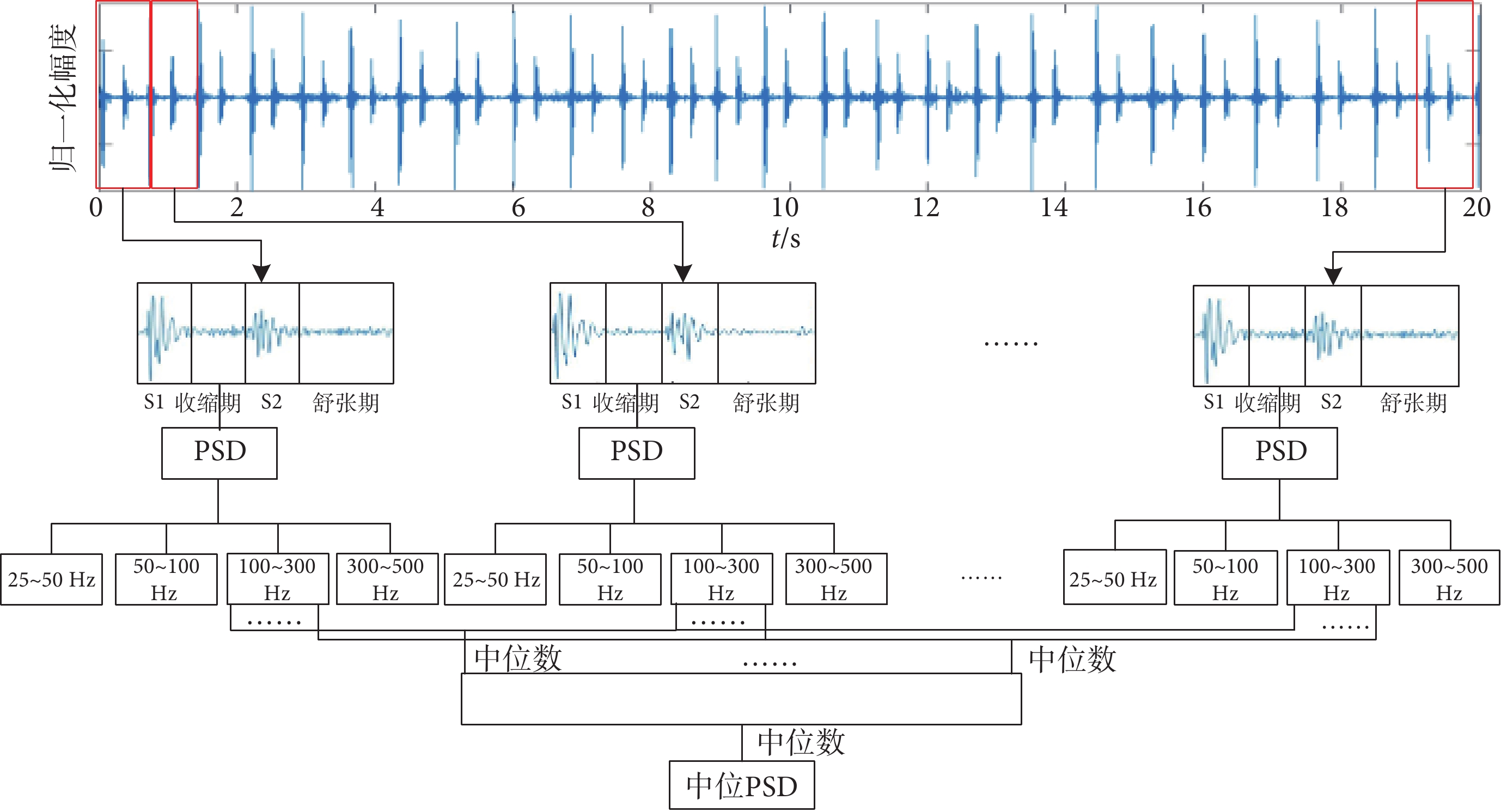圖3
中位功率譜密度特征提取流程圖
Figure3.
Extraction process for median power spectral density features
1.5 模糊神經網絡
ANFIS由自適應網絡和模糊推理系統組合而成[20]，擁有模糊推理系統可解釋性的特點和自適應網絡通過反向傳播學習的能力，可以根據先驗知識調整系統參數，使最終的輸出更契合真實情況。它集合了模糊控制理論和神經網絡的優點，在很多實際應用場景中，既保留了模糊控制對非精確性知識的經驗性表達，又擁有神經網絡自適應性學習權重參數的能力，二者相輔相成，具有學習、自適應、模糊和識別等功能[21-22]，能夠適應性地學習數據集的模糊性和非線性。心音信號的分類問題是一個典型的非線性問題，心音信號存在著大量的變異性和復雜性，包括來自于不同個體的生理差異、不同心臟病的病理差異等。ANFIS通過模糊化處理可以更好地處理這些變異性和復雜性。綜上，本文選擇了ANFIS作為分類器。
模糊神經網絡分類器利用訓練過程中提供的特征空間關系生成if-then規則，即模糊神經網絡的推理判斷規則。一般自適應模糊神經網絡的規則用偽代碼表述如下：
If x is A1 and y is B1，then f1 = p1x + q1y + r1
If x is A2 and y is B2，then f2 = p2x + q2y + r2
其中，
和
為輸入，
、
、
、
為模糊集合，
、
、
、
、
、
是線性設計參數，其中的線性設計參數具有自適應。
一般自適應模糊神經網絡共五層，見附件4。第一層為模糊層，將心音信號提出的特征分量
直接輸入到模糊層進行計算，其輸出為：
 |
式（5）中，
是信號的第
個特征分量，
代表一系列模糊集合，每一個集合在該節點都與一個語言變量的程度相關聯。這個程度可能是如“高”、“中”或“低”等描述。
是
屬于集合
的隸屬度，描述了
屬于
的程度。
常見的隸屬函數
有高斯型隸屬函數(Gaussmf)、廣義鐘型隸屬函數(Gbellmf)、S型隸屬函數(Sigmf)等。本文選擇的是Gaussmf，其公式如式(6)所示:
 |
其中x為輸入被模糊參數，
為正態分布的標準偏差，c為正態分布的均值，
、c是參數集。本文輸入MFCC和PSD作為特征，對兩種特征進行模糊化，得到每個特征在[0,1]的隸屬度。
第二層為規則層，將第一層輸出信號相乘來計算每個規則的觸發強度，即每個特征在每個規則上的觸發概率。
 |
第三層為歸一化層，對前一層的輸出數據進行歸一化，得到每個特征在此條規則上的觸發比重，其公式如式(8)所示。
 |
第四層為清晰化層，此層計算每條規則結果的加權平均數[23]，其公式如式(9)所示。
 |
第i條規則的輸出一般為一個一階多項式：
 |
其中，
和
是參數集，為規則Then的部分參數。
第五層對結果按照求和的方式進行降維，得到單個特征在每一個規則上的總和。
 |
本文的ANFIS的訓練參數見附件5，選擇2個特征作為輸入，隸屬函數的數量為3，形成的規則為9。如果增加隸屬函數的數量，相應地就會產生更多的規則，但是隨著規則增多，計算的復雜度增高，會花費更多時間來訓練模型，可能會導致內存耗盡。經過測試，增加隸屬函數數量并沒有增加分類精度，反而增加了網絡運算時間，因此本文采用了3個隸屬函數。本文網絡結構如圖4所示。
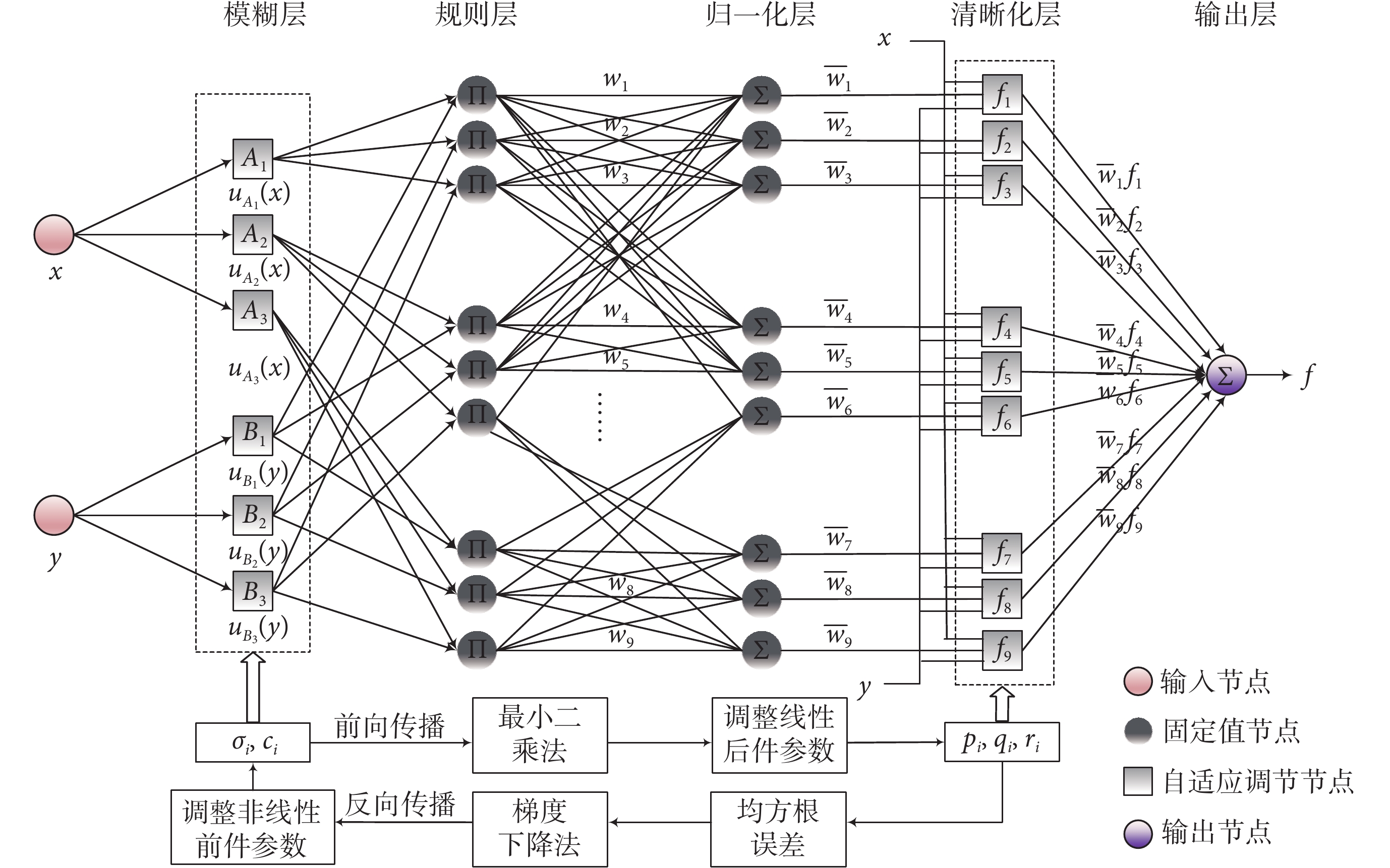圖4
網絡結構
Figure4.
Network structure
在本文的自適應模糊神經網絡中，第一層模糊層中的條件參數集{
、c}和第四層清晰化層中的結論參數集{
、
、
}是可調的，通過最小二乘法和梯度下降法混合學習進行訓練并確定。{
、c}通過反向傳播算法更新，結論參數通過最小二乘法更新求解。每一輪迭代流程中，先將輸入信號通過正向傳播至第四層，參數集{
、c}維持不變，{
、
、
}通過最小二乘法進行調節。信號繼續傳送至最后一層，得出預測結果值，將之與真實值進行對比，求出均方根誤差，通過梯度下降法進行反向傳播，調節第一層中的條件參數集。再通過前向傳播對第四層參數集進行最小二乘法估計，在反向傳播中對第一層的參數集進行更新。這種混合學習算法，可以大大減小搜索空間維數，提高參數收斂速度。
2 實驗設計
2.1 實驗環境
本文使用實驗環境硬件配置如下：深度學習框架為Tensorflow2.4.1（Google，美國），Python3.7（Python Software Foundation，美國），中央處理器（Ryzen 7 4800H with Radeon Graphics2.9GHz，AMD，美國），獨立顯卡（NVIDIA 2060 6GB，Nvidia，美國），內存（3 200 MHz，8Gx2，Micron，美國）。
2.2 評估指標
為了評估本文算法的性能，本次實驗共使用了五種評估指標，其中準確率（accuracy，Acc）、靈敏度（sensitivity，Se）、特異度（specificity，Sp）三種評估指標計算公式如式(12)～(14)所示：
 |
 |
 |
其中，TP表示真陽性，TN表示真陰性，FN表示假陰性，FP表示假陽性。
在本研究中，針對CHD的診斷，我們更注重降低假陰性率，以防止漏診可能導致的嚴重后果，因為相較于假陽性，假陰性會使患者失去及時治療的機會，對健康造成更嚴重的影響。因此，使用了F1分數作為衡量模型的指標，F1分數結合了精確率（precision，Pr）和召回率（recall，Re）[24]，其計算公式如式(17)所示。
 |
 |
 |
2.3 實驗設計與結果分析
在本研究中，選取5 000例PCG信號作為實驗數據，采用隨機抽樣方法將這些數據劃分成訓練集、驗證集和測試集。3 200例（64%）被分配到訓練集用于模型學習；800例（16%）分配到驗證集用于模型調參和驗證；剩下的1 000例（20%）作為測試集，用于最終的模型性能評估。所有數據在劃分前都經過了標準的預處理步驟，包括去噪和歸一化。并且，本實驗避免來自同一患者的數據被分到不同子集中，以防止數據泄露，確保實驗的有效性和結果的可靠性。
首先，為了對收縮期單一MFCC特征與MFCC的組合特征，也即MFCC與最佳PSD特征（100～300 Hz的中位PSD特征）進行區別，實驗一分別將這兩個特征放入網絡中訓練。隨后，其他條件不變，實驗二僅修改心音不同間期，尋找出包含更多病理性特征的心音間期。實驗三保持其他條件不變，修改PSD的頻率范圍，驗證不同頻率范圍的分類效果。實驗四選擇均值、標準差、方差、中位數四種不同統計參數的PSD進行對比，選取最優的PSD。實驗五特征不變，改變了ANFIS的隸屬函數，以期選擇出效果最好的隸屬函數。
2.3.1 實驗一：單一MFCC特征與MFCC結合PSD特征組合對比
在此次實驗中，在心音狀態和網絡等不變的情況下，主要對比僅使用MFCC與中位PSD結合MFCC組合特征的分類效果。由表1可見，組合特征分類效果更佳。
表1
不同時期頻率以及統計參數條件下的心音分類效果
Table1.
Heart sound classification outcomes under varying period frequencies and statistical parameters
2.3.2 實驗二：心音不同間期特征對比
在第一個實驗中，確定了MFCC和PSD特征效果比單個MFCC特征更好，本實驗研究在不同心音狀態對分類結果的影響，這個實驗可以找到最好心音狀態。由表1可見，收縮期的F1得分最高。
2.3.3 實驗三：不同頻率范圍PSD的分類效果對比
在此實驗中，選用了信號的收縮期MFCC和收縮期PSD，由于心音信號中不同頻率范圍包含了不同的病理性信號特征，因此選用四個頻率范圍的中位PSD作為對比。
由表1可知，在25～50 Hz的頻率范圍內，具有一定的病理性雜音，分類準確率在90%左右，在300～500 Hz頻率范圍內，分類效果與100～300 Hz頻率范圍相差不多。然而，經過詳細對比分析顯示，100～300 Hz頻率段的PSD中Acc、Pr、Sp、F1均比300～500 Hz高，具有較好的結果，由此可知在100～300 Hz頻率段更能找到心音信號中具有代表性的病理性特征。
2.3.4 實驗四：不同統計參數分類效果對比
實驗采用了均值PSD（Mean_PSD）、標準差PSD（Std_PSD）、方差PSD（Var_PSD）、中位PSD（Median_PSD）四種不同統計參數的PSD進行對比，以確定最佳統計參數。結果顯示，相比其他統計參數的PSD，中位PSD的F1值更高。
2.3.5 實驗五：不同隸屬函數分類對比
在這個階段中，選用了收縮期MFCC和100～300 Hz的中位PSD作為特征，輸入自適應模糊神經網絡中，根據1.5節所提出的Gsussmf、Gbellmf和Sigmf三種常見的隸屬函數對網絡進行訓練，得出最終的分類結果。可以看出Gsussmf的F1得分最高（見表2）。
表2
不同隸屬函數的ANFIS
Table2.
ANFIS with different membership functions
以上實驗結果表明，基于收縮期的MFCC和100～300 Hz的中位PSD組合特征有著更優的效果，并且證明了病理性雜音主要集中于收縮期和100～300 Hz頻率范圍內，提示此間期和頻率范圍對分類有著更大的幫助。
為了更直觀地顯示信號分類過程和分類效果，取出測試集中一例CHD疾病的心音信號，簡述其分類過程。此信號為PDA患者，男性，4歲，M點位。首先，使用小波去噪去除心音中多余的噪聲，對信號進行下采樣至1 000 Hz后，對信號進行分割，獲得了27個收縮期時期心音信號，提取收縮期信號的MFCC，同時計算出收縮期的中位PSD，將兩個特征輸入到ANFIS中，得出分類的異常概率為71%，判斷為異常。
3 結論
本文提出了一種將收縮期MFCC與中位PSD作為特征，使用ANFIS作為分類器的心音分類方法。首先對原始心音進行小波去噪，并將信號下采樣至1 000 Hz，使用HSMM模型分割信號，提取收縮期信號。然后對信號分幀加窗，提取MFCC特征，同時計算每一幀100～300 Hz內的中位PSD，將MFCC和PSD進行拼接。接著將特征輸入ANFIS，使用高斯函數作為隸屬函數對兩種特征模糊化，得到其對應隸屬度，將特征與隸屬度相乘，得到觸發強度，隨后經過歸一化得到觸發概率，最后去模糊化，對單個規則上的結果加權求和，得到二分類結果。本文選擇了五種評價指標，在測試集上的準確率達到了96.50%，綜合評價指標F1達到96.35%，與其他幾種方案相比性能最佳。實驗結果驗證了相對于其他時期，在收縮期內先心病病理性雜音的時頻特征具有更高的辨識度，同時，病理性雜音集中在100～300 Hz頻率范圍內。本研究顯示根據不同心音狀態、不同頻率的特征識別具有重要意義，這為先心病篩查提供了一種可行的思路。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻說明：汪琴負責實驗構思與設計、數據采集、數據分析和論文寫作；楊宏波負責醫學指導和數據收集；潘家華負責醫學指導和數據審查；田英杰負責實驗指導、論文寫作指導和數據收集；郭濤負責醫學指導；王威廉負責理論指導、實驗設計指導、論文整體審查和寫作指導。
倫理聲明：本文所使用的心音數據得到云南大學人體研究材料倫理委員會以及云南省阜外心血管病醫院倫理委員會批準采集并授權使用（CHSRE2021008，IRB2020-BG-028）。
本文附件見本刊網站的電子版本（biomedeng.cn）。
0 引言
先天性心臟病（congenital heart disease，CHD）是威脅嬰幼兒生命的主要疾病之一[1]。到目前為止心臟聽診依然是CHD初診或篩查的主要方式[2]。
心音分析流程[3]一般分為三個步驟：預處理、特征提取、分類。預處理通常是對心音進行去噪以及分割。目前，已經提出了許多不同的心音分割方法，例如基于多尺度的希爾伯特包絡分割、特征幅度閾值分割和隱馬爾可夫模型（hidden Markov model，HMM）分割。Springer等[4]使用隱藏半馬爾可夫模型（hidden semi-Markov mode，HSMM）分割S1和S2聲音，取得了（95.63 ± 0.85）%的平均F1得分；Sedighian等[5]也使用相同的分割模型，分別在分割S1和S2聲音時實現了（92.4 ± 1.1）%和（93.5 ± 1.1）%的精度。特征提取是心音分析中的重要一步，特征提取的好壞決定了分類結果的準確率。Milani等[6]使用線性判別分析（linear discriminant analysis，LDA）分別對時域特征、頻域特征、時頻域組合特征進行降維，再將特征放入人工神經網絡（artificial neural network，ANN）中，分類準確率分別為90%、83.33%和93.33%。Xiang等[7]分別使用對數梅爾譜圖、對數功率譜圖、心音波形圖和希爾伯特包絡圖四種不同特征進行對比，分別得到95.0%、94.7%、88.3%、89.4%的精確度。Roy等[8]提取熵、能量方差和標準差等特征，使用自適應模糊神經網絡（adaptive neuro-fuzzy inference system，ANFIS）檢測心臟的病理狀態，獲得98.33%的準確度。Asmare等[9]使用梅爾頻譜系數（mel-frequency spectral coefficients，MFSC）分量作為特征，使用卷積神經網絡（convolutional neural network，CNN）分類，準確率達到96.10%。Al-Naami等[10]使用了離散傅里葉變換（discrete Fourier transform，DFT）第三個累積量的實分量的平均值、標準差、方差、熵和對數熵作為特征，輸入ANFIS，使用1 837個數據樣本，最高得到了89%的準確率。
文獻[4-5]顯示了HSMM模型在分割上有著良好的表現。文獻[7]驗證了信號時頻域包含更多的信號特征并能獲得更好的分類效果，但是將心音分類轉換為圖像分類增加了計算復雜度，網絡運行較慢。文獻[8]信號共94例，測試集只有23例，樣本量過少，算法的魯棒性和穩定性有待商榷。文獻[9]中分類準確率較高，但是只有170例受試者，樣本數量不足。文獻[10]使用了五個特征輸入ANFIS，最終準確率為89％，準確率較低。
基于以上情況，本研究提出一種基于時頻組合特征和ANFIS的心音分類方法，并在大規模且正負樣本均衡的的數據集上進行驗證，以期為心臟疾病的早期診斷提供更為準確和可靠的工具。
1 算法模型與方法
1.1 數據來源與說明
本文使用心音信號來自昆明醫科大學附屬心血管病醫院與云南大學實驗室聯合采集的心音數據庫。每位被采集志愿者/監護人均簽署知情同意書。庫中數據都已通過云南大學人體研究材料倫理委員會和昆明醫科大學附屬心血管病醫院倫理委員會的審查與批準使用。庫中數據標簽均來自超聲心動圖確診結果。
本文共使用了1 000位志愿者的心音數據，每個人包含五條心音數據，分別來自五個采集點位，共5 000例數據，每條數據采集時間為20 s，采樣頻率為5 000 Hz。其中正常心音2 500例，異常心音2 500例。本研究為二分類，正常與異常的心音信號數量相等。異常心音主要包含了房間隔缺損（atrial septal defect，ASD）、室間隔缺損（ventricular septal defect，VSD）和動脈導管未閉（patent ductus arteriosus，PDA）等常見的異常心音類型。相對于其他的實驗，本實驗正負樣本數量均衡，且大部分信號采集自嬰幼兒和未成年志愿者，本數據集對先心病早期篩查的針對性強，樣本分布合理，保證了算法具有較強的魯棒性。
1.2 算法模型與流程
一個心動周期分為S1、收縮期、S2、舒張期，常見的CHD在收縮期有不同的病理性雜音。臨床上，ASD在收縮期有一種類似吹風的雜音；PDA在收縮期有持續存在的機械性雜音，聲音高亢；VSD有4～5級的收縮期雜音，向心前區傳導，伴收縮期細震顫[11]。因此，本實驗對收縮期心音信號做特征提取。完整算法模型框圖見附件1，具體步驟如下：① 標注心音數據集，將數據集分為訓練集、驗證集和測試集。② 利用小波變換對信號進行去噪，隨后對信號下采樣至1 000 Hz，以降低計算復雜度。③ 使用HSMM模型對心音圖（phonocardiogram，PCG）信號進行分割，提取S1、收縮期、S2、舒張期。④ 對收縮期信號提取頻率在100～300 Hz之間的中位PSD和MFCC。⑤ 將兩種特征輸入模糊神經網絡進行訓練和分類，得到算法模型。⑥ 對訓練出的模型進行性能評估。
1.3 信號預處理
為了降低噪聲對心音分割的影響，本文使用小波去噪去除高頻噪音。正常心音（S1和S2）主要集中在50～100 Hz頻段，而異常心音頻率往往具有較高的頻率特性[12]。經過實驗對比，選用db10小波函數進行5層分解，選擇軟閾值作為降噪閾值，最終有效去除了雜音并保留了病理性噪聲。
使用HSMM模型對PCG信號進行分割[13]。首先選用心音心電同步采集的信號，對R峰和T波進行位置標注，如圖1所示。
圖1
標記R峰與T波末端作為S1和S2起始點參考
Figure1.
Identification of R peak and end of T wave for S1 and S2 initiation
為了評估模型分割信號的能力，使用同步采集的PCG和心電圖（electrocardiograph，ECG）的標簽，評估模型在數據集上準確定位S1、收縮期、S2、舒張期的能力。以ECG的R峰和T波為參考位置，公差為50 ms，經過驗證分割準確率可達91.5%。心音-心電圖評估模型分割圖見附件2。
本文參考基于持續時間HMM的分割方法[13]，將每個心動周期四個組成部分的每一個持續時間作為特征，建立每個狀態持續時間的高斯混合模型，提供HSMM所需要的參數。建立HSMM模型，對模型進行訓練，通過估計每種狀態時間的概率密度來估計每個心音狀態的持續時間。使用擴展的維特比算法來解碼最優狀態序列，提高了收縮期雜音掩蓋S2時的分割效果，再提取收縮期信號。對于不同類型信號的分割結果如圖2所示。
圖2
各類信號分割結果
Figure2.
Segmentation results of various signals
1.4 特征提取
僅依靠時域信號可能較難洞察到信號的全部特性[14]，相比之下，時頻分析能夠在時間和頻率兩個維度上展現信號，因此能揭示更多的信號信息。MFCC是語音信號處理中一種常見的特征提取方式，是從低頻到高頻范圍內，設置一組從密集到稀疏的帶通濾波器對信號進行濾波，通過模仿人耳聽覺生理特征提取聲音特征[15]。PSD能準確反映信號功率分布和頻譜分布的相互關系,可以反映心音信號的輸出信號功率在頻域各個點上的功率分布情況[16-17]。基于以上原因，本文選擇MFCC和PSD作為特征。其特征提取流程圖見附件3。
1.4.1 提取MFCC特征
MFCC提取過程包含對心音信號的預處理和特征提取，首先對信號進行預加重，使信號頻譜變得平坦。由于漢明窗能夠減少旁瓣泄露，相比矩形窗等更適合心音信號的分幀，所以本次實驗中使用漢明窗作為窗函數。在每一幀信號乘上旁瓣衰減較大的漢明窗后，通過快速傅里葉變換（fast Fourier transform，FFT）得到心音信號的頻譜能量分布，通過能量分布來觀察信號特性。隨后將能量譜通過一組三角帶通濾波器，得到Mel頻率。最后經過離散余弦變換（discrete cosine transform，DCT）分離基音信號與聲道信號，提取基音信息，得到MFCC特征[18]。
1.4.2 提取中位PSD特征
心臟信號的頻域分析能夠顯示在一個頻率范圍內信號的能量是如何變化的，不同的能量分布代表了不同的心音特性。FFT [19]是一種分析音頻信號頻譜的常用方法，表達式如式(1)所示。
|
式(1)中的頻譜信息不能識別不同頻率隨時間的變化情況，因此，通過應用50%重疊的漢明窗，使用短時傅里葉變換進行時頻分析，如式(2)所示。
|
PSD是信號在頻域內的功率分布，顯示了在不同頻率范圍內的能量分布，對進一步的心音分析有一定價值。將信號分成重疊的窗口，并計算每個窗口的PSD，這些PSD提供了各個窗口的頻域信息。
設x為輸入信號，r(x)為輸入信號的自相關：
|
信號的PSD被視為信號自相關函數的傅里葉變換，并記為:
|
在提取心音特征時，對心音信號中每個心動周期的每個間期都提取了不同頻段的功率譜特征。本文將每個心動周期分割為S1、收縮期、S2、舒張期四個階段，隨后計算心音不同間期的PSD，再將所求的PSD分成25～50、50～100、100～300、300～500 Hz四個頻率段，計算不同頻段的均值PSD、方差PSD、標準差PSD和中位PSD。其中100～300 Hz中位PSD特征提取流程圖如圖3所示。一條心音信號時長為20 s，可分為22～35個心動周期，則一條心音信號可算出22～35個收縮期PSD，將每個收縮期相同位置的PSD進行排序，選擇中位數，將得出的中位數再進行排序提取最后的PSD中位數。
圖3
中位功率譜密度特征提取流程圖
Figure3.
Extraction process for median power spectral density features
1.5 模糊神經網絡
ANFIS由自適應網絡和模糊推理系統組合而成[20]，擁有模糊推理系統可解釋性的特點和自適應網絡通過反向傳播學習的能力，可以根據先驗知識調整系統參數，使最終的輸出更契合真實情況。它集合了模糊控制理論和神經網絡的優點，在很多實際應用場景中，既保留了模糊控制對非精確性知識的經驗性表達，又擁有神經網絡自適應性學習權重參數的能力，二者相輔相成，具有學習、自適應、模糊和識別等功能[21-22]，能夠適應性地學習數據集的模糊性和非線性。心音信號的分類問題是一個典型的非線性問題，心音信號存在著大量的變異性和復雜性，包括來自于不同個體的生理差異、不同心臟病的病理差異等。ANFIS通過模糊化處理可以更好地處理這些變異性和復雜性。綜上，本文選擇了ANFIS作為分類器。
模糊神經網絡分類器利用訓練過程中提供的特征空間關系生成if-then規則，即模糊神經網絡的推理判斷規則。一般自適應模糊神經網絡的規則用偽代碼表述如下：
If x is A1 and y is B1，then f1 = p1x + q1y + r1
If x is A2 and y is B2，then f2 = p2x + q2y + r2
其中，和為輸入，、、、為模糊集合，、、、、、是線性設計參數，其中的線性設計參數具有自適應。
一般自適應模糊神經網絡共五層，見附件4。第一層為模糊層，將心音信號提出的特征分量直接輸入到模糊層進行計算，其輸出為：
|
式（5）中，是信號的第個特征分量，代表一系列模糊集合，每一個集合在該節點都與一個語言變量的程度相關聯。這個程度可能是如“高”、“中”或“低”等描述。是屬于集合的隸屬度，描述了屬于的程度。
常見的隸屬函數有高斯型隸屬函數(Gaussmf)、廣義鐘型隸屬函數(Gbellmf)、S型隸屬函數(Sigmf)等。本文選擇的是Gaussmf，其公式如式(6)所示:
|
其中x為輸入被模糊參數，為正態分布的標準偏差，c為正態分布的均值，、c是參數集。本文輸入MFCC和PSD作為特征，對兩種特征進行模糊化，得到每個特征在[0,1]的隸屬度。
第二層為規則層，將第一層輸出信號相乘來計算每個規則的觸發強度，即每個特征在每個規則上的觸發概率。
|
第三層為歸一化層，對前一層的輸出數據進行歸一化，得到每個特征在此條規則上的觸發比重，其公式如式(8)所示。
|
第四層為清晰化層，此層計算每條規則結果的加權平均數[23]，其公式如式(9)所示。
|
第i條規則的輸出一般為一個一階多項式：
|
其中，和是參數集，為規則Then的部分參數。
第五層對結果按照求和的方式進行降維，得到單個特征在每一個規則上的總和。
|
本文的ANFIS的訓練參數見附件5，選擇2個特征作為輸入，隸屬函數的數量為3，形成的規則為9。如果增加隸屬函數的數量，相應地就會產生更多的規則，但是隨著規則增多，計算的復雜度增高，會花費更多時間來訓練模型，可能會導致內存耗盡。經過測試，增加隸屬函數數量并沒有增加分類精度，反而增加了網絡運算時間，因此本文采用了3個隸屬函數。本文網絡結構如圖4所示。
圖4
網絡結構
Figure4.
Network structure
在本文的自適應模糊神經網絡中，第一層模糊層中的條件參數集{、c}和第四層清晰化層中的結論參數集{、、}是可調的，通過最小二乘法和梯度下降法混合學習進行訓練并確定。{、c}通過反向傳播算法更新，結論參數通過最小二乘法更新求解。每一輪迭代流程中，先將輸入信號通過正向傳播至第四層，參數集{、c}維持不變，{、、}通過最小二乘法進行調節。信號繼續傳送至最后一層，得出預測結果值，將之與真實值進行對比，求出均方根誤差，通過梯度下降法進行反向傳播，調節第一層中的條件參數集。再通過前向傳播對第四層參數集進行最小二乘法估計，在反向傳播中對第一層的參數集進行更新。這種混合學習算法，可以大大減小搜索空間維數，提高參數收斂速度。
2 實驗設計
2.1 實驗環境
本文使用實驗環境硬件配置如下：深度學習框架為Tensorflow2.4.1（Google，美國），Python3.7（Python Software Foundation，美國），中央處理器（Ryzen 7 4800H with Radeon Graphics2.9GHz，AMD，美國），獨立顯卡（NVIDIA 2060 6GB，Nvidia，美國），內存（3 200 MHz，8Gx2，Micron，美國）。
2.2 評估指標
為了評估本文算法的性能，本次實驗共使用了五種評估指標，其中準確率（accuracy，Acc）、靈敏度（sensitivity，Se）、特異度（specificity，Sp）三種評估指標計算公式如式(12)～(14)所示：
|
|
|
其中，TP表示真陽性，TN表示真陰性，FN表示假陰性，FP表示假陽性。
在本研究中，針對CHD的診斷，我們更注重降低假陰性率，以防止漏診可能導致的嚴重后果，因為相較于假陽性，假陰性會使患者失去及時治療的機會，對健康造成更嚴重的影響。因此，使用了F1分數作為衡量模型的指標，F1分數結合了精確率（precision，Pr）和召回率（recall，Re）[24]，其計算公式如式(17)所示。
|
|
|
2.3 實驗設計與結果分析
在本研究中，選取5 000例PCG信號作為實驗數據，采用隨機抽樣方法將這些數據劃分成訓練集、驗證集和測試集。3 200例（64%）被分配到訓練集用于模型學習；800例（16%）分配到驗證集用于模型調參和驗證；剩下的1 000例（20%）作為測試集，用于最終的模型性能評估。所有數據在劃分前都經過了標準的預處理步驟，包括去噪和歸一化。并且，本實驗避免來自同一患者的數據被分到不同子集中，以防止數據泄露，確保實驗的有效性和結果的可靠性。
首先，為了對收縮期單一MFCC特征與MFCC的組合特征，也即MFCC與最佳PSD特征（100～300 Hz的中位PSD特征）進行區別，實驗一分別將這兩個特征放入網絡中訓練。隨后，其他條件不變，實驗二僅修改心音不同間期，尋找出包含更多病理性特征的心音間期。實驗三保持其他條件不變，修改PSD的頻率范圍，驗證不同頻率范圍的分類效果。實驗四選擇均值、標準差、方差、中位數四種不同統計參數的PSD進行對比，選取最優的PSD。實驗五特征不變，改變了ANFIS的隸屬函數，以期選擇出效果最好的隸屬函數。
2.3.1 實驗一：單一MFCC特征與MFCC結合PSD特征組合對比
在此次實驗中，在心音狀態和網絡等不變的情況下，主要對比僅使用MFCC與中位PSD結合MFCC組合特征的分類效果。由表1可見，組合特征分類效果更佳。
表1
不同時期頻率以及統計參數條件下的心音分類效果
Table1.
Heart sound classification outcomes under varying period frequencies and statistical parameters
2.3.2 實驗二：心音不同間期特征對比
在第一個實驗中，確定了MFCC和PSD特征效果比單個MFCC特征更好，本實驗研究在不同心音狀態對分類結果的影響，這個實驗可以找到最好心音狀態。由表1可見，收縮期的F1得分最高。
2.3.3 實驗三：不同頻率范圍PSD的分類效果對比
在此實驗中，選用了信號的收縮期MFCC和收縮期PSD，由于心音信號中不同頻率范圍包含了不同的病理性信號特征，因此選用四個頻率范圍的中位PSD作為對比。
由表1可知，在25～50 Hz的頻率范圍內，具有一定的病理性雜音，分類準確率在90%左右，在300～500 Hz頻率范圍內，分類效果與100～300 Hz頻率范圍相差不多。然而，經過詳細對比分析顯示，100～300 Hz頻率段的PSD中Acc、Pr、Sp、F1均比300～500 Hz高，具有較好的結果，由此可知在100～300 Hz頻率段更能找到心音信號中具有代表性的病理性特征。
2.3.4 實驗四：不同統計參數分類效果對比
實驗采用了均值PSD（Mean_PSD）、標準差PSD（Std_PSD）、方差PSD（Var_PSD）、中位PSD（Median_PSD）四種不同統計參數的PSD進行對比，以確定最佳統計參數。結果顯示，相比其他統計參數的PSD，中位PSD的F1值更高。
2.3.5 實驗五：不同隸屬函數分類對比
在這個階段中，選用了收縮期MFCC和100～300 Hz的中位PSD作為特征，輸入自適應模糊神經網絡中，根據1.5節所提出的Gsussmf、Gbellmf和Sigmf三種常見的隸屬函數對網絡進行訓練，得出最終的分類結果。可以看出Gsussmf的F1得分最高（見表2）。
表2
不同隸屬函數的ANFIS
Table2.
ANFIS with different membership functions
以上實驗結果表明，基于收縮期的MFCC和100～300 Hz的中位PSD組合特征有著更優的效果，并且證明了病理性雜音主要集中于收縮期和100～300 Hz頻率范圍內，提示此間期和頻率范圍對分類有著更大的幫助。
為了更直觀地顯示信號分類過程和分類效果，取出測試集中一例CHD疾病的心音信號，簡述其分類過程。此信號為PDA患者，男性，4歲，M點位。首先，使用小波去噪去除心音中多余的噪聲，對信號進行下采樣至1 000 Hz后，對信號進行分割，獲得了27個收縮期時期心音信號，提取收縮期信號的MFCC，同時計算出收縮期的中位PSD，將兩個特征輸入到ANFIS中，得出分類的異常概率為71%，判斷為異常。
3 結論
本文提出了一種將收縮期MFCC與中位PSD作為特征，使用ANFIS作為分類器的心音分類方法。首先對原始心音進行小波去噪，并將信號下采樣至1 000 Hz，使用HSMM模型分割信號，提取收縮期信號。然后對信號分幀加窗，提取MFCC特征，同時計算每一幀100～300 Hz內的中位PSD，將MFCC和PSD進行拼接。接著將特征輸入ANFIS，使用高斯函數作為隸屬函數對兩種特征模糊化，得到其對應隸屬度，將特征與隸屬度相乘，得到觸發強度，隨后經過歸一化得到觸發概率，最后去模糊化，對單個規則上的結果加權求和，得到二分類結果。本文選擇了五種評價指標，在測試集上的準確率達到了96.50%，綜合評價指標F1達到96.35%，與其他幾種方案相比性能最佳。實驗結果驗證了相對于其他時期，在收縮期內先心病病理性雜音的時頻特征具有更高的辨識度，同時，病理性雜音集中在100～300 Hz頻率范圍內。本研究顯示根據不同心音狀態、不同頻率的特征識別具有重要意義，這為先心病篩查提供了一種可行的思路。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻說明：汪琴負責實驗構思與設計、數據采集、數據分析和論文寫作；楊宏波負責醫學指導和數據收集；潘家華負責醫學指導和數據審查；田英杰負責實驗指導、論文寫作指導和數據收集；郭濤負責醫學指導；王威廉負責理論指導、實驗設計指導、論文整體審查和寫作指導。
倫理聲明：本文所使用的心音數據得到云南大學人體研究材料倫理委員會以及云南省阜外心血管病醫院倫理委員會批準采集并授權使用（CHSRE2021008，IRB2020-BG-028）。
本文附件見本刊網站的電子版本（biomedeng.cn）。
