針對先天性心臟病相關肺動脈高壓聽診特征不明顯，已有的機器輔助診斷算法相對復雜等問題，提出一種基于第二心音信號高頻分量統計特征的分析方法。首先，采用端點檢測自適應分割方法提取第二心音。其次，使用離散小波變換分解出高頻分量，并提取該分量的赫斯特（Hurst）指數、勒佩爾-齊夫（Lempel-Ziv）信息和樣本熵等統計特征。最后，使用這些特征訓練極端梯度提升算法（XGBoost）分類器，在三分類中準確率達到了80.45%。該方法無需進行降噪處理，特征提取速度快，且只需三個特征即可實現較好的多分類效果，有望用于先天性心臟病相關肺動脈高壓早期篩查。
引用本文： 楊炫鍇, 孫靜, 楊宏波, 郭濤, 潘家華, 王威廉. 基于第二心音統計特征的先天性心臟病相關肺動脈高壓診斷方法. 生物醫學工程學雜志, 2024, 41(1): 41-50. doi: 10.7507/1001-5515.202304037 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
肺動脈高壓（pulmonary arterial hypertension，PAH）是一種潛在致命性心血管疾病，其特征為肺動脈壓力升高，當壓力超過一定閾值時，會使得右心房擴大，最終導致右心衰竭[1]。然而，PAH的癥狀通常在疾病晚期才顯現，早期篩查很容易遺漏。PAH的病因復雜，其中約40%是由先天性心臟病（congenital heart disease，CHD）引起的[2]。CHD是一種胎兒時期發育異常導致的心血管畸形，心臟缺陷導致肺循環的壓力與容量超負荷，最終形成PAH。CHD相關PAH（CHD-associated PAH，CHD-PAH）由于同時夾雜著兩種癥狀，致死率更高。有創介入式的右心導管術是診斷PAH的金標準，但存在較大的風險。目前無創診斷最有價值的評估方法是超聲心動圖檢查，但在偏遠地區，由于缺乏設備和技術人員支持，且該設備不便攜帶，難以在大規模篩查中推廣。
心音是一種機械振動，是心臟血流動力學和心血管系統相互作用的結果。由于心音包含了大量有關心血管系統生理狀況的信息，因此可以用于評估心臟的健康狀況[3]。計算機智能輔助診斷（computer-aided diagnosis，CAD）通過提取心音信號的病理特征，進行機器學習訓練并構建模型用于疾病輔助診斷，能有效配合超聲心動圖，提高篩查效率，主要步驟分為信號預處理、特征提取、構建分類器等。
預處理階段主要為降噪與分割。降噪能抑制采集中的呼吸音、雜音等。Dwivedi等[4] 結合穩態小波變換與集合經驗模態分解（ensemble empirical mode decomposition，EEMD），來抑制環境音和噪聲，以提高后續分類準確率（accuracy，Acc）。Simonneau等[5]研究表明，第一心音（first heart sound，S1）和第二心音（second heart sound，S2）與PAH的嚴重程度相關。其中PAH患者的S2病理特征更明顯，會出現異常亢進與分裂，有助于提高PAH的診斷Acc [6]。但從心音中人工提取S2，困難且復雜[7]，而現有的心音分割算法則沒有提取S2，轉而通過分割出單個心動周期來研究病理特征，如基于多尺度的希爾伯特包絡分割[8]和持續時間隱馬爾可夫分割等[9]。因此，如果能高效準確地分割出S2，將是目前有助于促進PAH診斷的一個研究方向。
特征提取的質量會影響分類的結果，Kaddoura等[10]研究心音信號的聲學特征，估計心音信號的頻譜對數并進行傅里葉逆變換，以創建倒譜特征對PAH與正常心音進行二分類。Alqudah等[11]提取心音信號中S2的能量比作為特征，來區分PAH患者和健康受試者。Ge等[12]提取心動周期和S2的時頻域特征等150個特征用于后續分類。
分類階段，當數據集充足時神經網絡能有效提升分類Acc。Wang等[7]基于長短時記憶方法建立了一種小波散射卷積網絡，提取受試者的小波散射系數作為特征，來對正常心音與CHD二分類。對于CHD-PAH這樣的小樣本數據，經典的機器學習能夠有效根據信號特征對心音進行分類，不易受小數據量的影響而產生過擬合。已有研究報道，隨機森林（random forest，RF）[9]和K近鄰法（k-nearest neighbor，KNN）[13]在心音二分類上有一定效果。
目前大多數研究都是針對PAH和正常心音的二分類[5.10-11]，CHD-PAH的多分類問題仍有待改進，比如在預處理階段，降噪算法有可能濾除病理信息且耗時，達不到實際應用的要求。在心音分割中，大多數分割算法依賴于同步采集心電信號來對心音信號進行輔助分割，對信號采集要求高，只通過心音信號對S2部分進行分割是目前研究的難點。特征提取階段，目前的研究集中于提取心音的聲學和時頻域特征，如梅爾倒譜系數（Mel-scale frequency cepstral coefficients，MFCC）[14]和梅爾頻譜系數（Mel-frequency spectral coefficient，MFSC）[15]等。然而，聲學特征是針對語音信號設計的，而心音信號是由血液流動沖擊瓣膜所產生的信號，與語音信號存在一定的差異，并且在聽診中，PAH和CHD-PAH僅通過聽覺是很難區分，因為它們之間的聲學與時頻特征相似度高，分類效果不理想。此外，對于CHD-PAH的多分類診斷依賴于大量特征[12]，特征提取耗時長，不利于大規模的早期篩查任務。在分類器階段，由于CHD-PAH的數據量少，神經網絡在少量數據上容易出現過擬合的問題，傳統機器學習更適用于小樣本數據分類。
鑒于上述現狀，本文旨在建立一個快速有效的CHD-PAH診斷算法。在預處理階段，不進行降噪，使用自適應的雙閾值分割法得到心音S2部分，再提取S2高頻分量中的統計特征，包括赫斯特（Hurst）指數、勒佩爾-齊夫（Lempel-Ziv）復雜度（Lempel-Ziv complexity，LZC）和樣本熵（sample entropy，SampEn）。與傳統方法不同的是，本文算法專注于研究心音的高頻特性而非聲學相關特性，這些高頻分量被用來描述短而突然的變化特征雜音，能更有效地凸顯出PAH患者S2亢進、分裂的特征。最后，采用貝葉斯優化的極端梯度提升算法（extreme gradient boosting，XGBoost）對正常、CHD和CHD-PAH進行三分類診斷。
1 方法
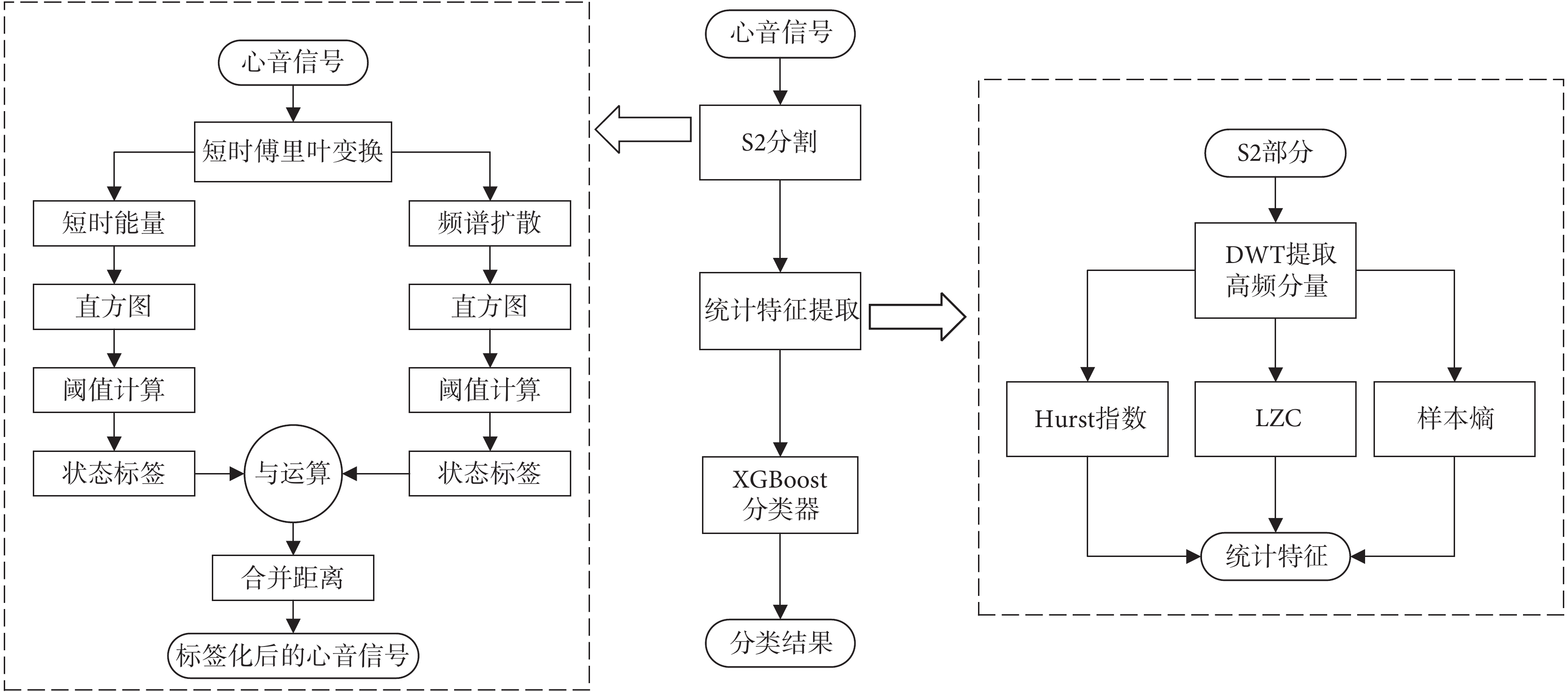
本文算法通過以下幾個步驟對CHD-PAH進行診斷：① 使用一種自適應分割方法來截取出心音信號中S2部分。② 對S2部分進行離散小波變換（discrete wavelet transformation，DWT）分解，提取出高頻分量。③ 使用Hurst指數、LZC和樣本熵進行復雜性度量，提取出S2高頻分量的統計特征。④ 特征通過XGboost分類器進行CHD-PAH的三分類診斷。CHD-PAH分類流程如圖1所示。
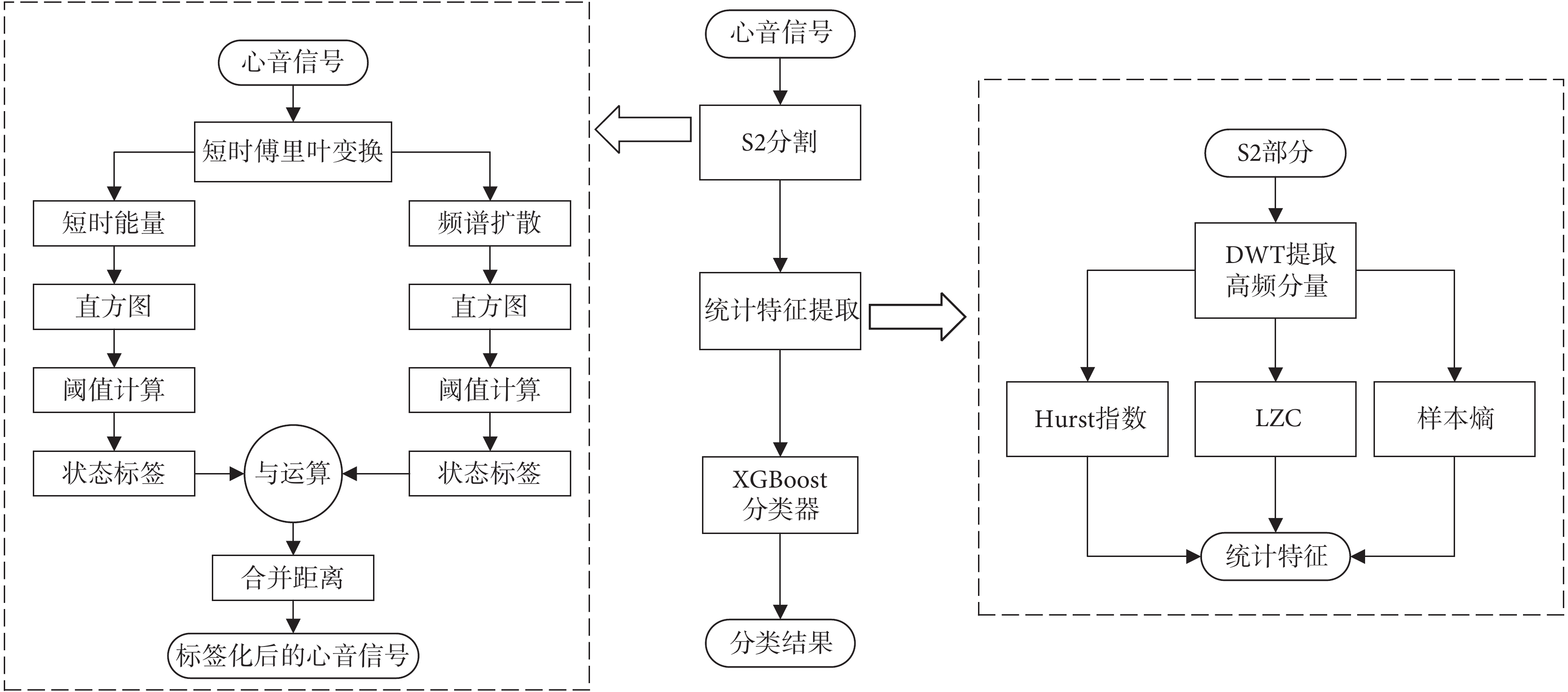圖1
CHD-PAH流程圖
Figure1.
CHD-PAH flow chart
1.1 預處理
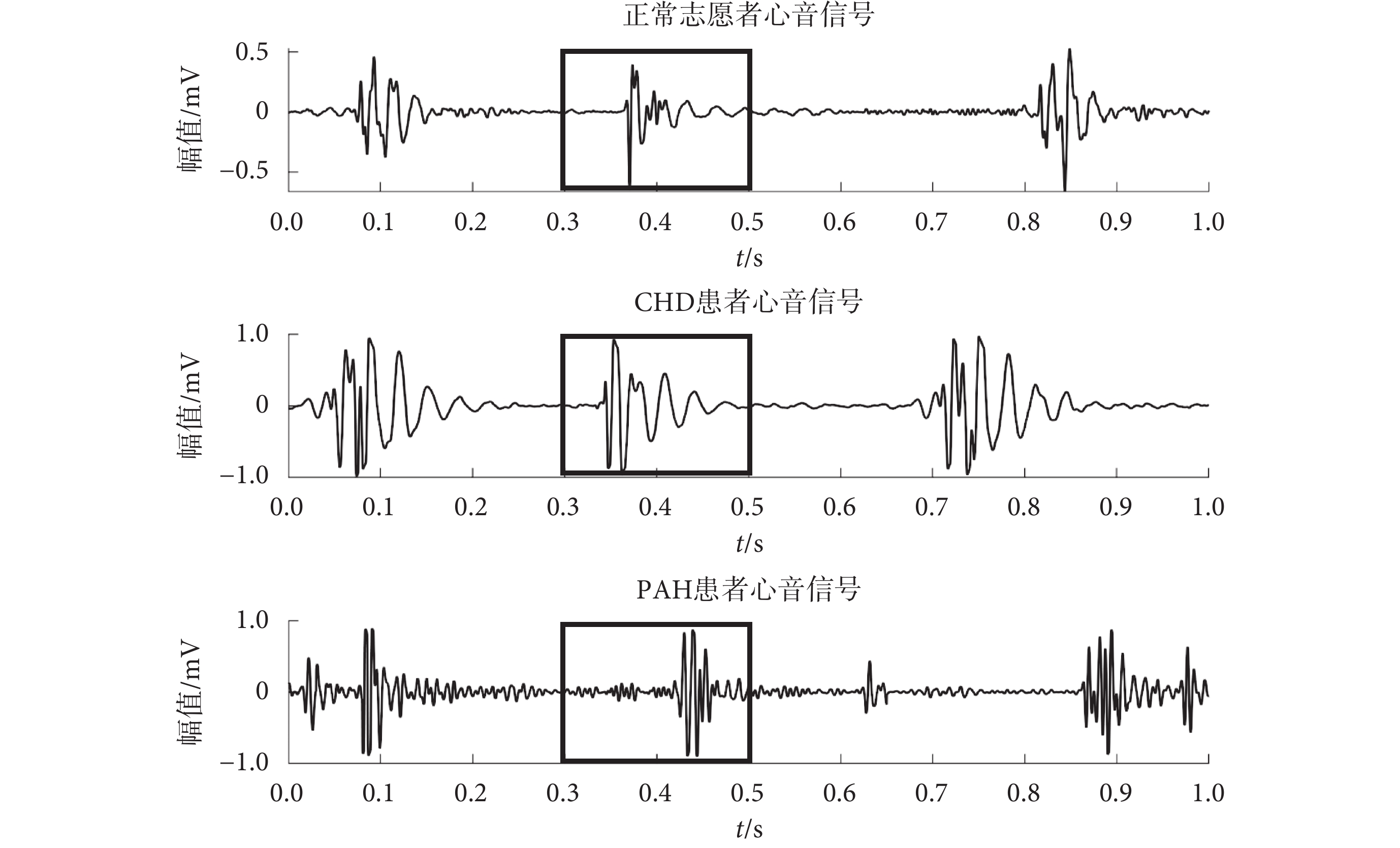
心臟跳動是一個近似于周期性的過程，通常分為S1、收縮期、S2和舒張期四個部分。在聽診PAH患者時，S2中肺部成分加重是其確診的主要特征之一[6]。如圖2所示，局部方框圈出部分波形即為S2，PAH患者表現為S2部分出現亢進與異常分裂。相比于整個心動周期，僅使用S2部分即能有效地凸顯出PAH的特征[13]。并且，將原始信號分割為單獨的S2部分后，還能提高特征提取速度。
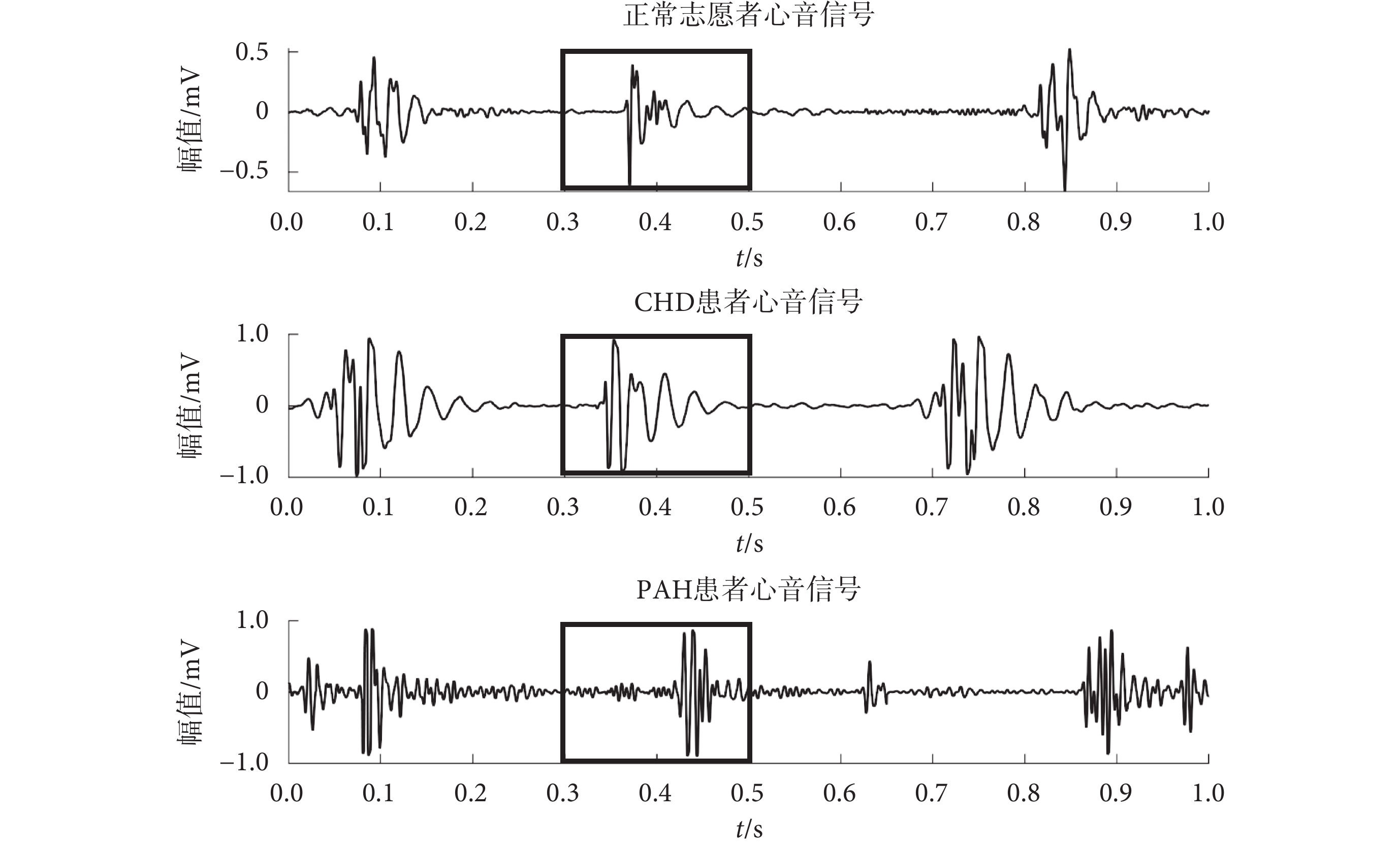圖2
CHD-PAH的S2部分出現異常
Figure2.
Anomalies in the S2 part of CHD-PAH
本文采用了一種閾值檢測算法分割S2，如圖1所示。首先對心音信號進行短時傅里葉變換（short-time Fourier transform，STFT），并使用漢明窗進行分幀，如式(1)所示：
 |
其中， t為時間，f為頻率，j為虛數，π為圓周率，x(τ) 為t = τ時的心音信號，ω(τ ? t)為窗函數。心音 x(τ)被分幀后，提取每一幀的短時能量Ei與頻譜擴散Si，如式(2)～式(3)所示：
 |
 |
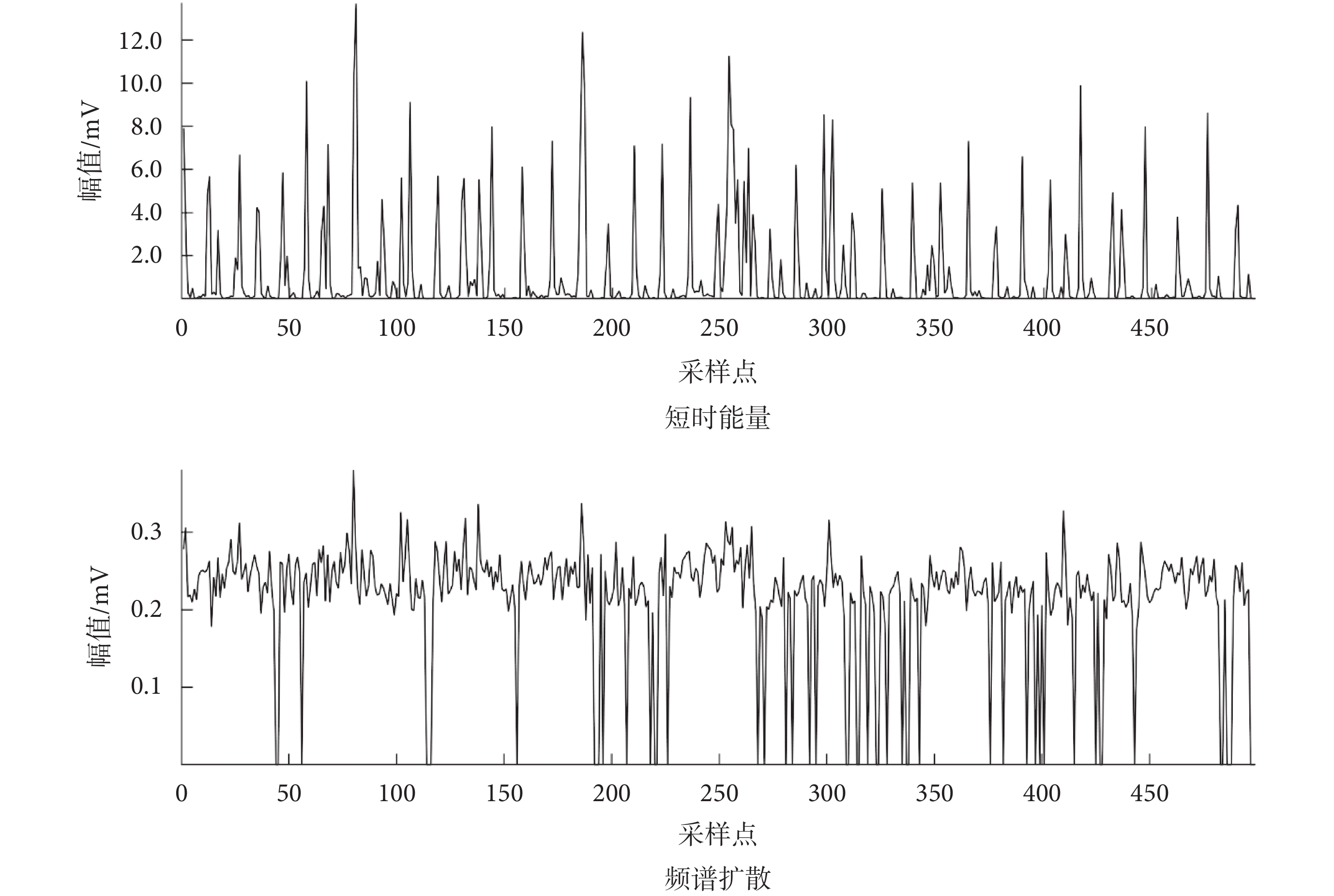
其中，xi(n)，n = 1, ···, N表示心音信號的第i幀，N為幀數長度，fi為第i幀的頻率，u1為頻譜中值，si為第i幀的頻譜值， b1與b2為頻譜邊界值。所得Ei與Si，如圖3所示。
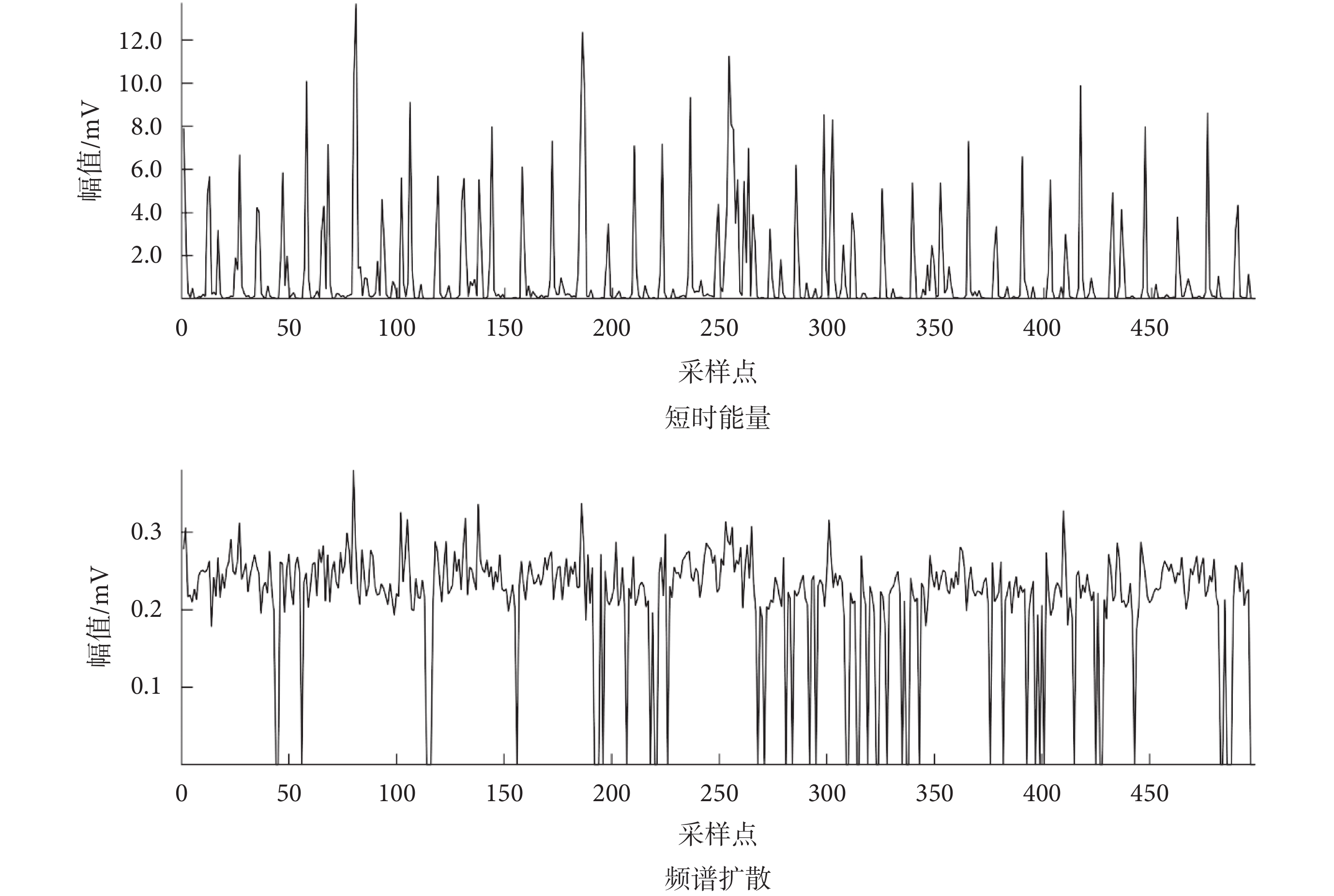圖3
短時能量與頻譜擴散
Figure3.
Short-time energy and spectral diffusion
計算短時能量與頻譜擴散對應的直方圖與直方圖閾值TE與TS，閾值計算如式(4)所示：
 |
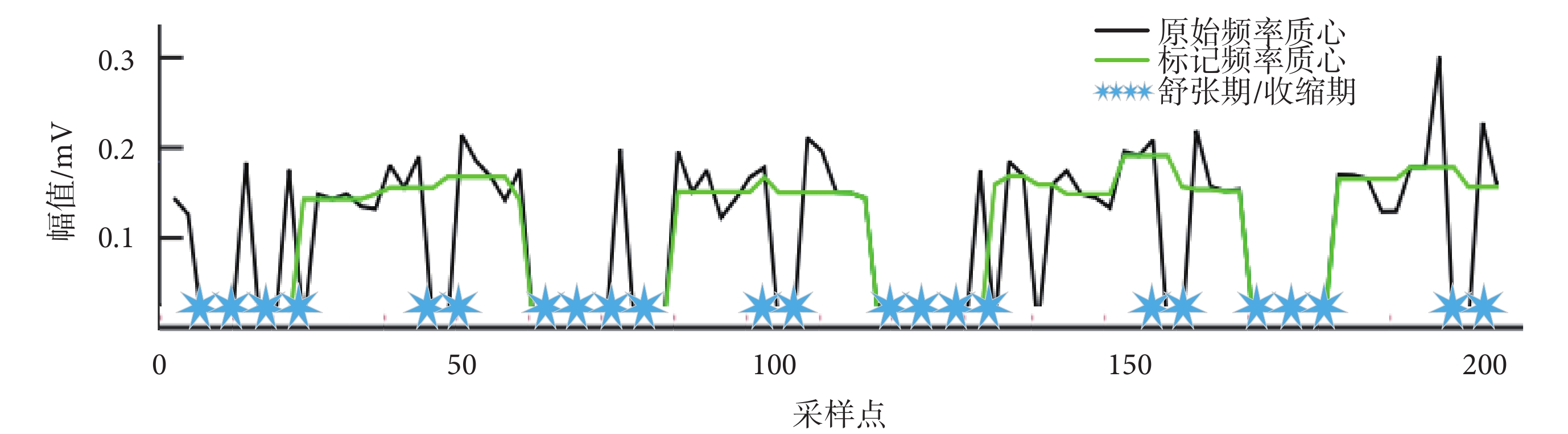
其中，M1、M2為直方圖中前兩個最大值的位置，W為設定值。根據閾值對序列進行判斷并標記。其中，滿足Ei ≥ TE的為標記點1（flag1），滿足Si ≥ TS的為標記點2（flag2），這些標記被認為是心音S1或S2分量，稱之為待定分量。如圖4所示，根據閾值判斷并標記序列，黑色波形是原始心音信號的頻率質心，綠色波形是待定分量，即被標記為心音S1或心音S2的頻率質心，藍色星號代表S1或S2頻率質心之間的距離，即舒張期或收縮期。
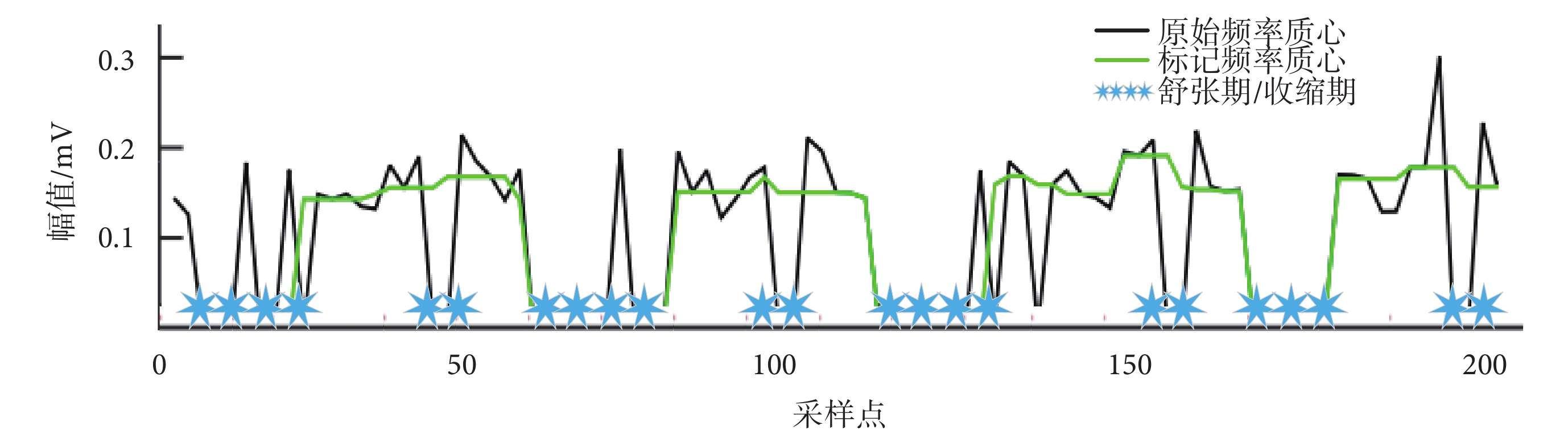圖4
心音待定分量標記
Figure4.
Suspected components of the heart sound waveform
計算這些待定分量之間的距離（distance，Dist）（以符號Dist表示），如式(5)所示：
 |
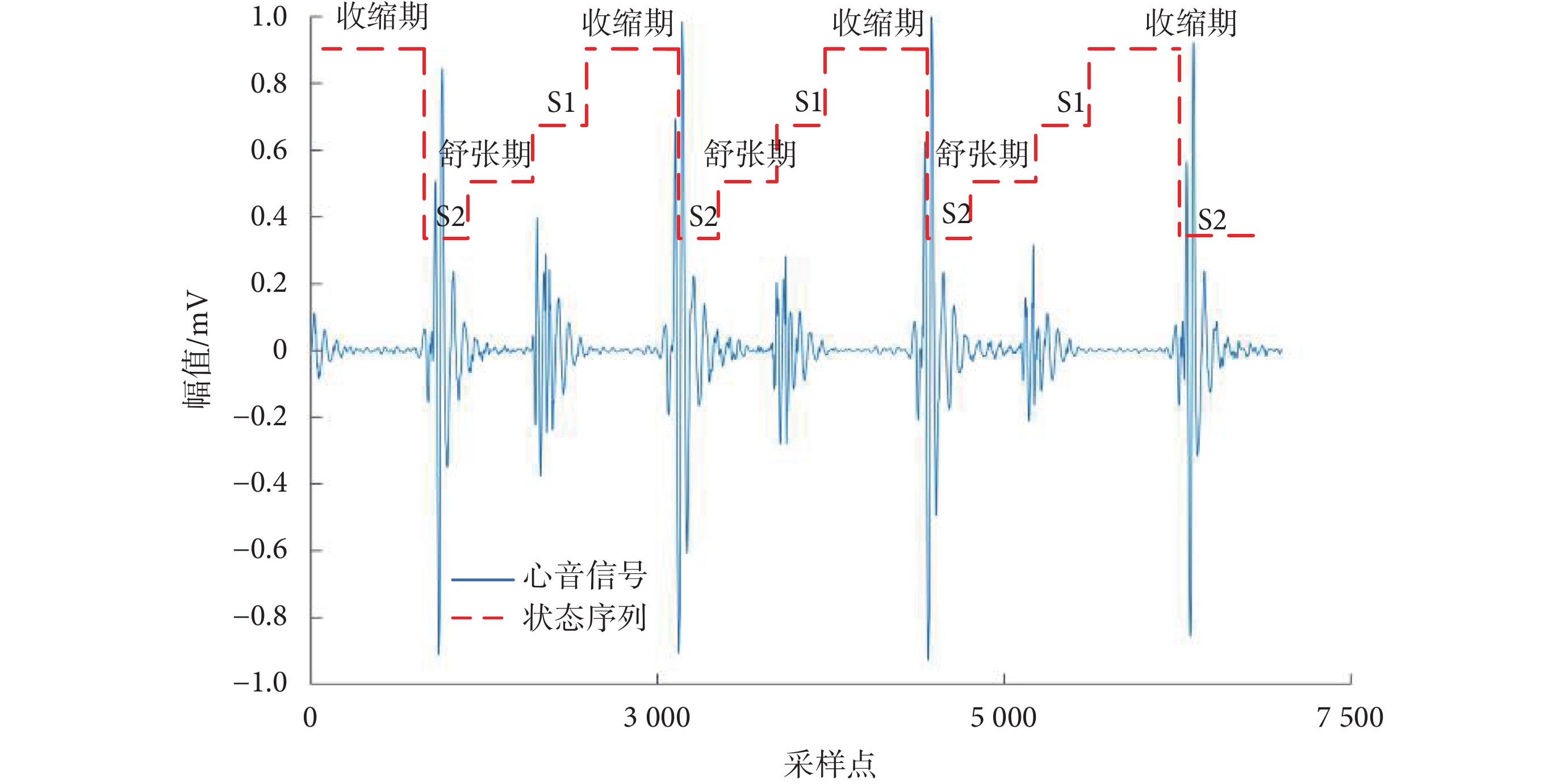
其中，{flags}表示標記點集合，flagx_i與flagx_i+1分別為兩個距離最近的標記點， Fs表示采樣率。一個心動周期中S1與S2之間的間隔通常小于58 ms[16]，因此實驗中設定了一個58 ms的判定距離。如果待定分量之間的距離小于判定距離，則這些分量會被判定為心音S1或S2。將序列映射到原始心音信號中，根據心音的生理特征，S2與S1之間的信號被定義為舒張期，具有最大的時間間隔[17]。如圖5所示，紅色虛線為狀態序列，根據狀態序列的長度進行選取，最長的一段為舒張期，將舒張期前的分量標記為S2，從而實現了對心音信號中S2部分的精準截取。
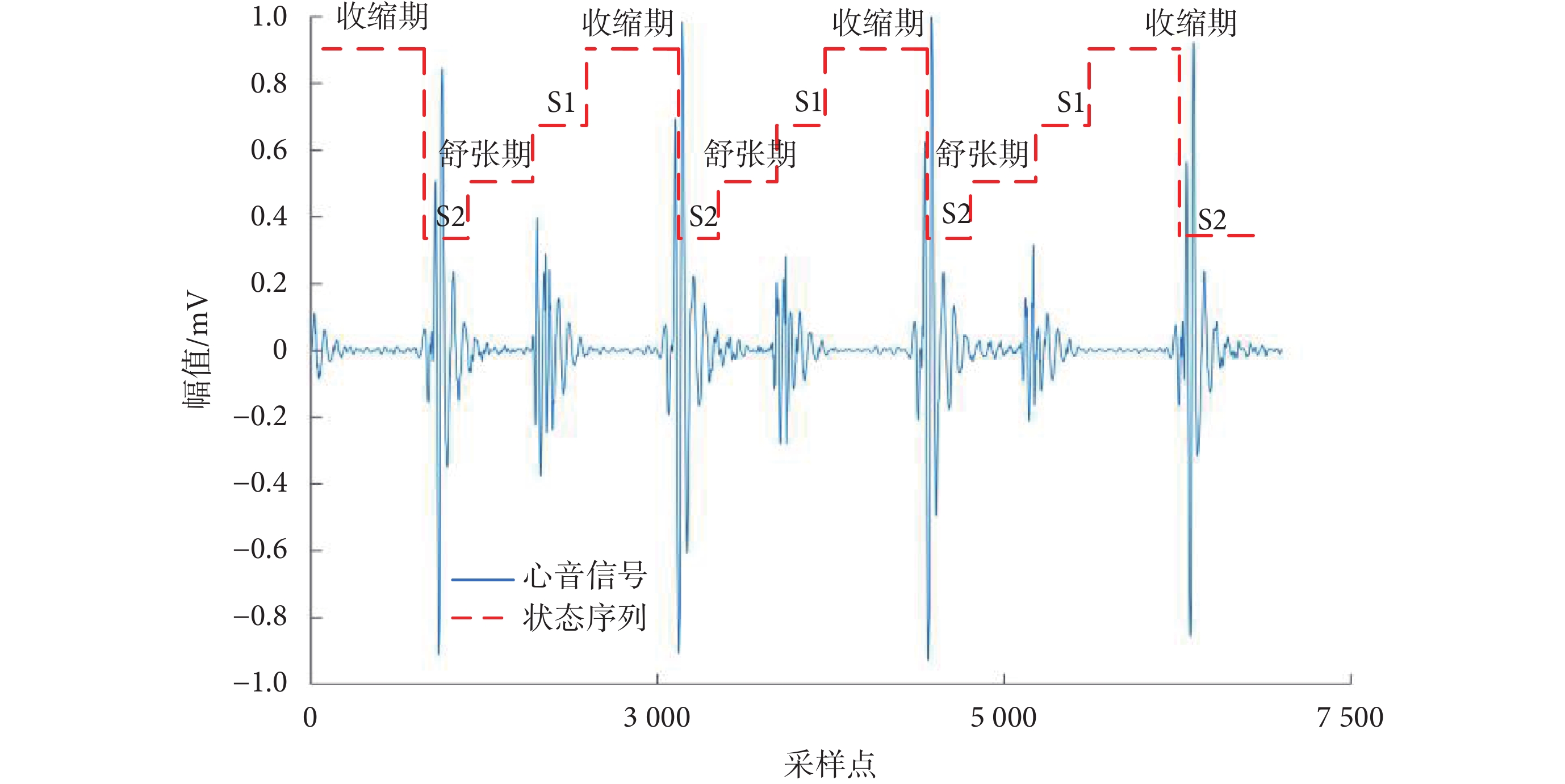圖5
心音分割標記圖
Figure5.
Heart sound segmentation marker chart
1.2 特征提取
心音是由心臟在收縮和開合時血流撞擊產生的振動信號組成[18]。心血管疾病導致心臟結構變化，使得心音出現病理特征。本文選取心音S2部分的長記憶性、信息內容和隨機性作為統計特征用于分類。
1.2.1 高頻分量的分解
DWT將信號分解成多個不同頻率的子帶，其中高頻子帶包含信號中的瞬時變化和細節信息[19]。對于心音信號，高頻分量包含著心臟收縮、瓣膜開合等短暫且快速的變化，因此選擇高頻分量可以很好地描述心音信號的動態特性。此外，直接提取高頻分量還可以避免低頻噪聲的影響[20]，去除降噪步驟，進一步提高算法的速度。DWT需要兩個基本小波來分析信號：父子波φ(t)和母子波ψ(t)。其中，φ(t)用于提取低頻部分，ψ(t)用于提取高頻部分。尺度j下的低頻振蕩v和高頻振蕩ω的離散形式分別由Sj和Dj表示，如式(6)～式(7)所示：
 |
 |
其中，k表示求和的下界，N表示上界，即從k = 1開始取值，一直取到N。多貝西小波四號（Daubechies-4）用于對S2部分進行三級分解，分解后將312.5 Hz以上的分量認為是高頻分量。在尺度j處，Sj表示信號的總體趨勢，Dj表示其詳細波動。后續的統計特征都是從高頻分量Dj提取的。
1.2.2 統計特征提取
統計特征主要包括Hurst指數、LZC與樣本熵。這些特征分別用于獲取心音高頻分量中的長期記憶性、信息內容和規律性[21]，能有效地描述心音信號S2部分的病理特征。
Hurst指數即有偏的隨機游走，用于衡量時間序列的長期記憶性。心音信號本質上是一種非平穩時間序列。Hurst值大于0.5，表示為一個具有持續性并且極度相關的時間序列；Hurst值等于0.5，表示為一個不相關的時間序列；Hurst值小于0.5，表示為一個非持續不相關的時間序列，本文用重標極差分析法計算Hurst指數。
給定的時間序列{I1, I2, ···, Iq}，有q個分量，對于任意正整數υ≥1(υ=1, 2, ···, n)，計算其平均值e(υ)與方差S(υ)，如式(8)、式(9)所示:
 |
 |
對q個分量，計算其累計差Z(q)與極差R(υ)，如式(10)、式(11)所示:
 |
 |
引入無量綱比，通過方差S(υ)與極差R(υ)來計算重標極差Rs(υ)，如式(12)所示:
 |
通過計算對應的對數方程，并求取對應的斜率即可得到Hurst系數，其中b是一個常數，H是Hurst指數，如式(13)所示:
 |
LZC可量化時間序列的隨機性和復雜性，適用于衡量非線性、非平穩信號的信息內容。LZC對信號中小擾動和噪聲不敏感，因此在生理檢測中可用于確定心音信號的基本模式與復雜性，正常心音通常以重復模式為特征，而異常心音則以缺乏重復模式為特征。
對于一個給定的信號{x1, x2, …, xN}，將其轉化為二進制，轉化公式如式(14)所示:
 |
閾值Td為信號{x1, x2, …, xN}平均值。得到yi以后，用c(n)作為yi的復雜度計數器來計算yi中不同字串的數目。c(n)存在著上限，通過b(n)進行歸一化得到LZC值C，如式(15)、式(16)所示:
 |
 |
樣本熵，是一種衡量時間序列信號復雜性的方法；熵值越低，表示信號具有更高的規律性和可預測性。在心音信號分析中，高的樣本熵值，可能表明心音的不規則性或變異性程度較高，并且相較于其它熵測量方法，樣本熵的優勢在于其穩定性，抗噪、抗干擾能力強。
定義一個長度為m的滑動窗口，從時間序列數據{s1, s2, ···, sN}中提取出所有長度為m的子序列{Sm(1), Sm(2), ···, Sm(N ? m + 1)}，其中Sm(i) = si, si + 1, ···, si + m ? 1，對于每個子序列，計算其它子序列與該子序列距離小于等于r的數量，表示為Cm(r)。其中，閾值r為原始信號的標準差與自定義權值w的乘積，如式(17)所示:
 |
對于長度為m+1的子序列，計算其它子序列與該子序列距離小于等于r的數量，表示為Cm+1(r)，計算樣本熵（以符號SampEn表示），如式(18)所示:
 |
1.3 分類識別
XGBoost，是一種高效的機器學習算法，它采用多個決策樹模型的集成來解決二分類和多分類問題。該算法通過構建一系列的決策樹模型，并進行結合，每個決策樹都基于前面決策樹的殘差誤差構建，因此，能夠不斷提高分類效果。XGBoost的數學描述如式(19)所示:
 |
其中，t=1, 2, …, T，T表示分類回歸樹的總數，a=1, 2, …, N，Za為輸入，ma為實際值，
為預測值，ft表示第t棵分類回歸樹。再設置XGBoost的目標函數obj(θ)，如式(20)所示：
 |
其中，
為損失函數，用于衡量實際值ma與預測值
的偏差值。
為正則項，對t個分類回歸樹的復雜度進行求和。
XGBoost不斷優化后，得到第k棵決策樹fk的模型fk(Za)，第k個決策樹的目標函數H(k)，如式(21)所示：
 |
貝葉斯優化算法，是一種高效的超參數優化算法，它利用先驗信息不斷優化目標函數，在短時間內找到更好的超參數組合。該算法具有快速找到最優解、強魯棒性和通用性的優點[22]。在預處理與特征提取后，本文采用貝葉斯優化算法來獲取合適的分類模型參數。
2 實驗與分析
2.1 數據與說明
實驗所用心音數據集采集于云南省阜外心血管病醫院，所用采集設備為實驗室自行研發的心音信號采集設備，傳感器為The ONE心音傳感器（Thinklabs Medical LLC Inc.，美國）。招募的志愿者年齡在6個月～18歲，未成年受試者監護人及成年受試者均已簽署知情同意書。每個志愿者按5個心臟聽診位置各采集20 s心音信號，采樣頻率為5 000 Hz。志愿者都經過超聲心動儀檢測，CHD-PAH患者還經過臨床醫生在術前與術中檢測患者的壓力進行確認，以保證數據的可靠性。本次研究所用的心音數據的采集通過了云南大學人體研究材料倫理委員會及云南省阜外心血管病醫院醫學倫理委員會的批準并授權使用（CHSRE2021008、IRB2020-BG-028）。
從前述采集的心音數據集中選取345名志愿者的1 725例心音數據，志愿者年齡限制18歲以下，這是為了保證訓練模型在青少年早期篩查中的有效性。其中，正常、CHD與CHD-PAH心音比例為1:1:1，以保證樣本的平衡性。CHD心音包括室間隔缺損、房間隔缺損、動脈導管未閉等常見疾病。將數據按7:2:1的比例劃分為訓練集、測試集、驗證集。
2.2 實驗環境
實驗所用配置：中央處理器i5-11400H@2.70GHz（Intel Inc.，美國)，獨立顯卡NVIDIA GeForce RTX3060（Nvidia Inc.，美國）。信號處理軟件Matlab2021b（MathWorks Inc.，美國），深度學習框架TensorFlow 2.0（Google Inc.，美國），編程語言Python 3.7（Python Software Foundation Inc.，美國）
2.3 評價指標
使用靈敏度（sensitivity，Se）、特異性（specificity，Sp）、精準率（precision，Pr）、Acc等指標用于評價分類器的性能，如式(22) ～ 式(25)所示：
 |
 |
 |
 |
其中，真陽性（true positive，TP）表示正類別中正確分類樣本的數目；真陰性（true negative，TN）表示負類別中正確分類樣本的數目；假陰性（false negative，FN）表示負類別中錯誤分類樣本的數目； 假陽性（false positive，FP）表示正類別中錯誤分類樣本的數目。
F1分數，是一種兼顧了Pr與召回率（recall, Re）的分類模型評價指標，如式(26)、式(27)所示：
 |
 |
修正Acc（modified Acc，MAcc）是根據復雜生理信號研究資源網（research resource for complex physiologic signals，PhysioNet）心音挑戰賽中所提出的，對Sp和Se指標添加不定權系數0.5，如式(28)所示：
 |
2.4 實驗方案設計
本文根據參數設置對結果的影響進行討論，貝葉斯參數尋優算法對結果的影響如圖6所示。為了凸顯本文算法速度的優勢，與小波降噪、EEMD去噪進行對比，計算處理1 725例心音的運行時間與分類結果，結果如表1所示。
圖6
貝葉斯參數優化算法尋優圖
Figure6.
Optimization by Bayesian parameter optimization algorithm
表1
預處理運行時間與分類效果
Table1.
Pre-treatment running time and classification results
為了驗證統計特征對分類的提升效果，本文還進行了特征消融實驗，分別使用三個特征單獨進行分類，來區分正常心音、CHD心音與CHD-PAH心音，分類結果總結如表2所示。與文獻[9, 13-15]中的聲學特征MFCC、MFSC進行對比，其中MFCC采用與人耳結構相似的三角濾波器組，MFSC更注重對信號在高低頻內的特征提取。分類模型選擇KNN與RF。KNN是一種基于距離度量的非參數分類方法，適用于小規模數據集；而RF通過構建多個決策樹來進行分類，能與XGBoost形成對比，分類結果如表3所示。
表2
消融實驗分類結果
Table2.
Classification results of ablation experiments
表3
聲學特征對比實驗分類評價指標
Table3.
Classification evaluation metrics for acoustic features comparison experiment
為了驗證本文算法的有效性，選取近兩年文獻[23-24]提及的心音分類算法，以本文數據集進行訓練，對比分類結果。文獻[23]對心音進行改進的自適應噪聲完全EEMD（the improved complete EEMD with adaptive noise，ICEEMDAN），提取分解后本征模態函數（intrinsic mode function，IMF）的多尺度樣本熵，通過邏輯回歸（logistic regression，LR)進行分類。文獻[24]中對心音進行自適應噪聲完備EEMD（complete EEMD with adaptive noise，CEEMDAN），提取IMF的排列熵與支持向量機（support vector machine，SVM）結合后實現分類，分類結果總結如表4所示。
表4
分類算法對比實驗分類評價指標
Table4.
Classification evaluation metrics for comparison of classification algorithms
所有實驗中，機器學習都通過貝葉斯優化算法進行參數尋優，XGBoost中決策樹的數量設為150，學習率設為0.1，最大深度設為5。KNN中k值設為7。RF中決策樹的數量設為300，最大深度設置為6。
2.5 實驗結果與分析
2.5.1 貝葉斯參數優化實驗
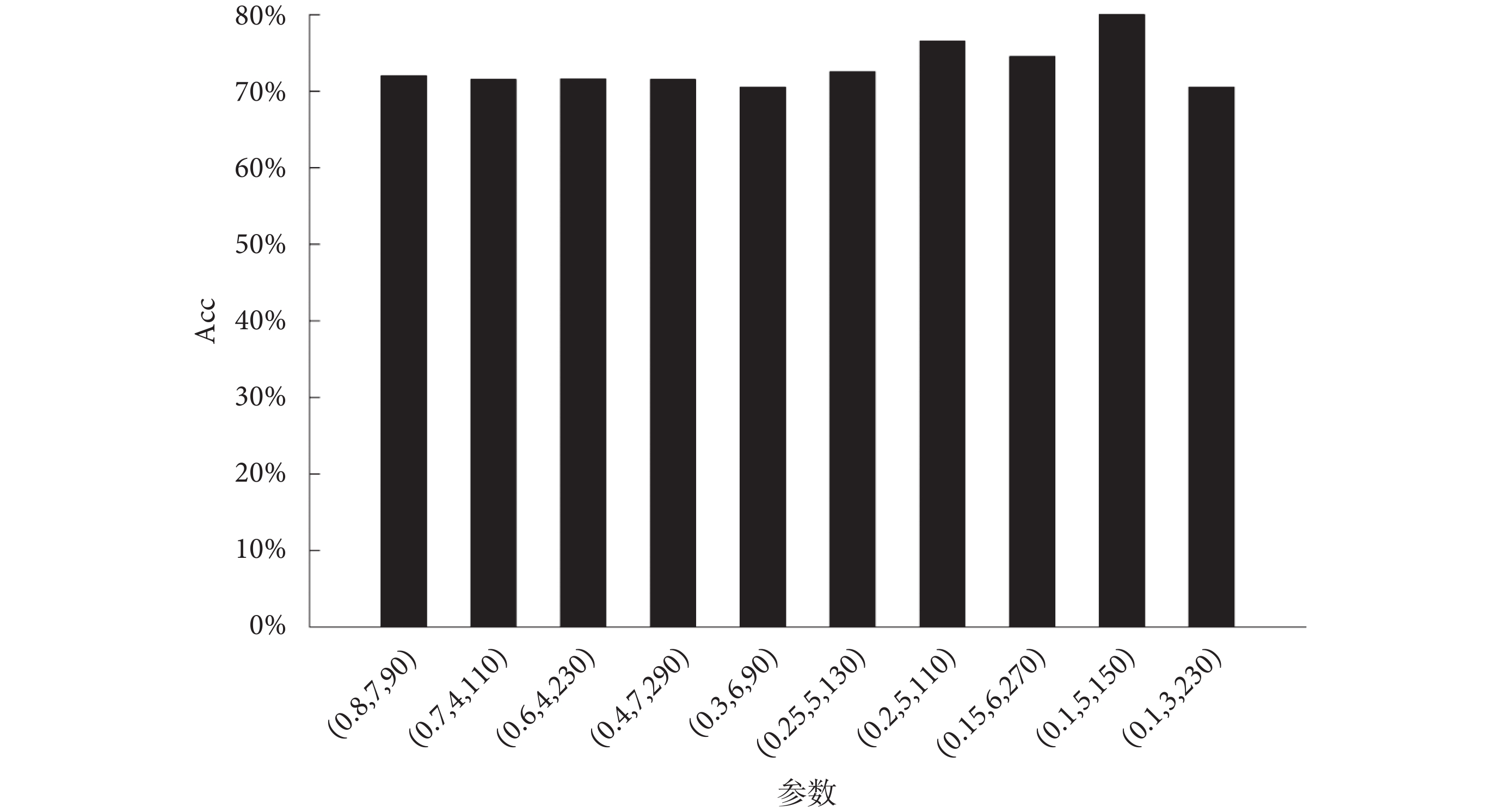
如圖6所示，對XGBoost的參數進行了貝葉斯優化算法尋優，其中學習率的范圍設定在0.1～1.0之間，最大深度設定在3～8，決策樹的數量設定在10～600。圖6中展示了10組尋優出來的參數以及對應的Acc，參數的順序為學習率、最大深度、決策樹的數量。貝葉斯優化算法在短時間對參數進行尋優，獲得了分類Acc較高的一組參數，即學習率0.1，最大深度5，決策樹數量150，Acc達到了80.45%。
2.5.2 預處理實驗
如表1所示，為本文算法（S2分割+高頻分量）與文獻[4]、文獻[20]中去噪算法的對比實驗，小波降噪與EEMD降噪是心音分類中有效的預處理算法。可以看出，由于直接提取高頻分量，省略了降噪步驟，本文模型在運行時間上遠低于小波降噪與EEMD降噪算法。同時，小波降噪與EEMD降噪過程中可能將一些微弱的病理信息去除，導致分類效果不佳。本文算法直接去除低頻分量，雖然會導致低頻中部分特征被舍棄，但高頻分量中的特征能保證Acc達到80%以上，實現了快速有效的診斷。
2.5.3 消融實驗
消融實驗結果如表2所示，Hurst指數、LZC和樣本熵三個特征都有效地提取了心音高頻分量的部分特征，在三分類實驗中具有一定的分類效果，其中LZC與樣本熵的Acc都達到了70%以上，但同時使用三個特征進行分類的Acc達到了80%以上，各項指標也遠高于單獨使用，驗證了三個特征組合后對分類效果的提升。
2.5.4 三分類實驗
三分類實驗結果如表3所示，對已經分割出S2部分的心音進行特征提取與分類，將不同的特征和分類器進行組合，得到分類結果與相關指標。基于高頻統計特征的XGBoost模型分類效果優于其它算法，表現為：① 高頻統計特征相比于MFCC與MFSC在Acc 、MAcc和F1三個評價指標上更優。MFCC的核心是構建一個非均勻分布的頻域濾波器組，其特點是低頻區域分布密集、高頻區域分布稀疏，忽略了信號的相位信息和高頻細節，因此在PAH與CHD-PAH的分類中效果不佳。通過對比Acc值，證實了高頻統計特征能更好地提取CHD-PAH的病理特征。通過對比MAcc值，表明該特征不易受環境噪聲影響。通過對比F1值，得出使用該特征進行分類得到的假陰性更少。② 聲學特征MFCC、MFSC與本文特征在XGBoost模型上各項評價指標都高于RF與KNN，體現了XGBoost在小樣本多分類任務上的優越性。
2.5.5 對比分類實驗
分類算法對比實驗結果如表4所示，將文獻[23-24]心音分類算法用于本文的CHD-PAH數據集上進行三分類實驗，并與本文算法進行比較。
從結果上看，三種算法采用的特征與分類器在三分類上都有一定效果，但本文算法在Acc、Pr、Re和 F1 值上都優于其它方法。① 對比Acc值，證實了分割S2來進行后續特征提取，能更好地提供病理信息，提高了篩查中的檢出率。② 通過對比MAcc值，表明直接提取高頻分量，去除低頻部分的噪聲，可提高算法抗噪聲能力。③ 通過對比F1值，得出使用S2的高頻統計特征相較多尺度樣本熵與排列熵，可提取到的病理信息更豐富，得到更少的假陰性病例。④ 采用多個決策樹模型的集成，XGBoost在小樣本的分類效果也要優于SVM與LR。
綜上所述，基于心音S2部分高頻分量的統計特征，有效提取了CHD-PAH的病理特征，結合XGBoost分類模型，在三分類綜合評價指標上相比現有算法有所提升。
3 結論
本研究的主要目的是設計一個計算機輔助診斷系統，以區分正常、CHD與CHD-PAH心音。本文通過自適應分割出心動周期中S2部分，能更好地凸顯CHD-PAH的病理特征，再利用S2的高頻分量統計特征來訓練貝葉斯優化算法調整的XGBoost模型。本研究的主要特點在于省略了預處理中降噪步驟，通過DWT將原始信號縮短并提取了其高頻分量的主要病理特征，這使得特征提取更為快速，整體算法所需時間與資源量低，在三分類上Acc達到80.45%，為CHD-PAH快速輔助診斷提供一種可行的思路。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：楊炫鍇負責實驗構思與設計、數據采集、數據分析和論文寫作；孫靜負責實驗指導、論文寫作指導和數據收集；楊宏波負責醫學指導和數據收集；郭濤負責醫學指導；潘家華負責醫學指導和數據審查；王威廉負責理論指導、實驗設計指導、論文整體審查和寫作指導。
倫理聲明：本文所使用的心音數據得到云南大學人體研究材料倫理委員會以及云南省阜外心血管病醫院倫理委員會批準采集并授權使用（CHSRE2021008、IRB2020-BG-028）。
0 引言
肺動脈高壓（pulmonary arterial hypertension，PAH）是一種潛在致命性心血管疾病，其特征為肺動脈壓力升高，當壓力超過一定閾值時，會使得右心房擴大，最終導致右心衰竭[1]。然而，PAH的癥狀通常在疾病晚期才顯現，早期篩查很容易遺漏。PAH的病因復雜，其中約40%是由先天性心臟病（congenital heart disease，CHD）引起的[2]。CHD是一種胎兒時期發育異常導致的心血管畸形，心臟缺陷導致肺循環的壓力與容量超負荷，最終形成PAH。CHD相關PAH（CHD-associated PAH，CHD-PAH）由于同時夾雜著兩種癥狀，致死率更高。有創介入式的右心導管術是診斷PAH的金標準，但存在較大的風險。目前無創診斷最有價值的評估方法是超聲心動圖檢查，但在偏遠地區，由于缺乏設備和技術人員支持，且該設備不便攜帶，難以在大規模篩查中推廣。
心音是一種機械振動，是心臟血流動力學和心血管系統相互作用的結果。由于心音包含了大量有關心血管系統生理狀況的信息，因此可以用于評估心臟的健康狀況[3]。計算機智能輔助診斷（computer-aided diagnosis，CAD）通過提取心音信號的病理特征，進行機器學習訓練并構建模型用于疾病輔助診斷，能有效配合超聲心動圖，提高篩查效率，主要步驟分為信號預處理、特征提取、構建分類器等。
預處理階段主要為降噪與分割。降噪能抑制采集中的呼吸音、雜音等。Dwivedi等[4] 結合穩態小波變換與集合經驗模態分解（ensemble empirical mode decomposition，EEMD），來抑制環境音和噪聲，以提高后續分類準確率（accuracy，Acc）。Simonneau等[5]研究表明，第一心音（first heart sound，S1）和第二心音（second heart sound，S2）與PAH的嚴重程度相關。其中PAH患者的S2病理特征更明顯，會出現異常亢進與分裂，有助于提高PAH的診斷Acc [6]。但從心音中人工提取S2，困難且復雜[7]，而現有的心音分割算法則沒有提取S2，轉而通過分割出單個心動周期來研究病理特征，如基于多尺度的希爾伯特包絡分割[8]和持續時間隱馬爾可夫分割等[9]。因此，如果能高效準確地分割出S2，將是目前有助于促進PAH診斷的一個研究方向。
特征提取的質量會影響分類的結果，Kaddoura等[10]研究心音信號的聲學特征，估計心音信號的頻譜對數并進行傅里葉逆變換，以創建倒譜特征對PAH與正常心音進行二分類。Alqudah等[11]提取心音信號中S2的能量比作為特征，來區分PAH患者和健康受試者。Ge等[12]提取心動周期和S2的時頻域特征等150個特征用于后續分類。
分類階段，當數據集充足時神經網絡能有效提升分類Acc。Wang等[7]基于長短時記憶方法建立了一種小波散射卷積網絡，提取受試者的小波散射系數作為特征，來對正常心音與CHD二分類。對于CHD-PAH這樣的小樣本數據，經典的機器學習能夠有效根據信號特征對心音進行分類，不易受小數據量的影響而產生過擬合。已有研究報道，隨機森林（random forest，RF）[9]和K近鄰法（k-nearest neighbor，KNN）[13]在心音二分類上有一定效果。
目前大多數研究都是針對PAH和正常心音的二分類[5.10-11]，CHD-PAH的多分類問題仍有待改進，比如在預處理階段，降噪算法有可能濾除病理信息且耗時，達不到實際應用的要求。在心音分割中，大多數分割算法依賴于同步采集心電信號來對心音信號進行輔助分割，對信號采集要求高，只通過心音信號對S2部分進行分割是目前研究的難點。特征提取階段，目前的研究集中于提取心音的聲學和時頻域特征，如梅爾倒譜系數（Mel-scale frequency cepstral coefficients，MFCC）[14]和梅爾頻譜系數（Mel-frequency spectral coefficient，MFSC）[15]等。然而，聲學特征是針對語音信號設計的，而心音信號是由血液流動沖擊瓣膜所產生的信號，與語音信號存在一定的差異，并且在聽診中，PAH和CHD-PAH僅通過聽覺是很難區分，因為它們之間的聲學與時頻特征相似度高，分類效果不理想。此外，對于CHD-PAH的多分類診斷依賴于大量特征[12]，特征提取耗時長，不利于大規模的早期篩查任務。在分類器階段，由于CHD-PAH的數據量少，神經網絡在少量數據上容易出現過擬合的問題，傳統機器學習更適用于小樣本數據分類。
鑒于上述現狀，本文旨在建立一個快速有效的CHD-PAH診斷算法。在預處理階段，不進行降噪，使用自適應的雙閾值分割法得到心音S2部分，再提取S2高頻分量中的統計特征，包括赫斯特（Hurst）指數、勒佩爾-齊夫（Lempel-Ziv）復雜度（Lempel-Ziv complexity，LZC）和樣本熵（sample entropy，SampEn）。與傳統方法不同的是，本文算法專注于研究心音的高頻特性而非聲學相關特性，這些高頻分量被用來描述短而突然的變化特征雜音，能更有效地凸顯出PAH患者S2亢進、分裂的特征。最后，采用貝葉斯優化的極端梯度提升算法（extreme gradient boosting，XGBoost）對正常、CHD和CHD-PAH進行三分類診斷。
1 方法
本文算法通過以下幾個步驟對CHD-PAH進行診斷：① 使用一種自適應分割方法來截取出心音信號中S2部分。② 對S2部分進行離散小波變換（discrete wavelet transformation，DWT）分解，提取出高頻分量。③ 使用Hurst指數、LZC和樣本熵進行復雜性度量，提取出S2高頻分量的統計特征。④ 特征通過XGboost分類器進行CHD-PAH的三分類診斷。CHD-PAH分類流程如圖1所示。
圖1
CHD-PAH流程圖
Figure1.
CHD-PAH flow chart
1.1 預處理
心臟跳動是一個近似于周期性的過程，通常分為S1、收縮期、S2和舒張期四個部分。在聽診PAH患者時，S2中肺部成分加重是其確診的主要特征之一[6]。如圖2所示，局部方框圈出部分波形即為S2，PAH患者表現為S2部分出現亢進與異常分裂。相比于整個心動周期，僅使用S2部分即能有效地凸顯出PAH的特征[13]。并且，將原始信號分割為單獨的S2部分后，還能提高特征提取速度。
圖2
CHD-PAH的S2部分出現異常
Figure2.
Anomalies in the S2 part of CHD-PAH
本文采用了一種閾值檢測算法分割S2，如圖1所示。首先對心音信號進行短時傅里葉變換（short-time Fourier transform，STFT），并使用漢明窗進行分幀，如式(1)所示：
|
其中， t為時間，f為頻率，j為虛數，π為圓周率，x(τ) 為t = τ時的心音信號，ω(τ ? t)為窗函數。心音 x(τ)被分幀后，提取每一幀的短時能量Ei與頻譜擴散Si，如式(2)～式(3)所示：
|
|
其中，xi(n)，n = 1, ···, N表示心音信號的第i幀，N為幀數長度，fi為第i幀的頻率，u1為頻譜中值，si為第i幀的頻譜值， b1與b2為頻譜邊界值。所得Ei與Si，如圖3所示。
圖3
短時能量與頻譜擴散
Figure3.
Short-time energy and spectral diffusion
計算短時能量與頻譜擴散對應的直方圖與直方圖閾值TE與TS，閾值計算如式(4)所示：
|
其中，M1、M2為直方圖中前兩個最大值的位置，W為設定值。根據閾值對序列進行判斷并標記。其中，滿足Ei ≥ TE的為標記點1（flag1），滿足Si ≥ TS的為標記點2（flag2），這些標記被認為是心音S1或S2分量，稱之為待定分量。如圖4所示，根據閾值判斷并標記序列，黑色波形是原始心音信號的頻率質心，綠色波形是待定分量，即被標記為心音S1或心音S2的頻率質心，藍色星號代表S1或S2頻率質心之間的距離，即舒張期或收縮期。
圖4
心音待定分量標記
Figure4.
Suspected components of the heart sound waveform
計算這些待定分量之間的距離（distance，Dist）（以符號Dist表示），如式(5)所示：
|
其中，{flags}表示標記點集合，flagx_i與flagx_i+1分別為兩個距離最近的標記點， Fs表示采樣率。一個心動周期中S1與S2之間的間隔通常小于58 ms[16]，因此實驗中設定了一個58 ms的判定距離。如果待定分量之間的距離小于判定距離，則這些分量會被判定為心音S1或S2。將序列映射到原始心音信號中，根據心音的生理特征，S2與S1之間的信號被定義為舒張期，具有最大的時間間隔[17]。如圖5所示，紅色虛線為狀態序列，根據狀態序列的長度進行選取，最長的一段為舒張期，將舒張期前的分量標記為S2，從而實現了對心音信號中S2部分的精準截取。
圖5
心音分割標記圖
Figure5.
Heart sound segmentation marker chart
1.2 特征提取
心音是由心臟在收縮和開合時血流撞擊產生的振動信號組成[18]。心血管疾病導致心臟結構變化，使得心音出現病理特征。本文選取心音S2部分的長記憶性、信息內容和隨機性作為統計特征用于分類。
1.2.1 高頻分量的分解
DWT將信號分解成多個不同頻率的子帶，其中高頻子帶包含信號中的瞬時變化和細節信息[19]。對于心音信號，高頻分量包含著心臟收縮、瓣膜開合等短暫且快速的變化，因此選擇高頻分量可以很好地描述心音信號的動態特性。此外，直接提取高頻分量還可以避免低頻噪聲的影響[20]，去除降噪步驟，進一步提高算法的速度。DWT需要兩個基本小波來分析信號：父子波φ(t)和母子波ψ(t)。其中，φ(t)用于提取低頻部分，ψ(t)用于提取高頻部分。尺度j下的低頻振蕩v和高頻振蕩ω的離散形式分別由Sj和Dj表示，如式(6)～式(7)所示：
|
|
其中，k表示求和的下界，N表示上界，即從k = 1開始取值，一直取到N。多貝西小波四號（Daubechies-4）用于對S2部分進行三級分解，分解后將312.5 Hz以上的分量認為是高頻分量。在尺度j處，Sj表示信號的總體趨勢，Dj表示其詳細波動。后續的統計特征都是從高頻分量Dj提取的。
1.2.2 統計特征提取
統計特征主要包括Hurst指數、LZC與樣本熵。這些特征分別用于獲取心音高頻分量中的長期記憶性、信息內容和規律性[21]，能有效地描述心音信號S2部分的病理特征。
Hurst指數即有偏的隨機游走，用于衡量時間序列的長期記憶性。心音信號本質上是一種非平穩時間序列。Hurst值大于0.5，表示為一個具有持續性并且極度相關的時間序列；Hurst值等于0.5，表示為一個不相關的時間序列；Hurst值小于0.5，表示為一個非持續不相關的時間序列，本文用重標極差分析法計算Hurst指數。
給定的時間序列{I1, I2, ···, Iq}，有q個分量，對于任意正整數υ≥1(υ=1, 2, ···, n)，計算其平均值e(υ)與方差S(υ)，如式(8)、式(9)所示:
|
|
對q個分量，計算其累計差Z(q)與極差R(υ)，如式(10)、式(11)所示:
|
|
引入無量綱比，通過方差S(υ)與極差R(υ)來計算重標極差Rs(υ)，如式(12)所示:
|
通過計算對應的對數方程，并求取對應的斜率即可得到Hurst系數，其中b是一個常數，H是Hurst指數，如式(13)所示:
|
LZC可量化時間序列的隨機性和復雜性，適用于衡量非線性、非平穩信號的信息內容。LZC對信號中小擾動和噪聲不敏感，因此在生理檢測中可用于確定心音信號的基本模式與復雜性，正常心音通常以重復模式為特征，而異常心音則以缺乏重復模式為特征。
對于一個給定的信號{x1, x2, …, xN}，將其轉化為二進制，轉化公式如式(14)所示:
|
閾值Td為信號{x1, x2, …, xN}平均值。得到yi以后，用c(n)作為yi的復雜度計數器來計算yi中不同字串的數目。c(n)存在著上限，通過b(n)進行歸一化得到LZC值C，如式(15)、式(16)所示:
|
|
樣本熵，是一種衡量時間序列信號復雜性的方法；熵值越低，表示信號具有更高的規律性和可預測性。在心音信號分析中，高的樣本熵值，可能表明心音的不規則性或變異性程度較高，并且相較于其它熵測量方法，樣本熵的優勢在于其穩定性，抗噪、抗干擾能力強。
定義一個長度為m的滑動窗口，從時間序列數據{s1, s2, ···, sN}中提取出所有長度為m的子序列{Sm(1), Sm(2), ···, Sm(N ? m + 1)}，其中Sm(i) = si, si + 1, ···, si + m ? 1，對于每個子序列，計算其它子序列與該子序列距離小于等于r的數量，表示為Cm(r)。其中，閾值r為原始信號的標準差與自定義權值w的乘積，如式(17)所示:
|
對于長度為m+1的子序列，計算其它子序列與該子序列距離小于等于r的數量，表示為Cm+1(r)，計算樣本熵（以符號SampEn表示），如式(18)所示:
|
1.3 分類識別
XGBoost，是一種高效的機器學習算法，它采用多個決策樹模型的集成來解決二分類和多分類問題。該算法通過構建一系列的決策樹模型，并進行結合，每個決策樹都基于前面決策樹的殘差誤差構建，因此，能夠不斷提高分類效果。XGBoost的數學描述如式(19)所示:
|
其中，t=1, 2, …, T，T表示分類回歸樹的總數，a=1, 2, …, N，Za為輸入，ma為實際值，為預測值，ft表示第t棵分類回歸樹。再設置XGBoost的目標函數obj(θ)，如式(20)所示：
|
其中，為損失函數，用于衡量實際值ma與預測值的偏差值。為正則項，對t個分類回歸樹的復雜度進行求和。
XGBoost不斷優化后，得到第k棵決策樹fk的模型fk(Za)，第k個決策樹的目標函數H(k)，如式(21)所示：
|
貝葉斯優化算法，是一種高效的超參數優化算法，它利用先驗信息不斷優化目標函數，在短時間內找到更好的超參數組合。該算法具有快速找到最優解、強魯棒性和通用性的優點[22]。在預處理與特征提取后，本文采用貝葉斯優化算法來獲取合適的分類模型參數。
2 實驗與分析
2.1 數據與說明
實驗所用心音數據集采集于云南省阜外心血管病醫院，所用采集設備為實驗室自行研發的心音信號采集設備，傳感器為The ONE心音傳感器（Thinklabs Medical LLC Inc.，美國）。招募的志愿者年齡在6個月～18歲，未成年受試者監護人及成年受試者均已簽署知情同意書。每個志愿者按5個心臟聽診位置各采集20 s心音信號，采樣頻率為5 000 Hz。志愿者都經過超聲心動儀檢測，CHD-PAH患者還經過臨床醫生在術前與術中檢測患者的壓力進行確認，以保證數據的可靠性。本次研究所用的心音數據的采集通過了云南大學人體研究材料倫理委員會及云南省阜外心血管病醫院醫學倫理委員會的批準并授權使用（CHSRE2021008、IRB2020-BG-028）。
從前述采集的心音數據集中選取345名志愿者的1 725例心音數據，志愿者年齡限制18歲以下，這是為了保證訓練模型在青少年早期篩查中的有效性。其中，正常、CHD與CHD-PAH心音比例為1:1:1，以保證樣本的平衡性。CHD心音包括室間隔缺損、房間隔缺損、動脈導管未閉等常見疾病。將數據按7:2:1的比例劃分為訓練集、測試集、驗證集。
2.2 實驗環境
實驗所用配置：中央處理器i5-11400H@2.70GHz（Intel Inc.，美國)，獨立顯卡NVIDIA GeForce RTX3060（Nvidia Inc.，美國）。信號處理軟件Matlab2021b（MathWorks Inc.，美國），深度學習框架TensorFlow 2.0（Google Inc.，美國），編程語言Python 3.7（Python Software Foundation Inc.，美國）
2.3 評價指標
使用靈敏度（sensitivity，Se）、特異性（specificity，Sp）、精準率（precision，Pr）、Acc等指標用于評價分類器的性能，如式(22) ～ 式(25)所示：
|
|
|
|
其中，真陽性（true positive，TP）表示正類別中正確分類樣本的數目；真陰性（true negative，TN）表示負類別中正確分類樣本的數目；假陰性（false negative，FN）表示負類別中錯誤分類樣本的數目； 假陽性（false positive，FP）表示正類別中錯誤分類樣本的數目。
F1分數，是一種兼顧了Pr與召回率（recall, Re）的分類模型評價指標，如式(26)、式(27)所示：
|
|
修正Acc（modified Acc，MAcc）是根據復雜生理信號研究資源網（research resource for complex physiologic signals，PhysioNet）心音挑戰賽中所提出的，對Sp和Se指標添加不定權系數0.5，如式(28)所示：
|
2.4 實驗方案設計
本文根據參數設置對結果的影響進行討論，貝葉斯參數尋優算法對結果的影響如圖6所示。為了凸顯本文算法速度的優勢，與小波降噪、EEMD去噪進行對比，計算處理1 725例心音的運行時間與分類結果，結果如表1所示。
圖6
貝葉斯參數優化算法尋優圖
Figure6.
Optimization by Bayesian parameter optimization algorithm
表1
預處理運行時間與分類效果
Table1.
Pre-treatment running time and classification results
為了驗證統計特征對分類的提升效果，本文還進行了特征消融實驗，分別使用三個特征單獨進行分類，來區分正常心音、CHD心音與CHD-PAH心音，分類結果總結如表2所示。與文獻[9, 13-15]中的聲學特征MFCC、MFSC進行對比，其中MFCC采用與人耳結構相似的三角濾波器組，MFSC更注重對信號在高低頻內的特征提取。分類模型選擇KNN與RF。KNN是一種基于距離度量的非參數分類方法，適用于小規模數據集；而RF通過構建多個決策樹來進行分類，能與XGBoost形成對比，分類結果如表3所示。
表2
消融實驗分類結果
Table2.
Classification results of ablation experiments
表3
聲學特征對比實驗分類評價指標
Table3.
Classification evaluation metrics for acoustic features comparison experiment
為了驗證本文算法的有效性，選取近兩年文獻[23-24]提及的心音分類算法，以本文數據集進行訓練，對比分類結果。文獻[23]對心音進行改進的自適應噪聲完全EEMD（the improved complete EEMD with adaptive noise，ICEEMDAN），提取分解后本征模態函數（intrinsic mode function，IMF）的多尺度樣本熵，通過邏輯回歸（logistic regression，LR)進行分類。文獻[24]中對心音進行自適應噪聲完備EEMD（complete EEMD with adaptive noise，CEEMDAN），提取IMF的排列熵與支持向量機（support vector machine，SVM）結合后實現分類，分類結果總結如表4所示。
表4
分類算法對比實驗分類評價指標
Table4.
Classification evaluation metrics for comparison of classification algorithms
所有實驗中，機器學習都通過貝葉斯優化算法進行參數尋優，XGBoost中決策樹的數量設為150，學習率設為0.1，最大深度設為5。KNN中k值設為7。RF中決策樹的數量設為300，最大深度設置為6。
2.5 實驗結果與分析
2.5.1 貝葉斯參數優化實驗
如圖6所示，對XGBoost的參數進行了貝葉斯優化算法尋優，其中學習率的范圍設定在0.1～1.0之間，最大深度設定在3～8，決策樹的數量設定在10～600。圖6中展示了10組尋優出來的參數以及對應的Acc，參數的順序為學習率、最大深度、決策樹的數量。貝葉斯優化算法在短時間對參數進行尋優，獲得了分類Acc較高的一組參數，即學習率0.1，最大深度5，決策樹數量150，Acc達到了80.45%。
2.5.2 預處理實驗
如表1所示，為本文算法（S2分割+高頻分量）與文獻[4]、文獻[20]中去噪算法的對比實驗，小波降噪與EEMD降噪是心音分類中有效的預處理算法。可以看出，由于直接提取高頻分量，省略了降噪步驟，本文模型在運行時間上遠低于小波降噪與EEMD降噪算法。同時，小波降噪與EEMD降噪過程中可能將一些微弱的病理信息去除，導致分類效果不佳。本文算法直接去除低頻分量，雖然會導致低頻中部分特征被舍棄，但高頻分量中的特征能保證Acc達到80%以上，實現了快速有效的診斷。
2.5.3 消融實驗
消融實驗結果如表2所示，Hurst指數、LZC和樣本熵三個特征都有效地提取了心音高頻分量的部分特征，在三分類實驗中具有一定的分類效果，其中LZC與樣本熵的Acc都達到了70%以上，但同時使用三個特征進行分類的Acc達到了80%以上，各項指標也遠高于單獨使用，驗證了三個特征組合后對分類效果的提升。
2.5.4 三分類實驗
三分類實驗結果如表3所示，對已經分割出S2部分的心音進行特征提取與分類，將不同的特征和分類器進行組合，得到分類結果與相關指標。基于高頻統計特征的XGBoost模型分類效果優于其它算法，表現為：① 高頻統計特征相比于MFCC與MFSC在Acc 、MAcc和F1三個評價指標上更優。MFCC的核心是構建一個非均勻分布的頻域濾波器組，其特點是低頻區域分布密集、高頻區域分布稀疏，忽略了信號的相位信息和高頻細節，因此在PAH與CHD-PAH的分類中效果不佳。通過對比Acc值，證實了高頻統計特征能更好地提取CHD-PAH的病理特征。通過對比MAcc值，表明該特征不易受環境噪聲影響。通過對比F1值，得出使用該特征進行分類得到的假陰性更少。② 聲學特征MFCC、MFSC與本文特征在XGBoost模型上各項評價指標都高于RF與KNN，體現了XGBoost在小樣本多分類任務上的優越性。
2.5.5 對比分類實驗
分類算法對比實驗結果如表4所示，將文獻[23-24]心音分類算法用于本文的CHD-PAH數據集上進行三分類實驗，并與本文算法進行比較。
從結果上看，三種算法采用的特征與分類器在三分類上都有一定效果，但本文算法在Acc、Pr、Re和 F1 值上都優于其它方法。① 對比Acc值，證實了分割S2來進行后續特征提取，能更好地提供病理信息，提高了篩查中的檢出率。② 通過對比MAcc值，表明直接提取高頻分量，去除低頻部分的噪聲，可提高算法抗噪聲能力。③ 通過對比F1值，得出使用S2的高頻統計特征相較多尺度樣本熵與排列熵，可提取到的病理信息更豐富，得到更少的假陰性病例。④ 采用多個決策樹模型的集成，XGBoost在小樣本的分類效果也要優于SVM與LR。
綜上所述，基于心音S2部分高頻分量的統計特征，有效提取了CHD-PAH的病理特征，結合XGBoost分類模型，在三分類綜合評價指標上相比現有算法有所提升。
3 結論
本研究的主要目的是設計一個計算機輔助診斷系統，以區分正常、CHD與CHD-PAH心音。本文通過自適應分割出心動周期中S2部分，能更好地凸顯CHD-PAH的病理特征，再利用S2的高頻分量統計特征來訓練貝葉斯優化算法調整的XGBoost模型。本研究的主要特點在于省略了預處理中降噪步驟，通過DWT將原始信號縮短并提取了其高頻分量的主要病理特征，這使得特征提取更為快速，整體算法所需時間與資源量低，在三分類上Acc達到80.45%，為CHD-PAH快速輔助診斷提供一種可行的思路。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：楊炫鍇負責實驗構思與設計、數據采集、數據分析和論文寫作；孫靜負責實驗指導、論文寫作指導和數據收集；楊宏波負責醫學指導和數據收集；郭濤負責醫學指導；潘家華負責醫學指導和數據審查；王威廉負責理論指導、實驗設計指導、論文整體審查和寫作指導。
倫理聲明：本文所使用的心音數據得到云南大學人體研究材料倫理委員會以及云南省阜外心血管病醫院倫理委員會批準采集并授權使用（CHSRE2021008、IRB2020-BG-028）。
