多窗口時頻重排有助于提升對心音進行巴克頻譜系數（BFSC）分析的時頻分辨率。為此，本文提出一種基于多窗口時頻重排的BFSC特征提取與深度學習結合的心音分類新算法。首先，對隨機截取的心音片段進行幅值歸一化等預處理，然后分別用多個正交窗口對心音做分幀處理，及計算基于短時傅里葉變換的時頻重排，將得到的各獨立頻譜通過算術平均計算出平穩的頻譜估計。最后，通過巴克濾波器組提取該重排頻譜的BFSC作為特征。本文采用卷積網絡與循環神經網絡作為分類器，對提取的特征進行模型比較與性能評估。最終，多窗口時頻重排改進BFSC的方法提取了更具有辨別力的特征，二分類準確率達到0.936，靈敏度為0.946，特異度為0.922。研究結果表明，本文所提算法無需分割心音，隨機截取心音片段，大大簡化了計算流程，有望用于先天性心臟病篩查。
引用本文： 夏軍, 孫靜, 楊宏波, 潘家華, 郭濤, 王威廉. 基于多窗口時頻重排的巴克頻譜系數心音分類算法研究. 生物醫學工程學雜志, 2024, 41(1): 51-59. doi: 10.7507/1001-5515.202212037 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
全球因心血管疾病死亡的人數占總死亡人數的31%，而在中國這一比例更高，因心血管疾病死亡的人數約占總死亡人數的40%[1]。先天性心臟病（congenital heart diseases，CHD）是一種嚴重影響青少年兒童身體健康的心血管疾病，若未得到及時治療，還會對患者的生命構成威脅，因此對嬰幼兒進行CHD早期篩查就顯得極為重要。然而，傳統對CHD進行早期篩查的人工聽診方式很容易忽略心音中的隱藏信息，所以近年來隨著計算機技術的發展，心音自動分析在識別先天性心臟結構缺失及心血管疾病醫療保健方面的應用越來越廣泛而深入。
心音自動分析的流程，包括：預處理、特征提取、分類識別。其中，特征提取一直是心音分類的重要研究內容。異常心音在時域或頻域上表現出與正常心音顯著不同的特征，而這種差異是影響異常心音識別的關鍵因素。因此，為了準確識別異常心音，必須選擇合適的特征表示方法進行特征提取。傳統的心音分類研究關注于從單個域（如時域、頻域、小波域等）提取特征[2-6]，但文獻[7]的研究表明，單獨的時域或頻域特征并不能很好地表征心臟的病理信息，所以近年來國內外的研究多采用時頻域特征進行分析。
Chen等[8]計算心音的短時傅里葉變換（short-time Fourier transform，STFT）并送入卷積神經網絡（convolutional neural networks，CNN）進行分類研究，在測試樣本上達到了0.954的準確率。Markaki等[9]采用了基于STFT的時頻重排頻譜作為特征，改善了頻譜時頻表示的分辨率，準確率達到了0.958。Lubis等[10]則是提取了巴克頻率倒譜系數（Bark-frequency cepstrum coefficient，BFCC）作為特征,分類準確率為0.791。Rubin等[11]對心音進行分割，提取梅爾頻率倒譜系數（Mel-frequency cepstrum coefficient，MFCC）并送入CNN進行分類，二分類準確率為0.848。Kui等[12]對分割的心音提取梅爾頻譜系數（Mel-frequency spectral coefficient，MFSC），然后用CNN對所提特征進行分類，最后采用多數投票算法得到最優分類結果，二分類準確率達到 0.938。上述算法仍有進一步改善分類性能的空間，比如：文獻[8]取得較好的分類性能但使用的數據量較少，且正負樣本比例不均衡，缺乏大量驗證，不利于推廣。文獻[9]使用時頻重排銳化了STFT頻譜，卻忽略了頻譜泄露引起的高方差問題。文獻[10]沒有改進BFCC對噪聲敏感的問題。文獻[10]和文獻[11]選擇了公開數據集，而公開數據集缺乏專門針對CHD兒童患者的相關數據。文獻[12]分割心音信號需要同步心電數據作為對照，過程較為繁瑣，且分割錯誤對分類準確率影響較大。
另一方面，分類器的選擇同樣是受到研究人員強烈關注的問題。深度神經網絡（deep neural network，DNN）是由機器學習發展而來的，通過堆疊更加復雜的網絡結構，從輸入中自動學習深度特征。文獻[11]和文獻[12]采用了CNN，而文獻[13]則采用了門控循環單元（gated recurrent unit，GRU），這些研究表明DNN在心音研究領域得到了廣泛的運用。
綜上考慮，本文提出了一種新的心音分類算法。該算法采用多窗口時頻重排（multiple window reassigned spectrogram，MWRS）與巴克頻譜系數（Bark-frequency spectral coefficient，BFSC）相結合的方式（MWRS-BFSC）提升特征的表達能力，并運用深度學習對算法的分類性能進行驗證評估。本文將MWRS與非均勻濾波器組相結合的方法運用到心音分析領域，由于無需分割心音，該算法的復雜度得到了簡化，有望提升性能并應用于CHD早期篩查。
1 方法
1.1 算法框架
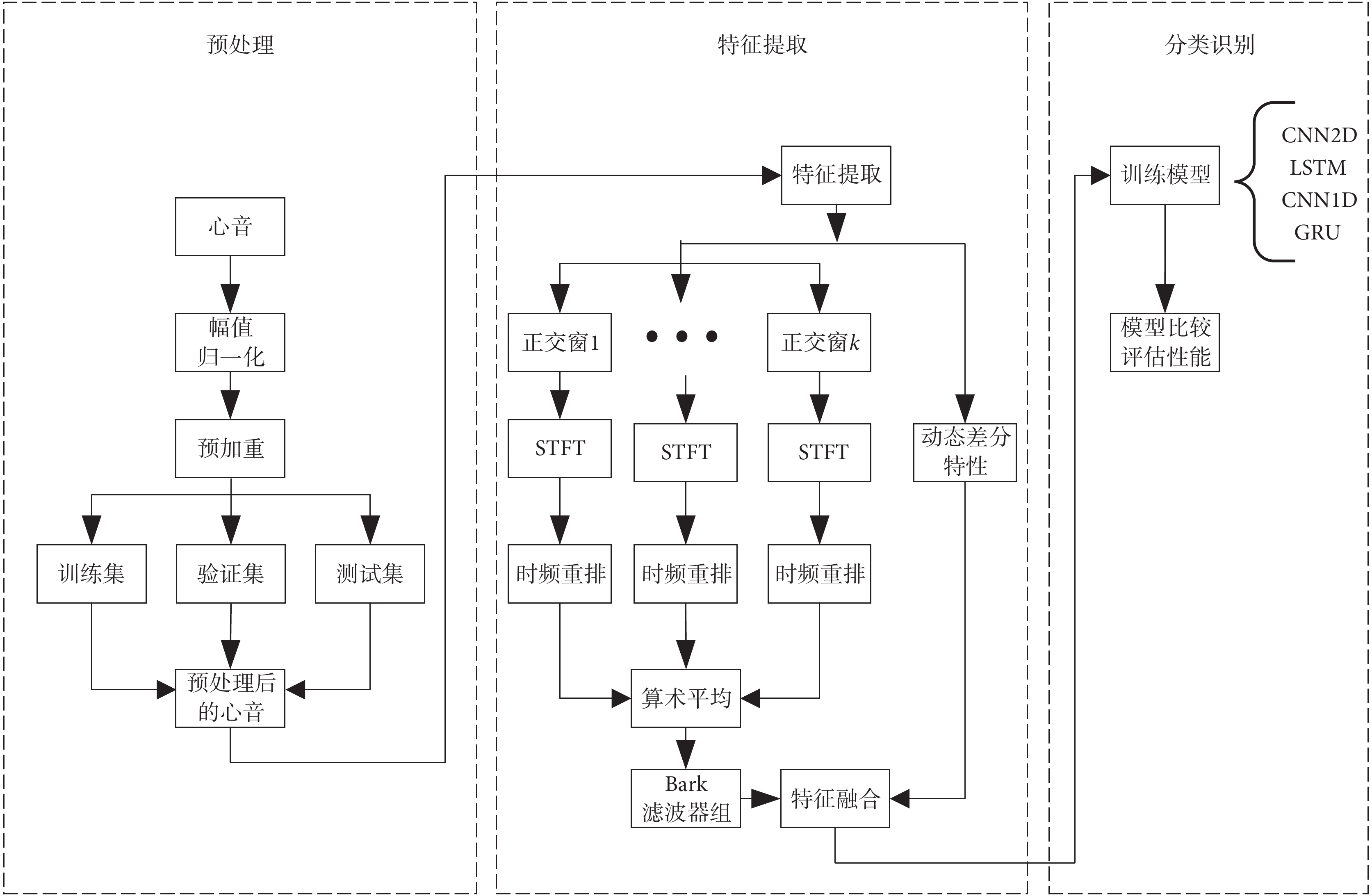
本文的分類算法流程如圖1所示，具體步驟為：① 對原始心音數據進行幅值歸一化、預加重處理。② 對預處理后的心音分別采用多個正交窗口（正交窗1～正交窗k）計算STFT。③ 對子頻譜計算時頻重排，得到各自的重排頻譜。④ 將得到的各重排頻譜進行算術平均。⑤ 使平均后的頻譜通過巴克（Bark）濾波器組，并且進行對數運算得到BFSC特征，再融合動態差分向量。⑥ 輸入分類網絡得到分類結果，并對結果進行評估。
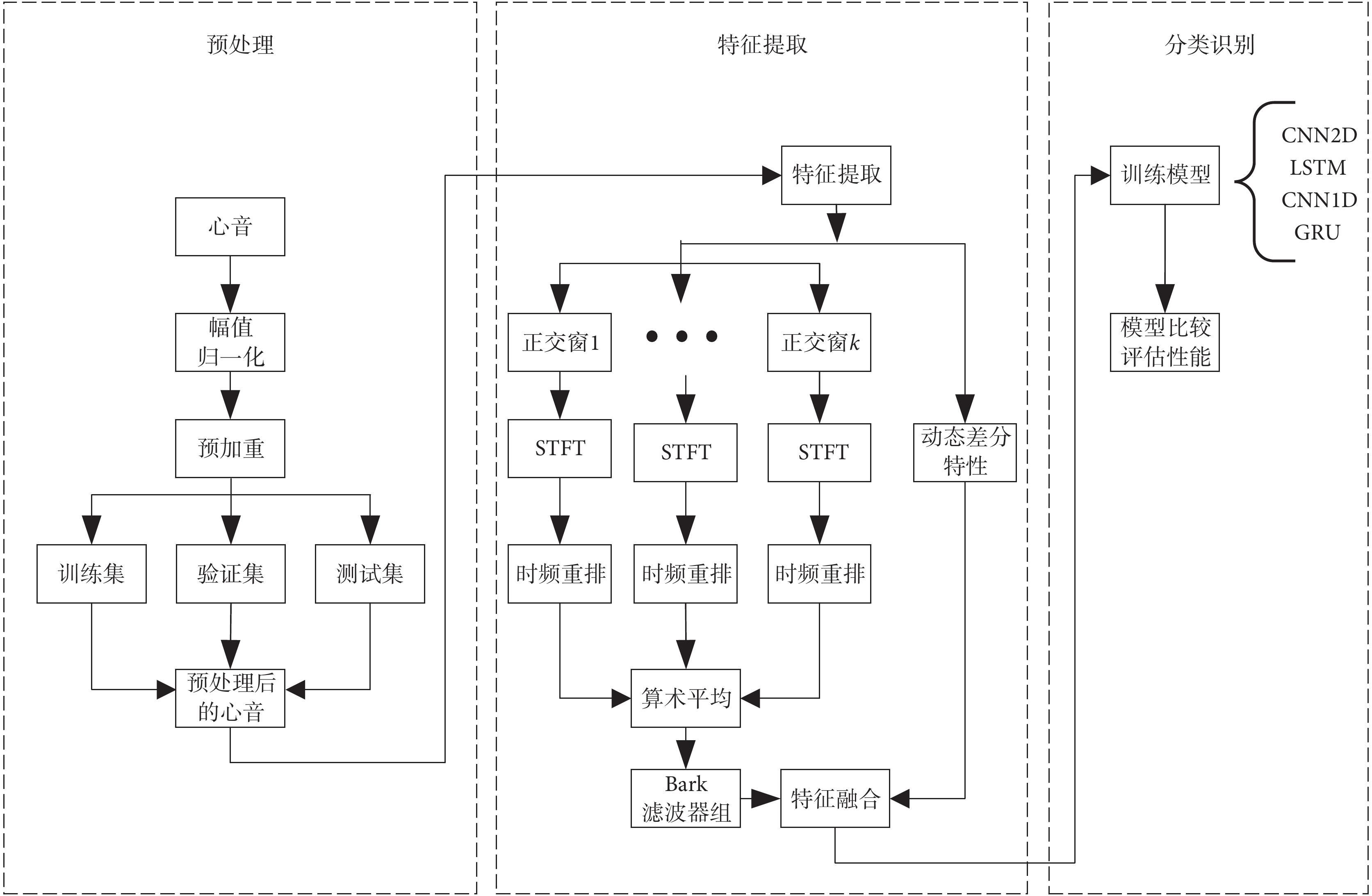圖1
算法流程圖
Figure1.
Algorithm flow chart
1.2 數據來源
研究數據源于課題組在云南阜外心血管病醫院以及云南省各地州開展CHD免費篩查救治活動中采集的心音數據所構建的數據庫。心音數據由課題組自主研發心音采集裝置與The ONE電子聽診器（Thinklabs Medical LLC，美國）進行采集。在安靜、溫暖的環境下，CHD患者保持仰臥位且保持胸部裸露，保證電子聽診器與患者胸壁直接接觸，完整記錄每位患者的五個心臟聽診區信息。每一例數據時長為20 s，采樣頻率為5 000 Hz。
本次實驗采用心音樣本共5 000例。心音樣本來自1 000名心音志愿者，志愿者年齡均在8個月至18歲，正常、異常樣本比例1∶1。正常數據是從健康人群所采集的心音，異常數據包括房間隔缺損、室間隔缺損、動脈導管未閉、卵圓孔未閉。實驗數據按照7∶2∶1的比例劃分為訓練集、驗證集和測試集。整個采集試驗的全過程通過了倫理審查，且全體志愿者均簽署知情同意書自愿提供心音樣本。研究所使用的心音數據已獲得云南大學人體研究材料倫理委員會（批文編號：CHSRE2021008）以及云南省阜外心血管病醫院倫理委員會（批文編號：IRB2020-BG-028）的授權使用。
1.3 預處理
傳統的心音預處理需要對心音的各成分進行準確分割，該步驟通常是基于同步心電信號來實現的。由于目前精準分割心音仍是尚未攻克的難題，且分割不準確會嚴重影響分類準確率。因此，本研究預處理采取隨機截取心音片段，并對信號進行幅值歸一化、預加重、分幀加窗操作。正常人群的心率為60～100 次/min，頻率范圍在20～500 Hz[14]，考慮到高頻成分與心臟異常產生的雜音有關，采用預加重突出高頻雜音成分信息。心音是非平穩信號，STFT的窗函數長度應該與心音的短時平穩時長相匹配。為了改善窗函數在邊界處產生的問題，需要在各幀之間設置重疊，保證幀與幀之間的關聯性。本文選擇幀長為256個采樣點（51.2 ms），幀移為128個采樣點，既保證窗內信號片段的平穩性，又可以獲得良好的時頻分辨率。
1.4 特征提取
MFCC能夠模擬人類聽覺感知，因此在語音信號處理領域被廣泛應用于提取聲學信號的特征。近年來，MFCC也被應用于心音分類領域，以識別異常心音。但心音相較于語音頻率偏低，其能量主要集中在低頻段，低頻信息相對重要。BFCC與MFCC相比，不僅同樣具有低頻排列密集、高頻排列稀疏的特點，而且在低頻段具有更強的頻率感知能力[15]。而BFSC作為BFCC的一種特殊形式，省略了離散余弦變換（discrete cosines transform，DCT），保留了更多相關信息。
1.4.1 BFSC
人耳對聲音頻率的感知是非線性的，Bark濾波器組模擬人耳聽覺感知特性，低頻排列密集、高頻排列稀疏，可以從心音信號中捕捉更具辨識度的特征，得到良好而緊湊的時頻表示。線性頻率轉換為Bark頻率（以符號B表示）的計算方法如式(1)所示：
 |
其中，f代表頻率，sinh(·)代表雙曲正弦函數。
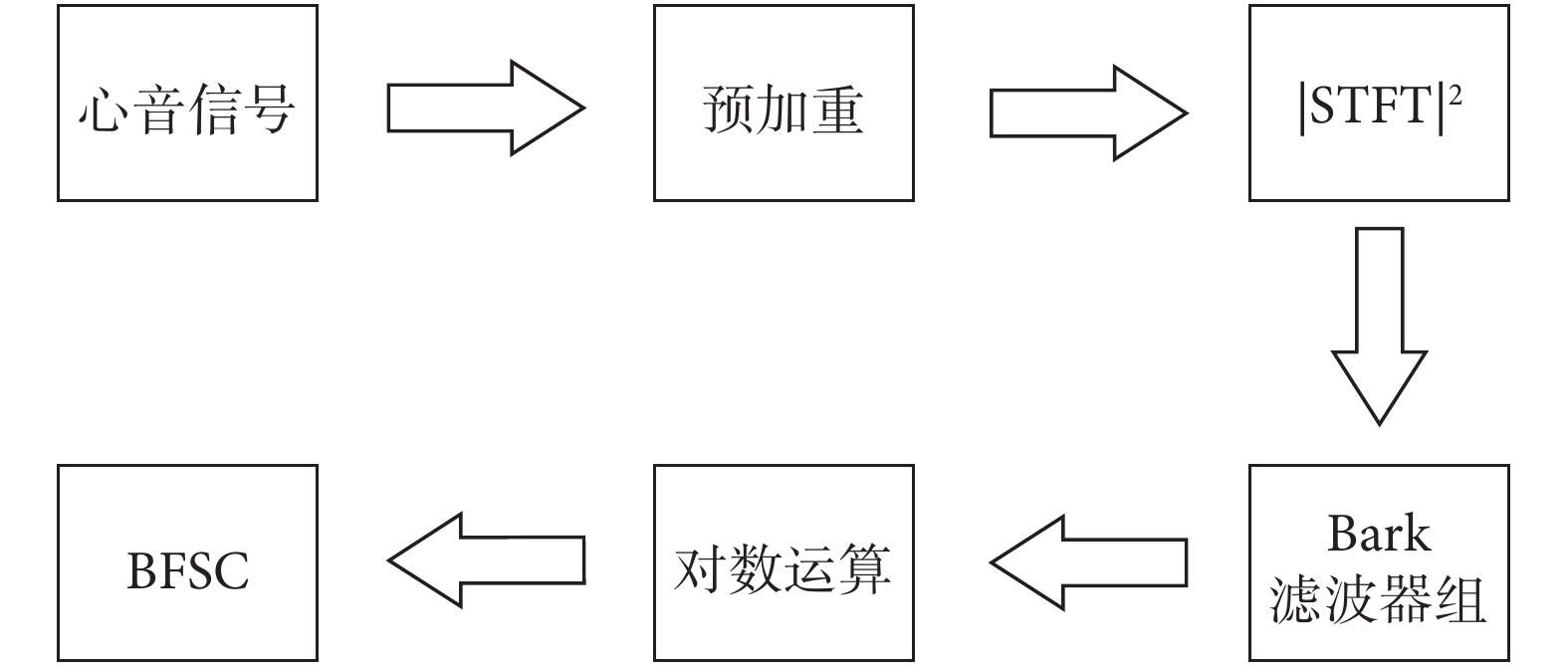
BFSC的提取步驟:首先對心音信號做預加重處理，再計算出信號的STFT，最后通過預先設定好的Bark濾波器組從頻譜中提取BFSC，具體流程如圖2所示。
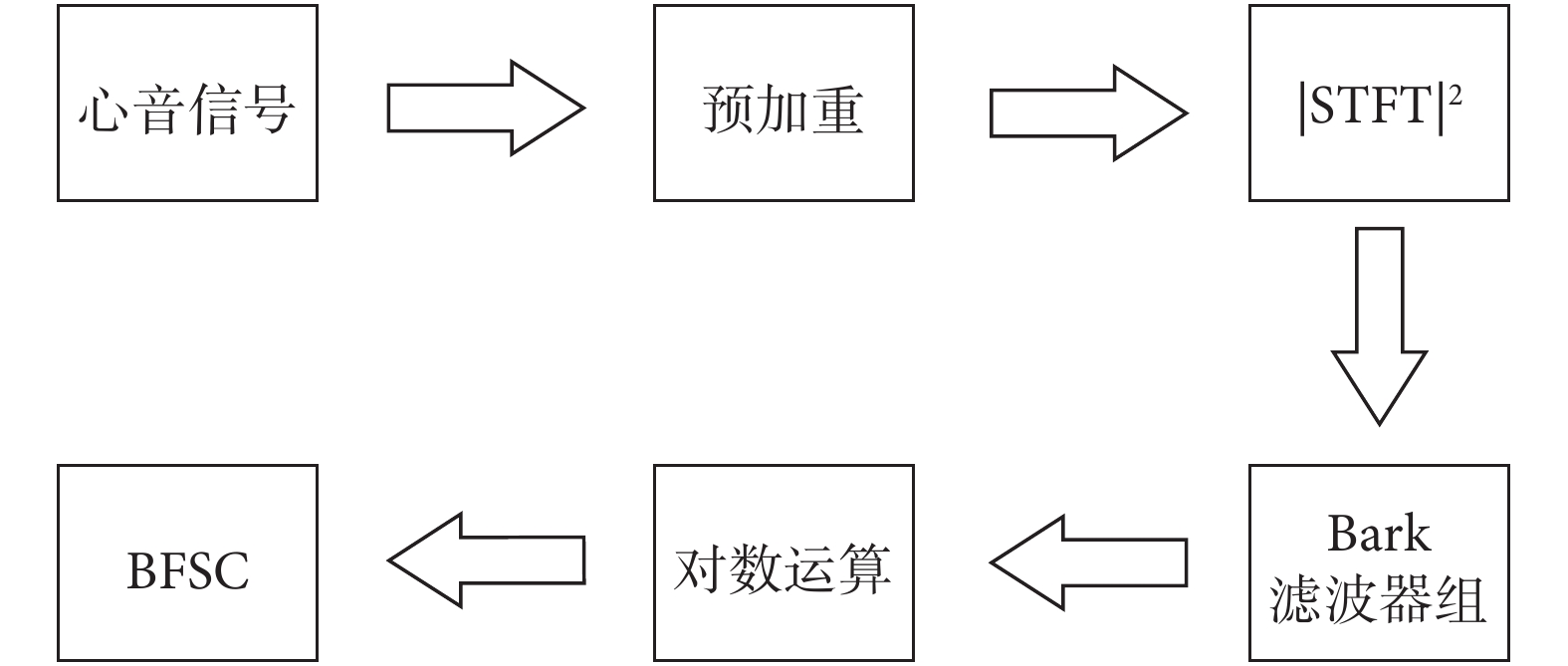圖2
BFSC算法流程圖
Figure2.
BFSC algorithm flow diagram
然而，BFSC存在一些問題，如對噪聲敏感、高方差的頻譜泄漏以及無法包含心音的動態細節等。針對上述問題，本研究對BFSC的提取過程進行了改進。
1.4.2 時頻重排
心音是一種非平穩信號，STFT作為傳統的時頻分析方法，被廣泛應用于心音信號的分析和特征提取。STFT（以符號S表示）的計算公式，如式(2)所示：
 |
其中，x(τ)代表心音信號，h(t)代表窗函數，j代表虛數單位，f代表頻率，π代表圓周率。相應的能量譜圖（以符號E表示）計算方法如式(3)所示：
 |
其中，t代表時間，w代表頻率，S代表STFT時頻譜圖，x代表心音信號，h代表窗函數。
然而，傳統時頻分析在時域和頻域受到限制，導致在第一心音、第二心音處的頻譜表現出能量彌散現象[16]。時頻重排是改善時頻能量彌散的重要方法[17]，其目的在于銳化時頻表示，提高時頻譜圖的分辨率。因此，本文采用時頻重排的方法來改善傳統時頻分析時頻域上的能量彌散問題，重點刻畫心音的病理信息。
首先，根據能量譜圖計算出每個點在時域、頻域上的偏移量，并將譜圖中每個點的能量值，按照其計算好的重排位置，分配到時頻重排后的譜圖中。時頻重排譜圖（以符號RS表示），計算方法如式(4)所示：
 |
其中，δ(·)代表沖激函數，
代表時間移位向量，
代表頻率移位向量，α、β為積分變量，表示能量譜圖在時頻域上的坐標。
時頻重排的時間、頻率向量計算公式如式(5)～式(6)所示：
 |
 |
其中，ζ(·)和Ψ(·)分別表示取實部與虛部，ct與cw分別代表時間移位向量與頻率移位向量的伸縮因子。
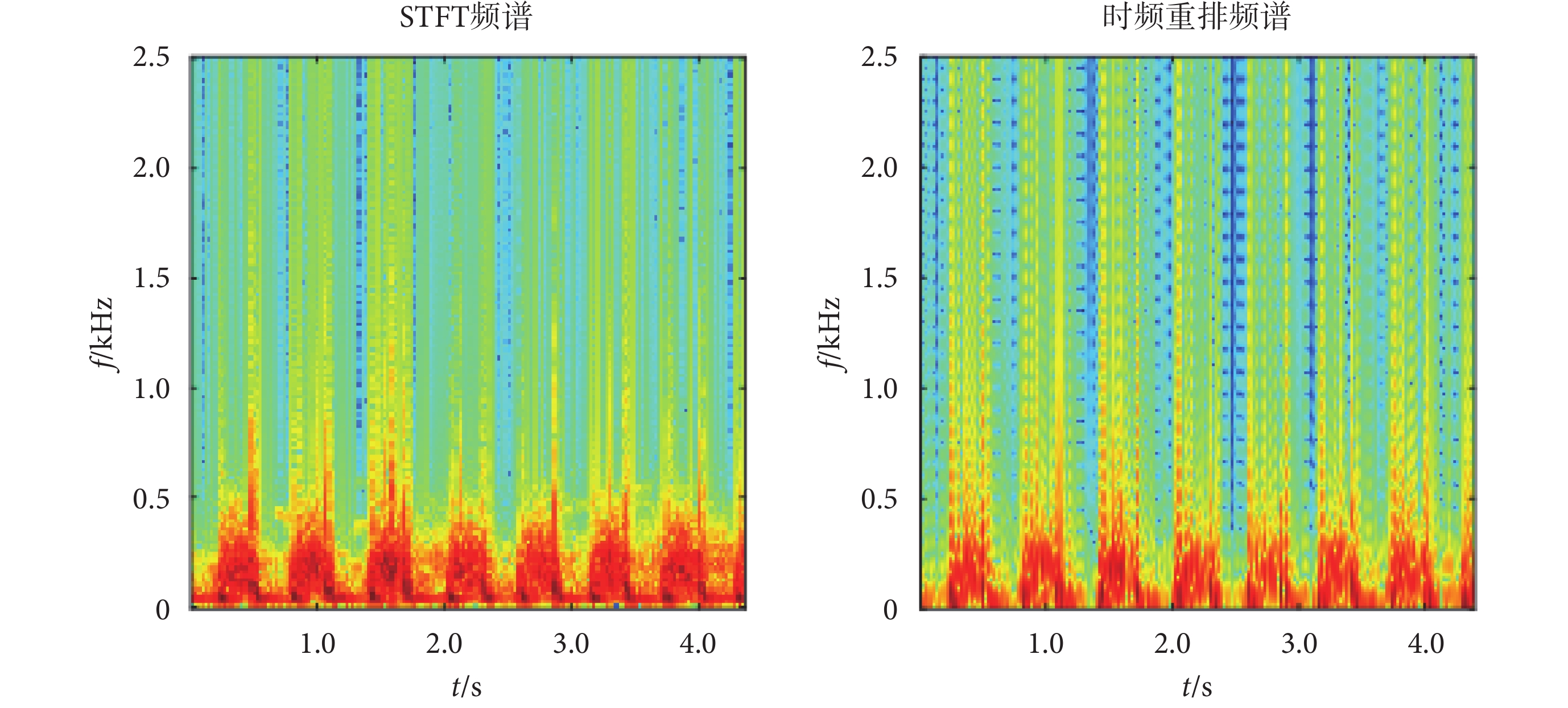
由式(4)～式(6)可以知道，時頻重排不以(t,w)作為時頻域的幾何中心進行分布，而是計算心音時頻譜圖中任意點附近的能量中心作為分布[18]。時頻重排頻譜如圖3所示。
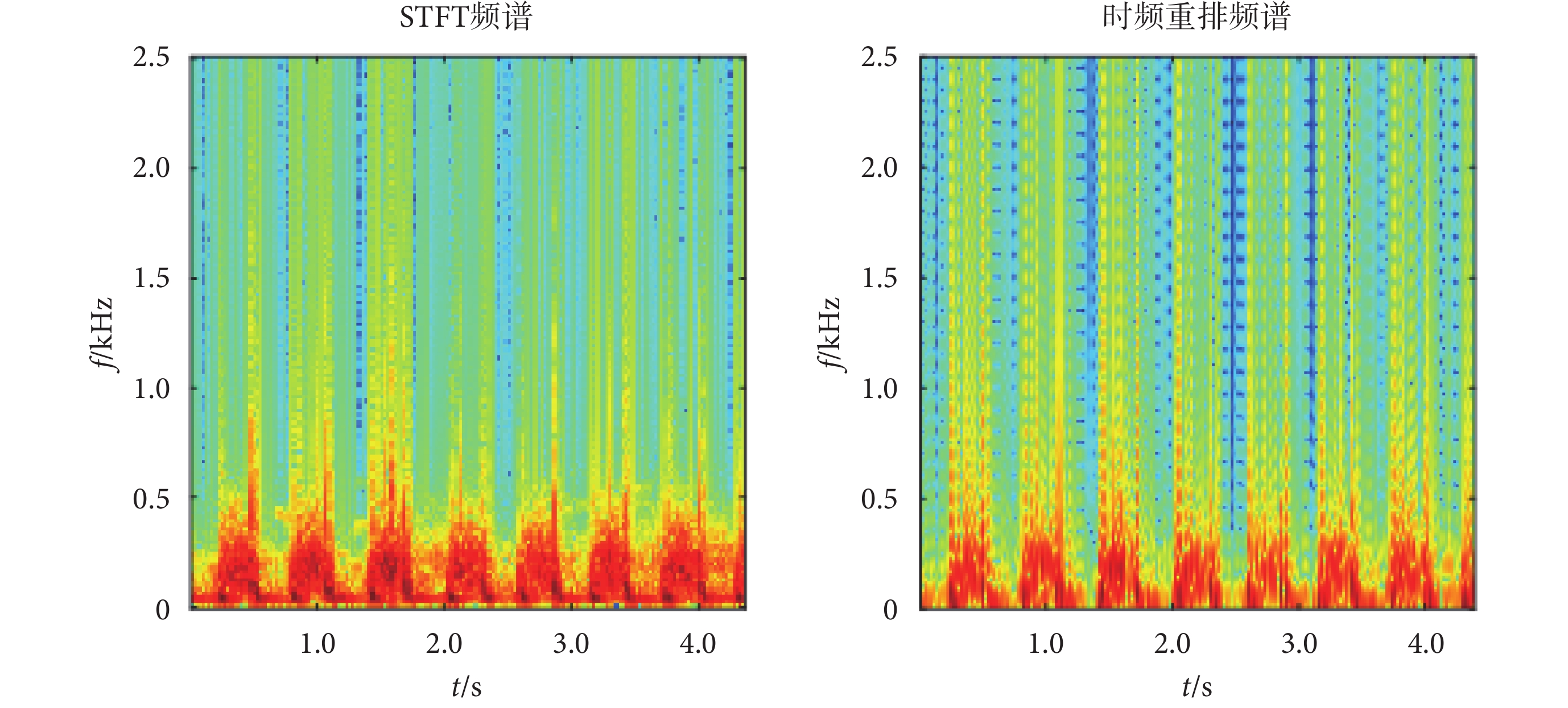圖3
重排頻譜對比圖
Figure3.
Comparison chart of reassignment spectrogram
由圖3可以知道，時頻重排提高了頻譜圖的分辨率，同時由于該方法保留了時間平移不變性以及能量守恒特性，可以更精確地表示信號的時頻特性，進而提高自動分類的準確率。
1.4.3 多窗譜分析
心音的時頻重排提高了頻譜的分辨率，卻仍存在一些問題，如頻譜泄露引起的高方差以及心音信號臨床采集過程中存在的噪聲干擾等。考慮到以上存在的問題，本文采用多窗譜分析改進時頻重排，提高頻譜估計的精度和可靠性。與單獨窗口的時頻重排相比，MWRS具有更強的噪聲魯棒性，并且能夠進一步改善頻譜的能量定位。
（1）正交窗函數
多窗譜分析最初使用的窗函數是長橢球函數，但是該窗函數對瞬態信號表現不好且在時頻域內并不是最佳能量集中，而在Daubechies[19]的研究中表明，埃米特（Hermite）函數作為時頻窗口能表現出更好的時頻集中效果。k次Hermite窗函數（以符號hk表示）定義如式（7）所示：
 |
可以證明Hermite窗函數具有正交性[20]，其正交性保證了各子頻譜之間較小相關性，算術平均后可減小頻譜方差。Hermite窗函數的正交性如式(8)所示：
 |
其中，m代表第一個窗函數的階數，n代表第二個窗函數的階數。
（2）計算流程
采用多個正交窗口對心音信號進行頻譜分析，對于每個窗函數得到的頻譜估計結果計算算術平均來減小頻譜估計方差，得到心音信號的平穩頻譜估計。這種方法在提高精度和減少震蕩方面有較好的改善。多窗譜（以符號M表示）計算公式如式(9)所示：
 |
其中，k代表窗口的個數，dk代表加權因子。
綜上所述，本文選擇正交Hermite窗函數，窗口數目k為4，加權因子dk采用平均加權的方式[21]。MWRS-BFSC以及其一階、二階差分向量進行融合，提高了特征對心音的表征能力，改善了分類性能。
1.5 分類識別
近年來，深度學習作為人工智能的主要發展方向，主要應用于圖像處理、多媒體學習、生物醫學、自然語言處理等方面。常見的傳統網絡結構有CNN與循環神經網絡（recurrent neural networks，RNN）；其中，二維（two-dimention，2D）CNN（CNN2D）被運用在圖像處理、目標檢測等領域，RNN與一維（one-dimention，1D）CNN（CNN1D）等則在處理時間序列領域取得良好的成果，三維CNN則被運用于視頻處理。
1.5.1 網絡搭建
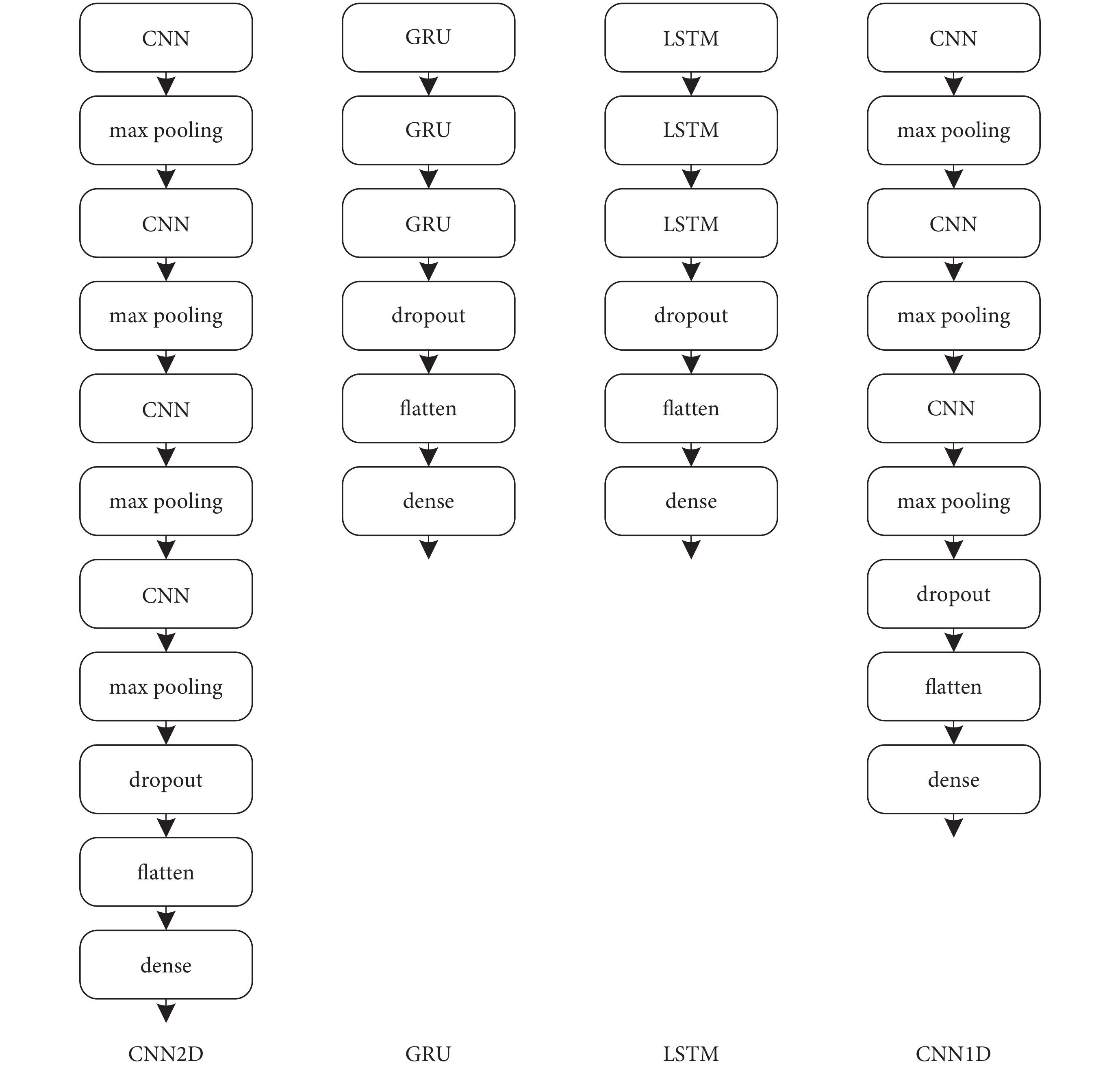
本文在評估上文所提取特征的分類性能時，考慮到不同的神經網絡對輸入特征的不同側重，搭建了四種不同的網絡結構：CNN2D、CNN1D、GRU、長短時記憶網絡（long short-term memory，LSTM）。四種網絡的結構如圖4所示。圖4的網絡結構中課題組已證實，每一個網絡結構經過驗證更多的層數不會帶來更好的分類效果，反而會增大過擬合風險。四種網絡結構中，CNN2D采用了四層卷積、池化結構，四層卷積層的卷積核的數量分別是32、64、64、128，卷積核大小為3 × 3，步長為1 × 1，激活函數為線性整流函數（rectified linear unit，ReLU）。CNN1D則采用三層卷積、池化結構，每一層卷積層的卷積核的數量為34，卷積核大小為3 × 1，步長為1 × 1，池化核大小為2。LSTM、GRU是RNN的常見結構，采用的RNN均選擇三層結構，每一層神經元個數為46，激活函數為雙曲正切函數（hyperbolic tangent，tanh）。圖4中四種網絡結構優化器均選擇自適應矩估計（adaptive moment estimation，Adam）來加快模型的擬合速度，提高模型性能，學習率為0.000 43。池化層均使用最大池化（maxpooling）。展平層（flatten）前都加入隨機失活層（dropout），數值均為0.5，并在最后連接了密集連接（dense）層。分類器均選擇S型生長曲線（sigmoid）函數。
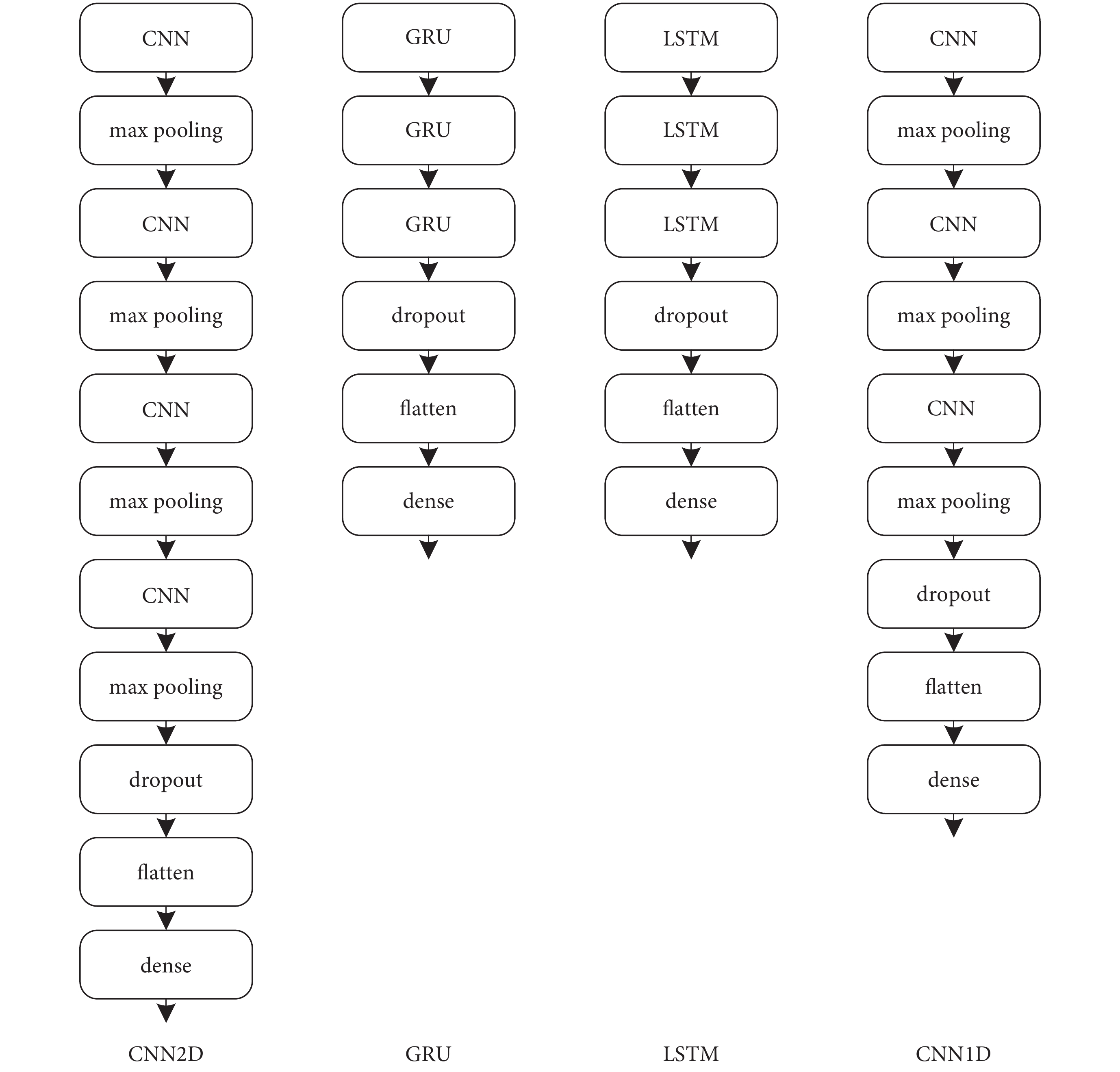圖4
深度學習網絡結構圖
Figure4.
Structure graph of deep learning network
2 實驗與分析
2.1 實驗環境
本實驗所用硬件配置為：中央處理器(Ryzen 7 5800H @ 3.20 GHz，AMD，美國)，獨立顯卡(NVIDIA GeForce RTX3060 6GB，Nvidia，美國)。深度學習框架為TensorFlow 2.4(Google，美國)，編程語言為Python 3.7(Python Software Foundation，美國)。
2.2 評價指標
本文采用四種評價指標評估模型性能，其中包括準確率（accuracy，Acc）、特異度（specificity，Sp）、靈敏度（sensitivity，Se）、F1分數。靈敏度是指具有金標準標簽的患病人群中，檢測出陽性的概率。特異度是指具有金標準標簽無病人群中，檢測出陰性的概率。理想情況下需要精準率與召回率數值都高，但實際上兩者存在制約關系，F1分數是精準率和召回率的調和平均數，可以更好地均衡精準率與召回率兩者的關系。
各項指標的具體計算公式如式（10）～式（15）所示，其中真陽性（true positive，TP）表示被模型預測為正類中正確分類樣本的數量；真陰性（true negative，TN）表示被模型預測為負類中正確分類樣本的數量；假陽性（false positive，FP）表示被模型預測為正類中錯誤分類樣本數量；假陰性（false negative，FN）是被模型預測為負類中錯誤分類樣本的數量；精準率（precision，Pre）表示正確預測為正的樣本數占所有被預測為正的樣本數的比例；召回率（recall，Rec）表示正確預測為正的樣本數占所有實際為正的樣本數的比例。
 |
 |
 |
 |
 |
 |
2.3 實驗設定
將數據集劃分為3 500例訓練集，1 000例驗證集，500例測試集，正常心音與異常心音比例為1∶1。采用本文所提出的MWRS-BFSC作為分類特征，提出四種網絡結構來進行性能分析與模型比較，選擇分類性能最好的神經網絡進行模型訓練，并與多種基于時頻分析的分類算法進行對比實驗，分析其優越性。
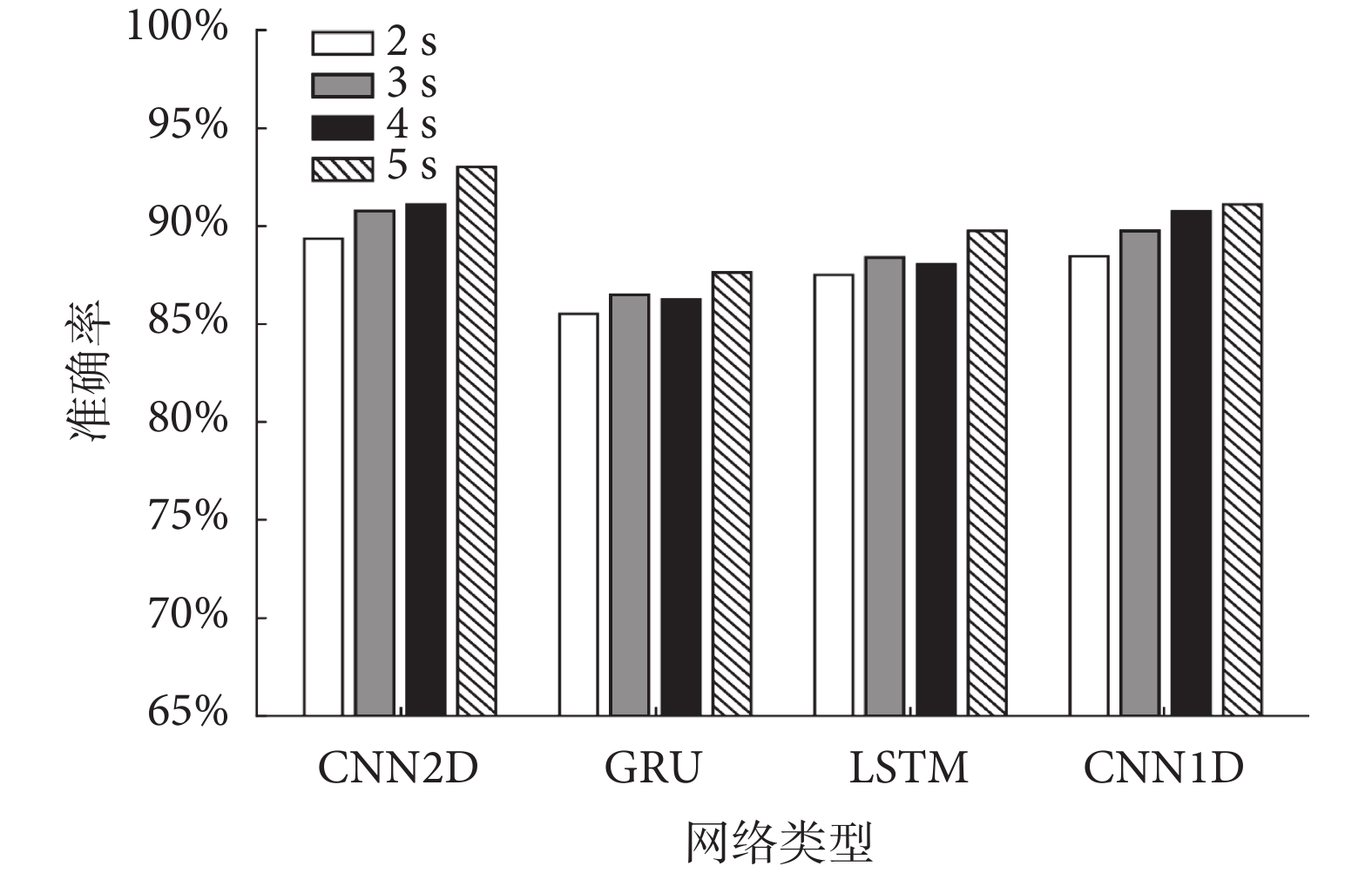
本文為對比隨機截取心音片段的長度對分類效果的影響，設置2、3、4、5 s四組時間變量，驗證心音持續時間對分類效果的影響。心音是準周期信號，一個心動周期平均為0.8 s且隨機截取2 s至少包含一個心動周期。為保證每個心音片段包含完整心動周期，隨機心音片段長度從2 s開始設置，而文獻[22]中表明識別異常心音所需心音片段的長度至少需要5 s。綜合考慮計算機的計算能力，設置了四組時間變量。由于深度學習隨機初始化的特性，每一次訓練模型存在一定的隨機波動問題現象，故在每一組時間變量上選擇10次實驗的平均值作為分析標準。
2.4 結果分析
如圖5所示，表明在無需心音分割的情況下，增加心音片段長度能夠提升分類性能。對于CNN而言，增加心音片段長度的提升效果比RNN更為顯著，且在RNN上更容易出現過擬合現象。當心音片段長度為5 s，CNN2D表現出最佳的分類性能。CNN是深度學習最具代表性的算法之一，既做到權值共享、減少網絡參數，同時又能有效提取局部特征。MWRS-BFSC特征具有較好的2D表征能力，輸入到CNN網絡中，可以得到可靠的分類性能。
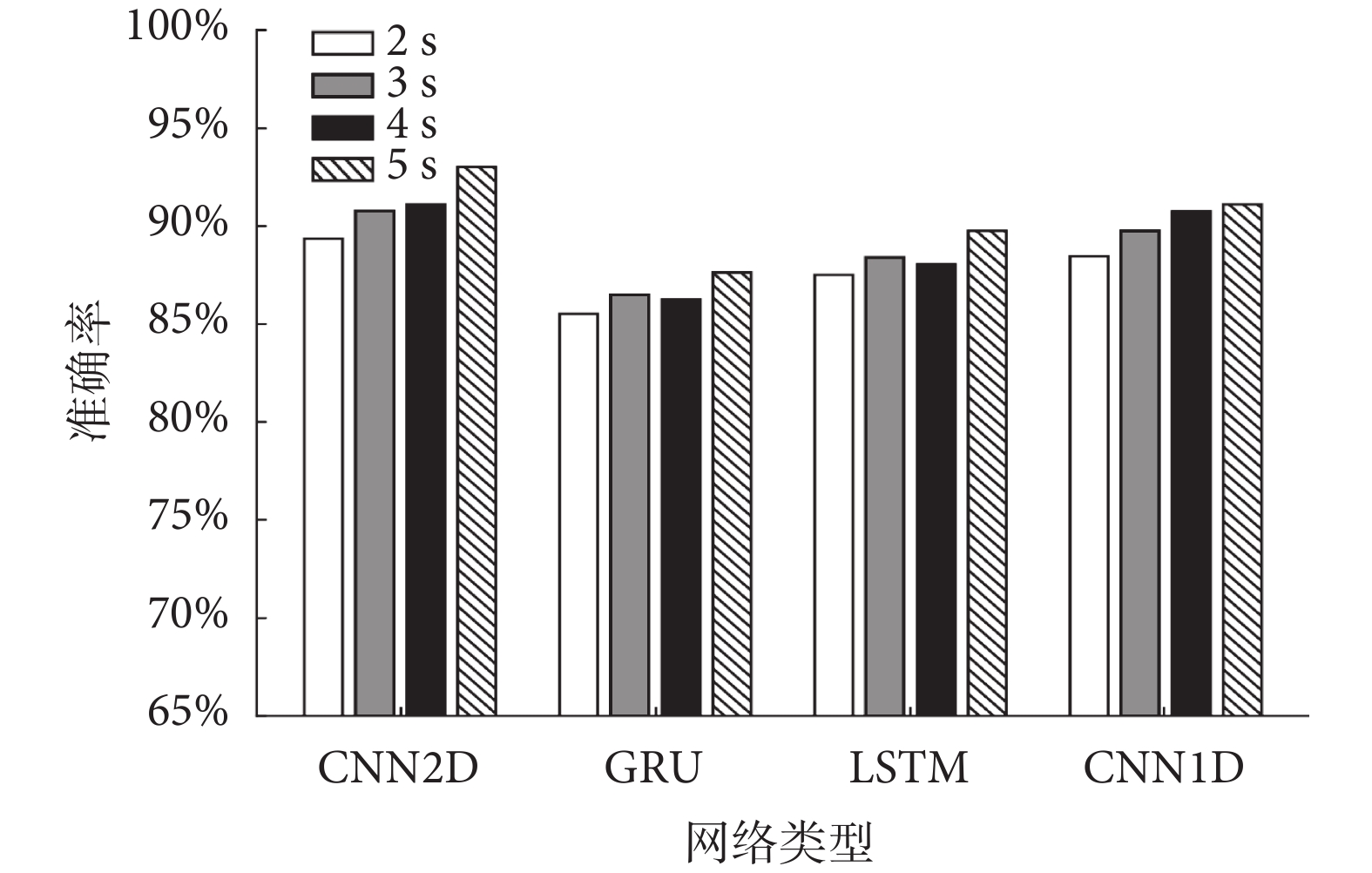圖5
心音片段長度分類效果對比
Figure5.
Comparison of the classification effect of heart sound fragment length
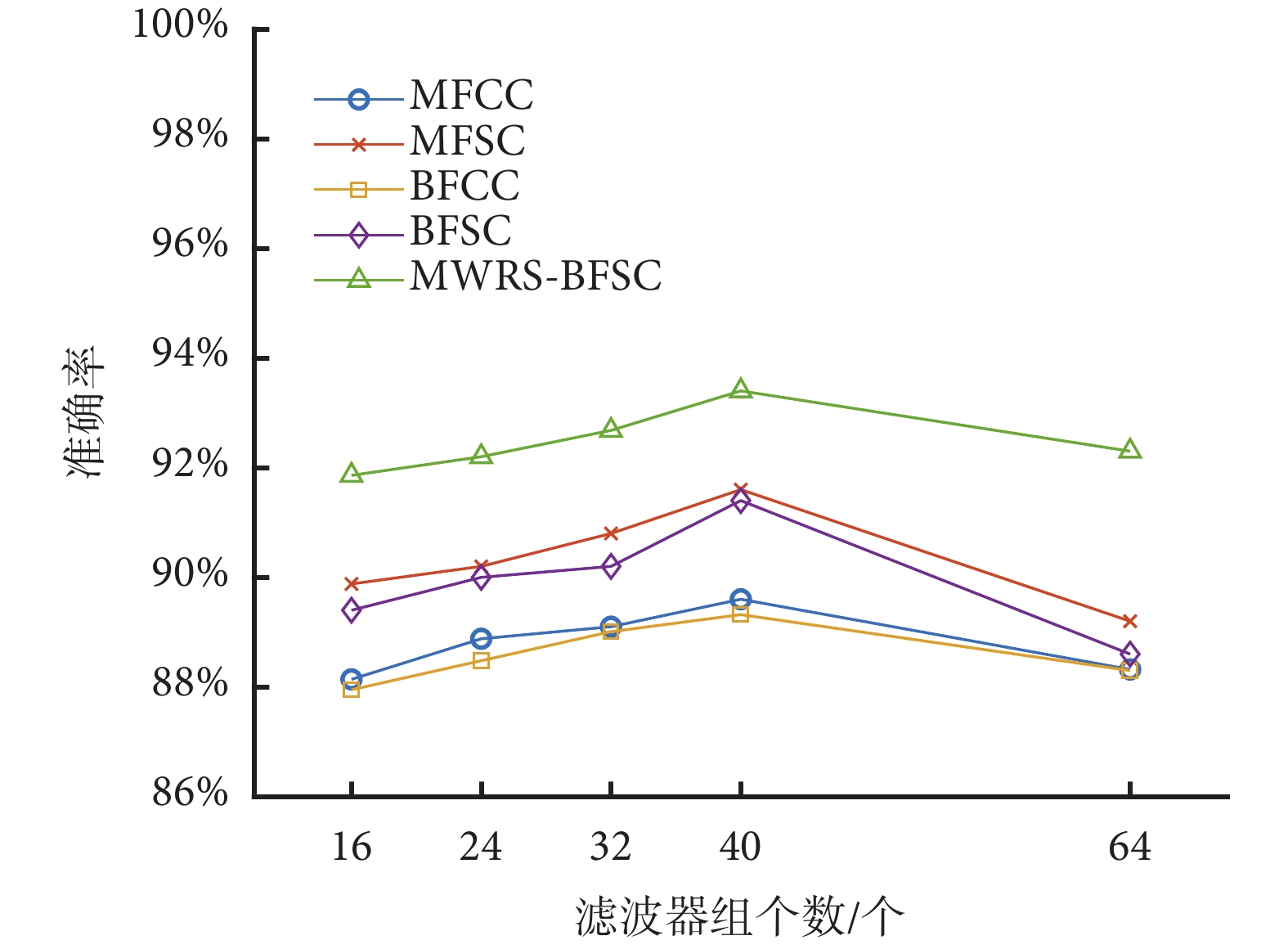
對比實驗中采用了多種時頻分析算法進行對比，而提取頻譜系數特征的濾波器個數是影響分類性能的重要因素。為比較濾波器組中濾波器的個數對分類效果的影響，本文采用固定心音片段長度、相同的網絡結構以及不同數量的濾波器組對不同時頻分析算法進行對比實驗。濾波器組個數分別選用16、24、32、40、64進行對比分析，具體分類效果如圖6所示。
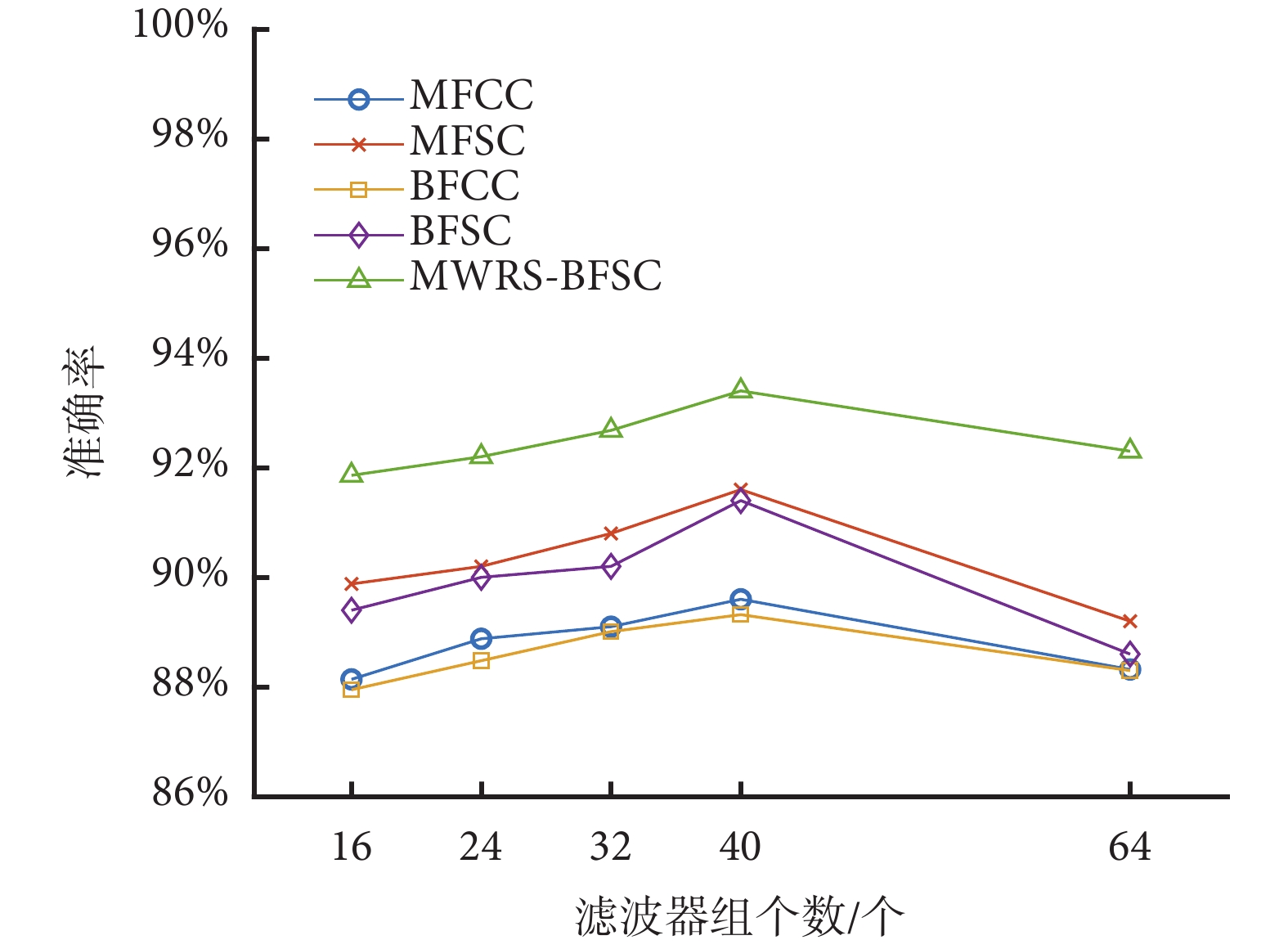圖6
濾波器組個數分類效果對比
Figure6.
Comparison of the classification effect of the number of filter banks
圖6結果表明，隨著濾波器數量的增加，特征的表達能力呈現出先增加后下降的趨勢。具體來說，當濾波器數量為40個時，MWRS-BFSC的分類性能最佳。濾波器數量增加到64個時，整體性能反而下降。原因可能是當濾波器數量逐漸增大時，捕獲頻率信息增多，對分類性能有提升作用，而當相同頻段內的濾波器組中濾波器的數量過多，會導致濾波器組中心頻率過于接近產生干擾，導致模型整體性能下降。
文獻[23]中表明，多窗譜分析的最佳窗口個數在2～8之間，增加窗口可以減低頻譜泄露引起的高方差問題，但隨著窗口個數的增加同樣會影響時頻表示的分辨率。故本文設置不同的窗口個數的對比實驗進行分析。如表1所示，正交窗口的個數為4時，既可以有效降低頻譜估計的方差，又可以保證較好的時頻分辨率。
表1
不同窗口個數的多窗口時頻重排BFSC性能對比
Table1.
Performance comparison of MWRS-BFSC with different number of windows
綜上分析，本文選擇性能最好的CNN2D作為分類模型。為對比所提出MWRS-BFSC特征的CHD分類效果，對比實驗所使用的網絡結構為文中所提出的CNN2D，具體網絡結構如圖7所示。
圖7
CNN網絡結構圖
Figure7.
CNN network structure diagram
本文選擇的對比算法為文獻[8-12]。文獻[8]與文獻[9]中分別使用了STFT和基于STFT的時頻重排方法，STFT是傳統時頻分析方法，而時頻重排使得STFT的能量表示更加聚集。文獻[10]采用了BFCC特征，該特征模擬人類心理聽覺，在情感識別領域廣泛運用。文獻[11]和文獻[12]分別選用了MFCC與MFSC的特征提取方法，MFSC省略了MFCC中DCT步驟，保留了更多相關信息。文獻[12]中對心音進行了分割，再提取特征，鑒于本文不依賴于心動周期的分割，故在對比實驗中選擇不分割的MFSC進行對比。
如表2、表3所示，分別是消融實驗與對比實驗，結果表明：① 從表2中可知，采用時頻重排之后，分類結果的靈敏度均高于特異度，證明銳化時頻表示對正常心音與異常心音的區分帶來優勢。② 從表2中可知，多個正交窗口取平均的方式有效降低了頻譜估計的方差，對分類性能有提升作用。③ 從表3中可知，MWRS與BFSC相結合可以提升特征的判別能力，MWRS-BFSC在準確率、靈敏度、特異度各方面都要優于其他模型。④ 在CNN網絡中，MFSC與BFSC的分類性能都要高于MFCC與BFCC。綜合以上顯示，最后一行的MWRS-BFSC要優于其他模型。
表2
消融實驗的性能對比
Table2.
Performance comparison of ablation experiments
表3
基于CNN模型的各算法性能對比
Table3.
Performance comparison of algorithms based on CNN model
3 結論
本文提出了一種MWRS-BFSC特征提取與深度學習結合的心音分類新算法，將MWRS與非均勻濾波器組相結合，提取更具判別能力的特征。將MWRS-BFSC特征輸入到四種分類模型中對比性能，篩選出性能最好的模型，并且提出了四種評價指標對算法進行評估。與其他基于時頻分析的算法相比，MWRS與非均勻濾波器組相結合的特征提取方式在各方面都具備優異的性能，增強了時頻分析對心音的細節表達能力，從而有利于更好地篩查出異常心音。本論文所提出的方法無需分割心音，大大簡化了計算流程，有望用于CHD大規模篩查，讓基層尤其是邊遠地區的CHD患兒得到及早的醫療救治。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：夏軍負責實驗設計與實踐、數據采集、數據分析和論文寫作；孫靜負責心音分析指導、論文寫作指導和數據收集；楊宏波負責醫學指導和數據收集；郭濤負責醫學指導和處理數據；潘家華負責醫學指導和數據審查；王威廉負責心音理論研究、論文整體審查潤色和論文寫作指導。
倫理聲明：本文所使用的心音數據庫得到云南大學人體研究材料倫理委員會（批文編號：CHSRE2021008）以及云南省阜外心血管病醫院倫理委員會（批文編號：IRB2020-BG-028）的授權使用。
0 引言
全球因心血管疾病死亡的人數占總死亡人數的31%，而在中國這一比例更高，因心血管疾病死亡的人數約占總死亡人數的40%[1]。先天性心臟病（congenital heart diseases，CHD）是一種嚴重影響青少年兒童身體健康的心血管疾病，若未得到及時治療，還會對患者的生命構成威脅，因此對嬰幼兒進行CHD早期篩查就顯得極為重要。然而，傳統對CHD進行早期篩查的人工聽診方式很容易忽略心音中的隱藏信息，所以近年來隨著計算機技術的發展，心音自動分析在識別先天性心臟結構缺失及心血管疾病醫療保健方面的應用越來越廣泛而深入。
心音自動分析的流程，包括：預處理、特征提取、分類識別。其中，特征提取一直是心音分類的重要研究內容。異常心音在時域或頻域上表現出與正常心音顯著不同的特征，而這種差異是影響異常心音識別的關鍵因素。因此，為了準確識別異常心音，必須選擇合適的特征表示方法進行特征提取。傳統的心音分類研究關注于從單個域（如時域、頻域、小波域等）提取特征[2-6]，但文獻[7]的研究表明，單獨的時域或頻域特征并不能很好地表征心臟的病理信息，所以近年來國內外的研究多采用時頻域特征進行分析。
Chen等[8]計算心音的短時傅里葉變換（short-time Fourier transform，STFT）并送入卷積神經網絡（convolutional neural networks，CNN）進行分類研究，在測試樣本上達到了0.954的準確率。Markaki等[9]采用了基于STFT的時頻重排頻譜作為特征，改善了頻譜時頻表示的分辨率，準確率達到了0.958。Lubis等[10]則是提取了巴克頻率倒譜系數（Bark-frequency cepstrum coefficient，BFCC）作為特征,分類準確率為0.791。Rubin等[11]對心音進行分割，提取梅爾頻率倒譜系數（Mel-frequency cepstrum coefficient，MFCC）并送入CNN進行分類，二分類準確率為0.848。Kui等[12]對分割的心音提取梅爾頻譜系數（Mel-frequency spectral coefficient，MFSC），然后用CNN對所提特征進行分類，最后采用多數投票算法得到最優分類結果，二分類準確率達到 0.938。上述算法仍有進一步改善分類性能的空間，比如：文獻[8]取得較好的分類性能但使用的數據量較少，且正負樣本比例不均衡，缺乏大量驗證，不利于推廣。文獻[9]使用時頻重排銳化了STFT頻譜，卻忽略了頻譜泄露引起的高方差問題。文獻[10]沒有改進BFCC對噪聲敏感的問題。文獻[10]和文獻[11]選擇了公開數據集，而公開數據集缺乏專門針對CHD兒童患者的相關數據。文獻[12]分割心音信號需要同步心電數據作為對照，過程較為繁瑣，且分割錯誤對分類準確率影響較大。
另一方面，分類器的選擇同樣是受到研究人員強烈關注的問題。深度神經網絡（deep neural network，DNN）是由機器學習發展而來的，通過堆疊更加復雜的網絡結構，從輸入中自動學習深度特征。文獻[11]和文獻[12]采用了CNN，而文獻[13]則采用了門控循環單元（gated recurrent unit，GRU），這些研究表明DNN在心音研究領域得到了廣泛的運用。
綜上考慮，本文提出了一種新的心音分類算法。該算法采用多窗口時頻重排（multiple window reassigned spectrogram，MWRS）與巴克頻譜系數（Bark-frequency spectral coefficient，BFSC）相結合的方式（MWRS-BFSC）提升特征的表達能力，并運用深度學習對算法的分類性能進行驗證評估。本文將MWRS與非均勻濾波器組相結合的方法運用到心音分析領域，由于無需分割心音，該算法的復雜度得到了簡化，有望提升性能并應用于CHD早期篩查。
1 方法
1.1 算法框架
本文的分類算法流程如圖1所示，具體步驟為：① 對原始心音數據進行幅值歸一化、預加重處理。② 對預處理后的心音分別采用多個正交窗口（正交窗1～正交窗k）計算STFT。③ 對子頻譜計算時頻重排，得到各自的重排頻譜。④ 將得到的各重排頻譜進行算術平均。⑤ 使平均后的頻譜通過巴克（Bark）濾波器組，并且進行對數運算得到BFSC特征，再融合動態差分向量。⑥ 輸入分類網絡得到分類結果，并對結果進行評估。
圖1
算法流程圖
Figure1.
Algorithm flow chart
1.2 數據來源
研究數據源于課題組在云南阜外心血管病醫院以及云南省各地州開展CHD免費篩查救治活動中采集的心音數據所構建的數據庫。心音數據由課題組自主研發心音采集裝置與The ONE電子聽診器（Thinklabs Medical LLC，美國）進行采集。在安靜、溫暖的環境下，CHD患者保持仰臥位且保持胸部裸露，保證電子聽診器與患者胸壁直接接觸，完整記錄每位患者的五個心臟聽診區信息。每一例數據時長為20 s，采樣頻率為5 000 Hz。
本次實驗采用心音樣本共5 000例。心音樣本來自1 000名心音志愿者，志愿者年齡均在8個月至18歲，正常、異常樣本比例1∶1。正常數據是從健康人群所采集的心音，異常數據包括房間隔缺損、室間隔缺損、動脈導管未閉、卵圓孔未閉。實驗數據按照7∶2∶1的比例劃分為訓練集、驗證集和測試集。整個采集試驗的全過程通過了倫理審查，且全體志愿者均簽署知情同意書自愿提供心音樣本。研究所使用的心音數據已獲得云南大學人體研究材料倫理委員會（批文編號：CHSRE2021008）以及云南省阜外心血管病醫院倫理委員會（批文編號：IRB2020-BG-028）的授權使用。
1.3 預處理
傳統的心音預處理需要對心音的各成分進行準確分割，該步驟通常是基于同步心電信號來實現的。由于目前精準分割心音仍是尚未攻克的難題，且分割不準確會嚴重影響分類準確率。因此，本研究預處理采取隨機截取心音片段，并對信號進行幅值歸一化、預加重、分幀加窗操作。正常人群的心率為60～100 次/min，頻率范圍在20～500 Hz[14]，考慮到高頻成分與心臟異常產生的雜音有關，采用預加重突出高頻雜音成分信息。心音是非平穩信號，STFT的窗函數長度應該與心音的短時平穩時長相匹配。為了改善窗函數在邊界處產生的問題，需要在各幀之間設置重疊，保證幀與幀之間的關聯性。本文選擇幀長為256個采樣點（51.2 ms），幀移為128個采樣點，既保證窗內信號片段的平穩性，又可以獲得良好的時頻分辨率。
1.4 特征提取
MFCC能夠模擬人類聽覺感知，因此在語音信號處理領域被廣泛應用于提取聲學信號的特征。近年來，MFCC也被應用于心音分類領域，以識別異常心音。但心音相較于語音頻率偏低，其能量主要集中在低頻段，低頻信息相對重要。BFCC與MFCC相比，不僅同樣具有低頻排列密集、高頻排列稀疏的特點，而且在低頻段具有更強的頻率感知能力[15]。而BFSC作為BFCC的一種特殊形式，省略了離散余弦變換（discrete cosines transform，DCT），保留了更多相關信息。
1.4.1 BFSC
人耳對聲音頻率的感知是非線性的，Bark濾波器組模擬人耳聽覺感知特性，低頻排列密集、高頻排列稀疏，可以從心音信號中捕捉更具辨識度的特征，得到良好而緊湊的時頻表示。線性頻率轉換為Bark頻率（以符號B表示）的計算方法如式(1)所示：
|
其中，f代表頻率，sinh(·)代表雙曲正弦函數。
BFSC的提取步驟:首先對心音信號做預加重處理，再計算出信號的STFT，最后通過預先設定好的Bark濾波器組從頻譜中提取BFSC，具體流程如圖2所示。
圖2
BFSC算法流程圖
Figure2.
BFSC algorithm flow diagram
然而，BFSC存在一些問題，如對噪聲敏感、高方差的頻譜泄漏以及無法包含心音的動態細節等。針對上述問題，本研究對BFSC的提取過程進行了改進。
1.4.2 時頻重排
心音是一種非平穩信號，STFT作為傳統的時頻分析方法，被廣泛應用于心音信號的分析和特征提取。STFT（以符號S表示）的計算公式，如式(2)所示：
|
其中，x(τ)代表心音信號，h(t)代表窗函數，j代表虛數單位，f代表頻率，π代表圓周率。相應的能量譜圖（以符號E表示）計算方法如式(3)所示：
|
其中，t代表時間，w代表頻率，S代表STFT時頻譜圖，x代表心音信號，h代表窗函數。
然而，傳統時頻分析在時域和頻域受到限制，導致在第一心音、第二心音處的頻譜表現出能量彌散現象[16]。時頻重排是改善時頻能量彌散的重要方法[17]，其目的在于銳化時頻表示，提高時頻譜圖的分辨率。因此，本文采用時頻重排的方法來改善傳統時頻分析時頻域上的能量彌散問題，重點刻畫心音的病理信息。
首先，根據能量譜圖計算出每個點在時域、頻域上的偏移量，并將譜圖中每個點的能量值，按照其計算好的重排位置，分配到時頻重排后的譜圖中。時頻重排譜圖（以符號RS表示），計算方法如式(4)所示：
|
其中，δ(·)代表沖激函數， 代表時間移位向量， 代表頻率移位向量，α、β為積分變量，表示能量譜圖在時頻域上的坐標。
時頻重排的時間、頻率向量計算公式如式(5)～式(6)所示：
|
|
其中，ζ(·)和Ψ(·)分別表示取實部與虛部，ct與cw分別代表時間移位向量與頻率移位向量的伸縮因子。
由式(4)～式(6)可以知道，時頻重排不以(t,w)作為時頻域的幾何中心進行分布，而是計算心音時頻譜圖中任意點附近的能量中心作為分布[18]。時頻重排頻譜如圖3所示。
圖3
重排頻譜對比圖
Figure3.
Comparison chart of reassignment spectrogram
由圖3可以知道，時頻重排提高了頻譜圖的分辨率，同時由于該方法保留了時間平移不變性以及能量守恒特性，可以更精確地表示信號的時頻特性，進而提高自動分類的準確率。
1.4.3 多窗譜分析
心音的時頻重排提高了頻譜的分辨率，卻仍存在一些問題，如頻譜泄露引起的高方差以及心音信號臨床采集過程中存在的噪聲干擾等。考慮到以上存在的問題，本文采用多窗譜分析改進時頻重排，提高頻譜估計的精度和可靠性。與單獨窗口的時頻重排相比，MWRS具有更強的噪聲魯棒性，并且能夠進一步改善頻譜的能量定位。
（1）正交窗函數
多窗譜分析最初使用的窗函數是長橢球函數，但是該窗函數對瞬態信號表現不好且在時頻域內并不是最佳能量集中，而在Daubechies[19]的研究中表明，埃米特（Hermite）函數作為時頻窗口能表現出更好的時頻集中效果。k次Hermite窗函數（以符號hk表示）定義如式（7）所示：
|
可以證明Hermite窗函數具有正交性[20]，其正交性保證了各子頻譜之間較小相關性，算術平均后可減小頻譜方差。Hermite窗函數的正交性如式(8)所示：
|
其中，m代表第一個窗函數的階數，n代表第二個窗函數的階數。
（2）計算流程
采用多個正交窗口對心音信號進行頻譜分析，對于每個窗函數得到的頻譜估計結果計算算術平均來減小頻譜估計方差，得到心音信號的平穩頻譜估計。這種方法在提高精度和減少震蕩方面有較好的改善。多窗譜（以符號M表示）計算公式如式(9)所示：
|
其中，k代表窗口的個數，dk代表加權因子。
綜上所述，本文選擇正交Hermite窗函數，窗口數目k為4，加權因子dk采用平均加權的方式[21]。MWRS-BFSC以及其一階、二階差分向量進行融合，提高了特征對心音的表征能力，改善了分類性能。
1.5 分類識別
近年來，深度學習作為人工智能的主要發展方向，主要應用于圖像處理、多媒體學習、生物醫學、自然語言處理等方面。常見的傳統網絡結構有CNN與循環神經網絡（recurrent neural networks，RNN）；其中，二維（two-dimention，2D）CNN（CNN2D）被運用在圖像處理、目標檢測等領域，RNN與一維（one-dimention，1D）CNN（CNN1D）等則在處理時間序列領域取得良好的成果，三維CNN則被運用于視頻處理。
1.5.1 網絡搭建
本文在評估上文所提取特征的分類性能時，考慮到不同的神經網絡對輸入特征的不同側重，搭建了四種不同的網絡結構：CNN2D、CNN1D、GRU、長短時記憶網絡（long short-term memory，LSTM）。四種網絡的結構如圖4所示。圖4的網絡結構中課題組已證實，每一個網絡結構經過驗證更多的層數不會帶來更好的分類效果，反而會增大過擬合風險。四種網絡結構中，CNN2D采用了四層卷積、池化結構，四層卷積層的卷積核的數量分別是32、64、64、128，卷積核大小為3 × 3，步長為1 × 1，激活函數為線性整流函數（rectified linear unit，ReLU）。CNN1D則采用三層卷積、池化結構，每一層卷積層的卷積核的數量為34，卷積核大小為3 × 1，步長為1 × 1，池化核大小為2。LSTM、GRU是RNN的常見結構，采用的RNN均選擇三層結構，每一層神經元個數為46，激活函數為雙曲正切函數（hyperbolic tangent，tanh）。圖4中四種網絡結構優化器均選擇自適應矩估計（adaptive moment estimation，Adam）來加快模型的擬合速度，提高模型性能，學習率為0.000 43。池化層均使用最大池化（maxpooling）。展平層（flatten）前都加入隨機失活層（dropout），數值均為0.5，并在最后連接了密集連接（dense）層。分類器均選擇S型生長曲線（sigmoid）函數。
圖4
深度學習網絡結構圖
Figure4.
Structure graph of deep learning network
2 實驗與分析
2.1 實驗環境
本實驗所用硬件配置為：中央處理器(Ryzen 7 5800H @ 3.20 GHz，AMD，美國)，獨立顯卡(NVIDIA GeForce RTX3060 6GB，Nvidia，美國)。深度學習框架為TensorFlow 2.4(Google，美國)，編程語言為Python 3.7(Python Software Foundation，美國)。
2.2 評價指標
本文采用四種評價指標評估模型性能，其中包括準確率（accuracy，Acc）、特異度（specificity，Sp）、靈敏度（sensitivity，Se）、F1分數。靈敏度是指具有金標準標簽的患病人群中，檢測出陽性的概率。特異度是指具有金標準標簽無病人群中，檢測出陰性的概率。理想情況下需要精準率與召回率數值都高，但實際上兩者存在制約關系，F1分數是精準率和召回率的調和平均數，可以更好地均衡精準率與召回率兩者的關系。
各項指標的具體計算公式如式（10）～式（15）所示，其中真陽性（true positive，TP）表示被模型預測為正類中正確分類樣本的數量；真陰性（true negative，TN）表示被模型預測為負類中正確分類樣本的數量；假陽性（false positive，FP）表示被模型預測為正類中錯誤分類樣本數量；假陰性（false negative，FN）是被模型預測為負類中錯誤分類樣本的數量；精準率（precision，Pre）表示正確預測為正的樣本數占所有被預測為正的樣本數的比例；召回率（recall，Rec）表示正確預測為正的樣本數占所有實際為正的樣本數的比例。
|
|
|
|
|
|
2.3 實驗設定
將數據集劃分為3 500例訓練集，1 000例驗證集，500例測試集，正常心音與異常心音比例為1∶1。采用本文所提出的MWRS-BFSC作為分類特征，提出四種網絡結構來進行性能分析與模型比較，選擇分類性能最好的神經網絡進行模型訓練，并與多種基于時頻分析的分類算法進行對比實驗，分析其優越性。
本文為對比隨機截取心音片段的長度對分類效果的影響，設置2、3、4、5 s四組時間變量，驗證心音持續時間對分類效果的影響。心音是準周期信號，一個心動周期平均為0.8 s且隨機截取2 s至少包含一個心動周期。為保證每個心音片段包含完整心動周期，隨機心音片段長度從2 s開始設置，而文獻[22]中表明識別異常心音所需心音片段的長度至少需要5 s。綜合考慮計算機的計算能力，設置了四組時間變量。由于深度學習隨機初始化的特性，每一次訓練模型存在一定的隨機波動問題現象，故在每一組時間變量上選擇10次實驗的平均值作為分析標準。
2.4 結果分析
如圖5所示，表明在無需心音分割的情況下，增加心音片段長度能夠提升分類性能。對于CNN而言，增加心音片段長度的提升效果比RNN更為顯著，且在RNN上更容易出現過擬合現象。當心音片段長度為5 s，CNN2D表現出最佳的分類性能。CNN是深度學習最具代表性的算法之一，既做到權值共享、減少網絡參數，同時又能有效提取局部特征。MWRS-BFSC特征具有較好的2D表征能力，輸入到CNN網絡中，可以得到可靠的分類性能。
圖5
心音片段長度分類效果對比
Figure5.
Comparison of the classification effect of heart sound fragment length
對比實驗中采用了多種時頻分析算法進行對比，而提取頻譜系數特征的濾波器個數是影響分類性能的重要因素。為比較濾波器組中濾波器的個數對分類效果的影響，本文采用固定心音片段長度、相同的網絡結構以及不同數量的濾波器組對不同時頻分析算法進行對比實驗。濾波器組個數分別選用16、24、32、40、64進行對比分析，具體分類效果如圖6所示。
圖6
濾波器組個數分類效果對比
Figure6.
Comparison of the classification effect of the number of filter banks
圖6結果表明，隨著濾波器數量的增加，特征的表達能力呈現出先增加后下降的趨勢。具體來說，當濾波器數量為40個時，MWRS-BFSC的分類性能最佳。濾波器數量增加到64個時，整體性能反而下降。原因可能是當濾波器數量逐漸增大時，捕獲頻率信息增多，對分類性能有提升作用，而當相同頻段內的濾波器組中濾波器的數量過多，會導致濾波器組中心頻率過于接近產生干擾，導致模型整體性能下降。
文獻[23]中表明，多窗譜分析的最佳窗口個數在2～8之間，增加窗口可以減低頻譜泄露引起的高方差問題，但隨著窗口個數的增加同樣會影響時頻表示的分辨率。故本文設置不同的窗口個數的對比實驗進行分析。如表1所示，正交窗口的個數為4時，既可以有效降低頻譜估計的方差，又可以保證較好的時頻分辨率。
表1
不同窗口個數的多窗口時頻重排BFSC性能對比
Table1.
Performance comparison of MWRS-BFSC with different number of windows
綜上分析，本文選擇性能最好的CNN2D作為分類模型。為對比所提出MWRS-BFSC特征的CHD分類效果，對比實驗所使用的網絡結構為文中所提出的CNN2D，具體網絡結構如圖7所示。
圖7
CNN網絡結構圖
Figure7.
CNN network structure diagram
本文選擇的對比算法為文獻[8-12]。文獻[8]與文獻[9]中分別使用了STFT和基于STFT的時頻重排方法，STFT是傳統時頻分析方法，而時頻重排使得STFT的能量表示更加聚集。文獻[10]采用了BFCC特征，該特征模擬人類心理聽覺，在情感識別領域廣泛運用。文獻[11]和文獻[12]分別選用了MFCC與MFSC的特征提取方法，MFSC省略了MFCC中DCT步驟，保留了更多相關信息。文獻[12]中對心音進行了分割，再提取特征，鑒于本文不依賴于心動周期的分割，故在對比實驗中選擇不分割的MFSC進行對比。
如表2、表3所示，分別是消融實驗與對比實驗，結果表明：① 從表2中可知，采用時頻重排之后，分類結果的靈敏度均高于特異度，證明銳化時頻表示對正常心音與異常心音的區分帶來優勢。② 從表2中可知，多個正交窗口取平均的方式有效降低了頻譜估計的方差，對分類性能有提升作用。③ 從表3中可知，MWRS與BFSC相結合可以提升特征的判別能力，MWRS-BFSC在準確率、靈敏度、特異度各方面都要優于其他模型。④ 在CNN網絡中，MFSC與BFSC的分類性能都要高于MFCC與BFCC。綜合以上顯示，最后一行的MWRS-BFSC要優于其他模型。
表2
消融實驗的性能對比
Table2.
Performance comparison of ablation experiments
表3
基于CNN模型的各算法性能對比
Table3.
Performance comparison of algorithms based on CNN model
3 結論
本文提出了一種MWRS-BFSC特征提取與深度學習結合的心音分類新算法，將MWRS與非均勻濾波器組相結合，提取更具判別能力的特征。將MWRS-BFSC特征輸入到四種分類模型中對比性能，篩選出性能最好的模型，并且提出了四種評價指標對算法進行評估。與其他基于時頻分析的算法相比，MWRS與非均勻濾波器組相結合的特征提取方式在各方面都具備優異的性能，增強了時頻分析對心音的細節表達能力，從而有利于更好地篩查出異常心音。本論文所提出的方法無需分割心音，大大簡化了計算流程，有望用于CHD大規模篩查，讓基層尤其是邊遠地區的CHD患兒得到及早的醫療救治。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：夏軍負責實驗設計與實踐、數據采集、數據分析和論文寫作；孫靜負責心音分析指導、論文寫作指導和數據收集；楊宏波負責醫學指導和數據收集；郭濤負責醫學指導和處理數據；潘家華負責醫學指導和數據審查；王威廉負責心音理論研究、論文整體審查潤色和論文寫作指導。
倫理聲明：本文所使用的心音數據庫得到云南大學人體研究材料倫理委員會（批文編號：CHSRE2021008）以及云南省阜外心血管病醫院倫理委員會（批文編號：IRB2020-BG-028）的授權使用。
