在超聲彈性成像中，準確重建組織彈性模量分布是一項重要挑戰。現有的基于深度學習的全監督重建方法在訓練中只使用了添加噪聲的計算機仿真位移數據，不能完全模擬在體超聲數據的復雜性和多樣性。因此，本研究在訓練中引入對在體超聲射頻信號追蹤得到的位移數據（即真實位移數據），對模型進行半監督訓練，旨在提高網絡的預測準確度。實驗結果顯示，在仿體實驗中，加入了真實位移數據的半監督模型的平均絕對誤差和平均相對誤差均在3%左右，而全監督模型的相應數據在5%左右。在處理真實位移數據時，半監督模型預測錯誤區域明顯少于全監督模型。本文研究結果證實了所提方法的有效性和實用性，為在體超聲數據在彈性模量分布重建的深度學習方法中的使用提供了新思路。
引用本文： 張瀟, 彭博, 王銳, 魏星月, 羅建文. 基于半監督神經網絡的彈性模量分布重建. 生物醫學工程學雜志, 2024, 41(2): 262-271. doi: 10.7507/1001-5515.202306008 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
組織的彈性模量分布是臨床診斷的重要依據[1-5]。通常情況下，組織的彈性模量與一定程度的病理改變有關。重建彈性模量分布可以幫助臨床醫生確定相應組織或器官病理狀態可能的發展，例如可以輔助識別乳腺腫瘤的特征和肝纖維化的分期[6-7]。
彈性模量重建是彈性問題中的反問題。相較于給定一組彈性模量分布和邊界條件，就可以通過有限元法求解出組織位移的正向問題[1-4]，反問題的求解往往需要大量迭代計算和高質量的組織位移，成本更高[5-7]。傳統的彈性模量分布重建方法分為迭代求解法和直接求解法。迭代求解法，通常分為兩步：首先，從形變前后的超聲射頻（radio frequency，RF）數據中追蹤位移；然后，以得到的位移作為輸入，通過求解反問題得到組織的彈性模量分布[8-10]。該方法由于需要迭代計算，計算效率低，難以實現實時成像。并且，迭代求解法還需進行正則化參數的選擇，參數的變動可能會極大地影響彈性重建結果，而不同數據的最佳參數并不相同，故在實際應用中很難確定出一組通用的最佳參數[11]。直接求解法，是通過直接估計，將位移輸入偏微分方程，也可直接求解該反問題[12-14]。直接求解法降低了計算成本，但在實際應用中由于估計誤差的影響，重建結果往往較差；且還需已知組織表面的彈性模量或位移/力邊界條件，這在臨床應用中往往難以實現[15]。
針對上述問題，Chen等[16]將彈性模量分布重建任務視為圖像翻譯任務，利用彈性本構關系和平衡方程作為深度神經網絡的先驗知識，通過最小化不平衡力圖的優化任務，實現了從應變圖像到彈性圖像的無監督學習。他們提出的深度學習模型可以實現在沒有測量的情況下預測彈性模量分布。然而，受超聲換能器的限制，臨床實際采集到的超聲信號往往具有較高的軸向分辨率和較低的橫向分辨率，導致無法提供高質量的橫向位移圖，進而無法提供該方法所需的高質量橫向應變圖，最終無法滿足無監督方法對訓練數據的需求。另外，由于預測的彈性模量分布沒有直接標簽，僅能通過平衡方程約束，導致無監督模型訓練往往非常緩慢，根據彈性模量分布的復雜程度，耗時20～80 min不等[16]，唯有通過有監督模型可以解決這一問題。Ni等[17]和Zhang等[18]分別以仿真應變圖像和仿真位移圖像為輸入，配對的彈性模量分布圖為標簽，通過實驗證明了深度神經網絡僅利用軸向應變或軸向位移即可預測出較為準確的模量分布。在上述有監督模型的工作中，模型訓練通常使用的是添加了噪聲的配對仿真位移數據。然而，由于機械和電子噪聲干擾、操作者采集手法無法保證統一、追蹤算法以及在體環境的復雜性等原因，仿真位移數據難以完全重現在體超聲的復雜性和多樣性。即便是添加了各種噪聲的大量仿真位移數據，依然無法完全替代追蹤在體超聲RF信號所得到的位移數據。值得借鑒的是，在超聲成像的很多領域，如超聲散斑運動追蹤深度神經網絡模型的相關研究工作中，已經證明了相比于只使用仿真位移數據，引入在體數據訓練模型能取得更好的性能[19-20]。基于上述原因，本文提出一種半監督的彈性模量分布重建深度神經網絡，通過在訓練過程中引入真實位移數據，可望進一步提升彈性模量分布重建模型對于真實位移數據的彈性模量分布重建的準確性，為臨床醫生準確診斷腫瘤或組織的病理發展提供可靠依據。
1 方法
1.1 半監督學習的最小二乘生成對抗網絡
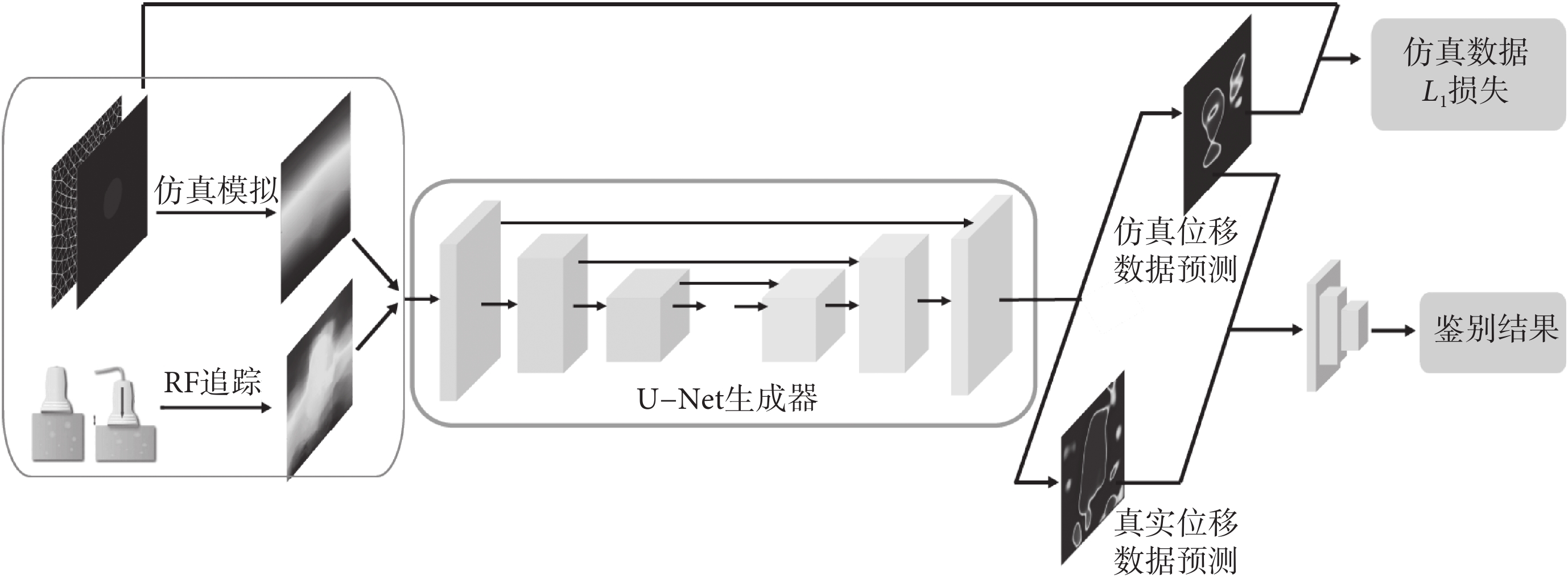
半監督學習是深度學習中訓練深度神經網絡模型的一種方法。在全監督學習中，模型只使用帶標簽的數據進行有監督的訓練，而半監督學習則允許模型在一部分數據上進行有監督的訓練，同時在另一部分數據上進行無監督的訓練。在本研究中，半監督模型不僅會學習帶有真實彈性模量分布的仿真位移數據，還會學習未知彈性模量分布的真實位移數據。半監督模型用最小二乘生成對抗網絡（least squares generative adversarial network，LSGAN）[21]來實現，網絡結構如圖1所示。LSGAN相比于常規生成對抗網絡，在許多方面表現出更優秀的性能[21-24]。LSGAN在圖像翻譯任務上，通過引入最小二乘損失函數，緩解了鑒別器訓練中梯度消失的問題，從而使得訓練更穩定，生成的圖像紋理更清晰，模態更豐富[21-22]。在醫學圖像重建任務上，半監督學習的LSGAN可以使用較少的標簽達到較好的重建質量[23-24]。如前所述，彈性模量分布重建任務可看作圖像翻譯任務，故本文采用LSGAN構建半監督神經網絡。LSGAN由一個生成器和一個鑒別器組成。在學習過程中，鑒別器對于仿真位移數據的生成器生成結果進行鑒別的同時，還會將生成結果與其對應的真實彈性模量分布圖作比較；而對于真實位移數據的生成器生成結果，僅有鑒別器鑒別真假，以此讓生成器提前適應真實位移數據，提高模型泛化性。
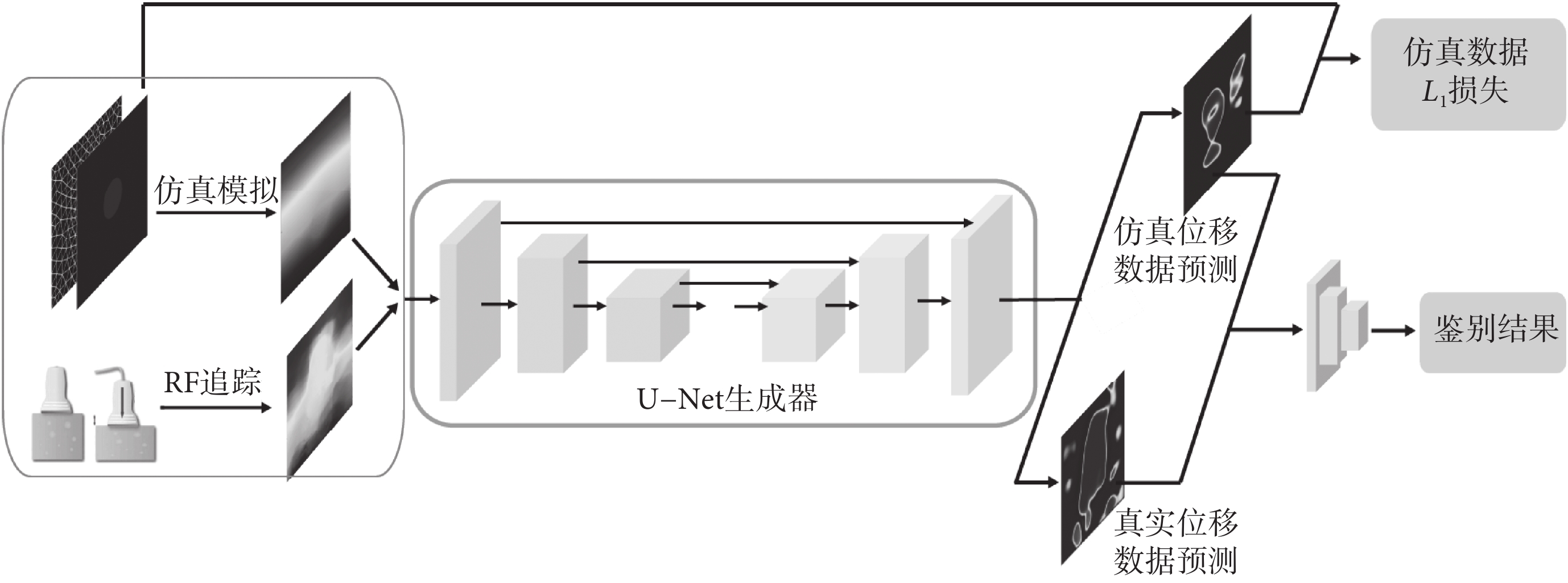圖1
半監督模型LSGAN的結構示意圖
Figure1.
Schematic structure of the semi-supervised LSGAN model
生成器是基于U型網絡（U-Net）的深度神經網絡，以單通道的軸向位移圖為輸入，通過多次卷積、下采樣、上采樣和跳躍鏈接后，輸出彈性模量分布圖。與原始工作相比，U-Net前四層卷積核被替換為了可變形卷積核，以更好地學習不規則的病變體形狀[25]；卷積層和輸出層激活函數都采用帶泄露修正線性單元（leaky rectified linear unit，LeakyReLU），其負數斜率為0.25，唯一不同的是輸出層，負數斜率為0.1；其余與原始U-Net相同。生成器的目標是學習位移與彈性模量分布之間的高維映射，輸出預測的彈性模量分布，希望欺騙鑒別器。對于真實位移數據，生成器僅需從鑒別結果中學習；而對于仿真位移數據，還需要額外學習生成結果與真實彈性模量分布圖的差異。
鑒別器取自馬爾可夫生成對抗網絡[26]，以單通道的模量圖為輸入，負責區分它是否是真實的彈性模量分布圖像。鑒別器前四層均由卷積層、歸一化層和激活函數LeakyReLU組成，每層的卷積核大小均為4 × 4，步長為2，輸出通道數分別為64、128、256、512。第五層是輸出層，是一個單獨的卷積層。卷積核大小為4 × 4，步長和輸出通道均為1。該鑒別器的鑒別結果和普通鑒別器僅輸出一個二元評價值（真或假）不同，其結果最終被映射到N×N的矩陣中，矩陣中每一個值代表其對應的感受野在鑒別器中的評價。相較于普通的鑒別器，該鑒別器擁有更強的鑒別能力，能夠緩解生成對抗網絡的梯度消失問題，更好地指導生成器[26]。
1.2 損失函數
1.2.1 生成器損失函數
生成器的損失函數由兩部分組成。一部分是鑒別器對生成結果圖和真實彈性模量分布圖的鑒別誤差，如式(1)和式(2)所示。另一部分來自于生成結果與真實彈性模量分布圖的L1損失，如式(3)所示：
 |
 |
 |
其中，dsimu和dreal分別是輸入生成器的仿真位移數據與真實在體位移數據；Lg_real代表鑒別器對真實位移數據的生成結果與實際彈性模量分布圖的鑒別差異；Lg_simu代表鑒別器對仿真位移數據的生成結果與實際彈性模量分布圖的鑒別差異； L1 代表生成結果與真實彈性模量分布圖的L1損失； G(?)代表生成器對于任一輸入的生成結果；D(?)是鑒別器對于任一輸入鑒別結果；y是dsimu的對應真實彈性模量分布圖。生成器總的損失函數Lg，定義如式(4)所示：
 |
其中，
和 
是權重，在本文研究中固定為0.01。
1.2.2 鑒別器損失函數
鑒別器的損失由兩部分組成，一部分來自于鑒別器對真實位移數據生成結果的鑒別（以符號Ld_real表示），如式(5)所示；另一部分來自于鑒別器對仿真位移數據生成結果和真實彈性分布的鑒別（以符號Ld_simu表示），如式(6)所示；鑒別器總的損失函數Ld，定義如式(7)所示：
 |
 |
 |
2 實驗
本研究將半監督模型LSGAN和Zhang等[18]提出的一種全監督模型進行比較，該全監督模型僅使用計算機仿真位移數據進行訓練。全監督模型采用深度卷積生成對抗網絡（deep convolution generative adversarial networks，DCGAN）作為網絡架構[27]，在訓練中僅使用仿真位移數據，并且所有仿真位移數據均有真實的彈性模量分布圖。為充分驗證本文所提方法的有效性，本研究通過計算機數字體模實驗、仿體體模實驗和在體乳腺試驗進行了定量和定性的比較。
在計算機數字體模實驗中，本研究首先采用量化指標評估兩種模型的重建結果與真實彈性模量分布圖像之間的誤差，以驗證預測的準確度。然后，通過對數字體模仿真實驗中的三組仿真位移數據，采用如2.1節中所述的方式對原始仿真位移添加1 000次噪聲，統計所有的預測誤差，以驗證提出的方法面對噪聲的魯棒性。最后，通過將不同尺寸的仿真位移數據輸入到本文所提出的方法中統計預測耗時，驗證本文所提方法在彈性模量分布重建的計算效率。
在仿體實驗中，本研究分別量化了兩種模型預測結果與真實彈性模量分布圖像之間的誤差。而在體試驗中，本研究將兩種模型重建的彈性模量分布圖像與現有臨床診斷結果進行比較分析。
2.1 訓練數據
在本研究中，訓練數據共包括162組真實位移數據和12 000組仿真位移數據，按照5∶1的比例劃分訓練集和測試集，最終訓練集中包含135組真實位移數據和10 000組仿真位移數據。
真實位移數據由追蹤在體超聲RF信號得到的162組位移數據組成。這些超聲RF數據來自27例經病理證實的乳腺病變受試者。數據采集均使用7.5 MHz的高頻線性陣列換能器（Siemens Medical Solution Inc., 美國）獲取，并得到了堪薩斯大學醫學中心人類受試者委員會（機構審查委員會）的批準，且獲得了患者的知情同意[28-30]。每個患者的超聲數據包含50～90 幀，從中隨機選擇6組相鄰的幀，采用具有局部多項式擬合的貝葉斯區域增長運動跟蹤算法（Bayesian region-growing motion tracking with local polynomial fitting，BRGMT-LPF）。該算法將貝葉斯推理與局部多項式擬合相結合，并納入區域增長塊匹配運動跟蹤框架，使用最大后驗概率密度函數來確定更加準確的位移向量。實驗結果表明，相較于原始區域增長運動跟蹤算法、貝葉斯推理區域增長和局部多項式擬合區域增長， BRGMT-LPF算法可以提供更加準確的運動跟蹤結果[28]，為后續神經網絡輸入高質量位移數據提供了基礎和保障。
仿真位移數據由仿真軟件MATLAB 2020a（The MathWorks Inc., 美國）偏微分方程工具箱生成。數字模體尺寸為40 mm × 40 mm × 1 mm，內部包裹一個橢圓包裹體。背景的楊氏模量固定為22 kPa。為了增加訓練數據的多樣性，本研究設計了半徑、楊氏模量和位置均為隨機值的橢圓包裹物。包裹物長軸范圍為5～10 mm，長軸與短軸之比為0.2～1.0的隨機數。包裹物的楊氏模量范圍為36～100 kPa。長軸與X軸夾角范圍為1°～180°。包裹物邊緣與數值體模邊緣之間的距離始終大于3 mm。泊松比設置為0.495，用以將組織視為一種幾乎不可壓縮的材料。數字體模在0.1%～5.0%的范圍內進行隨機軸向壓縮，這樣可以模擬超聲彈性成像中的大多數變形情況。在給定模量分布條件下，基于平面應變模型，采用有限元法計算模體相應的位移分布。為進一步增加訓練數據樣本和樣本的多樣性，在輸入深度神經網絡之前，對通過偏微分方程工具產生的仿真位移數據dsmooth進行隨機噪聲添加。最終，訓練輸入的仿真位移數據dsimu定義如式(8)所示：
 |
其中，avg(?)是均值函數，α是0.01～0.05的隨機數，σ是均值為0、方差為1的標準正態分布噪聲。需要說明的是，為適應網絡的輸入尺寸，本研究中的仿真位移數據、相對應的真實彈性模量分布圖和真實位移數據均被調整為256 × 256像素，對深度神經網絡進行半監督訓練。
2.2 計算機數字體模實驗數據
本研究在計算機數字體模實驗中使用了三組隨機選擇的仿真位移數據來驗證所提出的方法。如前一節所述，用于評價的位移和彈性數據與用于訓練的數據在生成方法上相同。以該位移數據作為輸入，重建出相應的彈性模量分布。最后利用生成器重建的彈性模量分布與真實彈性模量分布之間的差異來量化重建誤差。
2.3 仿體體模數據
本研究使用一臺配備L9-3線性陣列換能器的飛利浦iU22超聲系統（Philips Medical Systems Inc., 美國）徒手掃描乳房彈性成像仿體（model 059, CIRS Inc., 美國）獲取仿體實驗射頻數據。該仿體中分布有5個不同大小的球形包裹物，其硬度是背景的兩倍。實驗中，對仿體中直徑分別為4.1 mm和6.5 mm的包裹物進行掃描并采集射頻數據，得到的射頻數據的采樣頻率為32 MHz，每個射頻幀由320掃描線組成，軸向采樣間距和橫向采樣間距分別為0.01 mm和0.12 mm。
2.4 在體數據
在體試驗數據來自一名已經臨床診斷為浸潤性導管癌（invasive ductal carcinoma，IDC）的乳腺癌患者。該數據使用配有7.5 MHz線性陣列傳感器的掃描儀（Siemens Medical Solution Inc.，美國）獲得。采集時，醫生以徒手的方式壓縮乳房，用以產生1.0%～1.5%的應變。射頻數據采集頻率為36 MHz。軸向采樣間距和橫向采樣間距分別為0.021 mm和0.19 mm。數據采集同樣得到了堪薩斯大學醫學中心人類受試者委員會（機構審查委員會）的批準，并獲得了患者的知情同意[27-29]。本研究從連續采集的圖像幀中隨機選取兩幀連續的圖像幀來評估所提方法的性能。
2.5 評價指標
本研究使用平均絕對誤差（mean absolute error，MAE）和平均相對誤差（mean relative error，MRE）作為評價指標，來衡量深度學習模型預測的彈性模量分布圖像與計算機仿真得到的真實彈性模量分布圖像之間的全局相似度，以定量評價所提方法在彈性模量分布重建上的誤差，其定義如式(9)和式(10)所示：
 |
 |
其中，n和m分別是圖像的高度和寬度。G(x)(i, j)和y(i, j)分別是預測的彈性模量分布圖和真實彈性模量分布圖在該處的彈性值。
2.6 實現細節
本研究使用機器學習庫PyTorch 1.7.0（Facebook Inc.，美國）實現了本文方法和對比方法的深度神經網絡，并在配備圖形處理器NVIDIA GeForce RTX 3090（NVIDIA，Inc.，美國）的工作站上進行訓練。用于訓練的優化器是自適應矩估計（adaptive moment estimation，Adam）。批大小、訓練周期和學習率分別設置為16、400和5 × 10?5。
3 結果
為了更直觀地比較重建結果，本研究對模型預測的彈性模量分布結果進行了相對化處理。在實驗結果圖中，背景模量值始終為1，內部包裹物的模量值表現為背景模量的倍數，因此模量值不帶單位。
3.1 計算機數字體模實驗結果
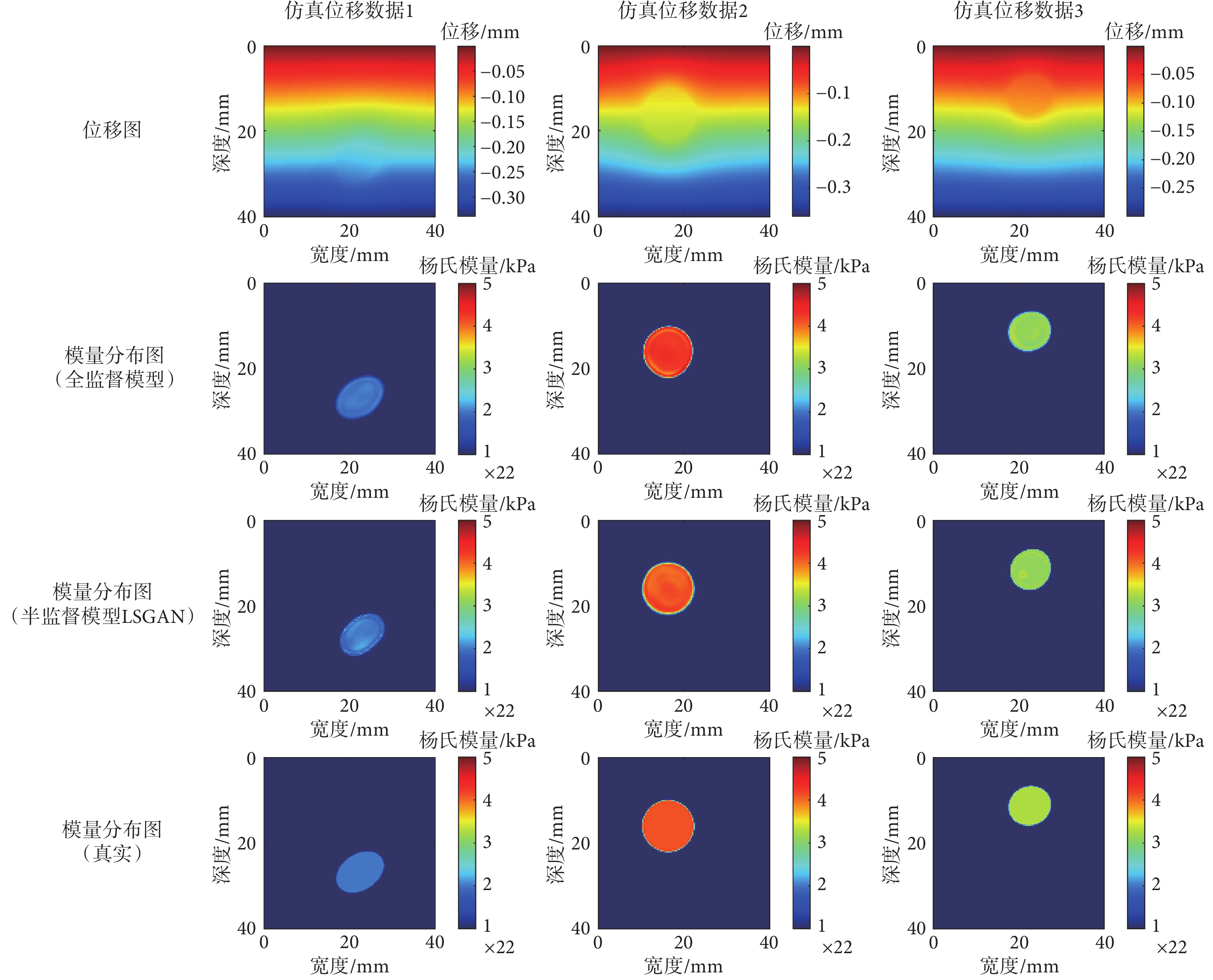
計算機數字體模的仿真實驗結果如圖2所示，其中縱列分別對應三組隨機選取的仿真位移數據（仿真位移數據1、仿真位移數據2、仿真位移數據3），橫排分別對應位移圖、全監督模型結果、半監督模型LSGAN結果和真實彈性模量分布圖。對于三組仿真位移數據，半監督模型LSGAN和全監督模型預測的橢球體的形狀與真實的橢球體形狀基本一致；同時從橢球體內部的模量數值來看，兩種模型預測的彈性模量數值也與真實彈性模量分布圖中橢球體的彈性模量值一致。
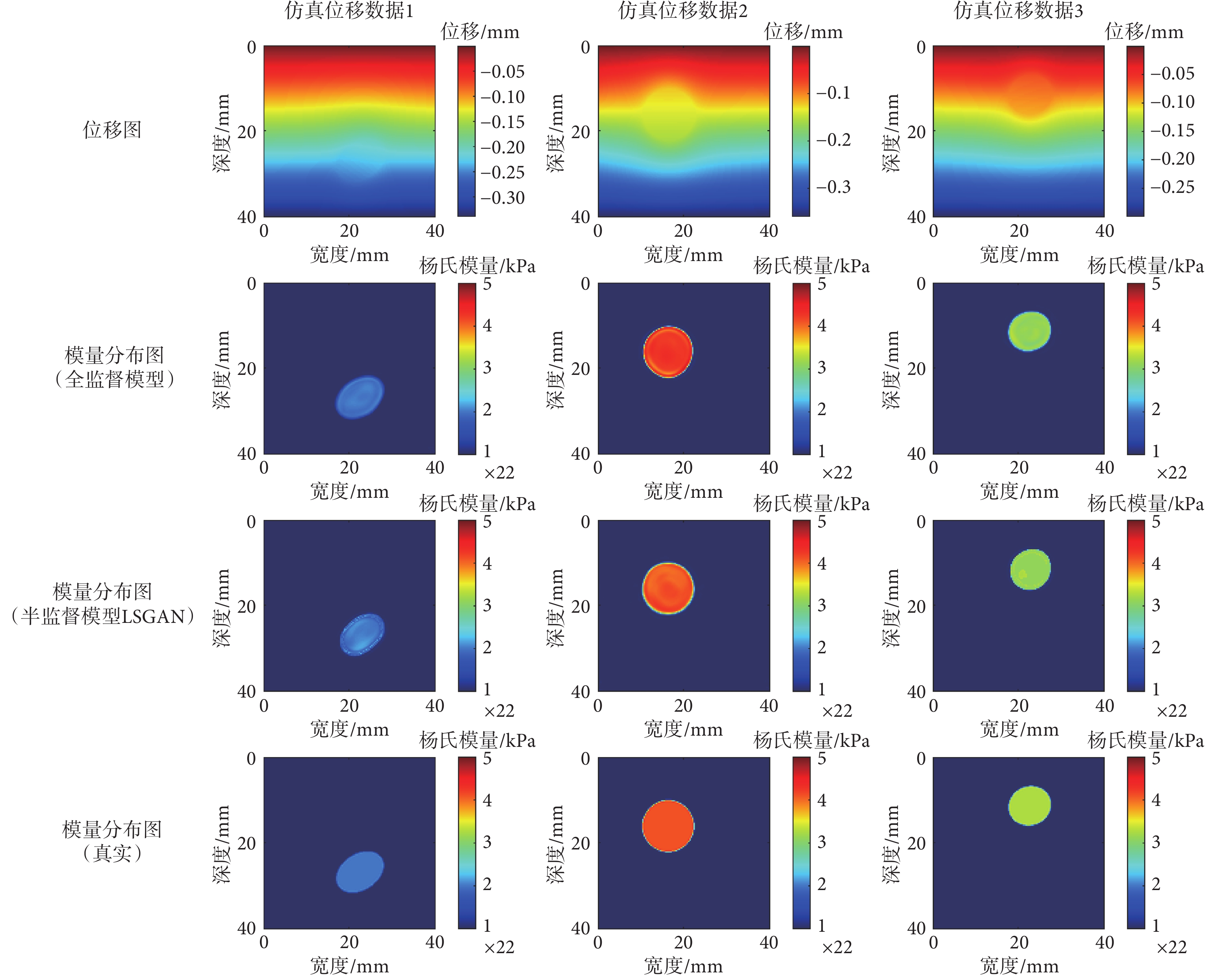圖2
仿真實驗結果
Figure2.
Results of simulation experiments
仿真實驗中半監督模型LSGAN和全監督模型預測的彈性模量值與真實彈性模量值之間的MAE和MRE如表1所示。對于三組仿真位移數據，半監督模型和全監督模型預測結果的MAE和MRE都在1.00%以內。兩種模型預測得到的彈性模量分布圖中的數值基本一致。這些結果證明了對于仿真位移數據，兩種模型都能夠準確預測彈性模量分布圖。
表1
仿真實驗中模型預測值與真實值的MAE和MRE
Table1.
MAE and MRE of model prediction value and real value in simulation experiments
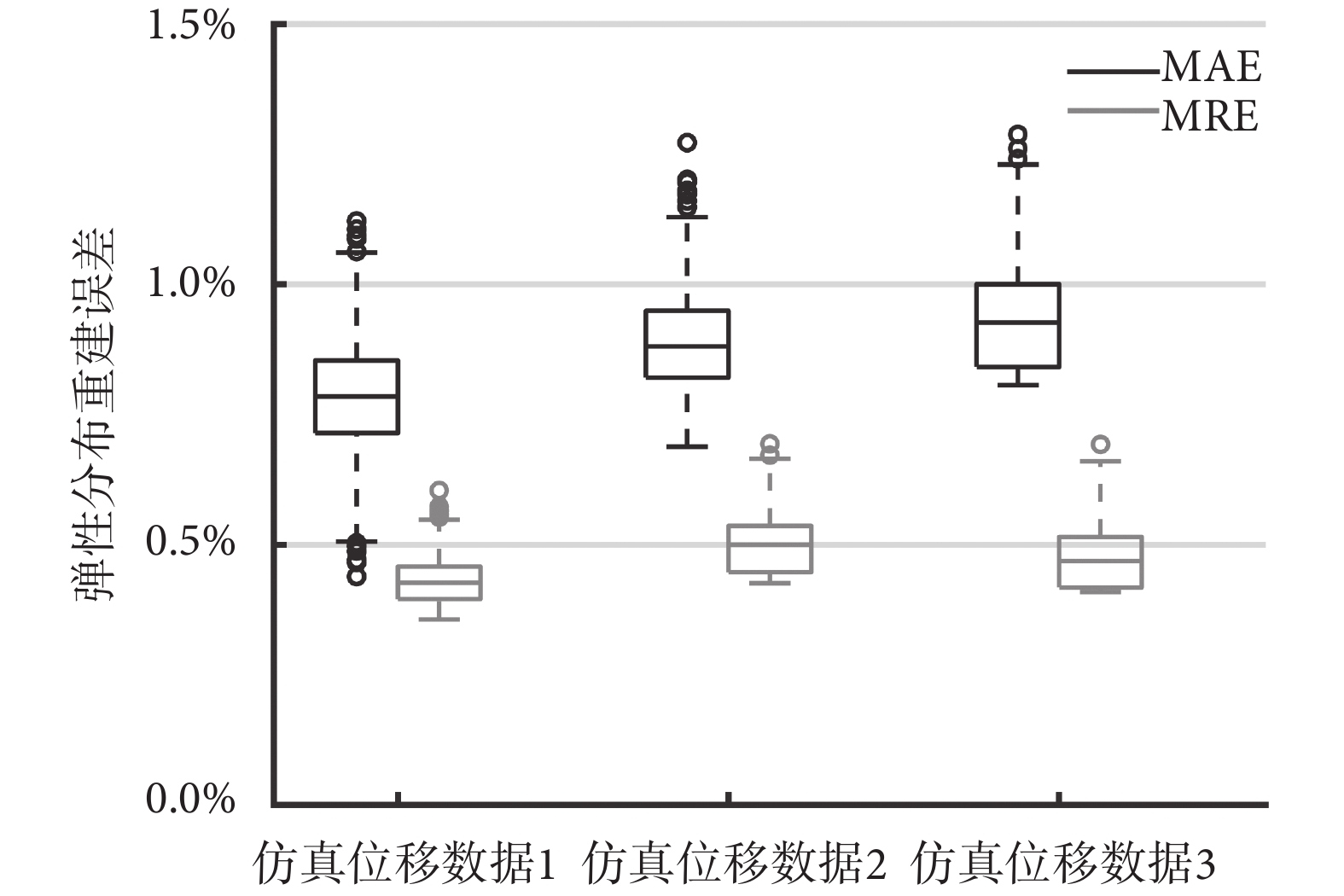
如圖3所示為本文提出的網絡在面對添加噪聲后仿真位移數據時的預測性能，噪聲添加方式如2.1節所述。對于仿真位移數據而言，當位移噪聲在1.0%～5.0%之間時，該網絡對仿真位移數據的預測結果的MAE和MRE均低于1.5%。其中大部分情況MAE低于1.0%，而MRE在0.5%上下浮動。總體上看，在輸入帶有噪聲數據的仿真位移數據時，本文所提出的網絡模型依然可以預測得到具有較高質量的彈性模量分布圖。
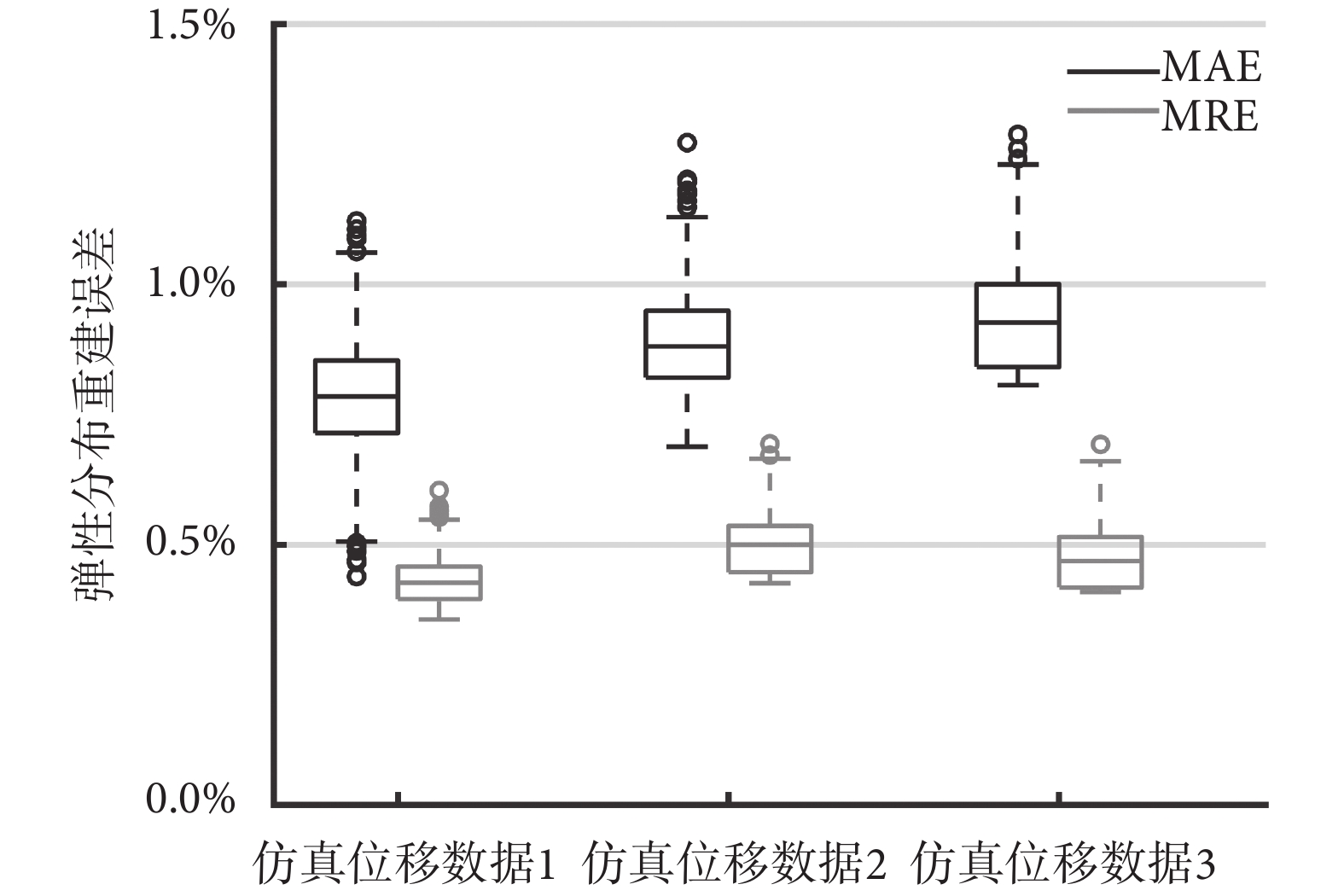圖3
彈性模量分布重建網絡面對噪聲位移時的性能表現
Figure3.
Performance of elastic distribution reconstruction network with noisy displacement
此外，網絡預測一個輸入所需時間如表2所示，基于U-Net的生成器對一個輸入進行預測僅需要不到0.1 s，因此該網絡對于彈性模量分布重建任務具有非常高的實時性。
表2
不同輸入尺寸下監督模型重建彈性模量分布所需時間
Table2.
Time required for elastic modulus distribution reconstruction by supervised model with different input size
3.2 仿體實驗結果
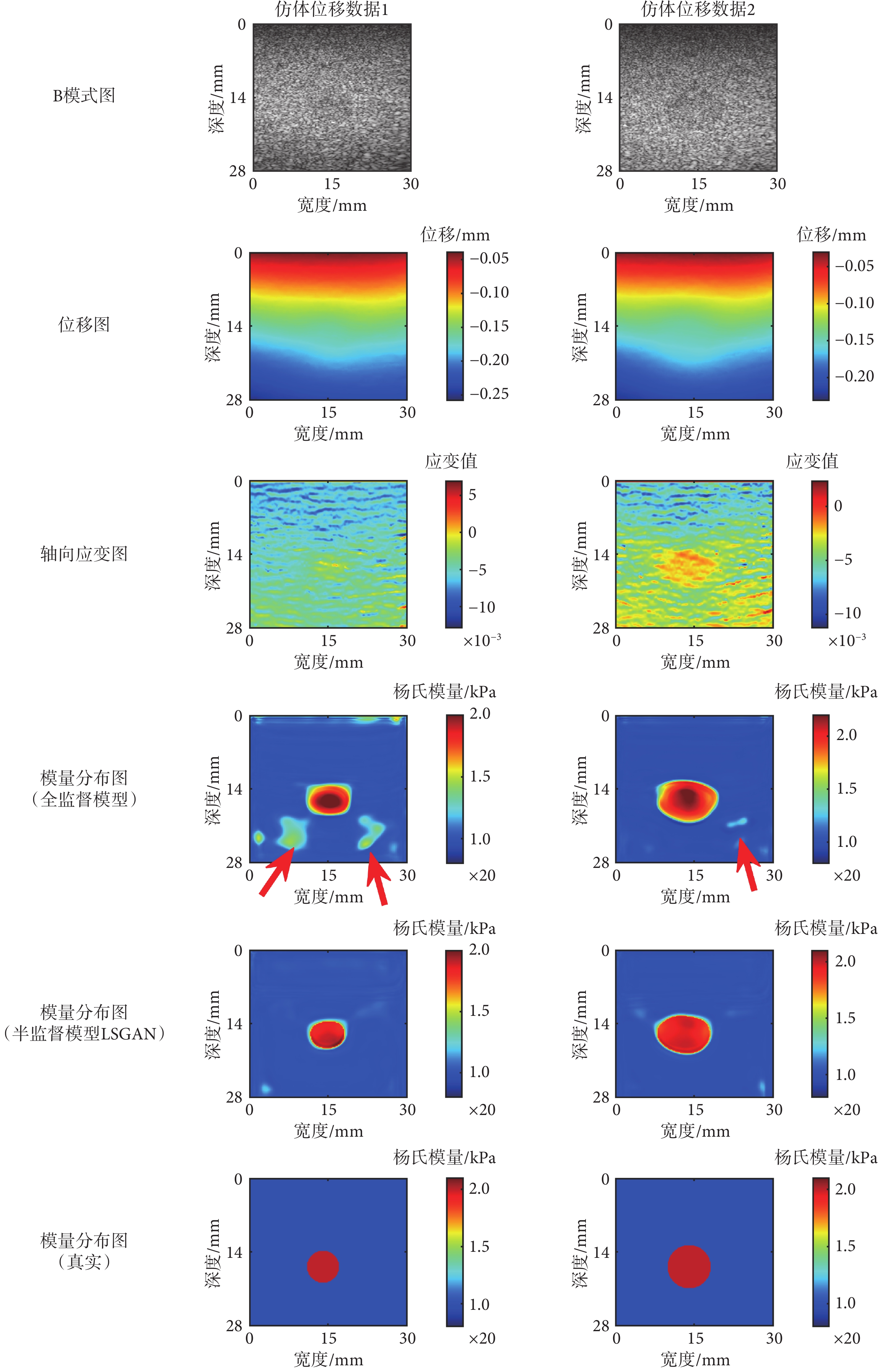
如圖4所示為兩個模型對仿體實驗數據預測的彈性模量分布重建結果，縱列展示了兩組不同的仿體數據實驗結果（仿體數據1、仿體數據2），橫排分別為B模式圖、位移圖、軸向應變圖、全監督模型結果、半監督模型LSGAN結果和真實彈性模量圖。從視覺上看，兩個模型預測結果的中間包裹物的形狀與大小與其對應的真實彈性模量分布較為一致。另外，對于全監督模型預測得到的彈性模量分布圖的背景區域出現了明顯的錯誤模量值（箭頭所指區域），而半監督模型LSGAN預測的彈性模量分布圖與真實彈性模量分布較為一致。同時，從圖4中可以看出，半監督模型LSGAN預測的彈性模量分布圖中包裹物硬度約為背景的2倍，這與仿體中已知的包裹體與背景的彈性模量比是一致的。
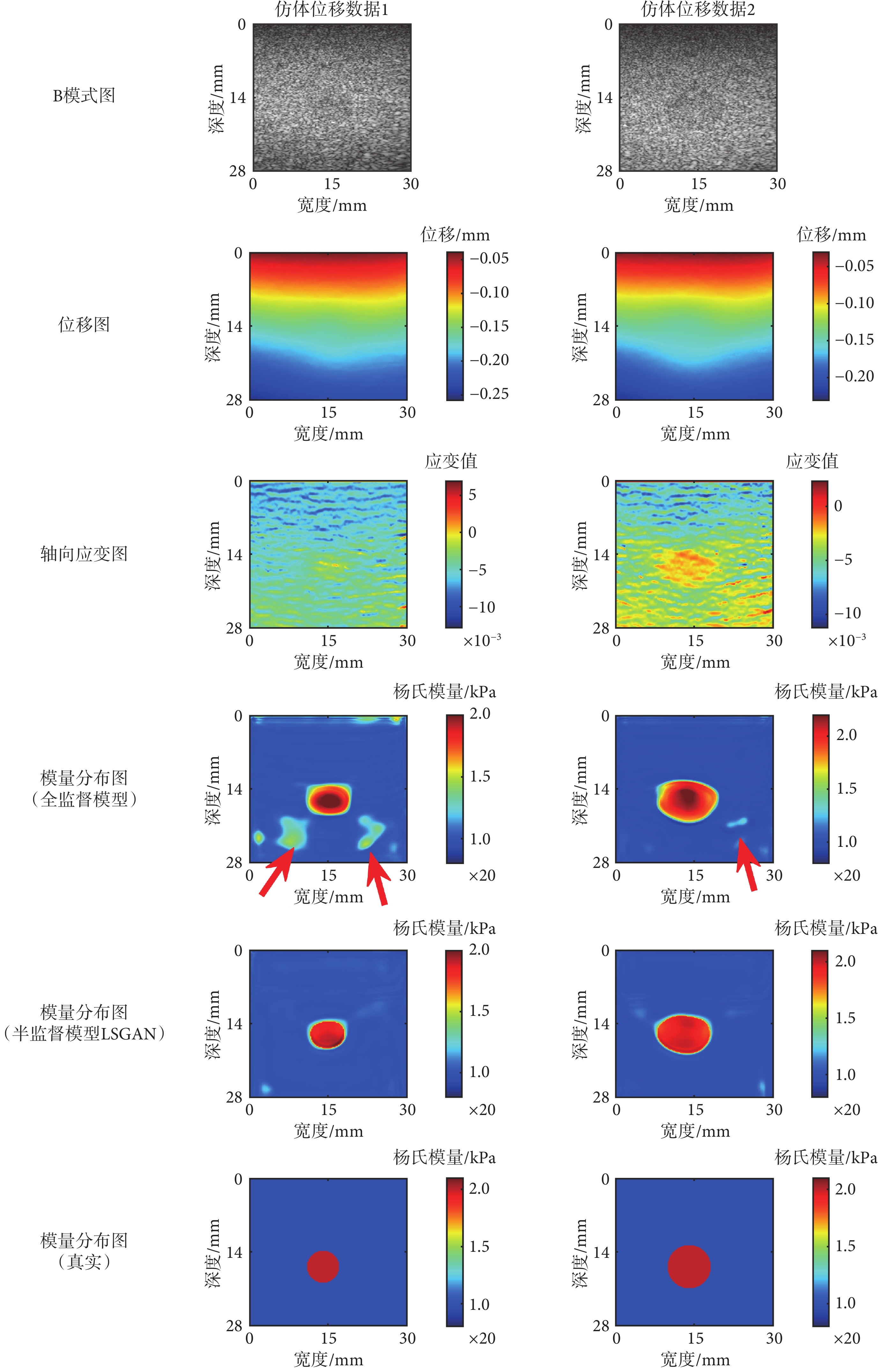圖4
仿體實驗結果
Figure4.
Results of phantom experiments
如表3所示為兩個模型預測的彈性模量分布與真實彈性模量分布之間的MAE和MRE。對于這兩組數據，半監督模型LSGAN預測結果均具有最低的 MAE 和 MRE。然而，值得注意的是，全監督模型也展現出了相當好的重建精度。從數據上看，兩種方法預測結果的MAE和MRE均未超過6%。尤其需要指出的是，對于這兩個仿體位移數據，半監督模型LSGAN預測結果的MAE分別僅為2.73%和3.79%，MRE分別僅為2.24%和3.25%。
表3
仿體實驗中模型預測值與真實值的MAE和MRE
Table3.
MAE and MRE of model prediction value and real value in phantom experiments
3.3 在體試驗結果
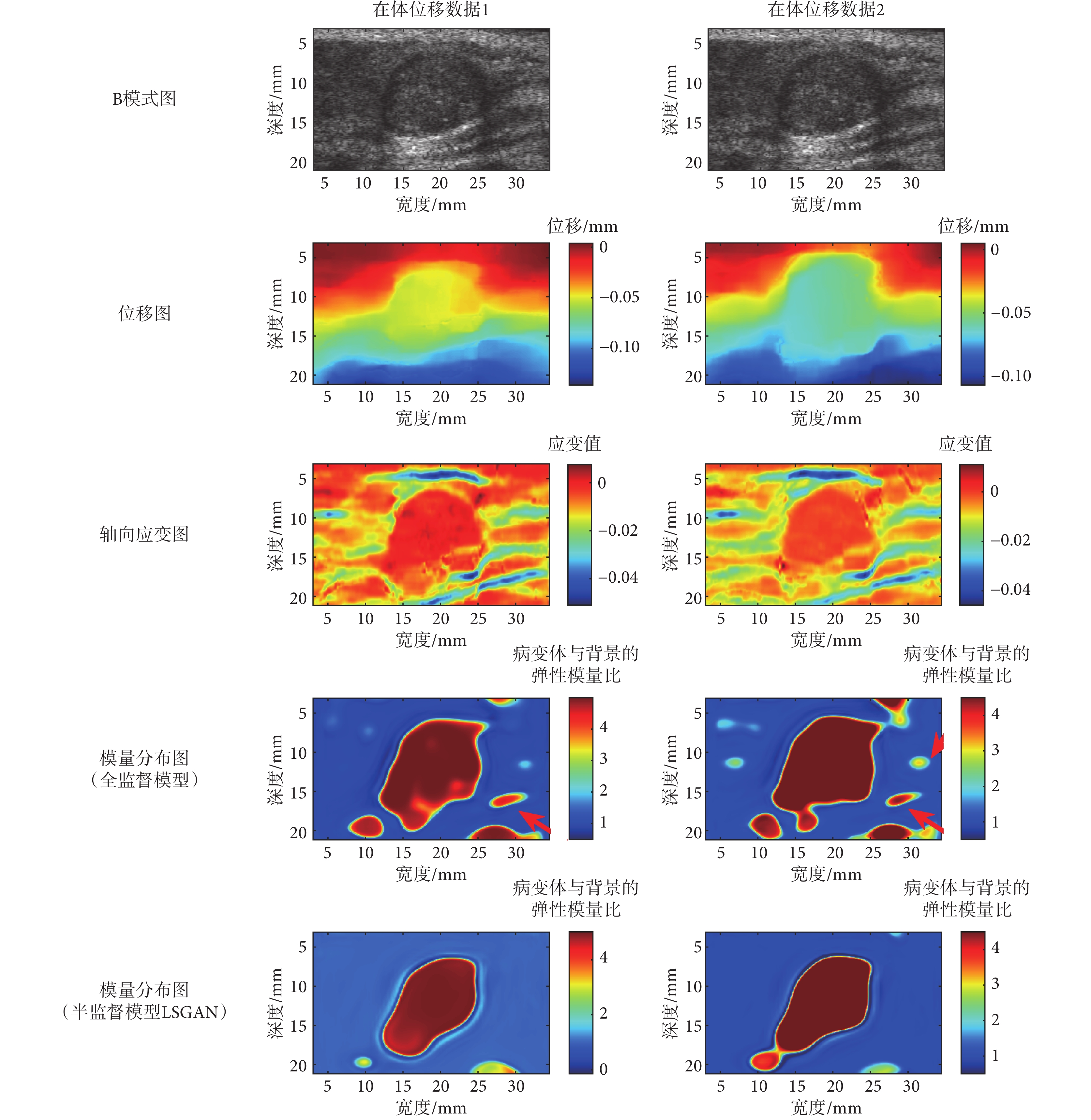
如圖5所示為兩個模型對在體數據進行彈性模量分布預測的結果，縱列分別展示了IDC病例在體乳房數據兩幀圖片試驗數據（在體位移數據1，在體位移數據2），橫排分別為B模式圖、位移圖、軸向應變圖、全監督模型結果和半監督模型LSGAN結果。從兩個網絡模型預測的彈性模量分布圖可以看出，病變體對應的彈性模量分布的位置、大小和形狀與其在B模式圖、軸向應變圖像中的對應位置、大小、形狀較吻合。從圖5中還可以分析出病變體與背景的彈性模量比約為4：1。在文獻[31]中，乳腺實質的楊氏模量為30～50 kPa，其中良性病變楊氏模量為（45.3 ± 41.1）kPa，惡性病變楊氏模量為（146.6 ± 40.05）kPa。基于以上知識，惡性病變與乳腺實質的比值大致在2.9～4.9之間。顯然，兩種模型預測的病變體的彈性模量分布圖像均顯示病變體是惡性的，符合臨床診斷。需要指出的是，僅使用仿真位移數據訓練得到的全監督模型的預測結果在背景中出現了較多的與臨床實際不符的區域（箭頭所指區域），而半監督模型LSGAN預測結果的背景區域能夠有效排除噪聲干擾，與該位置組織的真實彈性模量分布較為一致。
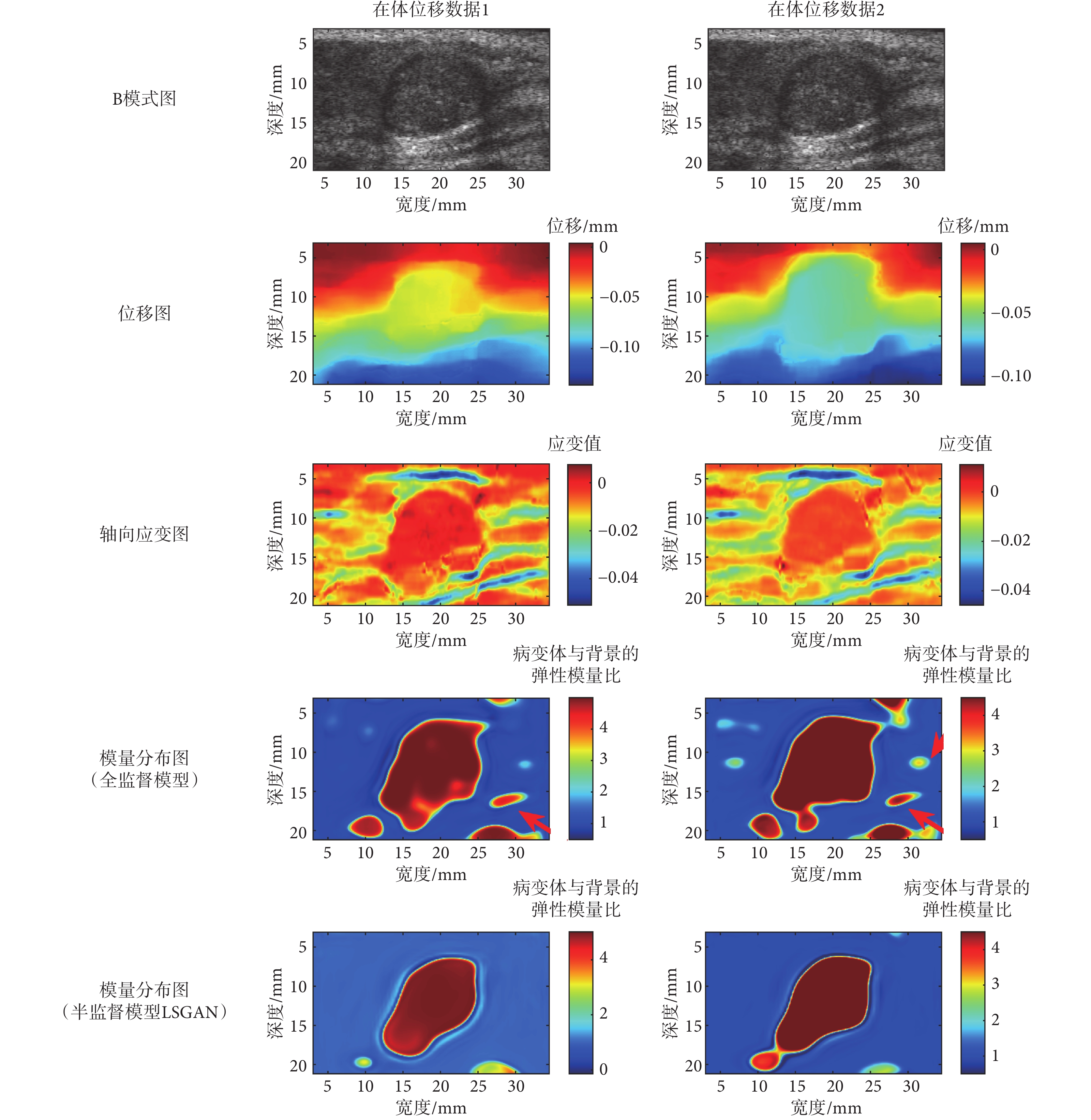圖5
在體乳腺試驗結果
Figure5.
Results of the in-vivo breast experiments.
4 討論與總結
本文提出了一種半監督的彈性模量分布重建深度神經網絡，將真實在體位移數據用于基于位移的彈性模量分布重建網絡訓練。實驗結果表明，相較于只是用了仿真位移數據訓練的全監督模型，引入了真實位移數據的半監督模型具有更好的彈性模量分布重建性能。
由于機械和電子噪聲干擾、操作者采集手法無法保證統一、追蹤算法以及在體環境的復雜性等原因，仿真位移數據難以完全重現在體超聲的復雜性和多樣性。即使通過添加噪聲等數據增強手段，仿真位移數據仍然不能完全替代真實在體位移數據。相比只使用仿真數據訓練的深度神經網絡模型，引入在體數據訓練的模型在超聲成像的很多領域都取得更好的性能。特別是在超聲散斑運動追蹤深度神經網絡模型中獲得了成功的應用。基于此，本文在彈性模量分布重建的深度學習模型訓練中引入真實位移數據，采用半監督學習的方法讓模型學習真實位移數據和仿真位移數據的差異，以提高模型的泛化性，減少重建結果中與臨床實際不符的區域。本文得到的模型進一步驗證了在超聲成像領域，使用在體數據可以進一步提升這些模型的性能。
本文所提出方法的泛化性是需要后續持續研究的一個問題，因為即使本文方法已經在訓練中引入了真實在體位移數據和添加噪聲的仿真位移數據一起訓練，但受限于真實位移數據的數量，依然無法完全彌補仿真位移數據和真實位移數據存在的差異。另外，受限于真實數據的病變類型，本研究使用的所有訓練數據均為病變的硬度高于背景硬度的數據。本文所得到的深度學習模型可能缺乏對較軟的病變、空腔等的重建彈性模量分布能力。因此，引入更多的真實在體數據繼續提升模型準確度將是下一步的研究方向。
還需要說明的是，本文的模型是將追蹤真實在體超聲數據得到的位移作為輸入，因此散斑追蹤算法的性能也會對本文所得到的模型結果有直接影響。鑒于前述基于光流的散斑追蹤深度神經網絡的成功，后續將基于光流的散斑追蹤深度神經網絡與本文所提方法構建為一個級聯網絡或者直接通過B模式圖像進行模型訓練以提升模型準確度也是一個重要的研究方向。
本文提出的基于半監督學習方法的彈性模量分布重建深度神經網絡，可以為深度神經網絡模型提供充足且具有更多復雜場景的訓練數據，進一步提高彈性模量分布重建深度神經網絡的魯棒性和泛化能力。本文所提出的方法在彈性模量分布重建領域主要的優勢在于：①能夠更準確進行彈性模量分布重建任務，減少重建錯誤；②相對于傳統方法不依賴于人工調參；③具有更快的重建速度，具有一定的臨床實際應用價值。未來的研究將繼續引入更多的沒有標簽的、具有不同病變類型的真實位移數據，使得到的模型具有更好的重建結果。
致謝
感謝威斯康星大學的Timothy Hall教授和密歇根理工大學的Jingfeng Jiang教授提供在體數據。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：彭博、羅建文負責設計整體研究方案；張瀟負責算法研究與實現，以及實驗、數據分析；張瀟、彭博負責撰寫論文；王銳、魏星月負責仿真位移數據算法的研究與實現。
倫理聲明：本研究通過了堪薩斯大學醫學中心人類受試者委員會機構倫理委員會的審批（批文編號：M1182）。
0 引言
組織的彈性模量分布是臨床診斷的重要依據[1-5]。通常情況下，組織的彈性模量與一定程度的病理改變有關。重建彈性模量分布可以幫助臨床醫生確定相應組織或器官病理狀態可能的發展，例如可以輔助識別乳腺腫瘤的特征和肝纖維化的分期[6-7]。
彈性模量重建是彈性問題中的反問題。相較于給定一組彈性模量分布和邊界條件，就可以通過有限元法求解出組織位移的正向問題[1-4]，反問題的求解往往需要大量迭代計算和高質量的組織位移，成本更高[5-7]。傳統的彈性模量分布重建方法分為迭代求解法和直接求解法。迭代求解法，通常分為兩步：首先，從形變前后的超聲射頻（radio frequency，RF）數據中追蹤位移；然后，以得到的位移作為輸入，通過求解反問題得到組織的彈性模量分布[8-10]。該方法由于需要迭代計算，計算效率低，難以實現實時成像。并且，迭代求解法還需進行正則化參數的選擇，參數的變動可能會極大地影響彈性重建結果，而不同數據的最佳參數并不相同，故在實際應用中很難確定出一組通用的最佳參數[11]。直接求解法，是通過直接估計，將位移輸入偏微分方程，也可直接求解該反問題[12-14]。直接求解法降低了計算成本，但在實際應用中由于估計誤差的影響，重建結果往往較差；且還需已知組織表面的彈性模量或位移/力邊界條件，這在臨床應用中往往難以實現[15]。
針對上述問題，Chen等[16]將彈性模量分布重建任務視為圖像翻譯任務，利用彈性本構關系和平衡方程作為深度神經網絡的先驗知識，通過最小化不平衡力圖的優化任務，實現了從應變圖像到彈性圖像的無監督學習。他們提出的深度學習模型可以實現在沒有測量的情況下預測彈性模量分布。然而，受超聲換能器的限制，臨床實際采集到的超聲信號往往具有較高的軸向分辨率和較低的橫向分辨率，導致無法提供高質量的橫向位移圖，進而無法提供該方法所需的高質量橫向應變圖，最終無法滿足無監督方法對訓練數據的需求。另外，由于預測的彈性模量分布沒有直接標簽，僅能通過平衡方程約束，導致無監督模型訓練往往非常緩慢，根據彈性模量分布的復雜程度，耗時20～80 min不等[16]，唯有通過有監督模型可以解決這一問題。Ni等[17]和Zhang等[18]分別以仿真應變圖像和仿真位移圖像為輸入，配對的彈性模量分布圖為標簽，通過實驗證明了深度神經網絡僅利用軸向應變或軸向位移即可預測出較為準確的模量分布。在上述有監督模型的工作中，模型訓練通常使用的是添加了噪聲的配對仿真位移數據。然而，由于機械和電子噪聲干擾、操作者采集手法無法保證統一、追蹤算法以及在體環境的復雜性等原因，仿真位移數據難以完全重現在體超聲的復雜性和多樣性。即便是添加了各種噪聲的大量仿真位移數據，依然無法完全替代追蹤在體超聲RF信號所得到的位移數據。值得借鑒的是，在超聲成像的很多領域，如超聲散斑運動追蹤深度神經網絡模型的相關研究工作中，已經證明了相比于只使用仿真位移數據，引入在體數據訓練模型能取得更好的性能[19-20]。基于上述原因，本文提出一種半監督的彈性模量分布重建深度神經網絡，通過在訓練過程中引入真實位移數據，可望進一步提升彈性模量分布重建模型對于真實位移數據的彈性模量分布重建的準確性，為臨床醫生準確診斷腫瘤或組織的病理發展提供可靠依據。
1 方法
1.1 半監督學習的最小二乘生成對抗網絡
半監督學習是深度學習中訓練深度神經網絡模型的一種方法。在全監督學習中，模型只使用帶標簽的數據進行有監督的訓練，而半監督學習則允許模型在一部分數據上進行有監督的訓練，同時在另一部分數據上進行無監督的訓練。在本研究中，半監督模型不僅會學習帶有真實彈性模量分布的仿真位移數據，還會學習未知彈性模量分布的真實位移數據。半監督模型用最小二乘生成對抗網絡（least squares generative adversarial network，LSGAN）[21]來實現，網絡結構如圖1所示。LSGAN相比于常規生成對抗網絡，在許多方面表現出更優秀的性能[21-24]。LSGAN在圖像翻譯任務上，通過引入最小二乘損失函數，緩解了鑒別器訓練中梯度消失的問題，從而使得訓練更穩定，生成的圖像紋理更清晰，模態更豐富[21-22]。在醫學圖像重建任務上，半監督學習的LSGAN可以使用較少的標簽達到較好的重建質量[23-24]。如前所述，彈性模量分布重建任務可看作圖像翻譯任務，故本文采用LSGAN構建半監督神經網絡。LSGAN由一個生成器和一個鑒別器組成。在學習過程中，鑒別器對于仿真位移數據的生成器生成結果進行鑒別的同時，還會將生成結果與其對應的真實彈性模量分布圖作比較；而對于真實位移數據的生成器生成結果，僅有鑒別器鑒別真假，以此讓生成器提前適應真實位移數據，提高模型泛化性。
圖1
半監督模型LSGAN的結構示意圖
Figure1.
Schematic structure of the semi-supervised LSGAN model
生成器是基于U型網絡（U-Net）的深度神經網絡，以單通道的軸向位移圖為輸入，通過多次卷積、下采樣、上采樣和跳躍鏈接后，輸出彈性模量分布圖。與原始工作相比，U-Net前四層卷積核被替換為了可變形卷積核，以更好地學習不規則的病變體形狀[25]；卷積層和輸出層激活函數都采用帶泄露修正線性單元（leaky rectified linear unit，LeakyReLU），其負數斜率為0.25，唯一不同的是輸出層，負數斜率為0.1；其余與原始U-Net相同。生成器的目標是學習位移與彈性模量分布之間的高維映射，輸出預測的彈性模量分布，希望欺騙鑒別器。對于真實位移數據，生成器僅需從鑒別結果中學習；而對于仿真位移數據，還需要額外學習生成結果與真實彈性模量分布圖的差異。
鑒別器取自馬爾可夫生成對抗網絡[26]，以單通道的模量圖為輸入，負責區分它是否是真實的彈性模量分布圖像。鑒別器前四層均由卷積層、歸一化層和激活函數LeakyReLU組成，每層的卷積核大小均為4 × 4，步長為2，輸出通道數分別為64、128、256、512。第五層是輸出層，是一個單獨的卷積層。卷積核大小為4 × 4，步長和輸出通道均為1。該鑒別器的鑒別結果和普通鑒別器僅輸出一個二元評價值（真或假）不同，其結果最終被映射到N×N的矩陣中，矩陣中每一個值代表其對應的感受野在鑒別器中的評價。相較于普通的鑒別器，該鑒別器擁有更強的鑒別能力，能夠緩解生成對抗網絡的梯度消失問題，更好地指導生成器[26]。
1.2 損失函數
1.2.1 生成器損失函數
生成器的損失函數由兩部分組成。一部分是鑒別器對生成結果圖和真實彈性模量分布圖的鑒別誤差，如式(1)和式(2)所示。另一部分來自于生成結果與真實彈性模量分布圖的L1損失，如式(3)所示：
|
|
|
其中，dsimu和dreal分別是輸入生成器的仿真位移數據與真實在體位移數據；Lg_real代表鑒別器對真實位移數據的生成結果與實際彈性模量分布圖的鑒別差異；Lg_simu代表鑒別器對仿真位移數據的生成結果與實際彈性模量分布圖的鑒別差異； L1 代表生成結果與真實彈性模量分布圖的L1損失； G(?)代表生成器對于任一輸入的生成結果；D(?)是鑒別器對于任一輸入鑒別結果；y是dsimu的對應真實彈性模量分布圖。生成器總的損失函數Lg，定義如式(4)所示：
|
其中， 和 是權重，在本文研究中固定為0.01。
1.2.2 鑒別器損失函數
鑒別器的損失由兩部分組成，一部分來自于鑒別器對真實位移數據生成結果的鑒別（以符號Ld_real表示），如式(5)所示；另一部分來自于鑒別器對仿真位移數據生成結果和真實彈性分布的鑒別（以符號Ld_simu表示），如式(6)所示；鑒別器總的損失函數Ld，定義如式(7)所示：
|
|
|
2 實驗
本研究將半監督模型LSGAN和Zhang等[18]提出的一種全監督模型進行比較，該全監督模型僅使用計算機仿真位移數據進行訓練。全監督模型采用深度卷積生成對抗網絡（deep convolution generative adversarial networks，DCGAN）作為網絡架構[27]，在訓練中僅使用仿真位移數據，并且所有仿真位移數據均有真實的彈性模量分布圖。為充分驗證本文所提方法的有效性，本研究通過計算機數字體模實驗、仿體體模實驗和在體乳腺試驗進行了定量和定性的比較。
在計算機數字體模實驗中，本研究首先采用量化指標評估兩種模型的重建結果與真實彈性模量分布圖像之間的誤差，以驗證預測的準確度。然后，通過對數字體模仿真實驗中的三組仿真位移數據，采用如2.1節中所述的方式對原始仿真位移添加1 000次噪聲，統計所有的預測誤差，以驗證提出的方法面對噪聲的魯棒性。最后，通過將不同尺寸的仿真位移數據輸入到本文所提出的方法中統計預測耗時，驗證本文所提方法在彈性模量分布重建的計算效率。
在仿體實驗中，本研究分別量化了兩種模型預測結果與真實彈性模量分布圖像之間的誤差。而在體試驗中，本研究將兩種模型重建的彈性模量分布圖像與現有臨床診斷結果進行比較分析。
2.1 訓練數據
在本研究中，訓練數據共包括162組真實位移數據和12 000組仿真位移數據，按照5∶1的比例劃分訓練集和測試集，最終訓練集中包含135組真實位移數據和10 000組仿真位移數據。
真實位移數據由追蹤在體超聲RF信號得到的162組位移數據組成。這些超聲RF數據來自27例經病理證實的乳腺病變受試者。數據采集均使用7.5 MHz的高頻線性陣列換能器（Siemens Medical Solution Inc., 美國）獲取，并得到了堪薩斯大學醫學中心人類受試者委員會（機構審查委員會）的批準，且獲得了患者的知情同意[28-30]。每個患者的超聲數據包含50～90 幀，從中隨機選擇6組相鄰的幀，采用具有局部多項式擬合的貝葉斯區域增長運動跟蹤算法（Bayesian region-growing motion tracking with local polynomial fitting，BRGMT-LPF）。該算法將貝葉斯推理與局部多項式擬合相結合，并納入區域增長塊匹配運動跟蹤框架，使用最大后驗概率密度函數來確定更加準確的位移向量。實驗結果表明，相較于原始區域增長運動跟蹤算法、貝葉斯推理區域增長和局部多項式擬合區域增長， BRGMT-LPF算法可以提供更加準確的運動跟蹤結果[28]，為后續神經網絡輸入高質量位移數據提供了基礎和保障。
仿真位移數據由仿真軟件MATLAB 2020a（The MathWorks Inc., 美國）偏微分方程工具箱生成。數字模體尺寸為40 mm × 40 mm × 1 mm，內部包裹一個橢圓包裹體。背景的楊氏模量固定為22 kPa。為了增加訓練數據的多樣性，本研究設計了半徑、楊氏模量和位置均為隨機值的橢圓包裹物。包裹物長軸范圍為5～10 mm，長軸與短軸之比為0.2～1.0的隨機數。包裹物的楊氏模量范圍為36～100 kPa。長軸與X軸夾角范圍為1°～180°。包裹物邊緣與數值體模邊緣之間的距離始終大于3 mm。泊松比設置為0.495，用以將組織視為一種幾乎不可壓縮的材料。數字體模在0.1%～5.0%的范圍內進行隨機軸向壓縮，這樣可以模擬超聲彈性成像中的大多數變形情況。在給定模量分布條件下，基于平面應變模型，采用有限元法計算模體相應的位移分布。為進一步增加訓練數據樣本和樣本的多樣性，在輸入深度神經網絡之前，對通過偏微分方程工具產生的仿真位移數據dsmooth進行隨機噪聲添加。最終，訓練輸入的仿真位移數據dsimu定義如式(8)所示：
|
其中，avg(?)是均值函數，α是0.01～0.05的隨機數，σ是均值為0、方差為1的標準正態分布噪聲。需要說明的是，為適應網絡的輸入尺寸，本研究中的仿真位移數據、相對應的真實彈性模量分布圖和真實位移數據均被調整為256 × 256像素，對深度神經網絡進行半監督訓練。
2.2 計算機數字體模實驗數據
本研究在計算機數字體模實驗中使用了三組隨機選擇的仿真位移數據來驗證所提出的方法。如前一節所述，用于評價的位移和彈性數據與用于訓練的數據在生成方法上相同。以該位移數據作為輸入，重建出相應的彈性模量分布。最后利用生成器重建的彈性模量分布與真實彈性模量分布之間的差異來量化重建誤差。
2.3 仿體體模數據
本研究使用一臺配備L9-3線性陣列換能器的飛利浦iU22超聲系統（Philips Medical Systems Inc., 美國）徒手掃描乳房彈性成像仿體（model 059, CIRS Inc., 美國）獲取仿體實驗射頻數據。該仿體中分布有5個不同大小的球形包裹物，其硬度是背景的兩倍。實驗中，對仿體中直徑分別為4.1 mm和6.5 mm的包裹物進行掃描并采集射頻數據，得到的射頻數據的采樣頻率為32 MHz，每個射頻幀由320掃描線組成，軸向采樣間距和橫向采樣間距分別為0.01 mm和0.12 mm。
2.4 在體數據
在體試驗數據來自一名已經臨床診斷為浸潤性導管癌（invasive ductal carcinoma，IDC）的乳腺癌患者。該數據使用配有7.5 MHz線性陣列傳感器的掃描儀（Siemens Medical Solution Inc.，美國）獲得。采集時，醫生以徒手的方式壓縮乳房，用以產生1.0%～1.5%的應變。射頻數據采集頻率為36 MHz。軸向采樣間距和橫向采樣間距分別為0.021 mm和0.19 mm。數據采集同樣得到了堪薩斯大學醫學中心人類受試者委員會（機構審查委員會）的批準，并獲得了患者的知情同意[27-29]。本研究從連續采集的圖像幀中隨機選取兩幀連續的圖像幀來評估所提方法的性能。
2.5 評價指標
本研究使用平均絕對誤差（mean absolute error，MAE）和平均相對誤差（mean relative error，MRE）作為評價指標，來衡量深度學習模型預測的彈性模量分布圖像與計算機仿真得到的真實彈性模量分布圖像之間的全局相似度，以定量評價所提方法在彈性模量分布重建上的誤差，其定義如式(9)和式(10)所示：
|
|
其中，n和m分別是圖像的高度和寬度。G(x)(i, j)和y(i, j)分別是預測的彈性模量分布圖和真實彈性模量分布圖在該處的彈性值。
2.6 實現細節
本研究使用機器學習庫PyTorch 1.7.0（Facebook Inc.，美國）實現了本文方法和對比方法的深度神經網絡，并在配備圖形處理器NVIDIA GeForce RTX 3090（NVIDIA，Inc.，美國）的工作站上進行訓練。用于訓練的優化器是自適應矩估計（adaptive moment estimation，Adam）。批大小、訓練周期和學習率分別設置為16、400和5 × 10?5。
3 結果
為了更直觀地比較重建結果，本研究對模型預測的彈性模量分布結果進行了相對化處理。在實驗結果圖中，背景模量值始終為1，內部包裹物的模量值表現為背景模量的倍數，因此模量值不帶單位。
3.1 計算機數字體模實驗結果
計算機數字體模的仿真實驗結果如圖2所示，其中縱列分別對應三組隨機選取的仿真位移數據（仿真位移數據1、仿真位移數據2、仿真位移數據3），橫排分別對應位移圖、全監督模型結果、半監督模型LSGAN結果和真實彈性模量分布圖。對于三組仿真位移數據，半監督模型LSGAN和全監督模型預測的橢球體的形狀與真實的橢球體形狀基本一致；同時從橢球體內部的模量數值來看，兩種模型預測的彈性模量數值也與真實彈性模量分布圖中橢球體的彈性模量值一致。
圖2
仿真實驗結果
Figure2.
Results of simulation experiments
仿真實驗中半監督模型LSGAN和全監督模型預測的彈性模量值與真實彈性模量值之間的MAE和MRE如表1所示。對于三組仿真位移數據，半監督模型和全監督模型預測結果的MAE和MRE都在1.00%以內。兩種模型預測得到的彈性模量分布圖中的數值基本一致。這些結果證明了對于仿真位移數據，兩種模型都能夠準確預測彈性模量分布圖。
表1
仿真實驗中模型預測值與真實值的MAE和MRE
Table1.
MAE and MRE of model prediction value and real value in simulation experiments
如圖3所示為本文提出的網絡在面對添加噪聲后仿真位移數據時的預測性能，噪聲添加方式如2.1節所述。對于仿真位移數據而言，當位移噪聲在1.0%～5.0%之間時，該網絡對仿真位移數據的預測結果的MAE和MRE均低于1.5%。其中大部分情況MAE低于1.0%，而MRE在0.5%上下浮動。總體上看，在輸入帶有噪聲數據的仿真位移數據時，本文所提出的網絡模型依然可以預測得到具有較高質量的彈性模量分布圖。
圖3
彈性模量分布重建網絡面對噪聲位移時的性能表現
Figure3.
Performance of elastic distribution reconstruction network with noisy displacement
此外，網絡預測一個輸入所需時間如表2所示，基于U-Net的生成器對一個輸入進行預測僅需要不到0.1 s，因此該網絡對于彈性模量分布重建任務具有非常高的實時性。
表2
不同輸入尺寸下監督模型重建彈性模量分布所需時間
Table2.
Time required for elastic modulus distribution reconstruction by supervised model with different input size
3.2 仿體實驗結果
如圖4所示為兩個模型對仿體實驗數據預測的彈性模量分布重建結果，縱列展示了兩組不同的仿體數據實驗結果（仿體數據1、仿體數據2），橫排分別為B模式圖、位移圖、軸向應變圖、全監督模型結果、半監督模型LSGAN結果和真實彈性模量圖。從視覺上看，兩個模型預測結果的中間包裹物的形狀與大小與其對應的真實彈性模量分布較為一致。另外，對于全監督模型預測得到的彈性模量分布圖的背景區域出現了明顯的錯誤模量值（箭頭所指區域），而半監督模型LSGAN預測的彈性模量分布圖與真實彈性模量分布較為一致。同時，從圖4中可以看出，半監督模型LSGAN預測的彈性模量分布圖中包裹物硬度約為背景的2倍，這與仿體中已知的包裹體與背景的彈性模量比是一致的。
圖4
仿體實驗結果
Figure4.
Results of phantom experiments
如表3所示為兩個模型預測的彈性模量分布與真實彈性模量分布之間的MAE和MRE。對于這兩組數據，半監督模型LSGAN預測結果均具有最低的 MAE 和 MRE。然而，值得注意的是，全監督模型也展現出了相當好的重建精度。從數據上看，兩種方法預測結果的MAE和MRE均未超過6%。尤其需要指出的是，對于這兩個仿體位移數據，半監督模型LSGAN預測結果的MAE分別僅為2.73%和3.79%，MRE分別僅為2.24%和3.25%。
表3
仿體實驗中模型預測值與真實值的MAE和MRE
Table3.
MAE and MRE of model prediction value and real value in phantom experiments
3.3 在體試驗結果
如圖5所示為兩個模型對在體數據進行彈性模量分布預測的結果，縱列分別展示了IDC病例在體乳房數據兩幀圖片試驗數據（在體位移數據1，在體位移數據2），橫排分別為B模式圖、位移圖、軸向應變圖、全監督模型結果和半監督模型LSGAN結果。從兩個網絡模型預測的彈性模量分布圖可以看出，病變體對應的彈性模量分布的位置、大小和形狀與其在B模式圖、軸向應變圖像中的對應位置、大小、形狀較吻合。從圖5中還可以分析出病變體與背景的彈性模量比約為4：1。在文獻[31]中，乳腺實質的楊氏模量為30～50 kPa，其中良性病變楊氏模量為（45.3 ± 41.1）kPa，惡性病變楊氏模量為（146.6 ± 40.05）kPa。基于以上知識，惡性病變與乳腺實質的比值大致在2.9～4.9之間。顯然，兩種模型預測的病變體的彈性模量分布圖像均顯示病變體是惡性的，符合臨床診斷。需要指出的是，僅使用仿真位移數據訓練得到的全監督模型的預測結果在背景中出現了較多的與臨床實際不符的區域（箭頭所指區域），而半監督模型LSGAN預測結果的背景區域能夠有效排除噪聲干擾，與該位置組織的真實彈性模量分布較為一致。
圖5
在體乳腺試驗結果
Figure5.
Results of the in-vivo breast experiments.
4 討論與總結
本文提出了一種半監督的彈性模量分布重建深度神經網絡，將真實在體位移數據用于基于位移的彈性模量分布重建網絡訓練。實驗結果表明，相較于只是用了仿真位移數據訓練的全監督模型，引入了真實位移數據的半監督模型具有更好的彈性模量分布重建性能。
由于機械和電子噪聲干擾、操作者采集手法無法保證統一、追蹤算法以及在體環境的復雜性等原因，仿真位移數據難以完全重現在體超聲的復雜性和多樣性。即使通過添加噪聲等數據增強手段，仿真位移數據仍然不能完全替代真實在體位移數據。相比只使用仿真數據訓練的深度神經網絡模型，引入在體數據訓練的模型在超聲成像的很多領域都取得更好的性能。特別是在超聲散斑運動追蹤深度神經網絡模型中獲得了成功的應用。基于此，本文在彈性模量分布重建的深度學習模型訓練中引入真實位移數據，采用半監督學習的方法讓模型學習真實位移數據和仿真位移數據的差異，以提高模型的泛化性，減少重建結果中與臨床實際不符的區域。本文得到的模型進一步驗證了在超聲成像領域，使用在體數據可以進一步提升這些模型的性能。
本文所提出方法的泛化性是需要后續持續研究的一個問題，因為即使本文方法已經在訓練中引入了真實在體位移數據和添加噪聲的仿真位移數據一起訓練，但受限于真實位移數據的數量，依然無法完全彌補仿真位移數據和真實位移數據存在的差異。另外，受限于真實數據的病變類型，本研究使用的所有訓練數據均為病變的硬度高于背景硬度的數據。本文所得到的深度學習模型可能缺乏對較軟的病變、空腔等的重建彈性模量分布能力。因此，引入更多的真實在體數據繼續提升模型準確度將是下一步的研究方向。
還需要說明的是，本文的模型是將追蹤真實在體超聲數據得到的位移作為輸入，因此散斑追蹤算法的性能也會對本文所得到的模型結果有直接影響。鑒于前述基于光流的散斑追蹤深度神經網絡的成功，后續將基于光流的散斑追蹤深度神經網絡與本文所提方法構建為一個級聯網絡或者直接通過B模式圖像進行模型訓練以提升模型準確度也是一個重要的研究方向。
本文提出的基于半監督學習方法的彈性模量分布重建深度神經網絡，可以為深度神經網絡模型提供充足且具有更多復雜場景的訓練數據，進一步提高彈性模量分布重建深度神經網絡的魯棒性和泛化能力。本文所提出的方法在彈性模量分布重建領域主要的優勢在于：①能夠更準確進行彈性模量分布重建任務，減少重建錯誤；②相對于傳統方法不依賴于人工調參；③具有更快的重建速度，具有一定的臨床實際應用價值。未來的研究將繼續引入更多的沒有標簽的、具有不同病變類型的真實位移數據，使得到的模型具有更好的重建結果。
致謝
感謝威斯康星大學的Timothy Hall教授和密歇根理工大學的Jingfeng Jiang教授提供在體數據。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：彭博、羅建文負責設計整體研究方案；張瀟負責算法研究與實現，以及實驗、數據分析；張瀟、彭博負責撰寫論文；王銳、魏星月負責仿真位移數據算法的研究與實現。
倫理聲明：本研究通過了堪薩斯大學醫學中心人類受試者委員會機構倫理委員會的審批（批文編號：M1182）。
