目前研發的新型國產正畸裝置中，托槽與形狀記憶合金（SMA）弓絲之間的止鎖機制是控制牙體精準矯正的關鍵。為滿足臨床治療中的止鎖力需求，止鎖螺栓的緊固扭角及所需要的扭矩大小需要精準設計。為此，本文開展止鎖機制的設計研究，分析緊固扭角與止鎖力的對應關系，確定有效的扭矩值，其中涉及復雜耦合的接觸、材料和幾何非線性特征。首先，針對SMA弓絲的三點彎曲實驗數據，開展基于參數正交實驗設計的仿真分析，確定SMA超彈性材料參數。其次，建立螺栓旋緊和弓絲拉拔的兩階段精細有限元仿真模型，通過關鍵接觸參數的優化設置，實現非線性分析收斂。最后，開展三種緊固扭角情況下的多組標定實驗。本研究通過設計分析與標定實驗的對比結果表明，各情況下止鎖力的設計分析值與標定均值的偏差在10%以內，設計分析方法有效可靠。本研究最終確定臨床應用的緊固扭角為10°，額定扭矩為2.8 N·mm。綜上，本文所得關鍵數據可用于新型正畸裝置的臨床方案設計和后續機械優化，研究方法可為包含SMA材料的醫療器械受力分析提供有益參考。
引用本文： 代清源, 吉利, 華嘉皓, 梁振宇, 余健文, 陳太聰. 微型正畸裝置形狀記憶合金弓絲非線性止鎖機制設計. 生物醫學工程學雜志, 2024, 41(4): 766-774. doi: 10.7507/1001-5515.202306051 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
佩戴牙齒矯治器是臨床正畸治療中矯正患者錯牙合畸形的主要手段。常見的矯治器由弓絲和托槽兩部分組成，其中托槽通過弓絲的牽引向人體組織傳遞矯治力，從而使錯位牙齒在牽引力和扭矩的作用下逐漸移動至理想位置[1-2]。相關研究表明，矯治力由弓絲變形產生，通過矯治器中止鎖裝置傳遞，其大小與作用方式對正畸治療的效率與效果影響顯著[3-5]。在口腔正畸領域，研究矯治器內部的弓絲止鎖機制對臨床正畸治療具有重要意義。
形狀記憶合金（shape memory alloy，SMA）作為一種新興智能材料，因其具有獨特的形狀記憶效應、超彈性效應和良好的生物相容性[6]，在生物醫療領域常被用在牙齒、骨骼和血管等相關的醫療器材中[7-9]。其中，在口腔正畸方面，SMA弓絲因能持續施加較輕的作用力，可縮短矯治時間，已逐漸成為應用主流弓絲。近年來，本課題組研發的新型球型自鎖托槽[10]，通過設計止鎖/止動系統，能與抗扭剛度較小的SMA弓絲結合，實現了輕力精準矯治[11]，具有正畸效率高、佩戴舒適等優越的臨床表現[12]，已成為具有國際競爭力的國產醫療器械。隨著該產品的臨床應用越來越廣泛，為了進一步達到更佳的矯治效果，有必要通過有限元等力學分析手段，實現新型托槽止鎖機制的優化設計。
現階段，口腔醫療領域的力學應用研究多集中于正畸裝置對牙齒和口腔組織的影響[13-16]，數據分析主要采用簡化的托槽模型，缺少對于托槽本身的機械性能研究[17-19]，而球型托槽止動系統的研究尚屬空白。其次，SMA弓絲的材料特性是力學分析的關鍵，使用不同成分、工藝制成的SMA材料性質差別明顯，供應商通常無法提供具體的相關材料模型參數，如果直接應用文獻參數則容易造成分析結果與實際差異較大。本課題組前期研發的裝置止鎖過程涉及復雜耦合的接觸、材料和幾何非線性特征，其中接觸參數對于分析收斂和精度具有決定性影響，相關設置也值得進一步深入研究。
針對上述問題，本文將開展新型托槽非線性止鎖機制的高精度設計分析方法的研究，具體包括：① 基于廠家提供的SMA弓絲三點彎曲實驗數據，通過多參數的正交實驗設計和相應仿真，確定SMA材料計算參數；② 建立螺栓旋緊和弓絲拉拔的兩階段精細有限元仿真模型，分辨關鍵接觸參數并進行優化設置，實現耦合非線性分析過程的有效收斂；③ 開展三種典型緊固扭角下的止鎖標定實驗，對比驗證本文分析方法的有效性，以期優化確定臨床應用的螺栓緊固扭角和扳手額定扭矩的設計值。
1 問題背景
1.1 球形自鎖托槽的工作原理
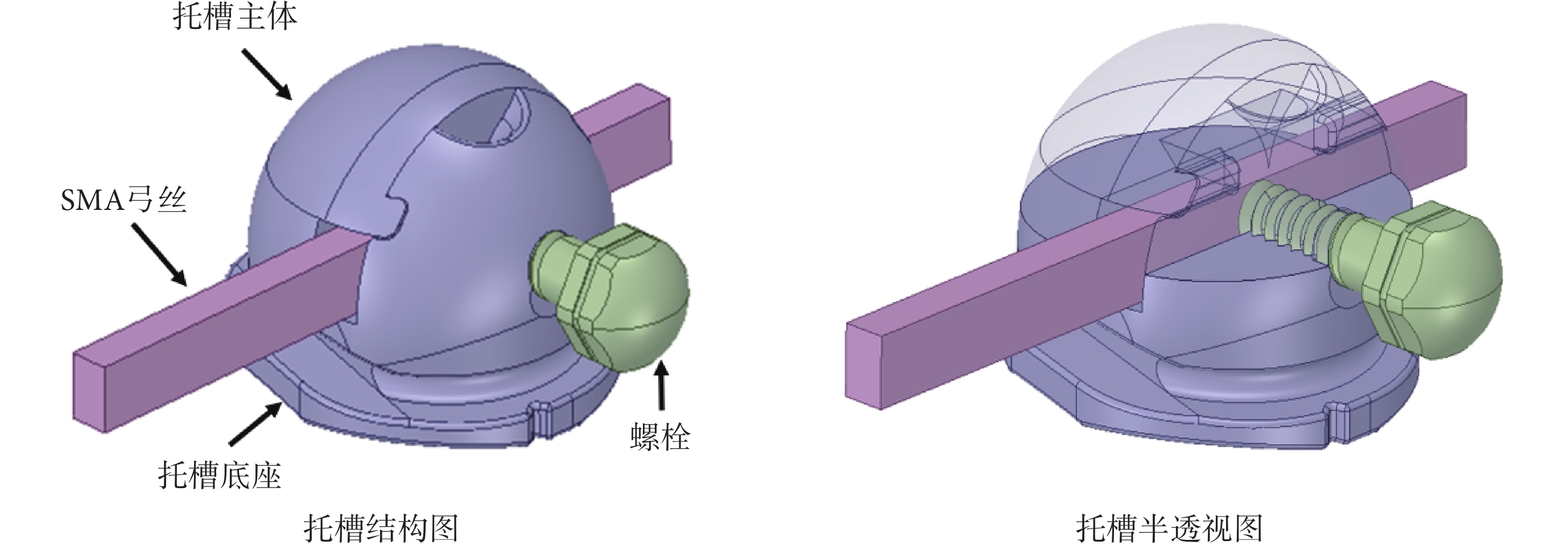
托槽是正畸矯治期間粘接于牙面的一種精密機械裝置，具有體積小、受荷大、制造精度高等特點。本文應用的球型自鎖托槽[10]，由底座、主體、SMA弓絲和螺栓四部分組成，如圖1所示。托槽底座長度和寬度約為3.5 mm，主體高約3 mm；SMA弓絲為矩形截面，高0.635 mm，寬0.406 mm。正畸治療中，托槽底部粘合在患者牙面上，SMA弓絲穿過托槽的槽溝，其中弓絲左側表面緊貼槽溝左側壁，弓絲下表面緊貼槽溝底壁，之后螺栓擰入托槽主體的栓道并壓緊弓絲實現緊固，最終通過弓絲的自恢復變形引導托槽攜帶牙齒移動。其中，當螺絲擰轉特定角度后，拉拔弓絲使之與螺栓之間發生相對滑動所需要的最小拉力，即定義為止鎖力，它等于托槽能提供給牙齒的最大牽引力，是該型托槽的重要性能指標。
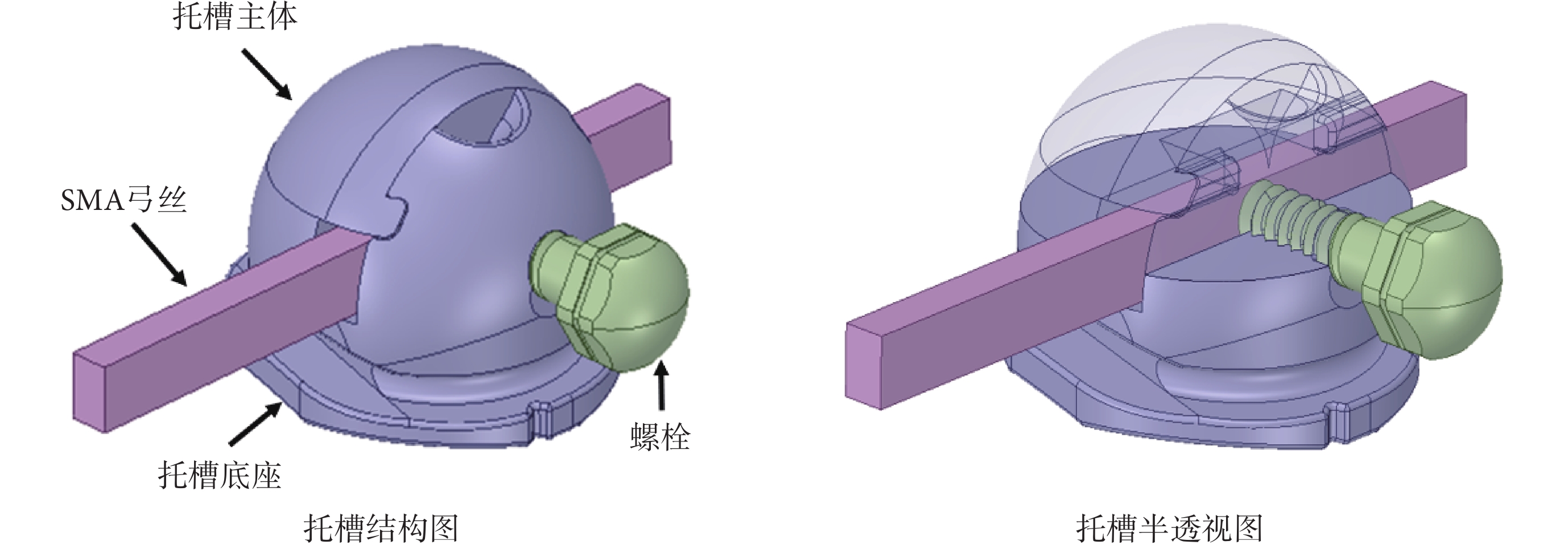圖1
球型自鎖托槽結構
Figure1.
Structure of spherical self-locking bracket
1.2 球形自鎖托槽的臨床應用問題
在球形托槽的臨床應用中，醫生通常使用微型扳手擰轉螺栓，使螺栓底面觸碰到弓絲右側表面，此時弓絲右側表面出現應力，扳手開始受力，然后繼續擰轉一定角度以緊固弓絲。這一后續擰轉角度定義為緊固扭角，其大小取決于扳手所施加的扭矩大小。臨床經驗發現，若扳手扭矩過小，導致緊固扭角偏小，則弓絲易發生滑動，不能為牙齒矯正提供足夠的牽引力；若扳手扭矩過大，導致緊固扭角偏大，則螺栓上部薄弱處易被擰斷。
為了能在實際臨床操作中獲得正畸所需的最佳牽引力，有必要預先確定不同緊固扭角與止鎖力的關系，以及相對應的扭矩大小，并在不損壞正畸裝置的前提下，優化設計緊固扭角和扭矩的取值。本課題組的托槽研發團隊前期開展了一系列實驗，測定不同緊固扭角下的弓絲拉拔力，實驗裝置如圖2所示，但由于正畸托槽過于微小，容易出現實驗結果數值不穩、離散度大等問題。此外，微型扳手的扭矩大小難以精確測量，僅能通過額定扭矩的設置來定義最大施加扭矩，無法精確控制不同緊固扭角對應的扭矩大小。
圖2
托槽止鎖力測試裝置
Figure2.
Test device of bracket locking force
因此，為了更精準地獲得上述量化關系和取值，本文研發團隊擬應用有限元的數值分析手段，對球形自鎖托槽的非線性止鎖機制開展仿真研究，分析確定不同緊固扭角下的各個部件的應力分布情況，以及相對應的SMA弓絲拉拔止鎖力，結合標定實驗對比，為球形自鎖托槽的臨床應用提供關鍵數據。
2 有限元分析的非線性特征
針對托槽止鎖機制的仿真分析，需要處理復雜的非線性關系，表現在：① 除了SMA弓絲的超彈性材料行為，托槽主體和螺栓材料也可能發生塑性屈服；② 在螺栓旋進和SMA弓絲拉拔過程中，各部件之間出現較大相對運動，模型計算構型需要隨時更新；③ 在托槽主體與螺栓之間、SMA弓絲底面與主體之間、SMA弓絲頂面與螺栓端頭之間存在大范圍的擠壓，接觸非線性效應明顯。
這些非線性關系高度耦合，主要出現在托槽主體和螺栓接觸的螺紋尖端，以及螺栓與弓絲接觸的螺栓端頭處，導致有限元計算極為耗時，給計算收斂造成巨大困難，最終影響計算精度，需要針對性定義和設置。
本次有限元仿真分析選擇通用工程仿真軟件ANSYS（version 19.2, ANSYS Inc., 美國）進行，其便于復雜機械建模，包含較為成熟的SMA材料本構模型，也支持多種非線性效應的耦合分析。下文將重點介紹弓絲SMA材料模型的參數標定方法，以及托槽止鎖的計算模型和分析方法。
3 SMA材料參數標定
3.1 SMA三點彎曲實驗
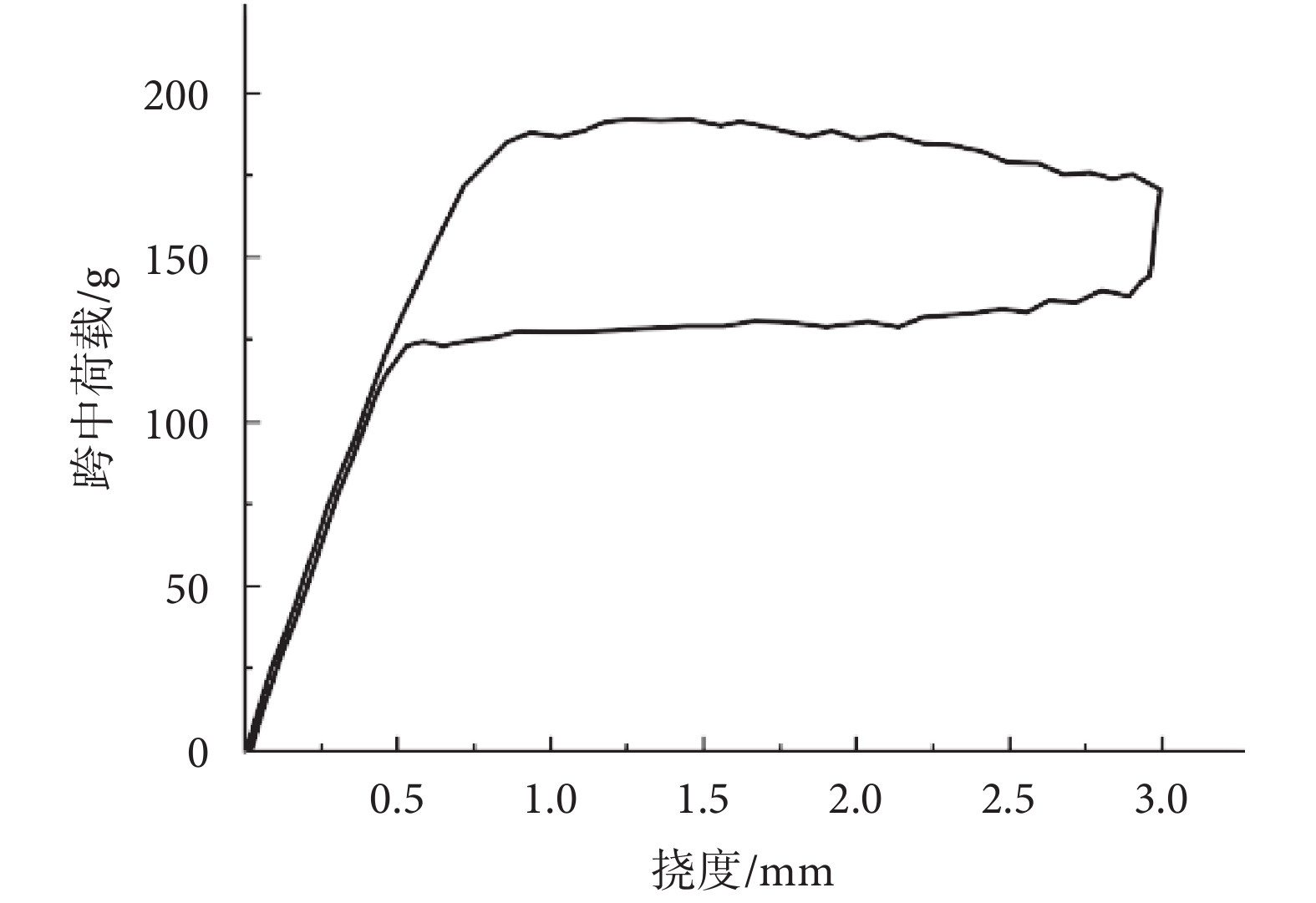
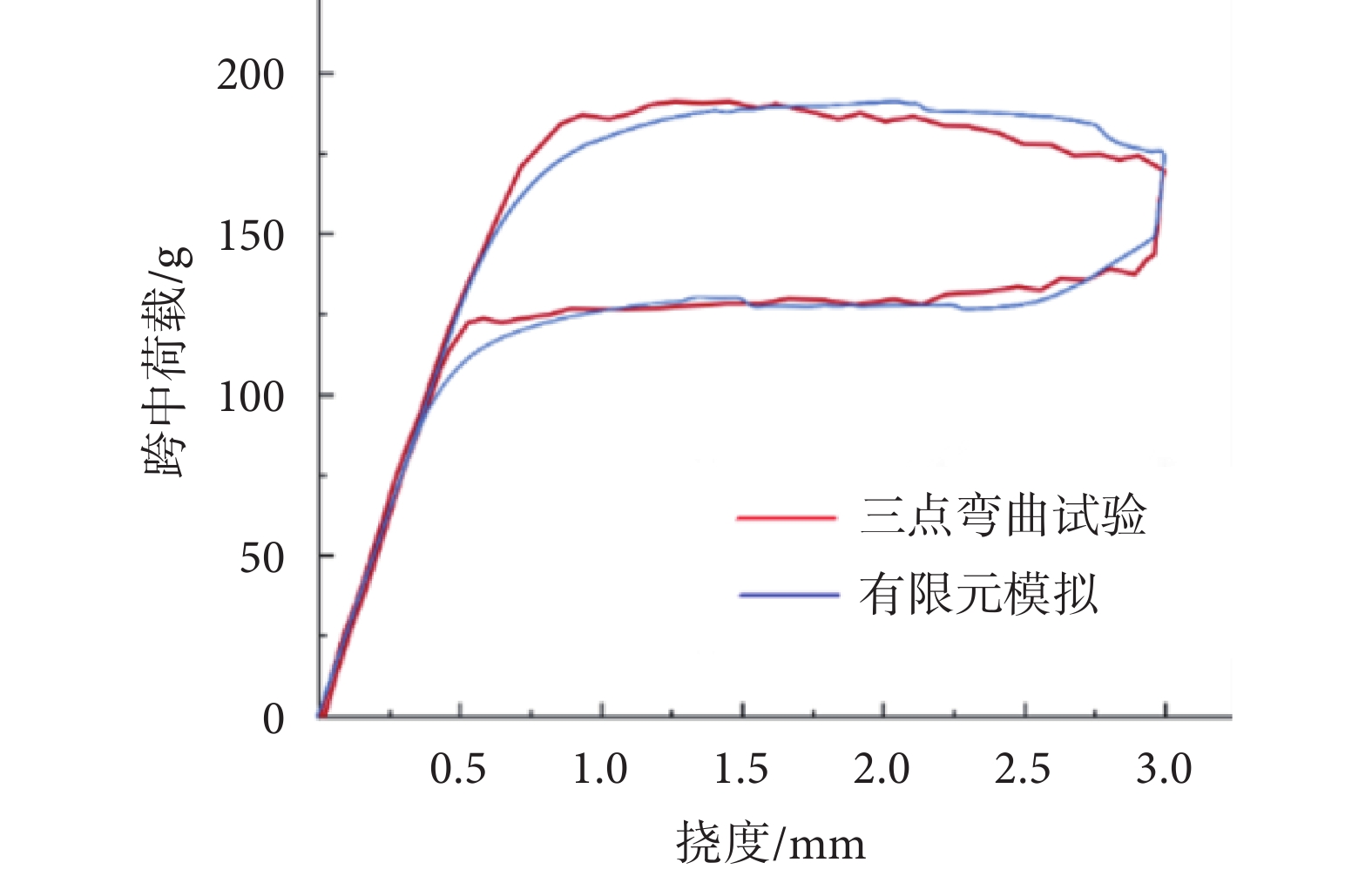
對于托槽所使用的SMA弓絲，材料供應商未提供具體組成和材性數據，只提供弓絲三點彎曲實驗數據。實驗采用直徑0.355 6 mm的SMA弓絲，在與人體溫度一致的37 °C環境溫度下進行，實驗裝置如圖3所示。兩支座間跨度為10 mm，在跨中進行位移加載，撓度達3 mm后卸載，最終得到的荷載—撓度關系曲線如圖4所示。
圖3
SMA弓絲的三點彎曲測試裝置
Figure3.
3-point bending test device of SMA archwire
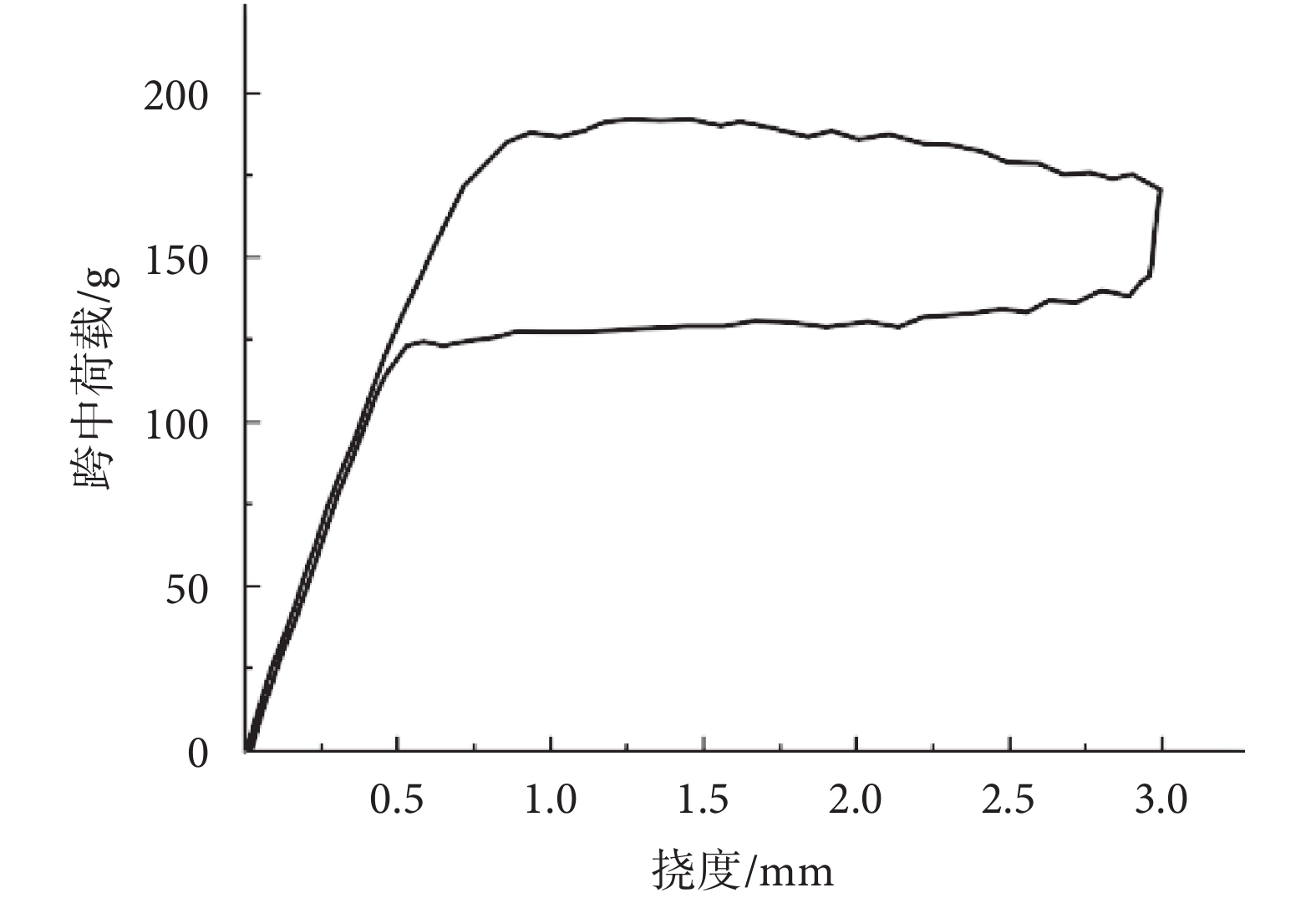圖4
三點彎曲實驗荷載—撓度曲線
Figure4.
Load-deflection curve from 3-point bending test
3.2 SMA本構模型
SMA材料的主要特征在于馬氏體與奧氏體之間的可逆相變，是由于剪切位移而改變晶體結構的切變型相變，分為由溫度誘導（形狀記憶效應）和由應力誘導（超彈性效應）兩種類型。由于人體口腔溫度幾乎恒定，因此在托槽止鎖機制應用中，SMA弓絲主要發揮超彈性效應。
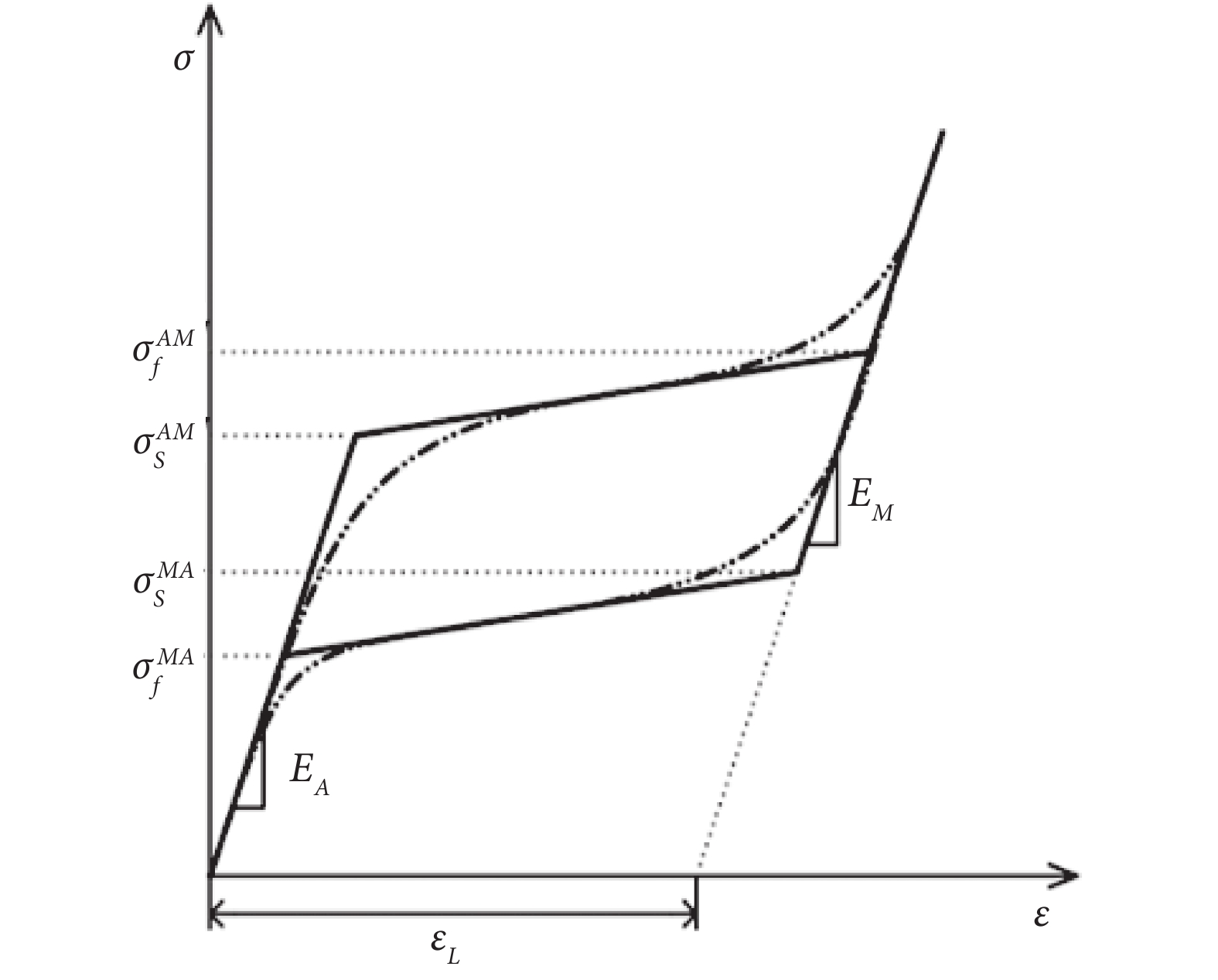
通用工程仿真軟件ANSYS（version 19.2，ANSYS Inc.，美國）采用宏觀唯象的奧利奇奧（Auricchio）模型[20]，通過9個參數設定SMA超彈性材料本構，各參數的物理意義如表1所示。前7個參數在單軸應力—應變曲線中的定義如圖5所示，其中，SMA材料的單軸拉伸實驗曲線實際為光滑曲線[21]，軟件中將其近似為多段折線，有利于計算分析。
表1
SMA超彈性材料的參數定義
Table1.
Parameter definition of SMA super-elastic material
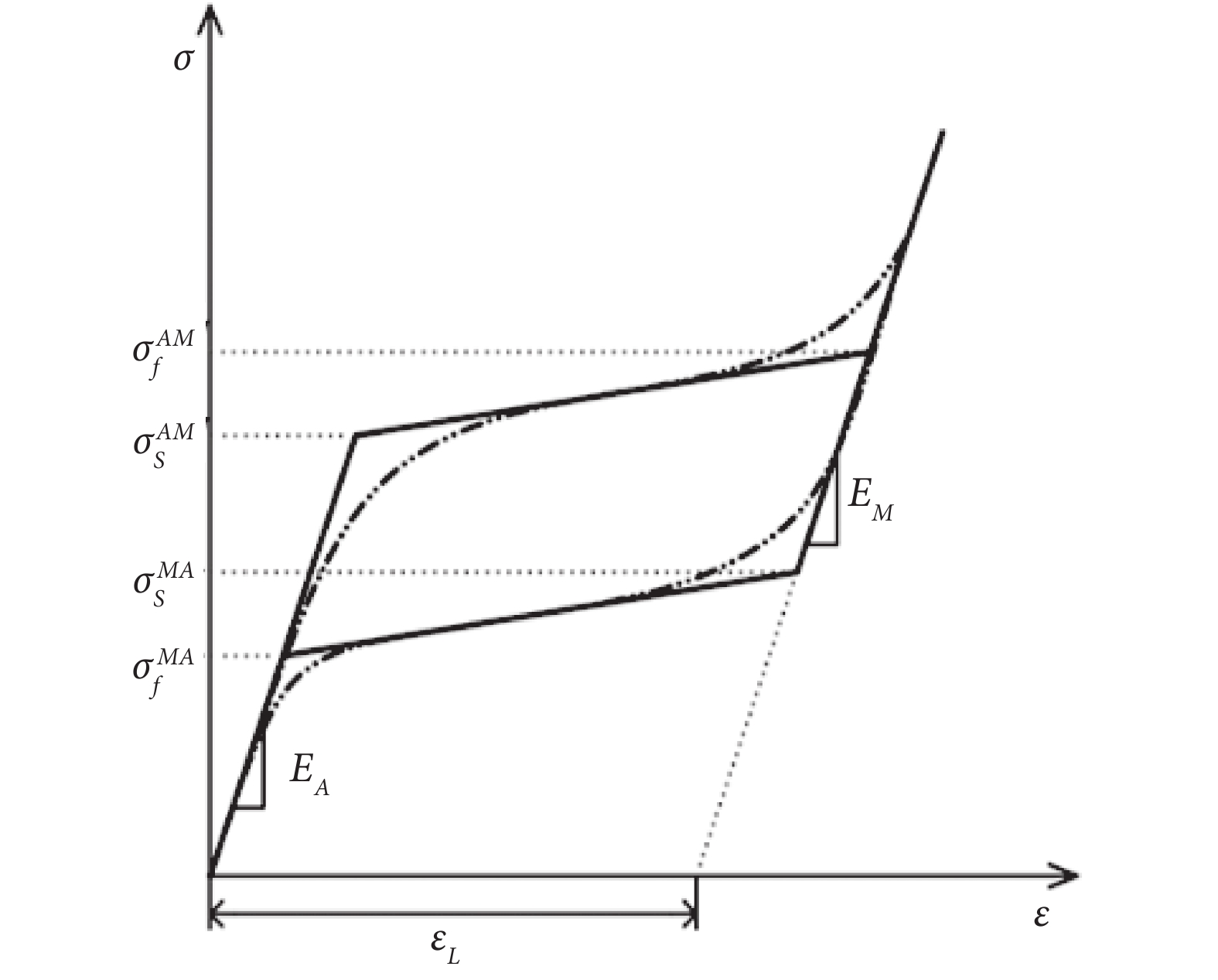圖5
ANSYS中的SMA單軸本構模型
Figure5.
SMA uniaxial constitutive model in ANSYS
3.3 彎曲實驗仿真與材料參數標定
為了應用弓絲三點彎曲實驗數據確定上述本構模型的9個參數，本文采用通用工程仿真軟件ANSYS（version 19.2, ANSYS Inc.，美國）建立SMA弓絲的三點彎曲實驗仿真實體有限元模型，如圖6所示。將SMA材料參數的不同取值組合代入有限元模型，按跨中位移分步加載方式，計算相應的仿真荷載—撓度曲線，并與如圖4所示的實驗曲線進行對比，最終通過平均誤差指標確定最佳參數組合。
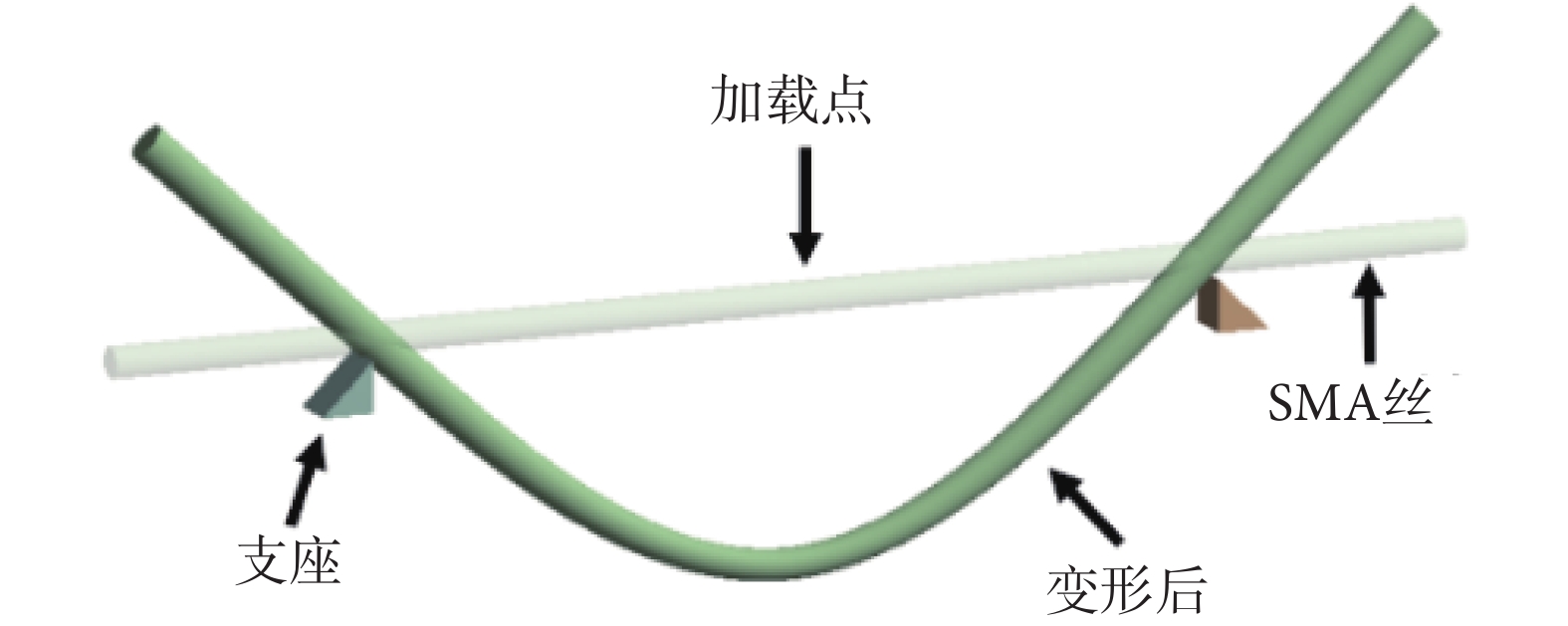圖6
三點彎曲實驗仿真模型
Figure6.
Simulation model of 3-point bending test
在實際操作時，在表1所列的9個參數中，部分參數可以提前確定。由于口腔中溫度恒定，因此馬氏體相變速率α取為0；材料泊松比
根據文獻[22-25]的建議值確定為0.33；奧氏體彈性模量
根據如圖4所示0～0.5 mm撓度的直線段，由線彈性有限元仿真計算確定，最終
取值為70 GPa。
剩余6個參數需要通過不同取值組合的有限元模型仿真試算確定。為了有效減少仿真試算的次數，本文提出兩階段正交實驗設計方法，進行這6個參數的標定，如表2所示：① 階段1，參考文獻[22-25]設定6個參數的變化范圍，繼而進行6個因素5個水平的正交實驗設計[26]，獲得25種取值組合，分別進行有限元模型仿真試算，確定初步優化參數組合；② 根據階段1獲得的初步優化參數組合，通過小范圍上浮和下調，進行6個因素3個水平的正交實驗設計[26]，獲得18種取值組合，分別進行有限元模型仿真試算，確定最優參數組合。表2中，粗體數字代表相應階段完成后的優化參數組合。
表2
SMA 6個參數的兩階段水平定義
Table2.
Level setting of six SMA parameters in two stages
最終標定得到的SMA材料的9個參數取值如表3所示，相應的仿真曲線與實驗曲線的對比如圖7所示。圖7中，兩曲線高度符合，僅在曲線拐點處有輕微差異，其主要來源于前述本構模型對實際光滑曲線的折線化近似處理。
表3
SMA九個參數的最終標定結果
Table3.
Final calibrated results of nine SMA parameters
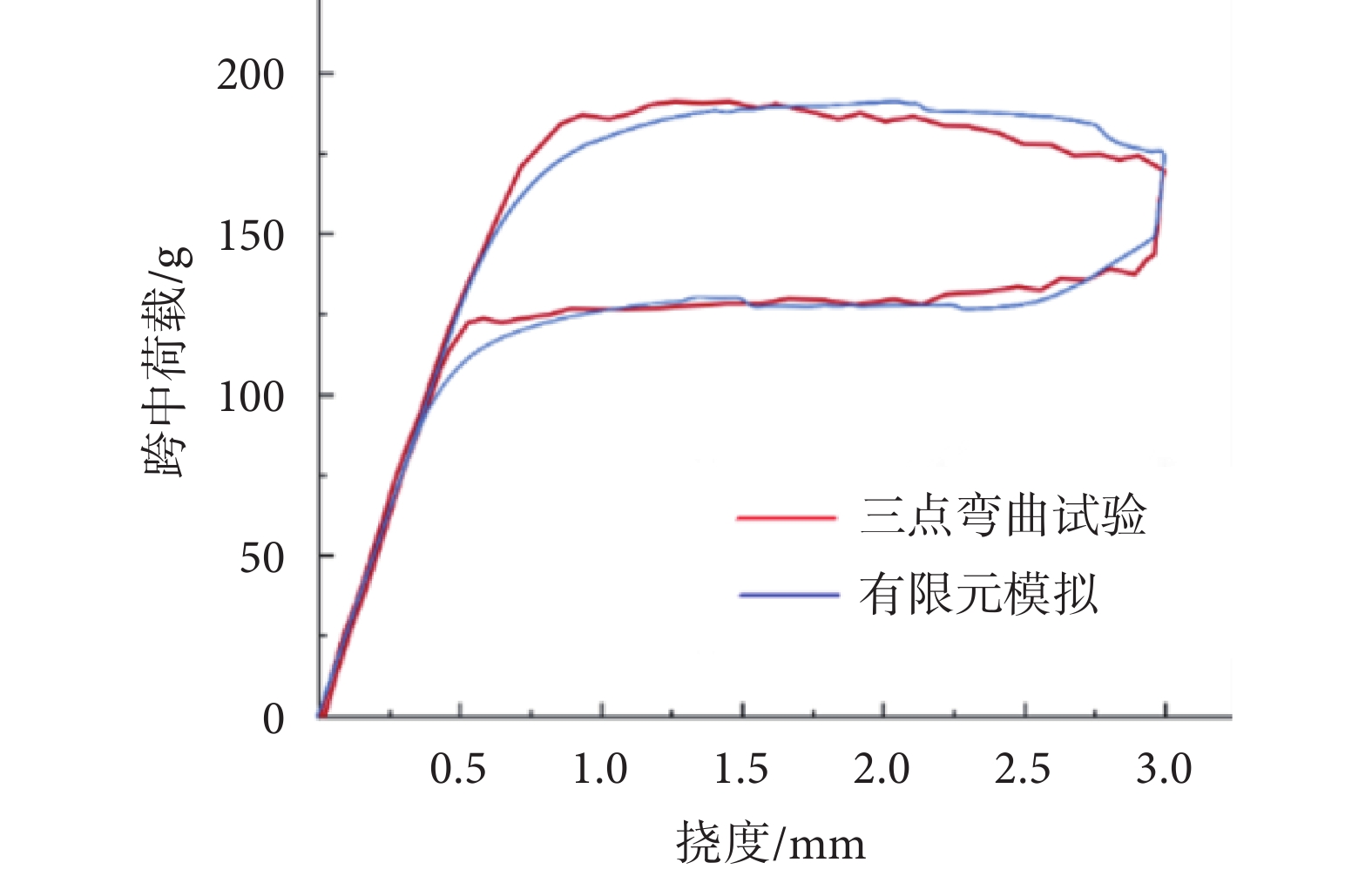圖7
實驗和仿真荷載—撓度曲線對比
Figure7.
Comparison of load-deflection curves from test and simulation
4 托槽止鎖計算分析
4.1 有限元計算方案
本研究采用擬動力分析方法，通過位移分步加載的方式，依次完成螺栓旋緊和弓絲拉拔兩個連續工況的有限元計算。
（1）幾何模型
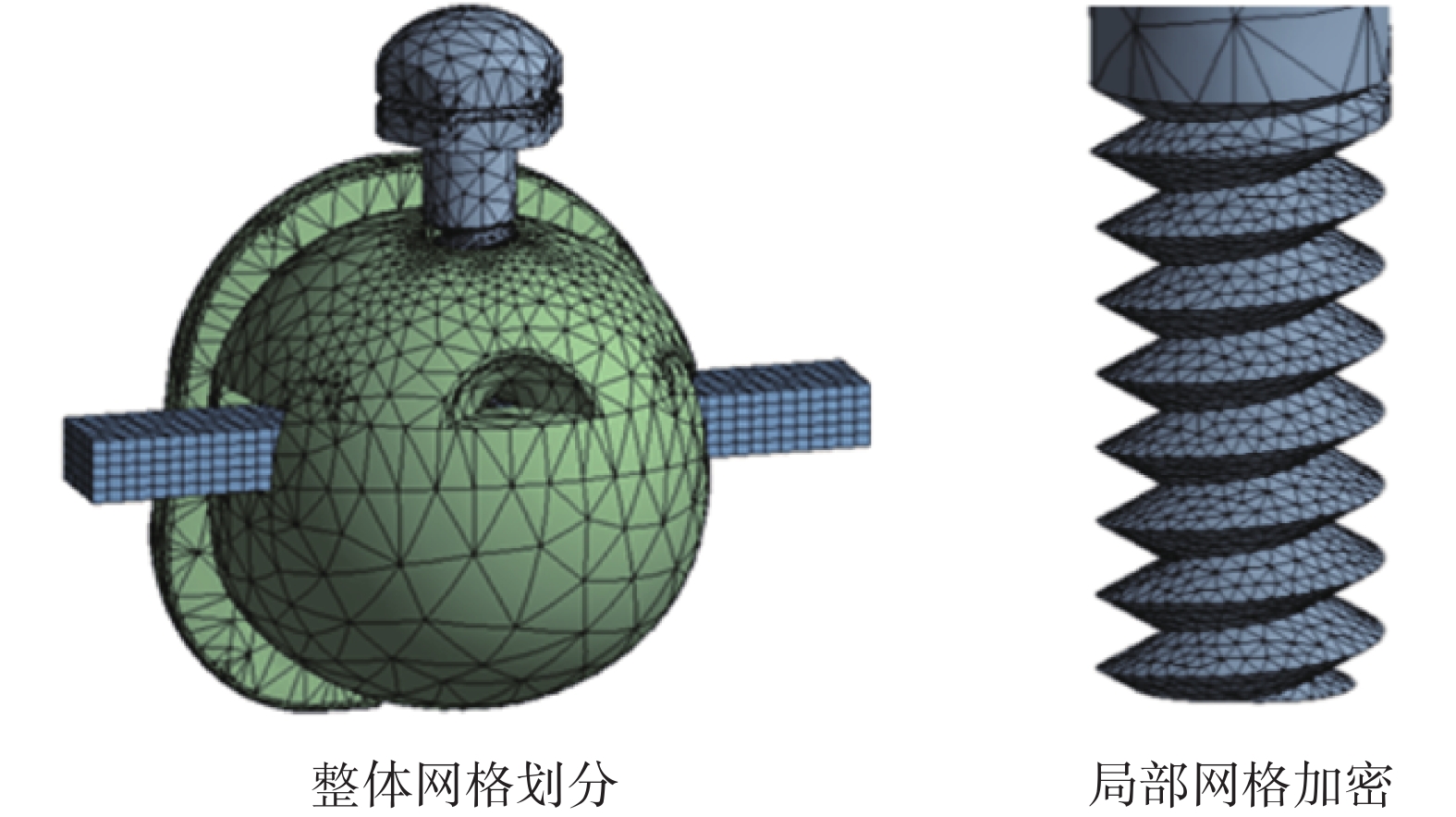
首先在工業建模軟件SolidWorks（version 2018, Dassault Systemes Inc., 美國）中完成托槽的復雜形體建模，繼而導入通用工程仿真軟件ANSYS（version 19.2, ANSYS Inc., 美國）進行仿真分析。在剖分計算網格時，由于螺紋咬合處形狀不規則、應力變化劇烈，同時涉及非線性接觸問題，因此在托槽主體和螺栓的螺紋部分均采用細化網格，以保證求解收斂和精度。為進一步保證計算精度，模型所有四面體和六面體單元均采用二階單元。最終分析模型如圖8所示，包含近7萬個單元，共33萬個自由度。
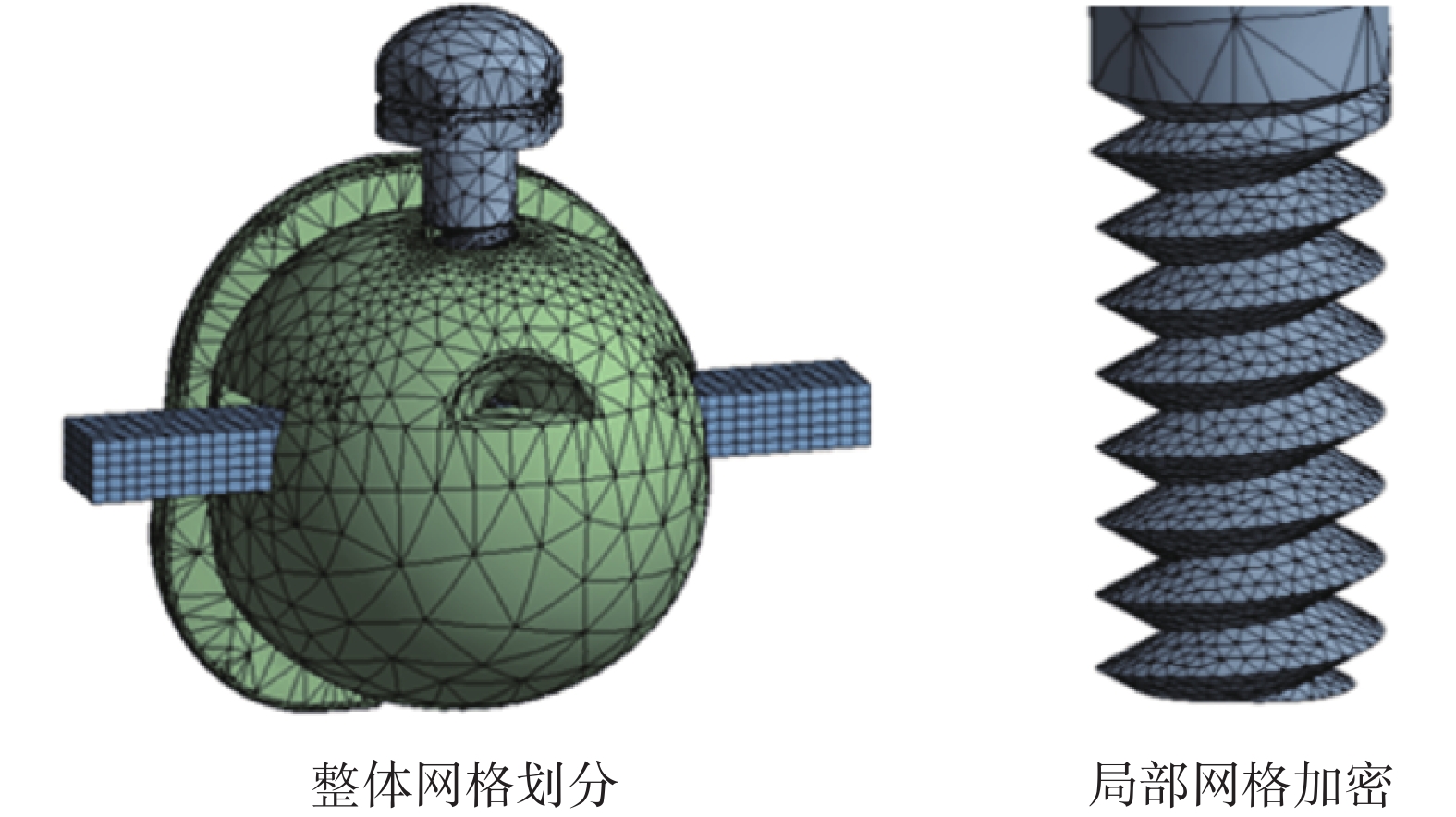圖8
模型網格劃分
Figure8.
Model meshing
（2）材料模型
除了弓絲采用SMA材料以外，托槽主體和止鎖螺栓分別采用金屬粉末注射成形（metal injection molding，MIM）材料與高強度303不銹鋼制造，且均采用雙折線金屬本構模型定義。材料參數定義如表4所示，其中MIM參數由材料供應商提供，高強度303不銹鋼參數取自日本機械學會力學實驗結果[27]。
表4
MIM與303不銹鋼材料參數設定
Table4.
Parameter setting of MIM and 303 stainless steel
（3）邊界條件
首先將托槽底座設置為固定支座，然后按照位移分步加載方式，依次定義如下兩個連續工況：① 螺栓旋緊工況，在螺帽處從0°開始施加4種緊固扭角（5、8、10、15°）的多步繞軸旋轉位移，步長為0.1°；② 弓絲拉拔工況，在弓絲的端截面處施加0～2 mm的多步拉拔位移，步長為0.01 mm。
其中需要說明的是，由于螺紋間咬合接觸的復雜性，螺栓緊固作用通常是有限元仿真分析實踐中的難點問題。傳統的簡化處理包括添加預擰緊力、設置初始過盈配合、耦合螺孔相關節點、直接固定螺紋連接等幾種方式[28-29]，雖然有利于計算收斂、加快計算速度，可為與螺栓連接的其它構件如梁、柱、板等的受力計算提供有效的邊界處理，但卻難以保證螺栓自身應力分布結果的準確性。
本文對螺栓與SMA弓絲間的止鎖機制進行研究，其中螺栓的受力情況是仿真分析的重點內容，因此需要精細模擬加載工況和邊界條件，包括直接在螺帽處施加旋轉位移，以模擬臨床中醫生使用扳手旋緊螺栓的實際情況，以及優化設置關鍵接觸參數來保證復雜耦合非線性分析的計算收斂和結果精度。
4.2 關鍵接觸參數設置
托槽主體、螺栓和弓絲之間的接觸均定義為摩擦型接觸，并參考文獻[30-32]，將螺栓與主體間的摩擦系數取為0.15，弓絲與主體、弓絲與螺栓間的摩擦系數均取為0.2。考慮3個部件之間的不同材料剛度，因此3組接觸行為均設置為非對稱接觸，相對剛度較小和較大的部件表面分別定義為接觸面和目標面，以滿足接觸面不能穿透目標面的計算要求。
由于螺栓緊固扭角為5～15°，主體與螺栓間的螺紋接觸面滑動量小，因此開啟小滑動假定開關，有利于快速收斂。而弓絲與主體、弓絲與螺栓間的接觸面滑動較大，應關閉小滑動假定開關，以保證計算精度。
法向接觸剛度對于計算收斂起決定性作用，可取值0.01～10.00，摩擦型接觸的程序控制默認值為1，其值越大，穿透量越小，計算結果越準確，但容易引起求解震蕩或發散。本研究手動設置初始值為3，根據迭代狀態自動更新剛度，可同時提高精度和收斂性。
此外，本研究采用兼顧計算精度和收斂性的增強拉格朗日接觸算法，替代程序控制默認的罰函數法，進行接觸反力的探測計算。其中，關鍵的穿透容差的設定如下：模型中螺栓的螺距為0.15 mm，當螺栓緊固扭角為5°時，理論上螺栓底部的無阻礙進深為5 ÷ 360 × 0.15 = 0.002 1 mm。為了避免螺栓過度穿透SMA弓絲導致計算結果失真，本研究將其降低一個數量級定義穿透容差，即取值為0.000 2 mm。
最終，模型中3組摩擦接觸的關鍵接觸參數設置總結如表5所示。基于這些優化參數，不同緊固扭角下的非線性仿真分析都能穩定收斂，從而計算得到止鎖力及各部件應力分布結果。
表5
3組摩擦接觸的關鍵接觸參數設置
Table5.
Setting of key contact parameters for three groups of frictional contact
4.3 模型計算結果與實驗比對
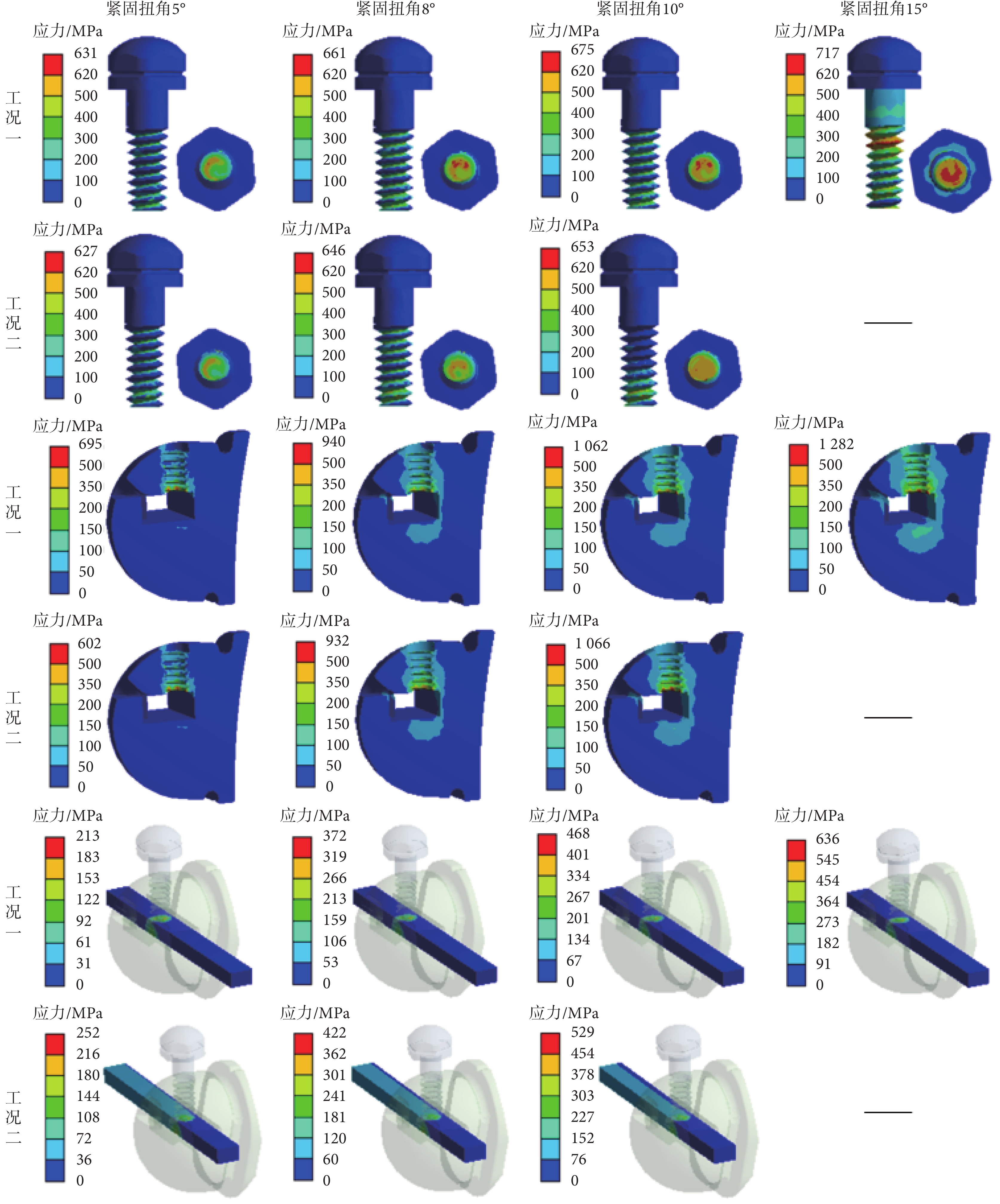
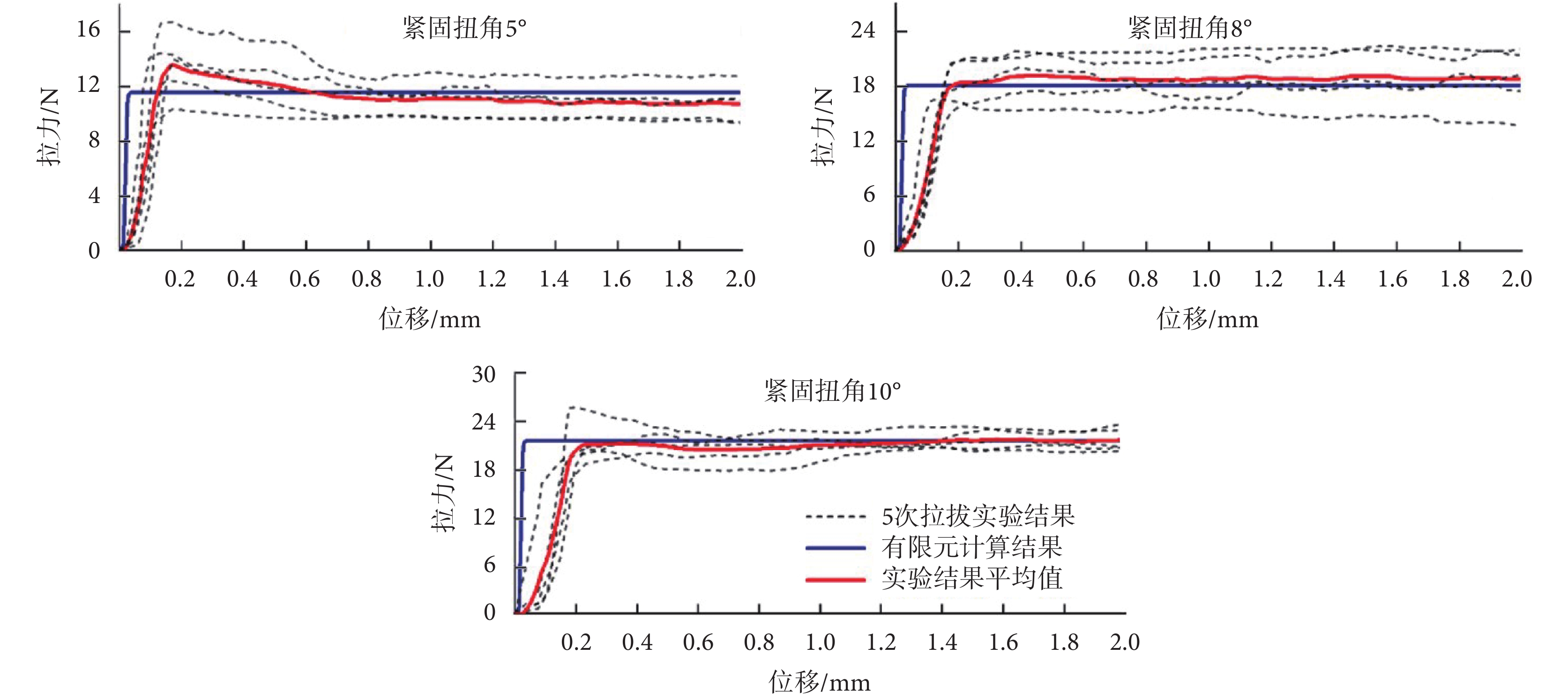
根據4種緊固扭角（5、8、10、15°），分別進行兩個連續工況的有限元計算，得到3個部件在不同工況下的應力分布如圖9所示，以及弓絲拉拔力—位移曲線如圖10所示，其中補充列出了5次拉拔實驗的實測曲線。如表6所示，總結列出了4種緊固扭角下有限元計算得到的扳手扭矩和螺栓止鎖力。
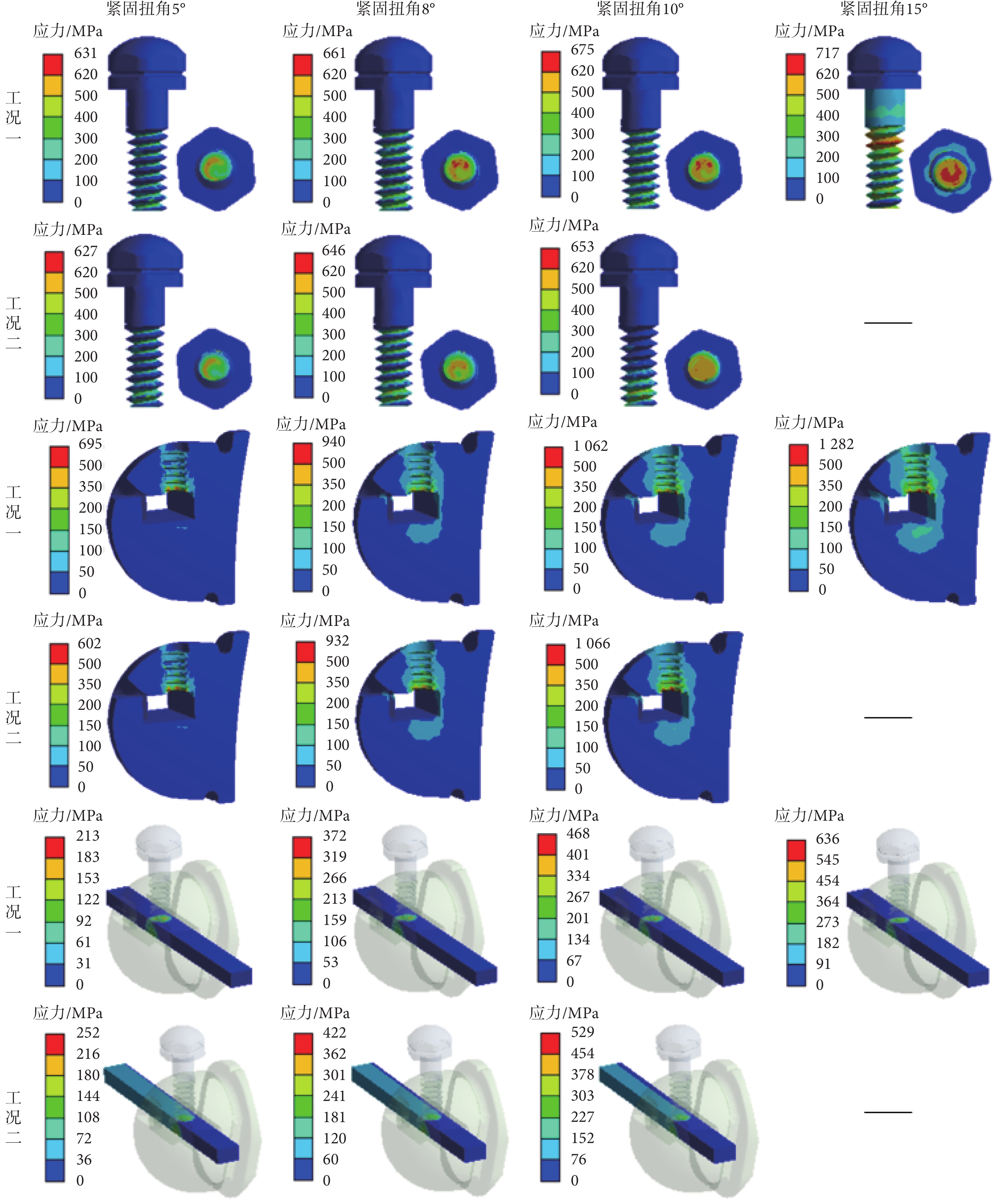圖9
兩工況下各部件應力分布
Figure9.
Stress distribution of each component in two stages
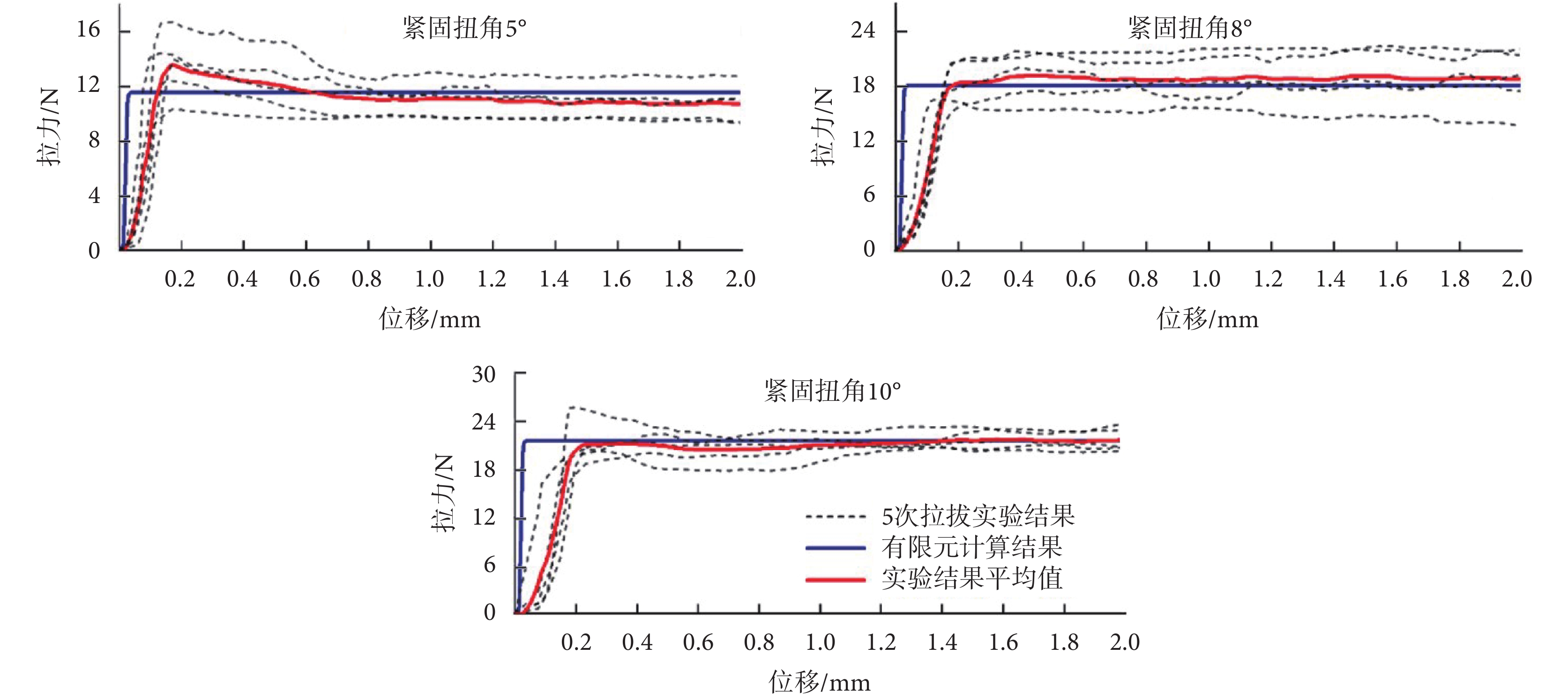圖10
弓絲拉拔實驗和仿真拉力—位移曲線對比
Figure10.
Comparison of tension-displacement curves from archwire pullout test and simulation
表6
止鎖力與緊固扭矩仿真結果
Table6.
Simulated results of locking force and tightening torque
如圖9所示，在螺栓方面：
（1）工況一時，隨著扭角增大，螺栓應力不斷增大，在10°扭角以下時，螺栓底面處出現局部屈服，螺身未出現屈服；在15°扭角時，除了螺栓底面出現局部破壞以外，螺栓上部的第二節螺紋處也出現破壞，導致截面斷裂，后續無法繼續加載。這與臨床操作中扭角過大情況下容易在第二、三節擰斷的實際觀測相符。
（2）工況二時，由于弓絲拉拔拖動螺栓底面發生一定移動，螺栓與另兩個部件之間的緊密擠壓有所松脫，導致螺栓應力略有下降。
在托槽主體方面：
（1）工況一時，隨著扭角增大，主體應力不斷增大，在10°扭角以下時，主體未出現屈服；在15°扭角時，主體近槽溝的栓道下邊緣處出現局部屈服和破壞。
（2）工況二時，由于主體與螺栓間的緊密擠壓有所松脫，導致主體應力略有下降。
在弓絲方面：
（1）工況一時，隨著扭角增大，SMA弓絲應力不斷增大，在10°扭角以下時，弓絲應力未達到正相變開始應力，沒有材料相變發生；在15°扭角時，弓絲應力超過正相變開始應力，表明有材料相變發生，材料彈性模量降低。
（2）工況二時，拉拔作用導致弓絲軸向應變增大，弓絲應力較工況一有所增加，但仍未達到正相變開始應力，沒有材料相變發生。
如圖10所示，同一緊固扭角下的5組實測曲線離散度大，實測最大拉力與實測平均值的最大偏差接近30%，而有限元計算值與實測平均值的偏差在10%以內。在曲線的上升段，實測平均值表現出的剛度要小于有限元計算值，其原因在于實測時的弓絲形狀并不是完全直線，如圖2所示，而是有一定彎曲的形狀，相應的抗拉剛度相比于有限元模型中的直線弓絲有所下降。
如表6所示，為了降低醫生在臨床操作時擰斷螺栓的風險，需要提前設定扳手的額定扭矩為2.8 N·mm，可在扭角未能精確控制下保證螺栓的安全。此設定也有利于將托槽主體最大應力控制在略低于屈服強度的水平，避免出現塑性變形，以及將弓絲最大應力控制在正相變開始應力以內，保持較大剛度。這一精準設計的思想可實現制造材料的充分利用，以及保障裝置各部件在整個正畸過程（1～2年）的正常使用。
5 結論
本文通過復雜耦合的非線性有限元仿真分析，實現了對微型正畸裝置內SMA弓絲止鎖機制的精準設計。作為口腔正畸醫療領域的首次嘗試，本文仿真分析為自鎖托槽臨床診療的方案設計提供了關鍵數據，包括緊固扭角—止鎖力的對應關系、扭矩扳手的額定扭矩設置。相關分析方法可為其他微型醫療器械的力學機制研究提供有益參考。需要說明，本文研究主要是根據裝置研發需求提出了螺栓緊固扭角與扳手扭矩的建議值，未來后續研究中將進一步結合臨床實踐和病患反應，提出更具操作性的指標。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：代清源主要負責材料參數標定、有限元模型建立、論文初稿撰寫；吉利主要負責研究技術路線輔助制定、標定實驗方案制定；華嘉皓與梁振宇主要負責有限元模型計算；余健文主要負責標定實驗開展與數據整理；陳太聰主要負責研究技術路線制定、有限元方案設計、論文審閱修訂。
0 引言
佩戴牙齒矯治器是臨床正畸治療中矯正患者錯牙合畸形的主要手段。常見的矯治器由弓絲和托槽兩部分組成，其中托槽通過弓絲的牽引向人體組織傳遞矯治力，從而使錯位牙齒在牽引力和扭矩的作用下逐漸移動至理想位置[1-2]。相關研究表明，矯治力由弓絲變形產生，通過矯治器中止鎖裝置傳遞，其大小與作用方式對正畸治療的效率與效果影響顯著[3-5]。在口腔正畸領域，研究矯治器內部的弓絲止鎖機制對臨床正畸治療具有重要意義。
形狀記憶合金（shape memory alloy，SMA）作為一種新興智能材料，因其具有獨特的形狀記憶效應、超彈性效應和良好的生物相容性[6]，在生物醫療領域常被用在牙齒、骨骼和血管等相關的醫療器材中[7-9]。其中，在口腔正畸方面，SMA弓絲因能持續施加較輕的作用力，可縮短矯治時間，已逐漸成為應用主流弓絲。近年來，本課題組研發的新型球型自鎖托槽[10]，通過設計止鎖/止動系統，能與抗扭剛度較小的SMA弓絲結合，實現了輕力精準矯治[11]，具有正畸效率高、佩戴舒適等優越的臨床表現[12]，已成為具有國際競爭力的國產醫療器械。隨著該產品的臨床應用越來越廣泛，為了進一步達到更佳的矯治效果，有必要通過有限元等力學分析手段，實現新型托槽止鎖機制的優化設計。
現階段，口腔醫療領域的力學應用研究多集中于正畸裝置對牙齒和口腔組織的影響[13-16]，數據分析主要采用簡化的托槽模型，缺少對于托槽本身的機械性能研究[17-19]，而球型托槽止動系統的研究尚屬空白。其次，SMA弓絲的材料特性是力學分析的關鍵，使用不同成分、工藝制成的SMA材料性質差別明顯，供應商通常無法提供具體的相關材料模型參數，如果直接應用文獻參數則容易造成分析結果與實際差異較大。本課題組前期研發的裝置止鎖過程涉及復雜耦合的接觸、材料和幾何非線性特征，其中接觸參數對于分析收斂和精度具有決定性影響，相關設置也值得進一步深入研究。
針對上述問題，本文將開展新型托槽非線性止鎖機制的高精度設計分析方法的研究，具體包括：① 基于廠家提供的SMA弓絲三點彎曲實驗數據，通過多參數的正交實驗設計和相應仿真，確定SMA材料計算參數；② 建立螺栓旋緊和弓絲拉拔的兩階段精細有限元仿真模型，分辨關鍵接觸參數并進行優化設置，實現耦合非線性分析過程的有效收斂；③ 開展三種典型緊固扭角下的止鎖標定實驗，對比驗證本文分析方法的有效性，以期優化確定臨床應用的螺栓緊固扭角和扳手額定扭矩的設計值。
1 問題背景
1.1 球形自鎖托槽的工作原理
托槽是正畸矯治期間粘接于牙面的一種精密機械裝置，具有體積小、受荷大、制造精度高等特點。本文應用的球型自鎖托槽[10]，由底座、主體、SMA弓絲和螺栓四部分組成，如圖1所示。托槽底座長度和寬度約為3.5 mm，主體高約3 mm；SMA弓絲為矩形截面，高0.635 mm，寬0.406 mm。正畸治療中，托槽底部粘合在患者牙面上，SMA弓絲穿過托槽的槽溝，其中弓絲左側表面緊貼槽溝左側壁，弓絲下表面緊貼槽溝底壁，之后螺栓擰入托槽主體的栓道并壓緊弓絲實現緊固，最終通過弓絲的自恢復變形引導托槽攜帶牙齒移動。其中，當螺絲擰轉特定角度后，拉拔弓絲使之與螺栓之間發生相對滑動所需要的最小拉力，即定義為止鎖力，它等于托槽能提供給牙齒的最大牽引力，是該型托槽的重要性能指標。
圖1
球型自鎖托槽結構
Figure1.
Structure of spherical self-locking bracket
1.2 球形自鎖托槽的臨床應用問題
在球形托槽的臨床應用中，醫生通常使用微型扳手擰轉螺栓，使螺栓底面觸碰到弓絲右側表面，此時弓絲右側表面出現應力，扳手開始受力，然后繼續擰轉一定角度以緊固弓絲。這一后續擰轉角度定義為緊固扭角，其大小取決于扳手所施加的扭矩大小。臨床經驗發現，若扳手扭矩過小，導致緊固扭角偏小，則弓絲易發生滑動，不能為牙齒矯正提供足夠的牽引力；若扳手扭矩過大，導致緊固扭角偏大，則螺栓上部薄弱處易被擰斷。
為了能在實際臨床操作中獲得正畸所需的最佳牽引力，有必要預先確定不同緊固扭角與止鎖力的關系，以及相對應的扭矩大小，并在不損壞正畸裝置的前提下，優化設計緊固扭角和扭矩的取值。本課題組的托槽研發團隊前期開展了一系列實驗，測定不同緊固扭角下的弓絲拉拔力，實驗裝置如圖2所示，但由于正畸托槽過于微小，容易出現實驗結果數值不穩、離散度大等問題。此外，微型扳手的扭矩大小難以精確測量，僅能通過額定扭矩的設置來定義最大施加扭矩，無法精確控制不同緊固扭角對應的扭矩大小。
圖2
托槽止鎖力測試裝置
Figure2.
Test device of bracket locking force
因此，為了更精準地獲得上述量化關系和取值，本文研發團隊擬應用有限元的數值分析手段，對球形自鎖托槽的非線性止鎖機制開展仿真研究，分析確定不同緊固扭角下的各個部件的應力分布情況，以及相對應的SMA弓絲拉拔止鎖力，結合標定實驗對比，為球形自鎖托槽的臨床應用提供關鍵數據。
2 有限元分析的非線性特征
針對托槽止鎖機制的仿真分析，需要處理復雜的非線性關系，表現在：① 除了SMA弓絲的超彈性材料行為，托槽主體和螺栓材料也可能發生塑性屈服；② 在螺栓旋進和SMA弓絲拉拔過程中，各部件之間出現較大相對運動，模型計算構型需要隨時更新；③ 在托槽主體與螺栓之間、SMA弓絲底面與主體之間、SMA弓絲頂面與螺栓端頭之間存在大范圍的擠壓，接觸非線性效應明顯。
這些非線性關系高度耦合，主要出現在托槽主體和螺栓接觸的螺紋尖端，以及螺栓與弓絲接觸的螺栓端頭處，導致有限元計算極為耗時，給計算收斂造成巨大困難，最終影響計算精度，需要針對性定義和設置。
本次有限元仿真分析選擇通用工程仿真軟件ANSYS（version 19.2, ANSYS Inc., 美國）進行，其便于復雜機械建模，包含較為成熟的SMA材料本構模型，也支持多種非線性效應的耦合分析。下文將重點介紹弓絲SMA材料模型的參數標定方法，以及托槽止鎖的計算模型和分析方法。
3 SMA材料參數標定
3.1 SMA三點彎曲實驗
對于托槽所使用的SMA弓絲，材料供應商未提供具體組成和材性數據，只提供弓絲三點彎曲實驗數據。實驗采用直徑0.355 6 mm的SMA弓絲，在與人體溫度一致的37 °C環境溫度下進行，實驗裝置如圖3所示。兩支座間跨度為10 mm，在跨中進行位移加載，撓度達3 mm后卸載，最終得到的荷載—撓度關系曲線如圖4所示。
圖3
SMA弓絲的三點彎曲測試裝置
Figure3.
3-point bending test device of SMA archwire
圖4
三點彎曲實驗荷載—撓度曲線
Figure4.
Load-deflection curve from 3-point bending test
3.2 SMA本構模型
SMA材料的主要特征在于馬氏體與奧氏體之間的可逆相變，是由于剪切位移而改變晶體結構的切變型相變，分為由溫度誘導（形狀記憶效應）和由應力誘導（超彈性效應）兩種類型。由于人體口腔溫度幾乎恒定，因此在托槽止鎖機制應用中，SMA弓絲主要發揮超彈性效應。
通用工程仿真軟件ANSYS（version 19.2，ANSYS Inc.，美國）采用宏觀唯象的奧利奇奧（Auricchio）模型[20]，通過9個參數設定SMA超彈性材料本構，各參數的物理意義如表1所示。前7個參數在單軸應力—應變曲線中的定義如圖5所示，其中，SMA材料的單軸拉伸實驗曲線實際為光滑曲線[21]，軟件中將其近似為多段折線，有利于計算分析。
表1
SMA超彈性材料的參數定義
Table1.
Parameter definition of SMA super-elastic material
圖5
ANSYS中的SMA單軸本構模型
Figure5.
SMA uniaxial constitutive model in ANSYS
3.3 彎曲實驗仿真與材料參數標定
為了應用弓絲三點彎曲實驗數據確定上述本構模型的9個參數，本文采用通用工程仿真軟件ANSYS（version 19.2, ANSYS Inc.，美國）建立SMA弓絲的三點彎曲實驗仿真實體有限元模型，如圖6所示。將SMA材料參數的不同取值組合代入有限元模型，按跨中位移分步加載方式，計算相應的仿真荷載—撓度曲線，并與如圖4所示的實驗曲線進行對比，最終通過平均誤差指標確定最佳參數組合。
圖6
三點彎曲實驗仿真模型
Figure6.
Simulation model of 3-point bending test
在實際操作時，在表1所列的9個參數中，部分參數可以提前確定。由于口腔中溫度恒定，因此馬氏體相變速率α取為0；材料泊松比根據文獻[22-25]的建議值確定為0.33；奧氏體彈性模量根據如圖4所示0～0.5 mm撓度的直線段，由線彈性有限元仿真計算確定，最終取值為70 GPa。
剩余6個參數需要通過不同取值組合的有限元模型仿真試算確定。為了有效減少仿真試算的次數，本文提出兩階段正交實驗設計方法，進行這6個參數的標定，如表2所示：① 階段1，參考文獻[22-25]設定6個參數的變化范圍，繼而進行6個因素5個水平的正交實驗設計[26]，獲得25種取值組合，分別進行有限元模型仿真試算，確定初步優化參數組合；② 根據階段1獲得的初步優化參數組合，通過小范圍上浮和下調，進行6個因素3個水平的正交實驗設計[26]，獲得18種取值組合，分別進行有限元模型仿真試算，確定最優參數組合。表2中，粗體數字代表相應階段完成后的優化參數組合。
表2
SMA 6個參數的兩階段水平定義
Table2.
Level setting of six SMA parameters in two stages
最終標定得到的SMA材料的9個參數取值如表3所示，相應的仿真曲線與實驗曲線的對比如圖7所示。圖7中，兩曲線高度符合，僅在曲線拐點處有輕微差異，其主要來源于前述本構模型對實際光滑曲線的折線化近似處理。
表3
SMA九個參數的最終標定結果
Table3.
Final calibrated results of nine SMA parameters
圖7
實驗和仿真荷載—撓度曲線對比
Figure7.
Comparison of load-deflection curves from test and simulation
4 托槽止鎖計算分析
4.1 有限元計算方案
本研究采用擬動力分析方法，通過位移分步加載的方式，依次完成螺栓旋緊和弓絲拉拔兩個連續工況的有限元計算。
（1）幾何模型
首先在工業建模軟件SolidWorks（version 2018, Dassault Systemes Inc., 美國）中完成托槽的復雜形體建模，繼而導入通用工程仿真軟件ANSYS（version 19.2, ANSYS Inc., 美國）進行仿真分析。在剖分計算網格時，由于螺紋咬合處形狀不規則、應力變化劇烈，同時涉及非線性接觸問題，因此在托槽主體和螺栓的螺紋部分均采用細化網格，以保證求解收斂和精度。為進一步保證計算精度，模型所有四面體和六面體單元均采用二階單元。最終分析模型如圖8所示，包含近7萬個單元，共33萬個自由度。
圖8
模型網格劃分
Figure8.
Model meshing
（2）材料模型
除了弓絲采用SMA材料以外，托槽主體和止鎖螺栓分別采用金屬粉末注射成形（metal injection molding，MIM）材料與高強度303不銹鋼制造，且均采用雙折線金屬本構模型定義。材料參數定義如表4所示，其中MIM參數由材料供應商提供，高強度303不銹鋼參數取自日本機械學會力學實驗結果[27]。
表4
MIM與303不銹鋼材料參數設定
Table4.
Parameter setting of MIM and 303 stainless steel
（3）邊界條件
首先將托槽底座設置為固定支座，然后按照位移分步加載方式，依次定義如下兩個連續工況：① 螺栓旋緊工況，在螺帽處從0°開始施加4種緊固扭角（5、8、10、15°）的多步繞軸旋轉位移，步長為0.1°；② 弓絲拉拔工況，在弓絲的端截面處施加0～2 mm的多步拉拔位移，步長為0.01 mm。
其中需要說明的是，由于螺紋間咬合接觸的復雜性，螺栓緊固作用通常是有限元仿真分析實踐中的難點問題。傳統的簡化處理包括添加預擰緊力、設置初始過盈配合、耦合螺孔相關節點、直接固定螺紋連接等幾種方式[28-29]，雖然有利于計算收斂、加快計算速度，可為與螺栓連接的其它構件如梁、柱、板等的受力計算提供有效的邊界處理，但卻難以保證螺栓自身應力分布結果的準確性。
本文對螺栓與SMA弓絲間的止鎖機制進行研究，其中螺栓的受力情況是仿真分析的重點內容，因此需要精細模擬加載工況和邊界條件，包括直接在螺帽處施加旋轉位移，以模擬臨床中醫生使用扳手旋緊螺栓的實際情況，以及優化設置關鍵接觸參數來保證復雜耦合非線性分析的計算收斂和結果精度。
4.2 關鍵接觸參數設置
托槽主體、螺栓和弓絲之間的接觸均定義為摩擦型接觸，并參考文獻[30-32]，將螺栓與主體間的摩擦系數取為0.15，弓絲與主體、弓絲與螺栓間的摩擦系數均取為0.2。考慮3個部件之間的不同材料剛度，因此3組接觸行為均設置為非對稱接觸，相對剛度較小和較大的部件表面分別定義為接觸面和目標面，以滿足接觸面不能穿透目標面的計算要求。
由于螺栓緊固扭角為5～15°，主體與螺栓間的螺紋接觸面滑動量小，因此開啟小滑動假定開關，有利于快速收斂。而弓絲與主體、弓絲與螺栓間的接觸面滑動較大，應關閉小滑動假定開關，以保證計算精度。
法向接觸剛度對于計算收斂起決定性作用，可取值0.01～10.00，摩擦型接觸的程序控制默認值為1，其值越大，穿透量越小，計算結果越準確，但容易引起求解震蕩或發散。本研究手動設置初始值為3，根據迭代狀態自動更新剛度，可同時提高精度和收斂性。
此外，本研究采用兼顧計算精度和收斂性的增強拉格朗日接觸算法，替代程序控制默認的罰函數法，進行接觸反力的探測計算。其中，關鍵的穿透容差的設定如下：模型中螺栓的螺距為0.15 mm，當螺栓緊固扭角為5°時，理論上螺栓底部的無阻礙進深為5 ÷ 360 × 0.15 = 0.002 1 mm。為了避免螺栓過度穿透SMA弓絲導致計算結果失真，本研究將其降低一個數量級定義穿透容差，即取值為0.000 2 mm。
最終，模型中3組摩擦接觸的關鍵接觸參數設置總結如表5所示。基于這些優化參數，不同緊固扭角下的非線性仿真分析都能穩定收斂，從而計算得到止鎖力及各部件應力分布結果。
表5
3組摩擦接觸的關鍵接觸參數設置
Table5.
Setting of key contact parameters for three groups of frictional contact
4.3 模型計算結果與實驗比對
根據4種緊固扭角（5、8、10、15°），分別進行兩個連續工況的有限元計算，得到3個部件在不同工況下的應力分布如圖9所示，以及弓絲拉拔力—位移曲線如圖10所示，其中補充列出了5次拉拔實驗的實測曲線。如表6所示，總結列出了4種緊固扭角下有限元計算得到的扳手扭矩和螺栓止鎖力。
圖9
兩工況下各部件應力分布
Figure9.
Stress distribution of each component in two stages
圖10
弓絲拉拔實驗和仿真拉力—位移曲線對比
Figure10.
Comparison of tension-displacement curves from archwire pullout test and simulation
表6
止鎖力與緊固扭矩仿真結果
Table6.
Simulated results of locking force and tightening torque
如圖9所示，在螺栓方面：
（1）工況一時，隨著扭角增大，螺栓應力不斷增大，在10°扭角以下時，螺栓底面處出現局部屈服，螺身未出現屈服；在15°扭角時，除了螺栓底面出現局部破壞以外，螺栓上部的第二節螺紋處也出現破壞，導致截面斷裂，后續無法繼續加載。這與臨床操作中扭角過大情況下容易在第二、三節擰斷的實際觀測相符。
（2）工況二時，由于弓絲拉拔拖動螺栓底面發生一定移動，螺栓與另兩個部件之間的緊密擠壓有所松脫，導致螺栓應力略有下降。
在托槽主體方面：
（1）工況一時，隨著扭角增大，主體應力不斷增大，在10°扭角以下時，主體未出現屈服；在15°扭角時，主體近槽溝的栓道下邊緣處出現局部屈服和破壞。
（2）工況二時，由于主體與螺栓間的緊密擠壓有所松脫，導致主體應力略有下降。
在弓絲方面：
（1）工況一時，隨著扭角增大，SMA弓絲應力不斷增大，在10°扭角以下時，弓絲應力未達到正相變開始應力，沒有材料相變發生；在15°扭角時，弓絲應力超過正相變開始應力，表明有材料相變發生，材料彈性模量降低。
（2）工況二時，拉拔作用導致弓絲軸向應變增大，弓絲應力較工況一有所增加，但仍未達到正相變開始應力，沒有材料相變發生。
如圖10所示，同一緊固扭角下的5組實測曲線離散度大，實測最大拉力與實測平均值的最大偏差接近30%，而有限元計算值與實測平均值的偏差在10%以內。在曲線的上升段，實測平均值表現出的剛度要小于有限元計算值，其原因在于實測時的弓絲形狀并不是完全直線，如圖2所示，而是有一定彎曲的形狀，相應的抗拉剛度相比于有限元模型中的直線弓絲有所下降。
如表6所示，為了降低醫生在臨床操作時擰斷螺栓的風險，需要提前設定扳手的額定扭矩為2.8 N·mm，可在扭角未能精確控制下保證螺栓的安全。此設定也有利于將托槽主體最大應力控制在略低于屈服強度的水平，避免出現塑性變形，以及將弓絲最大應力控制在正相變開始應力以內，保持較大剛度。這一精準設計的思想可實現制造材料的充分利用，以及保障裝置各部件在整個正畸過程（1～2年）的正常使用。
5 結論
本文通過復雜耦合的非線性有限元仿真分析，實現了對微型正畸裝置內SMA弓絲止鎖機制的精準設計。作為口腔正畸醫療領域的首次嘗試，本文仿真分析為自鎖托槽臨床診療的方案設計提供了關鍵數據，包括緊固扭角—止鎖力的對應關系、扭矩扳手的額定扭矩設置。相關分析方法可為其他微型醫療器械的力學機制研究提供有益參考。需要說明，本文研究主要是根據裝置研發需求提出了螺栓緊固扭角與扳手扭矩的建議值，未來后續研究中將進一步結合臨床實踐和病患反應，提出更具操作性的指標。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：代清源主要負責材料參數標定、有限元模型建立、論文初稿撰寫；吉利主要負責研究技術路線輔助制定、標定實驗方案制定；華嘉皓與梁振宇主要負責有限元模型計算；余健文主要負責標定實驗開展與數據整理；陳太聰主要負責研究技術路線制定、有限元方案設計、論文審閱修訂。
