為實現人體心率的非接觸式測量并提高其測量的精準度，本文提出一種基于多通道雷達數據融合的人體心率測量方法。雷達數據首先依次對每個通道數據進行人體位置識別、相位提取與解纏繞、相位差分、功率譜熵優化的帶通濾波以及快速獨立成分分析提取。再將四通道數據疊加融合后，使用霜冰優化的變分模態分解分離出心跳信號。最后引入線性調頻Z變換進行心率估計。經過40組數據驗證，本文方法的平均均方根誤差為2.35次/分，平均錯誤率為2.39%，皮爾遜相關系數為0.97，置信區間為[–4.78, 4.78]次/分，一致性誤差為–0.04次/分。實驗結果顯示，本文提出的測量方法在準確性、相關性、一致性方面表現出色，能夠實現人體心率的精準測量。
引用本文： 郭洪瑞, 曹匯敏, 楊克奇, 張朱珊瑩. 基于多通道雷達數據融合的人體心率精準測量. 生物醫學工程學雜志, 2024, 41(3): 461-468. doi: 10.7507/1001-5515.202307010 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
連續監測心率對于心率失常、猝死、心肌炎等心臟突發疾病的發現和預防尤為重要[1]。連續監測心率儀器分為接觸式與非接觸式兩種。傳統的接觸式儀器對于燒傷患者、嬰兒、受困人員等無法接觸人體的情況無能為力，而且長時間佩戴儀器也會引起人體不適[2]。而非接觸式儀器中的生物雷達因高穿透性、無光照影響、可連續性等優點被應用到人體心率檢測領域[3]。
生物雷達應用于連續監測心率領域的重點在于雷達信號分離，通常會使用數字濾波器[4]、經驗模式分解（empirical mode decomposition，EMD）[5]、變分模態分解（variational mode decomposition，VMD）[6]、小波分解[7]等方法。Higashi等[8]對多普勒雷達的時域信號使用維納濾波和多邏輯回歸，測量出的心率平均錯誤率為4.48%。胡錫坤等[9]利用自適應尺度小波從雷達信號分離出心跳信號，靜坐情況下25 s內的準確率保持在95%以上。Qi等[10]使用多階差分增強的VMD算法對超寬帶雷達信號提取人體心率，真實人體數據估計結果的平均錯誤率為4.24%。
現行國家標準GB 9706.227-2021中，心率監測的準確性應為±10%或±5次/分中的較大者[11]。為獲取更高的測量精準度，本文提出一種基于多通道雷達數據融合的人體心率精準測量方法。首先通過優化后的預處理方法得到多通道雷達數據，然后使用優化后的變分模態分解算法分離出心跳信號，最后通過線性調頻Z變換（cadmium zinc telluride，CZT）估計出心率[12]。本文將通過一系列實驗證實算法的可靠性、魯棒性和準確性。
1 雷達測量人體心率的原理
本文使用的雷達是調頻連續波（frequency modulation continuous wave，FMCW）雷達，具有信噪比高、指向精度高、多普勒靈敏度高等優勢。雷達發射信號是線性調頻脈沖（linear frequency modulation，LFM）信號，其最小單元稱之為脈沖，公式表示為：
 |
其中AT為脈沖的幅度，fc為起始的頻率，B為帶寬，Tc為周期，t為時間，φ(t)為相位噪聲。若人站在距離R米處，雷達回波信號與發射信號混頻后，得到的中頻（intermediate frequency，IF）信號為
 |
其中AR為回波信號幅度；IF信號的頻率fb = (4πBRt)/(cTc)，c為光速；IF信號的相位?b = (4πR)/λ，λ為波長，毫米波雷達的波長通常為1～10 mm。人體心臟跳動會伴隨著0.1～0.5 mm的胸腔伏動，通過計算不難發現IF信號的相位比頻率對微小伏動更加敏感，所以選用相位信號作為心率測量的原始信號[13-15]。
2 實驗方法
2.1 雷達數據的采集
實驗雷達數據使用德州儀器公司的IWR1642BOOST和DCA1000EVM進行采集。實驗中IWR1642BOOST雷達的起始頻率為77 GHz，調頻斜率為65 GHz/μs，快時間采樣點數為256，幀數為14 400，幀周期為5 ms，脈沖數為2。實驗中雷達使用1根發射天線和4根接收天線。不同接收天線具有不同方向的敏感度差異，可以保留目標的不同特征信息[16]。DCA1000EVM為高速數據采集卡，可將數據傳輸到電腦中，數據按照幀模式進行采集。實驗標準數據使用力康集團的KS-CM01血氧探頭進行采集，探頭每秒獲取一次心率，測量誤差符合YZB/粵0303-2014《血氧探頭》的標準要求。
實驗共招募無心血管疾病的志愿者20名，志愿者具體信息見附件1。采集時為避免志愿者大幅度晃動，每位志愿者坐在距離雷達0.4～0.5 m處，且胸部正對雷達。實驗采用舉啞鈴提升心率的方式保證心率分布范圍。每位志愿者連續進行兩次數據采集，每次采集72 s數據，總共收集40組雷達數據和標準數據，心率范圍為58～106次/分，數據編號參見附件1。在雷達和血氧探頭采集數據時，均會自動記錄開始時間戳，借此保證數據的時間對齊。由于雷達啟動前期性能不穩定，將刪除前2 s數據。在CZT頻率估計時，以10 s為滑窗進行心率估計，最終每組數據將獲取60 s的估計心率。
2.2 雷達信號的預處理
2.2.1 人體位置識別
靜態物體在不同時間的雷達回波相同，因此可采用相量均值相消算法去除靜態物體的回波[17]。將所有IF信號求算術平均得到參考IF信號，相量均值相消算法的數學表達為：
 |
其中m為快時間采樣點數，N為脈沖總數，Y為IF信號被采樣后的矩陣，大小為m × N。然后求取IF信號與參考IF信號的差值，得到相量均值相消后數據可表示為：
 |
人體位置識別普遍采用快速傅里葉變換（fast Fourier transform，FFT）法[18]。由于不同距離的目標物體會產生不同的多普勒頻移，所以不同的頻率對應著不同距離的物體。為隨時間變化準確地選取距離單元，以幀為組，取累加后幅度最大值時的復數數據，組成微動信號。
2.2.2 相位解纏繞方法及差分
對于復數類型的微動信號，利用反正切函數法即可得到其相位，公式為：
 |
其中，I(t)和Q(t)為微動信號的實部、虛部。但是反正切函數法得到的相位會出現跳躍大于或等于π弧度的情況，即相位纏繞。相位纏繞時不能反映相位的真實變化趨勢。因此選用線性解調（linear demodulation，LD）算法[19]進行相位解纏繞，算法是對實部和虛部組成的混合矩陣M進行奇異值分解（singular value decomposition，SVD），然后計算主成分矩陣，第一個主分量即為所求相位信號[20]，用公式可表示為：
 '/> |
其中，U、S、V分別是分解后的左奇異向量、奇異值、右奇異向量；Y是主成分矩陣。通過LD算法得到的信號容易存在波動性較大的問題，為降低這種不規則性波動并使信號趨于平穩，采取一階差分法優化后得到最終相位信號[10]。
2.2.3 帶通濾波器
心率的頻率范圍為0.8～3.0 Hz，為濾除其他頻率的噪聲并滿足極窄過渡帶寬和較小阻帶波動的需要，選用無限沖擊響應濾波器中的橢圓濾波器[21]。實驗所采用橢圓濾波器的具體參數以及幅頻與相頻特性曲線參見附件2。功率譜熵是一種表示信號復雜度的特征量，功率譜熵越小代表信號的混亂度越小[22]。所以功率譜熵越小的信號中，包含的噪聲越小，相位信號的信噪比越高。根據雷達幀周期、心率頻率以及奈奎斯特采樣定律，實驗將在10～200 Hz的范圍內搜索最優采樣率，確保較高的信噪比。
2.2.4 快速獨立成分分析
快速獨立成分分析（fast independent component analysis，FastICA）作為一種盲源分離技術，借助信號自身的非高斯性和獨立性進行分離。算法首先對輸入信號X(t)進行均值和白化處理，以此去除其相關性，再采用牛頓迭代的方法不斷修正解混矩陣W直至目標函數值滿足收斂條件λ。本文FastICA的目標函數是采用負熵，其中負熵的函數可簡化為：
 |
其中E[·]為均值運算，G(·)為非線性函數，W0為解混矩陣初始值，P為零均值的高斯隨機變量且與W0TZ具有相同協方差值[23–25]。因此可使用FastICA技術提取出雷達信號的主成分信號，去除其中高斯雜亂信號。
2.3 心跳信號的分離
2.3.1 變分模態分解
VMD算法[26–27]首先確定K個中心頻率為wk的模態分量（intrinsic mode functions，IMF），記作vk(t)，然后對vk(t)進行希爾伯特變換構造約束變分問題，過程由公式呈現為：
 |
其中，vk為模態分量，wk為模態分量的中心頻率，s為輸入信號。首先使用懲罰因子和拉格朗日乘子將問題變為無約束變分問題，同時保證嚴格約束條件，過程表示為
 |
其中α為懲罰因子，τ(t)為拉格朗日乘子。利用交替方向乘法迭代得到問題的最佳解，所有模態可表示為：
 |
其中ω為頻率，^為其傅里葉變換。迭代過程中模態中心頻率wkn + 1更新、拉格朗日乘子
n + 1(w)更新、迭代停止條件的數學表達分別為：
 |
 |
 |
VMD算法對不同的信號應當采用不同的模態數K和懲罰因子α，針對此問題本文采用霜冰優化算法對兩個參數進行優化。
2.3.2 霜冰優化算法
在2023年，Su等[28]以霧凇生長為靈感，提出霜冰（RIME）算法。算法整體由顆粒集群的初始化、軟霧凇搜索策略、硬霧凇穿刺機制和正貪婪選擇機制組成。五種顆粒凝結情形組成軟霧凇搜索策略，用公式表示為：
 |
其中Rijnew為第i個軟霧劑的第j個顆粒；Rbest,j為更新后的顆粒位置；r1為顆粒方向；h為附著力；Ubij和Lbij為上下界；r2為判定是否凝聚成軟霧劑的隨機值，取值范圍為(0, 1)；β = 1 ? [wt/T]/w為環境因素，w為分段數，[·]為取整函數，t為當前迭代次數，T為最大迭代次數。增強算法的收斂性與局部最優跳出性的硬霧凇穿刺機制，用公式表示為：
 |
其中Rijnew為更新后顆粒位置；r3為判定是否凝聚成軟霧劑的隨機值，取值范圍為(0, 1)；F(Si)為歸一化后最佳的適應度。針對每一組數據都進行VMD的參數優化，參數的搜索范圍為K
[2, 10]，α
[1 000, 20 000]。霜冰優化中通過設置適應度函數確定算法優化方向，適應度函數設置為與原信號相關性最大的IMF的功率譜熵[29]。
2.4 心率估計算法
CZT是對信號Z變換后的螺旋線周線上等間隔取點，以此達到對指定區間頻率進行細化的目的。本文使用CZT方法將心跳信號的0.8～3.0 Hz進行頻譜細化，同時以10 s為滑窗，完成對心跳信號的心率估計。
2.5 評價指標
實驗的評價指標主要采用均方根誤差（root mean square error，RMSE）和平均錯誤率（average error rate，ACE），其計算公式為：
 |
 |
其中t為估計時間長度，
為第i秒心率估計值，yi為第i秒的心率真實值。RMSE和ACE越小代表估計值越準確，算法越可靠[30]。本文采用40組RMSE和ACE的統計結果來整體評估算法性能，主要包括效果提升組數、效果提升率、效果提升組均值、效果降低組均值等。效果提升組數是指第二種算法相較于第一種算法在評價指標上有所優化的組別個數；效果提升率是指效果提升組數占總組數的比例；效果提升組均值是指所有效果提升組評價指標提升的平均值；效果降低組均值是指所有效果降低組評價指標降低的平均值。
3 結果展示與討論
3.1 結果展示
以01組數據為例，依次展示雷達信號的預處理、心跳信號分離的過程結果以及使用CZT算法得到預估心率的過程，具體流程如圖1所示。
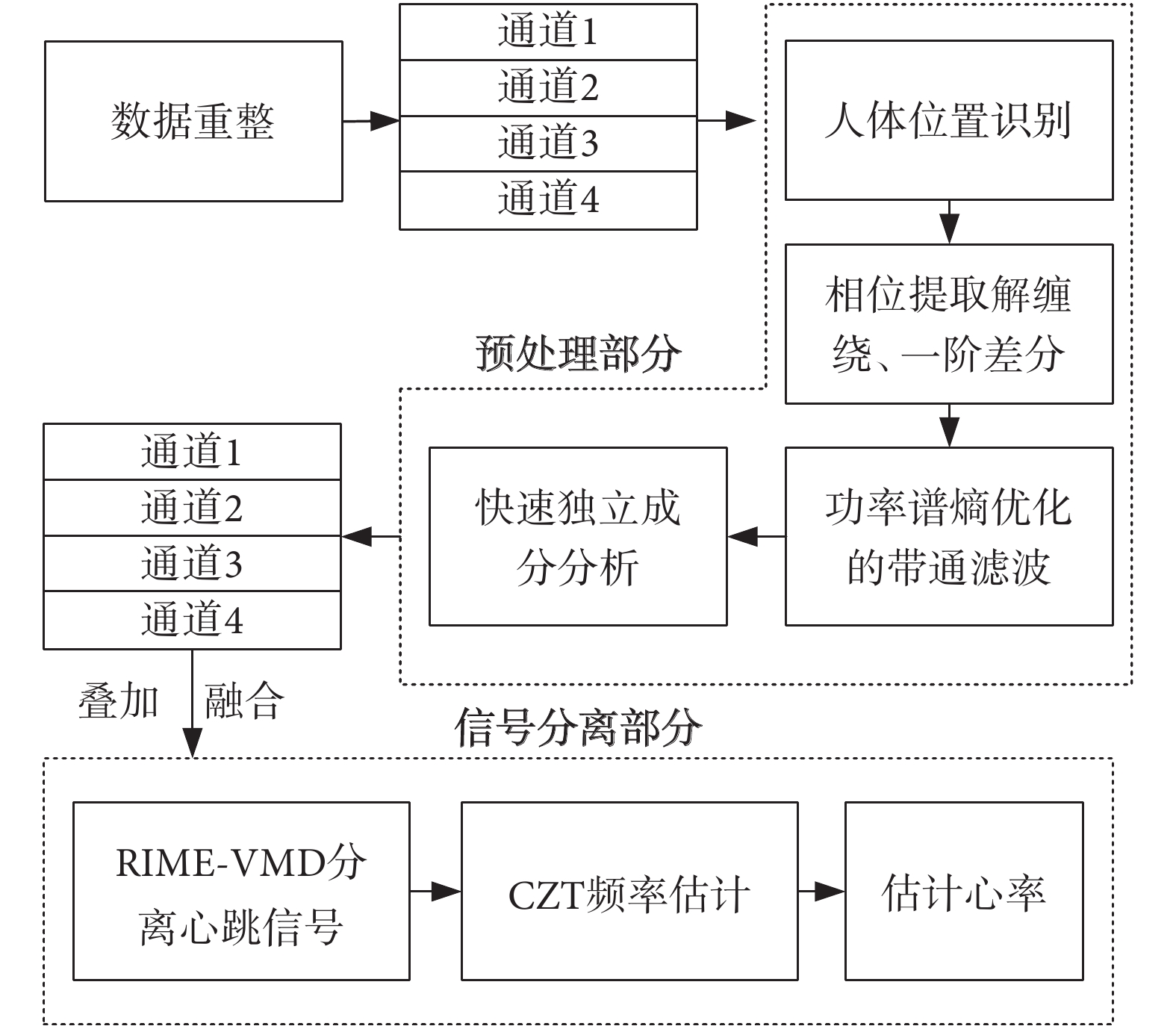圖1
算法整體流程圖
Figure1.
Overall flow chart of the algorithm
對01組數據的通道1先采用2.2.1小節的相量均值相消算法去除靜態物體回波（結果參見附件3），隨后以幀為組提取出通道1的微動信號（結果參見附件4）。然后根據反正切函數提取的相位信號，使用LD法進行解纏繞，并采取一階差分法降低通道1相位信號的無規則波動（結果參見附件5）。隨后使用2.2.3節的帶通濾波器，對通道1的相位信號進行濾波，再利用FastICA法得到通道1的主成分信號（結果參見附件6）。
為保留更多方向、速度特征信息和降低信噪比，以按照上述方式完成四個通道的主成分信號提取，并進行疊加處理得到多通道融合數據，結果如圖2的原信號所示。隨后使用RIME-VMD方法完成對多通道融合數據的分解，結果如圖2所示。其中，RIME優化后的模態數K為3，懲罰因子α為6 919。所有的模態分量中模態分量3的相關性最大，相關系數為0.591，因此選用模態分量3作為分離出的心跳信號。
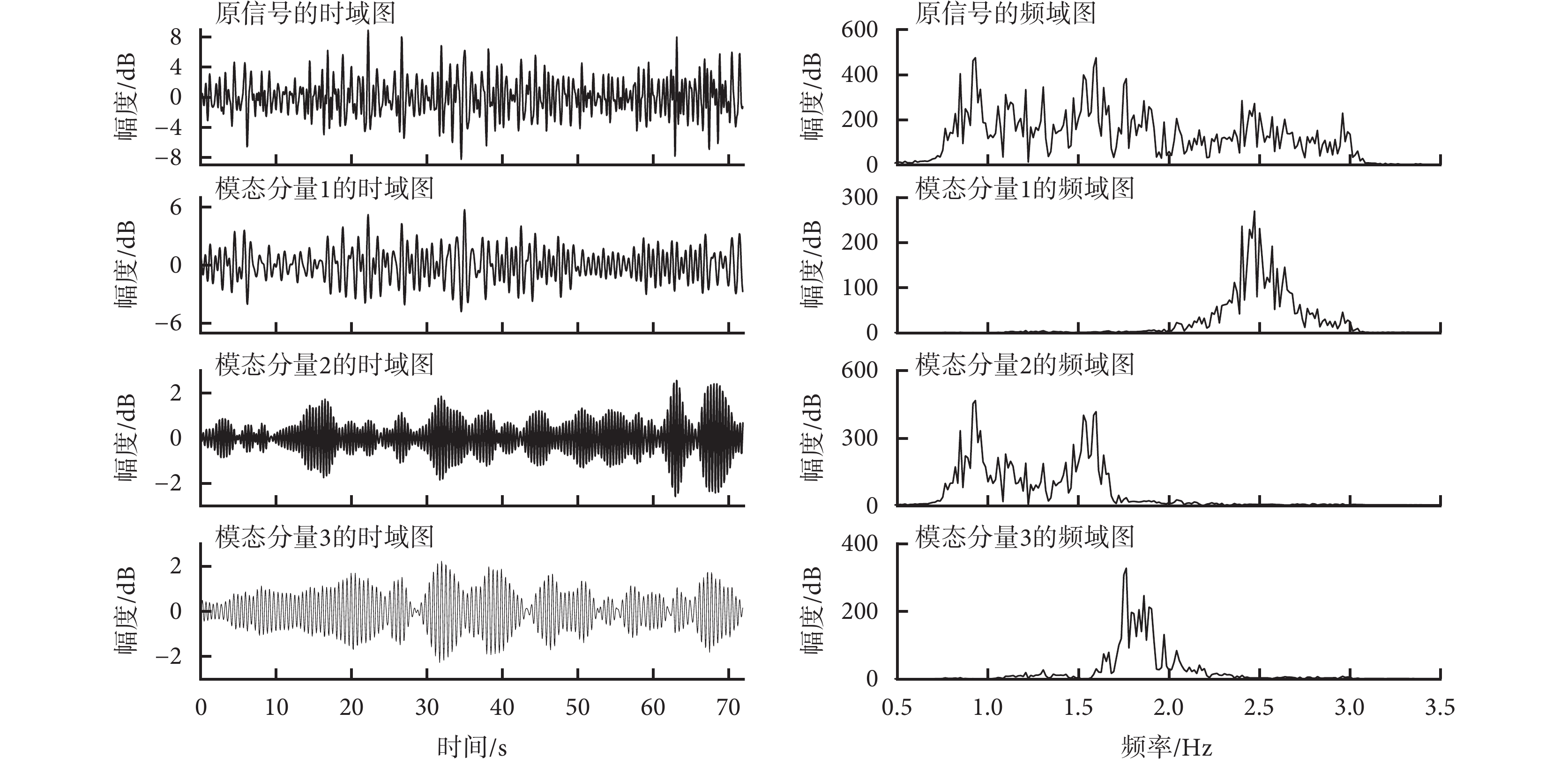圖2
RIME-VMD算法分解結果
Figure2.
RIME-VMD decomposition diagram
最后以10 s滑窗的方式，使用CZT法完成心率的估計。第1 s滑窗數據的頻譜圖如圖3左圖所示，其中最高峰的頻率為1.52 Hz，因此第1 s的估計心率為
次/分。以此類推，完成組01數據60 s的心率估計，結果如圖3右圖所示。
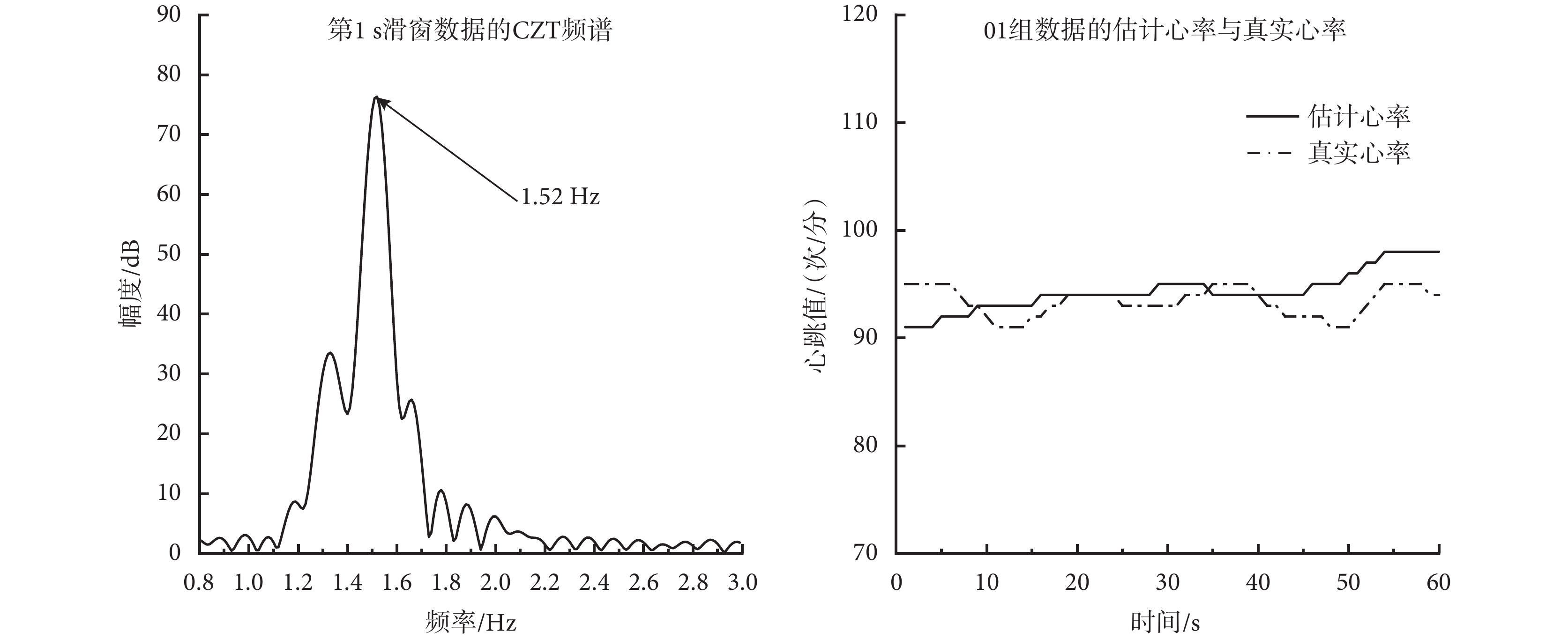圖3
01組數據心率估計過程以及結果
Figure3.
Heart rate estimation process and results for group 01 data
3.2 采樣率尋優驗證對比
根據奈奎斯特抽樣定律，心跳信號采樣率至少為1.6～6.0 Hz，才會不發生混疊現象。同時功率譜熵越小代表信號的混亂度越小，即信號越可能存在周期信號。因此以01、02組的單通道雷達數據為例，設置采樣率為10～200 Hz，計算濾波后信號的功率譜熵和算法的RMSE，歸一化處理后的結果如圖4所示。
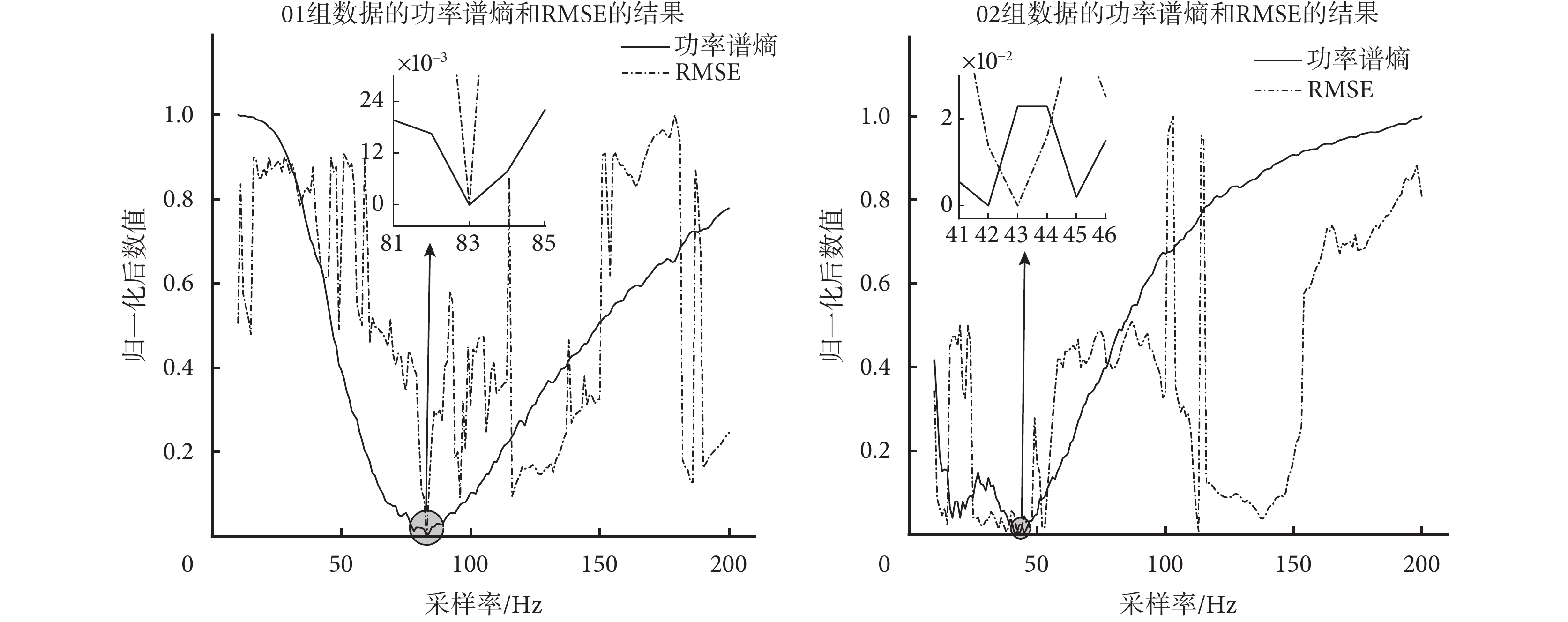圖4
歸一化的功率譜熵和RMSE關系圖
Figure4.
Normalized power spectrum entropy and RMSE plot
從圖4可知，01組在采樣率為83 Hz時，功率譜熵和RMSE均最小。02組在采樣率為42 Hz時功率譜熵最低，在采樣率為43 Hz時RMSE最低，盡管采樣率不一致，但十分接近。因此通過最小功率譜熵的方式確定采樣率可以減少信號的混亂度，從而提高整體算法精度。
3.3 FastICA算法驗證對比
使用FastICA算法能夠將獨立源信號分離出來，因此選取多通道融合數據為樣本，以是否使用FastICA算法為唯一變量，驗證采用FastICA算法的必要性，統計結果如表1所示，各組原始結果參見附件7。
表1
FastICA算法使用前后的統計結果
Table1.
Statistical results before and after using the FastICA algorithm
從表1可以看出，采用FastICA算法對于90%的數據都有提升效果，僅對于少量數據產生較小的不良影響。其中，效果提升組的RMSE平均降低10.29次/分，ACE平均降低11.96%；效果降低組的RMSE平均升高0.47次/分，ACE平均升高0.85%。總體而言，FastICA算法能夠提升心率估計的準確度，有效降低其他噪聲信號對實驗的不良影響。
3.4 單通道數據與多通道融合數據對比
多通道融合數據相較于單通道數據含有更多的信息，但同時也可能引入干擾。為驗證多通道融合數據的適用性和可靠性，實驗將對比單一通道數據的估計結果與多通道融合數據的估計結果，其中單一通道數據共計160個。統計結果如表2所示，各組原始實驗結果參見附件8。
表2
單通道數據與多通道融合數據的統計結果
Table2.
Statistical results of single-channel data and multi-channel fusion data
從表2可以看出，相比于單通道數據，78.80%的多通道融合數據都具有更好的估計效果，效果提升組的RMSE平均降低4.55次/分，ACE平均降低4.87%。反觀剩余單通道數據的RMSE平均升高0.31次/分，ACE平均升高0.47%。如果選用單通道數據，將無法保證每次都會有最優異的效果。綜上所述，多通道數據融合具有很好的適用性和可靠性，能夠保證后續算法的優異效果。
3.5 整體算法結果與討論
為驗證本文RIME-VMD算法的優劣性，將它與EMD算法、集合經驗模態分解（ensemble empirical mode decomposition，EEMD）算法進行對比。三種算法的實驗結果和對比如表3、表4所示，各組原始實驗結果參見附件9。
表3
RIME-VMD、EMD、EEMD的實驗結果
Table3.
Experimental results of RIME-VMD, EMD and EEMD
表4
RIME-VMD與EMD、EEMD的比較結果
Table4.
Comparison between RIME-VMD and EMD and EEMD
從表3和表4可以看出，RIME-VMD算法的平均RMSE為2.35次/分，平均ACE為2.39%，符合心電監護儀的國家標準，比引言中提到的算法具有更高的準確度。同時，RIME-VMD算法與EMD算法、EEMD算法相比在準確性上均有提升，其中RMSE平均降低14.35次/分、17.00次/分，ACE平均降低14.73%、17.47%。因此可以得出RIME-VMD算法效果優于EMD算法和EEMD算法的結論。但是，從平均運行時間來看，RIME-VMD算法需要更長的時間，所以在實時檢測時需要減少RIME-VMD算法尋優用時。此外，RIME-VMD算法相關性與一致性的結果，如圖5所示。
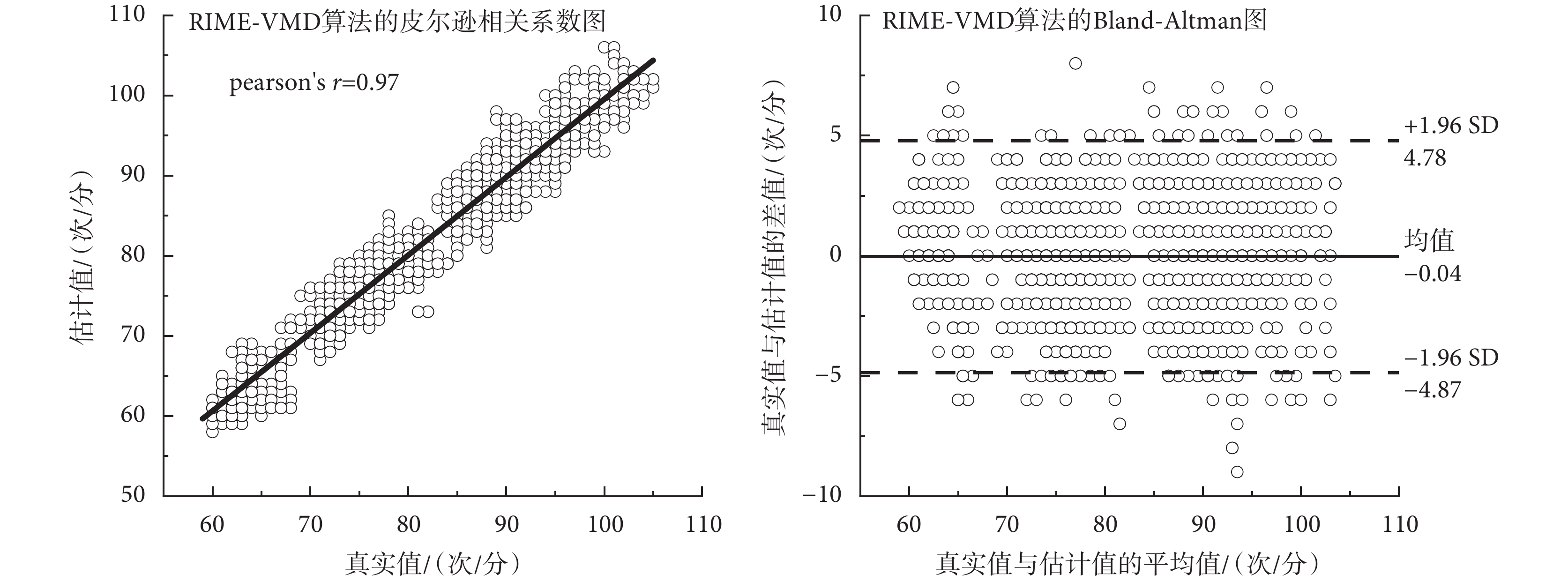圖5
RIME-VMD算法的相關性與一致性圖
Figure5.
Correlation and consistency graph of RIME-VMD
圖5左圖是RIME-VMD算法的皮爾遜相關系數圖，相關系數為0.97，說明估計值與真實值具有強相關性。圖5右圖為RIME-VMD算法的Bland-Altman圖，置信區間為[–4.78, 4.78]次/分，誤差值為–0.04次/分，大約有95.96%的數據在置信區間內，說明估計值與真實值具有極強的一致性。
4 結論
本文提出一種FMCW雷達的多通道融合心率測量方法，該方法首先對人體微動信號進行探究，使用以功率譜熵為優化指標的IIR帶通濾波器和FastICA算法分別對四通道數據進行降噪處理。然后將四通道數據疊加融合后，以功率譜熵作為RIME的適應度，采用RIME-VMD分離出心跳信號，最后使用CZT頻率估計心率。實驗結果顯示，40組心率估計結果RMSE平均值為2.35，ACE平均值為2.39%，皮爾遜相關系數為0.97，置信區間為[–4.78, 4.78]次/分，一致性誤差為–0.04次/分。綜上所述，本文提出的多通道融合心率測量算法有著優異的精準性、可靠性和魯棒性，同時也為雷達信號處理提供了一種新的思路和解決方案。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：郭洪瑞主要負責算法程序設計與編寫、數據記錄與分析以及論文撰寫；曹匯敏、張朱珊瑩主要負責實驗流程、協調溝通、計劃安排、提供實驗指導以及論文審閱修訂；楊克奇主要負責協助完成實驗以及數據的初步分析。
倫理聲明：本研究通過了中南民族大學科研倫理與科技安全委員會的審批（批文編號：2024-SCUEC-055）。
本文附件見本刊網站的電子版本（biomedeng.cn）。
0 引言
連續監測心率對于心率失常、猝死、心肌炎等心臟突發疾病的發現和預防尤為重要[1]。連續監測心率儀器分為接觸式與非接觸式兩種。傳統的接觸式儀器對于燒傷患者、嬰兒、受困人員等無法接觸人體的情況無能為力，而且長時間佩戴儀器也會引起人體不適[2]。而非接觸式儀器中的生物雷達因高穿透性、無光照影響、可連續性等優點被應用到人體心率檢測領域[3]。
生物雷達應用于連續監測心率領域的重點在于雷達信號分離，通常會使用數字濾波器[4]、經驗模式分解（empirical mode decomposition，EMD）[5]、變分模態分解（variational mode decomposition，VMD）[6]、小波分解[7]等方法。Higashi等[8]對多普勒雷達的時域信號使用維納濾波和多邏輯回歸，測量出的心率平均錯誤率為4.48%。胡錫坤等[9]利用自適應尺度小波從雷達信號分離出心跳信號，靜坐情況下25 s內的準確率保持在95%以上。Qi等[10]使用多階差分增強的VMD算法對超寬帶雷達信號提取人體心率，真實人體數據估計結果的平均錯誤率為4.24%。
現行國家標準GB 9706.227-2021中，心率監測的準確性應為±10%或±5次/分中的較大者[11]。為獲取更高的測量精準度，本文提出一種基于多通道雷達數據融合的人體心率精準測量方法。首先通過優化后的預處理方法得到多通道雷達數據，然后使用優化后的變分模態分解算法分離出心跳信號，最后通過線性調頻Z變換（cadmium zinc telluride，CZT）估計出心率[12]。本文將通過一系列實驗證實算法的可靠性、魯棒性和準確性。
1 雷達測量人體心率的原理
本文使用的雷達是調頻連續波（frequency modulation continuous wave，FMCW）雷達，具有信噪比高、指向精度高、多普勒靈敏度高等優勢。雷達發射信號是線性調頻脈沖（linear frequency modulation，LFM）信號，其最小單元稱之為脈沖，公式表示為：
|
其中AT為脈沖的幅度，fc為起始的頻率，B為帶寬，Tc為周期，t為時間，φ(t)為相位噪聲。若人站在距離R米處，雷達回波信號與發射信號混頻后，得到的中頻（intermediate frequency，IF）信號為
|
其中AR為回波信號幅度；IF信號的頻率fb = (4πBRt)/(cTc)，c為光速；IF信號的相位?b = (4πR)/λ，λ為波長，毫米波雷達的波長通常為1～10 mm。人體心臟跳動會伴隨著0.1～0.5 mm的胸腔伏動，通過計算不難發現IF信號的相位比頻率對微小伏動更加敏感，所以選用相位信號作為心率測量的原始信號[13-15]。
2 實驗方法
2.1 雷達數據的采集
實驗雷達數據使用德州儀器公司的IWR1642BOOST和DCA1000EVM進行采集。實驗中IWR1642BOOST雷達的起始頻率為77 GHz，調頻斜率為65 GHz/μs，快時間采樣點數為256，幀數為14 400，幀周期為5 ms，脈沖數為2。實驗中雷達使用1根發射天線和4根接收天線。不同接收天線具有不同方向的敏感度差異，可以保留目標的不同特征信息[16]。DCA1000EVM為高速數據采集卡，可將數據傳輸到電腦中，數據按照幀模式進行采集。實驗標準數據使用力康集團的KS-CM01血氧探頭進行采集，探頭每秒獲取一次心率，測量誤差符合YZB/粵0303-2014《血氧探頭》的標準要求。
實驗共招募無心血管疾病的志愿者20名，志愿者具體信息見附件1。采集時為避免志愿者大幅度晃動，每位志愿者坐在距離雷達0.4～0.5 m處，且胸部正對雷達。實驗采用舉啞鈴提升心率的方式保證心率分布范圍。每位志愿者連續進行兩次數據采集，每次采集72 s數據，總共收集40組雷達數據和標準數據，心率范圍為58～106次/分，數據編號參見附件1。在雷達和血氧探頭采集數據時，均會自動記錄開始時間戳，借此保證數據的時間對齊。由于雷達啟動前期性能不穩定，將刪除前2 s數據。在CZT頻率估計時，以10 s為滑窗進行心率估計，最終每組數據將獲取60 s的估計心率。
2.2 雷達信號的預處理
2.2.1 人體位置識別
靜態物體在不同時間的雷達回波相同，因此可采用相量均值相消算法去除靜態物體的回波[17]。將所有IF信號求算術平均得到參考IF信號，相量均值相消算法的數學表達為：
|
其中m為快時間采樣點數，N為脈沖總數，Y為IF信號被采樣后的矩陣，大小為m × N。然后求取IF信號與參考IF信號的差值，得到相量均值相消后數據可表示為：
|
人體位置識別普遍采用快速傅里葉變換（fast Fourier transform，FFT）法[18]。由于不同距離的目標物體會產生不同的多普勒頻移，所以不同的頻率對應著不同距離的物體。為隨時間變化準確地選取距離單元，以幀為組，取累加后幅度最大值時的復數數據，組成微動信號。
2.2.2 相位解纏繞方法及差分
對于復數類型的微動信號，利用反正切函數法即可得到其相位，公式為：
|
其中，I(t)和Q(t)為微動信號的實部、虛部。但是反正切函數法得到的相位會出現跳躍大于或等于π弧度的情況，即相位纏繞。相位纏繞時不能反映相位的真實變化趨勢。因此選用線性解調（linear demodulation，LD）算法[19]進行相位解纏繞，算法是對實部和虛部組成的混合矩陣M進行奇異值分解（singular value decomposition，SVD），然后計算主成分矩陣，第一個主分量即為所求相位信號[20]，用公式可表示為：
| '/> |
其中，U、S、V分別是分解后的左奇異向量、奇異值、右奇異向量；Y是主成分矩陣。通過LD算法得到的信號容易存在波動性較大的問題，為降低這種不規則性波動并使信號趨于平穩，采取一階差分法優化后得到最終相位信號[10]。
2.2.3 帶通濾波器
心率的頻率范圍為0.8～3.0 Hz，為濾除其他頻率的噪聲并滿足極窄過渡帶寬和較小阻帶波動的需要，選用無限沖擊響應濾波器中的橢圓濾波器[21]。實驗所采用橢圓濾波器的具體參數以及幅頻與相頻特性曲線參見附件2。功率譜熵是一種表示信號復雜度的特征量，功率譜熵越小代表信號的混亂度越小[22]。所以功率譜熵越小的信號中，包含的噪聲越小，相位信號的信噪比越高。根據雷達幀周期、心率頻率以及奈奎斯特采樣定律，實驗將在10～200 Hz的范圍內搜索最優采樣率，確保較高的信噪比。
2.2.4 快速獨立成分分析
快速獨立成分分析（fast independent component analysis，FastICA）作為一種盲源分離技術，借助信號自身的非高斯性和獨立性進行分離。算法首先對輸入信號X(t)進行均值和白化處理，以此去除其相關性，再采用牛頓迭代的方法不斷修正解混矩陣W直至目標函數值滿足收斂條件λ。本文FastICA的目標函數是采用負熵，其中負熵的函數可簡化為：
|
其中E[·]為均值運算，G(·)為非線性函數，W0為解混矩陣初始值，P為零均值的高斯隨機變量且與W0TZ具有相同協方差值[23–25]。因此可使用FastICA技術提取出雷達信號的主成分信號，去除其中高斯雜亂信號。
2.3 心跳信號的分離
2.3.1 變分模態分解
VMD算法[26–27]首先確定K個中心頻率為wk的模態分量（intrinsic mode functions，IMF），記作vk(t)，然后對vk(t)進行希爾伯特變換構造約束變分問題，過程由公式呈現為：
|
其中，vk為模態分量，wk為模態分量的中心頻率，s為輸入信號。首先使用懲罰因子和拉格朗日乘子將問題變為無約束變分問題，同時保證嚴格約束條件，過程表示為
|
其中α為懲罰因子，τ(t)為拉格朗日乘子。利用交替方向乘法迭代得到問題的最佳解，所有模態可表示為：
|
其中ω為頻率，^為其傅里葉變換。迭代過程中模態中心頻率wkn + 1更新、拉格朗日乘子n + 1(w)更新、迭代停止條件的數學表達分別為：
|
|
|
VMD算法對不同的信號應當采用不同的模態數K和懲罰因子α，針對此問題本文采用霜冰優化算法對兩個參數進行優化。
2.3.2 霜冰優化算法
在2023年，Su等[28]以霧凇生長為靈感，提出霜冰（RIME）算法。算法整體由顆粒集群的初始化、軟霧凇搜索策略、硬霧凇穿刺機制和正貪婪選擇機制組成。五種顆粒凝結情形組成軟霧凇搜索策略，用公式表示為：
|
其中Rijnew為第i個軟霧劑的第j個顆粒；Rbest,j為更新后的顆粒位置；r1為顆粒方向；h為附著力；Ubij和Lbij為上下界；r2為判定是否凝聚成軟霧劑的隨機值，取值范圍為(0, 1)；β = 1 ? [wt/T]/w為環境因素，w為分段數，[·]為取整函數，t為當前迭代次數，T為最大迭代次數。增強算法的收斂性與局部最優跳出性的硬霧凇穿刺機制，用公式表示為：
|
其中Rijnew為更新后顆粒位置；r3為判定是否凝聚成軟霧劑的隨機值，取值范圍為(0, 1)；F(Si)為歸一化后最佳的適應度。針對每一組數據都進行VMD的參數優化，參數的搜索范圍為K[2, 10]，α[1 000, 20 000]。霜冰優化中通過設置適應度函數確定算法優化方向，適應度函數設置為與原信號相關性最大的IMF的功率譜熵[29]。
2.4 心率估計算法
CZT是對信號Z變換后的螺旋線周線上等間隔取點，以此達到對指定區間頻率進行細化的目的。本文使用CZT方法將心跳信號的0.8～3.0 Hz進行頻譜細化，同時以10 s為滑窗，完成對心跳信號的心率估計。
2.5 評價指標
實驗的評價指標主要采用均方根誤差（root mean square error，RMSE）和平均錯誤率（average error rate，ACE），其計算公式為：
|
|
其中t為估計時間長度，為第i秒心率估計值，yi為第i秒的心率真實值。RMSE和ACE越小代表估計值越準確，算法越可靠[30]。本文采用40組RMSE和ACE的統計結果來整體評估算法性能，主要包括效果提升組數、效果提升率、效果提升組均值、效果降低組均值等。效果提升組數是指第二種算法相較于第一種算法在評價指標上有所優化的組別個數；效果提升率是指效果提升組數占總組數的比例；效果提升組均值是指所有效果提升組評價指標提升的平均值；效果降低組均值是指所有效果降低組評價指標降低的平均值。
3 結果展示與討論
3.1 結果展示
以01組數據為例，依次展示雷達信號的預處理、心跳信號分離的過程結果以及使用CZT算法得到預估心率的過程，具體流程如圖1所示。
圖1
算法整體流程圖
Figure1.
Overall flow chart of the algorithm
對01組數據的通道1先采用2.2.1小節的相量均值相消算法去除靜態物體回波（結果參見附件3），隨后以幀為組提取出通道1的微動信號（結果參見附件4）。然后根據反正切函數提取的相位信號，使用LD法進行解纏繞，并采取一階差分法降低通道1相位信號的無規則波動（結果參見附件5）。隨后使用2.2.3節的帶通濾波器，對通道1的相位信號進行濾波，再利用FastICA法得到通道1的主成分信號（結果參見附件6）。
為保留更多方向、速度特征信息和降低信噪比，以按照上述方式完成四個通道的主成分信號提取，并進行疊加處理得到多通道融合數據，結果如圖2的原信號所示。隨后使用RIME-VMD方法完成對多通道融合數據的分解，結果如圖2所示。其中，RIME優化后的模態數K為3，懲罰因子α為6 919。所有的模態分量中模態分量3的相關性最大，相關系數為0.591，因此選用模態分量3作為分離出的心跳信號。
圖2
RIME-VMD算法分解結果
Figure2.
RIME-VMD decomposition diagram
最后以10 s滑窗的方式，使用CZT法完成心率的估計。第1 s滑窗數據的頻譜圖如圖3左圖所示，其中最高峰的頻率為1.52 Hz，因此第1 s的估計心率為次/分。以此類推，完成組01數據60 s的心率估計，結果如圖3右圖所示。
圖3
01組數據心率估計過程以及結果
Figure3.
Heart rate estimation process and results for group 01 data
3.2 采樣率尋優驗證對比
根據奈奎斯特抽樣定律，心跳信號采樣率至少為1.6～6.0 Hz，才會不發生混疊現象。同時功率譜熵越小代表信號的混亂度越小，即信號越可能存在周期信號。因此以01、02組的單通道雷達數據為例，設置采樣率為10～200 Hz，計算濾波后信號的功率譜熵和算法的RMSE，歸一化處理后的結果如圖4所示。
圖4
歸一化的功率譜熵和RMSE關系圖
Figure4.
Normalized power spectrum entropy and RMSE plot
從圖4可知，01組在采樣率為83 Hz時，功率譜熵和RMSE均最小。02組在采樣率為42 Hz時功率譜熵最低，在采樣率為43 Hz時RMSE最低，盡管采樣率不一致，但十分接近。因此通過最小功率譜熵的方式確定采樣率可以減少信號的混亂度，從而提高整體算法精度。
3.3 FastICA算法驗證對比
使用FastICA算法能夠將獨立源信號分離出來，因此選取多通道融合數據為樣本，以是否使用FastICA算法為唯一變量，驗證采用FastICA算法的必要性，統計結果如表1所示，各組原始結果參見附件7。
表1
FastICA算法使用前后的統計結果
Table1.
Statistical results before and after using the FastICA algorithm
從表1可以看出，采用FastICA算法對于90%的數據都有提升效果，僅對于少量數據產生較小的不良影響。其中，效果提升組的RMSE平均降低10.29次/分，ACE平均降低11.96%；效果降低組的RMSE平均升高0.47次/分，ACE平均升高0.85%。總體而言，FastICA算法能夠提升心率估計的準確度，有效降低其他噪聲信號對實驗的不良影響。
3.4 單通道數據與多通道融合數據對比
多通道融合數據相較于單通道數據含有更多的信息，但同時也可能引入干擾。為驗證多通道融合數據的適用性和可靠性，實驗將對比單一通道數據的估計結果與多通道融合數據的估計結果，其中單一通道數據共計160個。統計結果如表2所示，各組原始實驗結果參見附件8。
表2
單通道數據與多通道融合數據的統計結果
Table2.
Statistical results of single-channel data and multi-channel fusion data
從表2可以看出，相比于單通道數據，78.80%的多通道融合數據都具有更好的估計效果，效果提升組的RMSE平均降低4.55次/分，ACE平均降低4.87%。反觀剩余單通道數據的RMSE平均升高0.31次/分，ACE平均升高0.47%。如果選用單通道數據，將無法保證每次都會有最優異的效果。綜上所述，多通道數據融合具有很好的適用性和可靠性，能夠保證后續算法的優異效果。
3.5 整體算法結果與討論
為驗證本文RIME-VMD算法的優劣性，將它與EMD算法、集合經驗模態分解（ensemble empirical mode decomposition，EEMD）算法進行對比。三種算法的實驗結果和對比如表3、表4所示，各組原始實驗結果參見附件9。
表3
RIME-VMD、EMD、EEMD的實驗結果
Table3.
Experimental results of RIME-VMD, EMD and EEMD
表4
RIME-VMD與EMD、EEMD的比較結果
Table4.
Comparison between RIME-VMD and EMD and EEMD
從表3和表4可以看出，RIME-VMD算法的平均RMSE為2.35次/分，平均ACE為2.39%，符合心電監護儀的國家標準，比引言中提到的算法具有更高的準確度。同時，RIME-VMD算法與EMD算法、EEMD算法相比在準確性上均有提升，其中RMSE平均降低14.35次/分、17.00次/分，ACE平均降低14.73%、17.47%。因此可以得出RIME-VMD算法效果優于EMD算法和EEMD算法的結論。但是，從平均運行時間來看，RIME-VMD算法需要更長的時間，所以在實時檢測時需要減少RIME-VMD算法尋優用時。此外，RIME-VMD算法相關性與一致性的結果，如圖5所示。
圖5
RIME-VMD算法的相關性與一致性圖
Figure5.
Correlation and consistency graph of RIME-VMD
圖5左圖是RIME-VMD算法的皮爾遜相關系數圖，相關系數為0.97，說明估計值與真實值具有強相關性。圖5右圖為RIME-VMD算法的Bland-Altman圖，置信區間為[–4.78, 4.78]次/分，誤差值為–0.04次/分，大約有95.96%的數據在置信區間內，說明估計值與真實值具有極強的一致性。
4 結論
本文提出一種FMCW雷達的多通道融合心率測量方法，該方法首先對人體微動信號進行探究，使用以功率譜熵為優化指標的IIR帶通濾波器和FastICA算法分別對四通道數據進行降噪處理。然后將四通道數據疊加融合后，以功率譜熵作為RIME的適應度，采用RIME-VMD分離出心跳信號，最后使用CZT頻率估計心率。實驗結果顯示，40組心率估計結果RMSE平均值為2.35，ACE平均值為2.39%，皮爾遜相關系數為0.97，置信區間為[–4.78, 4.78]次/分，一致性誤差為–0.04次/分。綜上所述，本文提出的多通道融合心率測量算法有著優異的精準性、可靠性和魯棒性，同時也為雷達信號處理提供了一種新的思路和解決方案。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：郭洪瑞主要負責算法程序設計與編寫、數據記錄與分析以及論文撰寫；曹匯敏、張朱珊瑩主要負責實驗流程、協調溝通、計劃安排、提供實驗指導以及論文審閱修訂；楊克奇主要負責協助完成實驗以及數據的初步分析。
倫理聲明：本研究通過了中南民族大學科研倫理與科技安全委員會的審批（批文編號：2024-SCUEC-055）。
本文附件見本刊網站的電子版本（biomedeng.cn）。
