在動脈疾病的診斷和治療中，有效評估血管壁局部生物力學特性至關重要。壓痕測量可用于評估動脈局部力學性能，但壓頭的幾何結構和分析理論對測量結果的影響尚不清楚。本文采用4種壓頭對豬的肺動脈、胸主動脈近心端和胸主動脈遠心端進行測量，并通過斯內登（Sneddon）和瑟爾吉（Sirghi）理論計算動脈彈性模量，探究壓頭幾何結構和分析理論對彈性模量測量值的影響。結果顯示，圓柱形壓頭測量的動脈彈性模量值低于球形壓頭測量值；其次，與Sirghi理論計算結果相比，通過不考慮黏附力的Sneddon理論獲得的動脈彈性模量值略大。綜上，本研究可為毫米級壓痕技術有效測量動脈局部力學特性提供參數支持。
引用本文： 曹祎凡, 高志鵬, 石怡柯, 李芬, 宋輝, 張倩倩, 趙雅威, 陳凌峰, 李曉娜, 陳維毅. 宏觀壓痕測量血管壁力學性能方法的研究. 生物醫學工程學雜志, 2024, 41(3): 469-475. doi: 10.7507/1001-5515.202310062 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
美國心臟病學會數據顯示，全球心血管患者從1990年的2.71億人增加到2019年的5.23億人，其中死亡人數從1990年的1 210萬增加到2019年的1 860萬[1]。心血管疾病已成為導致人類死亡和殘疾的主要原因。常見心血管疾病包括動脈粥樣硬化、動脈瘤和動脈夾層等，它們的發生和發展與血管壁局部力學性能的改變密切相關[2-6]。因此，有效評估動脈局部力學性能成為動脈疾病診斷和治療的關鍵，特別是在評估斑塊的發展、預測夾層破裂位置等方面尤為重要。
拉伸實驗[7-9]和灌流實驗[10]是測量動脈力學性能的常用方法，可表征實驗樣本的整體力學性能。與拉伸實驗和灌流實驗相比，壓痕實驗更適合測量動脈的局部力學性能。目前，壓痕技術在不同研究領域以及不同尺度上均有應用。其中，微米或納米級壓頭可以測量微觀組織力學性能，如動脈內皮細胞[11-13]、平滑肌細胞[14]以及細胞外基質[15]等；毫米級壓頭可以從宏觀角度測量組織力學性能，如動脈粥樣硬化中的纖維帽組織[16]和脂質組織[17]等。除此之外，毫米級壓痕實驗還能在傳統開放式手術中有效區分健康組織和病變組織，幫助外科醫生準確定位縫合線位置[18]。
隨著壓痕技術不斷發展，其應用也日益廣泛。在不同文獻報道中，使用壓痕技術測得的彈性模量值存在很大差異。例如，微米和納米級壓痕實驗中，Pesen等[11]測量的牛肺動脈內皮細胞彈性模量值在0.2～2.0 kPa之間；Viswanathan等[12]測量的人肺動脈內皮細胞平均彈性模量值為2.9 kPa；此外，Wang等[13]測量的人肺動脈內皮細胞細胞核、細胞質、細胞邊緣的彈性模量分別是26～29 kPa、18～19 kPa、4～6 kPa。據報道，微米和納米級壓痕實驗測量結果的差異主要源于不同的壓頭幾何結構[19-20]以及不同的分析理論[21]。相對而言，毫米級壓痕實驗中，壓頭幾何結構和分析理論對測量結果是否產生影響，目前尚不清楚。
為能在毫米級實驗中準確、有效地表征動脈組織局部力學性能，探究壓頭幾何結構和分析理論對壓痕測量結果的影響，本研究使用4種壓頭[包括：直徑為1 mm的圓柱形壓頭（圓柱形-1 mm）；直徑為0.5、1、2 mm的球形壓頭（球形-0.5 mm、球形-1 mm、球形-2 mm）]對豬的肺動脈、胸主動脈近心端和胸主動脈遠心端進行測量，并使用忽略黏附力的斯內登（Sneddon）理論[22]和考慮黏附力的瑟爾吉（Sirghi）理論[21]計算動脈彈性模量，并對測量結果進行統計分析。此外，本研究還通過壓痕實驗和拉伸實驗分別測量了動脈生物力學性能，驗證并比較兩種實驗方法測量結果的差異，以期更深入地了解動脈組織力學性能。
1 材料與方法
1.1 樣本的制備
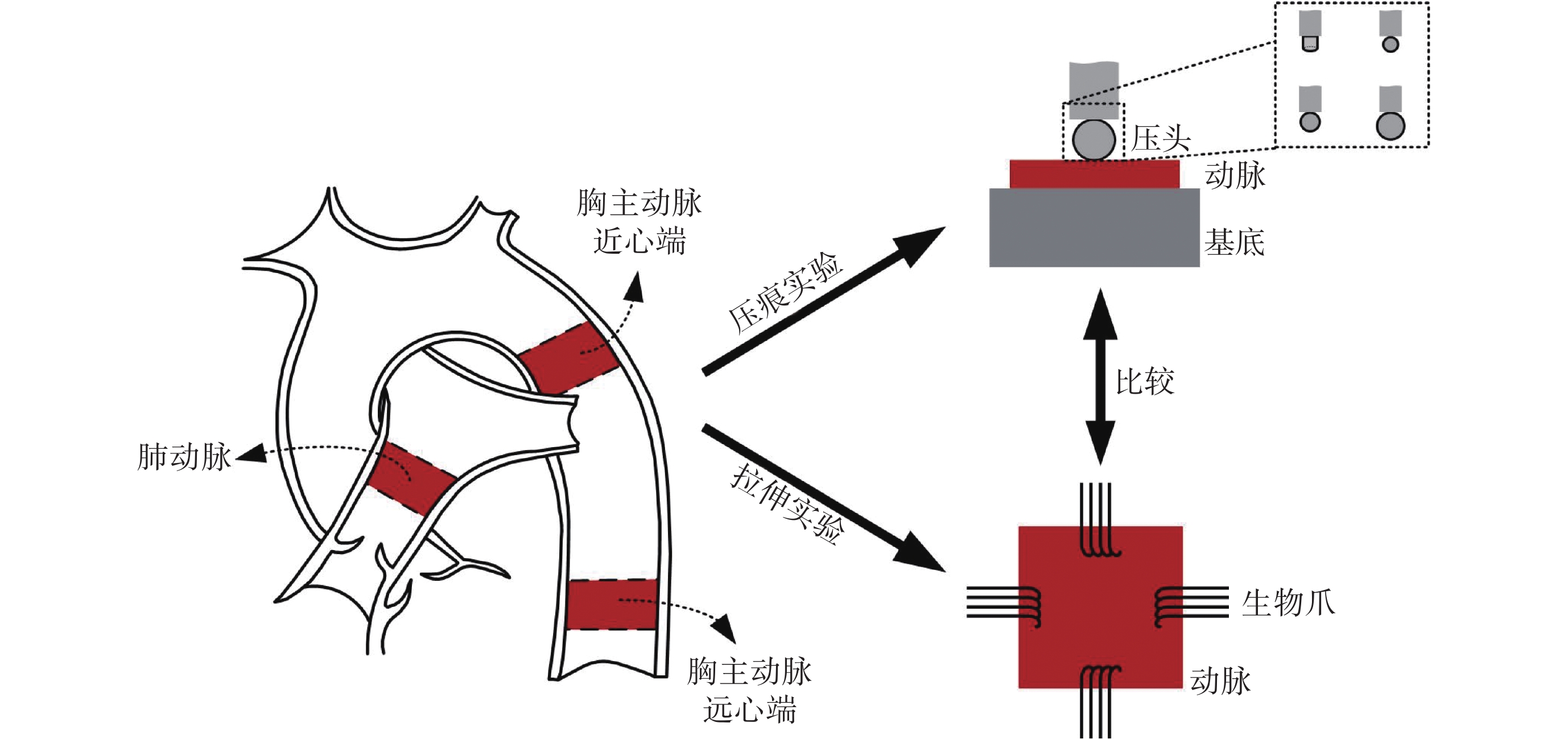
本研究使用當地屠宰場健康豬的動脈作為研究材料。如圖1所示，對豬肺動脈、胸主動脈近心端和胸主動脈遠心端進行力學實驗。實驗前，去除樣本上多余的脂肪和結締組織，并使用激光位移傳感器LK-G5000（Keyence Corp.，日本）測量樣本厚度。所有樣本在力學檢測前保存在4 °C生理鹽水中不超過6 h。
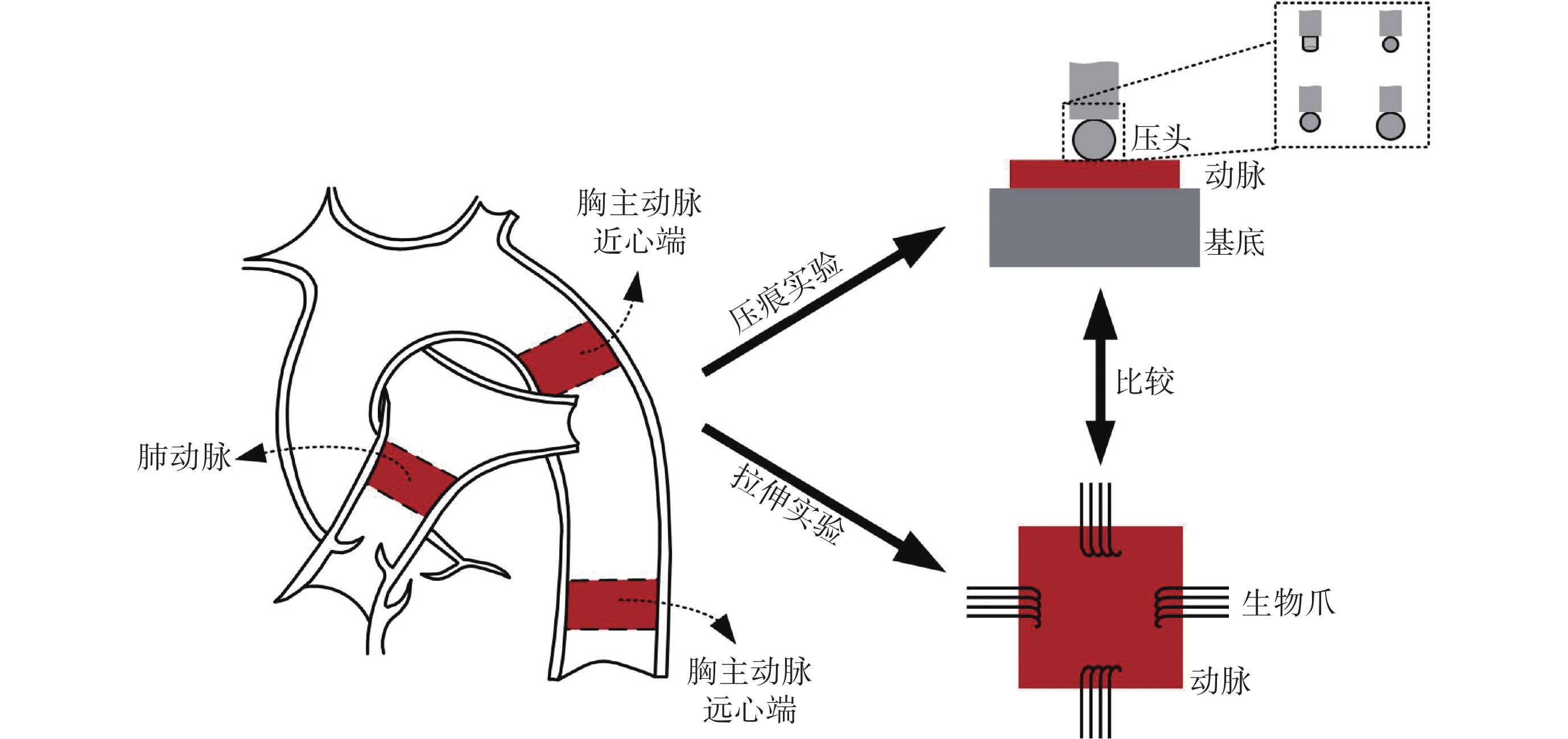圖1
動脈解剖示意圖及力學實驗示意圖
Figure1.
Schematic diagram of arterial anatomy and mechanical tests
1.2 力學實驗
1.2.1 壓痕實驗
使用力學實驗機5544（Instron Corp.，美國）進行測試，最大量程為5 N。為研究壓頭幾何結構對測量結果的影響，采用4種不同的壓頭（圓柱形-1 mm、球形-0.5 mm、球形-1 mm、球形-2 mm）對豬肺動脈、胸主動脈近心端和胸主動脈遠心端進行力學性能評估。實驗時需將樣本置于基底上，手動調整壓頭高度使其接近樣本且不相互接觸。為防止樣本干燥變硬，使用生理鹽水浸潤樣本。實驗中，壓頭以0.5 mm/min速率沿垂直于動脈內膜層方向施加載荷，最大加載位移（壓痕深度）為0.2 mm（小于樣本厚度的10%），隨后開始卸載，直至壓頭與樣本完全分離，記錄此過程中的載荷和位移數據。
1.2.2 拉伸實驗
本研究將樣本置于37 ℃生理鹽水中進行拉伸實驗，使用雙軸循環測試系統IPBF-300（凱爾測控試驗系統有限公司，中國）對豬肺動脈、胸主動脈近心端和胸主動脈遠心端進行測試，最大量程為5 N。如圖1所示，使用生物爪對樣本進行固定，并將水平和垂直方向與樣本的軸向和周向對齊。測試區域為20 mm×20 mm的正方形范圍。在水平與垂直兩個方向同時施加0%～5%應變范圍的預拉伸處理，共進行10次。正式實驗時采用等軸加載條件，收集20%應變范圍內的應力—應變曲線。預拉伸實驗和正式實驗均采用位移控制，拉伸速率為20 mm/min。
1.3 生物力學特性分析
1.3.1 壓痕實驗數據分析
樣本的彈性模量由壓痕實驗中獲得的力、位移數據計算得到。Sneddon[22]研究表明，使用軸對稱剛性壓頭測量各向同性半無限體材料生物力學性能時，如果材料發生小變形，則可根據壓頭所施加力F的絕對值和壓痕深度h獲得材料彈性模量E，其計算過程如式(1)所示：
 |
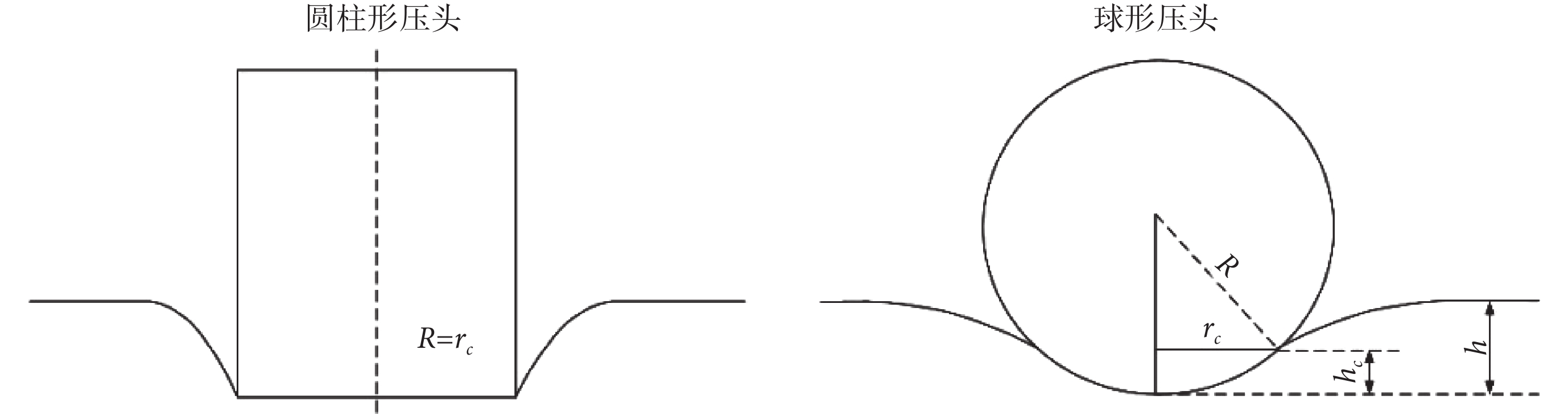
其中，S為材料剛度。υ是被測材料的泊松比，本研究假設動脈是不可壓縮材料，υ = 0.5。rc是壓頭與樣本的接觸半徑。如圖2所示，圓柱形壓頭接觸半徑rc = R，R是壓頭半徑[23]，則力F的絕對值如式(2)所示：
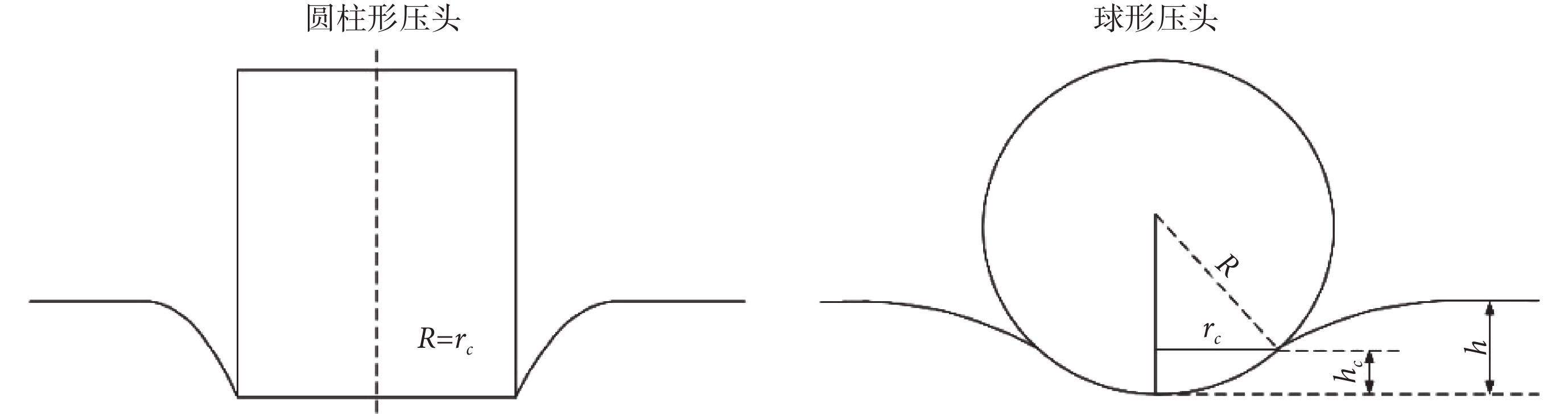圖2
壓頭與材料接觸輪廓圖
Figure2.
Contact profile between indenter and material
 |
球形壓頭壓痕實驗中壓頭與材料之間產生球形接觸，壓頭附近的材料下沉。根據Sneddon理論，球形壓頭與樣本的實際接觸深度hc = 0.5?h，接觸半徑rc如式(3)所示：
 |
則球形壓頭所施加力F的絕對值和材料壓痕深度h的關系如式(4)所示：
 |
上述理論忽略了壓頭與樣本之間的黏附力。當考慮黏附力時，根據Sirghi理論，外部載荷F由壓頭與樣本接觸部分的彈性力Fe與黏附力Fa組成，如式(5)所示：
 |
通過黏附力影響實驗測量繪制力—位移曲線，且黏附力可在卸載過程中觀察并測得[24]，因此本研究對卸載部分數據進行分析。考慮到壓頭與樣本接觸面積Ac和卸載過程中黏附能Wa不斷變化，黏附力Fa的絕對值如式(6)所示：
 |
黏附能Wa的計算過程如式(7)所示：
 |
其中，γa是壓頭與樣本之間的黏附功；π為圓周率。則黏附力Fa的絕對值如式(8)所示：
 |
綜上，對于球形壓頭，若不考慮壓頭與材料接觸區域的黏附力，外部施加載荷F的絕對值與壓痕深度h的關系如式(9)所示：
 |
若考慮壓頭與材料之間的黏附力，F的絕對值與h之間的關系如式(10)所示：
 |
1.3.2 拉伸實驗數據分析
拉伸實驗中樣本的工程應力σ（即載荷除以橫截面面積）如式(11)所示：
 |
樣本工程應變ε的絕對值（即位移除以樣品的初始厚度）如式(12)所示：
 |
其中，F為施加載荷，A0為樣本初始橫截面積，l0是樣本初始長度，l是實驗結束時的樣本長度。
根據樣本應力—應變曲線，可獲得應變為0.10時的動脈切線模量E，其計算過程如式(13)所示：
 |
1.4 統計學分析
彈性模量值用平均值±標準差表示。使用統計分析軟件SPSS v.24.0（International Business Machines Corp.，美國）進行統計學處理，兩組間比較采用獨立樣本t檢驗，多組間比較采用單因素方差分析和最小顯著差異法（least significant difference，LSD）、塔姆黑尼T2（Tamhane’s T2）事后多重比較；檢驗水準為0.05。
1.5 組織學染色
采用彈性范吉森染色法（elastica van Gieson staining，EVG）對動脈彈性纖維進行染色。首先用石蠟將樣本包埋切片，然后通過EVG染液浸染切片。使用顯微鏡IX71（Olympus Corp.，日本）觀察并采集染色圖像DP71（Olympus Corp.，日本），其中動脈彈性纖維呈黑色。
2 結果
2.1 壓頭幾何結構對動脈力學性能測量值的影響
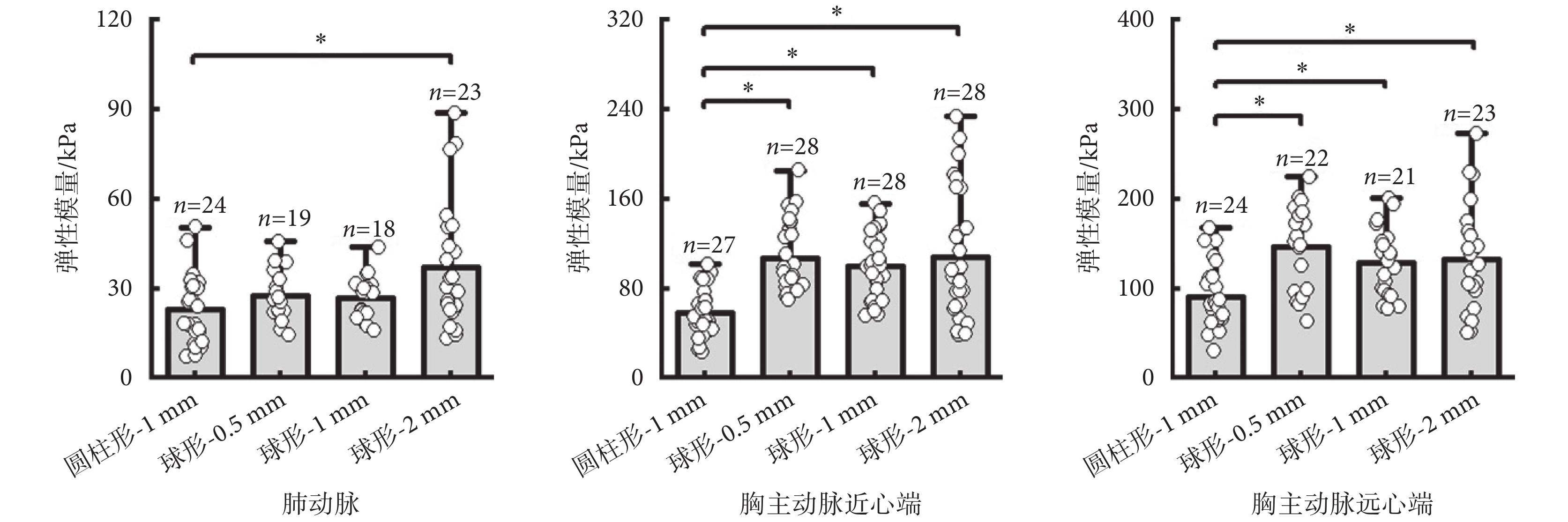
如圖3所示，在三個測量區域中，使用圓柱形-1 mm、球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量的彈性模量值之間均存在差異，并且該差異有統計學意義（肺動脈：F = 4.583，P < 0.01；胸主動脈近心端：F = 10.709，P < 0.01；胸主動脈遠心端：F = 16.024，P < 0.01）。在肺動脈處，使用球形-2 mm壓頭測量的彈性模量值大于圓柱形-1 mm壓頭測量的彈性模量值[MD = ? 14.361（? 28.323，? 0.399），P = 0.041]；在胸主動脈近心端，對比圓柱形-1 mm壓頭的彈性模量測量值，使用球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量的彈性模量值均較大[球形-0.5 mm：MD = ? 48.822（? 68.989，? 28.655），P < 0.01；球形-1 mm：MD = ? 6.867（? 60.570，? 22.947），P < 0.01；球形-2 mm：MD = ? 49.375（? 81.797，? 16.952），P < 0.01]；胸主動脈遠心端與胸主動脈近心端測量結果趨勢一致，均顯示使用球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量的彈性模量值大于圓柱形-1 mm壓頭測量值[球形-0.5 mm：MD = ? 55.044（? 89.623，? 20.465），P < 0.01；球形-1 mm：MD = ? 38.114（? 68.662，? 7.565），P < 0.01；球形-2 mm：MD = ? 41.046（? 81.604，? 0.488），P = 0.046]。
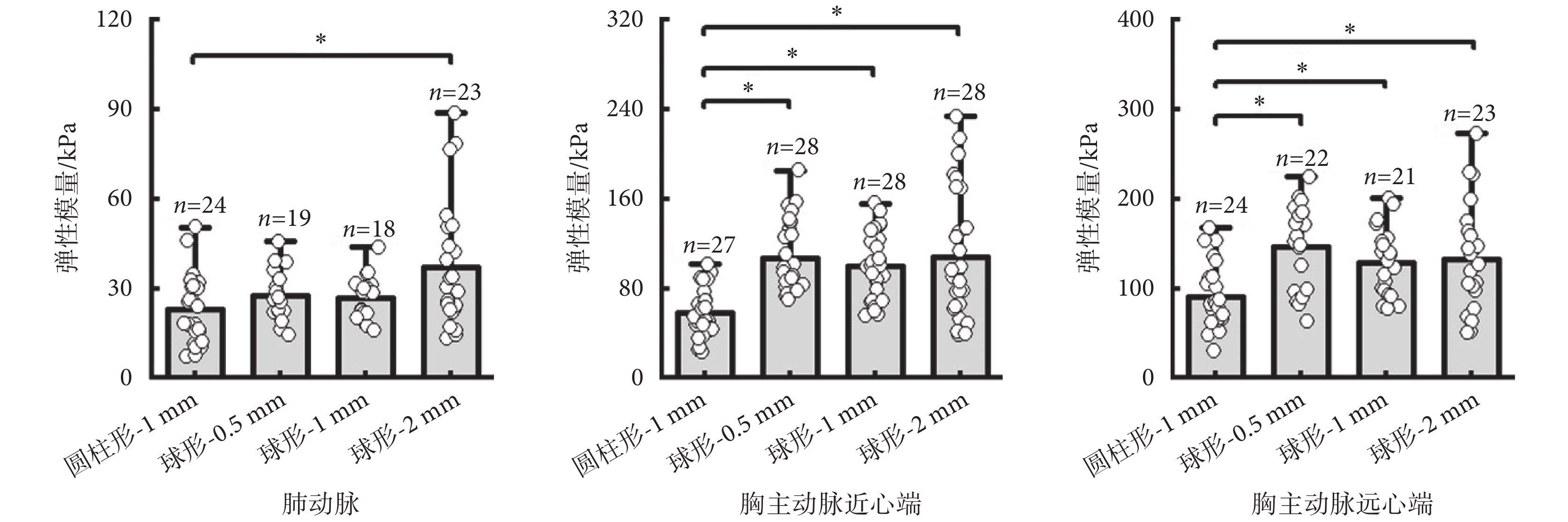圖3
使用4種壓頭測量的動脈彈性模量值
*
*
2.2 分析理論對動脈力學性能測量值的影響
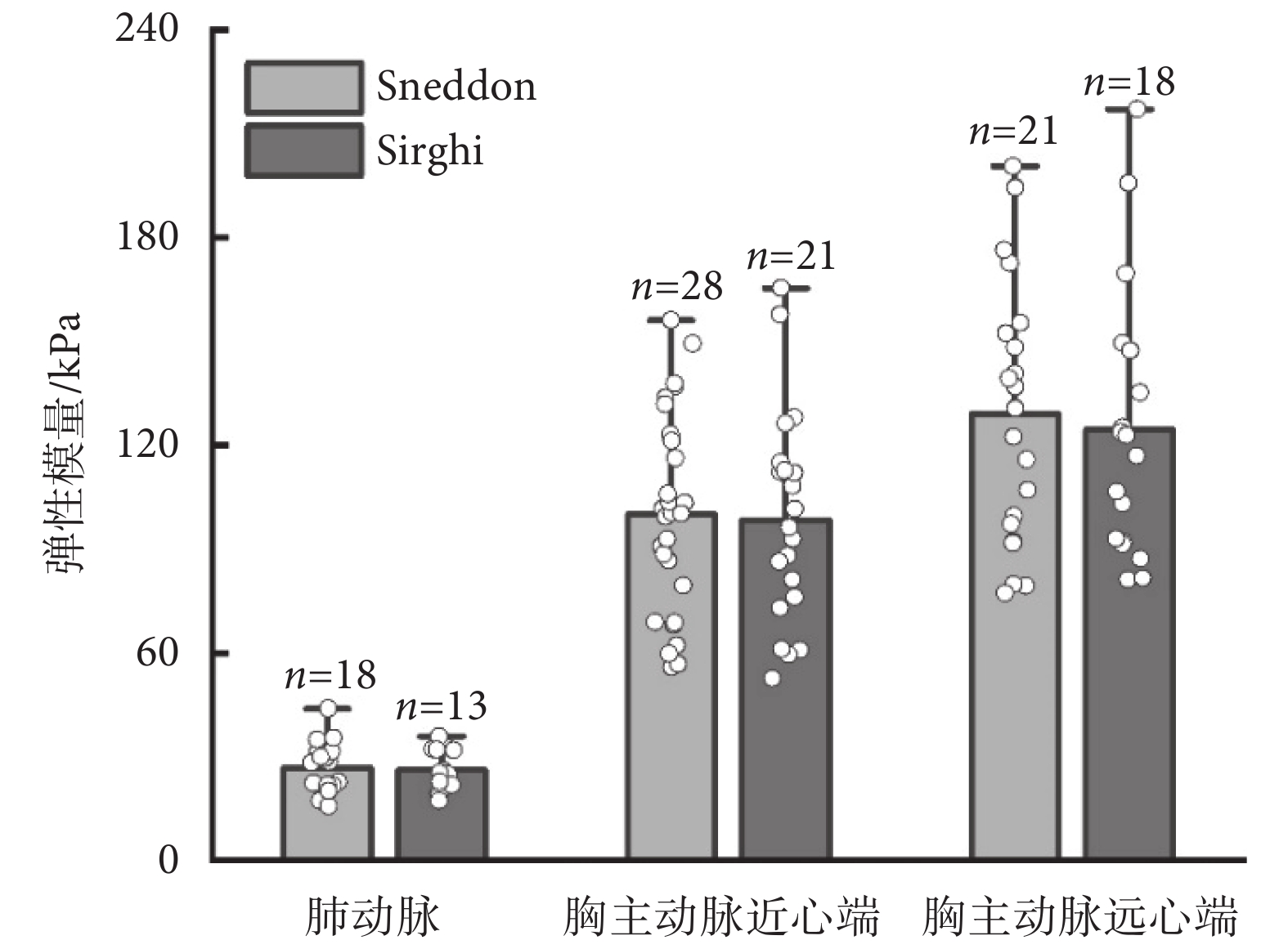
如圖4所示，使用兩種分析理論（忽略黏附力的Sneddon理論、考慮黏附力的Sirghi理論），分別計算球形-1 mm壓頭測量的動脈彈性模量值。結果顯示，與Sirghi理論計算結果相比，Sneddon理論獲得的動脈彈性模量值略大，差異無統計學意義（肺動脈：t = 0.211，P = 0.834；胸主動脈近心端：t = 0.181，P = 0.857；胸主動脈遠心端：t = 0.377，P = 0.708）。
2.3 壓痕實驗與拉伸實驗測量動脈力學性能值的對比
如表1所示，壓痕實驗測量的彈性模量和拉伸實驗測量的軸向、周向彈性模量值的差異有統計學意義（肺動脈：F = 43.756，P < 0.01；胸主動脈近心端：F = 88.720，P < 0.01；胸主動脈遠心端：F = 100.658，P < 0.01），且壓痕實驗測量的動脈彈性模量值小于拉伸實驗測量值；其中，拉伸實驗測量肺動脈軸向彈性模量值約是壓痕實驗測量值的4倍，胸主動脈近心端和胸主動脈遠心端軸向彈性模量值約是壓痕實驗測量值的3倍；拉伸實驗測量肺動脈、胸主動脈近心端周向彈性模量值約是壓痕實驗測量值的5倍，胸主動脈遠心端周向彈性模量值約是壓痕實驗測量值的4倍。此外，壓痕實驗和拉伸實驗測量結果均顯示，肺動脈、胸主動脈近心端和胸主動脈遠心端彈性模量值差異有統計學意義，表現為胸主動脈遠心端，胸主動脈近心端和肺動脈三者彈性模量依次減小。（壓痕實驗：F = 65.903，P < 0.01；軸向拉伸實驗：F = 17.934，P < 0.01；周向拉伸實驗：F = 52.945，P < 0.01）
表1
壓痕實驗和拉伸實驗測量的動脈彈性模量值
Table1.
The values of arterial elastic modulus (kPa) measured by the indentation test and the tensile test
2.4 動脈的組織學特征
如圖5所示，肺動脈、胸主動脈近心端和胸主動脈遠心端中的彈性纖維含量差異具有統計學意義（F = 40.471，P < 0.01），EVG染色圖和彈性纖維面積占比顯示，肺動脈彈性纖維含量低于胸主動脈近心端和胸主動脈遠心端[胸主動脈近心端：MD = ? 10.161（? 13.445，? 6.876），P < 0.01；胸主動脈遠心端：MD = ? 15.139（? 19.959，? 10.318），P < 0.01]，胸主動脈近心端彈性纖維含量低于胸主動脈遠心端[MD = ? 4.978（? 9.593，? 0.362），P = 0.032]。
圖5
動脈EVG染色圖及彈性纖維面積占比
*
*
3 討論
3.1 分析與討論
動脈局部力學性能的評估在動脈疾病的預測和治療方面具有重要意義。本研究旨在通過毫米級壓痕技術測量肺動脈、胸主動脈近心端和胸主動脈遠心端組織的局部力學性能，以評估壓頭幾何結構和分析理論對動脈彈性模量測量值的影響；此外，比較了壓痕實驗與拉伸實驗測量的動脈彈性模量，分析了兩種實驗方法獲得的測量值之間的差異。
壓痕實驗中，胸主動脈近心端和胸主動脈遠心端測量結果顯示，圓柱形-1 mm壓頭測量的彈性模量值低于球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量值。這可能是由于圓柱形壓頭邊緣與樣本表面接觸產生應力集中現象[25]，進而導致測量結果偏小。考慮到球形壓頭不易發生應力集中[26]，故其更適于測量動脈或其他軟組織的力學性能。結果顯示，使用球形-2 mm壓頭測量的彈性模量標準差在三個測量區域均大于球形-0.5 mm和球形-1 mm壓頭測量值。當樣本泊松比和壓痕深度確定時，壓頭與樣本之間的摩擦力與rc/h值呈正相關[27]，球形-2 mm壓頭與樣本表面會產生較大的摩擦力，導致彈性模量測量值的分散程度較大。此外，使用球形-0.5 mm壓頭測量時需要高精度傳感器和穩定的操作技術。綜上，使用球形-1 mm壓頭能相對方便、準確地測量動脈力學性能。
壓痕實驗結果顯示，與Sneddon[22]的理論結果相比，依據Sirghi等[21]的理論獲得的彈性模量測量值偏小，但兩者差異無統計學意義。差異產生的原因是由于Sirghi等[21]的理論假設外部載荷由彈性力和黏附力組成，黏附力會導致壓頭與樣本的接觸半徑增大[15]。同時，Sneddon[22]的理論表明，樣本彈性模量與接觸半徑成反比，因此忽略黏附力導致測量的動脈彈性模量值略大。
拉伸實驗測量的彈性模量值高于壓痕實驗測量值，這可能與動脈彈性纖維分布和實驗加載方式有關。動脈中膜含有豐富的彈性纖維[28]，其中71%以板層形態沿血管壁周向分布，27%包圍層間平滑肌細胞形成籠狀結構，剩余2%沿徑向分布連接彈性纖維板層[29]。徑向壓痕實驗中，部分纖維受外部載荷作用而產生小變形，而拉伸實驗中有更多的纖維響應載荷[30]，導致兩種實驗方法測得的動脈彈性模量值存在差異。此外，考慮到動脈更適合抵抗沿纖維方向的拉力[30]，壓痕實驗中載荷垂直于彈性纖維層，而拉伸實驗中載荷平行于彈性纖維層，這導致壓痕實驗彈性模量測量值偏小。
壓痕實驗和拉伸實驗結果顯示，肺動脈的彈性模量值低于胸主動脈近心端和遠心端，而胸主動脈近心端的彈性模量值又低于遠心端，這與之前的研究結果一致[31]。其原因在于肺動脈、胸主動脈近心端和遠心端的彈性纖維含量不同，導致了相應的彈性模量差異。同時，動脈微結構的差異也導致了壓痕實驗和拉伸實驗測量的相應動脈彈性模量值存在倍數差異。
3.2 研究局限性
在壓痕實驗測量動脈力學性能時，假設血管壁是各項同性材料，但動脈組織內部結構和性質通常是非均質的，這可能導致測量結果產生偏差。此外，本研究在室溫條件下對動脈進行壓痕實驗測試，未能考慮溫度對動脈壁生物力學性能的影響。最后，雖然本研究初步證實了壓痕實驗和拉伸實驗測量的動脈彈性模量值存在倍數關系，且隨著動脈在動脈樹中的位置而變化，但目前尚未確立兩種實驗方法所測動脈彈性模量值之間的轉化公式，這需要進行更深入的實驗驗證和數據分析。
4 結論
本研究探討了毫米級壓痕實驗中，壓頭幾何結構和分析理論對動脈彈性模量測量值的影響。結果表明，壓頭幾何結構明顯影響彈性模量測量值，而Sneddon[22]和Sirghi等[21]的理論對測量結果影響不大。通過球形-1 mm壓頭和Sneddon[22]理論能有效計算動脈彈性模量。本研究有助于理解不同文獻中報道的彈性模量值，并為使用壓痕技術有效測量動脈或其他軟組織彈性模量值提供參數支持。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：曹祎凡、高志鵬、陳凌峰主要負責實驗設計、數據記錄與分析；曹祎凡、石怡柯、趙雅威負責圖片繪制；曹祎凡主要負責論文撰寫；李芬、宋輝、張倩倩、陳凌峰、李曉娜、陳維毅負責論文審閱修訂。
0 引言
美國心臟病學會數據顯示，全球心血管患者從1990年的2.71億人增加到2019年的5.23億人，其中死亡人數從1990年的1 210萬增加到2019年的1 860萬[1]。心血管疾病已成為導致人類死亡和殘疾的主要原因。常見心血管疾病包括動脈粥樣硬化、動脈瘤和動脈夾層等，它們的發生和發展與血管壁局部力學性能的改變密切相關[2-6]。因此，有效評估動脈局部力學性能成為動脈疾病診斷和治療的關鍵，特別是在評估斑塊的發展、預測夾層破裂位置等方面尤為重要。
拉伸實驗[7-9]和灌流實驗[10]是測量動脈力學性能的常用方法，可表征實驗樣本的整體力學性能。與拉伸實驗和灌流實驗相比，壓痕實驗更適合測量動脈的局部力學性能。目前，壓痕技術在不同研究領域以及不同尺度上均有應用。其中，微米或納米級壓頭可以測量微觀組織力學性能，如動脈內皮細胞[11-13]、平滑肌細胞[14]以及細胞外基質[15]等；毫米級壓頭可以從宏觀角度測量組織力學性能，如動脈粥樣硬化中的纖維帽組織[16]和脂質組織[17]等。除此之外，毫米級壓痕實驗還能在傳統開放式手術中有效區分健康組織和病變組織，幫助外科醫生準確定位縫合線位置[18]。
隨著壓痕技術不斷發展，其應用也日益廣泛。在不同文獻報道中，使用壓痕技術測得的彈性模量值存在很大差異。例如，微米和納米級壓痕實驗中，Pesen等[11]測量的牛肺動脈內皮細胞彈性模量值在0.2～2.0 kPa之間；Viswanathan等[12]測量的人肺動脈內皮細胞平均彈性模量值為2.9 kPa；此外，Wang等[13]測量的人肺動脈內皮細胞細胞核、細胞質、細胞邊緣的彈性模量分別是26～29 kPa、18～19 kPa、4～6 kPa。據報道，微米和納米級壓痕實驗測量結果的差異主要源于不同的壓頭幾何結構[19-20]以及不同的分析理論[21]。相對而言，毫米級壓痕實驗中，壓頭幾何結構和分析理論對測量結果是否產生影響，目前尚不清楚。
為能在毫米級實驗中準確、有效地表征動脈組織局部力學性能，探究壓頭幾何結構和分析理論對壓痕測量結果的影響，本研究使用4種壓頭[包括：直徑為1 mm的圓柱形壓頭（圓柱形-1 mm）；直徑為0.5、1、2 mm的球形壓頭（球形-0.5 mm、球形-1 mm、球形-2 mm）]對豬的肺動脈、胸主動脈近心端和胸主動脈遠心端進行測量，并使用忽略黏附力的斯內登（Sneddon）理論[22]和考慮黏附力的瑟爾吉（Sirghi）理論[21]計算動脈彈性模量，并對測量結果進行統計分析。此外，本研究還通過壓痕實驗和拉伸實驗分別測量了動脈生物力學性能，驗證并比較兩種實驗方法測量結果的差異，以期更深入地了解動脈組織力學性能。
1 材料與方法
1.1 樣本的制備
本研究使用當地屠宰場健康豬的動脈作為研究材料。如圖1所示，對豬肺動脈、胸主動脈近心端和胸主動脈遠心端進行力學實驗。實驗前，去除樣本上多余的脂肪和結締組織，并使用激光位移傳感器LK-G5000（Keyence Corp.，日本）測量樣本厚度。所有樣本在力學檢測前保存在4 °C生理鹽水中不超過6 h。
圖1
動脈解剖示意圖及力學實驗示意圖
Figure1.
Schematic diagram of arterial anatomy and mechanical tests
1.2 力學實驗
1.2.1 壓痕實驗
使用力學實驗機5544（Instron Corp.，美國）進行測試，最大量程為5 N。為研究壓頭幾何結構對測量結果的影響，采用4種不同的壓頭（圓柱形-1 mm、球形-0.5 mm、球形-1 mm、球形-2 mm）對豬肺動脈、胸主動脈近心端和胸主動脈遠心端進行力學性能評估。實驗時需將樣本置于基底上，手動調整壓頭高度使其接近樣本且不相互接觸。為防止樣本干燥變硬，使用生理鹽水浸潤樣本。實驗中，壓頭以0.5 mm/min速率沿垂直于動脈內膜層方向施加載荷，最大加載位移（壓痕深度）為0.2 mm（小于樣本厚度的10%），隨后開始卸載，直至壓頭與樣本完全分離，記錄此過程中的載荷和位移數據。
1.2.2 拉伸實驗
本研究將樣本置于37 ℃生理鹽水中進行拉伸實驗，使用雙軸循環測試系統IPBF-300（凱爾測控試驗系統有限公司，中國）對豬肺動脈、胸主動脈近心端和胸主動脈遠心端進行測試，最大量程為5 N。如圖1所示，使用生物爪對樣本進行固定，并將水平和垂直方向與樣本的軸向和周向對齊。測試區域為20 mm×20 mm的正方形范圍。在水平與垂直兩個方向同時施加0%～5%應變范圍的預拉伸處理，共進行10次。正式實驗時采用等軸加載條件，收集20%應變范圍內的應力—應變曲線。預拉伸實驗和正式實驗均采用位移控制，拉伸速率為20 mm/min。
1.3 生物力學特性分析
1.3.1 壓痕實驗數據分析
樣本的彈性模量由壓痕實驗中獲得的力、位移數據計算得到。Sneddon[22]研究表明，使用軸對稱剛性壓頭測量各向同性半無限體材料生物力學性能時，如果材料發生小變形，則可根據壓頭所施加力F的絕對值和壓痕深度h獲得材料彈性模量E，其計算過程如式(1)所示：
|
其中，S為材料剛度。υ是被測材料的泊松比，本研究假設動脈是不可壓縮材料，υ = 0.5。rc是壓頭與樣本的接觸半徑。如圖2所示，圓柱形壓頭接觸半徑rc = R，R是壓頭半徑[23]，則力F的絕對值如式(2)所示：
圖2
壓頭與材料接觸輪廓圖
Figure2.
Contact profile between indenter and material
|
球形壓頭壓痕實驗中壓頭與材料之間產生球形接觸，壓頭附近的材料下沉。根據Sneddon理論，球形壓頭與樣本的實際接觸深度hc = 0.5?h，接觸半徑rc如式(3)所示：
|
則球形壓頭所施加力F的絕對值和材料壓痕深度h的關系如式(4)所示：
|
上述理論忽略了壓頭與樣本之間的黏附力。當考慮黏附力時，根據Sirghi理論，外部載荷F由壓頭與樣本接觸部分的彈性力Fe與黏附力Fa組成，如式(5)所示：
|
通過黏附力影響實驗測量繪制力—位移曲線，且黏附力可在卸載過程中觀察并測得[24]，因此本研究對卸載部分數據進行分析。考慮到壓頭與樣本接觸面積Ac和卸載過程中黏附能Wa不斷變化，黏附力Fa的絕對值如式(6)所示：
|
黏附能Wa的計算過程如式(7)所示：
|
其中，γa是壓頭與樣本之間的黏附功；π為圓周率。則黏附力Fa的絕對值如式(8)所示：
|
綜上，對于球形壓頭，若不考慮壓頭與材料接觸區域的黏附力，外部施加載荷F的絕對值與壓痕深度h的關系如式(9)所示：
|
若考慮壓頭與材料之間的黏附力，F的絕對值與h之間的關系如式(10)所示：
|
1.3.2 拉伸實驗數據分析
拉伸實驗中樣本的工程應力σ（即載荷除以橫截面面積）如式(11)所示：
|
樣本工程應變ε的絕對值（即位移除以樣品的初始厚度）如式(12)所示：
|
其中，F為施加載荷，A0為樣本初始橫截面積，l0是樣本初始長度，l是實驗結束時的樣本長度。
根據樣本應力—應變曲線，可獲得應變為0.10時的動脈切線模量E，其計算過程如式(13)所示：
|
1.4 統計學分析
彈性模量值用平均值±標準差表示。使用統計分析軟件SPSS v.24.0（International Business Machines Corp.，美國）進行統計學處理，兩組間比較采用獨立樣本t檢驗，多組間比較采用單因素方差分析和最小顯著差異法（least significant difference，LSD）、塔姆黑尼T2（Tamhane’s T2）事后多重比較；檢驗水準為0.05。
1.5 組織學染色
采用彈性范吉森染色法（elastica van Gieson staining，EVG）對動脈彈性纖維進行染色。首先用石蠟將樣本包埋切片，然后通過EVG染液浸染切片。使用顯微鏡IX71（Olympus Corp.，日本）觀察并采集染色圖像DP71（Olympus Corp.，日本），其中動脈彈性纖維呈黑色。
2 結果
2.1 壓頭幾何結構對動脈力學性能測量值的影響
如圖3所示，在三個測量區域中，使用圓柱形-1 mm、球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量的彈性模量值之間均存在差異，并且該差異有統計學意義（肺動脈：F = 4.583，P < 0.01；胸主動脈近心端：F = 10.709，P < 0.01；胸主動脈遠心端：F = 16.024，P < 0.01）。在肺動脈處，使用球形-2 mm壓頭測量的彈性模量值大于圓柱形-1 mm壓頭測量的彈性模量值[MD = ? 14.361（? 28.323，? 0.399），P = 0.041]；在胸主動脈近心端，對比圓柱形-1 mm壓頭的彈性模量測量值，使用球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量的彈性模量值均較大[球形-0.5 mm：MD = ? 48.822（? 68.989，? 28.655），P < 0.01；球形-1 mm：MD = ? 6.867（? 60.570，? 22.947），P < 0.01；球形-2 mm：MD = ? 49.375（? 81.797，? 16.952），P < 0.01]；胸主動脈遠心端與胸主動脈近心端測量結果趨勢一致，均顯示使用球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量的彈性模量值大于圓柱形-1 mm壓頭測量值[球形-0.5 mm：MD = ? 55.044（? 89.623，? 20.465），P < 0.01；球形-1 mm：MD = ? 38.114（? 68.662，? 7.565），P < 0.01；球形-2 mm：MD = ? 41.046（? 81.604，? 0.488），P = 0.046]。
圖3
使用4種壓頭測量的動脈彈性模量值
*
*
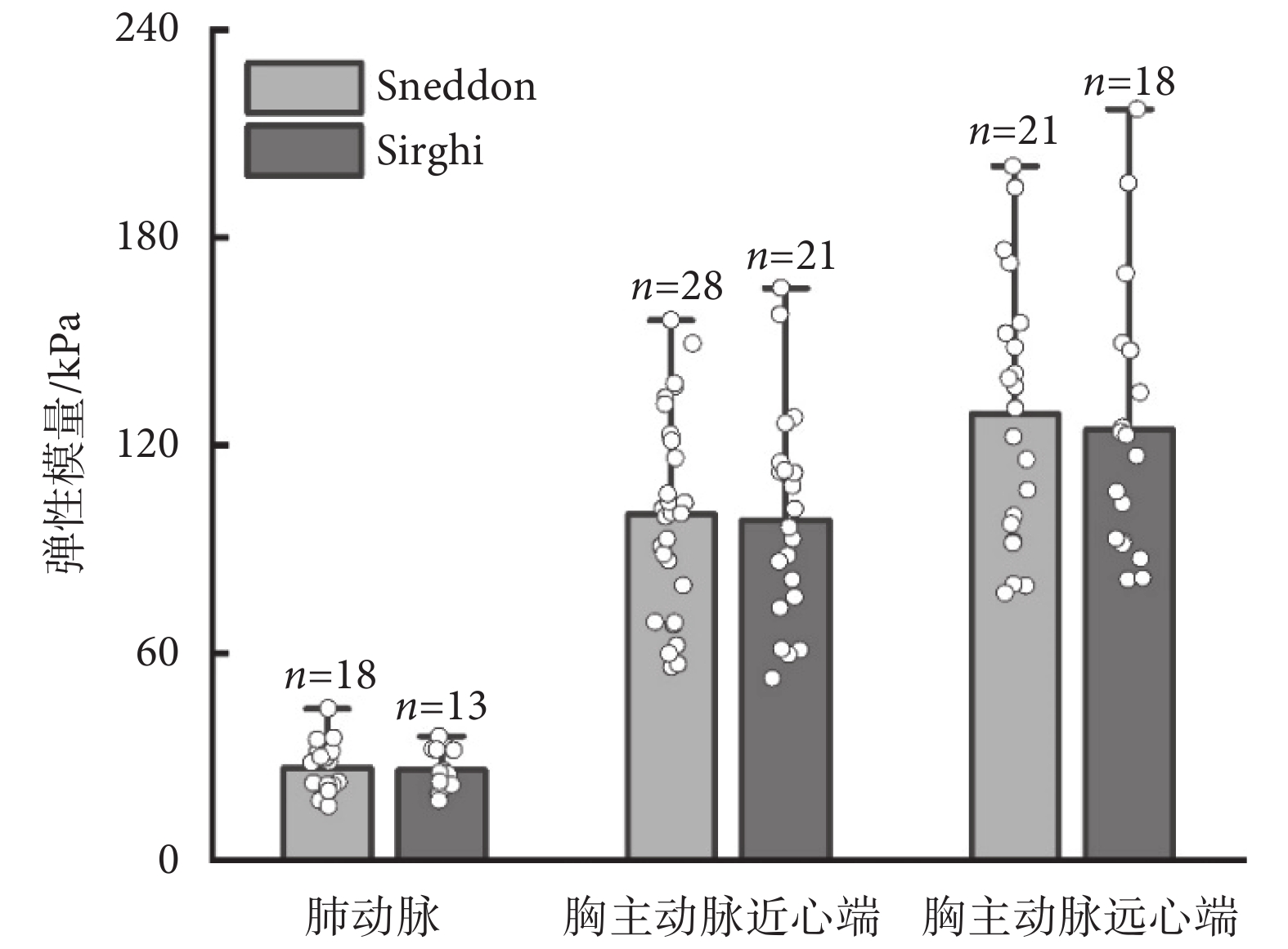
2.2 分析理論對動脈力學性能測量值的影響
如圖4所示，使用兩種分析理論（忽略黏附力的Sneddon理論、考慮黏附力的Sirghi理論），分別計算球形-1 mm壓頭測量的動脈彈性模量值。結果顯示，與Sirghi理論計算結果相比，Sneddon理論獲得的動脈彈性模量值略大，差異無統計學意義（肺動脈：t = 0.211，P = 0.834；胸主動脈近心端：t = 0.181，P = 0.857；胸主動脈遠心端：t = 0.377，P = 0.708）。
2.3 壓痕實驗與拉伸實驗測量動脈力學性能值的對比
如表1所示，壓痕實驗測量的彈性模量和拉伸實驗測量的軸向、周向彈性模量值的差異有統計學意義（肺動脈：F = 43.756，P < 0.01；胸主動脈近心端：F = 88.720，P < 0.01；胸主動脈遠心端：F = 100.658，P < 0.01），且壓痕實驗測量的動脈彈性模量值小于拉伸實驗測量值；其中，拉伸實驗測量肺動脈軸向彈性模量值約是壓痕實驗測量值的4倍，胸主動脈近心端和胸主動脈遠心端軸向彈性模量值約是壓痕實驗測量值的3倍；拉伸實驗測量肺動脈、胸主動脈近心端周向彈性模量值約是壓痕實驗測量值的5倍，胸主動脈遠心端周向彈性模量值約是壓痕實驗測量值的4倍。此外，壓痕實驗和拉伸實驗測量結果均顯示，肺動脈、胸主動脈近心端和胸主動脈遠心端彈性模量值差異有統計學意義，表現為胸主動脈遠心端，胸主動脈近心端和肺動脈三者彈性模量依次減小。（壓痕實驗：F = 65.903，P < 0.01；軸向拉伸實驗：F = 17.934，P < 0.01；周向拉伸實驗：F = 52.945，P < 0.01）
表1
壓痕實驗和拉伸實驗測量的動脈彈性模量值
Table1.
The values of arterial elastic modulus (kPa) measured by the indentation test and the tensile test
2.4 動脈的組織學特征
如圖5所示，肺動脈、胸主動脈近心端和胸主動脈遠心端中的彈性纖維含量差異具有統計學意義（F = 40.471，P < 0.01），EVG染色圖和彈性纖維面積占比顯示，肺動脈彈性纖維含量低于胸主動脈近心端和胸主動脈遠心端[胸主動脈近心端：MD = ? 10.161（? 13.445，? 6.876），P < 0.01；胸主動脈遠心端：MD = ? 15.139（? 19.959，? 10.318），P < 0.01]，胸主動脈近心端彈性纖維含量低于胸主動脈遠心端[MD = ? 4.978（? 9.593，? 0.362），P = 0.032]。
圖5
動脈EVG染色圖及彈性纖維面積占比
*
*
3 討論
3.1 分析與討論
動脈局部力學性能的評估在動脈疾病的預測和治療方面具有重要意義。本研究旨在通過毫米級壓痕技術測量肺動脈、胸主動脈近心端和胸主動脈遠心端組織的局部力學性能，以評估壓頭幾何結構和分析理論對動脈彈性模量測量值的影響；此外，比較了壓痕實驗與拉伸實驗測量的動脈彈性模量，分析了兩種實驗方法獲得的測量值之間的差異。
壓痕實驗中，胸主動脈近心端和胸主動脈遠心端測量結果顯示，圓柱形-1 mm壓頭測量的彈性模量值低于球形-0.5 mm、球形-1 mm、球形-2 mm壓頭測量值。這可能是由于圓柱形壓頭邊緣與樣本表面接觸產生應力集中現象[25]，進而導致測量結果偏小。考慮到球形壓頭不易發生應力集中[26]，故其更適于測量動脈或其他軟組織的力學性能。結果顯示，使用球形-2 mm壓頭測量的彈性模量標準差在三個測量區域均大于球形-0.5 mm和球形-1 mm壓頭測量值。當樣本泊松比和壓痕深度確定時，壓頭與樣本之間的摩擦力與rc/h值呈正相關[27]，球形-2 mm壓頭與樣本表面會產生較大的摩擦力，導致彈性模量測量值的分散程度較大。此外，使用球形-0.5 mm壓頭測量時需要高精度傳感器和穩定的操作技術。綜上，使用球形-1 mm壓頭能相對方便、準確地測量動脈力學性能。
壓痕實驗結果顯示，與Sneddon[22]的理論結果相比，依據Sirghi等[21]的理論獲得的彈性模量測量值偏小，但兩者差異無統計學意義。差異產生的原因是由于Sirghi等[21]的理論假設外部載荷由彈性力和黏附力組成，黏附力會導致壓頭與樣本的接觸半徑增大[15]。同時，Sneddon[22]的理論表明，樣本彈性模量與接觸半徑成反比，因此忽略黏附力導致測量的動脈彈性模量值略大。
拉伸實驗測量的彈性模量值高于壓痕實驗測量值，這可能與動脈彈性纖維分布和實驗加載方式有關。動脈中膜含有豐富的彈性纖維[28]，其中71%以板層形態沿血管壁周向分布，27%包圍層間平滑肌細胞形成籠狀結構，剩余2%沿徑向分布連接彈性纖維板層[29]。徑向壓痕實驗中，部分纖維受外部載荷作用而產生小變形，而拉伸實驗中有更多的纖維響應載荷[30]，導致兩種實驗方法測得的動脈彈性模量值存在差異。此外，考慮到動脈更適合抵抗沿纖維方向的拉力[30]，壓痕實驗中載荷垂直于彈性纖維層，而拉伸實驗中載荷平行于彈性纖維層，這導致壓痕實驗彈性模量測量值偏小。
壓痕實驗和拉伸實驗結果顯示，肺動脈的彈性模量值低于胸主動脈近心端和遠心端，而胸主動脈近心端的彈性模量值又低于遠心端，這與之前的研究結果一致[31]。其原因在于肺動脈、胸主動脈近心端和遠心端的彈性纖維含量不同，導致了相應的彈性模量差異。同時，動脈微結構的差異也導致了壓痕實驗和拉伸實驗測量的相應動脈彈性模量值存在倍數差異。
3.2 研究局限性
在壓痕實驗測量動脈力學性能時，假設血管壁是各項同性材料，但動脈組織內部結構和性質通常是非均質的，這可能導致測量結果產生偏差。此外，本研究在室溫條件下對動脈進行壓痕實驗測試，未能考慮溫度對動脈壁生物力學性能的影響。最后，雖然本研究初步證實了壓痕實驗和拉伸實驗測量的動脈彈性模量值存在倍數關系，且隨著動脈在動脈樹中的位置而變化，但目前尚未確立兩種實驗方法所測動脈彈性模量值之間的轉化公式，這需要進行更深入的實驗驗證和數據分析。
4 結論
本研究探討了毫米級壓痕實驗中，壓頭幾何結構和分析理論對動脈彈性模量測量值的影響。結果表明，壓頭幾何結構明顯影響彈性模量測量值，而Sneddon[22]和Sirghi等[21]的理論對測量結果影響不大。通過球形-1 mm壓頭和Sneddon[22]理論能有效計算動脈彈性模量。本研究有助于理解不同文獻中報道的彈性模量值，并為使用壓痕技術有效測量動脈或其他軟組織彈性模量值提供參數支持。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：曹祎凡、高志鵬、陳凌峰主要負責實驗設計、數據記錄與分析；曹祎凡、石怡柯、趙雅威負責圖片繪制；曹祎凡主要負責論文撰寫；李芬、宋輝、張倩倩、陳凌峰、李曉娜、陳維毅負責論文審閱修訂。
