當前體音聽診多采用基于最小均方誤差準則的雙通道自適應濾波算法實現環境音降噪;對于包含脈沖分量的非高斯信號,這類方法容易出現濾波器權值失調。與常用的變步長方法不同,本文引入線性預處理來克服這種現象。針對雙通道歸一化最小均方自適應降噪算法,分析線性預處理對于改善自適應降噪效果所起的作用,并探討預處理環節的設計原則。分析結果表明:濾波器的穩態均方權值偏差正比于體音的方差而反比于副通道環境噪音的方差,當線性預處理參數設置得當時,可抑制體音信號中的尖峰,大幅減小體音的方差和功率譜密度,而且不明顯地減小甚至可能增大副通道環境噪音的方差及其功率譜密度,如此即可減小權值失調從而顯著提升環境音降噪效果。最后以心音的環境音降噪為例說明了如何設計預處理環節,并解釋了它對于環境音降噪所起的作用。本文研究結果可為體音聽診的自適應降噪算法設計提供理論依據。
引用本文: 莫鴻強, 田翔, 李彬, 田軍章. 線性預處理改善體音聽診自適應降噪性能的分析. 生物醫學工程學雜志, 2024, 41(5): 969-976. doi: 10.7507/1001-5515.202307058 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
0 引言
隨著醫療保健服務需求的日益增長以及柔性材料[1]、微機電系統[2]和無線通信等技術的迅速發展,可穿戴生理參數采集設備的研發已成為當今熱點[1-4],具有自動降噪功能的體音信號采集設備和聽診設備就是其中的典型。無論是心音[4-5]、呼吸音[3, 5-6]還是腸鳴音[1, 7]聽診,環境噪音都是影響聽診效果的主要因素之一。當環境噪音超過66~70 dBA(A計權分貝)時,采用傳統聽診器就無法正常聽診[5, 8-9]。聽診過程中的環境噪音類型多樣,且幅值往往遠高于體音信號,會極大地妨礙人工聽診和異常體音的自動識別等[4-5]。另外,大部分環境噪音的時頻分布與體音信號的時頻分布高度重疊,其降噪難度較高[1, 3-6, 8-9]。
綜合考慮在線聽診要求以及成本、體積、可穿戴性及續航能力[5, 8]等因素的限制,目前常用雙通道自適應濾波方法進行實時降噪。其原理為:假設環境噪音為加性噪音,主通道測量帶噪體音,副通道采集環境噪音,副通道所測環境噪音經處理后用于抵消帶噪體音中的噪音而實現降噪[6, 10-12]。該方法實用性強,可應用于兒科診所[6]、救護車及直升機轉運[11]、航天器[12]等具高分貝環境噪音的場合。這些算法又可大致分為兩類:譜減法[6, 12]和基于最小均方誤差準則的自適應濾波算法。后者以最小均方(least mean square,LMS)算法、歸一化最小均方(normalized LMS,NLMS)算法[9-11]及其改進算法為代表[13-15],其計算復雜度顯著低于譜減法,實現成本低,特別適合于體音采集。
當前,聽診環境音自適應降噪算法的研究通常集中于如何設定或調節步長以在快速收斂和低失調(misalignment)之間實現平衡[9-11, 13-15],而較少考慮基于最小均方誤差準則的算法是否適用于所有的體音信號。以心音聽診為例,第一、第二心音這類周期性出現的大幅值、短時尖峰波形(即心音屬于含脈沖分量的信號)容易導致濾波器的權值周期性失調甚至發散,進而產生“額外的”輸出誤差。這些誤差易與一些高度瞬態的心音,如收縮期拍擊聲、異常的第三或第四心音等相混淆,增加聽診的難度。對于心音這類包含脈沖分量的體音信號,若能針對性地設計自適應濾波算法,將會大大提升降噪效果。
脈沖干擾在主動降噪[16]、回音抑制[17-18]、系統辨識[17, 19]等應用場合廣泛出現,最常見的解決辦法是建立合適的代價函數,使得脈沖干擾出現時濾波器權值不至于大幅調整,從而提高算法對于脈沖干擾的魯棒性[16-23]。例如:有的方法將脈沖干擾建模為α穩定分布過程[16, 20-21],分別基于輸出誤差的p范數均值[22]、輸出誤差的L1和L2范數組合[21]或特定約束下單步權值增量的L2范數[16]建立代價函數;有些方法以單步權值增量的L2范數限幅為約束條件,并分別基于后驗誤差的L2范數[18]或L1范數[19]建立代價函數;還有方法通過對輸出誤差引入非線性函數[17, 23]來構造代價函數。對這些代價函數進行優化,其結果往往形成變步長的自適應算法,但仍需要人為設定遺忘因子[16]、尺度縮放因子[17, 23]、單步權值增量閾值[16, 18-19]等參數,而對于聽診的自適應降噪,這些參數通常不易預先確定,因此,本文考慮采用與變步長方法不同的解決思路。
體音信號中的脈沖成分種類有限,僅幅值不確定,若能預先減小其中脈沖分量的幅值,則可大大簡化降噪算法的設計。本文前期研究[24-25]僅簡單地先對兩個通道的信號作線性預處理,再采用NLMS算法即顯著改善了環境音降噪性能,但文獻[24-25]均未解釋降噪效果改善的原因,無法在算法設計上形成指導性建議。鑒于此,本文將分析線性預處理對于改善自適應降噪效果所起的作用,并探討預處理環節的設計原則。
1 NLMS濾波算法
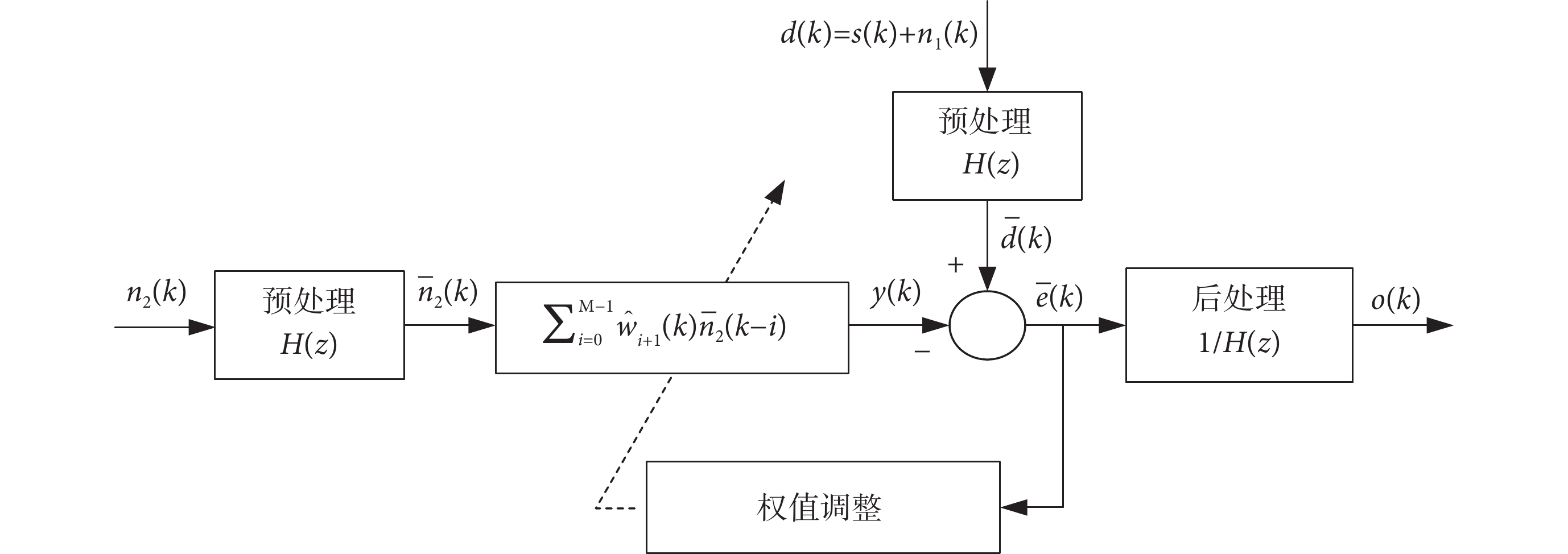
考慮到NLMS算法收斂速度快[26],后續分析主要圍繞雙通道NLMS濾波算法展開;其結構如圖1所示,其中的預處理 及后處理
及后處理 均采用線性濾波器實現,且
均采用線性濾波器實現,且 對應于算法不對信號作預處理。
對應于算法不對信號作預處理。
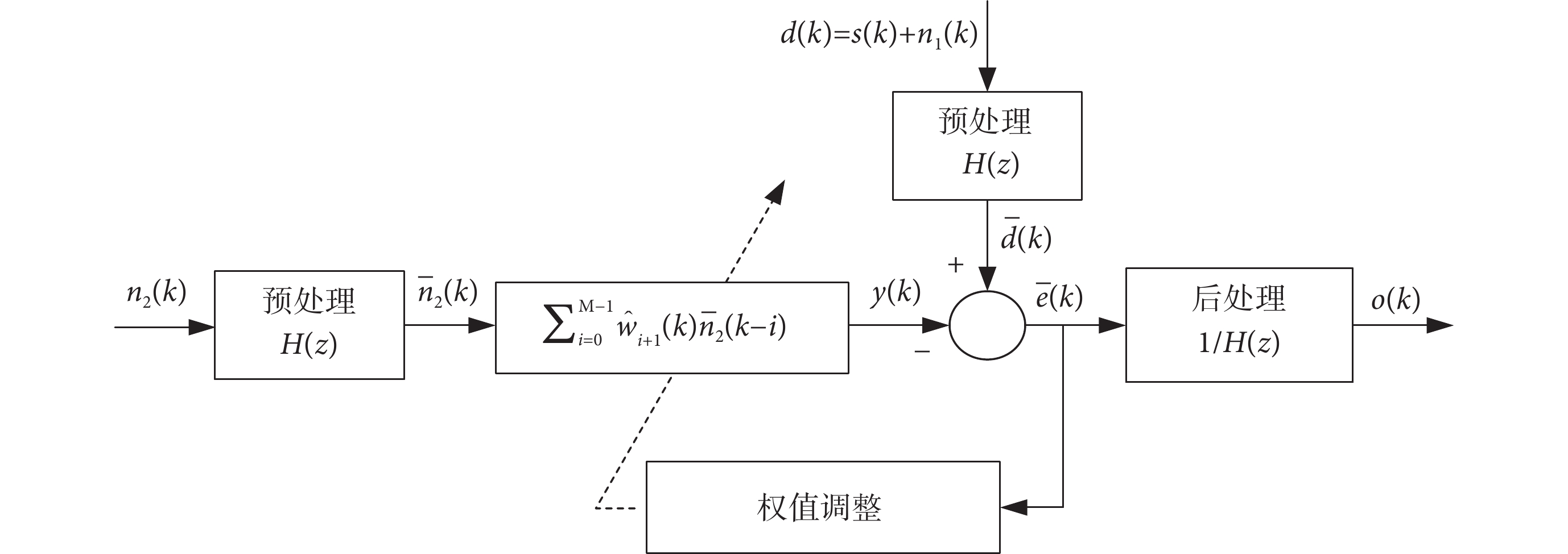 圖1
含線性預處理的NLMS濾波算法結構圖
Figure1.
The framework diagram of the NLMS algorithm with linear preprocessing
圖1
含線性預處理的NLMS濾波算法結構圖
Figure1.
The framework diagram of the NLMS algorithm with linear preprocessing
圖1中主通道信號為 ,其中
,其中 和
和 分別為第k時刻的體音和主通道環境噪音,且
分別為第k時刻的體音和主通道環境噪音,且 和
和 均未知。副通道信號為環境噪音
均未知。副通道信號為環境噪音 。信號
。信號 經
經 預處理后得
預處理后得 ,其中,
,其中, 和
和 分別對應于
分別對應于 和
和 經
經 預處理后所得結果。信號
預處理后所得結果。信號 經
經 預處理后得
預處理后得 。自適應濾波器的最終輸出為
。自適應濾波器的最終輸出為 。其余中間變量滿足式(1)和式(2)的約束。
。其余中間變量滿足式(1)和式(2)的約束。
 |
 |
其中, 為第
為第 時刻自適應濾波器權值向量,
時刻自適應濾波器權值向量, 為第k時刻預處理后副通道環境噪音向量,M為自適應濾波器的階數。
為第k時刻預處理后副通道環境噪音向量,M為自適應濾波器的階數。
權值向量 更新方式如式(3)所示,其中,
更新方式如式(3)所示,其中, 為步長控制參數。
為步長控制參數。
 |
2 預處理H(z)的作用及其設計原則
本節先在2.1小節給出理論推導的前提假設,并明確權值偏差的定義,然后在2.2小節分析線性預處理環節 對于降低穩態均方權值偏差所起的作用,進而形成
對于降低穩態均方權值偏差所起的作用,進而形成 的設計原則。
的設計原則。
2.1 假設與定義
根據體音采集/聽診過程的特點,可作如下假設:
假設1. 主、副通道的環境噪音信號 與
與 線性相關,且它們均獨立于體音信號
線性相關,且它們均獨立于體音信號 。
。
假設2.  、
、 和
和 均為均值為0的平穩遍歷信號。
均為均值為0的平穩遍歷信號。
對一特定位置進行聽診時,需將聽診器靜止按于相應位置一段時間;在該次聽診過程中,可認為 與
與 之間的互相關函數不會發生變化。相應地可作假設3。
之間的互相關函數不會發生變化。相應地可作假設3。
假設3. 主、副通道環境噪音 、
、 的互相關函數未知,但它不隨時間變化。
的互相關函數未知,但它不隨時間變化。
分別記 和
和 的z變換為
的z變換為 和
和 ;根據假設3可知,
;根據假設3可知, (后文稱為主、副通道環境噪音間的等效傳遞函數)不隨時間變化。分別記
(后文稱為主、副通道環境噪音間的等效傳遞函數)不隨時間變化。分別記 和
和 的z變換為
的z變換為 和
和 ,依圖1可知,
,依圖1可知, ,
, ,故
,故 ,即
,即 也與
也與 線性相關。
線性相關。
令 ;對于實際物理系統,成立
;對于實際物理系統,成立 ,故當M足夠大時,
,故當M足夠大時, 近似成立。因此,自適應濾波器的最佳權值向量為
近似成立。因此,自適應濾波器的最佳權值向量為 。相應地可作假設4。
。相應地可作假設4。
假設4. 自適應濾波器階數M足夠大時,
 |
當 時,主通道環境噪音可被完全抵消。故
時,主通道環境噪音可被完全抵消。故 與
與 之間的偏差可間接衡量環境音降噪效果。
之間的偏差可間接衡量環境音降噪效果。
自適應濾波器權值與其最佳權值之間的偏差,即 ,稱為權值偏差。
,稱為權值偏差。 稱為均方權值偏差,記為
稱為均方權值偏差,記為 。而
。而 稱為均方權值偏差陣。
稱為均方權值偏差陣。
易知, 的跡
的跡 ;而均方權值偏差
;而均方權值偏差 越小,環境音降噪效果越佳。
越小,環境音降噪效果越佳。
假設5. 步長控制參數 很小,等效步長
很小,等效步長 也很小。
也很小。
當接近穩態時,為降低均方權值偏差,通常 取很小的值,此時,假設5的條件成立。
取很小的值,此時,假設5的條件成立。
2.2 預處理H(z)的作用及其設計原則
依假設4和相關定義,可通過分析預處理 對
對 的影響來討論它在環境音降噪過程中所起的作用。
的影響來討論它在環境音降噪過程中所起的作用。
由式(2)~(4)可得
 |
記 ,則由式(5)可得:
,則由式(5)可得:
 |
根據假設1和假設2, 與
與 相互獨立,且
相互獨立,且 ,故
,故 。此外,當滿足假設5所述的小步長條件時,式(3)相當于對副通道環境噪音
。此外,當滿足假設5所述的小步長條件時,式(3)相當于對副通道環境噪音 和體音
和體音 作低通濾波;權值
作低通濾波;權值 ,進而權值偏差向量
,進而權值偏差向量 ,隨時間的變化將比
,隨時間的變化將比 和
和 隨時間的變化慢得多;換言之,
隨時間的變化慢得多;換言之, 及
及 各分量
各分量 的譜內容均與
的譜內容均與 各分量的譜內容存在顯著區別,故
各分量的譜內容存在顯著區別,故 的變化也比
的變化也比 快很多。因此,可采用直接平均法[27](direct-averaging method),將
快很多。因此,可采用直接平均法[27](direct-averaging method),將 的期望值代替其自身代入式(6),得
的期望值代替其自身代入式(6),得
 |
若 取值滿足
取值滿足 ,則由式(7)可知
,則由式(7)可知 ,即權值的估計無偏。依據相關定義,得到:
,即權值的估計無偏。依據相關定義,得到:
 |
再次運用直接平均法,考慮 與
與 相互獨立,可得式(8)等號右邊第2、3項均為0,而第4項
相互獨立,可得式(8)等號右邊第2、3項均為0,而第4項
 |
代入式(8)得
 |
進入穩態后, ,故由式(10)可得
,故由式(10)可得
 |
式(11)表明,穩態均方權值偏差 正比于步長控制參數的平方
正比于步長控制參數的平方 和體音信號的方差
和體音信號的方差 ,并且反比于副通道環境噪音向量的范數均方值
,并且反比于副通道環境噪音向量的范數均方值 。減小
。減小  、
、 或增大
或增大 ,均有助于降低穩態均方權值偏差,亦即有助于改善環境音降噪效果。
,均有助于降低穩態均方權值偏差,亦即有助于改善環境音降噪效果。
在線估計 和
和 并不方便,轉換至頻域更易于設計
并不方便,轉換至頻域更易于設計 。依假設2,
。依假設2, 和
和 均平穩遍歷,故經
均平穩遍歷,故經 處理后所得
處理后所得 和
和 亦為平穩遍歷信號。根據維納-辛欽定理,以下公式成立:
亦為平穩遍歷信號。根據維納-辛欽定理,以下公式成立:
 |
其中, 、
、 、
、 和
和 分別為
分別為 、
、 、
、 和
和 的功率譜密度。
的功率譜密度。
因 ,
, ,其中,
,其中, ,故若
,故若 能在降低
能在降低 的同時增大或至少不明顯減小
的同時增大或至少不明顯減小 ,即等效為在減小
,即等效為在減小 的同時增大或至少不明顯減小
的同時增大或至少不明顯減小 及
及 ,則可降低穩態均方權值偏差,從而改善環境音降噪效果。
,則可降低穩態均方權值偏差,從而改善環境音降噪效果。
綜上, 的設計原則為:經
的設計原則為:經 處理后,體音信號的功率譜密度
處理后,體音信號的功率譜密度 應顯著減小而副通道環境噪音信號的功率譜密度
應顯著減小而副通道環境噪音信號的功率譜密度 應增大或不明顯減小。
應增大或不明顯減小。
3 心音聽診案例討論
本節將以心音聽診的環境音降噪為例,說明如何設計 以及
以及 是如何改善降噪效果的。
是如何改善降噪效果的。
3.1 案例設計
案例設計包括兩個主要環節:主、副通道信號的生成以及兩通道環境噪音信號之間等效傳遞函數 的建立。兩個環節均盡可能與臨床應用時的體音采集和聽診情況相符。
的建立。兩個環節均盡可能與臨床應用時的體音采集和聽診情況相符。
3.1.1 等效傳遞函數 的建立
的建立
將自行研發的雙通道數字聽診器緊貼于大腿上,通過音箱播放M序列信號,分別測量主、副通道所拾取的信號并辨識得到 。其實現細節可參考文獻[28]。所得
。其實現細節可參考文獻[28]。所得 決定于聽診器的按壓力度、衣服材質等諸多因素。本節取其中一次的辨識結果
決定于聽診器的按壓力度、衣服材質等諸多因素。本節取其中一次的辨識結果 供后續分析用。
供后續分析用。
3.1.2 主、副通道信號的生成
環境噪音選用了兩類典型信號,一類為在多家醫院門診和體檢中心的候診大廳自行錄制的“醫院嘈雜環境音”,另一類為網上公開數據庫下載的“嬰兒啼哭聲”“說話聲”“兒童呼喊聲”“樂曲聲”。兩類信號均降采樣至8 kHz,且所有噪音文件拼接為一長段信號,記為 。
。
主通道環境噪音 的生成:以3.1.1節辨識所得的
的生成:以3.1.1節辨識所得的 為濾波器,對
為濾波器,對 進行濾波,所得結果為
進行濾波,所得結果為 。其中,
。其中, 模擬了環境噪音經人體進入聽診器主通道的傳輸特性。
模擬了環境噪音經人體進入聽診器主通道的傳輸特性。
副通道環境噪音 的生成:取
的生成:取 ,其時域曲線及語譜圖參見附件1。
,其時域曲線及語譜圖參見附件1。
心音信號 :對美國3M公司網站提供的正常心音信號欠采樣至8 kHz后作為
:對美國3M公司網站提供的正常心音信號欠采樣至8 kHz后作為 。取正常心音的原因在于其第一和第二心音相對明顯。
。取正常心音的原因在于其第一和第二心音相對明顯。
主通道信號 :
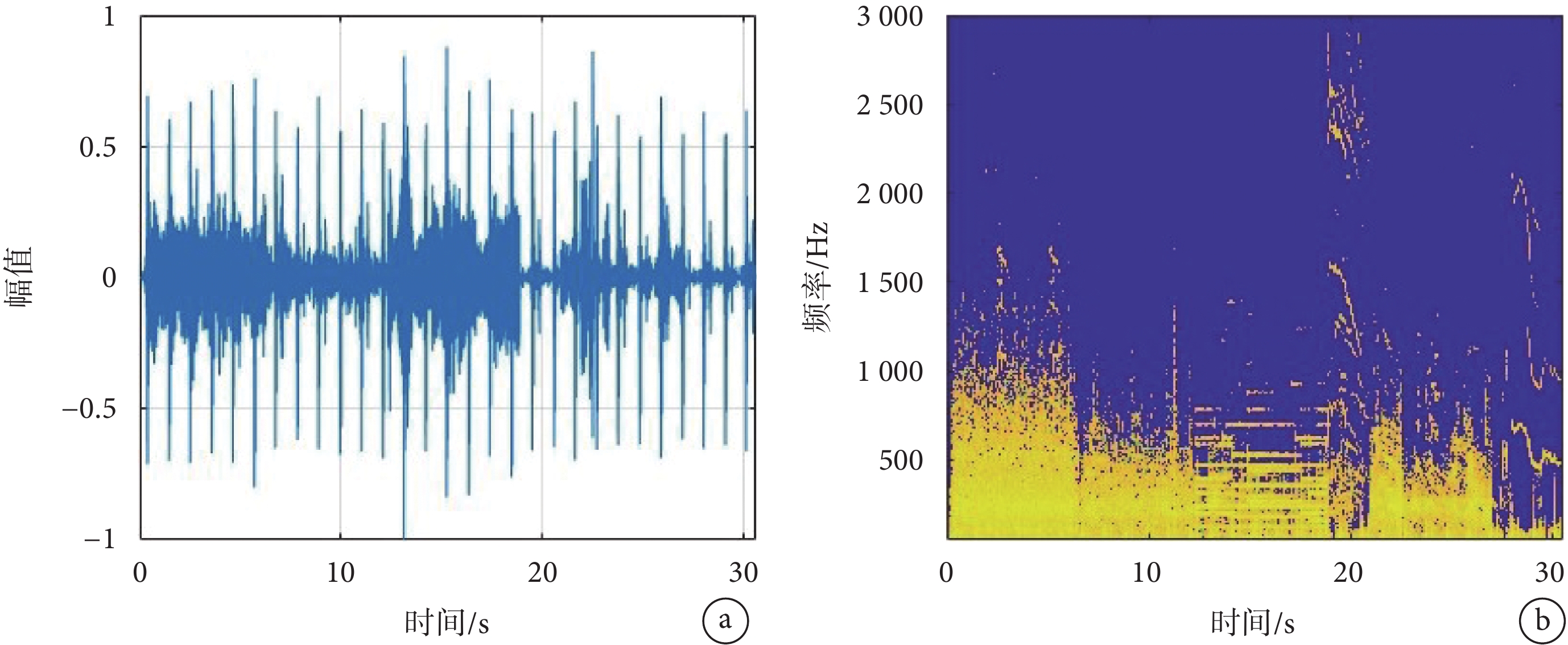
: ,其時域曲線及語譜圖分別如圖2a和圖2b所示。如圖2a所示,
,其時域曲線及語譜圖分別如圖2a和圖2b所示。如圖2a所示, 的時域曲線因第一、第二心音而周期性出現大幅值的脈沖分量。而在
的時域曲線因第一、第二心音而周期性出現大幅值的脈沖分量。而在 的語譜圖中,0~6.5 s、6.5~12 s分別因存在門診和體檢中心候診大廳處的環境噪音,信號能量廣泛分布于1 500 Hz(特別是1 000 Hz)以下較寬的頻段;12~19 s因受樂曲噪音的干擾,在200~1 000 Hz之間存在明顯的水平深色帶狀條紋;19~22 s因受兒童呼喊噪音干擾,在3 000 Hz以內多個頻段存在斜向下的深色帶狀條紋;22~27 s因受說話噪音干擾,在1 500 Hz以下存在斜向下的深色帶狀條紋;27~31 s則因受嬰兒啼哭噪音干擾,在500~2 500 Hz較寬的范圍內亦存在深色的瞬時頻率變化的條紋。
的語譜圖中,0~6.5 s、6.5~12 s分別因存在門診和體檢中心候診大廳處的環境噪音,信號能量廣泛分布于1 500 Hz(特別是1 000 Hz)以下較寬的頻段;12~19 s因受樂曲噪音的干擾,在200~1 000 Hz之間存在明顯的水平深色帶狀條紋;19~22 s因受兒童呼喊噪音干擾,在3 000 Hz以內多個頻段存在斜向下的深色帶狀條紋;22~27 s因受說話噪音干擾,在1 500 Hz以下存在斜向下的深色帶狀條紋;27~31 s則因受嬰兒啼哭噪音干擾,在500~2 500 Hz較寬的范圍內亦存在深色的瞬時頻率變化的條紋。
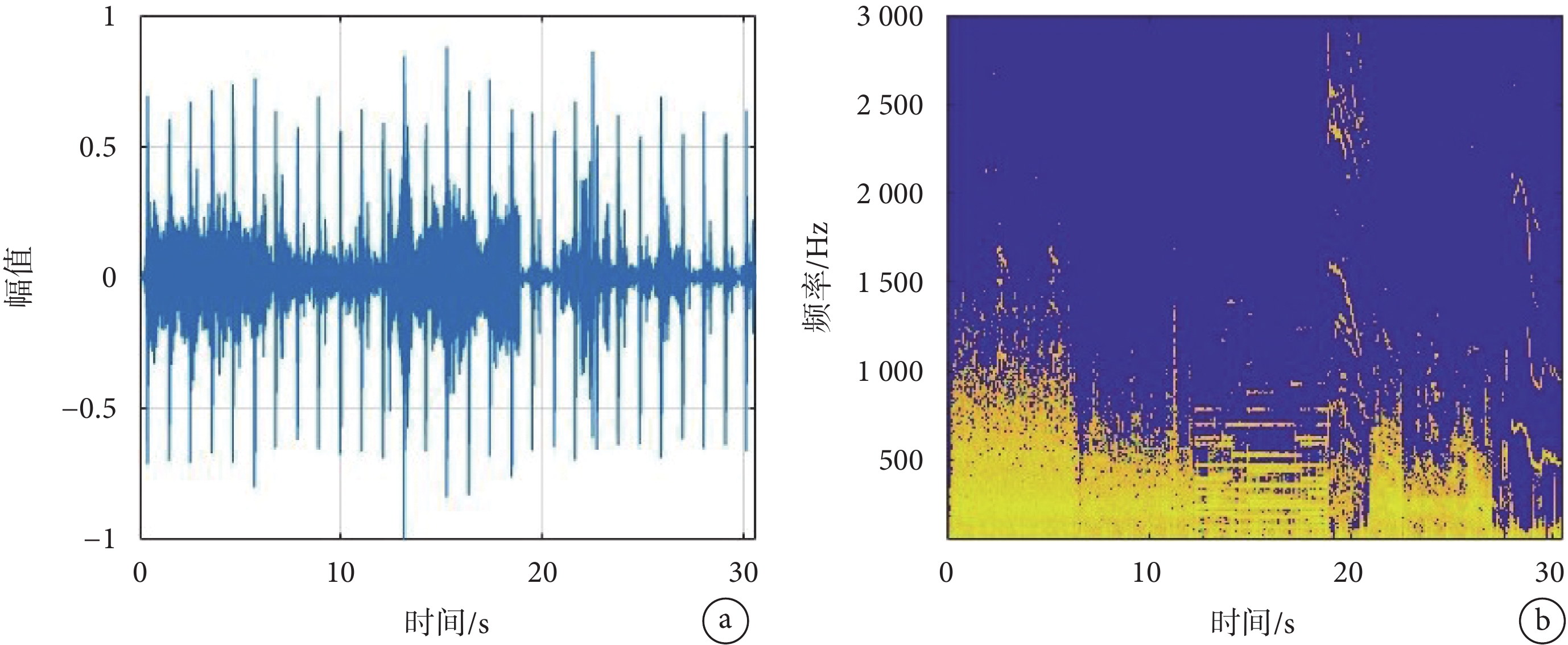 圖2
圖2
 的曲線及語譜圖
的曲線及語譜圖
a.的時域曲線;b.的語譜圖
Figure2. Curve and spectrogram of
a. curve of ; b. spectrogram of
3.1.3 最佳權值向量及權值偏差的度量
令 =
=  ,可求得
,可求得 的最大值為
的最大值為 ,且當
,且當 時,
時, ,近似為0。故濾波器階數M取為150,最佳權值向量
,近似為0。故濾波器階數M取為150,最佳權值向量 ,且
,且 為0.489。
為0.489。
定義對數權值失調 以衡量權值向量與最佳權值向量間的相對偏差,如式(12)所示。
以衡量權值向量與最佳權值向量間的相對偏差,如式(12)所示。
 |
3.2 預處理的設計
考慮到第一和第二心音主要能量通常集中于150 Hz以下的低頻段,而聽診過程中的典型環境噪音(例如語音、哭叫聲、音樂等)主要能量的頻段通常在150 Hz以上,采用了簡單的一階線性預處理 ,當采樣頻率為8 kHz時,可抑制150 Hz以下的信號而放大150 Hz以上的信號。
,當采樣頻率為8 kHz時,可抑制150 Hz以下的信號而放大150 Hz以上的信號。
經 預處理后,
預處理后, 的第一、第二心音幅值顯著減小,且150 Hz以下頻段的功率譜密度降低約20 dB。預處理后,
的第一、第二心音幅值顯著減小,且150 Hz以下頻段的功率譜密度降低約20 dB。預處理后, 不同時段的幅值有增有減,其功率譜密度在500 Hz以下頻段顯著降低,而在1 000 Hz以上頻段未減小,甚至在高頻段會增加。統計各信號的均方值或范數均方值以分別作為
不同時段的幅值有增有減,其功率譜密度在500 Hz以下頻段顯著降低,而在1 000 Hz以上頻段未減小,甚至在高頻段會增加。統計各信號的均方值或范數均方值以分別作為 、
、 、
、 和
和 的估計值,依次得
的估計值,依次得 、
、 、0.297和0.603。這些結果表明,
、0.297和0.603。這些結果表明, 的峰值和均值均分別遠小于
的峰值和均值均分別遠小于 的峰值和均值;但
的峰值和均值;但 既可能大于也可能不大于
既可能大于也可能不大于 ,兩者的均值差別不大,后者甚至稍大。各信號的曲線及功率譜密度曲線參見附件2,
,兩者的均值差別不大,后者甚至稍大。各信號的曲線及功率譜密度曲線參見附件2, 、
、 、
、 和
和 隨時間變化的曲線參見附件3。
隨時間變化的曲線參見附件3。
3.3 自適應濾波結果
本節分別針對固定步長控制參數的NLMS算法和一種變步長控制參數的自適應算法[19],比較其增加線性預處理前、后的濾波效果。
3.3.1 固定步長控制參數算法
前一種算法的步長控制參數 取0.06。分別對比圖2b帶噪心音信號
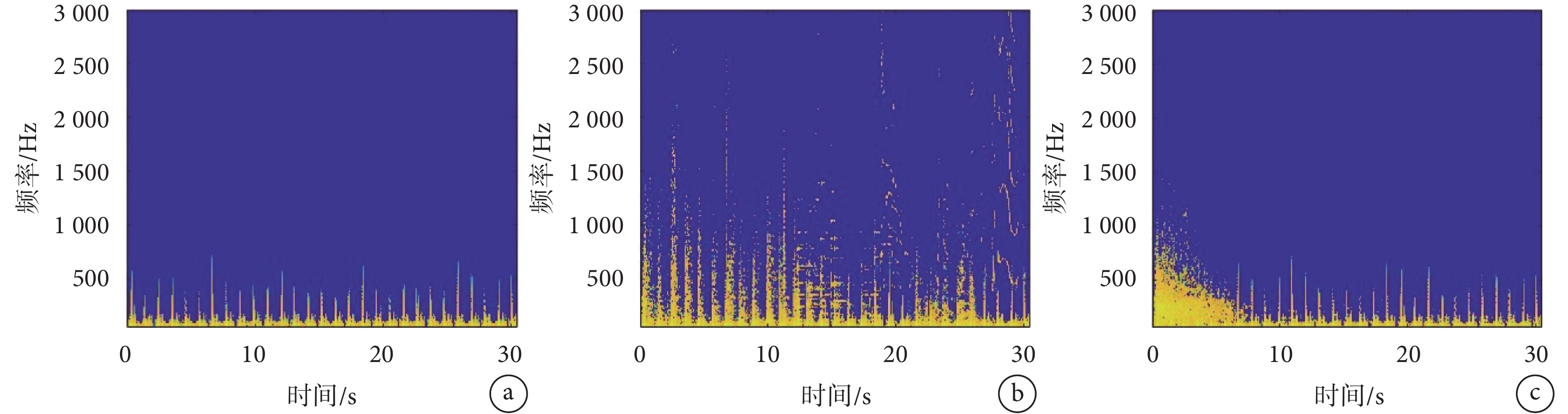
取0.06。分別對比圖2b帶噪心音信號 和圖3b及圖3c降噪后信號的語譜圖,均可發現,算法運行6 s后,環境噪音被顯著抑制,主要表現為環境噪音對應的圖2b中高亮的高頻分量被顯著抑制。此外,對比圖3a心音和圖3b無預處理自適應濾波后信號的語譜圖,可以發現濾波后依然殘余帶狀條紋,提示算法對嬰兒啼哭聲、說話聲和樂曲聲的抑制效果不夠理想;尤其是在第一、第二心音處,圖3a和圖3b的語譜圖差別更大,說明第一、第二心音對濾波器的權值更新產生負面影響。可見,無預處理的自適應降噪效果較差,無法有效抑制環境噪音。而對比圖3a心音和圖3c含預處理自適應濾波后信號的語譜圖,兩者當濾波器權值收斂后(第6 s后)差別很小,提示降噪效果較為理想。
和圖3b及圖3c降噪后信號的語譜圖,均可發現,算法運行6 s后,環境噪音被顯著抑制,主要表現為環境噪音對應的圖2b中高亮的高頻分量被顯著抑制。此外,對比圖3a心音和圖3b無預處理自適應濾波后信號的語譜圖,可以發現濾波后依然殘余帶狀條紋,提示算法對嬰兒啼哭聲、說話聲和樂曲聲的抑制效果不夠理想;尤其是在第一、第二心音處,圖3a和圖3b的語譜圖差別更大,說明第一、第二心音對濾波器的權值更新產生負面影響。可見,無預處理的自適應降噪效果較差,無法有效抑制環境噪音。而對比圖3a心音和圖3c含預處理自適應濾波后信號的語譜圖,兩者當濾波器權值收斂后(第6 s后)差別很小,提示降噪效果較為理想。
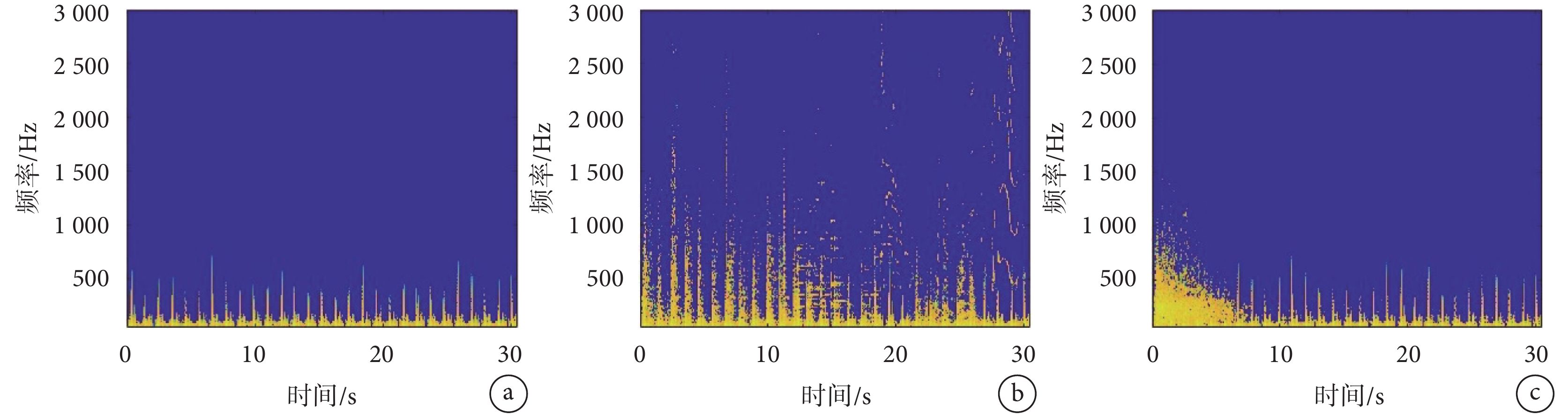 圖3
部分信號的語譜圖
圖3
部分信號的語譜圖
a.;b.無預處理時的;c.含預處理時的
Figure3. Spectrograms of certain signalsa.; b. when ; c. when
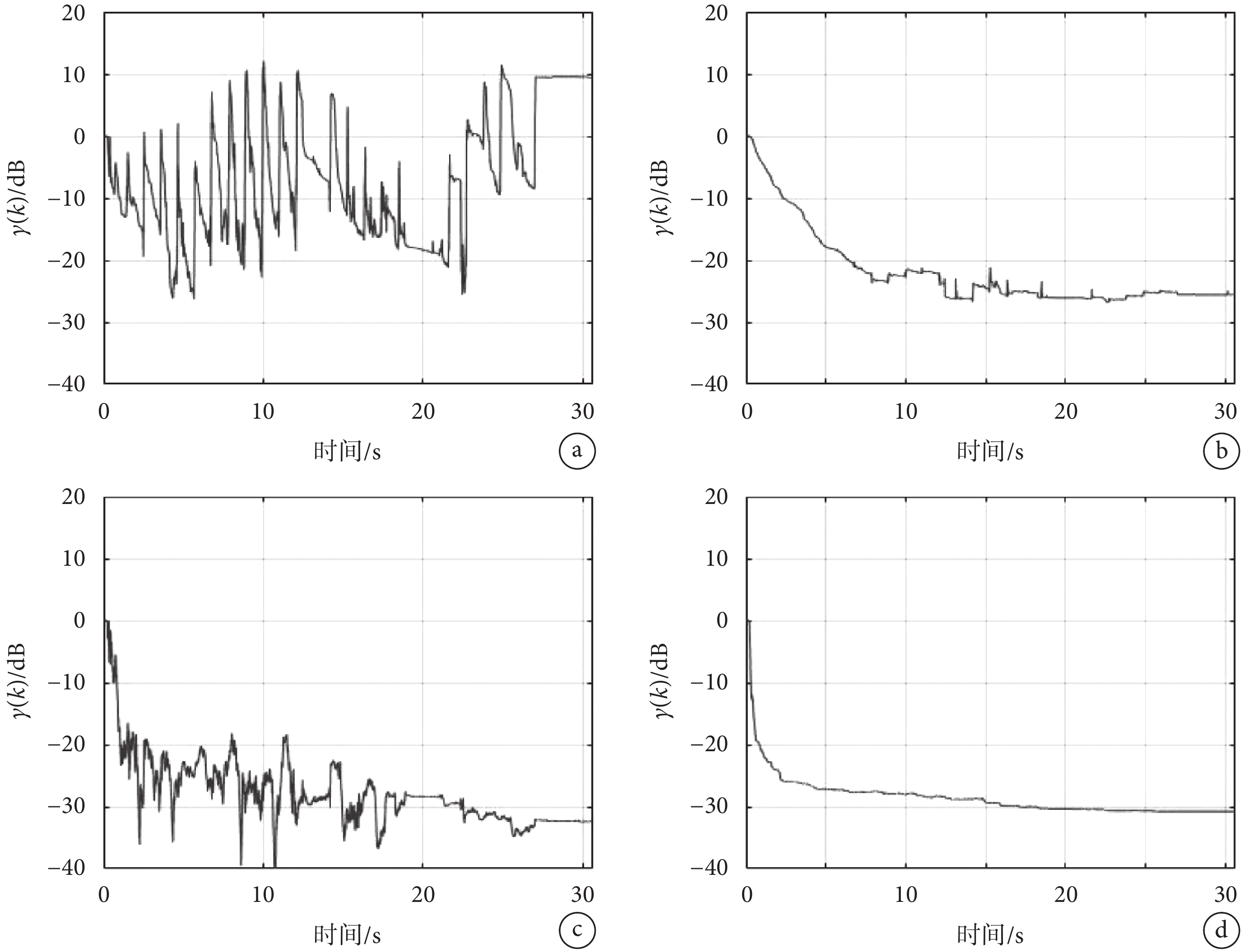
采用式(12)所定義的對數權值失調可更清晰地衡量權值偏差的相對大小及降噪效果。如圖4a和圖4b所示,無預處理和含預處理自適應降噪算法的 均可在6 s內減小到-20 dB以下。但隨后無預處理自適應濾波算法的
均可在6 s內減小到-20 dB以下。但隨后無預處理自適應濾波算法的 會出現周期性的大幅波動,且其波動的時間點恰好對應于第一、第二心音出現的時刻,表明濾波器權值因受第一、第二心音的影響而周期性產生失調;而含預處理自適應降噪算法的
會出現周期性的大幅波動,且其波動的時間點恰好對應于第一、第二心音出現的時刻,表明濾波器權值因受第一、第二心音的影響而周期性產生失調;而含預處理自適應降噪算法的 則持續減小且幾乎不出現波動,表明其濾波器權值的收斂幾乎不受第一、第二心音的影響。算法運行6 s后,統計各時刻
則持續減小且幾乎不出現波動,表明其濾波器權值的收斂幾乎不受第一、第二心音的影響。算法運行6 s后,統計各時刻 的均值以作為穩態均方權值偏差
的均值以作為穩態均方權值偏差 的估計值,無預處理和含預處理的自適應降噪算法的結果分別為:0.507和
的估計值,無預處理和含預處理的自適應降噪算法的結果分別為:0.507和 ,前者略大于
,前者略大于 ,后者則遠小于
,后者則遠小于 。由此可知,含預處理的自適應濾波器對于第一、第二心音這類脈沖分量的魯棒性要遠高于無預處理的自適應濾波器。
。由此可知,含預處理的自適應濾波器對于第一、第二心音這類脈沖分量的魯棒性要遠高于無預處理的自適應濾波器。
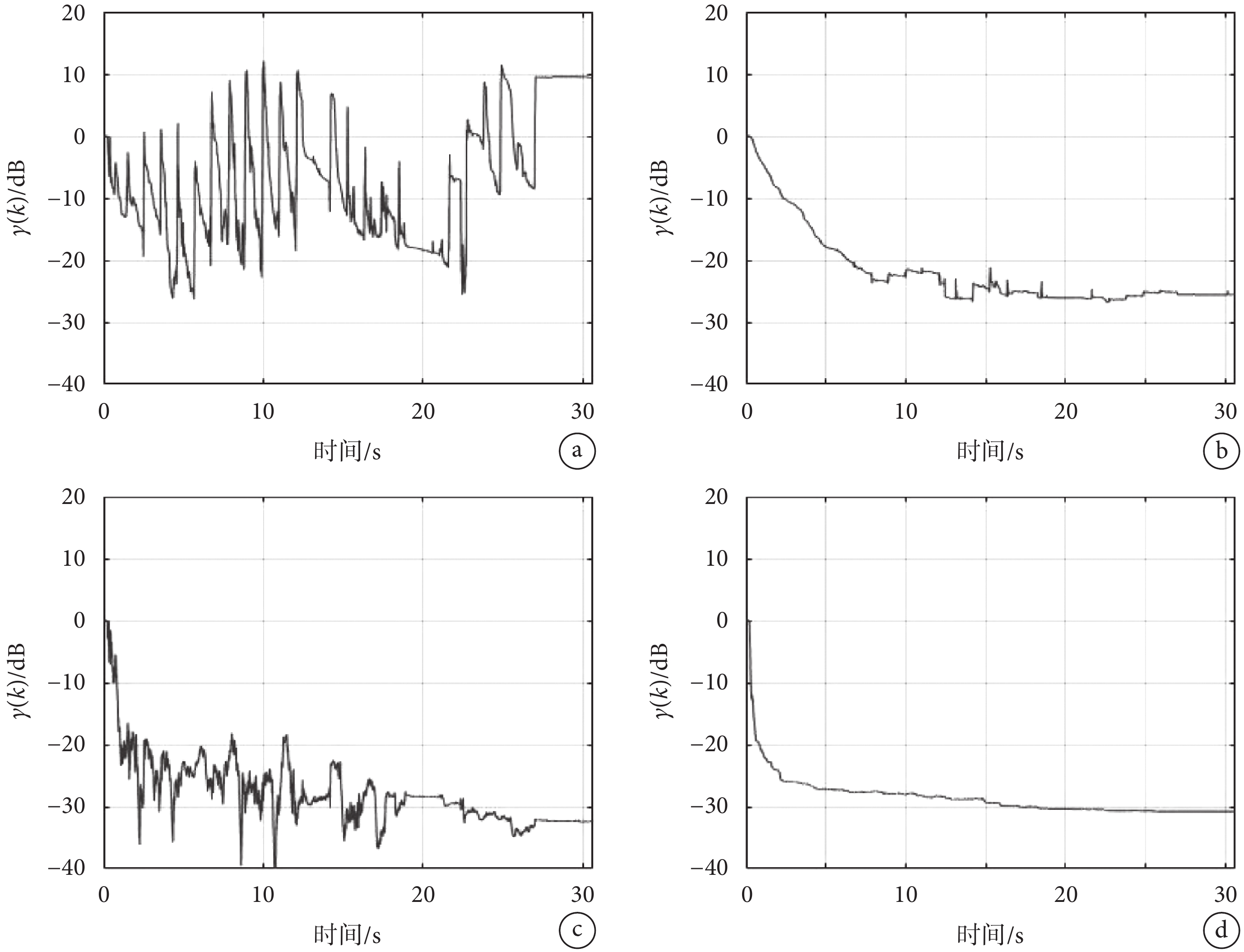 圖4
固定步長NLMS和VSS-RSA算法增加預處理前、后對數權值失調隨時間變化的曲線
圖4
固定步長NLMS和VSS-RSA算法增加預處理前、后對數權值失調隨時間變化的曲線
a. 固定步長NLMS且無預處理;b. 固定步長NLMS且含預處理;c. VSS-RSA算法且無預處理;d. VSS-RSA算法且含預處理
Figure4. Logarithmic weight misalignment of a NLMS filter and that of a VSS-RSA filter with and without preprocessinga. NLMS without preprocessing; b. NLMS with preprocessing; c. VSS-RSA without preprocessing; d. VSS-RSA with preprocessing
3.3.2 變步長控制參數算法
式(11)表明,減小步長控制參數 或
或 均有助于降低穩態均方權值偏差,且兩者的作用相對獨立。這意味著可以在預處理的基礎上增加變步長算法,以進一步減小權值偏差和輸出誤差,提升環境音降噪性能。本節變步長控制參數的自適應算法采用了文獻[19]提出的變步長魯棒飽和算法(variable step-size robust saturation algorithm,VSS-RSA),該算法按式(13)所示的方式更新權值:
均有助于降低穩態均方權值偏差,且兩者的作用相對獨立。這意味著可以在預處理的基礎上增加變步長算法,以進一步減小權值偏差和輸出誤差,提升環境音降噪性能。本節變步長控制參數的自適應算法采用了文獻[19]提出的變步長魯棒飽和算法(variable step-size robust saturation algorithm,VSS-RSA),該算法按式(13)所示的方式更新權值:
 |
其中, 為飽和函數,
為飽和函數, ,且
,且 ,飽和限估計值為
,飽和限估計值為
 |
其中,初始值 ,而
,而 為人工截除心音
為人工截除心音 中第一和第二心音片段后所得剩余部分信號的標準差。與文獻[19]中僅對
中第一和第二心音片段后所得剩余部分信號的標準差。與文獻[19]中僅對 取絕對值不同,為保證
取絕對值不同,為保證 不小于0,此處的式(14)對等式右邊的分子取絕對值。
不小于0,此處的式(14)對等式右邊的分子取絕對值。
對該變步長控制參數的VSS-RSA算法,增加預處理 前、后,對數權值失調
前、后,對數權值失調 隨時間變化的曲線分別如圖4c和圖4d所示。對比圖4b和圖4c可知,固定步長控制參數但增加預處理時,
隨時間變化的曲線分別如圖4c和圖4d所示。對比圖4b和圖4c可知,固定步長控制參數但增加預處理時, 收斂速度稍慢,但基本為單調減小而不會出現明顯的波動;而變步長控制參數但不作預處理時,
收斂速度稍慢,但基本為單調減小而不會出現明顯的波動;而變步長控制參數但不作預處理時, 收斂速度快,但會出現一定幅度的波動。此外,分別對比圖4b和圖4d、圖4c和圖4d可知,若同時采用變步長控制參數算法并增加預處理,則
收斂速度快,但會出現一定幅度的波動。此外,分別對比圖4b和圖4d、圖4c和圖4d可知,若同時采用變步長控制參數算法并增加預處理,則 不僅單調收斂而且收斂速度更快。
不僅單調收斂而且收斂速度更快。
4 結論
本文分析了線性預處理對于提升自適應濾波方法在聽診環境音降噪性能上所起的作用,主要貢獻為:針對雙通道NLMS自適應降噪算法,① 分析并闡明了自適應濾波器的穩態均方權值偏差與體音信號方差及環境噪音方差之間的量化關系;② 基于該量化關系解釋了線性預處理可改善環境音降噪效果的原因,并形成了線性預處理環節的設計原則。所形成的設計原則為:經其處理后,體音方差 或功率譜密度
或功率譜密度 顯著減小,而副通道環境噪音方差
顯著減小,而副通道環境噪音方差 或功率譜密度
或功率譜密度 不明顯減小甚至增大。基于該原則的頻域設計方法簡單易行,且便于引入“體音信號的頻譜特點”等先驗知識來確定預處理環節的參數。
不明顯減小甚至增大。基于該原則的頻域設計方法簡單易行,且便于引入“體音信號的頻譜特點”等先驗知識來確定預處理環節的參數。
第3節心音聽診環境音降噪的結果表明,不管采用的是變步長控制參數還是固定步長控制參數的算法,在其余參數相同的前提下,僅簡單地增加一階線性預處理,即可有效抑制第一和第二心音等脈沖分量對自適應濾波器穩態均方權值偏差的影響而顯著提升環境音降噪性能。因此,若計算資源有限,例如需要在運算能力低的單片機上實現,可只增加線性預處理,其計算量小,非常適合應用于體積和成本受限的可穿戴設備上;而若計算資源相對豐富,則可考慮同時增加變步長控制參數的自適應算法。
應指出的是,由于環境噪音和體音信號的頻譜存在重疊的頻段,線性預處理并不總能精細地區別對待,其靈活程度有限。本文的后續研究將針對各種體音信號,探索建立針對性更強的非線性預處理方法。
重要聲明
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
作者貢獻聲明:莫鴻強負責理論推導及數據分析;田翔負責算法實現及算法驗證方案設計;李彬負責算法分析;田軍章負責降噪需求分析及數據收集。四位作者共同參與了論文寫作。
本文附件見本刊網站的電子版本(biomedeng.cn)。
0 引言
隨著醫療保健服務需求的日益增長以及柔性材料[1]、微機電系統[2]和無線通信等技術的迅速發展,可穿戴生理參數采集設備的研發已成為當今熱點[1-4],具有自動降噪功能的體音信號采集設備和聽診設備就是其中的典型。無論是心音[4-5]、呼吸音[3, 5-6]還是腸鳴音[1, 7]聽診,環境噪音都是影響聽診效果的主要因素之一。當環境噪音超過66~70 dBA(A計權分貝)時,采用傳統聽診器就無法正常聽診[5, 8-9]。聽診過程中的環境噪音類型多樣,且幅值往往遠高于體音信號,會極大地妨礙人工聽診和異常體音的自動識別等[4-5]。另外,大部分環境噪音的時頻分布與體音信號的時頻分布高度重疊,其降噪難度較高[1, 3-6, 8-9]。
綜合考慮在線聽診要求以及成本、體積、可穿戴性及續航能力[5, 8]等因素的限制,目前常用雙通道自適應濾波方法進行實時降噪。其原理為:假設環境噪音為加性噪音,主通道測量帶噪體音,副通道采集環境噪音,副通道所測環境噪音經處理后用于抵消帶噪體音中的噪音而實現降噪[6, 10-12]。該方法實用性強,可應用于兒科診所[6]、救護車及直升機轉運[11]、航天器[12]等具高分貝環境噪音的場合。這些算法又可大致分為兩類:譜減法[6, 12]和基于最小均方誤差準則的自適應濾波算法。后者以最小均方(least mean square,LMS)算法、歸一化最小均方(normalized LMS,NLMS)算法[9-11]及其改進算法為代表[13-15],其計算復雜度顯著低于譜減法,實現成本低,特別適合于體音采集。
當前,聽診環境音自適應降噪算法的研究通常集中于如何設定或調節步長以在快速收斂和低失調(misalignment)之間實現平衡[9-11, 13-15],而較少考慮基于最小均方誤差準則的算法是否適用于所有的體音信號。以心音聽診為例,第一、第二心音這類周期性出現的大幅值、短時尖峰波形(即心音屬于含脈沖分量的信號)容易導致濾波器的權值周期性失調甚至發散,進而產生“額外的”輸出誤差。這些誤差易與一些高度瞬態的心音,如收縮期拍擊聲、異常的第三或第四心音等相混淆,增加聽診的難度。對于心音這類包含脈沖分量的體音信號,若能針對性地設計自適應濾波算法,將會大大提升降噪效果。
脈沖干擾在主動降噪[16]、回音抑制[17-18]、系統辨識[17, 19]等應用場合廣泛出現,最常見的解決辦法是建立合適的代價函數,使得脈沖干擾出現時濾波器權值不至于大幅調整,從而提高算法對于脈沖干擾的魯棒性[16-23]。例如:有的方法將脈沖干擾建模為α穩定分布過程[16, 20-21],分別基于輸出誤差的p范數均值[22]、輸出誤差的L1和L2范數組合[21]或特定約束下單步權值增量的L2范數[16]建立代價函數;有些方法以單步權值增量的L2范數限幅為約束條件,并分別基于后驗誤差的L2范數[18]或L1范數[19]建立代價函數;還有方法通過對輸出誤差引入非線性函數[17, 23]來構造代價函數。對這些代價函數進行優化,其結果往往形成變步長的自適應算法,但仍需要人為設定遺忘因子[16]、尺度縮放因子[17, 23]、單步權值增量閾值[16, 18-19]等參數,而對于聽診的自適應降噪,這些參數通常不易預先確定,因此,本文考慮采用與變步長方法不同的解決思路。
體音信號中的脈沖成分種類有限,僅幅值不確定,若能預先減小其中脈沖分量的幅值,則可大大簡化降噪算法的設計。本文前期研究[24-25]僅簡單地先對兩個通道的信號作線性預處理,再采用NLMS算法即顯著改善了環境音降噪性能,但文獻[24-25]均未解釋降噪效果改善的原因,無法在算法設計上形成指導性建議。鑒于此,本文將分析線性預處理對于改善自適應降噪效果所起的作用,并探討預處理環節的設計原則。
1 NLMS濾波算法
考慮到NLMS算法收斂速度快[26],后續分析主要圍繞雙通道NLMS濾波算法展開;其結構如圖1所示,其中的預處理 及后處理
及后處理 均采用線性濾波器實現,且
均采用線性濾波器實現,且 對應于算法不對信號作預處理。
對應于算法不對信號作預處理。
 圖1
含線性預處理的NLMS濾波算法結構圖
Figure1.
The framework diagram of the NLMS algorithm with linear preprocessing
圖1
含線性預處理的NLMS濾波算法結構圖
Figure1.
The framework diagram of the NLMS algorithm with linear preprocessing
圖1中主通道信號為 ,其中
,其中 和
和 分別為第k時刻的體音和主通道環境噪音,且
分別為第k時刻的體音和主通道環境噪音,且 和
和 均未知。副通道信號為環境噪音
均未知。副通道信號為環境噪音 。信號
。信號 經
經 預處理后得
預處理后得 ,其中,
,其中, 和
和 分別對應于
分別對應于 和
和 經
經 預處理后所得結果。信號
預處理后所得結果。信號 經
經 預處理后得
預處理后得 。自適應濾波器的最終輸出為
。自適應濾波器的最終輸出為 。其余中間變量滿足式(1)和式(2)的約束。
。其余中間變量滿足式(1)和式(2)的約束。
 |
 |
其中, 為第
為第 時刻自適應濾波器權值向量,
時刻自適應濾波器權值向量, 為第k時刻預處理后副通道環境噪音向量,M為自適應濾波器的階數。
為第k時刻預處理后副通道環境噪音向量,M為自適應濾波器的階數。
權值向量 更新方式如式(3)所示,其中,
更新方式如式(3)所示,其中, 為步長控制參數。
為步長控制參數。
 |
2 預處理H(z)的作用及其設計原則
本節先在2.1小節給出理論推導的前提假設,并明確權值偏差的定義,然后在2.2小節分析線性預處理環節 對于降低穩態均方權值偏差所起的作用,進而形成
對于降低穩態均方權值偏差所起的作用,進而形成 的設計原則。
的設計原則。
2.1 假設與定義
根據體音采集/聽診過程的特點,可作如下假設:
假設1. 主、副通道的環境噪音信號 與
與 線性相關,且它們均獨立于體音信號
線性相關,且它們均獨立于體音信號 。
。
假設2.  、
、 和
和 均為均值為0的平穩遍歷信號。
均為均值為0的平穩遍歷信號。
對一特定位置進行聽診時,需將聽診器靜止按于相應位置一段時間;在該次聽診過程中,可認為 與
與 之間的互相關函數不會發生變化。相應地可作假設3。
之間的互相關函數不會發生變化。相應地可作假設3。
假設3. 主、副通道環境噪音 、
、 的互相關函數未知,但它不隨時間變化。
的互相關函數未知,但它不隨時間變化。
分別記 和
和 的z變換為
的z變換為 和
和 ;根據假設3可知,
;根據假設3可知, (后文稱為主、副通道環境噪音間的等效傳遞函數)不隨時間變化。分別記
(后文稱為主、副通道環境噪音間的等效傳遞函數)不隨時間變化。分別記 和
和 的z變換為
的z變換為 和
和 ,依圖1可知,
,依圖1可知, ,
, ,故
,故 ,即
,即 也與
也與 線性相關。
線性相關。
令 ;對于實際物理系統,成立
;對于實際物理系統,成立 ,故當M足夠大時,
,故當M足夠大時, 近似成立。因此,自適應濾波器的最佳權值向量為
近似成立。因此,自適應濾波器的最佳權值向量為 。相應地可作假設4。
。相應地可作假設4。
假設4. 自適應濾波器階數M足夠大時,
 |
當 時,主通道環境噪音可被完全抵消。故
時,主通道環境噪音可被完全抵消。故 與
與 之間的偏差可間接衡量環境音降噪效果。
之間的偏差可間接衡量環境音降噪效果。
自適應濾波器權值與其最佳權值之間的偏差,即 ,稱為權值偏差。
,稱為權值偏差。 稱為均方權值偏差,記為
稱為均方權值偏差,記為 。而
。而 稱為均方權值偏差陣。
稱為均方權值偏差陣。
易知, 的跡
的跡 ;而均方權值偏差
;而均方權值偏差 越小,環境音降噪效果越佳。
越小,環境音降噪效果越佳。
假設5. 步長控制參數 很小,等效步長
很小,等效步長 也很小。
也很小。
當接近穩態時,為降低均方權值偏差,通常 取很小的值,此時,假設5的條件成立。
取很小的值,此時,假設5的條件成立。
2.2 預處理H(z)的作用及其設計原則
依假設4和相關定義,可通過分析預處理 對
對 的影響來討論它在環境音降噪過程中所起的作用。
的影響來討論它在環境音降噪過程中所起的作用。
由式(2)~(4)可得
 |
記 ,則由式(5)可得:
,則由式(5)可得:
 |
根據假設1和假設2, 與
與 相互獨立,且
相互獨立,且 ,故
,故 。此外,當滿足假設5所述的小步長條件時,式(3)相當于對副通道環境噪音
。此外,當滿足假設5所述的小步長條件時,式(3)相當于對副通道環境噪音 和體音
和體音 作低通濾波;權值
作低通濾波;權值 ,進而權值偏差向量
,進而權值偏差向量 ,隨時間的變化將比
,隨時間的變化將比 和
和 隨時間的變化慢得多;換言之,
隨時間的變化慢得多;換言之, 及
及 各分量
各分量 的譜內容均與
的譜內容均與 各分量的譜內容存在顯著區別,故
各分量的譜內容存在顯著區別,故 的變化也比
的變化也比 快很多。因此,可采用直接平均法[27](direct-averaging method),將
快很多。因此,可采用直接平均法[27](direct-averaging method),將 的期望值代替其自身代入式(6),得
的期望值代替其自身代入式(6),得
 |
若 取值滿足
取值滿足 ,則由式(7)可知
,則由式(7)可知 ,即權值的估計無偏。依據相關定義,得到:
,即權值的估計無偏。依據相關定義,得到:
 |
再次運用直接平均法,考慮 與
與 相互獨立,可得式(8)等號右邊第2、3項均為0,而第4項
相互獨立,可得式(8)等號右邊第2、3項均為0,而第4項
 |
代入式(8)得
 |
進入穩態后, ,故由式(10)可得
,故由式(10)可得
 |
式(11)表明,穩態均方權值偏差 正比于步長控制參數的平方
正比于步長控制參數的平方 和體音信號的方差
和體音信號的方差 ,并且反比于副通道環境噪音向量的范數均方值
,并且反比于副通道環境噪音向量的范數均方值 。減小
。減小  、
、 或增大
或增大 ,均有助于降低穩態均方權值偏差,亦即有助于改善環境音降噪效果。
,均有助于降低穩態均方權值偏差,亦即有助于改善環境音降噪效果。
在線估計 和
和 并不方便,轉換至頻域更易于設計
并不方便,轉換至頻域更易于設計 。依假設2,
。依假設2, 和
和 均平穩遍歷,故經
均平穩遍歷,故經 處理后所得
處理后所得 和
和 亦為平穩遍歷信號。根據維納-辛欽定理,以下公式成立:
亦為平穩遍歷信號。根據維納-辛欽定理,以下公式成立:
 |
其中, 、
、 、
、 和
和 分別為
分別為 、
、 、
、 和
和 的功率譜密度。
的功率譜密度。
因 ,
, ,其中,
,其中, ,故若
,故若 能在降低
能在降低 的同時增大或至少不明顯減小
的同時增大或至少不明顯減小 ,即等效為在減小
,即等效為在減小 的同時增大或至少不明顯減小
的同時增大或至少不明顯減小 及
及 ,則可降低穩態均方權值偏差,從而改善環境音降噪效果。
,則可降低穩態均方權值偏差,從而改善環境音降噪效果。
綜上, 的設計原則為:經
的設計原則為:經 處理后,體音信號的功率譜密度
處理后,體音信號的功率譜密度 應顯著減小而副通道環境噪音信號的功率譜密度
應顯著減小而副通道環境噪音信號的功率譜密度 應增大或不明顯減小。
應增大或不明顯減小。
3 心音聽診案例討論
本節將以心音聽診的環境音降噪為例,說明如何設計 以及
以及 是如何改善降噪效果的。
是如何改善降噪效果的。
3.1 案例設計
案例設計包括兩個主要環節:主、副通道信號的生成以及兩通道環境噪音信號之間等效傳遞函數 的建立。兩個環節均盡可能與臨床應用時的體音采集和聽診情況相符。
的建立。兩個環節均盡可能與臨床應用時的體音采集和聽診情況相符。
3.1.1 等效傳遞函數 的建立
的建立
將自行研發的雙通道數字聽診器緊貼于大腿上,通過音箱播放M序列信號,分別測量主、副通道所拾取的信號并辨識得到 。其實現細節可參考文獻[28]。所得
。其實現細節可參考文獻[28]。所得 決定于聽診器的按壓力度、衣服材質等諸多因素。本節取其中一次的辨識結果
決定于聽診器的按壓力度、衣服材質等諸多因素。本節取其中一次的辨識結果 供后續分析用。
供后續分析用。
3.1.2 主、副通道信號的生成
環境噪音選用了兩類典型信號,一類為在多家醫院門診和體檢中心的候診大廳自行錄制的“醫院嘈雜環境音”,另一類為網上公開數據庫下載的“嬰兒啼哭聲”“說話聲”“兒童呼喊聲”“樂曲聲”。兩類信號均降采樣至8 kHz,且所有噪音文件拼接為一長段信號,記為 。
。
主通道環境噪音 的生成:以3.1.1節辨識所得的
的生成:以3.1.1節辨識所得的 為濾波器,對
為濾波器,對 進行濾波,所得結果為
進行濾波,所得結果為 。其中,
。其中, 模擬了環境噪音經人體進入聽診器主通道的傳輸特性。
模擬了環境噪音經人體進入聽診器主通道的傳輸特性。
副通道環境噪音 的生成:取
的生成:取 ,其時域曲線及語譜圖參見附件1。
,其時域曲線及語譜圖參見附件1。
心音信號 :對美國3M公司網站提供的正常心音信號欠采樣至8 kHz后作為
:對美國3M公司網站提供的正常心音信號欠采樣至8 kHz后作為 。取正常心音的原因在于其第一和第二心音相對明顯。
。取正常心音的原因在于其第一和第二心音相對明顯。
主通道信號 :
: ,其時域曲線及語譜圖分別如圖2a和圖2b所示。如圖2a所示,
,其時域曲線及語譜圖分別如圖2a和圖2b所示。如圖2a所示, 的時域曲線因第一、第二心音而周期性出現大幅值的脈沖分量。而在
的時域曲線因第一、第二心音而周期性出現大幅值的脈沖分量。而在 的語譜圖中,0~6.5 s、6.5~12 s分別因存在門診和體檢中心候診大廳處的環境噪音,信號能量廣泛分布于1 500 Hz(特別是1 000 Hz)以下較寬的頻段;12~19 s因受樂曲噪音的干擾,在200~1 000 Hz之間存在明顯的水平深色帶狀條紋;19~22 s因受兒童呼喊噪音干擾,在3 000 Hz以內多個頻段存在斜向下的深色帶狀條紋;22~27 s因受說話噪音干擾,在1 500 Hz以下存在斜向下的深色帶狀條紋;27~31 s則因受嬰兒啼哭噪音干擾,在500~2 500 Hz較寬的范圍內亦存在深色的瞬時頻率變化的條紋。
的語譜圖中,0~6.5 s、6.5~12 s分別因存在門診和體檢中心候診大廳處的環境噪音,信號能量廣泛分布于1 500 Hz(特別是1 000 Hz)以下較寬的頻段;12~19 s因受樂曲噪音的干擾,在200~1 000 Hz之間存在明顯的水平深色帶狀條紋;19~22 s因受兒童呼喊噪音干擾,在3 000 Hz以內多個頻段存在斜向下的深色帶狀條紋;22~27 s因受說話噪音干擾,在1 500 Hz以下存在斜向下的深色帶狀條紋;27~31 s則因受嬰兒啼哭噪音干擾,在500~2 500 Hz較寬的范圍內亦存在深色的瞬時頻率變化的條紋。
 圖2
圖2
 的曲線及語譜圖
的曲線及語譜圖
a.的時域曲線;b.的語譜圖
Figure2. Curve and spectrogram of
a. curve of ; b. spectrogram of
3.1.3 最佳權值向量及權值偏差的度量
令 =
=  ,可求得
,可求得 的最大值為
的最大值為 ,且當
,且當 時,
時, ,近似為0。故濾波器階數M取為150,最佳權值向量
,近似為0。故濾波器階數M取為150,最佳權值向量 ,且
,且 為0.489。
為0.489。
定義對數權值失調 以衡量權值向量與最佳權值向量間的相對偏差,如式(12)所示。
以衡量權值向量與最佳權值向量間的相對偏差,如式(12)所示。
 |
3.2 預處理的設計
考慮到第一和第二心音主要能量通常集中于150 Hz以下的低頻段,而聽診過程中的典型環境噪音(例如語音、哭叫聲、音樂等)主要能量的頻段通常在150 Hz以上,采用了簡單的一階線性預處理 ,當采樣頻率為8 kHz時,可抑制150 Hz以下的信號而放大150 Hz以上的信號。
,當采樣頻率為8 kHz時,可抑制150 Hz以下的信號而放大150 Hz以上的信號。
經 預處理后,
預處理后, 的第一、第二心音幅值顯著減小,且150 Hz以下頻段的功率譜密度降低約20 dB。預處理后,
的第一、第二心音幅值顯著減小,且150 Hz以下頻段的功率譜密度降低約20 dB。預處理后, 不同時段的幅值有增有減,其功率譜密度在500 Hz以下頻段顯著降低,而在1 000 Hz以上頻段未減小,甚至在高頻段會增加。統計各信號的均方值或范數均方值以分別作為
不同時段的幅值有增有減,其功率譜密度在500 Hz以下頻段顯著降低,而在1 000 Hz以上頻段未減小,甚至在高頻段會增加。統計各信號的均方值或范數均方值以分別作為 、
、 、
、 和
和 的估計值,依次得
的估計值,依次得 、
、 、0.297和0.603。這些結果表明,
、0.297和0.603。這些結果表明, 的峰值和均值均分別遠小于
的峰值和均值均分別遠小于 的峰值和均值;但
的峰值和均值;但 既可能大于也可能不大于
既可能大于也可能不大于 ,兩者的均值差別不大,后者甚至稍大。各信號的曲線及功率譜密度曲線參見附件2,
,兩者的均值差別不大,后者甚至稍大。各信號的曲線及功率譜密度曲線參見附件2, 、
、 、
、 和
和 隨時間變化的曲線參見附件3。
隨時間變化的曲線參見附件3。
3.3 自適應濾波結果
本節分別針對固定步長控制參數的NLMS算法和一種變步長控制參數的自適應算法[19],比較其增加線性預處理前、后的濾波效果。
3.3.1 固定步長控制參數算法
前一種算法的步長控制參數 取0.06。分別對比圖2b帶噪心音信號
取0.06。分別對比圖2b帶噪心音信號 和圖3b及圖3c降噪后信號的語譜圖,均可發現,算法運行6 s后,環境噪音被顯著抑制,主要表現為環境噪音對應的圖2b中高亮的高頻分量被顯著抑制。此外,對比圖3a心音和圖3b無預處理自適應濾波后信號的語譜圖,可以發現濾波后依然殘余帶狀條紋,提示算法對嬰兒啼哭聲、說話聲和樂曲聲的抑制效果不夠理想;尤其是在第一、第二心音處,圖3a和圖3b的語譜圖差別更大,說明第一、第二心音對濾波器的權值更新產生負面影響。可見,無預處理的自適應降噪效果較差,無法有效抑制環境噪音。而對比圖3a心音和圖3c含預處理自適應濾波后信號的語譜圖,兩者當濾波器權值收斂后(第6 s后)差別很小,提示降噪效果較為理想。
和圖3b及圖3c降噪后信號的語譜圖,均可發現,算法運行6 s后,環境噪音被顯著抑制,主要表現為環境噪音對應的圖2b中高亮的高頻分量被顯著抑制。此外,對比圖3a心音和圖3b無預處理自適應濾波后信號的語譜圖,可以發現濾波后依然殘余帶狀條紋,提示算法對嬰兒啼哭聲、說話聲和樂曲聲的抑制效果不夠理想;尤其是在第一、第二心音處,圖3a和圖3b的語譜圖差別更大,說明第一、第二心音對濾波器的權值更新產生負面影響。可見,無預處理的自適應降噪效果較差,無法有效抑制環境噪音。而對比圖3a心音和圖3c含預處理自適應濾波后信號的語譜圖,兩者當濾波器權值收斂后(第6 s后)差別很小,提示降噪效果較為理想。
 圖3
部分信號的語譜圖
圖3
部分信號的語譜圖
a.;b.無預處理時的;c.含預處理時的
Figure3. Spectrograms of certain signalsa.; b. when ; c. when
采用式(12)所定義的對數權值失調可更清晰地衡量權值偏差的相對大小及降噪效果。如圖4a和圖4b所示,無預處理和含預處理自適應降噪算法的 均可在6 s內減小到-20 dB以下。但隨后無預處理自適應濾波算法的
均可在6 s內減小到-20 dB以下。但隨后無預處理自適應濾波算法的 會出現周期性的大幅波動,且其波動的時間點恰好對應于第一、第二心音出現的時刻,表明濾波器權值因受第一、第二心音的影響而周期性產生失調;而含預處理自適應降噪算法的
會出現周期性的大幅波動,且其波動的時間點恰好對應于第一、第二心音出現的時刻,表明濾波器權值因受第一、第二心音的影響而周期性產生失調;而含預處理自適應降噪算法的 則持續減小且幾乎不出現波動,表明其濾波器權值的收斂幾乎不受第一、第二心音的影響。算法運行6 s后,統計各時刻
則持續減小且幾乎不出現波動,表明其濾波器權值的收斂幾乎不受第一、第二心音的影響。算法運行6 s后,統計各時刻 的均值以作為穩態均方權值偏差
的均值以作為穩態均方權值偏差 的估計值,無預處理和含預處理的自適應降噪算法的結果分別為:0.507和
的估計值,無預處理和含預處理的自適應降噪算法的結果分別為:0.507和 ,前者略大于
,前者略大于 ,后者則遠小于
,后者則遠小于 。由此可知,含預處理的自適應濾波器對于第一、第二心音這類脈沖分量的魯棒性要遠高于無預處理的自適應濾波器。
。由此可知,含預處理的自適應濾波器對于第一、第二心音這類脈沖分量的魯棒性要遠高于無預處理的自適應濾波器。
 圖4
固定步長NLMS和VSS-RSA算法增加預處理前、后對數權值失調隨時間變化的曲線
圖4
固定步長NLMS和VSS-RSA算法增加預處理前、后對數權值失調隨時間變化的曲線
a. 固定步長NLMS且無預處理;b. 固定步長NLMS且含預處理;c. VSS-RSA算法且無預處理;d. VSS-RSA算法且含預處理
Figure4. Logarithmic weight misalignment of a NLMS filter and that of a VSS-RSA filter with and without preprocessinga. NLMS without preprocessing; b. NLMS with preprocessing; c. VSS-RSA without preprocessing; d. VSS-RSA with preprocessing
3.3.2 變步長控制參數算法
式(11)表明,減小步長控制參數 或
或 均有助于降低穩態均方權值偏差,且兩者的作用相對獨立。這意味著可以在預處理的基礎上增加變步長算法,以進一步減小權值偏差和輸出誤差,提升環境音降噪性能。本節變步長控制參數的自適應算法采用了文獻[19]提出的變步長魯棒飽和算法(variable step-size robust saturation algorithm,VSS-RSA),該算法按式(13)所示的方式更新權值:
均有助于降低穩態均方權值偏差,且兩者的作用相對獨立。這意味著可以在預處理的基礎上增加變步長算法,以進一步減小權值偏差和輸出誤差,提升環境音降噪性能。本節變步長控制參數的自適應算法采用了文獻[19]提出的變步長魯棒飽和算法(variable step-size robust saturation algorithm,VSS-RSA),該算法按式(13)所示的方式更新權值:
 |
其中, 為飽和函數,
為飽和函數, ,且
,且 ,飽和限估計值為
,飽和限估計值為
 |
其中,初始值 ,而
,而 為人工截除心音
為人工截除心音 中第一和第二心音片段后所得剩余部分信號的標準差。與文獻[19]中僅對
中第一和第二心音片段后所得剩余部分信號的標準差。與文獻[19]中僅對 取絕對值不同,為保證
取絕對值不同,為保證 不小于0,此處的式(14)對等式右邊的分子取絕對值。
不小于0,此處的式(14)對等式右邊的分子取絕對值。
對該變步長控制參數的VSS-RSA算法,增加預處理 前、后,對數權值失調
前、后,對數權值失調 隨時間變化的曲線分別如圖4c和圖4d所示。對比圖4b和圖4c可知,固定步長控制參數但增加預處理時,
隨時間變化的曲線分別如圖4c和圖4d所示。對比圖4b和圖4c可知,固定步長控制參數但增加預處理時, 收斂速度稍慢,但基本為單調減小而不會出現明顯的波動;而變步長控制參數但不作預處理時,
收斂速度稍慢,但基本為單調減小而不會出現明顯的波動;而變步長控制參數但不作預處理時, 收斂速度快,但會出現一定幅度的波動。此外,分別對比圖4b和圖4d、圖4c和圖4d可知,若同時采用變步長控制參數算法并增加預處理,則
收斂速度快,但會出現一定幅度的波動。此外,分別對比圖4b和圖4d、圖4c和圖4d可知,若同時采用變步長控制參數算法并增加預處理,則 不僅單調收斂而且收斂速度更快。
不僅單調收斂而且收斂速度更快。
4 結論
本文分析了線性預處理對于提升自適應濾波方法在聽診環境音降噪性能上所起的作用,主要貢獻為:針對雙通道NLMS自適應降噪算法,① 分析并闡明了自適應濾波器的穩態均方權值偏差與體音信號方差及環境噪音方差之間的量化關系;② 基于該量化關系解釋了線性預處理可改善環境音降噪效果的原因,并形成了線性預處理環節的設計原則。所形成的設計原則為:經其處理后,體音方差 或功率譜密度
或功率譜密度 顯著減小,而副通道環境噪音方差
顯著減小,而副通道環境噪音方差 或功率譜密度
或功率譜密度 不明顯減小甚至增大。基于該原則的頻域設計方法簡單易行,且便于引入“體音信號的頻譜特點”等先驗知識來確定預處理環節的參數。
不明顯減小甚至增大。基于該原則的頻域設計方法簡單易行,且便于引入“體音信號的頻譜特點”等先驗知識來確定預處理環節的參數。
第3節心音聽診環境音降噪的結果表明,不管采用的是變步長控制參數還是固定步長控制參數的算法,在其余參數相同的前提下,僅簡單地增加一階線性預處理,即可有效抑制第一和第二心音等脈沖分量對自適應濾波器穩態均方權值偏差的影響而顯著提升環境音降噪性能。因此,若計算資源有限,例如需要在運算能力低的單片機上實現,可只增加線性預處理,其計算量小,非常適合應用于體積和成本受限的可穿戴設備上;而若計算資源相對豐富,則可考慮同時增加變步長控制參數的自適應算法。
應指出的是,由于環境噪音和體音信號的頻譜存在重疊的頻段,線性預處理并不總能精細地區別對待,其靈活程度有限。本文的后續研究將針對各種體音信號,探索建立針對性更強的非線性預處理方法。
重要聲明
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
作者貢獻聲明:莫鴻強負責理論推導及數據分析;田翔負責算法實現及算法驗證方案設計;李彬負責算法分析;田軍章負責降噪需求分析及數據收集。四位作者共同參與了論文寫作。
本文附件見本刊網站的電子版本(biomedeng.cn)。