癲癇發作期腦電與發作間期癲癇樣放電具有近似的波形，有效提取癲癇發作的特征在理論和實踐上至關重要。本文分別在多個采樣間隔下，利用可見小圖構建狀態轉移網絡并挖掘網絡特征發現：發作期在采樣間隔變化的情況下更能維持特征波形，且采樣間隔變化較小時的特征網絡結構不易發生改變；而發作間期癲癇樣放電的特征網絡結構，則是在相對較大的采樣間隔范圍內不易改變；此外，發作期關鍵節點在時序上具有長程相關性，對調控系統行為起重要作用。本文研究還發現，對于500 Hz左右的立體定向腦電圖而言，當采樣間隔為0.032 s時，兩者特征差異最大。綜上，本文研究有效揭示了大腦系統病理變化特征與采樣間隔之間的關聯規律，這在臨床診斷上對癲癇的識別、分類與預測具有潛在的應用價值。
引用本文： 張鐳, 閻爽, 顧長貴. 采樣間隔依賴下癲癇信號的狀態轉移網絡特征提取. 生物醫學工程學雜志, 2024, 41(6): 1128-1136. doi: 10.7507/1001-5515.202406023 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
癲癇是一種因大腦節律改變導致的異質性疾病，通過研究電生理變化來準確識別、分類以及預測癲癇發作信號至關重要[1]。癲癇發作可以簡單地分為發作期與發作間期。其中，發作期是指癲癇持續性發作、臨床癥狀表現明顯的時間段，其腦電經典波形通常為棘波與慢波復合形成的棘慢波[2]。另一方面，在癲癇發作間期往往會出現癲癇樣放電（interictal epileptiform discharges，IED），這時腦電圖會出現多棘波、尖慢波、棘慢波等與發作期類似的波形[3]。由于癲癇發作的時間不可預測，通常需要對患者的腦電波進行長期監控，導致產生大量的患者腦電數據，而傳統的對患者腦電數據的視覺檢測方法高度依賴于醫生的個人經驗，具有很強的主觀性且非常耗時[4]。為了克服這些局限，近年來癲癇性發作的特征提取已經成為一個研究熱點。
立體定向腦電圖（stereo-electroencephalography，SEEG）通過一組立體分布的電極陣列探測三維大腦內電活動，能夠準確定位癲癇起源區，被廣泛用于癲癇患者的發作檢測[4]。SEEG包含了大腦系統中各個腦區或神經元集群的宏觀動力學規律以及其中多個元素之間的信息交互過程，其特征通常利用時域分析、頻域分析、時頻域分析、非線性分析和復雜網絡等方法提取[5-7]。傳統的時頻分析提取的特征具有高度的主觀性，依賴于數據分析者對該領域專業知識的掌握程度。非線性分析，例如功率譜密度、李雅普諾夫（Lyapunov）指數、排列熵等，雖然在癲癇發作的預測中具有巨大的潛力，但是依舊沒有系統地反映整體與局部之間特征變化規律[8-10]。此外，基于時間序列中順序采樣點之間可見性關系構建的網絡，即可見圖算法，也常用于檢測癲癇信號與正常信號的差異[11-13]；但是和傳統的復雜網絡方法類似，可見圖算法及其延伸算法通常是從宏觀的角度去刻畫時間序列的結構特征，卻忽略了介于局部（如節點和連邊）與整體（網絡）之間的基本結構塊的特征以及其對整體行為的調控作用。Ribeiro[14]以樂高玩具為例，認為識別構成復雜網絡基本構建塊，對發現相互聯系的模式并理解宏觀現象的行為有重要意義，于是研究者們將那些在網絡中出現頻率較高的基本結構塊定義為“模體（motif）”[15-17]。基于此，Stephen等[18]在2015年提出了基于可見小圖方法（visibility graphlet approach）來分析時間序列。該研究通過將不同的基本結構塊視為節點，構建一個“網絡的網絡”，或稱為狀態轉移網絡（state transfer network，STN），發現STN中模體在演化過程中的分布具有長程相關性，并認為這樣的性質結合STN的網絡結構能在宏觀時間尺度上預測復雜系統的行為。
大量研究表明，腦電信號往往具有分形特征，即腦電數據在不斷放大后依然呈現相似的結構和規律 [19-22]。于是，在多個采樣間隔下構建STN來分析癲癇信號的結構特征與時間尺度的關聯性的構想應運而生，以期揭示系統內部的基本原理和機制。Wang等[23]曾在由不同赫斯特指數（Hurst exponent）所模擬的分數階布朗運動序列上開展類似研究，即在多個采樣間隔下對比仿真序列的STN。研究發現，這些網絡結構都具有一個“主干模式”，而這一主干模式往往代表一類數據中出現次數最多的局部結構轉移過程，這在數據分類中具有實際的應用價值。例如，在羅斯勒（R?ssler）系統產生的混沌時間序列中，主干模式包含兩個自環，其連接強度隨采樣間隔的增大而單調減小，然后與其他節點產生一個較大的回路，最終達到穩定狀態[23]。非線性混沌仿真系統中的主干模式在多個采樣間隔下不同程度地影響或調控著系統動力學行為。但隨機現象在數據中普遍存在，這樣的主干模式往往包含著隨機序列的結構，因此，如何提取表征具體的一類數據的特征需要進一步探索。
為了去除分析過程中隨機成分的干擾，并找到區分發作期腦電波形與發作間期癲癇樣放電數據特征的最優采樣間隔，本文提出了在多個采樣間隔下利用可見小圖構建STN，并將強STN與打亂后序列的強STN作差集運算，分析網絡連邊和節點的特征提取方法。具體來說，即保留癲癇信號特有的轉移模式，除去與隨機序列STN相同的轉移過程所得到的網絡結構，并將其定義為差分狀態網絡。于是，在采樣間隔變化下，通過差分狀態網絡的連邊特征的變化以及模體在時間分布中出現的規律，可以判斷出兩類數據差異最大的采樣間隔，以期為準確識別、分類和預測癲癇發作信號提供理論依據。為了表述方便，后文統一將發作間期癲癇樣放電，簡述為：發作間期。
1 STN及其特征提取
1.1 可見小圖
可見小圖分析能保留數據拓撲結構的時間行為以及系統動力學機制。具體來說，令N表示數據長度，考慮時間序列{x1, x2, …, xN}，設置采樣因子（sampling factor）（以符號s表示），且s為自然數，分別對該時間序列進行降采樣，其中，原始時間序列s = 1。然后在不同采樣間隔下令長度為
的時間窗口沿序列連續滑動，得到新的片段集合為
= {xk, xk+1, …, xk + w ? 1}，k = 1, 2, …, N ? w + 1在每一個序列片段中，如果數據點xa和xb之間符合“可見法則”，反映在小圖中則認為xa和xb之間存在有向連邊，可見法則如式（1）所示：
 |
其中，a、b、c是片段集合
中任意數據點x位置下標，分別表示其先后順序。構造的可見小圖可以用一組維度為w × w的鄰接矩陣集{Lk}表示，k = 1, 2, …,N ? w + 1。
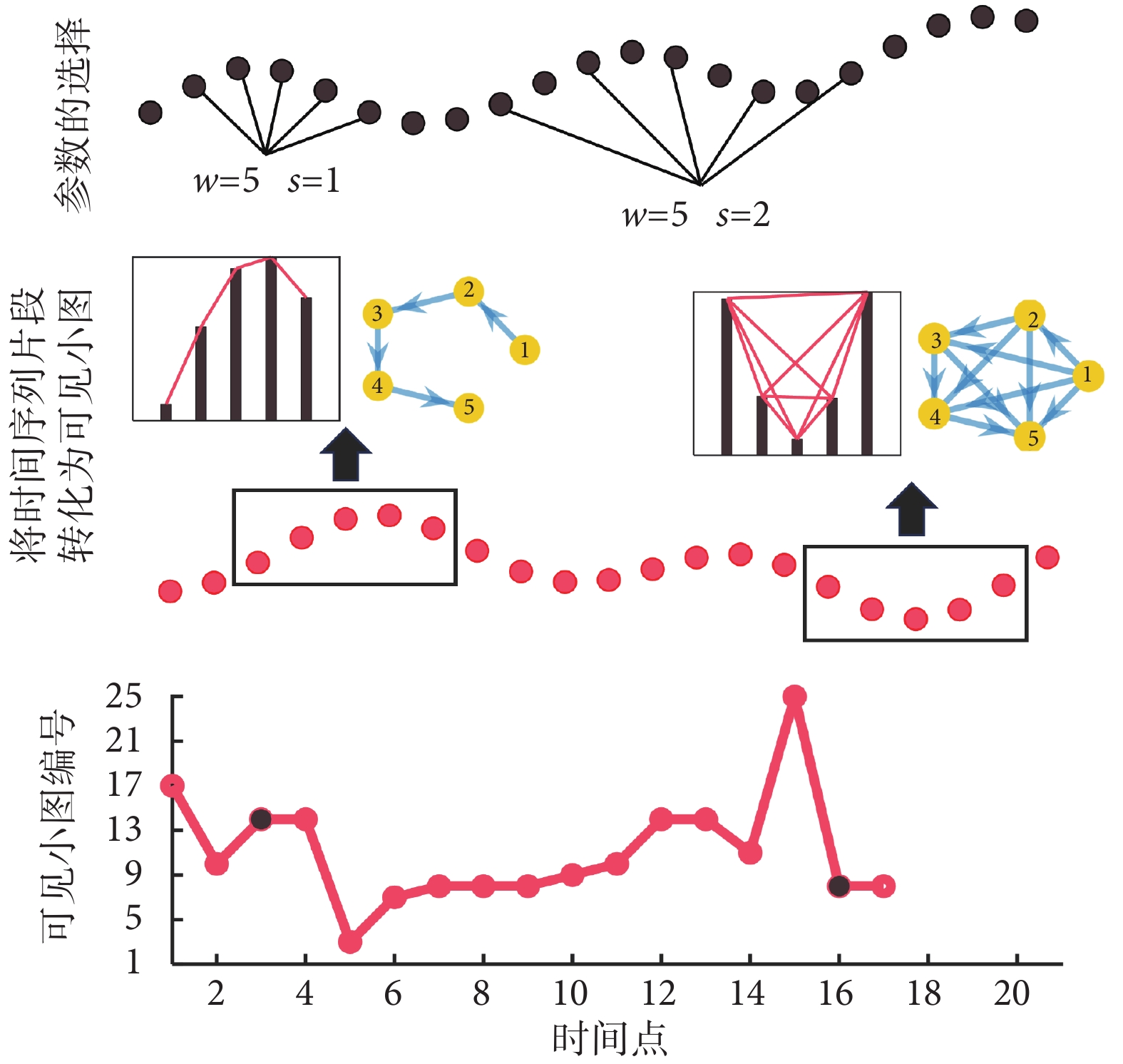
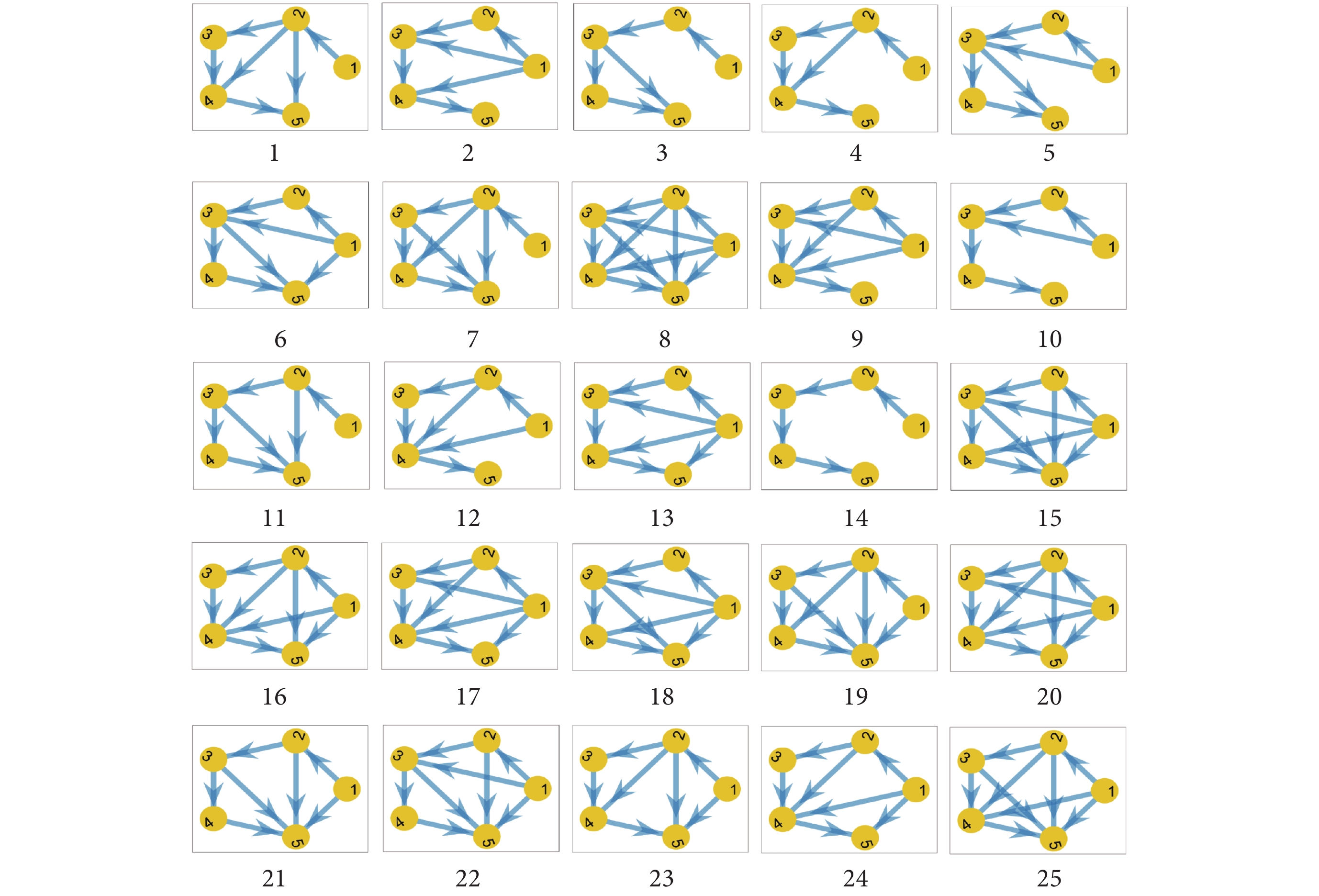
對于時間窗的選擇，Stephen等[18]認為w=5是最優的窗口長度，這在很大程度上是因為5個點確定了一條拋物線。通過這種方式，可見小圖揭示了數據局部波動程度的變化過程，并將相同程度的波動變化定義為同一種狀態或同一類可見小圖。即在序列{Lk}中，如果任意兩個小圖的鄰接矩陣相同，則將后一個小圖的編號替換為前一個小圖的編號。因此，可以得到在不同采樣間隔下，與序列{Lk}長度相同的新序列{Gpk}（p∈[1, M0] ），其中M0為所有互不相同的可見小圖類型數。具體算法流程如圖1所示，第一行展示了參數的選擇，w為選取的時間窗口，而s則代表了采樣間隔的選取過程。以5個時間點為窗口構造的可見小圖序列{Lk}中共有25種可見小圖類型，并且每個小圖都被分配了一個唯一的編號，如圖2所示。其中，可見小圖14和可見小圖8的片段序列，以及轉換后的新序列{Gpk}（p∈[1, 25]，k = 17），如圖1中的最后兩行所示。
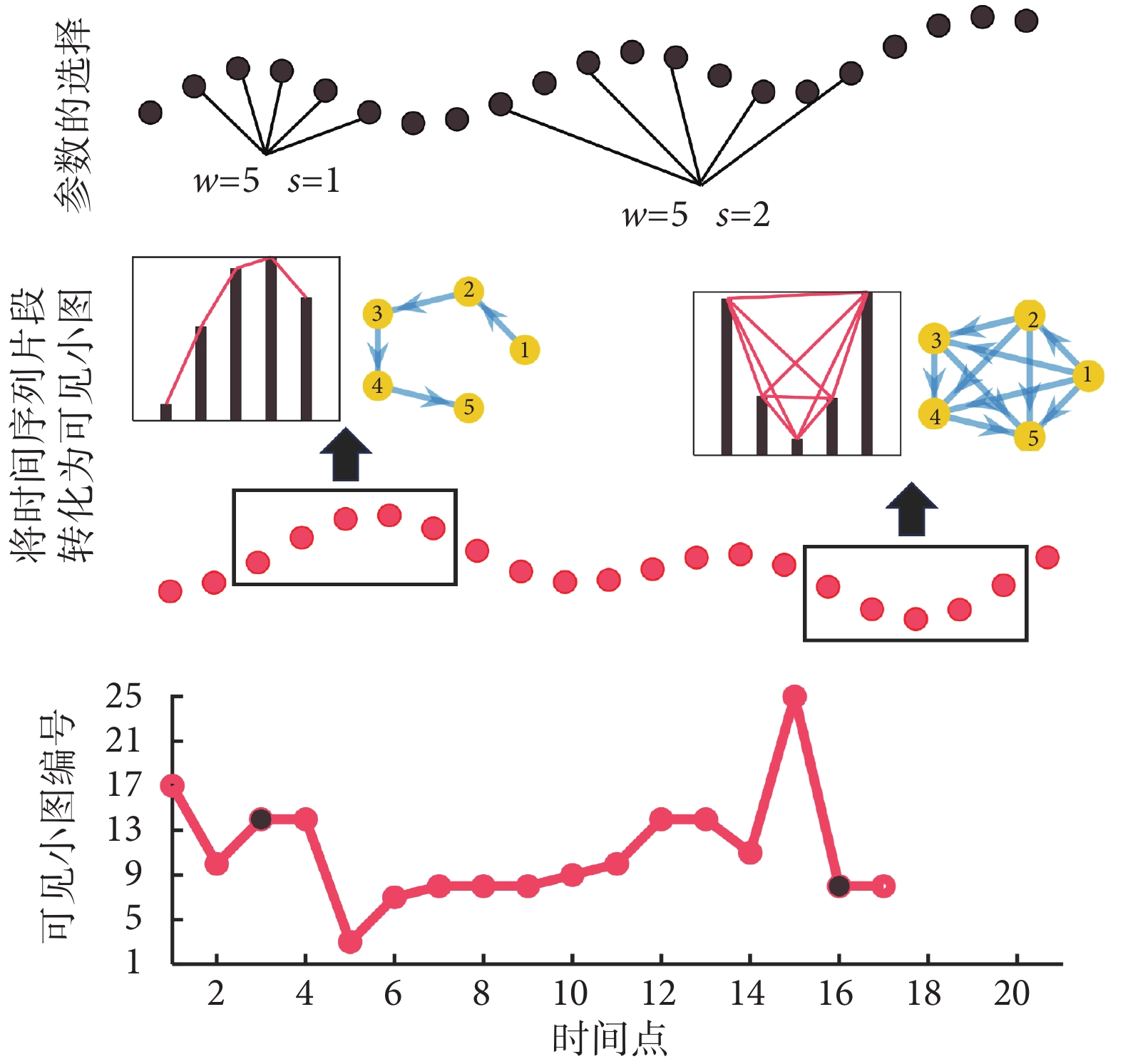圖1
可見小圖算法
Figure1.
Visibility graphlet algorithm
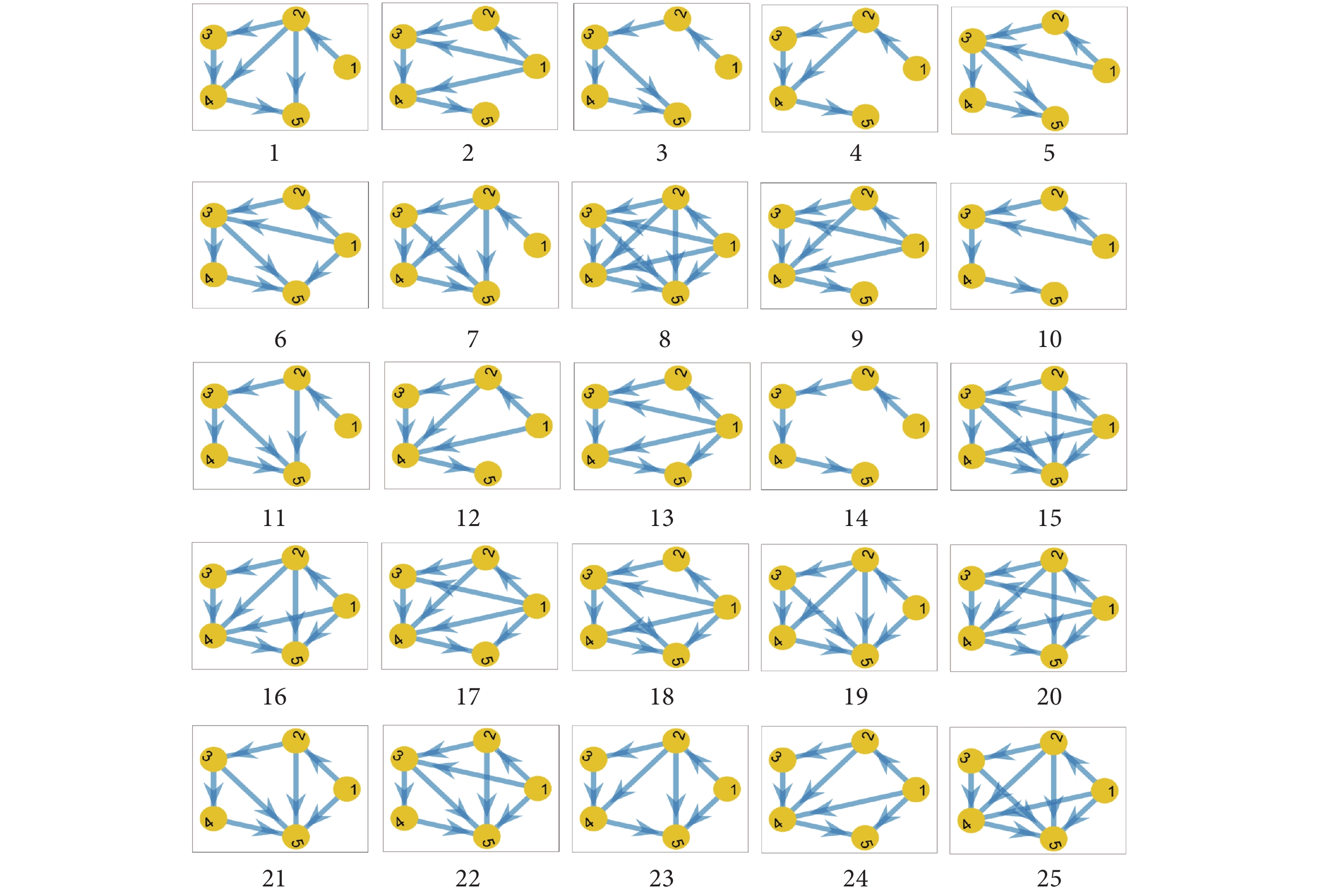圖2
25種可見小圖及其編號
Figure2.
25 types of visibility graphlets and their numbers
1.2 STN及其特征
本研究中STN的節點為25種可見小圖，有向連邊的權重定義為出現在序列{Gpk}（p∈[1, 25]）中連續兩個可見小圖出現的次數或占整個過程的比重。其中，強STN指的是保留最大的前20條連邊結構，如果第20 條連邊的權重與第21條連的邊權重相等，則一并保留。因此，通過在不同采樣間隔下利用可見小圖對癲癇信號局部特征的提取，可以有效模擬不同尺度下的離散空間中數據局部拓撲結構的“軌跡”。
1.2.1 差分狀態網絡
網絡中節點或可見小圖之間的強相關性，通常意味著一個時間序列中的兩類局部拓撲特征之間轉換的頻率較高，而且特定的一類數據往往具有與隨機網絡不同的轉移過程。為了找到這樣的特征網絡結構模式，在不同采樣間隔下構建所有數據的強STN和對應的打亂后序列的強STN，分別用SGori和SGshu表示。然后，作差集運算，得到該采樣間隔下的差分狀態網絡SGDSN，計算公式如式（2）所示：
 |
其中，link表示網絡中的任一有向連邊，差分狀態網絡SGDSN的權重代表了這一尺度下有多少數據具有這樣的有向連邊，而節點大小則反映了連邊度。由于任意兩個網絡都可由0-1鄰接矩陣Amn和Bmn表示，于是通過計算二維相關系數R來量化網絡結構的差異性，如式（3）所示：
 |
其中，
和
代表矩陣元素的平均值；而R ∈ [0,1]，其值越大代表相似度越高。
1.2.2 標度特征
從節點的角度來看，STN中節點或可見小圖出現的頻數稱為度，而模體是指在隨機網絡中出現的次數等于或大于真實網絡的概率P < 0.01的節點[14-16, 24]。模體在時間序列中的分布充分反映了組成復雜系統的局部特征對調節、控制系統演化行為的作用。因此，本研究利用重標極差分析法（rescaled range analysis，R/S）[25-26]計算了模體位置序列的長程相關性。通過在多個采樣間隔下記錄每一類模體出現的位置標記ωk（k = 1, 2, …, M，其中M為模體出現的頻數），得到位置序列{ωk + 1 ? ωk}（k = 1, 2, …, M?1）。以長度為n均分序列ωk為A個相鄰的子區間，即A×n ≈ M ? 1。如果對應位置序列存在標度不變性，則有極差與子區間標準差之比R/S(n)
nH，其中H為赫斯特指數。若H = 0.5，則表示模體在整個系統演化過程中是隨機出現的；如果H > 0.5，說明模體的出現是一個具有長程的持久性記憶過程；相反，如果H < 0.5，這意味著模體在時間維度上是反持續性的，亦稱為“均值回歸”，后續可能會出現反轉。
2 方法驗證與結果分析
2.1 實驗材料
本研究使用的SEEG信號來自美國國家心理健康研究所（National Institute of Mental Health，NIMH）贊助的神經元公開（OpenNeuro）數據庫，目前該數據庫由軟綿媒介公司（Squishymedia）開發、維護和托管。本文分析了8位共享在該公開數據庫上的受試者數據（編號為：060、112、116、117、130、133、134、138）[27]，共計28次發作，數據長度大約在5 min左右。然后，通過高通濾波器（截止頻率等于0.16 Hz，?3 dB）和一階低通濾波器（截止頻率等于97 Hz，?3 dB）對數據進行預處理。高通濾波器用于去除基線中非常緩慢的變化，一階低通濾波器用于避免混疊的情況發生。本文利用各頻段能量隨時間的動態變化對發作期所有的數據計算了致癇指數（epileptogenicity index，EI），即定量評估了致癇的程度[28]。最后，選取了109根EI有顯著波動的電極，和101根記錄發作間期腦電的電極進行深入的分析。受試者臨床信息如表1所示。
表1
本研究中OpenNeuro 數據集描述
Table1.
Description of OpenNeuro Dataset in this study
2.2 采樣間隔依賴下差分狀態網絡
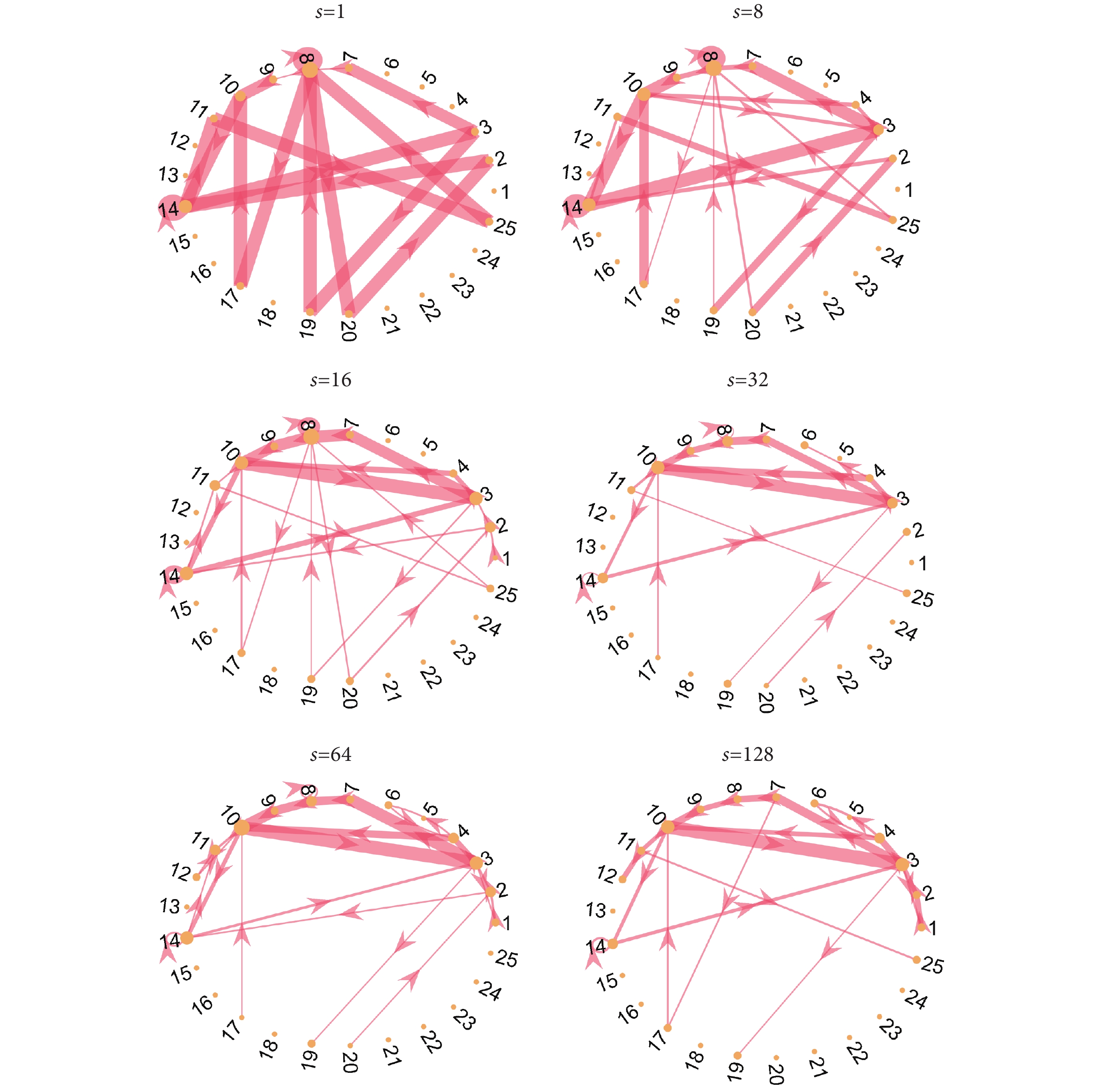
設置s
{1, 8, 16, 32, 64, 128}，對應的采樣間隔大約為：0.002、0.016、0.032、0.064、0.128、0.256 s。并利用可見小圖算法分別在不同的采樣因子下構建STN，然后對每一組癲癇信號強STN與打亂后的強STN做差后，得到的差分狀態網絡，如式（2）所示。網絡中，有向連邊的權重代表了109組發作期或101組發作間期數據中有多大比例的數據具有這樣的連邊。其中，發作期與發作間期腦電在不同采樣間隔下的差分狀態網絡分別如圖3和圖4所示。可以看到，在s=1或采樣間隔為0.002 s的時候，發作期與發作間期腦電的差分狀態網絡結構相同，只在部分結構統計出來的數量上（即連邊權重上）有些許差異。但隨著s變大時，與可見小圖8有關的特征結構8
、
、
、
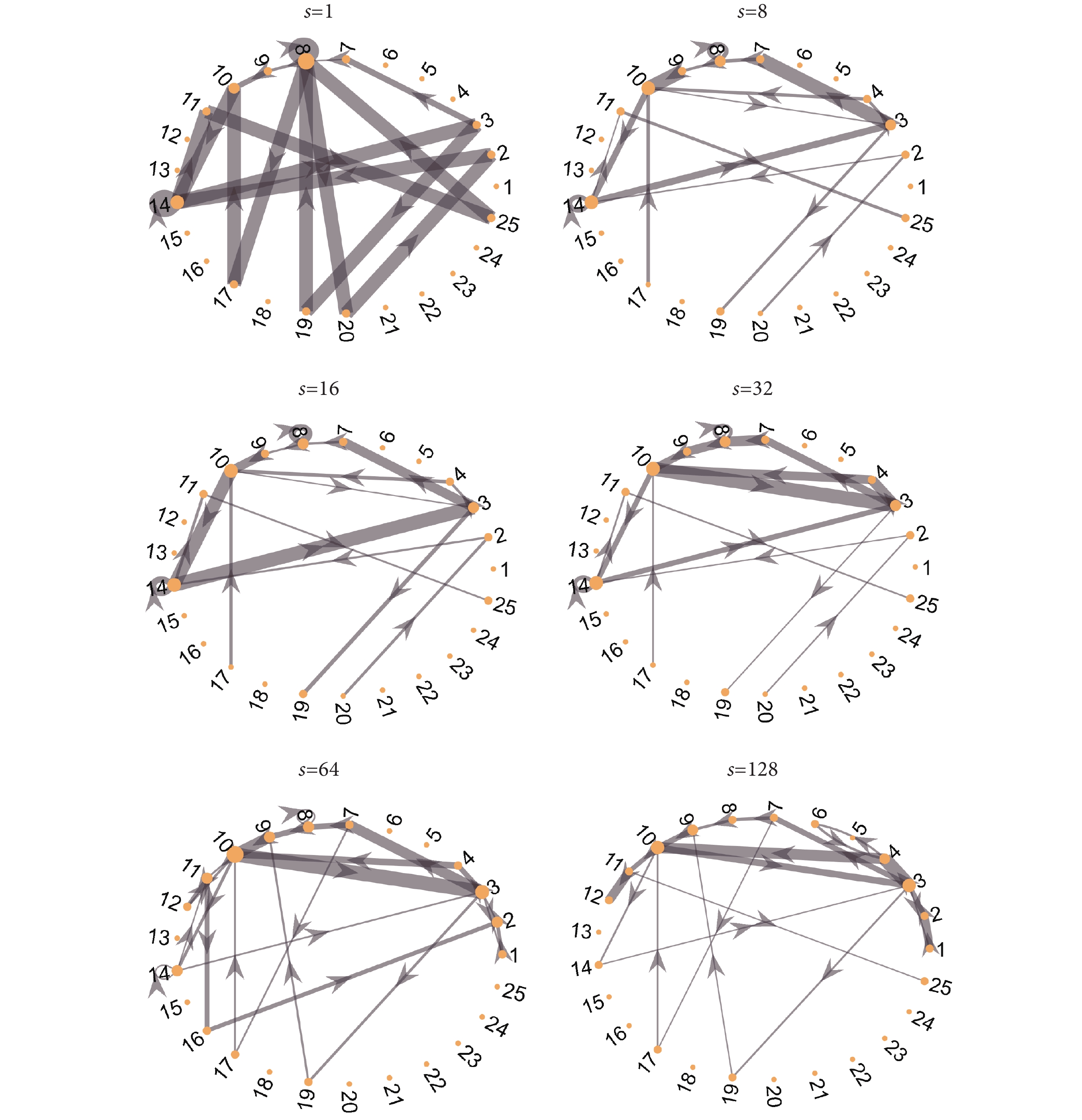
同步減小。到s=32時，該類結構便不屬于概率最大的前20條連邊之內；對比發作間期的差分狀態網絡，在s=8時即已不再屬于。類似的，隨采樣間隔變大，其出現概率同步減弱的結構還有8→8和14→14的自環，并且這兩個自環與利用R?ssler系統仿真的混沌時間序列中出現的兩個自環節點是相同的兩類可見小圖，其隨采樣因子變化的規律也類似[23]。這意味著，R?ssler系統下的非線性混沌時間序列可能與癲癇信號的動力學機制有相似的部分。總的來說，從差分狀態網絡結構演變的過程對比來看，發作期腦電STN中的網絡結構在較小的采樣間隔下的魯棒性更強，而發作間期的網絡結構則相對在較大采樣間隔范圍內保持不變。這表明了表征癲癇發作期與發作間期的腦電信號特點在不同的采樣間隔下有所分別。
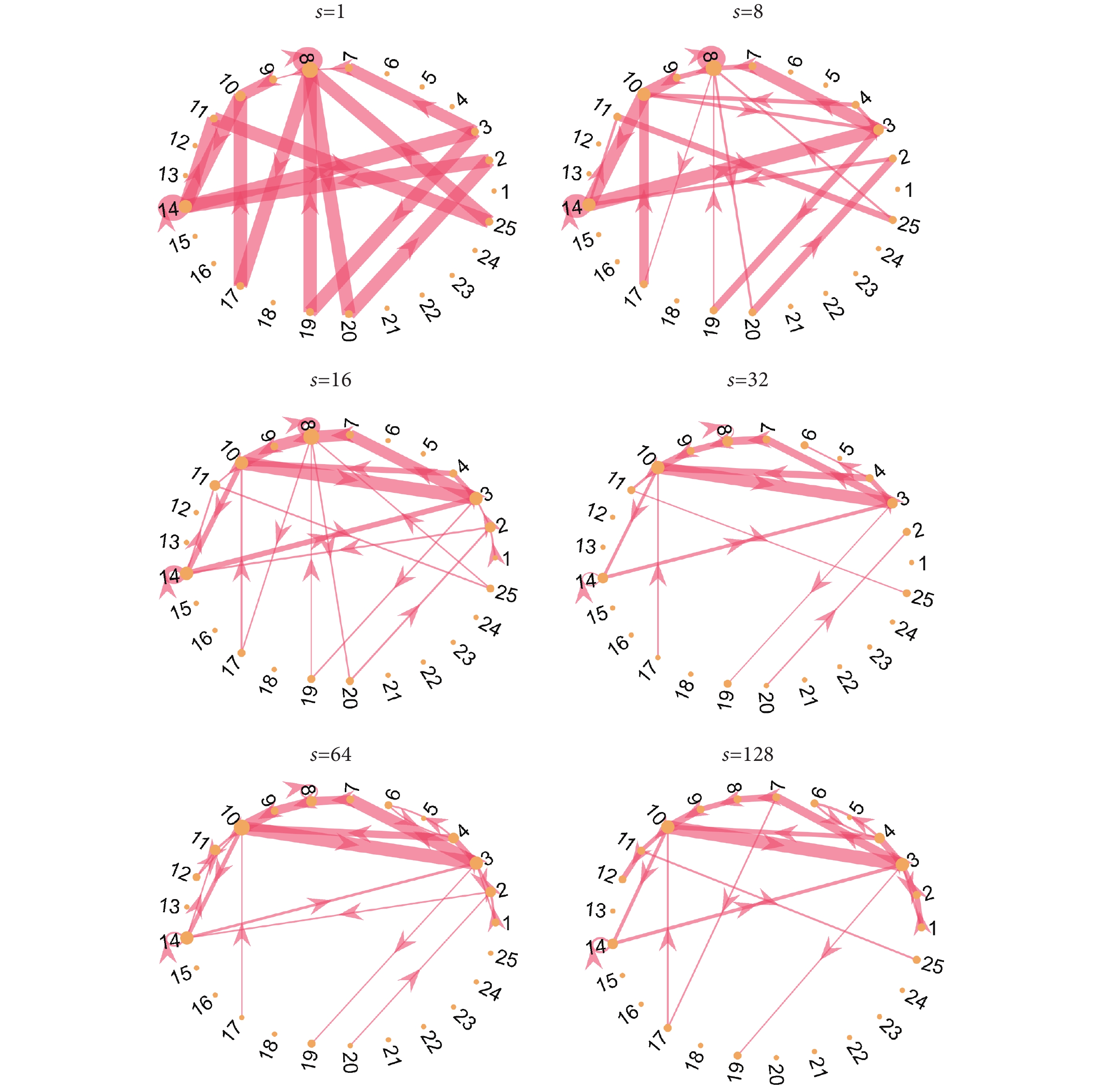圖3
不同采樣間隔下發作期的差分狀態網絡
Figure3.
Differential state network for ictal periods at different sampling intervals
圖4
不同采樣間隔下發作間期的差分狀態網絡
Figure4.
Differential state network for interictal periods at different sampling intervals
為了定量說明網絡結構的差異，通過計算如式（3）所示的兩個網絡鄰接矩陣之間的二維相關系數，可以量化在不同采樣間隔下以及不同發作類型之間的網絡結構相似度，最終分析結果如表2所示。符號Asind表示網絡鄰接矩陣，其中s為采樣因子，數據類型ind ∈{發作期，IED}。可以看到，采樣因子為1和128時，發作期差分狀態網絡的相關系數比發作間期的大，這意味著相比發作間期的數據，發作期數據的特征波形在采樣間隔變化的情況下相對穩定。通過連續的兩個采樣間隔發現，發作期腦電在較小的采樣間隔上網絡結構變化較慢，在采樣因子為16～32之間會有一個較大的差異，相關系數為0.78左右。相比之下，發作間期在采樣因子為1～8之間相似度較低，而在采樣因子為8～32之間網絡結構變化較慢，相關系數均在0.96附近。同時，本文還分析了同一采樣因子下兩類數據的差分狀態網絡結構，發現在s = 1時相關系數達到0.9以上，并不能很好地區分兩類數據。但在s = 16，即采樣間隔為0.032 s時兩者相似度最低。這一分析結果與圖3、圖4所展示的差分狀態網絡結構相吻合。
表2
差分狀態網絡結構相似性對比
Table2.
Correlation coefficient of two differential states network structures
2.3 采樣間隔依賴下STN的標度特征
2.3.1 模體的提取
模體在STN中類似于網絡中的關鍵節點具有較大的連邊度，同時在整個演化過程中比打亂后的STN中對應的節點更加頻繁地出現，且差異明顯。不同采樣間隔下癲癇信號STN平均后的節點度以及模體的選取如圖5所示。為了更好地進行對比，本研究將縱坐標數值大小映射到區間［1, 10］中，黃色虛線代表的是打亂后序列STN節點度，而紅色和黑色連線則是代表的發作期與發作間期STN的節點度，并且與之顏色對應的陰影部分則是標記的該發作類型中模體。從發作期與發作間期數據中25種可見小圖的節點度可以看出，當s∈{1, 8, 16, 32}時，發作期與發作間期數據的模體變化一致，都是由可見小圖8 和14 演化到可見小圖3、8、10 和14。但當采樣因子達到64之后，發作間期的模體已經有了明顯的不同，并且到s = 128時，節點度與打亂后網絡中對應節點度之間不再具有明顯的差異，也就不再有模體存在。但發作期STN中的模體在s = 64時依然為可見小圖3、8、10 和14，而到s = 128時只留下可見小圖3和10。
圖5
不同采樣間隔下的節點度以及模體
Figure5.
Degree and motifs at different sampling intervals
2.3.2 STN的標度性質
如圖6所示，展示的是通過R/S方法得到所有數據中模體位置序列赫斯特指數的平均值及其方差。可以看到當s=1時，由于采樣間隔較小，會捕獲更多精細結構，提取的信號會在子區間上重復，波動更為強烈，因此無論是發作期還是發作間期下的模體位置序列的赫斯特指數普遍偏低[20, 29]。降采樣后，當s∈{8, 16, 32, 64, 128}時，癲癇信號的原始特征波形開始凸顯，因此發作期STN中模體位置序列的赫斯特指數普遍大于0.5，具有長程相關性或分形結構。對比發作間期采樣間隔增加后，模體位置序列的赫斯特指數普遍接近0.5左右，意味著發作間期的模體在時間序列中是趨于隨機出現的，與發作期形成鮮明的對比。
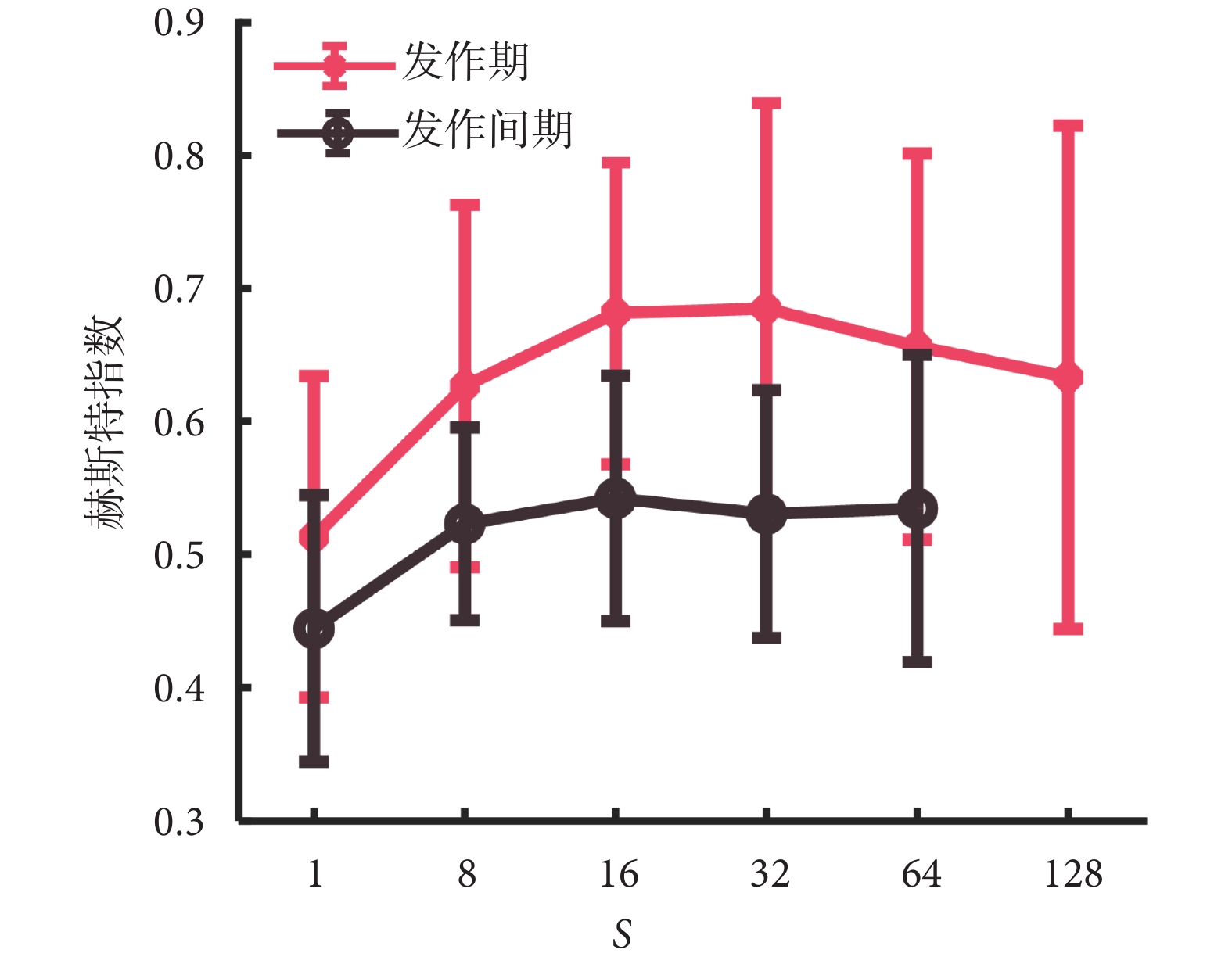圖6
不同采樣間隔下模體的赫斯特指數分布
Figure6.
The distribution of Hurst exponent of motifs at different sampling intervals
總的來說，在任意采樣間隔下，發作期中模體位置序列的赫斯特指數大于發作間期中的數值[21]。對比不同采樣因子下的分析結果可以發現，發作間期在s = 8時其赫斯特指數的分布就接近0.5，并隨采樣間隔增大繼續增加，依舊在0.5上下徘徊。而發作期則是在s = 16時基本達到穩定的區間內，但當采樣因子增加到64之后有所減弱，并有接近隨機分布的趨勢。而因此采樣因子為16，即0.032 s時，可以看作有效對比發作期與發作間期模體位置序列赫斯特指數的采樣尺度，這也對應了上文利用二維相關系數衡量網絡結構相似性中的分析結果。
3 結論
與健康受試者腦電圖相比，癲癇患者發作時正常腦電波活動減少或消失，腦電活動的頻率、節律、幅度和波形發生明顯變化，且時空分布明顯異常[29]。雖然目前有許多癲癇發作信號的特征提取方法，但是在采樣間隔發生變化下利用這些方法對特征演變過程的研究仍然是不足的[20, 29-30]。在多個尺度下分析系統的演化過程，是當前數據驅動下研究大腦系統動力學特性的有效途徑[31]。本文在多個采樣間隔下，利用可見小圖方法分析腦電信號的局部結構演變特征，并將同一類拓撲特征視為一種可見小圖，根據可見小圖之間的轉移概率構建不同采樣間隔下的STN，并分析兩類數據的STN網絡連邊特征和節點特征。最終，本文研究發現了病變大腦與健康大腦系統下的基本結構塊及其調控機制在采樣間隔變化下的規律，并找到兩者差異最大時的采樣間隔，有效揭示了健康和病理狀態下大腦的功能和活動。
本研究使用的是采樣率大約為500 Hz、持續時間約為5 min左右的癲癇SEEG數據。結果顯示，原始癲癇信號或者在采樣因子為1時，癲癇發作期與發作間期數據的差分狀態網絡結構類似，因此不能很好地區分這兩種數據。進一步改變采樣因子的大小，利用二維相關系數量化發作期與發作間期差分狀態網絡的結構差異，發現發作期網絡結構比發作間期網絡結構在采樣因子變化下更能維持特征波形；且在采樣間隔變化較小時，發作期差分狀態網絡結構不易改變；但發作間期的網絡結構在相對較大的采樣間隔下不易隨之而發生改變。對比來看，在采樣因子為16時，發作期與發作間期之間的特征差異最大。另一方面，通過分析網絡中的節點特征，發現在采樣因子大于1 時，發作期STN中模體的出現往往具有長程相關性，相比之下，發作間期的模體在時間維度上更傾向于隨機出現。且，從發作期與發作間期模體位置序列的赫斯特指數在多個采樣間隔下的分布來看，在s = 16時，即采樣間隔為0.032 s時，為較佳的采樣尺度。
擴散熵[32-33]、功能性網絡[34-35]、復雜度[36-37]等非線性方法都可運用于尋找大腦病理變化過程的特征，但這些方法沒有考慮尺度因素對結果的影響。在不同采樣間隔下研究STN，可以為人們提供新的標度行為，并用以區分不同發作類型的動力學機制，評估系統的狀態等。本文研究癲癇發作期與發作間期的STN在不同采樣間隔上的演化差異，為臨床診斷上用以分類或預測癲癇發作奠定了理論基礎。通過本文研究，希望可為其他類型的腦部疾病（如抑郁癥、阿爾茨海默癥、偏頭痛等）的研究提供新的思路。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：張鐳負責文獻調研、數據收集、提出研究問題和分析思路，以及文章的撰寫與修改；顧長貴，在分析數據的過程以及論文的撰寫和修改中進行了監督，并提出了批判性意見；閻爽，在論文的撰寫和修改中進行了指導。
0 引言
癲癇是一種因大腦節律改變導致的異質性疾病，通過研究電生理變化來準確識別、分類以及預測癲癇發作信號至關重要[1]。癲癇發作可以簡單地分為發作期與發作間期。其中，發作期是指癲癇持續性發作、臨床癥狀表現明顯的時間段，其腦電經典波形通常為棘波與慢波復合形成的棘慢波[2]。另一方面，在癲癇發作間期往往會出現癲癇樣放電（interictal epileptiform discharges，IED），這時腦電圖會出現多棘波、尖慢波、棘慢波等與發作期類似的波形[3]。由于癲癇發作的時間不可預測，通常需要對患者的腦電波進行長期監控，導致產生大量的患者腦電數據，而傳統的對患者腦電數據的視覺檢測方法高度依賴于醫生的個人經驗，具有很強的主觀性且非常耗時[4]。為了克服這些局限，近年來癲癇性發作的特征提取已經成為一個研究熱點。
立體定向腦電圖（stereo-electroencephalography，SEEG）通過一組立體分布的電極陣列探測三維大腦內電活動，能夠準確定位癲癇起源區，被廣泛用于癲癇患者的發作檢測[4]。SEEG包含了大腦系統中各個腦區或神經元集群的宏觀動力學規律以及其中多個元素之間的信息交互過程，其特征通常利用時域分析、頻域分析、時頻域分析、非線性分析和復雜網絡等方法提取[5-7]。傳統的時頻分析提取的特征具有高度的主觀性，依賴于數據分析者對該領域專業知識的掌握程度。非線性分析，例如功率譜密度、李雅普諾夫（Lyapunov）指數、排列熵等，雖然在癲癇發作的預測中具有巨大的潛力，但是依舊沒有系統地反映整體與局部之間特征變化規律[8-10]。此外，基于時間序列中順序采樣點之間可見性關系構建的網絡，即可見圖算法，也常用于檢測癲癇信號與正常信號的差異[11-13]；但是和傳統的復雜網絡方法類似，可見圖算法及其延伸算法通常是從宏觀的角度去刻畫時間序列的結構特征，卻忽略了介于局部（如節點和連邊）與整體（網絡）之間的基本結構塊的特征以及其對整體行為的調控作用。Ribeiro[14]以樂高玩具為例，認為識別構成復雜網絡基本構建塊，對發現相互聯系的模式并理解宏觀現象的行為有重要意義，于是研究者們將那些在網絡中出現頻率較高的基本結構塊定義為“模體（motif）”[15-17]。基于此，Stephen等[18]在2015年提出了基于可見小圖方法（visibility graphlet approach）來分析時間序列。該研究通過將不同的基本結構塊視為節點，構建一個“網絡的網絡”，或稱為狀態轉移網絡（state transfer network，STN），發現STN中模體在演化過程中的分布具有長程相關性，并認為這樣的性質結合STN的網絡結構能在宏觀時間尺度上預測復雜系統的行為。
大量研究表明，腦電信號往往具有分形特征，即腦電數據在不斷放大后依然呈現相似的結構和規律 [19-22]。于是，在多個采樣間隔下構建STN來分析癲癇信號的結構特征與時間尺度的關聯性的構想應運而生，以期揭示系統內部的基本原理和機制。Wang等[23]曾在由不同赫斯特指數（Hurst exponent）所模擬的分數階布朗運動序列上開展類似研究，即在多個采樣間隔下對比仿真序列的STN。研究發現，這些網絡結構都具有一個“主干模式”，而這一主干模式往往代表一類數據中出現次數最多的局部結構轉移過程，這在數據分類中具有實際的應用價值。例如，在羅斯勒（R?ssler）系統產生的混沌時間序列中，主干模式包含兩個自環，其連接強度隨采樣間隔的增大而單調減小，然后與其他節點產生一個較大的回路，最終達到穩定狀態[23]。非線性混沌仿真系統中的主干模式在多個采樣間隔下不同程度地影響或調控著系統動力學行為。但隨機現象在數據中普遍存在，這樣的主干模式往往包含著隨機序列的結構，因此，如何提取表征具體的一類數據的特征需要進一步探索。
為了去除分析過程中隨機成分的干擾，并找到區分發作期腦電波形與發作間期癲癇樣放電數據特征的最優采樣間隔，本文提出了在多個采樣間隔下利用可見小圖構建STN，并將強STN與打亂后序列的強STN作差集運算，分析網絡連邊和節點的特征提取方法。具體來說，即保留癲癇信號特有的轉移模式，除去與隨機序列STN相同的轉移過程所得到的網絡結構，并將其定義為差分狀態網絡。于是，在采樣間隔變化下，通過差分狀態網絡的連邊特征的變化以及模體在時間分布中出現的規律，可以判斷出兩類數據差異最大的采樣間隔，以期為準確識別、分類和預測癲癇發作信號提供理論依據。為了表述方便，后文統一將發作間期癲癇樣放電，簡述為：發作間期。
1 STN及其特征提取
1.1 可見小圖
可見小圖分析能保留數據拓撲結構的時間行為以及系統動力學機制。具體來說，令N表示數據長度，考慮時間序列{x1, x2, …, xN}，設置采樣因子（sampling factor）（以符號s表示），且s為自然數，分別對該時間序列進行降采樣，其中，原始時間序列s = 1。然后在不同采樣間隔下令長度為的時間窗口沿序列連續滑動，得到新的片段集合為 = {xk, xk+1, …, xk + w ? 1}，k = 1, 2, …, N ? w + 1在每一個序列片段中，如果數據點xa和xb之間符合“可見法則”，反映在小圖中則認為xa和xb之間存在有向連邊，可見法則如式（1）所示：
|
其中，a、b、c是片段集合中任意數據點x位置下標，分別表示其先后順序。構造的可見小圖可以用一組維度為w × w的鄰接矩陣集{Lk}表示，k = 1, 2, …,N ? w + 1。
對于時間窗的選擇，Stephen等[18]認為w=5是最優的窗口長度，這在很大程度上是因為5個點確定了一條拋物線。通過這種方式，可見小圖揭示了數據局部波動程度的變化過程，并將相同程度的波動變化定義為同一種狀態或同一類可見小圖。即在序列{Lk}中，如果任意兩個小圖的鄰接矩陣相同，則將后一個小圖的編號替換為前一個小圖的編號。因此，可以得到在不同采樣間隔下，與序列{Lk}長度相同的新序列{Gpk}（p∈[1, M0] ），其中M0為所有互不相同的可見小圖類型數。具體算法流程如圖1所示，第一行展示了參數的選擇，w為選取的時間窗口，而s則代表了采樣間隔的選取過程。以5個時間點為窗口構造的可見小圖序列{Lk}中共有25種可見小圖類型，并且每個小圖都被分配了一個唯一的編號，如圖2所示。其中，可見小圖14和可見小圖8的片段序列，以及轉換后的新序列{Gpk}（p∈[1, 25]，k = 17），如圖1中的最后兩行所示。
圖1
可見小圖算法
Figure1.
Visibility graphlet algorithm
圖2
25種可見小圖及其編號
Figure2.
25 types of visibility graphlets and their numbers
1.2 STN及其特征
本研究中STN的節點為25種可見小圖，有向連邊的權重定義為出現在序列{Gpk}（p∈[1, 25]）中連續兩個可見小圖出現的次數或占整個過程的比重。其中，強STN指的是保留最大的前20條連邊結構，如果第20 條連邊的權重與第21條連的邊權重相等，則一并保留。因此，通過在不同采樣間隔下利用可見小圖對癲癇信號局部特征的提取，可以有效模擬不同尺度下的離散空間中數據局部拓撲結構的“軌跡”。
1.2.1 差分狀態網絡
網絡中節點或可見小圖之間的強相關性，通常意味著一個時間序列中的兩類局部拓撲特征之間轉換的頻率較高，而且特定的一類數據往往具有與隨機網絡不同的轉移過程。為了找到這樣的特征網絡結構模式，在不同采樣間隔下構建所有數據的強STN和對應的打亂后序列的強STN，分別用SGori和SGshu表示。然后，作差集運算，得到該采樣間隔下的差分狀態網絡SGDSN，計算公式如式（2）所示：
|
其中，link表示網絡中的任一有向連邊，差分狀態網絡SGDSN的權重代表了這一尺度下有多少數據具有這樣的有向連邊，而節點大小則反映了連邊度。由于任意兩個網絡都可由0-1鄰接矩陣Amn和Bmn表示，于是通過計算二維相關系數R來量化網絡結構的差異性，如式（3）所示：
|
其中，和代表矩陣元素的平均值；而R ∈ [0,1]，其值越大代表相似度越高。
1.2.2 標度特征
從節點的角度來看，STN中節點或可見小圖出現的頻數稱為度，而模體是指在隨機網絡中出現的次數等于或大于真實網絡的概率P < 0.01的節點[14-16, 24]。模體在時間序列中的分布充分反映了組成復雜系統的局部特征對調節、控制系統演化行為的作用。因此，本研究利用重標極差分析法（rescaled range analysis，R/S）[25-26]計算了模體位置序列的長程相關性。通過在多個采樣間隔下記錄每一類模體出現的位置標記ωk（k = 1, 2, …, M，其中M為模體出現的頻數），得到位置序列{ωk + 1 ? ωk}（k = 1, 2, …, M?1）。以長度為n均分序列ωk為A個相鄰的子區間，即A×n ≈ M ? 1。如果對應位置序列存在標度不變性，則有極差與子區間標準差之比R/S(n)nH，其中H為赫斯特指數。若H = 0.5，則表示模體在整個系統演化過程中是隨機出現的；如果H > 0.5，說明模體的出現是一個具有長程的持久性記憶過程；相反，如果H < 0.5，這意味著模體在時間維度上是反持續性的，亦稱為“均值回歸”，后續可能會出現反轉。
2 方法驗證與結果分析
2.1 實驗材料
本研究使用的SEEG信號來自美國國家心理健康研究所（National Institute of Mental Health，NIMH）贊助的神經元公開（OpenNeuro）數據庫，目前該數據庫由軟綿媒介公司（Squishymedia）開發、維護和托管。本文分析了8位共享在該公開數據庫上的受試者數據（編號為：060、112、116、117、130、133、134、138）[27]，共計28次發作，數據長度大約在5 min左右。然后，通過高通濾波器（截止頻率等于0.16 Hz，?3 dB）和一階低通濾波器（截止頻率等于97 Hz，?3 dB）對數據進行預處理。高通濾波器用于去除基線中非常緩慢的變化，一階低通濾波器用于避免混疊的情況發生。本文利用各頻段能量隨時間的動態變化對發作期所有的數據計算了致癇指數（epileptogenicity index，EI），即定量評估了致癇的程度[28]。最后，選取了109根EI有顯著波動的電極，和101根記錄發作間期腦電的電極進行深入的分析。受試者臨床信息如表1所示。
表1
本研究中OpenNeuro 數據集描述
Table1.
Description of OpenNeuro Dataset in this study
2.2 采樣間隔依賴下差分狀態網絡
設置s{1, 8, 16, 32, 64, 128}，對應的采樣間隔大約為：0.002、0.016、0.032、0.064、0.128、0.256 s。并利用可見小圖算法分別在不同的采樣因子下構建STN，然后對每一組癲癇信號強STN與打亂后的強STN做差后，得到的差分狀態網絡，如式（2）所示。網絡中，有向連邊的權重代表了109組發作期或101組發作間期數據中有多大比例的數據具有這樣的連邊。其中，發作期與發作間期腦電在不同采樣間隔下的差分狀態網絡分別如圖3和圖4所示。可以看到，在s=1或采樣間隔為0.002 s的時候，發作期與發作間期腦電的差分狀態網絡結構相同，只在部分結構統計出來的數量上（即連邊權重上）有些許差異。但隨著s變大時，與可見小圖8有關的特征結構8、、、同步減小。到s=32時，該類結構便不屬于概率最大的前20條連邊之內；對比發作間期的差分狀態網絡，在s=8時即已不再屬于。類似的，隨采樣間隔變大，其出現概率同步減弱的結構還有8→8和14→14的自環，并且這兩個自環與利用R?ssler系統仿真的混沌時間序列中出現的兩個自環節點是相同的兩類可見小圖，其隨采樣因子變化的規律也類似[23]。這意味著，R?ssler系統下的非線性混沌時間序列可能與癲癇信號的動力學機制有相似的部分。總的來說，從差分狀態網絡結構演變的過程對比來看，發作期腦電STN中的網絡結構在較小的采樣間隔下的魯棒性更強，而發作間期的網絡結構則相對在較大采樣間隔范圍內保持不變。這表明了表征癲癇發作期與發作間期的腦電信號特點在不同的采樣間隔下有所分別。
圖3
不同采樣間隔下發作期的差分狀態網絡
Figure3.
Differential state network for ictal periods at different sampling intervals
圖4
不同采樣間隔下發作間期的差分狀態網絡
Figure4.
Differential state network for interictal periods at different sampling intervals
為了定量說明網絡結構的差異，通過計算如式（3）所示的兩個網絡鄰接矩陣之間的二維相關系數，可以量化在不同采樣間隔下以及不同發作類型之間的網絡結構相似度，最終分析結果如表2所示。符號Asind表示網絡鄰接矩陣，其中s為采樣因子，數據類型ind ∈{發作期，IED}。可以看到，采樣因子為1和128時，發作期差分狀態網絡的相關系數比發作間期的大，這意味著相比發作間期的數據，發作期數據的特征波形在采樣間隔變化的情況下相對穩定。通過連續的兩個采樣間隔發現，發作期腦電在較小的采樣間隔上網絡結構變化較慢，在采樣因子為16～32之間會有一個較大的差異，相關系數為0.78左右。相比之下，發作間期在采樣因子為1～8之間相似度較低，而在采樣因子為8～32之間網絡結構變化較慢，相關系數均在0.96附近。同時，本文還分析了同一采樣因子下兩類數據的差分狀態網絡結構，發現在s = 1時相關系數達到0.9以上，并不能很好地區分兩類數據。但在s = 16，即采樣間隔為0.032 s時兩者相似度最低。這一分析結果與圖3、圖4所展示的差分狀態網絡結構相吻合。
表2
差分狀態網絡結構相似性對比
Table2.
Correlation coefficient of two differential states network structures
2.3 采樣間隔依賴下STN的標度特征
2.3.1 模體的提取
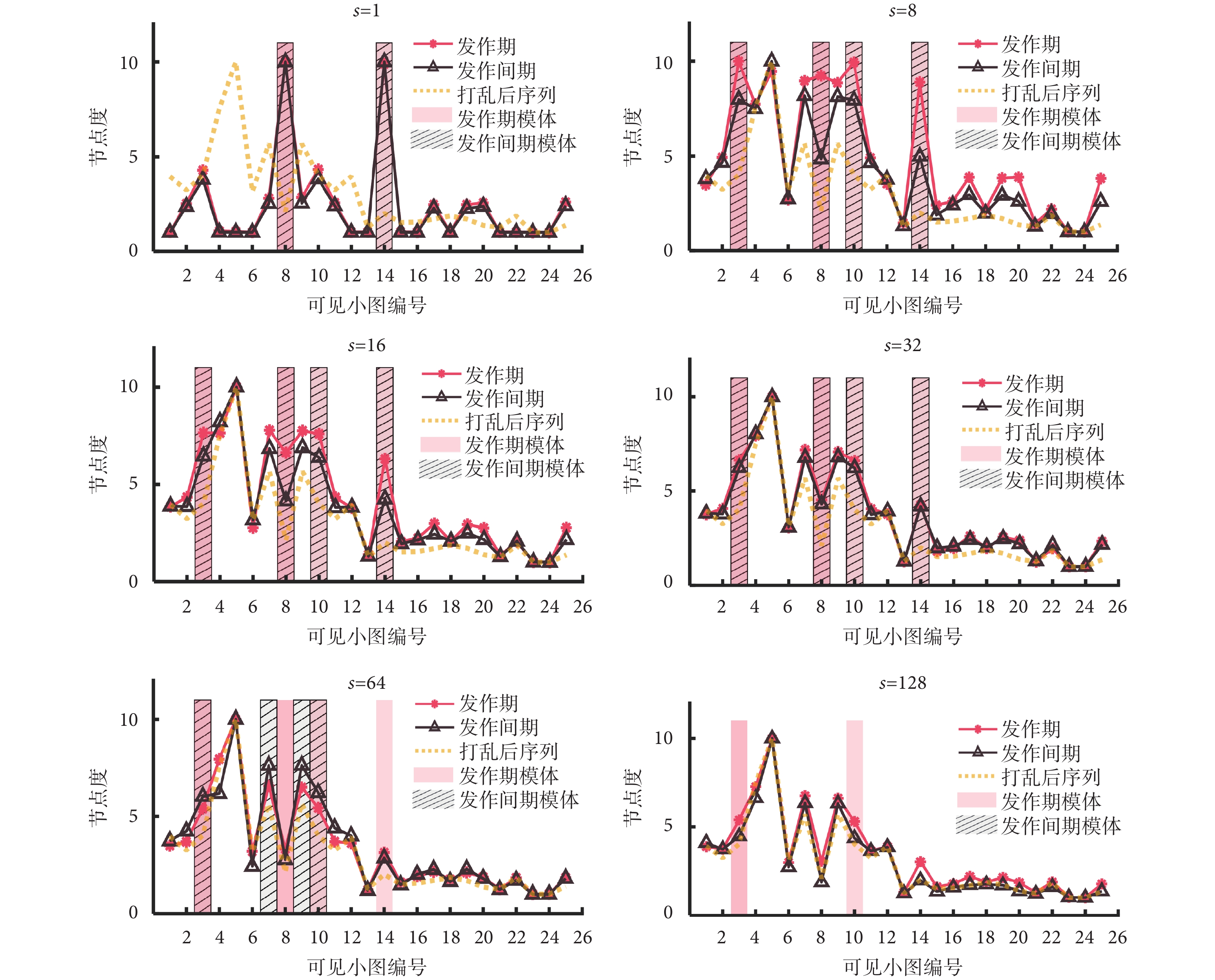
模體在STN中類似于網絡中的關鍵節點具有較大的連邊度，同時在整個演化過程中比打亂后的STN中對應的節點更加頻繁地出現，且差異明顯。不同采樣間隔下癲癇信號STN平均后的節點度以及模體的選取如圖5所示。為了更好地進行對比，本研究將縱坐標數值大小映射到區間［1, 10］中，黃色虛線代表的是打亂后序列STN節點度，而紅色和黑色連線則是代表的發作期與發作間期STN的節點度，并且與之顏色對應的陰影部分則是標記的該發作類型中模體。從發作期與發作間期數據中25種可見小圖的節點度可以看出，當s∈{1, 8, 16, 32}時，發作期與發作間期數據的模體變化一致，都是由可見小圖8 和14 演化到可見小圖3、8、10 和14。但當采樣因子達到64之后，發作間期的模體已經有了明顯的不同，并且到s = 128時，節點度與打亂后網絡中對應節點度之間不再具有明顯的差異，也就不再有模體存在。但發作期STN中的模體在s = 64時依然為可見小圖3、8、10 和14，而到s = 128時只留下可見小圖3和10。
圖5
不同采樣間隔下的節點度以及模體
Figure5.
Degree and motifs at different sampling intervals
2.3.2 STN的標度性質
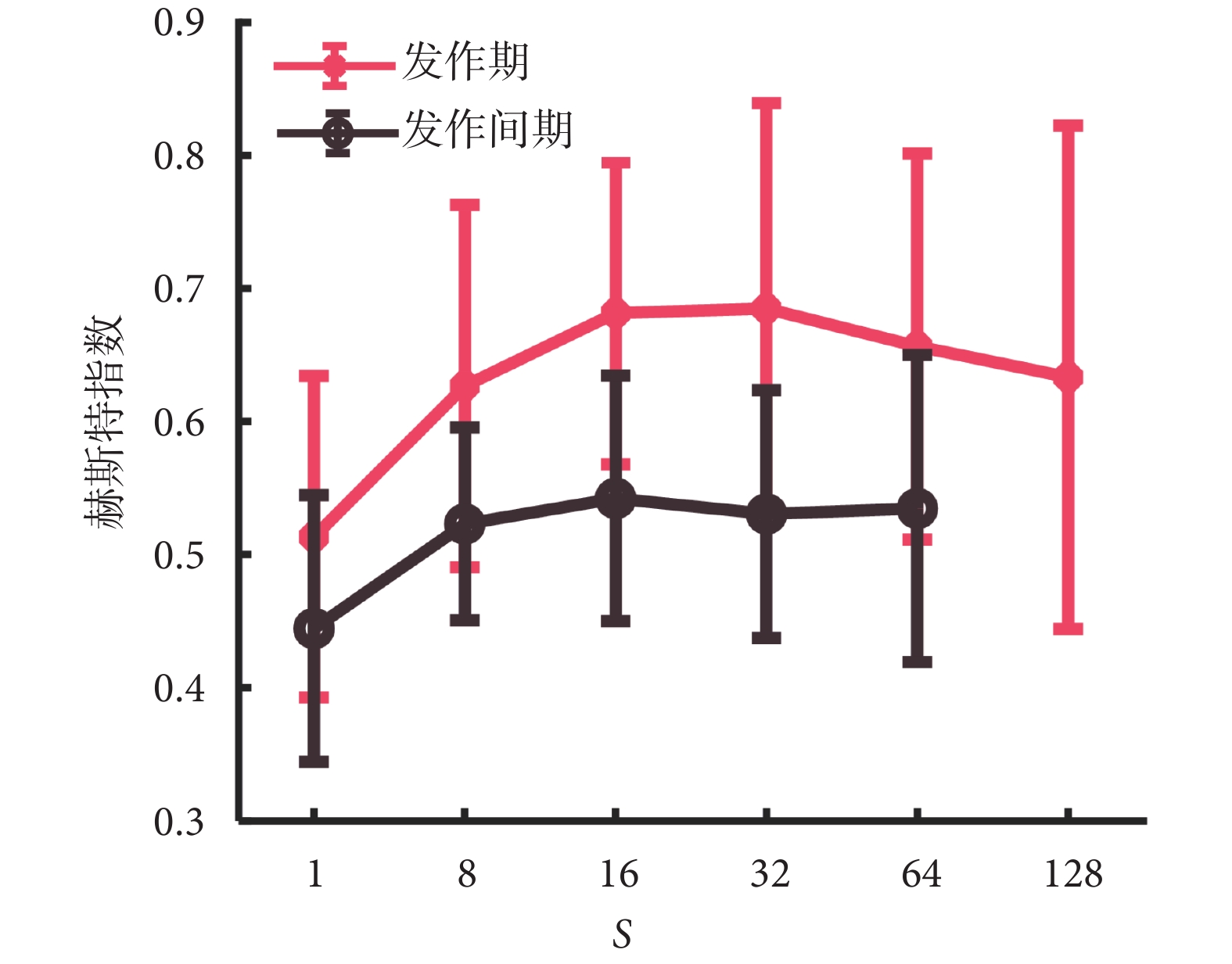
如圖6所示，展示的是通過R/S方法得到所有數據中模體位置序列赫斯特指數的平均值及其方差。可以看到當s=1時，由于采樣間隔較小，會捕獲更多精細結構，提取的信號會在子區間上重復，波動更為強烈，因此無論是發作期還是發作間期下的模體位置序列的赫斯特指數普遍偏低[20, 29]。降采樣后，當s∈{8, 16, 32, 64, 128}時，癲癇信號的原始特征波形開始凸顯，因此發作期STN中模體位置序列的赫斯特指數普遍大于0.5，具有長程相關性或分形結構。對比發作間期采樣間隔增加后，模體位置序列的赫斯特指數普遍接近0.5左右，意味著發作間期的模體在時間序列中是趨于隨機出現的，與發作期形成鮮明的對比。
圖6
不同采樣間隔下模體的赫斯特指數分布
Figure6.
The distribution of Hurst exponent of motifs at different sampling intervals
總的來說，在任意采樣間隔下，發作期中模體位置序列的赫斯特指數大于發作間期中的數值[21]。對比不同采樣因子下的分析結果可以發現，發作間期在s = 8時其赫斯特指數的分布就接近0.5，并隨采樣間隔增大繼續增加，依舊在0.5上下徘徊。而發作期則是在s = 16時基本達到穩定的區間內，但當采樣因子增加到64之后有所減弱，并有接近隨機分布的趨勢。而因此采樣因子為16，即0.032 s時，可以看作有效對比發作期與發作間期模體位置序列赫斯特指數的采樣尺度，這也對應了上文利用二維相關系數衡量網絡結構相似性中的分析結果。
3 結論
與健康受試者腦電圖相比，癲癇患者發作時正常腦電波活動減少或消失，腦電活動的頻率、節律、幅度和波形發生明顯變化，且時空分布明顯異常[29]。雖然目前有許多癲癇發作信號的特征提取方法，但是在采樣間隔發生變化下利用這些方法對特征演變過程的研究仍然是不足的[20, 29-30]。在多個尺度下分析系統的演化過程，是當前數據驅動下研究大腦系統動力學特性的有效途徑[31]。本文在多個采樣間隔下，利用可見小圖方法分析腦電信號的局部結構演變特征，并將同一類拓撲特征視為一種可見小圖，根據可見小圖之間的轉移概率構建不同采樣間隔下的STN，并分析兩類數據的STN網絡連邊特征和節點特征。最終，本文研究發現了病變大腦與健康大腦系統下的基本結構塊及其調控機制在采樣間隔變化下的規律，并找到兩者差異最大時的采樣間隔，有效揭示了健康和病理狀態下大腦的功能和活動。
本研究使用的是采樣率大約為500 Hz、持續時間約為5 min左右的癲癇SEEG數據。結果顯示，原始癲癇信號或者在采樣因子為1時，癲癇發作期與發作間期數據的差分狀態網絡結構類似，因此不能很好地區分這兩種數據。進一步改變采樣因子的大小，利用二維相關系數量化發作期與發作間期差分狀態網絡的結構差異，發現發作期網絡結構比發作間期網絡結構在采樣因子變化下更能維持特征波形；且在采樣間隔變化較小時，發作期差分狀態網絡結構不易改變；但發作間期的網絡結構在相對較大的采樣間隔下不易隨之而發生改變。對比來看，在采樣因子為16時，發作期與發作間期之間的特征差異最大。另一方面，通過分析網絡中的節點特征，發現在采樣因子大于1 時，發作期STN中模體的出現往往具有長程相關性，相比之下，發作間期的模體在時間維度上更傾向于隨機出現。且，從發作期與發作間期模體位置序列的赫斯特指數在多個采樣間隔下的分布來看，在s = 16時，即采樣間隔為0.032 s時，為較佳的采樣尺度。
擴散熵[32-33]、功能性網絡[34-35]、復雜度[36-37]等非線性方法都可運用于尋找大腦病理變化過程的特征，但這些方法沒有考慮尺度因素對結果的影響。在不同采樣間隔下研究STN，可以為人們提供新的標度行為，并用以區分不同發作類型的動力學機制，評估系統的狀態等。本文研究癲癇發作期與發作間期的STN在不同采樣間隔上的演化差異，為臨床診斷上用以分類或預測癲癇發作奠定了理論基礎。通過本文研究，希望可為其他類型的腦部疾病（如抑郁癥、阿爾茨海默癥、偏頭痛等）的研究提供新的思路。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：張鐳負責文獻調研、數據收集、提出研究問題和分析思路，以及文章的撰寫與修改；顧長貴，在分析數據的過程以及論文的撰寫和修改中進行了監督，并提出了批判性意見；閻爽，在論文的撰寫和修改中進行了指導。
