為了尋求一種對患者友好、成本低廉的腸道檢查方法，設計并制作了一種結構簡單的仿尺蠖氣動軟體腸道機器人。該腸道機器人由兩個用于錨定的徑向膨脹圓柱形橡膠薄膜氣囊和一個用于軸向伸縮的低密度聚乙烯薄膜氣囊構成，通過模仿尺蠖的爬行實現在腸道中的運動。對錨定氣囊內部氣壓和膨脹后自由變形尺寸的關系進行了理論推導，指出氣囊不均勻變形是一種由橡膠材料大變形引起的膨脹失穩現象。對腸道機器人在不同尺寸硬管和離體豬小腸中驗證了其運動性能，在離體豬小腸中運行速度為4.87 mm/s，駐留時錨固力為2.33 N，能夠順利通過90 °硬質彎管。這項工作有望為病患提供一種低痛苦、低費用的腸道檢查新方法。
引用本文： 何永勝, 孫志峻, 袁捷, 韋聰文, 韓國偉, 褚效成. 仿尺蠖氣動軟體腸道機器人的設計與研究. 生物醫學工程學雜志, 2024, 41(6): 1137-1144. doi: 10.7507/1001-5515.202409028 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
根據2022年全球癌癥統計數據[1]，消化道相關癌癥已成為世界上發病率最高的癌癥。小腸在消化道中檢查最為困難，它管腔較長（5～7 m）且迂曲折疊[2]，傳統小腸鏡檢查需要經肛和經口兩種方式，小腸鏡推進困難，對接成功率低，因此患者接受度很低。現有對小腸鏡的改造主要有單氣囊小腸鏡和雙氣囊小腸鏡[3]，雖提高了對接率，但未能解決檢查繁瑣及患者痛苦的問題。
以色列在2000年研發出膠囊內窺鏡[4]，略大于普通膠囊，吞服后可隨胃腸道蠕動而前進，同時將照片傳出體外。其主要缺點是運動不受控，無法拍攝指定位置，可能會漏檢。為此，學者還研究了磁控膠囊機器人[5]，但它對腸道的折疊和褶皺仍無能為力。鑒于以上檢查方式的缺點，國際上廣泛進行了自主推進式腸道機器人的研究[6]，早先有螺旋式[7]、螺旋槳式[8]、腿/槳式[9-10]、仿蝸牛爬行式[11]乃至電刺激腸道蠕動式[12]等，近年來出現的多為變徑履帶式[13]及仿尺蠖/蚯蚓式。
尺蠖因其運動方式成為了多種管道類機器人的仿生研究對象[14]。傳統分類方法主要根據腸道機器人運動方式進行分類，而本文根據與腸道接觸部分的剛度，將仿尺蠖腸道機器人分為軟接觸和硬接觸。硬接觸式腸道機器人結構復雜，成本較高，軟接觸式腸道機器人則結構簡單、成本低廉，具有較大的發展潛力[15]。軟接觸根據材料模量大小又分為軟材料接觸和軟結構接觸，或二者結合。軟材料接觸式機器人一般使用橡膠類超彈性材料與腸道直接接觸以保證接觸安全性，其錨定結構僅有材料自身變形[16]，而少有結構大變形，或變形后結構仍具有較大剛度[17]。軟結構接觸式機器人的材料模量較高，是通過結構大變形來保證安全性，如Li等[18]提出的檢查氣管用仿尺蠖運動機器人。
除以上兩種外，更多是將兩種接觸方式結合，以充氣橡膠薄膜作為錨定機構最具代表性。橡膠薄膜質地柔軟，膨脹后的大變形結構能夠很好地貼合腸道。文獻[19-23]均使用類似的橡膠氣囊作為錨定結構，區別主要在于中部伸縮氣囊的結構及整體的制作材料和方法。
為降低腸道檢查成本、減輕患者痛苦，以及降低已有腸道機器人的復雜度，本文提出了一種結構簡單的仿尺蠖運動氣動軟體腸道機器人，并進行了相關理論分析和實驗。
1 材料與方法
所提出的腸道機器人如圖1所示，由三個氣囊構成，其中氣囊1和氣囊3用于腸道內錨定，氣囊2用于伸縮。氣囊1和氣囊3由支撐結構及橡膠薄膜構成，氣囊2由低密度聚乙烯（low density polyethylene，LDPE）薄膜和聚氨酯（polyurethane，PU）彈簧管構成，與腸道接觸的所有結構（氣囊、硅橡膠軟管）均為高聚物材料，具有良好的生物相容性。
圖1
腸道機器人結構
Figure1.
The structure of intestinal robots
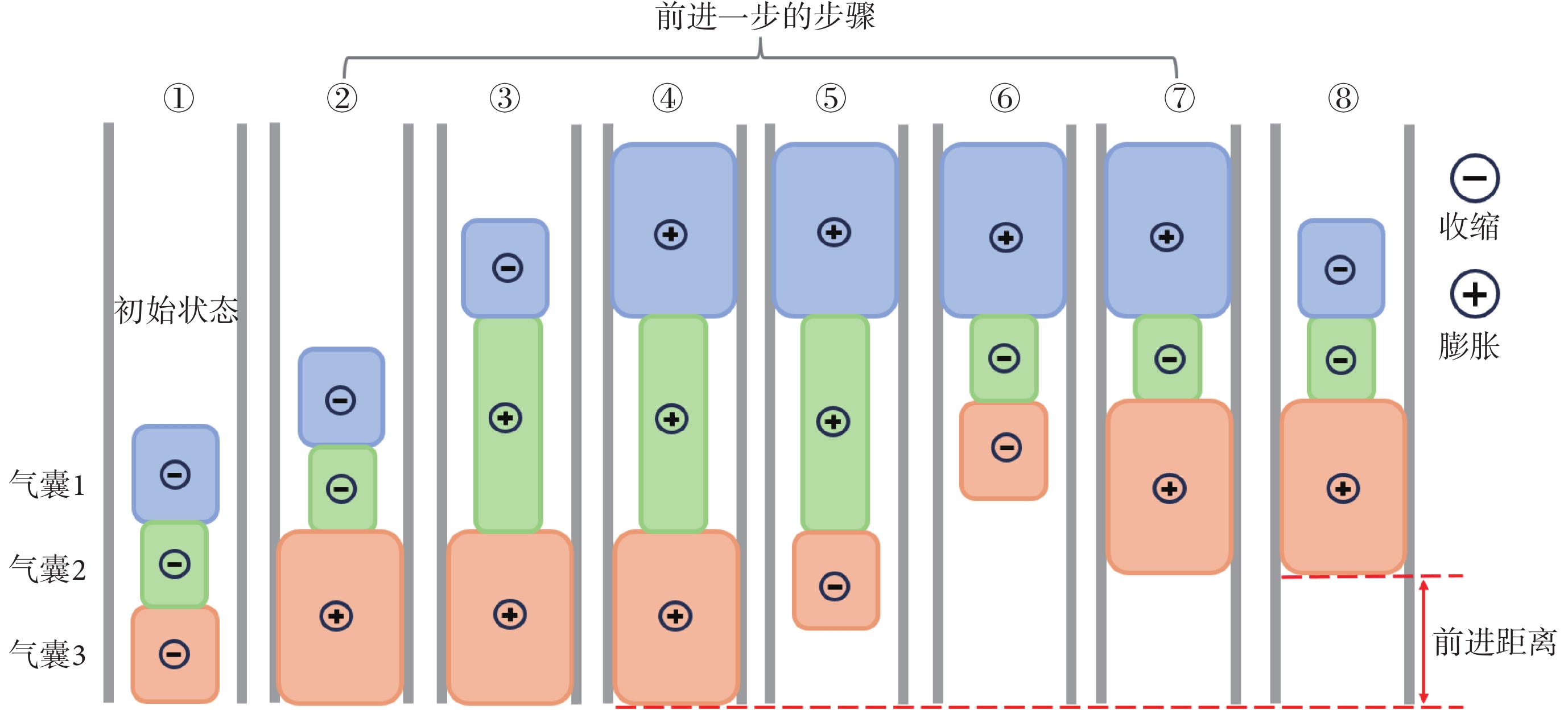
腸道機器人在腸道內前進的運動步驟如圖2所示，氣囊1和3膨脹時錨定，氣囊2膨脹時伸長，① 狀態時可放入或取出體內，②～⑦ 為一個運動循環，⑧ 狀態回到 ② 狀態，機器人前進一“步”，反向執行 ②～⑦ 步驟即可使腸道機器人倒退。
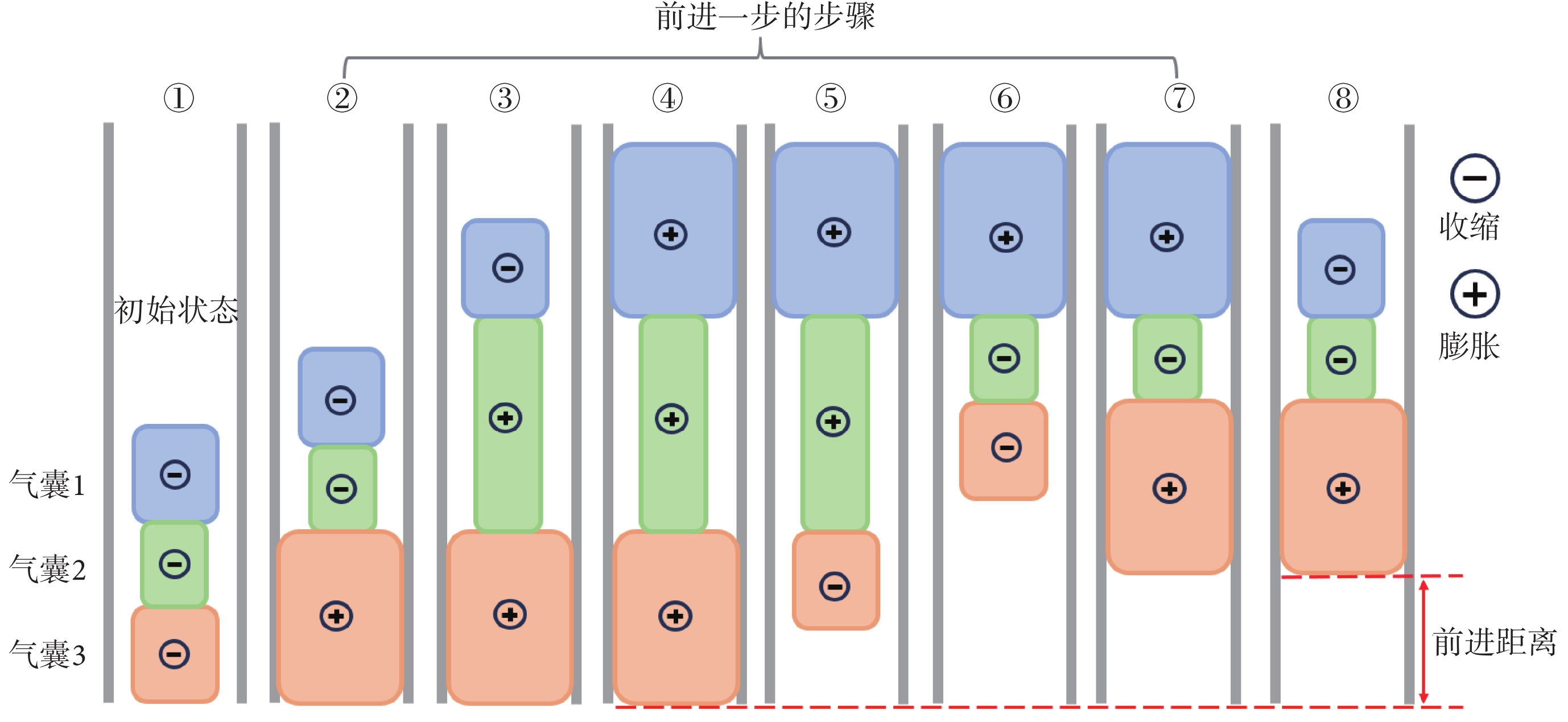圖2
運動過程
① 為完全收縮，②～⑦ 為運動步態，⑧ 為下一運動循環的初始狀態
Figure2. Movement process① complete contraction; ② - ⑦ movement gait; ⑧ initial state of the next movement cycle
氣囊2變形長度直接影響著腸道機器人前進速度，為使氣囊2能夠在伸縮時具有大行程，根據文獻[18]，PU彈簧管在伸長時的螺旋間距應當與圓筒形LDPE薄膜的直徑相同，若大于直徑，則薄膜收縮到一定程度會封閉氣道導致氣囊2無法繼續收縮，若小于直徑，過多的螺旋圈數亦使得氣囊2無法收縮到最短。
腸道機器人在未充氣時直徑小于人體小腸充盈后最小直徑15 mm[24]，借助柔順性通過腸道彎曲處，因此其長度不宜過長，否則容易折疊，但腸道機器人運動效率又與其單個周期的行程正相關[25]，綜合考慮后，將長度設計為162 mm，也可根據實際需要調整。
腸道機器人驅動部分的相關介紹參見附件1第1節。
2 錨定氣囊變形理論分析
錨定氣囊與腸道壁直接接觸，錨固力（靜摩擦力）與接觸壓力相關，為使錨定氣囊的變形能夠覆蓋人體結腸和小腸的尺寸變化范圍，需要計算錨定氣囊在氣壓下的變形。
2.1 幾何方程
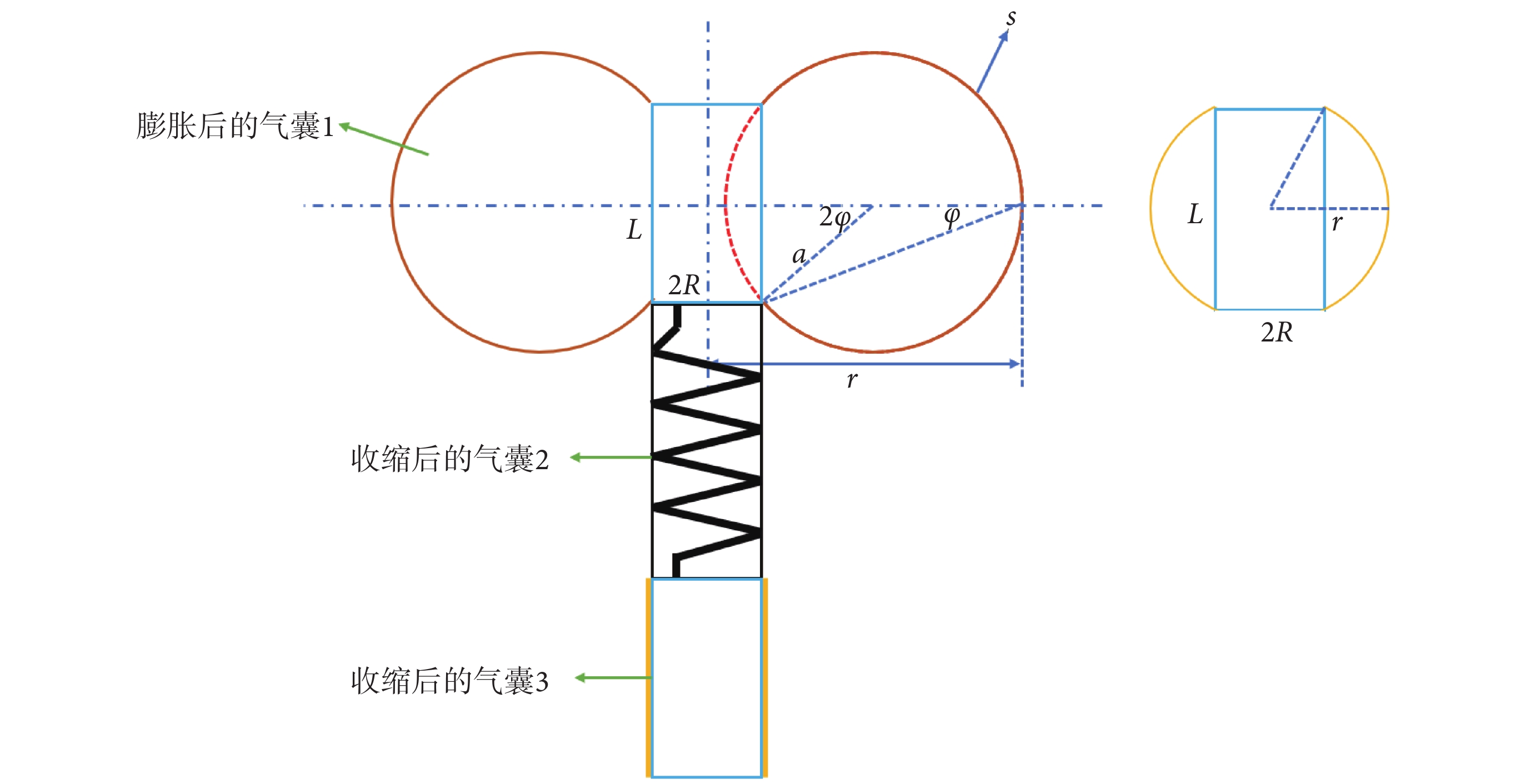
傳統的結構變形分析方法較為繁難，因此本文根據氣囊的實際變形情況進行一定簡化。觀察到錨定氣囊在變形后的截面形狀近似為圓弧，故假設變形后的錨定氣囊側面形狀為圓弧，如圖3所示。
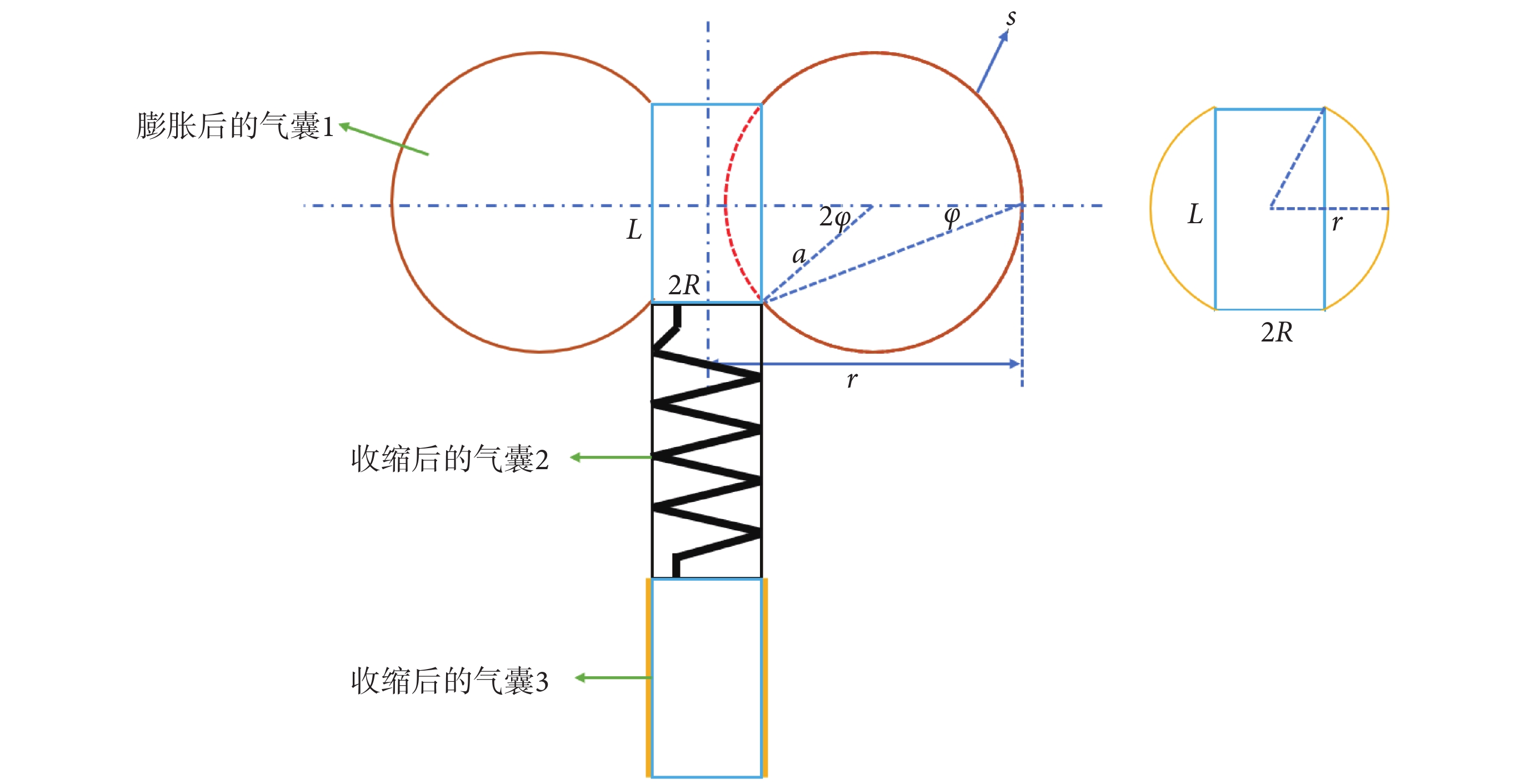圖3
氣囊變形截面的幾何關系
Figure3.
Geometric relationship of deformation cross-section of airbag
根據假設，未變形圓筒形橡膠薄膜的橫截面在變形后某一時刻會內接于一圓弧（見圖3右），內接條件為：
 |
r為錨定氣囊變形后半徑，R和L為圓柱形橡膠薄膜的初始半徑和長度，其中L = 14.5 mm，R = 6 mm，代入式(1)可得r = 9.4 mm，小于氣囊與腸道接觸時的半徑（約12 mm），未與腸道壁接觸，因此僅推導如圖3左所示變形的幾何關系如下：
緯度和經度方向的主拉伸：
 |
根據橡膠材料的不可壓縮性：
 |
h為橡膠薄膜變形后的厚度，H為其初始厚度，s為經度方向圓弧的長度，幾何關系如下：
 |
其中a為圓弧半徑，
為L/2對應的圓周角，a的計算公式為：
 |
的計算公式為：
 |
根據以上公式，在圓截面假設下，圓柱形橡膠薄膜在不同變形程度下的主拉伸
和
統一為變形半徑r的函數。
2.2 平衡方程
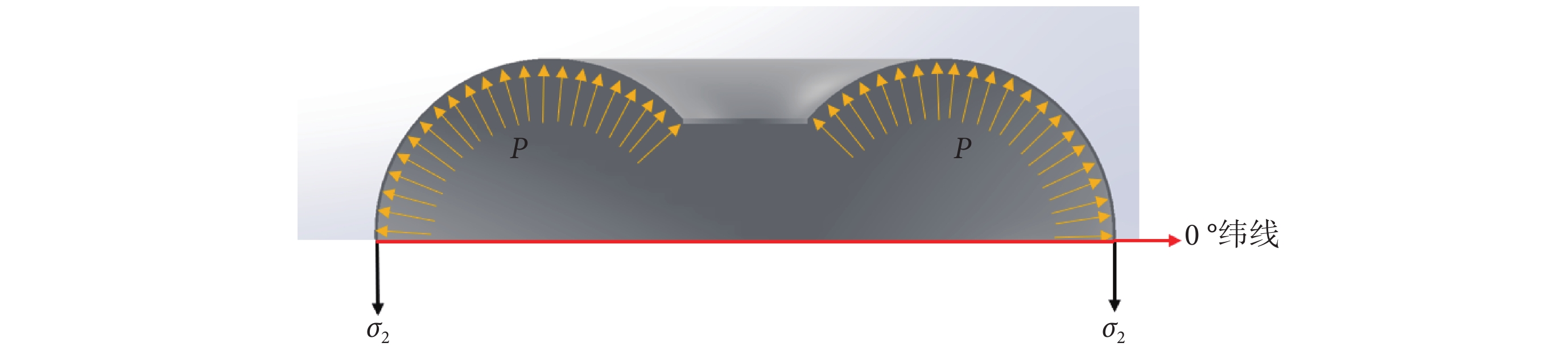
將變形后的錨定氣囊看作薄壁容器，其壁面壓力P與薄膜應力平衡，如圖4所示，考慮到氣囊變形后，不同緯度的薄膜周向拉伸程度不同，導致薄膜經向厚度分布不均勻，即0 °緯線上最薄，隨著緯度升高而逐漸變厚，因此將錨定氣囊沿0 °緯線剖開，根據對稱性，薄膜在該緯度上沿圓周方向均勻分布，由力的平衡得到平衡方程：
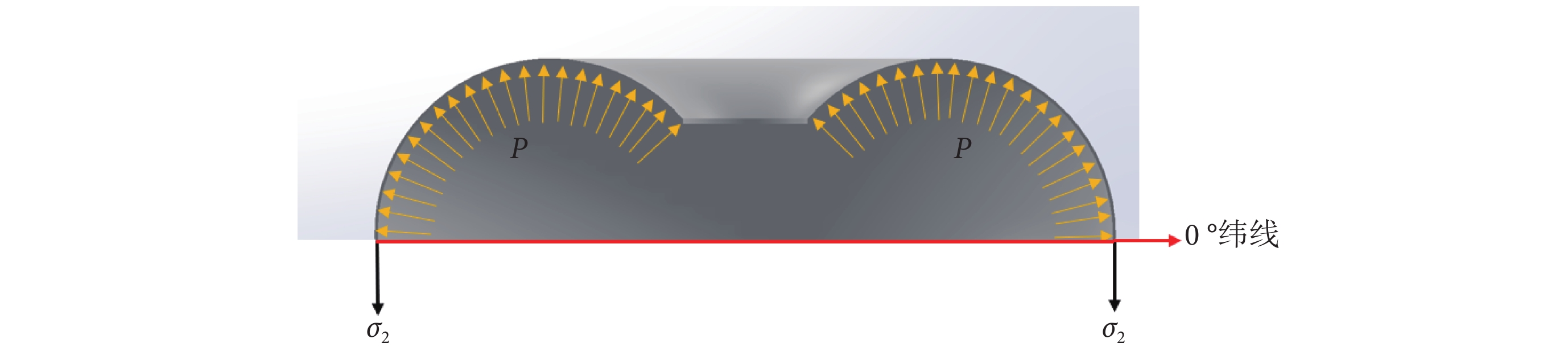圖4
氣囊受力平衡示意圖
Figure4.
Schematic diagram of airbag force balance
 |
其中
為沿主拉伸
方向的應力，可由下文物理方程求得。
2.3 本構方程
本構方程與橡膠材料的特性有關，不同的本構模型適用于不同的變形范圍和加載方式，基于使用的簡便性和計算準確性，采用三階Ogden模型[26]作為橡膠的本構模型。文獻[27]在忽略了薄膜厚度方向的應力后，使用橡膠的三階Ogden模型推導出橡膠薄膜本構方程：
 |
其中
、
為材料參數，
= 617 kPa，
= 1.86 kPa，
= ? 9.79 kPa，
= 1.65，
= 5.08，
= ? 2.0。在平衡方程中僅用到了
，故只需使用上式中第二式。
由平衡方程得到：
 |
將h和
的計算公式代入可得到壓強P關于變形半徑r的變化關系，即控制方程。
3 氣囊變形研究
3.1 錨定氣囊變形過程
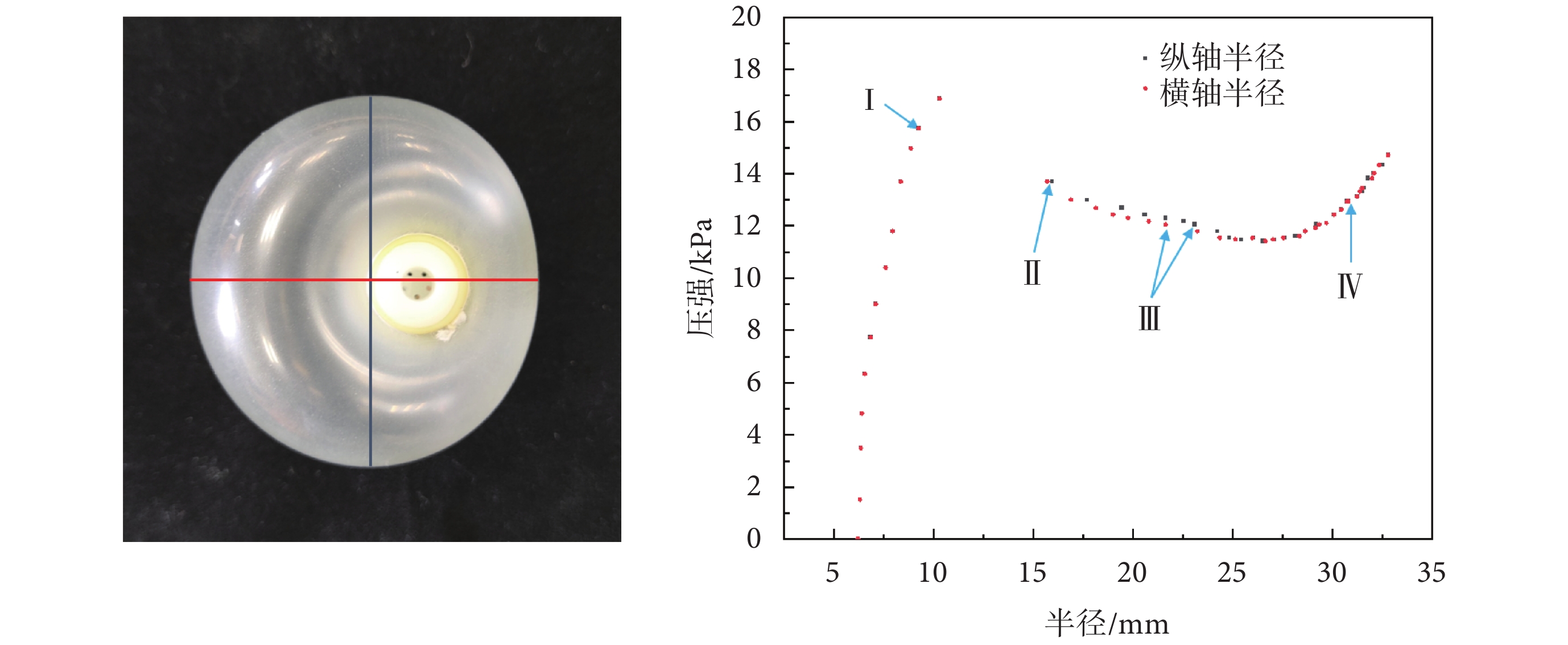
實驗測得錨定氣囊的氣壓-半徑關系如圖5右所示，變形過程如圖6所示，分為四個階段：Ⅰ. 開始充氣后，氣壓與半徑幾乎呈線性關系，氣囊的變形很小，但氣壓上升很快；Ⅱ. 到達某一氣壓后，氣囊外形產生局部突變，同時內部氣壓顯著降低，外觀表現為一大一小的不均勻變形，為方便描述，將大的部分記為A（左側氣囊），小的部分記為B（右側氣囊），氣囊的邊緣形狀近似為圓形，但內部支撐不在圓心處，測量如圖5左所示的長軸和短軸，二者尺寸相近，在圖5右中標記為同一氣壓下的紅點與黑點；Ⅲ. 繼續充氣，A部分變形較小，B部分變形較大，B部分變大使內部支撐逐漸移向圓心處，不均勻變形逐漸消失，氣壓隨半徑增大而變化較小；Ⅳ. 變形到最后階段，不均勻變形幾乎消失，氣壓隨半徑增大而上升。
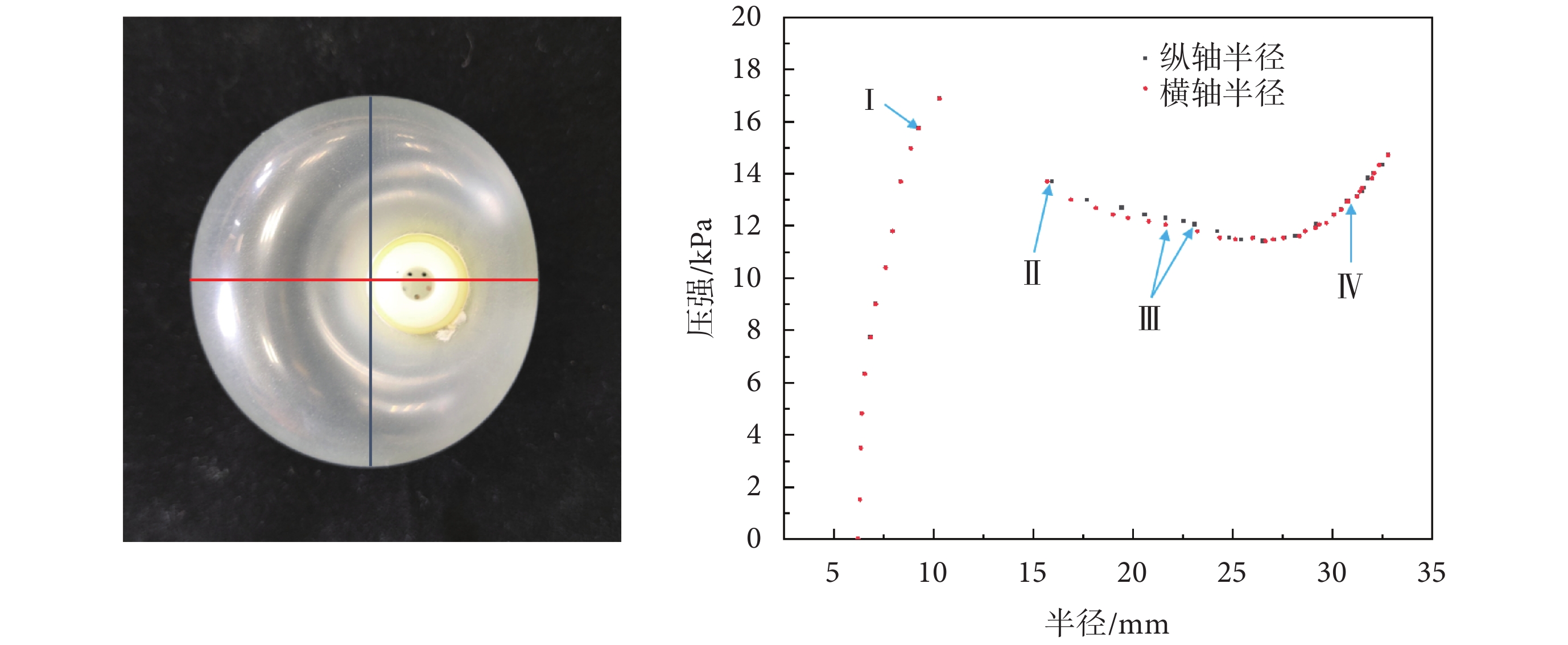圖5
錨定氣囊尺寸測量方式（左）及測量結果（右）
Figure5.
Measurement method for anchored airbag size (Left) and measurement results (Right)
圖6
錨定氣囊變形過程
Figure6.
Deformation process of anchored balloon
圖5右中，氣囊變化過程的實驗曲線最高點右端有一段空白即是氣囊變形發生局部突變所致。氣囊在不均勻變形階段氣壓變化小但半徑變化大，表明該階段的氣囊容易改變形狀，能夠更好地適應腸道的復雜結構。
氣囊變形過程中，不同變形可能會對應相同氣壓，因此，僅以氣壓作為反饋無法得知氣囊的變形，故氣囊的變形需要根據充氣體積確定，由于腸道環境的復雜性，仍需要氣壓反饋來保證充氣的安全性。氣囊變形的控制方法參見附件1第2節。
3.2 理論變形與實際變形的討論
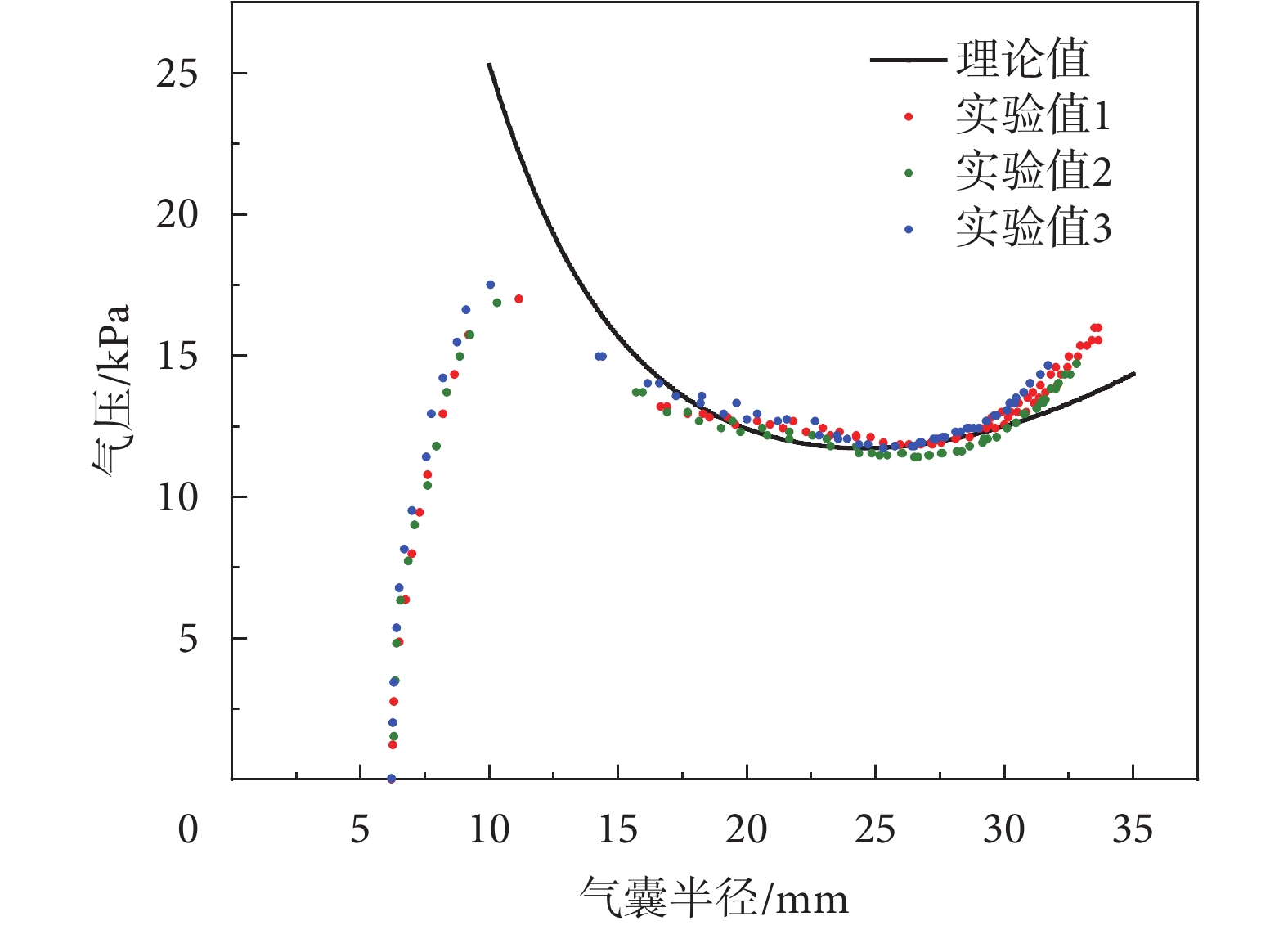
將理論計算得到的氣壓與氣囊半徑的關系曲線（
）與實驗測得的對應曲線進行比較，如圖7所示。在實驗中共測量了三個結構和尺寸相同的氣囊，其初始尺寸為L = 14.5 mm，H = 0.23 mm，R = 6.1 mm。
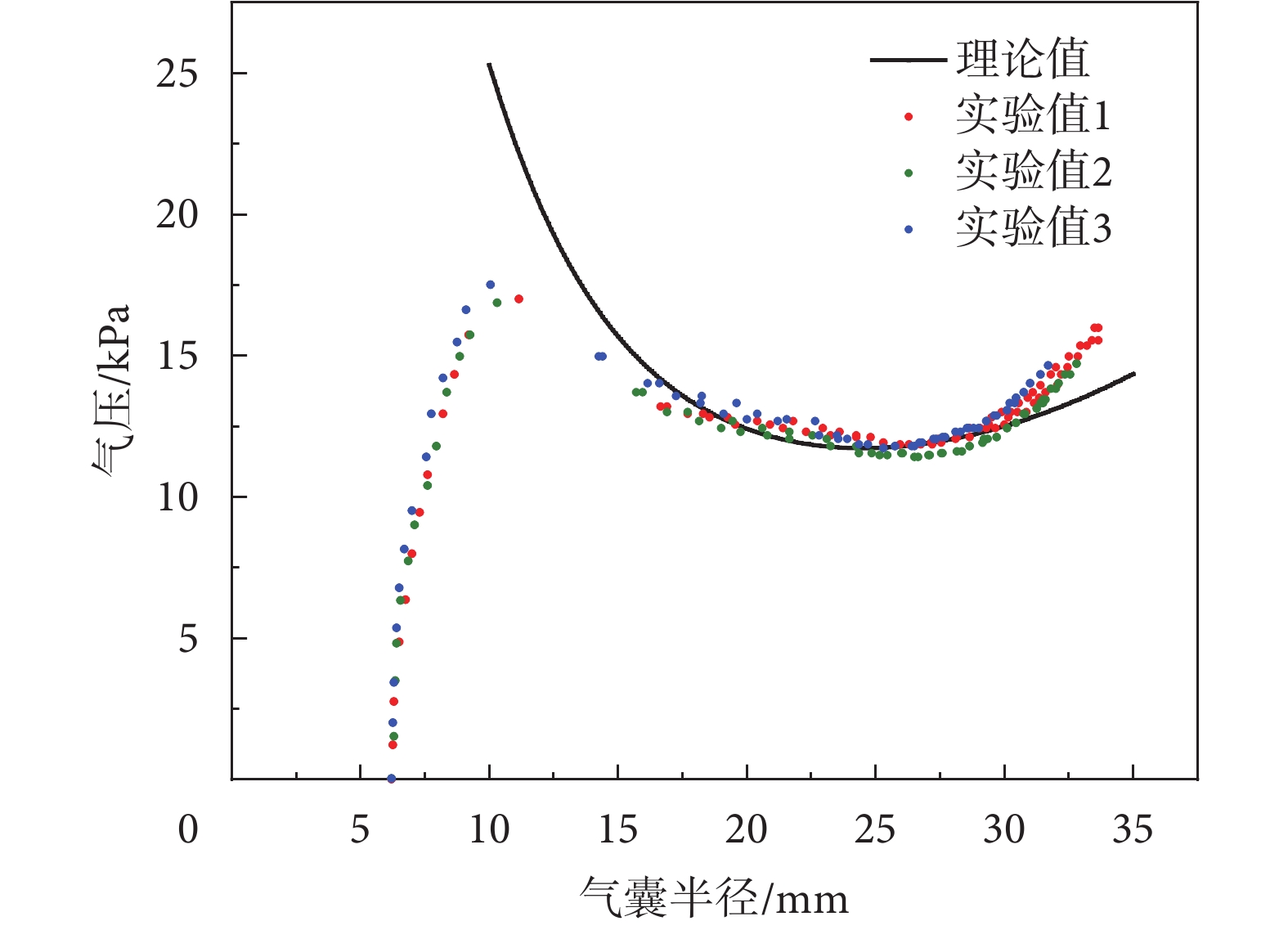圖7
氣囊變形的實驗值與理論值
Figure7.
Experimental and theoretical values of airbag deformation
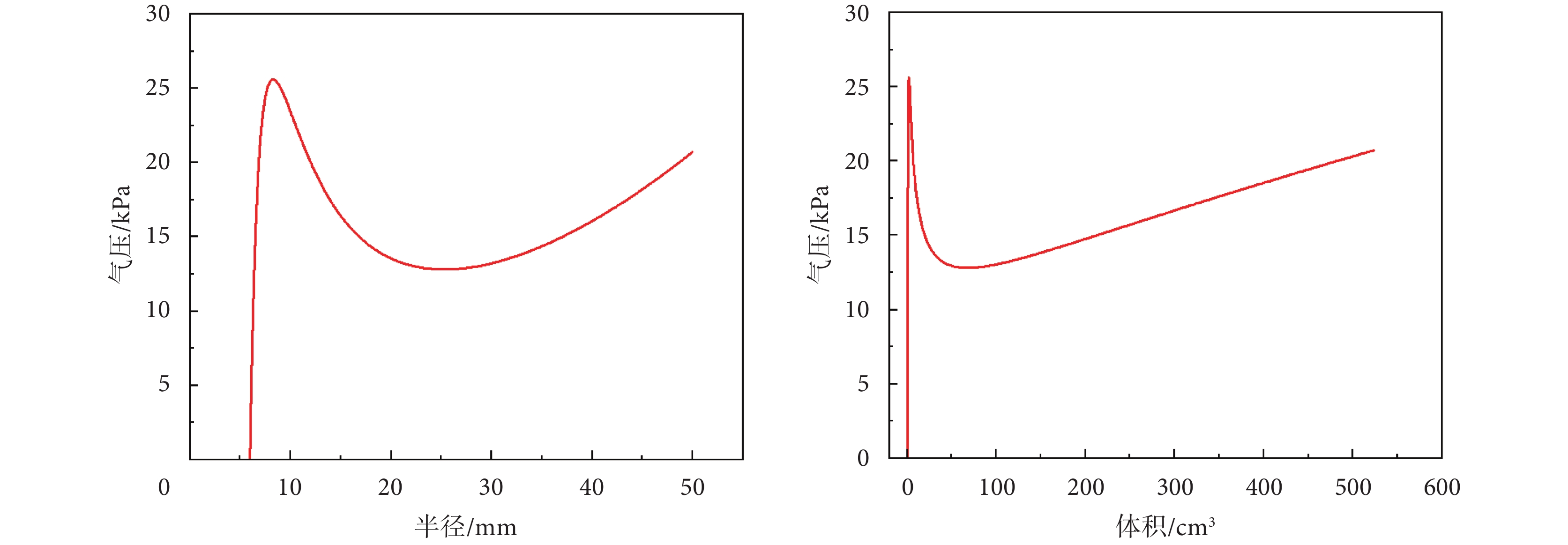
通過與球形氣囊的相關曲線對比來解釋實驗曲線，根據相同的分析方法，得到球形氣囊的氣壓-半徑變化曲線及氣壓-體積變化曲線如圖8所示，二者材料參數相同。球形氣囊結構對稱，其變形無需做出額外假設，即球形氣囊在充氣膨脹后仍為球形，圖8所示曲線為球形氣囊變形的精確解。
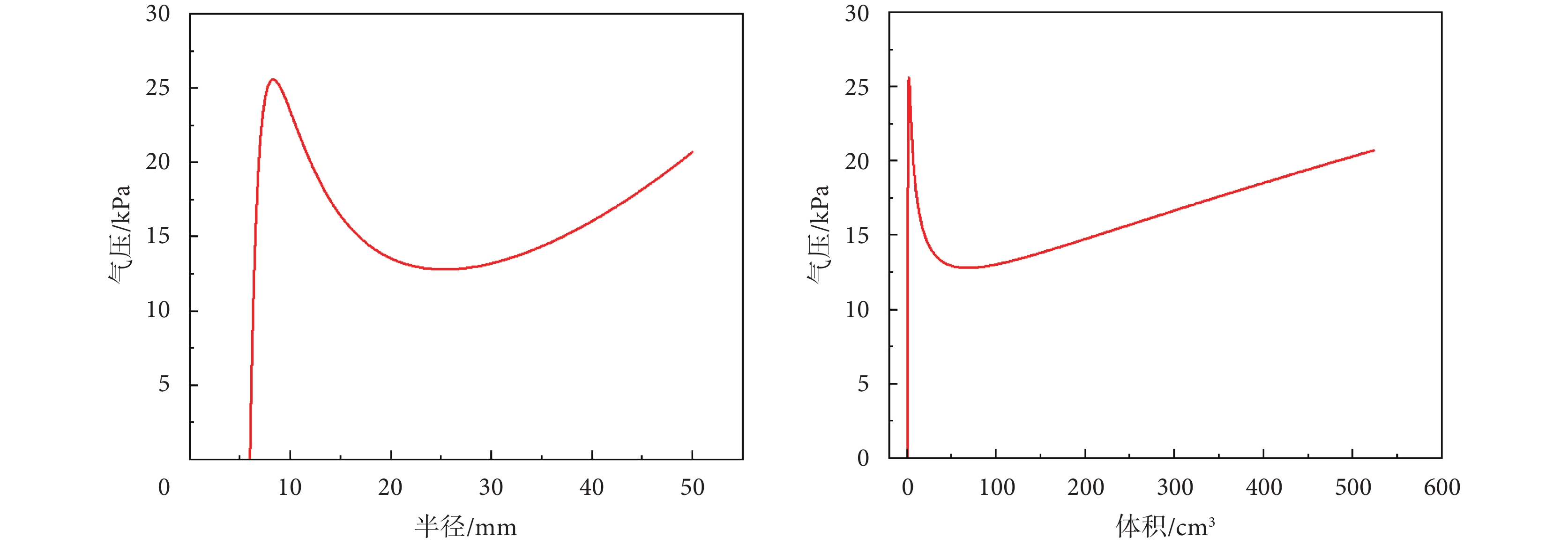圖8
球形氣囊壓強隨半徑（左）和體積（右）的變化規律
Figure8.
The variation of pressure of a spherical balloon with radius (left) and volume (right)
圖8左的變化趨勢與圖5右相似，在某一極值點后氣壓大幅下降而氣囊半徑大幅增加，通過氣壓-體積變化曲線（圖8右）可以更清楚地看到這一點，這是超彈性材料氣囊膨脹變形過程中的失穩現象[28-31]，因此錨定氣囊的不均勻變形是局部失穩現象，由橡膠材料自身特性決定，無法通過改進制作工藝等方式完全消除。本研究還對錨定球囊和醫用球囊變形過程進行了比較，醫用球囊同樣也出現了失穩現象，具體結果參見附件1第3節。
圖7中，理論曲線與實驗曲線在氣囊半徑較小（r < 13 mm）和半徑較大（r > 30 mm）時誤差較大，原因是為了消除橡膠的Mullins效應，錨定氣囊在測試前會經過大幅度的加載卸載，會產生殘余塑性應變，在小變形時形狀與圓弧有較大差距。在大變形時（r > 30 mm），緯度方向橡膠薄膜更早被拉伸硬化，因此與圓截面假設也有較大差距，導致理論與實驗數據偏離。理論曲線在中等變形（13 mm < r < 30 mm，200%～500%拉伸率）時與實驗曲線吻合較好，說明在中等變形時，氣囊截面形狀更符合理論推導所使用的圓截面假設。
4 腸道機器人相關實驗
4.1 錨定氣囊在不同管道中膨脹時內部氣壓變化
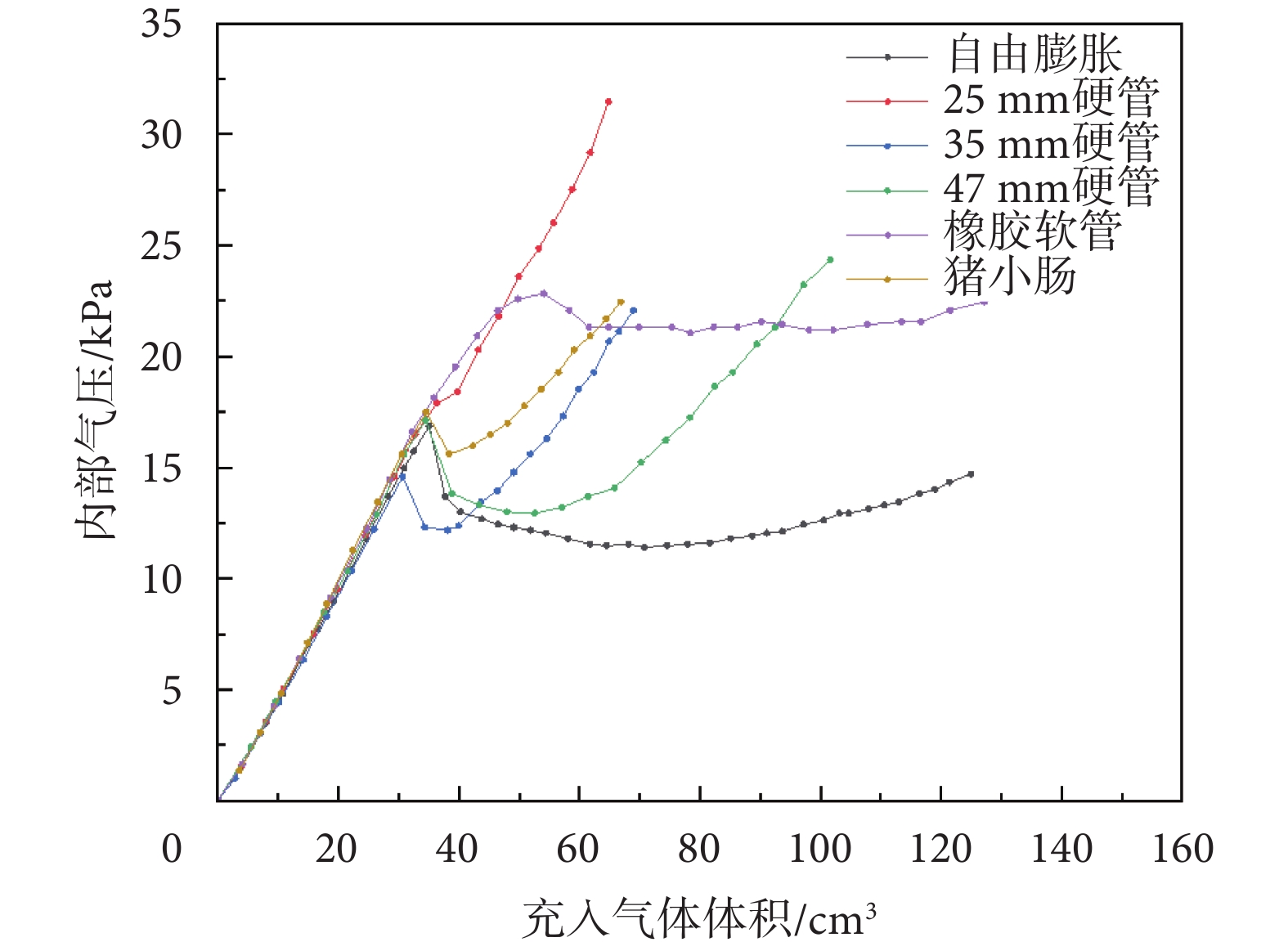
為區分錨定氣囊與多種實驗常用管道相互作用的異同，進行了錨定氣囊在內徑25、35、47 mm聚碳酸酯（polycarbonate，PC）硬管及直徑21 mm的橡膠軟管和離體豬小腸中的膨脹實驗，充入氣體體積和氣囊內部氣壓的關系如圖9所示，錨定氣囊自由膨脹的相應曲線亦在其中，以方便比較。
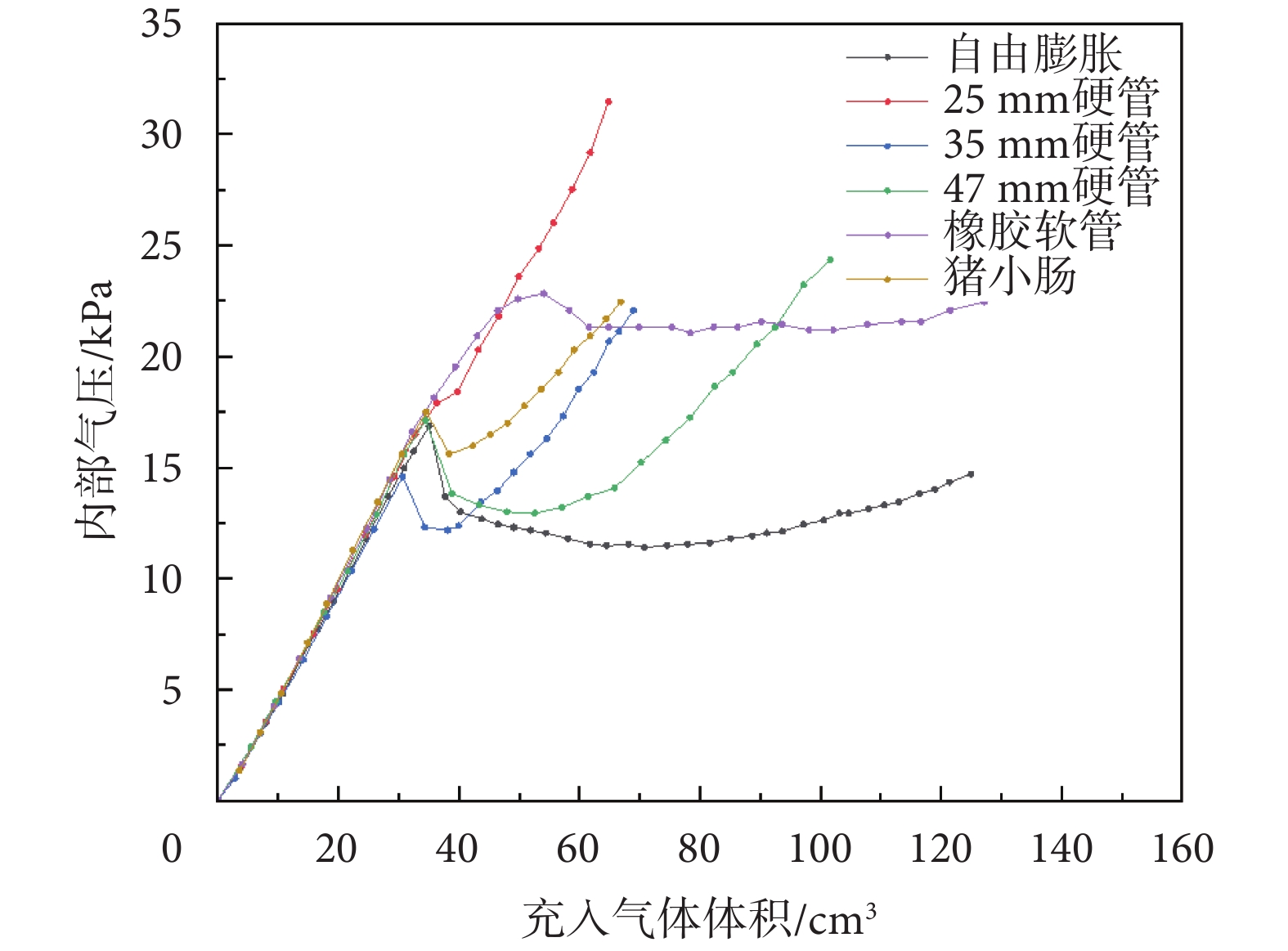圖9
氣囊在不同管道中的膨脹
Figure9.
Expansion of airbags in different pipelines
從圖中可以看出，對于硬管，氣囊與管壁接觸后，氣壓會迅速上升，管徑越小，上升速度越快，這也符合常規認知。氣囊在橡膠軟管中膨脹的曲線與自由膨脹的曲線形狀相似，但由于管道的約束，氣囊壁強度得到增強，內部能夠達到更高的氣壓。
氣囊在離體豬小腸中膨脹時，氣壓變化與在35 mm硬管中膨脹類似，而與橡膠薄膜軟管差別較大，在實驗過程中，感受到小腸薄而韌，延展性遠不及相近厚度的橡膠薄膜軟管。
4.2 氣囊錨固力測量
氣囊錨固力即靜摩擦力，與接觸壓力成正比，由于錨定氣囊的局部失穩不可避免，因而接觸面積難以進行理論推導，故通過實驗測量錨定氣囊在腸道內的錨固力。腸道僅能承受有限的徑向膨脹，錨定氣囊的接觸面積與徑向變形正相關，即錨固力與錨定氣囊徑向變形正相關。腸道組織的徑向拉伸極限為原直徑的1.85倍[32]，實驗中發現，離體豬小腸難以徑向拉伸至初始直徑的1.85倍，氣囊在腸道內膨脹到一定程度后會順應腸道形狀偏移位置，離體豬小腸初始充盈直徑在25 mm左右，最大能夠膨脹到約33 mm。
測量時，氣囊在腸道中膨脹到直徑約33 mm后，固定拉力計（卡西洛數顯拉力計），拖拽豬小腸，將測得數據上傳至上位機繪制為曲線，取曲線的峰值作為錨固力（即靜摩擦力）的典型值記錄。
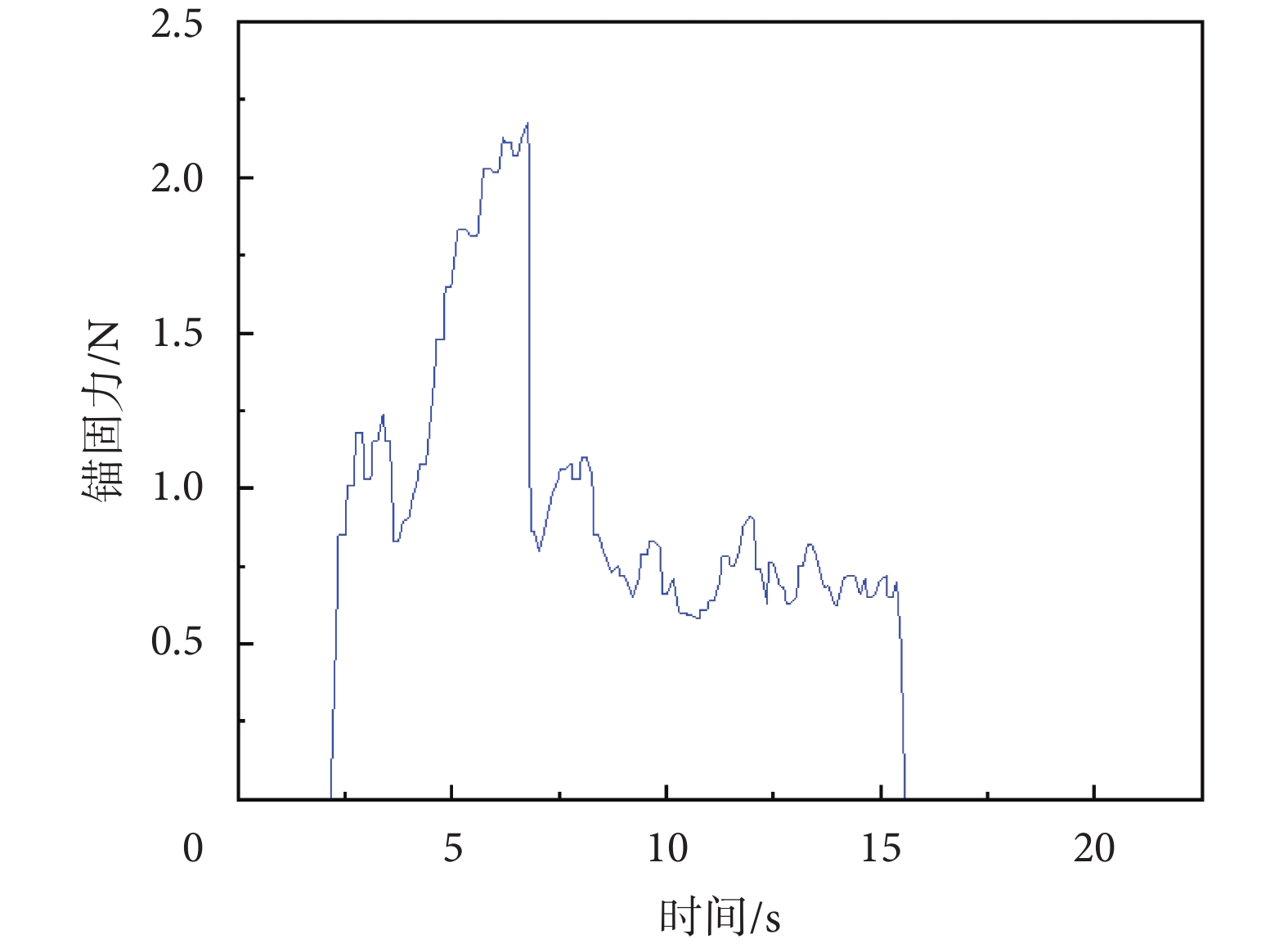
典型測試曲線如圖10所示，開始拖拽豬小腸時，曲線數值上升，上升到一定程度，錨定氣囊滑動，拉力驟降，繼續平穩地拖拽豬小腸，得到滑動摩擦曲線。共進行三次實驗，錨固力取最大靜摩擦力的平均值，約為2.33 N，滑動摩擦力平均值約為0.70 N。
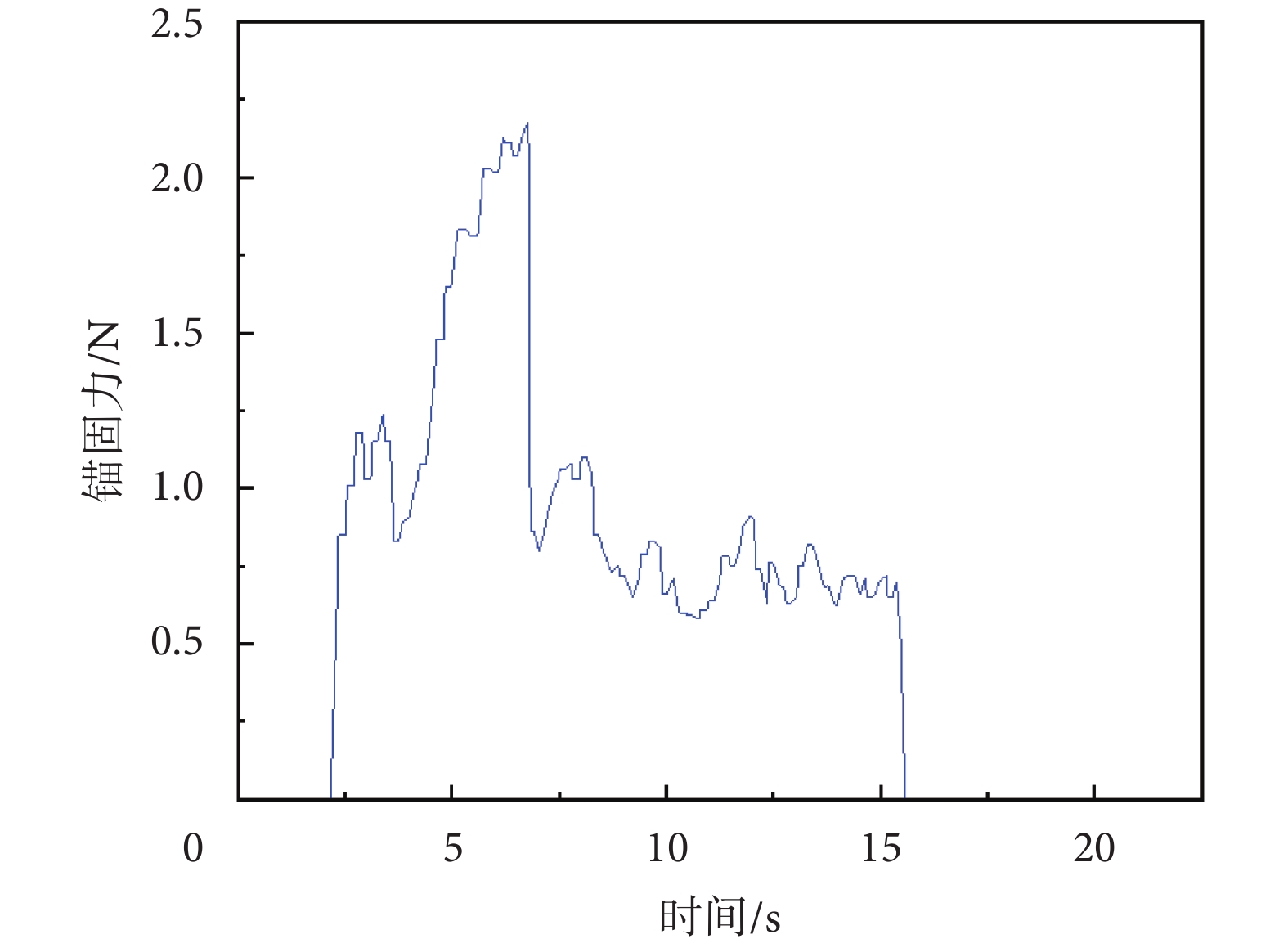圖10
錨固力典型測試曲線
Figure10.
Typical test curve of anchoring force
4.3 運行速度測量
為表征腸道機器人性能，分別測量它在內徑25、35、47 mm的PC硬直管和豬小腸中多次循環運動的時間和距離，得到其運行速度。
實驗中，腸道機器人在25、35 mm硬直管及豬小腸中運行正常，視頻參見附件2、3、4；但在47 mm直管未能正常運行，觀察到腸道機器人氣囊2在收縮后剛度很低，氣囊1與管壁自然接觸，當氣囊2充氣時，氣囊1與管壁間的摩擦力使氣囊2在充氣時發生翻折，導致腸道機器人無法正常前進，視頻參見附件5。在25 mm及35 mm硬直管中，剛開始同樣會有翻折的發生，但由于較小的管道直徑，后續的翻折被管壁所阻擋，而在豬小腸中，還存在濕滑導致摩擦力更小的原因，因此腸道機器人能夠在25 mm和35 mm硬管及豬小腸中正常運行，運行速度分別為8.46、7.27、4.87 mm/s。
在35 mm內徑硬直管中運行時，錨定氣囊需要充氣到更大的直徑，充氣時間增加導致運行速度較25 mm的管道略微下降。在豬小腸中運行時，氣囊2膨脹后，重力使豬小腸包裹在腸道機器人表面，氣囊2收縮后，腸道壁亦被摩擦力和粘滯力拖拽收縮，相對運動距離減少導致運行效率的下降，視頻參見附件4。
4.4 腸道機器人的彎道通過性
腸道機器人依靠其整體尤其是氣囊2的柔順性被動轉彎。氣囊2伸長時在氣壓作用下剛度也會增加，導致腸道機器人柔順性減小，因此，充氣時應使氣囊2完全伸長但內部氣壓不顯著增加，充氣量以氣囊2膨脹時體積減去PU彈簧管體積為宜。充氣前氣囊2內即存在部分空氣，在運動之前，應抽去空氣使它完全收縮，以使單次運動循環伸縮量最大。
將腸道機器人放置在90 °的拐彎中，使用水基潤滑劑潤滑彎道處管壁模仿腸液的潤滑，結果表明腸道機器人能夠依靠自身結構柔順性通過較大角度的硬質彎管，視頻參見附件6。
除以上實驗外，還在腸道機器人內部以兩種不同方式安裝了攝像頭并進行比較，選擇了不顯著增加腸道機器人剛度的安裝方式，具體內容參見附件1第4節。
5 結論與展望
本文提出了一種結構簡單、成本低廉的氣囊錨定式仿尺蠖運動氣動軟體腸道機器人，實現了腸道機器人在離體豬小腸中的自主運行。通過圓形截面假設，建立了氣囊內部氣壓與外部變形間的關系，較為準確地得到了圓柱狀橡膠薄膜在200%～500%徑向伸長率下的變形，為后續定量指導橡膠薄膜氣囊的制作提供了一定的理論基礎。與球形橡膠氣囊變形理論解比較，指出了錨定氣囊的不均勻變形是一種失穩現象。將腸道機器人放置在多種直徑的PC直管和離體豬小腸中測量其運行速度，其中在離體豬小腸中運行速度約為4.87 mm/s。在離體豬小腸中測得橡膠氣囊的錨固力約為2.33 N。
對腸道機器人的彎道通過性進行了相關實驗，表明它可通過90 °的硬質彎管，后續將對腸道機器人進行改進，以期通過更大角度的彎管（如180 °），同時搭建仿真人體腸道的實驗環境，對橡膠材料與腸道相互接觸的摩擦界面問題進行理論和實驗研究。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：何永勝主要負責設計制作、實驗數據采集與分析、論文寫作的工作；孫志峻主要負責研究經費提供、研究方向把控和內容審閱的工作；袁捷提供了實驗指導意見；韋聰文對于電路設計提供了指導；韓國偉和褚效成幫助進行了部分實驗。
本文附件見本刊網站的電子版本（biomedeng.cn）。
0 引言
根據2022年全球癌癥統計數據[1]，消化道相關癌癥已成為世界上發病率最高的癌癥。小腸在消化道中檢查最為困難，它管腔較長（5～7 m）且迂曲折疊[2]，傳統小腸鏡檢查需要經肛和經口兩種方式，小腸鏡推進困難，對接成功率低，因此患者接受度很低。現有對小腸鏡的改造主要有單氣囊小腸鏡和雙氣囊小腸鏡[3]，雖提高了對接率，但未能解決檢查繁瑣及患者痛苦的問題。
以色列在2000年研發出膠囊內窺鏡[4]，略大于普通膠囊，吞服后可隨胃腸道蠕動而前進，同時將照片傳出體外。其主要缺點是運動不受控，無法拍攝指定位置，可能會漏檢。為此，學者還研究了磁控膠囊機器人[5]，但它對腸道的折疊和褶皺仍無能為力。鑒于以上檢查方式的缺點，國際上廣泛進行了自主推進式腸道機器人的研究[6]，早先有螺旋式[7]、螺旋槳式[8]、腿/槳式[9-10]、仿蝸牛爬行式[11]乃至電刺激腸道蠕動式[12]等，近年來出現的多為變徑履帶式[13]及仿尺蠖/蚯蚓式。
尺蠖因其運動方式成為了多種管道類機器人的仿生研究對象[14]。傳統分類方法主要根據腸道機器人運動方式進行分類，而本文根據與腸道接觸部分的剛度，將仿尺蠖腸道機器人分為軟接觸和硬接觸。硬接觸式腸道機器人結構復雜，成本較高，軟接觸式腸道機器人則結構簡單、成本低廉，具有較大的發展潛力[15]。軟接觸根據材料模量大小又分為軟材料接觸和軟結構接觸，或二者結合。軟材料接觸式機器人一般使用橡膠類超彈性材料與腸道直接接觸以保證接觸安全性，其錨定結構僅有材料自身變形[16]，而少有結構大變形，或變形后結構仍具有較大剛度[17]。軟結構接觸式機器人的材料模量較高，是通過結構大變形來保證安全性，如Li等[18]提出的檢查氣管用仿尺蠖運動機器人。
除以上兩種外，更多是將兩種接觸方式結合，以充氣橡膠薄膜作為錨定機構最具代表性。橡膠薄膜質地柔軟，膨脹后的大變形結構能夠很好地貼合腸道。文獻[19-23]均使用類似的橡膠氣囊作為錨定結構，區別主要在于中部伸縮氣囊的結構及整體的制作材料和方法。
為降低腸道檢查成本、減輕患者痛苦，以及降低已有腸道機器人的復雜度，本文提出了一種結構簡單的仿尺蠖運動氣動軟體腸道機器人，并進行了相關理論分析和實驗。
1 材料與方法
所提出的腸道機器人如圖1所示，由三個氣囊構成，其中氣囊1和氣囊3用于腸道內錨定，氣囊2用于伸縮。氣囊1和氣囊3由支撐結構及橡膠薄膜構成，氣囊2由低密度聚乙烯（low density polyethylene，LDPE）薄膜和聚氨酯（polyurethane，PU）彈簧管構成，與腸道接觸的所有結構（氣囊、硅橡膠軟管）均為高聚物材料，具有良好的生物相容性。
圖1
腸道機器人結構
Figure1.
The structure of intestinal robots
腸道機器人在腸道內前進的運動步驟如圖2所示，氣囊1和3膨脹時錨定，氣囊2膨脹時伸長，① 狀態時可放入或取出體內，②～⑦ 為一個運動循環，⑧ 狀態回到 ② 狀態，機器人前進一“步”，反向執行 ②～⑦ 步驟即可使腸道機器人倒退。
圖2
運動過程
① 為完全收縮，②～⑦ 為運動步態，⑧ 為下一運動循環的初始狀態
Figure2. Movement process① complete contraction; ② - ⑦ movement gait; ⑧ initial state of the next movement cycle
氣囊2變形長度直接影響著腸道機器人前進速度，為使氣囊2能夠在伸縮時具有大行程，根據文獻[18]，PU彈簧管在伸長時的螺旋間距應當與圓筒形LDPE薄膜的直徑相同，若大于直徑，則薄膜收縮到一定程度會封閉氣道導致氣囊2無法繼續收縮，若小于直徑，過多的螺旋圈數亦使得氣囊2無法收縮到最短。
腸道機器人在未充氣時直徑小于人體小腸充盈后最小直徑15 mm[24]，借助柔順性通過腸道彎曲處，因此其長度不宜過長，否則容易折疊，但腸道機器人運動效率又與其單個周期的行程正相關[25]，綜合考慮后，將長度設計為162 mm，也可根據實際需要調整。
腸道機器人驅動部分的相關介紹參見附件1第1節。
2 錨定氣囊變形理論分析
錨定氣囊與腸道壁直接接觸，錨固力（靜摩擦力）與接觸壓力相關，為使錨定氣囊的變形能夠覆蓋人體結腸和小腸的尺寸變化范圍，需要計算錨定氣囊在氣壓下的變形。
2.1 幾何方程
傳統的結構變形分析方法較為繁難，因此本文根據氣囊的實際變形情況進行一定簡化。觀察到錨定氣囊在變形后的截面形狀近似為圓弧，故假設變形后的錨定氣囊側面形狀為圓弧，如圖3所示。
圖3
氣囊變形截面的幾何關系
Figure3.
Geometric relationship of deformation cross-section of airbag
根據假設，未變形圓筒形橡膠薄膜的橫截面在變形后某一時刻會內接于一圓弧（見圖3右），內接條件為：
|
r為錨定氣囊變形后半徑，R和L為圓柱形橡膠薄膜的初始半徑和長度，其中L = 14.5 mm，R = 6 mm，代入式(1)可得r = 9.4 mm，小于氣囊與腸道接觸時的半徑（約12 mm），未與腸道壁接觸，因此僅推導如圖3左所示變形的幾何關系如下：
緯度和經度方向的主拉伸：
|
根據橡膠材料的不可壓縮性：
|
h為橡膠薄膜變形后的厚度，H為其初始厚度，s為經度方向圓弧的長度，幾何關系如下：
|
其中a為圓弧半徑，為L/2對應的圓周角，a的計算公式為：
|
的計算公式為：
|
根據以上公式，在圓截面假設下，圓柱形橡膠薄膜在不同變形程度下的主拉伸和統一為變形半徑r的函數。
2.2 平衡方程
將變形后的錨定氣囊看作薄壁容器，其壁面壓力P與薄膜應力平衡，如圖4所示，考慮到氣囊變形后，不同緯度的薄膜周向拉伸程度不同，導致薄膜經向厚度分布不均勻，即0 °緯線上最薄，隨著緯度升高而逐漸變厚，因此將錨定氣囊沿0 °緯線剖開，根據對稱性，薄膜在該緯度上沿圓周方向均勻分布，由力的平衡得到平衡方程：
圖4
氣囊受力平衡示意圖
Figure4.
Schematic diagram of airbag force balance
|
其中為沿主拉伸方向的應力，可由下文物理方程求得。
2.3 本構方程
本構方程與橡膠材料的特性有關，不同的本構模型適用于不同的變形范圍和加載方式，基于使用的簡便性和計算準確性，采用三階Ogden模型[26]作為橡膠的本構模型。文獻[27]在忽略了薄膜厚度方向的應力后，使用橡膠的三階Ogden模型推導出橡膠薄膜本構方程：
|
其中、為材料參數， = 617 kPa， = 1.86 kPa， = ? 9.79 kPa， = 1.65， = 5.08， = ? 2.0。在平衡方程中僅用到了，故只需使用上式中第二式。
由平衡方程得到：
|
將h和的計算公式代入可得到壓強P關于變形半徑r的變化關系，即控制方程。
3 氣囊變形研究
3.1 錨定氣囊變形過程
實驗測得錨定氣囊的氣壓-半徑關系如圖5右所示，變形過程如圖6所示，分為四個階段：Ⅰ. 開始充氣后，氣壓與半徑幾乎呈線性關系，氣囊的變形很小，但氣壓上升很快；Ⅱ. 到達某一氣壓后，氣囊外形產生局部突變，同時內部氣壓顯著降低，外觀表現為一大一小的不均勻變形，為方便描述，將大的部分記為A（左側氣囊），小的部分記為B（右側氣囊），氣囊的邊緣形狀近似為圓形，但內部支撐不在圓心處，測量如圖5左所示的長軸和短軸，二者尺寸相近，在圖5右中標記為同一氣壓下的紅點與黑點；Ⅲ. 繼續充氣，A部分變形較小，B部分變形較大，B部分變大使內部支撐逐漸移向圓心處，不均勻變形逐漸消失，氣壓隨半徑增大而變化較小；Ⅳ. 變形到最后階段，不均勻變形幾乎消失，氣壓隨半徑增大而上升。
圖5
錨定氣囊尺寸測量方式（左）及測量結果（右）
Figure5.
Measurement method for anchored airbag size (Left) and measurement results (Right)
圖6
錨定氣囊變形過程
Figure6.
Deformation process of anchored balloon
圖5右中，氣囊變化過程的實驗曲線最高點右端有一段空白即是氣囊變形發生局部突變所致。氣囊在不均勻變形階段氣壓變化小但半徑變化大，表明該階段的氣囊容易改變形狀，能夠更好地適應腸道的復雜結構。
氣囊變形過程中，不同變形可能會對應相同氣壓，因此，僅以氣壓作為反饋無法得知氣囊的變形，故氣囊的變形需要根據充氣體積確定，由于腸道環境的復雜性，仍需要氣壓反饋來保證充氣的安全性。氣囊變形的控制方法參見附件1第2節。
3.2 理論變形與實際變形的討論
將理論計算得到的氣壓與氣囊半徑的關系曲線（）與實驗測得的對應曲線進行比較，如圖7所示。在實驗中共測量了三個結構和尺寸相同的氣囊，其初始尺寸為L = 14.5 mm，H = 0.23 mm，R = 6.1 mm。
圖7
氣囊變形的實驗值與理論值
Figure7.
Experimental and theoretical values of airbag deformation
通過與球形氣囊的相關曲線對比來解釋實驗曲線，根據相同的分析方法，得到球形氣囊的氣壓-半徑變化曲線及氣壓-體積變化曲線如圖8所示，二者材料參數相同。球形氣囊結構對稱，其變形無需做出額外假設，即球形氣囊在充氣膨脹后仍為球形，圖8所示曲線為球形氣囊變形的精確解。
圖8
球形氣囊壓強隨半徑（左）和體積（右）的變化規律
Figure8.
The variation of pressure of a spherical balloon with radius (left) and volume (right)
圖8左的變化趨勢與圖5右相似，在某一極值點后氣壓大幅下降而氣囊半徑大幅增加，通過氣壓-體積變化曲線（圖8右）可以更清楚地看到這一點，這是超彈性材料氣囊膨脹變形過程中的失穩現象[28-31]，因此錨定氣囊的不均勻變形是局部失穩現象，由橡膠材料自身特性決定，無法通過改進制作工藝等方式完全消除。本研究還對錨定球囊和醫用球囊變形過程進行了比較，醫用球囊同樣也出現了失穩現象，具體結果參見附件1第3節。
圖7中，理論曲線與實驗曲線在氣囊半徑較小（r < 13 mm）和半徑較大（r > 30 mm）時誤差較大，原因是為了消除橡膠的Mullins效應，錨定氣囊在測試前會經過大幅度的加載卸載，會產生殘余塑性應變，在小變形時形狀與圓弧有較大差距。在大變形時（r > 30 mm），緯度方向橡膠薄膜更早被拉伸硬化，因此與圓截面假設也有較大差距，導致理論與實驗數據偏離。理論曲線在中等變形（13 mm < r < 30 mm，200%～500%拉伸率）時與實驗曲線吻合較好，說明在中等變形時，氣囊截面形狀更符合理論推導所使用的圓截面假設。
4 腸道機器人相關實驗
4.1 錨定氣囊在不同管道中膨脹時內部氣壓變化
為區分錨定氣囊與多種實驗常用管道相互作用的異同，進行了錨定氣囊在內徑25、35、47 mm聚碳酸酯（polycarbonate，PC）硬管及直徑21 mm的橡膠軟管和離體豬小腸中的膨脹實驗，充入氣體體積和氣囊內部氣壓的關系如圖9所示，錨定氣囊自由膨脹的相應曲線亦在其中，以方便比較。
圖9
氣囊在不同管道中的膨脹
Figure9.
Expansion of airbags in different pipelines
從圖中可以看出，對于硬管，氣囊與管壁接觸后，氣壓會迅速上升，管徑越小，上升速度越快，這也符合常規認知。氣囊在橡膠軟管中膨脹的曲線與自由膨脹的曲線形狀相似，但由于管道的約束，氣囊壁強度得到增強，內部能夠達到更高的氣壓。
氣囊在離體豬小腸中膨脹時，氣壓變化與在35 mm硬管中膨脹類似，而與橡膠薄膜軟管差別較大，在實驗過程中，感受到小腸薄而韌，延展性遠不及相近厚度的橡膠薄膜軟管。
4.2 氣囊錨固力測量
氣囊錨固力即靜摩擦力，與接觸壓力成正比，由于錨定氣囊的局部失穩不可避免，因而接觸面積難以進行理論推導，故通過實驗測量錨定氣囊在腸道內的錨固力。腸道僅能承受有限的徑向膨脹，錨定氣囊的接觸面積與徑向變形正相關，即錨固力與錨定氣囊徑向變形正相關。腸道組織的徑向拉伸極限為原直徑的1.85倍[32]，實驗中發現，離體豬小腸難以徑向拉伸至初始直徑的1.85倍，氣囊在腸道內膨脹到一定程度后會順應腸道形狀偏移位置，離體豬小腸初始充盈直徑在25 mm左右，最大能夠膨脹到約33 mm。
測量時，氣囊在腸道中膨脹到直徑約33 mm后，固定拉力計（卡西洛數顯拉力計），拖拽豬小腸，將測得數據上傳至上位機繪制為曲線，取曲線的峰值作為錨固力（即靜摩擦力）的典型值記錄。
典型測試曲線如圖10所示，開始拖拽豬小腸時，曲線數值上升，上升到一定程度，錨定氣囊滑動，拉力驟降，繼續平穩地拖拽豬小腸，得到滑動摩擦曲線。共進行三次實驗，錨固力取最大靜摩擦力的平均值，約為2.33 N，滑動摩擦力平均值約為0.70 N。
圖10
錨固力典型測試曲線
Figure10.
Typical test curve of anchoring force
4.3 運行速度測量
為表征腸道機器人性能，分別測量它在內徑25、35、47 mm的PC硬直管和豬小腸中多次循環運動的時間和距離，得到其運行速度。
實驗中，腸道機器人在25、35 mm硬直管及豬小腸中運行正常，視頻參見附件2、3、4；但在47 mm直管未能正常運行，觀察到腸道機器人氣囊2在收縮后剛度很低，氣囊1與管壁自然接觸，當氣囊2充氣時，氣囊1與管壁間的摩擦力使氣囊2在充氣時發生翻折，導致腸道機器人無法正常前進，視頻參見附件5。在25 mm及35 mm硬直管中，剛開始同樣會有翻折的發生，但由于較小的管道直徑，后續的翻折被管壁所阻擋，而在豬小腸中，還存在濕滑導致摩擦力更小的原因，因此腸道機器人能夠在25 mm和35 mm硬管及豬小腸中正常運行，運行速度分別為8.46、7.27、4.87 mm/s。
在35 mm內徑硬直管中運行時，錨定氣囊需要充氣到更大的直徑，充氣時間增加導致運行速度較25 mm的管道略微下降。在豬小腸中運行時，氣囊2膨脹后，重力使豬小腸包裹在腸道機器人表面，氣囊2收縮后，腸道壁亦被摩擦力和粘滯力拖拽收縮，相對運動距離減少導致運行效率的下降，視頻參見附件4。
4.4 腸道機器人的彎道通過性
腸道機器人依靠其整體尤其是氣囊2的柔順性被動轉彎。氣囊2伸長時在氣壓作用下剛度也會增加，導致腸道機器人柔順性減小，因此，充氣時應使氣囊2完全伸長但內部氣壓不顯著增加，充氣量以氣囊2膨脹時體積減去PU彈簧管體積為宜。充氣前氣囊2內即存在部分空氣，在運動之前，應抽去空氣使它完全收縮，以使單次運動循環伸縮量最大。
將腸道機器人放置在90 °的拐彎中，使用水基潤滑劑潤滑彎道處管壁模仿腸液的潤滑，結果表明腸道機器人能夠依靠自身結構柔順性通過較大角度的硬質彎管，視頻參見附件6。
除以上實驗外，還在腸道機器人內部以兩種不同方式安裝了攝像頭并進行比較，選擇了不顯著增加腸道機器人剛度的安裝方式，具體內容參見附件1第4節。
5 結論與展望
本文提出了一種結構簡單、成本低廉的氣囊錨定式仿尺蠖運動氣動軟體腸道機器人，實現了腸道機器人在離體豬小腸中的自主運行。通過圓形截面假設，建立了氣囊內部氣壓與外部變形間的關系，較為準確地得到了圓柱狀橡膠薄膜在200%～500%徑向伸長率下的變形，為后續定量指導橡膠薄膜氣囊的制作提供了一定的理論基礎。與球形橡膠氣囊變形理論解比較，指出了錨定氣囊的不均勻變形是一種失穩現象。將腸道機器人放置在多種直徑的PC直管和離體豬小腸中測量其運行速度，其中在離體豬小腸中運行速度約為4.87 mm/s。在離體豬小腸中測得橡膠氣囊的錨固力約為2.33 N。
對腸道機器人的彎道通過性進行了相關實驗，表明它可通過90 °的硬質彎管，后續將對腸道機器人進行改進，以期通過更大角度的彎管（如180 °），同時搭建仿真人體腸道的實驗環境，對橡膠材料與腸道相互接觸的摩擦界面問題進行理論和實驗研究。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：何永勝主要負責設計制作、實驗數據采集與分析、論文寫作的工作；孫志峻主要負責研究經費提供、研究方向把控和內容審閱的工作；袁捷提供了實驗指導意見；韋聰文對于電路設計提供了指導；韓國偉和褚效成幫助進行了部分實驗。
本文附件見本刊網站的電子版本（biomedeng.cn）。
