運動想象腦電（EEG）的腦機接口因其無創采集和易用性等優勢，在神經康復領域展現了巨大潛力。然而，運動想象EEG具有較低的信噪比和時空分辨率，且傳統神經網絡僅關注其時空特征，導致運動想象任務的解碼識別率較低。為解決這一問題，本文從EEG信號的頻域和空間域角度出發，提出了一種基于空-頻特征圖學習的三維卷積神經網絡解碼方法。首先，利用Welch方法計算EEG的頻帶功率譜，結合電極空間拓撲分布的二維矩陣將時序EEG轉換為包含空-頻信息的腦地形圖。然后，設計一維和二維卷積串行結構的三維網絡，以有效學習EEG空-頻特征。最后，該方法與多種經典方法進行對比實驗，結果顯示平均解碼識別率達86.89%，較對照方法更優，驗證了該方法在運動想象EEG解碼領域的有效性。
引用本文： 吳雪健, 褚亞奇, 趙新剛, 趙憶文. 基于空-頻特征圖學習三維卷積神經網絡的運動想象腦電解碼方法. 生物醫學工程學雜志, 2024, 41(6): 1145-1152. doi: 10.7507/1001-5515.202407038 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
腦-機接口（brain-computer interface，BCI）能夠將腦部活動轉換為外部設備可解讀和響應的指令，實現大腦與外部設備的直接連接與控制。BCI不僅可幫助脊髓或肢體神經受損的患者提升生活質量，越來越多地應用于康復領域[1]，例如使用腦機接口康復手機器人幫助手障礙患者康復[2]，還廣泛地應用于機械臂[3]、游戲[4]和虛擬現實控制[5]等場景。
與誘發式腦電[6]相比，運動想象（motor imagery，MI）腦電具有自發性，這種性質在BCI技術中具備獨特優勢，能夠實現無外部環境干擾的控制[7]。在運動想象腦電信號（MI EEG）采集任務中，研究者發現實驗人員在執行不同的運動想象任務時會引起不同的大腦區域產生反應；同側運動與對側運動過程中，感覺運動皮質的電信號在α頻段（8～12 Hz）和β頻段（13～30 Hz）出現不同的振幅反應，分別被稱為事件相關同步化和事件相關去同步化[8]。利用這些現象，研究者提出了多種時域、頻域和空間域的特征提取方法，其中包括短時傅里葉變換、連續小波變換、共空間模式（common spatial pattern，CSP）及其他變種算法[9-11]，同時還有大量用于分類的算法例如人工神經網絡、支持向量機（support vector machine，SVM）和貝斯分類器等[12-15]。CSP是一種專注于空間域特征的提取算法，但它忽視了EEG在時域和頻域的特征，會影響解碼效果。
在深度學習解碼方面，卷積神經網絡（convolutional neural network，CNN）因能夠自動提取多層次的特征、減少參數的數量并提高計算效率而被廣泛應用于自然語言處理[16]和計算機視覺[17]等方面。近年來，CNN也被引入到運動想象EEG的分類解碼中，展現出優越的非線性特征提取能力和適應不同任務的架構靈活性。例如，Li等[18]通過結合CNN提取空間信息的能力和長短時記憶網絡對時間序列的建模能力提出一種CNN深度模型，達到87.68%的平均解碼識別率；褚亞奇等[19]提出一種CNN架構學習腦電信號的時空特征，在四分類任務上取得了優秀的效果；Zhang等[20]提出了一種多分支融合卷積網絡模型，使用兩種類型的CNN網絡分析腦電數據和時頻圖，實現了78.52%的平均識別率；Roy[21]使用了一種多尺度CNN，結合數據增強的方法，在不同的頻段上進行信息的提取，在BCI competition IV-2b數據集上達到了93.74%的識別率；Zhang等[22]提出一種帶有注意力的圖卷積神經網絡，在EEG Motor Movement/Imagery Dataset數據集上達到74.71%的識別率，優于當時的先進網絡。這些研究結果表明，深度學習方法對于EEG分類具有較好效果。然而，現有的研究主要集中在EEG的時域或時空域特征學習，并未充分利用EEG中蘊含的頻域和空間域信息，缺少對于充分高效利用EEG空-頻特征的探索和研究。
為了更好地利用EEG的多維特征，探究提高解碼EEG頻域、空間域特征的方法，本文構建了運動想象EEG的空-頻三維數據集，并設計了三維卷積神經網絡（three-dimensional CNN，3DCNN）框架進行解碼。本研究提出了以下創新點：① 針對傳統卷積網絡僅關注EEG信號時空特征，忽略空域、頻域特征的問題，采用將原始EEG轉化為二維空間頻譜特征圖像的方法提取EEG的空-頻特征。② 針對EEG空-頻特征解碼效果差的問題，構造了一種新型的3DCNN網絡架構以提取、解碼EEG的空-頻特征，提高對于EEG空-頻特征的解碼能力。③ 對EEG信號頻帶信息進行分析，選出與運動想象任務更相關的頻域特征，優化空-頻特征圖像。將所提方法與經典機器學習和深度學習模型在公開腦電數據集上進行對比測試和統計學分析，以驗證所提方法的有效性。
1 數據來源與數據轉化
1.1 實驗測試數據集
本文在公開數據集EEG Motor Movement/Imagery Dataset[23]上進行測試。該數據集由109名志愿者參與，記錄了他們執行各種運動和運動想象任務時的EEG數據。實驗過程如下：使用BCI2000系統，根據國際10-10標準從64個電極位點采集EEG信號，采樣率為160 Hz（不包含Nz、F9、F10、FT9、FT10、A1、A2、TP9、TP10、P9和P10電極）。受試者坐在顯示器前看到特定指令后，立即在腦中想象相應動作，實驗系統同時記錄運動想象EEG數據。每個受試者要重復多輪任務，兩次任務間有適當休息。運動想象任務為二分類任務：左拳和右拳。由于有5名受試者的EEG質量較差，本文最終使用了104名受試者的EEG數據進行實驗分析。
1.2 數據預處理
在信號數據的預處理環節，本文采用了分段和濾波的方法。為了提高處理速度，根據所選數據集的特點，將原始EEG數據劃分為持續4 s的短時間段，以針對運動想象任務的關鍵時間窗，便于后續的特征提取。為排除工頻噪聲等干擾，本文對分段后的EEG進行濾波處理。與運動想象任務相關的關鍵EEG頻段主要集中在μ節律和β節律[6]，本文使用帶通濾波器（5～35 Hz）對EEG數據進行濾波，以去除心電、眼動、不穩定呼吸等生理性偽跡干擾，從而提高信號整體的信噪比。
1.3 Welch功率譜密度估計
Welch功率譜密度估計是一種基于信號分段平均的頻譜估計方法，可以得到信號在不同頻率上的能量分布。Welch功率譜密度估計的原理如下[24]：
首先將長度為
的數據
分成L段，每段有M個數據，第i段數據表示為：
 |
然后利用快速傅里葉變換，把窗函數
加到每一個數據段上，求出每一時間段的功率譜密度，第i段的功率譜密度為：
 |
式（2）中，
被稱為歸一化因子：
 |
將每段信號的功率譜密度看成近似獨立，最后的功率譜估計即得到的Welch功率譜密度為：
 |
1.4 數據集轉化
數據集轉化的過程如圖1所示。原始EEG為64通道采集而成，首先使用滑動窗口技術對原始信號進行切片處理，得到短時間窗的EEG片段，然后針對這些EEG片段，采用Welch功率譜密度估計方法，計算出每個時間窗口內10～15 Hz頻段的功率譜密度特征。選擇10～15 Hz頻段是通過實驗得到的優化選擇結果，是與左右拳運動想象任務最相關的EEG頻段，具體選擇依據見3.1部分。
圖1
數據集轉化過程
Figure1.
Dataset conversion process
之后，將10～15 Hz頻段以0.5 Hz為步長劃分為10個子頻段，以細化頻率特征，從而更好地捕捉與運動想象任務相關的特征信息。每個頻段對應的信號值按照數據集中的64個電極的空間分布排列成二維矩陣。令單個信號值為
，此時
。創建空二維矩陣
，結合數據集的空間位置信息，將
轉化為二維矩陣
，如下所示：
 |
通過這種方法可以有效展現該頻段下不同電極位置的信號特征分布。EEG通常具有空間相關性，相鄰通道的信號變化趨勢相似，為了更好地體現電極的空間拓撲關系，本文利用MATLAB中基于三角剖分的三次插值技術，對生成的二維矩陣進行插值處理，在均勻坐標上生成110個和100個線性矢量，此時原來形狀為（11，10）的矩陣轉化成形狀為（110，100）的高分辨率矩陣。高分辨率矩陣模擬腦電極在大腦表面相對分散的分布，使EEG在后續圖像生成過程中具有更平滑的過渡，還原較真實的大腦表面生物電信號特征。然后通過高分辨率矩陣數據形成該子頻率特征下的二維腦電地形圖。插值前后數據生成的二維腦電地形圖如圖2所示。
圖2
插值前后數據生成的二維腦電地形圖
Figure2.
The two-dimensional EEG topographic maps generated before and after interpolation
如圖所示，通過插值，腦電地形圖的特征分辨率更高，更有利于EEG的解碼任務。最后，將10個子頻率對應的二維腦電地形圖整合為一個三維的空間-頻率圖像數據集。這種融合空-頻域特征的方式，可以更好地捕獲EEG信號復雜的特征，為后續的深度學習模型提供更豐富的輸入數據。
2 運動想象腦電解碼方法
2.1 基于空-頻特征學習的3DCNN解碼方法
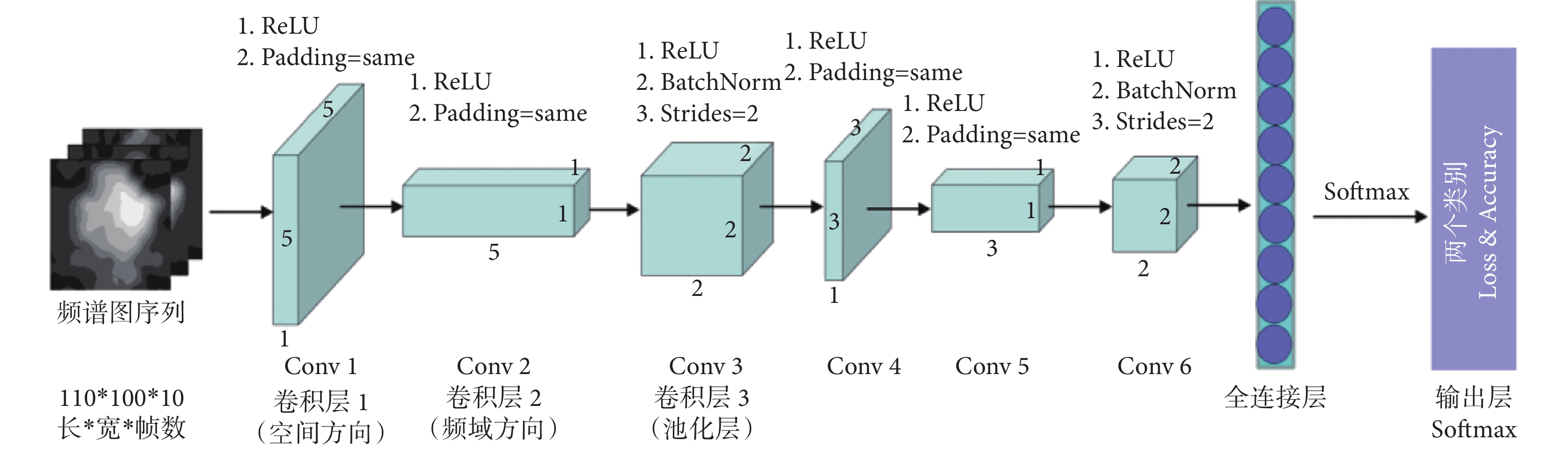
經典的卷積網絡模型局限于輸入的原始EEG類型，通常只能處理EEG的時頻或時空特征，缺少對空間域和頻域的探索。針對上述問題，本文提出了一種基于空-頻特征圖學習3DCNN的運動想象腦電解碼方法（Picture 3DCNN，P-3DCNN）。該方法利用卷積網絡的局部感受野和權值共享特性，通過設計頻域和空間方向的卷積結構，學習轉換后的二維EEG數據集的頻域和空間特征。同時，采用兩層三維卷積結構對空-頻特征進行抽象學習，從而充分捕捉EEG多維特征信息。整體網絡由四部分組成（見圖3）。
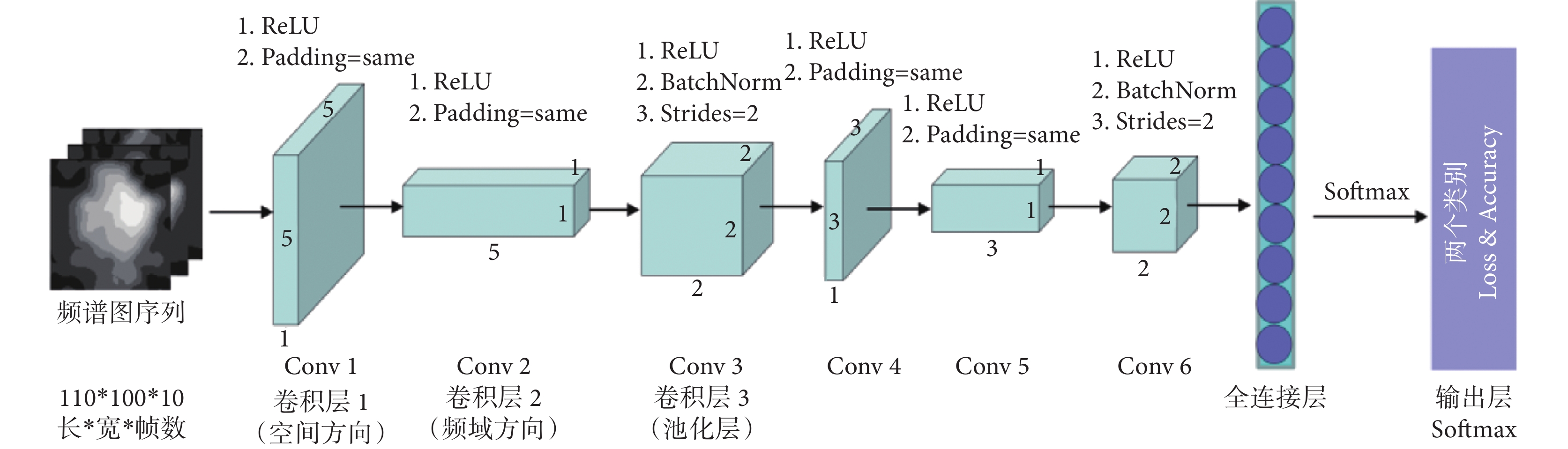圖3
基于空-頻特征圖學習的3DCNN架構（P-3DCNN）
Figure3.
The architecture of 3DCNN based on spatial-spectral feature pictures learning (P-3DCNN)
（1）輸入層：網絡的輸入是轉化完成的二維EEG空-頻圖數據集，每個樣本由110×100×10的數據矩陣組成，其中110和100為二維腦電圖x軸和y軸方向上像素點數量（代表EEG的空間信息），10為每個運動想象任務中所含的圖像幀數（代表EEG的頻域信息）。
（2）空間-頻域偽三維卷積模塊：該模塊獲取空-頻圖的空間和頻域特征信息。采用偽三維卷積實現二維卷積核功能，依次從空間方向和頻域方向對腦電圖序列進行卷積運算。為實現二維卷積在空間方向卷積，卷積層1的三維卷積核頻域方向上的參數被設置為1，空間方向的卷積核參數被設置為5 × 5。然后，卷積層2在頻域方向上的卷積核參數設置為5，空間方向上的卷積核參數設置為1 × 1，捕獲EEG頻域特征。最后，進行平方運算、三維卷積-池化模塊和對數運算，從而充分提取EEG樣本的空-頻特征。各卷積層采用非線性修正線性單元（ReLU）激活函數。
（3）三維卷積-池化模塊：該模塊用于對EEG空-頻特征進行降維處理，并學習更加抽象的高層次特征，達到多尺度學習的效果。通過三維卷積操作，可以改變數據結構的特性，在取消填充的同時將步長設置為2，從而實現池化降低特征圖大小的功能。同時，三維卷積會對空間-頻域三維卷積模塊提取的空-頻特征計算更加高級的特征表示。
（4）全連接層和Softmax輸出層：該部分將特征表示映射到最終的分類結果，以實現運動想象任務的分類。首先，將卷積-池化模塊提取的空-頻特征處理為特征向量，全連接層上神經元數量設定為256，每個神經元都與所有的特征向量相連接，采用ReLU非線性函數為激活函數。Softmax是一種廣泛應用于分類任務的輸出激活函數，Softmax層將輸入值歸一化為0到1之間的概率分布，進行最后的二分類任務。本文的Softmax層包括兩個神經元，分別對應左、右拳兩個運動想象任務。
（5）P-3DCNN網絡訓練與優化：為了實現P-3DCNN網絡的有效收斂，使模型的預測結果盡可能接近正確的分類，需要定義網絡的損失函數，并最小化損失函數。P-3DCNN網絡可以由映射函數
表示，其中
是網絡的給定輸入，
是P-3DCNN網絡中的所有參數，
是網絡的輸出類別數。計算網絡輸入
在不同的標簽
下的條件概率分布，計算公式如下：
 |
那么，可以通過計算所有樣本的損失之和的最小值，對
進行優化，為P-3DCNN確定最優參數，即：
 |
其中，
為樣本
的實際類別，
為損失函數，也稱之為類別的負對數似然函數：
 |
為了提升P-3DCNN網絡的訓練性能，本文采取了以下優化策略：首先，采用小批量隨機梯度下降法[25]對網絡參數進行更新，以提高模型的穩定性和泛化能力，同時優化內存使用，降低算力要求，節約解碼時間。然后，在第二層和第六層卷積后加入批歸一化（Batch Normalization），以防止模型過擬合并增強其魯棒性。最后，在第六層卷積之后添加50%概率的丟棄操作，進一步提升了模型的收斂速度和泛化性能。
2.2 評價指標及統計方法
對于每個被試的空-頻圖像數據集，利用python中的split函數設置隨機種子數為42，將整體數據集的數據予以打亂，然后以75%和25%的比例分為信號的訓練集和測試集。通過訓練集和測試集對多種機器學習和深度學習模型進行模型的訓練和性能的評估。主要的評價指標包括：
（1）每種模型在被試數據上的平均識別率；
（2）Kappa系數，用于反映分類結果與完全隨機分類的一致性程度，計算公式為：
 |
其中，
為總體識別率，
為隨機分類識別率（對于二分類問題，
= 0.5）；
（3）召回率（Recall），體現模型能夠識別正確樣本的能力，計算公式為：
 |
其中，TP（true positive）表示正確預測為正類的樣本數，FN（false negative）表示預測為負類的正類樣本數；
（4）F1是一個綜合了識別率和召回率的評價指標，計算公式為：
 |
其中，Precision（查準率）表示預測為正類的樣本中真正為正類的比例；
（5）計算各類運動想象EEG的混淆矩陣。除此之外，為了分析P-3DCNN和其他對比網絡的差異，采用威爾科克符號秩檢驗方法（Wilcoxon Signed-Rank Test）對網絡結果進行統計學分析，檢驗水準為0.05。
3 實驗結果與分析
3.1 特定頻段的優化選擇
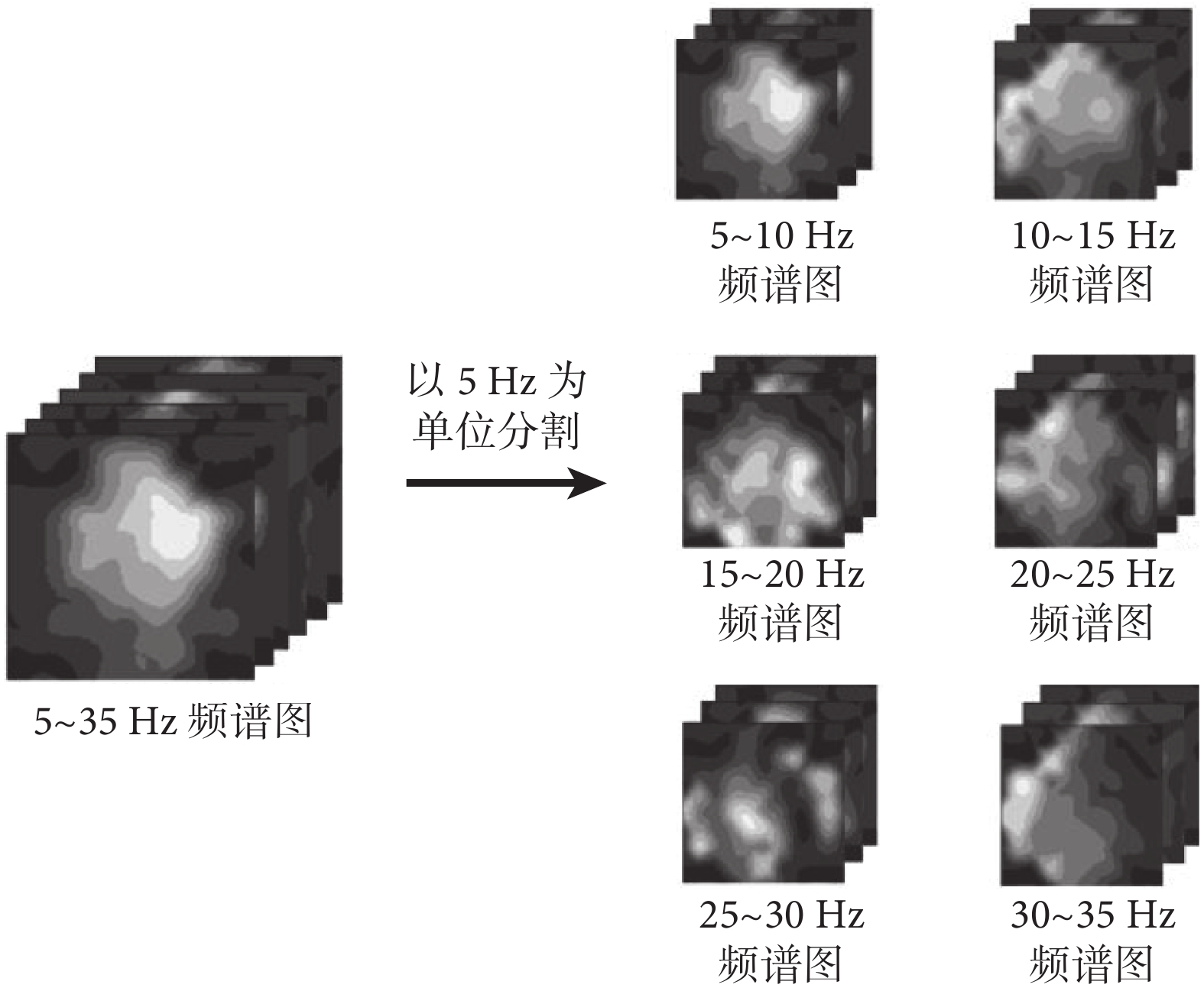
由于EEG本身較弱，在采集過程中難免會受到環境因素的干擾，如工頻噪聲、眼動偽跡等，即便在預處理階段盡力去除這些干擾偽跡，仍難以完全消除；同時，EEG轉化為空-頻特征圖的過程會增加計算負擔，采用全頻段或大頻段進行轉化解碼將降低計算效率。因此在將原始EEG轉換為二維腦電地形圖數據集之前，首先對不同頻段生成的腦電地形圖進行細分優化，選擇與左右拳運動想象任務最相關的頻帶進行解碼任務，以減少偽跡干擾和計算負擔，分割頻帶為每段5 Hz，如圖4所示。之后對這些細分數據進行預分類，分類結果如表1所顯示。
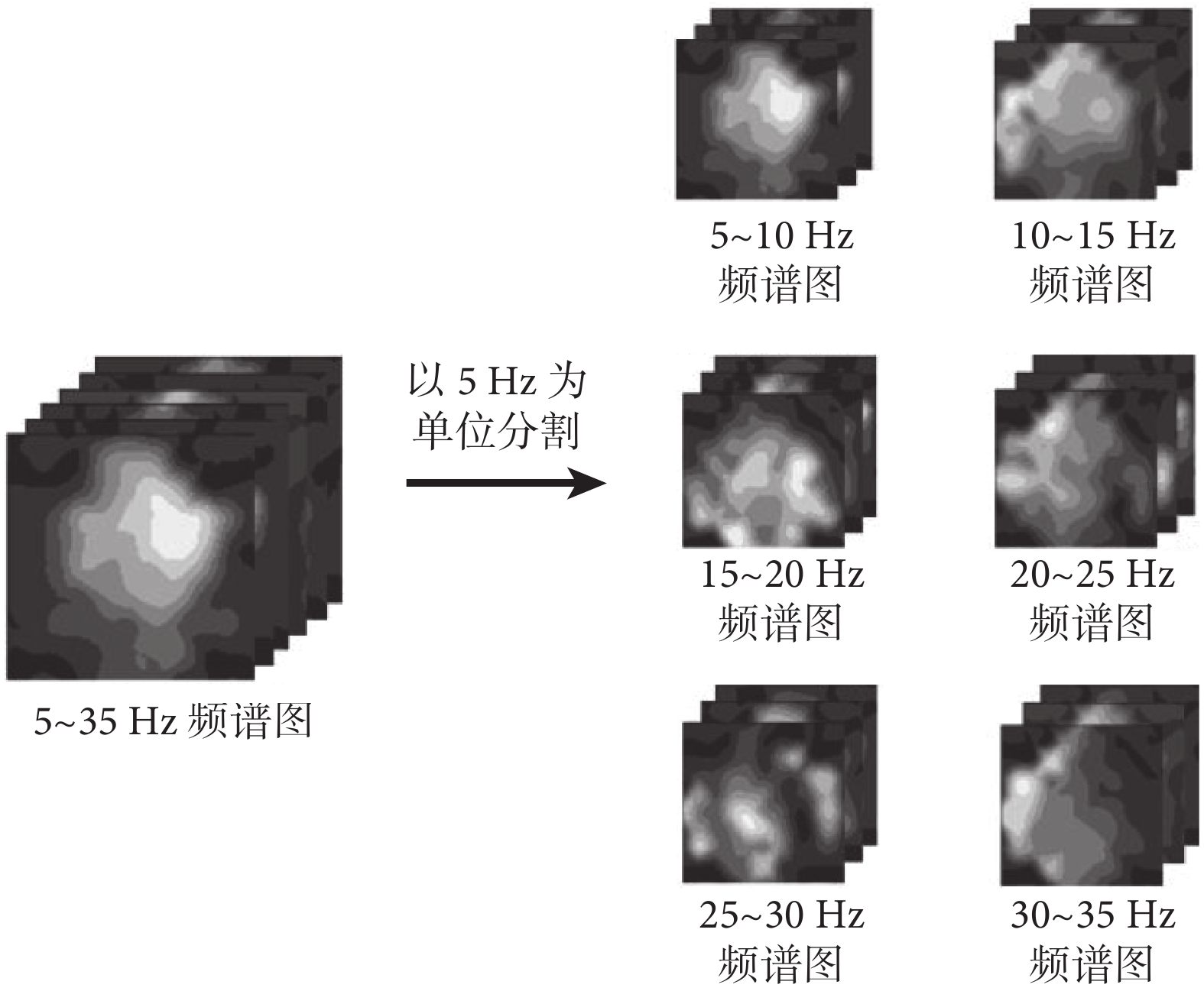圖4
頻帶分割方法
Figure4.
Frequency band segmentation method
表1
各頻帶下的平均識別率（%）
Table1.
The average recognition rate for each frequency band (%)
根據表1中的分類結果，10～15 Hz頻段的數據集表現更為出色，平均識別率高于其他頻段且具有較低的標準差，能夠擁有更穩定的識別效果。因此，本文采用10～15 Hz的頻段數據，作為后續EEG解碼分類的輸入。這一選擇不僅能充分利用該頻段內蘊含的顯著特征，而且可以有效降低解碼時間，同時也可以提升整體的分類性能。
3.2 解碼方法的結果對比
為了驗證P-3DCNN的解碼性能，本文將之與現有的先進算法進行比較，選擇了兩種傳統機器學習算法和五種深度學習算法。Antony等[26]利用在線遞歸的獨立成分分析和自適應SVM分類七種主成分；Yacine等[14]結合黎曼空間與人工神經網絡（artificial neural network，ANN），使用144個253維數據作為輸入，訓練迭代60次完成分類；褚亞奇等[19]采用四層卷積結構，在第二至第四層后加入池化層，實現高效的特征提取和分類；Li等[27]提出四層3DCNN結構，使用ReLU和Softmax激活函數以及批量歸一化技術，優化解碼能力；Lawhern等[28]提出EEGNet，利用一維卷積層和深度卷積層提取EEG特征，具有較好的實時性；Chaudhary等[29]構建DeepConvNet，并結合短時傅里葉變換增強對時頻特征的捕捉；Hermosilla等[30]提出ShallowConNet，使用兩層小卷積核的卷積層，具備快速解碼和易訓練的優勢；P-3DCNN（No-pic）是在不使用三維空-頻特征圖的情況下，直接利用本文提出的3DCNN進行解碼的方法。上述網絡基于公開數據集的解碼性能結果如表2所示。
表2
各方法的解碼性能
Table2.
The decoding performance for each method
從表2的對比結果來看，深度學習方法相較于傳統機器學習（如CSP+SVM、ANN）在解碼復雜的EEG時能夠提取更具價值的特征，從而提升EEG的解碼識別率和Kappa系數。其中，本文提出的P-3DCNN方法的平均識別率高達86.89%，能夠更好地捕捉到EEG空-頻特征并進行解碼，比傳統方法提高12%～31%。同時，P-3DCNN方法獲得的Kappa系數為0.751，表明結果具有高度的一致性。而在同類的對比方法中3DCNN的Kappa系數最高，為0.506，遠低于P-3DCNN。P-3DCNN的召回率和F1值同樣有較好的表現。綜上所述，與傳統方法相比，P-3DCNN全面提升了解碼性能，展現了在運動想象EEG解碼領域的有效性。統計分析顯示，104名參與者的實驗結果通過威爾科克符號秩檢驗，P-3DCNN在識別率和Kappa系數上均優于機器學習和深度學習中表現較好的ANN和3DCNN（P<0.05和P<0.001）。統計學檢驗的結果進一步驗證了P-3DCNN解碼方法的有效性。
進一步分析P-3DCNN（No-pic）網絡架構，結果表明，在考慮頻域和空間域信息的情況下，P-3DCNN（No-pic）較傳統CNN的平均識別率提高了13.83%，較3DCNN提高了1.54%。在本文采用生成三維頻譜圖方法的情況下，三維頻譜圖為網絡提供了蘊含更豐富空-頻特征信息的三維特征輸入，使模型在處理數據時實現了更高效的特征提取，學習到更多的有效特征，增強了模型對復雜信號的解碼能力。基于此，提出的P-3DCNN在P-3DCNN（No-pic）網絡基礎上，將平均識別率進一步提高了9.63%，且獲得了更高的Kappa系數、召回率和F1值。這充分表明，本文設計的P-3DCNN解碼方案在運動想象EEG解碼任務中的優良性能。
3.3 混淆矩陣結果分析
為了更全面地評估所提方法在各類運動想象EEG識別上的表現，本文計算了平均混淆矩陣，如圖5所示。混淆矩陣的行對應實際的運動想象類別（左拳、右拳），列對應預測的運動想象類別。矩陣中行與列對應的類別相同時，代表運動想象任務被正確識別分類的比例；不同時則代表被錯誤識別分類的比例。
圖5
深度學習解碼方式下的運動想象腦電類別混淆矩陣
Figure5.
The confusion matrix for motor imagery EEG classes with deep learning decoding method
從圖5中可以發現EEGNet、DeepConvNet、ShallowConvNet、CNN等網絡在本數據集上的識別率普遍不高，除ShallowConvNet在左拳的識別率為71%，其余均低于70%。而3DCNN的分類效果雖已具有較大的提升，但在左拳識別任務中仍未超過80%。這可能是由于左右手運動想象占據相同的運動感覺區，導致EEG信號在空間上的分辨率較低，3DCNN方法嘗試從高維時空域角度進行分析，但是其解碼效果仍不夠理想，未能充分利用空-頻域信息。顯然，即使采用了先進的深度學習算法，網絡對左右拳分類任務仍然存在一定的局限性，還有較大的改進空間。相比之下，本文所提出的P-3DCNN方法能夠提高左右拳分類任務的識別率，分別提升至86%和87%。這表明P-3DCNN方法能夠更好地提取二維頻譜圖中的空-頻域信息，通過分析較高分辨率的空-頻特征，獲得更優的解碼效果。
4 討論與結論
本研究提出了一種基于空間-頻率特征學習的偽三維CNN（P-3DCNN）結構，用于從運動想象EEG信號中提取更加可區分的特征，以提升EEG信號的分類識別性能。首先設計了頻域和空間域上的偽三維卷積層，用于從EEG信號中分別提取頻譜和空間分布特征。然后結合了兩層特殊的三維卷積結構，對這些空-頻特征進行聯合學習建模。最后，利用輸出層處理，實現對兩種運動想象任務的分類識別。
實驗結果表明，與經典機器學習和深度學習方法相比，P-3DCNN在平均識別率和Kappa系數等指標上均有提升。這說明頻域和空間域中蘊含著豐富的判別特征，通過融合這些特征可以大幅增強EEG信號的分類性能。相比于直接使用原始時域信號，本文通過有效特征提取和深度學習模型設計，充分解碼了EEG信號中的空-頻信息，提升了分類識別的準確性和可靠性。
未來的研究方向是針對現有數據量較少的問題，利用生成對抗網絡進行數據增強，提高數據集的特征數目，進一步優化P-3DCNN的泛化能力。另外，雖然本文采用了特定頻段的優化選擇方法提高計算效率，但仍然存在進一步提升的空間，未來可以通過調整網絡層數和神經元數量的方式簡化模型，并通過權重剪枝減少計算量，提高計算效率，增強P-3DCNN模型的實時性效果，為運動想象腦機接口的應用發展提供更加穩定、通用和高效快捷的算法支持。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：吳雪健負責實驗設計、數據集構建、方法建模和寫作；褚亞奇、趙新剛和趙憶文負責實驗指導和論文的審閱修訂。
0 引言
腦-機接口（brain-computer interface，BCI）能夠將腦部活動轉換為外部設備可解讀和響應的指令，實現大腦與外部設備的直接連接與控制。BCI不僅可幫助脊髓或肢體神經受損的患者提升生活質量，越來越多地應用于康復領域[1]，例如使用腦機接口康復手機器人幫助手障礙患者康復[2]，還廣泛地應用于機械臂[3]、游戲[4]和虛擬現實控制[5]等場景。
與誘發式腦電[6]相比，運動想象（motor imagery，MI）腦電具有自發性，這種性質在BCI技術中具備獨特優勢，能夠實現無外部環境干擾的控制[7]。在運動想象腦電信號（MI EEG）采集任務中，研究者發現實驗人員在執行不同的運動想象任務時會引起不同的大腦區域產生反應；同側運動與對側運動過程中，感覺運動皮質的電信號在α頻段（8～12 Hz）和β頻段（13～30 Hz）出現不同的振幅反應，分別被稱為事件相關同步化和事件相關去同步化[8]。利用這些現象，研究者提出了多種時域、頻域和空間域的特征提取方法，其中包括短時傅里葉變換、連續小波變換、共空間模式（common spatial pattern，CSP）及其他變種算法[9-11]，同時還有大量用于分類的算法例如人工神經網絡、支持向量機（support vector machine，SVM）和貝斯分類器等[12-15]。CSP是一種專注于空間域特征的提取算法，但它忽視了EEG在時域和頻域的特征，會影響解碼效果。
在深度學習解碼方面，卷積神經網絡（convolutional neural network，CNN）因能夠自動提取多層次的特征、減少參數的數量并提高計算效率而被廣泛應用于自然語言處理[16]和計算機視覺[17]等方面。近年來，CNN也被引入到運動想象EEG的分類解碼中，展現出優越的非線性特征提取能力和適應不同任務的架構靈活性。例如，Li等[18]通過結合CNN提取空間信息的能力和長短時記憶網絡對時間序列的建模能力提出一種CNN深度模型，達到87.68%的平均解碼識別率；褚亞奇等[19]提出一種CNN架構學習腦電信號的時空特征，在四分類任務上取得了優秀的效果；Zhang等[20]提出了一種多分支融合卷積網絡模型，使用兩種類型的CNN網絡分析腦電數據和時頻圖，實現了78.52%的平均識別率；Roy[21]使用了一種多尺度CNN，結合數據增強的方法，在不同的頻段上進行信息的提取，在BCI competition IV-2b數據集上達到了93.74%的識別率；Zhang等[22]提出一種帶有注意力的圖卷積神經網絡，在EEG Motor Movement/Imagery Dataset數據集上達到74.71%的識別率，優于當時的先進網絡。這些研究結果表明，深度學習方法對于EEG分類具有較好效果。然而，現有的研究主要集中在EEG的時域或時空域特征學習，并未充分利用EEG中蘊含的頻域和空間域信息，缺少對于充分高效利用EEG空-頻特征的探索和研究。
為了更好地利用EEG的多維特征，探究提高解碼EEG頻域、空間域特征的方法，本文構建了運動想象EEG的空-頻三維數據集，并設計了三維卷積神經網絡（three-dimensional CNN，3DCNN）框架進行解碼。本研究提出了以下創新點：① 針對傳統卷積網絡僅關注EEG信號時空特征，忽略空域、頻域特征的問題，采用將原始EEG轉化為二維空間頻譜特征圖像的方法提取EEG的空-頻特征。② 針對EEG空-頻特征解碼效果差的問題，構造了一種新型的3DCNN網絡架構以提取、解碼EEG的空-頻特征，提高對于EEG空-頻特征的解碼能力。③ 對EEG信號頻帶信息進行分析，選出與運動想象任務更相關的頻域特征，優化空-頻特征圖像。將所提方法與經典機器學習和深度學習模型在公開腦電數據集上進行對比測試和統計學分析，以驗證所提方法的有效性。
1 數據來源與數據轉化
1.1 實驗測試數據集
本文在公開數據集EEG Motor Movement/Imagery Dataset[23]上進行測試。該數據集由109名志愿者參與，記錄了他們執行各種運動和運動想象任務時的EEG數據。實驗過程如下：使用BCI2000系統，根據國際10-10標準從64個電極位點采集EEG信號，采樣率為160 Hz（不包含Nz、F9、F10、FT9、FT10、A1、A2、TP9、TP10、P9和P10電極）。受試者坐在顯示器前看到特定指令后，立即在腦中想象相應動作，實驗系統同時記錄運動想象EEG數據。每個受試者要重復多輪任務，兩次任務間有適當休息。運動想象任務為二分類任務：左拳和右拳。由于有5名受試者的EEG質量較差，本文最終使用了104名受試者的EEG數據進行實驗分析。
1.2 數據預處理
在信號數據的預處理環節，本文采用了分段和濾波的方法。為了提高處理速度，根據所選數據集的特點，將原始EEG數據劃分為持續4 s的短時間段，以針對運動想象任務的關鍵時間窗，便于后續的特征提取。為排除工頻噪聲等干擾，本文對分段后的EEG進行濾波處理。與運動想象任務相關的關鍵EEG頻段主要集中在μ節律和β節律[6]，本文使用帶通濾波器（5～35 Hz）對EEG數據進行濾波，以去除心電、眼動、不穩定呼吸等生理性偽跡干擾，從而提高信號整體的信噪比。
1.3 Welch功率譜密度估計
Welch功率譜密度估計是一種基于信號分段平均的頻譜估計方法，可以得到信號在不同頻率上的能量分布。Welch功率譜密度估計的原理如下[24]：
首先將長度為的數據分成L段，每段有M個數據，第i段數據表示為：
|
然后利用快速傅里葉變換，把窗函數加到每一個數據段上，求出每一時間段的功率譜密度，第i段的功率譜密度為：
|
式（2）中，被稱為歸一化因子：
|
將每段信號的功率譜密度看成近似獨立，最后的功率譜估計即得到的Welch功率譜密度為：
|
1.4 數據集轉化
數據集轉化的過程如圖1所示。原始EEG為64通道采集而成，首先使用滑動窗口技術對原始信號進行切片處理，得到短時間窗的EEG片段，然后針對這些EEG片段，采用Welch功率譜密度估計方法，計算出每個時間窗口內10～15 Hz頻段的功率譜密度特征。選擇10～15 Hz頻段是通過實驗得到的優化選擇結果，是與左右拳運動想象任務最相關的EEG頻段，具體選擇依據見3.1部分。
圖1
數據集轉化過程
Figure1.
Dataset conversion process
之后，將10～15 Hz頻段以0.5 Hz為步長劃分為10個子頻段，以細化頻率特征，從而更好地捕捉與運動想象任務相關的特征信息。每個頻段對應的信號值按照數據集中的64個電極的空間分布排列成二維矩陣。令單個信號值為，此時。創建空二維矩陣，結合數據集的空間位置信息，將轉化為二維矩陣，如下所示：
|
通過這種方法可以有效展現該頻段下不同電極位置的信號特征分布。EEG通常具有空間相關性，相鄰通道的信號變化趨勢相似，為了更好地體現電極的空間拓撲關系，本文利用MATLAB中基于三角剖分的三次插值技術，對生成的二維矩陣進行插值處理，在均勻坐標上生成110個和100個線性矢量，此時原來形狀為（11，10）的矩陣轉化成形狀為（110，100）的高分辨率矩陣。高分辨率矩陣模擬腦電極在大腦表面相對分散的分布，使EEG在后續圖像生成過程中具有更平滑的過渡，還原較真實的大腦表面生物電信號特征。然后通過高分辨率矩陣數據形成該子頻率特征下的二維腦電地形圖。插值前后數據生成的二維腦電地形圖如圖2所示。
圖2
插值前后數據生成的二維腦電地形圖
Figure2.
The two-dimensional EEG topographic maps generated before and after interpolation
如圖所示，通過插值，腦電地形圖的特征分辨率更高，更有利于EEG的解碼任務。最后，將10個子頻率對應的二維腦電地形圖整合為一個三維的空間-頻率圖像數據集。這種融合空-頻域特征的方式，可以更好地捕獲EEG信號復雜的特征，為后續的深度學習模型提供更豐富的輸入數據。
2 運動想象腦電解碼方法
2.1 基于空-頻特征學習的3DCNN解碼方法
經典的卷積網絡模型局限于輸入的原始EEG類型，通常只能處理EEG的時頻或時空特征，缺少對空間域和頻域的探索。針對上述問題，本文提出了一種基于空-頻特征圖學習3DCNN的運動想象腦電解碼方法（Picture 3DCNN，P-3DCNN）。該方法利用卷積網絡的局部感受野和權值共享特性，通過設計頻域和空間方向的卷積結構，學習轉換后的二維EEG數據集的頻域和空間特征。同時，采用兩層三維卷積結構對空-頻特征進行抽象學習，從而充分捕捉EEG多維特征信息。整體網絡由四部分組成（見圖3）。
圖3
基于空-頻特征圖學習的3DCNN架構（P-3DCNN）
Figure3.
The architecture of 3DCNN based on spatial-spectral feature pictures learning (P-3DCNN)
（1）輸入層：網絡的輸入是轉化完成的二維EEG空-頻圖數據集，每個樣本由110×100×10的數據矩陣組成，其中110和100為二維腦電圖x軸和y軸方向上像素點數量（代表EEG的空間信息），10為每個運動想象任務中所含的圖像幀數（代表EEG的頻域信息）。
（2）空間-頻域偽三維卷積模塊：該模塊獲取空-頻圖的空間和頻域特征信息。采用偽三維卷積實現二維卷積核功能，依次從空間方向和頻域方向對腦電圖序列進行卷積運算。為實現二維卷積在空間方向卷積，卷積層1的三維卷積核頻域方向上的參數被設置為1，空間方向的卷積核參數被設置為5 × 5。然后，卷積層2在頻域方向上的卷積核參數設置為5，空間方向上的卷積核參數設置為1 × 1，捕獲EEG頻域特征。最后，進行平方運算、三維卷積-池化模塊和對數運算，從而充分提取EEG樣本的空-頻特征。各卷積層采用非線性修正線性單元（ReLU）激活函數。
（3）三維卷積-池化模塊：該模塊用于對EEG空-頻特征進行降維處理，并學習更加抽象的高層次特征，達到多尺度學習的效果。通過三維卷積操作，可以改變數據結構的特性，在取消填充的同時將步長設置為2，從而實現池化降低特征圖大小的功能。同時，三維卷積會對空間-頻域三維卷積模塊提取的空-頻特征計算更加高級的特征表示。
（4）全連接層和Softmax輸出層：該部分將特征表示映射到最終的分類結果，以實現運動想象任務的分類。首先，將卷積-池化模塊提取的空-頻特征處理為特征向量，全連接層上神經元數量設定為256，每個神經元都與所有的特征向量相連接，采用ReLU非線性函數為激活函數。Softmax是一種廣泛應用于分類任務的輸出激活函數，Softmax層將輸入值歸一化為0到1之間的概率分布，進行最后的二分類任務。本文的Softmax層包括兩個神經元，分別對應左、右拳兩個運動想象任務。
（5）P-3DCNN網絡訓練與優化：為了實現P-3DCNN網絡的有效收斂，使模型的預測結果盡可能接近正確的分類，需要定義網絡的損失函數，并最小化損失函數。P-3DCNN網絡可以由映射函數表示，其中是網絡的給定輸入，是P-3DCNN網絡中的所有參數，是網絡的輸出類別數。計算網絡輸入在不同的標簽下的條件概率分布，計算公式如下：
|
那么，可以通過計算所有樣本的損失之和的最小值，對進行優化，為P-3DCNN確定最優參數，即：
|
其中，為樣本的實際類別，為損失函數，也稱之為類別的負對數似然函數：
|
為了提升P-3DCNN網絡的訓練性能，本文采取了以下優化策略：首先，采用小批量隨機梯度下降法[25]對網絡參數進行更新，以提高模型的穩定性和泛化能力，同時優化內存使用，降低算力要求，節約解碼時間。然后，在第二層和第六層卷積后加入批歸一化（Batch Normalization），以防止模型過擬合并增強其魯棒性。最后，在第六層卷積之后添加50%概率的丟棄操作，進一步提升了模型的收斂速度和泛化性能。
2.2 評價指標及統計方法
對于每個被試的空-頻圖像數據集，利用python中的split函數設置隨機種子數為42，將整體數據集的數據予以打亂，然后以75%和25%的比例分為信號的訓練集和測試集。通過訓練集和測試集對多種機器學習和深度學習模型進行模型的訓練和性能的評估。主要的評價指標包括：
（1）每種模型在被試數據上的平均識別率；
（2）Kappa系數，用于反映分類結果與完全隨機分類的一致性程度，計算公式為：
|
其中，為總體識別率，為隨機分類識別率（對于二分類問題， = 0.5）；
（3）召回率（Recall），體現模型能夠識別正確樣本的能力，計算公式為：
|
其中，TP（true positive）表示正確預測為正類的樣本數，FN（false negative）表示預測為負類的正類樣本數；
（4）F1是一個綜合了識別率和召回率的評價指標，計算公式為：
|
其中，Precision（查準率）表示預測為正類的樣本中真正為正類的比例；
（5）計算各類運動想象EEG的混淆矩陣。除此之外，為了分析P-3DCNN和其他對比網絡的差異，采用威爾科克符號秩檢驗方法（Wilcoxon Signed-Rank Test）對網絡結果進行統計學分析，檢驗水準為0.05。
3 實驗結果與分析
3.1 特定頻段的優化選擇
由于EEG本身較弱，在采集過程中難免會受到環境因素的干擾，如工頻噪聲、眼動偽跡等，即便在預處理階段盡力去除這些干擾偽跡，仍難以完全消除；同時，EEG轉化為空-頻特征圖的過程會增加計算負擔，采用全頻段或大頻段進行轉化解碼將降低計算效率。因此在將原始EEG轉換為二維腦電地形圖數據集之前，首先對不同頻段生成的腦電地形圖進行細分優化，選擇與左右拳運動想象任務最相關的頻帶進行解碼任務，以減少偽跡干擾和計算負擔，分割頻帶為每段5 Hz，如圖4所示。之后對這些細分數據進行預分類，分類結果如表1所顯示。
圖4
頻帶分割方法
Figure4.
Frequency band segmentation method
表1
各頻帶下的平均識別率（%）
Table1.
The average recognition rate for each frequency band (%)
根據表1中的分類結果，10～15 Hz頻段的數據集表現更為出色，平均識別率高于其他頻段且具有較低的標準差，能夠擁有更穩定的識別效果。因此，本文采用10～15 Hz的頻段數據，作為后續EEG解碼分類的輸入。這一選擇不僅能充分利用該頻段內蘊含的顯著特征，而且可以有效降低解碼時間，同時也可以提升整體的分類性能。
3.2 解碼方法的結果對比
為了驗證P-3DCNN的解碼性能，本文將之與現有的先進算法進行比較，選擇了兩種傳統機器學習算法和五種深度學習算法。Antony等[26]利用在線遞歸的獨立成分分析和自適應SVM分類七種主成分；Yacine等[14]結合黎曼空間與人工神經網絡（artificial neural network，ANN），使用144個253維數據作為輸入，訓練迭代60次完成分類；褚亞奇等[19]采用四層卷積結構，在第二至第四層后加入池化層，實現高效的特征提取和分類；Li等[27]提出四層3DCNN結構，使用ReLU和Softmax激活函數以及批量歸一化技術，優化解碼能力；Lawhern等[28]提出EEGNet，利用一維卷積層和深度卷積層提取EEG特征，具有較好的實時性；Chaudhary等[29]構建DeepConvNet，并結合短時傅里葉變換增強對時頻特征的捕捉；Hermosilla等[30]提出ShallowConNet，使用兩層小卷積核的卷積層，具備快速解碼和易訓練的優勢；P-3DCNN（No-pic）是在不使用三維空-頻特征圖的情況下，直接利用本文提出的3DCNN進行解碼的方法。上述網絡基于公開數據集的解碼性能結果如表2所示。
表2
各方法的解碼性能
Table2.
The decoding performance for each method
從表2的對比結果來看，深度學習方法相較于傳統機器學習（如CSP+SVM、ANN）在解碼復雜的EEG時能夠提取更具價值的特征，從而提升EEG的解碼識別率和Kappa系數。其中，本文提出的P-3DCNN方法的平均識別率高達86.89%，能夠更好地捕捉到EEG空-頻特征并進行解碼，比傳統方法提高12%～31%。同時，P-3DCNN方法獲得的Kappa系數為0.751，表明結果具有高度的一致性。而在同類的對比方法中3DCNN的Kappa系數最高，為0.506，遠低于P-3DCNN。P-3DCNN的召回率和F1值同樣有較好的表現。綜上所述，與傳統方法相比，P-3DCNN全面提升了解碼性能，展現了在運動想象EEG解碼領域的有效性。統計分析顯示，104名參與者的實驗結果通過威爾科克符號秩檢驗，P-3DCNN在識別率和Kappa系數上均優于機器學習和深度學習中表現較好的ANN和3DCNN（P<0.05和P<0.001）。統計學檢驗的結果進一步驗證了P-3DCNN解碼方法的有效性。
進一步分析P-3DCNN（No-pic）網絡架構，結果表明，在考慮頻域和空間域信息的情況下，P-3DCNN（No-pic）較傳統CNN的平均識別率提高了13.83%，較3DCNN提高了1.54%。在本文采用生成三維頻譜圖方法的情況下，三維頻譜圖為網絡提供了蘊含更豐富空-頻特征信息的三維特征輸入，使模型在處理數據時實現了更高效的特征提取，學習到更多的有效特征，增強了模型對復雜信號的解碼能力。基于此，提出的P-3DCNN在P-3DCNN（No-pic）網絡基礎上，將平均識別率進一步提高了9.63%，且獲得了更高的Kappa系數、召回率和F1值。這充分表明，本文設計的P-3DCNN解碼方案在運動想象EEG解碼任務中的優良性能。
3.3 混淆矩陣結果分析
為了更全面地評估所提方法在各類運動想象EEG識別上的表現，本文計算了平均混淆矩陣，如圖5所示。混淆矩陣的行對應實際的運動想象類別（左拳、右拳），列對應預測的運動想象類別。矩陣中行與列對應的類別相同時，代表運動想象任務被正確識別分類的比例；不同時則代表被錯誤識別分類的比例。
圖5
深度學習解碼方式下的運動想象腦電類別混淆矩陣
Figure5.
The confusion matrix for motor imagery EEG classes with deep learning decoding method
從圖5中可以發現EEGNet、DeepConvNet、ShallowConvNet、CNN等網絡在本數據集上的識別率普遍不高，除ShallowConvNet在左拳的識別率為71%，其余均低于70%。而3DCNN的分類效果雖已具有較大的提升，但在左拳識別任務中仍未超過80%。這可能是由于左右手運動想象占據相同的運動感覺區，導致EEG信號在空間上的分辨率較低，3DCNN方法嘗試從高維時空域角度進行分析，但是其解碼效果仍不夠理想，未能充分利用空-頻域信息。顯然，即使采用了先進的深度學習算法，網絡對左右拳分類任務仍然存在一定的局限性，還有較大的改進空間。相比之下，本文所提出的P-3DCNN方法能夠提高左右拳分類任務的識別率，分別提升至86%和87%。這表明P-3DCNN方法能夠更好地提取二維頻譜圖中的空-頻域信息，通過分析較高分辨率的空-頻特征，獲得更優的解碼效果。
4 討論與結論
本研究提出了一種基于空間-頻率特征學習的偽三維CNN（P-3DCNN）結構，用于從運動想象EEG信號中提取更加可區分的特征，以提升EEG信號的分類識別性能。首先設計了頻域和空間域上的偽三維卷積層，用于從EEG信號中分別提取頻譜和空間分布特征。然后結合了兩層特殊的三維卷積結構，對這些空-頻特征進行聯合學習建模。最后，利用輸出層處理，實現對兩種運動想象任務的分類識別。
實驗結果表明，與經典機器學習和深度學習方法相比，P-3DCNN在平均識別率和Kappa系數等指標上均有提升。這說明頻域和空間域中蘊含著豐富的判別特征，通過融合這些特征可以大幅增強EEG信號的分類性能。相比于直接使用原始時域信號，本文通過有效特征提取和深度學習模型設計，充分解碼了EEG信號中的空-頻信息，提升了分類識別的準確性和可靠性。
未來的研究方向是針對現有數據量較少的問題，利用生成對抗網絡進行數據增強，提高數據集的特征數目，進一步優化P-3DCNN的泛化能力。另外，雖然本文采用了特定頻段的優化選擇方法提高計算效率，但仍然存在進一步提升的空間，未來可以通過調整網絡層數和神經元數量的方式簡化模型，并通過權重剪枝減少計算量，提高計算效率，增強P-3DCNN模型的實時性效果，為運動想象腦機接口的應用發展提供更加穩定、通用和高效快捷的算法支持。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：吳雪健負責實驗設計、數據集構建、方法建模和寫作；褚亞奇、趙新剛和趙憶文負責實驗指導和論文的審閱修訂。
