腦出血是一種高發病率和高死亡率的嚴重腦血管疾病，及時診斷和治療至關重要。電阻抗斷層成像（EIT）作為一種功能性成像技術，能夠在腦部組織發病初期檢測電學特性的異常變化。然而，由于顱腦EIT圖像重建涉及不規則多層結構且各層導電特性存在差異，導致成像質量不高。針對這一問題，本文提出了一種基于改進密集全卷積神經網絡的腦出血圖像重建方法。在構建逼近人體頭部真實結構的三層顱腦模型基礎上，本文通過網絡訓練確定邊界電壓與電導率變化的非線性映射，避免了傳統靈敏度矩陣法逆問題求解引起的誤差，并在無噪、有噪及顱腦模型變化情況下對所提方法進行了評估。數值仿真和物理實驗結果表明，本文所提方法能準確重建顱內腦出血電導率分布，從而可為腦出血診斷和治療提供可靠依據，有助于推動電阻抗成像在腦部疾病診斷方面的應用。
引用本文： 施艷艷, 王孌珺, 李亞婷, 王萌, 楊濱, 付峰. 基于改進密集全卷積神經網絡的腦出血圖像重建方法研究. 生物醫學工程學雜志, 2024, 41(6): 1185-1194. doi: 10.7507/1001-5515.202406044 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
腦卒中是導致我國成人殘疾和死亡的首位病因[1]。在我國所有腦卒中類型中，腦出血患者的發病率為18.8%～47.6%[2]。腦出血主要由腦動脈破裂引起，并對神經組織造成不可逆的損害，其發病率高，死亡率約為40%[3]。為了降低死亡率和發病率，腦出血的早期診斷和積極治療至關重要。目前，計算機斷層掃描（computed tomography，CT）和磁共振成像（magnetic resonance imaging，MRI）是腦成像中使用最廣泛的醫學影像技術[4]。盡管這些技術可以提供高分辨率的腦出血圖像，但它們不可避免地存在以下缺點：CT和MRI設備龐大、造價昂貴、成像過程較慢。此外，這兩種技術均不可用于長期臨床實時監護，無法實現早期腦出血的診斷，尤其是因設備龐大，難以應用于突發事故現場[5]。作為一種功能性成像技術，電阻抗斷層成像（electrical impedance tomography，EIT）技術通過對目標場域施加小電流并測量相應的邊界電壓，隨后利用這些數據來計算被測對象內部的電導率分布，從而實現腦出血電導率圖像重建[6-7]。EIT技術具有體積小、成本低、快速無輻射且可實時監測等特點，能夠很好地彌補CT和MRI在醫學領域的不足之處[8]。此外，EIT不需要特別嚴苛的工作環境，在肺部呼吸成像、腦出血監測、乳腺癌檢測、細胞檢測等醫學檢測領域中具備很好的應用前景[9-12]。
然而，EIT圖像重建涉及到逆問題的求解，其求解過程具有嚴重的欠定性和病態特性[13]，其主要原因是測量的邊界電壓數量遠遠小于圖像重建的電導率的數量，這種情況下會導致求解得到的電導率的解不唯一。目前，已經有許多學者提出了一系列的圖像重建算法來獲得精確和穩定的解。文獻[14]提出了一種改進的吉洪諾夫（Tikhonov）正則化方法，可用于肺部癌癥及其轉移檢測。文獻[15]在分析雅可比矩陣基礎上，提出了一種基于嵌入保真度正則化和運動偽影影響抑制的圖像重建方法，在正則化中引入雅可比矩陣，利用運動偽影濾波器對噪聲數據進行穩定重構，實現了肺部圖像的高保真重建。為了實現腦出血圖像重建，文獻[16]中提出了一種迭代阻尼最小二乘法算法，解決了對具有不同電導率變化和不同干擾大小的目標進行成像時重建目標消失問題。文獻[17]提出了一種約束稀疏L1范數最小化模型，用于可視化腦出血引起的電導率變化，其采用增廣拉格朗日乘子法和交替最小化方案求解該模型，結果表明傳感區域的靈敏度顯著提高。在大多數圖像重建算法中，通過將邊界測量電壓和電導率分布之間的關系線性化來獲得唯一的解，這些方法嚴重依賴于靈敏度矩陣的精確計算。事實上，邊界測量電壓和電導率分布之間的關系是非線性的，使用線性方法難以反映出電導率分布和邊界測量之間的真實關系。近年來，由于深度學習具有強大的非線性映射能力，在求解EIT反問題方面顯示出突出的優勢[18]。與傳統的線性圖像重建算法相比，深度學習方法是一種不需要計算靈敏度矩陣的非線性方法。大多數深度學習方法采用卷積神經網絡（convolutional neural networks，CNN）直接學習邊界測量數據和電導率分布之間的非線性映射。文獻[19]提出了一種基于CNN與非線性傅里葉變換相結合的圖像重建方法，有效提高了肺部EIT圖像重建質量。文獻[20]中提出了一種用于肺部疾病成像的具有軟注意力門和殘差學習的條件生成對抗網絡，該方法能夠準確恢復肺部圖像中病灶的位置和邊界。
與肺部EIT成像和乳腺EIT成像相比，腦出血圖像重建面臨著更大的挑戰：顱腦具有各層電導率分布不均勻的特性，且顱骨電導率極低，僅為0.013 S/m，使得激勵電流大多被顱骨層屏蔽在外，嚴重阻礙了激勵電流的注入。因此，邊界測量電壓的變化不能很好地反映顱內電導率的分布，這進一步加劇了顱內電導率分布圖像重建逆問題的病態性。考慮到深度學習方法強大的非線性映射能力，有學者提出了基于深度學習方法的顱腦EIT圖像重建算法。文獻[21]中，在構建多層顱腦圓域仿真模型基礎上，提出了基于徑向基函數（radial basis function，RBF）神經網絡的成像算法，實現了腦損傷位置及大小的估計。文獻[22]中，為了實現顱腦阻抗分布模型中腦出血病灶目標檢測，提出了一種基于預處理模塊和改進U型網絡（U-Net）模型的多頻 EIT圖像重構方法。需要注意的是，以上圖像重建方法僅在顱腦簡單圓域模型上進行了驗證分析，然而真實顱腦結構模型要復雜得多。密集連接CNN（densely-connected CNN，DCNN）是近幾年提出的一種深度CNN，具有能緩解梯度消失、加強特征傳遞并減少訓練參數數量等優點[23-24]。為準確重建腦出血圖像，本文在構建逼近真實顱腦結構模型基礎上，提出了一種基于改進DCNN（improved DCNN，I-DCNN）的腦出血圖像重建方法，旨在準確映射腦成像中邊界測量電壓與電導率分布之間的關系。通過在原有的DCNN網絡的基礎上，增加3個并聯通道，以3種不同類型的卷積可以產生不同尺度的特征信息，從而提升網絡提取電導率特征信息的能力，進一步緩解梯度消失的問題，以期實現顱內腦出血電導率分布的準確重建。
1 顱腦電阻抗成像測量原理
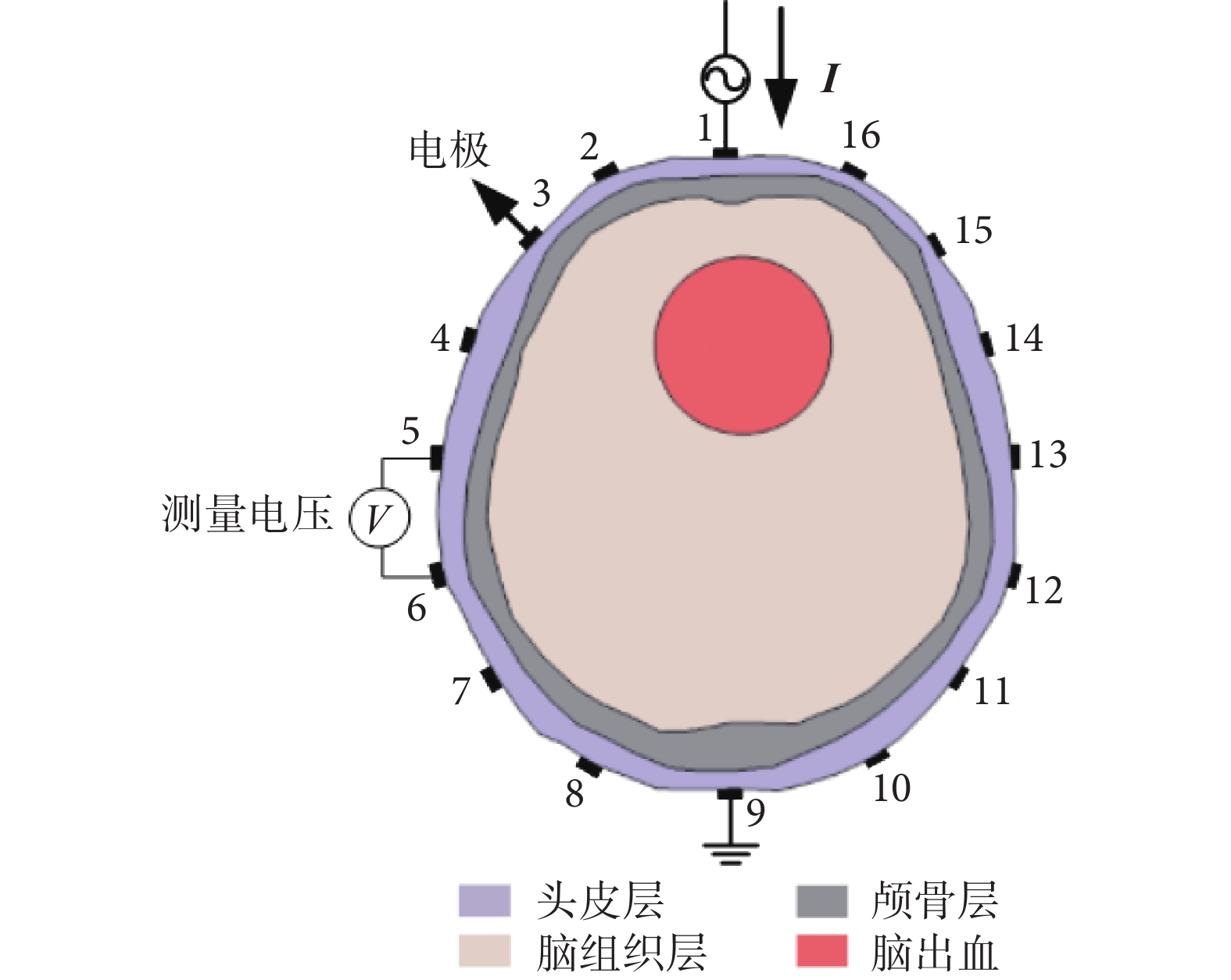
16電極顱腦EIT測量原理圖如圖1所示。本文中，采用相對激勵—相鄰測量模式，選擇相對的一對電極作為激勵，注入交流電流。然后，從其他相鄰電極進行邊界電壓測量。在所有電極對測量完成后，生成一幀數據。對于16電極顱腦EIT系統，總共包括192個邊界電壓測量。基于麥克斯韋方程，電導率分布和電勢分布之間的關系可表示為如式(1)所示：
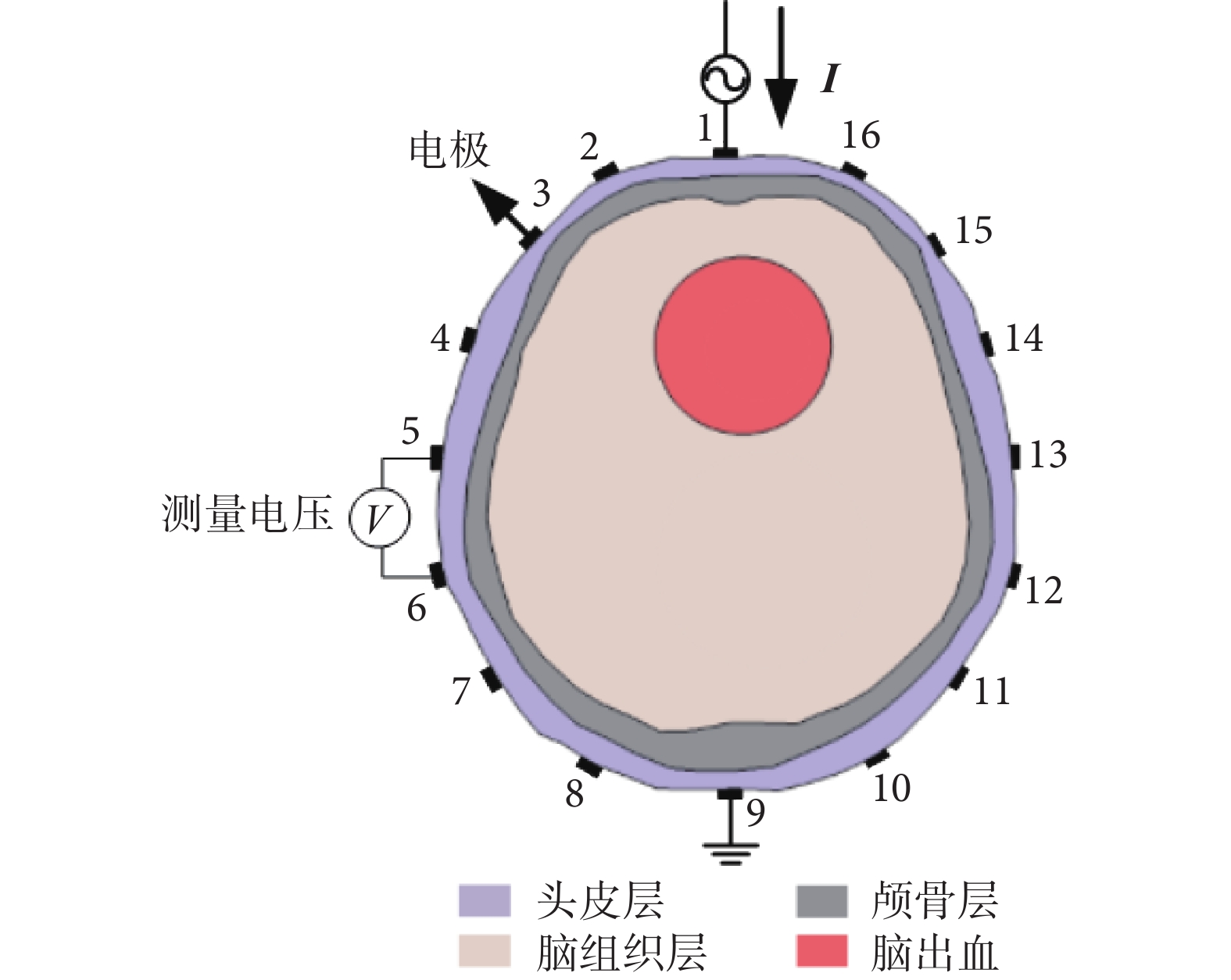圖1
16電極顱腦EIT測量原理圖
Figure1.
Measurement principle of EIT with 16 electrodes
 |
式中，σ(r)是電導率分布，?(r)是電位分布，r是空間位置，
表示檢測區域，▽和▽·分別表示梯度和散度。
為建立更準確、接近真實情況的數學模型，本文采用完全電極模型，其邊界條件的數學表達如式(2)所示[25]：
 |
式中，?是偏導數，n表示邊界上向外的法向量，el是第l個電極，∪表示并集，L是電極數量，zl是第l個電極的接觸阻抗，Ψl是第l個電極上的電勢，d為微分符號，S代表被測區域的邊界，Il是第l個電極上的注入電流，∫(·)dS表示對S積分。
注入電流和測量電位還應滿足的條件如式(3)所示：
 |
式中，
表示從I1到IL進行求和，
表示從Ψ1到ΨL進行求和。
根據式(1)～式(3)，可以計算出邊界測量電壓。邊界測量電壓和電導率分布之間的關系是非線性的，如式(4)所示：
 |
式中，f表示映射函數，Δσ是電導率分布的變化，ΔU是電壓差。
實際上，測量區域內的電導率分布是未知的。因此，EIT圖像重建過程涉及到逆問題的求解，即在已知被測場域邊界測量電壓條件下，反推顱腦域內電導率分布信息。
2 基于改進密集全卷積神經網絡的圖像重建方法
深度學習具有強大的非線性映射能力，在解決EIT逆問題方面表現出了優勢。基于深度學習方法，可以得到Δσ與ΔU之間的非線性映射。在數學上，基于深度學習的EIT圖像重建表示如式(5)所示：
 |
式中，Δσ*表示重建的電導率，Fθ代表映射函數，θ是訓練好的參數。
需要注意的是，在大多數圖像重建算法中，通常對邊界電壓和電導率分布之間的非線性關系近似線性化。此類方法需要在前向映射中計算靈敏度矩陣。與近似線性化的圖像重建方法相比，神經網絡能夠靈活地捕捉EIT中的非線性關系，從而實現電導率分布的更準確圖像重建。
2.1 改進密集全卷積神經網絡的結構
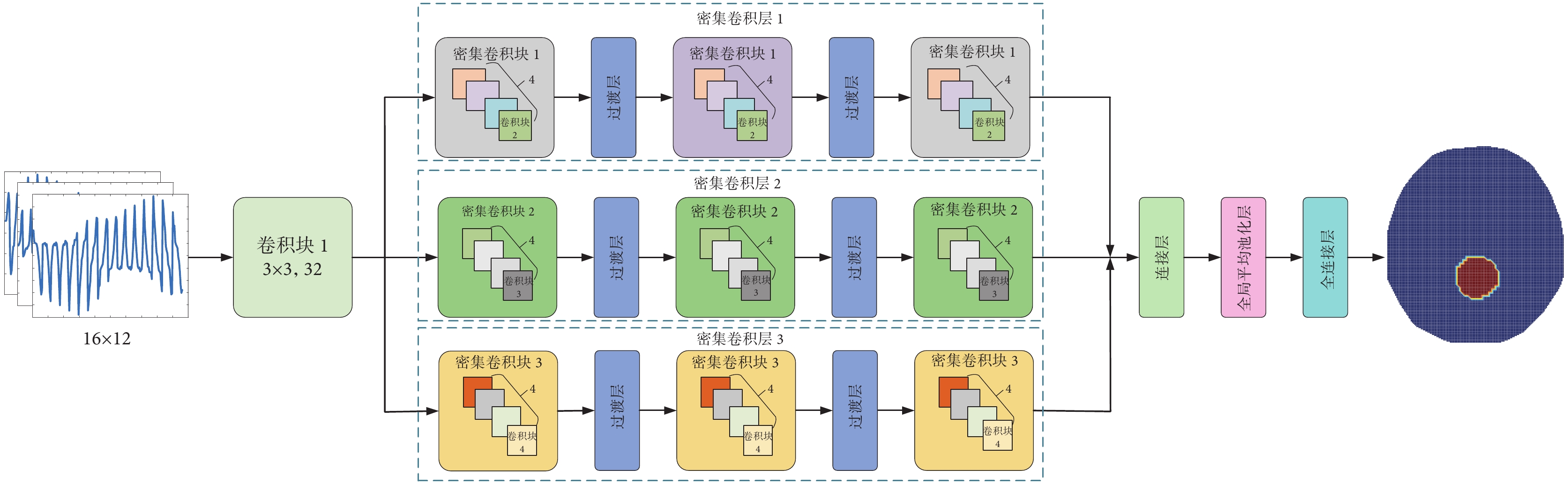
I-DCNN的整體結構如圖2所示，主要由卷積塊1、密集卷積層1～密集卷積層3、連接層、全局平均池化層以及全連接層組成，箭頭表示信息傳輸的方向。密集卷積層中有3種不同的密集卷積塊，每個密集卷積塊有4個層，屬于不同的類型。批歸一化（batch normalization，BN）、線性整流單元（rectified linear units，ReLU）和卷積在密集卷積塊中執行。每種密集卷積塊包含4個具有相同輸出的BN—ReLU—卷積結構，每個密集卷積層的3個密集卷積塊通過密集連接的結構保留了輸入特征。I-DCNN的作用是從不同尺度的數據中獲取信息。因此，網絡對輸入數據更加敏感，可獲取和保存不同的特征。如圖2所示，輸入端為尺寸16 × 12的邊界測量電壓，該數據首先輸送到卷積塊1進行卷積操作，該塊有32個濾波器，步幅為1，大小為3 × 3，采用全零填充法，以保持特征大小不變。數據經過卷積塊1卷積操作后，利用3組不同類型的密集卷積層來提高I-DCNN網絡提取特征信息的能力，每個密集卷積層包含3個相同的密集卷積塊和2個過渡層。其中，密集卷積塊1～密集卷積塊3分別由具有不同初始結構的卷積塊2～卷積塊4組成。
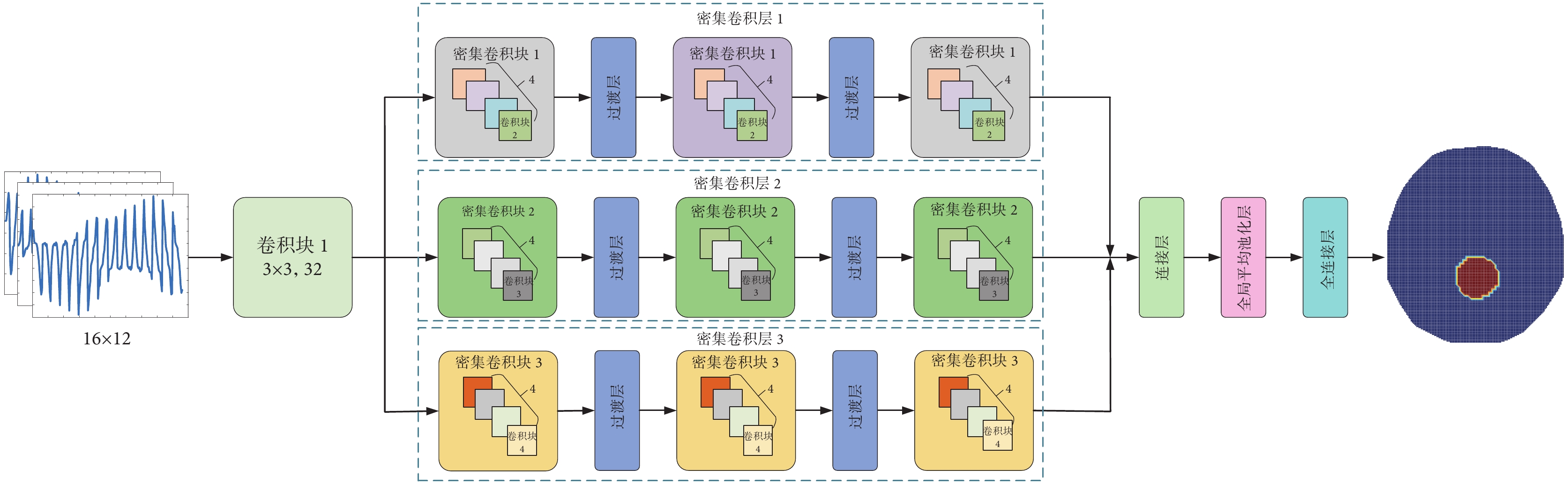圖2
I-DCNN神經網絡結構
Figure2.
Structure of the I-DCNN network
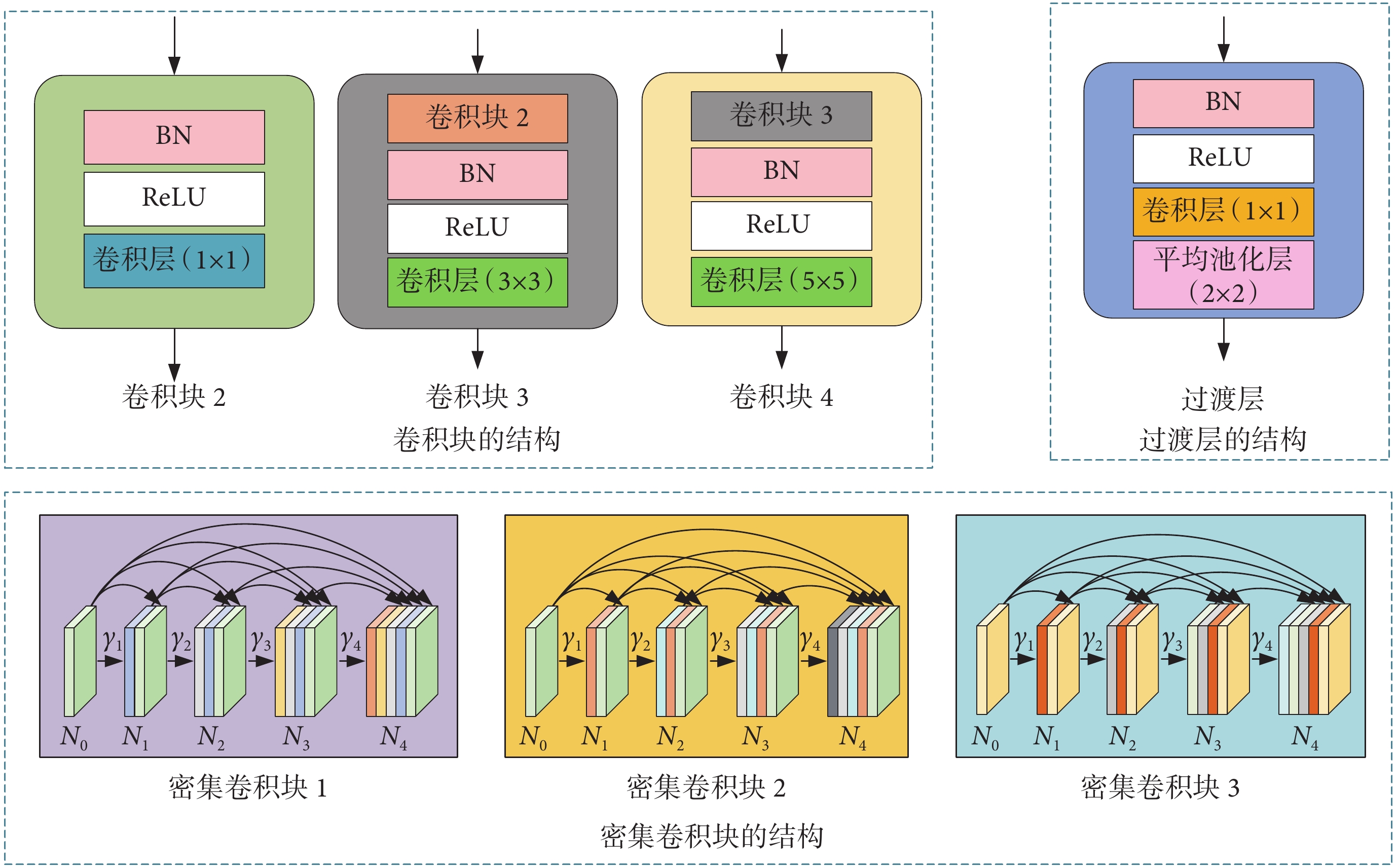
卷積塊2～卷積塊4、過渡層以及密集卷積塊的結構如圖3所示。在卷積塊2中，ReLU的輸出被送到1 × 1卷積層；在卷積塊3模塊中，數據首先通過與卷積塊2相同的1 × 1卷積層卷積操作，經BN層歸一化處理、ReLU層非線性變換后，進入3 × 3卷積層。在卷積塊4中，數據依次通過卷積塊3、BN層、ReLU層和5 × 5卷積層的計算，生成相應濾波器的信道數。過渡層結構由BN層、ReLU層、1 × 1卷積層、2 × 2平均池化層組成。最終，由求和層對相應通道的元素進行求和，得到卷積計算（convolution，Conv）結果。3種不同類型的卷積可以產生不同尺度的特征信息，有助于提高重建圖像的精度。在本文中，采用了預激活策略，使網絡更易得到訓練，提高了泛化性能。密集卷積塊的輸入由密集單位的輸出堆疊。在該結構中，淺層特征可以在一定程度上有效地緩解梯度的消失。在密集卷積塊中第i個密集單位層Ni的輸入與前面所有層的輸出γi有關，γi的表示如式(6)所示：
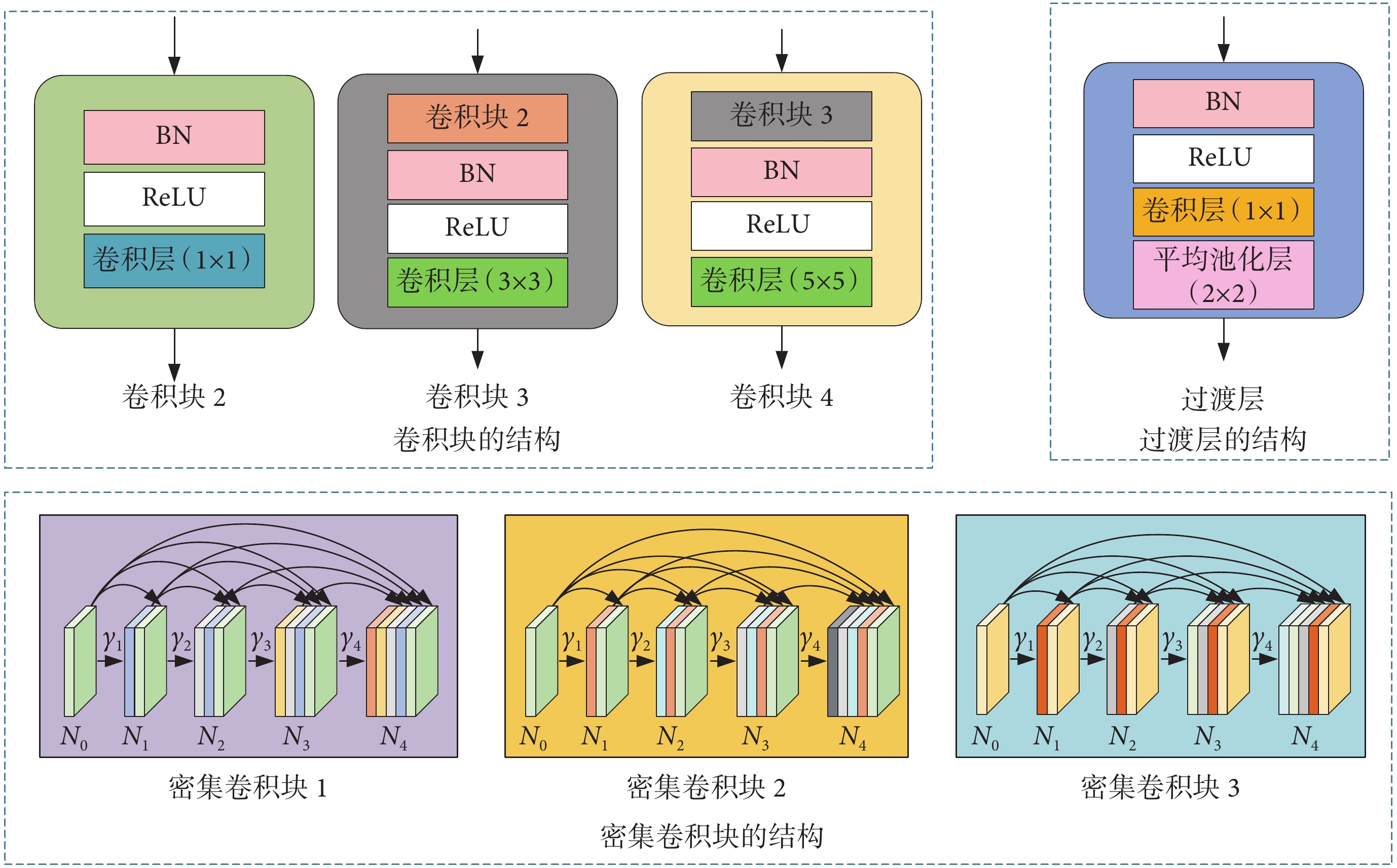圖3
I-DCNN結構細節圖
Figure3.
Details of I-DCNN structure
 |
式中，Wi（?）表示輸出與輸入之間的非線性映射，［γ1，γ2，
，γi?1］表示第N0到Ni-1層的輸出按特征拼接在一起，為BN、ReLU和卷積的組合。3組密集卷積層的輸出經過連接層和全局平均池化層的處理，最后使用全連接層進行數據映射。
2.2 數據的生成
通常情況下，訓練深度學習網絡需要大量的數據樣本。本文采用仿真的方法生成訓練數據集，在多物理場仿真軟件COMSOL Multiphysics 5.4（COMSOL Inc.，瑞典）中建立包含頭皮層、顱骨層和腦組織層的二維三層顱腦模型，各層電導率分別設定為0.440、0.013、0.150 S/m，腦出血的電導率設定為0.700 S/m[26]。其次，聯合數值計算與編程軟件MATLAB 2016a（MathWorks Inc.，美國），獲得了訓練及測試數據集。在腦組織層不同位置放置不同形狀的目標物模擬腦出血。腦出血形態多樣，具體形狀和大小會受到出血區域位置、出血量以及腦組織應力和反應的影響[27]。本文主要研究了圓形和橢圓形的腦出血模擬目標物。目標物的大小和位置是隨機生成的，圓形目標物直徑范圍為3～30 mm。對于橢圓形目標物，長軸和短軸從5～30 mm范圍之間變化。生成的訓練數據集包含
2.3 網絡的訓練
為了訓練所提出的I-DCNN，邊界電壓測量和真實電導率變化分別作為網絡的輸入和輸出，并通過最小化損失函數，學習最佳參數。在本文中，EIT圖像重建被建模為多標簽分類問題。因此，采用二元交叉熵損失（binary cross entropy loss，BCELoss）作為損失函數ρ(θ)，如式(7)所示：
 |
式中，N = 2 777是圖像重建中的單元個數，Δσi是Δσ的第i個單元，Δσi*是Δσ*的第i個單元，λ是正則化的超參數。
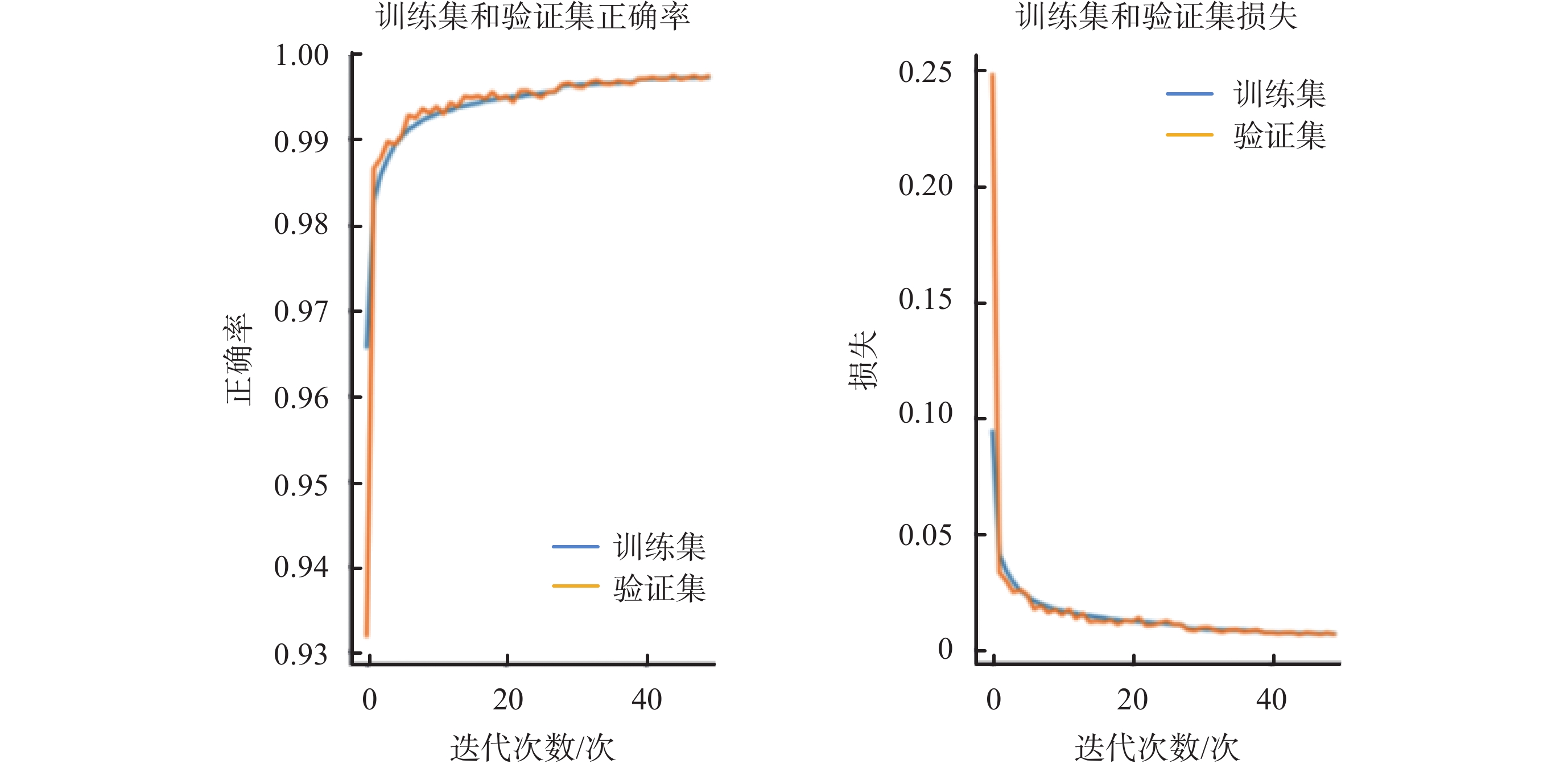
搭建模型的訓練和驗證通過一臺配置為16 GB內存和基頻為3.10 GHz的中央處理器（central processing unit，CPU）（i5-11300H，Intel? CoreTM，美國）的計算機進行。利用自適應矩估計算法在損失函數的反向傳播過程中對參數θ進行了更新，參數的選擇對網絡的精度和泛化能力有很大的影響。在網絡訓練過程中，采用經驗法進行參數確定：學習速率為0.000 1，正則化選擇為0.000 01，批大小（batch size）和輪次（epoch）分別設置為16和50。基于I-DCNN的腦出血圖像重建方法的訓練結果如圖4所示。可以看出，訓練集的正確率隨著迭代次數的增大而趨于1。迭代達到50次時，正確的速率緩慢增加，但仍呈上升趨勢。相應的，訓練集的損失減小并趨近于0。從驗證集正確性和損失曲線來看，曲線振蕩較小，說明所提出的基于I-DCNN的腦出血圖像重建方法得到了很好的訓練。
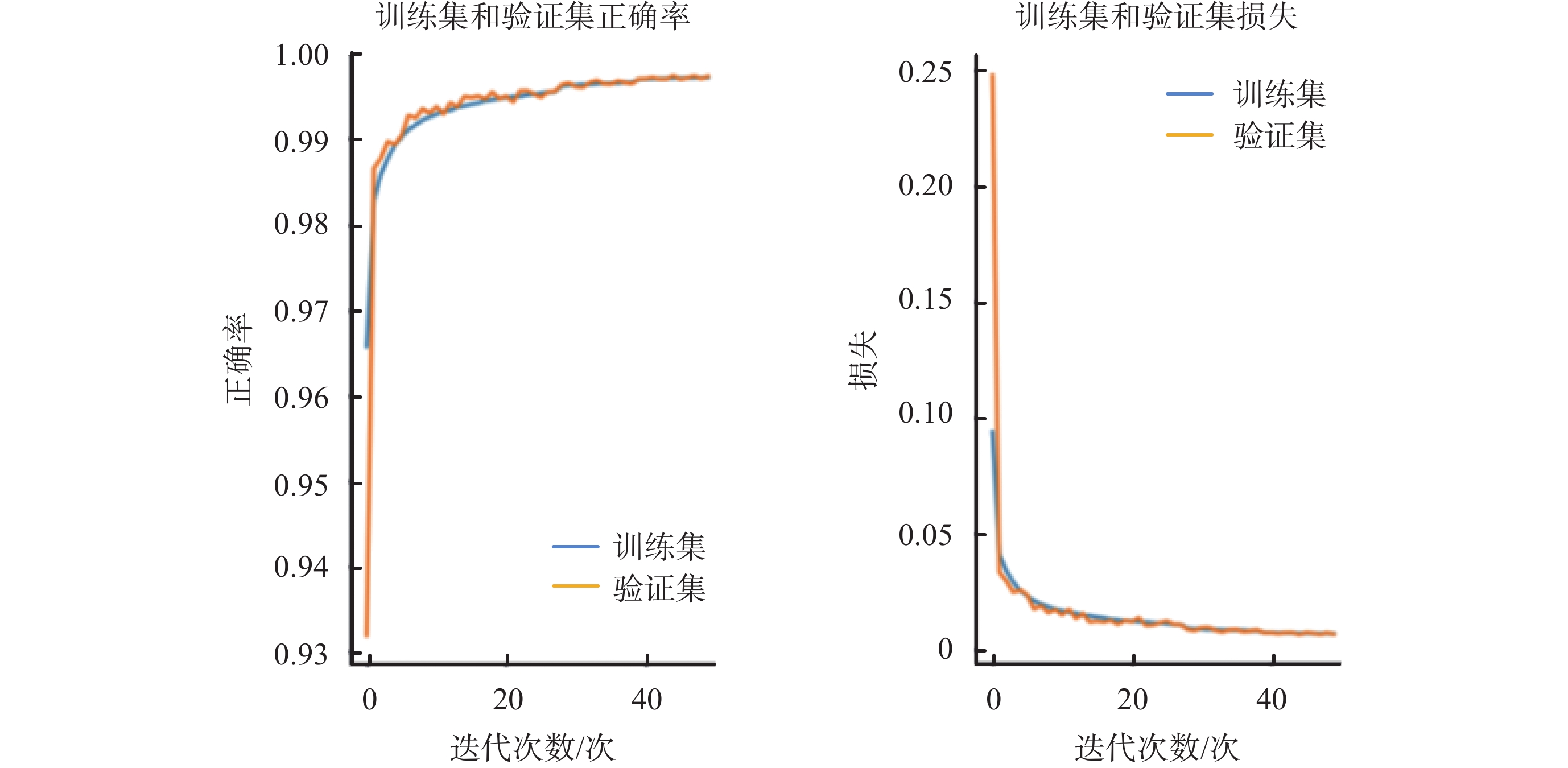圖4
基于I-DCNN的腦出血圖像重建方法的訓練結果
Figure4.
Training results of image reconstruction method for cerebral hemorrhage based on I-DCNN
3 圖像重建結果及討論
為了驗證本文所提方法在電導率分布圖像重建方面的性能，本節在無噪、噪聲及顱腦模型變化4種條件下開展了數值仿真研究，并與全連接神經網絡（fully connected neural network，FCNN）、CNN、DCNN等3種傳統的神經網絡成像方法進行比較，驗證了所提出的I-DCNN方法在重建腦出血圖像方面的優越性；然后，通過物理模型實驗進一步驗證了所提方法能夠提升顱內腦出血的電導率分布重建質量。為了定量比較不同方法的性能，對重建圖像的均方根誤差（root mean square error，RMSE）和相關系數（correlation coefficient，CC）進行了計算。RMSE和CC的表達式如式(8)～式(9)所示[28-29]：
 |
 |
式中，ge和
是真實電導率分布變化和預測電導率分布變化的第e個像素，
和
分別是真實電導率分布變化和預測電導率分布變化的平均值。
3.1 無噪條件下圖像重建結果
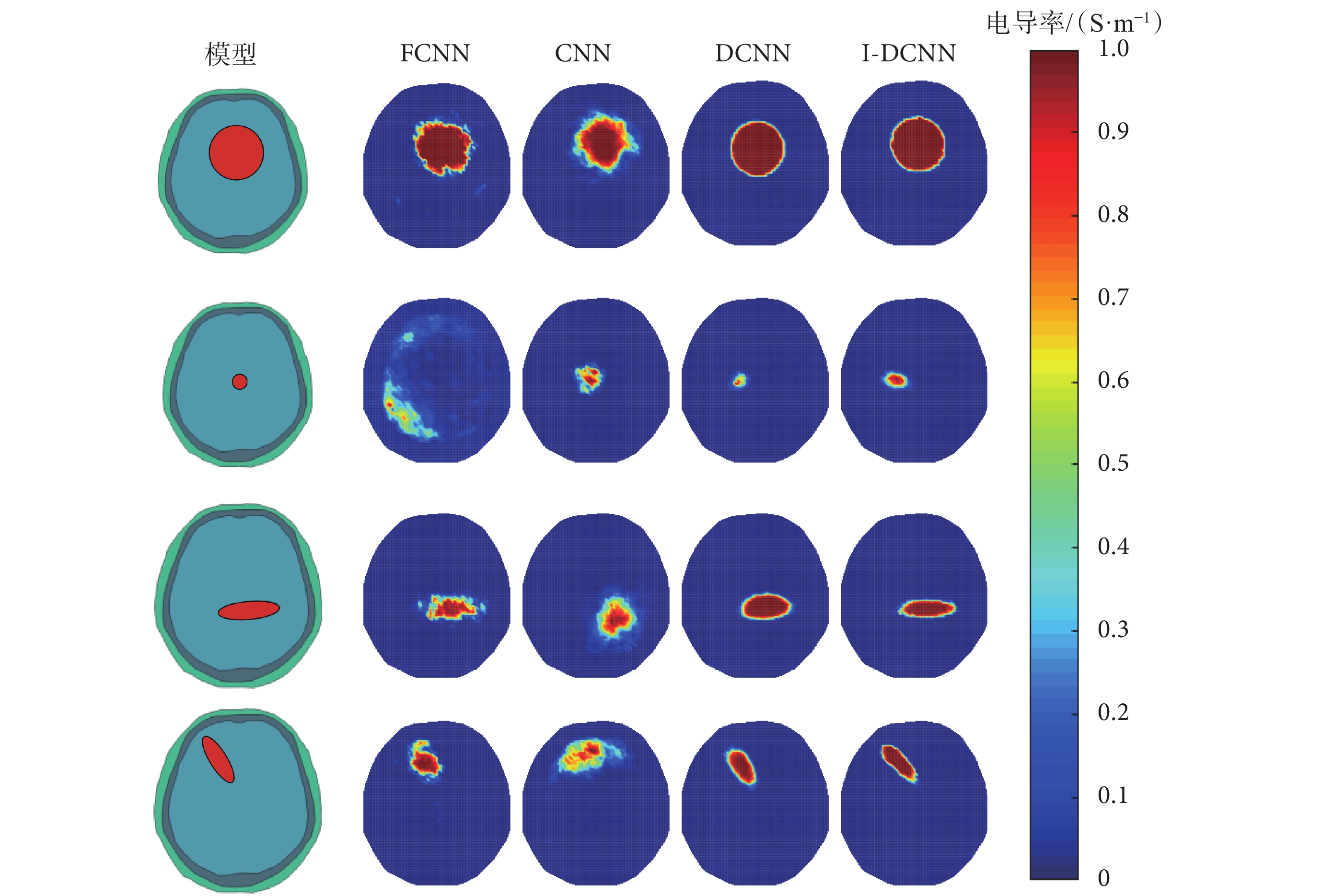
首先，在無噪聲條件下對基于不同方法的5種腦出血模型的圖像重建進行研究，圖像重建結果如圖5所示。可以看出，FCNN方法圖像重建背景有少量的偽影且重建目標物發生了嚴重形變。CNN方法重建的部分圖像中出現了大量的偽影，且腦出血的大小和形狀沒有得到好的重建。當目標物較大時，DCNN重建的腦出血形狀和大小較為準確，但當目標物較小時，DCNN的重建圖像不能真實反映腦出血的大小。在基于所提I-DCNN方法的重建圖像中，腦出血的位置重建效果較好；當出血點較小時，所提出方法仍然能夠較好地重建出出血點的大小和位置。結果表明，所提出的I-DCNN方法重建顱內腦出血電導率分布的性能優于其他3種傳統方法。
圖5
無噪條件下圖像重建結果
Figure5.
Reconstructed images under noise-free condition
重建圖像的CC和RMSE值如表1所示。可以觀察到，FCNN方法的CC值最低、RMSE值最高，這表明FCNN的圖像重建質量相對較差。DCNN方法的CC值比FCNN和CNN方法更高，而RMSE值偏小。與DCNN方法的CC值和RMSE值相比，本文所提出的I-DCNN方法的CC值有一定提高，RMSE值有所降低。特別是當目標物為橢圓形時，本文方法明顯優于DCNN法。
表1
無噪條件下的平均CC和RMSE值
Table1.
Average CC and RMSE values under noise-free condition
3.2 噪聲條件下的圖像重建結果
為評估所提出的方法在噪聲條件下的魯棒性，本研究中將高斯白噪聲添加到邊界測量電壓數據上，噪聲設置為20 dB。信噪比（signal-to-noise ratio，SNR）的計算方法如式(10)所示[30]：
 |
式中，e是均值為0、方差為1的噪聲。
噪聲條件下基于不同方法的4種模型的腦出血圖像重建結果如圖6所示。可以發現，FCNN和CNN方法重建的目標物形狀比無噪聲時的形狀略有變形，而DCNN方法重建的目標物形變稍微小一些。但在本文所提I-DCNN方法中，重建幾乎不受噪聲的影響。將圖5與圖6進行比較，可以發現，即使在噪聲的影響下，本文所提I-DCNN方法的圖像重建質量仍相較于其他3種方法更好。
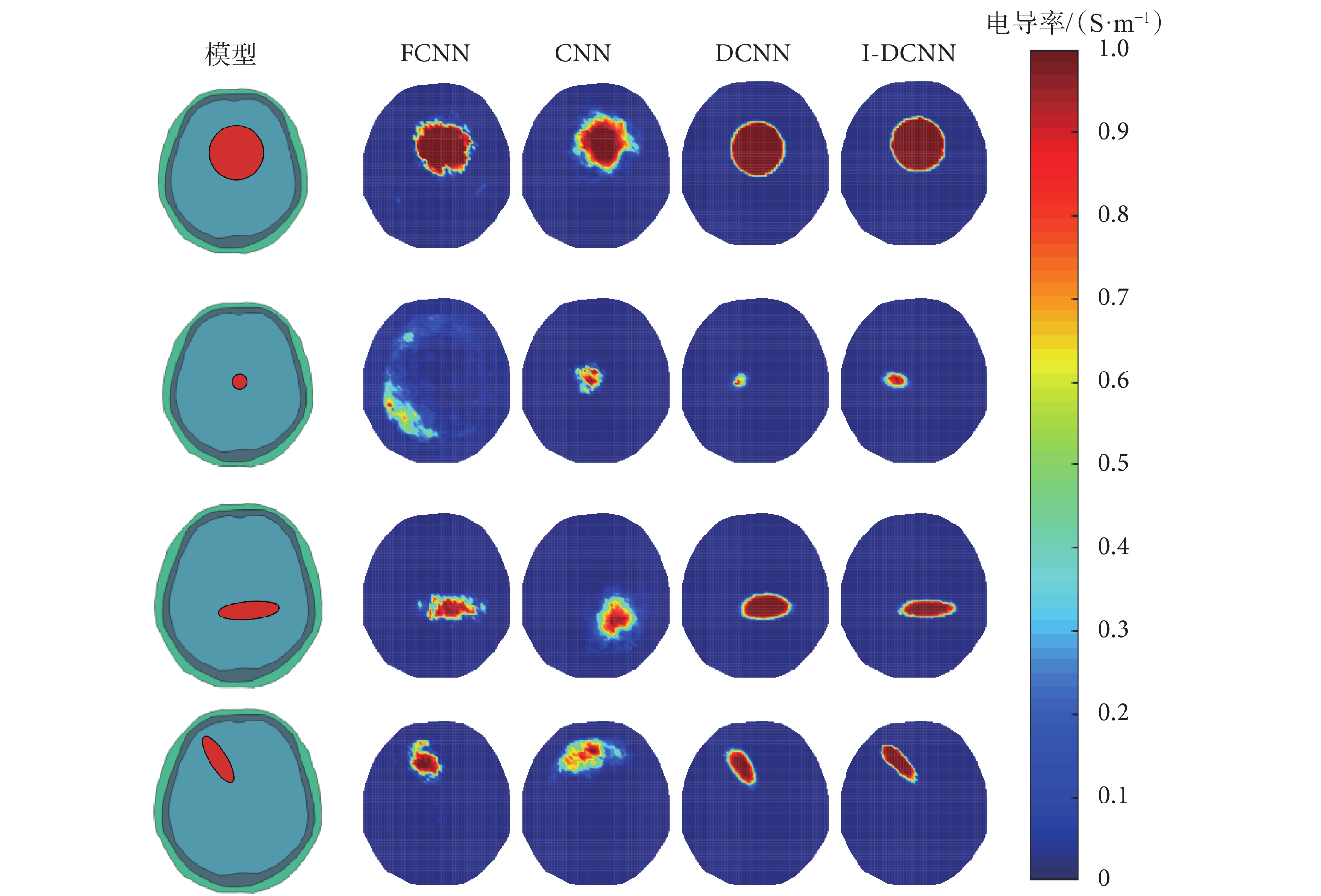圖6
噪聲條件下圖像重建結果
Figure6.
Image reconstruction results under noise condition
3.3 頭部模型形變條件下的圖像重建結果
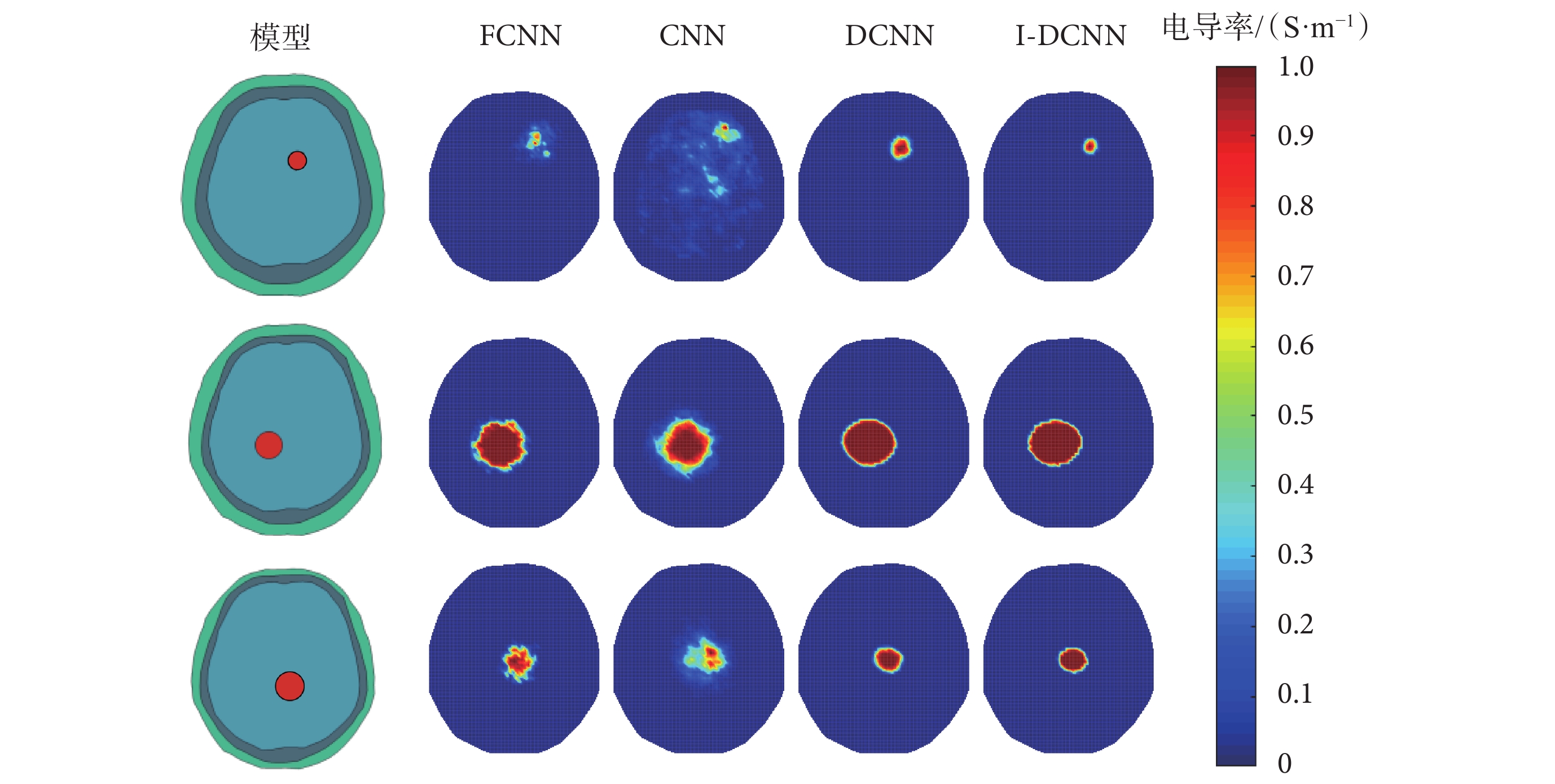
此外，不同患者的頭部可能與模擬中建立的模型不同。為驗證頭部形變的情況下本文所提出方法的性能，分別在3種頭部模型形變條件下生成了包含100個樣本的測試數據集。基于不同方法的3個頭部模型形變的圖像重建結果如圖7所示。可以發現，FCNN與CNN的圖像重建結果與真實腦出血目標物相比有較大的形變，DCNN網絡的圖像重建質量相較FCNN和CNN有所提升，但在目標物較小時的圖像重建結果不及所提出的I-DCNN方法，且本文所提I-DCNN方法重建出的圖像邊界清晰無偽影。定性評估表明，本文所提出的方法在頭部模型形變情況下具有較好的圖像重建質量。
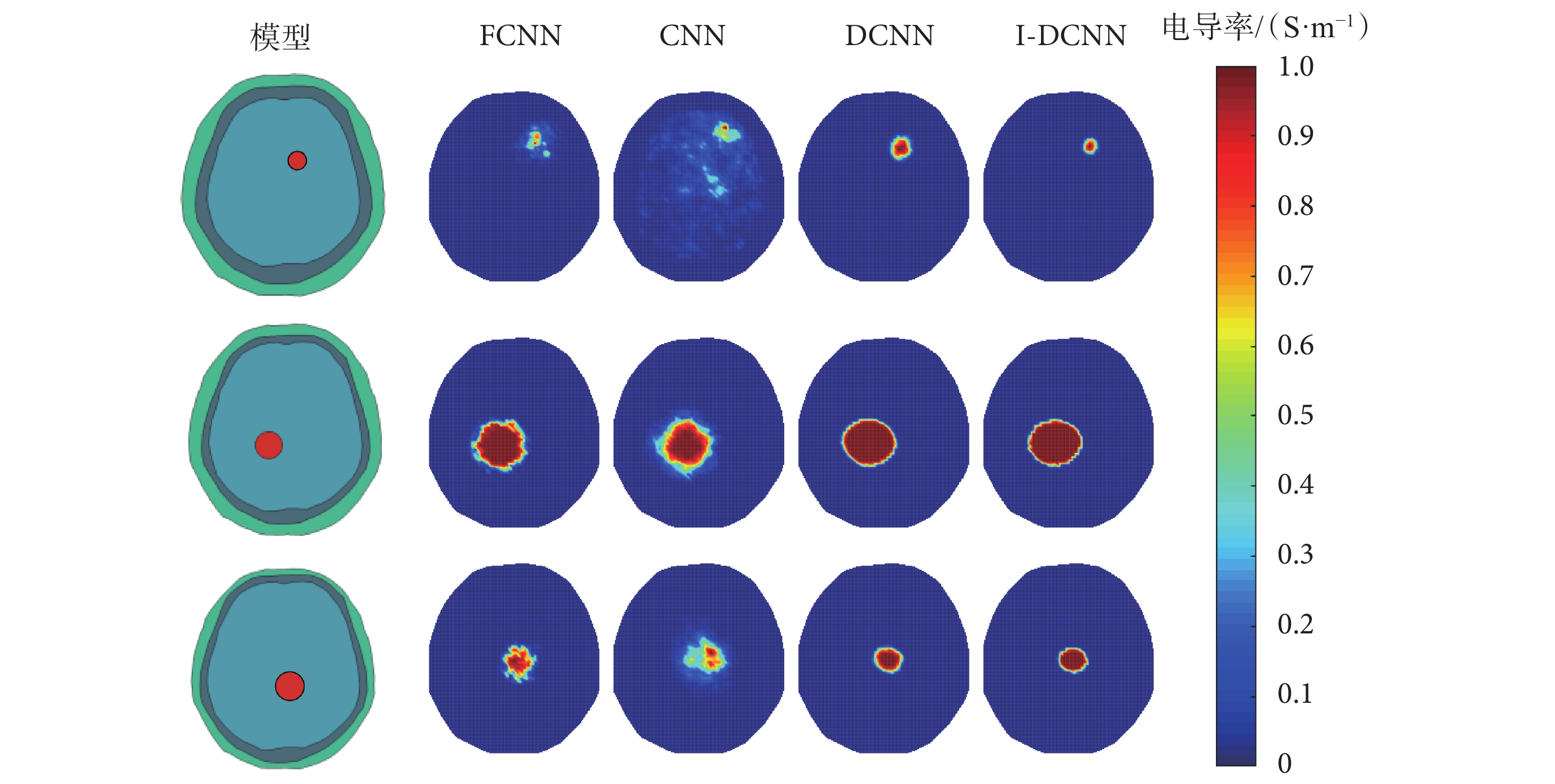圖7
頭部模型形變時的圖像重建結果
Figure7.
Image reconstruction when head model deforms
3.4 物理模擬實驗下的圖像重建結果
除了數值模擬研究外，還通過物理模型實驗對本文所提I-DCNN方法的圖像重建性能進行了評估。實驗系統采用課題組設計的16電極EIT系統，如圖8所示。實驗中采用了“相對—相鄰”激勵采集模式，激勵電流設置為1.25 mA，頻率為50 kHz[31]。制作了三層顱腦物理模型，使用瓊脂等材料制作了不同尺寸的瓊脂棒用于模擬腦出血，瓊脂棒的電導率配置為0.7 S/m。
圖8
物理模型實驗
Figure8.
Phantom experimental setup
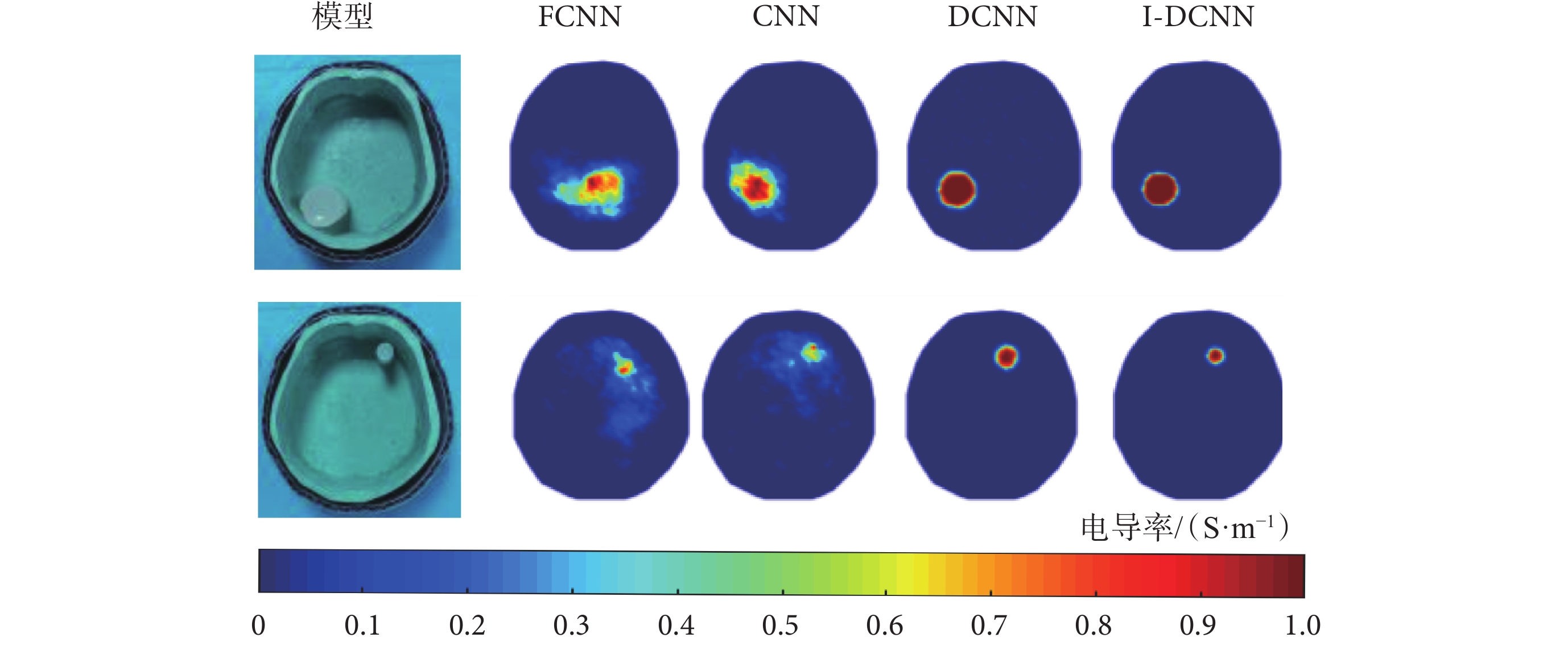
基于FCNN、CNN、DCNN與本文提出的I-DCNN這4種不同方法對兩個腦出血目標的電導率分布圖像重建結果如圖9所示。在I-DCNN網絡的訓練過程中，模擬腦出血的目標物直徑范圍為3 ～30 mm，也就是說經過網絡訓練后，該范圍的腦出血電導率分布圖像均可被很好地重建。由于過細的瓊脂棒不易制作且易漂浮在溶液中，實驗中制作的小瓊脂棒直徑為15 mm。同時，為了驗證網絡的泛化能力，模擬腦出血的大瓊脂棒直徑為40 mm。從圖9中可以得出，基于FCNN與CNN方法的重建圖像目標物形狀嚴重形變、背景有明顯偽影，且小目標物的圖像重建更加困難。與FCNN和CNN相比，DCNN方法圖像重建質量有較大提升，能夠重建出目標物的大小和形狀。對于本文所提I-DCNN方法在重建效果上優于DCNN方法，無論是對于大目標物還是小目標物，其重建結果都更接近真實情況，且重建圖背景清晰無偽影。實驗結果表明，本文I-DCNN方法比其他3種方法能更好地重建出腦出血圖像。
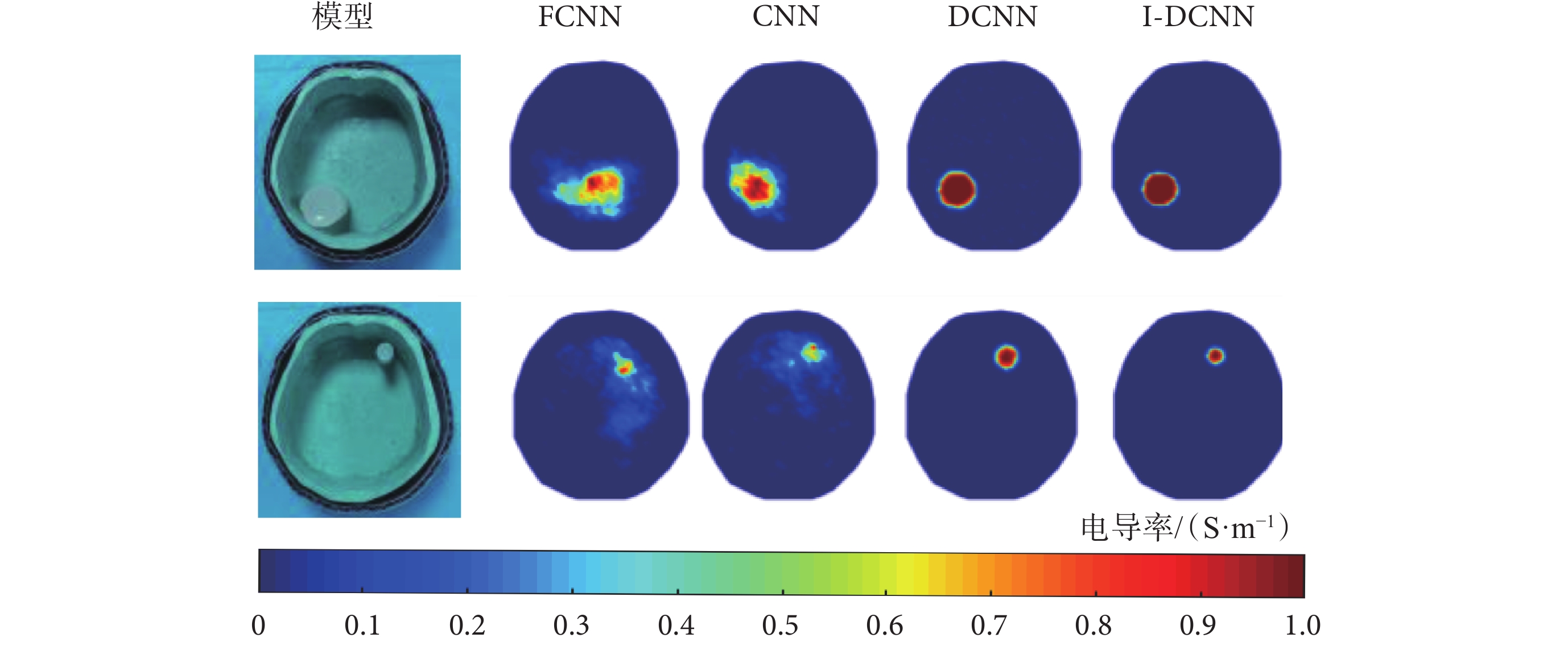圖9
基于實驗數據的圖像重建結果
Figure9.
Reconstructed images with phantom experimental data
4 結論
本文提出了一種基于I-DCNN的腦出血圖像重建方法，該方法在原有的DCNN網絡的基礎上，增加了3個并聯通道，并利用3種不同類型的卷積塊以產生不同尺度的特征信息，提升網絡對于提取電導率特征信息的能力，從而實現對腦出血的精準重建。本文通過數值仿真分別研究了無噪、有噪及顱腦模型變化3種條件下所提出I-DCNN方法在重建腦出血方面的性能，并與FCNN、CNN、DCNN這3種不同的圖像重建方法進行了比較。定性與定量評估均表明本文所提出方法在重建顱內腦出血方面的優良性能。此外，物理模擬實驗結果也表明本文所提方法能夠顯著提升顱內腦出血電導率分布變化的重建質量。然而，顱腦EIT臨床應用環境復雜，本文所提方法在臨床復雜環境中的適用性和可靠性仍需進一步深入研究。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：施艷艷、王孌珺負責本文算法程序設計、結果記錄分析以及論文撰寫；李亞婷負責實驗數據分析，王萌負責論文審閱及修訂；楊濱、付峰負責本文工作的實驗指導。
0 引言
腦卒中是導致我國成人殘疾和死亡的首位病因[1]。在我國所有腦卒中類型中，腦出血患者的發病率為18.8%～47.6%[2]。腦出血主要由腦動脈破裂引起，并對神經組織造成不可逆的損害，其發病率高，死亡率約為40%[3]。為了降低死亡率和發病率，腦出血的早期診斷和積極治療至關重要。目前，計算機斷層掃描（computed tomography，CT）和磁共振成像（magnetic resonance imaging，MRI）是腦成像中使用最廣泛的醫學影像技術[4]。盡管這些技術可以提供高分辨率的腦出血圖像，但它們不可避免地存在以下缺點：CT和MRI設備龐大、造價昂貴、成像過程較慢。此外，這兩種技術均不可用于長期臨床實時監護，無法實現早期腦出血的診斷，尤其是因設備龐大，難以應用于突發事故現場[5]。作為一種功能性成像技術，電阻抗斷層成像（electrical impedance tomography，EIT）技術通過對目標場域施加小電流并測量相應的邊界電壓，隨后利用這些數據來計算被測對象內部的電導率分布，從而實現腦出血電導率圖像重建[6-7]。EIT技術具有體積小、成本低、快速無輻射且可實時監測等特點，能夠很好地彌補CT和MRI在醫學領域的不足之處[8]。此外，EIT不需要特別嚴苛的工作環境，在肺部呼吸成像、腦出血監測、乳腺癌檢測、細胞檢測等醫學檢測領域中具備很好的應用前景[9-12]。
然而，EIT圖像重建涉及到逆問題的求解，其求解過程具有嚴重的欠定性和病態特性[13]，其主要原因是測量的邊界電壓數量遠遠小于圖像重建的電導率的數量，這種情況下會導致求解得到的電導率的解不唯一。目前，已經有許多學者提出了一系列的圖像重建算法來獲得精確和穩定的解。文獻[14]提出了一種改進的吉洪諾夫（Tikhonov）正則化方法，可用于肺部癌癥及其轉移檢測。文獻[15]在分析雅可比矩陣基礎上，提出了一種基于嵌入保真度正則化和運動偽影影響抑制的圖像重建方法，在正則化中引入雅可比矩陣，利用運動偽影濾波器對噪聲數據進行穩定重構，實現了肺部圖像的高保真重建。為了實現腦出血圖像重建，文獻[16]中提出了一種迭代阻尼最小二乘法算法，解決了對具有不同電導率變化和不同干擾大小的目標進行成像時重建目標消失問題。文獻[17]提出了一種約束稀疏L1范數最小化模型，用于可視化腦出血引起的電導率變化，其采用增廣拉格朗日乘子法和交替最小化方案求解該模型，結果表明傳感區域的靈敏度顯著提高。在大多數圖像重建算法中，通過將邊界測量電壓和電導率分布之間的關系線性化來獲得唯一的解，這些方法嚴重依賴于靈敏度矩陣的精確計算。事實上，邊界測量電壓和電導率分布之間的關系是非線性的，使用線性方法難以反映出電導率分布和邊界測量之間的真實關系。近年來，由于深度學習具有強大的非線性映射能力，在求解EIT反問題方面顯示出突出的優勢[18]。與傳統的線性圖像重建算法相比，深度學習方法是一種不需要計算靈敏度矩陣的非線性方法。大多數深度學習方法采用卷積神經網絡（convolutional neural networks，CNN）直接學習邊界測量數據和電導率分布之間的非線性映射。文獻[19]提出了一種基于CNN與非線性傅里葉變換相結合的圖像重建方法，有效提高了肺部EIT圖像重建質量。文獻[20]中提出了一種用于肺部疾病成像的具有軟注意力門和殘差學習的條件生成對抗網絡，該方法能夠準確恢復肺部圖像中病灶的位置和邊界。
與肺部EIT成像和乳腺EIT成像相比，腦出血圖像重建面臨著更大的挑戰：顱腦具有各層電導率分布不均勻的特性，且顱骨電導率極低，僅為0.013 S/m，使得激勵電流大多被顱骨層屏蔽在外，嚴重阻礙了激勵電流的注入。因此，邊界測量電壓的變化不能很好地反映顱內電導率的分布，這進一步加劇了顱內電導率分布圖像重建逆問題的病態性。考慮到深度學習方法強大的非線性映射能力，有學者提出了基于深度學習方法的顱腦EIT圖像重建算法。文獻[21]中，在構建多層顱腦圓域仿真模型基礎上，提出了基于徑向基函數（radial basis function，RBF）神經網絡的成像算法，實現了腦損傷位置及大小的估計。文獻[22]中，為了實現顱腦阻抗分布模型中腦出血病灶目標檢測，提出了一種基于預處理模塊和改進U型網絡（U-Net）模型的多頻 EIT圖像重構方法。需要注意的是，以上圖像重建方法僅在顱腦簡單圓域模型上進行了驗證分析，然而真實顱腦結構模型要復雜得多。密集連接CNN（densely-connected CNN，DCNN）是近幾年提出的一種深度CNN，具有能緩解梯度消失、加強特征傳遞并減少訓練參數數量等優點[23-24]。為準確重建腦出血圖像，本文在構建逼近真實顱腦結構模型基礎上，提出了一種基于改進DCNN（improved DCNN，I-DCNN）的腦出血圖像重建方法，旨在準確映射腦成像中邊界測量電壓與電導率分布之間的關系。通過在原有的DCNN網絡的基礎上，增加3個并聯通道，以3種不同類型的卷積可以產生不同尺度的特征信息，從而提升網絡提取電導率特征信息的能力，進一步緩解梯度消失的問題，以期實現顱內腦出血電導率分布的準確重建。
1 顱腦電阻抗成像測量原理
16電極顱腦EIT測量原理圖如圖1所示。本文中，采用相對激勵—相鄰測量模式，選擇相對的一對電極作為激勵，注入交流電流。然后，從其他相鄰電極進行邊界電壓測量。在所有電極對測量完成后，生成一幀數據。對于16電極顱腦EIT系統，總共包括192個邊界電壓測量。基于麥克斯韋方程，電導率分布和電勢分布之間的關系可表示為如式(1)所示：
圖1
16電極顱腦EIT測量原理圖
Figure1.
Measurement principle of EIT with 16 electrodes
|
式中，σ(r)是電導率分布，?(r)是電位分布，r是空間位置，表示檢測區域，▽和▽·分別表示梯度和散度。
為建立更準確、接近真實情況的數學模型，本文采用完全電極模型，其邊界條件的數學表達如式(2)所示[25]：
|
式中，?是偏導數，n表示邊界上向外的法向量，el是第l個電極，∪表示并集，L是電極數量，zl是第l個電極的接觸阻抗，Ψl是第l個電極上的電勢，d為微分符號，S代表被測區域的邊界，Il是第l個電極上的注入電流，∫(·)dS表示對S積分。
注入電流和測量電位還應滿足的條件如式(3)所示：
|
式中，表示從I1到IL進行求和，表示從Ψ1到ΨL進行求和。
根據式(1)～式(3)，可以計算出邊界測量電壓。邊界測量電壓和電導率分布之間的關系是非線性的，如式(4)所示：
|
式中，f表示映射函數，Δσ是電導率分布的變化，ΔU是電壓差。
實際上，測量區域內的電導率分布是未知的。因此，EIT圖像重建過程涉及到逆問題的求解，即在已知被測場域邊界測量電壓條件下，反推顱腦域內電導率分布信息。
2 基于改進密集全卷積神經網絡的圖像重建方法
深度學習具有強大的非線性映射能力，在解決EIT逆問題方面表現出了優勢。基于深度學習方法，可以得到Δσ與ΔU之間的非線性映射。在數學上，基于深度學習的EIT圖像重建表示如式(5)所示：
|
式中，Δσ*表示重建的電導率，Fθ代表映射函數，θ是訓練好的參數。
需要注意的是，在大多數圖像重建算法中，通常對邊界電壓和電導率分布之間的非線性關系近似線性化。此類方法需要在前向映射中計算靈敏度矩陣。與近似線性化的圖像重建方法相比，神經網絡能夠靈活地捕捉EIT中的非線性關系，從而實現電導率分布的更準確圖像重建。
2.1 改進密集全卷積神經網絡的結構
I-DCNN的整體結構如圖2所示，主要由卷積塊1、密集卷積層1～密集卷積層3、連接層、全局平均池化層以及全連接層組成，箭頭表示信息傳輸的方向。密集卷積層中有3種不同的密集卷積塊，每個密集卷積塊有4個層，屬于不同的類型。批歸一化（batch normalization，BN）、線性整流單元（rectified linear units，ReLU）和卷積在密集卷積塊中執行。每種密集卷積塊包含4個具有相同輸出的BN—ReLU—卷積結構，每個密集卷積層的3個密集卷積塊通過密集連接的結構保留了輸入特征。I-DCNN的作用是從不同尺度的數據中獲取信息。因此，網絡對輸入數據更加敏感，可獲取和保存不同的特征。如圖2所示，輸入端為尺寸16 × 12的邊界測量電壓，該數據首先輸送到卷積塊1進行卷積操作，該塊有32個濾波器，步幅為1，大小為3 × 3，采用全零填充法，以保持特征大小不變。數據經過卷積塊1卷積操作后，利用3組不同類型的密集卷積層來提高I-DCNN網絡提取特征信息的能力，每個密集卷積層包含3個相同的密集卷積塊和2個過渡層。其中，密集卷積塊1～密集卷積塊3分別由具有不同初始結構的卷積塊2～卷積塊4組成。
圖2
I-DCNN神經網絡結構
Figure2.
Structure of the I-DCNN network
卷積塊2～卷積塊4、過渡層以及密集卷積塊的結構如圖3所示。在卷積塊2中，ReLU的輸出被送到1 × 1卷積層；在卷積塊3模塊中，數據首先通過與卷積塊2相同的1 × 1卷積層卷積操作，經BN層歸一化處理、ReLU層非線性變換后，進入3 × 3卷積層。在卷積塊4中，數據依次通過卷積塊3、BN層、ReLU層和5 × 5卷積層的計算，生成相應濾波器的信道數。過渡層結構由BN層、ReLU層、1 × 1卷積層、2 × 2平均池化層組成。最終，由求和層對相應通道的元素進行求和，得到卷積計算（convolution，Conv）結果。3種不同類型的卷積可以產生不同尺度的特征信息，有助于提高重建圖像的精度。在本文中，采用了預激活策略，使網絡更易得到訓練，提高了泛化性能。密集卷積塊的輸入由密集單位的輸出堆疊。在該結構中，淺層特征可以在一定程度上有效地緩解梯度的消失。在密集卷積塊中第i個密集單位層Ni的輸入與前面所有層的輸出γi有關，γi的表示如式(6)所示：
圖3
I-DCNN結構細節圖
Figure3.
Details of I-DCNN structure
|
式中，Wi（?）表示輸出與輸入之間的非線性映射，［γ1，γ2，，γi?1］表示第N0到Ni-1層的輸出按特征拼接在一起，為BN、ReLU和卷積的組合。3組密集卷積層的輸出經過連接層和全局平均池化層的處理，最后使用全連接層進行數據映射。
2.2 數據的生成
通常情況下，訓練深度學習網絡需要大量的數據樣本。本文采用仿真的方法生成訓練數據集，在多物理場仿真軟件COMSOL Multiphysics 5.4（COMSOL Inc.，瑞典）中建立包含頭皮層、顱骨層和腦組織層的二維三層顱腦模型，各層電導率分別設定為0.440、0.013、0.150 S/m，腦出血的電導率設定為0.700 S/m[26]。其次，聯合數值計算與編程軟件MATLAB 2016a（MathWorks Inc.，美國），獲得了訓練及測試數據集。在腦組織層不同位置放置不同形狀的目標物模擬腦出血。腦出血形態多樣，具體形狀和大小會受到出血區域位置、出血量以及腦組織應力和反應的影響[27]。本文主要研究了圓形和橢圓形的腦出血模擬目標物。目標物的大小和位置是隨機生成的，圓形目標物直徑范圍為3～30 mm。對于橢圓形目標物，長軸和短軸從5～30 mm范圍之間變化。生成的訓練數據集包含
2.3 網絡的訓練
為了訓練所提出的I-DCNN，邊界電壓測量和真實電導率變化分別作為網絡的輸入和輸出，并通過最小化損失函數，學習最佳參數。在本文中，EIT圖像重建被建模為多標簽分類問題。因此，采用二元交叉熵損失（binary cross entropy loss，BCELoss）作為損失函數ρ(θ)，如式(7)所示：
|
式中，N = 2 777是圖像重建中的單元個數，Δσi是Δσ的第i個單元，Δσi*是Δσ*的第i個單元，λ是正則化的超參數。
搭建模型的訓練和驗證通過一臺配置為16 GB內存和基頻為3.10 GHz的中央處理器（central processing unit，CPU）（i5-11300H，Intel? CoreTM，美國）的計算機進行。利用自適應矩估計算法在損失函數的反向傳播過程中對參數θ進行了更新，參數的選擇對網絡的精度和泛化能力有很大的影響。在網絡訓練過程中，采用經驗法進行參數確定：學習速率為0.000 1，正則化選擇為0.000 01，批大小（batch size）和輪次（epoch）分別設置為16和50。基于I-DCNN的腦出血圖像重建方法的訓練結果如圖4所示。可以看出，訓練集的正確率隨著迭代次數的增大而趨于1。迭代達到50次時，正確的速率緩慢增加，但仍呈上升趨勢。相應的，訓練集的損失減小并趨近于0。從驗證集正確性和損失曲線來看，曲線振蕩較小，說明所提出的基于I-DCNN的腦出血圖像重建方法得到了很好的訓練。
圖4
基于I-DCNN的腦出血圖像重建方法的訓練結果
Figure4.
Training results of image reconstruction method for cerebral hemorrhage based on I-DCNN
3 圖像重建結果及討論
為了驗證本文所提方法在電導率分布圖像重建方面的性能，本節在無噪、噪聲及顱腦模型變化4種條件下開展了數值仿真研究，并與全連接神經網絡（fully connected neural network，FCNN）、CNN、DCNN等3種傳統的神經網絡成像方法進行比較，驗證了所提出的I-DCNN方法在重建腦出血圖像方面的優越性；然后，通過物理模型實驗進一步驗證了所提方法能夠提升顱內腦出血的電導率分布重建質量。為了定量比較不同方法的性能，對重建圖像的均方根誤差（root mean square error，RMSE）和相關系數（correlation coefficient，CC）進行了計算。RMSE和CC的表達式如式(8)～式(9)所示[28-29]：
|
|
式中，ge和是真實電導率分布變化和預測電導率分布變化的第e個像素，和分別是真實電導率分布變化和預測電導率分布變化的平均值。
3.1 無噪條件下圖像重建結果
首先，在無噪聲條件下對基于不同方法的5種腦出血模型的圖像重建進行研究，圖像重建結果如圖5所示。可以看出，FCNN方法圖像重建背景有少量的偽影且重建目標物發生了嚴重形變。CNN方法重建的部分圖像中出現了大量的偽影，且腦出血的大小和形狀沒有得到好的重建。當目標物較大時，DCNN重建的腦出血形狀和大小較為準確，但當目標物較小時，DCNN的重建圖像不能真實反映腦出血的大小。在基于所提I-DCNN方法的重建圖像中，腦出血的位置重建效果較好；當出血點較小時，所提出方法仍然能夠較好地重建出出血點的大小和位置。結果表明，所提出的I-DCNN方法重建顱內腦出血電導率分布的性能優于其他3種傳統方法。
圖5
無噪條件下圖像重建結果
Figure5.
Reconstructed images under noise-free condition
重建圖像的CC和RMSE值如表1所示。可以觀察到，FCNN方法的CC值最低、RMSE值最高，這表明FCNN的圖像重建質量相對較差。DCNN方法的CC值比FCNN和CNN方法更高，而RMSE值偏小。與DCNN方法的CC值和RMSE值相比，本文所提出的I-DCNN方法的CC值有一定提高，RMSE值有所降低。特別是當目標物為橢圓形時，本文方法明顯優于DCNN法。
表1
無噪條件下的平均CC和RMSE值
Table1.
Average CC and RMSE values under noise-free condition
3.2 噪聲條件下的圖像重建結果
為評估所提出的方法在噪聲條件下的魯棒性，本研究中將高斯白噪聲添加到邊界測量電壓數據上，噪聲設置為20 dB。信噪比（signal-to-noise ratio，SNR）的計算方法如式(10)所示[30]：
|
式中，e是均值為0、方差為1的噪聲。
噪聲條件下基于不同方法的4種模型的腦出血圖像重建結果如圖6所示。可以發現，FCNN和CNN方法重建的目標物形狀比無噪聲時的形狀略有變形，而DCNN方法重建的目標物形變稍微小一些。但在本文所提I-DCNN方法中，重建幾乎不受噪聲的影響。將圖5與圖6進行比較，可以發現，即使在噪聲的影響下，本文所提I-DCNN方法的圖像重建質量仍相較于其他3種方法更好。
圖6
噪聲條件下圖像重建結果
Figure6.
Image reconstruction results under noise condition
3.3 頭部模型形變條件下的圖像重建結果
此外，不同患者的頭部可能與模擬中建立的模型不同。為驗證頭部形變的情況下本文所提出方法的性能，分別在3種頭部模型形變條件下生成了包含100個樣本的測試數據集。基于不同方法的3個頭部模型形變的圖像重建結果如圖7所示。可以發現，FCNN與CNN的圖像重建結果與真實腦出血目標物相比有較大的形變，DCNN網絡的圖像重建質量相較FCNN和CNN有所提升，但在目標物較小時的圖像重建結果不及所提出的I-DCNN方法，且本文所提I-DCNN方法重建出的圖像邊界清晰無偽影。定性評估表明，本文所提出的方法在頭部模型形變情況下具有較好的圖像重建質量。
圖7
頭部模型形變時的圖像重建結果
Figure7.
Image reconstruction when head model deforms
3.4 物理模擬實驗下的圖像重建結果
除了數值模擬研究外，還通過物理模型實驗對本文所提I-DCNN方法的圖像重建性能進行了評估。實驗系統采用課題組設計的16電極EIT系統，如圖8所示。實驗中采用了“相對—相鄰”激勵采集模式，激勵電流設置為1.25 mA，頻率為50 kHz[31]。制作了三層顱腦物理模型，使用瓊脂等材料制作了不同尺寸的瓊脂棒用于模擬腦出血，瓊脂棒的電導率配置為0.7 S/m。
圖8
物理模型實驗
Figure8.
Phantom experimental setup
基于FCNN、CNN、DCNN與本文提出的I-DCNN這4種不同方法對兩個腦出血目標的電導率分布圖像重建結果如圖9所示。在I-DCNN網絡的訓練過程中，模擬腦出血的目標物直徑范圍為3 ～30 mm，也就是說經過網絡訓練后，該范圍的腦出血電導率分布圖像均可被很好地重建。由于過細的瓊脂棒不易制作且易漂浮在溶液中，實驗中制作的小瓊脂棒直徑為15 mm。同時，為了驗證網絡的泛化能力，模擬腦出血的大瓊脂棒直徑為40 mm。從圖9中可以得出，基于FCNN與CNN方法的重建圖像目標物形狀嚴重形變、背景有明顯偽影，且小目標物的圖像重建更加困難。與FCNN和CNN相比，DCNN方法圖像重建質量有較大提升，能夠重建出目標物的大小和形狀。對于本文所提I-DCNN方法在重建效果上優于DCNN方法，無論是對于大目標物還是小目標物，其重建結果都更接近真實情況，且重建圖背景清晰無偽影。實驗結果表明，本文I-DCNN方法比其他3種方法能更好地重建出腦出血圖像。
圖9
基于實驗數據的圖像重建結果
Figure9.
Reconstructed images with phantom experimental data
4 結論
本文提出了一種基于I-DCNN的腦出血圖像重建方法，該方法在原有的DCNN網絡的基礎上，增加了3個并聯通道，并利用3種不同類型的卷積塊以產生不同尺度的特征信息，提升網絡對于提取電導率特征信息的能力，從而實現對腦出血的精準重建。本文通過數值仿真分別研究了無噪、有噪及顱腦模型變化3種條件下所提出I-DCNN方法在重建腦出血方面的性能，并與FCNN、CNN、DCNN這3種不同的圖像重建方法進行了比較。定性與定量評估均表明本文所提出方法在重建顱內腦出血方面的優良性能。此外，物理模擬實驗結果也表明本文所提方法能夠顯著提升顱內腦出血電導率分布變化的重建質量。然而，顱腦EIT臨床應用環境復雜，本文所提方法在臨床復雜環境中的適用性和可靠性仍需進一步深入研究。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：施艷艷、王孌珺負責本文算法程序設計、結果記錄分析以及論文撰寫；李亞婷負責實驗數據分析，王萌負責論文審閱及修訂；楊濱、付峰負責本文工作的實驗指導。
