0.939）mm，醫師間平均誤差為（3.034±2.612）mm。 ② Cobb角標注：Swin-PGNet平均誤差為（2.062
1.352）°，醫師間平均誤差為（3.580
2.338）°；Swin-PGNet與3名醫師間誤差比較，差異均無統計學意義（P>0.05），但不同醫師間誤差比較差異有統計學意義（P<0.05）。③ 椎體滑移距離：Swin-PGNet平均誤差為（1.656
0.878）mm，醫師標注平均誤差為（1.884
1.612）mm；Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異均無統計學意義（P>0.05）。Swin-PGNet腰椎不穩判斷準確率為84.0%、醫師為75.3%，腰椎滑脫判斷準確率分別為71.3%、70.7%，Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異均無統計學意義（P>0.05）。④ 腰椎穩定性判定一致性分析：3名醫師標注椎間Cobb角的ICC為0.913 ［95%CI（0.898，0.934）］ （P<0.05），椎體滑移距離為0.741 ［95%CI（0.729，0.796）］ （P<0.05），說明3名醫師間標注具有一致性。Swin-PGNet-所有醫師間椎間Cobb角ICC為0.922 ［95%CI（0.891，0.938）］ （P<0.05），椎體滑移距離為0.748 ［95%CI（0.726，0.783）］（P<0.05），說明Swin-PGNet與醫師標注具有一致性。
引用本文： 胡厚民, 王賢帝, 楊恒, 張勁, 李康, 曾建成. 基于深度學習的腰椎穩定性自動診斷工具的研發及驗證. 中國修復重建外科雜志, 2023, 37(1): 81-90. doi: 10.7507/1002-1892.202209058 復制
版權信息： ?四川大學華西醫院華西期刊社《中國修復重建外科雜志》版權所有，未經授權不得轉載、改編
腰椎穩定性是判斷腰椎退變性疾病患者是否需要進行融合手術的關鍵指標，與患者腰背疼痛程度、生活質量具有緊密聯系[1-3]，因此準確判斷腰椎穩定性對于評估腰椎疾病狀態、術前規劃及術中決策至關重要[4]。目前，臨床通常以過屈、過伸位X線片上椎間Cobb角變化以及椎體滑移距離作為腰椎穩定性判斷標準，如椎間Cobb 角變化超過11° 即診斷為腰椎不穩，椎體滑移距離超過3 mm即診斷為腰椎滑脫[5]。椎間Cobb 角和椎體滑移距離測量主要由醫師手工或利用PACS系統測量工具完成，相關X線片測量參考點的選擇受醫師主觀影響較大，不同醫師間的測量一致性及穩定性較差，且耗時費力[6-11]。因此，開發一種客觀、穩定、可靠的脊柱穩定性判斷工具，對于構建腰椎退變性疾病標準化診療體系具有重要意義。
近年來，深度學習已成功應用于醫學圖像處理領域，在脊柱領域也有相關研究[12-18]。例如，Alukaev等[12]結合目標檢測和圖像分割，實現了Cobb角3.42° 的平均預測誤差；Wang等[13]提出結合冠狀面和矢狀面腰椎X線片預測Cobb角，實現了6.26° 的平均預測誤差；Fu等[14]使用編碼-解碼結構分割椎體，同時共享其權重用于回歸椎體4個角的坐標，將Cobb角平均預測誤差降至3.15°；Zhao等[15]提出一種U型結構網絡，上采樣中加入通道注意力機制，跳接模塊中加入殘差塊，在最深特征層提出卷積塊注意模塊，最終得到Cobb角平均預測誤差2.45° 的優秀性能。基于既往研究中的基礎算法，我們提出一種新的神經網絡Swin-PGNet，該網絡使用Swin-Transformer（ST）[19]與Resnet34 [20]共同對圖像進行下采樣，并利用局部-全局融合模塊（patch-global fusion block，PGFB）對不同深度特征進行融合，通過二階段方法直接對椎體關鍵點進行定位預測，從而自動測量患者過伸、過屈位X線片椎間Cobb角以及椎體滑移距離，判斷患者脊柱穩定性。報告如下。
1 材料與方法
1.1 腰椎X線片圖像數據庫的建立及標注
以2013年10月—2020年3月在四川大學華西醫院骨科因腰椎疾病接受經側前方L4、5椎間融合術的患者為研究對象，收集術前腰椎過伸、過屈位X線片（DICOM格式），采用自行編寫的脫敏工具對患者姓名、住院號、身份證號、聯系電話等敏感字段進行刪除脫敏。共153例患者306張X線片納入研究。
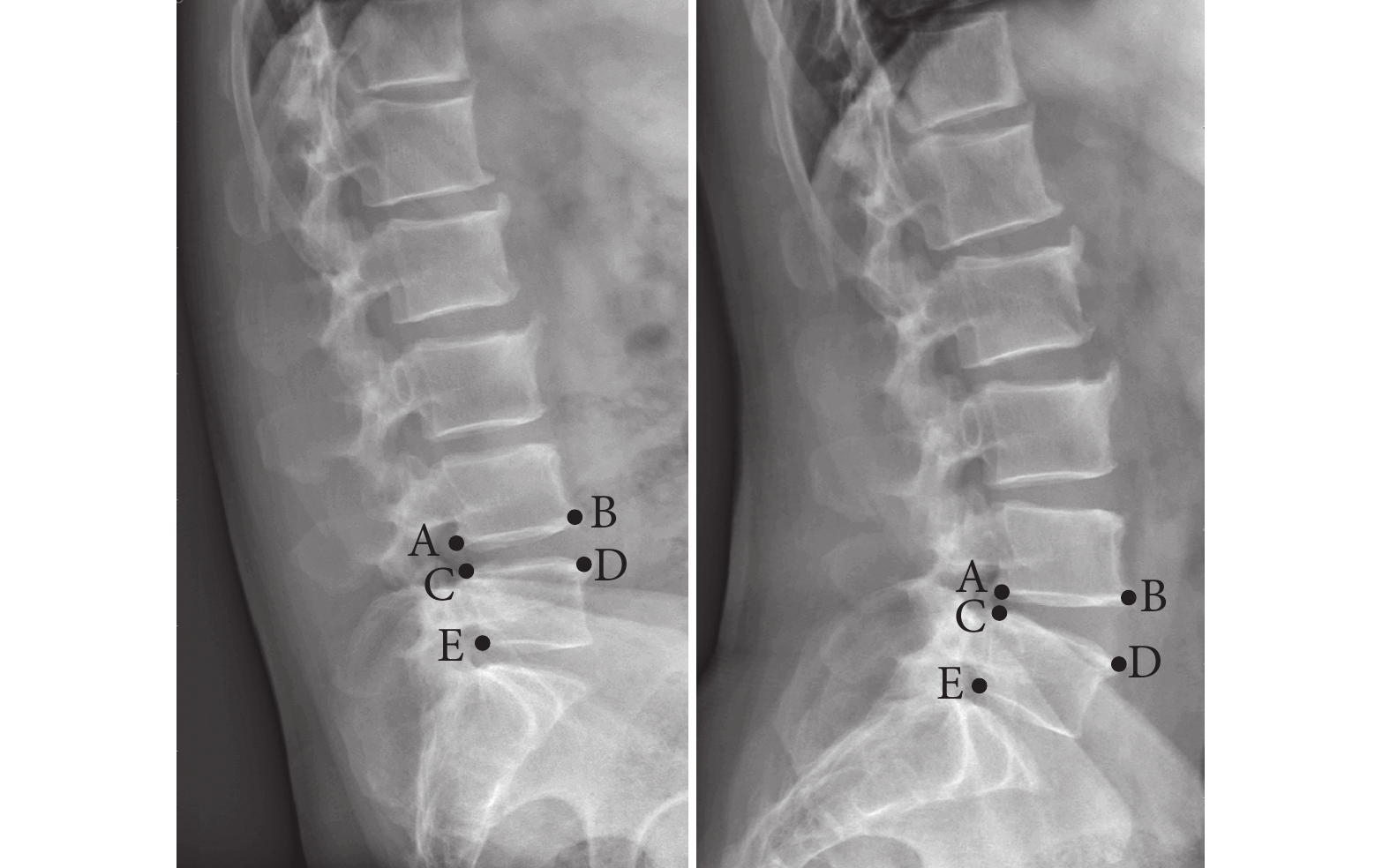
采用四川大學華西醫院研發的影像標注工具AI-Tutor，由3名骨科醫師（2名副主任醫師，1名主治醫師）對圖像進行人工標注。于每例患者過伸、過屈位X線片標注5個關鍵點，分別為L4后下角（A點）、前下角（B點）以及L5后上角（C點）、前上角（D點）、后下角（E點），見圖1。AI-Tutor工具可在標注后自動導出圖像以及與之對應的點坐標，訓練時圖像數據轉換為png格式，坐標信息保存在txt文件中。將306張X線片按照3∶1∶2比例，隨機分為訓練集（n=156）、驗證集（n=50）和測試集（n=100）。
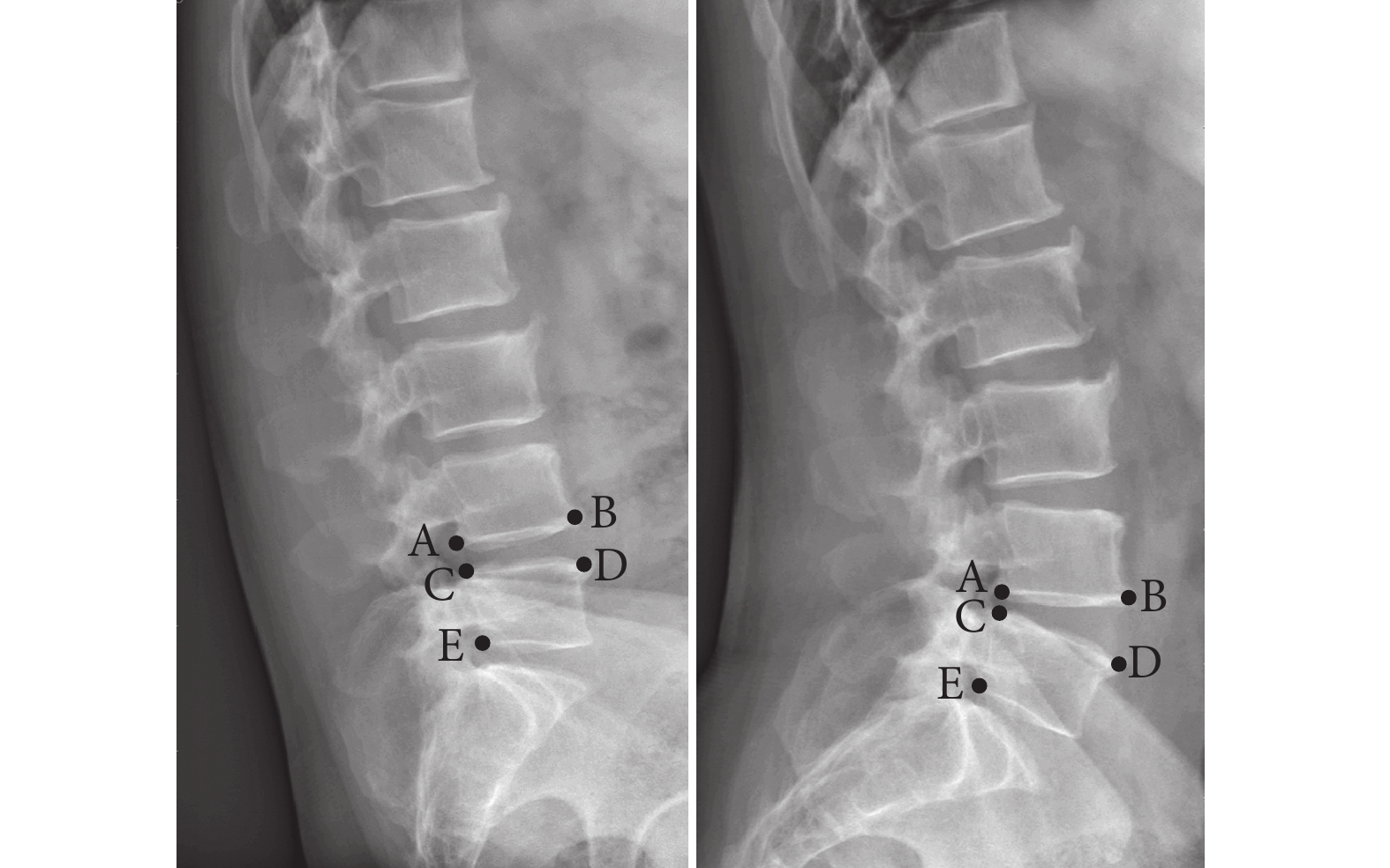圖1
過屈、過伸位X線片關鍵點
Figure1.
Key points on hyper-flexion and hyper-extension X-ray films
1.2 神經網絡結構與訓練
1.2.1 神經網絡結構
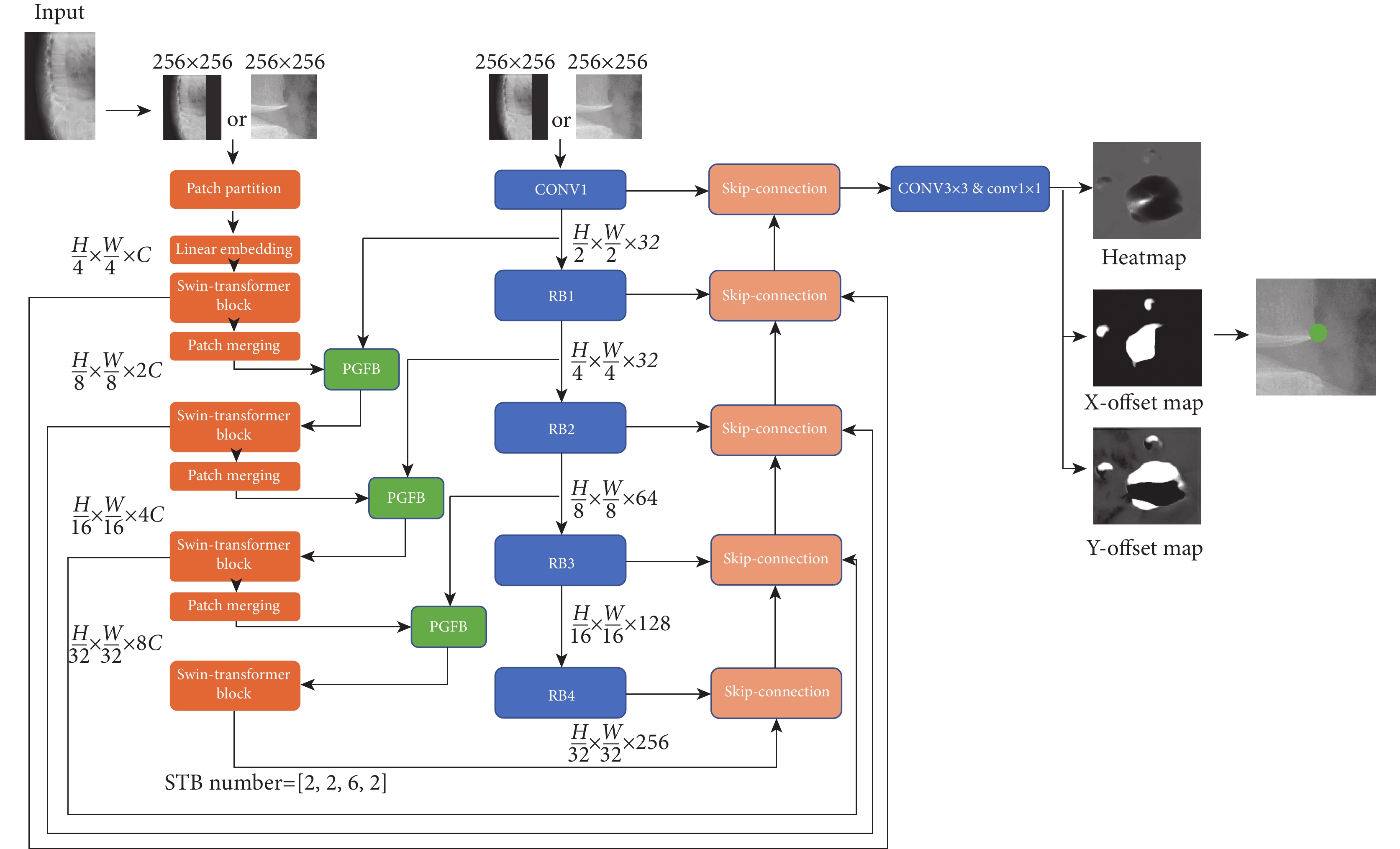
Swin-PGNet網絡結構總體類似U-net[21]的編碼-解碼結構，網絡輸出圖像和輸入圖像尺寸一致（圖2）。采用一種基于ST[19]和Resnet34[20]的雙編碼結構對圖像進行編碼。同時，兩條編碼分支用PGFB模塊融合信息，將卷積神經網絡不同深度的局部特征加入到ST編碼過程中，在解碼時兩條編碼分支深度相同的特征被拼接以后進行上采樣，一直到特征圖大小與原圖一致。
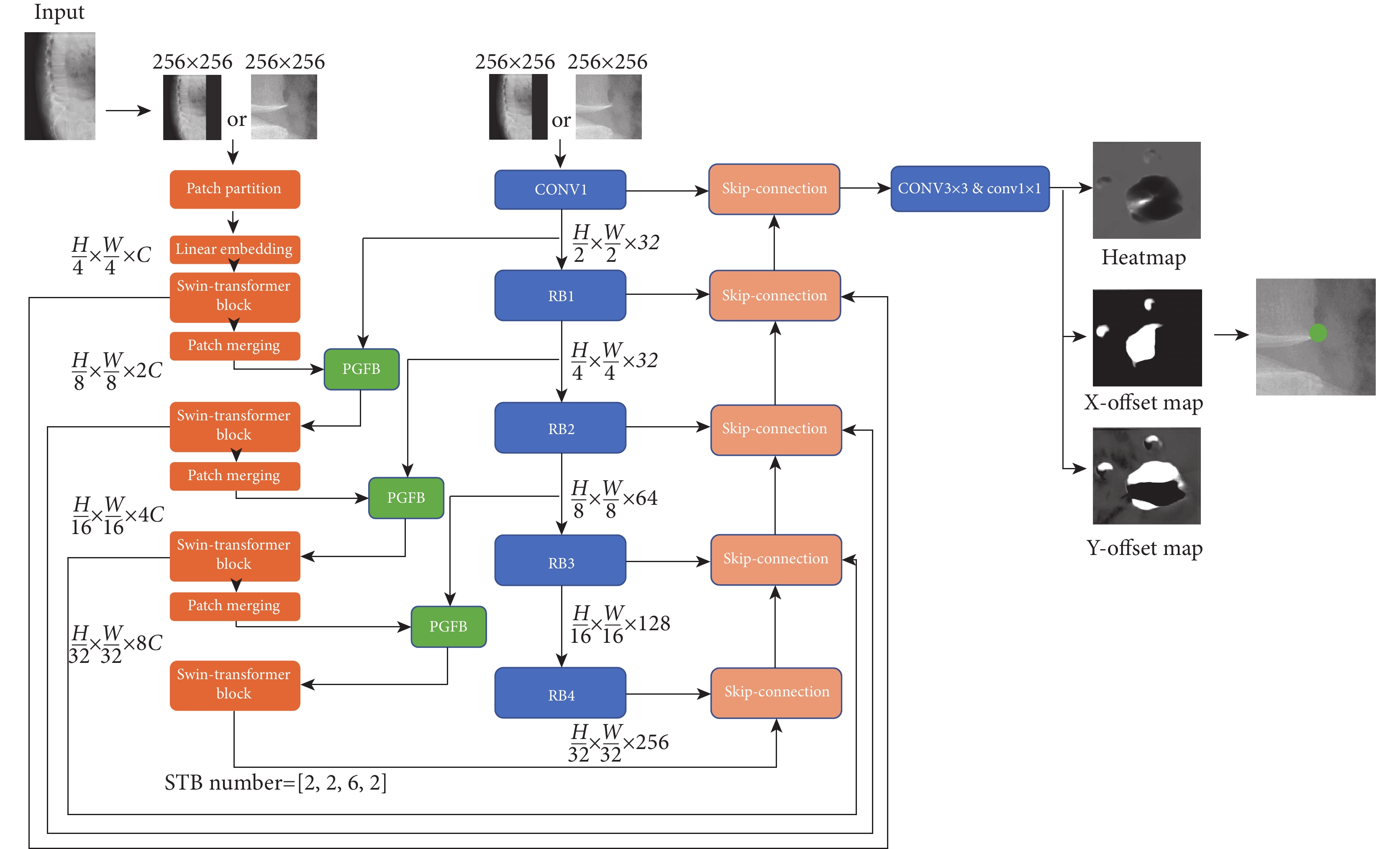圖2
Swin-PGNet網絡結構
Figure2.
Swin-PGNet network structure
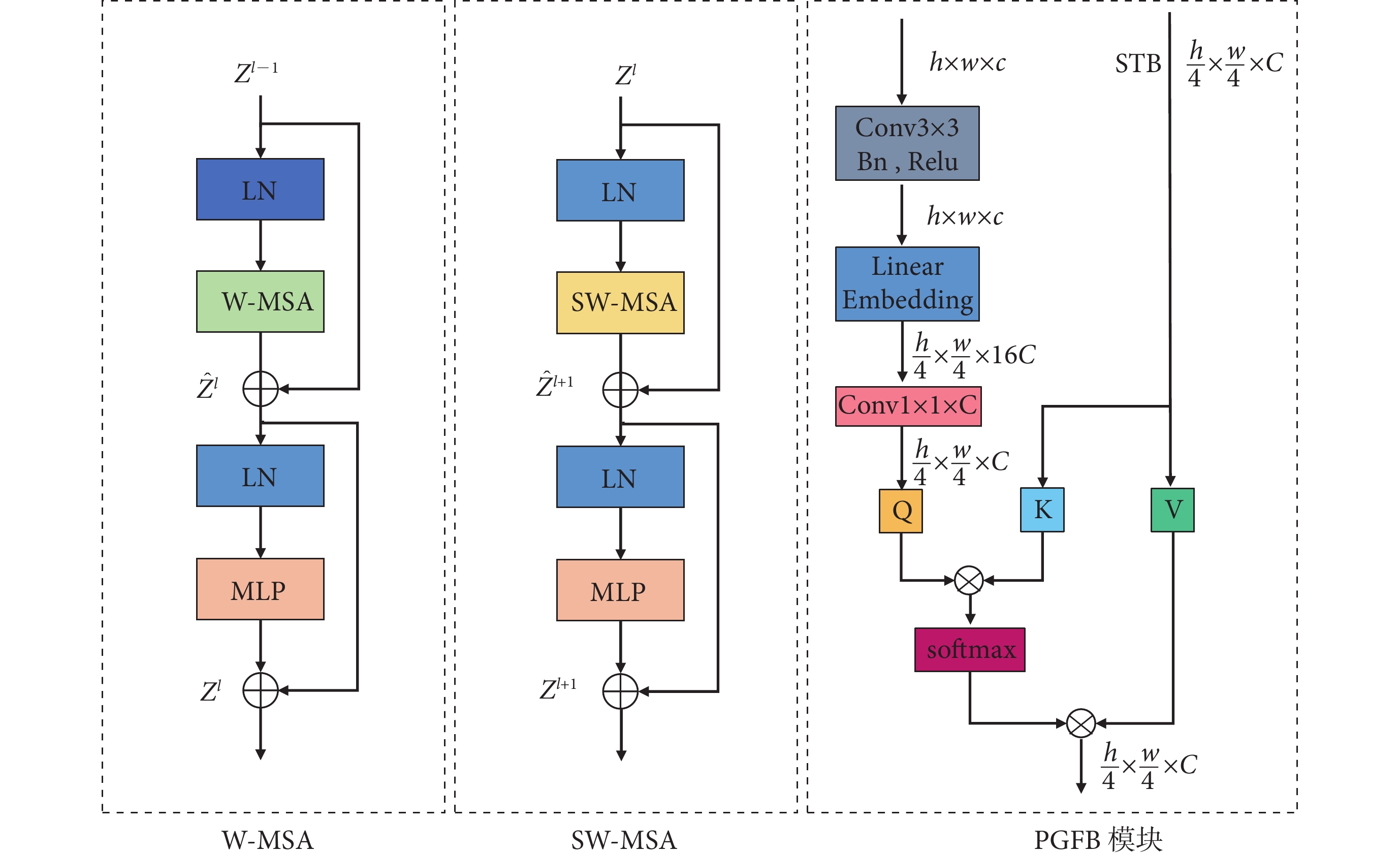
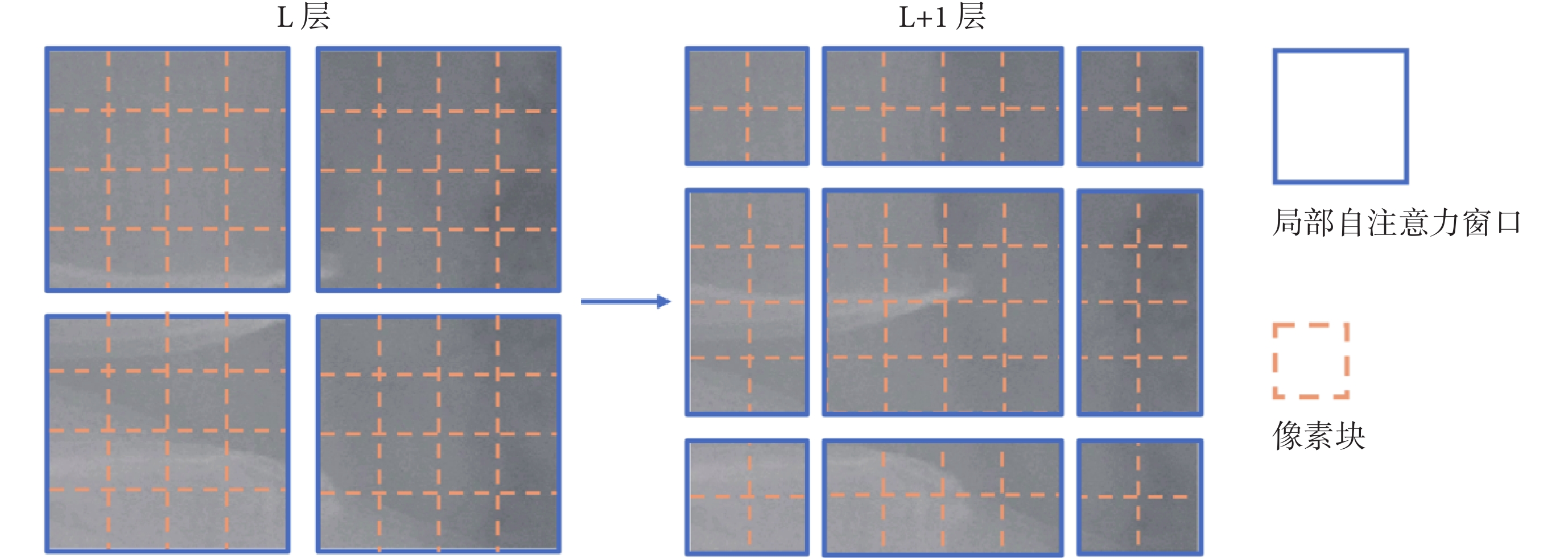
ST模塊由兩部分組成，第1部分為窗口多頭自注意力機制（window multi-head self-attention，W-MSA）、第2部分為移動W-MSA（shift W-MSA，SW-MSA），前者的輸出是后者的輸入（圖3）。圖像首先平均分成16塊，然后線性投射，在模塊內部依次經過線性歸一化層、多頭自注意力層、殘差連接和具有高斯誤差線性單元的多層感知機（multi-layer perceptron，MLP）。從上到下每個特征層的ST模塊堆疊數為 ［2，2，6，2］，多頭自注意力頭數為 ［4，8，16，32］，線性嵌入維度為96，窗口尺寸為8，每輪訓練時隨機選擇神經網絡中20%路徑不參與學習。其中，每個ST模塊中兩次窗口自注意力對圖像區域的選取如圖4所示，L層將特征圖分為4塊，并在每一塊內部計算其中元素相互之間的關聯程度；在L+1層中將特征層分為9塊，計算每一塊內部元素相互之間的關聯程度。ST模塊內部計算公式如下：
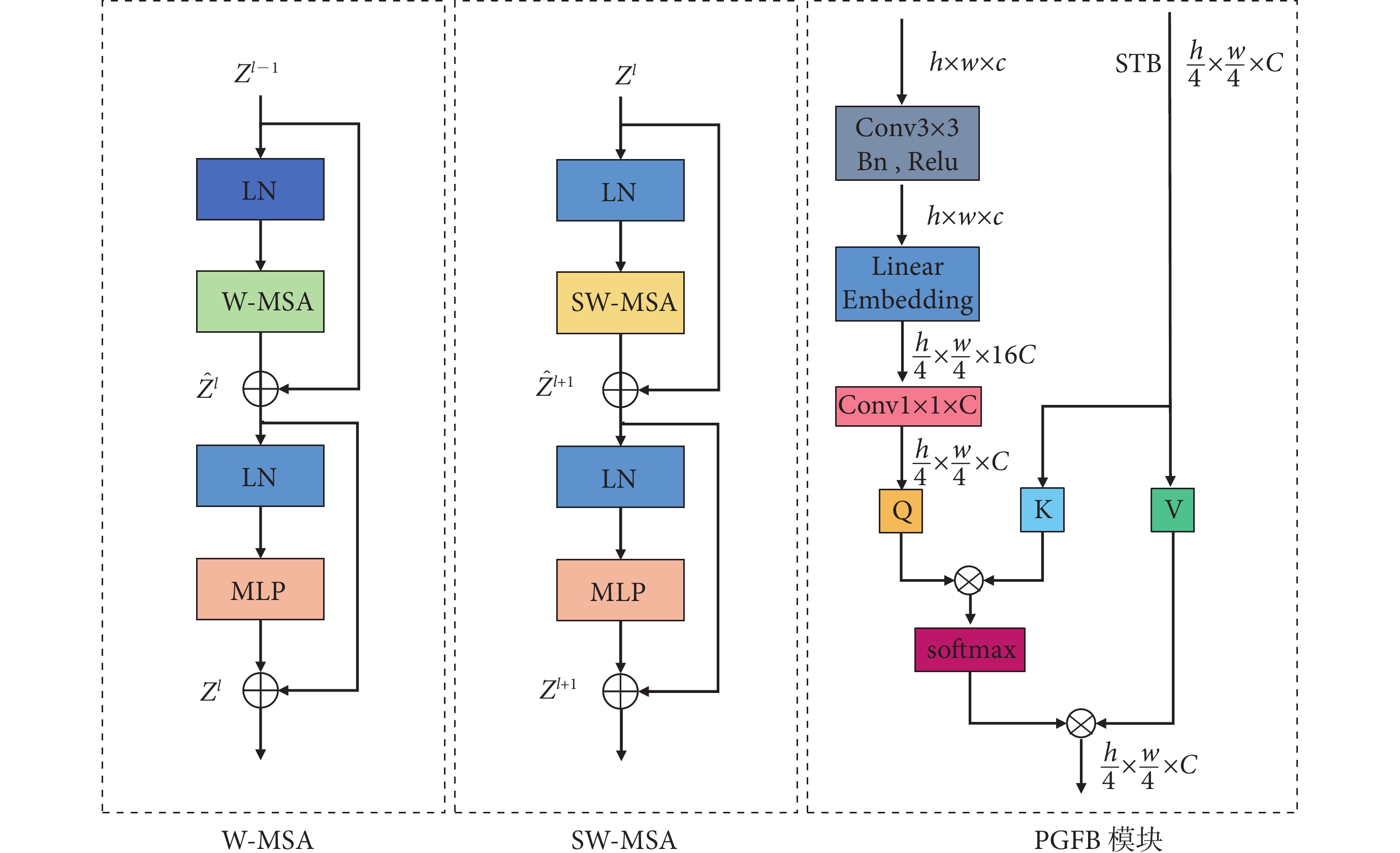圖3
ST模塊及PGFB模塊
Figure3.
ST module and PGFB module
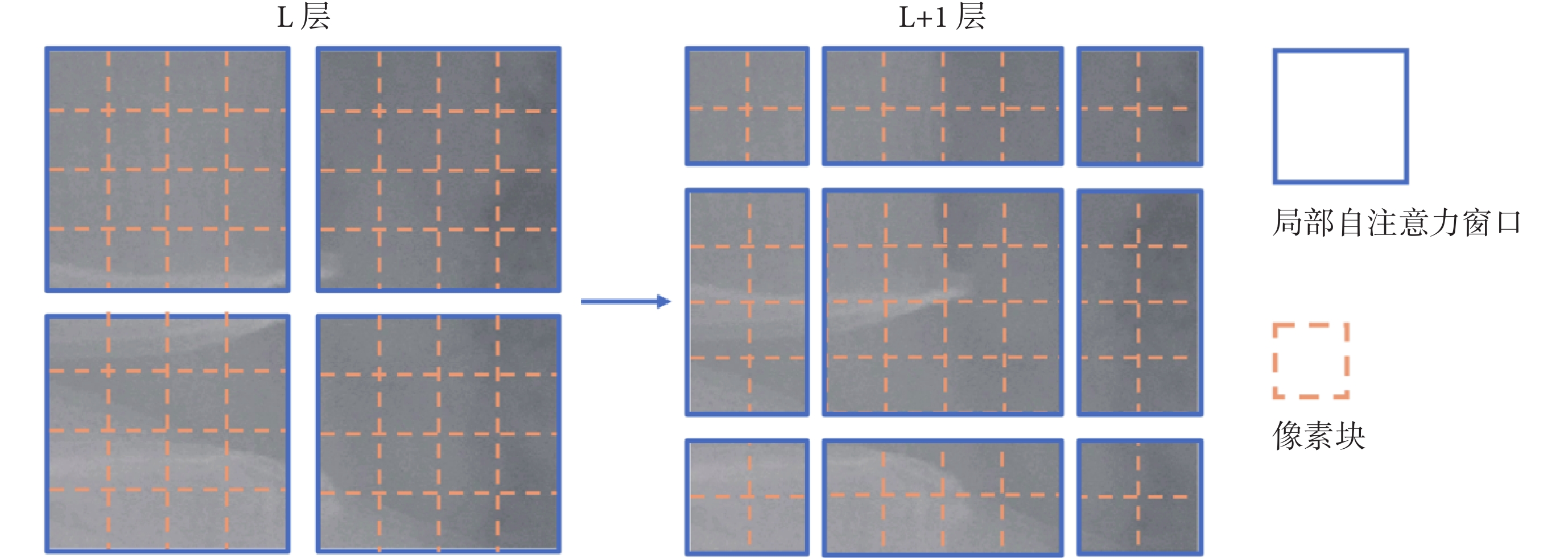圖4
移動窗口計算的圖片區域
Figure4.
Calculated picture area of shift window
 |
 |
 |
 |
其中，
和 
分別表示第 
個（S）W-MSA模塊的MLP輸出。參考既往研究[22-23]自注意力計算公式如下：
 |
其中，Q、K、
分別表示查詢、鍵和值的矩陣。
表示窗口中的分塊數量，
表示查詢或鍵的維度。此外，
中的值來自于偏置矩陣 
。
ST模塊下采樣過程中，圖像首先經過分塊層將
的圖片轉化成
的維度，線性投射層將其通道數轉化為預設的96，并且將其前兩個維度拉伸之后送入ST模塊。分塊融合層對特征圖兩倍下采樣，并將其原有通道數翻倍，具體方法為將特征圖均分4塊，然后在通道維度上拼接起來。
卷積神經網絡是經典的Resnet34，每一層通道數設置為 ［32，32，64，128，256］，每一個卷積之后都有一個批歸一化層和一個ReLU激活函數。將卷積編碼器
維度的特征和ST編碼器
維度的特征一并輸入PGFB模塊中，
［2，4，6］。
PGFB模塊中，卷積網絡輸入維度為
，ST模塊輸入維度為
。對于卷積網絡的輸入，首先經過 
的卷積層、批歸一化層以及ReLU層，再進入線性嵌入層，輸出維度為
，再通過
將其通道數和ST模塊輸入統一為C。將卷積層與ST模塊兩種特征圖做注意力機制后與ST模塊原本特征圖矩陣點乘后輸出。
跳接塊用于將來自ST編碼器、卷積編碼器相同深度特征層特征以及更深一層的跳接塊輸出特征在通道維度上進行拼接，三者拼接完成后使用上采樣將特征尺寸翻倍，再通過
將其通道數與Resnet當前深度的通道數統一，并將其輸出到下一個跳接塊中。最后的特征經過
和
將輸出維度設置為3，分別代表熱力圖、x方向偏移圖和y方向偏移圖。
1.2.2 標簽設置以及坐標計算
將熱力圖制定為分類問題，具體步驟為將真實關鍵點坐標距離25以內的像素點設置為1，其余為0，具體公式如下：
 |
最終偏移圖和熱力圖聯合計算關鍵點坐標方法和人體檢測普遍使用方法[24]類似：
 |
 |
 |
 |
 |
其中，
和
是圖上坐標，
是真實關鍵點坐標。
指熱力圖標簽，
是網絡輸出的熱力圖，
和
是x和y方向的修正圖，offsetmap指偏移圖，
是
的距離圖，
是分數圖，
和 
是網絡輸出的偏移圖，
最終預測坐標。
1.2.3 神經網絡的訓練
Swin-PGNet是二階段方法，第1階段進行粗定位，找出L4和L5區域；第2階段在前一階段得到的坐標周圍 
區域中對關鍵點精確定位。
第1階段將X線片像素空間值統一為0.1 mm/pixel，然后用0像素值將圖像填充至長寬比為1∶1，最后放縮至 256×256作為模型輸入；對關鍵點進行粗定位，定位L4和L5大致位置，以預測坐標為中心點取大小為512×512的區域，放縮圖像尺寸至256×256作為第2階段模型的輸入。第2階段訓練集制作，通過在關鍵點真實坐標半徑為50像素距離中隨機選取一點，以此點為中心截取大小為512×512 的局部圖像。每個點的預測均單獨進行，分為訓練粗定位和精細定位兩個階段模型，每次輸入圖片均為單通道灰度圖。
使用隨機梯度下降優化器訓練網絡，初始學習率為0.001，訓練批量為4。在第4、6和8個時期將學習率縮小1/10。使用python庫imgaug實現數據增強。圖像在x和y方向隨機平移最多10個像素；所有像素強度隨機縮放為0.5～1.0；放大或縮小圖像，使其在原始比例的 0.95～1.05 之間；將圖像逆時針或順時針旋轉最多 3°；最后對每個圖像進行彈性變換。ST模塊和卷積神經網絡均在ImageNet訓練集的預訓練權重上進行，在整個訓練集上訓練20個輪次，選擇驗證集上效果最好模型作為最終模型。負責輸出預測熱力圖的通道結果會通過一個sigmoid函數，并且對它使用交叉熵損失函數定義為 
。為訓練偏移回歸頭，懲罰預測偏移和真實偏移之間的差異，相應損失為：
 |
其中，
是Huber Robust損失， 
是真實關鍵點坐標位置，
是真實關鍵點坐標位置 
范圍內的點。最終損失函數表示如下：
 |
其中，
而 
，這樣可以平衡兩項損失。
1.3 神經網絡的評估
在100張腰椎X線片（50例患者過伸、過屈位腰椎X線片）測試集上對Swin-PGNet的預測結果進行評估，比較Swin-PGNet和醫師標注的關鍵點定位、L4、5椎間Cobb角、L4椎體滑移距離。評價指標包括關鍵點定位平均誤差、椎間Cobb角測量平均誤差、椎體滑移距離測量平均誤差，腰椎不穩及腰椎滑脫判斷準確率。
1.3.1 誤差定義
① 關鍵點定位誤差定義如下：
 |
其中，
表示關鍵點定位誤差（mm）；
和 
是關鍵點在圖像中的標注坐標，
和 
是關鍵點在圖像中的預測坐標；
是圖像中像素點對應的真實物理空間距離，預處理中統一成0.1 mm/pixel。
② 椎間Cobb角測量誤差定義如下：
 |
其中，
表示椎間Cobb角測量誤差，
表示醫師標注椎間Cobb角度，
表示 Swin-PGNet預測椎間Cobb角度。
③ 椎體滑移距離測量誤差定義如下：
 |
其中，
表示椎體滑移距離測量誤差，
表示醫師標注椎體滑移距離，
表示 Swin-PGNet預測椎體滑移距離。
1.3.2 臨床判斷分析
椎間Cobb角及椎體滑移距離測量方法：Cobb角為L4椎體下終板直線與L5椎體上終板直線夾角；過上位椎體后下角（A點）作下椎體后上角（C點）與后下角（E點）形成直線的平行線，兩條線距離即為椎體滑移距離。見圖5。以同一患者過伸、過屈位X線片上，椎間Cobb角變化超過11° 判定為腰椎不穩，椎體滑移距離超過3 mm判定為腰椎滑脫。
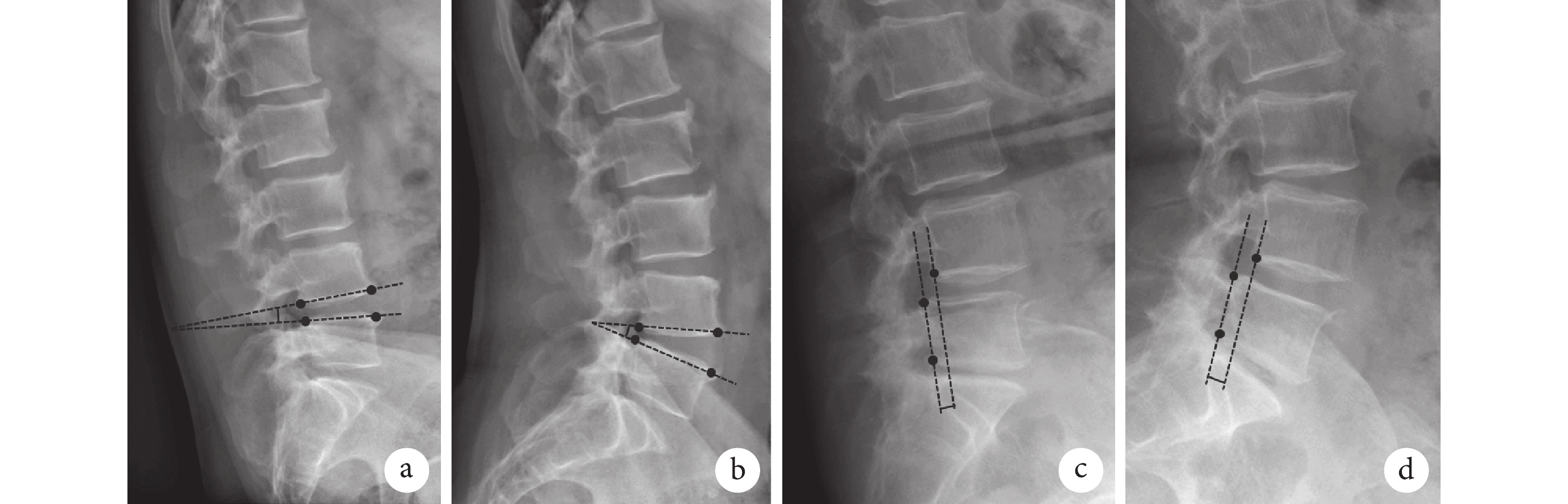圖5
基于腰椎過屈、過伸位X線片測量腰椎Cobb角以及椎體滑移距離示意圖
a、b. Cobb角；c、d. 椎體滑移距離
Figure5. Diagram for measuring Cobb angle and sliding distance of lumbar vertebrae based on hyper-flexion and hyper-extension X-rayfilmsa, b. Cobb angle; c, d. Sliding distance
對于關鍵點定位平均誤差、椎間Cobb角測量平均誤差和椎體滑移距離測量平均誤差3個評價指標，將每名醫師的標注單獨作為金標準分別對Swin-PGNet進行訓練，計算Swin-PGNet與該醫師標注的誤差，取Swin-PGNet與3名醫師標注誤差的平均值，得到Swin-PGNet平均誤差。同時，計算每 2 名醫師間誤差，取3組誤差的平均值作為醫師間平均誤差。最后，比較Swin-PGNet與醫師間的平均誤差，驗證Swin-PGNet在定位和測量任務中的精度是否超過醫師。
對于腰椎不穩、腰椎滑脫判斷準確率2個評價指標，同樣將每名醫師的標注單獨作為金標準對Swin-PGNet進行訓練，并根據臨床標準判斷患者是否存在腰椎不穩和腰椎滑脫，當Swin-PGNet測量結果與醫師一致時認為判斷正確，否則判斷錯誤，計算Swin-PGNet在3名醫師標簽上的平均準確率。同時，將每 2 名醫師的標注互相比較，對同一患者腰椎不穩/腰椎滑脫判斷一致則認為判斷正確，否則判斷錯誤，統計3個比較組的平均準確率。最后比較Swin-PGNet和醫師間對腰椎不穩以及腰椎滑脫判斷的準確率，驗證Swin-PGNet的診斷水平是否超過醫師水平。
1.4 統計學方法
采用Python軟件中的numpy包進行統計分析。計量資料經正態性檢驗均符合正態分布，數據以均數±標準差表示，組間比較采用方差分析，兩兩比較采用SNK檢驗；計數資料以率表示，組間比較采用χ2檢驗。
采用組內相關系數（intra-class correlation coefficient，ICC）分析不同醫師間以及Swin-PGNet與醫師測量一致性。檢驗水準α=0.05。
2 結果
2.1 關鍵點定位誤差分析
Swin-PGNet關鍵點定位平均誤差為（1.407±0.939）mm，Swin-PGNet與醫師在各關鍵點定位誤差的比較結果詳見表1。醫師間平均誤差為（3.034±2.612）mm，其中醫師1-2為（3.049±2.681）mm，醫師1-3為（3.207±2.783）mm，醫師2-3為（2.846±2.373）mm。
表1
Swin-PGNet與醫師在關鍵點定位的比較（n=100，
，mm）
Table1.
Comparison of Swin-PGNet with surgeons in key points localization (n=100, 
, mm)
2.2 臨床判斷分析
2.2.1 腰椎穩定性分析
① Cobb角：Swin-PGNet平均誤差為（2.062
1.352）°，醫師間平均誤差為（3.580
2.338）°；Swin-PGNet與3名醫師間誤差比較，差異均無統計學意義（P>0.05），但不同醫師間誤差比較差異有統計學意義（P<0.05），說明Swin-PGNet對醫師在Cobb角上的標注學習成功，但3名醫師在該任務上存在明顯差異。
② 椎體滑移距離：Swin-PGNet平均誤差為（1.656
0.878）mm，醫師標注平均誤差為（1.884
1.612）mm，Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異均無統計學意義（P>0.05），說明Swin-PGNet對醫師在椎體滑移距離上的標注學習成功，且3名醫師在該任務上無明顯差異。
Swin-PGNet腰椎不穩判斷準確率為84.0%，醫師為75.3%，Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異無統計學意義（P>0.05）；Swin-PGNet腰椎滑脫判斷準確率為71.3%，醫師為70.7%, Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異均無統計學意義（P>0.05），見表2。
表2
腰椎穩定性判斷比較（n=50）
Table2.
Comparison of lumbar stability judgments (n=50)
2.2.2 腰椎穩定性指標測量一致性分析
3名醫師標注椎間Cobb角的ICC為0.913 ［95%CI（0.898，0.934）］（P<0.05），椎體滑移距離為0.741 ［95%CI（0.729，0.796）］ （P<0.05） ，說明3名醫師間標注具有一致性。Swin-PGNet-所有醫師間椎間Cobb角ICC為0.922 ［95%CI（0.891，0.938）］ （P<0.05），椎體滑移距離為0.748 ［95%CI（0.726，0.783）］（P<0.05），說明Swin-PGNet標注結果與醫師標注具有一致性。見表3及圖6。
表3
腰椎穩定性判斷一致性比較
Table3.
Comparison of consistency of lumbar stability judgment
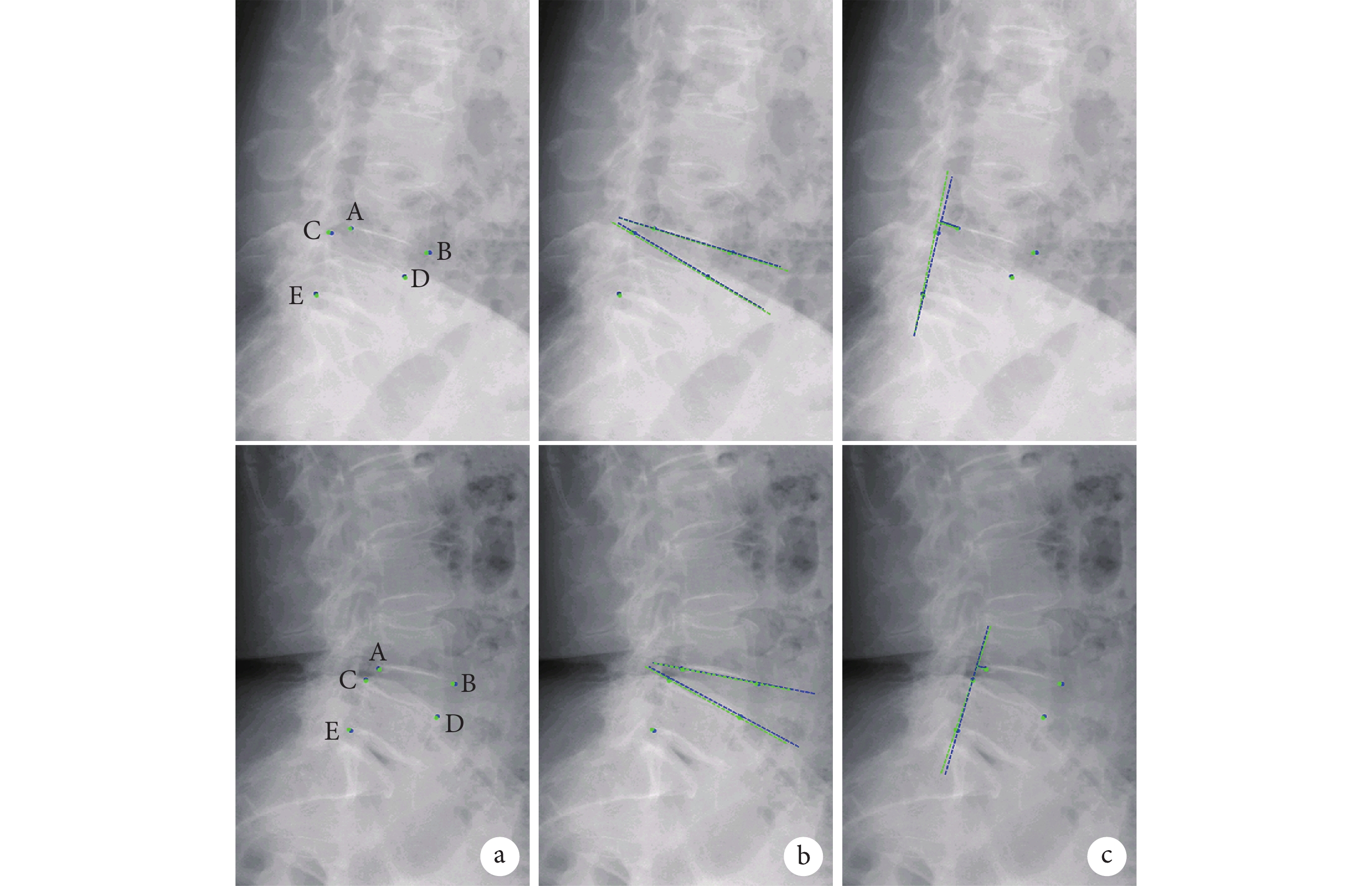
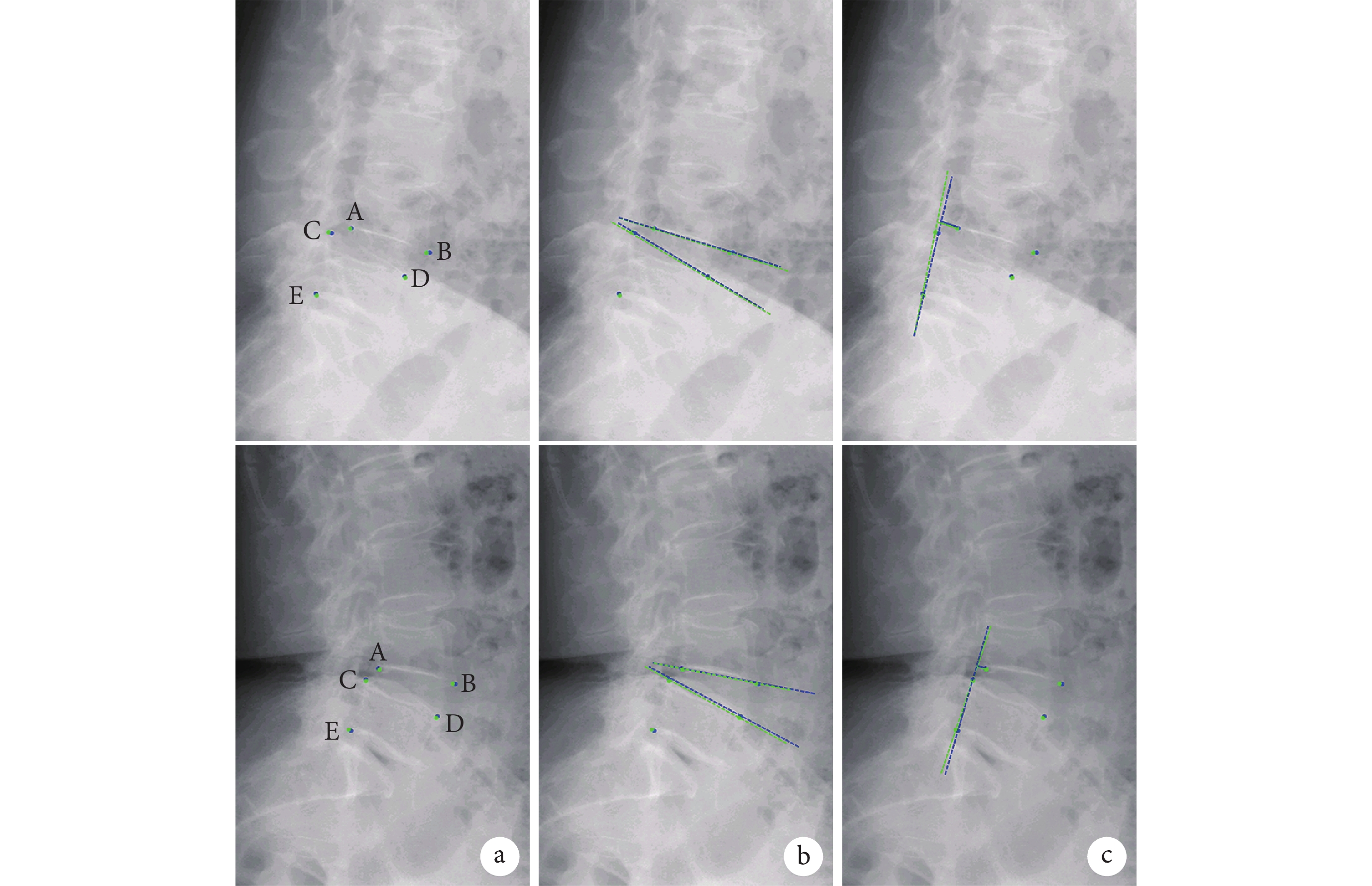圖6
患者，女，68歲，L4、 5椎間盤突出伴椎管狹窄，Swin-PGNet判斷為L4腰椎滑脫不伴節段性不穩，與醫師判斷相同
綠色為Swin-PGNet自動定位，藍色為人工標注；上為過屈位X線片，下為過伸位X線片 a. 關鍵點定位 ；b. Cobb角；c. 椎體滑移距離
Figure6. A 68-year-old female patient with L4, 5 intervertebral disc herniation with spinal stenosis, Swin-PGNet judged L4 lumbar spondylolisthesis without segmental instability, which was the same as the surgeon’s judgmentGreen for automatic location by Swin-PGNet, blue for manual marking; upper for hyper-flexion X-ray films, lower for hyper-extension X-ray films a. Key points location; b. Cobb angle; c. Sliding distance
3 討論
人工智能在醫學影像分析中有著廣泛應用，如胸部CT肺結節定位、識別，其精度已超過影像學醫師，且隨著數據積累，算法可自我迭代，以獲取更加優異表現。本研究采用的新的神經網絡Swin-PGNet，是結合ST [19]與Resnet34[20]算法共同對圖像進行下采樣，創新性地提出一種新的PGFB模塊，對不同深度特征進行融合，通過二階段方法直接對椎體關鍵點進行定位預測，從而實現了椎間Cobb角及椎體滑移距離的自動測量，并基于此對患者脊柱穩定性進行自動判斷。
Swin-PGNet采用了ST和Resnet的雙編碼結構來提取腰椎圖像特征，傳統卷積神經網絡擅長提取局部特征，而ST擅長獲取全局的長語義關系，使圖像每個像素點交互學習彼此語義信息。與此同時，使用PGFB模塊將卷積分支提取的局部特征加入到SW分支中，進一步提升網絡對關鍵點定位精度。在解碼過程中，網絡將兩個編碼器相同尺度的特征在通道方向上拼接后上采樣，融合圖像的全局信息和局部信息，進而將不同深度特征融合在一起，網絡可以學習到不同深度下局部特征相互之間的全局關系，降低定位誤差。
本研究算法采用了感興趣區域提取-關鍵點精細化定位的二階段流程。如果使用單階段直接預測，由于腰椎X線片尺寸大，無法輸入原尺寸圖片進入網絡訓練，因GPU顯存不足需要將圖片縮小后進行預測，預測結果按照縮放比例還原，存在不可避免的系統誤差。使用二階段方法可以在第一階段通過粗定位找出目標椎體的位置，提取出該位置附近的原始尺寸圖片放入第二階段進行精確定位，以減小甚至消除系統誤差。
我們對L4后下角、前下角以及L5后上角、前上角、后下角進行自動關鍵點定位，發現網絡在L4后下角、前下角以及L5前上角的定位效果較好，而在L5后上角、后下角的定位效果較差。這可能是前者在圖像中的形態更清晰，而后者由于髂嵴和椎弓影像的影響增大了關鍵點定位的難度。盡管如此，Swin-PGNet關鍵點定位平均誤差遠小于不同醫師間的平均誤差。這一點也反映在椎間Cobb角測量上，Swin-PGNet在椎間Cobb角測量任務中取得了（2.062±1.352）° 的平均誤差，而醫師間平均誤差為（3.580±2.338）°，說明Swin-PGNet在椎間Cobb角自動測量這一任務上表現優秀，進而在判斷腰椎不穩準確率上取得了84.0%的滿意結果，明顯優于人工測量的75.3%。在腰椎滑移距離測量任務上，Swin-PGNet僅稍好于人工測量，進而體現在對腰椎滑脫判斷的準確率（71.3% vs 70.7%），尤其在醫師3的標簽中，Swin-PGNet判斷準確率（68%）較人工測量（76%）降低了8%。我們分析這可能與本研究使用Quinnell法[25-26]計算腰椎椎體滑移距離有關。該測算方法是以L5后上角、后下角和L4后下角作為參考點，而Swin-PGNet對L5后上角、后下角關鍵點定位誤差較大。與此同時，我們從實例中觀察到Swin-PGNet對于腰椎上、下終板垂直方向的誤差小于水平方向的誤差，提示其學習到了關鍵點位置與椎體終板水平方向的關系，使定位誤差對于Cobb角測量的影響較小，但對采用Quinnell法測量椎體滑移距離中L5后上角與后下角連線方向影響較大。
統計分析結果顯示，Swin-PGNet在椎間Cobb角、椎體滑移距離測量以及腰椎不穩、椎體滑脫判斷方面與醫師標注無明顯差異（P>0.05），充分說明網絡對于任務的學習成功。3名醫師在Cobb角標注中存在差異性（P<0.05），但在腰椎不穩判斷上無明顯差異（P>0.05）。我們分析發現主要標注差異是椎間Cobb角平均值，這與標注Cobb角時醫師標注習慣不同有關。其中2名醫師傾向于椎體終板平行線末端，1名醫師傾向于椎體終板拐角最外側點。雖然椎間Cobb角標注存在差異，但腰椎不穩判斷是由患者過伸位和過屈位X線片上椎間Cobb角變化值決定的，醫師在兩個不同體位X線片中以同樣標準標注椎體角點，最終計算出的角度變化值相近。因此，關于腰椎不穩的判斷，3名醫師標注無明顯差異。此外，在Cobb角測量中，不同醫師間ICC為0.913（P<0.05），Swin-PGNet-所有醫師為0.922（P<0.05），而在椎體滑移距離任務中這兩項結果分別是0.741（P<0.05）和0.748（P<0.05），說明本研究采用的Cobb角測量方法較為可靠，而Quinnell法測量椎體滑移距離的方式本身可能存在系統誤差。
綜上述，本研究基于深度學習研發的腰椎穩定性自動診斷工具，在腰椎X線片關鍵點定位任務、Cobb角測量以及腰椎不穩判斷任務中優于醫師；在腰椎椎體滑移距離測量和腰椎滑脫判斷任務中，與醫師標注結果接近。該方法可以輔助臨床醫師進行診斷，同時提高工作效率。
利益沖突 在課題研究和文章撰寫過程中不存在利益沖突；經費支持沒有影響文章觀點和對研究數據客觀結果的統計分析及其報道
倫理聲明 研究方案經四川大學華西醫院生物醫學倫理審查委員會批準［2020年審（554）號］
作者貢獻聲明 胡厚民：算法設計、研究實施及撰寫文章；王賢帝：臨床分析及指導文章寫作；楊恒：患者數據采集和數據預處理；張勁：實驗思路指導；李康、曾建成：課題總體設計及文章審閱
腰椎穩定性是判斷腰椎退變性疾病患者是否需要進行融合手術的關鍵指標，與患者腰背疼痛程度、生活質量具有緊密聯系[1-3]，因此準確判斷腰椎穩定性對于評估腰椎疾病狀態、術前規劃及術中決策至關重要[4]。目前，臨床通常以過屈、過伸位X線片上椎間Cobb角變化以及椎體滑移距離作為腰椎穩定性判斷標準，如椎間Cobb 角變化超過11° 即診斷為腰椎不穩，椎體滑移距離超過3 mm即診斷為腰椎滑脫[5]。椎間Cobb 角和椎體滑移距離測量主要由醫師手工或利用PACS系統測量工具完成，相關X線片測量參考點的選擇受醫師主觀影響較大，不同醫師間的測量一致性及穩定性較差，且耗時費力[6-11]。因此，開發一種客觀、穩定、可靠的脊柱穩定性判斷工具，對于構建腰椎退變性疾病標準化診療體系具有重要意義。
近年來，深度學習已成功應用于醫學圖像處理領域，在脊柱領域也有相關研究[12-18]。例如，Alukaev等[12]結合目標檢測和圖像分割，實現了Cobb角3.42° 的平均預測誤差；Wang等[13]提出結合冠狀面和矢狀面腰椎X線片預測Cobb角，實現了6.26° 的平均預測誤差；Fu等[14]使用編碼-解碼結構分割椎體，同時共享其權重用于回歸椎體4個角的坐標，將Cobb角平均預測誤差降至3.15°；Zhao等[15]提出一種U型結構網絡，上采樣中加入通道注意力機制，跳接模塊中加入殘差塊，在最深特征層提出卷積塊注意模塊，最終得到Cobb角平均預測誤差2.45° 的優秀性能。基于既往研究中的基礎算法，我們提出一種新的神經網絡Swin-PGNet，該網絡使用Swin-Transformer（ST）[19]與Resnet34 [20]共同對圖像進行下采樣，并利用局部-全局融合模塊（patch-global fusion block，PGFB）對不同深度特征進行融合，通過二階段方法直接對椎體關鍵點進行定位預測，從而自動測量患者過伸、過屈位X線片椎間Cobb角以及椎體滑移距離，判斷患者脊柱穩定性。報告如下。
1 材料與方法
1.1 腰椎X線片圖像數據庫的建立及標注
以2013年10月—2020年3月在四川大學華西醫院骨科因腰椎疾病接受經側前方L4、5椎間融合術的患者為研究對象，收集術前腰椎過伸、過屈位X線片（DICOM格式），采用自行編寫的脫敏工具對患者姓名、住院號、身份證號、聯系電話等敏感字段進行刪除脫敏。共153例患者306張X線片納入研究。
采用四川大學華西醫院研發的影像標注工具AI-Tutor，由3名骨科醫師（2名副主任醫師，1名主治醫師）對圖像進行人工標注。于每例患者過伸、過屈位X線片標注5個關鍵點，分別為L4后下角（A點）、前下角（B點）以及L5后上角（C點）、前上角（D點）、后下角（E點），見圖1。AI-Tutor工具可在標注后自動導出圖像以及與之對應的點坐標，訓練時圖像數據轉換為png格式，坐標信息保存在txt文件中。將306張X線片按照3∶1∶2比例，隨機分為訓練集（n=156）、驗證集（n=50）和測試集（n=100）。
圖1
過屈、過伸位X線片關鍵點
Figure1.
Key points on hyper-flexion and hyper-extension X-ray films
1.2 神經網絡結構與訓練
1.2.1 神經網絡結構
Swin-PGNet網絡結構總體類似U-net[21]的編碼-解碼結構，網絡輸出圖像和輸入圖像尺寸一致（圖2）。采用一種基于ST[19]和Resnet34[20]的雙編碼結構對圖像進行編碼。同時，兩條編碼分支用PGFB模塊融合信息，將卷積神經網絡不同深度的局部特征加入到ST編碼過程中，在解碼時兩條編碼分支深度相同的特征被拼接以后進行上采樣，一直到特征圖大小與原圖一致。
圖2
Swin-PGNet網絡結構
Figure2.
Swin-PGNet network structure
ST模塊由兩部分組成，第1部分為窗口多頭自注意力機制（window multi-head self-attention，W-MSA）、第2部分為移動W-MSA（shift W-MSA，SW-MSA），前者的輸出是后者的輸入（圖3）。圖像首先平均分成16塊，然后線性投射，在模塊內部依次經過線性歸一化層、多頭自注意力層、殘差連接和具有高斯誤差線性單元的多層感知機（multi-layer perceptron，MLP）。從上到下每個特征層的ST模塊堆疊數為 ［2，2，6，2］，多頭自注意力頭數為 ［4，8，16，32］，線性嵌入維度為96，窗口尺寸為8，每輪訓練時隨機選擇神經網絡中20%路徑不參與學習。其中，每個ST模塊中兩次窗口自注意力對圖像區域的選取如圖4所示，L層將特征圖分為4塊，并在每一塊內部計算其中元素相互之間的關聯程度；在L+1層中將特征層分為9塊，計算每一塊內部元素相互之間的關聯程度。ST模塊內部計算公式如下：
圖3
ST模塊及PGFB模塊
Figure3.
ST module and PGFB module
圖4
移動窗口計算的圖片區域
Figure4.
Calculated picture area of shift window
|
|
|
|
其中，和 分別表示第 個（S）W-MSA模塊的MLP輸出。參考既往研究[22-23]自注意力計算公式如下：
|
其中，Q、K、分別表示查詢、鍵和值的矩陣。表示窗口中的分塊數量， 表示查詢或鍵的維度。此外，中的值來自于偏置矩陣 。
ST模塊下采樣過程中，圖像首先經過分塊層將的圖片轉化成的維度，線性投射層將其通道數轉化為預設的96，并且將其前兩個維度拉伸之后送入ST模塊。分塊融合層對特征圖兩倍下采樣，并將其原有通道數翻倍，具體方法為將特征圖均分4塊，然后在通道維度上拼接起來。
卷積神經網絡是經典的Resnet34，每一層通道數設置為 ［32，32，64，128，256］，每一個卷積之后都有一個批歸一化層和一個ReLU激活函數。將卷積編碼器維度的特征和ST編碼器維度的特征一并輸入PGFB模塊中，［2，4，6］。
PGFB模塊中，卷積網絡輸入維度為，ST模塊輸入維度為。對于卷積網絡的輸入，首先經過 的卷積層、批歸一化層以及ReLU層，再進入線性嵌入層，輸出維度為，再通過將其通道數和ST模塊輸入統一為C。將卷積層與ST模塊兩種特征圖做注意力機制后與ST模塊原本特征圖矩陣點乘后輸出。
跳接塊用于將來自ST編碼器、卷積編碼器相同深度特征層特征以及更深一層的跳接塊輸出特征在通道維度上進行拼接，三者拼接完成后使用上采樣將特征尺寸翻倍，再通過將其通道數與Resnet當前深度的通道數統一，并將其輸出到下一個跳接塊中。最后的特征經過和將輸出維度設置為3，分別代表熱力圖、x方向偏移圖和y方向偏移圖。
1.2.2 標簽設置以及坐標計算
將熱力圖制定為分類問題，具體步驟為將真實關鍵點坐標距離25以內的像素點設置為1，其余為0，具體公式如下：
|
最終偏移圖和熱力圖聯合計算關鍵點坐標方法和人體檢測普遍使用方法[24]類似：
|
|
|
|
|
其中，和是圖上坐標，是真實關鍵點坐標。指熱力圖標簽，是網絡輸出的熱力圖，和是x和y方向的修正圖，offsetmap指偏移圖，是的距離圖，是分數圖，和 是網絡輸出的偏移圖，最終預測坐標。
1.2.3 神經網絡的訓練
Swin-PGNet是二階段方法，第1階段進行粗定位，找出L4和L5區域；第2階段在前一階段得到的坐標周圍 區域中對關鍵點精確定位。
第1階段將X線片像素空間值統一為0.1 mm/pixel，然后用0像素值將圖像填充至長寬比為1∶1，最后放縮至 256×256作為模型輸入；對關鍵點進行粗定位，定位L4和L5大致位置，以預測坐標為中心點取大小為512×512的區域，放縮圖像尺寸至256×256作為第2階段模型的輸入。第2階段訓練集制作，通過在關鍵點真實坐標半徑為50像素距離中隨機選取一點，以此點為中心截取大小為512×512 的局部圖像。每個點的預測均單獨進行，分為訓練粗定位和精細定位兩個階段模型，每次輸入圖片均為單通道灰度圖。
使用隨機梯度下降優化器訓練網絡，初始學習率為0.001，訓練批量為4。在第4、6和8個時期將學習率縮小1/10。使用python庫imgaug實現數據增強。圖像在x和y方向隨機平移最多10個像素；所有像素強度隨機縮放為0.5～1.0；放大或縮小圖像，使其在原始比例的 0.95～1.05 之間；將圖像逆時針或順時針旋轉最多 3°；最后對每個圖像進行彈性變換。ST模塊和卷積神經網絡均在ImageNet訓練集的預訓練權重上進行，在整個訓練集上訓練20個輪次，選擇驗證集上效果最好模型作為最終模型。負責輸出預測熱力圖的通道結果會通過一個sigmoid函數，并且對它使用交叉熵損失函數定義為 。為訓練偏移回歸頭，懲罰預測偏移和真實偏移之間的差異，相應損失為：
|
其中，是Huber Robust損失， 是真實關鍵點坐標位置，是真實關鍵點坐標位置 范圍內的點。最終損失函數表示如下：
|
其中， 而 ，這樣可以平衡兩項損失。
1.3 神經網絡的評估
在100張腰椎X線片（50例患者過伸、過屈位腰椎X線片）測試集上對Swin-PGNet的預測結果進行評估，比較Swin-PGNet和醫師標注的關鍵點定位、L4、5椎間Cobb角、L4椎體滑移距離。評價指標包括關鍵點定位平均誤差、椎間Cobb角測量平均誤差、椎體滑移距離測量平均誤差，腰椎不穩及腰椎滑脫判斷準確率。
1.3.1 誤差定義
① 關鍵點定位誤差定義如下：
|
其中， 表示關鍵點定位誤差（mm）； 和 是關鍵點在圖像中的標注坐標，和 是關鍵點在圖像中的預測坐標；是圖像中像素點對應的真實物理空間距離，預處理中統一成0.1 mm/pixel。
② 椎間Cobb角測量誤差定義如下：
|
其中， 表示椎間Cobb角測量誤差， 表示醫師標注椎間Cobb角度，表示 Swin-PGNet預測椎間Cobb角度。
③ 椎體滑移距離測量誤差定義如下：
|
其中，表示椎體滑移距離測量誤差， 表示醫師標注椎體滑移距離，表示 Swin-PGNet預測椎體滑移距離。
1.3.2 臨床判斷分析
椎間Cobb角及椎體滑移距離測量方法：Cobb角為L4椎體下終板直線與L5椎體上終板直線夾角；過上位椎體后下角（A點）作下椎體后上角（C點）與后下角（E點）形成直線的平行線，兩條線距離即為椎體滑移距離。見圖5。以同一患者過伸、過屈位X線片上，椎間Cobb角變化超過11° 判定為腰椎不穩，椎體滑移距離超過3 mm判定為腰椎滑脫。
圖5
基于腰椎過屈、過伸位X線片測量腰椎Cobb角以及椎體滑移距離示意圖
a、b. Cobb角；c、d. 椎體滑移距離
Figure5. Diagram for measuring Cobb angle and sliding distance of lumbar vertebrae based on hyper-flexion and hyper-extension X-rayfilmsa, b. Cobb angle; c, d. Sliding distance
對于關鍵點定位平均誤差、椎間Cobb角測量平均誤差和椎體滑移距離測量平均誤差3個評價指標，將每名醫師的標注單獨作為金標準分別對Swin-PGNet進行訓練，計算Swin-PGNet與該醫師標注的誤差，取Swin-PGNet與3名醫師標注誤差的平均值，得到Swin-PGNet平均誤差。同時，計算每 2 名醫師間誤差，取3組誤差的平均值作為醫師間平均誤差。最后，比較Swin-PGNet與醫師間的平均誤差，驗證Swin-PGNet在定位和測量任務中的精度是否超過醫師。
對于腰椎不穩、腰椎滑脫判斷準確率2個評價指標，同樣將每名醫師的標注單獨作為金標準對Swin-PGNet進行訓練，并根據臨床標準判斷患者是否存在腰椎不穩和腰椎滑脫，當Swin-PGNet測量結果與醫師一致時認為判斷正確，否則判斷錯誤，計算Swin-PGNet在3名醫師標簽上的平均準確率。同時，將每 2 名醫師的標注互相比較，對同一患者腰椎不穩/腰椎滑脫判斷一致則認為判斷正確，否則判斷錯誤，統計3個比較組的平均準確率。最后比較Swin-PGNet和醫師間對腰椎不穩以及腰椎滑脫判斷的準確率，驗證Swin-PGNet的診斷水平是否超過醫師水平。
1.4 統計學方法
采用Python軟件中的numpy包進行統計分析。計量資料經正態性檢驗均符合正態分布，數據以均數±標準差表示，組間比較采用方差分析，兩兩比較采用SNK檢驗；計數資料以率表示，組間比較采用χ2檢驗。
采用組內相關系數（intra-class correlation coefficient，ICC）分析不同醫師間以及Swin-PGNet與醫師測量一致性。檢驗水準α=0.05。
2 結果
2.1 關鍵點定位誤差分析
Swin-PGNet關鍵點定位平均誤差為（1.407±0.939）mm，Swin-PGNet與醫師在各關鍵點定位誤差的比較結果詳見表1。醫師間平均誤差為（3.034±2.612）mm，其中醫師1-2為（3.049±2.681）mm，醫師1-3為（3.207±2.783）mm，醫師2-3為（2.846±2.373）mm。
表1
Swin-PGNet與醫師在關鍵點定位的比較（n=100，，mm）
Table1.
Comparison of Swin-PGNet with surgeons in key points localization (n=100, , mm)
2.2 臨床判斷分析
2.2.1 腰椎穩定性分析
① Cobb角：Swin-PGNet平均誤差為（2.0621.352）°，醫師間平均誤差為（3.5802.338）°；Swin-PGNet與3名醫師間誤差比較，差異均無統計學意義（P>0.05），但不同醫師間誤差比較差異有統計學意義（P<0.05），說明Swin-PGNet對醫師在Cobb角上的標注學習成功，但3名醫師在該任務上存在明顯差異。
② 椎體滑移距離：Swin-PGNet平均誤差為（1.6560.878）mm，醫師標注平均誤差為（1.8841.612）mm，Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異均無統計學意義（P>0.05），說明Swin-PGNet對醫師在椎體滑移距離上的標注學習成功，且3名醫師在該任務上無明顯差異。
Swin-PGNet腰椎不穩判斷準確率為84.0%，醫師為75.3%，Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異無統計學意義（P>0.05）；Swin-PGNet腰椎滑脫判斷準確率為71.3%，醫師為70.7%, Swin-PGNet與3名醫師間誤差比較以及不同醫師間誤差比較，差異均無統計學意義（P>0.05），見表2。
表2
腰椎穩定性判斷比較（n=50）
Table2.
Comparison of lumbar stability judgments (n=50)
2.2.2 腰椎穩定性指標測量一致性分析
3名醫師標注椎間Cobb角的ICC為0.913 ［95%CI（0.898，0.934）］（P<0.05），椎體滑移距離為0.741 ［95%CI（0.729，0.796）］ （P<0.05） ，說明3名醫師間標注具有一致性。Swin-PGNet-所有醫師間椎間Cobb角ICC為0.922 ［95%CI（0.891，0.938）］ （P<0.05），椎體滑移距離為0.748 ［95%CI（0.726，0.783）］（P<0.05），說明Swin-PGNet標注結果與醫師標注具有一致性。見表3及圖6。
表3
腰椎穩定性判斷一致性比較
Table3.
Comparison of consistency of lumbar stability judgment
圖6
患者，女，68歲，L4、 5椎間盤突出伴椎管狹窄，Swin-PGNet判斷為L4腰椎滑脫不伴節段性不穩，與醫師判斷相同
綠色為Swin-PGNet自動定位，藍色為人工標注；上為過屈位X線片，下為過伸位X線片 a. 關鍵點定位 ；b. Cobb角；c. 椎體滑移距離
Figure6. A 68-year-old female patient with L4, 5 intervertebral disc herniation with spinal stenosis, Swin-PGNet judged L4 lumbar spondylolisthesis without segmental instability, which was the same as the surgeon’s judgmentGreen for automatic location by Swin-PGNet, blue for manual marking; upper for hyper-flexion X-ray films, lower for hyper-extension X-ray films a. Key points location; b. Cobb angle; c. Sliding distance
3 討論
人工智能在醫學影像分析中有著廣泛應用，如胸部CT肺結節定位、識別，其精度已超過影像學醫師，且隨著數據積累，算法可自我迭代，以獲取更加優異表現。本研究采用的新的神經網絡Swin-PGNet，是結合ST [19]與Resnet34[20]算法共同對圖像進行下采樣，創新性地提出一種新的PGFB模塊，對不同深度特征進行融合，通過二階段方法直接對椎體關鍵點進行定位預測，從而實現了椎間Cobb角及椎體滑移距離的自動測量，并基于此對患者脊柱穩定性進行自動判斷。
Swin-PGNet采用了ST和Resnet的雙編碼結構來提取腰椎圖像特征，傳統卷積神經網絡擅長提取局部特征，而ST擅長獲取全局的長語義關系，使圖像每個像素點交互學習彼此語義信息。與此同時，使用PGFB模塊將卷積分支提取的局部特征加入到SW分支中，進一步提升網絡對關鍵點定位精度。在解碼過程中，網絡將兩個編碼器相同尺度的特征在通道方向上拼接后上采樣，融合圖像的全局信息和局部信息，進而將不同深度特征融合在一起，網絡可以學習到不同深度下局部特征相互之間的全局關系，降低定位誤差。
本研究算法采用了感興趣區域提取-關鍵點精細化定位的二階段流程。如果使用單階段直接預測，由于腰椎X線片尺寸大，無法輸入原尺寸圖片進入網絡訓練，因GPU顯存不足需要將圖片縮小后進行預測，預測結果按照縮放比例還原，存在不可避免的系統誤差。使用二階段方法可以在第一階段通過粗定位找出目標椎體的位置，提取出該位置附近的原始尺寸圖片放入第二階段進行精確定位，以減小甚至消除系統誤差。
我們對L4后下角、前下角以及L5后上角、前上角、后下角進行自動關鍵點定位，發現網絡在L4后下角、前下角以及L5前上角的定位效果較好，而在L5后上角、后下角的定位效果較差。這可能是前者在圖像中的形態更清晰，而后者由于髂嵴和椎弓影像的影響增大了關鍵點定位的難度。盡管如此，Swin-PGNet關鍵點定位平均誤差遠小于不同醫師間的平均誤差。這一點也反映在椎間Cobb角測量上，Swin-PGNet在椎間Cobb角測量任務中取得了（2.062±1.352）° 的平均誤差，而醫師間平均誤差為（3.580±2.338）°，說明Swin-PGNet在椎間Cobb角自動測量這一任務上表現優秀，進而在判斷腰椎不穩準確率上取得了84.0%的滿意結果，明顯優于人工測量的75.3%。在腰椎滑移距離測量任務上，Swin-PGNet僅稍好于人工測量，進而體現在對腰椎滑脫判斷的準確率（71.3% vs 70.7%），尤其在醫師3的標簽中，Swin-PGNet判斷準確率（68%）較人工測量（76%）降低了8%。我們分析這可能與本研究使用Quinnell法[25-26]計算腰椎椎體滑移距離有關。該測算方法是以L5后上角、后下角和L4后下角作為參考點，而Swin-PGNet對L5后上角、后下角關鍵點定位誤差較大。與此同時，我們從實例中觀察到Swin-PGNet對于腰椎上、下終板垂直方向的誤差小于水平方向的誤差，提示其學習到了關鍵點位置與椎體終板水平方向的關系，使定位誤差對于Cobb角測量的影響較小，但對采用Quinnell法測量椎體滑移距離中L5后上角與后下角連線方向影響較大。
統計分析結果顯示，Swin-PGNet在椎間Cobb角、椎體滑移距離測量以及腰椎不穩、椎體滑脫判斷方面與醫師標注無明顯差異（P>0.05），充分說明網絡對于任務的學習成功。3名醫師在Cobb角標注中存在差異性（P<0.05），但在腰椎不穩判斷上無明顯差異（P>0.05）。我們分析發現主要標注差異是椎間Cobb角平均值，這與標注Cobb角時醫師標注習慣不同有關。其中2名醫師傾向于椎體終板平行線末端，1名醫師傾向于椎體終板拐角最外側點。雖然椎間Cobb角標注存在差異，但腰椎不穩判斷是由患者過伸位和過屈位X線片上椎間Cobb角變化值決定的，醫師在兩個不同體位X線片中以同樣標準標注椎體角點，最終計算出的角度變化值相近。因此，關于腰椎不穩的判斷，3名醫師標注無明顯差異。此外，在Cobb角測量中，不同醫師間ICC為0.913（P<0.05），Swin-PGNet-所有醫師為0.922（P<0.05），而在椎體滑移距離任務中這兩項結果分別是0.741（P<0.05）和0.748（P<0.05），說明本研究采用的Cobb角測量方法較為可靠，而Quinnell法測量椎體滑移距離的方式本身可能存在系統誤差。
綜上述，本研究基于深度學習研發的腰椎穩定性自動診斷工具，在腰椎X線片關鍵點定位任務、Cobb角測量以及腰椎不穩判斷任務中優于醫師；在腰椎椎體滑移距離測量和腰椎滑脫判斷任務中，與醫師標注結果接近。該方法可以輔助臨床醫師進行診斷，同時提高工作效率。
利益沖突 在課題研究和文章撰寫過程中不存在利益沖突；經費支持沒有影響文章觀點和對研究數據客觀結果的統計分析及其報道
倫理聲明 研究方案經四川大學華西醫院生物醫學倫理審查委員會批準［2020年審（554）號］
作者貢獻聲明 胡厚民：算法設計、研究實施及撰寫文章；王賢帝：臨床分析及指導文章寫作；楊恒：患者數據采集和數據預處理；張勁：實驗思路指導；李康、曾建成：課題總體設計及文章審閱
