臨床試驗完成后,其結論一般取決于主要結局的統計分析結果,即假設檢驗中P值是否小于假設檢驗的水準α,通常α=0.05。P值的大小說明作出假設判斷的理由的充分程度,可解釋為某一結論是否具有統計學意義。但不涉及藥物效應或其他效應的差異程度。脆弱指數,即將統計上顯著的結果變為不顯著的結果所需的、由發生目標結局事件變為發生非目標結局事件的最小患者人數,脆弱指數的數值反映的是具有統計學意義的研究結果的穩健性,可用于輔助臨床試驗統計推斷結果的理解,輔助臨床決策。本文將對脆弱指數的概念、計算方法和臨床應用等方面進行論述,并建議在未來隨機對照試驗的結果中,考慮將脆弱指數作為敏感性分析的內容之一,以幫助患者、臨床醫生、政策制定者做出適當和最佳的決策。
引用本文: 羅慜婧, 劉芷含, 黃菁涵, 王映喬, 李一琳, 劉美君, 陶耘慈, 曹蕊, 王雅琪, 劉建平, 張穎, 費宇彤. 用于評估隨機對照試驗結果穩健性的脆弱指數. 中國循證醫學雜志, 2024, 24(2): 243-248. doi: 10.7507/1672-2531.202307022 復制
版權信息: ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有,未經授權不得轉載、改編
20世紀20年代Ronald Fisher在決策理論、概率論和最大似然理論的基礎上提出假設檢驗[1,2]的概念,是基于試驗樣本與總體之間或不同總體之間是否存在實質性差異而構建統計假設,根據在一次試驗中不可能發生小概率事件的原理和反證法的思想,通過對樣本提供的信息做出是否拒絕原假設的結論。此后,假設檢驗廣泛應用于臨床試驗的結果分析中,其結論一般取決于主要結局的統計分析結果,即假設檢驗中P值是否小于假設檢驗的水準α,通常α=0.05。P值的大小說明作出假設判斷的理由的充分程度,可解釋為某一結論是否具有統計學意義[3-5]。
現階段,統計學作為重要的分析手段已被廣大研究者所認同,而P值因易于計算,成為判斷研究結果的“金標準”[6-8],在生物醫學研究中被廣泛使用及被過度依賴。2016年JAMA發表了一篇研究,總結了1990—2015年數百萬篇生物醫學文獻中P值的報道頻率,發現摘要中P值的報道頻率由7.3%增長至15.6%,呈逐年上升趨勢,但大多數文章在報道P值時沒有同時報道效應量的置信區間[9,10]。在我國,有學者檢索統計了2014—2016年發表在中文核心期刊上的61篇隨機對照試驗(randomized controlled trial,RCT),結果均以α=0.05為檢驗水準,其中有55篇RCT均以P值大小做組間差異程度大小的結論推斷[8]。2016年,美國統計協會(American Statistical Association,ASA)發布了《ASA關于P值的聲明:背景、過程和目的》[11]。其中提到:“a P-value, or statistical significance, does not measure the size of an effect or the importance of a result”,即P值并不等同于測量效應的大小或研究結果的重要性。
可以明確的是,P值提供的信息有限,統計結果的顯著性可能會因為少數的目標結局事件的狀態改變而發生方向性的變化,這樣不穩健的結果可能會降低臨床醫生、政策制定者以及患者對真實治療效果的信心,因此數據統計分析不可止于一個P值的計算,同時臨床試驗在獲得主要結局指標的P值后,不可輕易做陽性或陰性的決斷結論,需要結合研究背景、研究設計、研究實施、多種數據分析結果做綜合的科學推斷。
1 RCT中脆弱指數(fragility index,FI)的概念
1990年,Feinstein教授團隊在Journal of Clinical Epidemiology上發表文章,提出“FI”的概念[12],即在兩組比較中,當結局指標為具有統計學意義的二分類變量時,如果依次迭加地將一個目標結局發生事件變為非目標結局發生事件,直至兩組比較Fisher精確檢驗的統計結果由具有顯著性差異變為無顯著性差異時,發生目標結局狀態轉變的最小事件數,數字越小表明結果越脆弱。此后,2014年,Walsh教授團隊將其用于臨床試驗穩健性的評價中,用來幫助患者、臨床醫生和政策制定者理解臨床試驗結果,輔助臨床決策[13]。
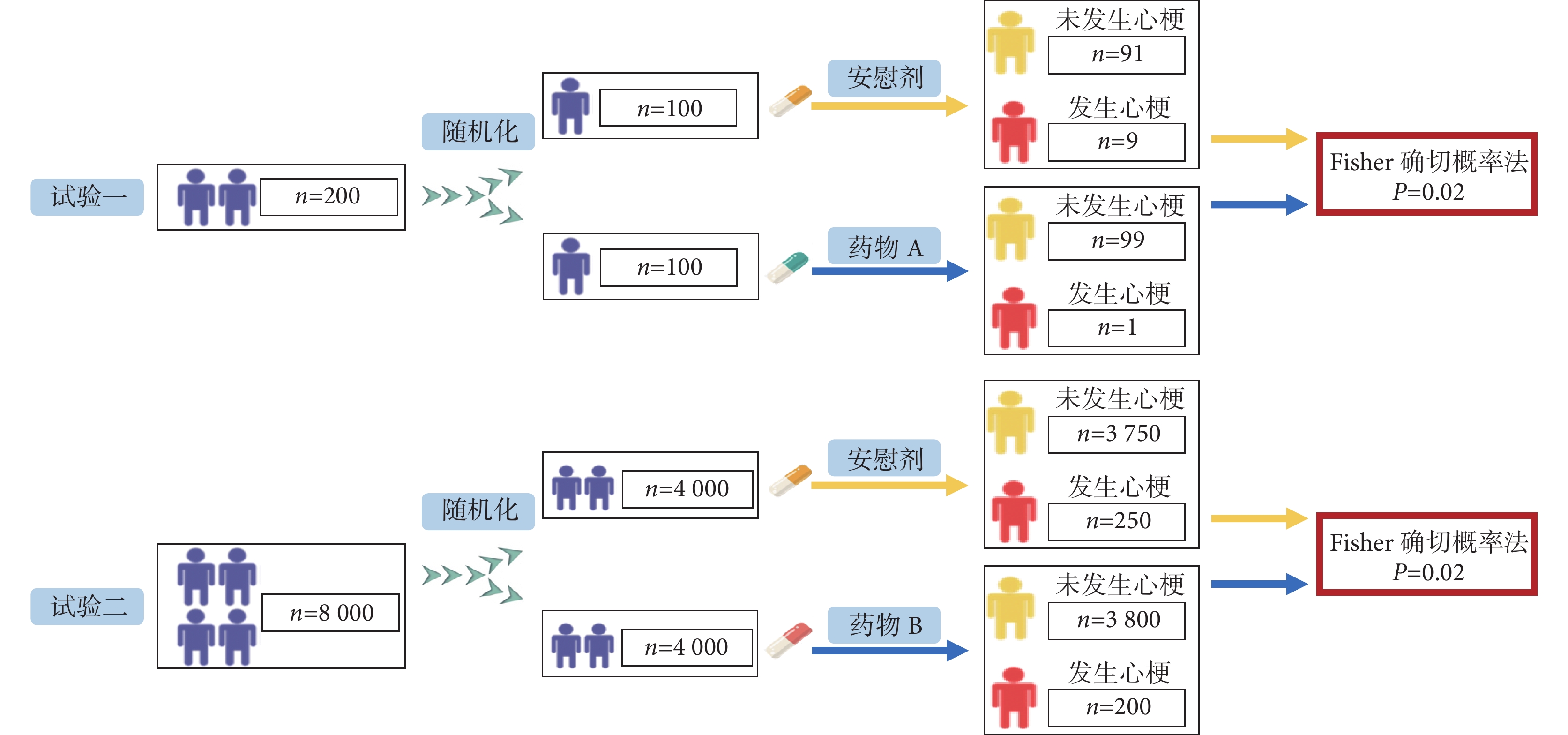
在研究藥物預防心肌梗死方面的作用時,假設有兩種不同的藥物分別與各自的模擬安慰劑進行比較,實施過程同樣嚴謹但規模不同(圖1)[13]。雖然兩個試驗的結果顯示出相同的P值(P=0.02),然而,第一個試驗的結果更容易受到結局發生事件數量的影響(FI=1)。如果在第一個試驗中,藥物A組中再多增加1例患者發生心肌梗死,則P值將變為0.06>0.05(即試驗結果變為:藥物A組發生2例心肌梗死 vs. 安慰劑組發生9例心肌梗死,Fisher精確檢驗,P=0.06),此時結果不再被認為具有統計學意義。相比之下,在第二個試驗中(FI=9),在治療組中再多增加一個結局事件對P值沒有顯著影響(即試驗結果變為:藥物B組發生201例心肌梗死 vs. 安慰劑組發生250例心肌梗死,Fisher精確檢驗,P=0.02)。因此,如果僅需少數事件就能將統計結果由具有統計學意義轉變為不具有統計學意義,那么表明這一療效結果的穩健性不高,這可能會影響臨床醫生、患者、政策制定者對干預措施真實治療效果的信心。
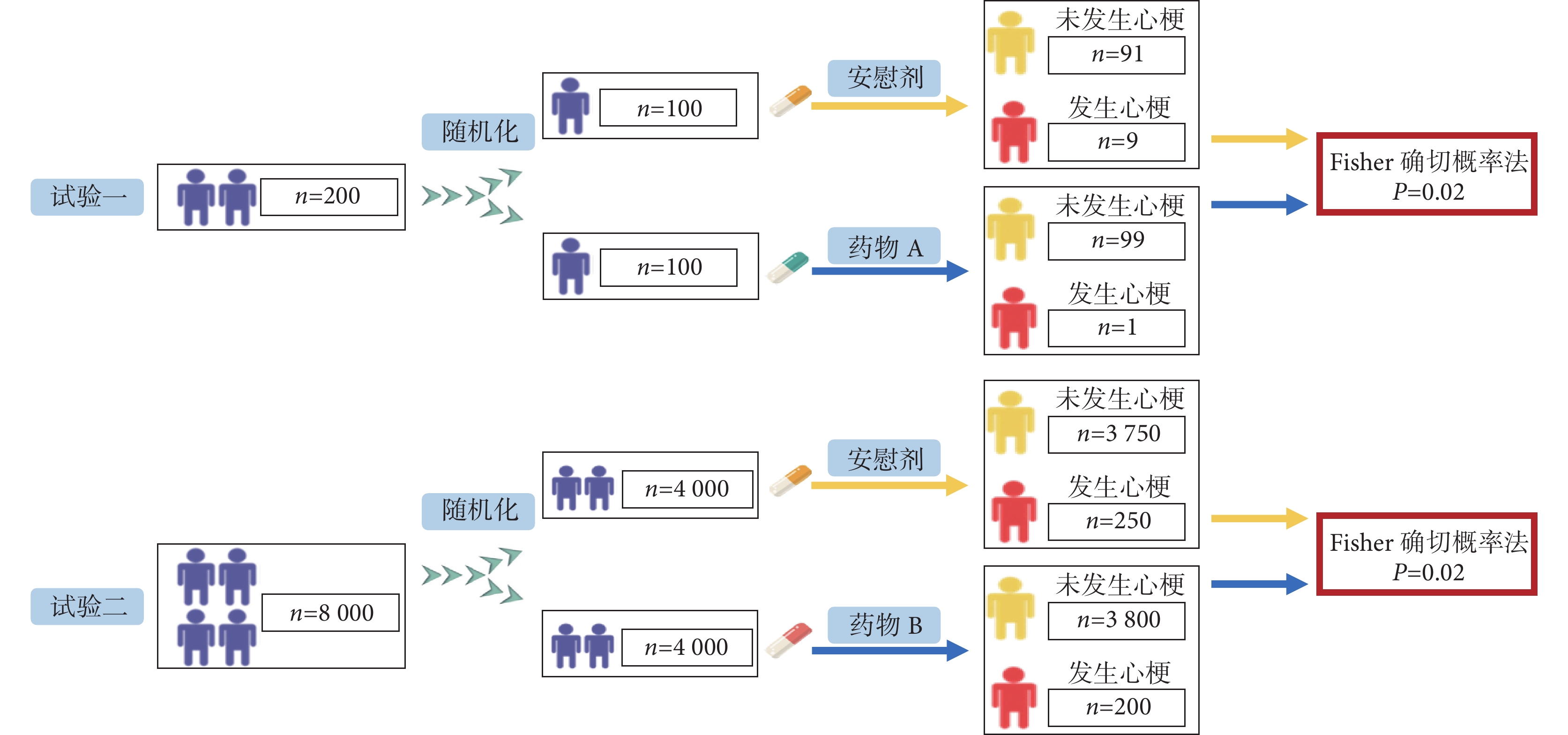 圖1
某兩種不同藥物預防心肌梗死臨床試驗設計示例
圖1
某兩種不同藥物預防心肌梗死臨床試驗設計示例
2 RCT中FI的計算方法
FI的計算通常需要臨床試驗具備以下條件:① 試驗設計為1∶1隨機分組;② 結局指標數據類型為二分類變量;③ 目標結局的統計分析結果具有統計學意義[13]。FI表示參與者結局事件發生數量在真實的試驗結果中結局發生數量的基礎上,假設試驗組再額外發生變化的最小參與者數量(根據干預措施的干預方向,其狀態從事件變為非事件或從非事件變為事件),每次迭加1例,直至該結局事件的統計學意義由顯著變為不顯著。FI越大,表明試驗結果不會因為額外發生較少結局事件數量而改變,即試驗結果越穩健[13]。
我們以“基于互聯網的行為激活療法結合接納與承諾療法治療抑郁的RCT”這項研究[14]為例,詳細介紹了FI的計算方法。該試驗將80名患者1∶1地隨機分為40例接受基于互聯網的行為激活療法結合接納與承諾療法,40例在等候名單中作為空白對照,結局事件為抑郁癥患者達到緩解的比例(定義為貝克抑郁量表II≤10),試驗結果為試驗組中有10例患者緩解(10/40) vs. 對照組中有2例患者緩解(2/40),結果具有統計學意義(P=0.025)。在治療組中,假設我們迭代地將1名達到緩解的患者狀態(結局事件)變為未達到緩解的狀態(非結局事件),并使用Fisher精確檢驗重新計算P值。連續迭代減少2例患者后,結果變得不顯著,即該試驗的FI為2,見表1。
3 用于評估RCT穩健性的FI“閾值”
目前,FI沒有固定的閾值來推斷試驗結果是脆弱的還是穩健的[15,16]。當FI較低時,結果的可信度可能會受到一些未知因素的影響,如患者的脫落率,當失訪的患者數量大于FI時,則應該對試驗結果持特別懷疑的態度[17,18]。Walsh教授團隊回顧了從2004—2010年發表在New England Journal of Medicine、Lancet、Journal of the American Medical Association、Annals of Internal Medicine和BMJ期刊上的399項RCT,發現它們的FI中位數為8(范圍:0~109)。25%的試驗FI≤3,在53%的試驗中,脫落患者的數量比試驗的FI大,提示試驗結果的脆弱[13]。在PubMed上檢索目前已發表的計算不同領域FI的研究,見表2。
在臨床試驗中,低FI是很常見的,這并不奇怪。因為在設計RCT時,為了最大限度地減少研究浪費,節省試驗成本,研究人員通常會提前進行樣本量計算,以估計實現主要結局指標的假陽性錯誤率為5%所需的最小樣本量[18],因此出現較低的FI并不意外。很多醫學研究都不屬于精確的科學研究范疇。從理論上講,P值為0.049和0.051之間的差異并不像我們所認為的那么大。與P值一樣,FI關注的是統計學意義,而不是臨床意義。它可以被認為是對研究結果統計顯著性的敏感性分析,作為傳達統計結論強度的指示性指標。
4 FI用于臨床決策的重要性
盡管經過精心設計的RCT結果代表了治療決策的金標準,但這樣的金標準也不總是完美的。越來越多的例子表明一項RCT的結果完全可能會被后續的RCT所推翻,因為后續試驗樣本量更大、更好地避免了偏倚、或結論更具有外推性[35]。即使是大樣本量的、很少或沒有明顯偏倚的、結果具有統計學顯著意義(P<0.05)的確證性的RCT,其結論也不一定能經受住考驗。對于偏倚風險較高、樣本量較小的RCT,即使結果具有統計學顯著意義,產生誤導性結果的可能性超過半數[35,36]。即使是引用率很高的RCT有時也會產生誤導,在1990—2003年發表的39項RCT,平均每項研究有1 000次以上的引用。然而,與隨后發表的更大規模、質量更高、結果更穩健的研究相比,發現其中9項研究的結果與真實情況相反[37]。一個典型的例子是關于治療革蘭氏陰性菌膿毒癥的內毒素單克隆抗體。該RCT納入了200名患者,結果發現該抗體可降低一半的死亡率(P=0.038,FI=1)[38]。然而,后續樣本量擴大10倍的另一個RCT發現該抗體對這些患者的死亡率沒有影響(P=0.864)[39]。樣本量不足、真實效應小、偏倚風險高、以及為求得陽性結果而過度挖掘數據,均可能產生虛假結論。
臨床醫生應謹慎對待治療效果格外顯著但臨床事件少的臨床試驗。通常情況下,出現一個非常顯著的治療效果是不合情理的,因為多數的疾病發病存在多重機制,而一種干預措施的治療通常針對其中1~2個機制[40]。如血管緊張素轉化酶抑制劑(angiotensin converting enzyme inhibitor,ACEI)、抗血小板藥、降脂藥和β受體阻滯劑在降低心肌梗死患者主要心血管不良事件(major adverse cardiovascular events,MACE)的協同作用方面充分說明了疾病發病機制的多樣性。由此可以推斷,單獨一種藥物降低MACE發生風險的作用通常不會十分顯著。例如在先前的一項研究[41]中,比較N-乙酰半胱氨酸與安慰劑預防造影劑腎損傷的療效,兩組分別入組41例和42例患者,分別有1例和9例患者發生終點事件。結果發現,N-乙酰半胱氨酸組發生造影劑腎損傷事件的相對風險為0.10[95%CI(0.02,0.90),P=0.01,FI=2],基于該研究結果,作者認為N-乙酰半胱氨酸是預防造影劑腎損傷的有效手段。在此之后的13年時間里,共有4項試驗[42-45],包括772名患者,均未顯示N-乙酰半胱氨酸的臨床獲益,隨后的一項系統評價證明相關研究的證據水平過于薄弱且異質性較大,無法支持N-乙酰半胱氨酸的臨床有效性。對于規模不小,但治療效果十分顯著的RCT,也應同樣謹慎解讀,因為其結果可能存在誤導性。即使那些事件不少且治療效果不甚顯著的研究,其結果仍有可能存在脆弱性[46]。
5 小結
FI為患者、臨床醫生、政策制定者提供了一種直觀的衡量指標(即患者個體的數量),是對臨床試驗統計結果中P值的一個解釋說明,可協助評估研究結論的強度,輔助臨床醫生解讀臨床試驗結果,并有助于識別不太穩健的結果[47]。
FI的應用存在一定的局限性[48]:① 因為FI僅以某一時間點對試驗結果穩健性進行評估,并未考慮到時間變量,因此在時間-事件分析中使用FI可能并不合適。② FI通常適用于1∶1隨機化,且具有統計學意義的二分類變量結局。③ 由于目前沒有閾值來判斷試驗結果是脆弱的還是穩健的,因此無法量化其數值大小的真實含義。④ FI采用Fisher精確概率法進行計算,其結果可能更偏保守,容易發生Ⅱ型錯誤。然而,FI的優點是非常簡單,易于計算也易于理解,可以增強醫生對于較小樣本量和較少結局事件發生數臨床試驗結果作為決策證據的信心。
提供高質量的臨床決策以獲得最佳的患者治療結果需要強有力的臨床研究證據作為基礎,而FI將有助于證據-決策過程。我們建議在未來RCT中考慮報告FI作為敏感性分析的內容之一,對于不具有統計學意義的二分類變量結局可以嘗試采用反向連續迭代增加一例發生狀態變化的事件數的方法,使結果從不具有統計學意義轉變為具有統計學意義,從而來計算反轉FI。對于連續變量類型的結局,可以嘗試通過逐個減少1個標準化效應量的方法,來計算FI,以幫助患者、臨床醫生、政策制定者做出適當和最佳的決策。同時建議在制訂臨床指南時考慮補充FI,以幫助臨床醫生確定指南建議是否可靠。在基于低FI(脫落的患者數量大于FI)RCT證據作出臨床實踐指導時,決策應特別謹慎。
20世紀20年代Ronald Fisher在決策理論、概率論和最大似然理論的基礎上提出假設檢驗[1,2]的概念,是基于試驗樣本與總體之間或不同總體之間是否存在實質性差異而構建統計假設,根據在一次試驗中不可能發生小概率事件的原理和反證法的思想,通過對樣本提供的信息做出是否拒絕原假設的結論。此后,假設檢驗廣泛應用于臨床試驗的結果分析中,其結論一般取決于主要結局的統計分析結果,即假設檢驗中P值是否小于假設檢驗的水準α,通常α=0.05。P值的大小說明作出假設判斷的理由的充分程度,可解釋為某一結論是否具有統計學意義[3-5]。
現階段,統計學作為重要的分析手段已被廣大研究者所認同,而P值因易于計算,成為判斷研究結果的“金標準”[6-8],在生物醫學研究中被廣泛使用及被過度依賴。2016年JAMA發表了一篇研究,總結了1990—2015年數百萬篇生物醫學文獻中P值的報道頻率,發現摘要中P值的報道頻率由7.3%增長至15.6%,呈逐年上升趨勢,但大多數文章在報道P值時沒有同時報道效應量的置信區間[9,10]。在我國,有學者檢索統計了2014—2016年發表在中文核心期刊上的61篇隨機對照試驗(randomized controlled trial,RCT),結果均以α=0.05為檢驗水準,其中有55篇RCT均以P值大小做組間差異程度大小的結論推斷[8]。2016年,美國統計協會(American Statistical Association,ASA)發布了《ASA關于P值的聲明:背景、過程和目的》[11]。其中提到:“a P-value, or statistical significance, does not measure the size of an effect or the importance of a result”,即P值并不等同于測量效應的大小或研究結果的重要性。
可以明確的是,P值提供的信息有限,統計結果的顯著性可能會因為少數的目標結局事件的狀態改變而發生方向性的變化,這樣不穩健的結果可能會降低臨床醫生、政策制定者以及患者對真實治療效果的信心,因此數據統計分析不可止于一個P值的計算,同時臨床試驗在獲得主要結局指標的P值后,不可輕易做陽性或陰性的決斷結論,需要結合研究背景、研究設計、研究實施、多種數據分析結果做綜合的科學推斷。
1 RCT中脆弱指數(fragility index,FI)的概念
1990年,Feinstein教授團隊在Journal of Clinical Epidemiology上發表文章,提出“FI”的概念[12],即在兩組比較中,當結局指標為具有統計學意義的二分類變量時,如果依次迭加地將一個目標結局發生事件變為非目標結局發生事件,直至兩組比較Fisher精確檢驗的統計結果由具有顯著性差異變為無顯著性差異時,發生目標結局狀態轉變的最小事件數,數字越小表明結果越脆弱。此后,2014年,Walsh教授團隊將其用于臨床試驗穩健性的評價中,用來幫助患者、臨床醫生和政策制定者理解臨床試驗結果,輔助臨床決策[13]。
在研究藥物預防心肌梗死方面的作用時,假設有兩種不同的藥物分別與各自的模擬安慰劑進行比較,實施過程同樣嚴謹但規模不同(圖1)[13]。雖然兩個試驗的結果顯示出相同的P值(P=0.02),然而,第一個試驗的結果更容易受到結局發生事件數量的影響(FI=1)。如果在第一個試驗中,藥物A組中再多增加1例患者發生心肌梗死,則P值將變為0.06>0.05(即試驗結果變為:藥物A組發生2例心肌梗死 vs. 安慰劑組發生9例心肌梗死,Fisher精確檢驗,P=0.06),此時結果不再被認為具有統計學意義。相比之下,在第二個試驗中(FI=9),在治療組中再多增加一個結局事件對P值沒有顯著影響(即試驗結果變為:藥物B組發生201例心肌梗死 vs. 安慰劑組發生250例心肌梗死,Fisher精確檢驗,P=0.02)。因此,如果僅需少數事件就能將統計結果由具有統計學意義轉變為不具有統計學意義,那么表明這一療效結果的穩健性不高,這可能會影響臨床醫生、患者、政策制定者對干預措施真實治療效果的信心。
 圖1
某兩種不同藥物預防心肌梗死臨床試驗設計示例
圖1
某兩種不同藥物預防心肌梗死臨床試驗設計示例
2 RCT中FI的計算方法
FI的計算通常需要臨床試驗具備以下條件:① 試驗設計為1∶1隨機分組;② 結局指標數據類型為二分類變量;③ 目標結局的統計分析結果具有統計學意義[13]。FI表示參與者結局事件發生數量在真實的試驗結果中結局發生數量的基礎上,假設試驗組再額外發生變化的最小參與者數量(根據干預措施的干預方向,其狀態從事件變為非事件或從非事件變為事件),每次迭加1例,直至該結局事件的統計學意義由顯著變為不顯著。FI越大,表明試驗結果不會因為額外發生較少結局事件數量而改變,即試驗結果越穩健[13]。
我們以“基于互聯網的行為激活療法結合接納與承諾療法治療抑郁的RCT”這項研究[14]為例,詳細介紹了FI的計算方法。該試驗將80名患者1∶1地隨機分為40例接受基于互聯網的行為激活療法結合接納與承諾療法,40例在等候名單中作為空白對照,結局事件為抑郁癥患者達到緩解的比例(定義為貝克抑郁量表II≤10),試驗結果為試驗組中有10例患者緩解(10/40) vs. 對照組中有2例患者緩解(2/40),結果具有統計學意義(P=0.025)。在治療組中,假設我們迭代地將1名達到緩解的患者狀態(結局事件)變為未達到緩解的狀態(非結局事件),并使用Fisher精確檢驗重新計算P值。連續迭代減少2例患者后,結果變得不顯著,即該試驗的FI為2,見表1。
3 用于評估RCT穩健性的FI“閾值”
目前,FI沒有固定的閾值來推斷試驗結果是脆弱的還是穩健的[15,16]。當FI較低時,結果的可信度可能會受到一些未知因素的影響,如患者的脫落率,當失訪的患者數量大于FI時,則應該對試驗結果持特別懷疑的態度[17,18]。Walsh教授團隊回顧了從2004—2010年發表在New England Journal of Medicine、Lancet、Journal of the American Medical Association、Annals of Internal Medicine和BMJ期刊上的399項RCT,發現它們的FI中位數為8(范圍:0~109)。25%的試驗FI≤3,在53%的試驗中,脫落患者的數量比試驗的FI大,提示試驗結果的脆弱[13]。在PubMed上檢索目前已發表的計算不同領域FI的研究,見表2。
在臨床試驗中,低FI是很常見的,這并不奇怪。因為在設計RCT時,為了最大限度地減少研究浪費,節省試驗成本,研究人員通常會提前進行樣本量計算,以估計實現主要結局指標的假陽性錯誤率為5%所需的最小樣本量[18],因此出現較低的FI并不意外。很多醫學研究都不屬于精確的科學研究范疇。從理論上講,P值為0.049和0.051之間的差異并不像我們所認為的那么大。與P值一樣,FI關注的是統計學意義,而不是臨床意義。它可以被認為是對研究結果統計顯著性的敏感性分析,作為傳達統計結論強度的指示性指標。
4 FI用于臨床決策的重要性
盡管經過精心設計的RCT結果代表了治療決策的金標準,但這樣的金標準也不總是完美的。越來越多的例子表明一項RCT的結果完全可能會被后續的RCT所推翻,因為后續試驗樣本量更大、更好地避免了偏倚、或結論更具有外推性[35]。即使是大樣本量的、很少或沒有明顯偏倚的、結果具有統計學顯著意義(P<0.05)的確證性的RCT,其結論也不一定能經受住考驗。對于偏倚風險較高、樣本量較小的RCT,即使結果具有統計學顯著意義,產生誤導性結果的可能性超過半數[35,36]。即使是引用率很高的RCT有時也會產生誤導,在1990—2003年發表的39項RCT,平均每項研究有1 000次以上的引用。然而,與隨后發表的更大規模、質量更高、結果更穩健的研究相比,發現其中9項研究的結果與真實情況相反[37]。一個典型的例子是關于治療革蘭氏陰性菌膿毒癥的內毒素單克隆抗體。該RCT納入了200名患者,結果發現該抗體可降低一半的死亡率(P=0.038,FI=1)[38]。然而,后續樣本量擴大10倍的另一個RCT發現該抗體對這些患者的死亡率沒有影響(P=0.864)[39]。樣本量不足、真實效應小、偏倚風險高、以及為求得陽性結果而過度挖掘數據,均可能產生虛假結論。
臨床醫生應謹慎對待治療效果格外顯著但臨床事件少的臨床試驗。通常情況下,出現一個非常顯著的治療效果是不合情理的,因為多數的疾病發病存在多重機制,而一種干預措施的治療通常針對其中1~2個機制[40]。如血管緊張素轉化酶抑制劑(angiotensin converting enzyme inhibitor,ACEI)、抗血小板藥、降脂藥和β受體阻滯劑在降低心肌梗死患者主要心血管不良事件(major adverse cardiovascular events,MACE)的協同作用方面充分說明了疾病發病機制的多樣性。由此可以推斷,單獨一種藥物降低MACE發生風險的作用通常不會十分顯著。例如在先前的一項研究[41]中,比較N-乙酰半胱氨酸與安慰劑預防造影劑腎損傷的療效,兩組分別入組41例和42例患者,分別有1例和9例患者發生終點事件。結果發現,N-乙酰半胱氨酸組發生造影劑腎損傷事件的相對風險為0.10[95%CI(0.02,0.90),P=0.01,FI=2],基于該研究結果,作者認為N-乙酰半胱氨酸是預防造影劑腎損傷的有效手段。在此之后的13年時間里,共有4項試驗[42-45],包括772名患者,均未顯示N-乙酰半胱氨酸的臨床獲益,隨后的一項系統評價證明相關研究的證據水平過于薄弱且異質性較大,無法支持N-乙酰半胱氨酸的臨床有效性。對于規模不小,但治療效果十分顯著的RCT,也應同樣謹慎解讀,因為其結果可能存在誤導性。即使那些事件不少且治療效果不甚顯著的研究,其結果仍有可能存在脆弱性[46]。
5 小結
FI為患者、臨床醫生、政策制定者提供了一種直觀的衡量指標(即患者個體的數量),是對臨床試驗統計結果中P值的一個解釋說明,可協助評估研究結論的強度,輔助臨床醫生解讀臨床試驗結果,并有助于識別不太穩健的結果[47]。
FI的應用存在一定的局限性[48]:① 因為FI僅以某一時間點對試驗結果穩健性進行評估,并未考慮到時間變量,因此在時間-事件分析中使用FI可能并不合適。② FI通常適用于1∶1隨機化,且具有統計學意義的二分類變量結局。③ 由于目前沒有閾值來判斷試驗結果是脆弱的還是穩健的,因此無法量化其數值大小的真實含義。④ FI采用Fisher精確概率法進行計算,其結果可能更偏保守,容易發生Ⅱ型錯誤。然而,FI的優點是非常簡單,易于計算也易于理解,可以增強醫生對于較小樣本量和較少結局事件發生數臨床試驗結果作為決策證據的信心。
提供高質量的臨床決策以獲得最佳的患者治療結果需要強有力的臨床研究證據作為基礎,而FI將有助于證據-決策過程。我們建議在未來RCT中考慮報告FI作為敏感性分析的內容之一,對于不具有統計學意義的二分類變量結局可以嘗試采用反向連續迭代增加一例發生狀態變化的事件數的方法,使結果從不具有統計學意義轉變為具有統計學意義,從而來計算反轉FI。對于連續變量類型的結局,可以嘗試通過逐個減少1個標準化效應量的方法,來計算FI,以幫助患者、臨床醫生、政策制定者做出適當和最佳的決策。同時建議在制訂臨床指南時考慮補充FI,以幫助臨床醫生確定指南建議是否可靠。在基于低FI(脫落的患者數量大于FI)RCT證據作出臨床實踐指導時,決策應特別謹慎。