階梯整群隨機試驗(SW-CRT)是近年來出現的、主要應用于公共衛生政策領域的一種整群隨機對照試驗方法,逐漸引起衛生領域工作者的關注。而目前在國內外,這一試驗方法的應用尚不廣泛,樣本量估算和統計學分析存在多種方式。本文介紹階梯整群隨機試驗原理、類別、與傳統隨機對照試驗的差異,概述樣本量估算及統計分析方法。總體而言,SW-CRT以群組、交叉設計、多個時間點的結果測量為特點;在樣本量估算方面,需區分群組大小相同及不同的情況,常用的樣本量估算程序可在Stata、R、SAS軟件及固定的在線網站中實現,包括“Steppedwedge”程序、“swCRTdesign”程序、“Swdpwr”程序、“CRTpowerdist”程序、“Shiny CRT Calculator”工具等;依據SW-CRT的設計特點,在統計分析中,研究者還應該考慮時間效應、重復測量的混雜因素,常以廣義線性混合模型(GLMM)和廣義估計方程(GEE)分析方法為主。然而以上模型多數基于橫斷面研究提出,目前還缺少針對隊列設計及存在過渡期的SW-CRT的統計方法,未來仍需開展更為全面的方法學探索。
引用本文: 董昱, 黃閃閃, 趙夢嬌, 張僑, 曾婧純, 陸麗明. 階梯整群隨機試驗的統計分析方法介紹. 中國循證醫學雜志, 2024, 24(3): 355-363. doi: 10.7507/1672-2531.202307125 復制
版權信息: ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有,未經授權不得轉載、改編
1 階梯整群隨機試驗概述
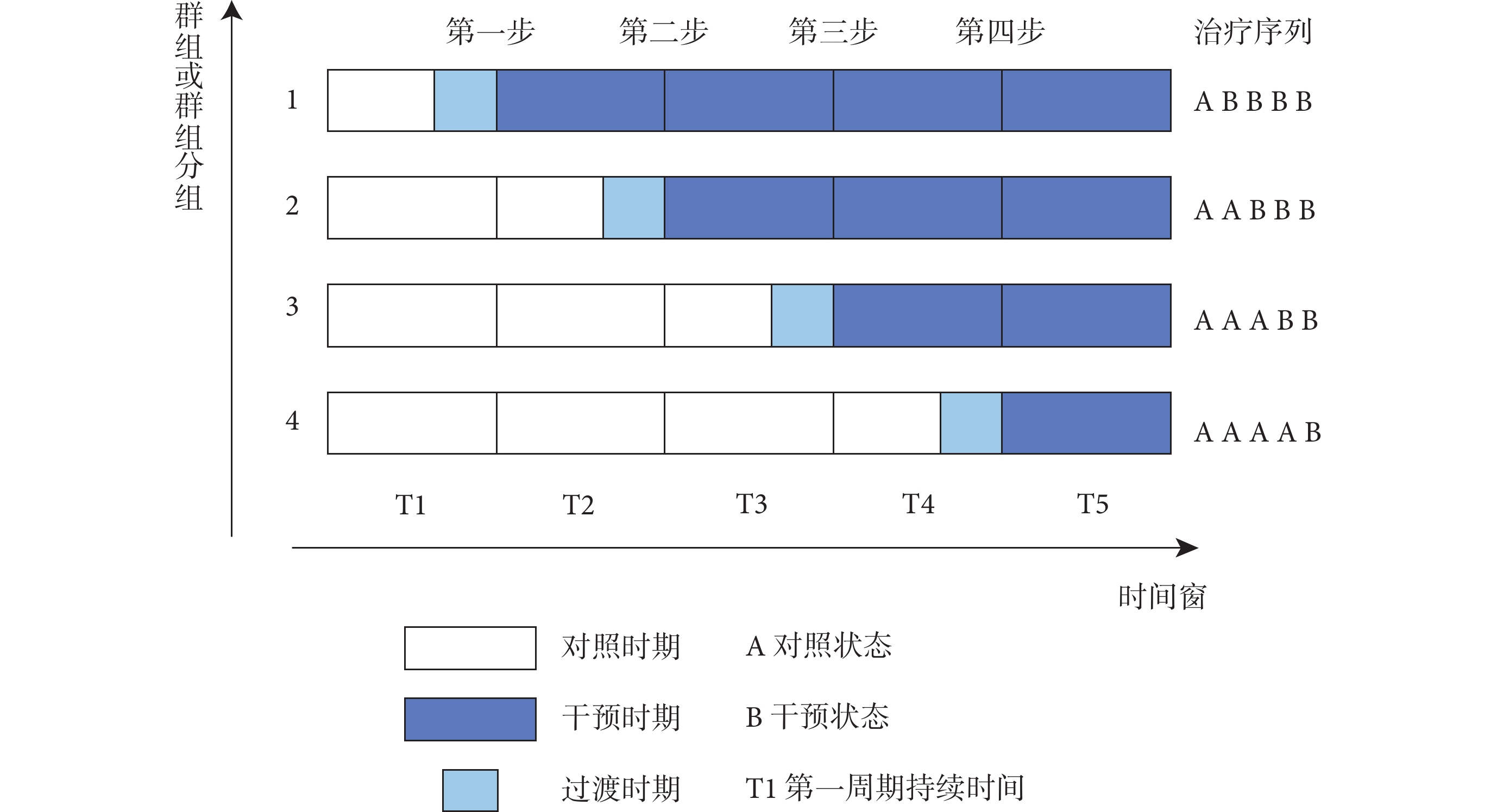
階梯整群隨機試驗(stepped wedge cluster randomised trials,SW-CRT)是一種特殊類型的整群隨機試驗(cluster randomized trials,CRT),其原理類似于“交叉設計”。試驗對象在干預開始前會被分為若干群組,不同的群組在不同的時間點接受從對照狀態切換至干預狀態的單向交叉處理[1]。在初始階段(基線期)沒有任何群組接受干預,隨后每隔一段時間或步驟,一個群(或一組群)會被隨機抽取接受干預,同一時間點可能有一個或多個群組開始接受干預,但這些群組開始接受干預的時間是隨機的,這一過程會依次進行,直至所有的群組都接受了干預[2,3](圖1)。SW-CRT依據不同的分類標準分為了不同的試驗類型,Hemming等[1]依據在不同的步驟或階段中集群數量及數據收集的差異,將其分為完整階梯設計和不完整階梯設計。而Copas等[4]依據不同的研究對象,將試驗分為固定隊列階梯設計(closed cohort design)、開放隊列階梯設計(open cohort design)和連續入組短期暴露階梯設計(continuous recruitment with short exposure)。
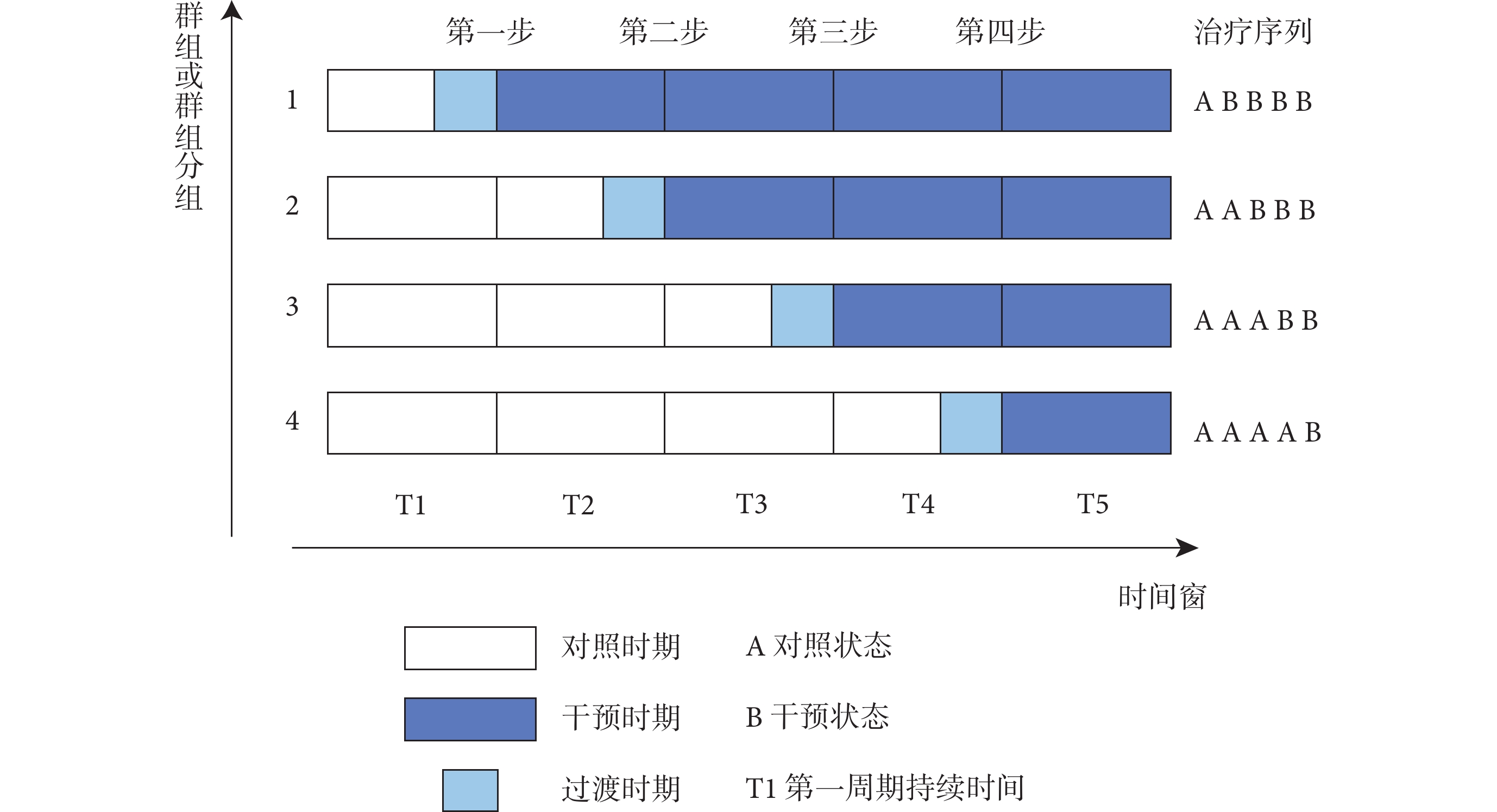 圖1
標準階梯整群隨機試驗示意圖
圖1
標準階梯整群隨機試驗示意圖
SW-CRT主要用來評估在日常實施過程中干預措施的有效性,特別是對于那些在更可控的研究環境中被證明有效的干預措施,或缺乏明確利大于弊的干預措施的有效性證據[5]。階梯整群隨機試驗的應用最早出現于20世紀80年代開展的一項岡比亞肝炎的干預研究[6]。流行病學調查表明,在發展中國家SW-CRT常用于針對HIV的干預措施的評估,其中,最常見的干預措施有疫苗接種、篩查、教育計劃出臺等[7]。近年來這一試驗方式的逐漸推廣,其使用領域也多種多樣,涉及癌癥、艾滋病、醫療保健、衛生政策制定等方面[5, 7]。就采取SW-CRT試驗方式的動機而言,多數研究都考慮到了試驗協調的靈活性、人力財力資源的限制、人群對于有利的干預方式的可接受性、倫理、干預措施在試驗多個集群中實施的難易程度、受試者失望效應(受試者因未被分配到干預組而產生的脫落)等[5, 8]。
隨著對SW-CRT試驗數量的增多,Hemming等學者使用Delphi調查和共識會議制定方法,制定了專門針對階梯整群隨機試驗的報告條目規范(reporting of stepped wedge cluster randomised trials: extension of the CONSORT 2010 statement with explanation and elaboration)[9],它作為臨床試驗報告規范(consolidated standards of reporting trials,CONSORT)聲明的擴展版,旨在為平行隨機對照試驗提供統一標準。目前,國內僅在急性冠脈綜合征患者[10]和自閉癥患兒[11]中開展了階梯整群隨機試驗,且仍缺乏對其統計分析方法和樣本量計算的介紹與解讀。本文將闡述SW-CRT的主要應用、辨析與傳統隨機對照試驗的區別,并著重從數據收集與分析方法、樣本量估算等統計學層面介紹SW-CRT。
2 SW-CRT與傳統隨機對照試驗
顧名思義,SW-CRT的名稱來源于圖1中明顯的階梯式楔形,它與傳統的(平行)整群隨機試驗和隨機對照試驗存在差異。傳統的(平行)整群隨機試驗是對群組隨機分組后,群組一直留在干預組或對照組直至研究結束。而SW-CRT擴展了試驗設計,每個集群均能提供觀察前后的數據,且會在不同的時間點從對照組切換到干預組[2],是一種交叉設計的方式。與傳統的隨機對照試驗不同,SW-CRT是以群組而非個體為研究對象,每個群組都會依次接受干預。需要特別注意的是,SW-CRT與以上兩種試驗方式都存在樣本量估算與統計學分析方法上的差異,表1對其進行了總結[12-14]。
由表1可見,SW-CRT在臨床試驗的實際應用中具有如下優勢:① 不需要專門設置對照組,減少了人力物力財力的投入;② 每個群組均會接受干預,受試者公平性得到保障,符合醫學倫理要求,是真實世界研究中的重要試驗方法之一;③ 以自身群體作為對照依據,減少了不同組別群體間個體化的差異對結果造成的影響,結論有更高可靠性。SW-CRT作為一種新興的定量研究設計方法,可以在真實世界研究中實施應用,作為一種循證實踐策略,能夠發揮真實世界中干預措施最大限度的效果[15]。
3 樣本量估算
3.1 樣本量估算方法
SW-CRT是聚類試驗的形式之一,故分析和設計需要考慮這種“聚類”屬性。SW-CRT的試驗過程是“單向轉換”的,即由對照狀態逐漸向干預狀態轉化。SW-CRT的受試者暴露于干預的集群比例會隨著時間的推移而逐漸增加。這些試驗設計的特點決定了SW-CRT的樣本量計算方式和參數并非是由個體的隨機對照試驗簡單修改而來的,而更需要將聚類效應、時間效應、重復測量幾項關鍵要素考慮在內。目前對已發表的SW-CRT樣本量估算情況的統計分析發現[12]:大多數研究考慮了聚類;但33項研究中只有15項研究考慮了時間效應;大多數研究未明確報告設計類型(隊列設計或橫斷面設計);在隊列設計的樣本量計算中,只有少數提及了重復測量。SW-CRT樣本量計算方法普遍存在質量較低、關鍵要素缺失的問題,亦沒有統一的計算方法。
樣本量估算與試驗的檢驗水準和檢驗效能密切相關,故必須設置合理的檢驗水準和檢驗效能[16]。檢驗水準為控制Ⅰ類錯誤的能力,用α表示,在多重檢驗中,為了減少假陽性錯誤,通常都需要設定檢驗水準在0.05以下;檢驗效能反應了根據當前的樣本量獲得組間有統計學差異的能力,用1-β來表示,實際中通常設置為0.8,當檢驗效能越高時,則所需的樣本量越多。SW-CRT涉及多個群組、多次的隨機分配和治療間隔時間,試驗過程相較其他傳統隨機對照試驗更為復雜,且SW-CRT樣本量易受集群大小影響,故本文將區分集群規模,從群間相關性、隨機化步驟、測量次數等對檢驗效能的影響來把握樣本量估算水平。
3.1.1 假設集群大小相同時的樣本量估算及檢驗效能影響因素
Hussey[3]等針對SW-CRT設計了樣本量計算的效能,并研究了不同的群間相關性、隨機化步驟數量和治療延遲對試驗效能的影響,發現試驗的效能受集群間相關性的影響相對較少,而測量次數的減少則會引起效能的損失。隨著SW-CRT在衛生服務評價中的應用越來越廣泛,目前已有SW-CRT的試驗設計大多數為橫斷面研究,即在某一時間段隨機分配相同數量的集群,在固定的時間段統一收集數據,假設納入研究的樣本在每個時間點都與其他時間點的樣本不同。基于此,Hemming等[1]從常規的SW-CRT中延伸了不同類型的試驗設計方式—完整階梯設計(傳統的階梯整群隨機設計)和不完整階梯設計(具有過渡周期的階梯整群隨機設計),且計算出試驗效能與群內相關性(intra-cluster correlation,ICC)沒有線性關系。對于較小的ICC值,試驗效能會隨著ICC的增加而降低;但對于較大的ICC值,試驗效能會隨著ICC值的增加而增加。
在平行的CRT中,常用設計效應(design effect,DE)進行樣本量估算,一些學者進而提出了基于DE推導的SW-CRT樣本量計算方法。Woertman等[17]假設結果測量是在多個離散時間點從每個集群獲得的,并且在每個交叉點測量的參與者數量在不同的時間和集群中是相同的,得出總樣本量計算公式為:
 |
nRCT:相應的平行RCT所需要的樣本量;B:基線測量次數;J:集群切換交叉到干預狀態的交叉點數量;T:每次交叉轉換期間的測量次數;CF:校正因子(correction factor)。
其中CF即為DE,受3個主要因素影響:每步的測量次數、基線測量次數和步數,任意一個因素的增加都會引起DE的降低。這一公式與Hussey等的模型相似,僅適用于橫斷面設計,每次測量都來自不同的個體參與者。然而公式中每次交叉轉換的集群數是相同的,每次交叉后的測量次數也不變。
隨后Hemming等又依據Hussey等建立的模型,調整了DE進行樣本量的估算,從而能夠計算集群數量給定時所需的集群大小[18],探索了樣本量計算的功效及其相關性。基于以上研究的理論框架和不同的情景設定,整理所得樣本量計算公式如下[19]:
① 當階梯步數(t)、每個觀察期每個集群的樣本量(m)以及集群內相關性ICC(ρ)已知,求總樣本量(N)
 |
N1:兩組等樣本隨機對照試驗所需樣本量。
② 當階梯步數(t)、總群數(k)、以及集群內相關性ICC(ρ)已知,求總樣本量(N)
 |
為了更好理解在集群大小相同時,樣本量的計算方式,本文運用贊比亞一項關于瘧疾預防工作的階梯整群隨機試驗案例[20],改編其中的數據,對樣本量估算進行演示。
示例:為了評估大規模檢測和治療(MTAT)干預對瘧疾患病率和衛生機構門診病例發病率的影響,贊比亞南部省開展了一項社區階梯整群隨機試驗。研究共設置了10個干預階梯,觀察時點為11個,以每個衛生設施集水區所在的家庭數量為一個群組,假設干預后干預組瘧疾門診病例發生率較對照組下降10%,ICC(ρ)為0.01,檢驗水準α=0.05,檢驗效能(1-β)為0.9,在兩個情景下分別計算需要的樣本量:
情況一:階梯步數t=10,ρ=0.01,假設每個群組的平均家庭數量數為50個(m=50),利用PASS軟件可計算出初步樣本量N1為1 038人,依據DE公式可得,DE=2.69,計算總樣本量N約為2 792人;集群數k為總樣本除以觀察時點數(t+1)和每個群組平均家庭數量(m),即k=N/[(t+1)m],此時,m=50,計算可得集群數k=5。
情況二:當階梯步數t=10,ρ=0.01,假設每個群組的平均家庭數量數為50個(m=50),集群數量(k)設置為5時,由公式2可計算出,總樣本量N約為2 750人。
3.1.2 假設集群大小不同時的樣本量估算及檢驗效能影響因素
在實施橫斷面研究的SW-CRT中,研究者可能會面臨所納入的集群大小不等的情況,曾有學者對101個SW-CRT的系統評價發現,48%的研究包括大小不同的集群[21],而忽略這一問題所帶來的影響尚不清楚。雖然在Hemming[1]構建的模型框架中說明了集群的大小變化不會導致連續結果較為顯著的效能損失,但這是基于只檢驗了一小部分參數得來的結果。基于此,Martin等研究了SW-CRT中不同集群大小的含義[22],發現橫斷面SW-CRT實際的功效可能較估計值并不穩定,尤其是當集群數量較少或集群大小的可變性很大時。Harrison等[23]推導了不同集群大小的橫斷面SW-CRT與單個隨機試驗相比的DE,計算了不同集群大小的橫斷面SW-CRT的預期相對效率(relative efficiency,RE)和校正樣本量計算的CF,提供了與集群大小變化相關的平均功率損失的公式,發現當集群數量較小或集群大小變異系數(coefficient of variation,CV)大于1時平均功效的損失更大。如果集群的數量足夠大,并在每一步均隨機分配幾個集群開始治療,其隨機分配的所有集群的總大小不會有明顯的不平等,則可以減少功效的損失[24]。
3.2 樣本功效的軟件實現方法
相較于SW-CRT復雜的樣本量計算,確定樣本功效相對容易,也有相應的軟件實現方式。而基于前期對于樣本量功效的計算理論,選擇合適的功效計算軟件,調整相應的參數值,能夠得出適合自身研究的樣本量。表2中總結了幾種常見的軟件實現方式及其優點與局限性。
3.2.1 Stata軟件中的樣本量估算
Hemming等在Stata軟件中開發了Steppedwedge命令[25],可計算完整和不完整的SW-CRT的可檢測差異和功效,包含一個訪問命令的對話框。可實現在雙側檢驗下的連續性變量、二分類變量和率(近似正態)的比較。在Stata軟件中,選擇結局變量的類型后(連續型數據、二分類型數據、比例型數據),輸入檢驗水準(α)、ICC、每步的階梯數、集群數量、時間點(不包含基線時期)、兩組值的比較(均數與標準差、比例、率),可完成功效的估算。
該命令存在優點與局限性。Steppedwedge命令可在Stata軟件中實現,且操作步驟簡單易懂,可實現性與可操作性強;與整群試驗的樣本量計算方法類似,都以ICC作為輸入參數。但該命令的假設前提基于集群大小相等,僅可計算固定樣本量的功效和可檢測差;命令和模型僅限于橫斷面研究,而不能用于隊列研究。
3.2.2 R軟件與SAS軟件的樣本量計算
Baio等[26]采用R軟件中分析和模擬訓練的函數,在假設橫斷面設計和封閉隊列設計,結局指標為連續和二分類變量的情況下,確定SW-CRT的樣本量。結局指標為連續型或二分類變量時,樣本的功效與ICC、集群交叉點、時間效應、隨機效應的關系也不盡相同。
Voldal等[27]運用R軟件開發了一個“swCRTdesign”程序包和一個shiny程序開發的基于web的圖形用戶界面(graphical user interface,GUI)。該程序使用隨機效應模型來解釋SW-CRT的數據相關性,來源包括集群、集群內的時間和集群內的治療。swCRTdesign包含了5個主要功能,其中swDsn(定義SW-CRT設計)和swPwr(計算功效)可實現功效的計算,GUI可以將功效的計算可視化。
Chen等[28]為不同結局變量類型、橫斷面研究和隊列研究、不同集群大小設置下的SW-CRT提供了適用的功效計算軟件swdpwr和Shiny應用程序,swdpwr可在SAS和R兩個平臺下實現,此外,Shiny應用程序還允許不能使用SAS或R的用戶直接在線實現功效的估算。該方法無需依賴于Hussey和Hughes[3]中的近似方法,而是采用了其他可提高計算效率的方法,如采用Fortran語言開發,保證了計算效率,還通過外部函數接口與SAS和R連接。此外,“CRTpowerdist”[29]也可以對連續、計數和二分類變量進行功效計算,但側重于橫斷面研究設計。
這些程序包應開發使功效的計算、數據的模擬繪制以及匯總SW-CRT數據變的更加容易,且對于不同的設計類型和不同的數據類型都進行了分析說明,不同背景的研究人員都能很好運用。
3.2.3 基于網絡的樣本量估算與功效計算
Hemming等[30]開發了一項基于網絡的樣本量估算工具Shiny CRT Calculator,用于集群試驗功效的計算,包括平行試驗、前后測量的平行設計、兩期交叉設計、多期交叉設計和階梯設計,研究者還可以上傳csv格式的文件,文件可以包含缺少的群集周期單元格,從而實現SW-CRT與其他高效試驗設計的結合。使SW-CRT的樣本量估算方法更加簡便,從而提升了試驗的完成效率。
4 統計學檢驗方法
SW-CRT的樣本量估算有多種方法,其統計檢驗方法也多種多樣。在SW-CRT中,所采取的統計分析原則為意向性分析(intention-to-treat,ITT),還需要考慮時間因素、重復測量、群組內沾染、治療效果與時間的交互作用等關鍵方法學問題。其一,干預采用群組隨機分組的順序依次進行介入,而這項過程是“單向交叉”的,即在試驗開展的這段時間,接受干預的集群比例逐漸增加,因此,在對照條件下收集到的觀測結果平均來說比在干預條件下收集到的觀測結果更早,在進行長期反復的結果測量時,受試者的健康狀況可能在研究期間變化,在統計分析時應考慮到時間的混雜影響。其二,SW-CRT針對每個群組都在隨時間進行一系列的測量,測量時會針對相同或不同的受試者,在分析時應考慮到數據并非是獨立的,而是隨著時間的變化而變化。其三,若群組暴露時間過長,部分受試者可能同時暴露對照和干預狀態下,此時為了避免群組沾染的產生,應盡早進行結局指標的評估。最后,SW-CRT可以評估許多不同形式的干預,包括一次性的干預和多次干預,分析時還應檢驗治療效果隨時間的改變。在SW-CRT中,由于每個集群是在隨機抽樣后產生的,必要時還需要對用于完全校正分析的重要預后因素進行預先指定(以減輕由于抽樣變異造成不平衡的可能性),并在適當的地方進行小樣本校正。
基于以上影響因素的考慮,目前,SW-CRT的統計分析方法主要包括以橫斷面研究為主的分析方法和更為復雜的混合模型,涉及了多水平回歸模型來考慮聚類和協變量問題(如時間延遲和長期趨勢)。多數研究者采用了廣義線性混合模型(generalised linear mixed model,GLMM)和廣義估計方程(generalized estimating equations,GEE),其余的分析方法包括卡方檢驗、Manne Whitney U檢驗、t檢驗、一般估計方程、Cox比例風險回歸模型、McNeMar檢驗、重復測量方差分析等[5, 13]。表3總結了SW-CRT幾種統計分析方法及示例[3,31-37]。
Moulton等[37]在一項目的為減少艾滋病毒門診人群中結核病的發病率的SW-CRT中,比較所有研究診所在任何時間點的結局,在考慮診所內相關性的情況下合并隨時間推移的結果,統計分析采用Cox比例風險回歸模型。這一分析方法利于探討干預方式的長期趨勢變化。
廣義線性混合模型可以看作廣義線性模型(generalized linear model,GLM)和線性混合模型(linear mixing model,LMM)的擴展,它可以將隨機效應和固定效應結合起來。通過在集群大小相同和集群大小不同模擬驗證,廣義線性混合模型[3]、廣義估計方程中的時間可作為每個步驟的固定效應被包括在內。對于連續性變量(符合正態分布)的結局數據,采用線性模型,集群具有隨機效應,每步具有固定效應;對于二分類結局,則采用聚類隨機效應、每步固定效應的logistic回歸模型,然而這一方法只適用于橫斷面研究。Twisk等[31]擴展了4種SW-CRT的線性混合模型分析方法(見表3),建議研究者應結合試驗特點選擇相應方法:當比較所有干預時間點與對照時點的數據時選擇方法1;當干預效果與時間無關時選擇方法3;分析結果不受時間影響時選擇方法2;比較受試者從對照期轉換為對照期、被試者從對照期轉換為干預期以及被試者從干預期轉換為干預期3種轉換期之間的差異選擇方法4[32]。
雖然多個學者均推薦使用GLMM和GEE的方法,但對于固定效應和隨機效應模型的運用仍存在不同的觀點。Fok等[38]提出了隨機截距模型,解釋了個人或群體水平單位內重復測量的聚類,當多個單位被分配在同一時間“步驟”或干預轉換時,時間的隨機效應可能包含在內,時間和干預之間的交互項作為固定效應。而Wyman等[39]則認為應該在隨機截距模型之外使用時間隨機效應。在實際分析過程中,應該依據試驗設計的具體方案選擇合適的分析方法。
5 總結
SW-CRT是一種實用的研究設計方法,對于涉及利益相關者持不同觀點的研究、或想減少因傳統試驗對聲譽帶來的不利影響和由于干預措施復雜不能整體實施時,SW-CRT凸顯了其在真實世界環境下“利大于弊”的研究特點,避免因資源不足而難以開展臨床研究的問題。在SW-CRT中,每個群組均會接受干預,不但可以評估干預效果,還可以評估干預時間的早晚對于干預有效性的影響,相同群組下的對比也減少了個體差異性對結果造成的影響。當研究者面臨著有開展大范圍試驗的需求卻又受資金、人力等限制的情況時,SW-CRT無疑是一個最優研究方式,它往往可以滿足偏向真實世界環境下所開展的研究,如公共衛生調查、衛生經濟學評估等。然而SW-CRT也存在缺點,由于試驗集群的復雜性、時間因素與干預措施之間的關聯性,在試驗設計和分析階段調整時間效應可能會導致統計損失效能;且它比傳統的研究更為復雜,試驗對象的群組較多、所涉及的試驗周期更長、統計學分析處理也更為復雜,研究者在完成試驗設計時需要全面考慮潛在的混雜因素。
本文主要總結了SW-CRT的樣本量估算和統計分析方法及其實現方式。檢驗效能與是樣本量估算中的一項重要參數,通過對樣本功效的計算進而可得出樣本量結果,對樣本量估算推薦以Stata軟件為主,操作簡便靈活,而由于目前樣本量估算仍以橫斷面研究為主,由此計算出的樣本量數量往往高于實際所需。SW-CRT受時間、集群的影響較大,故統計分析方法一般以廣義線性混合模型為主,可滿足受時間影響、非正態數據及集群大小不同的數據分析。
然而,樣本量估算及統計分析方法多為橫斷面研究或集群大小相同、結局為連續型數據時應用的模型,對于隊列設計、集群大小不等和二分類結局數據的情況卻鮮有涉及,未來還需要更多的精力投入其中。以期為這類試驗的開展和提高試驗的完整性及規范性提供參考。
聲明 所有作者均聲明不存在任何利益沖突。
1 階梯整群隨機試驗概述
階梯整群隨機試驗(stepped wedge cluster randomised trials,SW-CRT)是一種特殊類型的整群隨機試驗(cluster randomized trials,CRT),其原理類似于“交叉設計”。試驗對象在干預開始前會被分為若干群組,不同的群組在不同的時間點接受從對照狀態切換至干預狀態的單向交叉處理[1]。在初始階段(基線期)沒有任何群組接受干預,隨后每隔一段時間或步驟,一個群(或一組群)會被隨機抽取接受干預,同一時間點可能有一個或多個群組開始接受干預,但這些群組開始接受干預的時間是隨機的,這一過程會依次進行,直至所有的群組都接受了干預[2,3](圖1)。SW-CRT依據不同的分類標準分為了不同的試驗類型,Hemming等[1]依據在不同的步驟或階段中集群數量及數據收集的差異,將其分為完整階梯設計和不完整階梯設計。而Copas等[4]依據不同的研究對象,將試驗分為固定隊列階梯設計(closed cohort design)、開放隊列階梯設計(open cohort design)和連續入組短期暴露階梯設計(continuous recruitment with short exposure)。
 圖1
標準階梯整群隨機試驗示意圖
圖1
標準階梯整群隨機試驗示意圖
SW-CRT主要用來評估在日常實施過程中干預措施的有效性,特別是對于那些在更可控的研究環境中被證明有效的干預措施,或缺乏明確利大于弊的干預措施的有效性證據[5]。階梯整群隨機試驗的應用最早出現于20世紀80年代開展的一項岡比亞肝炎的干預研究[6]。流行病學調查表明,在發展中國家SW-CRT常用于針對HIV的干預措施的評估,其中,最常見的干預措施有疫苗接種、篩查、教育計劃出臺等[7]。近年來這一試驗方式的逐漸推廣,其使用領域也多種多樣,涉及癌癥、艾滋病、醫療保健、衛生政策制定等方面[5, 7]。就采取SW-CRT試驗方式的動機而言,多數研究都考慮到了試驗協調的靈活性、人力財力資源的限制、人群對于有利的干預方式的可接受性、倫理、干預措施在試驗多個集群中實施的難易程度、受試者失望效應(受試者因未被分配到干預組而產生的脫落)等[5, 8]。
隨著對SW-CRT試驗數量的增多,Hemming等學者使用Delphi調查和共識會議制定方法,制定了專門針對階梯整群隨機試驗的報告條目規范(reporting of stepped wedge cluster randomised trials: extension of the CONSORT 2010 statement with explanation and elaboration)[9],它作為臨床試驗報告規范(consolidated standards of reporting trials,CONSORT)聲明的擴展版,旨在為平行隨機對照試驗提供統一標準。目前,國內僅在急性冠脈綜合征患者[10]和自閉癥患兒[11]中開展了階梯整群隨機試驗,且仍缺乏對其統計分析方法和樣本量計算的介紹與解讀。本文將闡述SW-CRT的主要應用、辨析與傳統隨機對照試驗的區別,并著重從數據收集與分析方法、樣本量估算等統計學層面介紹SW-CRT。
2 SW-CRT與傳統隨機對照試驗
顧名思義,SW-CRT的名稱來源于圖1中明顯的階梯式楔形,它與傳統的(平行)整群隨機試驗和隨機對照試驗存在差異。傳統的(平行)整群隨機試驗是對群組隨機分組后,群組一直留在干預組或對照組直至研究結束。而SW-CRT擴展了試驗設計,每個集群均能提供觀察前后的數據,且會在不同的時間點從對照組切換到干預組[2],是一種交叉設計的方式。與傳統的隨機對照試驗不同,SW-CRT是以群組而非個體為研究對象,每個群組都會依次接受干預。需要特別注意的是,SW-CRT與以上兩種試驗方式都存在樣本量估算與統計學分析方法上的差異,表1對其進行了總結[12-14]。
由表1可見,SW-CRT在臨床試驗的實際應用中具有如下優勢:① 不需要專門設置對照組,減少了人力物力財力的投入;② 每個群組均會接受干預,受試者公平性得到保障,符合醫學倫理要求,是真實世界研究中的重要試驗方法之一;③ 以自身群體作為對照依據,減少了不同組別群體間個體化的差異對結果造成的影響,結論有更高可靠性。SW-CRT作為一種新興的定量研究設計方法,可以在真實世界研究中實施應用,作為一種循證實踐策略,能夠發揮真實世界中干預措施最大限度的效果[15]。
3 樣本量估算
3.1 樣本量估算方法
SW-CRT是聚類試驗的形式之一,故分析和設計需要考慮這種“聚類”屬性。SW-CRT的試驗過程是“單向轉換”的,即由對照狀態逐漸向干預狀態轉化。SW-CRT的受試者暴露于干預的集群比例會隨著時間的推移而逐漸增加。這些試驗設計的特點決定了SW-CRT的樣本量計算方式和參數并非是由個體的隨機對照試驗簡單修改而來的,而更需要將聚類效應、時間效應、重復測量幾項關鍵要素考慮在內。目前對已發表的SW-CRT樣本量估算情況的統計分析發現[12]:大多數研究考慮了聚類;但33項研究中只有15項研究考慮了時間效應;大多數研究未明確報告設計類型(隊列設計或橫斷面設計);在隊列設計的樣本量計算中,只有少數提及了重復測量。SW-CRT樣本量計算方法普遍存在質量較低、關鍵要素缺失的問題,亦沒有統一的計算方法。
樣本量估算與試驗的檢驗水準和檢驗效能密切相關,故必須設置合理的檢驗水準和檢驗效能[16]。檢驗水準為控制Ⅰ類錯誤的能力,用α表示,在多重檢驗中,為了減少假陽性錯誤,通常都需要設定檢驗水準在0.05以下;檢驗效能反應了根據當前的樣本量獲得組間有統計學差異的能力,用1-β來表示,實際中通常設置為0.8,當檢驗效能越高時,則所需的樣本量越多。SW-CRT涉及多個群組、多次的隨機分配和治療間隔時間,試驗過程相較其他傳統隨機對照試驗更為復雜,且SW-CRT樣本量易受集群大小影響,故本文將區分集群規模,從群間相關性、隨機化步驟、測量次數等對檢驗效能的影響來把握樣本量估算水平。
3.1.1 假設集群大小相同時的樣本量估算及檢驗效能影響因素
Hussey[3]等針對SW-CRT設計了樣本量計算的效能,并研究了不同的群間相關性、隨機化步驟數量和治療延遲對試驗效能的影響,發現試驗的效能受集群間相關性的影響相對較少,而測量次數的減少則會引起效能的損失。隨著SW-CRT在衛生服務評價中的應用越來越廣泛,目前已有SW-CRT的試驗設計大多數為橫斷面研究,即在某一時間段隨機分配相同數量的集群,在固定的時間段統一收集數據,假設納入研究的樣本在每個時間點都與其他時間點的樣本不同。基于此,Hemming等[1]從常規的SW-CRT中延伸了不同類型的試驗設計方式—完整階梯設計(傳統的階梯整群隨機設計)和不完整階梯設計(具有過渡周期的階梯整群隨機設計),且計算出試驗效能與群內相關性(intra-cluster correlation,ICC)沒有線性關系。對于較小的ICC值,試驗效能會隨著ICC的增加而降低;但對于較大的ICC值,試驗效能會隨著ICC值的增加而增加。
在平行的CRT中,常用設計效應(design effect,DE)進行樣本量估算,一些學者進而提出了基于DE推導的SW-CRT樣本量計算方法。Woertman等[17]假設結果測量是在多個離散時間點從每個集群獲得的,并且在每個交叉點測量的參與者數量在不同的時間和集群中是相同的,得出總樣本量計算公式為:
 |
nRCT:相應的平行RCT所需要的樣本量;B:基線測量次數;J:集群切換交叉到干預狀態的交叉點數量;T:每次交叉轉換期間的測量次數;CF:校正因子(correction factor)。
其中CF即為DE,受3個主要因素影響:每步的測量次數、基線測量次數和步數,任意一個因素的增加都會引起DE的降低。這一公式與Hussey等的模型相似,僅適用于橫斷面設計,每次測量都來自不同的個體參與者。然而公式中每次交叉轉換的集群數是相同的,每次交叉后的測量次數也不變。
隨后Hemming等又依據Hussey等建立的模型,調整了DE進行樣本量的估算,從而能夠計算集群數量給定時所需的集群大小[18],探索了樣本量計算的功效及其相關性。基于以上研究的理論框架和不同的情景設定,整理所得樣本量計算公式如下[19]:
① 當階梯步數(t)、每個觀察期每個集群的樣本量(m)以及集群內相關性ICC(ρ)已知,求總樣本量(N)
 |
N1:兩組等樣本隨機對照試驗所需樣本量。
② 當階梯步數(t)、總群數(k)、以及集群內相關性ICC(ρ)已知,求總樣本量(N)
 |
為了更好理解在集群大小相同時,樣本量的計算方式,本文運用贊比亞一項關于瘧疾預防工作的階梯整群隨機試驗案例[20],改編其中的數據,對樣本量估算進行演示。
示例:為了評估大規模檢測和治療(MTAT)干預對瘧疾患病率和衛生機構門診病例發病率的影響,贊比亞南部省開展了一項社區階梯整群隨機試驗。研究共設置了10個干預階梯,觀察時點為11個,以每個衛生設施集水區所在的家庭數量為一個群組,假設干預后干預組瘧疾門診病例發生率較對照組下降10%,ICC(ρ)為0.01,檢驗水準α=0.05,檢驗效能(1-β)為0.9,在兩個情景下分別計算需要的樣本量:
情況一:階梯步數t=10,ρ=0.01,假設每個群組的平均家庭數量數為50個(m=50),利用PASS軟件可計算出初步樣本量N1為1 038人,依據DE公式可得,DE=2.69,計算總樣本量N約為2 792人;集群數k為總樣本除以觀察時點數(t+1)和每個群組平均家庭數量(m),即k=N/[(t+1)m],此時,m=50,計算可得集群數k=5。
情況二:當階梯步數t=10,ρ=0.01,假設每個群組的平均家庭數量數為50個(m=50),集群數量(k)設置為5時,由公式2可計算出,總樣本量N約為2 750人。
3.1.2 假設集群大小不同時的樣本量估算及檢驗效能影響因素
在實施橫斷面研究的SW-CRT中,研究者可能會面臨所納入的集群大小不等的情況,曾有學者對101個SW-CRT的系統評價發現,48%的研究包括大小不同的集群[21],而忽略這一問題所帶來的影響尚不清楚。雖然在Hemming[1]構建的模型框架中說明了集群的大小變化不會導致連續結果較為顯著的效能損失,但這是基于只檢驗了一小部分參數得來的結果。基于此,Martin等研究了SW-CRT中不同集群大小的含義[22],發現橫斷面SW-CRT實際的功效可能較估計值并不穩定,尤其是當集群數量較少或集群大小的可變性很大時。Harrison等[23]推導了不同集群大小的橫斷面SW-CRT與單個隨機試驗相比的DE,計算了不同集群大小的橫斷面SW-CRT的預期相對效率(relative efficiency,RE)和校正樣本量計算的CF,提供了與集群大小變化相關的平均功率損失的公式,發現當集群數量較小或集群大小變異系數(coefficient of variation,CV)大于1時平均功效的損失更大。如果集群的數量足夠大,并在每一步均隨機分配幾個集群開始治療,其隨機分配的所有集群的總大小不會有明顯的不平等,則可以減少功效的損失[24]。
3.2 樣本功效的軟件實現方法
相較于SW-CRT復雜的樣本量計算,確定樣本功效相對容易,也有相應的軟件實現方式。而基于前期對于樣本量功效的計算理論,選擇合適的功效計算軟件,調整相應的參數值,能夠得出適合自身研究的樣本量。表2中總結了幾種常見的軟件實現方式及其優點與局限性。
3.2.1 Stata軟件中的樣本量估算
Hemming等在Stata軟件中開發了Steppedwedge命令[25],可計算完整和不完整的SW-CRT的可檢測差異和功效,包含一個訪問命令的對話框。可實現在雙側檢驗下的連續性變量、二分類變量和率(近似正態)的比較。在Stata軟件中,選擇結局變量的類型后(連續型數據、二分類型數據、比例型數據),輸入檢驗水準(α)、ICC、每步的階梯數、集群數量、時間點(不包含基線時期)、兩組值的比較(均數與標準差、比例、率),可完成功效的估算。
該命令存在優點與局限性。Steppedwedge命令可在Stata軟件中實現,且操作步驟簡單易懂,可實現性與可操作性強;與整群試驗的樣本量計算方法類似,都以ICC作為輸入參數。但該命令的假設前提基于集群大小相等,僅可計算固定樣本量的功效和可檢測差;命令和模型僅限于橫斷面研究,而不能用于隊列研究。
3.2.2 R軟件與SAS軟件的樣本量計算
Baio等[26]采用R軟件中分析和模擬訓練的函數,在假設橫斷面設計和封閉隊列設計,結局指標為連續和二分類變量的情況下,確定SW-CRT的樣本量。結局指標為連續型或二分類變量時,樣本的功效與ICC、集群交叉點、時間效應、隨機效應的關系也不盡相同。
Voldal等[27]運用R軟件開發了一個“swCRTdesign”程序包和一個shiny程序開發的基于web的圖形用戶界面(graphical user interface,GUI)。該程序使用隨機效應模型來解釋SW-CRT的數據相關性,來源包括集群、集群內的時間和集群內的治療。swCRTdesign包含了5個主要功能,其中swDsn(定義SW-CRT設計)和swPwr(計算功效)可實現功效的計算,GUI可以將功效的計算可視化。
Chen等[28]為不同結局變量類型、橫斷面研究和隊列研究、不同集群大小設置下的SW-CRT提供了適用的功效計算軟件swdpwr和Shiny應用程序,swdpwr可在SAS和R兩個平臺下實現,此外,Shiny應用程序還允許不能使用SAS或R的用戶直接在線實現功效的估算。該方法無需依賴于Hussey和Hughes[3]中的近似方法,而是采用了其他可提高計算效率的方法,如采用Fortran語言開發,保證了計算效率,還通過外部函數接口與SAS和R連接。此外,“CRTpowerdist”[29]也可以對連續、計數和二分類變量進行功效計算,但側重于橫斷面研究設計。
這些程序包應開發使功效的計算、數據的模擬繪制以及匯總SW-CRT數據變的更加容易,且對于不同的設計類型和不同的數據類型都進行了分析說明,不同背景的研究人員都能很好運用。
3.2.3 基于網絡的樣本量估算與功效計算
Hemming等[30]開發了一項基于網絡的樣本量估算工具Shiny CRT Calculator,用于集群試驗功效的計算,包括平行試驗、前后測量的平行設計、兩期交叉設計、多期交叉設計和階梯設計,研究者還可以上傳csv格式的文件,文件可以包含缺少的群集周期單元格,從而實現SW-CRT與其他高效試驗設計的結合。使SW-CRT的樣本量估算方法更加簡便,從而提升了試驗的完成效率。
4 統計學檢驗方法
SW-CRT的樣本量估算有多種方法,其統計檢驗方法也多種多樣。在SW-CRT中,所采取的統計分析原則為意向性分析(intention-to-treat,ITT),還需要考慮時間因素、重復測量、群組內沾染、治療效果與時間的交互作用等關鍵方法學問題。其一,干預采用群組隨機分組的順序依次進行介入,而這項過程是“單向交叉”的,即在試驗開展的這段時間,接受干預的集群比例逐漸增加,因此,在對照條件下收集到的觀測結果平均來說比在干預條件下收集到的觀測結果更早,在進行長期反復的結果測量時,受試者的健康狀況可能在研究期間變化,在統計分析時應考慮到時間的混雜影響。其二,SW-CRT針對每個群組都在隨時間進行一系列的測量,測量時會針對相同或不同的受試者,在分析時應考慮到數據并非是獨立的,而是隨著時間的變化而變化。其三,若群組暴露時間過長,部分受試者可能同時暴露對照和干預狀態下,此時為了避免群組沾染的產生,應盡早進行結局指標的評估。最后,SW-CRT可以評估許多不同形式的干預,包括一次性的干預和多次干預,分析時還應檢驗治療效果隨時間的改變。在SW-CRT中,由于每個集群是在隨機抽樣后產生的,必要時還需要對用于完全校正分析的重要預后因素進行預先指定(以減輕由于抽樣變異造成不平衡的可能性),并在適當的地方進行小樣本校正。
基于以上影響因素的考慮,目前,SW-CRT的統計分析方法主要包括以橫斷面研究為主的分析方法和更為復雜的混合模型,涉及了多水平回歸模型來考慮聚類和協變量問題(如時間延遲和長期趨勢)。多數研究者采用了廣義線性混合模型(generalised linear mixed model,GLMM)和廣義估計方程(generalized estimating equations,GEE),其余的分析方法包括卡方檢驗、Manne Whitney U檢驗、t檢驗、一般估計方程、Cox比例風險回歸模型、McNeMar檢驗、重復測量方差分析等[5, 13]。表3總結了SW-CRT幾種統計分析方法及示例[3,31-37]。
Moulton等[37]在一項目的為減少艾滋病毒門診人群中結核病的發病率的SW-CRT中,比較所有研究診所在任何時間點的結局,在考慮診所內相關性的情況下合并隨時間推移的結果,統計分析采用Cox比例風險回歸模型。這一分析方法利于探討干預方式的長期趨勢變化。
廣義線性混合模型可以看作廣義線性模型(generalized linear model,GLM)和線性混合模型(linear mixing model,LMM)的擴展,它可以將隨機效應和固定效應結合起來。通過在集群大小相同和集群大小不同模擬驗證,廣義線性混合模型[3]、廣義估計方程中的時間可作為每個步驟的固定效應被包括在內。對于連續性變量(符合正態分布)的結局數據,采用線性模型,集群具有隨機效應,每步具有固定效應;對于二分類結局,則采用聚類隨機效應、每步固定效應的logistic回歸模型,然而這一方法只適用于橫斷面研究。Twisk等[31]擴展了4種SW-CRT的線性混合模型分析方法(見表3),建議研究者應結合試驗特點選擇相應方法:當比較所有干預時間點與對照時點的數據時選擇方法1;當干預效果與時間無關時選擇方法3;分析結果不受時間影響時選擇方法2;比較受試者從對照期轉換為對照期、被試者從對照期轉換為干預期以及被試者從干預期轉換為干預期3種轉換期之間的差異選擇方法4[32]。
雖然多個學者均推薦使用GLMM和GEE的方法,但對于固定效應和隨機效應模型的運用仍存在不同的觀點。Fok等[38]提出了隨機截距模型,解釋了個人或群體水平單位內重復測量的聚類,當多個單位被分配在同一時間“步驟”或干預轉換時,時間的隨機效應可能包含在內,時間和干預之間的交互項作為固定效應。而Wyman等[39]則認為應該在隨機截距模型之外使用時間隨機效應。在實際分析過程中,應該依據試驗設計的具體方案選擇合適的分析方法。
5 總結
SW-CRT是一種實用的研究設計方法,對于涉及利益相關者持不同觀點的研究、或想減少因傳統試驗對聲譽帶來的不利影響和由于干預措施復雜不能整體實施時,SW-CRT凸顯了其在真實世界環境下“利大于弊”的研究特點,避免因資源不足而難以開展臨床研究的問題。在SW-CRT中,每個群組均會接受干預,不但可以評估干預效果,還可以評估干預時間的早晚對于干預有效性的影響,相同群組下的對比也減少了個體差異性對結果造成的影響。當研究者面臨著有開展大范圍試驗的需求卻又受資金、人力等限制的情況時,SW-CRT無疑是一個最優研究方式,它往往可以滿足偏向真實世界環境下所開展的研究,如公共衛生調查、衛生經濟學評估等。然而SW-CRT也存在缺點,由于試驗集群的復雜性、時間因素與干預措施之間的關聯性,在試驗設計和分析階段調整時間效應可能會導致統計損失效能;且它比傳統的研究更為復雜,試驗對象的群組較多、所涉及的試驗周期更長、統計學分析處理也更為復雜,研究者在完成試驗設計時需要全面考慮潛在的混雜因素。
本文主要總結了SW-CRT的樣本量估算和統計分析方法及其實現方式。檢驗效能與是樣本量估算中的一項重要參數,通過對樣本功效的計算進而可得出樣本量結果,對樣本量估算推薦以Stata軟件為主,操作簡便靈活,而由于目前樣本量估算仍以橫斷面研究為主,由此計算出的樣本量數量往往高于實際所需。SW-CRT受時間、集群的影響較大,故統計分析方法一般以廣義線性混合模型為主,可滿足受時間影響、非正態數據及集群大小不同的數據分析。
然而,樣本量估算及統計分析方法多為橫斷面研究或集群大小相同、結局為連續型數據時應用的模型,對于隊列設計、集群大小不等和二分類結局數據的情況卻鮮有涉及,未來還需要更多的精力投入其中。以期為這類試驗的開展和提高試驗的完整性及規范性提供參考。
聲明 所有作者均聲明不存在任何利益沖突。