引用本文： 錢迪, 金志超, 趙艷芳. 含時間依賴性治療變量預后預測模型構建策略的模擬研究. 中國循證醫學雜志, 2024, 24(4): 490-496. doi: 10.7507/1672-2531.202310209 復制
版權信息： ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有，未經授權不得轉載、改編
近年來，預測患者預后、預防疾病發生、個體化治療和患者共同參與得到越來越廣泛地認同，此理念的基礎是構建準確的臨床預后預測模型[1]。臨床預后預測模型是指根據患者已知的預測因子，依靠統計方法，計算患者發生某種結局的概率[2-4]。臨床醫師可以根據患者未來發生風險事件的概率進行臨床決策，相關研究表明，良好的預后預測模型給出的預測結果比臨床醫生根據臨床經驗的預測結果更準確[5]。
為了構建預測能力良好的預后預測模型，需要從研究目的、適用人群、預測因子、結局事件、統計方法、模型驗證等多方面進行考慮[6,7]。目前，大部分的研究者在構建預測模型時，納入預測因子時未考慮因果關系，著重考慮的是模型是否具有更好的預測效能。然而在一些特殊情況下，比如存在時間依賴性變量的情況下，不考慮相關因果可能會導致錯誤估計患者不良預后的概率。隨著因果推斷的理論發展和實際應用，越來越多的研究者在構建預測模型時將預測因子的因果關系納入考慮。從預測因子角度考慮，預測模型的預測效能欠佳主要是忽略了某些預測因子，更詳細了解因果關系有助于篩選合適的預測因子，從而提高模型預測效能[8]；從適用人群角度考慮，因果推斷框架下的臨床預后預測模型有助于提高模型在新環境或不同人群中的可移植性[9]；從研究目的角度考慮，因果推斷框架下的臨床預后預測模型預測的結果可以解釋患者采取某種治療前后發生不良預后概率變化的情況[10]。
預后預測模型的主要目的是指導臨床醫生進行臨床決策：在高風險患者中是否采取某種治療措施[11,12]。理想情況下，模型應該反映如果沒有干預，一個人發生危險事件的風險是什么，即“未經治療的風險”[13]，用
表示。構建預測模型的數據經常來自于觀察性研究，存在進入隊列時未采取治療的人群在隨訪過程中開始治療，這個現象被稱為“drop-in”[14]，使用傳統方法基于此類數據開發預后預測模型將導致發生錯誤的預測，預測結果為
。因此，該模型提供的對未來患者的風險預測會低估未治療結果的真實風險，導致決策錯誤。推而廣之，如果臨床醫生關心患者采用治療后發生風險的概率，用
表示。觀察性數據同樣存在進入隊列時采取治療的人群在隨訪過程中停止治療，因此可能存在高估治療的真實效果的問題。針對上述情況，相關研究建議，在開發預后預測模型時，應著重考慮治療的變化情況來提高預測效果[13,15]。然而，迄今為止，如何將治療納入預后預測模型還沒有明確的共識[16]。
基于觀察性研究數據構建臨床預后預測模型通常會采用縱向數據，分析存在時間依賴性變量的縱向數據，通常治療在基線后可能發生改變，如何處理治療的變化值是構建預后預測模型的難點之一[17,18]。例如，在一項關于齊多夫定治療對人類免疫缺陷病毒感染者死亡率影響的研究中，是否進行齊多夫定治療受CD4淋巴細胞計數影響，與此同時，CD4淋巴細胞計數本身受先前齊多夫定治療的影響，在此項研究中，構建人類免疫缺陷病毒感染受試者預后預測模型需考慮治療變量（齊多夫定）如何進行處理[19]。針對上述問題，Matthew Sperrin等提出了忽略治療模型（ignore treatment model，ITM）、基線無治療模型（treatment-na?ve model，TNM）、基線治療模型（treatment model，TM）、邊際結構預后預測模型（MSM-logistic model，MLM）四個方法對治療變量進行處理，通過模擬研究結果發現在兩個隨訪時間點情況下，MLM的預測效能較其余模型有所提升[20]；Nan van Geloven等提出忽略治療策略（ignore treatment strategy）、復合策略（composite strategy）、不治療策略（while untreated strategy）、假設策略（hypothetical strategy），通過實例驗證，發現四種策略可回答患者在不同情況下發生結局事件的可能性，對于指導臨床決策具有重大意義[21]。目前在構建預后預測模型時，對如何處理治療變量尚沒有明確共識，但越來越多的科研工作開始重視預后預測模型中治療變量的處理[13]。在實際的臨床研究中，治療的隨訪時間點往往大于2個，本研究在Matthew Sperrin等研究的基礎上，對隨訪時間點及模擬情景進行了擴展，以期解決多隨訪時間點、多種模擬情景下，時間依賴性治療變量的觀察性研究如何更好構建預后預測模型的問題。
1 方法
1.1 邊際結構模型（marginal structural model，MSM）
觀察性研究中，存在治療隨時間變化的情況，在估計治療效應時，會受到時依性混雜變量的影響。針對傳統統計方法無法解決時依性混雜的問題，Robins提出MSM這一方法[19]。
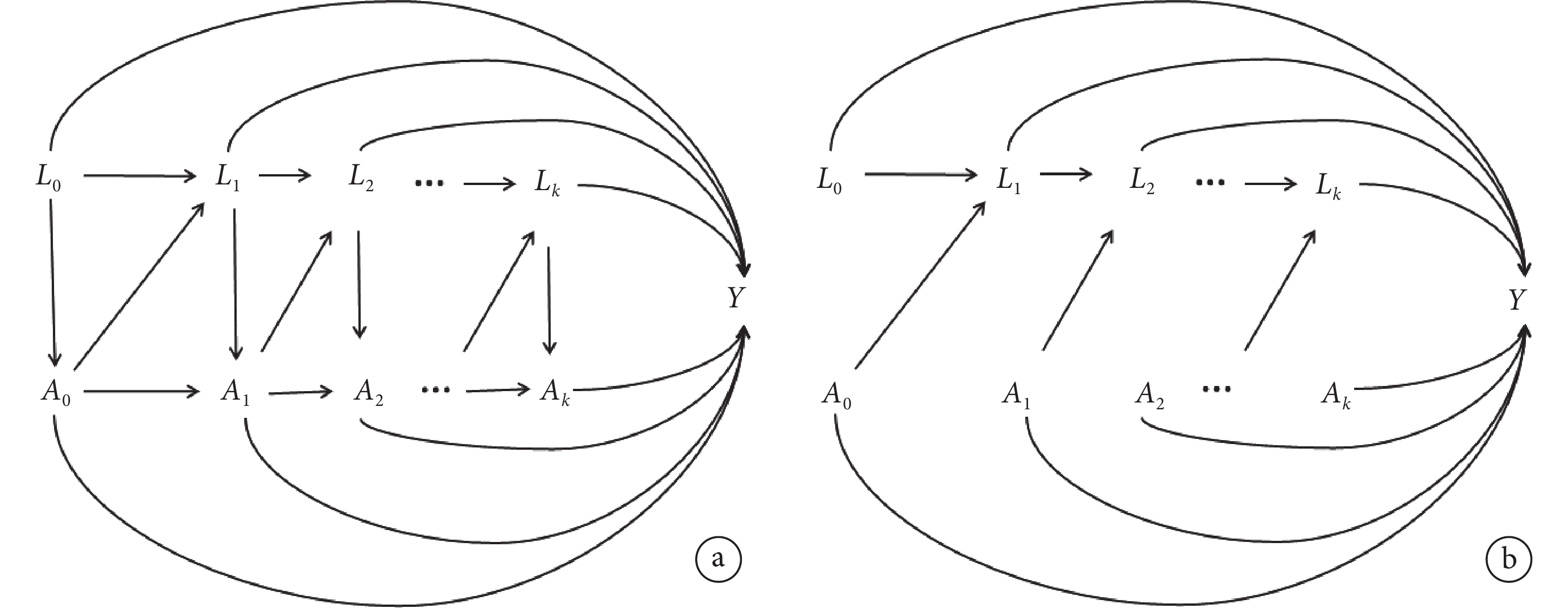
因果圖可以幫助研究者理解MSM，并有助于預后預測模型的構建[9]。假設存在K個隨訪時間，時間依賴性混雜變量為L，治療變量記為A，風險事件Y為二分類結局。根據上述假設指標，對校正時間依賴性變量前后分別繪制因果圖，見圖1。
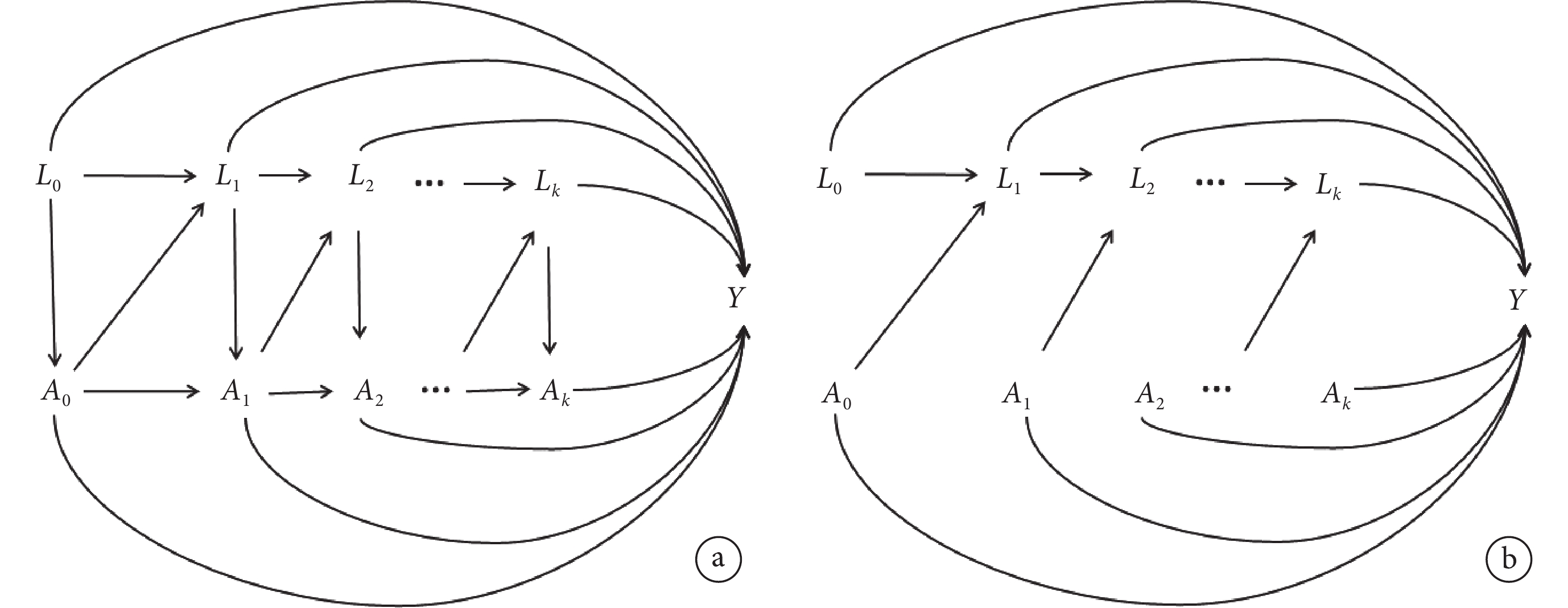圖1
校正時間依賴性變量前后的因果圖
a：校正前；b：校正后。
如圖1a所示，校正前基線治療情況A0受基線協變量L0的影響，第一次隨訪L1受L0與A0影響，A1受A0與L1的影響，以此類推，K個隨訪時間點時，Ak受Ak-1與Lk的影響。針對上述情況，無論是估計治療對于結局的效應還是構建預后預測模型，傳統方法均無法解決時間依賴性治療變量的問題。MSM采用逆概率加權法生成各對象組的偽分布，每組處理后的偽分布都相同，使得治療相對于時間依賴性變量獨立，反映在圖上就是刪除了影響該隨訪時間點治療的弧線，校正后的因果圖如圖1b所示。
1.2 MLM算法實現
在觀察性研究中，暴露變量可能受已觀測協變量（混雜因素）的影響。MSM正是通過構造已觀測協變量與暴露變量的模型，提出校正已觀測混雜偏倚的暴露變量逆概率權重，消除已觀測協變量的影響，從而獲得暴露變量與結局變量真實的因果關聯。
在時點研究中，研究對象i暴露的逆概率權重的計算公式為：
 |
其中：
表示研究對象
的已觀測協變量
的觀測值；
為研究對象
的暴露變量
的觀測值；
表示研究對象
在
的情況下，出現
的概率。
可通過擬合
與
的Logistic回歸模型獲得觀察對象接受暴露的概率。估計研究對象接受暴露概率的模型為：
 |
該模型可通過逆概率權重控制
造成的混雜偏倚，得到對因果關聯的無偏估計。
因果推斷與預測模型結合的要點是用因果關系取代關聯關系進行預測，因此邊際結構預測模型的核心思想是將MSM得出的因果關聯無偏估計帶入預測模型之中。構建邊際結構預測模型采取以下步驟：
首先，計算逆概率權重：
 |
其中，
表示模型
的估計值，
表示模型
的估計值。
其次，將計算所得的逆概率權重值帶入模型進行擬合：
 |
基于上述模型，可以得到類似傳統的Logistic回歸模型，并進行概率預測，得出患者發生不良預后的概率。
2 模擬研究
2.1 模擬概況
設置結局變量Y為二分類變量，處理變量A為二分類變量，時依性協變量X為連續性變量（可用于衡量疾病嚴重程度并作為治療的依據），同時設置4個固定協變量（包括2個連續型協變量、2個二分類協變量）。模擬研究設置2種不同的隨訪時間點（2、5次隨訪），64種不同的治療變量、時依性協變量、結局變量三者之間關系，共128種模擬情境（具體情景請參見附件1）。每個模擬情境模擬1 000次，每次模擬均基于訓練集采用ITM、TNM、TM、MLM4種方法進行建模，并在測試集進行驗證，比較4種方法在不同模擬情境下的表現。采用區分度和校準度對預測效果進行評價。本研究采用R 4.2.2進行數據模擬及統計分析，代碼見附件2。
2.2 模擬設計：數據生成機制
以兩個隨訪時間點為例，基于不同的治療與協變量、協變量與結局、治療與結局關系，生成樣本量為7 000的訓練數據集和3 000的驗證數據集，生成機制如下。
① 模擬生成隨訪時間點t=0時刻的協變量X0，X0~N（0，1）
② 模擬生成隨訪時間點t=0時刻的治療變量
，
 |
③ 模擬生成隨訪時間點t=1時刻的協變量
，
④ 模擬生成隨訪時間點t=1時刻的治療變量
，
 |
⑤ 模擬生成結局指標
，
 |
其中，
表示
時刻，
對
的影響，本次模擬研究中，
的取值范圍［log（2），log（3）］，表示協變量增加采取治療的概率；
表示
時刻，
對
的影響，本次模擬研究中，
的取值范圍（0，?1，?3，?5），表示治療可以降低協變量的數值；
表示
時刻，
對
的影響，本次模擬研究中，
的取值范圍［log（2），log（3）］，表示前一次治療對后一次采取治療概率的影響；
表示協變量
對結局變量
的影響，本次模擬研究中，
的取值范圍［log（2），log（4）］，表示協變量可以增加發生結局事件的概率；
表示治療變量
對結局變量
的影響，本次模擬研究中，
的取值范圍［log（0.4），log（0.5）］，表示治療可以降低發生結局事件的概率。
2.3 模型構建方法及效果評價
4種方法建模：
① ITM：只將基線協變量情況納入預測模型，不考慮治療情況。
 |
其中，
表示基線協變量情況。
② TNM：選取基線未發生治療的人群作為分析人群。
 |
其中，
表示基線協變量情況，
表示分析人群為基線未采取治療的人群。
③ TM：只將基線治療情況納入預測模型，不考慮治療變化的情況。
 |
其中，
表示基線協變量情況，
表示基線治療情況。
④ MLM：MSM與Logisitic回歸模型結合，將時依性治療變量的基線情況以及隨訪期間的治療變化情況納入預測模型。
 |
其中，
表示基線協變量情況，
表示治療情況，
表示第
個患者的逆概率權重。
建立樣本量為7 000的訓練集進行建模，所得模型帶入樣本量為3 000的驗證集進行驗證。采用區分度和校準度來評價模型的預測效能。通過設置一定的風險界值，高于界值判斷為發生事件，否則為不發生事件，從而正確區分個體是否會發生結局事件的能力稱為預測模型的區分度。校準度反映模型預測風險與實際發生風險的一致程度[22-24]。評價預測模型區分能力的指標，最常用的是ROC曲線下面積（area under the curve，AUC），AUC越大，說明預測模型的判別區分能力越好。一般認為AUC小于0.6則區分度較差，0.6～0.75認為模型有一定的區分力，大于0.75認為區分能力較好。概率預測的準確程度稱為校準度，是衡量模型預測出的概率和真實結果的差異的一種方式。常用的指標為Brier Score，它被計算為是概率預測相對于測試樣本的均方誤差。Brier Score的范圍是從0到1，分數越接近1校準程度越差，越接近0校準程度越好。
2.4 模擬研究結果
2.4.1 2個隨訪時間點
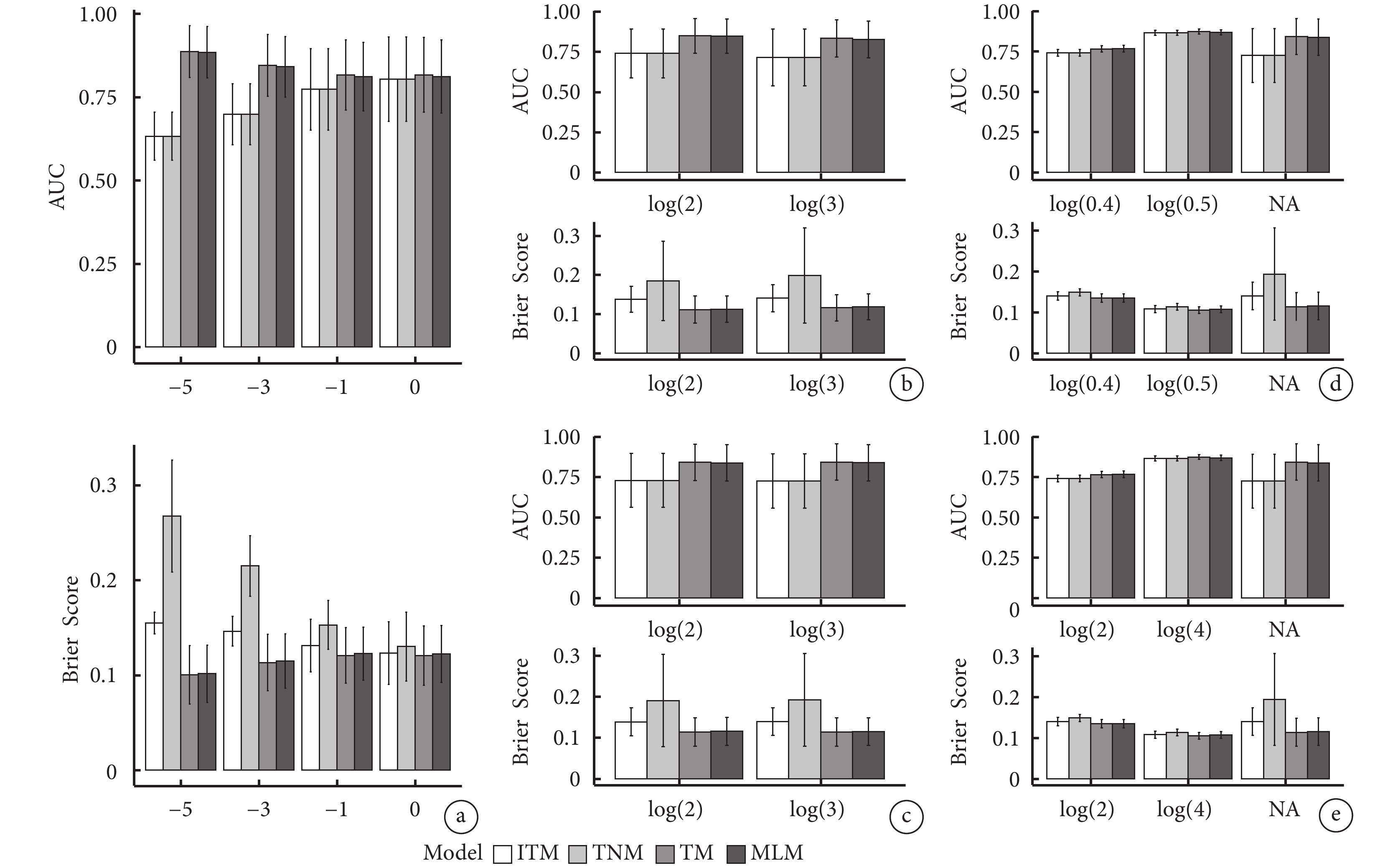
不同情境下不同模型的預測效能存在差異。圖2a顯示，當
取值發生改變，其余參數不變的情況下，ITM和TNM模型的AUC小于TM和MLM模型，ITM和TNM模型的AUC未見明顯差異，TM和MLM模型的AUC未見明顯差異，其中TM和MLM模型的AUC隨著
的增大而減小，當
=?5時，TM模型的AUC最大為0.889；TNM模型的Brier Score最大，ITM次之，TM和MLM模型的Brier Score最小且未見明顯差異。
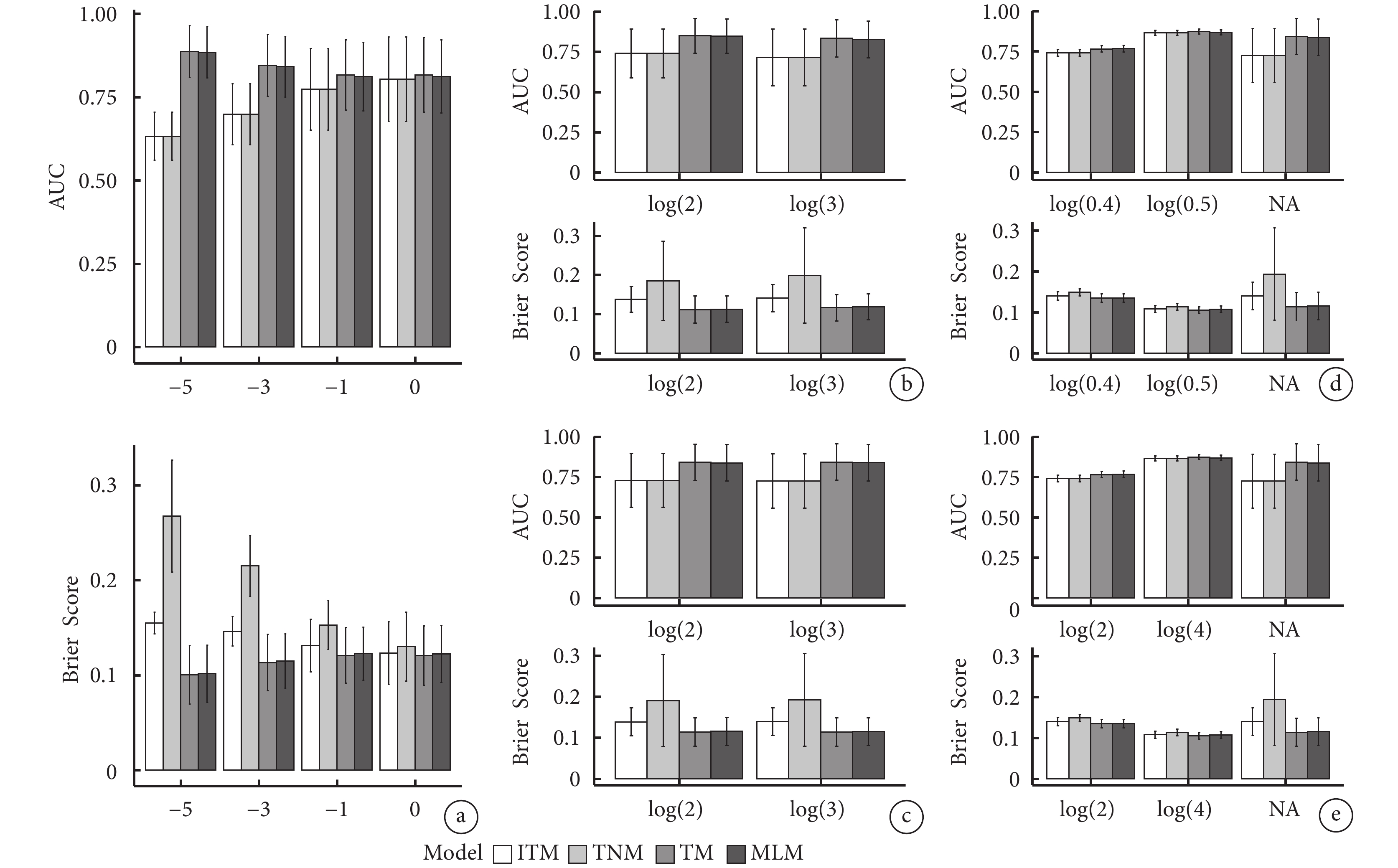圖2
2個隨訪時間點情況下不同模型預測效能比較
圖2b～圖2e分別顯示隨著
、
、
、
的取值分別增大，ITM和TNM模型的AUC始終小于TM和MLM模型，且TM和MLM模型的AUC隨數值增大而增大；TNM模型的Brier Score最大，ITM次之，TM和MLM模型的Brier Score最小且未見明顯差異。
2.4.2 5個隨訪時間點
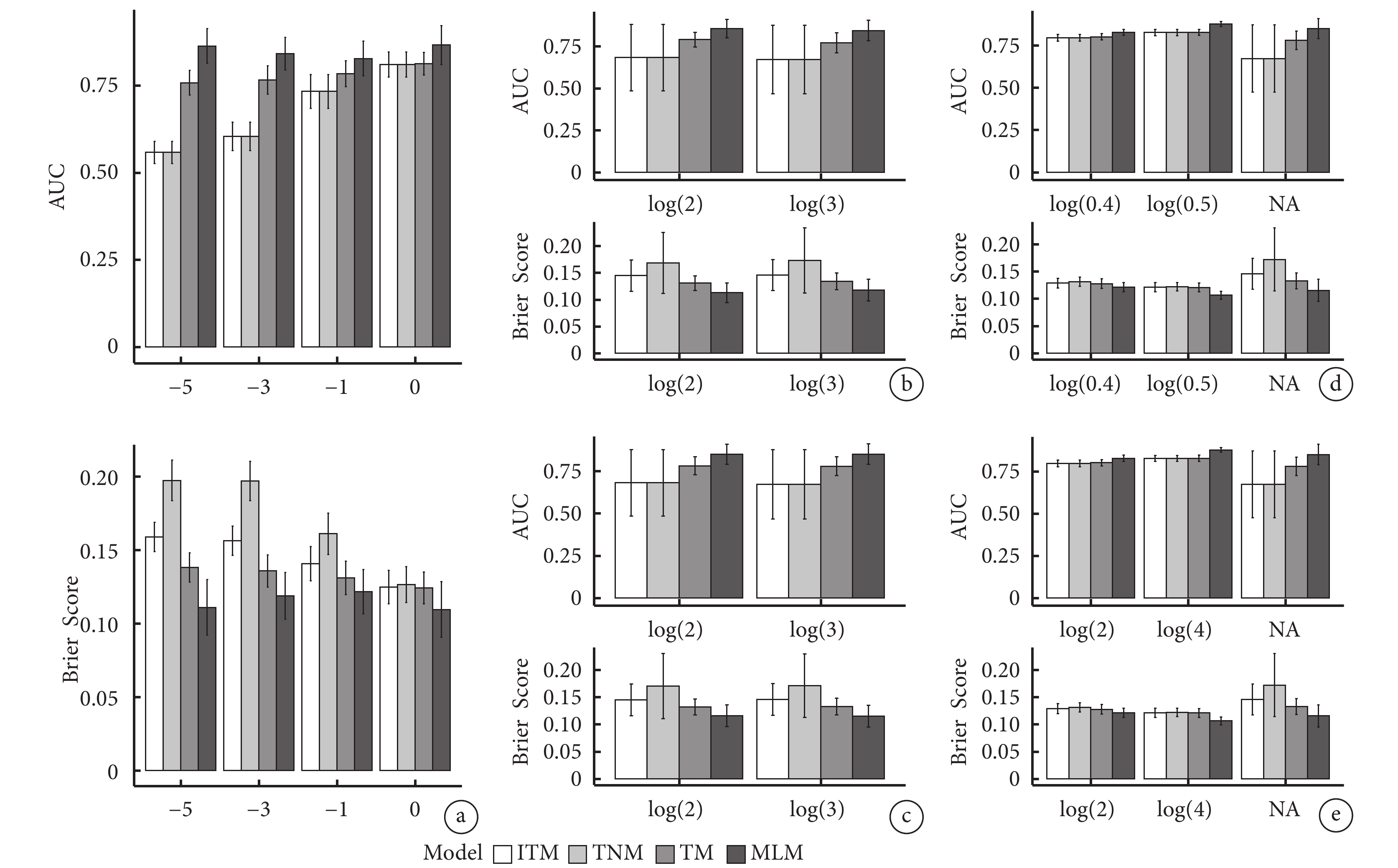
當各參數值固定不變時，不同模型的預測效能存在差異。圖3a顯示，當
取值發生改變，其余參數不變的情況下，MLM模型的AUC最高，TM次之，ITM和TNM模型的AUC最小，其中ITM、TNM、TM的AUC隨著
的增大而增大，而MLM模型未見明顯改變，當
=?5時，MLM模型的AUC最大為0.826～0.866；TNM模型的Brier Score最大，ITM次之，MLM模型的Brier Score最小。
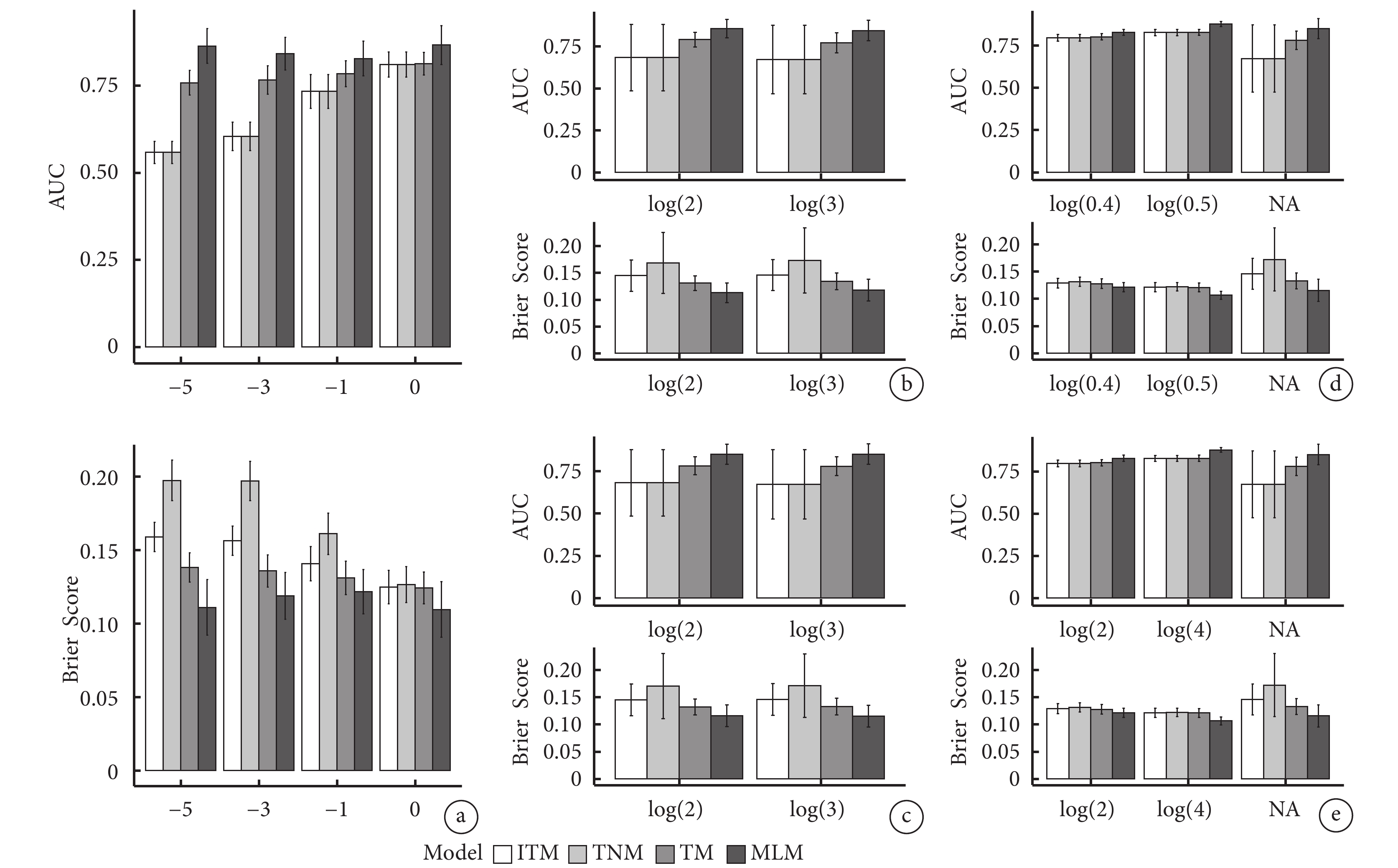圖3
5個隨訪時間點情況下不同模型預測效能比較
圖3b～圖3e分別表示隨著
、
、
、
的取值分別增大，MLM模型的AUC最高，TM次之，ITM和TNM模型的AUC最小，且各模型的AUC隨數值增大未見明顯變化；TNM模型的Brier Score最大，ITM次之，MLM模型的Brier Score最小。
3 結論
本研究探討因果框架下預后預測模型的合理性和邊際結構預測模型的構建方法，采用模擬研究的方法比較邊際結構預測模型與傳統模型的預測效能。基于因果關系構建的預后預測模型具有可解釋性，即可以解釋患者采取某種治療前后不良風險事件概率變化的情況，可以幫助臨床醫師進行臨床決策[25]；外推性，即模型在不同人群中的可移植性較傳統模型強[26]；預測效能，即可以在因果關系基礎上篩選更加合適的預測因子，從而提升模型預測效能[27]。在構建預后預測模型時，要充分考慮因果關系，可以采用有向循環圖、結構方程模型、既往研究等方法選取預測因子，Mitra等[28]認為因果推斷與精準醫療的融合是未來發展的趨勢之一。本研究在Matthew Sperrin等研究的基礎進一步拓展，增加隨訪時間點和模擬情景，通過模擬研究表明，在含有時間依賴性治療變量的隊列中建立預后預測模型，應該著重考慮治療變化情況。根據Nan van Geloven等提出的治療策略，在不同的臨床情景下，ITM、TNM、TM、MLM回答了不同的臨床問題。當患者想了解在不采取任何治療的情況下，自身發生結局事件的概率，采用TNM進行建模，可以得到患者不采取治療情況下發生結局事件的概率；當患者采取的治療方式為單次治療，如腎移植，在患病人群中采用TM進行建模，可以得到患者未來發生結局事件的概率；而通常在觀察性研究中，治療變量往往是多次，且建模人群的治療情況較為復雜，故在構建預后預測模型要考慮治療的復雜性，以期準確預測患者發生結局事件的概率。
針對觀察性研究構建預后預測模型如何處理時間依賴性治療變量這一難點，基于不同隨訪時間點不同情境下的模擬研究，對ITM、TNM、TM、MLM四種預后預測模型的預測效能進行比較，發現當隨訪時間點為2個情況下，MLM的預測效與TM未見明顯差異，當隨訪時間點為5個情況下，MLM的預測效能顯著高于其他模型。本研究對隨訪時間點為3、4個的情況也進行了分析，發現預測性隨著隨訪時間點增加能有所提升。在不同的臨床情景下，模擬研究
=?5，表明治療的療效較為顯著，此時忽略基線后治療變化情況，對于結局的預測效能最差，表明在治療的療效顯著情況下，建立預后預測模型更應該充分考慮基線后治療變化情況。基于多隨訪時間點的隊列構建預后預測模型，若治療變量為時間依賴性變量時，需要考慮基線后治療變化的情況，MLM較于傳統預后預測模型可以提升模型效能和模型的可解釋性。基于MLM，可以對臨床進行有效建議，如解答患者停止治療發生結局事件的概率，或者患者進行5次治療的獲益是否優于4次治療等臨床關注的問題。
本研究有以下幾點不足：第一，本研究提出構建預后預測模型需要考慮因果關系，但是對于高維數據，單純依靠有向循環圖、既往研究等現有方法無法解決預測因子的選擇問題，Mattia Prosperi等[29]認為，機器學習與因果推斷結合是下一步研究的方向；第二，本研究雖然提出隨著隨訪時間點的增加，構建預后預測模型需要著重考慮時間依賴性治療變量，但僅探究到5個隨訪時間點，隨著隨訪時間長期化，是否有必要將所有時間點納入考慮，這是下一步需要研究的重點。
近年來，預測患者預后、預防疾病發生、個體化治療和患者共同參與得到越來越廣泛地認同，此理念的基礎是構建準確的臨床預后預測模型[1]。臨床預后預測模型是指根據患者已知的預測因子，依靠統計方法，計算患者發生某種結局的概率[2-4]。臨床醫師可以根據患者未來發生風險事件的概率進行臨床決策，相關研究表明，良好的預后預測模型給出的預測結果比臨床醫生根據臨床經驗的預測結果更準確[5]。
為了構建預測能力良好的預后預測模型，需要從研究目的、適用人群、預測因子、結局事件、統計方法、模型驗證等多方面進行考慮[6,7]。目前，大部分的研究者在構建預測模型時，納入預測因子時未考慮因果關系，著重考慮的是模型是否具有更好的預測效能。然而在一些特殊情況下，比如存在時間依賴性變量的情況下，不考慮相關因果可能會導致錯誤估計患者不良預后的概率。隨著因果推斷的理論發展和實際應用，越來越多的研究者在構建預測模型時將預測因子的因果關系納入考慮。從預測因子角度考慮，預測模型的預測效能欠佳主要是忽略了某些預測因子，更詳細了解因果關系有助于篩選合適的預測因子，從而提高模型預測效能[8]；從適用人群角度考慮，因果推斷框架下的臨床預后預測模型有助于提高模型在新環境或不同人群中的可移植性[9]；從研究目的角度考慮，因果推斷框架下的臨床預后預測模型預測的結果可以解釋患者采取某種治療前后發生不良預后概率變化的情況[10]。
預后預測模型的主要目的是指導臨床醫生進行臨床決策：在高風險患者中是否采取某種治療措施[11,12]。理想情況下，模型應該反映如果沒有干預，一個人發生危險事件的風險是什么，即“未經治療的風險”[13]，用表示。構建預測模型的數據經常來自于觀察性研究，存在進入隊列時未采取治療的人群在隨訪過程中開始治療，這個現象被稱為“drop-in”[14]，使用傳統方法基于此類數據開發預后預測模型將導致發生錯誤的預測，預測結果為。因此，該模型提供的對未來患者的風險預測會低估未治療結果的真實風險，導致決策錯誤。推而廣之，如果臨床醫生關心患者采用治療后發生風險的概率，用表示。觀察性數據同樣存在進入隊列時采取治療的人群在隨訪過程中停止治療，因此可能存在高估治療的真實效果的問題。針對上述情況，相關研究建議，在開發預后預測模型時，應著重考慮治療的變化情況來提高預測效果[13,15]。然而，迄今為止，如何將治療納入預后預測模型還沒有明確的共識[16]。
基于觀察性研究數據構建臨床預后預測模型通常會采用縱向數據，分析存在時間依賴性變量的縱向數據，通常治療在基線后可能發生改變，如何處理治療的變化值是構建預后預測模型的難點之一[17,18]。例如，在一項關于齊多夫定治療對人類免疫缺陷病毒感染者死亡率影響的研究中，是否進行齊多夫定治療受CD4淋巴細胞計數影響，與此同時，CD4淋巴細胞計數本身受先前齊多夫定治療的影響，在此項研究中，構建人類免疫缺陷病毒感染受試者預后預測模型需考慮治療變量（齊多夫定）如何進行處理[19]。針對上述問題，Matthew Sperrin等提出了忽略治療模型（ignore treatment model，ITM）、基線無治療模型（treatment-na?ve model，TNM）、基線治療模型（treatment model，TM）、邊際結構預后預測模型（MSM-logistic model，MLM）四個方法對治療變量進行處理，通過模擬研究結果發現在兩個隨訪時間點情況下，MLM的預測效能較其余模型有所提升[20]；Nan van Geloven等提出忽略治療策略（ignore treatment strategy）、復合策略（composite strategy）、不治療策略（while untreated strategy）、假設策略（hypothetical strategy），通過實例驗證，發現四種策略可回答患者在不同情況下發生結局事件的可能性，對于指導臨床決策具有重大意義[21]。目前在構建預后預測模型時，對如何處理治療變量尚沒有明確共識，但越來越多的科研工作開始重視預后預測模型中治療變量的處理[13]。在實際的臨床研究中，治療的隨訪時間點往往大于2個，本研究在Matthew Sperrin等研究的基礎上，對隨訪時間點及模擬情景進行了擴展，以期解決多隨訪時間點、多種模擬情景下，時間依賴性治療變量的觀察性研究如何更好構建預后預測模型的問題。
1 方法
1.1 邊際結構模型（marginal structural model，MSM）
觀察性研究中，存在治療隨時間變化的情況，在估計治療效應時，會受到時依性混雜變量的影響。針對傳統統計方法無法解決時依性混雜的問題，Robins提出MSM這一方法[19]。
因果圖可以幫助研究者理解MSM，并有助于預后預測模型的構建[9]。假設存在K個隨訪時間，時間依賴性混雜變量為L，治療變量記為A，風險事件Y為二分類結局。根據上述假設指標，對校正時間依賴性變量前后分別繪制因果圖，見圖1。
圖1
校正時間依賴性變量前后的因果圖
a：校正前；b：校正后。
如圖1a所示，校正前基線治療情況A0受基線協變量L0的影響，第一次隨訪L1受L0與A0影響，A1受A0與L1的影響，以此類推，K個隨訪時間點時，Ak受Ak-1與Lk的影響。針對上述情況，無論是估計治療對于結局的效應還是構建預后預測模型，傳統方法均無法解決時間依賴性治療變量的問題。MSM采用逆概率加權法生成各對象組的偽分布，每組處理后的偽分布都相同，使得治療相對于時間依賴性變量獨立，反映在圖上就是刪除了影響該隨訪時間點治療的弧線，校正后的因果圖如圖1b所示。
1.2 MLM算法實現
在觀察性研究中，暴露變量可能受已觀測協變量（混雜因素）的影響。MSM正是通過構造已觀測協變量與暴露變量的模型，提出校正已觀測混雜偏倚的暴露變量逆概率權重，消除已觀測協變量的影響，從而獲得暴露變量與結局變量真實的因果關聯。
在時點研究中，研究對象i暴露的逆概率權重的計算公式為：
|
其中：表示研究對象的已觀測協變量的觀測值；為研究對象的暴露變量的觀測值；表示研究對象在的情況下，出現的概率。
可通過擬合與的Logistic回歸模型獲得觀察對象接受暴露的概率。估計研究對象接受暴露概率的模型為：
|
該模型可通過逆概率權重控制造成的混雜偏倚，得到對因果關聯的無偏估計。
因果推斷與預測模型結合的要點是用因果關系取代關聯關系進行預測，因此邊際結構預測模型的核心思想是將MSM得出的因果關聯無偏估計帶入預測模型之中。構建邊際結構預測模型采取以下步驟：
首先，計算逆概率權重：
|
其中，表示模型的估計值，表示模型的估計值。
其次，將計算所得的逆概率權重值帶入模型進行擬合：
|
基于上述模型，可以得到類似傳統的Logistic回歸模型，并進行概率預測，得出患者發生不良預后的概率。
2 模擬研究
2.1 模擬概況
設置結局變量Y為二分類變量，處理變量A為二分類變量，時依性協變量X為連續性變量（可用于衡量疾病嚴重程度并作為治療的依據），同時設置4個固定協變量（包括2個連續型協變量、2個二分類協變量）。模擬研究設置2種不同的隨訪時間點（2、5次隨訪），64種不同的治療變量、時依性協變量、結局變量三者之間關系，共128種模擬情境（具體情景請參見附件1）。每個模擬情境模擬1 000次，每次模擬均基于訓練集采用ITM、TNM、TM、MLM4種方法進行建模，并在測試集進行驗證，比較4種方法在不同模擬情境下的表現。采用區分度和校準度對預測效果進行評價。本研究采用R 4.2.2進行數據模擬及統計分析，代碼見附件2。
2.2 模擬設計：數據生成機制
以兩個隨訪時間點為例，基于不同的治療與協變量、協變量與結局、治療與結局關系，生成樣本量為7 000的訓練數據集和3 000的驗證數據集，生成機制如下。
① 模擬生成隨訪時間點t=0時刻的協變量X0，X0~N（0，1）
② 模擬生成隨訪時間點t=0時刻的治療變量，
|
③ 模擬生成隨訪時間點t=1時刻的協變量，
④ 模擬生成隨訪時間點t=1時刻的治療變量，
|
⑤ 模擬生成結局指標，
|
其中，表示時刻，對的影響，本次模擬研究中，的取值范圍［log（2），log（3）］，表示協變量增加采取治療的概率；表示時刻，對的影響，本次模擬研究中，的取值范圍（0，?1，?3，?5），表示治療可以降低協變量的數值；表示時刻，對的影響，本次模擬研究中，的取值范圍［log（2），log（3）］，表示前一次治療對后一次采取治療概率的影響；表示協變量對結局變量的影響，本次模擬研究中，的取值范圍［log（2），log（4）］，表示協變量可以增加發生結局事件的概率；表示治療變量對結局變量的影響，本次模擬研究中，的取值范圍［log（0.4），log（0.5）］，表示治療可以降低發生結局事件的概率。
2.3 模型構建方法及效果評價
4種方法建模：
① ITM：只將基線協變量情況納入預測模型，不考慮治療情況。
|
其中，表示基線協變量情況。
② TNM：選取基線未發生治療的人群作為分析人群。
|
其中，表示基線協變量情況，表示分析人群為基線未采取治療的人群。
③ TM：只將基線治療情況納入預測模型，不考慮治療變化的情況。
|
其中，表示基線協變量情況，表示基線治療情況。
④ MLM：MSM與Logisitic回歸模型結合，將時依性治療變量的基線情況以及隨訪期間的治療變化情況納入預測模型。
|
其中，表示基線協變量情況，表示治療情況，表示第個患者的逆概率權重。
建立樣本量為7 000的訓練集進行建模，所得模型帶入樣本量為3 000的驗證集進行驗證。采用區分度和校準度來評價模型的預測效能。通過設置一定的風險界值，高于界值判斷為發生事件，否則為不發生事件，從而正確區分個體是否會發生結局事件的能力稱為預測模型的區分度。校準度反映模型預測風險與實際發生風險的一致程度[22-24]。評價預測模型區分能力的指標，最常用的是ROC曲線下面積（area under the curve，AUC），AUC越大，說明預測模型的判別區分能力越好。一般認為AUC小于0.6則區分度較差，0.6～0.75認為模型有一定的區分力，大于0.75認為區分能力較好。概率預測的準確程度稱為校準度，是衡量模型預測出的概率和真實結果的差異的一種方式。常用的指標為Brier Score，它被計算為是概率預測相對于測試樣本的均方誤差。Brier Score的范圍是從0到1，分數越接近1校準程度越差，越接近0校準程度越好。
2.4 模擬研究結果
2.4.1 2個隨訪時間點
不同情境下不同模型的預測效能存在差異。圖2a顯示，當取值發生改變，其余參數不變的情況下，ITM和TNM模型的AUC小于TM和MLM模型，ITM和TNM模型的AUC未見明顯差異，TM和MLM模型的AUC未見明顯差異，其中TM和MLM模型的AUC隨著的增大而減小，當=?5時，TM模型的AUC最大為0.889；TNM模型的Brier Score最大，ITM次之，TM和MLM模型的Brier Score最小且未見明顯差異。
圖2
2個隨訪時間點情況下不同模型預測效能比較
圖2b～圖2e分別顯示隨著、、、的取值分別增大，ITM和TNM模型的AUC始終小于TM和MLM模型，且TM和MLM模型的AUC隨數值增大而增大；TNM模型的Brier Score最大，ITM次之，TM和MLM模型的Brier Score最小且未見明顯差異。
2.4.2 5個隨訪時間點
當各參數值固定不變時，不同模型的預測效能存在差異。圖3a顯示，當取值發生改變，其余參數不變的情況下，MLM模型的AUC最高，TM次之，ITM和TNM模型的AUC最小，其中ITM、TNM、TM的AUC隨著的增大而增大，而MLM模型未見明顯改變，當=?5時，MLM模型的AUC最大為0.826～0.866；TNM模型的Brier Score最大，ITM次之，MLM模型的Brier Score最小。
圖3
5個隨訪時間點情況下不同模型預測效能比較
圖3b～圖3e分別表示隨著、、、的取值分別增大，MLM模型的AUC最高，TM次之，ITM和TNM模型的AUC最小，且各模型的AUC隨數值增大未見明顯變化；TNM模型的Brier Score最大，ITM次之，MLM模型的Brier Score最小。
3 結論
本研究探討因果框架下預后預測模型的合理性和邊際結構預測模型的構建方法，采用模擬研究的方法比較邊際結構預測模型與傳統模型的預測效能。基于因果關系構建的預后預測模型具有可解釋性，即可以解釋患者采取某種治療前后不良風險事件概率變化的情況，可以幫助臨床醫師進行臨床決策[25]；外推性，即模型在不同人群中的可移植性較傳統模型強[26]；預測效能，即可以在因果關系基礎上篩選更加合適的預測因子，從而提升模型預測效能[27]。在構建預后預測模型時，要充分考慮因果關系，可以采用有向循環圖、結構方程模型、既往研究等方法選取預測因子，Mitra等[28]認為因果推斷與精準醫療的融合是未來發展的趨勢之一。本研究在Matthew Sperrin等研究的基礎進一步拓展，增加隨訪時間點和模擬情景，通過模擬研究表明，在含有時間依賴性治療變量的隊列中建立預后預測模型，應該著重考慮治療變化情況。根據Nan van Geloven等提出的治療策略，在不同的臨床情景下，ITM、TNM、TM、MLM回答了不同的臨床問題。當患者想了解在不采取任何治療的情況下，自身發生結局事件的概率，采用TNM進行建模，可以得到患者不采取治療情況下發生結局事件的概率；當患者采取的治療方式為單次治療，如腎移植，在患病人群中采用TM進行建模，可以得到患者未來發生結局事件的概率；而通常在觀察性研究中，治療變量往往是多次，且建模人群的治療情況較為復雜，故在構建預后預測模型要考慮治療的復雜性，以期準確預測患者發生結局事件的概率。
針對觀察性研究構建預后預測模型如何處理時間依賴性治療變量這一難點，基于不同隨訪時間點不同情境下的模擬研究，對ITM、TNM、TM、MLM四種預后預測模型的預測效能進行比較，發現當隨訪時間點為2個情況下，MLM的預測效與TM未見明顯差異，當隨訪時間點為5個情況下，MLM的預測效能顯著高于其他模型。本研究對隨訪時間點為3、4個的情況也進行了分析，發現預測性隨著隨訪時間點增加能有所提升。在不同的臨床情景下，模擬研究=?5，表明治療的療效較為顯著，此時忽略基線后治療變化情況，對于結局的預測效能最差，表明在治療的療效顯著情況下，建立預后預測模型更應該充分考慮基線后治療變化情況。基于多隨訪時間點的隊列構建預后預測模型，若治療變量為時間依賴性變量時，需要考慮基線后治療變化的情況，MLM較于傳統預后預測模型可以提升模型效能和模型的可解釋性。基于MLM，可以對臨床進行有效建議，如解答患者停止治療發生結局事件的概率，或者患者進行5次治療的獲益是否優于4次治療等臨床關注的問題。
本研究有以下幾點不足：第一，本研究提出構建預后預測模型需要考慮因果關系，但是對于高維數據，單純依靠有向循環圖、既往研究等現有方法無法解決預測因子的選擇問題，Mattia Prosperi等[29]認為，機器學習與因果推斷結合是下一步研究的方向；第二，本研究雖然提出隨著隨訪時間點的增加，構建預后預測模型需要著重考慮時間依賴性治療變量，但僅探究到5個隨訪時間點，隨著隨訪時間長期化，是否有必要將所有時間點納入考慮，這是下一步需要研究的重點。
