醫學研究的人群中常存在潛在亞人群具有與其他個體不同的特征或變化趨勢，但無法直接識別。潛變量混合模型基于“總體是由有限個亞群混合構成”的思想，可根據后驗概率為個體分配潛在類別組，既適用于橫斷面數據，也可用于縱向數據。本文從統計學角度出發，詳細闡述潛變量混合模型的4種常見方法的基本原理，總結基本建模流程，并結合既往案例和實際數據對其合理應用進行述評。潛變量混合模型是一種靈活的分類工具，可用于識別和分析研究人群中的潛在類別，深入探討影響潛在類別的預測因素或其對結局變量的影響，具有重要的臨床應用價值。
引用本文： 李秉哲, 姜棋競, 盧珍珍, 黃麗紅. 潛變量混合模型原理及其在臨床研究中的應用價值. 中國循證醫學雜志, 2024, 24(10): 1224-1230. doi: 10.7507/1672-2531.202402003 復制
版權信息： ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有，未經授權不得轉載、改編
人類認識世界往往首先將被認識的對象進行分類，分類學變成了人類認識世界的基礎科學。在醫學研究中，常存在潛在的亞人群在臨床癥狀、行為模式等方面具有相似的特征或變化趨勢。在橫斷面數據中表現為亞人群內部變量值接近，在縱向數據中表現為亞人群內部變量隨時間變化趨勢相似。為了能夠更精確識別個體特征的異質性和潛在亞人群，可采用潛變量混合模型（latent variable mixture modeling，LVMM）的分析方法。
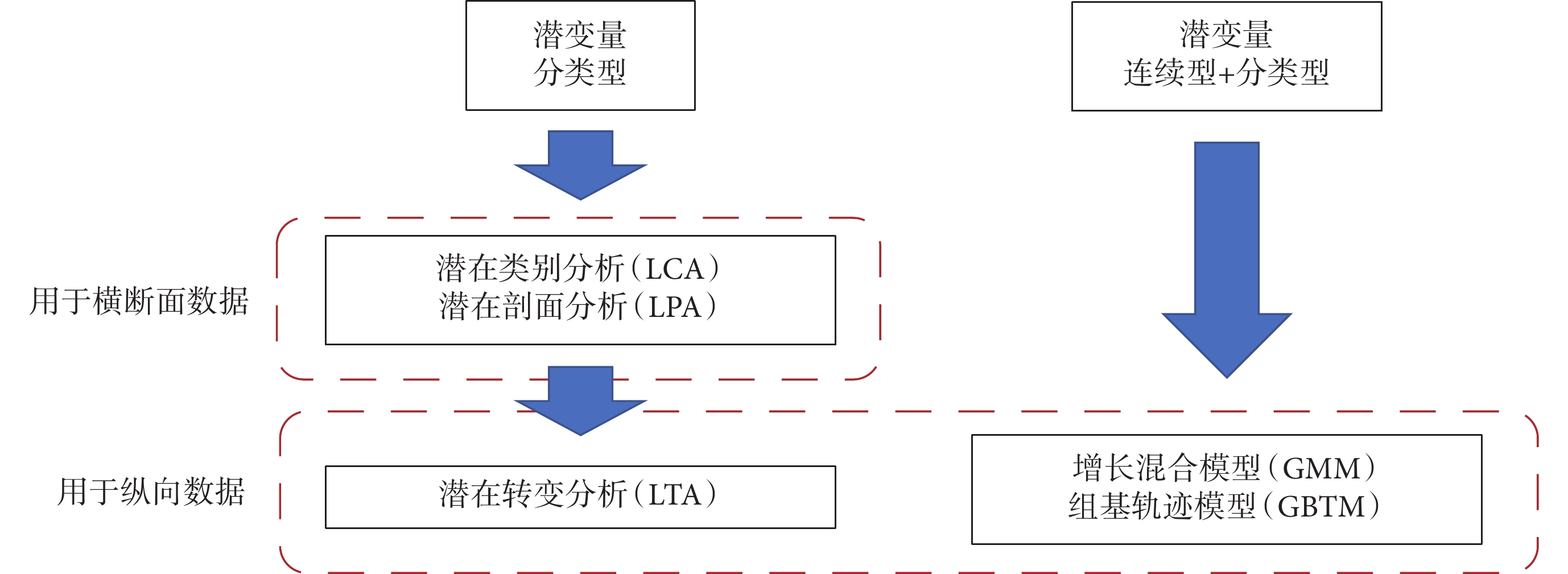
相較于傳統方法，LVMM基于個體數據，可清晰識別個體間的相似性和差異性，并據此將人群分為若干潛在亞人群，每個亞人群具有獨特的變量/趨勢特征[1]。其“潛變量”指那些未測量的，需要從已測量變量中推斷的變量，可分為連續型和分類型；“混合”即變量分布是由有限數量的亞人群混合而成，這也是LVMM的基本假設[2]。用于區分個體屬于哪個亞人群的分組變量稱為分類型潛變量。用于反映指標變量隨時間變化動態過程的變量稱為連續型潛變量，例如決定曲線變化趨勢的截距和斜率。2001年，Muthen[2]提出了LVMM框架，根據潛變量和數據的類型對建模方法進行分類（圖1）。
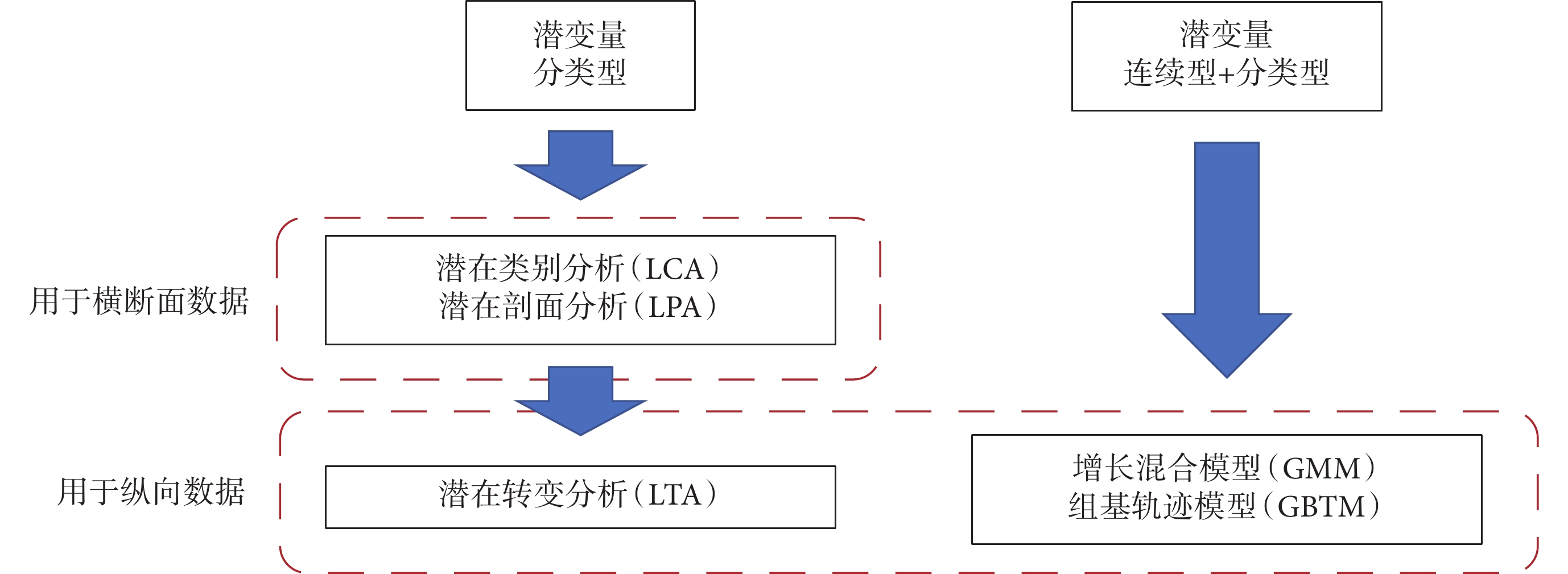圖1
潛變量混合模型框架
潛變量混合模型最先應用于心理和社會學領域，該領域通常研究個體行為的縱向發展軌跡，即人格發展或社會行為如何隨時間推移而變化。例如：Nagin等[3]研究青少年的攻擊性行為隨年齡的變化，Jackson等[4]研究酒精依賴情況隨時間的變化模式。近年來，此類方法也開始應用于醫學研究領域。本研究將詳細介紹常見LVMM方法的基本原理，總結基本建模流程，并結合實際案例對LVMM在醫學領域的應用進行解析。
1 LVMM的原理及常見類型
1.1 用于縱向重復測量數據的LVMM
1.1.1 模型基礎
潛在增長曲線模型（latent growth curve modeling，LGCM）是用于縱向數據的潛變量混合模型的理論基礎，用于研究個體觀測指標的動態變化趨勢。可表示為：
 |
 |
 |
y代表個體i在t個時間點的觀測值向量，連續型潛變量 α 和 β 分別代表個體i的潛在截距和潛在斜率。
和 
分別表示全部個體平均初始狀態和平均增長率，
和 
分別代表個體初始狀態和增長率的變異程度；
表示個體i在t時刻的殘差項。潛變量 α 和β 也稱為生長因子，通過因子載荷向量 
和 
與觀測指標相聯系。通常截距因子的載荷向量固定為1，表示每次測量的截距不變；斜率因子的載荷向量代表時間效應，可設定具體值，也可估算，不同的設定表示不同的時間函數或增長類型，若為等間距則代表線性變化。
在LGCM中，雖然允許個體間存在變異，但該方法假設所有個體來自同一人群，得到的結果是單個人群的平均軌跡，無法識別潛在亞人群[5]。為解決這一局限性，在LGCM的基礎上引入潛在類別的概念，衍生了用于重復測量數據的潛變量混合模型增長混合模型（growth mixture modeling，GMM）和組基軌跡模型（group-based trajectory modeling，GBTM）。
1.1.2 GMM
GMM是一種有限的混合參數模型。該模型假設總人群由有限數量的亞人群組成，同一亞人群中存在個體變異。研究目的是識別群體中某變量具有不同發展軌跡的亞群并描述亞群發展軌跡，可用于數值變量和分類變量。GMM根據后驗概率將個體分入不同的潛在類別，通過LGCM分別估計每個潛在類別的發展軌跡。
GMM的模型可表示如下：
 |
 |
 |
GMM在LGCM的基礎上引入了分類型潛變量c，
代表個體分配到潛在類別k的概率；當估計的潛分類數量等于1時，GMM簡化為LGCM。
使用GMM需要滿足模型假設，且變量具有至少三個時間點的測量值，個體的測量時間點可以相同或不同。其需要估計的參數較多，能夠較為準確地估計和識別分類。但當樣本量較小，或類間差異不夠明顯時，易出現收斂困難的問題[6]。且結果解釋相對復雜，因此在實際應用中，常常使用簡化的GBTM。
1.1.3 GBTM
GBTM也被稱作潛類別增長分析（latent class growth modeling，LCGM），是一種有限的混合半參數模型。GBTM假設人群是離散分布的，在人群中存在亞人群，但亞人群內部個體同質。GBTM的研究目的與使用條件與GMM相同，但在估計時限制所有時間點和所有類別的殘差方差相同[7]。
其與GMM的主要區別在于
和 
中無 
項，即單個潛在類別內所有個體具有相同的平均增長曲線。本質上，GBTM是GMM的一種特定情況下的簡化，優勢是可以簡化估計，其出現是為了平衡模型的復雜性和可理解性，便于識別和總結縱向數據中的復雜模式。Feldman等[8]從統計指標和可解釋性等方面比較了不同模型應用于青少年飲酒數據的建模結果，發現GBTM在模型擬合和可解釋性上要優于GMM。
1.2 用于橫斷面數據的LVMM
潛在類別分析（latent class analysis，LCA）和潛在剖面分析（latent profile analysis，LPA）是用于橫斷面數據分析的半參數模型。其假設存在潛在未觀察到的分類變量，根據一組預先指定的響應變量的整體特征將人群劃分為潛在亞人群。其研究目的為識別人群中的潛在類別，并描述亞人群響應變量的分布特征[9, 10]。LPA與LCA本質相同，但LCA的響應變量是一組分類變量，潛在類別間響應概率不同，而LPA的響應變量是一組連續變量，潛在類別間均值不同。
LCA模型可用如下公式表示：
 |
式中u代表響應變量；c代表潛在類別，共有k個分類。該模型基于個體對一組分類變量響應概率的相似性來識別亞人群。LCA中也可以納入協變量來探討其對個體歸屬于某個潛在類別概率的影響。
此外，對于重復測量數據，可使用潛在轉變分析（latent transition analysis，LTA）分析個體從一個時間點的潛在類別到下一個時間點潛在類別的轉換概率[11]。LTA是潛在類別分析的縱向擴展，目的在于研究LCA中個體所屬潛在類別隨時間推移的變化情況。該模型需要人群在多個時間點進行LCA的結果，并描述個體從前一個時間過渡到下一個時間的關于響應變量響應概率的過渡概率矩陣。通過每個時間的潛在類別歸屬和時間點之間響應概率的過渡概率矩陣共同描述個體潛在類別變化情況[12]。
以上方法的應用場景、優勢、局限性及可用軟件如表1所示。
表1
潛變量混合模型方法的優勢與局限性
2 LVMM建模框架
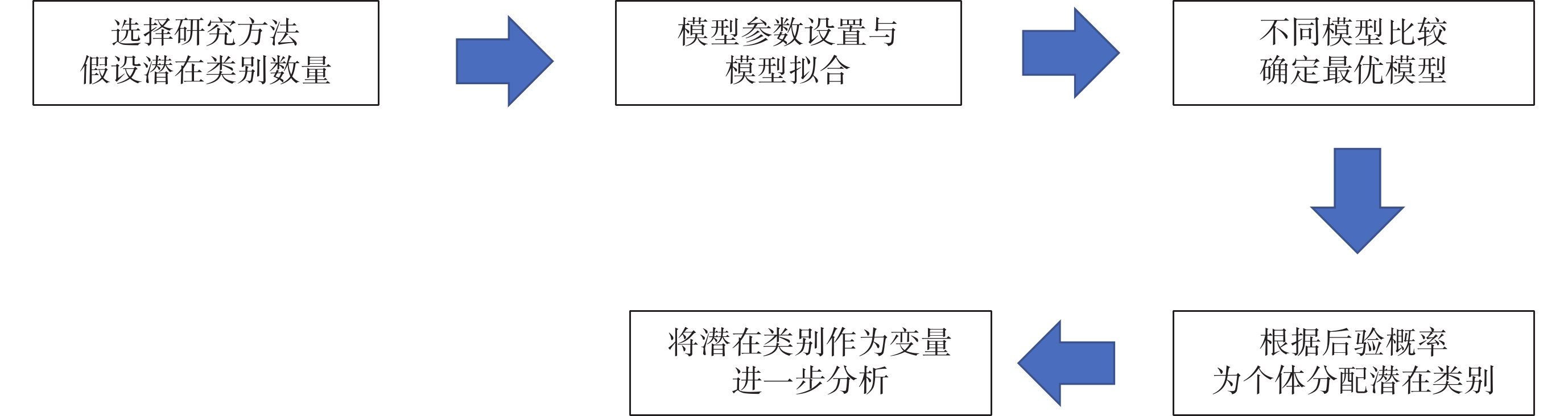
LVMM的建模流程如圖2示。關鍵決策點在于模型比較和模型選擇。
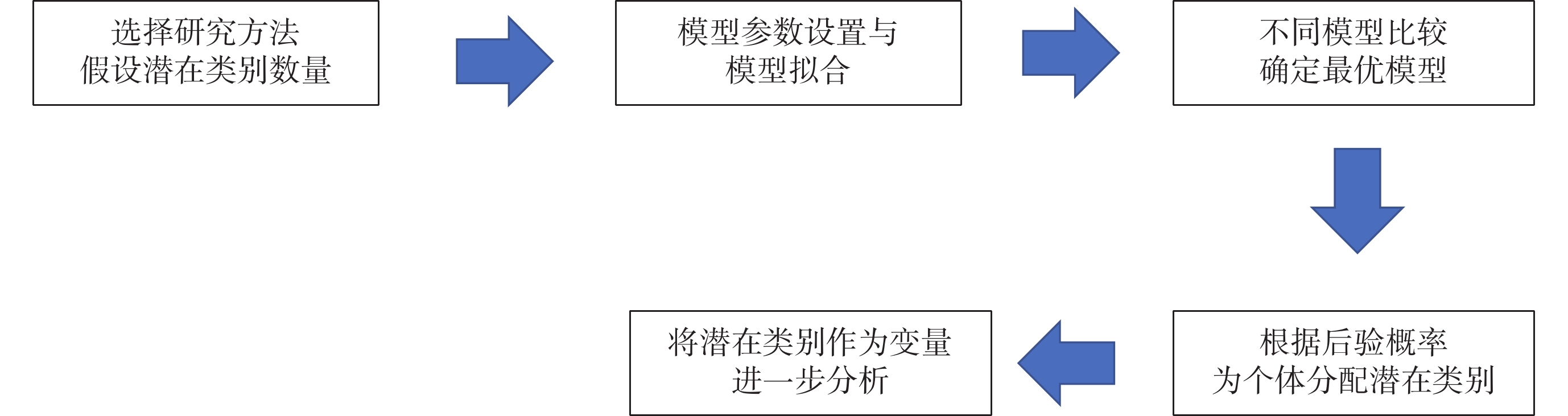圖2
潛變量混合模型建模流程
進行LVMM分析，首先需要根據研究問題和數據類型選擇分析方法，并根據先驗知識或描述性分析假設人群特征的潛在類別數量。橫斷面數據采用LCA等識別變量分布特征的潛在類別方法，縱向數據采用GMM、GBTM等識別變化軌跡潛在類別的方法。潛在類別數量的確定需要結合數據情況和文獻報道。此外，當數據真實來自K個類別的混合時需要預設多于K個類別來提取數據的主要特征[13]，通常初始設定1～7個潛在類別[14]。
在用于縱向數據的LVMM中，建模還需要考慮時間多項式的設置和方差結構的選擇。為了更好地擬合隨時間變化的軌跡，除最常用的線性關系外，還可以根據數據情況加入時間的二次項或三次項，以提高模型擬合效果。方差結構的設置需要權衡模型反映真實情況的能力、擬合難度和可解釋性。常見方差結構包括時間點和/或類別之間具有不同協方差結構，或約束殘差方差在時間點和/或類別之間相同。如果復雜的協方差結構模型擬合過程中出現收斂問題，可簡化為跨類同方差結構進行擬合[15]，但不適當的跨類相同方差結構更容易導致錯誤的分類結果[7]。通常對具有不同潛在類別組數、時間多項式設置和方差結構的模型分別估計，然后根據臨床可解釋性、簡約性和模型擬合優度指標進行綜合選擇。
模型選擇過程中最關鍵的是客觀統計學指標和主觀可解釋性的綜合權衡[14]。模型選擇需要同時考慮以下內容：① 簡約可解釋性和區分度：選擇軌跡組數量，要首先考慮該分組數量下的每個軌跡組是否具有臨床意義的可解釋性。同時，在比較k組和k+1組的選擇上，若多出來的一組與前面幾組區分度差，則不建議選擇k+1的組合。② 模型評價指標：評估模型擬合最常用的標準包括貝葉斯信息標準（Bayesian information criterion，BIC），Akaike信息準則（Akaike information criterion，AIC），羅-門德爾-魯賓似然比檢驗（Lo-Mendell-Rubin likelihood ratio test，LMR-LRT），自舉似然比檢驗（bootstrap likelihood ratio test，BLRT）和熵[16]。AIC和BIC值越低，表明模型擬合效果越好。LMR-LRT和BLRT檢驗比較了k類和k+1類模型之間的改進，并提供P值。熵是評價類別劃分準確性的指標，其范圍是0～1，熵值>0.8表明分類的可信度高，并且潛在類別之間有足夠的區分度[17]。在選擇評價指標相似的模型時，具有較高熵的模型更受青睞。基于信息準則的BIC和基于模型比較的BLRT通常是優選指標[16]。然而，有時由于過擬合，BIC值可能會隨著更多的組和參數的添加而減少，因此也需要考慮BIC值的減少幅度。③ 潛在類別成員平均后驗概率：各潛在類別所有個體平均最大后驗分配概率大于70%是可接受的[18]。④ 為了防止分組是由于過擬合或偶然產生的，同時也使分組具有實際意義，通常軌跡組成員數量要大于總人群的5%。
根據選擇的最優模型，將每個個體分入后驗概率最高的潛在類別作為個體分組結果。最終獲得潛在類別分組后通常有三種應用場景：① 對不同潛在類別組的發展軌跡或變量響應特征進行描述和比較；② 以潛在類別作為因變量，探討影響不同發展軌跡和變量響應模式的相關因素；③ 以潛在類別作為自變量，探討不同發展軌跡和變量響應模式對某個結局變量的影響。
3 應用案例
上述各類LVMM既往已有經典案例。Loupy等[19]利用法國國家登記中心和歐洲移植登記中心的1 301人10年隨訪隊列，使用GMM識別了四個同種異體心臟移植血管病變的潛在發展軌跡組，并進一步識別了六個對發展軌跡的早期預測因子。Zhang等[20]基于NHANES和UK Biobank數據庫，采用LCA方法，將家庭收入水平、職業、教育水平和健康保險歸納為了高、中、低社會經濟地位的三個潛在類別，并探討不同社會經濟地位對全因死亡率及心血管疾病死亡率和發病率的影響。Ni等[21]利用中國健康與退休縱向研究（CHARLS）的縱向數據，通過LCA識別了三個抑郁癥亞組并進一步通過LTA方法發現輕度抑郁和嚴重抑郁的個體均有較大概率轉變為缺乏積極情感的狀態。
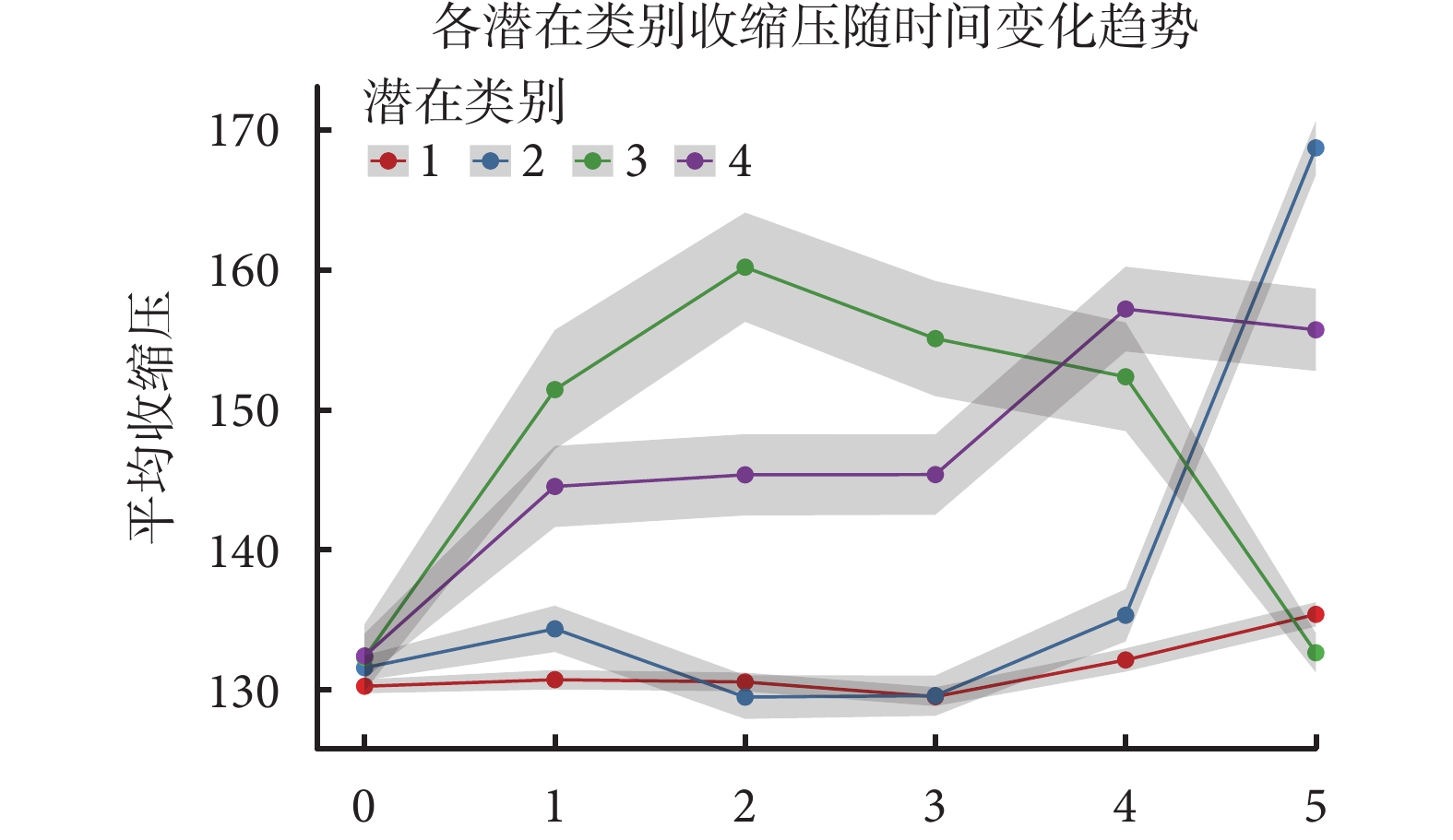
筆者以研究收縮壓逐年變化趨勢的潛變量混合模型為實際案例，展示模型的選擇過程和潛在類別的識別。案例數據來自社區的糖尿病居民自然人群隊列，包含1 000位60～75歲居民6年內每一年的血壓測量值。該人群6次測量的平均收縮壓值分別為131/134/134/133/137/143 mmHg，整體呈現穩定趨勢，在后兩年略有增加。但發現其中部分個體存在不同的收縮壓變化趨勢，因此采用用于重復測量數據的LVMM方法識別不同收縮壓發展軌跡并描述變化趨勢。同時采用GMM和GBTM建模，時間函數分別考慮線性、二次、三次函數，潛在類別數考慮1～5。模型的選擇根據似然值、AIC、BIC、熵和最小類別人數占比幾個指標進行綜合決策。GMM三次函數的4類建模具有最高的似然比，最低的AIC、BIC和可接受的熵值，且平均后驗概率均大于0.7，因此被選為最合適模型（表2）。最終所得收縮壓軌跡如圖3所示，四個潛在類別的軌跡組可以分別描述為“穩定組”“輕微下降后快速增加組”“先增加后下降組”“快速增加組”。
表2
模型評價指標比較
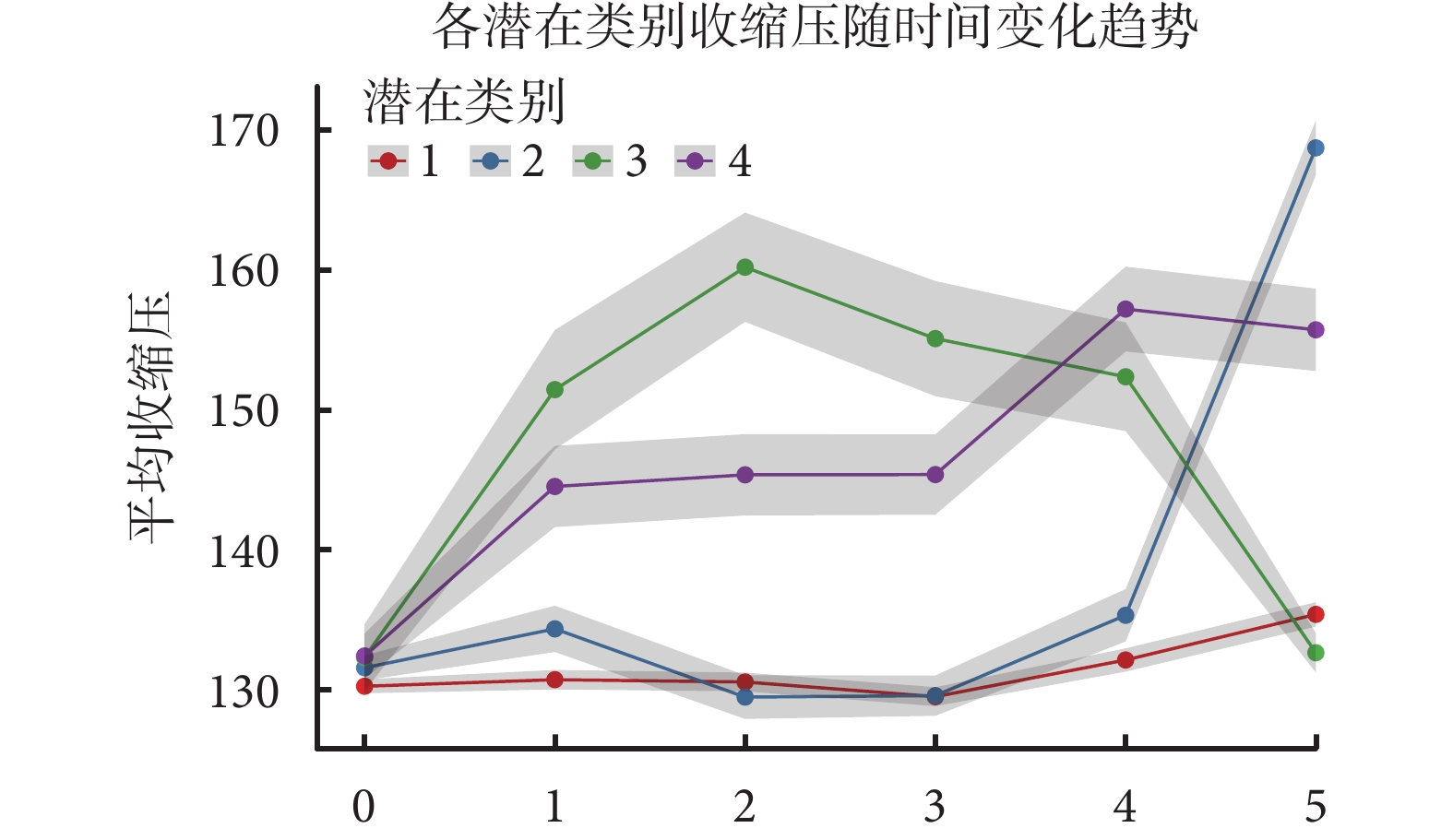圖3
四個潛在類別人群收縮壓在六次隨訪中的動態變化軌跡
4 討論
LVMM在醫學研究領域應用越發廣泛。該方法為橫斷面數據的分析提供了新的角度，且在縱向數據的處理上更具優勢，可從縱向數據中識別不同的發展軌跡并深入剖析其中個體發展情況。
使用LVMM分析也存在局限性。一方面是需注意前提假設：必須預先假設發展中不同的軌跡的存在，而不能檢驗它們的存在[22]。也需要對協方差結構做出假設，當假設與實際不符時會導致軌跡和方差參數的估計出現偏差以及收斂問題[23]。另一方面對模型的選擇和解釋需要謹慎，潛在變量分析往往需要構建多個模型并最終從中選擇一個合適的模型。雖然有客觀的統計學指標作為支撐，但仍需要結合主觀判斷來進行選擇，可能出現不同研究者對模型選擇意見的不一致。
除前文所述外，GMM和GBTM模型也可基于廣義線性混合模型的理論，通過鏈接函數將該模型的應用范圍拓展，不限于連續性的、具有高斯隨機偏差的縱向變量，也可用于如二元數據、泊松分布數據等。鏈接函數可選logit變換、泊松變換、貝塔分布的累積分布函數、具有n個節點的樣條函數來處理不同分布類型的數據[24]。Proust-Lima等[25]還提出了一種聯合建模方法處理生存資料的非隨機缺失數據。此外，在醫學研究中，有時會遇到關注多個縱向變量間的關聯，Proust等[25]提出了多軌跡聯合建模的方法，該方法假設多個變量隨時間變化的軌跡受一個共同的潛在過程影響，根據所有感興趣的變量來定義一個共同軌跡，并通過鏈接函數將多個結果關聯。
綜上所述，LVMM具有廣泛的應用范圍，且已在多個研究領域有成功的應用。隨著人們對醫療大數據認識的不斷深入，統計理論和軟件計算能力的提升，LVMM將在越來越多的醫學數據分析中被采用，為研究者提供科學合理的研究信息，具有重要的臨床應用價值。
聲明 所有作者均聲明無利益沖突。
人類認識世界往往首先將被認識的對象進行分類，分類學變成了人類認識世界的基礎科學。在醫學研究中，常存在潛在的亞人群在臨床癥狀、行為模式等方面具有相似的特征或變化趨勢。在橫斷面數據中表現為亞人群內部變量值接近，在縱向數據中表現為亞人群內部變量隨時間變化趨勢相似。為了能夠更精確識別個體特征的異質性和潛在亞人群，可采用潛變量混合模型（latent variable mixture modeling，LVMM）的分析方法。
相較于傳統方法，LVMM基于個體數據，可清晰識別個體間的相似性和差異性，并據此將人群分為若干潛在亞人群，每個亞人群具有獨特的變量/趨勢特征[1]。其“潛變量”指那些未測量的，需要從已測量變量中推斷的變量，可分為連續型和分類型；“混合”即變量分布是由有限數量的亞人群混合而成，這也是LVMM的基本假設[2]。用于區分個體屬于哪個亞人群的分組變量稱為分類型潛變量。用于反映指標變量隨時間變化動態過程的變量稱為連續型潛變量，例如決定曲線變化趨勢的截距和斜率。2001年，Muthen[2]提出了LVMM框架，根據潛變量和數據的類型對建模方法進行分類（圖1）。
圖1
潛變量混合模型框架
潛變量混合模型最先應用于心理和社會學領域，該領域通常研究個體行為的縱向發展軌跡，即人格發展或社會行為如何隨時間推移而變化。例如：Nagin等[3]研究青少年的攻擊性行為隨年齡的變化，Jackson等[4]研究酒精依賴情況隨時間的變化模式。近年來，此類方法也開始應用于醫學研究領域。本研究將詳細介紹常見LVMM方法的基本原理，總結基本建模流程，并結合實際案例對LVMM在醫學領域的應用進行解析。
1 LVMM的原理及常見類型
1.1 用于縱向重復測量數據的LVMM
1.1.1 模型基礎
潛在增長曲線模型（latent growth curve modeling，LGCM）是用于縱向數據的潛變量混合模型的理論基礎，用于研究個體觀測指標的動態變化趨勢。可表示為：
|
|
|
y代表個體i在t個時間點的觀測值向量，連續型潛變量 α 和 β 分別代表個體i的潛在截距和潛在斜率。 和 分別表示全部個體平均初始狀態和平均增長率， 和 分別代表個體初始狀態和增長率的變異程度； 表示個體i在t時刻的殘差項。潛變量 α 和β 也稱為生長因子，通過因子載荷向量 和 與觀測指標相聯系。通常截距因子的載荷向量固定為1，表示每次測量的截距不變；斜率因子的載荷向量代表時間效應，可設定具體值，也可估算，不同的設定表示不同的時間函數或增長類型，若為等間距則代表線性變化。
在LGCM中，雖然允許個體間存在變異，但該方法假設所有個體來自同一人群，得到的結果是單個人群的平均軌跡，無法識別潛在亞人群[5]。為解決這一局限性，在LGCM的基礎上引入潛在類別的概念，衍生了用于重復測量數據的潛變量混合模型增長混合模型（growth mixture modeling，GMM）和組基軌跡模型（group-based trajectory modeling，GBTM）。
1.1.2 GMM
GMM是一種有限的混合參數模型。該模型假設總人群由有限數量的亞人群組成，同一亞人群中存在個體變異。研究目的是識別群體中某變量具有不同發展軌跡的亞群并描述亞群發展軌跡，可用于數值變量和分類變量。GMM根據后驗概率將個體分入不同的潛在類別，通過LGCM分別估計每個潛在類別的發展軌跡。
GMM的模型可表示如下：
|
|
|
GMM在LGCM的基礎上引入了分類型潛變量c，代表個體分配到潛在類別k的概率；當估計的潛分類數量等于1時，GMM簡化為LGCM。
使用GMM需要滿足模型假設，且變量具有至少三個時間點的測量值，個體的測量時間點可以相同或不同。其需要估計的參數較多，能夠較為準確地估計和識別分類。但當樣本量較小，或類間差異不夠明顯時，易出現收斂困難的問題[6]。且結果解釋相對復雜，因此在實際應用中，常常使用簡化的GBTM。
1.1.3 GBTM
GBTM也被稱作潛類別增長分析（latent class growth modeling，LCGM），是一種有限的混合半參數模型。GBTM假設人群是離散分布的，在人群中存在亞人群，但亞人群內部個體同質。GBTM的研究目的與使用條件與GMM相同，但在估計時限制所有時間點和所有類別的殘差方差相同[7]。
其與GMM的主要區別在于 和 中無 項，即單個潛在類別內所有個體具有相同的平均增長曲線。本質上，GBTM是GMM的一種特定情況下的簡化，優勢是可以簡化估計，其出現是為了平衡模型的復雜性和可理解性，便于識別和總結縱向數據中的復雜模式。Feldman等[8]從統計指標和可解釋性等方面比較了不同模型應用于青少年飲酒數據的建模結果，發現GBTM在模型擬合和可解釋性上要優于GMM。
1.2 用于橫斷面數據的LVMM
潛在類別分析（latent class analysis，LCA）和潛在剖面分析（latent profile analysis，LPA）是用于橫斷面數據分析的半參數模型。其假設存在潛在未觀察到的分類變量，根據一組預先指定的響應變量的整體特征將人群劃分為潛在亞人群。其研究目的為識別人群中的潛在類別，并描述亞人群響應變量的分布特征[9, 10]。LPA與LCA本質相同，但LCA的響應變量是一組分類變量，潛在類別間響應概率不同，而LPA的響應變量是一組連續變量，潛在類別間均值不同。
LCA模型可用如下公式表示：
|
式中u代表響應變量；c代表潛在類別，共有k個分類。該模型基于個體對一組分類變量響應概率的相似性來識別亞人群。LCA中也可以納入協變量來探討其對個體歸屬于某個潛在類別概率的影響。
此外，對于重復測量數據，可使用潛在轉變分析（latent transition analysis，LTA）分析個體從一個時間點的潛在類別到下一個時間點潛在類別的轉換概率[11]。LTA是潛在類別分析的縱向擴展，目的在于研究LCA中個體所屬潛在類別隨時間推移的變化情況。該模型需要人群在多個時間點進行LCA的結果，并描述個體從前一個時間過渡到下一個時間的關于響應變量響應概率的過渡概率矩陣。通過每個時間的潛在類別歸屬和時間點之間響應概率的過渡概率矩陣共同描述個體潛在類別變化情況[12]。
以上方法的應用場景、優勢、局限性及可用軟件如表1所示。
表1
潛變量混合模型方法的優勢與局限性
2 LVMM建模框架
LVMM的建模流程如圖2示。關鍵決策點在于模型比較和模型選擇。
圖2
潛變量混合模型建模流程
進行LVMM分析，首先需要根據研究問題和數據類型選擇分析方法，并根據先驗知識或描述性分析假設人群特征的潛在類別數量。橫斷面數據采用LCA等識別變量分布特征的潛在類別方法，縱向數據采用GMM、GBTM等識別變化軌跡潛在類別的方法。潛在類別數量的確定需要結合數據情況和文獻報道。此外，當數據真實來自K個類別的混合時需要預設多于K個類別來提取數據的主要特征[13]，通常初始設定1～7個潛在類別[14]。
在用于縱向數據的LVMM中，建模還需要考慮時間多項式的設置和方差結構的選擇。為了更好地擬合隨時間變化的軌跡，除最常用的線性關系外，還可以根據數據情況加入時間的二次項或三次項，以提高模型擬合效果。方差結構的設置需要權衡模型反映真實情況的能力、擬合難度和可解釋性。常見方差結構包括時間點和/或類別之間具有不同協方差結構，或約束殘差方差在時間點和/或類別之間相同。如果復雜的協方差結構模型擬合過程中出現收斂問題，可簡化為跨類同方差結構進行擬合[15]，但不適當的跨類相同方差結構更容易導致錯誤的分類結果[7]。通常對具有不同潛在類別組數、時間多項式設置和方差結構的模型分別估計，然后根據臨床可解釋性、簡約性和模型擬合優度指標進行綜合選擇。
模型選擇過程中最關鍵的是客觀統計學指標和主觀可解釋性的綜合權衡[14]。模型選擇需要同時考慮以下內容：① 簡約可解釋性和區分度：選擇軌跡組數量，要首先考慮該分組數量下的每個軌跡組是否具有臨床意義的可解釋性。同時，在比較k組和k+1組的選擇上，若多出來的一組與前面幾組區分度差，則不建議選擇k+1的組合。② 模型評價指標：評估模型擬合最常用的標準包括貝葉斯信息標準（Bayesian information criterion，BIC），Akaike信息準則（Akaike information criterion，AIC），羅-門德爾-魯賓似然比檢驗（Lo-Mendell-Rubin likelihood ratio test，LMR-LRT），自舉似然比檢驗（bootstrap likelihood ratio test，BLRT）和熵[16]。AIC和BIC值越低，表明模型擬合效果越好。LMR-LRT和BLRT檢驗比較了k類和k+1類模型之間的改進，并提供P值。熵是評價類別劃分準確性的指標，其范圍是0～1，熵值>0.8表明分類的可信度高，并且潛在類別之間有足夠的區分度[17]。在選擇評價指標相似的模型時，具有較高熵的模型更受青睞。基于信息準則的BIC和基于模型比較的BLRT通常是優選指標[16]。然而，有時由于過擬合，BIC值可能會隨著更多的組和參數的添加而減少，因此也需要考慮BIC值的減少幅度。③ 潛在類別成員平均后驗概率：各潛在類別所有個體平均最大后驗分配概率大于70%是可接受的[18]。④ 為了防止分組是由于過擬合或偶然產生的，同時也使分組具有實際意義，通常軌跡組成員數量要大于總人群的5%。
根據選擇的最優模型，將每個個體分入后驗概率最高的潛在類別作為個體分組結果。最終獲得潛在類別分組后通常有三種應用場景：① 對不同潛在類別組的發展軌跡或變量響應特征進行描述和比較；② 以潛在類別作為因變量，探討影響不同發展軌跡和變量響應模式的相關因素；③ 以潛在類別作為自變量，探討不同發展軌跡和變量響應模式對某個結局變量的影響。
3 應用案例
上述各類LVMM既往已有經典案例。Loupy等[19]利用法國國家登記中心和歐洲移植登記中心的1 301人10年隨訪隊列，使用GMM識別了四個同種異體心臟移植血管病變的潛在發展軌跡組，并進一步識別了六個對發展軌跡的早期預測因子。Zhang等[20]基于NHANES和UK Biobank數據庫，采用LCA方法，將家庭收入水平、職業、教育水平和健康保險歸納為了高、中、低社會經濟地位的三個潛在類別，并探討不同社會經濟地位對全因死亡率及心血管疾病死亡率和發病率的影響。Ni等[21]利用中國健康與退休縱向研究（CHARLS）的縱向數據，通過LCA識別了三個抑郁癥亞組并進一步通過LTA方法發現輕度抑郁和嚴重抑郁的個體均有較大概率轉變為缺乏積極情感的狀態。
筆者以研究收縮壓逐年變化趨勢的潛變量混合模型為實際案例，展示模型的選擇過程和潛在類別的識別。案例數據來自社區的糖尿病居民自然人群隊列，包含1 000位60～75歲居民6年內每一年的血壓測量值。該人群6次測量的平均收縮壓值分別為131/134/134/133/137/143 mmHg，整體呈現穩定趨勢，在后兩年略有增加。但發現其中部分個體存在不同的收縮壓變化趨勢，因此采用用于重復測量數據的LVMM方法識別不同收縮壓發展軌跡并描述變化趨勢。同時采用GMM和GBTM建模，時間函數分別考慮線性、二次、三次函數，潛在類別數考慮1～5。模型的選擇根據似然值、AIC、BIC、熵和最小類別人數占比幾個指標進行綜合決策。GMM三次函數的4類建模具有最高的似然比，最低的AIC、BIC和可接受的熵值，且平均后驗概率均大于0.7，因此被選為最合適模型（表2）。最終所得收縮壓軌跡如圖3所示，四個潛在類別的軌跡組可以分別描述為“穩定組”“輕微下降后快速增加組”“先增加后下降組”“快速增加組”。
表2
模型評價指標比較
圖3
四個潛在類別人群收縮壓在六次隨訪中的動態變化軌跡
4 討論
LVMM在醫學研究領域應用越發廣泛。該方法為橫斷面數據的分析提供了新的角度，且在縱向數據的處理上更具優勢，可從縱向數據中識別不同的發展軌跡并深入剖析其中個體發展情況。
使用LVMM分析也存在局限性。一方面是需注意前提假設：必須預先假設發展中不同的軌跡的存在，而不能檢驗它們的存在[22]。也需要對協方差結構做出假設，當假設與實際不符時會導致軌跡和方差參數的估計出現偏差以及收斂問題[23]。另一方面對模型的選擇和解釋需要謹慎，潛在變量分析往往需要構建多個模型并最終從中選擇一個合適的模型。雖然有客觀的統計學指標作為支撐，但仍需要結合主觀判斷來進行選擇，可能出現不同研究者對模型選擇意見的不一致。
除前文所述外，GMM和GBTM模型也可基于廣義線性混合模型的理論，通過鏈接函數將該模型的應用范圍拓展，不限于連續性的、具有高斯隨機偏差的縱向變量，也可用于如二元數據、泊松分布數據等。鏈接函數可選logit變換、泊松變換、貝塔分布的累積分布函數、具有n個節點的樣條函數來處理不同分布類型的數據[24]。Proust-Lima等[25]還提出了一種聯合建模方法處理生存資料的非隨機缺失數據。此外，在醫學研究中，有時會遇到關注多個縱向變量間的關聯，Proust等[25]提出了多軌跡聯合建模的方法，該方法假設多個變量隨時間變化的軌跡受一個共同的潛在過程影響，根據所有感興趣的變量來定義一個共同軌跡，并通過鏈接函數將多個結果關聯。
綜上所述，LVMM具有廣泛的應用范圍，且已在多個研究領域有成功的應用。隨著人們對醫療大數據認識的不斷深入，統計理論和軟件計算能力的提升，LVMM將在越來越多的醫學數據分析中被采用，為研究者提供科學合理的研究信息，具有重要的臨床應用價值。
聲明 所有作者均聲明無利益沖突。
