本研究介紹了貝葉斯網絡個體化風險評估模型的構建方法,使用實例與傳統基于回歸的Logistic模型進行對比,對該模型的性能進行評價,并使用R語言進行演示說明,為研究者理解與應用貝葉斯網絡模型提供參考。
引用本文: 劉星雨, 饒慶雨, 劉祖婷, 莫佳麗, 嚴淳, 劉金, 杜慧杰, 盧依, 況杰. 基于貝葉斯網絡的個體化風險評估模型及R語言實現. 中國循證醫學雜志, 2024, 24(11): 1325-1331. doi: 10.7507/1672-2531.202405072 復制
版權信息: ?四川大學華西醫院華西期刊社《中國循證醫學雜志》版權所有,未經授權不得轉載、改編
隨著大量的醫療記錄轉變為電子格式,醫療領域積累了海量的臨床數據,為更加精準地評估患者疾病風險及選擇干預措施提供了機會。而從患者的角度出發,個體化風險評估具有廣泛的應用前景,可以幫助臨床醫生有針對性的為每個患者提供個性化的預防和治療方案,降低疾病的發生和死亡率。傳統的預測評估模型通常基于患者的臨床或非臨床特征,用于預測其在特定時間內發生特定健康狀況的風險和可能性[1]。然而,受限于所納入變量數[2]、大規模數據處理能力、模型復雜度以及難以捕捉預后因素之間的非線性關系[3]等原因難以滿足臨床需求。因此,機器學習方法受到越來越多的關注,該類方法在處理復雜數據上的優勢已使其廣泛應用于醫療衛生領域[4,5]。其中貝葉斯網絡(Bayesian networks,BN)模型通過構建有向無環圖(direct acyclic graph,DAG)和條件概率表,以其擅長闡明變量之間的潛在因果關系等優勢[6,7],為個體化風險評估研究提供了新途徑[8,9]。本研究旨在介紹BN的基本原理和模型構建步驟,并基于實例采用R語言實現個體化風險預測模型的構建,為幫助研究者更好理解、應用該方法提供參考。
1 BN基本原理
BN又稱信念網絡(belief network),由Judea Pear于1985年首次提出[10],是一種利用DAG表示隨機變量之間依賴關系的概率圖形模型,作為一種圖形化的建模工具,BN提供了一種表示變量之間因果關系的方法,用來發現隱藏在數據中的信息,BN將DAG與概率論有機結合,在不確定推理方面發揮了很大的優勢。
BN由兩部分組成,DAG和條件概率分布。DAG定性描述了變量之間的依賴和獨立關系,而條件概率分布則對變量與其父節點之間的依賴關系進行了定量描述,是聯合概率分布(joint probability distributions,JPD)的一種表現形式。JPD包含了所有的概率信息[11]。利用鏈式法則,JPD可以表示為:
 |
條件獨立性是BN的核心。DAG中的節點為隨機變量,表示為 ,有向邊表示變量之間的概率依賴關系,箭頭的指向是對變量之間的定性描述。當觀察到有向邊從
,有向邊表示變量之間的概率依賴關系,箭頭的指向是對變量之間的定性描述。當觀察到有向邊從 指向
指向 時,說明
時,說明 對
對 存在影響,在
存在影響,在 和
和 中,
中, 是父節點,而
是父節點,而 是子節點。每個節點都有一個條件概率分布表用來定量描述所有父節點對該節點的作用效果。假設
是子節點。每個節點都有一個條件概率分布表用來定量描述所有父節點對該節點的作用效果。假設 是
是 所有父節點的集合,即:
所有父節點的集合,即:
 |
 |
1.1 BN模型與傳統回歸模型優缺點比較
與傳統基于回歸的模型相比,BN模型是對JPD簡潔直觀的圖形表示,將與節點相關的條件概率分布分解為直接影響節點的變量,采用網絡的形式表示變量及其之間的復雜的相互作用關系,存在許多優勢,但仍存在一些不足[14]。具體比較內容見表1。
1.2 BN模型的學習
BN的學習過程主要分為結構學習和參數學習[15]。
結構學習是通過訓練集學習到相應的DAG結構,主要采用基于約束和基于分數的方法[11]。基于約束的方法利用數據中的條件獨立性推斷模型結構,例如Grow-Shrink算法。而基于評分的方法則引入評分函數評估每個候選模型,以找到最適合數據的模型結構,如禁忌搜索(tabu search)算法。另外,常用的方法還包括爬山算法(hill climbing algorithm),這是一種局部搜索算法,從空白網絡結構開始,通過添加、刪除或反轉變量之間的邊來搜索最優網絡結構,直到達到最優評分指標。同時,BN允許研究者將已知的時間關系、直接關系和直接因果關系納入成為結構的一部分。
參數學習旨在確定BN網絡模型各節點的條件概率分布,從而量化網絡中變量之間的依賴性。常見的學習方法包括最大似然估計(maximum likelihood estimation,MLE)方法和貝葉斯估計(Bayesian estimation,BE)方法等。MLE方法通過最大化觀測數據的似然函數來估計參數值,而BE方法則基于貝葉斯定理和先驗概率來計算后驗概率分布,從而得到參數的估計值。
2 BN個體化風險評估的R語言實現
2.1 數據來源
本研究采用來自Kaggle的卒中預測數據集[16]進行演示。該數據集的目標是根據患者臨床指標分析預測患者是否會發生卒中。數據集包含5 110個樣本,每個樣本有11個變量和一個結果變量。具體變量介紹見表2。
2.2 BN個體化風險評估建模思路
變量的選擇關系到BN模型的質量,本研究使用單因素分析方法與多因素Logistic回歸方法對變量進行篩選。數據按照7∶3的比例隨機分為訓練集和測試集,使用訓練集構建BN模型,使用測試集對模型進行驗證。為解決數據不平衡與防止數據泄露的問題,分別對訓練集和測試集使用了合成少數過采樣技術(synthetic minority oversampling technique,SMOTE)[17]。該方法不僅是對少數樣本進行重復,而是通過在附近實例之間插值,在算法上生成新的少數類實例,從而增強數據集平衡[18,19]。本研究以爬山算法構建BN結構,MLE方法進行參數學習。使用受試者工作特征(receiver operating characteristic,ROC)曲線下面積(area under the curve,AUC)、靈敏度、特異度和準確度對模型進行評價。同時,使用Delong檢驗比較BN模型與Logistic模型之間性能是否存在差異。所有統計分析使用R 4.2.2軟件進行,以雙側檢驗P<0.05為差異具有統計學意義。實現的R語言代碼見框1。
2.3 主要結果
2.3.1 缺血性腦卒中患者影響因素分析
數據集共納入5 110例患者,其中男性患者2 994例(58.59%),女性患者2 116例(41.41%)。對患者進行隨訪,IS患者249例(4.87%),非IS患者4 861例(95.13%)。Logistic回歸結果顯示年齡、高血壓史、心臟病史及平均血糖與缺血性腦卒中患者預后存在統計學意義(表3)。
2.3.2 BN模型構建
R軟件中,常使用bnlearn包進行學習BN圖形結構,并對參數進行估計。操作過程再在R Studio中進行。數據包加載完成后,對研究所需數據進行錄入。
本研究構建離散型BN模型,將連續型變量平均血糖分為正常(<3.9 mmol/L)和高血糖(≥3.9 mmol/L)。研究使用了爬山算法構建DAG。在此基礎上,結合相關文獻和專家經驗,對初始網絡結構進行了人工調整,包括刪除某些不合理的有向邊、增加必要的有向邊以及改變某些有向邊的方向。通常使用白名單(whitelist)和黑名單(blacklist)來進一步完善BN的結構。白名單指定了所需的有向邊存在,而黑名單指定了有向邊不存在。使用graphviz.plot()函數繪制所構建的BN結構。
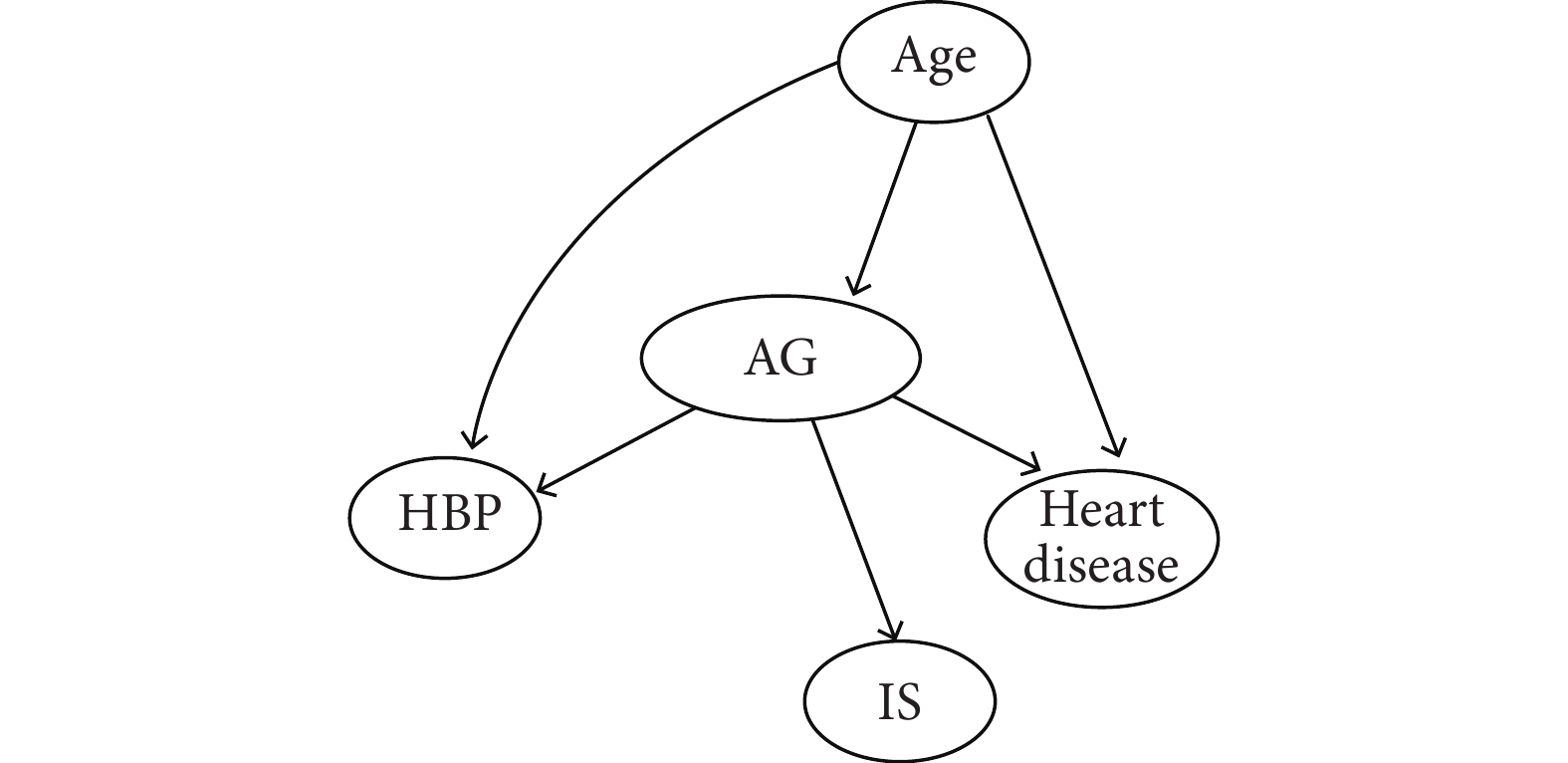
構建的BN模型結構如圖1所示。年齡、心臟病、高血壓和高血糖與IS直接相關。此外,年齡還可通過心臟病、高血壓和高血糖與IS間接相關,高血糖也可通過影響心臟病和高血壓,間接與IS相關。
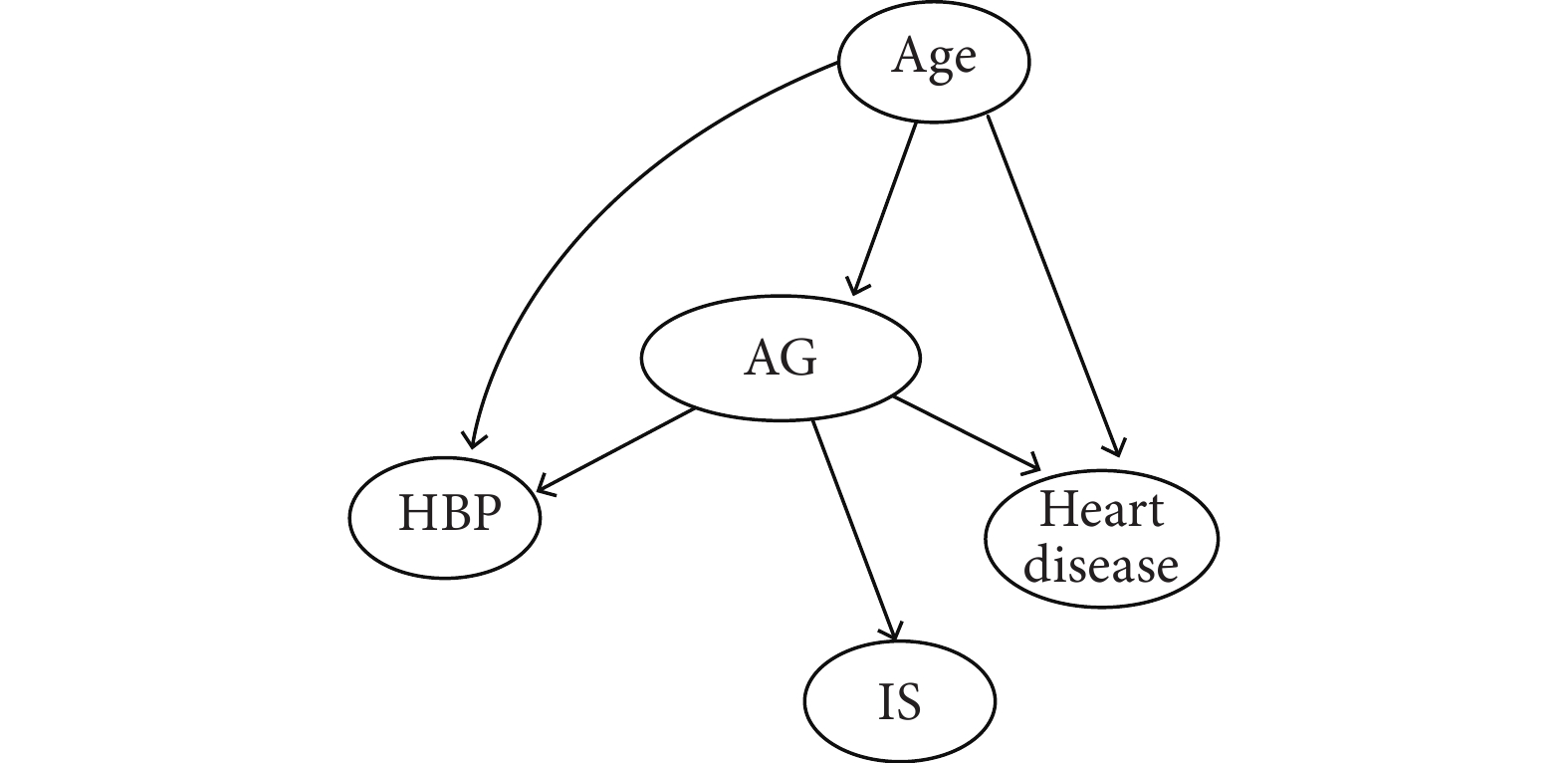 圖1
缺血性腦卒中發病的貝葉斯網絡模型結構
圖1
缺血性腦卒中發病的貝葉斯網絡模型結構
Age:年齡;AG:平均血糖;HBP:高血壓;Heart disease:心臟病;IS:缺血性腦卒中。
2.3.3 輸出條件概率表
構建BN結構后,需要對模型擬合參數。當所有節點都是離散變量時,這些參數被列在通常被稱為條件概率表的表格中[11]。本研究使用MLE對局部分布的參數進行擬合,使其形成條件概率表。bn.fit()函數默認使用MLE的方法,也可以根據method對方法進行更換,例如可以更換為method="bayes"使用BN。
fitted$IS可以輸出每個變量的條件概率表,在這里我們的目標節點是缺血性腦卒中。條件概率表如表4所示。60歲以上70歲以下,有高血壓、心臟病和高血糖的患者,缺血性腦卒中發病概率為0.870。而70歲以上,有高血壓和高血糖的患者,缺血性腦卒中發病概率為0.764。
2.3.4 BN交叉驗證
研究使用bnlearn包中的bn.cv()函數進行了10折交叉驗證。該函數提供了三種交叉驗證方法,包括k折交叉驗證(默認)、自定義折疊交叉驗證("custom-fold")和Hold-out交叉驗證("hold-out"),通過method對使用的交叉驗證方法進行修改。我們使用對數似然損失(log-likelihood loss)對BN模型性能進行評價,一般而言,期望損失值越低,表示模型在訓練集上的性能越好。本研究得到訓練集的期望損失為2.858,表明該模型在訓練集上表現良好。
2.3.5 模型效果評價
使用pROC包構建BN模型與Logistic回歸模型的ROC曲線,并分別計算AUC值、靈敏度、特異度和準確度,對模型效果進行評價(表5、圖2)。
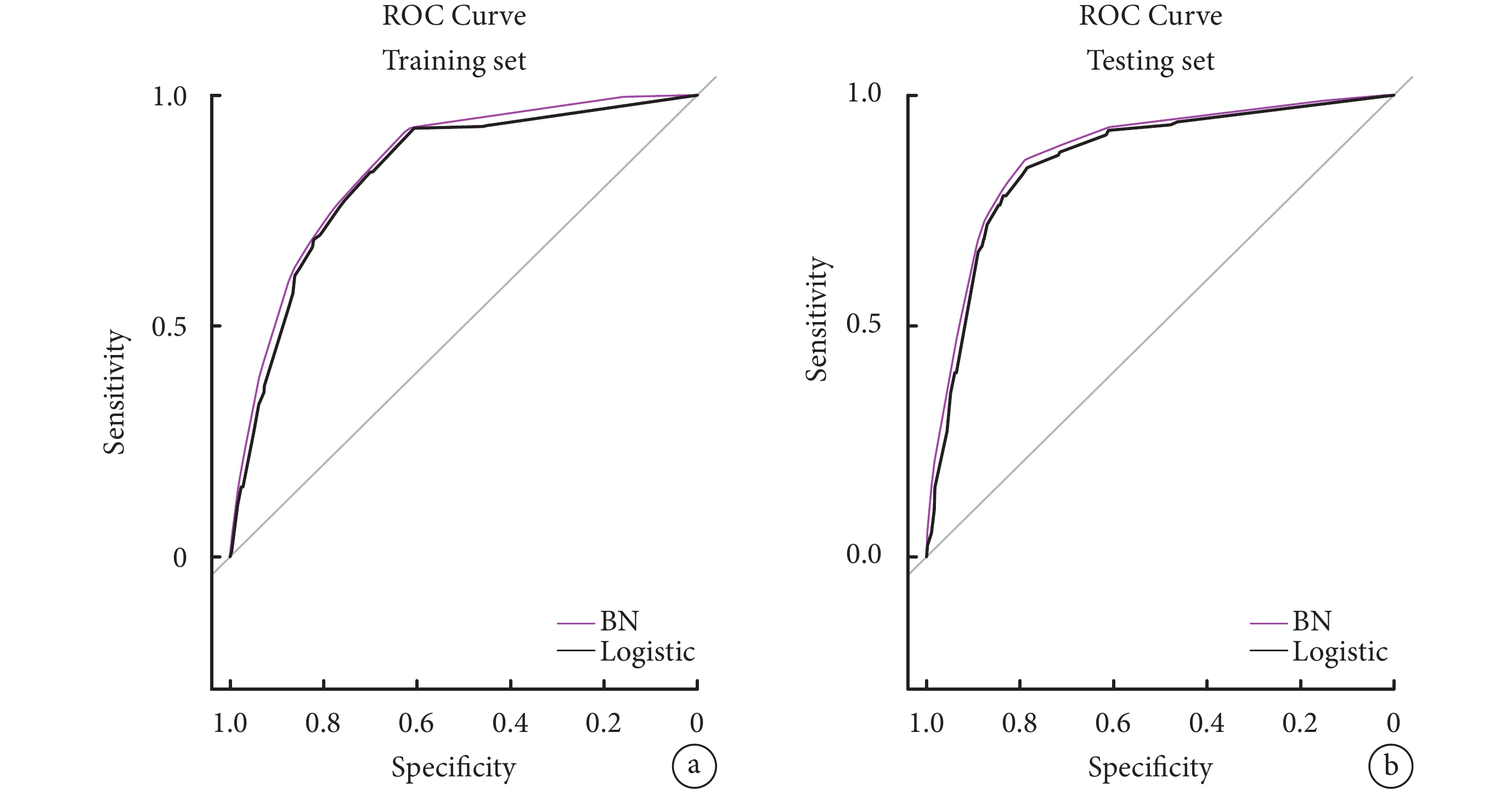 圖2
貝葉斯網絡模型與Logistic回歸模型的ROC曲線
圖2
貝葉斯網絡模型與Logistic回歸模型的ROC曲線
與Logistic回歸模型相比,在測試集和訓練集中BN模型均表現出更好的性能。在訓練集和測試集中,BN模型的準確率分別為79.37%和83.32%,AUC分別為0.85[95%CI(0.83,0.86)]和0.88[95%CI(0.86,0.89)],靈敏度分別為59.64%和72.80%,特異度分別為87.48%和87.59%。訓練集與測試集的Delong檢驗證實了兩個模型之間AUC之間存在統計學差異(P<0.05)。此外,BN模型的校準圖顯示,在訓練集和測試集中預測概率和實際觀測值之間較為一致,見圖3。
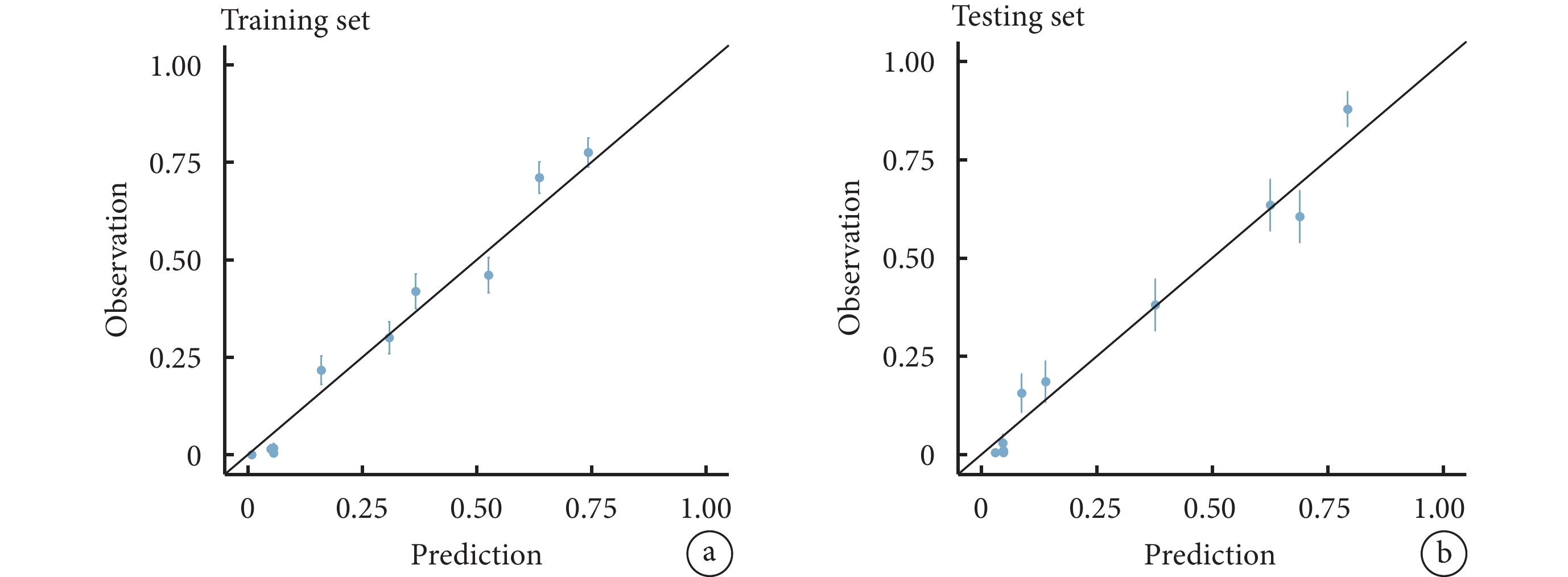 圖3
貝葉斯網絡模型校準曲線
圖3
貝葉斯網絡模型校準曲線
3 討論
本研究基于實例采用R語言實現個體化風險預測模型的構建,研究結果顯示,BN模型的預測性能優于傳統Logistic回歸模型。且通過DAG圖可以清晰的展示出變量之間的相互作用關系,年齡、心臟病、高血壓和高血糖與缺血性腦卒中發病直接相關。此外,年齡還可通過心臟病、高血壓和高血糖與缺血性腦卒中間接相關,高血糖也可通過影響心臟病和高血壓,間接與缺血性腦卒中相關。
基于BN的風險預測模型相較于統計回歸的方法具有多個優勢[20-22]。首先,BN模型通過其圖形結構和條件概率分布清晰地闡明了各變量之間復雜的相互作用關系,以及變量在網絡中的相對位置,描述了變量對結果的貢獻程度[7,23]。這種清晰的關系表達提高了對結果風險的評估準確性,并增強了結果的可解釋性[14]。其次,BN模型可以充分利用先驗知識和現有數據,有效地評估風險,并且在加入新數據時無需重新訓練模型[8,24],這使得其在個體化風險預測方面更加靈活和實用。隨著時間的推移,更多的病歷信息被納入,BN模型可以獲得進一步的提升。此外,BN模型能夠進行從原因到結果和從結果到原因的推理,以及處理變量間的線性和非線性關系,因而具有更廣泛的適用性[14]。
相比之下,基于回歸的方法局限于單一結果的預測,在加入新數據時需要重新估計,且在面對數據缺失或個體特異性較強的情況下,基于回歸的模型復雜程度較高且準確性有限。此外,基于回歸的方法在納入變量和結果之間的非線性關系時,通常涉及變量的轉換、加權等操作,往往使得結果難以解釋[14]。因此,BN模型在風險預測中展現出了顯著的優勢,并在實踐中得到了廣泛應用。
在臨床中,疾病的進展往往與時間密切相關,BN能夠與時間信息相結合,構成動態BN[25],從而更好地反映變量的發展變化規律。同時,BN也可以與多種機器學習技術和傳統統計方法結合使用,更好地處理數據,如與深度學習結合的貝葉斯深度學習模型[26],這為解決復雜問題提供了新的途徑。
BN為處理復雜的醫療衛生數據提供了一種強大且靈活的分析方法。數據規模的擴大、數據復雜性的增加等挑戰的不斷出現,傳統的數據分析方法面臨諸多限制。而BN能夠應對這些挑戰,不斷更新信息。隨著“精準醫學”時代的到來,新的風險評估與決策制定的方法逐漸引起人們的關注,而BN憑借其高度的靈活性、適應性以及強大的可解釋性,為大數據的分析提供了一種新的思路,值得進一步探索。本文提供了清晰的代碼和代碼解釋,以實例的形式進行演示,方便研究人員更好地理解和應用BN模型。
隨著大量的醫療記錄轉變為電子格式,醫療領域積累了海量的臨床數據,為更加精準地評估患者疾病風險及選擇干預措施提供了機會。而從患者的角度出發,個體化風險評估具有廣泛的應用前景,可以幫助臨床醫生有針對性的為每個患者提供個性化的預防和治療方案,降低疾病的發生和死亡率。傳統的預測評估模型通常基于患者的臨床或非臨床特征,用于預測其在特定時間內發生特定健康狀況的風險和可能性[1]。然而,受限于所納入變量數[2]、大規模數據處理能力、模型復雜度以及難以捕捉預后因素之間的非線性關系[3]等原因難以滿足臨床需求。因此,機器學習方法受到越來越多的關注,該類方法在處理復雜數據上的優勢已使其廣泛應用于醫療衛生領域[4,5]。其中貝葉斯網絡(Bayesian networks,BN)模型通過構建有向無環圖(direct acyclic graph,DAG)和條件概率表,以其擅長闡明變量之間的潛在因果關系等優勢[6,7],為個體化風險評估研究提供了新途徑[8,9]。本研究旨在介紹BN的基本原理和模型構建步驟,并基于實例采用R語言實現個體化風險預測模型的構建,為幫助研究者更好理解、應用該方法提供參考。
1 BN基本原理
BN又稱信念網絡(belief network),由Judea Pear于1985年首次提出[10],是一種利用DAG表示隨機變量之間依賴關系的概率圖形模型,作為一種圖形化的建模工具,BN提供了一種表示變量之間因果關系的方法,用來發現隱藏在數據中的信息,BN將DAG與概率論有機結合,在不確定推理方面發揮了很大的優勢。
BN由兩部分組成,DAG和條件概率分布。DAG定性描述了變量之間的依賴和獨立關系,而條件概率分布則對變量與其父節點之間的依賴關系進行了定量描述,是聯合概率分布(joint probability distributions,JPD)的一種表現形式。JPD包含了所有的概率信息[11]。利用鏈式法則,JPD可以表示為:
 |
條件獨立性是BN的核心。DAG中的節點為隨機變量,表示為 ,有向邊表示變量之間的概率依賴關系,箭頭的指向是對變量之間的定性描述。當觀察到有向邊從
,有向邊表示變量之間的概率依賴關系,箭頭的指向是對變量之間的定性描述。當觀察到有向邊從 指向
指向 時,說明
時,說明 對
對 存在影響,在
存在影響,在 和
和 中,
中, 是父節點,而
是父節點,而 是子節點。每個節點都有一個條件概率分布表用來定量描述所有父節點對該節點的作用效果。假設
是子節點。每個節點都有一個條件概率分布表用來定量描述所有父節點對該節點的作用效果。假設 是
是 所有父節點的集合,即:
所有父節點的集合,即:
 |
 |
1.1 BN模型與傳統回歸模型優缺點比較
與傳統基于回歸的模型相比,BN模型是對JPD簡潔直觀的圖形表示,將與節點相關的條件概率分布分解為直接影響節點的變量,采用網絡的形式表示變量及其之間的復雜的相互作用關系,存在許多優勢,但仍存在一些不足[14]。具體比較內容見表1。
1.2 BN模型的學習
BN的學習過程主要分為結構學習和參數學習[15]。
結構學習是通過訓練集學習到相應的DAG結構,主要采用基于約束和基于分數的方法[11]。基于約束的方法利用數據中的條件獨立性推斷模型結構,例如Grow-Shrink算法。而基于評分的方法則引入評分函數評估每個候選模型,以找到最適合數據的模型結構,如禁忌搜索(tabu search)算法。另外,常用的方法還包括爬山算法(hill climbing algorithm),這是一種局部搜索算法,從空白網絡結構開始,通過添加、刪除或反轉變量之間的邊來搜索最優網絡結構,直到達到最優評分指標。同時,BN允許研究者將已知的時間關系、直接關系和直接因果關系納入成為結構的一部分。
參數學習旨在確定BN網絡模型各節點的條件概率分布,從而量化網絡中變量之間的依賴性。常見的學習方法包括最大似然估計(maximum likelihood estimation,MLE)方法和貝葉斯估計(Bayesian estimation,BE)方法等。MLE方法通過最大化觀測數據的似然函數來估計參數值,而BE方法則基于貝葉斯定理和先驗概率來計算后驗概率分布,從而得到參數的估計值。
2 BN個體化風險評估的R語言實現
2.1 數據來源
本研究采用來自Kaggle的卒中預測數據集[16]進行演示。該數據集的目標是根據患者臨床指標分析預測患者是否會發生卒中。數據集包含5 110個樣本,每個樣本有11個變量和一個結果變量。具體變量介紹見表2。
2.2 BN個體化風險評估建模思路
變量的選擇關系到BN模型的質量,本研究使用單因素分析方法與多因素Logistic回歸方法對變量進行篩選。數據按照7∶3的比例隨機分為訓練集和測試集,使用訓練集構建BN模型,使用測試集對模型進行驗證。為解決數據不平衡與防止數據泄露的問題,分別對訓練集和測試集使用了合成少數過采樣技術(synthetic minority oversampling technique,SMOTE)[17]。該方法不僅是對少數樣本進行重復,而是通過在附近實例之間插值,在算法上生成新的少數類實例,從而增強數據集平衡[18,19]。本研究以爬山算法構建BN結構,MLE方法進行參數學習。使用受試者工作特征(receiver operating characteristic,ROC)曲線下面積(area under the curve,AUC)、靈敏度、特異度和準確度對模型進行評價。同時,使用Delong檢驗比較BN模型與Logistic模型之間性能是否存在差異。所有統計分析使用R 4.2.2軟件進行,以雙側檢驗P<0.05為差異具有統計學意義。實現的R語言代碼見框1。
2.3 主要結果
2.3.1 缺血性腦卒中患者影響因素分析
數據集共納入5 110例患者,其中男性患者2 994例(58.59%),女性患者2 116例(41.41%)。對患者進行隨訪,IS患者249例(4.87%),非IS患者4 861例(95.13%)。Logistic回歸結果顯示年齡、高血壓史、心臟病史及平均血糖與缺血性腦卒中患者預后存在統計學意義(表3)。
2.3.2 BN模型構建
R軟件中,常使用bnlearn包進行學習BN圖形結構,并對參數進行估計。操作過程再在R Studio中進行。數據包加載完成后,對研究所需數據進行錄入。
本研究構建離散型BN模型,將連續型變量平均血糖分為正常(<3.9 mmol/L)和高血糖(≥3.9 mmol/L)。研究使用了爬山算法構建DAG。在此基礎上,結合相關文獻和專家經驗,對初始網絡結構進行了人工調整,包括刪除某些不合理的有向邊、增加必要的有向邊以及改變某些有向邊的方向。通常使用白名單(whitelist)和黑名單(blacklist)來進一步完善BN的結構。白名單指定了所需的有向邊存在,而黑名單指定了有向邊不存在。使用graphviz.plot()函數繪制所構建的BN結構。
構建的BN模型結構如圖1所示。年齡、心臟病、高血壓和高血糖與IS直接相關。此外,年齡還可通過心臟病、高血壓和高血糖與IS間接相關,高血糖也可通過影響心臟病和高血壓,間接與IS相關。
 圖1
缺血性腦卒中發病的貝葉斯網絡模型結構
圖1
缺血性腦卒中發病的貝葉斯網絡模型結構
Age:年齡;AG:平均血糖;HBP:高血壓;Heart disease:心臟病;IS:缺血性腦卒中。
2.3.3 輸出條件概率表
構建BN結構后,需要對模型擬合參數。當所有節點都是離散變量時,這些參數被列在通常被稱為條件概率表的表格中[11]。本研究使用MLE對局部分布的參數進行擬合,使其形成條件概率表。bn.fit()函數默認使用MLE的方法,也可以根據method對方法進行更換,例如可以更換為method="bayes"使用BN。
fitted$IS可以輸出每個變量的條件概率表,在這里我們的目標節點是缺血性腦卒中。條件概率表如表4所示。60歲以上70歲以下,有高血壓、心臟病和高血糖的患者,缺血性腦卒中發病概率為0.870。而70歲以上,有高血壓和高血糖的患者,缺血性腦卒中發病概率為0.764。
2.3.4 BN交叉驗證
研究使用bnlearn包中的bn.cv()函數進行了10折交叉驗證。該函數提供了三種交叉驗證方法,包括k折交叉驗證(默認)、自定義折疊交叉驗證("custom-fold")和Hold-out交叉驗證("hold-out"),通過method對使用的交叉驗證方法進行修改。我們使用對數似然損失(log-likelihood loss)對BN模型性能進行評價,一般而言,期望損失值越低,表示模型在訓練集上的性能越好。本研究得到訓練集的期望損失為2.858,表明該模型在訓練集上表現良好。
2.3.5 模型效果評價
使用pROC包構建BN模型與Logistic回歸模型的ROC曲線,并分別計算AUC值、靈敏度、特異度和準確度,對模型效果進行評價(表5、圖2)。
 圖2
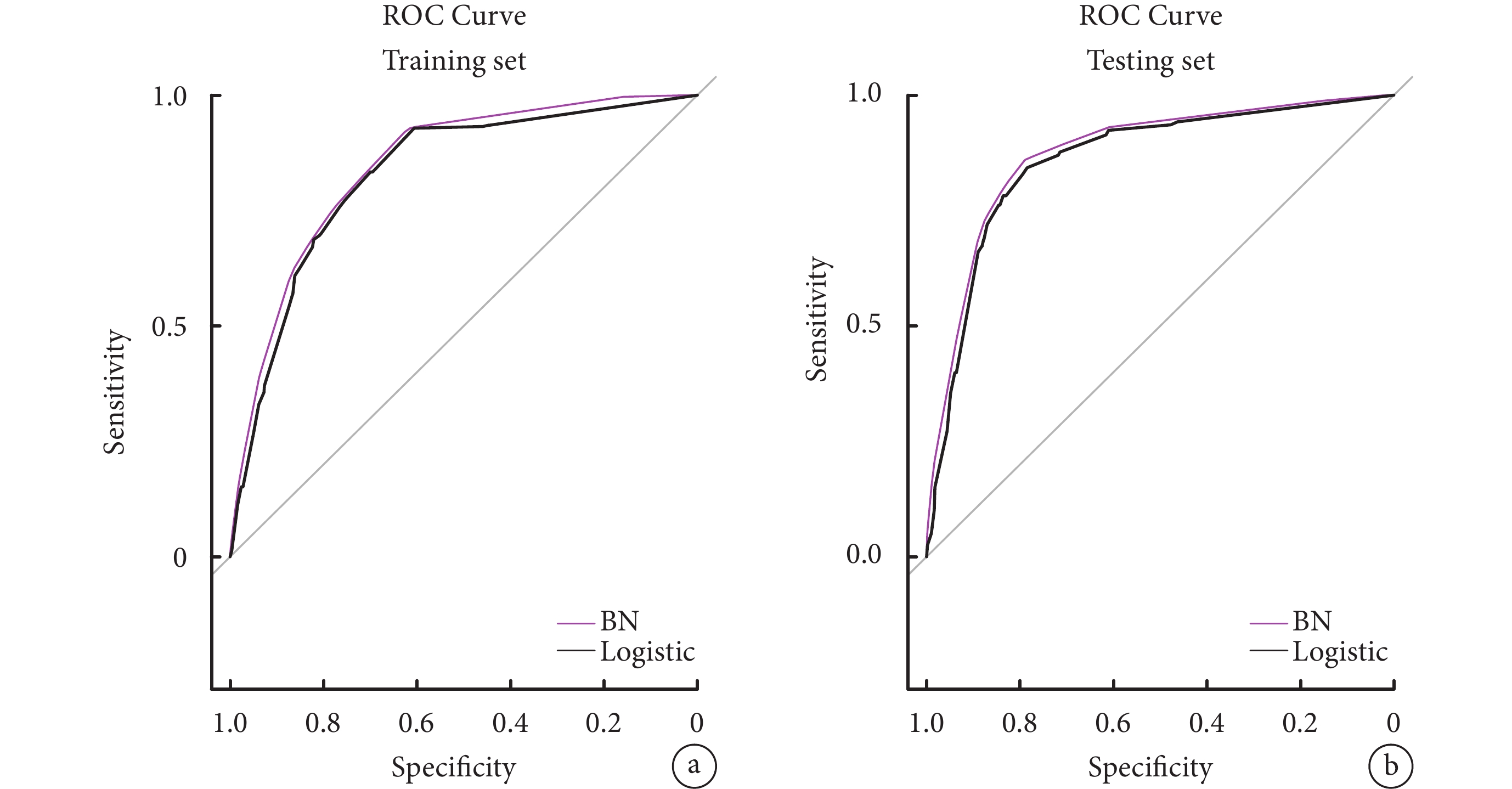
貝葉斯網絡模型與Logistic回歸模型的ROC曲線
圖2
貝葉斯網絡模型與Logistic回歸模型的ROC曲線
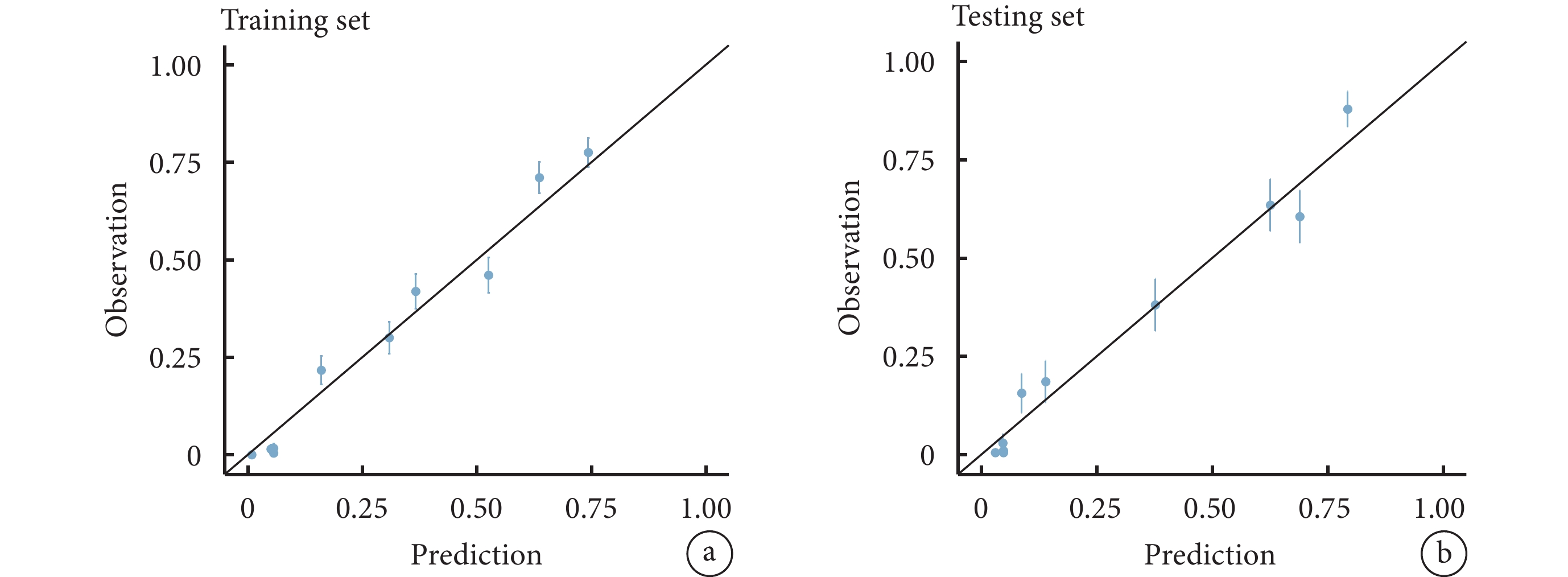
與Logistic回歸模型相比,在測試集和訓練集中BN模型均表現出更好的性能。在訓練集和測試集中,BN模型的準確率分別為79.37%和83.32%,AUC分別為0.85[95%CI(0.83,0.86)]和0.88[95%CI(0.86,0.89)],靈敏度分別為59.64%和72.80%,特異度分別為87.48%和87.59%。訓練集與測試集的Delong檢驗證實了兩個模型之間AUC之間存在統計學差異(P<0.05)。此外,BN模型的校準圖顯示,在訓練集和測試集中預測概率和實際觀測值之間較為一致,見圖3。
 圖3
貝葉斯網絡模型校準曲線
圖3
貝葉斯網絡模型校準曲線
3 討論
本研究基于實例采用R語言實現個體化風險預測模型的構建,研究結果顯示,BN模型的預測性能優于傳統Logistic回歸模型。且通過DAG圖可以清晰的展示出變量之間的相互作用關系,年齡、心臟病、高血壓和高血糖與缺血性腦卒中發病直接相關。此外,年齡還可通過心臟病、高血壓和高血糖與缺血性腦卒中間接相關,高血糖也可通過影響心臟病和高血壓,間接與缺血性腦卒中相關。
基于BN的風險預測模型相較于統計回歸的方法具有多個優勢[20-22]。首先,BN模型通過其圖形結構和條件概率分布清晰地闡明了各變量之間復雜的相互作用關系,以及變量在網絡中的相對位置,描述了變量對結果的貢獻程度[7,23]。這種清晰的關系表達提高了對結果風險的評估準確性,并增強了結果的可解釋性[14]。其次,BN模型可以充分利用先驗知識和現有數據,有效地評估風險,并且在加入新數據時無需重新訓練模型[8,24],這使得其在個體化風險預測方面更加靈活和實用。隨著時間的推移,更多的病歷信息被納入,BN模型可以獲得進一步的提升。此外,BN模型能夠進行從原因到結果和從結果到原因的推理,以及處理變量間的線性和非線性關系,因而具有更廣泛的適用性[14]。
相比之下,基于回歸的方法局限于單一結果的預測,在加入新數據時需要重新估計,且在面對數據缺失或個體特異性較強的情況下,基于回歸的模型復雜程度較高且準確性有限。此外,基于回歸的方法在納入變量和結果之間的非線性關系時,通常涉及變量的轉換、加權等操作,往往使得結果難以解釋[14]。因此,BN模型在風險預測中展現出了顯著的優勢,并在實踐中得到了廣泛應用。
在臨床中,疾病的進展往往與時間密切相關,BN能夠與時間信息相結合,構成動態BN[25],從而更好地反映變量的發展變化規律。同時,BN也可以與多種機器學習技術和傳統統計方法結合使用,更好地處理數據,如與深度學習結合的貝葉斯深度學習模型[26],這為解決復雜問題提供了新的途徑。
BN為處理復雜的醫療衛生數據提供了一種強大且靈活的分析方法。數據規模的擴大、數據復雜性的增加等挑戰的不斷出現,傳統的數據分析方法面臨諸多限制。而BN能夠應對這些挑戰,不斷更新信息。隨著“精準醫學”時代的到來,新的風險評估與決策制定的方法逐漸引起人們的關注,而BN憑借其高度的靈活性、適應性以及強大的可解釋性,為大數據的分析提供了一種新的思路,值得進一步探索。本文提供了清晰的代碼和代碼解釋,以實例的形式進行演示,方便研究人員更好地理解和應用BN模型。