腦電圖（EEG）分析對癲癇疾病的診斷具有重要的參考價值，對癲癇腦電信號的自動分類可以及時對患者的情況作出判斷，在臨床上有很重要的意義。為解決腦電信號采用單一特征識別率不高的問題，同時也為避免小波基函數的選取對分類結果的影響，本文提出了一種基于 S 變換和排列熵（PE）的癲癇腦電信號自動判別方法，首先將原始腦電信號進行離散 S 變換，再對變換后腦電信號各節律的系數分別求其波動指數，并與腦電信號的排列熵值共同組成特征向量送入 Real AdaBoost 分類器進行癲癇各時期的判別。本研究采用德國波恩大學癲癇研究中心數據庫，對正常人清醒睜眼，癲癇患者發病間歇期致癇灶內及發作期 3 組腦電信號數據進行方法有效性檢驗。研究結果表明，各節律的波動指數可有效表征正常、癲癇發作間期和癲癇發作期腦電信號，且多種特征的識別率明顯優于單一特征，平均識別率可達到 98.13%，相比于僅提取時頻特征或非線性特征，識別率分別提高了 1.2% 和 8.1% 以上，優于文獻中報道的多種方法。因此，本方法在癲癇疾病的診斷方面有較好的應用前景。
引用本文： 張健釗, 姜威, 元輝, 尚偉, 劉湜, 焦萍. 基于離散 S 變換和排列熵的癲癇腦電識別. 生物醫學工程學雜志, 2017, 34(5): 681-687. doi: 10.7507/1001-5515.201702034 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
引言
癲癇是大腦神經元異常放電，導致大腦功能障礙的一種慢性疾病，目前全世界患有癲癇的人數約占總人口數的 1%，且每年以 0.02%～0.05% 的速度增長[1]。癲癇是一種突發性疾病且難以治愈，給患者及患者家庭帶來沉重的精神負擔，若疾病持續發作而沒有得到及時的救治，甚至會有生命危險，因此該疾病長期以來倍受醫學界關注。癲癇疾病的預報與檢測是治療中首先要解決的問題，腦電圖（electroencephalogram，EEG）作為目前疾病檢測的主要手段已得到廣泛應用，醫學專家可以對腦電儀采集到的信息進行判讀從而確定是否有癲癇特征波出現。然而癲癇發作的不確定性和患者的個體差異給這一工作帶來了困難，采取人工的方式對腦電圖進行判讀不僅效率低下，也會因為專家的主觀經驗差異造成診斷結果的差異，因而腦電信號的自動檢測仍是當前生物醫學研究的熱點問題之一。
目前，時域、頻域及非線性動力學分析等方法均可用于處理腦電信號問題，其中基于小波變換的特征提取方法在腦電信號的時頻分析方面一直占有較為重要的地位[2-4]，而經驗模態分解（empirical mode decomposition，EMD）作為一種隨機序列的多尺度分析方法也在腦電信號相關問題的研究領域中顯現出了它的價值[5]。此外，非線性動力學分析也是解決生理信號分類的重要方法，常用的非線性動力學方法有 Hurst 指數[4]、近似熵（approximate entropy）[6]、樣本熵（sample entropy）等[7]。文獻[8]還將小波變換、樣本熵等方法相結合，共同應用于腦電信號的分類問題上，取得了 97.53% 的識別率。在模式識別方面，目前常用的分類方法有決策樹[9]、神經網絡（artificial neural network，ANN）[3]、支持向量機（support vector machine，SVM）[6]、極限學習機（extreme learning machine，ELM）等[8]。文獻[10]將神經網絡作為自適應提升（adaptive boosting，AdaBoost）算法的弱分類器，并將原始的 AdaBoost 算法進行了優化，取得了正常腦電信號 99.51%、癲癇腦電信號 96.11% 的識別率。腦電信號的時頻分析多采用小波變換，并在相應頻段提取特征；或者對腦電信號進行非線性動力學分析并在多個尺度上進行特征提取，但這些方法沒有考慮到多種特征相結合的優勢。雖然很多方法考慮在小波變換的基礎上對相應頻段進行非線性分析，但通過這種方法提取到的某些特征聚類效果不夠理想，對最終的分類無法起到較好的指導作用。另外，小波變換雖然是一種優秀的信號時頻分析方法，但其依賴于母小波函數的選擇，不同的母小波函數對特征提取效果會產生一定影響。
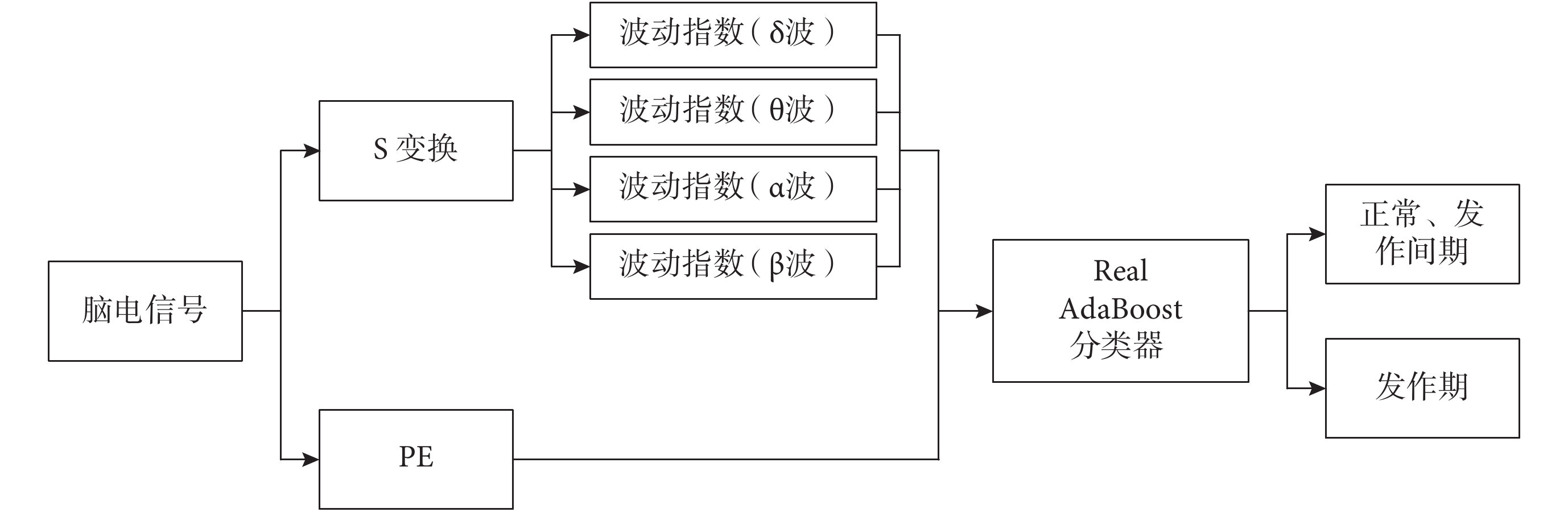
針對以上問題，本文結合腦電信號的非線性特征提取和時頻分析的優勢，嘗試將 S 變換和排列熵（permutation entropy，PE）理論共同用于對癲癇腦電信號的檢測中，S 變換結合了短時傅里葉變換和連續小波變換的優點，是一種新型的非線性信號分析方法。本文方法對原始腦電信號計算其 PE 值并進行離散 S 變換，根據人類腦電信號的節律特點將頻率分為相應的若干部分，提取變換各個頻帶系數的波動指數，并與 PE 共同組成特征向量。Real AdaBoost 是 AdaBoost 算法的改進，它引入置信度的概念作為最終分類的依據，對分類輸出的描述更為精細，因此本研究采用該方法作為分類器，整個系統流程如圖 1 所示。
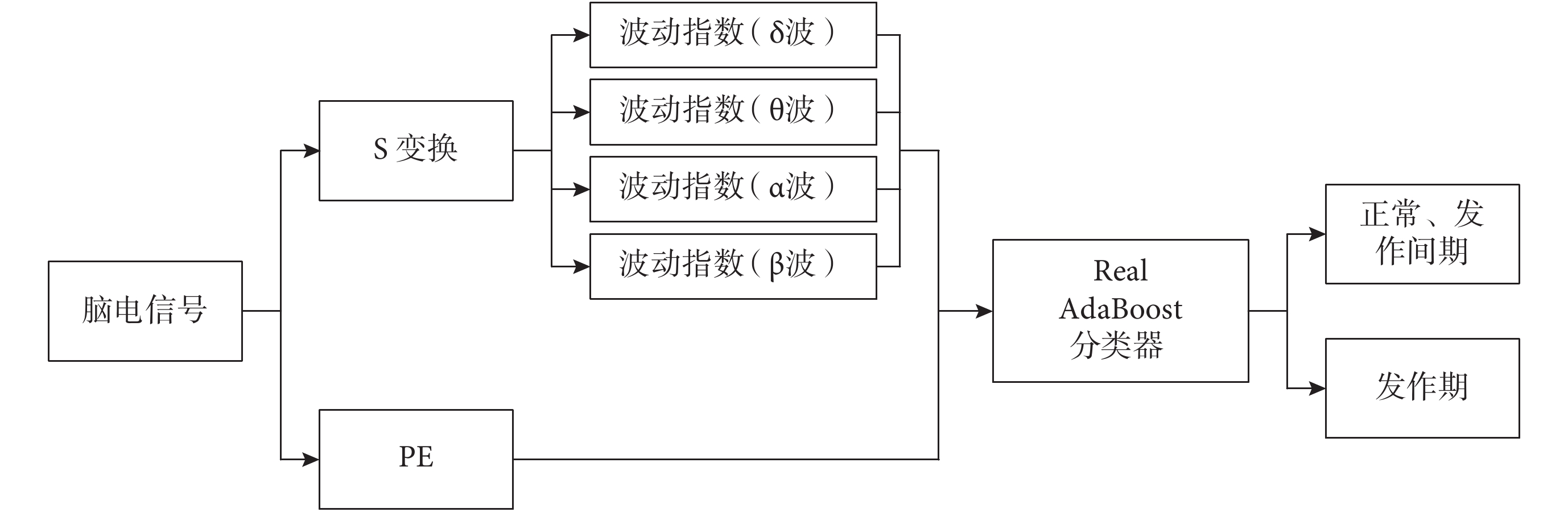圖1
腦電信號識別流程圖
Figure1.
Process of electroencephalogram signal recognition
1 特征提取方法
1.1 S 變換
Stockwell 等[11]在 1996 年提出了一種新型的時頻分析方法，稱為 S 變換，該方法可以看作是短時傅里葉變換和小波變換的延伸，即采用寬度可變的高斯窗函數替代傳統短時傅里葉變換中的窗函數。信號 h（t）的連續 S 變換定義為：
 |
其中：
 |
為窗口函數，τ 為時延因子。由高斯窗函數的表達式可以看出，隨著頻率的升高，窗函數的寬度減小，而低頻處的窗口相對較寬，這樣就在理論上達到了在低頻處有更好的頻率分辨率，高頻處有更好的時間分辨率的效果。在信號分析領域，常常采用 S 變換的離散形式。設 H（f）為 h（t）的傅里葉變換，則 h（t）的 S 變換也可寫成如下形式：
 |
若設信號的采樣間隔為 T，則采樣點數為 N = t/T。則根據（3）式，一維信號的離散 S 變換可表示為（k = 0，1，2，
，N—1，n = 1，2，
，N—1）：
 |
n = 0 時，
 |
變換結果為二維復矩陣，矩陣的行為頻率值，列為采樣時間點，這里取矩陣中元素的模值作為最終結果，即：
 |
由于離散 S 變換與短時傅里葉變換有一定的聯系，因此在實際計算時可采用快速傅里葉變換提高運算速度。
1.2 排列熵
PE 是由 Bandt 等[12]提出的一種衡量一維時間序列復雜度的方法。該方法在估計序列的復雜度方面具有計算方法簡單、抗噪聲能力強等特點，在隨機信號分析、信號突變檢測等方面有著廣泛的應用且具有良好的效果。設一維時間序列為{h（i），i = 1，2，
，N}，對其進行重構，得到一個新的相空間，即：
 |
m 為嵌入維度，τ 為時延因子，其中 1 ≤ i ≤ N —（ m — 1） τ，對每一個 i 值所對應的元素進行升序排列，即：
，其中 j1，j2，
，jm 為元素所在相空間矩陣中列的索引，若存在元素值相等的情況，則按照索引的大小進行升序排列，顯然，對于 m 個元素即存在 m! 種排列方式。定義 π 為序列的一種排列方式，πi 的出現概率為 pj（π），則 PE 的定義為：
 |
由于引入“熵”的概念作為復雜度的度量，因此理論上 PE 的值越低，時間序列越具有規律性，即信號產生新模式的概率較小；反之則表明序列越混亂無序，即信號產生新模式的概率越大。
2 分類方法
Real AdaBoost 算法是著名的集成學習算法 AdaBoost 算法的改進版本，由 Schapire 等[13]提出，目的是為了克服 AdaBoost 算法在輸出上較為粗糙的缺陷。其基本思想都是通過訓練若干個弱分類器，賦予其不同權重，最終組合成強分類器。而 Real AdaBoost 算法的優點主要在于，能夠將樣本屬于某一類的可能性通過置信度表示，而不像原始的 AdaBoost 算法只能輸出 —1 或 +1。該研究還通過實驗指出，Real AdaBoost 算法在訓練的收斂速度方面也要優于原始算法。該算法的基本步驟如下：
（1）假設訓練集合為 S = {（x 1，y1），（x 2，y2），
，（x n，yn）}，其中xi 為特征向量，yi 為類別標簽且 yi∈{+1，—1}。初始化樣本權重D1（i） = 1/n，i = 1，2，3，
，n；
（2）循環執行步驟①～④，t 為循環輪數，且 t = 1，2，3，
，T。
① 對樣本劃分為若干個互不相交的子空間，劃分后區間個數為 m。對每一區間計算 + 1 和 — 1 類的累計樣本權重，記為
和
，1 ≤ j ≤ m；
② 計算歸一化因子
，設弱分類器函數為 ht（x），對任意屬于某區間的x 有
（1 ≤ j ≤ m），ε 為一很小的正數，選擇
；
③ 更新樣本權重：
；
④ 當誤差率小于初始設定的值或等于最大迭代次數時，執行第（3）步，否則繼續執行循環體。
（3）輸出強分類器
。其中 b 為平滑因子，默認為 0。
3 實驗結果與分析
本文使用的實驗數據來源于德國波恩大學癲癇研究中心數據庫[14]。腦電信號的采樣頻率為 173.61 Hz，共有 5 組數據集，分別用 Z、O、N、F 和 S 表示。其中 Z 和 O 分別為正常人清醒時睜眼和閉眼時的腦電數據；N 和 F 分別為患者癲癇發作間期致癇灶外和致癇灶內的腦電數據；S 為患者癲癇發作期致癇灶內的腦電數據。每個數據集都包含 100 個樣本且每個樣本都包含 4 097 個采樣點。實驗前需要對數據進行預處理，把每個樣本的最后一個點舍棄并將其均分為 4 段，這樣每個數據集就得到了 400 個樣本。取 Z、F、S 共 3 組進行實驗，共計 1 200 個樣本。在本分類問題中，將 Z 組和 F 組標記為負類，S 組標記為正類。
首先對處理后的信號進行離散 S 變換，由于人類腦電信號主要集中于 0.3～30 Hz 的頻率范圍內，因此主要在該頻率段內對信號進行分析。如圖 2 所示，為 Z、F、S 3 組中隨機選出的 3 個腦電信號樣本及其 S 變換后的結果，變換結果用三維圖表示。由于直接將變換結果作為特征向量維數過高，因此根據腦電信號各個節律的頻段范圍，將整個頻段進一步劃分為 4 段，即 δ 波（0.3～4 Hz）、θ 波（4～8 Hz）、α 波（8～13 Hz）和 β 波（13～30 Hz），在每一個頻率段中對變換后的幅值求取波動指數，若信號序列為 s（t），則我們即可將相應頻段 i 的波動指數定義為[15]：
 |
其中 N 為信號長度。研究表明，癲癇發作期信號波動較為劇烈，其波動指數值遠區別正常期和發作間期。
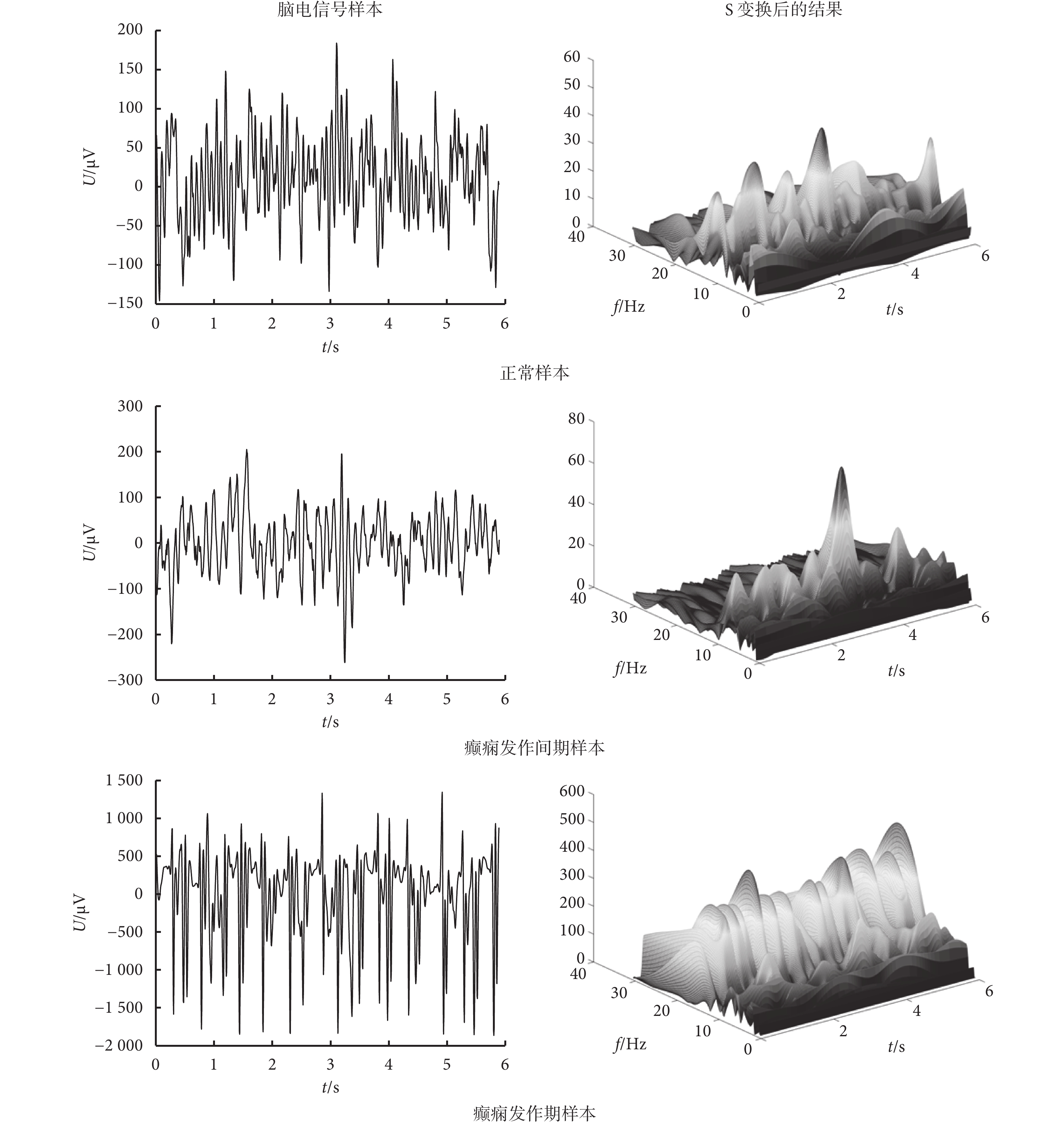圖2
處理后的腦電各時期樣本和離散 S 變換后的結果
Figure2.
The processed electroencephalogram samples and the results of discrete S transform
如圖 3 所示為 Z 組（正常）、F 組（發作間期）和 S 組（發作期）3 組信號 4 個節律的波動指數的箱線圖（每組隨機選取 100 個樣本），從中可以看出，正常信號和發作間期信號的波動指數值整體遠小于發作期信號，且波動指數的上下浮動范圍也遠小于發作期信號，因此適合作為分類依據。
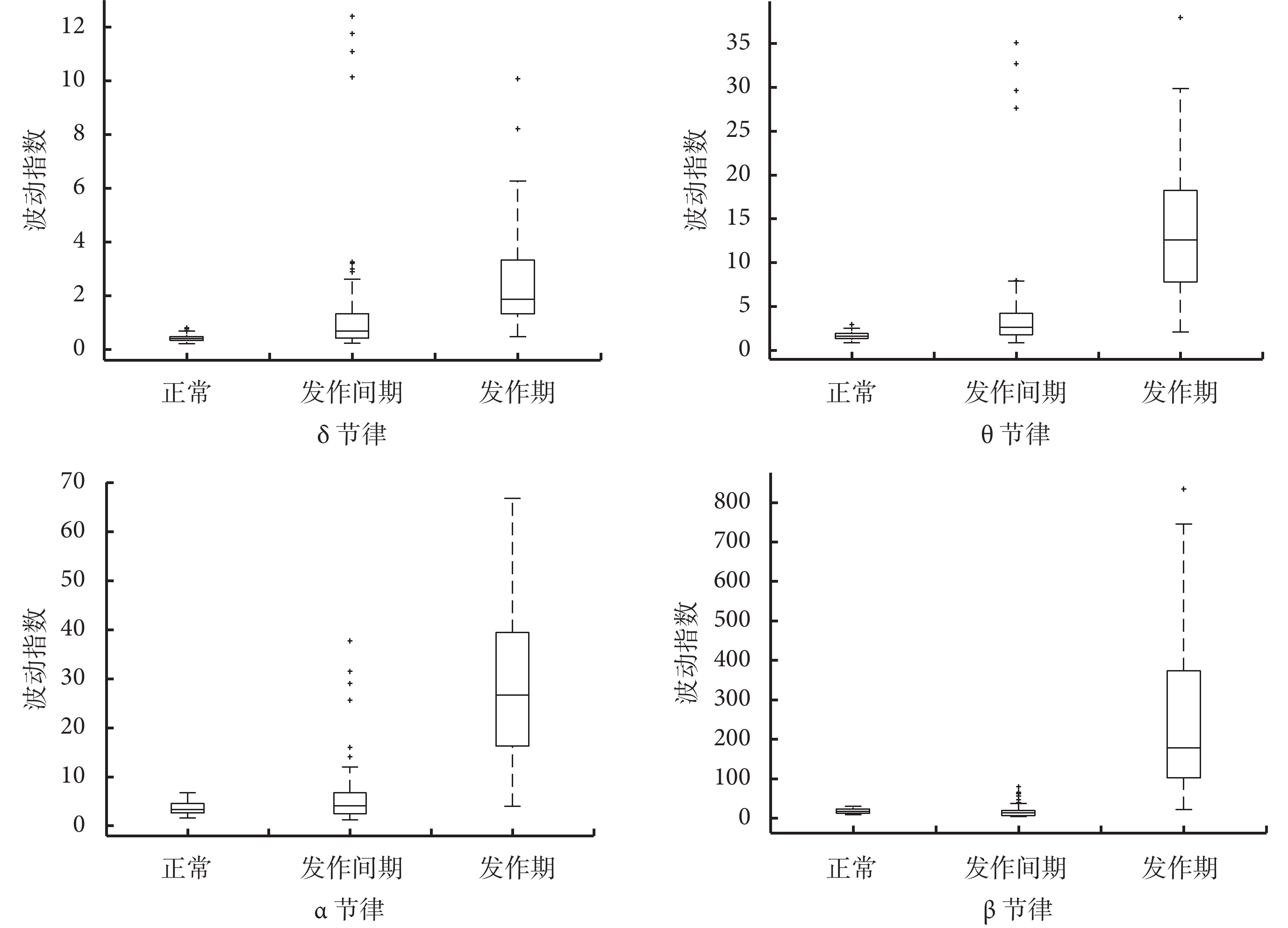圖3
正常、癲癇發作間期和癲癇發作期腦電信號不同節律下的波動指數
Figure3.
The fluctuation index of the electroencephalogram signals during normal，interictal and ictal periords of different rhythm
在對原始信號進行 PE 計算前需要確定最佳嵌入維度 m，不同 m 下 3 組腦電數據的 PE 均值及其標準差如圖 4 所示（時延因子 τ = 1），由圖 4 可以看出，正常和發作間期信號的 PE 值總體大于發作期，且隨著嵌入維度的增加，各時期 PE 均值的差距也不斷增大，但每個時期結果的標準差也隨之增大，說明當 m 過大時波動較為劇烈，聚類效果較差。綜合考慮，本實驗選取 m = 5 作為最終的嵌入維度。
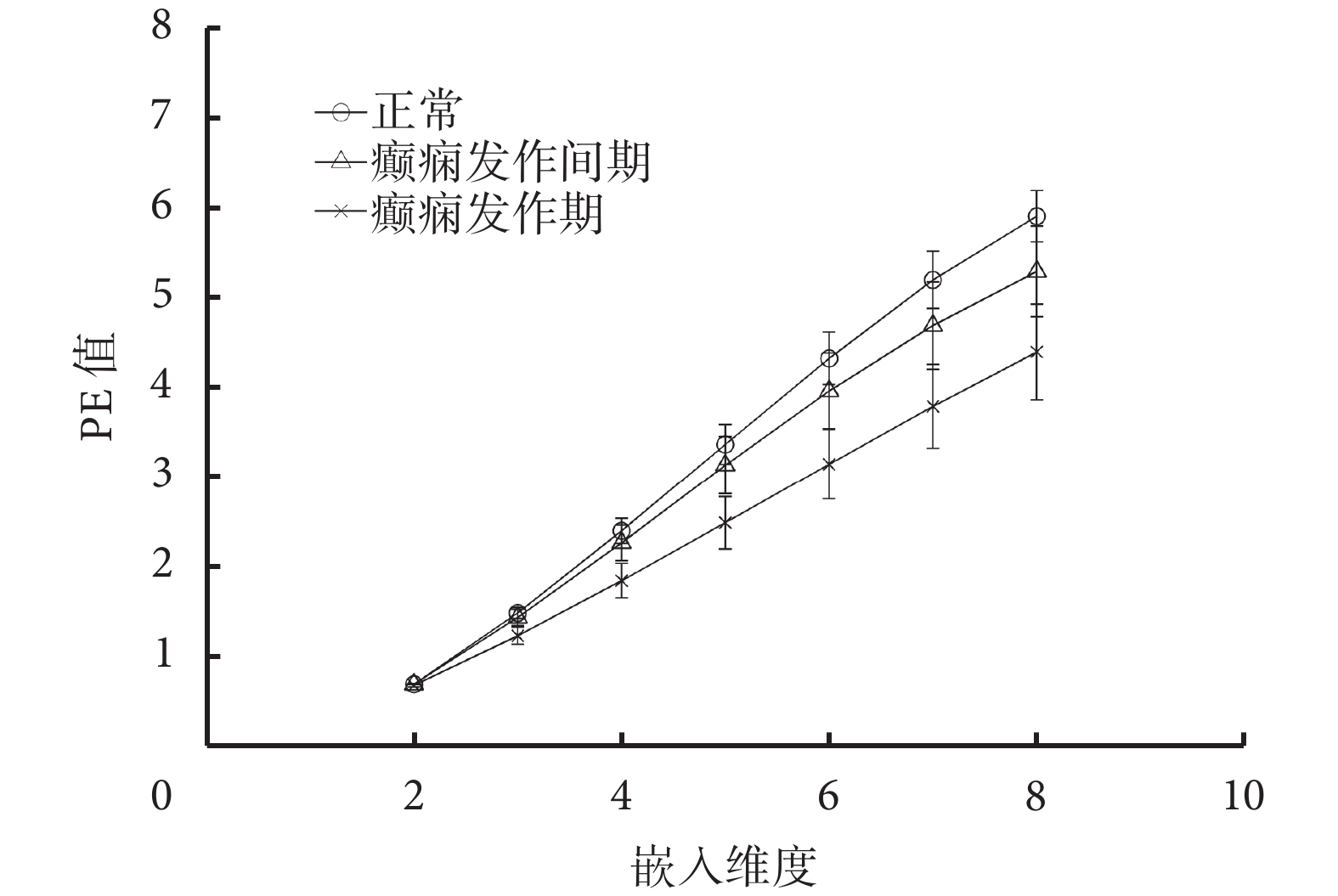圖4
腦電信號在不同時期不同嵌入維度下的 PE
Figure4.
The PE of electroencephalogram signals in different embedding dimensions and different periods
在得到信號各頻段波動指數和 PE 后，需要將這兩類特征共 5 維組成的特征向量送入分類器中進行訓練。實驗采取隨機抽取的方式，為避免正類和負類樣本在數量上差距過大，在 Z、F 數據集中各隨機選取 200 個樣本并與 S 數據集共同組成本實驗所需樣本集。訓練樣本和測試樣本的分配情況如表 1 所示。其中 Real AdaBoost 的弱分類器采用單層決策樹，最大迭代次數設為 100，識別率結果取 20 次實驗的平均值。
表1
各數據集訓練和測試樣本的數量分配情況
Table1.
Distribution of training samples and testing samples on each dataset
如表 2 所示，列出了采用不同特征得到的分類結果，結果用靈敏度（sensitivity）、特異性（specificity）和準確率（accuracy）表示，這其中包括了采用單一特征和多特征結合得到的識別率，其中 Fδ～Fβ 代表各個頻段的波動系數。從表 2 結果可以得出，僅采用單一特征得到的最終識別率均可以達到 84% 以上，經過 S 變換后，不同節律的波動指數所得到的分類效果不同，隨著頻段的升高，準確率也在逐步提高，其中 β 節律準確率最高，為 95.11%。另外，多個節律、多種特征結合得到的分類效果明顯優于單一特征，且時頻特征和非線性特征相結合所得到的效果最好，達到了 98.13% 的準確率。
表2
不同特征下腦電信號的分類結果比較
Table2.
comparison of classification results of electroencephalo-gram signals with different characteristics
如表 3 所示，列出了國內外相關問題所得到的識別準確率與本文方法的比較。可以看出，盡管所用的特征提取方法和分類方法不盡相同，但各方法所得到的識別率都較高。其中，文獻[7]僅利用樣本熵作為特征，文獻[16]從多尺度的角度對腦電信號進行樣本熵特征的提取，本文則采用時頻分析與熵特征相結合的方式，從而對腦電信號的描述更為精細，取得了更好的結果。在模式識別方面，AdaBoost 算法即使在數據樣本較大的情況下仍然可以保持較快的訓練速度，也克服了支持向量機對核函數的依賴。另外，本文方法在 3 個數據集的條件下仍能達到較高的識別準確率且優于其它方法，也說明了時頻分析和非線性動力學相結合進行腦電信號分類的可行性。
表3
部分同類問題在各數據集上的分類識別率
Table3.
Recognition rate of some similar problems on datasets used above
4 結論
時頻分析和非線性動力學方法在腦電信號分類問題中有著很重要的應用，S 變換一定程度上克服了短時傅里葉變換和小波變換的不足，是一種有效的時頻分析工具；PE 可以提取時間序列的復雜度信息并可以有效區分正常、癲癇發作間期和癲癇發作期腦電信號。本文首先將腦電信號進行離散 S 變換，并將變換后各節律系數的波動指數和原始信號的 PE 值共同作為特征向量輸入到基于 Real AdaBoost 算法的分類器中進行識別。實驗表明，S 變換可以有效提取腦電信號各個節律的特征且單一特征的識別率均可以達到 84% 以上，而各個節律特征和 PE 相結合作為特征的識別率最高，達到了 98.13%，體現出時頻分析和信號的非線性特征相結合的優勢，說明該方法在癲癇腦電信號判別問題中是可行的，可以在臨床上為癲癇各時期的判斷提供有力的依據。下一步我們將嘗試采用其它分類方法，并將此方法應用于其它數據集，爭取達到更為理想的結果。
引言
癲癇是大腦神經元異常放電，導致大腦功能障礙的一種慢性疾病，目前全世界患有癲癇的人數約占總人口數的 1%，且每年以 0.02%～0.05% 的速度增長[1]。癲癇是一種突發性疾病且難以治愈，給患者及患者家庭帶來沉重的精神負擔，若疾病持續發作而沒有得到及時的救治，甚至會有生命危險，因此該疾病長期以來倍受醫學界關注。癲癇疾病的預報與檢測是治療中首先要解決的問題，腦電圖（electroencephalogram，EEG）作為目前疾病檢測的主要手段已得到廣泛應用，醫學專家可以對腦電儀采集到的信息進行判讀從而確定是否有癲癇特征波出現。然而癲癇發作的不確定性和患者的個體差異給這一工作帶來了困難，采取人工的方式對腦電圖進行判讀不僅效率低下，也會因為專家的主觀經驗差異造成診斷結果的差異，因而腦電信號的自動檢測仍是當前生物醫學研究的熱點問題之一。
目前，時域、頻域及非線性動力學分析等方法均可用于處理腦電信號問題，其中基于小波變換的特征提取方法在腦電信號的時頻分析方面一直占有較為重要的地位[2-4]，而經驗模態分解（empirical mode decomposition，EMD）作為一種隨機序列的多尺度分析方法也在腦電信號相關問題的研究領域中顯現出了它的價值[5]。此外，非線性動力學分析也是解決生理信號分類的重要方法，常用的非線性動力學方法有 Hurst 指數[4]、近似熵（approximate entropy）[6]、樣本熵（sample entropy）等[7]。文獻[8]還將小波變換、樣本熵等方法相結合，共同應用于腦電信號的分類問題上，取得了 97.53% 的識別率。在模式識別方面，目前常用的分類方法有決策樹[9]、神經網絡（artificial neural network，ANN）[3]、支持向量機（support vector machine，SVM）[6]、極限學習機（extreme learning machine，ELM）等[8]。文獻[10]將神經網絡作為自適應提升（adaptive boosting，AdaBoost）算法的弱分類器，并將原始的 AdaBoost 算法進行了優化，取得了正常腦電信號 99.51%、癲癇腦電信號 96.11% 的識別率。腦電信號的時頻分析多采用小波變換，并在相應頻段提取特征；或者對腦電信號進行非線性動力學分析并在多個尺度上進行特征提取，但這些方法沒有考慮到多種特征相結合的優勢。雖然很多方法考慮在小波變換的基礎上對相應頻段進行非線性分析，但通過這種方法提取到的某些特征聚類效果不夠理想，對最終的分類無法起到較好的指導作用。另外，小波變換雖然是一種優秀的信號時頻分析方法，但其依賴于母小波函數的選擇，不同的母小波函數對特征提取效果會產生一定影響。
針對以上問題，本文結合腦電信號的非線性特征提取和時頻分析的優勢，嘗試將 S 變換和排列熵（permutation entropy，PE）理論共同用于對癲癇腦電信號的檢測中，S 變換結合了短時傅里葉變換和連續小波變換的優點，是一種新型的非線性信號分析方法。本文方法對原始腦電信號計算其 PE 值并進行離散 S 變換，根據人類腦電信號的節律特點將頻率分為相應的若干部分，提取變換各個頻帶系數的波動指數，并與 PE 共同組成特征向量。Real AdaBoost 是 AdaBoost 算法的改進，它引入置信度的概念作為最終分類的依據，對分類輸出的描述更為精細，因此本研究采用該方法作為分類器，整個系統流程如圖 1 所示。
圖1
腦電信號識別流程圖
Figure1.
Process of electroencephalogram signal recognition
1 特征提取方法
1.1 S 變換
Stockwell 等[11]在 1996 年提出了一種新型的時頻分析方法，稱為 S 變換，該方法可以看作是短時傅里葉變換和小波變換的延伸，即采用寬度可變的高斯窗函數替代傳統短時傅里葉變換中的窗函數。信號 h（t）的連續 S 變換定義為：
|
其中：
|
為窗口函數，τ 為時延因子。由高斯窗函數的表達式可以看出，隨著頻率的升高，窗函數的寬度減小，而低頻處的窗口相對較寬，這樣就在理論上達到了在低頻處有更好的頻率分辨率，高頻處有更好的時間分辨率的效果。在信號分析領域，常常采用 S 變換的離散形式。設 H（f）為 h（t）的傅里葉變換，則 h（t）的 S 變換也可寫成如下形式：
|
若設信號的采樣間隔為 T，則采樣點數為 N = t/T。則根據（3）式，一維信號的離散 S 變換可表示為（k = 0，1，2，
，N—1，n = 1，2，
，N—1）：
|
n = 0 時，
|
變換結果為二維復矩陣，矩陣的行為頻率值，列為采樣時間點，這里取矩陣中元素的模值作為最終結果，即：
|
由于離散 S 變換與短時傅里葉變換有一定的聯系，因此在實際計算時可采用快速傅里葉變換提高運算速度。
1.2 排列熵
PE 是由 Bandt 等[12]提出的一種衡量一維時間序列復雜度的方法。該方法在估計序列的復雜度方面具有計算方法簡單、抗噪聲能力強等特點，在隨機信號分析、信號突變檢測等方面有著廣泛的應用且具有良好的效果。設一維時間序列為{h（i），i = 1，2，
，N}，對其進行重構，得到一個新的相空間，即：
|
m 為嵌入維度，τ 為時延因子，其中 1 ≤ i ≤ N —（ m — 1） τ，對每一個 i 值所對應的元素進行升序排列，即：
，其中 j1，j2，
，jm 為元素所在相空間矩陣中列的索引，若存在元素值相等的情況，則按照索引的大小進行升序排列，顯然，對于 m 個元素即存在 m! 種排列方式。定義 π 為序列的一種排列方式，πi 的出現概率為 pj（π），則 PE 的定義為：
|
由于引入“熵”的概念作為復雜度的度量，因此理論上 PE 的值越低，時間序列越具有規律性，即信號產生新模式的概率較小；反之則表明序列越混亂無序，即信號產生新模式的概率越大。
2 分類方法
Real AdaBoost 算法是著名的集成學習算法 AdaBoost 算法的改進版本，由 Schapire 等[13]提出，目的是為了克服 AdaBoost 算法在輸出上較為粗糙的缺陷。其基本思想都是通過訓練若干個弱分類器，賦予其不同權重，最終組合成強分類器。而 Real AdaBoost 算法的優點主要在于，能夠將樣本屬于某一類的可能性通過置信度表示，而不像原始的 AdaBoost 算法只能輸出 —1 或 +1。該研究還通過實驗指出，Real AdaBoost 算法在訓練的收斂速度方面也要優于原始算法。該算法的基本步驟如下：
（1）假設訓練集合為 S = {（x 1，y1），（x 2，y2），
，（x n，yn）}，其中xi 為特征向量，yi 為類別標簽且 yi∈{+1，—1}。初始化樣本權重D1（i） = 1/n，i = 1，2，3，
，n；
（2）循環執行步驟①～④，t 為循環輪數，且 t = 1，2，3，
，T。
① 對樣本劃分為若干個互不相交的子空間，劃分后區間個數為 m。對每一區間計算 + 1 和 — 1 類的累計樣本權重，記為
和
，1 ≤ j ≤ m；
② 計算歸一化因子
，設弱分類器函數為 ht（x），對任意屬于某區間的x 有
（1 ≤ j ≤ m），ε 為一很小的正數，選擇
；
③ 更新樣本權重：
；
④ 當誤差率小于初始設定的值或等于最大迭代次數時，執行第（3）步，否則繼續執行循環體。
（3）輸出強分類器
。其中 b 為平滑因子，默認為 0。
3 實驗結果與分析
本文使用的實驗數據來源于德國波恩大學癲癇研究中心數據庫[14]。腦電信號的采樣頻率為 173.61 Hz，共有 5 組數據集，分別用 Z、O、N、F 和 S 表示。其中 Z 和 O 分別為正常人清醒時睜眼和閉眼時的腦電數據；N 和 F 分別為患者癲癇發作間期致癇灶外和致癇灶內的腦電數據；S 為患者癲癇發作期致癇灶內的腦電數據。每個數據集都包含 100 個樣本且每個樣本都包含 4 097 個采樣點。實驗前需要對數據進行預處理，把每個樣本的最后一個點舍棄并將其均分為 4 段，這樣每個數據集就得到了 400 個樣本。取 Z、F、S 共 3 組進行實驗，共計 1 200 個樣本。在本分類問題中，將 Z 組和 F 組標記為負類，S 組標記為正類。
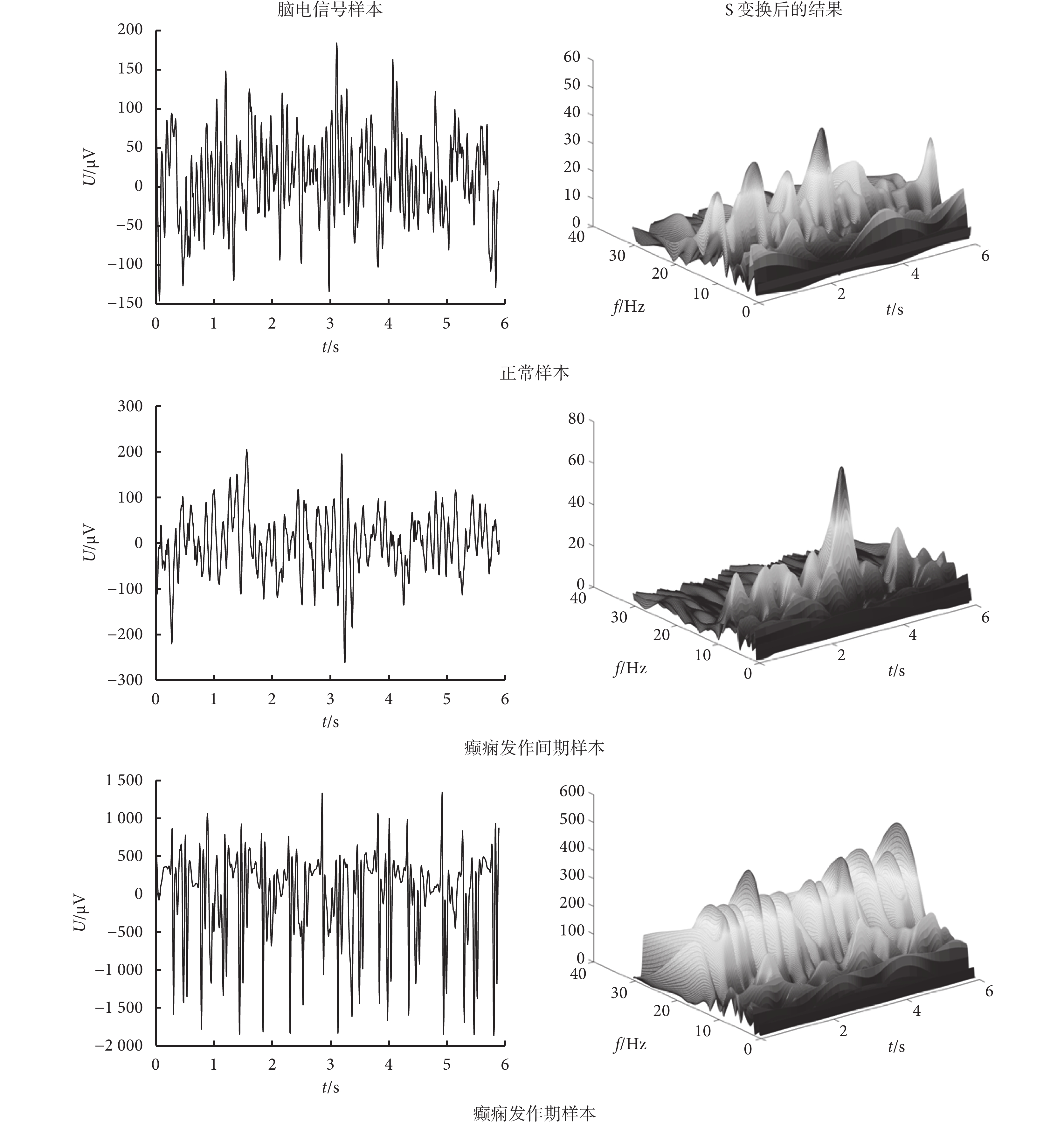
首先對處理后的信號進行離散 S 變換，由于人類腦電信號主要集中于 0.3～30 Hz 的頻率范圍內，因此主要在該頻率段內對信號進行分析。如圖 2 所示，為 Z、F、S 3 組中隨機選出的 3 個腦電信號樣本及其 S 變換后的結果，變換結果用三維圖表示。由于直接將變換結果作為特征向量維數過高，因此根據腦電信號各個節律的頻段范圍，將整個頻段進一步劃分為 4 段，即 δ 波（0.3～4 Hz）、θ 波（4～8 Hz）、α 波（8～13 Hz）和 β 波（13～30 Hz），在每一個頻率段中對變換后的幅值求取波動指數，若信號序列為 s（t），則我們即可將相應頻段 i 的波動指數定義為[15]：
|
其中 N 為信號長度。研究表明，癲癇發作期信號波動較為劇烈，其波動指數值遠區別正常期和發作間期。
圖2
處理后的腦電各時期樣本和離散 S 變換后的結果
Figure2.
The processed electroencephalogram samples and the results of discrete S transform
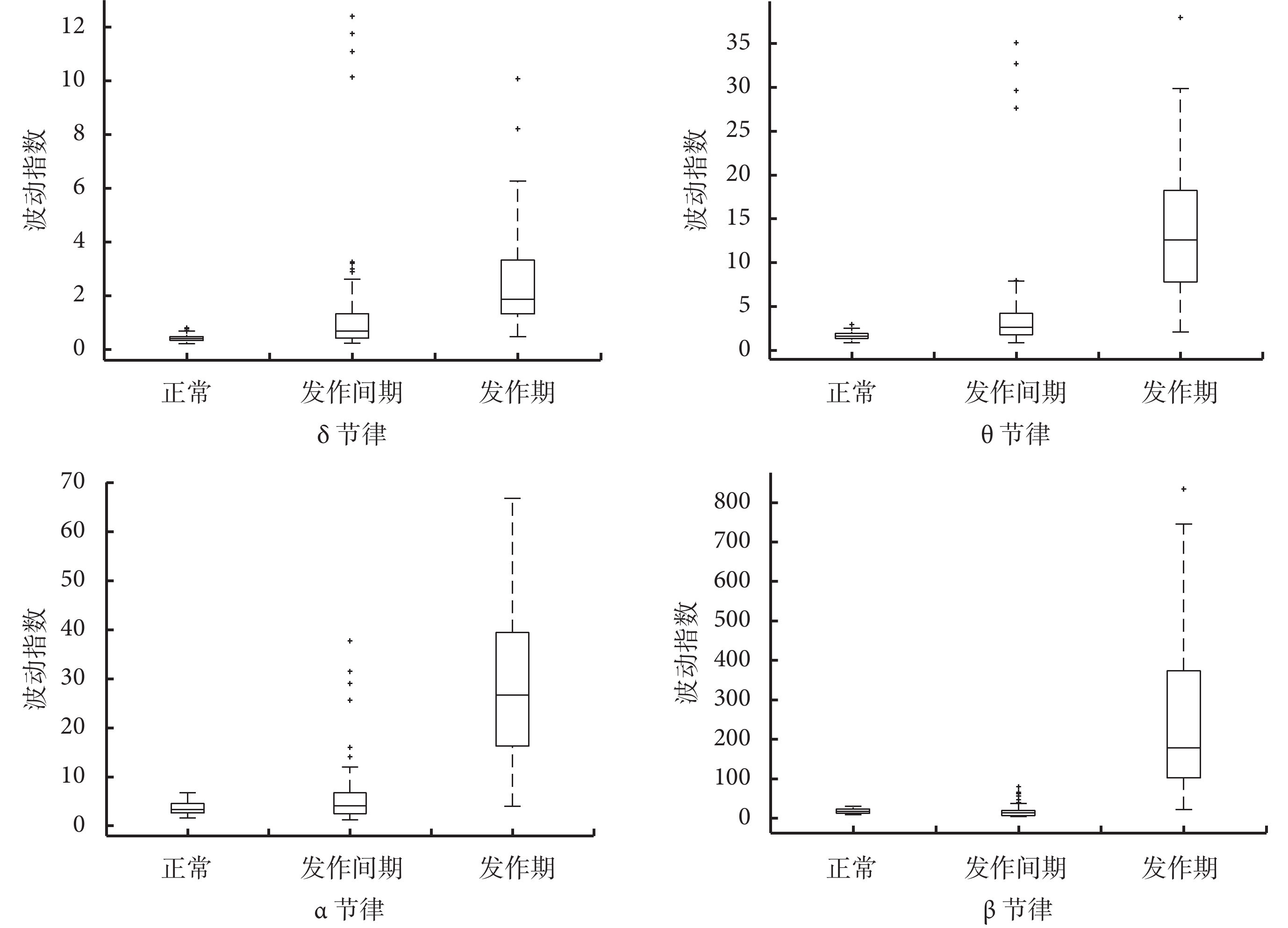
如圖 3 所示為 Z 組（正常）、F 組（發作間期）和 S 組（發作期）3 組信號 4 個節律的波動指數的箱線圖（每組隨機選取 100 個樣本），從中可以看出，正常信號和發作間期信號的波動指數值整體遠小于發作期信號，且波動指數的上下浮動范圍也遠小于發作期信號，因此適合作為分類依據。
圖3
正常、癲癇發作間期和癲癇發作期腦電信號不同節律下的波動指數
Figure3.
The fluctuation index of the electroencephalogram signals during normal，interictal and ictal periords of different rhythm
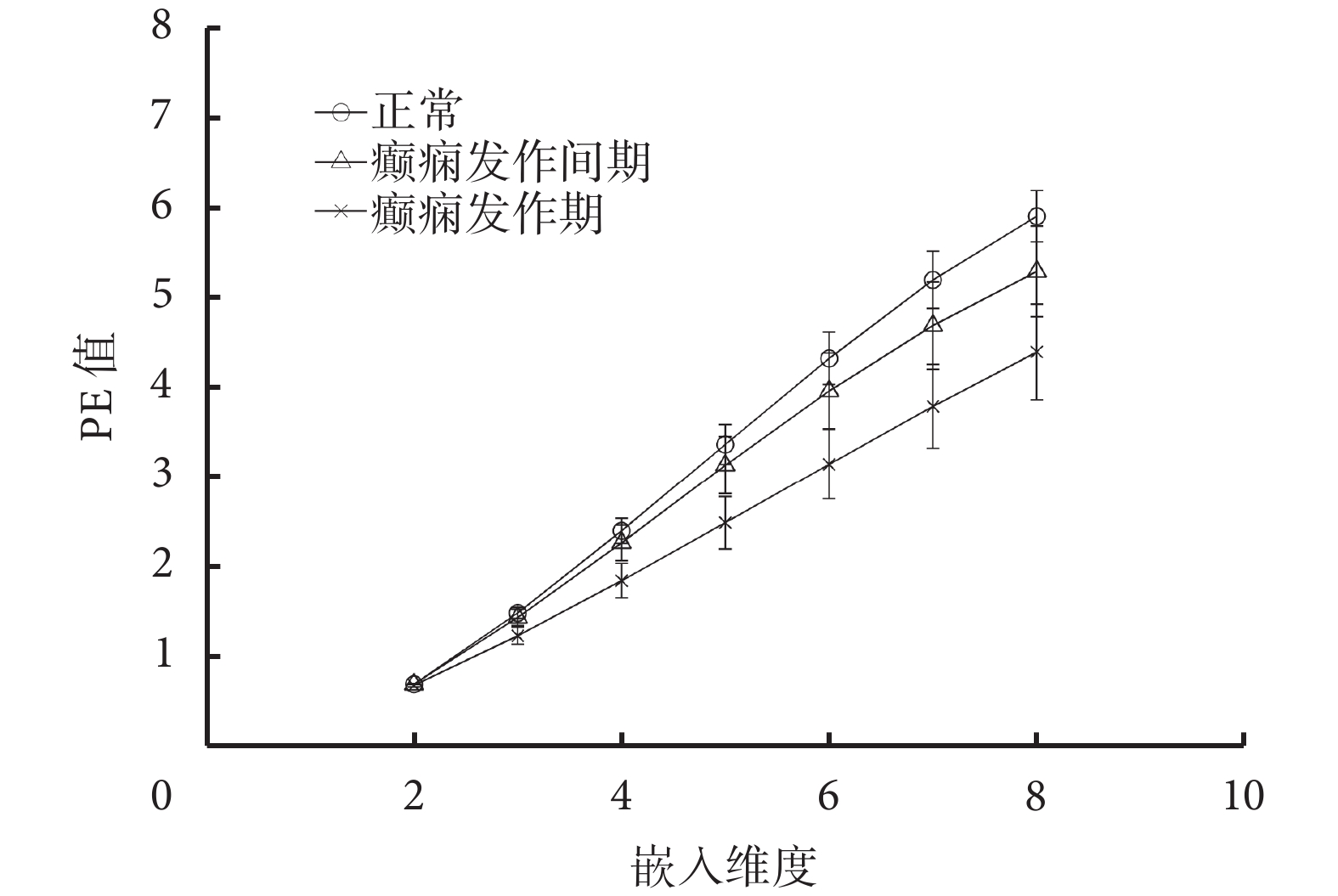
在對原始信號進行 PE 計算前需要確定最佳嵌入維度 m，不同 m 下 3 組腦電數據的 PE 均值及其標準差如圖 4 所示（時延因子 τ = 1），由圖 4 可以看出，正常和發作間期信號的 PE 值總體大于發作期，且隨著嵌入維度的增加，各時期 PE 均值的差距也不斷增大，但每個時期結果的標準差也隨之增大，說明當 m 過大時波動較為劇烈，聚類效果較差。綜合考慮，本實驗選取 m = 5 作為最終的嵌入維度。
圖4
腦電信號在不同時期不同嵌入維度下的 PE
Figure4.
The PE of electroencephalogram signals in different embedding dimensions and different periods
在得到信號各頻段波動指數和 PE 后，需要將這兩類特征共 5 維組成的特征向量送入分類器中進行訓練。實驗采取隨機抽取的方式，為避免正類和負類樣本在數量上差距過大，在 Z、F 數據集中各隨機選取 200 個樣本并與 S 數據集共同組成本實驗所需樣本集。訓練樣本和測試樣本的分配情況如表 1 所示。其中 Real AdaBoost 的弱分類器采用單層決策樹，最大迭代次數設為 100，識別率結果取 20 次實驗的平均值。
表1
各數據集訓練和測試樣本的數量分配情況
Table1.
Distribution of training samples and testing samples on each dataset
如表 2 所示，列出了采用不同特征得到的分類結果，結果用靈敏度（sensitivity）、特異性（specificity）和準確率（accuracy）表示，這其中包括了采用單一特征和多特征結合得到的識別率，其中 Fδ～Fβ 代表各個頻段的波動系數。從表 2 結果可以得出，僅采用單一特征得到的最終識別率均可以達到 84% 以上，經過 S 變換后，不同節律的波動指數所得到的分類效果不同，隨著頻段的升高，準確率也在逐步提高，其中 β 節律準確率最高，為 95.11%。另外，多個節律、多種特征結合得到的分類效果明顯優于單一特征，且時頻特征和非線性特征相結合所得到的效果最好，達到了 98.13% 的準確率。
表2
不同特征下腦電信號的分類結果比較
Table2.
comparison of classification results of electroencephalo-gram signals with different characteristics
如表 3 所示，列出了國內外相關問題所得到的識別準確率與本文方法的比較。可以看出，盡管所用的特征提取方法和分類方法不盡相同，但各方法所得到的識別率都較高。其中，文獻[7]僅利用樣本熵作為特征，文獻[16]從多尺度的角度對腦電信號進行樣本熵特征的提取，本文則采用時頻分析與熵特征相結合的方式，從而對腦電信號的描述更為精細，取得了更好的結果。在模式識別方面，AdaBoost 算法即使在數據樣本較大的情況下仍然可以保持較快的訓練速度，也克服了支持向量機對核函數的依賴。另外，本文方法在 3 個數據集的條件下仍能達到較高的識別準確率且優于其它方法，也說明了時頻分析和非線性動力學相結合進行腦電信號分類的可行性。
表3
部分同類問題在各數據集上的分類識別率
Table3.
Recognition rate of some similar problems on datasets used above
4 結論
時頻分析和非線性動力學方法在腦電信號分類問題中有著很重要的應用，S 變換一定程度上克服了短時傅里葉變換和小波變換的不足，是一種有效的時頻分析工具；PE 可以提取時間序列的復雜度信息并可以有效區分正常、癲癇發作間期和癲癇發作期腦電信號。本文首先將腦電信號進行離散 S 變換，并將變換后各節律系數的波動指數和原始信號的 PE 值共同作為特征向量輸入到基于 Real AdaBoost 算法的分類器中進行識別。實驗表明，S 變換可以有效提取腦電信號各個節律的特征且單一特征的識別率均可以達到 84% 以上，而各個節律特征和 PE 相結合作為特征的識別率最高，達到了 98.13%，體現出時頻分析和信號的非線性特征相結合的優勢，說明該方法在癲癇腦電信號判別問題中是可行的，可以在臨床上為癲癇各時期的判斷提供有力的依據。下一步我們將嘗試采用其它分類方法，并將此方法應用于其它數據集，爭取達到更為理想的結果。
