基于靜息態功能磁共振成像(fMRI)構建腦功能網絡是揭示人腦運作機制的有效手段,但是目前常見的腦功能網絡普遍包含大量噪聲從而導致錯誤的分析結果。本文使用壓縮感知中的最小絕對值收縮和選擇算子(LASSO)模型對腦功能網絡進行降噪重建,該模型利用 L1 范數懲罰項的稀疏性避免過擬合問題。然后,通過快速迭代閾值收縮算法(FISTA)求解,該算法在每一次迭代中通過一個收縮閾值操作來更新變量,從而收斂到全局最優解。實驗結果表明:與其他幾種方法相比,該方法可以將腦功能網絡降噪重建的準確率提高到 98% 以上,有效地抑制了噪聲,有助于即使在噪聲環境下也能很好地探索人腦的功能。
引用本文: 郭慶, 滕月陽, 仝燦, 李迪森, 王雪飛. 基于壓縮感知與快速迭代閾值收縮算法的腦功能網絡重建. 生物醫學工程學雜志, 2020, 37(5): 855-862. doi: 10.7507/1001-5515.201908024 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
引言
大腦是人體內結構和功能最復雜的器官,了解并掌握人腦的運作機制是腦科學研究領域的一項重大挑戰[1]。腦科學的研究成果不僅可以使人們更好地保護和開發大腦,同時也有助于治療各種腦部疾病,例如阿爾茲海默癥(Alzheimer disease,AD)、輕度認知障礙(mild cognitive impairment,MCI)和自閉癥譜系障礙(autism spectrum disorder,ASD)等[2-4]。目前,研究人員通過功能性磁共振成像(functional magnetic resonance imaging,fMRI)等非侵入式技術有效地探索了人腦結構及其運行機制[5-7]。其中,基于 fMRI 構建腦功能網絡就是一種重要的研究手段。在腦功能網絡中,通常將大腦皮層或感興趣區(region of interest,ROI)定義為節點,不同節點之間的連接用邊來表示,邊的大小,表示不同節點之間的連接權重。已有研究表明,許多精神疾病都與腦功能網絡的異常連接有關,表現為大腦區域之間的連接中斷或屬性異常[8-9]。例如,相對于健康人群而言,AD 患者的腦功能網絡連接會出現一些顯著的病理變化。
然而在腦功能成像過程中,心血管和呼吸運動不可避免會產生一些生理噪聲,這些噪聲通常服從高斯分布,會對血氧水平依賴(blood oxygen level dependent,BOLD)的 fMRI 造成很大影響[10]。這種影響會降低圖像的信噪比,進而使后續構建的腦功能網絡中包含大量高斯噪聲,導致對大腦的功能分析出現錯誤[11]。所以,如何從含有噪聲的數據中構建出真實的腦功能網絡,對于腦部疾病的診斷和人類大腦功能的探索具有重要意義。
壓縮感知理論指出:如果信號滿足稀疏性,即使該信號在傳輸和采集過程中受到噪聲影響,也能通過相應的算法對其進行恢復。最小絕對值收斂和選擇算子(least absolute shrinkage and selection operator,LASSO)是實現壓縮感知的一種有效方法[12]。為了求解 LASSO 問題,Daubechies 等[13]提出了一種迭代閾值收縮算法(iterative shrinkage-thresholding algorithm,ISTA)。該算法在每一次迭代過程中通過一個收縮閾值操作來更新待恢復的信號,但該算法收斂速度較慢,需要大量的時間才能獲得一個較好的結果。為了解決相同問題,Teng 等[14]采用一種平滑函數來逼近 L0 和 L1 范數,然后通過替代函數法求解該問題。
針對腦功能網絡噪聲問題,本文采用一種快速 ISTA(fast ISTA,FISTA)算法求解壓縮感知中的 LASSO 模型對腦功能網絡進行降噪重建的問題。該方法利用小波變換對待構建的腦功能網絡進行分解,從而把求解腦功能網絡問題轉化為求解小波基系數問題。由于小波基系數具有稀疏性,所以可以使用 LASSO 模型進行表達。最后通過 FISTA 求解,從而抑制噪聲。通過以上步驟,期望本文提出的方法可以對腦功能網絡進行有效地降噪重建,并為更好地探索不同腦區之間的連接關系奠定研究基礎。
1 材料及方法
1.1 數據獲取
本研究數據來自阿爾茨海默病神經影像學計劃(Alzheimer’s Disease Neuroimaging Initiative,ADNI)數據庫(http://www.loni.ucla.edu/ADNI)。該數據庫主要通過 fMRI、正電子發射斷層掃描(positron emission computed tomography,PET)等影像學檢查結合心理學評估,確定早期 AD 患者的特征,以幫助醫生制定治療方案并監測其有效性。由于 AD 患者和健康人群[即正常對照組(normal controls,NC)]的腦功能網絡結構明顯不同,為了證明本研究所提出的降噪重建方法對于兩組不同人群的腦功能網絡降噪均有效,本文從 ADNI 數據庫中選取了 3T 掃描的標準化數據集,其中 AD 組 18 例(男 10 例,女 8 例),NC 組 12 例(男 6 例,女 6 例),年齡范圍均為(78  6)歲。
6)歲。
1.2 數據預處理
本實驗使用神經影像腦連接組分析軟件 GRETNA-2.0.0(北京師范大學,中國)對數據進行預處理。具體的步驟包括:將醫學數字成像和通信(digital imaging and communications in medicine,DICOM)格式圖像轉換為神經影像信息學技術協議(neuroimaging informatics technology initiative,NIFTI)格式圖像;去除前 10 個時間點的信號以便于參與者適應測試環境;以時間層校正的方式校正層與層之間的時間差;剔除水平頭動超過 2 mm 和旋轉超過 2° 的數據;選用高斯核函數對標準化后的數據進行平滑。最后將圖像匹配到蒙特利爾神經學研究所(Montreal neurological institute,MNI)模板。本文選用 MNI 提供的自動解剖標記模板(automated anatomical labeling 90 atlas,AAL90)將大腦劃分成 90 個 ROI,每個 ROI 都當作腦功能網絡的一個節點[15]。
1.3 腦功能網絡構建
所有 ROI 之間的連接關系用連接矩陣表示,矩陣元素是各個 ROI 之間的連接強度[16]。本文使用 90 個 ROI 作為節點,獲得了 90 × 90 的腦功能網絡連接矩陣 I。為了能夠表達網絡的模塊化結構,對獲得的連接矩陣進行二值化處理:當矩陣元素大于設定的閾值時,將其設置為 1,否則設置為 0,處理方法如式(1)所示:
 |
其中,Iij 表示連接矩陣的第(i,j)個元素值,T 表示閾值。本文設定 T 為 0.8Imax,Imax 表示連接矩陣中最大的元素值。通過上述處理后得到 0、1 二值化矩陣,即為本文所需的原始腦功能網絡。
由于在腦功能成像的過程中,生理噪聲呈現高斯分布,所以本文通過對原始網絡添加高斯噪聲來表示含有噪聲的腦功能網絡,如式(2)所示:
 |
其中,Y 表示含有噪聲的腦功能網絡矩陣,n 表示強度是 0.01 的高斯噪聲。
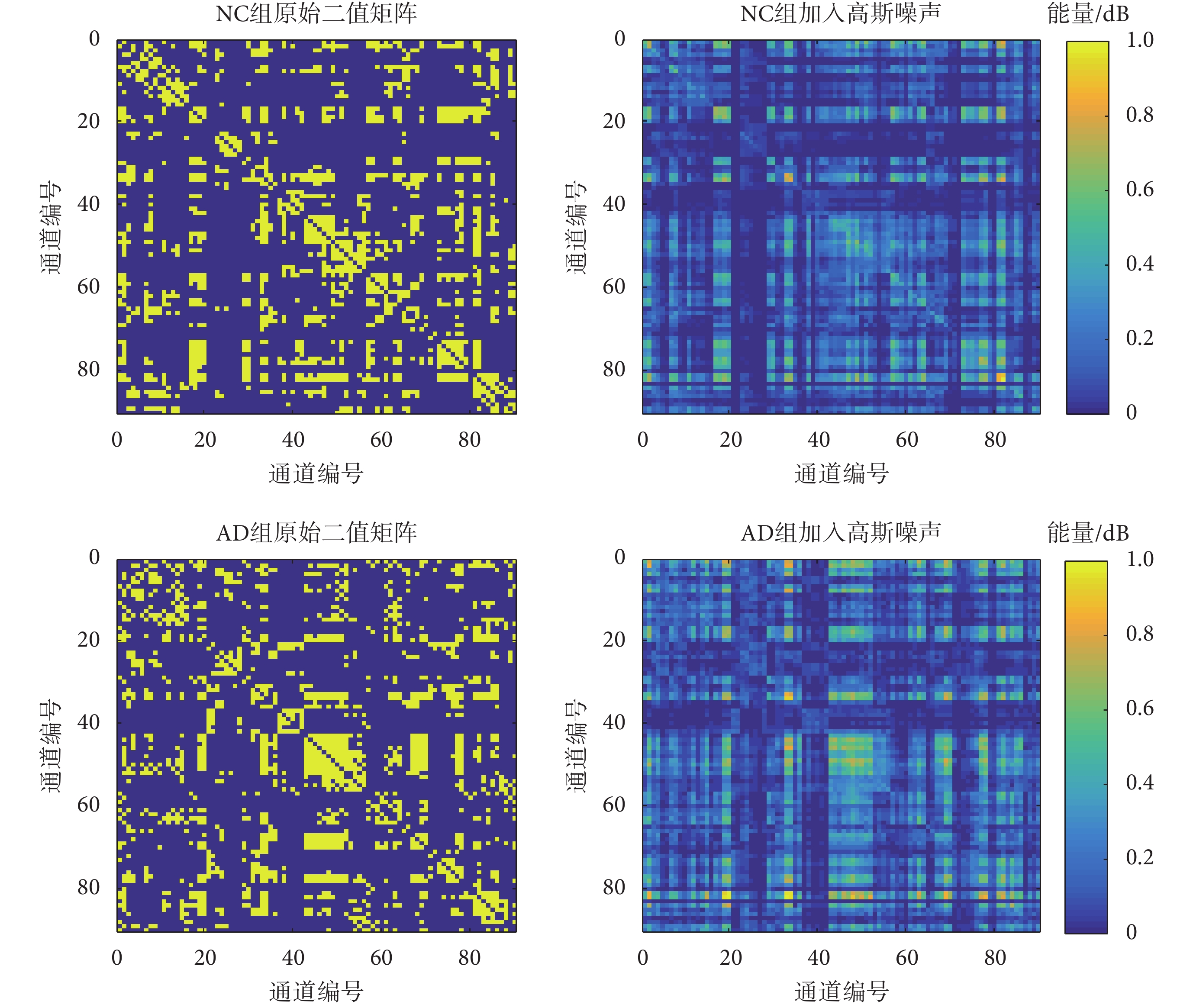
為了均衡表現所選兩組數據大腦 ROI 之間的連接關系,本文對 18 例 AD 組和 12 例 NC 組的腦功能網絡矩陣分別取每組的平均值,再將所得結果以二值矩陣的形式表現出來,最后將其加入高斯噪聲作為研究對象。如圖 1 所示,分別展示了每組的原始二值矩陣和加入高斯噪聲后的效果圖。其中,藍色表示二值矩陣中的元素為 0,即對應的兩個 ROI 之間沒有關聯;黃色表示二值矩陣中的元素為 1,即對應的兩個 ROI 之間有關聯。在受到高斯噪聲干擾后,原始二值矩陣變為多值矩陣。此時,已經難以有效判斷不同 ROI 之間的關聯情況,因此需要對其進行降噪重建。
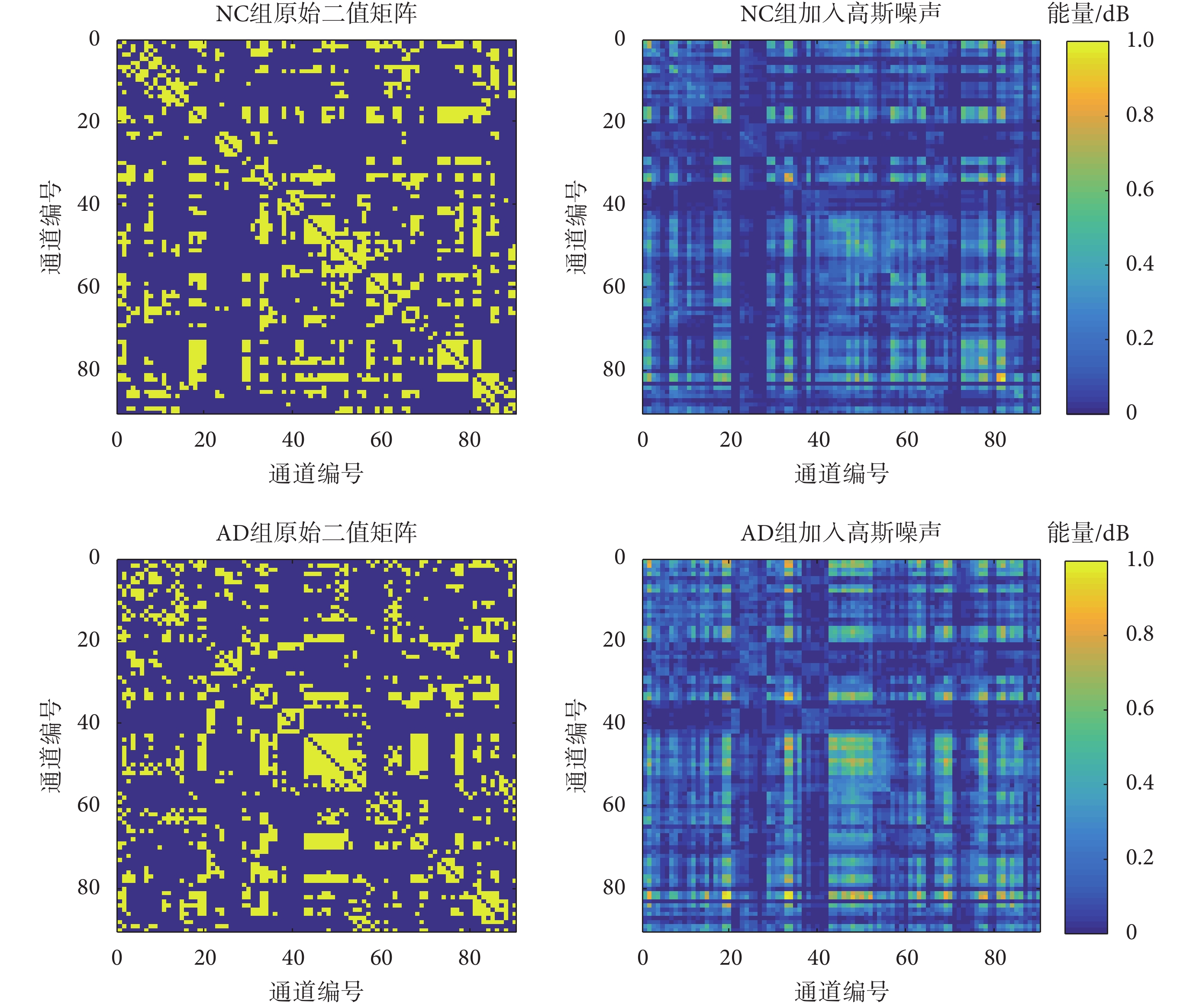 圖1
原始二值矩陣與含噪聲矩陣
Figure1.
Original binary matrix and noisy matrix
圖1
原始二值矩陣與含噪聲矩陣
Figure1.
Original binary matrix and noisy matrix
2 重建算法的原理
2.1 LASSO 模型和 FISTA 算法
LASSO 模型是壓縮感知理論中經典模型之一[17]。該模型的基本思想是在殘差平方和最小化過程中,引入稀疏約束。在該限制條件下,絕對值較小的回歸系數會約束到零,進而產生稀疏解,如式(3)所示:
 |
其中, 表示 L1 范數,
表示 L1 范數, 表示 L2 范數,b 表示測量信號,x 表示待恢復信號,A 表示給定的系統矩陣,λ 表示正則化參數。該模型可以保證在一定程度恢復原始信號的前提下,防止由于噪聲引起的過擬合現象。
表示 L2 范數,b 表示測量信號,x 表示待恢復信號,A 表示給定的系統矩陣,λ 表示正則化參數。該模型可以保證在一定程度恢復原始信號的前提下,防止由于噪聲引起的過擬合現象。
ISTA 是求解 LASSO 問題的一種有效算法,該算法是一種迭代優化算法,通過極小化替代函數保證原目標函數迭代下降。相較于 ISTA,FISTA 收斂速度更快,二者的區別在于迭代過程中替代函數起始點的選擇策略不同:ISTA 使用前一次迭代的替代函數最小值作為起始點;而 FISTA 則利用前兩次迭代值確定起始點,以此來加快收斂速度[18]。
對于式(3)所示的無約束優化問題,令  ,則該問題轉化為如式(4)所示:
,則該問題轉化為如式(4)所示:
 |
式(4)通過近端梯度方法可以得到 ISTA 算法的迭代公式,如式(5)所示:
 |
其中,k 表示迭代次數,tk 表示步長。
令  ,則可以對式(5)進行簡化,如式(6)所示:
,則可以對式(5)進行簡化,如式(6)所示:
 |
對式(6)進行求解,可以得到迭代公式,如式(7)所示:
 |
其中,xj 和 zj 分別表示 x 和 z 的第 j 個分量。
而 FISTA 的改進如式(8)~式(9)所示:
 |
 |
理論證明,ISTA 的收斂速度為 O(1/k),而 FISTA 的收斂速度為 O(1/k2)。
2.2 腦功能網絡降噪
在腦功能網絡降噪問題中,將含有噪聲的腦功能網絡 Y 看作測量信號,已知 Y 和測量矩陣 R,要想重建降噪后的網絡  ,可以通過如式(10)所示的優化模型求得[19]:
,可以通過如式(10)所示的優化模型求得[19]:
 |
其中,R 表示單位矩陣 E 與 Y 的克羅內克積,如式(11)所示:
 |
由于小波變換具有降噪的特性,可以對  進行小波分解,如式(12)所示:
進行小波分解,如式(12)所示:
 |
其中,W 表示小波基矩陣,α 表示小波基系數向量。將式(12)代入式(10)中,可以得到如式(13)所示:
 |
為求解該問題,需要對上式添加稀疏約束。最稀疏的解可以由 L0 范數得到,它度量了非 0 元素的個數,如式(14)所示:
 |
其中, 表示 L0 范數。由于 L0 范數最小化屬于組合優化問題,難以直接求解。所以,通常使用 L1 范數代替 L0 范數,獲得新的優化模型,如式(15)所示:
表示 L0 范數。由于 L0 范數最小化屬于組合優化問題,難以直接求解。所以,通常使用 L1 范數代替 L0 范數,獲得新的優化模型,如式(15)所示:
 |
最后,通過懲罰函數法將式(15)轉化為無約束優化問題,如式(16)所示:
 |
其中,正則化參數 λ 表示可接受的稀疏化程度。通過上述推導,可以將求解待重建網絡  轉化為求解小波基系數 α 的問題,由此證明 LASSO 模型可以用于腦功能網絡的降噪重建。
轉化為求解小波基系數 α 的問題,由此證明 LASSO 模型可以用于腦功能網絡的降噪重建。
3 結果與分析
3.1 小波基的選擇
小波基選擇的多樣性是小波變換的重要特點之一,本實驗使用重建準確率對 Haar、Db2、Db3、Db4、Coif1、Bior1.3、Bior1.5 七種不同小波基進行了對比。其中,重建準確率是正確恢復的矩陣元素與元素總數的百分比。為了避免重建信號失真過大,均采用一層分解。NC 組和 AD 組迭代 100 次時的重建準確率如表 1 所示。NC 組和 AD 組迭代 200 次時的重建準確率如表 2 所示。可以看出,無論是 100 次還是 200 次迭代,Haar 小波基在兩組實驗中均獲得了最高的重建準確率,而 Bior1.5 小波基所獲得的重建準確率最低。最終,選擇 Haar 小波對含有噪聲的腦功能網絡進行分解。
3.2 參數選擇
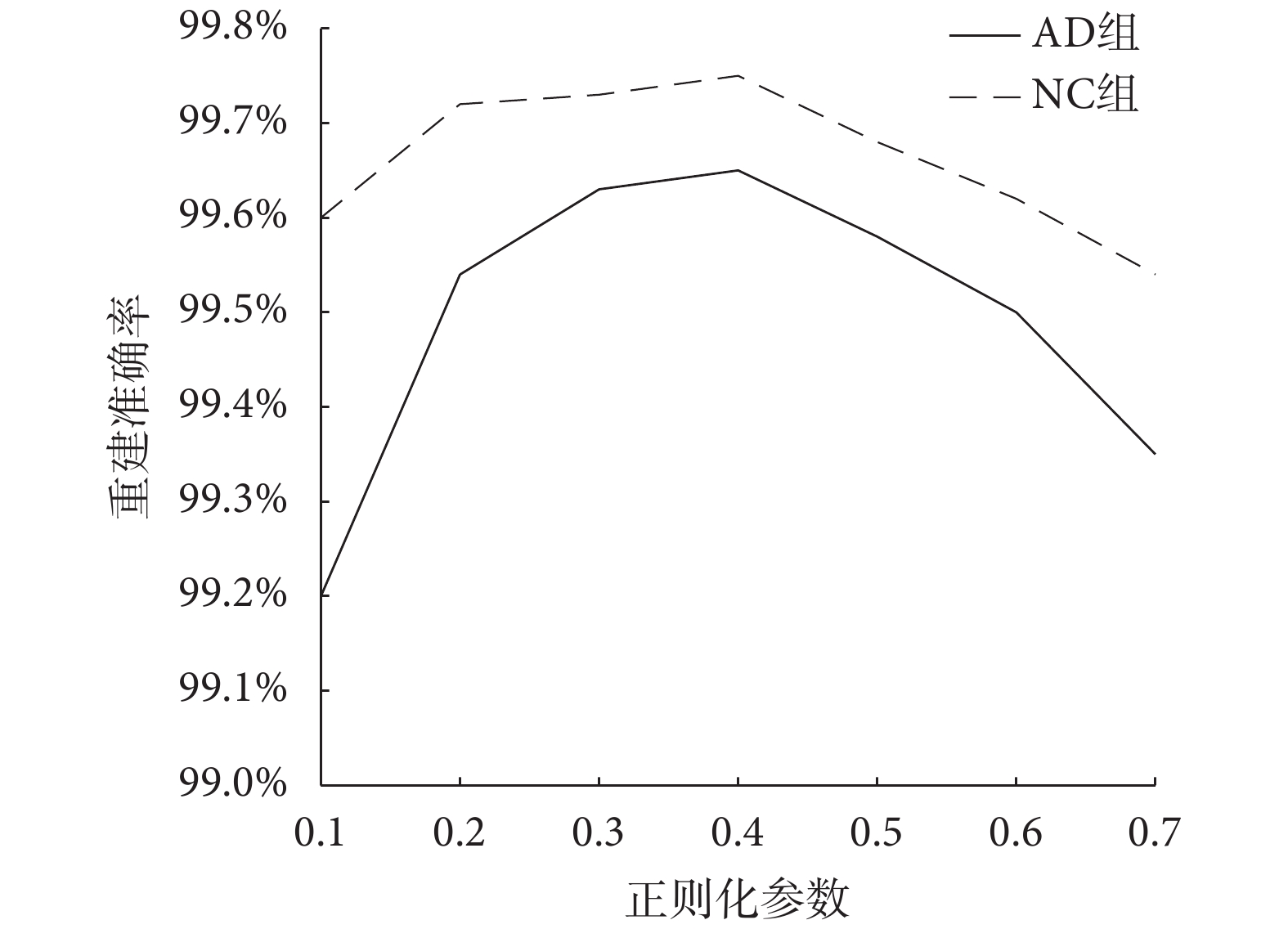
在 LASSO 模型中,參數 λ 的取值不同,會對重建效果產生不同的影響。當 λ 取值過大時,會使過多的矩陣元素置為 0,導致無法對原始腦功能網絡進行有效恢復。當 λ 取值過小時,容易造成過擬合,此時無法有效抑制噪聲。所以,選擇合適的參數 λ 是本實驗重要一步。本文分別對 NC 組和 AD 組選擇不同正則化參數進行比較,迭代次數設置為 200。如圖 2 所示,當  時,NC 組和 AD 組的重建準確率隨著 λ 的增大而上升。當
時,NC 組和 AD 組的重建準確率隨著 λ 的增大而上升。當  時,NC 組和 AD 組的重建準確率隨著 λ 的增大而降低。因此,設置
時,NC 組和 AD 組的重建準確率隨著 λ 的增大而降低。因此,設置  以獲得最好的實驗效果。
以獲得最好的實驗效果。
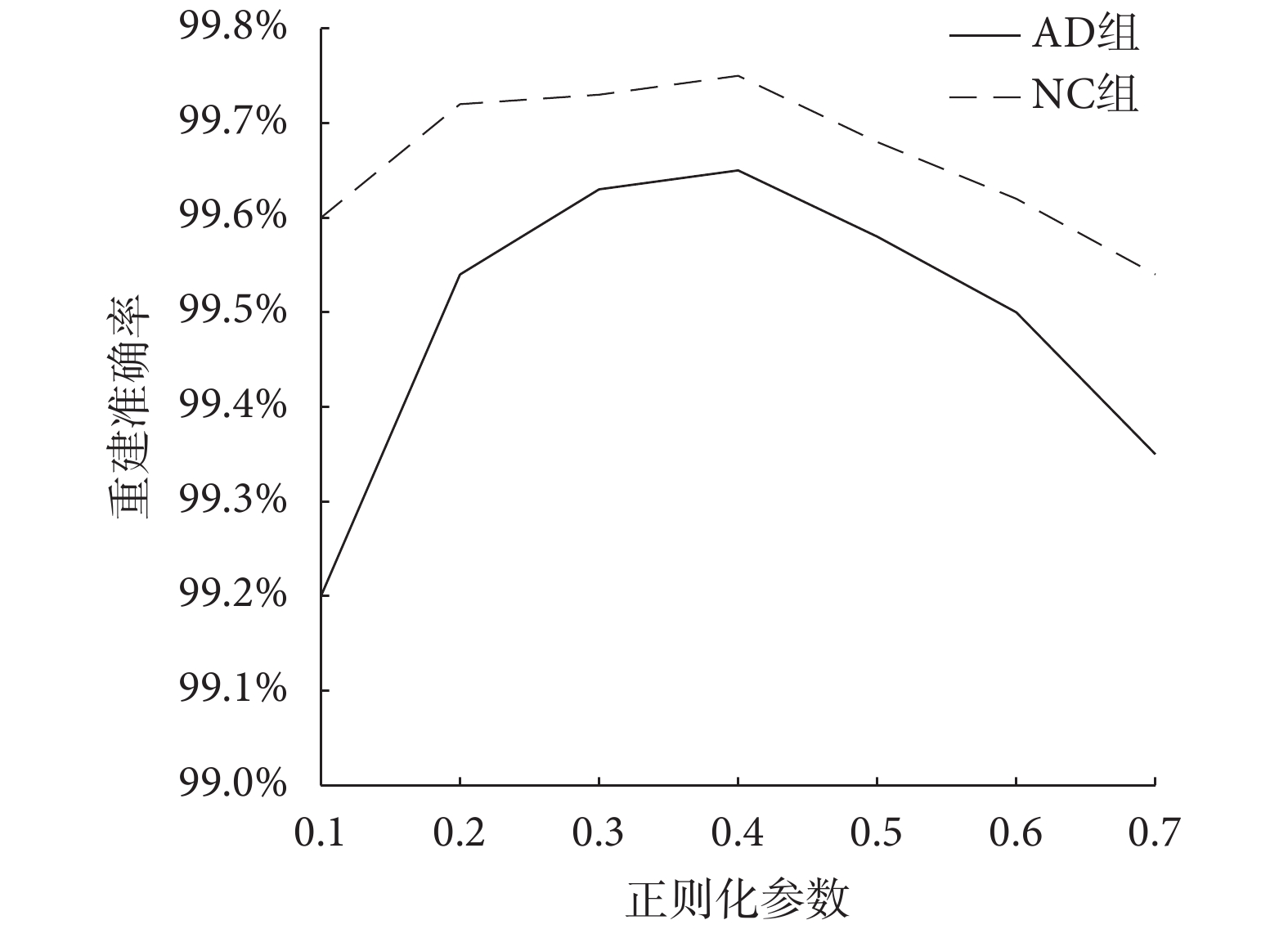 圖2
不同正則化參數對應的重建準確率
Figure2.
Reconstruction accuracy under different regularization parameters
圖2
不同正則化參數對應的重建準確率
Figure2.
Reconstruction accuracy under different regularization parameters
3.3 算法的重建效果
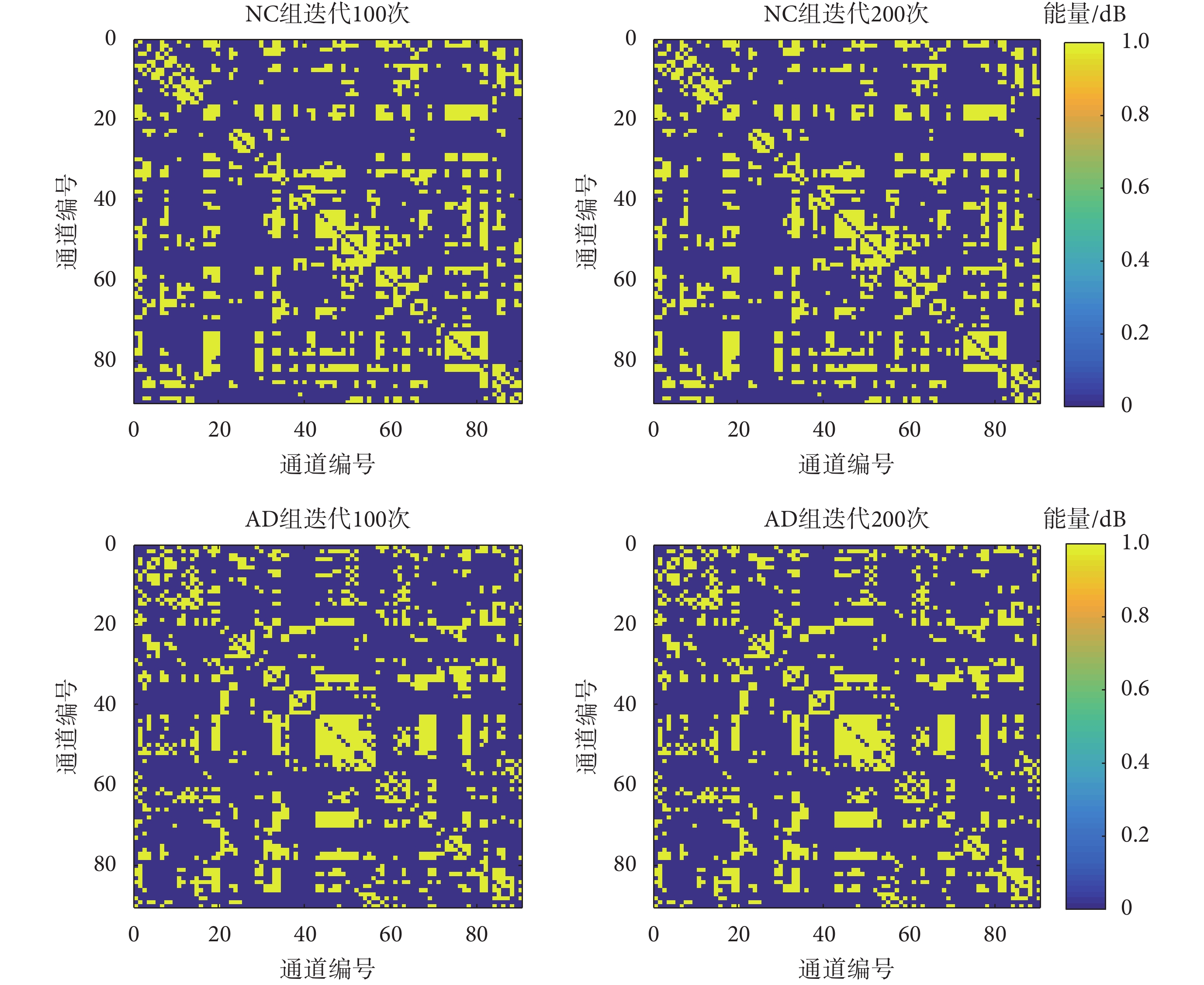
本文針對每組數據分別迭代 100 次和 200 次獲得重建結果。如圖 3 所示,無論 NC 組還是 AD 組,在 100 次迭代后,已經非常接近原始腦功能網絡。200 次迭代后,重建效果進一步提升。
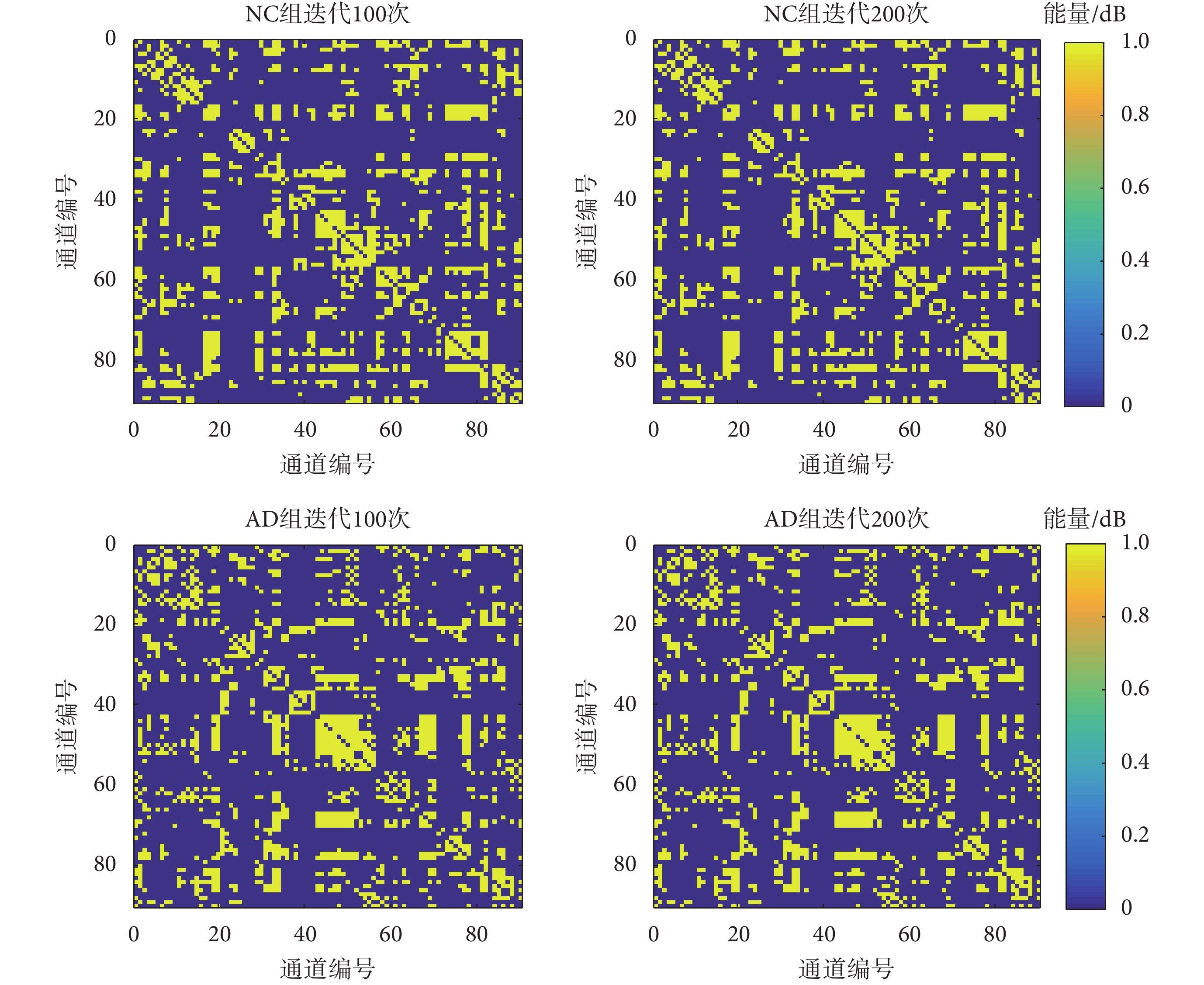 圖3
迭代 100 次、200 次后的二值矩陣
Figure3.
The binary matrix after 100 and 200 iterations
圖3
迭代 100 次、200 次后的二值矩陣
Figure3.
The binary matrix after 100 and 200 iterations
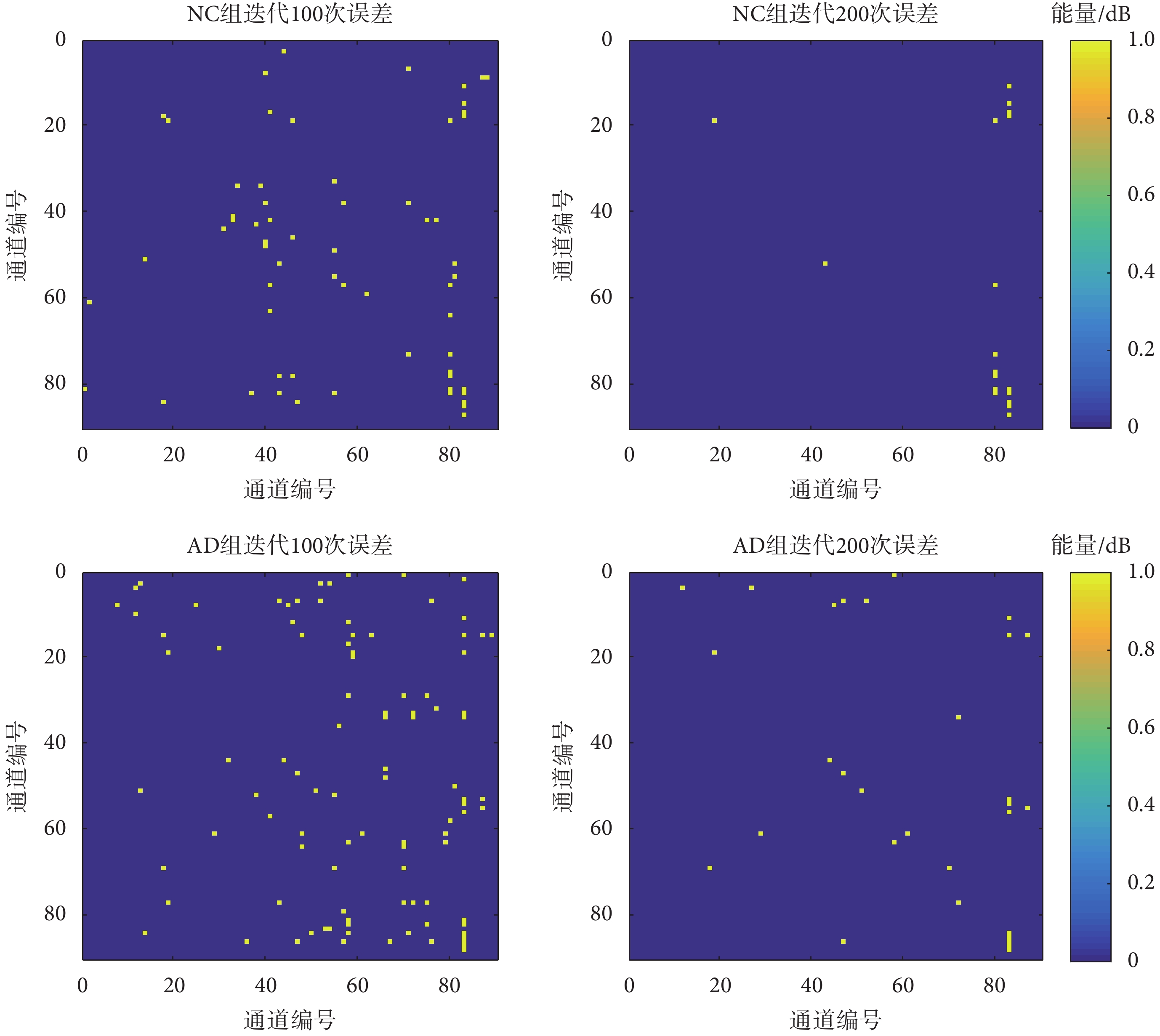
兩個實驗組迭代前后的差異如圖 4 所示。其中藍色表示重建正確的部分,黃色表示重建錯誤的部分。由于默認每個 ROI 與其自身的關聯為 0,所以在原始矩陣中對角線元素均為 0。當有噪聲干擾時,對角線上的 0 值更易受到影響,從而導致在重建結果中,對角線上數值更容易出現誤差。
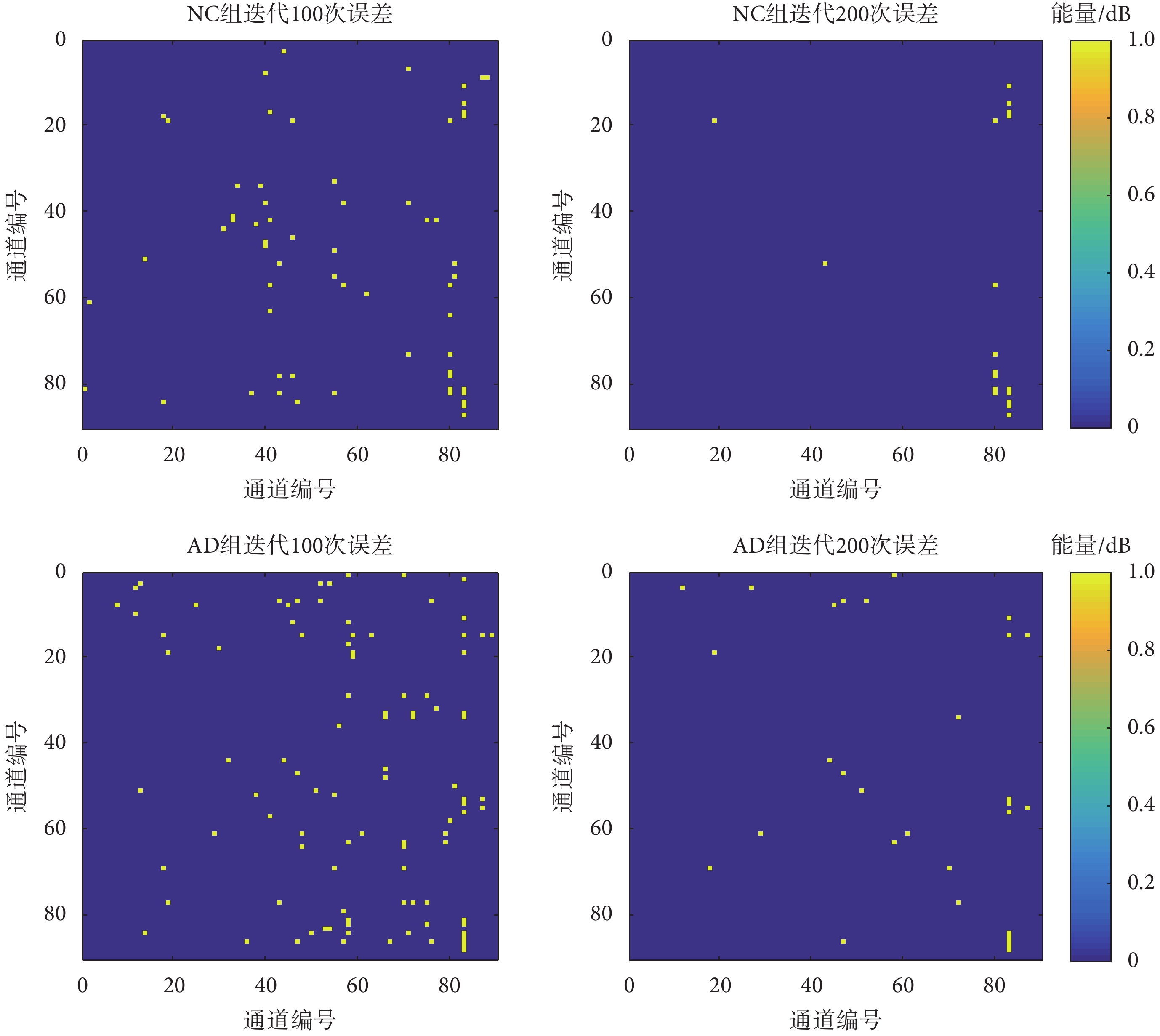 圖4
不同迭代次數的重建誤差
Figure4.
Reconstruction error after different times of iterations
圖4
不同迭代次數的重建誤差
Figure4.
Reconstruction error after different times of iterations
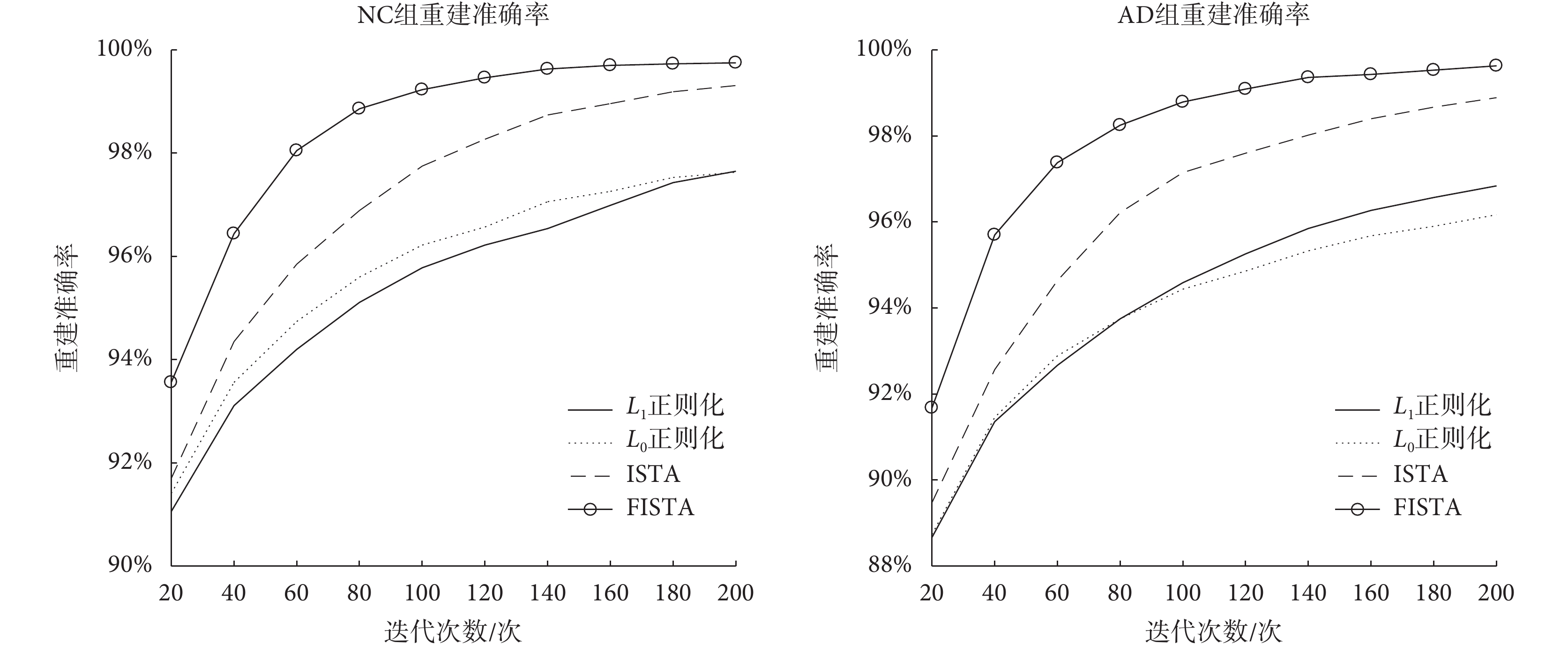
3.4 不同算法的性能比較
為了進一步評估所提出算法的性能,本文比較了 FISTA 與 ISTA、L0 正則化算法和 L1 正則化算法[14]在不同迭代次數時的重建準確率。每種方法都選取了最佳參數。對于 ISTA,λ = 0.4;對于 L0 正則化算法,λ = 0.5;對于 L1 正則化算法,λ = 0.000 1。如圖 5 所示,四種算法隨著迭代次數的增加,都達到了較高的重建準確率。其中 FISTA 在 NC 組和 AD 組的多次迭代中都取得了最好的效果,ISTA 次之,L0 正則化算法和 L1 正則化算法獲得的效果相對較差。具體重建準確率與迭代次數間的關系如表 3、表 4 所示。
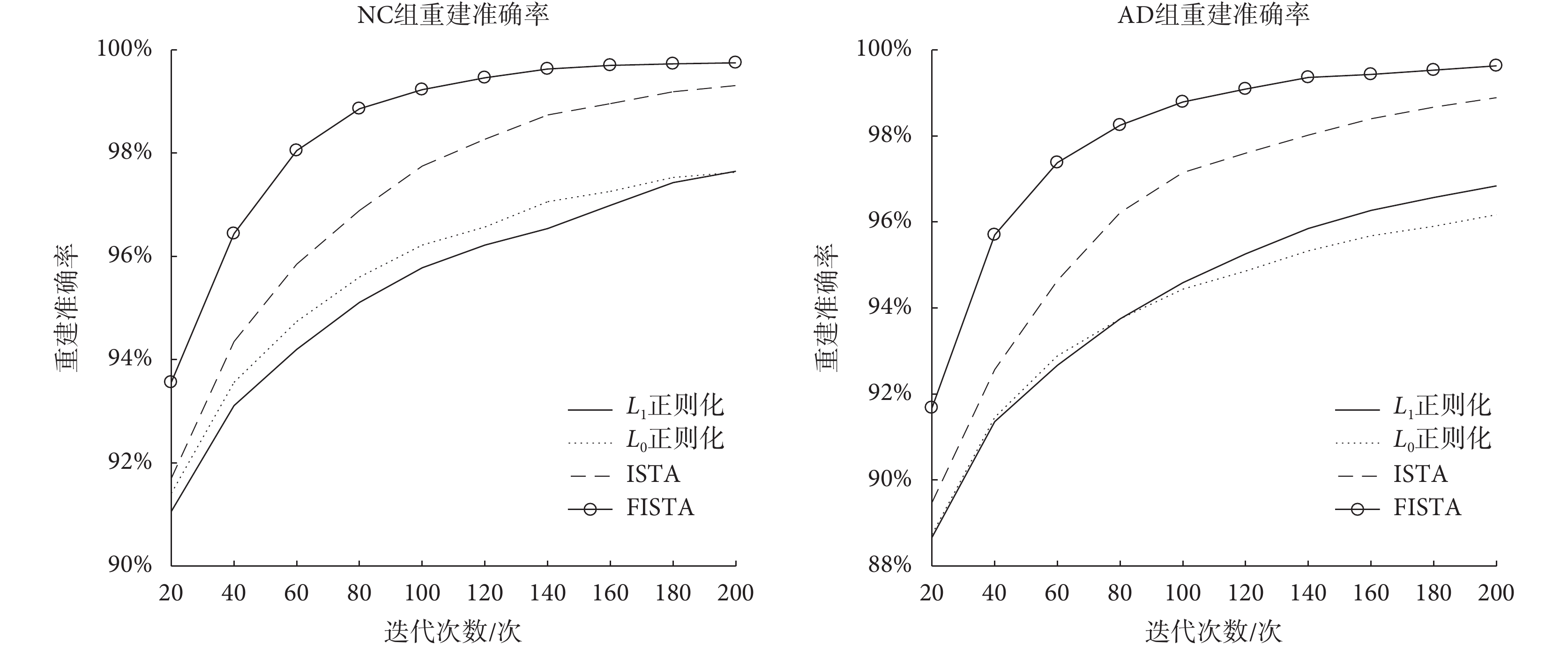 圖5
NC 組和 AD 組不同迭代次數的重建準確率
Figure5.
Reconstruction accuracy of NC and AD groups with different times of iterations
圖5
NC 組和 AD 組不同迭代次數的重建準確率
Figure5.
Reconstruction accuracy of NC and AD groups with different times of iterations
4 總結與展望
已有研究表明,壓縮感知已經成為腦功能網絡建模的一種有效方法[20-22]。本文針對腦功能網絡構建過程中存在的噪聲問題,提出了一種降噪重建方法。將 LASSO 模型結合 FISTA 算法引入到腦功能網絡重建中。結果表明,所提出方法具有良好的恢復效果,能夠有效抑制腦功能網絡中的噪聲。在兩個實驗組中,重建準確率均達到了 98% 以上。相較于其他三種算法而言,具有明顯的優勢。
雖然本文對腦功能網絡進行了有效恢復,但是該項工作仍存在不足。首先,在實驗過程中,如果采用不同的腦區模板,對最終的重建效果會有較大的影響。采用 AAL90 模板、哈佛-牛津模板(Harvard-Oxford 112 atlas,HOA112)和多森巴赫模板(Dosenbach 160 atlas,Dos160)的重建效果明顯不同[23-24]。其次,從實驗結果上看,AD 組的重建準確率在四種算法上都低于 NC 組,說明這些算法在處理異常的腦功能網絡連接時,能力都有待提高。以上這些問題,都將在未來的工作中進一步研究。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
引言
大腦是人體內結構和功能最復雜的器官,了解并掌握人腦的運作機制是腦科學研究領域的一項重大挑戰[1]。腦科學的研究成果不僅可以使人們更好地保護和開發大腦,同時也有助于治療各種腦部疾病,例如阿爾茲海默癥(Alzheimer disease,AD)、輕度認知障礙(mild cognitive impairment,MCI)和自閉癥譜系障礙(autism spectrum disorder,ASD)等[2-4]。目前,研究人員通過功能性磁共振成像(functional magnetic resonance imaging,fMRI)等非侵入式技術有效地探索了人腦結構及其運行機制[5-7]。其中,基于 fMRI 構建腦功能網絡就是一種重要的研究手段。在腦功能網絡中,通常將大腦皮層或感興趣區(region of interest,ROI)定義為節點,不同節點之間的連接用邊來表示,邊的大小,表示不同節點之間的連接權重。已有研究表明,許多精神疾病都與腦功能網絡的異常連接有關,表現為大腦區域之間的連接中斷或屬性異常[8-9]。例如,相對于健康人群而言,AD 患者的腦功能網絡連接會出現一些顯著的病理變化。
然而在腦功能成像過程中,心血管和呼吸運動不可避免會產生一些生理噪聲,這些噪聲通常服從高斯分布,會對血氧水平依賴(blood oxygen level dependent,BOLD)的 fMRI 造成很大影響[10]。這種影響會降低圖像的信噪比,進而使后續構建的腦功能網絡中包含大量高斯噪聲,導致對大腦的功能分析出現錯誤[11]。所以,如何從含有噪聲的數據中構建出真實的腦功能網絡,對于腦部疾病的診斷和人類大腦功能的探索具有重要意義。
壓縮感知理論指出:如果信號滿足稀疏性,即使該信號在傳輸和采集過程中受到噪聲影響,也能通過相應的算法對其進行恢復。最小絕對值收斂和選擇算子(least absolute shrinkage and selection operator,LASSO)是實現壓縮感知的一種有效方法[12]。為了求解 LASSO 問題,Daubechies 等[13]提出了一種迭代閾值收縮算法(iterative shrinkage-thresholding algorithm,ISTA)。該算法在每一次迭代過程中通過一個收縮閾值操作來更新待恢復的信號,但該算法收斂速度較慢,需要大量的時間才能獲得一個較好的結果。為了解決相同問題,Teng 等[14]采用一種平滑函數來逼近 L0 和 L1 范數,然后通過替代函數法求解該問題。
針對腦功能網絡噪聲問題,本文采用一種快速 ISTA(fast ISTA,FISTA)算法求解壓縮感知中的 LASSO 模型對腦功能網絡進行降噪重建的問題。該方法利用小波變換對待構建的腦功能網絡進行分解,從而把求解腦功能網絡問題轉化為求解小波基系數問題。由于小波基系數具有稀疏性,所以可以使用 LASSO 模型進行表達。最后通過 FISTA 求解,從而抑制噪聲。通過以上步驟,期望本文提出的方法可以對腦功能網絡進行有效地降噪重建,并為更好地探索不同腦區之間的連接關系奠定研究基礎。
1 材料及方法
1.1 數據獲取
本研究數據來自阿爾茨海默病神經影像學計劃(Alzheimer’s Disease Neuroimaging Initiative,ADNI)數據庫(http://www.loni.ucla.edu/ADNI)。該數據庫主要通過 fMRI、正電子發射斷層掃描(positron emission computed tomography,PET)等影像學檢查結合心理學評估,確定早期 AD 患者的特征,以幫助醫生制定治療方案并監測其有效性。由于 AD 患者和健康人群[即正常對照組(normal controls,NC)]的腦功能網絡結構明顯不同,為了證明本研究所提出的降噪重建方法對于兩組不同人群的腦功能網絡降噪均有效,本文從 ADNI 數據庫中選取了 3T 掃描的標準化數據集,其中 AD 組 18 例(男 10 例,女 8 例),NC 組 12 例(男 6 例,女 6 例),年齡范圍均為(78  6)歲。
6)歲。
1.2 數據預處理
本實驗使用神經影像腦連接組分析軟件 GRETNA-2.0.0(北京師范大學,中國)對數據進行預處理。具體的步驟包括:將醫學數字成像和通信(digital imaging and communications in medicine,DICOM)格式圖像轉換為神經影像信息學技術協議(neuroimaging informatics technology initiative,NIFTI)格式圖像;去除前 10 個時間點的信號以便于參與者適應測試環境;以時間層校正的方式校正層與層之間的時間差;剔除水平頭動超過 2 mm 和旋轉超過 2° 的數據;選用高斯核函數對標準化后的數據進行平滑。最后將圖像匹配到蒙特利爾神經學研究所(Montreal neurological institute,MNI)模板。本文選用 MNI 提供的自動解剖標記模板(automated anatomical labeling 90 atlas,AAL90)將大腦劃分成 90 個 ROI,每個 ROI 都當作腦功能網絡的一個節點[15]。
1.3 腦功能網絡構建
所有 ROI 之間的連接關系用連接矩陣表示,矩陣元素是各個 ROI 之間的連接強度[16]。本文使用 90 個 ROI 作為節點,獲得了 90 × 90 的腦功能網絡連接矩陣 I。為了能夠表達網絡的模塊化結構,對獲得的連接矩陣進行二值化處理:當矩陣元素大于設定的閾值時,將其設置為 1,否則設置為 0,處理方法如式(1)所示:
 |
其中,Iij 表示連接矩陣的第(i,j)個元素值,T 表示閾值。本文設定 T 為 0.8Imax,Imax 表示連接矩陣中最大的元素值。通過上述處理后得到 0、1 二值化矩陣,即為本文所需的原始腦功能網絡。
由于在腦功能成像的過程中,生理噪聲呈現高斯分布,所以本文通過對原始網絡添加高斯噪聲來表示含有噪聲的腦功能網絡,如式(2)所示:
 |
其中,Y 表示含有噪聲的腦功能網絡矩陣,n 表示強度是 0.01 的高斯噪聲。
為了均衡表現所選兩組數據大腦 ROI 之間的連接關系,本文對 18 例 AD 組和 12 例 NC 組的腦功能網絡矩陣分別取每組的平均值,再將所得結果以二值矩陣的形式表現出來,最后將其加入高斯噪聲作為研究對象。如圖 1 所示,分別展示了每組的原始二值矩陣和加入高斯噪聲后的效果圖。其中,藍色表示二值矩陣中的元素為 0,即對應的兩個 ROI 之間沒有關聯;黃色表示二值矩陣中的元素為 1,即對應的兩個 ROI 之間有關聯。在受到高斯噪聲干擾后,原始二值矩陣變為多值矩陣。此時,已經難以有效判斷不同 ROI 之間的關聯情況,因此需要對其進行降噪重建。
 圖1
原始二值矩陣與含噪聲矩陣
Figure1.
Original binary matrix and noisy matrix
圖1
原始二值矩陣與含噪聲矩陣
Figure1.
Original binary matrix and noisy matrix
2 重建算法的原理
2.1 LASSO 模型和 FISTA 算法
LASSO 模型是壓縮感知理論中經典模型之一[17]。該模型的基本思想是在殘差平方和最小化過程中,引入稀疏約束。在該限制條件下,絕對值較小的回歸系數會約束到零,進而產生稀疏解,如式(3)所示:
 |
其中, 表示 L1 范數,
表示 L1 范數, 表示 L2 范數,b 表示測量信號,x 表示待恢復信號,A 表示給定的系統矩陣,λ 表示正則化參數。該模型可以保證在一定程度恢復原始信號的前提下,防止由于噪聲引起的過擬合現象。
表示 L2 范數,b 表示測量信號,x 表示待恢復信號,A 表示給定的系統矩陣,λ 表示正則化參數。該模型可以保證在一定程度恢復原始信號的前提下,防止由于噪聲引起的過擬合現象。
ISTA 是求解 LASSO 問題的一種有效算法,該算法是一種迭代優化算法,通過極小化替代函數保證原目標函數迭代下降。相較于 ISTA,FISTA 收斂速度更快,二者的區別在于迭代過程中替代函數起始點的選擇策略不同:ISTA 使用前一次迭代的替代函數最小值作為起始點;而 FISTA 則利用前兩次迭代值確定起始點,以此來加快收斂速度[18]。
對于式(3)所示的無約束優化問題,令  ,則該問題轉化為如式(4)所示:
,則該問題轉化為如式(4)所示:
 |
式(4)通過近端梯度方法可以得到 ISTA 算法的迭代公式,如式(5)所示:
 |
其中,k 表示迭代次數,tk 表示步長。
令  ,則可以對式(5)進行簡化,如式(6)所示:
,則可以對式(5)進行簡化,如式(6)所示:
 |
對式(6)進行求解,可以得到迭代公式,如式(7)所示:
 |
其中,xj 和 zj 分別表示 x 和 z 的第 j 個分量。
而 FISTA 的改進如式(8)~式(9)所示:
 |
 |
理論證明,ISTA 的收斂速度為 O(1/k),而 FISTA 的收斂速度為 O(1/k2)。
2.2 腦功能網絡降噪
在腦功能網絡降噪問題中,將含有噪聲的腦功能網絡 Y 看作測量信號,已知 Y 和測量矩陣 R,要想重建降噪后的網絡  ,可以通過如式(10)所示的優化模型求得[19]:
,可以通過如式(10)所示的優化模型求得[19]:
 |
其中,R 表示單位矩陣 E 與 Y 的克羅內克積,如式(11)所示:
 |
由于小波變換具有降噪的特性,可以對  進行小波分解,如式(12)所示:
進行小波分解,如式(12)所示:
 |
其中,W 表示小波基矩陣,α 表示小波基系數向量。將式(12)代入式(10)中,可以得到如式(13)所示:
 |
為求解該問題,需要對上式添加稀疏約束。最稀疏的解可以由 L0 范數得到,它度量了非 0 元素的個數,如式(14)所示:
 |
其中, 表示 L0 范數。由于 L0 范數最小化屬于組合優化問題,難以直接求解。所以,通常使用 L1 范數代替 L0 范數,獲得新的優化模型,如式(15)所示:
表示 L0 范數。由于 L0 范數最小化屬于組合優化問題,難以直接求解。所以,通常使用 L1 范數代替 L0 范數,獲得新的優化模型,如式(15)所示:
 |
最后,通過懲罰函數法將式(15)轉化為無約束優化問題,如式(16)所示:
 |
其中,正則化參數 λ 表示可接受的稀疏化程度。通過上述推導,可以將求解待重建網絡  轉化為求解小波基系數 α 的問題,由此證明 LASSO 模型可以用于腦功能網絡的降噪重建。
轉化為求解小波基系數 α 的問題,由此證明 LASSO 模型可以用于腦功能網絡的降噪重建。
3 結果與分析
3.1 小波基的選擇
小波基選擇的多樣性是小波變換的重要特點之一,本實驗使用重建準確率對 Haar、Db2、Db3、Db4、Coif1、Bior1.3、Bior1.5 七種不同小波基進行了對比。其中,重建準確率是正確恢復的矩陣元素與元素總數的百分比。為了避免重建信號失真過大,均采用一層分解。NC 組和 AD 組迭代 100 次時的重建準確率如表 1 所示。NC 組和 AD 組迭代 200 次時的重建準確率如表 2 所示。可以看出,無論是 100 次還是 200 次迭代,Haar 小波基在兩組實驗中均獲得了最高的重建準確率,而 Bior1.5 小波基所獲得的重建準確率最低。最終,選擇 Haar 小波對含有噪聲的腦功能網絡進行分解。
3.2 參數選擇
在 LASSO 模型中,參數 λ 的取值不同,會對重建效果產生不同的影響。當 λ 取值過大時,會使過多的矩陣元素置為 0,導致無法對原始腦功能網絡進行有效恢復。當 λ 取值過小時,容易造成過擬合,此時無法有效抑制噪聲。所以,選擇合適的參數 λ 是本實驗重要一步。本文分別對 NC 組和 AD 組選擇不同正則化參數進行比較,迭代次數設置為 200。如圖 2 所示,當  時,NC 組和 AD 組的重建準確率隨著 λ 的增大而上升。當
時,NC 組和 AD 組的重建準確率隨著 λ 的增大而上升。當  時,NC 組和 AD 組的重建準確率隨著 λ 的增大而降低。因此,設置
時,NC 組和 AD 組的重建準確率隨著 λ 的增大而降低。因此,設置  以獲得最好的實驗效果。
以獲得最好的實驗效果。
 圖2
不同正則化參數對應的重建準確率
Figure2.
Reconstruction accuracy under different regularization parameters
圖2
不同正則化參數對應的重建準確率
Figure2.
Reconstruction accuracy under different regularization parameters
3.3 算法的重建效果
本文針對每組數據分別迭代 100 次和 200 次獲得重建結果。如圖 3 所示,無論 NC 組還是 AD 組,在 100 次迭代后,已經非常接近原始腦功能網絡。200 次迭代后,重建效果進一步提升。
 圖3
迭代 100 次、200 次后的二值矩陣
Figure3.
The binary matrix after 100 and 200 iterations
圖3
迭代 100 次、200 次后的二值矩陣
Figure3.
The binary matrix after 100 and 200 iterations
兩個實驗組迭代前后的差異如圖 4 所示。其中藍色表示重建正確的部分,黃色表示重建錯誤的部分。由于默認每個 ROI 與其自身的關聯為 0,所以在原始矩陣中對角線元素均為 0。當有噪聲干擾時,對角線上的 0 值更易受到影響,從而導致在重建結果中,對角線上數值更容易出現誤差。
 圖4
不同迭代次數的重建誤差
Figure4.
Reconstruction error after different times of iterations
圖4
不同迭代次數的重建誤差
Figure4.
Reconstruction error after different times of iterations
3.4 不同算法的性能比較
為了進一步評估所提出算法的性能,本文比較了 FISTA 與 ISTA、L0 正則化算法和 L1 正則化算法[14]在不同迭代次數時的重建準確率。每種方法都選取了最佳參數。對于 ISTA,λ = 0.4;對于 L0 正則化算法,λ = 0.5;對于 L1 正則化算法,λ = 0.000 1。如圖 5 所示,四種算法隨著迭代次數的增加,都達到了較高的重建準確率。其中 FISTA 在 NC 組和 AD 組的多次迭代中都取得了最好的效果,ISTA 次之,L0 正則化算法和 L1 正則化算法獲得的效果相對較差。具體重建準確率與迭代次數間的關系如表 3、表 4 所示。
 圖5
NC 組和 AD 組不同迭代次數的重建準確率
Figure5.
Reconstruction accuracy of NC and AD groups with different times of iterations
圖5
NC 組和 AD 組不同迭代次數的重建準確率
Figure5.
Reconstruction accuracy of NC and AD groups with different times of iterations
4 總結與展望
已有研究表明,壓縮感知已經成為腦功能網絡建模的一種有效方法[20-22]。本文針對腦功能網絡構建過程中存在的噪聲問題,提出了一種降噪重建方法。將 LASSO 模型結合 FISTA 算法引入到腦功能網絡重建中。結果表明,所提出方法具有良好的恢復效果,能夠有效抑制腦功能網絡中的噪聲。在兩個實驗組中,重建準確率均達到了 98% 以上。相較于其他三種算法而言,具有明顯的優勢。
雖然本文對腦功能網絡進行了有效恢復,但是該項工作仍存在不足。首先,在實驗過程中,如果采用不同的腦區模板,對最終的重建效果會有較大的影響。采用 AAL90 模板、哈佛-牛津模板(Harvard-Oxford 112 atlas,HOA112)和多森巴赫模板(Dosenbach 160 atlas,Dos160)的重建效果明顯不同[23-24]。其次,從實驗結果上看,AD 組的重建準確率在四種算法上都低于 NC 組,說明這些算法在處理異常的腦功能網絡連接時,能力都有待提高。以上這些問題,都將在未來的工作中進一步研究。
利益沖突聲明:本文全體作者均聲明不存在利益沖突。