通過二維圖像進行重建的三維模型，是目前術前規劃、人工關節定制的普遍需求。本文提出一種統計形狀模型與拉普拉斯曲面變形相結合的方法，應用于股骨圖像的三維重建，以優化傳統統計建模重建過程中特征不足和信息損失造成的精度問題。該方法將基于統計形狀模型的重建結果用能夠代表形狀特征的拉普拉斯算子表示，在拉普拉斯坐標系下進行曲面結點坐標變換，建立骨骼新特征，使重建模型與二維圖像充分擬合。最后選取50例股骨模型驗證本方法的有效性。結果表明，引入拉普拉斯曲面變形后的方法較傳統統計形狀模型的精度提升了16.8%～25.9%。該方法能夠以更高精度完成骨三維重建，為術前個性化假體設計及其精準定位與快速生物力學分析等研究提供模型基礎。
引用本文： 張祖佩, 張小剛, 張亞麗, 靳忠民. 基于拉普拉斯算子與統計形狀模型的股骨三維重建方法. 生物醫學工程學雜志, 2023, 40(6): 1168-1174. doi: 10.7507/1001-5515.202303024 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
在現代骨科醫療實踐中，有時需要獲得患者個體的三維（three-dimensional，3D）骨骼模型以進行輔助醫療，如術前方案規劃[1-2]、病情診斷[3]或運動動力學分析等[4]。傳統的骨骼三維重建為利用電子計算機斷層掃描（computed tomography，CT）圖像在Mimics等軟件中建模[5-7]。然而，CT圖像存在輻射量較大、重建時間長、受設備影響而無法重建出站立位或坐立位位姿等缺點，在骨骼三維模型的臨床與科學研究中有一定的局限性[8-10]。
近年來，利用如X線平片或超聲圖像等二維（two-dimensional，2D）醫學圖像[11]建立一定精度的患者個性化骨骼三維模型，成為解決上述問題的主流方法。例如，上海濤影醫療設計的Ti-WISH-IL雙平面Ｘ射線攝影系統，基于骨骼統計大數據庫進行三維重建，目前已應用于臨床診斷中。
基于統計形狀模型（statistical shape models，SSM）的三維重建[12-14]，也是目前應用廣泛的一種基于數據庫先驗信息的方法。它針對人體根骨[15]、顳骨[16]、肋骨[17]、股骨[14]、脊椎[18]、膝關節[19]等骨骼的三維重建在臨床診斷、強度計算、計算機輔助手術等領域都有應用。SSM在一定程度上優化了CT三維重建存在的問題。但是，SSM的原理是將控制骨骼形狀的結點通過主成分分析（principal components analysis，PCA）進行數據降維變為數十個形狀特征，一方面這些形狀特征完全是由數據庫決定的，若目標模型存在數據庫以外的特征，重建精度就會較差[14, 20-21]；另一方面，經過數據降維，這些特征通常僅包含數據庫中85.0%～95.0%的形狀信息，存在信息損失[21-23]。因此，重建結果不能完全擬合目標二維圖像，無法完全滿足高精度的術前規劃和個性化植入物設計需求。
拉普拉斯曲面變形（Laplacian surface deformation，LSD）是一種基于拉普拉斯算子的三維建模算法，最初主要應用于圖像處理和計算機視覺[24-25]，近年來被廣泛應用于三維表面形狀處理，包括人臉建模[26]、動畫建模[27]和生物醫學[28]等領域。LSD的優勢在于能夠在保持模型整體拓撲結構不變的情況下，將形狀擬合至目標位置[29]。將LSD用于基于SSM的重建模型，能在保持骨骼特征不變的前提下，充分擬合目標輪廓，提升重建精度。然而，目前還沒有將LSD作用于SSM的重建結果的研究。
本文提出一種基于SSM與LSD結合的方法（statistical shape and Laplacian models，SSLM），將LSD作用于SSM的重建結果，研究充分擬合二維信息的三維重建方法，為個性化假體設計與安裝定位、生物力學分析和術前規劃提供更高精度的模型基礎。
1 方法
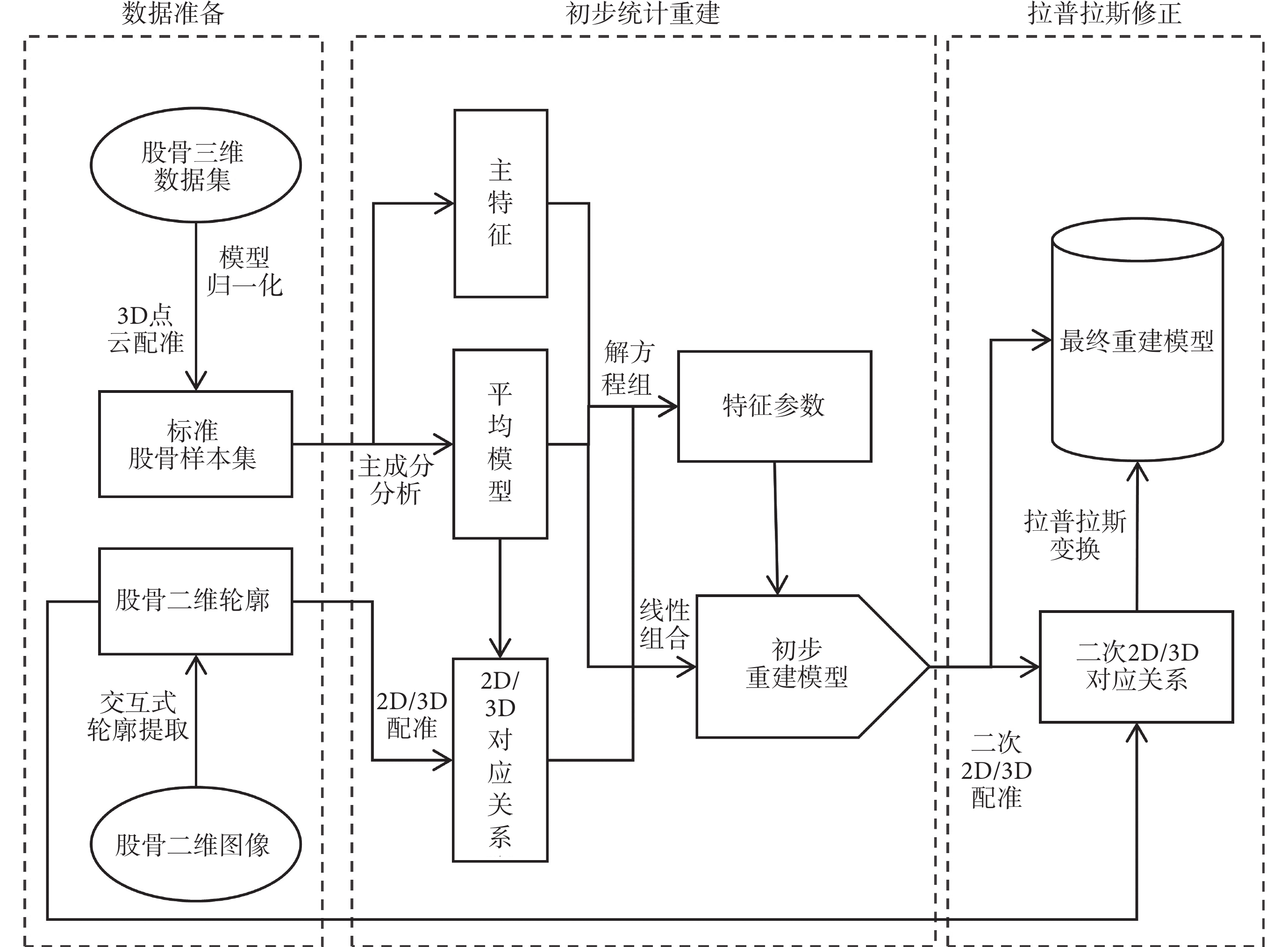
為了對股骨進行三維重建，在SSM的基礎上在拉普拉斯空間中對SSM的重建結果進行三維變形，使重建模型與二維圖像充分擬合。方法框架如圖1所示。SSLM將重建流程分為數據準備、初步統計重建和拉普拉斯修正。在數據準備階段對采集的三維數據集進行處理，對輸入的目標二維圖像進行輪廓提取；在初步統計重建時建立SSM，利用處理過的二維與三維數據初步建立二維/三維對應關系，進而求解出特征參數，通過平均模型、主特征及其特征參數的線性組合完成股骨初步重建；最后進行的拉普拉斯修正則是通過建立新的二維/三維對應關系，在拉普拉斯空間中進行三維變換以提升精度，得到最終的重建模型。
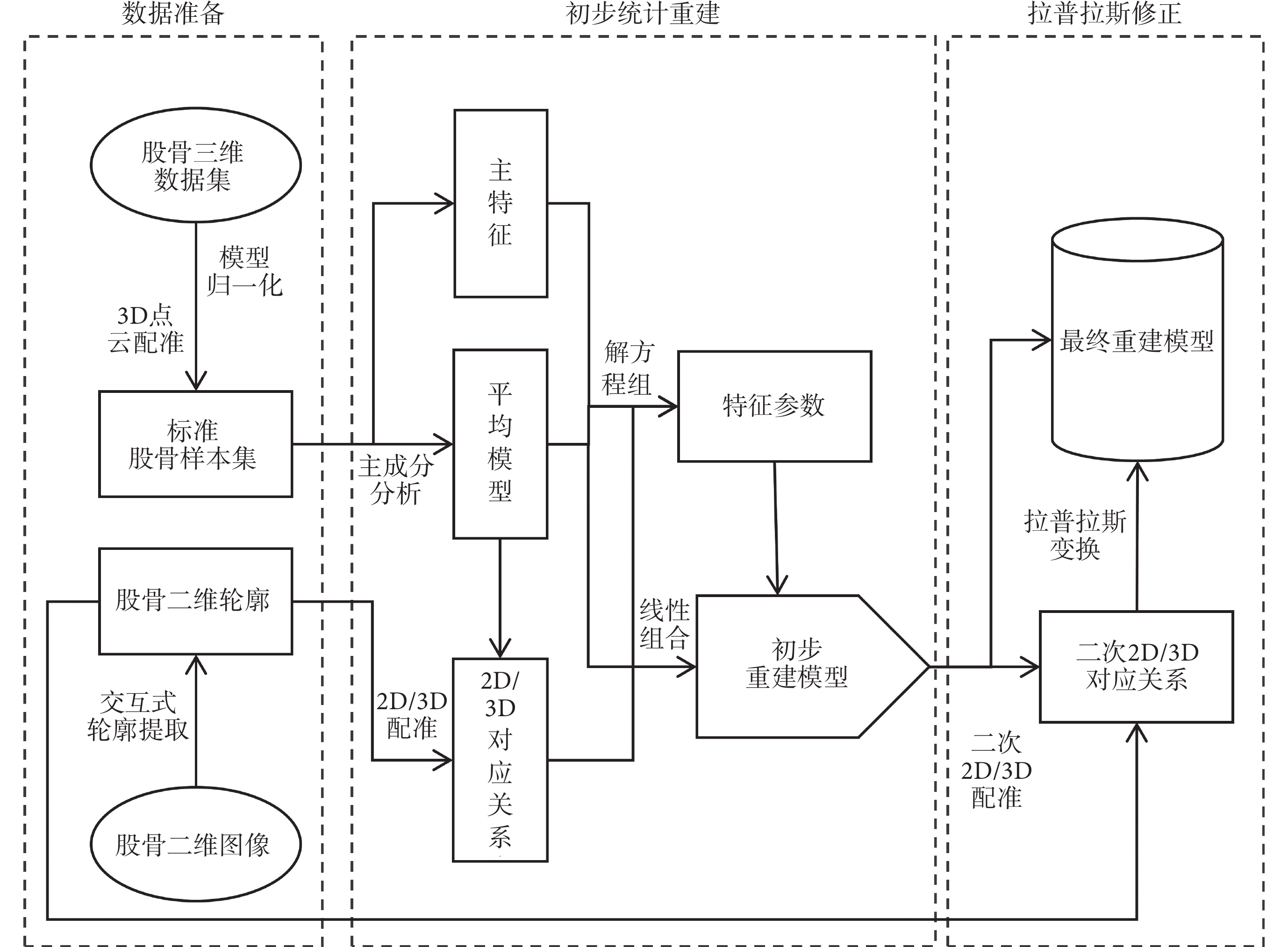圖1
SSLM方法框架及流程
Figure1.
The method framework and flowchart of SSLM
1.1 數據準備
數據準備階段包括對采集的二維輸入圖像和三維數據集的預處理。本文采用livewire算法提取股骨二維輪廓[30]。三維股骨的特征提取首先需由股骨數據集建立數據庫，將采集的股骨三維模型離散化，保存為三維點云模型及其三角面信息。采用線性縮放的方式對數據集進行模型歸一化處理，以突出股骨形狀特征，擬合患者的特異性模型，而后去中心化，采用最近點迭代（iterative closest point，ICP）算法[31]，將股骨三維點云位姿進行配準，使所有點云位姿與患者二維圖像采集位姿相擬合，統一坐標系，并找出股骨模型間的對應點，建立數據庫。
1.2 統計形狀建模
由所建立的股骨數據庫與提取的二維輪廓建立SSM。首先是用數據庫中已預處理的、點對應關系已知的股骨點云模型，基于主成分分析進行參數化處理，求解出數據庫中股骨的形狀特征主成分，并計算平均模型(1)。為求出數據庫中的主要特征，將數據庫表示為[
]矩陣，求出數據庫的協方差矩陣(2)，并求解出協方差矩陣的特征值 
和特征向量 
，按數值大小對特征值及其對應的特征向量由大到小進行排序，每個特征向量就表示股骨的一個主要形狀特征。按照特征值大小取85.0%～95.0%占比特征值所對應的特征向量作為此數據庫的主要形狀特征。由此任一股骨都可由一個平均模型和形狀特征及權重系數的線性組合表示(3)。各形狀特征對應的權重系數被限制在 
內[32]。將從二維輪廓上提取并映射到三維空間上的點與重建模型上建立二維/三維對應關系[20]，將對應點的平均距離(4)作為損失函數，求解出形狀特征參數，得到初步重建的股骨特征模型。
 |
 |
 '/> |
 '/> |
式中 
表示骨點云數據；
表示平均模型；p 表示數據庫中股骨點云數量；
表示協方差矩陣；{
}表示 
的特征向量，即股骨的主成分；{
}表示各主成分的權重參數；n 表示從提取的二維輪廓中均勻采樣的點的個數；
表示從二維輪廓映射到三維的對應點；
表示平均模型上與
對應的點；
表示第i個主成分上與第j個點所對應的值。
1.3 拉普拉斯修正
由于優化算法和SSM的局限性，初步重建的股骨三維模型并不能完全擬合所提取的二維輪廓信息，重建精度有一定的提升空間，這就需要在三維空間內對初步重建模型進行變換，使重建模型充分擬合二維信息。
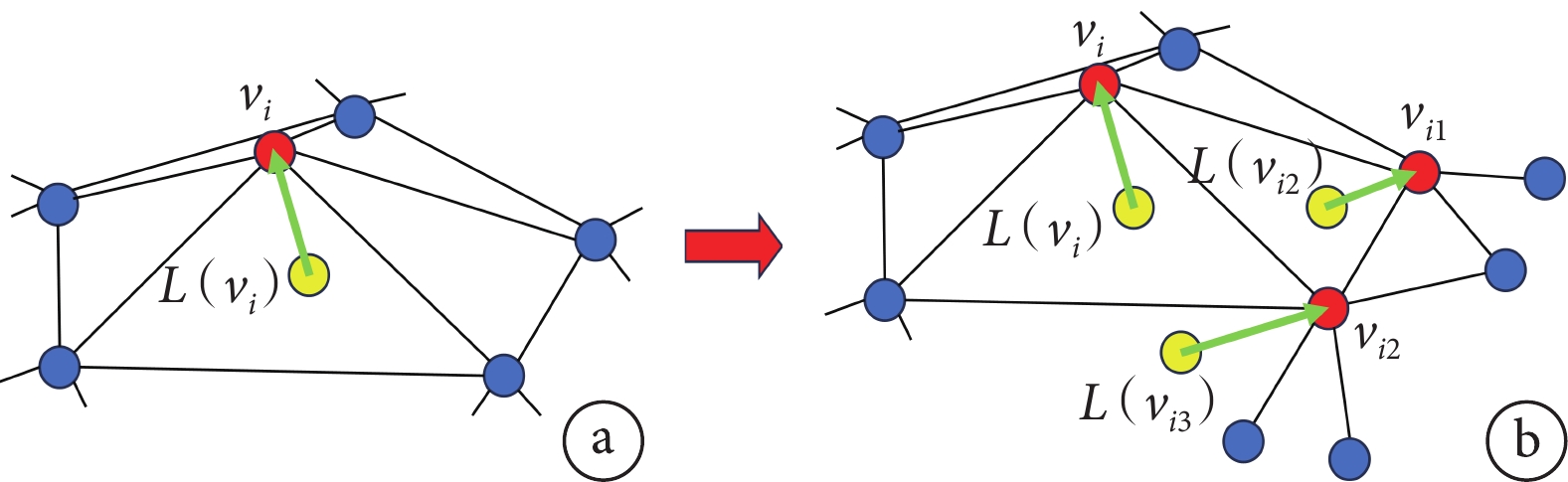
LSD基于拉普拉斯算子［見式(5)］[33]，如圖2a所示，算子將模型中的每個結點表示為該點與其所有鄰接點質心的差值向量，向量的模長表示曲面上該點的屈曲程度，方向為該點的曲面法向量。由此拉普拉斯算子可以表示模型中任意結點的局部表面形狀特征。三維網格模型結點拓撲結構間的連接性決定了拉普拉斯算子的傳遞性，如圖2b所示，某一結點的拉普拉斯算子改變，該結點鄰接點的局部形狀特征也會改變，并依次傳遞至所有相互連通的結點,從而影響整個模型。
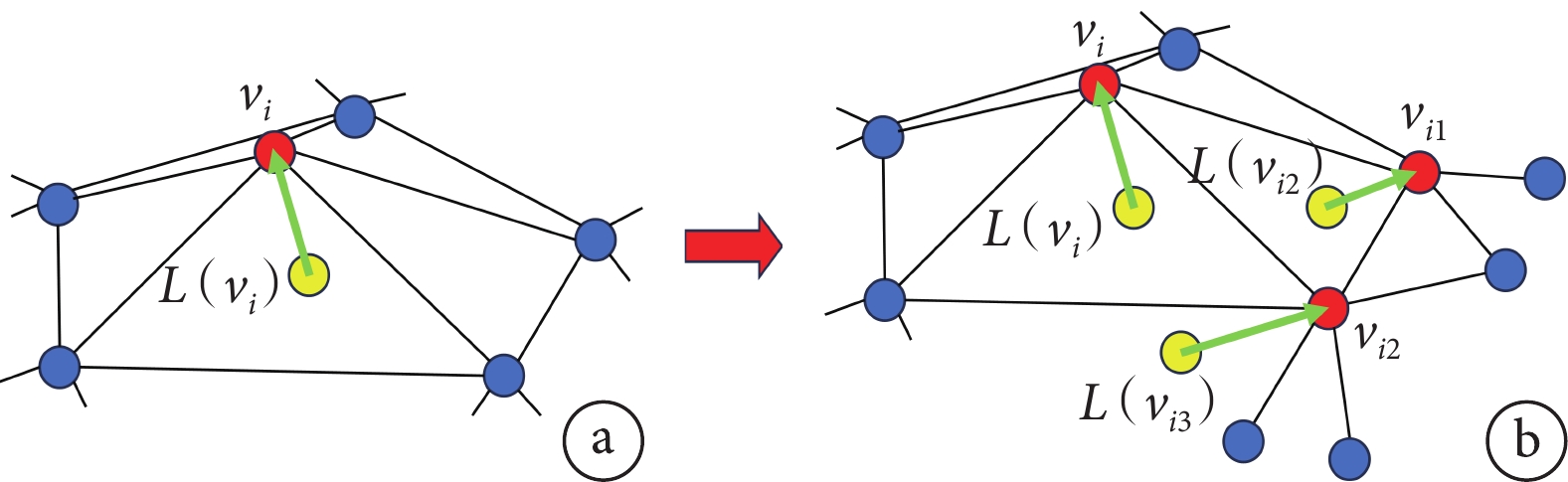圖2
拉普拉斯算子示意圖
a. 處的拉普拉斯算子；b. 及其鄰接點處的拉普拉斯算子
Figure2. Laplace operatora. the Laplace operator at ; b. the Laplace operator at and its neighbors
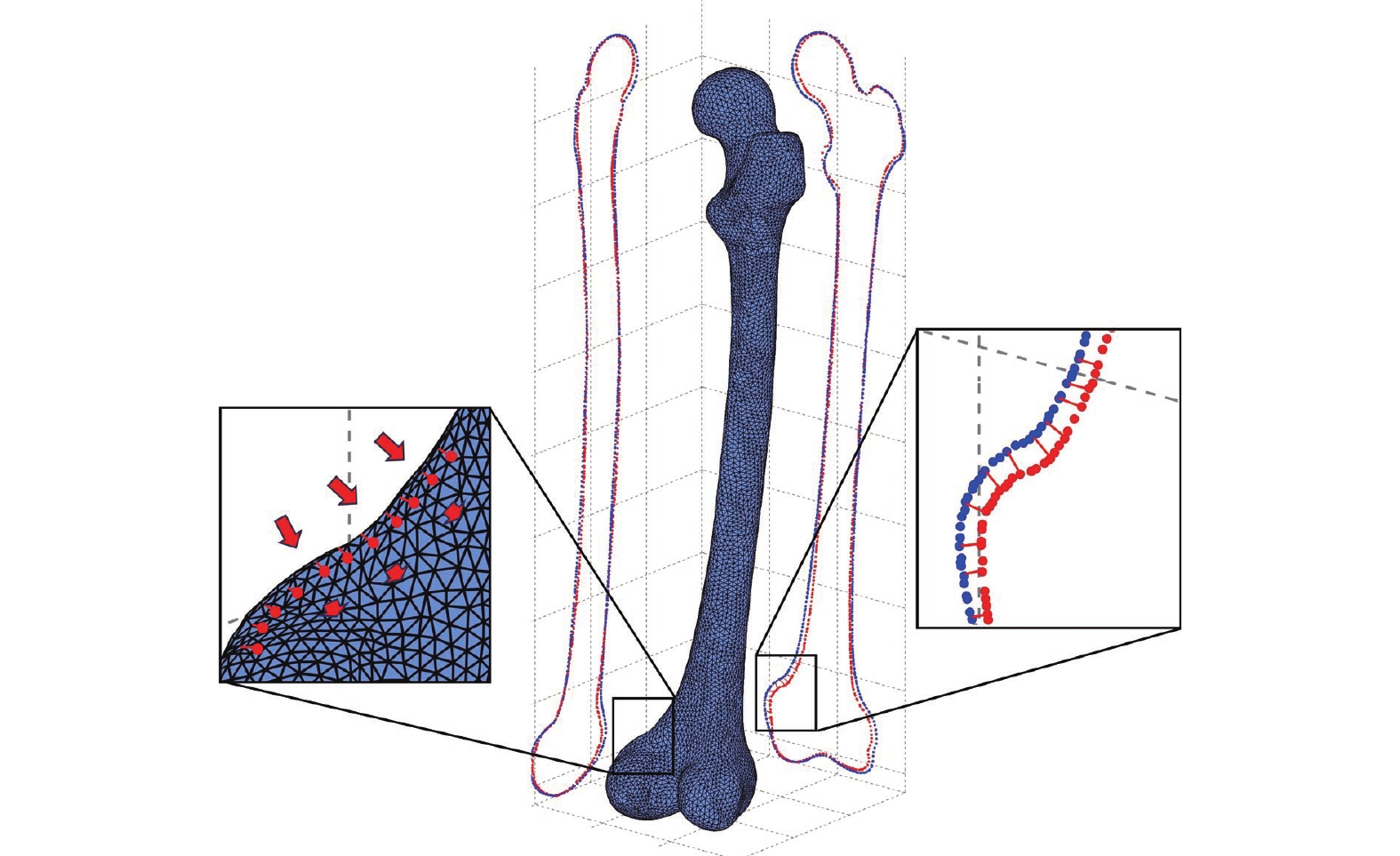
將LSD應用于基于SSM的股骨三維重建結果，就是將股骨形狀變換至目標位置的同時，將變換前后拉普拉斯算子的變化最小化［見式(6)］。如圖3所示，通過二次二維/三維對應關系，將局部的結點坐標變換拓展至整個股骨的三維形變中去，同時重建股骨的形狀特征不變。SSLM能在保持SSM重建結果中數據庫的先驗特征不變的情況下，將股骨曲面變形擬合出新特征，對二維圖像充分擬合，完成更高精度的三維重建。
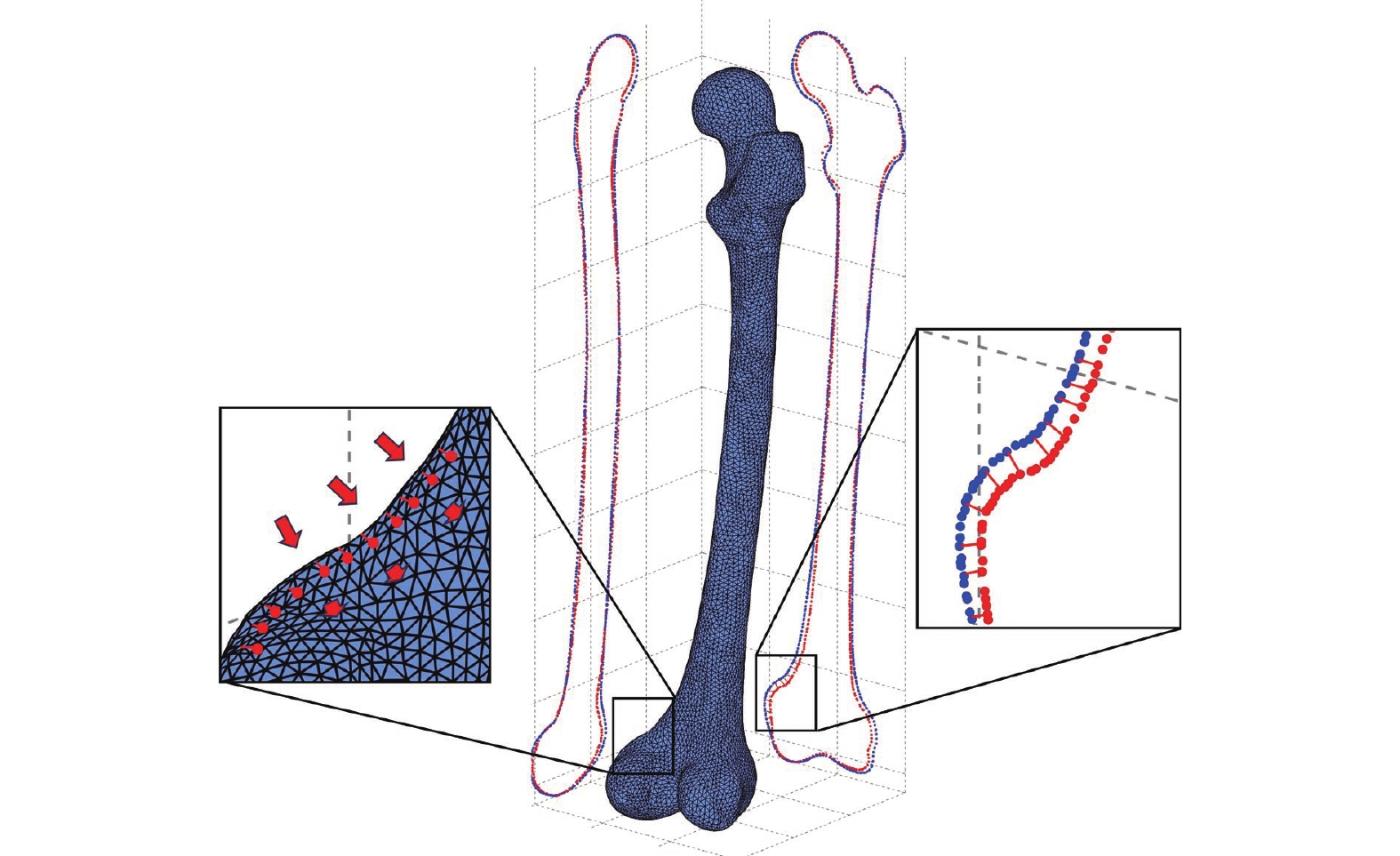圖3
股骨LSD示意圖
Figure3.
LSD of femur
 |
 '/> |
式中，
為點云模型中的點，
為 
的1鄰域內的點，
為 
鄰接點的數量，
、
分別表示變形前和變形后 
的拉普拉斯算子，
表示控制點變形后的坐標，
表示 
變形的目標坐標。
1.4 方法驗證
采用50例取自SMIR醫學圖像數據庫健康人的完整三維左股骨模型驗證方法的準確性，將第50例股骨作為目標真實模型，并基于上述數據準備階段進行模型處理。采用所有對應結點距離的平均絕對誤差（mean absolute error，MAE）、標準差（standard deviation，SD）來衡量重建模型的品質。以上述數據庫為基礎，分別使用三種方法對二維股骨圖像進行三維重建：基于SSM、基于LSD和基于SSLM，并將重建結果與真實模型進行比對，從不同特征數、不同信息量和不同二維圖像數量三個方面驗證方法的優化機制。三維重建過程在Matlab（2021b）軟件中完成。
2 結果與分析
2.1 不同特征數的股骨重建
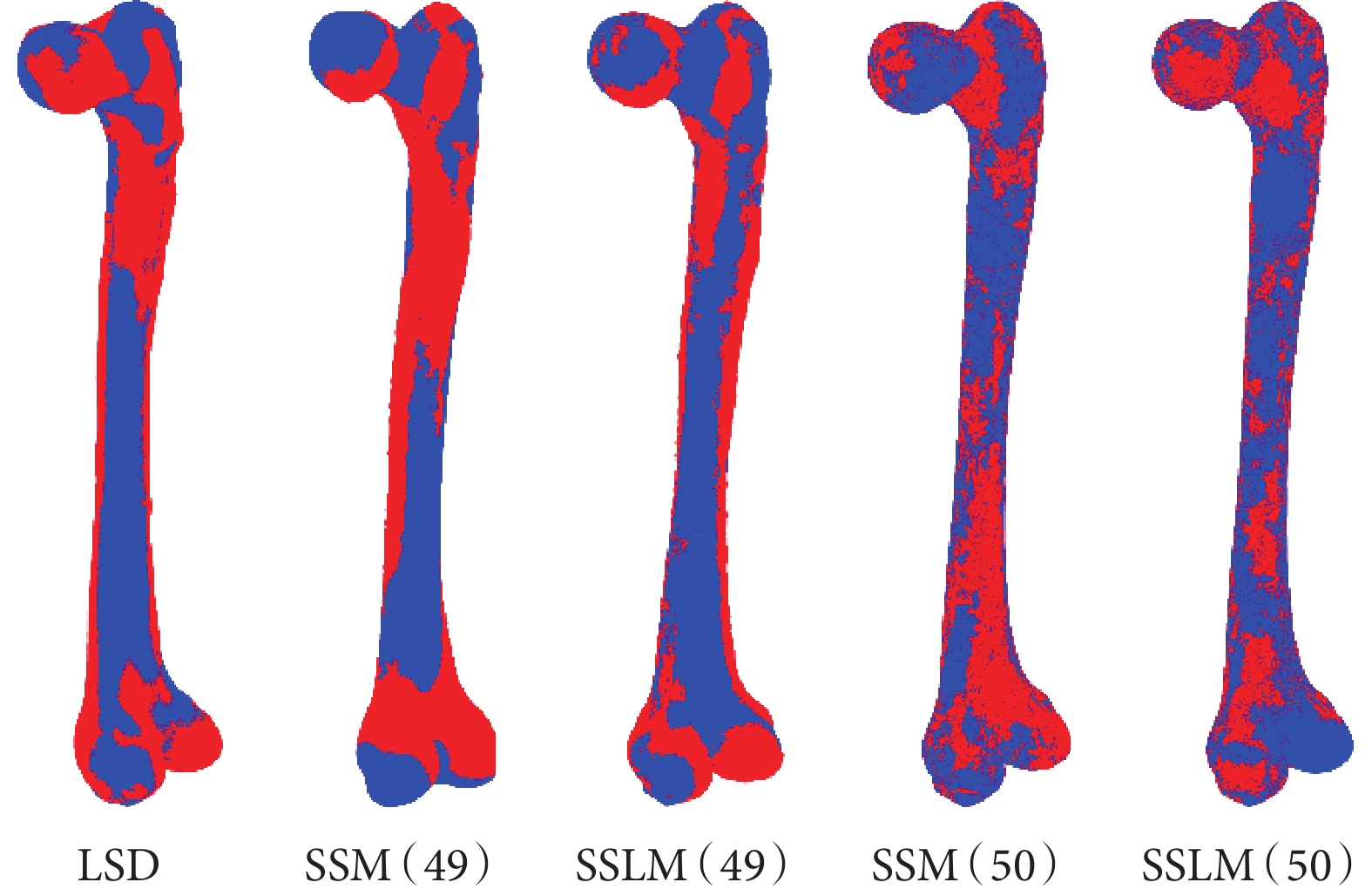
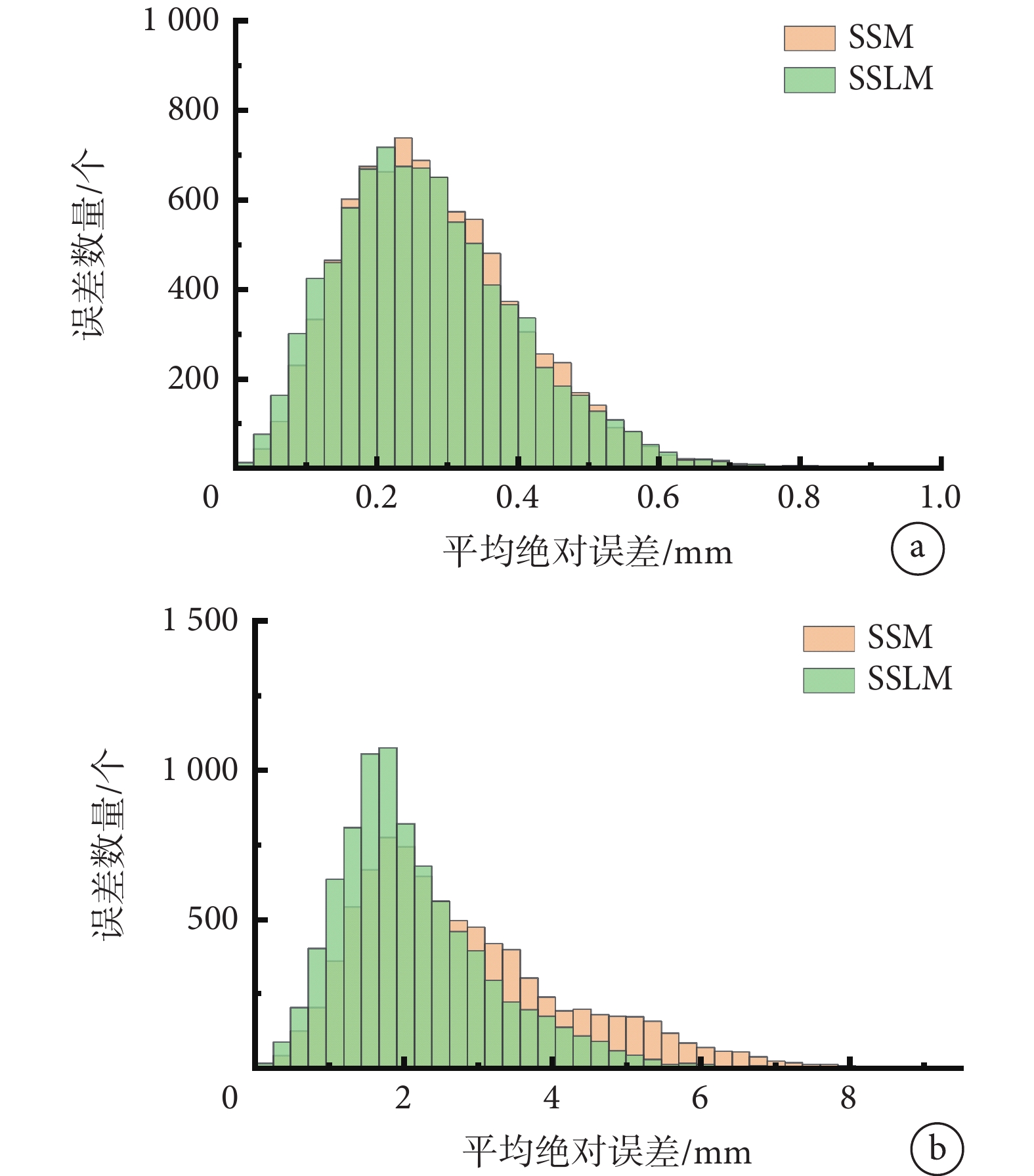
分別采用50例股骨和49例股骨建立數據庫，代表特征數充足與否的情況。LSD、49例股骨數據庫條下的SSM與SSLM、50例股骨數據庫條件下的SSM與SSLM重建效果如圖4所示。采用LSD進行重建時的重建模型的MAE為2.432 mm，SD為1.855 mm。在數據庫特征數較少或不包含目標股骨的特征時，SSM重建的MAE為2.342 mm，SD為1.237 mm，SSLM的MAE為1.736 mm，SD為0.987 mm，誤差分布如圖5b所示。此時，SSLM與SSM的重建結果相比，精度提了25.9%，誤差分布也更為集中。在數據庫特征數充足或包含目標圖像三維模型的特征時，SSM的MAE為0.283 mm，SSLM的MAE為0.275 mm。此時，SSLM相比SSM的精度提升2.8%，誤差分布如圖5a所示。
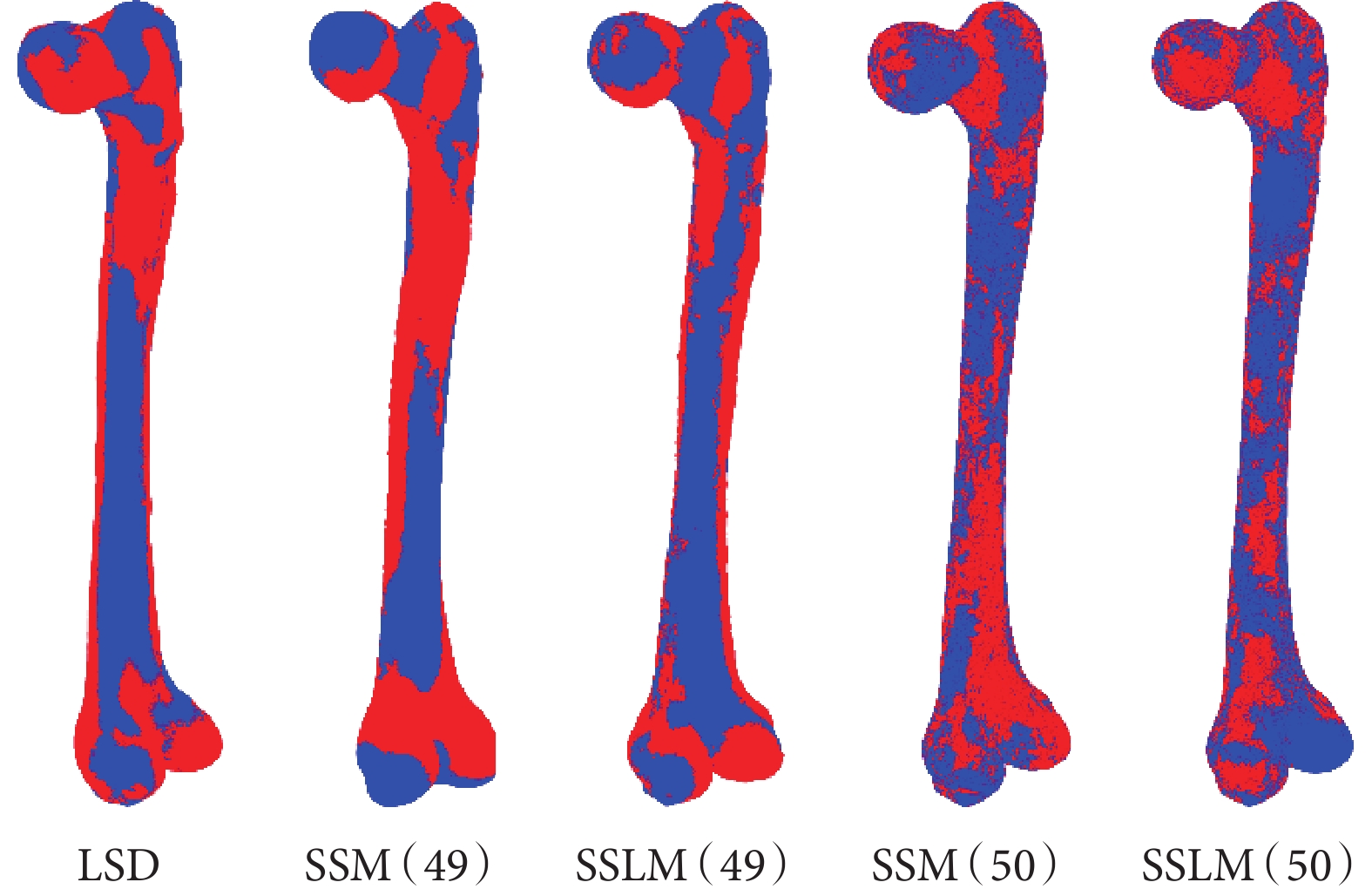圖4
股骨重建效果圖
紅色為重建模型，藍色為真實模型
Figure4. A rendering of the femoral reconstructionred is the reconstructed model and blue is the true model
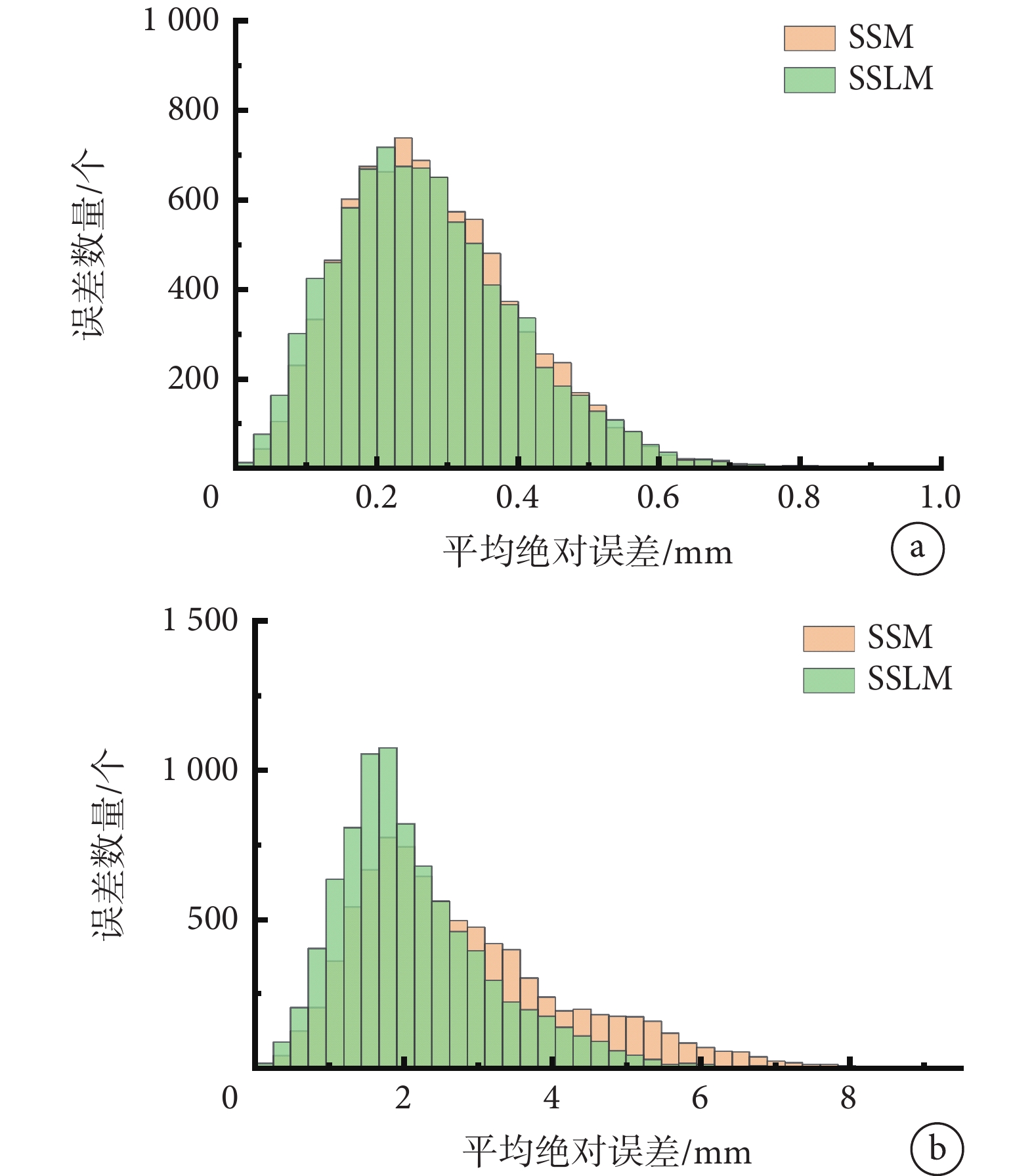圖5
三維重建誤差分布圖
a. 特征充足；b. 特征不足
Figure5. 3D reconstruction error distributiona. sufficient number of feature; b. insufficient number of features
2.2 不同信息量的股骨重建
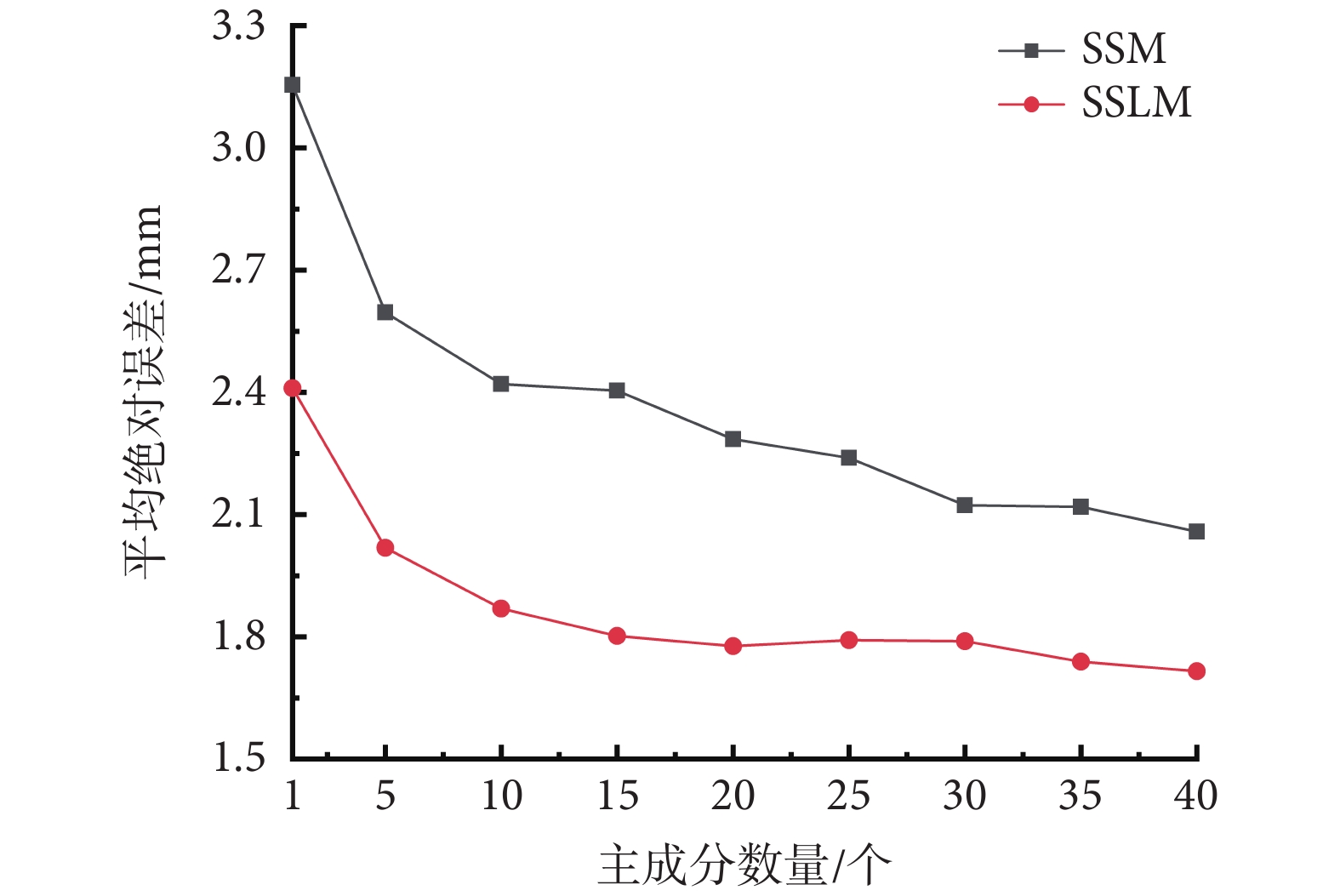
在特征數有限的數據庫條件下，建立SSM與SSLM模型，采用不同主成分數量即不同信息量的股骨三維重建結果誤差如圖6所示。隨著使用主成分數量的增多，重建誤差逐漸減少，在使用主成分數量超過10后，誤差減少的趨勢逐漸放緩。使用多于10個主成分的SSM重建的MAE在2.1～2.5 mm，SSLM重建的MAE在1.7～1.9 mm。使用40個主成分時，信息占比98.2%，SSM與SSLM的MAE分別為2.058 mm與1.712 mm，SSLM的精度提升效果為16.8%。使用5個主成分時，信息占比85.8%，SSM與SSLM的MAE分別為2.596 mm與2.018 mm，SSLM的精度提升效果為22.2%。
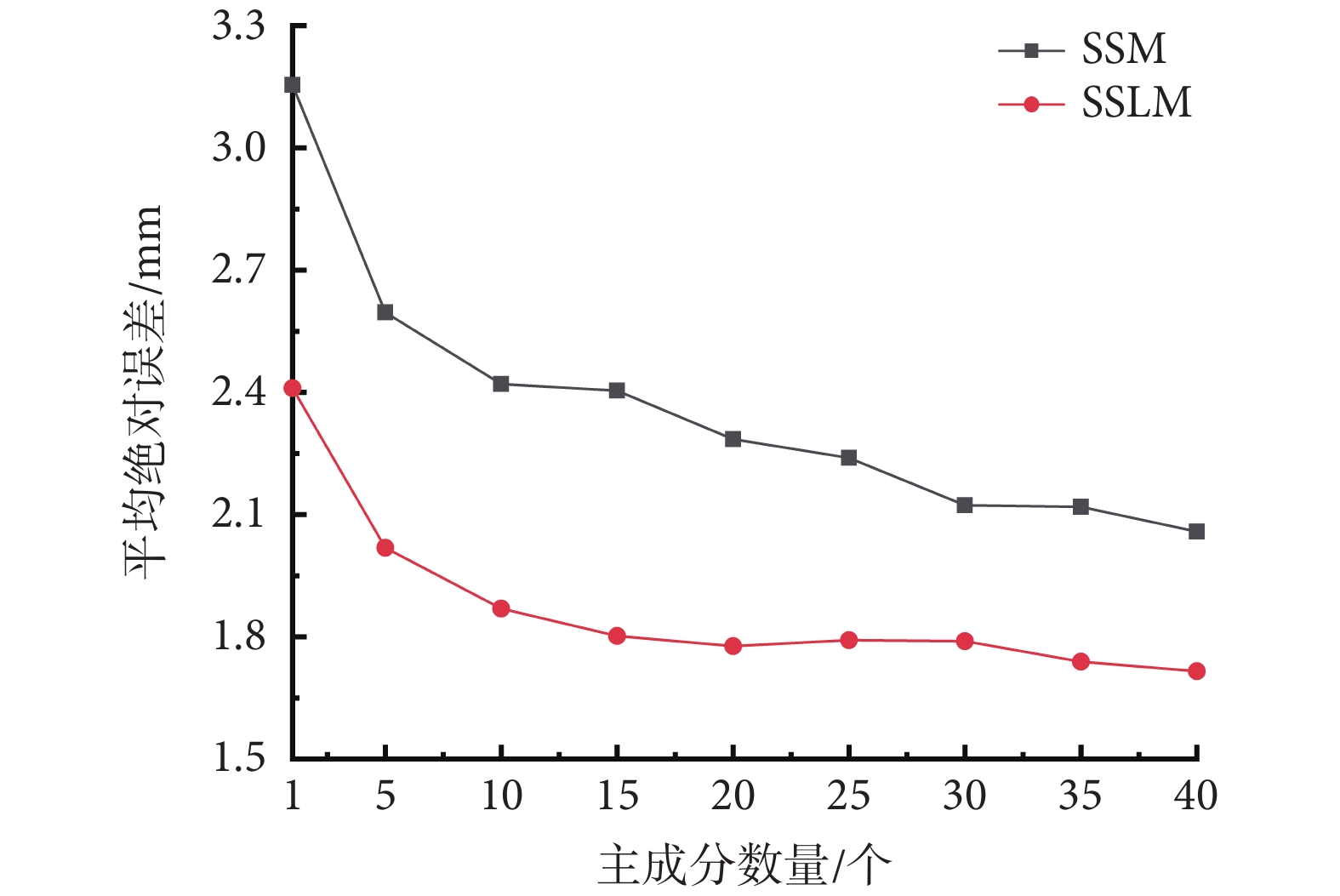圖6
重建誤差隨主成分數量變化圖
Figure6.
Reconstruction error change with feature number
2.3 不同二維圖像數量的股骨重建
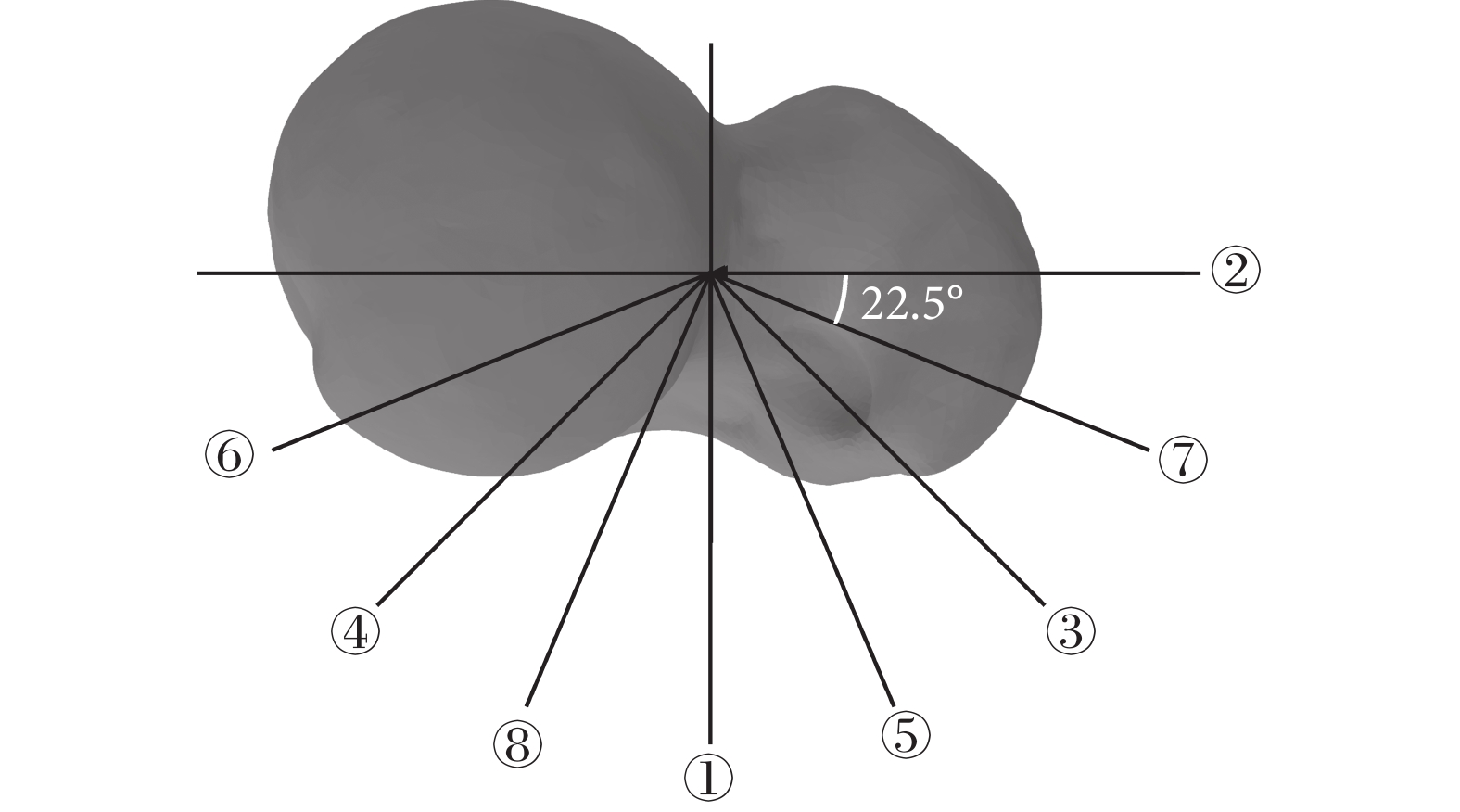
驗證在不同二維圖像數量下進行三維重建的精度規律，從正側位開始拍攝，每間隔22.5°取一張二維圖像（如圖7所示）。固定使用20個主成分，按1～8號圖像依次累加進行SSM和SSLM的三維重建。
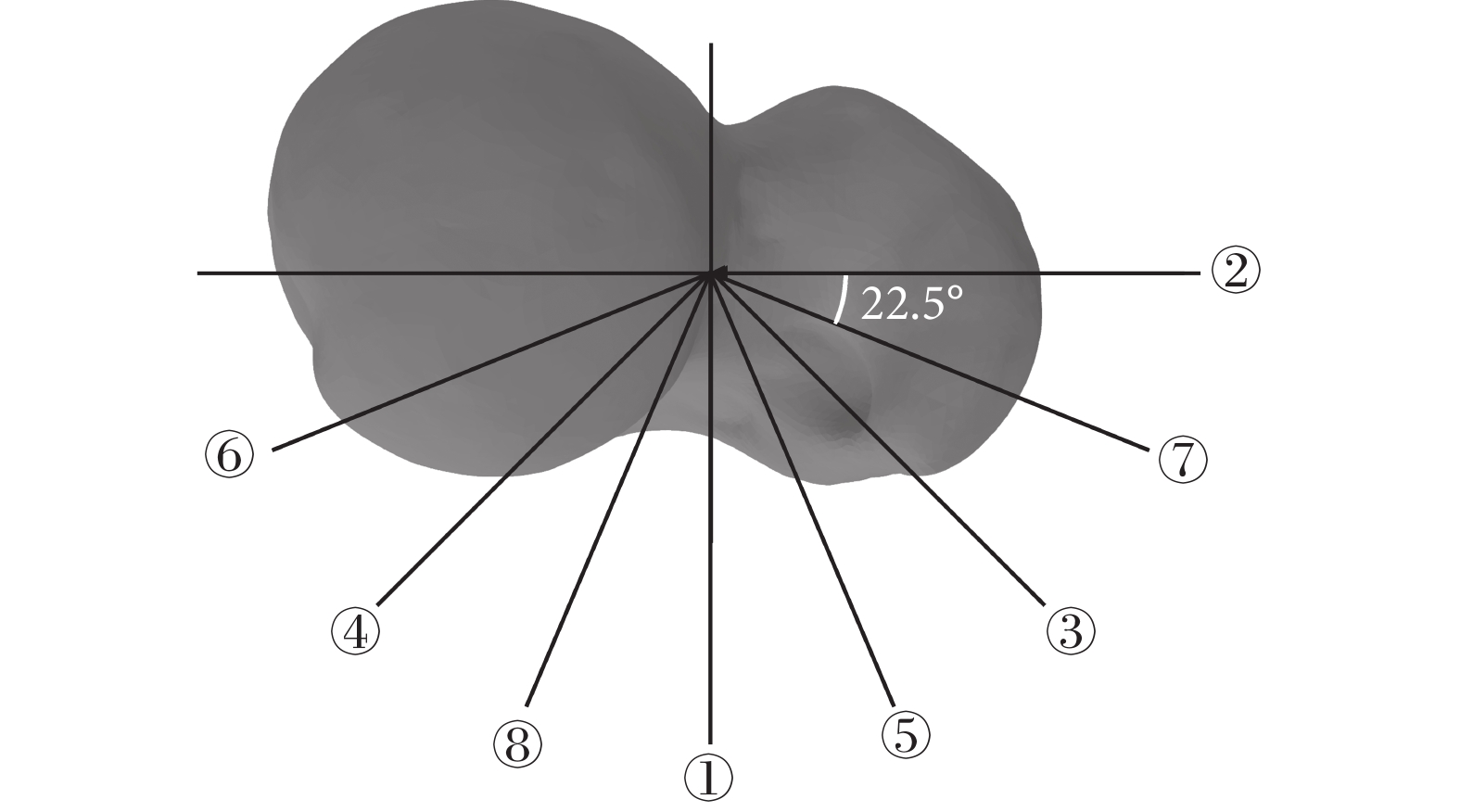圖7
二維圖像拍攝角度
Figure7.
The angle at which the 2D image was taken
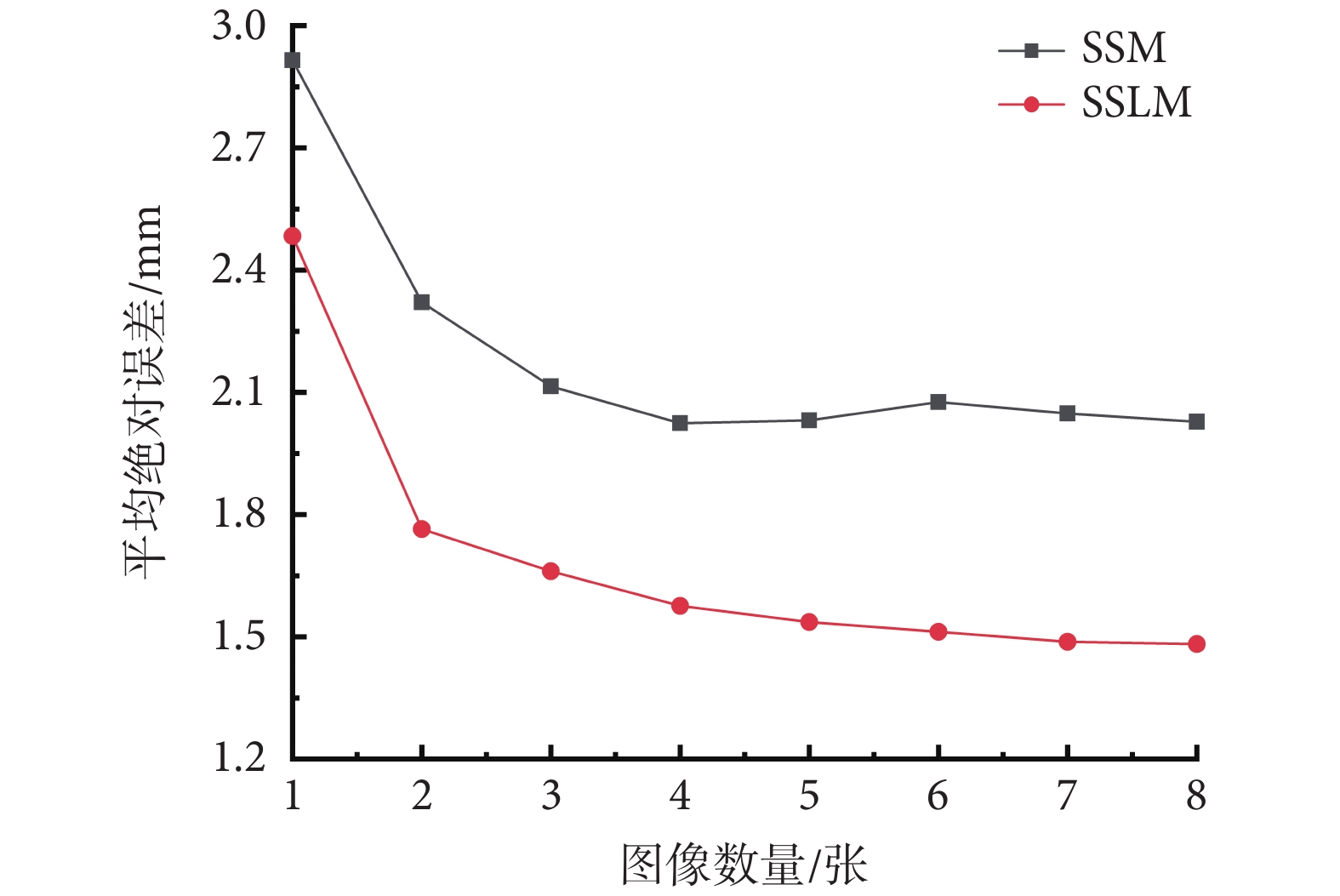
采用1～8張二維圖像的三維重建結果如圖8所示，在僅使用一張圖像時，SSM與SSLM的MAE均在2.5 mm以上；在使用正交的第二張圖像后，SSM的MAE減少至2.321 mm，SSLM的MAE減少至1.736 mm。但是，當繼續累加其他視角的二維圖像時，無論SSM還是SSLM的重建結果相比于其使用兩張圖像時的重建精度無明顯提高。
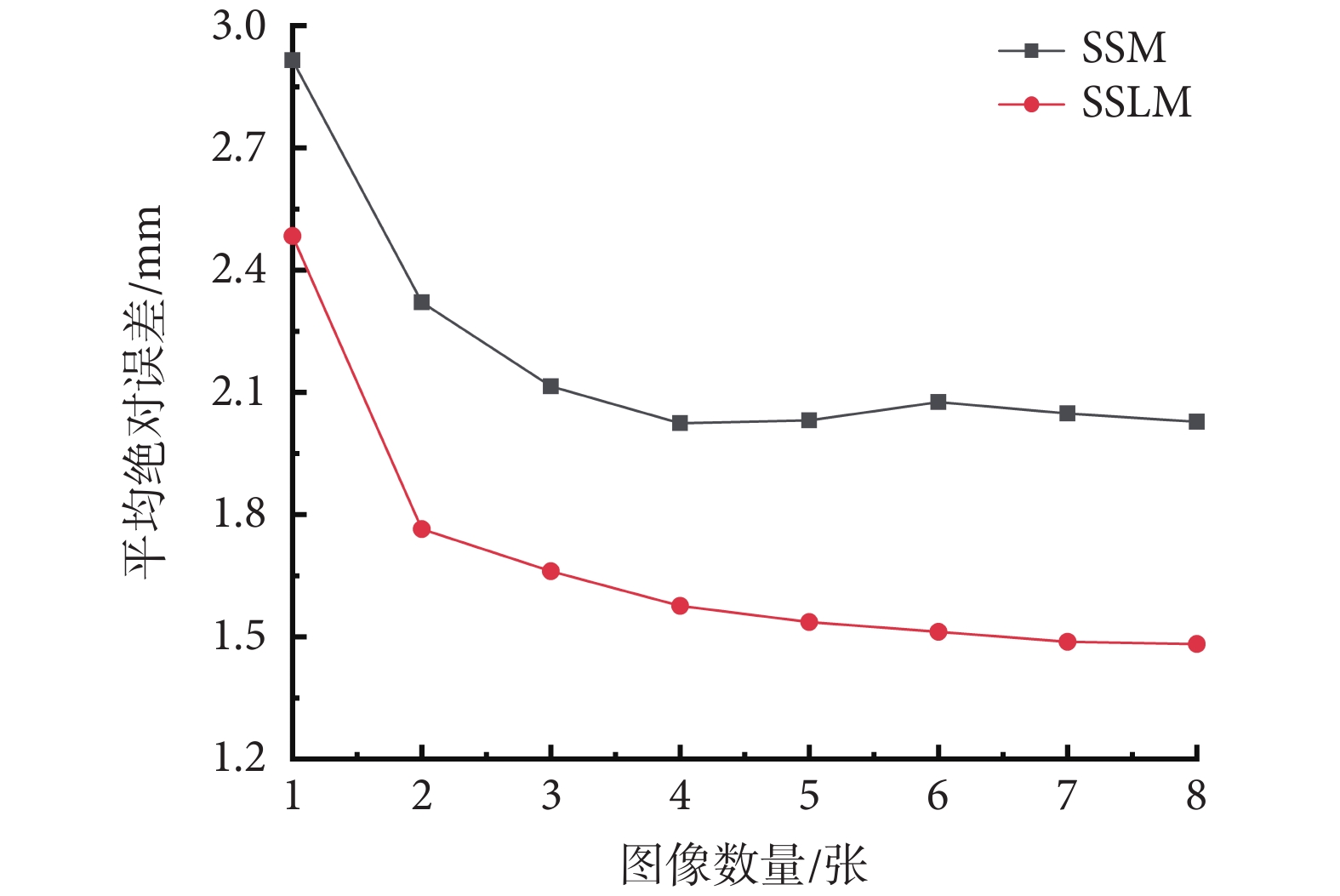圖8
重建誤差－圖像數量變化圖
Figure8.
Reconstruction error - the number of images change
3 討論
在之前基于SSM的三維重建的研究中，其原理主要是根據所建立的三維模型數據庫中的特征先驗信息，基于主成分分析將目標模型表示為85.0%～95.0%信息占比的主成分與平均模型的線性組合[34-35]。然而，通常情況下，由于特征不足與精度損失問題，SSM的重建精度仍有提升空間，曲面修正是目前改善此問題的方法之一。Zheng等[20]使用薄板樣條函數（thin plate splines，TPS）對SSM的重建結果進行修正后，精度提升了9.1%。相比于TPS基于能量公式對模型局部表面的變形[8, 36]，拉普拉斯算子是基于拓撲結構對整體模型的描述。LSD既保留了SSM數據庫中的先驗特征及計算出的信息參數，又擬合出了二維圖像中的新特征與新信息，使精度提升了16.8%～25.9%。驗證結果得出，在保持信息量不變時，數據庫中包含目標股骨的特征時，LSD對SSM的重建結果精度提升較少，僅有2.8%，此時尚不能完全重建真實模型，因為此處也存在信息損失。數據庫中不包含目標股骨的特征時，精度提升效果達到最大，達到25.9%。保持數據庫不變時，隨著使用信息量的減少，LSD的精度提升也增大。本研究驗證了LSD對特征不足與信息損失問題的優化效果。在驗證不同特征數時，前后精度提升效果相差23.1%，而驗證不同信息量時，前后精度提升效果僅相差5.4%，說明數據庫特征的缺失是造成SSM重建精度不足的主要原因。這也讓本方法能為如Ti-WISH-IL雙平面X射線攝影系統等基于統計數據庫的臨床三維重建方法的優化提供思路。
同時本研究也存在一定的局限性。首先本文僅針對股骨進行了三維重建并驗證，對諸如盆骨、肩胛骨等結構更為復雜的骨骼重建的適用性還有待驗證。其次，由于數據采集信息的缺失，本文對于數據庫中骨骼志愿者的年齡、性別、體重和身高等參數對重建的影響沒有考慮。在后續的研究中，一方面可以將方該法應用于其他骨骼的三維重建中；另一方面，可將數據庫中的骨骼根據各參數進行分類研究，進一步提升模型的重建精度。
4 結論
本文基于SSM與LSD結合模型，建立了利用患者正側位股骨二維圖像進行特異性三維重建的方法，在保留股骨特征的前提下擬合二維目標輪廓，優化在SSM及主成分參數求解過程中的特征不足和信息損失的問題。實驗結果表明，在特征數量有限時，傳統SSM的重建精度為2.058～2.342 mm，引入LSD后的SSLM的重建精度為1.712～1.736 mm，相比SSM的重建精度提升了16.8%～25.9%，能以更高精度重建出患者的特異性股骨三維模型，為建立膝關節有限元模型、患者個性化假體設計和臨床診斷提供了技術基礎。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：張祖佩和張小剛構思方案，張祖佩實施方案并處理數據，張祖佩、張小剛、張亞麗和靳忠民討論并修改了論文。
0 引言
在現代骨科醫療實踐中，有時需要獲得患者個體的三維（three-dimensional，3D）骨骼模型以進行輔助醫療，如術前方案規劃[1-2]、病情診斷[3]或運動動力學分析等[4]。傳統的骨骼三維重建為利用電子計算機斷層掃描（computed tomography，CT）圖像在Mimics等軟件中建模[5-7]。然而，CT圖像存在輻射量較大、重建時間長、受設備影響而無法重建出站立位或坐立位位姿等缺點，在骨骼三維模型的臨床與科學研究中有一定的局限性[8-10]。
近年來，利用如X線平片或超聲圖像等二維（two-dimensional，2D）醫學圖像[11]建立一定精度的患者個性化骨骼三維模型，成為解決上述問題的主流方法。例如，上海濤影醫療設計的Ti-WISH-IL雙平面Ｘ射線攝影系統，基于骨骼統計大數據庫進行三維重建，目前已應用于臨床診斷中。
基于統計形狀模型（statistical shape models，SSM）的三維重建[12-14]，也是目前應用廣泛的一種基于數據庫先驗信息的方法。它針對人體根骨[15]、顳骨[16]、肋骨[17]、股骨[14]、脊椎[18]、膝關節[19]等骨骼的三維重建在臨床診斷、強度計算、計算機輔助手術等領域都有應用。SSM在一定程度上優化了CT三維重建存在的問題。但是，SSM的原理是將控制骨骼形狀的結點通過主成分分析（principal components analysis，PCA）進行數據降維變為數十個形狀特征，一方面這些形狀特征完全是由數據庫決定的，若目標模型存在數據庫以外的特征，重建精度就會較差[14, 20-21]；另一方面，經過數據降維，這些特征通常僅包含數據庫中85.0%～95.0%的形狀信息，存在信息損失[21-23]。因此，重建結果不能完全擬合目標二維圖像，無法完全滿足高精度的術前規劃和個性化植入物設計需求。
拉普拉斯曲面變形（Laplacian surface deformation，LSD）是一種基于拉普拉斯算子的三維建模算法，最初主要應用于圖像處理和計算機視覺[24-25]，近年來被廣泛應用于三維表面形狀處理，包括人臉建模[26]、動畫建模[27]和生物醫學[28]等領域。LSD的優勢在于能夠在保持模型整體拓撲結構不變的情況下，將形狀擬合至目標位置[29]。將LSD用于基于SSM的重建模型，能在保持骨骼特征不變的前提下，充分擬合目標輪廓，提升重建精度。然而，目前還沒有將LSD作用于SSM的重建結果的研究。
本文提出一種基于SSM與LSD結合的方法（statistical shape and Laplacian models，SSLM），將LSD作用于SSM的重建結果，研究充分擬合二維信息的三維重建方法，為個性化假體設計與安裝定位、生物力學分析和術前規劃提供更高精度的模型基礎。
1 方法
為了對股骨進行三維重建，在SSM的基礎上在拉普拉斯空間中對SSM的重建結果進行三維變形，使重建模型與二維圖像充分擬合。方法框架如圖1所示。SSLM將重建流程分為數據準備、初步統計重建和拉普拉斯修正。在數據準備階段對采集的三維數據集進行處理，對輸入的目標二維圖像進行輪廓提取；在初步統計重建時建立SSM，利用處理過的二維與三維數據初步建立二維/三維對應關系，進而求解出特征參數，通過平均模型、主特征及其特征參數的線性組合完成股骨初步重建；最后進行的拉普拉斯修正則是通過建立新的二維/三維對應關系，在拉普拉斯空間中進行三維變換以提升精度，得到最終的重建模型。
圖1
SSLM方法框架及流程
Figure1.
The method framework and flowchart of SSLM
1.1 數據準備
數據準備階段包括對采集的二維輸入圖像和三維數據集的預處理。本文采用livewire算法提取股骨二維輪廓[30]。三維股骨的特征提取首先需由股骨數據集建立數據庫，將采集的股骨三維模型離散化，保存為三維點云模型及其三角面信息。采用線性縮放的方式對數據集進行模型歸一化處理，以突出股骨形狀特征，擬合患者的特異性模型，而后去中心化，采用最近點迭代（iterative closest point，ICP）算法[31]，將股骨三維點云位姿進行配準，使所有點云位姿與患者二維圖像采集位姿相擬合，統一坐標系，并找出股骨模型間的對應點，建立數據庫。
1.2 統計形狀建模
由所建立的股骨數據庫與提取的二維輪廓建立SSM。首先是用數據庫中已預處理的、點對應關系已知的股骨點云模型，基于主成分分析進行參數化處理，求解出數據庫中股骨的形狀特征主成分，并計算平均模型(1)。為求出數據庫中的主要特征，將數據庫表示為[]矩陣，求出數據庫的協方差矩陣(2)，并求解出協方差矩陣的特征值 和特征向量 ，按數值大小對特征值及其對應的特征向量由大到小進行排序，每個特征向量就表示股骨的一個主要形狀特征。按照特征值大小取85.0%～95.0%占比特征值所對應的特征向量作為此數據庫的主要形狀特征。由此任一股骨都可由一個平均模型和形狀特征及權重系數的線性組合表示(3)。各形狀特征對應的權重系數被限制在 內[32]。將從二維輪廓上提取并映射到三維空間上的點與重建模型上建立二維/三維對應關系[20]，將對應點的平均距離(4)作為損失函數，求解出形狀特征參數，得到初步重建的股骨特征模型。
|
|
| '/> |
| '/> |
式中 表示骨點云數據； 表示平均模型；p 表示數據庫中股骨點云數量； 表示協方差矩陣；{}表示 的特征向量，即股骨的主成分；{}表示各主成分的權重參數；n 表示從提取的二維輪廓中均勻采樣的點的個數； 表示從二維輪廓映射到三維的對應點； 表示平均模型上與 對應的點； 表示第i個主成分上與第j個點所對應的值。
1.3 拉普拉斯修正
由于優化算法和SSM的局限性，初步重建的股骨三維模型并不能完全擬合所提取的二維輪廓信息，重建精度有一定的提升空間，這就需要在三維空間內對初步重建模型進行變換，使重建模型充分擬合二維信息。
LSD基于拉普拉斯算子［見式(5)］[33]，如圖2a所示，算子將模型中的每個結點表示為該點與其所有鄰接點質心的差值向量，向量的模長表示曲面上該點的屈曲程度，方向為該點的曲面法向量。由此拉普拉斯算子可以表示模型中任意結點的局部表面形狀特征。三維網格模型結點拓撲結構間的連接性決定了拉普拉斯算子的傳遞性，如圖2b所示，某一結點的拉普拉斯算子改變，該結點鄰接點的局部形狀特征也會改變，并依次傳遞至所有相互連通的結點,從而影響整個模型。
圖2
拉普拉斯算子示意圖
a. 處的拉普拉斯算子；b. 及其鄰接點處的拉普拉斯算子
Figure2. Laplace operatora. the Laplace operator at ; b. the Laplace operator at and its neighbors
將LSD應用于基于SSM的股骨三維重建結果，就是將股骨形狀變換至目標位置的同時，將變換前后拉普拉斯算子的變化最小化［見式(6)］。如圖3所示，通過二次二維/三維對應關系，將局部的結點坐標變換拓展至整個股骨的三維形變中去，同時重建股骨的形狀特征不變。SSLM能在保持SSM重建結果中數據庫的先驗特征不變的情況下，將股骨曲面變形擬合出新特征，對二維圖像充分擬合，完成更高精度的三維重建。
圖3
股骨LSD示意圖
Figure3.
LSD of femur
|
| '/> |
式中， 為點云模型中的點， 為 的1鄰域內的點， 為 鄰接點的數量，、 分別表示變形前和變形后 的拉普拉斯算子， 表示控制點變形后的坐標， 表示 變形的目標坐標。
1.4 方法驗證
采用50例取自SMIR醫學圖像數據庫健康人的完整三維左股骨模型驗證方法的準確性，將第50例股骨作為目標真實模型，并基于上述數據準備階段進行模型處理。采用所有對應結點距離的平均絕對誤差（mean absolute error，MAE）、標準差（standard deviation，SD）來衡量重建模型的品質。以上述數據庫為基礎，分別使用三種方法對二維股骨圖像進行三維重建：基于SSM、基于LSD和基于SSLM，并將重建結果與真實模型進行比對，從不同特征數、不同信息量和不同二維圖像數量三個方面驗證方法的優化機制。三維重建過程在Matlab（2021b）軟件中完成。
2 結果與分析
2.1 不同特征數的股骨重建
分別采用50例股骨和49例股骨建立數據庫，代表特征數充足與否的情況。LSD、49例股骨數據庫條下的SSM與SSLM、50例股骨數據庫條件下的SSM與SSLM重建效果如圖4所示。采用LSD進行重建時的重建模型的MAE為2.432 mm，SD為1.855 mm。在數據庫特征數較少或不包含目標股骨的特征時，SSM重建的MAE為2.342 mm，SD為1.237 mm，SSLM的MAE為1.736 mm，SD為0.987 mm，誤差分布如圖5b所示。此時，SSLM與SSM的重建結果相比，精度提了25.9%，誤差分布也更為集中。在數據庫特征數充足或包含目標圖像三維模型的特征時，SSM的MAE為0.283 mm，SSLM的MAE為0.275 mm。此時，SSLM相比SSM的精度提升2.8%，誤差分布如圖5a所示。
圖4
股骨重建效果圖
紅色為重建模型，藍色為真實模型
Figure4. A rendering of the femoral reconstructionred is the reconstructed model and blue is the true model
圖5
三維重建誤差分布圖
a. 特征充足；b. 特征不足
Figure5. 3D reconstruction error distributiona. sufficient number of feature; b. insufficient number of features
2.2 不同信息量的股骨重建
在特征數有限的數據庫條件下，建立SSM與SSLM模型，采用不同主成分數量即不同信息量的股骨三維重建結果誤差如圖6所示。隨著使用主成分數量的增多，重建誤差逐漸減少，在使用主成分數量超過10后，誤差減少的趨勢逐漸放緩。使用多于10個主成分的SSM重建的MAE在2.1～2.5 mm，SSLM重建的MAE在1.7～1.9 mm。使用40個主成分時，信息占比98.2%，SSM與SSLM的MAE分別為2.058 mm與1.712 mm，SSLM的精度提升效果為16.8%。使用5個主成分時，信息占比85.8%，SSM與SSLM的MAE分別為2.596 mm與2.018 mm，SSLM的精度提升效果為22.2%。
圖6
重建誤差隨主成分數量變化圖
Figure6.
Reconstruction error change with feature number
2.3 不同二維圖像數量的股骨重建
驗證在不同二維圖像數量下進行三維重建的精度規律，從正側位開始拍攝，每間隔22.5°取一張二維圖像（如圖7所示）。固定使用20個主成分，按1～8號圖像依次累加進行SSM和SSLM的三維重建。
圖7
二維圖像拍攝角度
Figure7.
The angle at which the 2D image was taken
采用1～8張二維圖像的三維重建結果如圖8所示，在僅使用一張圖像時，SSM與SSLM的MAE均在2.5 mm以上；在使用正交的第二張圖像后，SSM的MAE減少至2.321 mm，SSLM的MAE減少至1.736 mm。但是，當繼續累加其他視角的二維圖像時，無論SSM還是SSLM的重建結果相比于其使用兩張圖像時的重建精度無明顯提高。
圖8
重建誤差－圖像數量變化圖
Figure8.
Reconstruction error - the number of images change
3 討論
在之前基于SSM的三維重建的研究中，其原理主要是根據所建立的三維模型數據庫中的特征先驗信息，基于主成分分析將目標模型表示為85.0%～95.0%信息占比的主成分與平均模型的線性組合[34-35]。然而，通常情況下，由于特征不足與精度損失問題，SSM的重建精度仍有提升空間，曲面修正是目前改善此問題的方法之一。Zheng等[20]使用薄板樣條函數（thin plate splines，TPS）對SSM的重建結果進行修正后，精度提升了9.1%。相比于TPS基于能量公式對模型局部表面的變形[8, 36]，拉普拉斯算子是基于拓撲結構對整體模型的描述。LSD既保留了SSM數據庫中的先驗特征及計算出的信息參數，又擬合出了二維圖像中的新特征與新信息，使精度提升了16.8%～25.9%。驗證結果得出，在保持信息量不變時，數據庫中包含目標股骨的特征時，LSD對SSM的重建結果精度提升較少，僅有2.8%，此時尚不能完全重建真實模型，因為此處也存在信息損失。數據庫中不包含目標股骨的特征時，精度提升效果達到最大，達到25.9%。保持數據庫不變時，隨著使用信息量的減少，LSD的精度提升也增大。本研究驗證了LSD對特征不足與信息損失問題的優化效果。在驗證不同特征數時，前后精度提升效果相差23.1%，而驗證不同信息量時，前后精度提升效果僅相差5.4%，說明數據庫特征的缺失是造成SSM重建精度不足的主要原因。這也讓本方法能為如Ti-WISH-IL雙平面X射線攝影系統等基于統計數據庫的臨床三維重建方法的優化提供思路。
同時本研究也存在一定的局限性。首先本文僅針對股骨進行了三維重建并驗證，對諸如盆骨、肩胛骨等結構更為復雜的骨骼重建的適用性還有待驗證。其次，由于數據采集信息的缺失，本文對于數據庫中骨骼志愿者的年齡、性別、體重和身高等參數對重建的影響沒有考慮。在后續的研究中，一方面可以將方該法應用于其他骨骼的三維重建中；另一方面，可將數據庫中的骨骼根據各參數進行分類研究，進一步提升模型的重建精度。
4 結論
本文基于SSM與LSD結合模型，建立了利用患者正側位股骨二維圖像進行特異性三維重建的方法，在保留股骨特征的前提下擬合二維目標輪廓，優化在SSM及主成分參數求解過程中的特征不足和信息損失的問題。實驗結果表明，在特征數量有限時，傳統SSM的重建精度為2.058～2.342 mm，引入LSD后的SSLM的重建精度為1.712～1.736 mm，相比SSM的重建精度提升了16.8%～25.9%，能以更高精度重建出患者的特異性股骨三維模型，為建立膝關節有限元模型、患者個性化假體設計和臨床診斷提供了技術基礎。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：張祖佩和張小剛構思方案，張祖佩實施方案并處理數據，張祖佩、張小剛、張亞麗和靳忠民討論并修改了論文。
