電阻抗成像（EIT）是一種無輻射、非侵入式的可視化診斷技術。為提高胸部電阻抗成像技術重建算法的成像分辨率和去偽影能力，本研究提出了一種利用Hadamard product優化多層神經網絡（MANN）的HMANN算法。將HMANN算法的重建圖像與廣義矢量模式匹配（GVSPM）算法、截斷奇異值分解（TSVD）算法、反向傳播（BP）神經網絡算法和傳統MANN算法的重建圖像進行對比，仿真結果表明：相對于MANN算法，HMANN算法重建圖像的相關系數在圓截面模型中可以提高17.30%，在肺截面模型中可以提高13.98%。雖然肺截面模型中HMANN算法重建圖像的部分相關系數會有所下降，但在所有模型中，HMANN算法保留了MANN算法的圖像信息，同時HMANN算法重建圖像的偽影更少，檢測目標與背景的可識別度比傳統MANN算法高。本研究可以提升重建圖像的相關系數，有效去除重建圖像的偽影，為EIT成像技術提供了一種有效提升重建圖像質量的新思路。
引用本文： 宋振忠, 李建平, 溫建明, 萬嫩, 馬繼杰, 張昱, 胡意立, 高增鋒. 基于Hadamard product優化多層神經網絡的胸部電阻抗成像研究. 生物醫學工程學雜志, 2024, 41(3): 439-446, 454. doi: 10.7507/1001-5515.202305047 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
電阻抗成像（electrical impedance tomography，EIT）技術是一種非侵入式、安全的新型可視化診斷技術[1-4]，通過測量場域的邊界電壓重建物體組織內部的電導率分布，從而評估物體組織內部結構是否發生病變。EIT技術在材料檢測、生物醫學等領域應用發展迅速[5-8]，在胸部肺功能監測方面具有很好的前瞻性。王慧泉等[9]通過仿真分析了磁探測EIT應用于呼吸監測的可行性；張靜等[10]利用EIT技術評價通氣模式對慢性阻塞性肺疾病急性加重患者的影響；Sella等[11]利用EIT技術尋求最佳呼吸末正壓值，監測肺塌陷和肺膨脹；Shono等[12]和Gibot等[13]利用EIT技術監測肺機械通氣過程，實現了COVID-19患者急性呼吸窘迫綜合征的個性化治療；Zamani等[14]提出了可識別氣道數生成校正因子的EIT圖像來準確估計充盈系數；李芳等[15]針對現有肺部監測系統基本依賴于PC平臺造成使用場合受限的問題，開發了一種面向肺功能檢測的便攜式EIT成像系統，實現了動態成像的功能。
利用重建算法重建EIT圖像，實質上是求解一個病態的逆問題。針對圓截面模擬試驗，李星等[16]提出了一種基于自診斷正則化的EIT圖像重建方法，提高了EIT圖像質量和抗噪聲能力；曹璐等[17]提出了多頻動態EIT算法，通過增加測量數據量改善逆問題的病態性；丁明亮等[18]提出基于鄰域信息和快速模糊C均值聚類的偽跡優化算法，提高了胸部EIT圖像的精確度；Wu等[19]設計了基于稀疏貝葉斯學習的BSBL算法用于EIT肺呼吸監測，該方法具有良好的建模能力和噪聲魯棒性，可以自適應地探索內部電導率分布。在深度學習方面，神經網絡具有較好的自適應與自組織能力、泛化能力、非線性映射能力，常被應用于EIT成像。Wu等[20]利用改進卷積神經網絡對胸部進行EIT成像，改進的卷積神經網絡收斂速度更快，提高了EIT成像的準確性和魯棒性；Zhu等[21]提出了基于數字孿生和深度學習的肺監測EIT成像算法，不僅可獲取更高精度的重建圖像，同時重建算法具有較好的抗噪性能；Wang等[22]利用粒子群算法優化反向傳播（backpropagation，BP）神經網絡，克服了BP神經網絡算法收斂緩慢和局部極值的局限性，有效提高了EIT圖像分辨率；戎舟等[23]設計了多層神經網絡的EIT求解方法，能迅速得到精度高的結果。優化重建算法是提高圖像質量和分辨率的重要舉措之一，但現有的重建算法獲取的圖像或多或少存在偽影，會影響對病變組織的評估甚至做出錯誤的判斷。因此，提高重建圖像的空間分辨率以及減少重建圖像的偽影是十分有必要的。
為提高胸部EIT圖像的分辨率，本研究提出了利用Hadamard product對多層神經網絡（multilayer artificial neural network，MANN）算法進行后處理優化的HMANN算法，通過10種圓截面模型和10種肺截面模型進行仿真，對比HMANN算法和MANN算法的成像效果，利用相關系數、均方根誤差作為評價指標評估重建圖像的質量；最后，利用MATLAB獲取4種圓截面模型和4種肺截面模型，從而評估多層神經網絡的泛化能力。
1 電阻抗圖像重建方法
EIT成像技術的圖像重建過程就是利用重建算法推導電導率分布的過程，邊界電壓與電導率分布的映射關系如下：
 |
式中：u和σ分別表示邊界電壓和電導率分布；S是一個M × N的靈敏度矩陣，M和N分別為邊界電壓和電導率的個數，靈敏度矩陣由EIT正問題求解獲得。傳統的非智能算法中，通常先求解靈敏度矩陣，再求解電導率分布；以神經網絡為主的智能算法中，并不需要求解靈敏度矩陣，只需提供大量數據樣本訓練神經網絡，使其自主尋找邊界電壓與電導率分布的映射關系。
目前，常見的EIT成像系統包含8電極系統、16電極系統、32電極系統等系統，隨著電極對的增加，測量的邊界電壓值個數增多，數據計算的難度也隨之增加。本研究采用8電極EIT成像系統驗證HMANN算法的圖像重建特性；利用EIDORS和MATLAB對整個場域進行有限元剖分，將場域全域均勻剖分為576個有限元，其次，利用相鄰激勵測量方式獲取場域的邊界電壓值[24]，若有m個電極，則可以獲取 m(m + 3) 個電壓值，本研究的8電極系統完成一次測量可以獲取40個電壓值，最終建立40個電壓值與576個有限元電導率值之間的映射關系。
1.1 MANN算法和BP神經網絡算法
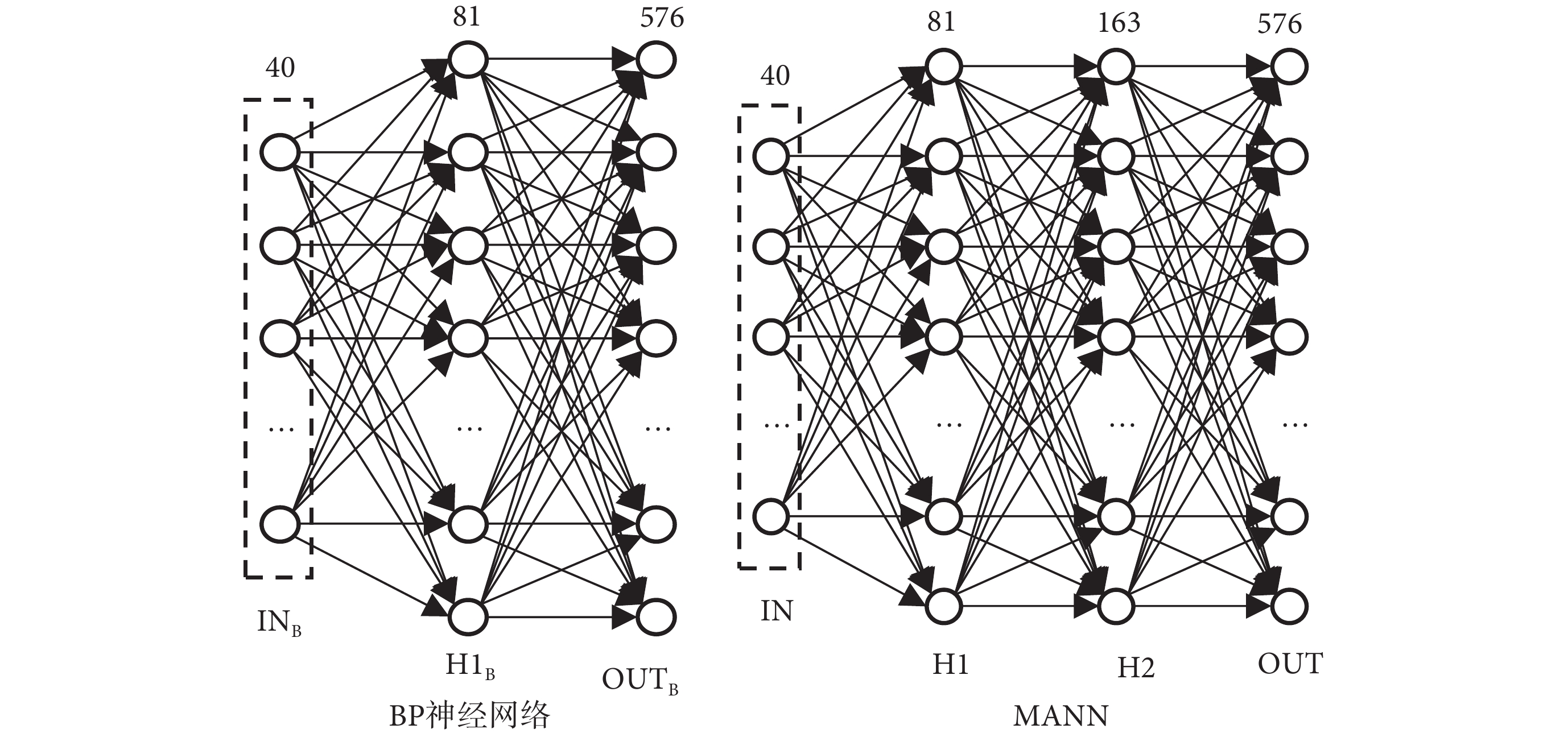
BP神經網絡具有很強的非線性映射能力和柔性的網絡結構，包括輸入層、隱藏層和輸出層，相鄰兩層神經元采用全連接方式映射，但是BP神經網絡會出現局部收斂等現象，導致最終解不一定是最優解。本研究將MANN算法作為EIT技術的圖像重建算法，并引用Hadamard product作為MANN算法的后處理方式，優化MANN算法的圖像重建效果。MANN結構和BP神經網絡結構如圖1所示。BP神經網絡結構的INB表示輸入層，H1B表示隱藏層，OUTB表示輸出層；MANN結構的IN表示輸入層，H1表示第一個隱藏層，OUT表示輸出層，H2為MANN的第二個隱藏層；BP神經網絡與MANN的輸入和輸出分別是邊界電壓值和電導率值，因此輸入層和輸出層的神經元分別為40個和576個。蔡榮輝等[25]探究三層BP神經網絡最佳隱藏層神經元個數時，通過手寫字母的仿真結果得出，先驗公式 h = 2m + 1 的識別率遠大于其他先驗公式；其次，輸入和輸出的維度相差較大，測量的邊界電壓值個數遠遠小于電導率值的未知數個數，采用先驗公式 h = 2m + 1可以避免相鄰兩層神經元之間的維度相差太大。因此，本研究隱藏層神經元的個數由先驗公式(2)確定[25]：
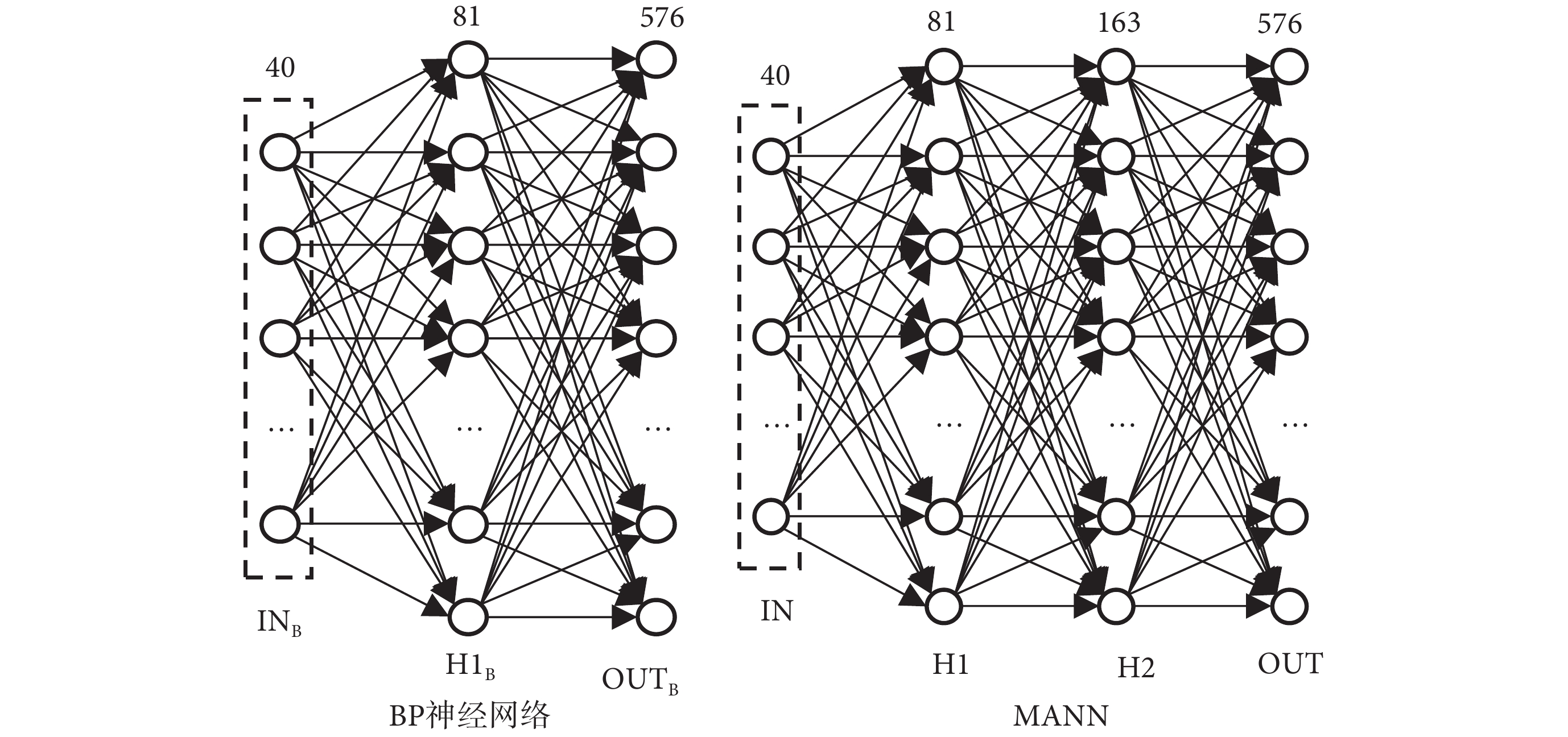圖1
神經網絡結構
Figure1.
Neural network structure
 |
式中：h表示隱藏層神經元的個數，m表示輸入層的神經元個數；BP神經網絡的隱藏層具有81個神經元，MANN的第一隱藏層具有81個神經元，第二隱藏層具有163個神經元；BP神經網絡結構和MANN結構除了隱藏層參數不一樣外，其他參數均一致。
1.2 HMANN算法
HMANN算法是利用Hadamard product優化MANN算法的圖像重建方法，Hadamard product[26-27]是矩陣的一類運算規則，若A = (aij)和B = (bij)是兩個同階矩陣，兩矩陣的Hadamard product為C = (cij)，且cij = aij × bij。如圖2所示，輸入數據IN后，經過MANN預測后輸出OUT，OUT2是OUT通過Hadamard product優化的結果，關系表達式如下：
圖2
HMANN算法和MANN算法
Figure2.
HMANN algorithm and MANN algorithm
 |
式中：σ1表示輸出OUT的電導率分布，σ2表示OUT2的電導率分布，（o）表示Hadamard product運算符號。若σj表示MANN算法重建電導率分布的一個有限元電導率值，則HMANN算法對應的有限元電導率值為σj2。
對數據集歸一化處理，重建圖像中背景區域有限元的電導率絕對值小于1，無限接近于0，同時目標物體的電導率絕對值大于背景區域的電導率絕對值，因此可以得到：
 |
 |
式中，σm和σn分別表示背景區域任意兩個有限元的電導率絕對值，由于σm < 1，故σm2 < σm，且σm2更加趨近于0；同時有σm + σn < 1，因此利用Hadamard product運算后，背景區域任意兩個有限元的電導率絕對值會變小。假設目標物體的電導率絕對值為σk，且有σk > σn，可以得到：
 |
從式(6)中可以看出，令f(σ) = ( σk2 ? σn2)/(σm2 ? σn2)，g(σ) = ( σk ? σn)/(σm ? σn)，則f(σ)/g(σ) 大于1，說明利用Hadamard product運算后，目標物體與背景區域的相對差異更加明顯，兩者的可區分性更高。
1.3 數據集模型
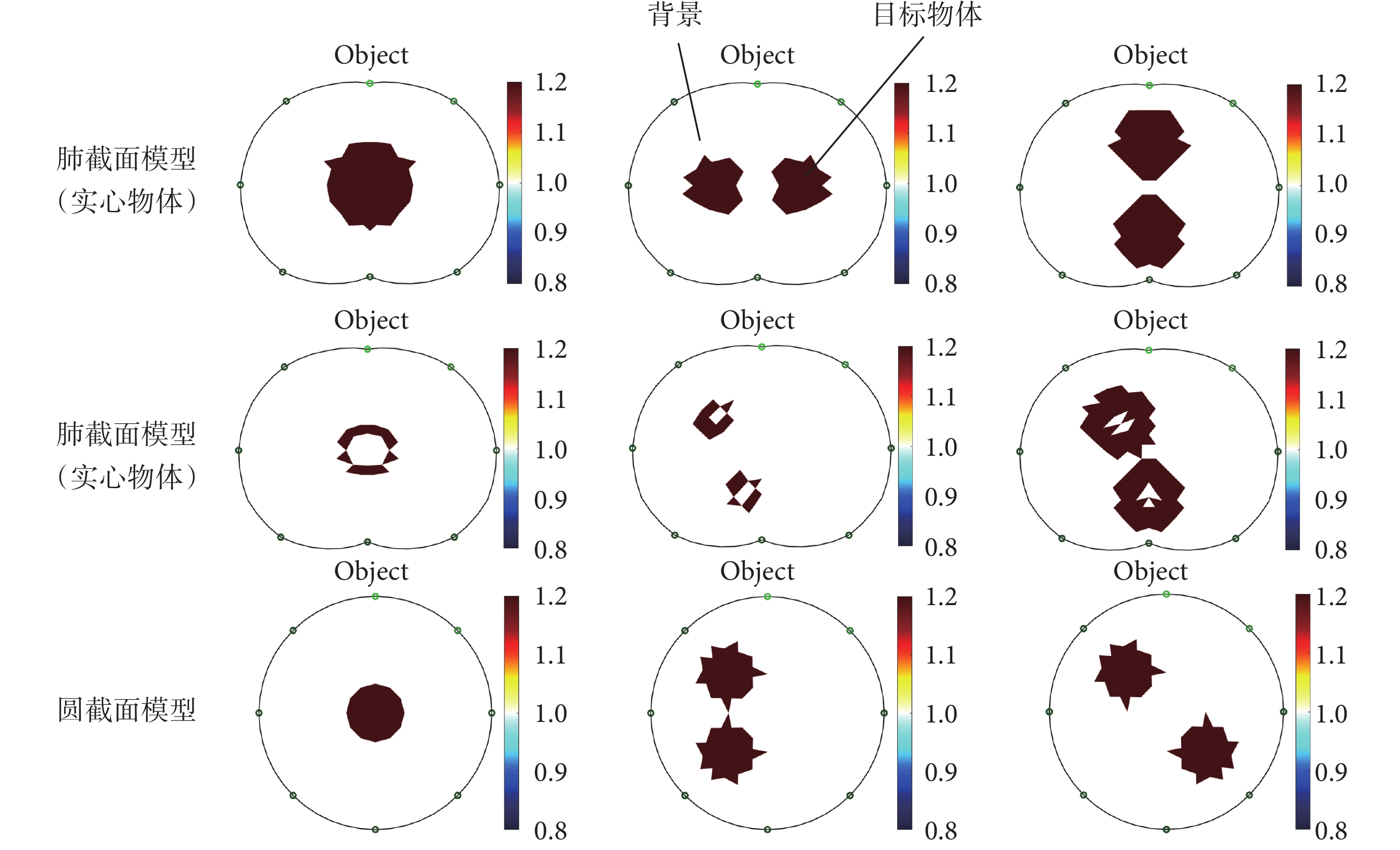
為了驗證HMANN算法的重建效果，本研究建立了肺截面模型和圓截面模型獲取訓練神經網絡的訓練樣本，如圖3所示。通過改變目標物體的大小、位置、電導率值等參數獲取大量的數據集，背景物體的電導率值設定為1 S/m，目標物體電導率值為1.2～2 S/m。在肺截面模型，目標物體的輪廓設定為圓形，且目標物體分為實心目標物體和空心目標物體；在圓截面模型中，目標物體的輪廓包含圓形、三角形和正方形（圖3中僅給出圓形目標物體）。利用有限元法對被測區域經行網格剖分后，若網格劃分比較粗糙，則目標物體的輪廓與設定的輪廓存在誤差，會出現尖端或者尖角的現象，圖3所示結果是被測區域被剖分為576個網格的模型結果。最終，獲取肺截面模型訓練樣本45 000個，圓截面模型訓練樣本75 000個，由于條件限制，兩種模型采集的訓練樣本分開作為兩神經網絡訓練。
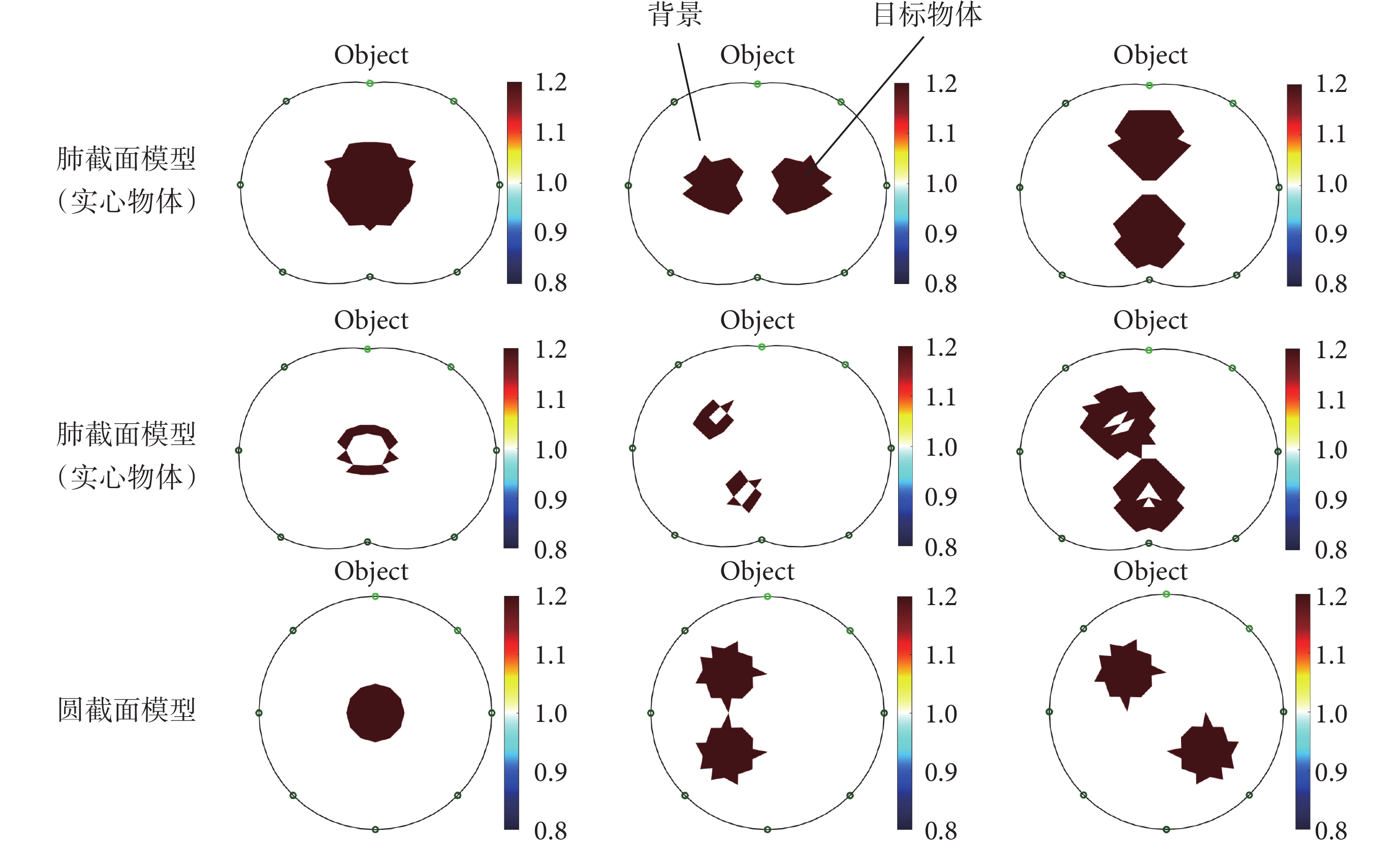圖3
訓練樣本模型
Figure3.
Training sample models
2 仿真結果
2.1 圓截面模型的仿真結果
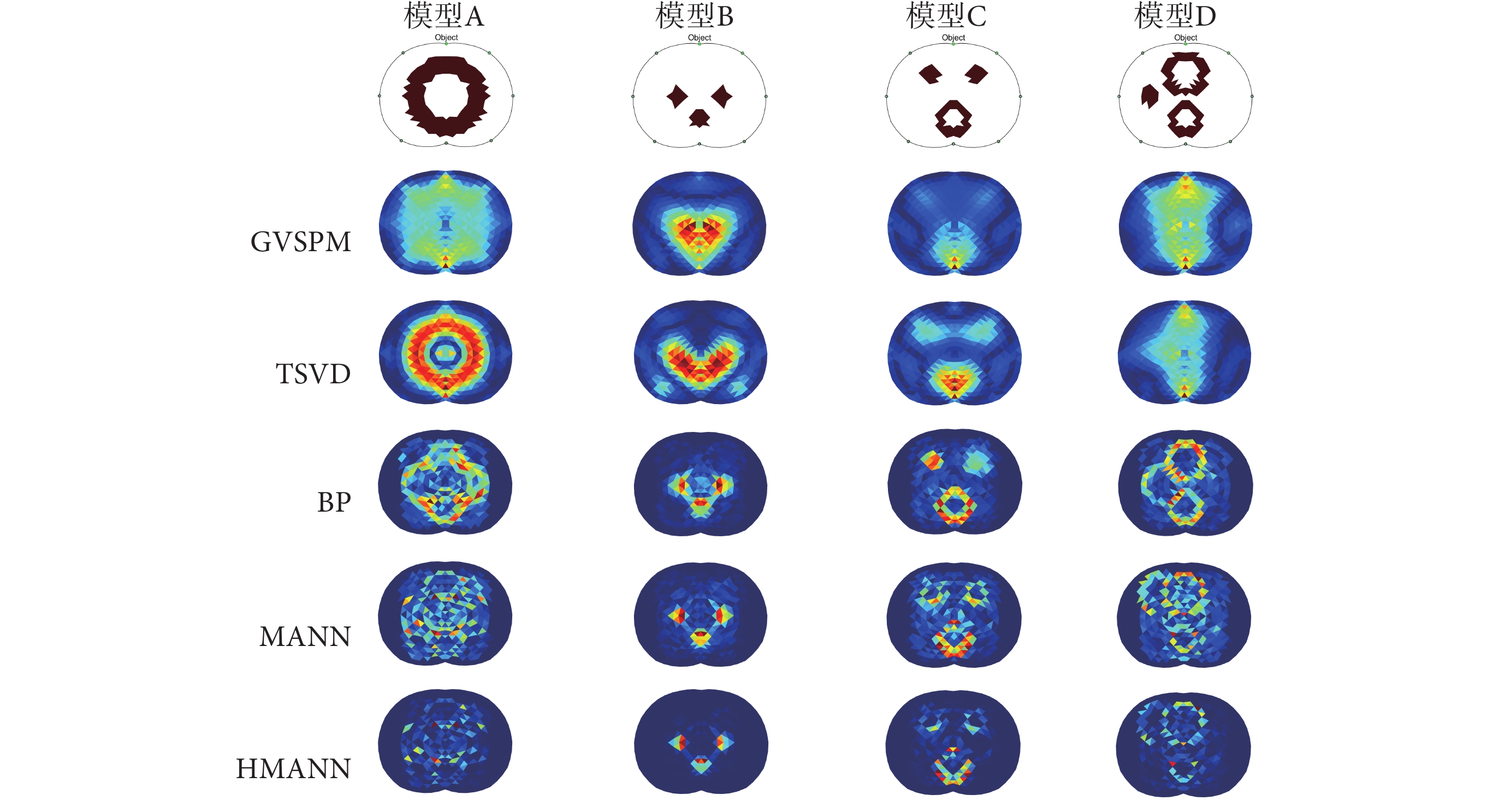
利用75 000個訓練樣本訓練BP神經網絡和MANN后，隨機選取10個樣本模型進行預測分析，將廣義矢量模式匹配（generalized vector sampled pattern matching，GVSPM）[28-29]算法和截斷奇異值分解（truncated singular value decomposition，TSVD）[30]算法作為對比算法，5種圖像重建算法的成像效果如圖4所示。
圖4
圓截面模型的仿真結果
Figure4.
Simulation results of the circular cross-section models
對于10種模型而言，TSVD算法和GVSPM算法重建的圖像存在大量偽影，重建圖像質量差；BP神經網絡算法重建的圖像偽影較少；MANN的成像效果比BP神經網絡成像效果更好，偽影也更少，重建圖像中目標物體的大小、位置幾乎與實際目標物體的大小、位置一致。但是，無論是TSVD算法和GVSPM算法，還是BP神經網絡算法和MANN算法，重建圖像依舊存在偽影，容易造成錯誤的診斷。HMANN算法的重建圖像基本沒有偽影，在目標物體區域外的背景區域中，區域的顏色分布基本一致。可見HMANN算法既保留了MANN算法的圖像信息，又減少了圖像的偽影，提高了背景區域與目標物體的可區分性。
本研究選取相關系數和均方根誤差評價重建算法的重建圖像質量，相關系數和均方誤差是評價重建圖像質量的常用參數[3-4]，適合于分析重建圖像的質量。相關系數越大，表示重建電導率分布趨勢與實際電導率分布趨勢相關性越好，重建圖像中目標物體的分布更接近于實際情況；均方根誤差越小，說明重建電導率與實際電導率的誤差更小，相關系數（correlation coefficient，CC）和均方根誤差（root mean square error，RMSE）的表達式如下所示：
 |
 |
式中：CC表示相關系數，RMSE表示均方根誤差；xi表示重建電導率中第i個有限元的電導率值，
表示重建電導率的平均值；yi表示實際電導率中第i個有限元的電導率值，
表示實際電導率的平均值；相關系數和均方根誤差計算結果如表1和表2所示。
表1
圓截面模型重建圖像的相關系數
Table1.
The correlation coefficients of reconstructed images for the circular cross-section models
表2
圓截面模型重建圖像的均方根誤差
Table2.
The root mean square error of reconstructed image for the circular cross-section models
表1是10種圓截面模型的相關系數，GVSPM算法重建圖像的相關系數在5種重建算法中是最低的，最大值僅為0.526 7；TSVD算法重建圖像的相關系數比GVSPM算法有所增加，但最大值也僅為0.606 0，說明GVSPM算法與TSVD算法重建電導率分布趨勢與實際電導率分布趨勢相關性較差，導致重建圖像中存在大量的偽影。BP神經網絡算法重建圖像的相關系數最大為0.788 3，相對于GVSPM算法和TSVD算法增加了49.67%和30.25%。MANN算法重建圖像的相關系數最大為0.829 9，相對于BP神經網絡算法增加了5.28%；HMANN算法重建圖像的相關系數在10種模型中始終比MANN算法大，在模型Ⅶ時相關系數最大，為0.870 1，相對于MANN算法而言，相關系數最大增加17.30%，最小增加0.84%。對于模型Ⅹ而言，5種重建算法重建圖像的相關系數都極低，但HMANN算法的相關系數比MANN算法大。
GVSPM算法重建圖像的均方根誤差較大，說明重建電導率與實際電導率的誤差較大；TSVD算法的均方根誤差在0.2范圍內波動，MANN算法的均方根誤差最小。從表2中可以看出，HMANN算法的均方根誤差比MANN算法大，因為在Hadamard product運算后，實際電導率與重建電導率的相關性會增加，同時實際電導率與重建電導率的差值會變大。假設重建電導率的第i個有限元值為xi，實際電導率為yi，且實際電導率的絕對值大于重建電導率的絕對值，兩者同為負值或者同為正值，電導率誤差等于重建電導率與實際電導率的差，由于|xi|小于1，可以得到|xi|大于|xi2|，因此，|xi2 ? yi|大于|xi ? yi|，故HMANN算法的均方根誤差比MANN算法大。
2.2 肺截面模型的仿真結果
本研究在肺截面模型的基礎上進行EIT成像，利用45 000個肺截面模型訓練樣本訓練神經網絡后，依然隨機選取10個樣本模型進行預測分析，結果同樣顯示，HMANN算法可重建圖像質量較好的肺EIT圖像（肺截面模型的具體仿真數據見附件1）。
3 神經網絡泛化能力
為了評估BP神經網絡和MANN神經網絡的泛化能力，以及HMANN的成像效果，本研究利用COMSOL與MATLAB仿真了4種圓截面模型，同時利用EIDORS與MATLAB仿真了4種肺截面模型，8種模型的數據均不在訓練神經網絡的樣本數據集中，仿真結果如圖5和圖6所示。
圖5
圓截面模型的仿真結果
Figure5.
Simulation results of the circular cross-section models
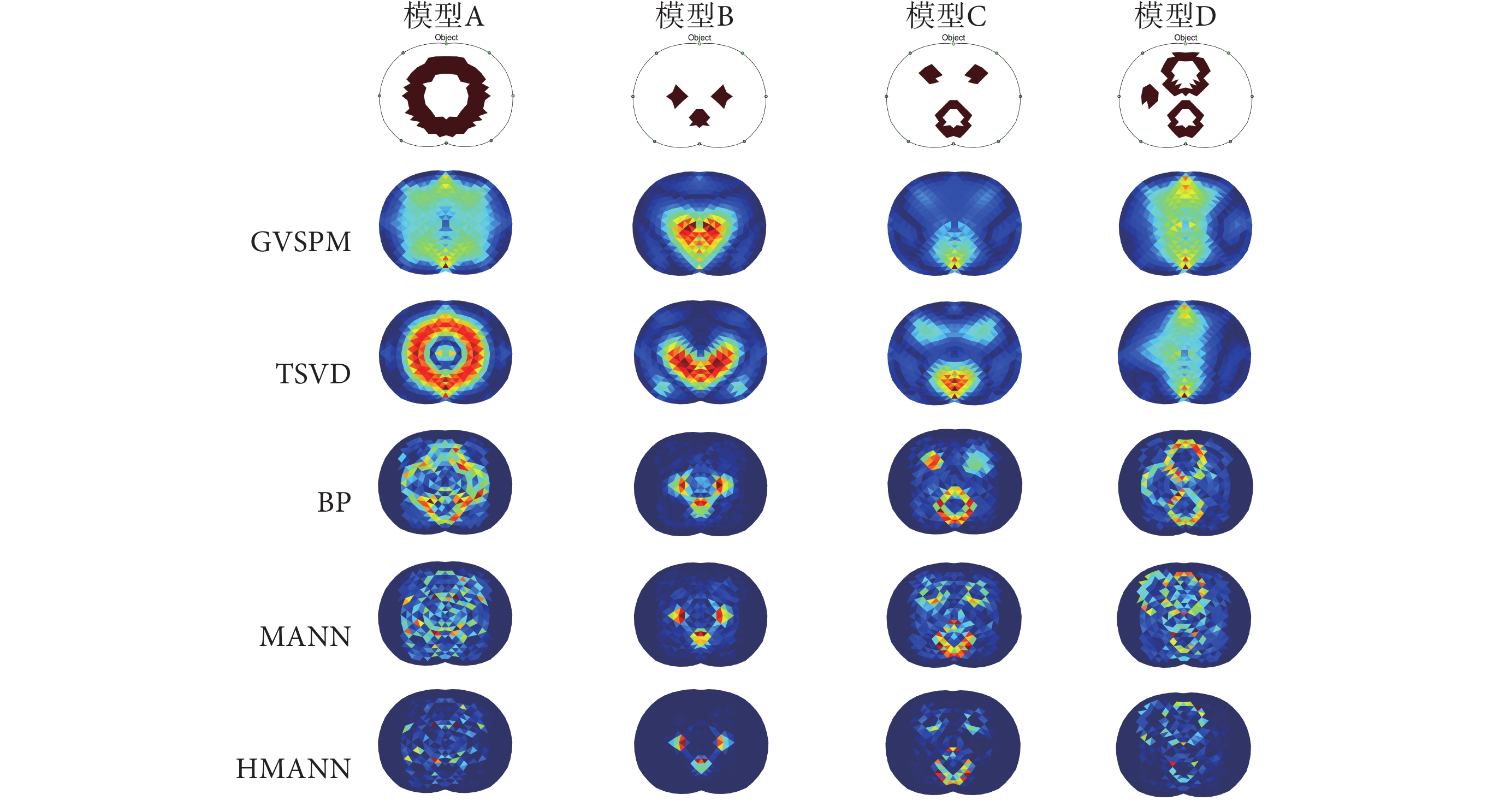圖6
肺截面模型的仿真結果
Figure6.
Simulation results of the lung cross-section model
從圖5可以看出，模型A中的目標物體是空心正方形，但GVSPM算法與TSVD算法重建圖像中目標物體的形狀類似于實心圓，兩者不相符；BP神經網絡算法、MANN算法和HMANN算法重建的目標物體基本是空心正方形，成像效果較好。在模型C中，當目標物體較小時，GVSPM算法與TSVD算法無法監測到目標物體的存在，三種神經網絡算法能監測到目標物體；HMANN算法重建圖像的較小目標物體電導率值基本接近于背景電導率值，不容易監測到小目標物體的存在，但是HMANN算法相對于MANN算法以及其他幾種算法而言，重建圖像中的偽影都極少。
圖6是4種肺截面模型的仿真結果，利用TSVD算法可以較好地重建模型A的目標物體，而GVSPM算法、MANN算法和HMANN算法存在失真現象。對于模型B而言，MANN算法和HMANN算法的泛化精度比BP神經網絡算法好，同時HMANN算法中的偽影比MANN算法少。模型C和模型D中，BP神經網絡的預測能力比其余4種算法好。原因是神經網絡訓練時，本研究獲取的訓練樣本45 000組數據還不足以充分地訓練神經網絡，使得MANN算法的泛化能力比BP神經網絡算法差。另外，圖5的重建圖像質量明顯不如圖4，主要因為圖5和圖6中的模型與網絡訓練集的模型無相似之處，主要驗證神經網絡的泛化能力，圖4的模型與訓練集中的模型有相似之處，因此，兩者會出現明顯的差異。在后續的研究中，將對BP神經網絡和HMANN進行結構優化，如參考遺傳算法（genetic algorithm，GA）優化的BP神經網絡（GA-BP）、粒子群優化算法（particle swarm optimization，PSO）優化的BP神經網絡（PSO-BP）等方法，提升BP神經網絡和HMANN的泛化應用能力。
EIT成像技術實現可視化成像時，是基于目標物體與背景區域的電導率值相差相對較大，而偽影的存在則是由于該處的電導率值有接近目標物體的趨勢，而利用Hadamard product可將偽影處的電導率值降低，使其與背景區域差異更小。通過泛化能力的對比和仿真結果表明，Hadamard product提高了重建圖像的質量。一方面，背景區域元素的電導率小于被測對象元素的電導率，采用Hadamard product運算后，背景區域元素的電導率值會更加接近于0。另一方面，如式（6）所示，被測對象元素的電導率與背景元素的電導率之間的差異變得相對容易區分，因此，Hadamard product有效地提高了本研究中重建圖像的相關性。HMANN算法建立在MANN算法的基礎上，在重建圖像過程中依賴于MANN算法，因此，HMANN算法網絡的泛化能力還需要進一步提升。HMANN算法的主要目的是有限去除重建圖像中的偽影，可為EIT成像技術在臨床監測、材料無損檢測等方面提供一種去偽影的參考方法。
4 結論
本研究利用Hadamard product 優化MANN算法得到HMANN算法，并與GVSPM算法、TSVD算法、BP神經網絡算法進行對比，通過仿真10種圓截面模型和10種胸部實驗模型評估HMANN算法的重建圖像效果，同時建立4種圓截面模型和4種胸部肺截面模型評估HMANN算法的泛化能力。仿真結果表明：當目標物體較小時，GVSPM算法和TSVD算法較難識別目標物體的實際大小和位置，BP神經網絡算法、MANN算法和HMANN算法基本能監測到目標物體的位置和大小；神經網絡訓練樣本為75 000組時，MANN算法的預測精度比BP神經網絡高，泛化能力也比BP神經網絡算法強；HMANN算法的成像效果好，既保留了MANN算法的圖像信息，又減少了圖像的偽影，提高了背景區域與目標物體的可區分程度。相對于MANN算法，HMANN算法重建的電導率分布與實際電導率分布的相關性在圓截面模型中可以提高17.30%，在肺截面模型中可以增加13.98%。當訓練樣本為45 000組時，MANN算法的預測精度比BP神經網絡高，但泛化能力比BP神經網絡算法差；HMANN算法的重建圖像相關系數在部分預測模型中有所下降，但重建圖像的偽影比MANN算法少，檢測目標與背景的可識別度更高。但是，目前肺EIT成像沒有公開的數據源作為支撐，沒辦法使用真實肺EIT成像的數據集驗證神經網絡的性能，輸出最真實的肺EIT成像，在后續的研究中，將結合CT等其他診斷方式重建真實肺輪廓的EIT圖像。
重要聲明
利益沖突聲明：本研究全體作者均聲明不存在利益沖突。
作者貢獻聲明：李建平、溫建明提出了本研究思路和結構；宋振忠、高增鋒完成了仿真測試；萬嫩、馬繼杰完成仿真數據的分析；張昱、胡意立對數據進行了回顧和分析；宋振忠根據數據完成論文的撰寫。
本文附件見本刊網站的電子版本（biomedeng.cn）。
0 引言
電阻抗成像（electrical impedance tomography，EIT）技術是一種非侵入式、安全的新型可視化診斷技術[1-4]，通過測量場域的邊界電壓重建物體組織內部的電導率分布，從而評估物體組織內部結構是否發生病變。EIT技術在材料檢測、生物醫學等領域應用發展迅速[5-8]，在胸部肺功能監測方面具有很好的前瞻性。王慧泉等[9]通過仿真分析了磁探測EIT應用于呼吸監測的可行性；張靜等[10]利用EIT技術評價通氣模式對慢性阻塞性肺疾病急性加重患者的影響；Sella等[11]利用EIT技術尋求最佳呼吸末正壓值，監測肺塌陷和肺膨脹；Shono等[12]和Gibot等[13]利用EIT技術監測肺機械通氣過程，實現了COVID-19患者急性呼吸窘迫綜合征的個性化治療；Zamani等[14]提出了可識別氣道數生成校正因子的EIT圖像來準確估計充盈系數；李芳等[15]針對現有肺部監測系統基本依賴于PC平臺造成使用場合受限的問題，開發了一種面向肺功能檢測的便攜式EIT成像系統，實現了動態成像的功能。
利用重建算法重建EIT圖像，實質上是求解一個病態的逆問題。針對圓截面模擬試驗，李星等[16]提出了一種基于自診斷正則化的EIT圖像重建方法，提高了EIT圖像質量和抗噪聲能力；曹璐等[17]提出了多頻動態EIT算法，通過增加測量數據量改善逆問題的病態性；丁明亮等[18]提出基于鄰域信息和快速模糊C均值聚類的偽跡優化算法，提高了胸部EIT圖像的精確度；Wu等[19]設計了基于稀疏貝葉斯學習的BSBL算法用于EIT肺呼吸監測，該方法具有良好的建模能力和噪聲魯棒性，可以自適應地探索內部電導率分布。在深度學習方面，神經網絡具有較好的自適應與自組織能力、泛化能力、非線性映射能力，常被應用于EIT成像。Wu等[20]利用改進卷積神經網絡對胸部進行EIT成像，改進的卷積神經網絡收斂速度更快，提高了EIT成像的準確性和魯棒性；Zhu等[21]提出了基于數字孿生和深度學習的肺監測EIT成像算法，不僅可獲取更高精度的重建圖像，同時重建算法具有較好的抗噪性能；Wang等[22]利用粒子群算法優化反向傳播（backpropagation，BP）神經網絡，克服了BP神經網絡算法收斂緩慢和局部極值的局限性，有效提高了EIT圖像分辨率；戎舟等[23]設計了多層神經網絡的EIT求解方法，能迅速得到精度高的結果。優化重建算法是提高圖像質量和分辨率的重要舉措之一，但現有的重建算法獲取的圖像或多或少存在偽影，會影響對病變組織的評估甚至做出錯誤的判斷。因此，提高重建圖像的空間分辨率以及減少重建圖像的偽影是十分有必要的。
為提高胸部EIT圖像的分辨率，本研究提出了利用Hadamard product對多層神經網絡（multilayer artificial neural network，MANN）算法進行后處理優化的HMANN算法，通過10種圓截面模型和10種肺截面模型進行仿真，對比HMANN算法和MANN算法的成像效果，利用相關系數、均方根誤差作為評價指標評估重建圖像的質量；最后，利用MATLAB獲取4種圓截面模型和4種肺截面模型，從而評估多層神經網絡的泛化能力。
1 電阻抗圖像重建方法
EIT成像技術的圖像重建過程就是利用重建算法推導電導率分布的過程，邊界電壓與電導率分布的映射關系如下：
|
式中：u和σ分別表示邊界電壓和電導率分布；S是一個M × N的靈敏度矩陣，M和N分別為邊界電壓和電導率的個數，靈敏度矩陣由EIT正問題求解獲得。傳統的非智能算法中，通常先求解靈敏度矩陣，再求解電導率分布；以神經網絡為主的智能算法中，并不需要求解靈敏度矩陣，只需提供大量數據樣本訓練神經網絡，使其自主尋找邊界電壓與電導率分布的映射關系。
目前，常見的EIT成像系統包含8電極系統、16電極系統、32電極系統等系統，隨著電極對的增加，測量的邊界電壓值個數增多，數據計算的難度也隨之增加。本研究采用8電極EIT成像系統驗證HMANN算法的圖像重建特性；利用EIDORS和MATLAB對整個場域進行有限元剖分，將場域全域均勻剖分為576個有限元，其次，利用相鄰激勵測量方式獲取場域的邊界電壓值[24]，若有m個電極，則可以獲取 m(m + 3) 個電壓值，本研究的8電極系統完成一次測量可以獲取40個電壓值，最終建立40個電壓值與576個有限元電導率值之間的映射關系。
1.1 MANN算法和BP神經網絡算法
BP神經網絡具有很強的非線性映射能力和柔性的網絡結構，包括輸入層、隱藏層和輸出層，相鄰兩層神經元采用全連接方式映射，但是BP神經網絡會出現局部收斂等現象，導致最終解不一定是最優解。本研究將MANN算法作為EIT技術的圖像重建算法，并引用Hadamard product作為MANN算法的后處理方式，優化MANN算法的圖像重建效果。MANN結構和BP神經網絡結構如圖1所示。BP神經網絡結構的INB表示輸入層，H1B表示隱藏層，OUTB表示輸出層；MANN結構的IN表示輸入層，H1表示第一個隱藏層，OUT表示輸出層，H2為MANN的第二個隱藏層；BP神經網絡與MANN的輸入和輸出分別是邊界電壓值和電導率值，因此輸入層和輸出層的神經元分別為40個和576個。蔡榮輝等[25]探究三層BP神經網絡最佳隱藏層神經元個數時，通過手寫字母的仿真結果得出，先驗公式 h = 2m + 1 的識別率遠大于其他先驗公式；其次，輸入和輸出的維度相差較大，測量的邊界電壓值個數遠遠小于電導率值的未知數個數，采用先驗公式 h = 2m + 1可以避免相鄰兩層神經元之間的維度相差太大。因此，本研究隱藏層神經元的個數由先驗公式(2)確定[25]：
圖1
神經網絡結構
Figure1.
Neural network structure
|
式中：h表示隱藏層神經元的個數，m表示輸入層的神經元個數；BP神經網絡的隱藏層具有81個神經元，MANN的第一隱藏層具有81個神經元，第二隱藏層具有163個神經元；BP神經網絡結構和MANN結構除了隱藏層參數不一樣外，其他參數均一致。
1.2 HMANN算法
HMANN算法是利用Hadamard product優化MANN算法的圖像重建方法，Hadamard product[26-27]是矩陣的一類運算規則，若A = (aij)和B = (bij)是兩個同階矩陣，兩矩陣的Hadamard product為C = (cij)，且cij = aij × bij。如圖2所示，輸入數據IN后，經過MANN預測后輸出OUT，OUT2是OUT通過Hadamard product優化的結果，關系表達式如下：
圖2
HMANN算法和MANN算法
Figure2.
HMANN algorithm and MANN algorithm
|
式中：σ1表示輸出OUT的電導率分布，σ2表示OUT2的電導率分布，（o）表示Hadamard product運算符號。若σj表示MANN算法重建電導率分布的一個有限元電導率值，則HMANN算法對應的有限元電導率值為σj2。
對數據集歸一化處理，重建圖像中背景區域有限元的電導率絕對值小于1，無限接近于0，同時目標物體的電導率絕對值大于背景區域的電導率絕對值，因此可以得到：
|
|
式中，σm和σn分別表示背景區域任意兩個有限元的電導率絕對值，由于σm < 1，故σm2 < σm，且σm2更加趨近于0；同時有σm + σn < 1，因此利用Hadamard product運算后，背景區域任意兩個有限元的電導率絕對值會變小。假設目標物體的電導率絕對值為σk，且有σk > σn，可以得到：
|
從式(6)中可以看出，令f(σ) = ( σk2 ? σn2)/(σm2 ? σn2)，g(σ) = ( σk ? σn)/(σm ? σn)，則f(σ)/g(σ) 大于1，說明利用Hadamard product運算后，目標物體與背景區域的相對差異更加明顯，兩者的可區分性更高。
1.3 數據集模型
為了驗證HMANN算法的重建效果，本研究建立了肺截面模型和圓截面模型獲取訓練神經網絡的訓練樣本，如圖3所示。通過改變目標物體的大小、位置、電導率值等參數獲取大量的數據集，背景物體的電導率值設定為1 S/m，目標物體電導率值為1.2～2 S/m。在肺截面模型，目標物體的輪廓設定為圓形，且目標物體分為實心目標物體和空心目標物體；在圓截面模型中，目標物體的輪廓包含圓形、三角形和正方形（圖3中僅給出圓形目標物體）。利用有限元法對被測區域經行網格剖分后，若網格劃分比較粗糙，則目標物體的輪廓與設定的輪廓存在誤差，會出現尖端或者尖角的現象，圖3所示結果是被測區域被剖分為576個網格的模型結果。最終，獲取肺截面模型訓練樣本45 000個，圓截面模型訓練樣本75 000個，由于條件限制，兩種模型采集的訓練樣本分開作為兩神經網絡訓練。
圖3
訓練樣本模型
Figure3.
Training sample models
2 仿真結果
2.1 圓截面模型的仿真結果
利用75 000個訓練樣本訓練BP神經網絡和MANN后，隨機選取10個樣本模型進行預測分析，將廣義矢量模式匹配（generalized vector sampled pattern matching，GVSPM）[28-29]算法和截斷奇異值分解（truncated singular value decomposition，TSVD）[30]算法作為對比算法，5種圖像重建算法的成像效果如圖4所示。
圖4
圓截面模型的仿真結果
Figure4.
Simulation results of the circular cross-section models
對于10種模型而言，TSVD算法和GVSPM算法重建的圖像存在大量偽影，重建圖像質量差；BP神經網絡算法重建的圖像偽影較少；MANN的成像效果比BP神經網絡成像效果更好，偽影也更少，重建圖像中目標物體的大小、位置幾乎與實際目標物體的大小、位置一致。但是，無論是TSVD算法和GVSPM算法，還是BP神經網絡算法和MANN算法，重建圖像依舊存在偽影，容易造成錯誤的診斷。HMANN算法的重建圖像基本沒有偽影，在目標物體區域外的背景區域中，區域的顏色分布基本一致。可見HMANN算法既保留了MANN算法的圖像信息，又減少了圖像的偽影，提高了背景區域與目標物體的可區分性。
本研究選取相關系數和均方根誤差評價重建算法的重建圖像質量，相關系數和均方誤差是評價重建圖像質量的常用參數[3-4]，適合于分析重建圖像的質量。相關系數越大，表示重建電導率分布趨勢與實際電導率分布趨勢相關性越好，重建圖像中目標物體的分布更接近于實際情況；均方根誤差越小，說明重建電導率與實際電導率的誤差更小，相關系數（correlation coefficient，CC）和均方根誤差（root mean square error，RMSE）的表達式如下所示：
|
|
式中：CC表示相關系數，RMSE表示均方根誤差；xi表示重建電導率中第i個有限元的電導率值，表示重建電導率的平均值；yi表示實際電導率中第i個有限元的電導率值，表示實際電導率的平均值；相關系數和均方根誤差計算結果如表1和表2所示。
表1
圓截面模型重建圖像的相關系數
Table1.
The correlation coefficients of reconstructed images for the circular cross-section models
表2
圓截面模型重建圖像的均方根誤差
Table2.
The root mean square error of reconstructed image for the circular cross-section models
表1是10種圓截面模型的相關系數，GVSPM算法重建圖像的相關系數在5種重建算法中是最低的，最大值僅為0.526 7；TSVD算法重建圖像的相關系數比GVSPM算法有所增加，但最大值也僅為0.606 0，說明GVSPM算法與TSVD算法重建電導率分布趨勢與實際電導率分布趨勢相關性較差，導致重建圖像中存在大量的偽影。BP神經網絡算法重建圖像的相關系數最大為0.788 3，相對于GVSPM算法和TSVD算法增加了49.67%和30.25%。MANN算法重建圖像的相關系數最大為0.829 9，相對于BP神經網絡算法增加了5.28%；HMANN算法重建圖像的相關系數在10種模型中始終比MANN算法大，在模型Ⅶ時相關系數最大，為0.870 1，相對于MANN算法而言，相關系數最大增加17.30%，最小增加0.84%。對于模型Ⅹ而言，5種重建算法重建圖像的相關系數都極低，但HMANN算法的相關系數比MANN算法大。
GVSPM算法重建圖像的均方根誤差較大，說明重建電導率與實際電導率的誤差較大；TSVD算法的均方根誤差在0.2范圍內波動，MANN算法的均方根誤差最小。從表2中可以看出，HMANN算法的均方根誤差比MANN算法大，因為在Hadamard product運算后，實際電導率與重建電導率的相關性會增加，同時實際電導率與重建電導率的差值會變大。假設重建電導率的第i個有限元值為xi，實際電導率為yi，且實際電導率的絕對值大于重建電導率的絕對值，兩者同為負值或者同為正值，電導率誤差等于重建電導率與實際電導率的差，由于|xi|小于1，可以得到|xi|大于|xi2|，因此，|xi2 ? yi|大于|xi ? yi|，故HMANN算法的均方根誤差比MANN算法大。
2.2 肺截面模型的仿真結果
本研究在肺截面模型的基礎上進行EIT成像，利用45 000個肺截面模型訓練樣本訓練神經網絡后，依然隨機選取10個樣本模型進行預測分析，結果同樣顯示，HMANN算法可重建圖像質量較好的肺EIT圖像（肺截面模型的具體仿真數據見附件1）。
3 神經網絡泛化能力
為了評估BP神經網絡和MANN神經網絡的泛化能力，以及HMANN的成像效果，本研究利用COMSOL與MATLAB仿真了4種圓截面模型，同時利用EIDORS與MATLAB仿真了4種肺截面模型，8種模型的數據均不在訓練神經網絡的樣本數據集中，仿真結果如圖5和圖6所示。
圖5
圓截面模型的仿真結果
Figure5.
Simulation results of the circular cross-section models
圖6
肺截面模型的仿真結果
Figure6.
Simulation results of the lung cross-section model
從圖5可以看出，模型A中的目標物體是空心正方形，但GVSPM算法與TSVD算法重建圖像中目標物體的形狀類似于實心圓，兩者不相符；BP神經網絡算法、MANN算法和HMANN算法重建的目標物體基本是空心正方形，成像效果較好。在模型C中，當目標物體較小時，GVSPM算法與TSVD算法無法監測到目標物體的存在，三種神經網絡算法能監測到目標物體；HMANN算法重建圖像的較小目標物體電導率值基本接近于背景電導率值，不容易監測到小目標物體的存在，但是HMANN算法相對于MANN算法以及其他幾種算法而言，重建圖像中的偽影都極少。
圖6是4種肺截面模型的仿真結果，利用TSVD算法可以較好地重建模型A的目標物體，而GVSPM算法、MANN算法和HMANN算法存在失真現象。對于模型B而言，MANN算法和HMANN算法的泛化精度比BP神經網絡算法好，同時HMANN算法中的偽影比MANN算法少。模型C和模型D中，BP神經網絡的預測能力比其余4種算法好。原因是神經網絡訓練時，本研究獲取的訓練樣本45 000組數據還不足以充分地訓練神經網絡，使得MANN算法的泛化能力比BP神經網絡算法差。另外，圖5的重建圖像質量明顯不如圖4，主要因為圖5和圖6中的模型與網絡訓練集的模型無相似之處，主要驗證神經網絡的泛化能力，圖4的模型與訓練集中的模型有相似之處，因此，兩者會出現明顯的差異。在后續的研究中，將對BP神經網絡和HMANN進行結構優化，如參考遺傳算法（genetic algorithm，GA）優化的BP神經網絡（GA-BP）、粒子群優化算法（particle swarm optimization，PSO）優化的BP神經網絡（PSO-BP）等方法，提升BP神經網絡和HMANN的泛化應用能力。
EIT成像技術實現可視化成像時，是基于目標物體與背景區域的電導率值相差相對較大，而偽影的存在則是由于該處的電導率值有接近目標物體的趨勢，而利用Hadamard product可將偽影處的電導率值降低，使其與背景區域差異更小。通過泛化能力的對比和仿真結果表明，Hadamard product提高了重建圖像的質量。一方面，背景區域元素的電導率小于被測對象元素的電導率，采用Hadamard product運算后，背景區域元素的電導率值會更加接近于0。另一方面，如式（6）所示，被測對象元素的電導率與背景元素的電導率之間的差異變得相對容易區分，因此，Hadamard product有效地提高了本研究中重建圖像的相關性。HMANN算法建立在MANN算法的基礎上，在重建圖像過程中依賴于MANN算法，因此，HMANN算法網絡的泛化能力還需要進一步提升。HMANN算法的主要目的是有限去除重建圖像中的偽影，可為EIT成像技術在臨床監測、材料無損檢測等方面提供一種去偽影的參考方法。
4 結論
本研究利用Hadamard product 優化MANN算法得到HMANN算法，并與GVSPM算法、TSVD算法、BP神經網絡算法進行對比，通過仿真10種圓截面模型和10種胸部實驗模型評估HMANN算法的重建圖像效果，同時建立4種圓截面模型和4種胸部肺截面模型評估HMANN算法的泛化能力。仿真結果表明：當目標物體較小時，GVSPM算法和TSVD算法較難識別目標物體的實際大小和位置，BP神經網絡算法、MANN算法和HMANN算法基本能監測到目標物體的位置和大小；神經網絡訓練樣本為75 000組時，MANN算法的預測精度比BP神經網絡高，泛化能力也比BP神經網絡算法強；HMANN算法的成像效果好，既保留了MANN算法的圖像信息，又減少了圖像的偽影，提高了背景區域與目標物體的可區分程度。相對于MANN算法，HMANN算法重建的電導率分布與實際電導率分布的相關性在圓截面模型中可以提高17.30%，在肺截面模型中可以增加13.98%。當訓練樣本為45 000組時，MANN算法的預測精度比BP神經網絡高，但泛化能力比BP神經網絡算法差；HMANN算法的重建圖像相關系數在部分預測模型中有所下降，但重建圖像的偽影比MANN算法少，檢測目標與背景的可識別度更高。但是，目前肺EIT成像沒有公開的數據源作為支撐，沒辦法使用真實肺EIT成像的數據集驗證神經網絡的性能，輸出最真實的肺EIT成像，在后續的研究中，將結合CT等其他診斷方式重建真實肺輪廓的EIT圖像。
重要聲明
利益沖突聲明：本研究全體作者均聲明不存在利益沖突。
作者貢獻聲明：李建平、溫建明提出了本研究思路和結構；宋振忠、高增鋒完成了仿真測試；萬嫩、馬繼杰完成仿真數據的分析；張昱、胡意立對數據進行了回顧和分析；宋振忠根據數據完成論文的撰寫。
本文附件見本刊網站的電子版本（biomedeng.cn）。
