本文研究髂動脈分叉幾何特性對脈搏波傳播特性的影響,應用多物理場分析軟件,分別建立了基于髂動脈的直管分叉和曲管分叉流-固雙向耦合有限元分析模型,對比分析了血管分叉角度對脈搏波傳播特性的影響。研究發現,分叉幾何特性對髂動脈脈搏波傳播有明顯影響,在一個心動周期內,這兩種模型預測的壓力脈搏波和速度脈搏波幅值在血管分叉前一致度較高;分叉后,曲管分叉模型預測的脈搏波幅值較低、壓降小,更符合人體實際情況。另外,分叉點處伴隨著血管壁的應力集中現象,速度脈搏波幅值出現瞬時增加,這與分叉部位容易出現動脈狹窄和硬化等現象相一致。本文的初步研究結果將為脈搏波形用于動脈疾病的診斷提供一定的參考。
引用本文: 孫雪航, 李本森, 盧意成, 繆馥星. 髂動脈的流-固耦合模型及脈搏波傳播特性分析. 生物醫學工程學雜志, 2024, 41(2): 351-359. doi: 10.7507/1001-5515.202306004 復制
版權信息: ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有,未經授權不得轉載、改編
0 引言
在心臟周期性收縮和舒張過程中,血液壓力、血流速度和血流量的脈動以及血管壁的變形在血管系統中的傳播統稱為脈搏波[1]。脈搏波蘊含著豐富的人體生理和病理信息[2],臨床上應用于評估高血壓、冠心病等患者的心血管狀況[3-6]。人體動脈血管的幾何結構多為帶有弧形的分叉型,比如髂動脈具有明顯的分叉特征,在分叉處極易血流受阻,發生病變,導致動脈粥樣硬化、血栓形成等[7-9]。髂動脈位于人體腹腔,發生病變時不易被發現,嚴重時會引起動脈破裂[10],導致大量出血,短時間內即可危及生命。因此,研究髂動脈的血流動力學及其脈搏波傳播特性,對其病變的早期預防、診斷和治療具有重要意義。
關于分叉血管血流動力學和脈搏波的研究,已有一些研究成果。譬如,Perktold等[11-12]對頸動脈血流動力學進行了數值模擬,發現頸動脈的分叉角度對其內部血液流場有很大影響,以及分叉角減小是頸動脈發生病變的原因之一。王青等[13]對出口流量分配比為6:4、7:3、8:2的分叉血管血液流場進行了三維數值模擬,重點分析了流量分配比和分叉幾何特征對血管局部血液動力學的影響。Kotmakova等[14]對髂動脈的血流也進行了數值分析,發現髂動脈的彈性對其血液流速以及血管內壁面應力有重要影響,動脈彈性下降會導致血管壁面應力增大。于風旭等[15]根據實驗用頸動脈分叉模型,建立了頸動脈分叉有限元分析模型,發現分叉動脈更易發生動脈粥樣硬化疾病。Abbasi等[16]通過影像技術研究了肺動脈分叉角對肺動脈栓塞疾病的影響,發現了肺動脈分叉角減小是診斷肺動脈栓塞的一個影像標準。彭紅梅等[17]分析了血流動力學特性的突變對雙分叉動脈血管病變發展的影響,發現雙分叉動脈主支管病變極易導致分支管分叉處粥樣斑塊病變。另外,張麗娜等[18]將脈搏波信號用于動脈硬化患者的無創檢測,提出了通過分析時域脈搏波信號輔助心血管疾病診斷的方法。然而,關于髂動脈分叉處分叉角對其血流動力學的影響和脈搏波傳播特性的分析,尚未見報道。
因此,本文計及血液粘性和可壓縮性,分別建立髂動脈的直管分叉和彎曲管分叉雙向流-固耦合分析模型,通過對比研究血管分叉對血液流場和脈搏波傳播速度的影響,探究髂動脈分叉角度與脈搏波傳播特性及血管壁損傷的關系。本文初步研究結果或可為髂動脈無創檢測的新方法提供理論指導,對髂動脈分叉前后病變的早期預防、診斷和治療具有重要意義。
1 髂動脈分叉血管的雙向流-固耦合分析模型
1.1 生物力學幾何模型構建
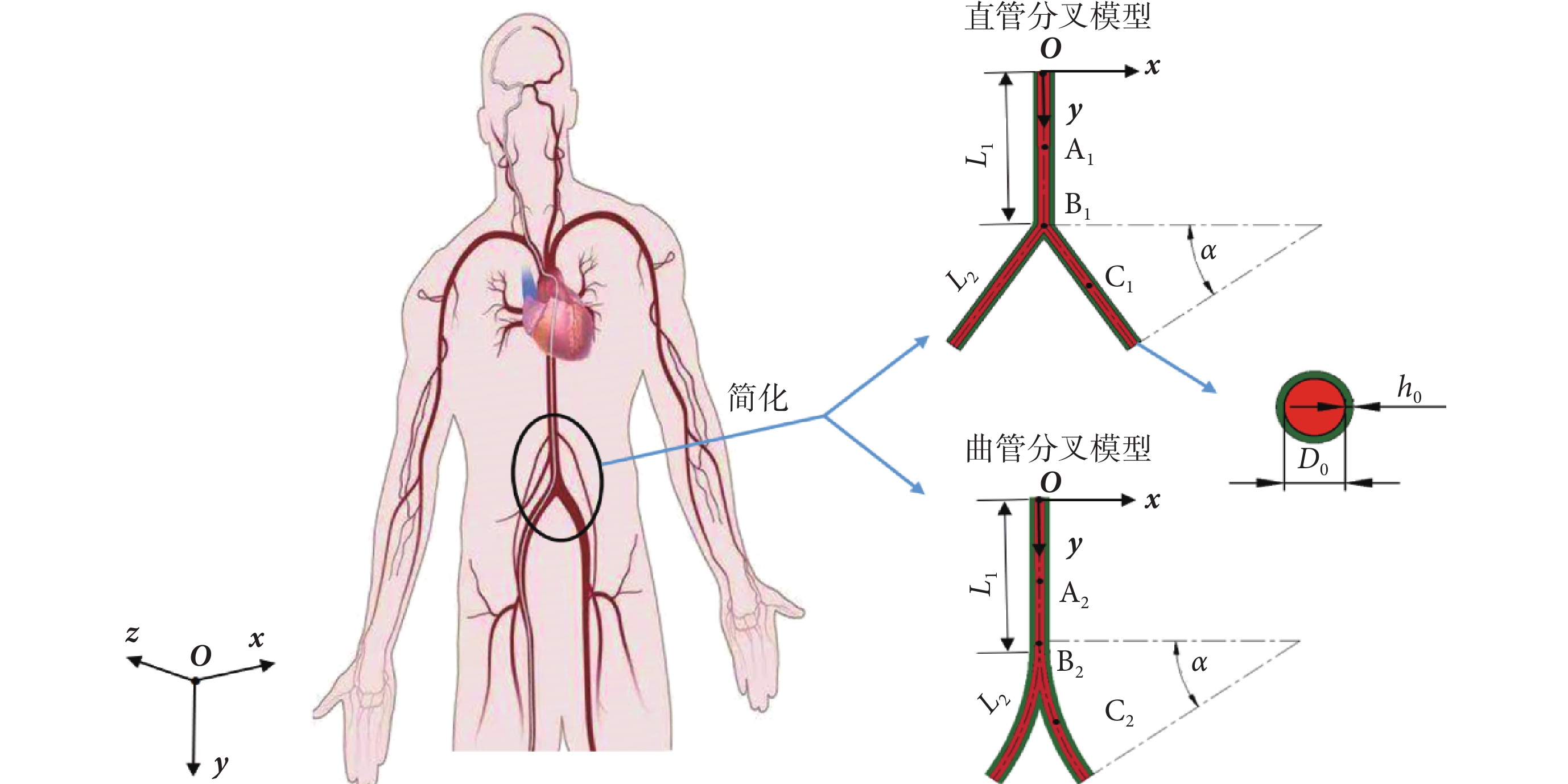
對于人體髂動脈分叉段,在動脈無特殊病變的情況下,本文視血管壁為薄壁管,只考慮血管壁外膜參數,根據如文獻[19-20]所述的人體髂動脈幾何尺寸,選取髂動脈分叉血管幾何模型參數,如表1所示,其中,D0、h0、L1、L2 分別為血管內徑、壁厚、分叉前軸線長度和分叉后軸線長度,并稱D0/h0為徑厚比,擬構建髂動脈分叉幾何模型。
為研究分叉角度對脈搏波傳播的影響,暫不考慮髂動脈的特殊結構以及其分支,根據文獻[21]對髂動脈的解剖分析,髂動脈單側分叉角范圍為20°~30°,由于分叉后動脈的彎曲對其內部的血流場有著重要影響,因此分別建立單側分叉角α為:20°、25°、30°的直管分叉模型和曲管分叉模型,并進行對比,如圖1所示。以直管中心為原點,模型關于yoz平面對稱,紅色、綠色區域分別表示血液和動脈壁。本研究選取直管分叉模型中的A1、B1、C1,以及曲管分叉模型中的A2、B2、C2作為監測點,分別位于髂動脈分叉前中點、分叉點、分叉管的中點。
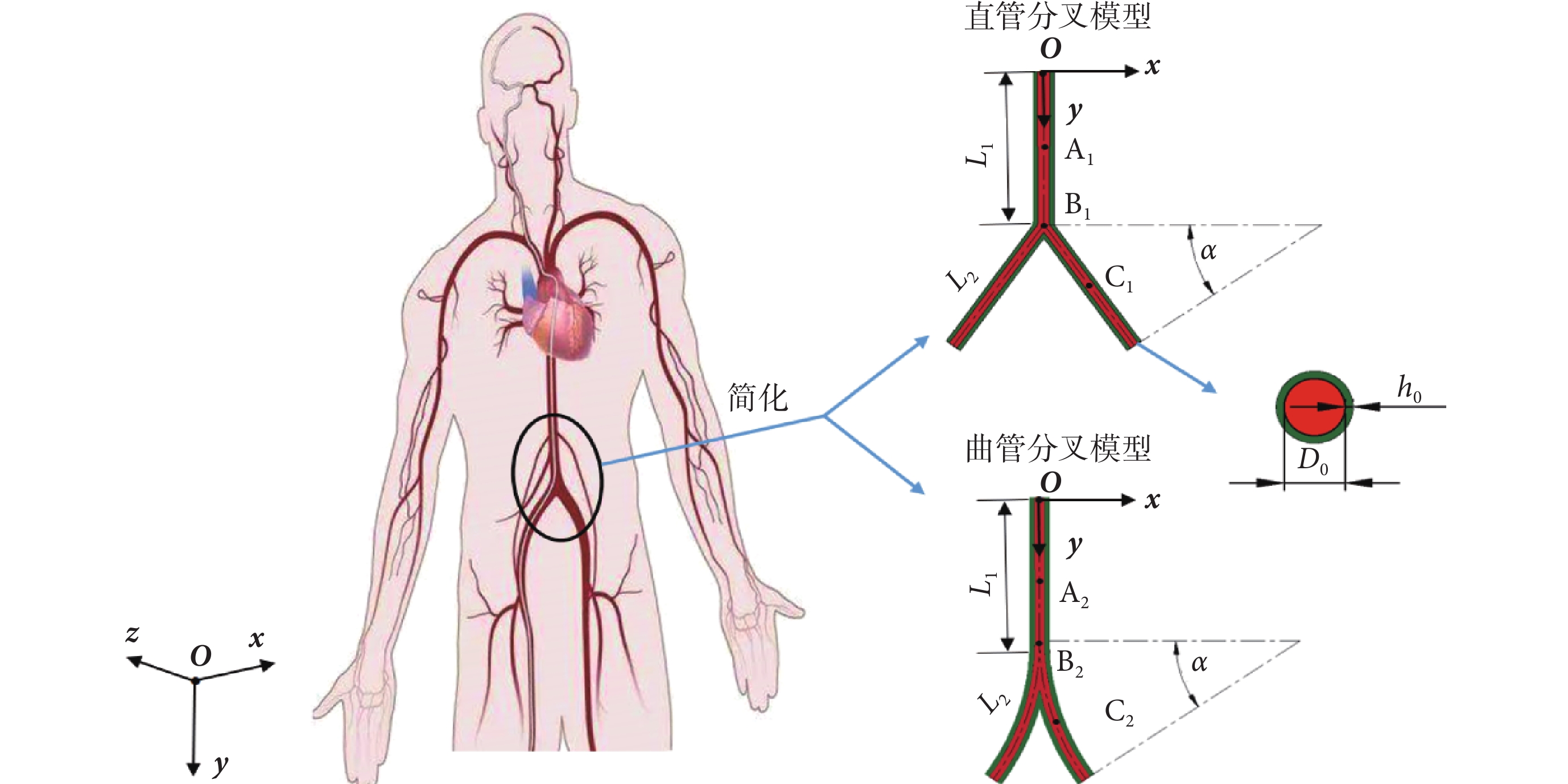 圖1
分叉血管幾何模型示意圖
Figure1.
The diagram of bifurcated vessels geometric model
圖1
分叉血管幾何模型示意圖
Figure1.
The diagram of bifurcated vessels geometric model
1.2 血流控制方程及動脈材料屬性描述
本文設血液為絕熱、可壓縮的粘性牛頓流體,根據文獻[22-24],取血液的體積模量Kb=2.5 GPa,動力粘度為0.004 Pa?s[25],血液的體積壓縮模量由血液密度ρb和壓力p的函數關系描述,下標b指血液(blood),如式(1)所示:
 |
根據文獻[26],血管壁用五參數超彈性本構關系,材料參數如表2所示,其中C10、C01、C20、C02、C11分別為五參數超彈性本構關系中的各個參數,用于描述血管壁材料的剛度與非線性特性。
根據流體動力學理論,人體血液流動遵循質量守恒定律、動量守恒定律以及能量守恒定律。血液體積力矢量為Fb、流動速度矢量為vb、流體壓力為p。則,血液流動的質量、動量、能量等守恒方程如式(2)~(4)所示:
 |
 |
 |
式中,t為血液流動時間,I為二階單位張量,τb為血液粘性應力張量,E為系統能量,Q為單位質量由熱輻射或內熱源傳給血液系統的熱量,q為熱通量。τb的表達式如式(5)所示:
 |
式中,μ表示血液動力粘性系數。本文不考慮重力作用以及血液流動過程中的熱量傳遞,且溫度保持恒定,即Fb = 0,Q = 0,q = 0。因此,式(4)可進一步簡化,如式(6)所示:
 |
在內壓p作用下,髂動脈血管壁薄壁模型的環向應力σθ和環向應變εθ分別如式(7)、式(8)所示:
 |
 |
式中,D為血管的外徑,D0為血管內徑,h0為壁厚。隨著心動,髂動脈血管壁面壓力發生變化,血管壁也發生變形;反之亦然。為此,血液與血管壁相接觸面即為流-固耦合界面,在此雙向流-固耦合有限元分析模型中,通過血液與血管壁的相互作用進行耦合分析。根據連續介質力學理論,在流-固耦合界面處,血液和血管壁應滿足位移連續和應力連續邊界條件,如式(9)所示:
 |
式中,ub、uv分別表示血液和血管壁的位移矢量,σb、σv分別為血液和血管壁的應力矩陣,下標v表示血管壁(vessel)。
1.3 實測脈搏波波形加載和邊界條件
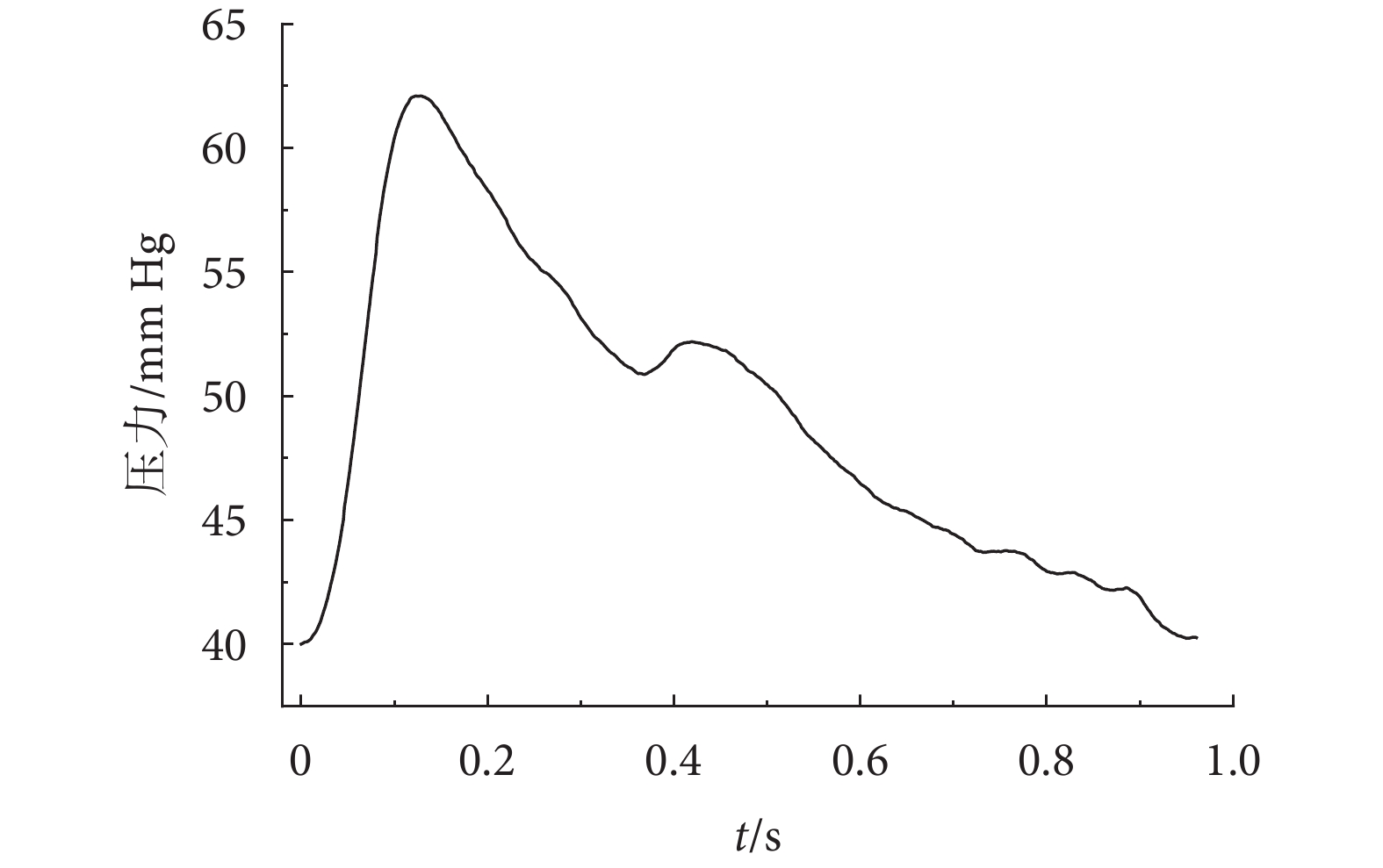
本研究在數值模擬中所加載的脈搏波波形數據采集于寧波市中醫院,所采用的設備為脈診儀(DS01-C,道生,中國)。招募的志愿者年齡在20~60周歲,受試者已簽署知情同意書,所使用的脈搏波波形數據通過了寧波市中醫院醫學倫理委員會的批準采集并授權使用(編碼:AF/SQ-01/03.1)。隨機選取采集到的一位健康志愿者單周期脈搏波波形如圖2所示,用于流-固雙向耦合分析模型的加載,即入口為壓力邊界,出口也為壓力邊界,其值為40 mm Hg,計算時間步長為10?4 s。在雙向流-固耦合分析模型中,本文設血液與血管壁內表面之間是無滑移層流流動,且血管壁的兩端無軸向位移,外表面為自由壁面。血液和血管壁均采用四面體單元,經過網格無關性驗證,選四面體單元為667 798個,網格節點為127 109個,誤差為不超過2%。
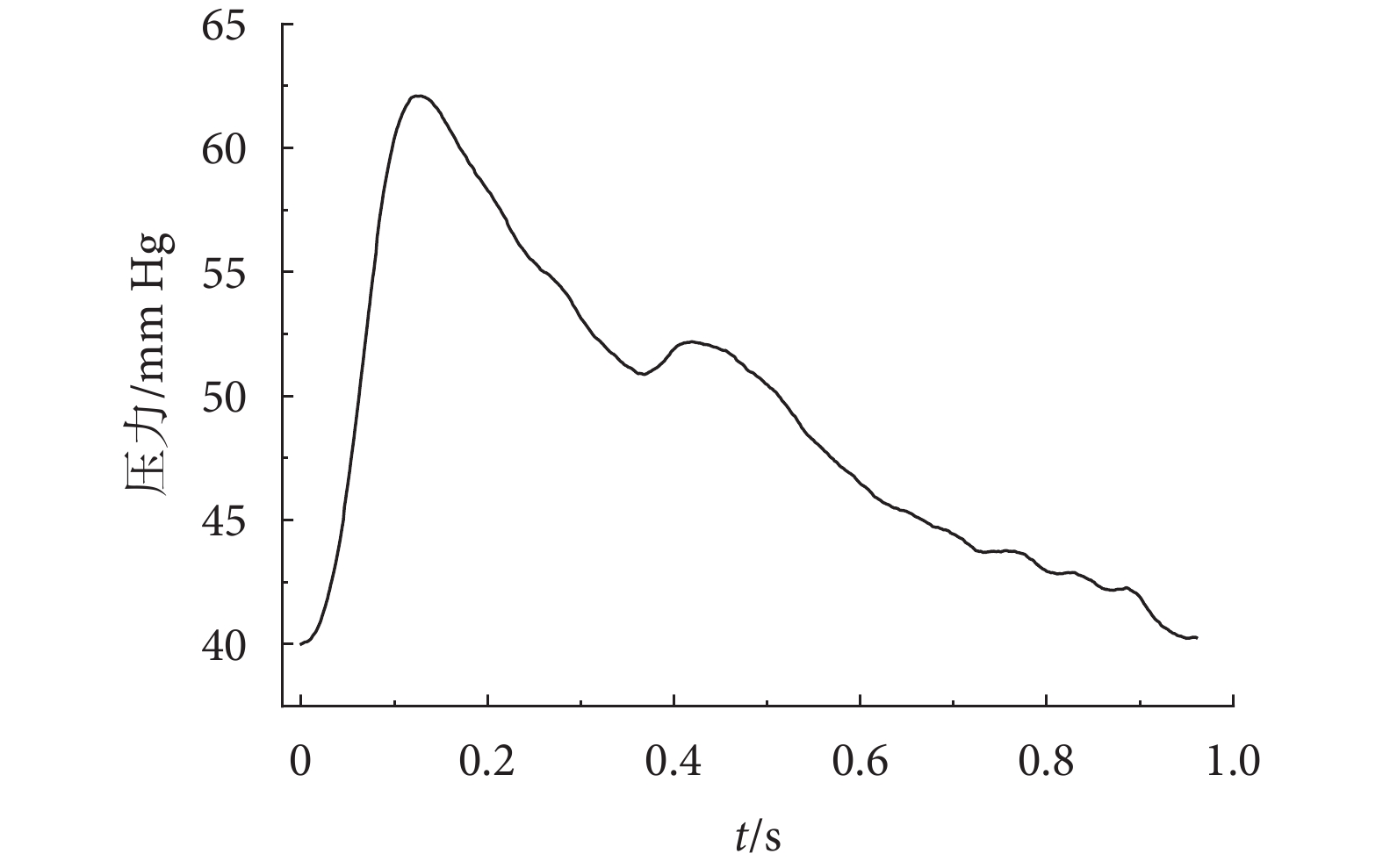 圖2
健康人體的壓力脈搏波波形
Figure2.
The pressure pulse wave of a healthy human
圖2
健康人體的壓力脈搏波波形
Figure2.
The pressure pulse wave of a healthy human
在相同情況下,本文定義血液中兩個相鄰監測點的變化幅度?d,如式(10)所示:
 |
式中,Pk(k = B1、B2、C1、C2)為監測點k的第一個波峰值,Pj(j = A1、A2、B1、B2)為監測點j的第一個波峰值,Pj0表示監測點j處,t = 0 s時的壓力值。
1.4 雙向流-固耦合模型驗證
為驗證本文雙向流-固耦合有限元模型,參照文獻[27]中分叉血管單向耦合的有限元模型,建立幾何模型,幾何參數包括:分叉前直管的直徑、長度分別為D0 = 6 mm和L1 = 10 mm,分叉管直徑和長度分別為D1 = 4.8 mm和L2 = 7 mm,壁厚為h0 = 0.4 mm。材料參數、邊界條件與節1.2和1.3中一致。在入口邊界處加載0.5 m/s的恒定速度波,網格類型為四面體,經網格無關性驗證,可選總共網格數為19 563個,誤差不超過2%。應用本文雙向流-固耦合模型進行數值模擬計算,可得到血液流速、壓力云圖如圖3所示。
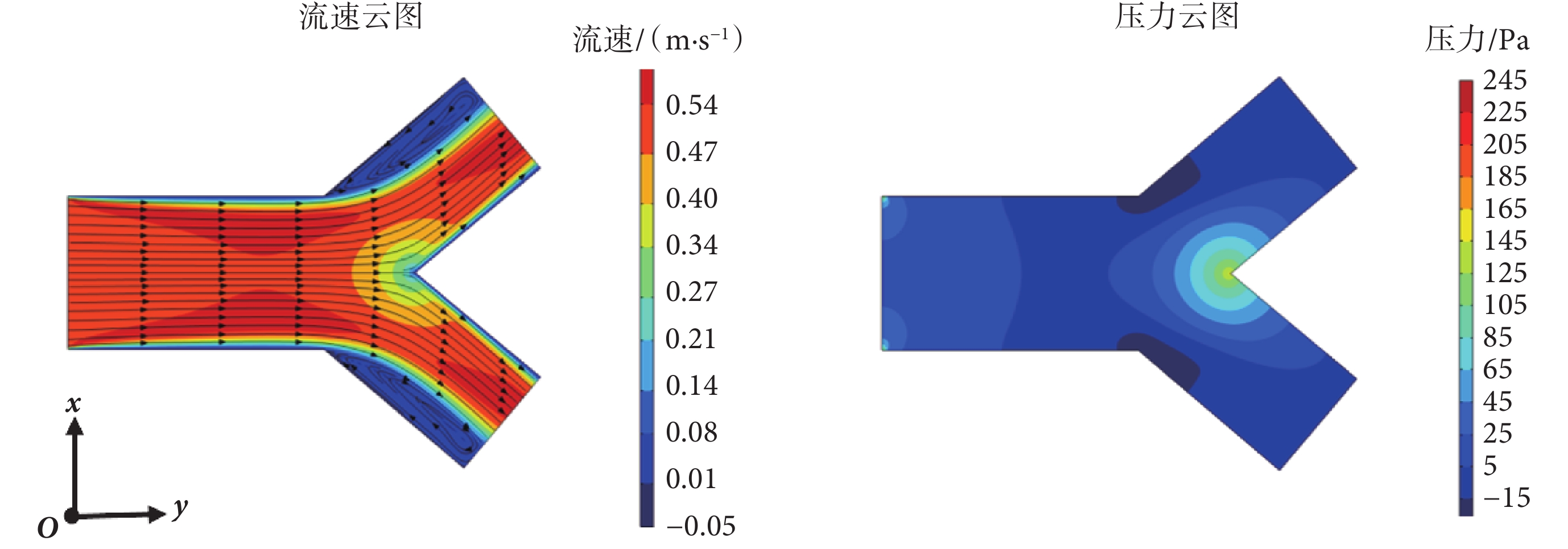 圖3
血液流速、壓力云圖
Figure3.
Cloud images of blood flow velocity and blood pressure
圖3
血液流速、壓力云圖
Figure3.
Cloud images of blood flow velocity and blood pressure
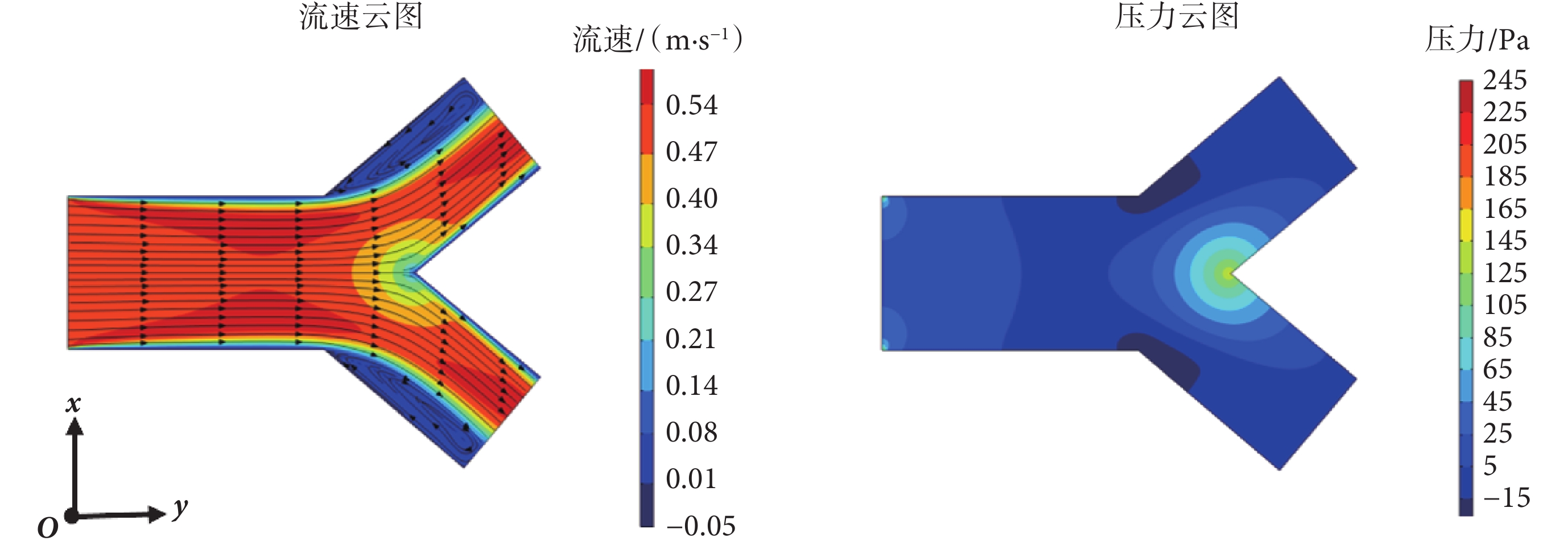
對比發現,本文雙向流-固耦合模型計算的分叉血管中的血液流速、流線、壓力的分布均與文獻[27]中一致,其中血液最大流速均為0.6 m/s,且在血管分叉位置處,血液流速會出現突變。這種突變導致血流在分叉處形成一個低速度區域,同時分叉處會引發局部的渦流。在分叉處血液壓力最大,這也說明了血管壁在分叉處出現應力集中現象。由此可見,本文血液-血管系統的雙向流-固耦合有限元分析模型可用于分叉血管中的血流動力學分析,也可用來研究分叉血管中的脈搏波傳播特性。
2 髂動脈分叉幾何特征對脈搏波傳播的影響
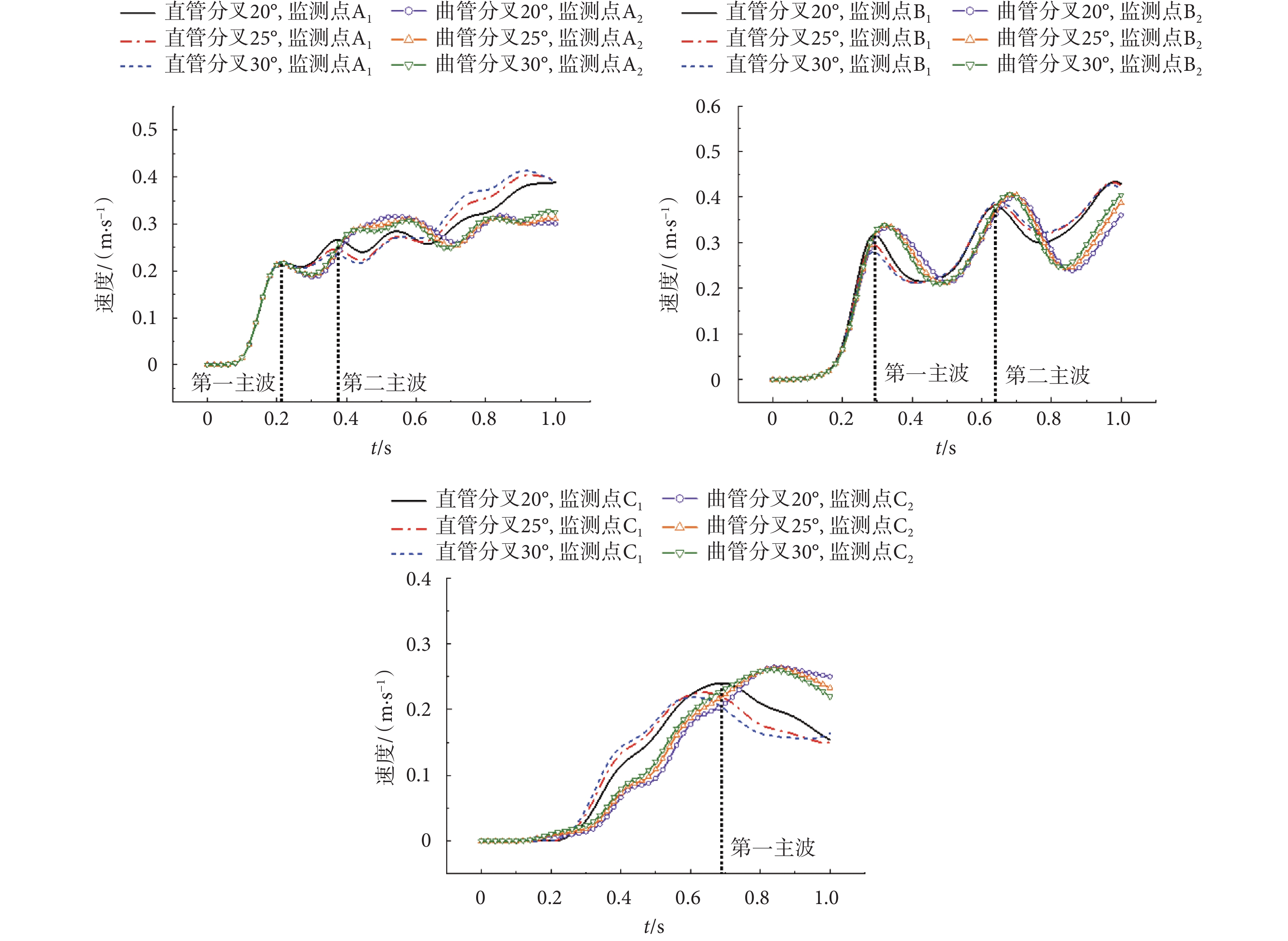
根據前文構建的髂動脈雙向流-固耦合有限元分析模型,本節探討分叉角對髂動脈中脈搏波傳播的影響,以壓力脈搏波與軸向速度脈搏波分析為例。此三種分叉角度下,髂動脈壓力脈搏波與軸向速度脈搏波傳播情況分別如圖4、圖5所示。
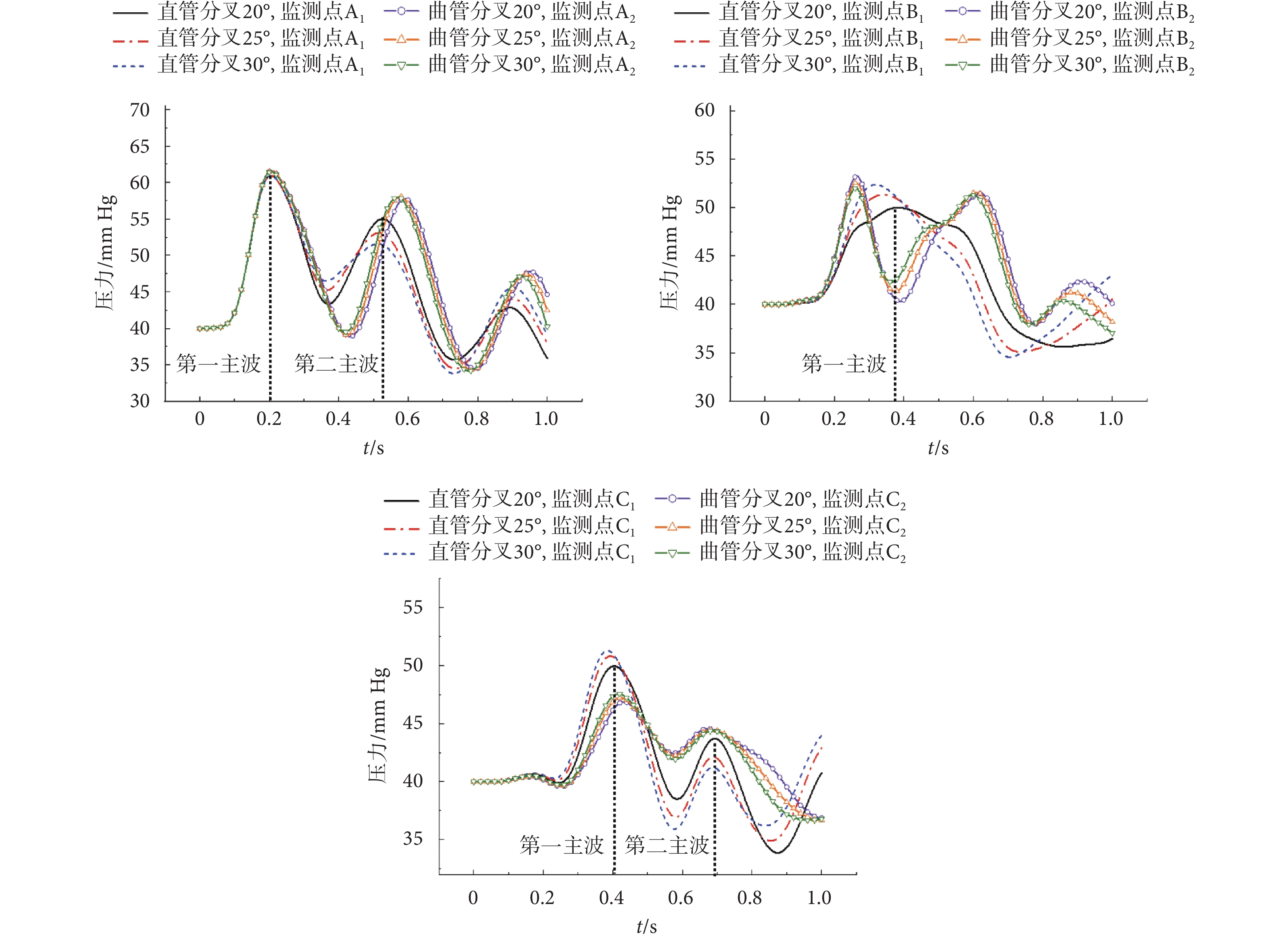 圖4
壓力脈搏波曲線
Figure4.
Pressure pulse wave curves
圖4
壓力脈搏波曲線
Figure4.
Pressure pulse wave curves
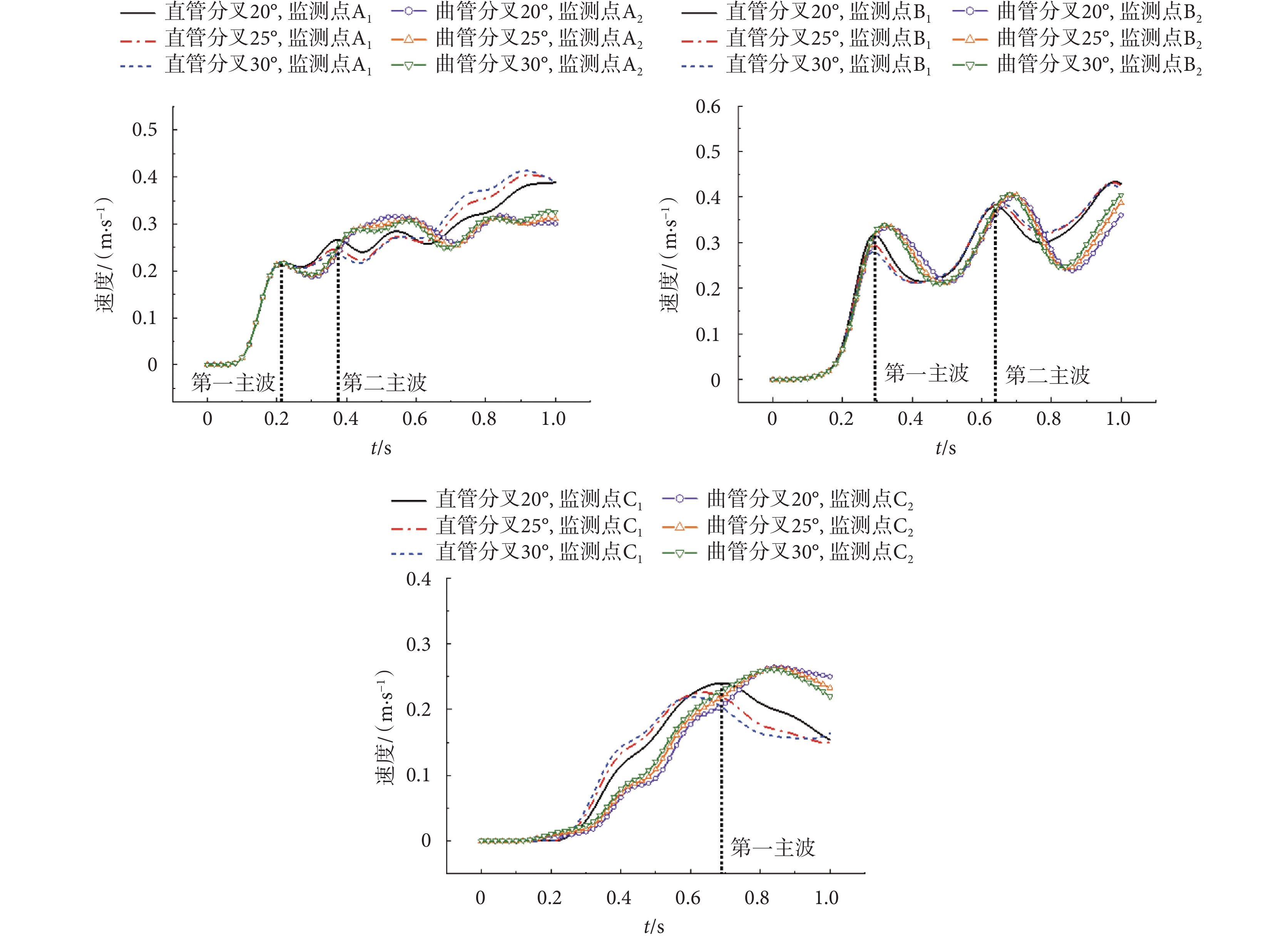 圖5
速度脈搏波曲線
Figure5.
Velocity pulse wave curves
圖5
速度脈搏波曲線
Figure5.
Velocity pulse wave curves
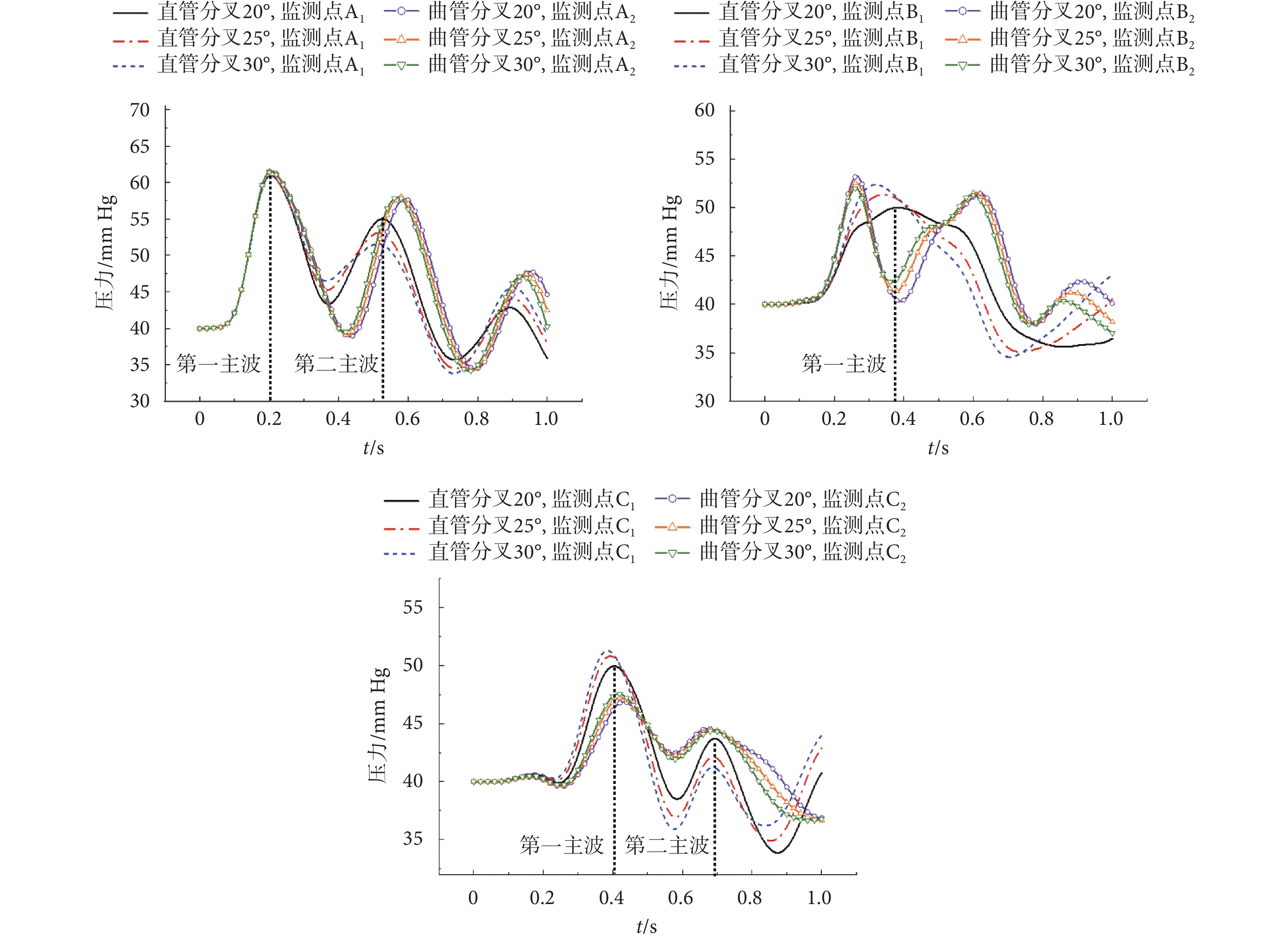
由圖4、圖5可以看出,直管分叉模型和曲管分叉模型所預測的壓力脈搏波和軸向速度脈搏波傳播特點有明顯差異,尤其是在分叉后的分支階段。對于分叉角為20°的模型,直管分叉和曲管分叉模型所預測的壓力脈搏波形,在分叉前直管段上,分別出現了3個波峰。大約過0.08 s后,相比分叉前的第一主波幅值,在分叉點處,監測點B1、B2的壓力脈搏波的第一主波幅值分別降低約52.31%、38.83%。而在分叉段上,監測點C1、C2壓力脈搏波的第一主波幅值分別降低約0.32%、47.89%;且曲管分叉模型下,分叉點處的主波波寬要比直管分叉模型下的小。對于直管分叉模型,在分叉前的直管段,分叉角度越大,第一主波壓力峰值衰減越小;在分叉后,分叉角度越大,峰值衰減越大;如:在分叉前,分叉20°和30°的情形下,分別衰減52.31%、41.05%;在分叉后則分別衰減了0.31%、8.71%。而曲管分叉模型預測的結果反之。對曲管分叉模型,在分叉前的直管段,分叉角度越大,壓力峰值衰減越大;對于分叉后的分支管,分叉角度越大,峰值衰減越小;如:在分叉前,分叉20°和30°的情形下,分別衰減38.83%、44.32%;在分叉后則分別衰減了47.89%、36.40%。
在分叉前,隨著分叉角度的增加,軸向速度脈搏波幅值的變化不大,明顯的變化是分叉前的軸向速度脈搏波形與分叉后的有較大不同,且分叉處速度脈搏波形振蕩明顯。分叉后軸向速度脈搏波的第一主波延遲約0.2 s,波形振蕩少、平緩。對于第一主波峰,在分叉處,監測點B1、B2的峰值相對A1、A2的峰值增大;如:對分叉20°的情形,直管分叉模型與曲管分叉模型預測的結果,分別增大44.98%、54.79%。而在分叉管中,監測點C1、C2的峰值相對B1、B2的峰值降低;如:分叉角20°的情形下,直管分叉模型與曲管分叉模型預測的結果,分別降低24.31%、23.19%。
3 結果與分析
3.1 髂動脈壓力脈搏波傳播特性分析
根據壓力脈搏波計算分析結果,監測點A1~B1、A2~B2、B1~C1、B2~C2的波速如表3所示。
由表3可知,直管分叉模型下,預測的血液在直管段傳播時壓力脈搏波波速要小于在分叉部分的壓力脈搏波波速。且對不同的分叉角度,在分叉前,隨著分叉角度增大,壓力脈搏波波速隨之增大,分叉30°情形的壓力脈搏波波速較分叉20°情形的大約56.33%;在分叉后,隨著分叉角增大,壓力脈搏波波速隨之減小。分叉30°情形的壓力脈搏波波速較分叉20°情形的小約68.19%。曲管分叉模型下,預測的血液在直管段傳播時壓力脈搏波波速大于分叉后支管段上的壓力脈搏波波速,并隨著分叉角增大,壓力脈搏波波速增大,在分叉前,分叉30°情形下的壓力脈搏波波速較分叉20°情形的大約5.45%;在分叉后,分叉30°情形的壓力脈搏波波速較20°情形的大約7.36%。
3.2 髂動脈軸向速度脈搏波傳播特性分析
根據速度脈搏波計算結果,可得出分叉血管中軸向速度脈搏波的傳播速度,監測點A1~B1、A2~B2、B1~C1、B2~C2的速度脈搏波速如表4所示。
由表4可知,兩種分析預測模型在分叉前的軸向速度脈搏波波速遠大于分叉后的,髂動脈分叉20°時,直管分叉模型與曲管分叉模型分別預測的軸向速度脈搏波波速,分叉前比分叉后要大約80.60%、77.14%。這說明血管的分叉幾何特性可明顯降低速度脈搏波的傳播速度。但不論是曲管分叉模型還是直管分叉預測模型,分叉20°情形時的軸向速度脈搏波波速最小。對于直管分叉預測模型,分叉前,分叉20°情形的比30°的小了約1.31%,而分叉后小了約18.45%;對于曲管分叉模型,在分叉前,分叉20°的情形的比30°的小了約11.76%,分叉后小了約2.04%。
3.3 髂動脈中的應力場分析
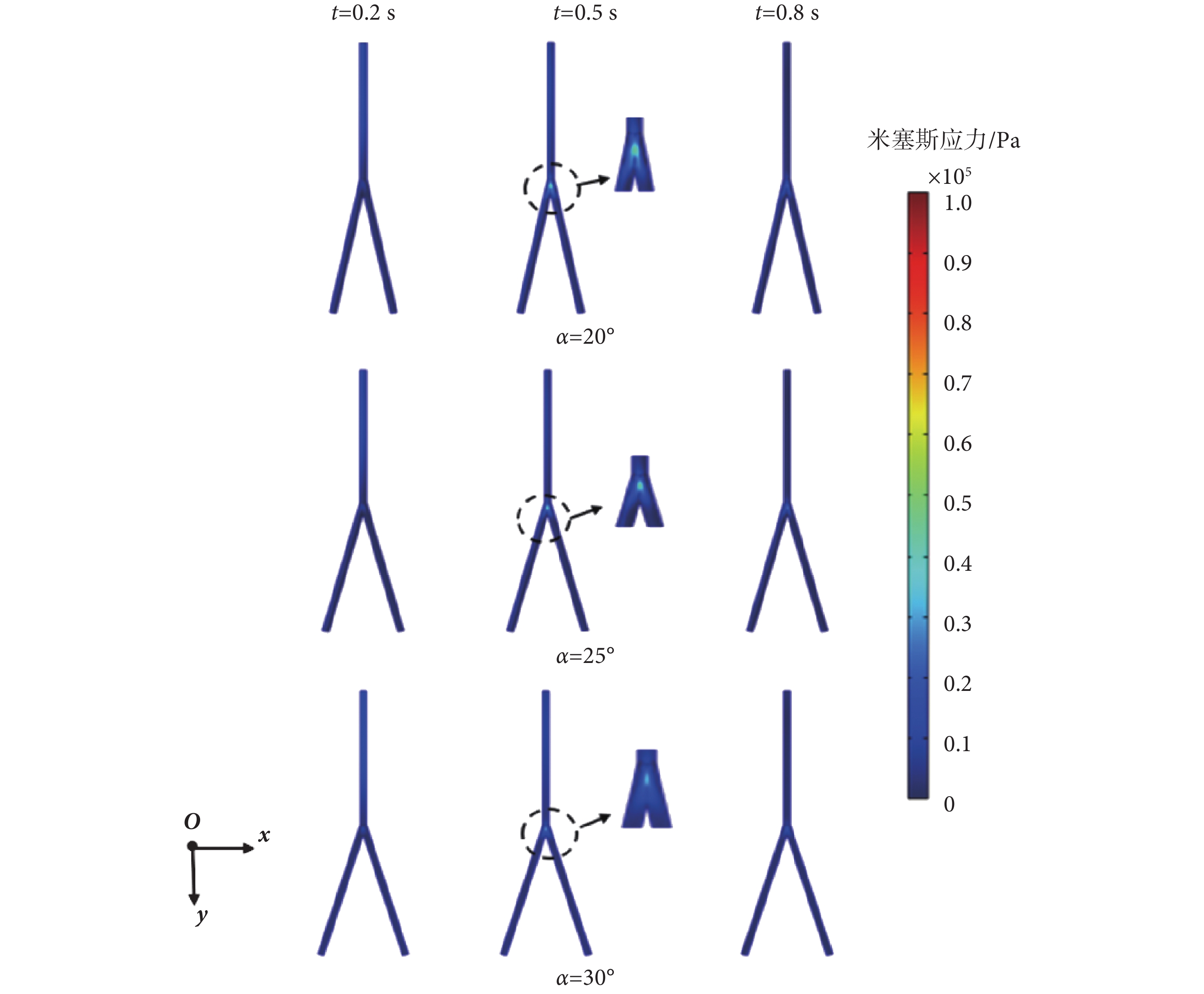
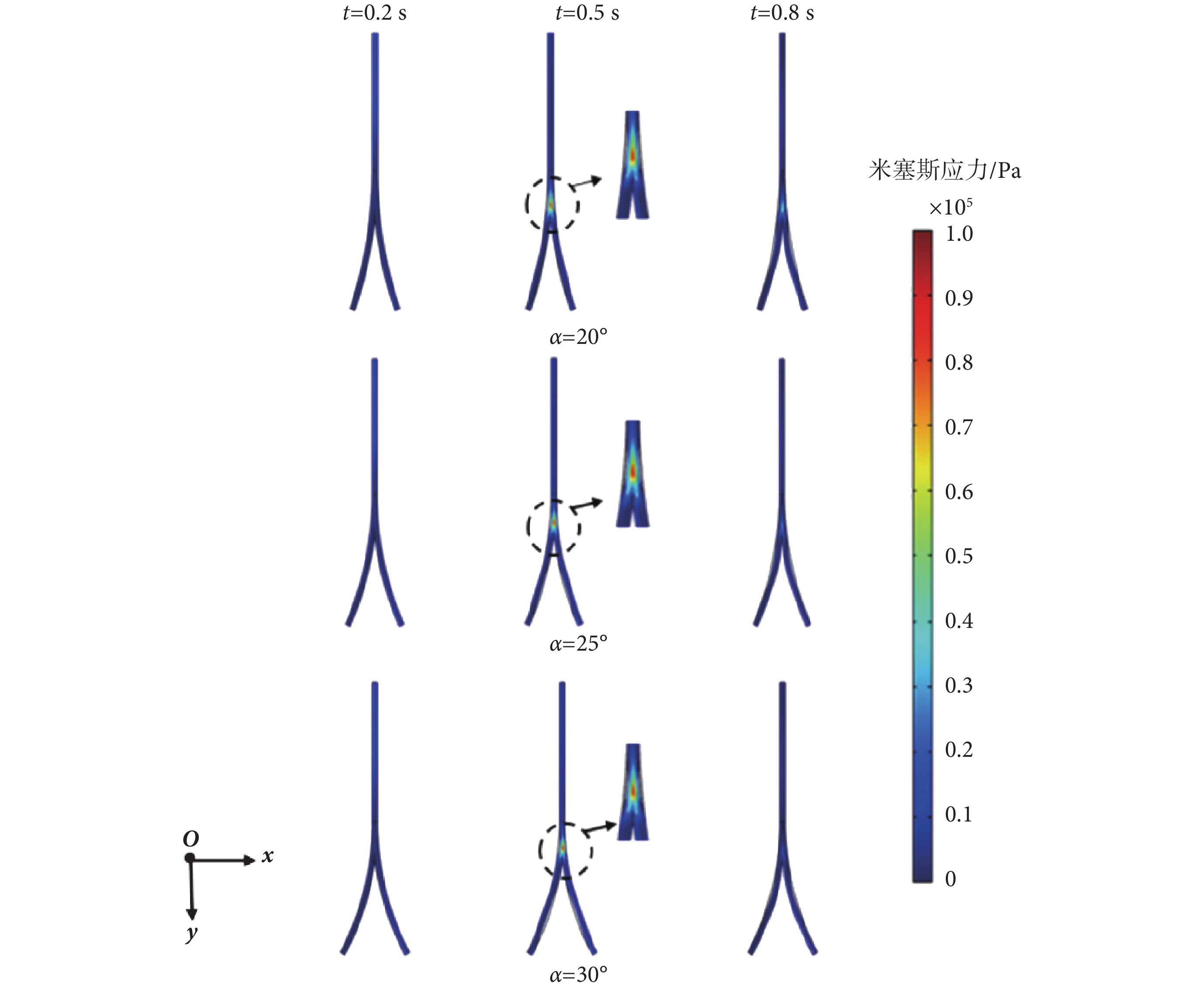
本節分析在一個心動周期內,髂動脈中的應力場分布情況,故選取分別代表一個心動周期的快速射血末期、收縮末期、舒張末期的0.2、0.5、0.8 s時刻點為例。在分叉血管分析預測模型下,血管壁上米塞斯應力云圖分別如圖6、圖7所示。由圖6、圖7可知,在0.2 s時,髂動脈中的脈搏波傳播仍在直管段部分,并沒有傳播到分叉點處和分叉管部分,此段上,并無應力集中現象,兩種模型下預測的最大的米塞斯應力值幾乎一致,數值較小。而當0.5 s時,脈搏波傳播至分叉點和分叉血管部位,此時在血管分叉處應力集中現象明顯。
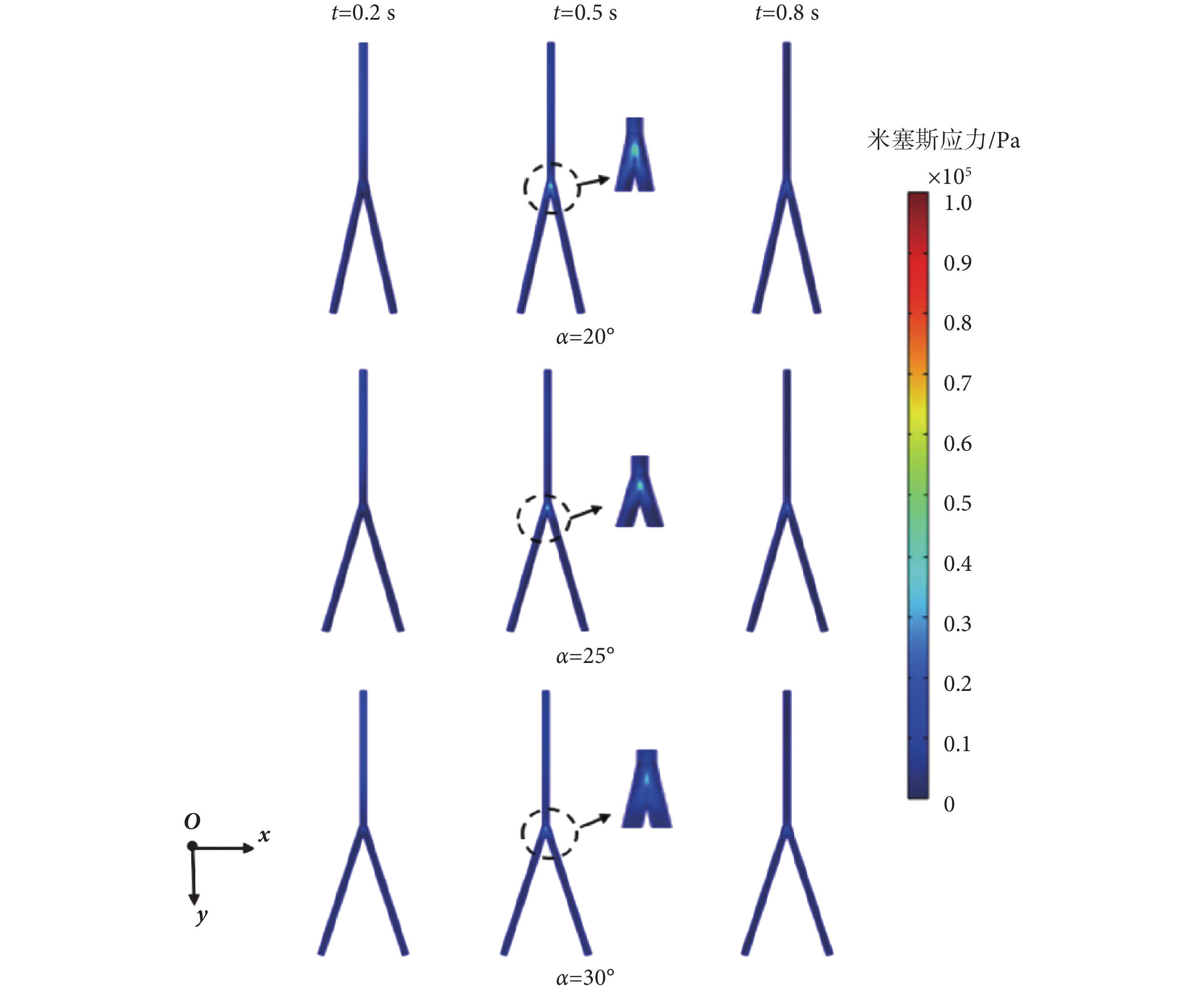 圖6
直管分叉模型下不同時刻米塞斯應力云圖
Figure6.
Von Mises stress distribution of straight bifurcated vessel model at different time
圖6
直管分叉模型下不同時刻米塞斯應力云圖
Figure6.
Von Mises stress distribution of straight bifurcated vessel model at different time
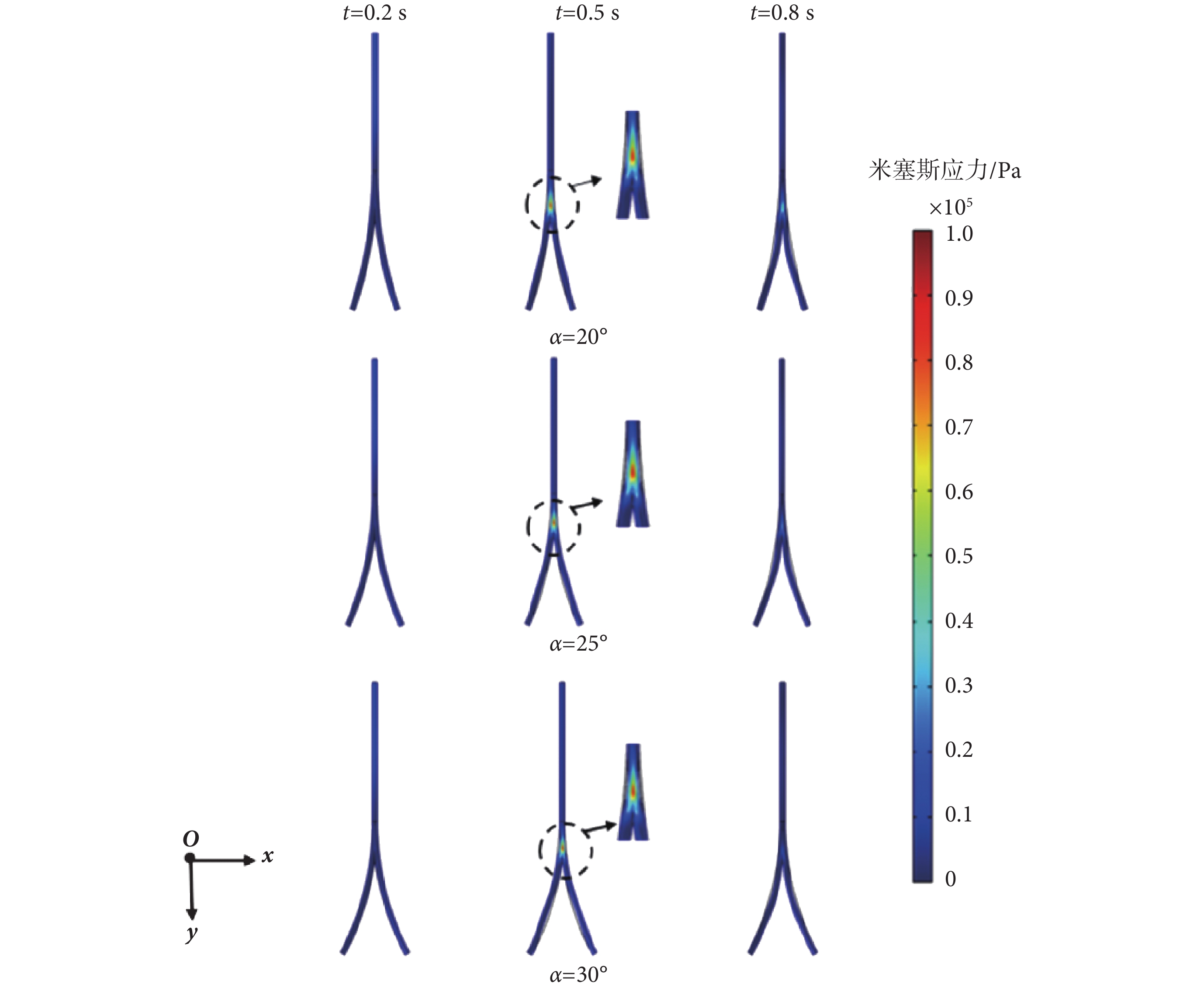 圖7
曲管分叉模型下,不同時刻的米塞斯應力云圖
Figure7.
Von Mises stress distribution of curvilinear bifurcated vessel model at different time
圖7
曲管分叉模型下,不同時刻的米塞斯應力云圖
Figure7.
Von Mises stress distribution of curvilinear bifurcated vessel model at different time
直管和曲管分叉模型在0.2、0.5、0.8 s時的最大米塞斯應力如表5所示。在髂動脈分叉處,其內部的血流形態也發生了變化,髂動脈常因不能抵抗管腔內血流壓力負荷而失衡,從而發生病變[28-29]。由表5可知,對曲管分叉與直管分叉分析預測模型而言,在一個心動周期內,均是分叉20°情形的米塞斯應力最大,分叉25°情形的次之,分叉30°情形的最小。對分叉20°情形,直管分叉模型和曲管分叉模型下分別較分叉30°情形的大約60.6%、16.13%。這表明,分叉角較小情形的髂動脈更易發生病變;具有不同分叉角度的髂動脈的最大應力部位均在髂動脈的分叉處,與其它部位相比,髂動脈在分叉處更易發生病變。
4 結 論
本文建立了血液-血管系統的流-固雙向耦合分析模型,經模擬分析發現,曲管分叉模型預測的壓力脈搏波和速度脈搏波波形要更接近于實際。在髂動脈分叉前,分叉角度越大,曲管分叉模型下的壓力脈搏波波幅衰減越大,而分叉后,波幅衰減越小。血管分叉后,軸向速度脈搏波隨之衰減。另外,髂動脈的分叉幾何特性對脈搏波傳播有明顯影響,且直管分叉模型和曲管分叉模型預測的脈搏波波形,在分叉前后有較大差別。對應一個心動周期內的心臟收縮區間,曲管分叉模型預測的壓力脈搏波和軸向速度脈搏波幅值,在分叉前后,更接近于實際情況。在分叉后的曲管段,分叉角越大,壓力脈搏波第一主波幅值越大,且隨著心臟的收縮和舒張,第二主波波幅逐漸越小,傳播速度也減小;軸向速度脈搏波幅值隨著分叉角增大,幅值減小;曲管分叉模型預測的幅值衰減幅度低。此外,分叉點處伴隨著血管壁的應力集中現象,這與髂動脈在分叉部位容易發生動脈狹窄和硬化等疾病的臨床現象相一致。
重要聲明
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
作者貢獻說明:孫雪航負責計算模型的后處理、論文寫作及修改,李本森、盧意成負責論文的選題及有限元模型的搭建,繆馥星提供論文指導以及論文的審閱修訂。
倫理聲明:本文所使用的脈搏波波形數據得到寧波市中醫院醫學倫理委員會的批準采集并授權使用(編碼:AF/SQ-01/03.1)。
0 引言
在心臟周期性收縮和舒張過程中,血液壓力、血流速度和血流量的脈動以及血管壁的變形在血管系統中的傳播統稱為脈搏波[1]。脈搏波蘊含著豐富的人體生理和病理信息[2],臨床上應用于評估高血壓、冠心病等患者的心血管狀況[3-6]。人體動脈血管的幾何結構多為帶有弧形的分叉型,比如髂動脈具有明顯的分叉特征,在分叉處極易血流受阻,發生病變,導致動脈粥樣硬化、血栓形成等[7-9]。髂動脈位于人體腹腔,發生病變時不易被發現,嚴重時會引起動脈破裂[10],導致大量出血,短時間內即可危及生命。因此,研究髂動脈的血流動力學及其脈搏波傳播特性,對其病變的早期預防、診斷和治療具有重要意義。
關于分叉血管血流動力學和脈搏波的研究,已有一些研究成果。譬如,Perktold等[11-12]對頸動脈血流動力學進行了數值模擬,發現頸動脈的分叉角度對其內部血液流場有很大影響,以及分叉角減小是頸動脈發生病變的原因之一。王青等[13]對出口流量分配比為6:4、7:3、8:2的分叉血管血液流場進行了三維數值模擬,重點分析了流量分配比和分叉幾何特征對血管局部血液動力學的影響。Kotmakova等[14]對髂動脈的血流也進行了數值分析,發現髂動脈的彈性對其血液流速以及血管內壁面應力有重要影響,動脈彈性下降會導致血管壁面應力增大。于風旭等[15]根據實驗用頸動脈分叉模型,建立了頸動脈分叉有限元分析模型,發現分叉動脈更易發生動脈粥樣硬化疾病。Abbasi等[16]通過影像技術研究了肺動脈分叉角對肺動脈栓塞疾病的影響,發現了肺動脈分叉角減小是診斷肺動脈栓塞的一個影像標準。彭紅梅等[17]分析了血流動力學特性的突變對雙分叉動脈血管病變發展的影響,發現雙分叉動脈主支管病變極易導致分支管分叉處粥樣斑塊病變。另外,張麗娜等[18]將脈搏波信號用于動脈硬化患者的無創檢測,提出了通過分析時域脈搏波信號輔助心血管疾病診斷的方法。然而,關于髂動脈分叉處分叉角對其血流動力學的影響和脈搏波傳播特性的分析,尚未見報道。
因此,本文計及血液粘性和可壓縮性,分別建立髂動脈的直管分叉和彎曲管分叉雙向流-固耦合分析模型,通過對比研究血管分叉對血液流場和脈搏波傳播速度的影響,探究髂動脈分叉角度與脈搏波傳播特性及血管壁損傷的關系。本文初步研究結果或可為髂動脈無創檢測的新方法提供理論指導,對髂動脈分叉前后病變的早期預防、診斷和治療具有重要意義。
1 髂動脈分叉血管的雙向流-固耦合分析模型
1.1 生物力學幾何模型構建
對于人體髂動脈分叉段,在動脈無特殊病變的情況下,本文視血管壁為薄壁管,只考慮血管壁外膜參數,根據如文獻[19-20]所述的人體髂動脈幾何尺寸,選取髂動脈分叉血管幾何模型參數,如表1所示,其中,D0、h0、L1、L2 分別為血管內徑、壁厚、分叉前軸線長度和分叉后軸線長度,并稱D0/h0為徑厚比,擬構建髂動脈分叉幾何模型。
為研究分叉角度對脈搏波傳播的影響,暫不考慮髂動脈的特殊結構以及其分支,根據文獻[21]對髂動脈的解剖分析,髂動脈單側分叉角范圍為20°~30°,由于分叉后動脈的彎曲對其內部的血流場有著重要影響,因此分別建立單側分叉角α為:20°、25°、30°的直管分叉模型和曲管分叉模型,并進行對比,如圖1所示。以直管中心為原點,模型關于yoz平面對稱,紅色、綠色區域分別表示血液和動脈壁。本研究選取直管分叉模型中的A1、B1、C1,以及曲管分叉模型中的A2、B2、C2作為監測點,分別位于髂動脈分叉前中點、分叉點、分叉管的中點。
 圖1
分叉血管幾何模型示意圖
Figure1.
The diagram of bifurcated vessels geometric model
圖1
分叉血管幾何模型示意圖
Figure1.
The diagram of bifurcated vessels geometric model
1.2 血流控制方程及動脈材料屬性描述
本文設血液為絕熱、可壓縮的粘性牛頓流體,根據文獻[22-24],取血液的體積模量Kb=2.5 GPa,動力粘度為0.004 Pa?s[25],血液的體積壓縮模量由血液密度ρb和壓力p的函數關系描述,下標b指血液(blood),如式(1)所示:
 |
根據文獻[26],血管壁用五參數超彈性本構關系,材料參數如表2所示,其中C10、C01、C20、C02、C11分別為五參數超彈性本構關系中的各個參數,用于描述血管壁材料的剛度與非線性特性。
根據流體動力學理論,人體血液流動遵循質量守恒定律、動量守恒定律以及能量守恒定律。血液體積力矢量為Fb、流動速度矢量為vb、流體壓力為p。則,血液流動的質量、動量、能量等守恒方程如式(2)~(4)所示:
 |
 |
 |
式中,t為血液流動時間,I為二階單位張量,τb為血液粘性應力張量,E為系統能量,Q為單位質量由熱輻射或內熱源傳給血液系統的熱量,q為熱通量。τb的表達式如式(5)所示:
 |
式中,μ表示血液動力粘性系數。本文不考慮重力作用以及血液流動過程中的熱量傳遞,且溫度保持恒定,即Fb = 0,Q = 0,q = 0。因此,式(4)可進一步簡化,如式(6)所示:
 |
在內壓p作用下,髂動脈血管壁薄壁模型的環向應力σθ和環向應變εθ分別如式(7)、式(8)所示:
 |
 |
式中,D為血管的外徑,D0為血管內徑,h0為壁厚。隨著心動,髂動脈血管壁面壓力發生變化,血管壁也發生變形;反之亦然。為此,血液與血管壁相接觸面即為流-固耦合界面,在此雙向流-固耦合有限元分析模型中,通過血液與血管壁的相互作用進行耦合分析。根據連續介質力學理論,在流-固耦合界面處,血液和血管壁應滿足位移連續和應力連續邊界條件,如式(9)所示:
 |
式中,ub、uv分別表示血液和血管壁的位移矢量,σb、σv分別為血液和血管壁的應力矩陣,下標v表示血管壁(vessel)。
1.3 實測脈搏波波形加載和邊界條件
本研究在數值模擬中所加載的脈搏波波形數據采集于寧波市中醫院,所采用的設備為脈診儀(DS01-C,道生,中國)。招募的志愿者年齡在20~60周歲,受試者已簽署知情同意書,所使用的脈搏波波形數據通過了寧波市中醫院醫學倫理委員會的批準采集并授權使用(編碼:AF/SQ-01/03.1)。隨機選取采集到的一位健康志愿者單周期脈搏波波形如圖2所示,用于流-固雙向耦合分析模型的加載,即入口為壓力邊界,出口也為壓力邊界,其值為40 mm Hg,計算時間步長為10?4 s。在雙向流-固耦合分析模型中,本文設血液與血管壁內表面之間是無滑移層流流動,且血管壁的兩端無軸向位移,外表面為自由壁面。血液和血管壁均采用四面體單元,經過網格無關性驗證,選四面體單元為667 798個,網格節點為127 109個,誤差為不超過2%。
 圖2
健康人體的壓力脈搏波波形
Figure2.
The pressure pulse wave of a healthy human
圖2
健康人體的壓力脈搏波波形
Figure2.
The pressure pulse wave of a healthy human
在相同情況下,本文定義血液中兩個相鄰監測點的變化幅度?d,如式(10)所示:
 |
式中,Pk(k = B1、B2、C1、C2)為監測點k的第一個波峰值,Pj(j = A1、A2、B1、B2)為監測點j的第一個波峰值,Pj0表示監測點j處,t = 0 s時的壓力值。
1.4 雙向流-固耦合模型驗證
為驗證本文雙向流-固耦合有限元模型,參照文獻[27]中分叉血管單向耦合的有限元模型,建立幾何模型,幾何參數包括:分叉前直管的直徑、長度分別為D0 = 6 mm和L1 = 10 mm,分叉管直徑和長度分別為D1 = 4.8 mm和L2 = 7 mm,壁厚為h0 = 0.4 mm。材料參數、邊界條件與節1.2和1.3中一致。在入口邊界處加載0.5 m/s的恒定速度波,網格類型為四面體,經網格無關性驗證,可選總共網格數為19 563個,誤差不超過2%。應用本文雙向流-固耦合模型進行數值模擬計算,可得到血液流速、壓力云圖如圖3所示。
 圖3
血液流速、壓力云圖
Figure3.
Cloud images of blood flow velocity and blood pressure
圖3
血液流速、壓力云圖
Figure3.
Cloud images of blood flow velocity and blood pressure
對比發現,本文雙向流-固耦合模型計算的分叉血管中的血液流速、流線、壓力的分布均與文獻[27]中一致,其中血液最大流速均為0.6 m/s,且在血管分叉位置處,血液流速會出現突變。這種突變導致血流在分叉處形成一個低速度區域,同時分叉處會引發局部的渦流。在分叉處血液壓力最大,這也說明了血管壁在分叉處出現應力集中現象。由此可見,本文血液-血管系統的雙向流-固耦合有限元分析模型可用于分叉血管中的血流動力學分析,也可用來研究分叉血管中的脈搏波傳播特性。
2 髂動脈分叉幾何特征對脈搏波傳播的影響
根據前文構建的髂動脈雙向流-固耦合有限元分析模型,本節探討分叉角對髂動脈中脈搏波傳播的影響,以壓力脈搏波與軸向速度脈搏波分析為例。此三種分叉角度下,髂動脈壓力脈搏波與軸向速度脈搏波傳播情況分別如圖4、圖5所示。
 圖4
壓力脈搏波曲線
Figure4.
Pressure pulse wave curves
圖4
壓力脈搏波曲線
Figure4.
Pressure pulse wave curves
 圖5
速度脈搏波曲線
Figure5.
Velocity pulse wave curves
圖5
速度脈搏波曲線
Figure5.
Velocity pulse wave curves
由圖4、圖5可以看出,直管分叉模型和曲管分叉模型所預測的壓力脈搏波和軸向速度脈搏波傳播特點有明顯差異,尤其是在分叉后的分支階段。對于分叉角為20°的模型,直管分叉和曲管分叉模型所預測的壓力脈搏波形,在分叉前直管段上,分別出現了3個波峰。大約過0.08 s后,相比分叉前的第一主波幅值,在分叉點處,監測點B1、B2的壓力脈搏波的第一主波幅值分別降低約52.31%、38.83%。而在分叉段上,監測點C1、C2壓力脈搏波的第一主波幅值分別降低約0.32%、47.89%;且曲管分叉模型下,分叉點處的主波波寬要比直管分叉模型下的小。對于直管分叉模型,在分叉前的直管段,分叉角度越大,第一主波壓力峰值衰減越小;在分叉后,分叉角度越大,峰值衰減越大;如:在分叉前,分叉20°和30°的情形下,分別衰減52.31%、41.05%;在分叉后則分別衰減了0.31%、8.71%。而曲管分叉模型預測的結果反之。對曲管分叉模型,在分叉前的直管段,分叉角度越大,壓力峰值衰減越大;對于分叉后的分支管,分叉角度越大,峰值衰減越小;如:在分叉前,分叉20°和30°的情形下,分別衰減38.83%、44.32%;在分叉后則分別衰減了47.89%、36.40%。
在分叉前,隨著分叉角度的增加,軸向速度脈搏波幅值的變化不大,明顯的變化是分叉前的軸向速度脈搏波形與分叉后的有較大不同,且分叉處速度脈搏波形振蕩明顯。分叉后軸向速度脈搏波的第一主波延遲約0.2 s,波形振蕩少、平緩。對于第一主波峰,在分叉處,監測點B1、B2的峰值相對A1、A2的峰值增大;如:對分叉20°的情形,直管分叉模型與曲管分叉模型預測的結果,分別增大44.98%、54.79%。而在分叉管中,監測點C1、C2的峰值相對B1、B2的峰值降低;如:分叉角20°的情形下,直管分叉模型與曲管分叉模型預測的結果,分別降低24.31%、23.19%。
3 結果與分析
3.1 髂動脈壓力脈搏波傳播特性分析
根據壓力脈搏波計算分析結果,監測點A1~B1、A2~B2、B1~C1、B2~C2的波速如表3所示。
由表3可知,直管分叉模型下,預測的血液在直管段傳播時壓力脈搏波波速要小于在分叉部分的壓力脈搏波波速。且對不同的分叉角度,在分叉前,隨著分叉角度增大,壓力脈搏波波速隨之增大,分叉30°情形的壓力脈搏波波速較分叉20°情形的大約56.33%;在分叉后,隨著分叉角增大,壓力脈搏波波速隨之減小。分叉30°情形的壓力脈搏波波速較分叉20°情形的小約68.19%。曲管分叉模型下,預測的血液在直管段傳播時壓力脈搏波波速大于分叉后支管段上的壓力脈搏波波速,并隨著分叉角增大,壓力脈搏波波速增大,在分叉前,分叉30°情形下的壓力脈搏波波速較分叉20°情形的大約5.45%;在分叉后,分叉30°情形的壓力脈搏波波速較20°情形的大約7.36%。
3.2 髂動脈軸向速度脈搏波傳播特性分析
根據速度脈搏波計算結果,可得出分叉血管中軸向速度脈搏波的傳播速度,監測點A1~B1、A2~B2、B1~C1、B2~C2的速度脈搏波速如表4所示。
由表4可知,兩種分析預測模型在分叉前的軸向速度脈搏波波速遠大于分叉后的,髂動脈分叉20°時,直管分叉模型與曲管分叉模型分別預測的軸向速度脈搏波波速,分叉前比分叉后要大約80.60%、77.14%。這說明血管的分叉幾何特性可明顯降低速度脈搏波的傳播速度。但不論是曲管分叉模型還是直管分叉預測模型,分叉20°情形時的軸向速度脈搏波波速最小。對于直管分叉預測模型,分叉前,分叉20°情形的比30°的小了約1.31%,而分叉后小了約18.45%;對于曲管分叉模型,在分叉前,分叉20°的情形的比30°的小了約11.76%,分叉后小了約2.04%。
3.3 髂動脈中的應力場分析
本節分析在一個心動周期內,髂動脈中的應力場分布情況,故選取分別代表一個心動周期的快速射血末期、收縮末期、舒張末期的0.2、0.5、0.8 s時刻點為例。在分叉血管分析預測模型下,血管壁上米塞斯應力云圖分別如圖6、圖7所示。由圖6、圖7可知,在0.2 s時,髂動脈中的脈搏波傳播仍在直管段部分,并沒有傳播到分叉點處和分叉管部分,此段上,并無應力集中現象,兩種模型下預測的最大的米塞斯應力值幾乎一致,數值較小。而當0.5 s時,脈搏波傳播至分叉點和分叉血管部位,此時在血管分叉處應力集中現象明顯。
 圖6
直管分叉模型下不同時刻米塞斯應力云圖
Figure6.
Von Mises stress distribution of straight bifurcated vessel model at different time
圖6
直管分叉模型下不同時刻米塞斯應力云圖
Figure6.
Von Mises stress distribution of straight bifurcated vessel model at different time
 圖7
曲管分叉模型下,不同時刻的米塞斯應力云圖
Figure7.
Von Mises stress distribution of curvilinear bifurcated vessel model at different time
圖7
曲管分叉模型下,不同時刻的米塞斯應力云圖
Figure7.
Von Mises stress distribution of curvilinear bifurcated vessel model at different time
直管和曲管分叉模型在0.2、0.5、0.8 s時的最大米塞斯應力如表5所示。在髂動脈分叉處,其內部的血流形態也發生了變化,髂動脈常因不能抵抗管腔內血流壓力負荷而失衡,從而發生病變[28-29]。由表5可知,對曲管分叉與直管分叉分析預測模型而言,在一個心動周期內,均是分叉20°情形的米塞斯應力最大,分叉25°情形的次之,分叉30°情形的最小。對分叉20°情形,直管分叉模型和曲管分叉模型下分別較分叉30°情形的大約60.6%、16.13%。這表明,分叉角較小情形的髂動脈更易發生病變;具有不同分叉角度的髂動脈的最大應力部位均在髂動脈的分叉處,與其它部位相比,髂動脈在分叉處更易發生病變。
4 結 論
本文建立了血液-血管系統的流-固雙向耦合分析模型,經模擬分析發現,曲管分叉模型預測的壓力脈搏波和速度脈搏波波形要更接近于實際。在髂動脈分叉前,分叉角度越大,曲管分叉模型下的壓力脈搏波波幅衰減越大,而分叉后,波幅衰減越小。血管分叉后,軸向速度脈搏波隨之衰減。另外,髂動脈的分叉幾何特性對脈搏波傳播有明顯影響,且直管分叉模型和曲管分叉模型預測的脈搏波波形,在分叉前后有較大差別。對應一個心動周期內的心臟收縮區間,曲管分叉模型預測的壓力脈搏波和軸向速度脈搏波幅值,在分叉前后,更接近于實際情況。在分叉后的曲管段,分叉角越大,壓力脈搏波第一主波幅值越大,且隨著心臟的收縮和舒張,第二主波波幅逐漸越小,傳播速度也減小;軸向速度脈搏波幅值隨著分叉角增大,幅值減小;曲管分叉模型預測的幅值衰減幅度低。此外,分叉點處伴隨著血管壁的應力集中現象,這與髂動脈在分叉部位容易發生動脈狹窄和硬化等疾病的臨床現象相一致。
重要聲明
利益沖突聲明:本文全體作者均聲明不存在利益沖突。
作者貢獻說明:孫雪航負責計算模型的后處理、論文寫作及修改,李本森、盧意成負責論文的選題及有限元模型的搭建,繆馥星提供論文指導以及論文的審閱修訂。
倫理聲明:本文所使用的脈搏波波形數據得到寧波市中醫院醫學倫理委員會的批準采集并授權使用(編碼:AF/SQ-01/03.1)。