三周期極小曲面（TPMS）可以通過公式精確地控制多孔支架的形態而被廣泛應用。本文構建一種I型包裝（I-WP）型多孔支架，采用有限元法研究壁厚和周期與支架形態和力學性能的關系，并進行壓縮和流體性能的研究。研究發現，不同壁厚（0.1～0.2 mm）、不同周期（I-WP 1～I-WP 5）的I-WP型支架孔隙率在68.01%～96.48%范圍內，等效彈性模量為0.655～18.602 GPa；隨著周期和壁厚的增加，支架應力分布趨于均勻；拓撲優化后I-WP型支架等效彈性模量基本不變，滲透性提升52.3%。綜上，對于I-WP型支架可以先調控周期參數，后調控壁厚參數，結合拓撲優化來達到設計要求。本文構建的I-WP型支架具有良好的力學性能，且滿足修復人體骨組織的需求，為人工骨小梁支架的設計提供一種新選擇。
引用本文： 門玉濤, 湯紹燦, 陳煒, 劉福龍, 張春秋. 基于三周期極小曲面法骨小梁支架的設計與性能研究. 生物醫學工程學雜志, 2024, 41(3): 584-594. doi: 10.7507/1001-5515.202310005 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
近年來，增材制造這一新興技術的快速發展，極大地促進了多孔骨植入物的研究[1]。增材制造技術是以計算機輔助設計（computer aided design，CAD）模型為依據，利用對材料逐層累加堆積的方法進行實體制造成型的一種技術[2]。很多傳統加工難以處理的復雜結構部件可以通過三維（three dimensional，3D）打印技術增材制造，其加工的多孔結構可以用作組織替代材料[3]。多孔支架可以根據人體骨骼彈性模量調整孔隙率、孔徑等參數，實現支架與自身骨骼力學性能的匹配，從而減少由實體植入物引起的應力遮擋效應，并降低術后并發癥的發生率[4]。已有研究表明，孔徑范圍為300～600 μm、孔隙率在50%～90%的相互連通的多孔結構通常被認為適合促進骨形成和毛細血管的形成[5]。多孔結構植入物還具有較大的比表面積和良好的連通性，可促進細胞遷移和黏附，有助于營養和氧氣流動，并能促進人體骨骼和其自身之間的生物固定[6]。鑒于孔隙率和比表面積是骨植入物的兩個重要參數，因此在對多孔支架進行設計時，研究結構的孔隙率和比表面積對力學性能的影響非常重要。
三周期極小曲面（triply periodic minimal surface，TPMS）是一種在三個獨立方向具有周期性且平均曲率為零的隱式等值曲面[7]。TPMS在自然界廣泛存在，將其作為骨組織植入體具有廣闊的前景[8]。TPMS可通過三角函數來表達，改變其閾值大小可以實現對孔徑參數的調整，實現多孔結構呈梯度變化[9]。TPMS最大的優勢是可以通過公式精確控制多孔支架孔形狀、孔徑尺寸、孔隙率、比表面積等內部孔隙結構參數[10]。目前，很多學者已經對基于TPMS方法的多孔結構展開研究。Wang[11]提出了一種基于TPMS的周期性曲面建模方法，實現了多孔支架的參數化建模。Yoo [12]提出了基于距離場的TPMS多孔支架設計方法，發現控制TPMS閾值可實現多孔支架孔隙率線性變化。Melchels等[13]構建了一種孔隙率梯度變化的螺旋二十四面體（gyroid，G）型多孔支架。鄧珍波等[14]構建了立方體（cube，C）、菱形（diamond，D）、G型3種支架，并進行力學實驗分析，發現80%左右孔隙率D型支架與天然骨組織的最大抗壓強度匹配性最好。Yang等[15-17]通過S形生長曲線函數（sigmoid function）和高斯徑向基函數（Gaussian radial basis function，GRBF）實現不同類型TPMS支架邊界融合過渡。劉佳辛等[18]構建了原始（primitive，P）、G、D型多孔支架，研究發現相同周期和壁厚的多孔支架中P型支架的孔隙率最大，應力分布更均勻。Liu等[19]將偏置測地B樣條曲線和測地線泰森網格相結合，設計了一種基于TPMS的復合多孔結構，并對不同周期和壁厚下的P型復合多孔結構孔隙率、最大應力和等效彈性模量進行研究；研究結果顯示，該方法不僅可以通過合理選擇TPMS的固有參數實現結構優化，而且可以根據應力分布，通過控制泰森位置分布和測地B樣條曲線的偏移來實現結構優化。由此可見，目前基于TPMS方法構建的P、D、G型支架的性能研究較多，而I型包裝（I-wrapped package，I-WP）、F-菱形十二面體（F-rhombic dodecahedra，FRD）、八面體-立方八面體-四方八面體（octahedra-cuboctahedra-tetragonal octahedron，OCTO）型支架函數表達式和結構較復雜，研究較少，其性能特性還不清楚。
為了解決上述問題，本文基于TPMS方法構建了I-WP型支架，與P、D、G、FRD、OCTO型支架進行比較，采用有限元方法研究多孔支架的壓縮性能和滲透性能，參數化分析曲面壁厚、周期對I-WP型多孔支架形態參數和力學性能的影響，利用變密度法對I-WP型支架進行拓撲優化，以提高支架的滲透性能。本研究期望構建的I-WP型支架具有良好的力學性能，作為一種潛在的骨科植入多孔結構，能滿足修復人體骨組織的要求，為構建適合骨組織工程需要的支架結構提供新選擇和參考數據。
1 材料和方法
1.1 TPMS參數化建模
1.1.1 TPMS數學模型
極小曲面是平均曲率為零的隱式等值曲面。與文獻[11]提及的參數化模型相比，TPMS更常采用隱式表達式描述[20]，如式(1)所示：
 |
其中，φ(r)為TPMS等值面數值；k為晶格數量；π為圓周率；Ak為振幅因子；λk為周期波長；r為歐式空間位置矢量；hk為倒數空間中第k個晶格矢量；Pk為相位偏移；C為閾值常量。
TPMS表達式中變量x、y、z前的參數分別控制對應方向上的孔徑，參數越大，孔徑越小，閾值C可以控制多孔支架孔隙率大小且呈現線性關系[16]。如表1所示，為6種TPMS表達式。
表1
TPMS表達式
Table1.
TPMS expression
1.1.2 TPMS支架參數化建模
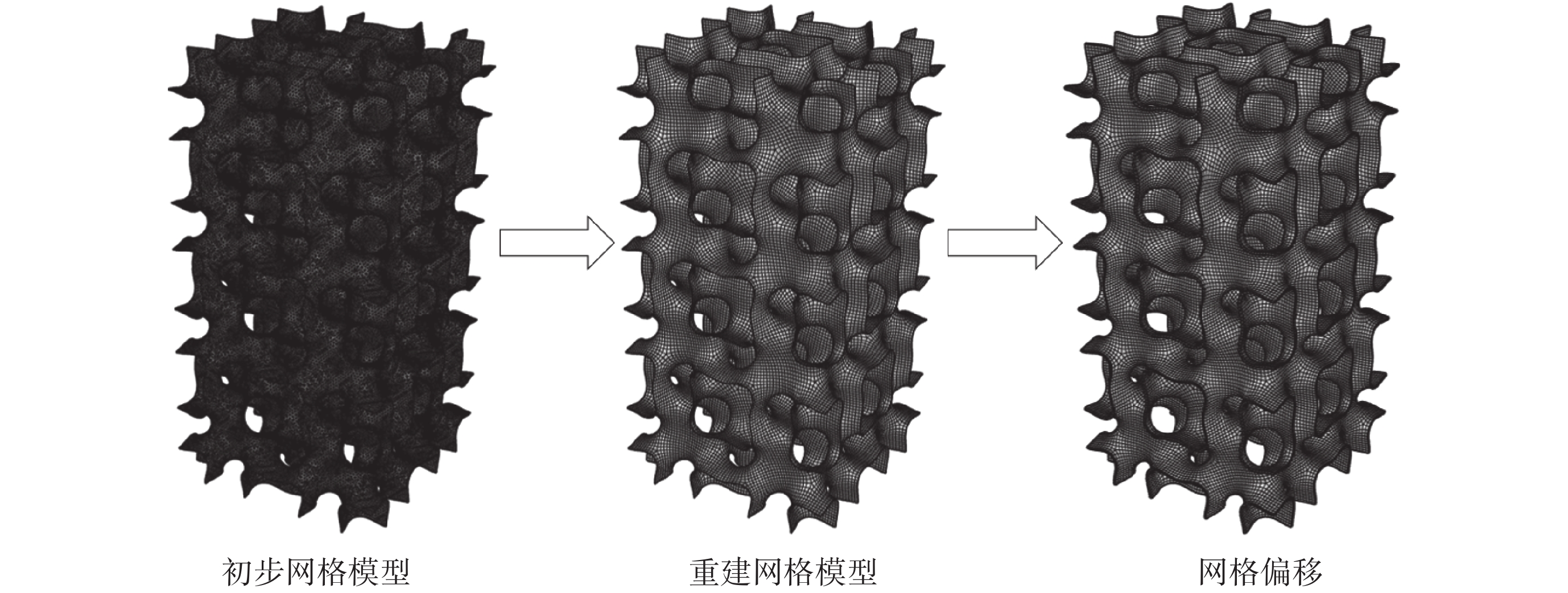
本文基于三維建模軟件Rhino7.0（Robert McNeel & Assoc.inc，美國）進行TPMS支架構建，并配合編程語言Grasshopper（Robert McNeel & Assoc.inc，美國）進行參數化控制。模型設計尺寸為10 × 10 × 20 mm3，周期為2，應用克拉克細分（Catmull-Clark）命令對模型進行細分，得到精度更高的平滑TPMS曲面模型。然后對模型進行網格重建，將重建后的零厚度TPMS曲面進行空間等距偏移加厚，獲得任意厚度的骨小梁多孔結構，如圖1所示。周期為2、壁厚為0.1 mm的6種類型的TPMS支架，如圖2所示。
圖1
TPMS支架創建流程
Figure1.
TPMS scaffold creation process
圖2
TPMS支架模型
Figure2.
TPMS scaffold model
1.2 壓縮仿真條件設置
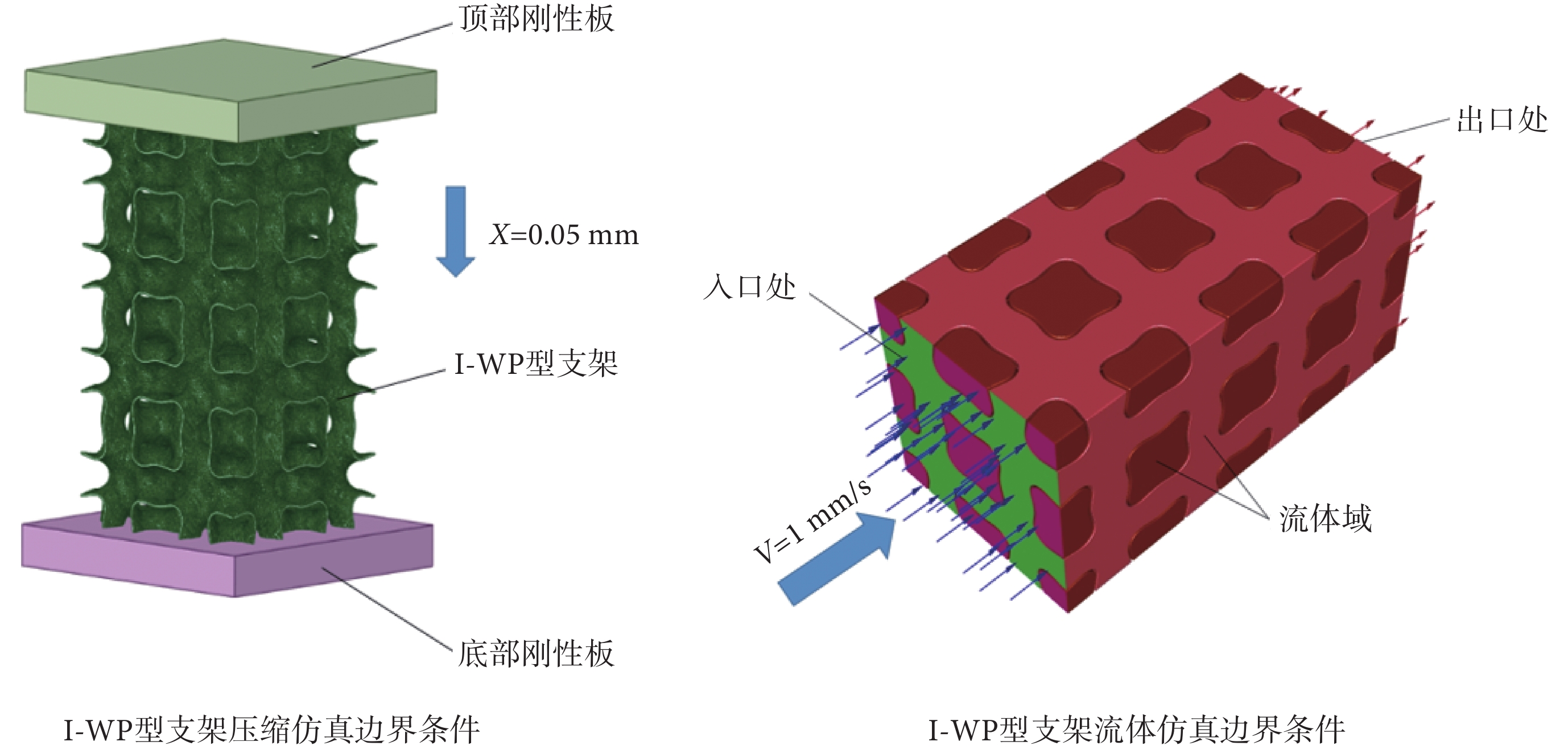
將6種TPMS支架模型導入有限元分析軟件ANSYS 2020 R2（ANSYS Inc.，美國）中進行有限元分析。支架采用醫療領域常用的鈦合金材料，密度為4 620 kg/m3，彈性模量為110 GPa，泊松比0.3，屈服強度為950 MPa[18]。將模型上下端面與剛體板施加接觸約束，摩擦系數0.45，為鈦合金與鑄鐵摩擦系數。在上剛體板面施加軸向位移（X = 0.05 mm），為支架軸向總長0.25%，支架處于彈性階段，如圖3左側所示。TPMS支架采用四面體單元，網格大小為0.15 mm。剛體板采用六面體單元，網格大小為0.3 mm。
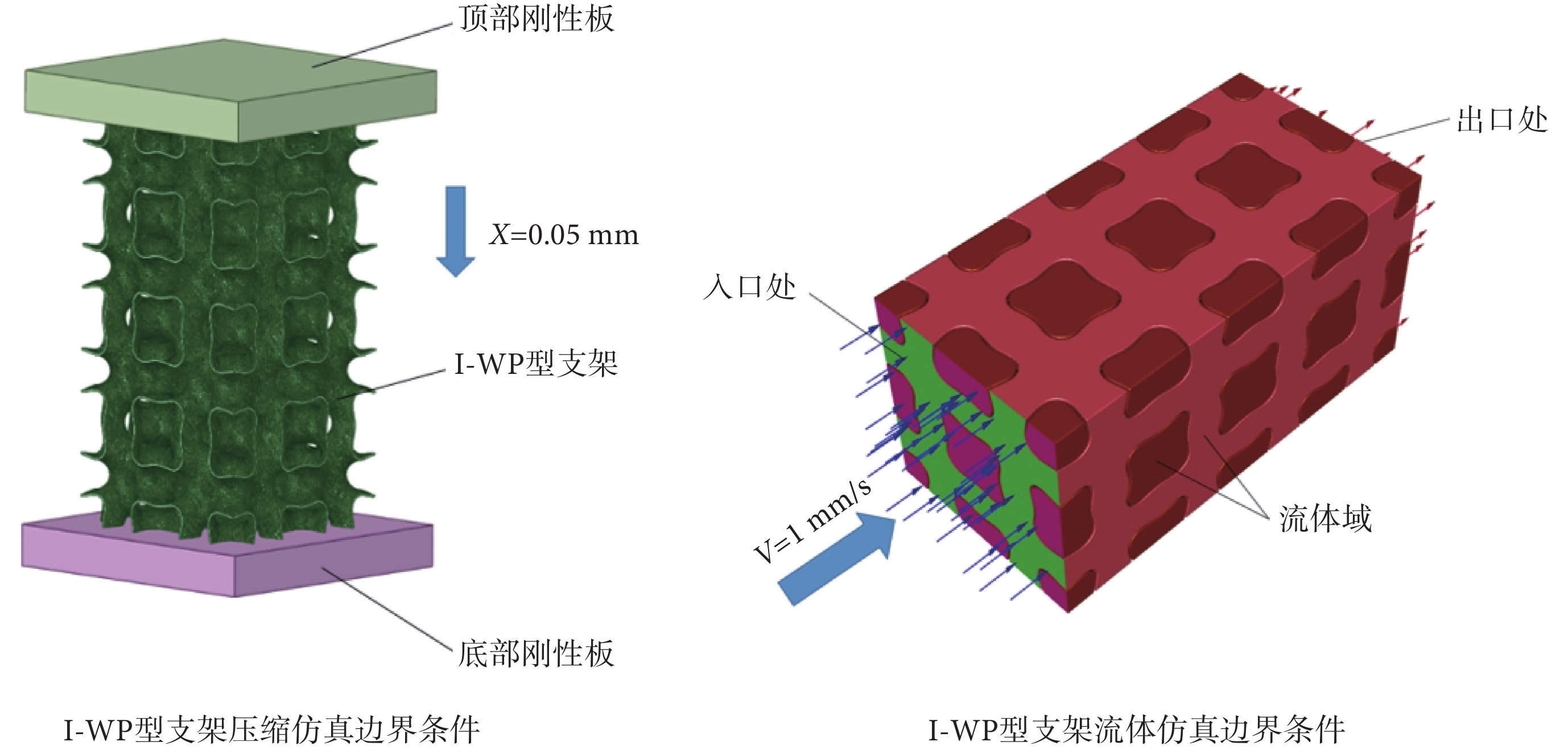圖3
I-WP型支架有限元仿真邊界條件
Figure3.
Boundary conditions for finite element simulation of I-WP type scaffold
1.3 拓撲優化
拓撲優化是一種根據設定的載荷大小、邊界約束和優化條件，對結構內材料分布進行優化設計的數學方法[21]。基于TPMS方法構建的I-WP型多孔支架，屬于體心立方結構，中心收縮，向頂點伸出8個支撐。由于I-WP型支架側壁由封閉曲面連接，不利于運輸營養物質，從而影響骨生長。本文基于變密度法對I-WP型支架進行拓撲優化，在支架結構剛度幾乎不變的條件下，提高結構滲透性，促進骨長入。變密度法采用固體各向同性材料懲罰（solid isotropic material with penalization，SIMP）模型[22]，通過密度函數關系對模型進行優化。
設定目標函數為支架剛度最大，設置拓撲區域和排除區域，設置質量分數97%為約束條件，得到拓撲優化后的支架模型。
1.4 流體仿真條件設置
將6種TPMS支架模型導入流體力學數值計算軟件Fluent 2020 R2（ANSYS Inc.，美國），進行流體性能仿真分析。支架的計算流體動力學（computational fluid dynamics，CFD）分析使用不可壓縮穩態層流的靜止納維-斯托克斯（Navier-Stokes）方程。液相部分使用杜爾貝科改良伊格爾培養基（Dulbecco’s modified Eagle medium，DMEM）在37 ℃（平均人體溫度）下的流體特性：動態粘度η = 1.45 × 10?3 Pa·s；密度ρ = 1 000 kg/m3[23]。
在達西定律的適用性范圍內，將入口液體流速V設置為1 mm/s，出口壓力設置為零，支架的壁面設置為無滑移條件，如圖3右側所示。達西定律數學表達式[24]如式(2)所示：
 |
其中，K為滲透率；L為支架的軸向長度；
為壓降；v為入口處的速度；
為DMEM的粘度。
2 結果
2.1 TPMS支架形態參數分析
2.1.1 不同類型TPMS對支架孔隙率、比表面積的影響
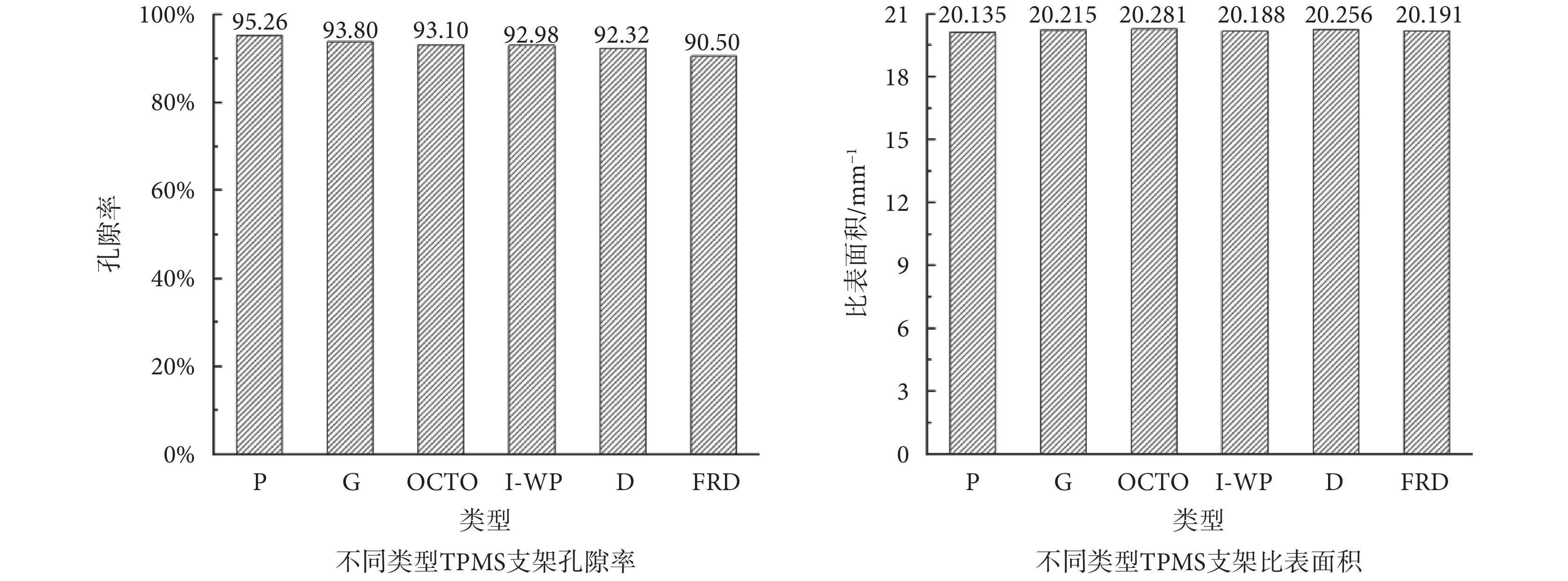
如圖4所示，周期為2、壁厚為0.1 mm的6種TPMS支架模型的孔隙率P > G > OCTO > I-WP > D > FRD，孔隙率在90.50%～95.26%范圍內。比表面積變化不大，變化范圍為20.135～20.281 mm?1。比表面積越大，越有利于細胞增殖和黏附，促進骨長入。由此趨勢可得，在構建相同曲面壁厚、周期的TPMS支架時，TPMS的類型是影響多孔結構孔隙率的重要因素。
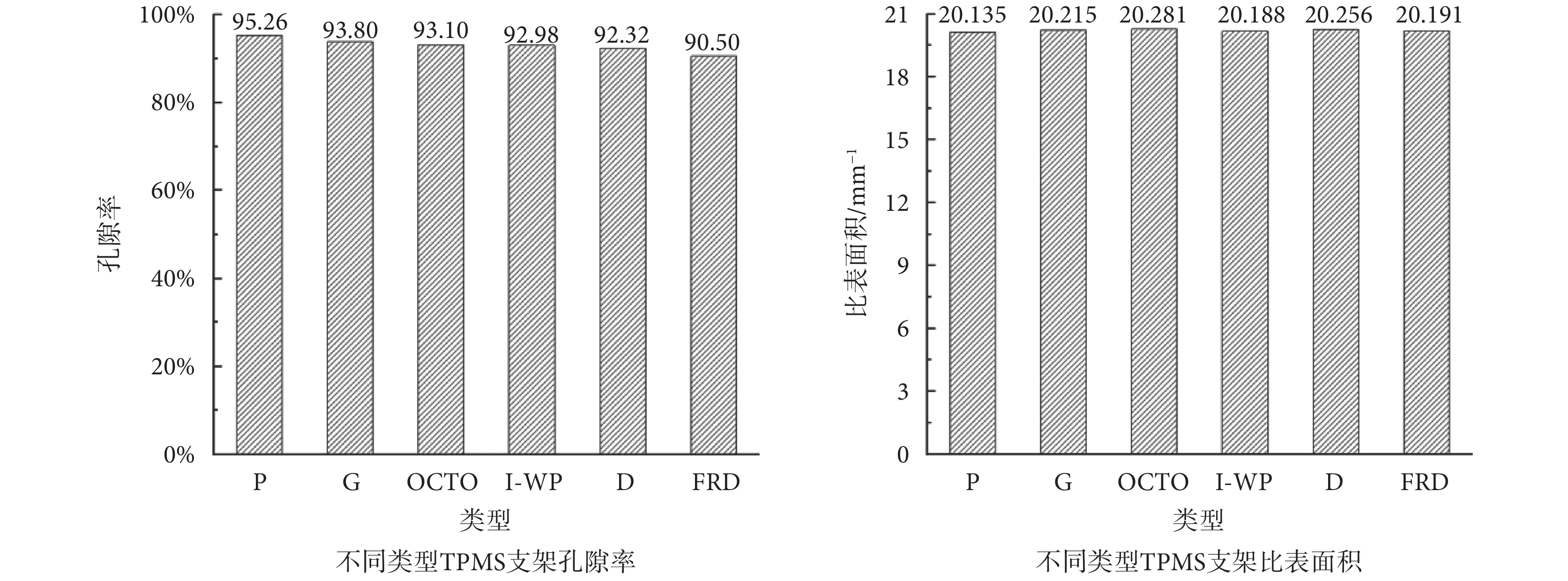圖4
不同類型TPMS支架孔隙率與比表面積
Figure4.
Porosity and specific surface area of different types of TPMS scaffolds
2.1.2 曲面壁厚、周期對I-WP型支架孔隙率、比表面積的影響
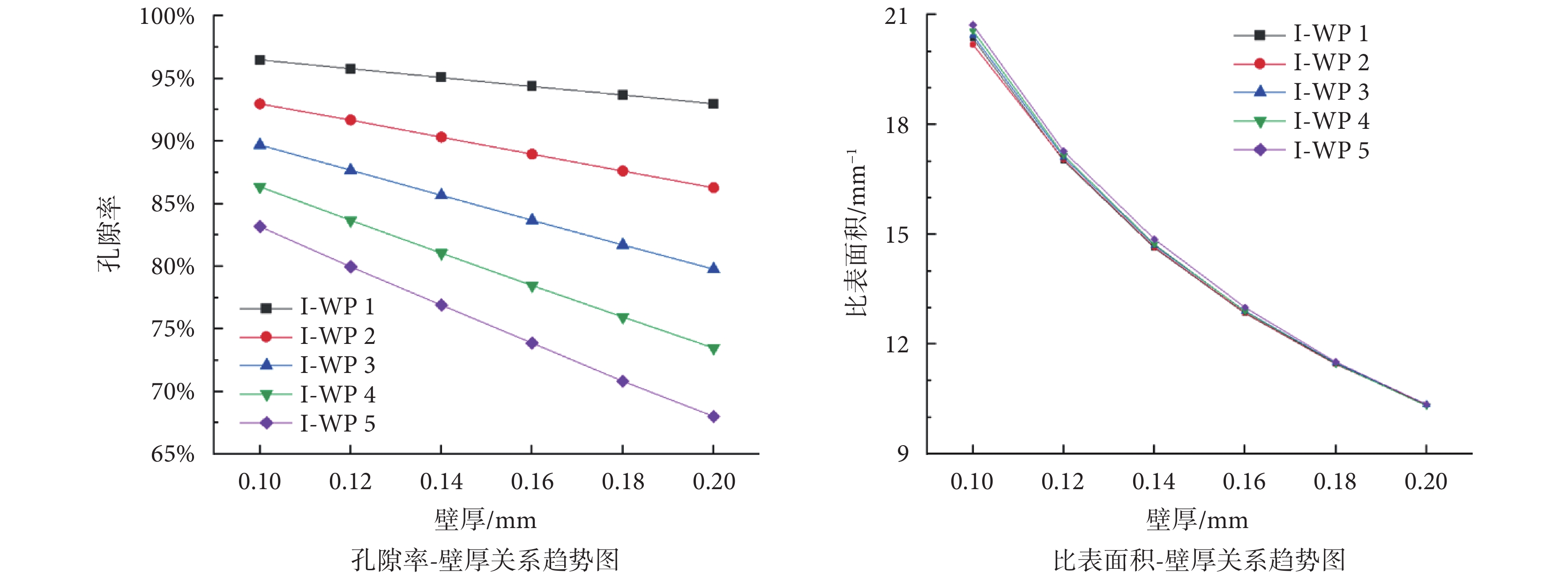
如圖5所示，不同周期（I-WP 1～I-WP 5）、不同壁厚（0.1～0.2 mm）的I-WP型支架孔隙率在68.01%～96.48%范圍內，比表面積在10.349～20.351 mm?1范圍內。如圖5左側所示，隨著壁厚的增加，I-WP型支架的孔隙率線性降低；隨著周期數增大，支架的孔隙率降低，且周期對孔隙率的影響程度大于厚度。如圖5右側所示，隨著壁厚的增加，I-WP型支架的比表面積降低；隨著周期數增大，支架的比表面積升高，但周期對I-WP型支架的比表面積影響很小，且隨著壁厚的增加，周期的影響越來越小。設計I-WP型支架應該優先考慮周期，后對厚度進行調整，可以很好地調節支架的孔隙率與比表面積。
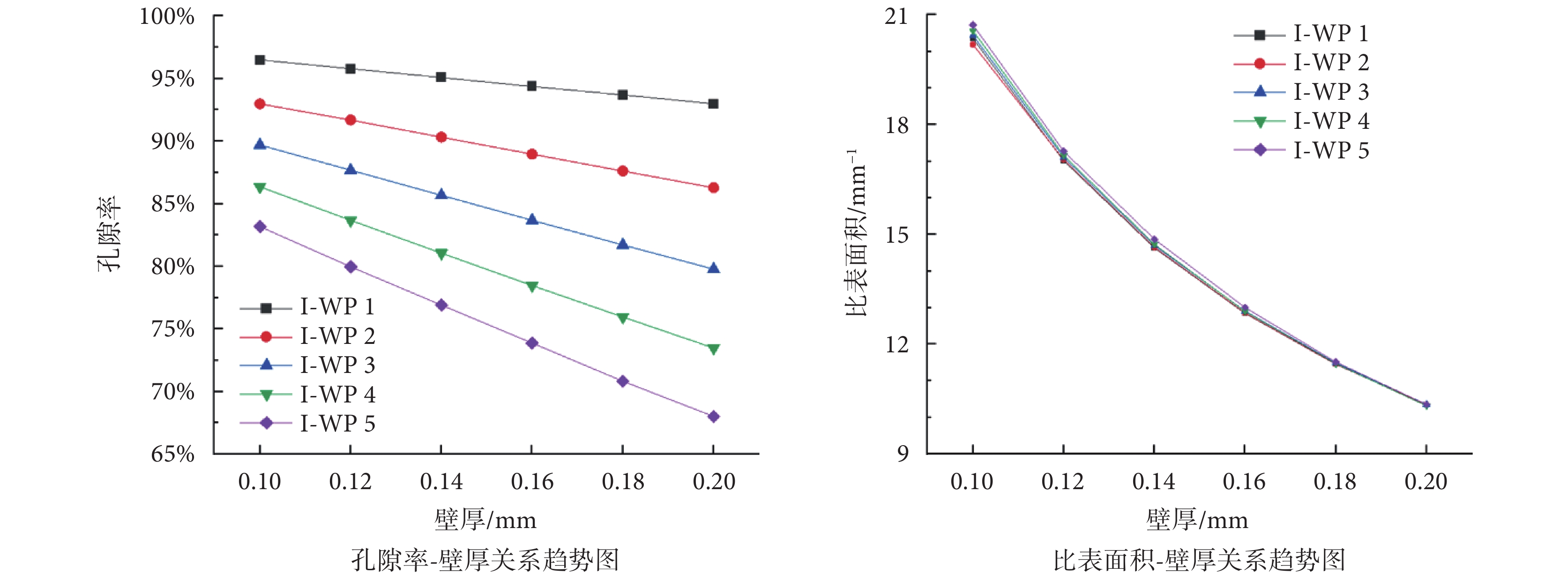圖5
曲面壁厚、周期對結構形態參數的影響
Figure5.
The influence of surface wall thickness and period on structural morphological parameters
2.2 TPMS支架壓縮性能
2.2.1 不同類型TPMS支架有限元結果分析
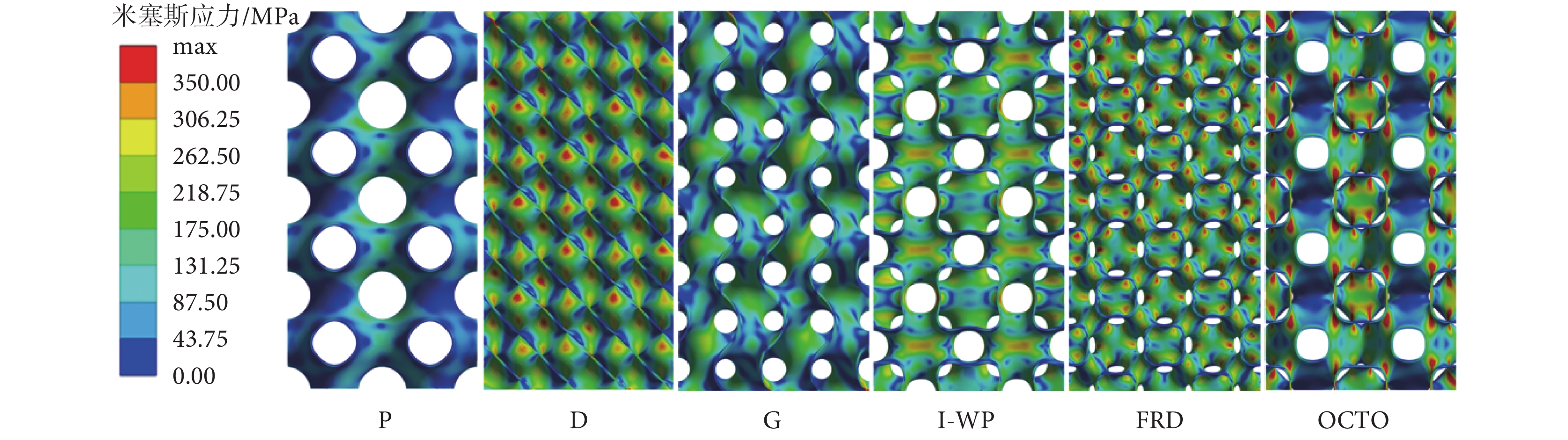
對周期為2、厚度為0.1 mm的不同類型TPMS支架施加軸向位移0.05 mm工況下的等效應力云圖，如圖6所示。可以看出，P、G、I-WP型支架相比D、FRD、OCTO型支架，應力集中區域不明顯。D、FRD、OCTO型支架應力集中區域較多，結構容易發生損壞，尤其是OCTO型支架有多處應力集中區域，容易發生斷裂和疲勞現象。G型支架在邊緣處出現應力集中現象，這是由于G型支架邊緣彎曲的曲面導致的。P型與I-WP型支架邊緣為近似圓環結構，可以很好地分散應力，減小應力集中。綜上，I-WP型支架應力分布均勻，支架強度更好，對提高支架強度具有一定的研究價值。
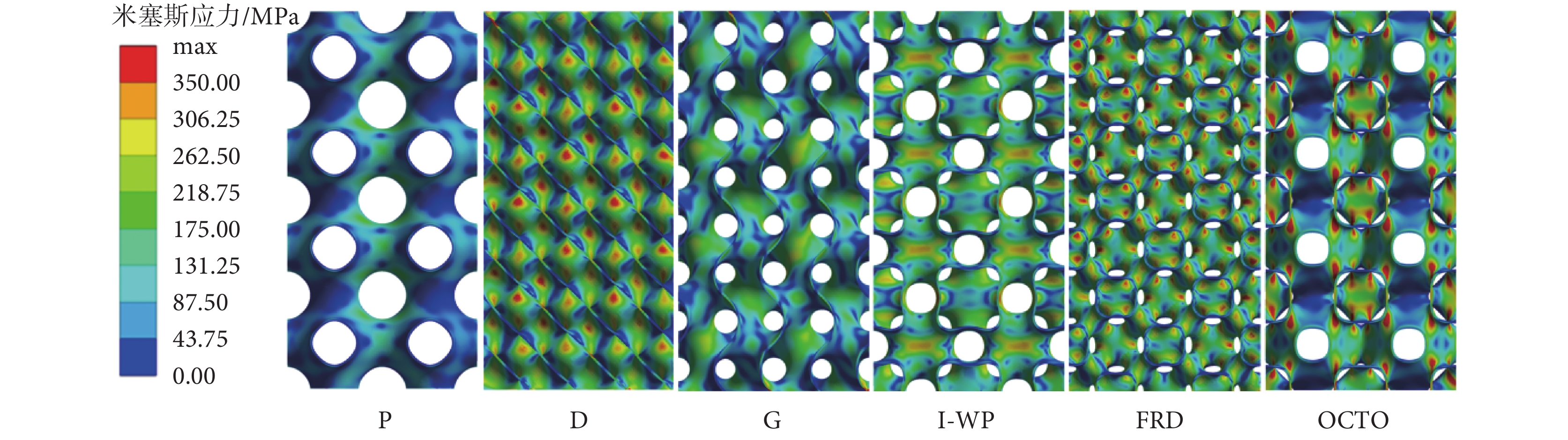圖6
不同類型TPMS支架的等效應力云圖
Figure6.
Von Mises stress nephogram of different types of TPMS scaffolds
2.2.2 I-WP型支架有限元結果分析
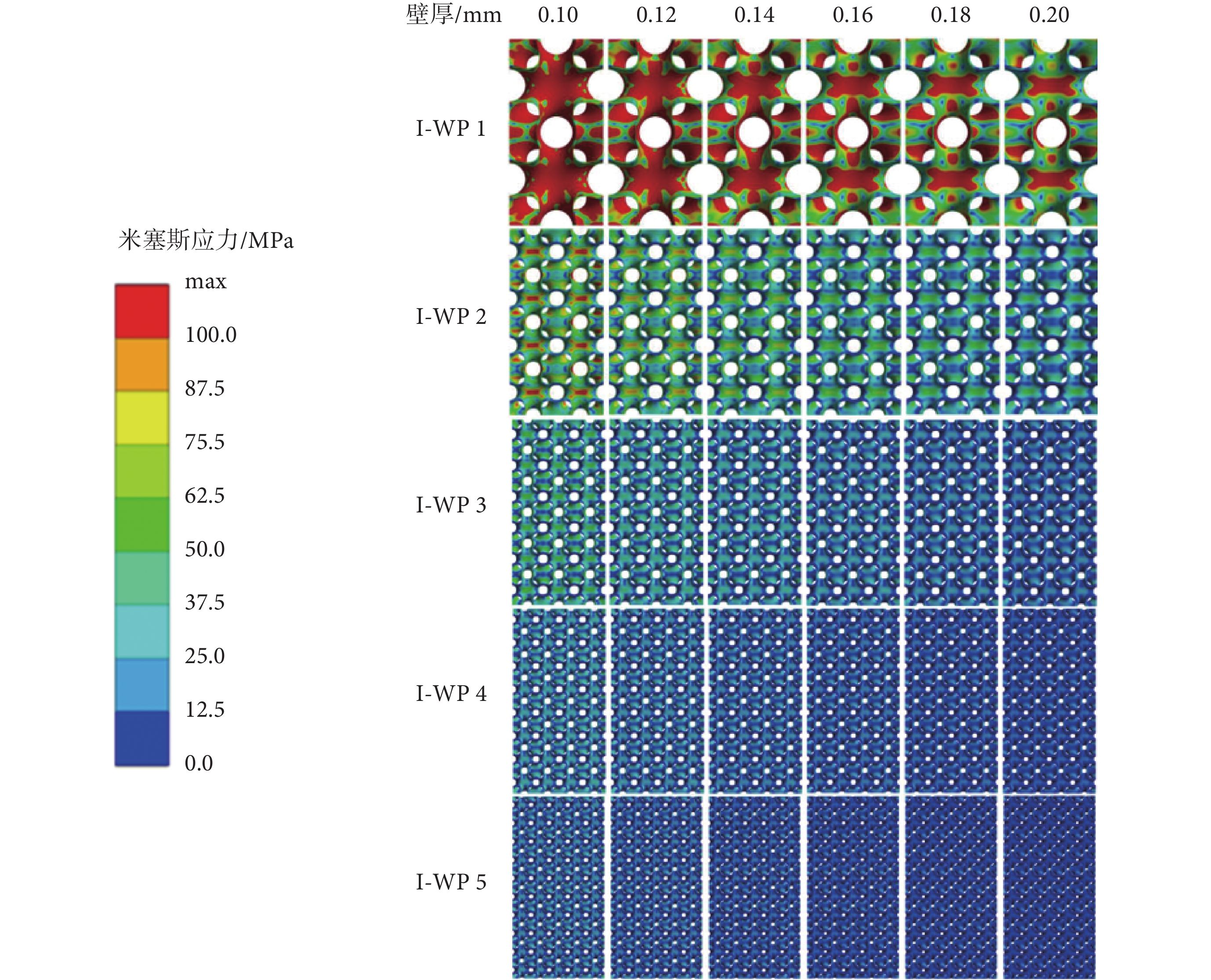
如圖7所示，為不同周期（I-WP 1～I-WP 5）、不同壁厚（0.1～0.2 mm）的I-WP型支架在200 N縱向壓力工況下的等效應力云圖。可以看出，I-WP 1支架應力集中較為明顯，尤其是結構中心收縮區域應力較高。隨著周期的增加，I-WP型支架應力分布趨于均勻，應力集中變得不明顯，支架結構穩定性增強；隨著厚度的增加，I-WP型支架應力分布基本不變，但高應力區域減小，低應力區域增大，基本沒有應力集中現象，支架結構穩定性增強。設計I-WP型支架應該優先調整周期，后對壁厚進行調整，可以很好地控制多孔結構的應力分布情況，避免應力集中。
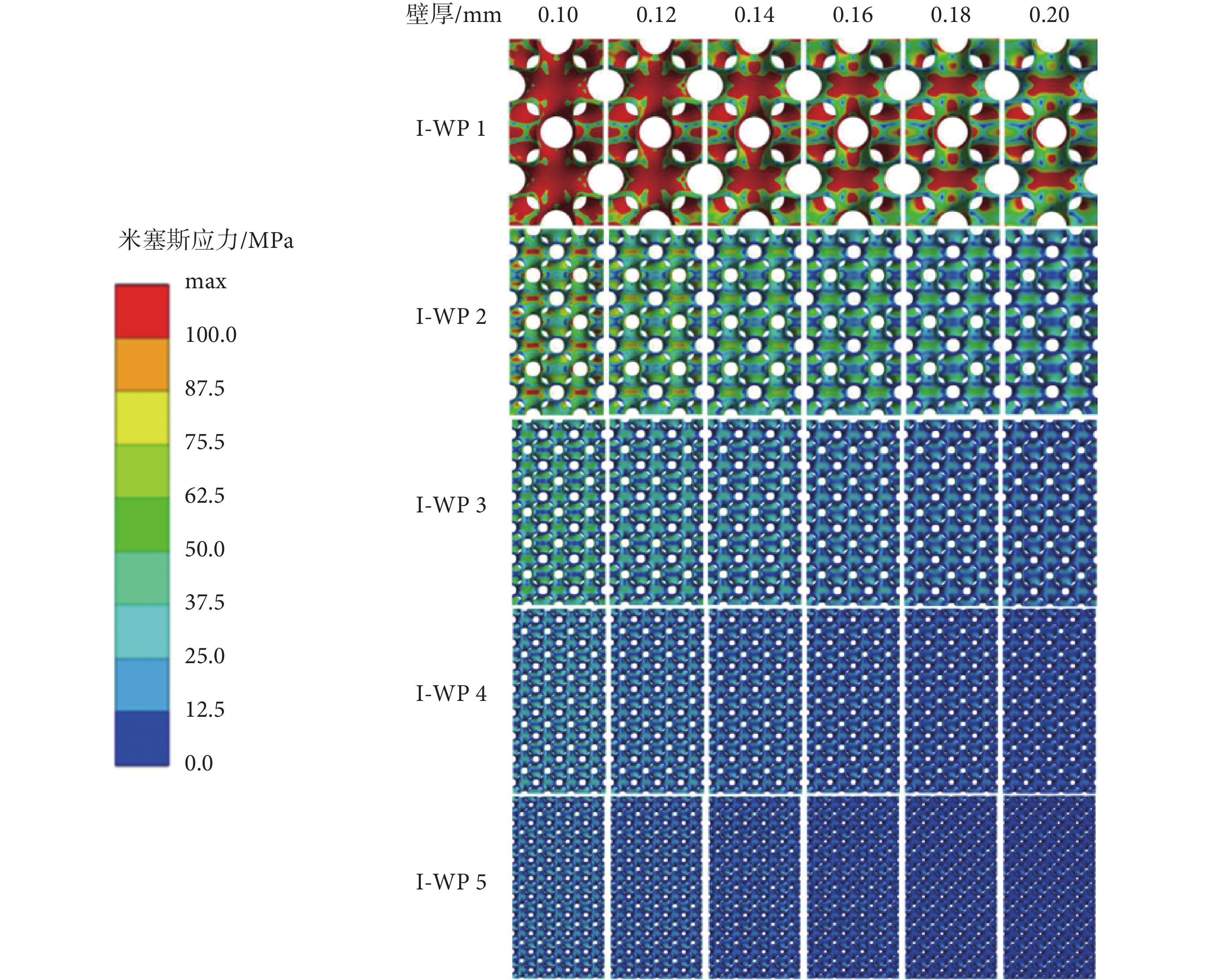圖7
不同I-WP型支架的等效應力云圖
Figure7.
Von Mises stress nephogram of different I-WP scaffolds
2.2.3 多孔結構力學性能分析
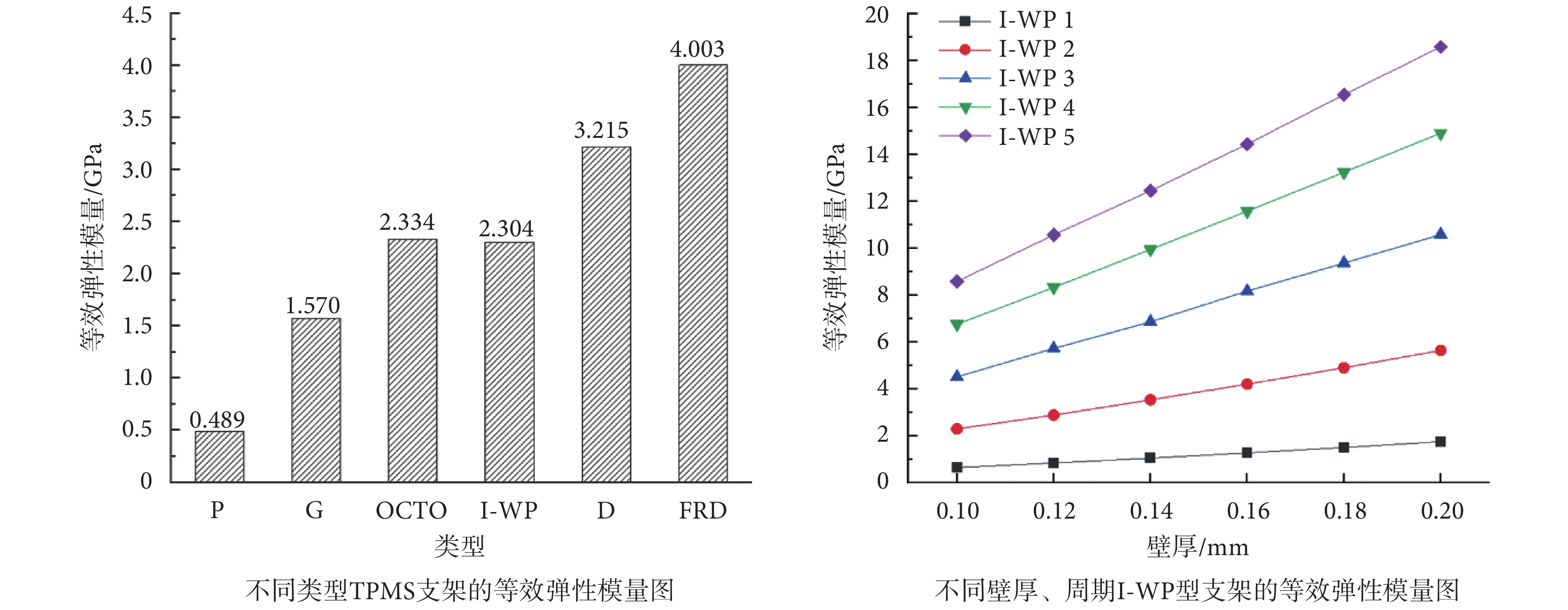
周期為2、厚度為0.1 mm的不同類型TPMS支架的等效彈性模量圖，如圖8左側所示。結合孔隙率圖，如圖4左側所示，比較不同類型TPMS支架的計算結果，發現在相同的周期和壁厚條件下，支架的等效彈性模量在0.489～4.003 GPa范圍內，等效彈性模量基本上隨著孔隙率的降低而升高，而I-WP型支架的等效彈性模量偏低，可以看出I-WP型支架在降低應力遮擋效應上更具有優勢。
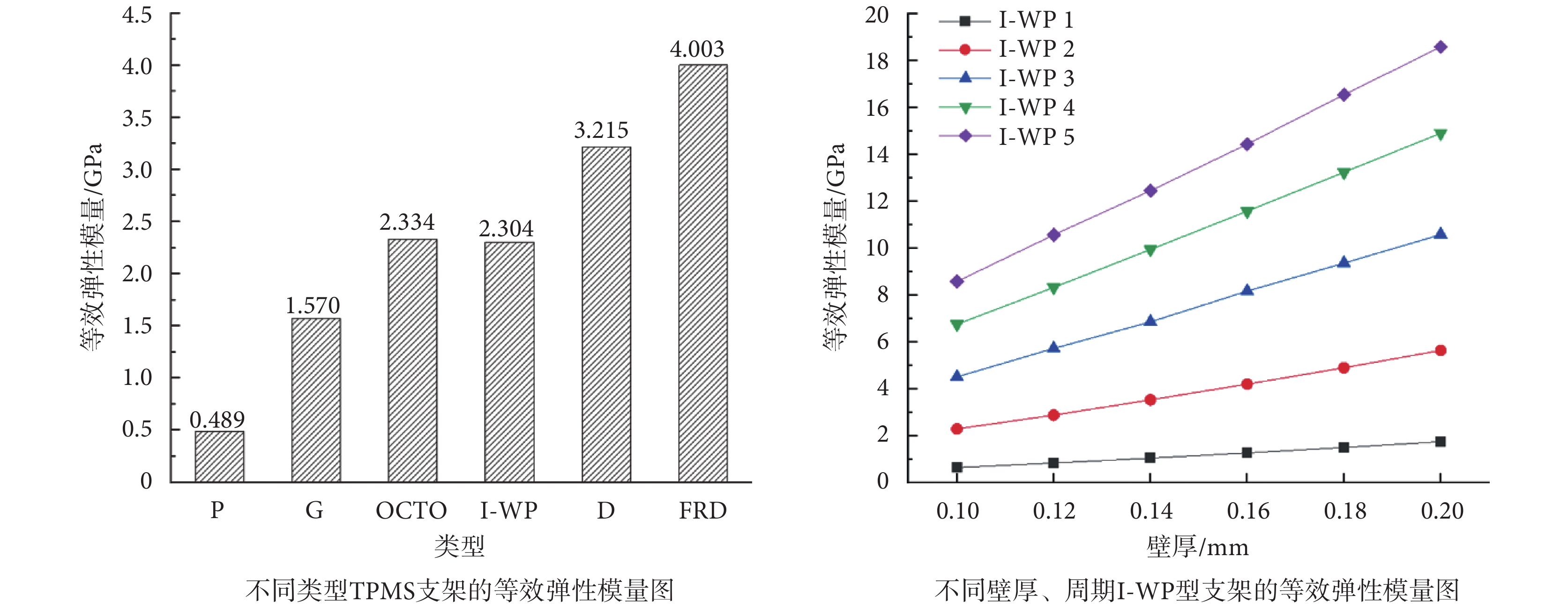圖8
多孔結構等效彈性模量比較圖
Figure8.
Comparison chart of equivalent elastic modulus of porous structures
如圖8右側所示，通過對比不同周期（I-WP 1～I-WP 5）、不同壁厚（0.1～0.2 mm）I-WP型支架等效彈性模量，發現隨著壁厚增大，等效彈性模量線性增大。隨著周期增大，等效彈性模量增大，且周期較大的多孔結構等效彈性模量變化范圍更大。本文設計的I-WP型支架等效彈性模量在0.655～18.602 GPa范圍內。
人松質骨的楊氏模量范圍為0.1～4.5 GPa，皮質骨的楊氏模量范圍為5～23 GPa [25-27]。綜上所述，I-WP型支架等效彈性模量在人體骨的彈性模量范圍內。
2.3 I-WP型支架拓撲優化
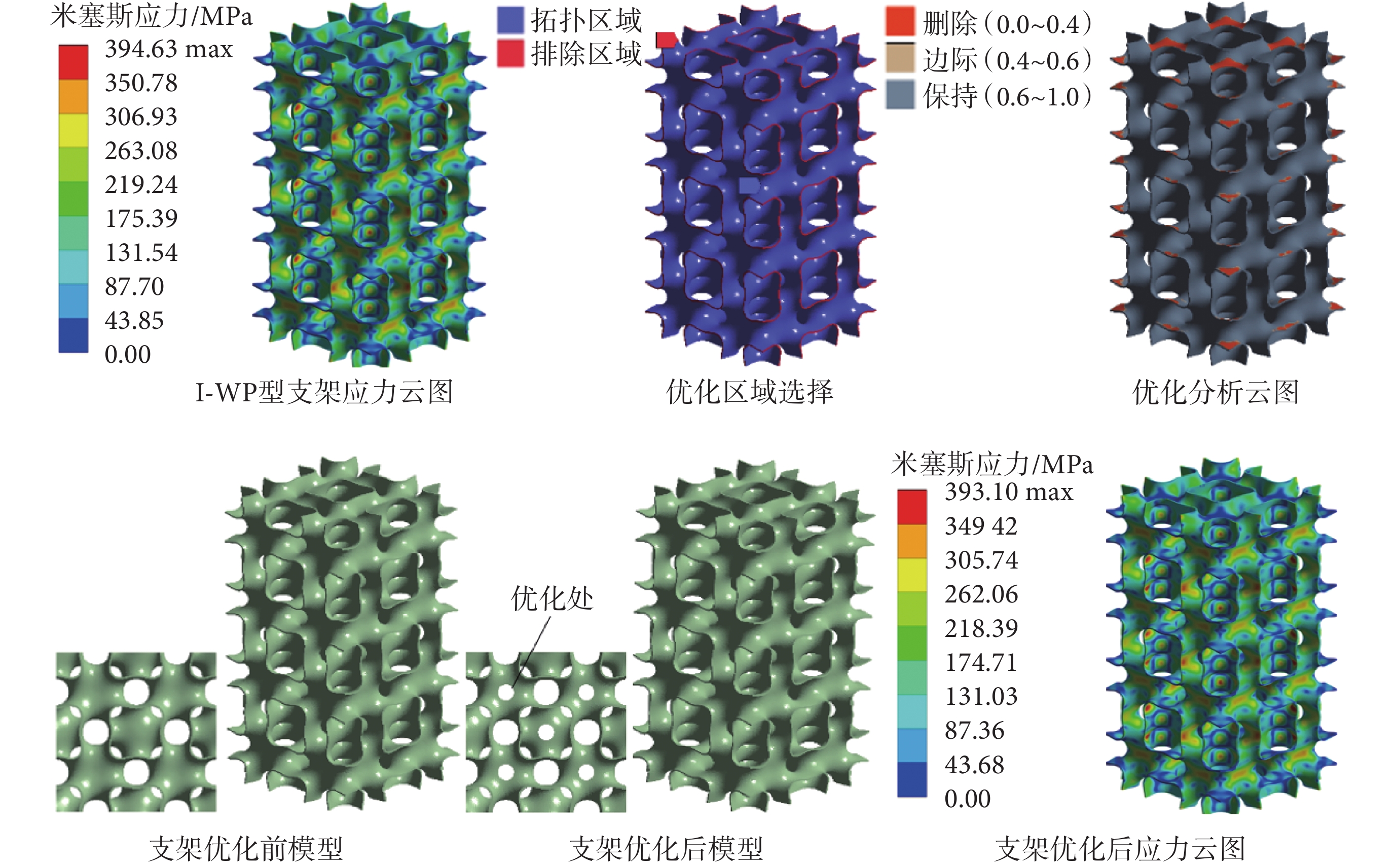
如圖9所示，I-WP型支架最大應力為394.63 MPa，設置優化目標為保留質量分數97%。為保證多孔單元結構的完整性和整體支架的尺寸不變，外邊界為排除區域。密度在0.0～0.4區域為可刪除區域，在軸向應力較小處增加開孔。經拓撲優化后，支架最大應力為393.10 MPa，減小了1.53 MPa，基本沒有出現應力集中現象，兩者最大應力值均小于鈦合金屈服強度950 MPa。拓撲優化后，支架質量由0.631 4 g降低到0.617 0 g，減小2.28%，即優化后質量是優化前質量的97.72%；支架等效彈性模量由2.304 GPa降低到2.271 GPa，減小1.43%，基本符合設計要求。
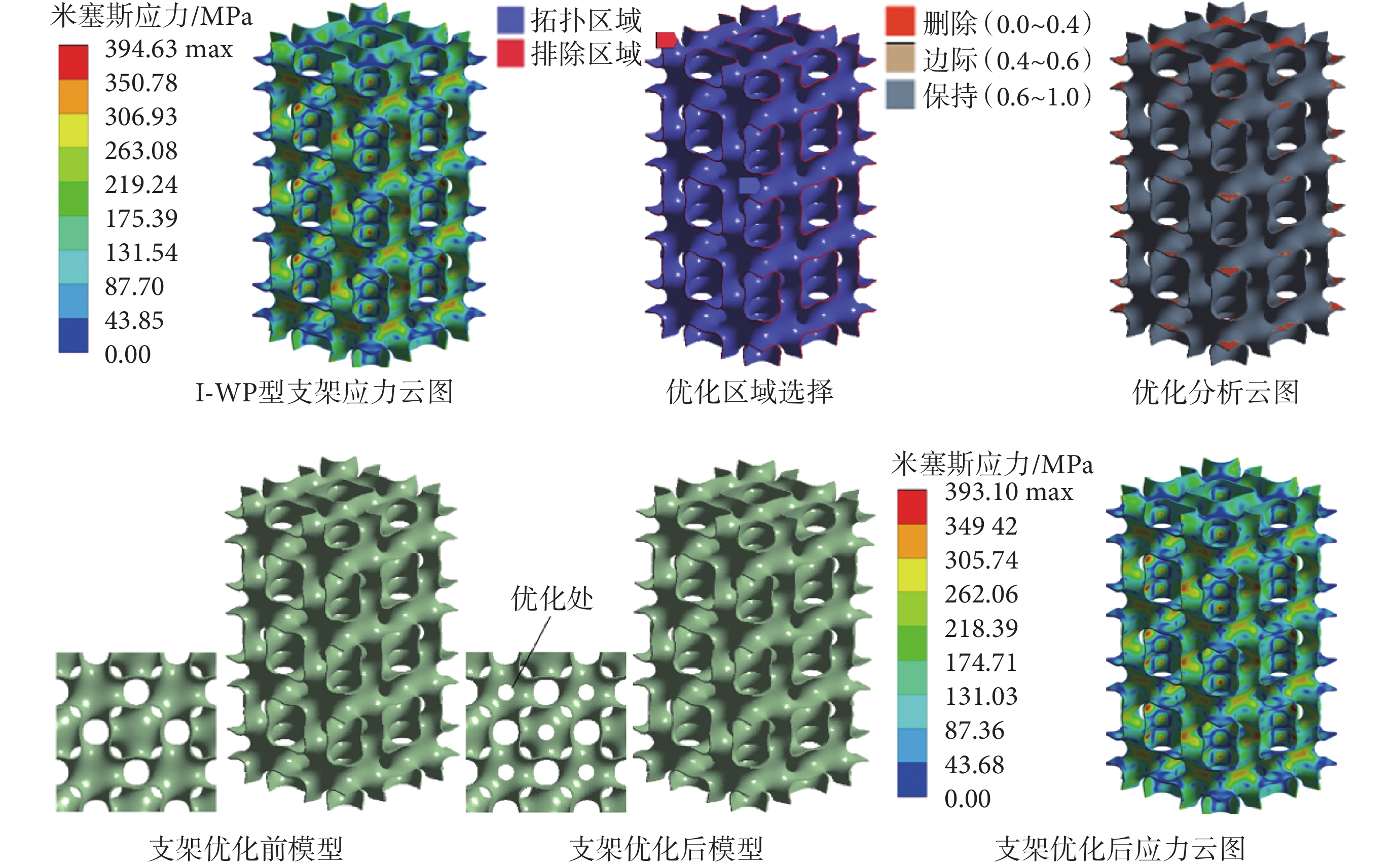圖9
拓撲優化
Figure9.
Topology optimization
2.4 TPMS支架流體力學分析
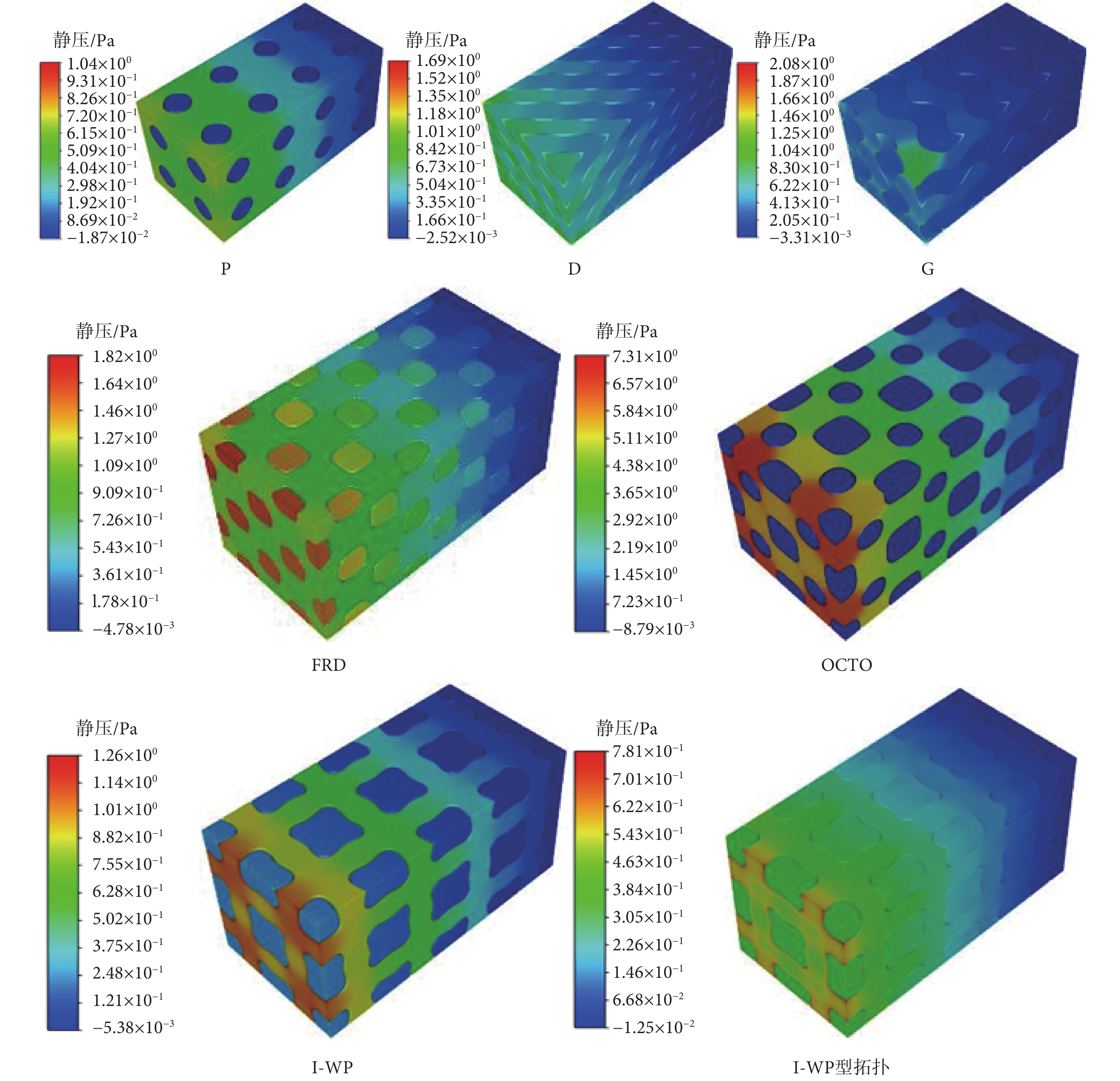
如圖10所示，隨著組織液的流入，壓力逐漸減小。入口處流體域靠近組織液，壓力較大，出口處壓力為零。TPMS支架有2個流體域，導致流體域之間流體壓力有一定差異，壓力云圖可以看出明顯的分層。FRD、OCTO型多孔支架壓力分布最不均勻，這是由于FRD、OCTO型支架相對復雜的內部結構引起的，并導致壓力分布差別較大，但支架的壓力對稱分布。D、G型支架流體壓力分布不對稱，有流體壓力較為集中的部分，這是由于D、G型支架結構受限于TPMS數學表達式，不對稱的多孔結構引起組織液聚集導致的。對比I-WP型與I-WP型拓撲骨小梁支架的壓力分布云圖，I-WP型拓撲骨小梁支架相互貫通，解決了多個流體域壓力差異大的問題，即I-WP型拓撲支架流體壓力分布較為均勻，且最大壓力減小了38%。
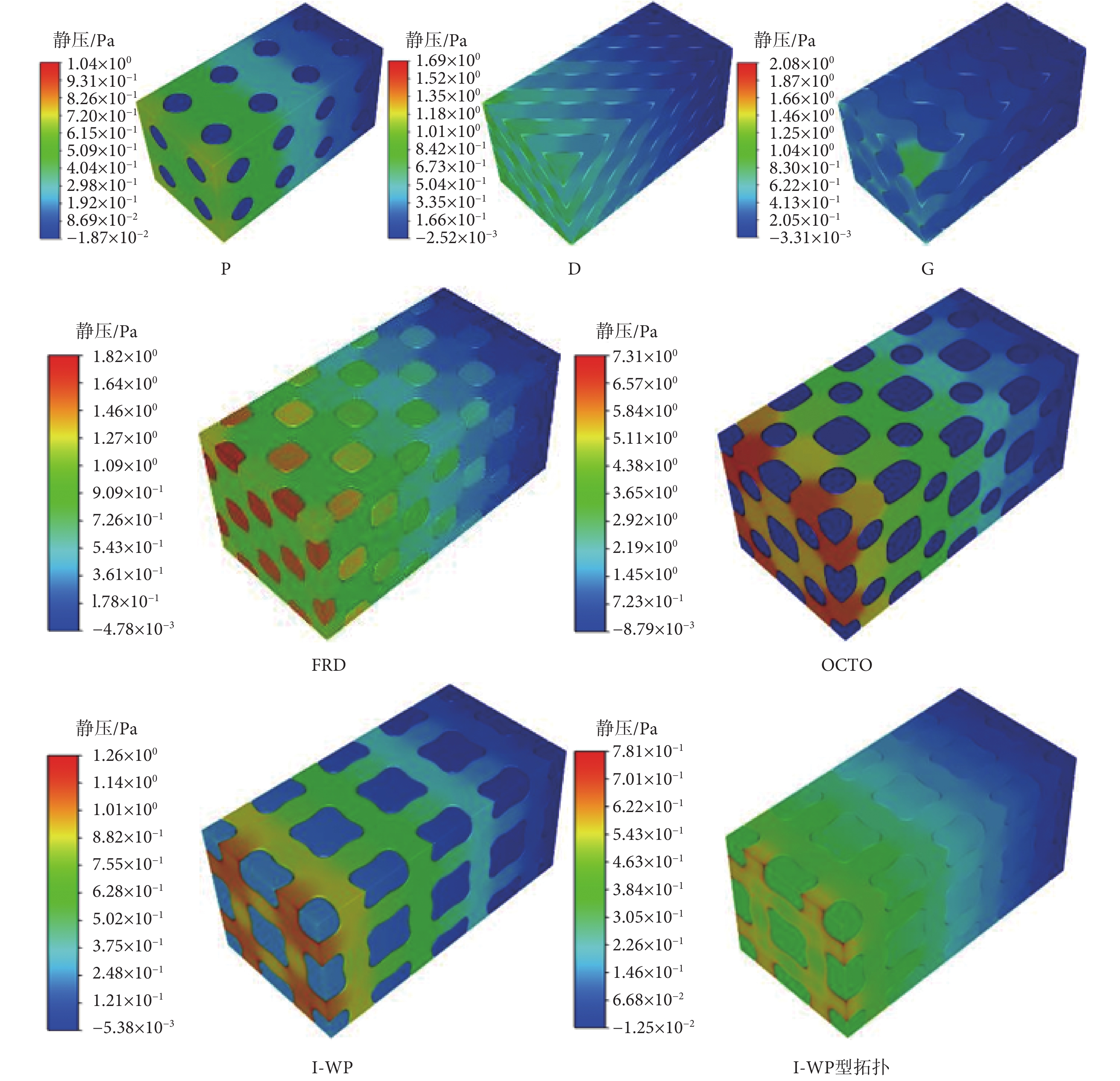圖10
TPMS支架壓力分布云圖
Figure10.
TPMS scaffolds pressure distribution nephograms
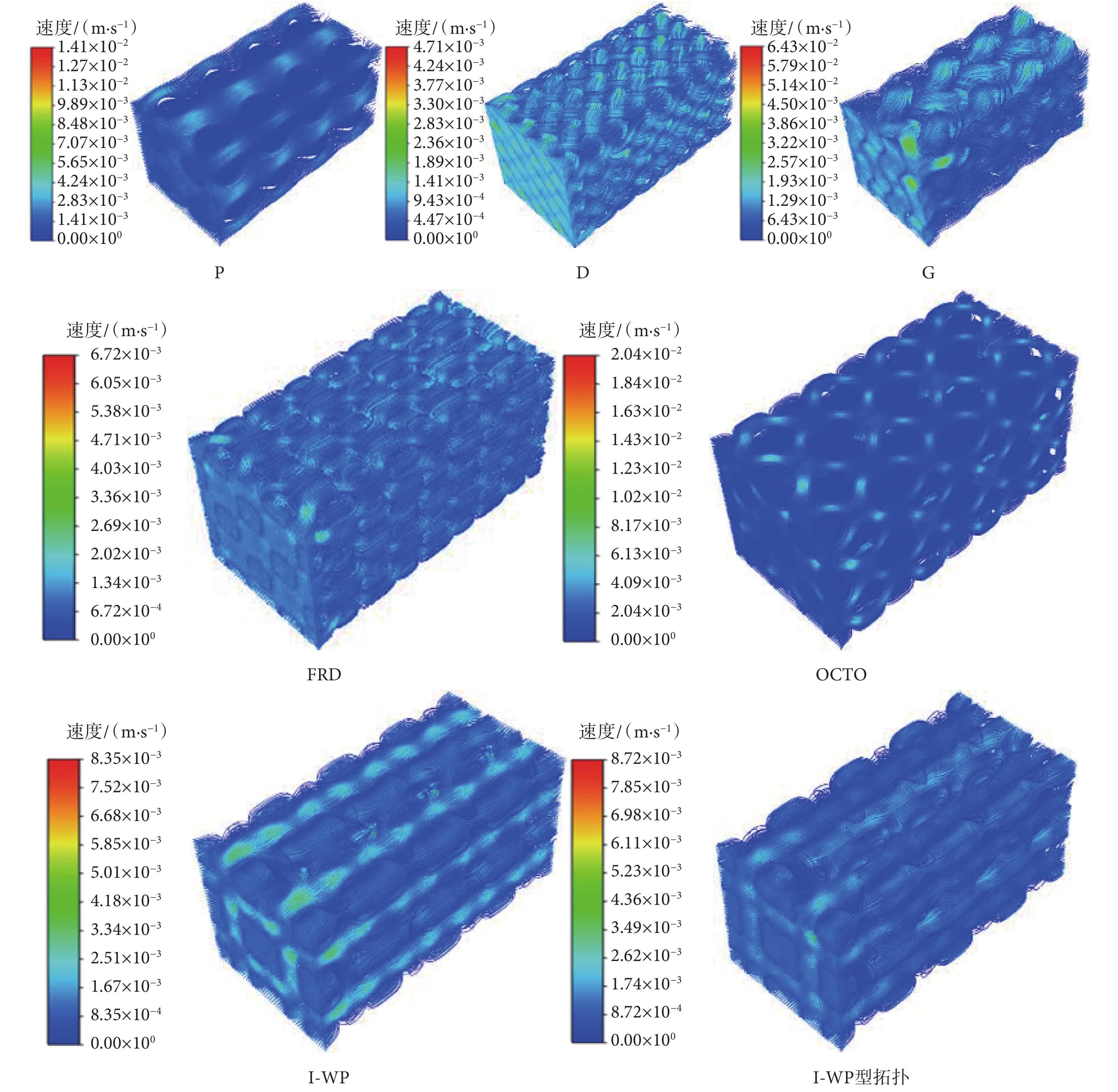
如圖11所示，TPMS支架內液體速度跡線規則，且相對均勻分布。D、G型支架速度跡線分布相對P、FRD、OCTO、I-WP型支架沒有那么均勻，這是由于D、G型支架不對稱的多孔結構導致流體多次轉向，速度變化較大。對比I-WP型與I-WP型拓撲支架的速度跡線圖，I-WP型拓撲支架流體速度均勻分布，最大流速變化不大，改善了I-WP型支架流體速度差異大的問題。
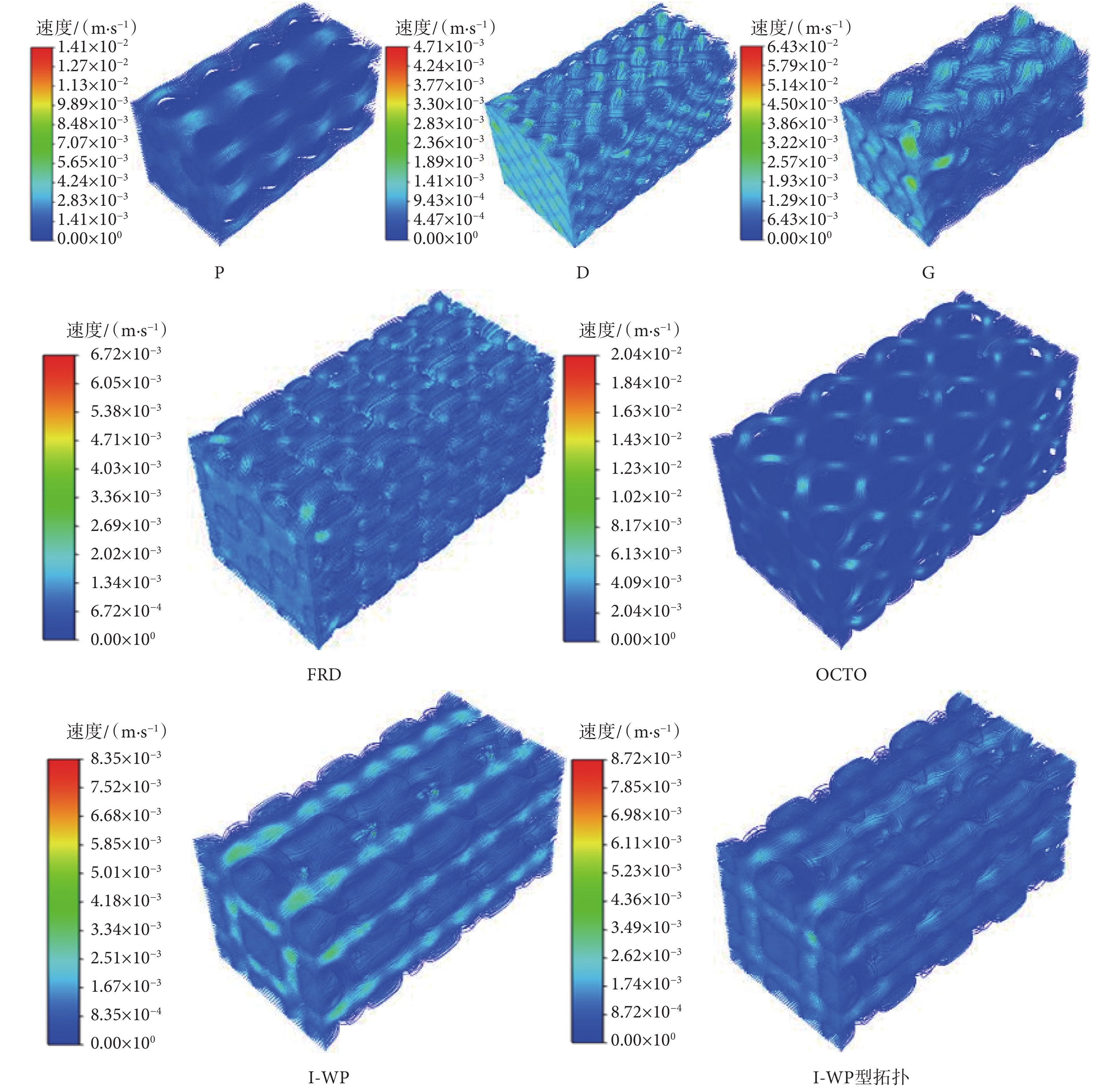圖11
TPMS支架速度跡線圖
Figure11.
TPMS scaffolds velocity trace diagram
7種TPMS支架的入口最大壓力、入口平均壓力和滲透率如表2所示。7種支架的滲透率都在10?8的數量級，基本符合天然人骨滲透性的范圍［0.5 × 10?8 m2 < K < 5 × 10?8 m2］[28]。P型、D型、G型、I-WP型支架減小孔隙率，滲透率減小，滲透率有很大的變化空間。如圖4所示，FRD型支架孔隙率90.5%，相比前面四種支架滲透率變化空間較小。OCTO型支架孔隙率93.1%，滲透率0.734 × 10?8 m2，滲透性能較差。I-WP型支架拓撲優化后滲透率比拓撲優化前提升了52.3%，滲透率變化空間更大，滲透性能更好，更有利于運輸營養物質及促進骨組織長入支架結構。
表2
TPMS支架滲透率
Table2.
TPMS scaffolds permeability
3 討論
目前，多孔生物支架的設計方法主要包括標準多面體法、拓撲優化法、隱式曲面法、泰森鑲嵌法、成型后體外處理法、醫學圖像設計法[29]。標準多面體法設計的結構相對簡單，制造效率高、制造成本低，但結構的力學性能和滲透性能較差[30-31]。拓撲優化法可以對多孔生物支架進行優化設計，提高支架的力學性能和滲透性能，但涉及變量多，模型計算量大[32]。泰森鑲嵌法可以模仿天然骨梯度多孔結構，但模型成本較高，需要著重考慮支柱直徑，避免過小的支柱對支架力學性能的影響[33]。成型后體外處理法主要用于支架的后處理，以提高支架的各項性能，對支架的材料有一定要求[34]。醫學圖像設計法適合于個性化醫療，可以設計和天然骨基本一樣的內部結構，但結構通用性極差，成本較高[35]。本文所提的TPMS支架，力學性能和滲透性較好，可以在此基礎上進行多種模型優化，提升支架性能。除此之外，TPMS支架具有各向異性，可以滿足不同方向上的性能要求[9]，所以本文選擇TPMS方法構建骨小梁多孔支架。
本文研究發現，相同曲面壁厚、相同周期的不同類型TPMS支架由于結構的差異導致孔隙率有所不同，但比表面積差別不明顯。本文重點以I-WP型支架為對象開展研究，發現周期對支架孔隙率的影響程度大于曲面壁厚，曲面壁厚對支架比表面積的影響程度大于周期。隨著周期的增加，應力分布趨于均勻；隨著壁厚的增加，應力分布基本不變，但高應力區域減小，低應力區域增大。通過調整I-WP型支架曲面壁厚、周期參數，支架孔隙率在68.01%～96.48%范圍內，等效彈性模量在0.655～18.602 GPa范圍內，滿足人體骨植入物力學性能的要求。對于I-WP型支架的設計，應該優先考慮調節支架周期，后調節支架壁厚，以滿足支架力學性能的要求。
對比不同類型TPMS支架，I-WP型支架應力分布、流體壓力分布均勻，不容易引起組織液聚集。對I-WP型支架進行拓撲優化后，支架質量由0.631 4 g降低到0.617 0 g，減小了2.28%；支架等效彈性模量由2.304 GPa降低到2.271 GPa，減小了1.43%。拓撲優化后的支架最大應力為393.1 MPa，減小1.53 MPa，基本沒有出現應力集中現象。I-WP型支架拓撲優化后的滲透率相比拓撲優化前提升了52.3%，最大流體壓力減小了38%，明顯提升了支架的滲透性能，更符合骨組織支架設計要求。
本文研究為骨植入物支架的設計提供了一種新的選擇，但本文目前只對I-WP型支架進行了壓縮力學性能和滲透性能的仿真分析，如果將I-WP多孔支架進行應用，還必須考慮使用環境和各向異性、彎曲、疲勞、沖擊、斷裂等的力學性能，并開展力學實驗和生物實驗等測試，對多孔支架的力學性能和生物相容性進行全面評價。
4 結論
本文基于TPMS方法參數化構建I-WP型多孔結構，為I-WP型多孔結構骨植入物的應用提供技術基礎。研究發現，I-WP型支架與P、D、G、FRD、OCTO型支架相比，具有良好的壓縮力學性能和滲透性能；不同曲面壁厚（0.1～0.2 mm）、不同周期（I-WP 1～I-WP 5）的I-WP型支架的孔隙率在68.01%～96.48%范圍內，等效彈性模量在0.655～18.602 GPa范圍內，符合人體骨的彈性模量（0.1～23.0 GPa）需求；對結構進行優化設計后，最大流體壓力減小了38%，滲透性提升了52.3%；周期對支架孔隙率的影響程度大于曲面壁厚，曲面壁厚對支架比表面積的影響程度大于周期；隨著周期的增加，應力分布趨于均勻，隨著曲面壁厚的增加，應力分布基本不變，但高應力區域減小，低應力區域增大。為了達到設定的力學性能要求，可以先調控周期參數，后調控壁厚參數。最后，期望通過本文研究能為多孔骨植入物的設計提供新的選擇和參考數據。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：湯紹燦負責骨小梁支架構建、有限元仿真和論文撰寫；門玉濤負責仿真與數據分析指導及論文審閱修訂；陳煒負責課題背景調研；劉福龍負責行文構思；張春秋負責文章主持與計劃安排。
0 引言
近年來，增材制造這一新興技術的快速發展，極大地促進了多孔骨植入物的研究[1]。增材制造技術是以計算機輔助設計（computer aided design，CAD）模型為依據，利用對材料逐層累加堆積的方法進行實體制造成型的一種技術[2]。很多傳統加工難以處理的復雜結構部件可以通過三維（three dimensional，3D）打印技術增材制造，其加工的多孔結構可以用作組織替代材料[3]。多孔支架可以根據人體骨骼彈性模量調整孔隙率、孔徑等參數，實現支架與自身骨骼力學性能的匹配，從而減少由實體植入物引起的應力遮擋效應，并降低術后并發癥的發生率[4]。已有研究表明，孔徑范圍為300～600 μm、孔隙率在50%～90%的相互連通的多孔結構通常被認為適合促進骨形成和毛細血管的形成[5]。多孔結構植入物還具有較大的比表面積和良好的連通性，可促進細胞遷移和黏附，有助于營養和氧氣流動，并能促進人體骨骼和其自身之間的生物固定[6]。鑒于孔隙率和比表面積是骨植入物的兩個重要參數，因此在對多孔支架進行設計時，研究結構的孔隙率和比表面積對力學性能的影響非常重要。
三周期極小曲面（triply periodic minimal surface，TPMS）是一種在三個獨立方向具有周期性且平均曲率為零的隱式等值曲面[7]。TPMS在自然界廣泛存在，將其作為骨組織植入體具有廣闊的前景[8]。TPMS可通過三角函數來表達，改變其閾值大小可以實現對孔徑參數的調整，實現多孔結構呈梯度變化[9]。TPMS最大的優勢是可以通過公式精確控制多孔支架孔形狀、孔徑尺寸、孔隙率、比表面積等內部孔隙結構參數[10]。目前，很多學者已經對基于TPMS方法的多孔結構展開研究。Wang[11]提出了一種基于TPMS的周期性曲面建模方法，實現了多孔支架的參數化建模。Yoo [12]提出了基于距離場的TPMS多孔支架設計方法，發現控制TPMS閾值可實現多孔支架孔隙率線性變化。Melchels等[13]構建了一種孔隙率梯度變化的螺旋二十四面體（gyroid，G）型多孔支架。鄧珍波等[14]構建了立方體（cube，C）、菱形（diamond，D）、G型3種支架，并進行力學實驗分析，發現80%左右孔隙率D型支架與天然骨組織的最大抗壓強度匹配性最好。Yang等[15-17]通過S形生長曲線函數（sigmoid function）和高斯徑向基函數（Gaussian radial basis function，GRBF）實現不同類型TPMS支架邊界融合過渡。劉佳辛等[18]構建了原始（primitive，P）、G、D型多孔支架，研究發現相同周期和壁厚的多孔支架中P型支架的孔隙率最大，應力分布更均勻。Liu等[19]將偏置測地B樣條曲線和測地線泰森網格相結合，設計了一種基于TPMS的復合多孔結構，并對不同周期和壁厚下的P型復合多孔結構孔隙率、最大應力和等效彈性模量進行研究；研究結果顯示，該方法不僅可以通過合理選擇TPMS的固有參數實現結構優化，而且可以根據應力分布，通過控制泰森位置分布和測地B樣條曲線的偏移來實現結構優化。由此可見，目前基于TPMS方法構建的P、D、G型支架的性能研究較多，而I型包裝（I-wrapped package，I-WP）、F-菱形十二面體（F-rhombic dodecahedra，FRD）、八面體-立方八面體-四方八面體（octahedra-cuboctahedra-tetragonal octahedron，OCTO）型支架函數表達式和結構較復雜，研究較少，其性能特性還不清楚。
為了解決上述問題，本文基于TPMS方法構建了I-WP型支架，與P、D、G、FRD、OCTO型支架進行比較，采用有限元方法研究多孔支架的壓縮性能和滲透性能，參數化分析曲面壁厚、周期對I-WP型多孔支架形態參數和力學性能的影響，利用變密度法對I-WP型支架進行拓撲優化，以提高支架的滲透性能。本研究期望構建的I-WP型支架具有良好的力學性能，作為一種潛在的骨科植入多孔結構，能滿足修復人體骨組織的要求，為構建適合骨組織工程需要的支架結構提供新選擇和參考數據。
1 材料和方法
1.1 TPMS參數化建模
1.1.1 TPMS數學模型
極小曲面是平均曲率為零的隱式等值曲面。與文獻[11]提及的參數化模型相比，TPMS更常采用隱式表達式描述[20]，如式(1)所示：
|
其中，φ(r)為TPMS等值面數值；k為晶格數量；π為圓周率；Ak為振幅因子；λk為周期波長；r為歐式空間位置矢量；hk為倒數空間中第k個晶格矢量；Pk為相位偏移；C為閾值常量。
TPMS表達式中變量x、y、z前的參數分別控制對應方向上的孔徑，參數越大，孔徑越小，閾值C可以控制多孔支架孔隙率大小且呈現線性關系[16]。如表1所示，為6種TPMS表達式。
表1
TPMS表達式
Table1.
TPMS expression
1.1.2 TPMS支架參數化建模
本文基于三維建模軟件Rhino7.0（Robert McNeel & Assoc.inc，美國）進行TPMS支架構建，并配合編程語言Grasshopper（Robert McNeel & Assoc.inc，美國）進行參數化控制。模型設計尺寸為10 × 10 × 20 mm3，周期為2，應用克拉克細分（Catmull-Clark）命令對模型進行細分，得到精度更高的平滑TPMS曲面模型。然后對模型進行網格重建，將重建后的零厚度TPMS曲面進行空間等距偏移加厚，獲得任意厚度的骨小梁多孔結構，如圖1所示。周期為2、壁厚為0.1 mm的6種類型的TPMS支架，如圖2所示。
圖1
TPMS支架創建流程
Figure1.
TPMS scaffold creation process
圖2
TPMS支架模型
Figure2.
TPMS scaffold model
1.2 壓縮仿真條件設置
將6種TPMS支架模型導入有限元分析軟件ANSYS 2020 R2（ANSYS Inc.，美國）中進行有限元分析。支架采用醫療領域常用的鈦合金材料，密度為4 620 kg/m3，彈性模量為110 GPa，泊松比0.3，屈服強度為950 MPa[18]。將模型上下端面與剛體板施加接觸約束，摩擦系數0.45，為鈦合金與鑄鐵摩擦系數。在上剛體板面施加軸向位移（X = 0.05 mm），為支架軸向總長0.25%，支架處于彈性階段，如圖3左側所示。TPMS支架采用四面體單元，網格大小為0.15 mm。剛體板采用六面體單元，網格大小為0.3 mm。
圖3
I-WP型支架有限元仿真邊界條件
Figure3.
Boundary conditions for finite element simulation of I-WP type scaffold
1.3 拓撲優化
拓撲優化是一種根據設定的載荷大小、邊界約束和優化條件，對結構內材料分布進行優化設計的數學方法[21]。基于TPMS方法構建的I-WP型多孔支架，屬于體心立方結構，中心收縮，向頂點伸出8個支撐。由于I-WP型支架側壁由封閉曲面連接，不利于運輸營養物質，從而影響骨生長。本文基于變密度法對I-WP型支架進行拓撲優化，在支架結構剛度幾乎不變的條件下，提高結構滲透性，促進骨長入。變密度法采用固體各向同性材料懲罰（solid isotropic material with penalization，SIMP）模型[22]，通過密度函數關系對模型進行優化。
設定目標函數為支架剛度最大，設置拓撲區域和排除區域，設置質量分數97%為約束條件，得到拓撲優化后的支架模型。
1.4 流體仿真條件設置
將6種TPMS支架模型導入流體力學數值計算軟件Fluent 2020 R2（ANSYS Inc.，美國），進行流體性能仿真分析。支架的計算流體動力學（computational fluid dynamics，CFD）分析使用不可壓縮穩態層流的靜止納維-斯托克斯（Navier-Stokes）方程。液相部分使用杜爾貝科改良伊格爾培養基（Dulbecco’s modified Eagle medium，DMEM）在37 ℃（平均人體溫度）下的流體特性：動態粘度η = 1.45 × 10?3 Pa·s；密度ρ = 1 000 kg/m3[23]。
在達西定律的適用性范圍內，將入口液體流速V設置為1 mm/s，出口壓力設置為零，支架的壁面設置為無滑移條件，如圖3右側所示。達西定律數學表達式[24]如式(2)所示：
|
其中，K為滲透率；L為支架的軸向長度；為壓降；v為入口處的速度；為DMEM的粘度。
2 結果
2.1 TPMS支架形態參數分析
2.1.1 不同類型TPMS對支架孔隙率、比表面積的影響
如圖4所示，周期為2、壁厚為0.1 mm的6種TPMS支架模型的孔隙率P > G > OCTO > I-WP > D > FRD，孔隙率在90.50%～95.26%范圍內。比表面積變化不大，變化范圍為20.135～20.281 mm?1。比表面積越大，越有利于細胞增殖和黏附，促進骨長入。由此趨勢可得，在構建相同曲面壁厚、周期的TPMS支架時，TPMS的類型是影響多孔結構孔隙率的重要因素。
圖4
不同類型TPMS支架孔隙率與比表面積
Figure4.
Porosity and specific surface area of different types of TPMS scaffolds
2.1.2 曲面壁厚、周期對I-WP型支架孔隙率、比表面積的影響
如圖5所示，不同周期（I-WP 1～I-WP 5）、不同壁厚（0.1～0.2 mm）的I-WP型支架孔隙率在68.01%～96.48%范圍內，比表面積在10.349～20.351 mm?1范圍內。如圖5左側所示，隨著壁厚的增加，I-WP型支架的孔隙率線性降低；隨著周期數增大，支架的孔隙率降低，且周期對孔隙率的影響程度大于厚度。如圖5右側所示，隨著壁厚的增加，I-WP型支架的比表面積降低；隨著周期數增大，支架的比表面積升高，但周期對I-WP型支架的比表面積影響很小，且隨著壁厚的增加，周期的影響越來越小。設計I-WP型支架應該優先考慮周期，后對厚度進行調整，可以很好地調節支架的孔隙率與比表面積。
圖5
曲面壁厚、周期對結構形態參數的影響
Figure5.
The influence of surface wall thickness and period on structural morphological parameters
2.2 TPMS支架壓縮性能
2.2.1 不同類型TPMS支架有限元結果分析
對周期為2、厚度為0.1 mm的不同類型TPMS支架施加軸向位移0.05 mm工況下的等效應力云圖，如圖6所示。可以看出，P、G、I-WP型支架相比D、FRD、OCTO型支架，應力集中區域不明顯。D、FRD、OCTO型支架應力集中區域較多，結構容易發生損壞，尤其是OCTO型支架有多處應力集中區域，容易發生斷裂和疲勞現象。G型支架在邊緣處出現應力集中現象，這是由于G型支架邊緣彎曲的曲面導致的。P型與I-WP型支架邊緣為近似圓環結構，可以很好地分散應力，減小應力集中。綜上，I-WP型支架應力分布均勻，支架強度更好，對提高支架強度具有一定的研究價值。
圖6
不同類型TPMS支架的等效應力云圖
Figure6.
Von Mises stress nephogram of different types of TPMS scaffolds
2.2.2 I-WP型支架有限元結果分析
如圖7所示，為不同周期（I-WP 1～I-WP 5）、不同壁厚（0.1～0.2 mm）的I-WP型支架在200 N縱向壓力工況下的等效應力云圖。可以看出，I-WP 1支架應力集中較為明顯，尤其是結構中心收縮區域應力較高。隨著周期的增加，I-WP型支架應力分布趨于均勻，應力集中變得不明顯，支架結構穩定性增強；隨著厚度的增加，I-WP型支架應力分布基本不變，但高應力區域減小，低應力區域增大，基本沒有應力集中現象，支架結構穩定性增強。設計I-WP型支架應該優先調整周期，后對壁厚進行調整，可以很好地控制多孔結構的應力分布情況，避免應力集中。
圖7
不同I-WP型支架的等效應力云圖
Figure7.
Von Mises stress nephogram of different I-WP scaffolds
2.2.3 多孔結構力學性能分析
周期為2、厚度為0.1 mm的不同類型TPMS支架的等效彈性模量圖，如圖8左側所示。結合孔隙率圖，如圖4左側所示，比較不同類型TPMS支架的計算結果，發現在相同的周期和壁厚條件下，支架的等效彈性模量在0.489～4.003 GPa范圍內，等效彈性模量基本上隨著孔隙率的降低而升高，而I-WP型支架的等效彈性模量偏低，可以看出I-WP型支架在降低應力遮擋效應上更具有優勢。
圖8
多孔結構等效彈性模量比較圖
Figure8.
Comparison chart of equivalent elastic modulus of porous structures
如圖8右側所示，通過對比不同周期（I-WP 1～I-WP 5）、不同壁厚（0.1～0.2 mm）I-WP型支架等效彈性模量，發現隨著壁厚增大，等效彈性模量線性增大。隨著周期增大，等效彈性模量增大，且周期較大的多孔結構等效彈性模量變化范圍更大。本文設計的I-WP型支架等效彈性模量在0.655～18.602 GPa范圍內。
人松質骨的楊氏模量范圍為0.1～4.5 GPa，皮質骨的楊氏模量范圍為5～23 GPa [25-27]。綜上所述，I-WP型支架等效彈性模量在人體骨的彈性模量范圍內。
2.3 I-WP型支架拓撲優化
如圖9所示，I-WP型支架最大應力為394.63 MPa，設置優化目標為保留質量分數97%。為保證多孔單元結構的完整性和整體支架的尺寸不變，外邊界為排除區域。密度在0.0～0.4區域為可刪除區域，在軸向應力較小處增加開孔。經拓撲優化后，支架最大應力為393.10 MPa，減小了1.53 MPa，基本沒有出現應力集中現象，兩者最大應力值均小于鈦合金屈服強度950 MPa。拓撲優化后，支架質量由0.631 4 g降低到0.617 0 g，減小2.28%，即優化后質量是優化前質量的97.72%；支架等效彈性模量由2.304 GPa降低到2.271 GPa，減小1.43%，基本符合設計要求。
圖9
拓撲優化
Figure9.
Topology optimization
2.4 TPMS支架流體力學分析
如圖10所示，隨著組織液的流入，壓力逐漸減小。入口處流體域靠近組織液，壓力較大，出口處壓力為零。TPMS支架有2個流體域，導致流體域之間流體壓力有一定差異，壓力云圖可以看出明顯的分層。FRD、OCTO型多孔支架壓力分布最不均勻，這是由于FRD、OCTO型支架相對復雜的內部結構引起的，并導致壓力分布差別較大，但支架的壓力對稱分布。D、G型支架流體壓力分布不對稱，有流體壓力較為集中的部分，這是由于D、G型支架結構受限于TPMS數學表達式，不對稱的多孔結構引起組織液聚集導致的。對比I-WP型與I-WP型拓撲骨小梁支架的壓力分布云圖，I-WP型拓撲骨小梁支架相互貫通，解決了多個流體域壓力差異大的問題，即I-WP型拓撲支架流體壓力分布較為均勻，且最大壓力減小了38%。
圖10
TPMS支架壓力分布云圖
Figure10.
TPMS scaffolds pressure distribution nephograms
如圖11所示，TPMS支架內液體速度跡線規則，且相對均勻分布。D、G型支架速度跡線分布相對P、FRD、OCTO、I-WP型支架沒有那么均勻，這是由于D、G型支架不對稱的多孔結構導致流體多次轉向，速度變化較大。對比I-WP型與I-WP型拓撲支架的速度跡線圖，I-WP型拓撲支架流體速度均勻分布，最大流速變化不大，改善了I-WP型支架流體速度差異大的問題。
圖11
TPMS支架速度跡線圖
Figure11.
TPMS scaffolds velocity trace diagram
7種TPMS支架的入口最大壓力、入口平均壓力和滲透率如表2所示。7種支架的滲透率都在10?8的數量級，基本符合天然人骨滲透性的范圍［0.5 × 10?8 m2 < K < 5 × 10?8 m2］[28]。P型、D型、G型、I-WP型支架減小孔隙率，滲透率減小，滲透率有很大的變化空間。如圖4所示，FRD型支架孔隙率90.5%，相比前面四種支架滲透率變化空間較小。OCTO型支架孔隙率93.1%，滲透率0.734 × 10?8 m2，滲透性能較差。I-WP型支架拓撲優化后滲透率比拓撲優化前提升了52.3%，滲透率變化空間更大，滲透性能更好，更有利于運輸營養物質及促進骨組織長入支架結構。
表2
TPMS支架滲透率
Table2.
TPMS scaffolds permeability
3 討論
目前，多孔生物支架的設計方法主要包括標準多面體法、拓撲優化法、隱式曲面法、泰森鑲嵌法、成型后體外處理法、醫學圖像設計法[29]。標準多面體法設計的結構相對簡單，制造效率高、制造成本低，但結構的力學性能和滲透性能較差[30-31]。拓撲優化法可以對多孔生物支架進行優化設計，提高支架的力學性能和滲透性能，但涉及變量多，模型計算量大[32]。泰森鑲嵌法可以模仿天然骨梯度多孔結構，但模型成本較高，需要著重考慮支柱直徑，避免過小的支柱對支架力學性能的影響[33]。成型后體外處理法主要用于支架的后處理，以提高支架的各項性能，對支架的材料有一定要求[34]。醫學圖像設計法適合于個性化醫療，可以設計和天然骨基本一樣的內部結構，但結構通用性極差，成本較高[35]。本文所提的TPMS支架，力學性能和滲透性較好，可以在此基礎上進行多種模型優化，提升支架性能。除此之外，TPMS支架具有各向異性，可以滿足不同方向上的性能要求[9]，所以本文選擇TPMS方法構建骨小梁多孔支架。
本文研究發現，相同曲面壁厚、相同周期的不同類型TPMS支架由于結構的差異導致孔隙率有所不同，但比表面積差別不明顯。本文重點以I-WP型支架為對象開展研究，發現周期對支架孔隙率的影響程度大于曲面壁厚，曲面壁厚對支架比表面積的影響程度大于周期。隨著周期的增加，應力分布趨于均勻；隨著壁厚的增加，應力分布基本不變，但高應力區域減小，低應力區域增大。通過調整I-WP型支架曲面壁厚、周期參數，支架孔隙率在68.01%～96.48%范圍內，等效彈性模量在0.655～18.602 GPa范圍內，滿足人體骨植入物力學性能的要求。對于I-WP型支架的設計，應該優先考慮調節支架周期，后調節支架壁厚，以滿足支架力學性能的要求。
對比不同類型TPMS支架，I-WP型支架應力分布、流體壓力分布均勻，不容易引起組織液聚集。對I-WP型支架進行拓撲優化后，支架質量由0.631 4 g降低到0.617 0 g，減小了2.28%；支架等效彈性模量由2.304 GPa降低到2.271 GPa，減小了1.43%。拓撲優化后的支架最大應力為393.1 MPa，減小1.53 MPa，基本沒有出現應力集中現象。I-WP型支架拓撲優化后的滲透率相比拓撲優化前提升了52.3%，最大流體壓力減小了38%，明顯提升了支架的滲透性能，更符合骨組織支架設計要求。
本文研究為骨植入物支架的設計提供了一種新的選擇，但本文目前只對I-WP型支架進行了壓縮力學性能和滲透性能的仿真分析，如果將I-WP多孔支架進行應用，還必須考慮使用環境和各向異性、彎曲、疲勞、沖擊、斷裂等的力學性能，并開展力學實驗和生物實驗等測試，對多孔支架的力學性能和生物相容性進行全面評價。
4 結論
本文基于TPMS方法參數化構建I-WP型多孔結構，為I-WP型多孔結構骨植入物的應用提供技術基礎。研究發現，I-WP型支架與P、D、G、FRD、OCTO型支架相比，具有良好的壓縮力學性能和滲透性能；不同曲面壁厚（0.1～0.2 mm）、不同周期（I-WP 1～I-WP 5）的I-WP型支架的孔隙率在68.01%～96.48%范圍內，等效彈性模量在0.655～18.602 GPa范圍內，符合人體骨的彈性模量（0.1～23.0 GPa）需求；對結構進行優化設計后，最大流體壓力減小了38%，滲透性提升了52.3%；周期對支架孔隙率的影響程度大于曲面壁厚，曲面壁厚對支架比表面積的影響程度大于周期；隨著周期的增加，應力分布趨于均勻，隨著曲面壁厚的增加，應力分布基本不變，但高應力區域減小，低應力區域增大。為了達到設定的力學性能要求，可以先調控周期參數，后調控壁厚參數。最后，期望通過本文研究能為多孔骨植入物的設計提供新的選擇和參考數據。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：湯紹燦負責骨小梁支架構建、有限元仿真和論文撰寫；門玉濤負責仿真與數據分析指導及論文審閱修訂；陳煒負責課題背景調研；劉福龍負責行文構思；張春秋負責文章主持與計劃安排。
