理想的骨折內固定植入物剛度應具有隨時間變化的性能，使骨折在不同愈合階段都能產生合理的力學刺激，可降解材料可以滿足這一性能。考慮到材料降解過程的時間依賴性，提出一種具有時變剛度的骨折內固定植入物復合結構拓撲優化設計方法。采用相對密度和降解殘留率描述兩種具有不同降解速度和彈性模量的材料分布和降解狀態，建立降解模擬-力學分析耦合數學模型；基于變密度法設計雙材料復合結構，使之具有時變剛度特性。以脛骨骨折治療用的接骨板為例，采用所提出方法設計具有時變剛度特性的復合結構接骨板，優化結果顯示高剛度的材料1形成柱狀的支撐結構，低剛度的材料2分布在降解邊界和內部。利用骨重塑模擬模型對優化后的接骨板進行評估，經過11個月重塑，使用可降解時變剛度接骨板、鈦合金接骨板和不銹鋼接骨板的骨痂平均彈性模量分別為8 634、8 521、8 412 MPa，表明使用可降解時變剛度接骨板可使骨痂取得更好的重塑效果。
引用本文： 孫浩, 丁曉紅, 徐世鵬, 段朋云, 熊敏, 張橫. 具有時變剛度的骨折內固定植入物結構設計及骨重塑效果評估. 生物醫學工程學雜志, 2024, 41(3): 595-603. doi: 10.7507/1001-5515.202311037 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
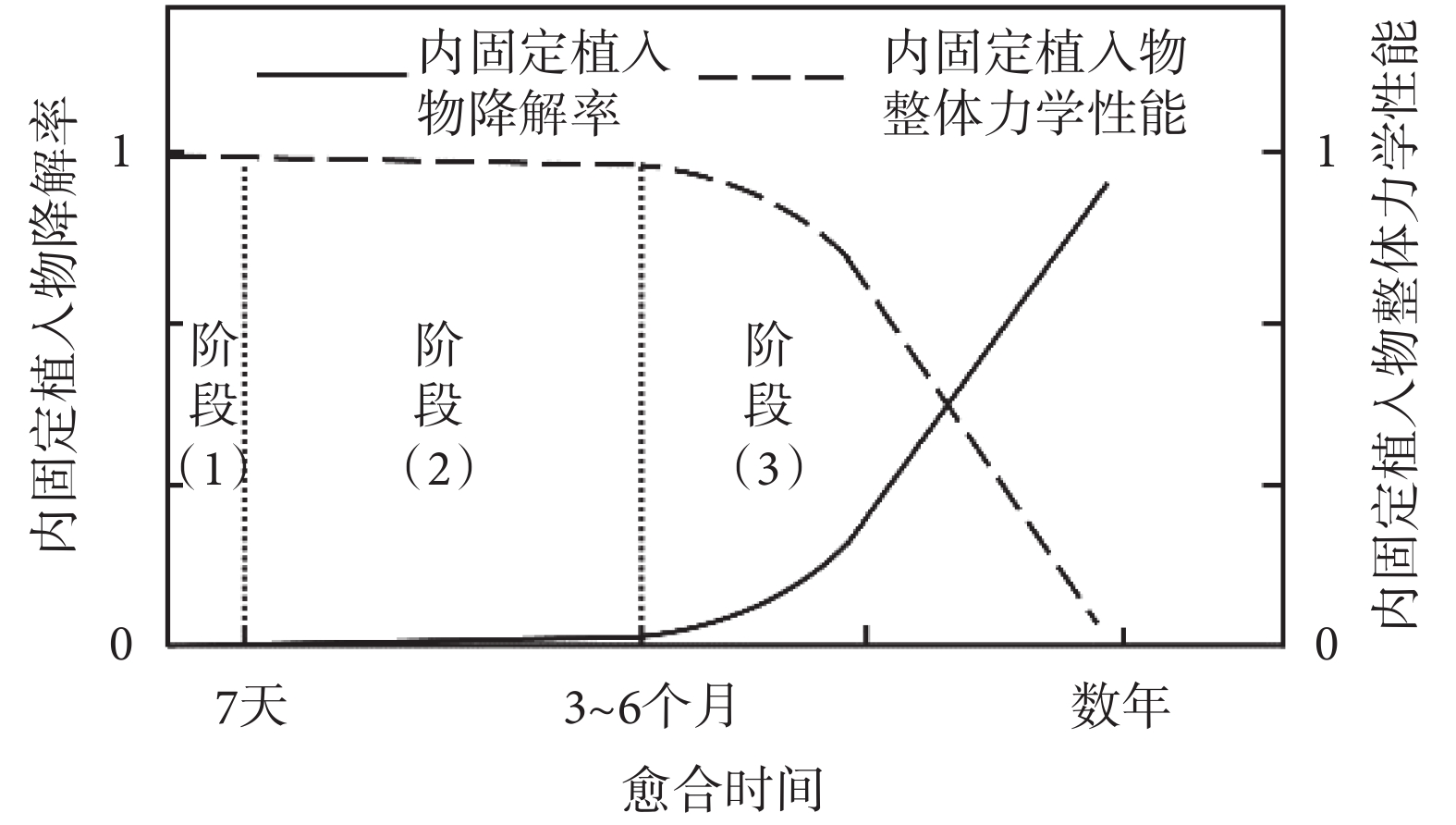
骨折是一種常見的創傷性疾病，內固定術是最為常用且有效的骨折治療方法。骨折愈合是一個力學調控和生物調控的復雜過程，骨折內固定植入物需要在治療初期提供足夠的支持和穩定性，隨著骨愈合的進行，內固定植入物的剛度逐漸降低，實現力流向斷骨處轉移，促進骨愈合[1-3]。這要求內固定植入物的剛度應隨時間發生變化（時變剛度），而使用可降解材料設計的植入物可滿足這一要求。參考文獻[4]，繪制具有時變剛度的理想可降解植入物的力學性能隨骨折愈合過程的變化趨勢圖（見圖1），骨愈合過程可以分為三個階段：炎癥期（階段1）、骨痂形成期（階段2）、骨痂重塑期（階段3）。內固定植入物的時變剛度如虛線所示，在炎癥期和骨痂形成期，骨折處血腫逐漸被肉芽組織代替，最終骨化成為編織骨，此時骨痂的彈性模量較低，植入物需要提供良好的固定穩定性；在骨痂重塑期，骨骼逐漸恢復到健康骨骼狀態，植入物剛度以較快的速率降低，使應力逐漸向骨痂轉移，在骨折完全愈合之后，內固定植入物的剛度接近零。因此如何設計內固定植入物結構，使其剛度特性符合骨愈合規律的要求是一個亟待解決的問題。
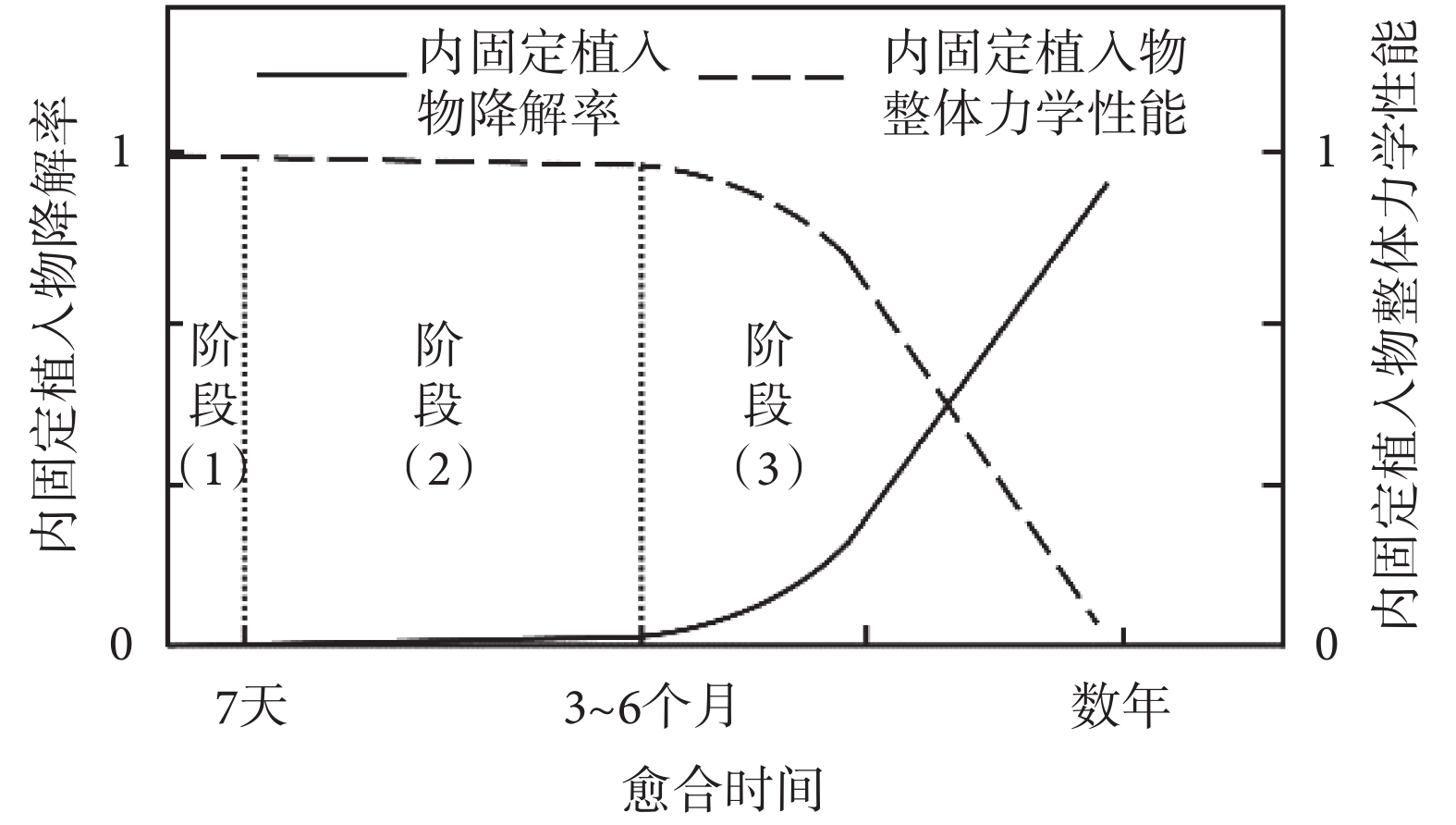圖1
理想骨折內固定植入物降解率與力學性能變化趨勢
Figure1.
The degradation rate and mechanical trend of ideal fracture internal fixation implants
目前可降解內固定植入物的設計主要通過合金化、冷加工、熱處理和表面改性等方法改變可降解材料的降解行為，使其具有與骨愈合相匹配的剛度[5-7]。結構拓撲優化設計方法通過設計結構的材料分布使結構得到所需的力學性能，Wu等[8]通過考慮骨重塑過程的時間依賴性，推導了時域的靈敏度，開發了一種新的下頜骨接骨板拓撲優化方法，但未考慮骨固定板降解；Chandra等[9]考慮到生物降解過程中鋼板的尺寸、均勻的降解率和整個過程中鋼板的固定穩定性，設計了一種可生物降解的植入鋼板，卻忽視了材料降解對結構的影響。由于內固定植入物的力學性能隨降解時間發生變化，而力學性能的變化會影響骨愈合效果，因此如何模擬降解過程，并量化材料降解對內固定植入物結構力學性能的影響，設計具有時變剛度的內固定植入物使之符合骨愈合規律的要求，具有重要的意義。目前，通過拓撲優化設計方法對可降解內固定植入物進行結構設計以改變可降解材料降解行為的研究仍較少[10-11]。
本文提出一種具有時變剛度的骨折內固定植入物復合結構拓撲優化設計方法，建立考慮結構降解的有限元模型，獲得降解過程中中間結構的力學性能，通過結構拓撲優化實現具有不同降解速度和彈性模量的雙材料可降解植入物，并利用骨重塑模擬模型對設計結果的時變剛度性能和骨重塑效果進行評估。
1 可降解結構的力學分析
1.1 具有時變剛度特性的復合結構設計構思
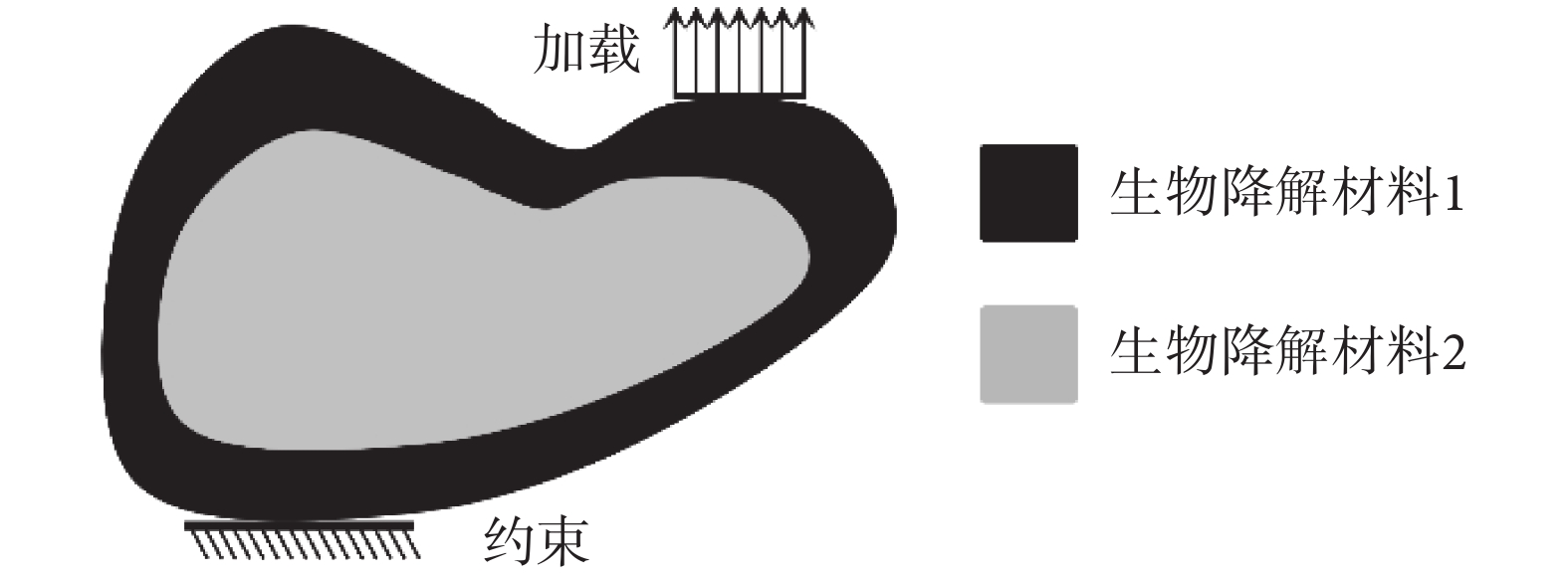
目前，單一材料的可降解內固定植入物的剛度很難與骨愈合周期相匹配，會出現降解過快發生固定失效和降解過慢導致應力屏蔽[12-14]，因此考慮采用兩種不同的可降解材料。如圖2所示，生物降解材料1降解速度慢、剛度大，材料2性能與其完全相反。在給定的邊界條件下，在設計域內確定兩種材料的最優布局，以實現在早期結構剛度緩慢降低，而后期結構剛度能夠以相對較快速率降低。
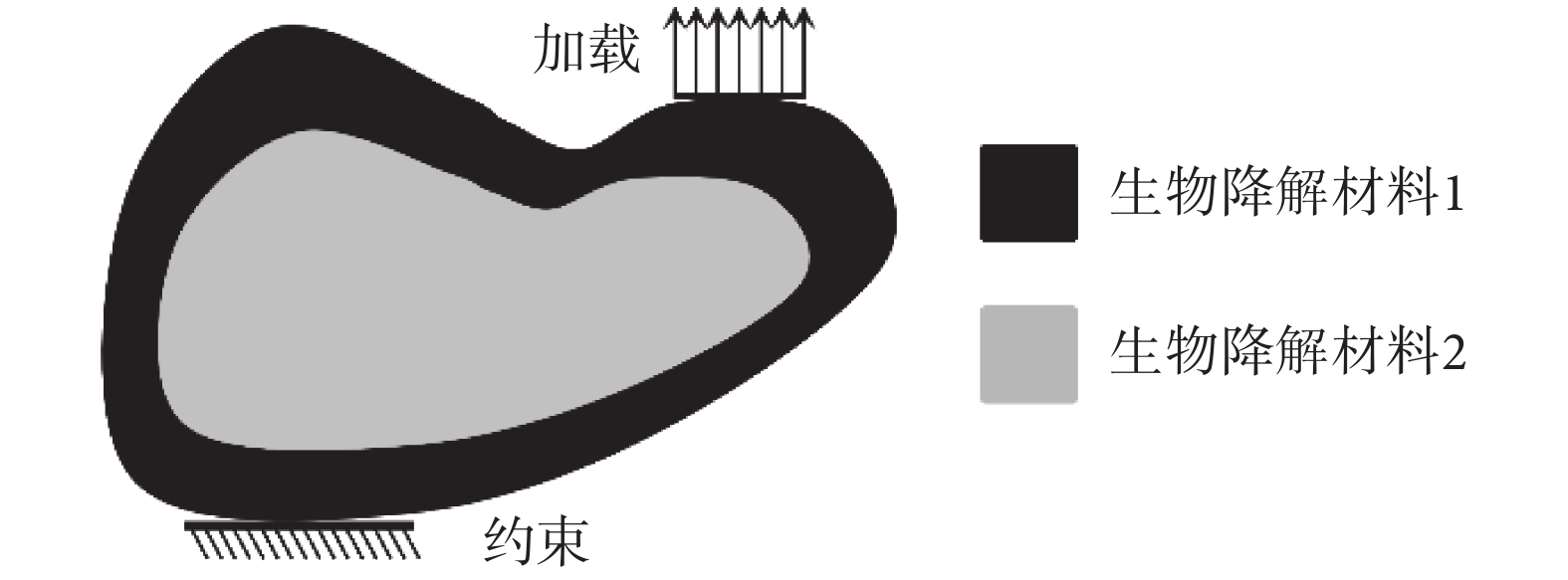圖2
考慮時變剛度特性的復合結構設計
Figure2.
Design of composite structures considering time-varying stiffness characteristics
1.2 問題描述
進行內固定植入物的拓撲優化設計，模擬結構的降解過程并量化材料降解對結構性能的影響是研究的關鍵。分別使用相對密度(xe)和降解殘留率(ye)描述兩種材料的分布和降解狀態，如式(1)～(2)所示。通過xe決定單元e為材料1還是材料2；通過ye表示降解狀態，ye = 1，代表單元e完全未降解，ye = ymin代表單元e完全降解。
 |
 |
式中，xmin和ymin取0.001；m為單元個數。
1.3 結構降解模擬-力學分析耦合模型
采用均勻腐蝕方法，以平均降解率模擬結構的降解[15-16]。為簡化模擬過程，假設：① 降解只發生在材料的固液交界處且均勻進行，降解邊界隨材料的降解而移動；② 材料的降解具有均一的降解速率，不考慮其他環境參數（如溫度、pH值等）；③ 腐蝕環境相同，忽略貼近骨面和貼近組織的兩面對降解速率的影響。需要說明的是，均勻腐蝕與實際腐蝕存在一定的差異，實際腐蝕是一個隨機過程，不僅和腐蝕環境有關，而且存在一定的不確定性。但降解實驗表明，以均勻腐蝕模擬結構的降解與降解實驗中隨機腐蝕降解的質量損失率差距在0.1%以內[17]，表明均勻降解模擬方法是可行的。
降解模擬過程如圖3所示，單元顏色由深到淺表示材料從未開始降解到完全降解，可降解邊界使用黑色粗虛線表示。圖3a為結構網格，圖3b為降解過程，降解過程示意如圖3b1～3b5所示。其中從b1到b3可降解邊界處的一層單元格顏色逐漸由深變淺，表示該層單元逐漸降解；從b3到b4，可降解邊界從外層單元移動到相鄰的內層單元；然后從b4到b5內層單元開始降解。在一個降解時間步完成后，對其降解結果進行結構性能分析，獲得結構性能隨時間的變化關系。單元降解的數學表達為：
圖3
降解過程示意圖
a. 結構網格；b. 降解過程；c. 單元
a. meshes of the structure; b. simulation of structure degradation; c. the location mark of element
 |
式中，i表示降解時間步，de表示單元e的降解速率，t為單位降解時間步的時間。
單元e和相鄰單元位置標記如圖3c所示，單元e的位置為(k, l)。通過判斷降解單元相鄰單元的狀態，來決定該單元是否發生降解，為了保證數值計算的穩定，設定yb=0.1，當相鄰單元的殘留率小于yb時可沿該單元方向進行降解，如當yk ? 1,l < yb時，認為單元e能夠從左側開始降解，當yk + 1,l < yb時，認為單元e可以從右側開始降解，上下方向類似[18]。通過對相鄰單元降解狀態的判斷，單元e的降解速率可以表示為：
 |
式中，Ω表示e相鄰單元的集合；α表示Ω中的第α個單元；d為材料的降解速率；Nα由式(5)得到：
 |
為了便于求導，使用Heaviside方程將式(4)近似為連續方程，單元的降解方程可以改寫為：
 |
階躍函數H為：
 |
式中，γ是一個常數。
由式(3)和式(6)，單元e殘留率的更新方程為：
 |
使用Kreisselmeier-Steinhauser函數將式(8)最大函數問題近似為連續方程[19-20]：
 |
式中，γ = 6，η = 6。
結構平衡方程如式(10)所示：
 |
式中，K是結構的整體剛度矩陣，由于材料的降解，K與時間相關；U為位移向量；F為力向量。
對于可降解結構，K由單元剛度矩陣ke與ye組裝得到，ye是關于降解速率d和降解時間i的函數。將材料降解對結構力學性能的影響耦合到有限元分析過程中，可降解結構的剛度矩陣為：
 |
式中，B表示幾何矩陣；D為彈性系數矩陣；Ωe為單元的體積。
降解模擬算法包括以下步驟。步驟1：初始化殘留率ye，使用k和l對單元e進行標記；步驟2：判斷相鄰單元的降解狀態；步驟3：使用式(6)計算單元e的降解速率de；步驟4：使用式(9)計算單元e的殘留率ye；步驟5：根據ye，使用式(10)進行有限元分析；重復步驟1～5，直到指定的時間步td。
2 雙材料可降解結構的拓撲優化
優化設計的目的是通過確定兩種具有不同可降解性能的材料的最佳分布，使復合結構在指定降解時間步中間結構的剛度之和最大。使用結構柔順度表征結構剛度，可降解復合結構柔順度最小的優化數學模型可以表示為：
 |
式中，X為設計變量的集合；C為結構柔順度，?為降解時間步的集合；v1為復合結構中材料1的最終體積，f是給定的體積分數，v0為總體積。
為獲得輪廓清晰的優化結構，使用基于固體各向同性材料懲罰模型（solid isotropic material with penalization，SIMP）的材料插值機制：
 |
 |
式中，E為彈性模量；p為懲罰系數，取3.0；下標1、2分別表示可降解材料1、2。
2.1 靈敏度分析
在每個降解時間步對結構進行有限元分析，計算結構柔順度，其靈敏度可以通過求導得到。目標函數對于設計變量X的靈敏度可以表示為：
 |
結構柔順度C是關于xe、ye和i的函數：
 |
式中，u表示單元位移矩陣；k0為單元剛度矩陣。
根據式(16)定義的柔順度，在降解時間步i對設計變量xe的導數為：
 |
其中：
 |
 |
 |
材料1的體積為：
 |
則材料1的體積對于設計變量xe的導數為：
 |
為克服棋盤格效應，采用基于Heaviside的靈敏度過濾方法使密度變量的值趨近0或1。使用如式(23)所示的Heaviside方程對中間密度場xei進行過濾，xei由式(24)計算得到。
 |
 |
式中，β為常數，控制函數的平滑度，如果β = 0，則是原始的密度過濾器，如果β接近于無窮大，則Heaviside為階躍函數。本文取β的初始值為1，每100次迭代對β的值加倍，最大值為512。
2.2 優化設計流程
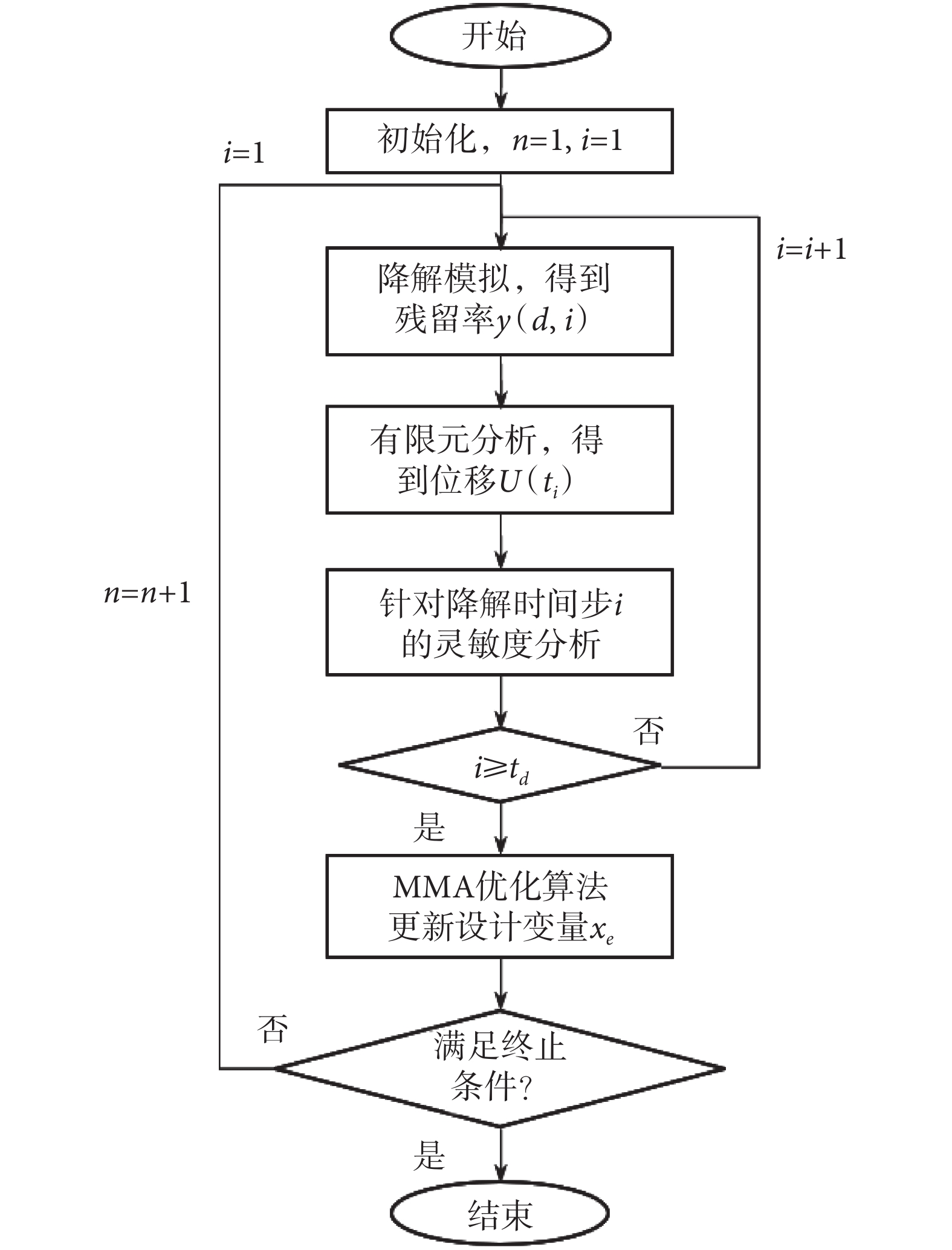
雙材料可降解結構的拓撲優化設計流程如圖4所示，主要步驟如下。
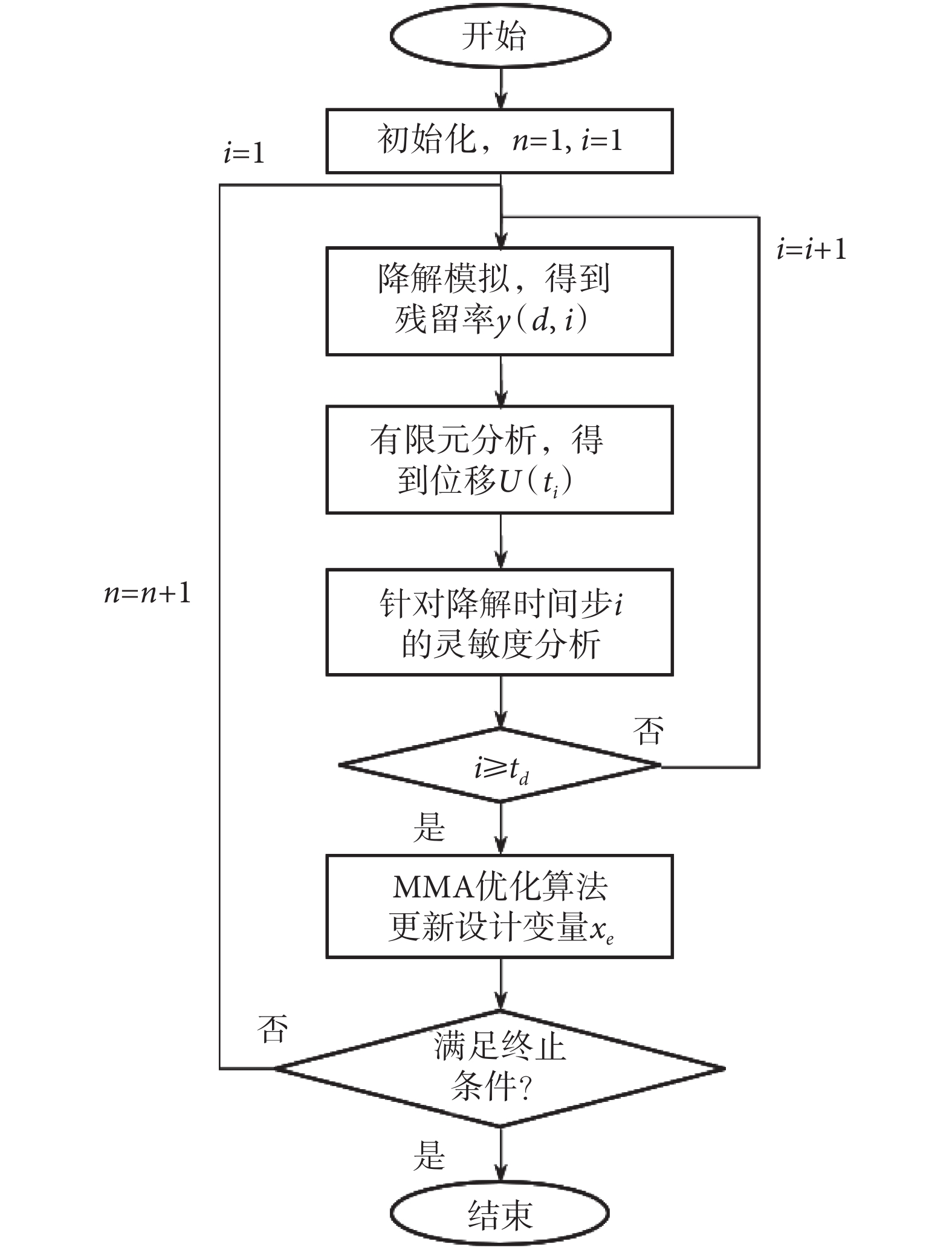圖4
雙材料可降解結構的拓撲優化設計流程
Figure4.
Topological optimization design process for dual material degradable structures
第一步：構造初始幾何模型并進行離散化。定義數學模型的參數，給定體積分數和過濾半徑，設置xe和ye的初始值，并定義可降解邊界、載荷和約束等邊界條件；第二步：根據式(9)進行降解模擬，計算得到殘留率；第三步：根據式(10)和(11)對考慮材料降解的復合結構進行有限元分析；第四步：根據式(15)進行靈敏度分析。重復第二步到第四步，直到指定的時間步。第五步：利用MMA優化算法更新設計變量；第六步：重復第二步到第五步，直到滿足約束條件或目標函數收斂。當滿足以下兩個條件之一時，迭代終止：① 連續兩次迭代的結構柔順度變化小于收斂判據；② 迭代步數達到指定值，本文中取100。
3 脛骨接骨板設計
3.1 設計模型及材料性能
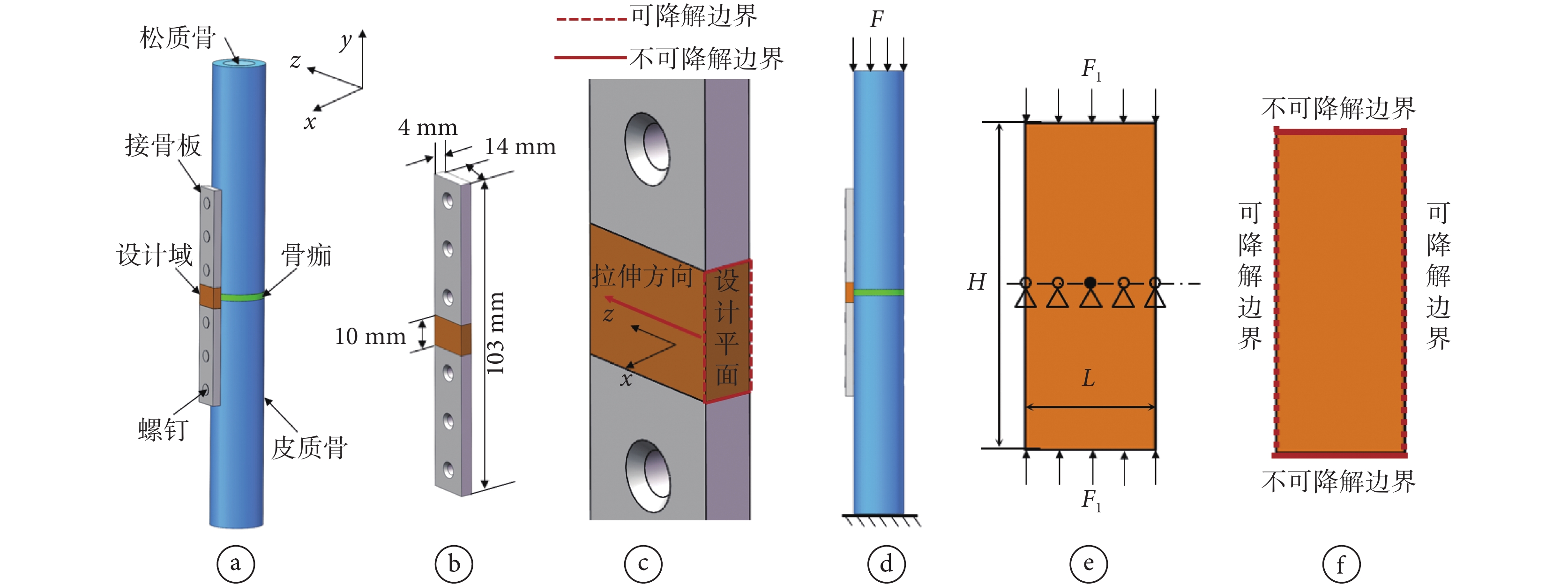
使用如圖5a所示的脛骨-接骨板系統簡化模型，接骨板的尺寸如圖5b所示，接骨板中間區域（橘黃色）為可降解結構，兩側（灰色）為不可降解結構。接骨板植入人體后，可降解結構垂直于x軸和z軸的四個面都能夠發生降解，其中垂直于x方向兩個面的面積較大，這兩個面的降解對結構剛度的影響也較大。為了將設計問題簡化，我們假定可降解結構僅能從垂直于x方向的兩個面發生降解，忽略垂直于z方向兩個面的降解。如圖5c所示，將垂直于z方向的面作為設計平面，利用考慮時變剛度特性的可降解復合結構拓撲優化設計方法對設計平面進行優化設計，然后沿z方向拉伸得到三維可降解復合結構，實現可降解接骨板的拓撲優化設計。
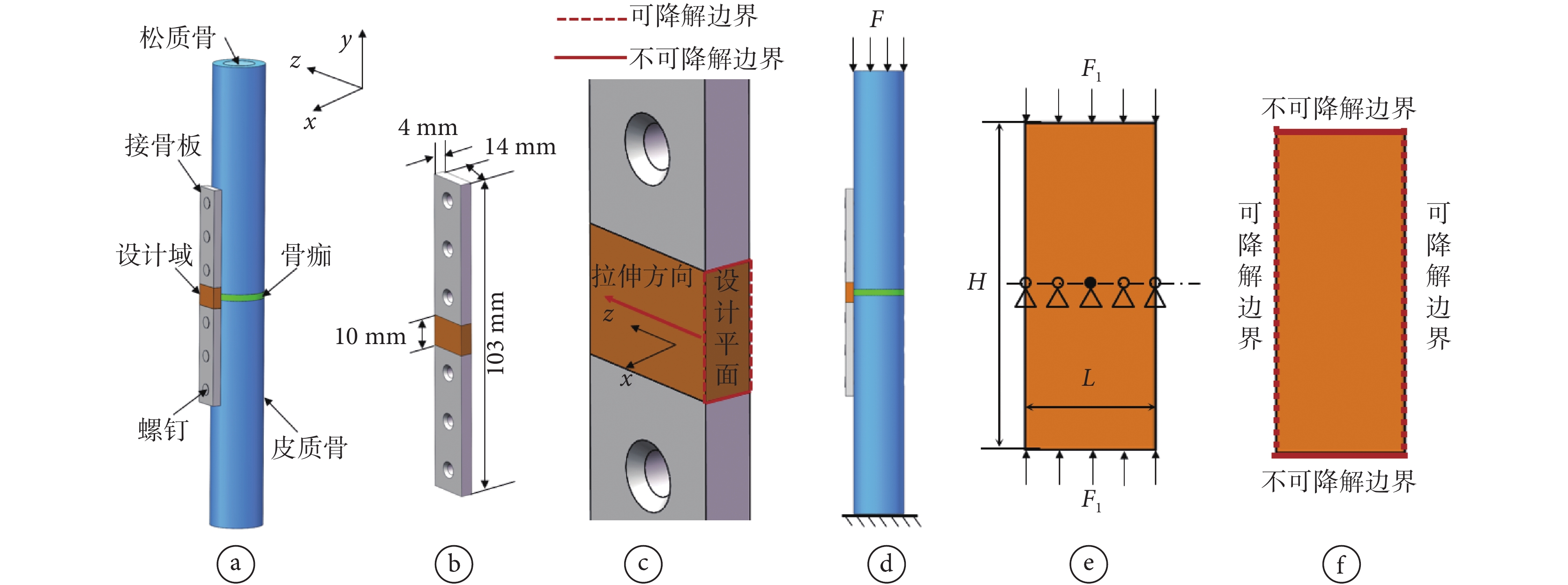圖5
脛骨-接骨板固定系統
a. 設計模型；b. 接骨板模型；c. 設計區域；d. 接骨板力學邊界條件；e. 接骨板的簡化模型；f. 降解邊界條件
Figure5. Bone and bone plate fixation systema. design model; b. bone plate model; c. design area; d. mechanical boundary conditions of bone plates; e. simplified model of bone plate; f. degradation boundary conditions
如圖5d所示，脛骨平臺的力學邊界條件可以簡化為底端全約束，頂端皮質骨受到垂直向下的載荷。骨愈合過程中，骨痂的剛度逐漸增大，但都遠小于接骨板的剛度，由于載荷分流，接骨板承擔大部分的載荷，設計平面的力學邊界條件簡化為圖5e所示，中心點全約束，中心線其余節點約束豎直方向自由度，上下邊受到垂直方向的壓力，F1 = 1 600 N。可降解邊界條件如圖5f所示，上下側為不可降解邊界，左右側為可降解邊界。根據文獻[12]，材料屬性如表1所示。
3.2 拓撲優化結果及其時變剛度特性分析
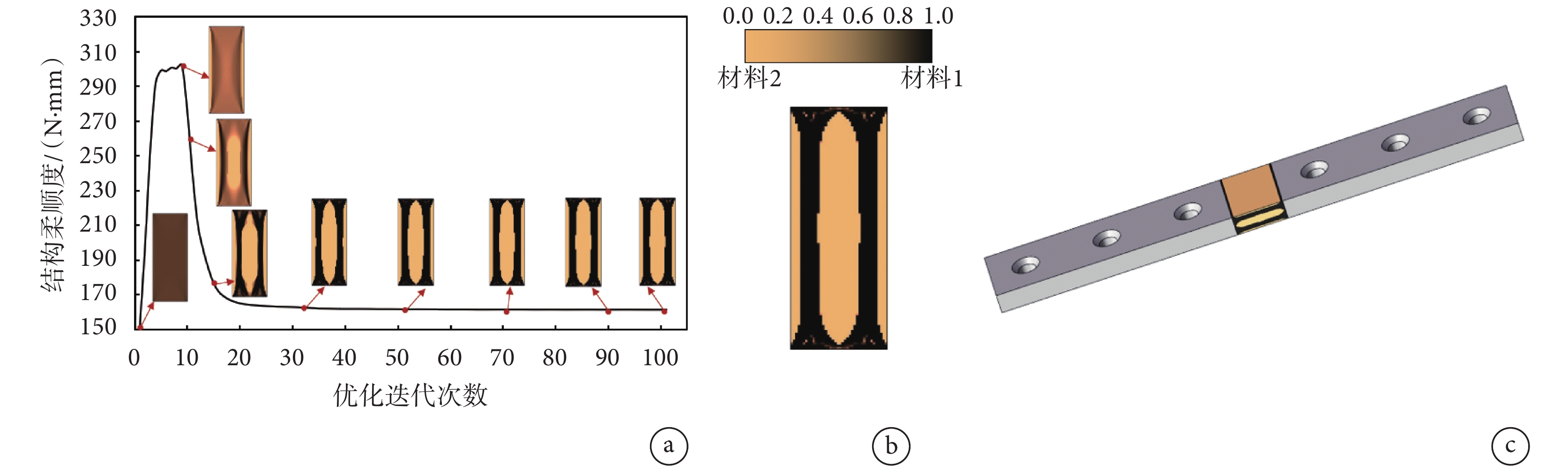
采用2.2小節的設計流程，使用尺寸為0.1 mm的四節點四邊形平面單元對設計域進行網格劃分，拓撲優化過濾半徑設置為單元尺寸的兩倍，材料1的體積分數為0.5，優化目標為第1和第90天中間結構柔順度之和最小。優化迭代歷程如圖6a所示，隨著迭代的進行逐漸獲得具有清晰邊界的材料分布輪廓，優化目標達到了收斂狀態。拓撲優化設計結果如圖6b所示，高剛度材料1（黑色）形成了柱狀的支撐結構，在可降解邊界處外層為材料2，結構左右呈現對稱性，高剛度材料1（黑色）主要分布在左右側可降解邊界處，在左右側中部形成V型開口，并在靠近加載側形成了類似X型的交叉結構，連接左右兩側的高剛度材料，提高了結構整體的穩定性。時變剛度接骨板設計結果如圖6c所示，兩側為惰性金屬，中間區域為可降解復合結構。需要說明的是，結構的最優拓撲形態主要與所受的載荷相關，本文采用了承受偏心壓力的圓柱模擬脛骨，考慮了實際脛骨承受的主要載荷為壓力和彎矩，因此圖6的設計結果具有合理性。
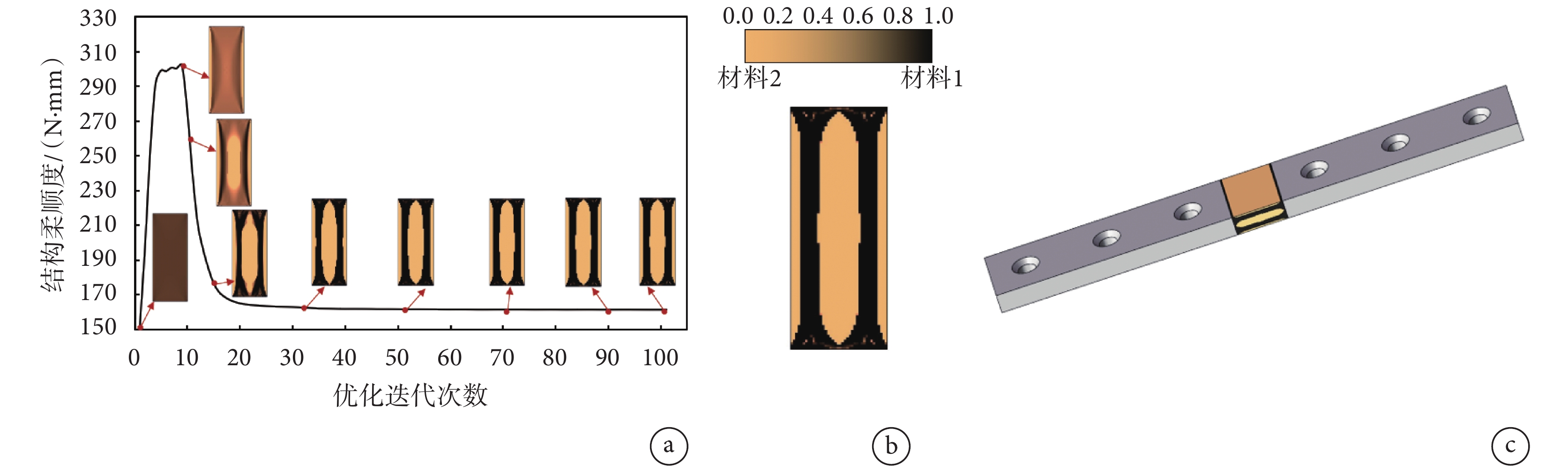圖6
拓撲優化設計結果
a. 拓撲優化迭代歷程；b. 二維設計結果；c. 可降解時變剛度接骨板
Figure6. Topology optimization design resulta. iteration history with two degradable interfaces; b. 2D design results; c. degradable time-varying stiffness plate
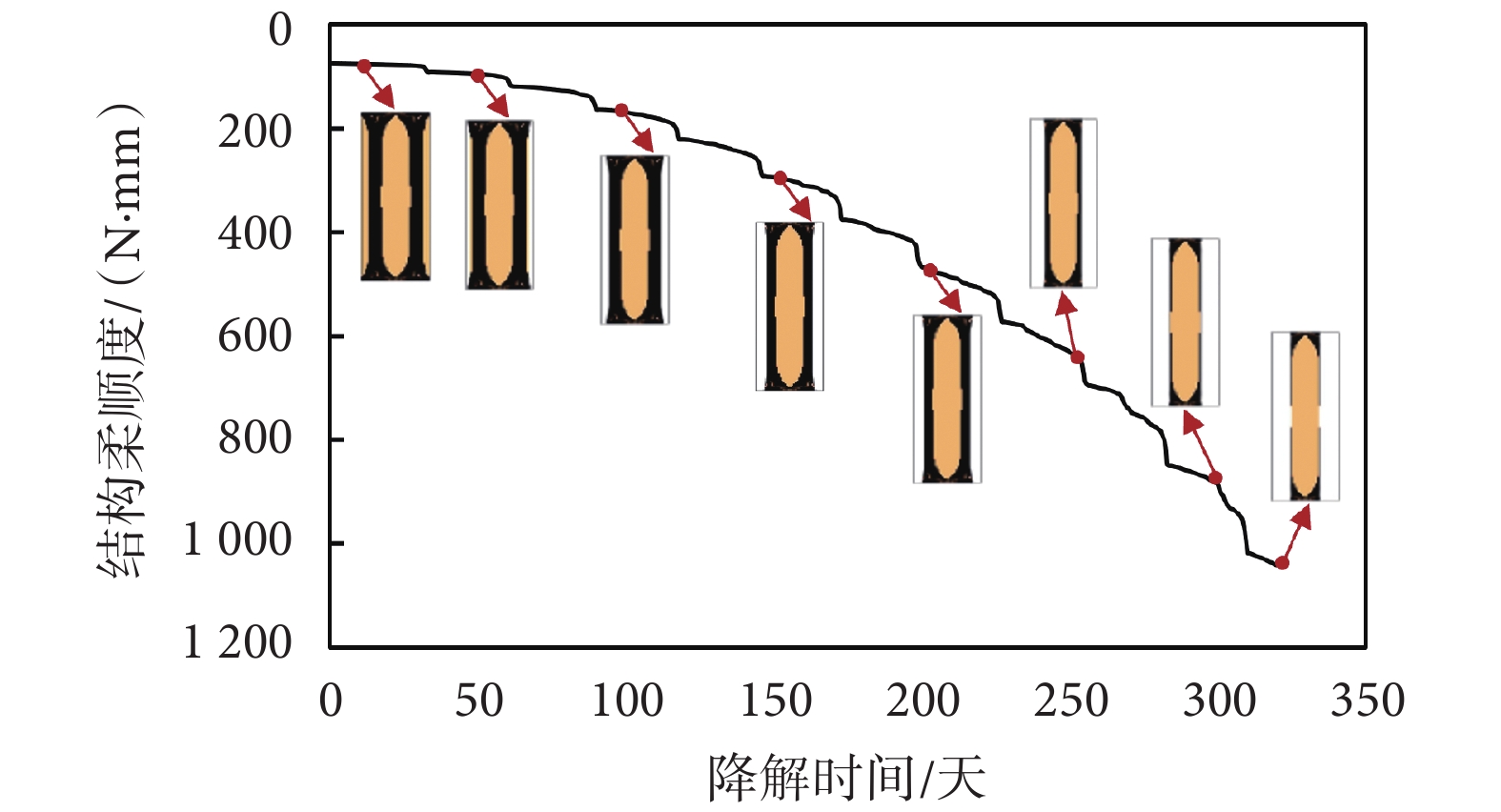
考慮時變剛度特性拓撲優化設計結果的降解過程如圖7所示。由于材料1剛度較大，其降解對結構剛度的影響程度較大。降解開始時，可降解邊界附近的材料2先逐漸降解，結構剛度緩慢下降。當外層的材料2降解完，結構內部的材料1開始降解，結構剛度下降的速度開始增大。
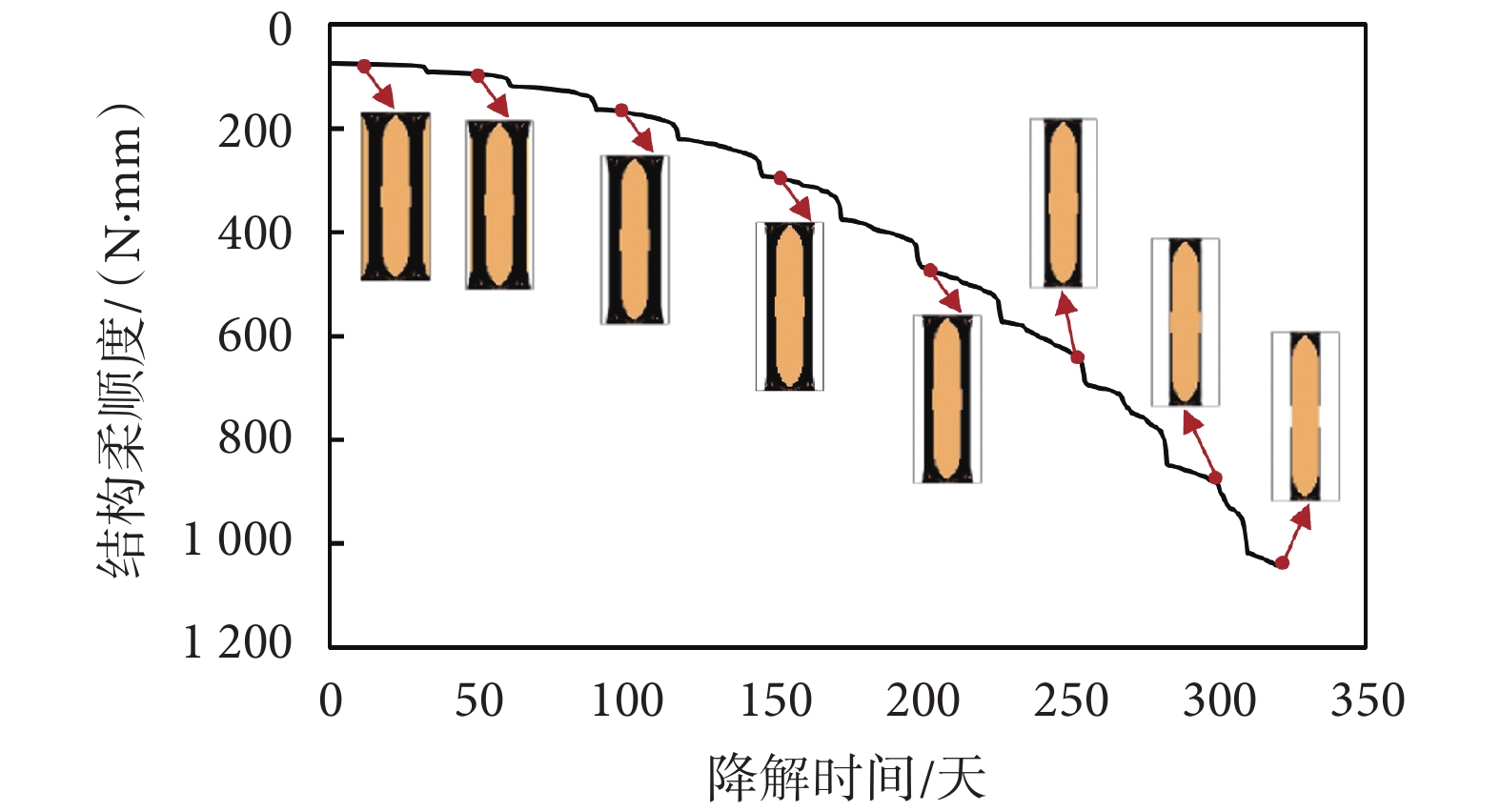圖7
考慮時變特性拓撲優化設計結果的降解過程
Figure7.
Degradation process of topology optimization design results considering time-varying characteristics
3.3 骨重塑效果評估
骨重塑是骨骼受到外部生物力學刺激時產生的一種自適應過程。骨重塑模擬模型能夠描述在生物力學刺激作用下骨密度隨時間的變化過程。利用應變能密度預測骨重塑過程[21-22]，力學刺激Ξ可以表示為：
 |
式中，U為應變能密度，ρ為骨密度。骨密度在一定時間間隔
t的變化量
ρ可以表示為：
 |
 |
 |
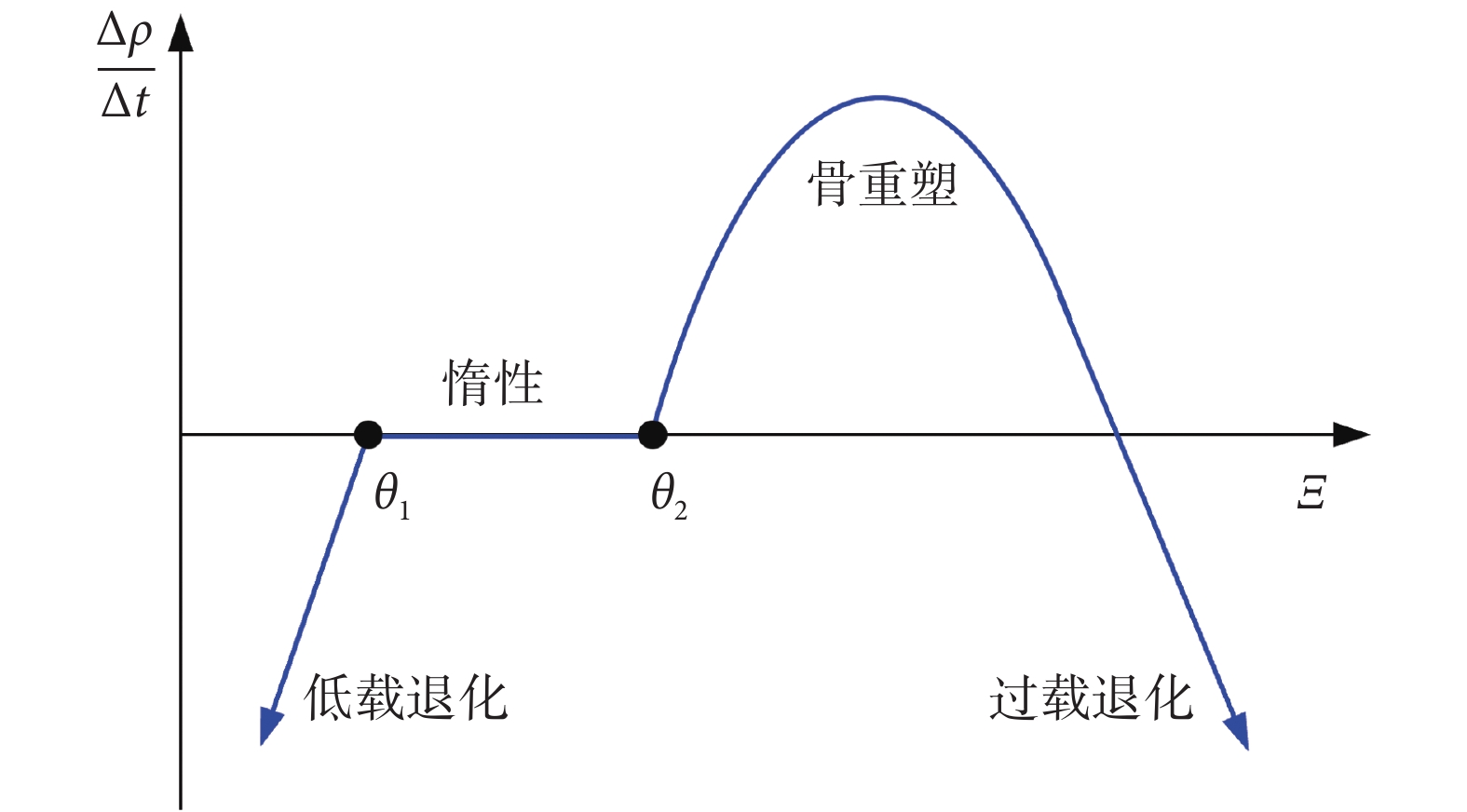
式中，t為時間；R1和R2為常數，分別取18 (g/cm3)2/(J/月)和600 (g/cm3)3/(J2/月)；θ1和θ2是力學刺激的閾值，分別由式(26)和(27)計算得到；s和δ為常數，分別取0.000 36 J/(g*cm3)和0.1。骨密度變化量與力學刺激之間的曲線描述如圖8所示，可以分為低載退化、惰性、骨重塑和過載退化四個區間。在低載退化和過載退化區間骨密度減小，在惰性區間骨密度不變，在骨重塑區間骨密度增大。
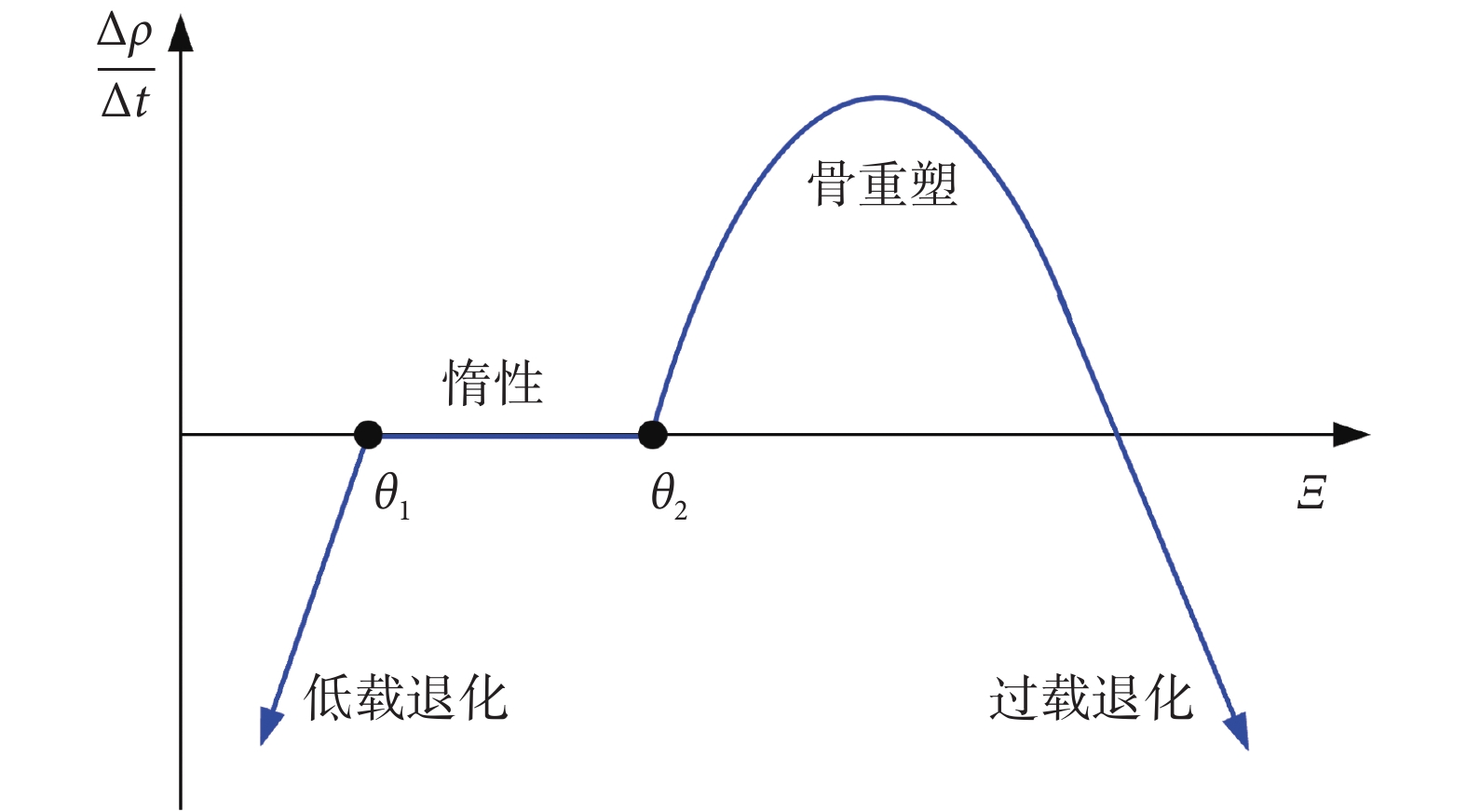圖8
骨密度變化率與力學刺激關系示意圖
Figure8.
The schematic of relationship between the rate of change in bone density and mechanical stimulus
假設發生骨重塑的骨材料屬性為各向同性，其彈性模量可以通過密度進行量化，經驗公式為：
 |
式中ζ為彈性模量；τ為常數，取3 790 MPa/(g/cm3)3。
使用圖5a所示的簡化模型模擬骨痂的重塑過程。邊界條件如圖5d所示，頂端受到垂直向下的載荷，底端全約束。載荷為普通人體重（70 kg）的三倍，即F = 2 100 N。骨痂的初始密度為1.0 g/cm3，最大為1.74 g/cm3，最小為0.1 g/cm3。接骨板除設計域外結構和螺釘為鈦合金，彈性模量為110 000 MPa。皮質骨和松質骨的彈性模量分別為15 750 MPa和1 100 MPa。不銹鋼的彈性模量為210 000 MPa。
采用彈性模量表征骨重塑過程的骨痂單元變化，平均彈性模量一定程度上能夠反映骨痂整體結構剛度的變化。骨痂的尺寸和初始狀態如圖9a所示，圖9b、c、d分別為使用可降解時變剛度接骨板、相同結構尺寸的鈦合金接骨板和不銹鋼接骨板固定時，經過6個月和11個月時的骨痂彈性模量分布云圖。接骨板位于骨痂的左側，由于接骨板造成的應力遮擋效應，靠近接骨板側的骨痂受到的力學刺激較小，因此彈性模量較低。與使用鈦合金接骨板和不銹鋼接骨板相比，使用可降解時變剛度接骨板時，骨痂重塑過程中左側彈性模量小于3 790 MPa的區域明顯較小。經過11個月重塑之后，使用可降解時變剛度接骨板時，骨痂彈性模量基本都大于3 790 MPa；而使用鈦合金接骨板和不銹鋼接骨板時，骨痂左側仍有部分區域彈性模量小于3 790 MPa。結果表明，使用可降解時變剛度接骨板可以使靠近接骨板側的骨痂在重塑過程中受到更多的力學刺激，有效地減緩應力遮擋效應，取得更好的重塑效果。對比相同重塑時間下使用三種接骨板的骨痂平均彈性模量的差值，結果如表2所示，隨著重塑的進行，三種骨板對應的骨痂的平均彈性模量均逐漸增大，使用可降解時變剛度接骨板時的骨痂平均彈性模量均高于鈦合金接骨板和不銹鋼接骨板，對比不同骨板的骨痂平均彈性模量的差值，隨著時間的增加差值逐漸變大，并且差值增大的速率也逐漸增大，說明可降解時變剛度接骨板的結構剛度減小的速率逐漸增大。
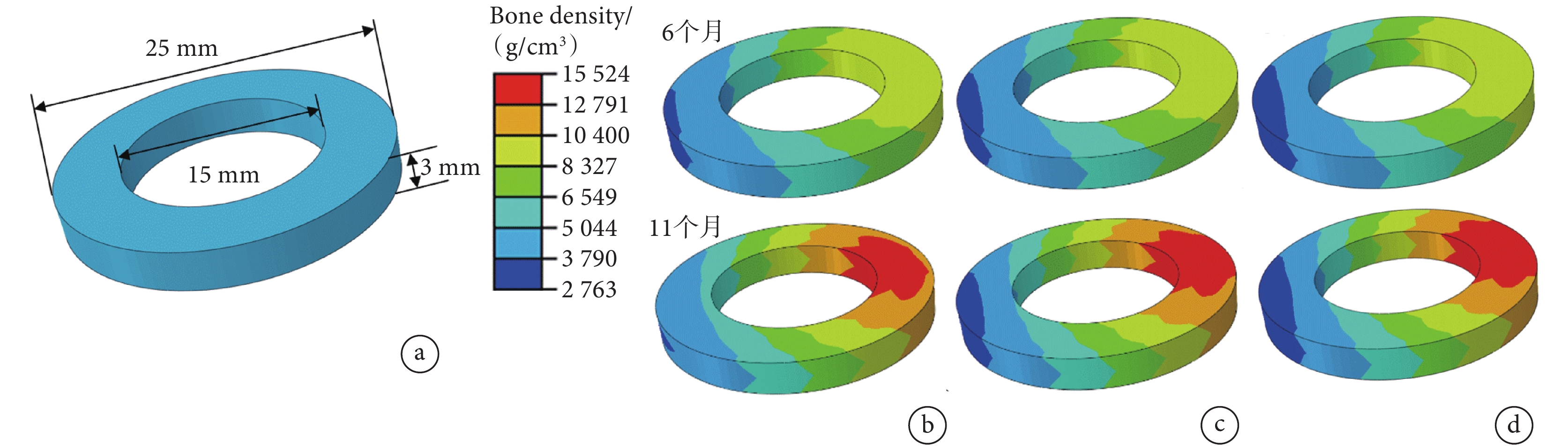圖9
骨痂彈性模量分布云圖
a. 初始狀態；b. 可降解時變剛度接骨板；c. 鈦合金接骨；d. 不銹鋼接骨板
Figure9. Distribution cloud map of elastic modulus of callusa. initial state; b. degradable time-varying stiffness bone plate; c. titanium alloy bone plate; d. stainless steel bone plate
表2
使用不同接骨板時重塑過程中骨痂平均彈性模量
Table2.
The average elastic modulus of callus during the reshaping process using different bone plates
4 結論
本文根據理想骨折內固定植入物的設計要求，提出了一種時變剛度骨折內固定植入物復合結構拓撲優化設計方法。通過設計可降解復合結構的構型，實現了對其時變剛度特性的調控設計，并利用骨重塑模擬模型進行了評估。優化的結果顯示，高剛度的材料1形成柱狀的支撐結構，低剛度的材料2分布在降解邊界和內部。降解初期分布在兩側降解邊界的材料2優先降解，結構剛度緩慢下降。當兩側的材料2降解完后，材料1開始降解，由于材料1作為主要的支撐，其降解導致結構剛度下降速度加快。因此設計出的可降解時變剛度接骨板可以在骨愈合前期提供良好的固定穩定性，而在愈合后期可以快速降解給予骨痂更多的生物力學刺激。與相同結構鈦合金接骨板和不銹鋼接骨板相比，可降解時變剛度接骨板能夠有效減緩應力遮擋效應，使骨痂取得更好的重塑效果，為基于生物力學的骨折內固定植入物的設計提供了參考。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：孫浩、丁曉紅負責算法程序設計、結果分析以及論文的撰寫和修改；徐世鵬、段朋云負責數據分析指導及論文審閱修訂；熊敏、張橫負責算法程序設計的指導。
0 引言
骨折是一種常見的創傷性疾病，內固定術是最為常用且有效的骨折治療方法。骨折愈合是一個力學調控和生物調控的復雜過程，骨折內固定植入物需要在治療初期提供足夠的支持和穩定性，隨著骨愈合的進行，內固定植入物的剛度逐漸降低，實現力流向斷骨處轉移，促進骨愈合[1-3]。這要求內固定植入物的剛度應隨時間發生變化（時變剛度），而使用可降解材料設計的植入物可滿足這一要求。參考文獻[4]，繪制具有時變剛度的理想可降解植入物的力學性能隨骨折愈合過程的變化趨勢圖（見圖1），骨愈合過程可以分為三個階段：炎癥期（階段1）、骨痂形成期（階段2）、骨痂重塑期（階段3）。內固定植入物的時變剛度如虛線所示，在炎癥期和骨痂形成期，骨折處血腫逐漸被肉芽組織代替，最終骨化成為編織骨，此時骨痂的彈性模量較低，植入物需要提供良好的固定穩定性；在骨痂重塑期，骨骼逐漸恢復到健康骨骼狀態，植入物剛度以較快的速率降低，使應力逐漸向骨痂轉移，在骨折完全愈合之后，內固定植入物的剛度接近零。因此如何設計內固定植入物結構，使其剛度特性符合骨愈合規律的要求是一個亟待解決的問題。
圖1
理想骨折內固定植入物降解率與力學性能變化趨勢
Figure1.
The degradation rate and mechanical trend of ideal fracture internal fixation implants
目前可降解內固定植入物的設計主要通過合金化、冷加工、熱處理和表面改性等方法改變可降解材料的降解行為，使其具有與骨愈合相匹配的剛度[5-7]。結構拓撲優化設計方法通過設計結構的材料分布使結構得到所需的力學性能，Wu等[8]通過考慮骨重塑過程的時間依賴性，推導了時域的靈敏度，開發了一種新的下頜骨接骨板拓撲優化方法，但未考慮骨固定板降解；Chandra等[9]考慮到生物降解過程中鋼板的尺寸、均勻的降解率和整個過程中鋼板的固定穩定性，設計了一種可生物降解的植入鋼板，卻忽視了材料降解對結構的影響。由于內固定植入物的力學性能隨降解時間發生變化，而力學性能的變化會影響骨愈合效果，因此如何模擬降解過程，并量化材料降解對內固定植入物結構力學性能的影響，設計具有時變剛度的內固定植入物使之符合骨愈合規律的要求，具有重要的意義。目前，通過拓撲優化設計方法對可降解內固定植入物進行結構設計以改變可降解材料降解行為的研究仍較少[10-11]。
本文提出一種具有時變剛度的骨折內固定植入物復合結構拓撲優化設計方法，建立考慮結構降解的有限元模型，獲得降解過程中中間結構的力學性能，通過結構拓撲優化實現具有不同降解速度和彈性模量的雙材料可降解植入物，并利用骨重塑模擬模型對設計結果的時變剛度性能和骨重塑效果進行評估。
1 可降解結構的力學分析
1.1 具有時變剛度特性的復合結構設計構思
目前，單一材料的可降解內固定植入物的剛度很難與骨愈合周期相匹配，會出現降解過快發生固定失效和降解過慢導致應力屏蔽[12-14]，因此考慮采用兩種不同的可降解材料。如圖2所示，生物降解材料1降解速度慢、剛度大，材料2性能與其完全相反。在給定的邊界條件下，在設計域內確定兩種材料的最優布局，以實現在早期結構剛度緩慢降低，而后期結構剛度能夠以相對較快速率降低。
圖2
考慮時變剛度特性的復合結構設計
Figure2.
Design of composite structures considering time-varying stiffness characteristics
1.2 問題描述
進行內固定植入物的拓撲優化設計，模擬結構的降解過程并量化材料降解對結構性能的影響是研究的關鍵。分別使用相對密度(xe)和降解殘留率(ye)描述兩種材料的分布和降解狀態，如式(1)～(2)所示。通過xe決定單元e為材料1還是材料2；通過ye表示降解狀態，ye = 1，代表單元e完全未降解，ye = ymin代表單元e完全降解。
|
|
式中，xmin和ymin取0.001；m為單元個數。
1.3 結構降解模擬-力學分析耦合模型
采用均勻腐蝕方法，以平均降解率模擬結構的降解[15-16]。為簡化模擬過程，假設：① 降解只發生在材料的固液交界處且均勻進行，降解邊界隨材料的降解而移動；② 材料的降解具有均一的降解速率，不考慮其他環境參數（如溫度、pH值等）；③ 腐蝕環境相同，忽略貼近骨面和貼近組織的兩面對降解速率的影響。需要說明的是，均勻腐蝕與實際腐蝕存在一定的差異，實際腐蝕是一個隨機過程，不僅和腐蝕環境有關，而且存在一定的不確定性。但降解實驗表明，以均勻腐蝕模擬結構的降解與降解實驗中隨機腐蝕降解的質量損失率差距在0.1%以內[17]，表明均勻降解模擬方法是可行的。
降解模擬過程如圖3所示，單元顏色由深到淺表示材料從未開始降解到完全降解，可降解邊界使用黑色粗虛線表示。圖3a為結構網格，圖3b為降解過程，降解過程示意如圖3b1～3b5所示。其中從b1到b3可降解邊界處的一層單元格顏色逐漸由深變淺，表示該層單元逐漸降解；從b3到b4，可降解邊界從外層單元移動到相鄰的內層單元；然后從b4到b5內層單元開始降解。在一個降解時間步完成后，對其降解結果進行結構性能分析，獲得結構性能隨時間的變化關系。單元降解的數學表達為：
圖3
降解過程示意圖
a. 結構網格；b. 降解過程；c. 單元
a. meshes of the structure; b. simulation of structure degradation; c. the location mark of element
|
式中，i表示降解時間步，de表示單元e的降解速率，t為單位降解時間步的時間。
單元e和相鄰單元位置標記如圖3c所示，單元e的位置為(k, l)。通過判斷降解單元相鄰單元的狀態，來決定該單元是否發生降解，為了保證數值計算的穩定，設定yb=0.1，當相鄰單元的殘留率小于yb時可沿該單元方向進行降解，如當yk ? 1,l < yb時，認為單元e能夠從左側開始降解，當yk + 1,l < yb時，認為單元e可以從右側開始降解，上下方向類似[18]。通過對相鄰單元降解狀態的判斷，單元e的降解速率可以表示為：
|
式中，Ω表示e相鄰單元的集合；α表示Ω中的第α個單元；d為材料的降解速率；Nα由式(5)得到：
|
為了便于求導，使用Heaviside方程將式(4)近似為連續方程，單元的降解方程可以改寫為：
|
階躍函數H為：
|
式中，γ是一個常數。
由式(3)和式(6)，單元e殘留率的更新方程為：
|
使用Kreisselmeier-Steinhauser函數將式(8)最大函數問題近似為連續方程[19-20]：
|
式中，γ = 6，η = 6。
結構平衡方程如式(10)所示：
|
式中，K是結構的整體剛度矩陣，由于材料的降解，K與時間相關；U為位移向量；F為力向量。
對于可降解結構，K由單元剛度矩陣ke與ye組裝得到，ye是關于降解速率d和降解時間i的函數。將材料降解對結構力學性能的影響耦合到有限元分析過程中，可降解結構的剛度矩陣為：
|
式中，B表示幾何矩陣；D為彈性系數矩陣；Ωe為單元的體積。
降解模擬算法包括以下步驟。步驟1：初始化殘留率ye，使用k和l對單元e進行標記；步驟2：判斷相鄰單元的降解狀態；步驟3：使用式(6)計算單元e的降解速率de；步驟4：使用式(9)計算單元e的殘留率ye；步驟5：根據ye，使用式(10)進行有限元分析；重復步驟1～5，直到指定的時間步td。
2 雙材料可降解結構的拓撲優化
優化設計的目的是通過確定兩種具有不同可降解性能的材料的最佳分布，使復合結構在指定降解時間步中間結構的剛度之和最大。使用結構柔順度表征結構剛度，可降解復合結構柔順度最小的優化數學模型可以表示為：
|
式中，X為設計變量的集合；C為結構柔順度，?為降解時間步的集合；v1為復合結構中材料1的最終體積，f是給定的體積分數，v0為總體積。
為獲得輪廓清晰的優化結構，使用基于固體各向同性材料懲罰模型（solid isotropic material with penalization，SIMP）的材料插值機制：
|
|
式中，E為彈性模量；p為懲罰系數，取3.0；下標1、2分別表示可降解材料1、2。
2.1 靈敏度分析
在每個降解時間步對結構進行有限元分析，計算結構柔順度，其靈敏度可以通過求導得到。目標函數對于設計變量X的靈敏度可以表示為：
|
結構柔順度C是關于xe、ye和i的函數：
|
式中，u表示單元位移矩陣；k0為單元剛度矩陣。
根據式(16)定義的柔順度，在降解時間步i對設計變量xe的導數為：
|
其中：
|
|
|
材料1的體積為：
|
則材料1的體積對于設計變量xe的導數為：
|
為克服棋盤格效應，采用基于Heaviside的靈敏度過濾方法使密度變量的值趨近0或1。使用如式(23)所示的Heaviside方程對中間密度場xei進行過濾，xei由式(24)計算得到。
|
|
式中，β為常數，控制函數的平滑度，如果β = 0，則是原始的密度過濾器，如果β接近于無窮大，則Heaviside為階躍函數。本文取β的初始值為1，每100次迭代對β的值加倍，最大值為512。
2.2 優化設計流程
雙材料可降解結構的拓撲優化設計流程如圖4所示，主要步驟如下。
圖4
雙材料可降解結構的拓撲優化設計流程
Figure4.
Topological optimization design process for dual material degradable structures
第一步：構造初始幾何模型并進行離散化。定義數學模型的參數，給定體積分數和過濾半徑，設置xe和ye的初始值，并定義可降解邊界、載荷和約束等邊界條件；第二步：根據式(9)進行降解模擬，計算得到殘留率；第三步：根據式(10)和(11)對考慮材料降解的復合結構進行有限元分析；第四步：根據式(15)進行靈敏度分析。重復第二步到第四步，直到指定的時間步。第五步：利用MMA優化算法更新設計變量；第六步：重復第二步到第五步，直到滿足約束條件或目標函數收斂。當滿足以下兩個條件之一時，迭代終止：① 連續兩次迭代的結構柔順度變化小于收斂判據；② 迭代步數達到指定值，本文中取100。
3 脛骨接骨板設計
3.1 設計模型及材料性能
使用如圖5a所示的脛骨-接骨板系統簡化模型，接骨板的尺寸如圖5b所示，接骨板中間區域（橘黃色）為可降解結構，兩側（灰色）為不可降解結構。接骨板植入人體后，可降解結構垂直于x軸和z軸的四個面都能夠發生降解，其中垂直于x方向兩個面的面積較大，這兩個面的降解對結構剛度的影響也較大。為了將設計問題簡化，我們假定可降解結構僅能從垂直于x方向的兩個面發生降解，忽略垂直于z方向兩個面的降解。如圖5c所示，將垂直于z方向的面作為設計平面，利用考慮時變剛度特性的可降解復合結構拓撲優化設計方法對設計平面進行優化設計，然后沿z方向拉伸得到三維可降解復合結構，實現可降解接骨板的拓撲優化設計。
圖5
脛骨-接骨板固定系統
a. 設計模型；b. 接骨板模型；c. 設計區域；d. 接骨板力學邊界條件；e. 接骨板的簡化模型；f. 降解邊界條件
Figure5. Bone and bone plate fixation systema. design model; b. bone plate model; c. design area; d. mechanical boundary conditions of bone plates; e. simplified model of bone plate; f. degradation boundary conditions
如圖5d所示，脛骨平臺的力學邊界條件可以簡化為底端全約束，頂端皮質骨受到垂直向下的載荷。骨愈合過程中，骨痂的剛度逐漸增大，但都遠小于接骨板的剛度，由于載荷分流，接骨板承擔大部分的載荷，設計平面的力學邊界條件簡化為圖5e所示，中心點全約束，中心線其余節點約束豎直方向自由度，上下邊受到垂直方向的壓力，F1 = 1 600 N。可降解邊界條件如圖5f所示，上下側為不可降解邊界，左右側為可降解邊界。根據文獻[12]，材料屬性如表1所示。
3.2 拓撲優化結果及其時變剛度特性分析
采用2.2小節的設計流程，使用尺寸為0.1 mm的四節點四邊形平面單元對設計域進行網格劃分，拓撲優化過濾半徑設置為單元尺寸的兩倍，材料1的體積分數為0.5，優化目標為第1和第90天中間結構柔順度之和最小。優化迭代歷程如圖6a所示，隨著迭代的進行逐漸獲得具有清晰邊界的材料分布輪廓，優化目標達到了收斂狀態。拓撲優化設計結果如圖6b所示，高剛度材料1（黑色）形成了柱狀的支撐結構，在可降解邊界處外層為材料2，結構左右呈現對稱性，高剛度材料1（黑色）主要分布在左右側可降解邊界處，在左右側中部形成V型開口，并在靠近加載側形成了類似X型的交叉結構，連接左右兩側的高剛度材料，提高了結構整體的穩定性。時變剛度接骨板設計結果如圖6c所示，兩側為惰性金屬，中間區域為可降解復合結構。需要說明的是，結構的最優拓撲形態主要與所受的載荷相關，本文采用了承受偏心壓力的圓柱模擬脛骨，考慮了實際脛骨承受的主要載荷為壓力和彎矩，因此圖6的設計結果具有合理性。
圖6
拓撲優化設計結果
a. 拓撲優化迭代歷程；b. 二維設計結果；c. 可降解時變剛度接骨板
Figure6. Topology optimization design resulta. iteration history with two degradable interfaces; b. 2D design results; c. degradable time-varying stiffness plate
考慮時變剛度特性拓撲優化設計結果的降解過程如圖7所示。由于材料1剛度較大，其降解對結構剛度的影響程度較大。降解開始時，可降解邊界附近的材料2先逐漸降解，結構剛度緩慢下降。當外層的材料2降解完，結構內部的材料1開始降解，結構剛度下降的速度開始增大。
圖7
考慮時變特性拓撲優化設計結果的降解過程
Figure7.
Degradation process of topology optimization design results considering time-varying characteristics
3.3 骨重塑效果評估
骨重塑是骨骼受到外部生物力學刺激時產生的一種自適應過程。骨重塑模擬模型能夠描述在生物力學刺激作用下骨密度隨時間的變化過程。利用應變能密度預測骨重塑過程[21-22]，力學刺激Ξ可以表示為：
|
式中，U為應變能密度，ρ為骨密度。骨密度在一定時間間隔t的變化量ρ可以表示為：
|
|
|
式中，t為時間；R1和R2為常數，分別取18 (g/cm3)2/(J/月)和600 (g/cm3)3/(J2/月)；θ1和θ2是力學刺激的閾值，分別由式(26)和(27)計算得到；s和δ為常數，分別取0.000 36 J/(g*cm3)和0.1。骨密度變化量與力學刺激之間的曲線描述如圖8所示，可以分為低載退化、惰性、骨重塑和過載退化四個區間。在低載退化和過載退化區間骨密度減小，在惰性區間骨密度不變，在骨重塑區間骨密度增大。
圖8
骨密度變化率與力學刺激關系示意圖
Figure8.
The schematic of relationship between the rate of change in bone density and mechanical stimulus
假設發生骨重塑的骨材料屬性為各向同性，其彈性模量可以通過密度進行量化，經驗公式為：
|
式中ζ為彈性模量；τ為常數，取3 790 MPa/(g/cm3)3。
使用圖5a所示的簡化模型模擬骨痂的重塑過程。邊界條件如圖5d所示，頂端受到垂直向下的載荷，底端全約束。載荷為普通人體重（70 kg）的三倍，即F = 2 100 N。骨痂的初始密度為1.0 g/cm3，最大為1.74 g/cm3，最小為0.1 g/cm3。接骨板除設計域外結構和螺釘為鈦合金，彈性模量為110 000 MPa。皮質骨和松質骨的彈性模量分別為15 750 MPa和1 100 MPa。不銹鋼的彈性模量為210 000 MPa。
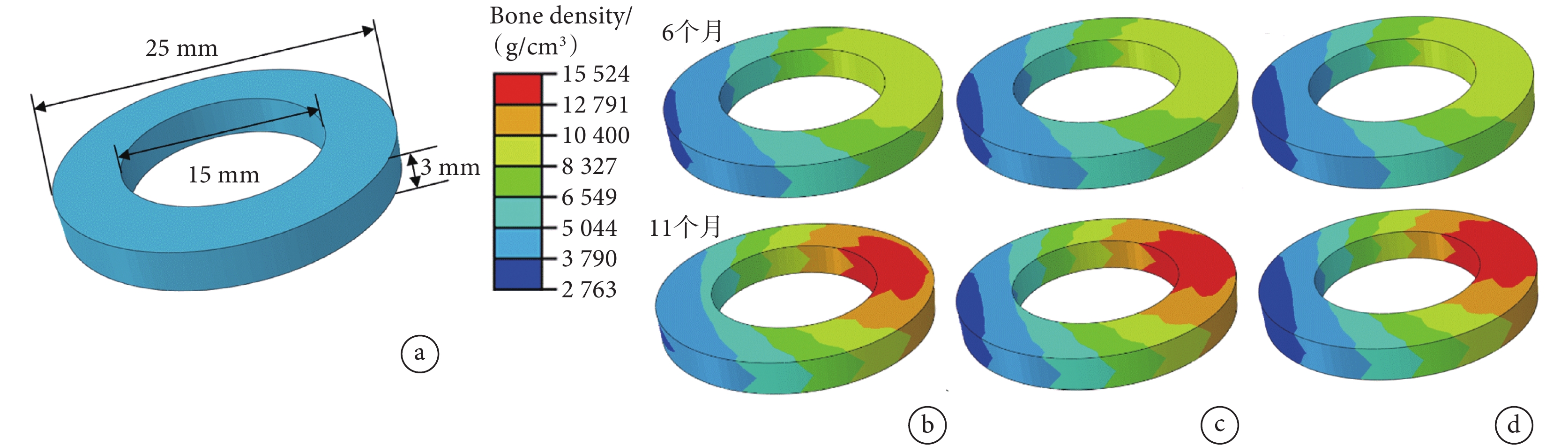
采用彈性模量表征骨重塑過程的骨痂單元變化，平均彈性模量一定程度上能夠反映骨痂整體結構剛度的變化。骨痂的尺寸和初始狀態如圖9a所示，圖9b、c、d分別為使用可降解時變剛度接骨板、相同結構尺寸的鈦合金接骨板和不銹鋼接骨板固定時，經過6個月和11個月時的骨痂彈性模量分布云圖。接骨板位于骨痂的左側，由于接骨板造成的應力遮擋效應，靠近接骨板側的骨痂受到的力學刺激較小，因此彈性模量較低。與使用鈦合金接骨板和不銹鋼接骨板相比，使用可降解時變剛度接骨板時，骨痂重塑過程中左側彈性模量小于3 790 MPa的區域明顯較小。經過11個月重塑之后，使用可降解時變剛度接骨板時，骨痂彈性模量基本都大于3 790 MPa；而使用鈦合金接骨板和不銹鋼接骨板時，骨痂左側仍有部分區域彈性模量小于3 790 MPa。結果表明，使用可降解時變剛度接骨板可以使靠近接骨板側的骨痂在重塑過程中受到更多的力學刺激，有效地減緩應力遮擋效應，取得更好的重塑效果。對比相同重塑時間下使用三種接骨板的骨痂平均彈性模量的差值，結果如表2所示，隨著重塑的進行，三種骨板對應的骨痂的平均彈性模量均逐漸增大，使用可降解時變剛度接骨板時的骨痂平均彈性模量均高于鈦合金接骨板和不銹鋼接骨板，對比不同骨板的骨痂平均彈性模量的差值，隨著時間的增加差值逐漸變大，并且差值增大的速率也逐漸增大，說明可降解時變剛度接骨板的結構剛度減小的速率逐漸增大。
圖9
骨痂彈性模量分布云圖
a. 初始狀態；b. 可降解時變剛度接骨板；c. 鈦合金接骨；d. 不銹鋼接骨板
Figure9. Distribution cloud map of elastic modulus of callusa. initial state; b. degradable time-varying stiffness bone plate; c. titanium alloy bone plate; d. stainless steel bone plate
表2
使用不同接骨板時重塑過程中骨痂平均彈性模量
Table2.
The average elastic modulus of callus during the reshaping process using different bone plates
4 結論
本文根據理想骨折內固定植入物的設計要求，提出了一種時變剛度骨折內固定植入物復合結構拓撲優化設計方法。通過設計可降解復合結構的構型，實現了對其時變剛度特性的調控設計，并利用骨重塑模擬模型進行了評估。優化的結果顯示，高剛度的材料1形成柱狀的支撐結構，低剛度的材料2分布在降解邊界和內部。降解初期分布在兩側降解邊界的材料2優先降解，結構剛度緩慢下降。當兩側的材料2降解完后，材料1開始降解，由于材料1作為主要的支撐，其降解導致結構剛度下降速度加快。因此設計出的可降解時變剛度接骨板可以在骨愈合前期提供良好的固定穩定性，而在愈合后期可以快速降解給予骨痂更多的生物力學刺激。與相同結構鈦合金接骨板和不銹鋼接骨板相比，可降解時變剛度接骨板能夠有效減緩應力遮擋效應，使骨痂取得更好的重塑效果，為基于生物力學的骨折內固定植入物的設計提供了參考。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：孫浩、丁曉紅負責算法程序設計、結果分析以及論文的撰寫和修改；徐世鵬、段朋云負責數據分析指導及論文審閱修訂；熊敏、張橫負責算法程序設計的指導。
